引言
空间机器人将在卫星维修、在轨装配、碎片清除等任务中发挥着重要作用. 典型的在轨演示试验如"Robot Technology Experiment (ROTEX)"、"Engineering Test Satellite VII (ETS-VII)"、"Orbital Express (OE)"和"凤凰号"等项目验证了空间机器人执行在轨服务任务的可行性[1 -4 ] . 然而, 在轨服务任务最具挑战性的工作之一是如何高效、可靠地抓捕目标卫星. 此外, 空间机械臂与基座之间的动力学耦合引起的非完整约束对于抓取规划提出了新的挑战.
过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解.
以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案.
前期研究在抓捕可行性和抓捕规划方面存在以下缺点: (1)空间机器人抓捕策略未充分考虑目标的运动和机器人的抓捕能力, 无法评估抓取可行性, 并确定最佳抓捕时机; (2)非合作目标的抓捕规划是一个多目标、多约束的非线性优化问题, 为评估抓捕规划策略的有效性, 在规划过程中须充分考虑捕获后的操作. 如何实现对翻滚目标的安全可靠抓捕对开展后续的在轨服务任务至关重要. 迄今为止, 空间机械臂的抓取规划仍然是一项极具挑战性的工作. 本文的目标是设计运动学冗余空间机械臂的抓捕规划策略, 同时充分考虑空间机械臂的抓捕能力、目标运动、关节限制和防碰撞等约束. 选择运动学冗余机械臂的原因在于其存在无穷多个逆运动学解, 可用于满足多约束条件, 例如最小化基座姿态干扰、防碰撞、最大化力可操作度等. 最终通过对抓捕策略的仿真验证, 为后续空间机器人抓捕动态非合作目标提供技术支撑.
1 动力学建模
1.1 空间机器人动力学
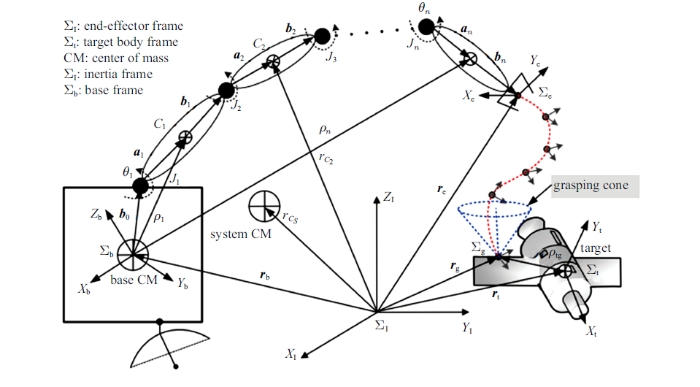
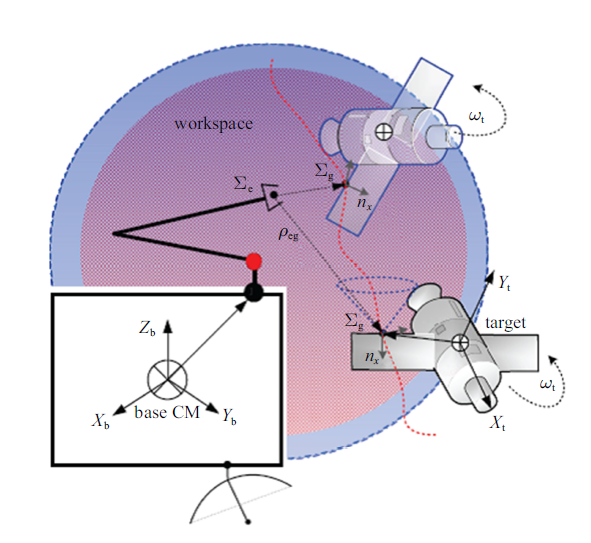
如图1 所示, 空间机器人系统由航天器基座与$n$个自由度的操作机械臂组成, 共包括$n+1$个对象. 基于Lagrange动力学方程, 空间机器人系统的动力学方程可表示如下
(1) $\begin{eqnarray} \label{eq1} \left[ {{\begin{array}{*{20}c} {{ H}_{\rm b} } & {{ H}_{\rm b} } \\ {{ H}_{\rm bm}^{\rm T} } & {{ H}_{m} } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{\ddot{{ x}}}_{\rm b} } \\ {{\ddot{{ \theta }}}} \\ \end{array} }} \right]+\left[ {{\begin{array}{*{20}c} { c_{\rm b} } \\ { c_{\rm m} } \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {{ h}_{\rm b} } \\ {{ \tau }} \\ \end{array} }} \right]+\left[ {{\begin{array}{*{20}c} {{ J}_{\rm b}^{\rm T} } \\ {{ J}_{\rm e}^{\rm T} } \\ \end{array} }} \right]{ h}_{\rm e} \end{eqnarray}$
其中${\ddot{{ x}}}_{\rm b} =\left( {{\ddot{{ r}}}_{\rm b} ,\dot{{\omega }}_{\rm b}} \right)$, ${\ddot{{ \theta}}}$表示机械臂的关节加速度. 自由漂浮模式下, ${ h}_{\rm b} ={\bf0}$和${ h}_{\rm e}={\bf0}$, 基座初始状态和末端执行器初始位姿已知, 无基座执行机构处于工作模式, 仅考虑机械臂关节的内力和内力矩. 因此, 整个系统可严格保持动量守恒. 假设${ L}_{0} $代表整个系统的初始线动量和角动量, ${ L}_{0} ={ H}_{\rm b} {\dot{{ x}}}_{\rm b} +{ H}_{\rm bm} {\dot{{ \theta }}}$, 假定${ L}_{0}={\bf0}$且${ H}_{\rm b} $是可逆, 基座运动可描述为
(2) $\begin{eqnarray} \label{eq2} {\dot{{ x}}}_{\rm b} ={ J}_{a} \dot{{\theta }}=-{ H}_{\rm b}^{-1} { H}_{\rm bm} \dot{{\theta }} \end{eqnarray}$
图1
图1
抓捕前空间机器人示意图
Fig.1
Schematic diagram of space robot in pre-capture phase
将式(2)代入末端执行器的运动学方程${\dot{{ x}}}_{\rm e} ={ J}_{\rm b} {\dot{{ x}}}_{\rm b} +{ J}_{\rm e} \dot{{\theta }}$, 可得
(3) $\begin{eqnarray} \label{eq3} {\dot{{ x}}}_{\rm e} ={ J}_{\rm g} \dot{{\theta }}=\left( {{ J}_{\rm e} -{ J}_{\rm b} { H}_{\rm b}^{\mbox{-1}} { H}_{\rm bm} } \right)\dot{{\theta }} \end{eqnarray}$
式中, ${ J}_{\rm g}$被称为广义雅可比矩阵[29 ] . 基于式(2)和式(3)可以看出, 自由漂浮模式下基座和末端执行器的运动仅依赖于关节轨迹及动力学耦合效应. 因此, 通过适当的抓捕策略规划可实现多个优化指标, 如末端执行器任务, 最小化基座干扰或最大化力可操作度等.
1.2 非合作目标动力学
(4) $\begin{eqnarray} \label{eq4} { H}_{\rm t} {\ddot{{ x}}}_{\rm t} + c_{\rm t} ={ h}_{\rm t} \end{eqnarray}$
其中${\dot{{ x}}}_{\rm t} \in \mathbb{R}^{6}$是目标的线速度${\dot{{ r}}}_{\rm t}$和角速度${\dot{{ \omega }}}_{\rm t} $. 广义惯量矩阵${ H}_{\rm t} $和非线性项$ c_{\rm t} $可以写成
(5) $\begin{eqnarray} \label{eq5} { H}_{\rm t} =\left[\begin{array}{c@{\ \ \ }c} {m_{\rm t} { E}_{3} } & {\bf0} \\ {\bf0} & {{ I}_{\rm t} } \\ \end{array} \right],\ \ c_{\rm t} =\left[\begin{array}{c@{\ \ \ }c} m_{\rm t} \omega_{\rm t} \times v_{\rm t}\\ \omega _{\rm t} \times I_{\rm t} \omega _{\rm t}\end{array}\!\!\!\right] \end{eqnarray}$
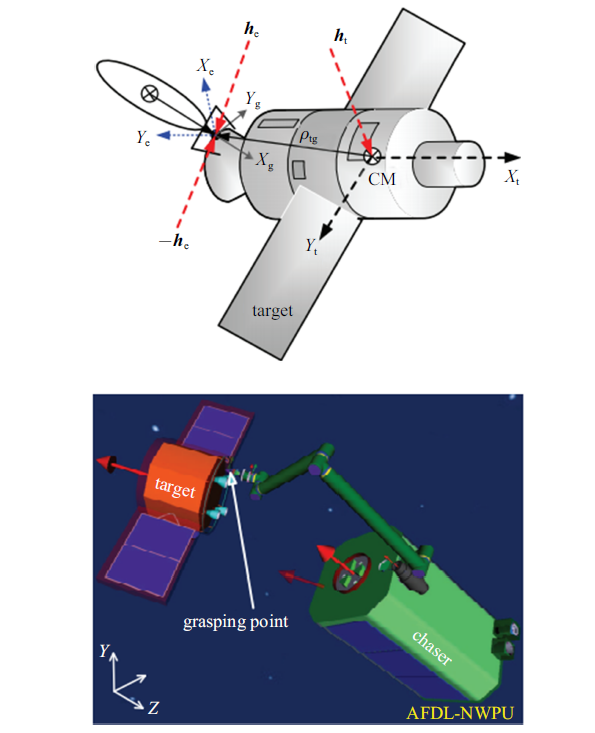
$m_{\rm t} $和${ I}_{\rm t} $分别为目标卫星的质量和惯性张量. ${ E}_{3}$是单位矩阵. 抓捕前阶段, 目标上的外力旋量${ h}_{\rm t}={\bf0}$, 目标捕获后, 外力旋量${ h}_{\rm t} ={ G}_{\rm te} { h}_{\rm e} $, ${ h}_{\rm e} \in \mathbb{R}^{6}$. 力旋量同时作用于末端执行器, 抓捕矩阵${ G}_{\rm te}$为
(6) $\begin{eqnarray} \label{eq6} { G}_{\rm te} =\left[ \begin{array}{c@{\ \ \ }c} -{ R}_{\rm e}^{\rm t} & {\bf0}_{3} \\ -{\tilde{{ \rho }}}_{\rm tg} { R}_{\rm e}^{\rm t} & -{ R}_{\rm t}^{\rm e} \\ \end{array}\right] \end{eqnarray}$
${ R}_{\rm e}^{\rm t} $是从末端执行器到目标本体的旋转矩阵, ${ \rho }_{\rm tg}$是抓捕点相对于目标质心的位置矢量. 对于任意向量${ \rho }=\left[ {\rho_{x} ,\rho_{y} ,\rho_{z} } \right]$, ${\tilde{{ \rho }}}$定义为
(7) $\begin{eqnarray} \label{eq7} {\tilde{{ \rho }}}=\left[ {{\begin{array}{*{20}c} 0 & {-\rho_{z} } & {\rho_{y} } \\ {\rho_{z} } & 0 & {-\rho_{x} } \\ {-\rho_{y} } & {\rho_{x} } & 0 \\ \end{array} }} \right] \end{eqnarray}$
图2
图2
抓捕后目标示意图
Fig.2
Schematic diagram of target in post-capture phase
1.3 动静态对偶性分析
根据虚功原理, 作用于末端执行器力旋量的虚功和关节力矩计算的虚功相等. 参考式(1), 末端执行器力旋量与关节力矩间的关系可通过广义雅可比矩阵的转置来建立
(8) $\begin{eqnarray} \label{eq8} { \tau }={ J}_{\rm g}^{\rm T} \left( {{ \theta }} \right){ h}_{\rm e} =\left( {{ J}_{\rm e}^{\rm T} -{ H}_{\rm bm}^{\rm T} { H}_{\rm b}^{-\rm T} { J}_{\rm b}^{\rm T} } \right){ h}_{\rm e} \end{eqnarray}$
结合式(3)与式(8), 可以给出动静态对偶性的关系. 目标一旦被捕获, 参考式(8)和${ h}_{\rm t} ={ G}_{\rm te} { h}_{\rm e} $, 可以得出
(9) $\begin{eqnarray} \label{eq9} { \tau }={ J}_{\rm g}^{\rm T} { G}_{\rm te}^{-1} { h}_{\rm t} ={ J}_{\rm c}^{\rm T} { h}_{\rm t} \end{eqnarray}$
${ J}_{\rm c} =\left( {{ J}_{\rm g}^{\rm T} { G}_{\rm tg}^{-1} } \right)^{\rm T}$是雅可比矩阵, 将目标上的力旋量映射到机械臂关节力矩. 运用动静态对偶性, 捕获后阶段目标的运动可以描述为
(10) $\begin{eqnarray} \label{eq10} {\dot{{ x}}}_{\rm t} ={ J}_{\rm c} {\dot{{ \theta }}}={ G}_{\rm te}^{-\rm T} { J}_{\rm g} {\dot{{ \theta }}} \end{eqnarray}$
考虑单位范数${\dot{{ \theta }}}^{\rm T}{\dot{{ \theta }}}=1$和${ \tau }^{\rm T}{ \tau}=1$, 其分别构成了关节速度空间与关节力矩空间中的单位超球面; 速度可操作椭球和力可操作椭球可分别定义如下
(11) $\begin{eqnarray} \label{eq11} &&{\dot{{ x}}}_{\ominus }^{\rm T} \left( {{ J}_{\odot } { J}_{\odot }^{\rm T} } \right)^{-1}{\dot{{ x}}}_{\ominus } =1 \end{eqnarray}$
(12) $\begin{eqnarray} \label{eq12} {\dot{{ h}}}_{\ominus }^{\rm T} \left( {{ J}_{\odot } { J}_{\odot }^{\rm T} } \right){\dot{{ h}}}_{\ominus } =1 \end{eqnarray}$
下标$\ominus $可以是e或t; 相应地, $\odot$可以对应设置为g或c. 从式(11)和式(12)可以看出, 力可操作椭球的主轴与速度可操作椭球的主轴一致, 而各轴的长度互为倒数. 根据动静态对偶性分析, 良好的力可操作性方向对应较差的速度可操作性方向, 反之亦然. 这些特征将用于后续抓捕规划策略设计中.
2 抓捕时机与可行性
一般而言, 空间非合作目标上没有固定的抓捕机构, 因此, 需要选择星上特定的结构作为可行的抓捕点. 非合作目标上可以抓捕的位置包括: 远地点发动机边缘、对接环、太阳能帆板支架等. 为了辅助构建空间机械臂的抓捕规划策略, 本文提出如下假设:
(1)空间机器人系统和目标均为刚体, 在执行抓捕任务之前, 空间机器人已通过轨道机动至相对于目标卫星的某一固定位姿;
(2)空间机器人系统的初始角动量为0, 抓捕过程中系统质量特性不发生变化, 目标的体坐标系处于目标质心处;
(3)空间机器人系统的运动状态和质量特性已知, 目标上的抓捕点事先已确定, 并在抓捕点上附着有抓捕坐标系;
(4)抓捕过程中忽略环境力(重力梯度、地磁、太阳光压等)以及相对轨道动力学效应.
2.1 抓捕能力图谱
针对单一机械臂, 其抓捕能力依赖于机械臂的运动学构型、安装位置等约束. 为了完成对目标的抓捕和操作, 机械臂需要更完备的抓捕能力描述. 因此, 结合机械臂的可达性和灵巧性概念[30 ] , 构建机械臂的抓捕能力图谱.
首先, 目标上的抓捕点需要位于机械臂的工作空间$WS$之中, 机械臂工作空间定义如下
(13) $\begin{eqnarray} \label{eq13} WS=\left\{ {{\cal F}{\cal K}\left( {{ \theta }} \right):{ \theta }\in {Q}} \right\}\subset SE\left( 3 \right) \end{eqnarray}$
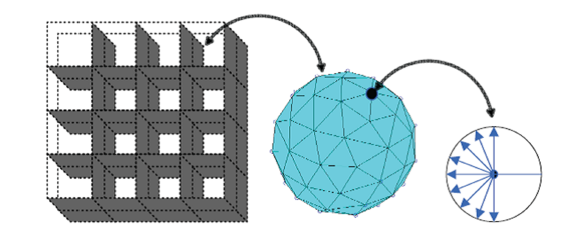
其中, ${ \theta }$是机械臂的构型空间, ${\cal F}{\cal K}\left( {{ \theta }}\right)$是正向运动学映射. 机械臂的可达性图谱描述了机器人工具中心点(TCP)坐标系能够到达的所有可能位姿. 如图3 所示, 该图谱的建立是通过在6自由度空间中结构化离散机械臂的工作空间完成的. 首先, ${\rm R}^{3}$中的可达工作空间被分割成等体积的立方体单元, 每个单元的姿态可达性通过单元内接球上均匀分布空间点来实现. 可达性图谱可存储为二进制矩阵, 每个块的值代表TCP局部区域的可达性, 值为1表示可达, 为0表示末端执行器不可达. 可达性图谱的计算可以基于机械臂的逆运动学. 本文中, 工作空间离散为$n_{v}$个立方体单元, 每个内接球上平均分布了$n_{d}$个点, 每个内接球上的点进行了$n_{z} $次旋转.
图3
图3
SE(3)离散化
Fig.3
Discretization of SE(3)
灵巧性为机械臂的操作能力提供了更为丰富的信息, 每个立方体单元的灵巧性指标可以定义如下
(14) $\begin{eqnarray} \label{eq14} D_{i} =\frac{\sum\nolimits_{a=1}^{n_{d} \times n_{z} } {V_{i} \left( a \right)} }{n_{d} \times n_{z} },\ \ i= 1,2,\cdots ,n_{v} \end{eqnarray}$
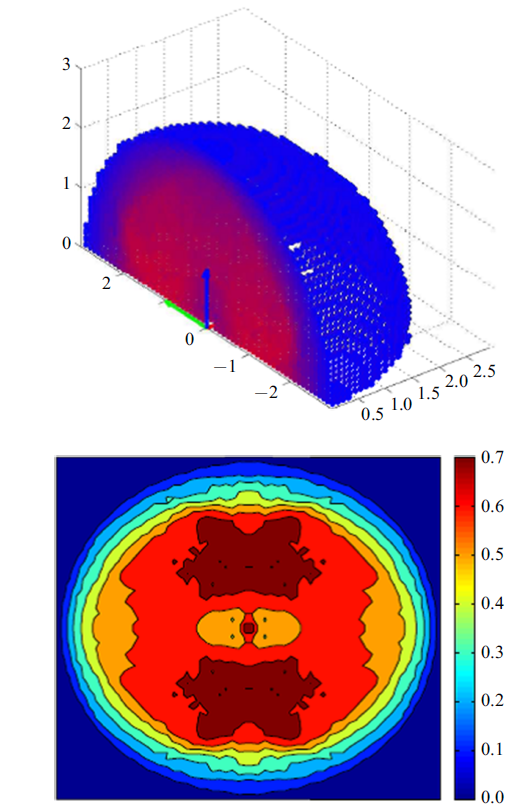
$V_{i} \left( a \right)$表示可达性图谱中第$i$个立方体单元的二进制值. $D_{i}$有效地给出了每个立方体单元中不同位姿的可达概率并给出了其灵巧性评估. 结合可达性与灵巧性, 将每个立方体单元的灵巧性值用相应的颜色表征, 可以构建机械臂的抓捕能力图谱, 如图4 所示. 抓捕能力图谱给出了机械臂工作空间中可以灵巧操作目标的程度, 结合目标的运动预测, 可以确定抓捕时间窗口并评估抓捕的可行性.
图4
图4
抓捕能力图谱及切面等高线图
Fig.4
Capability map and section contour map
2.2 抓捕时机确定
以往的研究未充分考虑抓捕过程中机械臂的抓捕能力、目标的运动、末端执行器的接近方向等问题, 如图5 所示, 抓捕时机确定依赖于机械臂的抓捕能力分析、初始构型、抓捕坐标系以及目标的运动预测. 首先, 基于工作空间$WS$分析, 确定抓捕时间窗口; 此后, 给定目标的初始运动条件, 搜索最优的未来时刻, 保证目标上的抓捕点位于能力图谱内且具有更高的灵活性指标, 此外, 末端执行器与抓捕点的距离要尽可能小, 位置矢量${ \rho }_{\rm eg} ={ r}_{\rm g} \left( t \right)-{ r}_{\rm e}^{\rm s}$和抓捕坐标系矢量$n_{x}$之间的夹角亦需尽可能小, 从而保证接近方向处于接近走廊内. 因此, 抓捕时机确定问题可描述如下
(15) $\begin{eqnarray} \label{eq15} &&t_{\rm g} =\arg \, \min_{t} \frac{1}{1+D_{i} \left( {{ r}_{\rm g} \left( t \right)} \right)}\left( {2\left\| {{ \rho }_{\rm eg} \left( t \right)} \right\|-{ n}_{x}^{\rm T} { \rho }_{\rm eg} } \right),\\&&\qquad n_{x}^{\rm T} { \rho }_{\rm eg} >0 \end{eqnarray}$
其中, $D_{i} \left( {{ r}_{\rm g} \left( t \right)}\right)$是抓捕点在工作空间$WS$的灵巧性指标, $n_{x} $是旋转矩阵${ R}_{\rm g}\left( t \right)$的第一列. 给定初始状态, ${ r}_{\rm g} \left( t\right)$和${ R}_{\rm g} \left( t \right)$的计算可以根据式(4)得到.
图5
图5
抓捕时机确定示意图
Fig.5
Schematic diagram of determining optimal grasping time
3 抓捕规划器设计
3.1 问题描述
空间机械臂的抓捕规划与控制受到动力学耦合的影响, 自由漂浮模式下由于非完整约束的存在, 机械臂各关节的构型是路径依赖的. 抓取规划策略的目标是确定最优的抓捕时机并生成可行的, 不违反各类约束的关节运动轨迹${ \theta }\left( t \right)$. 一般而言, 抓捕策略可描述为不等式约束$g_{i} \left({{ \theta }} \right)$与等式约束$h_{i} \left( {{ \theta }}\right)$下的非凸优化问题:
(16) $\left. \begin{array} \\ \mbox{minimize} & t_{\rm f} ,\varGamma \left( {{ \theta }\left( t \right)} \right) \\ \mbox{subject to}: & g_{i} \left( {{ \theta }\left( t \right)} \right)<0,i=1,2,\cdots ,n_{ie\rm q} \\ & h_{i} \left( {{ \theta }\left( t \right)} \right)=0,i=1,2,\cdots ,n_{ie\rm q} \\ \end{array} \right\}$
3.2 约束与目标函数
抓捕规划中的约束可以分为等式约束与不等式约束. 运动状态${ x}$带有上标s, f, d分别表示初始、终端和期望的位姿. 等式约束主要用于描述关节的初始位置、初始速度和初始加速度
(17) $\left. \begin{array} \\ { x}_{\rm b} \left( {t_{\rm s} } \right)={ x}_{\rm b}^{\rm s},\ \ { x}_{\rm e} \left( {t_{\rm s} } \right)={ x}_{\rm e}^{\rm s}\\ { \theta }\left( {t_{\rm s} } \right)={ \theta }^{\rm s},\ \ {\dot{{ \theta }}}\left( {t_{\rm s} } \right)={\ddot{{ \theta }}}\left( {t_{\rm s} } \right)=0 \\ \end{array} \right\}$
(1) 关节限幅: 抓捕过程中需要考虑关节的运动能力, 保证各关节不超出其运动范围
(18) $\begin{eqnarray} \label{eq18} { \theta }_{\min} \leqslant { \theta }\leqslant { \theta }_{\max} ,\ {\dot{{ \theta }}}_{\min} \leqslant {\dot{{ \theta }}}\leqslant {\dot{{ \theta }}}_{_{\max} } ,\ {\ddot{{ \theta }}}_{\min} \leqslant {\ddot{{ \theta }}}\leqslant \ddot{{ \theta }}_{\max} \end{eqnarray}$
(2) 抓捕走廊: 参考图1 , 末端执行器的接近方向必须限制在一个抓捕走廊内
(19) $\begin{eqnarray} \label{eq19} { n}_{x}^{\rm T} {\dot{{ r}}}_{\rm e}^{\rm f} -\left\| {{\dot{{ r}}}_{\rm e}^{\rm f} } \right\|\cos \gamma_{\rm g} \leqslant 0 \end{eqnarray}$
(3) 碰撞规避: 抓捕过程中需要保证机械臂与目标之间、各关节之间不发生碰撞
(20) $\begin{eqnarray} \label{eq20} d_{i} \left( {{ \theta }\left( t \right)} \right)>0.0 \ \ i=1,2,\cdots ,n_{\rm coll} \end{eqnarray}$
由于自由漂浮空间机器人非完整约束的存在, 航天器基座和末端执行器的终端状态不仅依赖于逆运动学, 也依赖于动力学耦合效应. 假定${ x}_{\rm e} =\left( {{ r}_{\rm e} ,{ q}_{\rm e} } \right)$和${ x}_{\rm b} =\left({{ r}_{\rm b} ,{ q}_{\rm b} }\right)$分别表示末端执行器和基座的位姿, 姿态描述采用四元数${ q}=\left\{{\eta ,\varepsilon } \right\}\in \mathbb{R}^{4}$表示, 相对四元数的计算公式如下
(21) $\begin{eqnarray} &&\left\{ {\delta_{\eta } ,\delta_{\varepsilon } } \right\}={ q}_{1} \ast { q}_{2}^{-1} =\\&&\qquad \left\{ {\eta_{1} \eta_{2} +\varepsilon_{1}^{\rm T} \varepsilon_{2} ,\eta_{2} \varepsilon_{1} -\eta_{1} \varepsilon_{2} -\tilde{{\varepsilon }}_{1} \varepsilon_{2} } \right\} \end{eqnarray}$
$\delta_{\varepsilon }=0$表示两个旋转坐标系重合. 基于单位四元数, 并考虑式(2)和式(3), 基座与末端执行器的终端位姿计算如下
(22) $\begin{eqnarray} \label{eq22} &&{ x}_{\rm b}^{\rm f} =\left[ \begin{array}{l} { r}_{\rm b}^{\rm f} \\ { q}_{\rm b}^{\rm f} \\ \end{array} \right]={ x}_{\rm b}^{\rm s} +\int_0^1 \left[ \begin{array}{cc} {{ E}_{3} } & {\bf0} \\ {\bf0} & {{ J}_{q} \left( {{ q}_{q} } \right)} \\ \end{array} \right] { J}_{a} \dot{{\bar{{ \theta }}}}{\rm d}u \end{eqnarray}$
(23) $\begin{eqnarray} \label{eq23} { x}_{\rm e}^{\rm f} =\left[ {\begin{array}{l} { r}_{\rm e}^{\rm f} \\ { q}_{\rm e}^{\rm f} \\ \end{array}} \right]={ x}_{\rm e}^{\rm s} +\int_0^1 {\left[ {{\begin{array}{cc} {{ E}_{3} } & {\bf0} \\ {\bf0} & {{ J}_{q} \left( {{ q}_{\rm e} } \right)} \\ \end{array} }} \right]} { J}_{\rm g} \dot{{\bar{{ \theta }}}}{\rm d}u \end{eqnarray}$
${ J}_{q} =\left[-\varepsilon\ \ \eta { E}_{3} +\tilde{{\varepsilon }}\right]^{\rm T}/2\in \mathbb{R}^{4\times 3}$且$\dot{{\bar{{ \theta }}}}={{\rm d}{ \theta }}/{{\rm d}u}$. 通过应用正向运动学, 避免了动力学奇异的发生. 终端位姿与期望位姿的偏差可计算如下
(24) $\left. \begin{array} \\ \delta { x}_{\rm b} =\left[ {{\begin{array}{*{20}c} {{ r}_{\rm b}^{\rm f} -{ r}_{\rm b}^{\rm d} } \hfill \\ {\eta_{\rm b}^{\rm d} \varepsilon_{\rm b}^{\rm f} -\eta_{\rm b}^{\rm f} \varepsilon_{\rm b}^{\rm d} -\tilde{{\varepsilon }}_{\rm b}^{\rm f} \varepsilon_{\rm b}^{\rm d} } \hfill \\ \end{array} }} \right]\\ \delta { x}_{\rm e} =\left[ {{\begin{array}{*{20}c} {{ r}_{\rm e}^{\rm f} -{ r}_{\rm e}^{\rm d} } \hfill \\ {\eta_{\rm e}^{\rm d} \varepsilon_{\rm e}^{\rm f} -\eta_{\rm e}^{\rm f} \varepsilon_{\rm e}^{\rm d} -\tilde{{\varepsilon }}_{\rm e}^{\rm f} \varepsilon_{\rm e}^{\rm d} } \hfill \\ \end{array} }} \right] \\ \end{array} \right\}$
基于上述分析, 空间机械臂抓捕规划策略考虑如下的优化指标.
(1) 调整末端执行器状态: 抓取规划要求机械臂末端执行器的终端位姿、速度要尽可能的与目标上的抓捕点相匹配. 因此, 定义如下的优化指标
(25) $\begin{eqnarray} \label{eq25} \varGamma_{1} \left( {\theta \left( t \right)} \right)=\left\| {\delta { x}_{\rm e} } \right\|_{{ Q}_{\rm e} } +\left\| {{\dot{{ x}}}_{\rm e}^{\rm f} -{\dot{{ x}}}_{\rm g}^{\rm f} } \right\|_{{ Q}_{v} } \end{eqnarray}$
(2) 最小化基座干扰: 为保持通信、观测等要求, 期望在抓捕过程中最小化基座干扰. 因此, 定义如下的优化指标
(26) $\begin{eqnarray} \label{eq26} \varGamma_{2} \left( {\theta \left( t \right)} \right)=\left\| {\delta { x}_{\rm b} } \right\|_{{ Q}_{\rm b} } \end{eqnarray}$
(3) 最大化力可操作度: 抓取完成后, 需要对目标进行消旋、调姿等操作, 因此, 需要最大化抓捕后的力可操作度
(27) $\begin{eqnarray} \label{eq27} \varGamma_{3} \left( {\theta \left( t \right)} \right)=\sqrt {\det \left( {{ J}_{\rm c} \left( {{ \theta }^{\rm f}} \right){ J}_{\rm c}^{\rm T} \left( {{ \theta }^{\rm f}} \right)} \right)} \end{eqnarray}$
3.3 关节参数化
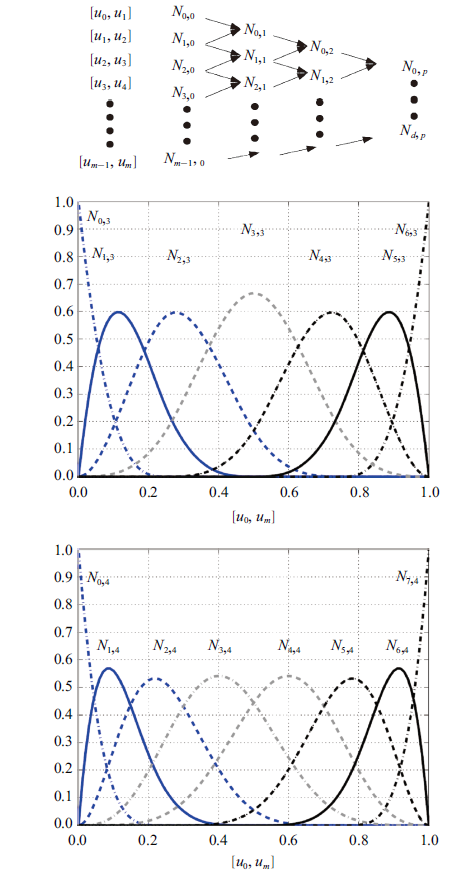
为保证抓取过程中关节位置、速度、加速度的连续性, 参考文献[14 ], 各关节的轨迹$\theta_{i} \left( t\right)$可以参数化为多项式曲线, 如Bezier曲线, 正弦多项式曲线等. 本文中, 采用B样条对关节进行参数化. B样条相比于Bezier曲线的构建需要更多的信息, 但是它具备如下优点: 首先, B样条曲线是一类Bezier曲线; 其次, B样条曲线具备Bezier曲线的所有特性; 再次, B样条曲线相比Bezier曲线提供了更好的控制灵活性. B样条曲线的阶次与其控制点的个数无关, 亦即, 可采用低阶曲线和更多控制点来构建运动曲线. 此外, B样条曲线具有局部修正特性, 改变某一个控制点并不会全局的改变曲线的形状, 此特性对于非线性优化过程中的求解十分有利.
给定$d+1$个控制点$P_{i,0} ,P_{i,1} ,\cdots ,P_{i,d} $和有$m+1$个节点的节点矢量${ U}=\left\{ {u_{0} ,u_{1} ,\cdots ,u_{m} }\right\}$, $u_{0} \leqslant u_{1} \leqslant \cdots \leqslant u_{m} $, 对于$p$阶次的Clamped B样条, 首节点与末节点具有重复度$p+1$, 因此, 对应于$m+1$个节点的节点矢量, $u_{0} =u_{1} =\cdots =u_{p} =0$和$u_{m-p} =u_{m-p+1} =\cdots =u_{m}=0$. 关节轨迹$\theta_{\rm i} \left( t \right)$可以描述为归一化的Clamped B样条曲线
(28) $\begin{eqnarray} \label{eq28} &&\theta_{i} \left( t \right)=C_{i} \left( u \right)=\displaystyle\sum\nolimits_{j=0}^d {N_{j,p} \left( u \right)P_{i,j} }\ \ {u\in \left[ {0,1} \right]},\\&&\qquad i=1,2,\cdots ,n \end{eqnarray}$
其中$N_{j,p} $是B样条的基函数, 可以递归计算如下
(29) $\begin{eqnarray} \label{eq29} &&N_{j,0} =\left\{ {{\begin{array}{l@{\ \ \ }l} {\mbox{1}}, & {\mbox{if } u_{j-1} \leqslant u\leqslant u_{j} } \\ {\mbox{0}}, & {\mbox{otherwise}} \\ \end{array} }} \right. \end{eqnarray}$
(30) $\begin{eqnarray} \label{eq30} N_{j,p} \left( u \right)=\frac{u-u_{j} }{u_{j+p} -u_{j} }N_{j,p-1} \left( u \right)+\\ \qquad\frac{u_{j+p+1} -u}{u_{j+p+1} -u_{j+1} }N_{j+1,p-1} \left( u \right) \end{eqnarray}$
上式通常被称为Cox-de Boor递归公式. 值得注意的是$d$, $m$和$p$满足$m=d+p+1$. 由于$u$是归一化时间, 对于轨迹的执行时间$T=t_{\rm f}-t_{\rm s} $, 如果定义$t=u\cdot T$, 关节速度和加速度可以计算如下
(31) $\begin{eqnarray} \label{eq31} &&\left. \begin{array}{l} \dot{{ \theta }}_{\rm i} =\dfrac{1}{T}\dfrac{{\rm d}\theta_{\rm i} }{{\rm d}u}=\dfrac{1}{T}{C}'_{\rm i} \left( u \right)=\\ \qquad \dfrac{1}{T}\displaystyle\sum\nolimits_{j=0}^{d-1} N_{j+1,p-1} \left( u \right)L_{i,j} \\ \ddot{{ \theta }}_{\rm i} =\dfrac{1}{T^{2}}\dfrac{{\rm d}^{2}\theta_{\rm i} }{{\rm d}u^{2}}=\dfrac{1}{T}{C}"_{\rm i} \left( u \right)=\\ \qquad \dfrac{1}{T^{2}}\displaystyle\sum\nolimits_{j=0}^{d-2} N_{j+2,p-2} \left( u \right)M_{i,j} \end{array} \right\} \end{eqnarray}$
$\begin{eqnarray} && L_{i,j} =\dfrac{p}{u_{j+p+1} -u_{j+1} }\left( {P_{i,j+1} -P_{i,j} } \right) &&M_{i,j} =\dfrac{p-1}{u_{j+p} -u_{j} }\left( {L_{i,j+1} -L_{i,j} } \right) \end{eqnarray}$
本文中, 选择四次Clamped B样条曲线$p=4,d=7,m=12$对关节轨迹进行参数化. B样条曲线的基函数计算可参考图6 . 式(18)中关节速度和加速度约束可通过调整执行时间满足
(32) $\begin{eqnarray} \label{eq32} T\geqslant \max \left( {\frac{\left| {{ {C}'}_{\max} } \right|}{{\dot{{ \theta }}}_{\max } },\sqrt {\frac{\left| {{ {C}"}_{\max} } \right|}{{\ddot{{ \theta }}}_{\max } }} } \right) \end{eqnarray}$
其中, ${ {C}'}={{\rm d}{ \theta }}/{{\rm d}u}$且${ {C}"}={{\rm d}^{2}{ \theta }}/{{\rm d}u^{2}}$. $t_{\rm g} -t_{\rm s} \geqslant T$意味着轨迹执行时间足够长且满足式(18), 终端时间可以设定为$t_{\rm f} =t_{\rm g} $; 否则, 需要更新$P_{i,j}$重新构建关节轨迹. 将式(17)中的等式约束代入式(28)和式(31)可得$P_{i,0}=P_{i,1} =P_{i,2} =\theta_{i}^{\rm s} $. 由于$\theta_{i}^{\rm s}$已知, 描述关节轨迹的Clamped B样条曲线形状仅依赖于剩余的控制点$P_{i,3},P_{i,4} ,\cdots ,P_{i,d} $. 考虑到空间机械臂的$n$个关节, 定义${ p}=\big[ P_{1,3} ,P_{1,4} ,\cdots , P_{1,d}$, $P_{2,3}$, $P_{2,4}$, $\cdots ,P_{n,3}$, $P_{n,4}, \cdots, P_{n,d} \big]^{\rm T}$作为设计变量, 一旦${ p}$确定, 即可确定每个关节的轨迹, 进而得到抓捕规划策略. 因此, 式(16)中的抓捕规划问题可转化为如下的优化问题
(33) $\left. \begin{array} \\ \mathop {\mbox{minimize}}\limits_{{ p}} & t_{\rm f} ,\varGamma \left( {{ p}} \right) \\ \mbox{subject to}: & g_{i} \left( {{ p}} \right)<0, \ h_{i} \left( {{ p}} \right)=0 \\ & { p}_{\min } \leqslant { p}\leqslant { p}_{\max } \\ \end{array} \right\}$
图6
图6
B样条基函数计算
Fig.6
B spline basic functions calculation
上述问题将利用自适应惯性权重的粒子群优化算法(PSO)进行求解, 算法基本步骤如下: 首先在可行的搜索区域内初始化具有随机初始值的粒子群. 单个粒子维度即为设计变量的维数. 然后, 各粒子对其适应度函数进行评估, 在搜索空间内搜索目前已知的自身最佳粒子(局部)和整群中的最佳粒子(全局). 各粒子的运动由局部及全局最佳粒子指导, 每一代更新一次. 当发现更好的粒子时, 就选作新一代粒子群运动的指导粒子. 此过程不断重复, 直到满足特定收敛条件或发现有更好的解决方案. PSO算法执行过程中, 需要考虑如何处理约束及选择合适的适应度函数, 参考文献[31 ,32 ], 采用修复不可行解集的方法处理本文中的不等式约束违反; 适应度函数选取式(25)用于评估每个粒子的优劣, 并存储可行的空间机械臂抓捕规划解集, 而后基于式(26)和式(27)进行多目标优化解集的选取与确定.
4 仿真结果
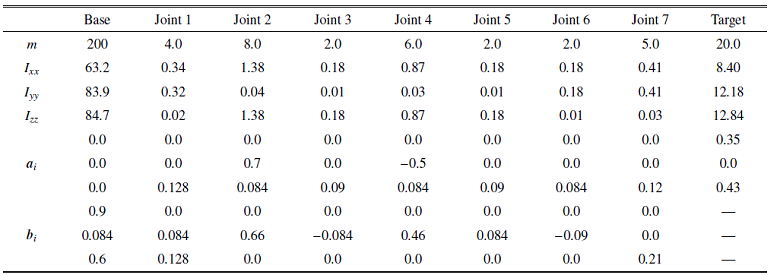
为验证本文提出的抓捕规划策略, 本节给出了抓捕翻滚目标的仿真验证. 空间机器人系统由一个7 DOF运动学冗余机械臂和6 DOF航天器组成, 运动学和动力学参数在表1 中给出, 其中${ a}_{i} $, ${ b}_{i} $和${ I}_{i} $在各运动体的体坐标系中进行描述. 在抓捕过程中, 首先基于机械臂的抓捕能力图谱、初始构型、目标运动预测等信息确定最优抓捕时机$t_{\rm g}$. 此后利用PSO算法搜索求解式(33), 构建基于Clamped B样条的关节轨迹, 生成空间机械臂的抓捕规划策略.
相对于目标体坐标系, 抓捕点的位姿可描述为${ x}_{\rm g}$ = $\Big\{ \rho _{\rm tg}$, ${ R}_{\rm t}^{\rm g}\Big\}$. 目标的初始状态为${ x}_{\rm t}^{\rm s}$ = (2.4, 0.0, $-0.5$, 0.717, 0.717, 0.0, 0.0), 目标绕三轴旋转, 旋转角速度$\omega_{\rm t}^{\rm s}$ = (8.594($^\circ$)/s, 2.865($^\circ$)/s, 0($^\circ$)/s). 基于机械臂能力分析、目标的运动预测, 最优抓捕时机为$t_{\rm f}=31.4$ s. 期望的末端执行器位姿可由此确定${ x}_{\rm e}^{\rm d}$ = (2.489, 0.197, $-1.010$, 0.761, $-0.498$, $-0.294$, $-0.294)$. 此外, 由于抓捕点的运动, 期望的末端执行器的速度为${\dot{{ x}}}_{\rm e}^{\rm d}$ = ($-0.013$, 0.075, 0.027, 0.132, $-0.008$, 0.086). 机械臂的初始构型及其对应的末端执行器位姿为${ \theta }^{\rm s}$ = ( 0, $-{\pi}/{3}$, 0 , ${\pi}/{4}$, 0, $-{\pi }/{12}$, 0) $\to$ ${ x}_{\rm e}^{\rm s}$ = (1.078, 0.252, $-1.853$, 1.0, 0.0, 0.0, 0.0). 基座的初始位姿为${ x}_{\rm b}^{\rm s} =$ (0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0), 利用式(25)中的适应度函数评估粒子群中单个粒子的优劣. ${ Q}_{\rm e}$和${ Q}_{v}$的确定取决于终端位姿、速度的要求. 本文中, 容许的位置误差为0.01 m, 姿态误差2$^\circ$, 线速度与角速度误差为0.01, 权重矩阵${ Q}_{\rm e} $和${ Q}_{v}$可确定如下
(34) $\left. \begin{array} \\ { Q}_{\rm e} =\left[\begin{array}{c@{\quad }c} 100{ E}_{3} & {\bf0}_{3}\\ {\bf0}_{3} & { E}_{3}/\sin\left(\dfrac{\pi}{180}\right)\\ \end{array} \right]\\ { Q}_{v} =\left[\begin{array}{c@{\quad }c} 100{ E}_{3} & {\bf0}_{3}\\ {\bf0}_{3} & 100{ E}_{3}\\ \end{array} \right] \\ \end{array} \right\}$
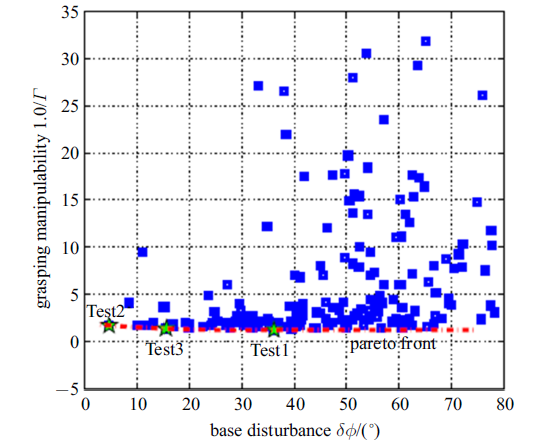
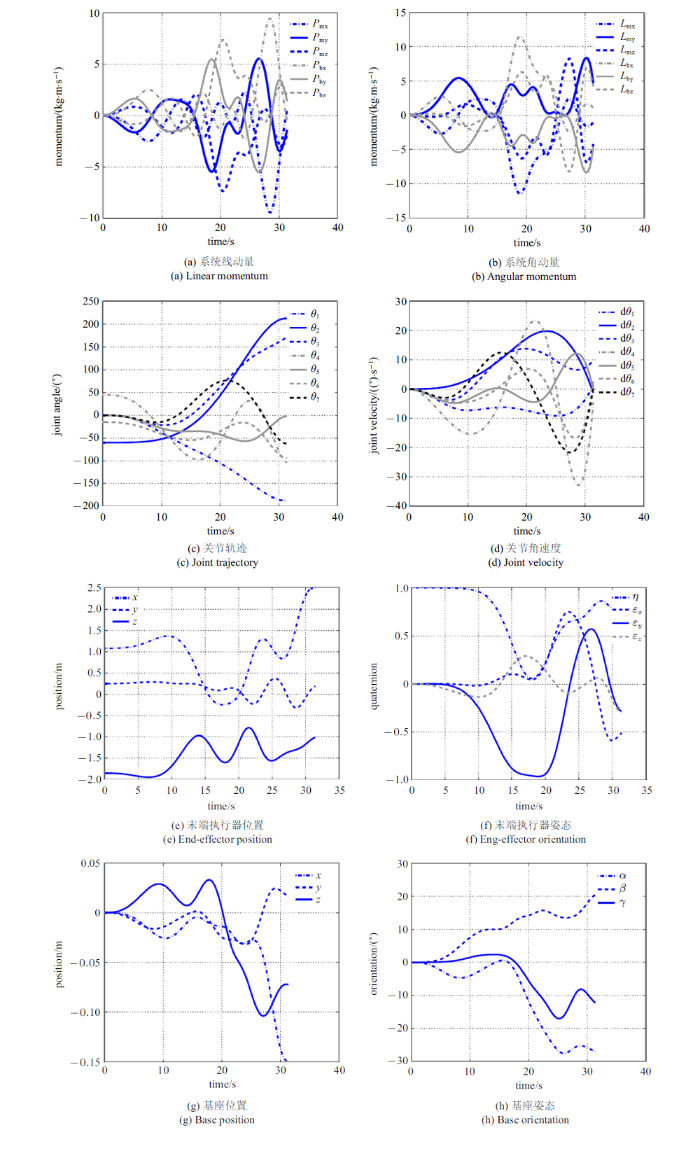
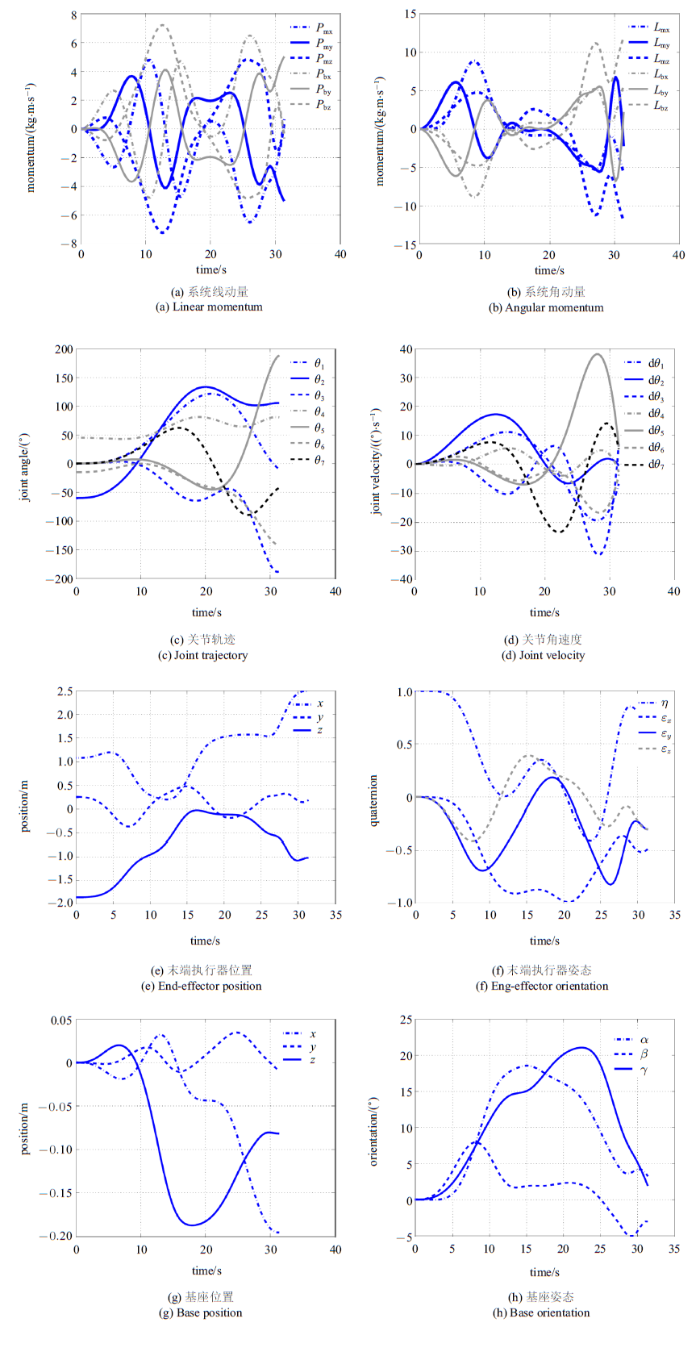
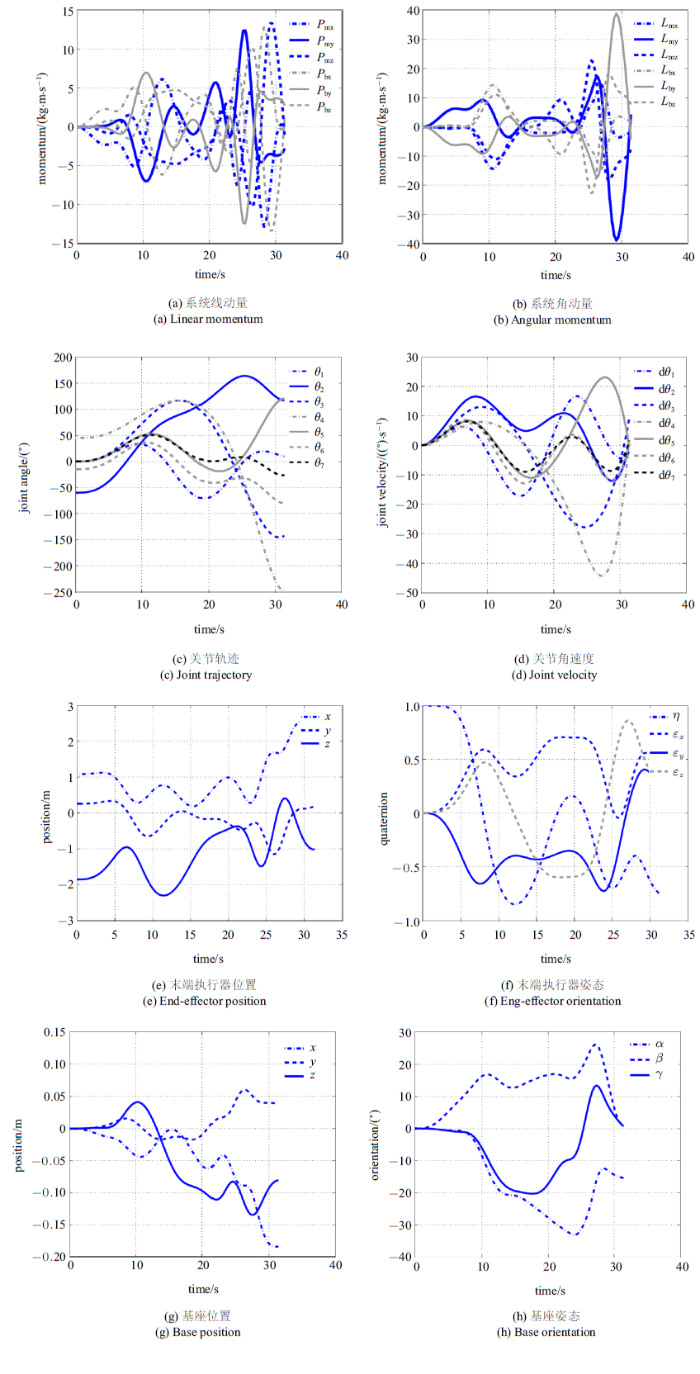
基于PSO的求解结果, 共选择三组记录来评价非合作目标抓捕规划策略. 三组记录对应的解集可参见表2 . 针对式(26)和式(27), 不同优化指标所构成的Pareto前沿如图7 所示. 图8 $\sim\!$图10 给出了三组不同解集对应的关节轨迹、末端执行器与基座的运动情形. 可以看出, 所有解集均满足仿真设定的终端状态误差要求. 此外, 抓捕过程中保证了空间机器人系统的动量守恒. 在终端抓捕时刻, 对于Test1, 最终的力可操作度为0.818, 总的基座姿态干扰为0.630; 对于Test2, 最终的力可操作度为0.588, 总的基座姿态干扰为0.083; 对于Test3, 最终的力可操作度为0.736, 总的基座姿态干扰为0.271. 可以看出, 末端执行器最终实现了对目标上抓捕点位姿和速度的匹配, 同时最小化基座姿态干扰和最大化末端执行器力可操作度两个优化指标均有考虑, 而选择不同的优化指标最终将影响空间机器人系统的终端状态.
图7
图7
Pareto前沿
Fig.7
Pareto front
图8
图8
Test1对应的关节轨迹、基座与末端执行器状态
Fig.8
Joint trajectories, base and end-effector's states for Test1
图9
图9
Test2对应的关节轨迹、基座与末端执行器状态
Fig.9
Joint trajectories, base and end-effector's states for Test2
图10
图10
Test3对应的关节轨迹、基座与末端执行器状态
Fig.10
Joint trajectories, base and end-effector's states for Test3
5 结论
空间机器人抓捕规划过程中, 需要考虑非合作目标的运动和机械臂的抓捕能力; 此外, 充分利用机械臂与基座间的动力学耦合特性, 可有效提高空间机器人系统的燃料利用率, 论文的主要工作列写如下:
(1)考虑机械臂抓捕能力、目标运动、末端执行器接近方向及TCP与抓捕点相对距离等因素, 确定了空间机械臂的最优抓捕时机, 并给出了抓捕点在抓捕时刻的终端位姿和速度;
(2)考虑自由漂浮空间机器人的非完整约束, 末端执行器的运动不仅依赖于逆运动学, 也依赖于历史运动路径. 由于本文所提方法无需对Jacobian矩阵求逆, 运动学与动力学奇异均得到了规避;
(3)采用Clamped B样条曲线对机械臂关节的轨迹进行参数化, 并对末端执行器的终端状态进行了优化; 此外, 将最小化基座干扰和最大化力可操作度作为抓捕后的优化指标.
仿真结果验证了所提算法可应用于抓捕时机的快速确定并生成优化的抓捕关节轨迹, 算法可有效扩展其应用于多臂机器人在轨抓捕过程之中. 具有测量和参数不确定性的鲁棒协调控制在本文中未充分考虑, 将是论文的未来工作之一.
参考文献
View Option
[1]
Hirzinger G Brunner B Dietrich J , et al . ROTEX--The first remotely controlled robot in space//Proceedings of the IEEE Conference on Robotics and Automation
San Diego, USA , 1994 , 2604 -2611
[本文引用: 1]
[2]
Inaba N Oda M . Autonomous satellite capture by a space robot//Proceedings of the IEEE Conference on Robotics and Automation
San Francisco, USA , 2000 , 1169 -1174
[3]
Ogilvie A Allport J Hannah M , et al . Autonomous satellite servicing using the orbital express demonstration manipulator system//Proceedings of the 9th International Symposium on Artificial Intelligence, Robotics and Automation in Space
Los Angeles, USA , 2008 , 25 -29
[4]
Rekleitis I Martin E Rouleau G . et al . Autonomous capture of a tumbling satellite
Journal of Field Robot 2007 ,23 :275 -296
[本文引用: 1]
[5]
Torres MA Dubowsky S . Minimizing spacecraft attitude disturbances in space manipulator systems
Journal of Guidance, Control, and Dynamics 1992 ,15 :1010 -1017
DOI
URL
[本文引用: 1]
[6]
Yoshida K Hashizume K Abiko S . Zeros reaction maneuver: flight validation with ETS-VII space robot and extension to kinematically redundant arm//Proceedings of the IEEE Conference on Robotics and Automation
Seoul, Korea , 2001 , 441 -446
[本文引用: 1]
[7]
Nguyen-Huynh T Sharf I . Adaptive reactionless motion for space manipulator when capturing an unknown tumbling target//Proceedings of the IEEE Conference on Robotics and Automation
Shanghai, China , 2011 , 4202 -4207
[本文引用: 1]
[8]
Wang MM Luo JJ Fang J . et al . Optimal trajectory planning of free-floating space manipulator using differential evolution algorithm
Advances in Space Research 2018 ,61 :1525 -1536
DOI
URL
[本文引用: 1]
[9]
Huang PF Xu YS Liang B . Dynamic balance control of multi-arm free-floating space robots
International Journal of Advanced Robotic Systems 2005 ,2 (2 ):117 -124
[本文引用: 1]
[10]
Wang MM Luo JJ Walter U . Novel synthesis method for minimizing attitude disturbance of the free-floating space robots
Journal of Guidance, Control, and Dynamics 2016 ,39 (3 ):695 -704
DOI
URL
[本文引用: 1]
[11]
Shah S Sharf I Misra A . Reactionless path planning strategies for capture of tumbling objects in space using a dual-arm robotic system//AIAA Conference on Guidance, Navigation, and Control
Boston, USA , 2013
[本文引用: 1]
[12]
Xu WF Peng JQ Liang B . et al . Hybrid modeling and analysis method for dynamic coupling of space robots
IEEE Transaction on Aerospace and Electronic Systems 2016 ,52 (1 ):85 -98
DOI
URL
[本文引用: 1]
[13]
Lampariello R Tuong D Castellini C , et al . Trajectory planning for optimal robot catching in real-time//Proceedings of the IEEE Conference on Robotics and Automation
Shanghai, China , 2011 , 3719 -3726
[本文引用: 1]
[14]
Wang MM Luo JJ Walter U . Trajectory planning of free-floating space robot using particle swarm optimization (PSO)
Acta Astronautica 2015 ,112 :77 -88
DOI
URL
[本文引用: 2]
[15]
介党阳 , 陆浩然 , 吴晗玲 等 . 空间大型机械臂系统载运轨迹优化方法
航空学报 , 2018 ,39 (S1 ):111 -119
[本文引用: 1]
( Jie Dangyang Lu Haoran Wu Hanling , et al . Transporting trajectory optimization method for large space manipulator system
Acta Aeronautica et Astronautica Sinica 2018 ,39 (S1 ):111 -119 (in Chinese))
[本文引用: 1]
[16]
Yamazaki K Tomono M Tsubouchi T , et al . A grasp planning for picking up an unknown object for a mobile manipulator//Proceedings of the IEEE Conference on Robotics and Automation
Orlando, USA , 2016 , 2143 -2149
[本文引用: 1]
[17]
Diankov R Ratliff N Ferguson D , et al . BiSpace planning: concurrent multi-space exploration//Robotics: Science and Systems
Zurich, Switzerland , 2008
[本文引用: 1]
[18]
余敏 , 罗建军 , 王明明 等 . 一种改进 RRT* 结合四次样条的协调路径规划方法
力学学报 , 2020 ,52 (4 ):1024 -1034
[本文引用: 1]
( Yu Min Luo Jianjun Wang Mingming , et al . Coordinated path planning by integrated improved RRT* and quartic spline
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (4 ):1024 -1034 (in Chinese))
[本文引用: 1]
[19]
Lin Y Sun Y . Robot grasp planning based on demonstrated grasp strategies
International Journal of Robotics Research 2015 ,34 (1 ):26 -42
DOI
URL
[本文引用: 1]
[20]
Yoshida K Dimitrov D Nakanishi H . On the capture of tumbling satellite by a space robot//Proceedings of the IEEE/RSJ Conference on Intelligent Robots and Systems
Beijing, China , 2006 , 4127 -4132
[本文引用: 1]
[21]
Aghili F . A prediction and motion-planning scheme for visually guided robotic capturing of free-floating tumbling objects with uncertain dynamics,
IEEE Transactions on Robotics 2012 ,28 (3 ):634 -649
DOI
URL
[本文引用: 1]
Visually guided robotic capturing of a moving object often requires long-term prediction of the object motion not only for a smooth capture but because visual feedback may not be continually available, e. g., due to vision obstruction by the robotic arm, as well. This paper presents a combined prediction and motion-planning scheme for robotic capturing of a drifting and tumbling object with unknown dynamics using visual feedback. A Kalman filter estimates the states and a set of dynamics parameters of the object needed for long-term prediction of the motion from noisy measurements of a vision system. Subsequently, the estimated states, parameters, and predicted motion trajectories are used to plan the trajectory of the robot's end-effector to intercept a grapple fixture on the object with zero relative velocity (to avoid impact) in an optimal way. The optimal trajectory minimizes a cost function, which is a weighted linear sum of travel time, distance, cosine of a line-of-sight angle (object alignment for robotic grasping), and a penalty function acting as a constraint on acceleration magnitude. Experiments are presented to demonstrate the robot-motion planning scheme for autonomous grasping of a tumbling satellite. Two robotics manipulators are employed: One arm drifts and tumbles the mockup of a satellite, and the other arm that is equipped with a robotic hand tries to capture a grapple fixture on the satellite using the visual guidance system.
[22]
郭闻昊 , 王天舒 . 空间机器人抓捕目标星碰撞前构型优化
宇航学报 , 2015 ,36 (4 ):390 -396
DOI
URL
[本文引用: 1]
空间双臂机器人抓捕目标星会导致碰撞,针对碰撞引起机器人系统基座姿态变化的问题,提出一种基于粒子群算法的碰撞前构型优化方法。该方法首先给出了碰撞前和碰撞后的动力学模型,然后根据冲量—动量方程推导出碰撞阶段动力学方程,最后提出基于粒子群算法的最优碰撞前构型规划数值方法,使碰撞对机器人系统角动量的影响尽量小。通过计算校验了该方法的有效性,找到了用于空间机器人抓捕目标星的较理想的碰撞前构型。
( Guo Wenhao Wang Tianshu . Pre-impact configuration optimization for a space robot capturing target satellite
Journal of Astronautics 2015 ,36 (4 ):390 -396 (in Chinese))
[本文引用: 1]
[23]
朱安 , 陈力 . 配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
力学学报 , 2019 ,51 (4 ):1156 -1169
[本文引用: 1]
( Zhu An Chen Li . Mechanical simulation and full order sliding collision avoidance complaint control based on neural network of dual-arm space robot with compliant mechanism capturing satellite
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (4 ):1156 -1169 (in Chinese))
[本文引用: 1]
[24]
艾海平 , 陈力 . 基于柔性机构捕捉卫星的空间机器人动态缓冲从顺控制
力学学报 , 2020 ,52 (4 ):975 -984
[本文引用: 1]
( Ai Haiping Chen Li . Buffer and compliant dynamic surface control of space robot capturing satellite based on compliant mechanism
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (4 ):975 -984 (in Chinese))
[本文引用: 1]
[25]
王明明 , 罗建军 , 王嘉文 等 . 空间机器人捕获非合作目标后的消旋策略及阻抗控制
机器人 , 2018 ,40 (5 ):750 -761
[本文引用: 1]
( Wang Mingming Luo Jianjun Wang Jiawen , et al . Detumbling strategy and impedance control for space robot after capturing an uncooperative target
Robot 2018 ,40 (5 ):750 -761 (in Chinese))
[本文引用: 1]
[26]
蓝启杰 , 刘宜成 , 张涛 . 基于位姿反馈的三臂空间机器人抓捕轨迹规划
中国机械工程 , 2018 ,29 (20 ):2495 -2501
[本文引用: 1]
( Lan Qijie Liu Yicheng Zhang Tao . Trajectory planning of a three-arm space robot based on pose feedback
China Mechanical Engineering 2018 ,29 (20 ):2495 -2501 (in Chinese))
[本文引用: 1]
[27]
彭键清 . 空间翻滚目标的位姿测量及其双臂捕获机器人的轨迹规划
[博士论文]. 哈尔滨: 哈尔滨工业大学 , 2018
[本文引用: 1]
( Peng Jianqing . Pose measurement of a space tumbling target and trajectory planning of dual-arm capture robot
[PhD Thesis]. Harbin: Harbin Institute of Technology , 2018 (in Chinese))
[本文引用: 1]
[28]
程靖 , 陈力 . 空间机器人双臂捕获卫星后辅助对接操作控制仿真
系统仿真学报 , 2018 ,30 (9 ):3429 -3436
[本文引用: 1]
( Cheng Jing Chen Li . Auxiliary docking maneuver control simulation of dual-arm space manipulator after capturing operation
Journal of System Simulation 2018 ,30 (09 ):3429 -3436 (in Chinese))
[本文引用: 1]
[29]
Umetani Y Yoshida K . Resolved motion rate control of space manipulators with generalized jacobian matrix
IEEE Transactions on Robotics and Automation 1989 ,5 (3 ):303 -314
DOI
URL
[本文引用: 1]
[30]
Porges O Lampariello R Artigas J , et al . Reachability and dexterity: Analysis and application for space robotics//Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk,
Netherlands , 2015
[本文引用: 1]
[31]
Helwig S . Particle swarms for constrained optimization
[PhD Thesis]. Erlangen, Germany: Erlangen University , 2010
[本文引用: 1]
[32]
Wang MM Luo JJ Yuan JJ . et al . Coordinated trajectory planning of dual-arm space robot using constrained particle swarm optimization
Acta Astronautica 2018 ,146 :259 -272
DOI
URL
[本文引用: 1]
ROTEX--The first remotely controlled robot in space//Proceedings of the IEEE Conference on Robotics and Automation
1
1994
... 空间机器人将在卫星维修、在轨装配、碎片清除等任务中发挥着重要作用. 典型的在轨演示试验如"Robot Technology Experiment (ROTEX)"、"Engineering Test Satellite VII (ETS-VII)"、"Orbital Express (OE)"和"凤凰号"等项目验证了空间机器人执行在轨服务任务的可行性[1 -4 ] . 然而, 在轨服务任务最具挑战性的工作之一是如何高效、可靠地抓捕目标卫星. 此外, 空间机械臂与基座之间的动力学耦合引起的非完整约束对于抓取规划提出了新的挑战. ...
Autonomous satellite capture by a space robot//Proceedings of the IEEE Conference on Robotics and Automation
0
2000
Autonomous satellite servicing using the orbital express demonstration manipulator system//Proceedings of the 9th International Symposium on Artificial Intelligence, Robotics and Automation in Space
0
2008
Autonomous capture of a tumbling satellite
1
2007
... 空间机器人将在卫星维修、在轨装配、碎片清除等任务中发挥着重要作用. 典型的在轨演示试验如"Robot Technology Experiment (ROTEX)"、"Engineering Test Satellite VII (ETS-VII)"、"Orbital Express (OE)"和"凤凰号"等项目验证了空间机器人执行在轨服务任务的可行性[1 -4 ] . 然而, 在轨服务任务最具挑战性的工作之一是如何高效、可靠地抓捕目标卫星. 此外, 空间机械臂与基座之间的动力学耦合引起的非完整约束对于抓取规划提出了新的挑战. ...
Minimizing spacecraft attitude disturbances in space manipulator systems
1
1992
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Zeros reaction maneuver: flight validation with ETS-VII space robot and extension to kinematically redundant arm//Proceedings of the IEEE Conference on Robotics and Automation
1
2001
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Adaptive reactionless motion for space manipulator when capturing an unknown tumbling target//Proceedings of the IEEE Conference on Robotics and Automation
1
2011
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Optimal trajectory planning of free-floating space manipulator using differential evolution algorithm
1
2018
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Dynamic balance control of multi-arm free-floating space robots
1
2005
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Novel synthesis method for minimizing attitude disturbance of the free-floating space robots
1
2016
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Reactionless path planning strategies for capture of tumbling objects in space using a dual-arm robotic system//AIAA Conference on Guidance, Navigation, and Control
1
2013
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Hybrid modeling and analysis method for dynamic coupling of space robots
1
2016
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Trajectory planning for optimal robot catching in real-time//Proceedings of the IEEE Conference on Robotics and Automation
1
2011
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
Trajectory planning of free-floating space robot using particle swarm optimization (PSO)
2
2015
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
... 为保证抓取过程中关节位置、速度、加速度的连续性, 参考文献[14 ], 各关节的轨迹$\theta_{i} \left( t\right)$可以参数化为多项式曲线, 如Bezier曲线, 正弦多项式曲线等. 本文中, 采用B样条对关节进行参数化. B样条相比于Bezier曲线的构建需要更多的信息, 但是它具备如下优点: 首先, B样条曲线是一类Bezier曲线; 其次, B样条曲线具备Bezier曲线的所有特性; 再次, B样条曲线相比Bezier曲线提供了更好的控制灵活性. B样条曲线的阶次与其控制点的个数无关, 亦即, 可采用低阶曲线和更多控制点来构建运动曲线. 此外, B样条曲线具有局部修正特性, 改变某一个控制点并不会全局的改变曲线的形状, 此特性对于非线性优化过程中的求解十分有利. ...
空间大型机械臂系统载运轨迹优化方法
1
2018
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
空间大型机械臂系统载运轨迹优化方法
1
2018
... 过往文献已提出多种空间机械臂轨迹规划方法. 增强干扰图(EDM)的概念[5 ] 首先被提出并应用于空间机器人的启发式轨迹规划问题求解. 然而, EDM很难计算, 尤其是对于具有较高自由度的空间机械臂. 此后, 文献[6 ]提出零反作用空间(RNS)的概念, 被应用于运动学非冗余和冗余空间机械臂的轨迹生成. 文献[7 ,8 ]考虑角动量守恒, 使用RNS的概念设计关节轨迹抓捕翻滚目标. 然而, 对于6自由度机械臂而言, RNS的体积十分有限. 文献[9 ]中, 提出等效平衡臂和动态平衡控制(DBC)相结合的方案减少基座姿态干扰. 文献[10 ]提出了一种新的组合策略, 将DBC和RNS集成到基于任务优先级的求解框架中. 此后, 文献[11 ]提出了空间双臂机器人点到点零反作用操作的规划策略. 文献[12 ]建模和分析了空间机器人系统的动力学耦合, 并将动力学耦合应用于最小化基座姿态干扰的运动轨迹规划. 此外, 可采用不同的关节轨迹参数化方法, 例如周期性均匀B样条[13 ] 、Bezier曲线[14 ] 等; 文献[15 ]给出了一种笛卡尔轨迹参数化方法, 使得自由漂浮空间机器人的轨迹规划问题转化为非线性优化问题. 非线性优化问题可以采用遗传算法、差分进化算法等进行求解. ...
A grasp planning for picking up an unknown object for a mobile manipulator//Proceedings of the IEEE Conference on Robotics and Automation
1
2016
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
BiSpace planning: concurrent multi-space exploration//Robotics: Science and Systems
1
2008
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
一种改进 RRT* 结合四次样条的协调路径规划方法
1
2020
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
一种改进 RRT* 结合四次样条的协调路径规划方法
1
2020
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
Robot grasp planning based on demonstrated grasp strategies
1
2015
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
On the capture of tumbling satellite by a space robot//Proceedings of the IEEE/RSJ Conference on Intelligent Robots and Systems
1
2006
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
A prediction and motion-planning scheme for visually guided robotic capturing of free-floating tumbling objects with uncertain dynamics,
1
2012
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
空间机器人抓捕目标星碰撞前构型优化
1
2015
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
空间机器人抓捕目标星碰撞前构型优化
1
2015
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
1
2019
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
1
2019
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
基于柔性机构捕捉卫星的空间机器人动态缓冲从顺控制
1
2020
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
基于柔性机构捕捉卫星的空间机器人动态缓冲从顺控制
1
2020
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
空间机器人捕获非合作目标后的消旋策略及阻抗控制
1
2018
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
空间机器人捕获非合作目标后的消旋策略及阻抗控制
1
2018
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
基于位姿反馈的三臂空间机器人抓捕轨迹规划
1
2018
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
基于位姿反馈的三臂空间机器人抓捕轨迹规划
1
2018
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
空间翻滚目标的位姿测量及其双臂捕获机器人的轨迹规划
1
2018
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
空间翻滚目标的位姿测量及其双臂捕获机器人的轨迹规划
1
2018
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
空间机器人双臂捕获卫星后辅助对接操作控制仿真
1
2018
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
空间机器人双臂捕获卫星后辅助对接操作控制仿真
1
2018
... 以上研究主要是解决捕获前阶段空间机械臂的轨迹规划问题, 而未考虑抓捕目标后的任务. 通常, 机械臂欲抓捕移动的目标, 需要感知环境并生成适当的抓捕策略, 最终实现机械臂末端执行器和目标抓捕点之间建立稳固的连接. 文献[16 ]描述了一种在真实环境中工作的移动机械手的抓捕规划方法, 利用当前物体模型优化机器人手的抓握位姿. 文献[17 ]提出了一种BiSpace规划算法, 结合了双向快速探索随机树(RRT)和RRT-JT算法, 通过同时探索多个空间来实现快速规划. 在此基础上, 文献[18 ]提出了改进的RRT*与四次样条曲线结合的协调路径规划方法. 文献[19 ]中提出了一种基于目标外形和操作任务, 学习人类抓取策略的抓捕集成方法. 前期的抓捕规划方法为在轨抓捕规划提供了参考. 通过在接近阶段使用偏置动量方法, 在接触碰撞阶段使用阻抗控制, 以及在捕获后阶段进行分布式动量控制, 文献[20 ]提出了一种可行的控制序列, 用于成功完成捕获操作. 文献[21 ]基于视觉反馈, 引入了一种引导操作机械臂先拦截, 后消旋的非合作目标抓捕策略, 形成了机器人捕获具有未知漂移和翻滚目标的预测和规划组合方案. 考虑抓捕过程中碰撞引起机器人基座姿态变化的问题, 文献[22 ]提出一种碰撞前的机械臂构型优化方法. 针对空间机械臂抓捕目标后的控制问题, 文献[23 ,24 ]设计了空间机器人在轨捕获非合作目标的柔性机构, 并分别基于神经网络的全阶滑模避障柔顺控制和动态缓冲柔顺控制, 实现抓捕过程的抗冲击与弹性振动主动抑制, 有效避免了机械臂关节电机的过载. 文献[25 ]设计了一类目标消旋策略并同时稳定基座的协调控制方法. 文献[26 ]以三臂空间机器人为对象, 提出一种基于位姿误差反馈的轨迹规划算法用于应对奇异位形出现时的位姿误差问题. 文献[27 ]系统地给出了空间双臂机器人的协同测量及轨迹规划方法. 文献[28 ]提出了空间双臂机器人捕获目标后辅助对接操作的协调控制方案. ...
Resolved motion rate control of space manipulators with generalized jacobian matrix
1
1989
... 式中, ${ J}_{\rm g}$被称为广义雅可比矩阵[29 ] . 基于式(2)和式(3)可以看出, 自由漂浮模式下基座和末端执行器的运动仅依赖于关节轨迹及动力学耦合效应. 因此, 通过适当的抓捕策略规划可实现多个优化指标, 如末端执行器任务, 最小化基座干扰或最大化力可操作度等. ...
Reachability and dexterity: Analysis and application for space robotics//Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk,
1
2015
... 针对单一机械臂, 其抓捕能力依赖于机械臂的运动学构型、安装位置等约束. 为了完成对目标的抓捕和操作, 机械臂需要更完备的抓捕能力描述. 因此, 结合机械臂的可达性和灵巧性概念[30 ] , 构建机械臂的抓捕能力图谱. ...
Particle swarms for constrained optimization
1
2010
... 上述问题将利用自适应惯性权重的粒子群优化算法(PSO)进行求解, 算法基本步骤如下: 首先在可行的搜索区域内初始化具有随机初始值的粒子群. 单个粒子维度即为设计变量的维数. 然后, 各粒子对其适应度函数进行评估, 在搜索空间内搜索目前已知的自身最佳粒子(局部)和整群中的最佳粒子(全局). 各粒子的运动由局部及全局最佳粒子指导, 每一代更新一次. 当发现更好的粒子时, 就选作新一代粒子群运动的指导粒子. 此过程不断重复, 直到满足特定收敛条件或发现有更好的解决方案. PSO算法执行过程中, 需要考虑如何处理约束及选择合适的适应度函数, 参考文献[31 ,32 ], 采用修复不可行解集的方法处理本文中的不等式约束违反; 适应度函数选取式(25)用于评估每个粒子的优劣, 并存储可行的空间机械臂抓捕规划解集, 而后基于式(26)和式(27)进行多目标优化解集的选取与确定. ...
Coordinated trajectory planning of dual-arm space robot using constrained particle swarm optimization
1
2018
... 上述问题将利用自适应惯性权重的粒子群优化算法(PSO)进行求解, 算法基本步骤如下: 首先在可行的搜索区域内初始化具有随机初始值的粒子群. 单个粒子维度即为设计变量的维数. 然后, 各粒子对其适应度函数进行评估, 在搜索空间内搜索目前已知的自身最佳粒子(局部)和整群中的最佳粒子(全局). 各粒子的运动由局部及全局最佳粒子指导, 每一代更新一次. 当发现更好的粒子时, 就选作新一代粒子群运动的指导粒子. 此过程不断重复, 直到满足特定收敛条件或发现有更好的解决方案. PSO算法执行过程中, 需要考虑如何处理约束及选择合适的适应度函数, 参考文献[31 ,32 ], 采用修复不可行解集的方法处理本文中的不等式约束违反; 适应度函数选取式(25)用于评估每个粒子的优劣, 并存储可行的空间机械臂抓捕规划解集, 而后基于式(26)和式(27)进行多目标优化解集的选取与确定. ...