引言
交通拥堵是当前各大城市的顽症. 有效地解决交通拥堵问题, 必须从整个道路交通网络的角度出发, 通过科学的交通诱导, 合理分配并使用道路资源. 随着计算机技术的发展和计算能力的迅速提高, 基于建模和仿真的动态交通流研究方法为解决城市交通拥堵问题提供了新的途径. 1992年Biham等[1]将真实道路网络简化为由正方形元胞组成的二维区域, 提出了描述网络交通流的元胞自动机模型, 即Biham-Middleton-Levine (BML)模型. 该模型可以再现自由流和全局堵塞两种状态, 表明当车辆密度超过临界密度后, 会发生从自由流相到堵塞相的一阶相变. 该模型提出后, 人们普遍认为该模型只存在自由流相和堵塞相. 直到2005年, D'Souza[2]在对系统尺寸更大的BML模型进行研究时发现还存在一种中间态, 在该中间态下自由流相和堵塞相可以同时存在. 此后在BML模型及其改进模型中发现新的交通流相成为一个引起广泛兴趣的问题.
在BML模型中, 每个元胞都是交叉路口, 完全忽略了相邻路口之间道路上交通流的演化过程. 该模型引入同步交通灯, 且交通周期$T$为1. 车辆仅有两个可能的运动方向(向东或向北), 在初始时刻随机产生, 且最大车速为1. 采取周期性边界条件. 每辆向东(北)的车只能沿水平(垂直)方向固定车道运动, 即每个水平(垂直)道路上向东(北)的车辆数是守恒的. 车辆运动采用并行更新方式. 很明显, BML模型是最简化的城市交通网络模型. 此后许多学者考虑到实际交通情况, 对BML模型进行了多方面的推广和改进. 在保证BML模型每条车道上的两个方向运动的车辆保持数目守恒的前提下, Chuang等[3]在BML模型中研究了失效的交通灯对道路通行能力的影响, 发现低密度下, 平均车速有所增大, 而临界密度减小. Sun等[4]研究了交通灯周期$T$对BML模型的影响, 发现当$T\geqslant 4$时会出现一种自由流相和堵塞相的共存相, 并解释了不同周期下系统相分离产生的原因. Xie等[5] 采用动态交通灯策略, 通过考虑不同方向车辆的动态空间构型, 利用局部车辆信息来控制城市交通, 车辆可以自组织成带装结构的新型中间状态. Ding等[6] 研究了BML模型中违反交通灯规则的驾驶员对系统的影响, 发现在自由流相中出现两种不同斜率的条状结构. Fukui等[7]研究了BML模型中两个方向具有不同最大速度的两种情况, 发现了介于自由流相和全局堵塞相之间的两种新交通流相. Ishibashi等[8]研究了BML模型的相图, 提出了中间拥堵流相的计算公式. 利用该公式得到了自由流与阻塞流相之间的相边界, 其中流量达到最大值. Fukui等[9]还研究了最大速度为2的BML模型, 发现系统临界密度可以由文献[8]中提出的流量公式拟合. Ding等[10]研究了采用随机更新方式的BML模型, 发现在开放边界条件下系统也会出现一种自由流相和堵塞相的共存相. Kuang等[11]将慢启动规则引入四向行驶的BML模型中, 发现多自由流条纹和多堵塞条纹共存的新的相分离现象. Pan等[12]提出了考虑合作意愿的BML模型, 提出了一种具有合作意愿的进化博弈方法来处理邻居间的冲突, 可以缓解交通网络的压力. Ding等[13-14]还考虑了天桥的影响.
部分学者放松了BML模型中对车辆运动的限制. Cuesta等[15]在BML模型中引入车辆的随机转向, 并首次将双向行驶规则扩展为四向行驶规则, 不同运动方向的车辆数目不再保持不变. Nagatani等[16]将随机转向规则加以改进, 规定车辆只有在遇到堵塞状态时才会以一定概率进行随机转向. 车辆可随机转向破坏了BML模型每个方向车辆数的守恒性. 盘薇[17]在采用随机更新方式的BML模型基础上引入了绕路策略, 当车辆遇到拥堵时, 会改变行驶方向来绕过拥堵区, 而绕过拥堵区域后则会再转回原行驶方向. Li等[18]研究了根据车辆信息控制车辆换道的BML模型, 发现系统可以在较大的密度范围内保持中间态. 虽然车辆可换道破坏了BML模型中车道车辆数守恒, 但是每个方向上车辆总数仍然不变. Moussa等[19]首次考虑了车辆的起点和终点(OD), 研究了车辆出行距离与出行时间之间的关系. Fang等[20]在模型中设定了办公区域, 考虑了车辆从居住区到达办公区域的不同路径选择对交通网络的影响. 这种车辆寻找路径的方式更接近实际, 车辆在行驶过程中会不断改变运动方向.
对BML模型的另外一个重要改进是考虑道路系统的实际网络结构, 逐渐从规则网络过渡到不规则的真实路网. Chowdhury等[21]在BML模型的基础上引入NaSch模型[22]描述相邻路口之间道路上的车流运动, 提出了ChSch模型. Scellato[23]建立了更接近真实交通网络的双向双车道路网模型. Chen等[24]在双向双车道模型中引入交通灯, 发现只提供局部路段上游道路信息可以最大限度的提升系统的交通性能. Huang等[25]研究了预信号在双向四车道系统中的影响. Wu等[26]在双向四车道系统中发现周界流量控制策略可以改善系统的通行状况. Ao等[27]在类曼哈顿模型中加入自适应交通灯, 显著提高了车辆的平均速度和到达率. 李浩等[28]在类曼哈顿城市系统中, 引入考虑平均速度和最小费用的路径选择策略.
即使更实际的道路交通网络是当前研究的热点, 类BML模型仍然是一个活跃的研究领域. 最近Hu等[29]将真实的城市交通路网直接映射到改进的BML模型中进行拥堵预测, 表明BML模型研究实际交通网络的拥堵仍可发挥重要作用. 以往由于技术手段的限制, 往往只能对局部路段交通流进行实测和建模[30-32], 随着大数据时代以及5G时代的来临, 为城市道路网络交通流的研究带来了新的契机. 驾驶员能够实时得到大量的道路信息(例如车道中车辆的平均速度、车道的平均密度以及车道上车辆的平均通行时间等), 从而能够根据道路信息选择道路, 因此将道路信息作为车辆换道依据是十分必要的. 本文将道路信息和转向灯影响引入BML模型中, 提出了综合考虑车道信息和前车转向灯影响的换道策略, 并在有(无)交通灯控制的BML模型中研究该换道策略对系统临界密度和通行能力的影响.
1 改进的BML模型
1.1 BML-I模型和BML-II模型
在Biham等的文章[1]中曾提出两种满足排斥体积效应的模型, 本文称为BML-I模型(有交通灯)和BML-II模型(无交通灯). 在BML-I模型中, 交通路网用$N\times N$的二维方形网格(元胞)表示, 采用周期性边界条件, 其中引入了同步交通灯. 每个元胞有3种状态: 被一辆北向或东向行驶的车辆占据、或空置. 在奇(偶)数时间步, 当东(北)向行驶车辆前方相邻元胞为空且交通灯允许其运动时, 则向前行驶一格占据该元胞, 否则该车辆保持静止; 北(东)向行驶车辆全部保持静止. 模拟结果显示, 随着系统车辆密度的增加, 该模型会发生由自由流状态到堵塞状态的一阶相变. 临界密度记为$\rho _{\rm c} $, 当系统密度$\rho <\rho _{\rm c} $时, 系统处于自由流状态, 车辆平均速度$<V>=1$; 当系统密度$\rho >\rho _{\rm c} $时, 系统处于堵塞状态, 车辆平均速度$<V>=0$. 在BML-II模型中, 则取消了交通灯, 北向和东向行驶车辆可以同时运动, 当不同方向行驶的车辆试图同时进入同一元胞而发生冲突. 此时通常以等概率选择其中一辆车进入目标元胞, 而另一辆车则保持静止. 由于缺少交通灯的调控, 不同方向行驶车辆之间的冲突会显著降低系统的通行效率, 从而导致BML-II模型的临界密度明显小于BML-I模型.
1.2 改进的BML-I模型和BML-II模型
本文首先改进了BML-II模型, 称为mBML-II模型. 该模型换道策略如下.
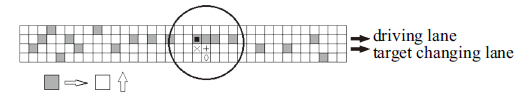
以东向行驶车辆为例, 其换道行为如图1所示. 图中黑色方块为所研究的向东行驶车辆, 此时由于前方相邻元胞被其他车辆占据, 若要继续前进则需进行换道. 在进行换道前, 司机需要判断相邻车道是否可以换道. 若司机想进行换道, 首先图中由"$\times $"标记的元胞必须为空, 否则车辆无法进入该车道, 其次由"+"和"0"标记的元胞都不能被北向行驶的车辆占据, 否则车辆换道后将无法继续前进. 北向行驶的车辆换道条件与此类似.
图 1
图 1
东向车辆换道示意图
Fig. 1
Sketch of lane-changing behavior for an eastbound vehicle
当满足换道条件后, 司机再根据前车转向灯和道路交通信息综合判断是否进行换道. 在本模型中, 北向行驶车辆换道时考虑左侧车道, 东向行驶车辆换道时考虑下侧车道. 在进行换道时, 首先根据当前车道与目标车道信息, 并考虑转向灯的状态后将这些交通信息量化如下
其中, $\rho _0 $表示当前车道的密度, 即当前车道上车辆总数目与该车道长度之比, $\rho _1 $表示目标车道的密度; $v_0 $表示当前车道的车辆平均速度, 即当前车道上运动车辆(包括离开当前车道的车辆)的总数与该车道上车辆总数之比, $v_1 $表示目标车道的车辆平均速度; $\tau $表示目标车道前方同向行驶车辆的转向灯状态, 当$\tau =0$ (1)时表示前方车辆无(有)转向行为, 且$\bar{{\tau }}=1-\tau $. $c$为系数, 在本文中取$c=2$. $m_0 $和$m_1$分别表示当前车道和目标车道的交通信息量化值.
在得到当前车道和目标车道的交通信息量化值后, 根据如下公式计算出车辆的换道概率
对于BML-I模型做类似的改进, 相应的模型称为mBML-I模型. 在mBML-I模型中, 仅增加了同步交通灯, 其余部分与mBML-II模型相同.
2 模拟结果与对比分析
本文对4种不同系统尺寸(包括$16\times 16$, $32\times 32$, $64\times 64$和$128\times 128)$进行了模拟. 模拟时间根据系统尺寸做相应调整: 当系统尺寸为$128\times 128$时, 每个样本共运行$10^6$个时间步, 取后$10^5$个时间步作为统计时间. 每个密度下重复计算20次, 再取速度的平均值.
2.1 mBML-II模型的模拟结果与分析
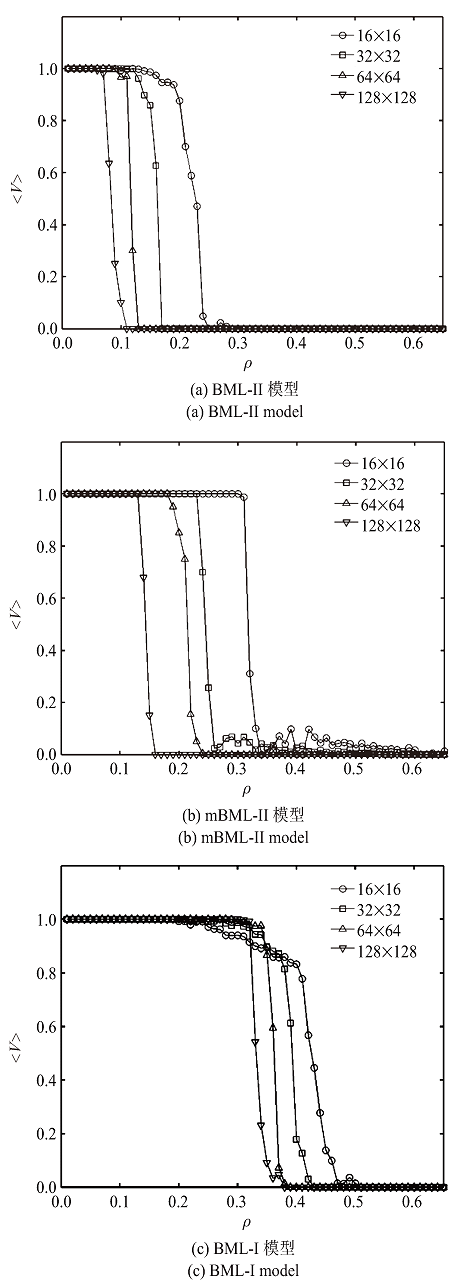
首先给出BML-II模型、mBML-II模型以及BML-I模型在不同系统尺寸下的速度-密度关系图. 从图2中可以看出这三种模型随着系统密度的增大, 都会发生从自由流到堵塞的一阶相变, 且相变的临界密度$\rho _{\rm c} $会随着系统尺寸的增大而减小. 在$\rho <\rho _{\rm c} $时, 3种模型都处于自由流状态, 系统平均速度$<V>=1$; 在$\rho >\rho _{\rm c} $时, BML-II模型以及BML-I模型处于堵塞状态, 系统平均密度接近于零, 而mBML-II模型由于引入了换道机制, 车辆在遇到堵塞时会通过换道绕过堵塞区域, 所以在较高密度下平均速度仍有波动. 值得注意的是, mBML-II模型在最小的系统尺寸($16\times 16)$下, 已经表现出明显的一阶相变特征, 而BML-I和BML-II模型都有一个相当大的相变过渡区域. 当系统尺寸较小时, mBML-II的临界密度与BML-I模型接近, 但随着系统尺寸的增大, 临界密度明显减小, 但仍比BML-II模型有明显增大.
图 2
图 2
BML-II模型、mBML-II模型以及BML-I模型在不同系统尺寸下的速度-密度关系
Fig. 2
Speed-density curves of BML-II model, mBML-II model and BML-I model at different system sizes
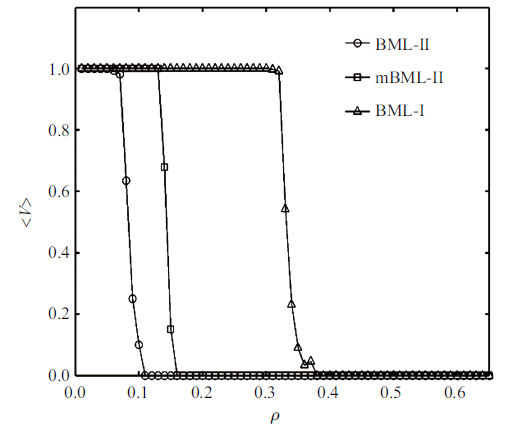
图3给出系统尺寸为$128\times 128$时, 3种模型的速密关系曲线, 此时系统尺寸较大, 呈现出明显的一阶相变特征, 且过渡区较小. 从图中可以看出BML-II模型的临界密度约为0.1, mBML-II模型的临界密度约为0.15, BML-I模型的临界密度约为0.35. 可以发现mBML-II模型相比于BML-II模型, 临界密度提升了50%. 由此可见, 引入换道策略可以提升交通网络的通行能力, 在一定程度上改善交通状况. 但是相比于BML-I模型, mBML-II模型的临界密度依然较小, 可见交通灯依然是改善交通状况更有效的策略.
图 3
图 3
系统尺寸为$128\times 128$时三个模型的速密变化曲线对比
Fig. 3
Comparison of the velocity-density curves in three models (when the system size is 128 × 128)
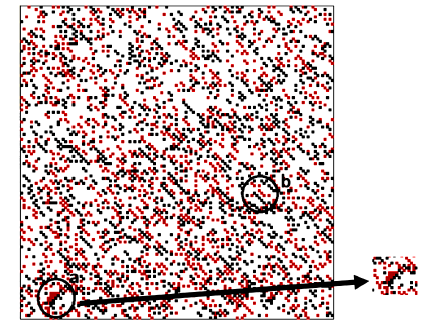
由图4(a)可知, 对于BML-II模型, 当$t=100$ s时, 系统中已经产生了多处局部拥堵; 当$t=1000$ s时, 系统演化为全局拥堵, 产生了从右上角到左下角延伸的拥堵带, 常呈现树枝状分叉结构. 对于mBML-II模型, 当$t=100$ s时, 系统自发演化成与水平轴成$135^{\circ}$的条状分布. 当$t=1000$ s时, 系统中产生了与水平轴成$45^{\circ}$的局部拥堵区域, 此时系统处于局部自由流与局部拥堵共存的状态. 随着时间的延长, 堵塞带逐渐扩展, 当演化时间继续延长时, 系统将处于全局拥堵状态, 产生了一条与水平轴成$45^{\circ}$的拥堵带. 通过对比, 可以看到在BML-II模型中, 全局拥堵状态下的堵塞带界限分明, 不同行驶方向的车辆被明显区分开, 仅有极少数车辆混杂在不同方向的车队中, 而在mBML-II模型中, 由于引入了换道规则, 全局拥堵状态下产生的堵塞带并没有明显界限, 不同行驶方向的车辆混杂在一起; 对于BML-I模型, 由于尚处于自由流范围, 系统自发的形成了与水平轴成$135^{\circ}$的有序条带, 见图4(c).
下面进一步讨论共存相的产生和演化机制. 本文所引入换道策略允许车辆选择路况更好的道路, 但在换道过程中, 换道的车辆可能会导致局域密度增大. 如图5所示, 在左下角处产生了车辆分布的密集区, 在此区域内车辆易产生换道. 由于车辆的换道行为, 在该密集区内会产生与自由流的有序条带方向相反的倒锯齿结构, 且此处车辆换道位置被占据, 无法通过换道而进行解锁. 当系统密度较高的情况下, 如果自锁未能及时解开, 当进入拥堵区的车辆多于离开的车辆时, 拥堵区不断向上游(右下方)传递, 局部拥堵最终发展为全局拥堵, 如图4(b)所示. 当系统尺寸足够大的时候, 一旦出现局部拥堵后, 最终演化为全局拥堵的概率显著增大, 因而在mBML-II模型中出现的自由流和局部堵塞共存相不能长时间保持, 临界密度也会进一步减小.
图 4
图 4
密度为0.2时, BML-II模型、mBML-II模型以及BML-I模型在不同时刻下的车辆空间分布图
Fig. 4
Space distributions of vehicles in BML-II model, mBML-II model and BML-I model at different times
图 5
图 5
mBML-II模型在尚未形成完全拥堵时的车辆空间分布图
Fig. 5
Spatial distribution of vehicles in mBML-II model before the global congestion occurs
2.2 mBML-I模型的结果与分析
图 6
图 6
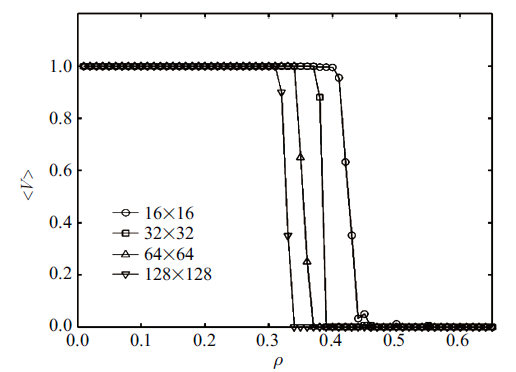
mBML-I模型在不同系统尺寸下的速密关系曲线
Fig. 6
Speed-density curves of mBML-I model under different system sizes
图7为系统密度为$\rho =0.5$时, 两种模型在不同时刻的车辆空间分布图. 此密度已经超过临界密度, 最终都会形成全局拥堵. 对比图4(a)与图4(b)未形成全局堵塞的车辆空间分布可以发现, mBML-I模型形成的局部堵塞带边界较为光滑, 而在BML-I模型中则较为粗糙, 在横向和纵向分别产生了许多细小的长条状拥堵. 在形成全局拥堵后的时空图中, 这种现象更加明显. 这是由于添加换道规则后, 处于细小长条状拥堵处的车辆会选择换道然后继续行驶. 与图4(b)产生全局拥堵的时空图相比, mBML-I模型在形成全局拥堵后, 北向车辆与东向车辆之间有明显的分界线, 不会产生mBML-II模型中不同方向车辆混杂的现象, 见图4(b). 总体而言, mBML-I模型和BML-I模型的定性性质类似. 这表明当考虑交通灯时, 换道虽然可以改变局部行为, 但不能改变系统的全局特征, 它主要由交通灯所确定.
图 7
图 7
密度为0.5时, BML-I模型、mBML-I模型在不同时刻下的车辆空间分布图
Fig. 7
Spatial distributions of vehicles in BML-I model and mBML-I model at different times ($\rho=0.5$)
图8分别为BML-I模型和mBML-I模型在小系统尺寸($16\times 16)$, 密度$\rho =0.4$时不同时刻的车辆空间分布图. 该密度略低于临界密度. 从图中可以看出, 当$t=100$ s时, 由于随机初始分布的影响, 两种模型车辆分布均呈现无规律的混乱状态. 随着时间$t$的不断增加, 这两种模型均会朝着与水平轴成$135^{\circ}$的条带状演化, 但演化所需要的时间不同. mBML-I模型会更快趋于规则的车辆空间分布状态, 而BML-I模型在$t=10 000$ s时车辆的空间分布仍较为随机, 难以观察到明显的规则斑图. 这也是BML-I模型平均速度略低于mBML-I模型的原因(比较图2(c)和图6). 由此可见, 引入换道规则有利于系统更快达到规则有序的分布, 从而导致系统的相变区域变窄.
图 8
图 8
密度$\rho =0.4$时, mBML-I模型和BML-I模型在不同时刻下的车辆空间分布图, 从上至下依次为$t=10^2$ s, $10^4$ s, $5\times 10^4$ s
Fig. 8
Spatial distribution of vehicles in mBML-I model and BML-I model at different times ($\rho =0.4$ and $t=10^2$ s, $10^4$ s, $5\times 10^4$ s)
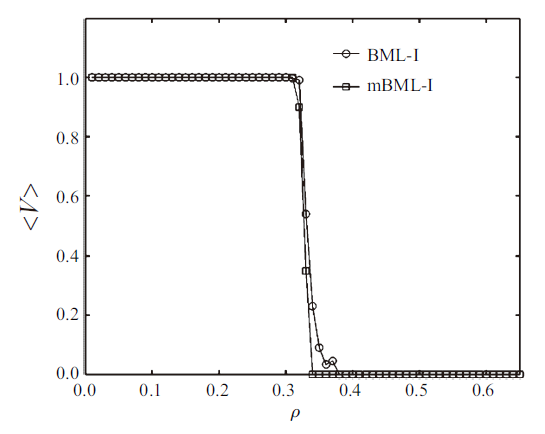
从图9中可以明显看出当系统尺度足够大时, BML-I模型和mBML-I模型的临界密度非常接近. 这说明交通灯在地面道路网络中起着关键的作用. 在有交通灯控制的系统中, 换道策略虽然能够影响系统中车辆演化过程, 但并不能有效改善整体交通状况, 因而无法有效提高临界密度, 但是mBML-I模型中的过渡区域更窄. 在现实交通中, 当密度过大时, 交通拥堵必然发生, 即使换道行驶, 依然难以避开拥堵.
图 9
图 9
系统尺寸为$128\times 128$时, BML-I模型与mBML-I模型的速密曲线
Fig. 9
Speed-density curves of BML-I model and mBML-I model when the system size is $128\times 128$
3 结束语
本文对BML模型进行推广, 引入了综合考虑转向灯影响和车道信息的换道机制, 并在周期性边界条件下进行模拟. 模拟结果表明对于mBML-II模型, 由于添加了换道机制, 相比于BML-II模型, 系统的临界密度明显增大, 交通运行状况有较大改善. 同时发现存在一种新的自由流和局部拥堵的临时共存相. 当密度超过临界密度后, 局部拥堵将逐渐扩展直至形成全局拥堵, 而当密度较小时, 局部拥堵则会消融并演化为自由流; 对于BML-I模型, 添加换道机制后, 系统临界密度并没有明显改变, 虽然局部车辆运动的特征有所改变. 总体而言, 引入换道机制以后, 系统由自由流状态到堵塞状态的相变过渡区域明显变窄, 即使在最小的系统尺度下依然呈现出明显的一阶相变特征, 这与BML模型有较大差异. 对于较小尺度的系统, 无交通灯的mBML-II模型的临界密度已接近有交通灯的BML-I模型, 说明引入换道机制的效果明显, 但对于系统尺寸较大的情况, 其临界密度要明显小于BML-I模型, 这是因为在更大的系统中, 局部拥堵更有可能发展成为全局拥堵. 如何避免由于换道引起的副作用, 更有效地提高交通网络通行能力, 还需要做进一步的研究.
参考文献
Self-organization and a dynamical transition in traffic-flow models
Coexisting phases and lattice dependence of a cellular automaton model for traffic flow
Two-dimensional traffic flow problems with faulty traffic lights
Timing of traffic lights and phase separation in two-dimensional traffic flow
Dynamical traffic light strategy in the Biham-Middleton-Levine model
Effect of violating the traffic light rule in the Biham-Middleton-Levine traffic flow model
Flow of cars crossing with unequal velocities in a two-dimensional cellular automaton model
Phase diagram of symmetric two-dimensional traffic model
Phase diagram of symmetric two-dimensional traffic model II. Higher-velocity case
Traffic flow in the Biham-Middleton-Levine model with random update rule
Effect of slow-to-start in the extended BML model with four-directional traffic
Biham-Middleton-Levine model in consideration of cooperative willingness
A two-dimensional BML model of traffic flow considering overpass configuration
Effect of overpasses in the Biham-Middleton-Levine traffic flow model with random and parallel update rule
Phase transitions in two-dimensional traffic-flow models
Effect of jam-avoiding turn on jamming transition in two-dimensional traffic flow model
城市交通网络元胞自动机模型的相变研究. [硕士论文]
Phase transition investigation of cellular automata urban traffic network models. [Master Thesis]
Effect of vehicle's changing lanes in the Biham-Middleton-Levine traffic flow model
Biham-Middleton-Levine traffic model with origin-destination trips
A two-dimensional CA traffic model with dynamic route choices between residence and workplace
Self-organization of traffic jams in cities: Effects of stochastic dynamics and signal periods
A cellular automaton model for freeway traffic
Traffic optimization in transport networks based on local routing
Effects of the amount of feedback information on urban traffic with advanced traveler information system
Effect of pre-signals in a Manhattan-like urban traffic network.
Perimeter control for urban traffic system based on macroscopic fundamental diagram
Network operation reliability in a Manhattan-like urban system with adaptive traffic lights
基于平均速度信息的城市交通路径诱导策略
Study on global route guidance strategy for urban traffic flow based on average speed information
Real-time traffic jams prediction inspired by Biham, Middleton and Levine(BML) model
基于实测数据的交通流模型比较研究
A comparative study on traffic flow models based on measured data
城市快速路交通流速密关系模型优化研究
Study on optimization of traffic flow velocity-density models for urban freeway
基于交通流实测数据的加速度研究
Study on the acceleration of traffic flow based on the empirical data
Advanced information feedback in intelligent traffic systems