引言
1990年,学者McGeer首次提出了"被动行走" (passive dynamic walking)的概念,描述了一类可以仅依靠自身重力以及结构特性在斜坡上实现稳定行走的机构[1].相比于具有复杂驱动与控制的双足机器人,被动行走器具有能量利用率高,行走步态自然的优点,因此在实验研究和理论研究层面都得到了广泛的关注.目前在实验研究层面已经取得了较多研究成果[2-9].例如,2005年由美国康奈尔大学、荷兰代尔夫特理工大学、美国麻省理工大学开展的 (准)被动行走器的研究工作发表在Science杂志上,简要介绍了被动行走器的实验研究进展,和基于被动行走机制改善双足机器人能效性的实验尝试[2].国内高校,诸如清华大学[3-4]、浙江大学[9-10]等高校的学者也开展了 (准)被动行走器的实验样机研究工作.上述研究中的部分 (准)被动行走器样机如图1所示[6-8].
图1
近年来,部分学者通过引入法向接触力模型与摩擦力模型描述圆弧足被动行走器足与地面间的接触力,通过数值仿真研究了平面圆弧足直腿被动行走器的步态,得到了支撑足与地面间有滑动或有弹起的步态[21-24]. 如段文杰等[24]利用牛顿碰撞恢复系数与库伦干摩擦模型描述支撑足与地面间的接触,采用时间步进法[25]分析了摩擦系数与碰撞恢复系数引起的圆弧足被动行走器行走步态的变化.祁峰等[23] 利用扩展的赫兹接触模型与修正的库伦摩擦模型描述支撑足与地面间的法向接触力与切向摩擦力,研究了圆弧足直腿被动行走器在不同接触参数条件下的步态变化. 郑旭东等[22]利用扩展的赫兹接触模型与库伦干摩擦模型描述支撑足与地面间的法向接触力与切向摩擦力,基于线性互补[26- 28]研究了圆弧足被动行走器的多种步态,弥补了原有模型中不能描述静摩擦力的不足.上述研究中尚未考虑圆弧足与地面间的滚动摩阻,滚动摩阻对被动行走器的动力学行为有何种影响是一个值得研究的问题.
综上所述,基于不同假设的研究都取得了一些有意义的研究进展,但也存在一定的局限性.例如,基于足与地面铰接模型的研究方法无法揭示被动行走器足的弹起或滑动过程;基于修正的库伦摩擦模型的研究方法难以仿真被动行走器静止站立的工况;基于库伦干摩擦模型的研究方法须用到试算法,或线性互补算法,这两种算法计算成本较高且繁琐;另外,忽略足与地面间的滚动摩阻是否合理尚需做进一步的探讨.为了弥补上述方法中的不足,本文在现有研究成果的基础上,首先采用扩展的赫兹接触模型和LuGre摩擦模型描述足地间的接触力,并考虑圆弧足的滚动摩阻;然后应用第二类Lagrange方程建立被动行走器的动力学方程;最后,将通过数值仿真方法分析支撑足与地面间的摩擦和滚动摩阻等非光滑因素对行走器动力学特性的影响.
1 力学建模
1.1 圆弧足被动行走器模型
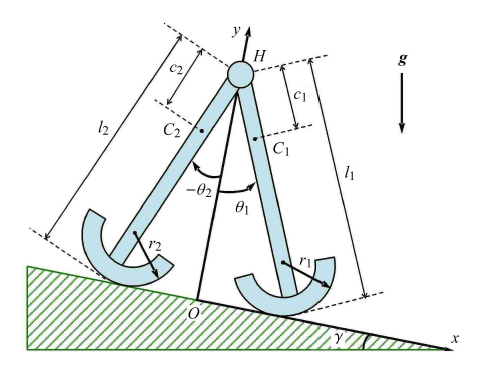
本文研究的圆弧足被动行走器模型如图2所示.
图2
设两腿在髋关节$H$处用光滑柱铰链连接,且分别记为腿1和腿2,$C_1 ,C_2$分别为两腿质心的位置,该模型的其余参数符号含义为:$m_1$,$m_2$分别为腿1、腿2的质量, $J_1$,$J_2$分别为腿1、腿2相对质心的转动惯量, $l_1$,$l_2 $分别为腿1、腿2的长度, $c_1$,$c_2$分别为腿1、腿2的质心与髋关节$H$的距离, $r_1$,$r_2 $分别为腿1、腿2的圆弧足半径,$\gamma $为斜面与水平面间的夹角, $g$为重力加速度.
在斜面上建立平面直角坐标系,其中$y$轴垂直于斜面向上,$x$轴沿斜面向下,设髋关节$H$的坐标为$\left({x_H ,y_H } \right)$, 两腿与$y$轴的夹角为$\theta _1 ,\theta_2 $ (逆时针为正),该系统的广义坐标可表示为
1.2 圆弧足与地面间的接触力建模
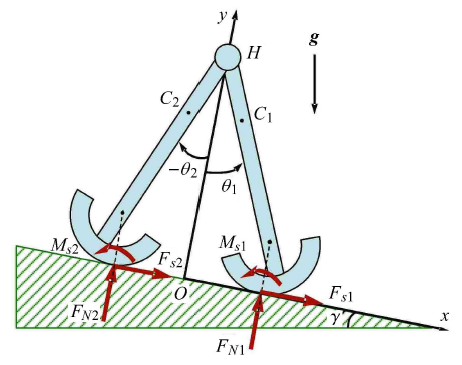
圆弧足被动行走器的支撑足$i \in \left\{ {1,2}\right\}$与地面接触时,会受到法向接触力$F_{Ni}$,切向摩擦力$F_{si} $以及滚阻力偶矩$M_{si}$的作用,如图3所示.
图3
(1) 圆弧足$i$与地面间的法向接触力
圆弧足$i$与地面间的法向接触力$F_{Ni} $ ($i=1,2$)采用扩展的赫兹接触力模型描述,其表达式为[29]
式中,$K,\chi $分别表示圆弧足与地面间的接触刚度系数与接触阻尼系数,$\delta _i $表示圆弧足与地面的相对压痕深度,$\dot {\delta }_i $表示圆弧足与地面的相对压痕深度的变化速率. 当圆弧足与地面接触时,根据几何关系,$\delta _i$,$\dot {\delta }_i (i= 1,2)$可表示为
(2) 圆弧足$i$与地面间的摩擦力
其中,$z_i ,\dot {z}_i$分别表示圆弧足$i$与地面的接触点处的平均鬃毛形变及形变速率;$\sigma _0 ,\sigma _1 ,\sigma _2 ,v_{\rm s}$分别表示鬃毛刚度系数、鬃毛阻尼系数、黏性摩擦系数、Stribeck速度;$\mu,\mu _0$分别表示动、静摩擦系数(通常情况下动摩擦系数大约是静摩擦系数的0.7~0.8倍).圆弧足被动行走器支撑足与地面的潜在接触点 (离斜面最近的点)的速度沿斜面$x$轴的投影可用系统的广义坐标及广义速度表示为
当$\delta _i \geqslant 0$时,则上式为实际接触点的相对切向速度.
(3) 圆弧足$i$与地面间的滚阻力偶矩
圆弧足被动行走器的支撑足$i$与地面间的滚阻力偶矩采用下列表达式描述[26]
其中,$\zeta _s $为滚动摩阻系数,$\dot {\theta }_i$为圆弧足$i$相对地面转动的角速度.
1.3 圆弧足被动行走器的动力学方程
利用第二类Lagrange方程推导可得被动行走器的动力学方程
其中,${\pmb Q}_g , {\pmb Q}_{F_N } , {\pmb Q}_{F_s } , {\pmb Q}_{M_s }$分别表示重力、法向接触力、摩擦力以及滚阻力偶的广义力.上式中各项的具体表达式如下所示
${\pmb M} = \left( \!\!\begin{array}{cccc} {m_1 + m_2 } & 0 & {m_1 c_1 \cos \theta _1 } & {m_2 c_2 \cos \theta _2 } \\ 0 & {m_1 + m_2 } & {m_1 c_1 \sin \theta _1 } & {m_2 c_2 \sin \theta _2 } \\ {m_1 c_1 \cos \theta _1 } & {m_1 c_1 \sin \theta _1 } & {J_1 + m_1 c_1^2 } & 0 \\ {m_2 c_2 \cos \theta _2 } & {m_2 c_2 \sin \theta _2 } & 0 & {J_2 + m_2 c_2^2 } \end{array} \!\! \right) $
${\pmb H} = \left(\!\!\begin{array}{c} {-m_1 c_1 \dot {\theta }_1 ^2\sin \theta _1-m_2 c_2 \dot {\theta }_2 ^2\sin \theta _2 } \\ {m_1 c_1 \dot {\theta }_1 ^2\cos \theta _1 + m_2 c_2 \dot {\theta }_2 ^2\cos \theta _2 } \\ 0 \\ 0 \end{array}\!\! \right)$
${\pmb Q}_g = \left(\!\!\begin{array}{c} {\left( {m_1 + m_2 } \right)g\sin \gamma } \\ {-\left( {m_1 + m_2 } \right)g\cos \gamma } \\ {-m_1 gc_1 \sin \left( {\theta _1-\gamma } \right)} \\ {-m_2 gc_2 \sin \left( {\theta _2-\gamma } \right)} \end{array}\!\! \right)$
${\pmb Q}_{F_N } = \left(\!\!\begin{array}{cccc} 0 & 1 & {\left( {l_1-r_1 } \right)\sin \theta _1 } & 0 \\ 0 & 1 & 0 & {\left( {l_2-r_2 } \right)\sin \theta _2 } \end{array} \!\! \right)^{\rm T} \left(\!\!\begin{array}{l} F_{N1} \\ F_{N2} \end{array}\!\! \right)$
${\pmb Q}_{F_s } = \left(\!\! \begin{array}{cccc} 1 & 1 \\ 0 & 0 \\ {\left( {l_1-r_1 } \right)\cos \theta _1 + r_1 } & 0 \\ 0 & {\left( {l_2-r_2 } \right)\cos \theta _2 + r_2 } \ \end{array} \!\! \right)\left(\!\! \begin{array}{l} F_{s1} \\ F_{s2} \end{array} \!\! \right)$
${\pmb Q}_{M_s } = \left(\!\! \begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \!\! \right)^{\rm T}\left(\!\! \begin{array}{l} M_{s1} \\ M_{s2} \end{array} \!\! \right)$
该方程为非线性常微分方程组,可通过数值仿真分析该系统的动力学特性.
2 数值仿真
2.1 算例1 LuGre摩擦模型参数的选取
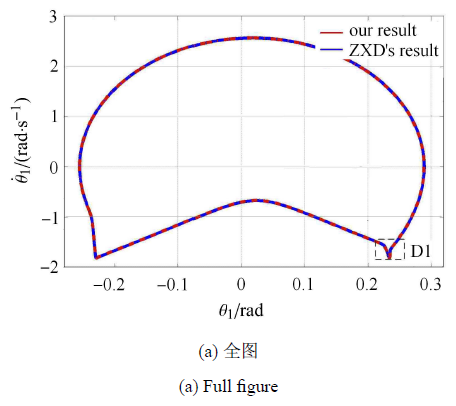
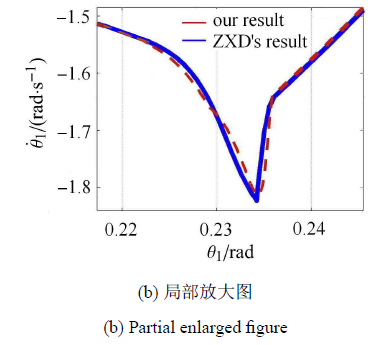
LuGre摩擦模型能够描述诸多的摩擦特性,且具有较好的连续性,目前对于不同材质的物体,该模型中的一些参数不易查找,如$\sigma _0 $和$\sigma _1 $. 本文通过数值仿真结果的对比来确定相关参数. 为了便于对比,本算例圆弧足被动行走器的参数和运动的初始条件与文献[22]中的相同.
被动行走器参数[22]:$m_1 = m_2 = 1.0$ kg,$J_1 = J_2 = 9.6\times 10^{-3}$ kg$\cdot$m$^2$,$l_1 = l_2 = 0.4$ m,$c_1 = c_2 = 0.1$ m,$r_1 = r_2 = 0.08$ m,$\gamma = 0.02$ rad,$g = 9.8$ m/s$^{2}$.
接触力参数[22]:$K = 1.0\times 10^6$ N/m$^{1.5}$,$\chi = 5.0\times 10^7$ N$\cdot$s/m$^{2.5}$,$\mu = 0.40$,$\mu _{0} = 0.50$,$v_{\rm s} = 1.0\times 10^{-4}$ m/s,$\sigma _2 = 0$ s/m,$\zeta _s = 0$ m.
初始条件[22]:$x_H = 0.0$ m,$y_H = 0.395 0$ m,$\theta _1 =0.165 5$ rad,$\theta _2=-0.247 9$ rad,$\dot {x}_H = 0.4971$ m/s,$\dot {y}_H =0.048 6$ m/s,$\dot {\theta }_1=-1.256 5$ rad/s,$\dot {\theta }_2 =0.005 2$ rad/s,$z_1 = 0$ m,$z_2 = 0$ m.
图4
图4
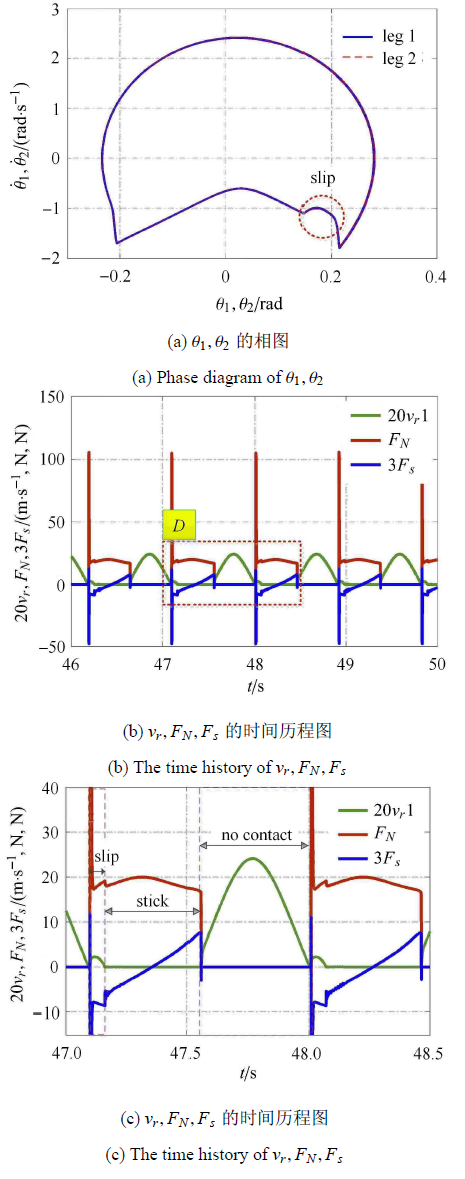
2.2 算例2 被动行走器的黏滞与滑移现象
在适当参数条件下,被动行走器在行走过程中会发生黏滞与滑移现象.本文中算例的仿真参数及初始条件如下,未列出的参数和算例1相同.
系统参数:$\mu = 0.15$,$\mu _{0} = 0.20$.
初始条件为: $x_H = 0.0$ m,$y_H = 0.399 1$ m, $\theta _1 = 0.032 9$ rad,$\theta _2 =0.017 0$ rad, $\dot {x}_H = 0.236 2$ m/s,$\dot {y}_H = 0.006 0$ m/s, $\dot {\theta }_1 = -0.590 9$ rad/s, $\dot {\theta }_2 = 2.386 2$ rad/s, $z_1 = 0$ m ,$z_2 = 0$ m.
图5
可以看出,LuGre摩擦模型可以很好地描述被动行走器的支撑足与地面间的滑动摩擦力和静摩擦力.
2.3 算例3动摩擦系数对被动行走器步态的影响
在下面的算例中,将通过数值仿真分析圆弧足与地面间的摩擦系数和滚阻系数对被动行走器动力学特性(如:$V$,$T$,$A$和$F_{\max } $)的影响.
本算例分析圆弧足与地面间的摩擦系数对被动行走器动力学特性的影响.仿真所用的参数及初始条件如下,未列出参数和算例1相同.
系统参数:$J_1 = J_2 = 6\times 10^{-3}$ kg$\cdot$m$^2$,$\gamma = 0.11$ rad,$\zeta _s = 0$ m.
初始条件:$x_H = 0.0$ m,$y_H = 0.373 7$ m,$\theta _1 = 0.389 3$ rad,$\theta _2 = -0.410 9$ rad,$\dot {x}_H = 0.236 2$ m/s,$\dot {y}_H = 0.316 2$ m/s,$\dot {\theta }_1 = -2.114 1$ rad/s,$\dot {\theta }_2 = -0.647 1$ rad/s,$z_1 = 0$ m,$z_2 = 0$ m.
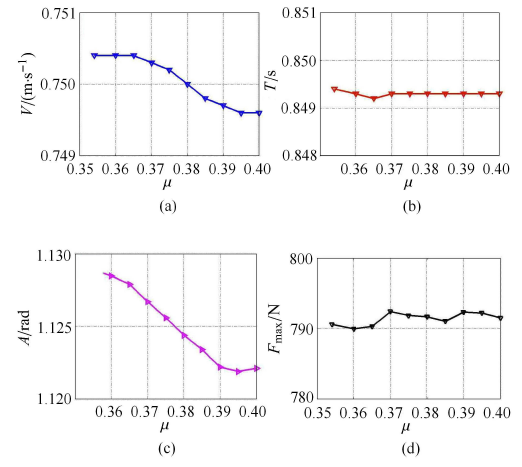
通过数值仿真发现,当$\mu <0.352$时,被动行走器会打滑摔倒,难以持续行走;当摩擦系数较大时,被动行走器的行走特征几乎不变.在此,通过数值仿真详细分析动摩擦系数$\mu \in[0.35,0.40]$对被动行走器动力学特性$V,T,A,F_{\max } $的影响.仿真时间历程为200 s,取后50 s (稳态解)的数据进行分析,数值结果如图6所示.
图6
图6
$V,T,A,F_{\max } $与$\mu $的关系
Fig. 6
Relationship between $V,T,A,F_{\max } $ and $\mu $
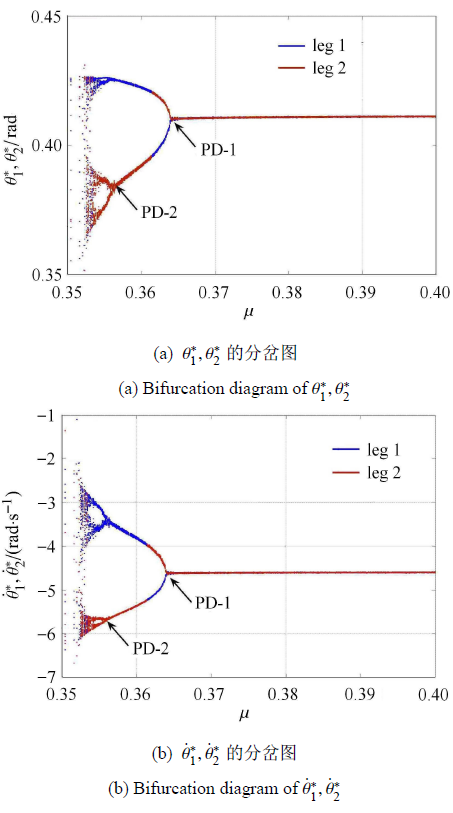
摩擦系数对行走器步态的$V,T,A,F_{\max } $的影响很小.但进一步的仿真结果表明:当摩擦系数逐步变小时,被动行走器的动力学特性会发生一项更显著的变化 (分岔现象).
图7
图7
动摩擦系数$\mu $导致的倍周期分岔现象
Fig. 7
Period-doubling bifurcation caused by the dynamic friction coefficient $\mu $
图8
2.4 算例4滚阻系数对被动行走器步态的影响
本算例分析圆弧足与地面间的滚阻系数对被动行走器动力学特性的影响,部分仿真参数如下,未列出的参数同算例1中对应参数.
系统参数:$J_1 = J_2 = 9.6\times 10^{-3}$ kg$\cdot$m$^2$,$\gamma = 0.02$ rad,$\mu = 0.40$,$\mu _0= 0.50$.
初始条件:$x_H = 0.0$ m,$y_H = 0.395 0$ m,$\theta _1 = 0.165 5$ rad,$\theta _2 = -0.247 9$ rad,$\dot {x}_H = 0.497 1$ m/s,$\dot {y}_H = 0.048 6$ m/s,$\dot {\theta }_1 = -1.256 5$ rad/s,$\dot {\theta }_2 = 0.005 2$ rad/s,$z_1 = 0$ m,$z_2 = 0$ m.
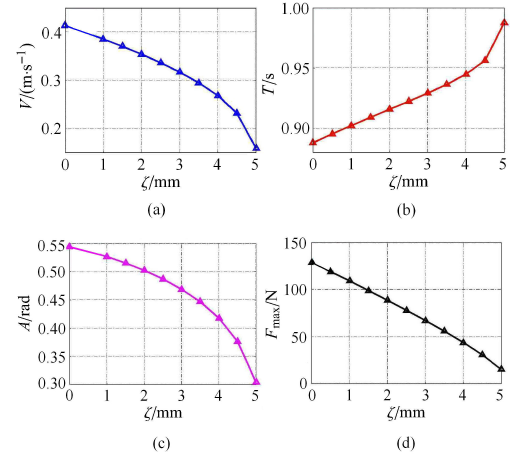
在本算例中,圆弧足与地面间的滚阻系数的取值范围为$\zeta \in [0.0 mm, 5.0 mm]$.设定仿真时间200 s,取后50 s (稳态解)的数据进行分析. 分析结果如图9所示.
图9
图9
不同滚阻系数下的步态特征: $V, T, A, F_{\max}$
Fig. 9
Gait characteristics under different rolling resistance coefficients: $V, T, A, F_{\max}$
不同于摩擦系数,滚阻系数对行走器的步态特征 ($V,T,A,F_{\max } $)的影响很大. 下面比较不同滚阻系数下被动行走器的运动状态.
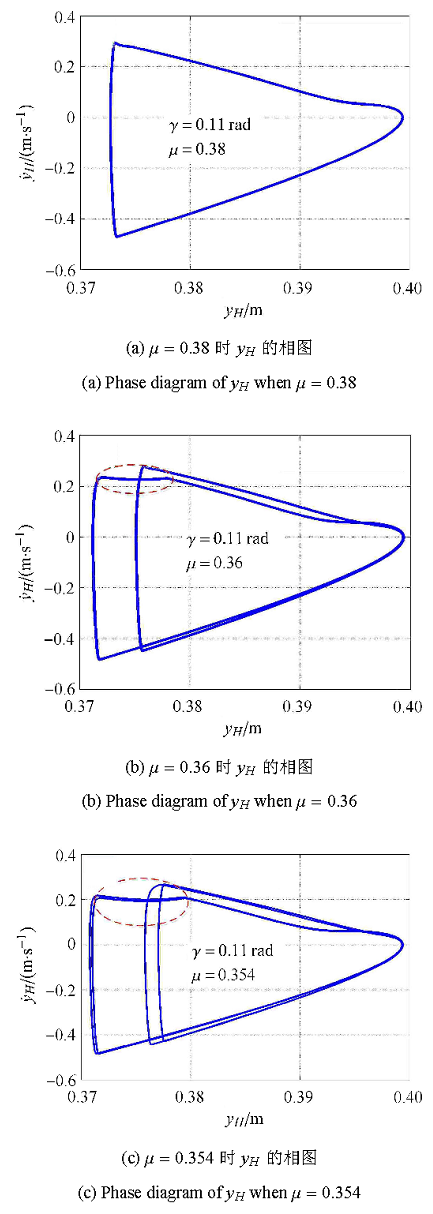
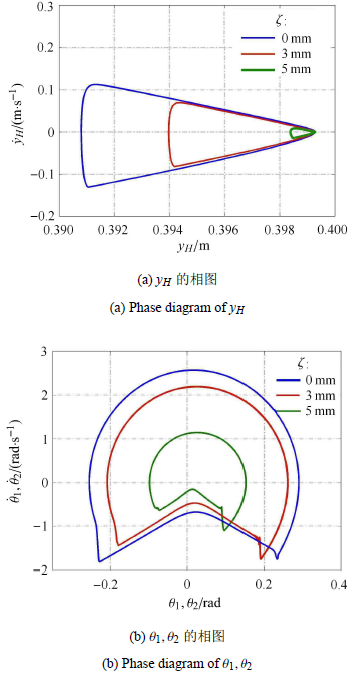
图10(a)和图10 (b)分别给出了滚阻系数 $\zeta $为0.0 mm, 3.0 mm,5.0 mm时被动行走器髋关节纵坐标$y_H$的相图以及双腿摆动角度$\theta _1 ,\theta _2 $的相图.从图中可以看出,虽然滚阻系数改变了,被动行走器仍以周期-1的步态行走.只是随着滚阻系数的增大,双腿摆动 角的幅值和角速度幅值都逐渐减小.
图10
图10
不同滚阻系数下的$(y_H, \dot y_H)$与$(\theta,\dot\theta)$相图
Fig.10
Phase diagram $(y_H, \dot y_H)$ and $(\theta,\dot\theta)$ under different rolling resistance coefficients
3 结论
本文首先采用扩展的赫兹接触模型、LuGre摩擦模型以及滚阻模型描述圆弧足与地面的接触力,然后通过第二类Lagrange方程得到
了被动行走器的动力学方程,最后通过数值仿真分析了摩擦系数和滚阻系数对被动行走器的运动特性的影响.
本文研究结果表明:
(1)与库伦干摩擦模型相比,采用LuGre摩擦模型描述足地间的摩擦,可降低判断stick-slip运动状态的计算成本,易于编程计算,但该模型的某些参数不易获取.
(2)当足地间的摩擦系数较大时,足地接触时无相对滑动,被动行走器的动力学特性不会随摩擦系数的改变而改变,但当摩擦系数较小时,足地间存在stick-slip切换,摩擦系数的变化对髋关节$H$点沿斜面的平均速度$V$、每行进一步所需的时间$T$、行进步幅$A$,以及足地间的最大法向接触力$F_{\max }$的影响很小;但会改变其步态类型,随着摩擦系数的不断减小,其行走步态会由周期-1步态变化为周期-2步态、由周期-2步态变化为周期-4步态,当摩擦系数减小到一定程度时,会产生混沌运动或摔倒.
(3) 滚阻系数对被动行走器某些动力学特性 ($V$,$T$,$A$,$F_{\max }$)的影响较大,但在足地间无滑动的情况下,不会改变其行走步态,无倍周期分岔现象.
后续有必要对含膝关节的被动行走器 (或欠驱动行走器) 进行研究.研究膝关节、髋关节处的非光滑因素对双足行走过程的影响,为双足机器人的设计和精度提高等提供有价值的指导意见.
参考文献
Efficient bipedal robots based on passive-dynamic walkers
The experimental study on the contact process of passive walking
Passive walker that can walk down steps: simulations and experiments
A three-dimensional passive-dynamic walking robot with two legs and knees
RABBIT: A testbed for advanced control theory
Passive-Based walking robot
First steps toward underactuated human-inspired bipedal robotic walking
双足机器人高效行走的自适应控制研究. [博士论文]
Adaptive walking control for under-actuated biped robots. [PhD Thesis]
基于步态切换的欠驱动双足机器人控制方法
Control method of an under-actuated biped robot based on gait transition
A study of the passive gait of a compass-like biped robot
Efficiency, speed, and scaling of two-dimensional passive-dynamic walking
Fully analytical solution to discrete behavior of hybrid zero dynamics in limit cycle walking with constraint on impact posture
Stability analysis of underactuated compass gait based on linearization of motion
The simplest walking model: stability, complexity, and scaling
Bifurcations and chaos in the semi-passive bipedal dynamic walking model under a modified OGY-based control approach
The simple chaotic model of passive dynamic walking
Walking dynamics of the passive compass-gait model under OGY-based control: Emergence of bifurcations and chaos
Walking dynamics of the passive compass-gait model under OGY-based state-feedback control: Analysis of local bifurcations via the hybrid Poincaré map.
Walking dynamics of the passive compass-gait model under OGY-based state-feedback control: Rise of the Neimark-Sacker bifurcation.
Dynamic bipedal walking under stick-slip transitions
LCP method for a planar passive dynamic walker based on an event-driven scheme
The elastic contact influences on passive walking gaits
圆弧足被动行走器非光滑动力学仿真研究
Simulation research of a passive dynamic walker with round feet based on non-smooth method
多体系统接触碰撞问题的牛顿-欧拉线性互补方法
Contact-impact analysis in multi-body systems based on newton euler LCP approach
Modeling and simulation of longitudinal dynamics coupled with clutch engagement dynamics for ground vehicles
浮放物体平面多刚体动力学建模与算法研究
Research on modeling and numerical method of free standing body on planar rigid multibody dynamics
含摩擦与碰撞平面多刚体系统动力学线性互补算法
A LCP method for the dynamics of planar multibody systems with impact and friction
A review of continuous contact-force models in multibody dynamics
Revisiting the LuGre friction model