引言
傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域.
CMG有两种机械结构, 单框架(SCMG)[7 ] 和双框架(double-gimbal control moment gyro, DCMG)[8 ] . 飞轮可调速时, CMG演化成变速控制力矩陀螺(variable-speed control moment gyro, VCMG), 按其机械结构分类, 有单框架变速控制力矩陀螺(single-gimbal variable-speed control moment gyro, SVCMG)[9 ] 和双框架变速控制力矩陀螺(double-gimbal variable-speed control moment gyro, DVCMG)[10 -11 ] . 相比于DCMG, SCMG机械结构简单, 但存在奇异性问题, 而前者机械结构和控制算法更加复杂, 两者同属于多体系统, 本文仅关注航天领域应用最广的SCMG.
通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等.
最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] .
本文不局限于Lappas假设条件, 建立SCMG输出力矩模型, 在全部可行域中对SCMG输出特性进行解析, 以期更加全面地理解SCMG动态输出特性, 为在工程实践中高效利用SCMG及其控制策略设计提供新思路.
1 SCMG输出力矩模型
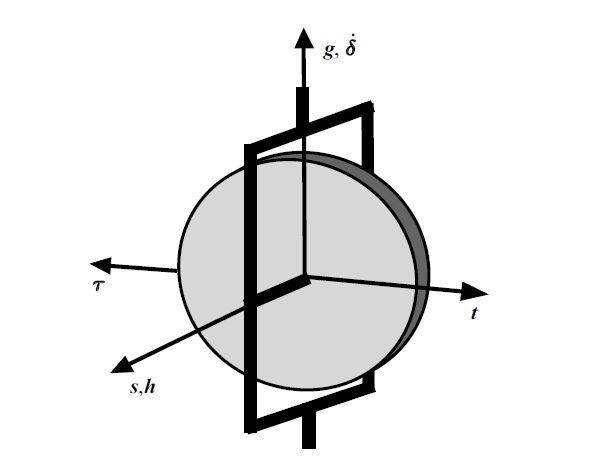
如图1 所示, 设SCMG的连体坐标系为${\cal F}( g, s, t)$, 坐标轴单位矢量为$ s$, $ g$和$ t$, 其中$ g$为安装轴. 定义飞轮角速度和角动量分别为 $ \varOmega $和$ h$, 框架相对基座的转动角速度为$\dot{{\delta }}$, 以致$\varOmega=\varOmega { s}$, ${ h}=h{ s}$, $ \delta =\delta { g}$和$\dot{{ \delta }}=\dot{{\delta }}{ g}$. 在连体坐标系中, 基座、飞轮和框架的角速度为
(1) $\begin{eqnarray} \label{eq1} \left. {\begin{array}{l} { \omega }=\{{ g},{ s},{ t}\}{ \omega }^{(0)}\\ { \omega }_{\rm f} =\{{ g},{ s},{ t}\}{ \omega}_{\rm f}^{(0)} \\ { \omega }_{\rm w} =\{{ g},{ s},{ t}\}{ \omega}_{\rm w}^{(0)} \\ \end{array}} \right\} \end{eqnarray}$
式中, ${ \omega }^{(0)}=\{\omega_{g}, \omega_{s} ,\omega_{t} \}^{\rm T}$, ${ \omega }_{\rm f}^{(0)}=\{\omega_{g} +\dot{{\delta }},\omega_{s},\omega_{t}\}^{\rm T}$和${ \omega }_{\rm w}^{(0)} =\{\omega_{g}+\dot{{\delta }},\omega_{s} +\varOmega ,\omega_{t}\}^{\rm T}$分别为角速度坐标.
图1
图1
SCMG模型
Fig.1
Model of SCMG
设飞轮与框架的惯量张量分别为${ J}_{\rm w} $和${ J}_{\rm f} $, ${ J}_{\rm w}^{(0)} ={\rm diag}[J_{{\rm w}g} ,J_{{\rm w}s} ,J_{{\rm w}t}]$和${ J}_{\rm f}^{(0)} ={\rm diag}[J_{{\rm f}g} ,J_{{\rm f}s},J_{{\rm f}t} ]$为惯性矩阵. 由于转子轴对称, 有$J_{{\rm w}g} =J_{{\rm w}t}=J$. SCMG的角动量${ h}_{\rm total} =[{ g},{ s},{ t}]({ J}_{\rm w}^{(0)} { \omega }_{\rm w}^{(0)} +{ J}_{\rm f}^{(0)} { \omega }_{\rm f}^{(0)} )$, 则SCMG输出力矩为
(2) $\begin{eqnarray} \label{eq2} { \tau }=-{\dot{{ h}}}_{\rm total} =\{{ g},{ s},{ t}\}\{\tau_{g} ,\tau_{s} ,\tau_{t} \}^{\rm T} \end{eqnarray}$
从式(2)可见, SCMG输出力矩沿$ s$, $ g$和$ t$三个方向, 而仅有$ g$和$ s$两个方向具有输入力矩, 即SCMG为二维输入三维输出系统.
将式(2)输出力矩分成两部分, 即${ \tau }={ \tau }_{0}+{ \tau }_{\rm c} $, 这里${ \tau }_{0} =\tau_{g0}{ g}+\tau_{s0} { s}+\tau_{t0} { t}$为不可调控输出力矩, 表示SCMG对基座的惯性影响, 只与基座角加速度和角速度有关, ${ \tau }_{\rm c} =\tau_{g\rm c} { g}+\tau_{s\rm c} { s}+\tau_{t\rm c} { t}$为可调控输出力矩. 令${ J}_{\rm cmg}^{(0)} ={ J}_{\rm w}^{(0)} +{ J}_{\rm f}^{(0)} ={\rm diag}[J_{g},J_{s} ,J_{t} ]$, 则
(3) $\begin{eqnarray} \label{eq3} &&\left. {\begin{array}{l} \tau_{g0} =-J_{g} { g}\cdot {\dot{{ \omega }}}-(J_{t} -J_{s} )\omega_{t} \omega_{s} \\ \tau_{s0} =-J_{s} { s}\cdot {\dot{{ \omega }}}-(J_{g} -J_{t} )\omega_{g} \omega_{t} \\ \tau_{t0} =-J_{t} { t}\cdot {\dot{{ \omega }}}-(J_{s} -J_{g} )\omega_{g} \omega_{s} \\ \end{array}} \right\} \end{eqnarray}$
(4) $\begin{eqnarray} \label{eq4} \left. {\begin{array}{l} \tau_{g{\rm c}} =-J_{g} \ddot{{\delta }}+J\varOmega \omega _{t} \\ \tau_{s{\rm c}} =-J\dot{{\varOmega }}-(J_{s} +J_{g} -J_{t} )\dot{{\delta }}\omega_{t} \\ \tau_{t{\rm c}} =-(J_{s} -J_{t} -J_{g} )\dot{{\delta }}\omega_{s} -J\varOmega (\omega_{g} +\dot{{\delta }}) \\ \end{array}} \right\} \end{eqnarray}$
2 SCMG输出输入力矩比
(5) $\begin{eqnarray} \label{eq5} { \tau }_{\rm in} =-\tau_{g} { g}+\tau_{s{\rm w}} { s} \end{eqnarray}$
式中, $\tau_{s\rm w} =-\tau_{s}|_{J_{{\rm f}g} =J_{{\rm f}s} =J_{{\rm f}t}=0}=J({ s}\cdot {\dot{{ \omega }}}+\dot{{\delta }}\omega_{t} +\dot{{\varOmega}})$. 记输出力矩为${ \tau }_{\rm out} $, 则输出与输入力矩比定义为
(6) $\begin{eqnarray} \label{eq6} K=\frac{\left| {{ \tau }_{\rm out} } \right|}{\left| {{ \tau }_{\rm in} } \right|}\end{eqnarray}$
令${ \tau }_{\rm c} ={ \tau }_{\rm c}^{\ast} +{ \tau}_{\rm r} $, ${ \tau }_{\rm c}^{\ast} $和${ \tau }_{\rm r}$分别为被利用和未利用的输出力矩, 这里${ \tau }_{\rm c}^{\ast}=n_{1} \tau_{t1} { t}+n_{2} \tau_{s1} { s}+n_{3} \tau_{g1}{ g}+n_{4} { \tau }_{c0}^{\ast } $, 其中
(7) $\begin{eqnarray} \label{eq7} \left. {\begin{array}{l} { \tau }_{\rm c0}^{\ast } =\tau_{g2} { g}+\tau _{s2} { s}+\tau_{t2} { t} \\ \tau_{g1} =-J_{g} \ddot{{\delta }},\ \ \tau_{g2} =J\varOmega \omega_{t} \\ \tau_{s1} =-J\dot{{\varOmega }},\ \ \tau_{s2} =-(J_{s} +J_{g} -J_{t} )\dot{{\delta }}\omega_{t} \\ \tau_{t1} =-J\varOmega \dot{{\delta }},\ \ \tau_{t2} =-[(J_{s} J_{t} -J_{g} )\dot{{\delta }}\omega_{s} +J\varOmega \omega_{g} ] \\ \end{array}} \right\} \end{eqnarray}$
因此, 当$n_{1}=1$且$n_{2} =n_{3} =n_{4} =0$时, 意指SCMG;当$n_{2}=1$且$n_{1} =n_{3} =n_{4}=0$时, 意指反作用轮;当$n_{1} =n_{2}=1$且$n_{3}=n_{4} =0$时, 则代表VSCMG; 当$n_{1} =n_{2}=n_{3}=1$且$n_{4} =0$或$n_{1} =n_{2} =n_{3} =n_{4}=1$时, 本文称为三维单框架控制力矩陀螺(three-dimensional single-gimbal control moment gyro, 3D-SCMG). 输出力矩可以为全部输出力矩、可调节输出力矩或者被利用输出力矩, 即
(8) $\begin{eqnarray} \label{eq8} K=\sqrt {\frac{\left| {{ \tau }_{\rm out} } \right|^{2}}{\tau_{g}^{2} +\tau_{s\rm w}^{2} }},\ \ { \tau }_{\rm out} ={ \tau } \ {\rm or} \ { \tau }_{\rm c} \ {\rm or} \ { \tau }_{\rm c}^{\ast} \end{eqnarray}$
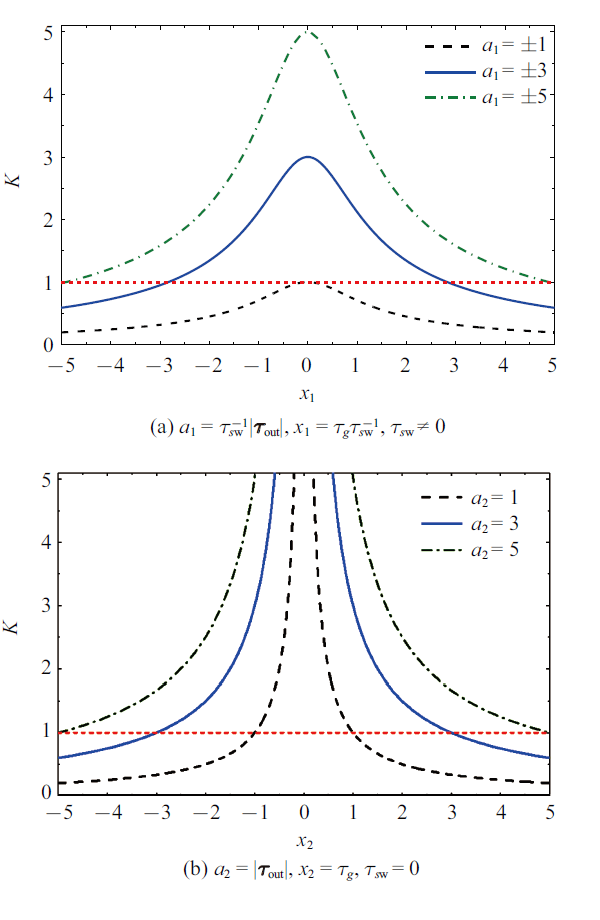
(9) $\begin{eqnarray} \label{eq9} K=\left\{ {\begin{array}{l} \sqrt {\dfrac{a_{1}^{2} }{1+x_{1}^{2} }} ,\ \ a_{1} =\tau _{s\rm w}^{-1} |{ \tau }_{\rm out} |,\ \ x_{1} =\tau_{g} \tau_{s\rm w}^{-1} ,\ \ \tau_{s\rm w} \ne 0 \\ a_{2} \left| {x_{2} } \right|^{-1},\ \ a_{2} =\vert { \tau}_{\rm out} |,\ \ x_{2} =\tau_{g} ,\ \ \tau_{s\rm w} =0 \\ \end{array}} \right. \end{eqnarray}$
式中, $a_{1}$为输出力矩幅值与$ s$方向输入力矩比值, $a_{2}$为输出力矩幅值, $x_{1}$为$ g$方向与$ s$方向输入力矩比值, $x_{2}$为$ g$方向输入力矩. 根据式(9), 可得输出与输入力矩之比的关系曲线, 如图2 所示. 从图2 可知, $K$值与SCMG的状态有关, 并不恒大于1, 即SCMG并不总有力矩放大效应.
图2
图2
SCMG输出输入力矩比
Fig.2
Torque ratio of SCMG's input to output
同理, 可以选择合适的独立参数, 对特定情形下的$K$值进行分析. 这里例举基座固定、输出力矩为全部力矩和三维控制力矩陀螺.
此时${ \omega }=0$, ${\dot{{ \omega }}}=0$, ${ \tau }_{\rm out} =-J_{g} \ddot{{\delta }}{ g}-J\dot{{\varOmega}}{ s}-J\varOmega \dot{{\delta }}{ t}$. 令$x_{3} =J\dot{{\varOmega}}/(J_{g} \ddot{{\delta }})$, $x_{4} =\dot{{\varOmega }}$, $a_{3} =J\varOmega \dot{{\delta }}/(J_{g} \ddot{{\delta}})$和$a_{4} =\varOmega \dot{{\delta }}$, 则
(10) $\begin{eqnarray} \label{eq10} K=\left\{ {\begin{array}{ll} \sqrt {1+a_{3}^{2} (1+x_{3}^{2} )^{-1}} ,&\ \ \ddot{{\delta }}=0 \\[3mm] \sqrt {1+a_{4}^{2} x_{4}^{-2} } ,&\ \ \ddot{{\delta }}\ne 0 \\ \end{array}} \right. \end{eqnarray}$
由式(10)可得SCMG的输出输入力矩比曲线, 结果如图3 所示. 从图3 可见, 基座固定的SCMG输出与输入力矩比$K\geqslant 1$. 当$a_{3} $或$a_{4} $为零时, $K=1$, 此时${ \tau }_{\rm out} $中陀螺力矩为零, 即等同于反作用轮.
图3
图3
基座固定的SCMG输出输入力矩比
Fig.3
Torque ratio of SCMG's input to output with the fixed base
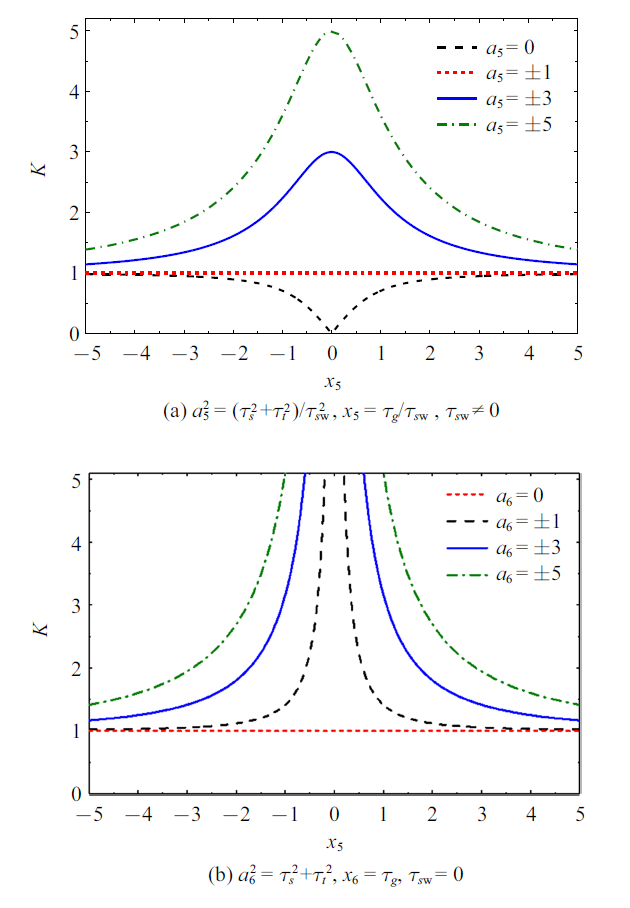
(11) $\begin{eqnarray} \label{eq11} K=\left\{ {{\begin{array}{ll} \sqrt {1+\dfrac{a_{5}^{2} -1}{x_{5}^{2} +1}},&\ \ \tau_{s\rm w} \ne 0\\ \sqrt {1+\dfrac{a_{6}^{2} }{x_{6}^{2} }},&\ \ \tau_{s\rm w} =0\\ \end{array} }} \right. \end{eqnarray}$
(2)输出力矩为全部力矩此时, 输出力矩${ \tau }_{\rm out} ={ \tau }$, 则
式中, $x_{5} =\tau_{g} /\tau_{s\rm w} $, $x_{6} =\tau _{g} $, $a_{5}^{2} =(\tau_{s}^{2} +\tau _{t}^{2} )/\tau_{s\rm w}^{2} $, $a_{6}^{2} =\tau _{s}^{2} +\tau_{t}^{2} $.
根据式(11), 可得输出输入力矩比曲线, 如图4 所示. 从图4 可知, 当$\tau_{s}^{2} +\tau_{t}^{2} \geqslant \tau_{s\rm w}^{2} $时, SCMG的输出与输入力矩比$K\geqslant 1$, 反之亦成立. 因为当$K\geqslant 1$时, 由式(11)可得$a_{5}^{2} \geqslant 1$, 即$\tau_{s}^{2} +\tau_{t}^{2} \geqslant \tau_{s\rm w}^{2} $.
图4
图4
SCMG输出输入力矩比
Fig.4
Torque ratio of SCMG's input to output with ${ \tau }_{\rm out} ={ \tau }$
(${ \tau }_{\rm out} ={ \tau }$)(3)三维控制力矩陀螺三维控制力矩陀螺情形, 即考虑${ \tau }_{\rm out} ={ \tau }_{\rm c}^{\ast} $, $n_{1} =n_{2} =n_{3}=1$且$n_{4} =0$, 则
(12) $\begin{eqnarray} \label{eq12} K=\sqrt {\frac{(J_{g} \ddot{{\delta }})^{2}+\dot{{\varOmega}}^{2}+(\varOmega \dot{{\delta }})^{2}}{(\tau_{g0} +\tau _{g2} )^{2}+(\tau_{s0} +\tau_{s2})^{2}+(\tau_{t0} +\tau_{t2} )^{2}}} \end{eqnarray}$
首先, 分析$\varOmega \dot{{\delta }}$对$K$的影响. 由式(12)可得
(13) $\begin{eqnarray} \label{eq13} K=\sqrt {\frac{b_{1}^{2} +(\varOmega \dot{{\delta }})^{2}}{(c_{1}-\varOmega \omega_{t} )^{2}+d_{1}^{2} }} \leqslant \sqrt {\frac{b_{1}^{2} +(\varOmega \dot{{\delta }})^{2}}{d_{1}^{2} }} \end{eqnarray}$
(14) $\begin{eqnarray} \label{eq14} \left. {\begin{array}{l} b_{1}^{2} =J_{g}^{2} \ddot{{\delta }}^{2}+\dot{{\varOmega }}^{2},\ \ d_{1}^{2} =({ s}\cdot {\dot{{ \omega }}}+\dot{{\delta }}\omega_{t} +\dot{{\varOmega }})^{2} \\ c_{1} =J_{g} { g}\cdot {\dot{{ \omega }}}+(J_{t} -J_{s} )\omega_{t} \omega_{s} +J_{g} \ddot{{\delta }} \\ \end{array}} \right\} \end{eqnarray}$
其次, 分析参数$\ddot{{\delta }}$对$K$的影响. 由式(12)可得
(15) $\begin{eqnarray} \label{eq15} K=\sqrt {\frac{b_{2}^{2} +(J_{g} \ddot{{\delta }})^{2}}{(c_{2} +J_{g} \ddot{{\delta }})^{2}+d_{2}^{2} }} \leqslant \sqrt {\frac{b_{2}^{2} +(J_{g} \ddot{{\delta }})^{2}}{d_{2}^{2} }} \end{eqnarray}$
(16) $\begin{eqnarray} \label{eq16} \left. {\begin{array}{l} b_{2}^{2} =\dot{{\varOmega }}^{2}+(\varOmega \dot{{\delta }})^{2},\ \ d_{2}^{2} =({ s}\cdot {\dot{{ \omega }}}+\dot{{\delta }}\omega_{t} +\dot{{\varOmega }})^{2} \\ c_{2} =J_{g} { g}\cdot {\dot{{ \omega }}}+(J_{t} -J_{s} )\omega_{t} \omega_{s} -\varOmega \omega_{t} \\ \end{array}} \right\} \end{eqnarray}$
最后, 分析参数$\dot{{\varOmega }}$对$K$的影响. 由式(12)可得
(17) $\begin{eqnarray} \label{eq17} K=\sqrt {\frac{b_{3}^{2} +\dot{{\varOmega }}^{2}}{(c_{3} +\dot{{\varOmega }})^{2}+d_{3}^{2} }} \leqslant \sqrt {\frac{b_{3}^{2} +\dot{{\varOmega }}^{2}}{d_{3}^{2} }} \end{eqnarray}$
(18) $\begin{eqnarray} \label{eq18} \left. {\begin{array}{l} b_{2}^{2} =\dot{{\varOmega }}^{2}+(\varOmega \dot{{\delta}})^{2},\ \ d_{2}^{2} =({ s}\cdot {\dot{{ \omega }}}+\dot{{\delta }}\omega_{t} +\dot{{\varOmega }})^{2} \\ c_{2} =J_{g} { g}\cdot {\dot{{ \omega }}}+(J_{t} -J_{s} )\omega_{t} \omega_{s} -\varOmega \omega_{t} \\ \end{array}} \right\} \end{eqnarray}$
设$p_{1} =\varOmega \dot{{\delta }}$, $p_{2} =\ddot{{\delta }}$, $p_{3} =\dot{{\varOmega }}$, 综合式(13)、式(15)和式(17), 可得$K$的上界为
(19) $\begin{eqnarray} \label{eq19} K_{{\rm m}i} =\sqrt {\frac{b_{i}^{2} +p_{i}^{2} }{d_{i}^{2} }} ,\ \ i=1,2,3 \end{eqnarray}$
$K_{{\rm m}i} $与参数$p_{i} $的关系如图5 所示. 由图5 可知, 上界$K_{{\rm m}i} $值随$|p_{i} |$值上升而增大, 且$K_{{\rm m}i}$的极小值随$b_{i}^{2} $值上升而增大.
图5
图5
不同参数的影响
Fig.5
Influence for different parameters
3 SCMG力矩利用率
设${ \tau }_{\rm c}^{\ast} $为SCMG被利用的力矩, 则未被利用的部分为${ \tau }-{ \tau }_{\rm c}^{\ast}$. 为衡量SCMG的力矩利用率, 定义
(20) $\begin{eqnarray} \label{eq20} \eta =\frac{|{ \tau }_{\rm c}^{\ast} |}{|{ \tau }-{ \tau }_{\rm c}^{\ast} |} \end{eqnarray}$
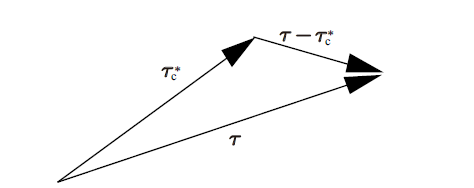
式中, 矢量${ \tau }={ \tau }_{\rm c}^{\ast} +({ \tau }-{ \tau }_{\rm c}^{\ast} )$, 几何关系如图6 所示.
图6
图6
矢量几何关系
Fig.6
Geometric relation diagram of vectors
由几何关系图6 可知, 当${ \tau }_{\rm c}^{\ast} $在${ \tau}$方向的投影值${ \tau }_{\rm c}^{\ast} \cdot$ ${ \tau }\cdot |{ \tau }|^{-1}>0.5|{ \tau }|$, 则$|{ \tau }_{\rm c}^{\ast} \vert>\vert { \tau }-{ \tau }_{\rm c}^{\ast}|$. 根据式(20), 即
(21) $\begin{eqnarray} \label{eq21} \left.\begin{array}{ll} \eta \geqslant 1, & \tau_{\rm c}^{\ast} \cdot \tau \geqslant 0.5| \tau |^{2} \\ \eta <1, & \tau_{\rm c}^{\ast} \cdot \tau <0.5| \tau |^{2} \\ \end{array} \right\} \end{eqnarray}$
由式(21)可得, 力矩利用率$\eta $与SCMG的状态有关, 并不恒大于1. 下面举例分析$\eta $. 取转子和框架以及基座处于匀速状态, 即$\dot{{\varOmega }}=\ddot{{\delta }}=0$, ${\dot{{ \omega }}}={\bf0}$, 此时被利用的力矩只有陀螺力矩, 即${ \tau }_{\rm c}^{\ast } =\varOmega \dot{{\delta }}$. 取$J_{g} =J_{s} =J_{t} =nJ$, 有
(22) $\begin{eqnarray} \label{eq22} |{ \tau }-{ \tau }_{\rm c}^{\ast} \vert =\sqrt {(\varOmega \omega_{t} )^{2}+(n\dot{{\delta }}\omega_{t} )^{2}+(\varOmega \omega_{g} -n\dot{{\delta }}\omega_{s} )^{2}} \end{eqnarray}$
将式(22)代入式(20), 利用不等式可得$\eta \leqslant \eta_{\rm m} $, 这里$\eta_{\rm m} $为$\eta $的上界. 令$p_{1} =\omega_{t} /\dot{{\delta}}$, $p_{2} =\varOmega /\dot{{\delta }}$, 即
(23) $\begin{eqnarray} \label{eq23} \eta_{\rm m} =\sqrt {\frac{p_{1}^{-2} }{1+n^{2}p_{2}^{-2} }} \end{eqnarray}$
式中, $p_{1}$为基座的角速度在$ t$方向分量与框架角速度值之比, $p_{2}$为转子转速值与框架角速度值之比, $n$表示转子在$ s$轴的惯量矩与基座主惯量矩之比.
根据式(23), 当$n=1$和$n=2$时, $\eta_{\rm m}$分别如图7 所示. 对比图7 (a)和图7 (b)可知, $\eta_{\rm m} $曲线关于$p_{2}=0$对称, 并在$p_{2} =0$取得峰值, 随$\left| {p_{1} }\right|$值上升而下降. 当$\left| {p_{1} } \right|>1$时, $\eta_{\rm m}$始终小于1, 可得此时$\eta $恒小于1. $n$不影响峰值大小, 但随$n$增大, 使得$\eta_{\rm m} $曲线的峰值变陡.
图7
图7
SCMG力矩利用率上界$\eta_{\rm m}$(${\dot{{ \omega }}}=0$, $\dot{{\varOmega }}=\ddot{{\delta }}={\bf0}$, $J_{g}=J_{s} =J_{t} =nJ$)
Fig.7
The upper bound of torque utilization in SCMG (${\dot{{ \omega }}}={\bf0}$, $\dot{{\varOmega }}=\ddot{{\delta }}=0$, $J_{g} =J_{s} =J_{t} =nJ$)
4 姿态控制
4.1 非对角奇异鲁棒操纵控制
考虑斜装两个VSCMG的航天器姿态控制, 安装角$\beta =\pi /6$, 第$i$个SCMG的转子对$ s$轴转动惯量为$J_{i} $, 其连体坐标系对航天器本体坐标系的转换矩阵为${ B}_{i}\ (i=1,2)$. 矢量或张量在航天器本体坐标系下的坐标加注上标(b), 则陀螺群的输出力矩在航天器本体坐标系中的坐标为
(24) $\begin{eqnarray} \label{eq24} { \tau }_{\rm c}^{\rm (b)} =\sum\limits_{i=1,2} {{ B}_{i} [0,-J_{i} \dot{{\varOmega }}_{i} ,-J_{i} \varOmega _{i} \dot{{\delta }}_{i} ]^{\rm T}} \end{eqnarray}$
$\begin{eqnarray*} { B}_{i} =\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {(-1)^{i+1}\sin \beta } & 0 & {(-1)^{i}\cos \beta } \\ {-\sin \delta_{i} \cos \beta } & {(-1)^{i+1}\cos \delta_{i} } & {-\sin \delta_{i} \sin \beta } \\ {\cos \delta_{i} \cos \beta } & {(-1)^{i+1}\sin \delta_{i} } & {\cos \delta_{i} \sin \beta } \\ \end{array} }} \right] \end{eqnarray*}$
令${ u}=\{\dot{{\delta }}_{1} ,\dot{{\varOmega }}_{1} ,\dot{{\delta }}_{2} ,\dot{{\varOmega }}_{2} \}^{\rm T}$, ${ \tau }_{\rm c}^{\rm (b)} ={ Q} u$. 航天器姿态四元数${ q}=\{q_{0} ,q_{1} ,q_{2} ,q_{3} \}^{\rm T}$, 这里$q_{0}$为姿态四元数的标量部分. ${ q}(0)$和${ q}_{\rm d}$分别为姿态四元数的初始值和目标值, ${ q}_{\rm d} =\{q_{\rm 0d} ,q_{\rm 1d} ,q_{\rm 2d} ,q_{\rm 3d} \}^{\rm T}$. 定义误差四元数
(25) $\begin{eqnarray} \label{eq25} { q}_{\rm e} =\left[ {{\begin{array}{*{20}c} {q_{\rm 0d} } & {q_{\rm 1d} } & {q_{\rm 2d} } & {q_{\rm 3d} } \\ {-q_{\rm 1d} } & {q_{\rm 0d} } & {q_{\rm 3d} } & {-q_{\rm 2d} } \\ {-q_{\rm 2d} } & {-q_{\rm 3d} } & {q_{\rm 0d} } & {q_{\rm 1d} } \\ {-q_{\rm 3d} } & {q_{\rm 2d} } & {-q_{\rm 1d} } & {q_{\rm 0d} } \\ \end{array} }} \right]{ q} \end{eqnarray}$
取${ q}_{\rm re} =\{q_{\rm 1e} ,q_{\rm 2e} ,q_{\rm 3e} \}^{\rm T}$, 令${ \omega }_{0} $和${ \omega }_{\rm d}$分别为航天器的角速度初始值和目标值, 则航天器姿态机动控制任务描述为$\mathop{\rm lim}\limits_{t\to \infty } { q}={ q}_{\rm d} $和$\mathop{\rm lim}\limits_{t\to \infty } { \omega }={ \omega }_{\rm d}$. 采用误差四元数反馈控制调整航天器姿态, 取$ K$和$ D$为正定矩阵, ${ T}_{\rm d}^{\rm (b)}$为干扰力矩, ${ \tau}_{\rm r}^{\rm (b)} $为SCMG群输出力矩中未利用的力矩, ${ \omega }^{{\rm (b)}\times}$表示航天器角速度的叉乘矩阵. 含SCMG的系统总惯量为
(26) $\begin{eqnarray} \label{eq26} { J}_{\rm all}^{\rm (b)} ={ J}^{\rm (b)}+\sum\limits_{i=1,2} {{ B}_{i} { J}_{{\rm cmg}i}^{(0)}{ B}_{i} } \end{eqnarray}$
(27) $\begin{eqnarray} \label{eq27} &&{ \tau }_{\rm c}^{\rm (b)} ={ \omega }^{{\rm (b)}\times}{ J}_{\rm all}^{\rm (b)} { \omega }^{\rm (b)}+{ K q}_{\rm re}+ \\&&\qquad{ D}({ \omega }_{\rm d}^{\rm (b)} -{ \omega }^{\rm (b)})-{ T}_{\rm d} ^{\rm (b)}-{ \tau }_{\rm r}^{\rm (b)} \end{eqnarray}$
取$\lambda =\lambda_{0} \exp [-\mu \det ({ Q Q}^{\rm T})]$, 这里$\lambda_{0} $和$\mu $为正实常数. 取对角元素$W_{i}(i=1$, 2, 3, 4)和非对角元素$\varepsilon_{i}$ $(i=1,2,3)$, 采用非对角奇异鲁棒操纵律[32 ] , 有
(28) \begin{eqnarray} \label{eq28} { u}={ W A}^{\rm T}({ A W A}^{\rm T}+{ V})^{-1}{ \tau }_{\rm c}^{\rm (b)} \end{eqnarray}
(29) $\begin{eqnarray} \label{eq29} { W}=\left[ {{\begin{array}{*{20}c} {W_{1} } & \lambda & \lambda & \lambda \\ \lambda & {W_{2} } & \lambda & \lambda \\ \lambda & \lambda & {W_{3} } & \lambda \\ \lambda & \lambda & \lambda & {W_{4} } \\ \end{array} }} \right],\ \ { V}=\lambda \left[ {{\begin{array}{*{20}c} 0 & {\varepsilon_{3} } & {\varepsilon_{2} } \\ {\varepsilon_{3} } & 0 & {\varepsilon_{1} } \\ {\varepsilon_{2} } & {\varepsilon_{1} } & 0 \\ \end{array} }} \right] \end{eqnarray}$
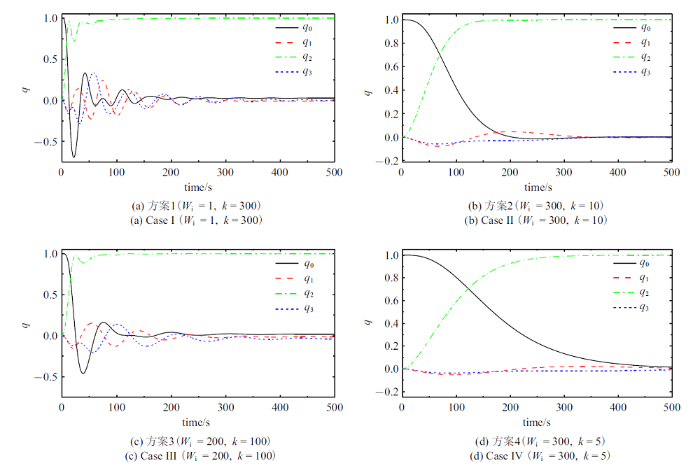
(30) $\begin{eqnarray} \label{eq30} \left. {\begin{array}{l} { q}_{\rm d} =\{0,0,1,0\}^{\rm T},\ \ { q}(0)=\{1,0,0,0\}^{\rm T} \\ { \omega }_{\rm d}^{\rm (b)} =\{0,0,0\}^{\rm T},\ \ { \omega }_{0}^{\rm (b)} =\{0,0,0\}^{\rm T} \\ \end{array}} \right\} \end{eqnarray}$
(31) $\begin{eqnarray} \label{eq31} \left. \begin{array}{l} { D}=300{\rm diag}[1,1,1],\ \ { K}=k{\rm diag}[1,1,1] \\ \lambda_{0} =10^{-3},\ \ \mu =100,\ \ \varepsilon_{1}=0.1\cos 0.1t \\ \varepsilon_{2} =0.1\cos (0.1t+2),\ \ \varepsilon_{3}=0.1\cos (0.1t+1) \\ \end{array} \right\} \end{eqnarray}$
令$J_{{\rm w}gi} =J_{{\rm w}ti} =0.4$ kg/m$^{2}$, $J_{i} =0.7$ kg/m$^{2}$, $J_{{\rm f}gi} =J_{{\rm f}si} =J_{{\rm f}ti} =0.1$ kg/m$^{2}$, 以及[33 ]
(32) $\begin{eqnarray} \label{eq32} { J}^{\rm (b)}=\left[ {{\begin{array}{*{20}c} {15053} & {3000} & {-1000} \\ {3000} & {6510} & {2000} \\ {-1000} & {2000} & {11122} \\ \end{array} }} \right] kg \cdot m^{-2} \end{eqnarray}$
取${ \tau }_{\rm out}= { \tau }_{\rm c}^{\ast} =\tau _{t1} { t}+\tau_{s1} { s}$.
选4种控制参数进行控制效果考核, 方案1: $W_{i} =1$, $k=300$; 方案2: $W_{i} =300$, $k=10$; 方案3: $W_{i} =200$, $k=100$; 方案4: $W_{i} =300$, $k=5$. 仿真控制结果如图8 和图9 所示. 可以看出, 4种方案均在500 s内趋于稳态, 其中方案1和3在初始有一段时间的波动后趋于稳态, 方案2和4相对平稳.
图8
图8
航天器姿态四元数时间历程
Fig.8
Time histories of the attitude quaternion about spacecraft
图9
图9
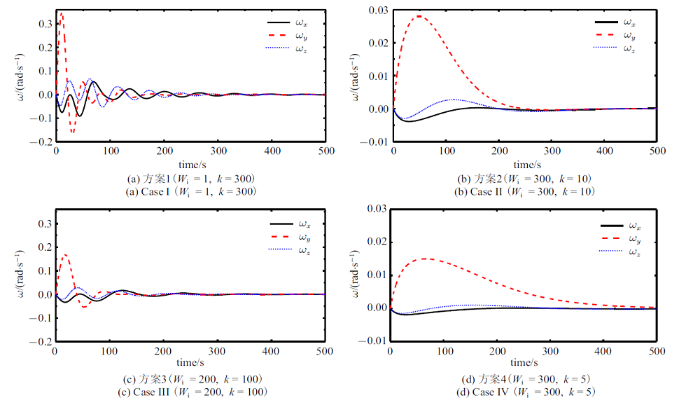
航天器的角速度时间历程
Fig.9
Time histories of the angular velocity about spacecraft
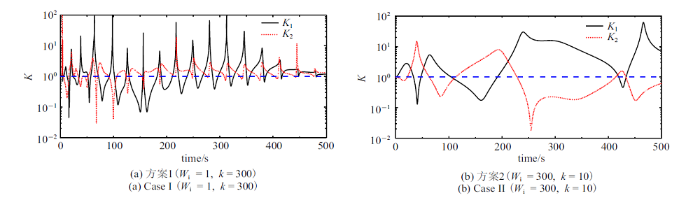
由式(8)和式(20)可得SCMG群的输出与输入力矩之比$K$和力矩利用率$\eta $, 如图10 $\sim\!$图12 所示. 可以看出, 在4种方案中, $K$和$\eta $均在等值线1上下波动, 表明SCMG并不恒有力矩放大效应和高效的力矩利用率, 这与理论结论一致. 方案1在等值线1上下波动次数最多, 总体控制效果欠佳, 与图8 (a)和图9 (a)表现出的控制效果吻合;方案3在等值线1上下波动次数仅次于方案1, 与图8 (c)和图9 (c)一致. 从图10 (b)和图11 (b)可见, 方案2的输出输入力矩比在等值线1以上的区域占优. 根据图8 和图9 所示的控制效果, 方案2收敛更快, 两者吻合;比较图12 (b)和图12 (d)可见, 方案3的力矩利用率$\eta$在等值线1以上的区域占优, 与图8 和图9 所示的平稳控制效果一致. 综上所述, 控制效果与输出输入力矩比$K$和力矩利用率$\eta $这两个参数密切相关.
图10
图10
输出与输入力矩比时间历程
Fig.10
Torque ratio of CMG's input to output vs time
图11
图11
输出与输入力矩比时间历程
Fig.11
Torque ratio of CMG's input to output vs time
图12
图12
力矩利用率时间历程
Fig.12
Torque utilization vs time
4.2 优化控制
使用两个SCMG对控制方案1进行优化, 其参数与4.1节相同. 这里考虑SCMG的运动参数约束[34 ] 为$|\varOmega _{i} |\leqslant 3000$ rad/s, $|\dot{{\varOmega }}_{i} |\leqslant 10$ rad/s$^{2}$, $|\dot{{\delta }}_{i} |\leqslant 10$ rad/s, $|\ddot{{\delta }}_{i} |\leqslant 10$ rad/s$^{2}$, ($i=1$, 2), ${ \tau }_{\rm out}= { \tau }_{\rm c}^{\ast} ={ \tau }_{\rm c} $, 仿真时长$t_{\rm f} =80$ s, 优化目标为
(33) $\begin{eqnarray} \label{eq33} { f}=\int_0^{t_{\rm f} } {({ e}^{\rm T}{ N e}+{ x}^{\rm T}{ M x}+{ u}^{\rm T}{ R u})\mbox{d}t} \end{eqnarray}$
(34) $\begin{eqnarray} \label{eq34} \left. {\begin{array}{l} { e}=\{q_{0} -q_{\rm 0d} ,q_{1} -q_{\rm 1d} ,q_{2} -q_{\rm 2d} ,q_{3} -q_{\rm 3d} \}^{\rm T} \\ { x}=\{\omega_{x} ,\omega_{y} ,\omega_{z} ,\dot{{\delta }}_{1} ,\dot{{\delta }}_{2} ,\varOmega_{1} ,\varOmega_{2} \}^{\rm T} \\ { u}=\{\ddot{{\delta }}_{1} ,\ddot{{\delta }}_{2} ,\dot{{\varOmega }}_{1} ,\dot{{\varOmega }}_{2} \}^{\rm T} \\ N =3000{ E}_{4} ,\ \ { M}=300{ E}_{7} ,\ \ { R}={ E}_{4} \\ \end{array}} \right\} \end{eqnarray}$
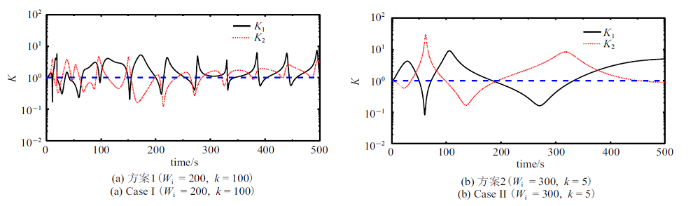
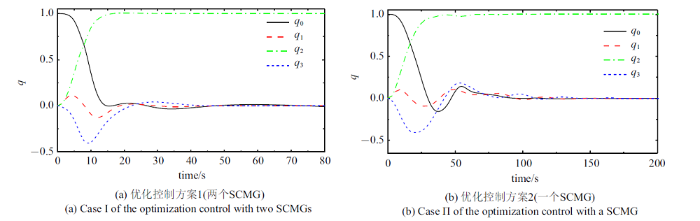
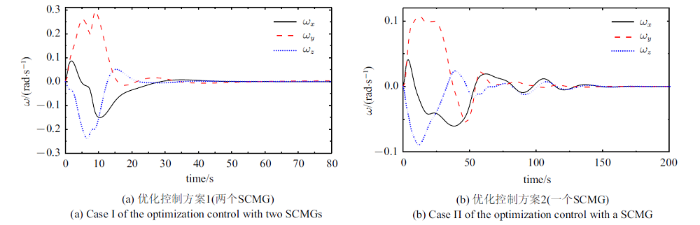
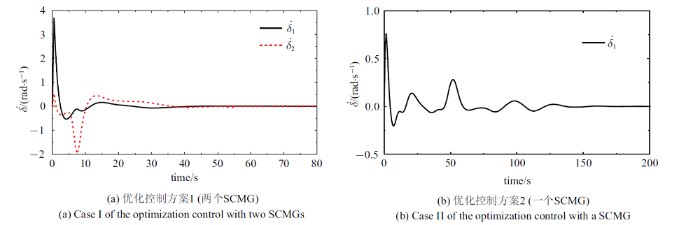
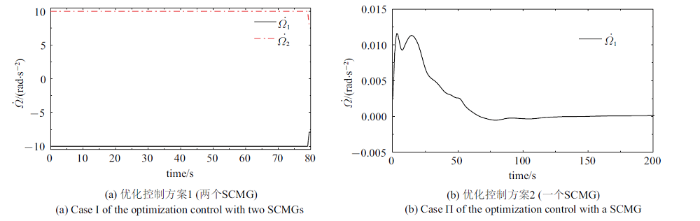
式中, ${ E}_{i} $表示$i\times i$阶单位矩阵. 方案1控制效果如图13 (a)和图14 (a)所示, 框架角速度和转子角加速度分别如图15 (a)和图16 (a)所示. 由式(8)和式(20)计算输出与输入力矩比和力矩利用率, 结果如图17 (a)和图18 (a)所示.
图13
图13
航天器姿态四元数时间历程
Fig.13
Time histories of the attitude quaternion about the spacecraft
图14
图14
航天器角速度时间历程
Fig.14
Time histories of the angular velocity about the spacecraft
图15
图15
框架角速度时间历程
Fig.15
Time histories of the gimbal rates
图16
图16
转子角加速度时间历程
Fig.16
Time histories of the angular acceleration about the flywheel
图17
图17
输出与输入力矩比时间历程
Fig.17
Torque ratio of CMG's input to output vs time
图18
图18
力矩利用率时间历程
Fig.18
Torque utilization vs time
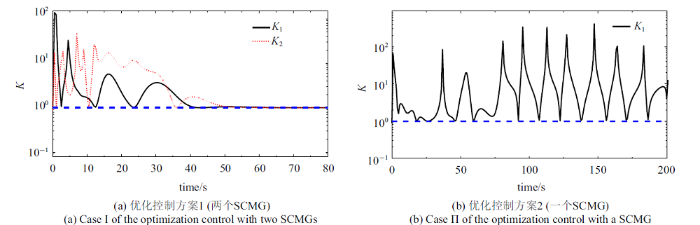
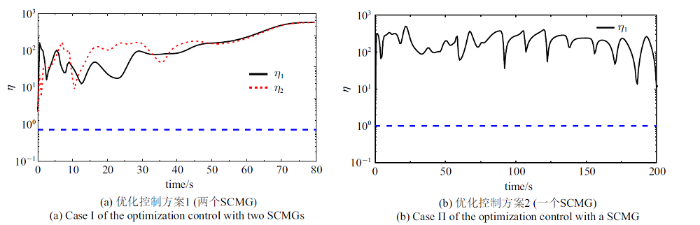
由式(3)和式(4)可知, SCMG为三维力矩输出, 单个SCMG即可实现航天器三维姿态控制. 因此, 优化控制方案2只保留优化方案1中第一个SCMG, 仿真时长$t_{\rm f} =200$ s, 其他仿真参数不变. 方案2仿真控制效果如图13 (b)和图14 (b)所示, 框架角速度和转子角加速度如图15 (b)和图16 (b)所示. 从式(8)和式(20)可得输出与输入力矩比和力矩利用率, 结果如图17 (b)和图18 (b)所示.
从图13 和图14 可见, 考虑到SCMG的运动参数受限, 两个优化控制方案均可完成控制任务, 控制过程比较平稳, 收敛效果良好. 对于收敛到目标的耗时, 方案1 (两个SCMG)约50 s, 方案2 (一个SCMG)约150 s, 后者用时略长, 前者航天器机动角速度明显高于后者, 因此收敛速度更快. 从图15 可见, 方案1的框架角速度幅值更大. 图15 (a)显示方案1在35 s以后$\dot{{\delta }}_{i} (i=1$, 2)已接近零, 即此时输出的陀螺力矩值非常有限. 由图16 可知, 方案1长时间利用转子变速输出力矩, 而方案2在50 s时已接近目标姿态, 之后就不再利用转子变速输出力矩, 但维持比较高的转子速度. 由图15 (b)可知, 方案2在50 s以后框架角速度在稳态期望值零上下波动, 通过输出陀螺力矩来调节航天器姿态. 上述两种优化控制方案的任务相同, 但图13 $\sim\!$图16 中两种控制方案表现出明显差异, 根本原因在于方案1有4个输入, 从控制的角度可理解其有一个冗余, 可行域更广;方案2仅有2个输入, 属于欠驱动, 可行域更窄. 由图17 和图18 可知, 在整个控制过程中, 两种优化控制方案的输出输入力矩比和力矩利用率始终位于等值线1以上, 表明在优化控制过程中SCMG始终有良好的输出特性, 即SCMG始终具有力矩放大效应和高效的力矩利用率.
5 结论
通过建立SCMG的两维输入三维输出模型, 将其输出力矩分解成可调控部分与不可调控部分, 进而定义SCMG的输入与输出力矩比和力矩利用率. 研究发现, SCMG不恒有力矩放大效应, 也不恒有高效的力矩利用率. 此外, SCMG输出特性确实与系统状态有关. 根据SCMG的三维输出特性, 借助一个SCMG的优化控制可实现航天器三轴姿态机动. 在提出的优化控制方案中, 可以始终确保SCMG具有力矩放大效应和高效的力矩利用率. 因此, 通过合理设计控制方案, 可以使SCMG具有良好的动态输出特性且控制效果最优.
参考文献
View Option
[1]
Tabarovskii AM . On the stability of motion of foucault gyroscopes with two degrees of freedom
Journal of Applied Mathematics & Mechanics 1960 ,24 (5 ):1206 -1213
[本文引用: 1]
[2]
Toriumi FY Angelico BA . Nonlinear controller design for tracking task of a control moment gyroscope actuator
IEEE/ASME Transactions on Mechatronics 2020 ,25 (1 ):438 -448
[本文引用: 1]
[3]
王恩美 , 邬树楠 , 吴志刚 . 在轨组装空间结构面向主动控制的动力学建模
力学学报 , 2020 ,52 (3 ):805 -817
[本文引用: 1]
( Wang Enmei Wu Shunan Wu Zhigang . Active-control-oriented dynamic modelling for on-orbit assembly space structure
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (3 ):805 -816 (in Chinese))
[本文引用: 1]
[4]
罗操群 , 孙加亮 , 文浩 等 . 多刚体系统分离策略及释放动力学研究
力学学报 , 2020 ,52 (2 ):503 -513
[本文引用: 1]
( Luo Caoqun Sun Jialiang Wen Hao , et al . Research on separation strategy and deployment dynamics of a space multi-rigid-body system
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (2 ):503 -513 (in Chinese))
[本文引用: 1]
[5]
Yoon H . Spacecraft attitude and power control using variable speed control moment gyros
[PhD Thesis]. Atlanta: Georgia Institute of Technology , 2004
[本文引用: 1]
[6]
Sasaki T Shimomura T Pullen S . et al . Attitude and vibration control with double-gimbal variable-speed control moment gyros
Acta Astronautica 2018 ,152 (11 ):740 -751
[本文引用: 1]
[7]
Valk L Berry A Vallery H , Directional singularity escape and avoidance for single-gimbal control moment gyroscopes
Journal of Guidance Control and Dynamics 2018 ,41 (5 ):1095 -1107
[本文引用: 1]
[8]
Sasaki T Alcorn J Schaub H . et al . Convex optimization for power tracking of double-gimbal variable-speed control moment gyroscopes
Journal of Spacecraft and Rockets 2018 ,55 (3 ):541 -551
[本文引用: 1]
[9]
Zhao H Liu F Yao Y . Optimization design steering law for VSCMGs with the function of attitude control and energy storage
Aerospace Science and Technology 2017 ,65 (6 ):9 -17
[本文引用: 1]
[10]
Sasaki T Shimomura T Schaub H . Robust attitude control using a double-gimbal variable-speed control moment gyroscope
Journal of Spacecraft and Rockets 2018 ,55 (5 ):1235 -1247
[本文引用: 1]
[11]
Stevenson D Schaub H . Nonlinear control analysis of a double-gimbal variable-speed control moment gyroscope
Journal of Guidance Control and Dynamics 2012 ,35 (3 ):787 -793
[本文引用: 1]
[12]
Hu QL Tan X . Dynamic near-optimal control allocation for spacecraft attitude control using a hybrid configuration of actuators
IEEE Transactions on Aerospace and Electronic Systems 2020 ,56 (2 ):1430 -1443
[本文引用: 1]
[13]
Guo JT Geng YH Kong XR . Pyramid-type single-gimbal control moment gyro system singularity avoidance using gimbal reorientation
Journal of Guidance Control and Dynamics 2020 ,43 (6 ):1180 -1189
[本文引用: 1]
[14]
Yoshikawa T . A Steering law for a roof type configuration of single gimbal control moment gyro system
IFAC Proceedings Volumes 1975 ,8 (1 ):361 -369
[本文引用: 1]
[15]
Tang L Xu SJ . Geometric analysis of singularity for single-gimbal control Moment gyro systems
Chinese Journal of Aeronautics 2005 ,18 (4 ):295 -303
[本文引用: 1]
[16]
Kawajiri S Matunaga S . Singularity avoidance/passage steering logic for a variable-speed double-gimbal control moment gyro based on inverse kinematics
Transactions of The Japan Society for Aeronautical and Space Sciences, Space Technology Japan 2018 ,16 (2 ):188 -194
[本文引用: 1]
[17]
Margulies G Aubrun JN . Geometric theory of single-gimbal control moment gyro system
Journal of the Astronnutical Sciences 1978 ,26 (2 ):159 -191
[本文引用: 1]
[18]
Wie B . Singularity analysis and visualization for single-gimbal control moment gyro systems
Journal of Guidance Control and Dynamics 2004 ,27 (2 ):271 -282
[本文引用: 1]
[19]
Kurokawa H . Constrained steering law of pyramid-type control moment gyros and ground tests
Journal of Guidance Control and Dynamics 1997 ,20 (3 ):445 -449
[本文引用: 1]
[20]
Leeghim H Lee CY Jin J . et al . A singularity-free steering law of roof array of control moment gyros for agile spacecraft maneuver
International Journal of Control Automation and Systems 2020 ,18 (7 ):1679 -1690
[本文引用: 1]
[21]
Guo YN Wang PY Ma GF . et al . Envelope oriented singularity robust steering law of control moment gyros for spacecraft attitude maneuver
Transactions of the Institute of Measurement and Control 2019 ,41 (4 ):954 -962
[本文引用: 1]
[22]
Pechev AN . Feedback-based steering law for control moment gyros
Journal of Guidance Control and Dynamics 2007 ,30 (3 ):848 -855
[本文引用: 1]
[23]
Meng T Matunaga S . Modified singular-direction avoidance steering for control moment gyros
Journal of Guidance Control and Dynamics 2012 ,34 (6 ):1915 -1920
[本文引用: 1]
[24]
Schaub H Junkins JL . Singularity avoidance using null motion and variable-speed control moment gyros
Journal of Guidance Control and Dynamics 2000 ,23 (1 ):11 -16
[本文引用: 1]
[25]
Kurokawa H . Survey of theory and steering laws of single-gimbal control moment gyros
Journal of Guidance Control and Dynamics 2007 ,30 (5 ):1331 -1340
[本文引用: 1]
[26]
Hoelscher BR Vadali SR . Optimal open-loop and feedback control using single gimbal control moment gyroscopes
Advances in the Astronautical Sciences 1994 ,42 (2 ):189 -206
[本文引用: 1]
[27]
Biggs JD Livornese G . Control of a thrust-vectoring cubeSat using a single variable-speed control moment gyroscope
Journal of Guidance Control and Dynamics 2020 ,43 (10 ):1865 -1880
[本文引用: 1]
[28]
曹登庆 , 白坤朝 , 丁虎 等 . 大型柔性航天器动力学与振动控制研究进展
力学学报 , 2019 ,51 (1 ):1 -13
[本文引用: 1]
( Cao Dengqing Bai Kunchao Ding Hu , et al . Advances in dynamics and vibration control of large-scale flexible spacecraft
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (1 ):1 -13 (in Chinese))
[本文引用: 1]
[29]
胡权 , 贾英宏 , 徐世杰 . 多体系统动力学Kane方法的改进
力学学报 , 2011 ,43 (5 ):968 -972
[本文引用: 1]
( Hu Quan Jia Yinghong Xu Shijie . An improved Kane's method for multibody dynamics
Chinese Journal of Theoretical and Applied Mechanics 2011 ,43 (5 ):968 -972 (in Chinese))
[本文引用: 1]
[30]
Lappas VJ Steyn WH Underwood CI . Torque amplification of control moment gyros
Electronics Letters 2002 ,38 (15 ):837 -839
[本文引用: 2]
[31]
Alcorn J Allard C Schaub H . et al . Fully coupled reaction wheel static and dynamic imbalance for spacecraft jitter modeling
Journal of Guidance Control and Dynamics 2018 ,41 (6 ):1380 -1388
[本文引用: 1]
[32]
Wie B . Singularity escape/avoidance steering logic for control moment gyro systems
Journal of Guidance Control & Dynamics 2005 ,28 (5 ):948 -956
[本文引用: 1]
[33]
Yoon H Tsiotras P . Singularity analysis of variable speed control moment gyros
Journal of Guidance Control and Dynamics 2004 ,27 (3 ):374 -386
[本文引用: 2]
[34]
Wu PC Wen H Chen T . et al . Model predictive control of rigid spacecraft with two variable speed control moment gyroscopes
Applied Mathematics and Mechanics (English Edition )2017 ,38 (11 ):1551 -1564
[本文引用: 1]
On the stability of motion of foucault gyroscopes with two degrees of freedom
1
1960
... 傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域. ...
Nonlinear controller design for tracking task of a control moment gyroscope actuator
1
2020
... 傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域. ...
在轨组装空间结构面向主动控制的动力学建模
1
2020
... 傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域. ...
在轨组装空间结构面向主动控制的动力学建模
1
2020
... 傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域. ...
多刚体系统分离策略及释放动力学研究
1
2020
... 傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域. ...
多刚体系统分离策略及释放动力学研究
1
2020
... 傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域. ...
Spacecraft attitude and power control using variable speed control moment gyros
1
2004
... 傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域. ...
Attitude and vibration control with double-gimbal variable-speed control moment gyros
1
2018
... 傅科(Foucault)于1852年首次提出"陀螺"概念[1 ] , 可利用陀螺的力学特性设计执行器, 称之为控制力矩陀螺(control moment gyroscope, CMG). 半个世纪以来, CMG广泛用于航天器姿态控制[2 ] , 并随着航天器控制任务的多样化[3 -4 ] , 从姿态控制逐渐延伸到能量存储[5 ] 、振动抑制[6 ] 等领域. ...
Directional singularity escape and avoidance for single-gimbal control moment gyroscopes
1
2018
... CMG有两种机械结构, 单框架(SCMG)[7 ] 和双框架(double-gimbal control moment gyro, DCMG)[8 ] . 飞轮可调速时, CMG演化成变速控制力矩陀螺(variable-speed control moment gyro, VCMG), 按其机械结构分类, 有单框架变速控制力矩陀螺(single-gimbal variable-speed control moment gyro, SVCMG)[9 ] 和双框架变速控制力矩陀螺(double-gimbal variable-speed control moment gyro, DVCMG)[10 -11 ] . 相比于DCMG, SCMG机械结构简单, 但存在奇异性问题, 而前者机械结构和控制算法更加复杂, 两者同属于多体系统, 本文仅关注航天领域应用最广的SCMG. ...
Convex optimization for power tracking of double-gimbal variable-speed control moment gyroscopes
1
2018
... CMG有两种机械结构, 单框架(SCMG)[7 ] 和双框架(double-gimbal control moment gyro, DCMG)[8 ] . 飞轮可调速时, CMG演化成变速控制力矩陀螺(variable-speed control moment gyro, VCMG), 按其机械结构分类, 有单框架变速控制力矩陀螺(single-gimbal variable-speed control moment gyro, SVCMG)[9 ] 和双框架变速控制力矩陀螺(double-gimbal variable-speed control moment gyro, DVCMG)[10 -11 ] . 相比于DCMG, SCMG机械结构简单, 但存在奇异性问题, 而前者机械结构和控制算法更加复杂, 两者同属于多体系统, 本文仅关注航天领域应用最广的SCMG. ...
Optimization design steering law for VSCMGs with the function of attitude control and energy storage
1
2017
... CMG有两种机械结构, 单框架(SCMG)[7 ] 和双框架(double-gimbal control moment gyro, DCMG)[8 ] . 飞轮可调速时, CMG演化成变速控制力矩陀螺(variable-speed control moment gyro, VCMG), 按其机械结构分类, 有单框架变速控制力矩陀螺(single-gimbal variable-speed control moment gyro, SVCMG)[9 ] 和双框架变速控制力矩陀螺(double-gimbal variable-speed control moment gyro, DVCMG)[10 -11 ] . 相比于DCMG, SCMG机械结构简单, 但存在奇异性问题, 而前者机械结构和控制算法更加复杂, 两者同属于多体系统, 本文仅关注航天领域应用最广的SCMG. ...
Robust attitude control using a double-gimbal variable-speed control moment gyroscope
1
2018
... CMG有两种机械结构, 单框架(SCMG)[7 ] 和双框架(double-gimbal control moment gyro, DCMG)[8 ] . 飞轮可调速时, CMG演化成变速控制力矩陀螺(variable-speed control moment gyro, VCMG), 按其机械结构分类, 有单框架变速控制力矩陀螺(single-gimbal variable-speed control moment gyro, SVCMG)[9 ] 和双框架变速控制力矩陀螺(double-gimbal variable-speed control moment gyro, DVCMG)[10 -11 ] . 相比于DCMG, SCMG机械结构简单, 但存在奇异性问题, 而前者机械结构和控制算法更加复杂, 两者同属于多体系统, 本文仅关注航天领域应用最广的SCMG. ...
Nonlinear control analysis of a double-gimbal variable-speed control moment gyroscope
1
2012
... CMG有两种机械结构, 单框架(SCMG)[7 ] 和双框架(double-gimbal control moment gyro, DCMG)[8 ] . 飞轮可调速时, CMG演化成变速控制力矩陀螺(variable-speed control moment gyro, VCMG), 按其机械结构分类, 有单框架变速控制力矩陀螺(single-gimbal variable-speed control moment gyro, SVCMG)[9 ] 和双框架变速控制力矩陀螺(double-gimbal variable-speed control moment gyro, DVCMG)[10 -11 ] . 相比于DCMG, SCMG机械结构简单, 但存在奇异性问题, 而前者机械结构和控制算法更加复杂, 两者同属于多体系统, 本文仅关注航天领域应用最广的SCMG. ...
Dynamic near-optimal control allocation for spacecraft attitude control using a hybrid configuration of actuators
1
2020
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Pyramid-type single-gimbal control moment gyro system singularity avoidance using gimbal reorientation
1
2020
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
A Steering law for a roof type configuration of single gimbal control moment gyro system
1
1975
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Geometric analysis of singularity for single-gimbal control Moment gyro systems
1
2005
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Singularity avoidance/passage steering logic for a variable-speed double-gimbal control moment gyro based on inverse kinematics
1
2018
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Geometric theory of single-gimbal control moment gyro system
1
1978
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Singularity analysis and visualization for single-gimbal control moment gyro systems
1
2004
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Constrained steering law of pyramid-type control moment gyros and ground tests
1
1997
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
A singularity-free steering law of roof array of control moment gyros for agile spacecraft maneuver
1
2020
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Envelope oriented singularity robust steering law of control moment gyros for spacecraft attitude maneuver
1
2019
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Feedback-based steering law for control moment gyros
1
2007
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Modified singular-direction avoidance steering for control moment gyros
1
2012
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Singularity avoidance using null motion and variable-speed control moment gyros
1
2000
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Survey of theory and steering laws of single-gimbal control moment gyros
1
2007
... 通常, 为实现航天器三轴姿态控制, 在只利用SCMG输出陀螺力矩[12 ] 的情况下, 要满足输出三维控制力矩, 则需要按一定构型配置多个SCMG, 如金字塔构型[13 ] 、屋顶构型[14 ] 和五棱锥构型[15 ] 等. VSCMG有两个输出, 只需两个VSCMG即可完成航天器三轴姿态控制. 力矩陀螺群存在操纵奇异性[16 ] 问题, 针对不同构型的力矩陀螺群, 许多学者分析了其奇异几何特性[17 -18 ] 和零运动存在性[19 ] , 提出诸如奇异逃离[20 ] 、奇异鲁棒[21 ] 、反馈[22 ] 、方向规避等操纵律[23 ] , 以及综合零运动与奇异逃离的混合操纵律[24 -25 ] 等. ...
Optimal open-loop and feedback control using single gimbal control moment gyroscopes
1
1994
... 最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] . ...
Control of a thrust-vectoring cubeSat using a single variable-speed control moment gyroscope
1
2020
... 最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] . ...
大型柔性航天器动力学与振动控制研究进展
1
2019
... 最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] . ...
大型柔性航天器动力学与振动控制研究进展
1
2019
... 最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] . ...
多体系统动力学Kane方法的改进
1
2011
... 最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] . ...
多体系统动力学Kane方法的改进
1
2011
... 最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] . ...
Torque amplification of control moment gyros
2
2002
... 最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] . ...
... [30 -31 ]. ...
Fully coupled reaction wheel static and dynamic imbalance for spacecraft jitter modeling
1
2018
... 最初, SCMG作为航天器的执行机构, 其输出模型仅考虑陀螺力矩[26 ] , 而VSCMG的飞轮可调速, 输出力矩比SCMG多一个反作用力矩[27 ] . 为分析柔性航天器的振动问题[28 ] , 胡权等[29 ] 基于Kane方程建立了适用于任意构型的多个柔性体系统递推算法, 这丰富了含SCMG的多体系统建模方法. 现有研究对SCMG的力矩输出特性不够关注, 一直停留于Lappas等[30 ] 关于SCMG基座角速度较小且转子角速度较大的假设基础之上, 并借鉴反作用轮原理获得SCMG的力矩放大效应[30 -31 ] . ...
Singularity escape/avoidance steering logic for control moment gyro systems
1
2005
... 取$\lambda =\lambda_{0} \exp [-\mu \det ({ Q Q}^{\rm T})]$, 这里$\lambda_{0} $和$\mu $为正实常数. 取对角元素$W_{i}(i=1$, 2, 3, 4)和非对角元素$\varepsilon_{i}$ $(i=1,2,3)$, 采用非对角奇异鲁棒操纵律[32 ] , 有 ...
Singularity analysis of variable speed control moment gyros
2
2004
... 取控制参数[33 ] 为 ...
... 令$J_{{\rm w}gi} =J_{{\rm w}ti} =0.4$ kg/m$^{2}$, $J_{i} =0.7$ kg/m$^{2}$, $J_{{\rm f}gi} =J_{{\rm f}si} =J_{{\rm f}ti} =0.1$ kg/m$^{2}$, 以及[33 ] ...
Model predictive control of rigid spacecraft with two variable speed control moment gyroscopes
1
2017
... 使用两个SCMG对控制方案1进行优化, 其参数与4.1节相同. 这里考虑SCMG的运动参数约束[34 ] 为$|\varOmega _{i} |\leqslant 3000$ rad/s, $|\dot{{\varOmega }}_{i} |\leqslant 10$ rad/s$^{2}$, $|\dot{{\delta }}_{i} |\leqslant 10$ rad/s, $|\ddot{{\delta }}_{i} |\leqslant 10$ rad/s$^{2}$, ($i=1$, 2), ${ \tau }_{\rm out}= { \tau }_{\rm c}^{\ast} ={ \tau }_{\rm c} $, 仿真时长$t_{\rm f} =80$ s, 优化目标为 ...