引言
对接机构技术是指能够在太空通过接触、缓冲、捕获和刚性联接等过程将两个飞行器在结构上形成一个整体的技术[1 ] .其中,在轨道上等待对接的飞行器称为目标飞行器,通过一系列变轨等运动控制与目标飞行器进行对接的飞行器称为主动飞行器.对接技术作为航天领域内的一项重大技术主要有以下几个作用.
(1) 大型航天器的在轨组装.由于对接技术首要的功能就是可以将两个航天器通过刚性联接固连为一个结构整体,这为一些需要在轨组装拼接的大型航天器提供了很大的优势[2 -3 ] .
(2) 航天员转移以及物资补给.大多数对接机构中都具有可供航天员转移以及物资补给用的通道[4 ] ,在两飞行器固连完成后,主动飞行器和目标飞行器的通道完整的联接[5 ] .
(3) 空间在轨服务.空间飞行器的低寿命问题一直是困扰航天工作者的一个重大难题,为了延长航天器在轨的工作寿命[6 -7 ] ,许多空间在轨维修以及更换等维护服务均依靠对接技术的支持得以实现[8 -10 ] .
(4) 深空探测等任务的技术支持.未来的载人登月以及深空探测等任务均需将飞行器送入更远的轨道中去[11 -12 ] ,利用对接技术手段通过多次发射,多次对接的方式来实现.
对接机构作为一项关键技术一直承担着重要的航天任务,但随着载人航天和深空探测任务的不断发展,目前对接机构难以满足未来建立月球轨道空间站的需求,其在功能和性能方面都具有一定的局限性,主要具体有以下几点.
(1) 现有对接机构捕获性能调整不灵活.由于月球轨道空间站的建设首先需要完成载人登月任务,根据目前载人登月工程综合论证工作,我国的载人登月任务拟采用"近地轨道一次对接+环月轨道两次对接''这种模式[13 -14 ] ,整个任务周期需要完成三次对接任务.其中,每次对接的主动飞行器与目标飞行器的吨位质量均不相同,大致从 18 吨与 3 吨对接至 18 吨与 80 吨对接,而现有对接机构因其刚度和阻尼等性能都需要在地面调试完成,故无法满足在轨多质量范围的对接需求[15 -17 ] .
(2) 现有对接机构质量较重.探月飞行器由于需要进入更高的飞行轨道,并同时要进行月面着陆和起飞等过程[18 -19 ] ,这便对整个对接系统质量要求高于传统的近地飞行器.我国现有在轨运作的对接机构在质量上约为 540 kg,其中主动件约为 320 kg,目标件约为 220 kg,相对较重,需要针对月球轨道空间站的任务在质量指标方面进行优化设计.
(3) 现有对接机构的通道直径无法满足需求.月球轨道空间站的搭建需要经历多次发射来对接进行在轨组装,同时为了方便仪器及设备在飞行器间的转移,这就对对接完成后内部通道的直径有了更大的需求,此外,目前在轨的对接机构的通道直径大约是 800 mm,其中某些部位由于结构影响使得直径更小,在航天员穿着航天服的情况下通过该通道较为勉强,故通道直径的需求也需要考量.
(4) 现有对接机构适应性无法满足日益苛刻的任务环境.载人探月飞行任务中,对接机构需要满足的空间环境更为苛刻,月球轨道环境与近地轨道环境有着较大的差异,载人登月对接机构能够承受满足近月空间环境的高真空特性,以及更宽的高低温 范围[20 ] .
(5) 现有对接机构捕获方式较为单一.由于现有对接机构的结构特性,在进行捕获前需要有一定的推力,致使对接环上的捕获锁在力的作用下成功捕获到目标飞行器,故不支持利用机械臂对对接机构进行停靠对接和摇操作[21 ] .
近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据.
1 结构设计
抱爪式对接机构采用周边式构型,内部通道在整个机构的中心部位,其余的传动以及捕获缓冲等部组件均安置在机构的周边,该设计能很好满足飞行器刚性联接之后形成内部通道的需要.同时采用了异体同构式结构,即主动对接机构与目标对接机构的结构设计完全相同,在对接任务中所有的机构运动一般由主动对接机构实现,目标对接机构属于冗余备份. 此外,异体同构式设计能实现主目标对接机构之间的互换.图1 为设计的抱爪式对接机构模型.
图1
图1
抱爪式对接机构模型及其外包络尺寸
Fig. 1
Outer envelope size of claw-type docking mechanism
原有在轨对接机构以靠两飞行器上的导向板互相接触再完成捕获,而导向板内翻式的实际会致使对接框的直径需要比通道直径大,从而加大了对接机构的质量. 从图1 抱爪式对接机构尺寸包络可以看到,由于设计的抱爪式对接机构完全取消了导向板的设计,故可以将对接框内径与通道直径一致,从而大幅降低了对接框的质量,与此同时,单个对接机构上的对接锁的数量也能减少. 整个抱爪式对接机构对轻量化的设计具有很大的优势,与国内外主要在轨工作过的主动对接机构质量对比如表1 所示.
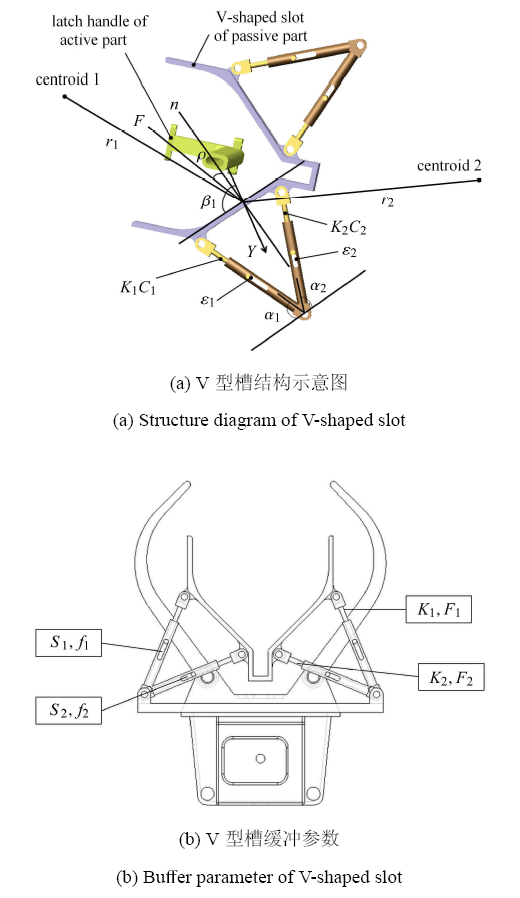
根据图1 中所示,V 型槽与爪钩组成了机构的捕获缓冲系统,在对目标飞行器捕获过程中,通过爪钩的运动将目标动飞行器上的锁柄抱住同时相互拉近直至完全捕获,V 型槽主要功能是缓冲对接过程中的碰撞力,其与底座之间安装有 4 个滑移杆,通过杆内的弹簧阻尼结构实现碰撞力的消耗.
2 捕获缓冲动力学分析
恢复系数是指两物体碰撞时的变形恢复能力的参数,其定义为碰撞前后两物体在接触点上的法向相对分离速度与法向相对接近速度之比,可表示为
(1) $S = \dfrac{V'_2 - V'_1 }{V_2 - V_1 }$
其中,$V_1 $ 和 $V_2 $ 分别表示两飞行器碰撞前速度,$V'_1 $ 和 $V'_2 $ 分别表示两飞行器碰撞后速度.
理想的弹性元件在碰撞后可以完全回到原始位置,或是说其能够恢复物体动能且无损耗,就如同绝对弹性撞击的情况一样,此时恢复系数 $S =1$. 当完全不考虑结构弹性时,此时的恢复系数 $S =0$. 自然界中不存在理想的弹性元件,对于实际缓冲器来说 $S$ 值是在这两个极限值之间,即 $0 \leqslant S < 1$.
为了设计缓冲器确定 $S$ 值,需要引入阻尼结构,对于能够产生与变形速度成正比的力,变形系数为 $K_n $ 的弹性元件和阻尼系数为 $C_n $ 的线性缓冲器来说,它的当量模型可用线性微分方程来描述
(2) $M_n \ddot {\varepsilon } + K_n \dot {\varepsilon } + C_n \varepsilon = 0$
其中,$M_n $ 为两飞行器的当量质量,$\varepsilon $ 为缓冲器变形量,令 $\varepsilon (t) = \bar {\varepsilon } {e}^{st}$,同时引入等效阻尼比 $\xi = \dfrac{C_n }{2\sqrt {K_n M_n } } = \dfrac{C_n }{2M_n \omega _n }$,则可以得到以下关系式
(3) $s_{1,2} = \left( { - \xi \pm \sqrt {\xi ^2 - 1} } \right)\omega _n$
将式 (3) 代入式 (2) 中,同时对缓冲器变形量的二阶导为零判定为分离时刻,据此求得恢复系数与等效阻尼比之间的关系式
(4) $S = \dfrac{1}{\sqrt {\xi ^2 - 1} }{e}^{\tfrac{\xi A}{\sqrt {\xi ^2 - 1} }}\left({ - \xi {sh} A + \sqrt {\xi ^2 - 1} {ch} A} \right)$
式中,双曲线表达式 ${sh} x = \dfrac{{e}^x - {e}^{ - x}}{2}$,${ch} x = \dfrac{{e}^x + {e}^{ - x}}{2}$,得出
(5) $A = \dfrac{1}{2} {In}\dfrac{2\xi ^2 - 1 + 2\xi \sqrt {\xi ^2 - 1} }{2\xi - 1 - 2\xi \sqrt {\xi ^2 - 1} }$
由此可见,缓冲器的特性决定了抱爪式对接机构撞击前后的恢复系数. 显然,若 $S =0$ 时,表示锁柄与沿着 V 型槽的母线方向滑动. V 型槽结构及相关参数标定见图2 ,假设在不考虑飞行器的主推力作用和在飞船间轴向夹角不超过限定值的条件下,保证锁柄能落入到 V 型槽底部,则得到如下公式
(6) $S < \dfrac{1}{1 / [k_1 {tg}\left( {\pi / 2 - 2\beta _k } \right)] - 1}$
(7) $K_1 = M_n \sum_{i = 1}^2 {\left[ {\sin \rho / m_i + r_i ^2\sin \beta _i \cos \left({\beta _i + \rho } \right) / I_{zi} } \right]}$
(8) $ 1 / M_n = {1 / m_i + \left( {r_{iy} \cos \alpha _{iz} - r_{iz} \cos \alpha _{iy} } \right)^2} /{I_{ix} } + \\ {\left( {r_{iz} \cos \alpha _{ix} - r_{ix} \cos _{iz} } \right)^2} / {I_{iy} } + \\ {\left( {r_{ix} \cos \alpha _{iy} - r_{iy} \cos \alpha _{ix} } \right)^2} /{I_{iz} } $
图2
图2
V 型槽结构
Fig. 2
Structure of V-shaped slot
假设作用点处滑动速度不改变方向且不等于零,则可以进一步减少自由度,简化当量数学模型和摩擦的计算.此时,作用点处的摩擦被看作是沿某一方向的常值,并与法向力具有正比例关系.因此,合反力 (摩擦力加上法向力) 与法线的夹角为 $\rho $,且 $\rho = \arctan \lambda $,其中 $\lambda$ 为摩擦系数. 在这种情况下,当量重量的表达式为
(9) $1/ M_n = \sum_{i = 1}^2 \left[ { {\cos \rho } / {m_i } + {r_i ^2\cos \beta _i \cos \left( {\beta _i + \rho }\right)} /{I_{iz} }} \right]$
其中 $\beta _i $ 为向量 $\overline {r_i } $ 与作用点处切线之间的夹角.
考虑最恶劣工况初始碰撞只有一个锁柄与 V 型槽相碰,轴向黏弹性缓冲器 (其参数相应地为 $C_1 $,$C_2 $,$K_1$,$K_2 $), 缓冲器的相应变形量为 $\varepsilon _1 $ 和 $\varepsilon _2 $,可以 得到
(10) $ M_n \left( {\varepsilon _1 \sin \beta _1 + \varepsilon _2 \cos \beta _1 } \right) =- {\left( {K_1 \varepsilon _1 + C_1 \varepsilon _1 } \right)} /{\sin \left( {\beta _1 + \rho } \right)}$
(11) $M_n \left( {\varepsilon _1 \sin \beta _1 + \varepsilon _2 \cos \beta _1 } \right) = - {\left( {K_2 \varepsilon _2 + C_2 \varepsilon _2 } \right)} /{\sin \left( {\beta _1 + \rho } \right)}$
从上式可以看出,缓冲器的变形可以由当量重量为 $M_n$ 的物体及其位移分别为 $\varepsilon _1 \cos \beta _1 $ 和 $\varepsilon _2 \cos\beta _2 $ 两个并联的缓冲器的撞击模型来描述,其变形系数相应为 ${\left( {K_1 + C_1 } \right)} /{\sin (\beta _1 + \rho )}$ 和 ${\left( {K_2 + C_2 } \right)} /{\sin (\beta _1 + \rho )}$
3 仿真计算
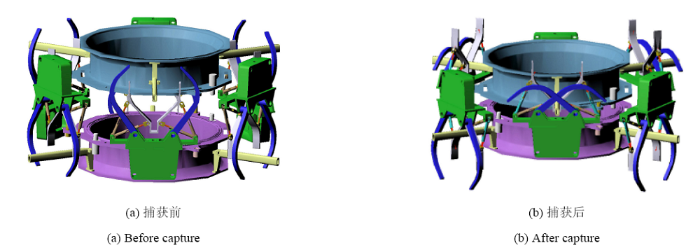
由于空间中主动飞行器和目标飞行器飞行位姿和精度的不同,对接初始条件也随之产生变化,不同工况下对接机构的捕获能力与缓冲能力均有所偏差.本文设计了两种不同且较为典型的对接初始条件工况,分别对抱爪式对接机构进行动力学仿真,分析其捕获缓冲过程的能量变化以及受力情况. 具体的对接初始条件工况如表2 所示.
从图3 工况 1 对接过程可以看到,抱爪机构成功将目标飞行器捕获,两飞行器校正完成.
图3
图3
工况 1 对接过程
Fig. 3
Process of docking of 1st working condition
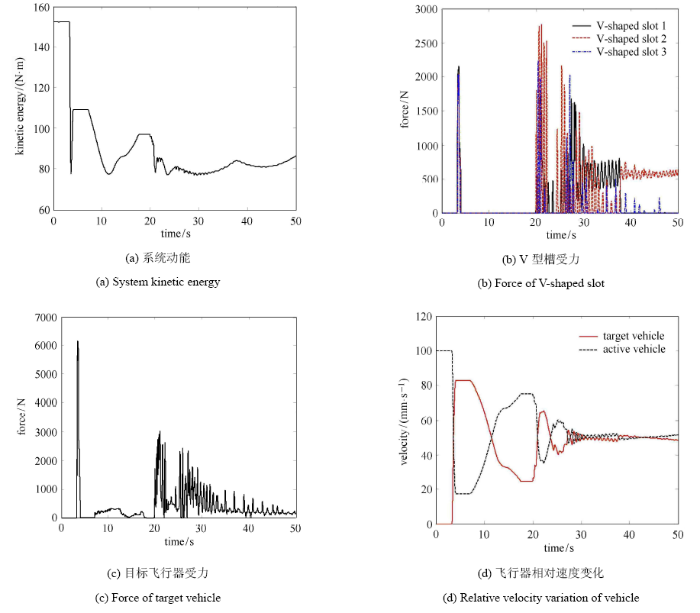
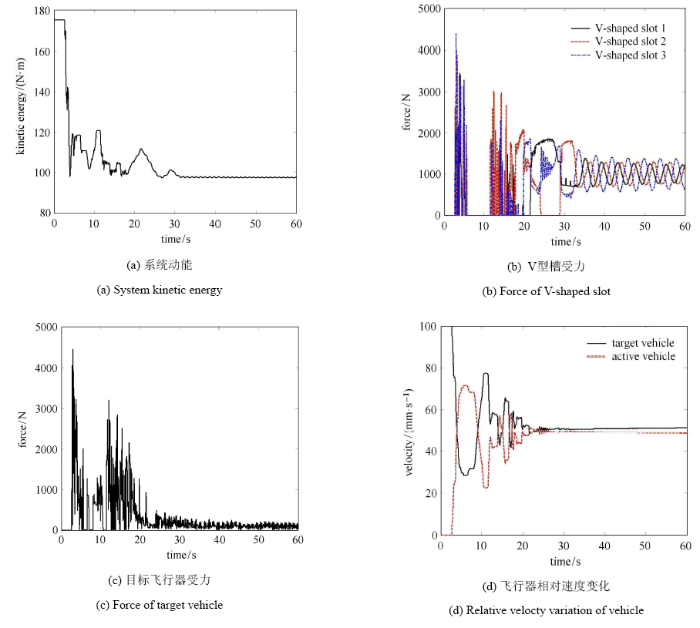
从图4 工况 1 仿真结果可以看到,系统在正碰下的动能在目标飞行器第一次接触 V 型槽并回弹后,动能从 152 N$\cdot$m 下降至 109 N$\cdot$m,系统动能下降了约 28.3%,校正完成后系统动能最终下降了 47.4%.3 个 V 型槽最大受力约 2700 N,且持续时间较短,最终 V 性槽 2 稳定在 600 N 左右.目标飞行器受力最大峰值为 6100 N 左右,出现在第一次接触时,此后的接触力不超过 3000 N,并随着校正过程逐渐减小至稳定. 根据飞行器相对速度变化情况可以得到第一次接触碰撞后的恢复系数约为 0.64.
图4
图4
工况 1 仿真结果
Fig. 4
Simulation result of 1st working condition
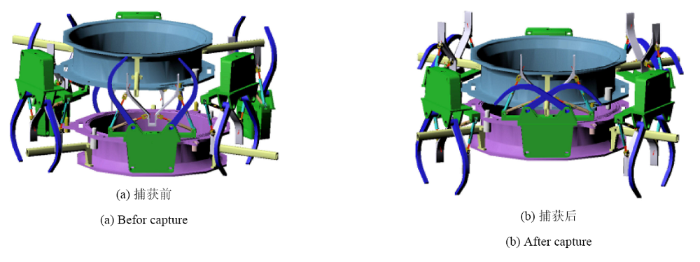
从图5 工况 2 对接过程可以看到,在此工况下抱爪成功将目标飞行器捕获,两飞行器校正完成.
图5
图5
工况 2 对接过程
Fig. 5
Process of docking of 2nd working condition
从图6 工况 2 仿真结果可以看到,系统在正碰下的动能在目标飞行器第一次接触V型槽并回弹后,动能从 175 Nm 下降至 120 Nm,系统动能下降了约 31.4%,校正完成后系统动能最终下降了 44.5%.3 个 V 型槽最大受力约 4300 N,且持续时间较短,V 型槽后期稳定在 500 N 至 1200 N 之间波动.目标飞行器受力最大峰值为 4400 N 左右,出现在第一次接触时,此后的接触力不超过 3200 N,并随着校正过程逐渐减小至稳定.根据飞行器相对速度变化情况可以得到第一次接触碰撞后的恢复系数约为 0.42.
图6
图6
工况 2 仿真结果
Fig. 6
Simulation result of 2nd working condition
4 结论
根据捕获缓冲机构动力学分析和仿真分析,可以得到以下结论:
抱爪式对接机构的飞行碰撞恢复系数对捕获功能具有一定的影响,需要根据机构构型尺寸设计满足任务需求的捕获缓冲系统边界条件,从而调整恢复系数保证捕获成功率;
根据对接初始条件的不同,工况 2 的初始动能比工况 1 大,而由于V型槽接触面与锁柄间的摩擦作用,工况 2 下的目标飞行器受力小于工况 1,由此可见在正碰以外的工况条件下,V 型槽与锁柄的摩擦系数对整体飞行器碰撞力具有较大影响;
抱爪机构在对目标飞行器锁柄完全抱拢后,锁柄在 V 型槽与爪钩仍有一定的运动间隙,从而导致校正后期 V 型槽仍具有一定的受力,但对实际捕获缓冲功能影响较小;
抱爪式对接机构的缓冲系统能很好消耗整个系统对接过程的动能,在抱爪爪钩的作用下能够稳定实现目标飞行器的捕获和校正功能. 两飞行器第一次接触后的动能下降约 30%,校正稳定后最终系统动能下降约 45%,能满足设计需求.
根据第一次接触碰撞后的飞行器相对速度变化情况,工况 1 的恢复系数大于工况 2,据此可知正碰工况对于捕获缓冲能力相对较弱,在非正碰工况下,V 型槽的斜面导向对最终的捕获起了很大作用.
参考文献
View Option
[1]
张崇峰 , 刘志 . 空间对接机构综述
上海航天 , 2016 ,33 (5 ):1 -11
[本文引用: 1]
( Zhang Chongfeng Liu Zhi . Review of space docking mechanism and its technology
Aerospace Shanghai 2016 ,33 (5 ):1 -11 (in Chinese))
[本文引用: 1]
[2]
沈晓凤 , 曾令斌 , 靳永强 等 . 在轨组装技术研究现状与发展趋势
载人航天 , 2017 ,23 (2 ):228 -235,244
[本文引用: 1]
( Shen Xiaofeng Zen Linbin Jin Yongqiang , et al . Status and prospect of on-orbit assembly technology
Manned Spaceflight 2017 ,23 (2 ):228 -235, 244 (in Chinese))
[本文引用: 1]
[3]
Saunders C Lobb D Sweeting M , et al . Building large telescopes in orbit using small satellites
Acta Astronautica 2017 ,141 :183 -195
[本文引用: 1]
[4]
蒋波 , 熊西军 , 彭志会 等 . 国际空间站物资管理系统的发展趋势及建议
遥测遥控 , 2012 ,33 (2 ):1 -6
[本文引用: 1]
( Jiang Bo Xiong Xijun Peng Zhihui , et al . Development and suggestion of inventory management system for International Space Station
Journal of Telemetry, Tracking and Command 2012 ,33 (2 ):1 -6 (in Chinese))
[本文引用: 1]
[5]
张崇峰 , 陈宝东 , 郑云青 等 . 航天器对接机构 . 北京 : 科学出版社 , 2016 : 187 -217
[本文引用: 1]
( Zhang Chongfeng Chen Baodong Zheng Yunqing , et al . Space Docking Mechanism . Beijing : Science Press , 2016 : 187 -217 (in Chinese))
[本文引用: 1]
[6]
陈萌 , 肖余之 , 张涛 . 空间服务与操控中的人工智能技术
载人航天 , 2018 ,24 (3 ):285 -291
[本文引用: 1]
( Chen Meng Xiao Yuzhi Zhang Tao . Artifical intelligence technology in space servicing and manipulation
Manned Spaceflight 2018 ,24 (3 ):285 -291 (in Chinese))
[本文引用: 1]
[7]
Chiu SW . Promoting international co-operation in the age of global space governance - A study on on-orbit servicing operations
Acta Astronautica 2019 ,161 :375 -381
[本文引用: 1]
[8]
侯鹏飞 . 面向航天器在轨维修任务的机械臂及其地面实验研究. [硕士论文]
哈尔滨: 哈尔滨工业大学 , 2015
[本文引用: 1]
( Hou Pengfei . Research on manipulator for on-orbit servicing tasks of spacecraft and its ground test. [Master Thesis]
Harbin: Harbin Institute of Technology , 2015 (in Chinese))
[本文引用: 1]
[9]
Ge XY Zhou QX Liu ZQ . Assessment of space station on-orbit maintenance task complexity
Reliability Engineering and System Safety 2019 ,193 :106661
[10]
朱安 , 陈力 . 配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
力学学报 , 2019 ,51 (4 ):1156 -1169
[本文引用: 1]
( Zhu An Chen Li . Mechanical simulation and full order sliding mode collision avoidance compliant control based on neural network of dual-arm space robot with compliant mechanism capturing satellite
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (4 ):1156 -1169 (in Chinese))
[本文引用: 1]
[11]
孙泽洲 , 孟林智 . 中国深空探测现状及持续发展趋势
南京航空航天大学学报 , 2015 ,47 (6 ):785 -791
[本文引用: 1]
( Sun Zezhou Meng Linzhi . Current situation and sustainable development trend of deep space exploration in China
Journal of Nanjing University of Aeronautics and Astronautics 2015 ,47 (6 ):785 -791 (in Chinese))
[本文引用: 1]
[12]
Stanley GL Ralph PH . Crew autonomy for deep space exploration: lessons from the antarctic search for meteorites
Acta Astronautica 2014 ,94 (1 ):83 -92
[本文引用: 1]
[13]
彭祺擘 , 李桢 , 李海阳 . 载人登月飞行方案研究
上海航天 , 2012 ,29 (5 ):14 -19
[本文引用: 1]
( Peng Qibo Li Zhen Li Haiyang . Analysis on manned lunar mission flight mode
Aerospace Shanghai 2012 ,29 (5 ):14 -19 (in Chinese))
[本文引用: 1]
[14]
Wang XH Mao LH Yue TX , et al . Manned lunar landing mission scale analysis and flight scheme selection based on mission architecture matrix
Acta Astronautica 2018 ,152 :385 -395
[本文引用: 1]
[15]
胡海岩 . 动力学与控制论力学系统的自由度
力学学报 , 2018 ,50 (5 ):1135 -1144
[本文引用: 1]
( Hu Haiyan . On the degrees of freedom of a mechanical system
Chinese Journal of Theoretical and Applied Mechani 2018 ,50 (5 ):1135 -1144 (in Chinese))
[本文引用: 1]
[16]
曹登庆 , 白坤朝 , 丁虎 等 . 大型柔性航天器动力学与振动控制研究进展
力学学报 , 2019 ,51 (1 ):1 -13
( Cao Dengqing Bai Kunchao Ding Hu , et al . Advances in dynamics and vibration control of large-scale flexible spacecraft
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (1 ):1 -13 (in Chinese))
[17]
孙加亮 , 田强 , 胡海岩 . 多柔体系统动力学建模与优化研究进展
力学学报 , 2019 ,51 (6 ):1565 -1586
[本文引用: 1]
( Sun Jialiang Tian Qiang Hu Haiyan . Advances in dynamic modeling and optimization of flexible multibody systems
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (6 ):1565 -1586 (in Chinese))
[本文引用: 1]
[18]
王闯 , 邓宗全 , 高海波 等 . 国内外月球着陆器研究状况
导弹与航天运载技术 , 2006 (4 ):31 -36
[本文引用: 1]
( Wang Chuang Deng Zongquan Gao Haibo , et al . Development status of lunar landers
Missile and Space Vehicle 2006 (4 ):31 -36 (in Chinese))
[本文引用: 1]
[19]
Cho D Lee D Bang H . Initial guess structure for the optimal lunar landing trajectory
// The Proceedings of 2010 Asia-Pacific International Symposium on Aerospace Technology(Vol. 2) , 2010 : 4
[本文引用: 1]
[20]
王赤 , 张贤国 , 徐欣锋 等 . 中国月球及深空空间环境探测
深空探测学报 , 2019 ,6 (2 ):105 -118
[本文引用: 1]
( Wang Chi Zhang Xianguo Xu Xinfeng , et al . The lunar and deep space enviroment exploration in China
Journal of Deep Space Exploration 2019 ,6 (2 ):105 -118 (in Chinese))
[本文引用: 1]
[21]
朱仁璋 , 郑安波 , 娄汉文 等 . 航天器联接系统发展综述
载人航天 , 2007 , (1 ):13 -23
[本文引用: 1]
( Zhu Renzhang Zheng Anbo Lou Hanwen , et al . A review of the development of spacecraft docking system
Manned Spaceflight 2007 , (1 ):13 -23 (in Chinese))
[本文引用: 1]
[22]
Dick BD Oesch C Rupp TW . Linear actuator for the NASA Docking System
https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20170005413.pdf, [2017 -4 -13 ]
URL
[本文引用: 1]
[23]
Motaghedi P Ghofranian S . Feasibility of the SIMAC for the NASA Docking System
https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20140009916.pdf, [2014 -9 -16 ]
URL
[24]
Motaghedi P Ghofranian S . Feasibility of the soft impact mating attenuation concept for the NASA docking system
Reports on Progress in Physics 2013 ,63 (62 ):1573 -1659
[本文引用: 1]
[25]
叶鹏达 , 尤晶晶 , 仇鑫 等 . 并联机器人运动性能的研究现状及发展趋势
南京航空航天大学学报 , 2020 ,52 (3 ):363 -377
[本文引用: 1]
( Ye Pengda You Jinjin Qiu Xin , et al . Research status and development trend of kinematic performance of parallel robots
Journal of Nanjing University of Aeronautics and Astronautics 2020 ,52 (3 ):363 -377 (in Chinese))
[本文引用: 1]
[26]
Feldman A Caporicci M Gracia O . et al . Advances in intelligent health reasoning and its application to IBDM
// Aerospace Conference, 2007 IEEE , 2007 . 219 -230
[本文引用: 1]
[27]
Hardt M Ayuso A Cocho D , et al . Multibody dynamic considerations in the redesign of the international berthing and docking mechanism (IBDM)
// 1st ESA Workshop on Multibody Dynamics for Space Applications . 2010
[本文引用: 1]
[28]
刘志 , 崔宇新 , 张崇峰 . 国际对接系统标准
载人航天 , 2014 ,20 (2 ):152 -158
[本文引用: 1]
( Liu Zhi Cui Xinyu Zhang Chongfeng . Study on international docking system standard
Manned Spaceflight 2014 ,20 (2 ):152 -158 (in Chinese))
[本文引用: 1]
[29]
Marco B Alessandro C Federico C , et al . Flexible electromagnetic leash docking system experiment from design to microgravity testing
// 66th International Astronautical Congress, Jerusalem, Israel: IAC-15 , 2015 : 1 -12
[本文引用: 1]
[30]
Lorenzo O Alessandro F . Design and test of a semiandrogynous docking mechanism for small satellites
Acta Astronautica 2016 ,122 :219 -230
[本文引用: 1]
[31]
徐敏 . 空间弱撞击对接机构设计与仿真分析. [硕士论文]
南京: 南京航空航天大学 , 2017
[本文引用: 1]
( Xu Ming . Design and simulation analysis of a low impact docking System. [Master Thesis]
Nanjing: Nanjing University of Aeronautics and Astronautics , 2017 (in Chinese))
[本文引用: 1]
[32]
解增辉 . 弱撞击空间对接机构及其主动柔顺控制的研究. [硕士论文]
哈尔滨: 哈尔滨工业大学 , 2017
[本文引用: 1]
( Xie Zenghui . Research on the low impact space docking mechanism and active compliant control. [Master Thesis]
Harbin: Harbin Institute of Technology , 2017 (in Chinese))
[本文引用: 1]
[33]
张玲瑄 , 邵济明 , 邹怀武 等 . 弱撞击式对接机构力传递及运动性能分析与优化
载人航天 , 2015 ,21 (5 ):462 -467
[本文引用: 1]
( Zhang Ling- xuan Shao Jiming Zhou Huaiwu , et al . Analysis and optimization of force transmissibility and kinematic performance of low impact docking mechanism
Manned Spaceflight 2015 ,21 (5 ):462 -467 (in Chinese))
[本文引用: 1]
[34]
姚文莉 , 岳嵘 . 有争议的碰撞恢复系数研究进展
振动与冲击 , 2015 ,34 (19 ):43 -48
URL
[本文引用: 1]
( Yao Wenli Yue Rong . Advance in controversial restitution coefficient study for impact problems
Journal of Vibration and Shock 2015 ,34 (19 ):43 -48 (in Chinese))
URL
[本文引用: 1]
[35]
Galeani S Menini L Tornambè A . Identification of the relationship between the coefficient of restitution and the impact velocity
IFAC Proceedings Volumes 2003 ,36 (2 ):275 -280
[本文引用: 1]
空间对接机构综述
1
2016
... 对接机构技术是指能够在太空通过接触、缓冲、捕获和刚性联接等过程将两个飞行器在结构上形成一个整体的技术[1 ] .其中,在轨道上等待对接的飞行器称为目标飞行器,通过一系列变轨等运动控制与目标飞行器进行对接的飞行器称为主动飞行器.对接技术作为航天领域内的一项重大技术主要有以下几个作用. ...
空间对接机构综述
1
2016
... 对接机构技术是指能够在太空通过接触、缓冲、捕获和刚性联接等过程将两个飞行器在结构上形成一个整体的技术[1 ] .其中,在轨道上等待对接的飞行器称为目标飞行器,通过一系列变轨等运动控制与目标飞行器进行对接的飞行器称为主动飞行器.对接技术作为航天领域内的一项重大技术主要有以下几个作用. ...
在轨组装技术研究现状与发展趋势
1
2017
... (1) 大型航天器的在轨组装.由于对接技术首要的功能就是可以将两个航天器通过刚性联接固连为一个结构整体,这为一些需要在轨组装拼接的大型航天器提供了很大的优势[2 -3 ] . ...
在轨组装技术研究现状与发展趋势
1
2017
... (1) 大型航天器的在轨组装.由于对接技术首要的功能就是可以将两个航天器通过刚性联接固连为一个结构整体,这为一些需要在轨组装拼接的大型航天器提供了很大的优势[2 -3 ] . ...
Building large telescopes in orbit using small satellites
1
2017
... (1) 大型航天器的在轨组装.由于对接技术首要的功能就是可以将两个航天器通过刚性联接固连为一个结构整体,这为一些需要在轨组装拼接的大型航天器提供了很大的优势[2 -3 ] . ...
国际空间站物资管理系统的发展趋势及建议
1
2012
... (2) 航天员转移以及物资补给.大多数对接机构中都具有可供航天员转移以及物资补给用的通道[4 ] ,在两飞行器固连完成后,主动飞行器和目标飞行器的通道完整的联接[5 ] . ...
国际空间站物资管理系统的发展趋势及建议
1
2012
... (2) 航天员转移以及物资补给.大多数对接机构中都具有可供航天员转移以及物资补给用的通道[4 ] ,在两飞行器固连完成后,主动飞行器和目标飞行器的通道完整的联接[5 ] . ...
1
2016
... (2) 航天员转移以及物资补给.大多数对接机构中都具有可供航天员转移以及物资补给用的通道[4 ] ,在两飞行器固连完成后,主动飞行器和目标飞行器的通道完整的联接[5 ] . ...
1
2016
... (2) 航天员转移以及物资补给.大多数对接机构中都具有可供航天员转移以及物资补给用的通道[4 ] ,在两飞行器固连完成后,主动飞行器和目标飞行器的通道完整的联接[5 ] . ...
空间服务与操控中的人工智能技术
1
2018
... (3) 空间在轨服务.空间飞行器的低寿命问题一直是困扰航天工作者的一个重大难题,为了延长航天器在轨的工作寿命[6 -7 ] ,许多空间在轨维修以及更换等维护服务均依靠对接技术的支持得以实现[8 -10 ] . ...
空间服务与操控中的人工智能技术
1
2018
... (3) 空间在轨服务.空间飞行器的低寿命问题一直是困扰航天工作者的一个重大难题,为了延长航天器在轨的工作寿命[6 -7 ] ,许多空间在轨维修以及更换等维护服务均依靠对接技术的支持得以实现[8 -10 ] . ...
Promoting international co-operation in the age of global space governance - A study on on-orbit servicing operations
1
2019
... (3) 空间在轨服务.空间飞行器的低寿命问题一直是困扰航天工作者的一个重大难题,为了延长航天器在轨的工作寿命[6 -7 ] ,许多空间在轨维修以及更换等维护服务均依靠对接技术的支持得以实现[8 -10 ] . ...
面向航天器在轨维修任务的机械臂及其地面实验研究. [硕士论文]
1
2015
... (3) 空间在轨服务.空间飞行器的低寿命问题一直是困扰航天工作者的一个重大难题,为了延长航天器在轨的工作寿命[6 -7 ] ,许多空间在轨维修以及更换等维护服务均依靠对接技术的支持得以实现[8 -10 ] . ...
面向航天器在轨维修任务的机械臂及其地面实验研究. [硕士论文]
1
2015
... (3) 空间在轨服务.空间飞行器的低寿命问题一直是困扰航天工作者的一个重大难题,为了延长航天器在轨的工作寿命[6 -7 ] ,许多空间在轨维修以及更换等维护服务均依靠对接技术的支持得以实现[8 -10 ] . ...
Assessment of space station on-orbit maintenance task complexity
0
2019
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
1
2019
... (3) 空间在轨服务.空间飞行器的低寿命问题一直是困扰航天工作者的一个重大难题,为了延长航天器在轨的工作寿命[6 -7 ] ,许多空间在轨维修以及更换等维护服务均依靠对接技术的支持得以实现[8 -10 ] . ...
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
1
2019
... (3) 空间在轨服务.空间飞行器的低寿命问题一直是困扰航天工作者的一个重大难题,为了延长航天器在轨的工作寿命[6 -7 ] ,许多空间在轨维修以及更换等维护服务均依靠对接技术的支持得以实现[8 -10 ] . ...
中国深空探测现状及持续发展趋势
1
2015
... (4) 深空探测等任务的技术支持.未来的载人登月以及深空探测等任务均需将飞行器送入更远的轨道中去[11 -12 ] ,利用对接技术手段通过多次发射,多次对接的方式来实现. ...
中国深空探测现状及持续发展趋势
1
2015
... (4) 深空探测等任务的技术支持.未来的载人登月以及深空探测等任务均需将飞行器送入更远的轨道中去[11 -12 ] ,利用对接技术手段通过多次发射,多次对接的方式来实现. ...
Crew autonomy for deep space exploration: lessons from the antarctic search for meteorites
1
2014
... (4) 深空探测等任务的技术支持.未来的载人登月以及深空探测等任务均需将飞行器送入更远的轨道中去[11 -12 ] ,利用对接技术手段通过多次发射,多次对接的方式来实现. ...
载人登月飞行方案研究
1
2012
... (1) 现有对接机构捕获性能调整不灵活.由于月球轨道空间站的建设首先需要完成载人登月任务,根据目前载人登月工程综合论证工作,我国的载人登月任务拟采用"近地轨道一次对接+环月轨道两次对接''这种模式[13 -14 ] ,整个任务周期需要完成三次对接任务.其中,每次对接的主动飞行器与目标飞行器的吨位质量均不相同,大致从 18 吨与 3 吨对接至 18 吨与 80 吨对接,而现有对接机构因其刚度和阻尼等性能都需要在地面调试完成,故无法满足在轨多质量范围的对接需求[15 -17 ] . ...
载人登月飞行方案研究
1
2012
... (1) 现有对接机构捕获性能调整不灵活.由于月球轨道空间站的建设首先需要完成载人登月任务,根据目前载人登月工程综合论证工作,我国的载人登月任务拟采用"近地轨道一次对接+环月轨道两次对接''这种模式[13 -14 ] ,整个任务周期需要完成三次对接任务.其中,每次对接的主动飞行器与目标飞行器的吨位质量均不相同,大致从 18 吨与 3 吨对接至 18 吨与 80 吨对接,而现有对接机构因其刚度和阻尼等性能都需要在地面调试完成,故无法满足在轨多质量范围的对接需求[15 -17 ] . ...
Manned lunar landing mission scale analysis and flight scheme selection based on mission architecture matrix
1
2018
... (1) 现有对接机构捕获性能调整不灵活.由于月球轨道空间站的建设首先需要完成载人登月任务,根据目前载人登月工程综合论证工作,我国的载人登月任务拟采用"近地轨道一次对接+环月轨道两次对接''这种模式[13 -14 ] ,整个任务周期需要完成三次对接任务.其中,每次对接的主动飞行器与目标飞行器的吨位质量均不相同,大致从 18 吨与 3 吨对接至 18 吨与 80 吨对接,而现有对接机构因其刚度和阻尼等性能都需要在地面调试完成,故无法满足在轨多质量范围的对接需求[15 -17 ] . ...
动力学与控制论力学系统的自由度
1
2018
... (1) 现有对接机构捕获性能调整不灵活.由于月球轨道空间站的建设首先需要完成载人登月任务,根据目前载人登月工程综合论证工作,我国的载人登月任务拟采用"近地轨道一次对接+环月轨道两次对接''这种模式[13 -14 ] ,整个任务周期需要完成三次对接任务.其中,每次对接的主动飞行器与目标飞行器的吨位质量均不相同,大致从 18 吨与 3 吨对接至 18 吨与 80 吨对接,而现有对接机构因其刚度和阻尼等性能都需要在地面调试完成,故无法满足在轨多质量范围的对接需求[15 -17 ] . ...
动力学与控制论力学系统的自由度
1
2018
... (1) 现有对接机构捕获性能调整不灵活.由于月球轨道空间站的建设首先需要完成载人登月任务,根据目前载人登月工程综合论证工作,我国的载人登月任务拟采用"近地轨道一次对接+环月轨道两次对接''这种模式[13 -14 ] ,整个任务周期需要完成三次对接任务.其中,每次对接的主动飞行器与目标飞行器的吨位质量均不相同,大致从 18 吨与 3 吨对接至 18 吨与 80 吨对接,而现有对接机构因其刚度和阻尼等性能都需要在地面调试完成,故无法满足在轨多质量范围的对接需求[15 -17 ] . ...
大型柔性航天器动力学与振动控制研究进展
0
2019
大型柔性航天器动力学与振动控制研究进展
0
2019
多柔体系统动力学建模与优化研究进展
1
2019
... (1) 现有对接机构捕获性能调整不灵活.由于月球轨道空间站的建设首先需要完成载人登月任务,根据目前载人登月工程综合论证工作,我国的载人登月任务拟采用"近地轨道一次对接+环月轨道两次对接''这种模式[13 -14 ] ,整个任务周期需要完成三次对接任务.其中,每次对接的主动飞行器与目标飞行器的吨位质量均不相同,大致从 18 吨与 3 吨对接至 18 吨与 80 吨对接,而现有对接机构因其刚度和阻尼等性能都需要在地面调试完成,故无法满足在轨多质量范围的对接需求[15 -17 ] . ...
多柔体系统动力学建模与优化研究进展
1
2019
... (1) 现有对接机构捕获性能调整不灵活.由于月球轨道空间站的建设首先需要完成载人登月任务,根据目前载人登月工程综合论证工作,我国的载人登月任务拟采用"近地轨道一次对接+环月轨道两次对接''这种模式[13 -14 ] ,整个任务周期需要完成三次对接任务.其中,每次对接的主动飞行器与目标飞行器的吨位质量均不相同,大致从 18 吨与 3 吨对接至 18 吨与 80 吨对接,而现有对接机构因其刚度和阻尼等性能都需要在地面调试完成,故无法满足在轨多质量范围的对接需求[15 -17 ] . ...
国内外月球着陆器研究状况
1
2006
... (2) 现有对接机构质量较重.探月飞行器由于需要进入更高的飞行轨道,并同时要进行月面着陆和起飞等过程[18 -19 ] ,这便对整个对接系统质量要求高于传统的近地飞行器.我国现有在轨运作的对接机构在质量上约为 540 kg,其中主动件约为 320 kg,目标件约为 220 kg,相对较重,需要针对月球轨道空间站的任务在质量指标方面进行优化设计. ...
国内外月球着陆器研究状况
1
2006
... (2) 现有对接机构质量较重.探月飞行器由于需要进入更高的飞行轨道,并同时要进行月面着陆和起飞等过程[18 -19 ] ,这便对整个对接系统质量要求高于传统的近地飞行器.我国现有在轨运作的对接机构在质量上约为 540 kg,其中主动件约为 320 kg,目标件约为 220 kg,相对较重,需要针对月球轨道空间站的任务在质量指标方面进行优化设计. ...
Initial guess structure for the optimal lunar landing trajectory
1
2010
... (2) 现有对接机构质量较重.探月飞行器由于需要进入更高的飞行轨道,并同时要进行月面着陆和起飞等过程[18 -19 ] ,这便对整个对接系统质量要求高于传统的近地飞行器.我国现有在轨运作的对接机构在质量上约为 540 kg,其中主动件约为 320 kg,目标件约为 220 kg,相对较重,需要针对月球轨道空间站的任务在质量指标方面进行优化设计. ...
中国月球及深空空间环境探测
1
2019
... (4) 现有对接机构适应性无法满足日益苛刻的任务环境.载人探月飞行任务中,对接机构需要满足的空间环境更为苛刻,月球轨道环境与近地轨道环境有着较大的差异,载人登月对接机构能够承受满足近月空间环境的高真空特性,以及更宽的高低温 范围[20 ] . ...
中国月球及深空空间环境探测
1
2019
... (4) 现有对接机构适应性无法满足日益苛刻的任务环境.载人探月飞行任务中,对接机构需要满足的空间环境更为苛刻,月球轨道环境与近地轨道环境有着较大的差异,载人登月对接机构能够承受满足近月空间环境的高真空特性,以及更宽的高低温 范围[20 ] . ...
航天器联接系统发展综述
1
2007
... (5) 现有对接机构捕获方式较为单一.由于现有对接机构的结构特性,在进行捕获前需要有一定的推力,致使对接环上的捕获锁在力的作用下成功捕获到目标飞行器,故不支持利用机械臂对对接机构进行停靠对接和摇操作[21 ] . ...
航天器联接系统发展综述
1
2007
... (5) 现有对接机构捕获方式较为单一.由于现有对接机构的结构特性,在进行捕获前需要有一定的推力,致使对接环上的捕获锁在力的作用下成功捕获到目标飞行器,故不支持利用机械臂对对接机构进行停靠对接和摇操作[21 ] . ...
Linear actuator for the NASA Docking System
1
2017
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
Feasibility of the SIMAC for the NASA Docking System
0
2014
Feasibility of the soft impact mating attenuation concept for the NASA docking system
1
2013
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
并联机器人运动性能的研究现状及发展趋势
1
2020
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
并联机器人运动性能的研究现状及发展趋势
1
2020
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
Advances in intelligent health reasoning and its application to IBDM
1
2007
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
Multibody dynamic considerations in the redesign of the international berthing and docking mechanism (IBDM)
1
2010
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
国际对接系统标准
1
2014
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
国际对接系统标准
1
2014
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
Flexible electromagnetic leash docking system experiment from design to microgravity testing
1
2015
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
Design and test of a semiandrogynous docking mechanism for small satellites
1
2016
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
空间弱撞击对接机构设计与仿真分析. [硕士论文]
1
2017
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
空间弱撞击对接机构设计与仿真分析. [硕士论文]
1
2017
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
弱撞击空间对接机构及其主动柔顺控制的研究. [硕士论文]
1
2017
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
弱撞击空间对接机构及其主动柔顺控制的研究. [硕士论文]
1
2017
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
弱撞击式对接机构力传递及运动性能分析与优化
1
2015
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
弱撞击式对接机构力传递及运动性能分析与优化
1
2015
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
有争议的碰撞恢复系数研究进展
1
2015
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
有争议的碰撞恢复系数研究进展
1
2015
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...
Identification of the relationship between the coefficient of restitution and the impact velocity
1
2003
... 近年来,各国许多航天单位与高校着手研制新型对接机构,美国航空航天局与波音公司联合研制弱撞击对接机构[22 -24 ] (NASA Docking System Block 1, NDSB1),其采用完全主动控制型的直线驱动机构,与对接环相连形成 stewart 并联机构[25 ] ,通过力反馈控制实现对接碰撞过程中的柔顺捕获. 欧空局也研制了国际停靠对接系统[26 -27 ] (international berthing docking mechanism, IBDM),其依托国际对接系统标准[28 ] ,目的用于未来的新飞船与国际空间站进行对接. Marco Buonomo[29 ] 等设计了一种磁吸附型对接机构,进行了吸附能力测试和磁铁球运动状态研究. Lorenzo Olivieri 等[30 ] 设计了一种针对小型卫星对接的对接机构并进行了动力学仿真分析. 国内徐敏[31 ] 提出了一种弱撞击式对接机构,并对其进行了机构设计与仿真分析. 解增辉[32 ] 对弱撞击式对接机构提出了两种主动柔顺控制算法. 张玲瑄等[33 ] 建立了弱撞击式对接机构运动学性能及力传递性能的优化模型. 上述研究大多集中在并联运动平台形式的对接机构,其结构复杂,加工生产难度大且质量较重. 基于现有对接机构的不足,设计了一种抱爪式对接机构. 本工作采用恢复系数方法[34 -35 ] ,推导了对接碰撞的影响因素,并加以仿真分析以期为后续工程研制提供参考数据. ...