引言
空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注.
近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题.
值得一提的是, 上述研究仅考虑空间机器人基座、臂、关节某一类或两类部件柔性的影响, 属于部分柔性空间机器人系统. 基座、臂、关节全柔性空间机器人系统是刚性运动与三重柔性振动高度耦合、高度非线性的时变系统, 其动力学模拟非常繁杂, 控制器设计面临着实现刚性轨迹跟踪, 抑制基座、臂、关节柔性振动四重功能共存的突出难点[25 ] . 这使得全柔性空间机器人动力学模拟与控制问题较难分析, 相关研究鲜有报道. 针对这些问题, 本文提出了柔性基座、两柔性杆、两柔性关节空间机器人的动力学建模方法, 以及系统刚性运动与三重柔性振动的解耦方案.
另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪.
基于上述两方面的分析, 本文提出基座、臂、关节全柔性空间机器人运动振动一体化输入受限重复学习控制器. 利用假设模态法与拉格朗日方程建立模型, 采用奇异摄动法分解模型, 将基座与关节的柔性等效在快变时标下分析, 刚性运动与臂的柔性等效在慢变时标下讨论. 而为了抑制慢变子系统中臂的柔性振动, 运用虚拟力的概念, 设计能实现刚性轨迹跟踪与臂柔性抑振的基于虚拟力的输入受限重复学习控制器. 对于快变子系统, 利用线性二次最优控制方案同时抑制基座与关节双重柔性振动. 最后仿真分析, 校验了算法的可行性.
1 全柔性空间机器人系统动力学模型
1.2 系统动力学简化模型
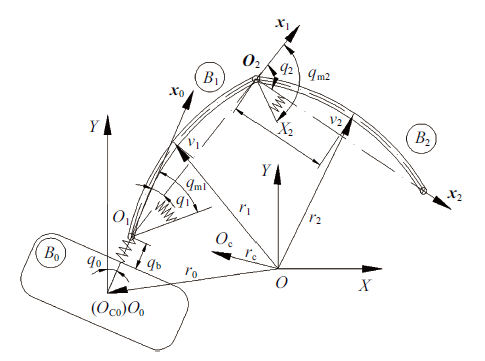
漂浮柔性基、柔性臂、柔性关节空间机器人结构模型如图1 所示, 由漂浮载体$B_0 $, 近载体端的柔性杆$B_1 $, 远载体端柔性杆$B_2 $组成. $O_{C0} $为载体$B_0$的质心, $O_C $为系统的总质心, $O_i $为连接$B_{i-1} $与$B_i$关节铰的几何中心$(i=1,2)$.建立惯性坐标系$OXY$与各分体的连体坐标系$O_i x_i y_i $, 令$x_i$轴的轴向单位向量为$e_i (i=0,1,2)$, 柔性杆$B_i$主轴坐标系$x_i $轴的径向单位向量为$e_i ^\prime \left( {i=1,2} \right)$, $O_0 $与$O_{C0} $重合. 假设系统在$OXY$平面内做平面运动. $r_0 $与$r_C$分别表示载体质心与系统总质心在惯性坐标系下的位置矢量, $r_i $表示柔性杆$B_i$上任意一点相对于$O$的矢径$\left( {i=1,2} \right)$. $q_{\rm b} $为载体与杆$B_1$铰接处载体柔性变形量, $q_0 $为惯性坐标系下基座相对于$Y$轴的转角, $q_i$为杆$B_i $的相对转角, $q_{{\rm m}i} $为关节电机转子转角$\left( {i=1,2} \right)$. $x_i $为柔性杆$B_i $主轴坐标系$x_i $上任意轴向距离, $v_i \left( {x_i ,t}\right)$为$t$时刻柔性杆$B_i $在$x_i $处径向柔性位移$\left( {i=1,2} \right)$. 基座无弹性变形时,$O_{C0} $与$O_1 $的距离为$l_0$, 载体质量为$m_0$, 转动惯量为$J_0$. 杆$B_i $初始长度为$l_i $, 密度为$\rho _i \left( {i=1,2} \right)$. 电机转子质量忽略不计, 转动惯量为$J_{{\rm m}i} $.
图 1
图 1
基座、臂、关节全柔性空间机器人系统
Fig. 1
Space robot system with flexible base, flexible links and flexible joints
本文将柔性基座与柔性关节分别等效为无质量的线性伸缩弹簧和线性扭转弹簧, 假设基座与关节的柔性系数均为定值, 分别用$k_{\rm b} $和$k_{{\rm m}i} $表示. 将两杆均等效为简支梁, 取其抗弯刚度$EI_i$为定值,杆径向变形表达式为$v_i\left( {x_i ,t} \right)=\sum\limits_{j=1}^n {\phi _{ij} \left({x_i } \right)\delta _{ij} \left( t \right)}$, $(0\leqslant x_i \leqslant l_i )$. 其中$\phi _{ij}$, $\delta _{ij} $分别表示杆$B_i$的第$j$阶模态函数与模态坐标,$\phi _{ij} \left( {x_i } \right)=\sin \left[ ({j\pi }/{l_i })x_i \right]$, $i,j=1,2$, $n$为保留模态数, 本文取$n=2$. 经计算, 杆$B_i$的等效刚度系数为$k_{\delta ij} =EI_i \int_0^{l_i } \ddot{\phi}_{ij}^2 (x_i){\rm d}x_i$, $i,j=1,2$.
1.2 系统动力学建模
(1) $ \begin{eqnarray} \label{eq1} \left. {\begin{array}{l} r_0 =\left( {x_0 ,y_0 } \right)^{\rm T} \\ r_1 =r_0 +\left( {l_0 +q_{\rm b} } \right)e_0 +x_1 e_1 +v_1 \left( {x_1 ,t} \right){e}'_1 \\ r_2 =r_0 +\left( {l_0 +q_{\rm b} } \right)e_0 +l_1 e_1 +x_2 e_2 +v_2 \left( {x_2 ,t} \right){e}'_2 \\ \end{array}} \right\} \end{eqnarray}$
其中, $x_0$, $y_0 $为载体质心坐标.
(2) $ \begin{eqnarray} \label{eq2} m=m_0 +\sum\limits_{i=1}^2 {\rho _i l_i } \end{eqnarray}$
(3) $ \begin{eqnarray} \label{eq3} m_0 r_0 +\sum\limits_{i=1}^2 {\int_0^{l_i } {\rho _i r_i } {\rm d}x_i } =mr_C \end{eqnarray}$
(4) $ \begin{eqnarray} \label{eq4} &&r_i =r_C +\varGamma _{i0} \left( {l_0 +q_{\rm b} } \right)e_0 +\varGamma _{i1} e_1 +\left[ \varGamma _{i2} \delta _{11} \left( t \right)+\right.\\&&\left.\qquad\varGamma _{i3} \delta _{12} \left( t \right) \right]{e}'_1 + \varGamma _{i4} e_2 +\left[ \varGamma _{i5} \delta _{21} \left( t \right)+\right.\\&&\left.\qquad\varGamma _{i6} \delta _{22} \left( t \right) \right]{e}'_2 ,\ \ i=0,1,2 \end{eqnarray}$
式中, $\varGamma _{00} \sim \varGamma _{26} $为惯性参数组合函数.
本文全柔性空间机器人系统的动能主要考虑基座、两杆及两电机转子的动能, 设系统初始动量为0, 即$\dot{r}_C =0$, 对式(4)求导, 得系统各分体动能为
(5) $ \begin{eqnarray} \label{eq5} \left. {\begin{array}{l} T_{{\rm r}0} =\dfrac{1}{2}m_0 \dot{{r}}_0^2 +\dfrac{1}{2}J_0 \dot{{q}}_0^2 \\ T_{{\rm r}i} =\dfrac{1}{2}\int_0^{l_i } {\rho _i \dot{{r}}_i^2 {\rm d}x_i } ,\ \ i=1,2\\ T_{{\rm m}i} =\dfrac{1}{2}J_{{\rm m}i} \dot{{q}}_{{\rm m}i}^2 ,\ \ i=1,2\\ \end{array}} \right\} \end{eqnarray}$
其中, $T_{{\rm r}0} $表示基座的动能, $T_{{\rm r}i} $表示杆$B_i $的动能, $T_{{\rm m}i} $表示关节铰$O_i $处电机转子的动能$\left( {i=1,2} \right)$.
(6) $ \begin{eqnarray} \label{eq6} T=T_{{\rm r}0} +\sum\limits_{i=1}^2 {T_{{\rm r}i} } +\sum\limits_{i=1}^2 {T_{{\rm m}i} } \end{eqnarray}$
忽略重力, 全柔性空间机器人系统的势能主要由基座、杆及关节的振动引起, 各部分势能如下
(7) $ \begin{eqnarray} \label{eq7} \left. \begin{array}{l} V_{\rm b} =\dfrac{1}{2}k_{\rm b} q_{\rm b}^2 \\ V_{{\rm a}i} =\dfrac{EI_i }{2}\int_0^{l_i } {\left( {\dfrac{\partial ^2v_i \left( {x_i ,t} \right)}{\partial x_i^2 }} \right)^2{\rm d}x_i } =\\\qquad \dfrac{1}{2}\sum \limits_{j=1}^2 {k_{\delta ij} \delta _{ij}^2 } , \ \ i=1,2\\ V_{{\rm m}i} =\dfrac{1}{2}k_{{\rm m}i} \left( {q_{{\rm m}i} -q_i } \right)^2,\ \ i=1,2\\ \end{array} \right\} \end{eqnarray}$
其中, $V_{\rm b} $表示柔性基座的势能, $V_{{\rm a}i} $表示杆$B_i $的势能, $V_{{\rm m}i}$表示$O_i $处柔性关节的势能$\left( {i=1,2} \right)$.
(8) $ \begin{eqnarray} \label{eq8} V=V_{\rm b} +\sum\limits_{i=1}^2 {V_{{\rm a}i} } +\sum\limits_{i=1}^2 {V_{{\rm m}i} } \end{eqnarray}$
令$L=T-V$为拉格朗日函数, 将式(6)、式(8)代入拉格朗日方程, 得载体姿态受控全柔性空间机器人动力学模型为
(9) $ \begin{eqnarray} \label{eq9} &&\left[ {{\begin{array} {D\left( {q_{\rm boj\delta } } \right)} & 0 \\ 0 & {J_{\rm m} } \\ \end{array} }} \right]\left[ {{\begin{array} {\ddot{{q}}_{\rm boj\delta } } \\ {\ddot{{q}}_{\rm m} } \\ \end{array} }} \right]+\left[ {{\begin{array} {h\left( {q_{\rm boj\delta } ,\dot{{q}}_{\rm boj\delta } } \right)} \\ {0_{2\times 1} } \\ \end{array} }} \right]+\\&&\left[ {{\begin{array} {{\begin{array} {k_{\rm b} q_{\rm b} } \\ 0 \\ {-K_{\rm m} \sigma } \\ {K_\delta \delta } \\ \end{array} }} \\ {K_{\rm m} \sigma } \\ \end{array} }} \right]=\left[ {{\begin{array} {{\begin{array} 0 \\ {\tau _0 } \\ {0_{6\times 1} } \\ \end{array} }} \\ {\tau _{\rm m} } \\ \end{array} }} \right] \end{eqnarray}$
式中, $D\left( {q_{\rm boj\delta } } \right)$为对称正定质量矩阵,$h\left( {q_{\rm boj\delta } ,\dot{{q}}_{\rm boj\delta } } \right)$表示离心力、科氏力列向量,$q_{\rm boj\delta } =\left[ {q_{\rm b} ,q_{\rm oj\delta }^{\rm T} } \right]^{\rm T}$, $q_{\rm oj\delta } =\left[ {q^{\rm T} ,\delta^{\rm T} } \right]^{\rm T}$,$q=\left[ {q_0,q_j^{\rm T} } \right]^{\rm T}$, $q_j =\left[ {q_1,q_2} \right]^{\rm T}$, $\delta =\left[\delta _{11},\delta _{12}, \delta _{21},\delta _{22} \right]^{\rm T}$,$q_{\rm m} =\left[{q_{\rm m1} ,q_{\rm m2} } \right]^{\rm T}$, $J_{\rm m} ={\rm dig}\left({J_{\rm m1} ,J_{\rm m2} } \right)$, $K_\delta ={\rm dig}\left(k_{\delta 11}, k_{\delta 12},k_{\delta 21} ,k_{\delta 22} \right)$, $K_{\rm m}={\rm dig}(k_{\rm m1} ,k_{\rm m2} )$, $\sigma=q_{\rm m} -q_j$.
(10) $ \begin{eqnarray} \label{eq10} &&D\left( {q_{\rm boj\delta } } \right)\ddot{{q}}_{\rm boj\delta } +H\left( {q_{\rm boj\delta } ,\dot{{q}}_{\rm boj\delta } } \right)\dot{{q}}_{\rm boj\delta } +\\&&\left[ {{\begin{array} {k_{\rm b} q_{\rm b} } \\ 0 \\ {-\tau } \\ {K_\delta \delta } \\ \end{array} }} \right]=\left[ {{\begin{array} 0 \\ {\tau _0 } \\ {0_{6\times 1} } \\ \end{array} }} \right] \end{eqnarray}$
(11) $ \begin{eqnarray} J_{\rm m} \ddot{{q}}_{\rm m} +\tau =\tau _{\rm m} \end{eqnarray}$
(12) $ \begin{eqnarray} \tau =K_{\rm m} \sigma \end{eqnarray}$
2 全柔性空间机器人模型分解及其特性
基座、臂、关节全柔性空间机器人运动振动主动控制问题中, 突出难点在于存在三重柔性, 主动抑制其中一类柔性会造成另一类的激振, 控制难度大. 为解决上述问题, 利用奇异摄动法, 将系统柔性等效在不同时标下考虑.
2.1 模型奇异摄动分解
(13) $ \begin{eqnarray} \label{eq13} \tau _{\rm m} =\left( {I+K_{\rm c} } \right)\tau _{\rm n} -K_{\rm c} \tau \end{eqnarray}$
式中, $I\in {\bf R}^{2\times 2}$为单位矩阵, $K_{\rm c} \in {\bf R}^{2\times2}$为对称正定柔性补偿矩阵, $\tau _{\rm n} \in {\bf R}^{2\times 1}$为待设计的控制器,
(14) $ \begin{eqnarray} \label{eq14} \tau _{\rm n} =\tau _{\rm ns} +\tau _{\rm nf} \end{eqnarray}$
式中, $\tau _{\rm ns} \in {\bf R}^{2\times 1}$为慢变子系统控制器, $\tau _{\rm nf} \in {\bf R}^{2\times 1}$为快变子系统控制器.
(15) $ \begin{eqnarray} \label{eq15} \ddot{{\sigma }}=J_{\rm m}^{-1} \left( {I+K_{\rm c} } \right)\left( {\tau _{\rm n} -\tau } \right)-\ddot{{q}}_j \end{eqnarray}$
(16) $ \begin{eqnarray} \label{eq16} &&\left[ {{\begin{array} {D_{\rm bb} } & {D_{\rm ba} } \\ {D_{\rm ab} } & {D_{\rm aa} } \\ \end{array} }} \right]\left[ {{\begin{array} {\ddot{{q}}_{\rm b} } \\ {\ddot{{q}}_{\rm oj\delta } } \\ \end{array} }} \right]+\left[ {{\begin{array} {H_{\rm bb} } & {H_{\rm ba} } \\ {H_{\rm ab} } & {H_{\rm aa} } \\ \end{array} }} \right]\left[ {{\begin{array} {\dot{{q}}_{\rm b} } \\ {\dot{{q}}_{\rm oj\delta } } \\ \end{array} }} \right]+\\&&\left[ \begin{array} {k_{\rm b} q_{\rm b} } \\ 0 \\ {-\tau } \\ {K_\delta \delta } \\ \end{array}\right]=\left[\begin{array} 0 \\ {\tau _0 } \\ {0_{2\times 1} } \\ {0_{4\times 1} } \\ \end{array} \right] \end{eqnarray}$
式中, $D_{\rm bb}$, $H_{\rm bb} \in {\bf R}^{1\times 1}$, $D_{\rm ba}$, $H_{\rm ba} \in {\bf R}^{1\times 7}$, $D_{\rm ab}$, $H_{\rm ab} \in {\bf R}^{7\times 1}$, $D_{\rm aa}$, $H_{\rm aa} \in {\bf R}^{7\times 7}$.
(17) $ \begin{eqnarray} \label{eq17} \left[ {{\begin{array} {N_{11} } & {N_{12} } \\ {N_{21} } & {N_{22} } \\ \end{array} }} \right]=\left[ {{\begin{array} {D_{\rm bb} } & {D_{\rm ba} } \\ {D_{\rm ab} } & {D_{\rm aa} } \\ \end{array} }} \right]^{-1} \end{eqnarray}$
令$q_{\rm oj\delta } $为慢变子变量, $q_{\rm b}$和$\sigma$为快变子变量, $\mu =1/\min \left( {k_{\rm b} ,k_{\rm m1} ,k_{\rm m2} } \right)$为奇异摄动因子. $k_{\rm bf} =\mu k_{\rm b} $, $K_{\rm mf} =\mu K_{\rm m} $, $q_{\rm bf} =q_{\rm b} /\mu $, $\sigma _{\rm f} =\sigma /\mu $. 将式(17)代入式(16)进行慢、快变子系统刚柔性解耦, 再将$k_{\rm bf}$, $q_{\rm bf}$, $K_{\rm mf}$, $\sigma _{\rm f}$表达式与$\mu =0$, $\tau _{\rm nf}=0$分别代入式(15)与解耦结果式得
(18) $ \begin{eqnarray} \label{eq18} &&K_{\rm mf} \bar{{\sigma }}_{\rm f} =\tau _{\rm ns} -\left( {I+K_{\rm c} } \right)^{-1}J_{\rm m} \ddot{{q}}_j \end{eqnarray}$
(19) $ \begin{eqnarray} && k_{\rm bf} \bar{{q}}_{\rm bf} =-\bar{{H}}_{\rm ba} \dot{{q}}_{\rm oj\delta } -\bar{{N}}_{11}^{-1} \bar{{N}}_{12} \bar{{H}}_{\rm aa} \dot{{q}}_{\rm oj\delta } +\\&&\bar{{N}}_{11}^{-1} \bar{{N}}_{12} \left[\begin{array} {\tau _0 } \\ {K_{\rm mf} \bar{{\sigma }}_{\rm f} } \\ {-K_\delta \delta } \\ \end{array}\right] \end{eqnarray}$
(20) $ \begin{eqnarray} && \ddot{{q}}_{\rm oj\delta } =-\bar{{N}}_{21} \bar{{H}}_{\rm ba} \dot{{q}}_{\rm oj\delta } -\bar{{N}}_{21} k_{\rm bf} \bar{{q}}_{\rm bf}-\\&&\bar{{N}}_{22} \bar{{H}}_{\rm aa} \dot{{q}}_{\rm oj\delta } +\bar{{N}}_{22} \left[\begin{array} {\tau _0 } \\ {K_{\rm mf} \bar{{\sigma }}_{\rm f} } \\ {-K_\delta \delta } \\ \end{array}\right] \end{eqnarray}$
其中, $\bar{{\Re}}$表示变量$\Re $中$\mu =0$时的表达式.
(21) $ \begin{eqnarray} \label{eq21} \left. \begin{array}{l} \bar{{D}}_{\rm aa} =\left( {\bar{{N}}_{22} -\bar{{N}}_{21} \bar{{N}}_{11}^{-1} \bar{{N}}_{12} } \right)^{-1} \\ \left[\begin{array} 0 \\ {\left( {I+K_{\rm c} } \right)^{-1}J_{\rm m} \ddot{{q}}_j } \\ {0_{4\times 1} } \\ \end{array} \right]=\left[\begin{array} 0 & {0_{1\times 2} } & {0_{1\times 4} } \\ {0_{2\times 1} } & {\left( {I+K_{\rm c} } \right)^{-1}J_{\rm m} } & {0_{2\times 4} } \\ {0_{4\times 1} } & {0_{4\times 2} } & {0_{4\times 4} }\\ \end{array} \right]\ddot{{q}}_{\rm oj\delta } \\ \end{array} \right\}\\&& \end{eqnarray}$
将式(18)、式(19)代入式(20), 再将式(21)代入结果式, 得慢变子系统动力学方程
(22) $ R(q_{oj\delta})\ddot{{q}}_{\rm oj\delta } +S( {q_{\rm oj\delta } ,\dot{{q}}_{\rm oj\delta } } )\dot{{q}}_{\rm oj\delta } + \left[ \begin{array}{ccc} {0_{3\times 1} } \\ {K_\delta \delta } \end{array}\right]=\left[\begin{array}{ccc} {\tau _{\rm oj} } \\ {0_{4\times 1} }\end{array} \right] $
\begin{eqnarray*} &&R\left( {q_{\rm oj\delta } } \right)=\bar{{D}}_{\rm aa} +\left[ \begin{array} 0 & {0_{1\times 2} } & {0_{1\times 4} } \\ {0_{2\times 1} } & {\left( {I+K_{\rm c} } \right)^{-1}J_{\rm m} } & {0_{2\times 4} } \\ {0_{4\times 1} } & {0_{4\times 2} } & {0_{4\times 4} }\\ \end{array}\right]\\ &&S\left( {q_{\rm oj\delta } ,\dot{{q}}_{\rm oj\delta } } \right)=\bar{{H}}_{\rm aa} , \quad \tau _{\rm oj} =\left[ {\tau _0 ,\tau _{\rm ns}^{\rm T} } \right]^{\rm T} \end{eqnarray*}
为便于基于虚拟力概念的控制器设计, 式(22)重新写为
(23) $ \left[{\begin{array}{ccc} {R_{11} } & {R_{12} } \\ {R_{21} } & {R_{22} } \\ \end{array}} \right] \left[ {{\begin{array}{ccc} {\ddot{{q}}} \\ {\ddot{{\delta }}} \\ \end{array} }} \right]+\left[ {{\begin{array}{ccc} {S_{11} } & {S_{12} } \\ {S_{21} } & {S_{22} } \\ \end{array} }} \right]\left[ {{\begin{array}{ccc} {\dot{{q}}} \\ {\dot{{\delta }}} \\ \end{array} }} \right]+\left[ {{\begin{array}{ccc} {0_{3\times 1} } \\ {{K}_\delta \delta } \\ \end{array} }} \right]=\left[ {{\begin{array}{ccc} {\tau _{\rm oj} } \\ {0_{4\times 1} } \\ \end{array} }} \right] $
其中, $R_{11}$, $S_{11} \in {\bf R}^{3\times 3}$, $R_{12}$, $S_{12} \in R^{3\times4}$, $R_{21}$, $S_{21} \in {\bf R}^{4\times 3}$, $R_{22}$, $S_{22} \in {\bf R}^{4\times 4}$.
(24) $ \begin{eqnarray} \label{eq24} &&R_{11} \ddot{{q}}+R_{12} \ddot{{\delta }}+S_{11} \dot{{q}}+S_{12} \dot{{\delta }}=\tau _{\rm oj} \end{eqnarray}$
(25) $ \begin{eqnarray} \label{eq25} R_{21} \ddot{{q}}+R_{22} \ddot{{\delta }}+S_{21} \dot{{q}}+S_{22} \dot{{\delta }}+{K}_\delta \delta =0_{4\times 1} \end{eqnarray}$
(26) $ \begin{eqnarray} \label{eq26} M\left( {\delta ,q} \right)\ddot{{q}}+C\left( {\delta ,\dot{{\delta}},q,\dot{{q}}} \right)\dot{{q}}+\kappa \left( {\delta ,\dot{{\delta }},q,\dot{{q}}} \right)=\tau _{\rm oj} \end{eqnarray}$
式中, $M\left( {\delta ,q} \right)=R_{11} -R_{12} R_{22}^{-1} R_{21}$, $C\left( {\delta ,\dot{{\delta }},q,\dot{{q}}} \right)=S_{11} -R_{12} R_{22}^{-1} S_{21}$, $\kappa \left( {\delta ,\dot{{\delta}},q,\dot{{q}}} \right)=\left( {S_{12} -R_{12} R_{22}^{-1} S_{22} }\right)\dot{{\delta }}-R_{12} R_{22}^{-1} {K}_\delta \delta$.
取快变时标$t_{\rm f} =t/\sqrt \mu $, 快变子系统状态变量$q_{\rm f} =\left[ {q_{f1} ,q_{f2} ,q_{f3}^{\rm T} ,q_{f4}^{\rm T} } \right]^{\rm T}$, 其中$q_{f1} =q_{\rm bf} -\bar{{q}}_{\rm bf} $, $q_{f2} = \sqrt \mu \dot{{q}}_{\rm bf} $, $q_{f3} =\sigma_{\rm f} -\bar{{\sigma }}_{\rm f} $, $q_{f4} =\sqrt \mu \dot{{\sigma }}_{\rm f} $. 将$q_{f1} ,q_{f3} $与式(19)代入式(16) 慢、快变子系统解耦结果式得
(27) $ \begin{eqnarray} \label{eq27} \mu \ddot{{q}}_{\rm bf} =-\bar{{N}}_{11} k_{\rm bf} q_{f1} +N_{12}^\ast K_{\rm mf} q_{f3} \end{eqnarray}$
其中, $N_{12}^\ast $是$\bar{{N}}_{12} $第二、三项元素组成的行向量.
将$q_{f3} $与式(14)、式(18)代入式(15)得
(28) $ \mu \ddot{{\sigma }}_{\rm f} =-J_{\rm m}^{-1} \left( {I+K_{\rm c} } \right)K_{\rm mf} q_{f3} +J_{\rm m}^{-1} \left( {I+K_{\rm c} } \right)\tau _{\rm nf} $
$q_{\rm f} $在快变时标下求微分, 并代入式(27)、式(28)得快变子系统动力学方程
(29) $ \begin{eqnarray} \label{eq29} {\rm d}q_{\rm f} /{\rm d}t_{\rm f} =A_{\rm f} q_{\rm f} +B_{\rm f} \tau _{\rm nf} \end{eqnarray}$
\begin{eqnarray*} &&B_{\rm f} =\left[ {0_{1\times 2}^{\rm T} ,\ \ 0_{1\times 2}^{\rm T} ,\ \ 0_{2\times 2} ,\left( {J_{\rm m}^{-1} \left( {I+K_{\rm c} } \right)} \right)^{\rm T}} \right]^{\rm T}\\ &&A_{\rm f} =\left[ {{\begin{array} 0 & 1 & {0_{1\times 2} } & {0_{1\times 2} } \\ {-\bar{{N}}_{11} k_{\rm bf} } & 0 & {N_{12}^\ast K_{\rm mf} } & {0_{1\times 2} } \\ {0_{2\times 1} } & {0_{2\times 1} } & {0_{2\times 2} }& {I_{2\times 2} } \\ {0_{2\times 1} } & {0_{2\times 1} } & {-J_{\rm m}^{-1} \left( {I+K_{\rm c} } \right)K_{\rm mf} } & {0_{2\times 2} } \\ \end{array} }} \right] \end{eqnarray*}
2.2 动力学模型特性
注意到式(26)是全驱动的动力学模型, 形式与刚性机械臂相似, 具有如下结构特性[34 -35 ] :
(30) $ \begin{eqnarray} \label{eq30} \lambda _{\rm m} (M )\left\| y \right\|^2\leqslant y^{\rm T}M(x)y\leqslant \lambda _{\rm M} ( M )\left\| y \right\|^2, \forall y\in {\bf R}^{3\times 1} \end{eqnarray}$
其中, $\lambda _{\rm m} \left( \cdot \right)$和$\lambda _{\rm M} \left( \cdot \right)$分别表示矩阵的最小和最大特征值, $\left\| \cdot \right\|$表示二范数.
特性2 科氏力、离心力矩阵$C\left( {x,y} \right)\in {\bf R}^{3\times 3}$满足
(31) $ C\left( {x,y} \right)z=C\left( {x,z} \right)y,\ \ \forall y,z\in {\bf R}^{3\times 1} $
(32) $ C_{\rm m} \left\| y \right\|\leqslant \left\| {C\left( {x,y} \right)} \right\|\leqslant C_{\rm M} \left\| y \right\|,\ \ \forall y\in {\bf R}^{3\times 1} $
式中, $C_{\rm m}$, $C_{\rm M} $是已知正常数.
特性3 $\dot{{M}}(x)-2C\left( {x,\dot{{x}}} \right)$为交错矩阵, 满足
(33) $ \begin{eqnarray} \label{eq33} y^{\rm T}\left[ {\dot{{M}}(x)-2C\left( {x,\dot{{x}}} \right)} \right]y={\bf0},\ \ \forall y\in {\bf R}^{3\times 1} \end{eqnarray}$
特性4 存在正常数$k_{\rm M}$, $k_{\rm C1}$, $k_{\rm C2} $对于任意矢量$x $, $y$, $z$, $x_1$, $y_1$, $x_2$, $y_2\in {\bf R}^{3\times 1}$满足关系式
(34) $ \begin{eqnarray} \label{eq34} &&\left\| {M(x)z-M\left( y \right)z} \right\|\leqslant k_{\rm M} \left\| {\mbox{tanh}\left( {x-y} \right)} \right\|\left\| z \right\| \end{eqnarray}$
(35) $ \begin{eqnarray} &&\left\| {C\left( {x_1 ,y_1 } \right)z-C\left( {x_2 ,y_2 } \right)z} \right\|\leqslant k_{\rm C1} \left\| {\mbox{tanh}\left( {y_1 -y_2 } \right)} \right\|\left\| z \right\|+\\&& k_{\rm C2} \left\| {y_1 } \right\|\left\| {\mbox{tanh}\left( {x_1 -x_2 } \right)} \right\|\left\| z \right\| \end{eqnarray}$
其中, $k_{\rm M}$, $k_{\rm C1}$, $k_{\rm C2}$的取值参考文献[34 ] , tanh$\left( \cdot\right)$如式(43)所定义.
特性5 $\kappa \left( {x,y} \right)$满足关系式
(36) $ \left\| {\kappa \left( {x_1 ,y_1 } \right)-\kappa \left( {x_2 ,y_2 } \right)} \right\|\leqslant k_{\rm C3} \left\| {y_1 -y_2 } \right\|+ \\ k_{\rm C4} \left\| {y_1 } \right\|\left\| {\mbox{tanh}\left( {x_1 -x_2 } \right)} \right\|, \\ \forall x_1 ,x_2 ,y_1 ,y_2 \in {\bf R}^{3\times 1} $
其中, $k_{\rm C3}$, $k_{\rm C4} $的取值参考Kelly等[34 ] .
3 控制器设计
3.1 慢变子系统输入受限重复学习控制器设计
连续可微周期期望轨迹$q_{\rm d} \left( t \right)$满足条件
(37) $ \begin{eqnarray} \label{eq37} &&q_{\rm d} \left( t \right),\ \ \dot{{q}}_{\rm d} \left( t \right),\ \ \ddot{{q}}_{\rm d} \left( t \right)\in l_\infty \end{eqnarray}$
(38) $ \begin{eqnarray} &&\left.\begin{array}{l}q_{\rm d} \left( t \right)=q_{\rm d} \left( {t-T} \right)\\\dot{{q}}_{\rm d} \left( t \right)=\dot{{q}}_{\rm d} \left( {t-T} \right)\\\ddot{{q}}_{\rm d} \left( t \right)=\ddot{{q}}_{\rm d} \left( {t-T} \right)\end{array}\right\} \end{eqnarray}$
(39) $ \begin{eqnarray} \left\| {\dot{{q}}_{\rm d} } \right\|\leqslant V_{\rm M},\ \ \left\| {\ddot{{q}}_{\rm d} } \right\|\leqslant A_{\rm M} \end{eqnarray}$
其中, $T$为已知周期, $V_{\rm M}$, $A_{\rm M} $为期望速度与加速度范数的上界.
结合式(26), 机器人期望输入力矩$\tau _{\rm d} $为
(40) $ \begin{eqnarray} \label{eq40} &&\tau _{\rm d} =M\left( {\delta ,q_{\rm d} } \right)\ddot{{q}}_{\rm d} +C\left( {\delta ,\dot{{\delta }},q_{\rm d} ,\dot{{q}}_{\rm d} } \right)\dot{{q}}_{\rm d} +\\&&\kappa \left( {\delta ,\dot{{\delta }},q_{\rm d} ,\dot{{q}}_{\rm d} } \right) \end{eqnarray}$
其中, $\tau _{\rm d} \left( t \right)$是以$T$为周期的周期函数, 用傅里叶级数展开为
(41) $ \begin{eqnarray} \label{eq41} \tau _{\rm d} \left( t \right)=\bar{{a}}_0 +\sum\limits_{k=1}^\infty {\left[{\bar{{a}}_k \cos \left( {k\omega t} \right)+\bar{{b}}_k \sin \left({k\omega t} \right)} \right]} \end{eqnarray}$
式中, $\omega =2\pi /T$为角频率$\bar{{a}}_0$, $\bar{{a}}_k$, $\bar{{b}}_k$为未知常矢量.
结合式(30)、式(32)、式(36)、式(37)、式(39)与式(40)得, $\tau _{\rm d} \left( t \right)$是有界函数, 满足
(42) $ \begin{eqnarray} \label{eq42} \left| {\tau _{{\rm d},i} \left( t \right)} \right|\leqslant \gamma _i,\ \ i=1,2,3 \end{eqnarray}$
其中, $\tau _{{\rm d},i} \left( t \right)$表示$\tau _{\rm d} \left( t\right)$的第$i$个元素, $\gamma =\left[ {\gamma _1 ,\gamma _2 ,\gamma _3 }\right]^{\rm T}$是已知的正常数矢量.
定义矢量sgn$\left( \cdot \right)\in {\bf R}^{3\times 1}$, $\mbox{tanh}\left( \cdot \right)\in {\bf R}^{3\times 1}$, sat$\left( \cdot \right)\in {\bf R}^{3\times 1}$为
(43) $ \begin{eqnarray} \label{eq43} \left. {\begin{array}{l} {\rm sgn}\left( \eta \right)=\left[ {{\rm sgn} {\eta _1 } , {\rm sgn}{\eta _2 }, {\rm sgn}{\eta _3 }} \right]^{\rm T} \\ {\rm tanh}\left( \eta \right)=\left[ {\tanh {\eta _1 },\tanh {\eta _2 },\tanh {\eta _3 }} \right]^{\rm T} \\ {\rm sat}\left( \eta \right)=\left[ {{\rm sat}{\eta _1 } ,{\rm sat} {\eta _2 },{\rm sat}{\eta _3 } } \right]^{\rm T}\\ \end{array}} \right\} \end{eqnarray}$
其中$\eta \in {\bf R}^{3\times 1}$ , 令输出误差$e,\dot{{e}}\in {\bf R}^{3\times 1}$为
(44) $ \begin{eqnarray} \label{eq44} e=q_{\rm d} -q, \ \ \dot{{e}}=\dot{{q}}_{\rm d} -\dot{{q}} \end{eqnarray}$
引入滑模变量$s\in {\bf R}^{3\times 1}$为
(45) $ \begin{eqnarray} \label{eq45} s=\dot{{e}}+\mbox{tanh}e \end{eqnarray}$
(46) $ \begin{eqnarray} \label{eq46} &&\tau _{\rm oj} =K_0 \mbox{tanh}s+K_1 \mbox{tanh}e+K_2{\rm sgn}\left( s \right)+\\&&{\rm sat}\left( {Q_0 z_0 +\sum\limits_{k=1}^N {Q_k \dot{{z}}_k } } \right) \end{eqnarray}$
(47) $ \begin{eqnarray} \left. {\begin{array}{l} \ddot{{z}}_k +k^2\omega ^2z_k =Q_k s,\ \ k=1,2,\cdots ,N \\ \dot{{z}}_0 =Q_0 s \\ \end{array}} \right\} \end{eqnarray}$
其中, $K_0$, $K_1$, $K_2$, $Q_0$ 和$Q_k$ $\left( {k=1,2, \cdots ,N} \right)$是$3\times 3$的常正定对角矩阵, $N$为谐振子数量. $Q_0 z_0 +\sum\limits_{k=1}^N {Q_k \dot{{z}}_k } $为重复学习控制器(repetitive learning controller, RC), sat$\left( \cdot \right)$为重复项饱和函数, 其元素为
(48) $ \begin{eqnarray} \label{eq48} {\rm sat}\left( {\eta _i } \right)=\left\{ {\begin{array}{ll} \eta _i ,&\left| {\eta _i } \right|\leqslant\gamma _i \\ \gamma _i {\rm sgn}\eta _i , & \left| {\eta _i } \right|>\gamma _i\\ \end{array}} \right.,\ \forall \eta _i \in {\bf R},\ \ i=1,2,3 \end{eqnarray}$
考虑双曲正切函数, 符号函数, 饱和函数的性质, 由式(46)得输入力矩满足关系式
(49) $ \begin{eqnarray} \label{eq49} \left| \tau _{{\rm oj},i} \right|\leqslant k_{0,i} +k_{1,i} +k_{2,i} +\gamma _i ,\ \ i=1,2,3 \end{eqnarray}$
其中, $\tau _{{\rm oj},i} $表示$\tau _{\rm oj} $的第$i$个元素, $k_{0,i}$, $k_{1,i}$, $k_{2,i} $分别为$K_0$, $K_1$, $K_2 $对角线上第$i$个元素. 假设$\tau _{{\rm oj},i,\max }$为空间机器人基座或关节最大控制力矩, 合理选择控制器参数, 可使系统满足输入受限条件, 即$k_{0,i} +k_{1,i} +k_{2,i} +\gamma _i \leqslant \tau _{{\rm oj},i,\max } $.
现求闭环系统方程, 式(45)对时间求导, 结果式两边同乘$M\left( {\delta ,q}\right)$, 并代入式(26)得
(50) $ \begin{eqnarray} \label{eq50} M\left( {\delta ,q} \right)\dot{{s}}=X+\tilde{{Y}}+\tau _{\rm d} -C\left( {\delta ,\dot{{\delta }},q,\dot{{q}}} \right)s-\tau _{\rm oj} \end{eqnarray}$
其中, $X=M\left( {\delta ,q} \right){\rm sech}\left( e \right)^2\dot{{e}}+C\left({\delta ,\dot{{\delta }},q,\dot{{q}}} \right)\dot{{q}}-C\left( \delta ,\dot{{\delta }},q,\dot{{q}}_{\rm d} \right)\dot{{q}}_{\rm d} +C\left( {\delta ,\dot{{\delta }},q,\dot{{q}}} \right)s$, $\tilde{{Y}}=M\left( {\delta ,q} \right)\ddot{{q}}_{\rm d} +C\left( \delta ,\dot{{\delta }}, q,\dot{{q}}_{\rm d} \right)\dot{{q}}_{\rm d} +\kappa \left( {\delta ,\dot{{\delta }},q,\dot{{q}}} \right)-\tau _{\rm d}$, sech$^2\eta ={\rm dig}\left( {\rm sech}^2\eta _1, {\rm sech}^2\eta _2, {\rm sech}^2\eta _3\right)$.
将式(31)、式(44)、式(45)代入$X$表达式得
(51) $ \begin{eqnarray} \label{eq51} &&X=M\left( {\delta ,q} \right){\rm sech}\left( e \right)^2\left( {s-\mbox{tanh}e} \right)-\\&&C\left( {\delta ,\dot{{\delta }},q,\dot{{q}}_{\rm d} }\right)\left(s-\mbox{tanh}e \right)+\\&&C\left( {\delta ,\dot{{\delta }},q,\mbox{tanh}e} \right)\left( {\dot{{q}}_{\rm d} +\mbox{tanh}e-s} \right) \end{eqnarray}$
(52) $ \begin{eqnarray} \label{eq52} &&\left\| X \right\|\leqslant \left[ {\lambda _{\rm M} ( M )+2C_{\rm M} V_{\rm M} +C_{\rm M} } \right]\left\| {\mbox{tanh}e} \right\|+ \left[ \lambda _{\rm M} ( M )+\right.\\&&\left.\qquad C_{\rm M} V_{\rm M} +C_{\rm M} \right]\left\| s\right\|\leqslant \lambda _1 \left\| h \right\| \end{eqnarray}$
对$\tilde{{Y}}$求范数, 并利用特性4得
(53) $ \begin{eqnarray} \label{eq53} &&\left\| {\tilde{{Y}}} \right\|\leqslant \left( {k_{\rm M} A_{\rm M} +k_{\rm C2} V_{\rm M}^2 +k_{\rm C4} V_{\rm M} } \right)\left\| {\rm tanh}e \right\|+\\&& k_{\rm C3} \left\| s \right\|\leqslant \lambda _2 \left\| h \right\| \end{eqnarray}$
其中, $h=\left[ {\mbox{tanh}^{\rm T}e,s^{\rm T}} \right]^{\rm T}$.
定理1 对于刚性子系统式(26), 在满足如式$k_{0,i} +k_{1,i} +k_{2,i} +\gamma _i \leqslant \tau _{{\rm oj},i,\max } $所示的输入受限条件下, 若控制器增益满足如下条件
(54) $ \begin{eqnarray} \label{eq54} \left. {\begin{array}{l} \lambda _{\rm m} \left( {K_0 } \right)\geqslant \dfrac{1}{\alpha _0 }\left( {\lambda _1 +\lambda _2 } \right) \\ \lambda _{\rm m} \left( {K_1 } \right)\geqslant \lambda _1 +\lambda _2 \\ \lambda _{\rm m} \left( {K_2 } \right)\geqslant \max \left\{ {d_1 ,d_2 } \right\} \\ \end{array}} \right\} \end{eqnarray}$
则输入受限重复学习控制器可确保$\mathop {\lim }\limits_{t\to \infty } e=0$, $\mathop {\lim }\limits_{t\to \infty } \dot{{e}}=0$, 其中$d_1$, $d_2$在证明中给出.
证明: (1) 当$\left|\left(Q_0Z_0+\displaystyle\sum\limits_{k=1}^NQ_k\dot{z}_k\right)_i\right|\leqslant \gamma_i$时
引入变量$\tilde{{z}}_k =z_k -z_k^\ast$, $k=0,1,2,\cdots N$, 定义
(55) $ \begin{eqnarray} \label{eq55} \left. \begin{array}{l} z_0^\ast =Q_0^{-1} \bar{{a}}_0 \\ z_k^\ast =\left( {k\omega } \right)^{-1}Q_k^{-1} \left[ {\bar{{a}}_k \sin \left( {k\omega t} \right)-\bar{{b}}_k \cos \left( {k\omega t} \right)} \right] \\ \end{array} \right\} \end{eqnarray}$
(56) $ \begin{eqnarray} \label{eq56} \ddot{z}_k^*=-(k\omega)^2{z}_k^* \end{eqnarray}$
将式(41)、式(46)、式(55)代入式(50), 得闭环系统误差方程, 为
(57) $ \begin{eqnarray} \label{eq57} &&M\left( {\delta ,q} \right)\dot{{s}}=-C\left( {\delta ,\dot{{\delta }},q,\dot{{q}}} \right)s-Q_0 \tilde{{z}}_0 -\sum\limits_{k=1}^N {Q_k \dot{{\tilde{{z}}}}_k } -\\&&K_2 {\rm sgn}\left( s \right)+X+\tilde{{Y}}-K_0 {\rm tanh}s-\\&&K_1 \mbox{tanh}e+\bar{{f}} \end{eqnarray}$
(58) $ \begin{eqnarray} \left. \begin{array}{l} \ddot{{\tilde{{z}}}}_k +k^2\omega ^2\tilde{{z}}_k =Q_k s,\ \ k=1,2,\cdots N \\ \dot{{\tilde{{z}}}}_0 =Q_0 s \\ \end{array} \right\} \end{eqnarray}$
(59) $ \begin{eqnarray} \bar{{f}}=\sum\limits_{k=N+1}^\infty {\left[ {\bar{{a}}_k \cos \left( {k\omega t} \right)+\bar{{b}}_k \sin \left( {k\omega t} \right)} \right]} \end{eqnarray}$
由式(41)、式(42)知, $\left\| {\bar{{f}}} \right\|\leqslant d_1$, $d_1$为已知正常数. 构造李雅普诺夫函数$V_1 $为
(60) $ \begin{eqnarray} \label{eq60} &&V_1 =\frac{1}{2}s^{\rm T}M\left( {\delta ,q} \right)s+\sum\limits_{i=1}^3 {k_{1,i} \ln \left( {\cosh e_i } \right)} +\frac{1}{2}\sum\limits_{k=1}^N {\dot{{\tilde{{z}}}}_k^{\rm T} \dot{{\tilde{{z}}}}_k } +\\&&\frac{1}{2}\sum\limits_{k=1}^N {k^2\omega ^2\tilde{{z}}_k^{\rm T} \tilde{{z}}_k } +\frac{1}{2}\tilde{{z}}_0^{\rm T} \tilde{{z}}_0 \end{eqnarray}$
合理选择$\alpha _0 $, 使满足以下关系式
(61) $ \begin{eqnarray} \label{eq61} s^{\rm T}K_0 {\rm tanh}s\geqslant \lambda _{\rm m} \left( {K_0 } \right)\alpha _0s^{\rm T}s \end{eqnarray}$
式(60)沿闭环轨迹式(57) ~式(59)求微分, 并代入特性3与式(45)得
(62) $ \begin{eqnarray} \label{eq62} &&\dot{{V}}_1 =s^{\rm T}X+s^{\rm T}\tilde{{Y}}-s^{\rm T}K_0{\rm tanh}s-s^{\rm T}K_2 {\rm sgn}s+ s^{\rm T}\bar{{f}}-\\&&{\rm tanh}^{\rm T}eK_1 \mbox{tanh}e \end{eqnarray}$
将式(52)、式(53)、式(61)代入式(62), 并在结果式中代入式$\left\| h \right\|^2=\left\| {\mbox{tanh}e} \right\|^2+\left\| s \right\|^2$, 得
(63) $ \begin{eqnarray} \label{eq63} &&\dot{{V}}_1 \leqslant -\left[ {\alpha _0 \lambda _{\rm m} \left( {K_0 } \right)-\left( {\lambda _1 +\lambda _2 } \right)} \right]\left\| s \right\|^2-\\&&\left[ {\lambda _{\rm m} \left( {K_2 } \right)-d_1 } \right]\left\| s \right\| -\left[ \lambda _{\rm m} \left( {K_1 } \right)-\right.\\&&\left.\qquad\left( {\lambda _1 +\lambda _2 } \right) \right]\left\| {\mbox{tanh}e} \right\|^2 \end{eqnarray}$
由式(54)可知$\dot{{V}}_1 \leqslant 0$. 定义$\varOmega _1 $为$\dot{{V}}_1 \leqslant 0$确定的点的集合, $R_1 $为$\varOmega _1 $内$\dot{{V}}_1 =0$确定的所有点的子集, 而$\dot{{V}}_1 =0$的解为$\dot{{e}}=0$, tanh$e=0$,所以上述等式确定的集合$M_1 $是$R_1 $内的最大不变集. 根据拉塞尔不变性原理, 对于$\varOmega _1 $内的任意初值$q\left( 0 \right),\dot{{q}}\left( 0 \right)$, 当$t\to \infty $都趋向于$M_1 $内, 即$\mathop {\lim }\limits_{t\to \infty }\dot{{e}}=0$, $\mathop {\lim }\limits_{t\to \infty } \mbox{tanh}e=0$, 再结合双曲正切函数的性质, 得$\mathop {\lim }\limits_{t\to \infty } e=0$, $\mathop {\lim }\limits_{t\to \infty } \dot{{e}}=0$.
(2) 当$\left| {\left( {Q_0 z_0 +\displaystyle\sum\limits_{k=1}^N {Q_k \dot{{z}}_k } } \right)_i } \right|>\gamma _i $时
(64) $ \begin{eqnarray} \label{eq64} && M\left( {\delta ,q} \right)\dot{{s}}=-C\left( {\delta ,\dot{{\delta }},q,\dot{{q}}} \right)s+\tau _{\rm d} +X+\tilde{{Y}}-\\&&\varGamma \cdot {\rm sgn}\left( Q_0 z_0 + \sum\limits_{k=1}^N {Q_k } {\dot{{z}}_k } \right)-K_0 {\rm tanh}s-\\&&K_1 {\rm tanh}e-K_2 {\rm sgn}s \end{eqnarray}$
其中, $\varGamma ={\rm diag}\left( {\gamma _1 ,\gamma _2 ,\gamma _3 } \right)$.
(65) $ \begin{eqnarray} \label{eq65} V_2 =\frac{1}{2}s^{\rm T}M\left( {\delta ,q} \right)s+\sum\limits_{i=1}^n {k_{1,i} \ln \left( {\cosh e_i } \right)} \end{eqnarray}$
(66) $ \begin{eqnarray} \label{eq66} &&\dot{{V}}_2 =s^{\rm T}\Bigg[ {\tau _{\rm d} } -\varGamma \cdot {\rm sgn}\left( Q_0 z_0 +\sum\limits_{k=1}^N {Q_k \dot{{z}}_k } \right)-K_0 {\rm tanh}s-\\&&K_2 {\rm sgn}s+X+\tilde{{Y}} \Bigg]-{\rm tanh}^{\rm T} eK_1 {\rm tanh}e \end{eqnarray}$
由于$\tau _{\rm d} \in l_\infty $, 结合范数性质得
(67) $ \begin{eqnarray} \label{eq67} \left\| {\tau _{\rm d} -\varGamma \cdot {\rm sgn}\left( {Q_0 z_0 +\sum\limits_{k=1}^N {Q_k \dot{{z}}_k } } \right)} \right\|\leqslant d_2 \end{eqnarray}$
将式(52)、式(53)、式(61)、式(67)代入式(66)得
(68) $ \dot{{V}}_2 \leqslant -\left[ {\alpha _0 \lambda _{\rm m} \left( {K_0 } \right)-\left( {\lambda _1 +\lambda _2 } \right)} \right]\left\| s \right\|^2-\left[ \lambda _{\rm m} \left( {K_2 } \right)-\right. \\ \left.\qquad d_2 \right]\left\| s \right\|-\left[ {\lambda _{\rm m} \left( {K_1 } \right)-\left( {\lambda _1 +\lambda _2 } \right)} \right]\left\| {\mbox{tanh}e} \right\|^2 $
由式(54)得$\dot{{V}}_2 \leqslant 0$, 根据拉塞尔不变性原理, 对于任意初值$q\left( 0 \right)$, $\dot{{q}}\left( 0 \right)$, 系统误差收敛, 即$\mathop {\lim }\limits_{t\to \infty } e={\bf 0}$, $\mathop {\lim }\limits_{t\to \infty }\dot{{e}}=0$. 证毕.
3.2 慢变子系统控制器设计
由于上节设计的输入受限重复学习控制器仅能保证慢变系统中刚性运动对期望轨迹的渐进跟踪, 而不能对两杆柔性振动主动抑制, 因此, 本节使用虚拟控制力原理, 对原有的期望轨迹进行修正, 生成同时反映臂柔性振动和刚性期望轨迹的混合轨迹$q_{\rm h}$. 然后设计基于虚拟力概念的输入受限重复学习控制器, 实现运动跟踪与两杆振动主动抑制双重功能. 引入虚拟力$F\in {\bf R}^{3\times 1}$, 期望轨迹与混合轨迹误差为$e_{\rm h} =q_{\rm d} -q_{\rm h} $, 由如下二阶指令发生器生成
(69) $ \begin{eqnarray} \label{eq69} \ddot{{e}}_{\rm h} +a\dot{{e}}_{\rm h} +be_{\rm h} =F \end{eqnarray}$
其中, $a,b\in {\bf R}^{3\times 3}$为正定常值对角矩阵.
定义混合误差$e_{\rm r} =q_{\rm h} -q$, 混合滑模变量为$s_{\rm r} =\dot{{e}}_{\rm r} +{\rm tanh}e_{\rm r}$, 将控制器式(46), 式(47)中$q_{\rm d}$, $e$分别替换为$q_{\rm h} $与$e_{\rm r} $, 得基于虚拟力的输入受限重复学习控制器为
(70) $ \begin{eqnarray} \label{eq70} &&\left( {\tau _{\rm oj} } \right)_{\rm r} =K_0 {\rm tanh}s_{\rm r} +K_1 {\rm tanh}e_{\rm r} +K_2 {\rm sgn} {s_{\rm r} } +\\&&{\rm sat}\left( {Q_0 z_{r0} +\sum\limits_{k=1}^N {Q_k \dot{{z}}_{{\rm r}k} } } \right) \end{eqnarray}$
(71) $ \begin{eqnarray} \left. {\begin{array}{l} \ddot{{z}}_{rk} +k^2\omega ^2z_{rk} =Q_k s_{\rm r} ,\ \ k=1,2,\cdots ,N\\ \dot{{z}}_{r0} =Q_0 s_{\rm r} \\ \end{array}} \right\} \end{eqnarray}$
将控制器式(70), 式(71)代入刚性系统式(26)得
(72) $ \begin{eqnarray} \label{eq72} \ddot{{e}}_{\rm r} +a\dot{{e}}_{\rm r} +be_{\rm r} =G \end{eqnarray}$
其中, $G=\ddot{q}_{\rm h} +M^{-1}(\delta ,q)\big[C(\delta,\dot{\delta },q,\dot{q})\dot{q}+ \kappa (\delta,\dot{\delta },q,\dot{q})-(\tau_{\rm oj})_{\rm r} \big]+a\dot{e}_{\rm r} +be_{\rm r}$.
(73) $ \begin{eqnarray} \label{eq73} \ddot{{e}}+a\dot{{e}}+be=F+G \end{eqnarray}$
由式(73)有$\ddot{{q}}=\ddot{{q}}_{\rm d} +a\dot{{e}}+be-\left( {F+G} \right)$, 将其代入式(25)得
(74) $ \begin{eqnarray} \label{eq74} &&\ddot{{\delta }}=-R_{22}^{-1} R_{21} \ddot{{q}}_{\rm d} -R_{22}^{-1} R_{21} a\dot{{e}}-R_{22}^{-1} R_{21} be+\\&&R_{22}^{-1} R_{21} \left( {F+G} \right)-R_{22}^{-1} S_{21} \dot{{q}}-\\&&R_{22}^{-1} S_{22} \dot{{\delta }}-R_{22}^{-1} {K}_\delta \delta \end{eqnarray}$
令$q_{\rm s} =\left[ {\delta ^{\rm T},e^{\rm T},\dot{{\delta }}^{\rm T},\dot{{e}}^{\rm T}} \right]^{\rm T}$, 由式(73)、式(74)得
(75) $ \begin{eqnarray} \label{eq75} \dot{{q}}_{\rm s} =A_{\rm s} q_{\rm s} +B_{\rm s} F+L_{\rm s} \end{eqnarray}$
\begin{eqnarray*} &&A_{\rm s} =\left[ {{\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c} {0_{4\times 4} } & {0_{4\times 3} } & {I_{4\times 4} } & {0_{4\times 3} } \\ {0_{3\times 4} } & {0_{3\times 3} } & {0_{3\times 4} } & {I_{3\times 3} } \\ {-R_{22}^{-1} {K}_\delta } & {-R_{22}^{-1} R_{21} b} & {-R_{22}^{-1} S_{22} } & {-R_{22}^{-1} R_{21} a} \\ {0_{3\times 4} } & {-b} & {0_{3\times 4} } & {-a} \\ \end{array} }} \right]\\&& B_{\rm s} =\left[ {{\begin{array} {0_{4\times 3} } \\ {0_{3\times 3} } \\ {R_{22} R_{21} } \\ {I_{3\times 3} } \\ \end{array} }} \right],\ \ L_{\rm s} =\left[ {{\begin{array} {0_{4\times 1} } \\ {0_{3\times 1} } \\ {R_{22}^{-1} R_{21} \left( {G-\ddot{{q}}_{\rm d} } \right)-R_{22}^{-1} S_{21} \dot{{q}}} \\ G \\ \end{array} }} \right] \end{eqnarray*}
定理2 对于状态方程$\dot{{q}}_{\rm s} =A_{\rm s} q_{\rm s} +B_{\rm s} F+L_{\rm s} $, 当$L_{\rm s} =0_{14\times 1}$或满足以下条件式(76), 取$F=-R_{\rm s}^{-1} B_{\rm s}^{\rm T} P_{\rm s} q_{\rm s} $, 则系统稳定.
(76) $ \begin{eqnarray} \label{eq76} &&\frac{\left\| {L_{\rm s} \left( t \right)} \right\|_{\rm E} }{\left\| {q_{\rm s} } \right\|_{\rm E} }\leqslant \frac{1}{2\left\| {N_{\rm s}^{-1} } \right\|_{\rm s} \left\| {P_{\rm s} } \right\|_{\rm s} }=\frac{\lambda _{\min } \left( {N_{\rm s} } \right)}{2\lambda _{\max } \left( {P_{\rm s} } \right)},\\&&\forall q_{\rm s} \in {\bf R}^{3\times 1} \end{eqnarray}$
其中, $N_{\rm s} =Q_{\rm s} +P_{\rm s} B_{\rm s} R_{\rm s}^{-1} B_{\rm s}^{\rm T} P_{\rm s} $, $\left\| \Re \right\|_{\rm E} $表示向量$\Re $的欧几里得范数, $\left\| {M} \right\|_{\rm s} $表示矩阵${M}$的谱范数.
证明: 当$L_{\rm s} =0_{14\times 1} $时, 对于系统$\dot{{q}}_{\rm s} =A_{\rm s} q_{\rm s} +B_{\rm s}F$构造性能指标函数为
(77) $ \begin{eqnarray} \label{eq77} J_{\rm s} =\frac{1}{2}\int_0^\infty {\left( {q_{\rm s}^{\rm T} Q_{\rm s} q_{\rm s} +F^{\rm T}R_{\rm s} F} \right)} {\rm d}t \end{eqnarray}$
其中,对称权阵$Q_{\rm s} \geqslant 0$, $R_{\rm s} >0$, 于任意矩阵$\Re _{\rm s} $, 有$\Re _{\rm s} \Re _{\rm s}^{\rm T} =Q_{\rm s} $, 若如下黎卡提方程式(78)的解$P_{\rm s} $对称正定, 则阵对$\left\{ {A_{\rm s} ,\Re _{\rm s} } \right\}$完全可观.
(78) $ \begin{eqnarray} \label{eq78} P_{\rm s} A_{\rm s} +A_{\rm s}^{\rm T} P_{\rm s} -P_{\rm s} B_{\rm s} R_{\rm s}^{-1} B_{\rm s}^{\rm T} P_{\rm s} +Q_{\rm s} ={\bf 0} \end{eqnarray}$
又因为阵对$\left\{ {A_{\rm s} ,B_{\rm s} } \right\}$完全可控, 所以系统存在最优控制
(79) $ \begin{eqnarray} \label{eq79} F=-R_{\rm s}^{-1} B_{\rm s}^{\rm T} P_{\rm s} q_{\rm s} \end{eqnarray}$
其中最优性能指标为$J_{\rm s}^\ast =q_{\rm s}^{\rm T} \left( 0 \right)P_{\rm s} q_{\rm s} \left( 0 \right)/2$.
当$L_{\rm s} \ne 0_{14\times 1} $时, 将式(79)代入式(75)得
(80) $ \begin{eqnarray} \label{eq80} \dot{{q}}_{\rm s} =\left( {A_{\rm s} -B_{\rm s} R_{\rm s}^{-1} B_{\rm s}^{\rm T} P_{\rm s} } \right)q_{\rm s} +L_{\rm s} \end{eqnarray}$
构造李雅普诺夫函数$V\left( {q_{\rm s} } \right)=q_{\rm s}^{\rm T} P_{\rm s} q_{\rm s}$, $V\left( {q_{\rm s} } \right)$对时间求导, 并代入式(80)及$N_{\rm s} $得
(81) $ \begin{eqnarray} \label{eq81} \dot{{V}}\left( {q_{\rm s} } \right)=\dot{{q}}_{\rm s}^{\rm T} P_{\rm s} q_{\rm s} +q_{\rm s}^{\rm T} P_{\rm s} \dot{{q}}_{\rm s} =-q_{\rm s}^{\rm T} N_{\rm s} q_{\rm s} +2L_{\rm s}^{\rm T} P_{\rm s} q_{\rm s} \end{eqnarray}$
(82) $ \begin{eqnarray} \label{eq82} &&L_{\rm s}^{\rm T} P_{\rm s} q_{\rm s} \leqslant \left\| {L_{\rm s}^{\rm T} } \right\|\left\| {P_{\rm s} q_{\rm s} } \right\|\leqslant \left\| {L_{\rm s} } \right\|\left\| {P_{\rm s} } \right\|\left\| {q_{\rm s} } \right\|\leqslant\\&& \frac{\lambda _{\min } \left( {N_{\rm s} } \right)}{2\lambda _{\max } \left( {P_{\rm s} } \right)}\left\| {P_{\rm s} } \right\|\left\| {q_{\rm s} } \right\|^2\leqslant \frac{1}{2}\lambda _{\min } \left( {N_{\rm s} } \right)\left\| {q_{\rm s} } \right\|^2 \end{eqnarray}$
(83) $ \begin{eqnarray} \label{eq83} \dot{{V}}\left( {q_{\rm s} } \right)\leqslant -\left( {q_{\rm s}^{\rm T} N_{\rm s} q_{\rm s} -\lambda _{\min } \left( {N_{\rm s} } \right)\left\| {q_{\rm s} } \right\|^2} \right)\leqslant 0 \end{eqnarray}$
3.3 快变子系统控制器设计
同上文分析, 快变子系统中, $q_{\rm f} $在快变时标$t_{\rm f} $下的状态方程如式(29). 构造性能指标函数
(84) $ \begin{eqnarray} \label{eq84} J_{\rm qf} =\frac{1}{2}\int_0^\infty {\left( {q_{\rm f}^{\rm T} Q_{\rm f} q_{\rm f} +\tau _{\rm nf}^{\rm T} R_{\rm f} \tau _{\rm nf} } \right)} {\rm d}t_{\rm f} \end{eqnarray}$
其中, 对称权阵$Q_{\rm f} \geqslant 0$, $R_{\rm f} >0$.
(85) $ \begin{eqnarray} \label{eq85} \tau _{\rm nf} =-R_{\rm f}^{-1} B_{\rm f}^{\rm T} P_{\rm f} q_{\rm f} \end{eqnarray}$
(86) $ \begin{eqnarray} \label{eq86} P_{\rm f} A_{\rm f} +A_{\rm f}^{\rm T} P_{\rm f} -P_{\rm f} B_{\rm f} R_{\rm f}^{-1} B_{\rm f}^{\rm T} P_{\rm f} +Q_{\rm f} =0 \end{eqnarray}$
4 仿真算例分析
为了验证式(13)、式(14)、式(70)、式(71)、式(85)构成的运动振动一体化输入受限重复学习控制器(an input limited repetitive learning controller with integration of motion and vibration, ILRCI)的有效性, 对图1 所示的系统进行仿真分析.全柔性空间机器人参数选取为: $m_0 =40$ kg, $l_0 =l_1 =l_2 =1.5$ m, $J_0 =30$ kg$\cdot$m$^2$, $\rho _1 =3.5$ kg$\cdot$m, $\rho _2 =1.1$ kg$\cdot$m, $J_{\rm m1} =J_{\rm m2} =0.1$ kg$\cdot$m$^2$, $EI_1 =EI_2 =100$ N/m$^2$, $k_{\rm m1} =k_{\rm m2} =50$ N$\cdot$m/rad, $k_{\rm b} =500$ N/m. 取控制参数: $K_0 ={\rm dig}\left( {200,40,20} \right)$, $K_1 ={\rm dig}\left( {10,5,1} \right)$,$K_2 ={\rm dig}\left( 10, 10, 2 \right)$, $K_C ={\rm dig}\left( 104, 88 \right)$, $Q_0 ={\rm dig}\left( 15,40, 25 \right)$, $Q_k ={\rm dig}\left( {20,20,20} \right)$, $k=1,2,\cdots ,N$, $N=3$, $a=b={\rm dig}\left( {5,} {5,5} \right)$.
广义坐标初值为$q_{{\rm boj}\delta} (0)=[0$ m, 1.9 rad, 0.7 rad, 0.5 rad, 0 m, 0 m, 0 m, 0 m]$^{\rm T}$, $q_{\rm m}(0)=[0.7$ rad, 0.5 rad]$^{\rm T}$, $\dot{q}_{{\rm boj}\delta}(0)= 0_{8\times 1}$, $\dot{q}_{\rm m}(0)=0_{2\times 1}$, $z_{{\rm r}k}(0)=0_{3\times 1}$, $\dot{z}_{{\rm r}k}(0)=0_{3\times 1}$.
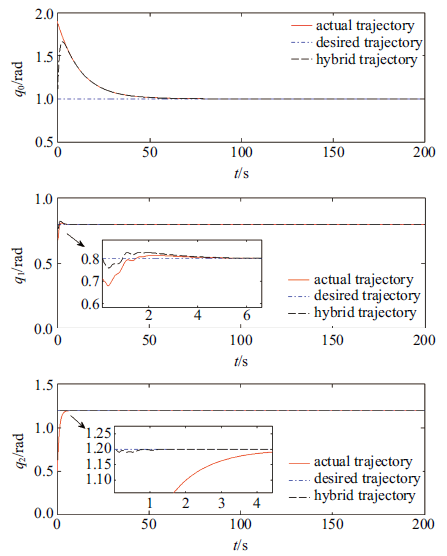
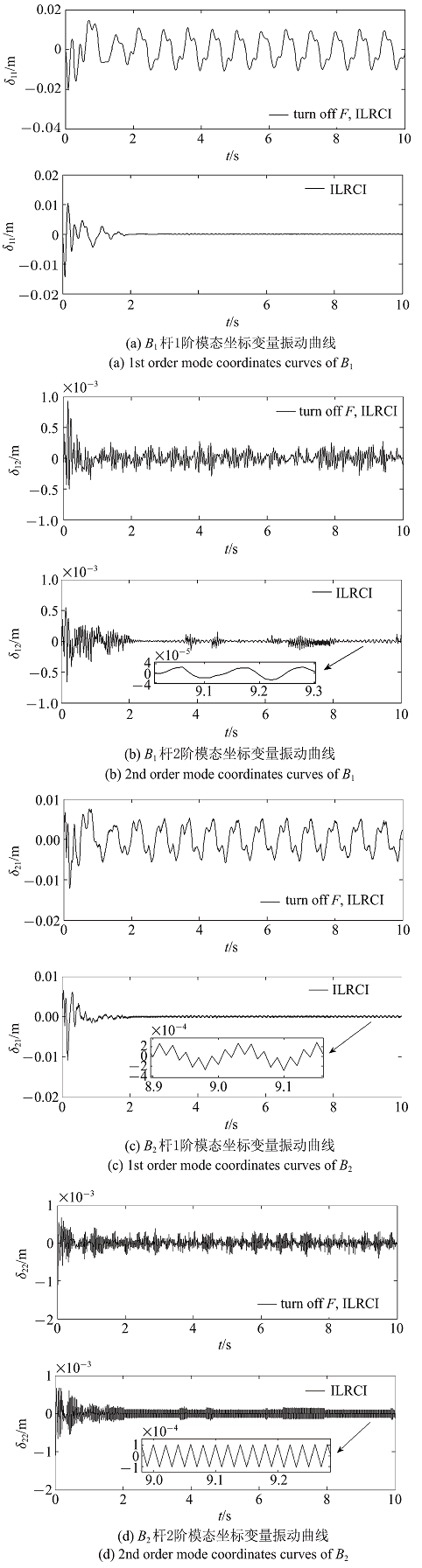
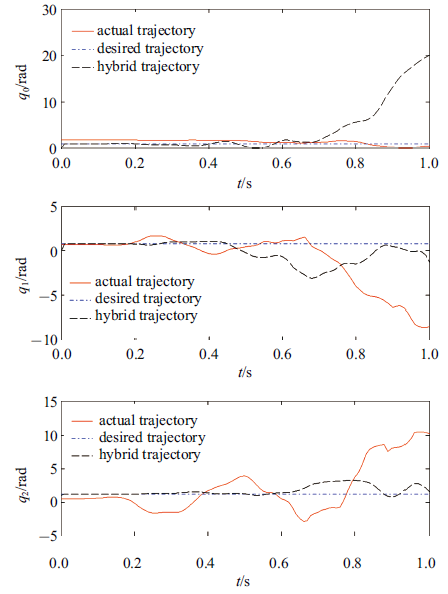
周期性期望轨迹为$q_{\rm d} =\left[1{\rm rad}, 0.8{\rm rad},1.2 {\rm rad} \right]^{\rm T}$, 仿真步长取0.01 s. 图2 给出了全柔性空间机器人基座姿态、关节在ILRCI控制下的轨迹追踪曲线.图3 为开启或关闭ILRCI控制中RC时, 基座姿态、关节的跟踪误差收敛曲线. 图4 为开启或关闭ILRCI控制中$\tau _{\rm nf} $时基座与关节的柔性抑振曲线. 为了对比验证虚拟力对杆的抑振效果, 采用式(13)、式(14)、式(46)、式(47)、式(85)构成的关闭虚拟力的ILRCI控制重新仿真.图5 为ILRCI控制中虚拟力对柔性杆$B_i$的抑振效果图.
图 2
图 2
ILRCI控制下基座姿态与关节角的轨迹追踪曲线
Fig. 2
Trajectory tracking curve of base attitude and joint angle under ILRCI
图 3
图 3
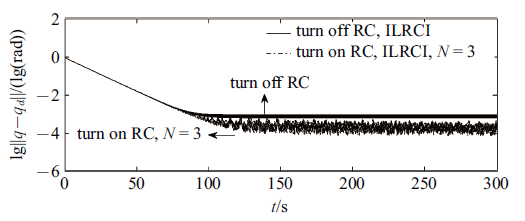
ILRCI控制与关闭RC后ILRCI控制的误差收敛曲线(单位: rad以10为底取对数)
Fig. 3
Error convergence curve of ILRCI and ILRCI without RC
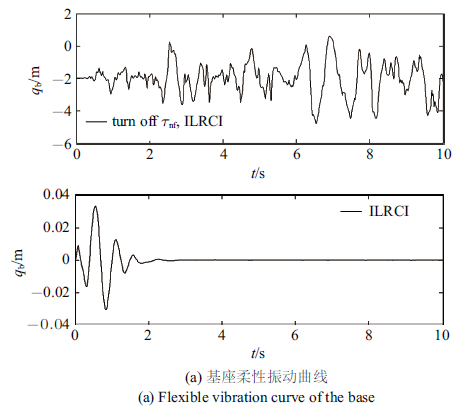
图3 表明, RC可以提高系统的轨迹跟踪精度. 图4 表明, 快变子系统控制器$\tau _{\rm nf} $能实现对系统基座、关节柔性振动的有效抑制. 图2 、图5 表明, 所提的ILRCI能确保轨迹精确追踪的同时, 实现对柔性杆振动的有效抑制.本文机器人关节柔性大, 所以采用关节柔性补偿间接增大其等效刚度. 关闭柔性补偿, 重新对系统进行仿真运算, 图6 为前1 s的仿真结果, 系统发散, 可见奇异摄动法仅适用于弱柔性非线性系统. 而本文设计的关节柔性补偿器,可实现对一般柔性非线性系统的奇异摄动分解与有效控制.
图 4
图 4
ILRCI控制与关闭$\tau _{\rm nf}$后ILRCI控制的仿真结果
Fig. 4
Simulation results of ILRCI and ILRCI without $\tau _{\rm nf}$
图 4
图 4
ILRCI控制与关闭$\tau _{\rm nf}$后ILRCI控制的仿真结果(续)
Fig. 4
Simulation results of ILRCI and ILRCI without $\tau _{\rm nf}$ (continued)
图 5
图 5
ILRCI控制与关闭虚拟力$F$后ILRCI控制的仿真结果
Fig. 5
Simulation results of ILRCI and ILRCI without virtual force $F$
图 6
图 6
关闭关节柔性补偿后ILRCI控制的仿真结果
Fig. 6
Simulation results of ILRCI after closing joint flexible compensation controller
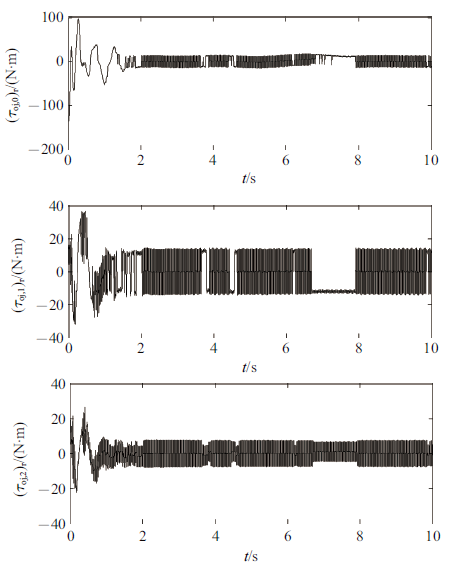
更进一步, 为了验证所提算法的力矩受限情况, 分析ILRCI控制所需的驱动力矩, 仿真结果如图7 所示. 可以看出, 实时力矩的最大上界$\left( {\tau _{\rm oj} } \right)_{\rm r} =\left[ {150,40,23} \right]^{\rm T}$, 根据式$k_{0,i} +k_{1,i} +k_{2,i} +\gamma _i \leqslant \tau _{{\rm oj},i,\max } $得, $\left( {\tau _{\rm oj,0,\max } } \right)_{\rm r} \geqslant 220,\left( {\tau _{\rm oj,1,\max } } \right)_{\rm r} \geqslant 55,\left( {\tau _{\rm oj,2,\max } } \right)_{\rm r} \geqslant 23$, 仿真运算中$\left( {\tau _{{\rm oj},i} } \right)_{\rm r} \leqslant \left( {\tau _{{\rm oj},i,\max } } \right)_{\rm r} $, 式中, $\left( {\tau _{{\rm oj},i} } \right)_{\rm r} $是矢量$\left( {\tau _{\rm oj} } \right)_{\rm r} $对应的元素, $i=1,2,3$, 所以力矩受限.
图 7
图 7
ILRCI控制的驱动力矩
Fig. 7
Torques of ILRCI
5 结论
利用假设模态法与拉格朗日第二类方程, 建立基座、臂、关节同时存在柔性的空间机器人动力学模型. 根据奇异摄动法, 将模型解耦为双时标下的慢变子系统与快变子系统. 对子系统分别设计控制器. 提出基于虚拟力概念的慢变子控制器, 具有如下优点: 第一, 控制器不基于模型信息设计; 第二, 适用于驱动力矩饱和情况; 第三, 能补偿周期重复出现的误差, 精确追踪周期信号; 第四, 可以有效抑制臂杆的柔性振动. 基于线性最优控制设计的快变子控制器, 可同时抑制基座与关节的柔性振动. 上述两种算法组成的一体化控制器中引入关节柔性补偿, 使系统动力学模拟与控制适用于一般柔性非线性系统. 仿真算例, 验证了算法的有效性.
参考文献
View Option
[1]
姚其家 , 戈新生 . 基于伪谱法的自由漂浮柔性空间机器人姿态运动规划与反馈控制
振动与冲击 , 2019 ,38 (7 ):20 -27
[本文引用: 1]
( Yao Qijia Ge Xinsheng . Attitude motion planning and feedback control for a free-floating flexible space robot based on pseudo-spectral method
Journal of Vibration and Shock , 2019 ,38 (7 ):20 -27 (in Chinese))
[本文引用: 1]
[2]
郭闻昊 , 王天舒 . 空间机器人抓捕目标星碰撞前构型优化
宇航学报 , 2015 ,36 (4 ):390 -396
( Guo Wenhao Wang Tianshu . Pre-impact configuration optimization for a space robot capturing target satellite
Journal of Astronautics , 2015 ,36 (4 ):390 -396 (in Chinese))
[3]
Yu YS Ding XL . Trajectory linearization control on SO(3) with application to aerial manipulation
Journal of the Franklin Institute-Engineering and Applied Mathematics , 2018 ,355 (15 ):7072 -7097
[4]
王一帆 , 孙汉旭 , 陈钢 等 . 基于分层结构的空间机械臂多约束任务规划
机械工程学报 , 2017 ,53 (11 ):104 -112
( Wang Yifan Sun Hanxu Chen Gang , et al . Hierarchical task planning for space manipulator with multi-constraint
Journal of Mechanical Engineering , 2017 ,53 (11 ):104 -112 (in Chinese))
[5]
Li JL Yan SZ . Thermally induced vibration of composite solar array with honeycomb panels in low earth orbit
Applied Thermal Engineering , 2014 ,71 (1 ):419 -432
[6]
尹婷婷 , 邓子辰 , 胡伟鹏 等 . 空间刚性杆-弹簧组合结构轨道、姿态耦合动力学分析
力学学报 , 2018 ,50 (1 ):87 -98
( Yin Tingting Deng Zichen Hu Weipeng , et al . Dynamic modelling and simulation of orbit and attitude coupling problems for structure combined of spatial rigid rods and spring
Chinese Journal of Theoretical and Applied Mechanics , 2018 ,50 (1 ):87 -98 (in Chinese))
[7]
Abdul Hafez A Mithun P Anurag V , et al . Reactionless visual servoing of a multi-arm space robot combined with other manipulation tasks
Robotics and Autonomous Systems , 2017 ,91 :1 -10
[本文引用: 1]
[8]
程靖 , 陈力 . 空间机器人双臂捕获卫星力学分析及镇定控制
力学学报 , 2016 ,48 (4 ):832 -842
[本文引用: 1]
( Cheng Jing Chen Li . Mechanical analysis and calm control of dual-arm space robot for capturing a satellite
Chinese Journal of Theoretical and Applied Mechanics , 2016 ,48 (4 ):832 -842 (in Chinese))
[本文引用: 1]
[9]
朱安 , 陈力 . 配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
力学学报 , 2019 ,51 (4 ):1156 -1169
[本文引用: 1]
( Zhu An Chen Li . Mechanical simulation and full order sliding mode collision avoidance compliant control based on neural network of dual-arm space robot with compliant mechanism capturing satellite
Chinese Journal of Theoretical and Applied Mechanics , 2019 ,51 (4 ):1156 -1169 (in Chinese))
[本文引用: 1]
[10]
Wang M Sun L Yin W , et al . Continuous robust control for series elastic actuator with unknown payload parameters and external disturbances.
IEEE/CAA Journal of Automatica Sinica , 2017 ,4 (4 ):620 -627
[本文引用: 1]
[11]
吴吉 , 章定国 , 黎亮 等 . 带集中质量的旋转柔性曲梁动力学特性分析
力学学报 , 2019 ,51 (4 ):1134 -1147
( Wu Ji Zhang Dingguo Li Liang , et al . Dynamic characteristics analysis of a rotating flexible curved beam with a concentrated mass
Chinese Journal of Theoretical and Applied Mechanics , 2019 ,51 (4 ):1134 -1147 (in Chinese))
[12]
Ramin M Mojtaba M . Maneuvering and vibrations control of a free-floating space robot with flexible arms.
Journal of Dynamic Systems, Measurement, and Control , 2011 ,133 (5 ):1 -8
[本文引用: 1]
[13]
Alessandro MG Christian O Alin AS . Coordinated control of spacecraft's attitude and end-effector for space robots
IEEE Robotics and Automation Letters , 2019 ,4 (2 ):2108 -2115
[本文引用: 1]
[14]
Meng ZJ Huang PF Guo J . Approach modeling and control of an autonomous maneuverable space net
IEEE Transactions on Aerospace and Electronic Systems , 2017 ,53 (6 ):2651 -2661
[15]
Dubanchet V Saussié D Alazard D , et al . Modeling and control of a space robot for active debris removal
CEAS Space Journal , 2015 ,7 (2 ):203 -218
[16]
Brian I Marco P . Robot motion planning in learned latent spaces
IEEE Robotics and Automation Letters , 2019 ,4 (3 ):2407 -2414
[17]
Gangapersaud Rabindra A Liu GJ de Ruiter Anton HJ . Detumbling of a non-cooperative target with unknown inertial parameters using a space robot
CEAS Space Journal , 2019 ,63 (12 ):3900 -3915
[本文引用: 1]
[18]
Kumar A Pathak PM Sukavanam N . Trajectory control of a two dof rigid-flexible space robot by a virtual space vehicle
Robotics and Autonomous Systems , 2013 ,61 (5 ):473 -482
[本文引用: 1]
[19]
Wang CQ Wu PF Zhou X , et al . Composite sliding mode control for a free-floating space rigid-flexible coupling manipulator system
International Journal of Advanced Robotic Systems , 2013 ,10 :1 -10
[本文引用: 1]
[20]
于潇雁 , 陈力 . 漂浮基柔性两杆空间机械臂基于状态观测器的鲁棒控制及振动控制
机械工程学报 , 2016 ,52 (15 ):28 -35
[本文引用: 1]
( Yu Xiaoyan Chen Li . Observer based robust control and vibration control for a free-floating flexible space manipulator
Journal of Mechanical Engineering , 2016 ,52 (15 ):28 -35 (in Chinese))
[本文引用: 1]
[21]
Nanos K Papadopoulos EG . On the dynamics and control of flexible joint space manipulators
Control Engineering Practice , 2015 ,45 (1 ):230 -243
[本文引用: 1]
[22]
Chu M Jia QX Sun HX . Backstepping control for flexible joint with friction using wavelet neural networks and L2-gain approach
Asian Journal of Control , 2017 ,20 (2 ):856 -866
[本文引用: 1]
[23]
谢立敏 , 陈力 . 漂浮基柔性空间机器人的鲁棒控制及振动抑制
力学学报 , 2012 ,44 (6 ):1058 -1065
[本文引用: 1]
( Xie Limin Chen Li . Robust control and vibration suppression of free-floating flexible space robot
Chinese Journal of Theoretical and Applied Mechanics , 2012 ,44 (6 ):1058 -1065 (in Chinese))
[本文引用: 1]
[24]
陈志勇 , 张婷婷 , 郭益深 . 弹性基和弹性关节空间机器人的自适应鲁棒抗扰控制及振动抑制
自动化学报 , 2018 ,44 (7 ):1271 -1281
[本文引用: 1]
( Chen Zhiyong Zhang Tingting Guo Yishen . Adaptive robust anti-interference control and vibration suppression for an elastic-base elastic-joint space robot
Journal of Mechanical Engineering , 2018 ,44 (7 ):1271 -1281 (in Chinese))
[本文引用: 1]
[25]
张登博 , 唐有绮 , 陈立群 . 非齐次边界条件下轴向运动梁的非线性振动
力学学报 , 2019 ,51 (1 ):218 -227
[本文引用: 1]
( Zhang Dengbo Tang Youqi Chen Liqun . Nonlinear vibrations of axially moving beams with nonhomogeneous boundary conditions
Chinese Journal of Theoretical and Applied Mechanics , 2019 ,51 (1 ):218 -227 (in Chinese))
[本文引用: 1]
[26]
张飞龙 , 贺云 , 李秋实 等 . 空间站载荷转移机构机器人的力加载控制方法
机器人 , 2018 ,40 (2 ):249 -256
[本文引用: 1]
( Zhang Feilong He Yun Li Qiushi , et al . The control method of force loading of robot on load transfer mechanism of space station
Robot , 2018 ,40 (2 ):249 -256 (in Chinese))
[本文引用: 1]
[27]
Liu JG Gao Q Liu ZW , et al . Attitude control for astronaut assisted robot in the space station
International Journal of Control Automation and Systems , 2016 ,14 (4 ):1082 -1095
[28]
Asaoka Y Akaike Y Komiya Y , et al . Energy calibration of CALET onboard the international space station
Social Science Quarterly , 2017 ,91 :1 -10
[本文引用: 1]
[29]
李鹤 , 孙明轩 . 一类不确定非线性系统的重复学习控制
自动化学报 , 2018 ,44 (10 ):1854 -1863
[本文引用: 1]
( Li He Sun Mingxuan . Repetitive learning control for a class of uncertain nonlinear systems
Acta Automatica Sinica , 2018 ,44 (10 ):1854 -1863 (in Chinese))
[本文引用: 1]
[30]
Califano F Bin M Macchelli A , et al . Stability analysis of nonlinear repetitive control schemes
IEEE Control Systems Letters , 2018 ,2 (4 ):773 -778
[本文引用: 1]
[31]
Verrelli C M . A larger family of nonlinear systems for the repetitive learning control
Automatica , 2016 ,71 :38 -43
[本文引用: 1]
[32]
Sun YG Qiang HY Mei X , et al . Modified repetitive learning control with unidirectional control input for uncertain nonlinear systems
Neural Computing & Applications , 2018 ,30 (6 ):2003 -2012
[本文引用: 1]
[33]
Verrelli CM . Repetitive learning control design and period uncertainties
Asian Journal of Control , 2015 ,17 (6 ):2417 -2426
[本文引用: 1]
[34]
Kelly R Santibanez V Loria A . Control of Robot Manipulators in Joint Space
London: Springer Verlag , 2005
[本文引用: 3]
[35]
Khalil H K . Nonlinear Systems.3rd ed
. Englewood Cliffs, NJ: Prentice Hall , 2002
[本文引用: 1]
基于伪谱法的自由漂浮柔性空间机器人姿态运动规划与反馈控制
1
2019
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
基于伪谱法的自由漂浮柔性空间机器人姿态运动规划与反馈控制
1
2019
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
Trajectory linearization control on SO(3) with application to aerial manipulation
2018
Thermally induced vibration of composite solar array with honeycomb panels in low earth orbit
2014
空间刚性杆-弹簧组合结构轨道、姿态耦合动力学分析
2018
空间刚性杆-弹簧组合结构轨道、姿态耦合动力学分析
2018
Reactionless visual servoing of a multi-arm space robot combined with other manipulation tasks
1
2017
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
空间机器人双臂捕获卫星力学分析及镇定控制
1
2016
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
空间机器人双臂捕获卫星力学分析及镇定控制
1
2016
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
1
2019
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
1
2019
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
Continuous robust control for series elastic actuator with unknown payload parameters and external disturbances.
1
2017
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
Maneuvering and vibrations control of a free-floating space robot with flexible arms.
1
2011
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
Coordinated control of spacecraft's attitude and end-effector for space robots
1
2019
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
Approach modeling and control of an autonomous maneuverable space net
2017
Modeling and control of a space robot for active debris removal
2015
Robot motion planning in learned latent spaces
2019
Detumbling of a non-cooperative target with unknown inertial parameters using a space robot
1
2019
... 空间探索进程中, 为减少太空作业风险, 需借助空间机器人代替宇航员完成舱外任务. 空间机器人是由航天器与机械臂构成的无根多体系统, 其动力学与控制的研究受到众多航天工作者重视[1 -7 ] . 机械臂安装于航天器桁架导轨上, 在极端恶劣的太空环境中, 机械臂易受到宇宙射线, 太阳风等的影响, 加之执行空间任务, 尤其在目标卫星的抓捕阶段, 由于碰撞极易造成基座轨道安装处振动[8 -9 ] ; 另外, 为减少发射载重以降低发射成本, 构成机械臂的各杆多选用轻质细长杆, 所以工作中臂杆易发生柔性变形; 而且, 空间机器人关节处多采用谐波减速器以驱动杆的运动, 具有轻质、大承载力与大减速比等显著优点, 但由于其本身的结构特性, 导致关节处电机的驱动转角与被驱动杆的实际转角不同步, 相当于在电机与杆之间设置了一个力矩滤波器, 引入了关节柔性[10 -12 ] . 因此, 空间机器人系统是一个刚性运动与基座、臂、关节柔性振动高度耦合的刚柔复合系统, 其各部件柔性严重影响机器人工作精度与性能. 为减少柔性对机器人控制精度的影响, 往往采用"低速, 缓动''操作模式, 这种模式下, 柔性振动影响不突出, 整个系统可看作刚性系统. 迄今为止, 刚性模型假设下的空间机器人动力学响应分析及运动控制相对成熟[13 -17 ] . 然而, 由于太空环境的特殊性, 对空间机器人可靠性要求非常高. 面对未知的太空环境与复杂的空间任务, 系统柔性很容易被激振, 一旦基座、臂、关节某部件柔性振动被激发, 可能导致系统所有柔性部件的振动, 在无阻尼的太空环境中衰减缓慢, 如果不对其进行有效抑制, 会使执行器发生剧烈振动甚至失效, 严重影响机器人工作可靠性. 因此, 考虑空间机器人基座、臂、关节的柔性效应并主动抑制其振动值得人们关注. ...
Trajectory control of a two dof rigid-flexible space robot by a virtual space vehicle
1
2013
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
Composite sliding mode control for a free-floating space rigid-flexible coupling manipulator system
1
2013
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
漂浮基柔性两杆空间机械臂基于状态观测器的鲁棒控制及振动控制
1
2016
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
漂浮基柔性两杆空间机械臂基于状态观测器的鲁棒控制及振动控制
1
2016
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
On the dynamics and control of flexible joint space manipulators
1
2015
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
Backstepping control for flexible joint with friction using wavelet neural networks and L2-gain approach
1
2017
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
漂浮基柔性空间机器人的鲁棒控制及振动抑制
1
2012
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
漂浮基柔性空间机器人的鲁棒控制及振动抑制
1
2012
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
弹性基和弹性关节空间机器人的自适应鲁棒抗扰控制及振动抑制
1
2018
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
弹性基和弹性关节空间机器人的自适应鲁棒抗扰控制及振动抑制
1
2018
... 近些年, 柔性空间机器人的研究取得一定进展. 针对臂杆柔性, Kumar等[18 ] 讨论了单柔性杆空间机器人的动力学模拟与控制问题; Wang等[19 ] 用假设模态法处理单柔性杆, 讨论了其动力学建模, 刚性控制与柔性振动抑振问题; 于潇雁等[20 ] 考虑两杆均存在柔性的情况下空间机器人动力学响应分析与振动主动抑制问题. 针对关节柔性, Nanos等[21 ] 讨论了双柔性关节空间机器人的动力学模拟与控制问题; Chu等[22 ] 针对高精度柔性关节伺服系统的位置控制问题, 提出了反推控制方案. 针对存在两类柔性部件系统, 谢立敏等[23 ] 讨论了单柔性杆、双柔性关节空间机器人的动力学建模与控制问题; 陈志勇等[24 ] 讨论了弹性基座、双柔性关节空间机器人的动力学模拟与双重振动抑振问题. ...
非齐次边界条件下轴向运动梁的非线性振动
1
2019
... 值得一提的是, 上述研究仅考虑空间机器人基座、臂、关节某一类或两类部件柔性的影响, 属于部分柔性空间机器人系统. 基座、臂、关节全柔性空间机器人系统是刚性运动与三重柔性振动高度耦合、高度非线性的时变系统, 其动力学模拟非常繁杂, 控制器设计面临着实现刚性轨迹跟踪, 抑制基座、臂、关节柔性振动四重功能共存的突出难点[25 ] . 这使得全柔性空间机器人动力学模拟与控制问题较难分析, 相关研究鲜有报道. 针对这些问题, 本文提出了柔性基座、两柔性杆、两柔性关节空间机器人的动力学建模方法, 以及系统刚性运动与三重柔性振动的解耦方案. ...
非齐次边界条件下轴向运动梁的非线性振动
1
2019
... 值得一提的是, 上述研究仅考虑空间机器人基座、臂、关节某一类或两类部件柔性的影响, 属于部分柔性空间机器人系统. 基座、臂、关节全柔性空间机器人系统是刚性运动与三重柔性振动高度耦合、高度非线性的时变系统, 其动力学模拟非常繁杂, 控制器设计面临着实现刚性轨迹跟踪, 抑制基座、臂、关节柔性振动四重功能共存的突出难点[25 ] . 这使得全柔性空间机器人动力学模拟与控制问题较难分析, 相关研究鲜有报道. 针对这些问题, 本文提出了柔性基座、两柔性杆、两柔性关节空间机器人的动力学建模方法, 以及系统刚性运动与三重柔性振动的解耦方案. ...
空间站载荷转移机构机器人的力加载控制方法
1
2018
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
空间站载荷转移机构机器人的力加载控制方法
1
2018
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
Attitude control for astronaut assisted robot in the space station
2016
Energy calibration of CALET onboard the international space station
1
2017
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
一类不确定非线性系统的重复学习控制
1
2018
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
一类不确定非线性系统的重复学习控制
1
2018
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
Stability analysis of nonlinear repetitive control schemes
1
2018
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
A larger family of nonlinear systems for the repetitive learning control
1
2016
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
Modified repetitive learning control with unidirectional control input for uncertain nonlinear systems
1
2018
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
Repetitive learning control design and period uncertainties
1
2015
... 另外, 考虑到太空任务复杂, 搭建空间站, 维护航天设备, 回收失效卫星, 清理轨道垃圾等任务中周期重复工作都占有很大比重[26 -28 ] . 而传统的控制器, 执行周期性任务, 可以实现渐进跟踪, 但对于周期重复出现的误差, 系统响应无法改善, 导致控制精度不高. 重复项的引入, 能补偿周期性误差, 提高控制精度[29 ] . 最近, 地面机器人重复学习控制研究相对成熟, Califano等[30 ] 提出指数稳定的重复学习算法, Verrelli等[31 ] 论证最小相位非线性系统的重复控制方法, Sun等[32 ] 提出了跟踪误差收敛于有限时间内的重复学习算法, Verrelli等[33 ] 提出不确定周期的重复控制算法. 然而, 作为高精度运动的有效控制策略, 其在全柔性空间机器人系统中的应用比较少见. 而且, 载人航天成本高昂, 机器人控制液宝贵, 由于驱动能量的有限与机械构造的限制, 其关节输入力矩是有饱和值的, 限制力矩输入就变得很有必要. 所以, 在运动控制方面, 设计了输入受限重复学习控制算法, 满足力矩受限要求的同时, 实现对周期信号的高精度追踪. ...
Control of Robot Manipulators in Joint Space
3
2005
... 注意到式(26)是全驱动的动力学模型, 形式与刚性机械臂相似, 具有如下结构特性[34 -35 ] : ...
... 其中, $k_{\rm M}$, $k_{\rm C1}$, $k_{\rm C2}$的取值参考文献[34 ] , tanh$\left( \cdot\right)$如式(43)所定义. ...
... 其中, $k_{\rm C3}$, $k_{\rm C4} $的取值参考Kelly等[34 ] . ...
Nonlinear Systems.3rd ed
1
2002
... 注意到式(26)是全驱动的动力学模型, 形式与刚性机械臂相似, 具有如下结构特性[34 -35 ] : ...