引 言
对于复合柔性结构,构成部件多为具有无限自由度的柔性体,描述其运动的动力学方程为偏微分方程. 无论是对系统的动力学特性进行分析,还是基于其动力学模型的状态空间进行控制器设计,都要建立具有有限自由度的动力学模型. 实际工程应用中,通常采用有限元法对复杂结构进行离散化处理,只有在结构相对简单(包括单一的索、杆、梁、板、壳等)时才采用解析方法建模.
有限元法可以离散具有复杂形状的复合柔性结构,在单元数量足够多的情况下,有限元模型所得到的结果可以达到较高的精度.因此,许多学者[5-9]采用有限元法,建立系统的有限元模型,进行动力学特性的分析和研究.例如,Al-Bedoor等[7]建立了含有柔性关节的柔性机械臂的有限元模型,并开展了柔性关节的扭转变形对于系统动力学的影响研究.采用有限元商业软件(如Ansys、Abaqus、Nastran等)建模,也是分析复合柔性结构固有特性的有效途径[10-13]. 例如,代颖等[12]采用软件Ansys建立了车用电机的有限元模型,分析了各结构部件对电机固有特性的影响.然而,有限元模型为了保证其精度,需要较多的单元数,导致系统的离散动力学模型出现维数过高的弊端,这为系统的控制器设计或非线性动态响应分析带来了困难;并且由有限元商业软件得到的系统全局模态是以数值形式给出的,对于存在非线性环节的复合结构,很难建立解析形式的非线性动力学模型.
相比于有限元离散方法,采用解析形式的模态函数导出复合柔性结构的模态方程,利用Galerkin截断可以有效地降低系统的维数[14],从而明显地提高求解系统动力学模型的计算效率. 因此,解析方法在多刚柔体系统动力学中得到了广泛的应用,尤其是在柔性航天器[15-18]的动力学建模与控制器设计. 解析方法的关键在于将柔性部件的位移表示为部件模态与模态坐标的线性组合,所建立的动力学模型的准确性依赖于所选模态的精确性和数量,也即所选模态越能准确地描述柔性部件的真实变形,其需要的模态数量就越少,同时所推导出的动力学模型的准确性也越高. Pan和Liu[19]通过钟摆和曲柄连杆机构的数例仿真结果,表明了边界为两端自由、简支或悬臂的振型函数适合于柔性多体系统的建模,能得到较好的结果. 但是,采用两端固支或具有超静定边界的振型函数可能导致系统动力学方程的计算结果出现较为严重的误差. Schwertassek等[20]通过结合柔性附件的静变形和特征函数,构造出合适的振型函数用于描述柔性体的变形,从而提高系统动力学模型的准确性和收敛性.
对于由多个柔性部件组成的复合结构,各柔性部件之间的弹性振动耦合效应不可忽略. 系统中单一柔性部件在悬臂、简支和自由等静定边界下的模态与其在整体结构中的真实模态有较大差异. 采用柔性部件的假设模态建模,可能会导致其动力学模型精度下降,甚至出现较大误差. 为此,针对由中心刚体和柔性附件组成的航天器,Hablani[21]指出,如果选取相同数量的模态,全局模态所得到的动力学模型比假设模态得到的模型具有更高的精度. 这是因为全局模态包含了系统中刚体的运动和全部柔性部件弹性振动的模态,选取少量的全局模态就能较好地描述系统的运动. 针对空间柔性机械臂系统,魏进等[22]分别采用假设模态和全局模态建立了系统的动力学模型,并对两种模型进行了对比研究. 将有限元结果作为参考值,对比分析的结果表明全局模态方法所得结果的精度远高于假设模态方法给出的结果.
鉴于采用全局模态进行离散具有优越性,已有一些学者通过全局模态离散,得到复合柔性结构的动力学离散模型.针对索——梁组合结构,Gattulli等[23-24]、赵跃宇等[25-26]和王志搴等[27-28]利用边界条件和连接点的匹配条件,获取系统的固有频率和全局模态,通过全局模态进行离散,建立了系统的动力学离散模型.Hablani等[29-31]采用系统的全局模态,建立了柔性航天器的动力学模型,并在此基础上对其动力学特性分析以及控制作了比较全面的研究.曲广吉[32]和繆炳祺等[33-34]通过求解系统的特征值问题或模态综合等方法,得到系统的全局模态,离散柔性部件的位移,由此基于伪坐标的拉格朗日方程导出了柔性航天器的动力学方程.
1 复合柔性结构全局模态解析提取方法
1.1 定义坐标系
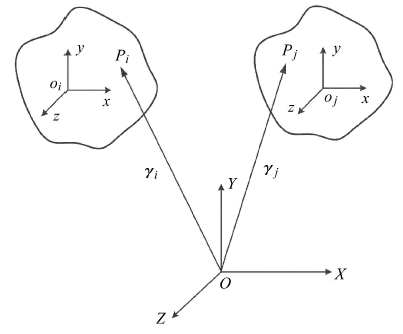
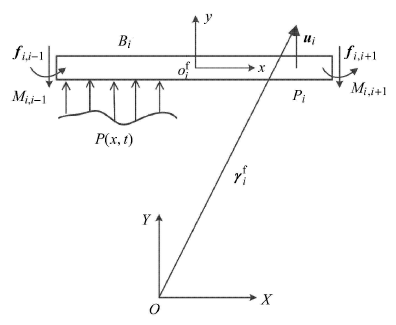
采用笛卡尔坐标描述系统的运动,一般以系统中每一个物体为单元,在刚体、柔性部件和连接部件上建立坐标系,其上每个部件的位形都相对于一个公共参考系进行定义,其位形坐标统一为笛卡尔坐标.如图1所示,在系统中第i个物体和第j个物体的质心上分别建立各自的坐标系为$o_i xyz$和$o_j xyz$,坐标系$OXYZ$为公共参考系. 这样,物体上任意一点$P_i$和$P_j$的位置矢量分别为$\gamma _i$和$\gamma _j$.
图1
1.2 系统的运动方程
对于由多个刚体和柔体组成的复合柔性结构中的刚体,采用牛顿-欧拉法建立动力学方程. 在系统的g个刚体 中取刚体$ A_i \ (i = 1,2, \cdots ,g)$为研究对象,它不仅受到系统构件相互之间的作用力和力矩,也可能受到外部的作用力和力矩.
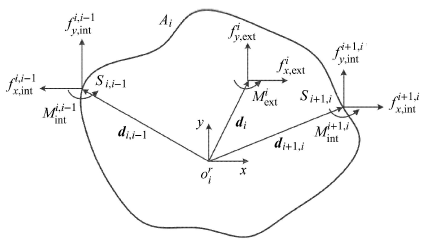
如图2所示,只考虑系统的平面运动,在刚体$A_i$的质心上建立坐标系,并命名为$o_i^r xy$. 在连接点$S_{i,i-1}$处,相邻物体作用在刚体$A_i$的力$f_{x,{\rm int}}^{i,i-1}$和$f_{y, {\rm int}}^{i,i-1}$分别沿坐标系$o_i^r xy$的x方向和y方向,力矩为$M_{\rm int}^{i,i-1}$. 在连接点$ S_{i + 1,i}$处,相邻物体作用在刚体$A_i$的力$f_{x, {\rm int}}^{i + 1,i}$和$f_{y, {\rm int}}^{i+1,i}$分别沿坐标系$o_i^r xy$的x方向和y方向,力矩为$M_{\rm int}^{i + 1,i}$. 刚体$A_i$受到的外部作用力$f_{x, {\rm ext}}^i$和$f_{y, {\rm ext}}^i$分别沿坐标系$o_i^r xy$的x方向和y方向,外部力矩为$M_{{\rm ext}}^i$.因此,在连接点$S_{i,i-1}$和$S_{i + 1,i}$上,相邻物体作用在刚体$A_i$的总力矩为
图2
其中,${\pmb d}_{i,i-1}$和${\pmb d}_{i+ 1,i}$分别是连接点$S_{i,i-1}$和$S_{i + 1,i}$的作用力到刚体$A_i$的质量中心的矢量,${\pmb i}$和${\pmb j}$分别为沿x方向和y方向的单位矢量. 刚体$A_i$受到外部作用的总力矩为
其中,${\pmb d}_i$为刚体$ {A}_i$受到的外部作用力到其质量中心的矢量.
通过牛顿-欧拉法,可以写出单个刚体$A_i$的动力学方程
其中,$m_i$和$J_i$分别为刚体$A_i$的质量和关于质心$o_i^r$的转动惯量,$x_i^r$和$y_i^r$分别为刚体$A_i$沿坐标系$o_i^r xy$的x方向和y方向的坐标,$\theta _i^r$为刚体$A_i$的绕质心$o_i^r$转动角位移.因此,刚体$A_i$的平动和转动可以用向量${\pmb\gamma}_i^r = \left[ {x_i^r ,y_i^r ,\theta _i^r } \right]^{\rm T}$来描述.
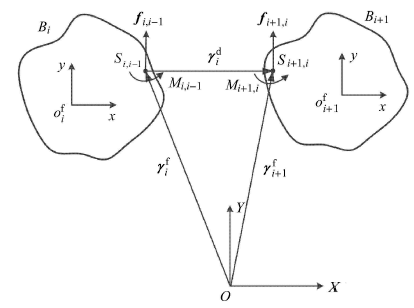
在复合柔性结构中,柔体具有连续分布的质量和弹性,且有无限多个自由度,其动力学方程为偏微分方程. 为了求解系统的固有频率和全局模态,需要确定系统的边界条件和相邻物体之间的力、力矩、位移和转角的匹配条件.由图3描述的相邻两个柔体$B_i$和$B_{i + 1}$,它们通过${\pmb\gamma}_i^{\rm d}$向量连接在一起. 在柔体$B_i$和$B_{i + 1}$上分别建立浮动坐标系,并命名为$o_i^{\rm f} xy$和$o_{i + 1}^{\rm f} xy$. 在连接点$S_{i,i-1}$处,柔体$B_{i + 1}$作用在$B_i$的力和力矩分别为$f_{i,i-1}$和$M_{i,i-1}$. 同样地,在连接点$S_{i + 1,i}$处,柔体$B_i$作用在$B_{i + 1}$的力和力矩分别为$f_{i + 1,i}$和$M_{i + 1,i}$. 在柔体的连接点$S_{i,i-1}$和$S_{i + 1,i}$处,柔体的矢量${\pmb\gamma}_i^{\rm f}$和${\pmb\gamma}_{i + 1}^{\rm f}$必须满足约束条件
图3
图3
刚性连接相邻柔体的约束关系
Fig.3
Constraint relationship of rigid connecting deformable bodies
如图3所示,当两个柔体$B_i$和$B_{i + 1}$为刚性连接时,连接向量满足
亦即
两个柔体$B_i$和$B_{i + 1}$相互之间的力和力矩也应满足关系式
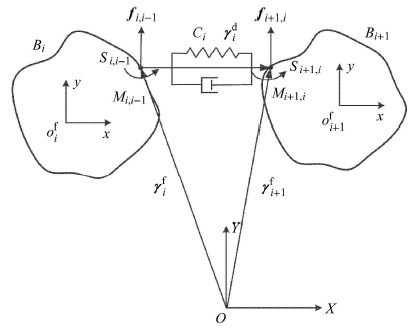
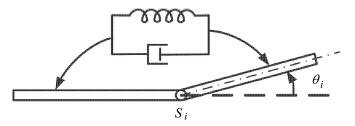
如图4所示,当两个柔体$B_i$和$B_{i + 1}$为弹性连接时,连接向量${\pmb\gamma}_i^{\rm d} \ne {\bf 0}$,且连接向量${\pmb\gamma}_i^{\rm d}$为弹性连接结构$C_i$的变形向量. 此时,弹性连接结构所受到的作用力$f_i$和力矩$M_i$可由自身的弹簧和线性阻尼构成的无质量系统来表达,即
图4
图4
弹性连接相邻柔体的约束关系
Fig.4
Constraint relationship of elastic connection deformable bodies
其中,$x_i^{\rm d} ,y_i^{\rm d}$和$\theta _i^{\rm d}$分别为连接结构变形向量${\pmb\gamma}_i^{\rm d}$的水平位移,垂直位移和转动角位移,其相对应方向的弹簧刚度系数为$k_{i,1} ,k_{i,2}$和$k_{i,3}$,阻尼系数为$c_{i,1} ,c_{i,2}$和$c_{i,3}$. 连接结构的变形向量${\pmb\gamma}_i^{\rm d}$可以表示为${\pmb\gamma} _i^{\rm d} =\left[ {x_i^{\rm d} , y_i^{\rm d} ,\theta _i^{\rm d} } \right]^{\rm T}$.
两个柔体在连接点$S_{i,i-1}$和$S_{i + 1,i}$的矢量${\pmb\gamma} _i^{\rm f}$和${\pmb\gamma }_{i + 1}^{\rm f}$满足的约束条件为
两个柔体$B_i$和$B_{i + 1}$相互之间的力和力矩也应满足关系式
为了便于理解,以欧拉——伯努利梁作为典型的柔体,推导复合柔性结构中单个柔体的动力学方程.如图5所示,在欧拉梁$B_i$的质心建立坐标系$o_i^f xy$,其点$o_i^f$固结在未变形前的梁$B_i$的中心,$B_i$的长度为$2l$. 梁$B_i$上任一点的变形向量为${\pmb u}_i$. 由于只考虑梁$B_i$在y方向上的运动,变形向量为${\pmb u}_i = \left[ {0, w_i } \right]$,$w_i$表示梁$B_i$上任一点在y方向上的位移. $B_i$上任一点的位置向量为自身的变形向量,可表示为
图5
根据欧拉——伯努利梁理论,可以得到其运动微分方程为
式中,$(')$表示对x求导数,梁的弹性模量为E,截面惯性矩为$I$,单位长度的质量为$\rho$,梁上各点的运动位移为, 作用在梁上沿长度方向的分布载荷为$p(x,t)$.
由图5所示,在$B_i$的连接点$S_{i,i-1}$和$S_{i,i + 1}$的位移分别为$w_i (-l,t)$和$w_i (l,t)$. 同样地,在$B_i$的连接点$S_{i,i-1}$和$S_{i,i + 1}$的转角分别为${w}'_i (-l,t)$和${w}'_i (l,t)$. 在$B_i$的连接点$S_{i,i-1}$和$S_{i,i + 1}$的剪力可表示为
在$B_i$的连接点$S_{i,i-1}$和$S_{i,i + 1}$的弯矩可表示为
1.3 系统的固有频率和全局模态
对于由多个刚体、柔体和弹性连接结构组成的复合柔性结构,可以简化为g个刚体,$h$个柔体以及M个弹性连接结构.仅考虑系统的平面运动,由1.2节给出的系统中各物体的动力学方程,刚体$A_i (i = 1,2, \cdots ,g)$的平动和转动用向量${\pmb\gamma} _i^r$描述,弹性连接结构$C_j (j = 1,2, \cdots ,h)$在平动和转动方向上的变形用向量${\pmb\gamma}_j^{\rm d}$描述,柔体$B_k (k = 1,2, \cdots ,m)$上任一点的位移用向量${\pmb\gamma} _k^{\rm f}$ (即弹性变形向量${\pmb u}_k$)描述.考虑系统的自由振动,根据系统具有与时间无关的确定振型的特性,可用分离变量法推导系统的特征方程.同时定义系统的各广义坐标以同一频率作谐振动. 系统中刚体$A_i$,弹性连接结构$C_j$和柔体$B_k$的广义坐标特解形式为
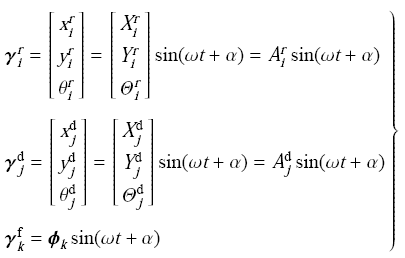
式中,$\omega$为系统的固有频率.
因为柔体是连续体,其变形是用偏微分方程来描述的,所以柔体$B_k$的振型矢量${\pmb\phi}_k$,是与空间位置有关的函数,根据柔体的类型不同,有其不同的形式.
如图5所示,当欧拉梁$B_k$在y方向上有位移时,其描述变形的偏微分方程如式(12)所示,那么描述欧拉梁$B_k$任一点的位置向量${\pmb\gamma} _k^{\rm f}$为自身的位移$w_k (x,t)$,其特解表示为
将式(16)代入方程(12)的自由振动形式,可得
式(17)的通解形式可写为
其中,$\beta = \left( {\frac{\rho \omega ^{2}}{EI}} \right)^{1 / 4}$. 令
将式(18)代入梁$B_k$在连接点$S_{i,i-1}$和$S_{i,i + 1}$的位移、转角、剪力和弯矩的匹配条件,将式(15)表示刚体运动和连接结构变形的广义坐标特解分别代入刚体的动力学方程(3)和弹性连接结构的匹配条件(10)可得
为了求解系统的固有频率,需保证方程(20)有非零解,即矩阵${\pmb H}(\omega )$的行列式必须等于零.通过行列式等于零可以解出系统的固有频率,进而确定${\pmb A}$中各项系数.将关于描述柔体弹性变形的振型函数系数$\psi _1 ,\psi _2 , \cdots ,\psi _m$代入到各自的振型中,可以得到系统的全局模态.
1.4 系统动力学模型
与多自由度系统的振型叠加法类似,系统的各个物体的位移响应可以用$N$个模态叠加的形式近似表示. 系统中各个物体的第$s$阶模态振型可表示为
式中,${\pmb A}_{i,s}^r$和${\pmb A}_{j,s}^{\rm d}$分别为刚体$A_i$,弹性连接结构$C_j$的第$s$阶模态振型,${\pmb\phi} _{ k,s}$为柔体$B_k$的第$s$阶模态振型,${\pmb\psi}_s$为系统第$s$阶全局模态振型.
系统中各个物体的位移可以表示为
将上式代入刚体的运动微分方程(3),弹性连接结构的变形表达式(8),描述柔体弹性变形的偏微分方程(例如式(12)),然后将刚体的运动微分方程,描述柔体弹性变形的偏微分方程分别乘以自身的第$n$阶模态,再将描述柔体弹性变形的偏微分方程进行空间积分,并利用系统全局模态的正交性关系,可以得到系统的模态方程为
式中,$M_n$为第$n$阶模态质量,$K_n$为第$n$阶模态刚度,$F_n(t)$为系统外激励.
2 应用算例
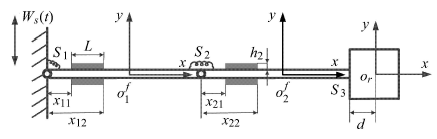
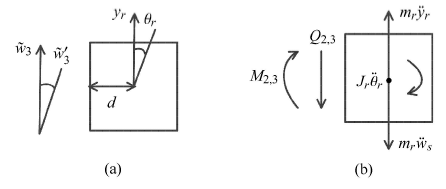
将图6所示的铰链连接双梁结构作为应用算例,图中的结构由两个欧拉——伯努利梁通过铰链连接而成,右端梁的自由端与刚体刚性连接.在该应用实例中,由于支撑平台移动,系统受到外部激励$w_s (t)$. 假定各个梁有着相同的截面和材料特性.同样地,各个铰链也是有着相同的几何参数和材料特性. 梁的长度为$2l$,宽度为$b$,厚度为$h_1$,单位长度的质量为$\rho$,弹性模量为E,截面惯性矩为$I$.分别在第i个梁上下表面粘贴一对压电片作为作动器,压电片的长度为$L$,厚度为$h_2$,宽度与梁相同,压电致动器在厚度方向(即图6所示y方向)分别施加输入电压为$U_i (t)$而产生的作动力矩$\hat {M}_i(x,t)$.$\theta _i$为描述第i个铰链的扭转变形的角位移.$m_r$和$J_r$分别为端部刚体的质量和关于质心$o_r$的转动惯量.d为连接点$S_{3}$到刚体质心$o_r$的距离. 令$o_i^{\rm f} xy$为第i个梁的坐标系,其坐标原点为梁的中心. 令$o_r xy$为端部刚体的坐标系,其坐标原点为刚体的质心.
图6
2.1 系统的运动方程
压电作动器在输入电压的作用下对第i个梁产生的力矩为[39]
式中,$C = bpE(h_1 + h_2 )$,$x_{i2} = x_{i1} + L$,$p$为压电常数,$H(x)$为Heaviside阶跃函数.
由欧拉——伯努利梁理论,图6所示的第i个梁的运动微分方程为
其中,$w_i$为第i个梁的垂向位移,$w_s (t)$为支撑平台的运动位移.$\xi _a$和$\eta$分别为梁的外阻尼和内阻尼系数,并且假定它们分别与其质量和刚度成比例关系,可以表示为
将式(24)代入方程(25)可得
又因$H(x)$的广义导数为${H}'(x) = \delta (x)$,${H}"(x) = {\delta }'(x)$,由此可得
式中,$c,k_L ,k_N$和$\mu$分别为铰链的线性阻尼系数,线性刚度系数,三次非线性刚度系数和摩擦力矩系数.
图7
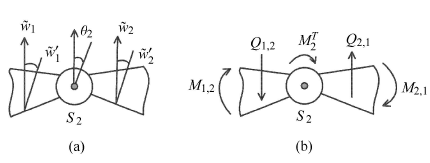
由图8(a)所示的铰链${S}_{2}$的几何条件,相对应的位移和转角可以表示为
图8
图8
铰链${S}_{2}$的(a) 几何条件 (b) 自然条件
Fig.8
(a) Geometric and (b) natural matching conditions at the joint${S}_{2}$
如图8(b)所示,$Q_{1,2}$和$Q_{2,1}$分别为铰链${S}_{2}$两边的剪力,$M_{1,2}$和$M_{2,1}$分别为铰链${S}_{2}$两边的弯矩,它们可以表示为
由图8所示的铰链匹配关系,根据柔体之间满足的位移和转角的匹配条件(9),力和力矩的匹配条件(10),由式(30)和式(31),可以得到铰链${S}_{2}$的匹配条件为
如图9(b)所示,端部刚体左边受到连接处${S}_{3}$的力$Q_{2,3}$和力矩$M_{2,3}$,它们可以表示为
图9
图9
刚体的(a) 几何条件 (b) 自然条件
Fig.9
(a) Geometric and (b) natural matching conditions on the rigid body
由式(33),根据牛顿-欧拉法得到的刚体动力学方程(3),基于图9(b)所示的力和力矩的平衡关系,可以得到端部刚体平移和转动的运动方程为
式中,$\xi _b$和$\xi _c$分别为中心刚体在y方向上平移和绕质心$o_r$转动的外阻尼系数,它们分别表示为
如图9(a)所示,端部刚体所对应的位移和转角可以表示为
由式(37),通过它们之间的位移和转角的匹配关系,可以得到端部刚体的几何匹配条件
在铰链${S}_1$,系统的边界条件为
2.2 系统的固有频率和全局模态
采用分离变量法,求解系统特征值问题. 将系统的位移表示为
式中,$\omega$为系统的固有频率. 将式(40)代入梁的无阻尼自由振动方程(25)可得
同样地,将式(40)代入系统中铰链${S}_{2}$的匹配条件(32)的线性表达式,得到
将式(40)代入端部刚体平移和转动的无阻尼自由振动方程,得到
将式(40)代入端部刚体的几何匹配条件(38),得到
将式(40)代入铰链$ {S}_1$的边界条件,得到
方程(41)的通解可以写为
其中$\beta = \left( {\frac{\rho \omega ^{2}}{EI}} \right)^{1 /4}$. 令
将式(47)代入铰链${S}_{2}$的匹配条件(42),刚体平移和转动的无阻尼自由振动方程(43)和(44),端部刚体的几何匹配条件(45)和铰链${S}_1$的边界条件(46),可以得到
其中,${\pmb H}(\omega ) \in {\bf R}^{12\times 12}$.为了求解系统的固有频率,需保证方程(49)具有非零解,即矩阵${\pmb H}(\omega )$的行列式必须等于零.通过行列式等于零可以解出系统的固有频率,进而确定A中各项系数. 将这些系数代入式(47),可以得到系统的全局模态.
2.3 系统全局模态的正交性
在一定的边界条件下,系统对应于任意两个不同的固有频率$\omega _j$和$\omega _k$的模态函数分别为${\pmb\phi} _{\;j} (x)$和${\pmb\phi}_{\;k} (x)$,即
根据方程(41),(43)和(44),可以有
方程(51)两边分别乘以$\varphi _i^k (x)$,加上所有方程,得到
方程(52)和(53)两边分别乘以$Y_r^k$和$\varTheta _r^k$,再加上所有方程,可以得到
对方程(54)部分积分,再加上方程(55),在系统的边界条件和匹配条件下,可以得到
方程(56)代入方程(54)的左边,可以得到
交换方程(57)的下标,可以得到
方程(58)与方程(57)相减有
由方程(59),可记下列积分为
式中,$M_k$为系统第k阶模态质量. 由方程(60)和方程(57),可记下列积分为
式中,$K_k$为系统第k阶模态刚度.
2.4 系统的状态空间模型
系统的位移可由全局模态乘以模态坐标的形式表示为
其中,$q_j (t)$为系统的模态坐标.
将式(62)分别代入梁的运动微分方程(25),铰链传递扭矩的非线性表达式(29),端部刚体的运动方程(34)和(35),可以得到
方程(63)的两边乘以$\phi _{i}^{ k}$,再沿梁的全长积分,方程(65)和(66)两边分别乘以$Y_r^k$和$\varTheta _r^k$,再加上所有方程,在系统的匹配条件和边界条件下,利用系统全局模态的正交性,可以得到
式中,$\alpha _k $为梁的模态阻尼,$\gamma _k$为铰链的阻尼,$e_k$为铰链的摩擦扭矩,方程(67)中各相关系数为
$$ \begin{array}{l} \alpha _k = {\left( {a / {\omega _k } + b \omega _k } \right)} / 2 ,\ \ \gamma _k = \frac{c}{M_k }\sum_{i = 1}^2 {\sum_{j = 1}^n {\Theta _i^j \Theta _i^k } } e_k = \frac{\mu }{M_k }\sum_{i = 1}^2 {\sum_{j = 1}^n {\Theta _i^k } } p_k = \frac{k_N }{M_k }\sum_{i = 1}^2 {\sum_{j = 1}^n {\sum_{r = 1}^n {\sum_{s = 1}^n {\varTheta _i^j \varTheta _i^r \varTheta _i^s \varTheta _i^k } } } } f_k (t) = \frac{\ddot {w}_s (t)}{M_k }\sum_{i = 1}^2 {\left[ {∫_{-l}^l {\rho \varphi _i^k } d x + m_r Y_r^k } \right]} \hat {B}_k (t) = \frac{C}{M_k }\sum_{i = 1}^2 {U_i } (t)\left[ {{\varphi }'_i (x_{i2} )-{\varphi }'_i (x_{i1} )} \right] \end{array} $$
引入状态向量
则系统的状态方程可表示为
其中
式(67)为系统的非线性动力学方程组,其方程组的线性部分相互独立,非线性部分相互耦合,这样就使得方程组适用于解析方法来研究系统产生的非线性振动. 同时,基于该方法构建的低维状态空间模型(69),可以方便地进行振动控制器设计.
2.5 模态提取方法的有效性验证
为了验证本文提出的全局模态提取方法,这里以有限元方法得出的结果作为参考值,将本文方法给出的固有频率与采用有限元方法计算出的结果进行对比,以验证本文方法的有效性和正确性. 铰链连接的双梁结构的几何尺寸和材料参数见表1.
表1 铰链连接的多梁结构的几何尺寸和材料参数
Table 1
| l/m | E/GPa | b/mm | h"mm |
|---|---|---|---|
| 0.15 | 210 | 50 | 5 |
| p/(kg.m-1) | kL/(Nm.rad-1) | mr /kg | J"(kg.m2) |
| 1.962 5 | 1000 | 0.353 3 | 1.33 x 10-4 |
式中,$\omega _i$和$\omega _i^{\rm ANS}$分别为由解析方法和Ansys得到的结构第i阶固有频率.
图10
图10
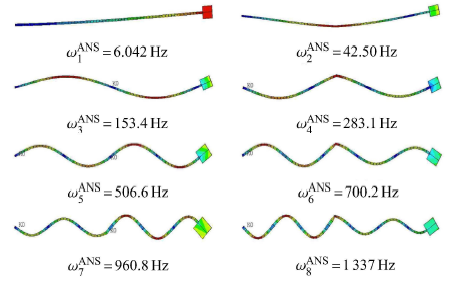
ANSYS得到的结构前八阶固有频率和振型
Fig.10
The first eight natural frequencies and mode shapes of the structure from Ansys
图11
图11
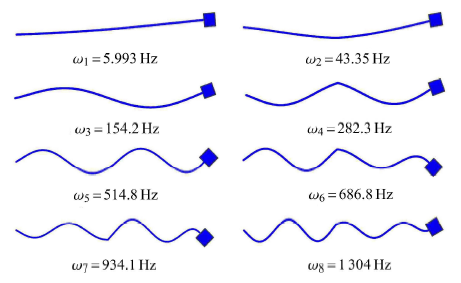
解析方法得到的结构前八阶固有频率和振型
Fig.11
The first eight natural frequencies and mode shapes of the structure from the analytic method
3 结 论
针对复合柔性结构,提出了获取系统全局模态的一般性解析方法. 采用笛卡尔坐标描述系统的运动,给出了建立系统模态方程的策略和步骤. 通过描述柔性部件弹性变形的偏微分方程、描述刚体的运动微分方程以及描述连接界面力、力矩、位移和转角的匹配条件以及系统的边界条件,利用分离变量法给出了统一形式的频率方程,据此获取系统的固有频率和反映结构动力学特征的全局模态. 该方法具有以下优点:
(1) 所求解的系统全局模态是反映系统中各个部件弹性振动的真实模态.在此基础上,方便于分析参数对系统全局模态的影响,从而更深入地揭示系统中各个部件之间的振动耦合关系.
(2)由于所求解的全局模态为系统的真实模态,相比采用单个柔性部件的假设模态得到的动力学模型,基于全局模态方法得到的动力学模型,其精度更高、自由度更少.
(3)在考虑非线性因素的情况下,基于全局模态方法得到的系统非线性振动方程,其方程的线性部分相互独立,非线性部分相互耦合.这可以为采用解析方法求解复合柔性结构的非线性动态响应提供有效的低阶动力学模型.
(4) 基于解析形式的全局模态函数可以方便地构建系统的低维状态空间模型,有利于主动振动控制器的设计.
参考文献
条带式太阳帆的结构动力学分析
Structural dynamic and stability analysis of a stripped solar sail
黏性流体环境下V 型悬臂梁结构流固耦合振动特性研究
V型悬臂梁结构在原子力显微镜、微纳机械传感器件中得到了广泛应用,该结构通常在黏性流体环境下实现精密检测、传感与性能表征,同时也会使得结构的流固耦合振动特性更为复杂,直接影响器件的动态性能.本文针对V型结构变截面、变刚度等复杂几何特征,建立了黏性流体环境下V型悬臂梁结构的流固耦合动力学模型,导出了基于截面孔宽比参数的梁结构的修正水动力函数,确定了截面孔宽比和频率参数影响下V型悬臂梁结构的水动力函数;理论分析得到了黏性流体中V型梁结构的频率响应特性.同时,设计了多种不同几何尺寸的V型梁结构,并在水环境中开展了实验验证,结果表明,实验所得频率响应与理论分析结果吻合较好,验证了V型梁结构水动力函数修正表达式及流固耦合动力学模型.此外,基于该流固耦合动力学模型,详细分析了不同流体黏度、V型梁角度及尺寸变化对耦合系统振动特性的影响.
Analysis of flexural vibration of V-shaped beams immersed in viscous fluids
V型悬臂梁结构在原子力显微镜、微纳机械传感器件中得到了广泛应用,该结构通常在黏性流体环境下实现精密检测、传感与性能表征,同时也会使得结构的流固耦合振动特性更为复杂,直接影响器件的动态性能.本文针对V型结构变截面、变刚度等复杂几何特征,建立了黏性流体环境下V型悬臂梁结构的流固耦合动力学模型,导出了基于截面孔宽比参数的梁结构的修正水动力函数,确定了截面孔宽比和频率参数影响下V型悬臂梁结构的水动力函数;理论分析得到了黏性流体中V型梁结构的频率响应特性.同时,设计了多种不同几何尺寸的V型梁结构,并在水环境中开展了实验验证,结果表明,实验所得频率响应与理论分析结果吻合较好,验证了V型梁结构水动力函数修正表达式及流固耦合动力学模型.此外,基于该流固耦合动力学模型,详细分析了不同流体黏度、V型梁角度及尺寸变化对耦合系统振动特性的影响.
大跨度Y 形柱地铁车站结构地震反应研究
<p>随着地铁建设的发展,出现了一种新型的结构形式-大跨度Y形柱地铁车站结构,与现有的地铁车站结构完全不同,其空间高大宽敞,环境舒适.为研究该新型地铁车站结构的抗震性能,以北京地铁6号线新华大街站为工程背景,使用FLAC<sup>3D</sup>软件建立土与地下结构三维有限差分动力模型,模拟其在新华大街人工波作用下的响应过程,重点分析了车站Y形柱和侧墙的加速度、位移、应变的规律,并与试验结果进行了对比分析,结果表明:数值模拟与振动台试验结果基本一致,体现出了相似的规律性;Y形柱加速度最大位置出现于柱顶端稍下位置,并非于柱顶端;Y形柱分叉位置处应变出现突变,此点相对于柱底的位移最大,且变化率较大,是抗震设计中需要加强的部位;Y形柱加速度、位移变化都会大于侧墙.上述研究成果对提高该类地铁车站结构抗震性能的认识及抗震设计水平提供了合理的参考与指导.</p>
Seismic response of subway station with large span and Y-shaped column
<p>随着地铁建设的发展,出现了一种新型的结构形式-大跨度Y形柱地铁车站结构,与现有的地铁车站结构完全不同,其空间高大宽敞,环境舒适.为研究该新型地铁车站结构的抗震性能,以北京地铁6号线新华大街站为工程背景,使用FLAC<sup>3D</sup>软件建立土与地下结构三维有限差分动力模型,模拟其在新华大街人工波作用下的响应过程,重点分析了车站Y形柱和侧墙的加速度、位移、应变的规律,并与试验结果进行了对比分析,结果表明:数值模拟与振动台试验结果基本一致,体现出了相似的规律性;Y形柱加速度最大位置出现于柱顶端稍下位置,并非于柱顶端;Y形柱分叉位置处应变出现突变,此点相对于柱底的位移最大,且变化率较大,是抗震设计中需要加强的部位;Y形柱加速度、位移变化都会大于侧墙.上述研究成果对提高该类地铁车站结构抗震性能的认识及抗震设计水平提供了合理的参考与指导.</p>
大型柔性航天器动力学与振动控制研究进展
颗粒材料在高应力环境下会发生颗粒破碎现象,颗粒破碎不仅影响颗粒材料的力学特性,同时与大量工程问题密切相关.目前的相关研究主要集中在唯象地描述颗粒破碎的演化以及破碎对力学特性的影响层面,对颗粒破碎演化路径的物理机制研究较少.本文基于热力学框架,采用细观力学中细观-宏观的均匀化方法推导了颗粒体系弹性能和破碎能量耗散,并在最大能量耗散的假设下,在热力学框架内,建立了理想化的无摩擦球体颗粒等向压缩过程的弹性-破碎模型,阐述了颗粒材料破碎演化路径细观热力学机制.由于模型的推导不依赖任何唯象的经验公式,因此模型中包含的参数均有明确的物理意义.模型预测与前人试验结果对比表明,材料的初始级配对弹性压缩模量和破碎应力的影响并不相同:不同分形维数级配对应的弹性体变模量存在极大值,而破碎应力却随着分形维数的增大单调递增;颗粒破碎的演化符合最大能量耗散原理,且颗粒材料的压缩曲线可以分为弹性-破碎-拟弹性3个机制不同的阶段.
Advances in dynamics and vibration control of large-scale flexible spacecraft
颗粒材料在高应力环境下会发生颗粒破碎现象,颗粒破碎不仅影响颗粒材料的力学特性,同时与大量工程问题密切相关.目前的相关研究主要集中在唯象地描述颗粒破碎的演化以及破碎对力学特性的影响层面,对颗粒破碎演化路径的物理机制研究较少.本文基于热力学框架,采用细观力学中细观-宏观的均匀化方法推导了颗粒体系弹性能和破碎能量耗散,并在最大能量耗散的假设下,在热力学框架内,建立了理想化的无摩擦球体颗粒等向压缩过程的弹性-破碎模型,阐述了颗粒材料破碎演化路径细观热力学机制.由于模型的推导不依赖任何唯象的经验公式,因此模型中包含的参数均有明确的物理意义.模型预测与前人试验结果对比表明,材料的初始级配对弹性压缩模量和破碎应力的影响并不相同:不同分形维数级配对应的弹性体变模量存在极大值,而破碎应力却随着分形维数的增大单调递增;颗粒破碎的演化符合最大能量耗散原理,且颗粒材料的压缩曲线可以分为弹性-破碎-拟弹性3个机制不同的阶段.
Finite element method in dynamics of flexible multibody systems: Modeling of holonomic constraints and energy conserving integration schemes
In this work we discuss an application of the finite elementmethod to modeling of flexible multibody systems employing geometricallyexact structural elements. Two different approaches to handleconstraints, one based on the Lagrange multiplier procedure and anotherbased on the use of release degrees of freedom, are examined in detail.The energy conserving time stepping scheme, which is proved to be wellsuited for integrating stiff differential equations, gouverning themotion of a single flexible link is appropriately modified and extendedto nonlinear dynamics of multibody systems.
大型空间柔性梁的有限元动力学建模方法研究
在精确描述柔性梁变形的基础上,针对具有大范围运动的大型空间柔性结构的动力学建模方法进行了研究。首先利用有限元方法对空间柔性梁结构进行离散,导出其动能、势能及广义力,然后采用Lagrange方程建立系统的精确动力学方程。该方程包含各个方向的变形、变形运动与大范围运动的相互耦合项。
Dynamics modeling of large spatial flexible beam with finite element method
在精确描述柔性梁变形的基础上,针对具有大范围运动的大型空间柔性结构的动力学建模方法进行了研究。首先利用有限元方法对空间柔性梁结构进行离散,导出其动能、势能及广义力,然后采用Lagrange方程建立系统的精确动力学方程。该方程包含各个方向的变形、变形运动与大范围运动的相互耦合项。
Dynamics of flexible-link and flexible-joint manipulator carrying a payload with rotary inertia
A dynamic model of a flexible-arm and flexible-joint manipulator carrying a payload with rotary inertia is presented. The Lagrangian approach in conjunction with the finite element method is employed in deriving the equations of motion, within the assumption of a small deformation theory. All the dynamic coupling terms between the system reference rotational motion, joint torsional deformations and arm bending deformations are accounted for. The dynamics of a payload with rotary inertia are incorporated in the model in a consistent manner. Furthermore, the effects of axial shortening due to beam and bending deformations and motions induced inertial forces as well as the effects of gravity are included in the model. The resulting model and simulation results have shown that the joint flexibility has a pronounced effect on the dynamic behavior of rotating flexible arms that should not be simply neglected. The effect is shown to be due to the nonlinear dynamic interaction between the joint torsional deformations, the arm bending deformations and the system reference rotational motion. Simulation results of the nonlinear and the linearized models are compared and the results are discussed. The effects of the payload are shown to be increasing the elastic deformations amplitudes and reducing the frequency of oscillations. Due to the model nonlinearity, different combinations of system parameters are expected to develop different effects. This makes the proposed model valid in the design process as well as in the performance evaluation.
作大范围空间运动柔性梁的刚——柔耦合动力学
研究带中心刚体的作大范围空间运动梁的刚-柔耦合动力学问题. 从精确的应变-位移关系式出发,在动力学变分方程中, 考虑了横截面转动的惯性力偶和与扭转变形有关的弹性力的虚功率,用速度变分原理建立了考虑几何非线性的空间梁的刚-柔耦合动力学方程,用有限元法进行离散. 通过对空间梁系统的数值仿真研究扭转变形和截面转动惯量对系统动力学性态的影响.
Rigid-flexible coupling dynamics of a flexible beam with three-dimensional large overall motion
研究带中心刚体的作大范围空间运动梁的刚-柔耦合动力学问题. 从精确的应变-位移关系式出发,在动力学变分方程中, 考虑了横截面转动的惯性力偶和与扭转变形有关的弹性力的虚功率,用速度变分原理建立了考虑几何非线性的空间梁的刚-柔耦合动力学方程,用有限元法进行离散. 通过对空间梁系统的数值仿真研究扭转变形和截面转动惯量对系统动力学性态的影响.
Dynamic analysis of a flexible hub-beam system with tip mass
For a dynamic system of a rigid hub and a flexible cantilever beam, the traditional hybrid coordinate model assumes the small deformation in structural dynamics where axial and transverse displacements at any point in the beam are uncoupled. This traditional hybrid coordinate model is referred as the zeroth-order approximation coupling model in this paper, which may result in divergence to the dynamic problem of some rigid lexible coupling systems with high rotational speed. In this paper, characteristics of a flexible hub-beam system with a tip mass is studied. Based on the Hamilton theory and the finite element discretization method, and in consideration of the second-order coupling quantity of the axial displacement caused by the transverse displacement of the beam, the rigid lexible coupling dynamic model (referred as the first-order approximation coupling (FOAC) model in this paper) and the corresponding model in non-inertial system for the flexible hub-beam system with a tip mass are presented firstly, then the dynamic characteristics of the system are studied through numerical simulations under twos cases: the large motion of the system is known and is unknown. Simulation and comparison studies using both the traditional zeroth-order model and the proposed first-order model show that even small tip mass may affect dynamic characteristics of the system significantly, which may result in the largening of vibrating amplitude and the descending of vibrating frequency of the beam, and may affect end position of the hub-beam system as well. The effect of the tip mass becomes large along with the increasing of rotating speed of large motion of the system. When the large motion of the system is at low speed, the traditional ZOAC model may lead to a large error, whereas the proposed FOAC model is valid. When the large motion is at high speed, the ZOAC model may result in divergence to the dynamic problem of the flexible hub-beam system, while the proposed second model can still accurately describe the dynamic hub-beam system.
航空发动机整机有限元模型转子动力学分析
现代航空发动机在工作中不断变化的机械激振,气动激振频率越来越复杂,这使得对航空发动机振动分析必须考虑各结构间的动力影响.因此,利用能够考虑陀螺力矩影响,基于NASTRAN中实体单元编制的转子动力特性计算程序,对发动机整机进行了动力特性计算.首先对转子支承结构传递函数(动刚度)进行计算,并进一步研究其对转子动力特性的影响;分析比较基于不同单元模型计算时,盘轴耦合振动及盘轴连接处的角刚度对转子动力特性的影响,证明了基于实体单元的整机模型能够准确考虑各种振动模态.最后,在分析中发现了高阶转子弯曲振动模态与机匣振动耦合现象及其变化规律,在计算分析的基础上研究了在考虑机匣振动耦合时转子系统临界转速的确定方法.
Rotor dynamic analysis of whole aero-engine models based on finite element method
现代航空发动机在工作中不断变化的机械激振,气动激振频率越来越复杂,这使得对航空发动机振动分析必须考虑各结构间的动力影响.因此,利用能够考虑陀螺力矩影响,基于NASTRAN中实体单元编制的转子动力特性计算程序,对发动机整机进行了动力特性计算.首先对转子支承结构传递函数(动刚度)进行计算,并进一步研究其对转子动力特性的影响;分析比较基于不同单元模型计算时,盘轴耦合振动及盘轴连接处的角刚度对转子动力特性的影响,证明了基于实体单元的整机模型能够准确考虑各种振动模态.最后,在分析中发现了高阶转子弯曲振动模态与机匣振动耦合现象及其变化规律,在计算分析的基础上研究了在考虑机匣振动耦合时转子系统临界转速的确定方法.
一种柔性铰链连接的柔性板结构振动模态分析
针对一种空间铰接柔性板结构的振动特性进行了分析,采用有限元分析方法给出通过柔性铰链连接的柔性板结构建模思路.利用有限元软件ANSYS对几种不同的铰链扭转刚度条件下铰接柔性板结构进行了模态分析,获得了模型结构的前五阶模态曲面及其模态频率.并比较了不同铰链刚度对铰接柔性板结构的模态振型和模态频率的影响.该分析有助于研究铰接柔性板结构的动力学和控制方案的设计、建模和分析. <a style="display: none" id="ChDivSummaryMore">更多</a><a style="display: none" id="ChDivSummaryReset">还原</a>
Vibration modal analysis of flexible plate structure connected by a flexible hinge
针对一种空间铰接柔性板结构的振动特性进行了分析,采用有限元分析方法给出通过柔性铰链连接的柔性板结构建模思路.利用有限元软件ANSYS对几种不同的铰链扭转刚度条件下铰接柔性板结构进行了模态分析,获得了模型结构的前五阶模态曲面及其模态频率.并比较了不同铰链刚度对铰接柔性板结构的模态振型和模态频率的影响.该分析有助于研究铰接柔性板结构的动力学和控制方案的设计、建模和分析. <a style="display: none" id="ChDivSummaryMore">更多</a><a style="display: none" id="ChDivSummaryReset">还原</a>
车用电机的有限元模态分析
<p>模态分析是一种确定结构振动特性的技术,是结构运动学的分析基础,固有频率是结构动力学特性分析中的重要指标。采用有限元法对电动汽车驱动用电机进行模态分析,通过对电机结构进行适当假设和等效,建立电机结构定子绕组、机壳、端盖以及转子和轴的模态有限元仿真模型,分析各结构部件对电机固有频率的影响。通过有限元仿真得到电机结构径向各阶模态的固有频率和模态振型,并通过锤击法模态实验和电机空载噪声频谱验证了有限元分析的准确性。</p>
Finite element method modal analysis of driving motor for electric vehicle
<p>模态分析是一种确定结构振动特性的技术,是结构运动学的分析基础,固有频率是结构动力学特性分析中的重要指标。采用有限元法对电动汽车驱动用电机进行模态分析,通过对电机结构进行适当假设和等效,建立电机结构定子绕组、机壳、端盖以及转子和轴的模态有限元仿真模型,分析各结构部件对电机固有频率的影响。通过有限元仿真得到电机结构径向各阶模态的固有频率和模态振型,并通过锤击法模态实验和电机空载噪声频谱验证了有限元分析的准确性。</p>
基于有限元模型的电机零部件与整机结构振动关联特性
针对电机由多个复杂零部件组合而成导致系统振动故障难以准确诊断的问题,推导了含定子绕组、铁芯、端盖、转轴等电机零部件系统结构动力学方程,采用有限元法构建了某型异步电机零部件与整机系统动力学模型,并运用锤击法验证了建模法的有效性。通过分析无相对位移连接组件与整机有限元模型的固有频率值,得出底板、定子绕组、转轴、铁芯、前端盖及后端盖零部件对整机前三阶模态的贡献程度依次增大;研究零部件间连接方式对电机固有频率的影响,发现电机各阶固有频率随着零部件间连接刚度值增大而增加规律,这些可为电机振动故障分析与动力学设计提供参考。
Structural vibration correlation feature analysis for parts and whole-machine of motor based on finite element model
针对电机由多个复杂零部件组合而成导致系统振动故障难以准确诊断的问题,推导了含定子绕组、铁芯、端盖、转轴等电机零部件系统结构动力学方程,采用有限元法构建了某型异步电机零部件与整机系统动力学模型,并运用锤击法验证了建模法的有效性。通过分析无相对位移连接组件与整机有限元模型的固有频率值,得出底板、定子绕组、转轴、铁芯、前端盖及后端盖零部件对整机前三阶模态的贡献程度依次增大;研究零部件间连接方式对电机固有频率的影响,发现电机各阶固有频率随着零部件间连接刚度值增大而增加规律,这些可为电机振动故障分析与动力学设计提供参考。
A reduced-order analytical model for the nonlinear dynamics of a class of flexible multi-beam structures
Nonlinearities in the differential equations of motion of dynamical systems can play, under certain conditions, such a dominant role that the motion described by linearized differential equations bears no resemblance to the actual motion exhibited by the systems. For a structure, nonlinearities are due to material behavior and to deformation. The latter are called eometric nonlinearities and, even for linear (i.e., Hookean) materials and small deformations, their effect can be dramatic. To investigate the nonlinear behavior of a dynamical system by making use of analytical techniques, one must start the analysis by formulating a set of mathematically consistent differential equations of motion for the system. Furthermore, the equations must be cast in a form that makes them amenable to the application of known analytical methods, such as perturbation techniques, to investigate the motion. The work presented in this paper addresses the formulation of such equations for a class of multi-beam structures. Each beam in the structure may have arbitrary cross section variation along its span, but behaves as inextensional. The structure may have any number of beams and supports, and may carry any number of lumped masses along its span.
Adaptive variable structure maneuvering control and vibration reduction of three-axis stabilized flexible spacecraft
This paper proposes a robust control algorithm for stabilization of a three-axis flexible spacecraft in the presence of model uncertainty, external disturbances and control input nonlinearities. This control algorithm is based on variable structure output feedback control design technique that explicitly accounts for the control input nonlinearities in the stability analysis. Asymptotically and exponentially stable design methods are investigated for constructing the controller to stabilized uncertain system with input nonlinearities. Two kinds of the controller are presented that both ensures the global reaching condition of the sliding mode of the spacecraft dynamics system. Moreover, in the sliding mode, the dynamics system under study still bears the insensitivity to the uncertainties and disturbances as the system with linear input. An additional attractive feature of the control method is that the structure of controller is independent of the elastic mode dynamics of the spacecraft, since in practice the measurement of flexible modes is not easy or feasible. It is also shown that an adaptive version of the proposed controller is achieved through removing requirements of knowing the bounds of the uncertainties and perturbations in advance. Furthermore, a modified adaptation control law is given to improve the adaptive performances such that a new controller is designed which can guarantee the boundedness of the closed-loop system. Numerical simulations show that the precise attitude and vibration suppression can be accomplished using the derived controller for both cases with and without adaptive control.
Input shaping and variable structure control for simultaneous precision positioning and vibration reduction of flexible spacecraft with saturation compensation
This paper treats the question of simultaneous robust attitude control and vibration suppression of orbiting spacecraft with flexible appendages. The spacecraft consists of a rigid body and two flexible appendages and the finite dimensional representation of the flexible spacecraft is assumed to be of arbitrary order. Robust nonlinear variable structure control (VSC) strategy integrated with input shaping technique is concerned for the pitch angle control and elastic vibration suppression under actuator saturation limit. More specially, the input shaper is implemented outside of the feedback loop, which is designed for the reference model and achieves the exact elimination of residual vibration; while for the feedback loop, the variable structure controller is designed to make the closed-loop system behave like the reference model with the input shaper in the presence of parametric uncertainty, external disturbances and actuator saturation. To prevent the presence of input saturation from destroying the system performance, a saturation compensator is designed as well for the variable structure attitude control system. For the synthesis of the attitude controller, only the pitch angel and its derivative are used. Simulation results are presented which show that in the closed loop, pitch angel control and elastic mode stabilization are accomplished in spite of uncertainty and external disturbance.
Active vibration suppression in flexible spacecraft attitude tracking
Abstract The active suppression of vibrations of spacecraft flexible appendages during attitude tracking or large-angle maneuvers is discussed. On the basis of a model obtained using the Lagrangian approach and the unitary quaternion parameterization,piezoelectric actuators are used to damp the vibration of flexible booms induced during the maneuvers: The results of simulation reveal the interest and the practical feasibility of such a control scheme. The control law requires only the measure of the attitude and the angular velocity. The absence of flexible displacement and velocity sensors is compensated for by the presence of appropriate dynamics in the controller.
挠性多体卫星姿态动力学与控制
三轴稳定卫星挠性附件的弹性振动和刚性部件的转动与卫星的姿态运动构成耦合的强非线性系统,因此须设计有效的控制律.该文研究了采用反作用飞轮作为执行机构、带有柔性附件和刚性转动部件的整星零动量三轴稳定卫星的姿态解耦控制问题.导出了卫星的多体系统动力学方程,并给出了部分线性化的形式.进一步利用反馈线性化方法将非线性耦合系统解耦,然后对线性化的系统模型进行状态反馈解耦和极点配置.数值仿真结果表明,该文所设计的控制方法具有很高的姿态控制精度和稳定度.
Attitude dynamics and control of a flexible multi-body satellite
三轴稳定卫星挠性附件的弹性振动和刚性部件的转动与卫星的姿态运动构成耦合的强非线性系统,因此须设计有效的控制律.该文研究了采用反作用飞轮作为执行机构、带有柔性附件和刚性转动部件的整星零动量三轴稳定卫星的姿态解耦控制问题.导出了卫星的多体系统动力学方程,并给出了部分线性化的形式.进一步利用反馈线性化方法将非线性耦合系统解耦,然后对线性化的系统模型进行状态反馈解耦和极点配置.数值仿真结果表明,该文所设计的控制方法具有很高的姿态控制精度和稳定度.
Investigation on the choice of boundary conditions and shape functions for flexible multi-body system
AbstractThe objective of this investigation is to examine the correctness and efficiency of the choice of boundary conditions when using assumed mode approach to simulate flexible multi-body systems. The displacement field due to deformation is approximated by the Rayleigh-Ritz assumed modes in floating frame of reference (FFR) formulation. The deformations obtained by the absolute nodal coordinate (ANC) formulation which are transformed by two sets of reference coordinates are introduced as a criterion to verify the accuracy of the simulation results by using the FFR formulation. The relationship between the deformations obtained from different boundary conditions is revealed. Numerical simulation examples demonstrate that the assumed modes with cantilevered-free, simply-supported and free-free boundary conditions without inclusion of rigid body modes are suitable for simulation of flexible multi-body system with large over all motion, and the same physical deformation can be obtained using those mode functions, differ only by a coordinate transformation. It is also shown that when using mode shapes with statically indeterminate boundary conditions, significant error may occur. Furthermore, the slider crank mechanism with rigid crank is accurate enough for investigating boundary condition problem of flexible multi-body system, which cost significant less simulating time. The project was supported by the National Natural Science Foundation of China (10872126) and the Research Fund of the Doctoral Program of Higher Education of China (20100073110007).
Flexible multibody simulation and choice of shape functions
The approach most widely used for the modelling of flexible bodies in multibody systems has been called the floating frame of reference formulation. In this methodology the flexible body motion is subdivided into a reference motion and deformation. The displacement field due to deformation is approximated by the Ritz method as a product of known shape functions and unknown coordinates depending on time only. The shape functions may be obtained using finite-element-models of flexible bodies in multibody systems, resulting in a detailed system representation and a high number of system equations. The number of system equations of such a nodal approach can be reduced considerably using a modal representation of deformation. This modal approach, however, leads to the fundamental problem of selecting the shape functions.The floating frame of reference formulation is reviewed here using a generic flexible body model, from which the various body models used in multibody simulations may be derived by formulation of specific constraint equations. Special attention is given in this investigation to the following subjects:61 The separation of flexible body motion into a reference motion and deformation requires the definition of a body reference frame, which in turn affects the choice of shape functions. Some alternatives will be outlined together with their advantages and disadvantages.61 Assuming the body deformation to be small, the system equations can be linearized. This may require considering geometric stiffening terms. The problem of how to compute these terms has been solved in literature on the instability of structures under critical loads. For finite element models the geometric stiffening terms are obtained from the tangential stiffness matrix.61 The generality of the flexible body model allows the definition of an object oriented data base to describe the system bodies. Such a data base includes a general interface between multibody- and finite-element-codes.61 By combining eigenfunctions and static deformation modes to represent body deformation one obtains a set of so-called quasi-comparison functions. When selected properly these functions can be shown to improve the representation of stresses significantly.
Constrained and unconstrained modes-some modeling aspects of flexible spacecraft
Not Available
Global mode method for dynamic modeling of a flexible-link flexible-joint manipulator with tip mass
In this paper, the global mode method (GMM) is proposed to obtain a reduced-order analytical dynamic model for a signal flexible-link flexible-joint (SFF) manipulator. Firstly, the nonlinear partial differential equations (PDE) that govern the motion of the flexible link and flexible joint, respectively, are derived by applying the Hamilton principle. By combining the linearized governing equations of motion for a flexible link and the equation of motion for the flexible joint, the characteristic equation is obtained for the whole system. The natural frequencies and global mode shapes of the linearized model of the SFF manipulator are determined, and orthogonality relations of the global mode shapes are established. Then, the global mode shapes and their orthogonality relations are used to truncate the nonlinear PDEs of the SFF manipulator to a nonlinear ordinary differential equation with a few degrees-of-freedom (DOF). For comparison, two other dynamic models of the SFF are derived by employing the assumed mode method (AMM) and finite element method (FEM). To verify the method proposed, the results from the GMM are compared with those obtained from the FEM. The effects of the link length and payload mass on the convergence of AMM model for the first two frequencies are investigated. Based on dynamic models, obtained by GMM and AMM, dynamical responses for the system with different numbers of modes are worked out numerically, which are compared with those obtained from FEM. These comparisons show a good agreement between the results of the GMM and that of the FEM model, which indeed proved the accuracy and applicability of the GMM model.
A parametric analytical model for non-linear dynamics in cable-stayed beam
Nonlinear interactions in the planar dynamics of cable-stayed beam
An analytical model is proposed to study the nonlinear interactions between beam and cable dynamics in stayed-systems. The integro-differential problem, describing the in-plane motion of a simple cable-stayed beam, presents quadratic and cubic nonlinearities both in the cable equation and at the boundary conditions. Mainly studied are the effects of quadratic interactions, appearing at relatively low oscillation amplitude. To this end an analysis of the sensitivity of modal properties to parameter variations, in intervals of technical interest, has evidenced the occurrence of one-to-two and two-to-one internal resonances between global and local modes. The interactions between the resonant modes evidences two different sources of oscillation in cables, illustrated by simple 2dof discrete models. In the one-to-two global ocal resonance, a novel mechanism is analyzed, by which cable undergoes large periodic and chaotic oscillations due to an energy transfer from the low-global to high-local frequencies. In two-to-one global ocal resonance, the well-known parametric-induced cable oscillation in stayed-systems is correctly reinterpreted through the autoparametric resonance between a global and a local mode. Increasing the load the saturation of the global oscillations evidences the energy transfer from high-global to low-local frequencies, producing large cable oscillations. In both cases, the effects of detuning from internal and external resonance are presented.
In-plane free vibration analysis of cable-arch structure
Cable-stayed arch bridge is a new type of composite bridge, which utilizes the mechanical characters of cable and arch. Based on the supporting members of cable-stayed arch bridge and of erection of arch bridge using of the cantilever construction method with tiebacks, we propose a novel mechanical model of cable–arch structure. In this model, the equations governing vibrations of the cable–arch are derived according to Hamilton's principle for dynamic problems in elastic body under equilibrium state. Then, the program of solving the dynamic governing equations is ultimately established by the transfer matrix method for free vibration of uniform and variable cross-section, and the internal characteristics of the cable–arch are investigated. After analyzing step by step, the research results approve that the program is accurate; meanwhile, the mechanical model and method are both valuable and significant not only in theoretical research and calculation but also in design of engineering.
索——梁组合结构中拉索的非线性响应
研究由桥面振动引起的斜拉索参数共振和亚谐波共振问题。首先,建立索-梁组合结构力学模型,推导了考虑拉索初始垂度的索-梁组合结构非线性动力学方程。然后利用多尺度方法研究斜拉索的参数共振和亚谐波共振,并对稳态解的稳定性进行了分析。最后对斜拉索参数共振和亚谐波共振进行数值模拟,得到不同阻尼及不同初始条件下的拉索时间历程曲线。数值模拟结果表明斜拉索振幅与阻尼有关,但不受拉索初始条件影响。
Nonlinear response of cables in cable-stayed bean structure
研究由桥面振动引起的斜拉索参数共振和亚谐波共振问题。首先,建立索-梁组合结构力学模型,推导了考虑拉索初始垂度的索-梁组合结构非线性动力学方程。然后利用多尺度方法研究斜拉索的参数共振和亚谐波共振,并对稳态解的稳定性进行了分析。最后对斜拉索参数共振和亚谐波共振进行数值模拟,得到不同阻尼及不同初始条件下的拉索时间历程曲线。数值模拟结果表明斜拉索振幅与阻尼有关,但不受拉索初始条件影响。
Modeling and nonlinear modal characteristics of the cable-stayed beam
61Considering the static configuration of the cable and beam, using the piecewise function, the mode shapes of the cable-stayed beam can be obtained precisely.61The nonlinear modal properties of the system have been investigated.61The nonlinear coupling term make a meaningful contribution of the modal properties.
索——梁组合结构的建模及面内动力特性分析
利用哈密顿变分原理以及结构动静态构型的影响,建立了索-梁组合结构的约化运动学控制方程.考虑到边界条件和耦合连接条件,我们研究了体系的面内特征值问题.根据求解得到的面内特征值方程,并通过分段函数的引入,结构的模态函数可以被直接确定.随后,我们研究了参数垂跨比f,刚度比K和质量比m对面内固有频率的影响.研究发现从结构的频率谱图中可以看出频率跳跃现象是存在的,另外,频率穿越现象也是十分明显.随后,考虑到局部模态和整体模态,结合之前确定的特征值方程及分段振型函数,我们研究了索-梁组合结构可能的模态形状.最后,我们讨论了索-梁组合结构可能发生的内共振形式,比如面内1:1内共振形式以及1:2内共振形式.研究表明梁的静态构型不仅直接影响到耦合力连接条件,还将影响索-梁组合结构频率的确定.
Modeling and in-plane dynamics analysis of the cable-stayed beam
利用哈密顿变分原理以及结构动静态构型的影响,建立了索-梁组合结构的约化运动学控制方程.考虑到边界条件和耦合连接条件,我们研究了体系的面内特征值问题.根据求解得到的面内特征值方程,并通过分段函数的引入,结构的模态函数可以被直接确定.随后,我们研究了参数垂跨比f,刚度比K和质量比m对面内固有频率的影响.研究发现从结构的频率谱图中可以看出频率跳跃现象是存在的,另外,频率穿越现象也是十分明显.随后,考虑到局部模态和整体模态,结合之前确定的特征值方程及分段振型函数,我们研究了索-梁组合结构可能的模态形状.最后,我们讨论了索-梁组合结构可能发生的内共振形式,比如面内1:1内共振形式以及1:2内共振形式.研究表明梁的静态构型不仅直接影响到耦合力连接条件,还将影响索-梁组合结构频率的确定.
Modal analysis of gyroscopic flexible spacecraft: a continuum approach
In the past, modal analyses of gyroscopic spacecraft have been performed after constructing a discrete model of the dynamics. This, however, obscures any momentum interaction between different parts of the spacecraft. This paper uses a continuum approach and gives a clear formulation of the complex gyroscopic vehicle modes. It is shown that unlike discrete modal analysis, special care is required while composing the phase space representation of the vehice dynamics for a continuum modal analysis. The motion of the vehicle is shown to consist of two phases. In the first phase the vehicle executes a rigid body rotation with respect to an inertial frame. This rotation depends on the instantaneous angular momentum of the vehicle and determines the location of the associated Tisserand's frame. The second phase accounts for deformation measured from the Tisserand's frame and is expressed as a superposition of infinite gyroscopic modes. This phase contributes zero overall angular momentum.
Hinges-free and hinges-locked modes of a deformable multibody space station-a continuum analysis
Not Available
Modal identities for multibody elastic spacecraft
Not Available
复合柔性结构航天器动力学建模研究
柔性航天器动力学建模的传统方法是采用混合坐标法,针对中心刚体带大型柔性附件类的航天器,这种方法在理论建模和工程应用方面都获得了极大的成功。在中心刚体加柔性附件类航天器柔性动力学研究成炎学模型,其软件系统DASFA2.0已初步用于工程分析设计。
Dynamics modeling of spacecraft with composite flexible structures
柔性航天器动力学建模的传统方法是采用混合坐标法,针对中心刚体带大型柔性附件类的航天器,这种方法在理论建模和工程应用方面都获得了极大的成功。在中心刚体加柔性附件类航天器柔性动力学研究成炎学模型,其软件系统DASFA2.0已初步用于工程分析设计。
关于柔性航天器动力学模型降阶问题
针对柔性航天器动力学模型的降阶问题,综述了动力学建模中几种常用的模态集,介绍了用于选择系统保留模态的有关准则.通常的模态价值分析和内平衡理论是用于航天器系统模态的选取,而不是直接用于动力学建模时的部件模态或系统结构弹性变形模态的选取,因而存在如何应用上述准则于动力学建模的问题.为此,提出了一个动力学建模时的降阶策略;还提供了一个数值例子,以对采用不同的模态集建模时的结果进行比较,并表明如何采用上述准则于航天器的动力学建模.
On the order reduction of dynamics models of flexible spacecraft
针对柔性航天器动力学模型的降阶问题,综述了动力学建模中几种常用的模态集,介绍了用于选择系统保留模态的有关准则.通常的模态价值分析和内平衡理论是用于航天器系统模态的选取,而不是直接用于动力学建模时的部件模态或系统结构弹性变形模态的选取,因而存在如何应用上述准则于动力学建模的问题.为此,提出了一个动力学建模时的降阶策略;还提供了一个数值例子,以对采用不同的模态集建模时的结果进行比较,并表明如何采用上述准则于航天器的动力学建模.
柔性航天器的模态综合——混合坐标动力学建模
针对由中心体和柔性附件组成的 柔性航天器 ,采用混合坐标法 ,通过伪坐标形式的拉格朗日方程 ,建立了全柔性航天器的混合坐标动力学方程。建模中采用模态综合理论的方法 ,由航天器结构的弹性正则模态和静变形模态组成的模态集表示结构变形 ,以便更有效的将结构变形的影响引入到航天器的动力学模型中。文中用由盒形中心体和两帆板组成的假想航天器系统为例 ,以此系统的有限元动力学模型为基准 ,比较了采用弹性正则模态和静变形模态的模态综合建模和单纯采用弹性正则模态的常规建模时得到的系统特征频率 ,表明引入静变形模态以后 ,所得到的动力学模型能更好反映柔性航天器的动力学特性。
Modal synthesis-hybrid coordinate dynamics modeling of flexible spacecrafts
针对由中心体和柔性附件组成的 柔性航天器 ,采用混合坐标法 ,通过伪坐标形式的拉格朗日方程 ,建立了全柔性航天器的混合坐标动力学方程。建模中采用模态综合理论的方法 ,由航天器结构的弹性正则模态和静变形模态组成的模态集表示结构变形 ,以便更有效的将结构变形的影响引入到航天器的动力学模型中。文中用由盒形中心体和两帆板组成的假想航天器系统为例 ,以此系统的有限元动力学模型为基准 ,比较了采用弹性正则模态和静变形模态的模态综合建模和单纯采用弹性正则模态的常规建模时得到的系统特征频率 ,表明引入静变形模态以后 ,所得到的动力学模型能更好反映柔性航天器的动力学特性。
Dynamic analysis of a micro-resonator driven by electrostatic combs
The dynamic response of a micro-resonator driven by electrostatic combs is investigated in this work. The micro-resonator is assumed to consist of eight flexible beams and three rigid bodies. The nonlinear partial differential equations that govern the motions of the flexible beams are obtained, as well as their boundary and matching conditions. The natural matching conditions for the flexible beams are the governing equations for the rigid bodies. The undamped natural frequencies and mode shapes of the linearized model of the micro-resonator are determined, and the orthogonality relation of the undamped global mode shapes is established. The modified Newton iterative method is used to simultaneously solve for the frequency equation and identify repeated natural frequencies that can occur in the micro-resonator and their multiplicities. The Gram-Schmidt orthogonalization method is extended to orthogonalize the mode shapes of the continuous system corresponding to the repeated natural frequencies. The undamped global mode shapes are used to spatially discretize the nonlinear partial differential equations of the micro-resonator. The simulation results show that the geometric nonlinearities of the flexible beams can have a significant effect on the dynamic response of the micro-resonator.
Modeling and analysis of the in-plane vibration of a complex cable-stayed bridge
The in-plane vibration of a complex cable-stayed bridge that consists of a simply-supported four-cable-stayed deck beam and two rigid towers is studied. The nonlinear and linear partial differential equations that govern transverse and longitudinal vibrations of the cables and transverse vibrations of segments of the deck beam, respectively, are derived, along with their boundary and matching conditions. The undamped natural frequencies and mode shapes of the linearized model of the cable-stayed bridge are determined, and orthogonality relations of the mode shapes are established. Numerical analysis of the natural frequencies and mode shapes of the cable-stayed bridge is conducted for various symmetrical and non-symmetrical bridge cases with regards to the sizes of the components of the bridge and the initial sags of the cables. The results show that there are very close natural frequencies when the bridge model is symmetrical and/or partially symmetrical, and the mode shapes tend to be more localized when the bridge model is less symmetrical. The relationships between the natural frequencies and mode shapes of the cable-stayed bridge and those of a single fixed ixed cable and the single simply-supported deck beam are analyzed. The results, which are validated by commercial finite element software, demonstrate some complex classical resonance behavior of the cable-stayed bridge.
Dynamics of a multi-beam structure connected with nonlinear joints: modelling and simulation
A dynamic modelling approach for a multi-beam structure connected with nonlinear joints is presented and subsequently used to obtain its reduced-order analytical model. Firstly, by applying the...
Dynamic modeling and simulation for flexible spacecraft with flexible jointed solar panels
This paper presents a dynamic modeling approach for flexible spacecraft with multiple solar panels and flexible joints. Firstly, the characteristic equation for the flexible spacecraft is derived in terms of the partial differential equations of motion for the solar panels, the ordinary differential equations of motion for the central rigid body, the matching conditions at the joints, and the boundary conditions. The natural frequencies and global mode shapes of the flexible spacecraft are determined, and orthogonality relations of the global mode shapes are established. Then, the global mode shapes and their orthogonality relations are used to truncate the dynamical equation of the flexible spacecraft to a set of ordinary differential equations with multiple-DOF. The validity of the derived model is verified by comparing the natural frequencies obtained from the characteristic equation with those obtained from FEM. For each global mode shape, a translation index and a set of rotation indexes are introduced to describe the interaction between the elastic deformation of the solar arrays and the displacements of the central rigid body. Based on the truncated dynamic model obtained in this paper, dynamical responses of the flexible spacecraft with flexible joints are worked out numerically for the cases of orbit control and attitude control, respectively. The corresponding results of the flexible spacecraft with rigid joints are given to illustrate the effects of flexible joints on the responses of the system. The results show that the joint flexibility has a significant effect on the dynamical responses of the flexible spacecraft, especially, in the case of very small stiffness of the joints.
压电柔性结构振动的鲁棒控制
针对具有多面体型参数不确定性和外界扰动的柔性悬臂梁系统,研究其振动的鲁棒控制问题.基于压电柔性悬臂梁系统的状态方程,利用一种扩展LMI(Linear Matrix Inequality),对柔性悬臂梁的振动提出了改进的 H<sub>2</sub>/H<sub>∞</sub> 综合状态反馈鲁棒控制方法.此方法针对多面体型参数不确定性系统引入不同的Lyapunov函数,降低了原来 H<sub>2</sub>/H<sub>∞</sub> 综合鲁棒控制方法中由于使用一个公共Lyapunov函数而产生的保守性.通过Matlab分别采用改进和未改进的 H<sub>2</sub>/H<sub>∞</sub> 鲁棒控制方法对柔性悬臂梁系统的振动控制进行了数值仿真.仿真结果表明,2种方法都使柔性悬臂梁的振动得到了良好控制,而改进方法的控制效果更好.
Robust vibration control of flexible piezoelectric structure
针对具有多面体型参数不确定性和外界扰动的柔性悬臂梁系统,研究其振动的鲁棒控制问题.基于压电柔性悬臂梁系统的状态方程,利用一种扩展LMI(Linear Matrix Inequality),对柔性悬臂梁的振动提出了改进的 H<sub>2</sub>/H<sub>∞</sub> 综合状态反馈鲁棒控制方法.此方法针对多面体型参数不确定性系统引入不同的Lyapunov函数,降低了原来 H<sub>2</sub>/H<sub>∞</sub> 综合鲁棒控制方法中由于使用一个公共Lyapunov函数而产生的保守性.通过Matlab分别采用改进和未改进的 H<sub>2</sub>/H<sub>∞</sub> 鲁棒控制方法对柔性悬臂梁系统的振动控制进行了数值仿真.仿真结果表明,2种方法都使柔性悬臂梁的振动得到了良好控制,而改进方法的控制效果更好.
太阳翼铰链结构的动力学实验与非线性动力学建模
<p>通过动力学实验获得真实的太阳翼板间铰链结构于不同激振频率下的振动响应参数,并采用力状态映射法建立板间铰链的非线性动力学模型。首先,采用单频激励信号模拟外扰对实际的板间铰链结构实施动力学实验;然后,基于其结构具有的多重非线性动力学特性,根据实验数据应用力状态映射法辨识结构的动力学参数,建立其非线性动力学模型;最后,对由太阳翼板间铰链连接的两段梁所构成的系统进行了冲击激励下的振动响应测试,同时进行了有限元动力学仿真,实验测试结果和数值仿真结果取得了较好的一致性。本文建立的太阳翼板间铰链非线性动力学模型能够较好地反映其动力学特性,对于实际太阳翼结构的动力学建模具有理论参考价值。</p>
Dynamic experiments and nonlinear dynamics modeling of joints in solar array
<p>通过动力学实验获得真实的太阳翼板间铰链结构于不同激振频率下的振动响应参数,并采用力状态映射法建立板间铰链的非线性动力学模型。首先,采用单频激励信号模拟外扰对实际的板间铰链结构实施动力学实验;然后,基于其结构具有的多重非线性动力学特性,根据实验数据应用力状态映射法辨识结构的动力学参数,建立其非线性动力学模型;最后,对由太阳翼板间铰链连接的两段梁所构成的系统进行了冲击激励下的振动响应测试,同时进行了有限元动力学仿真,实验测试结果和数值仿真结果取得了较好的一致性。本文建立的太阳翼板间铰链非线性动力学模型能够较好地反映其动力学特性,对于实际太阳翼结构的动力学建模具有理论参考价值。</p>