MULTI-OUTPUT PHYSICS-INFORMED NEURAL NETWORKS MODEL BASED ON THE RUNGE-KUTTA METHOD
-
摘要: 物理信息神经网络(physics-informed neural networks, PINN)由于嵌入了物理先验知识, 可以在少量训练数据的情况下获得自动满足物理约束的代理模型, 受到了智能科学计算领域的广泛关注. 但是, PINN的离散时间模型(PINN-RK)无法同时近似多个物理量相互耦合的偏微分方程系统, 限制了其处理复杂多物理场的能力. 为了打破这一限制, 文章提出了一种基于龙格库塔法的多输出物理信息神经网络(multi-output physics-informed neural networks based on the Runge-Kutta method, MO-PINN-RK), MO-PINN-RK模型在离散时间模型的基础上采用了并行输出的神经网络结构, 通过将神经网络划分为多个子网络, 建立了多个神经网络输出层. 采用不同输出层近似不同物理量的方式, MO-PINN-RK模型不仅可以同时表征多个物理量, 而且还能够实现求解偏微分方程系统的目的. 另外, MO-PINN-RK克服了PINN离散时间模型仅适用于一维空间的局限性, 将其应用范围扩展到了更为普遍的多维空间. 为了验证MO-PINN-RK的有效性, 文章对圆柱绕流问题进行了流场预测和参数辨识研究. 测试结果表明, 与PINN相比, MO-PINN-RK在流场预测问题中的准确性获得了提升, 其精度至少提高了2倍, 而在参数辨识问题中, MO-PINN-RK的相对误差降低了一个数量级. 这凸显了MO-PINN-RK在流体动力学领域的卓越能力, 为解决复杂问题提供了更准确、更有效的解决方案.Abstract: Physics-informed neural networks (PINN) have attracted considerable attention in the field of intelligent scientific computing primarily due to their capacity to incorporate prior knowledge of physics. This outstanding integration allows PINNs to automatically satisfy physical constraints even with limited or zero labeled data. As a result, the applicability and effectiveness of PINN are vastly developed across numerous domains. However, it is worth noting that the discrete time models of PINN, also known as PINN-RK, face a significant limitation in their ability to approximate multiple physical quantities and solve coupled partial differential equation systems simultaneously. This shortcoming hinders its ability to handle complex multi-physics fields, which is a crucial drawback in various practical scenarios. To overcome this limitation, a multi-output physics-informed neural network based on Runge-Kutta method (MO-PINN-RK) is proposed in this paper.MO-PINN-RK, building upon the success of PINN-RK, incorporates a sophisticated parallel neural network architecture, boasting multiple output layers for enhanced performance and accuracy. By associating each output layer with a sub-network and assigning it with different physical quantities, MO-PINN-RK can accurately solve the coupled partial differential equation system and predict multiple physical quantities simultaneously. The MO-PINN-RK proposed in this paper overcomes the limitation of PINN-RK that is only applicable to one dimensional problems extending its applicability to more general multi-dimensional problems. To demonstrate the effectiveness of MO-PINN-RK, it is then applied to the flow field prediction and parameter identification of flow around a cylinder. The outcomes unequivocally reveal that MO-PINN-RK surpasses PINN in terms of flow field prediction precision, achieving an enhancement of no less than 2 times. At the same time, MO-PINN-RK reduces the relative error by an order of magnitude in the context of parameter identification. This highlights the exceptional capabilities of MO-PINN-RK in the field of fluid dynamics, offering a more accurate and efficient solution for solving complex problems.
-
引 言
近年来, 随着计算资源和可用数据的暴发式增长, 机器学习技术不仅在计算机视觉[1]、自然语言处理[2]和智能推荐系统[3]等方面取得了革命性成果, 在智能计算领域也展现出了巨大潜力[4]. 目前, 机器学习技术已被广泛应用于各种常见的科学问题[5]和工程问题[6]. 例如, 基于高斯过程[7]求解线性和非线性偏微分方程(partial differential equations, PDE), 采用稀疏回归算法[8]从观测数据中反演物理系统的状态和属性, 以及基于深度学习方法对流场进行超分辨重构[9]等. 但是, 上述机器学习技术属于基于数据驱动的方法, 强大的代理模型需要建立在大量的训练数据之上. 而在现实应用场景中, 数据的获取通常伴随着昂贵的代价和成本, 这导致人们往往要在信息不完备的情况下对复杂系统做出预测和决策. 另外, 绝大多数先进的机器学习技术都是建立在概率统计上的一种黑箱模型[10], 缺乏对物理系统内部机理的合理解释. 在这种背景下, 物理信息神经网络[11](physics-informed neural networks, PINN)因其训练数据少和内嵌了物理先验知识而受到学术界的广泛关注.
PINN的基本原理是神经网络的函数通用近似定理[12], 核心思想是将PDE的残差形式嵌入到神经网络的损失函数中, 约束训练参数的求解空间. 该思想最早出现于1994年, Dissanayake等[13]基于神经网络强大的非线性近似能力, 将求解PDE的数值问题转化为无约束优化问题, 通过最小化损失函数实现了神经网络输出对PDE解的近似. 但是, 由于当时反向传播算法的落后以及计算资源的限制, 使用神经网络求解PDE的方法并未引起太多的关注. 近年来, 随着机器学习技术的崛起和自动微分技术[14]的出现, 该方法才再次走进科研人员的视野. 在2019年, Raissi等[11]采用自动微分技术代替了原始的手动求导方法, 极大地提升了神经网络的计算效率, 并正式将嵌入物理知识的神经网络命名为PINN. 并且, 为了应对不同的使用场景, Raissi进一步设计了连续时间模型和离散时间模型两种不同的神经网络模型.
PINN的概念自从被提出后, 迅速成为数据科学工程和人工智能领域的研究热点[15]. 为了提高PINN求解PDE问题的精度、加快收敛速度以及增强泛化性能, 研究人员从神经网络结构、损失函数类型和激活函数形式等方面展开了深入研究, 并提出了各种PINN的变体. Yu等[16]利用PDE的梯度信息, 将额外的梯度项嵌入到损失函数中, 提出了梯度增强型物理信息神经网络(gPINN)框架, 提高了神经网络的稳定性和泛化性. 针对PINN训练过程中存在梯度反向传播不平衡的问题, Wang等[17]提出了一种自适应学习率退火算法, 可以在PINN训练期间动态调节各个损失项的量级, 提高模型求解精度. Jagtap等[18]通过在激活函数中加入可缩放因子, 提出了一种自适应激活函数, 加快了PINN求解非线性PDE的收敛速度.
根据损失函数不同的构造方式, PINN可以分为连续时间模型和离散时间模型, 离散时间模型也被称为基于龙格库塔法的物理信息神经网络(physics-informed neural networks based on the Runge-Kutta method, PINN-RK). 为方便起见, 文中后续内容中的PINN将特指物理信息神经网络连续时间模型. 虽然PINN具有出色的高效性和灵活性, 但是仍存在两个局限性[19-23]. 在正问题中, 随着PDE维度的升高, 其施加物理约束所需的采样点数量呈指数级增长, 增加了计算负担. 在逆问题中, 其前提假设是采样数据在整个时空域内是连续可用的, 采样点能够取到求解域内的任意时空坐标点. 但是, 在实际的应用场景中, 该假设往往难以得到满足. 数据采集过程中, 传感器通常在固定位置上以固定时间间隔对系统进行采样. 并且, 对于采样空间较大的应用, 采样数据在时空域内往往呈现出稀疏离散的特点. 与PINN相比, PINN-RK的使用并不存在该假设限制, 更加符合实际应用场景, 约束点数量也不会随PDE维度的升高而呈现指数级增长. 但是, 迄今为止, 针对PINN-RK的研究少之又少, 且主要集中在一维非稳态问题上. 另外, 由于神经网络结构的限制, PINN-RK的输出仅能表征一种物理量, 无法同时反映多个物理量的状态, 导致现有的PINN-RK模型仅适用于求解单个PDE, 而无法求解相互耦合的PDE系统.
因此, 为了扩展PINN-RK的应用范围和实现对PDE系统的求解, 本文提出了一种基于龙格库塔法的多输出物理信息神经网络(multi-output physics-informed neural networks based on the Runge-Kutta method, MO-PINN-RK). MO-PINN-RK在PINN-RK的基础上采用了并行输出的神经网络结构, 通过将神经网络划分为多个子网络, 建立了多个神经网络输出层, 利用不同输出层近似不同的物理量, 并通过输出层共享的隐藏层捕捉不同物理量之间的耦合关系, 使MO-PINN-RK不仅可以同时预测多个物理量, 还可实现耦合PDE系统的求解. 为验证MO-PINN-RK的有效性, 本文将二维不可压缩流体的圆柱绕流问题作为测试案例. 基于观测数据, 使用MO-PINN-RK对流场预测和参数辨识两种问题展开研究, 并将模型预测解与基准解进行对比. 本工作采用并行的多输出神经网络结构, 构建了新型的PDE求解器, 以期为工程和科学领域的问题求解提供准确高效的解决方案.
1. 物理信息神经网络
1.1 PINN
一般情况下, 线性和非线性PDE的通用形式为
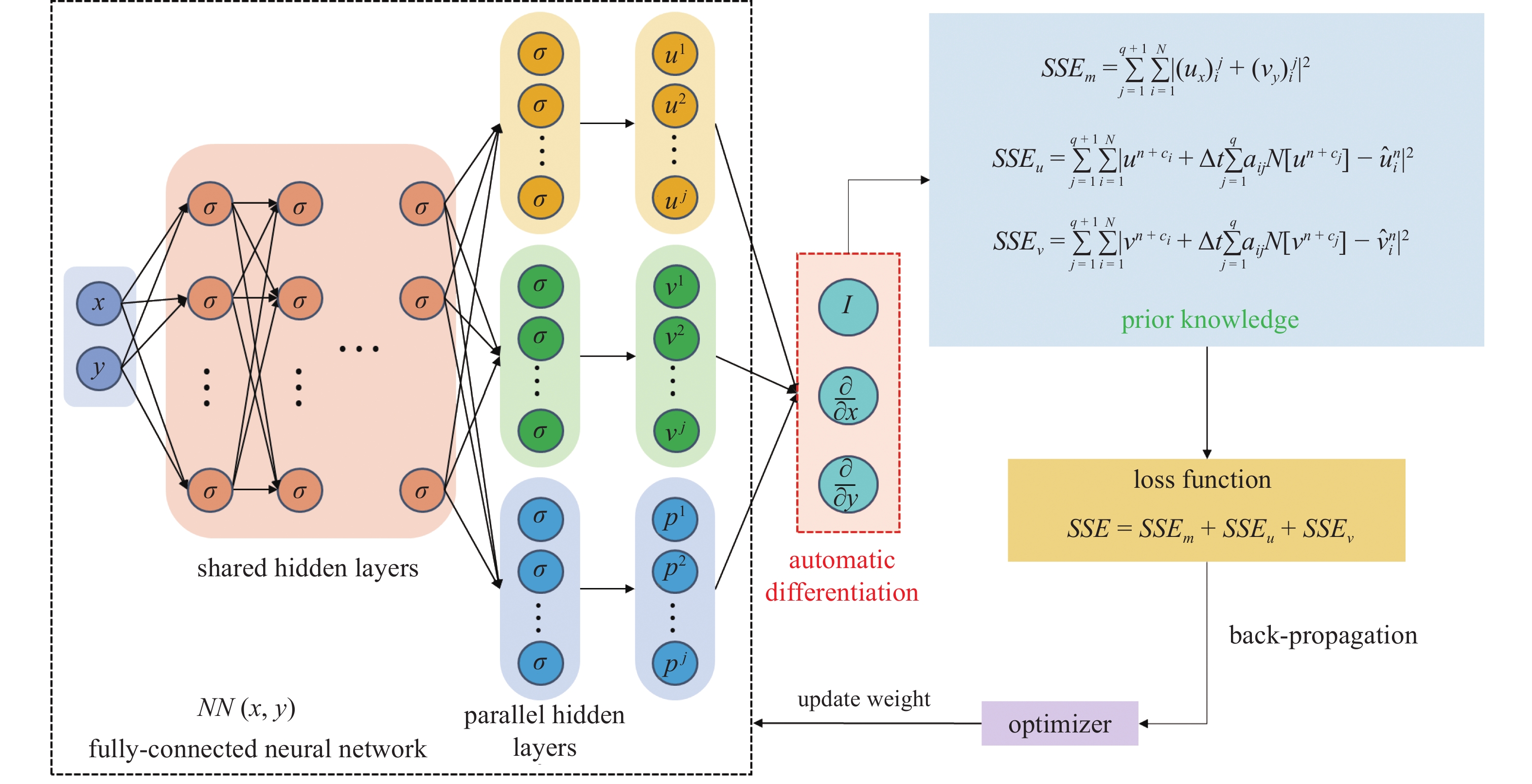
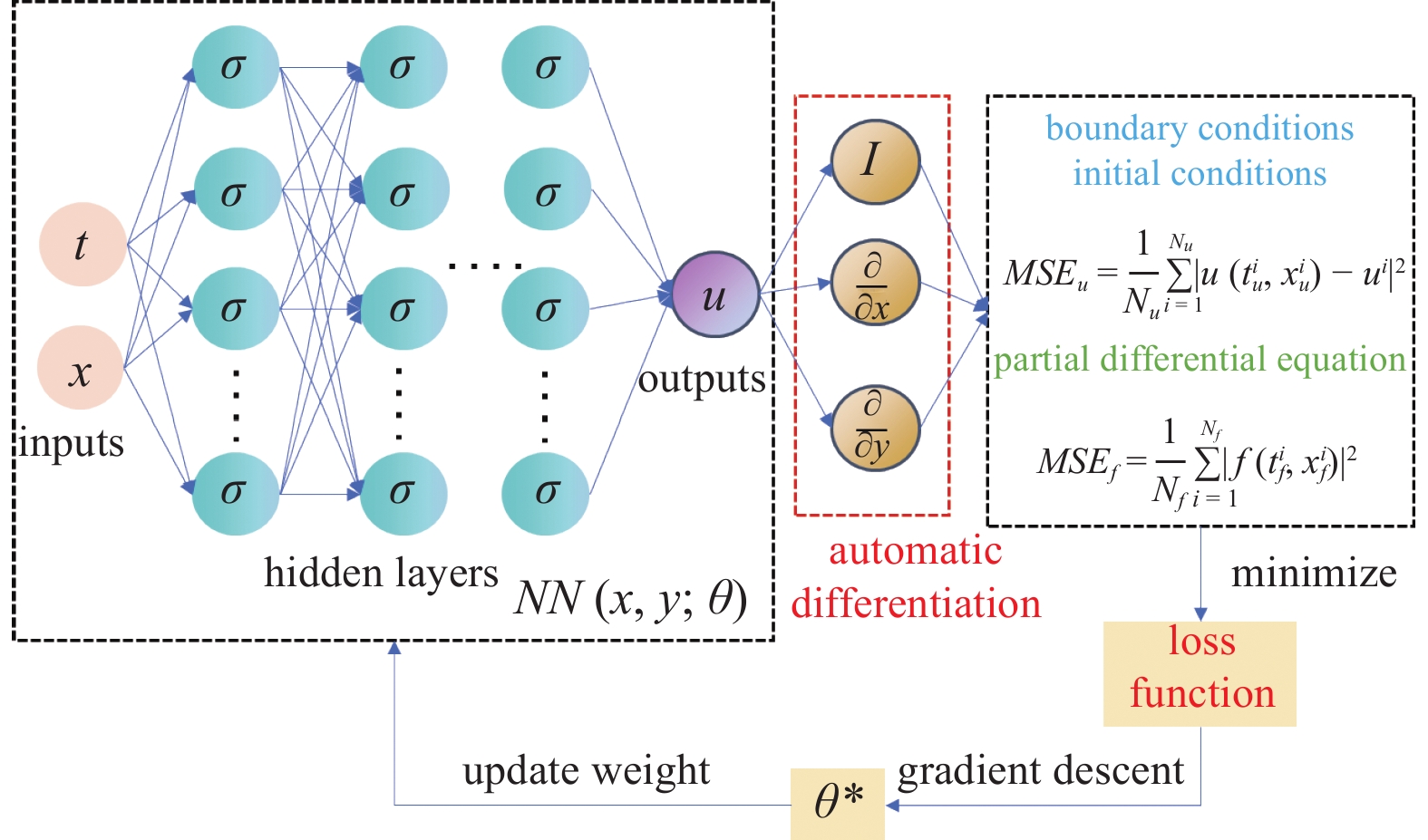
$$ {u_t}(t,x) + \mathcal{N}[u(t,x)] = 0\quad x \in \varOmega ,t \in [0,T] $$ (1) 其中, $ u(t,x) $表示PDE的解, 下标$ t $表示函数$ u(t,x) $对时间的偏导数, $ \mathcal{N}[\cdot] $表示线性或非线性微分算子, $\varOmega$为$ {\mathbb{R}^D} $的子集. 从神经网络的通用近似定理可知, 一个包含足够多神经元的单层神经网络模型可以以任意精度近似一个非线性函数. 基于该定理, 在大量训练数据的基础上, 可以通过神经网络的输出近似PDE的解. 然而, 很多科学问题和工程系统的数据采集较为困难, 基于大量数据的机器学习技术并不适用于这些小数据系统. 人们对于科学问题和工程应用却有着大量的先验知识, 这些先验知识的存在恰好可以弥补数据上的不足. 一般而言, 先验知识以PDE守恒方程的形式出现, 如式(1)所示. 与传统的神经网络不同, PINN是一种将物理先验知识嵌入到损失函数中的神经网络模型, 如图1所示.
PINN通过最小化损失函数的方式, 使用梯度下降算法不断更新神经网络的权重和偏差, 以实现近似PDE解的目的[24]. 将PDE的残差形式以惩罚项的方式加入到神经网络损失函数中, 可以为神经网络的优化学习指明方向, 减少可行解的参数空间, 降低训练代价. 当神经网络的权重参数不满足约束条件时, 惩罚项会导致损失函数的增加. 因此, 在神经网络优化过程中, 惩罚项会影响权重的调整, 以达到在约束条件下降低总损失值的目标. 先验知识的嵌入相当于人为地从数据中提取了物理规律, 代替机器学习模型进行了部分特征提取工作, 节省了优化算法自身进行数据挖掘的时间. 另外, 相比于优化算法主动学习隐藏在数据中的物理规律, 显式地将先验知识嵌入到神经网络中的做法可以进一步放大增强数据中的信息量[25], 更有益于模型朝着最优解的方向前进.
1.2 PINN-RK
龙格库塔法是一种高阶精度的数值方法, 常被用于科学计算和工程应用中. 该方法通过在每个时间步中计算多个中间节点加权和的方式逼近数值解, 可以有效地抑制数值发散等问题, 提高了数值求解过程的稳定性, 因此更适用于处理长时间跨度问题. PINN-RK是神经网络与龙格库塔法结合的产物. 将$ q $阶龙格库塔公式[26]应用到式(1), 可以得到
$$ {u^{n + {c_i}}} = {u^n} - \Delta t\sum\limits_{j = 1}^{q + 1} {{a_{ij}}} \mathcal{N}\left[ {{u^{n + {c_j}}}} \right],\quad i = 1,2, \cdots ,q,q + 1 $$ (2) 其中, $ q $为龙格库塔阶数, $ \Delta t $表示时间间隔, $ {a_{ij}} $为龙格库塔公式中的系数, 龙格库塔公式的显式格式和隐式格式由这些系数所决定. 由于隐式格式具有非常出色的稳定性, 本文后续计算均采用隐式龙格库塔公式. $ {c_i} $和$ {c_j} $为龙格库塔节点, $ {u^{n + {c_i}}} $和$ {u^{n + {c_j}}} $为龙格库塔采样值
$$ {{u^{n + {c_j}}}(x) = u({t^n} + {c_j}\Delta t,x)},\;\;{j = 1,2, \cdots , q} ,q + 1 $$ (3) 为了便于书写表达, 式(2)可以被转化为如下形式
$$ {u^n} = u_i^n,\quad i = 1,2, \cdots ,q,q + 1 $$ (4) 其中
$$ u_i^n: = {u^{n + {c_i}}} + \Delta t\sum\limits_{j = 1}^{q + 1} {{a_{ij}}} \mathcal{N}\left[ {{u^{n + {c_j}}}} \right],\quad i = 1,2, \cdots ,q,q + 1 $$ (5) 在PINN-RK中, 输出层神经元数量等于龙格库塔阶数$ q + 1 $, 具体形式如下所示
$$u^{n+c_i}= \left[ {{u^{n + {c_1}}}(x),{u^{n + {c_2}}}(x), \cdots ,{u^{n + {c_q}}}(x),{u^{n + 1}}(x)} \right] $$ (6) 其中, $ {u^n}(x) $表示PDE当前时刻的解, $ {u^{n + 1}}(x) $表示PDE下一时刻的解.
通过整合PINN框架、龙格库塔公式(5)和相应的PDE, 即可得到PINN-RK模型. 相比于PINN, PINN-RK的输入量仅为空间坐标$ x $, 不含任何时间变量$ t $. 时间变量通过龙格库塔公式被隐式地嵌入到了损失函数中, 能够显著提升求解过程中的稳定性. PINN-RK的输出为$ q $阶龙格库塔采样值与下一时刻PDE的解
$$ u_{q_i}^n=\left[ {u_1^n(x),u_2^n(x), \cdots ,u_q^n(x),u_{q + 1}^n(x)} \right] $$ (7) 从式(7)中可以看到, 由于龙格库塔公式的嵌入和神经网络结构的限制, PINN-RK的输出层只能表示单个物理量的龙格库塔采样值, 无法同时描述多个物理量. 这导致PINN-RK仅适用于求解单个PDE的问题, 无法处理相互耦合的PDE系统. 究其原因, 主要是因为PINN-RK中神经网络结构过于简单, 输出层个数仅为1, 使得神经网络表达能力较差, 难以准确近似多个物理量. 为此, 本文通过对PINN-RK结构的改进, 提出了MO-PINN-RK.
1.3 MO-PINN-RK
为了阐明MO-PINN-RK的构建方法, 本文将以N-S方程为例描述多输出神经网络的构建过程, 并详细介绍如何将物理先验知识嵌入到损失函数中. 通常情况下, 全连接神经网络包含一个输入层、多个隐藏层和一个输出层, 而在MO-PINN-RK中则采用了多个输出层的结构设计, 以实现同时求解耦合PDE的目的. 另外, 该模型还采用了并行的隐藏层结构, 能够捕获不同物理量之间的差异, 增强了神经网络模型的表达能力. MO-PINN-RK的输出层数量取决于PDE问题中的未知数个数. 对于二维流动问题N-S方程, 未知的物理量为$ u $, $ v $和$ p $, 因此输出层个数为3. 其次, 根据龙格库塔阶数确定输出层神经元个数, 每个输出层的神经元个数等于龙格库塔阶数$ q + 1 $. 最后, 以采样点的二维空间坐标$ (x,y) $作为神经网络的输入, 选择合适的隐藏层层数和神经元个数, 建立MO-PINN-RK模型, 如图2所示.
MO-PINN-RK模型隐藏层可以分为两个部分. 一部分为共享隐藏层, 另一部分为并行隐藏层. 共享隐藏层与神经网络常规的隐藏层相同, 均为全连接结构. 共享隐藏层可以学习到多个子任务之间的特征表示, 提取不同物理量之间的共同特征. 并行隐藏层则分为3个并行子网络, 不同子网络近似不同的物理量, 每个子网络中的隐藏层均为全连接结构, 不同子网络的隐藏层互不干扰. 并行隐藏层允许每个子网络根据其所要解决的任务特点, 自由设计隐藏层结构和参数. 这样的灵活性使得每个子网络可以更好地适应不同任务的复杂性和数据特点, 从而提高整体模型的性能.
采用多输出的神经网络结构, 可以利用不同的输出层表示不同的物理量, 提高了模型的准确性和泛化能力. 由于每个输出层专注于自己的任务, 神经网络可以学习每个物理量的特征, 并通过共享的隐藏层捕捉不同物理量之间的耦合关系, 使得MO-PINN-RK可以有效地求解耦合PDE系统, 更好地描述复杂的物理过程.
下列式子为本文所采用的N-S方程表达式
$$ {u_x} + {v_y} = 0 $$ (8) $$ {u_t} + u{u_x} + v{u_y} = - {p_x} + 0.01({u_{xx}} + {u_{yy}}) $$ (9) $$ {v_t} + u{v_x} + v{v_y} = - {p_y} + 0.01({v_{xx}} + {v_{yy}}) $$ (10) 其中, $ u $和$ v $分别表示流向速度分量和横向速度分量, $ p $表示压力. 下标$ t $, $ x $和$ y $分别表示函数对时间和空间的一阶偏导数, 下标$ xx $和$ yy $分别表示对空间的二阶偏导数. 为了将N-S方程嵌入MO-PINN-RK的损失函数中, 使用$ q $阶隐式龙格库塔公式对其进行离散化, 可得
$$ \left( {{u_x}} \right)_i^j + \left( {{v_y}} \right)_i^j = 0 $$ (11) $$ u_i^n: = {u^{n + {c_i}}} + \Delta t\sum\limits_{j = 1}^{q + 1} {{a_{ij}}} \mathcal{N}\left[ {{u^{n + {c_j}}}} \right],\quad i = 1,2, \cdots ,q,q + 1 $$ (12) $$ v_i^n: = {v^{n + {c_i}}} + \Delta t\sum\limits_{j = 1}^{q + 1} {{a_{ij}}} \mathcal{N}\left[ {{v^{n + {c_j}}}} \right],\quad i = 1,2, \cdots ,q,q + 1 $$ (13) $$\begin{split} & {\mathcal{N}\left[ {u_i^j} \right] = - \left( {{p_x}} \right)_i^j + 0.01\left[ {\left( {{u_{xx}}} \right)_i^j + \left( {{u_{yy}}} \right)_i^j} \right]}- \\ & \qquad{ \left( u \right)_i^j\left( {{u_x}} \right)_i^j - \left( v \right)_i^j\left( {{u_y}} \right)_i^j} \end{split} $$ (14) $$\begin{split} & \mathcal{N}\left[ {v_i^j} \right] = - \left( {{p_y}} \right)_i^j + 0.01\left[ {\left( {{v_{xx}}} \right)_i^j + \left( {{v_{yy}}} \right)_i^j} \right] - \\ & \qquad \left( u \right)_i^j\left( {{v_x}} \right)_i^j - \left( v \right)_i^j\left( {{v_y}} \right)_i^j \end{split} $$ (15) 其中, 下标$ i $表示不同的空间采样点, 取值范围由采样点数量决定, 上标$ j $表示龙格库塔阶数, $j = 1,2, \cdots ,q, q + 1$. 式(14)和式(15)分别为式(12)和式(13)的一部分, 表示不同采样点下不同龙格库塔节点处N-S方程的残差形式. 两式的作用是为神经网络的损失函数引入物理约束, 指导神经网络的训练朝着满足N-S方程的方向进行.
根据式(11) ~ 式(13)构建用于MO-PINN-RK的损失函数. 不同的损失函数形式会对训练结果产生不同的影响, 文中采用了平方误差和(sum of squared errors, SSE)形式. 总损失函数由3部分组成
$$ SSE = SS{E_m} + SS{E_u} + SS{E_v} $$ (16) $$ SS{E_m} = \sum\limits_{j = 1}^{q + 1} {\sum\limits_{i = 1}^N {{{\left| {\left( {{u_x}} \right)_i^j + \left( {{v_y}} \right)_i^j} \right|}^2}} } $$ (17) $$ SS{E_u} = \sum\limits_{j = 1}^{q + 1} {\sum\limits_{i = 1}^N {{{\left| {{u^{n + {c_i}}} + \Delta t\sum\limits_{j = 1}^{q + 1} {{a_{ij}}} \mathcal{N}\left[ {{u^{n + {c_j}}}} \right] - {{\hat u}_i}^n} \right|}^2}} } $$ (18) $$ SS{E_v} = \sum\limits_{j = 1}^{q + 1} {\sum\limits_{i = 1}^N {{{\left| {{v^{n + {c_i}}} + \Delta t\sum\limits_{j = 1}^{q + 1} {{a_{ij}}} \mathcal{N}\left[ {{v^{n + {c_j}}}} \right] - {{\hat v}_i}^n} \right|}^2}} } $$ (19) 其中, $ SS{E_m} $为连续性方程损失函数, $ SS{E_u} $为$ x $方向动量方程损失函数, $ SS{E_v} $为$ y $方向动量方程损失函数, $ N $为训练集中采样点个数, $ u_i^n $和$ v_i^n $表示神经网络输出, $ {\hat u_i}^n $和$ {\hat v_i}^n $表示已知的观测数据. MO-PINN-RK将以最小化损失函数SSE为目标, 通过优化器不断更新神经网络中权重, 直至损失函数低于设定的阈值.
为了更加深入地理解MO-PINN-RK的训练原理, 可以将其与自编码器中的编码神经网络和解码神经网络[27]进行类比. 在MO-PINN-RK中, 观测数据可视为编码神经网络中的输入特征向量, 前向传播过程则类似于对观测数据进行编码操作, 而输出层神经元所代表的变量则可视为编码神经网络所输出的潜在变量, 即解码神经网络的输入特征. MO-PINN-RK输出层应用龙格库塔公式的过程类似于解码网络中的解码操作. 为了最小化编码神经网络输入特性向量和解码神经网络输出特征之间的差异, 自编码器模型以最小化重构误差为目标进行训练. 在MO-PINN-RK中, 最小化损失函数的作用与最小化重构误差相同, 均用于指导神经网络的优化训练过程. 但是, 与之相比, MO-PINN-RK还嵌入了物理先验知识, 提高了模型的泛化性能. 此外, MO-PINN-RK中的解码过程由龙格库塔公式和描述物理守恒定律的PDE充当, 使得解码方式由隐式形式转化为了显式形式, 显著地增强了模型的可解释性, 提高了模型的鲁棒性. 同时, 这种转变也使MO-PINN-RK可以更加准确地求解复杂的PDE系统.
2. 数值实验
2.1 问题设置
圆柱绕流因几何形状简单而流动形态丰富、机理复杂, 一直作为流体力学中的经典问题被广泛研究[28]. 当流体流经圆柱体时会出现剪切流动, 产生边界层分离和涡的非对称脱落现象. 这种绕流现象广泛地存在于各种工程应用中, 例如跨海大桥的稳定性设计、热电厂输运管道的优化以及水利机械的制造等. 了解圆柱体周围的流动模式对这些结构的优化设计和性能提高具有至关重要的作用. 为此, 人们从理论、实验和数值模拟进行了各种研究.
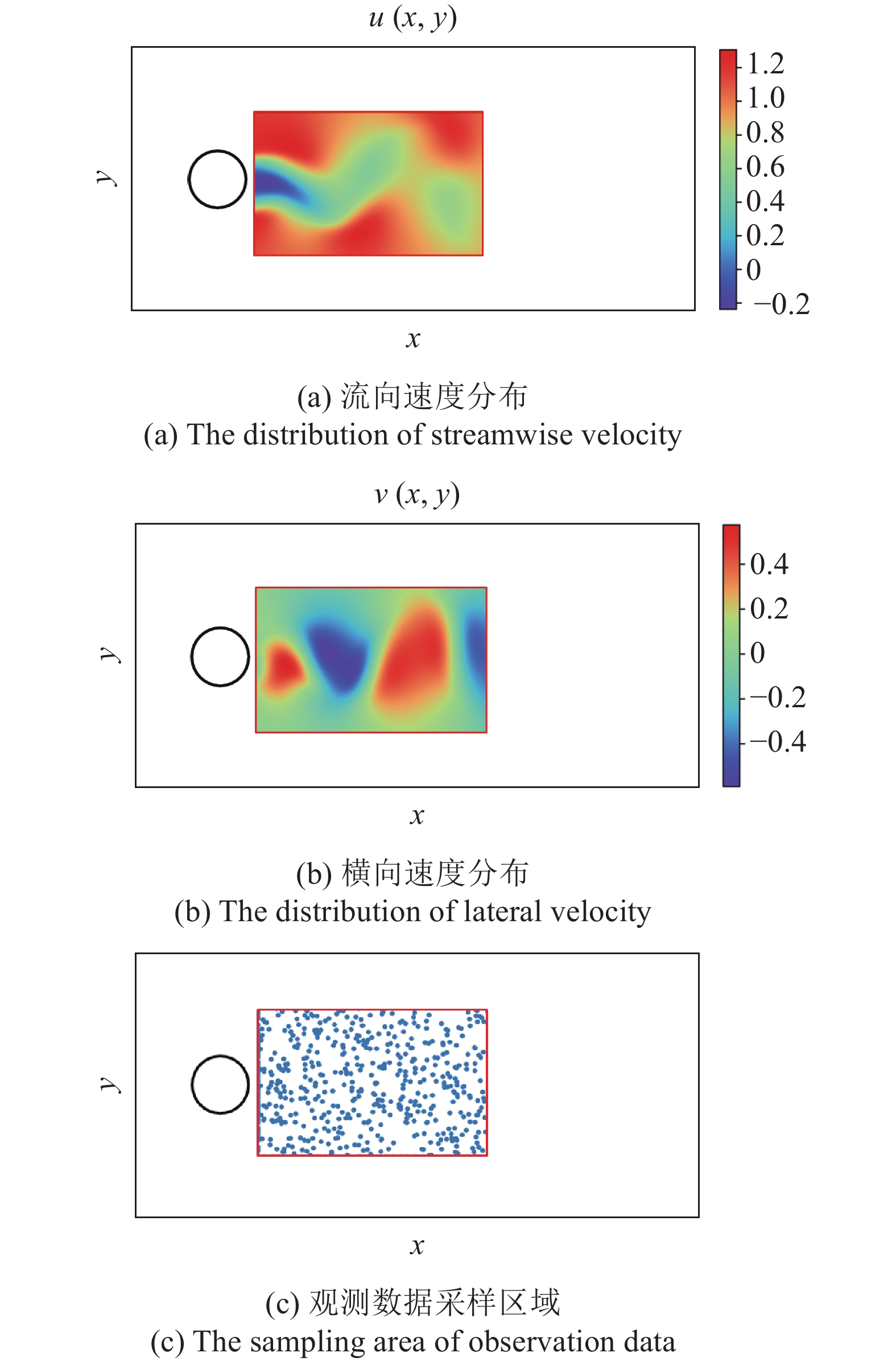
为了验证MO-PINN-RK的有效性, 本文使用该模型对二维不可压缩流体的圆柱绕流问题进行流场推断预测和参数辨识研究. 在圆柱绕流中, 圆柱尾迹的流动状态不仅展现出了丰富的流动现象, 如图3(a)和图3(b)所示, 而且还蕴含着深刻的物理规律, 因此本文只对圆柱下游特定的小矩形区域进行研究, 如图3(c)所示.
圆柱绕流现象背后的物理规律由N-S方程所控制. 为此, 根据前一节中阐述的方法, 建立如图2所示的MO-PINN-RK架构. 考虑到目前已有大量文献对圆柱绕流问题进行了数值模拟研究, 本文将直接使用文献[11]中提供的流场数据作为MO-PINN-RK的训练数据和测试数据, 以确保结果的可靠性. 对于流场分布预测问题, MO-PINN-RK以一个时间切片的速度观测值作为输入来预测另一个时间切片的速度分布. 从数值模拟数据的时空分布中随机选择某一时间点作为数据采集时刻$ t $, 并将该时刻下的流向速度分布$ u(x,y) $和横向速度分布$ v(x,y) $作为模型的数据集, 如图3(a)和图3(b)所示. 在圆柱下游特定矩形区域内进行数据集的随机采样操作, 总计采样5000个观测点, 采样区域如图3(c)所示. 设置损失函数中龙格库塔公式的时间步长为$ \Delta t $. 通过迭代训练和优化过程, MO-PINN-RK能够根据观测数据推断损失函数中N-S方程的解, 学习流体的时空动态行为, 并准确地提供未来$ t + \Delta t $时刻的速度分布.
对于参数辨识问题, MO-PINN-RK以时间间隔为$ \Delta t $的$ N $个速度观测值作为输入, 用于推测PDE中的未知参数. 在参数辨识中, MO-PINN-RK中的N-S方程并非完全已知, 而是存在部分未知参数$ {\lambda _1} $和$ {\lambda _2} $, 如下式所示. 参数$ {\lambda _1} $和$ {\lambda _2} $的真实值由文献[11]确定
$$ {u_t} + {\lambda _1}\left( {u{u_x} + v{u_y}} \right) = - {p_x} + {\lambda _2}({u_{xx}} + {u_{yy}}) $$ (20) $$ {v_t} + {\lambda _1}\left( {u{v_x} + v{v_y}} \right) = - {p_y} + {\lambda _2}({v_{xx}} + {v_{yy}}) $$ (21) 基于部分观测数据和不完备的物理知识, MO-PINN-RK通过最小化损失函数并采用梯度下降方法来进行优化训练, 以获取最优的参数估计. 经过充分训练后, MO-PINN-RK能够从观测数据中学习和理解系统的物理规律, 并准确地推断出未知参数的值. 这使得MO-PINN-RK成为了一种强大的工具, 可在缺乏部分信息的情况下, 通过结合物理先验知识和观测数据, 推断出系统的隐藏特性和未知参数, 并生成准确的预测结果.
2.2 神经网络配置
神经元中的非线性激活函数是神经网络能够具备强大表达能力和拟合性能的关键因素. 神经网络中常见的激活函数有ReLU, Tanh和Sigmoid等[29]. 在智能科学计算中, 由于损失函数中嵌入了物理约束PDE, 通常需要获得神经网络输出关于输入的导数信息. 由于Tanh激活函数具有无限可导的特点, 文中所有的隐藏层均采用Tanh激活函数. 但是, Tanh函数的输出范围仅为[−1,1]区间, 为了不限制神经网络的输出, 输出层不设置激活函数. 设定神经网络共享隐藏层数量为10, 并行隐藏层数量为2, 每个隐藏层包含20个神经元. 神经网络结构选择全连接神经网络, 权重初始化方式采用Glorot正态分布初始化.
MO-PINN-RK的训练过程是对PDE不断寻优求解的过程, 训练算法的好坏对神经网络的性能起到了决定性的作用. 本文将神经网络训练过程分为两个阶段, 前期使用随机梯度下降算法的变体Adam算法, 训练10000代, 后期则使用L-BFGS-B算法训练, 直至算法迭代收敛. Adam等[30]结合AdaGrad算法和RMSProp算法的优点, 并引入了动量的概念, 不仅能够自适应地调整学习率, 而且还能借助动量加速收敛, 逃离局部极小值. 但是, Adam算法对学习率的选择非常敏感, 过高的学习率会导致优化过程的不稳定. L-BFGS-B算法[31]是一种基于拟牛顿方法的优化算法, 通常比梯度下降等一阶优化算法更高效, 收敛速度更快, 且不需要手动调整学习率. 然而, L-BFGS-B算法在非凸优化问题中容易陷入局部极小值. 因此, 本文训练过程采用Adam和L-BFGS-B结合的方式, 先利用Adam尽可能地逼近全局最优点, 再使用L-BFGS-B加快神经网络的收敛. 文中的所有计算代码均基于TensorFlow2.9版本的Python库完成, 并在GeForce RTX3090显卡上进行运算.
3. 结果和讨论
3.1 流场预测
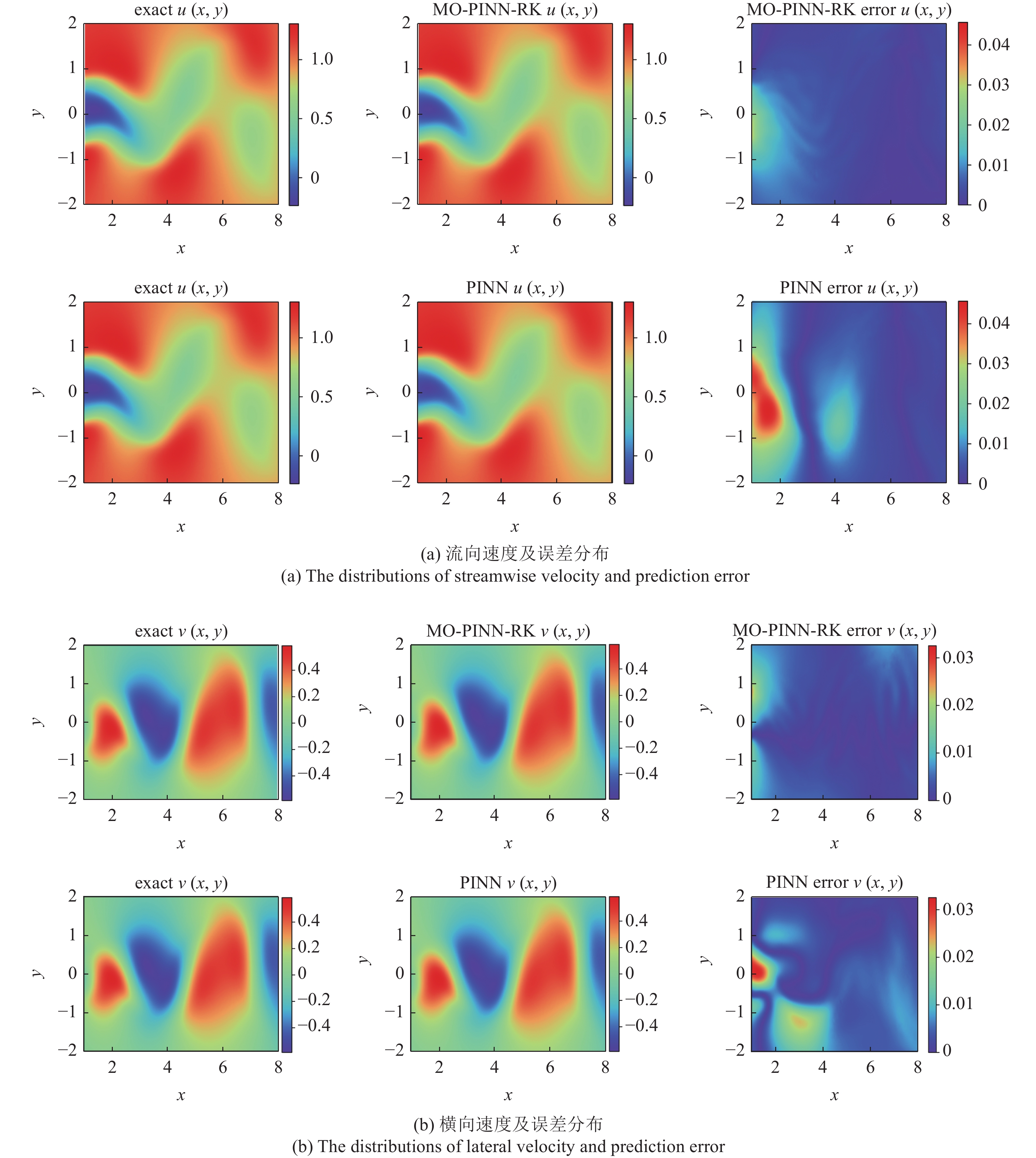
本小节将应用MO-PINN-RK和PINN两种模型对二维不可压缩流体的圆柱绕流问题进行流场预测研究, 并对模型预测结果展开深入讨论. 当预测时间间隔$ \Delta t $为0.1时, 由MO-PINN-RK和PINN模型所获得的速度云图如图4所示. 图中, 第1列对应着基准解, 第2列上下图分别为MO-PINN-RK和PINN模型的预测解, 第3列则展示了不同模型与基准解之间的绝对误差. 绝对误差公式为
![]()
图 4 MO-PINN-RK和PINN流场预测解与基准解对比 ($ \Delta t $ = 0.1)Figure 4. Comparison of the flow field predictions of MO-PINN-RK and PINN with the benchmark solutions ($ \Delta t $ = 0.1)$$ e_{{\rm{ab}}} = \left| {{{\hat u}_i} - {u_i}} \right| $$ (22) 其中, $ {\hat u_i} $为模型预测值, $ {u_i} $为基准值, $ i $为不同的样本点.
综合来看, 两种模型的预测解与基准解之间具有很好的一致性, 都能够成功地捕获到圆柱绕流中涡街脱落的形态和位置. 根据图4中的绝对误差分布图可以观察到, PINN的预测误差主要集中在圆柱下游的尾迹区域. 造成该现象的原因是尾迹区域的流动特性比较复杂, 常常涉及边界层分离和旋涡的相互作用. 这些因素增大了神经网络的训练难度, 导致预测结果与基准解间的误差增大. 然而, 相比于PINN, MO-PINN-RK在整个求解域内都表现出更低的绝对误差, 包括尾迹区域. 究其原因, 这主要是由于MO-PINN-RK中不仅嵌入了龙格库塔方法, 而且还使用了多输出的神经网络结构, 可以同时捕获系统的不同属性, 因此能够更好地学习尾迹区域的流动特性, 产生更精确的预测结果.
在较短的时间跨度内, 流动的演变幅度较小, 使得模型能够获得较好的预测精度. 但是, 随着时间的推移, 流动过程中的非线性特性会加剧系统的演变, 给模型的预测任务带来挑战. 为了对MO-PINN-RK的性能进行深入验证, 进一步推进模型预测的时间间隔. 图5展示了当预测时间间隔$ \Delta t $为0.4时, 由MO-PINN-RK和PINN所获得的速度云图. 从图5(a)可以观察到, PINN的预测解已经出现了偏离基准解的趋势, 产生了较大的预测误差. 然而, MO-PINN-RK仍能具备精确捕捉圆柱尾迹流动特性的能力, 展现出了出色的预测精度. 在面对长时间跨度的流体动态预测任务时, 由于龙格库塔法的融入, MO-PINN-RK不仅可以实现对流体动态过程的精确模拟, 而且还能根据初始观测数据优化模型的预测能力. 这种结合了数值方法和物理约束的深度学习框架使得MO-PINN-RK在预测流体行为和捕捉流场特性方面表现出了更高的准确性.
![]()
图 5 MO-PINN-RK和PINN流场预测解与基准解对比 ($ \Delta t $ = 0.4)Figure 5. Comparison of the flow field predictions of MO-PINN-RK and PINN with the benchmark solutions ($ \Delta t $ = 0.4)为了从定量的角度比较MO-PINN-RK和PINN的预测准确性, 本文采用模型预测解与基准解之间的$ {L_2} $相对误差作为衡量标准, 其计算公式如下所示
$$ e_{L_2}= \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{{{\left\| {{{\hat u}_i} - {u_i}} \right\|}_2}}}{{{{\left\| {{u_i}} \right\|}_2}}}} $$ (23) 其中, $ {\hat u_i} $表示模型预测值, $ {u_i} $表示基准值, $ N $表示采样点个数. 不同时间间隔下, 不同模型之间流场预测值和基准值的$ {L_2} $相对误差如表1所示.
表 1 MO-PINN-RK和PINN-RK流场预测值与基准值之间的L2相对误差Table 1. The$ {L_2} $relative errors between the flow field predictions of MO-PINN-RK and PINN-RK and the benchmark solutions$ \Delta t $ MO-PINN-RK PINN $ u $ $ v $ $ u $ $ v $ 0.1 0.006 5 0.016 5 0.013 5 0.027 1 0.2 0.007 5 0.021 8 0.027 8 0.057 2 0.3 0.011 9 0.027 6 0.037 3 0.091 6 0.4 0.026 2 0.038 9 0.058 5 0.128 7 根据表1提供的数据可以得出, 在各个预测时间间隔下, MO-PINN-RK的预测误差均比PINN低. 这一结果进一步验证了MO-PINN-RK在流场预测方面的优越性. 在预测流向速度分布时, MO-PINN-RK最大$ {L_2} $相对误差仅为0.026 2. 相比之下, PINN的预测误差约为MO-PINN-RK的2倍. 在对横向速度预测时, MO-PINN-RK的$ {L_2} $相对误差虽然略有升高, 但仍将最大误差控制在0.038 9. 而PINN的相对误差则为0.128 7, 约为MO-PINN-RK模型的3倍. 这表明经过足够的迭代次数, MO-PINN-RK能够逐渐学习真实系统的物理规律, 更加有效地捕捉流体流动的时间演化和动态行为, 具有较高的预测精度.
3.2 参数辨识
本小节将应用MO-PINN-RK和PINN两种模型对圆柱绕流问题进行参数辨识研究, 并对模型辨识结果展开深入讨论, 以评估不同模型的可行性和有效性. 在参数辨识问题中, 未知参数$ {\lambda _1} $和$ {\lambda _2} $是需要从给定的数据中推断或估计的参数. 未知参数$ {\lambda _1} $和$ {\lambda _2} $并非以显式的形式存在于神经网络的输出中, 而是借助TensorFlow库的功能, 以可训练参数的形式嵌入到神经网络中.
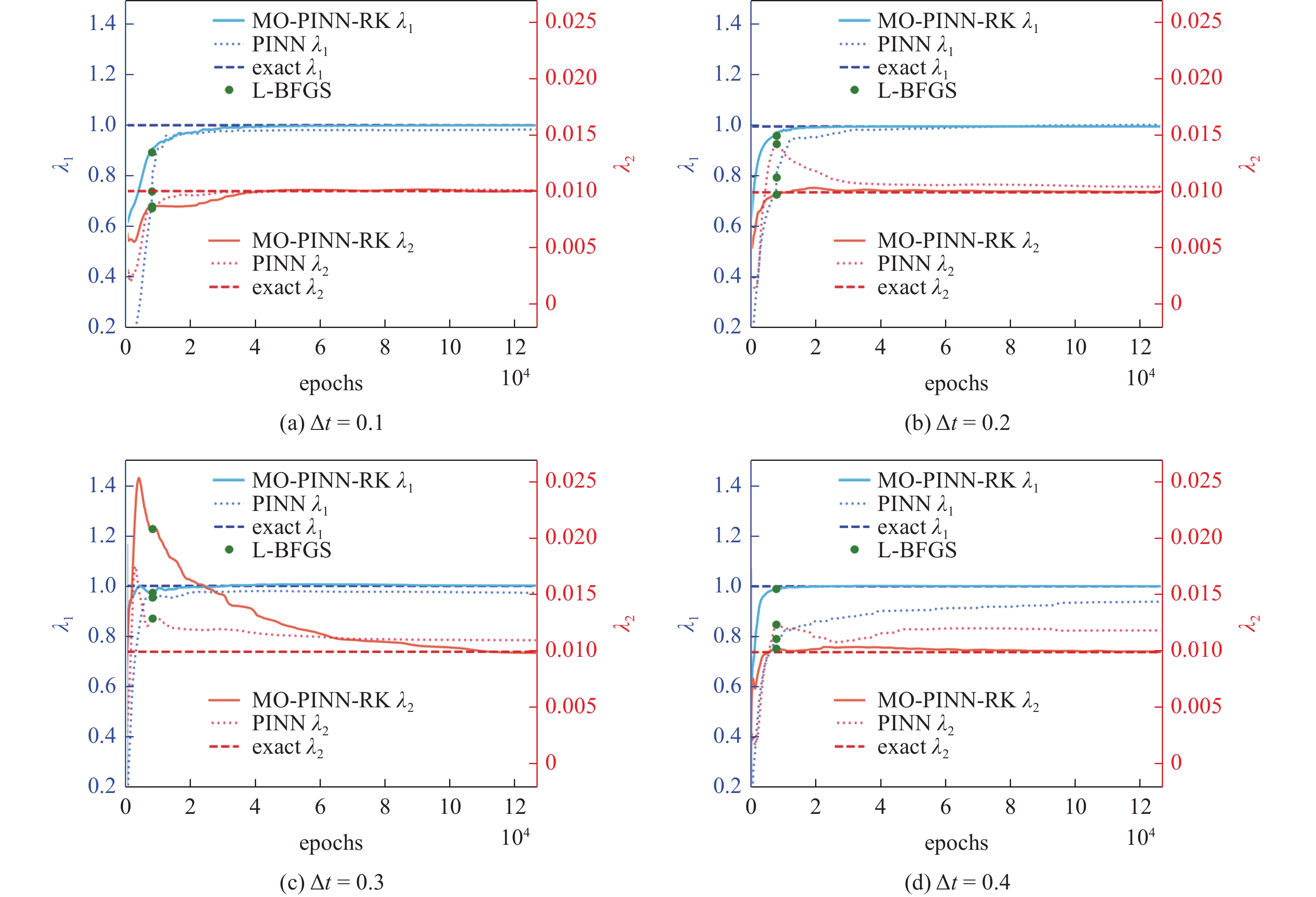
在模型的训练初期, 随机假设未知参数的初始值. 为了说明MO-PINN-RK的性能, 选择不同的采样时间间隔$ \Delta t $ = 0.1,0.2,0.3,0.4. 图6为MO-PINN-RK与PINN在不同采样时间间隔下对N-S方程中未知参数$ {\lambda _1} $和$ {\lambda _2} $的辨识结果. 图中, 蓝色虚线和红色虚线分别表示$ {\lambda _1} $和$ {\lambda _2} $的真实值, 蓝色实线和红色实线分别表示MO-PINN-RK对$ {\lambda _1} $和$ {\lambda _2} $的辨识结果, 蓝色点线和红色点线分别表示PINN对$ {\lambda _1} $和$ {\lambda _2} $的辨识结果, 绿色实点表示Adam算法的结束位置和L-BFGS算法的起始位置.
![]()
图 6 MO-PINN-RK和PINN参数辨识结果与真实值对比Figure 6. Comparison between the parameter identification results of the MO-PINN-RK and PINN with the true values整体上看, 在较短时间间隔内, 随着迭代次数的不断增加, 不同模型的辨识结果逐渐趋向于真实值. 但是, 随着采样时间间隔的增加, PINN的辨识结果开始逐渐偏离真实值, 产生了较大的预测误差. 与之相比, MO-PINN-RK的辨识结果一直具有较高的精度, 不随采样时间间隔的增大而偏离真实值. 这主要是因为MO-PINN-RK具有多个神经网络输出层, 可同时捕捉相互耦合的多变量信息, 具有更强的描述复杂流动形态的能力. 并且, 龙格库塔方法的嵌入使得该模型能够更好地处理长时间跨度问题. 相较于PINN, MO-PINN-RK可以高效地从稀疏离散的观测数据中学习潜在的物理规律, 具有更好的适应性.
为了从定量的角度比较MO-PINN-RK和PINN的辨识准确性, 本文采用模型辨识值与真实值之间的相对误差进行衡量, 其计算公式如下
$$ e = \frac{{\left| {\hat \lambda - \lambda } \right|}}{{\left| \lambda \right|}} \times 100\% $$ (24) 其中, $ \hat \lambda $表示神经网络模型的辨识值, $ \lambda $表示精确值.
不同采样时间间隔下, 由不同模型获得的辨识值与真实值的之间相对误差如表2所示. 从表中可以看到, PINN模型的相对误差随着采样时间的增加而增大, 且最大误差达到了19.38%, 大幅偏离了真实值. 与之相比, MO-PINN-RK能够准确地辨识出未知参数$ {\lambda _1} $和$ {\lambda _2} $, 且最大相对误差保持在低于1.11%的水平. 另外, 可以观察到, 无论是对参数$ {\lambda _1} $还是$ {\lambda _2} $的辨识, MO-PINN-RK的相对误差始终比PINN的相对误差低一个数量级. 这一结果表明, MO-PINN-RK在参数辨识方面具有更好的性能, 能够从流体复杂的动态演化过程中推测出数学模型中的未知参数, 对于推断流体系统的未知属性具有非常重要的意义.
表 2 MO-PINN-RK和PINN-RK辨识参数和真实参数的相对误差Table 2. The relative errors between the identified parameters by MO-PINN-RK, PINN-RK and the true values$ \Delta t $ MO-PINN-RK PINN ${\lambda _1}$/% ${\lambda _2}$/% ${\lambda _1}$/% ${\lambda _2}$/% 0.1 0.06 0.47 1.70 0.55 0.2 0.01 0.31 0.65 4.90 0.3 0.15 1.11 2.75 10.22 0.4 0.07 0.60 6.09 19.38 4. 结论
针对PINN-RK无法求解耦合PDE系统的问题, 本文提出了一种MO-PINN-RK. MO-PINN-RK在原始PINN-RK架构的基础上设计了并行的神经网络输出层, 通过采用不同输出层近似不同物理量、共享隐藏层捕捉不同物理量之间耦合关系的方式, 成功实现了在损失函数中嵌入多个PDE并同时求解的目的. 与PINN相比, MO-PINN-RK中嵌入了龙格库塔法的数值求解方法, 提高了神经网络的求解精度和泛化性能. 与PINN-RK相比, MO-PINN-RK增强了神经网络的表达能力, 实现了对耦合PDE系统的求解, 将PINN-RK的应用范围从一维空间扩展到了多维空间域.
为验证MO-PINN-RK的有效性, 本文选择二维不可压缩流体的圆柱绕流问题作为测试案例, 分别进行了流场预测和参数辨识研究. 测试结果表明, 在流场预测问题中, 定性上, MO-PINN-RK的预测解与基准解完全吻合. 定量上, MO-PINN-RK的$ {L_2} $相对误差保持在低于0.038 9的水平, 具有较高的准确性. 在参数辨识问题中, 定性上, MO-PINN-RK的辨识值会随着迭代次数的增加收敛于真实值, 且收敛行为不受采样时间间隔增大的影响. 定量上, MO-PINN-RK辨识值与真实值之间的最大相对误差仅为1.11%, 拥有极高的辨识性能. 因此, 本文所提出的MO-PINN-RK作为一种新型的物理信息神经网络架构, 无论是在流场预测还是参数辨识方面都具有非常大的潜力.
-
![]()
图 4 MO-PINN-RK和PINN流场预测解与基准解对比 ($ \Delta t $ = 0.1)
Figure 4. Comparison of the flow field predictions of MO-PINN-RK and PINN with the benchmark solutions ($ \Delta t $ = 0.1)
![]()
图 5 MO-PINN-RK和PINN流场预测解与基准解对比 ($ \Delta t $ = 0.4)
Figure 5. Comparison of the flow field predictions of MO-PINN-RK and PINN with the benchmark solutions ($ \Delta t $ = 0.4)
![]()
图 6 MO-PINN-RK和PINN参数辨识结果与真实值对比
Figure 6. Comparison between the parameter identification results of the MO-PINN-RK and PINN with the true values
表 1 MO-PINN-RK和PINN-RK流场预测值与基准值之间的L2相对误差
Table 1 The$ {L_2} $relative errors between the flow field predictions of MO-PINN-RK and PINN-RK and the benchmark solutions
$ \Delta t $ MO-PINN-RK PINN $ u $ $ v $ $ u $ $ v $ 0.1 0.006 5 0.016 5 0.013 5 0.027 1 0.2 0.007 5 0.021 8 0.027 8 0.057 2 0.3 0.011 9 0.027 6 0.037 3 0.091 6 0.4 0.026 2 0.038 9 0.058 5 0.128 7 
下载: 导出CSV
表 2 MO-PINN-RK和PINN-RK辨识参数和真实参数的相对误差
Table 2 The relative errors between the identified parameters by MO-PINN-RK, PINN-RK and the true values
$ \Delta t $ MO-PINN-RK PINN ${\lambda _1}$/% ${\lambda _2}$/% ${\lambda _1}$/% ${\lambda _2}$/% 0.1 0.06 0.47 1.70 0.55 0.2 0.01 0.31 0.65 4.90 0.3 0.15 1.11 2.75 10.22 0.4 0.07 0.60 6.09 19.38
下载: 导出CSV
-
[1] Esser P, Rombach R, Ommer B. Taming transformers for high-resolution image synthesis//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021
[2] Han X, Gao T, Lin Y, et al. More data, more relations, more context and more openness: A review and outlook for relation extraction. ArXiv: 200403186, 2020
[3] Balog K, Radlinski F, Karatzoglou A. On Interpretation and Measurement of Soft Attributes for Recommendation//Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, 2021
[4] 谢晨月, 袁泽龙, 王建春等. 基于人工神经网络的湍流大涡模拟方法. 力学学报, 2021, 53(1): 1-16 (Xie Chenyue, Yuan Zelong, Wang Jianchun, et al. Artificial neural network-based subgrid-scale models for large-eddy simulation of turbulence. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 1-16 (in Chinese) Xie Chenyue, Yuan Zelong, Wang Jianchun, Wan Minping, Chen Shiyi. Artificial neural network-based subgrid-scale models for large-eddy simulation of turbulence. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 1-16 (in Chinese)
[5] 蒋子超, 江俊扬, 姚清河等. 基于神经网络的差分方程快速求解方法. 力学学报, 2021, 53(7): 1912-1921 (Jiang Zichao, Jiang Junyang, Yao Qinghe, et al. A fast solver based on deep neural network for difference equation. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(7): 1912-1921 (in Chinese) doi: 10.6052/0459-1879-21-040 Jiang Zichao, Jiang Junyang, Yao Qinghe, Yang Gengchao. A fast solver based on deep neural network for difference equation. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(7): 1912-1921 (in Chinese) doi: 10.6052/0459-1879-21-040
[6] Blechschmidt J, Ernst OG. Three ways to solve partial differential equations with neural networks —A review. GAMM-Mitteilungen, 2021, 44(2): e202100006
[7] Rasmussen CE, Williams CK. Gaussian Processes for Machine Learning, vol 1. Cambridge, MA: MIT Press, 2006
[8] Chen Z, Liu Y, Sun H. Physics-informed learning of governing equations from scarce data. Nature Communications, 2021, 12(1): 6136 doi: 10.1038/s41467-021-26434-1
[9] Fukami K, Fukagata K, Taira K. Super-resolution reconstruction of turbulent flows with machine learning. Journal of Fluid Mechanics, 2019, 870: 106-120 doi: 10.1017/jfm.2019.238
[10] Willard J, Jia X, Xu S, et al. Integrating physics-based modeling with machine learning: A survey. ArXiv: 200304919, 2020
[11] Raissi M, Perdikaris P, Karniadakis GE. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 2019, 378: 686-707 doi: 10.1016/j.jcp.2018.10.045
[12] Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural Networks, 1989, 2(5): 359-366 doi: 10.1016/0893-6080(89)90020-8
[13] Dissanayake M, Phan-Thien N. Neural-network-based approximations for solving partial differential equations. Communications in Numerical Methods in Engineering, 1994, 10(3): 195-201 doi: 10.1002/cnm.1640100303
[14] Baydin AG, Pearlmutter BA, Radul AA, et al. Automatic differentiation in machine learning: a survey. Journal of Marchine Learning Research, 2018, 18: 1-43
[15] Cuomo S, DI Cola VS, Giampaolo F, et al. Scientific machine learning through physics–informed neural networks: where we are and what’s next. Journal of Scientific Computing, 2022, 92(3): 88 doi: 10.1007/s10915-022-01939-z
[16] Yu J, Lu L, Meng X, et al. Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems. Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114823
[17] Wang S, Teng Y, Perdikaris P. Understanding and Mitigating Gradient Flow Pathologies in Physics-Informed Neural Networks. SIAM Journal on Scientific Computing, 2021, 43(5): A3055-A3081 doi: 10.1137/20M1318043
[18] Jagtap AD, Kawaguchi K, Karniadakis GE. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. Journal of Computational Physics, 2020, 404: 109136
[19] Mao Z, Jagtap AD, Karniadakis GE. Physics-informed neural networks for high-speed flows. Computer Methods in Applied Mechanics and Engineering, 2020, 360: 112789
[20] Meng X, Li Z, Zhang D, et al. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Computer Methods in Applied Mechanics and Engineering, 2020, 370: 113250
[21] Jin X, Cai S, Li H, et al. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. Journal of Computational Physics, 2021, 426: 109951
[22] Babaee H, Perdikaris P, Chryssostomidis C, et al. Multi-fidelity modelling of mixed convection based on experimental correlations and numerical simulations. Journal of Fluid Mechanics, 2016, 809: 895-917 doi: 10.1017/jfm.2016.718
[23] 宋家豪, 曹文博, 张伟伟. FD-PINN: 频域物理信息神经网络. 力学学报, 2023, 55(5): 1195-1205 (Song Jiahao, Cao Wenbo, Zhang Weiwei. FD-PINN: Frequency domain physics-informed neural network. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(5): 1195-1205 (in Chinese) doi: 10.6052/0459-1879-23-169 Song Jiahao, Cao Wenbo, Zhang Weiwei. FD-PINN: Frequency domain physics-informed neural network. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(5): 1195-1205 (in Chinese) doi: 10.6052/0459-1879-23-169
[24] 查文舒, 李道伦, 沈路航等. 基于神经网络的偏微分方程求解方法研究综述. 力学学报, 2022, 54(3): 543-556 (Zha Wenshu, Li Daolun, Shen Luhang, et al. Review of neural network-based methods for solving partial differential equations. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(3): 543-556 (in Chinese) doi: 10.6052/0459-1879-21-617 Zha Wenshu, Li Daolun, Shen Luhang, Zhang Wen, Liu Xuliang. Review of neural network-based methods for solving partial differential equations. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(3): 543-556 (in Chinese) doi: 10.6052/0459-1879-21-617
[25] Karniadakis GE, Kevrekidis IG, Lu L, et al. Physics-informed machine learning. Nature Reviews Physics, 2021, 3(6): 422-440 doi: 10.1038/s42254-021-00314-5
[26] Iserles A. A First Course in the Numerical Analysis of Differential Equations. Cambridge: Cambridge University Press, 2009
[27] Michelucci U. An introduction to autoencoders. ArXiv: 220103898, 2022
[28] Zdravkovich MM, Bearman PW. Flow around circular cylinders—volume 1: Fundamentals. Journal of Fluids Engineering, 1998, 120(1): 216 doi: 10.1115/1.2819655
[29] Fan E. Extended tanh-function method and its applications to nonlinear equations. Physics Letters A, 2000, 277(4-5): 212-218 doi: 10.1016/S0375-9601(00)00725-8
[30] Kingma DP, Ba J. Adam: A method for stochastic optimization. ArXiv: 14126980, 2014
[31] Byrd RH, Lu P, Nocedal J, et al. A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing, 1995, 16(5): 1190-1208 doi: 10.1137/0916069
-
期刊类型引用(7)
1. 刘雪琪，王志远，魏强，王敏，孙小辉，王雪瑞，张剑波，尹邦堂，孙宝江. 物理信息神经网络驱动的井筒温度场求解方法. 石油学报. 2025(02): 413-425 . 
百度学术
2. 万志强，张珊珊，王晓喆，马靓，许翱，吴志刚，杨超. 弹性飞机机动载荷分析与减缓技术综述. 航空学报. 2025(03): 147-180 . 百度学术
3. 韦昌，樊昱晨，周永清，刘欣，李驰，王赫阳. 基于时间权重的物理信息神经网络求解非稳态偏微分方程. 力学学报. 2025(03): 755-766 . 本站查看
4. 任旭虎，王文倩，刘通，闫宇晴，吴鹏宇. 基于PSO的随机共振钻井返出液信号处理方法. 石油机械. 2025(03): 1-9 . 百度学术
5. 潘小果，王凯，邓维鑫. 基于NTK理论和改进时间因果的物理信息神经网络加速收敛算法. 力学学报. 2024(07): 1943-1958 . 本站查看
6. 张凌海，周彬，罗毅，冯俊. 物理信息神经网络的一种自适应配置点算法. 力学学报. 2024(10): 3069-3083 . 本站查看
7. 聂成，景万鹏，罗紫元，郑守海，王金玉. 同步发电机在变频启动柴油机中的应用研究. 国外电子测量技术. 2024(10): 153-159 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 1136
- HTML全文浏览量: 274
- PDF下载量: 271
- 被引次数: 11
