RESERCH ON UNIVERSAL SOLUTION OF TRANSFORMING SEPARABLE CONVEX PROGRAMMING TO DUAL PROGRAMMING WITH EXPLICIT MODEL
-
摘要: 文章旨在提升对偶规划显式模型(dual programming-explicit model, DP-EM)的建模和求解的境界. DP-EM模型从一类变量可分离凸规划的特点出发, 突破了对偶目标二阶采用近似的定势, 推导得出显式的对偶目标函数; 应用于ICM方法求解连续体结构拓扑优化问题时, 其求解效率比对偶序列二次规划方法(DSQP)和可移动渐近线方法(MMA)求解效率更高. 文章进一步把常见的一类显式模型抽象为普适的可分离凸规划列式, 在需要满足的一些条件下, 转换为DP-EM模型, 并且提出4种处理方法: (1)对偶变量迭代逼近法; (2)指数函数形式的解法; (3)幂函数形式的解法; (4)基于变换的精确解法. 为了进行数值验证, 做了广泛的计算, 限于篇幅, 文章列出了5个具有代表性的算例, 除了算例1属于纯数学问题, 其余4个算例皆基于ICM方法, 分别对于位移、应力、疲劳等约束和破损−安全的连续体结构拓扑优化问题, 基于所提出的方法进行建模和求解, 都显示了所提出方法的普适性及更高的求解效率. 工作的意义在于: (1)深度方面, 加深了结构优化对偶解法的研究; (2)广度方面, 对数学规划对偶理论的发展做出了新的贡献.Abstract: This paper aims to improve the modeling and solving level of DP-EM (dual programming-explicit model) method. Based on the characteristics of a class of convex programming with separable variables, the DP-EM model breaks through the usual way of using second-order approximation for the dual objective function, and derives an explicit dual objective function. The DP-EM method is more efficient than the dual sequential quadratic programming (DSQP) and the method of moving asymptotes (MMA) when it is applied to the ICM method solving the continuum topology optimization problems. In this paper, the common explicit models are abstracted into universal separable convex programming, and then converted into DP-EM models under certain conditions. Four processing methods are proposed: (1) The approximate solution of iterative approximation of dual variables; (2) The solution of objective and constraint functions with the exponential function form; (3) The solution of objective and constraint functions with the power function form; (4) Accurate solution based on variable transformation. In order to conduct numerical verification, extensive calculations have been carried out. Limited by paper space, five representative examples among them are listed. Example 1 is a pure mathematical problem, which is used to compare the efficiency of the processing method 1 and the processing method 4. The remaining four examples are all continuum topology optimization problems modeled and solved by the ICM (independent continuous and mapping) method, including displacement, stress, fatigue constraint problems and fail-safe optimization. Those four examples are illustrations of the processing method 3. All the results show the universality of the proposed method and the higher solving efficiency. The proposed method can used for different penalty functions in the variable density method and filtering functions in the ICM method. And the proposed method is more efficient than the MMA method. The contribution of the work is as follows: (1) In depth, it deepens the research on the dual solution of structural optimization; (2) In breadth, it makes a contribution to the dual theory of mathematical programming.
-
Keywords:
- structural topology optimization /
- mapping function /
- solving efficiency /
- ICM method
-
引言
Fleury首先将非线性对偶规划引到结构优化领域, 进行建立模型和求解算法的研究[1-3]. 钱令希团队用对偶序列二次规划算法求解结构优化问题[4]. 结构优化中经典的优化求解算法如CONLIN (convex linearization method )[5]是基于对偶算法. Svanberg[6]提出的移动渐近线法(MMA)也是基于对偶算法. Beekers等[7]和Hoppe等[8]均是较早研究了利用原−对偶算法解决结构优化问题. 隋允康等[9-10]结合累积迭代信息策略, 研究了对偶算法在结构优化中的方法和应用. 吴京等[11]和金鹏等[12]用对偶规划研究了钢管混凝土拱结构优化设计问题. Xuan等[13]在优化层应用对偶内点法的线性规划和在分析层应用二次规划法求解非光滑结构优化问题. Etman等[14]研究了利用对偶理论的近似对角二次规划法. Cronje等[15]探讨了序列对偶近似规划中约束的等效性. Liang等[16]通过序列整数规划和典范对偶理论求解结构拓扑优化问题.
多数结构拓扑优化方法对应的模型归结为非线性规划, 如均匀化方法[17], 变密度方法[18]、ICM(独立连续映射)方法[19-21]、水平集方法[22-23]、拓扑导数法[24-25]、MMC(可移动变形组件)方法[26]、CBS(close B-splines)方法[27]等, 可以采用基于非线性规划理论的各种求解算法. 如果采用数学规划对偶理论, 借助原−对偶变量的显式关系, 将大规模的原问题转化为小规模的对偶问题求解, 可以大幅度地提高算法的效率[19-21]. 然而, 对偶目标函数却是一个含参数的极小化问题, 难以求解出对偶目标函数的显式表达式, 只得转而求其1阶导数和2阶导数, 构造二次规划逼近对偶规划, 迭代求解, 最后由对偶问题最大解求出原问题的最小解.
隋允康等[28]从优化所建立的数学规划模型的特点出发, 针对一大类广泛遇见的变量可分离的凸规划问题, 突破了只是停留在对偶目标二阶近似的定势, 推导得出了显式的对偶目标函数. 在这一研究的基础上, 提出了便捷求解的对偶规划显式模型(dual programming-explicit model, DP-EM)方法, 并将其应用于ICM方法[19-21]求解连续体结构拓扑优化问题, 将DP-EM方法与基于DSQP算法及MMA算法[6]的方法进行计算效率对比, 结果显示DP-EM方法具有更高的求解效率.
本文的工作旨在进一步提升DP-EM方法的境界, 隋允康等[28]提出的DP-EM方法仅解决了优化模型中约束和目标函数的每一项均为幂函数形式的情况(对应于本文所列举的情况3: 幂函数形式的解法), 而本文把常见的一类变量可分离的凸规划模型抽象为普适的可分离规划列式, 在需要满足的一些条件下, 转换为DP-EM解法. 相关工作有4个具体的成果: (1)对偶变量迭代逼近法; (2)指数函数形式的解法; (3)幂函数形式的解法; (4)基于变换的精确解法. 这一工作有深度与广度两方面的意义: (1)深度方面, 加深了结构优化对偶解法的研究, 相关的结论在结构拓扑优化里得到了验证; (2)广度方面, 对数学规划对偶理论的发展做出了新贡献. 预期今后无论在数学规划寻优算法和结构拓扑优化的求解中, 都将会有进一步的应用.
1. 普适的可分离凸规划转换为DP-EM解法
可分离规划通常可以表达为
$$ \left. \begin{split} &\mathop {\min }\limits_{{{x}} \in {E^N}} {\text{ }}F{\text{(}}{\boldsymbol{x}}{\text{)}} = \sum\limits_{i = 1}^N {{f_i}(x_i^{})} \\ & {\rm{s.t.}}{\text{ }}{G_j}{\text{(}}{\boldsymbol{x}}{\text{)}} = \sum\limits_{i = 1}^N {{g_{ji}}(x_i^{}) - {{\bar g_j}} } \leqslant {\text{0}}\quad {\text{(}}j = 1,2, \cdots ,M) \\ &\quad\;\; \underline {{x_i}} \leqslant {x_i} \leqslant {{\bar x_i}} \quad (i = 1,2, \cdots ,N)\quad {\text{ }} \end{split} \right\} $$ (1) 其中$ {f_i} $和$ {g_{ji}} $为任意的单变量函数, 即目标函数与约束条件属于可分离函数形式.
式(1)的拉格朗日函数为
$$ L({\boldsymbol{x}}{\text{,}}{\boldsymbol{\lambda }}) = \sum\limits_{i = 1}^N {{f_i}(x_i^{})} + \sum\limits_{j = 1}^M {{\lambda _j}\left(\sum\limits_{i = 1}^N {{g_{ji}}(x_i^{}) - {{\bar g_j}} } \right)} $$ (2) 其中${\lambda _j}\;(j = 1,2,\cdots,M)$为拉格朗日乘子.
原问题(1)的对偶问题为
$$ \left.\begin{split} & \mathop {\max }\limits_{{\boldsymbol{\lambda }} \in {E^M}} {\text{ }}\varphi {\text{(}}{\boldsymbol{\lambda }}{\text{)}} \\ & {\rm{s.t.}}{\text{ }}{\lambda _j} \geqslant {\text{0}}\quad (j = 1, 2,\cdots ,M) \end{split}\right\} $$ (3) 其中
$$ \varphi ({\boldsymbol{\lambda }}) = \mathop {\min }\limits_{\underline {{x_i}} \leqslant {x_i} \leqslant {{\bar x_i}} } (L({\boldsymbol{x}},{\boldsymbol{\lambda }})) $$ (4) 式(4)的库恩−塔克条件为
$$ \frac{{{\text{d}}f_i(x_{_i}^ * )}}{{{\text{d}}{x_i}}} + \sum\limits_{j = 1}^M {{\lambda _j}\frac{{{\text{d}}{g_{ji}}(x_{_i}^ * )}}{{{\text{d}}{x_i}}}} \left\{ \begin{aligned} & < {\text{0 }}\quad (x_i^* = {{\bar x_i}} ) \\ & = {\text{0 }}\quad (\underline {{x_i}} < x_i^* < {{\bar x_i}} ) \\ & > 0 \quad (x_i^* = \underline {{x_i}} ) \end{aligned} \right. $$ (5) 式(5)表明存在如下的函数关系
$$ x_i^* = x_i^*({\boldsymbol{\lambda }}) $$ (6) 式(6)表达了抽象的原−对偶设计变量关系, 当对偶规划的最优解求出来之后, 需根据具体的原−对偶设计变量关系式(5)由对偶规划的最优解求出来对应的原规划最优解. 可以按如下两步求解式(5).
先得到如下非线性方程的解
$$ \frac{{{\text{d}}f_i(x_i^s)}}{{{\text{d}}{x_i}}} + \sum\limits_{j = 1}^M {{\lambda _j}\frac{{{\text{d}}{g_{ji}}(x_i^s)}}{{{\text{d}}{x_i}}} = {\text{0}}} $$ (7) 由式(7)的解得到
$$ x_i^* = \left\{\begin{split} & {{\bar x_i}} \quad {\text{ (if }}x_i^s > {{\bar x_i}} ) \\ & x_i^s \quad {\text{ (if }}\underline {{x_i}} < x_i^s < {{\bar x_i}} ) \\ & \underline {{x_i}} \quad {\text{(if }}x_i^s < \underline {{x_i}} ) \end{split} \right. $$ (8) 为了给推导对偶规划的海赛阵做准备, 先将式(6)代入式(5)得
$$ \frac{{{\text{d}}f_i(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}{x_i}}} + \sum\limits_{j = 1}^M {{\lambda _j}\frac{{{\text{d}}{g_{ji}}(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}{x_i}}}} \left\{ \begin{aligned} & < {\text{0 }}\quad (x_i^*{\text{ = }} {{\bar x_i}} ) \\ & {\text{ = 0 }}\quad (\underline {{x_i}} < x_i^* < {{\bar x_i}} ) \\ & > 0 \quad (x_i^*{\text{ = }}\underline {{x_i}} ) \end{aligned} \right. $$ (9) $$ \frac{{\partial \varphi ({\boldsymbol{\lambda }})}}{{\partial {\lambda _j}}} = {G_j}{\text{(}}{{\boldsymbol{x}}^*}{\text{(}}{\boldsymbol{\lambda }}{\text{))}} $$ (10) 由式(10)可列出对偶目标函数的梯度向量, 而其海赛阵的元素则可在式(10)继续求偏导数给出
$$ \frac{{{\partial ^2}\varphi ({\boldsymbol{\lambda }})}}{{\partial {\lambda _j}\partial {\lambda _k}}} = \frac{{\partial {G_j}{\text{(}}{{\boldsymbol{x}}^*}{\text{(}}{\boldsymbol{\lambda }}{\text{))}}}}{{\partial {\lambda _k}}} = \sum\limits_{i = 1}^N {\frac{{{\text{d}}{g_{ji}}{\text{(}}x_i^*{\text{(}}{\boldsymbol{\lambda }}{\text{))}}}}{{{\text{d}}{x_i}}}\frac{{\partial x_i^*{\text{(}}{\boldsymbol{\lambda }}{\text{)}}}}{{\partial {\lambda _k}}}} $$ (11) 为了求出$\dfrac{{\partial x_i^*{\text{(}}{\boldsymbol{\lambda }}{\text{)}}}}{{\partial {\lambda _k}}}$, 对式(9)的$\underline {{x_i}} < x_i^* < {{\bar x_i}}$即$ i \in {I_a} $, 求$ {\lambda _k} $的偏导数得
$$ \begin{split} & \frac{{{{\text{d}}^{\text{2}}}f_i(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}x_i^2}}\frac{{\partial x_i^*({\boldsymbol{\lambda}} )}}{{\partial {\lambda _k}}} + \frac{{\partial {\lambda _k}}}{{\partial {\lambda _k}}}\frac{{{\text{d}}{g_{ki}}(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}{x_i}}} + \\ &\qquad \sum\limits_{j = 1}^M {{\lambda _j}\frac{{{{\text{d}}^{\text{2}}}{g_{ji}}(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}x_i^2}}\frac{{\partial x_i^*({\boldsymbol{\lambda}} )}}{{\partial {\lambda _k}}}} = 0 \end{split} $$ (12) 由式(12)得
$$ \frac{{\partial x_i^*({\boldsymbol{\lambda}} )}}{{\partial {\lambda _k}}} = \dfrac{{ - \dfrac{{{\text{d}}{g_{ki}}(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}{x_i}}}}}{{\dfrac{{{{\text{d}}^{\text{2}}}f_i(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}x_i^2}} + \displaystyle\sum\limits_{j = 1}^M {{\lambda _j}\dfrac{{{{\text{d}}^{\text{2}}}{g_{ji}}(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}x_i^2}}} }} $$ (13) 式(13)是$ i \in {I_a} $的结果; 若$ i \notin {I_a} $, 则有
$$\qquad\qquad\quad x_i^* \equiv \left\{ \begin{gathered} {{\bar x_i}}\quad {\text{ (if }}x_i^* > {{\bar x_i}} ) \\ \underline {{x_i}} \quad {\text{(if }}x_i^* < \underline {{x_i}} ) \\ \end{gathered} \right. $$ (14) $$\qquad\qquad\quad \frac{{\partial x_i^*({\boldsymbol{\lambda }})}}{{\partial {\lambda _k}}} = 0 $$ (15) 于是, 若$ i \notin {I_a} $时, 将式(13)和式(15)代入式(11), 就得到了
$$ \frac{{{\partial ^2}\varphi ({\boldsymbol{\lambda }})}}{{\partial {\lambda _j}\partial {\lambda _k}}} = - \displaystyle\sum\limits_{i \in {I_a}}^{} {\dfrac{{\dfrac{{{\text{d}}{g_{ji}}{\text{(}}x_i^*{\text{(}}{\boldsymbol{\lambda}} {\text{))}}}}{{{\text{d}}{x_i}}}\dfrac{{{\text{d}}{g_{ki}}(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}{x_i}}}}}{{\dfrac{{{{\text{d}}^{\text{2}}}f(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}x_i^2}} + \displaystyle\sum\limits_{j = 1}^M {{\lambda _j}\dfrac{{{{\text{d}}^{\text{2}}}{g_{ji}}(x_i^*({\boldsymbol{\lambda}} ))}}{{{\text{d}}x_i^2}}} }}} $$ (16) 有了式(10)和式(16), 就可以构造对偶规划的近似2阶显式
$$ \begin{split} & \varphi ({\boldsymbol{\lambda }}) = {\nabla ^{\text{T}}}\varphi ({{\boldsymbol{\lambda }}^{(v)}})({\boldsymbol{\lambda }} - {{\boldsymbol{\lambda }}^{(v)}})+ \\ &\qquad \frac{1}{2}{({\boldsymbol{\lambda }} - {{\boldsymbol{\lambda }}^{(v)}})^{\text{T}}}{\nabla ^{\text{2}}}\varphi ({{\boldsymbol{\lambda }}^{(v)}})({\boldsymbol{\lambda }} - {{\boldsymbol{\lambda }}^{(v)}}) \end{split} $$ (17) 其中$ {{\boldsymbol{\lambda }}^{(v)}} $取上一次的最优解$ {{\boldsymbol{\lambda }}^*} $作为本次的初始点, 以便构造第v次的对偶二次规划模型.
当第v次寻优收敛后, 需要代入式(6)求出对应的原变量最优解. 不过式(6)只是理论上的表达, 具体将第v + 1次的最优解$ {{\boldsymbol{\lambda }}^{(v + 1)}} $代入式(7)求出$ {{\boldsymbol{x}}^s} $, 然后代入式(8)得到第$ \mu + 1 $次的原变量$ {{\boldsymbol{x}}^{(\mu + 1)}} $, 这里的$ \mu $与v不同, 它表示结构重分析的指标. 经过在$\boldsymbol{x}^{(\mu+1)}$的结构重分析之后, 重新构造新的对偶规划式(17), 其中梯度向量和海赛阵分别按式(10)和式(16)构造, 此时的式(17)中的v清零, 取$\lambda^{(0)}=\lambda^{(v+1)}$, 这里的$\lambda^{(v+1)}$是前一次的最优解, 开始新一轮的对偶规划寻优, 式(3)是一个迭代的寻优序列, 直到得到新一轮的最优解为止. 然后, 再求出新的原变量.
值得探讨一下式(7)的算法实现. 在求解式(7)时, 于具体的$\lambda$值, 除了可按变量$x_i$非线性方程式求解, 常常会遇到显式解, 更为方便.
由于式(16)中含有$\lambda_j\;(j=1, 2,\cdots, M)$, 因而需对此进行处理, 使对偶二阶导数不显含对偶变量. 下面给出4种处理方法, 分别是: (1)对偶变量迭代逼近法; (2)指数函数形式的解法; (3)幂函数形式的解法; (4)基于变换的精确解法.
1.1 对偶变量迭代逼近法
在迭代寻优过程中, 取式(13)中的${f_k}({\lambda }_{j}) = {(t_i)^\beta }$为上一次的变量, 于是海赛阵中就不显含本次的对偶变量了.
至于由对偶规划的最优解按式(7)和式(8)求出对应的原变量, 一般要求解N个变量$ {x_i} $各自的非线性方程解, 有时存在原−对偶变量之间的显函数关系可以利用, 从而勿需求解非线性方程.
1.2 指数函数形式的解法
若约束函数存在下述形式
$$ {g_{ji}}({x_i}) = {a_{ji}}{{\rm{e}}^{{b_i}{x_i}}}\;(i = 1,2,\cdots,N;j = 1,2,\cdots,M) $$ (18) 其中$a_{ji}$和${b_i}$为实数值.
将式(18)代入式(16)得
$$ \frac{\partial^2 \varphi({\boldsymbol{\lambda}})}{\partial \lambda_j \partial \lambda_k}=-\sum_{i \in I_a} \frac{a_{j i} a_{k i} b_i^2 {\rm{e}}^{2 b_i x_i^*}}{\dfrac{\mathrm{d}^2 f_i\left(x_i^*\right)}{\mathrm{d} x_i^2}+\displaystyle\sum_{j=1}^M \lambda_j a_{j i} b_i^2 {\rm{e}}^{b_i x_i^*}} $$ (19) 为了将式(19)中含$ {\lambda _j}\;(j = 1,\cdots,M) $的项消除, 现将式(18)代入到式(5), 得
$$ \sum_{j=1}^M \lambda_j a_{j i} b_i {\rm{e}}^{b_i x_i^*}=-\frac{\mathrm{d} f_i\left(x_i^*\right)}{\mathrm{d} x_i} \quad\left(i \in I_a\right) $$ (20) 将式(20)代入式(19)得
$$ \frac{{{\partial ^2}\varphi ({\boldsymbol{\lambda}} )}}{{\partial {\lambda _j}\partial {\lambda _k}}} = - \sum\limits_{i \in {I_a}}^{} {\dfrac{{{a_{ji}}{a_{ki}}b_i^2{{\rm{e}}^{2{b_i}x_i^*}}}}{{\dfrac{{{{\text{d}}^{\text{2}}}f_i(x_i^*)}}{{{\text{d}}x_i^2}} - b_i^{}\dfrac{{{\text{d}}f_i(x_i^*)}}{{{\text{d}}x_i^{}}}}}} $$ (21) 为了求出原−对偶变量的函数关系, 假定有
$$ f_i\left(x_i\right)=c_i {\rm{e}}^{d_i x_i} $$ (22) 将式(22)代入到式(20)得
$$ {\rm{e}}^{\left(d_i-b_i\right) x_i^*}=\frac{-\displaystyle\sum_{j=1}^M \lambda_j a_{j i} b_i}{c_i d_i} $$ (23) 若上式右边大于0能够保证, 则得到原−对偶变量的如下显式关系, 避免了非线性方程的求解
$$ x_i^*=\frac{1}{d_i-b_i} \ln \left(\frac{-\displaystyle\sum_{j=1}^M \lambda_j a_{j i} b_i}{c_i d_i}\right) $$ (24) 1.3 幂函数形式的解法
若约束函数存在下述形式
$$ g_{j i}\left(x_i\right)=a_{j i} x_i^{b_i}\;(i=1,2, \cdots, N ; j=1,2, \cdots, M) $$ (25) 其中$ {a_{ji}} $和${b_i}$为实数值.
同上一情况类似, 可以推导出
$$ \frac{{{\partial ^2}\varphi (\lambda )}}{{\partial {\lambda _j}\partial {\lambda _k}}} = - \sum\limits_{i \in {I_a}}^{} {\dfrac{{{a_{ji}}{a_{ki}}b_i^2{{(x_i^*)}^{2{b_i} - 2}}}}{{\dfrac{{{{\text{d}}^{\text{2}}}f_i(x_i^*)}}{{{\text{d}}x_i^2}} - \dfrac{{b_i^{} - 1}}{{{x_i}}}\dfrac{{{\text{d}}{f_i}(x_i^*)}}{{{\text{d}}x_i^{}}}}}} $$ (26) 为了求出原−对偶变量的函数关系, 假定有
$$ {f_i}(x_i^{}) = {c_i}x_i^{{d_i}} $$ (27) 将式(25)和式(27)代入式(5), 得到原−对偶变量的如下显式关系
$$ x_i^* = {\left(\frac{{ - {b_i}}}{{{c_i}{d_i}}}\sum\limits_{j = 1}^M {{\lambda _j}{a_{ji}}} \right)^{\tfrac{1}{{{d_i} - {b_i}}}}} $$ (28) 上式开方时必须注意实根的存在.
1.4 基于变换的精确解法
第2和第3种处理针对两种函数形式的情况, 能否给出约束函数更一般情况的处理?本文就如下情况予以回答.
若
$$ {g_{ji}}({x_i}) = {a_{ji}}{\theta _i}({x_i})\quad (i = 1,2,\cdots,N;j = 1,2,\cdots,M) $$ (29) 满足凸函数条件, 则将式(29)代入式(1)得
$$ \left. \begin{split} & \mathop {\min }\limits_{x \in {E^N}} {\text{ }}F{\text{(}}{\boldsymbol{x}}{\text{)}} = \sum\limits_{i = 1}^N {{f_i}(x_i^{})} \\ & {\rm{s.t.}}{\text{ }}{G_j}{\text{(}}{\boldsymbol{x}}{\text{)}} = \sum\limits_{i = 1}^N {{a_{ji}}{\theta _i}(x_i^{}) - {{\bar g_j}} } \leqslant {\text{0}}\,\;(j = 1,2, \cdots ,M) \\ &\quad\;\; \underline {{x_i}} \leqslant {x_i} \leqslant {{\bar x_i}} \;\,(i = 1, 2,\cdots ,N)\quad {\text{ }} \end{split} \right\} $$ (30) 引入变换及其逆变换
$$ {z_i} = {\theta _i}({x_i})\;,\quad {x_i} = \theta _i^{ - 1}({z_i})\; $$ (31) 代入式(30)得
$$ \left.\begin{split} & \mathop {\min }\limits_{{{z}} \in {E^N}} {\text{ }}F{\text{(}}{\boldsymbol{z}}{\text{)}} = \sum\limits_{i = 1}^N {{f_i}({z_i}\;)} \\ & {\rm{s.t.}}{\text{ }}{G_j}{\text{(}}{\boldsymbol{z}}{\text{)}} = \sum\limits_{i = 1}^N {{a_{ji}}{z_i} - {{\bar g_j}} } \leqslant {\text{0}}\;\,(j = 1,2, \cdots ,M) \\ &\quad\;\; \underline {{{{z}}_i}} \leqslant {z_i} \leqslant {{\bar z_i}} \;\,(i = 1,2, \cdots ,N)\quad {\text{ }} \end{split} \right\} $$ (32) 其中
$$ {f_i}({x_i}) = {f_i}(\theta _i^{ - 1}({z_i})\;) \text{, } \underline {{z_i}} = {\theta _i}(\underline {{z_i}} )\;\; \text{, } {{\bar z_i}} = {\theta _i}(\overline {{z_i}} )\; $$ (33) 仿前面的推导, 得如下结果
$$ \frac{{\partial \varphi ({\boldsymbol{\lambda }})}}{{\partial {\lambda _j}}} = {G_j}({z^*}({\boldsymbol{\lambda }})) $$ (34) $$ \frac{{{\partial ^2}\varphi ({\boldsymbol{\lambda }})}}{{\partial {\lambda _j}\partial {\lambda _k}}} = - \sum\limits_{i \in {I_a}}^{} {\frac{{{a_{ji}}{a_{ki}}}}{{\dfrac{{{{\text{d}}^{\text{2}}}f_i(z_i^*)}}{{{\text{d}}z_i^2}}}}} $$ (35) $$ \frac{{{\text{d}}f_i(z_i^*)}}{{{\text{d}}{z_i}}} + \sum\limits_{j = 1}^M {\lambda _j^{}{a_{ji}}} = 0 $$ (36) $$ z_i^* = \left\{\begin{aligned} & {{\bar z_i}} {\text{ (if }}z_i^s > {{\bar z_i}} ) \\ & z_i^s{\text{ (if }}\underline {{z_i}} < z_i^s < {{\bar z_i}} ) \\ & \underline {{z_i}} \;{\text{(if }}z_i^s < \underline {{z_i}} )\end{aligned} \right. $$ (37) 其中表达原−对偶变量关系的式(36)并不需要解非线性方程, 记
$$ \frac{{{\text{d}}{f_i}({\boldsymbol{z}})}}{{{\text{d}}{z_{{i}}}}} = {\varOmega _i}({z_{{i}}}) \text{, } {z^s} = {\varOmega ^{ - 1}}\left( - \sum\limits_{j = 1}^M {\lambda _j^{}{a_{ji}}} \right) $$ (38) 由式(37)解得$ z_i^* $后, 可得规划式(30)的解
$$ x_i^* = \theta _i^{ - 1}(z_i^*)\; $$ (39) 以上的4种处理尽量不采用第1种, 原因是多了一个对$ {\boldsymbol{\lambda }} $的迭代过程. 当分离的每一项函数形式为指数函数或幂函数时分别按第2种和第3种处理, 一般情况下可采用第4种处理.
2. 算例
本研究团队以往用对偶规划求解结构优化问题时, 多遇到幂函数的情况, 故多按第3种情况进行了处理, 当时的推导均为个案进行, 现以算例2至算例5中4类不同结构拓扑优化问题为例, 按本文的结果进行了验证. 算例1为特别设计的简单数学算例, 以比较按第1种情况和第4种情况处理的效率, 其它算例均是按第3种情况处理.
2.1 算例1: 普适处理的效果比较
取
$$ {f_i}(x_i^{}) = {c_i}\frac{{{x_i}}}{{1 + 2(1 - {x_i})}} \text{, } {g_{ji}}(x_i^{}) = {a_{ji}}\frac{{1 + 5(1 - {x_i})}}{{{x_i}}} $$ 计算如下可分离非线性优化问题
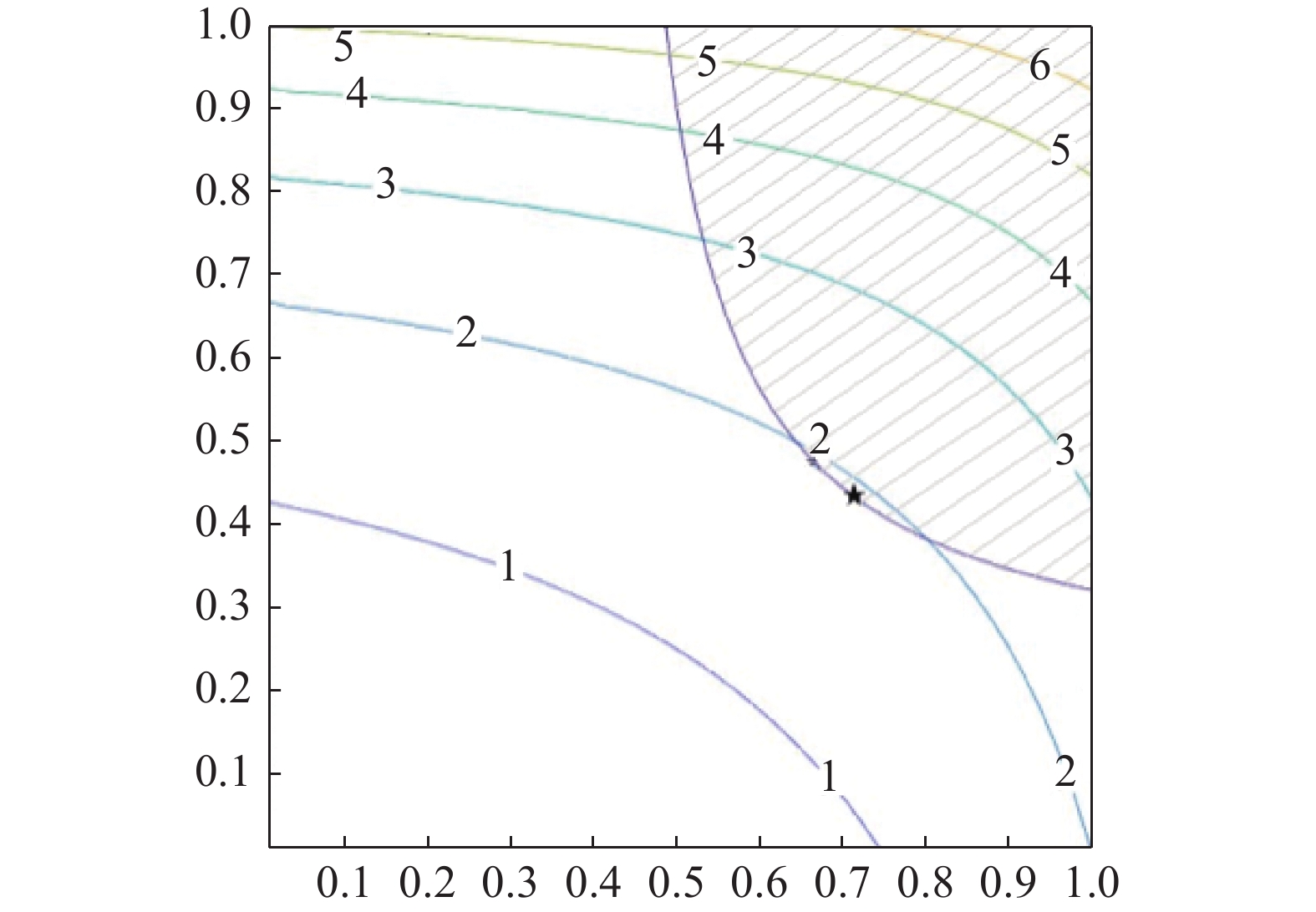
$$ \left.\begin{split} & \mathop {\min }\limits_{{x_1},{x_2}} {\text{ }}F{\text{(}}{x_1},{x_2}{\text{)}} = 2\frac{{{x_1}}}{{1 + 2(1 - {x_1})}} + 5\frac{{{x_2}}}{{1 + 2(1 - {x_2})}} \\ & {\rm{s.t.}}{\text{ }}{G_1}{\text{(}}{x_1},{x_2}{\text{)}} = 6\frac{{1 + 5(1 - {x_i})}}{{{x_i}}} + 3\frac{{1 + 5(1 - {x_i})}}{{{x_i}}} \leqslant {\text{47}} \\ &\quad\;\; 0.01 \leqslant {x_i} \leqslant 1\;\,(i = 1,2)\quad {\text{ }} \end{split} \right\}$$ (40) 取初值$ ({x_1},{x_2}) = (0.01,0.01) $, 按第1种情况处理, 迭代12次, 目标值1.9226, 最优点${({x_1},{x_2})^*} = (0.713\;7,0.433\;1)$. 按第4种情况处理, 迭代9次, 目标值最优点值相同. 第4种处理方式的迭代次数更少. 算例1的目标函数等值线及约束可行域如图1所示, 星号点为最优点.
2.2 算例2: 位移约束下连续体拓扑优化问题[19-21,28]
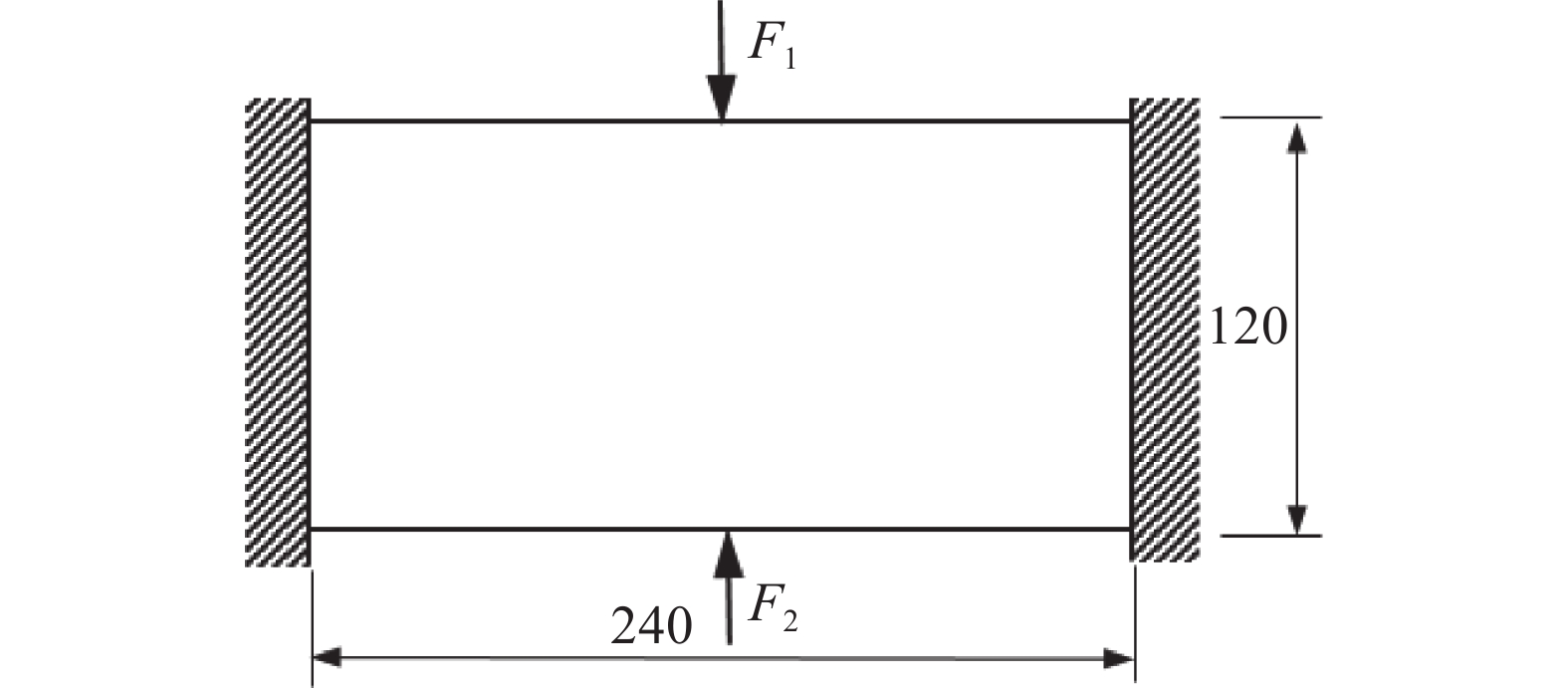
本算例以多工况位移约束下结构重量极小化结构拓扑优化问题为例, 比较MMA算法[6]与本文提出的DP-EM算法的计算效率. 算例数据如下.
如图2所示, 基结构尺寸为240 × 120 × 1的平面体, 材料弹性模量为E = 1, 泊松比为0.3. 左右边界固定, 工况1: 集中载荷F1 = −1竖直向下作用于上边界中点; 工况2: 集中载荷F2 = 1竖直向上作用于下边界中点(力以竖直向上为正). 计算网格为240 × 120个正方形单元. 初始位移为工况1沿集中载荷F1方向位移为−5.156, 工况2沿集中载荷F2方向位移为5.156 (位移方向竖直向上为正). 位移约束为: 工况1时约束集中载荷F1方向位移大于等于−15, 工况2时约束集中载荷F2方向位移小于等于15. 收敛精度取0.01.
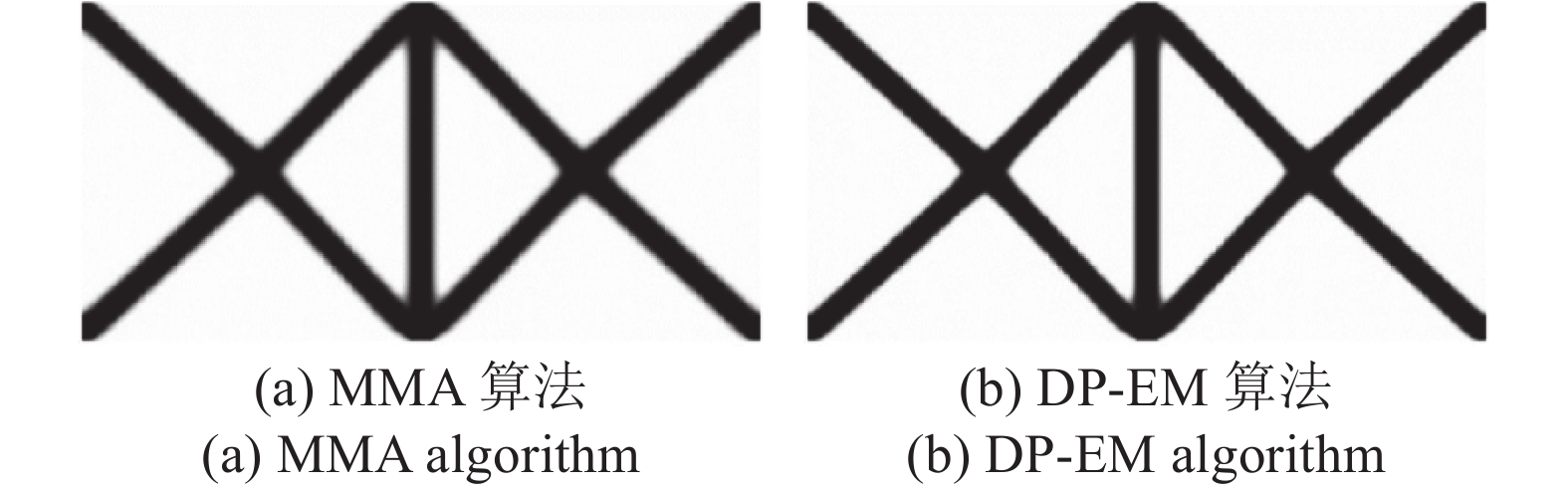
使用MMA算法经过80次迭代收敛, 历时247.904 s, 最优点结构体积比为24.88%, 上下结构边中点处约束点位移分别为−15.001和15.001, 最优拓扑图形如图3(a)所示. 使用DP-EM算法经过75次迭代收敛, 历时65.435 s, 最优点结构体积比为23.76%, 上下结构边中点处约束点位移分别为−14.999和14.999, 最优拓扑图形如图3(b)所示. MMA算法的用时是DP-EM算法的3.789倍. 结果显示DP-EM算法具有更高的求解效率.
2.3 算例3: 应力约束下连续体拓扑优化问题[29-31]
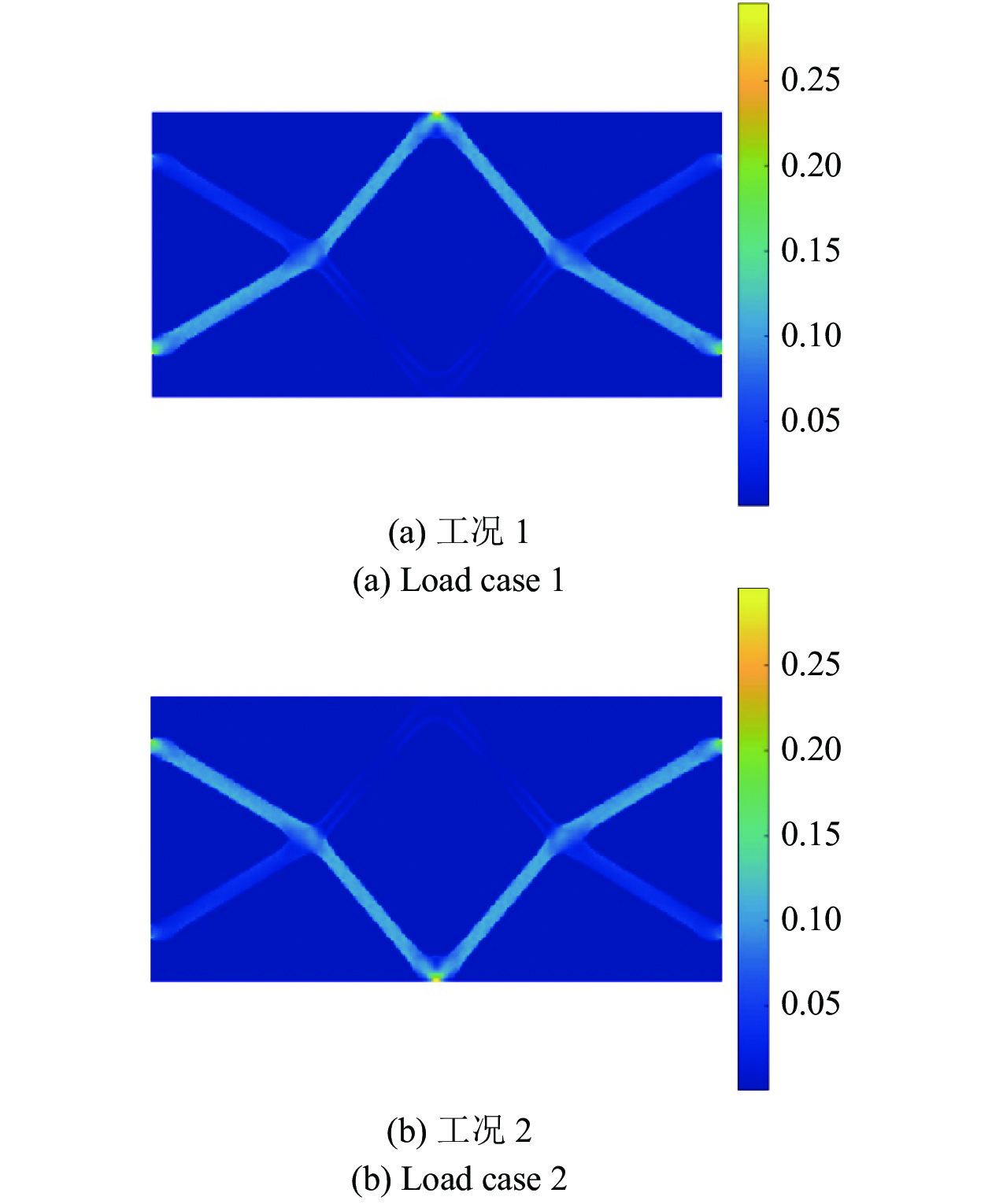
算例3的基结构及载荷与算例2相同, 只是为了避免集中力作用导致的应力集中, 将集中载荷分散布置在相邻的3个节点上. Mises应力约束小于或等于0.3.
取用本文算法, 迭代66次收敛, 最优点体积比15.42%, 最优拓扑图形如图4所示. 各工况的最大Mises应力为0.2957, 两个工况下的Mises应力分布图如图5所示, 满足应力约束条件.
比较算例2可知, 位移约束与应力约束下的结构拓扑优化得到的最优拓扑是不相同的.
2.4 算例4: 疲劳约束下连续体拓扑优化问题[30-31]
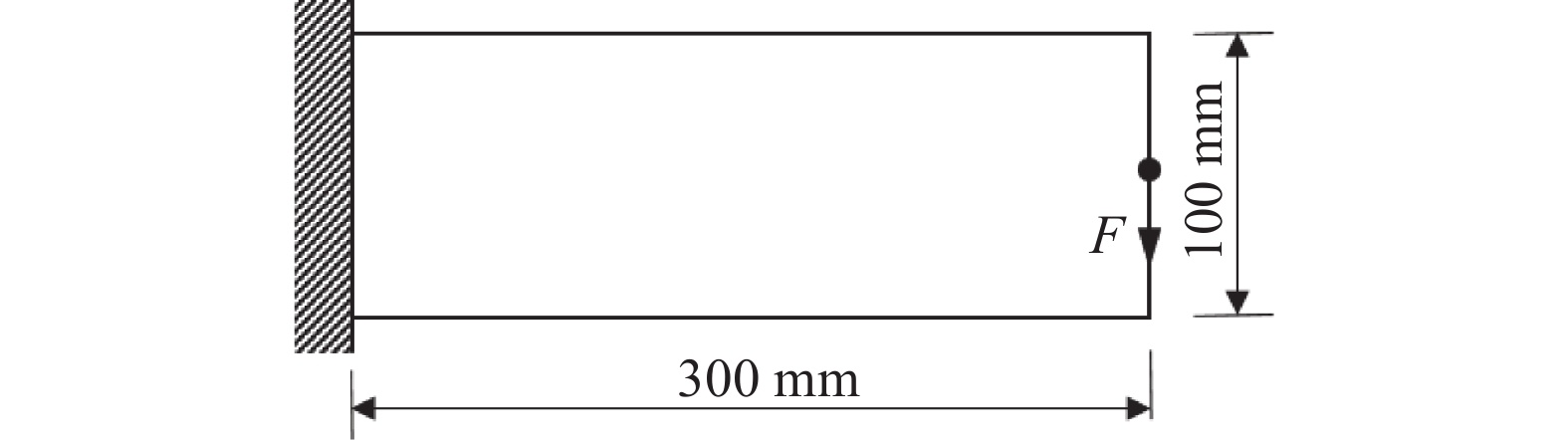
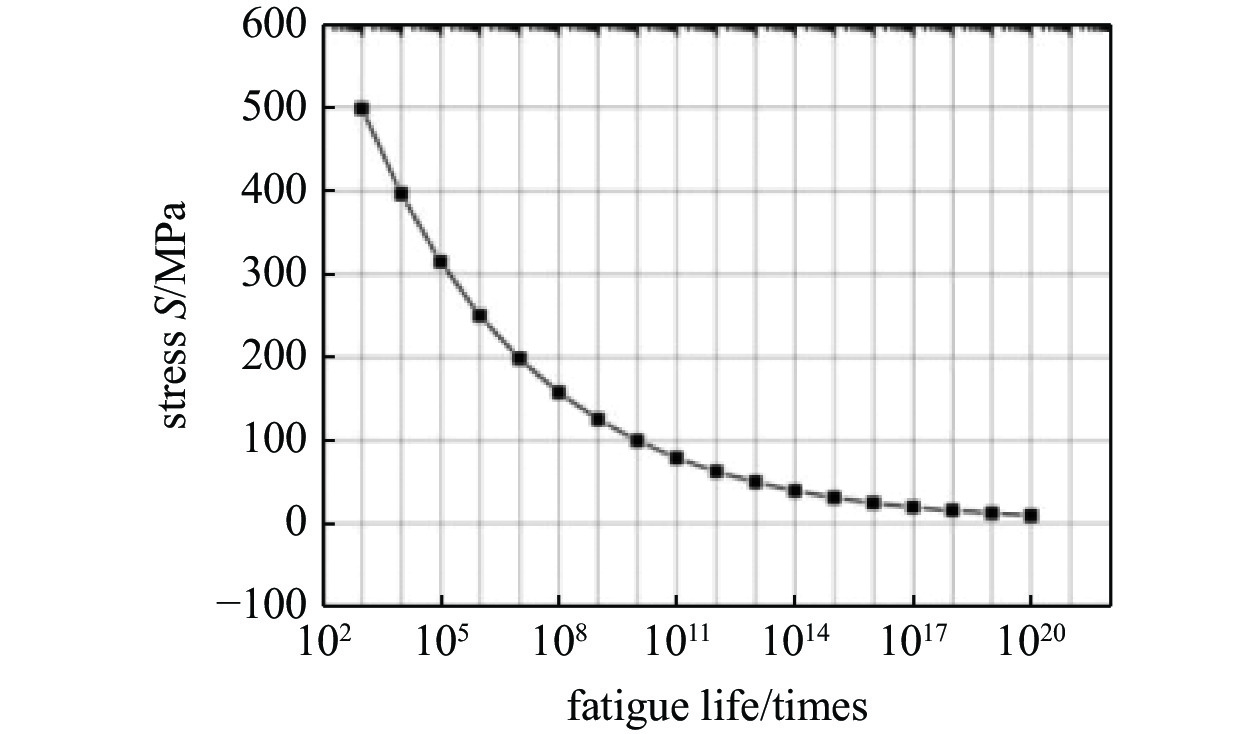
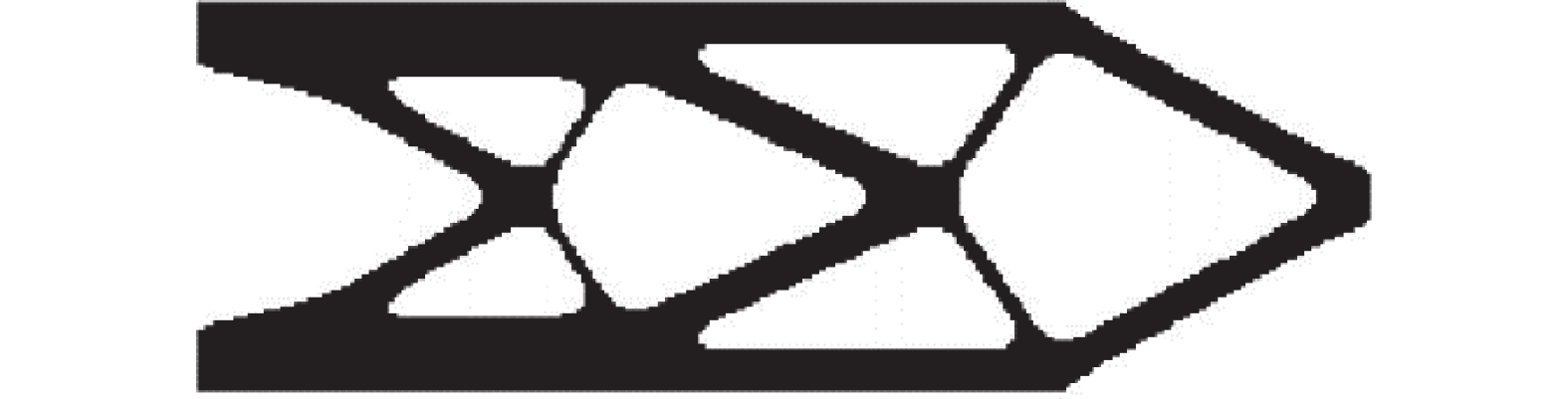
如图6所示, 材料弹性模量为$ E = 2.1 \times {10^5}{\text{ MPa}} $, 泊松比$ \nu = 0.3 $, 材料对应于循环次数$ 1.0 \times {10^6} $的疲劳极限为${\sigma _s} = 250{\text{ MPa}}$, 基结构为300 mm × 100 mm × 10 mm的平面体, 划分为300 × 100个正方形单元. 基结构的左边界固定, 正弦形式循环载荷F = 7500 N且均值为零, 相位角为零, 作用于基结构右边界的中心点, 为了避免应力集中将载荷施加在3个节点上. 疲劳寿命约束为大于或等于$ 1.0 \times {10^5} $次. 巴士昆公式$ \sigma = A{L^{ - m}} $中, $ \sigma $为疲劳循环下的材料应力, L为对应的疲劳寿命, A与m为材料给定的常数量, 此例中取值为m = 0.10, A = 995.3 MPa, S-N曲线如图7所示.
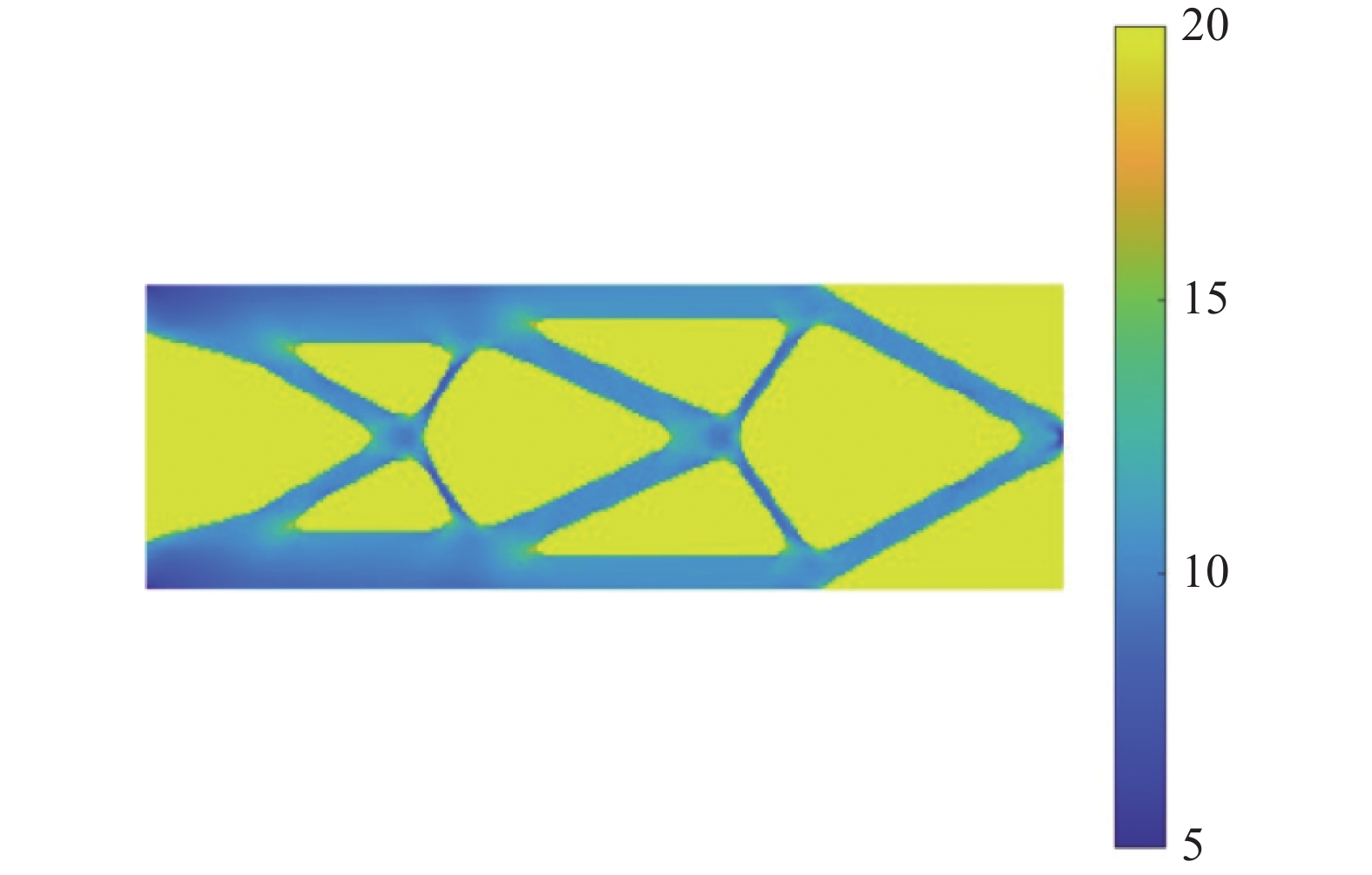
取用本文算法, 经过62次迭代收敛, 最优体积比为39.73%, 最大疲劳寿命为99163次. 得到的最优拓扑如图8所示, 对应的疲劳寿命以10为底的对数分布如图9所示.
2.5 算例5: 破损−安全拓扑优化问题[32]
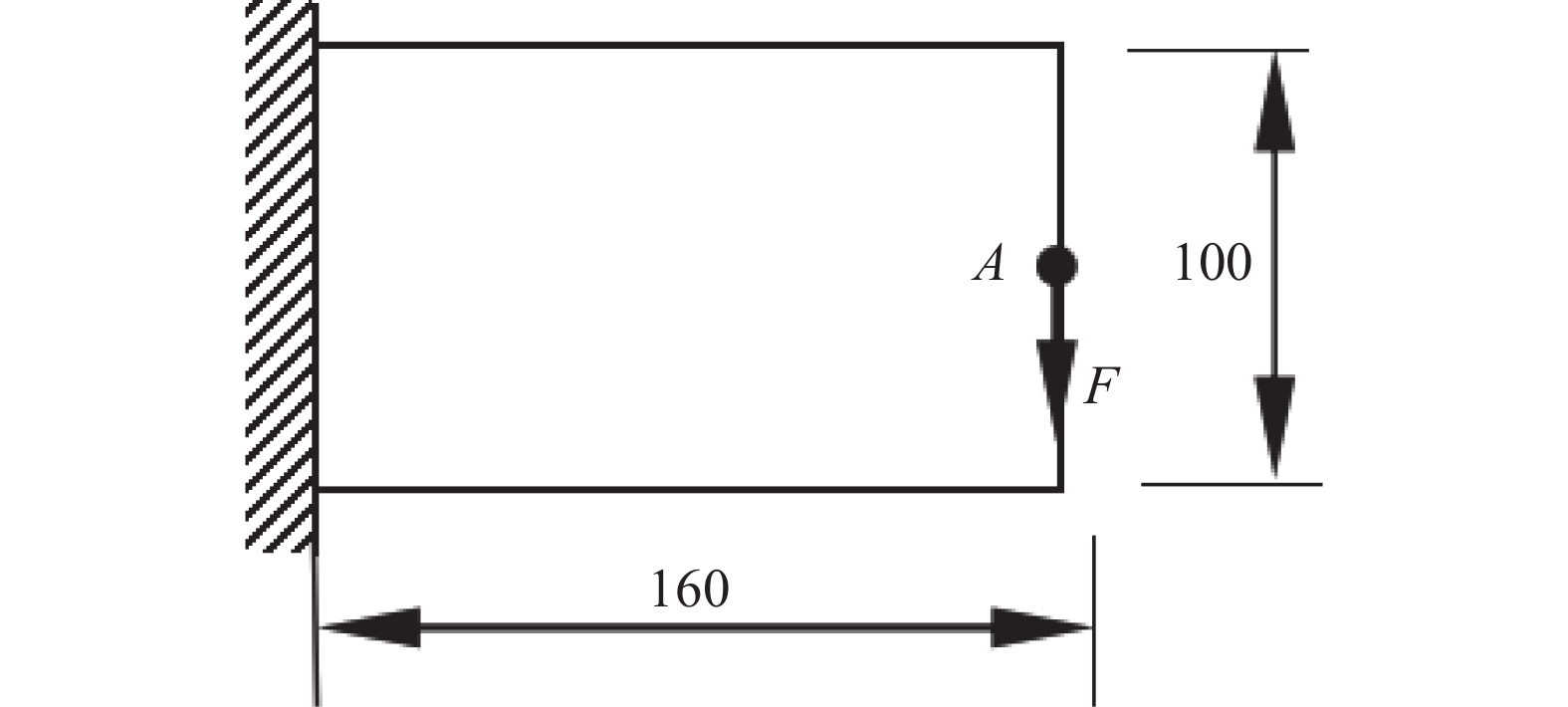
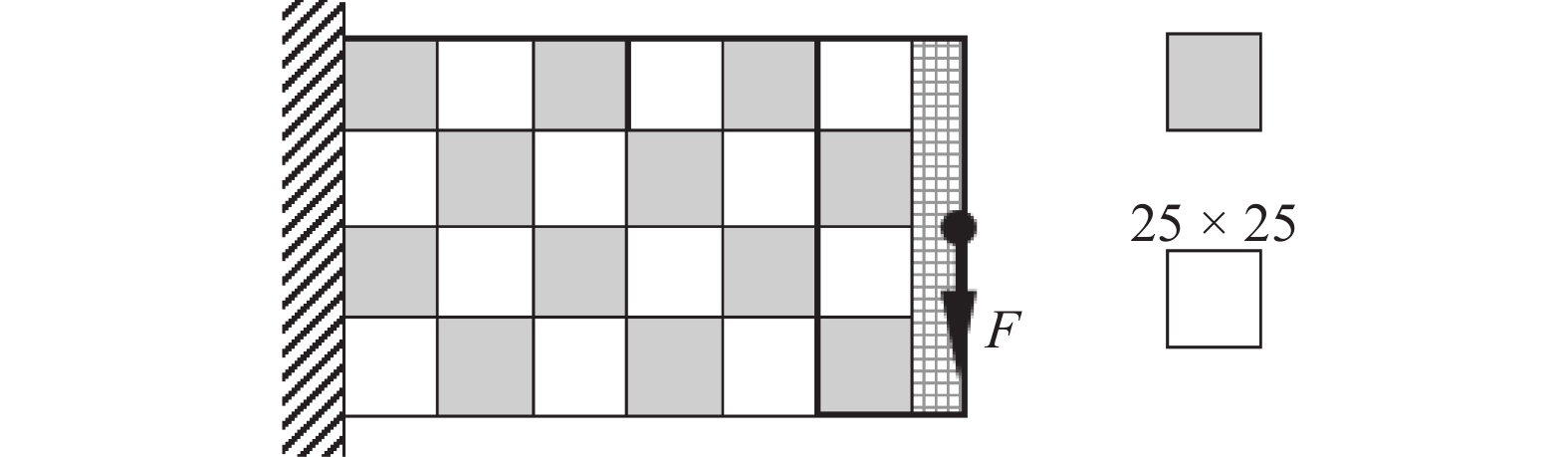
如图10所示, 基结构为160 × 100的平面体, 厚度为1, 材料弹性模量为1, 泊松比为0.3. 左边界固定, 一集中载荷F = 1作用于右边界中心位置. 采用25 × 25的正方形作为结构局部破损模式, 如图11中白色和灰色正方形所示, 采用无缝平铺的结构破损状况预估分布模式, 右边界附近区域为保留不发生破损的区域(如图11所示方格子图案填充部分). 有限元网格为160 × 100个正方形单元, 位移约束条件为A点的竖直向下位移值小于120.
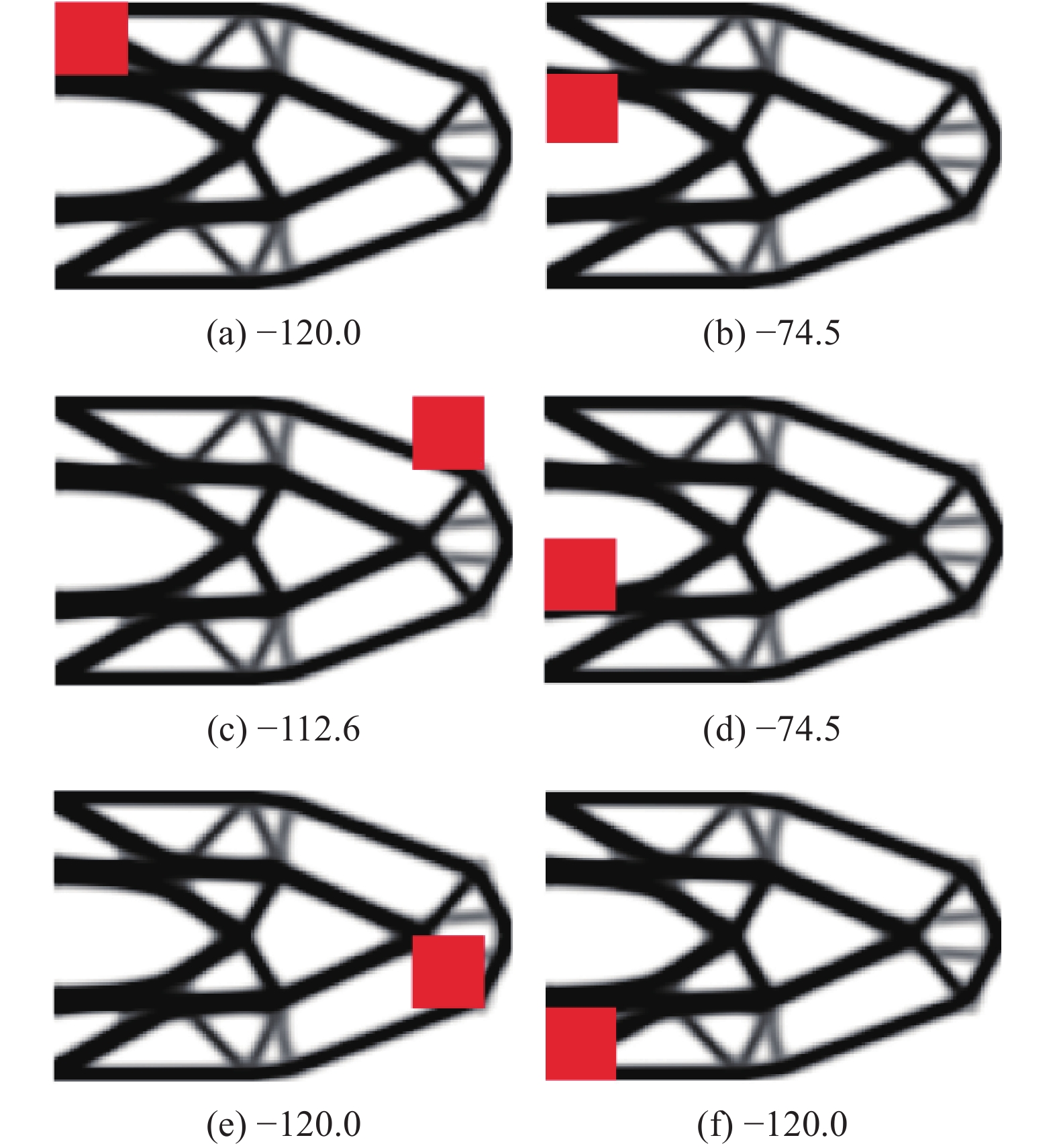
不考虑破损−安全, 按传统安全理念进行拓扑优化, 得到的最优点体积比为18.40%, 最优拓扑如图12(a)所示, 最优点时约束点位移值为−119.9, 满足位移约束条件. 考虑破损−安全的结构拓扑优化最优点体积比为38.12%, 最优拓扑如图12(b)所示. 可以看出, 考虑破损−安全之后得到的结构体积比更大, 结构拓扑更复杂, 但结构可满足所有破损情况下的安全. 图13为部分破损工况下的结构拓扑图及位移, 表1为最优点时所有各破损工况位移约束点的位移值, 表中各行列数据均与图11中的破损工况位置一一对应, 例如表中的第1行第1列数据(−120.0)对应于图11中第1行第1列破损位置发生破损, 如图13(a)所示. 可以看出有些破损工况是关键约束, 有些破损工况不是关键约束, 但所有破损工况均满足位移约束条件.
表 1 算例5最优点时各破损工况对应的约束点位移值Table 1. Displacements at constraint point for all failure cases at optimization of example 5Columns Rows 1 2 3 4 5 6 1 −120.0 −120.0 −120.0 −116.3 −112.6 −112.6 2 −74.5 −94.2 −120.0 −118.5 −120.0 −120.0 3 −74.5 −94.2 −120.0 −118.5 −120.0 −120.0 4 −120.0 −120.0 −120.0 −116.3 −112.6 −112.6 3. 结论
我们团队以往经常把对偶规划用于结构优化的建模和求解, 尤其用于结构拓扑优化问题, 以提高求解效率, 不过那时建立对偶规划的海赛阵, 均为对个案的推导.
本文阐述了普适的处理方法, 针对一类变量可分离凸规划模型, 给出了4种处理方法: (1)对偶变量迭代逼近法; (2)指数函数形式的解法; (3)幂函数形式的解法; (4)基于变换的精确解法. 其中方法(1)和方法(4)是普适的方法, 由于方法4不需要采用迭代逼近的近似求解, 比方法1的求解效率更高. 而方法2和方法3则示例了当函数形式给定后, 依据具体的函数形式, 同样可以给出直接解法, 而不需要如方法1中采取迭代解法.
不同于以往变密度法或ICM方法中针对某一具体惩罚函数或过滤函数形式所建立的优化模型给出个案的求解公式及算法, 本文针对一类变量可分离凸规划模型所阐述的普适处理方法, 对文献[28]的DP-EM方法进行了推广, 从原来的只处理幂函数形式推广为可处理任意函数形式, 因而保证今后惩罚函数或过滤函数采取不同函数形式时, 优化模型的求解有一套普遍适用的可靠理论和算法. 本文所提出方法相比广泛使用的MMA方法具有更高的求解效率. 这说明理论高度的提升会导致更有效和广泛的应用前景. 相信本文的工作也会对于同行有借鉴作用.
附录A
以下列举基于ICM方法建立的位移、应力、疲劳等约束下结构拓扑优化模型, 以及考虑破损−安全的结构拓扑优化模型.$\; $
采用幂函数形式的过滤函数, 单元重量及单元刚度用过滤函数识别
$$ {w_i} = {({t_i})^\alpha }w_i^0 ,\quad {{\boldsymbol{k}}_i} = {({t_i})^\beta }{\boldsymbol{k}}_i^0 \tag{A1}$$ 其中$ {w_i} $及$ {{\boldsymbol{k}}_i} $为单元重量及单元刚度阵, $ w_i^0 $及$ {\boldsymbol{k}}_i^0 $为单元固有重量及单元固有刚度阵. $ {f_w}({t_{_i}}) = {({t_i})^\alpha } $及$ {f_k}({t_{_i}}) = {({t_i})^\beta } $分别为单元重量及单元刚度的幂函数形式过滤函数.
结构总重量表达为
$$ {w_i} = \sum\limits_{i = 1}^N {{{({t_i})}^\alpha }w_i^0} \tag{A2}$$ 其中N表示单元拓扑设计变量的总数.
位移利用莫尔定理表达为
$$ {u_j} = \sum\limits_{i = 1}^N {\frac{{{{(t_i^{(k)})}^\beta }}}{{{{({t_i})}^\beta }}}} {[{({\boldsymbol{u}}_{ij}^{\text{V}})^{\text{T}}}{\boldsymbol{F}}_i^{\text{R}}]^{(k)}}= \sum\limits_{i = 1}^N {\frac{{{{(t_i^{(k)})}^\beta }{A_{ij}}}}{{{{({t_i})}^\beta }}}} = \sum\limits_{i = 1}^N {\frac{{{c_{ij}}}}{{{{({t_i})}^\beta }}}} \tag{A3}$$ 其中$ t_i^{(k)} $为第k步迭代时单元i对应的拓扑变量值, ${\boldsymbol{u}}_{ij}^{\text{V}}$及 $ {\boldsymbol{F}}_i^{\text{R}} $为单元i在第j个位移对应单位虚工况下的单元节点位移向量及在实工况下的单元节点力向量, j = 1, 2, ···, J, J = L × R为优化模型中位移约束条件总数, L为工况数, R为定义的位移约束总数. ${A_{ij}} = {[{({\boldsymbol{u}}_{ij}^{\text{V}})^{\text{T}}}{\boldsymbol{F}}_i^{\text{R}}]^{(k)}}$定义为第k次迭代时单元i对位移j的贡献系数, $ {c_{ij}} = {(t_i^{(k)})^\beta }{A_{ij}} $为位移j的约束近似方程系数.
用ICM法建立的拓扑优化模型表示为
$$ \left. \begin{split} & {{\text{find}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{t}} \in {E^N}{\text{ }}} \\ & {{\text{make}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} W = \sum\limits_{i = 1}^N {{{({t_i})}^\alpha }w_i^0 \to \min } } \\ & {{\text{s}}{\text{.t}}{\text{. }}\; \sum\limits_{i = 1}^N {\frac{{{c_{ji}}}}{{{{({t_i})}^\beta }}} \leqslant {{\bar u}_j}} {\kern 1pt} {\kern 1pt} } \\ & \qquad \underline {{t_i}{\kern 1pt} } \leqslant {t_i} \leqslant 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ & (i = 1, 2,\cdots ,N;{\kern 1pt} {\kern 1pt} j = 1,2, \cdots ,J) \end{split} \right\} \tag{A4}$$ 式中${\boldsymbol{t}} = {({t_1},{t_2}, \cdots ,{t_N})^{\text{T}}}$是单元拓扑设计变量向量$ {\bar u_j} $表示第j号位移约束的上限.
(2) 应力或疲劳局部性能约束连续体结构拓扑优化[30-31]
对结构重量(或体积)、结构局部性能如应力或疲劳寿命等, 均用过滤函数进行识别
$$ {w_i}({t_i}) = w_i^0{f_w}({t_i}) \text{, } {\bar \psi _i}({t_i}) = {f_\psi }({t_i})\bar \psi \tag{A5}$$ 式中, $ {f_w}({t_i}) $及$ {f_\psi }({t_i}) $分别为结构重量(或体积)及结构性能如应力或疲劳寿命等的过滤函数, $ w_i^0 $及$\bar \psi$分别为结构固有的重量(或体积)及结构性能如应力或疲劳寿命允许值等.
将N个约束应用K-S函数进行集成, 得到基于K-S函数集成的局部性能约束优化模型
$$ \left.\begin{split} &\text{find}: {\boldsymbol{t}}\in {E}^{N}\\ &\mathrm{min}: {\displaystyle \sum _{i = 1}^{N}{w}_{i}^{0}{f}_{w}({t}_{i})}\\ &\text{s}\text{.t}\text{. }\frac{1}{\rho }\text{ln}{\displaystyle \sum _{i = 1}^{N}\mathrm{exp}\left(\rho \frac{\underset{l = 1,2,\cdots,L}{\mathrm{max}}({\psi }_{il}^{(\nu )})}{{f}_{\psi }({t}_{i})}\right)}\leqslant \bar{\psi }\\ &\underline {{t}}\leqslant {t}_{i}\leqslant 1\end{split}\right\} \tag{A6}$$ 式中$\mathop {\max }\limits_{(l = 1,2,\cdots,L)} (\psi _{il}^{(\nu )}) = \psi _i^{(\nu )}$, 称此措施为多工况的“单工况化”处理. $ \rho $为K-S函数参数, $ \rho $值越大, K-S函数逼近效果越好.
(3) 考虑破损−安全的连续体结构拓扑优化[32]
应用ICM方法, 建立的结构拓扑优化模型为
$$ \left.\begin{split} & {\text{find }} {\boldsymbol{t}} \in {E^N} \\ & {\text{make }}V{\text{(}}{\boldsymbol{t}},{{\varPhi}} {\text{)}} = \mathop {{\text{max}}}\limits_{s = 1,2,\cdots,S} {V_s}{\text{(}} {\boldsymbol{t}}{\text{)}} \to \min \\ & {\rm{s.t.}}{\text{ }}{u_{jls}}{\text{(}}{\boldsymbol{t}}{\text{)}} \leqslant \overline {{u_j}} \; \\ &\quad {\text{ }}(j = 1,2,\cdots,J;\;l = 1,2,\cdots,L;\;s = 1,2,\cdots,S) \\ &\quad {\text{ }}\underline {{t_i}} \leqslant {t_i} \leqslant 1\;{\text{(}}\;i = 1, 2,\cdots ,N)\quad {\text{ }} \end{split} \right\} \tag{A7}$$ 其中, t为拓扑设计变量向量; $V{\text{(}}{\boldsymbol{t}},{{\varPhi }}{\text{)}}$为结构失效状况集合$ \varPhi $中所有结构失效状况中体积最大值; $ {u_{jls}}{\text{(}}t{\text{)}} $为结构失效状况集合${{\varPhi}}$中第s号结构失效状况$ {\varOmega _s} $在第l的载荷工况下的第j号位移约束函数, $ \overline {{u_j}} $为第j号位移约束值; J为位移约束总数, L为载荷工况总数; $ \underline {{t_i}} $为防止有限元分析时总刚度矩阵奇异而设置的拓扑变量下限值.
结构总体积及位移约束的显式化与1中的式(A1) ~ 式(A4)类似. 在此不再重复.
-
表 1 算例5最优点时各破损工况对应的约束点位移值
Table 1 Displacements at constraint point for all failure cases at optimization of example 5
Columns Rows 1 2 3 4 5 6 1 −120.0 −120.0 −120.0 −116.3 −112.6 −112.6 2 −74.5 −94.2 −120.0 −118.5 −120.0 −120.0 3 −74.5 −94.2 −120.0 −118.5 −120.0 −120.0 4 −120.0 −120.0 −120.0 −116.3 −112.6 −112.6 -
[1] Fleury C. Structural weight optimization by dual methods of convex programming. International Journal for Numerical Methods in Engineering, 1979, 14(2): 1761-1783
[2] Fleury C. Primal and dual methods in structural optimization. Journal of the Structural Division, 1980, 106(5): 1117-1133 doi: 10.1061/JSDEAG.0005418
[3] Fleury C, Braibant V. Structural optimization: A new dual method using mixed variables. International Journal for Numerical Methods in Engineering, 1986, 23(3): 409-428 doi: 10.1002/nme.1620230307
[4] 钱令希, 钟万勰, 程耿东等. 工程结构优化设计的一个新途径——序列二次规划SQP. 计算结构力学及其应用, 1984, 1(1): 7-20 (Qian Lingxi, Zhong Wanxie, Cheng Gengdong, Sui Yunkang. An approach to structural optimization—sequential quadratic programming SQP. Computational Structural Mechanics and Applications, 1984, 1(1): 7-20 (in Chinese) Qiang Lingxi, Zhong Wanxie, Cheng Gengdong, Sui Yunkang. An approach to structural optimization - sequential quadratic programming SQP [J]. Computational Structural Mechanics and Applications. 1984, 1(1): 7-20. (in Chinese
[5] Fleury C. CONLIN: An efficient dual optimizer based on convex approximation concepts. Structural Optimization, 1989, 1(2): 81-89 doi: 10.1007/BF01637664
[6] Svanberg K. The method of moving asymptotes—A new method for structural optimization. International Journal for Numerical Methods in Engineering, 1987, 24(2): 359-373 doi: 10.1002/nme.1620240207
[7] Beekers M, Fleury C. A primal-dual approach in truss topology optimization. Computers & Structures, 1997, 64(1-4): 77-88
[8] Hoppe RHW, Linsenmann C, Petrova SI. Primal-dual Newton methods in structural optimization. Computing and Visualization in Science, 2006, 9(2): 71-87
[9] 隋允康, 阳志光. 应用两点有理逼近改进的牛顿法和对偶法. 大连理工大学学报, 1994, 34(1): 1-9 (Sui Yunkang, Yang Zhiguang. Modified newton's method and dual method through rational approximation at two expanded points. Journal of Dalian University of Technology, 1994, 34(1): 1-9 (in Chinese) Sui Yunkang, Yang Zhiguang. Modified newton's method and dual method through rational approximation at two expanded points [J]. Journal of Dalian University of Technology. 1994, 34(1): 1-9. (in Chinese))
[10] 隋允康, 邢誉峰, 张桂明. 基于两点累积信息的原/倒变量展开的对偶优化方法. 力学学报, 1994, 26(6): 699-710 (Sui Yunkang, Xing Yufeng, Zhang Guiming. The dual optimization method by original/reciprocal variables' expansion based on cumulative information at two points. Acta Mechanica Sinica, 1994, 26(6): 699-710 (in Chinese) Sui Yunkang, Xing Yufeng, Zhang Guiming. The dual optimization method by original/reciprocal variables' expansion based on cumulative information at two points [J]. Acta Mechanica Sinica. 1994, 26(6): 699-710. (in Chinese))
[11] 吴京, 刘荣桂, 苏军. 对偶规划法在钢管混凝土拱桥结构优化设计中的应用. 工程力学, 1999, 16(4): 97-104 (Wu Jing, Liu Ronggui, Su Jun. Application of the dual theory to the CFST structure's optimization design. Engineering Mechanics, 1999, 16(4): 97-104 (in Chinese) Wu Jing, Liu Ronggui, Su Jun. Application of the dual theory to the CFST structure's optimization design [J]. Engineering Mechanics, 1999, 16(04): 97-104. (in Chinese))
[12] 金鹏. 对偶规划法在钢管混凝土拱结构优化设计中的应用. 建筑结构学报, 2001, 22(6): 59-63 (Jin Peng. Optimum design of concrete filled steel tubular arch structure using dual theory. Journal of Building Structures, 2001, 22(6): 59-63 (in Chinese) Jin Peng. Optimum design of concrete filled steel tubular arch structure using dual theory [J]. Journal of Building Structures. 2001, 22(06): 59-63. (in Chinese))
[13] Xuan ZC, Shao PG. A programming approach for nonsmooth structural optimization. Advances in Engineering Software, 2000, 31(2): 75-81 doi: 10.1016/S0965-9978(99)00049-6
[14] Etman LFP, Groenwold AA, Rooda JE. First-order sequential convex programming using approximate diagonal QP subproblems. Structural and Multidisciplinary Optimization, 2012, 45(4): 479-488 doi: 10.1007/s00158-011-0739-3
[15] Cronje M, Marthinus RN, Munro DP, et al. Brief note on equality constraints in pure dual SAO settings. Structural and Multidisciplinary Optimization, 2019, 59(5): 1853-1861 doi: 10.1007/s00158-018-2149-2
[16] Liang Y, Cheng GD. Topology optimization via sequential integer programming and Canonical relaxation algorithm. Computer Methods in Applied Mechanics and Engineering, 2019, 348(5): 64-96
[17] Bendsoe MP, Kikuchi N. Generating optimal topologies in structural design using a homogenization method. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224 doi: 10.1016/0045-7825(88)90086-2
[18] Mlejnek HP. Some aspects of the genesis of structures. Structural Optimization, 1992, 5(1-2): 64-69 doi: 10.1007/BF01744697
[19] 隋允康. 建模·变换·优化———结构综合方法新进展. 大连: 大连理工大学出版社, 1996 Sui Yunkang. Modelling, Transformation, and Optimization—New Developments of Structural Synthesis Method. Dalian: Dalian University of Technology Press, 1996 (in Chinese))
[20] 隋允康, 叶红玲. 连续体结构拓扑优化的ICM方法. 北京: 科学出版社, 2013 Sui Yunkang, Ye Hongling. Continuum Topology Optimization Methods ICM. Beijing: Science Press, 2013 (in Chinese))
[21] Sui YK Peng XR, Modeling, Solving and Application for Topology Optimization of Continuum Structures: ICM Method Based on Step Function. Cambridge: Elsevier Inc., 2018
[22] Osher S, Sethian J. Fronts propagating with curvature dependent speed-algorithms based on hamilton-jacobi formulations. J. Comput. Phys., 1988, 79(1): 12-49 doi: 10.1016/0021-9991(88)90002-2
[23] Wei P, Li ZY, Li XP, et al. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Structural and Multidisciplinary Optimization, 2018, 58(2): 831-849 doi: 10.1007/s00158-018-1904-8
[24] Norato J, Bendsøe M, Haber R, et al. A topological derivative method for topology optimization. Structural and Multidisciplinary Optimization, 2007, 33(4-5): 375-386 doi: 10.1007/s00158-007-0094-6
[25] Cai SY, Zhang WH. An adaptive bubble method for structural shape and topology optimization. Computer Methods in Applied Mechanics and Engineering, 2020, 360: 1-25
[26] Guo X, Zhang WS, Zhang J. Explicit structural topology optimization based on moving morphable components (MMC) with curved skeletons. Computer Methods in Applied Mechanics and Engineering, 2016, 310(10): 711-748
[27] Zhang WH, Zhao LY, Gao T, et al. Topology optimization with closed B-splines and Boolean operations. Computer Methods in Applied Mechanics and Engineering, 2017, 315(3): 652-670
[28] 隋允康, 彭细荣. 求解一类可分离凸规划的对偶显式模型DP-EM方法. 力学学报, 2017, 49(5): 1135-1144 (Sui Yunkang, Peng Xirong. A dual explicit model based DP-EM method for solving a class of separable convex programming. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(5): 1135-1144 (in Chinese) Sui Yunkang, Peng Xirong. A dual explicit model based DP-EM method for solving a class of separable convex programming [J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(5): 1135-1144. (in Chinese))
[29] 彭细荣, 隋允康, 叶红玲等. 比较基于化整交融应力拓扑优化诸解法的效果. 力学学报, 2022, 54(2): 459-470 (Peng Xirong, Sui Yunkang, Ye Hongling, et al. Effect comparison of globalization blend based-methods for stess topology optimization. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(2): 459-470 (in Chinese) doi: 10.6052/0459-1879-21-499 Peng Xirong, Sui Yunkang, Ye Hongling, TIE Jun. Effect comparison of globalization blend based-methods for stess topology optimization [J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(2): 459-470. (in Chinese)) doi: 10.6052/0459-1879-21-499
[30] 隋允康, 彭细荣, 叶红玲等. 结构拓扑优化局部性能约束下轻量化问题的互逆规划解法. 计算力学学报, 2021, 38(4): 479-486 (Sui Yunkang, Peng Xirong, Ye Hongling, et al. Reciprocal programming method for structural lightweight topology optimization with local performance constraints. Chinese Journal of Computational Mechanic, 2021, 38(4): 479-486 (in Chinese) doi: 10.7511/jslx20210515409 Sui Yunkang, Peng Xirong, Ye Hongling, Li Zonghan. Reciprocal programming method for structural lightweight topology optimization with local performance constraints [J]. Chinese Journal of Computational Mechanic, 2021, 38(04): 479-486. (in Chinese)) doi: 10.7511/jslx20210515409
[31] 彭细荣, 隋允康, 叶红玲等. K-S函数集成局部性能约束的结构拓扑优化二阶逼近解法. 固体力学学报, 2022, 43(3): 307-317 (Peng Xirong, Sui Yunkang, Ye Hongling, et al. Second-order approximation algorithm of using K-S function to integrate local performance constraints in structural topology optimization. Chinese Journal of Solid Mechnaics, 2022, 43(3): 307-317 (in Chinese) Peng Xirong, Sui Yunkang, Ye Hongling, Tie Jun. Second-order approximation algorithm of using K-S function to integrate local performance constraints in structural topology optimization [J]. Chinese Journal of Solid Mechnaics, 2022, 43(03): 307-317. (in Chinese))
[32] 彭细荣, 隋允康. 考虑破损−安全的连续体结构拓扑优化ICM方法. 力学学报, 2018, 50(3): 611-621 (Peng Xirong, Sui Yunkang. ICM method for fail-safe topology optimization of continuum structures. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(3): 611-621 (in Chinese) doi: 10.6052/0459-1879-17-366 Peng Xirong, Sui Yunkang. ICM method for fail-safe topology optimization of continuum structures [J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(3): 611-621. (in Chinese)) doi: 10.6052/0459-1879-17-366



 下载:
下载: