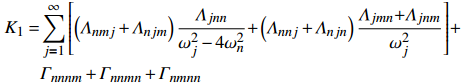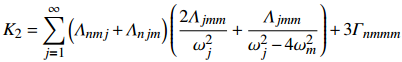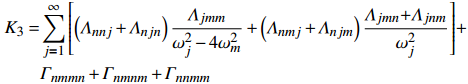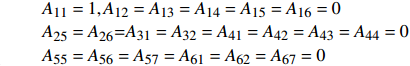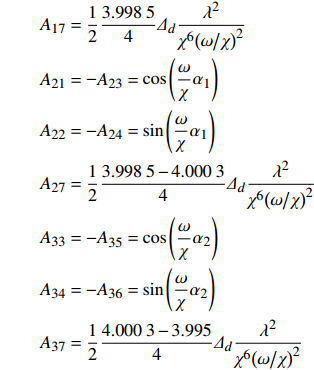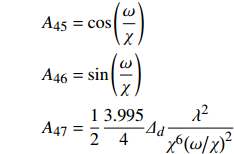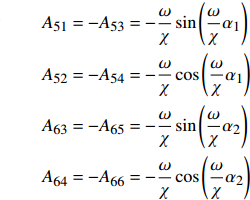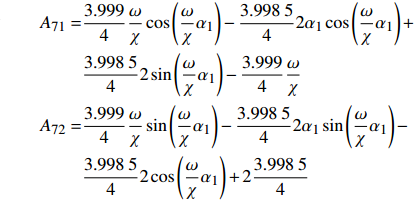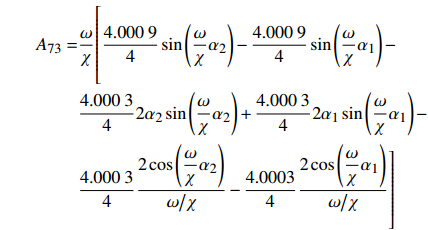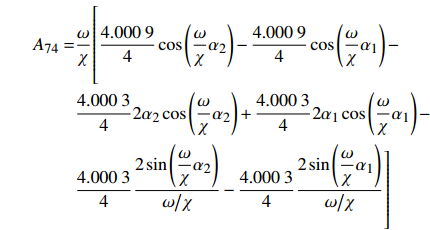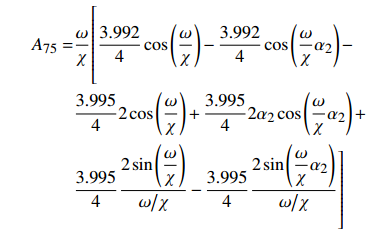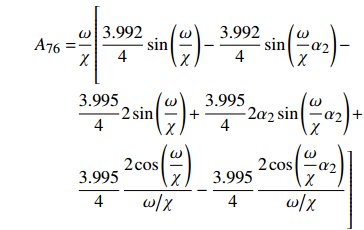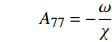STUDY ON NONLINEAR COUPLED VIBRATIONS OF DAMAGED SUSPENDED CABLES WITH SYMMETRY-BREAKING
-
摘要: 对称性是振动理论中5大美学特征之一, 然而对称性破缺又难以避免. 本文以工程中常见的易损结构—悬索为例, 探究当该系统遭遇非对称性损伤时, 对称性破缺对其面内耦合振动特性影响. 首先建立受损悬索面内非线性动力学模型, 并采用Galerkin法得到离散的无穷维微分方程. 利用多尺度法计算该非线性系统发生面内耦合共振响应的调谐方程. 截取前9阶模态, 利用数值计算方法得到无损和受损悬索的各类共振曲线及其稳定性, 通过计算最大李雅普诺夫指数来确定系统的混沌运动. 研究结果表明: 已有研究常采用抛物线模拟悬索静态构形, 然而一旦发生不对称损伤, 采用分段函数更能准确描述悬索受损后的静态构形; 对称性破缺会导致悬索固有频率之间的交点变为转向点, 其正、反对称模态均变为非对称模态; 受损后悬索的非线性相互作用系数会发生显著改变, 其内共振响应会产生明显变化; 当激励直接作用在高阶模态时, 无损系统会呈现出单模态解和内共振解, 而受损系统并没有呈现出明显的单模态解; 受损系统的分岔和混沌特性会发生改变, 系统将通过倍周期分岔产生混沌运动.Abstract: Symmetry is one of the five aesthetic characteristics in the vibration theory, but the symmetry-breaking is also inevitable. This paper takes a common vulnerable structure in engineering-the suspended cable-as an example, and the influences of symmetry-breaking on the planar coupled vibrations have been investigated when the asymmetric damage is occurred. Firstly, the in-plane nonlinear dynamical model of damaged suspended cable has been established, and the nonlinear infinite dimensional differential equations have been obtained by using the Galerkin method. The method of multiple scales has been adopted to obtain the modulation equations of the nonlinear systems’ in-plane coupled vibrations. The resonant curves of undamaged and damaged suspended cables including the first nine modes have been obtained by using the numerical methods, and the stabilities of solutions have also been determined. The largest Lyapunov exponent has been calculated to determine the system’s chaotic motions. The numerical results show that the classical parabolic curves have been often adopted to simulate the suspended cables’ static configurations. However, when the asymmetric damage occurs, the piecewise functions should be used to accurately describe the damaged cables’ static configurations. The symmetry-breaking causes crossover points between two natural frequencies of suspended cables to turn into veering points, and the symmetric/anti-symmetric mode shapes before damage are changed into the asymmetric ones after damaged. The nonlinear interaction coefficients are changed significantly, resulting in significant changes in internal resonant responses. When the excitation is directly applied to the higher-order modes, the single-mode solutions and internal resonant ones are obvious in the undamaged system, while the damaged system does not present the obvious single-mode solutions. The bifurcations and chaos of the damaged system are also changed obviously, and some chaotic motions around the period-doubling bifurcation are observed as to the damaged system.
-
引言
普遍存在于自然界中的对称性, 不仅是现代物理学的一个核心概念, 而且从分子结构到自然景观, 从艺术作品到建筑结构, 甚至诗词歌赋, 对称性也处处体现. 振动理论具有统一、简洁、整齐、对称和奇异等5大美学特征[1], 当中蕴含的美, 一方面具有客观存在性, 同时对其认识亦存在相对性. 对称让一切均衡有序, 结构固有的对称性, 不但可以大幅降低动力学建模和分析计算工作量, 还可以带来视觉上冲击和美感. 近年来随着奇异性理论和分岔理论等不断发展, 对于结构遭遇对称性破缺[2]或非齐次边界条件等问题[3], 一些奇异性现象逐渐被人们认识和理解. 由此可见对称性及其破缺是结构振动分析中不可忽视的关键因素.
以工程中常见的索结构为例[4], 两端水平自由悬挂的索具有明显的结构对称性. 但是这种对称性很容易被打破, 比如: 端点不在同一水平位置的斜拉索[5]; 包含非均匀分布的集中质量[6]; 存在非均匀损伤[7]等. 因此一旦索结构遭遇到对称性破缺, 系统固有特性将或多或少发生改变, 比如频率[8-10]. 具体而言, 水平悬索固有频率随着Irvine参数[11]增大, 会出现多个交点, 该处固有频率相等. 对于斜拉索, 由于对称性破缺, 频率间交点消失, 从而出现转向点. 此时随着Irvine参数不断增大, 两固有频率会不断接近然后迅速分开[12]. 对于各类动力系统或结构, 当其固有频率相等或近似相等时, 系统有可能会出现明显的模态耦合共振[13-17], 能量会在模态间发生传递, 导致系统产生更为复杂的动力学现象. 已有研究表明[18-19]: 对于悬索/斜拉索, 两者会呈现出截然不同的模态耦合共振响应. 由此可见, 频率交点/转向点附近的动力学现象丰富且复杂, 倘若进一步考虑系统对称性破缺, 其动力学特性将发生更多定性和定量的改变.
索是一类典型的易损构件[20-22], 不对称损伤是引发系统对称性破缺的重要因素之一. 对于受损拉索, Jiang等[23]建立考虑钢丝磨损和索内腐蚀分布的斜拉索的腐蚀疲劳模型, 分析了不同环境条件中拉索的腐蚀疲劳. Bouaanani[24]采用有限差分法研究损伤位置和范围对悬索模态灵敏度影响, 研究不同损伤情况下悬索的力学特性. Lepidi[25]基于受损悬索力学模型, 以面内频率为损伤指标, 识别悬索损伤. Sun等[26]建立了腐蚀拉索静力学模型和平面内自由振动的控制方程, 分析表明随着腐蚀时间增加, 拉索张力、垂度和固有频率将出现明显变化. Xu等[27]基于损伤拉索的微观力学模型, 提出了一种断丝拉索静、动力特性的分析方法, 考虑不同物理参数, 分析断丝损伤对拉索静动力特性影响. 王立彬等[28]通过推导拉索损伤后的索力和线形公式来分析损伤拉索的等效弹性模量. 兰成明等[29]对已经服役18年的拉索钢丝开展研究, 发现拉索腐蚀钢丝的屈服强度和极限应变都有所降低, 腐蚀钢丝与未腐蚀钢丝的弹性模量基本相同. Zhu等[30]采用同伦分析法研究斜拉梁中拉索受损后, 该系统的动力学行为.
上述研究主要关注拉索疲劳或腐蚀损伤的机理, 或分析损伤后的频率、振型和索力等. 对于受损悬索, 经典的对称抛物线构形已无法准确刻画对称性破缺后的分段构形. 因此如何采用分段函数拟合受损系统的悬链线构形?如何进一步从非线性动力学的角度去分析受损悬索的动力学行为?尤其是对称性破缺导致频率间交点变为转向点后, 受损系统多模态间的耦合共振响应特性又会发生哪些定量和定性的变化?这些问题值得进一步探索和研究.
本文基于受损悬索面内非线性动力学模型, 采用分段样条曲线描述损伤后的静态构形, 并利用多尺度法得到模态耦合共振的调谐方程. 通过数值算例, 探究受损悬索对称性破缺下的耦合振动特性.
1. 数学模型
假定悬索由均匀、连续的弹性材料构成, 且只考虑索横截面上均匀分布的拉应力和拉应变, 忽略剪切、抗弯和扭转刚度. 损伤悬索无应力状态下的构形如图1左图所示, 采用弧坐标s贯穿悬索全长, EA表示轴向刚度, EAd(s)表示受损后残余轴向刚度. 假设锈蚀部分的残余截面面积相等, 损伤区域为[a1, a2], 不对称分布. L0为无应力状态下索长, L表示水平跨度, bd 表示受损悬索的垂度. 无损和受损的悬索的静态、动态构形如图1右图所示, u(x,t)和v(x, t)分别表示轴向和竖向的位移分量.
引入以下3个无量纲参数分别描述悬索损伤的程度、范围和位置[7]
$$ \left.\begin{split} & \eta =\frac{EA-E{A}_{d}\left(s\right)}{EA}\\ &\delta =\frac{{a}_{2}-{a}_{1}}{{L}_{0}}\\ &\alpha =\frac{{a}_{1} + {a}_{2}}{2{L}_{0}} \end{split} \right\}$$ (1) 损伤程度在整个索长上变化用分段函数表示
$$ \zeta \left(s\right)=\left\{\begin{array}{l}\eta, \;\;\;{a}_{1} < s < {a}_{2}\\ 0,\;\;\;{\rm{other}}\end{array}\right. $$ (2) 损伤会导致悬索形成新的静力构形, 引起张力减小, 垂度增大. 因此本文引入悬索水平张力折减系数
$\chi ^{{2}}$ 和垂度增大系数$\kappa ^{{2}}$ [7]: Hd=χ2H, bd=κ2b. 式中Hd (H)分别表示受损(无损)悬索的初始水平张力, 通过求解其静力学平衡方程得到.损伤会改变水平悬索的静态构形, 倘若损伤呈现出明显不对称性, 此时抛物线就无法准确描述受损后的静态构形, 因此需要采用分段样条曲线来拟合 [7]. 节点之间每段曲线都由一个多项式函数yj(x)映射. 比如对于一段受损悬索的线形, 可以采用三段抛物线近似表示: 未损段y1(x) (0<x<a1), 受损段y2(x) (a1<x<a2), 未损段y3(x) (a2<x<L), 此时节点处需满足连续性条件
$$ \left. \begin{array}{l} {y_1}\left( {{a_1}} \right) = {y_2}\left( {{a_1}} \right)\\ {y_2}\left( {{a_2}} \right) = {y_3}\left( {{a_2}} \right) \\ {{y'}_1}\left( {{a_1}} \right) = {{y'}_2}\left( {{a_1}} \right)\\ {{y'}_2}\left( {{a_2}} \right) = {{y'}_3}\left( {{a_2}} \right) \end{array} \right\} $$ (3) 利用哈密顿变分原理, 可得悬索面内非线性运动微分方程
$$\;\;\;\;\;\;\;\;\;\begin{split} m\ddot u + &{c_u}\dot u - EA\left({1 - \zeta } \right) \cdot \\ & {{ }} {\left[ {u' + {\kappa ^2}{{y'}_j}v' + {{\left( {v'} \right)}^2}/2} \right]^\prime } = 0 \end{split} $$ (4) $$ \;\;\;\;\;\;\;\;\;\begin{split} m\ddot v + &{c_v}\dot v - {\chi ^{{2}}}Hv'' - EA\left( {1 - \zeta} \right)\left( {{\kappa ^2}{{y''}_j} + v''} \right) \cdot \\& {{ }} {\left[ {u' + {\kappa ^2}{{y'}_j}v' + {{\left( {v'} \right)}^2}/2} \right]^\prime } = {p_v}\cos (\varOmega t) \end{split} $$ (5) 式中, 点表示对t求导, 撇表示对x求导, m和
${c_v},{c_u}$ 分别为单位长度质量和阻尼系数, pv和Ω为外激励幅值和频率.系统的边界条件和连续条件表示为
$$ \left. \begin{array}{l} u(0) = 0,{{ }}{u_1}^ - = u_1^ + ,{{ }}u_2^ - = u_2^ + ,{{ }}u(L) = 0 \\ v(0) = 0,{{ }}{v_1}^ - = v_1^ + ,{{ }}v_2^ - = v_2^ + ,{{ }}v(L) = 0 \\ u_j^ \pm = \mathop {\lim }\limits_{\gamma \to 0} u\left( {{a_j} \pm \gamma } \right),v_j^ \pm = \mathop {\lim }\limits_{\gamma \to 0} v\left( {{a_j} \pm \gamma } \right) \\ \gamma > 0,j = 1,2 \\ \end{array} \right\} $$ (6) 由索轴向张力平衡可得以下连续性方程:
$ EA\varepsilon _1^ - = EA(1 - \eta )\varepsilon _1^ + ,{{ }}EA(1 - \eta )\varepsilon _2^ - = EA\varepsilon _2^ + $ , 其中ε1和ε2为拉格朗日应变.基于拟静态假设, 并结合索的轴向张力平衡方程, 得到损伤悬索轴向应变的拟静态解
$\varepsilon (x,t) = $ $ \left( {u' + {\kappa ^2}y'v' + {{v'}^2}/2} \right) = {{e(t)} \mathord{\left/ {\vphantom {{e(t)} {\left[ {1 - \zeta (x)} \right]}}} \right. } {\left[ {1 - \zeta (x)} \right]}} $ , 积分后$u\left( {x,t} \right) = $ $\displaystyle\int_0^x {{{e(t)} \mathord{\left/ {\vphantom {{e(t)} {\left[ {1 - \zeta (x)} \right]}}} \right. } {\left[ {1 - \zeta (x)} \right]}}} {{{\rm{d}}}}x - \displaystyle\int_0^x {\left( {{\kappa ^2}{{y'}_j}v' + {{v'}^2}/2} \right)} {{{\rm{d}}}}x$ , 再引入边界条件和连续条件(6)可得$$ e(t) = {\varDelta _d}\int_0^L {\left[ {{\kappa ^2}{{y'}_j}v' + {{\left( {v'} \right)}^2}/2} \right]} {{{\rm{d}}}}x $$ (7) 其中跟损伤相关的无量纲参数
${\varDelta _d} = \dfrac{{1 - \eta }}{{1 - \eta (1 - \delta )}}$ .因此受损悬索面内运动方程可以简化为
$$ \begin{split} m\ddot v + &{c_v}\dot v - EA/L\left( {{\kappa ^2}{{y''}_j} + v''} \right){\varDelta _d} \cdot \\ & \int_0^L {\left[ {{\kappa ^2}{{y'}_j}v' + {{\left( {v'} \right)}^2}/2} \right]} {{{\rm{d}}}}x - {\chi ^2}Hv'' = {p_v}\cos \left( {\varOmega t} \right) \end{split} $$ (8) 引入以下无量纲参数
$$ \left. \begin{array}{l} {v^ * } = \dfrac{v}{L},{\omega ^ * } = \dfrac{\omega }{L},{x^ * } = \dfrac{x}{L},y_j^ * = \dfrac{{{y_j}}}{L},{t^ * } = \sqrt {\dfrac{g}{{8b}}} t \\ {c_v}^ * = \sqrt {\dfrac{{8b}}{g}} \dfrac{{{{{c}}_v}}}{m},\varOmega ^ * = \sqrt {\dfrac{{8b}}{g}} {\varOmega},p_v^ * = \dfrac{{{p_v}L}}{H},\varTheta = \dfrac{{EA}}{H} \end{array} \right\} $$ (9) 可得无量纲化后的运动方程
$$ \begin{split} \ddot v + &{c_v}\dot v - {\chi ^2}v'' - \varTheta \left( {{\kappa ^2}{{y''}_j} + v''} \right){\varDelta _d} \cdot \\ & \displaystyle\int_0^1 {\left[ {{\kappa ^2}{{y'}_j}v' + {{\left( {v'} \right)}^2}/2} \right]} {{{\rm{d}}}}x = {p_v}\cos \left( {\varOmega t} \right) \end{split} $$ (10) 采用分离变量法:
$v\left( {x,t} \right) = {{{{\rm{e}}}}^{{{{\rm{i}}}}\omega t}}\varphi \left( x \right)$ , 忽略非线性项、阻尼项和激励项等, 通过线性化处理, 可得$$ {\chi ^2}{\left( {{\varphi ^j}} \right)^{\prime \prime }} + {\omega ^2}{\varphi ^j} = {k_j},\;j = 1,2,3 $$ (11) $$ \begin{split} {k_j} =& \varTheta {\varDelta _d}{{y''}_j} \cdot \\ & \left[ {\int_0^{{\alpha _1}} {{{y'_1}}{{\left( {{\varphi ^1}} \right)}^\prime }{{{\rm{d}}}}x + \int_{{\alpha _1}}^{{\alpha _2}} {{{y'_2}}{{\left( {{\varphi ^2}} \right)}^\prime }{{{\rm{d}}}}x + } \int_{{\alpha _2}}^1 {{{y'_3}}{{\left( {{\varphi ^3}} \right)}^\prime }{{{\rm{d}}}}x} } } \right] \end{split} $$ (12) 式中α1=a1/L, α2=a2/L. 可知特征函数的分段解为
$$ {\varphi ^j}\left( x \right) = {d_{1j}}\cos \left( {\frac{\omega }{\chi }x} \right) + {d_{2j}}\sin \left( {\frac{\omega }{\chi }x} \right) + \frac{{{k_j}}}{{{\omega ^2}}} $$ (13) 模态函数的边界条件和连续性如下
$$ \left. \begin{array}{l} {\varphi ^1}\left( 0 \right) = 0,{\left( {{\varphi ^1}} \right)^ + } = {\left( {{\varphi ^1}} \right)^ - },{\left( {{\varphi ^2}} \right)^ + } = {\left( {{\varphi ^2}} \right)^ - } \\ {\left( {{\varphi ^1}} \right)^\prime }^ + = {\left( {{\varphi ^1}} \right)^\prime }^ - ,{\left( {{\varphi ^2}} \right)^\prime }^ + = {\left( {{\varphi ^2}} \right)^\prime }^ - ,{\varphi ^3}\left( 1 \right) = 0 \end{array} \right\} $$ (14) 将式(13)代入式(12), 并将边界条件代入式(13),可得由未知系数d1j, d2j和特征频率ω组成的7 × 7系数矩阵.
利用Galerkin法对式(10)进行离散
$$ v\left( {x,t} \right) = \sum\limits_{n = 1}^\infty {{\varphi _n}\left( x \right){q_n}} \left( t \right) $$ (15) 其中
$\varphi_{{n}}{(}{x}{)}$ 表示模态函数,$ {{q}}_{{n}}{(}{t}{)} $ 为坐标函数.将式(15)代入式(10), 两边同时乘以
$\varphi_{{n}}{(}{x}{)}$ 后从0到L积分, 可得离散的无穷维方程$$ \begin{split} & {{\ddot q}_n} + \omega _n^2{q_n} + 2{\mu _n}{{\dot q}_n}{{ = }}\sum\limits_{i = 1}^\infty {\sum\limits_{j = 1}^\infty {{\varLambda _{nij}}{q_i}} } {q_j} + \\ &\qquad\quad \sum\limits_{i = 1}^\infty {\sum\limits_{j = 1}^\infty {\sum\limits_{h = 1}^\infty {{\varGamma _{nijh}}} } } {q_i}{q_j}{q_h}{{ + }}{f_n}\cos \left( {\varOmega t} \right) \end{split} $$ (16) 其中各项系数表达式如附录A所示.
2. 摄动分析
首先将二阶微分方程(16)改写为
$$ \left. \begin{array}{l} {{\dot q}_k} - {z_k}{{ = }}0 \\ {{\dot z}_k} + \omega _k^2{q_k} + 2{\mu _k}{z_k} = \displaystyle\sum\limits_{i = 1}^\infty {\displaystyle\sum\limits_{j = 1}^\infty {{\varLambda _{kij}}{q_i}} } {q_j} + \\ \qquad\quad \displaystyle\sum\limits_{i = 1}^\infty {\displaystyle\sum\limits_{j = 1}^\infty {\displaystyle\sum\limits_{h = 1}^\infty {{\varGamma _{kijh}}{q_i}{q_j}{q_h}} } } + {f_k}\cos \left( {\varOmega t} \right) \end{array} \right\} $$ (17) 采用多尺度法摄动分析, 设位移和速度坐标为
${{q}}_{{k}}{(}{t}{;}{ \epsilon }{)=}{\sum }_{{i}{=1}}^{{}}{{ \epsilon }}^{{i}}{{q}}_{{ki}}{(}{{T}}_{{0}}{,}{{T}}_{{1}}{,}{{T}}_{{2}}{)}$ ,$ {{z}}_{{k}}{(}{t}{;}{ \epsilon }{)=}{\sum }_{{i}{=1}}^{{\infty }}{{ \epsilon }}^{{i}}{{z}}_{{ki}}{(}{{T}}_{{0}}{,}{{T}}_{{1}}{,}{{T}}_{{2}}{)} $ , 其中,$ {{T}}_{{i}}{=}{{ \epsilon }}^{{i}}{t}{}\;{(}{i}{=0, 1, 2)} $ , 故$ {\partial }/{\partial t}{=}{\sum }_{{i=0}}^{{\infty }}{{ \epsilon }}^{{i}}{{D}}_{{i}} $ ,$ {{D}}_{{i}}{=}{\partial }/{\partial }{{T}}_{{i}} $ . 将位移和速度的广义坐标代入式(17)中, 可得各阶微分方程组.针对一阶微分方程组, 可以假设其解表示为
$ {{q}}_{{k}{1}}{=}{{A}}_{{k}}{(}{{T}}_{{1}}{,}{{T}}_{{2}}{)}{{{\rm{e}}}}^{{{\rm{i}}}{{ \omega }}_{{k}}{{T}}_{{0}}}{ + }{cc} $ ,$ {{z}}_{{k}{1}}{=}{{{\rm{i}}}{{ \omega }}_{{k}}{A}}_{{k}}{(}{{T}}_{{1}}{,}{{T}}_{{2}}{)}{{{\rm{e}}}}^{{{\rm{i}}}{{ \omega }}_{{k}}{{T}}_{{0}}}{ + cc} $ . 其中δkm和δkn为Delta函数, cc表示共轭复数项. 将一阶方程组的解代入二阶方程组中, 可求得二阶近似解. 对于系统固有频率相等或者近似相等, 可以引入调谐参数σ1(外)和σ2(内)描述频率接近的程度, 其关系式为:$ { \varOmega =}{{ \omega }}_{{j}}{ + \epsilon }{{\sigma }}_{{1}} $ 和$ {{ \omega }}_{{n}}{=}{{ \omega }}_{{m}}{ + \epsilon }{{\sigma }}_{{2}} $ ($ {j=m,}\;{}{n} $ ). 将二阶近似解代入三阶微分方程组中, 求得可解性条件, 再根据重组法得调谐方程如下$$ \left. \begin{array}{l} 2{{{\rm{i}}}}{\omega _m}\left( {{{\dot A}_m} + {\mu _m}{A_m}} \right) = {K_{mm}}A_m^2{{\bar A}_m} + \\ \qquad {K_{mn}}{A_m}{A_n}{{\bar A}_n} + {R_5}A_n^2{{\bar A}_n}{{{{\rm{e}}}}^{{{{\rm{i}}}}{\sigma _2}{T_2}}} + {R_6}{A_n}{A_m}{{\bar A}_m}{{{{\rm{e}}}}^{{{{\rm{i}}}}{\sigma _2}{T_2}}}+ \\ \qquad {R_7}A_m^2{{\bar A}_n}{{{{\rm{e}}}}^{ - {{{\rm{i}}}}{\sigma _2}{T_2}}} + {R_8}A_n^2{{\bar A}_m}{{{{\rm{e}}}}^{2{{{\rm{i}}}}{\sigma _2}{T_2}}} + {f_m}{\delta _{mi}}{{{{\rm{e}}}}^{{{{\rm{i}}}}{\sigma _1}{T_2}}}/2 \\ 2{{{\rm{i}}}}{\omega _n}\left( {{{\dot A}_n} + {\mu _n}{A_n}} \right) = {K_{nn}}A_n^2{{\bar A}_n} + {K_{nm}}{A_n}{A_m}{{\bar A}_m} + \\ \qquad {R_1}A_m^2{{\bar A}_m}{{{{\rm{e}}}}^{ - {{{\rm{i}}}}{\sigma _2}{T_2}}} + {R_2}{A_m}{A_n}{{\bar A}_n}{{{{\rm{e}}}}^{ - {{{\rm{i}}}}{\sigma _2}{T_2}}}+ \\ \qquad {R_3}A_m^2{{\bar A}_n}{{{{\rm{e}}}}^{ - 2{{{\rm{i}}}}{\sigma _2}{T_2}}} + {R_4}A_n^2{{\bar A}_m}{{{{\rm{e}}}}^{{{{\rm{i}}}}{\sigma _2}{T_2}}} + {f_n}{\delta _{ni}}{{{{\rm{e}}}}^{{{{\rm{i}}}}{\sigma _1}{T_2}}}/2 \end{array} \right\} $$ (18) 其中非线性系数Kij见附录B, 2K1=R2=2R4=2R5, 2K2=R6=2R1=2R7, K3=R3=R8. 将
$ {{A}}_{{j}} $ 表示为直角坐标形式:$ {{A}}_{{j}}{=}\left[{{p}}_{{j}}{(}{t}{)-}{{\rm{i}}}{{r}}_{{j}}{(}{t}{)}\right]{{{\rm{e}}}}^{{{\rm{i}}}{{\beta }}_{{j}}{(}{t}{)}}{/2,}{}{j}{=}{m,n} $ , 代入式(18)可得$$ \begin{split} {{\dot p}_m} =& - {\upsilon _m}{r_m} - {\mu _m}{p_m} - {K_{mm}}{r_m}\left( {p_m^2 + r_m^2} \right)/8{\omega _m} - \\ & {K_{mn}}{r_m}\left( {p_n^2 + r_n^2} \right)/8{\omega _m} - {K_1}{r_n}\left( {p_n^2 + r_n^2} \right)/8{\omega _m} - \\ & {K_2}\left( {{r_n}p_m^2{{ + }}2{p_m}{p_n}{r_m} + 3{r_n}r_m^2} \right)/8{\omega _m}+ \\ & {{ }}{K_3}\left( {p_n^2{r_m} - 2{p_n}{p_m}{r_n} - r_n^2{r_m}} \right)/8{\omega _m} \end{split} $$ (19) $$ \begin{split} {{\dot r}_m} =& {\upsilon _m}{p_m} - {\mu _m}{r_m}{{ + }}{K_{mm}}{p_m}\left( {p_m^2 + r_m^2} \right)/8{\omega _m} + \\ & {{ }}{K_{mn}}{p_m}\left( {p_n^2 + r_n^2} \right)/8{\omega _m}{{ + }}{K_1}{p_n}\left( {p_n^2 + r_n^2} \right)/8{\omega _m} + \\ & {{ }}{K_2}\left( {3{p_n}p_m^2 + 2{p_m}{r_m}{r_n} + r_m^2{p_n}} \right)/8{\omega _m}+ \\ & {{ }}{K_3}\left( {{p_m}p_n^2 + 2{p_n}{r_n}{r_m} - r_n^2{p_m}} \right)/8{\omega _m}{{ + }}{f_m}/2{\omega _m} \end{split} $$ (20) $$ \begin{split} {{\dot p}_n} =& - {\upsilon _n}{r_n} - {\mu _n}{p_n} - {K_{nn}}{r_n}\left( {p_n^2 + r_n^2} \right)/8{\omega _n} - \\ & {K_{nm}}{r_n}\left( {p_m^2 + r_m^2} \right)/8{\omega _n} - {K_2}{r_m}\left( {p_m^2 + r_m^2} \right)/8{\omega _n}- \\ & {K_1}\left( {p_n^2{r_m} + 2{p_n}{p_m}{r_n} + 3r_n^2{r_m}} \right)/8{\omega _n}+ \\ & {{ }}{K_3}\left( {p_m^2{r_n} - 2{p_m}{p_n}{r_m} - r_m^2{r_n}} \right)/8{\omega _n} \end{split} $$ (21) $$ \begin{split} {{\dot r}_n} =& {\upsilon _n}{p_n} - {\mu _n}{r_n} + {K_{nn}}{p_n}\left( {p_n^2 + r_n^2} \right)/8{\omega _n} + \\ & {{ }}{K_{nm}}{p_n}\left( {p_m^2 + r_m^2} \right)/8{\omega _n}{{ + }}{K_2}{p_m}\left( {p_m^2 + r_m^2} \right)/8{\omega _n} + \\ & {{ }}{K_1}\left( {3{p_m}p_n^2 + 2{p_n}{r_n}{r_m}{{ + }}r_n^2{p_m}} \right)/8{\omega _n} + \\ & {{ }}{K_3}\left( {{p_n}p_m^2 + 2{p_m}{r_m}{r_n} - r_m^2{p_n}} \right)/8{\omega _n}{{ + }}{f_n}/2{\omega _n} \end{split} $$ (22) 其中,
$ {a_j} = \sqrt {p_j^2 + r_j^2} ,j = m,n $ , 当激励直接作用在低阶模态时($ { \varOmega }{=}{{ \omega }}_{{m}} $ ),$ {{\nu}}_{{m}}{=}{{\sigma }}_{{1}} $ ,${{\nu}}_{{n}}{=}{{\sigma}}_{{1}}{-}{{\sigma}}_{{2}}$ ; 当激励直接作用在高阶模态时($ { \varOmega }{=}{{ \omega }}_{{n}} $ ),${{\nu}}_{{m}}{=}{{\sigma }}_{{1}}{ + }{{\sigma}}_{{2}}$ ,${{\nu}}_{{n}}{=}{{\sigma }}_{{1}}$ .3. 数值算例与分析
3.1 静态构形、频率及模态
悬索物理参数为: L = 200.0 m, A = 7.069 × 10−2 m2, E = 200 GPa以及ρ = 7800.0 kg/m3. 无量纲化后的阻尼系数分别为: μm = 0.005, μn = 0.006. 不对称的损伤参数为: 损伤程度η = 0.4、损伤范围δ = 0.3、损伤位置α = 0.7. 对于无损系统, 其构形可以采用抛物线描述y(x) = (−4x2 + 4x)f. 一旦遭遇非对称损伤, 此时对称性破缺, 需要采用样条曲线拟合受损悬索的悬链线构形. 经拟合, 可以得到以下分段函数
$$ {y_j}\left( x \right) = \left\{ \begin{gathered} \left( { - 3.998\;5{x^2} + 3.999x} \right) f,\;{{ 0}} \leqslant x \leqslant {\alpha _1} \\ \left( { - 4.000\;3{x^2} + 4.000\;9x - 0.000\;5} \right) f,\; {\alpha _1} \leqslant x \leqslant {\alpha _2} \\ \left( { - 3.995{x^2} + 3.992x + 0.003} \right) f,\;{\alpha _2} \leqslant x \leqslant 1 \end{gathered} \right. $$ 对比上述两组方程, 由于非对称损伤导致悬索构形函数发生改变, 用分段样条曲线表示的线形将不再具有对称性. 因此本文将重点分析和讨论对称性破缺的动力系统, 其线性和非线性振动特性.
首先, 图2给出了无损和受损悬索前六阶模态频率ω/π和Irvine参数λ2的关系曲线. 如图2(a)所示, 对于无损结构, 其模态频率分为正对称和反对称两类, 且随着Irvine参数的不断增大, 系统频率之间存在多个交点. 观察图2(b)可知: 悬索发生不对称损伤后, 系统模态频率之间交点将消失, 其频率轨迹会相互接近, 然后迅速分开, 形成频率转向点. 此时各阶频率ω包含在7 × 7的系数矩阵中, 如附录C所示.
值得一提的是, 此时由于模态振型不再严格区分正、反对称形式, 因此转向点附近模态振型失去了对称性. 针对《公路桥梁抗风设计规范》(JTG/T 3360-01-2018)中对于斜拉索频率面内频率计算, 如果严格从力学概念而言, 斜拉索和受损的水平悬索, 由于系统存在对称性破缺, 其频率和模态不宜再分为正、反对称两类形式.
3.2 激励响应幅值曲线/幅频响应曲线
表1给出了无损和受损悬索的参数以及非线性相互作用系数. 当系统的两个模态频率接近时, 在外激励作用下, 能量将在不同模态间传递, 导致系统发生1:1内共振. 由表1数据可知: 由于无损悬索具有对称性, 假设高阶为正对称模态, 低阶为反对称模态, 可得非线性相互作用系数K1=K2=0. 而损伤悬索由于其模态振型对称性破缺, 此时K1≠0和K2≠0. 表1中部分参数正负号也出现了截然相反的情况, 由此可见对称性破缺后, 随着非线性相互作用系数的改变, 系统非线性耦合动力学行为也发生变化. 此外损伤后悬索的频率呈现出明显下降的趋势, 这一特点与温度效应有所区别.
表 1 无损和受损悬索的参数与非线性相互作用系数Table 1. Parameters and nonlinear interaction coefficients of undamaged and damaged suspended cablesCable types m n λ2 ωm ωn Kmm Knn Kmn/ Knm K1 K2 K3 undamaged 1 2 40.373 6.2640 6.2830 −2650000 1329000 2079000 0 0 1368000 damaged 1 2 41.829 6.1535 6.1538 1091850 902357 −2365780 938598 1024960 −1028280 对于激励直接作用于高阶(Ω≈ω2), 图3给出了无损和受损悬索的激励响应幅值曲线. 其中实线为稳定解, 虚线为不稳定解, SN和HB分别表示鞍节点分岔和霍普夫分岔. 如图3(a)所示, 对于无损悬索, 稳态解可以明显分为两类: 单模态解和双模态解(内共振). 对于前者(a1=0), 随着外激励幅值f2不断增加, 直接激励响应幅值a2不断增大. 选取合适的初始条件, 可以得到第二类内共振解. 此时由于内共振而激发的低阶模态响应幅值a1明显要大于a2. 且随着f2不断减小, a1和a2逐渐降低, 直到SN1, 系统发生跳跃现象, 此处a2迅速增大, a1则直接变成0, 系统再次出现单模态解.
图3(b)给出了受损系统的激励响应幅值曲线. 此时系统不存在明显的单模态解, 随着f2的增大, a2会不断增加, 直到0.0008附近, 出现第一个鞍结点分岔SN1, 发生跳跃现象. 同时, a1也不断增大, 直到SN1. 倘若f2进一步增加, 此时a2不会一直增加, 而会出现一段饱和现象直至第二个霍普夫分岔HB2, 能量将不断通过内共振的形式传递到低阶模态, 导致a1不断增大. 倘若f2从大不断减小直到0, 对于稳定解而言, a2由于饱和现象, 会基本保持不变, a1则不断减小, 直到第3个鞍结点分岔SN3, 幅值发生明显的跳跃现象, 迅速下降. 此外选择合适的初始条件, 可以得到鞍结点分岔SN2与霍普夫分岔HB1之间小范围的稳定解.
如图3所示, 对比无损和受损悬索的鞍结点分岔, 悬索受损后, 分岔数量增加到3个, 由此导致跳跃现象增多, 系统响应幅值突然增大或减小变得更加频繁, 影响悬索的疲劳性质. 进而有可能导致悬索损伤程度、范围和位置的进一步扩展和增加, 严重影响索结构安全. 因此在索结构的施工、运营与维护阶段, 需要及时识别索的损伤, 并及时采取相应措施进行处理, 避免由于出现局部损伤后不断加剧, 最终导致整体结构安全受影响.
选取外激励幅值f2 = 0.002以及内调谐参数σ2 = 0.2, 图4描述了当外激励直接作用于高阶模态(Ω ≈ ω2)时, 无损和受损悬索的幅频响应曲线. 其中实线和虚线分别为稳定和不稳定解, PF为叉形分岔.
对于无损系统, 如图4(a)所示, 与激励响应幅值曲线类似, 系统会呈现出明显的单模态解和内共振解. 此时可以观察到两个叉形分岔PF1和PF2. 选择一定的初始条件, 系统会展现出明显的耦合共振. 当外调谐参数σ1的不断增加时, a1和a2均会不断减小, 直到第一个霍普夫分岔HB1. 此后系统出现不稳定解. 倘若σ1继续增加, 系统会出现第二个霍普夫分岔HB2, 此时系统重新出现稳定解. 如果σ1仍然继续增加, a1会呈现增大的趋势, 而a2基本不变.
对于受损系统, 其共振响应特性发生了显著改变, 如图4(b)所示. 随着外调谐参数σ1从−1.0开始不断增大, 对于稳定解, 虽然内共振响应幅值a1虽小, 但是其并不是恒等于零, 且幅频响应曲线中并没有叉形分岔PF, 而出现鞍结点分岔SN1, 此处系统发生跳跃现象. 对于系统的大幅振动, 一开始为不稳定解, 随着调谐参数σ1不断增大, 直到第一个霍普夫分岔HB1, 此时系统开始出现稳定解. 之后随着σ1继续增大, 与无损系统类似, 系统会经历两个霍普夫分岔HB2和HB3, 内共振响应幅值a1呈现出先减小后增大的趋势. 倘若σ1继续增加, 系统又将恢复稳定解, 直到第4个霍普夫分岔HB4. 对比图4(a)可知: 无损系统此时会出现鞍结点分岔SN1, 导致系统出现跳跃现象. 由此可见, 受损伤影响, 在交点和转向点附近, 系统模态间的耦合振动特性存在明显的定性和定量的区别.
3.3 分岔和混沌
图3和图4中, 无论是无损还是受损悬索, 都存在霍普夫分岔. 由于系统的非线性动力学行为在霍普夫分岔附近会发生明显的改变, 因此分别采用打靶法和Floquet理论求解霍普夫分岔点附近的动态解并判断其稳定性. 图5给出了受损系统在两个霍普夫分岔HB2和HB3间的动态解, 其中实心圆是稳定的, 空心圆是不稳定的. 显然HB3是一个超临界霍普夫分岔, HB1点首先出现稳定的周期解分支, 随着调谐参数σ1的减少, 系统会出现倍周期分岔PD1, 表明系统存在通往混沌的路径.
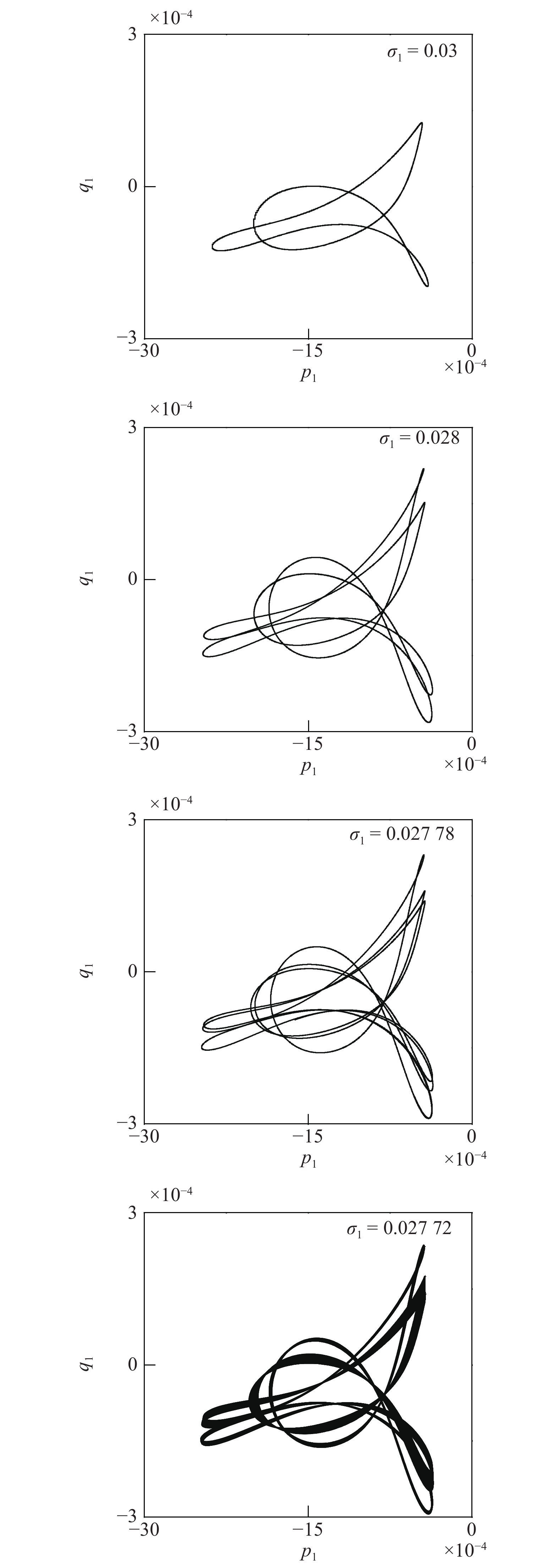
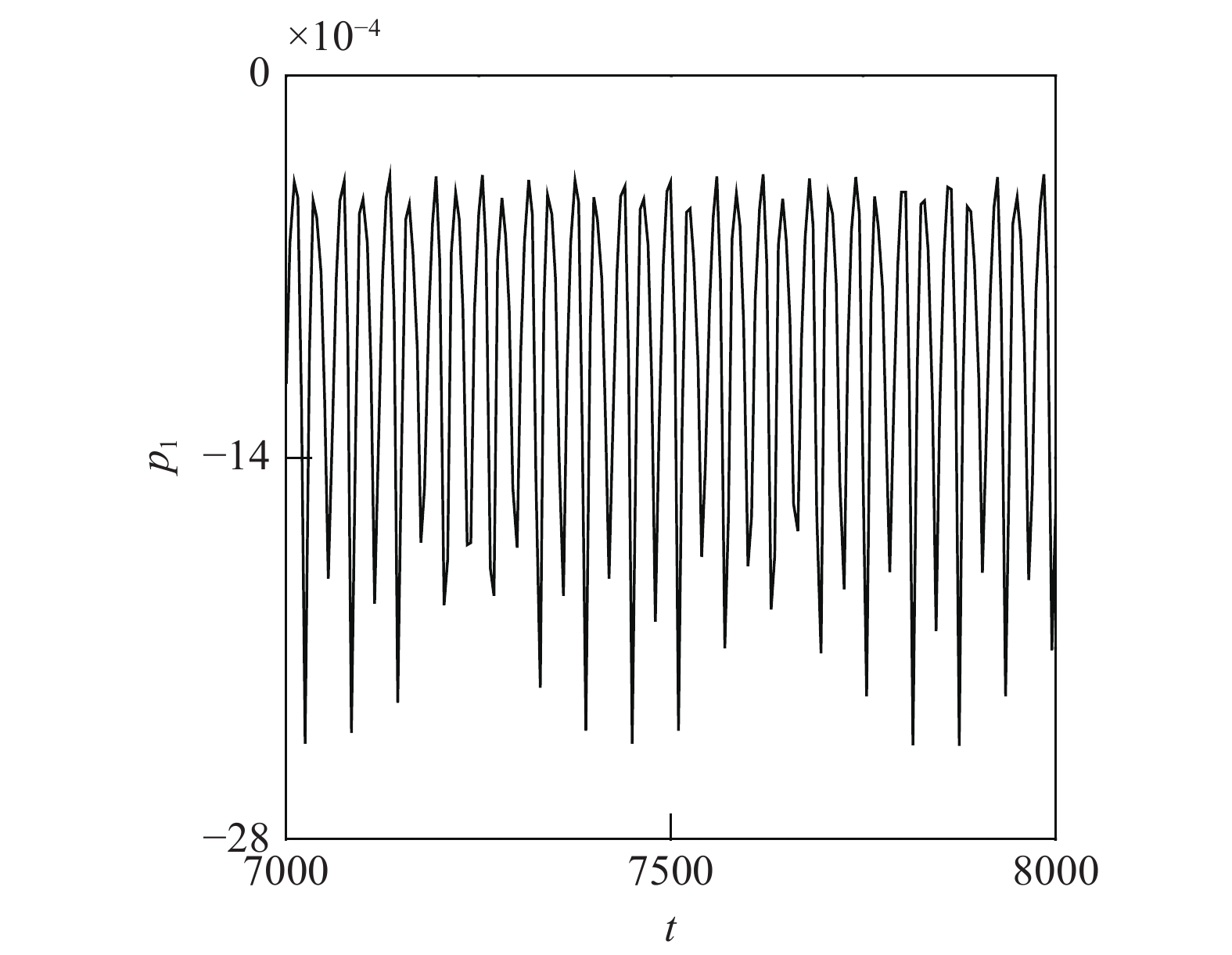
在PD1附近, 外调谐参数σ1从0.04不断减小, 依次选定为0.04→0.03→0.028→0.02778→0.02772, 图6给出了系统在对应调谐参数变化时的相位图. 如图所示, 随着调谐参数不断增加, 该动力系统会经历周期1→2→4→8→···→混沌解. 为了验证系统出现的混沌运动, 图7给出了系统的时程曲线、相位图、频率谱以及庞加莱截面, 并计算出系统的最大李雅普诺夫指数. 由时程曲线可以看出系统的波形呈现出明显的随机性, 此时的庞加莱截面具有分形的特点, 随机性强. 经计算可得其最大李雅普诺夫指数为0.00357, 据此可以判定为混沌吸引子.
4. 结 论
水平悬索遭遇不对称损伤后, 其固有对称性被打破, 如果仍采用一段抛物线来描述受损后的线形, 会出现细微差异. 因此需采用样条曲线拟合受损悬索的静态构形, 利用分段函数表示; 由于损伤导致对称性破缺, 水平悬索固有频率之间的交点变为转向点, 受损前正、反对称模态也变为受损后的非对称模态; 失去对称性后, 受损系统非线性相互作用系数亦会产生明显改变, 导致其内共振响应产生显著改变; 当激励直接作用在高阶模态时, 无损系统呈现出明显的单模态解和多模态解(即内共振), 但受损系统并没有呈现出明显的单模态解; 损伤会导致系统的鞍结点分岔数量增加, 导致系统可能发生的跳跃现象增多, 引发响应幅值发生突变, 影响索结构的疲劳性能; 受损系统的分岔和混沌特性会发生明显的改变, 将通过倍周期分岔产生混沌运动.
附录 A
$ \;$ $$ \begin{split} & 2{\mu _n} = {c_v}{{ }}\\ & {f_n} = \int_0^1 {{p_v}{\varphi _n}} \left( x \right){{{\rm{d}}}}x \\ & {\varLambda _{nijh}} = - \frac{\varTheta }{2}{\varDelta _d}\int_0^1 {\left[ {{{\varphi ''}_j}\left( x \right)\int_0^1 {{{\varphi '}_i}\left( x \right){{\varphi '}_h}\left( x \right){{{\rm{d}}}}x} } \right]{\varphi _n}\left( x \right){{{\rm{d}}}}x} \\ & {\varGamma _{nij}} = - {\kappa ^2}\varTheta {\varDelta _d}\int_0^1 {\left[ {{{\varphi ''}_j}\left( x \right)\int_0^1 {y'\left( x \right){{\varphi '}_i}\left( x \right){{{\rm{d}}}}x} } \right]{\varphi _n}\left( x \right){{{\rm{d}}}}x} \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{{{\kappa ^2}}}{2}\varTheta {\varDelta _d}\int_0^1 {y''\left( x \right)} \left[ {\int_0^1 {{{\varphi '}_i}\left( x \right){{\varphi '}_j}\left( x \right){{{\rm{d}}}}x} } \right]{\varphi _n}\left( x \right){{{\rm{d}}}}x \end{split} $$ 附录 B
$$ \begin{split} {K_{mn}}{\rm{ = }}&\sum\limits_{j = 1}^\infty {\left\{ {\left( {{\varLambda _{mmj}} + {\varLambda _{mjm}}} \right)\frac{{2{\varLambda _{jnn}}}}{{\omega _j^2}}{\rm{ + }}\left( {{\varLambda _{mnj}} + {\varLambda _{mjn}}} \right)} \right.} \cdot \\ & \left. {\left[ {\frac{{ {{\varLambda _{jmn}}{\rm{ + }}{\varLambda _{jnm}}} }}{{\omega _j^2 - {{\left( {{\omega _n} - {\omega _m}} \right)}^2}}}{\rm{ + }}\frac{{ {{\varLambda _{jmn}}{\rm{ + }}{\varLambda _{jnm}}} }}{{\omega _j^2 - {{\left( {{\omega _m} + {\omega _n}} \right)}^2}}}} \right]} \right\} + \\ & 2\left( {{\varGamma _{mnnm}} + {\varGamma _{mnmn}} + {\varGamma _{mmnn}}} \right) \end{split}$$ $$ \begin{split} {K_{nm}} =& \sum\limits_{j = 1}^\infty {\left\{ {\left( {{\varLambda _{nnj}} + {\varLambda _{njn}}} \right)\frac{{2{\varLambda _{jmm}}}}{{\omega _j^2}} + \left( {{\varLambda _{nmj}} + {\varLambda _{njm}}} \right) \cdot } \right.} \\ & \left. {\left[ {\frac{{ {{\varLambda _{jmn}}{\rm{ + }}{\varLambda _{jnm}}} }}{{\omega _j^2 - {{\left( {{\omega _n} - {\omega _m}} \right)}^2}}}{\rm{ + }}\frac{{ {{\varLambda _{jmn}}{\rm{ + }}{\varLambda _{jnm}}} }}{{\omega _j^2 - {{\left( {{\omega _m} + {\omega _n}} \right)}^2}}}} \right]} \right\} + \\ & 2\left( {{\varGamma _{nnmm}} + {\varGamma _{nmnm}} + {\varGamma _{nmmn}}} \right) \end{split}$$ $$ \begin{split} &{K_{mm}} = \sum\limits_{j = 1}^\infty {\left( {{\varLambda _{mmj}} + {\varLambda _{mjm}}} \right)\left( {\frac{{2{\varLambda _{jmm}}}}{{\omega _j^2}} + \frac{{{\varLambda _{jmm}}}}{{\omega _j^2 - 4\omega _m^2}}} \right)} {\rm{ + 3}}{\varGamma _{mmmm}}\\ & {K_{nn}} = \sum\limits_{j = 1}^\infty {\left( {{\varLambda _{nnj}} + {\varLambda _{njn}}} \right)\left( {\frac{{2{\varLambda _{jnn}}}}{{\omega _j^2}}{\rm{ + }}\frac{{{\varLambda _{jnn}}}}{{\omega _j^2 - 4\omega _n^2}}} \right)} {\rm{ + 3}}{\varGamma _{nnnn}} \end{split}$$ $$\begin{split} {K_1} = &\sum\limits_{j = 1}^\infty {\left[ {\left( {{\varLambda _{nmj}} + {\varLambda _{njm}}} \right)\frac{{{\varLambda _{jnn}}}}{{\omega _j^2 - 4\omega _n^2}}{\rm{ + }}\left( {{\varLambda _{nnj}} + {\varLambda _{njn}}} \right)\frac{{{\varLambda _{jmn}}{\rm{ + }}{\varLambda _{jnm}}}}{{\omega _j^2}}} \right]} + \\ & {\varGamma _{nnnm}} + {\varGamma _{nnmn}} + {\varGamma _{nmnn}} \end{split}$$ $$ {K_2} = \sum\limits_{j = 1}^\infty {\left( {{\varLambda _{nmj}} + {\varLambda _{njm}}} \right)\left( {\frac{{2{\varLambda _{jmm}}}}{{\omega _j^2}} + \frac{{{\varLambda _{jmm}}}}{{\omega _j^2 - 4\omega _m^2}}} \right)} + 3{\varGamma _{nmmm}} $$ $$ \begin{split} {K_3} = &\sum\limits_{j = 1}^\infty {\left[ {\left( {{\varLambda _{nnj}} + {\varLambda _{njn}}} \right)\frac{{{\varLambda _{jmm}}}}{{\omega _j^2 - 4\omega _m^2}} + \left( {{\varLambda _{nmj}} + {\varLambda _{njm}}} \right)\frac{{{\varLambda _{jmn}}{{ + }}{\varLambda _{jnm}}}}{{\omega _j^2}}} \right]} + \\ & {\varGamma _{nmmn}} + {\varGamma _{nmnm}} + {\varGamma _{nnmm}} \end{split} $$ 附录 C
7 × 7系数矩阵中每个元素Aij分别表示为
$$ \begin{gathered} {A_{11}} = 1,{A_{12}} = {A_{13}} = {A_{14}} = {A_{15}} = {A_{16}} = 0 \\ {A_{25}} = {A_{26}}{{ = }}{A_{31}} = {A_{32}} = {A_{41}} = {A_{42}} = {A_{43}} = {A_{44}} = 0 \\ {A_{55}} = {A_{56}} = {A_{57}} = {A_{61}} = {A_{62}} = {A_{67}} = 0 \\ \end{gathered} $$ $$ \begin{split} & {A_{17}} = \frac{1}{2}\frac{{3.998\;5}}{4}{\varDelta _d}\frac{{{\lambda ^2}}}{{{\chi ^6}{{\left( {{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }} \right)}^2}}} \\ & {A_{21}} = - {A_{23}} = \cos \left( {\frac{\omega }{\chi }{\alpha _1}} \right)\\ &{A_{22}} = - {A_{24}} = \sin \left( {\frac{\omega }{\chi }{\alpha _1}} \right) \\ & {A_{27}} = \frac{1}{2}\frac{{3.998\;5 - 4.000\;3}}{4}{\varDelta _d}\frac{{{\lambda ^2}}}{{{\chi ^6}{{\left( {{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }} \right)}^2}}} \\ & {A_{33}} = - {A_{35}} = \cos \left( {\frac{\omega }{\chi }{\alpha _2}} \right)\\ &{A_{34}} = - {A_{36}} = \sin \left( {\frac{\omega }{\chi }{\alpha _2}} \right) \\ & {A_{37}} = \frac{1}{2}\frac{{4.000\;3 - 3.995}}{4}{\varDelta _d}\frac{{{\lambda ^2}}}{{{\chi ^6}{{\left( {{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }} \right)}^2}}} \end{split} $$ $$ \begin{gathered} {A_{45}} = \cos \left( {\frac{\omega }{\chi }} \right) \\ {A_{46}} = \sin \left( {\frac{\omega }{\chi }} \right) \\ {A_{47}} = \frac{1}{2}\frac{{3.995}}{4}{\varDelta _d}\frac{{{\lambda ^2}}}{{{\chi ^6}{{\left( {{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }} \right)}^2}}} \\ \end{gathered} $$ $$ \begin{gathered} {A_{51}} = - {A_{53}} = - \frac{\omega }{\chi }\sin \left( {\frac{\omega }{\chi }{\alpha _1}} \right) \\ {A_{52}} = - {A_{54}} = - \frac{\omega }{\chi }\cos \left( {\frac{\omega }{\chi }{\alpha _1}} \right) \\ {A_{63}} = - {A_{65}} = - \frac{\omega }{\chi }\sin \left( {\frac{\omega }{\chi }{\alpha _2}} \right) \\ {A_{64}} = - {A_{66}} = - \frac{\omega }{\chi }\cos \left( {\frac{\omega }{\chi }{\alpha _2}} \right) \\ \end{gathered} $$ $$ \begin{split} {A_{71}} =& \frac{{3.999}}{4}\frac{\omega }{\chi }\cos \left( {\frac{\omega }{\chi }{\alpha _1}} \right) - \frac{{3.998\;5}}{4}2{\alpha _1}\cos \left( {\frac{\omega }{\chi }{\alpha _1}} \right) + \\ & \frac{{3.998\;5}}{4}2\sin \left( {\frac{\omega }{\chi }{\alpha _1}} \right) - \frac{{3.999}}{4}\frac{\omega }{\chi } \\ {A_{72}} =& \frac{{3.999}}{4}\frac{\omega }{\chi }\sin \left( {\frac{\omega }{\chi }{\alpha _1}} \right) - \frac{{3.998\;5}}{4}2{\alpha _1}\sin \left( {\frac{\omega }{\chi }{\alpha _1}} \right) - \\ & \frac{{3.998\;5}}{4}2\cos \left( {\frac{\omega }{\chi }{\alpha _1}} \right) + 2\frac{{3.998\;5}}{4} \\ \end{split} $$ $$ \begin{split} {A_{73}} = &\dfrac{\omega }{\chi }\Biggl[{23} {\dfrac{{4.000\;9}}{4}\sin \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right) - \dfrac{{4.000\;9}}{4}\sin \left( {\dfrac{\omega }{\chi }{\alpha _1}} \right) - } \\ & \dfrac{{4.000\;3}}{4}2{\alpha _2}\sin \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right) + \dfrac{{4.000\;3}}{4}2{\alpha _1}\sin \left( {\dfrac{\omega }{\chi }{\alpha _1}} \right) - \\ & {\dfrac{{4.000\;3}}{4}\dfrac{{2\cos \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right)}}{{{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }}} - \dfrac{{4.0003}}{4}\dfrac{{2\cos \left( {\dfrac{\omega }{\chi }{\alpha _1}} \right)}}{{{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }}}} \Biggl]{23} \end{split}$$ $$ \begin{split}{A_{74}} =& \dfrac{\omega }{\chi }\Biggl[{23} \dfrac{{4.000\;9}}{4}\cos \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right) - \dfrac{{4.000\;9}}{4}\cos \left( {\dfrac{\omega }{\chi }{\alpha _1}} \right)- \\ & \dfrac{{4.000\;3}}{4}2{\alpha _2}\cos \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right) + \dfrac{{4.000\;3}}{4}2{\alpha _1}\cos \left( {\dfrac{\omega }{\chi }{\alpha _1}} \right) - \\ & \dfrac{{4.000\;3}}{4}\dfrac{{2\sin \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right)}}{{{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }}} - \dfrac{{4.000\;3}}{4}\dfrac{{2\sin \left( {\dfrac{\omega }{\chi }{\alpha _1}} \right)}}{{{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }}} \Biggl]{23} \end{split} $$ $$ \begin{split} {A_{75}} = &\dfrac{\omega }{\chi }\Biggl[{23} \dfrac{{3.992}}{4}\cos \left( {\dfrac{\omega }{\chi }} \right) - \dfrac{{3.992}}{4}\cos \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right)- \\ & \dfrac{{3.995}}{4}2\cos \left( {\dfrac{\omega }{\chi }} \right) + \dfrac{{3.995}}{4}2{\alpha _2}\cos \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right) + \\ & \dfrac{{3.995}}{4}\dfrac{{2\sin \left( {\dfrac{\omega }{\chi }} \right)}}{{{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }}} - \dfrac{{3.995}}{4}\dfrac{{2\sin \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right)}}{{{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }}} \Biggl]{23} \end{split} $$ $$ \begin{split}{A_{76}} = &\dfrac{\omega }{\chi }\Biggl[{23} \dfrac{{3.992}}{4}\sin \left( {\dfrac{\omega }{\chi }} \right) - \dfrac{{3.992}}{4}\sin \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right) - \\ & \dfrac{{3.995}}{4}2\sin \left( {\dfrac{\omega }{\chi }} \right) + \dfrac{{3.995}}{4}2{\alpha _2}\sin \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right)+ \\ & \dfrac{{3.995}}{4}\dfrac{{2\cos \left( {\dfrac{\omega }{\chi }} \right)}}{{{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }}} - \dfrac{{3.995}}{4}\dfrac{{2\cos \left( {\dfrac{\omega }{\chi }{\alpha _2}} \right)}}{{{\omega \mathord{\left/ {\vphantom {\omega \chi }} \right. } \chi }}} \Biggl]{23} \end{split}$$ $$ {A_{77}} = - \frac{\omega }{\chi } $$ -
表 1 无损和受损悬索的参数与非线性相互作用系数
Table 1 Parameters and nonlinear interaction coefficients of undamaged and damaged suspended cables
Cable types m n λ2 ωm ωn Kmm Knn Kmn/ Knm K1 K2 K3 undamaged 1 2 40.373 6.2640 6.2830 −2650000 1329000 2079000 0 0 1368000 damaged 1 2 41.829 6.1535 6.1538 1091850 902357 −2365780 938598 1024960 −1028280 -
[1] 胡海岩. 对振动学及其发展的美学思考. 振动工程学报, 2000, 13(2): 161-169 (Hu Haiyan. Aesthetical consideration for vibration theory and its development. Journal of Vibration Engineering, 2000, 13(2): 161-169 (in Chinese) doi: 10.3969/j.issn.1004-4523.2000.02.001 [2] 胡海岩. 振动力学−研究性教程. 北京: 科学出版社 Hu Haiyan. Mechanics of Vibration—Research Course. Beijing: Science Press, 2020 (in Chinese)
[3] 张登博, 唐有绮, 陈立群. 非齐次边界条件下轴向运动梁的非线性振动. 力学学报, 2019, 51(1): 218-227 (Zhang Dengbo, Tang Youqi, Chen Liqun. Nonlinear vibrations of axially moving beams with nonhomogeneous boundary conditions. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(1): 218-227 (in Chinese) doi: 10.6052/0459-1879-18-189 [4] 康厚军, 郭铁丁, 赵跃宇等. 大跨度斜拉桥非线性振动模型与理论研究进展. 力学学报, 2016, 48(3): 519-535 (Kang Houjun, Guo Tieding, Zhao Yueyu, et al. Review on nonlinear vibration and modeling of large span cable-stayed bridge. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3): 519-535 (in Chinese) doi: 10.6052/0459-1879-15-436 [5] Triantafyllou MS, Grinfogel L. Natural frequencies and modes of inclined cables. Journal of Structural Engineering, 1986, 112(1): 139-148 doi: 10.1061/(ASCE)0733-9445(1986)112:1(139)
[6] Cheng SP, Perkins NC. Closed form vibration analysis of sagged cable/mass suspensions. Journal of Applied Mechanics, 1992, 59(4): 923-928 doi: 10.1115/1.2894062
[7] Lepidi M, Gattulli V, Vestroni F. Static and dynamic response of elastic suspended cables with damage. International Journal of Solids and Structures, 2007, 44: 8194-8212 doi: 10.1016/j.ijsolstr.2007.06.009
[8] Wu QX, Takahashi K, Nakamura S. Formulae for frequencies and modes of in-plane vibrations of small-sag inclined cables. Journal of Sound and Vibration, 2005, 279(3-5): 1155-1169 doi: 10.1016/j.jsv.2004.01.004
[9] 任伟新, 陈刚. 由基频计算拉索拉力的实用公式. 土木工程学报, 2005, 38(11): 26-31 (Ren Weixin, Chen Gang. Practical formulas to determine cable tension by using cable fundamental frequency. China Civil Engineering Journal, 2005, 38(11): 26-31 (in Chinese) doi: 10.3321/j.issn:1000-131X.2005.11.005 [10] 吴庆雄, 陈宝春. 塔桅结构的斜索面内固有振动计算的修正Irvine方程. 工程力学, 2007, 24(4): 18-23 (Wu Qingxiong, Chen Baochun. Modified Irvine equations for in-plane natural vibrations of inclined cables in tower and guyed mast structures. Engineering Mechanics, 2007, 24(4): 18-23 (in Chinese) doi: 10.3969/j.issn.1000-4750.2007.04.004 [11] Irvine HM. Cable Structures. Cambridge: MIT Press, 1981
[12] Srinil N, Rega G, Chucheepsakul S. Large amplitude three-dimensional free vibrations of inclined sagged elastic cables. Nonlinear Dynamics, 2003, 33(2): 129-154 doi: 10.1023/A:1026019222997
[13] 王浩宇, 吴勇军. 1: 1内共振对随机振动系统可靠性的影响. 力学学报, 2015, 47(5): 807-813 (Wang Haoyu, Wu Yongjun. The influence of one-to-one internal resonance on reliability of random vibration system. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(5): 807-813 (in Chinese) doi: 10.6052/0459-1879-15-058 [14] 吕敬, 李俊峰, 王天舒等. 充液挠性航天器俯仰运动1: 1: 1内共振动力学分析. 力学学报, 2007, 39(6): 804-812 (Lü Jing, Li Junfeng, Wang Tianshu, et al. Analytical study on 1: 1: 1 internal resonance nonlinear dynamics of a liquid-filled spacecraft with elastic appendages. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(6): 804-812 (in Chinese) doi: 10.3321/j.issn:0459-1879.2007.06.012 [15] 叶敏, 吕敬, 丁千等. 复合材料层合板1: 1参数共振的分岔研究. 力学学报, 2004, 36(1): 64-71 (Ye Min, Lü Jing, Ding Qian, et al. The bifurcation analysis of the laminated composite plate with 1: 1 parametrically resonance. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(1): 64-71 (in Chinese) doi: 10.3321/j.issn:0459-1879.2004.01.010 [16] 姜盼, 郭翔鹰, 张伟. 石墨烯三相复合材料板的非线性动力学研究. 动力学与控制学报, 2019, 17(3): 270-280 (Jiang Pan, Guo Xiangying, Zhang Wei. Nonlinear dynamics of a three-phase composite materials plate with grapheme. Journal of Dynamics and Control, 2019, 17(3): 270-280 (in Chinese) doi: 10.6052/1672-6553-2019-021 [17] 孙莹, 张伟. 1: 1内共振环形桁架天线的稳定性分析. 动力学与控制学报, 2018, 16(3): 281-288 (Sun Ying, Zhang Wei. Analysis on stability of circular mesh antenna with 1: 1 internal resonance. Journal of Dynamics and Control, 2018, 16(3): 281-288 (in Chinese) doi: 10.6052/1672-6553-2018-024 [18] Srinil N, Rega G. The effects of kinematic condensation on internally resonant forced vibrations of shallow horizontal cables. International Journal of Non-Linear Mechanics, 2007, 42(1): 180-195 doi: 10.1016/j.ijnonlinmec.2006.09.005
[19] Rega G, Srinil N. Nonlinear hybrid-mode resonant forced oscillations of sagged inclined cables at avoidances. Journal of Computational and Nonlinear Dynamics, 2007, 2(4): 324-336 doi: 10.1115/1.2756064
[20] Chen Z, Chen H, Liu H, et al. Corrosion behavior of different cables of large-span building structures in different environments. Journal of Materials in Civil Engineering, 2020, 32(11): 04020345 doi: 10.1061/(ASCE)MT.1943-5533.0003428
[21] Chen A, Yang YY, Ma RJ, et al. Experimental study of corrosion effects on high-strength steel wires considering strain influence. Construction and Building Materials, 2020, 240: 117910 doi: 10.1016/j.conbuildmat.2019.117910
[22] Wang Y, Zheng YQ, Zhang WH, et al. Analysis on damage evolution and corrosion fatigue performance of high strength steel wire for bridge cable: Experiments and numerical simulation. Theoretical and Applied Fracture Mechanics, 2020, 107: 102571 doi: 10.1016/j.tafmec.2020.102571
[23] Jiang C, Wu C, Cai CS, et al. Corrosion fatigue analysis of stay cables under combined loads of random traffic and wind. Engineering Structures, 2020, 206: 110153 doi: 10.1016/j.engstruct.2019.110153
[24] Bouaanani N. Numerical investigation of the modal sensitivity of suspended cables with localized damage. Journal of Sound and Vibration, 2006, 292(3-5): 1015-1030 doi: 10.1016/j.jsv.2005.09.013
[25] Lepidi M. Damage identification in elastic suspended cables through frequency measurement. Journal of Vibration and Control, 2009, 15(6): 867-896 doi: 10.1177/1077546308096107
[26] Sun HH, Xu J, Chen WZ, et al. Time-dependent effect of corrosion on the mechanical characteristics of stay cable. Journal of Bridge Engineering, 2018, 23(5): 04018019 doi: 10.1061/(ASCE)BE.1943-5592.0001229
[27] Xu J, Sun HH, Cai SY. Effect of symmetrical broken wires damage on mechanical characteristics of stay cable. Journal of Sound and Vibration, 2019, 461: 114920 doi: 10.1016/j.jsv.2019.114920
[28] 王立彬, 王达, 吴勇. 损伤拉索的等效弹性模量及其参数分析. 计算力学学报, 2015, 32(3): 339-345 (Wang Libin, Wang Da, Wu Yong. The equivalent elastic modulus of damaged cables and parameter analysis. Chinese Journal of Computational Mechanics, 2015, 32(3): 339-345 (in Chinese) doi: 10.7511/jslx201503007 [29] 兰成明, 李惠, 鞠杨. 平行钢丝拉索承载力评定. 土木工程学报, 2013, 46(5): 31-38 (Lan Chengming, Li Hui, Ju Yang. Bearing capacity assessment for parallel wire cables. China Civil Engineering Journal, 2013, 46(5): 31-38 (in Chinese) [30] Zhu J, Ye GR, Xiang YQ, et al. Dynamic behavior of cable-stayed beam with localized damage. Journal of Vibration and Control, 2011, 17(7): 1080-1089 doi: 10.1177/1077546310378028




 下载:
下载: