PSEUDO ARC-LENGTH NUMERICAL ALGORITHM FOR COMPUTATIONAL DYNAMICS
-
摘要: 动力学问题通常采用微分方程来描绘，但由于工程实际问题的复杂性，微分方程模型常伴随着解的不连续性、刚性或激波间断奇异性特点，传统方法很难求解，奇异性问题是计算动力学难点，同时也是国内外学者研究的热点。伪弧长数值算法是针对计算动力学中的奇异性问题所提出的，其基本思想为通过在解曲线上引入伪弧长参数，并增加一个约束方程，在伪弧长参数作用下，使得原始离散单元发生扭曲形变，从而达到消除或减弱奇异性的目的。本文首先介绍伪弧长方法求解定常对流-扩散方程的奇异性问题，并提出针对双曲守恒定律的局部伪弧长算法，其思想在于首先通过间断解的梯度变换来确定强间断所处位置，进而通过局部网格点重构以及数值修正来达到强间断处奇异性消除与降低的目的。针对高维问题，提出全局伪弧长方法，通过对整个计算区域内的网格点进行重构，使得所有网格点向奇异间断点处移动，从而降低间断点的影响域，达到降低奇异性的目的。重点讨论了三维全局伪弧长算法问题的计算难点，即三维空间网格扭曲大变形导致的数值算法不收敛，并提出在算法设计过程中采用分块重构与整体计算相结合的策略，实现了三维空间中的伪弧长数值算法，最后通过数值实验来验证伪弧长算法对于奇异性问题的有效性。Abstract: Differential equations are often used to describe the dynamic problems. Classical approaches are always hard to solve it in engineering practice due to its characteristics of strong discontinuity, rigidity and shock singularity, among which singularity problem is one of the most difficult and hot issues among scholars. Pseudo arc-length numerical algorithm is proposed for singularity problems in computational dynamics, whose basic idea is to introduce a pseudo arc-length parameter in the original governing equations so that a constraint equation is added. Under the action of a pseudo arc-length parameter, the original discrete elements are distorted to achieve the goal of eliminating or weakening singularity. Firstly, this paper gave an introduction about the pseudo arc-length method for solving the singularity problem in steady diffusion-convection equations. Then the local pseudo arc-length algorithm is proposed for hyperbolic conservation laws. This algorithm has two steps. The first step is to determine the location of the strong discontinuity and the second one aims to eliminate or reduce the singularity by reconstructing the local mesh. Secondly, a global pseudo arc-length algorithm is put forward for high dimensional problems, which can reconstruct the mesh in whole area. Since the reconstructed mesh can adaptively catch the singularity points, the singularity is greatly reduced. Thirdly, the threedimensional global pseudo arc-length algorithm and its computational difficulties in numerical algorithm convergence caused by large grid distortion in three-dimensional space are presented. Then the combination of block reconstruction and integral calculation strategy is adopted in the algorithm design process to achieve the pseudo arc-length numerical algorithm in three-dimensional space. Finally, numerical examples were employed to verify the validity of the pseudo arc-length algorithm.
-
Keywords:
- computational dynamics /
- pseudo arc-length /
- adaptive /
- explosion shock wave /
- three-dimensional
-
引言
计算动力学是利用科学计算方法来研究动力学现象与特性的科学[1].但由于动力学问题较复杂, 许多实验的开展面临着周期长、代价大等困难, 通过理论分析又难以获得大多数现实工程问题的解析解, 数值方法就成为一种有效的替代手段.特别是在第二次世界大战以后, 电子计算机的出现以及随后数十年中大型计算机的迅速普及和数值计算方法的迅猛发展[2], 为计算科学的发展提供了物质与理论基础.因为动力学问题常常伴随着时间和空间的演化, 所以计算动力学问题通常采用基于连续介质力学问题的微分方程模型来描述.而且由于工程实际问题的复杂性, 动力系统微分方程模型常伴随着解的不连续性、刚性或激波间断等奇异性特点.奇异性问题是计算力学中的难点, 同时也是国内外学者研究的热点[3-5]. 1979年, Riks[6]首次应用弧长法求解了带有参数的非线性方程中的极值问题. Boor证明了利用参数变换求解微分方程的可行性, 并且提出高阶逼近函数的方法[7].之后Crisfield [8]通过变分法将非线性几何问题的本构方程变换为非线性代数方程, 进而引入弧长参数, 建立了弧长算法的基本理论.此外Chan[9]在1984年通过引入伪弧长控制参数将其引申为伪弧长方法, 并将其应用于求解非线性方程的奇异性问题中.在此基础之上, 忻孝康等[10]、陈国谦等[11]将伪弧长方法推广，用于求解常微分方程动力系统的奇异性问题.受此启发, 武际可等[12]将常微分方程动力系统的伪弧长算法推广, 用来求解微分动力系统中的双曲偏微分方程的Burgers奇异性问题, 总结出伪弧长算法的基本思想.通过在解曲线上引入伪弧长参数, 并增加一个约束方程, 在伪弧长参数作用下, 使得原始离散单元发生扭曲形变, 达到消除或减弱奇异性的目的.此时双曲偏微分方程的伪弧长算法的框架思想已经基本形成.与此同时, 出现了一种以网格自适应为目的, 通过网格点的重新分布与数值解的重新插值来求解奇异双曲问题的数值算法-移动网格方法.该方法在1983年由Harten等[13]第一次提出. Ren等[14]对该方法进行了改进, 提出利用弧长参数来控制网格点的自适应移动.在此基础之上, Huang等[15]根据均分原则[16], 提出了结合伪弧长控制参数的移动网格控制方程.此后, 大量学者利用移动网格控制方程与双曲控制方程构成的耦合系统来研究移动网格方法[15, 17-18].对比分析伪弧长方法与移动网格方法的特点, 可以发现, 两种数值方法具有一定联系, 移动网格法就是一种具有伪弧长性质的双曲方程数值算法, 属于计算动力学中的伪弧长数值算法的一部分.对于双曲偏微分方程来说, 虽然伪弧长方法与移动网格方法的出发点不一样, 但是移动网格方法具有伪弧长数值算法的特点, 符合伪弧长算法的定义, 可以被称作是伪弧长移动网格算法.此外，由于移动网格方法的出发点是网格的移动重构, 缺乏网格的整体性与直观性, 特别是在三维问题的计算过程中, 认为六面体网格在移动后, 某个面发生畸变, 变形为非六面体, 从而导致计算失败.当前对三维问题都是采用工程的简化计算方法来完成的, 所获得的计算结果不可避免地会失去原有工程问题的物理本质.再者大多数工程实际问题都是三维问题，所以针对三维问题的大规模高效算法的研究是迫切与必要的.
近年来, 宁建国等将伪弧长算法用于求解爆炸冲击波问题, 先后发展出局部伪弧长算法与全局伪弧长移动网格算法[19-24], 通过伪弧长变换来捕捉爆炸冲击波阵面, 建立了爆炸冲击波问题的伪弧长算法的基础理论体系.先引入一般形式的Runge-Kutta法, 得到双曲守恒控制方程与网格映射控制方程所构成的限制微分动力系统[25-26], 进一步利用牛顿迭代法, 将非线性问题转化为类线性问题来处理, 继而对类线性问题的系数矩阵进行正则化归约分析, 建立了伪弧长数值算法的稳定性理论, 得到了伪弧长算法的收敛性结论[24].针对反应气体动力学模型源项的刚性特点以及反应区域的冲击波与稀疏波的复杂作用导致计算过程密度、压力等物理量出现负值的问题[27-28], 提出了伪弧长数值算法的保正性理论[23].
本文在研究计算动力学问题中的三类伪弧长算法的基础之上, 从伪弧长算法降低奇异性的特点出发, 提出了三维空间中六面体网格单元分割与整体结合的思想, 实现了三维空间中爆炸冲击问题的伪弧长法的数值模拟.进而针对二维、三维爆轰波对于板型障碍物的爆炸冲击问题进行数值模拟, 实现了网格对于爆轰波阵面的捕捉, 对障碍物后方的多个标定点处的压力大小进行分析, 得到障碍物后方的安全位置.
1. 定常对流-扩散问题中的伪弧长方法
定常对流-扩散问题广泛存在于化学工程、传热传质、大气和水质污染等领域中[29-30].其模型通常采用常微分方程描绘, 在数值计算中常常会出现伪振荡、非物理的负浓度解、激波层或边界层被拉宽等奇异性现象.采用伪弧长算法求解此类问题, 可以有效地避免与降低常微分方程的奇异性问题.定常对流-扩散方程的一维无量纲形式为
$$ \frac{{\partial (uc)}}{{\partial X}} = \frac{1}{{Pe}}\frac{{{\partial ^2}c}}{{\partial {X^2}}} + q,\quad a < x < b $$ (1) 其中，$u$为对流速度, $q$为源汇项, $c$为污染物的浓度, $Pe$称为Peclet数, 定义为
$$ Pe = \dfrac{U \cdot L}{\alpha } $$ (2) 式中，$U$为特征对流速度, $L$为特征长度, $\alpha $为扩散系数.
在大Peclet数情况下, 即$Pe \gg 1$, 可令
$$ \delta = \frac{1}{{Pe}} \ll 1 $$ (3) 方程 (1) 可以写成奇异摄动型的二阶常微分方程式
$$ \delta y'' + fy' + gy = h $$ (4) $$ y\left( a \right) = \alpha, \;\;y\left( b \right) = \beta $$ (5) 其中，$y = c$, $f$, $g$, $h$均可是$x$和$y (c)$的函数, $\alpha $, $\beta $为常数.
引入解曲线的弧长$s$, 则有
$$ {\rm{d}}s = \sqrt {1 + {{\left( {{\rm{d}}y/{\rm{d}}x} \right)}^2}} {\rm{d}}x $$ (6) 令$v = {\rm{d}} y / {\rm{d}} x$, 则式 (4) 可转化为如下一阶常微分方程组
$$ \left. \begin{array}{l} \frac{{{\rm{d}}x}}{{{\rm{d}}s}} = \frac{1}{{\sqrt {1 + {v^2}} }}\\ \frac{{{\rm{d}}y}}{{{\rm{d}}s}} = \frac{v}{{\sqrt {1 + {v^2}} }}\\ \frac{{{\rm{d}}v}}{{{\rm{d}}s}} = \frac{{\left( {h-fv-gy} \right)}}{{\delta \sqrt {1 + {v^2}} }} \end{array} \right\} $$ (7) 假设$x = a$端的弧长为零, $x = b$端的弧长为$S_{\max } $, 于是式 (5) 化为如下的边界条件
$$ \left. \begin{array}{l} x(0) = a, x\left( {{S_{\max }}} \right) = b\\ y(0) = \alpha, y\left( {{S_{\max }}} \right) = \beta \end{array} \right\} $$ (8) 因此, 奇异摄动两点边值问题式 (4) 和式 (5) 就转化为一阶常微分方程的边值问题式 (7) 和式 (8).对于方程组 (7) 通常采用Rosenbrock格式求解[31].对于边值问题式 (8) 可采用打靶法进行求解[32].
2. 非定常对流问题的伪弧长方法
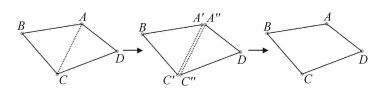
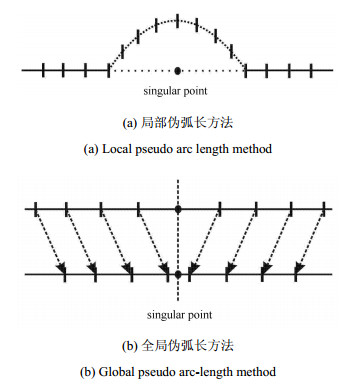
非定常对流问题通常采用双曲型偏微分方程来刻画[33].这类问题通常伴随着激波间断性而导致解出现强间断奇异性[34].数值求解这类奇异间断性问题的核心在于对间断处的精确捕捉与计算.对于这类问题的求解, 伪弧长方法包括局部伪弧长方法和全局伪弧长方法.局部伪弧长方法为伪弧长方法的早期形式, 其核心在于首先通过间断解的梯度变换来确定强间断所处位置, 进而通过局部网格点重构以及数值修正来达到强间断处奇异性消除与降低的目的, 如图 1(a)所示.而全局伪弧长方法 (伪弧长移动网格法) 则是通过对整个计算区域内的网格点进行重构, 使得所有网格点向奇异间断点处进行移动, 从而降低间断点的影响域, 进而达到降低奇异性的目的, 如图 1(b)所示.
![]()
图 1 双曲微分方程伪弧长方法示意图Figure 1. Schematic diagram for the hyperbolic differential equations pseudo arc-length method2.1 局部伪弧长方法
考虑一维双曲守恒系统
$$ \frac{{\partial U}}{{\partial t}} + \frac{{\partial F(U)}}{{\partial x}} = 0 $$ (9) $$ U{\rm{(}}x{\rm{, 0) = }}{U_{\rm{0}}}{\rm{ (}}x{\rm{)}} $$ (10) 利用雅克比矩阵$A (U) = \nabla _U F$, 守恒型方程可以转换到如下形式
$$ \frac{{\partial U}}{{\partial t}} + A(U)\frac{{\partial U}}{{\partial x}} = 0 $$ (11) 引入弧长参量$\xi $, 其满足关系式
$$ {\left( {{\rm{d}}\xi } \right)^2} = {\left( {{\rm{d}}x} \right)^2} + {\left( {{\rm{d}}u} \right)^2} $$ (12) 其中$u$是$U$的分量形式, 进而由上式可得
$$ x = \sqrt {1-{{\left( {\frac{{\partial u}}{{\partial \xi }}} \right)}^2}} {\rm{d}}\xi $$ (13) 进而联立控制方程 (10) 与伪弧长限制方程 (13) 可以得到
$$ \frac{{{\rm{d}}U}}{{{\rm{d}}t}} =-A\frac{{\partial U}}{{\partial \xi }}\frac{1}{{\sqrt {1-{{\left( {\frac{{\partial u}}{{\partial \xi }}} \right)}^2}} }} $$ (14) 上式中含有因子$\varPsi = 1/ \sqrt{1-(\partial u/\partial \xi )^2}$, 当$\sqrt {1-{\partial u}/{\partial \xi }^2 } $趋于$0$时, $\varPsi $趋于无穷大, 在实际计算中, 采用下式计算
$$ \psi {\rm{ = }}\left\{ \begin{array}{l} \psi, \;\;\;\;\left[{1-{{(\partial u/\partial \xi )}^2}} \right] > \varepsilon \\ 1/\varepsilon, \;\left[{1-{{(\partial u/\partial \xi )}^2}} \right] < \varepsilon \end{array} \right. $$ (15) 其中$\varepsilon $是一个小的正数.进而对式 (14) 进行空间离散, 得
$$ \begin{array}{l} \frac{{{\rm{d}}{u_i}}}{{{\rm{d}}t}} =- \left( {{u_i} + \frac{{\Delta {x_i}}}{{\Delta t}}} \right)\frac{{{u_{i + 1}}- {u_{i- 1}}}}{{2\Delta \xi }} \cdot \\ \frac{1}{{\sqrt {1 - {{\left[{\left( {{u_{i + 1}}-{u_{i-1}}} \right)/2\Delta \xi } \right]}^2}} }} \end{array} $$ (16) 在计算空间中可采用均匀网格, $u_i = u\left ({\xi _i, t} \right)$, $\Delta \xi = \xi _{i + 1}-\xi _i $为计算空间网格步长, 物理空间网格步长为$\Delta x_i = x\left ({\xi _i, \tau + \Delta \tau } \right)-x\left ({\xi _i, \tau } \right)$.进一步可对式 (16) 利用Runge-Kutta[35-36]进行时间离散求解.
为提高上述过程计算效率, 令参数
$$ \mathit{\Phi } = 1 - \Delta {u^2}/\left( {\Delta {u^2} + \Delta {x^2}} \right) $$ (17) 其中, $\Delta u = u\left ({x_{i + 1}, t} \right)-u\left ({x_i, t} \right)$, $\Delta x$为物理空间网格步长, 在求解过程中, 对于每个离散单元, 检验$\mathit{\Phi } $值, 当$\mathit{\Phi } \leqslant \mathit{\Phi } _0 $ (其中$\mathit{\Phi } _0 $为一个小的正数), 采用引入弧长变量$\xi $的方程, 而其他的单元仍采用原有的方程.
2.2 全局伪弧长方法
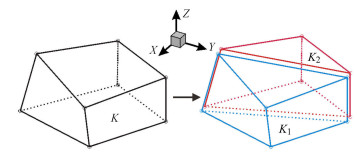
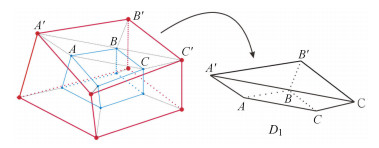
由于在高维空间中, 间断点的跟踪与控制方程在间断处的变形修正都是十分困难的, 因此相比于局部伪弧长算法, 全局伪弧长方法更适合处理二维、三维问题.在二维空间中, 网格变形如图 2所示, 在计算过程中需要保证每个单元网格面积大于零, 避免网格面积为零或为负值的出现, 相比于二维问题, 三维问题要复杂很多, 由于在三维空间中六面体单元畸变以后, 其外表面各点会出现不共面的情况, 如图 3所示, 这样会导致计算过程中的物理量重构不守恒, 以及扭曲变形后网格单元的控制方程演化失败.为解决这一难题, 本文采用分块重构与整体计算相结合的策略, 即在物理量重构阶段, 将六面体单元每个空间外表面拆分成两个面 (如图 4过程), 则每个六面体在$X, Y, Z$每个方向上被拆分成两个三棱柱分别进行处理 (如图 5所示).在网格移动与控制方程的演化计算阶段再回归整体单元区域进行计算.分块重构过程可以避免网格的重构过程中由于多个点不在一个平面导致物理量重构不守恒问题.整体移动与计算可以避免多个块体分别计算导致计算量过大以及多个块体的同时移动导致网格错位以及交叉网格的出现.
对于三维非定常、无黏、无热传导反应流体动力学问题, 考虑三维空间中一步反应流体欧拉方程组
$$ \dfrac{\partial }{\partial t}\boldsymbol{w} + \dfrac{\partial }{\partial \boldsymbol{x} }\boldsymbol{F}\left( \boldsymbol{w} \right) = \boldsymbol{s}\left( \boldsymbol{w} \right), \ t \geqslant 0 $$ (18) 其中, $\boldsymbol{x}$为三维物理空间向量；三维空间矩阵函数
$$ \boldsymbol{F}\left( \boldsymbol{w} \right) = \left( \!\!\begin{array}{ccc} {\rho u} & {\rho v} & {\rho w} \\ {\rho u^2 + p} & {\rho uv} & {\rho uw} \\ {\rho vu} & {\rho v^2 + p} & {\rho vw} \\ {\rho wu} & {\rho wv} & {\rho w^2 + p} \\ {\left( {E + p} \right)u} & {\left( {E + p} \right)v} & {\left( {E + p} \right)w} \\ {\rho uR} & {\rho vR} & {\rho wR} \end{array}\!\! \right) $$ 物理量$\boldsymbol{w} = \left ({\rho, \rho u, \rho v, \rho w, E, \rho R} \right)^{\rm T}$；化学反应源项函数为$\boldsymbol{s}\left (\boldsymbol{w} \right) = \left ({0, 0, 0, 0, 0, \omega } \right)^ {\rm T}$.对于一步Arrhenius化学反应模型$\omega $
$$ R \to P, \omega = - \tilde {K}\rho R\exp \left( { - \tilde {T} /T} \right) $$ 一步化学反应状态方程为
$$ E = \dfrac{1}{2}\rho { u}^2 + \dfrac{p}{\gamma - 1} + \rho qR $$ 引入弧长参数${\pmb \xi } = {\pmb \xi }\left ({\boldsymbol{x}, t} \right)$, 其满足弧长表达式
$$ \left( {\rm{d}}{\pmb \xi } \right)^2 = \left( {\rm{d}}\boldsymbol{x} \right)^2 + {\rm{d}}sum_n^{i = 1 } \lambda_i({\rm{d}} \boldsymbol{w}_i)^2 $$ (19) 进一步, 我们可以定义监视函数
$$ M\left( {\mathit{\boldsymbol{x}}, t} \right) = \sqrt {1 + \sum\limits_n^{i = 1} {{\lambda _i}{{\left( {\nabla \mathit{\boldsymbol{w}}} \right)}^2}} } $$ (20) 通过引入伪时间来得到多维空间中的网格移动速度的偏微分方程
$$ \boldsymbol{x}_t = \dfrac{1}{\tau }\dfrac{\partial }{\partial {\pmb \xi }} \Big(M\dfrac{\partial \boldsymbol{x}}{\partial {\pmb \xi }} \Big) $$ (21) 对上式可以采用Gauss-Seidel循环迭代求解
$$ \begin{array}{l} \sum\limits_{r = 1}^3 {\left[{\vartheta _{\tilde j_1^ +, \tilde j_2^ +, \tilde j_3^ + }^r\left( {\mathit{\boldsymbol{x}}_{\hat j_1^ +, \hat j_2^ +, \hat j_3^ + }^{\left[\kappa \right]} - \mathit{\boldsymbol{x}}_{{j_1}, {j_2}, {j_3}}^{\left[{\kappa + 1} \right]}} \right)} \right. - } \\ \;\;\;\;\;\;\;\left. {\vartheta _{\tilde j_1^ -, \tilde j_2^ -, \tilde j_3^ - }^r\left( {\mathit{\boldsymbol{x}}_{{j_1}, {j_2}, {j_3}}^{\left[{\kappa + 1} \right]} - \mathit{\boldsymbol{x}}_{\hat j_1^ -, \hat j_2^ -, \hat j_3^ - }^{\left[\kappa \right]}} \right)} \right] = \boldsymbol{0} \end{array} $$ (22) 其中
$$ \tilde j_{\tilde r}^ \pm = \left\{ {\begin{array}{*{20}{l}} {{j_r},}&{r \ne \tilde r}\\ {{j_r} \pm \frac{1}{2},}&{r = \tilde r} \end{array}} \right.,{\rm{ }}\hat j_{\tilde r}^ \pm = \left\{ {\begin{array}{*{20}{l}} {{j_r},}&{r \ne \tilde r}\\ {{j_r} \pm 1,}&{r = \tilde r} \end{array}} \right. $$ $\tilde {r} = 1, 2, 3$, $\kappa = 0, 1, 2, \cdots $为迭代次数
$$ \vartheta _{\tilde j_1^\pm, \tilde j_2^\pm, \tilde j_3^\pm}^r = M_{\tilde j_1^\pm, \tilde j_2^\pm , \tilde j_3^\pm}^{\left[r \right]} = \dfrac{1}{4}\sum\limits_{s_{r} = \tilde j_r^\pm \pm \tfrac{1}{2}\atop s_k = j_k \pm \tfrac{1}{2}} M_{S_1, S_2, S_3} $$ 其中，$r, k = 1, 2, 3$, $M_{j^1, j^2, j^3 } : = M\left ({\boldsymbol{w}_{ j^1, j^2, j^3 }^{\left[\kappa \right]} } \right)$.
对方程 (18) 在每个网格单元上$K$积分得到并化简得
$$ \left| K \right|\frac{\partial }{{\partial t}}\mathit{\boldsymbol{\overline w}} =-\sum\limits_{l = 1}^{12} \mathit{\boldsymbol{h}} \left( {\mathit{\boldsymbol{w}}_K^{{\rm{int}}\left( l \right)}, \mathit{\boldsymbol{w}}_K^{{\rm{ext}}\left( l \right)}, \mathit{\boldsymbol{n}}_K^l} \right)\left| {e_K^l} \right|-\left| K \right|\mathit{\boldsymbol{s}}\left( {\mathit{\boldsymbol{\overline w}} } \right) $$ (23) 其中
$$ \begin{array}{l} \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 1 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 2 \right)} = {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} + \\ \frac{1}{2}\psi \left( {{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i - 1,\bar j,\bar k}},{{\mathit{\boldsymbol{\bar w}}}_{\bar i + 1,\bar j,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}}} \right)\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 3 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 4 \right)} = {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} + \\ \frac{1}{2}\psi \left( {{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i + 1,\bar j,\bar k}},{{\mathit{\boldsymbol{\bar w}}}_{\bar i - 1,\bar j,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}}} \right)\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 5 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 6 \right)} = {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} + \\ \frac{1}{2}\psi \left( {{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j - 1,\bar k}},{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j + 1,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}}} \right)\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 7 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 8 \right)} = {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} + \\ \frac{1}{2}\psi ({{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j + 1,\bar k}},{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j - 1,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}})\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( 9 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( {10} \right)} = {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} + \\ \frac{1}{2}\psi \left( {{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k - 1}},{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k + 1}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}}} \right)\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( {11} \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{int}}\left( {12} \right)} = {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} + \\ \frac{1}{2}\psi \left( {{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k + 1}},{{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k - 1}} - {{\mathit{\boldsymbol{\bar w}}}_{\bar i,\bar j,\bar k}}} \right)\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 1 \right)} = \mathit{\boldsymbol{w}}_{\bar i + 1,\bar j,\bar k}^{{\rm{int}}\left( 3 \right)},\mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 2 \right)} = \mathit{\boldsymbol{w}}_{\bar i + 1,\bar j,\bar k}^{{\rm{int}}\left( 4 \right)}\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 3 \right)} = \mathit{\boldsymbol{w}}_{\bar i - 1,\bar j,\bar k}^{{\rm{int}}\left( 1 \right)},\mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 4 \right)} = \mathit{\boldsymbol{w}}_{\bar i - 1,\bar j,\bar k}^{{\rm{int}}\left( 2 \right)}\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 5 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j + 1,\bar k}^{{\rm{int}}\left( 7 \right)},\mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 6 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j + 1,\bar k}^{{\rm{int}}\left( 8 \right)}\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 7 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j - 1,\bar k}^{{\rm{int}}\left( 5 \right)},\mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 8 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j - 1,\bar k}^{{\rm{int}}\left( 6 \right)}\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( 9 \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k + 1}^{{\rm{int}}\left( {11} \right)},\mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( {10} \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k + 1}^{{\rm{int}}\left( {12} \right)}\\ \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( {11} \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k - 1}^{{\rm{int}}\left( 9 \right)},\mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k}^{{\rm{ext}}\left( {12} \right)} = \mathit{\boldsymbol{w}}_{\bar i,\bar j,\bar k - 1}^{{\rm{int}}\left( {10} \right)} \end{array} $$ 其中，$\boldsymbol{\bar w}$为单元$K$的物理量均值, $e_K^l $为单元$K$各外表面曲面. $\left| K \right|$为单元$K$体积, ${\pmb h} \left ({ *, *, * } \right)$为数值流通量, 计算中通常采用Lax-Friedrichs形式
$$ \boldsymbol{h} \left( {\boldsymbol{u}, \boldsymbol{v}, \boldsymbol{n}} \right) = \dfrac{1}{2}\left[{\boldsymbol{F}(\boldsymbol{u}) \cdot \boldsymbol{n} + \boldsymbol{F} (\boldsymbol{v} ) \cdot \boldsymbol{n}-a\left( {\boldsymbol{v}-\boldsymbol{u}} \right)} \right] $$ 其中，$a = \max \left ({\boldsymbol{F}(\boldsymbol{u}) \cdot \boldsymbol{n}, \boldsymbol{F}(\boldsymbol{v}) \cdot \boldsymbol{n}} \right)$, $\boldsymbol{n}_K^l $为单元$K$外表面$e_K^l $单位外法线向量, $\boldsymbol{w}_K^{{\rm int}\left (l \right)}$, $\boldsymbol{w}_K^{{\rm ext}\left (l \right)}$为外表面$e_K^l $内外侧函数值.可通过使用van Leer's限制器
$$ \psi \left( {a, b} \right) = \left( {{\rm{sign}}a + {\rm{sign}}b} \right)\frac{{\left| {ab} \right|}}{{\left| a \right| + \left| b \right| + \varepsilon }} $$ 对$\boldsymbol{w}_K^{{\rm int} \left (l \right)} $, $\boldsymbol{w}_K^{{\rm ext}\left (l \right)} $进行二阶近似.
进而可对系统式 (22) 和式 (23) 采用Runge-Kutta[35-36]耦合求解.耦合求解过程中, 要保证网格物理量值插值重构的守恒性
$$ \sum\limits_K | {\tilde A_K}|{\mathit{\boldsymbol{\tilde w}}_K} = \sum\limits_K | {A_K}|{\mathit{\boldsymbol{w}}_K} $$ (24) 其中, $\boldsymbol{w}_K $, $\boldsymbol{\tilde w}_K $为重构前后的物理量值, $A_K $, $\tilde {A}_K $为重构前后的网格体积.令$D_l $为式 (24) 一次循环求解后, 外表面$e_K^l $所扫过的体积.所以得到对于单个网格的守恒插值策略
$$ \left| {{{\tilde A}_K}} \right|{\mathit{\boldsymbol{\tilde w}}_K} = \left| {{A_K}} \right|{\mathit{\boldsymbol{w}}_K} + \sum\limits_{l = 1}^{12} {\mathop F\limits^\frown } \left( {\mathit{\boldsymbol{w}}_K^{{\rm{int}}\left( l \right)}, \mathit{\boldsymbol{w}}_K^{{\rm{ext}}\left( l \right)}} \right) $$ (25) 其中, ${\mathop{F}\limits^{ \frown }}_l \left ({\boldsymbol{u}, \boldsymbol{v}} \right)$为网格扭曲变形时, 外表面$e_K^l $扫过区域产生的物理量改变量, 对于${\mathop{F}\limits^{ \frown }}_l \left ({\boldsymbol{u}, \boldsymbol{v} } \right)$可以采用下式求解
$$ {\mathop F\limits^\frown _l}\left( {\mathit{\boldsymbol{u}}, \mathit{\boldsymbol{v}}} \right) = \max \left\{ {{D_l}, 0} \right\} \cdot \mathit{\boldsymbol{v}} + \min \left\{ {{D_l}, 0} \right\} \cdot \mathit{\boldsymbol{u}} $$ (26) 其中, $D_l $为外表面$e_K^l $扫过区域产生的体积改变量, 这里以计算$D_1 $为例, $D_1 $为图 6所示的三棱柱块体. $D_1 $可以分解为三个四面体进行求解, 因此可得
$$ \begin{array}{l} {D_1} = {V_{x_{i + 1, j, k + 1}^{\left[\kappa \right]}x_{i + 1, j, k + 1}^{\left[{\kappa + 1} \right]}x_{i + 1, j + 1, k + 1}^{\left[{\kappa + 1} \right]}x_{i, j, k + 1}^{\left[{\kappa + 1} \right]}}} + \\ \;\;\;\;\;\;\;{V_{x_{i + 1, j, k + 1}^{\left[\kappa \right]}x_{i + 1, j + 1, k + 1}^{\left[{\kappa + 1} \right]}x_{i, j, k + 1}^{\left[\kappa \right]}x_{i, j, k + 1}^{\left[{\kappa + 1} \right]}}} + \\ \;\;\;\;\;\;\;{V_{x_{i + 1, j, k + 1}^{\left[\kappa \right]}x_{i + 1, j + 1, k + 1}^{\left[{\kappa + 1} \right]}x_{i + 1, j + 1, k + 1}^{\left[\kappa \right]}x_{i, j, k + 1}^{\left[\kappa \right]}}} \end{array} $$ 通过四面体体积公式求解出每个四面体有向体积$ V_{OABC}$，即当$ABC$为逆时针排列时, 其值为正, 顺时针排列时, 其值为负.
除此之外, 对于化学反应流问题, 在计算过程中要应用保正性策略, 保证计算过程中的压力、密度、化学反应质量分数等为正.笔者在文献[23]已经讨论了二维空间中保正性问题, 建立了全局伪弧长保正性算法的体系结构.全局伪弧长算法的保正性理论包括两个方面: (1) 控制方程离散的保正性; (2) 物理量自适应重构的保正性.其实现步骤也包括两个方面: (1) 通过添加时间步长和网格移动步长的约束条件实现网格均值的保正性; (2) 通过补充算法实现网格的每个点物理量值的保正性.
3. 数值算例
算例1 首先通过具有解析解的一维Sod's问题来说明全局伪弧长算法能够降低激波间断奇异性.对于Euler方程 (18) 的一维初值问题
$$ \left( {\rho, u, p} \right) = \left\{ {\begin{array}{*{20}{l}} {\left( {1, 0, 0} \right), }&{x \le 0.5}\\ {\left( {0.125, 0, 0.1} \right), }&{x > 0.5} \end{array}} \right. $$ 计算域取$\left[{0, 1} \right]$, 最终计算时间为$ T = 0.2$.计算过程中取监视函数为
$$ M = \sqrt {1 + {\alpha _1}{{\left( {\frac{{{\rho _\xi }}}{{\mathop {\max }\limits_\xi \left( {{\rho _\xi }} \right)}}} \right)}^2} + {\alpha _2}{{\left( {\frac{{{s_\xi }}}{{\mathop {\max }\limits_\xi \left( {{s_\xi }} \right)}}} \right)}^2}} $$ 表 1中对比给出伪弧长法与固定网格 (fix mesh) 方法的计算效果.从表 1中可以看出, 利用伪弧长 (pseudo arc-length) 法50个网格点就可以获得比固定网格方法100个网格点更好的计算效果, 而且计算时间并没有增加.利用100个网格点的不同的弧长参数的伪弧长法可以获得比固定网格方法150, 200, 300个更好的计算效果.特别是$L^2$与$L^\infty $误差范数显著降低, 说明伪弧长算法对于激波间断奇异性问题有很好的计算效果.
表 1 伪弧长法与固定网格方法计算效果对比Table 1. Computational comparison for pseudo arc-length method and fixed grid method
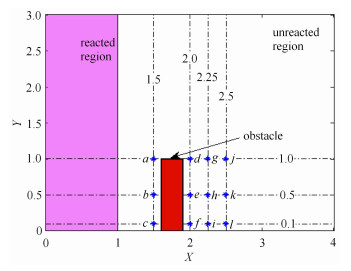
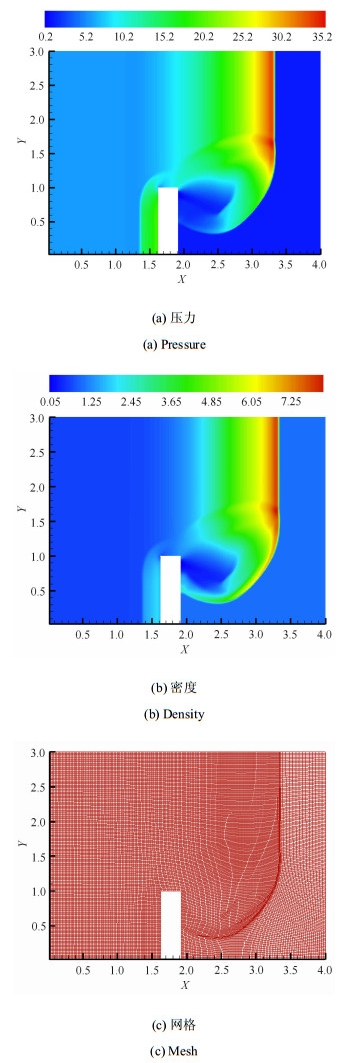
算例2 考虑二维板型障碍物爆轰衍射问题.计算域如图 7所示, 红色为障碍物区域, 其空间位置为$\left[{1.6, 1.9} \right]\times \left[{0, 1.0} \right]$.初始反应区选定为$X$方向的小于1的区域.计算过程中取未反应区$R$为$1$, 完全反应区$R$为$0$.指前因子$\tilde {K}$为$2 566.4$, 活化能$\tilde {T}$为$50$.一步化学反应状态方程为
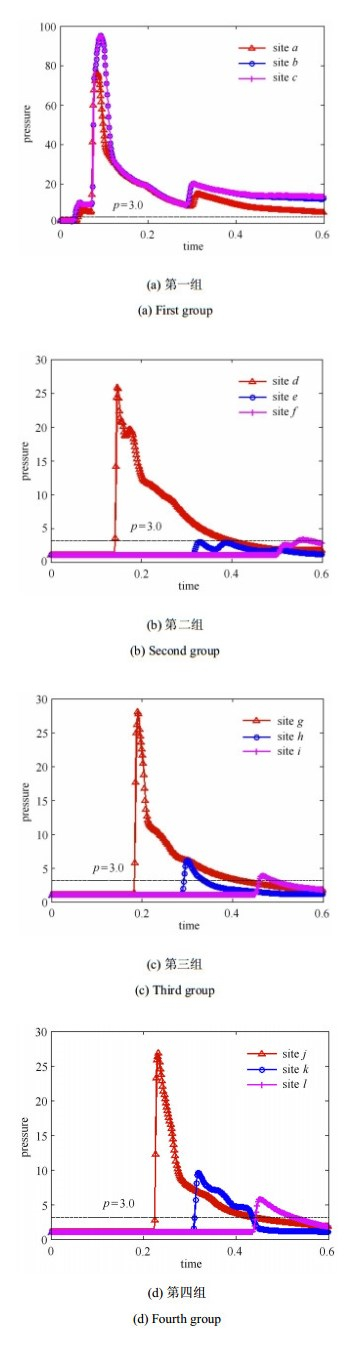
$$ E = \frac{1}{2}\rho {u^2} + \frac{p}{{\gamma-1}} + \rho qR $$ 其中, 热释放率$q$为$50$, 反应气体常数$\gamma $为$1.2$.以Zeldovich Neuman-Doring (ZND) 模型[37-38]解析解作为反应初值.初始计算域如图 7所示, 障碍物为刚性反射边界, 地面为刚性反射边界, 计算域前后及上方均为无限边界, 初始网格步长为$\Delta x = \Delta y = \dfrac{1}{50}$. 图 8给出了当$t = 0.35$时的模拟结果.结果表明, 网格随着爆轰波阵面而进行自适应变化, 实现了网格对爆炸冲击波阵面的捕捉.选定板型障碍物前后12个位置点, 根据位置点与障碍物的位置关系分成4组，考察其各点处的压力变化, 12点的位置如图 7中所示, 其压力变化如图 9所示.选定一般研究认为的压力安全线3.0为参考压力线.从图 9中可以看出, 在障碍物前方区域压力较高, 为危险区域.在障碍物后方区域中, 位置较高点的爆轰波压力较大, 位置较低的点压力相对较小, 且越靠近障碍物的后方区域, 其安全性越高.在本文所选取的12个点中, 安全性最高的是${ e}\left ({2.0, 0.5} \right)$位置的点. ${ f}\left ({2.0, 0.1} \right)$位置由于地面反射波的原因, 稍有危险.所以在爆炸发生时, 最安全的区域是障碍物后方的中部位置.
![]()
图 8 二维板型障碍物绕射问题Figure 8. Two-dimensional diffraction problem for plate-shape obstacle![]()
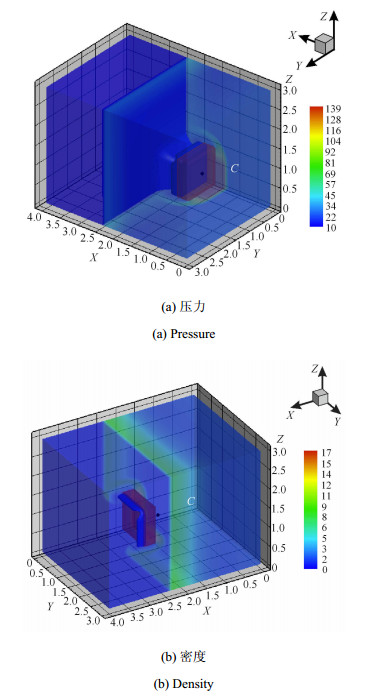
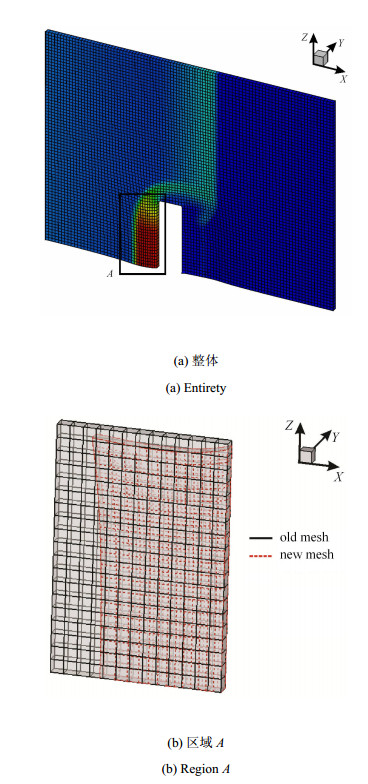
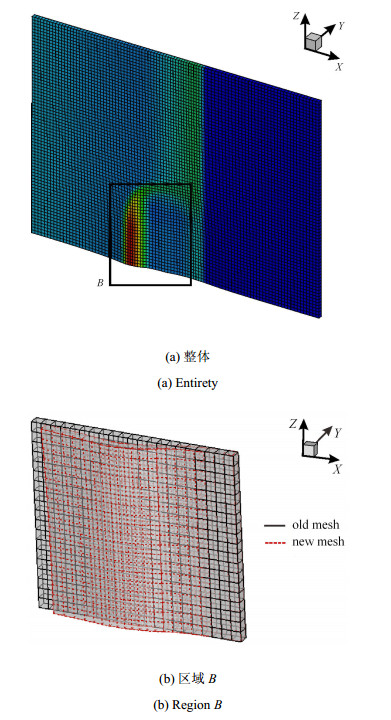
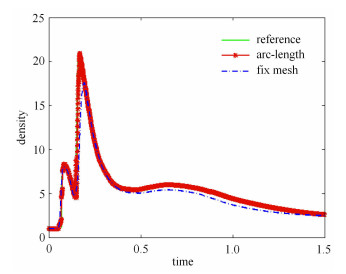
图 9 二维板型障碍物绕射各位置点压力变化Figure 9. Pressure history of typical locations in two-dimensional plate-shape obstacle diffraction problem算例3 下面分析考察三维空间中的板型障碍物绕射问题.计算域如图 10(a)所示, 红色为障碍物区域, 其空间位置为$\left[{1.6, 1.9} \right]\times \left[{0, 1.0} \right]\times \left[{0, 1.0} \right]$.初始反应区选定为$X$方向的小于1的区域, 其余为未反应区.计算过程中取未反应区$R$为$1$, 完全反应区$R$为$0$.计算参数与算例2相同, 并且同样以Zeldovich Neuman-Doring (ZND) 模型解析解作为反应初值.障碍物为刚性反射边界, 地面为刚性反射边界, 计算域前后左右及上方均为无限边界.计算中采用$100$万网格. 图 11中给出的是三维空间中压力与密度云图, 计算结果表明障碍物后方存在一个低密度区. 图 12中给出障碍物处切片的网格分布图, 特别是图 12(b)中给出图 12(a)中$A$部分的网格变形前后的对比图, 黑色为网格畸变前的, 红色表示网格畸变后的. 图 13中给出非障碍物处切片的网格分布图, 可以明显看出三维空间中网格的移动变形.计算结果表明, 伪弧长算法能够实现三维空间中网格的自适应变化. 图 14中, 给出图 11中点$C$处的密度计算效果对比, 其中参照解是采用2 000万网格的计算效果, 从图中可以看出, 伪弧长算法的计算效果与参照解的计算效果基本一致, 且明显优于固定网格算法的100万网格的计算效果.
![]()
图 11 三维板型障碍物绕射问题Figure 11. Three-dimensional diffraction problem for plate-shape obstacle![]()
图 12 三维板型障碍物绕射问题障碍物处切片Figure 12. Slices at obstacle for three-dimensional plate-shape obstacle diffraction problem![]()
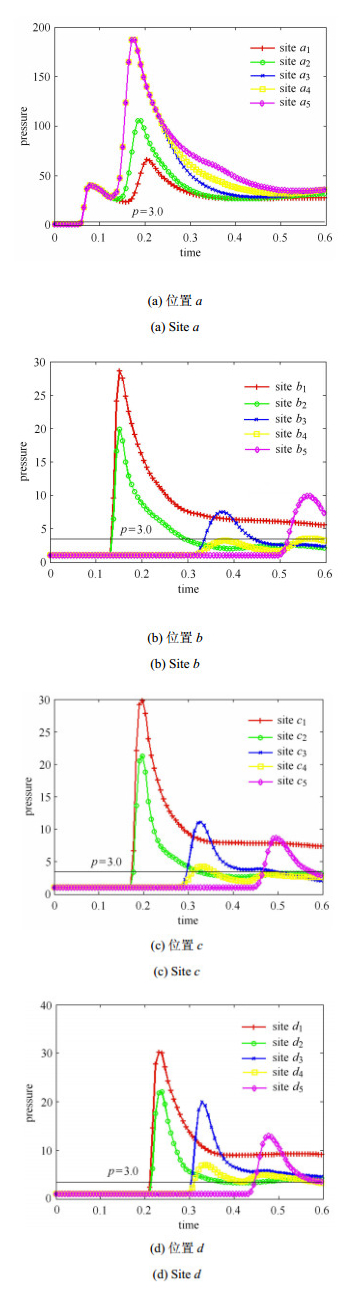
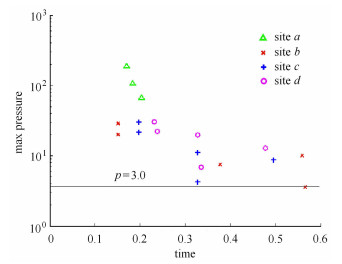
图 13 三维板型障碍物绕射问题非障碍物处切片Figure 13. Slices at non-obstacle for three-dimensional plate-shape obstacle diffraction problem进而选取障碍物前后$X$方向的$a, b, c, d$四个横切面, 如图 10(a)所示, 继而在每个横切面上选取5个位置点, 各点的选取如图 10(b)所示.根据数值模拟结果测定各个位置点处的压力变化, 如图 15所示. 图 15(a)中给出的是障碍物前方$a$位置处各点的压力变化曲线.从图中可以看出, 板前区域的压力普遍较大, 均远高于压力安全线3.0. 图 15(b)中给出的是障碍物后方临近障碍物$b$位置处的若干点的压力变化情况.从图中可以看出位置$b_4 $处的压力是处于安全线以下的. 图 15(c)和图 15(d)给出的是障碍物后方$c$位置和$d$位置各点的压力变化曲线.从图中可以看出, 其各点均处于危险区域中, 但是$d$位置处的最大压力峰值相对滞后. 图 16中给出了更为直观的各个位置点处的最大压力分布图, 从图中可以明显看出第一组的峰值压力高于其他各组, 最小的峰值压力在第二组中.
4. 总结与讨论
本文针对于计算动力学问题, 分析讨论了定常对流-扩散问题的伪弧长法以及求解非定常对流问题的伪弧长法.其中非定常对流问题的伪弧长法包括局部伪弧长法和全局伪弧长法.针对三维爆炸冲击奇异性问题的计算难点, 提出了爆炸冲击问题的三维全局伪弧长算法, 与前人研究的移动网格方法不同, 由于移动网格方法的出发点是网格的移动重构, 缺乏网格的整体性与直观性, 认为六面体网格移动后, 某个面发生畸变, 变形为非六面体, 从而导致计算失败.而伪弧长算法的计算目标不是网格移动, 而是减少奇异性.算例表明, 本文提出的六面体网格单元分割与整体结合的计算方法成功实现了三维空间中的爆炸与冲击问题的数值模拟.针对二维, 三维爆轰波对于板型障碍物的爆炸冲击问题, 本文得到了以下结论：
(1) 伪弧长算法可以有效实现网格对于爆轰波阵面的捕捉, 从而提高计算精度, 其计算精度要明显优于固定网格方法.
(2) 障碍物前方区域均为危险区域.
(3) 障碍物后方临近障碍物的区域会存在某些安全区域.
(4) 在障碍物后方临近障碍物的区域中, 远离障碍物边缘与地面的地方为最安全区域.在二维空间中, 最安全的区域是障碍物后方的中部位置.在三维空间中, 最安全的区域是障碍物后方离地面与边缘最远的位置.
-
![]()
图 1 双曲微分方程伪弧长方法示意图
Figure 1. Schematic diagram for the hyperbolic differential equations pseudo arc-length method
![]()
图 8 二维板型障碍物绕射问题
Figure 8. Two-dimensional diffraction problem for plate-shape obstacle
![]()
图 9 二维板型障碍物绕射各位置点压力变化
Figure 9. Pressure history of typical locations in two-dimensional plate-shape obstacle diffraction problem
![]()
图 11 三维板型障碍物绕射问题
Figure 11. Three-dimensional diffraction problem for plate-shape obstacle
![]()
图 12 三维板型障碍物绕射问题障碍物处切片
Figure 12. Slices at obstacle for three-dimensional plate-shape obstacle diffraction problem
![]()
图 13 三维板型障碍物绕射问题非障碍物处切片
Figure 13. Slices at non-obstacle for three-dimensional plate-shape obstacle diffraction problem
表 1 伪弧长法与固定网格方法计算效果对比
Table 1 Computational comparison for pseudo arc-length method and fixed grid method
下载: 导出CSV
-
[1] 马天宝, 任会兰, 李健等.爆炸与冲击问题的大规模高精度计算.力学学报, 2016, 48(3):599-608 http://lxxb.cstam.org.cn/CN/abstract/abstract145835.shtml Ma Tianbao, Ren Huilan, Li Jian, et al. Large scale high precision computation for explosion and impact problems. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3):599-608 (in Chinese) http://lxxb.cstam.org.cn/CN/abstract/abstract145835.shtml
[2] 杨露斯, 黎炼.论计算机发展史及展望.信息与电脑, 2010, 6(1):188-188 http://www.cnki.com.cn/Article/CJFDTOTAL-XXDL201006153.htm Yang Lusi, Li Lian. Theory of computer development and prospects. China Computer & Communication, 2010, 6(1):188-188 (in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-XXDL201006153.htm
[3] Luo ST, Tran HV, Yu Y. Some inverse problems in periodic homogenization of hamilton-jacobi equations. Archive for Rational Mechanics and Analysis, 2016, 221(3):1585-1617 doi: 10.1007/s00205-016-0993-z
[4] Deleuze Y, Chiang CY, Thiriet M, et al. Numerical study of plume patterns in a chemotaxis-diffusion-convection coupling system. Computers & Fluids, 2016, 126(1):58-70
[5] Tian DS. Multiple positive periodic solutions for second-order differential equations with a singularity. Acta Applicandae Mathematicae, 2016, 144(1):1-10 doi: 10.1007/s10440-015-0030-5
[6] Riks E. An incremental approach to the solution of snapping and buckling problems. International Journal of Solids & Structures, 1979, 15(7):529-551
[7] Boor CD. On local spline approximation by moments. Journal of Mathematics and Mechanics, 1968, 17(1):729-735
[8] Crisfield MA. An arc-length method including line searches and accelerations. International Journal for Numerical Methods in Engineering, 1983, 19(1):1268-1289
[9] Chan TF. Newton-like pseudo-arclength methods for computing simple turning points. Siam Journal on Scientific & Statistical Computing, 1984, 5(1):135-148
[10] 忻孝康, 唐登海.一维定常对流-扩散方程的伪弧长参数法.应用力学学报, 1988, 5 (1):45-54 http://www.cnki.com.cn/Article/CJFDTOTAL-YYLX198801005.htm Xin Xiaokang, Tang Denghai. An arc-length parameter technique for steady diffusion-convection equation. Chinese Journal of Applied Mechanics, 1988, 5 (1):45-54 (in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-YYLX198801005.htm
[11] 陈国谦, 高智.对流扩散方程的迎风变换及相应有限差分方法.力学学报, 1991, 23(4):418-425 http://lxxb.cstam.org.cn/CN/abstract/abstract140618.shtml Chen Guoqian, Gao Zhi. Transformation of the convective diffusion equation with corresponding finite difference method. Chinese Journal of Theoretical and Applied Mechanics, 1991, 23(4):418-425 (in Chinese) http://lxxb.cstam.org.cn/CN/abstract/abstract140618.shtml
[12] 武际可, 许为厚, 丁红丽.求解微分方程初值问题的一种弧长法.应用数学和力学, 1999, 20(8):875-880 http://www.cnki.com.cn/Article/CJFDTOTAL-YYSX908.013.htm Wu Jike, Xu Weihou, Ding Hongli. Arc-length method for differential equations. Applied Mathematics and Mechanics, 1999, 20(8):875-880 (in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-YYSX908.013.htm
[13] Harten A, Hyman JM. Self adjusting grid methods for onedimensional hyperbolic conservation laws. Journal of Computational Physics, 1983, 50(2):235-269 doi: 10.1016/0021-9991(83)90066-9
[14] Ren YH, Russell RD. Moving mesh techniques based upon equidistribution, and their stability. Siam Journal on Scientific & Statistical Computing, 1992, 13(6):1265-1286
[15] Huang WZ, Ren YH, Russell RD. Moving mesh partial differential equations (MMPDEs) based upon the equidistribution principle. Siam Journal on Numerical Analysis, 1994, 31(3):709-730 doi: 10.1137/0731038
[16] White AB. On selection of equidistributing meshes for two-point boundary-value problems. Siam Journal on Numerical Analysis, 1979, 16(3):472-502 doi: 10.1137/0716038
[17] Stockie JM, Mackenzie JA, Russell RD. A moving mesh method for one-dimensional hyperbolic conservation laws. Siam Journal on Scientific Computing, 2001, 22(5):1791-1813 doi: 10.1137/S1064827599364428
[18] Tang HZ, Tang T. Adaptive mesh methods for one-and twodimensional hyperbolic conservation laws. Siam Journal on Numerical Analysis, 2003, 41(2):487-515 doi: 10.1137/S003614290138437X
[19] Ning JG, Wang X, Ma TB, et al. Numerical simulation of shock wave interaction with a deformable particle based on the pseudo arclength method. Science China Technological Sciences, 2015, 58(5):848-857 doi: 10.1007/s11431-015-5800-9
[20] 王星, 马天宝, 宁建国.双曲偏微分方程的局部伪弧长方法研究.计算力学学报, 2014, 31(3):384-389 doi: 10.7511/jslx201403017 Wang Xing, Ma Tianbao, Ning Jianguo. Local pseudo arc-length method for hyperbolic partial differential equation. Chinese Journal of Computational Mechanics, 2014, 31(3):384-389 (in Chinese) doi: 10.7511/jslx201403017
[21] Wang X, Ma TB, Ning JG. A pseudo arc-length method for numerical simulation of shock waves. Chinese Physics Letter, 2014, 31(3):030201-030201 doi: 10.1088/0256-307X/31/3/030201
[22] Wang X, Ma TB, Ren HL, et al. A local pseudo arc-length method for hyperbolic conservation laws. Acta Mechanica Sinica, 2014, 30(6):956-965 doi: 10.1007/s10409-014-0091-0
[23] Ning JG, Yuan XP, Ma TB, et al. Positivity-preserving moving mesh scheme for two-step reaction model in two dimensions. Computers & Fluids, 2015, 123(1):72-86
[24] Yuan XP, Ning JG, Ma TB, et al. Stability of newton tvd runge-kutta scheme for one-dimensional Euler equations with adaptive mesh. Applied Mathematics & Computation, 2016, 282(1):1-16
[25] Sun LP, Cong YH, Kuang JX. Asymptotic behavior of nonlinear delay differential-algebraic equations and implicit Euler methods. Applied Mathematics & Computation, 2014, 228(1):395-403
[26] Harwood SM, Kai H, Barton PI. Efficient solution of ordinary differential equations with a parametric lexicographic linear program embedded. Numerische Mathematik, 2016, 133(4):623-653 doi: 10.1007/s00211-015-0760-3
[27] Perthame B, Shu CW. On positivity preserving finite volume schemes for Euler equations. Numerische Mathematik, 1996, 73(1):119-130 doi: 10.1007/s002110050187
[28] Wang C, Zhang X, Shu CW, et al. Robust high order discontinuous galerkin schemes for two-dimensional gaseous detonations. Journal of Computational Physics, 2012, 231(2):653-665 doi: 10.1016/j.jcp.2011.10.002
[29] 魏涛, 许明田, 汪引.求解对流扩散问题的积分方程法.化工学报, 2015, 66(10):3888-3894 doi: 10.11949/j.issn.0438-1157.20150364 Wei Tao, Xu Mingtian, Wang Yin. Integral equation approach to convection-diffusion problems. Ciesc Journal, 2015, 66(10):3888-3894 (in Chinese) doi: 10.11949/j.issn.0438-1157.20150364
[30] Zhou XF, Guo J, Li F. Stability, accuracy and numerical diffusion analysis of nodal expansion method for steady convection diffusion equation. Nuclear Engineering & Design, 2015, 295(1):567-575 https://www.researchgate.net/publication/285037521_Stability_accuracy_and_numerical_diffusion_analysis_of_nodal_expansion_method_for_steady_convection_diffusion_equation
[31] Sandu A. Rosenbrock methods with an explicit first stage. International Journal of Computer Mathematics, 2015, 93(6):1-18 https://www.researchgate.net/publication/226034423_Singly_Diagonally_Implicit_Runge-Kutta_Methods_with_an_Explicit_First_Stage
[32] 冯帆, 王自发, 唐晓.一个基于打靶法的大气污染源反演自适应算法.大气科学, 2016, 40(4):719-729 http://www.cnki.com.cn/Article/CJFDTOTAL-DQXK201604005.htm Feng Fan, Wang Zifa, Tang Xiao. Development of an adaptive algorithm based on the shooting method and its application in the problem of estimating air pollutant emissions. Chinese Journal of Atmospheric Sciences, 2016, 40(4):719-729 (in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-DQXK201604005.htm
[33] Chen Z, Huang H, Yan J. Third order maximum-principle-satisfying direct discontinuous galerkin methods for time dependent convection diffusion equations on unstructured triangular meshes. Journal of Computational Physics, 2015, 308(1):198-217 https://www.osti.gov/pages/biblio/1330548-third-order-maximum-principle-satisfying-direct-discontinuous-galerkin-methods-time-dependent-convection-diffusion-equations-unstructured-triangular-meshes
[34] 刘朝阳, 王振国, 孙明波, 等.一种求解激波问题的中心差分——WENO混合方法研究.推进技术, 2016, 37(8):1522-1528 http://www.cnki.com.cn/Article/CJFDTOTAL-TJJS201608016.htm Liu Chaoyang, Wang Zhenguo, Sun Mingbo, et al. Investigation of a hybrid central difference-WENO method for shock wave problems. Journal of Propulsion Technology, 2016, 37(8):1522-1528 (in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-TJJS201608016.htm
[35] Shu CW, Osher S. Efficient implementation of essentially nonoscillatory shock-capturing schemes. Journal of Computational Physics, 1989, 83(1):32-78 doi: 10.1016/0021-9991(89)90222-2
[36] Gotlieb S, Shu CW. Total variation diminishing Runge-Kutta schemes. Mathematics of Computation, 1996, 67(221):73-85 http://dl.acm.org/citation.cfm?id=870122
[37] Doring W. On detonation processes in gases. Annals of Physics, 1943, 43(9):421-436
[38] Fickett W, Wood WW. Flow calculations for pulsating onedimensional detonations. The Physics of Fluids, 1966, 9(5):903-916 doi: 10.1063/1.1761791
计量
- 文章访问数: 2374
- HTML全文浏览量: 546
- PDF下载量: 495
