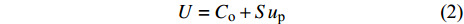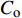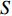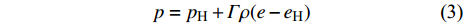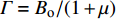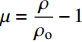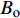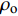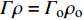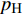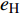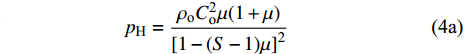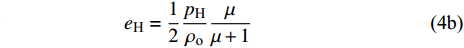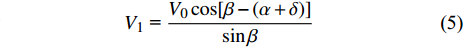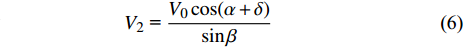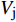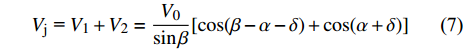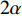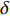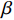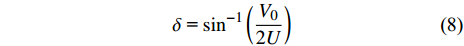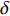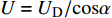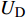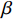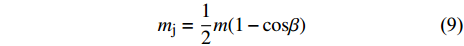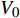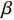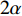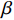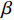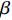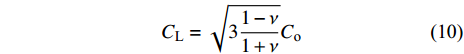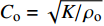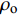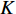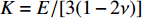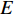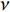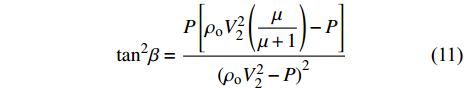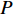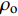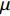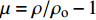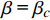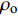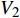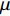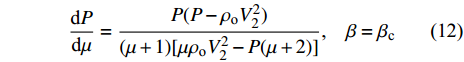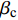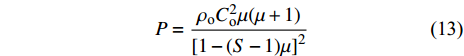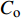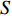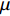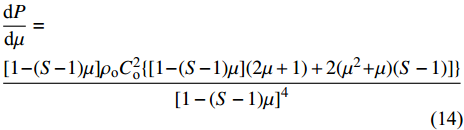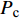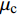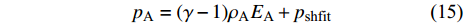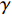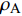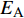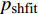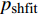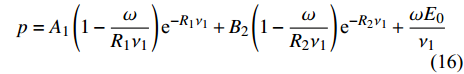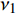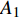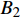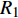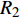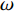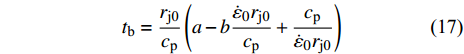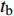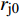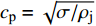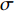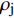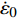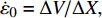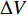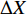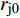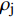FORMATION AND STABILITY OF SHAPED CHARGE LINER JET OF CrMnFeCoNi HIGH-ENTROPY ALLOY
-
摘要: 近年迅速兴起的多主元高熵合金因其具有很宽的成分-性能调控范围及一系列优异力学性能, 有望替代紫铜成为新一代药型罩材料. 本文基于CrMnFeCoNi五元高熵合金动态力学性能实验和数值模拟, 探索该合金用作药型罩的适用性. 基于分离式霍普金森拉杆和材料试验机研究了高熵合金不同应变率及温度下的力学行为, 获得了高熵合金Johnson-Cook热黏塑性动态本构. 利用流动速度与临界压垮角关系对凝聚性高熵合金射流形成边界进行界定. 结合数值模拟验证了高熵合金射流形成边界的合理性, 并进一步揭示了射流高速拉伸断裂演化规律. 研究表明: 射流断裂时间与材料强度成负相关, 材料动态强度增大, 将会引起射流断裂时间下降. 本工作可为新型高熵合金药型罩结构设计提供参考.Abstract: Recently emerging multi-principal component high-entropy alloy is expected to replace copper as a new generation of shaped charge liner material due to its wide composition/property control range and a series of excellent mechanical properties. Based on the experiments and numerical simulation of dynamic mechanical properties of five-element CrMnFeCoNi high-entropy alloy, the feasibility of this alloy as a shaped charge liner is explored. The mechanical behavior of high-entropy alloys at different strain rates and temperatures was studied via split Hopkinson tensile bar (SHTB) and material testing machine, and a Johnson-Cook thermal viscoplastic dynamic constitutive model of high-entropy alloys was established. The continuity condition of high-entropy alloy jet is explored based on the relationship between flow velocity and critical collapse angle. The continuity condition of high-entropy alloy jet is verified by finite element simulation, and the evolution law of high-speed tensile fracture of high-entropy alloy jet is further investigated. The results show that the jet break-up time is negatively correlated with the material tensile strength, and when the dynamic tensile strength increases, the jet break-up time will decrease. This work was provide references for the structural design of novel high-entropy alloy linev.
-
Keywords:
- high-entropy alloy /
- shaped charge liner /
- jet stability /
- jet break-up time
-
引言
破甲弹以内衬金属空腔(也称为药型罩)的聚能装药爆炸后形成的超高速金属射流实现对坦克装甲、混凝土工事等目标的毁伤破坏. 空心聚能装药破甲弹与动能穿甲弹也是常规武器系统中两类典型弹种[1-4], 空腔聚能装药的聚能效应现象最早在1888年由Munroe[5]发现, 在第二次世界大战期间得到广泛应用. 概括起来, 破甲弹从空心装药的起爆到对目标的侵彻破坏, 涉及3个基本过程: 药型罩受炸药爆轰压溃形成金属射流、金属射流的高速拉伸运动、射流对目标的高速侵彻. 因此药型罩材料是影响其侵彻性能的关键. 上个世纪70年代初到80年代末. 郑哲敏带领团队, 对破甲机理、破甲侵彻相似律、射流稳定性等开展了大量研究, 取得了丰富成果[6-10]. 在总结大量破甲实验结果与理论分析后, 从射流的成型与抑制射流失稳断裂的角度, 郑哲敏明确指出[8,10], 药型罩材料一般应有足够高的声速、充分的延展性、高的密度. 实际上二战以后, 为了改善射流的侵彻性能, 国内外研究者对药型罩材料进行了大量的积极探索. 紫铜以其高密度、高延性以及良好的加工性能成为广泛使用的药型罩材料. 然而紫铜药型罩自二战开始投入使用, 经过半个多世纪的发展, 其性能利用已经接近极限. 随着新型材料与加工技术的不断涌现, 寻找超越紫铜的新型药型罩材料进一步提升破甲弹的侵彻性能成为现今面临的主要问题. Held[11]针对高密度纯金属药型罩材料(如镍、钼、钽、钨、铀等)的应用前景进行评估分析, 破甲试验表明钨、钽药型罩的毁伤性能优于纯铜药型罩, 但加工成本限制其使用. 除了纯金属药型罩, 学者还针对合金材料药型罩[12-14]、复合材料药型罩[15]、粉末药型罩[16-17]、增材制造药型罩[18-19]等开展大量细致的研究工作, 这些新材料及加工手段扩展药型罩材料的应用范围, 同时也存在密度低, 强度低等问题, 难以具备全面超越铜的优势. 一些学者将研究方向转向锆基非晶药型罩, Walter等[20]将Zr基非晶合金作为药型罩, 研究聚能射流形态和破甲行为, 发现非晶合金侵彻时因具有良好的活性产生明显的横向破坏作用, 但大尺寸高质量的非晶合金制备及室温塑性差等问题仍然是目前急需克服的难题.
金属射流成型能力与稳定性是材料选择的最重要依据. 凝聚性与稳定性好的射流对炸高的适应性以及侵彻性能会更好. Walsh等[21]提出爆炸驱动金属板斜碰撞射流形成条件, 但研究中未对射流的凝聚性进行讨论, 此外该研究结果针对爆炸成型无法确定是否适用于药型罩压垮射流的形成. Chou等[22]提出了以流动速度、压垮角与材料声速为评价指标的聚能射流形成准则, 而且还预测射流的品质. Elshenawy等[23]应用该准则给出了锆基非晶合金药型罩形成连续射流、离散射流、无射流的边界条件. 针对金属射流失稳断裂的原因, 目前认为与材料的强度有关[24]. 郑哲敏[8-9]从理论上分别揭示了高速段与低速段射流断裂失稳机理, 认为低速段射流失稳断裂由材料强度控制, 高速段失稳断裂则源于高速空气扰动. 并通过量纲分析建立了聚能射流失稳判据与断裂时间预估模型.
高熵合金(high-entropy alloys, HEAs)也称多主元合金, 是近年迅速兴起的一类具有很宽成分与性能调控范围的新型金属材料. 其长程化学无序性和短程有序性的原子排布使其具有一些异于普通金属的力学特性[25-28]. 通过原子级别的“自由设计”和组合, 可以实现特定的应用需求. 例如, 最近作者团队基于高熵合金设计思想和团队前期在颗粒增强金属基复合材料剪切带应变梯度效应方面的研究认知[29-30], 突破传统钨合金缺乏侵彻自锐性的固有局限, 发明了具有高剪切自锐性能的多相钨高熵合金[31], 相同的动能条件下相比传统93W侵彻深度提高20%. 这表明, 通过成分设计有望满足药型罩应用所需的高密度、高声速、高延性及释能活性等特性[32-33], 高熵合金显示出应用于先进聚能药型罩的迷人前景.
最近, 我们对CoCrNi中熵合金药型罩射流侵彻进行了初步尝试[34]. 破甲射流侵彻实验结果显示, 这种中熵合金较紫铜材料有较好的横向扩孔效应, 但同时也发现高速侵彻过程中形成的富Cr的纳米析出相影响了射流稳定与侵彻深度. 因此, 在探索多主元高熵合金药型罩技术时, 首先要研究多主元合金的射流成型与稳定性, 这是制约射流侵彻威力的关键环节. 为此, 本文选择强塑性与声速比铜有明显优势的CrMnFeCoNi五元高熵合金, 探索其作为药型罩材料的适用性. 首先开展该类高熵合金的Johnson-Cook (J-C)动态本构模型的实验研究, 进一步建立了炸药爆轰压溃药型罩射流成型与高速运动的数值模型, 结合先前获得该合金激波压缩状态方程, 对射流成型与稳定性分析, 揭示了高熵合金射流高速拉伸断裂规律.
1. 高熵合金材料力学行为表征
1.1 材料本构模型
高熵合金药型罩材料在高应变率下的力学行为采用Johnson-Cook热黏塑性动态本构模型描述, 该本构模型中的三项分别表征材料的应变硬化、应变率和温度的影响. 可以描述材料在高速冲击条件下的力学行为, 具体形式如下
$$ Y = (A + B\varepsilon _{\text{p}}^{{n}})(1{\text{ + }}C{\text{ln}}{\dot \varepsilon _{\text{p}}})(1 - T_{\text{H}}^{{m}}) $$ (1) 式中,
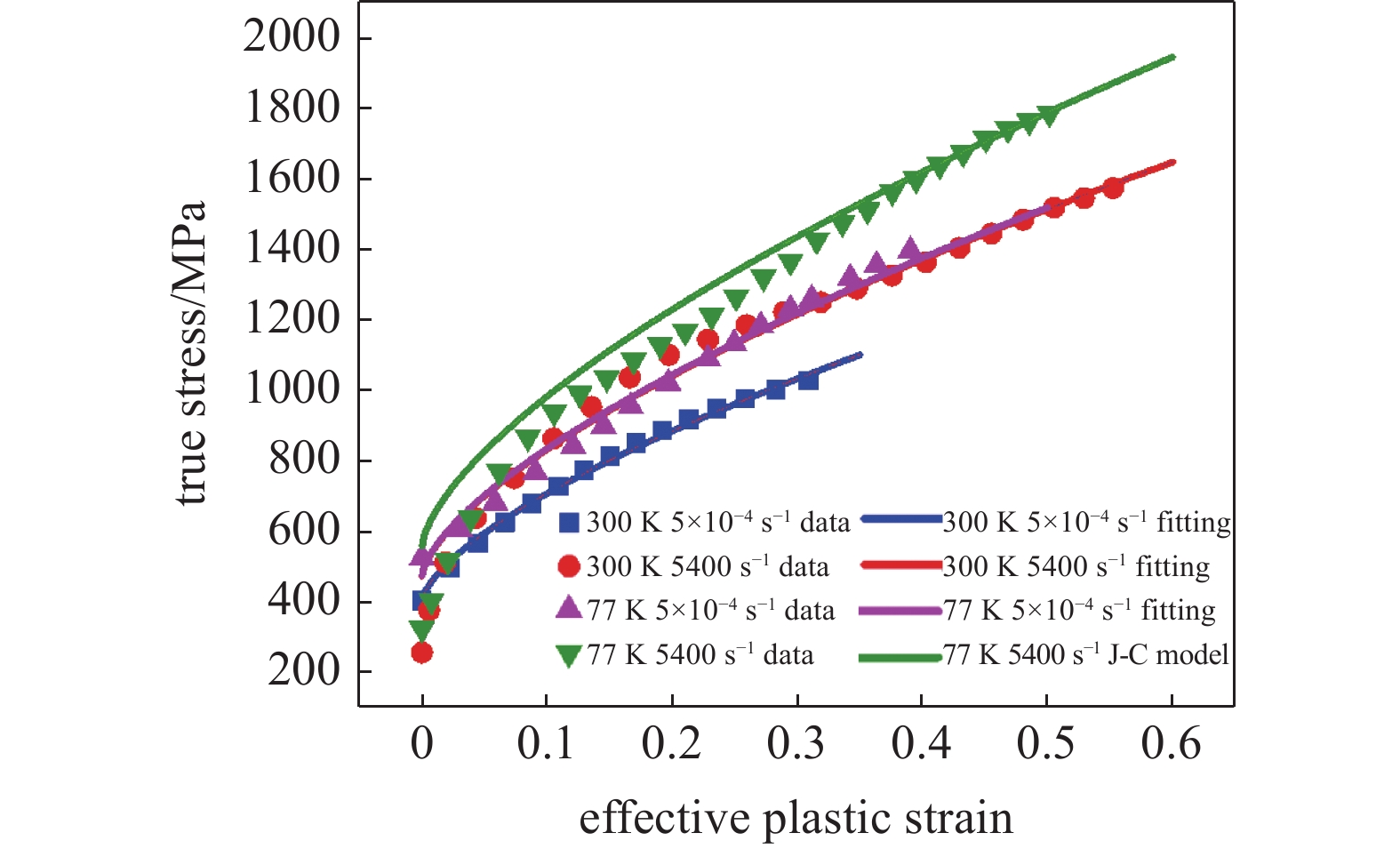
$ Y $ 为材料的流动应力;$ {\varepsilon _{\text{p}}} $ 为等效塑性应变;$ {\dot \varepsilon _{\text{p}}} = {{\dot \varepsilon } \mathord{\left/ {\vphantom {{\dot \varepsilon } {{{\dot \varepsilon }_{\text{o}}}}}} \right. } {{{\dot \varepsilon }_{\text{o}}}}} $ 为无量纲等效塑性应变率,$ {\dot \varepsilon _{\text{o}}} $ 为参考应变率(= 5.0 × 10−4 s−1),$ \dot \varepsilon $ 为实际的应变率;$ {T_{\text{H}}} = (T - {T_{{\text{room}}}})/({T_{{\text{melt}}}} - {T_{{\text{room}}}}) $ 为修正的无量纲温度,$ {T_{{\text{room}}}} $ 为室温,$ {T_{{\text{melt}}}} $ 为材料的熔化温度; A, B和n是材料常数, C是应变率相关系数, m是温度相关常数.为了确定高熵合金的J-C本构材料参数, 我们进行了一系列不同温度与应变率条件的拉伸实验. 准静态低应变率实验在配备温度环境箱的材料试验机进行, 高应变率的冲击拉伸实验在分离式霍普金森拉杆上进行, 霍普金森杆实验原理与技术最新发展参见文献[35], 实验布置见图1所示. 确定J-C本构参数, 需要选取参考应变率, 这里我们将参考应变率取准静态实验应变率5.0 × 10−4 s−1. 每个工况重复3~5次实验以保证数据可靠性. 不同实验工况下, 拟合获得的真实应力与塑性应变曲线如图2所示. 由图2实验结果可得, 与准静态(应变率5.0 × 10−4 s−1)拉伸条件相比, 动态冲击拉伸 (应变率为5400 s−1)条件下应变率效应明显, 随着塑性应变不断增大, 材料的强度与塑性均呈现增强. 此外与室温(300 K)条件进行比较, 随着塑性应变不断增大, 低温(77 K)加载环境下材料强度更大, 塑性也有所增加, 但是增加幅度不明显. 最终得到的CrMnFeCoNi高熵合金J-C动态本构材料参数如表1所示. 最后我们通过低温、动态(77 K, 5400 s−1)拉伸实验对拟合获得的J-C动态本构参数进行验证, 在塑性应变高于0.3时, 实验数据(绿色倒三角)与J-C曲线(绿色曲线)吻合较好; 当塑性应变低于0.3时, 实验数据与J-C曲线误差在5 %以内表明拟合获得的J-C动态本构参数的准确性.
![]()
图 2 CrMnFeCoNi高熵合金不同温度下静、动态J-C本构模型拟合曲线Figure 2. Static and dynamic J-C model fitting curves of the CrMnFeCoNi HEA at different temperatures表 1 CrMnFeCoNi高熵合金材料参数Table 1. Material parameters of the CrMnFeCoNi HEAρ/(g·cm−3) A/MPa B/MPa n C m Tmelt/K Cp/(J·kg−1·K−1) $ \dot{{\epsilon }_{0}} $/s−1 7.96 399 1396 0.6612 0.0099 0.9790 1561 452 5 × 10−4 1.2 材料激波压缩状态方程
为了便于开展高熵合金射流成型规律及数值模拟研究, 参考Jiang等[36]的工作, 本节对CrMnFeCoNi高熵合金激波压缩状态方程进行介绍. 激波压缩状态方程主要用于描述高熵合金材料在超高压条件下超出弹性极限的变形行为. 对于大多数不发生相变的固体, 激波速度与波阵面后粒子速度成线性关系, 具体形式为[2]
$$ U = {C_{\text{o}}} + S{u_{\text{p}}} $$ (2) 式中,
$ U $ 与$ {u_{\text{p}}} $ 分别为激波速度与波阵面后粒子速度,$ {C_{\text{o}}} $ 高熵合金材料体波波速,$ S $ 为线性Hugoniot斜率.基于冲击Hugoniot关系的Mie-Gruneisen状态方程可以表示为
$$ p = {p_{\text{H}}} + \varGamma \rho (e - {e_{\text{H}}}) $$ (3) 式中,
$ \varGamma = {B_{\text{o}}}/(1 + \mu ) $ 为Gruneisen Gamma系数,$ \mu = \dfrac{\rho }{{{\rho _{\text{o}}}}} - 1 $ 表征材料的可压缩性,$ {B_{\text{o}}} $ 为常数,$ {\rho _{\text{o}}} $ 为参考密度; 假定$ \varGamma \rho = {\varGamma _{\text{o}}}{\rho _{\text{o}}} $ =const.$ {p_{\text{H}}} $ 与$ {e_{\text{H}}} $ 分别为Hugoniot压力与能量$$ \qquad\qquad{p_{\text{H}}} = \frac{{{\rho _{\text{o}}}C_{\text{o}}^{\text{2}}\mu (1 + \mu )}}{{{{[1 - (S - 1)\mu ]}^2}}} \tag{4a}$$ $$\qquad\qquad {e_{\text{H}}} = \frac{1}{2}\frac{{{p_{\text{H}}}}}{{{\rho _{\text{o}}}}}\frac{\mu }{{\mu + 1}}\tag{4b} $$ Jiang等[36]利用中科院力学所非线性力学国家重点实验室101 mm口径一级轻气炮对面心立方结构的CrMnFeCoNi高熵合金进行了平板撞击加载实验, 采用激光干涉质点速度测量系统(photon doppler velocimetry, PDV)获得了撞击过程中的激波速度与粒子速度, 利用式(2)拟合实验数据, 首次获得了CrMnFeCoNi高熵合金的激波压缩状态方程, 相关参数如表2所示.
Material HEL/GPa Co/(m·s−1) S Γ CrMnFeCoNi 2.58 4500 1.39 1.78 2. 高熵合金射流成型规律
2.1 射流凝聚性准则
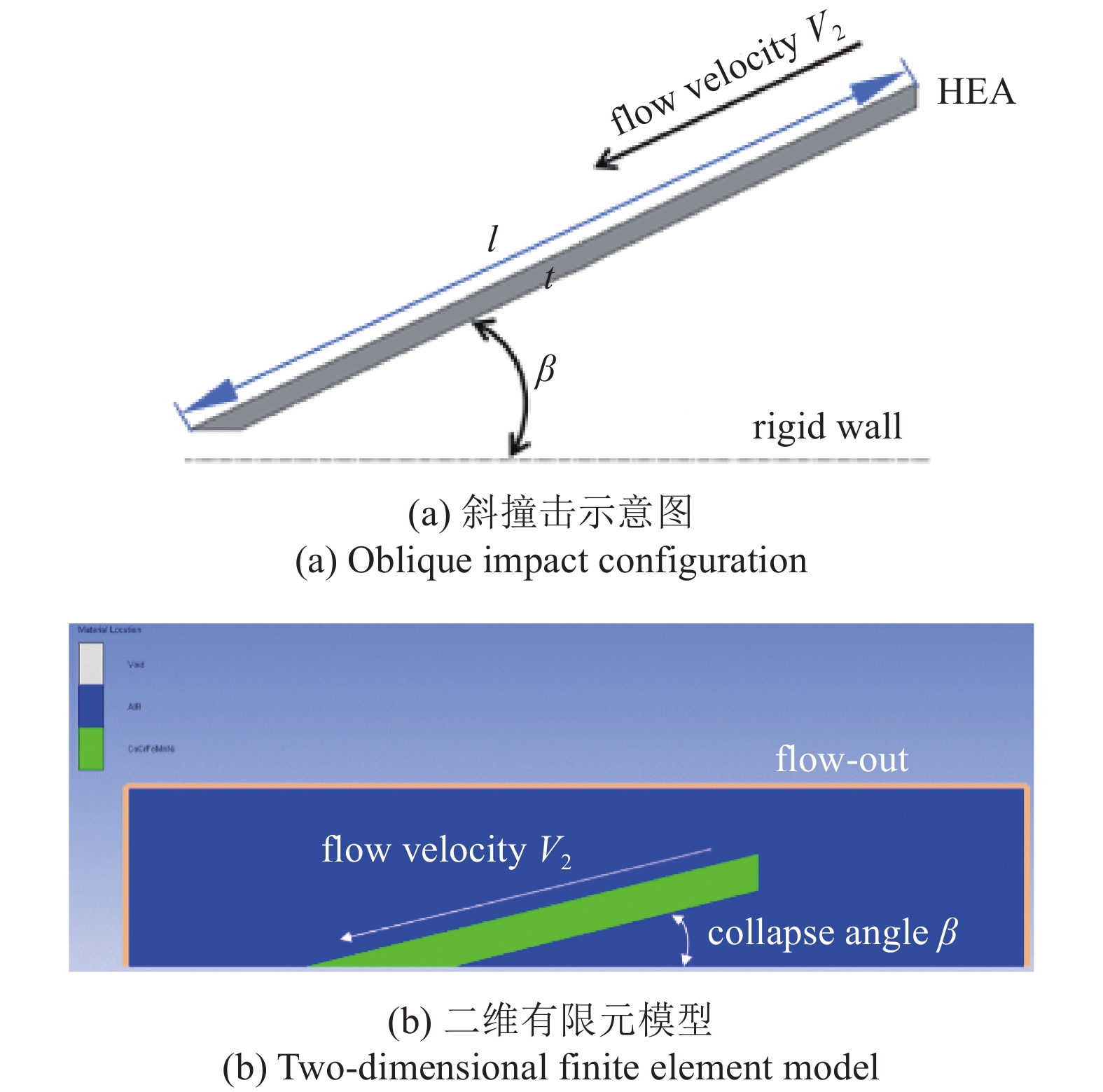
聚能装药起爆后, 爆炸波以极快的速度在炸药内部传播, 当爆轰波到达药型罩表面后, 在爆轰压力作用下被压溃, 迅速向其轴线处闭合, 形成高速射流侵彻体. 图3(a)所示为药型罩压垮过程, 射流的形成过程可以看作药型罩以恒定速度V2成β角高速斜撞击轴线, 在此过程中, 一部分药型罩材料形成杵体, 另一部分形成射流, 杵体、射流的质量分配以及速度与撞击角度β相关. 图3(b)为运动坐标系中射流流动速度V2, 驻点速度V1与压垮速度V0之间的关系.
根据一维准定常Pugh-Eichelberger-Rostoker(PER)理论[37], 碰撞点速度V1与流动速度V2关系为
$$ \qquad\qquad{V_1}{\text{ = }}\frac{{{V_0}\cos [\beta - (\alpha + \delta )]}}{{\sin \beta }} $$ $$ \qquad\qquad{V_2}{\text{ = }}\frac{{{V_0}\cos (\alpha + \delta )}}{{\sin \beta }} $$ (6) 射流速度
$ {V_{\text{j}}} $ 可以表示为$$ {V_{\text{j}}}{\text{ = }}{V_1} + {V_2} = \frac{{{V_0}}}{{\sin \beta }}[{\rm{cos}}(\beta - \alpha - \delta ) + {\rm{cos}}(\alpha + \delta )] $$ (7) 式中,
$ 2\alpha $ 为药型罩锥角,$ \delta $ 为Taylor抛散角,$ \,\beta $ 为压垮角, 见图3(a). 依据PER模型[37], 抛散角可以表示为$$ \delta {\text{ = }}{\sin ^{ - 1}}\left(\frac{{{V_0}}}{{2U}}\right) $$ (8) 式中,
$ \delta $ 的单位为度,$U = {U_{\text{D}}}/{\rm{cos}}\alpha$ ,$ {U_{\text{D}}} $ 为炸药的爆速.依据文献[37]中的描述, 射流微元质量mj与压垮角
$\, \beta $ 之间的关系为$$ {m_{\text{j}}} = \frac{1}{2}m(1 - {\rm{cos}}\beta ) $$ (9) 由式(7)可得, 随着压垮速度
$ {V_0} $ 增加, 压垮角$\, \beta $ 与药型罩锥角$ 2\alpha $ 的减小, 射流速度增加; 由式(9)可知, 随着压垮角$\, \beta $ 的增加, 射流质量增加; 表明压垮角$\, \beta $ 对射流速度与射流质量影响呈现相反的关系. 此外, 压垮角对射流的凝聚性存在重要的影响, Chou等[22]提出的射流凝聚性准则, 如表3所示, βc为临界压垮角, 决定形成的射流是否具有连续性. CL为药型罩材料纵向声速, 决定是否有射流的形成. 射流流动速度V2、压垮角$ \beta $ 与材料声速CL联合确定凝聚射流、离散射流以及无射流形成的边界.表 3 聚能射流凝聚性准则Table 3. Shaped charge jet criteriaFlow regime Collapse angle β Jet/not-jet Jet coherence supersonic
(V2＞CL)β ≤ βc no no β＞βc yes no subsonic(V2≤CL) all values yes yes 材料的纵向声速表达式为[2]
$$ {C_{\text{L}}} = \sqrt {3\frac{{1 - \nu }}{{1 + \nu }}} {C_{\text{o}}} $$ (10) 式中,
$ {C_{\text{o}}} = \sqrt {{K \mathord{\left/ {\vphantom {K {{\rho _{\text{o}}}}}} \right. } {{\rho _{\text{o}}}}}} $ ,$ {\rho _{\text{o}}} $ 为材料密度,$ K $ 为体积模量;$K = E/[3(1 - 2\nu )]$ ,$ E $ 为弹性模量,$ \nu $ 为材料泊松比.2.2 高熵合金射流流动速度与临界压垮角关系确定
Walsh等[21]将固体之间的高速碰撞作为流体动力学问题进行讨论, 采用临界碰撞角βc对有射流与无射流形成的条件进行界定. 参考其临界压垮角的确定方式, 我们建立CrMnFeCoNi高熵合金射流流动速度与临界压垮角之间的关系.
依据连续性方程与动量守恒方程, 建立了不同流速V2下临界压垮角β的解析模型[21]
$$ {\tan ^2}\beta = \frac{{P\left[{\rho _{\text{o}}}V_2^2\left(\dfrac{\mu }{{\mu + 1}}\right) - P\right]}}{{{{({\rho _{\text{o}}}V_2^2 - P)}^2}}} $$ (11) 式中,
$ P $ 为压力,$ {\rho _{\text{o}}} $ 为初始药型罩材料密度,$ \mu $ 表征材料的可压缩性($ \mu = \rho /{\rho _{\text{o}}} - 1 $ ).当
$\, \beta {\text{ = }}{\beta _c} $ ,$ {\text{d}}\beta /{\text{d}}\mu = {\text{d}}({\tan ^2}\beta )/{\text{d}}\mu = 0 $ 时, 保持$ {\rho _{\text{o}}} $ 与$ {V_2} $ 不变, 式(11)对$ \mu $ 求微分, 可得$$ \frac{\text{d}P}{\text{d}\mu }=\frac{P(P-{\rho }_{\text{o}}{V}_{2}^{2})}{(\mu + 1)[\mu {\rho }_{\text{o}}{V}_{2}^{2}-P(\mu + 2)]}\text{, }\text{ }\beta ={\beta }_{\text{c}} $$ (12) 将材料的激波压缩状态方程与式(12)联立求解, 即可建立流动速度V2与临界压垮角
$ {\beta _{\text{c}}} $ 之间的关系. 材料的激波压缩状态方程为$$ P = \frac{{{\rho _{\text{o}}}C_{\text{o}}^2\mu (\mu + 1)}}{{{{[1 - (S - 1)\mu ]}^2}}} $$ (13) 式中,
$ {C_{\text{o}}} $ 与$ S $ 分别为激波速度与粒子速度关系曲线的截距与斜率.式(13)对
$ \mu $ 进行求导可得$$ \begin{split} &\frac{{{\text{d}}P}}{{{\text{d}}\mu }} = \\ & \frac{{[1 - (S - 1)\mu ]{\rho _{\text{o}}}C_{\text{o}}^{\text{2}}\{[1 - (S - 1)\mu ](2\mu + 1) + 2({\mu ^2} + \mu )(S - 1)]\}}}{{{{[1 - (S - 1)\mu ]}^4}}} \end{split}$$ (14) 结合式(12)~式(14)并求解, 可以获得
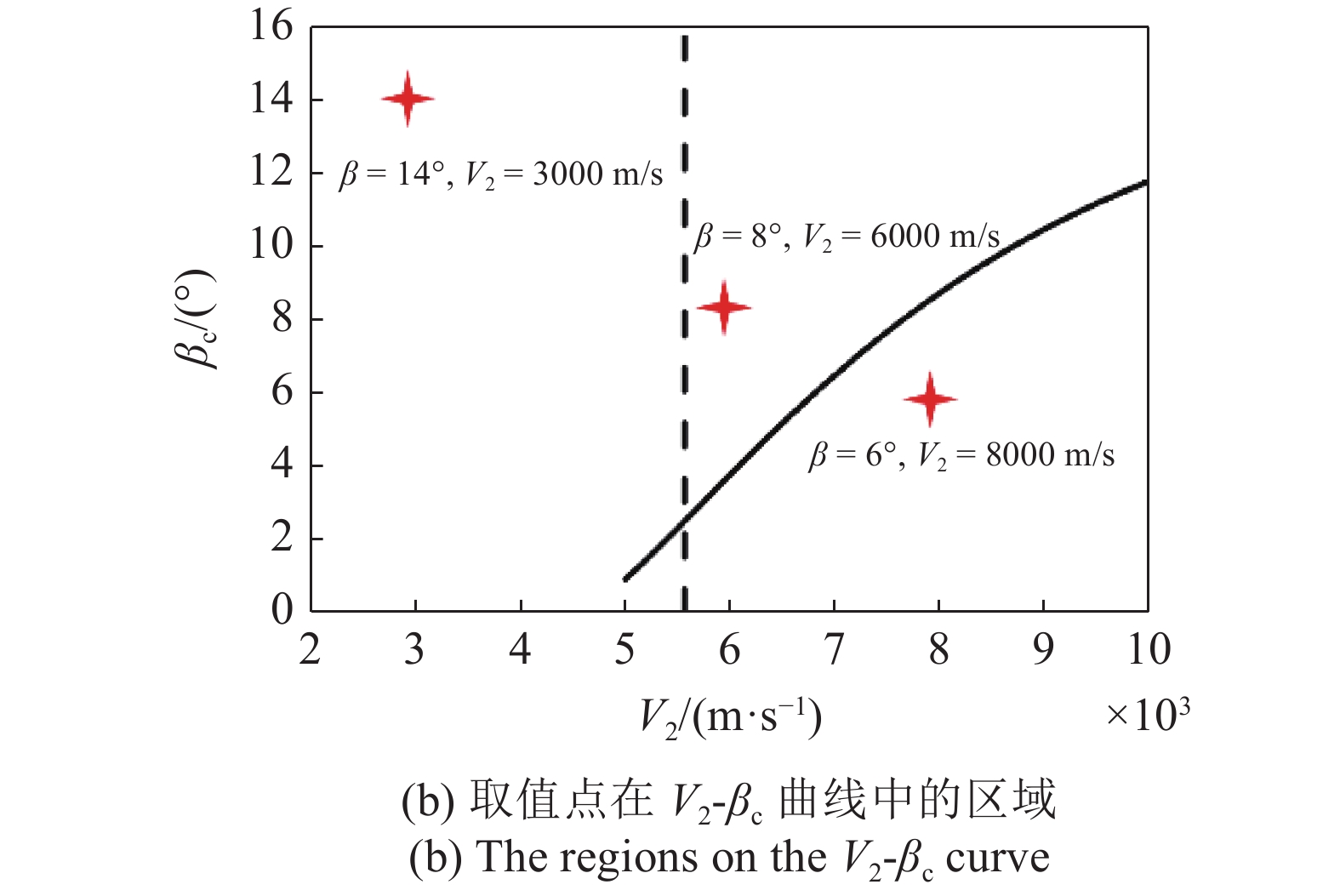
$ {P_{\text{c}}} $ 与$ {\mu _{\text{c}}} $ , 代入式(11)中即可建立流动速度V2与临界压垮角βc之间的关系.针对高熵合金(CrMnFeCoNi)与紫铜材料, 材料参数如表4所示[36,38], 根据上述计算流程, 建立两种材料流动速度V2与临界压垮角βc之间的关系. 如图4所示, V2-βc关系曲线(实线)与CL (虚线)将坐标空间分成3个区域, 若流动速度V2与压垮角βc取值位于最左边的区域, 将形成凝聚性射流; 在中间区域将产生非凝聚性射流; 位于右下角区域将不会形成射流. 相比于紫铜, CrMnFeCoNi声速更大, 凝聚射流取值范围更大, 此外高熵合金V2-β曲线位于紫铜下方, 无射流形成区域要小, 表明CrMnFeCoNi高熵合金材料相比与紫铜凝聚性射流形成能力更有优势.
表 4 CrMnFeCoNi高熵合金与紫铜材料参数Table 4. Material parameters of the CrMnFeCoNi HEA and copperMaterial ρ/(kg·m−3) S Co/(m·s−1) G/GPa ν CrMnFeCoNi 7960 1.390 4500 80 0.26 copper 8930 1.489 3940 47.8 0.34 ![]()
图 4 CrMnFeCoNi与紫铜材料流动速度与临界压垮角关系曲线Figure 4. Relationship between flow velocity and critical collapse angle of the CrMnFeCoNi and copper3. 射流凝聚性准则数值仿真验证
利用所获得高熵合金材料参数, 我们采用Autodyn-2D显式模块对射流凝聚性条件进行验证. 射流的形成过程可看成压溃后的药型罩以流动速度V2与轴线成β角高速斜撞击, Chou等[22]采用固体板壳高速斜撞击的方式对射流的凝聚性规律进行研究, 参考其研究方法对高熵合金射流的凝聚性规律进行分析. 假设射流为稳态流动, 分别在图4中凝聚射流、非凝聚射流与无射流3个区域对V2与β进行取值, 通过观察高熵合金药型罩撞击对称轴后的射流形态验证射流形成条件的合理性. 如图5(a)所示, 壁厚t为3.5 mm、母线l长为75 mm高熵合金药型罩以恒定速度V2斜撞击刚性壁面, 撞击角度为β. 药型罩采用欧拉网格进行划分, 空气域网格为0.2 mm × 0.2 mm均匀正方形网格, 在周围设置flow-out非反射边界条件消除边界效应的影响.
![]()
图 5 高熵合金药型罩压垮形成射流的数值计算Figure 5. Numerical computations for simulating the jet-formation of a HEA collapsing liner空气采用理想气体状态方程
$$ {p_{\text{A}}} =(\gamma - 1){\rho _{\text{A}}}{E_{\text{A}}} + {p_{{\text{shfit}}}} $$ (15) 式中,
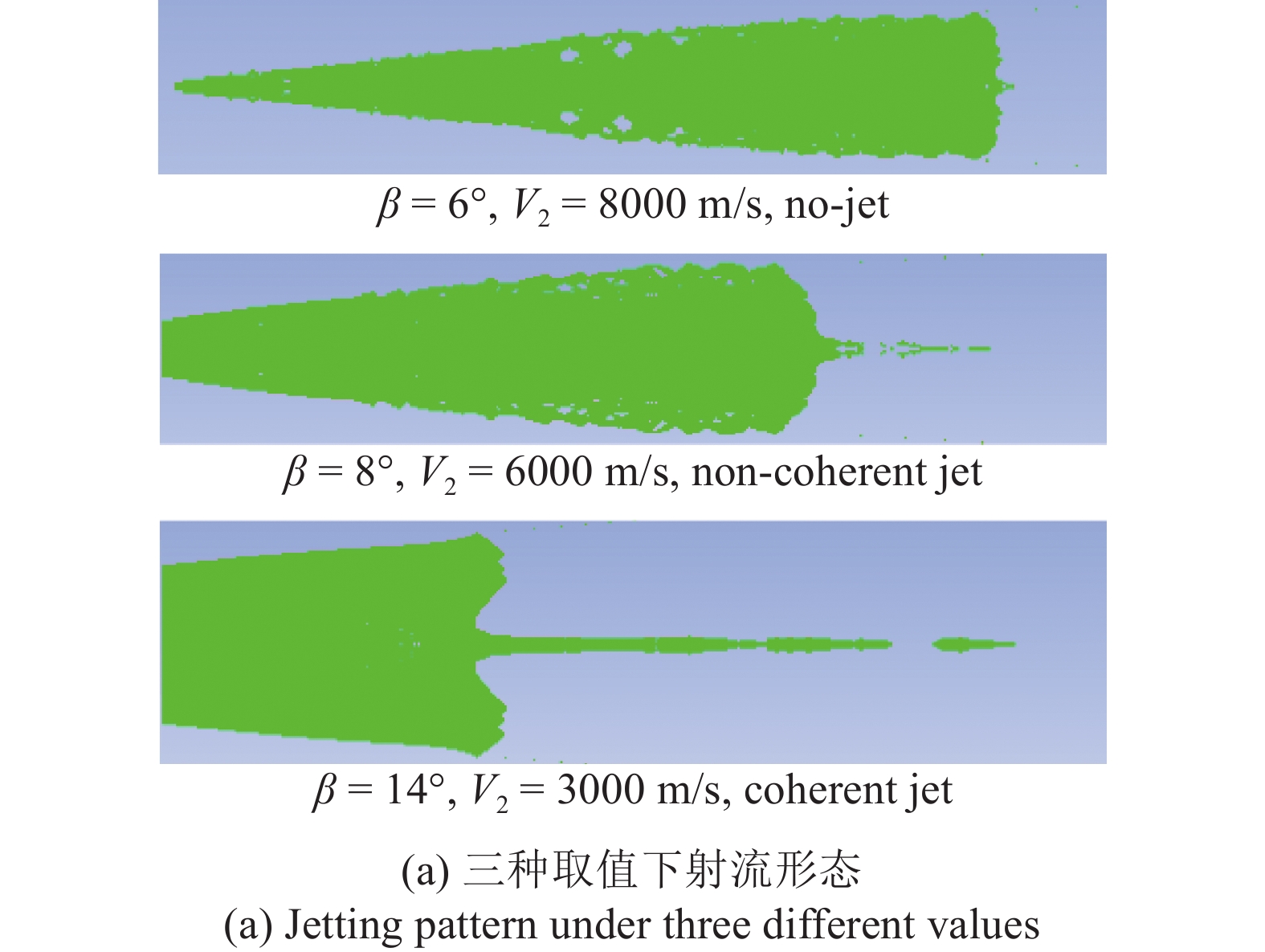
$ \gamma $ 为气体常数;$ {\rho _{\text{A}}} $ 为密度;$ {E_{\text{A}}} $ 为单位质量内能;$ {p_{{\text{shfit}}}} $ 为初始压力,$ {p_{{\text{shfit}}}} $ =0. 主要参数值见表5.图6为V2与β不同条件下高熵合金药型罩撞击刚性壁面仿真结果, 当流动速度与压垮角在最左边的区域取值(β=14°, V2=3000 m/s)时, 形成连续射流; 当取值点位于中间区域(β=8°, V2=6000 m/s)时, 形成的射流为离散形态; 当取值点位于右下角区域(β=6°, V2=8000 m/s)时, 没有射流产生. 表明利用V2-βc确定的高熵合金射流形成边界是合理的.
![]()
图 6 V2-βc曲线不同取值位置有限元仿真结果(续)Figure 6. Simulation results of different positions of V2-βc curve (continued)4. 高熵合金射流高速拉伸演化规律
4.1 材料参数与有限元模型
基于射流形成条件有效性的基础上, 采用Autodyn-2D显式分析软件对CrMnFeCoNi高熵合金射流拉伸演化规律进行研究. 图7(a)为高熵合金聚能装药结构示意图, 聚能装药结构由45#钢外壳、高熵合金药型罩以及8701高能炸药组成. 装药口径(charge diameter, CD)为90 mm, 药型罩的锥角为70°, 壁厚为3.5 mm. 有限元模型如图7(b)所示, 由于结构为完全对称结构, 建立1/2二维有限元模型, 中心点起爆, 壳体、药型罩与炸药均采用欧拉算法. 壳体外围为空气域欧拉网格, 空气域尺寸为60 mm × 500 mm, 并在其边界上设置flow-out非反射边界条件以消除边界效应的影响.
![]()
图 7 高熵合金药型罩聚能装药结构与仿真模型Figure 7. Structure and simulation model of shaped charge with HEA liner主装药为8701高能炸药, 其材料模型采用Jones-Wilkins-Lee (JWL)状态方程进行描述[40]
$$ p = {A_1}\left(1 - \frac{\omega }{{{R_1}\nu_1 }}\right){{\text{e}}^{ - {R_1}\nu_1 }} + {B_2}\left(1 - \frac{\omega }{{{R_2}\nu_1 }}\right){{\text{e}}^{ - {R_2}\nu_1 }} + \frac{{\omega {E_0}}}{\nu_1 } $$ (16) 式中, E0为初始比内能;
$ \nu_1 $ 为比体积;$ {A_1} $ ,$ {B_2} $ ,$ {R_1} $ ,$ {R_2} $ ,$ \omega $ 为常数. 其中方程式右端第1项在高压段起作用, 第2项在中压段起作用, 第3项主要在低压段起作用, 主要参数值见表6所示[41].表 6 8701炸药主要材料参数Table 6. Main material parameters of 8701 explosiveMaterial ρ/(g·cm−3) D/(m·s−1) PCJ/GPa A1/GPa B1/GPa R1 R2 ω v0 explosive 1.71 8.315 28.6 524.23 7.678 4.2 1.1 0.34 1.0 此外, 高熵合金药型罩与45#钢外壳采用Johnson-Cook强度模型与Shock状态方程进行表征. 高熵合金的材料参数如表1与2所示, 45#钢主要材料参数如表7所示[41].
表 7 45#钢材料参数Table 7. Material parameters of 45# steelρ/(g·cm−3) Γ C0/(m·s−1) S A/MPa B/MPa n C m Tmelt/K Cp/(J·kg−1·K−1) 7.83 2.17 4570 1.49 792 510 0.26 0.014 1.03 1793 452 4.2 基于数值仿真的高熵合金射流拉伸演化规律分析
4.2.1 网格敏感性分析
为了确定合适的模型网格划分标准, 本节开展网格密度对计算结果影响规律的研究. 采用0.2 mm, 0.25 mm, 0.4 mm, 0.6 mm, 1.0 mm 的四边形网格对欧拉空气域进行均匀划分, 观测点设置在距离药型罩90 mm处(1.0 CD). 观测点处沿轴线方向速度-时间曲线如图8所示, 曲线峰值反映网格尺寸对1.0 CD处射流头部速度的影响. 可知, 随着网格尺寸逐渐减小, 网格越精细, 射流头部速度越接近真值, 当网格尺寸从0.25 mm细化到0.2 mm, 射流头部速度之间的偏差为2.1 %, 但计算时间确增加2倍. 为了兼顾计算效率与精确度, 本文中确定0.25 mm为空气域网格尺寸划分的依据.
![]()
图 8 不同网格尺寸高熵合金射流观测点处(1.0 CD)速度-时间曲线Figure 8. Velocity-time histories for the HEA jet at the gauge point (1.0 CD) using different mesh sizes4.2.2 数值仿真结果分析
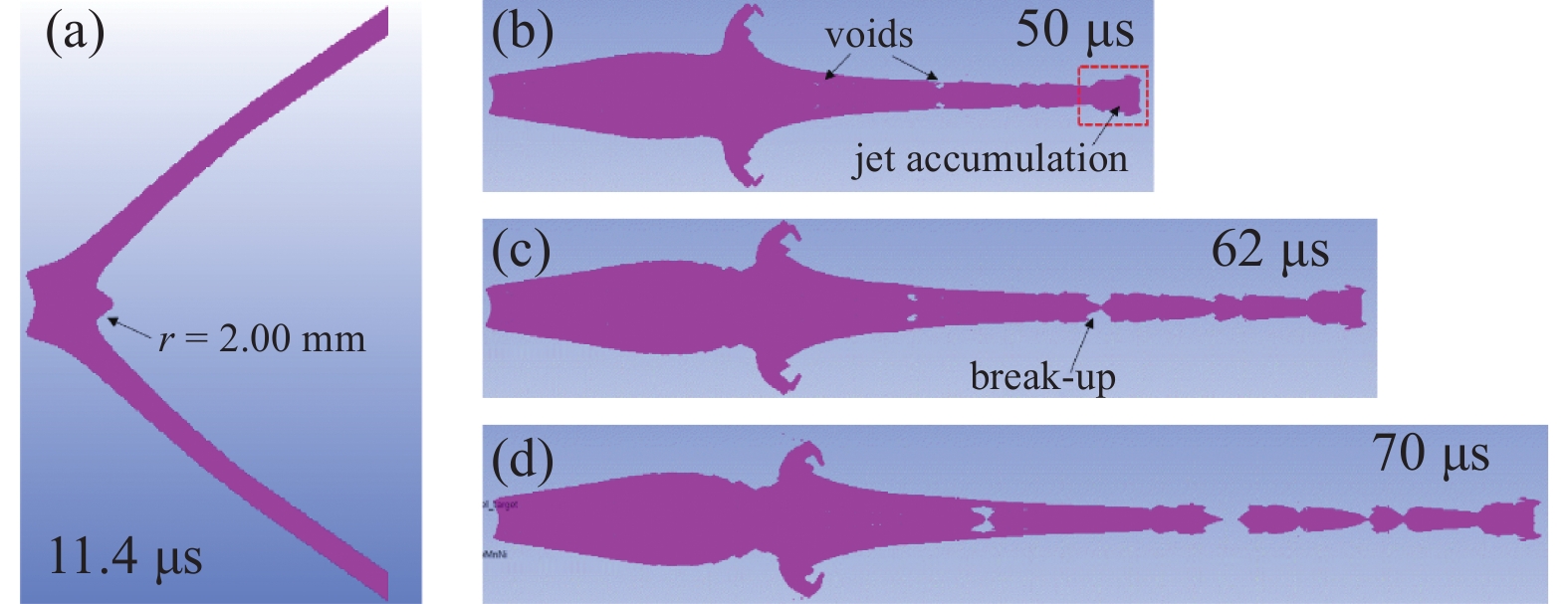
图9为CrMnFeCoNi高熵合金射流成型与拉伸演化时序图. 在射流头部出现射流堆积的现象, 是由“反向速度梯度”存在而引起[42]. 此外, 由于速度梯度的存在, 射流拉伸过程中出现空洞, 造成失稳, 在62 μs附近射流出现断裂(见图9(c)). 图10为t = 50 μs时高熵合金射流轴向速度分布, 可以看出射流尖端的速度明显高于杵体速度, 杵体速度为762 m/s, 射流头部速度为4855 m/s, 射流中存在明显的速度梯度. 速度梯度的形成是沿药型罩母线压垮速度不一致引起, 靠近药型罩顶部周围装药量大, 压垮速度越大; 而越靠近药型罩底部, 装药量小, 压垮速度也小. 通常射流侵彻体以速度为2000 m/s的射流微元为分界点[43], 左边部分为杵体, 右边部分为射流, 射流速度呈现出明显的线性分布, 速度梯度为34314.91 s−1.
![]()
图 9 CrMnFeCoNi高熵合金射流成型与拉伸演化时序图.(a) t =11.4 μs; (b) t =50 μs; (c) t =62 μs; (d) t =70 μsFigure 9. Sequence diagrams of jet formation and tensile evolution of CrMnFeCoNi HEA. (a) t =11.4 μs; (b) t =50 μs; (c) t =62 μs; (d) t =70 μs![]()
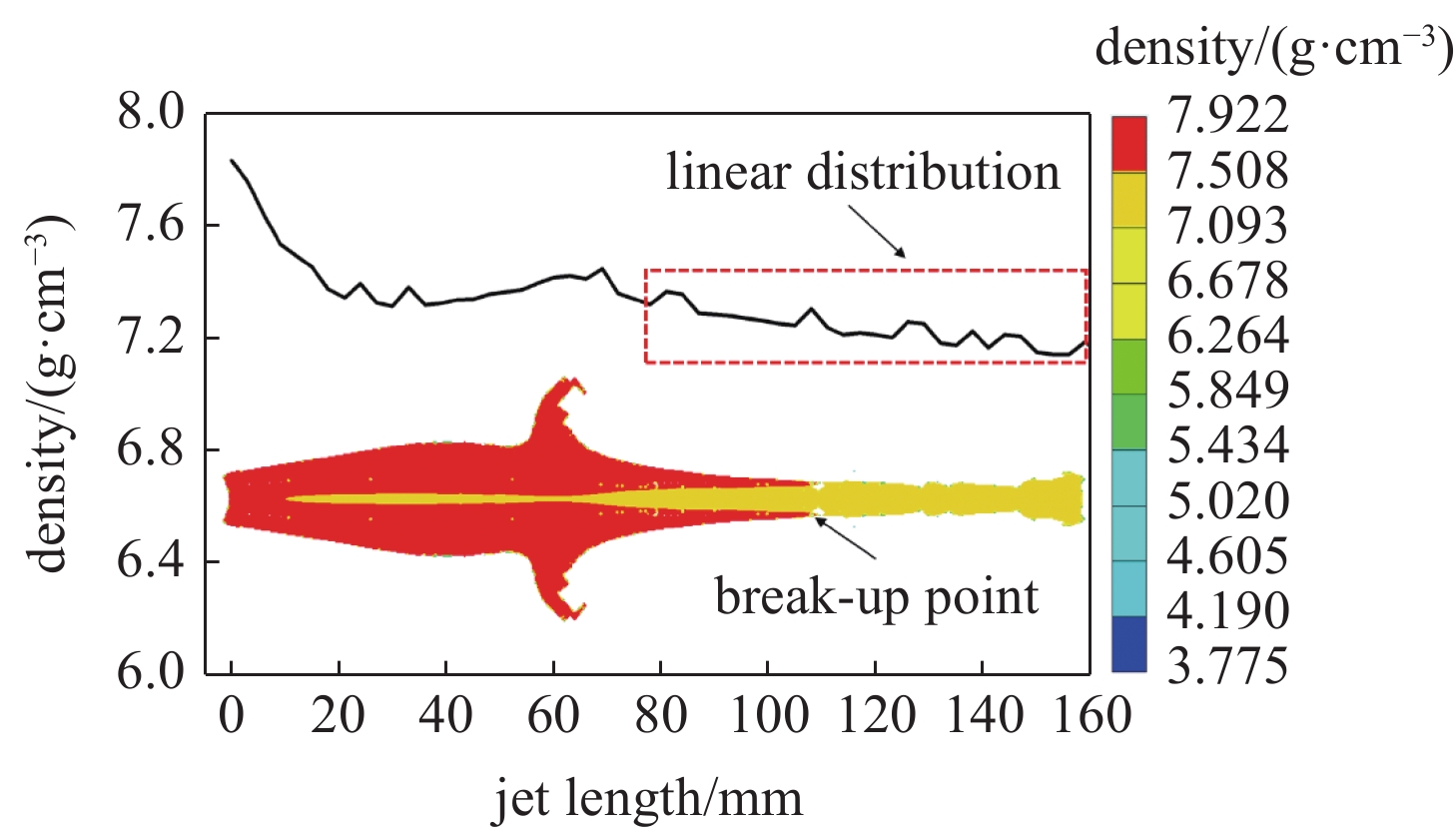
图 10 t = 50 μs时高熵合金射流轴线方向速度分布Figure 10. Velocity distribution along the axis of the HEA jet at t = 50 μs图11为t = 50 μs 时CrMnFeCoNi高熵合金射流密度沿轴线分布图. 密度从杵体到射流逐渐下降, 在杵体截面部分, 中心处的密度比两侧偏小. 此外, 射流轴线上密度逐渐减小呈现近似线性分布, 密度沿轴线变化的斜率为0.0257 g/cm−4. 在射流断裂点左侧射流截面密度由中心向两侧增大, 而断裂点右侧射流截面密度近似均匀分布. 分析原因为射流与杵体是由药型罩不同部分演化形成, 在演化形成过程中, 由于压力与温度不均匀, 造成应变率不均匀, 出现密度分布差异, 随之射流中也会形成空洞, 造成失稳断裂.
![]()
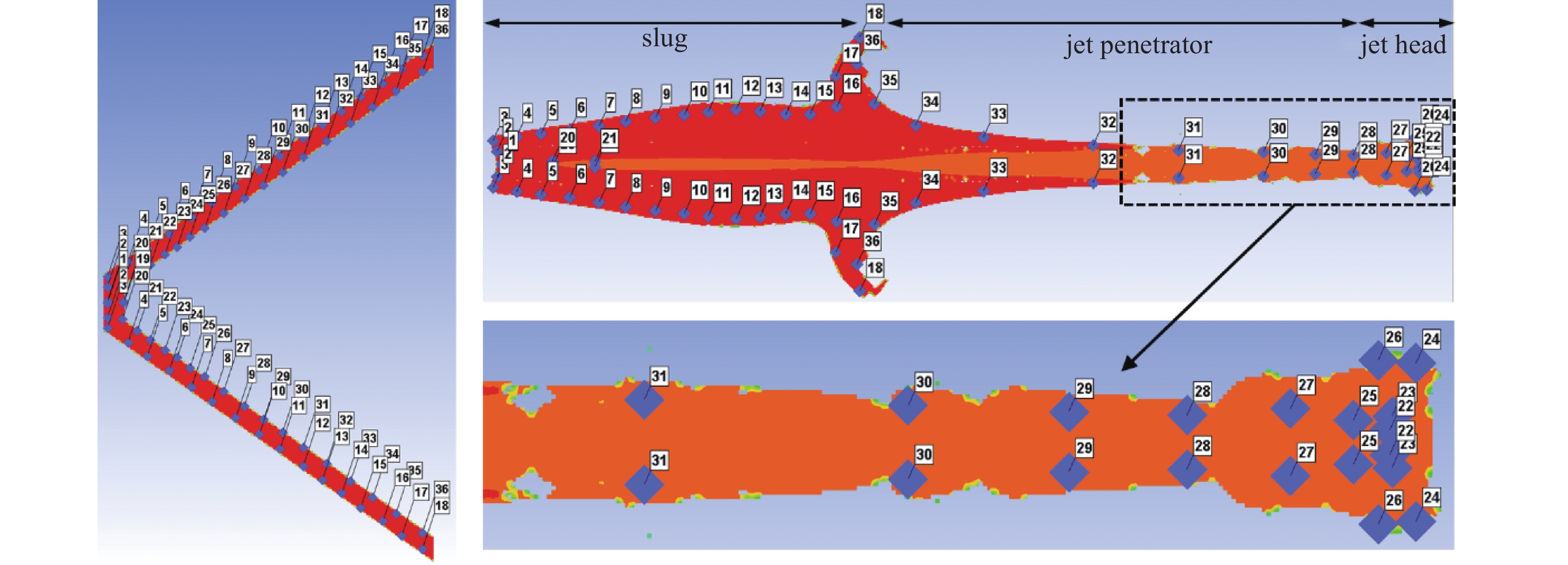
图 11 t = 50 μs时高熵合金射流轴线方向密度分布Figure 11. Density distribution along the axis of the HEA jet at t = 50 μs采用观测点示踪的方式对药型罩与射流形成对应关系进行研究. 如图12所示, 1 ~ 18号观测点位于药型罩外层, 19 ~ 39号观测点位于药型罩的内层. 由图12可知, 药型罩外层部分(1 ~ 18)演化形成杵体外层区域. 药型罩顶部内层部分(20 ~ 21)演化形成杵体内层, 药型罩顶部在爆轰波驱动下, 由于加速距离短, 未达到射流形成所需的压垮速度, 对该部分罩微元挤压速度小, 演化过程中在杵体内层部分即停止, 未形成射流. 此外, 靠近药型罩顶部的内层观测点(22 ~ 27)演化形成射流头部, 其观测点分布表明射流头部存在质量堆积, 同时也表明射流微元最大速度不是在药型罩顶部形成, 而是在药型罩22 ~ 27号节点处形成, 证实“反向速度梯度”的存在. 靠近药型罩底部的内层节点(28 ~ 38)形成射流侵彻体外层区域. 综上所述, 射流的形成主要由靠近药型罩顶部的内层节点在高能炸药爆轰驱动下挤压拉伸演化形成(图11中黄色区域). 此外药型罩底部内层节点演化形成过程中由于速度较低, 包覆在射流速度较低的区域, 出现在射流尾部区域外层. 爆轰驱动过程中, 由于压力、温度以及应变率的不均匀使射流中出现大量空洞(图11中黄色点)造成射流失稳, 最终产生拉伸断裂, 如果药型罩材质不均匀, 将会加剧空洞的形成, 使射流更易断裂.
![]()
图 12 观测点示踪高熵合金射流演化成型示意图Figure 12. Schematic diagram of high entropy alloy jet forming traced by observation points4.3 高熵合金射流断裂分析
4.3.1 射流断裂时间预估
郑哲敏[8-9]和Chou等[24,44]认为射流低速段失稳的主要原因是射流的强度效应, 他们分别给出了射流断裂时间预估公式. Chou等[44]给出的断裂时间预估表达式如下
$$ {t_{\text{b}}} = \frac{{{r_{{\text{j0}}}}}}{{{c_{\text{p}}}}}\left(a - b\frac{{{{\dot \varepsilon }_0}{r_{{\text{j0}}}}}}{{{c_{\text{p}}}}} + \frac{{{c_{\text{p}}}}}{{{{\dot \varepsilon }_0}{r_{{\text{j0}}}}}}\right) $$ (17) 式中, a = 3.75, b = 0.125.
$ {t_{\text{b}}} $ 为以爆轰波到达药型罩到射流断裂的时间;$ {r_{{\text{j0}}}} $ 为射流初始时刻半径; 塑性波速$ {c_{\text{p}}} = \sqrt {\sigma /{\rho _{\text{j}}}} $ ,$ \sigma $ 为屈服强度,$ {\rho _{\text{j}}} $ 为射流密度;$ {\dot \varepsilon _0} $ 为初始应变率,${\dot \varepsilon _0} = \Delta V/\Delta X,$ $ \Delta V $ 为射流速度变化,$ \Delta X $ 为射流长度变化, 下标0表征药型罩微元到达对称轴时的初始值.由式(17)可得, 射流断裂时间与射流密度和直径成正相关, 而与屈服强度和应变率成负相关. 针对本文CrMnFeCoNi高熵合金射流, 以图9(a)为初始时刻, 射流初始时刻的半径
$ {r_{{\text{j0}}}} $ 为2.0 mm, 射流密度成线性分布, 射流密度$ {\rho _{\text{j}}} $ 取平均值为7.21 g/cm3. 高熵合金的断裂强度[45]为524 MPa, 射流应变率为34314.9 s−1, 利用式(17)计算可得射流断裂时间为56.7 μs.仿真中爆轰波到达药型罩的时刻为9 μs, 射流断裂出现在62 μs处, 射流断裂时间为53.0 μs. 仿真与理论预估计算误差为6.5%.4.3.2 材料拉伸强度对射流断裂时间的影响
本节利用数值仿真探索了高熵合金材料拉伸强度对射流断裂时间影响规律. 高熵合金材料强度模型采用J-C本构模型进行表征. J-C本构模型中第一项为材料应变硬化项, 描述的是材料强度与塑性应变之间的关系, 由初始屈服强度A、硬化系数B及硬化指数n决定. 考虑到材料硬化指数n相比系数A与B在材料强度影响中占主导, 仿真中我们通过调节硬化指数n来研究材料的强度对高熵合金射流断裂时间的影响. 有限元模型、材料模型、边界条件及算法与前述一致. 仿真中硬化指数取n=k × n0 (n0 = 0.6612 ; k = 0.8, 1, 2, 3, 4, 5, 6, 7), 仿真结果如图13所示. 不同工况下, 具体的射流断裂时间与头部速度如表8所列, 射流头部速度均小于5000 m/s, 射流处于低速拉伸状态[8]. 由图13可知, 随着材料硬化指数逐渐增大, 射流断裂时间逐渐减小. 然而当k>5后, 射流断裂时间未呈现出减小的趋势, 原因为当材料强度过高, 射流微元之间的凝聚性变差, 已经不能形成正常的射流. 对图13(f)~图13(h)中射流形态观察发现, 射流头部均未出现射流堆积, 且射流内部形成大量的空洞, 这也证实未形成正常射流这一推测. 以上研究表明: 射流断裂时间与材料的强度成负相关, 此处材料强度指的是射流形成与演化过程中材料的动态拉伸强度, 材料被爆轰波压垮形成射流过程中会随着塑形应变、应变率及温度发生动态变化, 当动态拉伸强度出现增大, 射流断裂时间将呈现下降趋势, 这也与郑哲敏[8-9]和Chou等[24]从理论上给出的结论一致.
![]()
图 13 不同硬化指数射流形态对比Figure 13. Comparison of jet morphology with different hardening exponents表 8 不同硬化指数射流断裂时间及射流头部速度对比Table 8. Comparison of jet break-up time and tip velocity with different hardening exponentsk 0.8 1 2 3 4 5 6 7 break-up time t/μs 64 62 58 54 52 53 52 54 jet tip velocity vt/(m·s−1) 4857 4828 4788 4776 4773 4837 4916 4750 5. 结论
本文探索了CrMnFeCoNi高熵合金用作聚能药型罩的适用性. 研究了高熵合金材料不同温度与应变率拉伸加载下的力学行为, 建立了其动态本构关系. 最后采用数值模拟对高熵合金射流成型与高速拉伸断裂规律进行研究, 得出以下主要结论.
(1)开展了不同应变率、温度条件下拉伸实验, 建立了高熵合金Johnson-Cook动态本构关系.
(2)基于高熵合金激波压缩状态方程确立了高熵合金药型罩流动速度V2与临界压垮角βc之间的函数关系, 并界定了凝聚性高熵合金射流的形成边界.
(3)射流断裂时间与材料强度成负相关, 爆轰波压垮过程中材料强度会随着塑性应变、应变率及温度发生动态变化, 当材料动态强度增大, 将会引起射流断裂时间下降.
-
![]()
图 2 CrMnFeCoNi高熵合金不同温度下静、动态J-C本构模型拟合曲线
Figure 2. Static and dynamic J-C model fitting curves of the CrMnFeCoNi HEA at different temperatures
![]()
图 4 CrMnFeCoNi与紫铜材料流动速度与临界压垮角关系曲线
Figure 4. Relationship between flow velocity and critical collapse angle of the CrMnFeCoNi and copper
![]()
图 5 高熵合金药型罩压垮形成射流的数值计算
Figure 5. Numerical computations for simulating the jet-formation of a HEA collapsing liner
![]()
图 6 V2-βc曲线不同取值位置有限元仿真结果(续)
Figure 6. Simulation results of different positions of V2-βc curve (continued)
![]()
图 7 高熵合金药型罩聚能装药结构与仿真模型
Figure 7. Structure and simulation model of shaped charge with HEA liner
![]()
图 8 不同网格尺寸高熵合金射流观测点处(1.0 CD)速度-时间曲线
Figure 8. Velocity-time histories for the HEA jet at the gauge point (1.0 CD) using different mesh sizes
![]()
图 9 CrMnFeCoNi高熵合金射流成型与拉伸演化时序图.(a) t =11.4 μs; (b) t =50 μs; (c) t =62 μs; (d) t =70 μs
Figure 9. Sequence diagrams of jet formation and tensile evolution of CrMnFeCoNi HEA. (a) t =11.4 μs; (b) t =50 μs; (c) t =62 μs; (d) t =70 μs
![]()
图 10 t = 50 μs时高熵合金射流轴线方向速度分布
Figure 10. Velocity distribution along the axis of the HEA jet at t = 50 μs
![]()
图 11 t = 50 μs时高熵合金射流轴线方向密度分布
Figure 11. Density distribution along the axis of the HEA jet at t = 50 μs
![]()
图 12 观测点示踪高熵合金射流演化成型示意图
Figure 12. Schematic diagram of high entropy alloy jet forming traced by observation points
![]()
图 13 不同硬化指数射流形态对比
Figure 13. Comparison of jet morphology with different hardening exponents
表 1 CrMnFeCoNi高熵合金材料参数
Table 1 Material parameters of the CrMnFeCoNi HEA
ρ/(g·cm−3) A/MPa B/MPa n C m Tmelt/K Cp/(J·kg−1·K−1) $ \dot{{\epsilon }_{0}} $/s−1 7.96 399 1396 0.6612 0.0099 0.9790 1561 452 5 × 10−4 
下载: 导出CSV
Material HEL/GPa Co/(m·s−1) S Γ CrMnFeCoNi 2.58 4500 1.39 1.78
下载: 导出CSV
表 3 聚能射流凝聚性准则
Table 3 Shaped charge jet criteria
Flow regime Collapse angle β Jet/not-jet Jet coherence supersonic
(V2＞CL)β ≤ βc no no β＞βc yes no subsonic(V2≤CL) all values yes yes
下载: 导出CSV
表 4 CrMnFeCoNi高熵合金与紫铜材料参数
Table 4 Material parameters of the CrMnFeCoNi HEA and copper
Material ρ/(kg·m−3) S Co/(m·s−1) G/GPa ν CrMnFeCoNi 7960 1.390 4500 80 0.26 copper 8930 1.489 3940 47.8 0.34
下载: 导出CSV
ρ/(kg·m−3) γ EA/(kJ·kg−1) 1.225 1.4 2.068 × 105
下载: 导出CSV
表 6 8701炸药主要材料参数
Table 6 Main material parameters of 8701 explosive
Material ρ/(g·cm−3) D/(m·s−1) PCJ/GPa A1/GPa B1/GPa R1 R2 ω v0 explosive 1.71 8.315 28.6 524.23 7.678 4.2 1.1 0.34 1.0
下载: 导出CSV
表 7 45#钢材料参数
Table 7 Material parameters of 45# steel
ρ/(g·cm−3) Γ C0/(m·s−1) S A/MPa B/MPa n C m Tmelt/K Cp/(J·kg−1·K−1) 7.83 2.17 4570 1.49 792 510 0.26 0.014 1.03 1793 452
下载: 导出CSV
表 8 不同硬化指数射流断裂时间及射流头部速度对比
Table 8 Comparison of jet break-up time and tip velocity with different hardening exponents
k 0.8 1 2 3 4 5 6 7 break-up time t/μs 64 62 58 54 52 53 52 54 jet tip velocity vt/(m·s−1) 4857 4828 4788 4776 4773 4837 4916 4750
下载: 导出CSV
-
[1] Walters WP, Zukas J. Fundamentals of Shaped Charge. New York: Wiley Interscience Publication, 1989
[2] Meyers MA. Dynamic Behavior of Materials. New York: John Willey & Sons, 1994
[3] 焦文俊, 陈小伟. 长杆高速侵彻问题研究进展. 力学进展, 2019, 49(1): 312-391 doi: 10.6052/1000-0992-17-021 Jiao Wenjun, Chen Xiaowei. Review on long-rod penetration at hypervelocity. Advances in Mechanics, 2019, 49(1): 312-391 (in Chinese) doi: 10.6052/1000-0992-17-021
[4] 谈梦婷, 张先锋, 包阔等. 装甲陶瓷的界面击溃效应. 力学进展, 2019, 49(01): 392-427 doi: 10.6052/1000-0992-17-015 Tan Mengting, Zhang Xianfeng, Bao Kuo, et al. Interface defeat of ceramic armor. Advances in Mechanics, 2019, 49(1): 392-427 (in Chinese)) doi: 10.6052/1000-0992-17-015
[5] Munroe CE. Wave-like effects produced by detonation of gun-cotton. American Journal of Science, 1888, 36(211): 48-50
[6] 郑哲敏, 高举贤, 谈庆明等. 聚能射流侵彻过程模型律. 力学学报, 1974, 1: 1-10 Zheng Zhemin, Gao Juxian, Tang Qingming, et al. Scaling law in the penetration process of shaped chargejet. Chinese Journal of Theoretical and Applied Mechanics, 1974, 1: 1-10 (in Chinese)
[7] 郑哲敏, 谈庆明. 破甲机理的力学分析与简化模型 (631破甲机理课题研究进展报告). 科技参考资料, 1977, 6: 108-164 Zheng Zhemin, Tan Qingming. Mechanical analysis and simplified model of armor penetration mechanism (631 Research progress report of the armor penetration project). Science and Technology Reference Material, 1977, 6: 108-164 (in Chinese)
[8] 郑哲敏. 聚能射流的稳定性问题. 爆炸与冲击, 1981, (01): 6-17 Zheng Zhemin. Stability of jet produced by shaped charge. Explosion and Shock Waves, 1981, (01): 6-17 (in Chinese))
[9] 郑哲敏. 关于射流侵彻的几个问题. 兵工学报, 1980, 1: 13-22 Zheng Zhemin. Several problems on jet penetration. Acta Armamentarii, 1980, 1: 13-22 (in Chinese)
[10] 戴兰宏. 工程科学前沿的拓荒者——郑哲敏. 力学进展, 2013, 43(03): 265-294 doi: 10.6052/1000-0992-13-033 Dai Lanhong. A pioneer in the frontier of engineering science—Zhe-Min Zheng. Advances in Mechanics, 2013, 43(3): 265-294 (in Chinese)) doi: 10.6052/1000-0992-13-033
[11] Held M. Liners for shaped chapeds. Journal of Battlefield Technology, 2001, 4: 1-7
[12] 张晓伟, 段卓平, 张庆明. 钛合金药型罩聚能装药射流成型与侵彻实验研究. 北京理工大学学报, 2014, 34(12): 1229-1233 doi: 10.15918/j.tbit1001-0645.2014.12.004 Zhang Xiaowei, Duan Zhuoping, Zhang Qingming. Experimental study on the jet formation and penetration of conical shaped charged with titanium alloy liner. Transacctions of Beijing Institute of Technology, 2014, 34(12): 1229-1233 (in Chinese) doi: 10.15918/j.tbit1001-0645.2014.12.004
[13] 徐文龙, 王成, 徐斌. 超聚能射流形成过程机理研究. 兵工学报, 2018, 39(02): 261-268 doi: 10.3969/j.issn.1000-1093.2018.02.007 Xu Wenlong, Wang Cheng, Xu Bin. Investigation of Hyper Shaped Charge Jet Formation Theory. Acta Armamentarii, 2018, 39(02): 261-268 (in Chinese) doi: 10.3969/j.issn.1000-1093.2018.02.007
[14] Xi B, Liu J, Li S, et al. Effect of interaction mechanism between jet and target on penetration performance of shaped charge liner. Materials Science and Engineering A, 2012, 553: 142-148 doi: 10.1016/j.msea.2012.06.003
[15] 熊玮, 张先锋, 陈亚旭等. 冷轧成型Al/Ni多层复合材料力学行为与冲击释能特性研究. 爆炸与冲击, 2019, 39(05): 130-138 Xiong Wei, Zhang Xianfeng, Chen Yanxu, et al. Mechanical properties and shock-induced chemical reaction behaviors of cold-rolled Al/Ni multi-layered composites. Explosion and Shock Waves, 2019, 39(05): 130-138 (in Chinese)
[16] Wang HF, Guo HG, Geng B, et al. Application of PTFE/Al reactive materials for double-layered liner shaped charge. Materials, 2019, 12(17): 2768 doi: 10.3390/ma12172768
[17] Guo HG, Zheng YF, He S, et al. Reaction characteristic of PTFE/Al/Cu/Pb composites and application in shaped charge liner. Defence Technology, 2021, 472: 1-11
[18] 陈泽坤, 蒋佳希, 王宇嘉等. 金属增材制造中的缺陷、组织形貌和成形材料力学性能. 力学学报, 2021, 53(12): 3190-3205 doi: 10.6052/0459-1879-21-472 Chen Zekun, Jiang Jiaxi, Wang Yujia, et al. Defects, microstructures and mechanical properties of materials fabricated by metal additive manufacturing. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(12): 3190-3205 (in Chinese) doi: 10.6052/0459-1879-21-472
[19] 廉艳平, 王潘丁, 高杰等. 金属增材制造若干关键力学问题研究进展. 力学进展, 2021, 51(3): 648-701 doi: 10.6052/1000-0992-21-037 Lian Yanping, Wang Panding, Gao Jie, et al. Fundamental mechanics problems in metal additive manufacturing: A state-of-art review. Advances in Mechanics, 2021, 51(3): 648-701 (in Chinese)) doi: 10.6052/1000-0992-21-037
[20] Walters WP, Kecskes LJ, Pritchett JE. Investigation of a bulk metallic glass as a shaped charge liner material. Army Research Laboratory, No. ARL-TR-3864, 2006
[21] Walsh J, Shreffler R, Willig F. Limiting conditions for jet formation in high velocity collisions. Journal of Applied Physics, 1953, 24(3): 349-359 doi: 10.1063/1.1721278
[22] Chou PC, Carleone J, Karpp RR. Criteria for jet formation from impinging shells and plates. Journal of Applied Physics, 1976, 47(7): 2975-2981 doi: 10.1063/1.323038
[23] Elshenawy T, Li QM, Elbeih A. Experimental and numerical investigation of zirconium jet performance with different liner shapes design. Defence Technology, 2020, 18(1): 1-15
[24] Chou PC, Carleone J. The stability of shaped charge jets. Journal of Applied Physics, 1977, 48(10): 4187-4195 doi: 10.1063/1.323456
[25] Yeh JW, Chen SK, Lin SJ, et al. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Advanced Engineering Materials, 2004, 6(5): 299-303 doi: 10.1002/adem.200300567
[26] Cantor B, Chang ITH, Knight P, et al. Microstructural development in equiatomic multicomponent alloys. Materials Science and EngineeringA, 2004, 375-377: 213-218 doi: 10.1016/j.msea.2003.10.257
[27] George EP, Raabe D, Ritchie RO. High-entropy alloys. Nature Reviews Materials, 2019, 4(8): 515-534 doi: 10.1038/s41578-019-0121-4
[28] 卜叶强, 王宏涛. 多主元合金中的化学短程有序. 力学进展, 2021, 51( 4): 915-919 doi: 10.6052/1000-0992-21-027 Bu Ye qing, Wang Hongtao. Short-range order in multicomponent alloys. Advances in Mechanics, 2021, 51(4): 915-919 (in Chinese) doi: 10.6052/1000-0992-21-027
[29] Dai LH, Ling Z, Bai YL. A strain gradient-strengthening law for particle reinforced metal matrix composites. Scripta Materialia, 1999, 41(3): 245-251 doi: 10.1016/S1359-6462(99)00153-0
[30] Dai LH, Liu LF, Bai YL. Formation of adiabatic shear band in metal matrix composites. International Journal of Solids Structures, 2004, 41(22-23): 5979-5993 doi: 10.1016/j.ijsolstr.2004.05.023
[31] Liu XF, Tian Z, Zhang XF, et al. "Self-sharpening" tungsten high-entropy alloy. Acta Materialia, 2020, 186: 257-266 doi: 10.1016/j.actamat.2020.01.005
[32] 陈海华, 张先锋, 熊玮等. WFeNiMo高熵合金动态力学行为及侵彻性能研究. 力学学报, 2020, 52(05): 1443-1453 Chen Haihua, Zhang Xianfeng, Xiong Wei, et al. Dynamic mechanical behavior and penetration performance of WFeNiMo high-entropy alloy. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(05): 1443-1453 (in Chinese)
[33] 侯先苇, 熊玮, 陈海华等. 两种典型高熵合金冲击释能及毁伤特性研究. 力学学报, 2021, 53(09): 2528-2540 doi: 10.6052/0459-1879-21-327 Hou Xianwei, Xiong Wei, Chen Haihua, et al. Impact energy release and damage characteristics of two high-entropy alloys. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(9): 2528-2540 (in Chinese) doi: 10.6052/0459-1879-21-327
[34] Chen J, Liu TW, Cao FH, et al. Deformation behavior and microstructure evolution of CoCrNi medium-entropy alloy shaped charge liners. Metals, 2022, 12(5): 811 doi: 10.3390/met12050811
[35] 王维斌, 索涛, 郭亚洲等. 电磁霍普金森杆实验技术及研究进展. 力学进展, 2021, 51(4): 729-754 doi: 10.6052/1000-0992-20-024 (Wang Weibin, Suo Tao, Guo Yazhou, et al. Experimental technique and research progress of electromagnetic Hopkinson bar. Advances in Mechanics, 2021, 51(4): 729-754 in Chinese doi: 10.6052/1000-0992-20-024
[36] Jiang Z, He J, Wang H, et al. Shock compression response of high entropy alloys. Materials Research Letters, 2016, 4(4): 226-232 doi: 10.1080/21663831.2016.1191554
[37] Pugh EM, Eichelberger R, Rostoker N. Theory of jet formation by charges with lined conical cavities. Journal of Applied Physics, 1952, 23(5): 532-536 doi: 10.1063/1.1702246
[38] Xu W, Wang C, Chen D. Formation of a bore-center annular shaped charge and its penetration into steel targets. International Journal of Impact Engineering, 2019, 127: 122-134 doi: 10.1016/j.ijimpeng.2019.01.008
[39] Xu W, Wang C, Chen D. The jet formation and penetration capability of hypervelocity shaped charges. International Journal of Impact Engineering, 2019, 132: 103337 doi: 10.1016/j.ijimpeng.2019.103337
[40] Lee EL, Horning HC, Kury JW. Adiabatic expansion of high explosive detonation products. San Francisco: University of California. Technical Report, No. UCRL-50422, 1968
[41] Guo HG, Zheng Y, Tang L, et al. Effect of wave shaper on reactive materials jet formation and its penetration performance. Defence Technology, 2019, 15(4): 495-505 doi: 10.1016/j.dt.2019.05.005
[42] Carleone J, Jameson R, Chou PC. The tip origin of a shaped charge jet. Propellants, Explosives, Pyrotechnics, 1977, 2(6): 126-130 doi: 10.1002/prep.19770020604
[43] Guo HG, Su CH, Cai YQ, et al. Reactive jet density distribution effect on its penetration behavior. Defence Technology, 2022, in press
[44] Chou PC, Flis WJ. Recent developments in shaped charge technology. Propellants, Explosives, Pyrotechnics, 1986, 11(4): 99-114 doi: 10.1002/prep.19860110402
[45] Miracle DB, Senkov ON. A critical review of high entropy alloys and related concepts. Acta Materialia, 2017, 122: 448-511 doi: 10.1016/j.actamat.2016.08.081
-
期刊类型引用(10)
1. 李建林，黄天柱，张恒宾，邓华锋. 卸荷岩体力学试验研究进展与展望. 三峡大学学报(自然科学版). 2022(01): 1-13 . 
百度学术
2. 王云飞，宿辉，王立平，焦华喆，李震. 3种砂岩变形与强度特征对比分析. 煤炭学报. 2020(04): 1367-1374 . 百度学术
3. 王云飞，焦华喆，李震，宿辉. 白砂岩卸围压强度与损伤破坏特征. 煤炭学报. 2020(08): 2787-2794 . 百度学术
4. 马振乾，梁旭超，池恩安，张鹏冲，谢雄刚. 不同加载速率下煤的侧向变形特征研究. 应用力学学报. 2020(05): 2007-2012+2320 . 百度学术
5. 王如宾，徐波，徐卫亚，王伟，林志南，张久长. 不同卸荷路径对砂岩渗透性演化影响的试验研究. 岩石力学与工程学报. 2019(03): 467-475 . 百度学术
6. 韩强，屈展，叶正寅. 基于均匀化理论的页岩微观多孔黏土强度特性. 力学学报. 2019(03): 940-948 . 本站查看
7. 韩强，屈展，叶正寅，董广建. 基于微米力学实验的页岩Ⅰ型断裂韧度表征. 力学学报. 2019(04): 1245-1254 . 本站查看
8. 邹玉亮，薛凯喜，胡艳香，杨伟峰，何松，常留成. 不同侧限条件下红黏土竖向压缩性能响应试验分析. 科学技术与工程. 2017(11): 94-102 . 百度学术
9. 高江平，杨华，蒋宇飞，吴鹏阁，孙世界. 三剪应力统一强度理论研究. 力学学报. 2017(06): 1322-1334 . 本站查看
10. 武守信，魏吉瑞，杨舒蔚. 基于能量等效原理的应变局部化分析:Ⅱ.有限元解法. 力学学报. 2017(04): 880-893 . 本站查看
其他类型引用(6)
计量
- 文章访问数: 1304
- HTML全文浏览量: 472
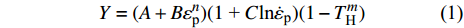
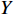
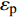
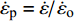
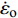
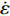
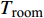
- PDF下载量: 291
- 被引次数: 16
