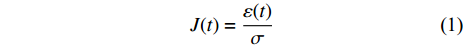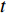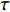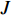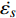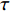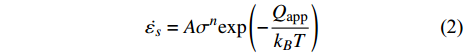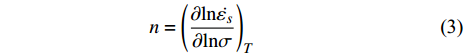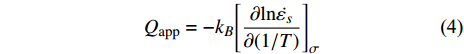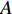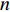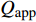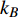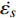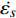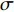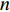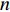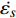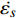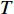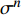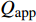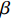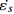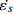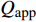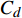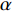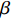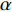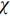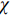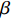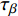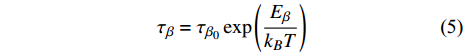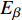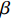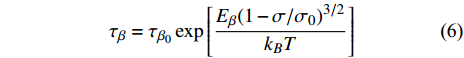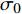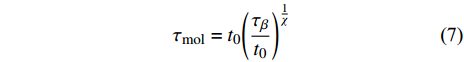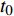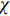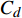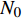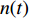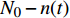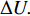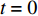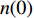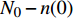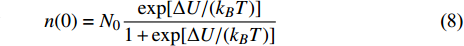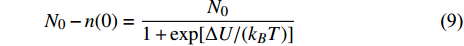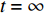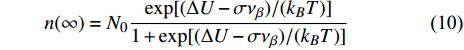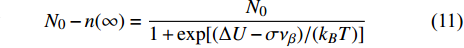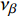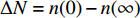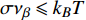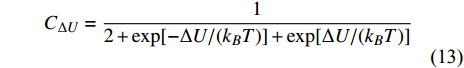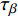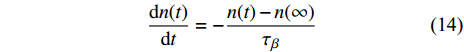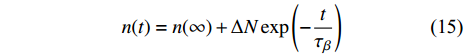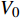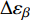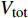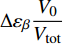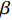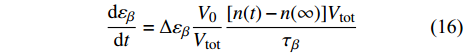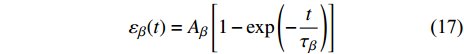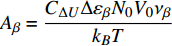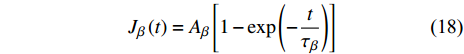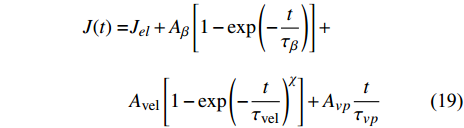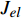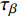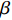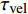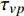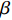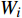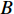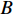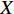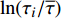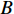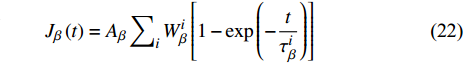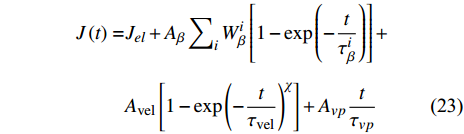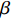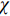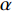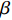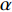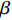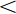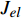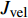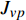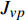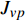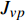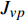PROBING INTO THE CREEP MECHANISM OF AMORPHOUS ALLOY BASED ON QUASI-POINT THEORY
-
摘要: 作为典型多体相互作用非平衡体系, 如何明晰非晶合金多场耦合激励下变形机制, 建立非晶合金变形行为、流动特性与微观结构特征本征关联始终是非晶合金力学性能的重要研究内容. 本文以具有显著
$ \beta $ 弛豫行为的La56.16Ce14.04Ni19.8Al10非晶合金作为研究载体, 通过开展宽温度应力窗口蠕变实验, 着重考查了蠕变柔量、准稳态蠕变速率、特征弛豫时间、蠕变应力指数及蠕变激活能演变规律, 系统研究了非晶合金蠕变行为与蠕变机制. 基于准点缺陷理论分析了非晶合金蠕变行为由弹性向黏弹性及黏塑性逐步转变的过程, 从微观结构演化角度构建了非晶合金蠕变行为完整物理图像. 研究结果表明, 非晶合金高温蠕变行为是一典型热力耦合、非线性过程, 其潜在蠕变机制受控于温度、应力与加载时间. 应力较低时, 非晶合金蠕变机制对应于热激活单粒子流动. 应力较高时, 蠕变机制则对应于应力诱导局部剪切变形增强与温度诱导原子扩散等复杂耦合过程. 非晶合金蠕变变形过程所涉及弹塑性转变源于非晶合金准点缺陷激活、微剪切畴经热力耦合激励形核长大、扩展与不可逆融合.Abstract: As a typical multi-body interaction and non-equilibrium system, how to clarify the deformation mechanism under multi-field coupling stimuli and then establish the intrinsic correlation among the deformation behavior, flow characteristics and microstructure evolution of amorphous alloys keep the fundamental topic. In the current work, a prototypical La56.16Ce14.04Ni19.8Al10 amorphous alloy which shows a pronounced slow$ \;\beta $ relaxation process was selected as the model system. Series of creep experiments of the amorphous alloy over wide temperature and stress range were carried out. Evolution of creep compliance$ J $ , quasi steady-state strain rate$ \dot{{\varepsilon }_{s}} $ , characteristic relaxation time$ \tau $ , stress index$ n $ along with the apparent activation energy for creep${Q}_{{\rm{app}}}$ were systematically investigated in order to probe into the deformation mechanism involved in the creep process of amorphous alloys. In parallel, a gradual transition of deformation mode from elasticity to viscoelasticity and viscoplasticity of amorphous alloys during creep was analyzed. In the framework of the quasi-point defects theory, a complete picture delineating the deformation process of amorphous creep was probed from the perspective of microstructure evolution. The results demonstrated that the creep deformation of amorphous alloy is a typical thermo-mechanical coupling and nonlinear mechanics process, which could be affected by experimental temperature, applied stress and loading time. The creep mechanism of amorphous alloy is dominated by the diffusion which is related to thermal particle flow when the applied stress is lower. On the other hand, when the stress is higher, the creep mechanism corresponds to more complicated synergistic actions consisting of both stress-induced collective rearrangements of atoms and temperature-induced thermal activation. In addition, the underlying physical background of the elastic-plastic transition of the amorphous alloy during creep deformation was described, which is correlated to the initiation of quasi-point defects as well as the formation, expansion and coalescence process of sheared micro-domains under thermo-mechanical stimuli.-
Keywords:
- amorphous alloy /
- creep /
- quasi-point theory /
- deformation mechanism /
- structural heterogeneity
-
引言
非晶合金(amorphous alloy)是一种兼具金属与玻璃双重特性的新型亚稳态金属材料, 具有高强度、高断裂韧性、超塑性、优良软磁特性以及耐腐蚀等一系列优异力学、物理和化学性能, 在基础科学和工程应用领域均具有广阔发展前景 [1-3]. 基于晶体周期化结构与相应结构缺陷信息, 传统金属材料微观结构决定宏观力学性能的研究范式已被广泛接受 [4-5]. 而非晶合金并无晶界、位错等典型结构缺陷, 在外载荷作用下表现出独特流变特性与能量耗散机制, 其微观结构特征、变形行为演化的物理图像仍不清晰. 近年来, 大量研究表明非晶合金微观结构是非均匀的且利用传统分析方法难以表征 [6-7]. 由此, 非晶合金力学行为与其微观结构非均匀性分布、演化形式的潜在联系仍未得到有效解决. 如何明晰非晶合金流动特性、变形机理进而合理自洽构建其微观结构非均匀性与宏观力学性能之间本征关联始终是固体力学研究领域一大挑战问题 [6, 8].
研究表明非晶合金力学行为与温度、应力、应变速率和加载方式等因素紧密相关 [9-10]. 非晶合金在高温、低应变速率条件下发生黏性流动, 表现为宏观均匀塑性流变模式; 而在低温、高应变速率条件下则发生局域非均匀变形, 变形高度集中于纳米尺度剪切带内 [11]. 同时, 非晶合金偏离平衡态并呈现一系列复杂而又独特非线性、非平衡特征 [12]. 长期以来有关其流变模式转变 [13]、弹塑性转变 [14]、韧脆转变 [15]及失稳断裂模式转变 [16]的研究持续深入进行. 目前, 研究非晶合金高温流变与塑性流动机制的传统实验手段主要包括拉伸 [17]、压缩 [18]、应力松弛 [19-20]、蠕变 [14, 21]与动力学弛豫 [22-23]. 蠕变在固定温度与恒定应力载荷下观察应变随时间演化, 由于其可直接反映材料微观结构在热力耦合过程中真实演化进程而备受关注. 此外, 蠕变可通过长时间静载引起非晶合金宏观尺度变形, 依托数值分析方法与分子动力学模拟处理其应变响应亦可精确反馈其动力学特征及能量状态信息 [24-25]. 基于此, 蠕变手段近年来已得到普遍应用并被广泛证明是定量研究非晶合金与时间相关结构弛豫、滞弹性与塑性变形、高温流变等关键科学问题的有效手段之一 [14, 21, 26].
基于平均场理论, Spaepen [27]提出以单原子跃迁为基础的“自由体积”模型用来解释非晶合金塑性流变行为, 建立了自由体积数量、原子跃迁速率与宏观剪切变形在非晶态物质流动过程中演化的物理图像. Argon [28]在此基础上结合肥皂泡筏实验创造性地提出了“剪切转变区”模型, 该模型借鉴晶体流变学研究思路, 认为非晶合金基本塑性流动单元是包含约100 ~ 600个原子的原子团簇或集团. 后经文献[29-31]进一步修正与优化, 剪切转变理论可以合理预测并解释非晶合金剪切高度局域化特征与宏观变形行为, 为揭示非晶合金塑性流变机制提供了新思路. 然而, 上述两种模型均建立在平均场理论基础上, 仅考虑了剪切变形对流动软化影响而忽略了非晶合金基本变形单元间相互作用. 为此, 从微观结构演化角度出发, Perez [32]将非晶合金宏观力学性能与微观原子/分子运动结合起来并提出了准点缺陷理论, 该理论引入微剪切畴形核、长大、收缩与融合过程, 可从物理角度描述非晶合金经热力耦合作用由滞弹性到屈服完整变形过程.
基于前期研究, 本文将以具有显著
$ \beta $ 弛豫行为的La56.16Ce14.04Ni19.8Al10非晶合金作为模型体系, 通过开展高温蠕变实验, 系统研究非晶合金在不同温度及应力状态蠕变柔量、准稳态蠕变速率、特征弛豫时间、蠕变应力指数与蠕变机制演化. 尤其重要的是, 本文将深入分析非晶合金变形过程中由弹性向黏弹性与黏塑性逐步转变过程, 并基于准点缺陷理论尝试从非晶合金微观结构非均匀角度出发揭示非晶合金蠕变的潜在物理机制. 本研究致力于明晰热力耦合激励下非晶合金宏观性能演变与微观结构响应, 并为进一步增进对非晶合金变形机理, 尤其是对非晶合金蠕变机理的认识提供必要理论指导与数据支撑.1. 实验方法
本研究选取具有显著
$ \;\beta $ 弛豫行为的La56.16-Ce14.04Ni19.8Al10非晶合金作为模型体系开展宽温度应力窗口蠕变实验. 实验样品为采用单辊甩带法制备的非晶合金薄带, 其尺寸约为7.00 mm (长度) × 0.60 mm (宽度) × 0.04 mm (厚度). 使用TA Q800型动态力学分析仪单轴拉伸模式, 采用3 MPa ~ 250 MPa间不同加载应力, 分别在315 K, 330 K, 350 K和370 K进行蠕变实验. 每组实验蠕变时间均为1 × 105 s且实验开始前样品均在测试温度等温处理5 min以达到温度平衡.2. 实验结果与讨论
2.1 LaCe基非晶合金蠕变行为
图1为不同加载应力条件下La56.16Ce14.04Ni19.8-Al10非晶合金蠕变曲线(测试温度分别为315 K和370 K). 为直观表征温度或应力潜在影响, 加载后引起瞬时弹性变形被移除, 仅保留非弹性变形数据. 本实验温度窗口内可清晰观察到非晶合金蠕变过程存在两个显著演化阶段, 即应变速率随时间推移迅速减小的初始蠕变阶段与应变随时间线性增加、应变速率几乎恒定的(准)稳态蠕变阶段. 研究表明, 传统金属材料稳态蠕变源于内部位错生成硬化与消失软化平衡过程 [33], 而非晶合金(准)稳态蠕变机制则与非晶体系内部应力诱导自由体积再生与原子跃迁诱导自由体积湮灭达到动态平衡有关 [34]. 同时注意到, 随时间延长, LaCe基非晶合金蠕变变形逐渐增大, 且这种影响呈现明显温度及应力依赖性, 即随温度升高或应力增加, 蠕变变形更加显著. 低温低应力状态下, LaCe基非晶合金具有较好抗蠕变性能, 较高弹性模量, 弹性变形主导蠕变进程. 当温度逐渐升高, 非晶合金强度降低, 抗蠕变性能急剧下降, 体系在应力作用下迅速经历弹塑性转变, 黏弹性(黏塑性)变形进一步主导蠕变变形.
2.2 基于柔量的LaCe基非晶合金蠕变机制分析
非晶合金弹塑性转变和流变模式转变等一系列力学行为均与实验温度、外部应力和加载方式等因素紧密相关 [9]. 基于上述实验结果, 温度和应力对LaCe基非晶合金蠕变行为影响程度非常显著. 然而, 由于热力耦合激励下各影响因素潜在影响机理尚不明晰, 深入研究非晶合金相关蠕变机制转变须全面且充分考虑多因素相互影响并一定程度实现变量解耦. 接下来, 尝试从不同角度深入探究应力与温度对非晶合金蠕变行为影响, 进而揭示非晶合金蠕变机制经热力耦合演化情况.
首先, 引入蠕变柔量(creep compliance), 其定义为材料蠕变过程中任意时刻t对应应变与应力之比值, 即
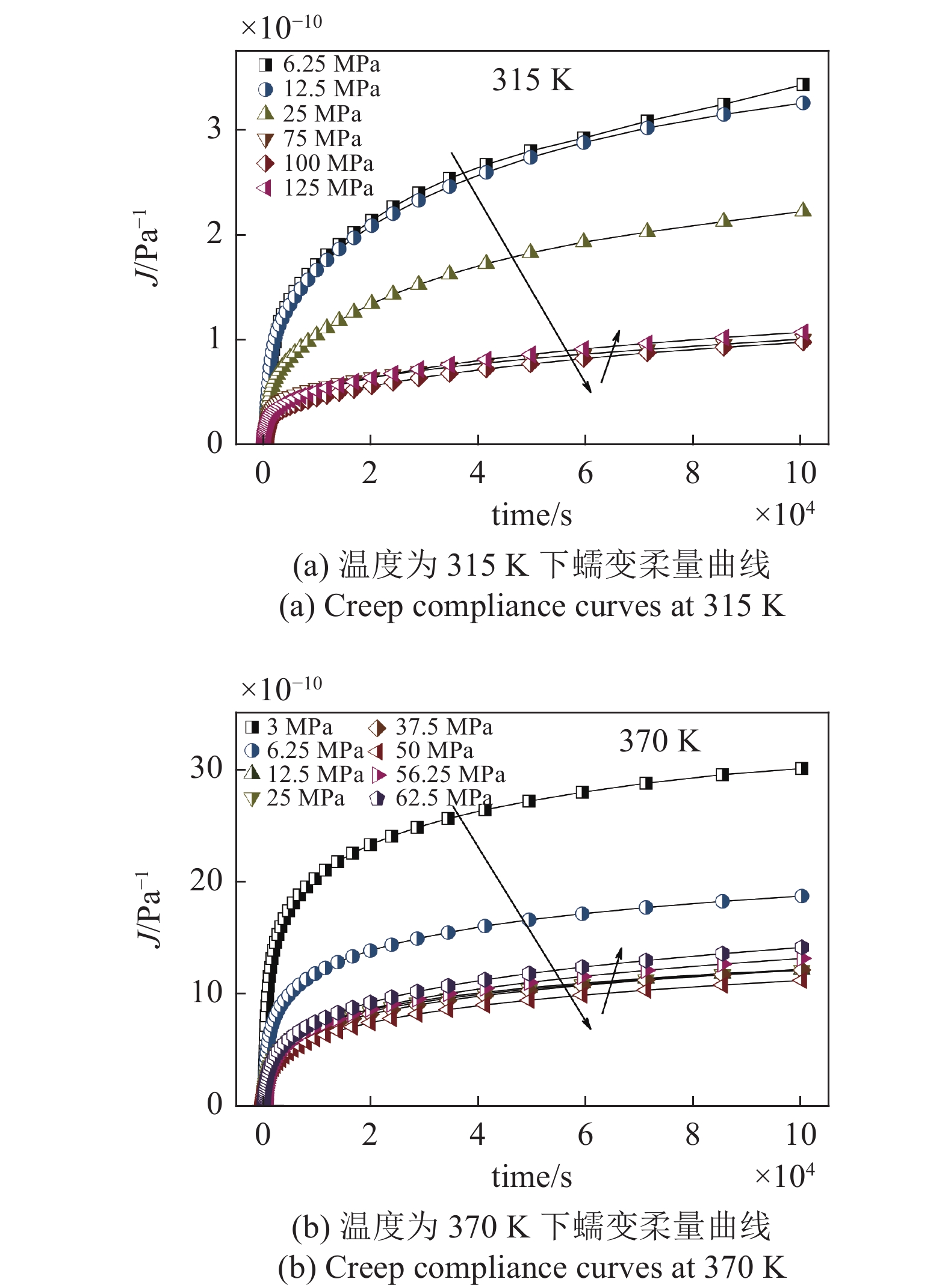
$$ J(t) = \frac{{\varepsilon (t)}}{\sigma } $$ (1) 图2为不同温度及应力状态La56.16Ce14.04Ni19.8Al10非晶合金蠕变柔量随时间演化(测试温度分别为315 K和370 K). 作为典型非线性变形过程, 非晶合金蠕变柔量仍随温度或应力显著变化. 在恒定应力下, 以
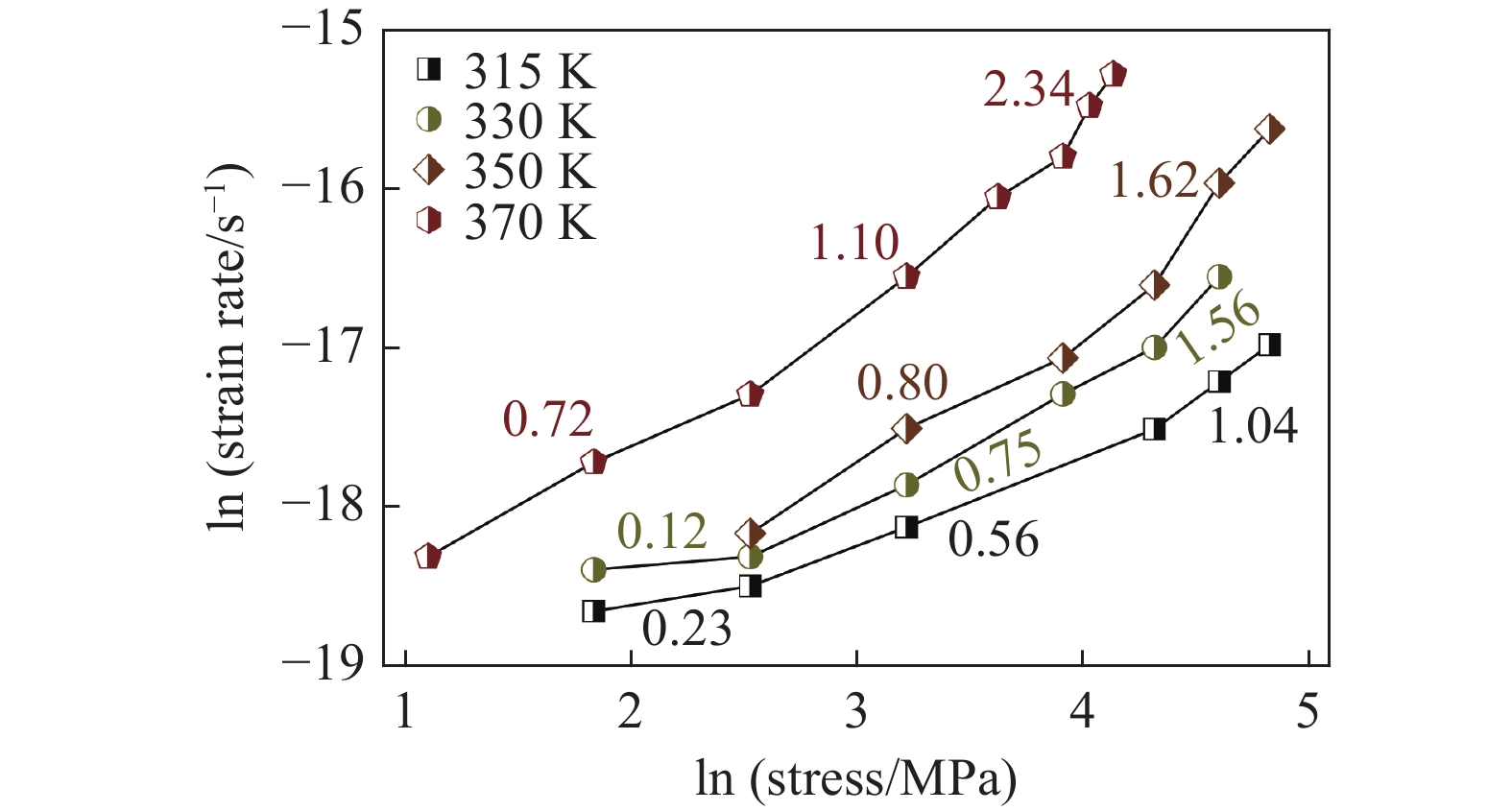
$ \sigma $ = 25 MPa, 蠕变结束时刻即$ t $ = 1 × 105 s时为例, 其终态蠕变柔量$ {J}_{{\rm{end}}} $ 由315 K的2.22 × 10−10 Pa−1迅速增大到370 K的1.21 × 10−9 Pa−1. 另一方面, 若恒定蠕变温度, 可以看到非晶合金蠕变柔量随应力增大呈现先降后升趋势, 且这一趋势随温度升高更加显著. 图3则更清晰直观地描述了终态蠕变柔量$ {J}_{{\rm{end}}} $ 随温度及应力演变情况. 需要注意的是, 其他含稀土元素非晶合金体系的蠕变柔量演化特征与之有所不同, 此前对La60Ni15Al25非晶合金蠕变行为的研究中发现, 在与本实验相似的温度区间内(340 K至400 K), 其蠕变柔量随应力不断增大始终显著上升, 且并未呈现图2所见明显转折 [14]. 对于本文模型体系La56.16Ce14.04Ni19.8Al10而言, 在温度较低时, 应力增加尚且不足以导致其出现更加显著蠕变变形, 即应变增幅低于应力增幅, 导致蠕变柔量随应力增加呈现下降趋势. 而当温度较高时, 应力对蠕变过程影响加剧, 随外加载荷不断增加, 非晶合金蠕变行为加剧, 应变增幅持续抬升并最终显著高于应力增幅, 导致蠕变柔量升高. 可见, 应力作用效果将在高温区域体现得更加明显. 这一结论也可由另一重要物理量准稳态蠕变速率$ \dot{{\varepsilon }_{s}} $ 演变情况加以说明. 材料的准稳态蠕变速率定义为相应蠕变-时间曲线上$ t $ = 8 × 104 s时刻蠕变应变增量对时间之导数. 如图4所示, 准稳态蠕变速率由低温低应力状态下仅1.0 × 10−8 s−1陡增至高温高应力状态下约2.1 × 10−7 s−1, 增幅超过2000%, 同时峰值向应力更低方向迁移.为获得更多精确描述非晶合金蠕变行为动力学信息, 研究了不同温度及应力模型合金特征弛豫时间分布情况. 图5为不同温度和应力状态La56.16Ce14.04Ni19.8Al10非晶合金蠕变过程特征弛豫时间分布强度谱. 弛豫时间
$ \tau $ 广泛分布于101 s至105 s范围内, 且其分布形式在不同应力及温度状态下存在较大差异, 表明非晶合金蠕变行为是涉及不同时间尺度变形单元结构演化的复杂过程. 图5(a)展示了加载应力为12.5 MPa, La56.16Ce14.04Ni19.8Al10非晶合金特征弛豫时间分布随温度分布情况. 随温度升高, 弛豫时间分布发生展宽, 由近乎离散分布逐步转变为连续分布. 而对于较高应力(100 MPa), 弛豫时间在不同温度下遵循相似分布方式, 在弛豫谱800 s, 5000 s与20000 s依次呈现规模由小渐大的三级弛豫峰. 通过对比, 可以发现低应力状态下LaCe基非晶合金弛豫时间分布对温度依赖性更强, 表明此状态下非晶合金蠕变机制主要由热激活主导. 而在高应力状态下, 温度影响甚微, 应力进一步主导非晶合金蠕变进程. 这一结论也可由恒定温度弛豫时间随应力演化特征所证实: 在图5(c)与图5(d)中, 确定弛豫时间分布形式的阈值应力由低温330 K时50 MPa降低至高温370 K时约25 MPa, 外加载荷一旦超过阈值, 弛豫时间均将遵循高度相似分布特征. 同时注意到, 超过50000 s较长弛豫时间对应于体系蠕变过程黏塑性响应, 3000 s左右较短弛豫时间对应于体系黏弹性响应, 而不足10 s最短弛豫时间则对应于体系瞬时弹性响应. 于是, 进一步观察到模型合金受控于温度与应力的蠕变变形模式转变过程. 低温低应力时, 较短弛豫时间规模相当可观, 此时黏弹性变形在非晶合金整体蠕变变形中起主导作用. 而随温度或应力增加, 弛豫时间谱较短一侧分布逐渐稀疏, 较长一侧分布强度则显著抬升, 表明非晶合金蠕变变形逐渐由黏塑性变形主导.结合蠕变柔量
$ J $ , 准稳态蠕变速率$ \dot{{\varepsilon }_{s}} $ 与弛豫时间$ \tau $ 演变特征, 初步揭示了温度与应力对La56.16Ce14.04Ni19.8Al10非晶合金蠕变机制潜在影响. 接下来, 尝试探寻衡量相关影响强度的更多定量判据. 对于金属材料, 其准稳态蠕变速率随温度演化遵循Arrhenius关系 [33]$$ \dot{{\varepsilon }_{s}}=A{\sigma }^{n}\mathrm{exp}\left(-\frac{{Q}_{{\rm{app}}}}{{k}_{B}T}\right) $$ (2) 当温度
$ T $ 或应力$ \sigma $ 恒定时, 得到$$ n={\left(\frac{\partial \mathrm{ln}\dot{{\varepsilon }_{s}}}{\partial \mathrm{ln}\sigma }\right)}_{T} $$ (3) $$ {Q}_{{\rm{app}}}=-{k}_{B}{\left[\frac{\partial \mathrm{ln}\dot{{\displaystyle {\varepsilon }_{s}}}}{\partial (1/T)}\right]}_{\sigma } $$ (4) 式中,
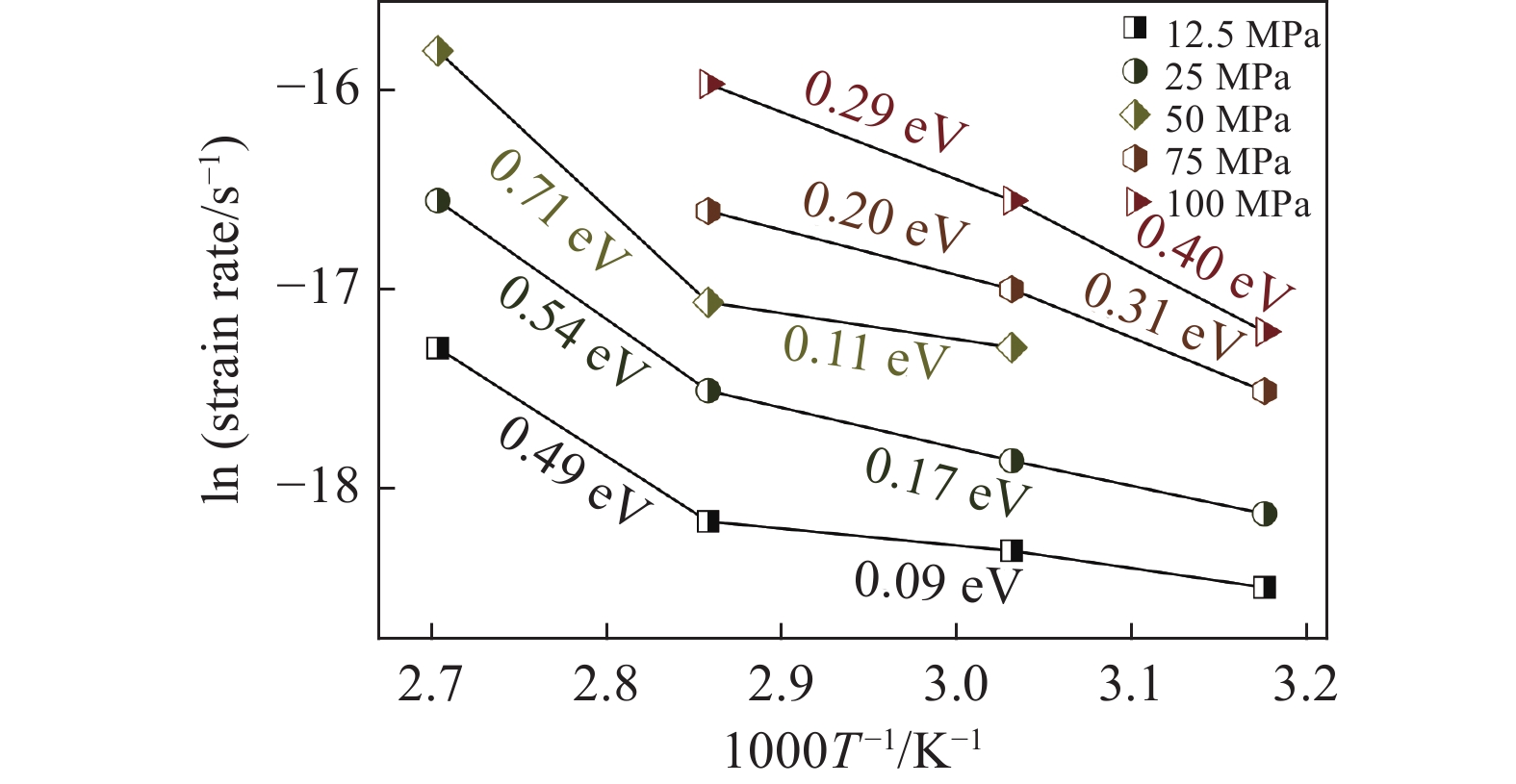
$ A $ 为材料常数,$ n $ 为蠕变应力指数,$ {Q}_{{\rm{app}}} $ 为名义蠕变激活能,$ {k}_{B} $ 为玻尔兹曼常数. 图6为不同温度时LaCe基非晶合金蠕变过程准稳态蠕变速率$ \dot{{\varepsilon }_{s}} $ 随应力演化情况,$ \dot{{\varepsilon }_{s}} $ 与应力$ \sigma $ 呈现明显非线性关系.对式 (3)两边取对数, 曲线斜率即为蠕变应力指数$ n $ . 可见, 不同温度时应力指数均大致服从三段分布特征, 应力指数随应力增加而明显增大. 一般地, 在蠕变型本构方程中, 应力指数$ n $ 直接反映了应力对体系蠕变行为的影响程度, 其数值大小更是应力影响权重的直接体现. 应力指数越大, 则应力因素对蠕变行为影响越强, 应力作用效果越明显. 在本研究中, 应力指数由低温低应力状态低于0.5增加到高温高应力状态超过2.3, 随温度升高或应力增加,应力逐渐占据主导, 并进一步主导蠕变进程. 另一方面, 根据式 (4), 应力恒定时, 准稳态蠕变速率$ \dot{{\varepsilon }_{s}} $ 与温度T之间符合Arrhenius关系, 根据曲线斜率即可求得名义蠕变激活能. 如图7所示, 显然,$ \dot{{\varepsilon }_{s}} $ 与1/$ T $ 并不能通过简单线性关系描述. 由于式 (4)建立在$ {\sigma }^{n} $ 为定值基础上, 即认为应力与应力指数均为温度不变量. 315 K至370 K温度区间内, 应力指数随温度与应力作显著变化, 因此, 将所得曲线分阶段计算蠕变激活能更加合理. 研究结果表明, LaCe基非晶合金名义蠕变激活能$ {Q}_{{\rm{app}}} $ 与应力指数呈现相似温度应力演化特征. 应力较低时, 蠕变激活能随温度变化更加明显, 其数值由低温0.10 eV左右迅速增大到高温0.55 eV (该数值与其$ \beta $ 弛豫激活能基本一致 [26]). 而应力较高时, 蠕变激活能对温度变化并不敏感, 数值基本维持在0.30 eV左右, 温度仅为影响其蠕变行为次要因素, 类似变化趋势在其他非晶合金蠕变行为研究中已有相关报道 [25, 35].传统金属材料蠕变物理机制主要通过蠕变扩散和蠕变位错两类行为解释 [33]. 低应力状态, 体系内位错运动停滞或缓慢进行, 金属原子受扩散因素影响连续移动而发生蠕变; 高应力状态, 蠕变变形则逐渐由内部结构缺陷如位错的滑移或攀移主导. 同时, 温度场通过产生热应力亦使应力场排布发生变化. 因此, 高温高应力材料蠕变行为是一包含热振动、单原子扩散与位错增殖等效应的复杂耦合过程. 对于非晶合金, 由于其内部缺乏晶界、位错等传统结构缺陷, 承载其塑性变形基本运动是能够适应剪切变形一系列原子团簇的局域重排. 本文应力指数n与名义蠕变激活能
$ {Q}_{{\rm{app}}} $ 随温度或应力演化趋势反映了非晶合金流变行为典型非线性响应, 这可能是非晶合金内单原子扩散与协同性剪切变形之间的非线性耦合结果. 应力较低时, 非晶合金蠕变机制对应于热激活单粒子流动, 温度在这一过程中起主导作用; 应力较高时, 非晶合金蠕变机制则对应于应力诱导局部剪切变形增强与温度诱导原子扩散等更为复杂过程, 应力在这一过程中起主导作用. 因此, 观察到上述蠕变柔量、特征弛豫时间以及蠕变应力指数独特的随应力演变特征. 同时, 随温度应力逐步升高以及加载时间延长, 非晶合金扩散效应加剧, 原子团簇局部剪切重排速率加快, 准稳态蠕变速率增大, 蠕变变形渐次由黏塑性变形主导.2.3 LaCe基非晶合金蠕变过程微观结构演化
非晶合金具有独特物理和力学性能, 研究表明其微观结构是非均匀的, 并且利用传统分析方法难以表征. 对其宏观变形机制的研究需要充分考虑内部变形单元间相互作用, 基于非晶固体微观结构演化而提出的准点缺陷理论紧密结合了非晶固体微观结构本质. 接下来, 借助准点缺陷理论对La56.16Ce14.04Ni19.8Al10非晶合金蠕变行为继续深入分析并尝试探寻上述表观现象背后潜藏的物理机制.
基于准点缺陷理论, 非晶固体中存在纳米尺度密度、焓和熵的起伏波动, 称之为准点缺陷. 需要指出, 与传统晶体点缺陷、晶界、位错等结构缺陷不同, 非晶固体中的缺陷很难通过传统实验方法被直接探测或表征, 往往仅表现为外场加载(温度场和应力场等)下的非均匀动力学响应, 如互不相同的特征弛豫时间与局部激活能垒分布等. 基于此, 该理论认为当温度低于玻璃转变温度时, 非晶固体处于构型被冻结状态, 即等构型态, 此时准点缺陷浓度
$ {C}_{d} $ 为一定值; 当温度高于玻璃转变温度时, 准点缺陷浓度随温度升高增长. 同时, 非晶固体分子/原子运动具有分级关联, 即最易发生运动的结构单元先运动, 随后引发一系列更加复杂的运动 [36]. 在非晶体系中, 通常认为$ \alpha $ 弛豫对应大规模分子/原子协同运动, 而小规模运动的$ \beta $ 弛豫为$ \alpha $ 弛豫前驱运动. 用于衡量分级运动关联强弱程度的参量由关联因子$ \mathrm{\chi } $ 表征, 其数值介于0至1之间,$ \mathrm{\chi } $ 值越小, 则代表体系内各分级运动关联性越强.在准点缺陷理论框架下, 对于LaCe基非晶合金, 其前驱运动为热激活
$ \beta $ 弛豫过程. 结构单元跃迁特征时间$ {\tau }_{\beta } $ 与温度T之间符合Arrhenius关系 [37]$$ {\tau _\beta } = {\tau _{{\beta _0}}}\exp \left(\frac{{{E_\beta }}}{{{k_B}T}}\right) $$ (5) 式中,
$ {E}_{\beta } $ 为$ \beta $ 弛豫激活能. 在应力场作用下, 非晶固体结构单元的激活服从 [37]$$ {\tau _\beta } = {\tau _{{\beta _0}}}\exp \left[\frac{{{E_\beta }{{(1 - \sigma /{\sigma _0})}^{3/2}}}}{{{k_B}T}}\right] $$ (6) 式中,
$ {\sigma }_{0} $ 为材料屈服极限. 非晶固体分子/原子移动性由$ {\tau }_{{\rm{mol}}} $ 表征, 其定义为体系结构单元完成所有运动的平均特征时间$$ {\tau _{{\rm{mol}}}} = {t_0}{\left(\frac{{{\tau _\beta }}}{{{t_0}}}\right)^{\frac{1}{\chi }}} $$ (7) 式中,
$ {t}_{0} $ 为时间尺度参数,$ \chi $ 为关联因子且其数值与非晶固体准点缺陷浓度$ {C}_{d} $ 线性相关.假设非晶固体单位体积内具有
$ {N}_{0} $ 个准点缺陷位点, 包含t时刻$ n(t) $ 个未激活位点以及$ {N_0} - n(t) $ 个已激活位点. 各位点基本运动过程中势阱能级变化与外加应力正相关. 无应力施加时, 两势阱处于热力学平衡状态, 能垒差异为$\Delta U.$ $ t = 0 $ 时刻未激活位点数目$ n(0) $ 与已激活位点数目$ {N_0} - n(0) $ 可分别表示为 [32]$$ n(0) = {N_0}\frac{{\exp [\Delta U/({k_B}T)]}}{{1 + \exp [\Delta U/({k_B}T)]}} $$ (8) $$ {N_0} - n(0) = \frac{{{N_0}}}{{1 + \exp [\Delta U/({k_B}T)]}} $$ (9) 应力场作用下,
$ t = \infty $ 时刻, 平衡状态下各点位数目可表示为 [32]$$ n(\infty ) = {N_0}\frac{{\exp [(\Delta U - \sigma {\nu _\beta })/({k_B}T)]}}{{1 + \exp [(\Delta U - \sigma {\nu _\beta })/({k_B}T)]}} $$ (10) $$ {N_0} - n(\infty ) = \frac{{{N_0}}}{{1 + \exp [(\Delta U - \sigma {\nu _\beta })/({k_B}T)]}} $$ (11) 式中,
$ {\nu }_{\beta } $ 为一与非晶原子构型有关常数. 伴随应力施加, 共有$ \Delta N = n(0) - n(\infty ) $ 个位点发生激活, 应力较小 ($ \sigma {\nu _\beta } \leqslant {k_B}T $ )时 [32]$$ \Delta N = \frac{{{C_{\Delta U}}{N_0}\sigma {\nu _\beta }}}{{{k_B}T}} $$ (12) $$ {C_{\Delta U}} = \frac{1}{{2 + \exp [ - \Delta U/({k_B}T)] + \exp [\Delta U/({k_B}T)]}} $$ (13) 结合各位点激活路径动力学特征, 即式 (5)中
$ {\tau }_{\beta } $ 演化信息, 可将位点数目与时间关系描述如下$$ \frac{{{\rm{d}}n(t)}}{{{\rm{d}}t}} = - \frac{{n(t) - n(\infty )}}{{{\tau _\beta }}} $$ (14) 对式 (14)积分得
$$ n(t) = n(\infty ) + \Delta N\exp \left( - \frac{t}{{{\tau _\beta }}}\right) $$ (15) 每一准点缺陷位点激活均引起体积为
$ {V_0} $ 微元大小为$ \Delta {\varepsilon _\beta } $ 的微小变形. 因此, 总体积$ {V_{{\rm{tot}}}} $ 中发生的总体宏观变形为$ \Delta {\varepsilon _\beta } \dfrac{{{V_0}}}{{{V_{{\rm{tot}}}}}} $ . 结合式 (14),$ \beta $ 弛豫过程对体系宏观应变速率贡献为$$ \frac{{{\rm{d}}{\varepsilon _\beta }}}{{{\rm{d}}t}} = \Delta {\varepsilon _\beta }\frac{{{V_0}}}{{{V_{{\rm{tot}}}}}} \frac{{[n(t) - n(\infty )] {V_{{\rm{tot}}}}}}{{{\tau _\beta }}} $$ (16) 将式 (15)代入得
$$ {\varepsilon _\beta }(t) = {A_\beta }\left[1 - \exp \left( - \frac{t}{{{\tau _\beta }}}\right)\right] $$ (17) 式中
${A_\beta } = \dfrac{{{C_{\Delta U}}\Delta {\varepsilon _\beta }{N_0}{V_0}{\nu _\beta }}}{{{k_B}T}}$ , 与$ \beta $ 弛豫强度密切相关, 以柔量形式表述, 即得$$ {J_\beta }\left(t\right) = {A_\beta }\left[1 - \exp \left( - \frac{t}{{{\tau _\beta }}}\right)\right] $$ (18) 在热力耦合激励下, 微剪切畴依次经历萌生、扩展以及不可逆融合过程. 非晶合金产生大量不可回复塑性变形. 变形过程中总柔量演化可描述为
$$ \begin{split} J(t) =& {J_{el}} + {A_\beta }\left[1 - \exp \left( - \frac{t}{{{\tau _\beta }}}\right)\right] +\\ &{A_{{\rm{vel}}}}\left[1 - \exp {\left( - \frac{t}{{{\tau _{{\rm{vel}}}}}}\right)^{\chi }}\right] + {A_{vp}}\frac{t}{{{\tau _{vp}}}} \end{split} $$ (19) 式中,
$ {J}_{el} $ 为瞬时弹性柔量且数值上等于模型合金未弛豫弹性模量之倒数,$ {\tau }_{\beta } $ 为$ \beta $ 弛豫过程特征时间,$ {\tau }_{{\rm{vel}}} $ 为黏弹性变形过程特征时间,$ {\tau }_{vp} $ 为黏塑性变形过程特征时间. 上式共包含四个分量, 其中第一项对应于初始瞬时弹性对总柔量贡献, 后三项则分别对应于$ \beta $ 弛豫、黏弹性与黏塑性过程对总柔量贡献.前已述及, 准点缺陷对应于非晶固体内部一系列密度、焓、熵的波动起伏. 结合非晶固体微观结构非均匀性物理本质, 不同准点缺陷尺寸、密度及能量分布各异, 特征时间往往跨越十几个数量级. 对非晶固体一系列动力学弛豫及高温流变行为的精确描述须合理且充分考虑特征时间分布情况. 在该理论框架下,
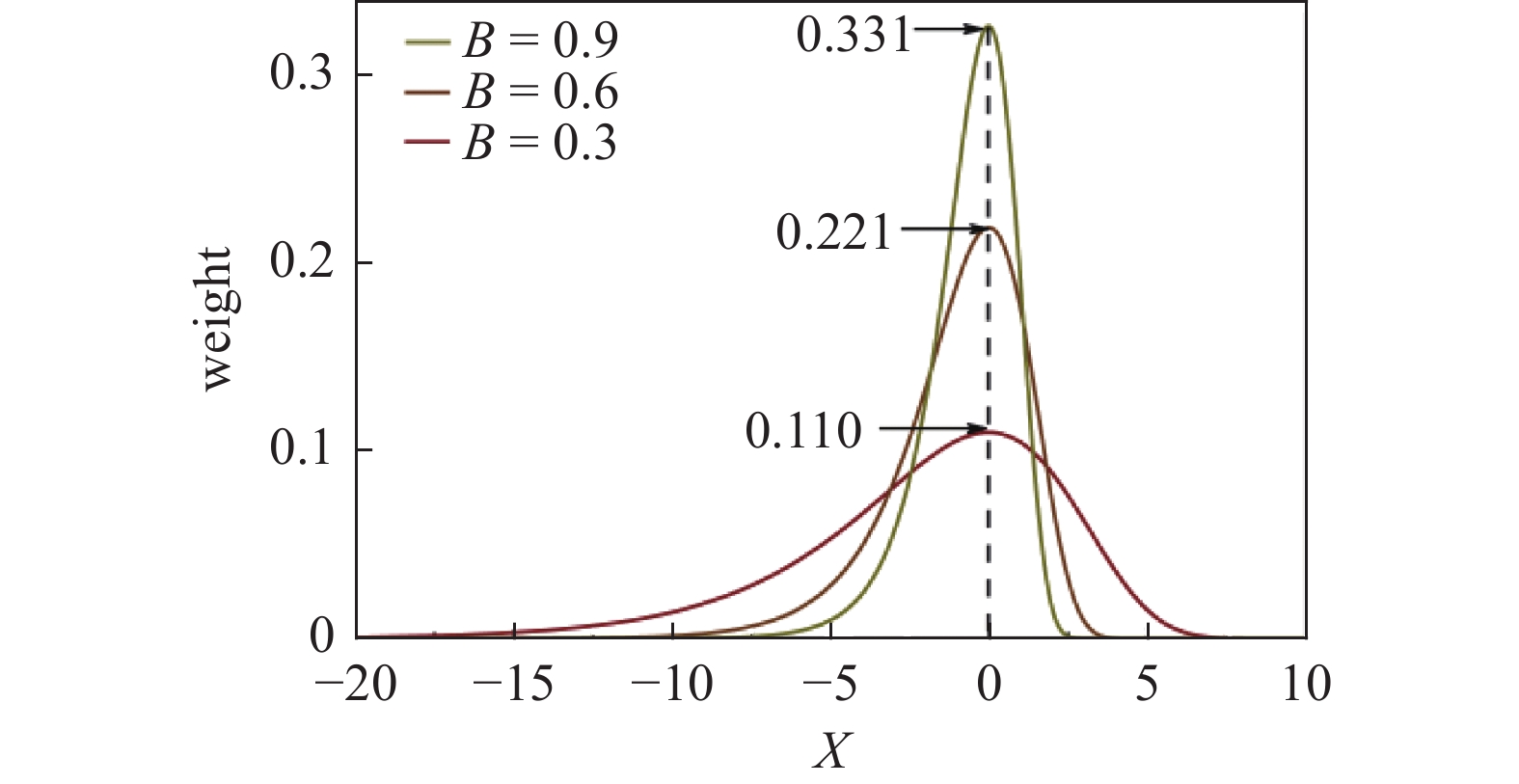
$ \beta $ 弛豫特征时间遵循Gumbel分布, 其基本分布形式为 [37]$$ {W_{{i}}} = \dfrac{{\exp \left[B\ln \dfrac{{{\tau _i}}}{{\overline \tau }} - \exp \left(B\ln \dfrac{{{\tau _i}}}{{\overline \tau }}\right)\right]}}{{\displaystyle\sum\nolimits_i {\exp \left[B\ln \dfrac{{{\tau _i}}}{{\overline \tau }} - \exp \left(B\ln \dfrac{{{\tau _i}}}{{\overline \tau }}\right)\right]} }} $$ (20) 式中,
$ {W}_{i} $ 为特征时间$ {\tau }_{i} $ 所对应概率权重,$ \overline \tau $ 为特征时间均值,$ B $ 为分布宽度参数, 通过改变$ B $ 取值即可实现对Gumbel分布调控. 如图8所示, 为清晰起见, 使用$ X $ 替代$ \ln ({\tau _i}/\overline \tau ) $ . 可见, 随分布宽度$ B $ 取值增大, 特征弛豫时间逐渐趋于集中分布, 而其独特非对称且“左密右疏”分布特征也客观反映了非晶合金$ \beta $ 弛豫动力学非均匀本质 [38]. 考虑$ \beta $ 弛豫特征时间分布, 式 (5)与式 (18)可分别进一步表示为$$ \tau _\beta ^i = \tau _{{\beta _0}}^i\exp \left(\frac{{E_\beta ^i}}{{{k_B}T}}\right) $$ (21) $$ {J_\beta }\left(t\right) = {A_\beta }\sum\nolimits_i {W_\beta ^i} \left[1 - \exp \left( - \frac{t}{{\tau _\beta ^i}}\right)\right] $$ (22) 进而, 总柔量表达式表述为
$$ \begin{split} J\left(t\right) =& {J_{el}} + {A_\beta }\sum\nolimits_i {W_\beta ^i} \left[1 - \exp \left( - \frac{t}{{\tau _\beta ^i}}\right)\right] +\\ &{A_{{\rm{vel}}}}\left[1 - \exp {\left( - \frac{t}{{{\tau _{{\rm{vel}}}}}}\right)^{\chi} }\right] + {A_{vp}}\frac{t}{{{\tau _{vp}}}} \end{split} $$ (23) 这里尝试利用准点缺陷理论从微观结构演化角度揭示LaCe基非晶合金独特的受控于温度、应力与加载时间等因素的变形模式及蠕变机制转变物理本质. 基于前期研究, La56.16Ce14.04Ni19.8Al10非晶合金
$ \beta $ 弛豫激活能约为0.76 eV [26], 结合式 (21)与式 (23), 将弛豫激活能信息与特征弛豫时间分布信息代入, 关联因子$ \mathrm{\chi } $ 取值为0.39 [39], 分布宽度$ B $ 取值为0.50, 于是便可相继获得描述LaCe基非晶合金动力学弛豫与高温蠕变行为理论曲线. 如图9(a)所示, 考虑到当前模型合金晶化温度较低(约418 K [26]), 在$ \alpha $ 弛豫发生前便已局域晶化, 进而导致实验数据偏离理论曲线. 如剔除这一影响因素, 可见准点缺陷理论可准确描述LaCe基非晶合金$ \beta $ 弛豫过程并合理预测随后对应于更高温度的$ \alpha $ 弛豫过程. 同时, 如图9(b)~图9(d)所示, 引入$ \beta $ 弛豫过程相关动力学信息, 基于前述柔量表达式的非晶合金蠕变行为理论曲线在低温段(315 K)和蠕变前期阶段($ < $ 20000 s)与实验数据基本吻合, 而随实验温度升高或加载时间延长, 物理时效对非晶合金蠕变行为作用效果尤为显著. 此时, 可以发现非晶合金蠕变过程受到抑制, 蠕变柔量演变略微偏离理论预测. 然而, 其偏离程度存在一定限度, 通过准点缺陷理论仍可构建非晶合金高温流变行为与其动态力学弛豫行为之间本征关联.依式 (23)解耦各变形分量, 便可获得不同温度及应力状态时瞬时弹性、黏弹性、黏塑性等各柔量分量对于总蠕变柔量贡献程度. 图10即为蠕变实验结束时刻(t = 1 × 105 s)各柔量分量随温度及应力变化情况. 显然, 弹性蠕变柔量$ {J}_{el} $ 与黏弹性蠕变柔量$ {J}_{{\rm{vel}}} $ 随温度应力变化并不显著, 其数值较小且仅略微波动. 相反, 黏塑性蠕变柔量$ {J}_{vp} $ 变化则更为显著, 其数值较大且呈跨数量级变化. 此外, 与前两者演变情况有所不同,$ {J}_{vp} $ 随应力的演变趋势在不同温度情况下存在较大差异. 低温状态下(330 K),$ {J}_{vp} $ 随应力增大小幅下降; 而在高温情况下(370 K),$ {J}_{vp} $ 则随应力增大显著上升. 黏塑性柔量分量$ {J}_{vp} $ 的相关演变趋势直观反映了非晶合金蠕变变形模式转变进程, 随外界温度或应力增大, 黏塑性变形逐渐主导非晶合金蠕变过程. 前述弛豫时间谱中曾发现随温度或应力增加, 弛豫时间将趋于向更长方向演变, 而$ {J}_{vp} $ 的独特演化特征则为这一受控于温度与应力的变形模式转变过程提供了更多定量解释.![]() 图 9 准点缺陷理论描述LaCe基非晶合金的(a)动态弛豫行为与(b)~(d)高温蠕变行为, 其中红色实线为理论预测曲线, 黑色实线为实验数据曲线Figure 9. Description of (a) dynamic relaxation behavior and (b)~(d) high temperature creep behavior of LaCe-based amorphous alloy in the framework of QPD theory. The red line represents the theoretical prediction curve and the black line represents the experimental results
图 9 准点缺陷理论描述LaCe基非晶合金的(a)动态弛豫行为与(b)~(d)高温蠕变行为, 其中红色实线为理论预测曲线, 黑色实线为实验数据曲线Figure 9. Description of (a) dynamic relaxation behavior and (b)~(d) high temperature creep behavior of LaCe-based amorphous alloy in the framework of QPD theory. The red line represents the theoretical prediction curve and the black line represents the experimental results准点缺陷对应于非晶合金内部一系列纳米尺度密度与能量起伏. 经热力耦合作用, 准点缺陷首先被激活, 发生局域性原子重排并在最大剪切面形成微剪切畴. 由于非晶合金固有微观结构非均匀性, 不同准点缺陷位点激活难易程度不同, 原子移动速率以及初始微剪切畴体积也不尽相同. 在外界应力持续作用下, 微剪切畴发生增殖扩展, 体积逐渐增大. 同时, 该过程与扩散作用紧密相关, 属于典型热激活过程, 此时温度起主导作用. 温度越高, 微剪切畴增殖速度越快. 然而, 由于空间有限以及周围弹性基体限制, 微剪切畴不可无限增殖长大. 随应力和温度升高以及加载时间延长, 微剪切畴尺寸达到临界值. 相邻微剪切畴边界接触并发生不可逆相互融合, 可以认为这就是非晶合金塑性变形的物理本源. 即低应力只会引起微剪切畴形核长大, 其彼此相互独立且范围很小, 数量与施加应力成正比. 去除应力后, 微剪切畴逐渐收缩并回到初始状态. 因此, 非晶合金在该阶段变形与时间相关, 属于典型黏弹性变形行为; 另一方面, 在高温和高应力状态, 微剪切畴将经历不可逆融合过程, 此阶段变形不可回复, 且由黏塑性变形主导. 伴随应力继续增大或温度持续升高, 体系黏度显著下降, 黏塑性分量占比进一步增多, 进而导致非晶合金蠕变行为呈现越来越显著非线性特征.
3. 结 论
本文以La56.16Ce14.04Ni19.8Al10非晶合金为研究载体, 通过开展不同温度及应力下拉伸蠕变实验, 综合考查蠕变柔量、特征弛豫时间、准稳态蠕变速率及蠕变应力指数演化规律, 明晰了非晶合金在热力耦合激励过程中的蠕变机制. 基于准点缺陷理论, 揭示了非晶合金弹塑性转变与其微观结构演化之间关联, 主要结论如下.
(1) LaCe基非晶合金蠕变行为表现出温度与应力强依赖性, 终态蠕变柔量与准稳态蠕变速率均随温度升高或应力增加显著提高, 蠕变过程呈现越来越显著非线性特征.
(2) 蠕变应力指数不断升高, 且在高温区域增幅更加明显, 表明随应力增加(温度升高), 应力逐渐主导蠕变进程. 应力较低时, 非晶合金蠕变机制对应于热激活单粒子流动. 应力较高时, 非晶合金蠕变机制则对应于应力诱导局部剪切变形增强与温度诱导原子扩散等复杂耦合过程.
(3) 基于准点缺陷理论获得的柔量型解析表达式可精确描述并合理预测LaCe基非晶合金高温蠕变行为, 非晶合金蠕变变形过程所涉及弹塑性转变源于准点缺陷的激活、微剪切畴经热力耦合激励的形核长大、扩展与不可逆融合. 研究结果表明, 非晶合金动力学弛豫行为与高温流变行为的物理图像均可在准点缺陷理论框架下系统讨论, 这为进一步构建非晶合金弛豫行为、变形机理与其微观结构演化潜在关联提供了新的出发点和切入口.
-
图 9 准点缺陷理论描述LaCe基非晶合金的(a)动态弛豫行为与(b)~(d)高温蠕变行为, 其中红色实线为理论预测曲线, 黑色实线为实验数据曲线
Figure 9. Description of (a) dynamic relaxation behavior and (b)~(d) high temperature creep behavior of LaCe-based amorphous alloy in the framework of QPD theory. The red line represents the theoretical prediction curve and the black line represents the experimental results
-
[1] 汪卫华. 非晶态物质的本质和特性. 物理学进展, 2013, 33(5): 177-351 (Wang Weihua. The nature and properties of amorphous matter. Progress in Physics, 2013, 33(5): 177-351 (in Chinese) Wang Weihua, The nature and properties of amorphous matter. Progress in Physics, 2013, 33(6): 177-351 (in Chinese)
[2] Wang WH. Dynamic relaxations and relaxation-property relationships in metallic glasses. Progress in Materials Science, 2019, 106: 100561 doi: 10.1016/j.pmatsci.2019.03.006
[3] Zhang C, Ouyang D, Pauly S, et al. 3D printing of bulk metallic glasses. Materials Science and Engineering: Reports, 2021, 145: 100625 doi: 10.1016/j.mser.2021.100625
[4] 管鹏飞, 王兵, 吴义成等. 不均匀性: 非晶合金的灵魂. 物理学报, 2017, 66(17): 176112 (Guan Pengfei, Wang Bing, Wu Yicheng, et al. Heterogeneity: the soul of metallic glasses. Acta Physica Sinica, 2017, 66(17): 176112 (in Chinese) Guan Pengfei, Wang Bing, Wu Yicheng, et al. Heterogeneity: the soul of metallic glasses, Acta Physica Sinica, 2017, 66(17): 176112 (in Chinese)
[5] 王云江, 魏丹, 韩懂等. 非晶态固体的结构可以决定性能吗? 力学学报, 2020, 52(2): 303-317 Wang Yunjiang, Wei Dan, Han Dong, et al. Does structure determine property in amorphous solids? Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(2): 303-317 (in Chinese)
[6] Qiao JC, Wang Q, Pelletier JM, et al. Structural heterogeneities and mechanical behavior of amorphous alloys. Progress in Materials Science, 2019, 104: 250-329 doi: 10.1016/j.pmatsci.2019.04.005
[7] 乔吉超, 张浪渟, 童钰等. 基于微观结构非均匀性的非晶合金力学行为. 力学进展, 2022, 52(1): 117-152 (Qiao Jichao, Zhang Langting, Tong Yu, et al. Mechancial properties of amorphous alloys: In the framework of the microstructure heterogeneity. Advances in Mechanics, 2022, 52(1): 117-152 (in Chinese) doi: 10.6052/1000-0992-21-038 Qiao Jichao, Zhang Langting, Tong Yu, et al. Mechancial properties of amorphous alloys: In the framework of the microstructure heterogeneity. Advances in Mechanics, 2022, 52(1): 117-152 (in Chinese) doi: 10.6052/1000-0992-21-038
[8] 郝奇, 乔吉超, Pelletier JM. 锆基非晶合金的动态弛豫机制和高温流变行为. 力学学报, 2020, 52(2): 360-368 (Hao Qi, Qiao Jichao, Pelletier JM. Dynamic relaxation characteristics and high temperature flow behavior of Zr-based bulk metallic glass. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(2): 360-368 (in Chinese) doi: 10.6052/0459-1879-20-004 Hao Qi, Qiao Jichao, Pelletier JM. Dynamic relaxation characteristics and high temperature flow behavior of Zr-based bulk metallic glass. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(2): 360-368 (in Chinese) doi: 10.6052/0459-1879-20-004
[9] Schuh C, Hufnagel T, Ramamurty U. Mechanical behavior of amorphous alloys. Acta Materialia, 2007, 55(12): 4067-4109 doi: 10.1016/j.actamat.2007.01.052
[10] Cheng YT, Hao Q, Pelletier JM. Modelling and physical analysis of the high-temperature rheological behavior of a metallic glass. International Journal of Plasticity, 2021, 146: 103107 doi: 10.1016/j.ijplas.2021.103107
[11] Greer AL, Cheng YQ, Ma E. Shear bands in metallic glasses. Materials Science and Engineering: Reports, 2013, 74(4): 71-132 doi: 10.1016/j.mser.2013.04.001
[12] Shen J, Sun YH, Orava J, et al. Liquid-to-liquid transition around the glass-transition temperature in a glass-forming metallic liquid. Acta Materialia, 2022, 225: 117588 doi: 10.1016/j.actamat.2021.117588
[13] Li N, Chen Y, Jiang MQ. A thermoplastic forming map of a Zr-based bulk metallic glass. Acta Materialia, 2013, 61(6): 1921-1931 doi: 10.1016/j.actamat.2012.12.013
[14] Qiao JC, Pelletier JM, Yao Y. Creep in bulk metallic glasses: Transition from linear to non linear regime. Materials Science and Engineering: A, 2019, 743: 185-189
[15] Sun BA, Yu HB, Jiao W. Plasticity of ductile metallic glasses: a self-organized critical state. Physical Review Letters, 2010, 105(3): 035501 doi: 10.1103/PhysRevLett.105.035501
[16] Gan KF, Jiang SS, Huang YJ. Elucidating how correlated operation of shear transformation zones leads to shear localization and fracture in metallic glasses: Tensile tests on CuZr based metallic-glass microwires, molecular dynamics simulations, and modelling. International Journal of Plasticity, 2019, 119: 1-20 doi: 10.1016/j.ijplas.2019.02.011
[17] Zhang LT, Wang YJ, Pineda E, et al. Sluggish dynamics of homogeneous flow in high-entropy metallic glasses. Scripta Materialia, 2022, 214: 114673 doi: 10.1016/j.scriptamat.2022.114673
[18] Yoo BG, Kim JY, Kim YJ. Increased time-dependent room temperature plasticity in metallic glass nanopillars and its size-dependency. International Journal of Plasticity, 2012, 37: 108-118 doi: 10.1016/j.ijplas.2012.04.005
[19] 陈迎红, 王云江, 乔吉超. La30Ce30Al15Co25金属玻璃应力松弛行为. 力学学报, 2020, 52(3): 740-748 (Chen Yinghong, Wang Yunjiang, Qiao Jichao. Stress relaxation of La30Ce30Al15Co25 metallic glass. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(3): 740-748 (in Chinese) doi: 10.6052/0459-1879-20-013 Chen Yinghong, Wang Yunjiang, Qiao Jichao. Stress relaxation of La30Ce30Al15Co25 metallic glass. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(3): 740-748 (in Chinese) doi: 10.6052/0459-1879-20-013
[20] Duan YJ, Qiao JC, Wada T, et al. Stress relaxation in high-entropy Pd20Pt20Cu20Ni20P20 metallic glass: Experiments, modeling and theory. Mechanics of Materials, 2021, 160: 103959 doi: 10.1016/j.mechmat.2021.103959
[21] Zhu W, Liu J, Mao S, et al. A new continuum model for viscoplasticity in metallic glasses based on thermodynamics and its application to creep tests. Journal of the Mechanics and Physics of Solids, 2021, 146: 104216 doi: 10.1016/j.jmps.2020.104216
[22] Zhang LT, Duan YJ, Crespo D. Dynamic mechanical relaxation and thermal creep of high-entropy La30Ce30Ni10Al20Co10 bulk metallic glass. Science China Physics, Mechanics & Astronomy, 2021, 64(9): 296111
[23] Tao K, Qiao JC, Zhang L, et al. Dynamic mechanical response of ZrCu-based bulk metallic glasses. International Journal of Mechanical Sciences, 2021, 211: 106770 doi: 10.1016/j.ijmecsci.2021.106770
[24] Herrero-Gomez C, Samwer K. Stress and temperature dependence of the avalanche dynamics during creep deformation of metallic glasses. Scientific Reports, 2016, 6: 33503 doi: 10.1038/srep33503
[25] Cao PH, Short MP, Yip S. Understanding the mechanisms of amorphous creep through molecular simulation. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(52): 13631-13636 doi: 10.1073/pnas.1708618114
[26] Xu ZR, Yang DS, Qiao JC, et al. Unified perspective on structural heterogeneity of a LaCe-based metallic glass from versatile dynamic stimuli. Intermetallics, 2020, 125: 106922 doi: 10.1016/j.intermet.2020.106922
[27] Spaepen F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metallurgica, 1977, 25: 407-415 doi: 10.1016/0001-6160(77)90232-2
[28] Argon AS. Plastic deformation in metallic glasses. Acta Metallurgica, 1979, 27: 47-58 doi: 10.1016/0001-6160(79)90055-5
[29] Langer JS. Microstructural shear localization in plastic deformation of amorphous solids. Physical Review E, 2001, 64(1): 011504 doi: 10.1103/PhysRevE.64.011504
[30] Johnson WL, Samwer K. A universal criterion for plastic yielding of metallic glasses with a (T/Tg)2/3 temperature dependence. Physical Review Letters, 2005, 95(19): 195501 doi: 10.1103/PhysRevLett.95.195501
[31] Lei TJ, DaCosta LR, Liu M, et al. Composition dependence of metallic glass plasticity and its prediction from anelastic relaxation—A shear transformation zone analysis. Acta Materialia, 2020, 195: 81-86 doi: 10.1016/j.actamat.2020.04.053
[32] Perez J. Physics and Mechanics of Amorphous Polymers. Rotterdam: A.A. Balkema, 1998: 123-125
[33] 穆霞英. 蠕变力学. 西安: 西安交通大学出版社, 1989: 8-10 Mu Xiaying. Creep Mechanics. Xi’an: Xi’an Jiaotong University Press, 1989: 8-10 (in Chinese)
[34] Heggen M, Spaepen F, Feuerbacher M. Creation and annihilation of free volume during homogeneous flow of a metallic glass. Journal of Applied Physics, 2005, 97(3): 033506
[35] Perez J. Homogeneous flow and anelastic/plastic deformation of metallic glasses. Acta Metallurgica, 1984, 32(12): 2163-2173 doi: 10.1016/0001-6160(84)90159-7
[36] Palmer RG, Stein DL, Abrahams E, et al. Models of hierarchically constrained dynamics for glassy relaxation. Physical Review Letters, 1984, 53(10): 958-961 doi: 10.1103/PhysRevLett.53.958
[37] Rinaldi R, Gaertner R, Chazeau L, et al. Modelling of the mechanical behaviour of amorphous glassy polymer based on the Quasi Point Defect theory — Part I: Uniaxial validation on polycarbonate. International Journal of Non-Linear Mechanics, 2011, 46(3): 496-506 doi: 10.1016/j.ijnonlinmec.2010.11.004
[38] Chabert E, Ershad Langroudi A, Gauthier C, et al. Mechanical response in amorphous and semicrystalline poly (ethylene terephtalate) and modelling in frame of quasi point defect theory. Plastics, Rubber and Composites, 2010, 30(2): 56-67
[39] Hao Q, Lyu GJ, Pineda E, et al. A hierarchically correlated flow defect model for metallic glass: Universal understanding of stress relaxation and creep. International Journal of Plasticity, 2022, 154: 103288 doi: 10.1016/j.ijplas.2022.103288
-
期刊类型引用(5)
1. 张剑,郝奇,邢光辉,乔吉超. La基非晶合金蠕变缺陷激活机制. 力学学报. 2024(04): 1037-1046 .  本站查看
本站查看
2. 朱凡,邢光辉,Jean-Marc Pelletier,乔吉超. Hf元素添加对Cu Zr基非晶合金动态弛豫的影响. 力学学报. 2024(08): 2282-2293 .  本站查看
本站查看
3. 张剑,郝奇,邢光辉,乔吉超. 基于应力松弛变形探索La基金属玻璃微观非均匀性. 力学学报. 2024(09): 2616-2624 .  本站查看
本站查看
4. 段亚娟,徐宗睿,郝奇,H.Kato,乔吉超. Pd_(20)Pt_(20)Cu_(20)Ni_(20)P_(20)高熵非晶合金蠕变机理研究. 力学学报. 2024(10): 2913-2923 .  本站查看
本站查看
5. 乔吉超,梁淑一,张浪渟. 黏弹性本构关系构建方法及应用举例. 力学与实践. 2022(06): 1411-1415 .  百度学术
百度学术
其他类型引用(0)











 下载:
下载: