引言
接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究.
在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力.
如上述文献研究可知, 接触约束法和LuGre模型在碰撞问题研究中有各自的优势, 然而目前柔性梁采用接触约束法结合LuGre摩擦模型对斜碰撞问题研究的文献相对尚少. 本文首先以刚柔耦合多体系统动力学理论为基础建立无碰撞时重力作用下旋转柔性梁的动力学方程; 其次在碰撞时引入法向加速度约束计算出法向碰撞力建立无摩擦的碰撞动力学方程, 在切向摩擦力计算上对于LuGre模型提出两种不同处理方法, 第一种是对LuGre摩擦模型在黏滞时建立接触约束方程引入拉格朗日乘子计算出黏滞时切向摩擦力, 滑动时根据摩擦系数和法向碰撞力计算出相应摩擦力(与Coulomb摩擦模型处理切向摩擦力的方法一致). 第二种是无论滑动还是黏滞状态直接使用LuGre摩擦模型的摩擦力计算方法, 碰撞全部过程采用相同的摩擦力计算方程. 最后基于系统动力学方程编写含摩擦的碰撞动力学仿真程序. 通过动力学仿真发现LuGre模型在黏滞状态下两种不同建模方式的动力学特性无差别, Coulomb摩擦模型建模方式的动力学特性随着碰撞次数增加与LuGre摩擦模型的逐渐产生区别.
1 力学模型描述
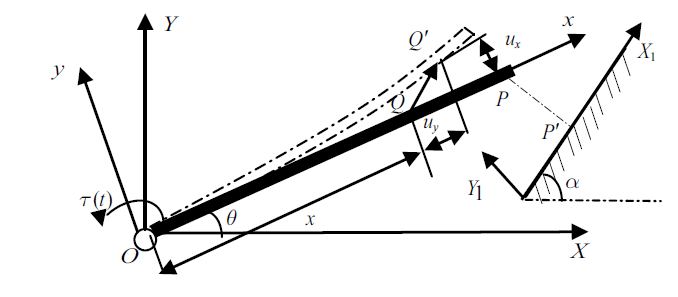
如图1 所述, 柔性梁绕铰$O$在重力场作用下作大范围定轴旋转运动, 柔性梁上任意一点$P$与刚性坡面上点${P}'$发生碰撞. 以铰$O$为惯性坐标系原点, 水平方向为惯性坐标系$X$轴, 建立惯性坐标系$OXY$. 在未变形时的柔性梁的中轴线为浮动坐标系的$x$轴, 铰$O$为原点建立单位矢量浮动坐标系$Oxy$. 惯性坐标系$OX$的轴和浮动坐标系$Ox$的夹角为柔性梁旋转运动时的转角$\theta $. 取刚性斜坡与水平面倾角斜率为$\alpha $, 设$O_{1} X_{1} $轴与斜坡重合建立碰撞面坐标系$O_{1} X_{1} Y_{1} $. 假设柔性梁为欧拉-伯努利梁, 忽略梁的轴向变形, 考虑横向弯曲变形引起的纵向缩短量(即非线性耦合变形量). 设柔性梁的物理参数分别为: 长度为$L$, 横截面为$S$, 密度为$\rho $, 弹性模量为$E$.
图1
图1
柔性梁碰撞模型图
Fig.1
Schematic of impact system of flexible beam
柔性梁在浮动坐标上任意一点$Q$变形后位移矢量表示为
(1) $\begin{eqnarray} \label{eq1} {u}=u_{x} (x,t){i}'+u_{y} (x,t){j}' \end{eqnarray} $
式(1)中是$u_{y} $表示任意点$Q$横向变形位移、 $u_{x} $表示为横向变形引起的纵向缩短量, 采用假设模态法将柔性变形位移离散表示为
(2) $u_{y} ={\varPhi }_{y} (x){B}(t) $
(3) $u_{x} =-\frac{1}{2}\int_0^x {\left( {\frac{\partial u_{y} }{\partial \xi }} \right)^{2}}{d}\xi =-\frac{1}{2}{B}^{T}(t){H}(x){B}(t) $
(4) $\begin{eqnarray} \label{eq4} {H}(x)=\int_0^x {\frac{\partial {\varPhi }_{y}^{T} (\xi )}{\partial \xi }} \frac{\partial {\varPhi }_{y} (\xi )}{\partial \xi }{d}\xi \end{eqnarray} $
式中, ${\varPhi }_{y} (x)$表示为柔性梁的横向振动模态函数的行阵, $B(t)$表示横向振动模态坐标列阵, $H(x)$表示耦合形函数矩阵.
2 碰撞动力学建模
2.1 无碰撞时刚柔耦合动力学方程
柔性梁上任意一点$Q$变形后位置矢量在惯性坐标下表示为
(5) $r=W({\rho }_{0} +u) $
(6) ${W}=\left[ {{\begin{array}{*{20}c} {\cos \theta } & {-\sin \theta } \\ {\sin \theta } & {\cos \theta } \\ \end{array} }} \right] $
(7) $\rho_{0} =(x,0)^{T} $
式中, $ W$表示惯性坐标到浮动坐标系的方向余弦矩阵, $\rho_{0}$表示任意点$Q$未变形前在浮动坐标系的位置. 柔性动能系统的动能为
(8) $\begin{eqnarray} \label{eq8} T=\frac{1}{2}\int_V {\rho {\dot{{r}}}^{T}{\dot{{r}}}{d}V} \end{eqnarray} $
(9) $\begin{eqnarray} \label{eq9} V=V_{E} +V_{G} =\frac{1}{2}\int_0^L {EI({B}{{\varPhi }"}_{y}^{T} {{\varPhi }"}_{y} {B})} {d}x-g^{T}{WR} \end{eqnarray} $
(10) $\begin{eqnarray} \label{eq10} {R}=\int_0^L {\rho S{h}(x){d}x} \end{eqnarray} $
式中, $V_{E} $和$V_{G}$分别为柔性梁的弹性势能和重力势能, $g$为惯性系下的重力加速度矢量阵, $h(x)$为任意点$Q$变形后在浮动坐标$Oxy$上的位置矢量阵. 将式(8)和式(9)代入第二类拉格朗日方程
(11) $\begin{eqnarray} \label{eq11} \frac{{d}}{{d}t}\left( {\frac{\partial T}{\partial {\dot{{q}}}}} \right)-\frac{\partial T}{\partial {q}}=-\frac{\partial V}{\partial {q}}+{F} \end{eqnarray} $
式中, ${F}$为非保守力对应的广义力, 其中$F=[\tau,{\bf0}]^{T}$, $\tau $为转动铰中的驱动力矩, 通过推导可得到系统的动力学方程
(12) $\begin{eqnarray} \label{eq12} \left[ {{\begin{array}{c@{\quad }c} {{M}_{11} } & {{M}_{12} } \\ {{M}_{21} } & {{M}_{22} } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\ddot{{\theta }}} \\ {{\ddot{{B}}}} \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {Q_{\theta } } \\ {{Q}_{{B}} } \\ \end{array} }} \right] \end{eqnarray} $
(13) ${M}_{11} =J_{ob} +{B}^{T}{M}_{2} {B}-{B}^{T}{DB} + \frac{1}{4}\int_0^L {\rho S{B}^{T}{HB}\cdot } {B}^{T}{HB}{d}x $
(14) ${M}_{21} ={M}_{12}^{T} ={S}_{y}^{T} +\int_0^L {\rho S{HB}{\varPhi }_{y} {B}{d}x} - \frac{1}{2}\int_0^L {\rho S{\varPhi }_{y}^{T} {B}^{T}{HB}{d}x} $
(15) ${M}_{22} ={M}_{2} +\int_0^L {\rho S{HBB}^{T}{H}{d}x} $
(16) $\begin{eqnarray} \label{eq16} && Q_{\theta } =\tau -2\dot{{\theta }}\left( {{B}^{T}{M}_{2} {\dot{{B}}}-{B}^{T}{\dot{{D}}B}} \right) - \\&& \dot{{\theta }}\int_0^L {\rho S{B}^{T}{HBB}^{T}{HB}{d}x}-\\&& \int_0^L {\rho A{\dot{{B}}}^{T}{\dot{{H}}B}{\varPhi }_{y} {B}{d}x} +g^{T}\frac{\partial {W}}{\partial \theta }{R} \end{eqnarray} $
(17) $\begin{eqnarray} \label{eq17} && {Q}_{B} =\dot{{\theta }}({M}_{2} -{D}){B}-{K}_{2} {B} +\\&& \int_0^L {\rho S\bigg(\frac{1}{2}\dot{{\theta }}{HBB}^{T}{HB}-{HB\dot{{B}}}^{T}{\dot{{H}}B}\bigg)} {d}x -\\&& \int_0^L {\rho S\left[ {2\dot{{\theta }}({HB}{\varPhi }_{y} {\dot{{B}}}-{\varPhi }_{y}^{T} {B}^{T}{\dot{{H}}B})} \right]} {d}x + \\&& \bigg(g^{T}{W}\frac{\partial {R}}{\partial {B}}\bigg)^{T} \end{eqnarray} $
(18) $J_{ob} =\int_0^L {\rho Sx^{2}{d}x} $
(19) $M_{2} =\int_0^L {\rho S\varPhi_{y}^{T} \varPhi_{y} {d}x} $
(20) ${S}_{y} =\int_0^L {\rho S{\varPhi }_{y} (x){d}x} $
(21) ${D}=\int_0^L {\rho Sx{H}(x){d}x} $
(22) ${K}_{2} =\int_0^L {EI{{\varPhi }"}_{y}^{T} {{\varPhi }"}_{y} {d}x} $
2.2 无摩擦系统碰撞动力学方程
梁上一点$P$与刚性斜坡上点${P}'$会发生碰撞, 碰撞面的单位法向量和切向量在惯性坐标系分别为 $n=[n_{x},n_{y} ]^{T}$和$\tau =[\tau_{x},\tau_{y} ]^{T}$, $W_{P} $为惯性坐标系到刚性斜坡坐标系的转换矩阵. 在发生碰撞时, 梁上碰撞点$P$相对于斜面接触点${P}'$的在斜坡法向上位移相同, 因此法向位移约束方程为
(23) $ \begin{eqnarray} \label{eq23} &&\varPsi =(n_{x} \cos \theta +n_{y} \sin \theta )\bigg(x_{P} -\frac{1}{2}B^{T}H(x_{P} )B\bigg) + \\ && (-n_{x} \sin \theta +n_{y} \cos \theta )\varPhi_{y} B -\\ && n_{P} (W_{P}r_{P} )=0 \end{eqnarray} $
假设碰撞面-刚性斜坡为静止, 则$W_{P} =r_{P} ={\bf0}$. 通过推导法向速度、法向加速度约束方程为
(24) $\dot{{\varPsi }}=\varPsi_{q} \dot{{q}}=0 $
(25) $\ddot{{\varPsi }}=\varPsi_{q} \ddot{{q}}+(\varPsi_{q} \dot{{q}})_{q} \dot{{q}}=\varPsi _{q} \ddot{{q}}+\dot{{\varPsi }}_{q} \dot{{q}}=0 $
(26) $\varPsi_{q} =[\varPsi_{\theta },\varPsi_{B_{1} },\varPsi_{B_{2} }, \cdots ,\varPsi_{B_{N} } ] $
(27) $\dot{{\varPsi }}_{q} =[\dot{{\varPsi }}_{\theta },\dot{{\varPsi }}_{B_{1} } ,\dot{{\varPsi }}_{B_{2} }, \cdots,\dot{{\varPsi }}_{B_{N} } ] $
(28) $\begin{eqnarray} \label{eq28} && \varPsi_{\theta } =(-n_{x} \sin \theta +n_{y} \cos \theta )\Bigg[x_{P} -\frac{1}{2}B^{T}H(x_{P} )B\Bigg] + \\&& (-n_{x} \cos \theta -n_{y} \sin \theta )\varPhi_{y} B \end{eqnarray} $
(29) $\begin{eqnarray} \label{eq29} && \varPsi_{B_{i} } =(n_{x} \cos \theta +n_{y} \sin \theta )\left[-\sum\limits_{j=1}^N {H_{ij} (x_{P} )B_{j} } \right] + \\&& (-n_{x} \sin \theta +n_{y} \cos \theta )\varPhi_{yi} (x_{P} ) \end{eqnarray} $
(30) $\begin{eqnarray} \label{eq30} && (\dot{{\varPsi }})_{\theta } =\Bigg\{(-n_{x} \cos \theta -n_{y} \sin \theta )\Bigg[x_{P} -\frac{1}{2}B^{T}H(x_{P} )B\Bigg] + \\&& (n_{x} \sin \theta -n_{y} \cos \theta )\varPhi _{y}^{T} (x_{P} )B\Bigg\}\dot{{\theta }} + \\&& (-n_{x} \sin \theta +n_{y} \cos \theta )(-B^{T}H(x_{P} )B) + \\&& (-n_{x} \cos \theta -n_{y} \sin \theta )\varPhi_{y} (x_{P} )\dot{{B}} \end{eqnarray} $
(31) $\begin{eqnarray} \label{eq31} && (\dot{{\varPsi }})_{B_{i} } =\Bigg\{(-n_{x} \sin \theta +n_{y} \cos \theta )\Bigg[-\sum\limits_{j=1}^N {H_{ij} (x_{P} )B_{j} }\Bigg] + \\&& (-n_{x} \cos \theta -n_{y} \sin \theta )\varPhi_{yi} (x_{P} )\Bigg\}\dot{{\theta }} + \\&& (n_{x} \cos \theta +n_{y} \sin \theta )\Bigg[-\sum\limits_{j=1}^N {H_{ij} (x_{P} )\dot{{B}}_{j} } \Bigg] \end{eqnarray} $
(32) $\begin{eqnarray} \label{eq32} \varPsi_{q} \ddot{{q}}=-(\dot{{\varPsi }})_{q} \dot{{q}}=\gamma_{n} \end{eqnarray} $
(33) $\left[ {{\begin{array}{*{20}c} M & {\varPsi_{q}^{T} } \\ {\varPsi_{q} } & 0 \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\ddot{{q}}} \\ {\lambda_{n} } \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} Q \\ {\gamma_{n} } \\ \end{array} }} \right] $
式(33)中, $\ddot{{q}}$为无碰撞时广义坐标阵, $M$和$Q$分别为无碰撞时柔性梁的广义质量阵和广义力阵; $\varPsi_{q} $为Jacobi矩阵, $\lambda_{n} $ 为Lagrange乘子表示接触约束反力.
式(33)碰撞动力学方程式为微分-代数混合方程组, 为了满足相容性条件; 采用Baumgarte违约修正方法引入违约数. 加速度的约束方程表示为
(34) $\begin{eqnarray} \label{eq34} \ddot{{\varPsi }}+2\chi \dot{{\varPsi }}-\beta^{2}\varPsi =0 \end{eqnarray} $
(35) $\left[ {{\begin{array}{*{20}c} M & {\varPsi_{q}^{T} } \\ {\varPsi_{q} } & 0 \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\ddot{{q}}} \\ {\lambda_{n} } \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} Q \\ {\gamma_{n}^{* } } \\ \end{array} }} \right] $
(36) $\gamma_{n}^{* } =\gamma_{n} -2\chi \dot{{\varPsi }}-\beta^{2}\varPsi $
由式(33), 式(35)和式(36) Lagrange乘子求解得
(37) $\begin{eqnarray} \label{eq35} \lambda_{n} =(\varPsi_{q} M^{-1}\varPsi_{q}^{T} )^{-1}(\varPsi_{q} M^{-1}Q-\gamma _{n}^{* } ) \end{eqnarray} $
将式(37)计算Lagrange乘子代回无摩擦碰撞动力学方程(35), 方程变为封闭的常微分方程组, 可以求此时刻的$\ddot{{q}}$初值, 进而通过求解得到下一时刻的$q$和$\dot{{q}}$. 则无摩擦时碰撞动力学方程可转化为
(38) $\begin{eqnarray} \label{eq38} M\ddot{{q}}=Q-\varPsi_{q}^{T} \lambda_{n} \end{eqnarray} $
2.3 碰撞的初始条件求解
在接触约束法中, 初始接触瞬间速度是不连续的, 在碰撞接触时直接添加约束会导致该时刻运动不协调从而导致违约计算困难的情况. 为了实现运动的协调, 在初始碰撞时刻需要实现无碰撞到碰撞的速度跳跃, 得出碰撞时刻添加约束的速度. 对于得出速度跳跃值, 许多学者进行了研究. Dong等[29 ] 根据连续介质力学的间断面理论得到碰撞初始速度, 段玥晨等[30 ] 利用冲量-动量法求出速度的跳跃值. 本文采用冲量动量法求出碰撞的初始速度
(39) $\begin{eqnarray} \label{eq39} \left[ {{\begin{array}{*{20}c} M & {-D_{n} } \\ {D_{n}^{T} } & 0 \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\Delta q} \\ I \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {{\bf 0}} \\ {-(1+e)v_{n0} } \\ \end{array} }} \right] \end{eqnarray} $
式中, $v_{n0} $为柔性梁上碰撞点$P$在碰撞前速度沿斜坡法向的投影, $I$为碰撞冲量, $D_{n} $为$n$维数组
(40) $D_{n} =[D_{n_{\theta } },D_{nB_{1} },D_{nB_{2} },\cdots,D_{nB_{N} } ]^{T} $
(41) $D_{n_{\theta } } =-\frac{\partial \hat{{V}}_{I} }{\partial \theta }/I=n\frac{\partial W}{\partial \theta }h_{F} $
(42) $D_{nB_{i} } =-\frac{\partial \hat{{V}}_{I} }{\partial B_{i} }/I=n\frac{\partial W}{\partial B_{i} }h_{F} $
式中,$\hat{{V}}_{I} $冲量势, $W$为惯性系到浮动坐标系的方向余弦阵, $n$为在惯性坐标系下斜坡的法向单位矢量. 相关方程如下
(43) $D_{n_{\theta } } =(-n_{x} \sin \theta +n_{y} \cos \theta )\Bigg[x_{P} -\frac{1}{2}B^{T}H(x_{P} )B\Bigg] + (-n_{x} \cos \theta -n_{y} \sin \theta )\varPhi_{y} B $
(44) $D_{nB_{i} } =(n_{x} \cos \theta +n_{y} \sin \theta )\Bigg[-\sum\limits_{j=1}^N {H_{ij} (x_{P} )B_{j} }\Bigg] + (-n_{x} \sin \theta +n_{y} \cos \theta )\varPhi_{yi} (x_{P} ) $
(45) $I=-(1+e)(D_{n}^{T} M^{-1}D_{n} )^{-1}v_{n0} $
(46) $\Delta q=M^{-1}D_{n} I $
(47) $\dot{{q}}\vert_{t^{+}} =\dot{{q}}\vert_{t^{+}} +\Delta\dot{{q}} $
(48) $q\vert_{t^{+}} =q\vert_{t^{-}} $
其中, $\dot{{q}}\vert_{t^{-}} $和$\dot{{q}}\vert_{t^{+}} $分别表示柔性梁上碰撞点初始时刻碰撞前后速度, $q\vert_{t^{+}} $和$q\vert _{t^{-}} $柔性梁上碰撞点碰撞前后广义位移.
2.4 黏滞状态时碰撞动力学方程
柔性梁上碰撞点$P$在碰撞过程中还包含切向的摩擦力作用. 切向运动可以分为黏滞状态和滑移状态, 在碰撞接触过程中满足一定条件可以相互切换. 在黏滞的状态下, 因为切向没有发生运动, 需要建立切向的约束方程求解摩擦力, 在滑移状态下, 需要根据摩擦系数来确定, 通过引入摩擦力势能求解.
当系统处于黏滞状态时, 柔性梁上碰撞点$P$和斜坡上接触点$P'$在斜坡上切向位移相同, 由此切向的约束方程为
(49) $\begin{eqnarray} \label{eq49} && \varGamma =(\tau_{x} \cos \theta +\tau_{y} \sin \theta )\Bigg[x_{P} -\frac{1}{2}B^{T}H(x_{P} )B\Bigg] + \\&& (-\tau_{x} \sin \theta +\tau_{y} \cos \theta )\varPhi_{y} B -\tau_{P} (W_{P} r_{P} )=0 \end{eqnarray} $
(50) $\dot{{\varGamma }}=\varGamma_{q} \dot{{q}}=0 $
(51) $\ddot{{\varGamma }}=\varGamma_{q} \ddot{{q}}+(\varGamma_{q} \dot{{q}})_{q} \dot{{q}}=\varGamma_{q} \ddot{{q}}+\dot{{\varGamma }}_{q} \dot{{q}}=0 $
(52) $\varGamma_{q} =[\varGamma_{\theta },\varGamma_{B_{1} },\varGamma_{B_{2} },\cdots,\varGamma_{B_{N} } ] $
(53) $\dot{{\varGamma }}_{q} =[\dot{{\varGamma }}_{\theta },\dot{{\varGamma }}_{B_{1} } ,\dot{{\varGamma }}_{B_{2} },\cdots,\dot{{\varGamma }}_{B_{N} } ] $
(54) $\varGamma_{\theta } =(-\tau_{x} \sin \theta +\tau_{y} \cos \theta )\Bigg[x_{P} -\frac{1}{2}B^{T}H(x_{P} )B\Bigg] +\\ (-\tau_{x} \cos \theta -\tau_{y} \sin \theta )\varPhi_{y} B $
(55) $\begin{eqnarray} \label{eq55} && \varGamma_{B_{i} } =(\tau_{x} \cos \theta +\tau_{y} \sin \theta )\Bigg[-\sum\limits_{j=1}^N {H_{ij} (x_{P} )B_{j} }\Bigg] +\\&& (-\tau_{x} \sin \theta +\tau_{y} \cos \theta )\varPhi_{yi} (x_{P} )\end{eqnarray} $
(56) $\begin{eqnarray} \label{eq56} && \dot{{\varGamma }}_{\theta } =\Bigg\{(-\tau_{x} \cos \theta -\tau_{y} \sin \theta )\Bigg[x_{P} -\frac{1}{2}B^{T}H(x_{P} )B\Bigg] +\\&& (\tau_{x} \sin \theta -\tau_{y} \cos \theta )\varPhi_{y} (x_{P} )B\Bigg\}\dot{{\theta }} +\\&& (-\tau_{x} \sin \theta +\tau_{y} \cos \theta )\Bigg[-B^{T}H(x_{P} )B\Bigg] + \\&& (-\tau_{x} \cos \theta -\tau_{y} \sin \theta )\varPhi_{y} (x_{P} )\dot{{B}} \end{eqnarray} $
(57) $\begin{eqnarray} \label{eq57} && \dot{{\varGamma }}_{B_{i} } =\Bigg\{(-\tau_{x} \sin \theta +\tau_{y} \cos \theta )\Bigg[-\sum\limits_{j=1}^N {H_{ij} (x_{P} )B_{j} }\Bigg] + \\&& (-\tau_{x} \cos \theta -\tau_{y} \sin \theta )\varPhi_{yi} (x_{P} )\Bigg\}\dot{{\theta }} + \\&& (\tau_{x} \cos \theta +\tau_{y} \sin \theta )\Bigg[-\sum\limits_{j=1}^N {H_{ij} (x_{P} )\dot{{B}}_{j} }\Bigg] \end{eqnarray} $
(58) $\begin{eqnarray} \label{eq58} \varGamma_{q} \ddot{{q}}=-(\dot{{\varGamma }})_{q} \dot{{q}}=\gamma_{\tau } \end{eqnarray} $
研究发现斜向碰撞过程和法向碰撞力和切向摩擦力变化同步[33 ] , 目前大多数学者认为切向碰撞力和法向摩擦力相互独立[10 ,34 ] . 可以将无摩擦动力学和切向接触约束方程结合, 黏滞状态的动力学方程为
(59) $\begin{eqnarray} \label{eq59} \left[ {{\begin{array}{c@{\quad }c@{\quad }c} M & {\varPsi_{q}^{T} } & {\varGamma_{q}^{T} } \\ {\varPsi_{q} } & 0 & 0 \\ {\varGamma_{q} } & 0 & 0 \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\ddot{{q}}} \\ {\lambda_{n} } \\ {\lambda_{\tau } } \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} Q \\ {\gamma_{n} } \\ {\gamma_{\tau } } \\ \end{array} }} \right] \end{eqnarray} $
为了同时满足位移、速度和加速度的约束方程, 分别对法向和切向接触约束方程和切向约束方程进行违约修正
(60) $\ddot{{\varPsi }}+2\chi \dot{{\varPsi }}-\beta^{2}\varPsi =0 $
(61) $\ddot{{\varGamma }}+2\chi \dot{{\varGamma }}+\beta^{2}\varGamma =0 $
(62) $\left[ {{\begin{array}{c@{\quad }c@{\quad }c} M & {\varPsi_{q}^{T} } & {\varGamma_{q}^{T} } \\ {\varPsi_{q} } & 0 & 0 \\ {\varGamma_{q} } & 0 & 0 \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\ddot{{q}}} \\ {\lambda_{n} } \\ {\lambda_{\tau } } \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} Q \\ {\gamma_{n}^{* } } \\ {\gamma_{\tau }^{* } } \\ \end{array} }} \right] $
(63) $\gamma_{n}^{* } =\gamma_{n} -2\chi \dot{{\varPsi }}-\beta^{2}\varPsi $
(64) $\gamma_{\tau }^{* } =\gamma_{\tau } -2\chi \dot{{\varGamma }}-\beta ^{2}\varGamma $
由黏滞状态下碰撞动力学方程求出, 即法向和切向的接触约束反力为
(65) $\lambda_{n} =(\varPsi_{q} M^{-1}\varPsi_{q}^{T} )^{-1}(\varPsi_{q} M^{-1}Q-\gamma _{n}^{* } ) $
(66) $\lambda_{\tau } =(\varGamma_{q} M^{-1}\varGamma_{q}^{T} )^{-1}(\varGamma_{q} M^{-1}Q-\gamma_{\tau }^{* } ) $
将求解得Lagrange乘子$\lambda_{n} $和$\lambda_{\tau } $代回式(62)中, 计算出此时的广义加速度$\ddot{{q}}$, 通过常微分方程的求解得出下一时刻$\dot{{q}}$和$q$. 则柔性梁碰撞时在黏滞状态下的动力学方程为
(67) $\begin{eqnarray} \label{eq67} M\ddot{{q}}=Q-\varPsi_{q}^{T} \lambda_{n} -\varGamma_{q}^{T} \lambda_{\tau } \end{eqnarray} $
2.5 滑动状态时碰撞动力学方程
在碰撞中发生滑移时, 碰撞点法向间距、速度、加速度始终为零, 而切向产生碰撞点的位移、速度、加速度不为零, 本文分别采用Coulomb摩擦模型和LuGre摩擦模型用来描述滑动过程中的实际摩擦系数. Coulomb摩擦模型取动摩擦系数$\mu_{d} $, LuGre模型摩擦系数为
(68) $\begin{eqnarray} \label{eq68} \left. {{\begin{array}{l} {u=\sigma_{0} z+\sigma_{1} \dot{{z}}+\sigma_{2} v_{\tau } } \\ {\dot{{z}}=v_{\tau } -\sigma_{0} \dfrac{\left| {v_{\tau } } \right|}{g(v_{\tau } )}z} \\ {g(v_{\tau } )=\mu_{d} +(\mu_{s} -\mu_{d} ){e}^{-({{v_{\tau } }/{v_{s} }})^{2}}} \\ \end{array} }} \right\} \end{eqnarray} $
式中, $z$和$\dot{{z}}$表示梁上碰撞点$P$与斜坡接触点${P}'$的平均鬃毛变形和变形速率; $\sigma_{0}$, $\sigma_{1}$, $\sigma_{2} $ 分别表示鬃毛刚度系数、鬃毛阻尼系数、黏性摩擦系数; $v_{s} $为 stribeck速率; $\mu_{d}$和$\mu_{s} $分别表示动摩擦系数、静摩擦系数.
(69) $\begin{eqnarray} \label{eq64} \left. \begin{array}{l@{\quad }l} {\lambda }'_{\tau } =-{sgn}(v_{\tau } )\mu_{{d}} \lambda_{N}, & \mbox{Coulomb model} \\ {\lambda }'_{\tau } =-\mu \lambda_{N}, & \mbox{LuGre model} \\ \end{array} \right\} \end{eqnarray} $
(70) $\begin{eqnarray} \label{eq65} V_{\tau } =\left\{\begin{array}{l@{\quad }l} -{sgn}(v_{\tau } )\mu_{{d}} \lambda_{N} \varGamma, & \mbox{Coulomb model} \\ -\mu \lambda_{N} \varGamma, & \mbox{LuGre model} \\ \end{array} \right. \end{eqnarray} $
(71) $\begin{eqnarray} \label{eq71} M\ddot{{q}}+\varPsi_{q}^{T} \lambda_{n} +\frac{\partial V_{\tau } }{\partial q}=Q \end{eqnarray} $
式(71)中$M$为无碰撞时动力学方程(12)中广义质量矩阵, $\varPsi_{q}^{T} $为法向约束.
(72) $Q^{\tau }=-\frac{\partial V_{\tau } }{\partial q} $
(73) $Q_{\theta }^{\tau } =-{\lambda }'_{\tau } \frac{\partial \varGamma }{\partial \theta }=-{\lambda }'\varGamma_{\theta } $
(74) $Q_{B_{i} }^{\tau } =-{\lambda }'_{\tau } \frac{\partial \varGamma }{\partial B_{i}}=-{\lambda }'_{\tau } \varGamma_{B_{i} } $
(75) $\begin{eqnarray} \label{eq75} M\ddot{{q}}=Q-\varPsi_{q}^{T} \lambda_{n} -\varGamma_{q}^{T} {\lambda }'_{\tau} \end{eqnarray} $
2.6 碰撞时状态的切换准则
接触/分离切换的准则是通过与斜坡的法向间距矢量和法向相对速度, 判断是否是碰撞接触状态需要同时满足:
黏滞/滑移状态切换准则:在切向接触状态中存在黏滞、正滑移、逆滑移现象, 在切向接触过程其滑动和黏滞的判断条件为
(76) $\left.\begin{array}{ll} \left|v_{\tau}\right| \leqslant D_{v}, \left|\mu \lambda_{n}\right| \leqslant\left|\lambda_{\tau}\right| ; & \text { stick } \\ \left|v_{\tau}\right|>D_{v}, \left|\mu \lambda_{n}\right|>\left|\lambda_{\tau}\right| ; & \text { slip } \\ v_{\tau}=0, \left|\mu \lambda_{n}\right|>\left|\lambda_{\tau}\right| ; & \text { stick } \rightarrow \text { slip } \\ \left|v_{\tau}\right|>D_{v}, \left|\mu \lambda_{n}\right| \leqslant\left|\lambda_{\tau}\right| ; & \text { slip } \rightarrow \text { stick } \end{array}\right\}$
其中, Coulomb模型中$\mu_{d} $和$\mu $相同, 因为零时刻速度程序难以获得, 当切向速度小于微小速度$D_{v} $时, 本文认为发生黏滞.
(1) Coulomb模型黏滞时考虑切向约束混合建模方式(即hybrid Coulomb model)和LuGre模型黏滞时考虑切向约束混合建模方式(即hybrid LuGre model).
(77) $\begin{eqnarray} \label{eq77} M\ddot{{q}}=Q-\varPsi_{q}^{T} \lambda_{n} -\varGamma_{q}^{T} \lambda_{\tau } \end{eqnarray} $
(78) $\begin{eqnarray} \label{eq78} M\ddot{{q}}=Q-\varPsi_{q}^{T} \lambda_{n} -\varGamma_{q}^{T} {\lambda }'_{\tau} \end{eqnarray} $
(2) LuGre模型黏滞时不考虑切向约束采用统一摩擦力公式建模方式(即LuGre model).
(79) $\begin{eqnarray} \label{eq79} M\ddot{{q}}=Q-\varPsi_{q}^{T} \lambda_{n} -\varGamma_{q}^{T} {\lambda }'_{\tau} \end{eqnarray} $
3 动力学仿真
3.1 与现有文献对比
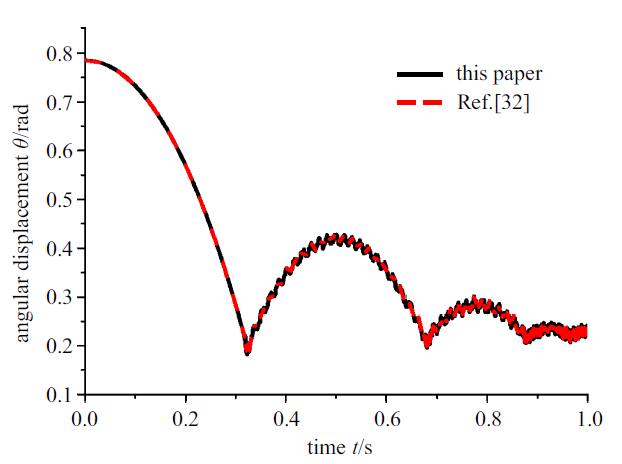
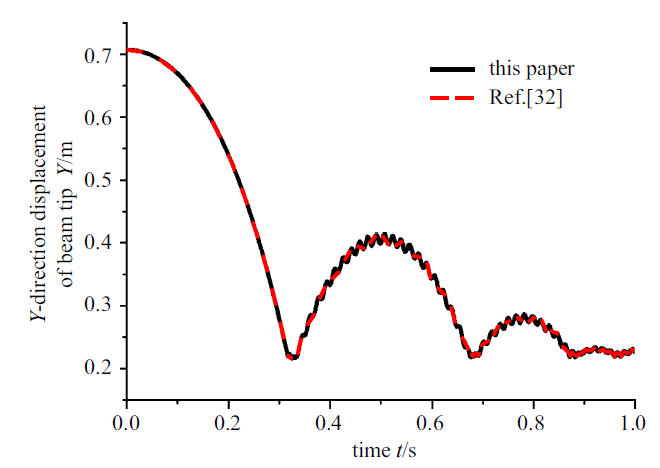
取柔性梁的参数为: $L=1.0$ m, $S=3.14\times 10^{-4}$ m$^{2}$, $\rho =27 667$ kg/m$^{3}$, $E=68.952$ GPa, $I=7.85\times 10^{-9}$. 假设柔性梁在初始状态处于静止和未变形状态; 柔性梁在初始角度$\theta ={\pi /4}$处在重力场下作自由下落. 旋转过程中柔性梁和原点位于(0.3, 0)处倾角$\alpha $为${\pi /{10}}$的刚性斜坡发生; 取动摩擦系数$\mu_{d} $为0.3, 如图2 和图3 所示柔性梁的角位移和末端$Y$方向位移与文献[32 ]仿真结果对比相同.
图2
图2
角位移
Fig.2
Angular displacement
图3
图3
梁末端末端$Y$方向位移
Fig.3
$Y$-direction displacement of beam tip
3.2 仿真结果分析
取柔性梁尺寸与材料参数如3.1节所示; 取违约数$\chi $和$\beta $为10和1000. 在惯性坐标系(0.5, 0)处取刚性斜坡坐标原点, 斜坡坡倾角为${\pi /{10}}$; 柔性梁在初始角度$\theta ={\pi /4}$处在重力场下作自由下落与斜坡发生碰撞. 取动摩擦系数$\mu_{d} $为0.4、最大静摩擦系数$\mu_{s} $为0.5, 通过对比取$\sigma_{0} $为$1.0\times 10^{5}$ N/m、$\sigma_{1} $为$1.0\times 10^{2}$ N$\cdot$s/m; 假设初始时刻柔性梁未发生变形, 未碰撞时和碰撞结束后鬃毛平均变形$z$和平均变形速率$\dot{{z}}$为0.
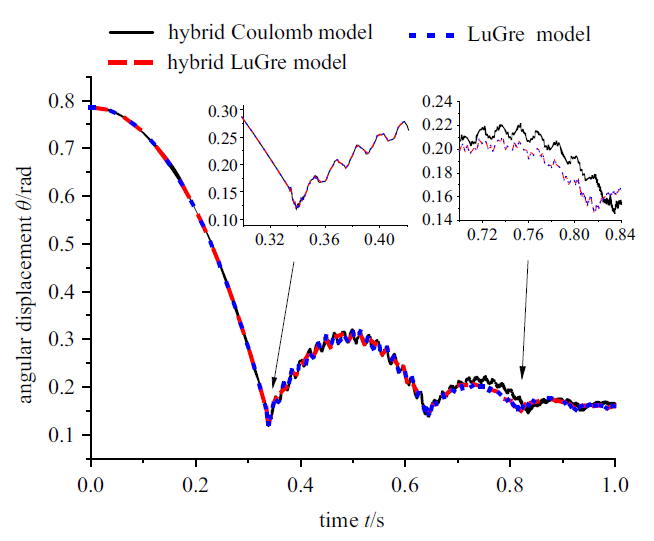
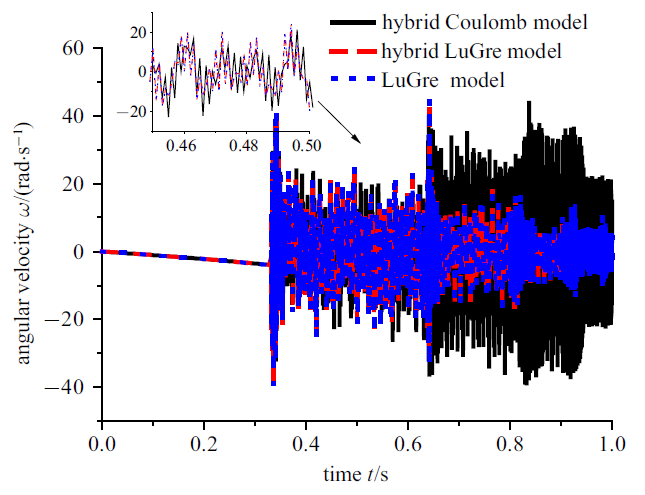
图4 和图5 分别表示旋转柔性梁在碰撞过程中角位移和角速度变化. 如图4 和图5 所示LuGre摩擦模型在仿真时考虑约束(黏滞时考虑切向约束方程混合建模方式 —— hybrid LuGre model)和不考虑约束(黏滞时不考虑切向约束方程建模方式 —— LuGre model)的角位移和角速度相同; 如图4 所示Coulomb摩擦模型(即hybrid Coulomb model)的角位移与LuGre摩擦模型考虑约束和不考虑约束的变化趋势相同, 但变化并不完全相同, 在第一次碰撞时和碰撞后3种摩擦模型基本相同, 第二次碰撞后Coulomb摩擦模型和LuGre摩擦模型(hybrid LuGre model和LuGre model)的角位移存在不同, 其反弹最大角位移相对偏大. 如图5 所示3种摩擦模型在碰撞后角速度曲线变化趋势相同, 在第一次碰撞后LuGre模型考虑约束和不考虑约束两者没有区别, Coulomb模型与LuGre模型考虑约束和不考虑约束的角速度有细微差别; 但是第二次以后碰撞Coulomb模型的速度变化范围相对于LuGre模型的区别较大. 碰撞过程黏滞状态时, LuGre模型考虑切向约束和不考虑的两种建模方式对旋转柔性梁的角位移和角速度无影响.
图4
图4
柔性梁角位移
Fig.4
Angular displacement of flexible beam
图5
图5
柔性梁角速度
Fig.5
Angular velocity of flexible beam
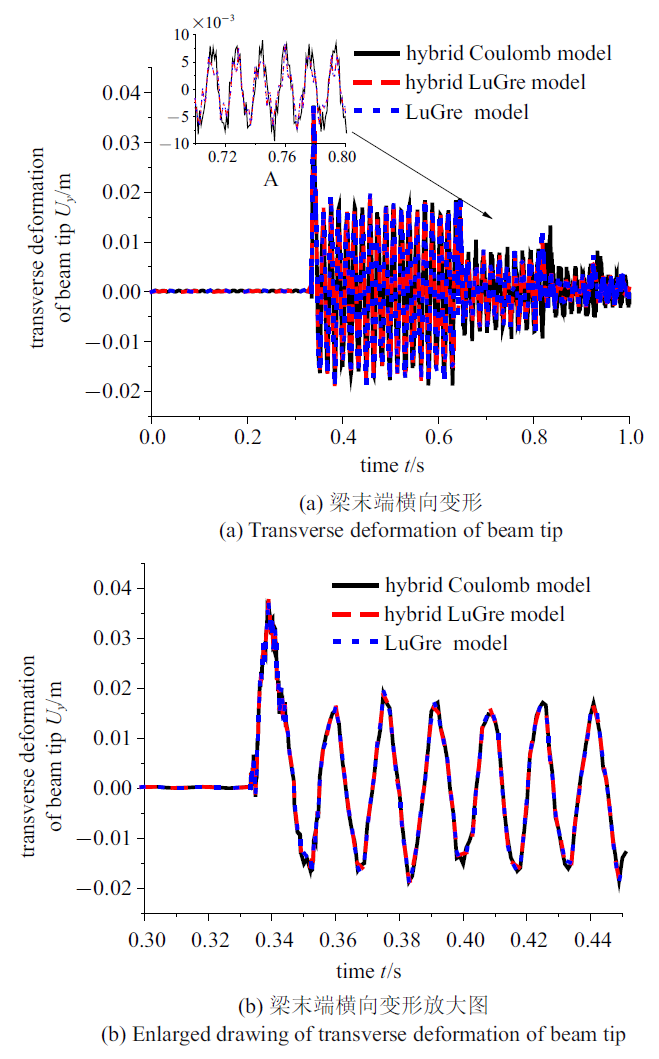
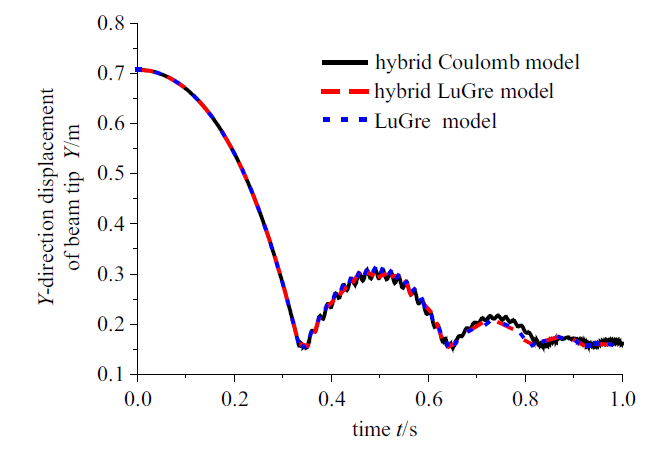
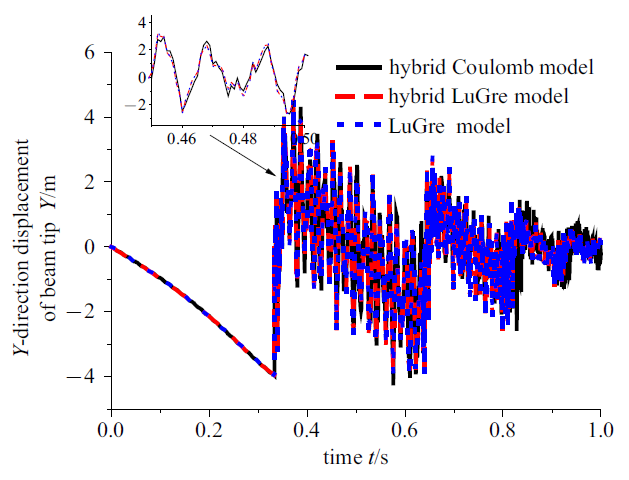
图6 所示为柔性梁末端横向变形, 由图6 (a)可知LuGre模型两种方式(即hybrid LuGre model和LuGre model)与Coulomb模型碰撞后的横向变形的曲线变化趋势相同. 由图6 (a)和图6 (b)看出在第一次碰撞后3种模型的末端变形曲线基本重合; 在第二次碰撞后, Coulomb模型相对LuGre模型两种方式柔性梁末端变形的变化基本相同但是变形量相对LuGre模型两种方式稍微偏大; 第三次碰撞后Coulomb模型变形量相对于LuGre模型有明显不同, 碰撞后末端横向变形量明显偏大. LuGre模型两种方式在多次碰撞中末端变形仍然相同. 图7 和图8 分别表示柔性梁末端$Y$方向的位移和速度, 从图7 和图8 可以看出, 3种模型方式(即hybrid Coulomb model, hybrid LuGre model和LuGre model)柔性梁末端在$Y$方向位移和速度变化基本相同. 在仿真时间内, LuGre模型两种方式$Y$方向位移和速度变化曲线重合, Coulomb模型随着碰撞次数增多和LuGre模型两种方式$Y$方向位移和速度曲线差别先变大后变小. LuGre模型考虑约束和不考虑约束柔性梁末端变形、位移、速度变化相同.
图6
图6
柔性梁末端横向变形图
Fig.6
Transverse deformation of flexible beam tip
图7
图7
柔性梁末端Y 方向位移
Fig. 7
Y -direction displacement of flexible beam tip
图8
图8
柔性梁末端$Y$方向速度
Fig.8
$Y$-direction velocity of flexible beam tip
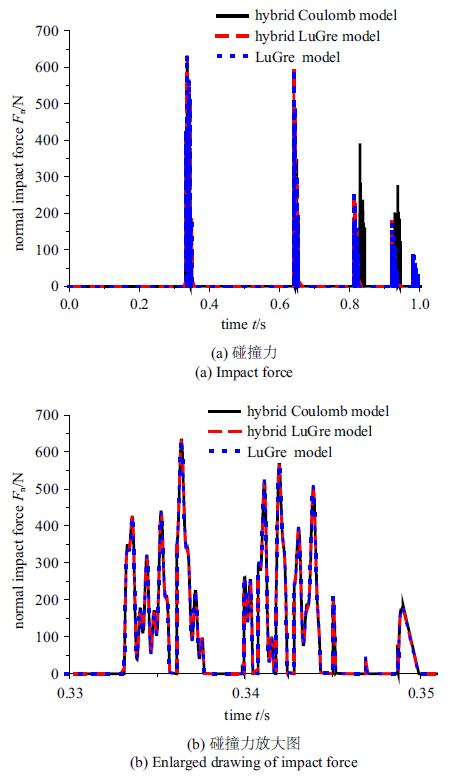
图9 表示3种摩擦模型方式柔性梁碰撞过程中法向碰撞力的变化图, 如图9 所示, 在第一次碰撞中法向的碰撞力完全相同, 随着碰撞次数增加3种模型碰撞时间和法向碰撞力大小出现明显区别. 在仿真时间内, LuGre模型黏滞时考虑约束和不考虑约束的碰撞力大小无明显区别, 而Coulomb模型随着碰撞次数增加碰撞力相对LuGre模型两种方式差异逐渐明显. 图10 表示3种摩擦模型柔性梁碰撞过程中切向摩擦力的变化, 由图10 (b)放大图可知, 切向摩擦力在第一次碰撞过程中变化曲线基本相同, 在碰撞开始阶段LuGre模型两种方式相对Coulomb模型摩擦力相对略微偏大, 随后3种方式曲线重合. LuGre模型的两种方式在多次碰撞中摩擦力没有明显区别, 而Coulomb摩擦力在多次碰撞后和LuGre模型出现明显差异. 说明LuGre模型黏滞状态考虑约束和不考虑约束方程两种碰撞建模方式不影响系统的碰撞力和摩擦力.
图9
图9
碰撞力变化图
Fig.9
Variation of impact force
图10
图10
摩擦力变化图
Fig.10
Variation of friction force
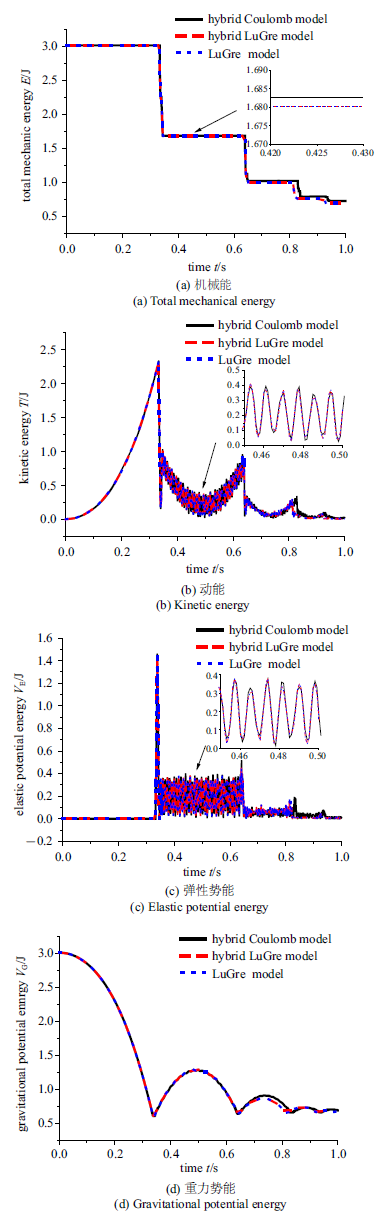
图11 表示柔性梁3种摩擦模型方式的能量变化, 从图11 (a)可以看出3种摩擦模型方式机械能整体变化的趋势相同, 随着碰撞次数增加, 每次碰撞过程损耗的机械能逐渐减少. 第一次碰撞过程中LuGre模型的两种方式消耗的能量比Coulomb模型略微多点但是不明显, 由于第一次碰撞过程中3种模型法向碰撞力相同, 能量差异只能是LuGre模型切向摩擦力和Coulomb模型出现略微不同而引起的. 随着碰撞次数增加, 柔性梁系统能量的大小变化差异呈现先增大后减小趋势, 但在仿真过程中LuGre模型考虑黏滞约束和不考虑黏滞约束方程机械能无明显区别. 从图11 (b)可以看出, 在碰撞过程中会引起动能的突变, 在第一碰撞后动能变化基本相同, 但是后面几次碰撞后逐渐可以看出Coulomb模型相对其他两种模型明显不同. 由图11 (c)看出, 3种模型方式的柔性梁弹性势能曲线趋势相同, 对比图6 可以看出在碰撞时柔性梁会出现大的变形随后引起高频振荡, 其弹性势能体现为在碰撞时产生大的突变、随后数值发生大范围周期变化. 随着能量的损耗, 弹性势能数值变化幅度能随着碰撞次数也逐渐减小、梁末端变形幅度也随着减小. Coulomb模型的弹性势能随着碰撞次数增加和其他两种方式逐渐产生区别后随着能量消耗区别减小, 在仿真过程中LuGre模型两种方式的弹性势能没有区别. 由图12 (d)看出, 重力势能变化趋势和角位移变化趋势基本相同, 重力势能的变化主要受刚性的转动影响, 在第二次碰撞后Coulomb模型和LuGre模型两种方式有明显区别, 柔性梁碰撞后Coulomb模型反弹高度相对较高, 机械能在反弹重力势能最大时刻能量以重力势能为主, 还有少部分机械能以弹性势能存在, 重力势能碰撞最大反弹高度区别能够反应出相同条件下Coulomb能量消耗略低而LuGre模型考虑约束和不考虑约束能量消耗相同. 反弹高度在第二次碰撞反弹同样影响碰撞力区别, 第三次碰撞由于前两次LuGre模型两种方式消耗能量大, 出现反弹高度小再次碰撞就出现碰撞力和摩擦力减小, LuGre模型两种方式能量损耗减小, 从而呈现3种摩擦模型方式能量之间差异减小的现象. 在仿真时间内LuGre模型黏滞状态下考虑约束和不考虑约束方程建模的两种方法所有能量曲线重合, 说明LuGre模型黏滞状态下引入计算切向约束反力和LuGre模型计算黏滞状态下摩擦力的能量损耗相同.
图11
图11
柔性梁能量变化图
Fig.11
Energy variation of flexible beam
图12
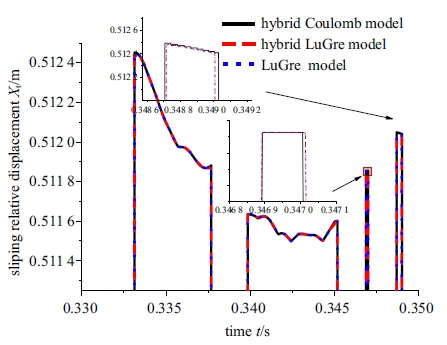
图12
第一次碰撞碰撞点相对斜坡原点切向位移
Fig.12
Tangential displacement of impact point relative to origin of slope in the first collision
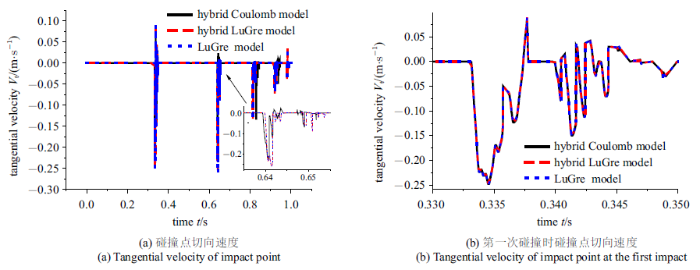
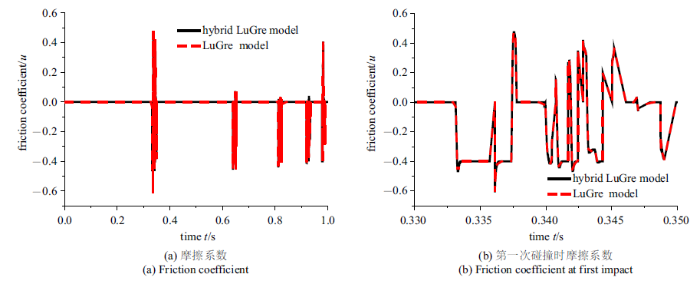
图12 表示第一次碰撞梁上碰撞点相对于斜坡原点的切向位移, 从图12 看出在第一次碰撞过程中3种模型方式的位移基本相同, 且在碰撞过程中都反映出正反滑移和黏滞现象. 其中LuGre无论是否考虑约束的滑动位移完全相同, 说明LuGre模型黏滞状态下不考虑约束同样能准确表现出该模型黏滞状态的位移. 图13 表示梁上碰撞点碰撞时在斜坡上切向滑动速度, 可以看出随着碰撞次数增加, Coulomb摩擦模型的速度相对于LuGre模型的两种方式逐渐产生区别. 图14 表示LuGre摩擦模型碰撞过程摩擦系数变化, 从图14 (a)和图14 (b)摩擦系数变化可知LuGre摩擦模型黏滞考虑约束和不考虑约束的建模的摩擦系数变化相同, 由图14 (b)第一次碰撞时摩擦系数变化可以看出, 在碰撞时摩擦系数会出现高于和低于动摩擦系数的值, 对比切向滑动位移和速度变化, 得出在开始滑动的阶段摩擦系数出现超过滑动摩擦系数(0.4)的现象, 这与实际情况相符,预滑动到宏观滑动时推力必须大于临界摩擦力. 这个现象反映在摩擦力上为碰撞开始阶段, LuGre模型的两种方式的摩擦力相对于Coulomb模型偏大. 图14 (b)和图12 结合同时看出, 在切向位移发生黏滞时(即位移不变时), 摩擦系数值出现小于或大于滑动摩擦系数(0.4)的现象, 这说明黏滞时摩擦力是小于当时状态最大静摩擦力而不是小于滑动摩擦力, 反应在摩擦力上在黏滞时出现LuGre模型的两种方式会出现大于Coulomb摩擦力. 因为摩擦系数不同会导致在碰撞开始阶段和黏滞状态下不同模型摩擦力不同, 因此不同模型能量损耗等动力学特性也不同. 采用Coulomb模型虽然第一次碰撞时滑动位移、速度等动力学特性与LuGre摩擦模型基本相同, 但是随着碰撞次数增加, 期间能量损耗逐渐累积的差异逐渐体现出来, Coulomb模型相对LuGre模型的两种方式动力特性区别也逐渐明显, 从而明显看出柔性梁末端变形差异、Coulomb模型能量损耗小、再次碰撞时间间隔较长等现象, 不过这种现象随着能量消耗趋于稳定值差异也逐渐减小. 如图5 柔性梁角速度的变化上亦能看出Coulomb模型和LuGre模型的区别, 第一次接触碰撞因切向摩擦力微小区别导致柔性梁角速度变化微小; 在第二次碰撞时, Coulomb模型的摩擦力相对于LuGre模型两种方式的有明显区别, 在碰撞反弹后柔性梁角速度产生差异; 在第三次及接下来的碰撞中由于多次碰撞累积效应, Coulomb模型碰撞力明显偏大, 导致碰撞时其柔性梁末端变形变大, 进而柔性梁的柔性作用反向影响柔性梁大范围旋转运动, 体现在柔性梁角速度变化上. 在切向摩擦力上考虑和未考虑黏滞的LuGre摩擦建模时摩擦系数、摩擦力和切向位移、速度并未出现差异, 说明LuGre摩擦模型能够反应出该模型的黏滞时摩擦力、位移和速度的变化. 在柔性梁斜向碰撞动力学建模时, 法向接触碰撞使用接触约束法, 符合碰撞过程中非嵌入的实际情况; 切向使用LuGre摩擦模型引入摩擦势能, 能够反应碰撞过程中切向运动的实际情况. 这样斜向碰撞动力建模相对于采用Hybrid LuGre model建模减少了计算程序中黏滞滑动的切换, 同样推导公式相对方便简洁.
图13
图13
碰撞时切向速度变化
Fig.13
Variation of tangential velocity during impact
图14
图14
碰撞时摩擦系数变化
Fig.14
Variation of friction coefficient during impact
4 结论
(1) 在碰撞接触过程中, 3种模型的动力学特性相似, 但随着碰撞次数的增加Coulomb摩擦模型和LuGre摩擦模型两种方式动力学特性差异逐渐明显, 后随碰撞时能量消耗柔性梁系统趋于稳定, 差异又逐渐减小.
(2) LuGre摩擦模型相对于Coulomb摩擦模型对于碰撞过程中的斜向摩擦描述更加准确, 可以描述预滑动到宏观滑动之间的临界摩擦力及在黏滞状态下介于正负最大静摩擦力之间的摩擦力变化.
(3) LuGre摩擦模型在黏滞状态下考虑约束和不考虑约束在仿真时间内动力学特性没有区别, 摩擦力、摩擦系数、碰撞时切向位移等均相同. 这些现象说明在黏滞状态下LuGre摩擦模型的动力学特性和切向约束描述的相同且减少了黏滞状态动力学方程的推导, 避免了计算程序中黏滞/滑动状态判断.
参考文献
View Option
[1]
Stolfi A Gasbarri P Sabatini M , et al . A parametric analysis of a controlled deployable space manipulator for capturing a non-cooperative flexible satellite
Acta Astronautica 2018 : 317 -326
DOI
URL
PMID
[本文引用: 1]
[2]
李海泉 , 梁建勋 , 吴爽 等 . 空间机械臂柔性捕获机构建模与实验研究
力学学报 , 2020 ,52 (5 ):1465 -1474
(Li Haiquan Liang Jianxun Wu Shuang et al . Dynamics modeling and experiment of a flexible capturing mechanism in a space manipulator
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (5 ):1465 -1474 (in Chinese))
[3]
沈涛 , 张崇峰 , 王卫军 等 . 基于抱爪式对接机构捕获缓冲系统动力学仿真研究
力学学报 , 2020 ,52 (6 ):1590 -1598
[本文引用: 1]
(Shen Tao Zhang Chongfeng Wang Weijun et al . Dynamic simulation analysis of capture and buffer system based on claw-type docking mechanism
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (6 ):1590 -1598 (in Chinese))
[本文引用: 1]
[4]
Li H Yu Z Guo S , et al . Investigation of joint clearances in a large-scale flexible solar array system
Multibody System Dynamics 2018 ,44 (3 ):277 -292
[本文引用: 1]
[5]
邱雪松 , 任志博 , 桂朋 等 . 含多间隙柔性可展帆板动力学建模及仿真
宇航学报 , 2018 ,39 (7 ):724 -731
[本文引用: 1]
(Qiu Xuesong Ren Zhibo Gui Peng et al . Dynamic modeling and simulation of a flexible deployable solar array with multiple clearances
Journal of Astronautics 2018 ,39 (7 ):724 -731 (in Chinese))
[本文引用: 1]
[6]
Tong R Quan Z Wan Q , et al . A new impact dynamics model of a clearance joint considering the adhesive effects in space environment
MATEC Web of Conferences 2020 ,306 :01005
[本文引用: 1]
[7]
秦睿贤 , 周俊先 , 陈秉智 . 基于柔性单元的一维列车碰撞模型及参数校正
铁道学报 , 2019 ,41 (11 ):58 -64
[本文引用: 1]
(Qin Ruixian Zhou Junxian Chen Bingzhi One-dimensional train collision model based on flexible element and parameters calibration
Journal of the China Railway Society 2019 ,41 (11 ):58 -64 (in Chinese))
[本文引用: 1]
[8]
袁晗 , 王小军 , 张宏剑 等 . 重复使用火箭着陆结构稳定性分析
力学学报 , 2020 ,52 (4 ):1007 -1023
[本文引用: 1]
(Yuan Han Wang Xiaojun Zhang Hongjian et al . Stability analysis of reusable launch vehicle landing structure
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (4 ):1007 -1023 (in Chinese))
[本文引用: 1]
[9]
Docquier N Lantsoght O Dubois F , et al . Modelling and simulation of coupled multibody systems and granular media using the non-smooth contact dynamics approach
Multibody System Dynamics 2020 ,49 (1 ):1 -22
[本文引用: 1]
[10]
丁千 , 翟红梅 . 机械系统摩擦动力学研究进展
力学进展 , 2013 ,43 (1 ):112 -131
[本文引用: 3]
(Ding Qian Zhai Hongmei The advance in researches of friction dynamics in mechanics system
Advances in Mechanics 2013 ,43 (1 ):112 -131 (in Chinese))
[本文引用: 3]
[11]
Qian Z Zhang D Jin C , et al . A regularized approach for frictional impact dynamics of flexible multi-link manipulator arms considering the dynamic stiffening effect
Multibody System Dynamics 2018 ,43 (3 ):229 -255
[本文引用: 2]
[12]
Chen ZQ Qian LF . Nonlinear dynamic characteristics analysis of planar flexible rotating beams with clearance joint
Journal of the Brazilian Society of Mechanical Sciences and Engineering 2020 ,42 (6 ):333
[13]
Tang L Liu J . Frictional contact analysis of sliding joints with clearances between flexible beams and rigid holes in flexible multibody systems
Multibody System Dynamics 2020 ,49 :155 -179
[本文引用: 1]
[14]
Zheng X Zhang F Wang Q . Modeling and simulation of planar multibody systems with revolute clearance joints considering stiction based on an LCP method
Mechanism and Machine Theory 2018 ,130 :184 -202
[本文引用: 2]
[15]
Brogliato B Kovecses J Acary V . The contact problem in Lagrangian systems with redundant frictional bilateral and unilateral constraints and singular mass matrix. The all-sticking contacts problem
Multibody System Dynamics 2020 ,48 (2 ):151 -192
[16]
Wang X Lv J . Modeling and simulation of dynamics of a planar-motion rigid body with friction and surface contact
International Journal of Modern Physics B 2017 ,31 :16 -19
[17]
Gholami F Nasri M Kovecses J , et al . A linear complementarity formulation for contact problems with regularized friction
Mechanism and Machine Theory 2016 ,105 :568 -582
[本文引用: 1]
[18]
Zheng X Li J Wang Q , et al . A methodology for modeling and simulating frictional translational clearance joint in multibody systems including a flexible slider part
Mechanism and Machine Theory 2019 ,142 :103603
[本文引用: 3]
[19]
Nan G Lou J Song C , et al . A new approach for solving rub-impact dynamic characteristics of shrouded blades based on macroslip friction model
Shock and Vibration 2020 (8 ):1 -9
[20]
Xu Z Wang Q Wang Q . Numerical method for dynamics of multi-body systems with two-dimensional Coulomb dry friction and nonholonomic constraints
Applied Mathematics and Mechanics $($English Edition$)$ 2017 ,38 (12 ):1733 -1752
[21]
Aghili F . Energetically consistent model of slipping and sticking frictional impacts in multibody systems
Multibody System Dynamics 2020 ,48 (2 ):193 -209
[本文引用: 2]
[22]
Kane TR Levinson DA . Dynamics Theory and Applications
New York: Mcgraw Hill , 1985
[本文引用: 1]
[23]
刘占生 , 张敏 , 张广辉 等 . 基于LuGre摩擦模型的叶片碰撞摩擦特性研究
振动与冲击 , 2012 ,31 (12 ):172 -178
[本文引用: 1]
(Liu Zhansheng Zhang Min Zhang Guanghui et al . Characteristics of impact-contact and friction between tips of blades based on LuGre model
Journal of Vibration and Shock 2012 ,31 (12 ):172 -178 (in Chinese))
[本文引用: 1]
[24]
Muvengei O Kihiu J Ikua B W , et al . Dynamic analysis of planar rigid-body mechanical systems with two-clearance revolute joints
Nonlinear Dynamics 2013 ,73 (1 ):259 -273
[25]
王晓军 , 吕敬 , 王琪 . 含摩擦滑移铰平面多刚体系统动力学的数值算法
力学学报 , 2019 ,51 (1 ):209 -217
(Wang Xiaojun Lv Jing Wang Qi A numerical method for dynamics of planar multi-rigid-body system with frictional translational joints based on LuGre friction model
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (1 ):209 -217 (in Chinese))
[26]
郑鹏 , 王琪 , 吕敬 等 . 摩擦与滚阻对被动行走器步态影响的研究
力学学报 , 2020 ,52 (1 ):162 -170
(Zheng Peng Wang Qi Lü Jing et al . Study on the influence of friction and rolling resistance on the gait of passive dynamic walker
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):162 -170 (in Chinese))
[27]
杨玉维 , 李彬 , 周海波 等 . 计及非完美运动副的移动并联机械手动力学分析
机械工程学报 , 2019 ,55 (15 ):208 -216
[本文引用: 1]
(Yang Yuwei Li Bin Zhou Haibo et al . Dynamic Analysis of a Mobile Parallel Manipulator with Imperfect Kinematic Joints
Journal of Mechanical Engineering 2019 ,55 (15 ):208 -216 (in Chinese))
[本文引用: 1]
[28]
Qian Z Jin C Zhang D , et al . Multiple frictional impact dynamics of threshing process between flexible tooth and grain kernel
Computers and Electronics in Agriculture 2017 ,141 :276 -285
[本文引用: 1]
[29]
Dong FX Hong JZ Zhu K , et al . Numerical and experimental studies on impact dynamics of a planar flexible multibody system
Acta Mechanica Sinica 2010 ,26 (4 ):635 -642
[本文引用: 1]
[30]
段玥晨 , 章定国 , 洪嘉振 . 作大范围运动柔性梁的一种碰撞动力学求解方法
机械工程学报 , 2012 ,48 (19 ):95 -102
[本文引用: 2]
(Duan Yuechen Zhang Dingguo Hong Jiazhen Method for solving the impact problem of a flexible beam with large overall motion
Journal of Mechanical Engineering 2012 ,48 (19 ):95 -102 (in Chinese))
[本文引用: 2]
[31]
钱震杰 , 章定国 , 金诚谦 . 柔性多体系统含摩擦碰撞stick-slip过程动力学仿真
振动与冲击 , 2017 ,36 (23 ):32 -37
(Qian Zhenjie Zhang Dingguo Jin Chengqian Dynamic simulation for flexible multibody systems containing frictional impact and stick- slip processes
Journal of Vibration and Shock 2017 ,36 (23 ):32 -37 (in Chinese))
[32]
Yuan W Li L Zhang DG , et al . New method for oblique impact dynamics research of a flexible beam with large overall motion considering impact friction force
Acta Mechanica Sinica 2016 ,32 (4 ):720 -730
[本文引用: 3]
[33]
Johnson KL . Contact Mechanics . Cambridge : Cambridge University Press , 1985
[本文引用: 1]
[34]
Lewis AD Rogers RJ . Experimental and numerical study of forces during oblique impact
Journal of Sound & Vibration 1988 ,125 (3 ):403 -412
[本文引用: 1]
A parametric analysis of a controlled deployable space manipulator for capturing a non-cooperative flexible satellite
1
2018
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
空间机械臂柔性捕获机构建模与实验研究
0
2020
空间机械臂柔性捕获机构建模与实验研究
0
2020
基于抱爪式对接机构捕获缓冲系统动力学仿真研究
1
2020
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
基于抱爪式对接机构捕获缓冲系统动力学仿真研究
1
2020
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
Investigation of joint clearances in a large-scale flexible solar array system
1
2018
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
含多间隙柔性可展帆板动力学建模及仿真
1
2018
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
含多间隙柔性可展帆板动力学建模及仿真
1
2018
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
A new impact dynamics model of a clearance joint considering the adhesive effects in space environment
1
2020
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
基于柔性单元的一维列车碰撞模型及参数校正
1
2019
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
基于柔性单元的一维列车碰撞模型及参数校正
1
2019
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
重复使用火箭着陆结构稳定性分析
1
2020
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
重复使用火箭着陆结构稳定性分析
1
2020
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
Modelling and simulation of coupled multibody systems and granular media using the non-smooth contact dynamics approach
1
2020
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
机械系统摩擦动力学研究进展
3
2013
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
... [10 -11 ]. 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
... 研究发现斜向碰撞过程和法向碰撞力和切向摩擦力变化同步[33 ] , 目前大多数学者认为切向碰撞力和法向摩擦力相互独立[10 ,34 ] . 可以将无摩擦动力学和切向接触约束方程结合, 黏滞状态的动力学方程为 ...
机械系统摩擦动力学研究进展
3
2013
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
... [10 -11 ]. 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
... 研究发现斜向碰撞过程和法向碰撞力和切向摩擦力变化同步[33 ] , 目前大多数学者认为切向碰撞力和法向摩擦力相互独立[10 ,34 ] . 可以将无摩擦动力学和切向接触约束方程结合, 黏滞状态的动力学方程为 ...
A regularized approach for frictional impact dynamics of flexible multi-link manipulator arms considering the dynamic stiffening effect
2
2018
... 接触碰撞是工程界普遍存在的现象, 例如航天器的对接和抓取[1 -3 ] 、太阳能帆板的展开[4 -5 ] 、旋转关节的间隙碰撞[6 ] 、车辆碰撞[7 ] 、火箭的回收着陆[8 ] 、工程机械作业[9 -10 ] . 由于碰撞过程存在法向碰撞和切向摩擦作用, 具有非光滑、不连续的特性[10 -11 ] . 因此, 有必要对高效精确的接触碰撞建模方法进行研究. ...
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
Nonlinear dynamic characteristics analysis of planar flexible rotating beams with clearance joint
0
2020
Frictional contact analysis of sliding joints with clearances between flexible beams and rigid holes in flexible multibody systems
1
2020
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
Modeling and simulation of planar multibody systems with revolute clearance joints considering stiction based on an LCP method
2
2018
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
... [14 ]. 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
The contact problem in Lagrangian systems with redundant frictional bilateral and unilateral constraints and singular mass matrix. The all-sticking contacts problem
0
2020
Modeling and simulation of dynamics of a planar-motion rigid body with friction and surface contact
0
2017
A linear complementarity formulation for contact problems with regularized friction
1
2016
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
A methodology for modeling and simulating frictional translational clearance joint in multibody systems including a flexible slider part
3
2019
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
... [18 -21 ]提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
... 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
A new approach for solving rub-impact dynamic characteristics of shrouded blades based on macroslip friction model
0
2020
Numerical method for dynamics of multi-body systems with two-dimensional Coulomb dry friction and nonholonomic constraints
0
2017
Energetically consistent model of slipping and sticking frictional impacts in multibody systems
2
2020
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
... ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
Dynamics Theory and Applications
1
1985
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
基于LuGre摩擦模型的叶片碰撞摩擦特性研究
1
2012
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
基于LuGre摩擦模型的叶片碰撞摩擦特性研究
1
2012
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
Dynamic analysis of planar rigid-body mechanical systems with two-clearance revolute joints
0
2013
含摩擦滑移铰平面多刚体系统动力学的数值算法
0
2019
含摩擦滑移铰平面多刚体系统动力学的数值算法
0
2019
摩擦与滚阻对被动行走器步态影响的研究
0
2020
摩擦与滚阻对被动行走器步态影响的研究
0
2020
计及非完美运动副的移动并联机械手动力学分析
1
2019
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
计及非完美运动副的移动并联机械手动力学分析
1
2019
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
Multiple frictional impact dynamics of threshing process between flexible tooth and grain kernel
1
2017
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
Numerical and experimental studies on impact dynamics of a planar flexible multibody system
1
2010
... 在接触约束法中, 初始接触瞬间速度是不连续的, 在碰撞接触时直接添加约束会导致该时刻运动不协调从而导致违约计算困难的情况. 为了实现运动的协调, 在初始碰撞时刻需要实现无碰撞到碰撞的速度跳跃, 得出碰撞时刻添加约束的速度. 对于得出速度跳跃值, 许多学者进行了研究. Dong等[29 ] 根据连续介质力学的间断面理论得到碰撞初始速度, 段玥晨等[30 ] 利用冲量-动量法求出速度的跳跃值. 本文采用冲量动量法求出碰撞的初始速度 ...
作大范围运动柔性梁的一种碰撞动力学求解方法
2
2012
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
... 在接触约束法中, 初始接触瞬间速度是不连续的, 在碰撞接触时直接添加约束会导致该时刻运动不协调从而导致违约计算困难的情况. 为了实现运动的协调, 在初始碰撞时刻需要实现无碰撞到碰撞的速度跳跃, 得出碰撞时刻添加约束的速度. 对于得出速度跳跃值, 许多学者进行了研究. Dong等[29 ] 根据连续介质力学的间断面理论得到碰撞初始速度, 段玥晨等[30 ] 利用冲量-动量法求出速度的跳跃值. 本文采用冲量动量法求出碰撞的初始速度 ...
作大范围运动柔性梁的一种碰撞动力学求解方法
2
2012
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
... 在接触约束法中, 初始接触瞬间速度是不连续的, 在碰撞接触时直接添加约束会导致该时刻运动不协调从而导致违约计算困难的情况. 为了实现运动的协调, 在初始碰撞时刻需要实现无碰撞到碰撞的速度跳跃, 得出碰撞时刻添加约束的速度. 对于得出速度跳跃值, 许多学者进行了研究. Dong等[29 ] 根据连续介质力学的间断面理论得到碰撞初始速度, 段玥晨等[30 ] 利用冲量-动量法求出速度的跳跃值. 本文采用冲量动量法求出碰撞的初始速度 ...
柔性多体系统含摩擦碰撞stick-slip过程动力学仿真
0
2017
柔性多体系统含摩擦碰撞stick-slip过程动力学仿真
0
2017
New method for oblique impact dynamics research of a flexible beam with large overall motion considering impact friction force
3
2016
... 在接触碰撞过程中存在法向接触速度跳跃、能量突变和切向摩擦的滑动-黏滞互相切换等问题. 对于解决柔性体接触碰撞过程中含切向黏滞/滑动状态摩擦的碰撞非光滑问题, 国内外学者提出了光滑化方法[11 -13 ] , 该方法采用光滑曲线来描述Coulomb摩擦模型滑动-黏滞的切换过程, 有效解决了切换引起的稳定性问题, 然而该方法存在失去黏滞时动力学特征的缺陷, 针对光滑化方法存在的缺陷, 国内外学者提出建立互补关系来求解接触碰撞非光滑问题[14 -17 ] . 互补关系算法通过Hertz接触理论描述法向接触力, 在切向上建立正负加速和正负摩擦余量的互补关系从而通过求解出摩擦余量得出静摩擦力[14 ] . 然而互补算法需要计算互补方程同时还需要进行状态切换条件的判断, 相对增加了计算求解时间[18 ] , 有学者[18 -21 ] 提出直接根据接触碰撞过程黏滞/滑移条件进行程序判断计算的方法. 文献[18 ]对柔性滑块接触问题研究中, 采用弹簧阻尼模型计算碰撞力, 以微小速度差作为滑动和黏滞的切换判断条件, 黏滞时直接以滑块受到的外力作为静摩擦力, 并且对于多节点接触问题求解不需要建立和计算互补方程, 通过两个仿真案例说明该方法有效可行. 文献[21 ]基于时间步进法直接引入预碰撞速度二次函数判别碰撞前黏滞/滑动状态, 并对 Kane[22 ] 案例进行研究证明其方法的正确性. 以上文献对于接触碰撞过程通常采用Coulomb摩擦模型进行描述, 当对柔性梁接触碰撞的非光滑问题进行研究时, 为了对柔性梁碰撞中黏滞时摩擦力的准确描述需要引入约束方程进行计算. 而LuGre摩擦模型可通过平均鬃毛变形来反应实时摩擦系数变化, 其包含了运动过程中最大静摩擦、预滑动、黏滞等现象, 直接避免黏滞/滑动切换的判断, 减少建模过程中动力学方程的推导, 且能完整描述预滑动阶段的摩擦特性, 有学者[23 -27 ] 将LuGre模型用于多体系统接触碰撞中, 证明该模型能够解决接触碰撞过程中的非光滑问题. 以上文献对于接触碰撞过程中法向接触力的计算通常采用连续接触法, 该方法需要进行嵌入假设, 而接触碰撞过程的实际情况应该是非嵌入的, 此时更符合工程实际情况的附加约束法被国内外学者提出[28 -32 ] . 段玥晨等[30 ] 证明该方法能够方便准确求解出法向碰撞力并与连续接触法的作对比. Yuan等[32 ] 针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
... [32 ]针对柔性梁和刚性斜面斜碰撞问题进行研究, 在法向碰撞时引入约束方程求解碰撞力, 在切向上根据滑动/黏滞判断条件分别采用切向接触约束法直接求解静摩擦力和Coulomb模型计算滑动摩擦力的混合建模方法, 并与采用修正库伦模型和无摩擦模型作对比证明该方法能够相对准确描述碰撞时的摩擦力. ...
... 取柔性梁的参数为: $L=1.0$ m, $S=3.14\times 10^{-4}$ m$^{2}$, $\rho =27 667$ kg/m$^{3}$, $E=68.952$ GPa, $I=7.85\times 10^{-9}$. 假设柔性梁在初始状态处于静止和未变形状态; 柔性梁在初始角度$\theta ={\pi /4}$处在重力场下作自由下落. 旋转过程中柔性梁和原点位于(0.3, 0)处倾角$\alpha $为${\pi /{10}}$的刚性斜坡发生; 取动摩擦系数$\mu_{d} $为0.3, 如图2 和图3 所示柔性梁的角位移和末端$Y$方向位移与文献[32 ]仿真结果对比相同. ...
1
1985
... 研究发现斜向碰撞过程和法向碰撞力和切向摩擦力变化同步[33 ] , 目前大多数学者认为切向碰撞力和法向摩擦力相互独立[10 ,34 ] . 可以将无摩擦动力学和切向接触约束方程结合, 黏滞状态的动力学方程为 ...
Experimental and numerical study of forces during oblique impact
1
1988
... 研究发现斜向碰撞过程和法向碰撞力和切向摩擦力变化同步[33 ] , 目前大多数学者认为切向碰撞力和法向摩擦力相互独立[10 ,34 ] . 可以将无摩擦动力学和切向接触约束方程结合, 黏滞状态的动力学方程为 ...