基于压电纤维复合材料的旋转叶片主动控制1)

doi:10.6052/0459-1879-20-448

基于压电纤维复合材料的旋转叶片主动控制¹⁾

张博^,^*^,^†^,²⁾, 丁虎^†, 陈立群^,^**^,³⁾

^*长安大学理学院, 西安 710064

^†上海大学力学与工程科学学院, 上海 200444

^**哈尔滨工业大学(深圳)理学院力学系, 广东深圳 518055

ACTIVE VIBRATION CONTROL OF A ROTATING BLADE BASED ON MACRO FIBER COMPOSITE¹⁾

Zhang Bo^,^*^,^†^,²⁾, Ding Hu^†, Chen Liqun^,^**^,³⁾

^*School of Science, Chang'an University, Xi'an 710064, China

^†School of Mechanics and Engineering Sciences, Shanghai University, Shanghai 200444, China

^**School of Science, Harbin Institute of Technology, Shenzhen 518055, Guangdong, China

通讯作者: 2)张博, 讲师, 主要研究方向: 非线性动力学与振动控制. E-mail:zhang_bo@chd.edu.cn;3)陈立群, 教授, 主要研究方向: 非线性动力学和振动控制. E-mail:chenliqun@hit.edu.cn

收稿日期: 2020-12-24 接受日期: 2021-02-8 网络出版日期: 2021-04-08

基金资助:

1)国家自然科学基金.  11702033
国家自然科学基金.  11872159
中央高校基本科研业务费专项资金.  300102120106
上海市教委创新项目.  2017-01-07-00-09-E00019

Received: 2020-12-24 Accepted: 2021-02-8 Online: 2021-04-08

作者简介 About authors

摘要

旋转叶片结构的振动失效占据了航空发动机整机故障的相当比重. 发展针对旋转叶片结构的减振技术对于减轻叶片重量, 提升叶片性能, 延长叶片寿命具有重要意义. 通过引入压电纤维复合材料(macro fiber composite, MFC)传感器和作动器, 研究预变形旋转叶片2:1内共振的主动控制. 建立考虑时滞效应的旋转叶片比例微分闭环控制系统运动方程. 通过摄动分析推导出受控叶片的演化方程, 并结合延拓法揭示速度增益、位移增益、时滞量等系统参数对受控系统稳态响应及稳定性的影响规律. 理论研究结果与数值结果得到相互验证. 研究发现时滞量对系统稳定性影响显著, 当时滞超过某临界值时, 演化方程原有的平衡点失稳, 闭环受控系统将缓慢进入一个大振幅的周期运动, 从而丧失控制效果. 位移增益存在一个范围使得系统出现多值稳态响应, 进而破坏了增益平面内系统稳定区和非稳定区域的直线边界. 不恰当的速度增益和位移增益会给受控系统引入新的共振. 研究结果为叶片结构的减振提供了理论基础.

关键词： 压电纤维复合材料 ; 预变形旋转叶片 ; 主动控制 ; 稳定性 ; 多尺度法

Abstract

For a long time, blade vibration failure occupies a quite large proportion of the total failure of the complete aeroengine. Developing the vibration reduction technology is of great importance for reducing the weight, improving the performance and extending the life for the rotating blade structure. In the present paper, the active vibration control is investigated in the presence of the 2:1 internal resonance of a pre-deformed rotating blade through introducing the sensors and actuators made of macro fiber composite (MFC). The equations of motion of the proportional-derivative feedback closed-loop control system are established with the effects of the time delay. The evolution equations of the controlled system are derived via the perturbation analysis. The effects of the velocity gain, the displacement gain, the time delay and some other system parameters on the steady-state response and the stabilities of the controlled system are revealed by the application of the continuation method. The analytic solutions are in good agreement with those obtained from the numerical integration. The main findings of the present study are as followings: the time delay has a significant effect on the stabilities of the controlled system. When the time delay exceeds a certain value, the equilibrium points of the evolution equations lose their stability. At the same time, the closed-loop control system enters a new period motion with a large vibration amplitude. There exists a range of displacement gain in which the multi-valued phenomenon appears in the steady-state response of the controlled system. Moreover, the straight borderline between the stable and the unstable regions in the gains plane is destroyed due to this range. Inappropriate assignments of the velocity gain and the displacement gain will cause a new resonance in the close-loop control system. The research results lay the theoretical foundations for the vibration reduction of the blade structure.

Keywords： macro fiber composite ; pre-deformed rotating blade ; active vibration control ; stabilities ; multiple scales method

PDF (1213KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张博, 丁虎, 陈立群. 基于压电纤维复合材料的旋转叶片主动控制¹⁾. 力学学报[J], 2021, 53(4): 1093-1102 DOI:10.6052/0459-1879-20-448

Zhang Bo, Ding Hu, Chen Liqun. ACTIVE VIBRATION CONTROL OF A ROTATING BLADE BASED ON MACRO FIBER COMPOSITE¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(4): 1093-1102 DOI:10.6052/0459-1879-20-448

引言

旋转叶片结构是航空发动机、重型燃气轮机等国家核心装备制造业的关键热端部件. 恶劣的服役条件往往会导致叶片发生大幅非线性振动, 出现多种共振形式, 加速损耗了叶片乃至整机的疲劳寿命. 亟需精准把握旋转叶片结构的运动规律并发展高效稳定的振动控制方法, 避免叶片因大幅振动而造成过早损毁.

首先, 需要针对典型的旋转叶片结构建立精确的动力学模型, 准确预测这类结构的运动规律. 大多数研究^[1-7]通常将叶片抽象为中轴线为直线的梁、板或壳, 建立线性或非线性动力学方程描述旋转叶片的运动规律, 研究其动力学特性以及非线性动力学行为. 然而叶片服役时所处的热梯度环境, 导致这类结构预变形是不可避免的. 20世纪90年代初, 日本学者Takabatake^[8]报道了恒载(dead load)引起的预变形对结构的动力学行为存在显著影响. 为了建立更为精确的动力学模型, Zhang和Li^[9]考虑了温度梯度引起的预变形, 从而将旋转叶片考虑为一个非对称振动系统, 建立了考虑预变形的旋转叶片非线性动力学方程. 在此模型基础上, 文献[10,11,12,13,14]研究了预变形旋转叶片2:1内共振、3:1内共振、参数共振、谐波共振等多种不同形式共振可能性以及所蕴含的丰富动力学现象.

其次, 针对旋转叶片结构, 发展相应的被动或主动振动控制方法对于减轻叶片重量, 提升叶片性能, 延长叶片寿命具有重要意义. 被动控制具有成本低, 易于维护等优点^[15-16]. 但通常存在工作频带窄, 不便调节, 产生较大的附加质量等缺陷^[17]. 因此, 很多学者开始将目光转向探索主动控制方法. 在主动控制中, 时滞效应对受控系统稳定性影响是一个重要问题. 由于信号采集测量、传输延迟、信号滤波、数据运算以及作动器响应等过程, 时滞效应很难避免. 王在华和胡海岩^[18-19]针对不同的简化动力学模型, 研究了比例微分(proportional derivative, PD)控制中时滞量对控制系统稳定的复杂影响. 早期学者们^[20]大多采用压电陶瓷材料作为主动控制装置的主要材料. 但压电陶瓷材料的柔韧性差强度低等缺点限制了其在工程中的广泛应用. 压电纤维复合材料由交叉指形电极、环氧树脂、压电陶瓷纤维三部分组成, 显著提升了传感和驱动性能, 且能更好地适用于曲面结构. 近年来, 基于MFC设计的主动控制设备越来越多, 学者们广泛将其应用到梁^[21]、平板^[22]、复合材料板^[23]等典型结构的振动抑制中. 最近, 孙杰等^[24]采用MFC驱动器实现了含间隙铰接航天器姿态运动与结构振动的协调控制. 2013年, NASA格伦研究中心通过实验验证和多物理场有限元仿真证明了压电片可显著降低叶片振动^[25]. 文献[26,27,28]在Yao模型上引入非线性饱和控制器, 正位置反馈控制器等, 实现了对空心压缩机叶片的振动控制. 唐冶等^[29]采用压电材料对脉动旋转悬臂梁进行主动振动控制, 得到了压电旋转悬臂梁在谐波共振时的稳定性边界.

虽然基于压电复合材料的振动控制取得一些进展, 但针对旋转叶片的主动振动控制方面, 目前相关研究还比较少^[30-31]. 本文采用MFC作为传感器和作动器, 与旋转叶片组成具有一定时滞效应的闭环控制系统. 并在叶片发生2:1内共振条件下, 探究控制器各主要参数对叶片振动控制效率及稳定性的影响规律.

1 模型描述和控制系统运动方程

本文研究的基于MFC的旋转叶片振动控制系统如图1所示. 在叶背和叶盆两侧对称地布置MFC传感器和MFC作动器. 控制器工作时, MFC传感器测量叶片弦向(chordwise)位移信号并传输给计算机, 经过分析运算后得到控制信号, 并将控制力信号输出给MFC作动器, 通过作动器的响应实现对旋转叶片的振动控制.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 包含MFC传感器和作动器的旋转叶片振动控制示意图

Fig.1 Schematic diagram of rotating blade controller system with MFC sensors and MFC actuators

文献[9,10]使用Lagrange原理结合假模态设法, 再通过模态变换, 得到了线性部分解耦的热梯度环境下旋转预扭叶片的动力学方程. 本文在上述方程的基础上引入具有时滞效应的PD反馈控制. 另外, 根据文献[10, 14]立方非线性对叶片2:1内共振影响十分微弱, 因此本文忽略立方非线性项, 最终得到受控叶片系统在模态空间下的运动微分方程为

(1)$\ddot{{q}}_{1} +c_{d} \dot{{q}}_{1} +\omega_{1}^{2} q_{1} =f_{1} \cos (\omega t)+\eta_{11} q_{1}^{2}+\eta_{12} q_{1} q_{2}+\eta_{13} q_{2}^{2}+u\left( t \right) $

(2)$\ddot{{q}}_{2} +c_{d} \dot{{q}}_{2} +\omega_{2}^{2} q_{2} =f_{2} \cos (\omega t)+\eta_{21} q_{1}^{2}+\eta_{22} q_{1} q_{2}+\eta_{23} q_{2}^{2} $

其中$q_{1}$, $q_{2}$分别为弦向和翼向模态坐标, $c_{d}$为无量纲阻尼系数. $\omega_{1}$, $\omega_{2}$为叶片前两阶无量纲固有频率, 叶片转速通过离心效应, 显著影响叶片的低阶固有频率, 在一定的转速条件下, $\omega_{1}$与$\omega_{2}$之间会出现可公度关系, 使得系统存在内共振的可能性^[13]. $f_{1}$, $f_{2}$为模态空间下的激振力, 与简谐变化的燃气压力的幅值成正比例关系. $\eta_{11}$, $\eta_{12}$, $\eta_{13}$, $\eta_{21}$, $\eta_{22}$, $\eta_{23}$为系统平方非线性项系数, 是由于考虑了叶片在服役环境下的预变形效应而产生的, 平方非线性项系数的大小与预变形程度成正比关系. 以上参数的具体定义可参考文献[14]. $u(t)$为PD控制器输出的控制力, 这里为了简化分析, 假设控制力仅是叶片弦向位移信号和速度信号的线性反馈, 且仅作用在弦向位移上, 通过系统内共振引入的前两阶模态间的能量交换机制, 实现对整个预扭叶片的振动控制. $u(t)$具体表达为

(3)$\begin{eqnarray} \label{eq3} u\left( t \right)=-k_{p} q_{1} \left( {t-\tau } \right)-k_{d} \dot{{q}}_{1} \left( {t-\tau } \right) \end{eqnarray} $

其中, $k_{p}$为位移反馈增益, $k_{d}$为速度反馈增益, $\tau$为信号采集、传输、运算、响应等环节产生的时间延迟, 通常是一个小量. 理论上讲, 位移通道和速度通道反馈时滞均可以是任意值^[32-33], 这里为了简便, 仅考虑最简单的一种情形, 即认为位移时滞与速度时滞相等.

2 基于多尺度法的摄动分析

对控制方程进行重刻度, 并引入两个时间尺度

(4)$\begin{eqnarray} \label{eq4} \left.\begin{array}{l} q_{1,2} \leftrightarrow \varepsilon q_{1,2} ,\ \ c_{d} \leftrightarrow \varepsilon c_{d},\ \ f_{1,2} \leftrightarrow \varepsilon^{2}f_{1,2}\\ k_{p} \leftrightarrow \varepsilon k_{p},\ \ k_{d} \leftrightarrow \varepsilon k_{d},\ \ T_{0} =t,\ \ T_{1} =\varepsilon t \\ \end{array}\right\} \end{eqnarray} $

其中$\varepsilon $为无量纲小参数. 采用多尺度法, 假设方程(1)和(2)的解为

(5)$\begin{eqnarray} \label{eq5} \left.\begin{array}{l} q_{1} \left( t \right)=q_{10} \left( {T_{0} ,T_{1} } \right)+\varepsilon q_{11} \left( {T_{0} ,T_{1} } \right) \\ q_{2} \left( t \right)=q_{20} \left( {T_{0} ,T_{1} } \right)+\varepsilon q_{21} \left( {T_{0} ,T_{1} } \right) \\ \end{array}\right\} \end{eqnarray} $

则考虑延迟效应下, 采集到的弦向位移信号

(6)$\begin{eqnarray} \label{eq6} && q_{1} \left( {t-\tau } \right)=q_{10} \left( {T_{0} -\tau ,T_{1} -\varepsilon \tau } \right)+\varepsilon q_{11\tau } \left( {T_{0} -\tau ,T_{1} -\varepsilon \tau } \right)=q_{10\tau } \left( {T_{0} ,T_{1} } \right)+ \varepsilon q_{11\tau } \left( {T_{0} ,T_{1} } \right) \end{eqnarray} $

将式(5)和式(6)代入方程(1)和(2), 对比$\varepsilon $同幂次系数, 可得$\varepsilon^0 $项

(7)$\begin{eqnarray} \label{eq7} \left.\begin{array}{l} \mbox{D}_{0}^{2} q_{10} +\omega_{1}^{2} q_{10} =0 \\ \mbox{D}_{0}^{2} q_{20} +\omega_{2}^{2} q_{20} =0 \\ \end{array}\right\} \end{eqnarray} $

$\varepsilon^{1}$项

(8)$\begin{eqnarray} \label{eq8} \left.\begin{array}{l} D_{0}^{2} q_{11} +\omega_{1}^{2} q_{11} =-2D_{1} D_{0} q_{10} -c_{d} D_{0} q_{10} +\eta_{11} q_{10}^{2}+ \\[1mm] \qquad \eta_{12} q_{10} q_{20} +\eta_{13} q_{20}^{2} +\dfrac{1}{2}f_{1} ({e}^{{i}\omega T_{0} }+{e}^{-{i}\omega T_{0} })- \\ \qquad k_{p} q_{10\tau } -k_{d} D_{0} q_{10\tau } \\ D_{0}^{2} q_{21} +\omega_{2}^{2} q_{21} =-2D_{1} D_{0} q_{20} -c_{d} D_{0} q_{20} +\eta_{21} q_{10}^{2}+ \\[1mm] \qquad \eta_{22} q_{10} q_{20} +\eta_{23} q_{20}^{2} +\dfrac{1}{2}f_{2} ({e}^{{i}\omega T_{0} }+{e}^{-{i}\omega T_{0} }) \\ \end{array}\right\} \end{eqnarray} $

方程(8)右侧最后两项是跟控制力相关的项. 齐次方程(7)的通解为

(9)$\begin{eqnarray} \label{eq9} \left.\begin{array}{l} q_{10} =A_{1} \left( {T_{1} } \right){e}^{{i}\omega_{1} T_{0} }+cc \\ q_{20} =A_{2} \left( {T_{1} } \right){e}^{{i}\omega_{2} T_{0} }+cc \\ \end{array}\right\} \end{eqnarray} $

其中$cc$代表前面各项的共轭, $A_{1}$, $A_{2}$为$T_{1}$的复函数, 写成极坐标形式

(10)$\begin{eqnarray} \label{eq10} A_{r} \left( {T_{1} } \right)=\dfrac{1}{2}a_{r} \left( {T_{1} } \right)\exp \left( {{i}\beta_{r} \left( {T_{1} } \right)} \right),\ \ r=1,2 \end{eqnarray} $

由式(6)和式(9)得

(11)$\begin{eqnarray} \label{eq11} && q_{10\tau } \left( {T_{0} ,T_{1} } \right)=A_{1} \left( {T_{1} -\varepsilon \tau } \right){e}^{{i}\omega_{1} \left( {T_{0} -\tau } \right)}+cc = A_{1\tau } {e}^{{i}\omega_{1} \left( {T_{0} -\tau } \right)}+cc \end{eqnarray} $

根据Taylor展开

(12)$\begin{eqnarray} \label{eq12} &&A_{1\tau } \left( {T_{1} } \right)=A_{1} \left( {T_{1} -\varepsilon \tau } \right)=A_{1} \left( {T_{1} } \right)-\varepsilon \tau D_{1} A_{1} +O\left( {\varepsilon^{2}} \right) \end{eqnarray} $

本文重点讨论旋转叶片2:1内共振条件下的一阶主共振, 为此引入解谐参数

(13)$\begin{eqnarray} \label{eq13} \omega_{2} = 2\omega_{1} +\varepsilon \sigma_{1} ,\ \ \omega =\omega _{1} +\varepsilon \sigma_{1} \end{eqnarray} $

将式(9) $\sim\!$式(13)代入式(8), 并分离实部和虚部, 得到受控系统自治演化方程

(14)$D_{1} a_{1} =-\dfrac{1}{2}c_{d} a_{1} +\dfrac{1}{4\omega_{1} }\eta_{12} a_{1} a_{2} \sin \phi _{1}+ \dfrac{1}{2\omega_{1} }f_{1} \sin\phi_{2}+\dfrac{1}{2\omega_{1}}k_{p} a_{1} \sin \left( {\omega_{1} \tau } \right)- \dfrac{1}{2}k_{d} a_{1} \cos \left( {\omega_{1} \tau } \right) $

(15)$D_{1} \phi_{1} =\sigma_{1} +\dfrac{1}{2\omega_{1} }\eta_{12} a_{2} \cos \left( {\phi_{1} } \right)-\dfrac{\eta _{21} a_{1}^{2}}{4a_{2} \omega_{2} }\cos \left( {\phi_{1} } \right)+ \dfrac{f_{1} }{a_{1} \omega_{1} }\cos \phi_{2}-\dfrac{\cos \left( {\omega_{1} \tau } \right)k_{p} }{\omega_{1} }-k_{d} \sin \left( {\omega_{1} \tau } \right) $

(16)$D_{1} a_{2} =-\dfrac{c_{d} }{2}a_{2} -\dfrac{\eta _{21} }{4\omega_{2} }a_{1}^{2}\sin \phi_{1} $

(17)$D_{1} \phi_{2} =\sigma_{2} +\dfrac{\eta_{12} }{4\omega_{1} }a_{2} \cos \phi_{1}+\dfrac{f_{1} }{2a_{1} \omega_{1} }\cos \phi_{2}- \dfrac{\cos \left( {\omega_{1} \tau } \right)k_{p}}{2\omega_{1} }-\dfrac{1}{2}\sin \left( {\omega_{1} \tau } \right)k_{d} $

其中$\phi_{1} = \sigma_{1}T_{1} - 2\beta_{1} + \beta _{2}$, $\phi_{2}=\sigma_{2}T_{1}-\beta_{1}$. 为了研究该受控系统的稳态响应, 令受控系统演化方程(14) $\sim$ (17)等号左侧为0. 系统的稳定性可由李雅普诺夫运动稳定性理论确定. 本文采用数值延拓与分岔分析工具包Matcont, 对受控系统的动力学行为进行研究.

3 受控系统响应演化规律

本文动力学方程采用文献[9,10]中的参数: $\sigma_{1}= 0$, $\sigma _{2} = 1.5$, $c_{d} =0.1$, $\varepsilon =0.01$, $\omega_{1}= 4.487 3$, $\eta_{11} =-922.70$, $\eta_{12} =4.093 0\times10^3$, $\eta _{13} =-3.983 5\times10^2$, $\eta_{21} =1.934 8\times10^3$, $\eta_{22} =-75 322\times10^2$, $\eta_{23} =3.725 9\times10^3$, $f_{1} =2.553 0\times10^{-3}$, $f_{2} =7.803 1\times10^{-3}$. 由演化方程(14) $\sim$ (17)分析旋转叶片发生2:1内共振附近时, 受控旋转预变形叶片的稳态动力学响应.

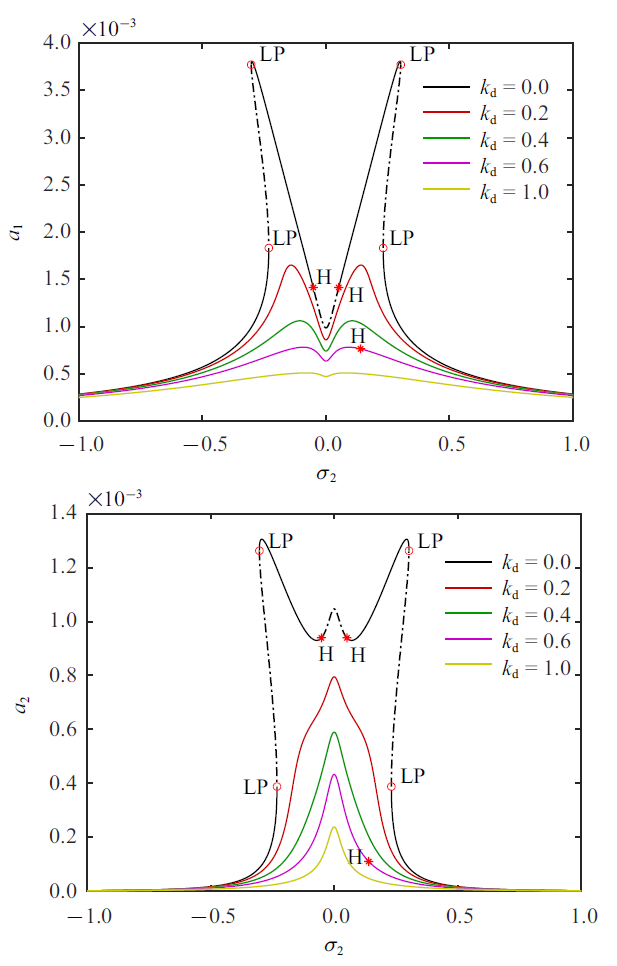
如图2所示, 当无控制($k_{d} =0$)时,系统频响曲线呈现典型的双跳跃现象^[9], 在两侧跳跃附近分别存在一个极限点(用圆圈和字母LP表示), 两个极限点之间的分支是不稳定的, 在完全外共振($\sigma_{2} =0$)附近系统存在一个Hopf分岔(用星号和字母H表示). 后面为了整洁, 略去表示分岔点类型的字母, 仅用点型来区分. 系统引入速度增益后, 跳跃现象被抑制, Hopf分岔消失, 响应峰值明显降低, 频响曲线变得更加平坦. 从受控系统动力学方程(1)和(3)来看, 若忽略时滞效应, 速度增益的作用类似于给系统引入新的阻尼.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不同速度增益$k_{d}$下受控系统频响曲线($k_{p} =0$)

Fig.2 Frequency response curves of controlled system for different velocity gain $k_{d}$ ($k_{p} =0$)

如图3所示, 随着位移增益增大, 频响曲线呈现硬化现象, 1阶响应增大, 2阶响应减小, 即系统前两阶模态响应耦合降低, 响应峰值向高频方向移动. 由此说明位移增益必须恰当选取, 否则会引起系统新的共振. 实际上, 从受控系统动力学方程看, 若忽略时滞效应, 位移增益的作用类似于给系统引入新的刚度, 系统原有的2:1内共振条件被打破.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同位移增益$k_{p}$下受控系统频响曲线($k_{d} =0$)

Fig.3 Frequency response curves of controlled system for different displacement gain $k_{p}$ ($k_{d} =0$)

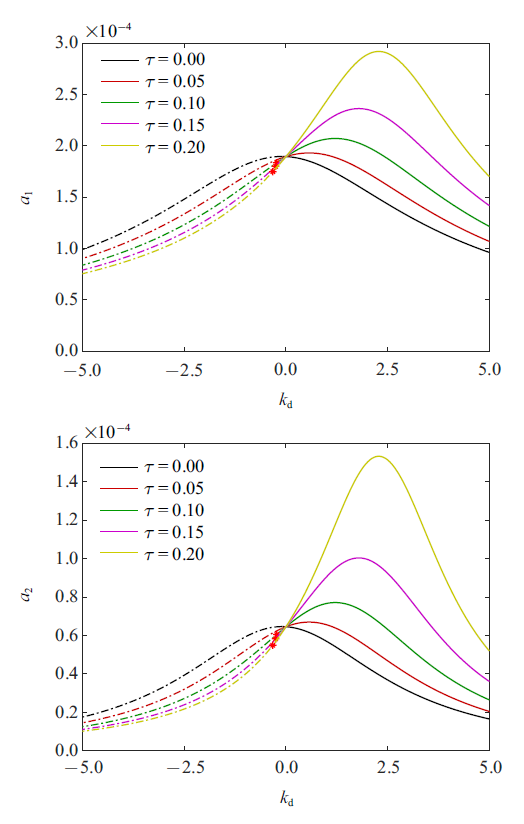
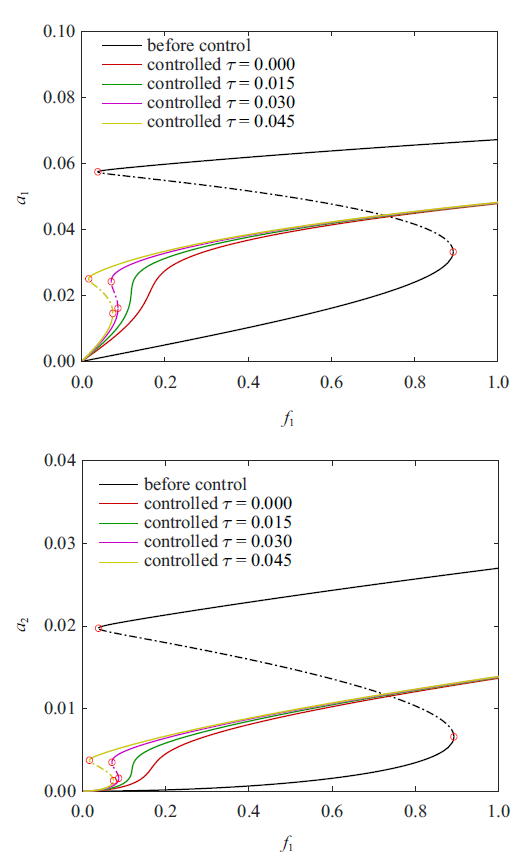
由图4可见, 速度增益跨越0附近, 存在一个Hopf分岔, 负的$k_{d}$使得系统丧失稳定性. 小延迟下的速度增益对系统响应抑制效果更为明显. 由图5所示, 当位移增益$k_{p}$变化中, 存在一个范围使得系统响应存在多值现象, 两个极限点之间的分支系统稳态响应是不稳定的. 且不稳定区域将会被时滞效应放大. 系统稳态响应随位移增益的演变对时滞效应十分敏感, 对于较大时滞, 系统有可能会出现Hopf分岔, 失去稳定性. 如果不恰当选取位移增益, 会使得系统响应迅速增长, 丧失控制效果.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同时滞量下受控系统稳态响应随速度增益($k_{d}$)的演变情况($k_{p} =0$)

Fig.4 Variation of the controlled system steady response with velocity gain $k_{d}$ for different time delay ($k_{p} =0$)

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同时滞量下受控系统稳态响应随位移增益($k_{p}$)的演变情况($k_{d} =0$)

Fig.5 Variation of the controlled system steady response with displacement gain $k_{p}$ for different time delay ($k_{d} =0$)

4 时滞量对控制器稳定性的影响

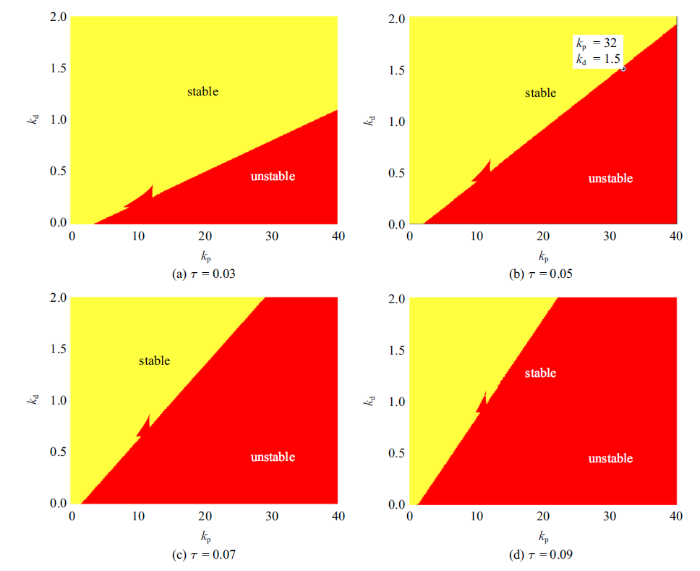
图6绘制了不同时滞量下, 受控系统在增益平面($k_{p}$, $k_{d})$内稳定区域. 显然时滞越大稳态区域越小. 稳定性区域和非稳定区域的分界线大致呈现一条直线, 该直线的斜率随时滞量增大而增大. $k_{p}$在8 $\sim$ 12附近, 非稳定区域出现一块戟形隆起. 这一隆起和系统随$k_{p}$演变过程中的多值现象相关. 这一隆起随时滞增大而向上移动且面积缩小.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同时滞量下受控系统增益稳定性区域

Fig.6 Stability regions of the controlled system for different time delay

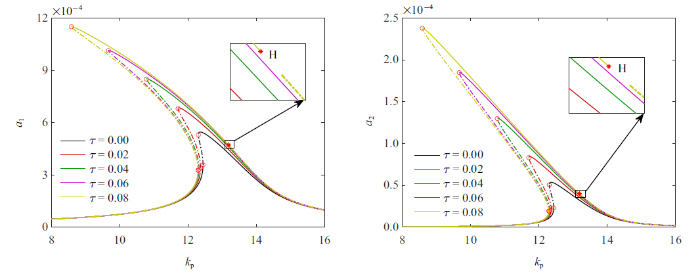
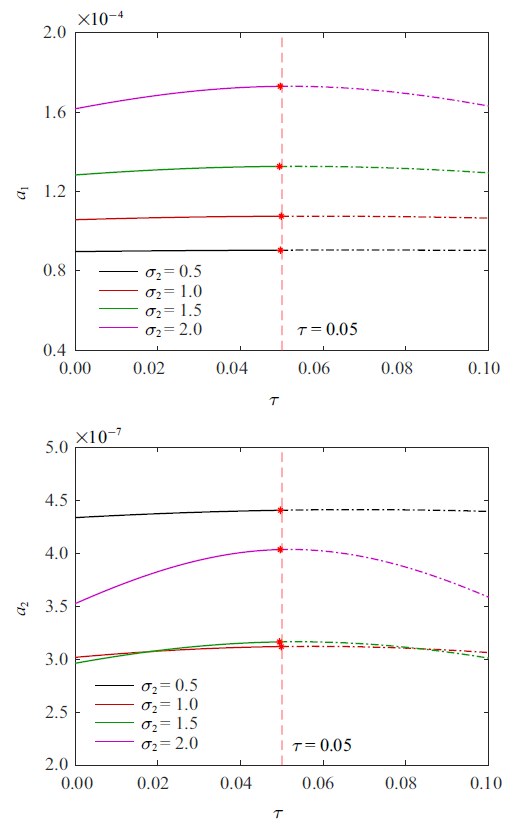
在图6(b)稳定性区域和非稳定区域的分界线上找一点$k_{p} =32$, $k_{d} =1.5$, 细致讨论. 图7给出了受控前后, 系统力响应曲线. 控制前系统力响应曲线存在两个极限点, 有明显的滞后现象. 加入反馈控制后, 系统的滞后现象被显著抑制, 仅在较大的时滞下出现跳跃现象. 下面以时滞为变量, 以零时滞为起点, 对系统平衡点做延拓分析, 如图8所示. 时滞较小时受控系统具有稳定的平衡点, 滞效应对系统稳态响应大小影响很微弱. 在$\tau =0.05$附近出现Hopf分岔, 表明系统稳定平衡点失稳而产生极限环, 出现新的周期运动. 深入研究将发现, Hopf分岔后, 受控系统会缓慢进入新的周期运动, 在新的周期运动下系统振动幅值远远大于分岔前. 因此本文将Hopf分岔时的时滞量, 称为临界时滞. 由图8可见, 不同外调谐参数$\sigma_{2}$下, 临界时滞大致相同.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 控制前($k_{p} =0$, $k_{d} =0$)与控制后($k_{p} =32$, $k_{d} =1.5$)系统的力响应曲线($\sigma_{2} =4.5$)

Fig.7 Force response curves of the system before($k_{p} =0$, $k_{d}= 0$) and after ($k_{p} =32$, $k_{d} =1.5$) control ($\sigma_{2} =4.5$)

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 受控系统稳态响应随时滞量的演变情况($k_{p} =32$, $k_{d} =1.5$)

Fig.8 Variation of the controlled system steady response with time delay ($k_{p} =32$, $k_{d} =1.5$)

为了验证多尺度分析的正确性, 对原系统(1)和(2)受控前后进行Runge-Kutta数值积分, 其中控制力项(3)采用差分法处理. 由图9(a) $\sim\!$图9(c)可见, 不同时滞量下, 受控系统进入稳态后响应幅值几乎不变, 印证了图8得到的结论. 此外, 时滞越小, 系统进入稳态所用的时间越短, 符合物理预期. 当时滞接近或大于临界时滞(0.05)时, 系统将缓慢进入新的周期运动, 为了能清晰展示新的周期运动, 在图9(f)中将$\tau=0.051$条件下的时间积分长度延长20倍, 发现此时受控系统十分缓慢的进入新的周期运动, 且振动幅值放大了近三个数量级, 受控前的系统响应历程被完全被淹没, 控制器失去控制效果, 与前文采用多尺度法计算得到的图6、图8展示的结果吻合.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同时滞量下原受控系统响应的时间历程 ($k_{p} =32$, $k_{d} =1.5$)

Fig.9 Time history of the controlled system for different time delay ($k_{p} =32$, $k_{d} =1.5$)

5 结论

本文针对基于压电复合材料的预变形旋转叶片闭环控制系统, 采用多尺度法得到了系统发生2:1内共振条件下受控系统的演化方程, 采用延拓法得到了系统稳态响应随速度增益、位移增益等系统参数的演化规律, 揭示了时滞量对系统稳定性的影响. 通过分析得到如下结论:

(1)速度增益的作用类似于阻尼, 具有抑制跳跃, 降低响应峰值的作用.

(2)频响曲线随位移增益向高频方向移动, 不恰当选取位移增益会给控制系统引入新的共振, 位移增益存在一个范围使得系统响应出现多值现象.

(3)增益平面内稳定性区域和非稳定区域的分界线大致呈现一条直线, 非稳定区域出现一块跟多值现象相关的隆起.

(4)时滞量对系统稳定性影响显著, 超过临界时滞时, 系统将缓慢进入一个大振幅的周期运动, 从而丧失控制效果.

(5)通过数值仿真验证了解析解的正确性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Yoo

, Park

Vibration analysis of rotating pre-twisted blades

Computers & Structures, 2001,79(19):1811-1819