三相驱动下非光滑振动驱动系统的动力学分析1)

doi:10.6052/0459-1879-20-177

三相驱动下非光滑振动驱动系统的动力学分析¹⁾

朱诗慧, 周震, 吕敬^,²⁾, 王琪

北京航空航天大学航空科学与工程学院, 北京 100083

KINETICS ANALYSIS OF NON-SMOOTH VIBRATION-DRIVEN SYSTEM WITH THREE-PHASE CONTROL ¹⁾

Zhu Shihui, Zhou Zhen, Lü Jing^,²⁾, Wang Qi

School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China

通讯作者: 2) 吕敬, 副教授, 主要研究方向: 动力学与控制. E-mail:lvjing@buaa.edu.cn

收稿日期: 2020-05-30 接受日期: 2020-08-20 网络出版日期: 2020-11-18

基金资助:

1) 国家自然科学基金项目. 11772021
国家自然科学基金项目. 11972055

Received: 2020-05-30 Accepted: 2020-08-20 Online: 2020-11-18

作者简介 About authors

摘要

可移动式机器人已成为机器人研究领域的重要分支,为实现其在狭小特殊环境中的运动, 学者们提出并研究了振动驱动移动系统.本文基于二维LuGre摩擦模型和拉格朗日方程,给出了一类振动驱动系统在各向同性摩擦环境中的动力学建模方法和数值算法.这类振动驱动系统结构简单且密封性好,依靠箱体与地面间的摩擦力实现自身的定向运动.该系统由一个外部箱体和两个内部质量块构成,两个质量块在箱体内的两个平行轨道上作三相振动驱动,箱体通过三个刚性支撑足与地面保持接触. 二维LuGre摩擦模型的利用,可有效避免库伦摩擦模型的不连续性给动力学方程的数值求解带来的困难,且可有效揭示该系统在运动过程中的黏滞-滑移切换现象. 数值仿真结果表明,通过调整其内部质量块的驱动参数,可实现箱体的直线平移、定轴转动和平面一般运动,且箱体在移动和转动过程中会出现擦滑、穿滑、回滑和不黏等4种现象; 另外,通过调节驱动参数, 不仅可以改变箱体移动和转动的快慢,还可以改变箱体形心运动轨迹的曲率半径.

关键词： 振动驱动系统 ; 三相驱动 ; 黏滞-滑移 ; LuGre摩擦模型

Abstract

Mobile robot has become an important branch in the domain of robotics. In order to achieve its movement in some narrow and special environments, the vibration-driven system has been proposed and researched by domestic and foreign scholars. In this paper, such a vibration-driven system consisting of an external rigid box and two internal mass blocks which are driven by three-phase control on two parallel orbits is researched. And the box is always in contact with the rough ground via three rigid support elements. This kind of vibration-driven system has simple structure, good sealing performance, and relies on the friction force between the box and the rough ground to realize its directional movement. Based on the two-dimensional LuGre friction model and Lagrange equations of the second kind, the dynamic modeling method and numerical algorithm of the vibration-driven system are presented in an isotropic friction environment. The use of the two-dimensional LuGre friction model can effectively avoid the difficulty of solving the dynamic equations caused by the discontinuity of the Coulomb friction model, and can accurately reveal the stick-slip switching phenomenon during the movement of vibration-driven systems. The numerical simulation results show that the driving parameters of the internal mass blocks can be adjusted to realize rectilinear translation, rotation about a fixed-axis and general plane motion of the rigid box. And four types of stick-slip motion with different sliding regions can occur during the translation and rotation of the rigid box, such as grazing sliding, crossing sliding, switching sliding and no stick. In addition, the translational speed and rotational speed of the box body and the radius of curvature of the box centroid trajectory can be changed by adjusting the driving parameters.

Keywords： vibration-driven system ; three-phase control ; stick-slip ; LuGre friction model

PDF (942KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

朱诗慧, 周震, 吕敬, 王琪. 三相驱动下非光滑振动驱动系统的动力学分析¹⁾. 力学学报[J], 2020, 52(6): 1755-1764 DOI:10.6052/0459-1879-20-177

Zhu Shihui, Zhou Zhen, Lü Jing, Wang Qi. KINETICS ANALYSIS OF NON-SMOOTH VIBRATION-DRIVEN SYSTEM WITH THREE-PHASE CONTROL ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(6): 1755-1764 DOI:10.6052/0459-1879-20-177

引言

近年来可移动式机器人的发展受到了广泛关注,其运动方式仍然是以轮式或腿式为主^[1-2],但是在管道清理、灾后救援等特殊情况下,这些运动方式并不能很好的满足人们的需求. Chernous'ko^[3-4]提出了振动驱动移动系统,这类系统依靠内部质量块的周期性振动来驱动外部箱体在有阻力环境中移动,具有结构简单、易于密封化和微型化等优点.

学者们在振动驱动系统的直线平移运动特性方面做了大量研究,其中Sergey等^[5]指出振动驱动系统的定向运动依赖于"非对称的摩擦力"或"非对称的内部驱动方式";Chernous'ko^[6-7]引入非对称驱动方式: 两相驱动和三相驱动,分别对内部质量块施加速度控制模式和加速度控制模式,分析了系统实现周期性稳态运动的条件.Li等^[8]和Sobolev等^[9]分别通过倒摆车和含多个转子的振动驱动实验模型验证了直线平移的相关理论.方虹斌等^[10-12]运用平均法得到了三相驱动下振动驱动系统在黏性摩擦环境中运动速度的近似解,并从滑移分岔的角度分析了其在库伦干摩擦作用下的运动情况.Du等^[13]通过压电悬臂梁实验对简谐振动驱动系统的黏滑运动进行了实验验证,观察到了明显的黏滞-滑移现象. 陈祺等^[14-15]基于一维库伦干摩擦模型(为便于计算假设动、静摩擦系数相等),首次分析了系统不同黏滑运动的分岔条件.

目前, 对于作平面一般运动振动驱动系统的运动特性研究得较少^[16-21],其中Volkva ^[16]等研究了这样一类振动驱动系统,它借助外部4个倾斜的支撑足与地面保持刚性接触, 内部有两个做正弦运动的质量块,在各向异性(前后运动的摩擦系数不相同)的黏性摩擦力作用下可以实现S形的折线运动.殷蓬勃等^[17]在此基础上分析了三相驱动下系统的平面运动特性,通过调节两个质量块的振动周期比和相位差实现了外部箱体上某点的运动轨迹在直线和圆弧间的切换.占雄等^[18-19]引入各向异性的库伦干摩擦模型,研究了一类振动驱动系统(滑道垂直, 正弦激励), 其外部箱体与地面间保持面接触;并假设箱体在运动过程中, 其纵轴始终与箱体形心的运动轨迹相切;揭示了箱体平动和转动中出现的黏滞-滑移切换现象.

这类振动驱动系统箱体的运动是通过外部的摩擦力实现的.干摩擦的不连续性带来的黏滞-滑移效应的存在^[22-23],使得系统的运动情况更为复杂, 但充分利用其特性可以有效提高系统运动效率.以往的研究大多采用库伦干摩擦模型分析系统直线平移运动中的黏滞-滑移切换现象^[13].在研究箱体作平面一般运动问题时, 若采用库伦模型处理多点摩擦问题,数值求解难度较大^[24-25].

近年来, LuGre摩擦模型也得到了广泛的应用^[26-27].它可反映库伦干摩擦、黏性摩擦和Stribeck摩擦等多种摩擦特性^[28],在降低数值计算难度的同时较为全面地揭示摩擦特性. 该模型的参数较多且不易选取,在工程手册上也难以查到, 但可借助一些经验公式^[29-30]进行选取.若模型参数选取不合适时, 会导致计算仿真结果失真.

本文将借鉴文献^{[14,15,16,17,18]}的研究方法研究三相振动驱动系统的动力学特性;为弥补原有研究中所采用的摩擦模型的不足,文中将采用LuGre摩擦模型描述箱体与地面接触点的二维摩擦,能更好地反映静摩擦特性对黏滞-滑移运动的影响, 且便于计算; 利用Lagrange方程,给出振动驱动系统作平面一般运动的动力学模型和算法;分析三相驱动参数的变化对系统运动特性的影响,为振动驱动型机器人的设计和控制提供理论支撑.

1 振动驱动系统

1.1 力学模型

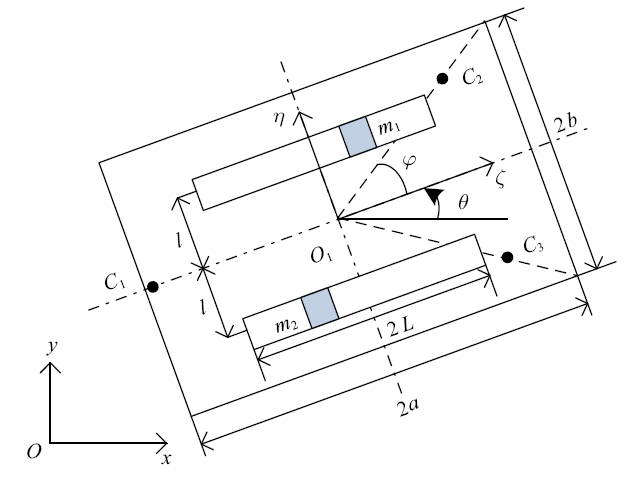
设振动驱动系统由质量为$M$的均质刚性箱体和质量分别为$m_1$, $m_2$的质量块(视为质点)组成,其中质量块在箱体内的两条平行滑道中相对箱体作周期运动,箱体通过三个刚性支撑足$C_i$ $(i=1,2,3)$始终与地面保持接触, 如图1所示.箱体的长和宽分别为$2a$和$2b$, 高度不计. 长度均为$2L$的两个平行滑道平行于箱体的对称轴, 到对称轴的距离均为$l$.支撑足到箱体形心$O_1 $的距离$O_1 C_i =a$, 且$\tan \varphi =b/a$.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 三足支撑的振动驱动系统模型

Fig. 1 The model of vibration-driven system with tripod support

设$Oxy$为惯性坐标系, $O_1 \xi \eta $为固连在箱体上的动坐标系, $\theta$表示轴$O_1 \xi $与轴$Ox$间的夹角, 以逆时针为正; $(x_M ,y_M )$是箱体形心$O_1$在惯性坐标系中的坐标, 则系统的广义坐标可表示为

(1)$q=(x_M ,y_M ,\theta )^{T}$

1.2 三相驱动

三相驱动是指将质量块相对箱体的运动周期$T^\ast $分为$\tau _1$, $\tau _2$, $\tau_3$三段, 在每个时间段, 质量块相对箱体作匀变速直线运动, 其相对运动的数学表达式为^[3]

(2)$\ddot{{\xi }}(t)=\left\{ {\begin{array}{l@{\quad }l} w_1, & t\in [0,\tau _1 ) \\ -w_2, & t\in [\tau _1 ,\tau _1 +\tau _2 ) \\ w_3, & t\in [\tau _1 +\tau _2 ,T^\ast ) \\ \end{array}} \right.$

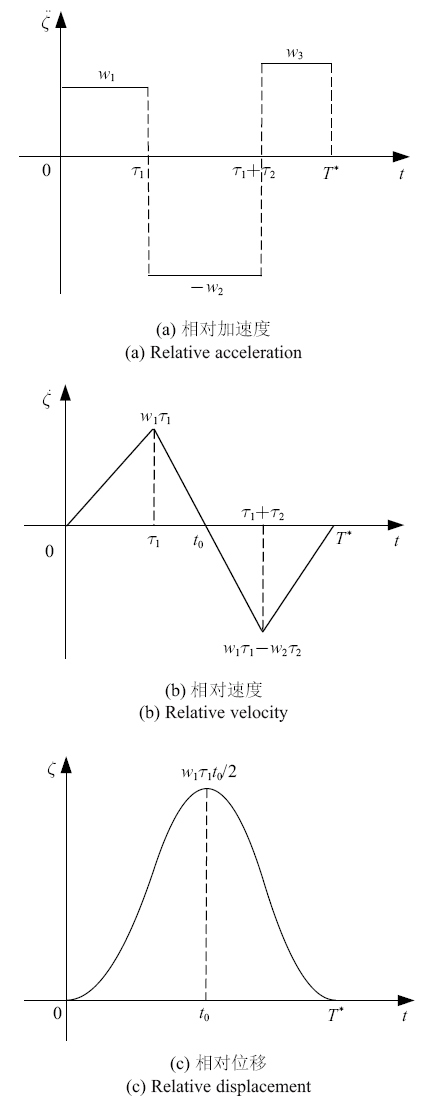
其中, $w_k >0$ $(k=1,2,3)$称为驱动参数, $T^\ast =\tau _1 +\tau _2 +\tau _3 $. 图2给出了该三相驱动方式下质量块的运动特征.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 三相驱动下质量块的运动特征

Fig. 2 Movement characteristics of a mass under three-phase control

设$t$时刻质量块相对于箱体的横坐标为$\xi _j (t)$ $(j=1,2)$, 且满足

(3)$-L\leqslant \xi _j (t)\leqslant L$

以质量块在区间$[0,L]$上的正向运动为例, 分析其运动时的参数特征. 为避免质量块与箱体间发生碰撞, 并满足周期性运动条件, 可得

(4)$\left. \begin{array}{l} \xi _j (0)=\xi _j (T^\ast )=0 \\ \dot{{\xi }}_j (0)=\dot{{\xi }}_j (T^\ast )=0 \\ \end{array} \right\}$

且存在某个时刻$t_{0j} $有

(5)$\xi _j (t_{0j} )=L,\ \ \dot{{\xi }}_j (t_{0j} )=0$

对于质量块$m_j$ $(j=1,2)$, 式(2)中的$w_1$, $w_2$, $w_3 $分别定义为$w_{1j}$, $w_{2j}$, $w_{3j}$, 由式(2)~式(5)可以导出^[3,7]

(6)$\left. {\begin{array}{l} \tau _{1j} =\sqrt {\dfrac{2Lw_{2j} }{w_{1j} (w_{1j} +w_{2j} )}} \\ \tau _{2j} =\sqrt {\dfrac{2L}{w_{2j} }} (\sqrt {\dfrac{w_{3j} }{w_{2j} +w_{3j} }} +\sqrt {\dfrac{w_{1j} }{w_{1j} +w_{2j} }} ) \\ \tau _{3j} =\sqrt {\dfrac{2Lw_{2j} }{w_{3j} (w_{2j} +w_{3j} )}} \\ t_{0j} =\sqrt {\dfrac{2L(w_{1j} +w_{2j} )}{w_{1j} w_{2j} }} \\ \end{array}} \right\}$

2 动力学方程及其算法

2.1 箱体接触足的摩擦力

动坐标系$O_1 \xi \eta $与惯性坐标系$Oxy$的转换矩阵可表示为

(7)${A}=\left[\begin{array}{cc} \cos \theta & -\sin \theta\\ \sin \theta & \cos \theta\\ \end{array}\right]$

由图1可知, 支撑足$C_i$ $(i=1,2,3)$相对箱体的位置向量可表示为

(8)$\left. {\begin{array}{l} r_{O_1 C_1 } =\left[ {-a,0} \right]^{T} \\ r_{O_1 C_2 } =\left[ {a\cos \varphi ,b\cos \varphi } \right]^{T} \\ r_{O_1 C_3 } =\left[ {a\cos \varphi ,-b\cos \varphi } \right]^{T} \\ \end{array}} \right\}$

支撑足在惯性系中的位置向量可表示为

(9)$r_{C_i } =r_{O1} +{A}\cdot r_{O_1 C_i }$

其中${r}_{O_1 } =\left[ {x_M ,y_M } \right]^{T}$, 将上式对时间求导可得其速度${v}_{C_i } ={\dot{{r}}}_{C_i} $.

用二维LuGre摩擦模型^[31-32]描述支撑足与地面间的摩擦力, 其表达式为

(10)$F_{T_i } =-\mu _i F_{N_i }$

其中, $F_{T_i } =[F_{T_i x} ,F_{T_i y} ]^{T}$为支撑足$C_i $的摩擦力向量, $F_{N_i } $为支撑力. $\mu _i =[\mu _{ix} ,\mu _{iy}]^{T}$为LuGre摩擦系数矩阵, 其表达式为

(11)$\left. {{\begin{array}{l} {\mu _i =\sigma _0 z_i +\sigma _1 \dot{{z}}_i +\sigma _2 v_{C_i } } \\ {\dot{{z}}_i =v_{C_i } -\sigma _0 \dfrac{\left\| {v_{C_i } } \right\|}{g(v_{C_i } )}z_i } \\ {g(v_{C_i } )=\mu _C +(\mu _S -\mu _C ){e}^{-({\| {v_{C_i } } \|} / {v_{s} })^2}} \\ \end{array} }} \right\}$

其中, $z_i =[z_{ix} ,z_{iy} ]^{T}$ $(i=1,2,3)$是鬃毛的平均变形量列向量;$\sigma _0 $和$\sigma _1 $为鬃毛刚度和阻尼系数, $\sigma _2 $为黏性系数, $\mu_c $, $\mu _s $分别为动/静摩擦系数, $v_{s} $为Stribeck速度.

2.2 振动驱动系统的动力学方程

设质量块$m_1$, $m_2$在动坐标系中的相对位置向量为

(12)${r}_{O_1 1} =\left[ {\xi _1 ,l} \right]^{T},\ \ {r}_{O_1 2} =\left[ {\xi _2 ,-l} \right]^{T}$

则质量块$m_j$ $(j=1,2)$的绝对位置向量为

(13)${r}_j =\left[ {r_{jx} ,r_{jy} } \right]^{T}={r}_{O1} +{A}\cdot {r}_{O_1 j}$

由第二类拉格朗日方程可得该系统的动力学方程

(14)$\frac{{d}}{{d}t}(\frac{\partial T}{\partial {\dot{{q}}}})-\frac{\partial T}{\partial {q}}={Q}_{q}$

其中, ${Q}_{q} $为系统广义力列向量. $T$为系统动能, 且$T=T_M +T_1+T_2 $, 其具体表达式为

(15)$\left.\begin{array}{l} T_M =\dfrac{1}{2}M(\dot{{x}}_M ^2+\dot{{y}}_M ^2)+\dfrac{1}{2}J_M \dot{{\theta }}^2 \\ T_j =\dfrac{1}{2}m_i \left( {\dot{{r}}_{jx} ^2+\dot{{r}}_{jy} ^2}\right),\ \ j=1,2 \\ \end{array} \right\}$

其中$J_M =M(a^2+b^2)$/3.

系统的广义力${Q}_{q} $可表示为

(16)${Q}_{q} =\left[ {Q_x ,Q_y ,Q_\theta } \right]^{T}=\left[{F_{Tx} ,F_{Ty} ,M_T } \right]^{T}$

其中, $F_{Tx} $和$F_{Ty} $是3个支撑足的摩擦力向点$O_1 $简化的主矢${F}_T$在$x$轴和$y$轴上的投影, $M_T$是这些摩擦力向点$O_1 $简化的主矩.

当不考虑箱体高度时, 支撑力可由下列方程求得

(17)$\left[ {{\begin{array}{ccc} 1 & 1 & 1 \\ a & {-a\cos \varphi } & {-a\cos \varphi } \\ 0 & {b\cos \varphi } & {-b\cos \varphi } \\ \end{array} }} \right]\left[ {{\begin{array}{c} {F_{N1} } \\ {F_{N2} } \\ {F_{N3} } \\ \end{array} }} \right]=\left[ {\begin{array}{l} (M+m_1 +m_2 )g \\ -(m_1 \xi _1 +m_2 \xi _2 )g \\ (m_1 -m_2 )gl \\ \end{array}} \right]$

将求出的支撑力代入式(10)得到摩擦力, 并代入式(16), 利用动力学方程(14), 通过数值仿真可分析该系统的动力学特性.

3 算例分析

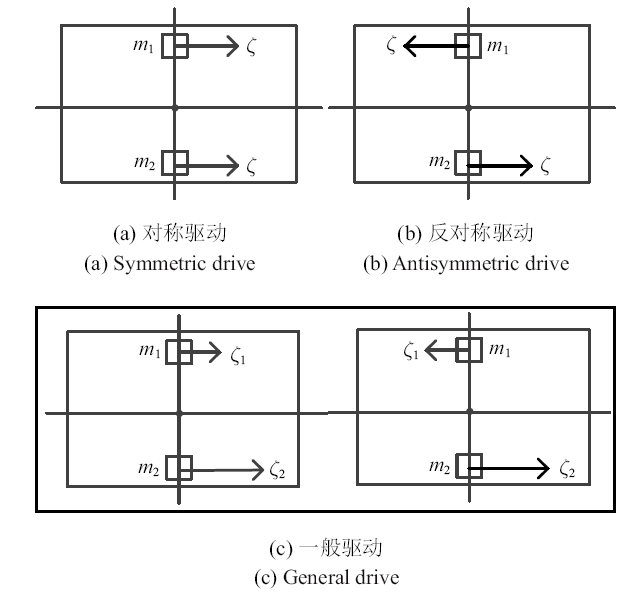
设箱体内的质量块按照图3给出的4种方式进行驱动, 分别就箱体直线平移和平面一般运动进行动力学分析,算例中系统的基本参数如下^[14,20]: $a=0.05$ m, $b=0.03$ m, $L=0.01$ m, $l=0.02$ m, $M=0.1$ kg, $m_1 =m_2 =0.03$ kg, $g=10$ m/s$^{2}$, $\mu _s =0.30$, $\mu _c =0.25$, $v_{s} =0.004$ m/s, $\sigma _0 =10^6$ /m, $\sigma _1 =10^3$ s/m, $\sigma _2 =0$ s/m.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 质量块的不同驱动方式

Fig. 3 Different methods of mass-driven

3.1 直线平移运动的仿真与分析

首先, 设两个质量块的驱动参数相同, 即$w_{k1} =w_{k2}$ $(k=1,2,3)$, $\xi _1 =\xi_2 =\xi $, 如图3(a)所示. 由于驱动的对称性, 以及质量分布与受力的对称性, 系统沿$x$轴作直线平移运动.

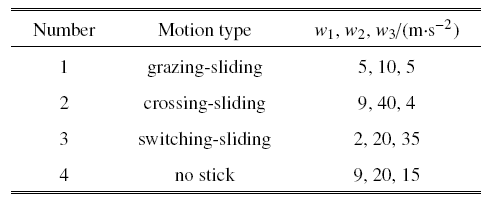
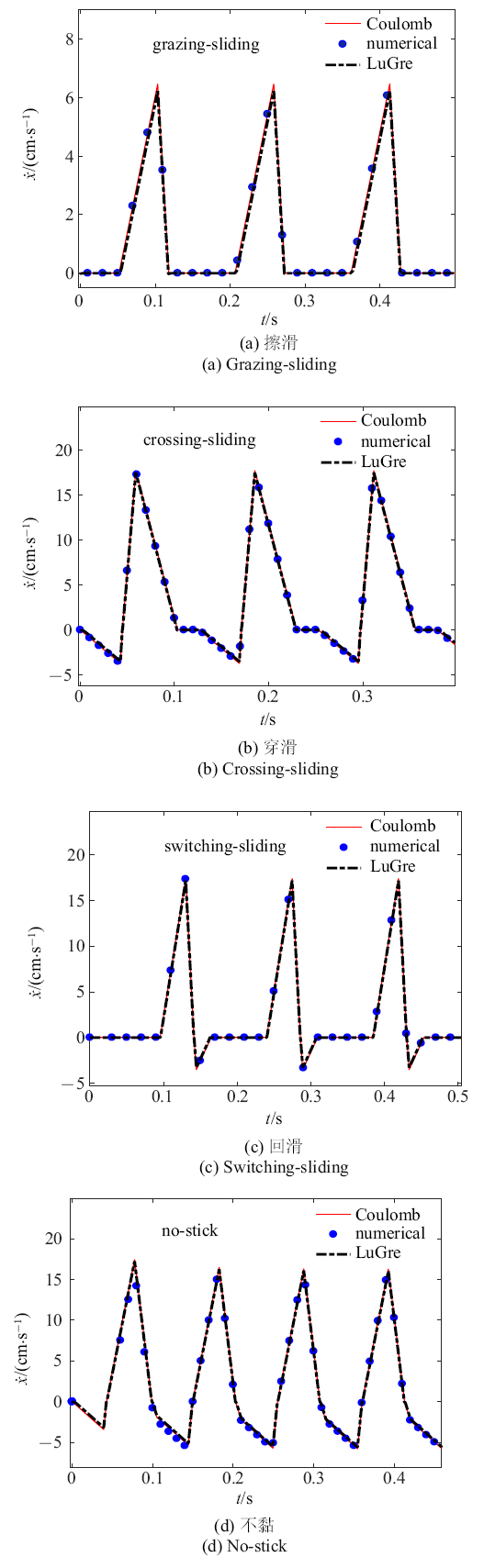
当$w_{k1} =w_{k2}$ $(k=1,2,3)$, 其值取表1给出的值. 由于摩擦的存在, 箱体稳态的周期性运动有4种类型^[14,33]:擦滑、穿滑、回滑和不黏(grazing-sliding、crossing-sliding、switching-sliding, no-stick).

表1 不同运动类型的驱动参数

Table 1 Different drive parameters

新窗口打开| 下载CSV

图4给出了箱体4种运动类型下的速度时间历程图, 其中黑虚线是基于LuGre摩擦模型的仿真结果, 红线是基于库伦摩擦模型的仿真结果,篮圈是由文献^[15]得到的理论解析结果. 3种结果完全一致, 验证了本文方法的有效性.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 四种运动类型箱体移动速度的时间历程图

Fig. 4 Time history diagram of box moving-velocity in four motion types

由图4可以看出, 当系统是擦滑运动类型时, 箱体时而向前运动, 时而保持静止, 但不存在倒退现象. 而其他运动类型, 箱体均存在着倒退现象.

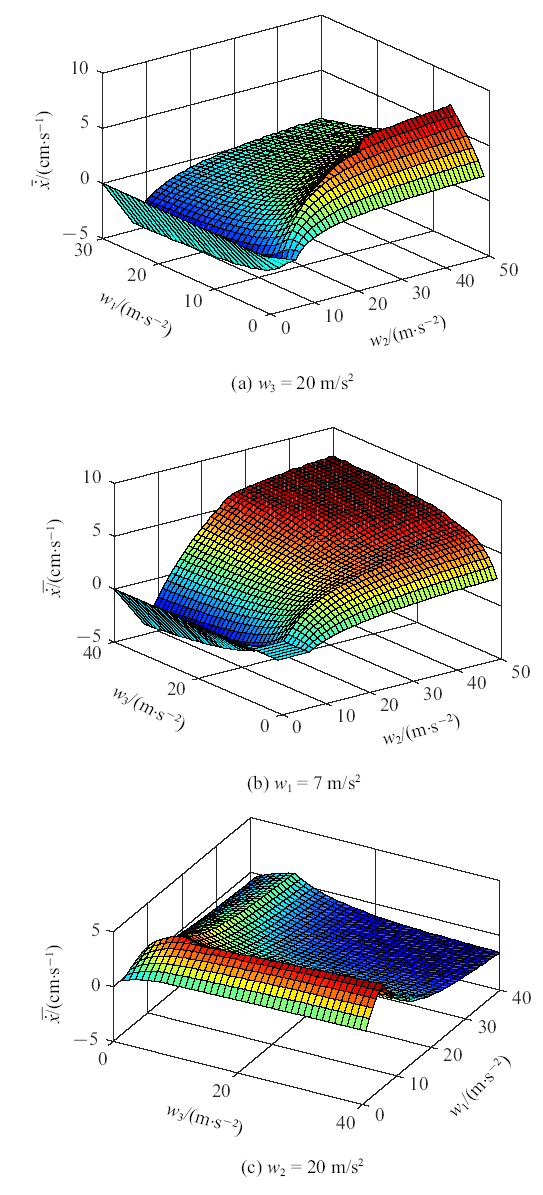
以在一个运动周期内箱体平移的平均速度$\overline{\dot{{x}}} $为指标, 分析三相驱动参数对该指标数的影响. 图5给出了驱动参数的变化对平均速度的影响.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 驱动参数与$\overline{\dot{{x}}} $的关系图

Fig. 5 The relationship between $\overline{\dot{{x}}} $ and the drive parameters

从图5可以发现, 存在明显的脊线. 当$w_1$, $w_2 $取脊线上的值时, 其对应的$\overline {\dot{{x}}} $值大于两侧的值; 且有$\overline {\dot{{x}}} $随$w_2 $的增大而增大. 因此当$w_2 $的值给定时(如图5(c)所示), 在脊线的交界处,$\overline {\dot{{x}}} $取得最大值.

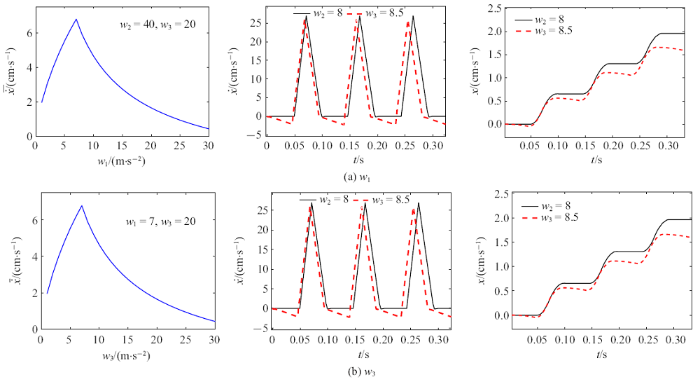
图6(a)和图6(b)分别展示了$w_1 $和$w_3 $对$\overline {\dot{{x}}} $的影响, 以及箱体的位置和速度随驱动参数变化的区别. 在转折点处所对应的驱动参数是箱体由擦滑运动类型转为其他运动类型的临界点, 这时系统的移动效率最优, 避免了后退运动的出现, 减少了能量的消耗.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 驱动参数$w_1$, $w_3$对$\overline {\dot{{x}}} $的影响

Fig. 6 The effect of drive parameters $w_1$, $w_3$ on the $\overline {\dot{{x}}} $

3.2 平面一般运动的仿真与分析

3.2.1 定轴转动

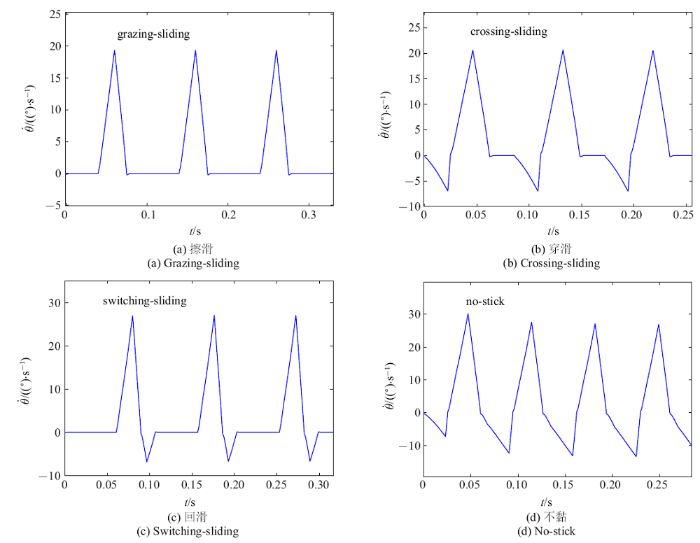
当按照图3(b)所示的模式驱动时, 即$w_{k1} =-w_{k2}$ $(k=1,2,3)$, $\xi _1 =-\xi _2 $, 由于驱动的反对称性, 若初始系统静止, 3个支撑足处摩擦力的主矢${F}_T =0$, 向箱体形心简化的主矩$M_T \ne 0$, 箱体绕其形心作定轴转动. 同样其转动运动类型也有4种, 即擦滑、穿滑、回滑和不黏, 如图7所示.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 四种运动类型箱体转动速度的时间历程图

Fig. 7 Time history diagram of box rotation-velocity in four motion types

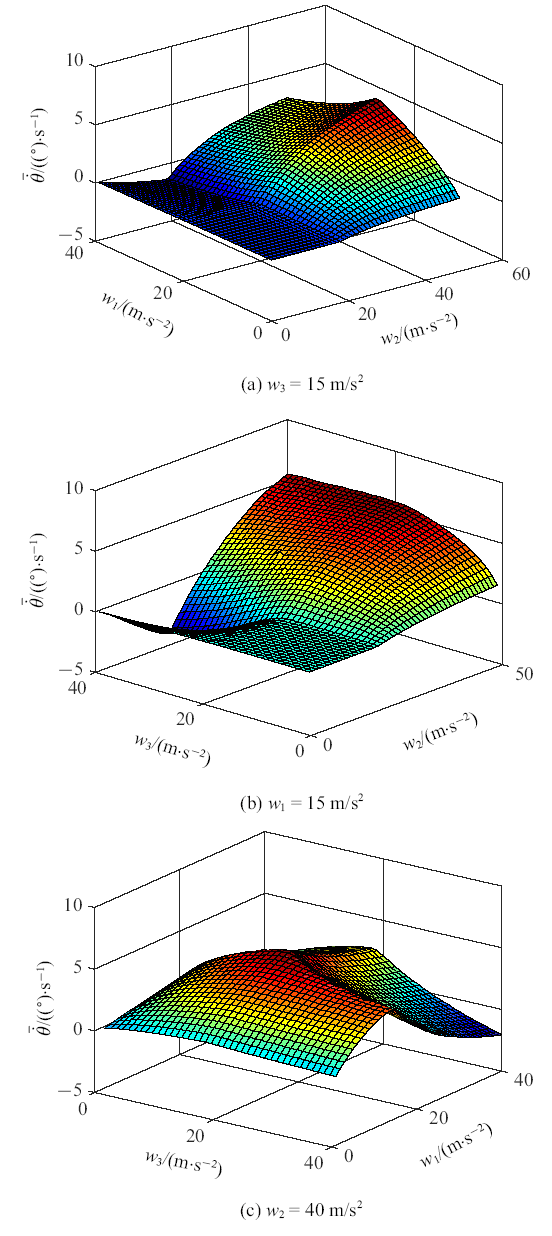
以箱体在一个振动周期内转动的平均角速度$\overline {\dot{{\theta }}} $为指标, 图8给出了驱动参数对$\overline {\dot{{\theta }}} $值的影响.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 驱动参数与$\overline{\dot{{\theta }}} $的关系图

Fig. 8 The relationship between $\overline{\dot{{\theta }}} $ and the drive parameters

在图8中, 同样可以看到脊线, 当驱动参数取脊线对应的数值时, $\overline{\dot{{\theta }}} $取得最大值; 脊线对应的驱动参数也是擦滑运动类型与其他运动类型的分界值.

3.2.2 平面一般运动

当按照图3(c)所示的模式驱动时, 即$\left| {w_{k1} } \right|\ne \left| {w_{k2} } \right|(k=1,2,3)$, 令$n={w_{k2}}/{w_{k1}}$, 箱体形心运动轨迹为圆周. 箱体作平面一般运动.

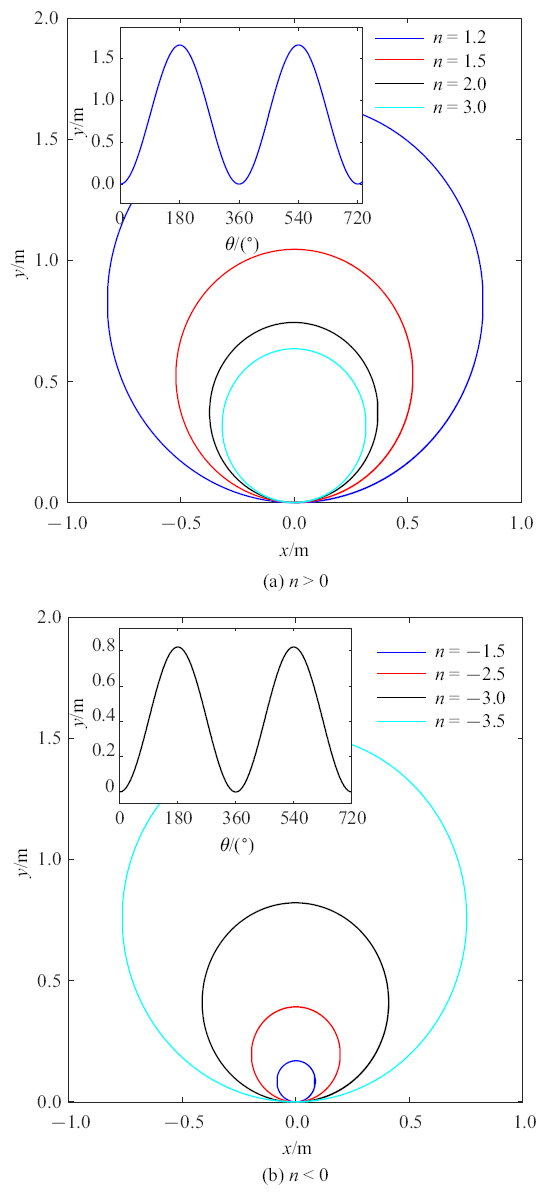
若$w_{11} =w_{31} =8$ m/s$^{2}$, $w_{21} =30$ m/s$^{2}$, 取不同的比值$n$, 箱体形心运动轨迹为半径不同的圆周, 如图9所示. 并描绘了$n=1.2$及$n=-3$时, 形心的$y$坐标与箱体转动角度的关系图. 可见, 箱体形心运动一周, 箱体转动一周.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同$n$值的形心运动轨迹

Fig. 9 The centroid-trajectory at different values of $n$

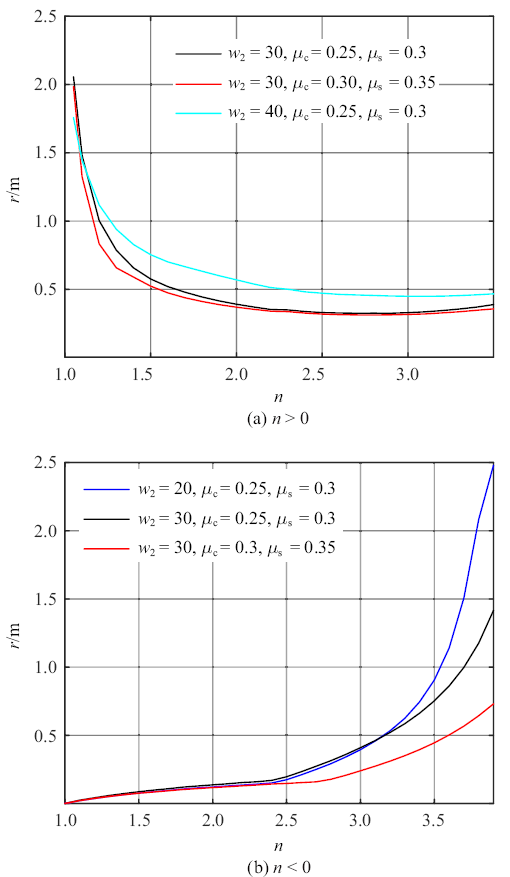
图10给出了不同驱动参数和不同摩擦系数情况下, 箱体形心运动轨迹的曲率半径$r$.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 曲率半径$r$与参数比$n$的关系图

Fig. 10 The relationship between radius of curvature $r$ and parameters ratio $n$

通过上述算例的分析可知, 根据不同的摩擦系数, 通过调整驱动参数可改变箱体的运动形式和形心运动轨迹.

4 结论

本文研究了一类内部受两个相互平行的三相驱动激励的振动驱动系统, 在各向同性的二维干摩擦环境中的平面运动规律. 首先,建立了具有3个足支撑的振动驱动系统的力学模型; 采用二维LuGre摩擦模型描述支撑足与地面间的摩擦, 用拉格朗日方程建立了该系统的动力学方程. 然后, 通过数值仿真对该系统的动力学特性进行了分析:(1)利用系统做直线平移运动的理论解和基于库伦摩擦的数值仿真解, 校验了基于LuGre摩擦模型的数值仿真结果, 表明了本文的建模方法与数值算法的合理性; (2)通过调整驱动参数, 实现了箱体的平移运动、定轴转动和平面一般运动,揭示了箱体平动和转动过程中均存在擦滑、穿滑、回滑和不黏4种运动类型; (3)不仅分析了驱动参数对箱体移动速度的影响,还分析了其对箱体转动快慢和箱体形心运动轨迹曲率半径的影响. 分析结果表明,这类振动驱动系统拥有丰富的黏滞-滑移动力学行为和形式多样的平面运动能力.本文给出的方法可为该类型的移动机器人的设计和研究提供一种方法.后续可以进一步研究振动驱动型机器人在三维空间的建模方法、数值算法和动力学特性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

朱磊磊, 陈军.

轮式移动机器人研究综述

机床与液压, 2009,37(8):242-247