引言
自行车具有结构简单,使用方便等特点,同时它的动力学行为与一些复杂的力学和数学问题密切相关. 静态来看,自行车很难 通过前后轮与路面的接触实现稳定直立. 因此,其物理本质与“倒立摆”结构类似,都属于一类静态不稳定系统[2]. 但当自行车在适当的运动速度条件下,却能够实现动态自稳定的直立“自行”. 这种自行稳定性现象在历史上引起了众多学者的研究兴趣,并出现了多种多样的理论解释. Rankine[3]将自行车简化为只包含车轮偏转角的单自由度动力学系统,粗略地认为自行车的平衡源于骑行者对车把转角的控制;Bourlet[4]建立了考虑车轮陀螺效应的自行车简单动力学模型,并认为自行车的自稳定性与车轮的陀螺效应有关;文献[5,6,7,8]也 建立了各自的自行车等效动力学模型,但这些模型在反映自行车的自稳定特征时均存在一定程度上的不足. 1899 年法国数学家 Carvallo[9]和英国剑桥大学 Whipple[10]应用刚体动力学理论,并引入一些线性化的假设,分别独立地建立了自行车做匀速直线运动时的线性化摄动动力学模型. 特别是,两位研究者首次将自行车简化为由 4 个刚体组成的简单构型,并给定了标准的几何和物理参数. 该简化的自行车构型被后来的研究者广泛采用[11-15],称之为“Carvallo-Whipple 自行车构型”或简称为“Whipple 构型”.
在动力学方面,自行车涉及的问题主要包括:(1) 由于两个接触体的运动约束涉及运动物体轮廓面 (线) 上的一对动点的运动学关系,建立自行车在复杂曲面上的完整和非完整约束方程需要较为复杂的数学表述;(2) 经典力学提供了丰富的动力学建模方法和手段,但是不同建模方法将会导致自行车动力学模型具有不同的表现方式. 因此,应理解不同动力学模型之间的内在关联关系,揭示自行车内在的动力学规律;(3) 自行车的稳定性分析;(4) 动力学实验和自行车相关的控制问题. 本文将围绕以上 4 个方面,期望对自行车动力学的研究进展给出较为全面的综述.
论文的结构如下:第 2 节简要描述了 Whipple 自行车构型,并对自行车动力学研究中涉及到的完整约束和非完整约束进行了概述;第 3 节系统总结了自行车动力学建模中的各类方法;第 4 节对自行车 3 种动态平衡状态的稳定性问题的研究进行了总结;最后,展望了自行车动力学的研究前景.
1 自行车构型描述及约束方程
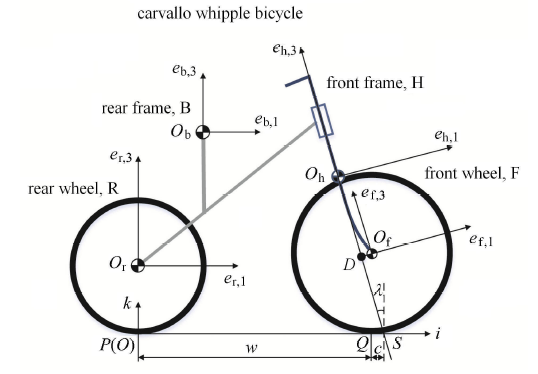
图1为通常采用的 Carvallo-Whipple 自行车构型系统. 该系统主要由前后框架 H 和 B (骑行人作为刚体固结于后框架)、前车轮 F 和后车轮 R 四个刚体组成. 忽略铰接处的间隙、摩擦、阻尼等因素,并在建模过程中考虑以下几个方面的假设:
图1
图1
Carvallo-Whipple 自行车构型图
Fig.1
The benchmark Carvallo-Whipple bicycle in an upright, straight reference configuration
(1) 前、后轮边缘为刀刃型结构,与地面的接触关系为点接触;
(2) 前、后轮是圆周对称结构,其质心与各自圆心重合;
(3) 假设前轮和后轮与地面之间的最大静摩擦系数足够大,以保证前后轮运动时处于纯滚动状态,即与地面无任何滑移;
(4) 前框架和后框架分别关于前轮和后轮所在的平面对称,一是几何对称,二是质量分布对称.
为了描述自行车的运动状态,定义空间惯性坐标系 $F_{I} = \{ O-ijk \}$,并将坐标原点设置在后车轮与路面的接触点 $P$ 处,$i$ 轴的正向指向前车轮,$k$ 轴正向背离地面,$j$ 轴正向指向骑行者的左侧. 分别在 4 个刚体质心处建立固连坐标系
$ F_{\rm b} = \{O_{\rm b} - e_{\rm b,1} e_{\rm b,2} e_{\rm b,3} \}, \ \ F_{\rm r} = \{O_{\rm r} - e_{\rm r,1} e_{\rm r,2} e_{\rm r,3} \} \\ F_{\rm h} = \{O_{\rm h} - e_{\rm h,1} e_{\rm h,2} e_{\rm h,3} \}, \ \ F_{\rm f} = \{O_{\rm f} - e_{\rm f,1} e_{\rm f,2} e_{\rm f,3} \} $
自行车的 4 个刚体通过 3 个理想铰链连接,当不考虑路面对车轮的约束时,描述自行车自由运动需要 9 个 ($4\times 6- 3\times 5 = 9$) 广义坐标. Xiong等[27-28]将 9 个广义坐标定义如下:选择前叉转轴与前框架坐标轴的交点 $D$ 为参考点,其在惯性坐标系 $F_{I}$ 中的 3 个坐标分量 $(x,y,z)$ 作为系统的 3 个广义坐标. 遵循 3-1-2 的旋转顺序,选择后框架固连坐标系 $F_{\rm b}$ 相对于惯性坐标系 $F_{\rm I}$ 的 3 个欧拉角 $(\psi ,\theta ,\varphi)$ 为系统的另外 3 个广义坐标,其中 $\psi $ 为绕着 $z$ 轴的偏航转角,$\theta $ 为绕着 $x$ 轴的倾斜角,$\varphi $ 为绕着 $y$ 轴的俯仰角. 另外 3 个广义坐标分别为车把转角 $\delta $ (前框架相对于后框架的转角),后、前轮相对于后、前框架的转角 $\phi _{\rm r} $ 和 $\phi _{\rm f}$. 这 9 个广义坐标可用向量表示为: $q = [x,y,z,\psi ,\theta ,\varphi ,\delta ,\phi _{\rm r} ,\phi _{\rm f} ]^{\rm T}$.
另外,描述 Whipple 自行车构型需 9 个几何参数和 16 个质量参数. 这 9 个几何参数包括:自行车的轴距 $w$,前轮尾迹 $c$ (即前叉转轴延长线与地面的交点和地面接触点 $Q$ 之间的距离,当该交点在 $Q$ 点右侧时,$c$ 为正值,否则为负值), 前叉转轴相对于竖直线的倾斜角 $\lambda $,前后轮的半径 $(r_{\rm f} ,r_{\rm r} )$,前框架质心 位置 $(x_{\rm h} ,y_{\rm h})$ 和后框架质心位置 $(x_{\rm b} ,y_{\rm b})$. 16 个质量惯性参数包括:4 个刚体 的质量 $(m_{\rm b}, m_{\rm h }, m_{\rm r} , m_{\rm f})$ 以及它们相对于各自质心的惯量 张量 $(I_{\rm b},I_{\rm h},I_{\rm r},I_{\rm f} )$ (共有 $4\times 2 + 2\times 2 = 12$ 个非零 分量). Whipple 自行车构型的经典参数可参考文献[17]. 根据车轮纯滚动的假设条件,容易理解自行车是一个 同时受完整和非完整约束的多刚体系统. 然而,与 Chaplygin 雪橇[29]和独轮机器人[30]等传统的非完整系统相比,自行车中的约束方程不易用显式方程来描述. 由于通过铰链约束连接的前后车轮的轮心和前后框架之间形成了复杂的链式传递关系,接触点处的几何约束往往是隐式和非线性的. 为建立 Whipple 自行车构型下的线性化动力学模型,Meijaard[17]对非线性约束方程进行了线性化近似处理;Psiaki[13]利用解析几何的方法首次推导了完整约束方程的解析形式,其为四次代数方程,且具有高度非线性;Basu-Mandal 等[18]基于寻找两个车轮的最低点为参考条件推导了约束方程;类似地,Peterson 和 Hubbard[31-32]考虑轮胎的形状,采用直观的解析几何方法建立了完整和非完整约束方程;Wang 等[33]对两个车轮圆周进行参数化,利用极值条件 (车轮与地面的接触点为轮缘的最低点) 推导出车轮的完整约束方程.
以上两个方程分别是广义坐标 $z$ 和 $\varphi $ 关于广义坐标 $(\theta ,\delta )$ 的隐式函数,详细推导过程参见文献[28]. 显然,根据以上两个几何约束关系,$z$ 和 $\varphi$ 不再是独立的广义坐标,从而可以将自行车构型空间的维数由 9 维降为 7 维,且定义降维后的独立广义坐标向量为 $\tilde {\pmb q} = [x,y,\psi ,\theta ,\delta ,\phi _{\rm r},\phi _{\rm f} ]^{\rm T}$.
假设自行车在水平面上作纯滚动,即每个接触点处速度为零. 这一速度条件使得每个接触点处对应两个独立的速度约束:该接触点的速度在水平面上的两个分量为零. 考虑自行车有两个接触点,故自行车系统共有 4 个纯滚动约束.
为恰当表示以上 4 个滚动约束方程,需要在接触点处建立局部的接触坐标系. 该坐标系不一定要求是正交的,但要求局部接触坐标系中的一个坐标轴对应接触点处共切面的公法线方向[34]. 利用接触条件得到的接触体的轮廓参数关于广义坐标的函数关系,然后利用两个接触体在接触点处的相对速度的运动学关系,并将该相对速度为零的矢量条件映射到所建立的局部接触坐标系上. 这样,在每个接触点处可以建立 3 个速度约束方程. 容易证明,沿两个接触点处公法线方向的两个速度约束方程一定是两个几何约束方程(1)的全微分形式. 自行车两个接触点引起的独立的速度约束方程仅有 4 个,它们对应 4 个独立的非完整约束方程[30]. 同时,这也意味着自行车系统的自由度为 $ 3$,(这里的自由度采取分析力学中的传统定义,即系统的独立虚位移数[35]).
对受约束的多体系统来说,可以将几何约束和微分约束在速度空间中进行统一表示[36]. 对 Whipple 自行车系统来说,可以直接利用两个接触点相对速度为零的条件,并将以上条件映射到接触点的局部坐标系中,进而可以将相应的完整和非完整约束统一表示为
其中,$\dot {\pmb q} = [\dot {x},\dot {y},\dot {z},\dot {\psi },\dot {\theta },\dot {\delta },\dot {\varphi },\dot {\phi }_{\rm r}, \dot {\phi }_{\rm f} ]^{\rm T}$,$W(q)$ 是一个 $6\times 9$ 的矩阵,其具体表达式见文献[28] 的附录 B.
当自行车在曲面上运动时,由于曲面接触点处的几何参数与描述自行车构型之间的广义坐标存在非常复杂的函数关系,通常需要采用计算机符号运算得到系统的约束方程. 这一过程可以按照如下的流程进行: 在两个接触点 $P$ 和 $Q$ 处分别定义三个曲面曲线参数,记为 ${\pmb p}_i = [p_{i,1} ,p_{i,2} ,p_{i,3} ]^{\rm T}$, $i= {\rm r, f}$,其中,前两个曲面参数表征接触点在路面上的位置信息,最后一个曲线参数表征接触点在轮缘上的位置信息. 根据文献[34] 给出的接触几何条件,可以建立以上 6 个参数 $p = \left[ {{\pmb p}_{\rm r}^{\rm T},{\pmb p}_{\rm f}^{\rm T}} \right]^{\rm T}$ 与系统广义坐标 $q$ 之间的函数关系以及两个几何约束方程如下
结合以上关系,并利用接触点处相对速度等于零的条件,将接触点的相对速度表示在局部接触坐标系中,可以得到自行车在任意曲面上运动时的速度约束方程[28]
2 动力学建模
在经典动力学框架内,存在多种不同的力学原理和方法建立系统的动力学模型. 然而,不同方法可能导致动力学方程的表现形式存在很大不同[37]. 在缺乏计算机符号运算等便利分析工具的年代,如何建立自行车系统完备的动力学模型是一个具有挑战性的问题[12,17,19,33]. Getz 和 Marsden[21]采用几何力学的方法建立了一个极为简化的自行车动力学模型,并研究了自行车控制问题. Neimark 和 Fufaev[14]由于对自行车势能分析时的错误,得到了一组错误的动力学方程组;Papadopoulos 等[16]为建立摄动后的系统线性化动力学方程,手工推演时不得不引入一些直观的假设;Meajaard 等[17]系统地综述了历史上各种形式的自行车动力学建模方法,并针对经典的 Whipple 自行车构型,不仅采用计算机符号推导了自行车在平面上运动的非线性动力学方程组,而且与手工推导得到的线性化动力学模型进行对比,验证了模型的正确性. 论文中还提供了在 Whipple 自行车构型经典参数下,所得到的线性化方程的系数矩阵的具体表达式以及线性系统的具体特征值,并将其作为其他模型校验基准. Basu-Mandal 等[18]采用矢量力学中的 Newton-Euler 方法和分析力学中的 Euler-Lagrange 方法,并结合计算机符号运算,得到 Whipple 自行车完备的非线性微分代数方程组,并通过数值结果验证了两种模型的等效性. 作者还通过研究自行车做匀速直线运动时的线性化方程验证模型的正确性和精度. 在此基础上给出了自行车在水平面上做匀速圆周运动的动态平衡解的完备描述. Wang 等[33]同样采用欧拉-拉格朗日方法建立了 Whipple 自行车的非线性模型,并通过符号运算工具消除了完整约束和非完整约束,由此得到约化的动力学模型; Huang 等[38]利用 Kane 方法推导自行车的控制微分方程. Sharp[12]考虑车轮滑动作用建立了自行车线性化方程;Meijaard 和 Schwab[39]在建立自行车动力学模型时考虑了轮胎几何、路况以及系统阻尼等因素;Boyer 和 Porez[40]从几何力学角度研究了自行车动力学问题,并通过主纤维丛上的一般约化方法建立动力学模型. 由于自行车中所包含的约束方程以及动力学方程组的表现形式异常复杂,人们往往需要通过数值计算[41-42]或实验[32,43-44]验证模型的正确性.
其中,系数 $c_i^{i,k} (q)$ 是关于广义坐标$q$的函数,$P_i (q)$ 为广义力. 通过数学软件 MAPLE 符号运算可以发现,方程 (5) 中的系数具有如下性质:
(1) 各项系数只与 $\sigma _1 $ 和 $\sigma _2 $ 有关,即 $m_{ij} = m_{ij} (\sigma _1 ,\sigma _2 )$, $c_i^{jk} = c_i^{jk} (\sigma _1 ,\sigma _2 )$, $P_i = P_i (\sigma _1 ,\sigma _2 )$;
(2) $m_{ij} (\sigma _1 ,\sigma _2 ) = m_{ji} (\sigma _1 ,\sigma _2 )$;
(3) $c_3^{3,3} (\sigma _1 ,\sigma _2 ) \equiv 0$;
(4) $P_3 (\sigma _1 ,\sigma _2 ) \equiv 0$.
然而,这些性质 (除了性质 (2) 是平凡的) 很难根据 Gibbs-Appell 方程或其他经典力学方程如 Lagrange 方程的结构去严格地证明. 事实上,这些性质来源于自行车系统内在的对称性,而要阐述对称性,则需要用到几何力学中的一些基本概念[46]. 对于平面自行车系统,在考虑两个几何约束方程 (1) 之后,其构型空间是一个七维微分流形,同时受到 4 个非完整约束作用,这就形成了该构型空间上的一个约束分布[20]. 自行车运动在构型空间切丛上形成的相轨迹始终限制在该约束分布之上. 取李群 $G = {\rm SE}(2)\times S^1\times S^1$ 为对称群,它是 3 个李子群 $ {\rm SE}(2)$,$S^1$ 和 $S^1$ 的直积,分别代表自行车后框架的平面刚体运动、后轮的转动以及前轮的转动. 在 $G$ 作用下,自行车系统具有 Lagrangian 不变性以及约束分布不变性[20]. 可以看到,在构型空间每一点处,约束允许的速度子空间与群轨道切空间之和张成了该点的切空间,同时二者交集为一维子空间. 在这基础之上,可以应用所谓的非完整 Lagrange-d'Alembert 方程以得到约化约束空间上的约化动力学方程[20,47-48]. 该方程本质上与 Gibbs-Appell 方程是等价的,但其考虑了对称性,结构较 Gibbs-Appell 方程更为清晰. 利用该方程,前述性质很容易得到证明,其中性质 (1) 是 Lagrangian 不变性和约束分布不变性的直接结果,而性质 (3) 和 (4) 除了这两个不变性之外,主要来源于前述两个子空间的交集是一维的.
其中,${\pmb F}({\pmb q},\dot {\pmb q})$ 与自行车的重力和惯性力有关,${\pmb A}= [ A_{i,j}^k ] \in \mathbb{R}^{6\times 9}$ 是完整约束和非完整约束的系数矩阵,$\varLambda = [\lambda _{i,j} ] \in \mathbb{R}^{6\times 1}$ 是前后车轮在接触点处与完整约束和非完整约束相对应的 6 个拉格朗日乘子.
3 自行车的相对平衡点及其稳定性
目前关于自行车的相对平衡点及其稳定性的研究主要有 3 种情况:
(1) 自行车在水平面上的匀速直线运动;
(2) 自行车在水平面上的匀速圆周运动;
(3) 自行车在旋转曲面上的匀速圆周运动.
为研究以上动态运动的稳定性,首先需要通过系统的动力学方程,得到其对应的平衡解,然后在平衡位置附近建立线性化动力学模型,通过分析该线性系统的 Lyapunov 稳定性问题,确定系统相对平衡点的稳定性. 历史上,人们对 Whipple 自行车做匀速直线运动情况的稳定性问题研究的较多[17,50-51]. Carvallo[9]和 Whipple[10]于 1899 年分别独立 推导出自行车的线性化方程组,并针对具体的模型参数计算了自行车自稳定的速度范围. 文献 [11,15,17,42] 相继针对 Carvallo-Whipple 自行车构型,分别采用 Lagrange 方法和矢量力学方法推导出了线性化方程. Schwab[42]与 Meijaard[17]还利用多体系统动力学计算软件分别求出了线性化方程的系数,并与手算结果进行了对比验证. Lennartsson[52]和 Aström[53]利用多体动力学软件 Sophia 得到的非线性动力学方程在平衡位置附近进行线性化处理,也得到了相应的线性化方程组. Basu-Mandal[18]利用对带乘子的 Lagrange 方程线性化, Moore[25]对 Kane 方法得到的非线性动力学方程线性化. 以上方法均得到了自行车做匀速直线运动时正确的线性化方程组,它具有如下的标准格式
其中,${\pmb\eta} = [\theta ,\delta ]^{\rm T}$,${\pmb f} = [P_1 ,P_2 ]^ {\rm T}$,$\omega _0 $ 是自行车匀速直线运动时后轮的角速度. 其他系数矩阵 ${\pmb M}$, ${\pmb K}_0 $, ${\pmb C}$ 和 ${\pmb D}$ 是与自行车几何和惯量参数相关的常数矩阵. 具体表达式见文献[28] 的附录.
为了得到自行车在水平面上的匀速直线运动和匀速圆周运动的统一描述,并进行更加严格的稳定性分析,Xiong 等[28]基于 Gibbs-Appell 方程对这两种运动进行了研究. 这两种运动在某种意义上都可以看作是自行车动力系统的平衡点. 注意到 $\sigma _3 = \phi _r $ 是循环坐标,可以将式 (5) 改写成一阶常微分方程组的形式
其中 $x= (\sigma _1, \sigma _2, \dot {\sigma }_1, \dot {\sigma }_2, \dot {\sigma }_3 )$. 设 $x_0 $ 是方程 (8) 的平衡点,即其满足 $f(x_{0} ) = 0$,则必有 $x_0= (\theta _0,\delta _0,0,0,\omega _0)$,其中$\theta _0,\delta _0,\omega _0 $ 是 3 个常数. 根据前文提到的方程 (5) 系数所具有的性质,这 3 个常数只需要满足两个代数方程. 因此,在这两个代数方程独立的情况下,这样的平衡点不是孤立的,而是以单参数解族的形式存在的. 进一步,平衡点可以分为两类. 第一类平衡点为 $x_0 = (0,0,0,0,\omega _0)$,其中 $\omega _0 $ 为任意常数,这样的平衡点代表自行车的匀速直线运动. 第二类平衡点的 $\theta _0 ,\delta _0 $ 不同时为零,这样的平衡点代表自行车的匀速圆周运动. 利用 Whipple 自行车的经典参数[17],Xiong 等[28]得到了四族单参数圆周解,与 Basu-Mandal[18]及 Wang 等[33]的结果完全一致.
对于一些特殊的动力学系统[64],其平衡点的 Lyapunov 稳定性可以通过构造 Lyapunov 函数,即采用 Lyapunov 直接方法[65] 进行判断. 但是,对于自行车系统,其动力学方程组系数 的复杂性, 导致相应的 Lyapunov 函数不易被求解. 因此,Xiong 等[28] 基于 Lyapunov 间接方法,即根据系统 (8) 在平衡点处 Jacobi 矩阵的特征根分布来判断平衡点的 Lyapunov 稳定性,并且首次给出了自行车匀速直线运动和匀速圆周运动的非线性稳定性分析. 事实上,由于 $x_0 $ 是非孤立的,可以证明该点的 Jacobi 矩阵必有一个零特征根,这意味着 $x_0 $ 是非双曲的平衡点. 因此,$x_0 $ 的非线性稳定性与线性稳定性并不直接等价[66]. Xiong 等[28]结合中心流形定理[67],第一次严格地证明了如果平衡点 $x_0 $ 处的 Jacobi 矩阵其余 4 个特征根均具有负实部,则 $x_0 $ 是稳定的,但不是渐近稳定的.
对于自行车在旋转曲面上匀速圆周运动的稳定性,Xiong 等[27]亦开展了相关研究. 首先,他们给出了自行车在旋转曲面上圆周 解的定义. 该定义给定了广义坐标 $q$,曲面曲线参数 $p$ 以及 Lagrange 乘子 $A$ 随时间变化的规律,其中一共有 21 个待定常数,由微分代数方程组 (6) 确定. 为了消除时变变量,他们引入了一系列旋转变化,将圆周解等价转化为了一个新的微分代数方程组的平衡解,其中一共有 21 个待定常数. 同时他们发现,这 21 个常数只需要满足 20 个代数方程. 因此与在水平路面上运动的情形一样,这样的平衡点一般来说不是孤立的,而是以单参数解族的形式存在的. 他们以旋转抛物面 $\zeta = \alpha (\xi ^2 + \eta ^2)$,$\alpha \geqslant 0$ 为对象,在不同的曲面系数下都找到了 4 个单参数圆周解族. 这些圆周解族的结构随着旋转曲面参数的变化而演化,其中包含了不同解族之间的相互碰撞、分裂等现象.
旋转曲面上匀速圆周运动的稳定性指的是相应平衡解的 Lyapunov 稳定性. 在平衡点处将新的微分代数方程组线性化,并利 用线性约束方程消去非独立的变量,可以得到一个 7 维的线性系统. 同样,平衡点的非孤立性意味着该线性系统必有一个零特征根. 结合中心流形定理可以证明,如果线性系统的其余 6 个特征根都具有负实部,则该平衡点是稳定的,但不是渐近稳定的. 数值计算结果发现,随着旋转抛物面系数 $\alpha$ 增大,稳定圆周解的区间越来越小. 当 $\alpha$ 增大到某个临界值时,所有的圆周解都是不稳定的.
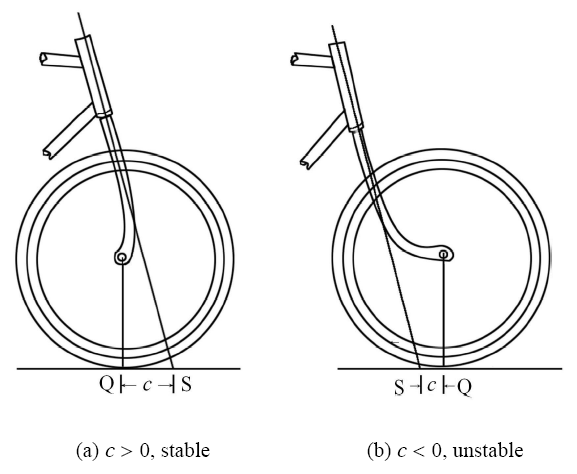
自行车的自稳定性研究除了基于解析模型的定量分析外,还可以从物理角度得到更直观的认识[26,68]. 历史上,对自行 车稳定性的观点主要有 3 种:一是以 Appell [69]、Timoshenko 和 Young[8]为代表的离心力观点,即前轮朝车体倾斜方向转动使车体转为曲线运动,所产生的离心惯性力平衡了重力的倾覆作用;二是以 Klein 和 Sommerfeld[70]为代表的陀螺效应观点 (如图2 所示),即车轮旋转产生的陀螺力矩在自稳定现象中起到了重要作用;三是以 Grammel [71]为代表的"脚轮效应"观点 (如图3 所示),即前轮尾迹 $c$ 是影响自行车稳定性的关键因素,当 $c > 0$ 时,前轮的法向支撑力产生对前叉转轴的力矩,推动车把朝倾斜方向转动,使离心力效应的稳定作用自动实现. Jones[72]安装了一个与前轮并列反向旋转的副车轮,以消除陀螺力矩作用,用实验否定了陀螺效应,验证了脚轮效应. 刘延柱[73]通过简化的力学分析对这三种效应都作出了解释. 在另一篇文献[74] 中,他经过估算发现在受控情况下,车轮的陀螺效应仅占稳定性因素的 3% 左右.
图2
图3
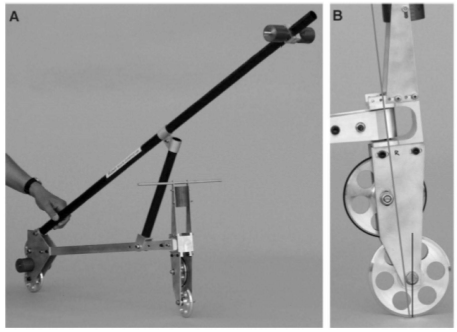
但是,Kooijman 等[26]则否认了陀螺效应和脚轮效应是保证自行车实现稳定性的必要条件. 他们设计了一款 "TBS 自行车" (如图 4 所示),该 "自行车" 同样包括车身、前叉、前轮和后轮 4 个刚体,但是车身和前叉简化为各自带有集中质量的杆件. 在该实验自行车中,一方面通过在前轮附近利用反向旋转的副轮彻底消除陀螺效应,另一方面前叉转轴延长线与地面的交点位于前轮触地点的后方,与 Jones[72]的自行车正好相反,以此消除脚轮效应. 通过实验发现该"自行车"仍然可以实现自稳定,因此,他们认为陀螺效应和脚轮效应不是自行车实现自稳定的必要条件,但也不能否认这两个条件对自稳定的影响效应. 他们同时验证了自行车的其他参数,如前车架质量分布,各个几何参数的相互耦合作用等等,均对自行车自稳定性有重要影响. 刘延柱[75]认为 Kooijman 等[26]的自行车并非无脚轮效应,他通过理论分析发现,由于其重心高度远大于普通自行车,前轮的侧向摩擦力的正面作用超过法向支撑力的负面作用,由此推动前叉朝脚轮效应正确方向转动.
图4
为了明确自行车各个参数对稳定性的影响程度,Xiong 等[28]对自行车匀速直线运动状态下各物理参数对稳定性的敏感性进行了理论分析. 他们发现轴距 $w$ 越大,自行车在水平面上作匀速直线运动时的自稳定区域越小;前轮尾迹 $c$ 越大,自稳定区域越大,这与Jones[72]的观点基本一致;前叉转轴倾角 $\lambda $ 影响相对较小,意味着该参数对自稳定具有很好的鲁棒性;前框架和后框架质心在惯性系中的水平位置对自稳定具有显著影响,这与 Kooijman[26]的观点一致;而对于自行车的车轮参数而言,增大前车轮半径,减小后车轮半径则有助于提高自行车的自稳定性;与陀螺效应有关联的前轮惯量参数对自稳定起相反作用. 另外,Doria[35]一方面基于方差的敏感度分析方法对自行车不同几何参数对稳定指数的影响进行了分析,另一方面利用相关分析方法,根据不同的相关系数判断几何参数对自行车系统整体稳定指标的影响规律. Tak 等[76]基于自行车线性动力学模型,研究了不同设计参数对自行车偏转速度和车把摇摆速度的灵敏度,结果发现在自行车的 25 个参数中有 7 个参数对稳定性影响明显.
4 自行车实验研究及控制
图5
近年来,人们也开展了一系列关于自行车控制的研究. Lowell 和 McKell[83]综合考虑了前文所述的自行车的3个稳定因素,将驾车人对前叉的控制用简单的比例规律替代,建立数学模型计算,却得出不稳定的结果. 刘延柱[84]对控制规律作了一些修改,即考虑前叉转轴的阻尼因素,且控制规律中除车体倾斜的角度信息以外,还计入了角速度信息,这样计算结果即转变为渐近稳定. 有的学者通过在自行车上增加外置平衡装置,如飞轮[85-86]和平衡块[87]实现自行车的稳定持续前行. Tanaka[88]以车把转角为控制变量,采用 PD 控制器研究自行车的稳定行驶. Keo[89]提出了 output-zeroing 控制器的方法实现自行车在速度为零时的直立状态的稳定性; Owczarkowski[90]和 Anjumol[91]采用 LQR 控制方法实现自行车的直线跟踪控制;Toshiyuki 和 Zhang 等[92]采用带扰动观测器的滑模控制方法研究运动稳定性,Chen 等[93]采用滑模控制器研究自行车的车轮转动角跟踪控制问题. 除以之外,有些学者[23,94-98]以电动摩托车为对象,开展了相关动力学的实验研究工作,为未来新型自行车的研制和实验提供了必要的借鉴资料.
5 结论与展望
本文较详细地总结了自行车自发明以来,不同学者对其动力学建模、稳定性分析以及实验验证的研究工作. 作为典型的多刚体动力系统,自行车简单的机械结构蕴藏着丰富的动力学现象,在不同路面行驶过程中受到的复杂完整约束和非完整约束导致了其动力学模型的复杂性. 为了明晰自行车的自稳定性本质,不同学者采用不同方法分析了不同几何参数和质量参数对稳定性的影响机理,而且通过实验验证了所提出的不同模型的正确性和有效性. 研究自行车的稳定性不仅可以探索这个百年来至今都未有明确解释的"自行"问题,而且还可以更深入研究人作为主动控制输入时,人、机与环境之间的复杂耦合关系,通过定量分析和物理直观解释对自行车的自稳定有进一步的认识,对未来真正无人自行车的实现提供一定的参考价值.
参考文献
A review on bicycle dynamics and rider control
On the dynamical principles of the motion of velocipedes
Étude théorique sur la bicyclette
Aperçu sur la théorie de la bicyclette
Complément à une étude récente concernant la théorie de la bicyclette: Influence, sur l'équilibre, des mouvements latéraux spontanés du cavalier
über die Theorie des Kreisels: Einführung in die Kinematik und Kinetik des Kreisels
Advanced Dynamics
Théorie du movement du monocycle, part 2: Théorie de la bicyclette
The stability of the motion of a bicycle
Cours De Mécanique Rationnelle Et Expérimentale, Librairie Ch
.
The stability and control of motorcycles
Bicycle stability: A mathematical and numerical analysis
[B.A. Thesis].
Comparisons and stability analysis of linearized equations of motion for a basic bicycle model
[Master Thesis].
Bicycle steering dynamics and self-stability: a summary report on work in progress
Linearized dynamics equations for the balance and steer of a bicycle: A benchmark and review
Hands-free circular motions of a benchmark bicycle
Symbolic linearization of equations of motion of constrained multibody systems
Nonholonomic mechanics//Nonholonomic Mechanics and Control
Control for an autonomous bicycle//Proceedings of 1995 IEEE International Conference on Robotics and Automation
A study of the effects of input parameters on the dynamics and required power of an electric bicycle
A robust two-stage active disturbance rejection control for the stabilization of a riderless bicycle
A bicycle can be self-stable without gyroscopic or caster effects
A riderless bicycle can automatically steer itself so as to recover from falls. The common view is that this self-steering is caused by gyroscopic precession of the front wheel, or by the wheel contact trailing like a caster behind the steer axis. We show that neither effect is necessary for self-stability. Using linearized stability calculations as a guide, we built a bicycle with extra counter-rotating wheels (canceling the wheel spin angular momentum) and with its front-wheel ground-contact forward of the steer axis (making the trailing distance negative). When laterally disturbed from rolling straight, this bicycle automatically recovers to upright travel. Our results show that various design variables, like the front mass location and the steer axis tilt, contribute to stability in complex interacting ways.
Bicycle dynamics and its circular solution on a revolution surface
Stability analysis for the Whipple bicycle dynamics
Hamel's formalism for infinite-dimensional mechanical systems
Inverse dynamics and energy optimal trajectories for a wheeled mobile robot
Analysis of the Holonomic Constraint in the Whipple Bicycle Model (P267)
//
Bicycle dynamics: modelling and experimental validation
Development of efficient nonlinear benchmark bicycle dynamics for control applications
Contact constraints and dynamical equations in Lagrangian systems
动力学与控制论力学系统的自由度
On the degrees of freedom of a mechanical system
Stability analysis of bicycles by means of analytical models with increasing complexity
分析动力学中的基本方程与非完整约束
Analytical mechanics is established based on d'Almbert-Lagrange Principle, Gauss principle, Jourdian principle and Hamilton principle, to deal with the dynamics of mechanical systems subject to holonomic or nonholonomic constraints. The governing equation of the systems are derived either by introducing Lagrange's multipliers to adjoin with the limitation equations for the virtual displacements, or by directly eliminating the constraint equations to achieve minimal formulations. The author presents a survey for the history of analytical mechanics, and explains some basic concepts, such as virtual displacement, ideal constraint, and the correlations between the Lagrange multipliers and the real constraint forces.
The fundamental equations in analytical mechanics for nonholonomic systems
Analytical mechanics is established based on d'Almbert-Lagrange Principle, Gauss principle, Jourdian principle and Hamilton principle, to deal with the dynamics of mechanical systems subject to holonomic or nonholonomic constraints. The governing equation of the systems are derived either by introducing Lagrange's multipliers to adjoin with the limitation equations for the virtual displacements, or by directly eliminating the constraint equations to achieve minimal formulations. The author presents a survey for the history of analytical mechanics, and explains some basic concepts, such as virtual displacement, ideal constraint, and the correlations between the Lagrange multipliers and the real constraint forces.
Dynamic modeling of a bicycle robot with front-wheel drive based on Kane's method
//
Linearized equations for an extended bicycle mode l//III European Conference on Computational Mechanics
Reduced dynamics of the non-holonomic Whipple bicycle
A bicycle model for education in multibody dynamics and real-time interactive simulation
This paper describes the use of a bicycle model to teach multibody dynamics. The bicycle motion equations are first obtained as a DAE system written in terms of dependent coordinates that are subject to holonomic and non-holonomic constraints. The equations are obtained using symbolic computation. The DAE system is transformed to an ODE system written in terms of a minimum set of independent coordinates using the generalised coordinates partitioning method. This step is taken using numerical computation. The ODE system is then numerically linearised around the upright position and eigenvalue analysis of the resulting system is performed. The frequencies and modes of the bicycle are obtained as a function of the forward velocity which is used as continuation parameter. The resulting frequencies and modes are compared with experimental results. Finally, the non-linear equations of the bicycle are used to create an interactive real-time simulator using Matlab-Simulink. A series of issues on controlling the bicycle are discussed. The entire paper is focussed on teaching engineering students the practical application of analytical and computational mechanics using a model that being simple is familiar and attractive to them.
Benchmark results on the linearized equations of motion of an uncontrolled bicycle
Comparison of experimental data to a model for bicycle steady-state turning
The steady-state turning of a bicycle arises when the bicycle/rider system negotiates a constant radius turn with constant speed and roll angle. This paper explores steady-state turning by employing a bicycle instrumented to measure steering torque, steering angle, and bicycle speed, acceleration, and angular velocity. We report data obtained from 134 trials using two subjects executing steady turns defined by nine different radii, three speeds, and three rider lean conditions. A model for steady-state turning, based on the Whipple bicycle model, is used to interpret the experimental results. Overall, the model explains 95.6% of the variability in the estimated bicycle roll angle, 99.4% of the variability in the measured steering angle, and 6.5% of the variability in the measured steering torque. However, the model explains 56.6% of the variability in steering torque for the subset of trials without exaggerated rider lean relative to the bicycle frame. Thus, the model, which assumes a rigid and non-leaning rider, reasonably predicts bicycle roll and steering angles for all rider lean conditions and steering torque without exaggerated rider lean. The findings demonstrate that lateral shifting of the bicycle/rider centre of mass strongly influences the steering torque, suggesting that rider lean plays an important role in bicycle control during steady-state turning. By contrast, the required steering angle is largely insensitive to rider lean, suggesting that the steering angle serves as a superior cue for bicycle control relative to the steering torque.
Experimental validation of a model of an uncontrolled bicycle
In this paper, an experimental validation of some modelling aspects of an uncontrolled bicycle is presented. In numerical models, many physical aspects of the real bicycle are considered negligible, such as the flexibility of the frame and wheels, play in the bearings, and precise tire characteristics. The admissibility of these assumptions has been checked by comparing experimental results with numerical simulation results.
Lateral dynamics and stability of the skateboard
Introduction to mechanics and symmetry: A basic exposition of classical mechanical systems
Nonholonomic mechanical systems with symmetry
Integrability and stability of nonholonomic systems
含摩擦滑移铰平面多刚体系统动力学的数值算法
A numerical method for dynamics of planar multi- rigid-body system with frictional translational joints based on lugre friction model
Some recent developments in bicycle dynamics and control
//
On the stability and control of the bicycle
Bicycle dynamics and control: Adapted bicycles for education and research
A review on bicycle and motorcycle rider control with a perspective on handling qualities
Jump rule for edge impacts of rolling prisms
On the influence of tyre and structural properties on the stability of bicycles
Wobble of a racing bicycle with a rider hands on and hands off the handlebar
On the wobble mode of a bicycle
Wheel shimmy and wobble are well-known dynamic phenomena at automobiles, aeroplanes and motorcycles. In particular, wobble at the motorcycle is an (unstable) eigenmode with oscillations of the wheel about the steering axis, and it is no surprise that unstable bicycle wobble is perceived unpleasant or may be dangerous, if not controlled by the rider in time. Basic research on wobble at motorcycles within the last decades has revealed a better understanding of the sudden onset of wobble, and the complex relations between parameters affecting wobble have been identified. These fundamental findings have been transferred to bicycles. As mass distribution and inertial properties, rider influence and lateral compliances of tyre and frame differ at bicycle and motorcycle, models to represent wobble at motorcycles have to prove themselves, when applied to bicycles. For that purpose numerical results are compared with measurements from test runs, and parametric influences on the stability of the wobble mode at bicycles have been evolved. All numerical analysis and measurements are based on a specific test bicycle equipped with steering angle sensor, wheel-speed sensor, global positioning system (GPS) 3-axis accelerometer, and 3-axis angular velocity gyroscopic sensor.
Wobble of a racing bicycle with a rider hands on and hands off the handlebar
Identification of the mechanical properties of bicycle tyres for modelling of bicycle dynamics
Influence of tire side forces on bicycle self-stability
Some effects of crosswind on the lateral dynamics of a bicycle
An advanced model of bicycle dynamics
用具有负定矩阵的梯度系统构造稳定的变质量力学系统
Stable variable mass mechanical systems constructed by using a gradient system with negative-definite matrix
A Mathematical Introduction to Robotic Manipulation
Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering
Historical review of thoughts on bicycle self-stability
关于自行车的稳定性
叙述自行车稳定性传统理论受到质疑和新理论提出的过程. 解释影响自行车稳定性的离心力效应、陀螺效应, 和新提出的脚轮效应的力学原理.
The stability of a bicycle
叙述自行车稳定性传统理论受到质疑和新理论提出的过程. 解释影响自行车稳定性的离心力效应、陀螺效应, 和新提出的脚轮效应的力学原理.
自行车的受控运动
本文以自行车和驾车人组成的多刚体系统为对象,考虑驾车人对车把的主动控制作用,导出稳定性条件,从而对自行车运动作出符合实际情况的动力学解释。
The controlled movement of a bicycle
本文以自行车和驾车人组成的多刚体系统为对象,考虑驾车人对车把的主动控制作用,导出稳定性条件,从而对自行车运动作出符合实际情况的动力学解释。
自稳定的无人自行车
叙述对自行车稳定性的各种理论的发展过程. 对一种特殊设计的所谓科伊曼自行车无人驾驶也能自行稳定的现象给出理论解释.
Self-stable bicycle without rider
叙述对自行车稳定性的各种理论的发展过程. 对一种特殊设计的所谓科伊曼自行车无人驾驶也能自行稳定的现象给出理论解释.
Design sensitivity analysis of bicycle stability and experimental validation
//
Bicycle Dynamics: Tire Characteristics and Rider Modeling
Computer simulation of bicycle dynamics
//
A digital computer simulation of bicycle dynamics
Study on construction of a rider robot for two-wheeled vehicle
Experimental validation of a model of an uncontrolled bicycle
In this paper, an experimental validation of some modelling aspects of an uncontrolled bicycle is presented. In numerical models, many physical aspects of the real bicycle are considered negligible, such as the flexibility of the frame and wheels, play in the bearings, and precise tire characteristics. The admissibility of these assumptions has been checked by comparing experimental results with numerical simulation results.
Validation of multibody modeling and simulation using an instrumented bicycle: from the computer to the road
The stability of bicycles
再谈无人自行车的自稳定性
Revisit of self-stabilization of unmanned bicycle
Experimental results for stabilizing of a bicycle with a flywheel balancer
//
Gyroscopic stabilization of an unmanned bicycle
//
Experimental study of automatic control of bicycle with balancer
//
Self sustaining bicycle robot with steering Controller
//
Controlling balancer and steering for bicycle Stabilization
//
Dynamic modeling and simulation of a bicycle stabilized by LQR control. Methods and Models in Automation and Robotics (MMAR)
//
Optimal stabilization and straight line tracking of an electric bicycle
//
Dynamic modeling and balance control of human/bicycle Systems
//
Fuzzy control for equilibrium and roll-angle tracking of an unmanned bicycle
This study presents steady turning motion and roll-angle tracking controls for an unmanned bicycle. The equations of motion describing the dynamics of a bicycle are developed using Lagrange's equations for quasi-coordinates. Pure rolling without slipping constraints between the ground and two wheels are also considered in this model. These constraints introduce four holonomic and four non-holonomic constraint equations to the model. For the developed bicycle dynamics, one PID and one fuzzy controller that create steering torque are derived to recover the balance of the bicycle from a near-fall state. Furthermore, another fuzzy controller is added for controlling the bicycle to a desired roll angle which leads to its steady circular motion. The bicycle can track a given roll angle while maintaining its balance. The effectiveness of the control schemes is proved by simulation results.
An evaluation of the performance and handling qualities of bicycles
Die Stabilität von Einspurfahrzeugen
Man-machine dynamics in the stabilization of single-track vehicles
Experimental study of motorcycle transfer functions for evaluating handling
The modal analysis of a motorcycle in straight running and on a curve
The vibrational modes (generalized) of a two-wheel vehicle are studied in several trim configurations. The modal analysis is carried out on a 3D non-linear mathematical model, developed using the natural coordinates approach. A special procedure for evaluating the steady state solutions in straight running and on a curve is proposed. The paper presents detailed results of the modal analysis for a production sports motorcycle. Furthermore, the influence of speed and lateral (centripetal) acceleration on stability, shape and modal interactions (coupling) is highlighted. Finally, consistency between the first experimental tests and simulation results is shown.
/
| 〈 |
|
〉 |