引言
近年来,国内外学者对高速列车的气动噪声开展了大量研究工作[8-9],目前对高速列车气动噪声的研究, 除了进行沿线实际观测外,主要通过风洞试验和数值模拟计算.但由于高速列车气动噪声问题的复杂性,大多数研究强调了高速列车某一部位的气动噪声, 主要集中在车头[10-11]、车厢连接处[12]、转向架[13-14]和受电弓[14-17]等主要致声部件的噪声.如刘加利等[18]数值研究了高速列车头车表面的气动噪声源,肖友刚等[19]研究了头车曲面对头部气动噪声的影响,孙振旭等[20]数值研究了列车头部、车厢连接处、尾部等的气动噪声分布及贡献,喻华华等[21]数值研究了受电弓、以及不同头型的气动噪声,安翼等[22]研究了头型长细比对气动噪声的影响, 等等.而对于高速列车整车气动噪声的研究, 由于计算条件的限制,大都将列车长度做了大幅简化.如袁磊等[23]简化计算了仅包括一个头车和一个尾车构成的模型车的气动噪声源,孙振旭等[20], Yang等[24], 张军等[25-26]将高速列车简化为包括一个头车、一个中间车和一个尾车的计算模型,数值研究了列车的近场和远场噪声.由于气动噪声数值求解的巨大计算量[27],目前对长编组真实列车气动噪声的数值模拟仍存在着较大的困难.
为此, 本文基于CRH380A 高速列车,抽象简化出代表列车主体结构特征的细长结构体,研究细长体结构长度对其气动噪声的影响,探讨高速列车气动噪声与车体长度之间的关系,分析当前噪声评估过程中广泛使用的三节车编组列车的合理性,并由此探讨对真实长度列车气动噪声的快速评估的近似方法和途径,以期为列车设计和优化提供理论参考和新方法.
1 数值模拟方法
针对高速列车气动噪声的复杂性, 本文数值模拟中,将模拟计算区域分为非线性声源区(近场流动区)和线性声传播区,采用计算流体力学/计算气动声学(hybridCFD/CAA)的混合算法进行模拟求解. 对于近场流动区,针对高速列车为细长流线体, 流动不稳定性较弱的特点, 选用Batten等[30-31]提出的计算量较低的非线性声学求解器(non-linearacoustics solver, NLAS). 即首先运用湍流(cubic$k\mbox{-}\varepsilon $RANS)模型求解N-S方程,得到流动的统计定常解,再采用非线性声学求解器(NLAS)求解流动的非定常时空演化和压力脉动,由此得到近场流场和噪声源信息. 而对于远场噪声则采用声比拟法,即采用FW-H方程[31], 通过在控制面积分得到远场噪声.该模拟方法及其验证已在我们的前期工作[22]有较详细论述,本文不再赘述.这里仅简要给出非线性声学解算器采用的控制方程和FW-H方程的时域积分解.
由Batten提出的非线性声学求解器是一种求解统计定常状态流动中声的产生与传播的数值算法,其控制方程为由N-S方程的扰动推导而来的非线性扰动方程(NLDE)[30]
其中
$$\bar { q} = \left[ {{\begin{array}{*{20}c} \bar {\rho } \\ {\bar {\rho }\bar {u}_j } \\ \bar {e} \\ \end{array} }} \right],\quad F_i = \left[ {{\begin{array}{*{20}c} {\bar {\rho }\bar {u}_i } \\ {\bar {\rho }\bar {u}_i \bar {u}_j + \bar {p}\delta _{ij} } \\ {\bar {u}_i (\bar {e} + \bar {p}\_} \\ \end{array} }} \right] \\ F_i^v = \left[ {{\begin{array}{*{20}c} 0 \\ {\bar {\tau }_{ij} } \\ { - \bar {\theta }_i + \bar {u}_k \bar {\tau }_{ki} } \\ \end{array} }} \right] \\ { q}' = \left[ {{\begin{array}{*{20}c} \rho \\ {\bar {\rho }{u}'_j + {\rho }'\bar {u}_j + {\rho }'{u}'_j } \\ {e}' \\ \end{array} }} \right] \\ ( F_i^v {)}' = \left[ {{\begin{array}{*{20}c} 0 \\ {{\tau }'_{ij} } \\ { - {\theta }'_i + {u}'_k \bar {\tau }_{ki} + \bar {u}_k {\tau }'_{ki} } \\ \end{array} }} \right] \\ { F}'_i = \left[ {{\begin{array}{*{20}c} {\bar {\rho }{u}'_i + {\rho }'\bar {u}_i } \\ {{\rho }'\bar {u}_i \bar {u}_j + \bar {\rho }\bar {u}_i {u}'_j + \bar {\rho }{u}'_i \bar {u}_j + {p}'\delta _{ij} } \\ {{u}'_i (\bar {e} + \bar {p}) + \bar {u}_i ({e}' + {p}')} \\ \end{array} }} \right]+ \\ \qquad \left[ {{\begin{array}{*{20}c} {{\rho }'{u}'_i } \\ {\bar {\rho }{u}'_i {u}'_j + {\rho }'{u}'_i \bar {u}_j + {\rho }'\bar {u}_i {u}'_j + {\rho }'{u}'_i {u}'_j } \\ {{u}'_i ({e}' + {p}')} \\ \end{array} }} \right] $$
式中, $\rho $为流体密度, $u$为速度, $e$为能量, $\tau $为切应力,$p$为压强.
忽略密度扰动, 对方程组取时间平均,可消去时间演化项和所有线性通量项, 得到$\overline { {LHS}} =\overline { {RHS}} = {\partial R_i }/ {\partial x_i }$
式(2)中的各物理量对应于雷诺应力张量和湍流热通量项,由RANS方法求解得出.
远场声压的模拟计算, 采用Farassat[33]给出的基于FW-H方程的时域积分解
式中, $L_i = p\hat {n}_i + \rho u_i (u_j - v_j )n_j $, $Q_i = (\rho _\infty - \rho )v_i + \rho u_i $; $\rho _\infty $和$c_\infty$分别为远场流体的密度和声速, $u_i $和$v_i$分别为当地流速和物体表面速度; $\hat {n}_i $和$\hat {r}_i$分别为物面单位法向矢量n和单位发射矢量$(x- y)/r$的坐标分量, $r$为观测点与声源间距离. 符号[ ]$_{ret}$代表在延迟时间$\tau = t - r / c_\infty $下取值, $t$和$\tau$分别为声源发出声波和声波到达观测点的时间; $M_r = v_i \hat {r}_i /c_\infty $为声源与观测点方向上的马赫数.
2 计算列车模型与设置
2.1 列车模型
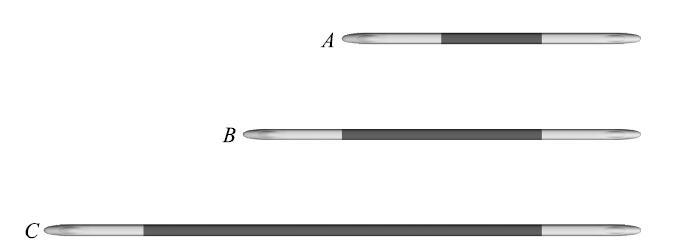
基于我国自主研发的高速列车外形,抽象简化出代表列车主体结构特征的细长结构体,作为本文研究的列车模型. 模型列车由头车、中间车厢和尾车组成,且去掉了车间间隙、受电弓和转向架等非顺滑曲面结构.为了研究细长体的气动噪声与其车体长度之间的关系,本文采用三种车体长度的细长结构体模型, 分别用$A,B,C$进行标识,其中, 模型$A$由一节头车、一节中间车厢和一节尾车组成, 而模型$B$和$C $具有与模型$A$相同的头、尾车, 但分别具有两节和四节中间车厢,如图1所示. 列车模型的单节车体长度$L_{\rm s }= 26$m,车体宽度W $\approx $3 m, 高度H$\approx $3.5m, $A,B,C$三种模型车的长度分别为78 m, 104 m, 156 m.
图1
图1
三种车体长度的细长结构体模型
Fig. 1
Simplified models of three trains with different lengths
2.2 计算条件
对于三种不同长度的列车模型,计算区域的原点均取在与尾车邻接车厢下底面的面心处, 从而$A$, $B$, $C$三种模型车的车体在$x$轴上的坐标范围分别为[$-$39 m, 39 m]、[$-$65m, 39 m] 和[$-$117 m, 39 m]. 在长度方向上,三种列车模型的计算区域, 前段为从头车前端向外延伸$3L_{\rm s}$后端为从尾车尾端向外延伸9$L_{\rm s}$, 宽度方向取$y \in [ -4L_{\rm s} ,\;4L_{\rm s} ]$, 高度方向取$z \in [ - h,\;4L_{\rm s}]$, 其中, $h= 0.371$m 为车体下底面距离地面的高度.
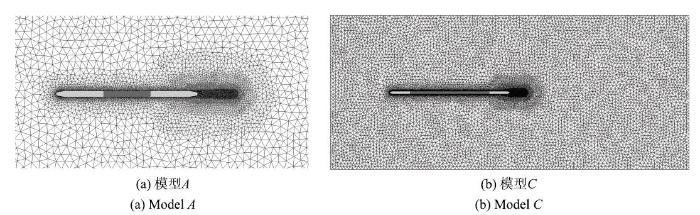
三种模型车的数值计算网格皆采用四面体非结构网格.壁面附近区域的网格分辨率约为205 {cells}/$L_{\rm s}$,对车体尾流区域的网格加密, 分辨率约为500 {cells}/$L_{\rm s}$.车体壁面边界层采用棱柱网格, 第一层网格高度对应的$y^{ + }$$\approx $150, 网格沿壁面法向共生长了5 层,增长率为1$.$6. 网格生成过程中, 三种模型车具有相似的的网格拓扑,其中, 三节车体模型$A $与六节车体模型$C $的网格如图2所示.
图2
模拟计算时, 对列车车体边界条件采用绝热无滑移固壁条件,而地面边界条件采用无滑移运动固壁条件, 其速度为来流速度350 km/h.其他外围边界条件均采用均匀来流的远场边界条件,其温度和压力分别取为298.5 K和101 325 Pa.流场的非定常计算采用隐式双重时间步, 瞬态时间步长$t $= 5$\times$10$^{ - 5}$s. 可解析的信号最高频率$f_{\max }$= 1/(2$\Delta t)$=25 000 Hz.
3 计算结果
3.1 近场流场
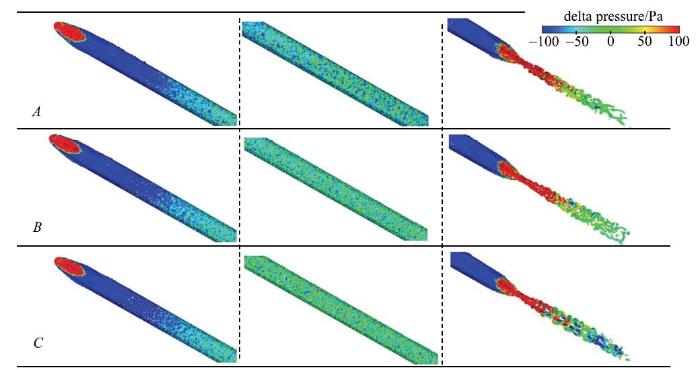
流动过程中产生的漩涡与势流以及漩涡之间的相互作用是流动致声的根本原因和内在机制[34].一般可以通过Q判据$({{Q}} = (\varOmega _{ij} \varOmega _{ij} -S_{ij} S{ }_{ij}) / 2$, $\varOmega = (\partial u_i / \partial u_j- \partial u_j /\partial u_i ) / 2$, $S = (\partial u_i / \partial u_j + \partial u_j /\partial u_i ) / 2)$来表征流场中的涡湍流结构, 并由此判别噪声源的强弱信息.为此, 我们基于Q判据分析了三种模型车的涡结构分布.图3给出了三种长度列车周围流场的Q判据等值面, $Q$的取值为($U_{\infty}$/$H)^{2}$, 其中, $U_{\infty }$为来流速度350 km/h,$H$为车体高度3.5 m. Q判据等值面由当地压力$p$与来流压力$p_{\infty}$= 101 325 Pa 的差值$\Delta p$渲染和着色,为了能更清楚地对比压力的相对大小, $\Delta p$取值限制在区间[$-$100Pa, 100 Pa] 内.
图3
图3
由$\Delta p =p-p_{\infty }$着色渲染的不同长度列车Q判据等值面$Q $= ($U_{\infty }$/$H)^{2}$
Fig. 3
Isosurface of Q criterion of different trains colored by $\Delta p =p-p_{\infty , }Q $= ($U_{\infty }$/$H)^{2}$
由图3的数值模拟结果可见, 不同车体长度的三种列车的周围流场,其Q判据等值面具有相似的空间分布, 主要分布于车体表面附近和尾流区域.中间车体的周围流动较为稳定, 流动状态与自由来流状态相近,相互间没有明显区别.车体长度的增加对头尾车附近的压力分布并明显影响,仅对尾流区域的Q判据等值面上的压力分布有一定影响, 但也无太明显影响.这总体上说明,列车长度的增大并不会对头、尾车的流动和涡湍流结构产生明显影响,而且各中间车体周围的流场结构无明显 区别.
3.2 远场噪声
远场噪声基于近场声源面的FW-H积分进行求解. 为获得远场噪声,在近场流动的非定常计算中需要设定声源面, 用于收集近场的声源信息.对于三种列车模型, 在长度方向上, 声源面都为从车体前端向外延拓1 m和从车体尾端向外延拓21 m, 即$A$, $B$, $C$的声源面在长度方向上的取值范围分别为[$-$40 m, 60 m]、[$-$66 m, 60m] 和[$-$118 m, 60 m], 各声源面具有相同的宽度和高度,宽度区间均为[$-$3 m, 3 m], 高度区间均为[0, 5.5 m]. 其中,六节车体的模型$C$的声源面如图4所示.各列车沿线噪声的总声压级及其分布特性通过图5所示的沿车体长度方向分布的声压探点获得,探点位于距离车体中心平面25 m, 高3.5 m 的直线上,沿车体长度方向等间距分布, 相邻探点间的距离为10 m.
图4
图5
图5
沿细长结构体长度方向分布的声压探点
Fig. 5
Location of sound pressure probes along with the trains
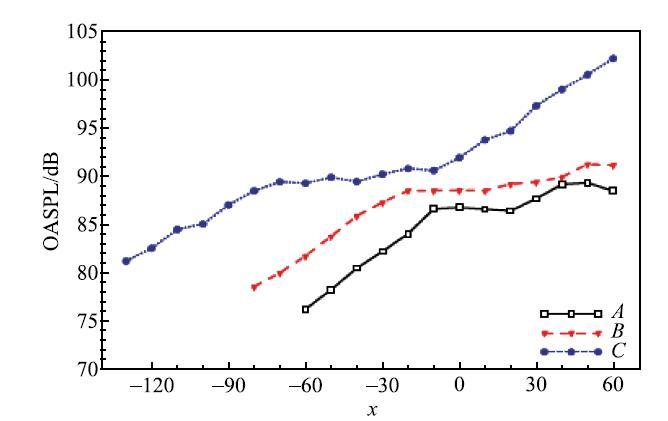
图6给出了三种列车模型在各沿线探点的总声压级的模拟计算结果.结果表明, 沿线噪声在车体长度方向具有相似的空间分布特征,即在头车及头车前部, 沿线噪声近似于线性增长,而在车体中部沿线噪声的变化趋于平缓, 当进入尾车及尾流附近区域时,沿线噪声将再次明显上升. 由此可知,车体长度的增加并不会明显改变沿线噪声的分布规律,但从声压级量值上的对比可知, 会导致沿线噪声的声压级显著增大.
图6
图6
三种车体长度的列车的沿线噪声总声压级
Fig. 6
Overall sound pressure level profile along the trains of different lengths
图7
图8
4 分析和讨论
从上述计算结果可知, 无论近场流动形态还是远场噪声特性,车体的长度都会影响特定物理量的数值,致使用短编组列车模型计算的气动噪声,与长编组列车的气动噪声之间存在着一定的差别.但车体长度的增加并不会显著改变声和流动的原有规律与特性.若能找寻和建立列车车体各组成部分噪声之间的联系,以及不同编组的列车, 其对应部位噪声之间的关联,则可通过对短编组列车的噪声求解结果,为长编组列车噪声的快速评估提供 可能.
4.1 列车各组成部分的噪声特征及其关联
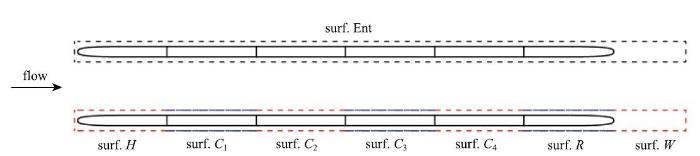
为探讨同一车体各部分之间的远场噪声关系,以及对比不同车体的对应部位之间的噪声特性, 对$A,B,C$三种模型车的头车、各节中间车厢, 以及尾车和尾流区域,分别设定相应的近场声源面, 以分析各组成部分的气动噪声特征.以模型$C$为例, 其近场声源面的设定如图9所示.列车各个部位的声源面为对整体声源面surf. Ent的分割,详细设置为:头车声源积分面surf. $H$, 中部车厢的声源面surf. $C$,其中, 模型$B $具有两节车厢, 车厢积分面分别编号为1和2, 而模型$C$具有四节车厢, 其编号为$1\sim 4$; surf. $R$为尾车的对应的声源面,而surf. $W$为包裹尾流区域的声源面.
图9
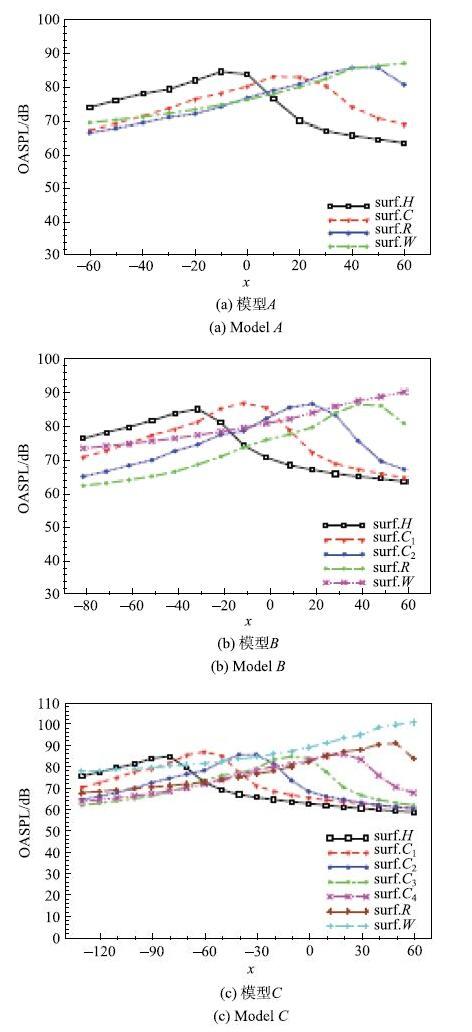
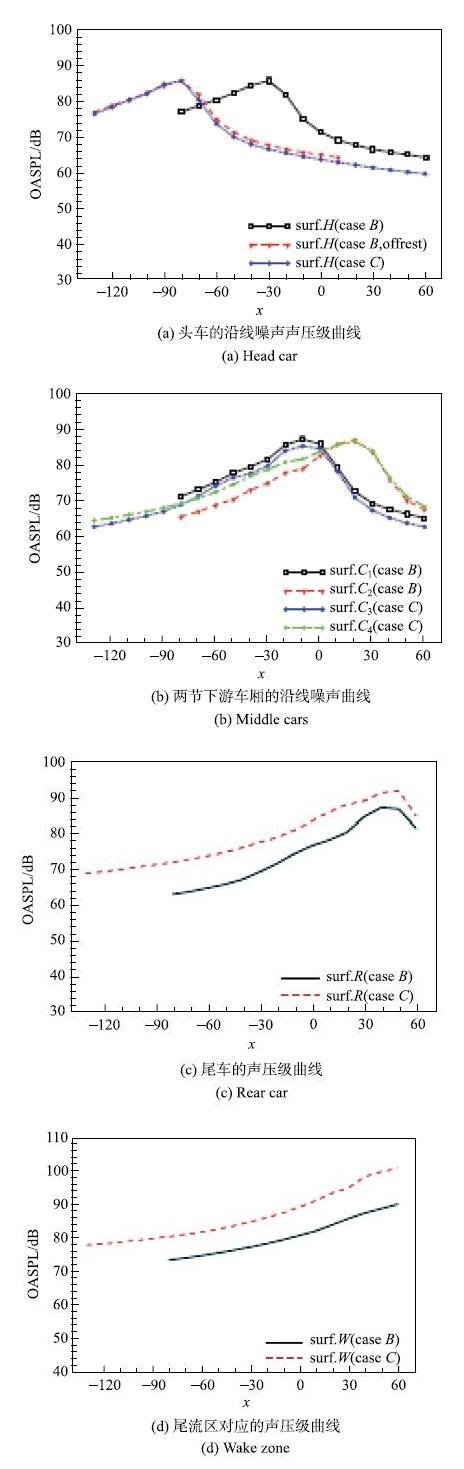
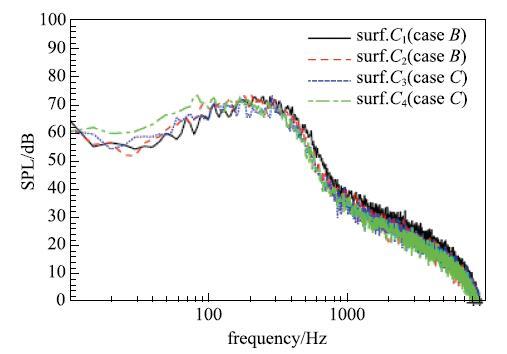
由此, 可得到三种列车模型各部位的沿线噪声声压级的分布特征(图10).结果显示, 各声压级曲线的峰值出现在对应部位的下游端, 除了尾流区域,各车体部位具有近似的声压级分布曲线, 以及声压级峰值(86 $\pm $1)dB.进一步分析不同列车模型对应部位之间噪声特性的关联性, 图11给出了模型$B$与模型$C$的头车、尾车、尾流区以及两节下游车厢沿线噪声的比较结果.其中, 以更加直观地对比, 图11(a)同时还给出了模型$B$头车的沿线噪声曲线的偏移曲线. 从图可知,不同车体长度的模型$B$和模型$C$,其头车沿线噪声的空间分布特征以及沿线噪声声压级十分相近,这可能与头车位于最上游端, 受下游车体影响较小有关. 同时,两声压级曲线的偏移距离近似等于两节车长, 与模型$B$和模型$C$的头车在空间上相差的距离一致.对比模型$B$和模型$C$具有相同空间位置的两节下游车厢的沿线噪声,由于上游车体长度存在差异, 导致边界层沿车体有着不同的发展距离,从而噪声声压级间存在小的差异,但两两对应的峰值和总体声压级分布具有很好的一致性.而模型$B$和模型$C$的尾车和尾流区对应的声压级曲线,虽然分布规律相近, 但量值上存在较大差异, 最大相差约6 dB,这一方面如前所述, 是由于车身加长后,导致尾流存在一定的差异而形成的; 另一方面, 由于计算量限制,噪声面不能取的离车体过远,进而导致边界层与噪声面有切割而产生了虚假的声源信息,也是产生较大差异的另一原因. 这提示我们在应用本文原理和方法时,应当注意在计算量和噪声面选取之前取得平衡.图12给出了图11(b)中四条沿线噪声声压级曲线的峰值所对应探点的声压级频谱,可以发现, 不同车体长度的列车模型,其对应车厢间的远场噪声不仅具有相近的总声压级, 同时,它们的远场噪声频谱亦十分吻合, 且声压级在50 dB以上的噪声主要集中于500 Hz 以内的中低频段内.
图10
图11
图11
模型$B$与模型$C$各部位的沿线噪声的对比
Fig. 11
OASPL profile comparison car by car for model $B${\&} $C$
图12
图12
两节下游车厢的沿线噪声曲线峰值探点的声压级频谱
Fig. 12
Spectrum of SPL for middle cars at the given location
4.2 近似评估长编组列车噪声的简化方法
由前文分析可知, 不仅同一车体模型的各部位具有近似的声压级分布曲线,以及声压级峰值, 而且对于不同车体长度的三种模型,各自对应的车体部位之间的声压级亦具有相一致的规律.这就使得基于短编组列车的噪声计算结果,对长编组列车噪声进行近似评估成为可能. 不同车体长度的列车,其差异往往主要体现在车厢的数量上, 要实现更长列车的噪声评估,如何获得待评估列车的各车厢部位的声压级分布, 是最主要的问题之一.
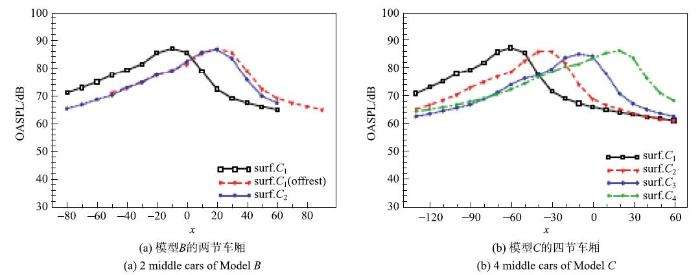
图13给出了四节车模型$B$与六节车模型$C$各自车厢之间的沿线噪声声压级的分布特征,其中, 为更加清晰地对比, 在模型$B$的噪声计算结果中(图13a), 对其中一节车厢的沿线噪声曲线进行了偏移.从各车厢的沿线噪声结果可知, 同一列车模型的各节车厢,它们的沿线噪声有着相似的空间分布, 同时, 在量值上亦十分接近,只是主峰位置会随着车厢的空间位置的不同而相应地发生偏移, 且偏移距离与相应车厢间的空间距离一致,如相邻车厢的沿线噪声曲线的偏移距离近似等于单节车厢的长度.而前面已说明了不同车体长度列车, 其对应车厢间噪声的近似性. 从而,当得到待评估列车的某单节车厢的远场噪声曲线时,则其他车厢的沿线噪声特性可由已知车厢的远场噪声曲线通过合适的空间偏移而得到.
图13
图13
模型$B$与模型$C$各车厢沿线噪声的声压级对比
Fig. 13
OASPL profile along the train for different cars of model
当通过对短编组列车的噪声求解以及合适的空间偏移处理,获得长编组列车对应的头车、中部车厢、尾车及尾流区的噪声特性,以及通过已得到的车厢噪声重构出长编组列车其他车厢的噪声分布后,最终长编组列车整体噪声的获得还需基于如下条件:各车体部位的远场噪声应满足线性叠加原理.从远场噪声求解的FW-H 方程可知, 由于FW-H 方程是线性波动方程,从而各列车部位的远场噪声是可线性叠加的,列车的整体噪声可通过各车体部位的远场噪声叠加得到.
由上述分析讨论可知,同一列车模型的各节车厢的远场噪声具有相似的空间分布特性,某一车厢的远场噪声可由已知车厢的远场噪声曲线通过合适的空间偏移得到.同时, 不同列车模型的对应部位之间的远场噪声特性具有很强的关联性,它们的远场噪声具有接近的总声压级和吻合的噪声频谱. 从而可以推知,通过对短编组列车远场噪声的求解,获取其各重要组成部分的远场噪声特性, 随后,借助已有噪声结果及其合适的处理, 如空间偏移等,可以重构出长编组列车(如真实车体长度的高速列车)的远场噪声结果,从而极大地降低列车气动噪声问题的求解难度,实现真实车长列车模型的气动噪声的快速评估.
需要指出的是, 由于空间偏移操作将导致对应测点位置移动,因此对于拟偏移噪声面的积分测点,应当在常规设置的远场噪声测点基础上, 补充更远场的积分测点,以便在偏移后的叠加过程中, 每个叠加测点处均有各车厢噪声贡献的数据.在本文中,考虑到重构模型偏移后测点声压远小于当地车厢贡献的声压(如图13(a)显示,本例中该差异接近10 dB), 因此, 在本例的叠加过程中, 为了简化计算,忽略了偏移后远端噪声测点的贡献. 在实际应用中,对于拟偏移声源还是应当尽可能获得更远的积分测点数据,以便得到更加合理和准确的结果.或者可以通过直接偏移噪声源面的方式进行远场积分,由于远场积分的线性特性, 上述两种处理结果是等价的.
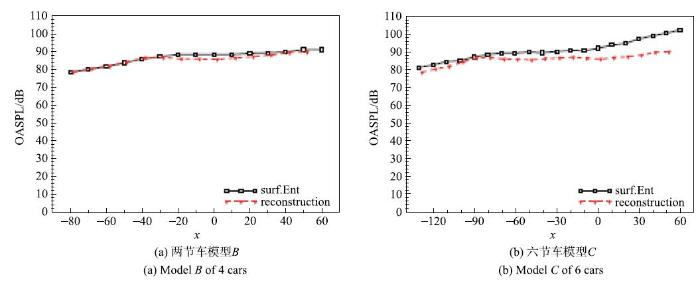
运用上述原理和方法,通过对三节车模型$A$各车体部位的沿线噪声计算结果进行适当偏移,重构出模型$B$与$C$的各相应车体部位的远场沿线噪声,进而通过线性叠加, 分别获得了四节车$B$与六节车$C$总的沿线噪声结果,与直接计算结果进行对比, 如图14所示.
图14
图14
基于三节车模型$A$的计算结果重构出的模型$B$与$C$的远场沿线噪声
Fig. 14
Reconstructed OASPL profile along the train for model $B$& $C$using data from the simulation of model $A$
从对比结果可知, 基于三节车计算结果,重构得到的四节车与六节车的沿线噪声, 可以较好地反映其实际噪声特性.其中, 重构得到的四节车结果与模型$B $的直接计算结果吻合很好,最大差异出现在列车中部附近, 约为3 dB.而重构得到的六节车结果与模型$C$的直接计算结果在列车中后部差异较大. 可见,采用该方法可以利用短编组列车的噪声模拟结果重构长编组列车的噪声,对列车前段噪声的模拟结果要好于对后段. 其原因,主要是长编组列车的尾流部分与短编组列车的尾流部分有一定的差异,使得利用短编组尾车的噪声模拟结果, 来重构长编组列车的尾车噪声,存在的较明显的差异. 但总体上,可以利用该方法基于短编组列车噪声模拟结果,对长编组列车沿线噪声进行快速的近似评估.
5 结 论
本文通过对三种不同长度列车模型的气动性能和噪声数值模拟,分析了车体长度对列车气动噪声的影响, 得到如下主要结论:
(1) 车体长度的增大基本不会改变列车远场噪声的分布规律,但将显著增加远场噪声的声压级,说明用短编组模型计算得到的噪声明显低估了长编组列车的气动噪声.
(2) 同一列车模型的各节车厢具有相似的沿线噪声,其噪声曲线在量值上十分接近,只是主峰位置会随着车厢空间位置的不同而相应地发生偏移,且偏移距离与相应车厢间的空间距离一致.当得到模型的某单节车厢的远场噪声曲线时,则其他车厢的远场噪声特性可由已知车厢的远场噪声曲线通过合适的空间偏移得到.
(3) 不同长度编组列车对应部位之间的远场噪声特性具有较强的关联性,它们的远场噪声具有接近的总声压级和相吻合的噪声频谱,为基于短编组列车远场噪声结果重构长编组列车的远场噪声提供了可能性.
(4) 基于三节车编组列车噪声的数值计算结果,重构得到的四节车与六节车的沿线噪声, 与直接数值计算的结果吻合较好,由此说明, 基于短编组列车噪声结果, 通过重构和叠加,可以实现对更长编组列车
噪声的近似评估. 但需注意应在计算量和噪声面选取之前取得平衡,以改善对列车后段, 特别是尾流区的噪声模拟,并进一步探讨车身加长对尾车尾流及噪声的影响规律,更好地改进该文提出的近似评估方法.
参考文献
Aerodynamic noise: A critical survey
High speed train noise emission: Latest investigation of the aerodynamic/rolling noise contribution
高速列车的关键力学问题
Research progress on the mechanics of high speed rails
国内高速列车气动噪声研究进展概述
Overview of the research progress on aerodynamic noise of high speed trains in China
日本新干线列车噪声声源分布及主动降噪实车试验研究综述
Overview of research on noise source distribution and active noise reduction of Shinkansen Trains in Japan
CIT500车外噪声源频谱分解模型的试验研究
Experimental study on frequency spectrum component model of noise source outside CIT500 train
Combined effects of high-speed railway noise and ground vibrations on annoyance
Aerodynamic noise generated by shinkansen cars
Study on numerical optimization of cross-sectional panhead shape for high-speed train
高速列车头型近场与远场噪声预测
Prediction of near field and far field noise for high-speed train head shape
车头长度对高速列车气动特性与声场特性影响的数值分析及降噪研究
Numerical analysis of influence of head length on aerodynamic and sound field characteristics of g-series high-speed train and research on noise reduction
车端风挡类型对高速列车气动噪声影响规律的研究
Investigation on the influence of inter-car windshield types on the aerodynamic noise of high speed trains
The effect of a moving ground on the flow and aerodynamic noise behaviour of a simplified high-speed train bogie
Investigation of the aeroacoustic behavior and aerodynamic noise of a high-speed train pantograph
Numerical modeling and investigation on aerodynamic noise characteristics of pantographs in high-speed trains
高速列车受电弓气动噪声特性研究
Study on the aerodynamic noise characteristics of the pantograph of the high-speed train
高速动车组受电弓气动噪声数值仿真分析
Numerical simulation analysis of aerodynamic noise for pantographs of high-speed trains
高速列车车头的气动噪声数值分析
Numerical analysis on aerodynamics noise of the high-speed train head
高速列车车头曲面气动噪声的数值预测
Numerical prediction of aerodynamics noise radiated from high-speed train head surface. Journal of
CRH3型高速列车气动噪声数值模拟研究
Numerical simulation of aerodynamics noise generated by CRH3 high-speed train
On aerodynamic noises radiated by the pantograph system of high-speed trains
高速列车头型长细比对气动噪声的影响
Study on the influence of the nose slenderness ratio of high-speed train on the aerodynamic noise
高速列车气动噪声及影响
Aerodynamics noise of high-speed train and its impact
A numerical study on aerodynamics noise sources of high-speed train
高速列车气动噪声数值仿真
Research on numerical simulation of aerodynamics noise for high-speed train
高速列车整车气动噪声及分布规律研究
Research on aerodynamics noise radiated from whole body surface of high-speed train and its distribution
结合并行策略与距离减缩法的搜索算法及其在CAA中的应用
A search algorithm coupling parallel strategy and distance decreasing method applied to CAA
Sound generation by turbulence and surfaces in arbitrary motion. Philosophical Transactions of the Royal Society of London,
Discontinuities in aerodynamics and aeroacoustics: The concept and applications of generalized derivatives
Theory of vortex sound