引 言
在文物"修旧如旧"的保护理念下,常用"锚固"这种隐蔽的力学稳定性控制技术来处理土遗址稳定问题[5-6].不同于传统岩土体锚固,土遗址具有岩土体与文物双重属性,多以竹、木等传统材料作为锚杆基材,配合强度略高于土体的改性浆体进行粘接.当前针对此类锚固系统的研究主要集中于现场与室内拉拔试验方面,以快速抢险加固为目的,对于锚固界面传力机理的研究十分匮乏,而界面间的接触与相互作用正是影响锚固性能的关键[7-9],仅凭借实践经验或参考传统岩土锚固领域技术规范已不能适应正在大规模开展的土遗址锚固需求,因此,针对土遗址锚固界面传力过程的研究亟待开展,这将有助于明确土遗址锚固系统的传力特点与规律,避免因过度加固而对土遗址造成不必要的"二次伤害".
土遗址保护工作者自20世纪80年代开始,进行了大量室内与现场拉拔试验来测试不同锚杆材料在土遗址锚固中的适用性,达成了以竹、木做为锚杆基材的共识[10\mbox-12].对竹木锚固系统的试验研究发现,锚固系统的失效主要是由杆体-浆体界面或浆体-土体界面的滑移引起,且前者滑动量远大于后者[2].在此类破坏模式下,锚固界面的剪应力分布及演化规律是准确预测极限锚固力和确定适合锚固长度的关键.此外,张景科等[13 \mbox-16]研究指出:不同锚固浆体(如:PS-F、PS-(F+C)、SH-(F+C)、改性糯米灰浆、烧料姜石(CGN)改性浆体等)强度对锚固系统性能有重要影响,因此在传力机理分析中应同时考虑浆体抗剪强度的影响;竹木锚固界面应力呈单峰或双峰特点,且随载荷增大应力峰值逐渐向锚固端转移,表明此类锚固界面应力沿锚杆轴向的非均匀分布特征[17 \mbox-18].毛筱霏[19]的试验研究同样验证了剪应力的非均匀分布特征,同时指出传统岩土体锚固力计算方法将会过高估计锚固系统的锚固力.张艳军等[20]从符合材料力学角度分析了锚固系统工作机理,认为筋材与楠竹的弹性模量之比、锚固剂剪切模量等对锚固界面传力性能影响较大.张虎元等[21]通过室内拉拔试验分析了楠竹加筋复合锚杆钢绞线-内粘剂界面的粘结-滑移模型,指出此过程可分为指数上升段与残余应力段,但楠竹-土体界面的粘结-滑移模型仍不明确.
近几十年来,国内外学者对全长粘结式锚杆传力机理的理论解析研究取得了许多重要成果.Farmer[22],Andan等[23],Hyett等[24]以及张季如等[25]研究均指出,锚杆轴力与界面剪应力均沿锚杆轴向自加载端向锚固端指数衰减,但这些分析均未涉及界面完全脱粘现象.Yazicit和Kaiser[26]认为极限锚固力与岩石-砂浆刚度比、浆体强度、锚杆-浆体界面粗糙度等因素密切相关,而忽略了界面间的粘结强度,这与实际情况有所差异.谢晶晶[27]和高丹盈[28]采用界面应力在软化段指数衰减的粘结-滑移模型对界面传力机理进行了分析,但相关参数需要通过迭代算法进行求解,不便于工程应用.Ma等[29 \mbox-31]考虑锚固端的滑移和锚固界面的完全脱粘现象,推导了界面应力应变的分布以及载荷-位移曲线,但对锚固界面传力全过程研究不足.Zheng和Dai[32 \mbox-33]采用微积分法与传递矩阵法分析了不同边界条件下FRP-岩石界面的力学行为,为锚固界面传力机理研究提供了新的思路.Ren等[34]参照Yuan等[35]的算法,基于岩体锚固工程常用的三线型粘结-滑移模型,分段求解了锚固界面剪应力、载荷-位移曲线等封闭解,但该模型定义滑移量超过一定值后界面残余应力保持为定值,这与竹木锚固系统现场拉拔试验结果[36]有所差异.
综上可以看出,以往对锚固界面传力过程的研究主要是基于三线型、双线型或指数型锚固界面粘结-滑移模型进行的,但上述方法均忽略了浆体本身抗剪强度的影响,且采用的界面力学模型并不完全适用于土遗址竹木锚固界面.针对上述问题,基于前期对竹木锚固界面力学行为的现场试验研究[36],考虑浆体剪切强度,采用含完全脱粘段的改进三线型粘结-滑移模型,将锚固界面粘结-滑移全过程分为6个连续阶段,着重分析了轴向拉拔载荷作用下锚固界面的应力分布规律与传递过程,推导了锚杆轴向变形、界面滑移量、界面剪应力、界面剪应变等参数的封闭解,同时给出了极限锚固力和有效锚固长度的计算方法,以期为土遗址锚固机理研究与锚固参数设计提供参考.
1 控制方程
前期试验研究结果显示,楠竹锚固系统在拉拔载荷作用下最主要的破坏模式为锚杆-改性泥浆或改性泥浆-土体界面间的滑移破坏,且前者发生的频率和相对滑移量均远大于后者(26个楠竹锚固试样中,除一个试样由端头劈裂破坏外,其余均由锚杆-改性泥浆界面滑移导致破坏,少数试样还伴随有改性泥浆-土体界面的滑移,但后者的滑移量仅为前者的1/50~1/10)[2].这主要是由于:(1)改性泥浆材性与土体相近,浆体渗入土体中,固化后增大了界面强度;(2)浆体为散粒体,而杆体为纤维材料,两者材性差异较大,更易导致滑移.因此,楠竹-改性泥浆界面的力学行为是影响锚固系统性能的决定因素,是锚固系统的主控面.
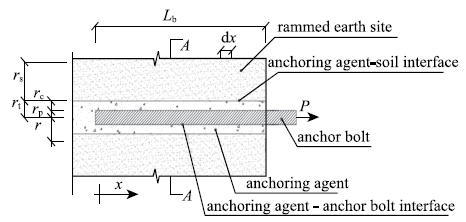
锚杆与锚固剂界面粘结-滑移的全过程分析需要考虑多方面的因素,以便确定合适的控制方程,进而准确地识别界面粘结-滑移的各个阶段.为便于分析,本文基于如下假设对锚固系统进行简化:(1)楠竹锚杆选取通体笔直,杆体无缺陷,直径(35$\pm$3)mm的楠竹杆材中段制成,直径变化微小,因此本文假设锚杆为等截面直杆;(2)土遗址失稳主要由水平地震作用导致,水平力对遗址稳定最为不利,因此本文假定锚杆与锚固剂仅承受轴向载荷;(3)土遗址锚固注浆前先采用改性硅丙乳液专用加固剂对孔壁进行加固,并采用对中支架确保杆体位于锚孔中央,而后采用二次压力注浆工艺完成注浆,保证了浆体与杆体、土体的有效粘结,因此本文假定锚杆与锚固剂界面粘结良好,不存在空鼓、漏浆等缺陷;(4)为简化计算,本文忽略泊松比影响,假定锚固界面仅承受剪应力.如图1所示为锚杆与锚固剂界面粘结-滑移计算简图,其中,锚固段总长度为$L_{\rm b}$,锚杆半径$r_{\rm p}$,锚固剂厚度$r_{\rm c}$,在锚杆端部作用拉拔载荷$P$.需要说明的是,实际土体厚度可视为无穷大,但为便于理论分析,先假设土体厚度为$r_{\rm s}$.
图1
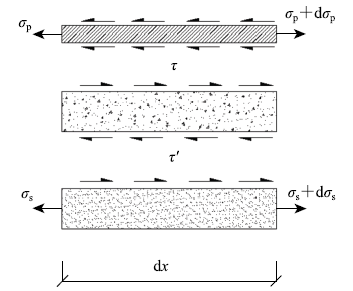
取锚固段中长度为dx的微元进行分析,各材料受力情况如图2所示,图中$\tau$为锚杆与锚固剂界面剪应力,$\tau '$为锚固剂与土体界面剪应力,$\sigma$p为锚杆轴向应力,$\sigma$s为土体轴向应力.根据受力平衡条件,存在如下基础方程
图2
图2
锚固材料受力:锚杆、浆体、土体
Fig.2
Anchorage material stress: anchor bolt, anchor agent and soil
根据锚杆受力平衡条件有
其中,$\sigma$$_{\rm p}$为锚杆轴向应力,$\tau$为锚杆-锚固剂界面剪应力.考虑锚杆的线弹性行为,存在如下应力应变关系
其中,$E_{\rm p}$和$U_{\rm p}$分别为锚杆的弹性模量与轴向位移,$\varepsilon$$_{\rm p}$为锚杆的轴向应变. 将式(2)代入式(1)可得
同理,根据土体微段平衡条件,可求得关于土体轴向位移$u_{\rm s}$的微分方程
根据之前假设,锚固剂仅受剪力作用,在$r_{\rm p} \le r \le r_{\rm c}$的任意位置,根据锚固剂的受力平衡,半径r处锚固剂剪应力$\tau$$_{\rm m}$均可表示为
其中,$\tau _{\rm m}$为锚固剂在距锚杆中心r处的剪应力. 当$r =r_{\rm t }= r_{\rm p}+r_{\rm c}$时(即锚固剂与土体界面处),有
将式(6)代入式(4)中,可得
考虑锚固剂的线弹性行为,存在如下应力应变关系
其中,$G_{\rm c}$ 为锚固剂的剪切模量. 将式(5)代入式(8)可得
对式(9)中r从$r_{\rm p}$到$r_{\rm t}$积分,可得
假设锚固剂与土体粘结良好,根据变形协调条件,土体轴向位移与锚固剂在$r=r_{\rm t}$处的轴向位移相等,有
根据假定,材料间的相对位移差异即为界面的滑移量,则锚杆与锚固剂界面滑移量$s$可以表示为
将式(11)与式(12)代入式(10),有
实际锚固工程中,土层厚度可以视为无限大,即$r_{\rm s} \to \infty$,则$u_{\rm s} \to$0,式(13)可化为
2 考虑完全脱粘的粘结-滑移模型
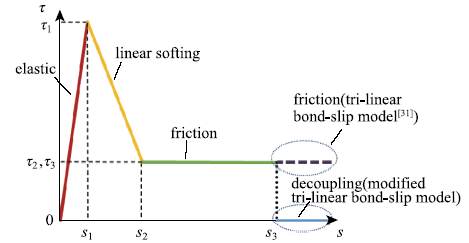
课题组前期采用现场拉拔试验方法,通过对土遗址楠竹锚固系统载荷位移关系,界面应力应变分布规律及滑移特征的分析,研究了此类锚固界面的力学行为,结果表明:当载荷较大时,加载端附近界面存在完全脱粘现象[37].因此,本文采用考虑完全脱粘现象的改进三线型粘结-滑移模型(如图3所示)[36]对锚杆-锚固剂界面的粘结-滑移全过程进行分析.该模型将传统三线型粘结-滑移模型摩擦段(图3中绿色实线与紫色虚线段)修正为有限长(仅绿色段),并加入完全脱粘段(图3中蓝色段,即$s>s_{3}$的部分).模型中,界面粘结应力$\tau$随滑移量$s$增大而增大,直至滑移量达到$s_{1}$,此时界面粘结应力达到最大值$\tau$1;随后,界面表现出软化行为,界面剪应力随滑移量进一步增大而线性减小,当$s=s_{2}$时此阶段结束;最后,当滑移量处于$s_{2}$至$s_{3}$之间时,界面剪应力保持为残余摩擦应力$\tau$2;当滑移量超过$s_{3}$时,锚固界面完全脱粘,界面粘结作用完全消失($\tau$=0).
图3
图3所示考虑完全脱粘现象的改进三线型粘结-滑移模型可由下式表达
$$ \tau \left( s \right) = \left\{ {{\begin{array}{lll} \frac{\tau _1 }{s_1 }s,& {0 \le s \le s_1 } &\rm (a1)\\[1mm] \frac{\tau _1 s_2-\tau _2 s_1 }{s_2-s_1 }-\frac{\tau _1-\tau _2 }{s_2-s_1 } s, & {s_1 < s \le s_2 } &\rm (a2)\\ {\tau _2 ,} & {s_1 < s \le s_2 } & \rm {(a3)} \\ {0,} & {s \ge s_3 } & \rm {(a4)} \end{array} }} \right.$$
可以看出,改进模型可分为4段:(1) 弹性段,此段滑移量$0<s \le s_{1}$;(2)软化段,此段界面粘结应力随滑移量增加线性衰减,直至$s \ge s_{2}$;(3)摩擦段,此段界面粘结应力不随滑移量的增大而改变,其值恒等于$\tau$2,直至$s \ge s_{3}$;(4)完全脱粘段,当$s \ge s_{3}$时材料界面无剪应力传递,$\tau$$(s)$恒等于0.
3 锚固界面传力过程分析
依据改进的界面三线型粘结-滑移本构模型,通过求解控制方程即可得到锚杆-锚固剂界面的滑移量分布和应力、应变分布封闭解.
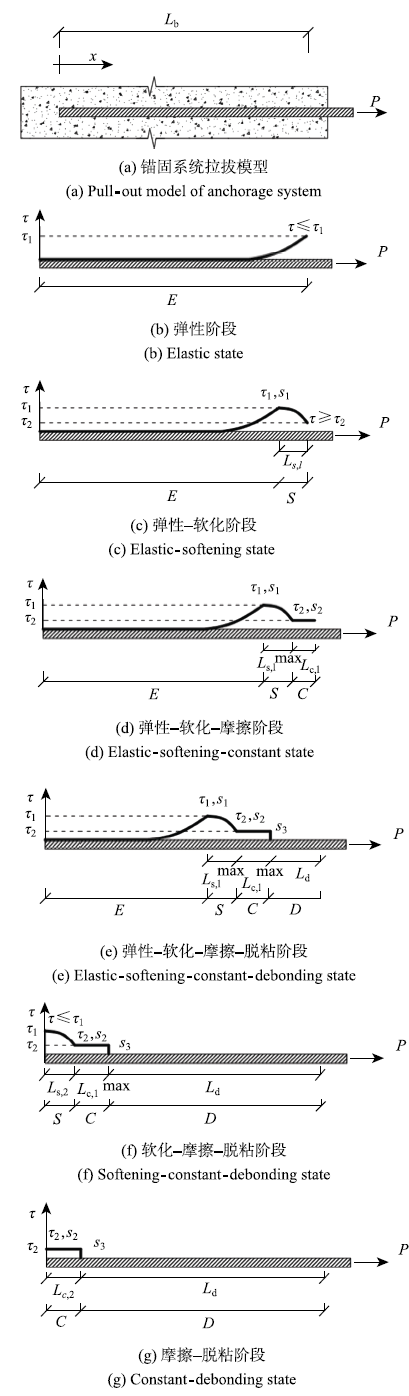
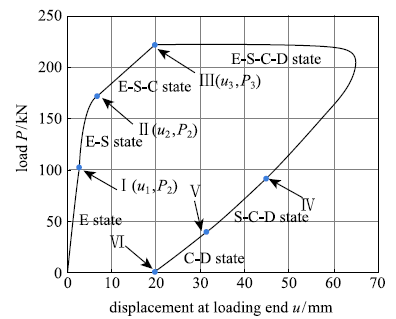
图4所示为锚杆-锚固剂界面粘结滑移全过程的各个阶段受力状态示意图.图中界面粘结-滑移全过程需要经历6个阶段,即:弹性阶段(E state)、弹 性-软化阶段(E-S state)、弹性-软化-摩擦阶段(E-S-C state)、弹性-软化-摩擦-完全脱粘阶段(E-S-C-D state)、软化-摩擦-完全脱粘阶段(S-C-D state)和摩擦-完全脱粘阶段(C-D state).本节所有分析均基于锚固长度足够的假设进行.
图4
图4
锚固界面传力过程的6个阶段
Fig.3
Six states of force transfer process in anchorage interface
3.1 弹性阶段
当载荷较小时,锚固界面全长均处于弹性状态,如图4(b)所示.加载端附近界面粘结应力最大,并随锚固深度增大逐渐呈指数衰减.当界面最大粘结应力在$x=L_{\rm b}$处达到$\tau$1时,此阶段结束.将界面粘结-滑移模型公式(a1),代入式(14)可得
将式(15)代入式(3)可得
其中
此阶段存在以下边界条件
求解微分方程(16)可得锚杆弹性段轴向位移$u_{\rm p}$
将式(20)分别代入式(2)和式(3)可解得锚杆的轴向应变$\varepsilon$$_{\rm p}$和切应力$\tau$为
将式(22)代入式(a1)即可求得界面相对滑移 量$s$
当$x=L_{\rm b}$处的最大粘结应力达到$\tau$1时此阶段结束,此时对应的界面滑移量为$s_{1}$,通过求解式(23)可获得此阶段的最大拉拔载荷$P_{\rm max,1}$
当锚固长度足够长时,粘结长度$L_{\rm b} \to \infty$,则tanh$(\alpha_1 L_{\rm b}) \to 1$,式(24)可简化为
3.2 弹性-软化阶段
当$x=L_{\rm b}$处的最大粘结应力达到$\tau$1(相应滑移量为$s_{1})$时,加载端附近锚杆与锚固剂界面开始出现软化现象,此时,锚固界面被分为两部分,即弹性段和软化段,如图4(c)所示.在软化段中,粘结应力从$\tau$1开始逐渐减小,但仍始终大于$\tau$2. 当界面粘结应力小于等于$\tau$2(相应滑移量为$s_{2})$时,此阶段结束.
将式(a2)代入式(14),可得
将式(26)代入式(3)可得
其中
此阶段中边界条件式(18)和式(19)仍然适用,且还存在以下连续条件
由边界条件式(18)、式(19)、式(30)和式(31)求解微分方程(16)可得弹性段($0 \le x \le L_{\rm b}-L_{\rm s} )$锚杆轴向位移$u_{\rm p}$
将式(32)分别代入式(2)和式(3)可解得锚杆弹性段的轴向应变$\varepsilon$$_{\rm p}$和切应力$\tau$为
将式(34)代入式(a1)即可求得弹性段界面相对滑移量$s$
由边界条件式(19)和式(30)求解微分方程(27)可得软化段($L_{\rm b}-L_{\rm s} \le x \le L{ }_{\rm b})$锚杆轴向位移$u_{\rm p}$(式(36)),将式(36)分别代入式(2)和式(3)可解得锚杆软化段轴向应变$\varepsilon$$_{\rm p}$ (式(37))和切应力$\tau$(式(38)),将式(38)代入式(a2)即可求得软化段界面相对滑移量$s$(式(39))
假设界面粘结应力在$x=L_{\rm b}-L_{\rm s,1}$处达到$\tau$1,且将总锚固长度$L_{\rm b}$视为无穷大,利用式(39)即可求得此阶段锚杆的软化长度$L_{\rm s,1}$
当界面粘结应力在$x=L_{\rm b}$处达到$\tau$2时,软化段长度达到最大,将总锚固长度$L_{\rm b}$视为无穷大,利用式(39)即可求得此阶段锚杆的最大软化长度$L_{\rm s,1}^{\max}$
3.3 弹性-软化-摩擦阶段
根据改进的界面粘结-滑移模型,此阶段中,粘结界面全长被分为三个部分,即弹性段、软化段和摩擦段,其中摩擦段内的界面相对滑移量$s_{2}\le s \le s_{3}$,且剪应力保持为定值($\tau$=$\tau$$_{2})$,如图4(d)所示.随软化段长度不断增大,峰值剪应力逐渐向锚固端转移,锚固深处的界面粘结强度逐渐被调动以抵抗拉拔载荷.
将式(a3)代入式(3),可得
其中
此阶段中边界条件式(18)和式(19)仍然适用,且还存在以下边界条件
由边界条件式(18)和式(46)求解微分方程式(16)可得弹性段($0 \le x \le L{ }_{\rm b}-L_{\rm s,1}^{\max }-L_{\rm c} )$锚杆轴向位移$u_{\rm p}$
将式(48)分别代入式(2)和式(3)可解得锚杆弹性段的轴向应变$\varepsilon$$_{\rm p}$和切应力$\tau$
将式(34)代入式(a1)即可求得弹性段界面相对滑移量$s$
由边界条件式(45)和式(47)求解微分方程(27)可得软化段($L_{\rm b}-L_{\rm s,1}^{\max }-L_{\rm c,1} \le x \le L_{\rm b}-L_{{\rm c},1} )$锚杆轴向位移$u_{\rm p}$ (式(52)),将式(52)分别代入式(2)和式(3)可解得锚杆软化段的轴向应变$\varepsilon$$_{\rm p}$ (式(53))和切应力$\tau$式(54)
将式(54)代入式(a2)即可求得弹性段界面相对滑移量$s$(式(55)),由边界条件式(19)和式(44)求解微分方程(42)可得摩擦段($L_{\rm b}-L_{\rm c,1} \le x \le L_{\rm b} )$锚杆轴向位移$u_{\rm p}$(式(56))
将式(52)代入式(2)可解得锚杆摩擦段的轴向应变$\varepsilon$$_{\rm p}$为
同时,易知摩擦段界面剪应力$\tau$
将式(56)和式(58)代入式(14)可得摩擦段界面相对滑移量$s$
当界面相对滑移量在$x=L_{\rm b}-L_{\rm c,1}$处达到$s_{2}$时,加载端载荷$P$由弹性软化段与摩擦段两部分的界面剪应力平衡,假设弹性软化段承受载荷为$P_{1}$,摩擦段承受载荷为$P_{2}$,那么此时加载端载荷$P$可表示为
其中摩擦段所承受载荷$P_{2}$可通过将摩擦段长度内界面上的剪应力$\tau$2积分得到
将式(61)代入式(60)可得摩擦段长度$L_{\rm c,1}$的表达式
假定界面锚固长度$L_{\rm b}$足够,E-S-C阶段所承受的载荷$P_{1}$与E-S阶段所能承受的最大载荷相等,考虑$L=L_{\rm b}$处界面剪应力$\tau$=$\tau$2,求解式(38),并令$L_{\rm s,1} = L_{\rm s,1}^{\max }$,有
将式(63)代入式(62)可解得E-S-C阶段摩擦段长度$L_{\rm c,1}$
当界面相对滑移量在$x=L_{\rm b}$处达到$s_{3}$时,摩擦段长度达到最大,之后进入下一阶段,此时将总锚固长度$L_{\rm b}$视为无穷大,利用式(59)即可求得此阶段锚杆的最大摩擦段长度$L_{\rm c,1}^{\max }$
3.4 弹性-软化-摩擦-脱粘阶段
此阶段中,加载端锚固界面开始出现完全脱粘,界面由四部分组成:弹性段、软化段、摩擦段与完全脱粘段.此阶段是粘结-滑移全过程中受力最复杂的一个阶段,如图4(e)所示.当加载端($x=L_{\rm b})$界面相对滑移量达到$s_{3}$时开始进入此阶段,界面剪应力随完全脱粘段长度的增大逐渐向锚固端转移(即$\tau$1与$\tau$2的位置逐渐向x=0处移动),因此,仅需将E-S-C阶段解析结果中的$L_{\rm b}$用$L_{\rm b}-L_{\rm d}$代换,即可得到本阶段的界面粘结应力与相对滑移量分布的解析解.
将锚杆考虑为线弹性材料,则锚固界面完全脱粘段的相对滑移量分布可以由下式表示
由界面滑移量分布式(66)与改进的界面粘结-滑移模型式(a4),可知完全脱粘段界面粘结应力$\tau$始终保持为零. 上述结论可通过将式(66)与式(14)代入式(3)进行验证.
在E-S-C-D阶段结束时,弹性段完全消失,在x=0处界面粘结应力$\tau$=$\tau$1,随后进入下一阶段,此时总锚固长度$L_{b}$可以由下式表示
3.5 软化-摩擦-脱粘阶段
当x=0处界面粘结应力$\tau$=$\tau$1时(即弹性段完全消失),界面开始进入软化-摩擦-脱粘阶段.此阶段中,界面峰值剪应力为$\tau$$_{1}(x$=0),之后随拉拔载荷的增加,界面总相对滑移量快速增大,而界面峰值剪应力逐渐减小,如图4(f)所示.
此阶段由式(27)与式(42)控制,存在如下边界条件
由边界条件式(69)和式(71),并考虑式(14),求解微分方程(42)可得摩擦段($L_{\rm s,2}^{\max } \le x \le L_{\rm s,2}^{\max } + L_{\rm c,1}^{\max })$锚杆轴向位移$u_{\rm p}$
将式(72)代入式(2)可解得锚杆摩擦段的轴向应变$\varepsilon$$_{\rm p}$
同时易知摩擦段界面剪应力$\tau$
由边界条件式(68)和式(70),并考虑式(73),求解微分方程(27),可得软化段($0 \le x \le L_{\rm s,2} )$锚杆轴向位移$u_{\rm p}$ (式(75)),将式(75)分别代入式(2)和式(3)可解得锚杆软化段的轴向应变$\varepsilon$$_{\rm p}$ (式(76))和切应力$\tau$ (式(77)), 将式(77)代入式(a2)可得摩擦段界面相对滑移量$s$ (式(78))
假定在$x=L_{\rm s,2}$处,有界面粘结应力$\tau$=$\tau$2,将其代入式(77)可得界面软化段长度$L_{\rm s,2}$
脱粘段最早出现于E-S-C-D阶段,随载荷增大,脱粘段长度也将持续增大,此时界面脱粘段的滑移量亦可通过式(66)解得,脱粘段长度$L_{\rm d}$可通过下式获得
当界面软化段消失时(即$L_{\rm s,2}$=0时),S-C-D阶段结束,此时,由式(80)可得
将式(43)代入式(81)可得
根据平衡条件,式(82)可通过将剪应力在摩擦段上积分进行验证
3.6 摩擦-脱粘阶段
摩擦-脱粘阶段出现在界面完全脱粘之前,此时软化段已完全消失,仅存在摩擦段与完全脱粘段,如图4(g)所示.该阶段的控制方程同式(42),且存在如下边界条件
由边界条件式(84)和式(85)求解微分方程式(42),可得摩擦段($0 \le x \le L_{\rm c,2} )$锚杆轴向位移$u_{\rm p}$
将式(86)代入式(2)可解得锚杆摩擦段的轴向应变$\varepsilon$$_{\rm p}$
同时易知摩擦段界面剪应力$\tau$
将式(86)和式(88)代入式(14)可得摩擦段界面相对滑移量$s$
考虑残余摩擦段长度$L_{\rm c,2}$上界面粘结应力始终保持为$\tau$2,其余部分粘结应力为零,根据平衡条件,拉拔载荷$P$可由下式表示
由式(91)可知,当$P$=0时,摩擦段长度$L_{\rm c,2}$=0,此时摩擦段消失,锚固界面全部进入完全脱粘状态,界面任一点剪应力均为零,锚固系统失效.
4 粘结-滑移模型特征点参数标定
由于当前土遗址的保护工作处于"抢险加固"阶段,尚无相关标准、规范可供参考,因此,本文以"先救命、后治病"为原则,以快速工程应用为目的,给出标定锚固界面粘结-滑移模型关键参数的半经验、半理论方法,以方便工程应用.
图5
图5
锚固系统粘结-滑移全过程载荷-位移曲线及特征点位置
Fig.5
Load-displacement curve of anchorage system and the feature point position
在求解$\tau$1和$\tau$2时,可将Ⅰ($u_{1}$,$P_{1})$代入式(24)或(25),并考虑式(17),解得界面峰值粘结应力$\tau$1,将Ⅱ($u_{2}$,$P_{2})$代入式(38)和式(41),并考虑软化段范围$L_{\rm b}-L_{\rm s} \le x \le L_{\rm b}$,可解得界面残余摩擦应力$\tau$2.
5 理论结果验证
5.1 载荷-位移曲线
本节选取2组土遗址锚杆拉拔试验数据,首先对界面的粘结-滑移模型特征参数进行标定,而后计算锚固系统加载端载荷-位移关系,并与试验结果进行对比,验证本文锚固界面粘结-滑移全过程理论解析方法的可靠性.由于现场试验条件与设备测试能力限制,两组试验均未能准确测得峰值载荷后的载荷-位移关系,因此本节仅对峰值载荷前的载荷-位移曲线进行对比.
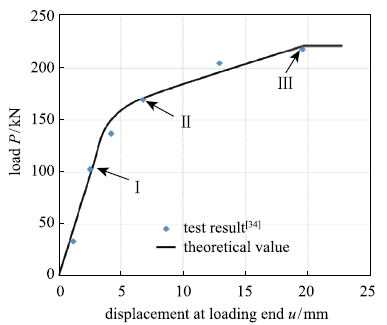
第一组数据取自楠竹锚杆拉拔试验结果[36].材料物理力学参数如下:楠竹直径35 mm,轴向抗拉强度106.5 MPa,弹性模量6.6 GPa;钻孔直径85 mm;改性泥浆抗压强度5.63 MPa,剪切模量23.56 MPa. 粘结-滑移模型参数为:$\tau$1=1.89 MPa,$\tau$2=0.44 MPa,$s_{1}$=3.34 mm,$s_{2}$=10.73 mm,$s_{3}$=22.56 mm.图6所示为楠竹-改性泥浆锚固系统载荷-位移曲线试验值与理论值的对比,其中实测数据取自长锚试样(CB-L-2000a和CB-L-3000b).结果显示:E-S阶段载荷理论值较试验值略微偏高,其他阶段吻合较好;两个试样均达到了极限拉拔载荷且与理论值相近.Ⅲ点对应E-S-C阶段的结束和E-S-C-D阶段的开始,由于试验条件限制此阶段后的数据未能准确获得.
图6
图6
加载端载荷-位移曲线理论值与锚固长度为2 m和3 m试样(楠竹锚固系统)的试验值对比
Fig.6
Comparison of the load-displacement curve at loading end between the theoretical solutions and the specimens with the anchorage lengths of 2 m and 3 m (bamboo anchorage system)
图7所示为复合锚杆加载端($x=L_{\rm b}$处)载荷-位移曲线试验值与理论值的对比,结果显示:本文理论值与现场试验值吻合良好,最大差异仅为6.8%,说明本文理论能够较精确地预测该界面的粘结-滑移过程.
图7
图7
复合锚杆锚固系统加载端载荷-位移曲线试验值与理论值对比
Fig.7
Comparison of the load-displacement curve at loading end between the theoretical solutions and the experimental result (composite bolt anchorage system)
5.2 锚固界面剪应力分布与传递规律
需要说明的是,由于天然竹材两端截面尺寸略有差异,导致试验中锚固端(截面略大于加载端)附近锚杆出现压变现象,应变值波动较大,与本文理论假设存在一定差异,因此,为便于对比,本节中将这些点处的应变值修正为零.
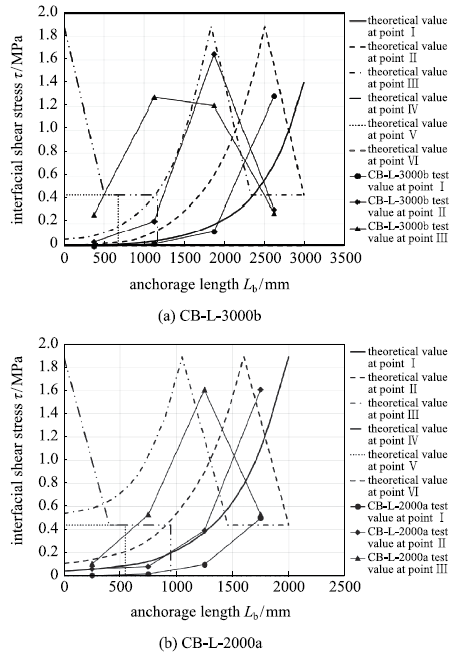
图8所示为粘结-滑移过程中各阶段界面剪应力沿锚固长度的分布理论值与试验值对比.其中界面剪应力试验值基于相邻应变监测点间的平均剪应力假定获得.根据锚固微段平衡条件,有
图8
图8
界面剪应力沿锚固长度分布的理论值与锚固长度为2 m和3 m试样(楠竹锚固系统)的试验值对比
Fig.8
Comparison of interfacial shear stress distribution along anchor length between the theoretical solutions and the specimens with the anchorage lengths of 2 m and 3 m (bamboo anchorage system)
上式可化为
其中,$E_{\rm p}$和$r_{\rm p}$分别为锚杆轴向刚度与半径,$\varepsilon$$_{i + 1}$和$\varepsilon$$_{i}$分别为第i个和第i+1个应变片测得的应变值,$x_{i + 1}-x_{i}$为相邻应变片间距,$\tau (x)$为相邻应变片间的平均剪应力.
图8中分别包含了两个试样(CB-L-2000a和CB-L-3000b)在粘结-滑移过程中的6个点(Ⅰ~Ⅵ)处的剪应力分布理论值和初始阶段3个点(Ⅰ~Ⅲ)处的试验值.对比结果显示,剪应力分布的试验值与理论值的吻合程度与粘结-滑移过程所处的阶段直接相关,试验值与理论值在初始阶段吻合较好,当软化现象出现后剪应力分布呈现较大差异,这可能是由于现场试验条件下不确定因素较多,且在试验值换算时采用了平均剪应力假定造成的.另外,对比不同阶段的试验值或理论值均可明显识别出剪应力峰值随粘结-滑移过程自加载端向锚固端转移的现象.
5.3 锚固参数敏感度分析
本节着重分析锚固长度、锚杆轴向刚度作对锚固系统性能的影响.计算中的相关参数取自文献[34]的试验数据.
5.3.1 锚固长度
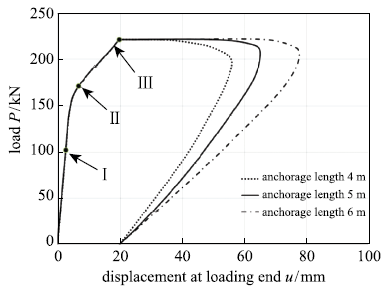
分别取锚固长度为4 m, 5 m, 6 m进行对比分析,计算结果如图9所示.
图9
图9
锚固长度对载荷-位移关系的影响
Fig.9
Effect of the bond length on the load-displacement relationship
Ⅰ, Ⅱ, Ⅲ点分别对应E阶段、E-S阶段、E-S-C阶段的末尾.由图可以看出,在Ⅲ点之前,3种锚固长度下锚杆所能达到的极限拉拔载荷值均相同,与锚固长度无关,因此,可认为这3种锚固长度均大于有效锚固长度($L_{\rm b} \ge L_{\rm eff})$.Ⅲ点后的载荷-位移曲线随锚固长度的变化呈现一定差异:锚固长度越长则加载端的极限滑移量越大,且在Ⅲ点之后有较长平稳段,表现出更强的柔性特征.之后,随着完全脱粘现象的发生,加载端位移$u$与载荷值$P$均持续降低,最终锚固段全长均进入完全脱粘,界面滑移量最终保持为$s_{3}$.
综上所述,在考虑界面完全脱粘现象时,锚固长度仅在$L_{\rm b}<L_{\rm eff}$ 时对锚固系统的极限抗拔力产生影响,而当$L_{\rm b} \ge L_{\rm eff}$时,增加锚固长度仅能提高锚杆的极限滑移量,增强锚固系统延展性.因此,在工程设计中应综合考虑安全性与经济性来确定锚固长度值.
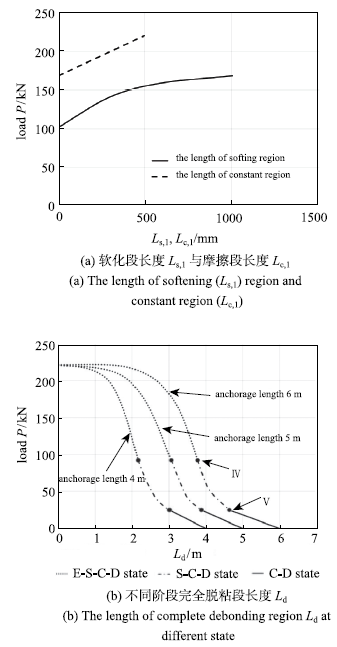
图10所示为$L_{\rm b} \ge L_{\rm eff}$时不同锚固长度下界面粘结-滑移过程各阶段的软化段、摩擦段、脱粘段长度随拉拔载荷的变化趋势.
图10
图10
不同锚固长度下各阶段的软化段、摩擦段、脱粘段长度随载荷的变化趋势
Fig.10
The variation trend of the length of softening region, friction region and debonding region of each state under pull-out load
弹性段的有效锚固长度$L_{\rm e}$(当锚杆界面总粘结力达到弹性段极限拉拔载荷的97%时所对应的锚固长度)可根据式(25)的假定确定,即为了保证tanh($\alpha$1,$L_{\rm b})$=1,可假定tanh(2)$ \approx$1,其误差小于4%[32]. 因此,弹性段有效锚固长度
至此,锚固界面弹性段、软化段和摩擦段的最大长度可由式(41)、式(65)和式(97)完全确定.经计算,本例中各段最大锚固长度分别为$L_{e}^{max}$ = 1851.85 mm,$L_{s,1}^{max}$ = 1004.78 mm,$L_{c,1}^{max}$ = 498.06 mm,三者之和即为界面总有效锚固长度:$L_{eff} = L_{e}^{max} + L_{s,1}^{max } + L_{c,1}^{max}$ = 3354.69 mm. 此结果同样验证了以上3种锚固长度(4 m, 5 m, 6 m)均大于总有效锚固长度$L_{eff}$的结论,均能够达到锚固系统的最大锚固力.
5.3.2 锚杆轴向刚度
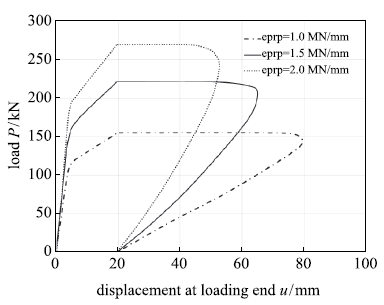
为明确锚杆轴向刚度对粘结-滑移过程的影响,选取锚杆弹性模量$E_{\rm p}$与锚杆半径$r_{\rm p}$的乘积$E_{\rm p }\cdot r_{\rm p}$作为变量,取值分别为1.0 MN/mm,1.5 MN/mm、2.0 MN/mm,计算所得载荷-位移曲线如图11所示.
图11
图11
锚杆轴向刚度对载荷-位移关系的影响
Fig.11
Effect of the bolt axial stiffness on the load-displacement relationship
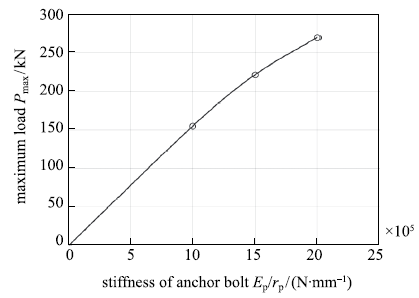
图12
图12
锚杆轴向刚度对极限拉拔载荷的影响
Fig.12
Effect of the bolt axial stiffness on the ultimate pull-out load
6 结 论
本文基于考虑完全脱粘现象的改进三线型粘结-滑移模型,将楠竹锚杆锚固界面粘结-滑移全过程分为六个连续阶段进行理论解析,推导了各阶段对应的锚杆轴向变形$u_{\rm p}$、界面滑移量$s$、界面剪应力$\tau$、界面剪应变$\varepsilon$、弹性段长度$L_{\rm e}$、软化段长度$L_{\rm \rm s,1}$、摩擦段长度$L_{\rm \rm c,1}$、有效锚固长度限值$L_{\rm eff}$等参数的封闭解,同时给出了粘结-滑移模型特征点参数标定方法.得到如下结论:
(1)楠竹-改性泥浆锚固系统受拉拔载荷作用时,其锚固界面存在弹性、软化、摩擦和完全脱粘四种状态;当锚固系统完全失效时其抗拔力为零,锚固界面全部进入完全脱粘状态,锚固界面滑移量均等于$s_{3}$.
(2)本文解析方法能够较精确地计算有效锚固长度与载荷峰值前(Ⅲ点前)加载端载荷-位移曲线,并能对峰值后(Ⅲ点后)的载荷-位移关系进行预测.
(3)锚固系统有效锚固长度与锚杆轴向刚度、锚固剂剪切模量以及粘结-滑移模型等因素相关,例如:当锚杆轴向刚度增大时有效锚固长度也将随之增大.
(4)锚固界面剪应力分布试验值与理论值的吻合程度与粘结-滑移过程所处的阶段直接相关;界面剪应力峰值随载荷的持续增加逐渐自锚杆加载端向锚固端转移.
(5)当实际锚固长度大于有效锚固长度时,锚杆所能承受的极限拉拔载荷值、锚固界面软化段长度和摩擦段长度均与锚固长度无关,但锚固系统延展性将随锚固长度的增大而改善.
(6)锚杆轴向刚度的增加有利于提高锚固系统的极限抗拔力,但同时会降低锚固系统的延展性,在设计时应综合考虑.
参考文献
Experimental studies on earthen architecture sites consolidated with BS materials in arid regions
干旱环境下土遗址夯补支顶加固变形机制室内试验研究
在自然力和人为活动影响下,地处干旱半干旱地区的长城、交河故城、北庭故城等土遗址,其墙体根部因掏蚀而大面积悬空,甚至造成局部区域坍塌。针对夯土遗址根部严重掏蚀问题,采用夯筑支顶加固措施既符合文物保护的基本原则,也遵循保存原材料与原工艺的要求,且加固效果显著。然而大体积夯筑支顶体在固结和失水干缩作用下,与原遗址墙体之间形成较大的裂隙,宽度达1~3 cm。如何控制和减小夯补体与原遗址体之间的收缩缝隙,成为实现大体积夯筑砌补加固的关键。基于固结理论和失水收缩特性,在室内制作不同密度和级配的试块进行固结试验,以及不同形状土样试验的失水收缩量的数据统计,对比分析不同密度、级配条件固结变形、干缩变形的特征,拟合基于传统夯筑工艺的夯补支顶体固结、干缩变形的阈值,初步摸索出了预控大体积垂直方向变形的经验式,为预判大体积夯筑支顶体沉降机制提供可靠的理论依据。
Laboratory test of deformation mechanism of rammed roof-propping reinforcement at earthen heritage sites in arid environment
在自然力和人为活动影响下,地处干旱半干旱地区的长城、交河故城、北庭故城等土遗址,其墙体根部因掏蚀而大面积悬空,甚至造成局部区域坍塌。针对夯土遗址根部严重掏蚀问题,采用夯筑支顶加固措施既符合文物保护的基本原则,也遵循保存原材料与原工艺的要求,且加固效果显著。然而大体积夯筑支顶体在固结和失水干缩作用下,与原遗址墙体之间形成较大的裂隙,宽度达1~3 cm。如何控制和减小夯补体与原遗址体之间的收缩缝隙,成为实现大体积夯筑砌补加固的关键。基于固结理论和失水收缩特性,在室内制作不同密度和级配的试块进行固结试验,以及不同形状土样试验的失水收缩量的数据统计,对比分析不同密度、级配条件固结变形、干缩变形的特征,拟合基于传统夯筑工艺的夯补支顶体固结、干缩变形的阈值,初步摸索出了预控大体积垂直方向变形的经验式,为预判大体积夯筑支顶体沉降机制提供可靠的理论依据。
Investigations on the structural behaviour of archaeological heritage in Peru: From survey to seismic assessment
The conservation of archaeological heritage is of major importance for preserving the scientific, ethnographic and artistic values of past cultures. Once archaeological sites are exposed after being buried for centuries, they are subjected to natural hazards, which should be studied with up-to-date techniques. Moreover, conservation works are primarily focused on aesthetic aspects or on solving localized problems. In earthquake-prone areas, it is of extreme importance to carry out structural analysis studies for assessing the actual behaviour of archaeological constructions, and for proposing adequate intervention measures. This paper presents an extensive study on structural behaviour of archaeological building remains in Peru, based on in-situ non-destructive testing as well as on numerical approaches. The case of the Chokepukio Archaeological Site is presented, which was built between 1000 and 1450 AD in the Pre-Columbian era, with a mixed masonry of stone units and earthen mortar. The paper begins with a comprehensive description of the historical, architectural and structural aspects of the archaeological site. The possibility of applying operational modal analysis tests is then explored with reference to a representative wall of Chokepukio. The results of the experimental field campaign are used to develop calibrated finite element models of the wall, and to indirectly estimate mechanical characteristics of the masonry. Basing on the investigations performed, potential failure mechanisms are identified for the wall and validated by pushover analysis. Finally, the mechanisms are evaluated through kinematic limit analysis, to proceed with the seismic assessment.
隧道及地下工程的基本问题及其研究进展
<p>作为隧道及地下工程学科的3个基本问题,隧道围岩稳定性、支护——围岩相互作用和结构体系的动力响应一直都是本学科研究的核心问题,本文围绕上述问题重点分析了隧道围岩力学特性及其载荷效应,建立了深浅层围岩结构力学模型,并通过分析深层围岩中结构层稳定性得到了围岩特性曲线的解析公式,提出了围岩结构性特点及载荷效应的计算方法;通过对隧道支护与围岩作用关系的分析,将支护与围岩的动态作用分为4个阶段:即自由变形、超前支护、初期支护和二次衬砌阶段.由此提出了动态作用全过程的描述方法;基于广义与狭义载荷的理念,提出隧道支护具有调动和协助围岩承载基本功能的观点,明确了两种功能的实现方式,即通过围岩加固、超前加固及锚杆支护实现调动围岩承载,通过支护结构协助围岩承载;针对复杂的隧道支护结构体系,提出了多目标、分阶段协同作用动态优化概念,可使各种支护结构的施作实现时间和空间上的协调,提高可靠性;针对极不稳定的复杂隧道围岩的安全性特点,建立了3种模式的安全事故机理模型,基于工程响应特点提出了安全性分级的新理念,并形成了分级指标体系和分级方法;针对水下隧道及富水围岩条件,建立了3种模式的隧道突涌水机理模型,提出了基于围岩变形控制的安全性控制理论和方法.最后,对本学科发展的热点和核心问题进行了分析和展望.</p>
Essential issues and their research progress in tunnel and underground engineering
<p>作为隧道及地下工程学科的3个基本问题,隧道围岩稳定性、支护——围岩相互作用和结构体系的动力响应一直都是本学科研究的核心问题,本文围绕上述问题重点分析了隧道围岩力学特性及其载荷效应,建立了深浅层围岩结构力学模型,并通过分析深层围岩中结构层稳定性得到了围岩特性曲线的解析公式,提出了围岩结构性特点及载荷效应的计算方法;通过对隧道支护与围岩作用关系的分析,将支护与围岩的动态作用分为4个阶段:即自由变形、超前支护、初期支护和二次衬砌阶段.由此提出了动态作用全过程的描述方法;基于广义与狭义载荷的理念,提出隧道支护具有调动和协助围岩承载基本功能的观点,明确了两种功能的实现方式,即通过围岩加固、超前加固及锚杆支护实现调动围岩承载,通过支护结构协助围岩承载;针对复杂的隧道支护结构体系,提出了多目标、分阶段协同作用动态优化概念,可使各种支护结构的施作实现时间和空间上的协调,提高可靠性;针对极不稳定的复杂隧道围岩的安全性特点,建立了3种模式的安全事故机理模型,基于工程响应特点提出了安全性分级的新理念,并形成了分级指标体系和分级方法;针对水下隧道及富水围岩条件,建立了3种模式的隧道突涌水机理模型,提出了基于围岩变形控制的安全性控制理论和方法.最后,对本学科发展的热点和核心问题进行了分析和展望.</p>
基于D-P准则的盾构隧道围岩与衬砌结构相互作用分析
<p>在进行盾构隧道管片衬砌结构载荷计算时,常采用全土柱或压力拱理论计算围岩松动压力,但当盾构隧道面临深埋条件且需计入形变压力时,该方法难以适用.鉴于此,基于Drucker-Prager屈服准则,推导了考虑渗流效应影响下围岩与衬砌结构相互作用的弹塑性解析解,给出了围岩弹、塑性区应力与位移、塑性区半径等关键参数与支护阻力间关系的解析式.阐述了上述解析结果在确定衬砌结构载荷中的应用,即建立围岩与衬砌结构静力平衡状态并求二者对应曲线的交点.进一步地,考虑接头引起管片衬砌结构整体刚度降低对围岩与衬砌结构相互作用的影响,引入刚度折减系数,并在衬砌结构围岩压力确定中对施工期流固耦合效应的影响和渗流力对衬砌结构支护特性曲线的影响进行了简化处理.最后,通过算例将解析解与水下盾构隧道载荷实测值和数值计算值进行了比较.结果表明:用解析方法得到的施工期和稳定期的管片衬砌结构围岩压力比现场实测值分别大28%和12%,稳定期围岩压力比数值计算值大5%,可为类似工程的设计施工提供一定的参考价值.</p>
Theoretical analysis of interaction between surrounding rocks and linging strcture of shield tunnel based on Drucker-Prager yield criteria
<p>在进行盾构隧道管片衬砌结构载荷计算时,常采用全土柱或压力拱理论计算围岩松动压力,但当盾构隧道面临深埋条件且需计入形变压力时,该方法难以适用.鉴于此,基于Drucker-Prager屈服准则,推导了考虑渗流效应影响下围岩与衬砌结构相互作用的弹塑性解析解,给出了围岩弹、塑性区应力与位移、塑性区半径等关键参数与支护阻力间关系的解析式.阐述了上述解析结果在确定衬砌结构载荷中的应用,即建立围岩与衬砌结构静力平衡状态并求二者对应曲线的交点.进一步地,考虑接头引起管片衬砌结构整体刚度降低对围岩与衬砌结构相互作用的影响,引入刚度折减系数,并在衬砌结构围岩压力确定中对施工期流固耦合效应的影响和渗流力对衬砌结构支护特性曲线的影响进行了简化处理.最后,通过算例将解析解与水下盾构隧道载荷实测值和数值计算值进行了比较.结果表明:用解析方法得到的施工期和稳定期的管片衬砌结构围岩压力比现场实测值分别大28%和12%,稳定期围岩压力比数值计算值大5%,可为类似工程的设计施工提供一定的参考价值.</p>
粗糙表面接触力学问题的重新分析,
为了克服基于统计学参数的接触模型的尺度依赖性以及现有接触分形模型推导过程中初始轮廓表征受控于接触面积或取样长度的不足,基于粗糙表面轮廓分形维数D、尺度系数G和最大微凸体轮廓基底尺寸l,建立了新的粗糙表面接触分形模型,探讨了微凸体变形机制、粗糙表面的真实接触面积和接触载荷的关系,揭示了接触界面的孔隙率和真实接触面积随端面形貌、表面接触压力等参数变化的规律,给出了不同形貌界面被压实的最大变形量.结果表明:微凸体变形从弹性变形开始,并随着平均接触压力pm的增大逐步向弹塑性变形和完全塑性变形转变;接触界面的初始孔隙率0随D的增大而增大,压实孔隙所需要的最大变形量也随之增大;接触压力pc增大,孔隙率减小,并随着D的增大和G减小,快速减小,直至填实,变为零;D较小时,G的增大对真实接触面积的增大影响较小;D较大时,G的增大对真实接触面积的增大作用明显.研究成果为端面摩擦副的润滑与密封设计提供了理论基础.
Reanalysis of the contact mechanics for rough surfaces
为了克服基于统计学参数的接触模型的尺度依赖性以及现有接触分形模型推导过程中初始轮廓表征受控于接触面积或取样长度的不足,基于粗糙表面轮廓分形维数D、尺度系数G和最大微凸体轮廓基底尺寸l,建立了新的粗糙表面接触分形模型,探讨了微凸体变形机制、粗糙表面的真实接触面积和接触载荷的关系,揭示了接触界面的孔隙率和真实接触面积随端面形貌、表面接触压力等参数变化的规律,给出了不同形貌界面被压实的最大变形量.结果表明:微凸体变形从弹性变形开始,并随着平均接触压力pm的增大逐步向弹塑性变形和完全塑性变形转变;接触界面的初始孔隙率0随D的增大而增大,压实孔隙所需要的最大变形量也随之增大;接触压力pc增大,孔隙率减小,并随着D的增大和G减小,快速减小,直至填实,变为零;D较小时,G的增大对真实接触面积的增大影响较小;D较大时,G的增大对真实接触面积的增大作用明显.研究成果为端面摩擦副的润滑与密封设计提供了理论基础.
连接结构接触界面非线性力学建模研究
连接界面上存在的跨尺度、多物理场和非线性行为是引起结构复杂非线性动力学的主要原因.由于连接界面的力学行为的复杂性,以及难以对连接界面进行直接试验观测,连接界面的力学建模一直是非常具有挑战性的科学问题.本文首先从分析结合面的跨尺度物理机理入手,将名义的光滑平面视作凹凸不平的粗糙面,考虑单个微凸体的黏滑摩擦行为,建立接触载荷与变形的非线性关系,然后采用GW(Greenwood and Williamson)模型数理统计方法建立整个粗糙界面的跨尺度力学模型,并与公开文献中试验结果进行对比.考虑连接界面具有典型非线性特征,提出一种改进的Iwan唯象模型,利用精细有限元方法获得非线性特征结果,采用系统辨识理论建立连接结构的降阶力学模型,并利用有限元结果进行模型验证.结果表明,本文提出的粗糙界面跨尺度模型在法向载荷较小时与试验结果吻合较好,改进的Iwan模型能够较好描述连接界面的非线性特征,并与有限元结果吻合较好.
Nonlinear mechanics modeling for joint interface of assembled structure
连接界面上存在的跨尺度、多物理场和非线性行为是引起结构复杂非线性动力学的主要原因.由于连接界面的力学行为的复杂性,以及难以对连接界面进行直接试验观测,连接界面的力学建模一直是非常具有挑战性的科学问题.本文首先从分析结合面的跨尺度物理机理入手,将名义的光滑平面视作凹凸不平的粗糙面,考虑单个微凸体的黏滑摩擦行为,建立接触载荷与变形的非线性关系,然后采用GW(Greenwood and Williamson)模型数理统计方法建立整个粗糙界面的跨尺度力学模型,并与公开文献中试验结果进行对比.考虑连接界面具有典型非线性特征,提出一种改进的Iwan唯象模型,利用精细有限元方法获得非线性特征结果,采用系统辨识理论建立连接结构的降阶力学模型,并利用有限元结果进行模型验证.结果表明,本文提出的粗糙界面跨尺度模型在法向载荷较小时与试验结果吻合较好,改进的Iwan模型能够较好描述连接界面的非线性特征,并与有限元结果吻合较好.
基于改性糯米灰浆的3种锚杆锚固性能对比研究
锚固浆液的类型及其与杆体、土体的兼容协调性问题是土遗址锚固领域的研究焦点。由糯米浆为胶凝主材和由黏土、粉煤灰为填充料组成的改性糯米灰浆与木锚杆、玻璃纤维增强塑料锚杆、钢筋锚杆组成了3种锚固系统。通过对3种锚固系统的原位锚固、拉拔试验和界面应力-应变监测,分析比较了3种锚固系统的破坏模式、极限荷载、荷载-位移特征,剖析了杆体-浆体界面应力分布传递规律和界面测点应变对荷载时步的响应程度。在初步分析其锚固机制的基础上,最终得出了此类基于改性糯米灰浆的3种锚固系统的锚固性能的优劣完全取决于杆体-浆体的受力机制、变形和强度特征所决定的力学兼容性的结论。该研究成果为以糯米浆为主材的改性浆液在土遗址锚固领域中的应用提供了依据和参考。
Comparative study of anchorage performance of three types of bolts fully grouted by modified glutinous rice mortar
锚固浆液的类型及其与杆体、土体的兼容协调性问题是土遗址锚固领域的研究焦点。由糯米浆为胶凝主材和由黏土、粉煤灰为填充料组成的改性糯米灰浆与木锚杆、玻璃纤维增强塑料锚杆、钢筋锚杆组成了3种锚固系统。通过对3种锚固系统的原位锚固、拉拔试验和界面应力-应变监测,分析比较了3种锚固系统的破坏模式、极限荷载、荷载-位移特征,剖析了杆体-浆体界面应力分布传递规律和界面测点应变对荷载时步的响应程度。在初步分析其锚固机制的基础上,最终得出了此类基于改性糯米灰浆的3种锚固系统的锚固性能的优劣完全取决于杆体-浆体的受力机制、变形和强度特征所决定的力学兼容性的结论。该研究成果为以糯米浆为主材的改性浆液在土遗址锚固领域中的应用提供了依据和参考。
胶木棒锚杆在唐皇城含光门土遗址锚杆锚固中的应用
针对唐皇城墙含光门土遗址出现 的夯土脱落、变形裂隙、建筑工艺裂隙等病害现状,对该遗址的土体性能进行了测试分析,设计了适宜于半干旱、半湿润地区土遗址的胶木棒锚固锚杆。结果表明: 对比其他土遗址类锚杆,采用均匀分布阻力棒的胶木棒锚杆具有抗腐蚀、强度大、韧性好等特点;此胶木棒锚杆性能优异,已成功应用于唐皇城墙含光门土遗址等重 要文物的保护工程中。
Application of bakelite rod anchor in protection of Tang Hanguangmen Entrance remains
针对唐皇城墙含光门土遗址出现 的夯土脱落、变形裂隙、建筑工艺裂隙等病害现状,对该遗址的土体性能进行了测试分析,设计了适宜于半干旱、半湿润地区土遗址的胶木棒锚固锚杆。结果表明: 对比其他土遗址类锚杆,采用均匀分布阻力棒的胶木棒锚杆具有抗腐蚀、强度大、韧性好等特点;此胶木棒锚杆性能优异,已成功应用于唐皇城墙含光门土遗址等重 要文物的保护工程中。
南竹加筋复合锚杆加固土遗址研究
The bamboo-steel composite anchor is a kind of new anchor that is designed for aiming at the bulk earthen sites. According to the test,the reinforcement of earthen sites accords with the principle of the heritage sites protection by adopting the PS series of grout material and the bamboo-steel composite anchor. If adopting the cement mortar as grout material,its anchoring unit power can be adopted 30 kN/m;if adopting the PS-(F+C) as grout material,its anchoring unit power can be adopted 20 kN/m. When reinforcing the earthen sites by the bamboo-steel composite anchor,its weak interface exists between anchor body and anchoring solid. The strengths of cement-mortar and PS-F slurry are adopted for anchoring by the bamboo-steel composite anchor. The standard value of cohesive strength averages 187 kPa,the eigenvalue averages 85 kPa between the cement-mortar and anchor body. The standard value of cohesive strength averages 114 kPa,the eigenvalue averages 52 kPa between the 12% PS-F and anchor body.
Study on reinforcement of earthen sites by bamboo-steel composite anchor
The bamboo-steel composite anchor is a kind of new anchor that is designed for aiming at the bulk earthen sites. According to the test,the reinforcement of earthen sites accords with the principle of the heritage sites protection by adopting the PS series of grout material and the bamboo-steel composite anchor. If adopting the cement mortar as grout material,its anchoring unit power can be adopted 30 kN/m;if adopting the PS-(F+C) as grout material,its anchoring unit power can be adopted 20 kN/m. When reinforcing the earthen sites by the bamboo-steel composite anchor,its weak interface exists between anchor body and anchoring solid. The strengths of cement-mortar and PS-F slurry are adopted for anchoring by the bamboo-steel composite anchor. The standard value of cohesive strength averages 187 kPa,the eigenvalue averages 85 kPa between the cement-mortar and anchor body. The standard value of cohesive strength averages 114 kPa,the eigenvalue averages 52 kPa between the 12% PS-F and anchor body.
夯筑土遗址中基于PS–(F+C)浆液的木锚杆锚固性能
基于室内物理模型试验和原位锚固试验,对基于高模数硅酸钾溶液-(粉煤灰+粉土)(PS-(F+C))浆液的木锚杆锚固系统在夯土介质中进行了拉拔测试与杆体-浆体界面应变监测,研究了该锚固系统的锚固性能与破坏模式、杆体-浆体界面剪应力分布与传递特征。结果表明:该锚固系统室内试验极限锚固力(24~38 k N)远大于现场试验值(2.5~8 k N);锚固系统具有低弹性强塑性特征,表现出极强的延性;在荷载进程中杆体-浆体界面的应力分布与传递特征具有多峰值分布、高值往往出现在锚固末端、压应力出现等特征,表明该锚固系统兼有拉力型和压力型全长黏结性锚固系统的特点;该系统适合于夯筑土遗址锚固,与遗址具有良好的物理力学兼容性。
Anchor performance of wood bolt fully grouted by PS–(F+C) slurry in rammed earth sites
基于室内物理模型试验和原位锚固试验,对基于高模数硅酸钾溶液-(粉煤灰+粉土)(PS-(F+C))浆液的木锚杆锚固系统在夯土介质中进行了拉拔测试与杆体-浆体界面应变监测,研究了该锚固系统的锚固性能与破坏模式、杆体-浆体界面剪应力分布与传递特征。结果表明:该锚固系统室内试验极限锚固力(24~38 k N)远大于现场试验值(2.5~8 k N);锚固系统具有低弹性强塑性特征,表现出极强的延性;在荷载进程中杆体-浆体界面的应力分布与传递特征具有多峰值分布、高值往往出现在锚固末端、压应力出现等特征,表明该锚固系统兼有拉力型和压力型全长黏结性锚固系统的特点;该系统适合于夯筑土遗址锚固,与遗址具有良好的物理力学兼容性。
夯土介质中基于PS浆液的楠竹锚杆锚固特性
基于PS溶液的楠竹锚杆锚固系统在夯筑土遗址加固中得到了成功的应用,然而其锚固机理研究还未开展。运用室内物理模型试验,针对该锚固系统开展了拉拔测试与杆体-浆体界面应变监测,研究了该锚固系统的锚固性能与破坏模式、杆体-浆体界面剪应变分布与传递特征。试验结果表明基于PS-F浆液锚固系统和基于PS-(C+F)浆液锚固系统均为杆体-浆体界面失效模式,极限锚固力分别为10~15kN和8~16kN;锚固系统均具有较强的延性;在荷载进程中杆体-浆体界面的应变分布具有单峰值及双峰值特点,荷载增加时界面应力向锚固末端传递、压应力出现在锚固段末端及峰值局部出现在末端等特征。研究结论表明,锚固系统的力学性能适用于夯筑土遗址加固,但在杆材耐久性和完整性保证方面还需要进一步探究。
Anchor performance of bamboo bolt grouted by PS solution-based slurry among rammed earth medium
基于PS溶液的楠竹锚杆锚固系统在夯筑土遗址加固中得到了成功的应用,然而其锚固机理研究还未开展。运用室内物理模型试验,针对该锚固系统开展了拉拔测试与杆体-浆体界面应变监测,研究了该锚固系统的锚固性能与破坏模式、杆体-浆体界面剪应变分布与传递特征。试验结果表明基于PS-F浆液锚固系统和基于PS-(C+F)浆液锚固系统均为杆体-浆体界面失效模式,极限锚固力分别为10~15kN和8~16kN;锚固系统均具有较强的延性;在荷载进程中杆体-浆体界面的应变分布具有单峰值及双峰值特点,荷载增加时界面应力向锚固末端传递、压应力出现在锚固段末端及峰值局部出现在末端等特征。研究结论表明,锚固系统的力学性能适用于夯筑土遗址加固,但在杆材耐久性和完整性保证方面还需要进一步探究。
烧料礓石改性浆体-遗址土体界面抗剪性能试验,
为研究土遗址锚固系统中浆体–土体界面抗剪性能,揭示锚固系统内部受力机制。试验选择目前土遗址锚固工程中常用的烧料礓石、粉煤灰、石英砂及遗址土作为主要浆体材料,同原状遗址土制成黏结试样。根据实际工作条件,对试样进行室外土体掩埋养护。通过浆体–土体界面直接剪切试验,得到不同配比浆体–土体界面的剪应力–位移关系曲线、抗剪强度参数及浆体–土体界面剪应力–位移拟合曲线。试验结果表明,浆体–土体界面未能有效黏结,界面抗剪强度主要依靠滑动摩擦及咬合摩擦承担;烧料礓石改性遗址土浆体与遗址土体黏结试样内摩擦角最大,浆体材料兼容性对界面抗剪强度的提高具有重要意义。室外掩埋养护土体温湿度的频繁波动和PS溶液的固化作用对界面黏结能力影响显著。因此,土遗址锚固工艺是保证锚固质量的关键因素之一。
Experiment on shear resistance behavior of interface between slurry modified by calcined ginger nuts and soil mass of earthen sites
为研究土遗址锚固系统中浆体–土体界面抗剪性能,揭示锚固系统内部受力机制。试验选择目前土遗址锚固工程中常用的烧料礓石、粉煤灰、石英砂及遗址土作为主要浆体材料,同原状遗址土制成黏结试样。根据实际工作条件,对试样进行室外土体掩埋养护。通过浆体–土体界面直接剪切试验,得到不同配比浆体–土体界面的剪应力–位移关系曲线、抗剪强度参数及浆体–土体界面剪应力–位移拟合曲线。试验结果表明,浆体–土体界面未能有效黏结,界面抗剪强度主要依靠滑动摩擦及咬合摩擦承担;烧料礓石改性遗址土浆体与遗址土体黏结试样内摩擦角最大,浆体材料兼容性对界面抗剪强度的提高具有重要意义。室外掩埋养护土体温湿度的频繁波动和PS溶液的固化作用对界面黏结能力影响显著。因此,土遗址锚固工艺是保证锚固质量的关键因素之一。
基于SH-(C+F)浆液锚杆锚固性能与机理研究
锚固技术在土遗址稳定性控制领域已得到了广泛应用,然而锚固浆液的缺乏成为制约土遗址锚固技术和理论发展的关键问题之一。对质量浓度分别为0.5%、1.0%、1.5%的SH与黏土、粉煤灰拌和组成SH混合浆液试块进行物理、力学、声波特性测试以及基于该类型混合浆液分别同木锚杆、玻璃纤维锚杆、钢筋锚杆组成的不同锚固系统的原位锚固、拉拔测试和杆体-浆体界面应力-应变监测。获取了3种锚固系统的破坏模式、锚固性能和杆体-浆体界面应力-应变的时空分布规律。试验结果表明:SH锚固浆液拥有良好的物理、力学性能,与土遗址构筑材料性能兼容;基于SH锚固浆液全长灌浆的3种锚固系统的锚固性能优良;木锚杆锚固系统锚固性能在SH浓度为1.0%时达到最优,而玻璃纤维和钢筋锚杆锚固系统锚固性能良好度随着SH的浓度升高而升高。研究结果为以SH为主材的改性浆液在土遗址锚固领域中的应用提供了依据和参考。
Performance and mechanism of bolts fully grouted with SH-( C+F) slurry
锚固技术在土遗址稳定性控制领域已得到了广泛应用,然而锚固浆液的缺乏成为制约土遗址锚固技术和理论发展的关键问题之一。对质量浓度分别为0.5%、1.0%、1.5%的SH与黏土、粉煤灰拌和组成SH混合浆液试块进行物理、力学、声波特性测试以及基于该类型混合浆液分别同木锚杆、玻璃纤维锚杆、钢筋锚杆组成的不同锚固系统的原位锚固、拉拔测试和杆体-浆体界面应力-应变监测。获取了3种锚固系统的破坏模式、锚固性能和杆体-浆体界面应力-应变的时空分布规律。试验结果表明:SH锚固浆液拥有良好的物理、力学性能,与土遗址构筑材料性能兼容;基于SH锚固浆液全长灌浆的3种锚固系统的锚固性能优良;木锚杆锚固系统锚固性能在SH浓度为1.0%时达到最优,而玻璃纤维和钢筋锚杆锚固系统锚固性能良好度随着SH的浓度升高而升高。研究结果为以SH为主材的改性浆液在土遗址锚固领域中的应用提供了依据和参考。
夹双筋体复合锚杆锚固性能与界面力学传递特征
在世界最大的生土遗址-交河故城开展现场试验,选用2种长度的锚杆按照基本试验的要求开展拉拔试验,同时在各界面层布设应变监测点。结果表明:8 m长锚杆锚固力达408 kN,满足大体量土遗址锚固的需求;随着长度增加,极限锚固力增长,但平均锚固力减小;复合锚杆各界面剪应力沿着杆长呈现单峰值或多峰值的空间分布特征,随着荷载的增加,界面各点剪应力增加并且向锚固末端传递,峰值剪应力亦同时向锚固末端偏移;试验过程中在较高荷载下出现界面剪应力状态转化的现象。
Anchorage performance and interfacial mechanics transfer characteristics of composite bolt with double-strand
在世界最大的生土遗址-交河故城开展现场试验,选用2种长度的锚杆按照基本试验的要求开展拉拔试验,同时在各界面层布设应变监测点。结果表明:8 m长锚杆锚固力达408 kN,满足大体量土遗址锚固的需求;随着长度增加,极限锚固力增长,但平均锚固力减小;复合锚杆各界面剪应力沿着杆长呈现单峰值或多峰值的空间分布特征,随着荷载的增加,界面各点剪应力增加并且向锚固末端传递,峰值剪应力亦同时向锚固末端偏移;试验过程中在较高荷载下出现界面剪应力状态转化的现象。
夹$\varPhi$22 mm钢筋体复合锚杆原位锚固特性分析
加钢筋体复合锚杆在土遗址载体锚固得到了较为成功的应用,但研究该类型锚杆机制刚刚起步.选择交河故城开展了夹φ22 mm钢筋复合体锚杆现场锚固测试,包括锚固性能测试和锚杆各界面层应变监测.锚固性能试验表明,3m长复合锚杆极限锚固力可达190 kN,而且杆体表现出较强塑性变形.锚杆各界面层应变监测结果表明,钢筋-复合材料界面层轴向应变远大于其他界面层,锚固失效在该层;由于杆体的非均直性,楠竹-复合材料界面表现出轴向应变的非规律性,局部出现受压状态;楠竹-浆体界面剪应变与荷载变化一致,在较高荷载下出现剪应变向锚固末端的传递特征;鉴于杆体的多圈层构造,受力过程中出现明显的横向传递和剪胀特征.其研究成果可为复合锚杆的优化与工艺完善奠定基础.
Analysis of in-situ anchoring characteristics of composite anchor containing steel bar($\varPhi$22 mm)
加钢筋体复合锚杆在土遗址载体锚固得到了较为成功的应用,但研究该类型锚杆机制刚刚起步.选择交河故城开展了夹φ22 mm钢筋复合体锚杆现场锚固测试,包括锚固性能测试和锚杆各界面层应变监测.锚固性能试验表明,3m长复合锚杆极限锚固力可达190 kN,而且杆体表现出较强塑性变形.锚杆各界面层应变监测结果表明,钢筋-复合材料界面层轴向应变远大于其他界面层,锚固失效在该层;由于杆体的非均直性,楠竹-复合材料界面表现出轴向应变的非规律性,局部出现受压状态;楠竹-浆体界面剪应变与荷载变化一致,在较高荷载下出现剪应变向锚固末端的传递特征;鉴于杆体的多圈层构造,受力过程中出现明显的横向传递和剪胀特征.其研究成果可为复合锚杆的优化与工艺完善奠定基础.
楠竹加筋复合锚杆应力传递理论模型
楠竹加筋复合锚杆是一种用于土遗址土体加固的新型锚杆。本文从复合材料力学的角度分析了楠竹复合锚杆内部系统的工作机理,推导了复合锚杆内部系统层间切应力的传递模型。复合锚杆的内部工作机理研究表明,管材的弹性模量与杆材的弹性模量比值、内粘结剂的剪切模量等对楠竹复合锚杆内部荷载传递影响较大。通过分析认为,可以通过改变管材与杆材弹性模量的比值、调整内粘结剂的配比等措施,从而使复合锚杆内部层间应力传递曲线达到最优化状态。
Stress transfer model of bamboo-steel composite anchor
楠竹加筋复合锚杆是一种用于土遗址土体加固的新型锚杆。本文从复合材料力学的角度分析了楠竹复合锚杆内部系统的工作机理,推导了复合锚杆内部系统层间切应力的传递模型。复合锚杆的内部工作机理研究表明,管材的弹性模量与杆材的弹性模量比值、内粘结剂的剪切模量等对楠竹复合锚杆内部荷载传递影响较大。通过分析认为,可以通过改变管材与杆材弹性模量的比值、调整内粘结剂的配比等措施,从而使复合锚杆内部层间应力传递曲线达到最优化状态。
楠竹加筋复合锚杆内部界面粘结滑移模型
楠竹加筋复合锚杆已经应用于中国西北丝绸之路上留存的古代土遗址保护加固工程中。该锚杆截面积大,可以获得足够大的锚固力。针对现场拉拔试验中钢绞线从内黏结剂中拔出的破坏形式,设计了专门的试件及夹具,试验研究了钢绞线与内黏结剂间的力学行为。试验结果表明,钢绞线与内黏结剂的黏结滑移分为指数上升阶段、软化下降阶段和残余应力阶段3个阶段,可以用简化模型和精确模型描述。试验还表明,钢绞线与内黏结剂接触界面上应力分布不均匀,靠近加载端的应力较大,且有应力峰,应力峰随荷载的逐渐增大向远离加载端的方向移动;钢绞线与内黏结剂间平均剪切应力随锚杆的长度增大呈指数衰减。通过理论分析,给出了界面黏结滑移微分方程及相关曲线,结果表明,钢绞线轴力及界面相对滑移沿钢绞线均呈不均匀分布,且随着距加载端的距离增加其值急剧下降,该规律可以指导锚杆设计及工程应用。
Bond-slip model for bamboo-steel cable composite anchor
楠竹加筋复合锚杆已经应用于中国西北丝绸之路上留存的古代土遗址保护加固工程中。该锚杆截面积大,可以获得足够大的锚固力。针对现场拉拔试验中钢绞线从内黏结剂中拔出的破坏形式,设计了专门的试件及夹具,试验研究了钢绞线与内黏结剂间的力学行为。试验结果表明,钢绞线与内黏结剂的黏结滑移分为指数上升阶段、软化下降阶段和残余应力阶段3个阶段,可以用简化模型和精确模型描述。试验还表明,钢绞线与内黏结剂接触界面上应力分布不均匀,靠近加载端的应力较大,且有应力峰,应力峰随荷载的逐渐增大向远离加载端的方向移动;钢绞线与内黏结剂间平均剪切应力随锚杆的长度增大呈指数衰减。通过理论分析,给出了界面黏结滑移微分方程及相关曲线,结果表明,钢绞线轴力及界面相对滑移沿钢绞线均呈不均匀分布,且随着距加载端的距离增加其值急剧下降,该规律可以指导锚杆设计及工程应用。
Stress distribution along a resin grouted rock anchor
The paper compares theoretical shear-stress distribution along a loaded resin grouted rock anchor, with computed shear-stress distributions obtained from tests on instrumented anchors in concrete, limestone and chalk. The results show that whilst at lower anchor loads in the concrete, the observed shear-stress distribution is similar to the theoretical shear-stress distribution; in the weaker limestone and chalk there is evidence of significant debonding. It is concluded that the anchor resistance in these rocks comprised mainly fully mobilised shear resistance.
Load bearing capacity and stress distribution in/along rockbolts with inelastic behaviour of interfaces
//
Load distribution along fully grouted bolts, with emphasis on cable bolt reinforcement
锚杆载荷传递机理分析的双曲函数模型
假定锚固体与锚杆周围岩 (土 )体之间的剪力与剪切位移呈线性增加关系 ,建立锚杆荷载传递的双曲函数模型 ,获得了锚杆摩阻力和剪切位移沿锚固长度的分布规律及其影响因素。根据埋设于黏性土中 4根灌浆锚杆的现场抗拔试验成果 ,分析了锚杆的荷载传递特性 ,计算与实测结果对比 ,二者较为吻合
Hyperbolic function model to analyze load transfer mechanism on bolts
假定锚固体与锚杆周围岩 (土 )体之间的剪力与剪切位移呈线性增加关系 ,建立锚杆荷载传递的双曲函数模型 ,获得了锚杆摩阻力和剪切位移沿锚固长度的分布规律及其影响因素。根据埋设于黏性土中 4根灌浆锚杆的现场抗拔试验成果 ,分析了锚杆的荷载传递特性 ,计算与实测结果对比 ,二者较为吻合
Bond strength of grouted cable bolts
A conceptual model for fully-grouted cable bolts is presented explaining the development of the bond strength. According to the theory, the bond strengths of bolts is primarily frictional and depends on the pressure at the bolt-grout interface. The pressure increase at this interface is a function of the grout dilation or radial movement caused by the rough surfaces of twisted cables. The formation of this dilational pressure during axial loading is explained using models of elasticity, brittle cracking of grout and dilative bolt-grout interface. The study shows that the mechanical and elastic properties of rock and grout, the geometry of the borehole and the bolt are all relevant parameters in the development of the bolt-grout interface pressure. The theory explains load drop often observed during short bond length pull-out tests as the consequence of unstable crack propagation. It is found that these load drops should disappear if the ratio of rock to grout stiffness exceeds 0.68. It is concluded that the bond strength increases with the stiffness ratio (rock-to-grout), the strength of grout, the friction coefficient between bolt and grout, and decreases with the diameter of the borehole. The results confirmed that grouted cables can develop more bond strength in stiff than in soft rocks and therefore conventional cable bolts may not be effective in soft rocks or disturbed rock masses. The theory presented in this paper constitutes the background for a companion paper on the effect of field stress changes on bond strength.
纤维增强塑料锚杆锚固性能的数值分析
<FONT face=Verdana>以建立的纤维增强塑料锚杆在岩土体中的粘结锚固基本方程为基础,结合纤维增强塑料锚杆的连续光滑粘结–滑移本构关系模式,提出了纤维增强塑料锚杆锚固性能分析的数值计算方法,并通过与FRP锚杆锚固试验结果对比确定有关参数。将数值计算结果与锚固试验结果以及理论计算结果进行了对比分析,验证了数值模拟方法的正确性。</FONT>
Numerical analysis of anchorage behavior of fiber reinforced plastic bolts
<FONT face=Verdana>以建立的纤维增强塑料锚杆在岩土体中的粘结锚固基本方程为基础,结合纤维增强塑料锚杆的连续光滑粘结–滑移本构关系模式,提出了纤维增强塑料锚杆锚固性能分析的数值计算方法,并通过与FRP锚杆锚固试验结果对比确定有关参数。将数值计算结果与锚固试验结果以及理论计算结果进行了对比分析,验证了数值模拟方法的正确性。</FONT>
An analytical model of fully grouted rock bolts subjected to tensile load
An analytical model for fully encapsulated rock bolts subjected to tensile load in pull-out tests is presented. This model is based on the bond–slip relationship describing the mechanical interaction at the bolt–grout interface. The model takes into account the residual shear stress in addition to the complete decoupling mechanisms. Formulations are also derived for the load–displacement curve, shear stress distribution at the bolt–joint interface and axial load distribution in the bolt. The model was validated with experimental results from both the laboratory experiments and in situ studies.
Analytical model for rock bolts reaching free end slip
This paper presents the difference of behaviour between fully grouted bolts with and without free end slip when loaded in tension. An analytical approach is proposed for fully encapsulated bolts when the free end of the bolt slips. This model is based on the existing bond–slip relationship of bolt–grout interface with no free end slip. The derived analytical solutions of load–slip relationship, slip distribution, the shear stress and strain distributions presented in this paper are all connected with free end slip. The analytical approach is validated by experimental results. Free end slip has a significant influence on rock bolt behaviour and should not be ignored.
A numerical model of fully grouted bolts considering the tri-linear shear bond-slip model
A numerical model of fully grouted bolts is proposed in this study by implementing the tri-linear bond–slip relationship of bolts into the numerical framework presented by Hyett et al. (1996). The bond–slip relationship of bolt–rock interface is simplified and represented by the tri-linear model. The proposed numerical model is characterized by (1) its ability in modeling decoupling mechanism of bolt–rock interface, i.e. the degradation of the interfacial shear bond stress along bolts; (2) its easy implementation in a numerical code. The proposed numerical model is verified with the pullout tests, and good agreements with the experimental results can be observed in terms of axial stress distributions in the bolt, shear stress distributions along the bolt and load–displacement relationship. The proposed model also gives a reasonable prediction on the behavior of bolts installed in the field.
Analytical solution for the full-range pull-out behavior of FRP ground anchors
This paper attempts to predict the nonlinear pull-out response of fiber reinforced polymer (FRP) rods embedded in steel tubes filled with cement grout. Based on a tri-linear bond鈥搒lip model, the whole FRP rod is divided into three zones: linear elastic, softening, and frictional. In each zone, a set of two second-order ordinary differential equations are established in terms of the displacements of the FRP rod and steel tube and solved in an analytical manner. When the thickness of the steel tube approaches infinity, the solution can be applied to the problem of FRP rods embedded in rock. Based on the derived solution, the interfacial bond properties and snapback phenomenon are discussed. After the analytical solution is validated by comparisons with four sets of experimental data, the effects of the radius and length of FRP rods, the local peak bond stress and the residual frictional strength on the maximum pull-out load are evaluated through sensitivity analysis.
Prediction of the nonlinear pull-out response of FRP ground anchors using an analytical transfer matrix method
Fiber-reinforced polymer (FRP) rods have been increasingly used in grouted ground anchors due to their high strength-to-weight ratio, excellent corrosion resistance, and convenience in incorporating the fiber sensing technology. To establish their pull-out capacity, FRP rods are usually embedded within a grouted steel tube and then subjected to pull-out in the laboratory. The aim of this paper is to develop a numerical method for predicting the nonlinear pull-out response of FRP rods embedded in steel tubes filled with cement grout. In the method, the cement grout is assumed to be subject to simple shear, the local interfacial bond stress lip model of the bar-to-grout interface is represented by a piece-wise curve comprising elastic, softening, and frictional stages, and the unloading effect is also taken into account. A set of two second-order ordinary differential equations are derived in terms of the displacements of the FRP rod and steel tube and solved analytically to formulate the element transfer matrix. When the thickness of the steel tube approaches infinity, this method can be applied to the problem of FRP rods embedded in rock. Based on the developed numerical method, the interfacial bond properties and snapback phenomenon are analyzed. After the method is validated by comparisons with four sets of experimental data, the effects of the radius and length of FRP rods, the local peak bond stress and the residual frictional strength on the maximum pull-out load are evaluated in a quantitative manner.
An analytical analysis of the full-range behaviour of grouted rockbolts based on a tri-linear bond-slip model
This paper presents an analytical solution for predicting the full-range mechanical behaviour of grouted rockbolts in tension based on a realistic tri-linear bond-slip model with residual bond strength at the grout-bolt interface. The full-range behaviour consists of five consecutive stages: elastic stage, elastic-softening stage, elastic-softening-debonding stage, softening-debonding stage and debonding stage. For each stage, closed-form solutions for the load-displacement relationship, interfacial shear stress distribution and bolt axial stress distribution along the bond length were derived. The ultimate load and the effective anchor length were also obtained. The analytical model was calibrated and validated against two pullout experimental studies. The predicted load-displacement curves as well as the distributions of the interfacial shear stress and the bolt axial stress are in close agreement with test results. A parametric study is also presented, providing insights into the behaviour of the rockbolts. [All rights reserved Elsevier].
Full-range behavior of FRP-to-concrete bonded joints
External bonding of fiber reinforced polymer (FRP) composites has become a popular technique for strengthening concrete structures all over the world. The performance of the interface between FRP and concrete is one of the key factors affecting the behavior of the strengthened structure, and has been widely studied using simple shear tests on FRP plate/sheet-to-concrete bonded joints. While a great deal of research is now available on the behavior of these bonded joints, no closed-form analytical solution has been presented which is capable of predicting the entire debonding propagation process. This paper presents such an analytical solution, in which the realistic bi-linear local bond–slip law is employed. Expressions for the interfacial shear stress distribution and load–displacement response are derived for different loading stages. It is also shown how experimental load–displacement responses of these joints can be used to quantify interfacial properties, including the interfacial fracture energy and parameters of the local bond–slip relationship. The debonding process is discussed in detail and the analytical results are compared with experimental data. Finally, results from the analytical solution are presented to illustrate how the bond length and the plate stiffness affect the behavior of such bonded joints. While the emphasis of the paper is on FRP-to-concrete joints, the analytical solution is equally applicable to similar joints between thin plates of other materials (e.g. steel and aluminum) and concrete.
Experimental study on bond-slip behavior of bamboo bolt-modified slurry interface under pull-out load
A new analytical solution to the mechanical behaviour of fully grouted rockbolts subjected to pull-out tests
A new analytical approach able to predict the mechanical behaviour of fully grouted rockbolts subjected to pull-out tests is proposed in this paper. Input parameters of such approach are: bolt radius, bolt’s Young modulus, displacement of the free end of the bolt and the constitutive law of the rockbolt–grout joint interface. The limited circumstances under which it is accurate to determine such constitutive law from pull-out tests are also presented. A solution for the load–displacement curve obtained during pull-out tests has been developed and is detailed in the case of a tri-linear bond-slip model. Comparison with experimental results obtained via in situ pull-out tests has led to the validation of this approach.