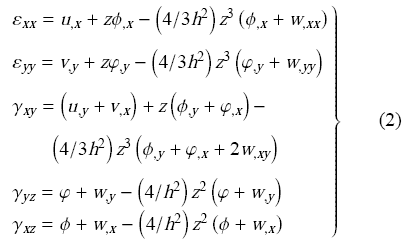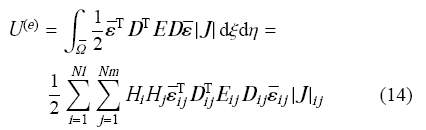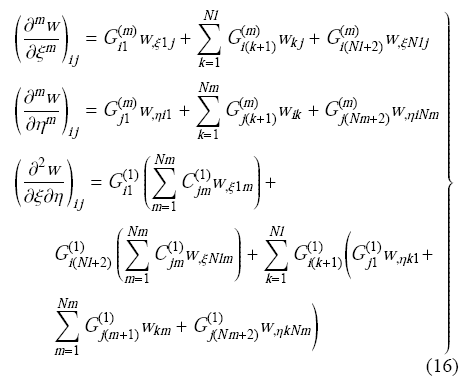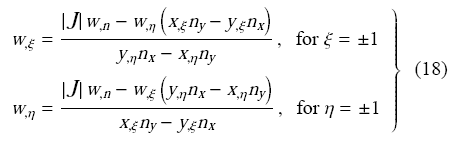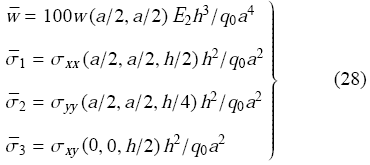引 言
板结构是工程实践中常见的一类结构形式,特别是近年来随着各类高性能复合材料和功能梯度材料的出现,由这些新型材料所构成的板结构在航空航天、土木工程以及军事防护领域得到了 广泛的应用[1 -2 ] .该类板结构的显著特点是其材料性能沿板厚变化,需合理考虑其横向剪切变形,而经典板理论假设横向剪切应变为零、一阶剪切变形理论则假设横向剪切应变沿板厚方向为常量,往往不适用于该类新型材料板结构的力学分析.在这种情况下,高阶剪切变形理论[2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析.
由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切.
弱形式求积元法(weak form quadrature element method) 简称 求积元法,是一种基于待求解问题的弱形式,利用统一的单元节点计算问题控制泛函中积分和微分的新型高阶数值方法[23 ] ,具有准确高效、步骤直接、前后处理过程简便等优点,在处理复杂几何形状、非均匀材料、强几何非线性问题上相比传统低阶有限元具有独特的优势[24 -28 ] .利用该方法,Zhong和Yue[26 ] 基于经典板理论对等厚度三角形板、方板及变厚度环板进行了弯曲和自由振动分析;Zhong和Wang[27 ] 对均质材料高阶梁的弯曲、自由振动及特征值屈曲进行了分析;作者则基于Euler梁理论,对考虑界面滑移效应的楔形变截面组合梁弯曲和自由振动问题进行了分析[29 ] .
本文基于Reddy高阶剪切变形理论,建立$C^{1}$连续的四边形求积元板单元.对典型均质材料、复合材料、功能梯度材料构成的等厚度矩形板、变厚度矩形板及等厚度斜板的弯曲和自由振动问题进行计算分析,通过与现有文献中相应计算结果进行对比,考察求积元板单元的计算效率.
1 四边形求积元板单元的建立
1.1 高阶剪切变形理论
考虑空间中某任意四边形板,板的各边边长分别为$a$,$b$,$c$和$d$,厚度为$h\left( {x,y}\right)$,同时建立参考坐标系$O - XYZ$,$XOY$平面与板几何中性面重合,如图1 所示.
图1 空间中的四边形板
Fig.1 A quadrilateral plate in physical domain
依据Reddy提出的高阶剪切变形理论,板的位移场可表示为
$${\pmb d} = \left[\!\! \begin{array}{c} {u + z\phi - \left( {4/{3h^2}} \right)z^3\left( {\phi + w_{,x} } \right)} {v + z\varphi - \left( {4 /{3h^2}} \right)z^3\left( {\varphi + w_{,y} } \right)} \hfill w \end{array} \!\! \right] (1)$$
式中,$u$, $v$和$w$分别为板几何中性面上物质点沿$X$, $Y$和$Z$向的位移,$\phi $, $ - \varphi$分别为该点处中性面法线绕$Y$, $X$轴转角. $w_{,x} $, $w_{,y}$表示$w$对$x$和$y$的偏导数,下同. 则板的应变场即可依据线性小应变理论表示为
并与相应的应力分量通过本构关系加以联系,即
$$\left[ \!\!\begin{array}{c} {\sigma _{xx} } {\sigma _{yy} } {\sigma _{xy} } \end{array} \!\! \right] = {\pmb E}_{\rm p} \left[\!\!\begin{array}{c} {\varepsilon _{xx} } {\varepsilon _{yy} } {\gamma _{xy} }\end{array} \!\! \right]\,, \quad\left[\!\!\begin{array}{c} {\sigma _{yz} } {\sigma _{xz} }\end{array} \!\!\right] = {\pmb E}_{\rm t} \left[\!\!\begin{array}{c} {\varepsilon _{yz} } {\gamma _{xz} }\end{array} \!\!\right] (3)$$
式中,${\pmb E}_{\rm p} $和${\pmb E}_{\rm t}$是由弹性模量等常数构成的矩阵,其具体形式与板的构成材料有关. 如对于均质各向同性材料
$$\left. \!\!{\pmb E}_{\rm p} = \dfrac{E}{1 - v^2}\left[\!\!\begin{array}{ccc} 1 & v & 0 v & 1 & 0 0 & 0 & (1 - v) / 2 \end{array}\!\!\right] {\pmb E}_{\rm t} = \dfrac{E}{1 - v^2}\left[\!\!\begin{array}{cc} {(1 - v)} / 2 & 0 0 & {{(1 - v)} /2}\end{array}\!\!\right] \right\} (4)$$
式中,$E$, $\nu $分别为材料的杨氏模量与泊松比. 而对于其他如正交各向异性材料、复合材料及功能梯度材料,${\pmb E}_{\rm p} $和${\pmb E}_{\rm t}$略微复杂,也可沿板厚变化,具体的表达形式可参阅相关教材或文献[1 ] .
1.2 求积元板单元
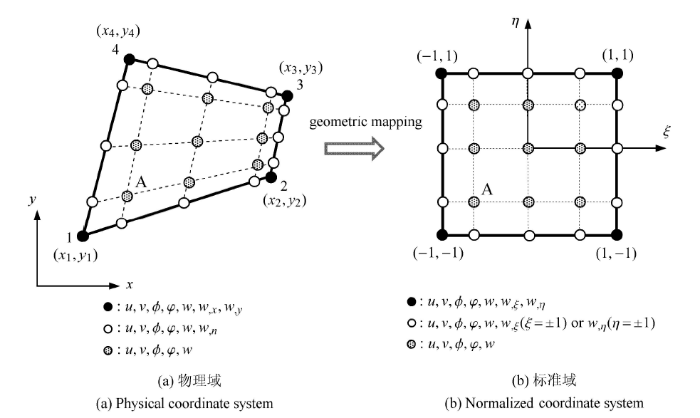
物理域中四边形求积元板单元如图2 (a)所示,4个角点按逆时针方向依次编号(图中编为1$\sim$4),与之相应标准域板单元如图2 (b)所示.
图2 四边形求积元板单元几何变换及自由度设置
Fig. 2 The geometric mapping and degrees of freedom for quadrilateral quadrature plate element
该单元$e$的应变能$U^{(e)}$可表示为
$$U^{(e)} = \int_\varOmega \dfrac{1}{2}{\pmb\varepsilon}^{\rm T}{\pmb E}{\pmb\varepsilon} d xd y (5)$$
式中, $\varOmega $为物理域板单元中性面区域. ${\pmb\varepsilon } $和${E}$为广义应变向量与弹性模量矩阵,分别为
$$ {\pmb \varepsilon} = [ {u_{,x} } \ \ {v_{,y} } \ \ {u_{,y} + v_{,x} } \ \ {\phi _{,x} } \ \ {\varphi _{,y} } \ \ {\phi _{,y} + \varphi _{,x} } \qquad {w_{,xx} } \ \ {w_{,yy} } \ \ {2w_{,xy} } \ \ {\phi _y + w_{,y} } \ \ {\phi _x + w_{,x} } ]^{\rm T} (6)$$
及
$${\pmb E} = \int_{ - h /2}^{h /2} \left[ \!\!\begin{array}{cccc} {{\pmb E}_{\rm p} } & {\alpha _1 {\pmb E}_{\rm p} } & {\alpha _2 {\pmb E}_{\rm p} } & {\bf 0} {\alpha _1 {\pmb E}_{\rm p} } & {\alpha _1^2 {\pmb E}_{\rm p} } & {\alpha _1 \alpha _2 {\pmb E}_{\rm p} } & {\bf 0} {\alpha _2 {\pmb E}_{\rm p} } & {\alpha _1 \alpha _2 {\pmb E}_{\rm p} } & {\alpha _2^2 {\pmb E}_{\rm p} } & {\bf 0} {\bf 0} & {\bf 0} & {\bf 0} & {\alpha _3^2 {\pmb E}_{\rm t} } \end{array} \!\!\right] d z (7)$$
式中
$$\alpha _1 = z - \dfrac{4}{3h^2}z^3\,, \ \ \alpha _2 = - \dfrac{4}{3h^2}z^3\,, \ \ \alpha _3 = 1 -\dfrac{4}{h^2}z^2 (8)$$
对于本文涉及的直边四边形板,可利用简单的线性变换,将问题的求解从物理域转换到标准域,即
$$x = \sum_{k = 1}^4 {S_k \left( {\xi ,\eta } \right)x_k } \,, \ y = \sum_{k = 1}^4 {S_k \left( {\xi ,\eta } \right)y_k } (9)$$
式中,($x_k , y_k $)为物理域四边形角点坐标,如图2 (a)所示,$k = 1, 2, 3, 4$,且
$$\left. \begin{array}{l} S_1 \left( {\xi ,\eta } \right) = {\left( {1 - \xi } \right)\left( {1 - \eta } \right)} / 4 S_2 \left( {\xi ,\eta } \right) = {\left( {1 + \xi } \right)\left( {1 - \eta } \right)} /4 S_3 \left( {\xi ,\eta } \right) = {\left( {1 + \xi } \right)\left( {1 + \eta } \right)} / 4 {S_4 \left( {\xi ,\eta } \right) = {\left( {1 - \xi } \right)\left( {1 + \eta } \right)} / 4}\end{array} \,, \ { - 1 \leqslant \xi ,\eta \leqslant 1} \right \} (10)$$
并将${\pmb\varepsilon} $中变量对相应物理域坐标的导数转化到标准域,即
$${\pmb\varepsilon} ={\pmb D}\bar {\varepsilon } (11)$$
其中,标准域中的应变向量定义为
$$ \bar {\pmb\varepsilon } = [ {u_{,\xi } } \ \ {u_{,\eta } } \ \ {v_{,\xi } } \ \ {v_{,\eta } } \ \ \phi \ \ {\phi _{,\xi } } \ \ {\phi _{,\eta } } \ \ \varphi \ \ {\varphi _{,\xi } } \ \ {\varphi _{,\eta } } \qquad {w_{,\xi } } \ \ {w_{,\eta } } \ \ {w_{,\xi \xi } } \ \ {w_{,\eta \eta } } \ \ {w_{,\xi \eta} } ]^{\rm T} (12)$$
矩阵${\pmb D}\left( {11\times 15} \right)$的非零元素为
式中所涉及的对物理域的各阶导数可利用式(9)并结合链式法则显式计算.
利用Gauss-Lobatto 数值积分[30 ] 计算单元应变能式(5)
其中,$\bar {\varOmega }$为标准域内板单元中性面区域. ${Nl}$为板单 $\xi $ 向积分点数,$Nm$为 $\eta $ 向积分点数,变量右下标$ij$表示该变量在该积分点处的值,$H_{i}$, $H_{j}$为相应积分点对应的积分权系数,${\pmb J}$为线性变换(9)的 Jacobi 矩阵.
利用微分求积法则和广义微分求积法则[31 ] ,将式(14)中$\bar{\varepsilon }_{ij}$所含积分点处的导数表示为积分点处基本自由度的线性加权代数和. 轴向位移$u$, $v$和转动$\phi $, $\varphi $的导数采用微分求积法则离散,如
$$\left( {u_{,\xi } } \right)_{ij} = \sum_{k = 1}^{Nl} {C_{ik}^{\left( 1 \right)} u_{kj} } \,, \ \ \left( {u_{,\eta } } \right)_{ij} = \sum_{k = 1}^{Nm} {C_{jk}^{\left( 1 \right)} u_{ik} } (15)$$
考虑到问题$C^{1}$连续的特点,横向位移对$\xi $向和$\eta $向的导数采用广义微分求积法则离散,对$\xi $向和$\eta $向二阶混合导数采用广义微分求积法结合传统微分求积法计算
式(15)和式(16)中,$C_{ij}^{(m)} $, $G_{ij}^{(m)}$分别为$m$阶微分求积及广义微分求积系数.
上述过程可以简洁的表示为
$$ \bar {\pmb \varepsilon }_{ij} = {\pmb B}_{ij} \bar{\pmb d}^{(e)} (17) $$
式中,${\pmb B}_{ij} $是由微分求积及广义微分求积系数构成的矩阵. $\bar{\pmb d}^{(e)}$为标准域中单元自由度向量,每个积分点均设置$u,v,\phi ,\varphi,w$自由度,标准域角点增设$w_{,\xi } ,w_{,\eta } $自由度,除角点外的边点增设$w_{,\xi } (\xi = \pm 1) $或$w_{,\eta } (\eta = \pm 1)$自由度,如图2 所示. 所有自由度经合理排列后构成标准域自由度向量$\bar {\pmb d}^{(e)}$.
为便于单元拼接和施加边界条件,物理域单元自由度向量${\pmb d}^{(e)}$按如下方式设置:每个积分点均设置$u,v,\phi ,\varphi ,w$自由度,物理域角点增设$w_{,x} ,w_{,y}$自由度,除角点外的边点增设$w_{,n} $自由度,${\pmb n}$为预先设定的单元边界法线方向. 角点处自由度$w_{,\xi } ,w_{,\eta } $可利用线性变换(9)的Jacobi矩阵与$w_{,x} ,w_{,y} $相联系,而边点自由度$w_{,\xi } (\eta = \pm 1) $或$w_{,\eta } (\xi = \pm 1)$可利用方向导数的计算方式与$w_{,n} $相联系,即
式 中,$n_{x}$, $n_{y}$分别为单元边界法线关于$X$轴、$Y$轴的方向余弦,等式右端$w_{,\xi } $, $w_{,\eta } $的计算也需运用微分求积法则. 最终$\bar {\pmb d}^{(e)}$可表示为
$$\bar{\pmb d}^{(e)} = {\pmb T}{\pmb d}^{(e)} (19)$$
利用式(17),则式(14)可进一步表示为
$ U^{(e)} = \dfrac{1}{2}\bar {\pmb d}^{(e) \rm T}\left( {\sum_{i = 1}^{Nl} \sum_{j = 1}^{Nm} H_i H_j {\pmb B}_{ij}^{\rm T} {\pmb D}_{ij}^{\rm T} {\pmb E}_{ij} {\pmb D}_{ij} {\pmb B}_{ij} \left| {\pmb J} \right|_{ij} } \right)\bar{\pmb d}^{(e)} =$
类似地,单元的外力势能$V^{(e)} $、动能$T^{(e)} $均可采用相同的步骤进行离散.在单元水平运用Hamilton原理
$$\delta \int_{t_1 }^{t_2 } {\left( {T^{(e)} - U^{(e)} - V^{(e)}} \right)} d t = 0 (21)$$
并将$U^{(e)} $, $V^{(e)} $, $T^{(e)} $代入,可得
$$\bar{\pmb M}^{\,(e)}{\mathop{\bar{\pmb d}^{\,(e)}}\limits^{\cdot\cdot \ \ \ }}+\bar{\pmb K}^{\,(e)}\bar{d}^{\,(e)} =\bar{\pmb F}^{\,(e)} (22)$$
相应地,物理域中的单元运动方程
$${\pmb M}^{\,(e)}\ddot {\pmb d}^{\,(e)} + {\pmb K}^{\,(e)} {\pmb d}^{\,(e)} ={\pmb F}^{\,(e)} (23)$$
可利用式(19)得到. 式(23)中,$\ddot{\pmb d}^{(e)}$表示单元自由度向量对时间的二阶导数,${\pmb M}^{(e)}$, ${\pmb K}^{(e)} $和${\pmb F}^{(e)}$分别为单元质量矩阵、刚度矩阵以及载荷向量.
如有必要,可进行单元拼接,得到总体刚度矩阵. 对于弯曲问题,式(23)转化为线性代数方程组. 对于自由振动问题,式(23)转化为广义代数特征值问题.
1.3 边界条件
求积元板单元的建立过程基于问题的弱形式描述,因而只需考虑位移边界条件. 后文中提及的边界条件定义如下. 简支边界
$$w = 0\,, \ \ u_s = 0\,, \ \ \phi _s = 0 (24)$$
固支边界
$$w = w_n = u_s = u_n = \phi _s = \phi _n = 0 (25)$$
自由边界则不约束任何自由度. 式(24)和式(25)中,$u_s $和$u_n$分别表示沿单元边线切向和法向的位移,$\phi _s $和$\phi _n$分别表示中性面法线绕单元边线法向和切向的转角. 单元边线的切向${\pmb s}$和法向${\pmb n}$应预先合理定义. 具体计算中,针对不同的边界条件利用下述关系
将${\pmb d}^{(e)}$中相应自由度进行转换,方可准确施加边界条件. 式(26)中,$s_{x}$, $s_{y}$分别为单元边界切线关于$X$轴、$Y$轴的方向余弦.
2 数值算例
通过对典型均质材料、复合材料、功能梯度材料构成的等/变厚度矩形板及等厚度斜板进行受荷弯曲和自由振动分析,并与文献中相关结果进行比较,考察求积元板单元的计算效率.
2.1 等厚度矩形板的弯曲和自由振动分析
(1)均质材料板
考察一等厚各向同性均质材料矩形板(边长分别为$a$,$b$;泊松比$\nu =0.3$)受均布载荷$q_{0}$的弯曲和自由振动问题,将整块板划分为1个求积元单元进行计算.
表1 和表2 分别给出了四边简支条件下,不同高跨比($h/a$)时,方板($a=b$)板中的无量纲挠度与弯矩.为便于比较,表中同时给出 了基于相同力学模型的有限元计算结果[15 ] 与Reddy给出的Navier解[32 ] . 表中 "QEM 7$\times $7''表示,采用1个求积元板单元,积分点数${Nl}= {Nm}=7$,下同.
观察表1 和表2 可知,随着积分点数的增加,位移和弯矩的求积元解均能较快地收敛于解析解,随着板厚的增大,收敛速度略有降低,采用9个积分点即能得到满意的计算结果. Sheikh等[15 ] 利用512个的6节点(每节点7自由度)三角形有限元单元未能得到与解析解一致的计算结果.
表3 给出了两对边简支($x=0$,$x=a$),$y=0$边固支,$y=b$边自由的边界条件下,不同高跨比($h/a$)和长宽比($b$/$a$)时板中的无量纲挠度$10{wEh^3}/ {q_0 a^4(1 - \nu ^2)}$、自由边板中弯矩${M_x } / {q_0 a^2}$、固支边板中弯矩${M_y }/{q_0 a^2}$.观察表3 可知,对于挠度,求积元计算结果与有限元较为一致;而对于弯矩,求积元的计算结果略高于有限元. 原因除单元理论不同外,两种方法对于应力(内力)的恢复计算(后处理)方式也存在差异.求积元利用高阶插值的方式得到单元域内任意点应变,进而通过本构关系计算应力;而传统有限元在利用形函数计算单元应变及应力后,也会采取平滑化处理技术改善应力分布.
表4 给出了四边简支方板,高跨比$h/a=0.1$时的横向无量纲自振频率.为便于比较,表中同时列出了基于相同力学模型的有限元(64个9节点矩形单元,每节点7个自由度)计算结果[13 ] 、Reddy给出的Navier解[34 ] 以及Shufrin给出的扩展Kantorovich法解[33 ] .模态栏"1,1''表示$X$向,$Y$向的半波数,下同.
观察表4 可知,求积元单元的计算结果与现有文献吻合较好,与文献[33 ] 计算结果一致.随着积分点数的增加,各阶自振频率均能 较快地收敛,对于基频的计算,采用9个积分点即能得到满意的计算结果.
(2)复合材料层合板
考虑一四边简支的正方形复合材料层合板,其边长为$a$. 铺层层数为4,铺层方式为(0$^\circ$/90$^\circ$)$_{\rm s}$,各层材料均为相同的正交各向异性材料且层厚相等,材料常数关系为
$$ \left. {E_1 }/{E_2 } = 25\,, \ \ {G_{12} } / {E_2 } = 0.5\,, \ \ {G_{23} }/ {E_2 } = 0.2 \nu _{12} = 0.25\,, \ \ G_{12} = G_{13}\,, \ \ \rho = 1 \right\} (27) $$
该板承受正弦分布载荷,$q = q_0 \sin \left( {{\pi x} / a} \right)\sin\left( {{\pi y}/ a} \right)$.
考虑到问题的对称性以及与现有文献进行直接对比,分别用1/4几何模型和全模型进行计算,两种模型均划分为1个求积元单元.表5 给出了不同高跨比时,板中挠度及相应位置处应力分量的无量纲计算值. 无量纲量计算方式为
为便于比较,表中同时列出了基于相同力学模型的有限元协调元[6 ] 和非协调元[7 ] 计算结果以及Reddy给出的Navier解[32 ] ,其中协调元为16个4节点矩形单元,每节点8个自由度;非协调元为25个4节点矩形单元,每节点7个自由度.
观察表5 可知,随着积分点的增加,挠度和应力的求积元的计算结果均能较快地收敛于解析解[32 ] ,采用9个积分点即能得到满意的计算结果. 14几何模型和全模型没有显著差异,下文中均采用全模型进行计算. 同时,两类有限元的计算结果未能收敛至解析解.
将该板的铺层方式变为$(45^\circ/-45^\circ )_{4}$,层数为8,各层材料层厚相等. 表6 给出了不同高跨比时,板中挠度及相应位置处应力分量的无量纲计算值,具体计算方式为
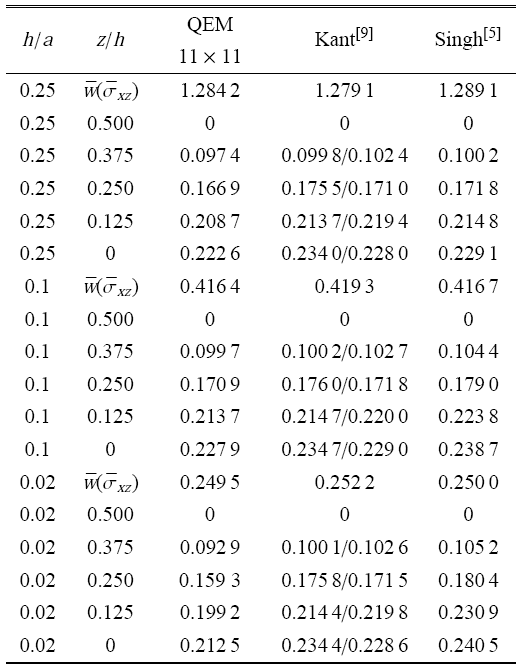
$$\left. \bar {w} = 100w\left( {a /2,a / 2} \right){E_2 h^3}/{q_0 }a^4 \bar {\sigma }_{xz} = \sigma _{xz} \left( {0,a /2,z} \right)h/{q_0 }a \right\} (29)$$
表中同时列出基于相同力学模型的有限元协调元[5 ] 和$C^{0}$单元[9 ] 计算结果,其中协调元为4个4节点矩形单元,每节点14个自由度;$C^{0}$单元为16个9节点矩形单元,每节点7个自由度.观察表6 可知,对于挠度而言,求积元的计算结果与协调元吻合度较好;而对于应力,求积元的计算结果略低于协调元.
考察一四边简支矩形复合材料软芯三明治层合板的自由振动问题,其层数为7,边长分别为$a$和$b$. 铺层方式为0$^\circ$90$^\circ$0$^\circ$/芯层0$^\circ$90$^\circ$0$^\circ$,除芯层外各层材料均为相同的正交各向异性聚酯树脂材料,材料常数为:$E_{1}=24.51$,GPa,$E_{2}=7.77$,GPa,$G_{12}=G_{13}=3.34$,GPa,$G_{23}=1.34$,GPa, $\nu_{12}=0.078$, $\rho =1,800$,kg/m$^{3}$. 芯层材料为聚氯乙烯泡沫,$E_{\rm c}=103.63$,MPa,$G_{\rm c}=50$,MPa, $\nu _{\rm c}=0.32$, $\rho_{\rm c}=130$,kg/m$^{3}$. 芯层厚度$h_{\rm c}=0.88h$,其余各层厚度相同.
表7 给出了不同高跨比、长宽比时,前三阶无量纲自振频率的计算值. 表中同时列出了基于相同力学模型的有限元$C^{0}$单元[13 ] 和阶谱单元的[18 ] 计算结果,其中$C^{0}$单元为36个9节点矩形单元,每节点7个自由度;阶谱单元为1个矩形单元,阶谱项数为14. 观察表7 可知,求积元方法的计算结果与阶谱单元近乎一致,而$C^{0}$单元的计算结果与前二者差异较大,最大相对差异为5.6%.
2.2 变厚度矩形板的自由振动
考察一各向同性均质材料正方形板(边长为$a$, 泊松比 $\nu =0.3$)的自由振动问题,该板厚度沿$X$方向以四类方式(式(30))单向变化,如图3 所示.
$$\left. \begin{array}{l} {\rm I}: h\left( x \right) = h_0 \left( {1 - x /{2a}} \right) {\rm II}:h\left( x \right) = h_0 \left( {1 - {x^2}/ {2a^2}} \right) {\rm III}: h\left( x \right) = h_0 \left({1 + {x^2}/ {2a^2} - x / a} \right) {\rm IV}: h\left( x \right) = h_0 \left( {1 + 2{x^2} /{a^2} - 2x /a} \right) \end{array}\!\!\right\} (30)$$
表8 给出了四边简支方形板($h_{0}$/$a$=0.2)在I类厚度变化条件下的前6阶横向无量纲自振频率. 表8 同时列出了Shufrin等基于一阶剪切变形理论(FSDT)[35 ] 以及Bacciocchi等基于一般高阶剪切变形理论(HSDT)[36 ] 得出的计算结果. 观察表8 可知,求积元单元仅需9个积分点即可使前四阶自振频率收敛,其计算结果高于一阶剪切变形理论,低于一般高阶剪切变形理论.
图3 板厚沿$X$方向变化的4种类型
Fig.3 4 different thickness profiles of the plate along $X$ direction
表9 给出了四边固支方形板($h_{0}/a =0.1$)在II、III、IV类厚度变化条件下的前6阶横向无量纲自振频率. 同时也给出了基于相同力学模型的扩展Kantorovich法解[35 ] 以及基于一阶剪切变形理论的广义微分求积法解[36 ] . 观察表9 可知,求积元法与文献[35 ] 计算结果吻合较好,最大相对误差0.2%,二者计算结果高于一阶剪切变形理论[36 ] .
2.3 等厚度斜板的弯曲和自由振动分析
平行四边形斜板如图4 所示,相邻两边边长为$a$,板厚为$h$,相邻边一边与$X$轴平行,另一边与$Y$轴夹角为$\alpha $.
图4 斜板的几何尺寸与坐标系
Fig. 4 The geometry and configuration of a skew plate
考虑一承受均布载荷$q_{0}$的复合材料层合板,其层数为3,铺层方式为0$^\circ$/90$^\circ$/0$^\circ$,各层材料均为相同的正交各向异性材料,材料常数关系见式(27).仍将整块板划分为一个求积元单元,随着夹角 $\alpha $ 的增大,所需积分点数逐步增加. 当 $\alpha=60^\circ$时,为得到较为理想的计算结果,需使用15个积分点.表10 给出了不同高跨比及夹角条件下四边简支板板中挠度及应力的无量纲计算值,具体计算方式为
$$\left. \bar {w} = 100w [a\left( {1 + \sin \alpha } \right) /2,{a\cos \alpha } /2] {E_2 h^3} / (q_0 a^4) \bar {\sigma }_1 = \sigma _{xx} [a\left( {1 + \sin \alpha } \right) /2,{a\cos \alpha } /2,h/2] {h^2} /(q_0 a^2) \bar {\sigma }_2 = \sigma _{xx} [a\left( {1 + \sin \alpha } \right) / 2,{a\cos \alpha } /2,h /6] {h^2}/ (q_0 a^2) \right\} (31)$$
同时,表中给出了Sheikh等[15 ] 利用512个的6节点(每节点7自由度)三角形有限元单元的计算结果. 观察表10 可知,对于挠度而言,求积元的计算结果与有限元吻合度较好;而对于应力,求积元的计算结果略高于有限元.
考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果.
观察表11 和表12 可知,求积元的计算结果与有限元吻合较好,最大相对差异小于3.5%.由于文献[12 ] 中提供的信息有限,无 法保证两类方法计算过程中除单元外的其他步骤完全一致,如对式(7)中沿厚度积分的具体计算方式,这些因素也将导致计算结果的差异.
3 结 论
本文基于Reddy高阶剪切变形理论,建立了$C^{1}$连续的四边形求积元板单元. 利用该单元对典型均质材料、复合材料、功能梯度材料构成的等厚度矩形板、变厚度矩形板及等厚度斜板的线弹性弯曲和自由振动问题进行了计算分析,并与现有文献中相应的计算结果进行了对比. 主要结论如下:
(1)基于高阶剪切变形理论的四边形求积元板单元具有较高的计算效率和良好的适应性,对于本文中涉及的各类材料等变厚度矩形板,等厚度斜板均只需一个求积元单元即可得到理想的计算结果.
(2)对于等/变厚度矩形板,使用1个求积元单元9$\times$9个积分点即可得到满意的计算结果. 对于等厚度斜板,随着夹角$\alpha $的增大,所需积分点的数目逐渐增多至15$\times$15.
(3)本文建立的四边形求积元板单元可进一步应用于新型复合材料板的非线性分析.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Jones RM. Mechanics of composite materials. CRC Press , 2014
[本文引用: 2]
[2]
刘人怀 , 薛江红 . 复合材料层合板壳非线性力学的研究进展
. 力学学报 , 2017 , 49 (3 ): 487 -506
[本文引用: 2]
(Liu Renhuai Xue Jianghong Development of nonlinear mechanics for laminated composite plates and shells
. Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (3 ): 487 -506 (in Chinese))
[本文引用: 2]
[3]
段铁城 , 李录贤 . 厚板的高阶剪切变形理论研究
. 力学学报 , 2016 , 48 (5 ): 1096 -1113
[本文引用: 1]
(Duan Tiecheng Li Luxian Study on higher-order shear deformation theories of thick-plate
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (5 ): 1096 -1113 (in Chinese))
[本文引用: 1]
[4]
Reddy JN A refined nonlinear theory of plates with transverse shear deformation
. International Journal of Solids and Structures , 1984 , 20 (9-10 ): 881 -896
[本文引用: 1]
[5]
Singh G Rao GV Iyengar NGR Large deflection of shear deformable composite plates using a simple higher-order theory
. Composites Engineering , 1993 , 3 (6 ): 507 -525
[本文引用: 2]
[6]
Liu IW An element for static, vibration and buckling analysis of thick laminated plates
. Computers & Structures , 1996 , 59 (6 ): 1051 -1058
[本文引用: 4]
[7]
Phan ND Reddy JN Analysis of laminated composite plates using a higher-order shear deformation theory
. International Journal for Numerical Methods in Engineering , 1985 , 21 (12 ): 2201 -2219
[本文引用: 4]
[8]
Ren JG Hinton E The finite element analysis of homogeneous and laminated composite plates using a simple higher order theory
. Communications in Applied Numerical Methods , 1986 , 2 (2 ): 217 -228
[本文引用: 1]
[9]
Kant T Pandya BN A simple finite element formulation of a higher-order theory for unsymmetrically laminated composite plates
. Composite Structures , 1988 , 9 (3 ): 215 -246
[本文引用: 2]
[10]
Pervez T Seibi AC Al-Jahwari FKS Analysis of thick orthotropic laminated composite plates based on higher order shear deformation theory
. Composite Structures , 2005 , 71 (3-4 ): 414 -422
[本文引用: 1]
[11]
Shankara CA Iyengar NGR A C0element for the free vibration analysis of laminated composite plates
. Journal of Sound and Vibration , 1996 , 191 (5 ): 721 -738
[本文引用: 1]
[12]
Ansari MI Kumar A Barnat-Hunek D et al .Static and Dynamic Response of FG-CNT-Reinforced Rhombic Laminates
. Applied Sciences , 2018 , 8 (5 ): 834
[本文引用: 9]
[13]
Nayak AK Moy SSJ Shenoi RA Free vibration analysis of composite sandwich plates based on Reddy's higher-order theory
. Composites Part B: Engineering , 2002 , 33 (7 ): 505 -519
[本文引用: 5]
[14]
Nayak AK Moy SSJ Shenoi RA Quadrilateral finite elements for multilayer sandwich plates
. The Journal of Strain Analysis for Engineering Design , 2003 , 38 (5 ): 377 -392
[本文引用: 1]
[15]
Sheikh AH Chakrabarti A A new plate bending element based on higher-order shear deformation theory for the analysis of composite plates
. Finite Elements in Analysis and Design , 2003 , 39 (9 ): 883 -903
[本文引用: 16]
[16]
Taj MNAG Chakrabarti A Sheikh AH Analysis of functionally graded plates using higher order shear deformation theory
. Applied Mathematical Modelling , 2013 , 37 (18-19 ): 8484 -8494
[本文引用: 1]
[17]
Putcha NS Reddy JN A mixed shear flexible finite element for the analysis of laminated plates
. Computer Methods in Applied Mechanics and Engineering , 1984 , 44 (2 ): 213 -227
[本文引用: 1]
[18]
Serdoun SMN Hamza Cherif SM Free vibration analysis of composite and sandwich plates by alternative hierarchical finite element method based on Reddy's C1 HSDT
. Journal of Sandwich Structures & Materials , 2016 , 18 (4 ): 501 -528
[本文引用: 3]
[19]
Asadi E Fariborz SJ Free vibration of composite plates with mixed boundary conditions based on higher-order shear deformation theory
. Archive of Applied Mechanics , 2012 , 82 (6 ): 755 -766
[本文引用: 1]
[20]
王伟 , 伊士超 , 姚林泉 . 分析复合材料层合板弯曲和振动的一种有效无网格方法
. 应用数学和力学 , 2015 , 36 (12 ): 1274 -1284
[本文引用: 1]
(Wang Wei Yi Shi-Chao Yao Linquan An effective meshfree method for bending and vibration analyses of laminated composite plates
. Applied Mathematics & Mechanics , 2015 , 36 (12 ):1274 -1284 (in Chinese))
[本文引用: 1]
[21]
Selim BA Zhang LW Liew KM Impact analysis of CNT-reinforced composite plates based on Reddy's higher-order shear deformation theory using an element-free approach
. Composite Structures , 2017 , 170 : 228 -242
[本文引用: 1]
[22]
赵寿根 , 王静涛 , 黎康 等 . 考虑辐射散热叠层板热诱发振动的有限元分析
. 力学学报 , 2010 , 42 (5 ): 978 -982
[本文引用: 1]
(Zhao Shougen Wang Jingtao Li Kang et al .Finite element method analysis of thermally induced vibration of laminated plates considering radiation
. Chinese Journal of Theoretical and Applied Mechanics , 2010 , 42 (5 ): 978 -982 (in Chinese))
[本文引用: 1]
[23]
Zhong H Yu T Flexural vibration analysis of an eccentric annular Mindlin plate
. Archive of Applied Mechanics , 2007 , 77 (4 ): 185 -195
[本文引用: 1]
[24]
Shen Z Zhong H Static and vibrational analysis of partially composite beams using the weak-form quadrature element method
. Mathematical Problems in Engineering , 2012 , 2012 : 974023
[本文引用: 1]
[25]
Xiao N Zhong H Non-linear quadrature element analysis of planar frames based on geometrically exact beam theory. International Journal of
Non-Linear Mechanics , 2012 , 47 (5 ): 481 -488
[26]
Zhong HZ Yue ZG Analysis of thin plates by the weak form quadrature element method. Science China Physics,
Mechanics and Astronomy , 2012 , 55 (5 ): 861 -871
[本文引用: 1]
[27]
Zhong H Wang Y Weak form quadrature element analysis of Bickford beams
. European Journal of Mechanics-A/Solids , 2010 , 29 (5 ): 851 -858
[本文引用: 1]
[28]
Wang X Yuan Z Jin C Weak form quadrature element method and its applications in science and engineering: a state-of-the-art review
. Applied Mechanics Reviews , 2017 , 69 (3 ): 030801
[本文引用: 1]
[29]
申志强 , 夏军 , 吴克刚 等 . 楔形变截面钢$\!$-$\!$-$\!$混凝土组合梁弯曲和自由振动的求积元分析
. 国防科技大学学报 , 2018 , 40 (1 ): 42 -48
[本文引用: 1]
(Shen Zhiqiang Xia Jun Wu Kegang et al .Flexural and free vibrational analysis of tapered partially steel-concrete composite beams using the weak form quadrature element method
. Journal of National University of Defense Technology , 2018 , 40 (1 ): 42 -48 (in Chinese))
[本文引用: 1]
[30]
Davis PJ Rabinowitz P Methods of Numerical Integration
. Courier Corporation , 2007
[本文引用: 1]
[31]
Wang X Differential Quadrature and Differential Quadrature Based Element Methods: Theory and
Applications. Butterworth-Heinemann , 2015
[本文引用: 1]
[32]
Reddy JN A simple higher-order theory for laminated composite plates
. Journal of Applied Mechanics , 1984 , 51 (4 ): 745 -752
[本文引用: 7]
[33]
Shufrin I Eisenberger M Stability and vibration of shear deformable plates---first order and higher order analyses
. International Journal of Solids and Structures , 2005 , 42 (3-4 ): 1225 -1251
[本文引用: 3]
[34]
Reddy JN Phan ND Stability and vibration of isotropic, orthotropic and laminated plates according to a higher-order shear deformation theory
. Journal of Sound and Vibration , 1985 , 98 (2 ): 157 -170
[本文引用: 2]
[35]
Shufrin I Eisenberger M Vibration of shear deformable plates with variable thickness---first-order and higher-order analyses
. Journal of Sound and Vibration , 2006 , 290 (1-2 ): 465 -489
[本文引用: 7]
[36]
Bacciocchi M Eisenberger M Fantuzzi N et al .Vibration analysis of variable thickness plates and shells by the generalized differential quadrature method
. Composite Structures , 2016 , 156 : 218 -237
[本文引用: 7]
[37]
Wang ZX Shen HS Nonlinear vibration of nanotube-reinforced composite plates in thermal environments
. Computational Materials Science , 2011 , 50 (8 ): 2319 -2330
[本文引用: 1]
2
2014
... 板结构是工程实践中常见的一类结构形式,特别是近年来随着各类高性能复合材料和功能梯度材料的出现,由这些新型材料所构成的板结构在航空航天、土木工程以及军事防护领域得到了 广泛的应用[1 -2 ] .该类板结构的显著特点是其材料性能沿板厚变化,需合理考虑其横向剪切变形,而经典板理论假设横向剪切应变为零、一阶剪切变形理论则假设横向剪切应变沿板厚方向为常量,往往不适用于该类新型材料板结构的力学分析.在这种情况下,高阶剪切变形理论[2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析. ...
... 式中,$E$, $\nu $分别为材料的杨氏模量与泊松比. 而对于其他如正交各向异性材料、复合材料及功能梯度材料,${\pmb E}_{\rm p} $和${\pmb E}_{\rm t}$略微复杂,也可沿板厚变化,具体的表达形式可参阅相关教材或文献[1 ] . ...
复合材料层合板壳非线性力学的研究进展
2
2017
... 板结构是工程实践中常见的一类结构形式,特别是近年来随着各类高性能复合材料和功能梯度材料的出现,由这些新型材料所构成的板结构在航空航天、土木工程以及军事防护领域得到了 广泛的应用[1 -2 ] .该类板结构的显著特点是其材料性能沿板厚变化,需合理考虑其横向剪切变形,而经典板理论假设横向剪切应变为零、一阶剪切变形理论则假设横向剪切应变沿板厚方向为常量,往往不适用于该类新型材料板结构的力学分析.在这种情况下,高阶剪切变形理论[2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析. ...
... [2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析. ...
复合材料层合板壳非线性力学的研究进展
2
2017
... 板结构是工程实践中常见的一类结构形式,特别是近年来随着各类高性能复合材料和功能梯度材料的出现,由这些新型材料所构成的板结构在航空航天、土木工程以及军事防护领域得到了 广泛的应用[1 -2 ] .该类板结构的显著特点是其材料性能沿板厚变化,需合理考虑其横向剪切变形,而经典板理论假设横向剪切应变为零、一阶剪切变形理论则假设横向剪切应变沿板厚方向为常量,往往不适用于该类新型材料板结构的力学分析.在这种情况下,高阶剪切变形理论[2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析. ...
... [2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析. ...
厚板的高阶剪切变形理论研究
1
2016
... 板结构是工程实践中常见的一类结构形式,特别是近年来随着各类高性能复合材料和功能梯度材料的出现,由这些新型材料所构成的板结构在航空航天、土木工程以及军事防护领域得到了 广泛的应用[1 -2 ] .该类板结构的显著特点是其材料性能沿板厚变化,需合理考虑其横向剪切变形,而经典板理论假设横向剪切应变为零、一阶剪切变形理论则假设横向剪切应变沿板厚方向为常量,往往不适用于该类新型材料板结构的力学分析.在这种情况下,高阶剪切变形理论[2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析. ...
厚板的高阶剪切变形理论研究
1
2016
... 板结构是工程实践中常见的一类结构形式,特别是近年来随着各类高性能复合材料和功能梯度材料的出现,由这些新型材料所构成的板结构在航空航天、土木工程以及军事防护领域得到了 广泛的应用[1 -2 ] .该类板结构的显著特点是其材料性能沿板厚变化,需合理考虑其横向剪切变形,而经典板理论假设横向剪切应变为零、一阶剪切变形理论则假设横向剪切应变沿板厚方向为常量,往往不适用于该类新型材料板结构的力学分析.在这种情况下,高阶剪切变形理论[2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析. ...
A refined nonlinear theory of plates with transverse shear deformation
1
1984
... 板结构是工程实践中常见的一类结构形式,特别是近年来随着各类高性能复合材料和功能梯度材料的出现,由这些新型材料所构成的板结构在航空航天、土木工程以及军事防护领域得到了 广泛的应用[1 -2 ] .该类板结构的显著特点是其材料性能沿板厚变化,需合理考虑其横向剪切变形,而经典板理论假设横向剪切应变为零、一阶剪切变形理论则假设横向剪切应变沿板厚方向为常量,往往不适用于该类新型材料板结构的力学分析.在这种情况下,高阶剪切变形理论[2 -3 ] (higher-order shear deformation theory)越来越受到学术界关注.在一般的高阶剪切变形理论中,板的位移场被表示为板厚坐标$z$多项式或其他函数形式,可利用板上下表面横向剪应变为零的条件确定各项系数间的关系,横向剪应力的计算不需要像一阶剪切变形理论那样人为地引入剪切修正因子.在各类高阶剪切变形理论中,由Reddy等[4 ] 提出的位移描述形式(式(1))不仅具有一般高阶剪切变形理论的优点,同时用于描述位移场的独立自由度物理意义明确,且计算成本较低,被广泛地应用于各类复合材料、功能梯度材料中厚板的分析. ...
Large deflection of shear deformable composite plates using a simple higher-order theory
2
1993
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
... 表中同时列出基于相同力学模型的有限元协调元[5 ] 和$C^{0}$单元[9 ] 计算结果,其中协调元为4个4节点矩形单元,每节点14个自由度;$C^{0}$单元为16个9节点矩形单元,每节点7个自由度.观察表6 可知,对于挠度而言,求积元的计算结果与协调元吻合度较好;而对于应力,求积元的计算结果略低于协调元. ...
An element for static, vibration and buckling analysis of thick laminated plates
4
1996
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
... 为便于比较,表中同时列出了基于相同力学模型的有限元协调元[6 ] 和非协调元[7 ] 计算结果以及Reddy给出的Navier解[32 ] ,其中协调元为16个4节点矩形单元,每节点8个自由度;非协调元为25个4节点矩形单元,每节点7个自由度. ...
... The dimensionless deflection and stress of the laminated plate
h/a Method $\bar{w}$ $\bar{\sigma_1}$ $\bar{\sigma_2}$ $\bar{\sigma_3}$ 0.1 1/4 model QEM 7 x 7 0.7156 0.5470 0.3893 0.0268 0.1 1/4 model QEM 9 x 9 0.7147 0.545 6 0.388 8 0.0268 0.1 1/4 model QEM 11 x 11 0.7147 0.545 6 0.388 8 0.0268 0.1 full model QEM 7 x 7 0.7147 0.545 5 0.3888 0.0268 0.1 full model QEM 9 x 9 0.7147 0.545 6 0.3888 0.0268 0.1 full model QEM 11 x 11 0.7147 0.545 6 0.3888 0.0268 0.1 Reddy[32 ] 0.7147 0.545 6 0.3888 0.0268 0.1 1/4 model Phan[7 ] 0.7161 0.5427 0.385 5 0.0266 0.1 1/4 model Liu[6 ] 0.7176 0.541 3 0.3873 0.0266 0.01 1/4 model QEM 7 x 7 0.4343 0.5387 0.2708 0.021 3 0.01 full model QEM 7 x 7 0.4349 0.5401 0.271 1 0.021 5 0.01 full model QEM 9 x 9 0.4343 0.5387 0.2708 0.021 3 0.01 full model QEM 11 x 11 0.4343 0.5387 0.2708 0.021 3 0.01 Reddy[32 ] 0.4343 0.5387 0.2708 0.021 3 0.01 1/4 model Phan[7 ] 0.4320 0.5301 0.2664 0.021 1 0.01 1/4 model Liu[6 ] 0.4408 0.5349 0.2670 0.021 1
观察表5 可知,随着积分点的增加,挠度和应力的求积元的计算结果均能较快地收敛于解析解[32 ] ,采用9个积分点即能得到满意的计算结果. 14几何模型和全模型没有显著差异,下文中均采用全模型进行计算. 同时,两类有限元的计算结果未能收敛至解析解. ...
... [
6 ]
0.4408 0.5349 0.2670 0.021 1 观察表5 可知,随着积分点的增加,挠度和应力的求积元的计算结果均能较快地收敛于解析解[32 ] ,采用9个积分点即能得到满意的计算结果. 14几何模型和全模型没有显著差异,下文中均采用全模型进行计算. 同时,两类有限元的计算结果未能收敛至解析解. ...
Analysis of laminated composite plates using a higher-order shear deformation theory
4
1985
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
... 为便于比较,表中同时列出了基于相同力学模型的有限元协调元[6 ] 和非协调元[7 ] 计算结果以及Reddy给出的Navier解[32 ] ,其中协调元为16个4节点矩形单元,每节点8个自由度;非协调元为25个4节点矩形单元,每节点7个自由度. ...
... The dimensionless deflection and stress of the laminated plate
h/a Method $\bar{w}$ $\bar{\sigma_1}$ $\bar{\sigma_2}$ $\bar{\sigma_3}$ 0.1 1/4 model QEM 7 x 7 0.7156 0.5470 0.3893 0.0268 0.1 1/4 model QEM 9 x 9 0.7147 0.545 6 0.388 8 0.0268 0.1 1/4 model QEM 11 x 11 0.7147 0.545 6 0.388 8 0.0268 0.1 full model QEM 7 x 7 0.7147 0.545 5 0.3888 0.0268 0.1 full model QEM 9 x 9 0.7147 0.545 6 0.3888 0.0268 0.1 full model QEM 11 x 11 0.7147 0.545 6 0.3888 0.0268 0.1 Reddy[32 ] 0.7147 0.545 6 0.3888 0.0268 0.1 1/4 model Phan[7 ] 0.7161 0.5427 0.385 5 0.0266 0.1 1/4 model Liu[6 ] 0.7176 0.541 3 0.3873 0.0266 0.01 1/4 model QEM 7 x 7 0.4343 0.5387 0.2708 0.021 3 0.01 full model QEM 7 x 7 0.4349 0.5401 0.271 1 0.021 5 0.01 full model QEM 9 x 9 0.4343 0.5387 0.2708 0.021 3 0.01 full model QEM 11 x 11 0.4343 0.5387 0.2708 0.021 3 0.01 Reddy[32 ] 0.4343 0.5387 0.2708 0.021 3 0.01 1/4 model Phan[7 ] 0.4320 0.5301 0.2664 0.021 1 0.01 1/4 model Liu[6 ] 0.4408 0.5349 0.2670 0.021 1
观察表5 可知,随着积分点的增加,挠度和应力的求积元的计算结果均能较快地收敛于解析解[32 ] ,采用9个积分点即能得到满意的计算结果. 14几何模型和全模型没有显著差异,下文中均采用全模型进行计算. 同时,两类有限元的计算结果未能收敛至解析解. ...
... [
7 ]
0.4320 0.5301 0.2664 0.021 1 0.01 1/4 model Liu[6 ] 0.4408 0.5349 0.2670 0.021 1 观察表5 可知,随着积分点的增加,挠度和应力的求积元的计算结果均能较快地收敛于解析解[32 ] ,采用9个积分点即能得到满意的计算结果. 14几何模型和全模型没有显著差异,下文中均采用全模型进行计算. 同时,两类有限元的计算结果未能收敛至解析解. ...
The finite element analysis of homogeneous and laminated composite plates using a simple higher order theory
1
1986
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
A simple finite element formulation of a higher-order theory for unsymmetrically laminated composite plates
2
1988
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
... 表中同时列出基于相同力学模型的有限元协调元[5 ] 和$C^{0}$单元[9 ] 计算结果,其中协调元为4个4节点矩形单元,每节点14个自由度;$C^{0}$单元为16个9节点矩形单元,每节点7个自由度.观察表6 可知,对于挠度而言,求积元的计算结果与协调元吻合度较好;而对于应力,求积元的计算结果略低于协调元. ...
Analysis of thick orthotropic laminated composite plates based on higher order shear deformation theory
1
2005
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
A C0element for the free vibration analysis of laminated composite plates
1
1996
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
Static and Dynamic Response of FG-CNT-Reinforced Rhombic Laminates
9
2018
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
... 考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果. ...
... The dimensionless frequencies of the FG-CNTRC skew plate (UD)
Mode 1 2 3 4 5 6 α =15° QEM 15 x 15 13.746 18.278 18.327 22.576 28.358 33.426 Ref.[12 ] 14.088 18.320 18.895 22.618 29.333 33.641 α = 30° QEM 15 x 15 14.519 18.668 20.719 28.286 32.165 34.834 Ref.[12 ] 14.898 18.830 21.372 28.432 33.108 35.118 α = 45° QEM 15 x 15 16.707 20.197 26.207 36.689 38.864 39.160 Ref.[12 ] 17.186 20.512 26.990 37.014 39.632 39.657
表12 斜板无量纲自振频率(FG-O)$\omega {a^2} / h\sqrt {{\rho _m }/ {E_m }} $ ...
... [
12 ]
14.898 18.830 21.372 28.432 33.108 35.118 α = 45° QEM 15 x 15 16.707 20.197 26.207 36.689 38.864 39.160 Ref.[12 ] 17.186 20.512 26.990 37.014 39.632 39.657 表12 斜板无量纲自振频率(FG-O)$\omega {a^2} / h\sqrt {{\rho _m }/ {E_m }} $ ...
... [
12 ]
17.186 20.512 26.990 37.014 39.632 39.657 表12 斜板无量纲自振频率(FG-O)$\omega {a^2} / h\sqrt {{\rho _m }/ {E_m }} $ ...
... The dimensionless frequencies of the FG-CNTRC skew plate (FG-O)
Mode 1 2 3 4 5 6 α = 15° QEM 15 x 15 11.548 16.756 18.326 22.635 27.174 29.610 Ref.[12 ] 11.225 16.857 18.273 22.561 27.702 28.690 α = 30° QEM 15 x 15 12.379 18.718 19.190 28.361 30.548 31.116 Ref.[12 ] 12.113 18.775 19.364 28.356 30.314 30.780 α = 45° QEM 15 x 15 14.661 20.253 24.547 35.709 36.336 36.789 Ref.[12 ] 14.520 20.439 24.733 35.270 36.212 36.901
观察表11 和表12 可知,求积元的计算结果与有限元吻合较好,最大相对差异小于3.5%.由于文献[12 ] 中提供的信息有限,无 法保证两类方法计算过程中除单元外的其他步骤完全一致,如对式(7)中沿厚度积分的具体计算方式,这些因素也将导致计算结果的差异. ...
... [
12 ]
12.113 18.775 19.364 28.356 30.314 30.780 α = 45° QEM 15 x 15 14.661 20.253 24.547 35.709 36.336 36.789 Ref.[12 ] 14.520 20.439 24.733 35.270 36.212 36.901 观察表11 和表12 可知,求积元的计算结果与有限元吻合较好,最大相对差异小于3.5%.由于文献[12 ] 中提供的信息有限,无 法保证两类方法计算过程中除单元外的其他步骤完全一致,如对式(7)中沿厚度积分的具体计算方式,这些因素也将导致计算结果的差异. ...
... [
12 ]
14.520 20.439 24.733 35.270 36.212 36.901 观察表11 和表12 可知,求积元的计算结果与有限元吻合较好,最大相对差异小于3.5%.由于文献[12 ] 中提供的信息有限,无 法保证两类方法计算过程中除单元外的其他步骤完全一致,如对式(7)中沿厚度积分的具体计算方式,这些因素也将导致计算结果的差异. ...
... 观察表11 和表12 可知,求积元的计算结果与有限元吻合较好,最大相对差异小于3.5%.由于文献[12 ] 中提供的信息有限,无 法保证两类方法计算过程中除单元外的其他步骤完全一致,如对式(7)中沿厚度积分的具体计算方式,这些因素也将导致计算结果的差异. ...
Free vibration analysis of composite sandwich plates based on Reddy's higher-order theory
5
2002
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
... 表4 给出了四边简支方板,高跨比$h/a=0.1$时的横向无量纲自振频率.为便于比较,表中同时列出了基于相同力学模型的有限元(64个9节点矩形单元,每节点7个自由度)计算结果[13 ] 、Reddy给出的Navier解[34 ] 以及Shufrin给出的扩展Kantorovich法解[33 ] .模态栏"1,1''表示$X$向,$Y$向的半波数,下同. ...
... The dimensionless frequencies of the square plate
Mode QEM QEM 10 x 10 QEM 11 x 11 Reddy [34 ] Shufrin[33 ] [13 ] 1,1 0.093 0 0.0930 0.093 0 0.093 1 0.0930 0.0930 1,2 0.222 0 0.2220 0.2220 0.2222 0.2220 0.2222 2,2 0.3406 0.3406 0.3406 0.341 1 0.3406 0.341 2 1,3 0.4090 0.4151 0.4151 0.4158 0.4151 0.4169 2,3 0.511 2 0.5208 0.5208 0.5221 0.5208 0.5231 1,4 0.569 4 0.6455 0.6526 0.6545 — 0.6599
观察表4 可知,求积元单元的计算结果与现有文献吻合较好,与文献[33 ] 计算结果一致.随着积分点数的增加,各阶自振频率均能 较快地收敛,对于基频的计算,采用9个积分点即能得到满意的计算结果. ...
... 表7 给出了不同高跨比、长宽比时,前三阶无量纲自振频率的计算值. 表中同时列出了基于相同力学模型的有限元$C^{0}$单元[13 ] 和阶谱单元的[18 ] 计算结果,其中$C^{0}$单元为36个9节点矩形单元,每节点7个自由度;阶谱单元为1个矩形单元,阶谱项数为14. 观察表7 可知,求积元方法的计算结果与阶谱单元近乎一致,而$C^{0}$单元的计算结果与前二者差异较大,最大相对差异为5.6%. ...
... The dimensionless frequencies of the rectangular laminated plate
Mode h/a = 0.2h/a = 0.05 a/b = 0.5a/b = 1.0a/b = 1.5a/b = 0.5a/b = 1.0a/b = 1.5 QEM 1 7.50 9.71 12.83 13.94 19.36 29.22 2 9.71 16.31 18.80 19.36 42.11 51.86 13 X 13 3 10.21 16.81 20.41 29.22 45.52 72.21 1 7.50 9.71 12.83 13.94 19.36 29.22 Ref.[18 ] 2 9.72 16.31 18.80 19.36 42.11 51.86 3 10.21 16.81 20.41 29.22 45.52 72.21 1 7.29 9.42 12.36 13.85 19.23 28.97 Ref.[13 ] 2 9.43 15.56 17.74 19.24 41.70 51.12 3 10.20 15.96 20.41 29.16 44.88 71.17
2.2 变厚度矩形板的自由振动 考察一各向同性均质材料正方形板(边长为$a$, 泊松比 $\nu =0.3$)的自由振动问题,该板厚度沿$X$方向以四类方式(式(30))单向变化,如图3 所示. ...
Quadrilateral finite elements for multilayer sandwich plates
1
2003
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
A new plate bending element based on higher-order shear deformation theory for the analysis of composite plates
16
2003
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
... 表1 和表2 分别给出了四边简支条件下,不同高跨比($h/a$)时,方板($a=b$)板中的无量纲挠度与弯矩.为便于比较,表中同时给出 了基于相同力学模型的有限元计算结果[15 ] 与Reddy给出的Navier解[32 ] . 表中 "QEM 7$\times $7''表示,采用1个求积元板单元,积分点数${Nl}= {Nm}=7$,下同. ...
... The dimensionless deflection at the center of the plate
A/a 0.001 0.01 0.10 0.20 0.25 QEM 7x7 0.406 4 0.406 6 0.4274 0.490 3 0.537 3 QEM 9x9 0.406 2 0.406 5 0.4273 0.490 3 0.537 5 QEM 1x11 0.406 2 0.406 4 0.4273 0.490 3 0.537 3 QEM3x13 0.406 2 0.406 4 0.4273 0.490 3 0.537 4 Sheikh[15 ] 0.406 4 0.406 6 0.4274 0.490 5 0.537 5 Reddy[32 ] 0.406 2 0.406 4 0.4273 0.490 3 0.537 4
表2 方板板中无量纲弯矩$10{M_x } / {q_0 a^2}$ ...
... The dimensionless moment at the center of the plate
h/a 0.001 0.01 0.10 0.20 0.25 QEM 7x7 0.4785 0.478 5 0.478 4 0.478 2 0.478 2 QEM 9x9 0.4789 0.478 9 0.478 8 0.478 9 0.478 8 QEM 11x11 0.4789 0.478 9 0.478 9 0.478 8 0.478 8 QEM 13x13 0.4789 0.478 9 0.478 9 0.478 9 0.478 9 Sheikh[15 ] 0.478 8 0.478 8 0.478 8 0.478 8 0.478 8 Reddy[32 ] 0.4789 0.478 9 0.478 9 0.478 9 0.478 9
观察表1 和表2 可知,随着积分点数的增加,位移和弯矩的求积元解均能较快地收敛于解析解,随着板厚的增大,收敛速度略有降低,采用9个积分点即能得到满意的计算结果. Sheikh等[15 ] 利用512个的6节点(每节点7自由度)三角形有限元单元未能得到与解析解一致的计算结果. ...
... 观察表1 和表2 可知,随着积分点数的增加,位移和弯矩的求积元解均能较快地收敛于解析解,随着板厚的增大,收敛速度略有降低,采用9个积分点即能得到满意的计算结果. Sheikh等[15 ] 利用512个的6节点(每节点7自由度)三角形有限元单元未能得到与解析解一致的计算结果. ...
... The dimensionless deflection and moment of the rectangular plate
b/a h/a Method $\bar{w}$ $\bar{ Mx }$ $\bar{ My }$ 1.5 0.01 QEM 9x9 0.142 6 0.123 3 0.1236 1.5 0.01 QEM 11x11 0.141 6 0.123 3 0.1237 1.5 0.01 QEM 13x13 0.141 6 0.123 2 0.1237 1.5 0.01 Sheikh[15 ] 0.141 7 0.123 1 0.1177 1.5 0.1 QEM 9x9 0.1478 0.1202 0.1188 1.5 0.1 QEM 11x11 0.148 1 0.1198 0.1187 1.5 0.1 QEM 13x13 0.148 1 0.1198 0.1187 1.5 0.1 Sheikh[15 ] 0.148 1 0.1170 0.115 8 2.0 0.01 QEM 9x9 0.1496 0.1305 0.1246 2.0 0.01 QEM 11x11 0.1496 0.1305 0.1246 2.0 0.01 QEM 13x13 0.1496 0.1304 0.1246 2.0 0.01 Sheikh[15 ] 0.1500 0.131 4 0.115 2 2.0 0.1 QEM 9x9 0.155 2 0.1279 0.1201 2.0 0.1 QEM 11x11 0.155 6 0.1273 0.1198 2.0 0.1 QEM 13x13 0.155 8 0.1271 0.1196 2.0 0.1 Sheikh[15 ] 0.155 8 0.1262 0.1136
表4 给出了四边简支方板,高跨比$h/a=0.1$时的横向无量纲自振频率.为便于比较,表中同时列出了基于相同力学模型的有限元(64个9节点矩形单元,每节点7个自由度)计算结果[13 ] 、Reddy给出的Navier解[34 ] 以及Shufrin给出的扩展Kantorovich法解[33 ] .模态栏"1,1''表示$X$向,$Y$向的半波数,下同. ...
... [
15 ]
0.148 1 0.1170 0.115 8 2.0 0.01 QEM 9x9 0.1496 0.1305 0.1246 2.0 0.01 QEM 11x11 0.1496 0.1305 0.1246 2.0 0.01 QEM 13x13 0.1496 0.1304 0.1246 2.0 0.01 Sheikh[15 ] 0.1500 0.131 4 0.115 2 2.0 0.1 QEM 9x9 0.155 2 0.1279 0.1201 2.0 0.1 QEM 11x11 0.155 6 0.1273 0.1198 2.0 0.1 QEM 13x13 0.155 8 0.1271 0.1196 2.0 0.1 Sheikh[15 ] 0.155 8 0.1262 0.1136 表4 给出了四边简支方板,高跨比$h/a=0.1$时的横向无量纲自振频率.为便于比较,表中同时列出了基于相同力学模型的有限元(64个9节点矩形单元,每节点7个自由度)计算结果[13 ] 、Reddy给出的Navier解[34 ] 以及Shufrin给出的扩展Kantorovich法解[33 ] .模态栏"1,1''表示$X$向,$Y$向的半波数,下同. ...
... [
15 ]
0.1500 0.131 4 0.115 2 2.0 0.1 QEM 9x9 0.155 2 0.1279 0.1201 2.0 0.1 QEM 11x11 0.155 6 0.1273 0.1198 2.0 0.1 QEM 13x13 0.155 8 0.1271 0.1196 2.0 0.1 Sheikh[15 ] 0.155 8 0.1262 0.1136 表4 给出了四边简支方板,高跨比$h/a=0.1$时的横向无量纲自振频率.为便于比较,表中同时列出了基于相同力学模型的有限元(64个9节点矩形单元,每节点7个自由度)计算结果[13 ] 、Reddy给出的Navier解[34 ] 以及Shufrin给出的扩展Kantorovich法解[33 ] .模态栏"1,1''表示$X$向,$Y$向的半波数,下同. ...
... [
15 ]
0.155 8 0.1262 0.1136 表4 给出了四边简支方板,高跨比$h/a=0.1$时的横向无量纲自振频率.为便于比较,表中同时列出了基于相同力学模型的有限元(64个9节点矩形单元,每节点7个自由度)计算结果[13 ] 、Reddy给出的Navier解[34 ] 以及Shufrin给出的扩展Kantorovich法解[33 ] .模态栏"1,1''表示$X$向,$Y$向的半波数,下同. ...
... 同时,表中给出了Sheikh等[15 ] 利用512个的6节点(每节点7自由度)三角形有限元单元的计算结果. 观察表10 可知,对于挠度而言,求积元的计算结果与有限元吻合度较好;而对于应力,求积元的计算结果略高于有限元. ...
... The dimensionless deflection and stress at the center of the skew laminated plate
h/a α Method $\bar{w}$ $\bar{sigma_{1}}$ $\bar{sigma_{2}}$ 0.01 30° QEM 15x15 0.546 5 0.6592 0.2802 0.01 30° Ref.[15 ] 0.5452 0.6444 0.2629 0.01 45° QEM 15x15 0.3633 0.4488 0.3197 0.01 45° Ref.[15 ] 0.3631 0.4421 0.3007 0.01 60° QEM 15x15 0.1464 0.2025 0.2723 0.01 60° Ref.[15 ] 0.1455 0.201 1 0.2572 0.10 30° QEM 15x15 0.861 6 0.6749 0.3896 0.10 30° Ref.[15 ] 0.8621 0.661 7 0.3709 0.10 45° QEM 15x15 0.5708 0.4602 0.3980 0.10 45° Ref.[15 ] 0.5707 0.4543 0.3786 0.10 60° QEM 15x15 0.2503 0.2059 0.3152 0.10 60° Ref.[15 ] 0.2505 0.2058 0.3023
考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果. ...
... [
15 ]
0.3631 0.4421 0.3007 0.01 60° QEM 15x15 0.1464 0.2025 0.2723 0.01 60° Ref.[15 ] 0.1455 0.201 1 0.2572 0.10 30° QEM 15x15 0.861 6 0.6749 0.3896 0.10 30° Ref.[15 ] 0.8621 0.661 7 0.3709 0.10 45° QEM 15x15 0.5708 0.4602 0.3980 0.10 45° Ref.[15 ] 0.5707 0.4543 0.3786 0.10 60° QEM 15x15 0.2503 0.2059 0.3152 0.10 60° Ref.[15 ] 0.2505 0.2058 0.3023 考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果. ...
... [
15 ]
0.1455 0.201 1 0.2572 0.10 30° QEM 15x15 0.861 6 0.6749 0.3896 0.10 30° Ref.[15 ] 0.8621 0.661 7 0.3709 0.10 45° QEM 15x15 0.5708 0.4602 0.3980 0.10 45° Ref.[15 ] 0.5707 0.4543 0.3786 0.10 60° QEM 15x15 0.2503 0.2059 0.3152 0.10 60° Ref.[15 ] 0.2505 0.2058 0.3023 考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果. ...
... [
15 ]
0.8621 0.661 7 0.3709 0.10 45° QEM 15x15 0.5708 0.4602 0.3980 0.10 45° Ref.[15 ] 0.5707 0.4543 0.3786 0.10 60° QEM 15x15 0.2503 0.2059 0.3152 0.10 60° Ref.[15 ] 0.2505 0.2058 0.3023 考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果. ...
... [
15 ]
0.5707 0.4543 0.3786 0.10 60° QEM 15x15 0.2503 0.2059 0.3152 0.10 60° Ref.[15 ] 0.2505 0.2058 0.3023 考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果. ...
... [
15 ]
0.2505 0.2058 0.3023 考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果. ...
Analysis of functionally graded plates using higher order shear deformation theory
1
2013
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
A mixed shear flexible finite element for the analysis of laminated plates
1
1984
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
Free vibration analysis of composite and sandwich plates by alternative hierarchical finite element method based on Reddy's C1 HSDT
3
2016
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
... 表7 给出了不同高跨比、长宽比时,前三阶无量纲自振频率的计算值. 表中同时列出了基于相同力学模型的有限元$C^{0}$单元[13 ] 和阶谱单元的[18 ] 计算结果,其中$C^{0}$单元为36个9节点矩形单元,每节点7个自由度;阶谱单元为1个矩形单元,阶谱项数为14. 观察表7 可知,求积元方法的计算结果与阶谱单元近乎一致,而$C^{0}$单元的计算结果与前二者差异较大,最大相对差异为5.6%. ...
... The dimensionless frequencies of the rectangular laminated plate
Mode h/a = 0.2h/a = 0.05 a/b = 0.5a/b = 1.0a/b = 1.5a/b = 0.5a/b = 1.0a/b = 1.5 QEM 1 7.50 9.71 12.83 13.94 19.36 29.22 2 9.71 16.31 18.80 19.36 42.11 51.86 13 X 13 3 10.21 16.81 20.41 29.22 45.52 72.21 1 7.50 9.71 12.83 13.94 19.36 29.22 Ref.[18 ] 2 9.72 16.31 18.80 19.36 42.11 51.86 3 10.21 16.81 20.41 29.22 45.52 72.21 1 7.29 9.42 12.36 13.85 19.23 28.97 Ref.[13 ] 2 9.43 15.56 17.74 19.24 41.70 51.12 3 10.20 15.96 20.41 29.16 44.88 71.17
2.2 变厚度矩形板的自由振动 考察一各向同性均质材料正方形板(边长为$a$, 泊松比 $\nu =0.3$)的自由振动问题,该板厚度沿$X$方向以四类方式(式(30))单向变化,如图3 所示. ...
Free vibration of composite plates with mixed boundary conditions based on higher-order shear deformation theory
1
2012
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
分析复合材料层合板弯曲和振动的一种有效无网格方法
1
2015
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
分析复合材料层合板弯曲和振动的一种有效无网格方法
1
2015
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
Impact analysis of CNT-reinforced composite plates based on Reddy's higher-order shear deformation theory using an element-free approach
1
2017
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
考虑辐射散热叠层板热诱发振动的有限元分析
1
2010
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
考虑辐射散热叠层板热诱发振动的有限元分析
1
2010
... 由于传统的解析方法仅适用于特定载荷、几何形式及边界条件问题的求解,国内外学者基于高阶剪切变形理论,利用各类数值方法对众多新型材料结构如碳纤维增强复合材料层合板、陶瓷$\!$-$\!$-$\!$金属功能梯度板、功能梯度碳纳米管增强复合材料板的相关力学问题进行了大量研究,这些数值方法中最为常见的是有限元法. 观察式(1)不难发现,$w_{,x} $项和$w_{,y}$项的存在要求单元$C^{1}$连续. 针对这一要求,一方面可通过构造较为复杂的协调板元或者非协调板元予以解决.如Singh等[5 ] 和Liu等[6 ] 利用Hermite插值,分别构造了矩形四节点协调元;Phan等[7 ] 和Ren等[8 ] 则构造了矩形四节点非协调元. 另一方面,不少学者通过变量替换,将原问题转化为$C^{0}$连续以简化单元的构造.如Kant等[9 ] 和Pervez等[10 ] 令$\theta _x^\ast = - \left( {4 / {3h^2}} \right)\left( {\phi + w_{,x} }\right)$, Shankara等[11 ] 和Ansari 等[12 ] 则令$\theta _x^\ast = w_{,x}$,Nayakc等[13 -14 ] 和Sheikh 等[15 -16 ] 则令$\theta _x^\ast = \left( {\phi +w_{,x} } \right)$, 分别构造了$C^{0}$型矩形单元或三角形单元,这样做虽可避开$C^{1}$连续要求,但也牺牲了单元的计算精度.同时,也有学者通过构造位移$\!$-$\!$-$\!$力混合单元[17 ] 或阶谱单元[18 ] 的方式来解决这一问题,这在一定程度上增加了问题的复杂度.此外,微分求积法[19 ] 、无网格方法[20 -21 ] 等新型数值方法及商业有限元软件[22 ] 也被用于高阶板的力学分析.目前这一领域的研究仍十分活跃,满足$C^{1}$连续的单元相对较少,对于简单高效数值计算方法的需求依然迫切. ...
Flexural vibration analysis of an eccentric annular Mindlin plate
1
2007
... 弱形式求积元法(weak form quadrature element method) 简称 求积元法,是一种基于待求解问题的弱形式,利用统一的单元节点计算问题控制泛函中积分和微分的新型高阶数值方法[23 ] ,具有准确高效、步骤直接、前后处理过程简便等优点,在处理复杂几何形状、非均匀材料、强几何非线性问题上相比传统低阶有限元具有独特的优势[24 -28 ] .利用该方法,Zhong和Yue[26 ] 基于经典板理论对等厚度三角形板、方板及变厚度环板进行了弯曲和自由振动分析;Zhong和Wang[27 ] 对均质材料高阶梁的弯曲、自由振动及特征值屈曲进行了分析;作者则基于Euler梁理论,对考虑界面滑移效应的楔形变截面组合梁弯曲和自由振动问题进行了分析[29 ] . ...
Static and vibrational analysis of partially composite beams using the weak-form quadrature element method
1
2012
... 弱形式求积元法(weak form quadrature element method) 简称 求积元法,是一种基于待求解问题的弱形式,利用统一的单元节点计算问题控制泛函中积分和微分的新型高阶数值方法[23 ] ,具有准确高效、步骤直接、前后处理过程简便等优点,在处理复杂几何形状、非均匀材料、强几何非线性问题上相比传统低阶有限元具有独特的优势[24 -28 ] .利用该方法,Zhong和Yue[26 ] 基于经典板理论对等厚度三角形板、方板及变厚度环板进行了弯曲和自由振动分析;Zhong和Wang[27 ] 对均质材料高阶梁的弯曲、自由振动及特征值屈曲进行了分析;作者则基于Euler梁理论,对考虑界面滑移效应的楔形变截面组合梁弯曲和自由振动问题进行了分析[29 ] . ...
Non-linear quadrature element analysis of planar frames based on geometrically exact beam theory. International Journal of
2012
Analysis of thin plates by the weak form quadrature element method. Science China Physics,
1
2012
... 弱形式求积元法(weak form quadrature element method) 简称 求积元法,是一种基于待求解问题的弱形式,利用统一的单元节点计算问题控制泛函中积分和微分的新型高阶数值方法[23 ] ,具有准确高效、步骤直接、前后处理过程简便等优点,在处理复杂几何形状、非均匀材料、强几何非线性问题上相比传统低阶有限元具有独特的优势[24 -28 ] .利用该方法,Zhong和Yue[26 ] 基于经典板理论对等厚度三角形板、方板及变厚度环板进行了弯曲和自由振动分析;Zhong和Wang[27 ] 对均质材料高阶梁的弯曲、自由振动及特征值屈曲进行了分析;作者则基于Euler梁理论,对考虑界面滑移效应的楔形变截面组合梁弯曲和自由振动问题进行了分析[29 ] . ...
Weak form quadrature element analysis of Bickford beams
1
2010
... 弱形式求积元法(weak form quadrature element method) 简称 求积元法,是一种基于待求解问题的弱形式,利用统一的单元节点计算问题控制泛函中积分和微分的新型高阶数值方法[23 ] ,具有准确高效、步骤直接、前后处理过程简便等优点,在处理复杂几何形状、非均匀材料、强几何非线性问题上相比传统低阶有限元具有独特的优势[24 -28 ] .利用该方法,Zhong和Yue[26 ] 基于经典板理论对等厚度三角形板、方板及变厚度环板进行了弯曲和自由振动分析;Zhong和Wang[27 ] 对均质材料高阶梁的弯曲、自由振动及特征值屈曲进行了分析;作者则基于Euler梁理论,对考虑界面滑移效应的楔形变截面组合梁弯曲和自由振动问题进行了分析[29 ] . ...
Weak form quadrature element method and its applications in science and engineering: a state-of-the-art review
1
2017
... 弱形式求积元法(weak form quadrature element method) 简称 求积元法,是一种基于待求解问题的弱形式,利用统一的单元节点计算问题控制泛函中积分和微分的新型高阶数值方法[23 ] ,具有准确高效、步骤直接、前后处理过程简便等优点,在处理复杂几何形状、非均匀材料、强几何非线性问题上相比传统低阶有限元具有独特的优势[24 -28 ] .利用该方法,Zhong和Yue[26 ] 基于经典板理论对等厚度三角形板、方板及变厚度环板进行了弯曲和自由振动分析;Zhong和Wang[27 ] 对均质材料高阶梁的弯曲、自由振动及特征值屈曲进行了分析;作者则基于Euler梁理论,对考虑界面滑移效应的楔形变截面组合梁弯曲和自由振动问题进行了分析[29 ] . ...
楔形变截面钢$\!$-$\!$-$\!$混凝土组合梁弯曲和自由振动的求积元分析
1
2018
... 弱形式求积元法(weak form quadrature element method) 简称 求积元法,是一种基于待求解问题的弱形式,利用统一的单元节点计算问题控制泛函中积分和微分的新型高阶数值方法[23 ] ,具有准确高效、步骤直接、前后处理过程简便等优点,在处理复杂几何形状、非均匀材料、强几何非线性问题上相比传统低阶有限元具有独特的优势[24 -28 ] .利用该方法,Zhong和Yue[26 ] 基于经典板理论对等厚度三角形板、方板及变厚度环板进行了弯曲和自由振动分析;Zhong和Wang[27 ] 对均质材料高阶梁的弯曲、自由振动及特征值屈曲进行了分析;作者则基于Euler梁理论,对考虑界面滑移效应的楔形变截面组合梁弯曲和自由振动问题进行了分析[29 ] . ...
楔形变截面钢$\!$-$\!$-$\!$混凝土组合梁弯曲和自由振动的求积元分析
1
2018
... 弱形式求积元法(weak form quadrature element method) 简称 求积元法,是一种基于待求解问题的弱形式,利用统一的单元节点计算问题控制泛函中积分和微分的新型高阶数值方法[23 ] ,具有准确高效、步骤直接、前后处理过程简便等优点,在处理复杂几何形状、非均匀材料、强几何非线性问题上相比传统低阶有限元具有独特的优势[24 -28 ] .利用该方法,Zhong和Yue[26 ] 基于经典板理论对等厚度三角形板、方板及变厚度环板进行了弯曲和自由振动分析;Zhong和Wang[27 ] 对均质材料高阶梁的弯曲、自由振动及特征值屈曲进行了分析;作者则基于Euler梁理论,对考虑界面滑移效应的楔形变截面组合梁弯曲和自由振动问题进行了分析[29 ] . ...
Methods of Numerical Integration
1
2007
... 利用Gauss-Lobatto 数值积分[30 ] 计算单元应变能式(5) ...
Differential Quadrature and Differential Quadrature Based Element Methods: Theory and
1
2015
... 利用微分求积法则和广义微分求积法则[31 ] ,将式(14)中$\bar{\varepsilon }_{ij}$所含积分点处的导数表示为积分点处基本自由度的线性加权代数和. 轴向位移$u$, $v$和转动$\phi $, $\varphi $的导数采用微分求积法则离散,如 ...
A simple higher-order theory for laminated composite plates
7
1984
... 表1 和表2 分别给出了四边简支条件下,不同高跨比($h/a$)时,方板($a=b$)板中的无量纲挠度与弯矩.为便于比较,表中同时给出 了基于相同力学模型的有限元计算结果[15 ] 与Reddy给出的Navier解[32 ] . 表中 "QEM 7$\times $7''表示,采用1个求积元板单元,积分点数${Nl}= {Nm}=7$,下同. ...
... The dimensionless deflection at the center of the plate
A/a 0.001 0.01 0.10 0.20 0.25 QEM 7x7 0.406 4 0.406 6 0.4274 0.490 3 0.537 3 QEM 9x9 0.406 2 0.406 5 0.4273 0.490 3 0.537 5 QEM 1x11 0.406 2 0.406 4 0.4273 0.490 3 0.537 3 QEM3x13 0.406 2 0.406 4 0.4273 0.490 3 0.537 4 Sheikh[15 ] 0.406 4 0.406 6 0.4274 0.490 5 0.537 5 Reddy[32 ] 0.406 2 0.406 4 0.4273 0.490 3 0.537 4
表2 方板板中无量纲弯矩$10{M_x } / {q_0 a^2}$ ...
... The dimensionless moment at the center of the plate
h/a 0.001 0.01 0.10 0.20 0.25 QEM 7x7 0.4785 0.478 5 0.478 4 0.478 2 0.478 2 QEM 9x9 0.4789 0.478 9 0.478 8 0.478 9 0.478 8 QEM 11x11 0.4789 0.478 9 0.478 9 0.478 8 0.478 8 QEM 13x13 0.4789 0.478 9 0.478 9 0.478 9 0.478 9 Sheikh[15 ] 0.478 8 0.478 8 0.478 8 0.478 8 0.478 8 Reddy[32 ] 0.4789 0.478 9 0.478 9 0.478 9 0.478 9
观察表1 和表2 可知,随着积分点数的增加,位移和弯矩的求积元解均能较快地收敛于解析解,随着板厚的增大,收敛速度略有降低,采用9个积分点即能得到满意的计算结果. Sheikh等[15 ] 利用512个的6节点(每节点7自由度)三角形有限元单元未能得到与解析解一致的计算结果. ...
... 为便于比较,表中同时列出了基于相同力学模型的有限元协调元[6 ] 和非协调元[7 ] 计算结果以及Reddy给出的Navier解[32 ] ,其中协调元为16个4节点矩形单元,每节点8个自由度;非协调元为25个4节点矩形单元,每节点7个自由度. ...
... The dimensionless deflection and stress of the laminated plate
h/a Method $\bar{w}$ $\bar{\sigma_1}$ $\bar{\sigma_2}$ $\bar{\sigma_3}$ 0.1 1/4 model QEM 7 x 7 0.7156 0.5470 0.3893 0.0268 0.1 1/4 model QEM 9 x 9 0.7147 0.545 6 0.388 8 0.0268 0.1 1/4 model QEM 11 x 11 0.7147 0.545 6 0.388 8 0.0268 0.1 full model QEM 7 x 7 0.7147 0.545 5 0.3888 0.0268 0.1 full model QEM 9 x 9 0.7147 0.545 6 0.3888 0.0268 0.1 full model QEM 11 x 11 0.7147 0.545 6 0.3888 0.0268 0.1 Reddy[32 ] 0.7147 0.545 6 0.3888 0.0268 0.1 1/4 model Phan[7 ] 0.7161 0.5427 0.385 5 0.0266 0.1 1/4 model Liu[6 ] 0.7176 0.541 3 0.3873 0.0266 0.01 1/4 model QEM 7 x 7 0.4343 0.5387 0.2708 0.021 3 0.01 full model QEM 7 x 7 0.4349 0.5401 0.271 1 0.021 5 0.01 full model QEM 9 x 9 0.4343 0.5387 0.2708 0.021 3 0.01 full model QEM 11 x 11 0.4343 0.5387 0.2708 0.021 3 0.01 Reddy[32 ] 0.4343 0.5387 0.2708 0.021 3 0.01 1/4 model Phan[7 ] 0.4320 0.5301 0.2664 0.021 1 0.01 1/4 model Liu[6 ] 0.4408 0.5349 0.2670 0.021 1
观察表5 可知,随着积分点的增加,挠度和应力的求积元的计算结果均能较快地收敛于解析解[32 ] ,采用9个积分点即能得到满意的计算结果. 14几何模型和全模型没有显著差异,下文中均采用全模型进行计算. 同时,两类有限元的计算结果未能收敛至解析解. ...
... [
32 ]
0.4343 0.5387 0.2708 0.021 3 0.01 1/4 model Phan[7 ] 0.4320 0.5301 0.2664 0.021 1 0.01 1/4 model Liu[6 ] 0.4408 0.5349 0.2670 0.021 1 观察表5 可知,随着积分点的增加,挠度和应力的求积元的计算结果均能较快地收敛于解析解[32 ] ,采用9个积分点即能得到满意的计算结果. 14几何模型和全模型没有显著差异,下文中均采用全模型进行计算. 同时,两类有限元的计算结果未能收敛至解析解. ...
... 观察表5 可知,随着积分点的增加,挠度和应力的求积元的计算结果均能较快地收敛于解析解[32 ] ,采用9个积分点即能得到满意的计算结果. 14几何模型和全模型没有显著差异,下文中均采用全模型进行计算. 同时,两类有限元的计算结果未能收敛至解析解. ...
Stability and vibration of shear deformable plates---first order and higher order analyses
3
2005
... 表4 给出了四边简支方板,高跨比$h/a=0.1$时的横向无量纲自振频率.为便于比较,表中同时列出了基于相同力学模型的有限元(64个9节点矩形单元,每节点7个自由度)计算结果[13 ] 、Reddy给出的Navier解[34 ] 以及Shufrin给出的扩展Kantorovich法解[33 ] .模态栏"1,1''表示$X$向,$Y$向的半波数,下同. ...
... The dimensionless frequencies of the square plate
Mode QEM QEM 10 x 10 QEM 11 x 11 Reddy [34 ] Shufrin[33 ] [13 ] 1,1 0.093 0 0.0930 0.093 0 0.093 1 0.0930 0.0930 1,2 0.222 0 0.2220 0.2220 0.2222 0.2220 0.2222 2,2 0.3406 0.3406 0.3406 0.341 1 0.3406 0.341 2 1,3 0.4090 0.4151 0.4151 0.4158 0.4151 0.4169 2,3 0.511 2 0.5208 0.5208 0.5221 0.5208 0.5231 1,4 0.569 4 0.6455 0.6526 0.6545 — 0.6599
观察表4 可知,求积元单元的计算结果与现有文献吻合较好,与文献[33 ] 计算结果一致.随着积分点数的增加,各阶自振频率均能 较快地收敛,对于基频的计算,采用9个积分点即能得到满意的计算结果. ...
... 观察表4 可知,求积元单元的计算结果与现有文献吻合较好,与文献[33 ] 计算结果一致.随着积分点数的增加,各阶自振频率均能 较快地收敛,对于基频的计算,采用9个积分点即能得到满意的计算结果. ...
Stability and vibration of isotropic, orthotropic and laminated plates according to a higher-order shear deformation theory
2
1985
... 表4 给出了四边简支方板,高跨比$h/a=0.1$时的横向无量纲自振频率.为便于比较,表中同时列出了基于相同力学模型的有限元(64个9节点矩形单元,每节点7个自由度)计算结果[13 ] 、Reddy给出的Navier解[34 ] 以及Shufrin给出的扩展Kantorovich法解[33 ] .模态栏"1,1''表示$X$向,$Y$向的半波数,下同. ...
... The dimensionless frequencies of the square plate
Mode QEM QEM 10 x 10 QEM 11 x 11 Reddy [34 ] Shufrin[33 ] [13 ] 1,1 0.093 0 0.0930 0.093 0 0.093 1 0.0930 0.0930 1,2 0.222 0 0.2220 0.2220 0.2222 0.2220 0.2222 2,2 0.3406 0.3406 0.3406 0.341 1 0.3406 0.341 2 1,3 0.4090 0.4151 0.4151 0.4158 0.4151 0.4169 2,3 0.511 2 0.5208 0.5208 0.5221 0.5208 0.5231 1,4 0.569 4 0.6455 0.6526 0.6545 — 0.6599
观察表4 可知,求积元单元的计算结果与现有文献吻合较好,与文献[33 ] 计算结果一致.随着积分点数的增加,各阶自振频率均能 较快地收敛,对于基频的计算,采用9个积分点即能得到满意的计算结果. ...
Vibration of shear deformable plates with variable thickness---first-order and higher-order analyses
7
2006
... 表8 给出了四边简支方形板($h_{0}$/$a$=0.2)在I类厚度变化条件下的前6阶横向无量纲自振频率. 表8 同时列出了Shufrin等基于一阶剪切变形理论(FSDT)[35 ] 以及Bacciocchi等基于一般高阶剪切变形理论(HSDT)[36 ] 得出的计算结果. 观察表8 可知,求积元单元仅需9个积分点即可使前四阶自振频率收敛,其计算结果高于一阶剪切变形理论,低于一般高阶剪切变形理论. ...
... The dimensionless frequencies of the square plate with variable thickness (Type I)
Mode 1 2 3 4 5 6 QEM 1.374 9 3.1150 3.1331 4.6741 5.451 5 5.5566 9x9 QEM 1.374 9 3.1150 3.1331 4.6741 5.5050 5.5829 10 x 10 QEM 1.374 9 3.1150 3.1331 4.6741 5.5047 5.5839 11 x 11 Ref.[35 ] 1.373 8 3.1096 3.1276 4.661 3 5.4883 5.5657 Ref.[36 ] 1.378 7 3.1324 3.1500 4.6923 5.5509 5.631 0
表9 给出了四边固支方形板($h_{0}/a =0.1$)在II、III、IV类厚度变化条件下的前6阶横向无量纲自振频率. 同时也给出了基于相同力学模型的扩展Kantorovich法解[35 ] 以及基于一阶剪切变形理论的广义微分求积法解[36 ] . 观察表9 可知,求积元法与文献[35 ] 计算结果吻合较好,最大相对误差0.2%,二者计算结果高于一阶剪切变形理论[36 ] . ...
... 表9 给出了四边固支方形板($h_{0}/a =0.1$)在II、III、IV类厚度变化条件下的前6阶横向无量纲自振频率. 同时也给出了基于相同力学模型的扩展Kantorovich法解[35 ] 以及基于一阶剪切变形理论的广义微分求积法解[36 ] . 观察表9 可知,求积元法与文献[35 ] 计算结果吻合较好,最大相对误差0.2%,二者计算结果高于一阶剪切变形理论[36 ] . ...
... [35 ]计算结果吻合较好,最大相对误差0.2%,二者计算结果高于一阶剪切变形理论[36 ] . ...
... The dimensionless frequencies of the square plate with variable thickness (Type II, III, IV)
Mode 1 2 3 4 5 6 Type II QEM 13x13 2.7450 5.3082 5.421 8 7.6561 9.0295 9.1302 Ref.[35 ] 2.7454 5.3031 5.4186 7.6483 9.0192 9.1099 Ref.[36 ] 2.7392 5.2879 5.4007 7.6143 8.9747 9.0768 Type III QEM 13x13 2.2846 4.3393 4.5317 6.4331 7.3198 7.7467 Ref.[35 ] 2.2850 4.3375 4.5294 6.4291 7.311 8 7.7358 Ref.[36 ] 2.281 8 4.3298 4.5207 6.4107 7.2945 7.7157 Type IV QEM 13x13 2.4382 4.2238 4.800 9 6.5089 6.9839 8.0295 Ref.[35 ] 2.4384 4.2222 4.7987 6.5044 6.9782 8.021 2 Ref.[36 ] 2.4356 4.2163 4.789 4 6.4882 6.9645 7.9971
2.3 等厚度斜板的弯曲和自由振动分析 平行四边形斜板如图4 所示,相邻两边边长为$a$,板厚为$h$,相邻边一边与$X$轴平行,另一边与$Y$轴夹角为$\alpha $. ...
... [
35 ]
2.2850 4.3375 4.5294 6.4291 7.311 8 7.7358 Ref.[36 ] 2.281 8 4.3298 4.5207 6.4107 7.2945 7.7157 Type IV QEM 13x13 2.4382 4.2238 4.800 9 6.5089 6.9839 8.0295 Ref.[35 ] 2.4384 4.2222 4.7987 6.5044 6.9782 8.021 2 Ref.[36 ] 2.4356 4.2163 4.789 4 6.4882 6.9645 7.9971 2.3 等厚度斜板的弯曲和自由振动分析 平行四边形斜板如图4 所示,相邻两边边长为$a$,板厚为$h$,相邻边一边与$X$轴平行,另一边与$Y$轴夹角为$\alpha $. ...
... [
35 ]
2.4384 4.2222 4.7987 6.5044 6.9782 8.021 2 Ref.[36 ] 2.4356 4.2163 4.789 4 6.4882 6.9645 7.9971 2.3 等厚度斜板的弯曲和自由振动分析 平行四边形斜板如图4 所示,相邻两边边长为$a$,板厚为$h$,相邻边一边与$X$轴平行,另一边与$Y$轴夹角为$\alpha $. ...
Vibration analysis of variable thickness plates and shells by the generalized differential quadrature method
7
2016
... 表8 给出了四边简支方形板($h_{0}$/$a$=0.2)在I类厚度变化条件下的前6阶横向无量纲自振频率. 表8 同时列出了Shufrin等基于一阶剪切变形理论(FSDT)[35 ] 以及Bacciocchi等基于一般高阶剪切变形理论(HSDT)[36 ] 得出的计算结果. 观察表8 可知,求积元单元仅需9个积分点即可使前四阶自振频率收敛,其计算结果高于一阶剪切变形理论,低于一般高阶剪切变形理论. ...
... The dimensionless frequencies of the square plate with variable thickness (Type I)
Mode 1 2 3 4 5 6 QEM 1.374 9 3.1150 3.1331 4.6741 5.451 5 5.5566 9x9 QEM 1.374 9 3.1150 3.1331 4.6741 5.5050 5.5829 10 x 10 QEM 1.374 9 3.1150 3.1331 4.6741 5.5047 5.5839 11 x 11 Ref.[35 ] 1.373 8 3.1096 3.1276 4.661 3 5.4883 5.5657 Ref.[36 ] 1.378 7 3.1324 3.1500 4.6923 5.5509 5.631 0
表9 给出了四边固支方形板($h_{0}/a =0.1$)在II、III、IV类厚度变化条件下的前6阶横向无量纲自振频率. 同时也给出了基于相同力学模型的扩展Kantorovich法解[35 ] 以及基于一阶剪切变形理论的广义微分求积法解[36 ] . 观察表9 可知,求积元法与文献[35 ] 计算结果吻合较好,最大相对误差0.2%,二者计算结果高于一阶剪切变形理论[36 ] . ...
... 表9 给出了四边固支方形板($h_{0}/a =0.1$)在II、III、IV类厚度变化条件下的前6阶横向无量纲自振频率. 同时也给出了基于相同力学模型的扩展Kantorovich法解[35 ] 以及基于一阶剪切变形理论的广义微分求积法解[36 ] . 观察表9 可知,求积元法与文献[35 ] 计算结果吻合较好,最大相对误差0.2%,二者计算结果高于一阶剪切变形理论[36 ] . ...
... [36 ]. ...
... The dimensionless frequencies of the square plate with variable thickness (Type II, III, IV)
Mode 1 2 3 4 5 6 Type II QEM 13x13 2.7450 5.3082 5.421 8 7.6561 9.0295 9.1302 Ref.[35 ] 2.7454 5.3031 5.4186 7.6483 9.0192 9.1099 Ref.[36 ] 2.7392 5.2879 5.4007 7.6143 8.9747 9.0768 Type III QEM 13x13 2.2846 4.3393 4.5317 6.4331 7.3198 7.7467 Ref.[35 ] 2.2850 4.3375 4.5294 6.4291 7.311 8 7.7358 Ref.[36 ] 2.281 8 4.3298 4.5207 6.4107 7.2945 7.7157 Type IV QEM 13x13 2.4382 4.2238 4.800 9 6.5089 6.9839 8.0295 Ref.[35 ] 2.4384 4.2222 4.7987 6.5044 6.9782 8.021 2 Ref.[36 ] 2.4356 4.2163 4.789 4 6.4882 6.9645 7.9971
2.3 等厚度斜板的弯曲和自由振动分析 平行四边形斜板如图4 所示,相邻两边边长为$a$,板厚为$h$,相邻边一边与$X$轴平行,另一边与$Y$轴夹角为$\alpha $. ...
... [
36 ]
2.281 8 4.3298 4.5207 6.4107 7.2945 7.7157 Type IV QEM 13x13 2.4382 4.2238 4.800 9 6.5089 6.9839 8.0295 Ref.[35 ] 2.4384 4.2222 4.7987 6.5044 6.9782 8.021 2 Ref.[36 ] 2.4356 4.2163 4.789 4 6.4882 6.9645 7.9971 2.3 等厚度斜板的弯曲和自由振动分析 平行四边形斜板如图4 所示,相邻两边边长为$a$,板厚为$h$,相邻边一边与$X$轴平行,另一边与$Y$轴夹角为$\alpha $. ...
... [
36 ]
2.4356 4.2163 4.789 4 6.4882 6.9645 7.9971 2.3 等厚度斜板的弯曲和自由振动分析 平行四边形斜板如图4 所示,相邻两边边长为$a$,板厚为$h$,相邻边一边与$X$轴平行,另一边与$Y$轴夹角为$\alpha $. ...
Nonlinear vibration of nanotube-reinforced composite plates in thermal environments
1
2011
... 考虑一四边简支的功能梯度碳纳米管增强复合材料板的自由振动问题. ${\pmb E}_{\rm p}$和${\pmb E}_{\rm t}$按照文献[37 ] 介绍的扩展混合律模型进行计算,基体材料参数为:$E_{\rm m}=2.1$\,GPa,$\rho_{\rm m}=1\,150$\,kg/m$^{3}$,$\nu_{\rm m}=0.34$. 碳纳米管材料参数为:$E_{11}=5.646\,6$\,TPa,$E_{22}=7.080\,0$\,TPa,$G_{12}=1.944\,5$\,TPa,$\nu_{12}=0.175$,$\rho =1\,400$\,kg/m$^{3}$. 表11 和表12 分别给出了高跨比$h/a=0.1$,碳纳米管平均体积含量为0.11时,碳纳米管沿厚度均匀分布(UD)与O型分布(FG-O)时的前6阶无量纲自振频率. 表中同时给出了Ansari等[12 ] 利用256个9节点(每节点7自由度)矩形有限元单元的计算结果. ...