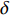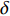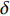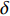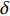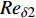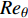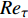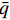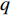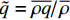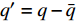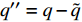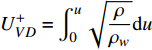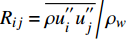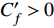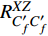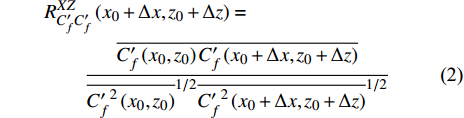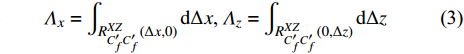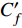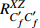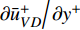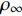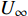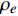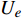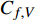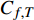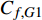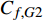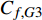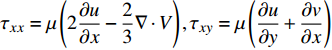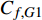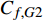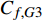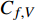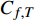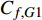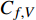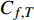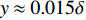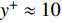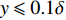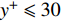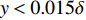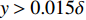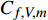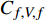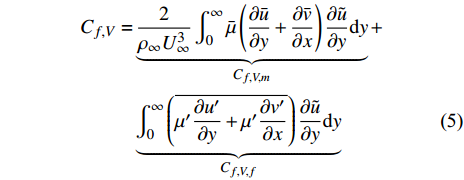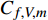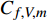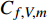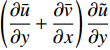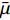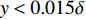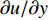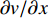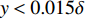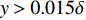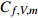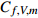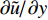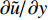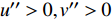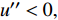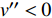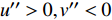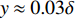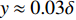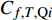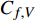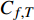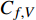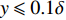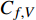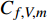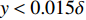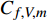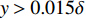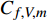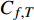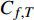ANALYSES ON GENERATION MECHANISM OF SKIN FRICTION IN HIGH ENTHALPY TURBULENT BOUNDARY LAYER
-
摘要: 高超飞行器在中低空以极高马赫数飞行时, 飞行器表面会遇到湍流与高温非平衡效应耦合作用的新问题. 这种高焓湍流边界层壁面摩阻产生机制是新型高超声速飞行器所关注的基础科学问题, 厘清此产生机制可以为减阻方法的设计提供指导, 具有重要的工程实用价值. 本文选取高超声速飞行时楔形体头部斜激波后的高焓流动状态, 开展了考虑高温非平衡效应的湍流边界层直接数值模拟研究, 并设置同等边界层参数下的低焓完全气体湍流边界层流动作为对比, 采用RD (Renard & Deck)分解技术研究了高焓湍流边界层摩阻的主要产生机制, 对摩阻产生的主要贡献项积分函数分布进行了详细分析, 研究了高温非平衡效应对摩阻产生的影响规律; 采用象限分析技术, 研究了摩阻分解湍动能生成项的主导流动事件. 计算结果表明, 高温非平衡效应会使得壁面摩阻脉动条带的流向和展向尺寸均减小. 分子黏性耗散项和湍动能生成项是高焓湍流边界层摩阻生成的主要流动过程. 分子黏性耗散项主要作用在近壁区, 高焓流动的分布与低焓流动存在差异. 象限分析表明, 上抛和下扫运动是影响摩阻分解中湍动能生成项的主导事件.Abstract: When flying in low or medium attitude at very high Mach number, the surface of new hypersonic vehicles will encounter the interaction between turbulence and chemical non-equilibrium, which makes the flying environment more complicated. Generation mechanism of skin friction in such high enthalpy turbulent boundary layer is the fundamental scientific problem. The clarification of this mechanism can serve guidance for the drag reduction design, which has a significant engineering practical value. This work chose the flow condition after the leading shock of a cone in hypersonic flight, and performed direct numerical simulation (DNS) of turbulent boundary including chemical non-equilibrium effect. The low enthalpy case under the same boundary condition was set as a comparison. The RD (Renard & Deck) decomposition was utilized to analyse the dominant generation process of skin friction. The profiles of the integrand functions of main contributors were compared in detail. The influence of chemical non-equilibrium on the generation mechanism of skin friction was investigated. Furtherly, quadrant analysis technique was utilized to analyse the dominant flow events of turbulence kinetic energy production term in RD decomposition. The results show that the steaks scales of skin friction fluctuation are reduced both in streamwise and spanwise directions due to the chemical non-equilibrium effect. The molecular viscous dissipation term and the turbulence kinetic energy production term are the two main contributors to the generation of skin friction. The former mainly works in the near wall region, and the influence of high enthalpy is applied through its average portion. The profile of the integrand function of the molecular viscous dissipation term is different between high- and low enthalpy cases. The results of quadrant analysis show that the ejection and sweep events are the dominant processes for the latter term.
-
Keywords:
- high enthalpy /
- turbulent boundary layer /
- skin friction /
- RD decomposition /
- quadrant analysis
-
引 言
高超声速飞行器在以极高马赫数飞行时, 飞行器周围会产生较强的激波并压缩来流空气, 使其温度急剧升高. 温度的升高会激发复杂的热力学过程, 比如振动能激发和气体分子离解, 使飞行器表面的气体处于非平衡状态[1]. 当飞行器在低空稠密大气高速飞行时, 飞行器表面流动会发生转捩并形成湍流. 湍流会使得壁面摩阻升高数倍[2], 损害飞行器飞行性能. 湍流与非平衡效应耦合在一起, 使得表面摩阻的预测更加困难, 高温非平衡效应对壁面摩阻产生机制的影响也尚不清楚.
目前同时考虑高温化学非平衡效应和湍流流动的研究尚处于起步阶段, 相关报道还十分有限, 且均是采用直接数值模拟方法(direct numerical simulation, DNS)进行分析研究. Duan和 Martin[3-4]使用5 组分空气反应模型进行了DNS, 结果表明高焓化学非平衡条件下基于Morkovin 假设的大部分相关尺度关系仍然成立, 并评估了湍流对化学反应速率的影响. Kim[5]使用单一组分的O2或N2, 并考虑热化学非平衡过程, 发现半当地尺度可以较好地消除热化学非平衡效应的影响. 刘朋欣等[6-7]发现在边界层的对数区, 各流动参数的拓展自相似理论的相对标度指数基本符合标度规律. 吴正园等[8]的研究表明湍流边界层中的高温气体效应对壁面平均压强和脉动压强有显著的增加效果. Renzo和Urzay [9-10]研究了含化学非平衡的边界层转捩过程, 并基于模拟结果分析了壁面摩阻、热流的流向演化. Passiatore等[11]对比了两种不同气体模型(冻结流动和化学非平衡流动)下的湍流边界层, 发现吸热反应会使得温度脉动和密度脉动低于冻结流模型, 但化学非平衡效应对速度的一阶和二阶统计量影响较小, 并简单地采用RD (Renard & Deck)方法对摩阻进行了分解研究. Volpiani[12]开发了一套模拟高超声速激波/化学非平衡湍流边界层相互的直接数值模拟程序, 发现化学非平衡效应使得激波干扰区的流动特性发生了显著变化.
上述研究结果表明, 高温非平衡效应会显著影响流场热力学特性分布. 温度分布的改变又会直接影响黏性系数的大小, 继而对摩阻分布产生影响. 因此有必要研究高温非平衡效应下的壁面摩阻产生机制. 目前高温非平衡湍流边界层的研究大都关注于湍流边界层宏观统计特性规律. 而对工程中较为关心的摩阻特性缺乏深入分析.
摩阻分解技术将壁面摩阻的产生与流动机制结合起来, 是分析摩阻产生机理的一种有效手段. 目前常见的有FIK分解[13]和RD分解[14]. Fukagata等[13]通过对平均动量方程的连续三次积分, 建立了摩阻系数与雷诺应力之间的关系, 将摩阻分解为层流部分的贡献和湍流部分的贡献. 后续的改进工作提升了公式的易用性[15-16], 并将该公式推广至任意复杂外形[17]. Renard和Deck指出[14]FIK公式没有明确的物理意义, 并提出了另外一种摩阻分解方法, 即RD分解该方法在假设远离壁面附近流体保持静止的绝对参考坐标系下, 通过对流向动量方程做变换和积分, 将摩阻的产生分为分子黏性耗散作用和湍动能生成作用, 具有更明确的物理意义. 此方法在旋涡结构输运过程[18]、大尺度湍流运动[19]和破碎[20]对摩阻的影响研究得到了应用. Li等[21-22]将其推广至可压缩湍流中, 并研究了雷诺数效应对摩阻产生的影响.
本文利用RD摩阻分解技术, 分析了高温化学非平衡湍流边界层摩阻生成机制, 给出了对摩阻生成起主要作用的流动过程; 通过设置低焓完全气体模型对比算例, 从摩阻空间分布特点、热力学和流动特性方面分析了高焓效应对主要摩阻产生项的影响.
1. 数值方法与算例设置
1.1 控制方程
低焓算例工质为空气, 采用完全气体模型, 控制方程为可压缩Naiver-Stokes (N-S); 高焓算例由于需要考虑空气的化学非平衡效应, 采用含化学反应的N-S方程作为控制方程. 后者的形式如下
$$ \left. \begin{array}{l} \dfrac{{\partial \rho }}{{\partial t}} = - \dfrac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}} \right) \hfill \\ \dfrac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} = - \dfrac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j} + p{\delta _{ij}}} \right) + \dfrac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} \hfill \\ \dfrac{{\partial E}}{{\partial t}} = - \dfrac{\partial }{{\partial {x_j}}}\left[ {\left( {E + p} \right){u_j}} \right] + \dfrac{\partial }{{\partial {x_j}}}\Bigg( {u_j}{\tau _{ij}} + K\dfrac{{\partial T}}{{\partial {x_j}}} + \\ \qquad\qquad \displaystyle\sum\limits_{k = 1}^{ns} {\rho {D_k}{h_k}\dfrac{{\partial {f_k}}}{{\partial {x_j}}}} \Bigg) \hfill \\ \dfrac{{\partial \left( {\rho {f_k}} \right)}}{{\partial t}} = - \dfrac{\partial }{{\partial {x_j}}}\left( {\rho {f_k}{u_j}} \right) + \dfrac{\partial }{{\partial {x_j}}}\left( {\rho {D_k}\dfrac{{\partial {f_k}}}{{\partial {x_j}}}} \right) + {S_k}\\ \qquad\qquad k = 1,\;2,\;\cdots, \;ns - 1 \hfill \end{array} \right\} $$ (1) 其中
$ \rho $ 和$ p $ 是密度和压力;$ {u_j} $ 为分速度;$ {f_k} $ 是第$ k $ 种组分的质量分数;$ E $ 为单位体积的总内能;$ {h_k} $ 是比焓, 通过温度的多项式拟合得到;$ {S_k} $ 是第$ k $ 种组分的生成速率;$ {\tau _{ij}} $ 为黏性应力;$ K $ 和$ {D_k} $ 分别为热传导系数和组分质量扩散系数. 在完全气体计算中, 通常取$ Pr $ =0.72, 比热比$ \gamma $ =1.4, 黏性系数采用Sutherland公式计算. 而对于多组分气体, 则首先通过Lennard-Jones分子黏性系数计算公式求得各组分的黏性系数, 并通过Wilke公式计算混合物黏性系数;$ \gamma $ 也不再为常数; 通过$ Pr $ 数和$ Sc $ 数与黏性系数的关系式来计算$ K $ 和$ {D_k} $ . 多组分输运系数(黏性系数、热传导系数和组分扩散系数)具体计算公式可参考文献[23].1.2 数值方法
计算采用课题组发展的Inhouse程序. 该计算程序已经成功开展大量的可压缩湍流[24-25]、激波/边界层干扰 [26-27]、旋转爆震精细流场结构[28]、高温非平衡湍流边界层[6-7]等复杂流动的数值模拟, 计算精度和鲁棒性均得到了充分验证. 在本文计算中, 无黏通量采用了7阶有限差分格式WENO-Z[29], 黏性项采用4阶中心差分格式, 时间推进采用具有TVD性质的3阶Runge-Kutta方法. 高焓算例计算不考虑温度非平衡效应, 且只考虑空气组分的离解过程, 化学反应源项求解采用Gupta等[30]提出的5组分(N2, O2, N, O, NO) 6基元反应模型.
1.3 算例设置
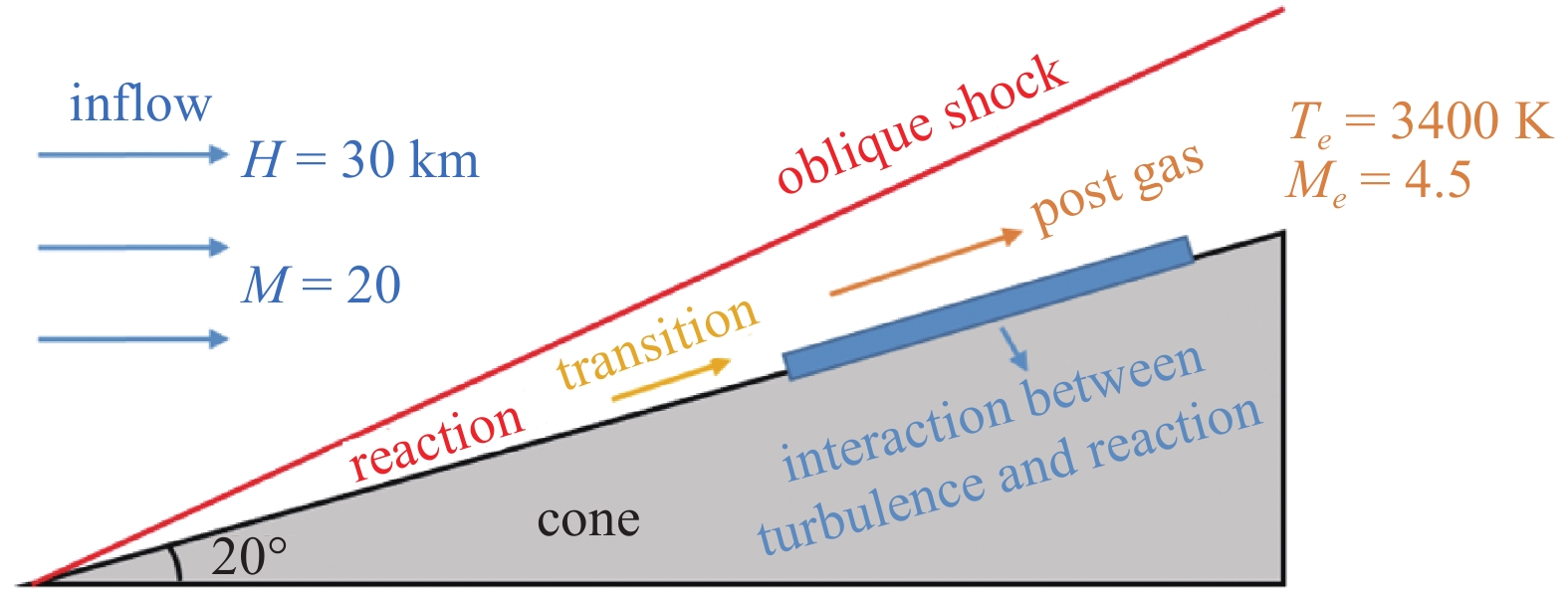
高焓算例的计算状态示意图见图1. 为了激发空气的化学非平衡态, 选择30 km高空以马赫数20飞行的楔形体, 其头部产生一道斜激波. 斜激波后的温度较高且已经足够激发空气发生化学反应, 选择此状态作为湍流边界层外缘流动状态. 高焓算例来流组分质量分数设置为f(O2)=0.2675, f(N2)=0.7325, 并使用空气化学反应模型模拟化学非平衡过程, 记为TH算例. 作为对比, 设置同等边界层参数下的低焓算例, 以评估高温非平衡效应对湍流边界层统计特性和摩阻的影响, 并记为TL算例. 两算例的来流状态及壁温设置见表1.
表 1 来流状态及壁温设置Table 1. Inflow condition and wall temperatureCase Me ρe/(kg·m−3) Te/K Tw/K Tw/ Taw TH 4.5 0.1025 3400 3400 0.206 TL 4.5 0.1025 300 300 0.215 Note: the recovery temperature ${T_{aw} } = {T_e}\left[ {1 + 0.9 \times \dfrac{ {\left( {\gamma - 1} \right)} }{2}M_e^2} \right]$ 计算初场采用相同来流状态下RANS[31]计算结果的剖面生成. 入口的脉动通过数字滤波合成湍流方法[32]产生; 出口采用特征边界条件; 上边界固定为初始值; 壁面采用黏性等温条件; 展向采用周期性边界条件.
计算域设置为20
$\delta $ × 4$\delta $ × 2$\delta $ (流向 × 法向 × 展向,$\delta $ 为边界层名义厚度), 相应的网格为901 × 161 × 301. 流向和展向网格均匀, 法向网格在壁面附近加密. 文献[6]进行了同等工况下的网格无关性验证, 本文所采用的网格可以满足直接数值模拟的要求. 湍流充分发展段的网格分辨率及边界层厚度和雷诺数见表2. 此时的边界层厚度$\delta $ 约为5 mm. 保持两个算例的$ {{Re} _{\delta 2}} $ 一致, 且可以发现${{Re} _\theta }$ 和$ {{Re} _\tau } $ 也相差不大. 分析所采用流向位置如图2(b)中黑色实线所示. 且如无特殊说明, 下文中分析默认基于此流向截面处的流场. 在下文的表述中约定,$ \bar q $ 代表变量$ q $ 的Reynolds平均,$ \tilde q = {{\overline {\rho q} } \mathord{\left/ {\vphantom {{\overline {\rho q} } {\overline \rho }}} \right. } {\overline \rho }} $ 表示Favre平均. 两种平均方式所对应的脉动量分别为:$ q' = q - \bar q $ ,$ q'' = q - \tilde q $ .表 2 边界层厚度、雷诺数和网格尺度Table 2. Thickness, Reynold number and grid resolutionCase Reθ Reτ Reδ2 θ/mm δ/mm ∆x + ∆y2 + ∆z + TH 2451.1 802.5 2396.8 0.452 4.793 18.6 0.34 5.6 TL 2483.7 868.3 2483.7 0.458 4.975 19.3 0.35 5.8 Note: θ is momentum thickness, the different types of Reynolds number are defined as$ {{Re} _\theta } = {{{\rho _\delta }{u_\delta }\theta } \mathord{\left/ {\vphantom {{{\rho _\delta }{u_\delta }\theta } {{\mu _\delta }}}} \right. } {{\mu _\delta }}} $, $ {{Re} _\tau } = {{{\rho _w}{u_\tau }\delta } \mathord{\left/ {\vphantom {{{\rho _w}{u_\tau }\delta } {{\mu _w}}}} \right. } {{\mu _w}}} $, $ {{Re} _{\delta 2}} = {{{\rho _\delta }{u_\delta }\theta } \mathord{\left/ {\vphantom {{{\rho _\delta }{u_\delta }\theta } {{\mu _w}}}} \right. } {{\mu _w}}} $ 2. 结果分析与讨论
2.1 湍流边界层瞬时与统计结果
图2给出了瞬时流场旋涡结构和密度梯度分布图. 从图中可以看出, 在入口添加的扰动, 经过一段距离的发展, 形成了充分发展的湍流, 流动结构变得紊乱无序. 从整体上看, 高焓算例和低焓算例的流动结构没有明显的变化, 说明化学非平衡过程对流动运动过程影响较小, 并不会显著改变流场结构特性.
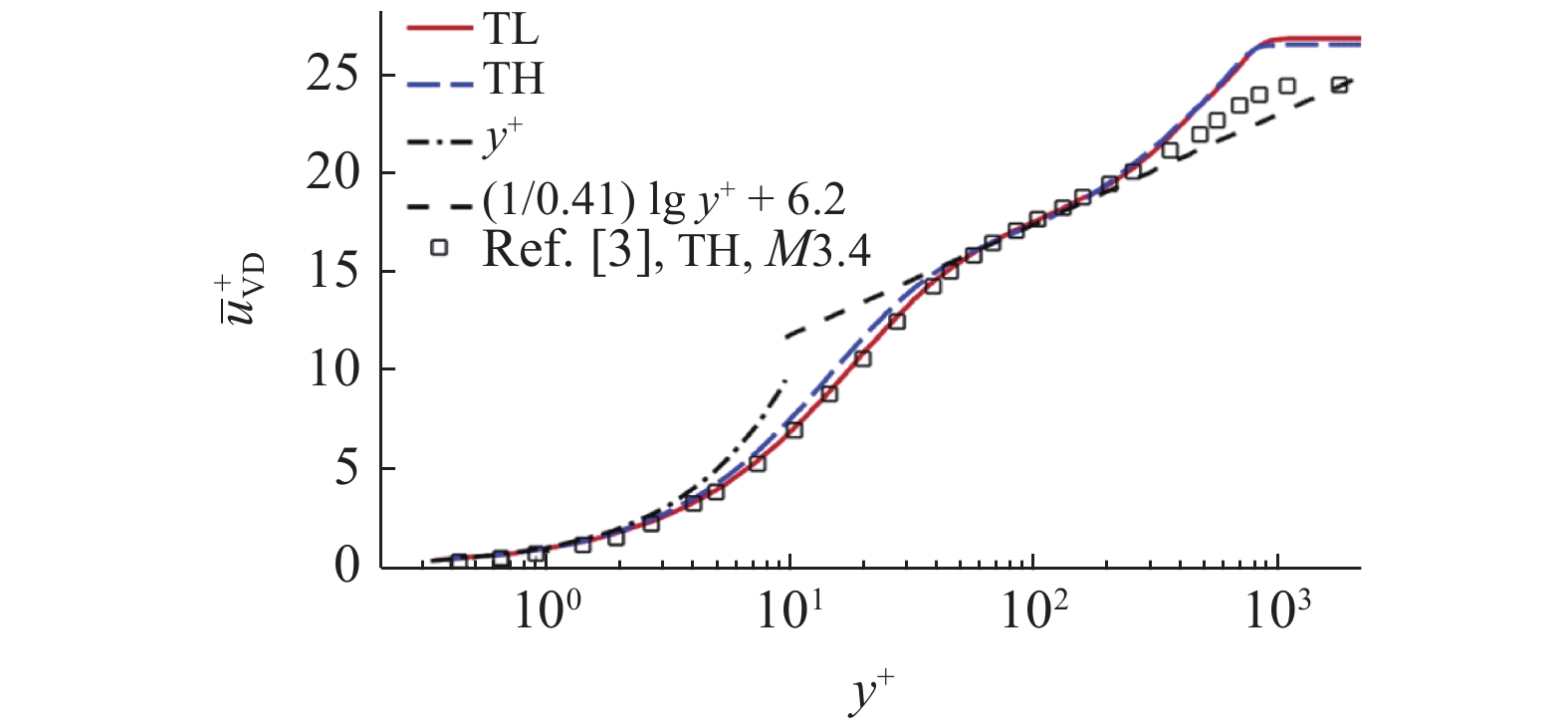
图3和图4分别给出了平均流向速度和雷诺应力分布. Van Driest 变换的定义为:
$ U_{VD}^ + = \displaystyle\int_0^u {\sqrt {\dfrac{\rho }{{{\rho _w}}}} {\rm{d}}u} $ . 从图3中可以看出, 此时速度边界层仍然存在明显的线性区、缓冲区和对数区, 只不过截距有所增大, 与文献中高焓算例[3]结果符合较好. 除了在缓冲区, 高焓算例的平均流向速度略高于低焓算例之外, 焓值并不会明显改变湍流边界层速度剖面的整体分布特性. 从图4中可以看出, 经过密度加权的雷诺应力$ {R_{ij}} = {{\overline {\rho u_i^{''}u_j^{''}} } \mathord{\left/ {\vphantom {{\overline {\rho u_i^{''}u_j^{''}} } {{\rho _w}}}} \right. } {{\rho _w}}} $ 分布具有相似的分布趋势, 与文献完全气体结果[33]及高焓算例结果[3]符合较好. 高焓效应对雷诺应力分布的影响不大, 并没有对湍流速度脉动产生明显影响, 这与图2中的瞬时流场结构对比结果是一致的.2.2 湍流边界层摩阻空间分布
本节首先对比高低焓值下摩阻的空间分布, 分析高温非平衡效应对摩阻分布的整体影响. 图5中给出了不同焓值工况下的局部瞬时摩阻系数在壁面上的分布, 从图中可以看出瞬时摩阻的分布是相似的, 都呈现出局部高摩阻斑点, 并且存在一些摩阻较弱的条带结构. 另外, 高焓情况下的条带结构尺度有减小趋势.
图6给出了摩阻脉动的概率分布函数(probability distribution function, PDF), 使用其均方根进行归一化, 并与高斯分布函数进行对比. 结果表明, 高焓非平衡流动和低焓流动的PDF曲线均呈现出倾斜趋势; 两者分布基本一致且均偏离高斯分布的中心位置, 峰值位置约在−0.5处; 高焓算例的峰值略低于低焓算例, 但两者的峰值概率密度略高于高斯分布; 计算结果与文献[34]完全气体模型(Reθ=2300)较为一致. 这说明摩阻脉动的PDF受化学非平衡效应的影响有限. PDF曲线向负方向一侧倾斜, 说明当地低速条带发生的概率较大;
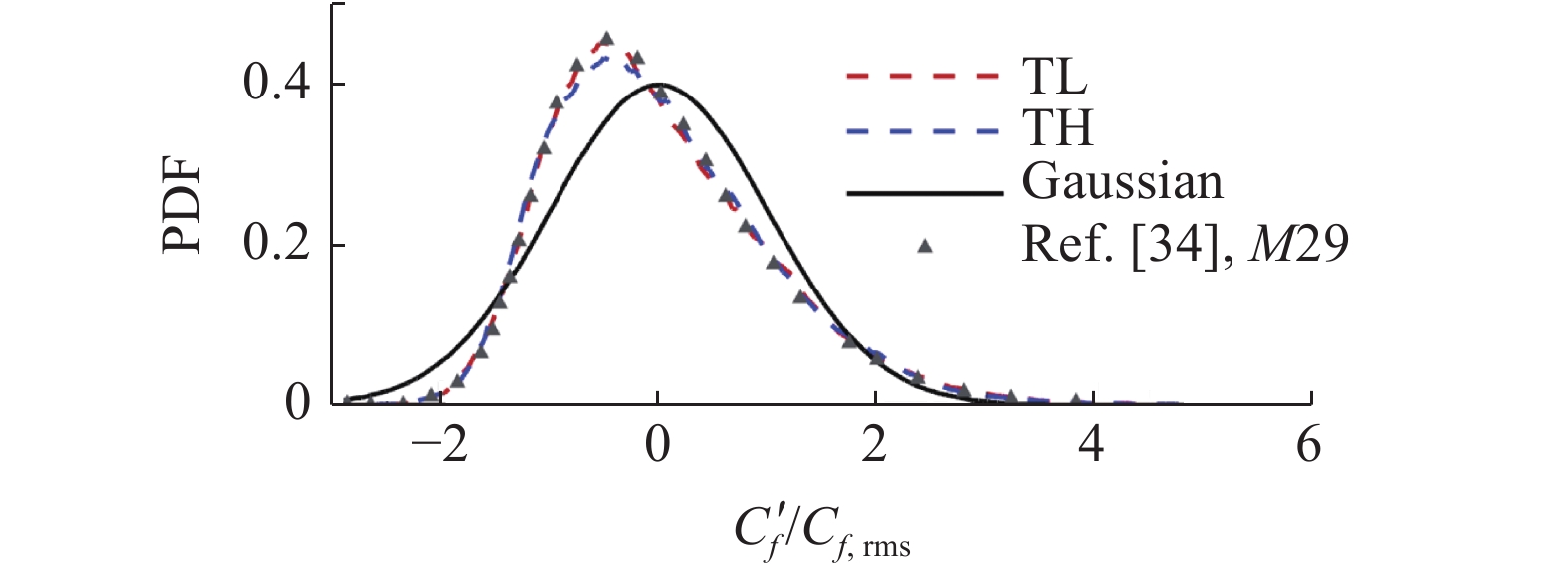
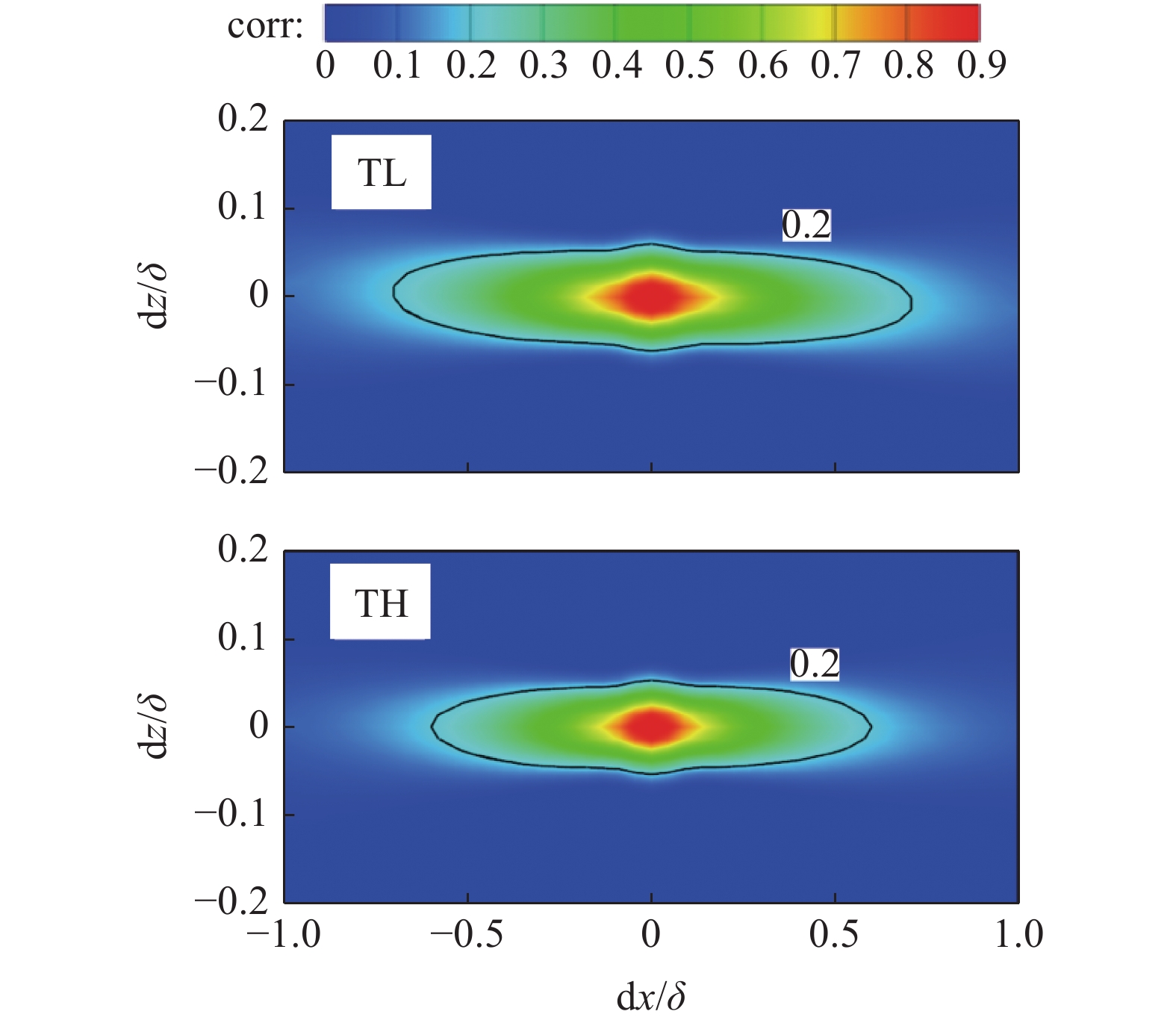
$ C_f' > 0 $ 对应于高速条带流动事件, 且摩阻脉动的幅值达到4左右, 表明高速条带产生的脉动更强.图5的结果表明, 摩阻脉动的高低值条带在尺寸上存在差异. 进一步可以通过摩阻脉动的空间两点相关系数来定量分析高温非平衡效应对摩阻脉动条带尺度的影响. 壁面上相关系数
$ R_{C_f'C_f'}^{XZ} $ 定义为$$ \begin{split} & R_{C_f'C_f'}^{XZ}\left( {{x_0} + \Delta x,{z_0} + \Delta z} \right) =\\ & \qquad \frac{{\overline {C_f'\left( {{x_0},{z_0}} \right)C_f'\left( {{x_0} + \Delta x,{z_0} + \Delta z} \right)} }}{{{{\overline {C{{_f'}^2}\left( {{x_0},{z_0}} \right)} }^{1/2}}{{\overline {C{{_f'}^2}\left( {{x_0} + \Delta x,{z_0} + \Delta z} \right)} }^{1/2}}}} \end{split}$$ (2) $$ {\varLambda _x} = \int_{R_{C_f'C_f' }^{XZ}\left({\Delta x,0} \right)} {{\rm{d}}\Delta x} \text{, } {\varLambda _z} = \int_{R_{C_f'C_f'}^{XZ}\left( {0,\Delta z} \right)} {{\rm{d}}\Delta z} $$ (3) 其中
$ C_f' $ 代表摩阻脉动,$ \Delta x,\Delta z $ 分别代表流场和展向间距,$ \left( {{x_0},{z_0}} \right) $ 在所选流向站位的展向中间位置. 式(3)是指摩阻脉动的空间两点相关系数值等于0.2的流向尺度和展向尺度.图7给出了相关系数的分布云图. 不同焓值下的相关系数均呈现出椭圆形分布, 且流向尺度远大于展向尺度. 高焓流动的分布范围在流向和展向两个方向上均小于低焓流动. 这与图5中瞬时摩阻脉动的条带尺寸一致. 沿两个方向进行长度尺度积分[34], 可以得到定量的尺寸, 具体见式(3). 低焓流动的流向尺度为1.41δ, 展向尺度为0.12δ; 高焓流动的流向尺度为1.20δ, 展向尺度为0.11δ. 可见高焓算例的流向尺度减小了14.9%, 展向尺度减小了8.3%.
![]()
图 7 壁面摩阻脉动两点相关系数空间分布Figure 7. Maps of two-point correlation coefficient$ R_{C_f'C_f'}^{XZ} $ on the wall进一步, 采用壁面黏性尺度δv进行对比. 低焓流动的流向尺度为1130.6δv, 展向尺度为96.0δv; 高焓流动的流向尺度为993.5δv, 展向尺度为95.5δv. 可见高焓算例的流向尺度减小了12.1%, 展向尺寸基本一致.
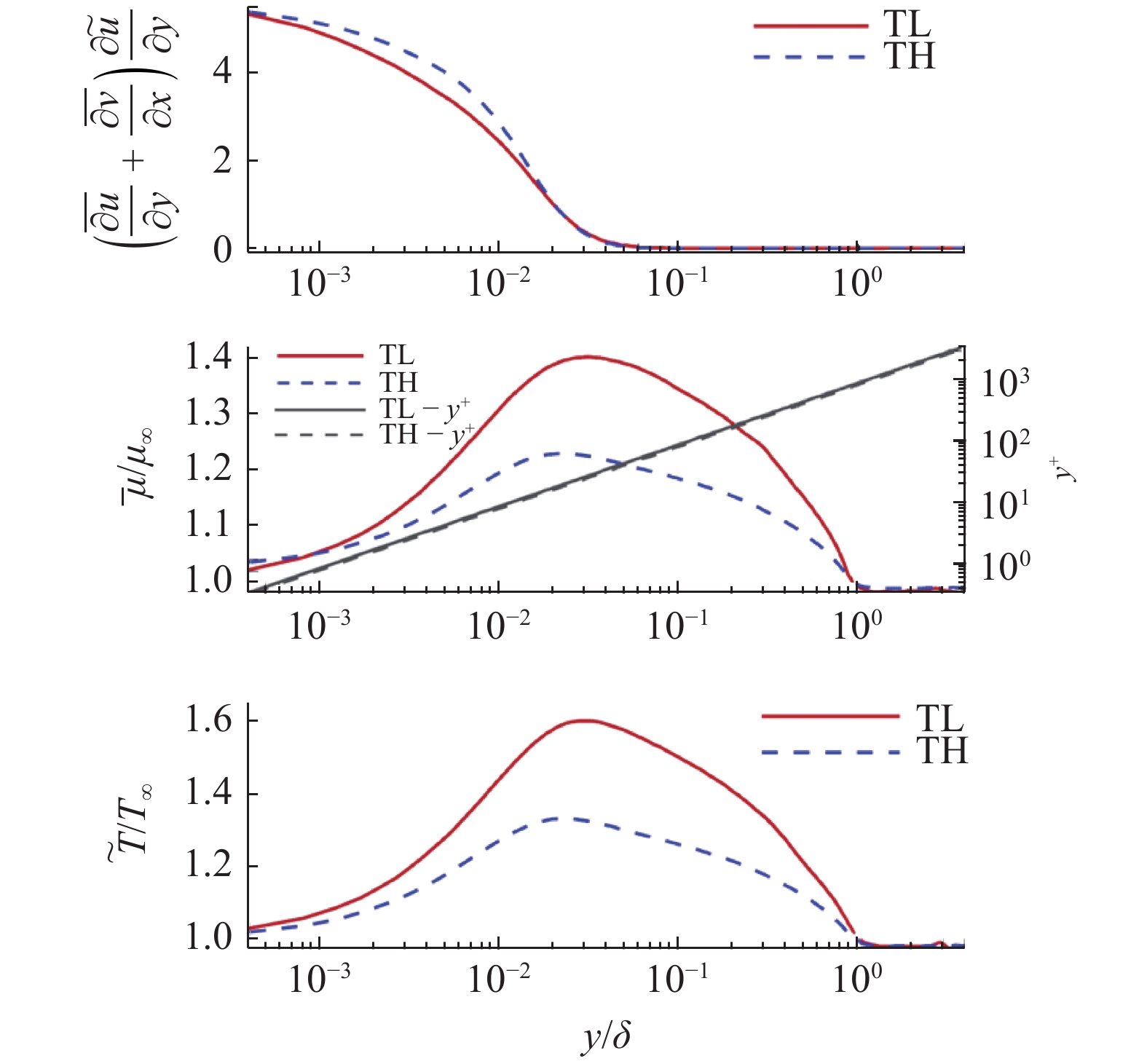
高焓条件下摩阻条带结构尺度减小的原因可能来自于高温非平衡效应. 热力学量的脉动引起局部流向速度梯度增大, 如图3中所示
$ {{\partial \bar u_{VD}^ + } \mathord{\left/ {\vphantom {{\partial \bar u_{VD}^ + } {\partial {y^ + }}}} \right. } {\partial {y^ + }}} $ 在缓冲区较高, 条带结构的能量更高. 相较低焓流动, 输运相同能量, 高焓边界层条带结构更小. 具体原因还需要进一步验证.2.3 湍流边界层摩阻分解
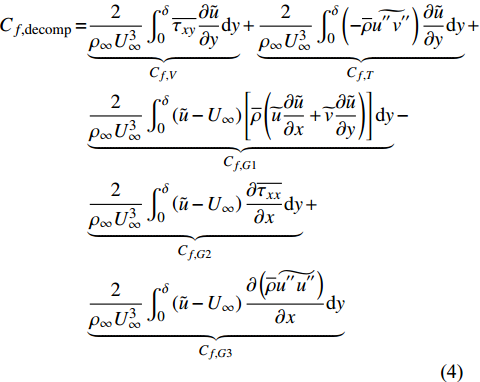
研究摩阻的产生机理以及与之相关的近壁区动力学过程, 对于基础研究和工程实际都有重要意义, 可以为减阻方法的设计提供指导. 对于可压缩壁湍流, 假设展向均匀, 可将壁面摩阻写成如下分解积分关系式[22]
$$\begin{split} {C_{f,{\rm{decomp}}}} = & \underbrace {\frac{2}{{{\rho _\infty }U_\infty ^3}}\int_0^\delta {\overline {{\tau _{xy}}} } \frac{{\partial \tilde u}}{{\partial y}}{\rm{d}}y}_{{C_{f,V}}} + \underbrace {\frac{2}{{{\rho _\infty }U_\infty ^3}}\int_0^\delta {\left( { - \overline \rho \widetilde {{u^{''}}{v^{''}}}} \right)\frac{{\partial \tilde u}}{{\partial y}}{\rm{d}}y} }_{{C_{f,T}}} + \\ & \underbrace {\frac{2}{{{\rho _\infty }U_\infty ^3}}\int_0^\delta {\left( {\tilde u - {U_\infty }} \right)\left[ {\overline \rho \left( {\widetilde u\frac{{\partial \tilde u}}{{\partial x}} + \widetilde v\frac{{\partial \tilde u}}{{\partial y}}} \right)} \right]{\rm{d}}y} }_{{C_{f,G1}}} - \\ & \underbrace {\frac{2}{{{\rho _\infty }U_\infty ^3}}\int_0^\delta {\left( {\tilde u - {U_\infty }} \right) {\frac{{\partial \overline {{\tau _{xx}}} }}{{\partial x}}} {\rm{d}}y} }_{{C_{f,G2}}} + \\ & \underbrace {\frac{2}{{{\rho _\infty }U_\infty ^3}}\int_0^\delta {\left( {\tilde u - {U_\infty }} \right) {\frac{{\partial \left( {\overline \rho \widetilde {{u^{''}}{u^{''}}}} \right)}}{{\partial x}}} {\rm{d}}y} }_{{C_{f,G3}}} \end{split} $$ (4) 其中
$ {\rho _\infty } $ 和$ {U_\infty } $ 分别为来流的密度和速度, 本算例中分别等于$ {\rho _e} $ 和$ {U_e} $ .$ {C_{f,V}} $ 代表分子黏性耗散项;$ {C_{f,T}} $ 代表湍动能生成项;$ {C_{f,G1}} $ 表示平均流向动能的变化项;$ {C_{f,G2}} $ 表示流向黏性正应力不均匀性项,$ {C_{f,G3}} $ 表示流向雷诺正应力不均匀性项, 两者合起来称为流向不均匀项. 其中${\tau }_{xx}=\mu \left(2\dfrac{\partial u}{\partial x}-\dfrac{2}{3}\nabla \cdot {V}\right),{\tau }_{xy}=\mu \left(\dfrac{\partial u}{\partial y} + \dfrac{\partial v}{\partial x}\right)$ .在对湍流边界层摩阻空间分布分析的基础上, 本节继续采用摩阻分解式(4)来分析边界层中摩阻生成机制. 表3比较了采用摩阻分解技术得到的摩阻平均值(Cf,decomp)、直接采用时间平均得到的摩阻值(Cf,avg)以及两者之间的相对误差. 相对误差的定义为error=(Cf,decomp−Cf,avg)/ Cf,avg. 结果显示, 本文实现的摩阻分解具有较高的精度, 相对误差均在1.5%以下.
表 3 摩阻分解公式相对误差Table 3. Relative error of decomposition formulaCase Cf,decomp Cf,avg error/% TH 2.19×10−3 2.16×10−3 1.4 TL 1.99×10−3 2.01×10−3 −0.98 表4给出了式(4)中不同流动和输运过程对摩阻产生的贡献比例. 可以看出, 分子黏性耗散项(
$ {C_{f,V}} $ )和湍动能生成项($ {C_{f,T}} $ )所占比例最大, 基本上在40%以上; 其次是平均流向动能的变化项($ {C_{f,G1}} $ ), 比例在10%; 流向黏性正应力不均匀性项($ {C_{f,G2}} $ )和流向雷诺正应力不均匀性项($ {C_{f,G3}} $ )占比很小, 基本上可以忽略. 对比不同焓值算例可以发现, 高焓值情况下,$ {C_{f,V}} $ 和$ {C_{f,T}} $ 的占比略有下降, 减少的这部分贡献基本上由$ {C_{f,G1}} $ 补上. 摩阻分解分析表明, 湍流边界层中对摩阻生成起主要作用的流动过程是$ {C_{f,V}} $ 和$ {C_{f,T}} $ . 下面将进一步分析两者产生的原因以及高低焓值边界层摩阻产生差异的原因.表 4 摩阻分解公式中各项贡献Table 4. Contributions of different terms to skin frictionTerm TH TL Cf,V/ Cf,decomp 0.397 0.415 Cf,T / Cf,decomp 0.464 0.482 Cf,G1 / Cf,decomp 0.142 0.097 Cf,G2/ Cf,decomp −3.3×10−5 −5.7×10−5 Cf,G3 / Cf,decomp −0.003 0.006 Cf,V,m/ Cf,decomp 0.394 0.410 Cf,V,f/ Cf,decomp 0.003 0.006 2.4 分子黏性耗散项对壁面摩阻的贡献分析
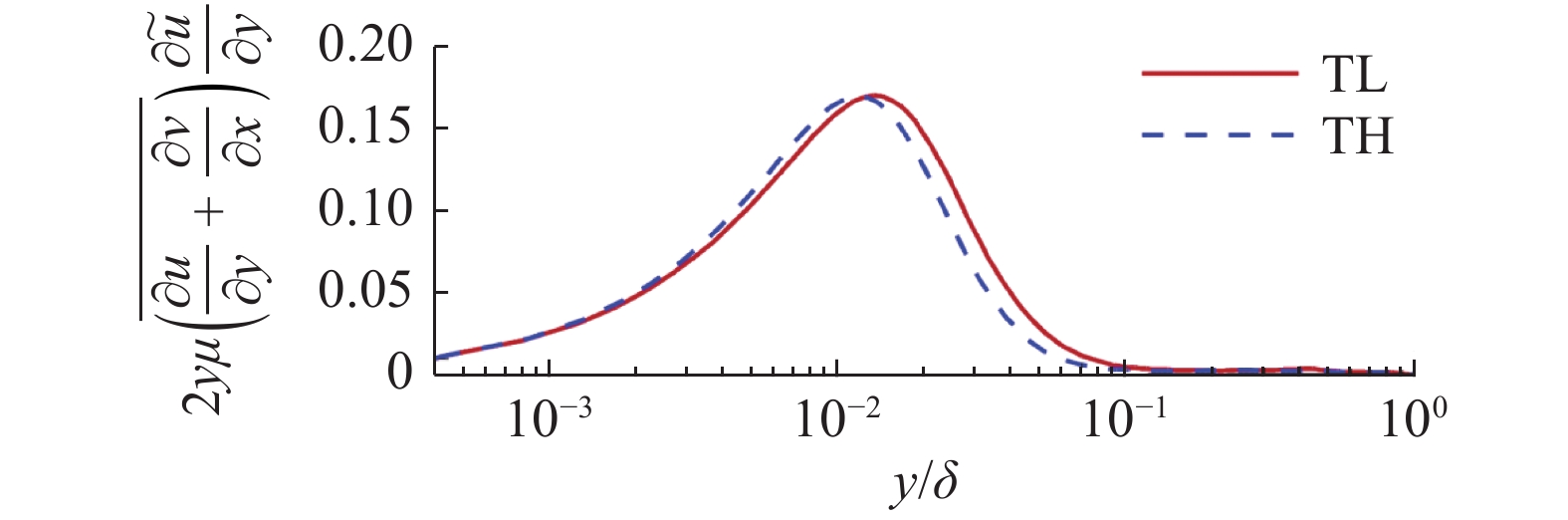
分子黏性耗散过程是壁面摩阻产生的主要流动过程之一. 图8给出了分子黏性耗散项预乘积分函数沿法向的分布. 两算例的分布趋势较为一致, 约在
$ y \approx 0.015\delta $ ($ {y^ + } \approx 10 $ )处达到峰值. 且分子黏性耗散项的主要作用区域在$ y \leqslant 0.1\delta $ ($ {y^ + } \leqslant 30 $ )的近壁区, 而在外区基本没有贡献. 这与文献中基于槽道、平板湍流[21-22]的分析结果一致. 高焓会使得$ y < 0.015\delta $ 以内的近壁区分子黏性耗散略大于低焓流动; 而在$ y > 0.015\delta $ 的区域中略小于低焓流动.进一步可以将分子黏性耗散项分解为平均部分
$ {C_{f,V,m}} $ 和脉动部分$ {C_{f,V,f}} $ [21]$$ \begin{split} {C_{f,V}} = & \underbrace {\frac{2}{{{\rho _\infty }U_\infty ^3}}\int_0^\infty {\bar \mu \left( {\frac{{\partial \bar u}}{{\partial y}} + \frac{{\partial \bar v}}{{\partial x}}} \right)\frac{{\partial \tilde u}}{{\partial y}}{\rm{d}}y} }_{{C_{f,V,m}}}+ \\ &\underbrace {\int_0^\infty {\left( {\overline {\mu '\frac{{\partial u'}}{{\partial y}} + \mu '\frac{{\partial v'}}{{\partial x}}} } \right)\frac{{\partial \tilde u}}{{\partial y}}{\rm{d}}y} }_{{C_{f,V,f}}} \end{split} $$ (5) 表4中给出了两部分的占比. 可以发现,
$ {C_{f,V,m}} $ 占据了分子黏性耗散项的绝大部分, 占比高达95%以上. 这就说明焓值对分子黏性耗散项的影响主要通过$ {C_{f,V,m}} $ 项体现.将
$ {C_{f,V,m}} $ 的积分函数分为两部分:$\left( {\dfrac{{\partial \bar u}}{{\partial y}} + \dfrac{{\partial \bar v}}{{\partial x}}} \right)\dfrac{{\partial \tilde u}}{{\partial y}}$ 和$ \bar \mu $ , 分别体现了流动特性和热力学特性的作用. 图9给出了两者沿壁面法向的分布, 并给出了温度的分布, 均采用无穷远处参数作为无量纲参考值. 从流动特性可以看出, 高焓使得近壁区($ y < 0.015\delta $ )的$\partial u/\partial y$ 增大(${\partial v}/{\partial x}$ 较小, 影响可以忽略); 而对外区的流动特性影响很小. 从热力学特性可以看出, 高焓对整个边界层内的黏性系数都有较大影响, 基本上均低于低焓算例的黏性系数. 黏性系数主要受到温度的影响, 两者的分布具有明显的一致性. 当高焓时, 边界层内发生空气化学非平衡过程, 离解反应会吸收一部分热量, 使得高焓边界层内的黏性系数低于低焓边界层. 综合流动特性和热力学特性的分布, 可以发现, 在$ y < 0.015\delta $ 时, 流动特性起到主导作用, 导致高焓流动黏性耗散项贡献略大于低焓流动; 而在$ y > 0.015\delta $ 时, 热力学特性起到主要作用, 导致低焓流动黏性耗散项贡献略大于高焓流动.![]()
图 9$ {C_{f,V,m}} $ 积分函数分解及温度分布Figure 9. Integrand parts of$ {C_{f,V,m}} $ and the temperature distribution2.5 湍动能生成项对壁面摩阻的贡献分析
湍动能生成项是壁面摩阻产生的另一个重要部分. 图10给出了湍动能生成项预乘积分函数沿法向的分布. 两算例的分布趋势较为一致; 但低焓流动时, 峰值位置更加远离壁面. 结合图4中雷诺应力分布基本一致的情况来看, 峰值位置的外移应该来自于
$ {{\partial \tilde u} \mathord{\left/ {\vphantom {{\partial \tilde u} {\partial y}}} \right. } {\partial y}} $ 的分布不同; 结合图9来看, 高焓流动在预乘积分函数附近的$ {{\partial \tilde u} \mathord{\left/ {\vphantom {{\partial \tilde u} {\partial y}}} \right. } {\partial y}} $ 要大于低焓流动. 两算例在边界层外区均出现了二次峰值, 这与较高雷诺数下的槽道流动[21]一致. 二次峰值的产生是由于较高雷诺数下, 边界层外区存在大尺度湍流运动导致. 大尺度湍流运动会引起外区产生大量湍动能, 从而通过摩阻的湍动能生成项影响摩阻; 且外区大尺度湍流流动对内区小尺度湍流运动具有调制作用, 促发湍动能在内外区的重新分配[35].为了进一步分析湍动能生成项中起主导作用的流动事件, 本节采用象限分析技术[36-37]将边界层中的主导流动事件与摩阻分解相结合以分析不同流动事件对摩阻中湍动能生成项的影响.
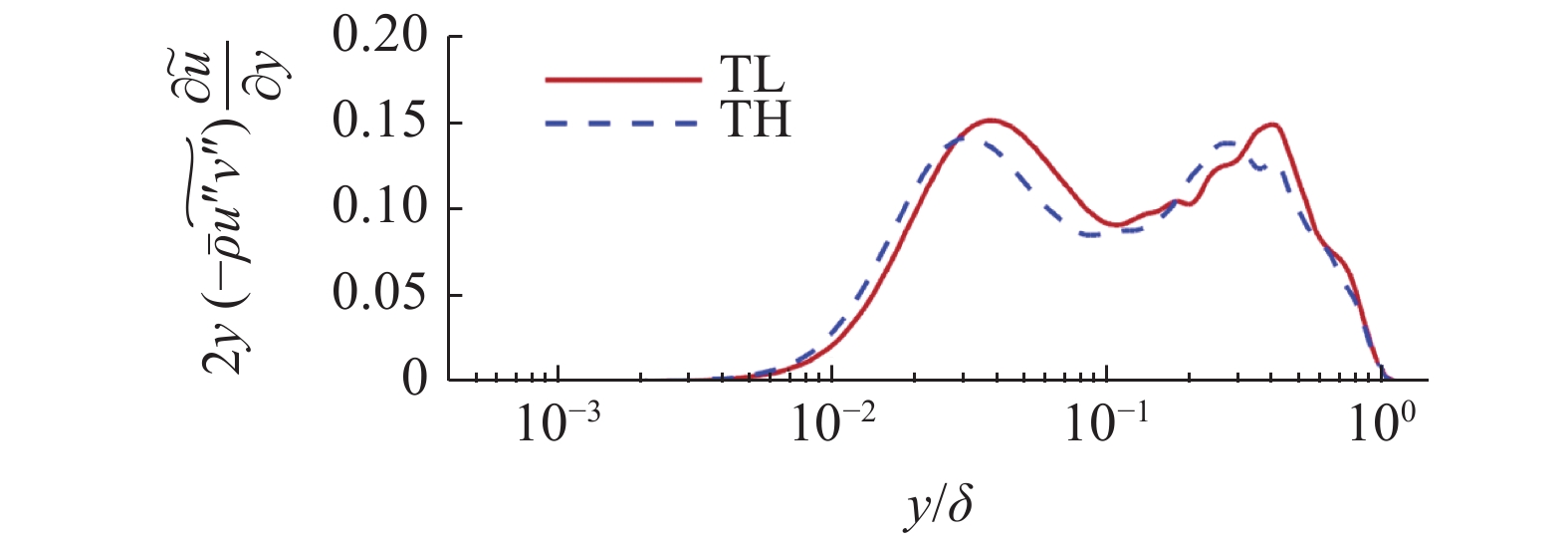
在边界层中, 可以按照脉动的正负将流向速度脉动和法向速度脉动分解到4个象限中. 第1象限:
$ u'' > 0,v'' > 0 $ 表示外向运动(outward motion); 第2象限:$ u'' < 0,v'' > 0 $ 表示上抛运动; 第3象限:$ u'' < 0, $ $ v'' < 0 $ 表示内向运动(inward motion); 第4象限:$ u'' > 0,v'' < 0 $ 表示下扫运动. 图11给出了Q1~Q4事件在边界层内发生的概率. 不同焓值下不同事件的概率分布曲线是相似的. Q2和Q4发生的概率显著大于Q1和Q3.图12中给出了不同事件对应的雷诺应力与总雷诺切应力的比值. 可以看出, 不同焓值的比值曲线很好的重合在一起, 说明该比值对焓值变化不敏感; Q2和Q4事件是雷诺切应力的主要贡献项, 并且在
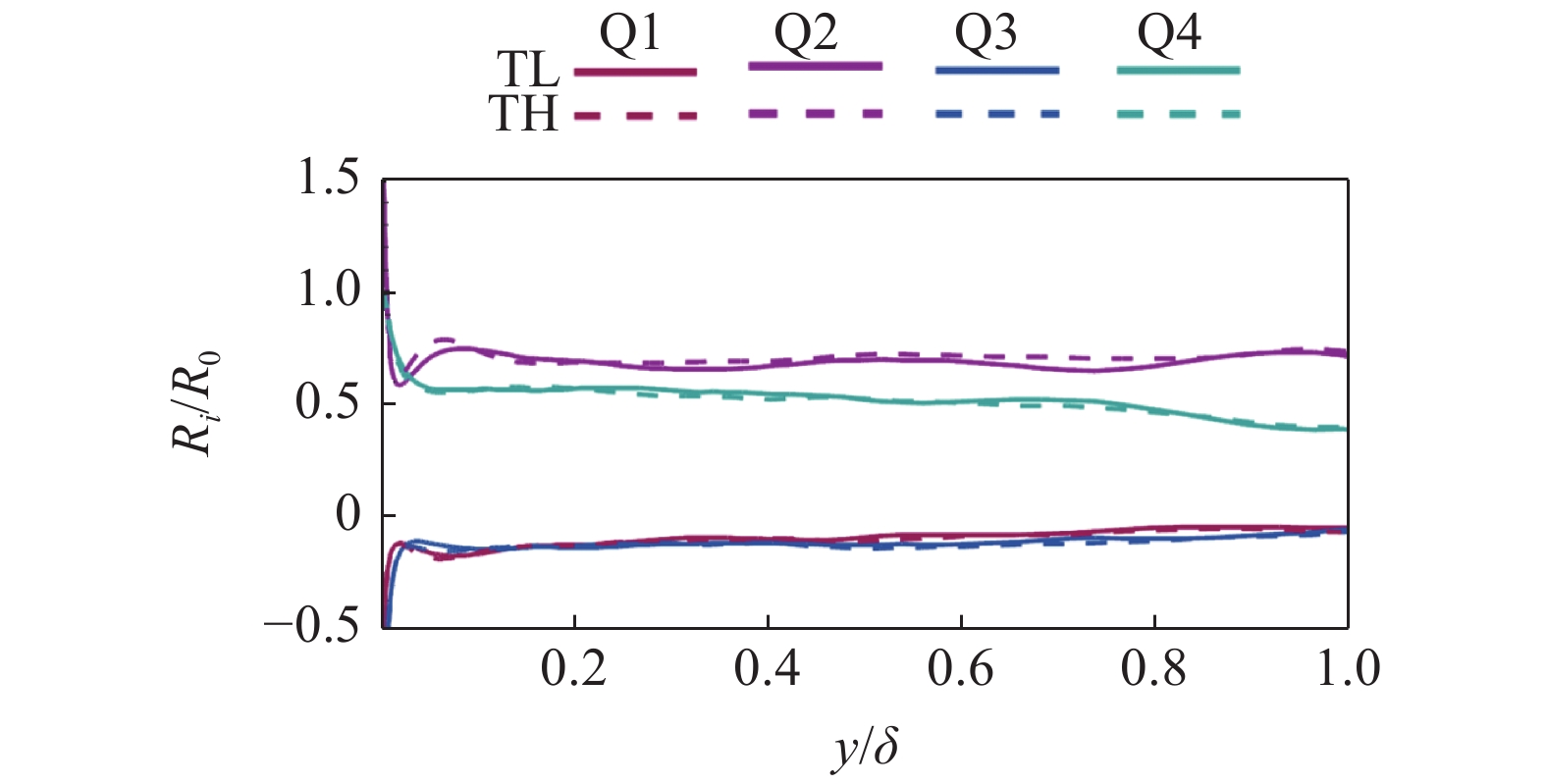
$ y \approx 0.03\delta $ 以内, Q4事件的比值要大于Q2事件; 在$ y \approx 0.03\delta $ 以外, Q2事件的比值大于Q4事件, 且这一趋势会在整个边界层范围内得到保持.![]()
图 12 Q1~Q4事件对湍动能生成项的贡献Figure 12. Contributions of Q1~Q4 events to TKE production terms表5定量给出了不同事件的湍动能生成项贡献的摩阻与整体摩阻的比值, 表中以
$ {C_{f,T,{\rm{Q}}i}} $ 表示Qi事件对湍动能生成项的贡献. 可以看出, Q2和Q4事件起到绝对主导作用, 且Q2贡献要略大于Q4事件, 这与图12中所指出的Q2对雷诺应力的贡献大于Q4一致. 且Q1和Q3对壁面摩阻的贡献为负, 两者的值基本相同, 且都远小于Q2和Q4.表 5 Q1~Q4湍流生成项对壁面摩阻的贡献Table 5. Contributions of TKE production terms produced by Q1~Q4 to the time-averaged value$\dfrac{ { {C_{f,T} } } }{ { {C_{f,{\rm{decomp}}} } } }$ $\dfrac{ { {C_{f,T,{\rm{Q}}1} } } }{ { {C_{f,{\rm{decomp}}} } } }$ $\dfrac{ { {C_{f,T,{\rm{Q}}2} } } }{ { {C_{f,{\rm{decomp}}} } } }$ $\dfrac{ { {C_{f,T,{\rm{Q}}3} } } }{ { {C_{f,{\rm{decomp}}} } } }$ $\dfrac{ { {C_{f,T,{\rm{Q}}4} } } }{ { {C_{f,{\rm{decomp}}} } } }$ TH 0.464 −0.006 0.326 −0.007 0.271 TL 0.482 −0.006 0.330 −0.007 0.285 图13给出了不同事件的被积函数沿法向的分布, 以考察主要起作用的边界层区域范围. 可以看出, 不同焓值下, 被积函数的曲线分布趋势都是相似的, 高焓效应仅会稍微改变幅值; Q4事件的峰值位置要比Q2事件更为靠内; Q1和Q3在整个边界层范围内的值都是负值.
![]()
图 13 Q1~Q4湍流生成项预乘积分函数Figure 13. Pre-multiplied integrand of TKE production terms produced by Q1~Q43. 结 论
本文通过采用直接数值模拟方法, 研究了高焓湍流边界层壁面摩阻产生机制, 并通过设置同等边界层参数下的低焓算例, 对比分析了高温化学非平衡效应对摩阻产生的影响, 可以得到以下结论.
(1)不同焓值下的摩阻脉动条带尺寸存在差异. 高焓流动的条带尺寸在流向和展向两个方向上均小于低焓流动.
(2)湍流边界层中对摩阻生成起主要作用的流动过程是分子黏性耗散项
$ {C_{f,V}} $ 和湍动能生成项$ {C_{f,T}} $ .(3)分子黏性耗散项
$ {C_{f,V}} $ 的主要作用区域在$ y \leqslant 0.1\delta $ 的近壁区. 焓值的影响主要通过$ {C_{f,V}} $ 的平均部分$ {C_{f,V,m}} $ 项体现. 且在$ y < 0.015\delta $ 时, 流动特性(速度梯度)起到主导作用, 导致高焓流动$ {C_{f,V,m}} $ 略大于低焓流动; 而在$ y > 0.015\delta $ 时, 热力学特性(黏性系数)起到主要作用, 导致低焓流动$ {C_{f,V,m}} $ 略大于高焓流动.(4)边界层中的上抛和下扫运动是影响摩阻分解湍动能生成项
$ {C_{f,T}} $ 的主导事件, 外向运动和内向运动对$ {C_{f,T}} $ 的影响很小, 且起到负贡献. -
![]()
图 7 壁面摩阻脉动两点相关系数空间分布
Figure 7. Maps of two-point correlation coefficient
$ R_{C_f'C_f'}^{XZ} $ on the wall![]()
图 9
$ {C_{f,V,m}} $ 积分函数分解及温度分布Figure 9. Integrand parts of
$ {C_{f,V,m}} $ and the temperature distribution![]()
图 12 Q1~Q4事件对湍动能生成项的贡献
Figure 12. Contributions of Q1~Q4 events to TKE production terms
![]()
图 13 Q1~Q4湍流生成项预乘积分函数
Figure 13. Pre-multiplied integrand of TKE production terms produced by Q1~Q4
表 1 来流状态及壁温设置
Table 1 Inflow condition and wall temperature
Case Me ρe/(kg·m−3) Te/K Tw/K Tw/ Taw TH 4.5 0.1025 3400 3400 0.206 TL 4.5 0.1025 300 300 0.215 Note: the recovery temperature ${T_{aw} } = {T_e}\left[ {1 + 0.9 \times \dfrac{ {\left( {\gamma - 1} \right)} }{2}M_e^2} \right]$ 
下载: 导出CSV
表 2 边界层厚度、雷诺数和网格尺度
Table 2 Thickness, Reynold number and grid resolution
Case Reθ Reτ Reδ2 θ/mm δ/mm ∆x + ∆y2 + ∆z + TH 2451.1 802.5 2396.8 0.452 4.793 18.6 0.34 5.6 TL 2483.7 868.3 2483.7 0.458 4.975 19.3 0.35 5.8 Note: θ is momentum thickness, the different types of Reynolds number are defined as$ {{Re} _\theta } = {{{\rho _\delta }{u_\delta }\theta } \mathord{\left/ {\vphantom {{{\rho _\delta }{u_\delta }\theta } {{\mu _\delta }}}} \right. } {{\mu _\delta }}} $, $ {{Re} _\tau } = {{{\rho _w}{u_\tau }\delta } \mathord{\left/ {\vphantom {{{\rho _w}{u_\tau }\delta } {{\mu _w}}}} \right. } {{\mu _w}}} $, $ {{Re} _{\delta 2}} = {{{\rho _\delta }{u_\delta }\theta } \mathord{\left/ {\vphantom {{{\rho _\delta }{u_\delta }\theta } {{\mu _w}}}} \right. } {{\mu _w}}} $
下载: 导出CSV
表 3 摩阻分解公式相对误差
Table 3 Relative error of decomposition formula
Case Cf,decomp Cf,avg error/% TH 2.19×10−3 2.16×10−3 1.4 TL 1.99×10−3 2.01×10−3 −0.98
下载: 导出CSV
表 4 摩阻分解公式中各项贡献
Table 4 Contributions of different terms to skin friction
Term TH TL Cf,V/ Cf,decomp 0.397 0.415 Cf,T / Cf,decomp 0.464 0.482 Cf,G1 / Cf,decomp 0.142 0.097 Cf,G2/ Cf,decomp −3.3×10−5 −5.7×10−5 Cf,G3 / Cf,decomp −0.003 0.006 Cf,V,m/ Cf,decomp 0.394 0.410 Cf,V,f/ Cf,decomp 0.003 0.006
下载: 导出CSV
表 5 Q1~Q4湍流生成项对壁面摩阻的贡献
Table 5 Contributions of TKE production terms produced by Q1~Q4 to the time-averaged value
$\dfrac{ { {C_{f,T} } } }{ { {C_{f,{\rm{decomp}}} } } }$ $\dfrac{ { {C_{f,T,{\rm{Q}}1} } } }{ { {C_{f,{\rm{decomp}}} } } }$ $\dfrac{ { {C_{f,T,{\rm{Q}}2} } } }{ { {C_{f,{\rm{decomp}}} } } }$ $\dfrac{ { {C_{f,T,{\rm{Q}}3} } } }{ { {C_{f,{\rm{decomp}}} } } }$ $\dfrac{ { {C_{f,T,{\rm{Q}}4} } } }{ { {C_{f,{\rm{decomp}}} } } }$ TH 0.464 −0.006 0.326 −0.007 0.271 TL 0.482 −0.006 0.330 −0.007 0.285
下载: 导出CSV
-
[1] Candler GV. Rate effects in hypersonic flows. Annual Review of Fluid Mechanics, 2019, 51: 379-402 doi: 10.1146/annurev-fluid-010518-040258
[2] Wright R, Zoby E. Flight boundary layer transition measurements on a slender cone at Mach 20. AIAA Paper, No. 77-719, 1977
[3] Duan L, Martin MP. Direct numerical simulation of hypersonic turbulent boundary layers. Part 4: Effect of high enthalpy. Journal of Fluid Mechanics, 2011, 684: 25-59
[4] Duan L, Martin MP. Assessment of turbulence–chemistry interaction in hypersonic turbulent boundary layers. AIAA Journal, 2011, 49(1): 172-184 doi: 10.2514/1.J050605
[5] Kim P. Non-equilibrium effects on hypersonic turbulent boundary layers. [PhD Thesis]. Los Angeles: University of California, 2016
[6] 刘朋欣, 袁先旭, 孙东等. 高温化学非平衡湍流边界层直接数值模拟. 航空学报, 2020, doi: 10.7527/S1000-6893.24877 Liu Pengxin, Yuan Xianxu, Sun Dong, et al. DNS of high-temperature turbulent boundary layer with chemical nonequilibrium. Acta Aeronautica et Astronautica Sinica, 2020, doi: 10.7527/S1000-6893.24877 (in Chinese)
[7] 刘朋欣, 李辰, 孙东等. 高温化学非平衡湍流边界层统计特性分析. 空气动力学报, 2021, doi: 10.7638/kqdlxxb-2020.0178 Liu Pengxin, Li Chen, Sun Dong, et al. Statistical properties of high-temperature turbulent boundary layer including chemical nonequilibrium. Acta Aerodynamica Sinica, 2021, doi: 10.7638/kqdlxxb-2020.0178 (in Chinese)
[8] 吴正园, 莫凡, 高振勋等. 湍流边界层与高温气体效应耦合的直接数值模拟. 空气动力学报, 2020, 38(6): 1111-1119 (Wu Zhengyuan, Mo Fan, Gao Zhenxun, et al. Direct numerical simulation of turbulent and high-temperature gas effect coupled flow. Acta Aerodynamica Sinica, 2020, 38(6): 1111-1119 (in Chinese) [9] Renzo MD, Urzay J. Direct numerical simulation of a hypersonic transitional boundary layer at suborbital enthalpies. Journal of Fluid Mechanics, 2021, 912: A29 doi: 10.1017/jfm.2020.1144
[10] Urazay J, Renzo MD. Engineering aspects of hypersonic turbulent flows at suborbital enthalpies. In: Annual Research Briefs, Center for Turbulence Research, Stanford University, 2021: 7-32
[11] Passiatore D, Sciacovelli L, Cinnella P, et al. Finite-rate chemistry effects in turbulent hypersonic boundary layers: a direct numerical simulation study. Physical Review Fluids, 2021, 6: 054604 doi: 10.1103/PhysRevFluids.6.054604
[12] Volpiani PS. Numerical strategy to perform direct numerical simulations of hypersonic shock/boundary-layer interaction in chemical nonequilibrium. Shock Waves, 2021, 31: 361-378 doi: 10.1007/s00193-021-01018-6
[13] Fukagata K, Iwamoto K, Kasagi N. Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Physics of Fluids, 2002, 14(11): 73-76 doi: 10.1063/1.1516779
[14] Renard N, Deck S. A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer. Journal of Fluid Mechanics, 2016, 790: 339-367 doi: 10.1017/jfm.2016.12
[15] Mehdi F, White CM. Integral form of the skin friction coefficient suitable for experimental data. Experiments in Fluids, 2011, 50(1): 43-51 doi: 10.1007/s00348-010-0893-1
[16] Mehdi F, Johansson TG, White CM, et al. On determining wall shear stress in spatially developing two-dimensional wall-bounded flows. Experiments in Fluids, 2014, 50(1): 1656
[17] Modesti D, Priozzoli S, Orlandi P, et al. On the role of secondary motions in turbulent square duct flow. Journal of Fluid Mechanics, 2018, 847: 11-111
[18] Yoon M, Ahn J, Hwang J, et al. Contribution of velocity-vorticity correlations to the frictional drag in wall-bounded turbulent flows. Physics of Fluids, 2016, 28(8): 081702 doi: 10.1063/1.4961331
[19] Hwang J, Sung HJ. Influence of large-scale motions on the frictional drag in a turbulent boundary layer. Journal of Fluid Mechanics, 2017, 829: 751-779 doi: 10.1017/jfm.2017.579
[20] Kim JS, Hwang J, Yoon M, et al. Influence of a large-eddy breakup device on the frictional drag in a turbulent boundary layer. Physics of Fluids, 2017, 29(6): 065103 doi: 10.1063/1.4984602
[21] Li WP, Fan YT, Modesti D, et al. Decomposition of the mean skin-friction drag in compressible turbulent channel flows. Journal of Fluid Mechanics, 2019, 875: 101-123 doi: 10.1017/jfm.2019.499
[22] Fan YT, Li WP, Priozzoli S. Decomposition of the mean friction drag in zero-pressure-gradient turbulent boundary layers. Physics of Fluids, 2019, 31: 086105 doi: 10.1063/1.5111009
[23] Li Q, Liu PX, Zhang HX. Further investigations on the interface instability between fresh injections and burnt products in 2-D rotating detonation. Computers and Fluids, 2018, 170: 261-272 doi: 10.1016/j.compfluid.2018.05.005
[24] Sun D, Guo QL, Li C, et al. Assessment of optimized symmetric fourth-order weighted essentially non-oscillatory scheme in direct numerical simulation of compressible turbulence. Computers and Fluids, 2020, 197: 104383 doi: 10.1016/j.compfluid.2019.104383
[25] Sun D, Guo QL, Yuna XX, et al. Decomposition formula for the wall heat flux of a compressible boundary layer. Advances in Aerodynamics, 2021, 3: 33
[26] Sun D, Guo QL, Yuan XX, et al. Direct numerical simulation of effects of a micro-ramp on a hypersonic shock wave/boundary layer interaction. Physics of Fluids, 2019, 31(12): 126101 doi: 10.1063/1.5123453
[27] Sun D, Chen JQ, Li C, et al. On the wake structure of a micro-ramp vortex generator in hypersonic flow. Physics of Fluids, 2020, 32(12): 126111 doi: 10.1063/5.0030975
[28] Liu PX, Guo QL, Sun D, et al. Wall effect on the flow structures of three-dimensional rotating detonation wave. International Journal of Hydrogen Energy, 2020, 45(53): 29546-29559 doi: 10.1016/j.ijhydene.2020.07.196
[29] Castro M, Costa B, Don WS. High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws. Journal of Computational Physics, 2011, 230: 1766-1792 doi: 10.1016/j.jcp.2010.11.028
[30] Gupta RN, Yos JM, Thomson RA, et al. A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30000 K. NASA RP-1232, 1990
[31] Menter FR. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal, 1994, 32(8): 1598-1605 doi: 10.2514/3.12149
[32] Adler MC, Gonzalez DR, Stack CM, et al. Synthetic generation of equilibrium boundary layer turbulence from modeled statistics. Computers and Fluids, 2018, 165: 127-143 doi: 10.1016/j.compfluid.2018.01.003
[33] Prozzoli S, Bernardini M, Grasso F. Characterization of coherent vortical structures in a supersonic turbulent boundary layer. Journal of Fluid Mechanics, 2008, 613: 2005-2031
[34] Tong FL, Chen JQ, Sun D, et al. Wall-shear stress fluctuations in a supersonic turbulent boundary layer over an expansion corner, Journal of Turbulence, 2020, 21(7): 1-20
[35] Hutchins N, Marusic I. Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. Journal of Fluid Mechanics, 2007, 579: 1-28 doi: 10.1017/S0022112006003946
[36] Lu SS, Willmarth WW. Measurements of the structure of the Reynolds stress in a turbulent boundary layer. Journal of Fluid Mechanics, 1973, 60: 481-511
[37] Tichenor NR, Humble RA, Bowersox RDW. Response of a hypersonic turbulent boundary layer to favorable pressure gradients. Journal of Fluid Mechanics, 2013, 722: 187-213
计量
- 文章访问数: 828
- HTML全文浏览量: 254
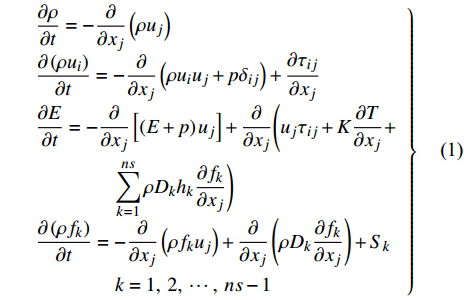
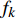
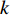
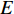
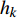
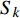
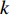
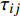
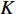
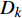
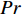
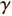
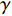
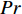
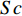
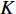
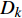
- PDF下载量: 188
