KEY MECHANICS ISSUES IN THE ANALYSIS, DESIGN, AND EVALUATION OF REUSABLE THERMAL STRUCTURES OF FIBER-REINFORCED CERAMIC MATRIX COMPOSITES
-
摘要: 新一代空天往返飞行器在全寿命周期内经历多次飞行-再入过程, 在此过程中经受严苛的气动热/力/振动等多物理耦合载荷作用, 在此类极端瞬态热力耦合载荷作用下纤维增强陶瓷基复合材料(ceramic matrix composites, CMC)热结构的力学行为及损伤失效机制亟需明晰. 本文从多物理场耦合视角揭示了CMC热结构在循环服役环境中的损伤演化机理, 辨识出瞬态热机械载荷是材料结构在重复使用条件下性能退化的主控因素之一, 构建了一套完整的高温瞬态大温度温度梯度下热机械诱导裂纹的预测与分析框架. 通过建立热传导-力学响应耦合模型, 实现了材料内部温度场、应力场及裂纹能量释放率(ERR)时空演化的定量表征. 研究表明, 瞬态热载荷导致的非均匀温度梯度是诱发亚表层应力状态反转(拉压转换)的核心诱因, 其与材料微结构相互作用使得最大ERR出现于迎风面侧的亚表面区域, 且弯曲约束条件可使ERR峰值提升至无约束工况的2倍. 基于参数化分析, 提出了以低ERR为指标的可重复设计准则, 明确了梯度模量化、高导热、低热膨胀和薄壁化为CMC热结构的优化方向. 通过自主搭建的1500 °C/1.5 kN级力热联合试验平台, 验证了C/SiC机翼前缘热结构在10次以上的循环加载后仍保持结构完整性, 无损检测未发现界面脱黏或基体裂纹. 本研究为可重复使用CMC热结构的材料/结构协同优化设计和损伤容限设计提供了理论-实验协同的创新方法论, 对突破高超声速飞行器热防护系统设计瓶颈具有重要工程意义.
-
关键词:
- 可重复使用高超声速飞行器 /
- 陶瓷基复合材料 /
- 能量释放率 /
- 大温度梯度 /
- 高温瞬态效应
Abstract: The next-generation reusable space vehicles undergo multiple flight-reentry cycles throughout their entire service life, during which they are subjected to extreme aerodynamic, thermal, mechanical, and vibrational loads. These loads involve complex multi-physics interactions, including severe transient thermo-mechanical coupling. The mechanical behavior and damage failure mechanisms of fiber-reinforced ceramic matrix composites (CMC) under such extreme conditions need to be clearly understood. This study investigates the damage evolution mechanisms of CMC thermal structures in cyclic service environments from the perspective of multi-physics coupling. It identifies transient thermo-mechanical loads as one of the primary factors influencing performance degradation under repeated use conditions. A comprehensive predictive and analytical framework for thermomechanical-induced cracking under high-temperature transient large thermal gradients is proposed. By developing a coupled thermal conduction-mechanical response model, we achieve quantitative characterization of the spatiotemporal evolution of the internal temperature field, stress field, and crack energy release rate (ERR) in the material. The results indicate that the non-uniform temperature gradients caused by transient thermal loads are the primary drivers of subsurface stress state reversal (tension-compression conversion). This, in turn, interacts with the material microstructure, leading to the maximum ERR occurring in the subsurface region on the windward side. Furthermore, bending constraints can double the peak ERR compared to unconstrained conditions. Based on parametric analysis, design guidelines for repeatable use, focusing on low ERR, are proposed. These guidelines highlight the optimization directions for CMC thermal structures, including gradient modulus, high thermal conductivity, low thermal expansion, and thin-walled designs. Experimental validation using a 1500 °C/1.5 kN thermomechanical test platform demonstrates that the C/SiC ceramic matrix composite-wing leading-edge (CMC-WLEs) thermal structure maintains its integrity after over ten cycles of loading, with no delamination or matrix cracking detected through nondestructive testing. This study offers an innovative theoretical-experimental methodology for the synergistic optimization of materials and structures in reusable CMC thermal structures and damage-tolerant design, which is of significant engineering importance for overcoming the design challenges in hypersonic vehicle thermal protection systems. -
引 言
高超声速飞行器(Ma > 5)作为可重复使用天地往返运输技术的重要组成部分, 是突防与全球打击的最重要军事手段之一, 是国际复杂形势下国家战略安全的支撑力量, 是国家2035年远景目标的建议中所列的8个重点前沿领域之一, 是“新域新质”力量建设的重要组成部分. 随着空天技术的快速发展, 新一代高超声速飞行器热结构的典型特征是服役温度更高(> 1650 °C)、过载系数更大(> 10g)、服役时间更长和可靠性要求更高[1-4]. 目前, 以连续纤维增强陶瓷基复合材料(ceramic matrix composites, CMC)为代表的高温复合材料, 由于其轻质、抗氧化烧蚀和优异的高温力学性能, 已成为高超声速飞行器的关键结构材料.
可重复使用高超声速飞行器热结构在全寿命周期内经历多次飞行-再入过程, 每次飞行-再入阶段, 热结构均承受严苛的气动热/力/强振动等多物理场耦合载荷作用. 尤其是, CMC系统具有较低的导热率(通常比金属材料低一个数量级), 剧烈的瞬态热对流导致CMC热结构表面温度迅速升高, 导致在壁板结构厚度方向存在大温度梯度, 材料内部产生比稳态飞行阶段更高的热应力. 虽然连续纤维的增韧作用使CMC的抗热瞬态冲击阻力有所提高, 不会发生瞬态断裂, 但在强瞬态热力耦合作用过程中CMC微结构会产生不可逆的改变, 尤其在热结构的自由边界处、几何不连续处、局部强约束处会产生很高的内应力, 导致材料发生分层、基体裂纹和褶皱等损伤, 如图1所示. 更为重要的是, 基于高超声速飞行器的可重复使用要求, 瞬态热力载荷的循环效应会加剧材料性能的劣化, 这会对高超声速飞行器热结构的寿命和可靠性产生非常不利的影响. 因此, CMC热结构设计方法亟需从传统高安全裕度包覆不确定的强度设计方法, 进入以多物理场多过程耦合分析为基础的可重复分析-设计-评价新阶段.
![]()
图 1 CMC系统在服役环境中可能的损伤失效模式Figure 1. A general CMC system common failure modes under operating environment瞬态热机械载荷下CMC热-力响应涉及到非平衡、强化、软化、多尺度损伤和能量耗散等, 建立相应的力学理论和方法极为困难[5-8]. 瞬态热机械载荷的高度非线性性质, 结合CMC的多组分、非均质和各向异性特性, 使得材料的损伤失效机理极为复杂[9]. 对CMC热结构与服役环境耦合特征的认识不充分, 空天往返飞行器热结构百次以上重复使用的重大需求和已掌握的科学理论间存在着巨大的差距, 照搬现有的设计规范, 难以保障飞行器的安全.
因此, 破解重复使用环境下陶瓷基复合材料热结构力学行为的机理与演变规律、每次服役过程中热力载荷与热结构耦合机制等的关键力学问题, 开展空天服役环境载荷及其与CMC热结构的耦合特性的基础研究, 必要而迫切.
1. 可重复使用评价的科学内涵
可重复使用性能评价, 是高超声速飞行器热结构在流固耦合强烈相互作用过程中发生损伤与累积过程的准确刻画与预测问题. 不同于传统的疲劳理论, 其载荷具有冲击荷载特征, 且有限次数重复. 因此, 不能“生搬硬套”传统金属疲劳理论. 另外, 空天环境中热结构的热力载荷呈现瞬态效应和热力强耦合特性, 需从力学原理出发, 对空天环境热力荷载的“动边界、动载荷、动响应以及动强度”的内涵进行科学的阐释, 从而给出热结构可重复使用的判据.
1.1 面临的挑战
可重复使用评价问题给现有的力学基本理论、实验技术、计算方法和研究范式带来了巨大的挑战, 主要体现在以下几个方面.
1.1.1 难以精准捕捉热力载荷时空特征
高超声速飞行器在服役环境中, 其极端服役条件中的一种形式是强瞬态热流“轰击”材料表面, 使材料结构表面温度迅速升温, 进而产生瞬态热应力, 并诱发材料微结构变化和累积, 最终导致材料结构损伤甚至失效[10-13]. 模拟高超声速飞行器强瞬态热冲击问题, 精确捕捉热力载荷的时空特征, 是准确刻画材料热力响应行为的关键.
首先要准确评价材料在极端热环境下抗热冲击能力. 通常的做法是先对材料进行热冲击试验, 然后对经历了热冲击的试样进行剩余力学表征. 根据瞬变温度的正负, 可以分为2种试验: (1)热冲击, 由冷态突然升高到热态(ΔT > 0)的快速加热试验; (2)冷冲击, 由热态突然降低到冷态(ΔT < 0)的快速降温试验.
高温试样快速降温试验, 通常将高温试样浸入淬火介质中(淬火介质通常是室温水, 也有沸水、室温空气和液氮等)[14], 试验操作相对简单, 试样和冷却介质之间温差ΔT明确. 然而, 试样表面传热系数很难评估, 尤其试样淬火到水中, 沸腾对试样表面与水的传热系数影响很大, 更为重要的是, 材料表面传热系数并非常数, 而是随着试样温度的变化而变化的, 且与试样表面粗糙度相关[15-16]. 因此, 以水淬实验为代表的快速降温试验, 适用于定性地比较材料的抗热冲击性能, 但很难量化冲击过程中热力载荷历程.
快速加热试验, 将试样指定区域通过等离子体射流、激光辐射、高能电子束、热气射流、电弧放电和氢氧火焰等高通量热源快速加热[17-18]. 快速加热试验导致试样中的应力分布与淬火试验不同, 两者之间是否具有等同性存疑. 另外, 高通量热源加热通常导致被加热区域的温度分布不均匀, 被加热区域与非加热区域的温度梯度极高, 导致失效区域往往在大温度梯度区域.
通常, 高温试样快速降温试验比快速加热试验诱发的热冲击严重得多. 材料的抗热冲击能力可通过测量裂纹萌生的临界温差、材料失效时高通量热源的临界功率或测量温度梯度并计算相应的应力强度因子来评估[19].
综上所述, 针对循环热冲击下CMC力学行为的研究, 沿用了表征超高温陶瓷抗热冲击性能的研究思路, 工作大多集中在两个方面: 一是分析CMC热冲击后微结构损伤模式, 确定临界热冲击温差、热冲击损伤性参数等; 二是热冲击对CMC性能的影响通过破坏性和非破坏性测试方法进行评估. 通常采用适当尺寸的热冲击试样的弯曲或拉伸试验来获得热冲击后材料剩余强度/刚度等退化规律. 事实上, CMC与超高温陶瓷的抗热冲击的损伤失效机制有很大不同, 亟需发展针对纤维增强CMC的抗热冲击性能表征的新理论和试验方法. 但受现有的实验手段在时间和空间的分辨率上的限制, 无法从宏观和微观角度同时观测循环热冲击过程中材料温度-损伤-变形时空演变.
1.1.2 缺乏结构时变分析方法及力学模型
高超声速飞行器在飞行过程中承受严酷的气动力和气动热效应, 且高热通量的热机械载荷呈现明显的瞬态性特征. 由于复合材料热传导特性和高温升速率的双重约束, 结构表面气动热流输入与内部传导热流不平衡, 输入热量会在材料表面快速积累, 使得表面温度急剧升高. 在高温瞬态环境下材料表面温度历程呈现“高温”特征; 由于CMC低热传导特性, 材料沿厚度温度分布呈现“高温度梯度”特征.
研究人员开发了多种方法来研究材料在瞬态热机械载荷下的响应, 包括实验测试、数值模拟和理论建模. Sundaram等[20]考虑了温度梯度和快速热表面冷却的影响, 系统地研究了影响热障涂层开裂能量释放率和模式混合的因素, 后来, Jackson等[21]扩展了上述瞬变效应影响的研究, 提出了避免热障涂层开裂的关键冷却速率, 现有的工作为材料在高温瞬态条件下的热力学行为提供了基础的理解. Liang等[22]基于热-力等效理论开展了热冲击和热失配下界面层裂的试验研究, 建立了跨尺度力学理论参数的关系, 发展了热冲击下材料热-力响应的数值计算方法. Shen[23]通过泰勒展开引入二阶速率和特征时间, 在亥姆霍兹能量框架下提出了连续介质的瞬态热-力-化耦合模型. Wang等[24]研究了非均匀材料在热-机等多物理场下随时间的波动特征和耦合行为, 并建立了非均匀材料热冲击阻力的评价方法. Huang等[25]在梯度损伤理论框架下建立了热力学一致的梯度损伤模型热力耦合框架, 并提出了具可变拉压强度比的改进Mazars准则. 然而, 考虑到CMC的多元素性质和固有的异质性和各向异性, 必须扩展当前的分析框架, 以全面研究和揭示CMC内部的损伤机制, 特别是在热梯度和非稳态热条件的影响下的损伤机制. Yang等[26]前期研究发现, 微时间尺度的瞬态效应, 会导致材料局部区域在极短时间内发生应力状态的改变, 如图2所示, 特别是材料的亚表面层, 可能承受拉伸/压缩和剪切的耦合作用, 增大了CMC的损伤率.
![]()
图 2 (a)瞬态大温度梯度作用下CMC贯穿厚度截面的非均匀温度分布(t = 0.50 s); (b)材料局部区域在极短时间内应力状态改变; (c)贯穿厚度截面上的热机械损伤分布Figure 2. (a) The temperature distribution along the thickness of the CMC subjected to thermal gradients and transients (t = 0.50 s), (b) the stress state in localized regions of the material changes within a very short time frame, and (c) the thermomechanical damage distribution along the thickness鉴于此, 传统的基于准稳态高温载荷发展而来的结构热强度设计准则, 主要关注结构温度趋于稳定后的高温(T)对材料性能劣化的影响, 并未考虑温度时变dT/dt 和温度梯度dT/ds “双重效应”对材料性能的影响, 导致其精确性和安全性存疑, 为面向高温瞬态环境的CMC结构高可靠设计和安全运行带来了极大的挑战.
1.1.3 匮乏循环热冲击下CMC的损伤演化规律
与传统的超高温陶瓷材料相比, CMC在循环热冲击过程中热-力耦合作用下的多尺度损伤演化机理及变形行为更为复杂. CMC的“陶瓷”属性和制备工艺导致其内部含有大量孔隙等初始缺陷, 加之组分材料之间的各向异性、离散性、热不匹配性及不均匀性[26-27], 为准确描述和预测循环热冲击下CMC的损伤-变形行为带来极大的挑战. 首先, 循环热冲击过程中瞬态热应力诱发的微结构损伤与增强纤维相互作用, 改变了基体裂纹萌生与扩展行为, 使得基体起裂后材料的非线性力学行为难以描述与预测; 纤维/基体热膨胀系数不匹配导致材料内部产生附加热应力, 再加上纤维/基体间复杂的界面作用, 使得纤维/基体界面脱黏行为难以准确描述.
而目前理论研究工作很少考虑循环热冲击(热冲击次数N > 1)对CMC损伤-变形行为的影响, 尤其缺乏揭示循环热冲击下CMC基体裂纹/界面脱黏等微结构损伤演化与力学性能退化之间内在关联机制的研究工作[26, 28]. 循环热冲击本质上是一种热冲击疲劳, 微结构损伤随着热冲击累积循环周次的增加而非线性累积[28], 这将彻底改变现有的针对单调纯机械载荷下的CMC损伤演化与变形行为的评价方法. 目前大多数研究集中于机械载荷下CMC的损伤-变形机理[29-32], 但由循环热冲击引起的CMC热机械损伤-变形机理与由应力控制/应变控制的机械载荷下的损伤-变形机理有很大的不同. 循环热冲击会诱发材料产生微结构损伤, 且损伤会随着热冲击累积周次的增加而累积. 在此过程中, 材料应变能不断耗散, 热冲击引起的热应力不断减小, 基体和界面裂纹扩展阻力增大, 并最终使得材料内损伤累积达到饱和. 在每一次热冲击过程中, 材料内部应力状态、微结构损伤累积、以及相应状态下的材料力学性能退化三者之间存在着极强的非线性耦合关系, 如图3所示. 因此, 需要发展循环热冲击下多损伤机制耦合的CMC细观损伤演化模型来准确预测材料的细观损伤-变形行为.
综上所述, 热结构从高安全裕度设计方法进入有限寿命设计方法面临严峻挑战, 从简单的强度校核变为可重复使用性能分析与评价, 设计技术与运营保障发生根本变化.
![]()
图 3 循环热冲击下CMC的损伤非线性累积与演化Figure 3. Damage non-linear accumulation and evolution of CMC under cyclic thermal shock1.2 可重复使用评价的关键
面对严酷的气动力/热/结构时空强耦合作用, 量化循环瞬态热机械载荷对材料结构性能退化是可重复使用高超声速飞行器热结构重复使用评价和预测的重要内容.
首先, 需要创新性地发展能模拟高超声速飞行器热结构服役环境的材料结构高温测试与试验方法, 与极端、原位、全场、在线试验和表征技术相结合, 获取材料结构在模拟环境中热力响应信息, 充分借助于先进的实验和数值技术, 发展能够描述材料瞬态传热特性、高温本构和失效行为的“多场、多尺度”建模和分析, 强调模型的试验验证, 从而捕捉到材料结构在模拟环境的热力荷载特征, 最终提高预测方法的置信度和精度.
其次, 亟需突破传统的准静态预测理论, 综合考虑给定构型热结构、材料和气动热/力等的相互作用, 形成热力时空关联的统一的数理模型.
再次, 从模型中提炼出耐受给定条件热力载荷的材料体系, 发展材料概率寿命预测和损伤容限分析方法[33], 把对材料高温行为的理解集成到结构尺度模拟中, 实现基于非确定性框架下的结构尺度高置信度失效模拟.
最终, 与材料制备-结构设计-计算力学多学科交叉, 将“高温物理效应”和“计算材料学”结合[34-36], 从根本上, 设计和优化出具备可重复潜力的新型陶瓷基复合材料热结构.
Yang等[26]基于高超风洞集成原位测试系统, 观测到了高温瞬态环境中, CMC损伤机制从单一模式转变为更标准的剪切破坏模式, 热梯度诱导的表面损伤显示出一种非常复杂的拓扑结构, 这在传统的准稳态热机械诱发的断裂损伤中是看不到的, 从而揭示了高温瞬态环境下CMC热结构的损伤失效机理与演变规律, 进而辨识出瞬态热机械载荷是材料在重复使用条件下性能退化的主控因素之一.
鉴于此, 本工作重点从局部高温度梯度和材料微结构相互作用的物理本质出发, 建立了可重复使用评价分析的理论框架, 推导了材料结构在瞬态大温度梯度下的可能发生损伤失效的能量释放率, 并以此作为可重复使用设计与评价指标, 设计并研制了纤维增强C/SiC复合材料机翼前缘热结构, 并在热力联合试验台架上开展10次以上的热力联合试验, 为CMC热结构可重复使用分析、设计与评价提供试验数据和技术支撑.
2. 可重复使用评价的分析框架
面对CMC热结构可重复使用评价, 笔者提出从能量视角审查CMC系统的损伤失效机制, 以尝试解决在空天服役环境中所涉及的高温瞬态与CMC多层级结构耦合作用带来的新挑战. 为此, 提出了CMC结构在高温瞬态大温度梯度下的损伤失效机理的分析框架[26], 其目的在于建立温变速度、裂纹起裂和分层等损伤位置以及损伤发生时刻之间的关系. 瞬态热力载荷下CMC结构的损伤模型由两部分组成: 瞬态热分析和随后的热力耦合分析, 以此预测由于各种实际工况所产生的非均匀温度场对材料性能的影响.
2.1 基本假设
该分析框架采用如下的基本假设.
(1) CMC薄板的厚度尺度远小于材料在面内两个方向上的长度尺度, 因此, 该模型假设材料的温度和变形都只在贯穿厚度的方向上发生变化, 即温度、应变和应力均可以表达为材料在厚度方向上的函数, 分别记为T = T(z), ɛ = ɛ (z)和σ = σ (z), 且材料在变形过程中始终保持平面应力状态.
(2) 在初始状态下, 假设材料内部的温度分布是均匀的, 且不存在残余应力. 材料的温度分布不受材料变形状态的影响, 仅取决于给定的一维热传导定解问题.
(3) 材料的变形以及裂纹的扩展达到稳态所需的时间尺度远小于温度变化的时间尺度, 因此, 可以认为在任一瞬态温度分布下材料的变形状态仅取决于当下的温度分布, 而与温度的时间梯度无关.
2.2 瞬态传热分析
材料结构的实际换热形式各异, 但材料结构的热边界可统一简化为强制对流换热模型. 在分析框架中, 目前只考虑与材料表面温度相关的情况, 即H = H[T(h, t)], 将材料上下表面与外界的换热系数分别记为Hh和H0, 与材料发生对流换热气体的温度记为$ {T}_{h}{}^{{\mathrm{gas}}}(t)和{T}_{\text{0}}{}^{{\mathrm{gas}}}(t) $, 这样, 材料结构的瞬态温度分布可以归结为以下定解问题, 材料结构的热边界条件可写为
$$ \left.\begin{aligned} & {{k_1}(T)\frac{{\partial T\left( {0,t} \right)}}{{\partial z}} = - {H_0}\left[ {{T_{\text{0}}}^{{\mathrm{gas}}}\left( t \right) - T(0,t)} \right]} \\ & {{k_n}(T)\frac{{\partial T\left( {h,t} \right)}}{{\partial z}} = - {H_h}\left[ {{T_h}^{{\mathrm{gas}}}\left( t \right) - T(h,t)} \right]} \end{aligned} \right\} $$ (1) 其中, 单层材料内部控制方程为
$$ \left.\begin{split} &\rho \frac{{\partial c\left( T \right)T}}{{\partial t}} = \frac{\partial }{\partial }\left[ {k(T)\frac{{\partial T}}{{\partial x}}} \right]\\ &\frac{{\left( {i - 1} \right)h}}{n} \leqslant x \leqslant \frac{{ih}}{n}{\text{, }}i{{ = 1,\; 2,\;}}\cdots{\text{,}\;}n \end{split}\right\}$$ (2) 2.3 由瞬态热引起的应力分析
根据第2.2节中获得的材料结构温度的时空分布, 求解3种约束条件下的材料结构的应力分布: (1)无弯曲约束; (2)单面弯曲约束; (3)双面弯曲约束. 每种约束情况都有相应的应变函数. 假设材料结构每层的热膨胀系数为温度的函数, 可以表示为αi(T), 那么在上述3种情况下, 材料的应变函数可以以不同的形式表示. 根据实验或实际使用环境的不同, 可使用合适的场景来分析和计算材料结构的真实变形. 本文中, 假设材料的总应变在厚度方向上服从线性分布, 这样, 可得到材料在厚度方向的应力分布, 进一步将应力在厚度上方向上积分, 得到主矢量和力矩的平衡方程, 从而确定应力在厚度方向上分布. 具体的应变方程和平衡方程如表1所示.
表 1 在三种边界条件下CMC结构的应变方程和平衡控制方程Table 1. The strain equation and equilibrium control equation of the CMC structure under three boundary conditionsConstraint type Bilateral bending constraint Unilateral bending constraint No bending constraint diagram 
strain distribution $\begin{aligned}& {\varepsilon ^M}\left( {x,t} \right) = {\varepsilon ^0}(t) - {\varepsilon ^{th}}\left( {x,t} \right)= \\&\qquad {\varepsilon ^0}\left( t \right) - \alpha (T)\left[ {T\left( {x,t} \right) - T\left( {x,0} \right)} \right]\end{aligned}$ $\begin{aligned}& {\varepsilon ^M}\left( {x,t} \right) = {\varepsilon ^0}\left( t \right) - {\varepsilon ^{th}}\left( {x,t} \right)= \\&\qquad {\varepsilon ^0}\left( t \right) + K\left( t \right)x - \alpha \left( T \right)\left[ {T\left( {x,t} \right) - T\left( {x,0} \right)} \right]\end{aligned}$ $ \begin{aligned}& {\varepsilon ^M}\left( {x,t} \right) = {\varepsilon ^0}(t) - {\varepsilon ^{th}}\left( {x,t} \right) = \\&\qquad {\varepsilon ^0}(t) + K(t)x - \alpha (T)\left[ {T\left( {x,t} \right) - T\left( {x,0} \right)} \right] \end{aligned}$ equilibrium equations $\displaystyle\int_{\tfrac{{(i - 1)h}}{n}}^{\tfrac{{ih}}{n}} {\Sigma \left[ {{\varepsilon ^M}(t,x)} \right]} {{\mathrm{d}}} x = 0$ $\begin{aligned}& {\int_{{{\mathrm{thk}}} 1} {\Sigma \left[ {{\varepsilon _1}^M(t,x)} \right]{\text{d}}x} = 0} \\ & {\int_{{{\mathrm{thk}}} 2} {\Sigma \left[ {{\varepsilon _2}^M(t,x)} \right]{\text{d}}x} = 0} \\ & {\int_{{{\mathrm{thk}}} 1 + {{\mathrm{thk}}} 2} {\Sigma \left[ {{\varepsilon ^M}(t,x)} \right]x{\text{d}}x} = 0} \end{aligned}$ $\begin{aligned}& {\int_0^h {\Sigma \left[ {{\varepsilon ^M}(t,x)} \right]} {{\mathrm{d}}} x = 0} \\ & {\int_0^h {\Sigma \left[ {{\varepsilon ^M}(t,x)} \right]} x{{\mathrm{d}}} x = 0} \end{aligned}$ 需要指出的是, 分析仅关注由气动加热引起的应力分布变化, 不考虑初始状态下的残余应力. 在裂纹后方, 材料起裂后的每个部分都需要满足主矢量和力矩的平衡方程, 对于起裂后但仍相互接触的部分, 需要按照求解单面弯曲约束下材料变形的方法重新列方程求解.
2.4 裂纹能量释放率
当从材料边缘或开放的垂直裂纹发出的裂纹足够长时, 可以认为此时材料裂纹达到稳态. 在稳态裂纹状态下, 可以利用同一时刻从裂纹尖端前方(无损材料)到后方(稳态裂纹材料)的能量变化来计算材料的裂纹/分层能量释放率(energy release rate, ERR). 根据前述假设, 裂纹发展所需的时间尺度远小于温度变化的时间尺度, 在这一假设下可以认为在快速加热过程中的任意时刻, 材料中的裂纹都已经充分发展达到稳态, 那么裂纹尖端前后材料的应变能之差即可视为材料的应变能释放率.
裂纹尖端前方较远处的无损材料的应变能与面积之比为
$$ {U_{{\text{ahead}}}} = \int_0^{{h_1} + {h_2}} {\left(\int {\sigma {\mathrm{d}}\varepsilon } \right){{\mathrm{d}}} x} $$ (3) 裂纹尖端后方较远处的无损材料的应变能与面积之比为
$$ {U_{{\text{behind}}}} = \int_0^{{h_1}} {\left( {\int {\sigma {{\mathrm{d}}} \varepsilon } } \right){{\mathrm{d}}} x} + \int_{{h_1}}^{{h_1} + {h_2}} {\left( {\int {\sigma {{\mathrm{d}}} \varepsilon } } \right){{\mathrm{d}}} x} $$ (4) 材料的裂纹/分层能量释放率可写为
$$ G = {U_{{\text{ahead}}}} - {U_{{\text{behind}}}} $$ (5) 该模型求解了任意位置的半无限界面裂纹的稳态ERR.
3. 典型场景下CMC系统热力响应分析与讨论
3.1 典型场景
前期研究发现[26, 28], CMC表面随着瞬态热机械循环的增加而逐渐损伤至失效. 微观结构变化和变形机制之间的相互作用取决于总温、加热速率和累积循环次数. 在实际的快速气动加热过程中, 材料的损伤与破坏集中于迎风面及其亚表层中, 其余部分则基本保持了无损状态, 因此, 可认为材料在快速气动加热的过程中只在某单一位置发生损伤, CMC系统的本征参量可以由材料的弹性模量E、泊松比v、热膨胀系数α、热传导系数k以及热扩散率κ来表示, 对于只考虑单一位置损伤的CMC系统, 只需要以裂纹界面(包括分层和隧道裂纹等)位置为界, 将材料分为上下两部分进行分析, 计算材料在该位置发生界面裂纹的能量释放率.
文中所使用的CMC体系为C/SiC复合材料, 其热物理参数如表2所示.
表 2 C/SiC复合材料的热物性参数Table 2. Properties used in the C/SiC compositesThermophysical properties Room temperture 1273 K 1473 K thermal expansion α/(10−6·K−1) 0.08 1.18 1.31 specific heat capacity c/[J·(g∙K)−1] 0.82 2.26 2.04 thermal conductivity
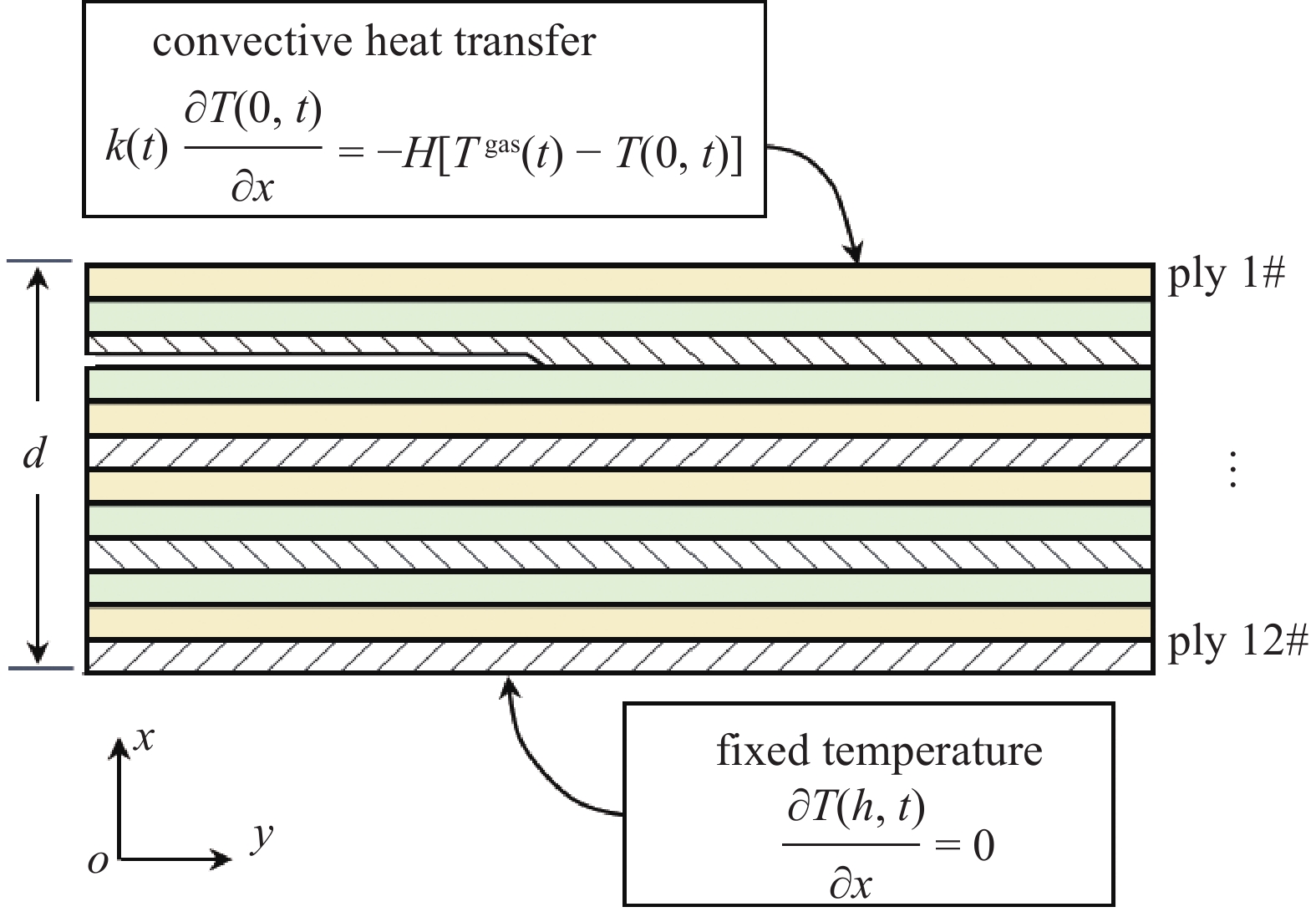
k/[W·(m∙K)−1]6.97 9.58 8.28 材料结构初始温度以及气动加热过程中的热边界条件如图4所示, 在初始状态下, 认为材料内部的温度分布是定常的, 因此, 材料内部的温度分布也是线性的, T2表示材料下表面的温度, T1表示材料上表面的温度. 将加热过程简化为一维热传导过程, 材料壁板的迎风面与高温气体发生强制对流换热, 背风面绝热. 材料迎风面的换热系数和气体温度是已知的: 换热系数记为H, 气体温度记为Tgas.
材料的初始温度T(x) = 300 K, 高温气体的温度Tgas(x) = 1473 K, 表面换热系数H =
40000 /1173·(1473 − T) W·m−2·K−1. 迎风面的换热系数对加热初期的能量释放率的峰值有显著影响. 因为迎风面换热系数越大, 表面加热速度越快, 相对于其余部分材料的温度上升越大, 表层中应力越大, 能量释放率也越大. 然而, 随着材料迎风面温度的快速升高, 表面的换热量会迅速下降, 因此在应力和能量释放率达峰之后, 表面换热系数对这两项指标的影响则会逐渐减弱直至消失.材料迎风面和背风面的热边界条件为
$$ \left. \begin{aligned} & {k\left( T \right)\frac{{\partial T\left( {0,t} \right)}}{{\partial x}} = - H\left[ {{T^{{\mathrm{gas}}}}\left( t \right) - T\left( {0,t} \right)} \right]} \\ &{\frac{{\partial T\left( {h,t} \right)}}{{\partial x}} = 0} \end{aligned} \right\} $$ (6) 材料内部的控制方程为
$$ \rho \frac{{\partial c\left( T \right)T}}{{\partial t}} = \frac{\partial }{\partial }\left[ {k\left( T \right)\frac{{\partial T}}{{\partial x}}} \right]{\text{, }}\quad 0 \leqslant x \leqslant h $$ (7) 需要说明的是, 此处给出的气体温度和表面换热系数只用来表征加热过程中宏观上的热边界, 并不一定满足材料在气动加热过程中的真实传热情况. 但在CMC热结构设计的初始阶段, 将表面的对流换热系数进行参数化分析, 可获取到材料结构温度时空分布的包线, 以便考察其对可重复设计的影响.
3.2 瞬态温度场分布
CMC典型各层的瞬态温度分布演变如图5所示. 在瞬态加热开始后的0.1 s内, 材料迎风面的温度迅速升高到1004 K, 而背风面的温升则不明显. 在这一阶段内, 材料中的高温区域体现出高温度和高温度梯度的双重特征, 整体的温度分布近似为双线性, 随着加热过程的进行, 材料中的温度分布逐渐趋近于线性稳态. 快速加热阶段发生在加热开始后的第0.2 s内, 在此阶段中, 高温区相对于低温区大幅度的温度上升会导致材料中产生较大的热应力和能量释放率, 从而促使材料发生基体裂纹、界面脱黏甚至分层等损伤.
加热过程中材料迎风面和背风面的温度变化情况如图5(b)所示. 通过第3.1节给出的热边界条件计算得到的温度分布如图5(b)的实线所示, 而前期结合流热固耦合计算和风洞试验测试结果, 对所计算的温度场时空分布进行了对比分析, 计算结果表明, 所提的一维解析计算结果比流热固耦合计算更加保守, 即背风面温度上升速度较慢, 这是由于将背风面设定为绝热条件, 热惯性效应导致背风面的温度历程有一个平台, 且最终温度较低. 而流热固耦合计算的结果更加贴合实际操作条件, 但需要指出的是, 背风面强制对流换热系数的确定仍然存在盲区. 无论本文的计算结果还是热流耦合计算结果, 相较于实验结果具有更显著的不均匀性, 因此能量释放率的计算结果相对于实验中的真实情况也会偏高.
3.3 应力场分布
第3.1节给出的典型场景下CMC薄板在瞬态加热过程中的应力变化情况如图6所示.
![]()
图 6 CMC薄板内瞬态应力演化情况: (a) ~ (c)双面弯曲约束; (d) ~ (f)无弯曲约束Figure 6. Transient stress variations in the CMC thin plate for (a) ~ (c) bilateral bending constraint and (d) ~ (f) no bending constraint裂纹尖端前方较远处的无损伤材料中各层材料的应力随时间的变化规律如图6(a) ~ 图6(c)所示, 由于表面相对于材料其他区域快速升温, 导致材料在表面区域中产生了非常大的压应力, 压应力的峰值出现在加热过程的第0.2 s内, 随着材料内部的温度逐渐趋于均匀, 温度梯度在逐渐降低, 材料表面和亚表面的压应力则快速下降. 有趣的是, 在快速加热过程的前0.3 s内, 由于材料低热传导特性, 材料的亚表面(其位置约在x/d∈(0.17 ~ 0.33))的温度较低, 因此在材料表面压缩应力的约束下, 该位置呈现出拉伸应力状态; 然而, 随着材料亚表面层的温度升高, 它们的应力状态则迅速由拉伸状态转换为压缩状态, 具体的应力变化如图6(b)所示. 这一应力状态的快速转变导致在材料裂纹的萌生与扩展不在材料的表面而是在亚表面处.
在受弯曲约束的情况下, CMC薄板的表面及其亚表面区域的应力水平较大. 这里需要指出的是, 材料表面的峰值拉伸应力发生在0.5 s时, 此时材料中性层及以下区域的温度开始发生显著变化, 但材料始终处于拉伸应力状态, 且最大应力值并不高, 其驱动产生的裂纹往往呈现I型(张开型)裂纹.
为揭示弯曲约束对材料的影响, 在第3.1节给出的典型场景下, CMC薄板不再受弯曲约束, 其瞬态应力的时空演化曲线如图6(d) ~ 图6(f)所示. 在无弯曲约束的情况下, 材料最大的表面应力发生在冷却开始后的第0.1 s内. 其最大应力值仅为653 MPa, 然后应力慢慢下降, 但是相比于弯曲约束情况, 其值小了近1/3, 说明弯曲约束效应对材料内部各层的应力分布有着显著影响. 同样地, 材料的亚表面(其位置约在x/d∈(0.17 ~ 0.25))处的应力状态发生了由拉伸状态转换为压缩状态, 且发生拉压转换的时间比弯曲约束状态提前到了0.05 s左右, 因为, 无弯曲约束情况下材料的拉压状态位置出现的更加靠近材料表面.
另外, 材料中性层及以下区域的弯曲会显著降低材料表面和亚表面层区域的应力. 相比之下, 在无弯曲约束的情况下, 材料表面和亚表面层的应力较高. 这似乎在暗示, 在有和没有弯曲应变的情况下, 应力分布的差异会导致材料能量释放率的巨大差异. 应力分布取决于CMC薄板经历整体弯曲的程度, 而整体弯曲又是材料厚度及其约束方式的函数. 这说明弯曲约束对材料内部各层的应力分布起到了重要的调节作用.
3.4 能量释放率演化
双面弯曲约束情况下, 材料的能量释放率计算结果如图7所示. 从图7中看到, 由于CMC表面的快速升温和表面内相关的很大的压缩应力, 另外, 双层弯曲约束应变的最大能量释放率大约是无约束情况的两倍. 这种重要影响主要是由于CMC中的较高应力抵抗弯曲.
![]()
图 7 弯曲约束下材料中的能量释放率演化Figure 7. Transient variation of the energy release rate for bending constraint对于双面弯曲约束情况, 最大能量释放率发生在冷却开始后约0.5 s (见图7(a)), 其分层裂纹的位置在0.25 ~ 0.33之间. 最大能量释放率的时间提前和裂纹的位置更加靠近被加热表面, 说明了弯曲约束从一定程度上限制了材料整体的变形.
在弯曲约束的情况下, 材料在快速加热过程中各个位置的能量释放率变化如图7(b)所示, 最大的分层能量释放率出现在第3层和第4层的位置. 能量释放率一方面受到材料中应力的影响, 另一方面也受到分层位置两侧材料厚度的影响. 将图7的结果与前述应力分布(图6)的计算结果进行比对, 可以发现, 材料中能量释放率最大的位置, 正是出现明显的拉-压应力状态发生转换的位置. 事实上, 后续改变条件后再进行同样的分析, 也得到了同样的结果.
但是, 无论对于有弯曲约束还是无弯曲约束情况, 裂纹的主要型式是II型(滑移型)裂纹. 因为快速加热表面呈现压缩应力, 而中性层及以下的部分虽然承受一定的拉应力, 但是其值小于材料的基体开裂应力或者界面脱黏应力. 当整个材料在逐渐达到热态即热平衡(约8 s), 能量释放率单调下降到一个极限, 该极限远低于仍具有模式I的主要分量的渐近模式混合的最大值.
在大多数情况下, 对分层裂纹能量释放率的主要贡献是CMC层合板快速加热的表面及其亚表面层中的弹性能. 能量释放率不大于表面及亚表面应变能的10%, 说明即使没有弯曲约束, 材料的表面及亚表面中的弹性能量对能量释放速率提供了最主要的贡献. 中性层及以下的层板提供的能量要少得多. 尽管如此, 在产生分层裂纹时并不是表面和亚表面中的所有弹性能量都被释放, 除非在那一刻温度分布恰好是严格线性的.
4. CMC热结构可重复使用设计方法及示例
4.1 材料本征参量的参数化分析
4.1.1 材料厚度的影响
图8给出了改变材料厚度得到的最大能量释放率. 从图8(a)中可以看到, 在保持材料的热边界条件和初始温度不变的情况下, 降低材料厚度可以使能量释放率明显降低, 从而显著降低分层裂纹的驱动力. 一方面, 随着材料厚度的降低, 材料整体的刚度会下降, 内部可存储的应变能也会降低; 另一方面, 随着材料厚度的降低, 在加热过程中材料中的热不均匀性也会下降. 另外, 较低的材料厚度的减小会导致热梯度的降低, 不仅会带来更低的能量释放率, 而且能量释放率在达到峰值之后也会更快速地下降, 这一效应相比于峰值的降低更加显著. 通过降低材料厚度, 可以有效减少能量释放率并降低分层损伤的形成.
![]()
图 8 不同材料厚度对CMC裂纹能量释放速率的影响Figure 8. The effect of the thickness of different meterial on the crack energy release rate for CMC4.1.2 迎风面材料模量的影响
在第3节的分析中, 发现对于厚度为3 mm的陶瓷基复合材料层合板, 其最大能量释放率出现在x/d = 0.25位置处. 鉴于此, 将材料沿厚度方向的模量进行优化设计, 使得迎风面材料表面到亚表面x/d = 0.25处的模量通过工艺适当调整, 提出了“梯度模量”的概念, 将其定义为迎风面材料表面到亚表面x/d = 0.25处的模量与整体弹性模量的比(E/E0). 考察梯度模量的改变对能量释放率影响. 由于材料的本构关系是非线性的, 因此, 将图8(b)显示了模量对材料中最大能量释放率的影响, 其他各项参数保持不变. 可以看出, 最大能量释放率都与模量呈现出近似的线性关系.
4.1.3 材料热传导系数的影响
只改变材料的热传导系数, 其他各项参数保持与原始条件相同, 得到最大能量释放率曲线如图8(c)所示. 由于热传导系数是温度的线性函数, 考虑采用控制比值的方法改变热传导系数. 可以看出, 提高热传导系数和降低材料厚度对能量释放率和应力的影响是相似的, 更高的热传导系数使加热过程中材料的温度分布更加均匀, 因此材料的能量释放率具有更低的峰值, 且达到峰值后以更快的下降速率下降.
4.1.4 热膨胀系数的影响
材料的热膨胀系数与温度相关, 采用控制比值的方法来改变材料的热膨胀系数, 其余条件保持不变. 图8(d)显示了热膨胀系数对材料中最大能量释放率的影响. 可以看出, 与改变模量的影响类似, 最大应力的比值与材料热膨胀系数的比值成线性关系, 但是最大能量释放率比值则与材料的热膨胀系数比值保持平方关系. 从这一点上来说, 改变材料的热膨胀系数比改变材料的模量对于降低能量释放率有更好的效果.
4.2 可重复使用设计指标
在传统的CMC热结构热强度设计基础上, 以低ERR作为材料结构具有可重复使用结构的分析和设计指标, 设计和筛选出具有低ERR的材料体系, 该材料体系应具有如下的基本特征: (1)较高的热导率; (2)较低的热膨胀系数; (3)迎风面表面较低的弹性模量; (4)较低的壁板厚度. 这样CMC结构系统在气动加热过程中具有较低的ERR, 从而能尽可能避免在服役过程中材料内部发生热机械损伤, 从而具有可重复使用潜力. 需要指出的是, 热结构壁板厚度不仅关系到飞行器整体结构刚度等静态性能, 而且也关系到整个结构的固有频率和模态特性等, 因此, 需要综合考虑结构总体性能进行协同优化设计.
对具有可重复使用潜力的CMC体系进行优化筛选, 从而将可重复使用分析、设计和评价的物理理解集成到构件级设计中, 将“设计-结构-材料-制造”协同迭代集成. 通过碳纤维预制体编织成型、织物高温热处理、化学气相渗透制备界面相及基体、高温热处理、特种前驱体浸渍-固化和高温裂解(precursor impregnation pyrolysis, PIP)等制造工艺, 研制了能够在高温瞬态服役环境下可重复使用C/SiC复合材料机翼前缘热结构样件, 如图9所示, 结构的平面尺寸为500 mm × 150 mm × 90 mm, 机翼前缘半径为7.46 mm, 壁厚为3 mm.
![]()
图 9 陶瓷基复合材料机翼前缘热结构样件实物图Figure 9. Physical model of the fully ceramic matrix composite-wing leading edges (CMC-WLEs) thermal structure4.3 可重复使用热结构试验验证
可重复使用高超声速飞行器多次往返的特点, 导致其载荷历程的复杂性, 目前尚未看到真实飞行试验数据和飞行后热结构无损检测数据分析报道. 为在地面有效模拟CMC热结构高温瞬态服役环境, 实现对飞行器CMC热结构可重复使用有效评价, 笔者搭建了具有全自主知识产权的基于高功率石英灯共聚焦辐射加热的力热联合加载试验与测试系统, 实现长时间随飞行历程变化的气动热环境地面等效模拟, 如图10所示. 该系统包括辐射加热系统、材料试验机/机械加载系统、高温3D数字图像相关系统、红外测温系统和声发射监测系统. 其中, 辐射加热系统包含基于辐射热流解析和冷却流道协同优化的石英灯辐射加热器、冷却系统和相应随形加热台架构成, 可实现系统长时工作温度达1500 °C, 被测试样表面的温度控制读数判别精度可达0.1 °C, 温升速率最高可达200 °C/s. 红外成像系统可实时(30 Hz)捕获热结构表面温度时空演化情况. 在对结构试验件加热的同时, 可以通过机械加载系统同时加载分布载荷、集中载荷等力学环境条件, 施加的最大机械载荷可达15 kN.
![]()
图 10 热力耦合加载条件下CMC机翼前缘结构测试: (a)机翼前缘高温散斑, (b)高温DIC-力热联合试验测试现场, (c)某典型时刻前缘端面温度场, (d)带冷却系统的光学窗口和(e)某典型时刻两加载点之间的全场应变分布Figure 10. Testing of the structure of CMC-WLEs under thermal-mechanical coupling loading conditions: (a) high temperature speckle at the CMC-WLEs, (b) high temperature DIC-force thermal joint test site, (c) temperature field of the CMC-WLEs at a typical moment, (d) optical window with cooling systems, and (e) full field strain distribution between two loading points at a typical moment针对实验条件要求的瞬态模拟环境特点, 发展了耦合补偿的热/力协同控制方法, 按照给定热结构所经历的温度-时间历程和载荷-时间历程, 实时精确施加多通道热/力载荷历程, 实现瞬态热环境的模拟. 与此同时, 实时监测和测量热结构温度、应力、变形和位移等物理参数.
为获得力热联合加载条件下CMC机翼前缘热结构的原位三维变形, 在热结构表面制作高温散斑, 如图10(a)所示, 该测量系统配置了数字CCD相机, 该相机采集的图像为分辨率4096 pixel × 2160 pixel的8 bit灰度图像. 另外, 为消除光学玻璃-空气-光学玻璃等多层介质对光线折射、畸变造成的误差影响, 利用VRO复杂畸变校正算法, 对含光线折射修正、畸变修正, 以获得精度更好的测试数据.
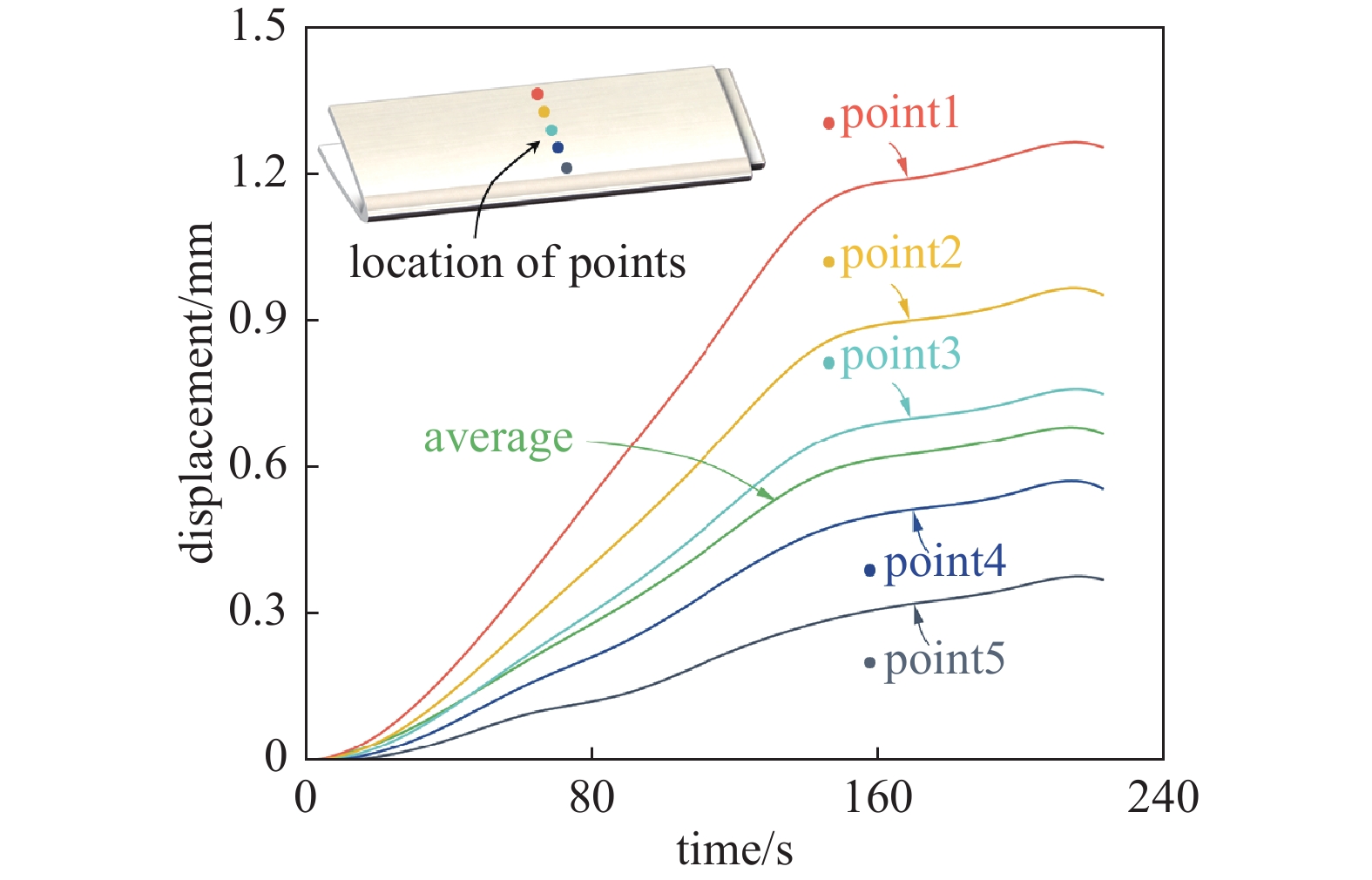
图11给出了由高温DIC技术获取的CMC机翼前缘热结构在第14次力热耦合载荷作用下典型位置处的位移随时间变化曲线. 试验结果表明, 在1200 °C下施加1500 N的法向机械载荷, CMC热结构仍具有很好的刚度. 试验结束后, 对其进行无损检测, 未发现损伤, 表明所设计和研制的CMC机翼前缘热结构初步具备可重复使用能力.
![]()
图 11 在力热耦合载荷作用下CMC机翼前缘结构典型位置处的位移随时间变化曲线Figure 11. The displacement over time at typical locations on the CMC-WLEs under thermo-mechanical coupling loads5. 结论与展望
面向高超声速飞行器CMC热结构的可重复使用分析、设计与评价问题, 从理论力学建模、实践CMC热结构研制、地面多次重复力热联合试验与测试3个维度, 开展了系统的研究工作, 具体包括可重复使用评价的科学内涵阐释, 可重复使用评价的理论分析框架, 典型场景下CMC系统热力响应计算与分析, CMC热结构可重复使用设计方法和可重复使用热结构地面试验验证等几个方面, 并着重介绍了可重复使用CMC热结构评价中涉及的关键力学问题, 形成结论如下.
(1)在快速气动加热过程中, 材料温度分布的不均匀性直接导致了材料中应力的产生, 温度梯度越高的区域, 材料中的应力越大; 而材料中间的某些位置会出现拉-压应力状态转化的现象. 材料的能量释放率受出现损伤位置两侧材料的应力和厚度的影响. 然而, 观察到具有最高能量释放率的位置与发生拉/压应力状态转变的位置高度重叠. 表明了解应力分布对于预测和控制材料中的能量释放率至关重要.
(2)发展了一套融合瞬态热传导解析解、分布式裂纹能量释放率计算和原位多场测试的“理论-仿真-实验”闭环评价体系, 形成了循环高温瞬态载荷与热结构的耦合特性分析理论, 并在原位高超风洞试验台进行了试验验证; 通过改善迎风面附近的材料属性, 可有效地降低材料在气动加热过程中的应力和能量释放率, 提升材料可重复使用的潜能.
(3)阐明了材料本征参量对稳态能量释放率的影响规律, 提出以低能量释放率作为材料结构具有可重复使用结构的设计指标, 给出了具有可重复使用能力材料结构应具备的特征;
(4)搭建了“1500 °C高温−1.5 × 103 kg法向载荷−0.1 s级捕捉”的力热联合试验系统, 可在地面上对热结构的可重复使用性能开展原位测试与检测.
CMC热结构可重复使用分析、设计与评价问题是高超热结构/热防护领域的前沿, 未来亟需瞄准飞行器热结构重复使用的重大需求, 融合仿真、地面试验和历时飞行等多源数据, 建立飞行器结构损伤在线监测系统, 构建“地面试验-在轨监测-飞行数据”联动数据库, 推动可重复使用CMC热结构从定性评价向数字孪生驱动的精准设计范式转变.
-
![]()
图 1 CMC系统在服役环境中可能的损伤失效模式
Figure 1. A general CMC system common failure modes under operating environment
![]()
图 2 (a)瞬态大温度梯度作用下CMC贯穿厚度截面的非均匀温度分布(t = 0.50 s); (b)材料局部区域在极短时间内应力状态改变; (c)贯穿厚度截面上的热机械损伤分布
Figure 2. (a) The temperature distribution along the thickness of the CMC subjected to thermal gradients and transients (t = 0.50 s), (b) the stress state in localized regions of the material changes within a very short time frame, and (c) the thermomechanical damage distribution along the thickness
![]()
图 3 循环热冲击下CMC的损伤非线性累积与演化
Figure 3. Damage non-linear accumulation and evolution of CMC under cyclic thermal shock
![]()
图 6 CMC薄板内瞬态应力演化情况: (a) ~ (c)双面弯曲约束; (d) ~ (f)无弯曲约束
Figure 6. Transient stress variations in the CMC thin plate for (a) ~ (c) bilateral bending constraint and (d) ~ (f) no bending constraint
![]()
图 7 弯曲约束下材料中的能量释放率演化
Figure 7. Transient variation of the energy release rate for bending constraint
![]()
图 8 不同材料厚度对CMC裂纹能量释放速率的影响
Figure 8. The effect of the thickness of different meterial on the crack energy release rate for CMC
![]()
图 9 陶瓷基复合材料机翼前缘热结构样件实物图
Figure 9. Physical model of the fully ceramic matrix composite-wing leading edges (CMC-WLEs) thermal structure
![]()
图 10 热力耦合加载条件下CMC机翼前缘结构测试: (a)机翼前缘高温散斑, (b)高温DIC-力热联合试验测试现场, (c)某典型时刻前缘端面温度场, (d)带冷却系统的光学窗口和(e)某典型时刻两加载点之间的全场应变分布
Figure 10. Testing of the structure of CMC-WLEs under thermal-mechanical coupling loading conditions: (a) high temperature speckle at the CMC-WLEs, (b) high temperature DIC-force thermal joint test site, (c) temperature field of the CMC-WLEs at a typical moment, (d) optical window with cooling systems, and (e) full field strain distribution between two loading points at a typical moment
![]()
图 11 在力热耦合载荷作用下CMC机翼前缘结构典型位置处的位移随时间变化曲线
Figure 11. The displacement over time at typical locations on the CMC-WLEs under thermo-mechanical coupling loads
表 1 在三种边界条件下CMC结构的应变方程和平衡控制方程
Table 1 The strain equation and equilibrium control equation of the CMC structure under three boundary conditions
Constraint type Bilateral bending constraint Unilateral bending constraint No bending constraint diagram strain distribution $\begin{aligned}& {\varepsilon ^M}\left( {x,t} \right) = {\varepsilon ^0}(t) - {\varepsilon ^{th}}\left( {x,t} \right)= \\&\qquad {\varepsilon ^0}\left( t \right) - \alpha (T)\left[ {T\left( {x,t} \right) - T\left( {x,0} \right)} \right]\end{aligned}$ $\begin{aligned}& {\varepsilon ^M}\left( {x,t} \right) = {\varepsilon ^0}\left( t \right) - {\varepsilon ^{th}}\left( {x,t} \right)= \\&\qquad {\varepsilon ^0}\left( t \right) + K\left( t \right)x - \alpha \left( T \right)\left[ {T\left( {x,t} \right) - T\left( {x,0} \right)} \right]\end{aligned}$ $ \begin{aligned}& {\varepsilon ^M}\left( {x,t} \right) = {\varepsilon ^0}(t) - {\varepsilon ^{th}}\left( {x,t} \right) = \\&\qquad {\varepsilon ^0}(t) + K(t)x - \alpha (T)\left[ {T\left( {x,t} \right) - T\left( {x,0} \right)} \right] \end{aligned}$ equilibrium equations $\displaystyle\int_{\tfrac{{(i - 1)h}}{n}}^{\tfrac{{ih}}{n}} {\Sigma \left[ {{\varepsilon ^M}(t,x)} \right]} {{\mathrm{d}}} x = 0$ $\begin{aligned}& {\int_{{{\mathrm{thk}}} 1} {\Sigma \left[ {{\varepsilon _1}^M(t,x)} \right]{\text{d}}x} = 0} \\ & {\int_{{{\mathrm{thk}}} 2} {\Sigma \left[ {{\varepsilon _2}^M(t,x)} \right]{\text{d}}x} = 0} \\ & {\int_{{{\mathrm{thk}}} 1 + {{\mathrm{thk}}} 2} {\Sigma \left[ {{\varepsilon ^M}(t,x)} \right]x{\text{d}}x} = 0} \end{aligned}$ $\begin{aligned}& {\int_0^h {\Sigma \left[ {{\varepsilon ^M}(t,x)} \right]} {{\mathrm{d}}} x = 0} \\ & {\int_0^h {\Sigma \left[ {{\varepsilon ^M}(t,x)} \right]} x{{\mathrm{d}}} x = 0} \end{aligned}$ 
下载: 导出CSV
表 2 C/SiC复合材料的热物性参数
Table 2 Properties used in the C/SiC composites
Thermophysical properties Room temperture 1273 K 1473 K thermal expansion α/(10−6·K−1) 0.08 1.18 1.31 specific heat capacity c/[J·(g∙K)−1] 0.82 2.26 2.04 thermal conductivity
k/[W·(m∙K)−1]6.97 9.58 8.28
下载: 导出CSV
-
[1] Padture NP. Advanced structural ceramics in aerospace propulsion. Nature Materials, 2016, 15(8): 804-809 doi: 10.1038/nmat4687
[2] Bale HA, Haboub A, MacDowell AA, et al. Ritchie. Real-time quantitative imaging of failure events in materials under load at temperatures above 1600 °C. Nature Materials, 2013, 12(1): 40-46
[3] Glass D. Ceramic matrix composite (CMC) thermal protection systems (TPS) and hot structures for hypersonic vehicles//15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. 2008: 2682
[4] Poovathingal SJ, Chen H. Microscale modeling of particle impact on thermal protection system materials during high-speed entry. AIAA Journal, 2022, 60(8): 4976-4990
[5] Wilkins PH, Lynch SP, Thole KA, et al. Experimental heat transfer and boundary layer measurements on a ceramic matrix composite surface. Journal of Turbomachinery, 2021, 143(6): 061010 doi: 10.1115/1.4050314
[6] Brouwer KR, Perez RA, Beberniss TJ, et al. Experiments on a thin panel excited by turbulent flow and shock/boundary-layer interactions. AIAA Journal, 2021, 59(7): 2737-2752 doi: 10.2514/1.J060114
[7] Pichon T, Barreteau R, Soyris P, et al. CMC thermal protection system for future reusable launch vehicles: Generic shingle technological maturation and tests. Acta Astronautica, 2009, 65(1-2): 165-176 doi: 10.1016/j.actaastro.2009.01.035
[8] Buffenoir F, Zeppa C, Pichon T, et al. Development and flight qualification of the C/SiC thermal protection systems for the IXV. Acta Astronautica, 2016, 124: 85-89
[9] Davies P. Environmental degradation of composites for marine structures: new materials and new applications. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2016, 374(2071): 20150272 doi: 10.1098/rsta.2015.0272
[10] Lu TJ, Fleck NA. The thermal shock resistance of solids. Acta Materialia, 1998, 46(13): 4755-4768 doi: 10.1016/S1359-6454(98)00127-X
[11] Dong X, Shin YC. Coupled thermomechanical multiscale modeling of alumina ceramics to predict thermally induced fractures under laser heating. Journal of the American Ceramic Society, 2015, 98(3): 920-928
[12] Hutchinson JW, Evans AG. On the delamination of thermal barrier coatings in a thermal gradient. Surface and Coatings Technology, 2002, 149(2-3): 179-184 doi: 10.1016/S0257-8972(01)01451-7
[13] 熊启林, 田晓耕, 沈亚鹏等. 瞬态热冲击下层合材料板界面的热弹性行为. 力学学报, 2011, 43(3): 630-634 (Xiong Qilin, Tian Xiaogeng, Shen Yapeng, et al. Thermoelastic behavior of interface of composite plate under thermal shock. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 630-634 (in Chinese) doi: 10.6052/0459-1879-2011-3-lxxb2010-284 Xiong Qilin, Tian Xiaogeng, Shen Yapeng, et al. Thermoelastic behavior of interface of composite plate under thermal shock. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 630-634 (in Chinese) doi: 10.6052/0459-1879-2011-3-lxxb2010-284
[14] 吴华, 邹绍华, 徐成辉等. 广义热弹模型的热力学基础与瞬态响应. 力学学报, 2022, 54(10): 2796-2807 (Wu Hua, Zou Shaohua, Xu Chenghui, et al. Thermodynamic basis and transient response of generalized thermos-elasticity. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(10): 2796-2807 (in Chinese) doi: 10.6052/0459-1879-22-225 Wu Hua, Zou Shaohua, Xu Chenghui, et al. Thermodynamic basis and transient response of generalized thermos-elasticity. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(10): 2796-2807 (in Chinese) doi: 10.6052/0459-1879-22-225
[15] Zhang XH, Wang Z, Hong CQ, et al. Modification and validation of the thermal shock parameter for ceramic matrix composites under water quenching condition. Materials & Design, 2009, 30(10): 4552-4556
[16] Bednarcyk BA, Ricks TM, Pineda EJ, et al. Gustafson. Multiscale recursive micromechanics of three-dimensional woven composite thermal protection materials thermal conductivities. AIAA Journal, 2022, 60(12): 6506-6519
[17] Spottswood SM, Mignolet MP. Experimental nonlinear response of tapered ceramic matrix composite plates to base excitation. AIAA Journal, 2002, 40(8): 1682-1687
[18] Appleby MP, Zhu DM, Morscher GN. Mechanical properties and real-time damage evaluations of environmental barrier coated SiC/SiC CMCs subjected to tensile loading under thermal gradients. Surface & Coatings Technology, 2015, 284: 318-326
[19] Wang H, Singh RN, Lowden RA. Thermal shock behavior of two-dimensional woven fiber-reinforced ceramic composites. Journal of the American Ceramic Society, 1996, 79(7): 1783-1792
[20] Sundaram S, Lipkin DM, Johnson CA, et al. The influence of transient thermal gradients and substrate constraint on delamination of thermal barrier coatings. Journal of Applied Mechanics, 2013, 80(1): 011002 doi: 10.1115/1.4007727
[21] Jackson RW, Begley MR. Critical cooling rates to avoid transient-driven cracking in thermal barrier coating (TBC) systems. International Journal of Solids and Structures, 2014, 51(6): 1364-1374
[22] Liang LH, Li MZ, Qin FQ, et al. Temperature effect on elastic modulus of thin films and nanocrystals. Philosophical Magazine, 2013, 93(6): 574-583 doi: 10.1080/14786435.2012.725950
[23] Shen SP. Transient continuum mechanics and chemomechanics. Journal of Applied Mechanics, 2022, 89(6): 061004 doi: 10.1115/1.4054061
[24] Wang BL, Li J, Yang CH. Thermal shock fracture mechanics analysis of a semi-infinite medium based on the dual-phase-lag heat conduction model. Proceedings of the Royal Society A-Mathematical Physical and Engineering Sciences, 2015, 471(2174): 20140595
[25] Huang HW, Yu H, Xu WL, et al. A thermo-mechanical localizing gradient damage model with modified Mazars strain. International Journal for Numerical Methods in Engineering, 2025, 126: 7652 doi: 10.1002/nme.7652
[26] Yang ZM, Wang JT, Yang R, et al. Thermomechanical - induced cracking model for ceramic matrix composite laminates subjected to thermal gradients and transients. International Journal of Solids and Structures, 2024, 300: 112927
[27] Cox BN, Bale HA, Begley M, et al. Stochastic virtual tests for high-temperature ceramic matrix composites. Annual Review of Materials Research, 2014, 44: 479-529 doi: 10.1146/annurev-matsci-122013-025024
[28] Wang JT, Yang ZM, Yue LJ, et al. Representation of thermomechanical damage in fiber-reinforced ceramic composites at high thermal gradients. AIAA Journal, 2024, 62(6): 2331-2341
[29] 杨成鹏, 林江嵘, 贾斐等. 2D-C/SiC复合材料的高温非线性本构模型. 力学学报, 2023, 55(8): 1721-1731 (Yang Chengpeng, Lin Jiangrong, Jia Fei, et al. Nonlinear constitutive model for 2D-C/SiC composites at elevated temperatures. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(8): 1721-1731 (in Chinese) doi: 10.6052/0459-1879-23-120 Yang Chengpeng, Lin Jiangrong, Jia Fei, et al. Nonlinear constitutive model for 2D-C/SiC composites at elevated temperatures. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(8): 1721-1731 (in Chinese) doi: 10.6052/0459-1879-23-120
[30] Yang ZM, Yuan H, Liu H. Evolution and characterization of cyclic thermal shock-induced thermomechanical damage in oxide/oxide ceramics matrix composites. International Journal of Fatigue, 2019, 120: 150-161 doi: 10.1016/j.ijfatigue.2018.11.006
[31] 杨正茂, 刘晖, 杨俊杰. 含热冲击预损伤的陶瓷基复合材料损伤本构模型. 力学学报, 2016, 51(6): 1797-1809 (Yang Zhengmao, Lui Hui, Yang Junjie. Damage constitutive model for thermal shocked-ceramic matrix composite. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(6): 1797-1809 (in Chinese) Yang Zhengmao, Lui Hui, Yang Junjie. Damage constitutive model for thermal shocked-ceramic matrix composite. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(6): 1797-1809 (in Chinese)
[32] Kastritseas C, Smith PA, Yeomans JA. Thermal shock fracture in cross-ply fibre-reinforced ceramic-matrix composites. Philosophical Magazine, 2010, 90(31-32): 4209-4226
[33] Yang ZM, Li WH, Chen Y, et al. Life assessment of thermomechanical fatigue in a woven SiC/SiC ceramic matrix composite with an environmental barrier coating at elevated temperature. International Journal of Fatigue, 2023, 172: 107584 doi: 10.1016/j.ijfatigue.2023.107584
[34] Cox BN, Sridhar N, Yang QD. An analytic traction-displacement model for a reinforcing ligament bridging a crack at an arbitrary angle, including elastic, frictional, snubbing, yielding, creep, and fatigue phenomena. Journal of the Mechanics and Physics of Solids, 2024, 193: 105879 doi: 10.1016/j.jmps.2024.105879
[35] 朱继宏, 张亦飞, 张亚辉等. 空天结构保形设计: 从几何特征到能量疏导. 航空学报, 2025, 46(1): 1-36 (Zhu Jihong, Zhang Yifan, Zhang Yahui, et al. Shape preserving design of aerospace structure: From geometric feature to energy channeling. Acta Aeronautica et Astronautica Sinica, 2025, 46(1): 1-36 (in Chinese) Zhu Jihong, Zhang Yifan, Zhang Yahui, et al. Shape preserving design of aerospace structure: From geometric feature to energy channeling. Acta Aeronautica et Astronautica Sinica, 2025, 46(1): 1-36 (in Chinese)
[36] Fish JG, Wagner J, Keten S. Mesoscopic and multiscale modelling in materials. Nature Materials, 2021, 20(6): 774-786
计量
- 文章访问数: 77
- HTML全文浏览量: 52
- PDF下载量: 45
