引 言

镍钛形状记忆合金因其特殊的超弹性和形状记忆效应广泛应用于工业和医学等各个领域. 在一些服役场景下, 镍钛形状记忆合金不可避免地处在富氢环境中. 例如, 在口腔整形外科领域, 镍钛合金经常被制成正畸丝^[1-6], 对需要矫正的牙齿进行施力, 使其移动到预期的位置. 然而许多镍钛正畸丝在使用几个月后就发生断裂, 即实际使用寿命远远小于其设计使用寿命. 这是因为口腔中的氢离子被吸收到镍钛正畸丝中, 导致其超弹性退化和脆化, 从而提前发生断裂^[7]. 另外, 在一些潮湿的服役环境中, 由于镍钛合金的保护层被破坏后发生电化学反应, 氢离子会进入镍钛合金内部. 除此之外, 在一些富含氢气的环境中, 氢气可以自发地扩散到镍钛合金的内部. 镍钛合金器件在富氢环境中的力学行为决定了其可靠性和服役寿命. 因此, 研究富氢环境下镍钛合金的变形行为对相关器件设计及优化起到至关重要的作用.

目前已有一些学者研究了氢对镍钛合金宏观力学行为的影响. Lachiguer等^[8]通过实验发现, 氢扩散提高了马氏体相变平台的应力、减少了最大相变应变. Elkhal等^[7]研究了氢扩散对镍钛合金丝材循环相变行为的影响, 观察到了镍钛合金在循环变形过程中的功能退化现象. 随着充氢时间的增加, 功能性退化现象变得更加明显. 同时, 他们还发现氢扩散显著降低了镍钛合金的延展性、拉伸强度和疲劳寿命, 并导致形状记忆效应的丧失. Sarraj等^[9]通过不同应变幅值的循环实验发现, 氢扩散会显著加剧镍钛合金在循环变形过程中残余应变的积累.

理论研究方面, 已有大量学者针对形状记忆合金的超弹性和形状记忆效应建立了宏观和细观本构模型^[10-14]. 然而, 这些模型并没有考虑氢扩散及其对相变行为的影响. 近年来, 一些学者针对镍钛合金建立了相应的力−扩散耦合本构模型. 例如, Lachiguer等^[8]将氢浓度作为变量引入本构模型, 根据实验结果, 将最大相变应变和相变温度视为平均氢浓度的函数. 该模型^[8]准确地预测了不同充氢时间下镍钛合金丝材的应力−应变响应. Elkhal等^[15]在Lagoudas模型^[12]的基础上, 发展了一个新的本构模型来预测在原位和非原位充氢下镍钛合金丝材的应力−应变响应, 其在该模型中考虑了弹性、热膨胀、氢扩散和相变对镍钛合金总变形的贡献. Ulff等^[4]考虑了马氏体相变和重取向机制, 引入氢浓度的影响, 对氢环境下镍钛合金丝材的力学响应进行了描述. Jiang等^[16]基于实验观察, 构建了一个考虑弹性、相变、相变诱发塑性和氢致膨胀的力−扩散耦合本构模型. Yu等^[17]建立了一个考虑力−扩散耦合的多尺度晶体塑性本构模型. 该模型首先建立在晶粒尺度上, 并将氢原子浓度分成了两部分, 用来描述晶格氢浓度和被缺陷捕获的氢浓度; 同时, 建立了力−扩散耦合自洽均匀化方法, 通过两级尺度过渡, 获得了镍钛合金丝材的整体力学响应. 需要指出的是, 这些模型仅仅关注镍钛合金在单次加−卸载下的响应, 无法描述该类合金在多级或循环载荷下的变形行为.

作为工程结构的核心部件, 镍钛合金弹簧常用作阻尼器^[18]、驱动器^[1,19]等. Savi等^[20]通过实验研究了弹簧的几何非线性行为, 并揭示了材料非线性和几何非线性耦合对弹簧刚度的影响. Attanasi等^[21]通过实验研究了拉伸和压缩历史对形状记忆合金弹簧力学行为的影响. Tobushi等^[22]研究了形状记忆合金弹簧的循环变形行为, 发现在大峰值位移下, 残余变形的累积主要发生在循环变形早期. Sakuma等^[23]研究了镍含量和热处理温度对形状记忆合金弹簧循环变形的影响. Mohammad等^[24]研究了加载率和位移幅值对形状记忆合金弹簧疲劳寿命的影响, 发现疲劳寿命取决于耗散能的大小. 为了描述镍钛合金弹簧的变形行为, Rao等^[25]构建了一个考虑弹簧扭转模式的理论模型. 该模型能够准确描述形状记忆合金弹簧在小位移幅值下的变形行为. Enemark等^[26]构建了能够同时考虑弹簧弯曲和扭转两种变形模式的半解析模型, 从而实现了对弹簧在大位移幅值下变形行为的准确描述. Zhang等^[10]在Enemark模型^[26]的基础上进一步考虑了偏心扭转, 更为准确地描述了马氏体体积分数在弹簧横截面上的分布. 然而, 这些研究并未涉及氢扩散对形状记忆合金弹簧变形行为的影响.

本文拟开展富氢环境下镍钛形状记忆合金弹簧变形行为的实验和理论研究. 通过对弹簧充氢后的多级加−卸载实验, 揭示氢扩散对镍钛合金弹簧变形行为的影响. 然后, 基于不可逆热力学框架, 建立考虑氢影响的镍钛形状记忆合金的力−扩散本构模型, 进而发展同时考虑弯曲、扭转以及氢扩散的弹簧半解析模型, 以期为镍钛合金器件的设计及优化提供参考.

1.   实验研究

1.1   实验材料和实验工况

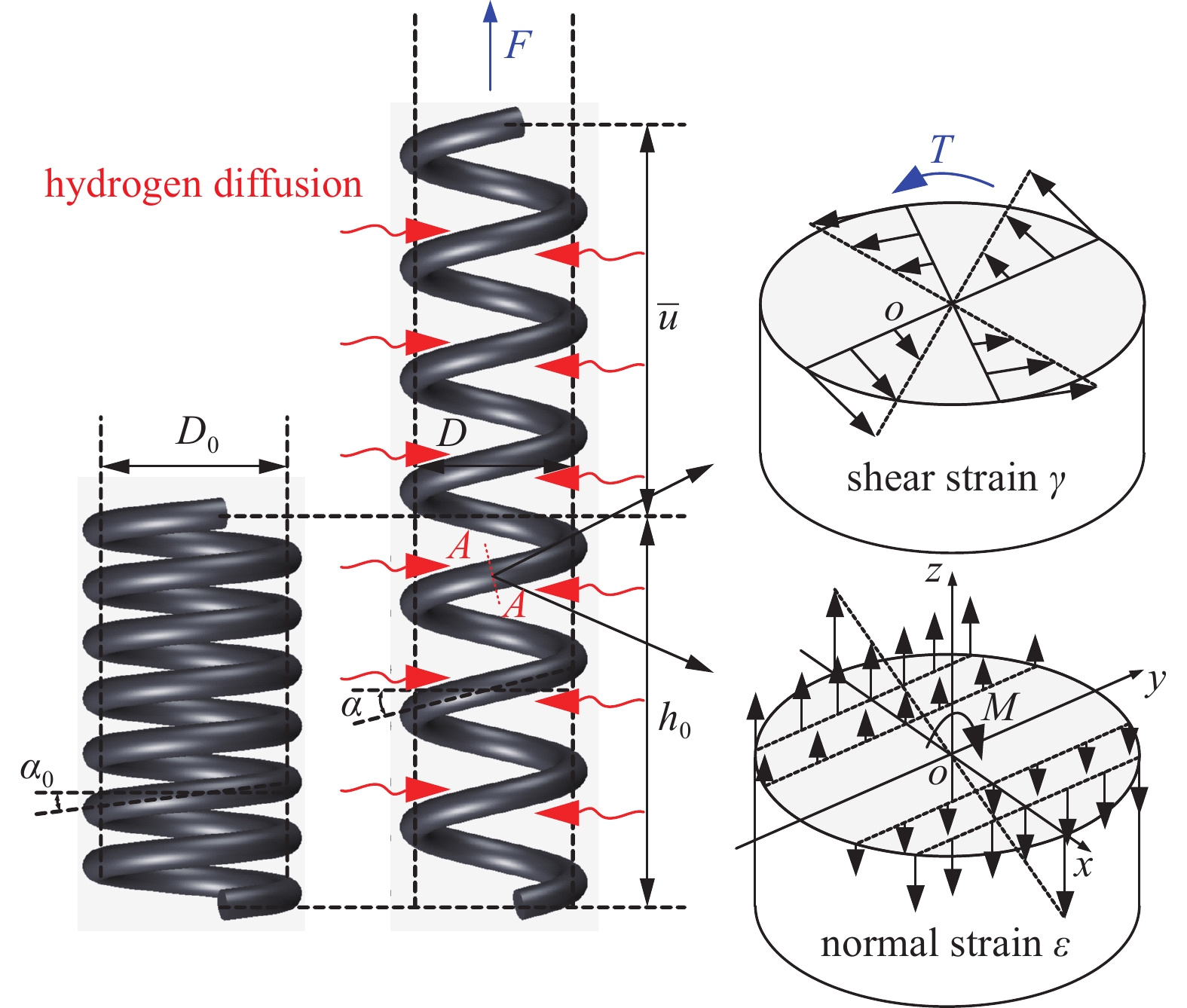
本文实验所采用的镍钛合金弹簧购自中国江阴豪露镍钛新材料有限公司. 弹簧试样由镍钛形状记忆合金丝材制成, 如图1所示, 该丝材的直径为d₀ = 1.41 mm. 弹簧根据缠绕直径D₀的不同分为两种尺寸: D₀ = 12 mm和D₀ = 16.5 mm. 两种弹簧的弹簧指数(C = D₀/d₀)分别可计算为8.5和11.7. 为方便起见, 下文中分别用C_8.5和C_11.7来表示这两种弹簧. 本文实验温度设定为299 K, 高于弹簧材料的奥氏体相变结束温度(A_f, 284 K). 因此, 形状记忆合金弹簧的初始相为奥氏体, 在变形过程中呈现超弹性.

图  1  镍钛形状记忆合金弹簧的示意图(D₀: 弹簧的缠绕直径, d₀: 镍钛合金丝的横截面直径)

Figure  1.  Schematic diagram of the NiTi SMA spring (D₀: the coil diameter of the spring, ${d_0}$: the cross-sectional diameter of the NiTi alloy wire)

下载: 全尺寸图片 幻灯片

本文采用电解法对弹簧试样进行充氢, 充氢所用的电解液是0.5 mol/L H₂SO₄ + 2 g/L CH₄N₂S溶液. 电解所用的电流为1 A, 充氢时间为30 min, 并设置了未充氢弹簧作为对照组.

机械加载实验在MTS 858试验机上进行, 加载模式为位移控制的3级加−卸载, 加−卸载速率为0.1 mm/s. 对于第i级加−卸载, 首先将弹簧加载到峰值位移u_i,max, 而后卸载到响应力为0的状态. 考虑到两种弹簧的相变程度差异, 对于C_8.5弹簧, 3级加载的峰值位移分别设置为40, 60和80 mm; 对于C_11.7弹簧, 3级加载的峰值位移分别为50, 70和90 mm, 具体工况如表1所示.

表  1  不同弹簧的3级加−卸载工况设置

Table  1.  Multi-step loading conditions for the two types of springs

	C8.5	C11.7
u1,max/mm	40	50
u2,max/mm	60	70
u3,max/mm	80	90

下载: 导出CSV 

| 显示表格

1.2   实验结果及分析

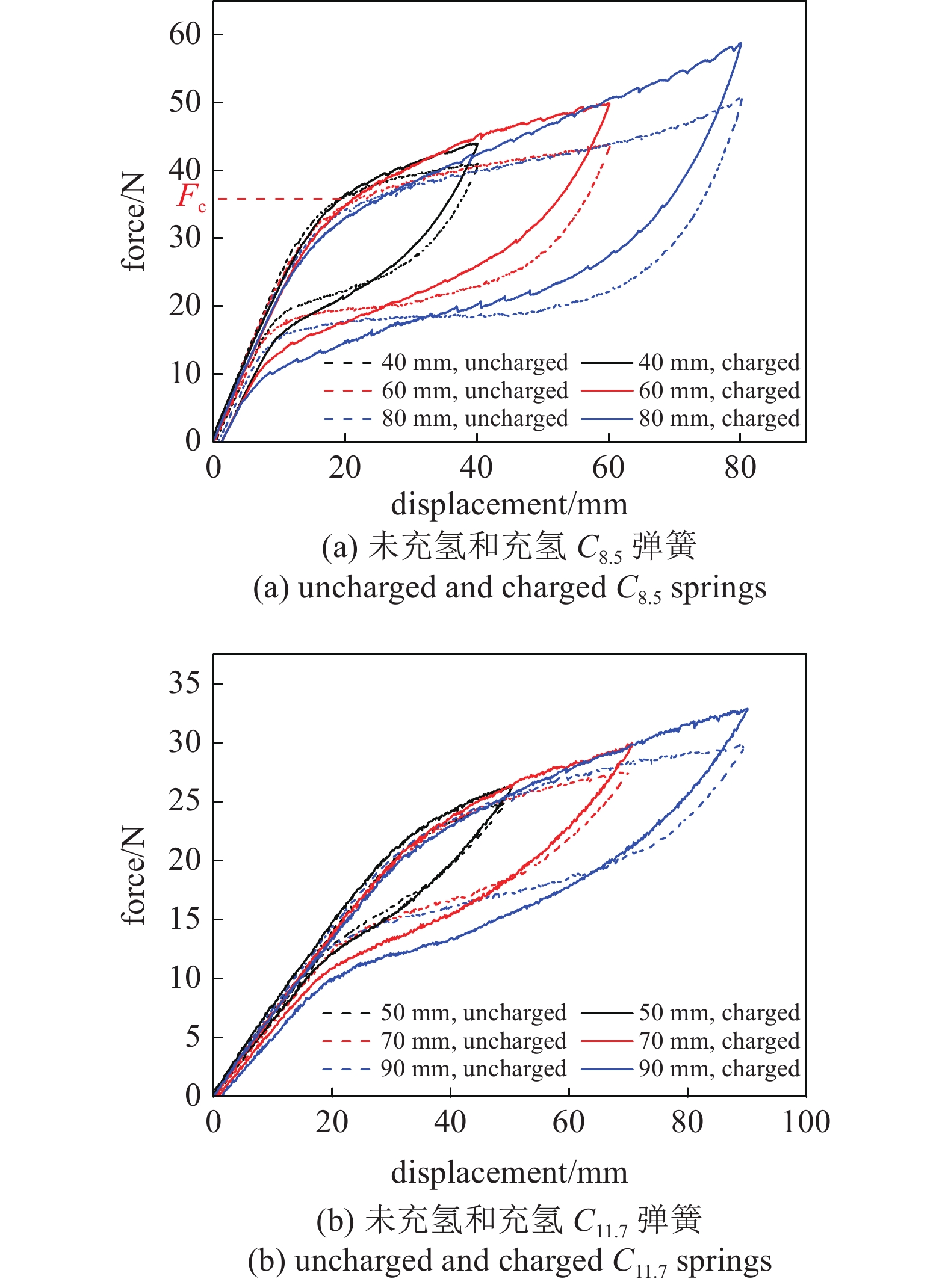
图2给出了两种弹簧在未充氢和充氢条件下的实验结果. 图2(a)为未充氢和充氢C_8.5弹簧的多级力−位移响应. 从图中可以看出, 对于未充氢弹簧, 在驱动力小于30 N时, 弹簧的响应近似呈现线性, 这表明此时的主导变形机制是弹性变形. 随着驱动力的增加, 弹簧刚度显著降低, 并呈现非线性响应. 此时弹簧逐渐由弹性变形转变为马氏体相变主导的非弹性变形. 在卸载过程中, 弹簧首先经历一段近似线性的弹性变形, 进而转入马氏体逆相变主导的非弹性变形, 并可观察到明显的滞回环. 在外载完全卸载后, 绝大部分的变形都能够回复, 仅有少量因相变诱发塑性机制(位错滑移)所导致的残余变形无法回复^[11]. 由此可见, 本文所采用的镍钛合金弹簧展示出了良好的超弹性特性. 需要指出的是, 在每一级的变形过程中, 马氏体相变发生的临界力(${F_c}$)都会低于上一级的情形, 如图2(a)所示. 这是由于相变诱发塑性变形产生的内应力能够促进马氏体形核, 从而降低了形核临界力^[27]. 图2(a)也给出了充氢后C_8.5弹簧的多级力−位移响应. 相比于未充氢情形, 其力学响应变化主要体现在以下3个方面: (1)充氢后弹簧的相变硬化行为显著高于未充氢情形. 例如, 同样在峰值位移为80 mm的情形下未充氢和充氢弹簧的响应力分别为50 N和58.8 N. 这表明, 氢扩散会增加马氏体相变扩展的阻力. 这是由于氢不同程度地改变了奥氏体和马氏体的相变温度, 使奥氏体相更加稳定, 马氏体相变行为因此受到了抑制^[28]; (2)充氢弹簧在多级加载过程中马氏体临界力降低的程度显著高于未充氢弹簧. 例如, 相比于第一级加载, 未充氢和充氢弹簧在第3级加载时的相变临界力分别下降了2 N和3.7 N. 这表明, 氢扩散会加剧内应力产生, 从而进一步促进马氏体形核. 这导致了形核临界力的进一步降低, 故充氢弹簧的马氏体相变临界力下降更为迅速; (3)充氢弹簧在变形结束时的残余应变显著大于未充氢情形. 这表明, 氢扩散会促进镍钛合金的位错滑移.

图  2  多级加载下弹簧的力−位移响应曲线

Figure  2.  Force-displacement responses of springs under multi-stage loading

下载: 全尺寸图片 幻灯片

图2(b)给出了未充氢和充氢C_11.7弹簧的多级力−位移响应. 对比图2(a)可以发现, 弹簧的响应强烈依赖于其几何构型(弹簧指数), 在相同加载位移情形下, 弹簧的响应力随着弹簧指数的增加而显著下降. 图2(b)中充氢后C_11.7弹簧的多级力−位移响应表明, 氢扩散对C_11.7弹簧的影响规律与C_8.5弹簧类似.

2.   理论模型

本节首先建立了超弹性镍钛形状记忆合金力−扩散耦合本构模型, 然后, 将Enemark等^[26]提出的螺旋弹簧半解析模型拓展到了考虑氢扩散情形, 最终得到能够描述镍钛合金弹簧在富氢环境中变形行为的理论模型.

2.1   本构模型

针对弹簧中的任意一个材料点, 其总应变可以分解为3个部分, 即

其中, $ {{\boldsymbol{\varepsilon }}^{\text{e}}} $为弹性应变, $ {{\boldsymbol{\varepsilon }}^{{\text{tr}}}} $为相变应变, $ {{\boldsymbol{\varepsilon }}^{\text{h}}} $为氢致膨胀应变. 正如实验中所观察到的, 相较于相变应变, 镍钛合金弹簧的塑性变形很小. 简化起见, 本文将不再考虑塑性变形机制.

应力和弹性应变之间的关系可用胡克定律表示

其中, $ {\boldsymbol{D}}\left( \xi \right) $是弹性刚度张量, $ \xi $为马氏体体积分数. 因为镍钛合金中奥氏体弹性模量和马氏体弹性模量有所不同, 因此$ {\boldsymbol{D}}\left( \xi \right) $是马氏体体积分数$ \xi $的函数, 可用如下混合律表示

式中, $ {{\boldsymbol{D}}^{\text{A}}} $和$ {{\boldsymbol{D}}^{\text{M}}} $分别为奥氏体和马氏体的弹性张量.

参考Lagoudas等^[12]的工作, 相变应变率与马氏体体积分数率是线性相关的, 即

其中, $ {{\boldsymbol{\varLambda }}^{{\text{tr}}}} $为相变方向张量, $ {H_{\max }} $是最大相变应变, $ {{\boldsymbol{\sigma }}^{{\text{dev}}}} $是偏应力张量, $ {{\boldsymbol{B}}_{{\text{tr}}}} $是内应力张量, ${{\boldsymbol{\varepsilon}} }_{{r}}^{{\text{tr}}}$是逆相变发生时的相变应变张量. $ \dot \xi > 0 $代表正相变过程, $ \dot \xi < 0 $代表逆相变过程. 正如实验中观察到的, 相变诱发塑性变形和氢扩散均会促进马氏体形核, 从而降低形核临界力. 为了描述这些现象, 本文引入内应力张量$ {{\boldsymbol{B}}_{{\text{tr}}}} $, 并进一步将其分解为以下两个部分

其中, $ {h_1} $, $ {h_2} $, ${l_B}$和$l$是材料参数. ${\xi ^{{\rm{accum}}}}$代表循环变形过程中累积的马氏体体积分数, 即${\dot \xi ^{{\rm{accum}}}} = \left| {\dot \xi } \right|$. 在式(6)中, 第1项代表的是在无氢环境下相变过程中由缺陷产生的内应力, 第2项代表氢对内应力演化的促进作用.

氢致膨胀应变$ {{\boldsymbol{\varepsilon }}^{\text{h}}} $与氢浓度$\omega $有如下线性关系^[15]

其中, $ {\boldsymbol{\beta }} $是氢膨胀系数张量, $ \omega $是当前氢浓度.

本文提出的本构模型建立在不可逆热力学框架下. 采用Helmholtz自由能$ \psi $来表征材料点的热力学状态, $ \psi $可进一步分解为

其中, $ {\psi ^{\text{e}}} $, $ {\psi ^{\text{T}}} $, ${\psi ^{{{\rm{int}}} }}$, $ {\psi ^{{\text{tr}}}} $, $ {\psi ^{\text{h}}} $分别为弹性能、与温度相关的内能、内应力能、相变硬化能和氢扩散相关的化学能.

弹性能可表示为弹性应变张量的二次函数

温度相关的内能可以用如下混合律表示

其中, $ \psi _{\text{A}}^{\text{T}} $和$ \psi _{\text{M}}^{\text{T}} $分别为奥氏体和马氏体的内能, 参考Yu等^[29]的工作, $ \psi _{\text{A}}^{\text{T}} $和$ \psi _{\text{M}}^{\text{T}} $可以写为如下形式

其中, ${c_{\text{A}}}$, $ s_{\text{0}}^{\text{A}} $和$ u_{\text{0}}^{\text{A}} $分别是奥氏体的热容、平衡温度处的参考熵和参考内能. 同理, ${c_{\text{M}}}$, $ s_{\text{0}}^{\text{M}} $和$ u_{\text{0}}^{\text{M}} $分别是马氏体的热容、平衡温度处的参考熵和参考内能.

内应力能和相变硬化能分别可以写为^[29]

其中, $ {\tau _{{\text{tr}}}} $为相变抗力. 为了描述相变平台的演化, 本文提出了一个新的相变抗力演化方程

其中, $ K_{}^{\text{I}} $, $ K_{}^{{\text{II}}} $和${n_{{\text{tr}}}}$是材料参数, $ K_{}^{\text{I}} $描述相变的线性硬化行为, $ K_{}^{{\text{II}}}{\left( {{\xi \mathord{\left/ {\vphantom {\xi {{\xi _{\text{r}}}}}} \right. } {{\xi _{\text{r}}}}}} \right)^{{n_{{\text{tr}}}}}} $描述逆相变的非线性硬化行为. 为了反映氢对镍钛合金相变硬化行为的影响, $ K_{}^{\text{I}} $可以表示为

氢扩散相关的化学能可以表示为^[30]

其中, $ R $为气体常数, $ T $为材料点的温度, $ {\mu _0} $为平衡温度处的参考化学势.

热通量$ {\boldsymbol{q}} $与温度以及氢通量$ {\boldsymbol{J}} $与化学势之间的关系可分别用Fourier定律和Fick定律描述

其中, $k$是热传导系数, $M$是氢迁移率, $M = \dfrac{{D\omega }}{{RT}}$, $D$代表氢的扩散率.

热力学耗散能不等式(Clausius-Duhem inequality)可以写为

其中, $ s $和$ \mu $分别代表熵和化学势.

将式(8) ~ 式(17)代入上式, 可得

为了让上式对于任意$ {{\boldsymbol{\dot \varepsilon }}^{\text{e}}} $, $ \dot T $和$ \dot \omega $都满足非负, 可以得到

式(22)、式(23)和式(24)分别给出的是应力−弹性应变关系、熵−温度−氢浓度关系和化学势−氢浓度−温度关系. 将式(18)和式(19)代入到式(21)等式右边的第5、第6项, 即满足$- {{\left( {{\boldsymbol{q}} \cdot \nabla T} \right)} \mathord{\left/ {\vphantom {{\left( {{\boldsymbol{q}} \cdot \nabla T} \right)} T}} \right. } T} = {{k{{\left( {\nabla T} \right)}^2}} \mathord{\left/ {\vphantom {{k{{\left( {\nabla T} \right)}^2}} T}} \right. } T} \geqslant 0$, 且也满足$ - {\boldsymbol{J}} \cdot \nabla \mu = M{\left( {\nabla \mu } \right)^2} \geqslant 0 $. 所以, 式(21)可以被缩减至

将式(9) ~ 式(17)代入上式, 可得

其中, $\Delta c = {c_{\text{M}}} - {c_{\text{A}}}$, $\Delta {s_0} = s_{\text{0}}^{\text{M}} - s_{\text{0}}^{\text{A}}$. 上式也可以写为

其中, 相变热力学驱动力${\pi _{{\text{tr}}}}$的形式为

由于式(27)是对马氏体体积分数演化的约束, 为了满足其严格成立, 提出如下幂律形式描述马氏体体积分数的演化

其中, $Y > 0$是表征马氏体相变耗散的参数. ${m_{{\text{tr}}}}$代表相变的黏性, 根据Grabe等^[31]的工作, 镍钛合金的相变黏性非常低, 因此, 在该模型中${m_{{\text{tr}}}}$可以设置成一个很大的值, 即${m_{{\text{tr}}}} = 100$.

氢的质量守恒方程可以表示为

将式(19)和式(24)代入上式, 即可得到氢浓度演化方程

需要指出的是, $\nabla \cdot \left[ {\dfrac{{D\omega }}{{RT}}\nabla \left( {{\boldsymbol{\sigma }}:{\boldsymbol{\beta }}} \right)} \right]$ 项代表应力场对氢扩散行为的影响. 然而, 由于镍钛合金的氢膨胀系数较小, Jiang等^[16]已揭示这一项对氢浓度演化的贡献很小. 为了简化起见, 可以忽略不计.

至此, 已完成了形状记忆合金力−扩散耦合本构模型的构建, 进一步结合力的平衡方程、变形协调方程, 即可得到求解镍钛合金结构力−扩散耦合问题的主控方程组

其中, ${\boldsymbol{u}}$是位移场. 需要指出的是, 本文并非直接求解方程组(32) ~ (35), 而是结合弹簧的几何特点对方程(32), (33)和(35)进行简化, 进而获取富氢环境下弹簧变形的半解析模型, 这将在2.2小节中进行详细讨论.

2.2   弹簧变形的半解析模型

正如引言中所提到的, 在螺旋弹簧承受较大位移时, 除了扭转变形模式之外, 弯曲变形也是需要考虑的另一种变形模式. Enemark等 ^[26]模型合理地考虑了这两种变形模式, 从而能够对弹簧在大位移幅值下的变形行为进行准确描述. 因此, 本文在Enemark等^[26]模型的基础上, 考虑了氢扩散这一物理过程, 得到了描述弹簧力−扩散耦合变形的半解析模型.

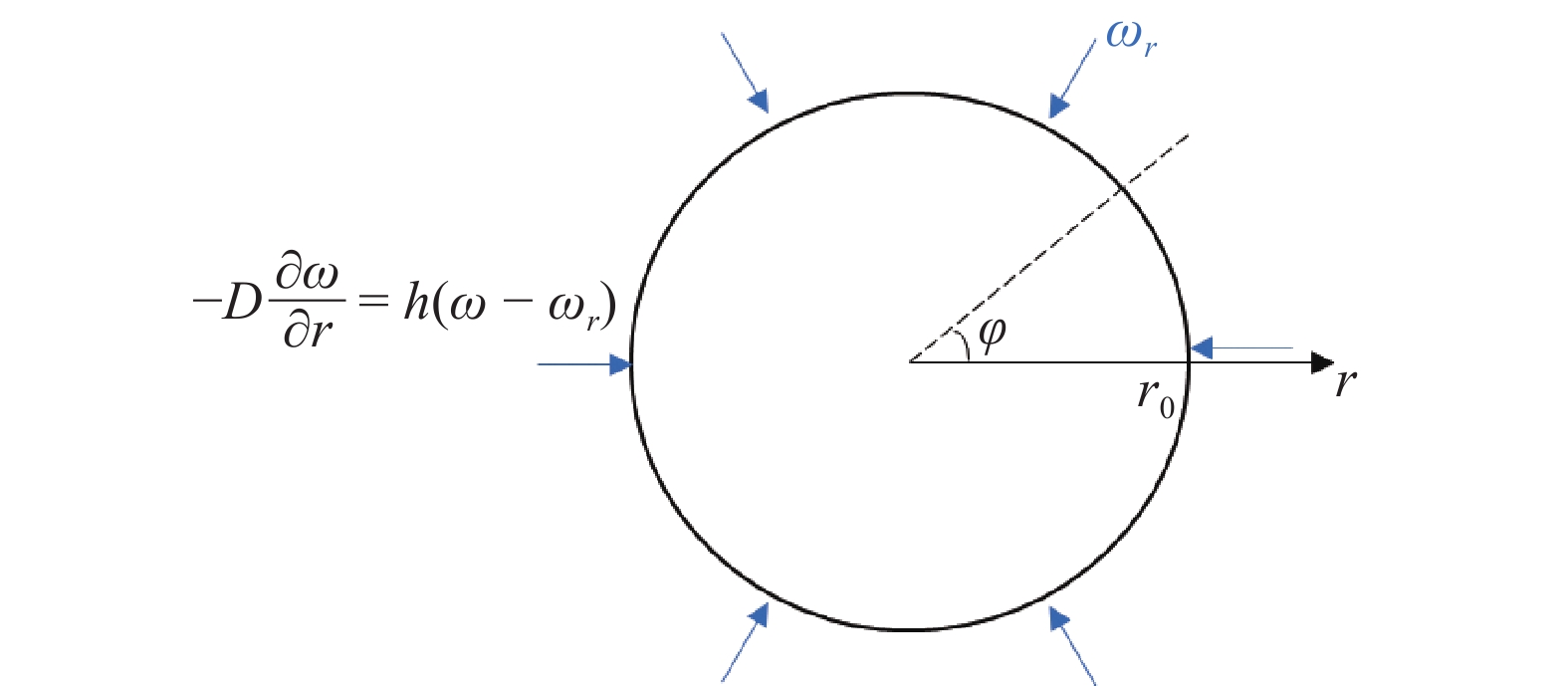
考虑弹簧的任意一横截面, 如图3所示为镍钛合金弹簧截面的氢扩散示意图.

图  3  镍钛合金弹簧截面的氢扩散示意图

Figure  3.  Schematic diagram of hydrogen diffusion in the cross section of the NiTi spring

下载: 全尺寸图片 幻灯片

在富氢环境下, 根据圆形截面的轴对称性, 氢扩散方程、边界条件和初始条件可表示为

其中, $ h $是界面氢扩散系数, $ {\omega _r} $是环境氢浓度, $ \omega \left( {r,t} \right) $是$ t $时刻距螺旋线中心轴$ r $处的材料点氢浓度. 该扩散方程的解为

其中, $H = \dfrac{h}{D}$, ${{\rm{J}}_0}(x) = \displaystyle\sum\limits_{k = 0}^\infty {\frac{{{{\left( { - 1} \right)}^k}}}{{k!\varGamma \left( {k + 1} \right)}}{{\left( {\frac{x}{2}} \right)}^{2 k}}}$是第1类0阶Bessel函数, ${\beta _m}$为方程${\beta _m}{\rm{J}}'_0\left( {{\beta _m}{r_0}} \right) + H{{\rm{J}}_0}\left( {{\beta _m}{r_0}} \right) = 0$的正根.

图4给出了弹簧变形前后的三维示意图. 变形前弹簧的平均缠绕半径和长度分别表示为R₀和h₀. 变形后弹簧的平均缠绕半径和长度分别表示为R和h. 弹簧的轴向力、弹簧截面的扭矩和弯矩分别表示为F, T和M.

图  4  镍钛合金弹簧拉伸前后的三维示意图以及横截面的平衡条件(用下标 "0 "表示未变形的状态)

Figure  4.  Schematic diagram for 3D configurations of NiTi spring before/after strentch and the balance conditions of the cross-section (the quantities are denoted with the subscript “0” when referred to the undeformed configuration)

下载: 全尺寸图片 幻灯片

弹簧的初始长度L₀和变形后长度L可以分别计算为${L_0} = \sqrt {h_0^2 + {{\left( {2\text{π} N{R_0}} \right)}^2}} $和$L = \sqrt {{h^2} + {{\left( {2\text{π} NR} \right)}^2}} $. 弹簧线圈的初始倾斜角和当前倾斜角分别为${\alpha _0} = \arctan \left( {\dfrac{{{h_0}}}{{2\text{π} N{R_0}}}} \right)$和$\alpha = \arctan \left( {\dfrac{h}{{2\text{π} NR}}} \right)$.

忽略截面的轴向变形, 变形后弹簧的平均缠绕半径R可以由下式得到

当弹簧的轴向变形为$\Delta x$时, 当前的线圈倾斜角可以表示为

对于A-A截面, 该截面的扭矩T和弯矩M可以通过截面上材料点的法向应力$\sigma \left( y \right)$和剪应力$\tau \left( r \right)$分布得到, 即

其中, $\tau \left( r \right)$是距离横截面圆心为r处的切应力, $\sigma \left( y \right)$是距离横截面中性轴为y处的正应力. 弹簧沿加载方向的轴向力F可由扭矩和弯矩合成得到, 即

切应变和正应变可以表示为

3.   模型验证

本节将通过理论模型的预测结果和实验结果的对比来验证新发展模型的合理性.

模型中的材料参数可以完全通过C_8.5弹簧的力−位移响应来标定. 根据未充氢弹簧的力−位移曲线中线性段的斜率可以确定弹性模量E_A和E_M. 根据Elkhal等^[15]的工作, 泊松比ν和氢膨胀系数β分别定为$0.3$和$1.2 \times {10^{ - 7}}{{\text{ m}}^{\text{3}}} / {\text{mol}}$. 根据Yu等^[29]的工作, $h$和 D分别定为$3 \times {10^{ - 9}}{\text{ m}} / {{\text{s}}}$和$8.6 \times {10^{ - 13}}{{\text{ m}}^{\text{2}}} / {{\text{s}}}$. 平衡温度T₀为室温($299{\text{ K}}$). 摩尔气体常数R为$8.314{\text{ J}} / ({\text{mol}} \cdot {{\text{K}})}$. 最大相变应变H_max可以通过u_3,max级加载的力−位移曲线获得. h₁, h₂, l_B和l与相变诱发内应力相关,可以通过充氢弹簧和未充氢弹簧的相变临界力演化确定. K_f^I, K_f^II, K^II和n_tr可以通过未充氢弹簧的力−位移曲线的非线性段拟合得到. h₃可以通过对比充氢弹簧和未充氢弹簧曲线的非弹性段演化得到. Y通过u_3,max级加载的力−位移曲线的滞回环宽度得到. Y_H则通过u_3,max级加载下充氢弹簧和未充氢弹簧的力−位移曲线的滞回环宽度差异得到. 由此可见, 绝大部分材料参数是通过未充氢C_8.5弹簧加载至u_1,max和u_3,max工况标定的, 少数材料参数需结合充氢C_8.5弹簧加载至u_1,max和u_3,max的工况确定. 以上为材料参数的标定方法, 详细参数取值如表2所示.

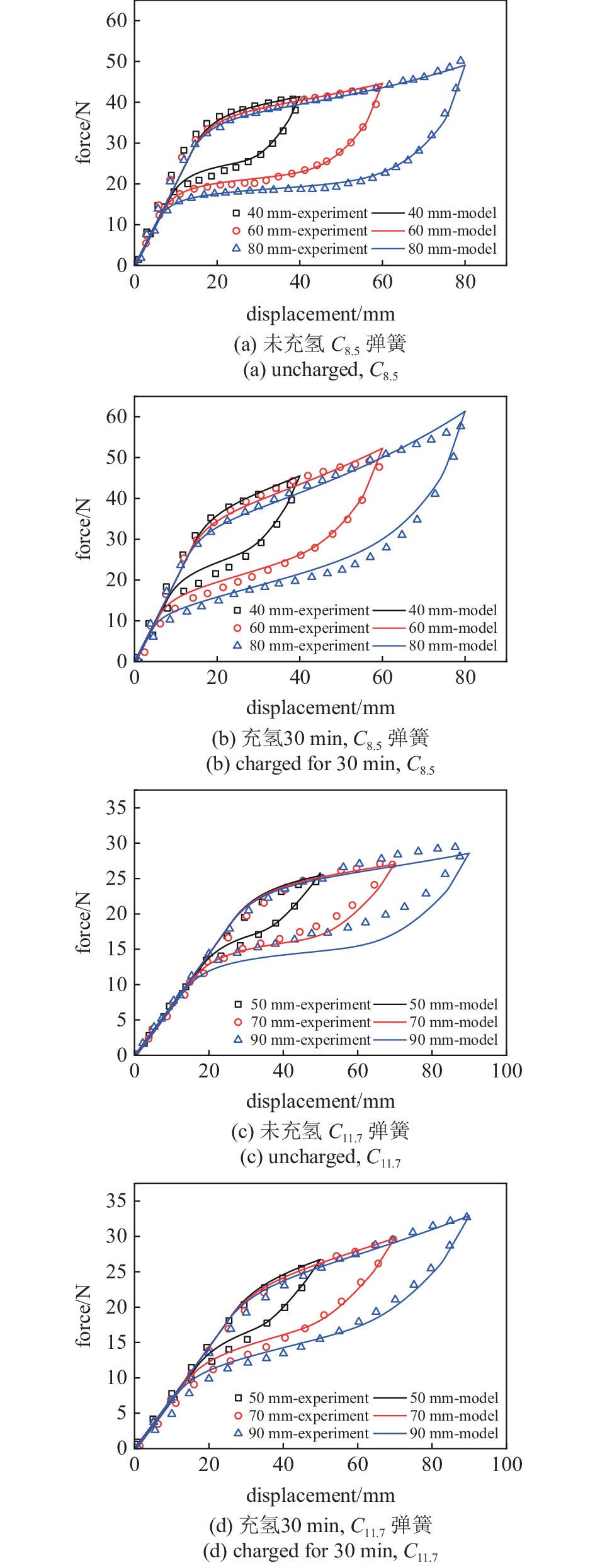
表  2  材料参数

Table  2.  Material parameters

Parameter	Value
${E_{\text{A}}}$, ${E_{\text{M}}}$	$90{\text{ GPa} }$, ${\text{70 GPa}}$
$\beta $, ${T_0}$	$1.2 \times {10^{ - 7} }{ {\text{ m} }^{\text{3} } }/{\text{mol} }$, $299{\text{ K} }$
$\upsilon $, ${H_{\max }}$,$R$	$0.3$, $0.09$, $8.314{\text{ J} }/( {\text{mol} } \cdot { {\text{K} }) }$
${h_1}$, ${h_2}$, ${h_3}$	$6{\text{ MPa} }$, $1.6 \times {10^4}{\text{ N} } \cdot {\text{m} } / {\text{mol} }$, $1.25 \times {10^5}{\text{ N} } \cdot {\text{m} } / {\text{mol} }$
${l_{\text{B}}}$, $l$, ${n_{{\text{tr}}}}$	0.5, 1, 10
$\Delta {s_0}$	$- 0.9{\text{ MPa} }/ { {\text{K} }}$
$ K_{}^{\text{I}} $, $ {K^{{\text{II}}}} $	$25{\text{ MPa} }$, $11{\text{ MPa} }$
$h$, $D$	$3 \times {10^{ - 9} }{\text{ m} }/ { {\text{s} } }$, $8.6 \times {10^{ - 13} }{ {\text{ m} }^{\text{2} } } / { {\text{s} } }$
${m_{{\text{tr}}}}$, $Y$	$100$, $4.8{\text{ MPa} }$

下载: 导出CSV 

| 显示表格

图5给出了两种镍钛合金弹簧在未充氢和充氢条件下多级力−位移响应的预测结果. 根据图5(a)和图5(b)可以发现, 本文提出的理论模型能准确地描述弹簧的主要变形特征, 并且能够很好地捕捉到氢致相变硬化的现象, 也能反映氢扩散会加剧内应力产生的现象.

图  5  弹簧的力−位移响应模型预测结果与实验结果的比较

Figure  5.  Comparison of the prediction results of the model for the force-displacement response with the experimental results

下载: 全尺寸图片 幻灯片

根据图5(c)和图5(d)中C_11.7弹簧的预测结果可以看出, 该模型能够反映出弹簧响应对于几何构型的依赖性. 在相同加载位移情形下, 弹簧的响应力随着弹簧指数增加而显著下降. 此外, 该预测结果也能说明, 氢扩散对不同构型弹簧的影响规律是类似的.

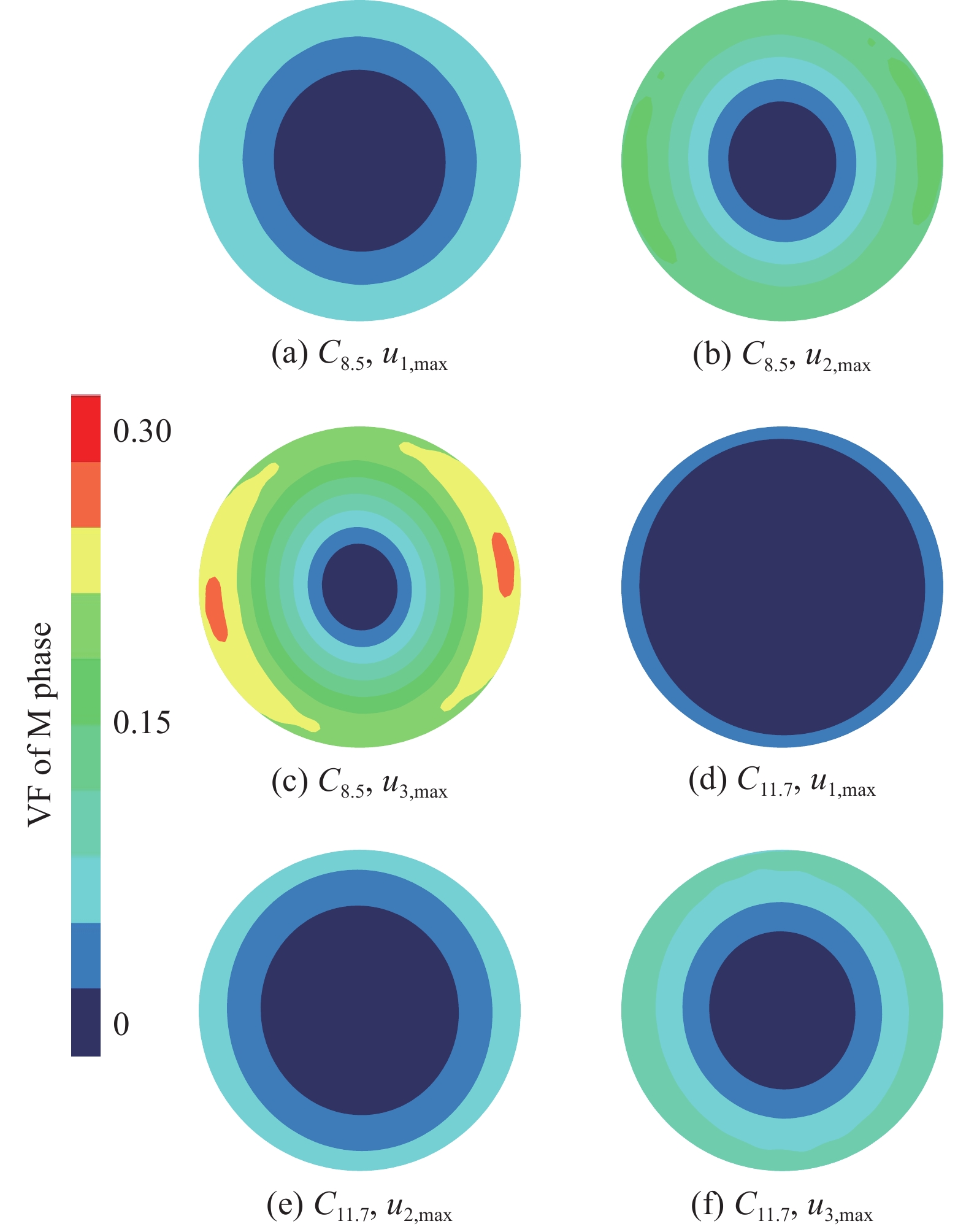
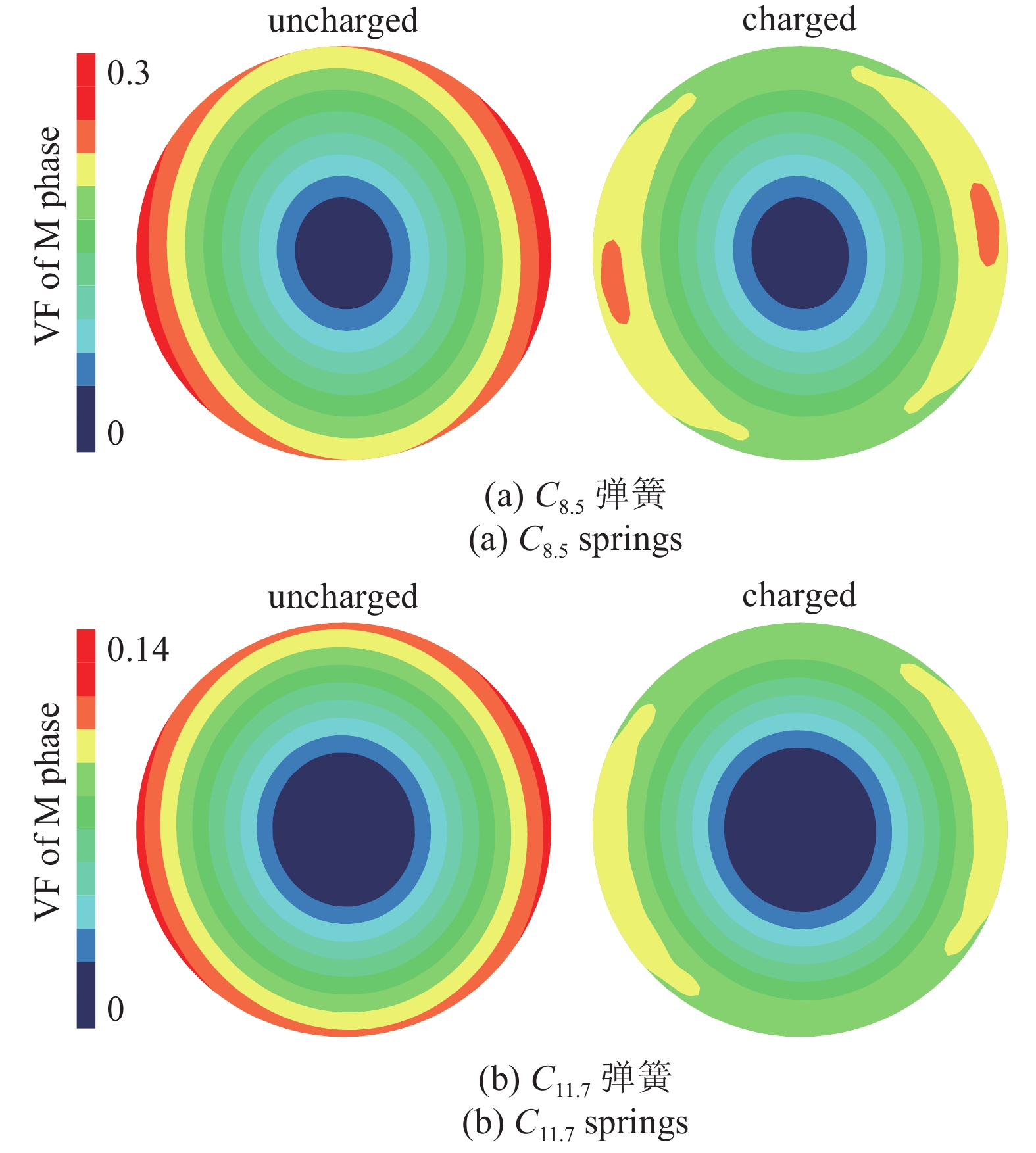
图6给出了充氢C_8.5和C_11.7弹簧在第3级加载峰值位移处的横截面马氏体体积分数分布. 对比C_8.5和C_11.7弹簧的结果, 可以发现弹簧的几何构型对马氏体相变行为存在很大影响. C_8.5弹簧在第1级加载时, 截面的马氏体体积分数呈现近似轴对称分布, 这表明其主要变形模式是扭转变形. 随着峰值位移逐渐增加, 马氏体体积分数的分布不再呈现近似轴对称, 这表明弯曲变形成为主导变形模式之一. 与C_8.5弹簧相比, C_11.7弹簧的马氏体体积分数始终呈现近似轴对称分布, 这表明其主要变形模式是扭转变形. 为了直观地对比充氢对弹簧相变行为的影响, 图7给出了充氢和未充氢条件下C_8.5和C_11.7弹簧在3级加载峰值位移处时横截面马氏体体积分数的分布云图. 可以发现, 在承受相同的外部位移条件下, 充氢弹簧的马氏体体积分数小于未充氢弹簧, 这表明氢对NiTi合金的马氏体相变行为有阻碍作用.

图  6  充氢弹簧加载至峰值位移u_i,max时弹簧截面的马氏体体积分数分布云图

Figure  6.  Distribution for the martensite volume fraction of the spring cross-section when the hydrogen-charged spring is loaded to the peak displacement u_i,max

下载: 全尺寸图片 幻灯片

图  7  充氢和未充氢弹簧加载至峰值位移u_3,max时弹簧截面的马氏体体积分数分布云图

Figure  7.  Distribution for the martensite volume fraction of the spring cross-section when the charged and uncharged springs are loaded to the peak displacement u_3,max

下载: 全尺寸图片 幻灯片

需要指出的是, 虽然本文实验部分仅研究了C_8.5和C_11.7这两种弹簧的变形行为, 但提出的理论模型能够对宽广弹簧指数范围下镍钛合金弹簧的力−扩散耦合变形行为进行预测.

4.   结 论

本文从实验和理论方面研究了富氢环境下超弹性镍钛合金弹簧的变形行为. 在实验方面, 首先对两种不同尺寸的弹簧进行了电解充氢. 然后, 对弹簧进行了不同峰值位移的多级拉伸−卸载实验, 揭示了氢扩散对镍钛合金弹簧变形行为的影响. 在理论方面, 基于不可逆热力学框架, 建立了力−扩散耦合本构模型并进一步发展考虑扭转、弯曲和氢扩散的弹簧半解析模型. 主要结论如下:

(1) 相较于未充氢弹簧, 氢扩散会增加马氏体相变的阻力, 导致充氢弹簧的相变硬化行为显著高于未充氢弹簧;

(2) 在多级加载的过程中, 相较于未充氢弹簧, 充氢弹簧的相变临界力下降得更为迅速, 说明氢会造成镍钛合金内应力的加速演化;

(3) 由于合理地考虑了氢扩散对镍钛合金马氏体相变的影响, 以及弹簧的弯曲、扭转变形模式, 本文提出的半解析理论模型能很好地描述富氢环境下镍钛形状记忆合金弹簧的变形行为.