THE THEORETICAL ANALYSIS AND EXPERIMENTAL INVESTIGATION OF SUB-WAVELENGTH FOCUSING VIA CONCAVE LENS
-
摘要: 为了提升传统平面透镜的聚焦效果, 增加焦点处的能量, 缩小焦斑尺寸, 实现亚波长聚焦, 文章基于厚度变化设计了用于聚焦平面弯曲波的凹透镜. 首先, 基于Timoshenko梁理论求解了弯曲波在经历厚度变化后的透射系数及相位变化, 并基于此完成了凹透镜的结构设计; 其次, 应用有限元软件COMSOL Multiphysics的结构力学模块开展了该透镜频域内的工作性能分析, 包括聚焦位置及焦点处能量、焦斑尺寸等, 并与传统平面透镜的情况进行对比; 最后, 实验验证了凹透镜设计的合理性和正确性. 研究结果表明: 文章所设计的凹透镜使平面入射的弯曲波聚焦在预先设定位置, 且其性能优于传统的平面透镜, 焦点处的能量更高、焦斑尺寸更小; 凹透镜的焦斑尺寸小于工作波长的0.5倍, 属于亚波长聚焦; 此外, 该透镜还具有一定的工作频率带宽, 在结构参数不变的情况下能够在设计频率附近正常工作. 提出的透镜设计方法易于工程实现, 且聚焦性能优越, 设计思想也能为声波、光波等领域相关透镜的设计提供借鉴.Abstract: In order to improve working performance of traditional plane lens, i.e., increase energy at focal point, reduce focusing size, and achieve subwavelength focusing, a concave lens for focusing incident flexural wave is designed based on the plate thickness variation. Firstly, the transmission coefficient and phase variation are obtained by utilizing the Timoshenko beam theory, based on which the lens design is performed. After that, the working performance of concave lens designed is simulated via the frequency analysis in structural mechanics module of COMSOL multiphysics software, including the focal position, energy distribution, focusing size, and so forth, which are further compared with the traditional plane lens. Finally, the experimental measurements are carried out to further validate and conform the design scheme. It is demonstrated that the concave lens can focus the incident flexural wave at the specific position, with its performance better than the plane lens, because energy concentrated is higher and the focusing size is smaller. Specifically, it exhibits subwavelength focusing phenomenon with the focusing size smaller than half wavelength. Additionally, the concave lens is broadband, which can work at a frequency region centered at designed frequency even if the whole structure is maintained. The present design scheme is easy realized for engineering application, and the concave lens exhibits better performance, which can also provide guidance for the lens design in acoustics and optics.
-
Keywords:
- focusing lens /
- flexural wave /
- subwavelength focusing
-
引 言
作为声子晶体和超材料的一种典型结构, 透镜具有聚焦、偏转和定向传输等功能[1], 是实现声波和弹性波操控的有效工具. 以会聚透镜为例, 它能够收集声波和弹性波的能量, 使其会聚在近场或远场的特定位置, 具有很多工程应用. 例如, 超声聚焦成像技术既可以用于研制高分辨率成像声呐, 还能够用于生物医学中的无损创伤治疗[2]. 弹性波的会聚透镜, 可以会聚声波或固体介质中的弹性波, 有利于能量的回收及再利用. 因此, 研究固体介质中透镜的结构设计及弹性波的人为操纵问题, 受到了国内外学者的广泛关注.
透镜大致分为两种, 即梯度折射率透镜和超表面透镜[3]. 折射率数值上等于波在背景场和局部结构中传播速度的比值. 梯度折射率透镜一般是基于声子晶体的概念设计而成, 通过改变局部单胞沿特定方向的几何结构或材料属性(如晶格尺寸或散射体的尺寸、材料及填充率)从而改变波传播的速度, 使其折射率沿空间坐标满足特定的函数规律[4-10], 从而使波在透镜中会沿着不同的弯曲轨迹进行传播. 常见的梯度折射率透镜包括Maxwell鱼眼透镜(Maxwell fish-eye lens)[4]、Luneburg透镜(Luneburg lens)[5-7]、贝塞尔透镜(Bessel lens)[8]、90°反转透镜(90° rotating lens)[9]和Eaton透镜(Eaton lens)[9]等. 这些透镜一般呈圆形, 折射率关于圆心对称分布, 所以呈现出较好的全向性. 此外, 还有一种矩形的梯度折射率透镜, 其折射率沿波传播方向保持恒定, 而垂直于波传播方向以双曲正切函数变化[11-13], 当波通过该透镜时, 可会聚在透镜内部的固定位置. 超表面(metasurface), 有时也被称之为“超构表面”, 是人工设计的几何厚度远小于工作波长的声学和光学结构[14]. 超表面透镜一般为矩形, 是通过人为设计的微结构来调控波的相位分布, 使波同时到达聚焦点或在焦点处发生相干干涉从而实现聚焦效果[15-16]. 关于超表面透镜的结构设计, 其本质在于设计组成透镜的微结构. 一般说来, 超表面透镜的设计会遵照以下原则[17-20]: (1)通常会将透镜人为地分为若干子通道, 波在各个子通道内各自独立传播, 互不干扰[18-19]; (2)当设计微结构时, 其几何结构或材料属性的改变要使波相位的变化能够覆盖[0, 2π]区间[17-19]; (3)当应用超表面调控透射波时, 既要满足相位分布, 同时还要在不同几何结构或材料属性下获取尽可能高的透射率[20], 以保证绝大多数的入射波能够通过透镜.
现阶段, 绝大多数超表面透镜只能实现正常聚焦, 即焦斑尺寸大于0.5λ (其中λ为工作波长), 焦斑尺寸相对较大, 不利于能量回收及点源成像. 为了缩小焦斑尺寸, 实现亚波长聚焦, 即使焦斑尺寸小于0.5λ, 一些方法被相继提出, 如利用各向异性材料的隧道谐振效应[21], 将倏逝波转化为行波[22], 利用双曲线型或抛物线型等频率线云图的特定频率区间[23]等; 但这些方法只适用于光波和声波, 并不适用于结构中的弯曲波. 为了提升传统矩形透镜的工作性能, 缩小焦斑尺寸, 实现亚波长聚焦, 本文提出了曲面弯曲波透镜的设计方法, 这是本文的一大创新. 这种设计方法使得焦点处能够接收到更多方向的透射波, 并间接地缩短了透镜与焦点之间的距离, 进而缩小焦斑尺寸, 提升聚焦效果.
首先, 本文利用透镜与焦点间的几何关系, 介绍了超表面凹透镜的设计原理; 其次, 应用Timoshenko梁方程得到了厚度与相位的定量化关系, 以此完成透镜的结构设计; 再次, 通过与传统矩形透镜的对比, 从有限元仿真和实验测试两个角度验证了本文设计方案的正确性和可靠性; 最后, 本文详细分析了凹透镜的宽频特性. 本文的设计方法能为声波、光波等领域相关透镜的设计提供借鉴.
1. 凹透镜的设计原理
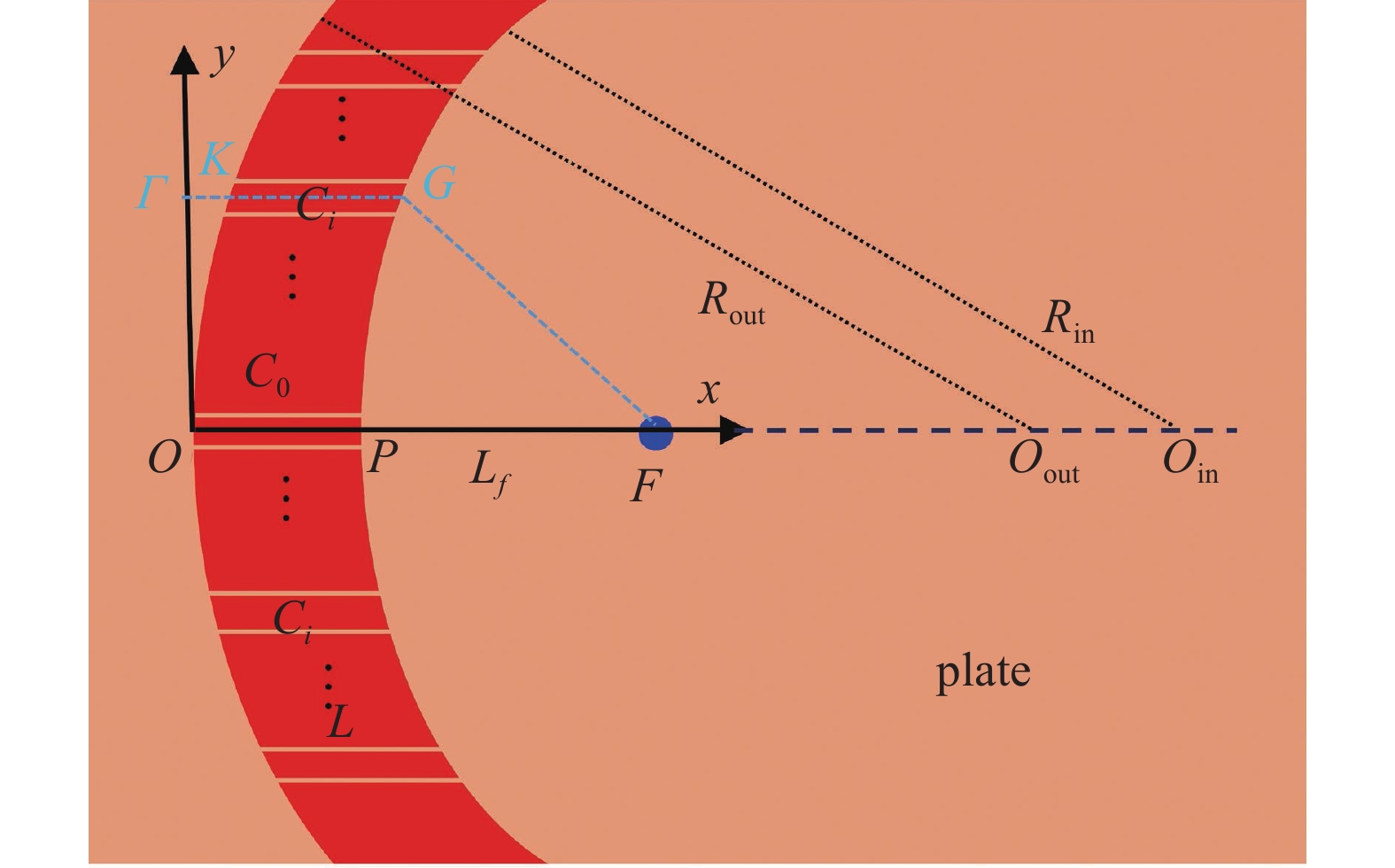
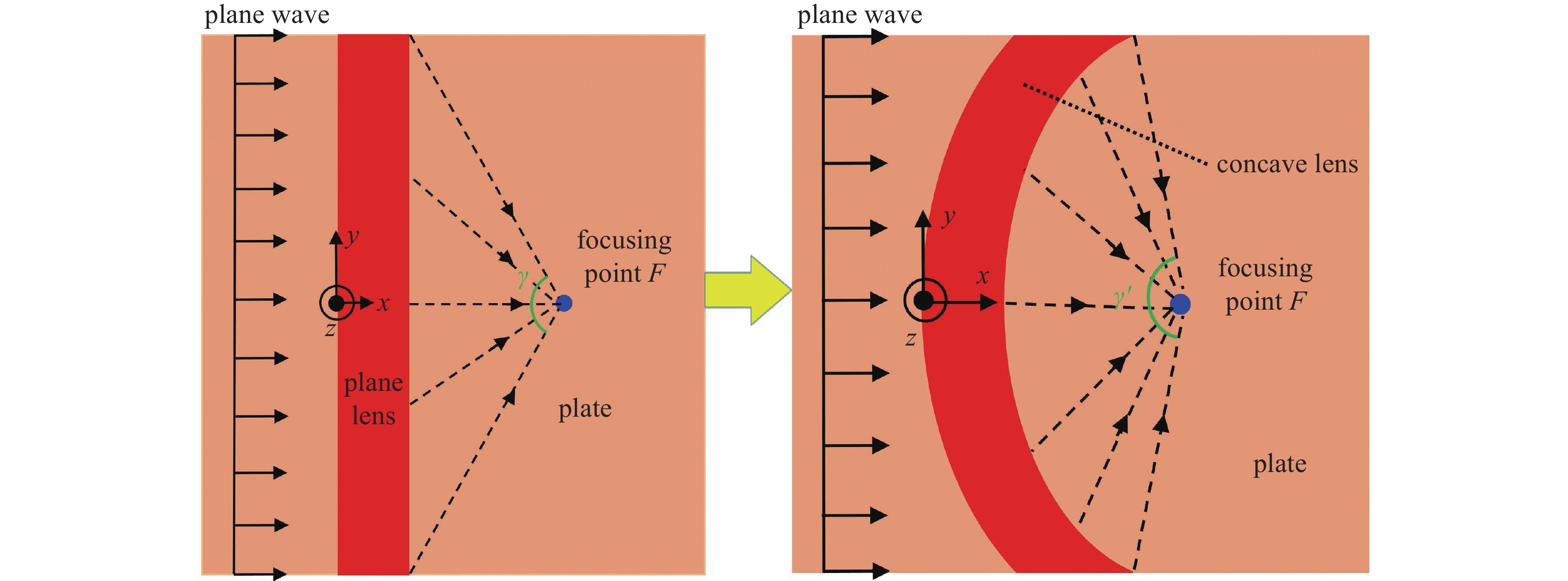
为了能够使入射的平面弯曲波聚集到指定位置, 通常会在焦点之前设计一个平面透镜, 如图1所示, 通过改变波传播的速度或相位, 使波同时到达焦点位置或在焦点位置发生相干干涉, 从而实现聚焦. 这种透镜一般能够实现正常聚焦, 即垂直于波传播方向的焦斑尺寸大于0.5λ[15-16, 24-25]. 为了提升聚焦效果, 本文将传统的平面透镜改进为等长度的凹透镜. 这种设计使得焦点处能够接收到更多方向的透射波, 如图1中$\gamma ' > \gamma $(这里$\gamma '$和$\gamma $为透镜边缘与焦点之间所形成的夹角); 同时由于透镜发生了弯曲, 与平面透镜相比, |y| > 0区域的透镜到焦点的距离也随之减小. 在上述这两方面因素的共同作用下, 焦斑尺寸将被缩小, 同时焦点处的能量将得到提高, 进而提升聚焦效果.
为了方便分析, 这里将聚焦位置设在x轴上, 则透镜关于y = 0对称. 在设计凹透镜过程中, 将整个透镜沿弧形方向划分为2N + 1个独立的子通道Ci (i = 0, 1, 2,···, N)[18-19], 如图2所示. 于是, 当弯曲波在透镜中传播时, 各通道之间互不干扰. 设凹透镜的内外径分别为Rin和Rout; 透镜的宽度为L; 焦点距离透镜右侧Lf处, 为了使平面入射的弯曲波经过透镜后聚焦在(L + Lf, 0)处, 这里令波沿OPF和ΓKGF两条路径传播的时间相同, 由此可得
$$ \frac{{{L_{OP}}}}{{{c_0}}} + \frac{{{L_{PF}}}}{{{{\bar c}_0}}} = \frac{{L_ {{\varGamma K}} + {L_{GF}}}}{{{{\bar c}_0}}} + \frac{{{L_{KG}}}}{{{c_i}}} $$ (1) 其中, c0和ci分别表示弯曲波在通道C0和Ci内传播的相速度; ${\bar c_0}$为波在平板中传播的相速度.
由式(1)可得
$$ {\phi _i} = {\phi _0} + \frac{\omega }{{{{\bar c}_0}}}\left( {{L_f} - L_ {{\varGamma K}} - {L_{GF}}} \right) $$ (2) 其中, $\phi_0 $和$\phi_i $分别表示弯曲波在通道C0和Ci内传播的相位变化; ω为角频率; LΓK和LGF分别为
$$ \left. \begin{split} & L_{{\varGamma K}} = {R_{{\rm{out}}}} - \sqrt {R_{{\rm{out}}}^2 - y_i^2} \\ & {L_{GF}} = \sqrt {y_i^2{\text{ + }}{{\left( {{L_f} - {R_{{\rm{in}}}} + \sqrt {R_{{\rm{in}}}^2 - y_i^2} } \right)}^{\text{2}}}} \end{split} \right\} $$ (3) 这里yi表示通道Ci的纵坐标. 本文的目的就是要通过结构设计使凹透镜各通道的相位分布满足式(2). 这里需要说明的是: 波在通过透镜的各通道后, 并不会只沿着图1中的路径进行传播, 而是以各通道的右端点为新的波源向四周辐射, 本文采用式(2)进行透镜的结构设计, 本质上是要求弯曲波能够在焦点处发生相干干涉, 从而形成能量的聚焦. 弹性平板中的弯曲波是频散的, 其速度与板的厚度直接相关, 因此可以通过改变透镜各通道的厚度, 进而改变相位以满足式(2). 本文接下来将通过理论模型获取透射波相位与厚度的定量关系.
2. 理论建模
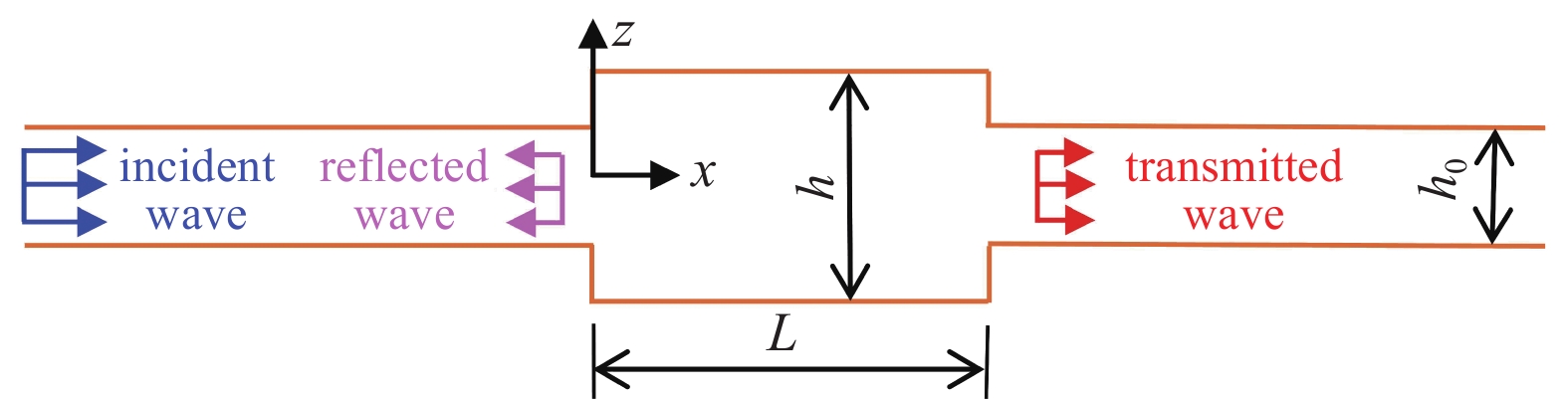
在厚度为h0的板中传播的弯曲波, 当遇到厚度为h的透镜子通道时会发生反射和透射, 如图3所示. 为了求解透射波的幅值和相位信息, 本文采用Timoshenko梁模型开展理论分析, 其控制微分方程为[26]
$$ \begin{split} & \frac{{EI}}{{\rho A}}\frac{{{\partial ^4}w(x,t)}}{{\partial {x^4}}} - \frac{I}{A}\left( {1 + \alpha } \right)\frac{{{\partial ^4}w(x,t)}}{{\partial {x^2}\partial {t^2}}} + \frac{{{\partial ^2}w(x,t)}}{{\partial {t^2}}}+ \\ &\qquad \frac{I}{A}\frac{\alpha }{{E/\rho }}\frac{{{\partial ^4}w(x,t)}}{{\partial {t^4}}} = 0 \end{split} $$ (4) 其中, $w(x,t)$为梁的挠度; 横截面的面积和惯性矩分别为A = bh和I = bh3/12 (这里b和h分别为梁的宽度和厚度); E和ρ分别为杨氏模量和密度; α = 2(1 + ν)/κ (这里ν和κ分别为泊松比和剪切修正因子); t代表时间. 当挠度确定后, 梁的转角$\varphi (x,t)$可通过下式得到[26-28]
$$ \frac{{\partial \varphi (x,t)}}{{\partial x}} = \frac{{{\partial ^2}w(x,t)}}{{\partial {x^2}}} - \frac{\alpha }{{E/\rho }}\frac{{{\partial ^2}w(x,t)}}{{\partial {t^2}}} $$ (5) 由此可得梁的弯矩$M(x,t)$和剪力$V(x,t)$分别为
$$ \left.\begin{split} & M(x,t) = - EI\frac{{\partial \varphi (x,t)}}{{\partial x}} \\ & V(x,t) = \frac{{EA}}{\alpha }\left( {\frac{{\partial w(x,t)}}{{\partial x}} - \varphi (x,t)} \right) \end{split} \right\} $$ (6) 式(4)的解可以在国内外很多文献中查阅到, 为了节省篇幅, 这里直接给出其解的表达形式, 即
$$ w(x,t) = \sum\limits_{j = 1}^4 {{G_j}} \exp \left[ {{\rm{i}}\left( {{k_j}x - \omega t} \right)} \right] $$ (7) 其中, Gj表示待定系数; i是虚数单位; 波速kj通过下式计算得到
$$ {k^4} - \frac{{{\omega ^2}}}{{E/\rho }}\left( {1 + \alpha } \right){k^2} + \frac{{{\omega ^2}}}{{E/\rho }}\left( {\frac{{\alpha {\omega ^2}}}{{E/\rho }} - \frac{A}{I}} \right) = 0 $$ (8) 这里为了方便分析, 用k1和k2分别代表沿x正向和负向传播的行波的波数, 用k3和k4分别代表沿x正向和负向传播的衰减波的波数. 基于式(4)和式(5), 相应的转角、弯矩和剪力分别为
$$ \left. \begin{split} & \varphi (x,t) = {\rm{i}}\left( {{k_j} - \frac{{\alpha {\omega ^2}}}{{{k_j}E/\rho }}} \right)w(x,t)= \\ & \qquad \sum\limits_{j = 1}^4 {{\rm{i}}\left( {{k_j} - \frac{{\alpha {\omega ^2}}}{{{k_j}E/\rho }}} \right){G_j}} \exp \left[ {{\rm{i}}\left( {{k_j}x - \omega t} \right)} \right] \\ & M(x,t) = EI\sum\limits_{j = 1}^4 {\left( {k_j^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right){G_j}} \exp \left[ {{\rm{i}}\left( {{k_j}x - \omega t} \right)} \right] \\ & V(x,t) = {\rm{i}}\rho A{\omega ^2}\sum\limits_{j = 1}^4 {\frac{{{G_j}}}{{{k_j}}}} \exp \left[ {{\rm{i}}\left( {{k_j}x - \omega t} \right)} \right] \end{split} \right\} $$ (9) 对于x < 0的入射波和反射波区域以及对于x > L的透射波区域, 其理论解分别如式(10)和式(11)所示[27-28]. 其中, R和T分别代表反射波和透射波的幅值; R′和T′分别代表x = 0和x = L处沿x轴负向和正向传播的衰减波的幅值; 为了避免与0 < x < L的物理量重复, 这里将波数添加了上标“−”加以区分. 此外, 为了满足x = 0和x = L处挠度、转角、弯矩和剪力的连续性条件, 将上述理论解代入, 可以得到式(12)所示的边界条件
$$ \left. \begin{split} & w(x,t) = \left( {{{\rm{e}}^{{\rm{i}}{{\bar k}_1}x}} + R{{\rm{e}}^{{\rm{i}}{{\bar k}_2}x}} + R'{{\rm{e}}^{{\rm{i}}{{\bar k}_4}x}}} \right){\rm{e}}^ { - {\rm{i}}\omega t} \\ & \varphi (x,t) = \left[ {\rm{i}}\left( {{{\bar k}_1} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_1}E/\rho }}} \right){{\rm{e}}^{{\rm{i}}{{\bar k}_1}x}} + {\rm{i}}\left( {{{\bar k}_2} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_2}E/\rho }}} \right)R{{\rm{e}}^{{\rm{i}}{{\bar k}_2}x}} +\right. \\ &\qquad \left.{\rm{i}}\left( {{{\bar k}_4} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_4}E/\rho }}} \right)R'{{\rm{e}}^{{\rm{i}}{{\bar k}_4}x}} \right]{\rm{e}}^ { - {\rm{i}}\omega t} \\ & M(x,t) = E\bar I\left[ \left( {\bar k_1^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right){{\rm{e}}^{{\rm{i}}{{\bar k}_1}x}} + \left( {\bar k_2^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right)R{{\rm{e}}^{{\rm{i}}{{\bar k}_2}x}} + \right.\\ &\qquad \left.\left( {\bar k_4^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right)R'{{\rm{e}}^{{\rm{i}}{{\bar k}_4}x}} \right]{\rm{e}}^ { - {\rm{i}}\omega t} \\ & V(x,t) = {\rm{i}}\rho \bar A{\omega ^2}\left( {\frac{1}{{{{\bar k}_1}}}{{\rm{e}}^{{\rm{i}}{{\bar k}_1}x}} + \frac{1}{{{{\bar k}_2}}}R{{\rm{e}}^{{\rm{i}}{{\bar k}_2}x}} + \frac{1}{{{{\bar k}_4}}}R'{{\rm{e}}^{{\rm{i}}{{\bar k}_4}x}}} \right){\rm{e}}^ { - {\rm{i}}\omega t} \end{split} \right\} $$ (10) $$ \left.\begin{split} & w(x,t) = \left( {T{{\rm{e}}^{{\rm{i}}{{\bar k}_1}\left( {x - L} \right)}} + T'{{\rm{e}}^{{\rm{i}}{{\bar k}_3}\left( {x - L} \right)}}} \right){\rm{e}}^ { - {\rm{i}}\omega t} \\ & \varphi (x,t) = \left[ {\rm{i}}\left( {{{\bar k}_1} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_1}E/\rho }}} \right)T{{\rm{e}}^{{\rm{i}}{{\bar k}_1}\left( {x - L} \right)}} +\right. \\ &\qquad \left.{\rm{i}}\left( {{{\bar k}_3} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_3}E/\rho }}} \right)T'{{\rm{e}}^{{\rm{i}}{{\bar k}_3}\left( {x - L} \right)}} \right]{\rm{e}}^ { - {\rm{i}}\omega t} \\ & M(x,t) = E\bar I\left[ \left( {\bar k_1^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right)T{{\rm{e}}^{{\rm{i}}{{\bar k}_1}\left( {x - L} \right)}} + \right.\\ &\qquad \left.\left( {\bar k_3^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right)T'{{\rm{e}}^{{\rm{i}}{{\bar k}_3}\left( {x - L} \right)}} \right]{\rm{e}}^ { - {\rm{i}}\omega t} \\ & V(x,t) = {\rm{i}}\rho \bar A{\omega ^2}\left( {\frac{1}{{{{\bar k}_1}}}T{\text{ + }}\frac{1}{{{{\bar k}_3}}}T'} \right){\rm{e}}^ { - {\rm{i}}\omega t} \end{split}\right\} $$ (11) $$ \left. \begin{split} & 1 + R + R' = \sum\limits_{j = 1}^4 {{G_j}}\cdot \\ & \left( {{{\bar k}_1} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_1}E/\rho }}} \right) + \left( {{{\bar k}_2} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_2}E/\rho }}} \right)R + \left( {{{\bar k}_4} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_4}E/\rho }}} \right)R' =\\ &\qquad \sum\limits_{j = 1}^4 {\left( {{k_j} - \frac{{\alpha {\omega ^2}}}{{{k_j}E/\rho }}} \right){G_j}} \\ & \frac{{\bar I}}{I}\left[ {\left( {\bar k_1^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right) + \left( {\bar k_2^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right)R + \left( {\bar k_4^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right)R'} \right] =\\ &\qquad \sum\limits_{j = 1}^4 {\left( {k_j^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right){G_j}} \\ & \frac{{\bar A}}{A}\left( {\frac{1}{{{{\bar k}_1}}} + \frac{1}{{{{\bar k}_2}}}R + \frac{1}{{{{\bar k}_4}}}R'} \right){\text{ = }}\sum\limits_{j = 1}^4 {\frac{{{G_j}}}{{{k_j}}}} \end{split} \right\} \tag{12a}$$ $$ \left. \begin{split} & \sum\limits_{j = 1}^4 {{G_j}} \exp ({\rm{i}}{k_j}L) = T + T{'} \\ & \sum\limits_{j = 1}^4 {\left( {{k_j} - \frac{{\alpha {\omega ^2}}}{{{k_j}E/\rho }}} \right){G_j}} \exp ({\rm{i}}{k_j}L) = \left( {{{\bar k}_1} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_1}E/\rho }}} \right)T +\\ &\qquad \left( {{{\bar k}_3} - \frac{{\alpha {\omega ^2}}}{{{{\bar k}_3}E/\rho }}} \right)T{'} \\ & \sum\limits_{j = 1}^4 {\left( {k_j^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right){G_j}} \exp ({\rm{i}}{k_j}L){\text{ = }}\frac{{\bar I}}{I}\left[ \left( {\bar k_1^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right)T +\right.\\ &\qquad \left.\left( {\bar k_3^2 - \frac{{\alpha {\omega ^2}}}{{E/\rho }}} \right)T{'} \right] \\ & \sum\limits_{j = 1}^4 {\frac{{{G_j}}}{{{k_j}}}} \exp ({\rm{i}}{k_j}L){\text{ = }}\frac{{\bar A}}{A}\left( {\frac{1}{{{{\bar k}_1}}}T{\text{ + }}\frac{1}{{{{\bar k}_3}}}T{'}} \right) \end{split} \right\} \tag{12b}$$ 式(12a)和式(12b)可以表示成如下的矩阵形式
$$ {{{{\boldsymbol{F}}_0}}} + {{{\boldsymbol{F}}_r}} {\left\{ {R,\;R'} \right\}^{\rm{T}}} = { {{{\boldsymbol{Q}}_r}} }{\left\{ {{G_1},\;{G_2},\;{G_3},\;{G_4}} \right\}^{\rm{T}}} \tag{13a}$$ $$ { {{{\boldsymbol{Q}}_t}}}{\left\{ {{G_1},\;{G_2},\;{G_3},\;{G_4}} \right\}^{\rm{T}}} = { {{{\boldsymbol{F}}_t}} }{\left\{ {T,\;T'} \right\}^{\rm{T}}} \tag{13b}$$ 其中, 上标T表示矩阵的转置; F0, Fr, Qr, Qt和Ft的具体表达式参见附录A. 综合式(13a)和式(13b)可得
$$ \begin{split} &\left[ {\begin{array}{*{20}{c}} { - {{ {{{\boldsymbol{F}}_r}} }},}&{{{{{{\boldsymbol{Q}}_r}} }} {{{\boldsymbol{Q}}_t}}^{ - 1}{{ {{{\boldsymbol{F}}_t}} }}} \end{array}} \right]\cdot\\ &\qquad {\left\{ {R,\;R',\;T,\;T'} \right\}^{\rm{T}}} ={ {{{\boldsymbol{F}}_0}} } \end{split}$$ (14) 式(14)为四元一次线性非齐次方程组, 从中可以求解得到反射波和透射波. T确定之后, x = L处透射波的相位φ可由通过下式计算得到[29], 即
$$ \phi = \left\{ \begin{split} & \arctan {\frac{{{\rm{Im}}(T)}}{{{\rm{Re}}(T)}}} + \frac{\text{π} }{2},\;{\rm{if}}\;{\rm{Re}}(T) > 0 \\ & \arctan {\frac{{{\rm{Im}}(T)}}{{{\rm{Re}}(T)}}} + \frac{{3\text{π} }}{2},\;{\rm{if}}\;{\rm{Re}}(T) < 0 \end{split} \right. $$ (15) 本文后续将应用式(15)进行凹透镜的结构设计.
3. 透镜的结构设计及聚焦效果
3.1 透镜设计及有限元仿真
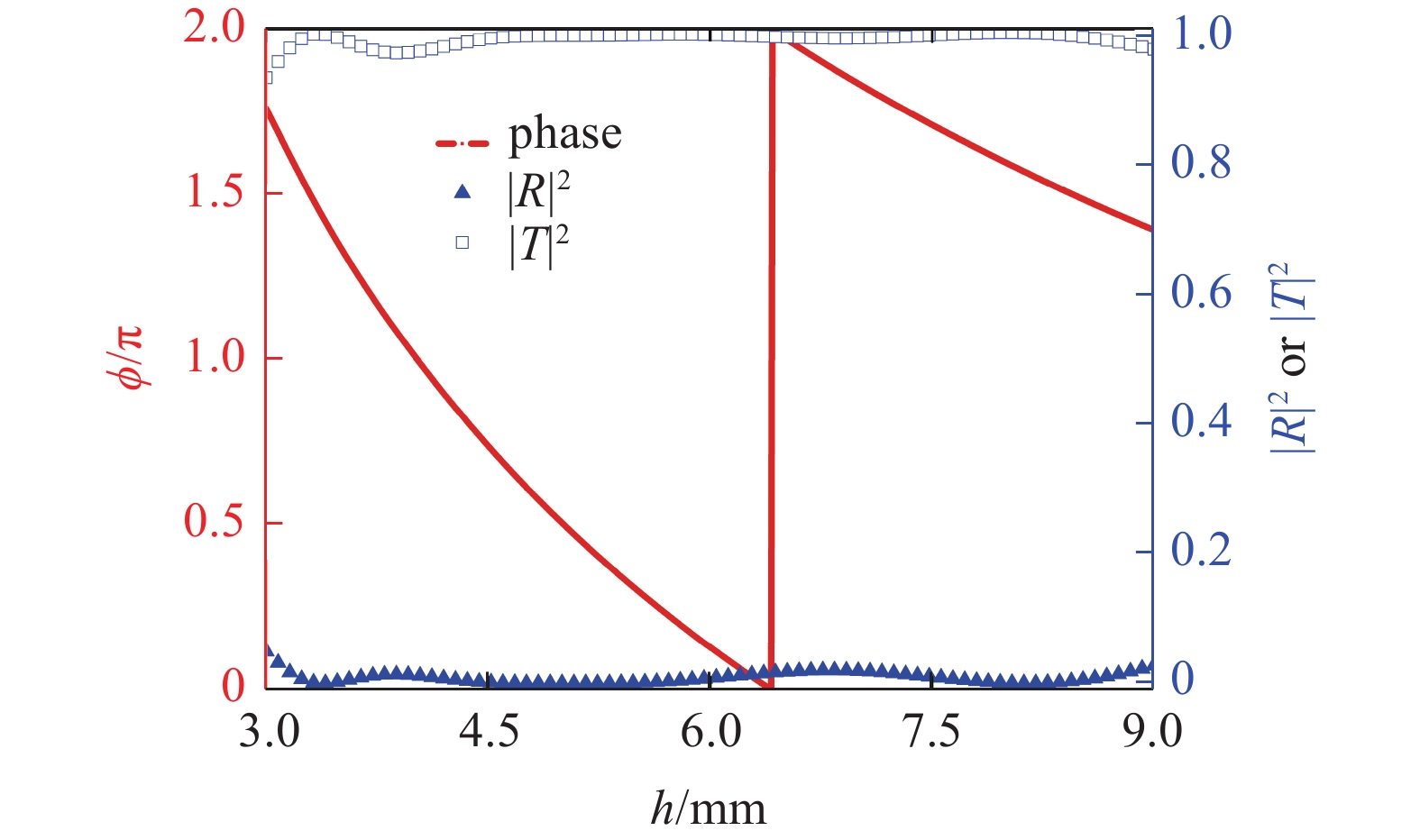
本文以结构健康监测和无损检测领域中常用的铝板作为研究对象, 其杨氏模量、泊松比和密度分别为E = 70 GPa, ρ = 2700 kg/m3, ν = 0.3[25, 30-31]. 板的厚度h0 = 5 mm, 透镜的内外径Rin = Rout = 0.3 m, 单通道的长度L = 0.1 m, 焦距Lf = 0.1 m, 入射波频率选择为f = 20 kHz, 此时工作波长λ = 4.8 cm. 当厚度h变化时, 反射系数|R|2、透射系数|T|2及相位φ随h的变化规律如图4所示, 由此可见: |R|2 + |T|2 = 1, 符合能量守恒, 说明本文的仿真结果是正确的; 此外, 当厚度h在[3, 7.5] mm范围内改变时, 相位变化范围为[0, 2π], 且在此范围内弯曲波始终保持较高的透射率. 因此, 本文将应用这一厚度变化范围进行透镜的结构设计.
![]()
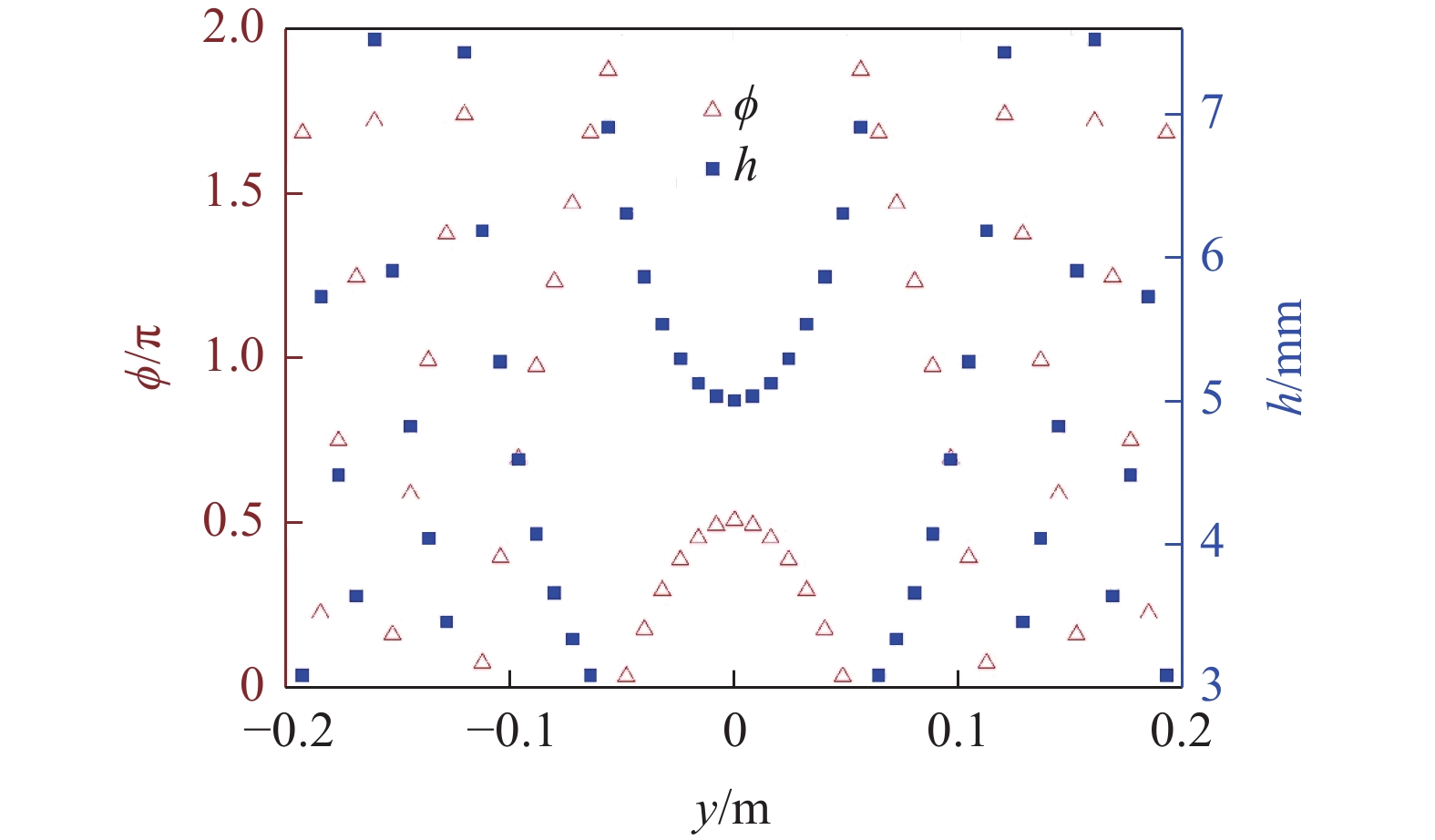
图 4 工作频率f = 20 kHz情况下相位、透射系数和反射系数随厚度的变化趋势Figure 4. Variations of phase and transmission coefficient versus thickness when f = 20 kHz本文将凹透镜沿y方向的总长度取为0.4 m, 总共划分为49 (即N = 24)个通道, 通道之间间隔1 mm, 此时由式(3)计算得到的各通道的相位分布及利用图4得到的相应厚度值如图5所示. 由此可见: 透镜关于x = 0对称, 且相位沿y轴的变化趋势与厚度相反, 这是因为低频情况下弯曲波的速度与厚度成反比.
![]()
图 5 透镜各通道的相位及厚度Figure 5. Phase and thickness values of individual elements of the curving lens designed在确定了透镜尺寸之后, 本文应用有限元软件COMSOL multiphysics的结构力学模块开展频域性能仿真. 仿真过程中使用四面体单元, 最大单元尺寸为3 mm, 并沿板厚度方向设置8个单元以确保仿真结果的准确性. 在距离透镜左侧0.3 m的直线位置施加沿z方向的位移, 用于激发板中的弯曲波, 并在板的四周增加1 m长的完美匹配层, 以模拟无穷远边界条件. 图6(a)为仿真得到的20 kHz时透镜附近的|w|2云图, 为了对比, 这里还给出了平面透镜及不包括透镜情况下板中相同位置的|w|2云图. 由此可见: 弯曲波经过透镜后聚焦在(0.193, 0) m, 与理论设计值(0.2, 0) m相差很小, 这充分说明了本文透镜设计方法的正确性; 此外, 与平面透镜相比, 本文所设计的凹透镜使得焦点处能够接收到更多方向的透射波, 所以焦点处的能量得到了提升.
为了进一步进行量化分析, 图6(b)给出了|w|2沿x和y轴的变化趋势, 由此可见: 与矩形透镜相比, 凹透镜可提升焦点处的能量, 并缩小焦斑尺寸. 相同条件下, 凹透镜在焦点处的能量峰值为1.257 × 10−12 m2, 约为平面透镜焦点峰值9.15 × 10−13 m2的1.37倍; 与此同时, 凹透镜在x和y方向的焦斑尺寸分别为1.36λ和0.48λ, 小于矩形透镜的1.91λ和0.54λ. 这里需要特别强调的是, 凹透镜在y方向的焦斑尺寸为0.48λ, 小于0.5λ, 属于亚波长聚焦. 这是因为与平面透镜相比, 焦点到 ± y轴上透镜的距离变小, 一些衰减波的分量没有完全衰减至零, 所以焦斑尺寸小于0.5λ.
3.2 实验验证
为了进一步验证凹透镜的工作性能, 还开展了相关的实验研究. 在透镜加工阶段, 采用精密机械加工方式, 分别加工厚度如图5所示的49个通道, 并将这些通道以胶接方式内嵌至铝板中, 各通道之间预留1 mm间隙以防止波在不同通道内传播时的相互干扰. 实验的测试系统如图7所示, 包括信号发生器、功率放大器、示波器和换能器等. 为了激发入射的平面弯曲波, 在透镜左侧金属板的表面布置1列(17个)压电片PZT5 A, 每个压电片之间间隔3 cm. 实验过程中, 首先采用20 kHz的五波峰脉冲信号, 由信号发生器激发并经过功率放大器放大, 接着对并联压电阵列进行信号激励, 形成近似的平面波; 其次, 平面波通过透镜后在其右侧聚焦, 为了验证其聚焦效果, 本文重点关注理论设计位置(0.2, 0) m附近的振动信号; 再次, 采用换能器对信号进行采集并将其转换为电压信号, 再通过示波器即可观测到采集的时域信号; 最后, 将时域信号进行快速傅里叶变换后得到频域信号进行分析. 这里需要强调的是: 课题组在铝板四周粘贴了阻尼胶进行吸波, 如图7所示, 以减小边界反射波对检测信号的影响; 实验过程中铝板放置在镂空的实验台上, 以尽量减小铝板与实验台的接触条件所引起的误差. 此外, 本文进行了凹透镜和平面透镜两组对比实验, 透镜加工及实验过程中, 除两种透镜的各通道厚度外, 其他工况(包括金属板的尺寸、压电阵列的布局、激励电压、阻尼胶的布置和检测位置等)都尽量保持一致.
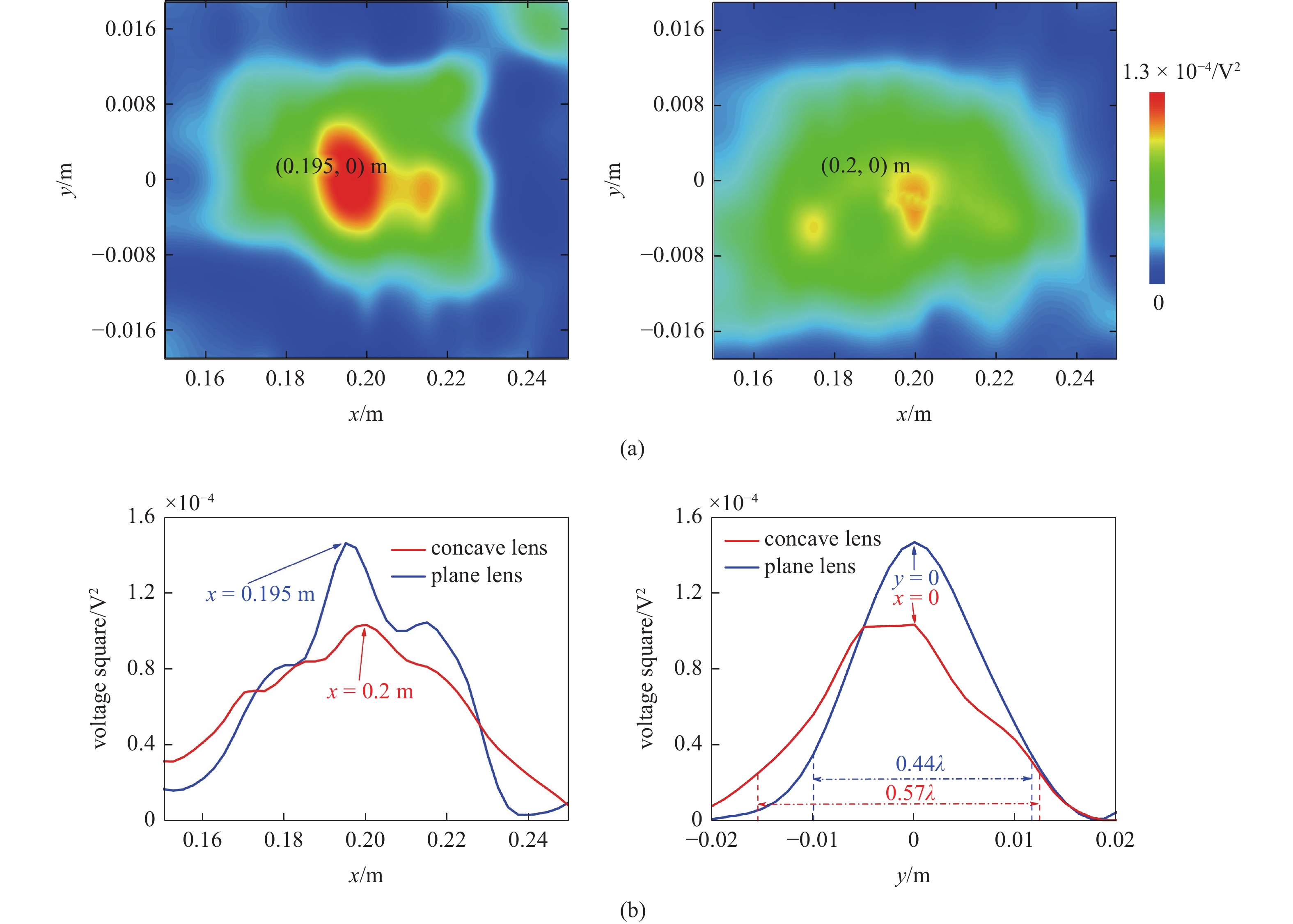
提取20 kHz频率下(0.2, 0) m附近各采样点的电压值, 考虑到电压与位移成正比, 本文应用各采样点的电压的平方值, 绘制如图8(a)所示的能量云图; 相应地, 电压平方的峰值沿x轴和y轴的分布如图8(b)所示. 由此可以看出, 对于凹透镜和平面透镜, 聚焦的位置分别为(0.195, 0) m和(0.2, 0) m, 这与理论设计值十分吻合; 对于凹透镜来说, 焦点处电压的平方值分别为1.46V2, 约为平面透镜1.03V2的1.42倍; 凹透镜y方向的焦斑尺寸为0.44λ, 小于平面透镜的0.57λ, 且属于亚波长聚焦.
![]()
图 8 实验结果: (a) 凹透镜(左)和平面透镜(右)在焦点附近电压平方的云图; (b) 电压平方沿x轴(左)和y轴(右)的分布Figure 8. Results from experimental measurement: (a) The contour distributions of voltage square near the concave lens (left) and plane lens (right); (b) The distributions of voltage square along x (left) and y (right) directions, respectively综合上述, 实验结果与仿真结果基本保持一致, 但会有一定的误差, 主要取决于以下几个方面: 首先, 本文是先加工透镜的各个通道, 而后通过人工胶接的方式将这些通道内嵌至铝板当中, 不可避免地会导致透镜结构的不完全对称, 所以图8中检测的结果沿y轴并不是对称的; 其次, 数值模拟中是针对工作频率20 kHz进行仿真的, 但实验中激励信号是以20 kHz为中心的五波峰信号, 存在一定的带宽; 再次, 本文虽然将金属板放置在中间镂空的实验台架上, 但并不能保证金属板处于完全应力自由状态; 最后, 本文采用换能器进行信号采集, 换能器与金属板之间存在一定的接触面积, 所提取的电压是该接触面积的电压和[32-33], 而不是接触中心的电压值, 这也会给检测结果带来误差. 尽管如此, 上述实验结果充分证明了本文所设计的凹透镜具有良好的聚焦效果, 其焦点处的能量及焦斑尺寸较平面透镜均有一定程度的改善.
3.3 透镜的工作带宽
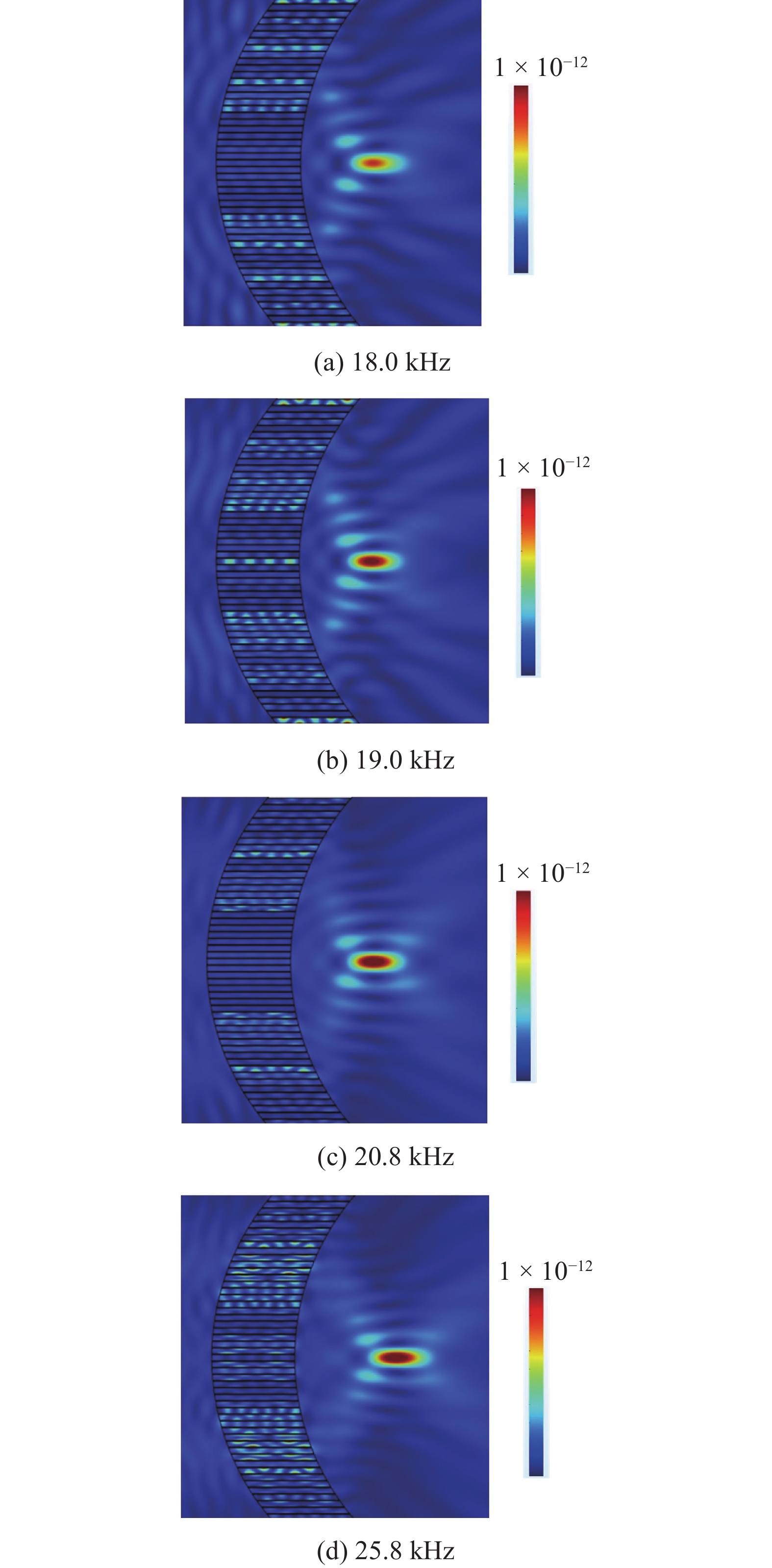
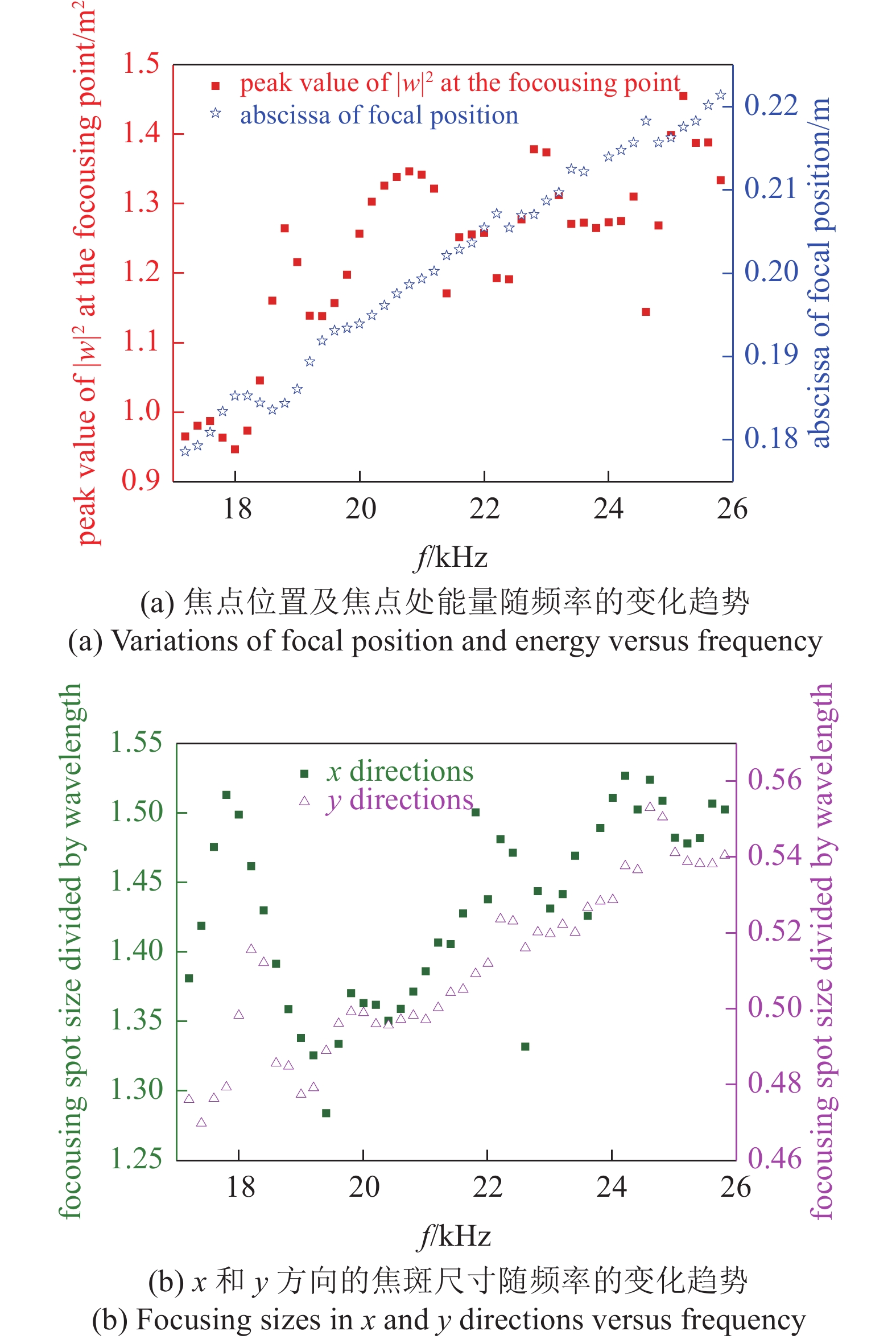
虽然该透镜的工作频率为20 kHz, 但由弯曲波的传播特性可知, 当频率在20 kHz附近发生微小改变时, 其速度变化并不显著[25, 34]. 由此可以预测: 在结构参数不变的情况下, 当工作频率在20 kHz附近发生改变时, 此透镜仍具有一定的聚焦效果. 为了验证这一推测, 本文对该凹透镜进行了扫频分析, 结果如图9和图10所示. 由图10(a)可知: 在20 kHz工作频率附近, 透镜均能将入射的平面弯曲波聚焦; 且随着频率的增加, 焦点的位置逐渐远离透镜, 这是因为频率越高, 各通道内弯曲波的传播速度越大, 相同时间内其传播的距离就越远. 为了量化, 本文选择|Ff−0.2|≤0.5λf来约束该透镜的工作频率范围(其中Ff表示不同频率下的聚焦位置坐标; 0.2 m为理论设计值; λf表示不同频率下的波长). 如果该式满足, 则认为该频率下透镜能够正常工作, 反之亦然. 应用此判断准则, 本文凹透镜的工作频率区间为[17.2, 25.8] kHz; 在此频率区间内, 随频率的增大, x和y方向无量纲的焦斑尺寸逐渐增大, 如图10(b)所示, 且当频率小于19.6 kHz时, 除个别频率外, y方向的焦斑尺寸均小于0.5λf, 属于亚波长聚焦.
![]()
图 9 不同频率下透镜的聚焦效果Figure 9. Working performance of the concave lens designed when f varies![]()
图 10 透镜的性能指标随频率的变化规律Figure 10. Performance indices of the concave lens designed versus frequency4. 结 论
本文基于Timoshenko梁理论, 利用厚度变化设计了凹透镜, 用于聚焦入射的平面弯曲波, 数值模拟和实验结果表明: 该透镜聚焦位置准确, 焦点能量较高, 聚焦效果优于传统平面透镜, 主要体现在如下两个方面.
(1) 由于焦点处可以接收到更多方向的透射波, 焦点处的能量约为普通平面透镜的1.3倍;
(2) 透镜到焦点的距离有所减小, 因此凹透镜的焦斑尺寸比平面透镜小, 对于本文的凹透镜, 其焦斑尺寸小于0.5λ, 属于亚波长聚焦.
此外, 本文的透镜在结构参数不变的情况下能够在设计频率附近工作. 由于本文仅利用了厚度变化来进行结构设计, 透镜结构相对简单, 由单相材料组成, 工程易于实现, 可避免多相材料所导致的加工复杂及阻抗不匹配等问题. 此外, 本文的设计思路及结果还可为透镜在无损检测和能量回收等领域的应用提供借鉴和参考.
附录A
F0, Fr, Qr, Qt和Ft的具体表达式如下所示$\; $
$$ {{\boldsymbol{F}}}_0=\left[1\quad \bar{k}_1-\frac{\alpha \omega^2}{\bar{k}_1 E / \rho}\quad \frac{\bar{I}}{I}\left(\bar{k}_1^2-\frac{\alpha \omega^2}{E / \rho}\right) \quad \frac{\bar{A}}{A} \frac{1}{\bar{k}_1}\right]^{\mathrm{T}} \tag{A1}$$ $$ \boldsymbol{F}_r=\left[\begin{array}{cc} 1 & 1 \\ \bar{k}_2-\dfrac{\alpha \omega^2}{\bar{k}_2 E / \rho} & \bar{k}_4-\dfrac{\alpha \omega^2}{\bar{k}_4 E / \rho} \\ \bar{I}\left(\bar{k}_2^2-\dfrac{\alpha \omega^2}{E / \rho}\right) & \bar{I}\left(\bar{k}_4^2-\dfrac{\alpha \omega^2}{E / \rho}\right) \\ \dfrac{\bar{A}}{A} \dfrac{1}{\bar{k}_2} & \bar{A} \dfrac{1}{\overline{k_4}} \end{array}\right] \tag{A2}$$ $$ \boldsymbol{F}_t=\left[\begin{array}{cc} 1 & 1 \\ \bar{k}_1-\dfrac{\alpha \omega^2}{\bar{k}_1 E / \rho} & \bar{k}_3-\dfrac{\alpha \omega^2}{\bar{k}_3 E / \rho} \\ \dfrac{\bar{I}}{I}\left(\bar{k}_1^2-\dfrac{\alpha \omega^2}{E / \rho}\right) & \bar{I}\left(\bar{k}_3^2-\dfrac{\alpha \omega^2}{E / \rho}\right) \\ \dfrac{\bar{A}}{A} \dfrac{1}{\bar{k}_1} & \dfrac{\bar{A}}{A} \dfrac{1}{\bar{k}_3} \end{array}\right] \tag{A3}$$ $$\boldsymbol{Q}_r=\left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ k_1-\dfrac{\alpha \omega^2}{k_1 E / \rho} & k_2-\dfrac{\alpha \omega^2}{k_2 E / \rho} & k_3-\dfrac{\alpha \omega^2}{k_3 E / \rho} & k_4-\dfrac{\alpha \omega^2}{k_4 E / \rho} \\ k_1^2-\dfrac{\alpha \omega^2}{E / \rho} & k_2^2-\dfrac{\alpha \omega^2}{E / \rho} & k_3^2-\dfrac{\alpha \omega^2}{E / \rho} & k_4^2-\dfrac{\alpha \omega^2}{E / \rho} \\ \dfrac{1}{k_1} & \dfrac{1}{k_2} & \dfrac{1}{k_3} & \dfrac{1}{k_4} \end{array}\right] \tag{A4}$$ $$ \boldsymbol{Q}_t=\left[\begin{array}{llll} \exp \left({\rm{i}} k_1 L\right) & \left(k_1-\dfrac{\alpha \omega^2}{k_1 E / \rho}\right) \exp \left({\rm{i}} k_1 L\right) & \left(k_1^2-\dfrac{\alpha \omega^2}{E / \rho}\right) \exp \left({\rm{i}} k_1 L\right) & \dfrac{1}{k_1} \exp \left({\rm{i}} k_1 L\right) \\ \exp \left({\rm{i}} k_2 L\right) & \left(k_2-\dfrac{\alpha \omega^2}{k_2 E / \rho}\right) \exp \left({\rm{i}} k_2 L\right) & \left(k_2^2-\dfrac{\alpha \omega^2}{E / \rho}\right) \exp \left({\rm{i}} k_1 L\right) & \dfrac{1}{k_2} \exp \left({\rm{i}} k_2 L\right) \\ \exp \left({\rm{i}} k_3 L\right) & \left(k_3-\dfrac{\alpha \omega^2}{k_3 E / \rho}\right) \exp \left({\rm{i}} k_3 L\right) & \left(k_3^2-\dfrac{\alpha \omega^2}{E / \rho}\right) \exp \left({\rm{i}} k_1 L\right) & \dfrac{1}{k_3} \exp \left({\rm{i}} k_3 L\right) \\ \exp \left({\rm{i}} k_4 L\right) & \left(k_4-\dfrac{\alpha \omega^2}{k_4 E / \rho}\right) \exp \left({\rm{i}} k_4 L\right) & \left(k_4^2-\dfrac{\alpha \omega^2}{E / \rho}\right) \exp \left({\rm{i}} k_1 L\right) & \dfrac{1}{k_4} \exp \left({\rm{i}} k_4 L\right) \end{array}\right]^{\mathrm{T}} \tag{A5}$$ -
![]()
图 4 工作频率f = 20 kHz情况下相位、透射系数和反射系数随厚度的变化趋势
Figure 4. Variations of phase and transmission coefficient versus thickness when f = 20 kHz
![]()
图 5 透镜各通道的相位及厚度
Figure 5. Phase and thickness values of individual elements of the curving lens designed
![]()
图 8 实验结果: (a) 凹透镜(左)和平面透镜(右)在焦点附近电压平方的云图; (b) 电压平方沿x轴(左)和y轴(右)的分布
Figure 8. Results from experimental measurement: (a) The contour distributions of voltage square near the concave lens (left) and plane lens (right); (b) The distributions of voltage square along x (left) and y (right) directions, respectively
![]()
图 9 不同频率下透镜的聚焦效果
Figure 9. Working performance of the concave lens designed when f varies
-
[1] 姜恒, 黄国良. 弹性波与力学超材料设计与应用专题序. 力学学报, 2022, 54(10): 2676-2677 (Jiang Heng, Huang Guoliang. Preface of theme articles on design and application of elastic wave and mechanical metamaterials. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(10): 2676-2677 (in Chinese) doi: 10.6052/0459-1879-22-481 Jiang Heng, Huang Guoliang. Preface of theme articles on design and application of elastic wave and mechanical metamaterials. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(10): 2676-2677 (in Chinese) doi: 10.6052/0459-1879-22-481
[2] 夏建平, 葛勇, 孙宏祥等. 基于近零折射率材料的声非对称聚焦透镜. 声学学报, 2019, 44(4): 765-771 (Xia Jianping, Ge Yong, Sun Hongxiang, et al. Acoustic asymmetric focusing lens by near-zero refractive index material. Acta Acustica, 2019, 44(4): 765-771 (in Chinese) doi: 10.15949/j.cnki.0371-0025.2019.04.038 Xia Jianping, Ge Yong, Sun Hongxiang, et al. Acoustic asymmetric focusing lens by near-zero refractive index material. Acta Acustica, 2019, 44(4): 765-771 (in Chinese) doi: 10.15949/j.cnki.0371-0025.2019.04.038
[3] 王丹凤, 任致远, 庄国志. 梯度折射率超材料透镜. 科学通报, 2022, 67(12): 1279-1289 (Wang Danfeng, Ren Zhiyuan, Zhuang Guozhi. A review of gradient index metamaterials lenses. Chinese Science Bulletin, 2022, 67(12): 1279-1289 (in Chinese) doi: 10.1360/TB-2021-0523 Wang Danfeng, Ren Zhiyuan, Zhuang Guozhi. A review of gradient index metamaterials lenses. Chinese Science Bulletin, 2022, 67(12): 1279-1289 (in Chinese) doi: 10.1360/TB-2021-0523
[4] Hu CJ, Xue SW, Yin YH, et al. Acoustic super-resolution imaging based on solid immersion 3D Maxwell's fish-eye lens. Applied Physics Letters, 2022, 120: 192202 doi: 10.1063/5.0093339
[5] Zhao LX, Lai CQ, Yu M. Modified structural Luneburg lens for broadband focusing and collimation. Mechanical Systems and Signal Processing, 2020, 144: 106868 doi: 10.1016/j.ymssp.2020.106868
[6] Zhao LX, Horiuchi T, Yu M. Broadband acoustic collimation and focusing using reduced aberration acoustic Luneburg lens. Journal of Applied Physics, 2021, 130: 214901 doi: 10.1063/5.0064571
[7] Ma TX, Li ZY, Zhang CZ, et al. Energy harvesting of Rayleigh surface waves by a phononic crystal Luneburg lens. International Journal of Mechanical Sciences, 2022, 227: 107435 doi: 10.1016/j.ijmecsci.2022.107435
[8] Zhu HF, Semperlotti F. Anomalous refraction of acoustic guided waves in solids with geometrically tapered metasurfaces. Physcial Review Letters, 2016, 117: 034302 doi: 10.1103/PhysRevLett.117.034302
[9] Climente A, Torrent D, Sánchez-Dehesa J. Gradient index lenses for flexural waves based on thickness variations. Applied Physics Letters, 2014, 105: 064101 doi: 10.1063/1.4893153
[10] 史惠琦, 王惠明. 一种新型介电弹性体仿生可调焦透镜的变焦分析. 力学学报, 2020, 52(6): 1719-1729 (Shi Huiqi, Wang Huiming. Theoretical nonlinear analysis of a biomimetic tunable lens driven by dielectric elastomer. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1719-1729 (in Chinese) doi: 10.6052/0459-1879-20-212 Shi Huiqi, Wang Huiming. Theoretical nonlinear analysis of a biomimetic tunable lens driven by dielectric elastomer. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1719-1729 (in Chinese) doi: 10.6052/0459-1879-20-212
[11] Wang ZY, Zhang P, Nie XF, et al. Focusing of liquid surface waves by gradient index lens. Europhysics Letters, 2014, 108: 24003 doi: 10.1209/0295-5075/108/24003
[12] Darabi A, Leamy MJ. Analysis and experimental validation of an optimized gradient-index phononic-crystal lens. Physical Review Applied, 2018, 10: 024045 doi: 10.1103/PhysRevApplied.10.024045
[13] Jin YB, Djafari-Rouhani B, Torrent D. Gradient index phononic crystals and metamaterials. Nanophonics, 2019, 8: 685-701
[14] Yu NF, Genevet P, Kats MA, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science, 2011, 334: 333-337 doi: 10.1126/science.1210713
[15] Li Y, Liang B, Gu ZM, et al. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Scientific Reports, 2013, 3: 2546 doi: 10.1038/srep02546
[16] Zhang H, Xiao Y, Wen JH, et al. Ultra-thin smart acoustic metasurface for low-frequency sound insulation. Applied Physics Letters, 2016, 108: 141902 doi: 10.1063/1.4945664
[17] Wang YF, Wang Y, Wu B, et al. Tunable and active phononic crystals and metamaterials. Applied Mechanics Reviews, 2020, 72: 040801 doi: 10.1115/1.4046222
[18] Mei J, Wu Y. Controllable transmission and total reflection through an impedance-matched acoustic metasurface. New Journal of Physics, 2014, 16: 123007 doi: 10.1088/1367-2630/16/12/123007
[19] Zhang J, Su XS, Liu YL, et al. Metasurface constituted by thin composite beams to steer flexural waves in thin plates. International Journal of Solids and Structures, 2019, 162: 14-20 doi: 10.1016/j.ijsolstr.2018.11.025
[20] Cao LY, Yang ZC, Xu YL, et al. Pillared elastic metasurface with constructive interference for flexural wave manipulation. Mechanical Systems and Signal Processing, 2021, 146: 107035 doi: 10.1016/j.ymssp.2020.107035
[21] Shen C, Xie YB, Sui N, et al. Broadband acoustic hyperbolic metamaterial. Physical Review Letters, 2015, 115: 254301 doi: 10.1103/PhysRevLett.115.254301
[22] Jia H, Ke MZ, Hao R, et al. Subwavelength imaging by a simple planar acoustic superlens. Applied Physics Letters, 2010, 97: 173507 doi: 10.1063/1.3507893
[23] Liu AP, Zhou XM, Huang GL, et al. Super-resolution imaging by resonant tunneling in anisotropic acoustic metamaterials. The Journal of the Acoustical Society of America, 2012, 132: 2800-2806 doi: 10.1121/1.4744932
[24] Qi SB, Li Y, Assouar B. Acoustic focusing and energy confinement based on multilateral metasurfaces. Physical Review Applied, 2017, 7: 054006 doi: 10.1103/PhysRevApplied.7.054006
[25] 宋世超, 王彬, 李鹏等. A0模态Lamb波聚焦透镜的结构设计及实验研究. 声学学报, 2023, 48(1): 154-161 (Song Shichao, Wang Bin, Li Peng, et al. The structural design and experimental investigation of focusing lens of A0 mode Lamb waves. Acta Acustica, 2023, 48(1): 154-161 (in Chinese) Song Shichao, Wang Bin, Li Peng, et al. The structural design and experimental investigation of focusing lens of A0 mode Lamb waves. Acta Acustica, 2023, 48(1): 154-161 (in Chinese)
[26] Liu L, Hussein MI. Wave motion in periodic flexural beams and characterization of the transition between Bragg scattering and local resonance. Journal of Applied Mechanics, 2012, 79: 011003 doi: 10.1115/1.4004592
[27] Geng Q, Wang T, Wu L, et al. Defect coupling behavior and flexural wave energy harvesting of phononic crystal beams with double defects in thermal environments. Journal of Physics D: Applied Physics, 2021, 54(22): 225501 doi: 10.1088/1361-6463/abe1e7
[28] Li P, Qian Z, Dong B, et al. A novel method for sub-wavelength focusing of flexural waves. International Journal of Mechanical Sciences, 2023, 248: 108206 doi: 10.1016/j.ijmecsci.2023.108206
[29] Xu YL, Cao LY, Yang ZC. Deflecting incident flexural waves by nonresonant single-phase meta-slab with subunits of graded thicknesses. Journal of Sound and Vibration, 2019, 454: 51-62 doi: 10.1016/j.jsv.2019.04.028
[30] Belanger P, Boivin G. Development of a low frequency omnidirectional piezoelectric shear horizontal wave transducer. Smart Materials and Structures, 2016, 25: 045024 doi: 10.1088/0964-1726/25/4/045024
[31] Huan Q, Miao HC, Li FX. Generation and reception of shear horizontal waves using the synthetic face-shear mode of a thickness-poled piezoelectric wafer. Ultrasonics, 2018, 86: 20-27 doi: 10.1016/j.ultras.2018.01.009
[32] Raghavan A, Cesnik CES. Finite-dimensional piezoelectric transducer modeling for guided wave based structural health monitoring. Smart Materials and Structures, 2005, 14(6): 1448-1461 doi: 10.1088/0964-1726/14/6/037
[33] Koduru JP, Rose JL. Transducer arrays for omnidirectional guided wave mode control in plate like structures. Smart Materials and Structures, 2012, 22(1): 15010
[34] Li P, Qian Z, Zhang YH, et al. The energy focusing of reflected flexural waves via two adjacent phase-modulation-based lenses. Energy, 2023, 267: 126523 doi: 10.1016/j.energy.2022.126523
-
期刊类型引用(0)
其他类型引用(1)
下载:
计量
- 文章访问数: 607
- HTML全文浏览量: 199
- PDF下载量: 105
- 被引次数: 1
