ADAPTIVE ISOGEOMETRIC BUCKLING ANALYSIS OF STIFFENED PANELS DRIVEN BY STIFFENER PATHS
-
摘要: 加筋薄壁结构常被用于航空航天结构的轻量化设计. 随着结构尺寸和几何特征的增加, 需要更加精细的网格来满足分析精度的要求. 传统的等几何方法采用NURBS张量积形式的拓扑结构, 使得在分析过程中难以实现局部细化, 而全局细化则会增加不必要的自由度. 为了提升加筋板壳结构的数值分析精度和效率, 提出一种基于RPHT (rational polynomial splines over hierarchical T-meshes)样条的加筋板壳自适应等几何屈曲分析方法. 样条网格可以沿着加筋路径进行自适应的局部细化, 有效提升低自由度下加筋板壳结构等几何屈曲分析的精度. 首先, 蒙皮和筋条分别采用RPHT样条曲面和NURBS样条曲线进行建模, 几何建模与数值仿真采用统一的几何语言, 实现建模与分析的一体化. 其次, 采用几何投影算法和样条插值算法实现筋条与蒙皮之间的高效高精度强耦合, 并建立基于加筋路径驱动自适应网格细化方法. 最后, 曲线加筋板和网格加筋壳两个算例验证本方法的高效性和鲁棒性, 通过与基于NURBS的等几何分析进行对比, 本方法能够明显降低分析模型的总自由度.Abstract: The stiffened thin-walled structures are broadly used in the lightweight design of aerospace structures. With the increase in structure size and geometric characteristics, more refined meshes are needed to meet the requirements of analysis accuracy. The conventional isogeometric method adopts the topological structure in the form of NURBS tensor product, which makes it challenging to achieve local refinement in the analysis process, and global refinement will increase unnecessary degrees of freedom. In order to improve the accuracy and efficiency of numerical analysis of stiffened plate and shell structures, an adaptive isogeometric buckling analysis method based on RPHT-spline (rational polynomial splines over hierarchical T-meshes) for stiffened structures is presented in this paper. The spline mesh can be refined locally and adaptively along the stiffener paths, which effectively improves the accuracy of isogeometric buckling analysis of stiffened panels with low degrees of freedom. Firstly, the skins and stiffeners are modelled using RPHT-spline surfaces and NURBS curves, respectively. The geometric modeling and numerical simulation adopt a unified geometric language to achieve the integration of modelling and analysis. Secondly, the geometric projection algorithm and spline interpolation algorithm are used to achieve the high-efficiency and high-precision strong coupling between skins and stiffeners. In addition, an adaptive mesh refinement method driven by the stiffener paths is established. Finally, two numerical examples, a curve stiffened plate and a grid stiffened shell, verify the efficiency and robustness of the proposed method. Compared with NURBS-based isogeometric analysis, the proposed method can significantly reduce the total degrees of freedom of the analysis model.
-
Keywords:
- isogeometric analysis /
- PHT-spline /
- adaptive mesh refinement /
- stiffened panels /
- buckling analysis
-
引 言
加筋板壳结构具有比刚度高、重量轻、设计多样性强等特点, 因而得到工程领域的广泛应用. 随着轻量化指标和结构功能性要求的提升, 加筋板壳结构设计正朝着复杂几何方向转变[1-2], 包括曲线型筋条[3-4]和复杂曲面蒙皮[5]. 具有复杂几何特征的加筋板壳结构给基于有限元软件的设计带来3个难点: (1)筋条网格节点与蒙皮网格节点不匹配; (2)复杂结构难以实现自动网格划分; (3)曲线和曲面的多项式离散存在几何离散误差. 加筋结构的建模与分析是轻量化设计的基础, 模型复杂度和分析复杂度的增加不利于结构优化. 此外, 航天轻质承载薄壁结构主要承受轴压载荷, 该载荷下加筋板壳最主要的失效形式是屈曲失稳. 因此, 加筋板壳结构的屈曲分析亟需更先进的数值方法. Cottrell等[6]提出的等几何分析是一种先进的数值计算范式, 该方法使用一致的数学表达将几何建模与数值模拟无缝集成, 有效消除了传统多项式插值网格引起的几何离散误差, 被公认为“一种替代标准多项式有限元分析的数值方法”[7]. Kirchhoff-Love[8]和Reissner-Mindlin[9]等一系列薄壁结构分析中常见的单元理论均在等几何范式下得到了扩展. Breitenberger等[10]直接利用CAD中标准B-Rep模型进行薄壁结构的等几何分析. Hao等[5, 11]面向变刚度板壳结构建立了系列先进的等几何设计/分析/优化一体化方法.
筋条作为加筋板壳的子结构, 可采用壳单元进行建模. 但是NURBS张量积的特性造成了四边拓扑限制, 导致加筋板壳结构必须使用多片样条几何的等几何分析. 多片样条几何的等几何耦合算法主要包括: 罚函数法、拉格朗日乘子法和Nitsche法. Guo等[12]基于Nitsche方法的非对称变体, 提出一种等几何Kirchhoff-Love壳单元的无参数变分耦合方法, 并将其应用于加筋圆柱壳的模态分析. Reissner-Mindlin壳理论适用于中厚壳, 且更易于应用多片耦合. Adam等[13]介绍一种用于等几何Reissner-Mindlin壳耦合的mortar方法. 作者讨论mortar空间的选择和适当的积分法则. 这种方法解决大量的学术和工业问题. Dornisch等[14]提出一种非协调NURBS面片的mortar耦合方法, 文中的加筋结构非线性分析证明了该耦合方法适用于等几何Reissner-Mindlin壳.
对于网格加筋结构, 使用壳模型对筋条进行建模的成本极高. 使用梁单元可以有效地减少分析变量, 且这一优势会随着筋条数量的增加而扩大. 因此, 基于梁模型的加筋板壳分析方法得到了广泛的研究. 石鹏等[15-16]和Qin等[17]使用插值算法建立梁单元变量和壳单元变量之间的耦合关系, 作者随后将其扩展到标准有限元分析[16]和等几何分析[17], 均取得了较高的计算精度. Saeedi等[18]使用相同的耦合方法, 研究不同参数对加筋板屈曲和弯曲行为的影响, 如弯曲刚度、相对质量、横截面和筋条形状. 为了实现与退化壳单元的耦合, Hao等[19]提出一种NURBS样条加筋单元, 该单元基于三维空间退化梁单元, 利用NURBS可以精确获取筋条的局部坐标系, 改进的投影算法大幅提升了筋条到蒙皮映射的鲁棒性和高效性. 通过详细对比大量数值算例, 该方法的性能明显优于商业有限元软件.
加筋结构数值分析中的另一个难点在于大部分加筋结构并不是规则几何, 例如曲线筋条和非均匀筋条. 这可能导致各向异性物理场, 此情况下使用各向同性参数化(结构化网格)在减少数值误差的层面上可能不是最优的. 因此, 自适应网格参数化技术在等几何分析中逐渐兴起, 包括h自适应、p自适应、k自适应和R自适应. 其中, h自适应方法是指具有局部细化能力的样条工具, 该方法试图在结构特征复杂的区域增加自由度, 在处理存在局部特征的问题时表现出显著的性能. Nguyen-Thanh等[20]基于PHT样条基函数提出二维问题的求解方法. Qin等[21]基于PHT样条实现加筋结构的模态和屈曲分析. 此外, 还研究加强筋的方向、曲率、位置和截面尺寸对固有频率和屈曲载荷的影响. Wang等[22]推导一种基于RPHT样条基函数的残差后验误差估计方法, 自适应地指导局部细化过程. 秦晓晨等[23]基于PHT样条实现复合材料加筋板结构的屈曲分析, 并讨论铺层数量和铺层角度对屈曲性能的影响.
针对基于张量积形式的NURBS基函数无法处理加筋结构分析局部细分问题, 本文基于等几何范式, 将RPHT样条引入加筋结构的屈曲分析并提出一种加筋路径驱动的板壳自适应等几何屈曲分析方法, 主要针对筋条和蒙皮连接处存在的复杂局部几何特征, 对与加筋路径关联的蒙皮单元开展自适应多层级细化. 由于RPHT样条允许网格存在T型节点, 可以实现局部网格的多级细分, 能够减少在实际分析过程中非必要控制变量的数量, 在保证分析精度的前提下降低结构的总自由度, 从而达到提高计算效率的目的.
1. PHT样条
1.1 T网格和层次T网格
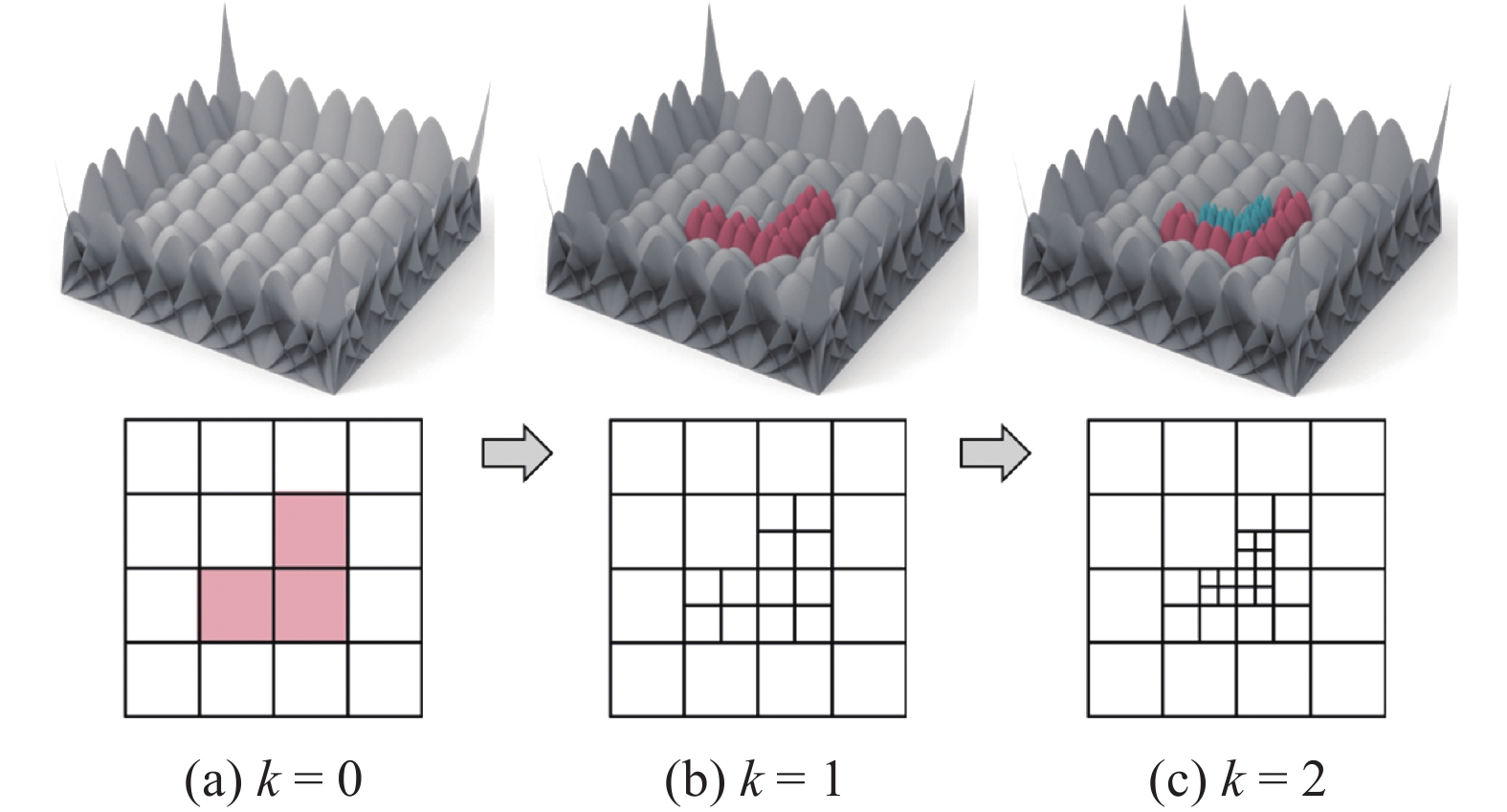
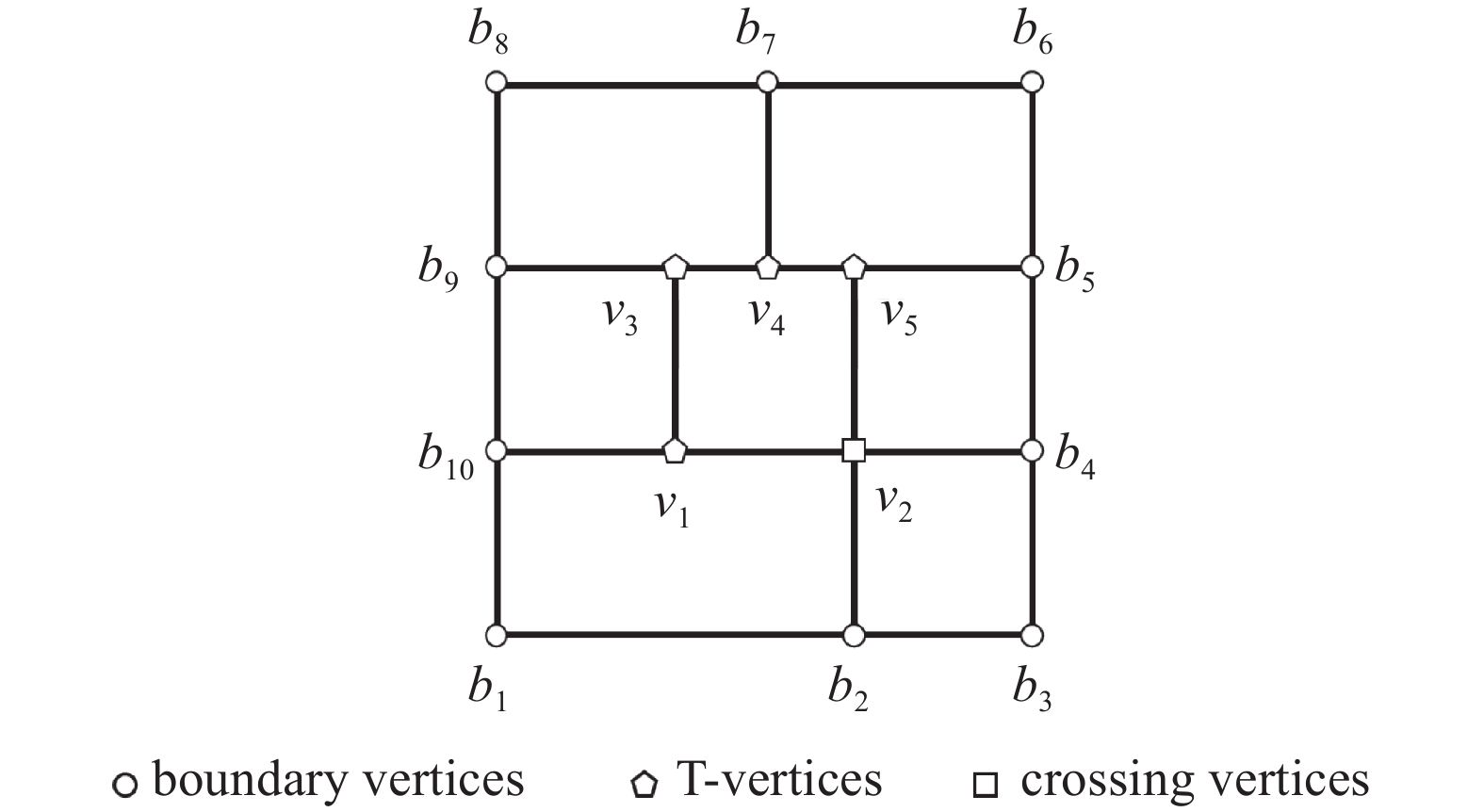
T网格是一种允许存在T型连接点的矩形网格[24-25], T网格要求网格端点必须落在其他网格线上, 并且所有胞腔的形状必须是矩形. 图1是一个典型的T网格, 在T网格中存在两种网格点, 一种是落在矩形边界上的边界节点, 另一种是落在矩形内部的内部节点, 包含十字型节点和T型节点两种形式. 其中, 将十字型点和边界节点称为T网格的基点, T型节点称为非基点.
层次T网格是一种具有层次结构的特殊T网格. 通常情况下, 将张量积网格设置为初始网格, 然后对待细分的胞腔进行十字插入剖分, 将一个胞腔细分成4个子胞腔, 得到一个新的T网格. 如此重复
$k$ 次, 最终得到最大层数为$k$ 的层次T网格. 图2展示了生成层次T网格的过程, 其中初始网格是标准的张量积网格, 图2(a)中的红色区域是待细化区域, 然后对指定网格进行逐级细化, 从基函数图像中可以看出细分区域的基函数数量随着网格级别的增加逐渐增多, 说明局部细化算法能够为结构指定区域增添更多的控制点和自由度, 从而提升计算精度.![]()
图 2 不同层级的二维层次T网格及其对应的基函数Figure 2. 2-D hierarchical T-meshes of different levels and their corresponding basis functions1.2 PHT样条曲面
PHT样条[26]是一种在层次T网格上构造的分片多项式样条, 不仅继承了T样条的众多优良性质, 例如: 凸包性、线性无关性、非负性、单位剖分性以及局部支撑性等, 同时还具备简单高效的局部细化能力, 因此, PHT样条在模型处理与仿真分析等方面均具有广泛的应用. 给定一个二维T网格
$\mathcal{T}$ , 那么层次T网格上的多项式样条空间定义为$$ \begin{split} & S(m,n,\alpha ,\beta ,\mathcal{T}): = \\ &\qquad \left\{ {s(x,y) \in \mathop C\nolimits^{\alpha ,\beta } (\varOmega ){{\left| {s(x,y)} \right|}_\phi } \in \mathop P\nolimits_{m,n} ,\forall \phi \in \varPhi } \right\} \end{split} $$ (1) 其中,
$\varPhi$ 为所有矩形胞腔的集合,$\varOmega$ 为网格$\mathcal{T}$ 所在的区域,$ \mathop P\nolimits_{m,n} $ 是次数为$(m,n)$ 的多项式空间,$\mathop C\nolimits^{\alpha ,\beta } (\varOmega )$ 表示函数在$x$ 和$y$ 方向分别$\alpha $ 阶和$\beta $ 阶连续. 当次数$m \geqslant 2\alpha + 1$ 且$n \geqslant 2\beta + 1$ 时, Deng等[26]基于B网方法推导出了双变量样条空间$ S(m,n,\alpha ,\beta ,\mathcal{T}) $ 的维度计算公式$$ \begin{split} & \dim S(m,n,\alpha ,\beta ,\mathcal{T}) = \\ &\qquad F(m + 1)(n + 1) - \mathop E\nolimits_h (m + 1)(\beta + 1) - \\ &\qquad \mathop E\nolimits_v (\alpha + 1)(n + 1) + V(\alpha + 1)(\beta + 1) \end{split} $$ (2) 其中,
$F$ 代表剖腔的个数,$E_{\rm{h}}$ 代表水平边的条数,$E_{\rm{v}}$ 代表竖直边的条数,$ V $ 代表内部网格点的数量. PHT样条曲面是指在层次T网格上的样条空间$ S(m,n,\alpha ,\beta ,\mathcal{T}) $ 中定义的多项式样条曲面, 本文主要研究双三次且具有${C^1}$ 连续性的PHT样条空间$ S(3,3,1,1,\mathcal{T}) $ , 由式(2)推导可得到其维度计算公式$$ \dim S(3,3,1,1,\mathcal{T}) = 4\left( {{V^{\rm{b}}} + {V^ + }} \right) $$ (3) 其中,
${V^{\rm{b}}}$ 和${V^ + }$ 分别是层次T网格$\mathcal{T}$ 上的边界点个数和十字点个数, 即为基点个数, 由式(3)的维度公式可知, 双三次${C^1}$ 连续的PHT样条曲面中每个基点对应4个基函数. 定义$ {b_{i,j}}\left( {\xi ,\eta } \right) $ 为$ S(3,3,1,1,\mathcal{T}) $ 样条空间的基函数, 其推导过程已在文献[27]中详细给出, 那么PHT样条曲面${S_{{\rm{pht}}}}$ 具体表示为如下形式$$ {S_{{\rm{pht}}}}(\xi ,\eta ) = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^4 {{b_{i,j}}\left( {\xi ,\eta } \right)} } {C_{i,j}},{\text{ }}\left( {\xi ,\eta } \right) \in \varOmega $$ (4) 其中,
$i$ 是基点的编号,$j$ 是每个基点对应的基函数编号,$n$ 是基点的总数量,$ \left( {\xi ,\eta } \right) $ 是PHT样条曲面${S_{{\rm{pht}}}}$ 上的参数坐标,${C_{i,j}}$ 是每个基函数对应的控制顶点坐标系数.1.3 RPHT样条曲面
由于PHT样条具有多项式样条的特性, 导致其无法精确描述圆锥曲面以及二次曲线等常见的工程形状, 例如圆、圆柱、球面和锥面等曲面. 因此, 需要将PHT样条扩展为有理形式, 也被称为有理PHT样条(RPHT样条), 具体做法是在原有PHT样条曲面的基础上, 为每个控制点坐标赋予一个权重系数
${w_{i,j}}$ , 加权后的控制点坐标定义为$ C_{i,j}^w = \left( {{w_{i,j}}{C_{i,j}},{w_{i,j}}} \right) $ , 那么齐次坐标系描述的RPHT样条曲面$S_{{\rm{rpht}}}^w$ 可以表示为如下$$ S_{{\rm{rpht}}}^w(\xi ,\eta ) = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^4 {{b_{i,j}}\left( {\xi ,\eta } \right)} } C_{i,j}^w,{\text{ }}\left( {\xi ,\eta } \right) \in \varOmega $$ (5) 通过将齐次坐标曲面转化为笛卡尔坐标曲面, 式(5)可以改写为另一种形式
$$ {S_{{\rm{rpht}}}}(\xi ,\eta ) = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^4 {{R_{i,j}}\left( {\xi ,\eta } \right){C_{i,j}}} } ,{\text{ }}\left( {\xi ,\eta } \right) \in \varOmega $$ (6) 其中,
$ {R_{i,j}}\left( {\xi ,\eta } \right) $ 是RPHT样条曲面的基函数, 定义如下$$ {R_{i,j}}\left( {\xi ,\eta } \right) = \frac{{{b_{i,j}}\left( {\xi ,\eta } \right){w_{i,j}}}}{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^4 {{b_{i,j}}\left( {\xi ,\eta } \right){w_{i,j}}} } }} $$ (7) 2. 基于RPHT样条的加筋板等几何分析
2.1 退化壳单元的等几何格式
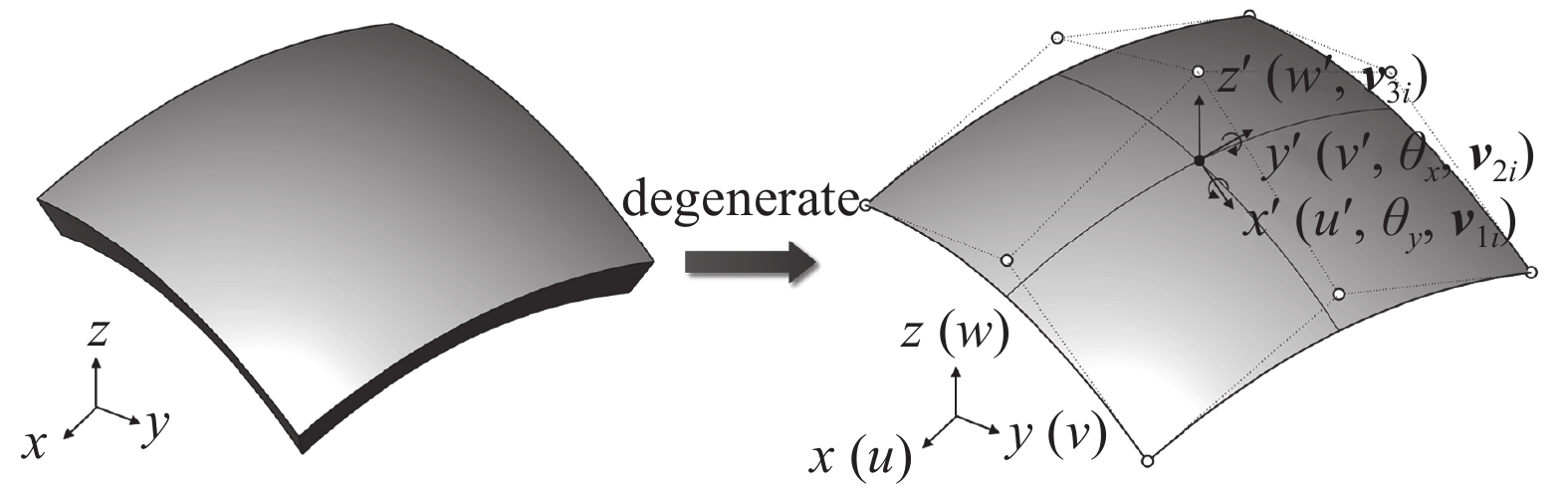
加筋结构的蒙皮采用RPHT样条曲面建模, 仿真采用基于RPHT样条的退化壳单元. 在我们先前的工作中已经大量使用了基于NURBS的退化壳单元[5], 本文将NURBS替换为RPHT样条重新推导了退化壳单元. 退化壳单元基于一阶剪切变形理论, 该单元避开了复杂的壳体理论, 直接通过连续介质力学进行推导. 退化壳体理论同时适用于薄壳和中厚壳. 当用于中厚壳时, 高阶NURBS基函数能够有效削弱剪切自锁现象, 这极大增加了该单元的适用范围. 下面简要介绍一下该单元的等几何格式. 如图3所示, 在退化壳单元中, 任意点的全局坐标可以近似表示为控制点坐标的插值形式, 全局位置坐标向量的定义如下
![]()
图 3 基于二阶基函数的退化壳单元的局部坐标系及控制变量Figure 3. Local coordinate system and control variables of degenerated shell element based on second order basis function$$ {\boldsymbol{x}} = \left\{ \begin{gathered} x \\ y \\ z \\ \end{gathered} \right\} = \sum\limits_{i = 1}^n {{{\bar R}_i}\left( {\xi ,\eta } \right)\left( {{{\left\{ \begin{gathered} {x_i} \\ {y_i} \\ {z_i} \\ \end{gathered} \right\}}_{{\rm{mid}}}}{\text{ + }}\frac{{t\zeta }}{2}{{\boldsymbol{v}}_{3i}}} \right)} $$ (8) 其中,
$ {\bar R_i}\left( {\xi ,\eta } \right) $ 为编号合并后的RPHT样条曲面基函数, 将基点的编号以及每个基点所对应4个基函数的编号合并到一个编号,$i = 1,2, \cdots ,n\left( {n = 4 m} \right)$ 为RPHT样条曲面基函数编号, 也代表每个控制点的编号.$\zeta $ 为壳体厚度方向上的参数坐标,$ t $ 为壳体厚度,${{\boldsymbol{v}}_{3 i}}{\text{ = }} \left[ {{l_{3 i}},{m_{3 i}},{n_{3 i}}} \right]$ 为壳体局部法向向量.曲面上任意点的位移向量
$ {\boldsymbol{u}} $ 都可以通过中间曲面控制点基于全局坐标系的平移自由度$\left( {{u_i},{v_i},{w_i}} \right)$ 和基于局部坐标系的转动自由度$\left( {{\theta _{xi}},{\theta _{yi}}} \right)$ 来定义$$ {\boldsymbol{u}} = \left\{ \begin{gathered} u \\ v \\ w \\ \end{gathered} \right\} = \sum\limits_{i = 1}^n {{{\bar R}_i}\left( {\xi ,\eta } \right)\left( {\left\{ \begin{gathered} {u_i} \\ {v_i} \\ {w_i} \\ \end{gathered} \right\} + \frac{{\zeta {t_i}}}{2}[{{\boldsymbol{v}}_{1i}}, - {{\boldsymbol{v}}_{2i}}]\left\{ \begin{gathered} {\theta _{xi}} \\ {\theta _{yi}} \\ \end{gathered} \right\}} \right)} $$ (9) 其中
${{\boldsymbol{v}}_{1 i}} = \left[ {{l_{1 i}},{m_{1 i}},{n_{1 i}}} \right]$ 和${{\boldsymbol{v}}_{2 i}} = \left[ {{l_{2 i}},{m_{2 i}},{n_{2 i}}} \right]$ 为壳体曲面的局部方向矢量, 定义如下$$\left. \begin{split} & {\rm{if}}{\text{ }}{\boldsymbol{i}} \times {{\boldsymbol{v}}_{3i}} \ne {\boldsymbol{0}},{\text{ }}{{\boldsymbol{v}}_{1i}} = \frac{{{\boldsymbol{i}} \times {{\boldsymbol{v}}_{3i}}}}{{\left| {{\boldsymbol{i}} \times {{\boldsymbol{v}}_{3i}}} \right|}},{\text{ }}{{\boldsymbol{v}}_{2i}} = \frac{{{{\boldsymbol{v}}_{3i}} \times {{\boldsymbol{v}}_{1i}}}}{{\left| {{{\boldsymbol{v}}_{3i}} \times {{\boldsymbol{v}}_{1i}}} \right|}} \\ & {\rm{if}}{\text{ }}{\boldsymbol{i}} \times {{\boldsymbol{v}}_{3i}} = {\boldsymbol{0}},{\text{ }}{{\boldsymbol{v}}_{1i}} = \frac{{{\boldsymbol{j}} \times {{\boldsymbol{v}}_{3i}}}}{{\left| {{\boldsymbol{j}} \times {{\boldsymbol{v}}_{3i}}} \right|}},{\text{ }}{{\boldsymbol{v}}_{2i}} = \frac{{{{\boldsymbol{v}}_{3i}} \times {{\boldsymbol{v}}_{1i}}}}{{\left| {{{\boldsymbol{v}}_{3i}} \times {{\boldsymbol{v}}_{1i}}} \right|}} \end{split}\right\} $$ (10) 任意点处的位移向量可以表示为矩阵运算形式
$$ {\boldsymbol{u}} = \sum\limits_{i = 1}^n {{{\boldsymbol{R}}_i}{{\boldsymbol{\delta }}_i}} $$ (11) 其中
$$ {{\boldsymbol{R}}_i} = \left[ {\begin{array}{*{20}{c}} {{{\bar R}_i}}&0&0&{{{\bar R}_i}\zeta \dfrac{t}{2}{l_{1i}}}&{ - {{\bar R}_i}\zeta \dfrac{t}{2}{l_{2i}}} \\ 0&{{{\bar R}_i}}&0&{{{\bar R}_i}\zeta \dfrac{t}{2}{m_{1i}}}&{ - {{\bar R}_i}\zeta \dfrac{t}{2}{m_{2i}}} \\ 0&0&{{{\bar R}_i}}&{{{\bar R}_i}\zeta \dfrac{t}{2}{n_{1i}}}&{ - {{\bar R}_i}\zeta \dfrac{t}{2}{n_{2i}}} \end{array}} \right] $$ (12) 此外,
$ {{\boldsymbol{\delta }}_i} = {\left[ {{u_i},{v_i},{w_i},{\theta _{xi}},{\theta _{yi}}} \right]^{\text{T}}} $ 表示控制点的控制变量向量. 根据壳体理论中${\sigma _{z'}} = 0$ 的假设, 需要在局部坐标系$\left( {x' - y' - z'} \right)$ 内建立计算壳体变形时所涉及的应变, 局部应变向量$ {\boldsymbol{\varepsilon '}} $ 和局部位移向量$ {\boldsymbol{u'}} $ 之间的关系定义如下$$ {\boldsymbol{\varepsilon '}} = {{\bf{L}}_{\text{L}}}{\boldsymbol{u'}} $$ (13) 其中,
${{\bf{L}}_{\text{L}}}$ 是微分算子, 定义如下$$ {{\bf{L}}_{\text{L}}} = {\left\{ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x'}}}&0&{\dfrac{\partial }{{\partial y'}}}&0&{\dfrac{\partial }{{\partial z'}}} \\ 0&{\dfrac{\partial }{{\partial y'}}}&{\dfrac{\partial }{{\partial x'}}}&{\dfrac{\partial }{{\partial z'}}}&0 \\ 0&{{\kern 1pt} 0}&0&{\dfrac{\partial }{{\partial y'}}}&{\dfrac{\partial }{{\partial x'}}} \end{array}} \right\}^{\text{T}}} $$ (14) 此外, 局部应变向量表示为
${\boldsymbol{\varepsilon '}} = \{ {\varepsilon _{x'}},{\varepsilon _{y'}},{\gamma _{x'y'}},{\gamma _{y'z'}}, {\gamma _{x'z'}}\} ^{\text{T}}$ , 局部位移向量表示为$ {\boldsymbol{u'}} = \left\{ {u',v',w'} \right\} $ , 如图3所示. 为了使用全局控制变量来表示局部坐标系下的应变向量, 需要对全局控制变量进行坐标变换, 并且将全局坐标系下位移的偏导数转换为局部坐标系下的位移的偏导, 主要涉及全局位置向量和全局位移向量的坐标系转换, 如下所示$$ {\boldsymbol{x'}} = {{\boldsymbol{\theta }}^{\text{T}}}{\boldsymbol{x}},{\text{ }}{\boldsymbol{u'}} = {{\boldsymbol{\theta }}^{\text{T}}}{\boldsymbol{u}} $$ (15) 其中,
$ {\boldsymbol{x'}} = \left[ {x',y',z'} \right] $ 是局部坐标向量,$ {\boldsymbol{\theta }} = \left[ {{{\boldsymbol{v}}_1},{{\boldsymbol{v}}_2},{{\boldsymbol{v}}_3}} \right] $ 是坐标变换矩阵. 通过将式(11)和式(15)代入式(13), 可以获得退化壳单元局部坐标系下的应变向量, 矩阵形式定义如下$$ {\boldsymbol{\varepsilon }}'{\text{ = }}{{\bf{L}}_{\text{L}}}\left\{ {{{\boldsymbol{\theta }}^{\text{T}}}{{\boldsymbol{R}}_i}{{\boldsymbol{\delta }}_i}} \right\} = \sum\limits_{i = 1}^n {{{\boldsymbol{B}}_i}{{\boldsymbol{\delta }}_i}} $$ (16) 其中
$ {{\boldsymbol{B}}_i} $ 定义为$$ {{\boldsymbol{B}}_i}{\text{ = }}{{\bf{L}}_{\text{L}}}\left\{ {{{\boldsymbol{\theta }}^{\text{T}}}{{\boldsymbol{R}}_i}} \right\} $$ (17) 利用线弹性平面应力关系定义局部坐标系下的应变
$$ {\boldsymbol{\varepsilon }}' = {\boldsymbol{D\sigma }}' $$ (18) $$ {\boldsymbol{D}} = \frac{E}{{1 - {v^2}}}\left[ {\begin{array}{*{20}{c}} 1&v&0&0&0 \\ v&1&0&0&0 \\ 0&0&{\dfrac{{1 - v}}{2}}&0&0 \\ 0&0&0&{\dfrac{{1 - v}}{{2k}}}&0 \\ 0&0&0&0&{\dfrac{{1 - v}}{{2k}}} \end{array}} \right] $$ (19) 式中,
${\boldsymbol{D}}$ 为弹性矩阵,$E$ 为杨氏模量,$ v $ 为泊松比,$k$ 是考虑剪应力沿厚度方向不均匀分布的影响而引入的修正系数, 本文中$k = {2 \mathord{\left/ {\vphantom {2 3}} \right. } 3}$ . 整理后可得到退化壳的总体刚度阵, 如下所示$$ {\boldsymbol{K}} = \sum {\left( {\int {{{\boldsymbol{B}}^{\rm{T}}}{\boldsymbol{DB}}\left| {\boldsymbol{J}} \right|{\text{d}}\xi {\text{d}}\eta {\text{d}}\zeta } } \right)} $$ (20) 其中,
$ {\boldsymbol{J}} $ 为雅可比矩阵, 用于将壳体位移向量到坐标向量的偏导数转换为参数坐标空间的偏导数. 根据式(8), 退化壳单元的雅可比矩阵表示如下$$ {\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial x}}{{\partial \xi }}}&{\dfrac{{\partial y}}{{\partial \xi }}}&{\dfrac{{\partial z}}{{\partial \xi }}} \\ {\dfrac{{\partial x}}{{\partial \eta }}}&{\dfrac{{\partial y}}{{\partial \eta }}}&{\dfrac{{\partial z}}{{\partial \eta }}} \\ {\dfrac{{\partial x}}{{\partial \zeta }}}&{\dfrac{{\partial y}}{{\partial \zeta }}}&{\dfrac{{\partial z}}{{\partial \zeta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\left\{ {\displaystyle\sum\limits_{i = 1}^n {\dfrac{{\partial {{\bar R}_i}}}{{\partial \xi }}({x_i} + \dfrac{{t\zeta }}{2}{{\boldsymbol{v}}_{3i}}} )} \right\}}^{\text{T}}}} \\ {{{\left\{ {\displaystyle\sum\limits_{i = 1}^n {\dfrac{{\partial {{\bar R}_i}}}{{\partial \eta }}({x_i} + \dfrac{{t\zeta }}{2}{{\boldsymbol{v}}_{3i}}} )} \right\}}^{\text{T}}}} \\ {{{\left\{ {\displaystyle\sum\limits_{i = 1}^n {\dfrac{t}{2}{{\bar R}_i}{{\boldsymbol{v}}_{3i}}} } \right\}}^{\text{T}}}} \end{array}} \right] $$ (21) 对于线性屈曲分析, 需要在局部坐标系下建立应变能的表达式
$$ {U_\sigma } = \frac{1}{2}\int {{\boldsymbol{\varepsilon }}_g^{\rm{T}}{\boldsymbol{\tau }}{{\boldsymbol{\varepsilon }}_g}{\text{d}}V} $$ (22) 其中
$$\begin{split} &{{\boldsymbol{\varepsilon }}_g} =\\ &{\left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial u'}}{{\partial x'}}} & {\dfrac{{\partial u'}}{{\partial y'}}} & {\dfrac{{\partial u'}}{{\partial z'}}} & {\dfrac{{\partial v'}}{{\partial x'}}} & {\dfrac{{\partial v'}}{{\partial y'}}} & {\dfrac{{\partial v'}}{{\partial z'}}} & {\dfrac{{\partial w'}}{{\partial x'}}} & {\dfrac{{\partial w'}}{{\partial y'}}} & {\dfrac{{\partial w'}}{{\partial z'}}} \end{array}} \right]^{\text{T}}}\end{split} $$ (23) 此外, 式中的初始应力矩阵
$ {\boldsymbol{\tau }} $ 定义如下$$ {\boldsymbol{\tau }} = \left[ {\begin{array}{*{20}{c}} {{{{{\boldsymbol{\tau}} }}^1}}&0&0 \\ 0&{{{{{\boldsymbol{\tau}} }}^1}}&0 \\ 0&0&{{{{{\boldsymbol{\tau}} }}^1}} \end{array}} \right]{\text{ , }}{{\boldsymbol{\tau }}^1} = \left[ {\begin{array}{*{20}{c}} {\sigma' _x}&{\tau '_{xy}}&{\tau' _{xz}} \\ {\tau '_{xy}}&{\sigma' _y}&{\tau' _{yz}} \\ {\tau' _{xz}}&{\tau' _{yz}}&0 \end{array}} \right] $$ (24) 几何应变矢量
$ {{\boldsymbol{\varepsilon }}_g} $ 可通过局部位移向量$ {\boldsymbol{u'}} $ 和非线性偏微分算子${{\bf{L}}_{\text{N}}}$ 以矩阵形式进行定义$$ {{\boldsymbol{\varepsilon }}_g} = {{\bf{L}}_{\text{N}}}{\boldsymbol{u'}} $$ (25) 其中
$$ {{\bf{L}}_{\text{N}}} = {\left\{ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x'}}}&{\dfrac{\partial }{{\partial y'}}}&{\dfrac{\partial }{{\partial z'}}}&0&0&0&0&0&0 \\ 0&0&0&{\dfrac{\partial }{{\partial x'}}}&{\dfrac{\partial }{{\partial y'}}}&{\dfrac{\partial }{{\partial z'}}}&0&0&0 \\ 0&0&0&0&0&0&{\dfrac{\partial }{{\partial x'}}}&{\dfrac{\partial }{{\partial y'}}}&{\dfrac{\partial }{{\partial z'}}} \end{array}} \right\}^{\rm{T}}} $$ (26) 将式(11)和式(15)代入到式(25), 得到由蒙皮控制点的位移向量表示的几何应变矢量
$$ {{\boldsymbol{\varepsilon }}_g}{\text{ = }}{{\bf{L}}_{\text{N}}}\left\{ {{{\boldsymbol{\theta }}^{\text{T}}}{{\boldsymbol{R}}_i}{{\boldsymbol{\delta }}_i}} \right\} = \sum\limits_{i = 1}^n {{{\boldsymbol{B}}_{Gi}}{{\boldsymbol{\delta }}_i}} $$ (27) 其中
$ {{\boldsymbol{B}}_{Gi}} $ 定义为$$ {{\boldsymbol{B}}_{Gi}}{\text{ = }}{{\bf{L}}_{\text{N}}}\left\{ {{{\boldsymbol{\theta }}^{\text{T}}}{{\boldsymbol{R}}_i}} \right\} $$ (28) 最终, 整理得到退化壳的总体几何刚度阵, 表达如下
$$ {{\boldsymbol{K}}_G} = \sum {\left( {\int {{\boldsymbol{B}}_G^{\text{T}}{\boldsymbol{\tau }}{{\boldsymbol{B}}_G}\left| {\boldsymbol{J}} \right|{\text{d}}\xi {\text{d}}\eta {\text{d}}\zeta } } \right)} $$ (29) 2.2 退化筋条单元的等几何格式
本文中筋条建模采用NURBS曲线, 仿真采用退化筋条单元. 退化筋条单元是由三维曲梁单元改进而来[19, 28], 三维曲梁单元直接与退化壳单元进行耦合会引起面内存在过度的刚度约束, 这是由于梁单元假设与壳单元假设之间存在冲突所造成的. 梁单元假设截面形状不变, 且存在z方向局部转动自由度. 而壳单元则是允许发生面内的变形. 因此筋条单元中忽略了筋条截面宽度方向的变形, 并去掉了
$z$ 方向的局部转动自由度, 基于NURBS曲线基函数, 可通过控制点的几何参数获得全局坐标系中任意点的位置. 与壳单元相同, 筋条单元中任意点的位移由控制点的位移变量插值获得.图4展示了筋条单元的局部坐标系、截面参数及其与壳单元相对位置关系. 筋条上任意一点的位置向量和位移向量定义为
![]()
图 4 筋条单元的局部坐标系、截面参数及其与壳单元相对位置关系Figure 4. The local coordinate system, section parameters and relative position relationship with shell element of the stiffener element$$ \begin{split} &{{\boldsymbol{x}}_s} = \left\{ \begin{gathered} x \\ y \\ z \\ \end{gathered} \right\} = \sum\limits_{i = 1}^n {R_{si}}(\xi )\left( {{\left\{ \begin{gathered} {x_i} \\ {y_i} \\ {z_i} \\ \end{gathered} \right\}}_{{\rm{mid}}}} +\right.\\ &\qquad \left.\left( {\frac{{\zeta {a_s}}}{2} + e} \right){\boldsymbol{v}}_{3i}^s + \frac{{\eta {b_s}}}{2}{\boldsymbol{v}}_{2i}^s \right)\end{split} $$ (30) $$\begin{split} &{{\boldsymbol{u}}_s} = \left\{ \begin{gathered} u \\ v \\ w \\ \end{gathered} \right\} = \sum\limits_{i = 1}^n {R_{si}}(\xi )\left( {{{\boldsymbol{T}}_{vi}}} \left\{ \begin{gathered} {u_i} \\ {v_i} \\ {w_i} \\ \end{gathered} \right\} + \left( {\frac{{\zeta {a_s}}}{2} + e} \right)\right. \\ &\qquad \left.[{{\boldsymbol{v}}_{1i}}, - {{\boldsymbol{v}}_{2i}}]\left\{ \begin{gathered} {\theta _{xi}} \\ {\theta _{yi}} \\ \end{gathered} \right\} \right)\end{split} $$ (31) 其中,
$\left( {x - y - z} \right)$ 为筋条的全局坐标系,$\left( {x' - y' - z'} \right)$ 为筋条的局部坐标系,$ {R_{si}}(\xi ) $ 为NURBS曲线基函数,$ \xi $ 为中性轴方向参数坐标,$ \eta $ 为筋条宽度方向参数坐标,$ \zeta $ 为筋条高度方向参数坐标,$ {\boldsymbol{v}}_{3 i}^s $ 为筋条截面局部法向向量(为了保证每一处筋条截面均与蒙皮保持垂直关系, 筋条的法向向量与蒙皮的法向向量相等),$ {a_s} $ 为筋条截面高度,$ {b_s} $ 为筋条截面宽度,$ e $ 为筋条偏置距离(筋条中性轴到蒙皮中面的距离),${{\boldsymbol{T}}_{vi}}$ 为筋条截面位移转换矩阵, 定义如下$$ \left.\begin{split} & {{\boldsymbol{T}}_{vi}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{v}}_{1i}^s}&0&{{\boldsymbol{v}}_{3i}^s} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{v}}_{1i}^s}&{{\boldsymbol{v}}_{2i}^s}&{{\boldsymbol{v}}_{3i}^s} \end{array}} \right]^{\text{T}}} \\ & {\boldsymbol{v}}_{3i}^s = \left[ {l_{3i}^s,m_{3i}^s,n_{3i}^s} \right] = {{\boldsymbol{v}}_{3i}} \\ & {\boldsymbol{v}}_{1i}^s = \left[ {l_{1i}^s,m_{1i}^s,n_{1i}^s} \right] = {{\boldsymbol{C}}^{\left( 1 \right)}}\left( \xi \right)/\left| {{{\boldsymbol{C}}^{\left( 1 \right)}}\left( \xi \right)} \right| \\ & {\boldsymbol{v}}_{2i}^s = \left[ {l_{2i}^s,m_{2i}^s,n_{2i}^s} \right] = \frac{{{\boldsymbol{v}}_{3i}^s \times {\boldsymbol{v}}_{1i}^s}}{{\left| {{\boldsymbol{v}}_{3i}^s \times {\boldsymbol{v}}_{1i}^s} \right|}} \end{split}\right\} $$ (32) 其中,
$ {{\boldsymbol{C}}^{\left( 1 \right)}}\left( \xi \right) $ 是NURBS曲线$ {\boldsymbol{C}}\left( \xi \right) $ 的一阶偏导矢. 将筋条上任意点处的位移向量表示为矩阵运算形式, 定义如下$$ {{\boldsymbol{u}}_s} = \sum\limits_{i = 1}^n {{\boldsymbol{R}}_i^s{\boldsymbol{\delta }}_i^s} $$ (33) $$ \begin{split} &{\boldsymbol{R}}_i^s =\\ &{R_{si}}{\left[ {\begin{array}{*{20}{c}} {{{\left( {l_{1i}^s} \right)}^2} + {{\left( {l_{3i}^s} \right)}^2}}&{l_{1i}^sm_{1i}^s + l_{3i}^sm_{3i}^s}&{l_{1i}^sn_{1i}^s + l_{3i}^sn_{3i}^s} \\ {l_{1i}^sm_{1i}^s + l_{3i}^sm_{3i}^s}&{{{\left( {m_{1i}^s} \right)}^2} + {{\left( {m_{3i}^s} \right)}^2}}&{m_{1i}^sn_{1i}^s + m_{3i}^sn_{3i}^s} \\ {l_{1i}^sn_{1i}^s + l_{3i}^sn_{3i}^s}&{m_{1i}^sn_{1i}^s + m_{3i}^sn_{3i}^s}&{{{\left( {n_{1i}^s} \right)}^2} + {{\left( {n_{3i}^s} \right)}^2}} \\ {\left( {\dfrac{{\zeta {a_s}}}{2} + e} \right){l_{1i}}}&{\left( {\dfrac{{\zeta {a_s}}}{2} + e} \right){m_{1i}}}&{\left( {\dfrac{{\zeta {a_s}}}{2} + e} \right){n_{1i}}} \\ { - \left( {\dfrac{{\zeta {a_s}}}{2} + e} \right){l_{2i}}}&{ - \left( {\dfrac{{\zeta {a_s}}}{2} + e} \right){m_{2i}}}&{ - \left( {\dfrac{{\zeta {a_s}}}{2} + e} \right){n_{2i}}} \end{array}} \right]^{\rm{T}}}\end{split} $$ (34) 其中,
$ {\boldsymbol{\delta }}_i^s = {\left[ {u_i^s,v_i^s,w_i^s,\theta _{xi}^s,\theta _{yi}^s} \right]^{\text{T}}} $ 是筋条单元的控制变量. 根据三维曲梁单元的基本假设, 需在筋条的局部坐标系$\left( {x' - y' - z'} \right)$ 下确定应力和应变. 局部坐标系下的应变与位移的关系定义如下$$ {\boldsymbol{\varepsilon '}} = {\bf{L}}_{\text{L}}^s{{\boldsymbol{u}}'_s} $$ (35) 其中
${\bf{L}}_{\text{L}}^s$ 为微分算子$$ {\bf{L}}_{\text{L}}^s = \left\{ {\begin{array}{*{20}{c}} {\dfrac{\partial }{{\partial x'}}}&0&0 \\ {\dfrac{\partial }{{\partial y'}}}&{\dfrac{\partial }{{\partial x'}}}&0 \\ {\dfrac{\partial }{{\partial z'}}}&0&{\dfrac{\partial }{{\partial x'}}} \end{array}} \right\} $$ (36) 另外,
$ {\boldsymbol{\varepsilon '}} = {\{ {\varepsilon _{x'}},{\gamma _{x'y'}},{\gamma _{x'z'}}\} ^{\text{T}}} $ 是局部坐标系下的应变向量.${{\boldsymbol{u}}'_s} = \left\{ {{u'_s},{v'_s},{w'_s}} \right\}$ 是局部坐标系下的位移向量, 如图4所示, 局部坐标系下的位移可通过控制点的控制变量插值表示, 结合坐标变换可以得到$$ {\boldsymbol{\varepsilon '}}{\text{ = }}{\bf{L}}_{\text{L}}^s\left\{ {{{\left[ {{{\boldsymbol{\theta }}^s}} \right]}^{\text{T}}}{\boldsymbol{R}}_i^s{\boldsymbol{\delta }}_i^s} \right\} = \sum\limits_{i = 1}^n {{\boldsymbol{B}}_i^s{\boldsymbol{\delta }}_i^s} $$ (37) 其中,
${\boldsymbol{B}}_i^s{\text{ = }}{\bf{L}}_{\text{L}}^s\left\{ {{{\left[ {{{\boldsymbol{\theta }}^s}} \right]}^{\text{T}}}{\boldsymbol{R}}_i^s} \right\}$ ,${{\boldsymbol{\theta }}^s} = \left[ {{\boldsymbol{v}}_1^s,{\boldsymbol{v}}_2^s,{\boldsymbol{v}}_3^s} \right]$ 为坐标转换矩阵,${\boldsymbol{R}}_i^s$ 是控制变量与任意点全局位移之间的插值矩阵. 材料矩阵$ {{\boldsymbol{D}}^s} $ 定义如下$$ {{\boldsymbol{D}}^s} = \left[ {\begin{array}{*{20}{c}} E&0&0 \\ 0&{{G_s}}&0 \\ 0&0&{{G_s}} \end{array}} \right] $$ (38) 其中
$E$ 是杨氏模量,$ {G_s} $ 是筋条单元的剪切修正系数[28]. 根据线弹性本构方程可得到局部坐标系中的应力−应变关系$$ {\boldsymbol{\varepsilon '}} = {{\boldsymbol{D}}^s}{\boldsymbol{\sigma '}} $$ (39) 整理后可得到筋条的总体刚度阵, 如下所示
$$ {{\boldsymbol{K}}^s} = \sum {\left( {\int {{{\left[ {{{\boldsymbol{B}}^s}} \right]}^{\text{T}}}{{\boldsymbol{D}}^s}{{\boldsymbol{B}}^s}\left| {{{\boldsymbol{J}}^s}} \right|{\text{d}}\xi {\text{d}}\eta {\text{d}}\zeta } } \right)} $$ (40) 其中,
$ {{\boldsymbol{J}}^s} $ 为筋条单元的雅可比矩阵, 用于将筋条位移向量到坐标向量的偏导数转换为参数坐标空间的偏导数. 根据式(30)整理后$ {{\boldsymbol{J}}^s} $ 表示如下$$ {{\boldsymbol{J}}^s} = \left[ {\begin{array}{*{20}{c}} {{{\left\{ {\displaystyle\sum\limits_{i = 1}^n {\frac{{\partial {{\bar R}_i}}}{{\partial \xi }}\left[ {{{\boldsymbol{x}}_i} + \left( {\frac{{\zeta {a_s}}}{2} + e} \right){\boldsymbol{v}}_{3i}^s + \frac{{\eta {b_s}}}{2}{\boldsymbol{v}}_{2i}^s} \right]} } \right\}}^{\text{T}}}} \\ {{{\left\{ {\displaystyle\sum\limits_{i = 1}^n {\frac{{{b_s}}}{2}{\boldsymbol{v}}_{2i}^s} } \right\}}^{\text{T}}}} \\ {{{\left\{ {\displaystyle\sum\limits_{i = 1}^n {\frac{{{a_s}}}{2}{\boldsymbol{v}}_{3i}^s} } \right\}}^{\text{T}}}} \end{array}} \right] $$ (41) 对于筋条的线性屈曲分析, 首先在局部坐标系中建立应变能方程
$$ {U_\sigma } = \frac{1}{2}\int {{{\left[ {{\boldsymbol{\varepsilon }}_g^s} \right]}^{\text{T}}}{{\boldsymbol{\tau }}^s}{\boldsymbol{\varepsilon }}_g^s{\text{d}}V} $$ (42) 不同于壳体单元, 退化筋条单元的初始应力矩阵为
$$ {{\boldsymbol{\tau }}^s} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\tau }}^{1s}}}&0&0 \\ 0&{{{\boldsymbol{\tau }}^{1s}}}&0 \\ 0&0&{{{\boldsymbol{\tau }}^{1s}}} \end{array}} \right]{\text{, }}{{\boldsymbol{\tau }}^{1s}} = \left[ {\begin{array}{*{20}{c}} {\sigma' _x}&{\tau' _{xy}}&{\tau' _{xz}} \\ {\tau' _{xy}}&0&0 \\ {\tau' _{xz}}&0&0 \end{array}} \right] $$ (43) 退化筋条单元的几何应变矢量可以由局部位移向量
$ {\boldsymbol{u'}} $ 和非线性偏微分算子${{\bf{L}}_{\text{N}}}$ 以矩阵形式表示为$$ {\boldsymbol{\varepsilon }}_g^s = {\bf{L}}_{\text{N}}^{}{{\boldsymbol{u'}}_s} $$ (44) 将式(33)代入到式(44), 结合坐标变换, 由筋条控制点的位移向量表示的几何应变向量为
$$ {\boldsymbol{\varepsilon }}_g^s{\text{ = }}{{\bf{L}}_{\text{N}}}\left\{ {{{\boldsymbol{\theta }}^{\text{T}}}{\boldsymbol{R}}_i^s{\boldsymbol{\delta }}_i^s} \right\} = \sum\limits_{i = 1}^n {{\boldsymbol{B}}_{{{G}}i}^s{\boldsymbol{\delta }}_i^s} $$ (45) 其中
$$ {\boldsymbol{B}}_{{{G}}i}^s = {{\bf{L}}_{\text{N}}}\left\{ {{{\boldsymbol{\theta }}^{\text{T}}}{\boldsymbol{R}}_i^s} \right\} $$ (46) 最终, 整理可得到筋条的总体几何刚度阵, 表达如下
$$ {\boldsymbol{K}}_G^s = \sum {\left( {\int {{{\left[ {{\boldsymbol{B}}_G^s} \right]}^{\text{T}}}{{\boldsymbol{\tau }}^s}{\boldsymbol{B}}_G^s\left| {{{\boldsymbol{J}}^s}} \right|{\text{d}}\xi {\text{d}}\eta {\text{d}}\zeta } } \right)} $$ (47) 2.3 筋条单元与壳单元的强耦合关系
对于具有复杂几何形状的加筋板壳, 筋条的网格与蒙皮网格之间一般是非协调关系, 因此, 筋条和蒙皮之间的耦合不能通过简单地匹配相邻控制点的变量来处理. 本文参考Prusty等[29]提出的方法, 首先将筋条的控制点投影到壳体表面, 投影采用Hao等[19]建立的改进样条投影算法, 然后将筋条的控制变量(自由度变量)与投影点的变量进行耦合, 投影点的变量可以通过蒙皮的控制变量插值获得. 最终, 筋条的控制变量全部转移到了蒙皮的控制变量, 这属于一种强耦合方法[19].
图5展示了参数空间内RPHT样条曲面(蒙皮)和NURBS曲线(筋条)之间的强耦合关系, 蓝色虚线代表筋条曲线的离散多边形,
$A,B,C$ 三个三角形分别代表筋条曲线控制点在蒙皮上的投影点, 黑色圆点代表蒙皮曲面控制点在蒙皮参数域的配置点. 其中,$\left( {{\xi _A},{\eta _A}} \right),\left( {{\xi _B},{\eta _B}} \right),\left( {{\xi _C},{\eta _C}} \right)$ 分别是3个投影点与之对应的蒙皮参数空间内的参数坐标, 以及①②③, 3个彩色方格分别代表了3个投影点所在的蒙皮节点空间(knot spans). 通过寻找筋条曲线控制点的投影点所在的蒙皮节点空间获取与之关联的蒙皮控制点编号, 并利用蒙皮单元在投影点处的位移插值函数, 最终建立筋条单元与蒙皮单元控制变量之间的位移耦合关系. 以图5中的红色筋条投影点A为例进一步解释该耦合关系, 点A落在$ ① $ 号蒙皮节点区间, 投影点A处的位移可以由该节点区间的红色配置点插值获得, 投影点A对应的筋条控制点位移$ {\boldsymbol{u}}_s^A $ 可表示为以下的插值形式![]()
图 5 蒙皮参数空间内的强耦合关系Figure 5. The strong coupling relationship in the skin parameter space$$ {\boldsymbol{u}}_s^A = \sum\limits_{i = 1}^{\tilde n} {{{\bar R}_i}({\xi _A},{\eta _A}){{\boldsymbol{u}}_i}} $$ (48) 其中,
$\tilde n$ 是当前筋条单元控制点的投影点所关联的蒙皮控制点数量. 那么, 筋条控制点的控制变量与蒙皮单元得控制变量之间存在以下插值关系$$\left. \begin{split} & {{{\boldsymbol{\delta }}^s} = {{\boldsymbol{N}}_{ps}}{\boldsymbol{\delta }}} \\ & {{{\boldsymbol{\delta }}^s} = {{\left[ {u_A^s,v_A^s,w_A^s,\theta _{xA}^s,\theta _{yA}^s, \cdots ,u_C^s,v_C^s,w_C^s,\theta _{xC}^s,\theta _{yC}^s} \right]}^{\text{T}}}} \\ & {{{\boldsymbol{\delta }}^{}} = {{\left[ {u_1^k,v_1^k,w_1^k,\theta _{x1}^k,\theta _{y1}^k, \cdots ,u_9^k,v_9^k,w_9^k,\theta _{x9}^k,\theta _{y9}^k} \right]}^{\text{T}}}}\\ &\qquad {{\text{where }}k{\text{ in }}l,m,n} \end{split}\right\} $$ (49) 其中,
$ {{\boldsymbol{\delta }}^s} $ 是一个筋条单元的控制变量集合,$ {\boldsymbol{\delta }} $ 是与筋条控制点相关联的蒙皮控制点的控制变量集合,$ l,m,n $ 是蒙皮节点空间标号,$ {{\boldsymbol{N}}_{ps}} $ 是由NURBS曲面插值基函数组成的转换矩阵, 其具体形式如下$$\begin{split} &{{\boldsymbol{N}}_{ps}} = \\ &{\left[ {\begin{array}{*{20}{c}} {{{\bar R}_1}\left( {{\xi _A},{\eta _A}} \right){{\boldsymbol{I}}_{5 \times 5}}}&0&0 \\ 0&{{{\bar R}_1}\left( {{\xi _B},{\eta _B}} \right){{\boldsymbol{I}}_{5 \times 5}}}&0 \\ 0&0&{{{\bar R}_1}\left( {{\xi _C},{\eta _C}} \right){{\boldsymbol{I}}_{5 \times 5}}} \\ \cdots & \cdots & \cdots \\ {{{\bar R}_{\tilde n}}\left( {{\xi _A},{\eta _A}} \right){{\boldsymbol{I}}_{5 \times 5}}}&0&0 \\ 0&{{{\bar R}_{\tilde n}}\left( {{\xi _B},{\eta _B}} \right){{\boldsymbol{I}}_{5 \times 5}}}&0 \\ 0&0&{{{\bar R}_{\tilde n}}\left( {{\xi _C},{\eta _C}} \right){{\boldsymbol{I}}_{5 \times 5}}} \end{array}} \right]^{\text{T}}}{{{{\boldsymbol{H}}}}}\end{split} $$ (50) 其中, H是用于组装
$ {{\boldsymbol{N}}_{ps}} $ 并消除重复控制点的矩阵, 定义如下$$ {\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {\delta _{1,1}^A{{\boldsymbol{I}}_{5 \times 5}}}&{\delta _{1,2}^A{{\boldsymbol{I}}_{5 \times 5}}}& \cdots &{\delta _{1,\tilde m}^A{{\boldsymbol{I}}_{5 \times 5}}} \\ {\delta _{1,1}^B{{\boldsymbol{I}}_{5 \times 5}}}&{\delta _{1,2}^B{{\boldsymbol{I}}_{5 \times 5}}}& \cdots &{\delta _{1,\tilde m}^B{{\boldsymbol{I}}_{5 \times 5}}} \\ {\delta _{1,1}^C{{\boldsymbol{I}}_{5 \times 5}}}&{\delta _{1,2}^C{{\boldsymbol{I}}_{5 \times 5}}}& \cdots &{\delta _{1,\tilde m}^C{{\boldsymbol{I}}_{5 \times 5}}} \\ \vdots & \vdots &{\text{ }}& \vdots \\ {\delta _{\tilde n,1}^A{{\boldsymbol{I}}_{5 \times 5}}}&{\delta _{\tilde n,2}^A{{\boldsymbol{I}}_{5 \times 5}}}& \cdots &{\delta _{\tilde n,\tilde m}^A{{\boldsymbol{I}}_{5 \times 5}}} \\ {\delta _{\tilde n,1}^B{{\boldsymbol{I}}_{5 \times 5}}}&{\delta _{\tilde n,2}^B{{\boldsymbol{I}}_{5 \times 5}}}& \cdots &{\delta _{\tilde n,\tilde m}^B{{\boldsymbol{I}}_{5 \times 5}}} \\ {\delta _{\tilde n,1}^C{{\boldsymbol{I}}_{5 \times 5}}}&{\delta _{\tilde n,2}^C{{\boldsymbol{I}}_{5 \times 5}}}& \cdots &{\delta _{\tilde n,\tilde m}^C{{\boldsymbol{I}}_{5 \times 5}}} \end{array}} \right] $$ (51) 下面详细解释H矩阵的含义, 已知
$\tilde n$ 是一个蒙皮单元包含的控制点数量, 单个二次NURBS筋条单元具有3个控制点, 那么每个筋条单元最多与$3\tilde n$ 个蒙皮控制点进行关联, 去掉可能共用的蒙皮控制点, 假定一个筋条单元总共关联$\tilde m$ 个蒙皮控制点.${\boldsymbol{H}}$ 矩阵中的$ \delta _{\tilde i,\tilde j}^A $ 起到消除重复关联的控制点的作用, 其中$\tilde i = 1,2, \cdots, \tilde n$ 对应筋条投影点A所在蒙皮单元的控制点编号,$\tilde j = 1,2, \cdots ,\tilde m$ 对应单个筋条单元所关联的非重复控制点编号, 如果$ \tilde i = \tilde j $ , 那么$ \delta _{\tilde i,\tilde j}^A = 1 $ , 反之$ \delta _{\tilde i,\tilde j}^A = 0 $ . 此外, 利用$ {{\boldsymbol{N}}_{ps}} $ 矩阵还实现了筋条位移向量坐标系的转换, 转换后的筋条刚度矩阵和几何刚度矩阵定义如下$$ \left.\begin{split} & {{\boldsymbol{K}}^s} = \sum {{{\left\{ {{{\boldsymbol{N}}_{ps}}} \right\}}^{\text{T}}}\left( {\int {{{\left[ {{{\boldsymbol{B}}^s}} \right]}^{\text{T}}}{{\boldsymbol{D}}^s}{{\boldsymbol{B}}^s}\left| {{{\boldsymbol{J}}^s}} \right|{\text{d}}\xi {\text{d}}\eta {\text{d}}\zeta } } \right){{\boldsymbol{N}}_{ps}}} \\ & {\boldsymbol{K}}_G^s = \sum {{{\left\{ {{{\boldsymbol{N}}_{ps}}} \right\}}^{\text{T}}}\left( {\int {{{\left[ {{\boldsymbol{B}}_G^s} \right]}^{\text{T}}}{{\boldsymbol{\tau }}^s}{\boldsymbol{B}}_G^s\left| {{{\boldsymbol{J}}^s}} \right|{\text{d}}\xi {\text{d}}\eta {\text{d}}\zeta } } \right){{\boldsymbol{N}}_{ps}}} \end{split}\right\} $$ (52) 可以发现, 该转换矩阵将筋条的刚度扩散到了蒙皮的刚度上, 对于加筋板壳结构的线性屈曲分析, 总体平衡方程定义如下
$$ \left[ {\left( {{\boldsymbol{K}} + {{\boldsymbol{K}}^s}} \right) - \lambda \left( {{{\boldsymbol{K}}_G} + {\boldsymbol{K}}_G^s} \right)} \right]{\boldsymbol{\varphi }} ={\boldsymbol{ 0}} $$ (53) 式中,
$ \lambda $ 为屈曲载荷系数,$ {\boldsymbol{\varphi }} $ 是屈曲模式. 可以发现, 最终刚度矩阵的自由度与蒙皮刚度矩阵相同, 实现了筋条刚度的“抹平”, 这大幅降低了数值仿真模型的计算规模, 有助于提升分析效率.2.4 加筋路径驱动的自适应网格细化
在网格细化之前, 需要寻找与筋条曲线相关联的蒙皮单元, 这里我们选择筋条的控制点作为参考点, 并搜寻参考点在蒙皮上的投影点参数坐标, 通常做法是使用牛顿迭代法处理这个问题, 然而牛顿迭代并不总是稳定收敛的, 初值的选择直接决定了结果的收敛性, Piegl等[30]的做法是先将NURBS曲面划分为多个节区间, 选择距离最小的作为候选, 而后基于向量余弦构建线性方程, 并使用数值方法迭代求解投影点. 该方法每次迭代均需要计算点到曲面的法向投影, 这涉及曲面的一阶和二阶导数, 控制点较多会导致计算量偏大. 另一种是求解最近距离点的方法, 点在曲面上可能有多个法向投影点, 但是在曲面上总能找到唯一的最近距离点, 当该点与法向投影点之间的距离小于该点与曲面的所有边界之间的距离时, 法向投影点就是最近点. 因此使用最近点搜索方法的鲁棒性更高, 具体做法可参见Hao等[19]建立的投影算法. 在获取到投影点之后, 需要将投影点所在的蒙皮节点区间视为与筋条曲线相关联的蒙皮单元, 利用RPHT样条的局部细分算法对指定的蒙皮单元进行十字剖分细化, 在完成所有与筋条曲线关联的蒙皮单元的细分之后, 可以选择重复上述操作, 重新搜索待细化的蒙皮单元并继续进行细分操作, 如此循环
$\widetilde {lv}$ 次便可以得到$\widetilde {lv}$ 级RPHT样条曲面. 加筋路径驱动的自适应网格细化流程如图6所示.![]()
图 6 加筋路径驱动的自适应网格细化流程图Figure 6. The flowchart of adaptive mesh refinement driven by stiffener paths如图7所示是加筋路径驱动的自适应网格细化过程的示意图, 已知红色筋条投影点A的参数坐标, 搜寻到投影点A所在的蒙皮单元(红色区域)并对此单元进行逐级细化, 在
$A,B,C$ 三个投影点处分别展示了不同层级的细化结果.![]()
图 7 加筋路径驱动的自适应网格细化示意图Figure 7. The diagram of adaptive mesh refinement driven by stiffener paths3. 数值算例
为了验证本文提出的加筋路径驱动的板壳自适应等几何屈曲分析的有效性和鲁棒性. 本节构造了两个典型算例: 曲线加筋板和1/4加筋圆柱壳. 基于RPHT样条对算例中的模型进行不同层级的局部细化, 验证加筋路径驱动自适应细化算法的正确性. 对基于双三次RPHT样条的自适应等几何模型和基于双三次NURBS样条的经典等几何模型进行一阶线性屈曲载荷的收敛性分析, 验证本方法的有效性和高效性, 本文中的算例均为学术性验证算例, 因此模型参数均为无量纲, 两个算例采用相同的材料, 弹性模量为72504 MPa, 泊松比为0.3.
3.1 曲线加筋平板
本节将介绍一个典型的曲线加筋板, 模型的原型来自NASA兰利研究中心[31]的结构, 后经过我们的简化改造, 曲线加筋板的几何形状如图8(a)所示. 矩形板边长为
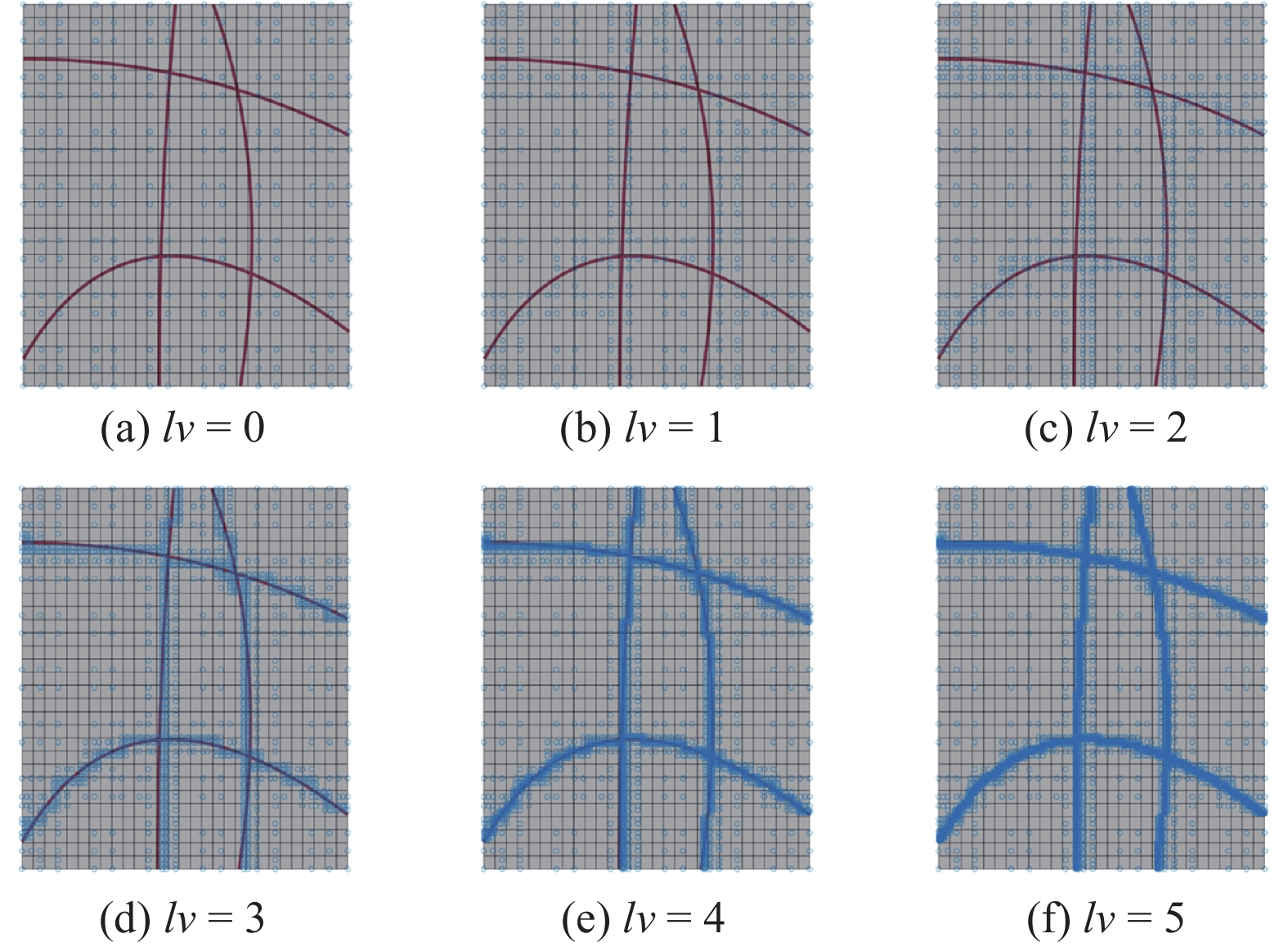
${L_1} = 70$ ,${L_2} = 60$ , 厚度为$t = 0.4$ . 筋条截面的高度为${a_s} = 2$ ,宽度为${b_s} = 1$ , 曲线加筋板的筋条偏心距离为$ e = \left( {{a_s} + t} \right)/2 = 1.2 $ . 载荷和边界条件如图8(b)所示. 参考压剪联合载荷作为飞机结构中常见的设计载荷条件, 我们选择在平板边缘施加压缩-剪切耦合的单位载荷.![]()
图 8 曲线加筋平板的几何信息以及载荷和边界条件Figure 8. The geometry information, load and boundary conditions of the plate with curvilinear stiffeners曲线筋条导致局部几何特征的复杂化, 同时还伴随着筋条和蒙皮网格数量的不匹配问题, 基于NURBS样条网格的结构化细化方法在减少数值误差方面很难达到最优. 局部细化方法能够针对性地解决因局部复杂几何特征带来的网格精细化要求, 进而有效消除了冗余的自由度. 图9清晰地展示了曲筋平板对应的层次T网格细化过程, 初始网格的规模设定为6 × 7. 如图9(b) ~ 图9(f)所示, 网格的细化层级从左至右逐级递增, 最大等级为5级. 从图中的网格分布可以观察到, 随着网格细化层级的提升, 沿筋条路径附近的蒙皮网格被逐级细分, 网格布局呈现出来的筋条形状逐渐清晰, 证明了加筋路径驱动的自适应细化算法的有效性.
![]()
图 9 沿加筋路径逐层级细化的平板蒙皮网格Figure 9. The plate mesh refined level by level along the stiffener paths使用RPHT样条自适应局部细化的目的是在结构特征复杂的区域增加控制变量的数量进而提高计算精度. 图10(a) ~ 图10(f)展示了在网格细化过程中蒙皮平板控制点的分布变化情况, 其中红色的曲线代表着筋条曲线, 蓝色圆点代表着蒙皮平板的控制点. 观察控制点分布的变化趋势能够发现, 局部网格的多层级细化可以为筋条附近的蒙皮增加更多的控制点, 同时也为局部区域物理场的精确表征提供了更多的控制变量以逼近真实的物理场.
![]()
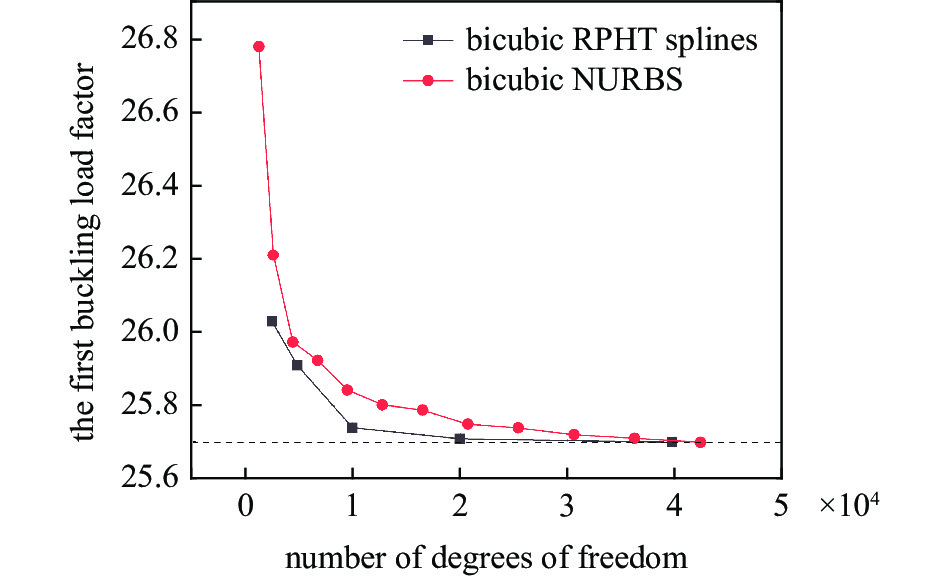
图 10 网格细化过程的蒙皮控制点分布Figure 10. Distribution of skin control points in the mesh refinement process表1的前3项展示了基于RPHT样条基函数的曲筋平板线性屈曲分析结果, 包括3级、4级和5级网格细化层级模型的1阶屈曲模态和屈曲载荷系数
${\lambda _1}$ . 从结果中可以看出, 在不同细化层级网格下, 曲线加筋平板的屈曲模态云图基本相同, 当自由度数量到达19960时, 1阶屈曲载荷系数已经完全收敛, 最终的一阶屈曲载荷系数为25.71. 同时, 为了验证本文提出的局部网格细化方法相比于全局细化网格在曲线加筋板结构上的优势, 将基于双三次${C^1}$ 连续RPHT样条的自适应等几何分析模型与基于双三次${C^1}$ 连续NURBS的经典等几何分析模型的收敛性曲线进行对比. 通过比较表中基于NURBS基函数的结果数据, 基于NURBS的一阶屈曲载荷在42400自由度时才接近于收敛, 并且从图11中收敛曲线趋势的对比, 不难发现, 相较于均匀网格, 非均匀网格对于加筋板结构的屈曲分析具有更好的收敛表现.表 1 基于双三次RPHT样条和双三次NURBS基函数的1/4加筋圆柱壳的1阶屈曲模态Table 1. The first-order buckling mode for the curved stiffened plate based on bicubic RPHT splines and bicubic NURBS basis functions3-level mesh
bicubic RPHT
splines (number of
degrees
of freedom:
9990)4-level mesh
bicubic RPHT
splines (number of
degrees of
freedom: 19960)5-level mesh
bicubic RPHT
splines (number
of degrees of
freedom: 39760)Bicubic
NURBS
(number of
degrees of
freedom:
42400)
${\lambda _1} = 25.74$ ${\lambda _1} = 25.71$ ${\lambda _1} = 25.70$ ${\lambda _1} = 25.70$ ![]()
图 11 基于双三次RPHT样条和双三次NURBS基函数的曲线加筋平板的1阶线性屈曲载荷系数收敛曲线Figure 11. Convergence curves of the first-order linear buckling load factor for the curved stiffened plate based on bicubic RPHT splines and bicubic NURBS basis functions3.2 1/4加筋圆柱壳
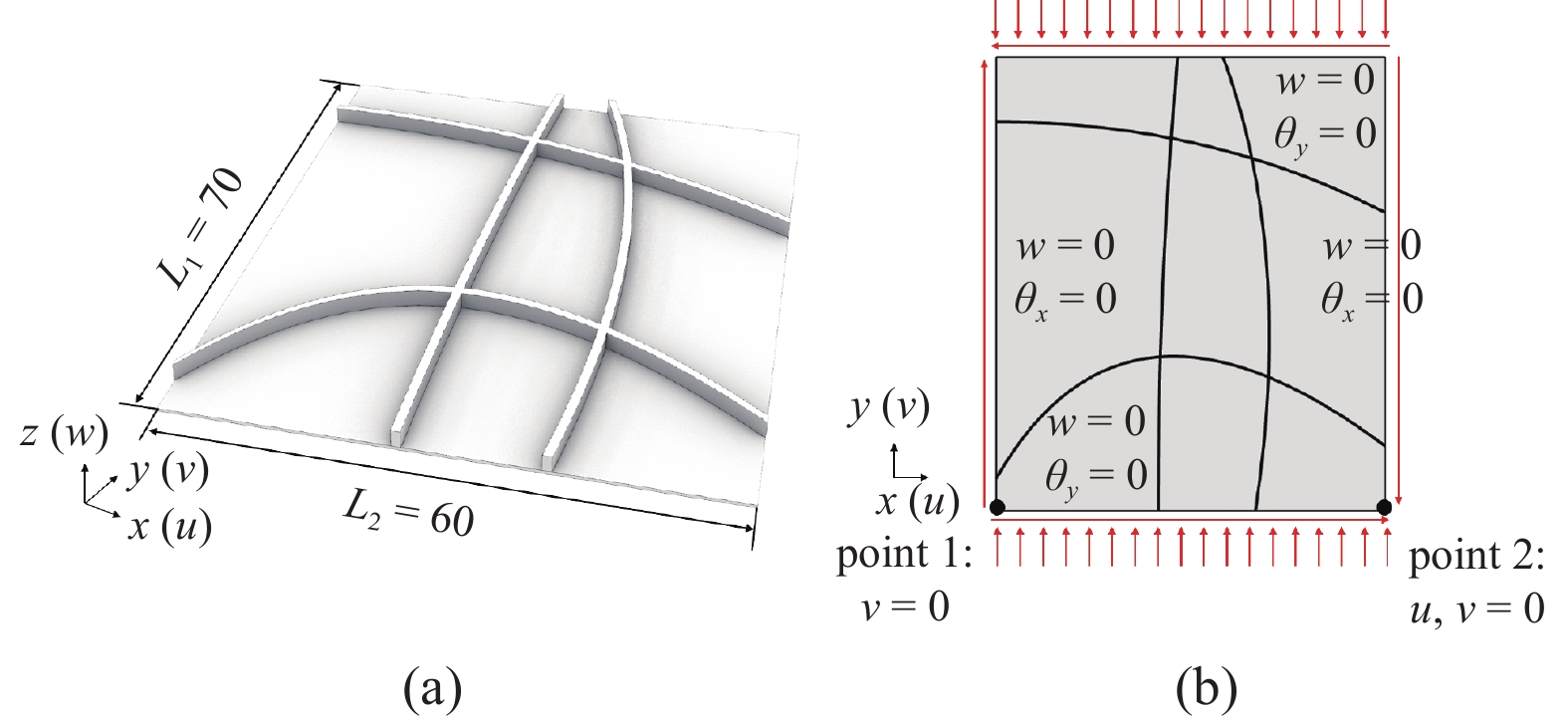
本节介绍的是一个1/4的X型网格加筋圆柱壳. 该模型的几何形状、载荷和边界约束如图12所示. 柱壳的高度为
$h = 60$ , 半径为$r = 50$ . 柱壳的厚度为$t = 0.4$ , 圆心角为$ \theta = {90^ \circ } $ . 筋条截面的高度为${a_s} = 1.2$ , 宽度为${b_s} = 0.6$ , 筋条中性轴无偏心$e = 0$ . 载荷工况是在柱壳的上边缘处施加单位均布轴压.![]()
图 12 1/4加筋圆柱壳的几何信息以及载荷和边界条件Figure 12. The geometry information, load and boundary conditions of quarter stiffened cylindrical shell曲面壳体加剧了局部几何特征的复杂度, 最直观的表现是曲面壳体的局部坐标系不再是固定形式. 相对于平板结构, 曲面蒙皮的局部坐标系随空间位置发生变动, 导致筋条曲线局部坐标系的法线方向也随之变化. 这些变化使得曲面加筋结构对网格精度的要求更为苛刻, 尤其是位于筋条附近的蒙皮单元. 另外, 由于梁壳单元耦合算法的加入, 筋条单元的位移、应力−应变等物理属性将与依附的蒙皮单元紧密联系, 粗网格导致的误差可能被放大. 因此对于复杂的曲面壳体, 筋条附近的蒙皮单元需要额外增加局部的细化处理. 图13(a) ~ 图13(f)具体展示了1/4圆柱壳所对应的自适应网格细化过程, 初始网格的规模预设为8 × 6, 网格的细化层级从左至右逐级递增, 最大级数为5级. 从图中的网格分布情况可以发现, 随着网格细化层级的不断提升, 细化后的网格稳定地呈现出明显的X形状, 这与筋条的布局完全吻合, 说明本文提出的自适应局部网格细化方法对于更为复杂的曲面壳体依然有效.
![]()
图 13 沿加筋路径逐级细化的圆柱壳蒙皮网格Figure 13. The cylindrical shell mesh refined level by level along the stiffener paths网格的局部细化改变了蒙皮曲面控制点的位置分布, 图14具体展示了在网格进行细化过程中蒙皮柱壳控制点的分布变化情况, 其中红色曲线代表着筋条曲线, 蓝色的圆点代表着蒙皮曲面的控制点. 筋条附近的蒙皮控制点分布随着网格的细化程度逐渐密集, 代表局部范围控制点的自由度数量提升, 更加精细的网格能够缓解因复杂几何特征导致的分析精度下降.
![]()
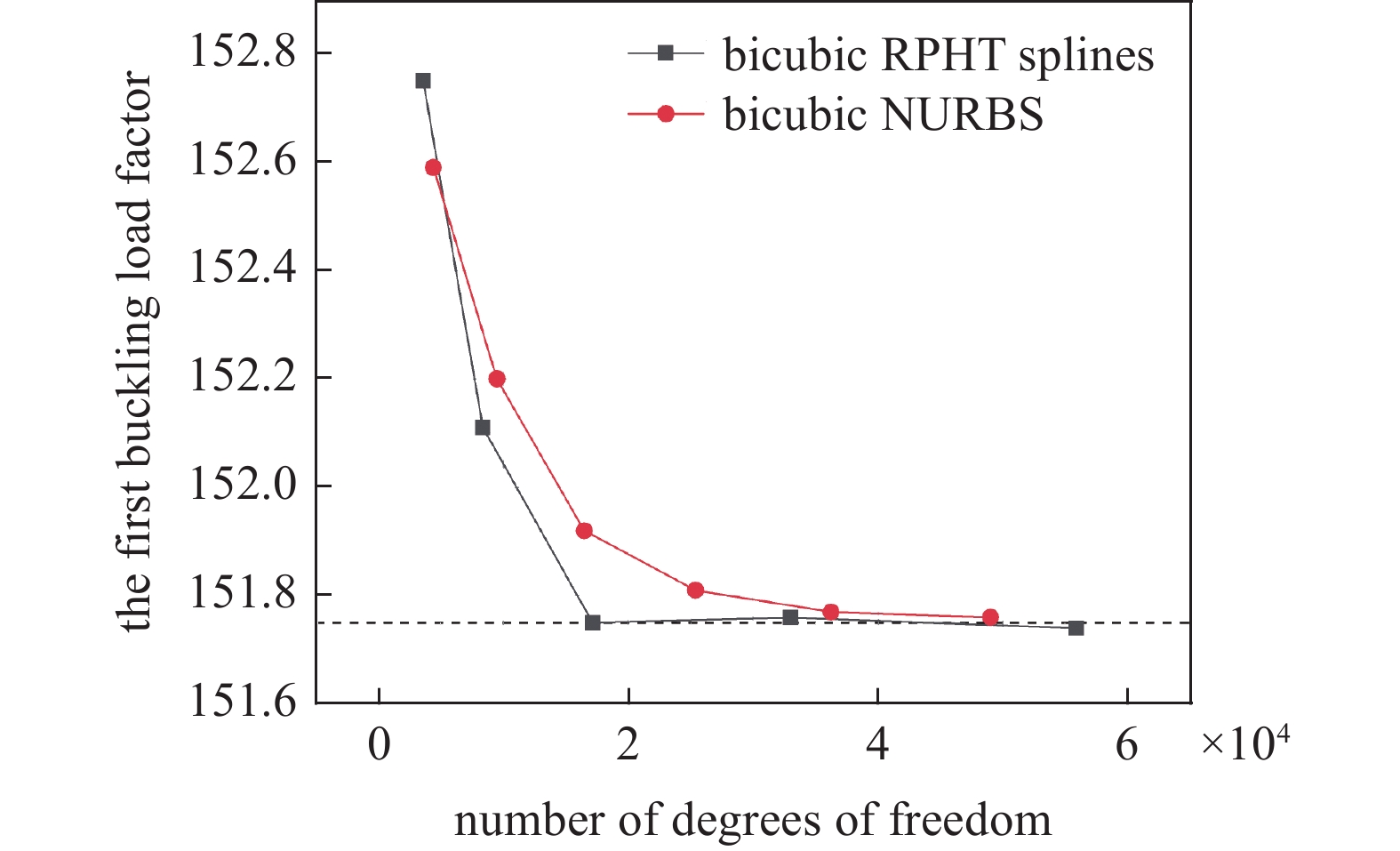
图 14 网格细化过程的蒙皮控制点分布Figure 14. Distribution of control points in the mesh subdivision process表2的前3项展示了基于RPHT样条基函数的1/4圆柱壳的线性屈曲分析结果, 包括3级、4级和5级网格细化层级模型的1阶屈曲模态和屈曲载荷系数
${\lambda _1}$ . 从1阶屈曲载荷系数来看, 3级、4级和5级网格细化层级的屈曲载荷系数基本相同, 说明已经趋近于收敛网格. 为了验证本文提出的局部网格细化方法相比于全局细化网格在复杂曲面加筋板结构上的优势, 将基于双三次${C^1}$ 连续RPHT样条的屈曲分析结果与基于双三次${C^1}$ 连续的NURBS的结果展开对比. 基于NURBS基函数的屈曲分析结果数据表明, 其一阶屈曲载荷在49020自由度时才接近于收敛, 相较于接近收敛的3级RPHT样条的细化网格, 同时参考图15中收敛曲线趋势的对比, 进一步验证了非均匀网格对于复杂曲面加筋板壳结构的屈曲分析具有更好的收敛表现.表 2 基于双三次RPHT样条和双三次NURBS基函数的1/4加筋圆柱壳的1阶屈曲模态Table 2. The first-order buckling mode for the quarter stiffened cylindrical shell based on bicubic RPHT splines and bicubic NURBS basis functions3-level mesh bicubic
RPHT splines
(number of
degrees of
freedom: 17160)4-level mesh
bicubic RPHT
splines (number of
degrees of freedom:
32980)5-level mesh
bicubic RPHT
splines (number
of degrees of
freedom:
55920)Bicubic
NURBS
(number of
degrees of
freedom:
49020)
${\lambda _1} = {\text{151}}{\text{.75}}$ ${\lambda _1} = 151.76$ ${\lambda _1} = 151.74$ ${\lambda _1} = {\text{151}}{\text{.76}}$ ![]()
图 15 基于双三次RPHT样条和双三次NURBS基函数的1/4加筋圆柱壳的1阶线性屈曲载荷系数收敛曲线Figure 15. Convergence curves of the first-order linear buckling load factor for the quarter stiffened cylindrical shell based on bicubic RPHT splines and bicubic NURBS basis functions4. 结 论
本文提出了一种加筋路径驱动的板壳自适应等几何屈曲分析方法, 利用RPHT样条支持局部细分的特性, 实现了与加筋路径关联蒙皮单元的自适应多层级细化. 自适应局部细化网格能够改善因复杂局部几何特征带来的各项异性物理场问题, 通过对结构特征复杂区域增加额外控制点以提高分析精度. 曲线加筋板和网格加筋圆柱壳这两个算例验证了本方法的高效性和鲁棒性, 经过算例对比证明了使用RPHT样条局部细化可以有效降低分析模型的自由度数量, 相较基于NURBS的经典等几何分析方法, 局部细化网格的方式更加灵活, 对于复杂的加筋板壳结构能够提供更加适合的网格布局, 有效提高了加筋板壳屈曲分析的收敛速率, 这对于提升加筋结构的设计效率具有十分重要的意义.
-
![]()
图 2 不同层级的二维层次T网格及其对应的基函数
Figure 2. 2-D hierarchical T-meshes of different levels and their corresponding basis functions
![]()
图 3 基于二阶基函数的退化壳单元的局部坐标系及控制变量
Figure 3. Local coordinate system and control variables of degenerated shell element based on second order basis function
![]()
图 4 筋条单元的局部坐标系、截面参数及其与壳单元相对位置关系
Figure 4. The local coordinate system, section parameters and relative position relationship with shell element of the stiffener element
![]()
图 5 蒙皮参数空间内的强耦合关系
Figure 5. The strong coupling relationship in the skin parameter space
![]()
图 6 加筋路径驱动的自适应网格细化流程图
Figure 6. The flowchart of adaptive mesh refinement driven by stiffener paths
![]()
图 7 加筋路径驱动的自适应网格细化示意图
Figure 7. The diagram of adaptive mesh refinement driven by stiffener paths
![]()
图 8 曲线加筋平板的几何信息以及载荷和边界条件
Figure 8. The geometry information, load and boundary conditions of the plate with curvilinear stiffeners
![]()
图 9 沿加筋路径逐层级细化的平板蒙皮网格
Figure 9. The plate mesh refined level by level along the stiffener paths
![]()
图 10 网格细化过程的蒙皮控制点分布
Figure 10. Distribution of skin control points in the mesh refinement process
![]()
图 11 基于双三次RPHT样条和双三次NURBS基函数的曲线加筋平板的1阶线性屈曲载荷系数收敛曲线
Figure 11. Convergence curves of the first-order linear buckling load factor for the curved stiffened plate based on bicubic RPHT splines and bicubic NURBS basis functions
![]()
图 12 1/4加筋圆柱壳的几何信息以及载荷和边界条件
Figure 12. The geometry information, load and boundary conditions of quarter stiffened cylindrical shell
![]()
图 13 沿加筋路径逐级细化的圆柱壳蒙皮网格
Figure 13. The cylindrical shell mesh refined level by level along the stiffener paths
![]()
图 14 网格细化过程的蒙皮控制点分布
Figure 14. Distribution of control points in the mesh subdivision process
![]()
图 15 基于双三次RPHT样条和双三次NURBS基函数的1/4加筋圆柱壳的1阶线性屈曲载荷系数收敛曲线
Figure 15. Convergence curves of the first-order linear buckling load factor for the quarter stiffened cylindrical shell based on bicubic RPHT splines and bicubic NURBS basis functions
表 1 基于双三次RPHT样条和双三次NURBS基函数的1/4加筋圆柱壳的1阶屈曲模态
Table 1 The first-order buckling mode for the curved stiffened plate based on bicubic RPHT splines and bicubic NURBS basis functions
3-level mesh
bicubic RPHT
splines (number of
degrees
of freedom:
9990)4-level mesh
bicubic RPHT
splines (number of
degrees of
freedom: 19960)5-level mesh
bicubic RPHT
splines (number
of degrees of
freedom: 39760)Bicubic
NURBS
(number of
degrees of
freedom:
42400)${\lambda _1} = 25.74$ ${\lambda _1} = 25.71$ ${\lambda _1} = 25.70$ ${\lambda _1} = 25.70$ 
下载: 导出CSV
表 2 基于双三次RPHT样条和双三次NURBS基函数的1/4加筋圆柱壳的1阶屈曲模态
Table 2 The first-order buckling mode for the quarter stiffened cylindrical shell based on bicubic RPHT splines and bicubic NURBS basis functions
3-level mesh bicubic
RPHT splines
(number of
degrees of
freedom: 17160)4-level mesh
bicubic RPHT
splines (number of
degrees of freedom:
32980)5-level mesh
bicubic RPHT
splines (number
of degrees of
freedom:
55920)Bicubic
NURBS
(number of
degrees of
freedom:
49020)${\lambda _1} = {\text{151}}{\text{.75}}$ ${\lambda _1} = 151.76$ ${\lambda _1} = 151.74$ ${\lambda _1} = {\text{151}}{\text{.76}}$
下载: 导出CSV
-
[1] 张卫红, 章胜冬, 高彤. 薄壁结构的加筋布局优化设计. 航空学报, 2009, 30(11): 2126-2131 (Zhang Weihong, Zhang Shengdong, Gao Tong. Stiffener layout optimization of thin walled structures. Acta Aeronautica et Astronautica Sinica, 2009, 30(11): 2126-2131 (in Chinese) doi: 10.3321/j.issn:1000-6893.2009.11.018 [2] 王博, 田阔, 郝鹏等. 变截面加筋板尺寸−布局一体化设计. 固体火箭技术, 2017, 40(2): 208-213, 227 (Wang Bo, Tian Kuo, Hao Peng, et al. Size-layout integrated cross-section optimization of variable stiffened panels. Journal of Solid Rocket Technology, 2017, 40(2): 208-213, 227 (in Chinese) doi: 10.7673/j.issn.1006-2793.2017.02.014 [3] Wang D, Abdalla MM, Wang ZP, et al. Streamline stiffener path optimization (SSPO) for embedded stiffener layout design of non-uniform curved grid-stiffened composite (NCGC) structures. Computer Methods in Applied Mechanics and Engineering, 2019, 344: 1021-1050 doi: 10.1016/j.cma.2018.09.013
[4] Alhajahmad A, Mittelstedt C. Minimum weight design of curvilinearly grid-stiffened variable-stiffness composite fuselage panels considering buckling and manufacturing constraints. Thin-Walled Structures, 2021, 161: 107526
[5] Hao P, Liu X, Wang Y, et al. Collaborative design of fiber path and shape for complex composite shells based on isogeometric analysis. Computer Methods in Applied Mechanics and Engineering, 2019, 354: 181-212 doi: 10.1016/j.cma.2019.05.044
[6] Cottrell JA, Hughes TJR, Bazilevs Y. Isogeometric analysis: toward integration of CAD and FEA. John Wiley and Sons, 2009, 141(5): 299-325
[7] Hughes TJR, Cottrell JA, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 2005, 194(39-41): 4135-4195 doi: 10.1016/j.cma.2004.10.008
[8] Kiendl J, Bletzinger KU, Linhard J, et al. Isogeometric shell analysis with Kirchhof-Love elements. Computer Methods in Applied Mechanics and Engineering, 2009, 198(49-52): 3902-3914 doi: 10.1016/j.cma.2009.08.013
[9] Benson DJ, Bazilevs Y, Hsu MC, et al. Isogeometric shell analysis: the Reissner–Mindlin shell. Computer Methods in Applied Mechanics and Engineering, 2010, 199(5-8): 276-289 doi: 10.1016/j.cma.2009.05.011
[10] Breitenberger M, Apostolatos A, Philipp B, et al. Analysis in computer aided design: nonlinear isogeometric B-Rep analysis of shell structures. Computer Methods in Applied Mechanics and Engineering, 2015, 284: 401-457 doi: 10.1016/j.cma.2014.09.033
[11] Hao P, Yuan X, Liu C, et al. An integrated framework of exact modeling, isogeometric analysis and optimization for variable-stiffness composite panels. Computer Methods in Applied Mechanics and Engineering, 2018, 339: 205-238 doi: 10.1016/j.cma.2018.04.046
[12] Guo Y, Ruess M, Schillinger D. A parameter-free variational coupling approach for trimmed isogeometric thin shells. Computational Mechanics, 2017, 59(4): 693-715 doi: 10.1007/s00466-016-1368-x
[13] Adam N, Le Tallec P, Zarroug M. Multipatch isogeometric mortar methods for thick shells. Computer Methods in Applied Mechanics and Engineering, 2020, 372: 113403 doi: 10.1016/j.cma.2020.113403
[14] Dornisch W, Vitucci G, Klinkel S. The weak substitution method - an application of the mortar method for patch coupling in NURBS-based isogeometric analysis. International Journal for Numerical Methods in Engineering, 2015, 103(3): 205-234 doi: 10.1002/nme.4918
[15] 石鹏. 曲型加筋板、壳结构的建模方法与分析研究. [博士论文]. 北京: 北京理工大学, 2015 Shi Peng. Modeling and analysis of curvilinearly stiffened plates and shells. [PhD Thesis]. Beijing: Beijing Institute of Technology, 2015 (in Chinese))
[16] Shi P, Kapania RK, Dong CY. Vibration and buckling analysis of curvilinearly stiffened plates using finite element method. American Institute of Aeronautics and Astronautics Joural, 2015, 53(5): 1319-1335 doi: 10.2514/1.J053358
[17] Qin XC, Dong CY, Wang F, et al. Static and dynamic analyses of isogeometric curvilinearly stiffened plates. Applied Mathematical Modelling, 2017, 45: 336-364 doi: 10.1016/j.apm.2016.12.035
[18] Saeedi A, Hassani B, Farzam A. Simultaneous modeling and structural analysis of curvilinearly stiffened plates using an isogeometric approach. Acta Mechanica, 2020, 231(8): 3473-3498 doi: 10.1007/s00707-020-02725-4
[19] Hao P, Wang Y, Tang H, et al. A NURBS-based degenerated stiffener element for isogeometric static and buckling analysis. Computer Methods in Applied Mechanics and Engineering, 2022, 398: 115245 doi: 10.1016/j.cma.2022.115245
[20] Nguyen-Thanh N, Nguyen-Xuan H, Bordas SPA, et al. Isogeometric analysis using polynomial splines over hierarchical T-meshes for two-dimensional elastic solids. Computer Methods in Applied Mechanics and Engineering, 2011, 200(21-22): 1892-1908 doi: 10.1016/j.cma.2011.01.018
[21] Qin XC, Dong CY, Yang HS. Isogeometric vibration and buckling analyses of curvilinearly stiffened composite laminates. Applied Mathematical Modelling, 2019, 73: 72-94 doi: 10.1016/j.apm.2019.03.045
[22] Wang P, Xu J, Deng J, et al. Adaptive isogeometric analysis using rational PHT-splines. Computer-Aided Design, 2011, 43(11): 1438-1448 doi: 10.1016/j.cad.2011.08.026
[23] 秦晓陈, 李晨, 陈程等. 基于等几何分析方法的复合材料加筋板屈曲分析. 复合材料科学与工程, 2022, 5: 21-27 (Qin Xiaochen, LiChen, Chen Cheng, et al. Buckling analysis of composite stiffened plates based on IGA method. Composites Science and Engineering, 2022, 5: 21-27 (in Chinese) [24] Sederberg TN, Zheng JM, Bakenov A, et al. T-splines and T-NURCCs. ACM Transactions on Graphics, 2003, 22(3): 477-484 doi: 10.1145/882262.882295
[25] Deng J, Chen F, Li X, et al. Polynomial splines over hierarchical T-meshes. Graphical Models, 2008, 70(4): 76-86 doi: 10.1016/j.gmod.2008.03.001
[26] Deng J, Chen F, Feng Y. Dimensions of spline spaces over T-meshes. Journal of Computational and Applied Mathematics, 2006, 194(2): 267-283 doi: 10.1016/j.cam.2005.07.009
[27] 许金兰. 等几何分析中的若干问题研究. [博士论文]. 合肥: 中国科学技术大学, 2015 Xu Jinlan. Some problems in isogeometric analysis. [PhD Thesis]. Hefei: University of Science and Technology of China, 2015 (in Chinese))
[28] Patel SN, Datta PK, Sheikh AH. Buckling and dynamic instability analysis of stiffened shell panels. Thin-Walled Structures, 2006, 44(3): 321-333 doi: 10.1016/j.tws.2006.03.004
[29] Prusty BG, Satsangi SK. Analysis of stiffened shell for ships and ocean structures by finite element method. Ocean Engineering, 2001, 28(6): 621-638 doi: 10.1016/S0029-8018(00)00021-4
[30] Piegl L, Tiller W. The NURBS Book. New York: Springer Science and Business Media, 1996
[31] Slemp WCH, Bird RK, Kapania RK, et al. Design, optimization, and evaluation of integrally stiffened Al-7050 panel with curved stiffeners. Journal of Aircraft, 2011, 48(4): 1163-1175 doi: 10.2514/1.C031118
-
期刊类型引用(3)
1. 孟凡哲，范天峰，田亚锋，黄诚，李银河. 自行防空武器校轴装备构型与力学分析. 兵器装备工程学报. 2024(04): 184-190 . 
百度学术
2. 齐栋梁. 靶向精细化分析的鲁棒等几何无网格配点法. 力学学报. 2024(08): 2313-2326 . 本站查看
3. 王英俊，李璟慧. 等几何分析中局部固定约束的精确施加方法. 华南理工大学学报(自然科学版). 2024(12): 65-78 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 739
- HTML全文浏览量: 234
- PDF下载量: 159
- 被引次数: 4
