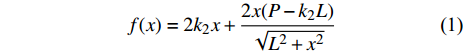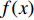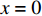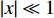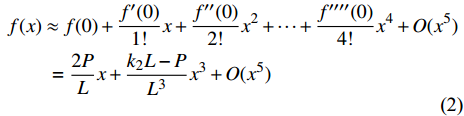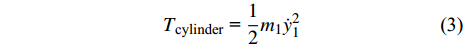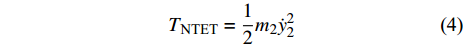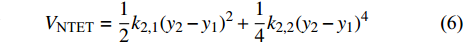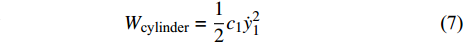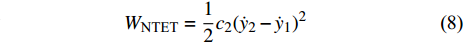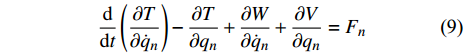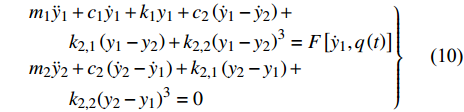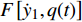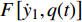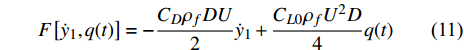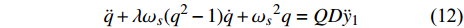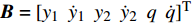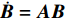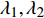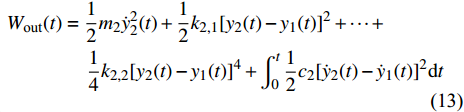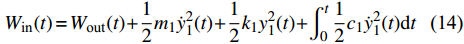THEORETICAL AND EXPERIMENTAL STUDY ON VORTEX-INDUCED VIBRATION SUPPRESSION BASED ON NONLINEAR TARGETED ENERGY TRANSFER
-
摘要: 流致振动现象广泛存在于机械、航空、土木和石油等重要工程领域, 为防止工程结构因流致振动行为而造成疲劳破坏, 有必要对稳定性、动力学响应及其振动控制做深入研究. 本文提出了一种由弹簧和质量块构成的非线性吸能器(nonlinear targeted energy transfer, NTET), 研究了该非线性吸能器对弹性支承圆柱体涡激振动的被动控制影响机制. 基于能量法推导了圆柱体涡激振动非线性被动控制的耦合动力学方程, 通过设计非线性弹簧−质量块构型的NTET, 进一步开展了涡激振动控制的实验研究, 并与理论预测结果进行了较好的对比, 获得提升涡激振动控制效果的最佳参数值. 研究发现, NTET的质量、弹簧刚度以及弹簧预应力等参数会对涡激振动控制效果产生显著的影响. 本文研究结果表明, 该耦合系统中圆柱体和NTET均表现出周期性的稳态振动响应, NTET质量的改变会显著影响系统的耦合频率. 在无预应力状态下, NTET质量越大、刚度越小时, 有更好的减振效果. 当弹簧预应力逐渐增大时, NTET的非线性刚度逐渐变弱, 会降低涡激振动控制性能. 参数分析表明: 随着涡激振动控制性能的提升, 圆柱体的振幅逐渐较小, NTET的振幅逐渐增大, 能量传递效率逐渐提高. 研究结果可为工程中涡激振动控制策略的高效设计提供有用的理论支撑和实验数据.Abstract: Flow-induced vibration of the structure widely occurs in many important engineering fields such as mechanical, aerospace, civil and petroleum. In order to prevent fatigue and failure of the engineering structures due to flow-induced vibrations, it’s necessary to do deep researches on stability, dynamic responses and vibration controls. In this paper, a nonlinear targeted energy transfer (NTET) model composed of linear springs and mass block is proposed. The passive control mechanism of nonlinear energy absorbers on the vortex-induced vibration of an elastically supported cylinder is investigated. Firstly, based on the energy method, the coupling dynamic equations for the nonlinear passive control on vortex-induced vibration of a cylinder are established. Then, experimental study is conducted by designing the nonlinear spring-mass configuration of NTET. Good agreements are obtained by comparing experimental results with theoretical predictions. Finally, the optimal parameters of the NTET for improving the control performance of vortex-induced vibrations are obtained. It is found that some NTET parameters such as mass, spring stiffness and spring prestress have significant impacts on the control performance. The results show that both the cylinder and NTET exhibit periodic steady-state vibration responses. Changes in the mass of NTET can significantly affect the coupling frequency of the system. In the case of no spring prestress, larger mass, lower stiffness of the NTET can produce a better vibration suppression. But when the spring prestress is increased, the nonlinear stiffness of the NTET becomes weak, resulting in a reduction of control effect on the vortex-induced vibration. Parametric analysis shows that with the enhancement of vortex-induced vibration control effect, the vibration amplitude of cylinder can be decreased while the NTET’s amplitude is gradually increased, indicating the improvement of the energy transfer efficiency. The present research results can provide very useful theoretical support and experimental data for efficiently designing control strategies on vortex-induced vibrations in engineering fields.
-
非线性吸能器, 简称NTET (nonlinear targeted energy transfer), 由于它可以从振动系统中吸收能量, 因此在振动控制工程中得到了广泛的应用, 以降低或抑制结构振幅[1-3]. NTET通常由三部分组成: 一是非线性刚度元件, 可使其与主系统产生共振行为; 二是线性阻尼器, 用于耗散通过共振相互作用传递的振动能量; 三是其自身质量, 它对主系统的耦合频率和减振效果有重要影响. 因此, NTET可以从宽频瞬态激励中吸收振动能量且具有快速、能量转移不可逆等显著优点. 使用NTET成为工程中隔离和抑制振动和冲击的一种有效的控制方法[4-8].
早期, 研究人员主要针对瞬态或受迫激励下结构的振动响应设计非线性吸能器进行减隔振处理, 并取得了一些重要的研究成果[9-15]. Vakakis等[11]在研究梁结构上附加局部非线性能量阱(nonlinear energy sink, NES)的动力学特性时, 最早提出了NES减振控制器, 可用于消除或降低小型或大型柔性结构的冲击和振动干扰. Mao等[12]提出了一种扭转型的NES, 对含简支边界条件的弹性梁的弯曲振动进行控制, 取得较好的抑制效果; 为抑制柔性机翼的振动行为, Hubbard等[14]设计了一种紧凑型的NES, 大幅降低了机翼的振动幅值; Andersen等[15]还研究了具有几何非线性黏性阻尼的吸能器, 用于控制结构在基础激励下的振动行为.
然而, 实际工程中除了基础激励引起结构的振动以外, 还经常会出现流体诱发结构的振动现象, 即流致振动, 它具有导致桥梁倒塌、结构颤振、以及管道疲劳失效等的潜在危险[16-20]. 因此, 针对流致振动引起的结构响应, 国内外研究者相继提出了大量的被动或主动控制策略, 取得了有效的控制效果[21-36]. 比如, Lee等[21]对双自由度机翼系统中的气动弹性不稳定性进行了研究, 通过利用NES, 可以实现目标物宽带能量的被动传输, 结果表明, 非线性能量阱可显著提高机翼系统的气动弹性稳定性. 后来, Tumkur等[23-24]利用NES对弹性支撑圆柱体涡激振动进行了振动控制研究, 研究表明, 选择合适的NES参数值可以显著抑制圆柱体的涡激振动响应. 在此基础上, Dai等[3, 27-28]通过建立耦合系统的理论模型, 研究了NES对涡激振动和驰振的锁频区域、起振流速以及振动幅值的影响, 发现NES的质量、阻尼和刚度等参数的变化对耦合系统的频率、振动幅值以及动力学行为有显著影响, 且有最优参数值使得系统的振动控制达到最佳效果. 最近, Ding等[8]系统而全面地阐述了非线性能量阱在工程振动控制中的应用, 为非线性振动控制器的设计、研发及分析提供了重要指导意义.
从以上研究可知, 目前国内外学者对于流致振动控制的研究取得了重要成果, 为后续研究工作提供了有益的借鉴. 但关于圆柱体涡激振动控制的实验研究鲜有报道, 大多是基于理论建模研究耦合控制系统的非线性特性及其减振效果. 鉴于此, 本文基于非线性弹簧−质量块构型设计了非线性吸能器, 从理论和实验两方面研究该非线性吸能器对弹性支撑圆柱体涡激振动的控制机理, 并通过关键的参数分析揭示非线性吸能器的影响规律.
1. 动力学理论建模
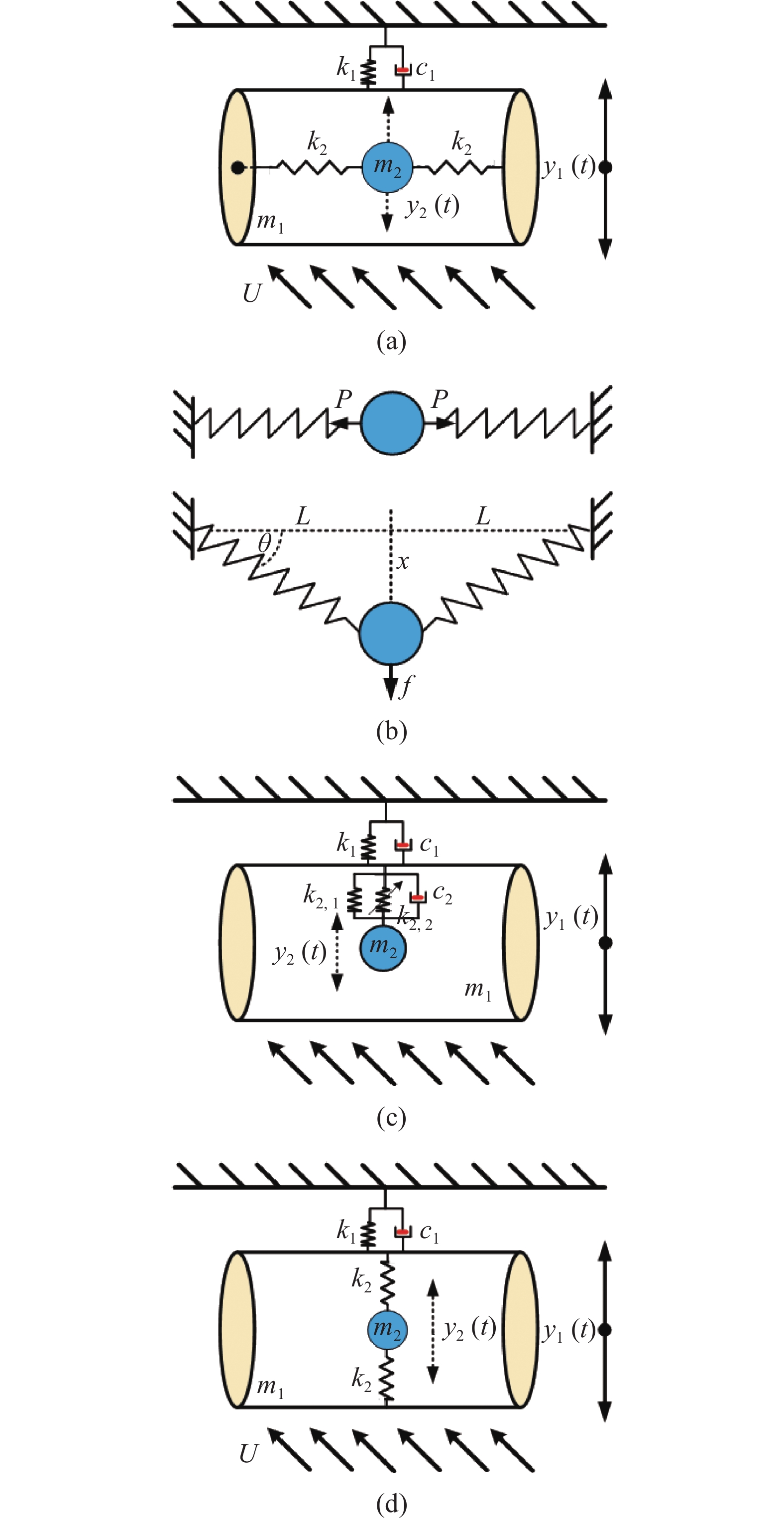
本文研究对象是直径为D的弹性支撑圆柱体, 在横向外流U作用下, 当流体脱落频率接近圆柱体固有频率时, 圆柱会发生涡激振动行为, 共振流速区域被称为锁频区域[37-38]. 圆柱体质量、阻尼和刚度分别为m1, c1和k1, 并假设圆柱体在受到横向(z)均匀来流作用时只在竖直(y)方向振动, 结构如图1(a)所示.
![]()
图 1 (a)涡激振动非线性控制模型示意图; (b)非线性吸能器示意图;(c)非线性吸能器控制等效模型示意图和(d)涡激振动线性吸能器模型示意图Figure 1. (a) Model diagram of the vortex-induced vibrations nonlinear control. (b) Model diagram of the nonlinear targeted energy transfer. (c) Equivalent model diagram of the nonlinear targeted energy transfer. (d) Model diagram of the vortex-induced vibrations linear control为降低圆柱体涡激振动响应, 引入非线性吸能器(NTET). 该吸能器由质量块m2和原长为L0、阻尼为c2的弹簧组成, 如图1(b)所示. 需要注意的是, NTET放置在圆柱体内. 此外, 当NTET的质量块处于初始位置时, 对应的弹簧长度为L, 刚度为k2, 则预应力P = k2(L−L0). 由于受重力影响, 弹簧变形后与初始水平位置的夹角为θ, 且弹簧变形后的长度为L′. 因此, 质量块m2在运动过程会受到非线性弹簧力的作用. 由几何和受力平衡关系可以求出非线性力为
$$ f(x) = 2{k_2}x + \frac{{2x(P - {k_2}L)}}{{\sqrt {{L^2} + {x^2}} }} $$ (1) 其中x为NTET质量块偏离水平位置的位移, 将
$f(x)$ 在$x = 0$ 处泰勒展开($\left| x \right| \ll 1$ )得到$$ \begin{gathered} f(x) \approx f(0) + \frac{{f'(0)}}{{1!}}x + \frac{{f''(0)}}{{2!}}{x^2} + \cdots + \frac{{f''''(0)}}{{4!}}{x^4} + O({x^5}) \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \frac{{2P}}{L}x + \frac{{{k_2}L - P}}{{{L^3}}}{x^3} + O({x^5}) \\ \end{gathered} $$ (2) 通过方程(2)可以看出, NTET具有线性和非线性刚度特性, 线性项系数为k2,1 = 2P/L, 非线性项系数为k2,2 = (k2L−P)/ L3, 控制等效模型如图1(c)所示. 值得一提的是, 如果弹簧竖直放置, 则吸能器只有线性刚度, 简化模型如图1(d)所示.
设圆柱体和NTET的振动幅值分别为y1(t)和y2(t), 则它们的动能表达式分别为
$$ {T_{{\text{cylinder}}}}{\text{ = }}\frac{1}{2}{m_1}\dot y_1^2 $$ (3) $$ {T_{{\text{NTET}}}} = \frac{1}{2}{m_2}\dot y_2^2 $$ (4) 势能表达式分别为
$$ {V_{{\text{cylinder}}}} = \frac{1}{2}{k_1}y_1^2 $$ (5) $$ {V_{{\text{NTET}}}} = \frac{1}{2}{k_{2,1}}{({y_2} - {y_1})^2} + \frac{1}{4}{k_{2,2}}{({y_2} - {y_1})^4} $$ (6) 阻尼做的功分别为
$$ {W_{{\text{cylinder}}}} = \frac{1}{2}{c_1}\dot y_1^2 $$ (7) $$ {W_{{\text{NTET}}}} = \frac{1}{2}{c_2}{({\dot y_2} - {\dot y_1})^2} $$ (8) 基于能量法和拉格朗日方程[39]
$$ \frac{{\rm{d}}}{{{\rm{d}}t}}\left(\frac{{\partial T}}{{\partial {{\dot q}_n}}}\right) - \frac{{\partial T}}{{\partial {q_n}}} + \frac{{\partial W}}{{\partial {{\dot q}_n}}} + \frac{{\partial V}}{{\partial {q_n}}} = {F_n} $$ (10) 其中, T, V和W分别代表耦合系统的总动能、总势能和总耗散能. qn表示系统的广义坐标, 分别取q1 = y1, q2 = y2, Fn为广义力. 将各项表达式代入式(10)中, 可得到基于非线性吸能器的圆柱体涡激振动控制耦合方程
$$\left. \begin{split} & {m_1}{{\ddot y}_1} + {c_1}{{\dot y}_1} + {k_1}{y_1} + {c_2}\left( {{{\dot y}_1} - {{\dot y}_2}} \right) +\\ &\qquad {k_{2,1}}\left( {{y_1} - {y_2}} \right) + {k_{2,2}}{\left( {{y_1} - {y_2}} \right)^3} = F\left[ {{{\dot y}_1},q\left( t \right)} \right] \\ & {m_2}{{\ddot y}_2} + {c_2}\left( {{{\dot y}_2} - {{\dot y}_1}} \right) + {k_{2,1}}\left( {{y_2} - {y_1}} \right) + \\ &\qquad{k_{2,2}}{\left( {{y_2} - {y_1}} \right)^3} = 0 \end{split} \right\}$$ (11) 式中, “ · ”表示关于时间的导数. x(t) = y2−y1为质量块对圆柱体的相对位移, 质量块与圆柱体之间的质量比β = m2/m1. 应当指出, 式(11)中m1应包含圆柱体质量和附加流体质量, 由于所考虑的流体为空气, 因此可忽略附加流体对质量m1的影响.
$F\left[ {{{\dot y}_1},q(t)} \right]$ 表示作用在圆柱体上的涡激力, 该力取决于圆柱的振动速度和升力系数q(t), 根据文献[40-41]的研究, 圆柱体上的气动载荷主要由两部分组成: 一是与结构阻力系数和圆柱体振动速度相关的流体效应; 二是与脉动升力系数有关的涡流对圆柱体的影响. 因此, 涡激力$F\left[ {{{\dot y}_1},q(t)} \right]$ 可以表示为以下形式$$ F\left[ {{{\dot y}_1},q(t)} \right] = - \frac{{{C_D}{\rho _f}DU}}{2}{\dot y_1} + \frac{{{C_{L0}}{\rho _f}{U^2}D}}{4}q(t) $$ (12) 其中CL0和CD分别是稳态升力系数和阻力系数, 根据Facchinetti[41]的研究, CL0 = 0.3和CD = 1.2. ρf表示流体密度, 取1.2 kg/m3. 尾流变量q(t)由下式给出
$$ \ddot q + \lambda {\omega _s}({q^2} - 1)\dot q + {\omega _s}^2q = QD{\ddot y_1} $$ (13) 其中λ和Q为经验参数[41], 值分别为0.24和15. ωs为漩涡脱落频率, 其表达式为ωs = 2πStU/D, 其中St为斯特劳哈尔数, 取值为0.2.
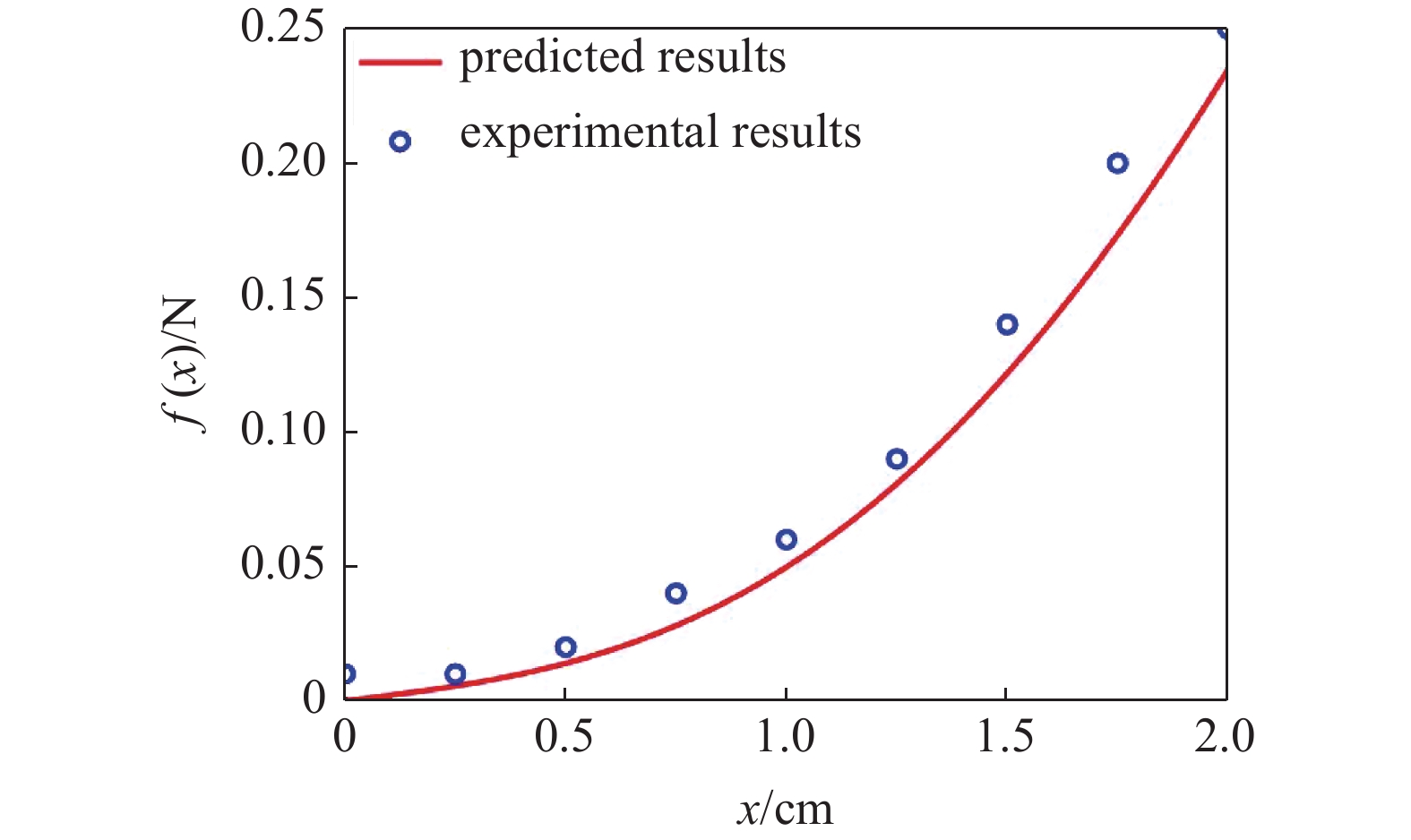
此外, 为了验证图1(b)所示模型以及非线性力表达式, 设计了模型实验测量NTET结构中的非线性力, 理论预测和实验结果对比如图2所示.
![]()
图 2 NTET结构中非线性力理论预测与实验结果对比Figure 2. Comparison of the nonlinear force in NTET between theoretical predictions and experimental results.2. 结果分析与讨论
2.1 理论模型的验证
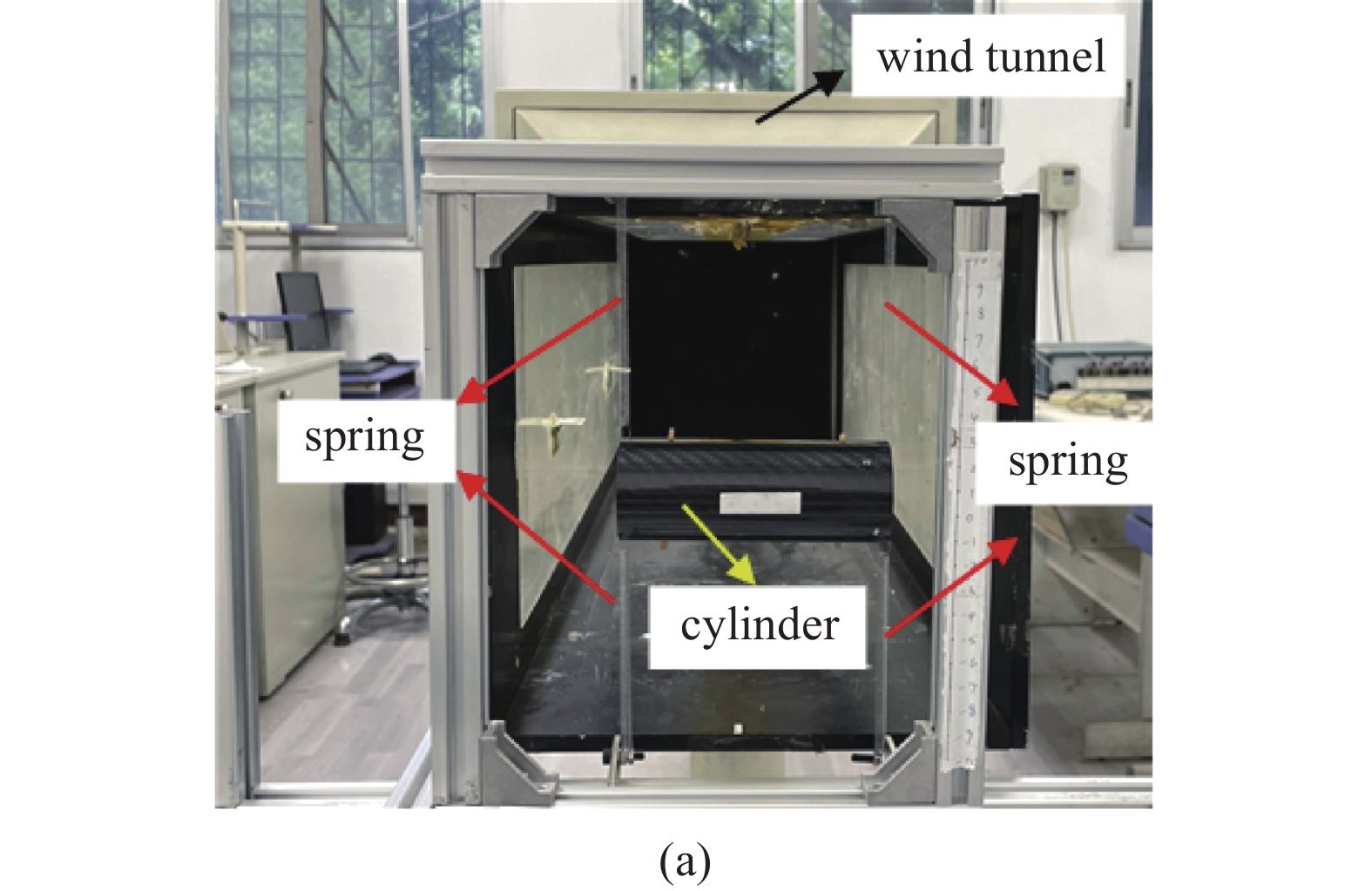
为验证理论模型, 设计了模型实验, 对比结果如图3所示. 图3(a)和图3(b)给出了实验模型的正视图和侧视图, 图3(c)给出了理论和实验对比结果. 实验中圆柱的物理参数为: m1 = 0.016 kg, D = 0.045 m, c1 = 0.01 N·s/m, k1 = 30 N/m. 初始条件设置为y1(t) = 0.001, NTET的参数为: β = 0.05, c2 = 0.02 N·s/m, k2 = 30 N/m, L ≈ L0=0.03 m, P = 0.03 N. 为了突出NTET的减振效果, 设计了线性吸能器(linear targeted energy transfer, LTET)减振实验. LTET的参数为: β = 0.05, c2 = 0.02 N·s/m, k2 = 30 N/m, L ≈ L0 = 0.02 m, P = 0.03 N. 通过图3(c)可以看出, 当不安装吸能器时(黑实线和圆圈), 圆柱体振动幅值在共振流速区域有较大的幅值. 安装了NTET后(红点线和方形), 圆柱体发生涡激振动的幅值有大幅减小, 且锁频区域明显变窄, 说明有显著的振动控制效果. 虽然安装 LTET(蓝虚线和菱形)有一定的减振效果, 但不明显. 理论预测和实验结果对比较好, 通过设计NTET结构可有效抑制圆柱体涡激振动行为, 且减振效果要明显优于LTET.
![]()
图 3 (a) 实验模型(正视图); (b) 实验模型(侧视图)和(c) 理论预测与实验结果对比Figure 3. (a) Experimental model (front view). (b) Experimental model (side view). (c) Comparison between theoretical predictions and experimental results![]()
3 (a) 实验模型(正视图); (b) 实验模型(侧视图)和(c) 理论预测与实验结果对比 (续)3. (a) Experimental model (front view). (b) Experimental model (side view). (c) Comparison between theoretical predictions and experimental results (continued)2.2 参数分析
下面研究NTET的质量、刚度以及预应力等参数对圆柱体涡激振动控制的影响, 旨在设计出更有效的NTET结构. 应当注意的是, 如Mehmood等[25]所述, 阵风和湍流引起的初始条件可能会对圆柱体涡激振动产生影响, 本文在此不考虑这种影响.
2.2.1 NTET质量对涡激振动控制的影响
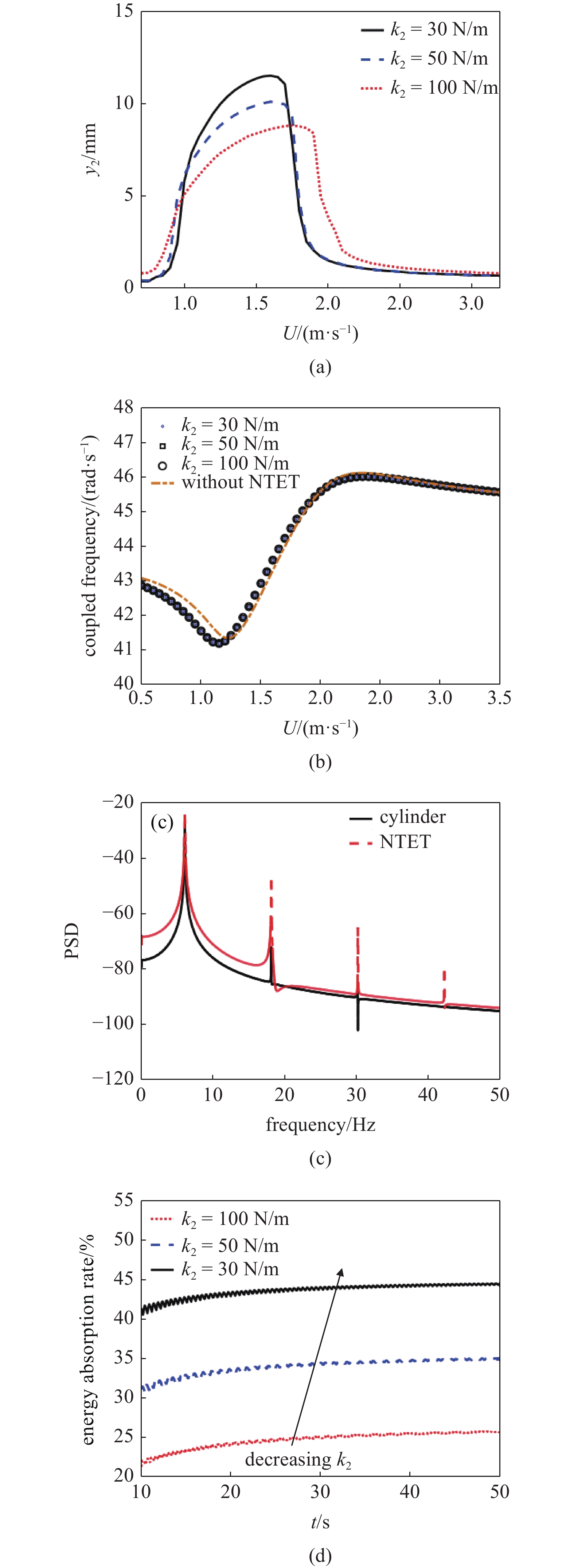
本小节着重讨论NTET质量对涡激振动的影响. 为避免NTET质量对主体结构质量的影响, 保持质量比β较小(β < 0.1), 同时控制β为单一变量. 由式(2)和式(11)可知, 预应力P的取值会影响方程中线性项和非线性项的大小, 从而改变方程的解, 因此本节只讨论无预应力下NTET结构质量对圆柱体涡激振动的影响. 开展变质量比的实验和理论研究, 实验参数如下: m1 = 0.016 kg, D = 0.045 m, c1 = 0.01 N·s/m, k1 = 30 N/m, c2 = 0.02 N·s/m, k2 = 10 N/m, L ≈ L0 = 0.04 m. 图4给出了不同质量比下实验和理论对比的结果图, 对比结果较好. 随着质量比的增大, 圆柱体振幅逐渐减小. 此外, 锁频区域随着质量比增大有减小并向左移动趋势. 说明增大NTET的质量可有效控制圆柱体涡激振动行为.
![]()
图 4 不同质量比下实验结果和理论预测对比图Figure 4. Comparisons between theoretical predictions with experimental results for different values of mass ratio图5(a)给出了不同质量比下NTET的振幅y2随风速变化曲线. 从图中可以看出, 在锁定区域内, NTET的振幅随质量比增大而增大. 从能量传递角度可以看出, 安装NTET后, 主结构圆柱体的能量会部分转移到NTET上, NTET振幅越大, 说明转移能量越多, 吸能效果越好. 因此, 圆柱体振幅也越小. 此外, 耦合频率为耦合系统的线性特征之一, 受控制方程中线性项的影响. 令矩阵
${\boldsymbol{B }}= {[{y_1}\;\; {\dot y_1}\;\; {y_2}\;\; {\dot y_2}\;\; q\;\; \dot q]^{\rm{T}}}$ , 根据控制方程式(11)和式(12)写出矩阵A使得$\dot {\boldsymbol{B}} = {\boldsymbol{AB}}$ , 求出矩阵A的所有特征值后, 能找到一组实部总为负数的复共轭特征值${\lambda _1},{\lambda _2}$ , 这一组特征值的实部的绝对值即为系统的耦合频率值. 锁频区域随着质量比的增大有向左迁移趋势, 这是因为系统的耦合频率随质量比增大有所减小, 耦合频率随着风速变化出现了先较小后增大的趋势, 如图5(b)所示. 图5(c)给出了β = 0.05, U = 1.4 m/s时的圆柱体和NTET的功能谱密度, 圆柱体和NTET的振动周期与功能谱曲线中第一个共振峰对应的频率值相同, 这说明圆柱体和NTET的振动频率一致, 它们发生的是单周期响应, 且保持同步行为.![]()
图 5 不同质量比下, (a) NTET振动幅值; (b) 系统的耦合频率; (c) 圆柱体和NTET的功率谱密度和(d) NTET的能量传递效率Figure 5. (a) Vibration amplitude of NTET, (b) the coupled frequency, (c) power spectra density and (d) energy transfer efficiency for different values of the mass ratio为进一步分析质量比对吸能效率的影响, 深入研究了流固耦合控制系统的能量耗散问题[42]. 通过引入变量η = Wout(t)/Win(t)表示能量传递效率, Win(t)表示输入系统的总能量, Wout(t)表示NTET的总能量, 其表达式由以下给出
$$ \begin{gathered} {W_{{\text{out}}}}(t) = \frac{1}{2}{m_2}\dot y_2^2(t) + \frac{1}{2}{k_{2,1}}{[{y_2}(t) - {y_1}(t)]^2} + \cdots + \\ \quad \quad \quad \quad \frac{1}{4}{k_{2,2}}{[{y_2}(t) - {y_1}(t)]^4} + \int_0^t {\frac{1}{2}{c_2}{{[{{\dot y}_2}(t) - {{\dot y}_1}(t)]}^2}} {\rm{d}}t \\ \end{gathered} $$ (14) $$ {W_{{\text{in}}}}(t) = {W_{{\text{out}}}}(t) + \frac{1}{2}{m_1}\dot y_1^2(t) + \frac{1}{2}{k_1}y_1^2(t) + \int_0^t {\frac{1}{2}{c_1}\dot y_1^2(t)} {\rm{d}}t $$ (15) 图5(d)给出了U = 1.4 m/s不同质量比下的能量传递效率随时间变化曲线. 可以看出, 质量比越大, 能量传递效率越高. 当系统振动达到稳态之后, 能量传递效率也保持在稳定水平. 因此, 在预应力P接近于零时, 随着质量比β的增加, 会使得NTET的振幅增大, 能量传递效率提高, 从而圆柱体的振幅减小, 减振效果得到增强.
2.2.2 NTET弹簧刚度对涡激振动控制的影响
接下来着重讨论NTET的弹簧刚度k2对圆柱体涡激振动控制的影响规律. 若弹簧初始状态为拉伸状态, 那么改变弹簧刚度k2会导致预应力P改变. 为了控制弹簧刚度k2为单一变量, 使弹簧初始状态长度L接近其原长L0, 此时预应力P ≈ 0. 开展变刚度的实验研究, 实验参数如下: m1 = 0.016 kg, D = 0.045 m, c1 = 0.01 N·s/m, k1 = 30 N/m, c2 = 0.02 N·s/m, L ≈ L0 = 0.03 m, β = 0.05. k2分别取30 N/m, 50 N/m和100 N/m. 实验和理论对比结果如图6所示, 可以看出, 在不同弹簧刚度下圆柱体振动随流速变化表现出明显的共振响应, 该共振响应流速区域随刚度增大没有发生明显变化. 此外, 随着刚度k2的增大, 圆柱体振动幅值在增大, 这说明NTET减振效果在减小.
![]()
图 6 不同弹簧刚度下实验结果和理论预测对比图Figure 6. Comparisons between theoretical predictions and experimental results图7(a)给出了不同刚度k2下NTET的振幅y2随流速变化曲线, 可以看出, 锁频区域没有发生明显改变, 在1 m/s ~ 2 m/s风速范围内. 这是因为刚度k2的变化只影响控制方程非线性项系数, 对耦合频率没有影响, 如图7(b)所示. 此外, 随着刚度k2的增加, NTET的振幅y2明显降低, 说明减振效果在减弱. 从能量耗散角度上看, 弹簧刚度k2越大, 弹簧发生形变越困难, 振子m2振动响应越小, 传递到NTET上的能量也越小. 若假设刚度k2→∞, 弹簧形变几乎为零, 此时NTET可视为集中质量跟随主结构圆柱体一起振动, 从而失去了减振效果. 图7(c)给出了k2 = 50 N/m, U = 1.6 m/s时圆柱体和NTET的功能谱密度. 同样地, 容易发现圆柱体与NTET的振幅频率一致, 且保持同步行为. 它们的振动频率与第一个峰值对应的频率相同, 说明发生的是极限环振动. 图7(d)给出了刚度k2对能量传递效率的影响规律, 当刚度增大时, 能量传递效率显著下降. 当k2 > 30 N/m时, 振动达到稳态之后, 传递效率已经跌至50%以下. 因此, 在预应力P接近于零时, 随着NTET弹簧刚度k2的增大, NTET的振幅减小, 能量传递效率降低, 从而圆柱体的振幅增大, 减振效果变弱.
![]()
图 7 不同弹簧刚度下, (a) NTET振动幅值; (b) 系统的耦合频率; (c) 圆柱体和NTET的功率谱密度和(d) NTET的能量传递效率Figure 7. (a) Vibration amplitude of NTET, (b) the coupled frequency, (c) power spectra density and (d) energy transfer efficiency of NTET for different values of k22.2.3 弹簧预应力对涡激振动控制的影响
根据P = k2(L−L0), 得知预应力P的大小与NTET弹簧刚度k2及其初始状态伸长量∆L = L−L0有关, 且预应力P随着∆L的增大而增大. 为控制单一变量, 本节针对相同弹簧刚度k2, 不同初始伸长量∆L的情况研究NTET预应力对圆柱体涡激振动的影响. 也就是说, 通过调节弹簧初始伸长量来改变NTET的预应力大小. 物理参数如下: m1 = 0.016 kg, D = 0.045 m, c1 = 0.01 N·s/m, k1 = 30 N/m, β = 0.05, L0 = 0.03 m, k2 = 10 N/m, c2 = 0.02 N·s/m.
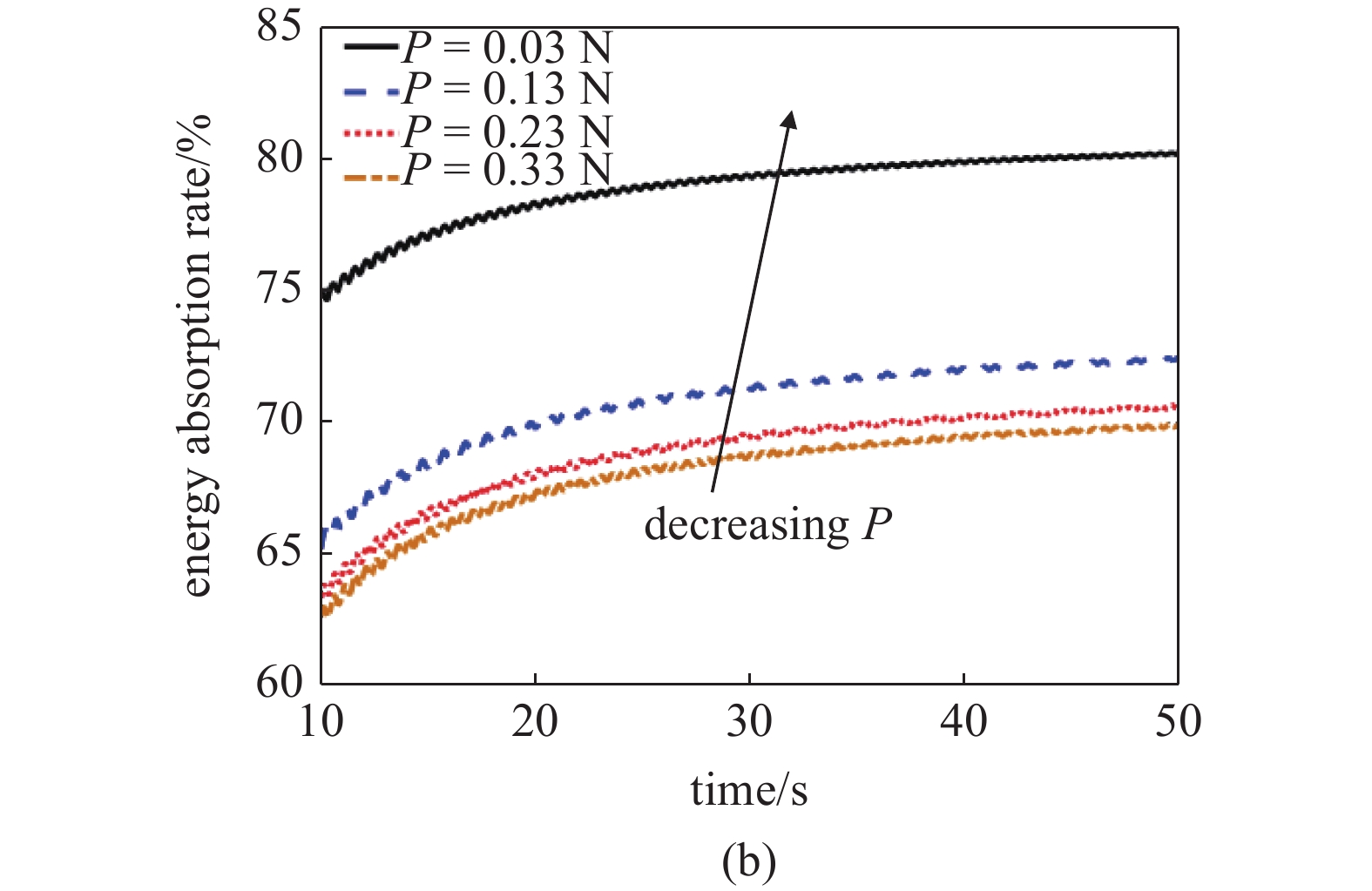
图8(a)给出了不同预应力下圆柱体振动幅值随流速变化曲线, 可以看出随着预应力的增大, 圆柱体振幅在锁频区域逐渐增大, 说明减振效果在降低. 由式(2)可知, 当∆L增大时, 预应力增大, NTET中的非线性刚度系数k2,2在减小, 因此减振性能变弱. 图8(b)给出了不同预应力下NTET的能量传递效率曲线. 随着预应力增大, 能量传递效率在逐渐降低. 当预应力P从0.23 N继续增大到0.33 N时, 圆柱体振幅几乎不再增大, NTET能量传递效率的下降速度也在变缓, 说明减振效果不再显著减弱.
![]()
8 不同预应力P下, (a) 圆柱体振动幅值和(b) NTET的能量传递效率8. (a) Vibration amplitude of the cylinder and (b) energy transfer efficiency of NTET for different values of P3. 结论
本文提出了一种非线性吸能器的涡激振动控制方法, 首先基于能量法建立了非线性吸能器与圆柱体涡激振动耦合的动力学理论模型; 然后通过设计实验装置, 研究了非线性吸能器对涡激振动的控制效果, 与理论预测进行了对比, 验证了理论模型的有效性; 最后通过参数分析, 研究了非线性吸能器各物理参数对圆柱体涡激振动控制的影响规律, 揭示了非线性吸能器的控制机理, 得到如下重要结论.
(1)理论预测和实验结果显示, 非线性吸能器对涡激振动的减振降幅效果要明显优于线性吸能器.
(2)在无预应力或低预应力条件下, 非线性吸能器的质量越大、弹簧刚度越小, 则能量传递效率越高, 减振效果越好.
(3)在有预应力条件下, 非线性吸能器弹簧预应力越小, 导致线性刚度越小、非线性刚度越大, 从而增大能量吸收效率, 提高减振性能.
-
![]()
图 1 (a)涡激振动非线性控制模型示意图; (b)非线性吸能器示意图;(c)非线性吸能器控制等效模型示意图和(d)涡激振动线性吸能器模型示意图
Figure 1. (a) Model diagram of the vortex-induced vibrations nonlinear control. (b) Model diagram of the nonlinear targeted energy transfer. (c) Equivalent model diagram of the nonlinear targeted energy transfer. (d) Model diagram of the vortex-induced vibrations linear control
![]()
图 2 NTET结构中非线性力理论预测与实验结果对比
Figure 2. Comparison of the nonlinear force in NTET between theoretical predictions and experimental results.
![]()
图 3 (a) 实验模型(正视图); (b) 实验模型(侧视图)和(c) 理论预测与实验结果对比
Figure 3. (a) Experimental model (front view). (b) Experimental model (side view). (c) Comparison between theoretical predictions and experimental results
![]()
3 (a) 实验模型(正视图); (b) 实验模型(侧视图)和(c) 理论预测与实验结果对比 (续)
3. (a) Experimental model (front view). (b) Experimental model (side view). (c) Comparison between theoretical predictions and experimental results (continued)
![]()
图 4 不同质量比下实验结果和理论预测对比图
Figure 4. Comparisons between theoretical predictions with experimental results for different values of mass ratio
![]()
图 5 不同质量比下, (a) NTET振动幅值; (b) 系统的耦合频率; (c) 圆柱体和NTET的功率谱密度和(d) NTET的能量传递效率
Figure 5. (a) Vibration amplitude of NTET, (b) the coupled frequency, (c) power spectra density and (d) energy transfer efficiency for different values of the mass ratio
![]()
图 6 不同弹簧刚度下实验结果和理论预测对比图
Figure 6. Comparisons between theoretical predictions and experimental results
![]()
图 7 不同弹簧刚度下, (a) NTET振动幅值; (b) 系统的耦合频率; (c) 圆柱体和NTET的功率谱密度和(d) NTET的能量传递效率
Figure 7. (a) Vibration amplitude of NTET, (b) the coupled frequency, (c) power spectra density and (d) energy transfer efficiency of NTET for different values of k2
-
[1] Lee YS, Vakakis AF, Bergman LA, et al. Passive non-linear targeted energy transfer and its applications to vibration absorption: A review. Journal of Multi-body Dynamics, 2008, 222(2): 77-134 doi: 10.1243/14644193JMBD118
[2] Gourdon E, Alexander NA, Taylor CA, et al. Nonlinear energy pumping under transient forcing with strongly nonlinear coupling: Theoretical and experimental results. Journal of Sound and Vibration, 2007, 300(3-5): 522-551 doi: 10.1016/j.jsv.2006.06.074
[3] Dai HL, Abdelkefi A, Wang L. Vortex-induced vibrations mitigation through a nonlinear energy sink. Communications in Nonlinear Science and Numerical Simulation, 2017, 42: 22-36 doi: 10.1016/j.cnsns.2016.05.014
[4] Vakakis AF, Gendelman OV, Bergman LA, et al. Nonlinear targeted energy transfer: state of the art and new perspectives. Nonlinear Dynamics, 2022, 108(2): 711-741 doi: 10.1007/s11071-022-07216-w
[5] Saeed AS, Al-Shudeifat MA, Vakakis AF, et al. Rotary-impact nonlinear energy sink for shock mitigation: analytical and numerical investigations. Archive of Applied Mechanics, 2020, 90(3): 495-521 doi: 10.1007/s00419-019-01622-0
[6] Zhang Z, Zhang YW, Ding H. Vibration control combining nonlinear isolation and nonlinear absorption. Nonlinear Dynamics, 2020, 100(3): 2121-2139 doi: 10.1007/s11071-020-05606-6
[7] 陆泽琦, 陈立群. 非线性被动隔振的若干进展. 力学学报, 2017, 49(3): 550-564 (Lu Zeqi, Chen Liqun. Some recent progresses in nonlinear passive isolations of vibrations. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 550-564 (in Chinese) doi: 10.6052/0459-1879-17-064 [8] Ding H, Chen LQ. Designs, analysis, and applications of nonlinear energy sinks. Nonlinear Dynamics, 2020, 100(4): 3061-3107 doi: 10.1007/s11071-020-05724-1
[9] Lee YS, Kerschen G, Vakakis AF, et al. Complicated dynamics of a linear oscillator with a light, essentially nonlinear attachment. Physica D: Nonlinear Phenomena, 2005, 204(1-2): 41-69 doi: 10.1016/j.physd.2005.03.014
[10] Kerschen G, Lee YS, Vakakis AF, et al. Irreversible passive energy transfer in coupled oscillators with essential nonlinearity. SIAM Journal on Applied Mathematics, 2005, 66(2): 648-679 doi: 10.1137/040613706
[11] Georgiades F, Vakakis AF. Dynamics of a linear beam with an attached local nonlinear energy sink. Communications in Nonlinear Science and Numerical Simulation, 2007, 12(5): 643-651 doi: 10.1016/j.cnsns.2005.07.003
[12] Mao XY, Ding H, Chen LQ. Nonlinear torsional vibration absorber for flexible structures. Journal of Applied Mechanics, 2019, 86(2): 021006
[13] Jiang X, McFarland DM, Bergman LA, et al. Steady state passive nonlinear energy pumping in coupled oscillators: Theoretical and experimental results. Nonlinear Dynamics, 2003, 33(1): 87-102 doi: 10.1023/A:1025599211712
[14] Hubbard SA, McFarland DM, Bergman LA, et al. Targeted energy transfer between a model flexible wing and nonlinear energy sink. Journal of Aircraft, 2010, 47(6): 1918-1931 doi: 10.2514/1.C001012
[15] Andersen D, Starosvetsky Y, Vakakis A, et al. Dynamic instabilities in coupled oscillators induced by geometrically nonlinear damping. Nonlinear Dynamics, 2011, 67(1): 807-827
[16] Dai HL, Abdelkefi A, Wang L. Modeling and nonlinear dynamics of fluid-conveying risers under hybrid excitations. International Journal of Engineering Science, 2014, 81: 1-14 doi: 10.1016/j.ijengsci.2014.03.009
[17] Dai HL, Wang L, Ni Q. Dynamics of a fluid-conveying pipe composed of two different materials. International Journal of Engineering Science, 2013, 73: 67-76 doi: 10.1016/j.ijengsci.2013.08.008
[18] Dai HL, Wang L, Qian Q, et al. Vortex-induced vibrations of pipes conveying fluid in the subcritical and supercritical regimes. Journal of Fluids and Structures, 2013, 39: 322-334 doi: 10.1016/j.jfluidstructs.2013.02.015
[19] Dai HL, Wang L, Qian Q, et al. Vortex-induced vibrations of pipes conveying pulsating fluid. Ocean Engineering, 2014, 77: 12-22 doi: 10.1016/j.oceaneng.2013.12.006
[20] Feng Z, Jiang N, Zang F, et al. Nonlinear characteristics analysis of vortex-induced vibration for a three-dimensional flexible tube. Communications in Nonlinear Science and Numerical Simulation, 2016, 34: 1-11 doi: 10.1016/j.cnsns.2015.10.007
[21] Lee YS, Vakakis AF, Bergman LA, et al. Suppression aeroelastic instability using broadband passive targeted energy transfers, Part 1: Theory. AIAA Journal, 2007, 45(3): 693-711 doi: 10.2514/1.24062
[22] Wang L, Liu WB, Dai HL. Aeroelastic galloping response of square prisms: The role of time-delayed feedbacks. International Journal of Engineering Science, 2014, 75: 79-84 doi: 10.1016/j.ijengsci.2013.11.008
[23] Tumkur RKR, Domany E, Gendelman OV, et al. Reduced-order model for laminar vortex-induced vibration of a rigid circular cylinder with an internal nonlinear absorber. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(7): 1916-1930 doi: 10.1016/j.cnsns.2012.11.028
[24] Tumkur RKR, Calderer R, Masud A, et al. Computational study of vortex-induced vibration of a sprung rigid circular cylinder with a strongly nonlinear internal attachment. Journal of Fluids and Structures, 2013, 40: 214-232 doi: 10.1016/j.jfluidstructs.2013.03.008
[25] Mehmood A, Nayfeh AH, Hajj MR. Effects of a non-linear energy sink (NES) on vortex-induced vibrations of a circular cylinder. Nonlinear Dynamics, 2014, 77(3): 667-680 doi: 10.1007/s11071-014-1329-x
[26] Mehmood A, Abdelkefi A, Akhtar I, et al. Linear and nonlinear active feedback controls for vortex-induced vibrations of circular cylinders. Journal of Vibration and Control, 2012, 20(8): 1137-1147
[27] Dai HL, Abdelkefi A, Wang L, et al. Time-delay feedback controller for amplitude reduction in vortex-induced vibrations. Nonlinear Dynamics, 2014, 80(1-2): 59-70
[28] Dai HL, Abdelkefi A, Wang L. Usefulness of passive non-linear energy sinks in controlling galloping vibrations. International Journal of Non-Linear Mechanics, 2016, 81: 83-94 doi: 10.1016/j.ijnonlinmec.2016.01.007
[29] 郭梓龙, 王琳, 倪樵等. 接地惯容式减振器对悬臂输流管稳定性和动态响应的影响研究. 力学学报, 2021, 53(6): 1769-1780 (Guo Zilong, Wang Lin, Ni Qiao, et al. Research on the influence of grounded inerter-based absorber on the stability and dynamic response of cantilevered pipe conveying fluid. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(6): 1769-1780 (in Chinese) doi: 10.6052/0459-1879-21-105 [30] 马烨璇, 宋志友, 徐万海. 基于能量传递规律的海洋立管涡激振动抑制研究. 力学学报, 2022, 54(4): 901-911 (Ma Yexuan, Song Zhiyou, Xu Wanhai. Study on vortex-vibration suppression of marine riser based on energy transfer. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(4): 901-911 (in Chinese) doi: 10.6052/0459-1879-21-664 [31] 易浩然, 周坤, 代胡亮等. 含集中质量悬臂输流管的稳定性与模态演化特性研究. 力学学报, 2020, 52(6): 1800-1810 (Yi Haoran, Zhou Kun, Dai Huliang, et al. Study on stability and modal evolution characteristics of the cantilevered fluid-conveying pipe attached with the lumped mass. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1800-1810 (in Chinese) doi: 10.6052/0459-1879-20-280 [32] Chen YY, Qian ZC, Zhao W, et al. A magnetic Bi-stable nonlinear energy sink for structural seismic control. Journal of Sound and Vibration, 2020, 473: 115233 doi: 10.1016/j.jsv.2020.115233
[33] Dekemele K, Van Torre P, Loccufier M. Design, construction and experimental performance of a nonlinear energy sink in mitigating multi-modal vibrations. Journal of Sound and Vibration, 2020, 473: 115243 doi: 10.1016/j.jsv.2020.115243
[34] Koroleva IP, Manevitch LI. Stationary and non-stationary dynamics of discrete square membrane. Communications in Nonlinear Science and Numerical Simulation, 2020, 84: 105174 doi: 10.1016/j.cnsns.2020.105174
[35] Lund A, Dyke SJ, Song W, et al. Identification of an experimental nonlinear energy sink device using the unscented Kalman filter. Mechanical Systems and Signal Processing, 2020, 136: 106512 doi: 10.1016/j.ymssp.2019.106512
[36] Strozzi M, Smirnov VV, Manevitch LI, et al. Nonlinear normal modes, resonances and energy exchange in single-walled carbon nanotubes. International Journal of Non-Linear Mechanics, 2020, 120: 103398 doi: 10.1016/j.ijnonlinmec.2019.103398
[37] Zhou K, Dai HL, Abdelkefi A, et al. Theoretical modeling and nonlinear analysis of piezoelectric energy harvesters with different stoppers. International Journal of Mechanical Sciences, 2020, 166: 105233
[38] Dai HL, Abdelkefi A, Wang L. Piezoelectric energy harvesting from concurrent vortex-induced vibrations and base excitations. Nonlinear Dynamics, 2014, 77(3): 967-981 doi: 10.1007/s11071-014-1355-8
[39] Sun W, Jiang Z, Xu X, et al. Electromechanical coupling modeling and analysis of contact-separation mode triboelectric nanogenerators. International Journal of Non-Linear Mechanics, 2021, 136: 103773 doi: 10.1016/j.ijnonlinmec.2021.103773
[40] Govardhan R, Williamson CHK. Modes of vortex formation and frequency response of a freely vibrating cylinder. Journal of Fluid Mechanics, 2000, 420: 85-130 doi: 10.1017/S0022112000001233
[41] Facchinetti ML, de Langre E, Biolley F. Coupling of structure and wake oscillators in vortex-induced vibrations. Journal of Fluids and Structures, 2004, 19(2): 123-140 doi: 10.1016/j.jfluidstructs.2003.12.004
[42] Zhang YW, Lu YN, Zhang W, et al. Nonlinear energy sink with inerter. Mechanical Systems and Signal Processing, 2019, 125: 52-64 doi: 10.1016/j.ymssp.2018.08.026
-
期刊类型引用(0)
其他类型引用(4)
下载:
计量
- 文章访问数: 962
- HTML全文浏览量: 353
- PDF下载量: 157
- 被引次数: 4
