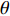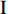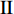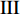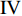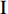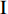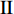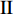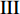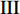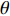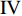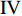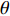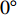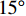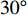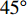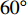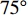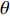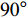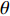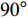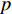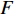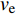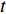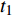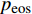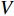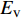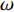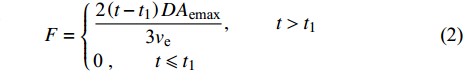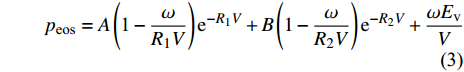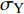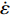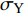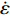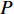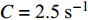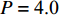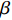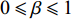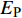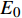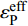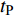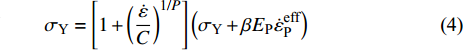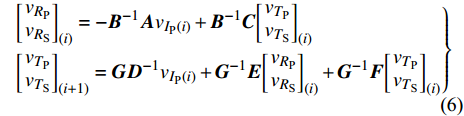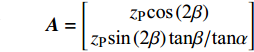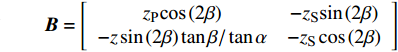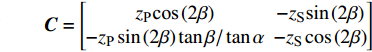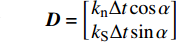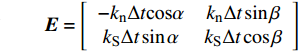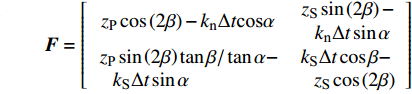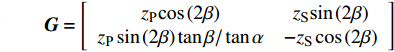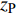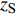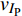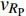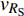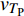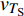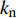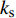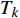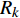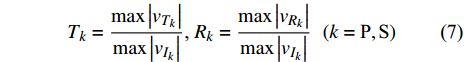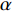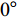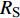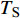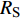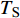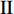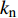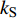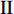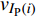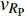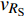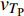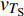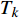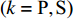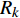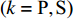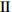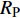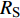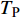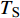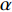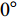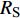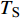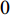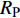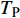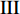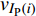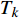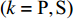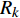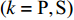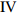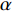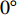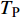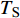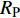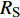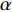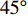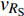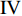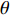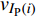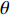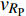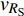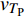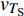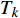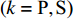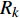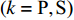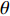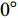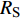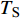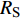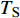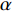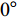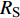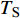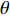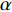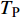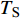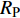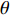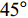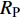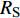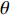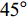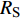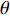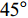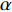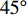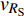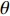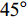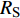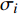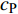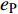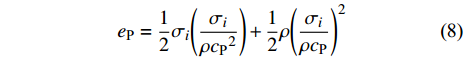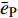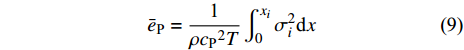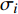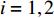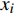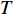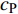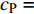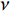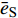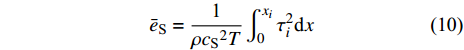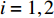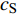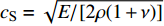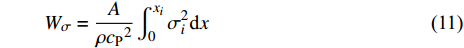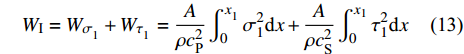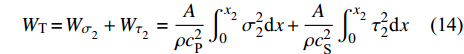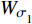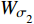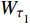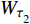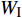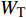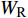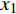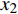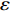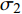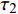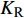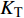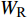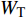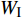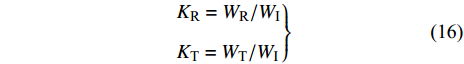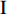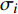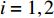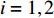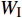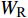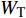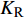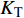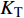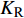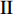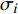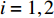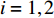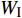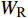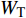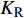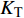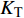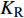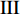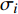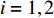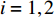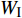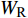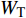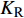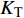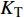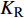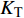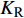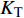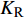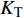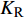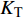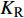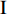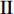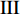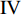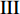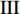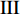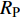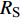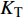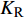NUMERICAL STUDY ON CRACK PROPAGATION AND STRESS WAVE PROPAGATION DURING BLASTING OF JOINTED ROCK MASS
-
摘要: 岩体中存在着大量自然形成的节理, 这些节理导致岩体的力学性质、振动、渗透、能量传递等多种性能发生改变. 爆炸应力波在含节理岩体中的传播与衰减也随着发生改变, 进而影响工程爆破的效果及安全性. 对含节理岩体的爆生裂纹扩展与爆炸应力波传播规律进行研究, 通过建立含节理岩体的爆炸数值模型得到节理两侧岩体的有效应力和振动速度, 并利用应力波的波动理论与能量密度理论计算出节理的透反射系数和透反射能量比. 在此基础上研究节理几何参数(节理填充物厚度D、爆源到节理的法向距离R、爆源到节理的竖向距离H、节理倾角
$ \theta $ )对含节理岩体爆生裂纹扩展的影响以及上述参数与节理的透反射系数和透反射能量比关系. 结果表明当节理位于裂纹区且爆源到节理的竖向距离H与法向距离R之比H/R = 1时, 节理的反射系数及反射能量比处于最大值, 切应力成为此范围内影响节理面损伤的主要因素; 节理近爆侧岩体的破碎区域面积与节理填充物厚度D成正相关; 节理近爆侧岩体的破碎区域面积与爆源到节理的法向距离R和爆源到节理的竖向距离H成负相关; 当节理位于裂纹区时, 节理对岩体的爆破碎岩效果影响最大.Abstract: There are a large number of naturally formed joints in natural rock mass, which lead to changes in the mechanical properties, vibration, permeability, energy transfer and other properties of rock mass. The propagation and attenuation of blast stress waves in the rock mass with joints also change, which affects the effect and safety of engineering blasting. The explosion crack propagation and explosion stress wave propagation law of the jointed rock mass are studied, and the effective stress and vibration velocity of the rock mass on both sides of the joint are obtained by establishing the explosion numerical model of the jointed rock mass. The transmission and reflection coefficient and the transmission and reflection energy ratio of the joint are calculated by using the stress wave wave theory and energy density theory. On this basis, the effects of joint geometric parameters (joint filler thickness D, normal distance R from blast source to joint, vertical distance H from blast source to joint, joint inclination$ \theta $ ) on the expansion of blast cracks at different positions of the joint were studied. And the relationship between the above-mentioned joint geometric parameters and the joint's transmission and reflection coefficient and transmission and reflection energy ratio. The results show that when the joint is located in the crack area and the ratio H/R of the vertical distance H from the blast source to the joint to the normal distance R is equal to 1, the reflection coefficient and reflected energy ratio of the joint are at the maximum value, and shear stress becomes the main factor affecting the damage of joint surface within this range. The fracture area of the rock mass near the explosion side of the joint is positively correlated with the thickness D of the joint filler. The fractured area of the rock mass near the blast side of the joint is negatively correlated with the normal distance R from the blast source to the joint and the vertical distance H from the blast source to the joint. When the joint is located in the crack area, the joint has the greatest impact on the blasting effect of the rock mass. -
引 言
由于天然岩体中存在着大量自然形成的节理、裂纹、层理和断层等构造, 这些构造导致岩体的力学性质、振动、渗透、能量传递等多种性能发生改变[1-3]. 爆炸应力波在这些含节理、裂纹和断层的岩体中的传播与衰减也随着发生改变, 进而影响工程爆破的效果及安全性[4-6]. 因此研究爆炸载荷下含节理岩体的爆生裂纹扩展规律与应力波传播规律, 对提高岩体工程的爆破能量利用效率、破岩效果及安全性具有重要意义[7]. 国内外学者[8-10]对爆炸应力波在含节理岩体的传播规律做了不少研究工作, 通过研究爆炸应力波穿透节理时节理两侧的应力、质点振动速度和能量的变化, 得到不同节理几何参数下含节理岩体的应力波的传播规律, 如Gu等[11]通过应力波的波动方程计算出了节理的透反射系数, 得出了不同节理参数下节理对岩体爆破效果的影响. 鞠杨等[12]通过多组岩石冲击试验, 探讨了爆炸应力波穿透节理时节理两侧的透反射能量比与应力强度变化关系. 柴少波等[13]将爆炸应力波在含交叉节理岩体的传播理论与数值模型进行对比, 进一步探讨了爆炸应力波在含交叉节理岩体的传播规律. 汪书敏等[14]引入Poyting-Thomson模型作为位移不连续条件, 基于时域递归方法推导出应力波通过一组平行黏弹性节理的传播方程, 探究黏弹性节理对应力波在岩体中传播的影响. Li等[15]对节理的透反射系数进行参数分析, 研究了不同节理参数下入射波的波形转换与节理的相互作用关系. Miller[16]利用近似分析方法, 对弹性波在岩体与节理边界处的透射和反射规律进行了研究.
部分学者通过数值模拟方法, 研究节理对岩体爆生裂纹扩展与应力波传播的影响, 如王举等[17]采用离散元软件UDEC研究了不同节理倾角下爆炸应力波在含节理岩体中的传播规律和波型转换规律. 谢冰等[18]通过将有限元软件AUTODYN 2D与离散元软件UDEC相结合的方法, 研究了节理几何特征对预裂爆破的影响. 孙宁新等[19]利用数值模拟方法, 探讨了软弱夹层厚度、位置及角度对爆炸应力波传播的影响. 朱亮等[20]根据白鹤滩水电站现场的柱状节理分布统计资料生成数值模型, 研究了边坡开挖轮廓爆破下含柱状节理岩体的开裂特质. 刘婷婷等[21]通过离散元数值模拟研究了间距不同的平行填充节理中的爆炸应力波传播规律. 璩世杰等[22]运用LS-DYNA研究了不同节理倾角下节理对预裂爆破效果的影响. 魏晨慧等[23]针对含节理岩体爆破过程开展数值模拟, 研究地应力条件和节理角度对爆生裂纹萌生、扩展过程的影响机理.
在前人研究的基础上, 继续探索含节理岩体爆破过程中裂纹扩展和爆炸应力波传播规律. 本文利用有限元软件构建含节理岩体的爆炸模型, 提取节理不同位置处的振动速度和有效应力, 通过应力波波动理论与能量密度理论得出节理的透反射系数和透反射能量比, 定量分析节理几何参数与节理的透反射系数、透反射能量比和位移差之间的关系, 研究不同节理几何参数下含节理岩体的爆生裂纹扩展规律与应力波传播规律.
1. 数值模型的建立
1.1 模型参数设定
爆炸应力波穿透岩体中的节理时, 会在节理面发生复杂的透射与反射, 当入射波的夹角
$ \Delta \alpha $ 足够小时, 其波阵面可看作平面, 即此情况下入射柱面波等同于平面波, 如图1所示,$ {I_{\text{P}}} $ 为爆炸产生的入射P波,$ {R_{\text{P}}} $ 和$ {R_{\text{S}}} $ 分别为入射P波接触节理近爆面产生的反射P波和反射S波,$ {T_{\text{P}}} $ 和$ {T_{\text{S}}} $ 分别为入射P波穿透节理背爆面产生的透射P波和透射S波,$ \alpha $ 为入射P波与节理法线的夹角,$ {\alpha _{\text{1}}} $ 为透射P波与节理法线的夹角,$ \beta $ 为透射S波与节理法线的夹角, “−”和“+”分别代表节理的近爆侧与背爆侧.节理的几何特征包括节理的条数、节理长度、节理倾角、节理填充物厚度和爆源到节理法向距离等, 本文以节理填充物厚度D、爆源到节理的法向距离R、爆源到节理的竖向距离H和节理倾角
$ \theta $ 作为研究对象, 利用ANSYS/LS-DYNA有限元软件构建了研究上述四个节理几何特征的含节理岩体爆炸模型, 分别命名为模型$ {\rm I} $ 、模型$ {\rm I}{\rm I} $ 、模型$ {\rm I}{\rm I}{\rm I} $ 和模型$ {\rm I}{\text{V}} $ . 为研究节理填充物厚度D对爆炸应力波传播和爆生裂纹扩展的影响而构建模型$ {\rm I} $ , 模型$ {\rm I} $ 采用单孔爆破, 装药半径r = 0.1 m, 模型尺寸为22r × 4r. 根据张奇[24]对应力波在节理处传递过程的研究, 当节理填充物厚度远小于爆炸应力波波长时, 应力波穿透节理不受节理填充物厚度D影响, 选取的节理填充物厚度D应该大于应力波波长, 因此节理填充物厚度D分别取0.1r, 0.2r, 0.3r, 0.4r, 0.5r, 0.6r, 0.7r和0.8r. 为研究爆源到节理法向距离R对爆炸应力波传播和爆生裂纹扩展的影响而构建模型$ {\rm I}{\rm I} $ , 模型$ {\rm I}{\rm I} $ 采用单孔爆破, 装药半径r = 0.1 m, 模型尺寸为22r × 4r. 冷振东等[25]对爆炸作用分区的研究指出, 粉碎区半径ra通常为1.2 ~ 5倍装药半径, 裂纹区半径rb通常为8 ~ 15倍装药半径, 根据爆炸作用分区范围取爆源到节理法向距离R分别为4r, 6r, 8r, 10r, 12r, 14r和16r. 为研究爆源到节理竖向距离H对爆炸应力波传播和爆生裂纹扩展的影响而构建模型$ {\rm I}{\rm I}{\rm I} $ , 模型$ {\rm I}{\rm I}{\rm I} $ 采用单孔爆破, 装药半径r = 0.1 m, 模型尺寸为40r × 40r, 取爆源到节理竖向距离H分别为2r, 4r, 6r, 8r, 10r, 12r, 14r, 16r, 18r, 20r. 为研究爆源到节理倾角$ \theta $ 对爆炸应力波传播和爆生裂纹扩展的影响而构建模型$ {\rm I}{\text{V}} $ , 模型$ {\rm I}{\text{V}} $ 采用单孔爆破, 装药半径r = 0.1 m, 模型尺寸为40r × 40r. 选取节理倾角$ \theta $ 分别为${0^\circ }$ ,${15^\circ }$ ,${30^\circ }$ ,${45^\circ }$ ,${60^\circ }$ 和${75^\circ }$ , 当节理倾角$ \theta $ 为${\text{9}}{{\text{0}}^\circ }$ 时节理贯穿炮孔, 因此不选取节理倾角$ \theta $ 为${\text{9}}{{\text{0}}^\circ }$ 的情况.上述模型均采用准三维模型, 即厚度方向只有一个单元格, 四周边界均施加无反射边界条件, 节理和岩体为共节点接触, 具体模型信息如表1 ~ 表4所示.
表 1 模型$ {\rm I} $ 的信息表Table 1. Information of model$ {\rm I} $ Parameter Explosion model Monitoring unit location D R 4r 
1.2 状态方程设定
炸药为2号岩石乳化炸药, 采用*MAT_HIGH_EXPLOSION_BURN关键字定义, 任意时刻爆源内压力采用JWL状态方程定义[26], 如式(1) ~ 式(3)所示, 其中
$ p $ 为爆炸压力, Pa;$ F $ 为炸药化学能释放率;$ D $ 为炸药爆速, m/s;$ {A_{{\text{emax}}}} $ 为炸药最大横截面积, m2;$ {v_{\rm{e}}} $ 为炸药最大体积, m3;$ t $ 和$ {t_1} $ 分别为当前时间和炸药起爆时间, s;$ {p_{{\rm{eos}}}} $ 为炸药的爆轰压力, Pa;$ V $ 为相对体积;$ {E_{\text{v}}} $ 为内能参数, Pa; A, B,$ \omega $ , R1, R2均为常数$$ p = F{p_{{\rm{eos}}}} $$ (1) $$ F = \left\{ \begin{gathered} \frac{{2\left( {t - {t_1}} \right)D{A_{{\text{emax}}}}}}{{{\text{3}}{v_{\text{e}}}}},{\text{ }}\qquad t \gt {t_1} \\ {\text{0 }},\qquad t \leqslant {t_1} \\ \end{gathered} \right. $$ (2) $$ {p_{{\text{eos}}}} = A\left( {{\text{1}} - \frac{\omega }{{{R_1}V}}} \right){{\rm{e}}^{ - {R_1}V}} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){{\rm{e}}^{ - {R_2}V}} + \frac{{\omega {E_{\text{v}}}}}{V} $$ (3) 岩体为砂质岩, 节理填充介质为碳质板岩, 皆采用*MAT_PLASTIC_KINEMATIC关键字定义, 岩体屈服应力
$ {\sigma _{\text{Y}}} $ 与应变率$ \dot \varepsilon $ 的关系如式(4) ~ 式(5)所示[27], 式中$ {\sigma _{\text{Y}}} $ 为初始屈服应力, Pa;$ \dot \varepsilon $ 为应变率, s−1;$ C $ 和$ P $ 为应变率参数, 对沙质岩取$ C = {\text{2}}{\text{.5}}\;{{\text{s}}^{ - {\text{1}}}} $ 和$ P = {\text{4}}{\text{.0}} $ ;$ \beta $ 为硬化参数$ {\text{0}} \leqslant \beta \leqslant {\text{1}} $ ;$ {E_{\text{P}}} $ 为塑性硬化模量, Pa;$ {E_0} $ 为弹性模量, Pa;$ \varepsilon _{\text{P}}^{{\text{eff}}} $ 为岩体有效塑性应变, m;$ {t_{\text{P}}} $ 为发生塑性变形应变累计时间, s; 岩体和节理填充物的爆生裂纹扩展采用*MAT_ADD_EROSION失效关键字定义, 由于岩体和节理填充物的最大抗压强度和最大抗拉强度不同, 两者的失效关键字参数设定不相同. 其中炸药、岩体和节理的强度参数与变形参数分别如表5 ~ 表7所示[19]$$ {\sigma _{\text{Y}}} = \left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{C}} \right)}^{{\text{1/}}P}}} \right]\left( {{\sigma _{\text{Y}}} + \beta {E_{\text{P}}}\dot \varepsilon _{\text{P}}^{{\text{eff}}}} \right) $$ (4) $$ \dot \varepsilon _{\text{P}}^{{\text{eff}}} = \int_{\text{0}}^{{t_{\text{P}}}} {{\text{d}}\varepsilon _{\text{P}}^{{\text{eff}}}} $$ (5) Material $ \rho /\left( {{\text{g}} \cdot {\text{c}}{{\text{m}}^{ - 3}}} \right) $ $ A/{\text{GPa}} $ $ B/{\text{GPa}} $ $ {R_1} $ $ {R_2} $ $ \omega $ $ {E_0}/{\text{GPa}} $ $ V/{\text{c}}{{\text{m}}^3} $ Explosive 1.78 214 18.2 4.1 1 0.35 4.19 1 Material $ \rho /\left( {{\text{g}} \cdot {\text{c}}{{\text{m}}^{ - 3}}} \right) $ $ {E_0}/{\text{GPa}} $ $ \mu $ $ \sigma /{\text{GPa}} $ $ {E_{\tan }} $ $ \beta $ C P Rock 2.73 58 0.228 0.5 0.02 0.5 2.63 3.96 Material $ \rho /\left( {{\text{g}} \cdot {\text{c}}{{\text{m}}^{ - 3}}} \right) $ ${E_0}/{\text{GPa} }$ $ \mu $ $\sigma /{\text{GPa} }$ $ {E_{\tan }} $ $ \beta $ Joints 2.20 28 0.241 0.25 0.025 0.5 2. 爆炸应力波在含线弹性节理岩体的传播理论
2.1 在线弹性节理中爆炸应力波的速度传播
根据文献[15]的时域递归方法得到了波入射线弹性节理后透反射波的表达式为
$$ \left. \begin{gathered} {\left[ \begin{gathered} {v_{{R_{\text{P}}}}} \\ {v_{{R_{\text{S}}}}} \\ \end{gathered} \right]_{\left( i \right)}} = - {{\boldsymbol{B}}^{ - 1}}{\boldsymbol{A}}{v_{{I_{\text{P}}}\left( i \right)}} + {{\boldsymbol{B}}^{ - 1}}{\boldsymbol{C}}{\left[ \begin{gathered} {v_{{T_{\text{P}}}}} \\ {v_{{T_{\text{S}}}}} \\ \end{gathered} \right]_{\left( i \right)}} \\ {\left[ \begin{gathered} {v_{{T_{\text{P}}}}} \\ {v_{{T_{\text{S}}}}} \\ \end{gathered} \right]_{\left( {i + 1} \right)}} = {\boldsymbol{G}}{{\boldsymbol{D}}^{ - 1}}{v_{{I_{\text{P}}}\left( i \right)}} + {{\boldsymbol{G}}^{ - 1}}{\boldsymbol{E}}{\left[ \begin{gathered} {v_{{R_{\text{P}}}}} \\ {v_{{R_{\text{S}}}}} \\ \end{gathered} \right]_{\left( i \right)}} + {{\boldsymbol{G}}^{ - 1}}{\boldsymbol{F}}{\left[ \begin{gathered} {v_{{T_{\text{P}}}}} \\ {v_{{T_{\text{S}}}}} \\ \end{gathered} \right]_{\left( i \right)}} \\ \end{gathered} \right\} $$ (6) 其中
$$ {\boldsymbol{A}} = \left[ \begin{gathered} {{{z}}_{\text{P}}}{\text{cos}}\left( {{\text{2}}\beta } \right) \\ {{{z}}_{\text{P}}}{\text{sin}}\left( {{\text{2}}\beta } \right){\text{tan}}\beta /{\text{tan}}\alpha \\ \end{gathered} \right]$$ $$ {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{z_{\text{P}}}{\text{cos}}\left( {{\text{2}}\beta } \right)}&{ - {z_{\text{S}}}{\text{sin}}\left( {{\text{2}}\beta } \right)} \\ { - z\sin \left( {2\beta } \right)\tan \beta /\tan \alpha }&{ - {z_{\text{S}}}\cos \left( {{\text{2}}\beta } \right)} \end{array}} \right]$$ $$ {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{z_{\text{P}}}{\text{cos}}\left( {{\text{2}}\beta } \right)}& { - {z_{\text{S}}}{\text{sin}}\left( {{\text{2}}\beta } \right)} \\ { - {z_{\text{P}}}\sin \left( {2\beta } \right)\tan \beta /\tan \alpha }& { - {z_{\text{S}}}\cos \left( {{\text{2}}\beta } \right)} \end{array}} \right]$$ $$ {\boldsymbol{D}} = \left[ \begin{gathered} {k_{\text{n}}}\Delta t\cos \alpha \\ {k_{\text{S}}}\Delta t\sin \alpha \\ \end{gathered} \right]$$ $$ {\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} { - {k_{\text{n}}}\Delta t{\text{cos}}\alpha }&{{k_{\text{n}}}\Delta t\sin \beta } \\ {{k_{\text{S}}}\Delta t\sin \alpha }&{{k_{\text{S}}}\Delta t\cos \beta } \end{array}} \right]$$ $$ {\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {{z_{\text{P}}}\cos \left( {2\beta } \right) - {k_{\text{n}}}\Delta t{\text{cos}}\alpha }&\begin{gathered} {z_{\text{S}}}\sin \left( {2\beta } \right)- \\ \;\;\; {k_{\text{n}}}\Delta t\sin \alpha \\ \end{gathered} \\ \begin{gathered} {z_{\text{P}}}\sin \left( {2\beta } \right)\tan \beta /\tan \alpha - \\ \;\;\; {k_{\text{S}}}\Delta t\sin \alpha \\ \end{gathered} &\begin{gathered} {k_{\text{S}}}\Delta t\cos \beta - \\ \;\;\; {z_{\text{S}}}\cos \left( {2\beta } \right) \\ \end{gathered} \end{array}} \right]$$ $$ {\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {{z_{\text{P}}}{\text{cos}}\left( {{\text{2}}\beta } \right)}&{{z_{\text{S}}}{\text{sin}}\left( {{\text{2}}\beta } \right)} \\ {{z_{\text{P}}}\sin \left( {2\beta } \right)\tan \beta /\tan \alpha }&{ - {z_{\text{S}}}\cos \left( {{\text{2}}\beta } \right)} \end{array}} \right]$$ 式中,
$ {z_{\text{P}}} $ 为纵波的波阻抗;$ {z_{\text{S}}} $ 为横波的波阻抗;$ {v_{{I_{\text{P}}}}} $ 为P波入射节理近爆面引起的质点振动速度, m/s;$ {v_{{R_{\text{P}}}}} $ 为P波反射出节理近爆面引起的质点振动速度, m/s;$ {v_{{R_{\text{S}}}}} $ 为S波反射出节理近爆面引起的质点振动速度, m/s;$ {v_{{T_{\text{P}}}}} $ 为P波透射出节理背爆面引起的质点振动速度, m/s;$ {v_{{T_{\text{S}}}}} $ 为S波透射出节理背爆面引起的质点振动速度, m/s;$ {k_{\text{n}}} $ 为节理的法向刚度, Pa/m;$ {k_{\text{s}}} $ 为节理的切向刚度, Pa/m.相应的透射系数
$ {T_k} $ 与反射系数$ {R_k} $ 可以由下式算得$$ {T_k} = \frac{{\max \left| {{v_{{T_k}}}} \right|}}{{\max \left| {{v_{{I_k}}}} \right|}} \text{, } {R_k} = \frac{{\max \left| {{v_{{R_k}}}} \right|}}{{\max \left| {{v_{{I_k}}}} \right|}} \;\; \left( {k = {\text{P}},{\text{S}}} \right) $$ (7) 由于爆炸应力波射入监测单元M1时, 爆炸应力波入射角
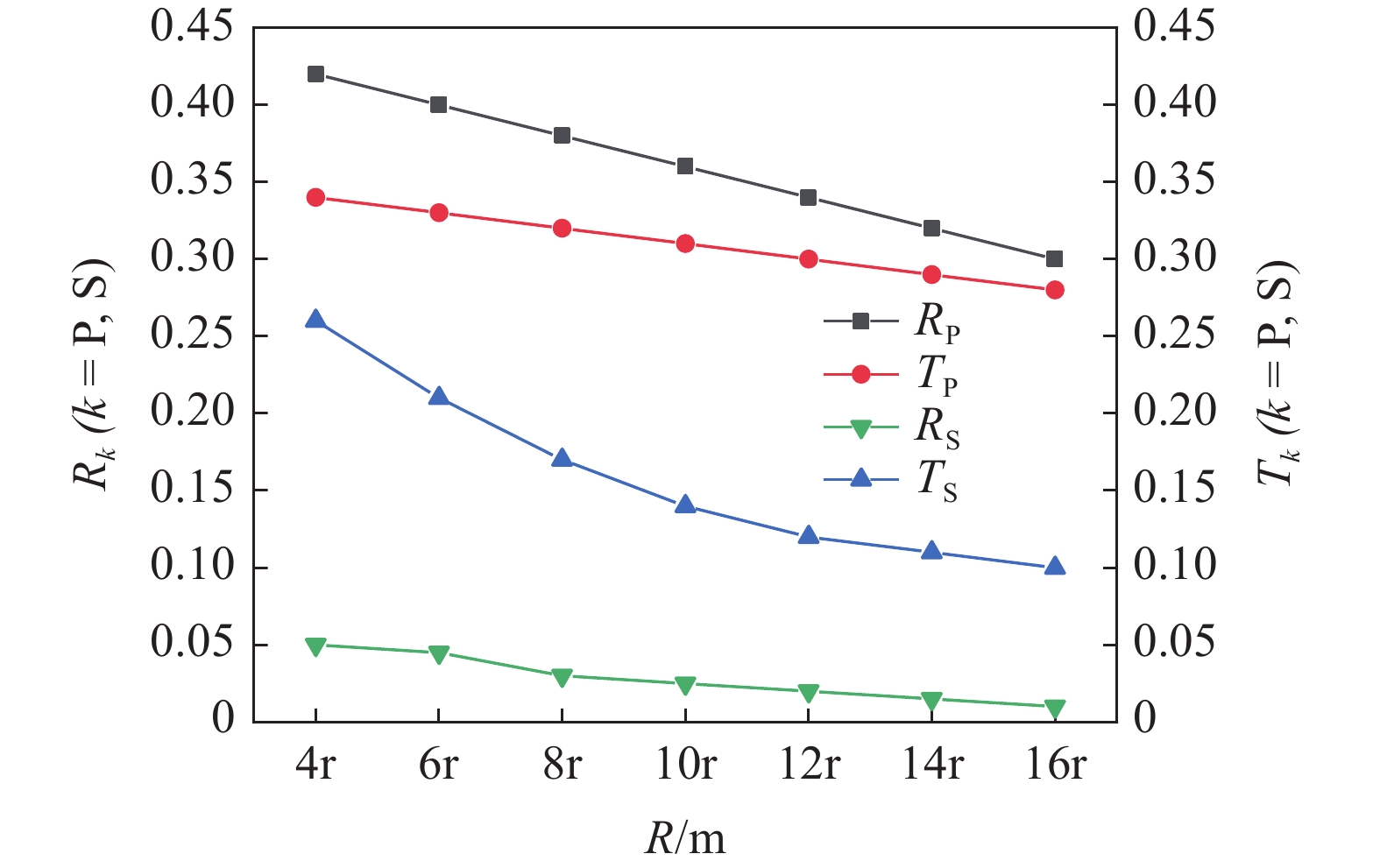
$ \alpha $ 为$ {{\text{0}}^ \circ } $ , 此时爆炸应力波在节理处不产生反射S波和透射S波, 因此反射系数$ {R_{\text{S}}} $ 和透射系数$ {T_{\text{S}}} $ 皆为0. 为方便研究反射系数$ {R_{\text{S}}} $ 和透射系数$ {T_{\text{S}}} $ 与爆源到节理的法向距离R的关系, 从模型$ {\rm I}{\rm I} $ 选取监测单元N1作为研究对象, 如表2所示. 取节理的法向刚度$ {k_{\text{n}}} $ 和切向刚度$ {k_{\text{S}}} $ 分别为2.9 GPa/m, 1.1 GPa/m, 从模型$ {\rm I}{\rm I} $ 的结果文件中提取当爆源到节理的法向距离R不同的情况下近爆侧监测单元N1的振动速度$ {v_{{I_{\text{P}}}\left( i \right)}} $ 并代入到式(6), 通过迭代计算得到当爆源节理填充物厚度D = 0.2r时, 爆源到节理的法向距离R不同的情况下监测单元N1的$ {v_{{R_{\text{P}}}}} $ ,$ {v_{{R_{\text{S}}}}} $ ,$ {v_{{T_{\text{P}}}}} $ 和$ {v_{{T_{\text{S}}}}} $ . 并将上述的计算结果代入式(7)计算得到相应的透射系数$ {T_k} $ $ (k = {\text{P}},{\text{S)}} $ 与反射系数$ {R_k} $ $ (k = {\text{P}},{\text{S)}} $ , 如图2所示.表 2 模型$ {\rm I}{\rm I} $ 的信息表Table 2. Information of model$ {\rm I}{\rm I} $ Parameter Explosion model Monitoring unit location R D 0.2r 
![]()
图 2 不同爆源到节理的法向距离R的透反射系数Figure 2. Transmission and reflection coefficients of different normal distances R from blast sources to joints由图2可知, 随着爆源到节理的法向R增大, 爆炸应力波在传播过程中随着距离的增加而发生几何衰减, 因此随着爆源到节理的法向R增大, 反射系数
$ {R_{\text{P}}} $ 和$ {R_{\text{S}}} $ 缓慢减小并逐渐趋于稳定, 透射系数$ {T_{\text{P}}} $ 和$ {T_{\text{S}}} $ 缓慢减小并逐渐趋于稳定. 且随着爆源到节理的法向R增大, 爆炸应力波的入射角$ \alpha $ 逐渐趋近于$ {{\text{0}}^ \circ } $ , 所以反射系数$ {R_{\text{S}}} $ 和透射系数$ {T_{\text{S}}} $ 亦逐渐趋近于$ {\text{0}} $ , 反射系数$ {R_{\text{P}}} $ 和透射系数$ {T_{\text{P}}} $ 则逐渐趋近于同一值. 这与柴少波等[28]研究的波源和节理的法向距离对透反射系数的变化规律一致, 只不过递减的变化速率不同, 其原因是对于岩体属性和节理属性的定义不同所导致的.从模型
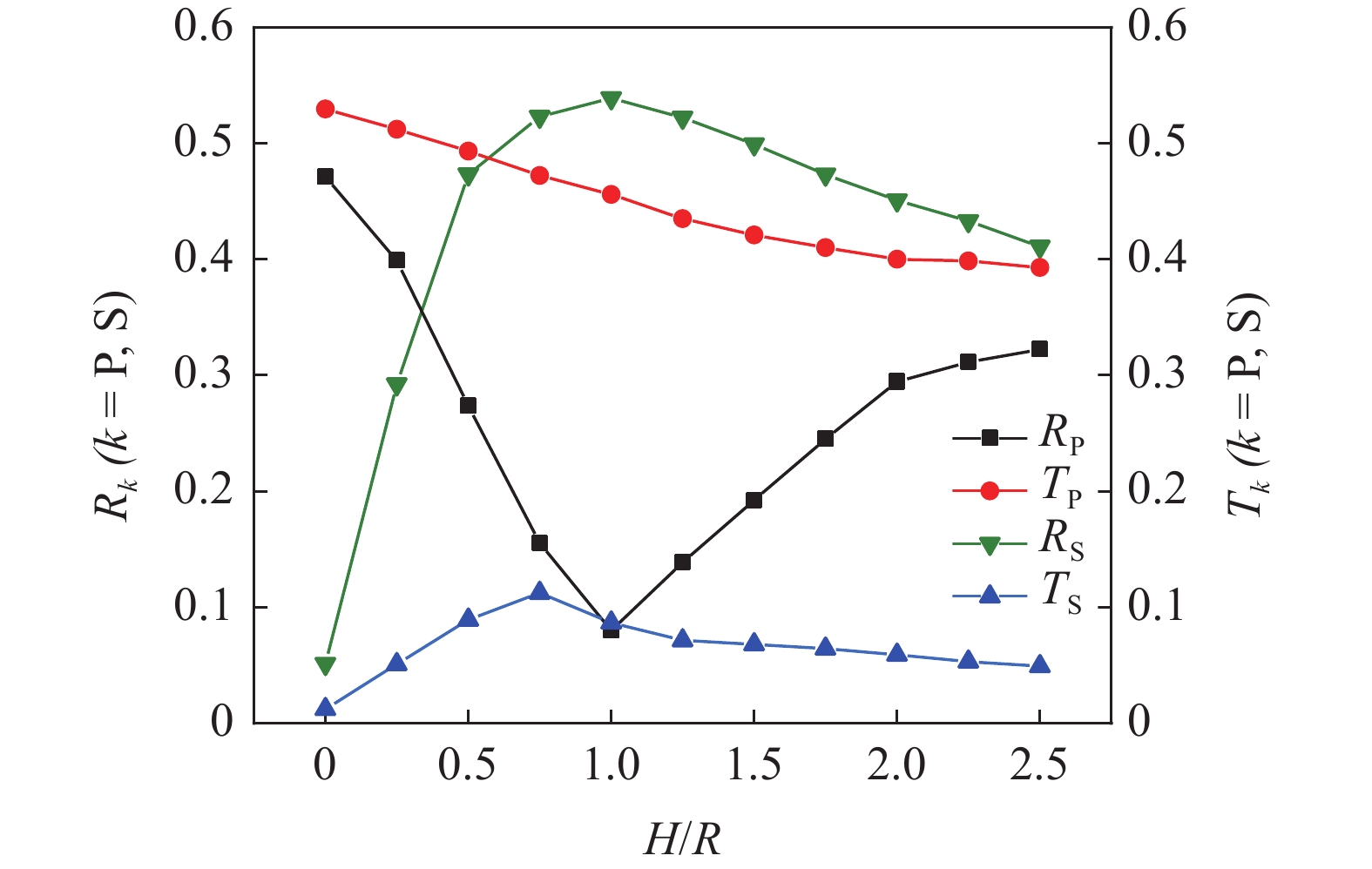
$ {\rm I}{\rm I}{\rm I} $ 中对节理近爆面沿竖向选取11个测点, 每一个测点间隔0.2 m, 并提取节理近爆面测点的振动速度$ {v_{{I_{\text{P}}}\left( i \right)}} $ , 监测单元的位置如表3所示. 取爆源到节理任意一点的竖向距离H与法向距离R之比为H/R, 经式(6) ~ 式(7)计算得到当R = 4r, D = 0.2r时, 节理在爆源与节理竖向上的透射系数$ {T_k} $ $ (k = {\text{P}},{\text{S)}} $ 与反射系数$ {R_k} $ $ (k = {\text{P}},{\text{S)}} $ , 如图3所示.表 3 模型$ {\rm I}{\rm I}{\rm I} $ 的信息表Table 3. Information of model$ {\rm I}{\rm I}{\rm I} $ Parameter Explosion model Monitoring unit location D 0.2r 0.4r 0.8r R 4r 
8r 16r 表 4 模型$ {\rm I}{\text{V}} $ 的信息表Table 4. Information of model$ {\rm I}{\text{V}} $ Parameter Explosion model Monitoring unit location $ \theta $ R 8r 
当R = 4r时, 此时节理位于压碎区, 随H/R的增大, 爆炸应力波的入射角
$ \alpha $ 由$ {0^ \circ } $ 逐渐增大,$ {T_{\text{P}}} $ 缓慢减小后趋于平缓,$ {T_{\text{S}}} $ 缓慢增大后缓慢减小.$ {R_{\text{P}}} $ 迅速减小并在H/R = 1时达到最小值后迅速增大,$ {R_{\text{S}}} $ 则先迅速增大并在H/R = 1时达到最大值后缓慢减小, 在H/R = 1时对应的入射角$ \alpha $ 为$ {45^ \circ } $ , 此时$ {v_{{R_{\text{S}}}}} $ 为最大值, 而剪切应力直接决定由反射波引起的质点速度, 因此在H/R=1时剪切应力对节理面损伤的影响最大.从模型
$ {\rm I}{\text{V}} $ 的结果文件中提取不同节理倾角$ \theta $ 下近爆侧监测单元O1的振动速度$ {v_{{I_{\text{P}}}\left( i \right)}} $ 并代入到式(6), 通过迭代计算得到当爆源节理填充物厚度D = 0.2r和爆源与节理法向距离R为8r时, 不同节理倾角$ \theta $ 下监测单元O1的$ {v_{{R_{\text{P}}}}} $ ,$ {v_{{R_{\text{S}}}}} $ ,$ {v_{{T_{\text{P}}}}} $ 和$ {v_{{T_{\text{S}}}}} $ . 并将上述得到的计算结果代入式(7)计算得到相应的透射系数$ {T_k} $ $ (k = {\text{P}},{\text{S)}} $ 与反射系数$ {R_k} $ $ (k = {\text{P}},{\text{S)}} $ , 如图4所示.![]()
图 4 不同节理倾角θ的透反射系数Figure 4. Transmission and reflection coefficients of different joint inclination angles θ由图4可知, 当节理倾角
$ \theta $ =$ {{\text{0}}^ \circ } $ 时, 反射系数$ {R_{\text{S}}} $ 和透射系数$ {T_{\text{S}}} $ 皆为最小值且$ {R_{\text{S}}} $ =$ {T_{\text{S}}} $ =0, 因为此时爆炸应力波入射角$ \alpha $ 为$ {{\text{0}}^ \circ } $ , 爆炸应力波在节理处不产生反射S波和透射S波, 所以反射系数$ {R_{\text{S}}} $ 和透射系数$ {T_{\text{S}}} $ 皆为0. 随着节理倾角$ \theta $ 逐渐增大, 爆炸应力波射入监测单元O1的入射角度$ \alpha $ 也逐渐增大, 透射系数$ {T_{\text{P}}} $ 和透射系数$ {T_{\text{S}}} $ 缓慢增大, 反射系数$ {R_{\text{P}}} $ 缓慢减小并在节理倾角$ \theta $ =$ {\text{4}}{{\text{5}}^ \circ } $ 时达到最小值,$ {R_{\text{P}}} $ = 0.22, 随后缓慢增大, 反射系数$ {R_{\text{S}}} $ 则先迅速增大并在节理倾角$ \theta $ =$ {\text{4}}{{\text{5}}^ \circ } $ 达到最大值,$ {R_{\text{S}}} $ = 0.42, 随后逐渐减小, 这是因为在节理倾角$ \theta $ =$ {\text{4}}{{\text{5}}^ \circ } $ 时, 对应的入射角$ \alpha $ 为$ {45^ \circ } $ , 此时$ {v_{{R_{\text{S}}}}} $ 为最大值, 而切向应力直接决定由反射波引起的质点速度, 因此在节理倾角$ \theta $ =$ {\text{4}}{{\text{5}}^ \circ } $ 时切向应力对节理面损伤的影响最大. 这与图3中当H/R = 1时反射系数$ {R_{\text{S}}} $ 最大的规律一致.2.2 在线弹性节理中爆炸应力波的能量
在平面内, 设定一强度为
$ {\sigma _i} $ 的平面纵波以$ {c_{\text{P}}} $ 速度沿平面内任意方向传播, 则该波具有的瞬时能量密度$ {e_{\text{P}}} $ 为$$ {e_{\text{P}}} = \frac{1}{2}{\sigma _i} {\left({\frac{{{\sigma _i}}}{{\rho {c_{\text{P}}}^2}}}\right)} + \frac{1}{2}\rho {\left( {\frac{{{\sigma _i}}}{{\rho {c_{\text{P}}}}}} \right)^2} $$ (8) 即纵波的平均能量密度
$ {\bar e_{\text{P}}} $ 为$$ {\bar e_{\text{P}}} = \frac{{\text{1}}}{{\rho {c_{\text{P}}}^2T}}\int_0^{{x_i}} {\sigma _i^2{\text{d}}x} $$ (9) 式中,
$ {\sigma _i} $ ($ i = 1,2 $ )为选取测点的法向应力, MPa;$ {x_i} $ 为被选取节理测点到爆源的距离, m;$ T $ 为应力波的整个作用过程, s;$ {c_{\text{P}}} $ 为纵波波速, m/s,${c_{\text{P}}} = \sqrt {{{E(1 - v)} \mathord{\left/ {\vphantom {{E(1 - v)} {\rho (1 + v)(1 - 2 v)}}} \right. } {[\rho (1 + v)(1 - 2 v)]}}}$ ; E为弹性模量;$ \nu $ 为泊松比. 相应地, 横波的平均能量密度$ {\bar e_{\text{S}}} $ 为$$ {\bar e_{\text{S}}} = \frac{{\text{1}}}{{\rho {c_{\text{S}}}^2T}}\int_0^{{x_i}} {\tau _i^2{\text{d}}x} $$ (10) 式中,
$ {\tau _i} $ ($ i = 1,2 $ )为选取质点的切向应力, MPa;$ {c_{\text{S}}} $ 为横波波速, m/s,${c_{\text{S}}} = \sqrt {{E \mathord{\left/ {\vphantom {E {{\text{2}}\rho (1 + \nu )}}} \right. } {[{\text{2}}\rho (1 + \nu )]}}}$ . 纵波与横波的能量公式分别为$$ {W_\sigma } = \frac{A}{{\rho {c_{\text{P}}}^2}}\int_0^{{x_i}} {\sigma _i^2} {\text{d}}x $$ (11) $$ {W_\tau } = \frac{A}{{\rho {c_{\text{S}}}^2}}\int_0^{{x_i}} {\tau _i^2} {\text{d}}x $$ (12) 数值模型中的岩石和节理皆为线弹性材料, 在线弹性材料中应力波动过程是等温过程, 与外部没有热交换, 因此, 根据热力学第一定律, 应力波动过程中入射波, 反射波与透射波的能量公式分别为
$$ {W_{\text{I}}} = {W_{{\sigma _{{}_1}}}} + {W_{{\tau _{_1}}}} = \frac{A}{{\rho c_{\text{P}}^2}}\int_0^{{x_{_1}}} {\sigma _1^2} {\text{d}}x + \frac{A}{{\rho c_{\text{S}}^2}}\int_0^{{x_1}} {\tau _1^2} {\text{d}}x $$ (13) $$ {W_{\text{T}}} = {W_{{\sigma _{_2}}}} + {W_{{\tau _{_2}}}} = \frac{A}{{\rho c_{\text{P}}^2}}\int_0^{{x_{_2}}} {\sigma _2^2} {\text{d}}x + \frac{A}{{\rho c_{\text{S}}^2}}\int_0^{{x_{_2}}} {\tau _2^2} {\text{d}}x $$ (14) $$ {W_{\text{R}}} = {W_{\text{I}}} - {W_{\text{T}}} $$ (15) 式中,
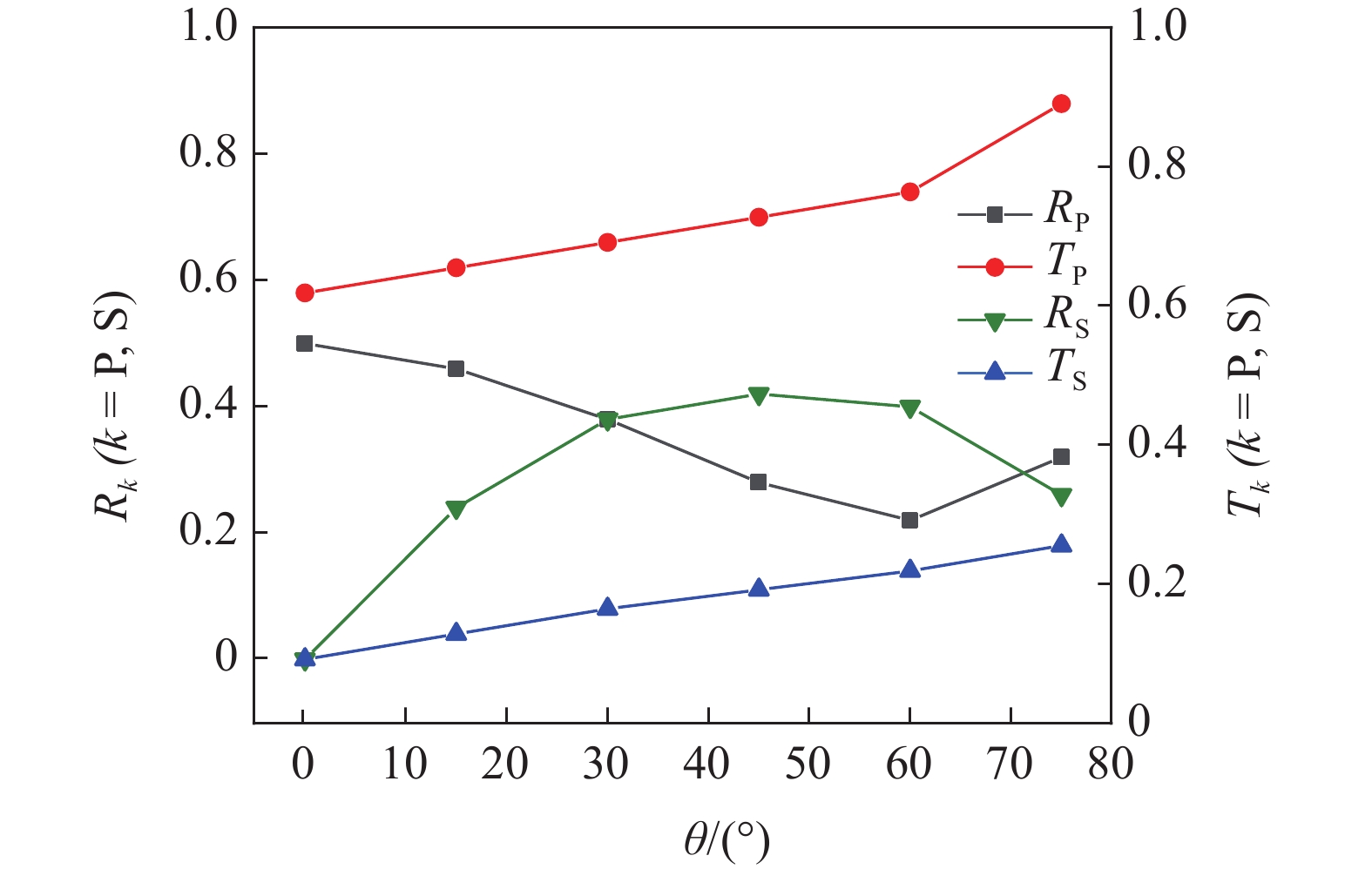
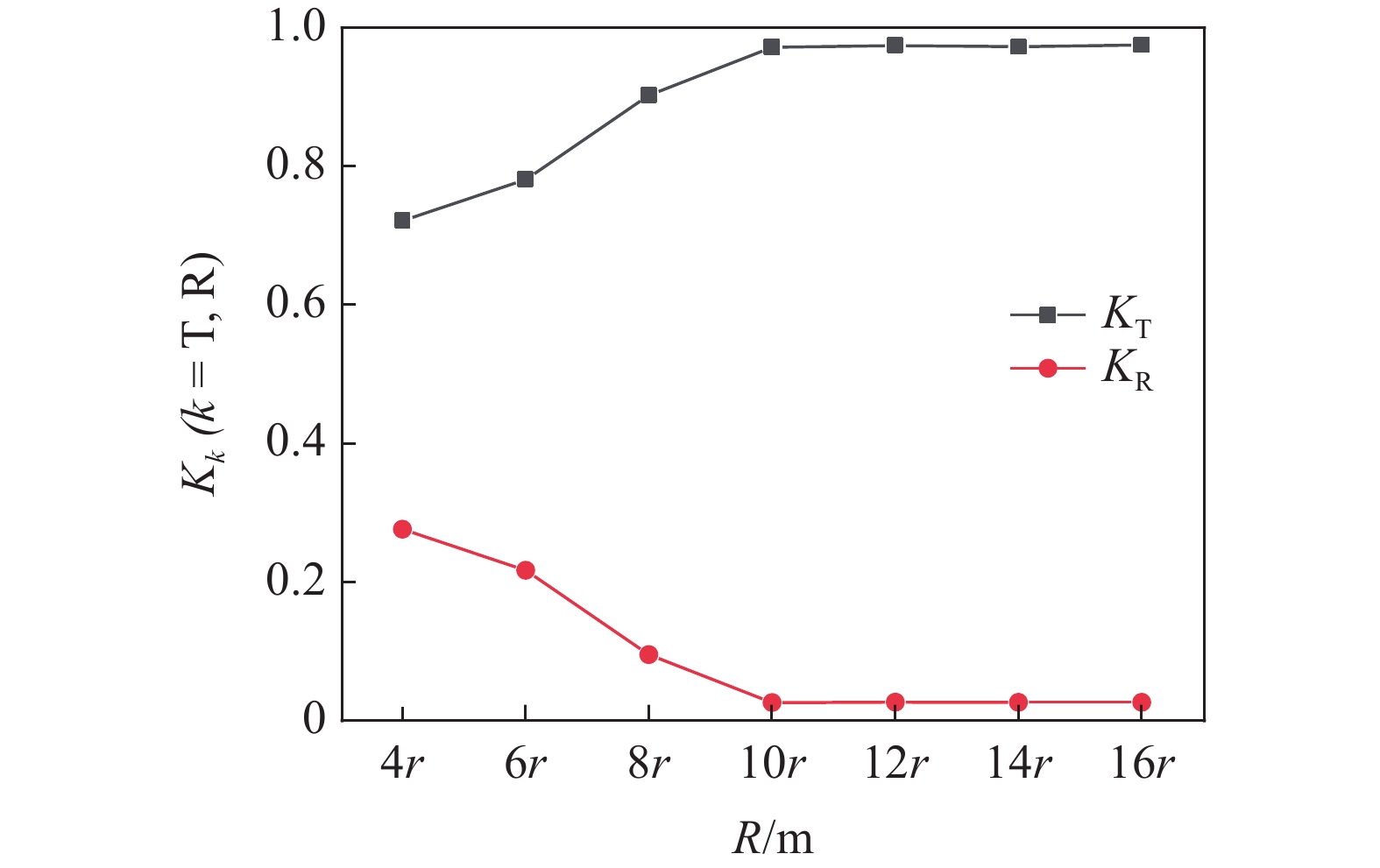
$ {W_{{\sigma _{_1}}}} $ ,$ {W_{{\sigma _{_2}}}} $ 分别为节理近爆面纵波的能量与节理背爆面纵波的能量;$ {W_{{\tau _{_{\text{1}}}}}} $ ,$ {W_{{\tau _{_{\text{2}}}}}} $ 分别为节理近爆面横波的能量与节理背爆面横波的能量;$ {W_{\text{I}}} $ ,$ {W_{\text{T}}} $ ,$ {W_{\text{R}}} $ 分别为入射波、反射波与透射波的能量; A为选取岩体单元的面积, m2;$ {x_1} $ 为节理近爆面测点到爆源的距离, m;$ {x_2} $ 为节理背爆面测点到爆源的距离, m;$ \varepsilon $ 为岩体单元的应变, m;$ {\sigma _{\text{1}}} $ 为节理近爆面测点的法向应力, MPa;$ {\sigma _{\text{2}}} $ 为节理背爆面测点的法向应力, MPa;$ {\tau _{\text{1}}} $ 为节理近爆面测点的切向应力, MPa;$ {\tau _{\text{2}}} $ 为节理背爆面测点的切向应力, MPa.对比时采用量纲为一的反射能量比
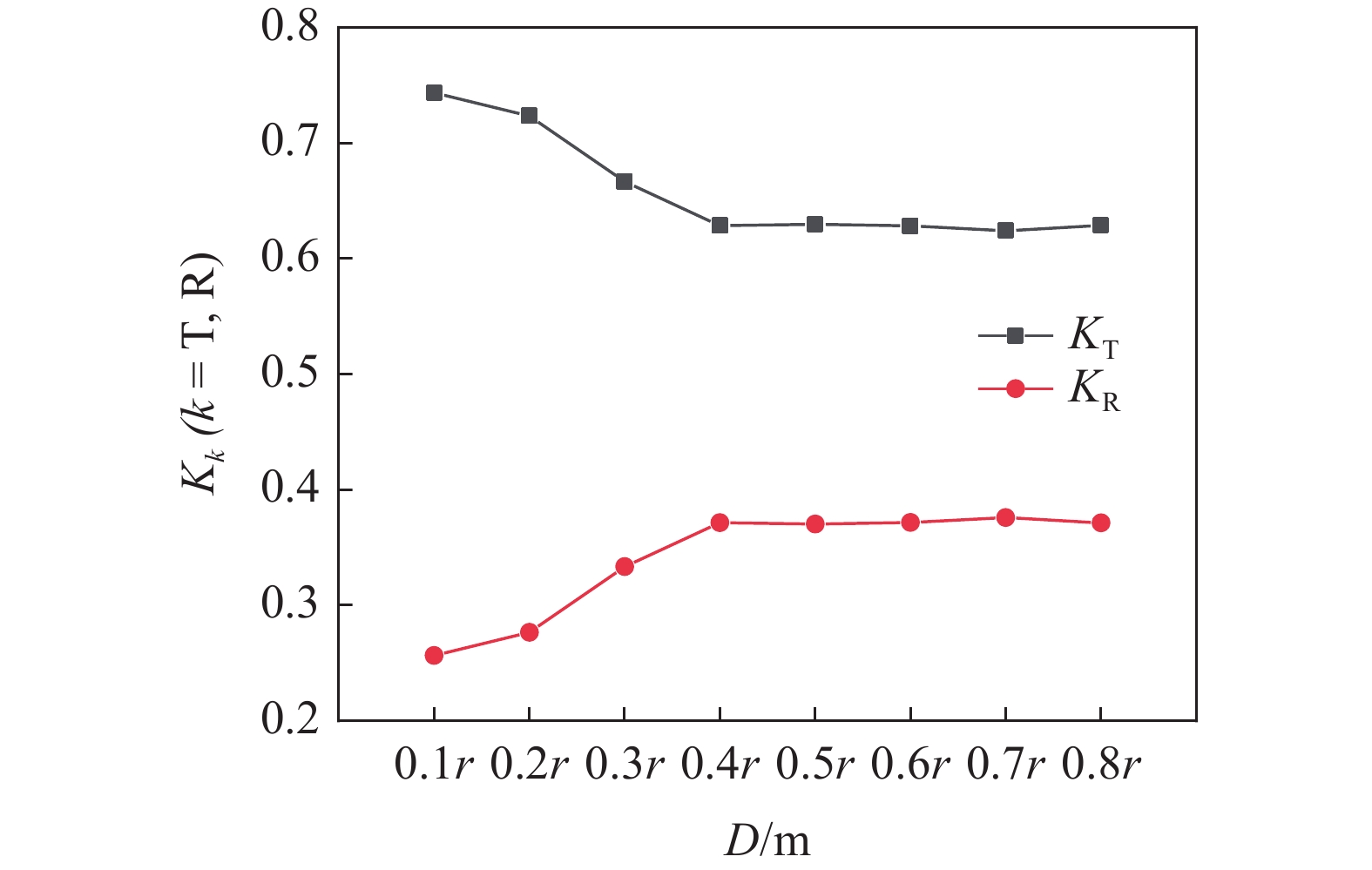
$ {K_{\text{R}}} $ 和透射能量比$ {K_{\text{T}}} $ , 分别为反射能量$ {W_{\text{R}}} $ 和透射能量$ {W_{\text{T}}} $ 占入射能量$ {W_{\text{I}}} $ 的比例, 如式(16)所示$$ \left. \begin{gathered} {K_{\text{R}}} = {W_{\text{R}}}/{W_{\text{I}}} \\ {K_{\text{T}}} = {W_{\text{T}}}/{W_{\text{I}}} \\ \end{gathered} \right\} $$ (16) 从数值模型
$ {\rm I} $ 中提取监测单元L1和监测单元L2的法向应力$ {\sigma _i} $ ($ i = 1,2 $ )和切向应力$ {\tau _i} $ ($ i = 1,2 $ ), 经式(13) ~ 式(15)分别计算得到当爆源到节理法向距离R = 4r时, 不同节理填充物厚度D下入射波能量$ {W_{\text{I}}} $ , 反射波能量$ {W_{\text{R}}} $ 和透射波能量$ {W_{\text{T}}} $ , 进而通过式(16)求得不同节理填充物厚度D下的反射能量比$ {K_{\text{R}}} $ 和透射能量比$ {K_{\text{T}}} $ , 结果曲线分别如图5所示.![]()
图 5 节理填充物厚度D对透反射能量比的影响Figure 5. Influence of joint filler thickness D on energy ratio of transmission and reflection由结果曲线可知, 随节理填充物厚度D增大, 透射能量比
$ {K_{\text{T}}} $ 逐渐减小并趋于稳定, 反射能比$ {K_{\text{R}}} $ 逐渐增加并趋于稳定, 这表明随着节理填充物厚度D增大, 爆炸应力波从节理面反射的能量增加, 透过节理的能量减小. 因此节理对近爆侧岩体的能量聚集作用和节理对爆炸应力波能量传播的阻碍作用随填充物厚度D增大而增强. 该变化规律与杨阳等[29]通过压杆试验得到的关于反射、透射和耗散能量比与节理厚度的关系的变化规律一致, 不过透反射能量比变化速率不同, 其原因是本文对于节理属性的定义不同所导致的.从数值模型
$ {\rm I}{\rm I} $ 中提取监测单元M1和监测单元M2的法向应力$ {\sigma _i} $ ($ i = 1,2 $ )与切向应力$ {\tau _i} $ ($ i = 1,2 $ ), 经式(13) ~ 式(15)分别计算得到当节理填充物厚度D = 0.2r时, 爆源到节理法向距离R不同的情况下入射波能量$ {W_{\text{I}}} $ , 反射波能量$ {W_{\text{R}}} $ 和透射波能量$ {W_{\text{T}}} $ , 进而通过式(16)求得当爆源到节理填充物厚度D = 0.2r时, 爆源到节理法向距离R不同的情况下反射能量比$ {K_{\text{R}}} $ 和透射能量比$ {K_{\text{T}}} $ , 结果曲线分别如图6所示.![]()
图 6 爆源到节理法向距离R对透反射能量比的影响Figure 6. Influence of the normal distance R from the blast source to the joint on the energy ratio of transmission and reflection由结果曲线可知, 随着爆源到节理法向距离R增大, 透射能量比
$ {K_{\text{T}}} $ 逐渐增大并趋于稳定, 反射能量比$ {K_{\text{R}}} $ 逐渐减小并趋于稳定, 这是因为随着爆源到节理法向距离R增大, 爆炸应力波在向监测单元传播过程中的几何衰减也越大, 根据潘长春等[30]的研究, 波的频率越低, 波的透射越强, 而爆炸应力波在传播过程中爆炸应力波的频率会随着爆炸应力波的衰减而逐渐衰减. 因此爆源到节理法向距离R越大, 爆炸应力波透过节理的能量越大, 反射的能量越小, 节理对爆炸应力波的反射效应也越小. 所以当爆源到节理法向距离R越大, 爆炸应力波也更容易穿透节理, 节理对爆炸应力波能量传播的阻碍作用也越弱.从数值模型
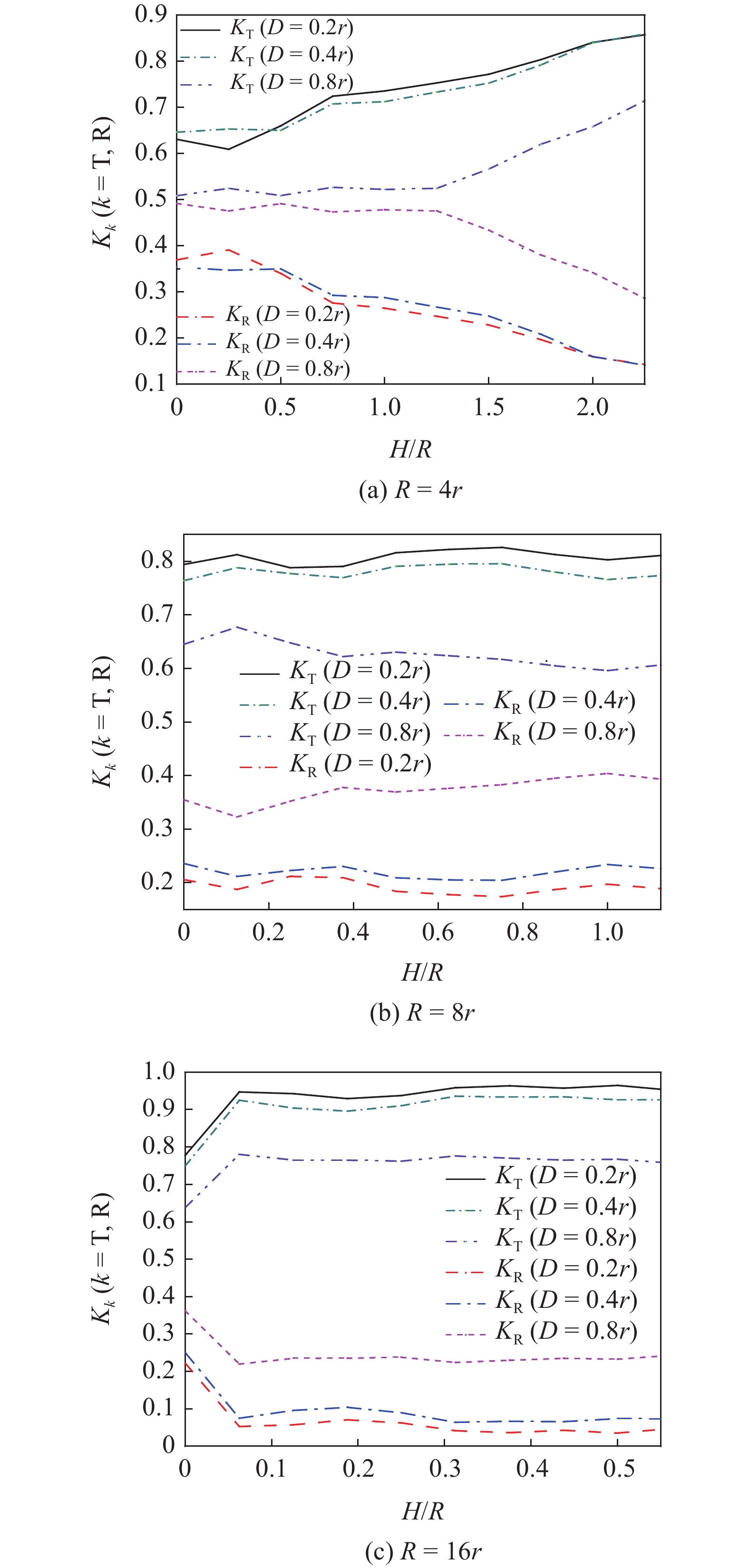
$ {\rm I}{\rm I}{\rm I} $ 中提取节理近爆侧监测单元和背爆侧监测单元的法向应力$ {\sigma _i} $ ($ i = 1,2 $ )与切向应力$ {\tau _i} $ ($ i = 1,2 $ ), 经式(13) ~ 式(15)分别计算得到不同H/R下入射波能量$ {W_{\text{I}}} $ , 反射波能量$ {W_{\text{R}}} $ 和透射波能量$ {W_{\text{T}}} $ , 进而通过式(16)求得不同H/R下节理的反射能量比$ {K_{\text{R}}} $ 和透射能量比$ {K_{\text{T}}} $ , 结果曲线分别如图7所示.![]()
图 7 H/R对透反射能量比的影响Figure 7. The energy ratio of transmission and reflection under different H/R由图7可知, 在爆源到节理法向距离R不同的情况下, 随着H/R增大, 透射能量比
$ {K_{\text{T}}} $ 和反射能量比$ {K_{\text{R}}} $ 的变化规律并不相同. 当爆源到节理的法向距离R = 4r时, 此时节理位于压碎区范围内, 随着H/R增大, 透射能量比$ {K_{\text{T}}} $ 逐渐增加, 反射能量比$ {K_{\text{R}}} $ 逐渐减小. 当R = 8r和R = 16r时, 此时节理位于裂纹区范围内, 随H/R增大, 透射能量比$ {K_{\text{T}}} $ 和反射能量比$ {K_{\text{R}}} $ 变化平缓. 对比节理在不同爆炸作用分区的透反射能量比, 节理位于压碎区时, 透射能量比$ {K_{\text{T}}} $ 和反射能量比$ {K_{\text{R}}} $ 在H/R上变化明显, 此时爆源到节理的竖向距离H对透射能量比$ {K_{\text{T}}} $ 和反射能量比$ {K_{\text{R}}} $ 的影响最大.3. 应力波在节理面的反射拉伸效应和节理岩体裂纹扩展
3.1 爆炸应力波在节理面的反射拉伸效应分析
从模型
$ {\rm I} $ 、模型$ {\rm I}{\rm I} $ 、模型$ {\rm I}{\rm I}{\rm I} $ 和模型$ {\rm I}{\text{V}} $ 结果文件中分别提取上述模型的裂纹扩展应力云图, 如表8所示. 以模型$ {\rm I}{\rm I}{\rm I} $ 的裂纹扩展应力云图为例, 将模型$ {\rm I}{\rm I}{\rm I} $ 中节理填充物厚度D = 0.2r, 爆源到节理的法向距离R = 8r的情况和不含节理的情况作对比, 爆炸应力波传播到节理面会发生反射与透射, 这种反射会使节理近爆面的岩体发生应力集中, 进而加剧节理近爆侧岩体的损伤, 而这种损伤的加剧在数值模型计算结果上具体表现为节理近爆侧岩体产生沿节理面竖向延伸的层状裂纹并与径向裂纹相互贯通, 该裂纹扩展特征在不含节理模型的裂纹扩展应力云图中没有出现. 并且由于反射波带走了一部分爆炸应力波的能量, 所以在节理背爆侧的岩体的裂纹数量和延伸距离也会减小.表 8 模型I、模型II、模型III和模型IV的裂纹扩展应力云图表Table 8. Fracture propagation stress nephogram chart for model I, model II, model III and model IVTime t = 2.38 ms t = 5.56 ms t = 10.09 ms model I 
model II 
model III 
model IV 
model without joint 
3.2 不同节理几何参数下含节理岩体裂纹扩展分析
为进一步研究节理几何参数对含节理岩体裂纹扩展的影响, 以模型
$ {\rm I}{\rm I}{\rm I} $ 为例, 分别提取9组含节理岩体爆生裂纹扩展图, 如图8所示, 分析节理填充物厚度D、爆源到节理法向距离R和爆源到节理竖向距离H对节理两侧岩体和节理填充物内爆生裂纹扩展的影响.当爆源到节理法向距离R = 4r时, 如图8(a) ~ 图8(c)所示, 此时节理位于压碎区, 根据Prasanth等[31]的研究, 压碎区内节理主要受压缩剪切破坏, 此时节理填充物不仅受到压应力的破坏, 还受剪切力产生环向裂纹. 在爆源到节理的竖向距离H = 0的节理位置处, 爆炸应力波垂直射入节理近爆面, 不产生剪切波, 爆炸主裂纹贯穿节理并在节理背爆面岩体延伸距离最大. 随着节理填充物厚度D增大, 节理背爆侧的岩体的径向裂纹数量减小, 节理对爆炸应力波的阻碍作用也越强, 这与图5中透射能力比随着节理填充物厚度D增大而减小的规律一致; 当爆源到节理法向距离R = 8r时, 如图8(d) ~ 图8(f)所示, 此时节理位于裂纹区, 由于节理近爆侧岩体内径向裂纹与层状裂纹相互贯通, 节理近爆侧岩体的破岩效果最好. 当爆源到节理法向距离R = 16r时, 如图8(g) ~ 图8(i)所示, 由于爆炸应力波在传播过程中的衰减, 节理近爆侧岩体的弧状裂纹区域面积随之减小, 节理背爆侧岩体的裂纹数量减少.
![]()
图 8 不同几何参数下含节理岩体的爆生裂纹扩展图Figure 8. Fracture propagation diagram of rock mass with joint under different geometric parameters4. 结 论
基于数值模型, 应力波波动理论与应力波能量密度理论, 得出节理的透反射系数与透反射能量比, 研究了爆炸载荷下节理不同位置处的裂纹扩展规律与应力波传播规律, 得出结论如下.
(1)当H/R = 1时反射系数
$ {R_{\text{P}}} $ 最小和反射系数$ {R_{\text{S}}} $ 最大, 此时切向应力对节理面损伤的影响最大.(2)随着节理填充物厚度D增大, 爆炸应力波从节理面反射的能量增加, 透过节理的能量减小, 节理对爆炸应力波能量传播的阻碍也越大. 爆源到节理法向距离R越大, 爆炸应力波透过节理的能量越大, 反射的能量越小. 当节理位于压碎区时, 爆源到节理的竖向距离H对透射能量比
$ {K_{\text{T}}} $ 和反射能量比$ {K_{\text{R}}} $ 的影响最大.(3)节理填充物厚度D越大, 节理近爆侧岩体的破岩效果就越好, 节理背爆侧岩体的破岩效果就越差. 爆源到节理上任意点的距离越大, 节理对岩体的爆炸效果影响就越小. 当节理法向距离位于裂纹区时, 由于爆炸应力波在节理前的反射拉伸效应, 节理近爆侧岩体产生向节理竖向延伸的层状裂纹, 并且层状裂纹会与径向裂纹相互贯通, 这会使节理近爆侧岩体的爆破碎岩效果加强.
-
![]()
图 2 不同爆源到节理的法向距离R的透反射系数
Figure 2. Transmission and reflection coefficients of different normal distances R from blast sources to joints
![]()
图 4 不同节理倾角θ的透反射系数
Figure 4. Transmission and reflection coefficients of different joint inclination angles θ
![]()
图 5 节理填充物厚度D对透反射能量比的影响
Figure 5. Influence of joint filler thickness D on energy ratio of transmission and reflection
![]()
图 6 爆源到节理法向距离R对透反射能量比的影响
Figure 6. Influence of the normal distance R from the blast source to the joint on the energy ratio of transmission and reflection
![]()
图 7 H/R对透反射能量比的影响
Figure 7. The energy ratio of transmission and reflection under different H/R
![]()
图 8 不同几何参数下含节理岩体的爆生裂纹扩展图
Figure 8. Fracture propagation diagram of rock mass with joint under different geometric parameters
表 1 模型
$ {\rm I} $ 的信息表Table 1 Information of model
$ {\rm I} $ Parameter Explosion model Monitoring unit location D R 4r 
下载: 导出CSV
Material $ \rho /\left( {{\text{g}} \cdot {\text{c}}{{\text{m}}^{ - 3}}} \right) $ $ A/{\text{GPa}} $ $ B/{\text{GPa}} $ $ {R_1} $ $ {R_2} $ $ \omega $ $ {E_0}/{\text{GPa}} $ $ V/{\text{c}}{{\text{m}}^3} $ Explosive 1.78 214 18.2 4.1 1 0.35 4.19 1
下载: 导出CSV
Material $ \rho /\left( {{\text{g}} \cdot {\text{c}}{{\text{m}}^{ - 3}}} \right) $ $ {E_0}/{\text{GPa}} $ $ \mu $ $ \sigma /{\text{GPa}} $ $ {E_{\tan }} $ $ \beta $ C P Rock 2.73 58 0.228 0.5 0.02 0.5 2.63 3.96
下载: 导出CSV
Material $ \rho /\left( {{\text{g}} \cdot {\text{c}}{{\text{m}}^{ - 3}}} \right) $ ${E_0}/{\text{GPa} }$ $ \mu $ $\sigma /{\text{GPa} }$ $ {E_{\tan }} $ $ \beta $ Joints 2.20 28 0.241 0.25 0.025 0.5
下载: 导出CSV
表 2 模型
$ {\rm I}{\rm I} $ 的信息表Table 2 Information of model
$ {\rm I}{\rm I} $ Parameter Explosion model Monitoring unit location R D 0.2r
下载: 导出CSV
表 3 模型
$ {\rm I}{\rm I}{\rm I} $ 的信息表Table 3 Information of model
$ {\rm I}{\rm I}{\rm I} $ Parameter Explosion model Monitoring unit location D 0.2r 0.4r 0.8r R 4r 8r 16r
下载: 导出CSV
表 4 模型
$ {\rm I}{\text{V}} $ 的信息表Table 4 Information of model
$ {\rm I}{\text{V}} $ Parameter Explosion model Monitoring unit location $ \theta $ R 8r
下载: 导出CSV
表 8 模型I、模型II、模型III和模型IV的裂纹扩展应力云图表
Table 8 Fracture propagation stress nephogram chart for model I, model II, model III and model IV
Time t = 2.38 ms t = 5.56 ms t = 10.09 ms model I model II model III model IV model without joint
下载: 导出CSV
-
[1] 夏文俊, 卢文波, 陈明等. 白鹤滩坝址柱状节理玄武岩爆破损伤质点峰值振速安全阈值研究[J]. 岩石力学与工程报, 2019, 38(S1): 2997-3007 Xia Wenjun, Lu Wenbo, Chen Ming, et al. Study on safety threshold of peak particle velocity about blasting damage of columnar jointed basalt rock mass in Baihetan Dam site. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S1): 2997-3007(in Chinese))
[2] Varma M, Maji VB, Boominathan A. Influence of rock joints on longitudinal wave velocity using experimental and numerical techniques. International Journal of Rock Mechanics and Mining Sciences, 2021, 141: 104699 doi: 10.1016/j.ijrmms.2021.104699
[3] Wang ZL, Konietzky H. Modelling of blast-induced fractures in jointed rock masses. Engineering Fracture Mechanics, 2009, 76(12): 1945-1955 doi: 10.1016/j.engfracmech.2009.05.004
[4] Yang P, Lei QH, Xiang JH, et al. Numerical simulation of blasting in confined fractured rocks using an immersed-body fluid-solid interaction model. Tunnelling and Underground Space Technology, 2020, 98: 103352 doi: 10.1016/j.tust.2020.103352
[5] Wang ZL, Wang HC, Wang JG, et al. Finite element analyses of constitutive models performance in the simulation of blast-induced rock cracks. Computers and Geotechnics, 2021, 135: 104172 doi: 10.1016/j.compgeo.2021.104172
[6] Zhu JB, Zhao XB, Li JC, et al. Normally incident wave propagation across a joint set with the virtual wave. Journal of Applied Geophysics, 2011, 73(3): 283-288 doi: 10.1016/j.jappgeo.2011.01.012
[7] Do TN, Wu JH. Verifying discontinuous deformation analysis simulations of the jointed rock mass behavior of shallow twin mountain tunnels. International Journal of Rock Mechanics and Mining Sciences, 2020, 130: 104322 doi: 10.1016/j.ijrmms.2020.104322
[8] Zhao J, Cai JG. Transmission of elastic P-wave across single fracture with a nonlinear normal deformation behavior. Rock Mechanics and Rock Engineering, 2001, 34(1): 3-22 doi: 10.1007/s006030170023
[9] Lu WB, Yang JH, Yan P, et al. Dynamic response of rock mass induced by the transient release of in-situ stress. International Journal of Rock Mechanics and Mining Sciences, 2012, 53: 129-141 doi: 10.1016/j.ijrmms.2012.05.001
[10] 楼晓明, 周文海, 简文彬等. 岩石破碎机理的微差爆破最佳延时控制. 哈尔滨工业大学学报, 2017, 49(02): 158-163 Lou Xiaoming, Zhou Wenhai, Jian Wenbin, et al. Millisecond blasting optimal time delay control based on rock breaking mechanism. Journal of Harbin Institute of Technology, 2017, 49(02): 158-163(in Chinese))
[11] Gu BL, Suárez‐Rivera R , Nihei KT, et al. Incidence of plane waves upon a fracture. Journal of Geophysical Research Solid Earth, 1996, 101(B11): 25337-25346
[12] 鞠杨, 李业学, 谢和平等. 节理岩石的应力波动与能量耗散. 岩石力学与工程学报, 2006(12): 2426-2434 doi: 10.3321/j.issn:1000-6915.2006.12.007 Ju Yang, Li Yexue, Xie Heping, et al. Stress wave propagation and energy dissipation in jointed Rocks. Chinese Journal of Rock Mechanics and Engineering, 2006(12): 2426-2434(in Chinese)) doi: 10.3321/j.issn:1000-6915.2006.12.007
[13] 柴少波, 李建春, 赵均海等. P波在非线性交叉节理岩体中的传播特性研究. 岩石力学与工程学报, 2019, 38(06): 1149-1157 doi: 10.13722/j.cnki.jrme.2018.1085 Chai Shaobo, Li Jianchun, Zhao Junhai, et al. Study on stress P-wave propagation across intersecting rock joints with nonlinear deformation. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(06): 1149-1157(in Chinese)) doi: 10.13722/j.cnki.jrme.2018.1085
[14] 汪书敏, 王志亮, 贾帅龙等. 黏弹性节理岩体中应力波的传播特性分析. 哈尔滨工业大学学报, 2022, 54(2): 99-107 Wang Shumin, Wang Zhiliang, Jia Shuailong, et al. Analysis of propagation characteristics of stress waves in viscoelastic jointed rock mass. Journal of Harbin Institute of Technology, 2022, 54(2): 99-107 (in Chinese))
[15] Li JC, Ma GW. Analysis of blast wave interaction with a rock joint. Rock Mechanics and Rock Engineering, 2010, 43(6): 777-787 doi: 10.1007/s00603-009-0062-0
[16] Miller RK. An approximate method of analysis of the transmission of elastic waves through a frictional boundary. Journal of Applied Mechanics, 1977, 44(4): 652-656 doi: 10.1115/1.3424152
[17] 王举, 杨风威, 唐旭. 地震荷载作用下含节理岩质边坡的破坏机理. 水利与建筑工程学报, 2017, 15(05): 171-177 doi: 10.3969/j.issn.1672-1144.2017.05.031 Wang Ju, Yang Fengwei, Tang Xu. Failure Mechanism of Rock Slope with Joint Under the Seismic Load. Journal of Water Resources and Architectural Engineering, 2017, 15(05): 171-177(in Chinese)) doi: 10.3969/j.issn.1672-1144.2017.05.031
[18] 谢冰, 李海波, 王长柏等. 节理几何特征对预裂爆破效果影响的数值模拟. 岩土力学, 2011, 32(12): 3812-3820 doi: 10.3969/j.issn.1000-7598.2011.12.044 Xie Bing, Li Haibin, Wang Changbai, et al. Numerical simulation of presplit blasting influenced by geometrical characteristics of joints. Rock and Soil Mechanics, 2011, 32(12): 3812-3820(in Chinese)) doi: 10.3969/j.issn.1000-7598.2011.12.044
[19] 孙宁新, 雷明锋, 张运良等. 软弱夹层对爆炸应力波传播过程的影响研究. 振动与冲击, 2020, 39(16): 112-119 + 147 doi: 10.3969/j.issn.1000-3835.2014.02.005 Sun Ningxin, Lei Mingfeng, Zhang Yunliang, et al. A study on the influence of weak inter-layer on the propagation process of explosion stress wave. Journal of Vibration and Shock, 2014, 31(02): 26-31.15(in Chinese)) doi: 10.3969/j.issn.1000-3835.2014.02.005
[20] 朱亮, 陈明, 卢文波等. 轮廓爆破下柱状节理岩体开裂过程的数值模拟. 爆炸与冲击, 2015, 35(04): 555-560 doi: 10.11883/1001-1455(2015)04-0555-06 Zhu Liang, Chen Ming, Lu Wenbo, et al. Numerical simulation on the cracking process of columnar jointed rock masses in contour blasting. Explosion and Shock Waves, 2015, 35(04): 555-560(in Chinese)) doi: 10.11883/1001-1455(2015)04-0555-06
[21] 刘婷婷, 李新平, 李海波等. 应力波在充填节理岩体中传播规律的数值研究. 岩石力学与工程学报, 2016, 35(S2): 3552-3560 Liu Tintin, Li Xinping, Li Haibo, et al. Numerical study on wave propagation across filled joints. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S2): 3552-3560(in Chinese))
[22] 璩世杰, 刘际飞. 节理角度对预裂爆破成缝效果的影响研究. 岩土力学, 2015, 36(01): 189-194 + 204 Qu Shijie, Liu Jifei. Numerical analysis of joint angle effect on cracking with presplit blasting. Rock and Soil Mechanics, 2015, 36(01): 189-194 + 204(in Chinese))
[23] 魏晨慧, 朱万成, 白羽等. 不同节理角度和地应力条件下岩石双孔爆破的数值模拟. 力学学报, 2016, 48(04): 926-935 doi: 10.6052/0459-1879-15-259 Wei Chenhui, Zhu Wancheng, Bai Yu, et al. Numerical simulation two-hole blasting of rock under different joint angle and in-situ stress conditions. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(04): 926-935(in Chinese)) doi: 10.6052/0459-1879-15-259
[24] 张奇. 应力波在节理处的传递过程. 岩土工程学报, 1986(06): 99-105 doi: 10.3321/j.issn:1000-4548.1986.06.011 Zhang Qi. The transfer process of stress wave at joint. Chinese Journal of Geotechnical Engineering, 1986(06): 99-105(in Chinese)) doi: 10.3321/j.issn:1000-4548.1986.06.011
[25] 冷振东, 卢文波, 陈明等. 岩石钻孔爆破粉碎区计算模型的改进. 爆炸与冲击, 2015, 35(01): 101-107 doi: 10.11883/1001-1455(2015)01-0101-07 Leng Zhendon, Lu Wenbo, Chen Min, et al. Improved calculation model for the size of crushed zone around blasthole. Explosion and Shock Waves, 2015, 35(01): 101-107. (in Chinese)) doi: 10.11883/1001-1455(2015)01-0101-07
[26] Liu L, Katsabanis PD. Development of a continuum damage model for blasting analysis. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(2): 217-231 doi: 10.1016/S0148-9062(96)00041-1
[27] LS-DYNA Keyword User's Manual. California: Livemore Software Technology Corporation, 2003
[28] 柴少波, 李建春, 李海波. 柱面波在节理岩体中的传播特性. 岩石力学与工程学报, 2014, 33(03): 523-530 Cai SB, Li J, Li HB. Propagation characteristics of cylindrical wave in joint rock masses. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(03): 523-530(in Chinese))
[29] 杨阳, 杨仁树, 王建国. 节理厚度对岩石动力特性影响的模拟试验[J]. 中国矿业大学学报, 2016, 45(02): 211-216 + 309 Yang Yang, Yang Renshu, Wang Jianguo. Simulation material experiment on dynamic mechanical properties of jointed rock affected by joint thickness. Journal of China University of Mining & Technology, 2016, 45(02): 211-216 + 309(in Chinese))
[30] 潘长春, 徐颖, 宗琦. 基于单孔爆破的节理裂隙减振模型试验研究[J]. 振动与冲击, 2017, 36(07): 255-261 Pang Changchun, Xu Ying, Zong Qi. Test for vibration reduction model of joint fracture based on single-hole blasting. Journal of Vibration and shock, 2017, 36(07): 255-261(in Chinese))
[31] Prasanth TK, Mittal S. Vortex-induced vibration of two circular cylinders at low Reynolds number. Journal of Fluids and Structures, 2009, 25(4): 731-741 doi: 10.1016/j.jfluidstructs.2008.12.002
计量
- 文章访问数: 832
- HTML全文浏览量: 368
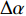
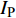
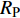
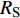
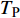
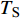
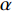
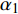
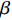
- PDF下载量: 149
