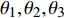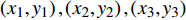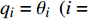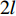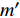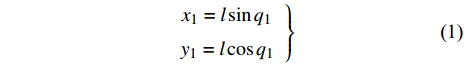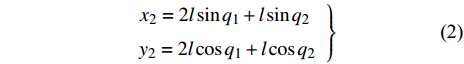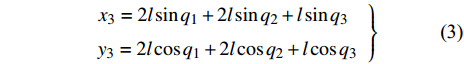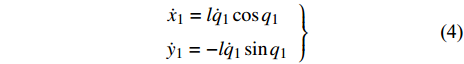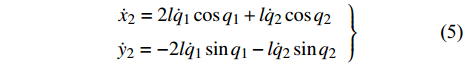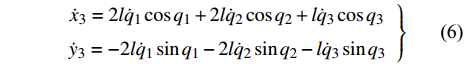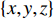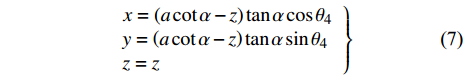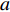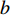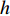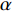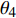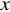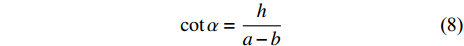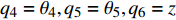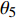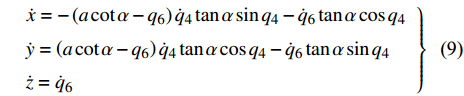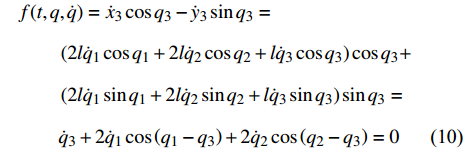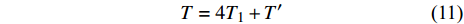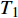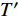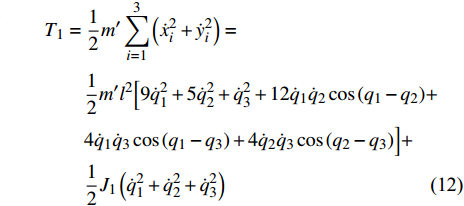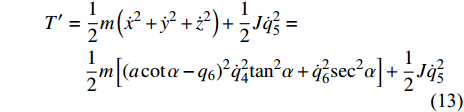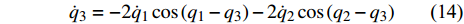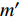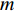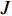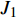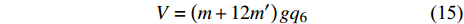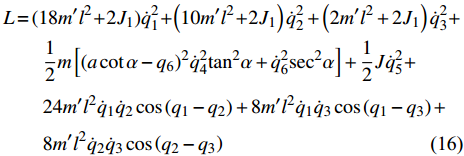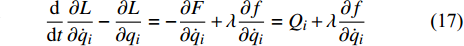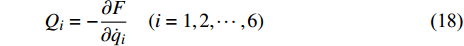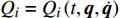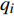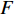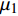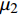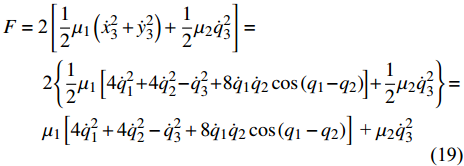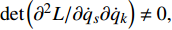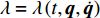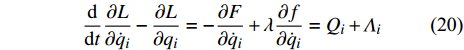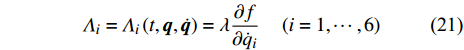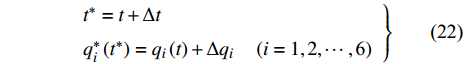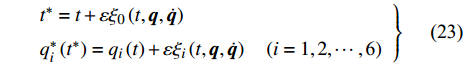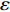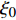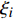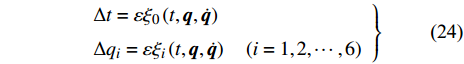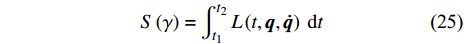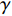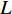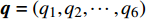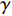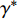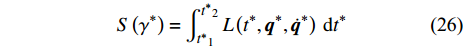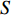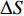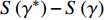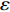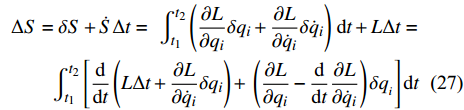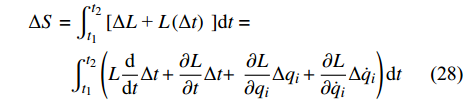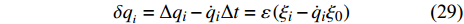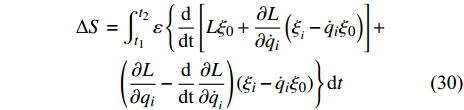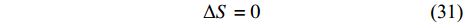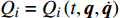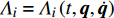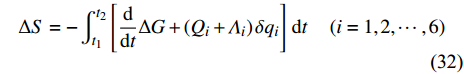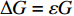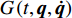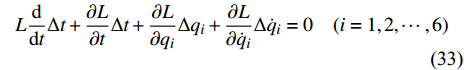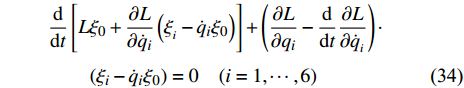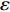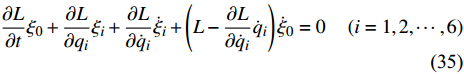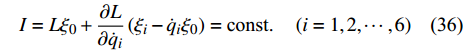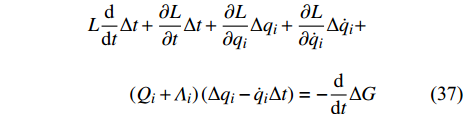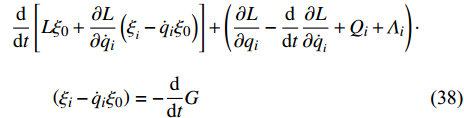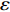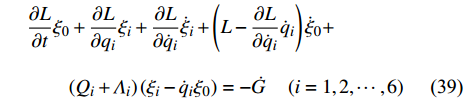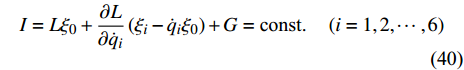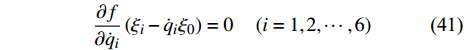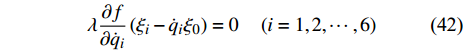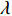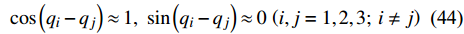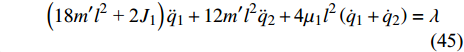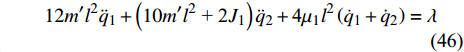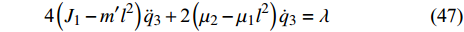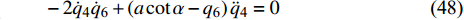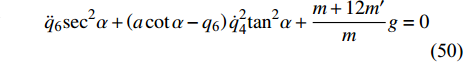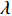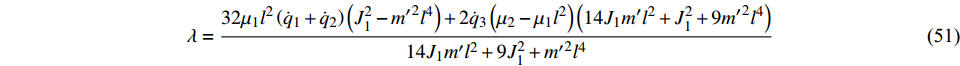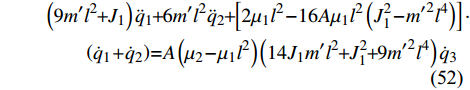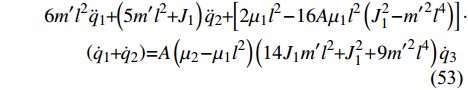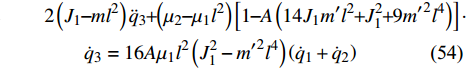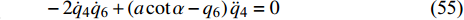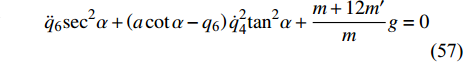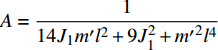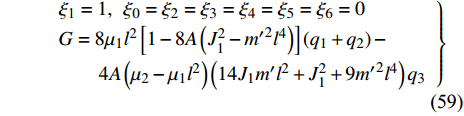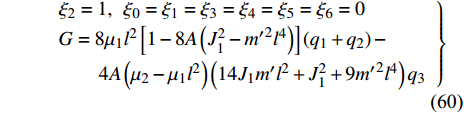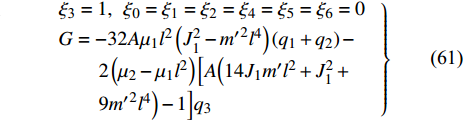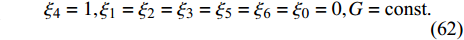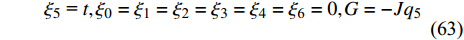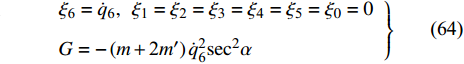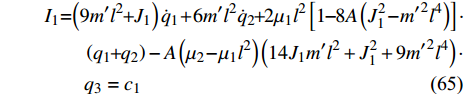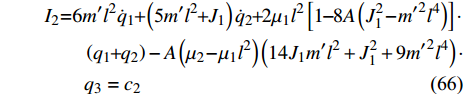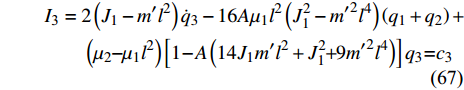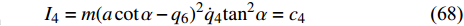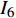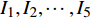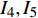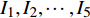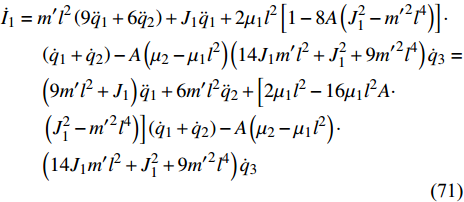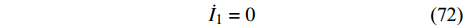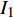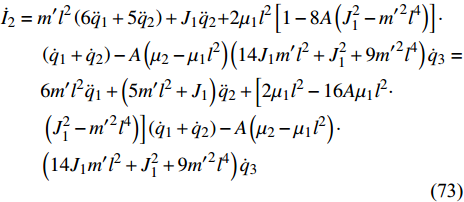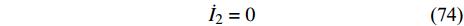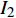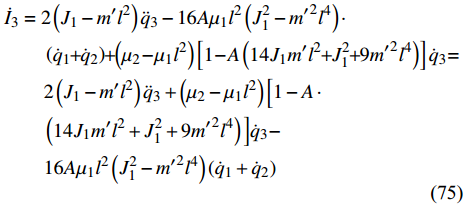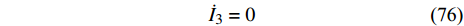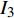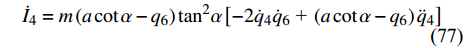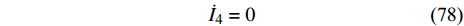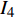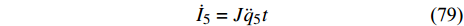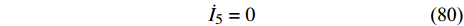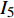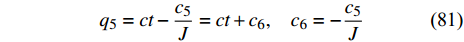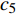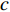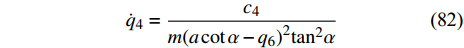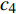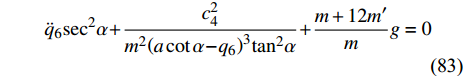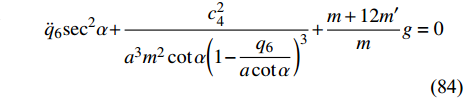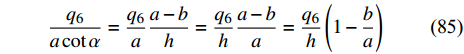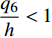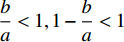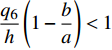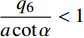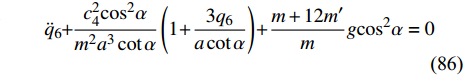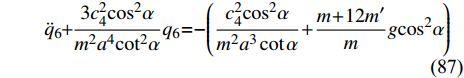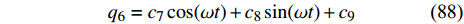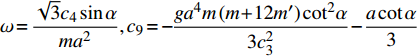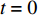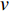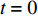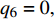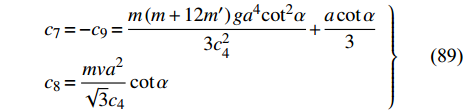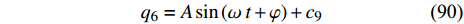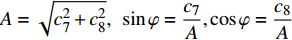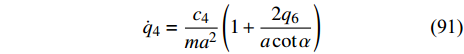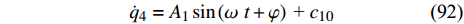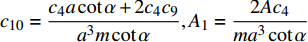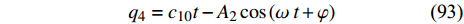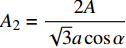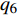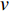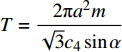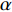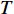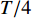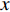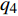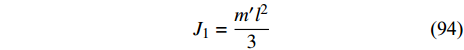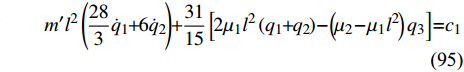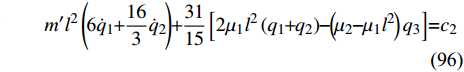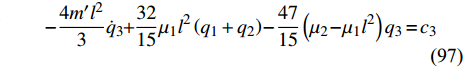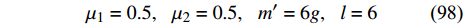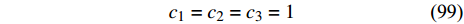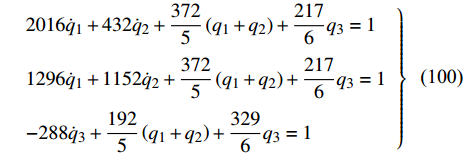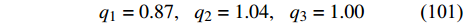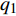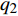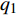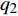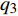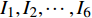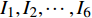NOETHER SYMMETRIES AND CONSERVED QUANTITIES OF WALL CLIMBING ROBOT SYSTEM
-
摘要: 爬壁机器人的运动是一种模仿壁虎爬行的运动, 爬壁机器人的运动可分解为四肢带动身体的运动, 先前的研究都是基于牛顿力学的方法. 本文采用Lagrange 力学的方法建立爬壁机器人系统的运动方程, 并运用Lie群分析方法建立该系统的Noether对称性理论, 得出爬壁机器人的运动规律. 首先, 给出非完整爬壁机器人系统的动能、势能和Lagrange函数以及所受的非完整约束, 从而建立了非完整爬壁机器人系统的Lagrange方程; 其次, 引入关于时间和广义坐标的无限小变换, 提出了非完整爬壁机器人系统的Hamilton作用量和Hamilton作用量的基本变分公式; 第三, 给出爬壁机器人系统 Noether对称性变换和广义准对称变换的定义, 判据和存在的Noether守恒量, 并提出了非保守完整系统和非保守非完整爬壁机器人系统的Noether定理; 最后, 以圆锥面上爬壁机器人为例, 对给出的守恒量直接进行积分给出圆锥面上爬壁机器人整体运动的精确解和四肢运动的数值解, 发现了该爬壁机器人的运动规律, 很好地验证了非完整爬壁机器人系统的Noether对称性理论. 本文的研究为Lie群分析方法应用于其他复杂的机器人系统以及柔性机器人系统的对称性求解提出了一种新的对称性求解方法.Abstract: The wall climbing robot's motion is a kind of imitation gecko's crawling motion. The wall climbing robot's motion can be divided into four limbs driving the body's movement. The previous research is based on Newton's mechanics. In this paper, Lagrange mechanics method is used to establish the motion equation of the wall climbing robot system, and the Noether symmetry theory of the system is established by using the Lie group analysis method, and the motion law of the wall climbing robot is obtained. Firstly, the kinetic energy, potential energy, Lagrange functions and nonholonomic constraints of nonholonomic wall climbing robot system are given, and the Lagrange equation of nonholonomic wall climbing robot system is established. Secondly, by introducing infinitesimal transformation of time and generalized coordinates, the basic variational formulas of Hamilton action and Hamilton action of nonholonomic wall climbing robot system are proposed. Thirdly, the wall climbing robot system is given The definition, criterion and existing Noether conserved quantity of Noether symmetry transformation and generalized quasi symmetry transformation are introduced. The Noether theorem of non conservative holonomic system and non conservative nonholonomic wall climbing robot system is proposed. Finally, taking the wall climbing robot on the conic surface as an example, the given conserved quantity is directly integrated, and the exact solution of the whole motion of the wall climbing robot on the conical surface and the motion of the limbs are given The numerical results show that the motion law of the wall climbing robot is found and the Noether symmetry theory of the nonholonomic wall climbing robot system is well verified. This paper proposes a new symmetry solution method for Lie group analysis method applied to other complex robot systems and flexible robot systems.
-
Keywords:
- wall climbing robot /
- Noether symmetry /
- Lagrange function /
- motion law
-
1. 引言
柔性机器人可以应用到很多复杂和危险的环境中. 关于柔性机器人的研究已经逐渐成为数学、力学、物理学、生物学、材料学等学科的热门研究课题[1-7].
在柔性机器人的研究中, 一种爬壁机器人受到关注. 21世纪初期, 人们揭示了壁虎能够攀爬在墙面上的原理[8], 并掀起了制造爬壁机器人的浪潮. 在国际上, 爬壁机器人制造原理主要是通过模仿壁虎的运动[9]. 目前爬壁机器人按移动功能区分主要有吸盘式、车轮式和履带式三种机器人. 吸盘式能跨越很小的障碍, 但移动速度慢; 车轮式移动速度快、控制灵活, 但维持一定的吸力较困难; 履带式对壁面适应性强, 着地面积大, 但不易转弯[10]. 斯坦福大学通过模仿壁虎的行走原理, 研发了StickyBot以及StickyBotⅢ[11]的仿壁虎机器人, 模仿的是壁虎自身的行走原理[12-13], 该机器人从吸附原理、运动形式都比较接近真实的壁虎. CMU (Carnegie Mellon University)微小型机器人实验室研制了两种结构形式的爬壁机器人[14], 即Waalbot机器人和履带式爬壁机器人, 其中Waalbot机器人是想寻求一种可以借助新的材料, 利用粘附原理使爬壁机器人在竖直面上行走; 另外一种履带式壁虎机器人, 试图找到一种可以粘附在接触面上的材料, 使得履带机器人像壁虎一样在墙面上行走. 虽然履带式爬壁机器人可以承受较大的负载, 但不能实现转弯. 加州大学伯克利分校与 iRobot 合作开发了Mecho-Gecko爬壁机器人, 它是两轮驱动的四轮式机器人, 通过在足上预装粘合剂和剥离粘合剂来实现对壁面的吸附, 其结构相对比较复杂, 他们后面又设计了6腿的爬壁机器人Hexa-Gecko[9]. 美国克利夫兰大学设计了一种轮腿式爬壁机器人Mini-Whegs[15], 这是一种轮式机器人但只能前进不能够后退和转弯等, 所以几乎不能够在实际中应用. 为了实现各种法向面的灵活过渡, 东京工艺研究院和 Isikawajima-Harima重工业有限公司联合设计开发了“忍者 ”机器人[16], 这是一种吸盘式爬壁机器人, 该机器人可以很方便地实现前进后退, 也可以横向移动, 也很容易实现墙面过渡, 但是控制的过程特别复杂.
国内在关于爬壁机器人的研究上也做了很多工作. 中科院采用模板法已经成功制成了类似壁虎绒毛的微纳米分叉结构[17]. 上海大学设计开发的采用真空吸附方式和腿足式移动机构, 可以适应不同曲率半径的曲面, 并可以跨越300 mm的障碍[18]. 北京航空航天大学研究的“蓝天洁士”系列是采用真空吸附技术的爬壁清洗机器人[19]. 南京航空航天大学研制了每个腿具有三个自由度的 IBSS系列机器人[20-22], 但这个机器人质量比较大, 载重能力不足, 且身体的柔性不足, 限制过多. 近几年中国科学院合肥物理科学研究院和中国科学技术大学联合提出“抓取 + 粘附 + 吸附”的爬壁机器人, 相对于先前的爬壁机器人, 该机器人可以实现在壁面上稳定的附着同时可以满足在多个壁面上爬行. 操纵过程也得到进一步的优化[23-24].
爬壁机器人在进入环境复杂的壁面进行工作时, 它的柔性状态尤其重要. 要建立柔性爬壁机器人的动力学方程, 必须对爬壁机器人的运动形态进行分析. 虽然国内外有很多实验室开发研究做出了不同类型的爬壁机器人. 但是对于爬壁机器人的动力学研究基本上仅限于牛顿力学方法, 由于爬壁机器人结构复杂, 约束过多, 使得研究十分困难. 而基于能量和广义坐标的拉格朗日力学方法对于解决复杂和多约束的问题具有优势. 邵洁[25]利用Lagrange方法建立了爬壁机器人后肢的Lagrange方程, 这个工作显然很不完善.
另一方面, 李群理论为求解复杂的微分方程提出了对称性分析方法[26]. 其中两种基本的Noether对称性方法和Lie对称性方法已经成为求解复杂工程问题的有效工具[27]. 众所周知, Noether对称性方法是基于系统的Hamilton作用量在变换Lie群下的不变性给出的一种对称性, 来寻找系统存在的守恒量, Noether对称性方法给出了系统存在的对称性和守恒量(即第一积分, 运动常数)之间的一一对应关系. 近年来复杂约束力学系统的Noether对称性理论已趋于完善[28-39], 并在物理、连续体, 量子力学及诸多工程中得到应用[40-42].
本文拟研究接近于真实壁虎爬行运动的腿式爬壁机器人的Lagrange方程和Noether对称性理论. 首先, 建立爬壁机器人系统的四肢的一个平面简化模型, 对爬壁机器人系统引入恰当的广义坐标, 并将直角坐标表示为广义坐标的函数, 给出爬壁机器人系统的动能和势能从而给出爬壁机器人系统的Lagrange函数, 采用不定乘子法, 推导出非完整爬壁机器人系统的Lagrange方程; 其次, 引入关于时间和广义坐标的无限小变换, 给出爬壁机器人系统 Noether对称性的定义、判据和存在的Noether守恒量; 再者, 基于爬壁机器人系统存在的守恒量, 给出了该系统的精确解; 最后, 以在圆锥壁面上爬壁机器人为例, 很好地验证了给出的爬壁机器人系统的对称性理论, 并进一步给出了该爬壁机器人系统的机身精确解以及四肢的数值解, 即得到了该爬壁机器人系统的运动规律.
2. 爬壁机器人的动力学分析
爬壁机器人大体上分为履带式, 轮式, 腿式. 其中运动原理最接近壁虎行走过程的是腿式机器人, 该机器人是通过模仿壁虎在行走过程中的形态建立起的爬壁机器人模型. 本文主要研究腿式机器人, 一方面腿式机器人较其他类型机器人的应用范围要广; 另一方面, 在运动过程中腿式机器人是最贴合壁虎的运动过程的. 本文将分析腿式爬壁机器人(如图1所示)的运动.
爬壁机器人的运动可以看成是四肢带动身体的一种运动, 每条腿上有四个电机驱动, 腿部采用杆来连接. 该爬壁机器人从运动形式和吸附原理都接近于真实的壁虎. 爬壁机器人的工作环境一般是在竖直面, 圆柱面以及圆锥面等. 本文所讨论的爬壁机器人的工作环境为圆锥壁面, 因为圆锥壁面较其他壁面更为复杂, 因此只要爬壁机器人可以实现在圆锥壁面上的行走, 那么在其余的工作环境也可以行走.
2.1 爬壁机器人四肢运动学
首先计算爬壁机器人在圆锥壁面上四肢相对于身体的坐标和速度.
考虑爬壁机器人的运动, 根据爬壁机器人的肢体形态特点, 为简化起见, 将爬壁机器人四肢各关节看成是一个自由度的转动关节. 并将爬壁机器人的单支腿简化为如图2所示, 简化结构由身体0、股骨1、胫骨2和脚掌3组成. 构件1和构件0的连接处为髋关节, 构件1和构件2的连接处为膝关节, 构件2和构件3的连接处为踝关节.
$ {\theta _1},{\theta _2},{\theta _3} $ 分别为股骨1、胫骨2和脚掌3与铅垂线的夹角(规定关节与铅垂线逆时针的夹角为正, 顺时针的夹角为负). 股骨1、胫骨2和脚掌3的质心坐标分别为$ \left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right) $ . 令${q_i} = {\theta _i}\; \;(i = 1,2,3)$ 作为广义坐标, 并用广义坐标表示直角坐标.为简便起见, 假设爬壁机器人腿部股骨、胫骨和脚掌长度, 质量相等. 分别记为
$ 2 l $ 和$ m' $ . 那么, 爬壁机器人的股骨相对于身体的质心坐标可用广义坐标表示为$$ \left.\begin{array}{l} {x_1} = l\sin {q_1} \hfill \\ {y_1} = l\cos {q_1} \end{array} \right\}$$ (1) 胫骨相对于身体的质心坐标可用广义坐标表示为
$$ \left.\begin{array}{l} {x_2} = 2l\sin {q_1} + l\sin {q_2} \hfill \\ {y_2} = 2l\cos {q_1} + l\cos {q_2} \end{array} \right\}$$ (2) 脚掌相对于身体的坐标可用广义坐标表示为
$$ \left.\begin{array}{l} {x_3} = 2l\sin {q_1} + 2l\sin {q_2} + l\sin {q_3} \hfill \\ {y_3} = 2l\cos {q_1} + 2l\cos {q_2} + l\cos {q_3} \end{array} \right\} $$ (3) 因此股骨相对于身体的速度为
$$ \left.\begin{array}{l} {{\dot x}_1} = l{{\dot q}_1}\cos {q_1} \hfill \\ {{\dot y}_1} = - l{{\dot q}_1}\sin {q_1} \end{array} \right\} $$ (4) 胫骨相对于身体的速度为
$$ \left.\begin{array}{l} {{\dot x}_2} = 2l{{\dot q}_1}\cos {q_1} + l{{\dot q}_2}\cos {q_2} \hfill \\ {{\dot y}_2} = - 2l{{\dot q}_1}\sin {q_1} - l{{\dot q}_2}\sin {q_2} \end{array} \right\} $$ (5) 脚掌相对于身体的速度为
$$ \left.\begin{array}{l} {{\dot x}_3} = 2l{{\dot q}_1}\cos {q_1} + 2l{{\dot q}_2}\cos {q_2} + l{{\dot q}_3}\cos {q_3} \hfill \\ {{\dot y}_3} = - 2l{{\dot q}_1}\sin {q_1} - 2l{{\dot q}_2}\sin {q_2} - l{{\dot q}_3}\sin {q_3} \end{array} \right\} $$ (6) 2.2 爬壁机器人机身运动学
接下来研究爬壁机器人在运动过程中机身重心位置坐标以及重心位置的速度变化. 爬壁机器人的工作壁面为圆锥曲面, 如图3所示.
在地面中心创建一个固定的笛卡尔坐标系
$ \left\{ {x,y,z} \right\} $ , 则在圆锥壁面工作环境下, 爬壁机器人的质心位置根据几何学可以表示为$$ \left.\begin{array}{l} x = \left( {a\cot \alpha - z} \right)\tan \alpha \cos {\theta _4} \hfill \\ y = \left( {a\cot \alpha - z} \right)\tan \alpha \sin {\theta _4} \hfill \\ z = z \end{array} \right\} $$ (7) 其中,
$ a $ 为圆锥壁面底面圆的半径,$ b $ 为圆锥壁面顶面圆的半径,$ h $ 为圆锥壁面的高度,$ \alpha $ 为圆锥顶角的一半,$ {\theta _4} $ 为爬壁机器人在底面投影与原点距离的连线与坐标系$ x $ 轴之间的夹角. 其中$$ \cot \alpha = \frac{h}{{a - b}} $$ (8) 选取
$ {q_4} = {\theta _4},{q_5} = {\theta _5},{q_6} = z $ 为爬壁机器人在圆锥壁面上爬行的机身重心广义坐标, 其中$ {\theta _5} $ 为爬壁机器人机身的转动角, 则爬壁机器人的机身重心位置的速度为$$ \left.\begin{array}{l} \dot x = - \left( {a\cot \alpha - {q_6}} \right){{\dot q}_4}\tan \alpha \sin {q_4} - {{\dot q}_6}\tan \alpha \cos {q_4} \hfill \\ \dot y = \left( {a\cot \alpha - {q_6}} \right){{\dot q}_4}\tan \alpha \cos {q_4} - {{\dot q}_6}\tan \alpha \sin {q_4} \hfill \\ \dot z = {{\dot q}_6} \end{array} \right\} $$ (9) 2.3 爬壁机器人系统动力学分析
通过对壁虎运动的研究发现[33], 在攀爬的过程中, 壁虎的四条腿并不是同时运动, 而是以图4这种方式向上爬行.
图中黄色圆点表示脚掌与壁面接触. 因为所研究的爬壁机器人系统是建立在壁虎的仿生学基础上, 所以对壁虎的运动步态研究就等价于对爬壁机器人系统的步态研究. 图2~图4表明, 爬壁机器人系统在攀爬过程中始终有两个脚掌是与壁面接触的, 并且在爬行过程中均采用的是对角步态, 即左侧前脚与右侧后脚同时运动, 右侧前脚与左侧后脚同时运动. 同时, 通过观察发现, 爬壁机器人系统在运动过程中, 支撑腿在运动时带动身体运动, 同时另外对角两条腿也运动. 并且发现, 两条支撑腿相对应的各个关节的运动广义坐标角度基本上是相等的. 因此为简便起见可将四肢的动能看成是相等的.
设爬壁机器人系统在爬壁中不发生滑动, 只存在静摩擦, 那么可以得到爬壁机器人的非完整约束条件为
$$ \begin{split}& f(t,q,\dot q) = {{\dot x}_3} \cos {q_3} - {{\dot y}_3}\sin {q_3} =\hfill \\& \qquad \left( {2l{{\dot q}_1}\cos {q_1} + 2l{{\dot q}_2}\cos {q_2} + l{{\dot q}_3}\cos {q_3}} \right)\cos {q_3}+ \hfill \\&\qquad \left( {2l{{\dot q}_1}\sin {q_1} + 2l{{\dot q}_2}\sin {q_2} + l{{\dot q}_3}\sin {q_3}} \right)\sin {q_3}= \hfill \\&\qquad {{\dot q}_3} + 2{{\dot q}_1}\cos \left( {{q_1} - {q_3}} \right) + 2{{\dot q}_2}\cos \left( {{q_2} - {q_3}} \right) = 0 \end{split} $$ (10) 为方便起见, 假设爬壁机器人系统在爬壁过程中四肢的动能相同. 由此非完整爬壁机器人系统的动能为
$$ T = 4{T_1} + T' $$ (11) 其中,
$ {T_1} $ 为非完整爬壁机器人系统相对于身体单条腿的动能,$ T' $ 为爬壁机器人系统机身的动能, 分别为$$ \begin{split}& {T_1} = \frac{1}{2}m'\sum\limits_{i = 1}^3 {\left( {\dot x_i^2 + \dot y_i^2} \right)}= \\&\qquad \frac{1}{2}m'{l^2}\Big[ {9\dot q_1^2 + 5\dot q_2^2 + \dot q_3^2 + 12{{\dot q}_1}{{\dot q}_2}\cos \left( {{q_1} - {q_2}} \right)} +\\&\qquad { 4{{\dot q}_1}{{\dot q}_3}\cos \left( {{q_1} - {q_3}} \right) + 4{{\dot q}_2}{{\dot q}_3}\cos \left( {{q_2} - {q_3}} \right)} \Big] + \\&\qquad \frac{1}{2}{J_1}\left( {\dot q_1^2 + \dot q_2^2 + \dot q_3^2} \right) \end{split} $$ (12) $$ \begin{split}& T' = \frac{1}{2}m\left( {{{\dot x}^2} + {{\dot y}^2} + {{\dot z}^2}} \right) + \frac{1}{2}J{{\dot q}^2}_{\text{5}}= \hfill \\&\qquad \frac{1}{2}m\left[ {{{\left( {a\cot \alpha - {q_{\text{6}}}} \right)}^2}{{\dot q}^2}_{\text{4}}{{\tan }^2}\alpha + \dot q_{\text{6}}^2{{\sec }^2}\alpha } \right] + \frac{1}{2}J{{\dot q}^2}_{\text{5}} \end{split} $$ (13) 由式(10)可得
$$ {\dot q_3} = - 2{\dot q_1}\cos \left( {{q_1} - {q_3}} \right) - 2{\dot q_2}\cos \left( {{q_2} - {q_3}} \right) $$ (14) 在式(12)和式(13)中,
$m' $ 为单条腿一关节的质量,$m$ 为爬壁机器人系统机身的质量,$ J$ 为爬壁机器人系统身体的转动惯量,$ {J_1} $ 为爬壁机器人系统单条腿中关节的转动惯量(本文假设爬壁机器人系统单支腿各个关节的转动惯量相等).非完整爬壁机器人系统的势能为
$$ V = \left( {m + 12m'} \right)g{q_6} $$ (15) 由此非完整爬壁机器人系统的Lagrange函数为
$$ \begin{split}& L = (18{m'}{l^2} + 2{J_1})\dot q_1^2 + \left( {10{m'}{l^2} + 2{J_1}} \right)\dot q_2^2 + \left( {2{m'}{l^2} + 2{J_1}} \right)\dot q_3^2+ \hfill \\& \qquad \frac{1}{2}m\left[ {{{\left( {a\cot \alpha - {q_{\text{6}}}} \right)}^2}{{\dot q}^2}_{\text{4}}{{\tan }^2}\alpha + \dot q_{\text{6}}^2{{\sec }^2}\alpha } \right] + \frac{1}{2}J{{\dot q}^2}_{\text{5}}+ \hfill \\& \qquad 24m'{l^2}{{\dot q}_1}{{\dot q}_2}\cos \left( {{q_1} - {q_2}} \right) + 8m'{l^2}{{\dot q}_1}{{\dot q}_3}\cos \left( {{q_1} - {q_3}} \right) +\hfill \\& \qquad 8m'{l^2}{{\dot q}_2}{{\dot q}_3}\cos \left( {{q_2} - {q_3}} \right) \\[-10pt] \end{split} $$ (16) 非完整爬壁机器人系统的运动微分方程, 即Routh方程为
$$\frac{{\rm{d}}}{{\rm{d}} t} \frac{\partial L}{\partial \dot{q}_{i}}-\frac{\partial L}{\partial q_{i}}=-\frac{\partial F}{\partial \dot{q}_{i}}+\lambda \frac{\partial f}{\partial \dot{q}_{i}}=Q_{i}+\lambda \frac{\partial f}{\partial \dot{q}_{i}} $$ (17) $$ Q_{i}=-\frac{\partial F}{\partial \dot{q}_{i}} \quad (i=1,2, \cdots, 6) $$ (18) 其中,
$ {Q_i} = {Q_i}\left( {t,{\boldsymbol{q}},\dot {\boldsymbol{q}}} \right)$ 为非完整爬壁机器人系统的非势广义力,$ {q_i}$ 为选定的广义坐标,$ F $ 为爬壁机器人系统脚掌贴附在壁面上的摩擦耗散函数. 假设爬壁机器人在壁面上缓慢爬行, 那么爬壁机器人所受的阻力可以看成是关于速度的正比例函数. 设爬壁机器人系统脚掌与地面之间的平动和转动的摩擦系数分别为$ {\mu _1} $ 和$ {\mu _2} $ . 因此爬壁机器人系统的摩擦耗散函数为$$ \begin{split}& F = {\text{2}}\left[ {\frac{1}{2}{\mu _1}\left( {\dot x_3^2 + \dot y_3^2} \right) + \frac{1}{2}{\mu _2}\dot q_3^2} \right]= \\ &\qquad {\text{2}} \left\{ {\frac{1}{2}{\mu _1}\left[ {4\dot q_1^2 + 4\dot q_2^2 - \dot q_3^2 + 8{{\dot q}_1}{{\dot q}_2}\cos \left( {{q_1} - {q_2}} \right)} \right] + \frac{1}{2}{\mu _2}\dot q_3^2} \right\} = \\ &\qquad {\mu _1}\left[ {4\dot q_1^2 + 4\dot q_2^2 - \dot q_3^2 + 8{{\dot q}_1}{{\dot q}_2}\cos \left( {{q_1} - {q_2}} \right)} \right]{\text{ + }}{\mu _2}\dot q_3^2 \end{split} $$ (19) 设系统(17)非奇异, 即
$\det \left( {{\partial ^2}L/\partial {{\dot q}_s}\partial {{\dot q}_k}} \right) \ne 0, (s,k = 1,2, \cdots ,6)$ , 则由方程式(10)和式(17)可求出$\lambda = \lambda \left( {t,{\boldsymbol{q}},\dot {\boldsymbol{q}}} \right)$ , 因此方程(17)写为$$ \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial {{\dot q}_i}}} - \frac{{\partial L}}{{\partial {q_i}}} = - \frac{{\partial F}}{{\partial {{\dot q}_i}}} + \lambda \frac{{\partial f}}{{\partial {{\dot q}_i}}} = {Q_i} + {\varLambda _i} $$ (20) 其中
$$ {\varLambda }_{i}={\varLambda }_{i}\left(t,{\boldsymbol{q}},\dot{{\boldsymbol{q}}}\right)=\lambda \frac{\partial f}{\partial {\dot{q}}_{i}} \quad\left(i=1,\cdots ,6\right) $$ (21) 为广义约束反力. 方程(20)为非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Lagrange方程. 非保守非完整爬壁机器人系统的运动微分方程的解可在方程(20)的解中找到. 当爬壁机器人系统在运动过程中满足非完整约束条件(10), 则方程(20)的解便可给出非完整爬壁机器人系统(17)的运动规律.
3. 爬壁机器人系统的Noether对称性和Noether守恒量
引入关于时间和广义坐标的无限小变换
$$ \left. \begin{array}{l} {t^*} = t + \Delta t \hfill \\ {q^*_i}\left( {{t^*}} \right) = {q_i}\left( t \right) + \Delta {q_i} \quad\left( {i = 1,2, \cdots ,{\text{6}}} \right) \end{array} \right\} $$ (22) 方程(22)可展开为
$$ \left. \begin{array}{l} {t^*} = t + \varepsilon {\xi _0}\left( {t,{\boldsymbol{q}},\dot {\boldsymbol{q}}} \right) \hfill \\ {q^*_i}\left( {{t^*}} \right) = {q_i}\left( t \right) + \varepsilon {\xi _i}\left( {t,{\boldsymbol{q}},\dot {\boldsymbol{q}}} \right)\quad(i = 1,2, \cdots ,{\text{6}}) \end{array} \right\} $$ (23) 其中,
$ \varepsilon $ 为无限小参数,$ {\xi _0} $ 和$ {\xi _i} $ 为无限小变换生成元$$\left. \begin{array}{l} \Delta t = \varepsilon {\xi _0}\left( {t,{\boldsymbol{q}},\dot {\boldsymbol{q}}} \right) \\ \Delta {q_i} = \varepsilon {\xi _i}\left( {t,{\boldsymbol{q}},\dot {\boldsymbol{q}}} \right)\quad \left( {i = 1,2, \cdots ,6} \right) \end{array}\right\} $$ (24) 引入爬壁机器人系统的Hamilton作用量
$$ S\left( \gamma \right) = \int_{{t_1}}^{{t_2}} {L\left( {t,{\boldsymbol{q}},{\boldsymbol{\dot q}}} \right){\text{ }}} {\rm{d}}t $$ (25) 其中,
$ \gamma $ 为某曲线,$ L $ 为爬壁机器人系统的拉格朗日函数,${\boldsymbol{q}} = \left( {{q_1},{q_2}, \cdots ,{q_6}} \right)$ . 在变换式(23)下, 曲线$ \gamma $ 将变为相靠近的曲线$ {\gamma ^*} $ , 爬壁机器人系统相应的Hamilton作用量变换为$$ S\left( {{\gamma ^*}} \right) = \int_{{t^*}_1}^{{t^*}_2} {L\left( {{t^*},{{\boldsymbol{q}}^*},{{\dot {\boldsymbol{q}}}^*}} \right){\text{ }}} {\rm{d}}{t^*} $$ (26) 作用量
$ S $ 的变分$ \Delta S $ 为差$ S\left( {{\gamma ^*}} \right) - S\left( \gamma \right) $ 的相对$ \varepsilon $ 的主线性部分, 根据全变分和等时变分之间关系, 有$$ \begin{split}& \Delta S = \delta S + \dot S\Delta t = {\text{ }}\int_{{t_1}}^{{t_2}} {\left( {\frac{{\partial L}}{{\partial {q_i}}}\delta {q_i} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\delta {{\dot q}_i}} \right)} {\text{ }}{\rm{d}}t + L\Delta t = \hfill \\ &\qquad \int_{{t_1}}^{{t_2}} {\left[ {\frac{\rm{d}}{{\rm{d}}{{t}}}\left( {L\Delta t + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\delta {q_i}} \right) + } \right.} \left. {\left( {\frac{{\partial L}}{{\partial {q_i}}} - \frac{\rm{d}}{{\rm{d}}{{{t}}}}\frac{{\partial L}}{{\partial {{\dot q}_i}}}} \right)\delta {q_{_i}}} \right]{\rm{d}}t \end{split} $$ (27) 及
$$ \begin{split}& \Delta S = \int_{{t_1}}^{{t_2}} {\left[ {\Delta L{\text{ + }}L\left( {\Delta t} \right){\text{ }}} \right]} {\rm{d}}t = \hfill \\ &\qquad \int_{{t_1}}^{{t_2}} {\left( {L\frac{\rm{d}}{{\rm{d}}{t}} {\Delta t} + \frac{{\partial L}}{{\partial t}}\Delta t + } \right.} \left. {\frac{{\partial L}}{{\partial {q_i}}}\Delta {q_i} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\Delta {{\dot q}_i}} \right){\rm{d}}t \end{split} $$ (28) 将式(23)代入式(27)并注意到
$$ \delta {q_{_i}} = \Delta {q_i} - {\dot q_i}\Delta t = \varepsilon \left( {{\xi _i} - {{\dot q}_i}{\xi _0}} \right) $$ (29) 得到
$$ \begin{split}& \Delta S = \int_{{t_1}}^{{t_2}} {\varepsilon \left\{ {\frac{\rm{d}}{{\rm{d}t}}\left[ {L{\xi _0} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\left( {{\xi _{_i}} - {{\dot q}_i}{\xi _0}} \right)} \right] + } \right.} \\&\qquad \left. {\left( {\frac{{\partial L}}{{\partial {q_i}}} - \frac{\rm{d}}{{\rm{d}t}}\frac{{\partial L}}{{\partial {{\dot q}_{_i}}}}} \right)\left( {{\xi _i} - {{\dot q}_i}{\xi _0}} \right)} \right\}{\rm{d}}t \end{split} $$ (30) 式(28)和式(30)就是完整爬壁机器人系统的Hamilton作用量变分的基本公式.
定义1 如果爬壁机器人系统的Hamilton作用量是无限小变换式(22)或式(23)下的不变量, 即无限小变换满足
$$ \Delta S = 0 $$ (31) 则无限小变换是完整爬壁机器人系统的Noether对称性变换.
定义2对于受到非势广义力
${Q_i} = {Q_i}\left( {t,{\boldsymbol{q}},\dot {\boldsymbol{q}}} \right)$ 和广义非完整约束力${\varLambda _i} = {\varLambda _i}\left( {t,{\boldsymbol{q}},\dot {\boldsymbol{q}}} \right)$ 的非保守非完整爬壁机器人系统的Hamilton作用量是无限小变换式(22)或式(23)下的不变量, 即无限小变换满足$$ \Delta S = - \int_{{t_1}}^{{t_2}} {\left[ {\frac{\rm{d}}{{\rm{d}}{t}} {\Delta G} + \left( {{Q_i} + {\varLambda _i}} \right)\delta {q_i}} \right]} {\text{ }}{\rm{d}}t\quad\left( {i = 1,2, \cdots ,6} \right) $$ (32) 这里
$ \Delta G = \varepsilon G $ ,$G\left( {t,{\boldsymbol{q}},{\boldsymbol{\dot q}}} \right)$ 为规范函数, 则无限小变换是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(20)的广义Noether准对称性变换.由定义公式(31)和基本公式(28)和(30)可以得到完整爬壁机器人系统的如下判据:
判据 1对于无限小群变换式(22), 如果满足条件
$$ L\frac{\rm{d}}{{\rm{d}}{t}}{\Delta t} + \frac{{\partial L}}{{\partial t}}\Delta t + \frac{{\partial L}}{{\partial {q_i}}}\Delta {q_i} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\Delta {\dot q_i} = 0\quad(i = 1,2, \cdots ,6) $$ (33) 则变换式(22)是完整爬壁机器人系统的Noether对称变换.
判据 2对于无限小群变换式(23), 如果满足条件
$$ \begin{split}& \frac{\rm{d}}{{\rm{d}}{t}}\left[ {L{\xi _0} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\left( {{\xi _{_i}} - {{\dot q}_i}{\xi _0}} \right)} \right] + \left( {\frac{{\partial L}}{{\partial {q_i}}} - \frac{\rm{d}}{{\rm{d}}{t}}\frac{{\partial L}}{{\partial {{\dot q}_{_i}}}}} \right) \cdot \\& \qquad \left( {{\xi _i} - {{\dot q}_i}{\xi _0}} \right) = 0\quad(i = 1, \cdots ,6) \end{split} $$ (34) 则变换式(23)为完整爬壁机器人系统的Noether对称变换.
利用关系(24), 由于
$ \varepsilon $ 独立性可以得到完整爬壁机器人系统的Noether恒等式$$ \frac{{\partial L}}{{\partial t}}{\xi _{\text{0}}} + \frac{{\partial L}}{{\partial {q_i}}}{\xi _i} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}{\dot \xi _i} + \left( {L - \frac{{\partial L}}{{\partial {{\dot q}_i}}}{{\dot q}_i}} \right){\dot \xi _0} = 0\quad\left( {i = 1,2, \cdots ,6} \right) $$ (35) Noether定理1 如果无限小变换式(23)是完整爬壁机器人系统的Noether对称变换, 则该系统存在如下形式的守恒量
$$ I = L{\xi _0} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\left( {{\xi _i} - {{\dot q}_i}{\xi _0}} \right) = {\text{const}}.\quad \left( {i = 1,2, \cdots ,6} \right) $$ (36) Noether定理1也可以表示为Noether定理2.
Noether定理2: 对于完整爬壁机器人系统, 如果无限小变换式(22)或式(23)满足Noether恒等式(35), 则完整爬壁机器人系统存在守恒量(36).
用定义公式(32)及基本公式(28)和(30)可以得到非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(10)和(20)广义Noether准对称性的如下判据:
判据 3 对于无限小群变换式(22), 如果满足条件
$$\begin{split} & L\frac{\rm{d}}{{\rm{d}}{t}} {\Delta t} + \frac{{\partial L}}{{\partial t}}\Delta t + \frac{{\partial L}}{{\partial {q_i}}}\Delta {q_i} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\Delta {\dot q_i} +\\&\qquad \left( {{Q_i} + {\varLambda _i}} \right)\left( {\Delta {q_i} - {{\dot q}_i}\Delta t} \right) = - \frac{\rm{d}}{{\rm{d}}{t}} {\Delta G} \end{split} $$ (37) 则变换式(22)是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的广义Noether准对称变换.
判据 4 对于无限小群变换式(23), 如果满足条件
$$\begin{split} & \frac{\rm{d}}{{\rm{d}}{t}}\left[ {L{\xi _0} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\left( {{\xi _{_i}} - {{\dot q}_i}{\xi _0}} \right)} \right] + \left( {\frac{{\partial L}}{{\partial {q_i}}} - \frac{\rm{d}}{{\rm{d}}{t}}\frac{{\partial L}}{{\partial {{\dot q}_{_i}}}} + {Q_i} + {\varLambda _i}} \right) \cdot \\& \qquad \left( {{\xi _i} - {{\dot q}_i}{\xi _0}} \right) = - \frac{\rm{d}}{{\rm{d}}{t}}G \end{split} $$ (38) 则变换式(23)为非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的广义Noether准对称变换.
利用关系(24), 由于
$ \varepsilon $ 独立性可以得到非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(10)和(20)的Noether恒等式$$ \begin{split} & \frac{{\partial L}}{{\partial t}}{\xi _{\text{0}}} + \frac{{\partial L}}{{\partial {q_i}}}{\xi _i} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}{\dot \xi _i} + \left( {L - \frac{{\partial L}}{{\partial {{\dot q}_i}}}{{\dot q}_i}} \right){\dot \xi _0} + \\& \qquad \left( {{Q_i} + {\varLambda _i}} \right)\left( {{\xi _i} - {{\dot q}_i}{\xi _0}} \right) = - \dot G\quad\left( {i = 1,2, \cdots ,6} \right) \end{split} $$ (39) Noether定理3: 如果存在规范函数
$ G $ , 使得无限小变换式(23)是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(10)和(20)的广义Noether准对称变换, 则该系统存在如下形式的守恒量$$ I = L{\xi _0} + \frac{{\partial L}}{{\partial {{\dot q}_i}}}\left( {{\xi _i} - {{\dot q}_i}{\xi _0}} \right) + G = {\text{const}}. \quad \left( {i = 1,2, \cdots ,6} \right) $$ (40) Noether定理3可以表示为Noether定理4.
Noether定理4: 对于非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(10)和(20), 如果存在规范函数
$ G $ 使得无限小变换式(22)或式(23)满足Noether恒等式(39), 则该系统存在守恒量(40).定义3如果无限小变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的广义Noether准对称性变换, 且变换还满足条件
$$ \frac{{\partial f}}{{\partial {{\dot q}_i}}}\left( {{\xi _i} - {{\dot q}_i}{\xi _0}} \right) = 0\quad \left( {i = 1,2, \cdots ,6} \right) $$ (41) 则称变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的强广义Noether准对称变换.
Noether定理5: 如果存在规范函数
$ G $ 使得无限小变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的强广义Noether准对称变换, 则该系统存在守恒量(40).当条件(41)放宽为以下条件
$$ \lambda \frac{\partial f}{\partial {\dot{q}}_{i}}\left({\xi }_{i}-{\dot{q}}_{i}{\xi }_{0}\right)=0 \quad \left(i=1,2,\cdots ,6\right) $$ (42) 便可以得出非完整爬壁机器人系统(10)和(17)的弱广义Noether准对称变换.
定义4如果无限小变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的广义Noether准对称性变换, 且变换还满足条件(42)则称变换式(23)为非保守非完整爬壁机器人系统(10)和(17)的弱广义Noehter准对称变换.
Noether定理6: 如果存在规范函数
$ G $ 使得无限小变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的弱广义Noether准对称变换, 则该系统存在守恒量(40).由Noether守恒量(40)再给定初始条件便可得出非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统在圆锥壁面上爬壁过程中的运动规律.
4. 利用爬壁机器人系统的Noether守恒量求其运动规律
在分析力学领域, 近30年来我国梅凤翔教授带领众多学者从事约束力学系统的Noether对称性和Lie对称性的研究工作[27,43-59], 并提出了约束力学系统的形式不变性(也称梅对称性)理论[60,61], 建立了约束力学系统的对称性理论, 在国际上产生一定影响. 然而在先前的工作中, 一般是根据系统的某种对称性给出系统存在的守恒量(第一积分或运动常数), 很少进一步由守恒量给出系统的精确解. 事实上, 当得出第一积分(守恒量, 它是一阶微分方程), 那么守恒量的求解已经没有困难, 对于专门从事于对称性理论研究的人员来说, 关于守恒量的求解不需继续进行. 然而, 近几年来一些学者对此提出异议, 并建议将约束力学系统对称性理论应用于多体系统、非线性系统、连续介质系统和工程实际中, 因为该方法可为复杂系统提供一个更好的解决思路和方向. 下面以复杂的非完整爬壁机器人系统为例, 由爬壁机器人系统存在的守恒量, 给出爬壁机器人系统的解, 即给出爬壁机器人系统的运动规律.
Bluman对从微分方程的对称性给出特征方程, 再得到方程对应的多个第一积分方法进行了系统研究[26]. 方法表明, 如果微分方程的阶数和守恒量的数目相等, 便可积分给出微分方程的解.
前面爬壁机器人系统给出的Noether守恒量都是一阶方程, 当给定初始条件时, 利用直接积分的方法, 便可解出非保守非完整爬壁机器人系统的解, 即给出非保守非完整爬壁机器人系统的运动规律.
5. 算例
通过以上讨论, 已经得出非保守非完整爬壁机器人系统在圆锥壁面上的Lagrane函数以及非保守非完整爬壁机器人系统的运动微分方程, 并给出了爬壁机器人系统的Noether对称性理论, 下面以圆锥壁面上爬壁机器人为例, 给出相应的Lagrange方程, Noether对称性和Noether守恒量, Noether定理, 以验证爬壁机器人Noether对称性理论. 并由圆锥壁面上爬壁机器人的守恒量给出精确解, 即运动规律.
5.1 圆锥面上爬壁机器人的Lagrange方程
将式(10), 式(16)及式(19)代入到式(17)和式(18)中得
$$ \left. \begin{array}{l} \left( { 18m'{l^2} + 2{J_1} } \right) {{\ddot q}_1} + m'{l^2}\Big[12{{\ddot q}_2}\cos \left( {{q_1} - {q_2}} \right) + \\\qquad 12\dot q_2^2\sin \left( {{q_1} - {q_2}} \right)\Big] + 4{\mu _1}{l^2}\left[ {{\dot q}_1} + {{\dot q}_2}\cos \left( {q_1} - \right. \right. \\\qquad \left.\left. {q_2} \right) \right] =\lambda \cos \left( {{q_1} - {q_2}} \right)\\ \left( {10m'{l^2} + 2{J_1}} \right){{\ddot q}_2} + m'{l^2} \cdot \\\qquad \left[ {12{{\ddot q}_1}\cos \left( {{q_1} - {q_2}} \right) - 12\dot q_1^2\sin \left( {{q_1} - {q_2}} \right)} \right] + \\\qquad 4{\mu _1}{l^2}\left[ {{{\dot q}_1} + {{\dot q}_2}\cos \left( {{q_1} - {q_2}} \right)} \right] = \lambda \cos \left( {{q_2} - {q_3}} \right)\\ 4\left( { - m'{l^2} + {J_1}} \right){{\ddot q}_3} + 2\left( {{\mu _2} - {\mu _1}{l^2}} \right){{\dot q}_3} = \lambda \\ - 2{{\dot q}_{\rm{4}}}{{\dot q}_{\rm{6}}} + \left( {a\cot \alpha - {q_{\rm{6}}}} \right){{\ddot q}_{\rm{4}}} = 0\\ J{{\ddot q}_{\rm{5}}} = 0\\ {{\ddot q}_{\rm{6}}}{\sec ^2}\alpha + \left( {a\cot \alpha - {q_{\rm{6}}}} \right)\dot q_{\rm{4}}^2{\tan ^2}\alpha +\\ \qquad {\dfrac{{m + 12m'}}{m}} g = 0 \end{array} \right\} $$ (43) 式(43)是非保守非完整爬壁机器人系统在圆锥壁面上的Routh方程. 但如果直接对式(43)求Lagrang乘子
$ \lambda $ 是非常复杂的. 为了简便起见, 现假设在圆锥面上爬壁机器人单支腿任意两个广义坐标中有如下关系$$ \cos \left( {{q_i} - {q_j}} \right) \approx 1 ,\;\;\sin \left( {{q_i} - {q_j}} \right) \approx 0\;\left( {i,j = 1,2,3};\;{i \ne j} \right) $$ (44) 此时非保守非完整爬壁机器人系统在圆锥壁面上的Routh方程(43)可化简为
$$ \left( {18m'{l^2}{\text{ + 2}}{J_1}} \right){\ddot q_1} + 12m'{l^2}{\ddot q_2} + {\text{4}}{\mu _1}{l^2}\left( {{{\dot q}_1} + {{\dot q}_2}} \right) = \lambda $$ (45) $$ 12m'{l^2}{\ddot q_1} + \left( {10m'{l^2}{\text{ + 2}}{J_1}} \right){\ddot q_2} + {\text{4}}{\mu _1}{l^2}\left( {{{\dot q}_{\text{1}}} + {{\dot q}_{\text{2}}}} \right) = \lambda $$ (46) $$ {\text{4}}\left( {{J_1} - m'{l^2}} \right){\ddot q_3} + {\text{2}}\left( {{\mu _2} - {\mu _1}{l^2}} \right){\dot q_3} = \lambda $$ (47) $$ - 2{\dot q_{\text{4}}}{\dot q_{\text{6}}} + \left( {a\cot \alpha - {q_{\text{6}}}} \right){\ddot q_{\text{4}}} = 0 $$ (48) $$ J{\ddot q_{\text{5}}} = 0 $$ (49) $$ {\ddot q_{\text{6}}}{\sec ^2}\alpha + \left( {a\cot \alpha - {q_{\text{6}}}} \right)\dot q_{\text{4}}^2{\tan ^2}\alpha + {\frac{{m + 12m'}}{m}} g = 0 $$ (50) 式(45) ~ 式(50)便是化简后非保守非完整爬壁机器人系统在圆锥壁面上的Routh方程.
由式(45) ~ 式(47)解出Lagrange乘子
$ \lambda $ 即$$ \lambda = \frac{{ {32{\mu _1}{l^2}\left( {{{\dot q}_1} + {{\dot q}_2}} \right)\left( {J_1^2 - {{m'}^2}{l^4}} \right) + 2{{\dot q}_3}\left( {{\mu _2} - {\mu _1}{l^2}} \right)\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^{\text{2}}}{l^4}} \right)} }}{{14{J_1}m'{l^2} + 9J_1^2 + {{m'}^2}{l^4}}} $$ (51) 将乘子(51)代入到方程式(45) ~ 式(47), 即可得到非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Lagrange方程
$$ \begin{split}& \left( {9m'{l^2} + {J_1}} \right){{\ddot q}_1} + 6m'{l^2}{{\ddot q}_2} + \left[ {2{\mu _1}{l^2} - 16A{\mu _1}{l^2}\left( {J_1^2 - {{m'}^2}{l^4}} \right)} \right]\cdot \\& \qquad \left( {{{\dot q}_1} + {{\dot q}_2}} \right) = A\left( {{\mu _2} - {\mu _1}{l^2}} \right)\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^{\text{2}}}{l^4}} \right){{\dot q}_3} \end{split} $$ (52) $$ \begin{split}& 6m'{l^2}{{\ddot q}_1} + \left( {5m'{l^2} + {J_1}} \right){{\ddot q}_2} + \left[ {2{\mu _1}{l^2} - 16A{\mu _1}{l^2}\left( {J_1^2 - {{m'}^2}{l^4}} \right)} \right] \cdot\\& \qquad \left( {{{\dot q}_1} + {{\dot q}_2}} \right) = A\left( {{\mu _2} - {\mu _1}{l^2}} \right)\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^{\text{2}}}{l^4}} \right){{\dot q}_3} \end{split} $$ (53) $$ \begin{split}& 2\left( {{J_1} - m{l^2}} \right){{\ddot q}_3} + \left( {{\mu _2} - {\mu _1}{l^2}} \right)\left[ {1 - A\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^{\text{2}}}{l^4}} \right)} \right]\cdot \\& \qquad{{\dot q}_3} = 16A{\mu _1}{l^2}\left( {J_1^2 - {{m'}^2}{l^4}} \right)\left( {{{\dot q}_1} + {{\dot q}_2}} \right) \end{split} $$ (54) $$ - 2{\dot q_{\text{4}}}{\dot q_{\text{6}}} + \left( {a\cot \alpha - {q_{\text{6}}}} \right){\ddot q_{\text{4}}} = 0$$ (55) $$ J{\ddot q_{\text{5}}} = 0 $$ (56) $$ {\ddot q_{\text{6}}}{\sec ^2}\alpha + \left( {a\cot \alpha - {q_{\text{6}}}} \right)\dot q_{\text{4}}^2{\tan ^2}\alpha + {\frac{{m + 12m'}}{m}}g = 0 $$ (57) 其中
$A = \dfrac{1}{{14{J_1}m'{l^2} + 9 J_1^2 + {{m'}^2}{l^4}}}$ .5.2 爬壁机器人的Noether等式和Noether守恒量
将式(10)、式(16)、式(19)和式(51)代入式(39), 并由假设(44)得到非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Noether恒等式为
$$ \begin{split}& - m\left[ {\left( {a\cot \alpha - {q_6}} \right)\dot q_4^2{{\tan }^2}\alpha + {\frac{{m + 12m'}}{m}} g} \right]{\xi _6} + \\&\qquad 4\left[ {\left( {9m'{l^2} + {J_{\rm{1}}}} \right){{\dot q}_1} + 6m'{l^2}{{\dot q}_2}} \right]{{\dot \xi }_1} + \\&\qquad 4\left[ {6m'{l^2}{{\dot q}_1} + \left( {5m'{l^2} + {J_{\rm{1}}}} \right){{\dot q}_2}} \right]{{\dot \xi }_2} + \\&\qquad 4\left( {{J_{\rm{1}}} - m'{l^2}} \right){{\dot q}_3}{{\dot \xi }_3} + m{\left( {a\cot \alpha - {q_6}} \right)^2} \cdot \\&\qquad {{\dot q}_4} {{\dot \xi }_4}{\tan ^2}\alpha + J{{\dot q}_5}{{\dot \xi }_5} + m{{\dot q}_6} {{\dot \xi }_6}{\sec ^2}\alpha - \Big\{2m'{l^2} \cdot \\&\qquad \left( {9\dot q_1^2 + 5\dot q_2^2 - \dot q_3^2 + 12{{\dot q}_1}{{\dot q}_2}} \right) + 2{J_{\rm{1}}}\left( {\dot q_1^2 + \dot q_2^2 + \dot q_3^2} \right) + \frac{1}{2}J\dot q_{\rm{5}}^2 + \\&\qquad \frac{1}{2}m\left[ {{{\left( {a\cot \alpha - {q_{\rm{6}}}} \right)}^2}{{\dot q}^2}_{\rm{4}}{{\tan }^2}\alpha + \dot q_{\rm{6}}^2{{\sec }^2}\alpha } \right] - \\&\qquad \left( {m + 12m'} \right)g{q_{\rm{6}}}\Big\} {{\dot \xi }_0} + A\left( {{\xi _3} - {{\dot q}_3}{\xi _0}} \right)\left[ - 2\left( {{\mu _2} - {\mu _1}{l^2}} \right){{\dot q}_3} \cdot \right.\\&\qquad \left( {14{J_1}m'{l^{\rm{2}}} + 9J_1^2 + {{m'}^2}{l^{\rm{4}}}} \right) + 32{\mu _1}{l^2}\left( {{{\dot q}_1} + {{\dot q}_2}} \right)\left( {J_1^2 - {{m'}^2}{l^4}} \right) + \\&\qquad \left.2{{\dot q}_3}\left( {{\mu _2} - {\mu _1}{l^2}} \right) \left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^{\rm{2}}}{l^4}} \right)\right] + 2A\left( {{\xi _1} - {{\dot q}_1}{\xi _0}} +\right.\\&\qquad {{\xi _2} - {{\dot q}_2}{\xi _0}} ) \Big[ - 4{\mu _1}{l^2}\left( {{{\dot q}_1} + {{\dot q}_2}} \right)\left( {14{J_1}m'{l^{\rm{2}}} + 9J_1^2 + {{m'}^2}{l^{\rm{4}}}} \right)+\\&\qquad 32{\mu _1}{l^2}\left( {{{\dot q}_1} + {{\dot q}_2}} \right)\left( {J_1^2 - {{m'}^2}{l^4}} \right) + 2{{\dot q}_3}\left( {{\mu _2} - {\mu _1}{l^2}} \right) \cdot \\&\qquad \left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^{\rm{2}}}{l^4}} \right)\Big] = - \dot G \end{split}$$ (58) 取无限小变换生成元和规范函数为
$$ \left. \begin{array}{l} {\xi }_{\text{1}}=1,\;\;{\xi }_{0}={\xi }_{2}={\xi }_{3}={\xi }_{4}={\xi }_{5}={\xi }_{6}=0\text{ }\\ G=8{\mu }_{1}{l}^{2}\left[1-8A\left({J}_{1}^{2}-{{m}^{\prime }}^{2}{l}^{4}\right)\right]\left({q}_{1} + {q}_{2}\right)-\\ \qquad 4A\left({\mu }_{2}-{\mu }_{1}{l}^{2}\right)\left(14{J}_{1}{m}^{\prime }{l}^{2} + {J}_{1}^{2} + 9{{m}^{\prime }}^{2}{l}^{4}\right){q}_{3} \end{array} \right\}$$ (59) $$ \left. \begin{array}{l} {\xi }_{\text{2}}=1,\;\;{\xi }_{0}={\xi }_{\text{1}}={\xi }_{3}={\xi }_{4}={\xi }_{5}={\xi }_{6}=0\text{ }\\ G=8{\mu }_{1}{l}^{2}\left[1-8A\left({J}_{1}^{2}-{{m}^{\prime }}^{2}{l}^{4}\right)\right]\left({q}_{1} + {q}_{2}\right)-\\ \qquad 4A\left({\mu }_{2}-{\mu }_{1}{l}^{2}\right)\left(14{J}_{1}{m}^{\prime }{l}^{2} + {J}_{1}^{2} + 9{{m}^{\prime }}^{2}{l}^{4}\right){q}_{3} \end{array} \right\}$$ (60) $$ \left. \begin{array}{l} {\xi }_{\text{3}}=1,\;\;{\xi }_{0}={\xi }_{\text{1}}={\xi }_{\text{2}}={\xi }_{4}={\xi }_{5}={\xi }_{6}=0\text{ }\\ G=-32A{\mu }_{1}{l}^{2}\left({J}_{1}^{2}-{{m}^{\prime }}^{2}{l}^{4}\right)\left({q}_{1} + {q}_{2}\right)-\\\qquad 2\left({\mu }_{2}-{\mu }_{1}{l}^{2}\right)\Big[A\Big(14{J}_{1}{m}^{\prime }{l}^{2} + {J}_{1}^{2} +\Big.\Big.\\ \Big.\Big. \qquad 9{{m}^{\prime }}^{2}{l}^{4}\Big)-1\Big]{q}_{3} \end{array} \right\}$$ (61) $$ {\xi _{\text{4}}} = 1,{\xi _{\text{1}}} = {\xi _{\text{2}}} = {\xi _3} = {\xi _{\text{5}}} = {\xi _{\text{6}}} = {\xi _0} = 0,G = {\text{const}}. $$ (62) $$ {\xi _5}{\text{ = }}t,{\xi _0} = {\xi _{\text{1}}} = {\xi _{\text{2}}} = {\xi _3} = {\xi _4} = {\xi _{\text{6}}} = 0,G = - J{q_{\text{5}}} $$ (63) $$ \left. \begin{array}{l} {\xi _{\text{6}}} = {\dot q_{\text{6}}},\;\;{\xi _{\text{1}}} = {\xi _{\text{2}}} = {\xi _3} = {\xi _{\text{4}}} = {\xi _{\text{5}}} = {\xi _0} = 0\\ G = - \left( {m + {\text{2}}m'} \right)\dot q_{\text{6}}^{\text{2}}{\sec ^2}\alpha \end{array} \right\}$$ (64) 以上得到的生成元和规范函数是对应于非保守非完整爬壁机器人系统相应非保守完整圆锥壁面上爬壁机器人系统的广义准对称变换.
将无限小变换式(59) ~ 式(64)分别代入到式(41)和式(42)中. 其中无限小变换式(59) ~ 式(61)不满足式(41)及式(42), 无限小变换式(62) ~ 式(64)满足式(41). 因此无限小变换式(62) ~ 式(64)对应非保守非完整爬壁机器人系统的强广义准对称变换.
对无限小变换式(59) ~ 式(61), 由Noether定理3的守恒量(40)分别给出为
$$ \begin{split}& {I_1} = \left( {9m'{l^2} + {J_1}} \right){{\dot q}_1} + 6m'{l^2}{{\dot q}_2}{{ + 2}}{\mu _1}{l^2}\left[ {1 - 8A\left( {J_1^2 - {{m'}^2}{l^4}} \right)} \right] \cdot \\&\qquad\left( {{q_1} + {q_2}} \right) - A\left( {{\mu _2} - {\mu _1}{l^2}} \right)\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right) \cdot \\&\qquad{q_3} = {c_1} \end{split} $$ (65) $$ \begin{split}& {I_2} = 6m'{l^2}{{\dot q}_1} + \left( {{\text{5}}m'{l^2} + {J_1}} \right){{\dot q}_2}{{ + 2}}{\mu _1}{l^2}\left[ {1 - 8A\left( {J_1^2 - {{m'}^2}{l^4}} \right)} \right] \cdot \\&\qquad \left( {{q_1} + {q_2}} \right) \hfill - A\left( {{\mu _2} - {\mu _1}{l^2}} \right)\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right)\cdot\\&\qquad {q_3} = {c_2} \end{split} $$ (66) $$ \begin{split}& {I_{\text{3}}} = 2\left( {{J_1} - m'{l^2}} \right){{\dot q}_3} - 16A{\mu _1}{l^2}\left( {J_1^2 - {{m'}^2}{l^4}} \right)\left( {{q_1} + {q_2}} \right)+ \hfill \\& \qquad \left( {{\mu _2} - {\mu _1}{l^2}} \right)\left[ {1 - A\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right)} \right]{q_3} = {c_3} \end{split} $$ (67) 对无限小变换式(62) ~ 式(64), 由Noether定理4的守恒量(40)分别给出为
$$ {I_4} = m{\left( {a\cot \alpha - {q_6}} \right)^2}{\dot q_4}{\tan ^2}\alpha = {c_4}$$ (68) $$ {I_5} = J{\dot q_5}t - J{q_5} = {c_5} $$ (69) $$ {I_6} = 0 $$ (70) 显然, 守恒量
$ {I_6} $ 是平庸的. 其中守恒量$ {I}_{1}, {I}_{2},\cdots, {I}_{5} $ 是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Noether守恒量.$ {I_4},{I_5} $ 是非保守非完整爬壁机器人系统的Noether守恒量.下面验证
$ {I_1},{I_2}, \cdots ,{I_5} $ 的守恒性. 式(65)对时间求导得$$ \begin{split}& {{\dot I}_1} = m'{l^2}\left( {9{{\ddot q}_1} + 6{{\ddot q}_2}} \right) + {J_1}{{\ddot q}_1} + 2{\mu _1}{l^2}\left[ {1 - 8A\left( {J_1^2 - {{m'}^2}{l^4}} \right)} \right]\cdot\\&\qquad \left( {{{\dot q}_1} + {{\dot q}_2}} \right) - A\left( {{\mu _2} - {\mu _1}{l^2}} \right)\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right){{\dot q}_3} = \\&\qquad \left( {9m'{l^2} + {J_1}} \right){{\ddot q}_1} + 6m'{l^2}{{\ddot q}_2} + \left[2{\mu _1}{l^2} - 16{\mu _1}{l^2}A \cdot \right.\\&\qquad \left. \left( {J_1^2 - {{m'}^2}{l^4}} \right)\right]\left( {{{\dot q}_1} + {{\dot q}_2}} \right) - A\left( {{\mu _2} - {\mu _1}{l^2}} \right) \cdot \\&\qquad \left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right){{\dot q}_3} \end{split} $$ (71) 由式(52)得
$$ {\dot I_1} = 0 $$ (72) 即
$ {I_1} $ 是一个守恒量.将式(66)对时间求导得
$$ \begin{split}& {{\dot I}_2} = m'{l^2}\left( {{\rm{6}}{{\ddot q}_1} + {\rm{5}}{{\ddot q}_2}} \right) + {J_1}{{\ddot q}_{\rm{2}}}{\rm{ + 2}}{\mu _1}{l^2}\left[ {1 - 8A\left( {J_1^2 - {{m'}^2}{l^4}} \right)} \right] \cdot \\&\qquad \left( {{{\dot q}_1} + {{\dot q}_2}} \right) - A\left( {{\mu _2} - {\mu _1}{l^2}} \right)\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right){{\dot q}_3} = \\& \qquad 6m'{l^2}{{\ddot q}_1} + \left( {5m'{l^2} + {J_1}} \right){{\ddot q}_{\rm{2}}} + \left[{\rm{2}}{\mu _1}{l^2} - 16A{\mu _1}{l^2} \cdot \right.\\&\qquad\left. \left( {J_1^2 - {{m'}^2}{l^4}} \right)\right] \left( {{{\dot q}_1} + {{\dot q}_2}} \right) - A\left( {{\mu _2} - {\mu _1}{l^2}} \right) \cdot \\&\qquad \left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right){{\dot q}_3} \end{split} $$ (73) 由式(53)得
$$ {\dot I_2} = 0 $$ (74) 即
$ {I_2} $ 是一个守恒量.将式(67)对时间求导得
$$ \begin{split}& {{\dot I}_{\rm{3}}} = 2\left( {{J_1} - m'{l^2}} \right){{\ddot q}_3} - 16A{\mu _1}{l^2}\left( {J_1^2 - {{m'}^2}{l^4}} \right) \cdot \\&\qquad \left( {{{\dot q}_1} + {{\dot q}_2}} \right) + \left( {{\mu _2} - {\mu _1}{l^2}} \right)\left[ {1 - A\left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right)} \right]{{\dot q}_3} = \\&\qquad 2\left( {{J_1} - m'{l^2}} \right){{\ddot q}_3} + \left( {{\mu _2} - {\mu _1}{l^2}} \right)\Big[1 - A \cdot \Big.\\&\qquad \Big. \left( {14{J_1}m'{l^2} + J_1^2 + 9{{m'}^2}{l^4}} \right)\Big]{{\dot q}_3} - \\&\qquad 16A{\mu _1}{l^2}\left( {J_1^2 - {{m'}^2}{l^4}} \right)\left( {{{\dot q}_1} + {{\dot q}_2}} \right) \end{split} $$ (75) 由式(54)得
$$ {\dot I_3} = 0 $$ (76) 即
$ {I_3} $ 是一个守恒量.将式(68)对时间求导得
$$ {\dot I_4} = m\left( {a\cot \alpha - {q_6}} \right){\tan ^2}\alpha \left[ { - 2{{\dot q}_4}{{\dot q}_6}{\text{ + }}\left( {a\cot \alpha - {q_6}} \right){{\ddot q}_4}} \right] $$ (77) 由式(55)得
$$ {\dot I_4} = 0$$ (78) 即
$ {I_4} $ 是一个守恒量.将式(69)对时间求导得
$$ {\dot I_5} = J{\ddot q_5}t $$ (79) 由式(56)得
$$ {\dot I_5} = 0 $$ (80) 即
$ {I_5} $ 是一个守恒量.可见式(65) ~ 式(67)是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Noether守恒量. 式(68) ~ 式(70)是非保守非完整爬壁机器人系统的Noether守恒量.
5.3 圆锥壁面上爬壁机器人机身的运动规律
利用非保守非完整爬壁机器人的守恒量(68)和(69), 可以得出非保守非完整爬壁机器人系统在圆锥壁面上机身的运动规律.
对Noether守恒量(69)积分可得
$$ {q_5} = ct - \frac{{{c_5}}}{J} = ct + {c_6},\;\;\;\;{c_6} = - \frac{{{c_5}}}{J} $$ (81) 其中,
$ {c_5} $ 为Noether守恒量(69)的常数,$ c $ 为不定积分常量. 由上式可以看出, 爬壁机器人在圆锥壁面上机身的旋转角与时间成正比.由式(68)得
$$ {\dot q_4} = \frac{{{c_4}}}{{m{{\left( {a\cot \alpha - {q_6}} \right)}^2}{{\tan }^2}\alpha }} $$ (82) 其中,
$ {c_4} $ 为Noether守恒量(68)中的常数. 将式(82)代入到式(57)中得$$ {\ddot q_6}{\sec ^2}\alpha + \frac{{c_4^2}}{{{m^2} {{\left( {a\cot \alpha - {q_6}} \right)}^3}{{\tan }^2}\alpha}} + {\frac{{m + 12m'}}{m}} g = 0 $$ (83) $$ {\ddot q_6}{\sec ^2}\alpha + \frac{{c_4^2}}{{{a^3}{m^2}\cot \alpha {{\left( {1 - \dfrac{{{q_6}}}{{a\cot \alpha }}} \right)}^3}}} + {\frac{{m + 12m'}}{m}} g = 0 $$ (84) 其中
$$ \frac{{{q_6}}}{{a\cot \alpha }} = \frac{{{q_6}}}{a} \frac{{a - b}}{h} = \frac{{{q_6}}}{h}\frac{{a - b}}{a} = \frac{{{q_6}}}{h}\left( {1 - \frac{b}{a}} \right) $$ (85) 因为
$ \dfrac{{{q_6}}}{h} < 1 $ 且$ \dfrac{b}{a} < 1,1 - \dfrac{b}{a} < 1 $ , 所以$ \dfrac{{{q_6}}}{h}\left( {1 - \dfrac{b}{a}} \right) < 1 $ . 因此$ \dfrac{{{q_6}}}{{a\cot \alpha }} < 1 $ .对式(84)利用泰勒公式展开同时精确到一阶无穷小量可以得到
$$ {\ddot q_6} + \frac{{c_4^2{{\cos }^2}\alpha }}{{{m^2}{a^3}\cot \alpha }}\left( {1 + \frac{{3{q_6}}}{{a\cot \alpha }}} \right) + {\frac{{m + 12m'}}{m}} g{\cos ^2}\alpha = 0 $$ (86) $$ {\ddot q_6} + \frac{{3c_4^2{{\cos }^2}\alpha }}{{{m^2}{a^4}{{\cot }^2}\alpha }}{q_6} = - \left( {\frac{{c_4^2{{\cos }^2}\alpha }}{{{m^2}{a^3}\cot \alpha }} + {\frac{{m + 12m'}}{m}} g{{\cos }^2}\alpha } \right)$$ (87) 求解式(87)得
$$ {q_6} = {c_7}\cos (\omega t) + {c_8}\sin( \omega t) + {c_9} $$ (88) 其中
$\omega = \dfrac{{\sqrt 3 {c_4}\sin \alpha }}{{m{a^2}}},{c_9} = - \dfrac{{g{a^4} m\left( {m + 12 m'} \right){{\cot }^2}\alpha}}{{3 c_3^2}} - \dfrac{{a\cot \alpha }}{3}$ 为常数.假设非保守非完整爬壁机器人在
$ t = 0 $ 时以初速度$ v $ 沿着壁面从底部向上爬行. 即$ t = 0 $ 时,${q_6} = 0, {\dot q_6} = v\cos \alpha$ 根据初始条件可得$$\left.\begin{array}{l} {c_7} = - {c_9} = \dfrac{{m\left( {m + 12m'} \right)g{a^4}{{\cot }^2}\alpha }}{{3c_4^2}} + \dfrac{{a\cot \alpha }}{3}\\ {c_8} = \dfrac{{mv{a^2}}}{{\sqrt 3 {c_4}}}\cot \alpha \end{array}\right\}$$ (89) 为分析运动规律将式(88)化简得
$$ {q_6} = A\sin \left( {\omega {\kern 1pt} {\kern 1pt} t + \varphi } \right) + {c_9} $$ (90) 其中
$A = \sqrt {c_7^2 + c_8^2}, \;\;\sin \varphi = \dfrac{{{c_7}}}{A},\cos \varphi = \dfrac{{{c_8}}}{A}$ 为常数.同样利用泰勒公式展开式(83)得
$$ {\dot q_4} = \frac{{{c_4}}}{{m{a^2}}}\left( {1 + \frac{{2{q_6}}}{{a\cot \alpha }}} \right) $$ (91) 将式(90)代入到式(91)可得
$$ {\dot q_4} = {A_1}\sin \left( {\omega {\kern 1pt} {\kern 1pt} {\kern 1pt} t + \varphi } \right){\text{ + }}{c_{10}} $$ (92) 其中
$ {c_{10}} = \dfrac{{{c_4}a\cot \alpha + 2{c_4}{c_9}}}{{{a^3}m\cot \alpha }},{A_1} = \dfrac{{2 A{c_4}}}{{m{a^3}\cot \alpha }} $ 为常数.对式(92)积分可得
$$ {q_4} = {c_{10}}t - {A_2}\cos \left( {\omega {\kern 1pt} {\kern 1pt} t + \varphi } \right) $$ (93) 其中
${A_2} = \dfrac{{2 A}}{{\sqrt 3 a\cos \alpha }}$ 为常数.从式(90)可以看到非保守非完整爬壁机器人在爬壁过程中高度
$ {q_6} $ 和初始速度$ v $ , 爬壁机器人总体的重量, 圆锥壁面的顶角以及底面圆的半径有关. 并且该式的周期为$T = \dfrac{{2\text{π} {a^2}m}}{{\sqrt 3 {c_4}\sin \alpha }}$ , 一般情况下, 爬壁机器人机身的重量是非常大的, 并且圆锥壁面$ \alpha $ 角一般来说比较小, 即$ T $ 是一个非常大的数, 不妨假设爬壁机器人在爬壁过程中在$ {T}/{4} $ 时间内就足以爬到顶峰. 这个结论说明, 爬壁机器人在爬壁过程中的高度随时间呈非线性递增.从式(93)可以看出非保守非完整爬壁机器人在爬壁过程中, 非保守非完整爬壁机器人在底面投影与原点距离的连线与坐标系
$ x $ 轴之间的夹角$ {q_4} $ 和时间之间呈非线性关系.5.4 圆锥壁面上爬壁机器人四肢运动规律
利用非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的守恒量(65) ~ (67), 便可以得出非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统在圆锥壁面上四肢的运动规律.
为方便研究非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统在圆锥壁面上的四肢运动规律, 将爬壁机器人系统四肢的各个关节看成是细直杆. 由细直杆的转动惯量[62]可以得知各关节中心位置的转动惯量为
$$ {J_1} = \frac{{m'{l^2}}}{3} $$ (94) 将式(94)代入式(65)~式(67)得
$$ m'{l^2}\left( {\frac{{28}}{3}{{\dot q}_1} + 6{{\dot q}_2}} \right) + \frac{{31}}{{15}}\left[ {2{\mu _1}{l^2}\left( {{q_1} + {q_2}} \right) - \left( {{\mu _2} - {\mu _1}{l^2}} \right){q_3}} \right] = {c_1} $$ (95) $$ m'{l^2}\left( {{\text{6}}{{\dot q}_1} + \frac{{16}}{3}{{\dot q}_2}} \right) + \frac{{31}}{{15}}\left[ {2{\mu _1}{l^2}\left( {{q_1} + {q_2}} \right) - \left( {{\mu _2} - {\mu _1}{l^2}} \right){q_3}} \right] = {c_2} $$ (96) $$ { - \frac{{4m'{l^2}}}{3}}{\dot q_3} + \frac{{32}}{{15}}{\mu _1}{l^2}\left( {{q_1} + {q_2}} \right) - \frac{{47}}{{15}}\left( {{\mu _2} - {\mu _1}{l^2}} \right){q_3} = {c_3} $$ (97) 通过查阅相关文献[35], 同时考虑到计算的简便可设相应参数的值为
$$ {\mu _1} = 0.5,\;\;\;{\mu _2} = 0.5,\;\;\;m' = 6g,\;\;\;l = 6 $$ (98) 同时假设式(65) ~ 式(67)中守恒量的常数为
$$ {c_1} = {c_2} = {c_3} = 1 $$ (99) 将式(98)和式(99)代入到式(95) ~ 式(97)后可得
$$\left. \begin{array}{l} 2016{{\dot q}_1} + 432{{\dot q}_2} + \dfrac{{372}}{5}\left( {{q_1} + {q_2}} \right) + \dfrac{{217}}{6}{q_3} = 1 \hfill \\ 1296{{\dot q}_1} + 1152{{\dot q}_2} + \dfrac{{372}}{5}\left( {{q_1} + {q_2}} \right) + \dfrac{{217}}{6}{q_3} = 1 \hfill \\ - 288{{\dot q}_3} + \dfrac{{192}}{5}\left( {{q_1} + {q_2}} \right) + \dfrac{{329}}{6}{q_3} = 1 \end{array} \right\}$$ (100) 假设初始状态下
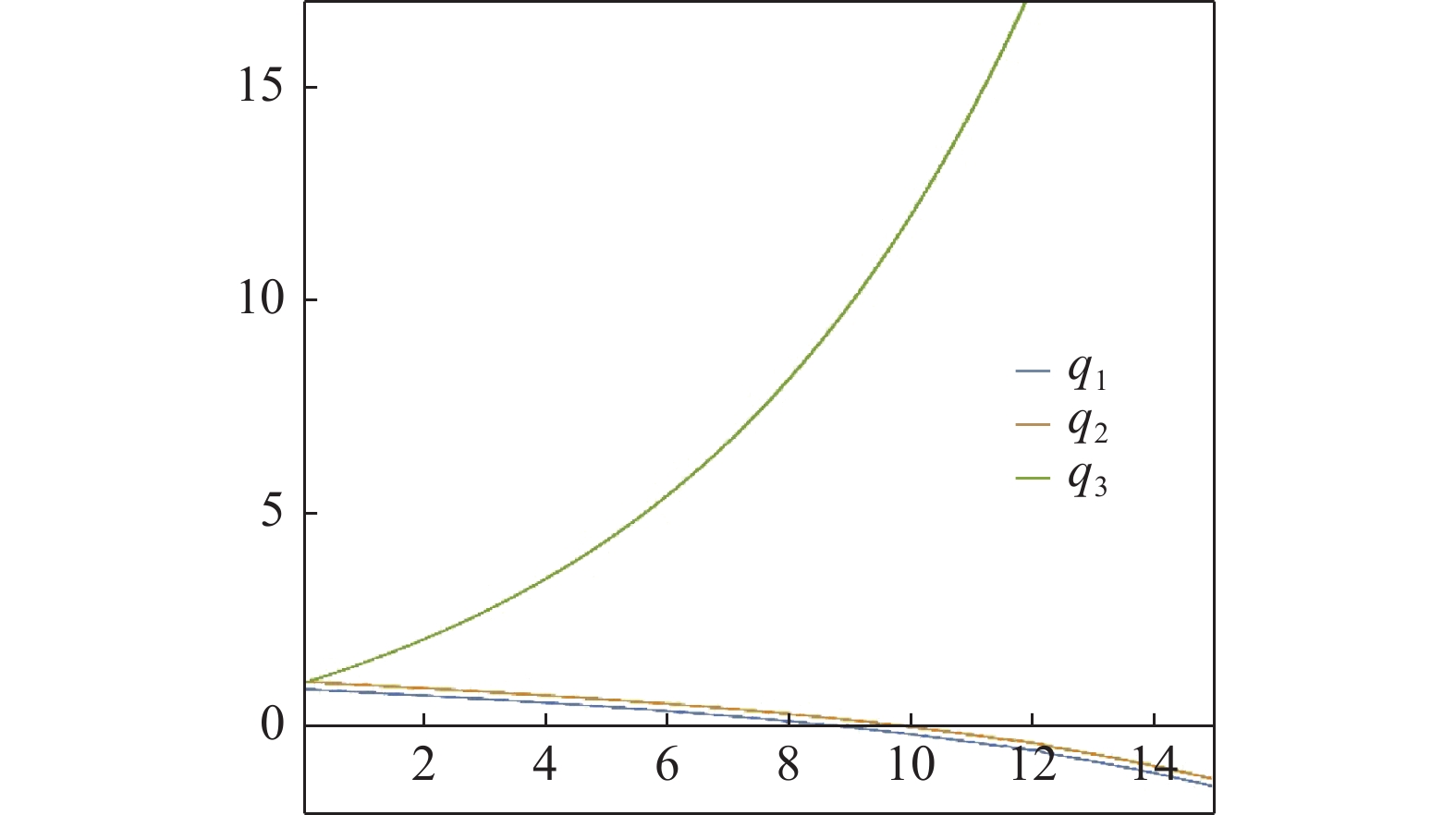
$$ {q_1} = 0.87,\;\;\;{q_2} = 1.04,\;\;\;{q_3} = 1.00 $$ (101) 可以得到图5所示的数值解.
通过图5可以得出在运动过程中随着时间的增加, 非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的股骨, 胫骨与铅垂线的夹角
$ {q_1} $ 和${q_2} $ 越来越小并单调递减. 这里负值表示爬壁机器人的各关节与铅垂线顺时针方向的夹角. 因此单看广义坐标$ {q_1} $ 和${q_2} $ 夹角的度数来说是先减少后增加, 即爬壁机器人在爬壁过程中的股骨和胫骨是左右摆动的.最后, 非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统中脚掌与铅垂线的夹角呈单调递增. 并且通过图像发现, 广义坐标
$ {q_3} $ 的夹角的增长速度呈现指数上升的趋势. 这也就说明爬壁机器人在爬壁过程中, 其脚掌的灵活性要比股骨和胫骨的灵活性高, 同时表现出爬壁机器人在爬壁过程中的四肢各个关节中, 脚掌的作用力起着重要作用. 这也与文献[43]中壁虎四肢的运动规律一致.6. 结论
综合本文的研究, 给出如下结论.
(1) 对爬壁机器人这一复杂的动力学系统, 本文基于其动能和势能构建了Lagrange函数, 选择恰当的广义坐标, 建立了系统的Lagrange方程; 引入Lie群方法, 基于爬壁机器人系统的Hamilton作用量在变换Lie群下的不变性, 建立了系统的Noether对称性理论, 找到了系统存在的一系列守恒量; 基于给出的守恒量进行了详细的求解, 给出了爬壁机器人系统机身的精确解和四肢的数值解, 发现了在圆锥壁面上爬壁机器人的运动规律.
(2) 爬壁机器人是一个多体非完整约束系统, 采用的Lagrange力学方法比牛顿力学方法优势明显, 方法简介: 首次将Lie群分析方法用于复杂的爬壁机器人系统, 建立了Noether对称性理论, 发现了该系统在运动过程中存在的守恒量, 为Lie群分析方法应用于其他机器人系统奠定了基础; 通过利用爬壁机器人系统存在的守恒量, 给出了系统的精确解和数值解, 为约束力学系统的Noether对称性理论应用于其他机器人系统展示了美好前景.
(3) 提出爬壁机器人系统的Routh方程, 求出Lagrange乘子(51), 建立了圆锥曲面上爬壁机器人系统的Lagrange方程(52) ~ (57).
(4) 系统建立了爬壁机器人系统的Noether对称性理论. 定义爬壁机器人系统的Hamilton作用量, 给出了Hamilton作用量的基本变分公式(28)和(30); 引入关于爬壁机器人系统的广义坐标和时间的无限小变换(Lie群变换), 基于Hamilton作用量在变换Lie群下的不变性, 提出了完整爬壁机器人系统的Noether定理1和Noether定理2, 在此基础上提出了非保守非完整爬壁机器人系统相应于非保守完整爬壁机器人系统的Noether定理3和Noether定理4, 同时提出了非保守非完整爬壁机器人系统的Noether定理5和Noether定理6; 基于给出的Noether定理, 求出圆锥面上爬壁机器人的Noether恒等式(58)和一系列对称性的变换Lie群(59) ~ (64); 发现了圆锥面上爬壁机器人存在的守恒量
$ {I_1},{I_2}, \cdots ,{I_6} $ .(5) 基于给出的守恒量
$ {I_1},{I_2}, \cdots ,{I_6} $ , 给出了圆锥曲面上爬壁机器人机身运动的精确解(81)、(90)和(93)以及四肢在特定参数下运动的数值解(100), 即解图5. 发现了圆锥曲面上爬壁机器人在爬壁过程中的股骨和胫骨是左右摆动的, 其脚掌的灵活性要比股骨和胫骨的灵活性高, 同时表现出爬壁机器人在爬壁过程中的四肢各个关节中, 脚掌的作用力起着重要作用, 这个结论与壁虎爬壁过程中四肢运动规律结论一致.(6) 研究表明对于一般的爬壁机器人系统的Lagrange方程存在突出的非线性项, 要给出对称性的一般解(精确解)是困难的, 只能给出对称性的数值解.
(7) 本文基于爬壁机器人系统的Hamilton作用量在变换Lie群下的不变性建立了系统的Noether对称性理论, 接下来考虑爬壁机器人系统的Lagrange方程在变换Lie群下的不变性, 建立系统的Lie对称性理论, 并研究在相空间中爬壁机器人系统的Noether对称性理论和Lie对称性理论.
(8) 本文给出的方法可以推广应用于其他柔性机器人系统.
-
[1] Wang W, Ahn SH. Shape memory alloy-based soft gripper with variable stiffness for compliant and effective grasping. Soft Robotics, 2017, 4(4): 379-389 doi: 10.1089/soro.2016.0081
[2] 方五益, 郭晛, 黎亮等. 柔性铰柔性杆机器人动力学建模、仿真和控制. 力学学报, 2020, 52(4): 965-974 (Fang Wuyi, Guo Jian, Li Liang, Zhang DG. Dynamic modeling, simulation and control of flexible articulated flexible link robot. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(4): 965-974 (in Chinese) Fang Wuyi, Guo Jian, Li Liang, Zhang DG. Dynamic modeling, simulation and control of flexible articulated flexible link robot, Chinese Journal of Theoretical and Applied Mechanics, 2020, 52 (4): 965-974(in Chinese)
[3] Miriyev A, Stack K, Lipson H. Soft material for soft actuators. Nature Communications, 2017, 8(1): 1-8 doi: 10.1038/s41467-016-0009-6
[4] Valentin TM, Dubois EM, Machnicki CE, et al. 3D printed self-adhesive Pegda-paa hydrogels as modular components for soft actuators and microfluidics. Polymer Chemistry, 2019, 10(16): 2015-2028 doi: 10.1039/C9PY00211A
[5] Park J, Lee Y, Barbee MH, et al. A hierarchical nanoparticle-in-micropore architecture for enhanced mechanosensitivity and stretch ability in mechanochromic electronic skins. Advanced Materials, 2019, 31(25): 1-10
[6] Cangialosi A, Yoon CK, Liu J, et al. DNA sequence-directed shape change of photopatterned hydrogels via high-degree swelling. Science, 2017, 357(6356): 1126-1130 doi: 10.1126/science.aan3925
[7] Fei Y, Wang J, Pang W. A novel fabric-based versatile and stiffness-tunable soft gripper integrating soft pneumatic fingers and wrist. Soft Robotics, 2019, 6(1): 1-20 doi: 10.1089/soro.2018.0015
[8] Autumn K, Liang YA, Hsieh ST, et al. Adhesive force of a single gecko foot-hair. Nature, 2000, 405: 681-685 doi: 10.1038/35015073
[9] 程思敏, 陈韦宇, 丛培杰. 爬壁机器人的研究现状. 机电工程技术, 2019, 48(9): 6-10 (Cheng Simin, Chen Weiyu, Cong Peijie. Research status of wall climbing robot. Electromechanical Engineering Technology, 2019, 48(9): 6-10 (in Chinese) doi: 10.3969/j.issn.1009-9492.2019.09.003 Cheng Simin, Chen Weiyu, Cong Peijie. Research status of wall climbing robot, Electromechanical Engineering Technology, 2019, 48 (9): 6-10(in Chinese) doi: 10.3969/j.issn.1009-9492.2019.09.003
[10] 章旭君. 仿壁虎机器人的机构设计与仿真. [硕士论文]. 南京: 南京航空航天大学, 2005 Zhang Xujun. Mechanism design and simulation of gecko like robot. [Master's Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005 (in Chinese))
[11] Qian ZY, Zhao YZ, Fu Z, et al. Design and realization of a non-actuated glass-curtain wall-cleaning robot prototype with dual suction cups. International Journal of Advance Manufacturing Technology, 2006, 30(2): 147-155
[12] Sangbae K, Spenko M, Trujillo S, et al. Smooth vertical surface climbing with directional adhesion. IEEE Transaction on Robotic, 2008, 24(1): 65-74 doi: 10.1109/TRO.2007.909786
[13] Cutkosky MR, Sangbae K. Design and fabrication of multimaterial structures for bioinspired robots. Philosophical Transactions of the Royal Society, 2009, 367(13): 1799-1813
[14] Carlo M, Metin S. Gecko inspired surface climbing robots//IEEE Internation Conference on Robotics and Biomimetics. Shenyang, China. 2004: 618-619
[15] Daltorio KA, Wei TE, Gorb SN, et al. Passive foot design and contact area analysis for climbing mini-whegs//Proceedings of the IEEE International Conference on Robotics and Automation. Roma, Italy. 2007: 1274-1279
[16] Cepolina F, Michelini RC, Razzoli RP, et al. Gecko, a climbing robot for walls cleaning//Proceedings of the 1st International Workshop on Advances in Services Robotics. http://www.dimec.unige.it/PMAR/pages/down load/papers/zoppi11, 2003
[17] Zhao A, Mei T, et al. Fabrication and characterization of tree-like nanorod arrays for bionic gecko foot-hairs//Proceedings of 7th IEEE international Conference on Nanotechnology. Hongkong, China. 2007: 259-262
[18] 谈士力, 王建成, 苏建良等. 球面移动机器人机构研制. 机床与液压, 2003(2): 19-22 (Tan Shili, Wang Jiancheng, Su Jianliang, et al. Development of spherical mobile robot. Mechanism Machine Tools and Hydraulics, 2003(2): 19-22 (in Chinese) doi: 10.3969/j.issn.1001-3881.2003.02.008 Tan SL, Wang JC, Su JL, et al. Development of spherical mobile robot, mechanism Machine tools and hydraulics, 2003 (2): 19-2(in Chinese) doi: 10.3969/j.issn.1001-3881.2003.02.008
[19] 王巍, 宗光华. 气动擦窗机器人的控制和环境检测. 液压与气动, 2001, 1: 4-7 (Wang Wei, Zong Guanghua. Control and environment detection of pneumatic window cleaning robot. Hydraulic and Pneumatic, 2001, 1: 4-7 (in Chinese) doi: 10.3969/j.issn.1000-4858.2001.01.006 Wang W, Zong GH. Control and environment detection of pneumatic window cleaning robot, Hydraulic and pneumatic, 2001, 1: 4-7(in Chinese) doi: 10.3969/j.issn.1000-4858.2001.01.006
[20] 李冰. 柔性仿壁虎机器人的研究. [硕士论文]. 合肥: 中国科学技术大学, 2011 Li Bing. Research on flexible gecko like robot. [Master's Thesis]. Hefei: University of Science and Technology of China, 2011 (in Chinese)
[21] Guo C, Cai L, Xie HR, et al. The divisional and hierarchical innervations of gecko's toes to motion and reception. Chinese Science Bulletin, 2009, 54(16): 2880-2887
[22] Li HK, Dai ZD, Shi AJ, et al. Angular observation of joints of geckos moving on horizontal and vertical surfaces. Chinese Science Bulletin, 2009, 54(4): 592-598 doi: 10.1007/s11434-009-0077-7
[23] Liu JF, Xu LS, Xu JJ, et al. Analysis and optimization of the wall-climbing robot with an adsorption system and adhesive belts. International Journal of Advanced Robotic Systems, 2020, 17(3): 1-14
[24] Liu JF, Xu LS, Xu JJ, et al. Design, modeling and experimentation of a biomimetic wall-climbing robot for multiple surfaces. Journal of Bionic Engineering, 2020, 17(3): 523-538 doi: 10.1007/s42235-020-0042-3
[25] 邵洁. 基于壁虎形态仿生的爬壁机器人技术研究. [博士论文]. 北京: 北京理工大学, 2014 Shao Jie. Research on wall climbing robot technology based on gecko morphology bionics. [PhD thesis]. Beijing: Beijing University of Technology, 2014 (in Chinese)
[26] Bluman GW, Anco SC. Symmethy and Integration Methods for Differential Equations. New York: Springer-Verlag, 2002
[27] 梅凤翔. 李群李代数对约束力学系统的应用. 北京: 科学出版社, 1999 Mei Fengxiang. Application of Lie Group Lie Algebra to Constrained Mechanical System. Beijing: Science Press, 1999 (in Chinese)
[28] Noether E. Invariant variation problems. Transport Theory and Statistical Physics, 1971, 1(3): 186-207 doi: 10.1080/00411457108231446
[29] Candotti E. On the inversion of Noether’s theorem in classical dynamical systems. American Journal of Physics, 1972, 40(3): 424-429 doi: 10.1119/1.1986566
[30] Djukic DDS, Vujanovic BD. Noether's theory in classical nonconservative mechanic. Acta Mechanica, 1975, 23(1): 17-27
[31] 李子平. 约束系统的变换性质. 物理学报, 1981, 30(12): 1659-1671 (Li Ziping. Transformation properties of constrained systems. Actaf Physica Sinica, 1981, 30(12): 1659-1671 (in Chinese) doi: 10.3321/j.issn:1000-3290.1981.12.012 Li ZP. Transformation properties of constrained systems, Actaf physica Sinica, 1981, 30 (12): 1659-1671(in Chinese) doi: 10.3321/j.issn:1000-3290.1981.12.012
[32] Djukic DS, Sreauss AM. Noether’s theory for nonconservative generalised mechanical systems. Journal of Physics A: General Physics, 1980, 13(2): 431-435
[33] Djukic DS, Sutela T. Integrating factors and conservation laws for nonconservative dynamical systems. International Journal of Non-Linear Mechanics, 1984, 19(4): 331-339 doi: 10.1016/0020-7462(84)90061-1
[34] Mei FX. Exchange relations in nonholonomic systems mechanics. Mechanics in Engineering, 1979, 1(3): 37-38
[35] Mei FX. Stability of equilibrium for the autonomous Birkhoff system. Science Bulletin, 1993, 23(10): 816-819
[36] Mei FX. One type of integrals for the equations of motion of higher order nonholonomic systems. Applied Mathematics and Mechanics, 1991, 12(8): 799-806 doi: 10.1007/BF02458170
[37] Giachetta G. First integrals of nonholonomic systems and their generators. Journal of Physics A:General Physics, 2000, 33(30): 53-69
[38] Cai PP, Fu JL, Guo YX. Noether symmetries of the nonconservative and nonholonomic systems on time scales. Science China: Physics, Mechanics & Astronomy, 2013, 56(5): 1-12
[39] 梅凤翔. 关于Noether定理—分析力学札记之三十. 力学与实践, 2020, 42(1): 66-74 (Mei Fengxiang. About Noether's theorem−thirty notes on analytical mechanics. Mechanics and Practice, 2020, 42(1): 66-74 (in Chinese) doi: 10.6052/1000-0879-19-332 Mei FX. About Noether's theorem -- thirty notes on analytical mechanics, Mechanics and practice, 2020, 42 (1): 66-74(in Chinese) doi: 10.6052/1000-0879-19-332
[40] 李子平. 经典和量子约束系统及其对称性质. 北京: 北京工业大学出版社, 1993 Li Ziping. Classical and Quantum Constrained Systems and Their Symmetry Properties. Beijing: Beijing University of Technology Press,1993 (in Chinese)
[41] Fu JL, Chen BY, Fu H, et al. Velocity-dependent symmetries and non-Noether conserved quantities of electromechanical systems. Science China: Physics, Mechanics and Astronomy, 2011, 54(2): 288-295 doi: 10.1007/s11433-010-4173-0
[42] 傅景礼, 陈立群, 陈本永. 非规范格子离散机电耦合动力系统的 Noether 理论. 中国科学(G辑), 2010, 40(2): 133-145 (Fu Jingli, Chen Liqun, Chen Benyong. Noether theory of irregular lattice discrete electromechanical coupling dynamic system. Chinese Science (Series G) , 2010, 40(2): 133-145 (in Chinese) Fu JL, Chen LQ, Chen BY. Noether theory of irregular lattice discrete electromechanical coupling dynamic system, Chinese Science (Series G), 2010, 40 (2): 133-145(in Chinese)
[43] 王周义. 大壁虎斜面运动力学脚趾外翻脱附力学及其仿生研究. [博士论文]. 南京: 南京航空航天大学, 2015 Wang ZY. Kinematics of gecko's inclined plane, mechanics of toe valgus and desorption and its bionic research investigate. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015 (in Chinese)
[44] 赵跃宇, 梅凤翔. 关于力学系统的对称性和守恒量. 力学进展, 1993, 23(3): 360-372 (Zhao Yueyu, Mei Fengxiang. On the symmetry and conserved quantity of mechanical system. Mechanical Progress, 1993, 23(3): 360-372 (in Chinese) doi: 10.3321/j.issn:1000-0992.1993.03.010 Zhao YY, Mei FX. On the symmetry and conserved quantity of mechanical system, Mechanical Progress,1993, 23(3): 360-372(in Chinese) doi: 10.3321/j.issn:1000-0992.1993.03.010
[45] 赵跃宇. 非保守力学系统的Lie对称性和守恒量. 力学学报, 1994, 26(3): 380-384 (Zhao Yueyu. Lie symmetries and conserved quantities of nonconservative mechanical systems. Chinese Journal of Theoretical and Applied Mechanics, 1994, 26(3): 380-384 (in Chinese) Zhao Yueyu. Lie symmetries and conserved quantities of nonconservative mechanical systems, Chinese Journal of Theoretical and Applied Mechanics, 1994,26 (3): 380-38446.(in Chinese)
[46] Fu JL, Chen LQ, Yang XD. Lie symmetries and conserved quantities of controllable nonholonomic dynamical systems. Chinese Physics B, 2003, 12(7): 695-699 doi: 10.1088/1009-1963/12/7/301
[47] Fu JL, Chen LQ, Chen BY. Noether-type theory for discrete mechanico-electrical dynamical systems with nonregular lattices. Science China: Physics, Mechanics & Astronomy, 2010, 53(9): 1687-1698
[48] 张毅. Caputo导数下分数阶Birkhoff系统的准对称性与分数阶Noether定理. 力学学报, 2017, 49(3): 693-702 (Zhang Yi. Quasi symmetry and fractional Noether theorem of fractional Birkhoff system under Caputo derivative. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 693-702 (in Chinese) Zhang Y. Quasi symmetry and fractional Noether theorem of fractional Birkhoff system under Caputo derivative, Chinese journal of Theoretical and Applied Mechanics, 2017, 49 (3): 693-702(in Chinese)
[49] 梅凤翔. 约束力学系统的对称性与守恒量. 北京: 北京理工大学出版社, 2004 Mei Fengxiang. Symmetry and Conserved Quantities of Constrained Mechanical Systems. Beijing: Beijing Institute of Technology Press, 2004 (in Chinese)
[50] Song CJ, Zhang Y. Noether symmetry and conserved quantity for fractional Birkhoffian mechanics and its applications. Fractional Calculus & Applied Analysis, 2018, 21(2): 509-526
[51] Cai PP, Fu JL, Guo YX. Lie symmetries and conserved quantities of the constraint mechanical systems on time scales. Reports on Mathematical Physics, 2017, 79(3): 279-296 doi: 10.1016/S0034-4877(17)30045-9
[52] Fu JL, Fu LP, Chen BY, et al. Lie symmetries and their inverse problems of nonholonomic Hamilton systems with fractional derivatives. Physics Letters A, 2016, 380(1): 15-21
[53] Zhang Y, Zhai XH. Perturbation to Lie symmetry and adiabatic invariants for Birkhoffian systems on time scales. Communication in Nonlinear Science and Numerical Simulation, 2019, 75: 251-261 doi: 10.1016/j.cnsns.2019.04.005
[54] Fu JL, Chen BY, Chen LQ. Noether symmetries of discrete nonholonomic dynamical systems. Physics Letters A, 2009, 373(4): 409-412 doi: 10.1016/j.physleta.2008.11.039
[55] 傅景礼, 陈立群, 陈本永. 非规范格子离散非保守系统的 Noether 理论. 中国科学(G 辑), 2009, 39(9): 1320-1329 (Fu Jingli, Chen Liqun, Chen Benyong. Noether's theory of discrete nonconservative systems with non canonical lattices. Chinese Science (Series G) , 2009, 39(9): 1320-1329 (in Chinese) Fu JL, Chen LQ, Chen BY. Noether's theory of discrete nonconservative systems with non canonical lattices, Chinese Science (Series G), 2009, 39 (9): 1320-1329(in Chinese)
[56] Zhang HB. Lie symmetries and conserved quantities of nonholonomic mechanical systems with unilateral Vacco constraints. Chinese Physics, 2002, 11(1): 1-4 doi: 10.1088/1009-1963/11/1/301
[57] 梅凤翔. 非完整系统力学基础. 北京: 北京工业学院出版社, 1985 [58] Fu JL, Zhang LJ, Khalique CM, and Guo ML. Motion equations and non-Noether symmetries of Lagrangian systems with the conformable fractional derivatives. Thermal Science, 2021, 25(2B): 1365-1372
[59] Feng K, Qin MZ. Symplectic Geometric Algorithms for Hamiltonian Systems. New York: Springer, 2010
[60] Zhao GL, Chen LQ, Fu JL. Mei symmetries and conservation laws of discrete nonholonomic dynamical systems with regular and irregular lattices. Chinese Physics B, 2013, 22(3): 54-60
[61] Zhao L, Fu JL, Chen BY. A new type of conserved quantity of Mei symmetry for the motion of mechanico-electrical coupling dynamical systems. Chinese Physics B, 2011, 20(4): 1-4
[62] 谢传峰, 王琪. 理论力学, 第2版. 北京: 高等教育出版社, 2015 Xie Chuanfeng, Wang Qi. Theoretical Mechanics (2nd Edition). Beijing: Higher Education Press, 2015 (in Chinese)
-
期刊类型引用(5)
1. 张毅. 非保守广义Chaplygin系统的Herglotz型Noether定理. 力学学报. 2024(09): 2695-2702 .  本站查看
本站查看
2. 吕桂志,王鹏,李国红,陆峰,戴圣龙. 爬壁机器人动力学模型的模块化构建研究. 机械传动. 2024(11): 24-31 .  百度学术
百度学术
3. 董欣畅,张毅. 含时滞非完整系统的对称性与Herglotz型守恒量. 力学学报. 2024(11): 3302-3311 .  本站查看
本站查看
4. 张毅. 二阶非完整Vacco动力学及其Noether定理. 苏州科技大学学报(自然科学版). 2023(03): 29-35 .  百度学术
百度学术
5. 徐宏,傅景礼. 基于伺服电机驱动的进给传动系统扭转振动的Lie群分析方法. 力学学报. 2023(09): 2000-2009 .  本站查看
本站查看
其他类型引用(3)




 下载:
下载: