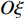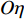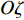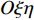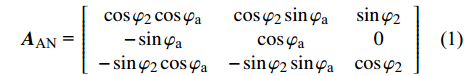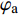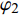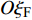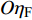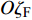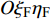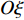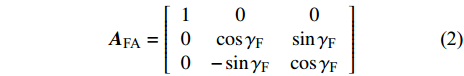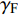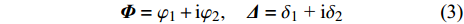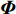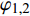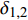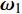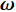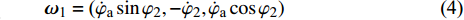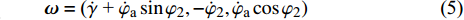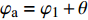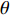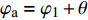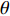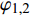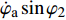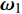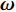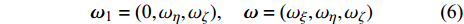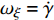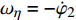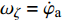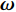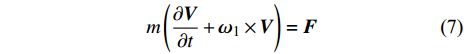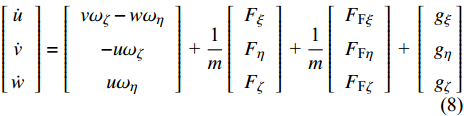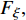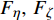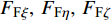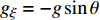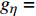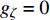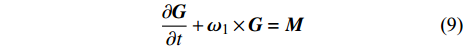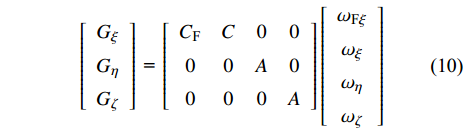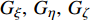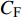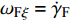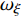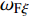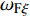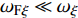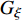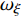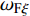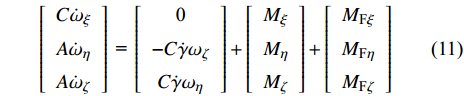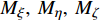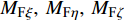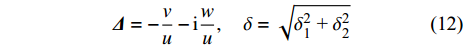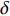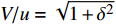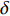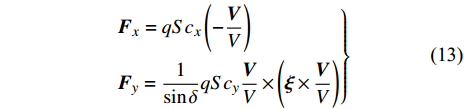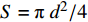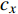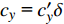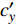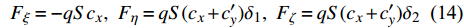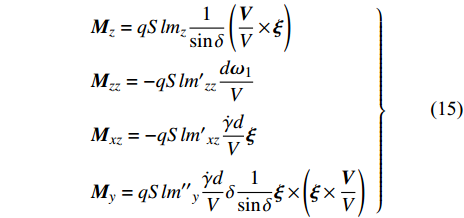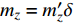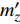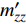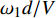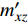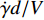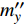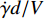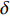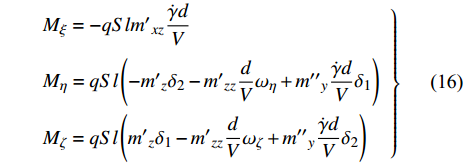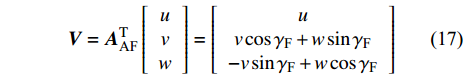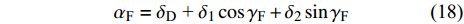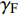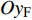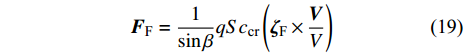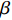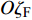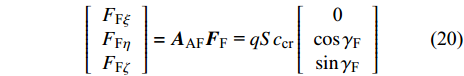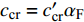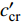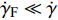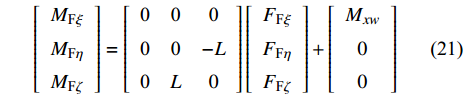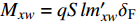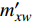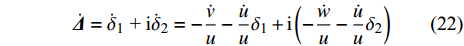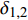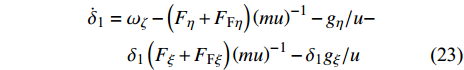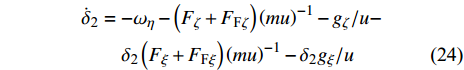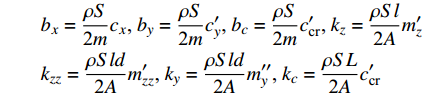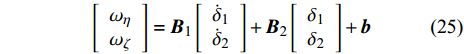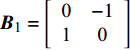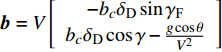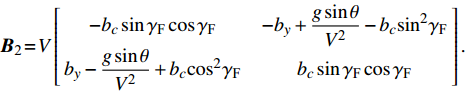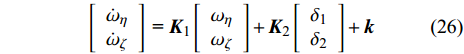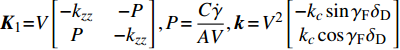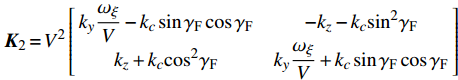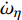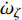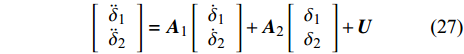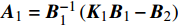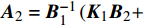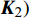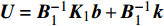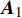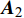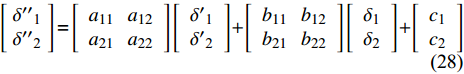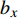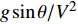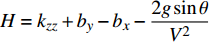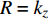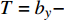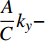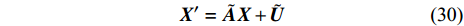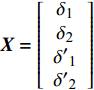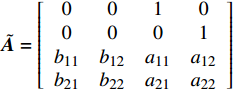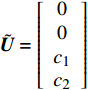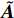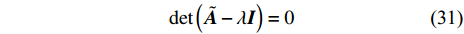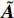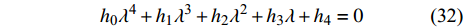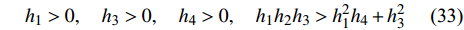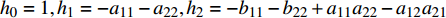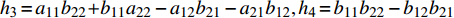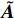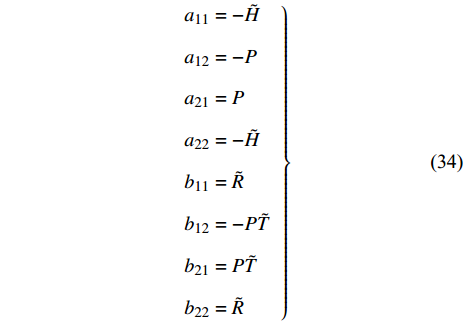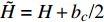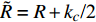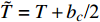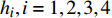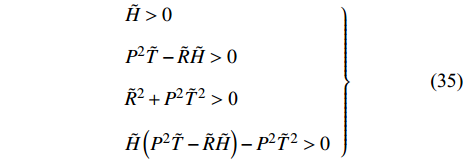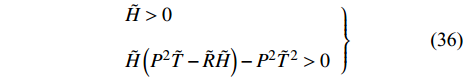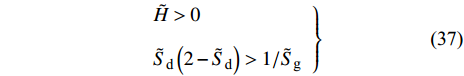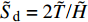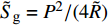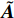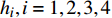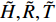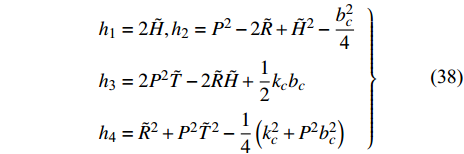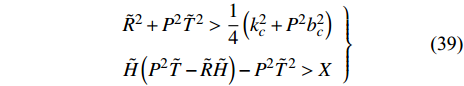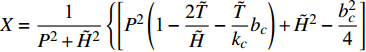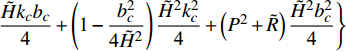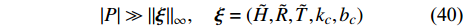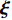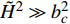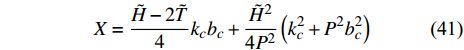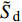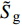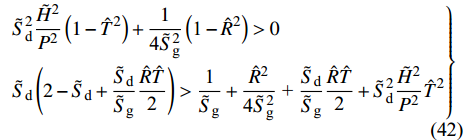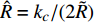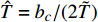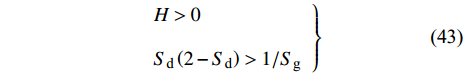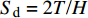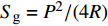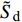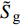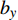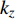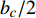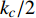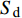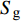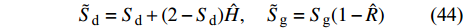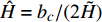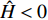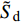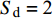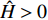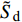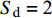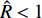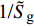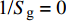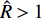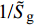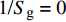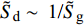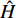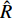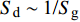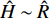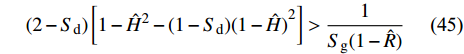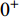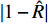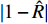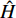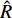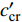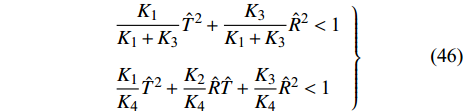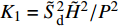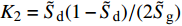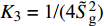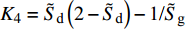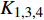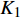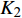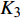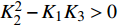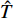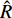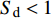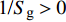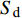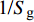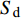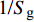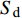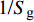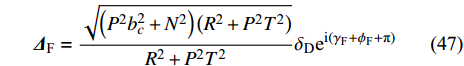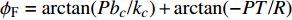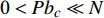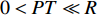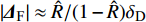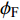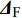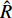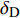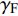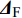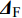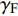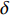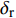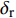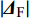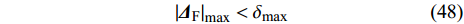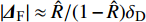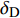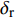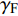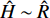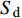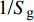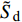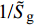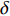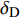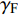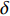DYNAMIC STABILITY AND INFLUENCE FACTORS OF THE WHOLE TRAJECTORY OF FIXED CANARD DUAL-SPIN PROJECTILES
-
摘要: 为研究固定鸭舵双旋弹全弹道飞行时的动态稳定性问题, 在小攻角条件下建立复攻角运动的状态空间模型, 并应用霍尔维茨方法导出其特征根实部皆负的一般性条件. 针对起控前/后前体滚转角的运动特点, 利用常规旋转弹的稳定性分析方法, 建立固定鸭舵双旋弹在不同飞行状态下的动态稳定性判据, 其与常规旋转弹的形式相似, 无控飞行时在升力和静力矩项中对应增加了舵面控制力和力矩项; 有控飞行时进一步增加了有关项相对增量的影响. 据此在后体参数确定的条件下推导舵面参数约束条件, 并分析操纵舵控制力系数导数、安装位置和舵偏角对动态稳定性的影响, 揭示了该类炮弹动不稳定形成的原因. 对复攻角运动在不同条件下的仿真分析结果表明, 当舵面引起的有关项相对增量同时位于无控和有控飞行的边界曲线内时, 固定鸭舵双旋弹全弹道飞行动态稳定, 验证了本文推导的动态稳定性判据和舵面参数约束条件合理, 为该类炮弹的研制提供了理论依据与设计参考.Abstract: To research the dynamic stability of fixed canard dual-spin projectiles in full trajectory flight, the state space model of the complex attack angle motion is established under the condition of small attack angle, and the general condition that the real parts of the characteristic roots are all negative is derived by using the Hurwitz method. Based on the motion characteristics of the front body’s rolling angle before/after starting control, the dynamic stability criterion of fixed canard dual-spin projectiles under different flight conditions is proposed by using the stability analysis method of the conventional rotating projectiles, whose form is similar to that of the conventional rotating projectiles. When flying without control, the control force and moment terms of control canard are added correspondingly in the lift force and static moment terms. Controlled flight further increases the relative increment effect of relevant terms. Accordingly, the constraint on canard parameters of control surface is deduced under the condition that the parameters of projectile body are determined, the effects of the control force coefficient’s derivative, the installation position and the deflection angle of control canard on the dynamic stability are discussed, and the reasons for the formation of the dynamic instability of this kind of projectile are revealed. The simulation analysis results of the complex attack angle motion under different conditions show that when the relative increment caused by control surface is within the boundary of both uncontrolled and controlled flight, the full trajectory flight of the fixed canard dual-spin projectile is dynamically stable, which verifies that the dynamic stability criterion and the constraint on canard parameters deduced in this paper are reasonable and feasible, and provides a theoretical basis and design reference for the design and development of this type of projectile.
-
引 言
随着现代战争对弹药精确打击能力需求的提高, 兼顾作战性能和制造成本, 设法改善常规弹药射击精度成为兵器弹箭发展的重要方向之一[1]. 在此背景下, 为研制具有二维弹道修正能力的旋转稳定弹, 一种对常规旋转弹加装弹道修正组件改进而来的固定鸭舵双旋弹应运而生[2]. 该类弹丸采用前/后体双自旋结构, 通过使装有修正机构的前体在弹道初始段快速减旋, 从原理上消除了后体转速过快对姿态测量和机构动作等的不利影响[3].
自文献[4]提出双旋弹的概念以来, 国内外机构和学者围绕气动数值模拟与实验[5-11]、动力学建模及仿真[12-15]、修正与控制系统研究[16-22]等开展了大量工作, 并取得一些成果. 随着研究的深入, 近年来相关学者逐步对双旋弹的角运动特性和稳定性理论展开研究. 文献[23]针对舵面偏角可调节的情况, 分析了双旋弹的飞行稳定性; 常思江等[24-25]研究了鸭舵控制力和重力作用下双旋弹的动态响应规律, 并针对鸭舵周期性干扰引起的强迫运动, 讨论了舵面偏角、安装位置和极转动惯量比对共振幅值的影响; 史金光等[26-27]通过建立双旋弹复攻角运动方程, 分析了不同控制力作用下弹丸攻角和速度偏角的运动特性, 阐释了其角运动形成机理和弹道修正的力学本质; Zhu等[28]将攻角引起的舵面升力与后体空气体动力一体化考虑, 研究了固定鸭舵双旋弹的动态稳定性条件; 马国梁等[29]针对前体滚转角快速时变的动态稳定性问题, 利用范数概念导出了固定鸭舵双旋弹的绝对稳定性判据; 李佳迅等[30]初步分析了双旋弹的非线性角运动特性.
上述研究主要围绕双旋弹的角运动理论以及无控飞行时的稳定性问题展开, 所得结果为该类炮弹的飞行稳定性判别提供了参考, 但有关舵面参数对动态稳定性影响机理的分析较少, 尤其是针对有控飞行时的动态稳定性问题, 尚未形成有效判别方法. 本文拟进一步研究固定鸭舵双旋弹的全弹道动态稳定性及其影响因素, 通过分析该类弹丸动力学特性, 在小攻角条件下建立复攻角运动的状态空间模型, 导出状态矩阵特征根实部皆负的一般性条件. 据此利用常规旋转弹的稳定性分析方法, 分别提出固定鸭舵双旋弹无控和有控飞行时的动态稳定性判据, 并在后体参数确定的条件下推导舵面参数约束条件, 讨论操纵舵控制力系数导数、安装位置和舵偏角对动态稳定性的影响, 揭示该类弹丸动不稳定形成的原因. 最后通过对复攻角运动在不同条件下的弹道仿真, 验证本文推导的动态稳定性判据和舵面参数约束条件的合理性, 以期为该类炮弹的研制和前体结构设计与优化提供理论参考.
1. 动力学建模
1.1 物理模型
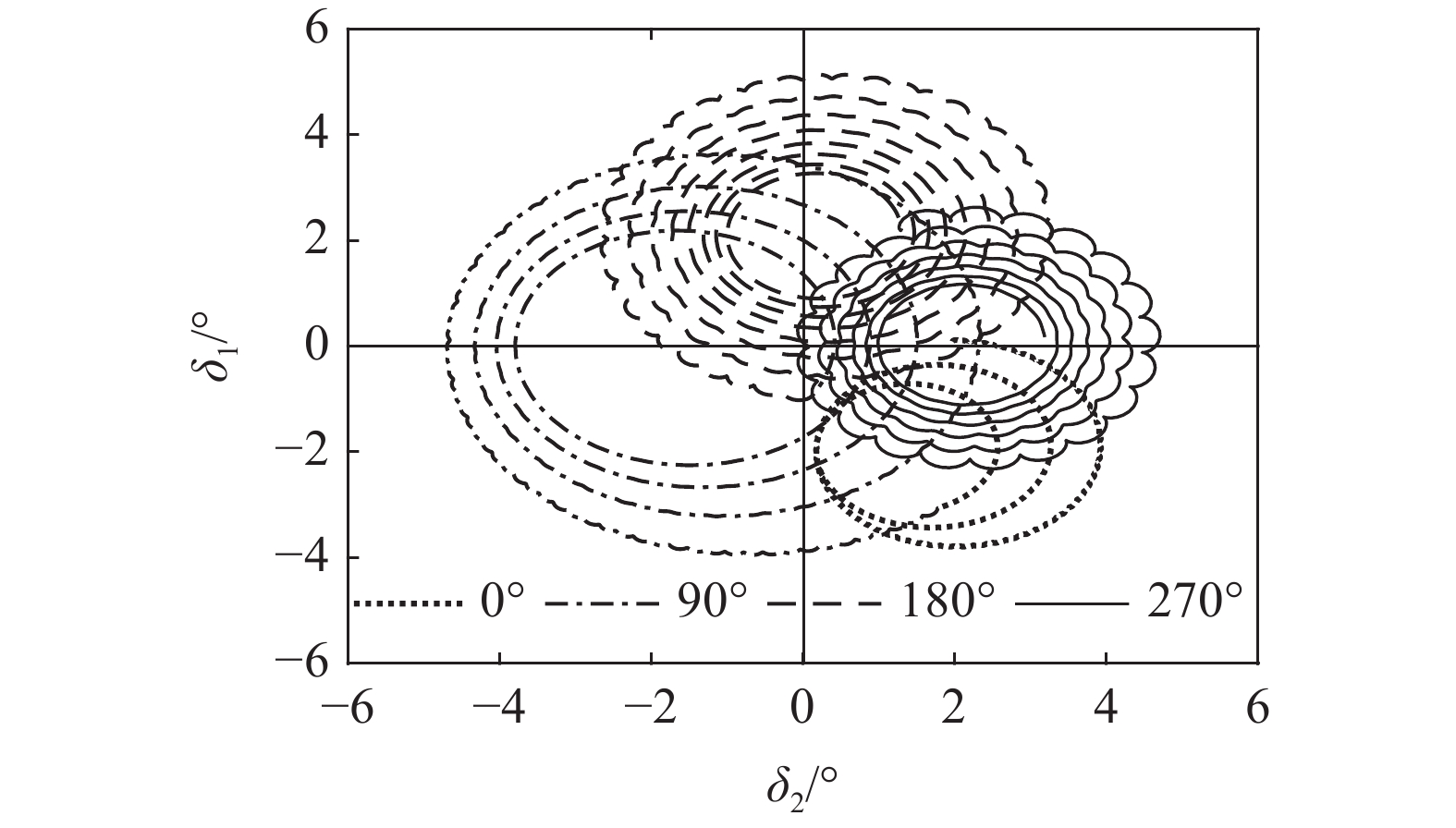
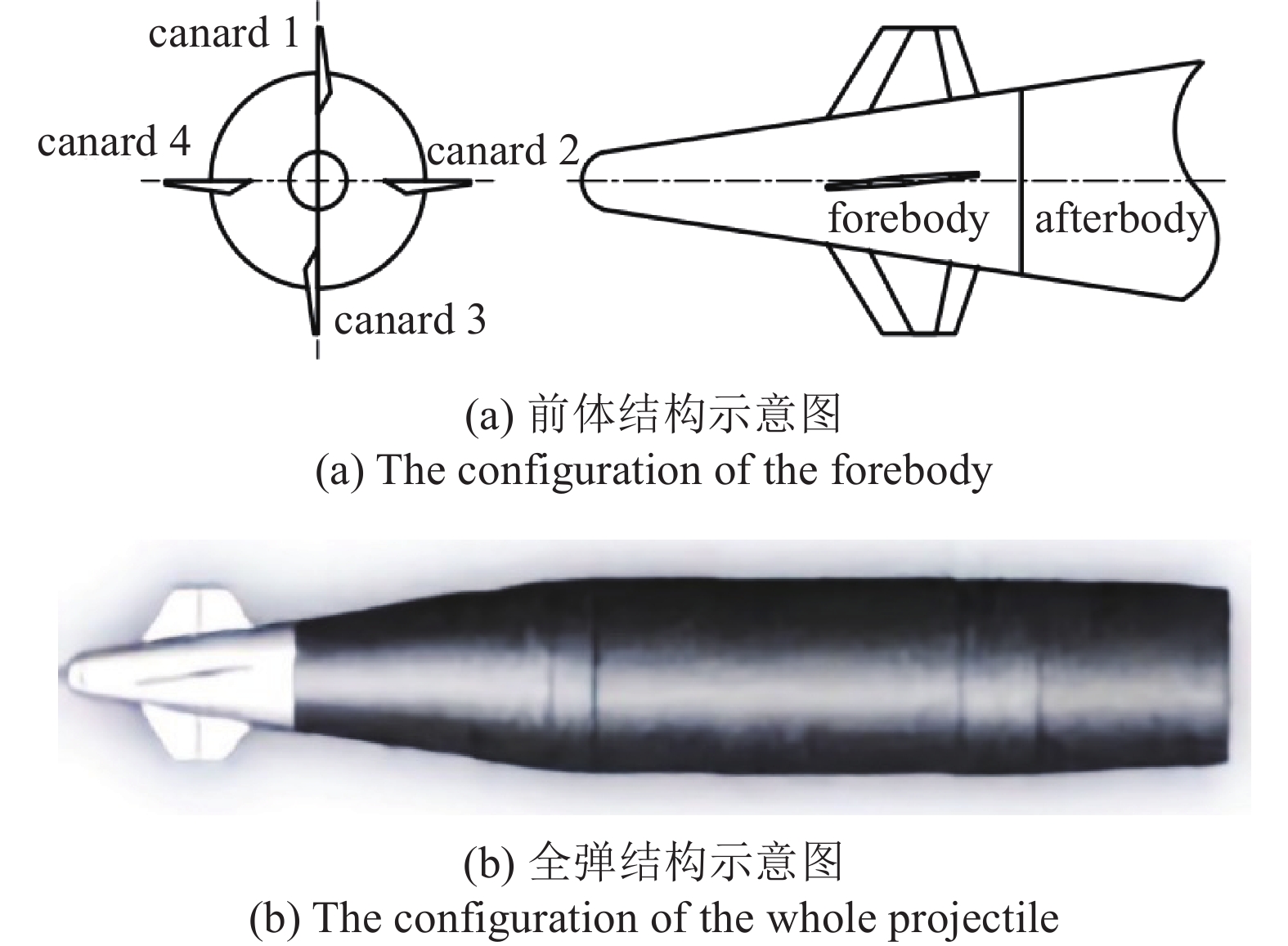
固定鸭舵双旋弹的结构如图1所示, 其由前体和后体两部分构成, 在弹道飞行时通过调节前体滚转角控制方位, 对弹道进行一次或若干次修正. 其中前体上差动布置的舵片1和3为减旋舵, 产生反转力矩使前体滚转角速度在出炮口后快速下降, 斜置角为
${\delta _{\text{F}}}$ ; 同向布置的舵片2和4为操纵舵, 提供弹道修正所需的控制力和力矩, 舵偏角为${\delta _{\text{D}}}$ .固定鸭舵双旋弹出炮口后无控飞行, 前体滚转角在反转力矩作用下快速下降到某一平衡转速, 其值可以通过调节前/后体的滚转阻尼力矩和减旋舵的舵面参数进行设计, 一般为5 ~ 20 r/s; 飞行一段时间后有控飞行, 通过分析后续弹道诸元与预定弹道诸元的偏差, 前体滚转角在驱动电机作用下进行切换, 并在一段时间内保持不变.
1.2 坐标系定义及转换
1.2.1 基准坐标系
由地面坐标系平移至弹丸质心O而来, 记为N. Ox轴沿水平线指向射击方向, Oy轴竖直向上, Oz轴按右手定则垂直于Oxy面向右.
1.2.2 弹轴坐标系
用于确定弹轴的空间方位, 记为A.
$O\xi $ 轴沿弹轴方向,$O\eta $ 轴在铅直平面内垂直于弹轴向上,$O\zeta $ 轴按右手定则垂直于$O\xi \eta $ 面向右. 该坐标系可由基准坐标系旋转两次而来, 转换矩阵为$$ {{\boldsymbol{A}}_{{\text{AN}}}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {\cos {\varphi _2}\cos {\varphi _{\text{a}}}}&{\cos {\varphi _2}\sin {\varphi _{\text{a}}}}&{\sin {\varphi _2}} \\ { - \sin {\varphi _{\text{a}}}}&{\cos {\varphi _{\text{a}}}}&0 \\ { - \sin {\varphi _2}\cos {\varphi _{\text{a}}}}&{ - \sin {\varphi _2}\sin {\varphi _{\text{a}}}}&{\cos {\varphi _2}} \end{array}} \right] $$ (1) 式中,
$ {\varphi _{\text{a}}} $ 为弹轴高低角,$ {\varphi _{\text{2}}} $ 为弹轴方向角.1.2.3 前体坐标系
用于确定前体的滚转角方位, 记为F.
$O{\xi _{\text{F}}}$ 轴沿弹轴方向,$O{\eta _{\text{F}}}$ 轴在前体纵向对称面内垂直于弹轴向上,$O{\zeta _{\text{F}}}$ 轴按右手定则垂直$ O{\xi _{\text{F}}}{\eta _{\text{F}}} $ 面向右. 该坐标系可由弹轴坐标系绕$O\xi $ 旋转而来, 转换矩阵为$$ {{\boldsymbol{A}}_{{\text{FA}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos {\gamma _{\text{F}}}}&{\sin {\gamma _{\text{F}}}} \\ 0&{ - \sin {\gamma _{\text{F}}}}&{\cos {\gamma _{\text{F}}}} \end{array}} \right] $$ (2) 式中,
$ {\gamma _{\text{F}}} $ 为前体滚转角.1.3 动力学模型
依据外弹道学理论, 在小扰动条件下认为旋转稳定弹的刚体弹道偏离理想弹道程度不大, 故可以在复数平面下定义
$$ {{{{\varPhi}}}} = {\varphi _1} + {\rm{i}}{\varphi _2},\quad {{{{\varDelta}}}} = {\delta _{\text{1}}}{\text{ + }}{\rm{i}}{\delta _2} $$ (3) 式中,
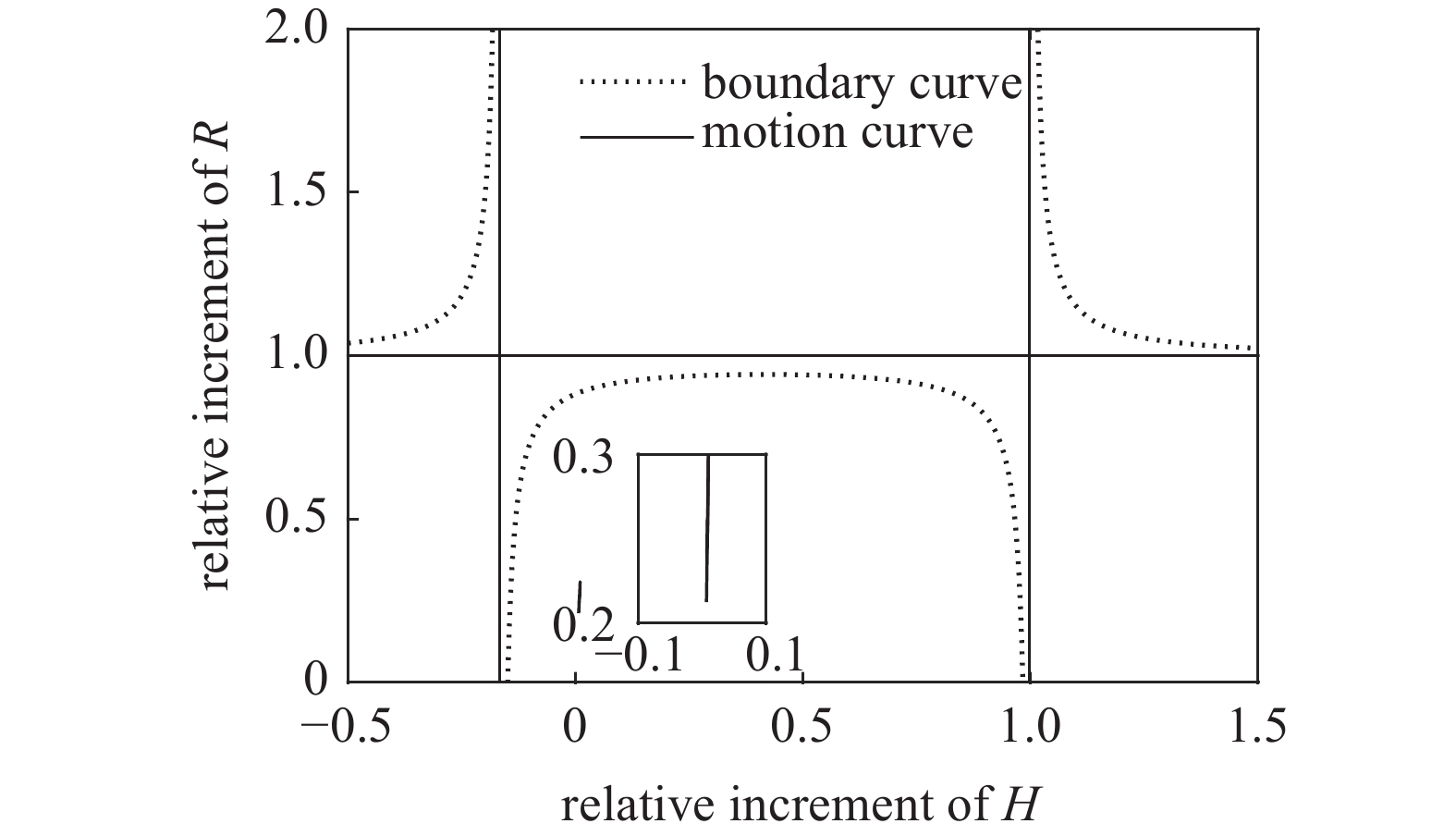
${{{{\varPhi}} }}$ 为复摆动角,${{{{\varDelta}} }}$ 为复攻角, 分别描述弹轴相对理想弹道切线和速度矢量的空间方位;$ {\varphi }_{\text{1}, \text{2}} $ 和$ {\delta }_{\text{1}, \text{2}} $ 均为小量.定义
$ {{\boldsymbol{\omega}} _{\text{1}}} $ 为弹轴坐标系的转动角速度,${\boldsymbol{ \omega}} $ 为弹丸绕质心的转动角速度, 其在弹轴坐标系下的分量形式分别为$$ {{\boldsymbol{\omega }}_{\text{1}}} = {\text{(}}{\dot \varphi _{\text{a}}}\sin {\varphi _2}, \;- {\dot \varphi _2},\;{\dot \varphi _{\text{a}}}\cos {\varphi _2}) $$ (4) $$ {\boldsymbol{\omega}} = {\text{(}}\dot \gamma {\text{ + }}{\dot \varphi _{\text{a}}}\sin {\varphi _2}, \;- {\dot \varphi _2},\;{\dot \varphi _{\text{a}}}\cos {\varphi _2}) $$ (5) 式中,
$ {\varphi _{\text{a}}} = {\varphi _1} + \theta $ ,$ \theta $ 为理想弹道倾角;$ \gamma $ 为弹丸滚转角. 根据$ {\varphi _{\text{a}}} = {\varphi _1} + \theta $ , 由于$ \theta $ 变化较慢, 故当$ {\varphi }_{\text{1}, \text{2}} $ 均为小量时,$ {\dot \varphi _{\text{a}}}\sin {\varphi _2} $ 为高阶小量,$ {{\boldsymbol{\omega}} _{\text{1}}} $ 和$ {\boldsymbol{\omega}} $ 则可简化为$$ {{\boldsymbol{\omega}} _{\text{1}}} = {\text{(0}},\;{\omega _\eta },\;{\omega _\zeta }),\quad {\boldsymbol{\omega}} = {\text{(}}{\omega _\xi },\;{\omega _\eta },\;{\omega _\zeta }) $$ (6) 式中,
$ {\omega _\xi } = \dot \gamma $ ,$ {\omega _\eta } = - {\dot \varphi _2} $ ,$ {\omega _\zeta } = {\dot \varphi _{\text{a}}} $ 为$ {\boldsymbol{\omega}} $ 在弹轴坐标系下的分量.1.3.1 质心运动方程
对于固定鸭舵双旋弹的质心运动方程, 学者们普遍认为其与常规旋转稳定弹的相似, 只不过增加了舵面空气动力的影响[17,25,27,28], 在弹轴坐标系下的表达式为
$$ m\left( {\frac{{\partial {\boldsymbol{V}}}}{{\partial t}} + {{\boldsymbol{\omega}} _{\text{1}}} \times {\boldsymbol{V}}} \right) = {\boldsymbol{F}} $$ (7) 式中, m为弹丸质量, V为速度矢量, F为合外力矢量.
将式(6)代入式(7), 整理得到
$$ \left[ {\begin{array}{*{20}{c}} {\dot u} \\ {\dot v} \\ {\dot w} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {v{\omega _\zeta } - w{\omega _\eta }} \\ { - u{\omega _\zeta }} \\ {u{\omega _\eta }} \end{array}} \right]{\text{ + }}\frac{{\text{1}}}{m}\left[ {\begin{array}{*{20}{c}} {{F_\xi }} \\ {{F_\eta }} \\ {{F_\zeta }} \end{array}} \right]{\text{ + }}\frac{{\text{1}}}{m}\left[ {\begin{array}{*{20}{c}} {{F_{{\text{F}}\xi }}} \\ {{F_{{\text{F}}\eta }}} \\ {{F_{{\text{F}}\zeta }}} \end{array}} \right]{\text{ + }}\left[ {\begin{array}{*{20}{c}} {{g_\xi }} \\ {{g_\eta }} \\ {{g_\zeta }} \end{array}} \right] $$ (8) 式中, u, v, w为速度在弹轴坐标系下的分量;
$ {F}_{\xi },\; $ $ {F}_{\eta }, \;{F}_{\zeta } $ 为后体空气动力在弹轴坐标系下的分量;$ {F}_{\text{F}\xi },\; {F}_{\text{F}\eta },\; {F}_{\text{F}\zeta } $ 为前体空气动力在弹轴坐标系下的分量;$ {g_\xi } = - g\sin \theta $ ,$ {g_\eta } = $ $ g\cos \theta $ ,$ {g_\zeta } = 0 $ 为重力加速度在弹轴坐标系下的分量.1.3.2 绕质心运动方程
固定鸭舵双旋弹的绕质心运动相对复杂, 一些学者将前体滚转角运动单独考虑, 建立了4自由度绕质心运动方程[25,27]; 另一些则认为受反转力矩、滚转阻尼力矩和驱动电机等综合作用, 前体滚转角运动相对独立, 故可以略去并建立了3自由度绕质心运动方程[17,28]. 本文重点关心弹丸的复攻角运动特性, 主要借鉴第二种思路, 在弹轴坐标系下建立其绕质心运动方程为
$$ \frac{{\partial {\boldsymbol{G}}}}{{\partial t}} + {{\boldsymbol{\omega }}_{\text{1}}} \times {\boldsymbol{G}} = {\boldsymbol{M}} $$ (9) 式中, G为弹丸对质心的动量矩; M为合外力对质心的力矩.
为便于研究, 忽略动不平衡, 得到G在弹轴坐标系下的分量形式为
$$ \left[ {\begin{array}{*{20}{c}} {{G_\xi }} \\ {{G_\eta }} \\ {{G_\zeta }} \end{array}} \right]{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{C_{\text{F}}}}&C&0&0 \\ 0&0&A&0 \\ 0&0&0&A \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\omega _{{\text{F}}\xi }}} \\ {{\omega _\xi }} \\ {{\omega _\eta }} \\ {{\omega _\zeta }} \end{array}} \right] $$ (10) 式中,
$ {G}_{\xi }, \;{G}_{\eta }, \;{G}_{\zeta } $ 为动量矩在弹轴坐标系下的分量;$ {C_{\text{F}}} $ , C, A为前体极转动惯量、后体极转动惯量和弹丸赤道转动惯量;$ {\omega _{{\text{F}}\xi }} = {\dot \gamma _{\text{F}}} $ 为前体滚转角速度.又由于固定鸭舵双旋弹发射后, 后体高速旋转以维持弹丸飞行稳定(
$ {\omega _\xi } $ 约为300 r/s); 前体则会快速减旋到某一平衡转速($ {\omega _{{\text{F}}\xi }} $ 一般为5 ~ 20 r/s), 并在有控飞行时固定于某一滚转角方位保持不变($ {\omega _{{\text{F}}\xi }} $ 近似为0). 由量级大小比较可知${\omega _{{\text{F}}\xi }} \ll {\omega _\xi }$ , 则式(10)中${G_\xi }$ 主要由$ {\omega _\xi } $ 决定, 因此可以略去其中$ {\omega _{{\text{F}}\xi }} $ 的影响, 并将其代入式(9), 整理得到$$ \left[ {\begin{array}{*{20}{c}} {C{{\dot \omega }_\xi }} \\ {A{{\dot \omega }_\eta }} \\ {A{{\dot \omega }_\zeta }} \end{array}} \right]{\text{ = }}\left[ {\begin{array}{*{20}{c}} {\text{0}} \\ { - C\dot \gamma {\omega _\zeta }} \\ {C\dot \gamma {\omega _\eta }} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{M_\xi }} \\ {{M_\eta }} \\ {{M_\zeta }} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{M_{{\text{F}}\xi }}} \\ {{M_{{\text{F}}\eta }}} \\ {{M_{{\text{F}}\zeta }}} \end{array}} \right] $$ (11) 式中,
$ {M}_{\xi },\;{M}_{\eta },\;{M}_{\zeta } $ 为作用在后体上的外力矩在弹轴坐标系下的分量;$ {M}_{\text{F}\xi },\;{M}_{\text{F}\eta },\;{M}_{\text{F}\zeta } $ 为作用在前体上的外力矩在弹轴坐标系下的分量.1.4 作用在后体上的空气动力和力矩
为便于确定作用在后体上的空气动力和力矩矢量, 首先给出复攻角在弹轴坐标系下的表达式为
$$ {{{{\varDelta}} }} = - \frac{v}{u} - {\rm{i}}\frac{w}{u},\quad \delta = \sqrt {\delta _{\text{1}}^{\text{2}}{\text{ + }}\delta _{\text{2}}^{\text{2}}} $$ (12) 式中,
$ \delta $ 为复攻角的幅值; 由于$V/u = \sqrt {1 + {\delta ^2}} $ , 且$ \delta $ 为小量, 故可以近似认为$ V = u $ .1.4.1 后体空气动力
忽略较小的马格努斯力, 作用在后体上的空气动力主要包括: 沿速度反方向的阻力、在攻角平面内垂直于速度且在弹轴一侧的升力, 表达式分别为
$$ \left. \begin{gathered} {{\boldsymbol{F}}_x} = qS{c_x}\left( { - \frac{{\boldsymbol{V}}}{V}} \right) \hfill \\ {{\boldsymbol{F}}_y} = \frac{1}{{\sin \delta }}qS{c_y}\frac{{\boldsymbol{V}}}{V} \times \left( {{\boldsymbol{\xi}} \times \frac{{\boldsymbol{V}}}{V}} \right) \hfill \\ \end{gathered} \right\} $$ (13) 式中, q为来流动压; V为速度的模;
$S = {\text{π}}{d^2}/4$ 为特征面积, d为弹径;$ {c_x} $ 为后体阻力系数;${c_y}{\text{ = }}{c'_y}\delta $ 为后体升力系数,${c'_y}$ 为后体升力系数导数.忽略高阶小量, 后体空气动力在弹轴坐标系下的分量形式为
$$ {F_\xi } = - qS{c_x},\;\;{F_\eta } = qS({c_x} + {c'_y}){\delta _1},\;\;{F_\zeta } = qS({c_x} + {c'_y}){\delta _2} $$ (14) 1.4.2 后体空气动力矩
忽略气动偏心和动不平衡的影响, 高旋后体在外弹道飞行过程中受到的空气动力矩主要包括: 静力矩、赤道阻尼力矩、极阻尼力矩和马格努斯力矩, 表达式分别为
$$ \left. \begin{array}{l} {{\boldsymbol{M}}_z} = qSl{m_z}\dfrac{1}{{\sin \delta }}\left( {\dfrac{{\boldsymbol{V}}}{V} \times {\boldsymbol{\xi }}} \right) \hfill \\ {{\boldsymbol{M}}_{zz}} = - qSl{{m'}_{zz}}\dfrac{{d{{\boldsymbol{\omega}} _1}}}{V} \hfill \\ {{\boldsymbol{M}}_{xz}} = - qSl{{m'}_{xz}}\dfrac{{\dot \gamma d}}{V}{\boldsymbol{\xi}} \hfill \\ {{\boldsymbol{M}}_y} = qSl{{m''}_y}\dfrac{{\dot \gamma d}}{V}\delta \dfrac{1}{{\sin \delta }}{\boldsymbol{\xi }} \times \left( {{\boldsymbol{\xi }} \times \dfrac{{\boldsymbol{V}}}{V}} \right) \end{array} \right\} $$ (15) 式中, l为特征长度;
${m_z} = {m'_z}\delta $ 为静力矩系数,${m'_z}$ 为静力矩系数导数;${m'_{zz}}$ 为赤道阻尼力矩系数对${\omega _1}d/V$ 的导数;$ {m'_{xz}} $ 为极阻尼力矩系数对$\dot \gamma d/V$ 的导数;$ {m''_y} $ 为马格努斯力矩系数对$\dot \gamma d/V$ 和$\delta $ 的联合偏导数.忽略高阶小量, 后体空气动力矩在弹轴坐标系下的分量形式为
$$ \left. \begin{array}{l} {M_\xi } = - qSl{{m'}_{xz}}\dfrac{{\dot \gamma d}}{V} \hfill \\ {M_\eta } = qSl\left( { - {{m'}_z}{\delta _2} - {{m'}_{zz}}\dfrac{d}{V}{\omega _\eta } + {{m''}_y}\dfrac{{\dot \gamma d}}{V}{\delta _1}} \right) \hfill \\ {M_\zeta } = qSl\left( {{{m'}_z}{\delta _1} - {{m'}_{zz}}\dfrac{d}{V}{\omega _\zeta } + {{m''}_y}\dfrac{{\dot \gamma d}}{V}{\delta _2}} \right) \end{array} \right\} $$ (16) 1.5 作用在前体上的空气动力和力矩
为便于确定作用在前体上的空气动力和力矩矢量, 给出速度矢量在前体坐标系下的分量表达式为
$$ {\boldsymbol{V}} = {\boldsymbol{A}}_{{\text{AF}}}^{\rm T}\left[ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} u \\ {v\cos {\gamma _{\text{F}}} + w\sin {\gamma _{\text{F}}}} \\ { - v\sin {\gamma _{\text{F}}} + w\cos {\gamma _{\text{F}}}} \end{array}} \right]$$ (17) 据此可得操纵舵的有效攻角为
$$ {\alpha _{\text{F}}} = {\delta _{\text{D}}}{\text{ + }}{\delta _1}\cos {\gamma _{\text{F}}} + {\delta _2}\sin {\gamma _{\text{F}}} $$ (18) 1.5.1 前体空气动力
将仅由弹丸复攻角决定的前体空气动力合并到后体上, 单独考虑由操纵舵产生的随
${\gamma _{\text{F}}}$ 周期性变化的控制力, 其在纵向对称面内垂直于V且在$O{y_{\text{F}}}$ 轴一侧, 表达式为$$ {{\boldsymbol{F}}_{\text{F}}} = \frac{1}{{\sin \beta }}qS{c_{{\text{cr}}}}\left( {{{\boldsymbol{\zeta}} _{\text{F}}} \times \frac{{\boldsymbol{V}}}{V}} \right) $$ (19) 式中,
$\beta $ 为$O{\zeta _{\text{F}}}$ 轴与速度矢量的夹角. 忽略高阶小量, 在弹轴坐标系下的分量形式为$$ \left[ {\begin{array}{*{20}{c}} {{F_{{\text{F}}\xi }}} \\ {{F_{{\text{F}}\eta }}} \\ {{F_{{\text{F}}\zeta }}} \end{array}} \right] = {{\boldsymbol{A}}_{{\text{AF}}}}{{\boldsymbol{F}}_{\text{F}}}{\text{ = }}qS{c_{{\text{cr}}}}\left[ {\begin{array}{*{20}{c}} {\text{0}} \\ {\cos {\gamma _{\text{F}}}} \\ {\sin {\gamma _{\text{F}}}} \end{array}} \right] $$ (20) 式中,
$ {c_{{\text{cr}}}} = {c'_{{\text{cr}}}}{\alpha _{\text{F}}} $ 为操纵舵的控制力系数,$ {c'_{{\text{cr}}}} $ 为操纵舵的控制力系数导数.1.5.2 前体空气动力矩
依据
${\dot \gamma _{\text{F}}} \ll \dot \gamma $ , 忽略较小的前体马格努斯力矩和前体极阻尼力矩, 作用在前体上的空气动力矩主要包括: 控制力引起的控制力矩和沿弹轴方向的反转力矩, 在弹轴坐标系下的分量形式为$$ \left[ {\begin{array}{*{20}{c}} {{M_{{\text{F}}\xi }}} \\ {{M_{{\text{F}}\eta }}} \\ {{M_{{\text{F}}\zeta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{ - L} \\ {\text{0}}&L&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{F_{{\text{F}}\xi }}} \\ {{F_{{\text{F}}\eta }}} \\ {{F_{{\text{F}}\zeta }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{M_{xw}}} \\ 0 \\ 0 \end{array}} \right] $$ (21) 式中, L为操纵舵安装位置, 即弹丸质心沿弹轴方向到操纵舵压心的距离;
$ {M_{xw}} = qSl{m'_{xw}}{\delta _{\text{F}}} $ 为减旋舵产生的反转力矩,$ {m'_{xw}} $ 为反转力矩系数导数.2. 动态稳定性分析
2.1 线性化状态方程
根据式(12)中复攻角在弹轴坐标系下的表达式, 导出复攻角运动方程为
$$ \dot {{{{\varDelta}}}} = {\dot \delta _{\text{1}}}{\text{ + }}{\rm{i}}{\dot \delta _2} = { - \frac{{\dot v}}{u} - \frac{{\dot u}}{u}{\delta _{\text{1}}}} + {\rm{i}}\left( { - \frac{{\dot w}}{u} - \frac{{\dot u}}{u}{\delta _{\text{2}}}} \right) $$ (22) 利用式(8)将上式展开, 并略去小量
$ {\delta }_{\text{1}, \text{2}} $ 的乘积项, 整理得到$$ \begin{split} & {{\dot \delta }_{\text{1}}} = {\omega _\zeta } - \left( {{F_\eta } + {F_{{\text{F}}\eta }}} \right){\left( {mu} \right)^{ - 1}} - {g_\eta }/u -\\ &\qquad {\delta _{\text{1}}}\left( {{F_\xi } + {F_{{\text{F}}\xi }}} \right){\left( {mu} \right)^{ - 1}} - {\delta _{\text{1}}}{g_\xi }/u \end{split} $$ (23) $$ \begin{split} & {{\dot \delta }_{\text{2}}} = - {\omega _\eta } - \left( {{F_\zeta } + {F_{{\text{F}}\zeta }}} \right){\left( {mu} \right)^{ - 1}} - {g_\zeta }/u -\\ &\qquad {\delta _{\text{2}}}\left( {{F_\xi } + {F_{{\text{F}}\xi }}} \right){\left( {mu} \right)^{ - 1}} - {\delta _{\text{2}}}{g_\xi }/u \end{split} $$ (24) 为便于分析, 引入组合参数
$$ \begin{split} & {b_x} = \frac{{\rho S}}{{{\text{2}}m}}{c_x} \text{, } {b_y} = \frac{{\rho S}}{{{\text{2}}m}}{c'_y} \text{, } {b_c} = \frac{{\rho S}}{{{\text{2}}m}}{c'_{{\text{cr}}}} \text{, } {k_z} = \frac{{\rho Sl}}{{{\text{2}}A}}{m'_z} \\ & {k_{zz}} = \frac{{\rho Sld}}{{{\text{2}}A}}{m'_{zz}} \text{, } {k_y} = \frac{{\rho Sld}}{{{\text{2}}A}}{m''_y} \text{, } {k_c} = \frac{{\rho SL}}{{{\text{2}}A}}{c'_{{\text{cr}}}} \end{split}$$ 将作用在弹丸上的外力代入式(23)和式(24), 可得
$$ \left[ {\begin{array}{*{20}{c}} {{\omega _\eta }} \\ {{\omega _\zeta }} \end{array}} \right] = {{\boldsymbol{B}}_{\text{1}}}\left[ {\begin{array}{*{20}{c}} {{{\dot \delta }_{\text{1}}}} \\ {{{\dot \delta }_{\text{2}}}} \end{array}} \right] + {{\boldsymbol{B}}_{\text{2}}}\left[ {\begin{array}{*{20}{c}} {{\delta _{\text{1}}}} \\ {{\delta _{\text{2}}}} \end{array}} \right] + {\boldsymbol{b}} $$ (25) 式中,
$ {{\boldsymbol{B}}_{\text{1}}} = \left[ {\begin{array}{*{20}{c}} {\text{0}}&{ - 1} \\ {\text{1}}&{\text{0}} \end{array}} \right] $ ,${\boldsymbol{b}} = V\left[ {\begin{array}{*{20}{c}} { - {b_c}{\delta _{\text{D}}}\sin {\gamma _{\text{F}}}} \\ {{b_c}{\delta _{\text{D}}}\cos \gamma - \dfrac{{g\cos \theta }}{{{V^{\text{2}}}}}} \end{array}} \right]$ ,$$ {{\boldsymbol{B}}_{\text{2}}} = V\left[ {\begin{array}{*{20}{c}} { - {b_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}}}&{ - {b_y} + \dfrac{{g\sin \theta }}{{{V^{\text{2}}}}} - {b_c}{{\sin }^2}{\gamma _{\text{F}}}} \\ {{b_y} - \dfrac{{g\sin \theta }}{{{V^{\text{2}}}}} + {b_c}{{\cos }^2}{\gamma _{\text{F}}}}&{{b_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}}} \end{array}} \right] .$$ 将作用在弹丸上的外力矩代入式(11), 可得
$$ \left[ {\begin{array}{*{20}{c}} {{{\dot \omega }_\eta }} \\ {{{\dot \omega }_\zeta }} \end{array}} \right]{\text{ = }}{{\boldsymbol{K}}_{\text{1}}}\left[ {\begin{array}{*{20}{c}} {{\omega _\eta }} \\ {{\omega _\zeta }} \end{array}} \right] + {{\boldsymbol{K}}_{\text{2}}}\left[ {\begin{array}{*{20}{c}} {{\delta _{\text{1}}}} \\ {{\delta _{\text{2}}}} \end{array}} \right] + {\boldsymbol{k}} $$ (26) 式中,
${{\boldsymbol{K}}_{\text{1}}} = V\left[ {\begin{array}{*{20}{c}} { - {k_{zz}}}&{ - P} \\ P&{ - {k_{zz}}} \\\end{array}} \right], P = \dfrac{{C\dot \gamma }}{{AV}},{\boldsymbol{ k}} = {V^{\text{2}}}\left[ {\begin{array}{*{20}{c}} { - {k_c}\sin {\gamma _{\text{F}}}{\delta _{\text{D}}}} \\ {{k_c}\cos {\gamma _{\text{F}}}{\delta _{\text{D}}}} \end{array}} \right]\\ $ ,$$\begin{split} {{\boldsymbol{K}}_{\text{2}}} = {V^{\text{2}}}\left[ {\begin{array}{*{20}{c}} {{k_y}\dfrac{{{\omega _\xi }}}{V} - {k_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}}}&{ - {k_z} - {k_c}{{\sin }^2}{\gamma _{\text{F}}}} \\ {{{{k}}_z} + {k_c}{{\cos }^2}{\gamma _{\text{F}}}}&{{k_y}\dfrac{{{\omega _\xi }}}{V} + {k_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}}} \end{array}} \right]. \end{split}$$ 将式(25)对时间求导, 并利用式(25)和式(26)消去其中
$ {\dot \omega _\eta } $ ,$ {\dot \omega _\zeta } $ ,$ {\omega _\eta } $ 和$ {\omega _\zeta } $ 项, 整理得到$$ \left[ {\begin{array}{*{20}{c}} {{{\ddot \delta }_{\text{1}}}} \\ {{{\ddot \delta }_{\text{2}}}} \end{array}} \right] = {{\boldsymbol{A}}_{\text{1}}}\left[ {\begin{array}{*{20}{c}} {{{\dot \delta }_{\text{1}}}} \\ {{{\dot \delta }_{\text{2}}}} \end{array}} \right] + {{\boldsymbol{A}}_{\text{2}}}\left[ {\begin{array}{*{20}{c}} {{\delta _{\text{1}}}} \\ {{\delta _{\text{2}}}} \end{array}} \right] + {\boldsymbol{U}} $$ (27) 式中,
$ {{\boldsymbol{A}}_{\text{1}}} = {\boldsymbol{B}}_1^{ - 1}\left( {{{\boldsymbol{K}}_{\text{1}}}{{\boldsymbol{B}}_{\text{1}}} - {{\boldsymbol{B}}_{\text{2}}}} \right) $ ,$ {{\boldsymbol{A}}_2} = {\boldsymbol{B}}_1^{ - 1}\left( {{{\boldsymbol{K}}_{\text{1}}}{{\boldsymbol{B}}_2} + } \right. $ $ \left. {{{\boldsymbol{K}}_{\text{2}}}} \right) $ ,$ {\boldsymbol{U}} = {\boldsymbol{B}}_1^{ - 1}{{\boldsymbol{K}}_{\text{1}}}{\boldsymbol{b}} + {\boldsymbol{B}}_1^{ - 1}{\boldsymbol{k}} $ .为消去
$ {{\boldsymbol{A}}_{\text{1}}} $ 和$ {{\boldsymbol{A}}_{\text{2}}} $ 中的公因子V和${V^2}$ , 将式(27)改写为对弧长的导数, 得到非齐次复攻角方程为$$ \left[ {\begin{array}{*{20}{c}} {{{\delta ''}_{\text{1}}}} \\ {{{\delta ''}_{\text{2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}} \\ {{a_{21}}}&{{a_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\delta '}_{\text{1}}}} \\ {{{\delta '}_{\text{2}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{b_{11}}}&{{b_{12}}} \\ {{b_{21}}}&{{b_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\delta _{\text{1}}}} \\ {{\delta _{\text{2}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{c_{\text{1}}}} \\ {{c_{\text{2}}}} \end{array}} \right] $$ (28) 对于旋转稳定弹, 由于
${b_x}$ 等组合参数和$g\sin \theta /{V^2}$ 的量级较小, 故略去上述参数间的乘积项, 式(28)中各参数可以写为$$ \left. \begin{array}{l} {a_{11}} = - H - {b_c}{\cos ^2}{\gamma _{\text{F}}}\\ {a_{12}} = - P - {b_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}} \\ {a_{21}} = P - {b_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}}\\ {a_{22}} = - H - {b_c}{\sin ^2}{\gamma _{\text{F}}} \\ {b_{11}} = R - P{b_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}} + {k_c}{\cos ^2}{\gamma _{\text{F}}} \\ {b_{12}} = - PT - P{b_c}{\sin ^2}{\gamma _{\text{F}}} + {k_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}} \\ {b_{21}} = PT + P{b_c}{\cos ^2}{\gamma _{\text{F}}} + {k_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}} \\ {b_{22}} = R + P{b_c}\sin {\gamma _{\text{F}}}\cos {\gamma _{\text{F}}} + {k_c}{\sin ^2}{\gamma _{\text{F}}} \\ {c_1} = \left( { - P{b_c}\sin {\gamma _{\text{F}}} + {k_c}\cos {\gamma _{\text{F}}}} \right){\delta _{\text{D}}} \\ {c_2} = \left( {P{b_c}\cos {\gamma _{\text{F}}} + {k_c}\sin {\gamma _{\text{F}}}} \right){\delta _{\text{D}}} - Pg\cos \theta /{V^{\text{2}}} \end{array} \right\} $$ (29) 式中,
$H = {k_{zz}} + {b_y} - {b_x} - \dfrac{{2 g\sin \theta }}{{{V^2}}}$ ,$ R = {k_z} $ ,$ T = {b_y} - $ $ \dfrac{A}{C}{k_y} - $ $ \dfrac{{g\sin \theta }}{{{V^{\text{2}}}}} $ .2.2 动态稳定性条件
为便于研究固定鸭舵双旋弹的动态稳定性, 将式(28)转换得复攻角运动的状态空间模型为
$$\boldsymbol X' = \tilde {\boldsymbol {A}} {\boldsymbol{X}} + \tilde{ \boldsymbol U }$$ (30) 式中,
${\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{\delta _{\text{1}}}} \\ {{\delta _{\text{2}}}} \\ {{{\delta '}_{\text{1}}}} \\ {{{\delta '}_{\text{2}}}} \end{array}} \right]$ ,$ \tilde {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&0&1&0 \\ 0&0&0&1 \\ {{b_{11}}}&{{b_{12}}}&{{a_{11}}}&{{a_{12}}} \\ {{b_{21}}}&{{b_{22}}}&{{a_{21}}}&{{a_{22}}} \end{array}} \right] $ ,$\tilde {\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ {{c_1}} \\ {{c_2}} \end{array}} \right]$ .当状态矩阵
$ \tilde {\boldsymbol{A}} $ 为缓变系统时, 采用“系数冻结法”讨论式(30)的稳定性, 由霍尔维茨条件可知其动态稳定的充要条件是特征方程的根实部均为负数. 定义I为四阶单位矩阵, 根据$$ \det \left( {\tilde {\boldsymbol{A}} - \lambda {\boldsymbol{I}}} \right) = 0 $$ (31) 得到
$ \tilde {\boldsymbol{A}} $ 的特征方程为$$ {h_{\text{0}}}{\lambda ^{\text{4}}} + {h_1}{\lambda ^{\text{3}}} + {h_2}{\lambda ^{\text{2}}} + {h_3}\lambda + {h_{\text{4}}} = 0 $$ (32) 特征根实部皆负的充要条件为
$$ {h_1} > 0,\quad {h_{\text{3}}} > 0,\quad {h_{\text{4}}} > 0,\quad {h_1}{h_2}{h_3} > h_1^2{h_4} + h_3^2 $$ (33) 式中,
$ {h}_{0}=1, {h}_{\text{1}}=-{a}_{11}-{a}_{22}, {h}_{\text{2}}=-{b}_{11}-{b}_{22} + {a}_{11}{a}_{22}-{a}_{12}{a}_{21} $ ,${h}_{\text{3}}={a}_{11}{b}_{22} + {b}_{11}{a}_{22}-{a}_{12}{b}_{21}-{a}_{\text{21}}{b}_{\text{12}}, {h}_{\text{4}}={b}_{11}{b}_{22}-{b}_{12}{b}_{21}$ .2.2.1 无控飞行时的动态稳定性判据
无控飞行时, 前体滚转角运动在反转力矩和滚转阻尼力矩的作用下自由转动, 其转速相对复攻角的慢圆运动频率较大[27], 故在一个慢圆运动周期内可以对
$ \tilde {\boldsymbol{A}} $ 中元素平均处理得到$$ \left. \begin{array}{l} {a_{11}} = - \tilde H,\; {a_{12}} = - P\\ {a_{21}} = P,\; {a_{22}} = - \tilde H \hfill \\ {b_{11}} = \tilde R,\; {b_{12}} = - P\tilde T\\ {b_{21}} = P\tilde T,\; {b_{22}} = \tilde R \end{array} \right\}$$ (34) 式中,
$ \tilde H = H + {b_c}{\text{/2}} $ ,$ \tilde R = R + {k_c}{\text{/2}} $ ,$ \tilde T = T + {b_c}{\text{/2}} $ .将式(34)代入
$ {h}_{i}, i=1,2,3,4 $ , 由式(33)导出无控飞行时, 特征根实部皆负的充要条件为$$ \left.\begin{array}{l}\tilde{H} > 0\\ {P}^{2}\tilde{T}-\tilde{R}\tilde{H} > 0\\ {\tilde{R}}^{2} + {P}^{2}{\tilde{T}}^{2} > \text{0}\\ \tilde{H}\left({P}^{2}\tilde{T}-\tilde{R}\tilde{H}\right)-{P}^{2}{\tilde{T}}^{2} > 0\end{array} \right\}$$ (35) 由于第3式一定成立, 且第1式和第4式成立时第2式也成立, 故可以将式(35)简化为
$$ \left. \begin{array}{l} \tilde H > 0\; \hfill \\ \tilde H\left( {{P^2}\tilde T - \tilde R\tilde H} \right) - {P^2}{{\tilde T}^2} > 0 \hfill \end{array} \right\} $$ (36) 沿袭常规旋转弹稳定性理论, 改写得到固定鸭舵双旋弹无控飞行时的动态稳定性判据为
$$ \left.\begin{array}{l} \tilde H > 0 \hfill \\ {{\tilde S}_{\text{d}}}\left( {2 - {{\tilde S}_{\text{d}}}} \right) > 1/{{\tilde S}_{\text{g}}} \end{array} \right\} $$ (37) 式中,
${\tilde S_{\text{d}}} = 2\tilde T{\text{/}}\tilde H$ ,${\tilde S_{\text{g}}} = {P^2}/(4\tilde R)$ 分别为固定鸭舵双旋弹的动态稳定因子和陀螺稳定因子.2.2.2 有控飞行时的动态稳定性判据
有控飞行时, 前体滚转角控制方位在驱动电机作用下固定不变, 则
$ \tilde {\boldsymbol{A}} $ 中元素均可视为缓变量. 将式(29)代入$ {h}_{i}, i=1,2,3,4 $ , 利用$ \tilde{H}, \tilde{R}, \tilde{T} $ 改写得到$$ \left. \begin{array}{l} {h_1} = 2\tilde H\hfill \\ {h_{\text{2}}} = {P^2} - 2\tilde R + {{\tilde H}^2} - \dfrac{{b_c^2}}{{\text{4}}} \hfill \\ {h_{\text{3}}} = 2{P^2}\tilde T - {\text{2}}\tilde R\tilde H + \dfrac{1}{2}{k_c}{b_c} \hfill \\ {h_{\text{4}}} = {{\tilde R}^2} + {P^2}{{\tilde T}^2} - \dfrac{1}{4}\left( {k_c^2 + {P^2}b_c^2} \right) \end{array} \right\}$$ (38) 将上式代入式(33), 在满足无控飞行时动态稳定性判据的基础上, 进一步考虑前体滚转角运动状态改变对弹丸动态特性的影响, 导出有控飞行时特征根实部皆负的充要条件为
$$ \left. \begin{array}{l} {{\tilde R}^2} + {P^2}{{\tilde T}^2} > \dfrac{1}{4}\left( {k_c^2 + {P^2}b_c^2} \right) \hfill \\ \tilde H\left( {{P^2}\tilde T - \tilde R\tilde H} \right) - {P^2}{{\tilde T}^2} > X \hfill \end{array} \right\} $$ (39) 式中,
$X = \dfrac{{\text{1}}}{{{P^2} + {{\tilde H}^2}}}\left\{ {\left[ {{P^2}\left( {{\text{1}} - \dfrac{{2\tilde T}}{{\tilde H}} - \dfrac{{\tilde T}}{{{k_c}}}{b_c}} \right) + {{\tilde H}^{\text{2}}} - \dfrac{{b_c^2}}{{\text{4}}}} \right]} \right. \cdot$ $\left. { \dfrac{{\tilde H{k_c}{b_c}}}{{\text{4}}}+ \left( {{\text{1}} - \dfrac{{b_c^2}}{{{\text{4}}{{\tilde H}^2}}}} \right)\dfrac{{{{\tilde H}^2}k_c^2}}{{\text{4}}} + \left( {{P^2} + \tilde R} \right)\dfrac{{{{\tilde H}^2}b_c^2}}{{\text{4}}}} \right\}$ .依据外弹道学理论, 旋转稳定弹的陀螺力矩项远大于静力矩项和赤道阻尼力矩项, 重力项、升力项、阻力项和马格努斯力矩项更小[31], 所以在控制力和力矩较小的条件下满足关系式
$$ \left| P \right| \gg {\left\| {\boldsymbol{\xi }} \right\|_\infty },\quad{\boldsymbol{ \xi}} = (\tilde H,\tilde R,\tilde T,{k_c},{b_c}) $$ (40) 由于
${\boldsymbol{ \xi }}$ 中各元素均为小量, 且$ {\tilde H^2} \gg b_c^2 $ , 故略去X中相对高阶小量, 化简得到$$ X = \frac{{\tilde H - 2\tilde T}}{4}{k_c}{b_c} + \frac{{{{\tilde H}^2}}}{{{\text{4}}{P^2}}}\left( {k_c^2 + {P^2}b_c^2} \right) $$ (41) 将上式代入式(39), 由
${\tilde S_{\text{d}}}$ 和${\tilde S_{\text{g}}}$ 改写得到固定鸭舵双旋弹有控飞行时的动态稳定性判据为$$ \left. \begin{gathered} \tilde S_{\text{d}}^2\frac{{{{\tilde H}^{\text{2}}}}}{{{P^2}}}\left( {1 - {{\hat T}^2}} \right) + \frac{1}{{{\text{4}}\tilde S_{\text{g}}^2}}\left( {{\text{1}} - {{\hat R}^2}} \right) > 0 \hfill \\ {{\tilde S}_{\text{d}}}\left( {2 - {{\tilde S}_{\text{d}}} + \frac{{{{\tilde S}_{\text{d}}}}}{{{{\tilde S}_{\text{g}}}}}\frac{{\hat R\hat T}}{{\text{2}}}} \right) > \frac{{\text{1}}}{{{{\tilde S}_{\text{g}}}}} + \frac{{{{\hat R}^{\text{2}}}}}{{{\text{4}}\tilde S_{\text{g}}^2}}{\text{ + }}\frac{{{{\tilde S}_{\text{d}}}}}{{{{\tilde S}_{\text{g}}}}}\frac{{\hat R\hat T}}{{\text{2}}} + \tilde S_{\text{d}}^2\frac{{{{\tilde H}^{\text{2}}}}}{{{P^2}}}{{\hat T}^2} \end{gathered} \right\} $$ (42) 式中,
$ \hat R = {k_c}/(2\tilde R) $ 为R项的相对增量;$ \hat T = {b_c}/(2\tilde T) $ 为T项的相对增量.2.3 舵面参数对动态稳定性的影响
为便于分析舵面参数对动态稳定性的影响, 假设加装修正组件不改变后体气动参数, 在此补充原常规旋转稳定弹(后文简称原弹)的动态稳定性判据为
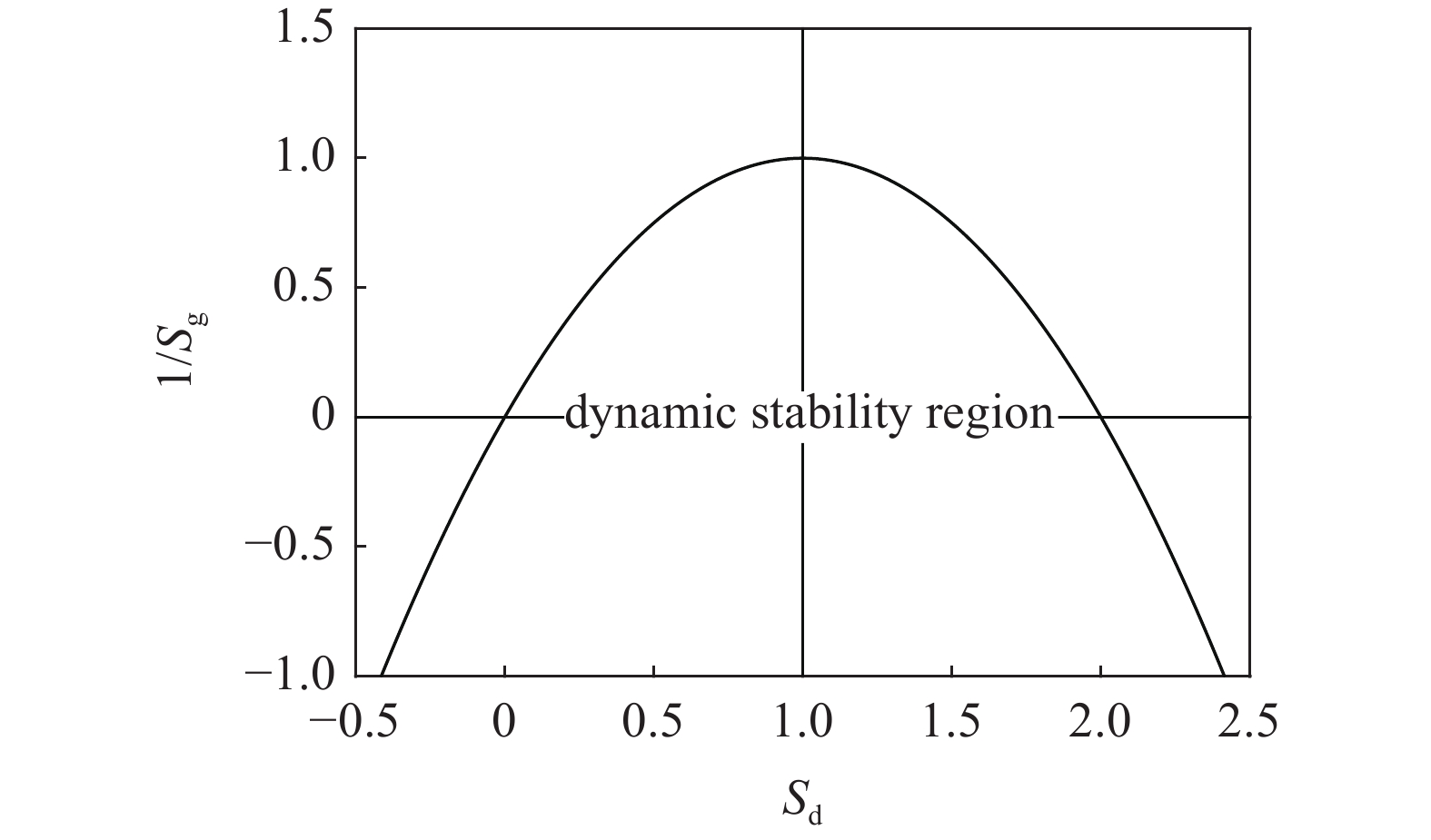
$$ \left. \begin{array}{l} H > 0 \hfill \\ {S_{\text{d}}}\left( {2 - {S_{\text{d}}}} \right) > 1/{S_{\text{g}}} \end{array} \right\} $$ (43) 式中,
${S_{\text{d}}} = 2 T{\text{/}}H$ ,$ {S_{\text{g}}} = {P^2}/(4 R) $ , 分别为原弹的动态稳定因子和陀螺稳定因子, 对应的动态稳定边界如图2所示.对比式(37)和式(43)可知, 固定鸭舵双旋弹无控飞行时的动态稳定性判据与原弹的形式一致, 只不过在
${\tilde S_{\text{d}}}$ 和${\tilde S_{\text{g}}}$ 中, 与$ {b_y} $ 及$ {k_z} $ 有关的项对应增加了$ {b_c}/2 $ 和$ {k_c}/2 $ , 利用${S_{\text{d}}}$ 和${S_{\text{g}}}$ 改写得到$$ {\tilde S_{\text{d}}} = {S_{\text{d}}} + ({\text{2}} - {S_{\text{d}}})\hat H,\quad {\tilde S_{\text{g}}} = {S_{\text{g}}}(1 - \hat R) $$ (44) 式中,
$ \hat H = {b_c}/({\text{2}}\tilde H) $ , 为H项的相对增量. 结合图2可知,$\hat H < 0$ 使${\tilde S_{\text{d}}}$ 远离${S_{\text{d}}} = {\text{2}}$ ,$\hat H > 0$ 使${\tilde S_{\text{d}}}$ 靠近${S_{\text{d}}} = {\text{2}}$ ;$\hat R < {\text{1}}$ 使${\text{1/}}{\tilde S_{\text{g}}}$ 远离${\text{1/}}{S_{\text{g}}} = 0$ ,$\hat R > {\text{1}}$ 使${\text{1/}}{\tilde S_{\text{g}}}$ 穿过${\text{1/}}{S_{\text{g}}} = 0$ .上述分析表明, 原弹在安装弹道修正组件后, 可能会使
${\tilde S_{\text{d}}}\sim{\text{1/}}{\tilde S_{\text{g}}}$ 移动到动态稳定域外, 因此为了保证固定鸭舵双旋弹无控飞行时动态稳定, 必须对$\hat H$ 和$\hat R$ 的取值进行限制. 在已知原弹气动参数, 即${S_{\text{d}}}\sim{\text{1/}}{S_{\text{g}}}$ 确定的条件下, 将式(44)代入式(37), 导出$\hat H \sim \hat R$ 须满足关系式$$(2 - {S_{\rm{d}}})\left[ {1 - {{\hat H}^2} - (1 - {S_{\rm{d}}}){{(1 - \hat H)}^2}} \right] > \dfrac{{\rm{1}}}{{{S_{\rm{g}}}(1 - \hat R)}} $$ (45) 式中, 不等式左边趋于
${{\text{0}}^ + }$ 时,$ {\text{|1}} - \hat R{\text{|}} $ 的最小取值须快速增大; 不等式左边小于0, 且绝对值逐渐增大时,$ {\text{|1}} - \hat R{\text{|}} $ 的最大取值须快速趋近于0. 易见, 当$ \hat H $ 使不等式左边趋于0时, 要求$\hat R$ 的边界取值快速变化, 这可能导致操纵舵的安装位置超出前体结构限制, 故$ {c'_{{\text{cr}}}} $ 不宜接近某一界限值, 该值由弹体气动参数和结构允许的L取值限度综合确定.在满足无控飞行时动态稳定性条件的基础上, 进一步分析舵面参数对固定鸭舵双旋弹有控飞行时动态稳定性的影响, 根据式(42)导出气动参数相对增量还须满足关系式
$$ \left. \begin{array}{l} \dfrac{{{K_1}}}{{{K_{\text{1}}} + {K_{\text{3}}}}}{{\hat T}^2} + \dfrac{{{K_3}}}{{{K_{\text{1}}} + {K_{\text{3}}}}}{{\hat R}^{\text{2}}} < {\text{1}} \hfill \\ \dfrac{{{K_1}}}{{{K_{\text{4}}}}}{{\hat T}^2} + \dfrac{{{K_2}}}{{{K_{\text{4}}}}}\hat R\hat T + \dfrac{{{K_3}}}{{{K_{\text{4}}}}}{{\hat R}^{\text{2}}} < {\text{1}} \end{array} \right\} $$ (46) 式中,
$ {K_1} = \tilde S_{\text{d}}^2{\tilde H^{\text{2}}}/{P^2} $ ,$ {K_2} = {\tilde S_{\text{d}}}(1 - {\tilde S_{\text{d}}})/({\text{2}}{\tilde S_{\text{g}}}) $ ,$ {K_3} = {\text{1/}}({\text{4}}\tilde S_{\text{g}}^2) $ ,$ {K_4} = {\tilde S_{\text{d}}}\left( {2 - {{\tilde S}_{\text{d}}}} \right) - {\text{1/}}{\tilde S_{\text{g}}} $ . 由于$ {K}_{1, 3, 4} $ 均大于0, 且$ {K_1} $ 相对$ {K_{\text{2}}} $ 和$ {K_{\text{3}}} $ 为高阶小量, 满足$ K_{\text{2}}^{\text{2}} - {K_1}{K_3} > 0 $ , 故有控飞行时的$\hat T$ ~$\hat R$ 取值应在第1式定义的椭圆内以及第2式定义的双曲线之间.3. 弹道数值计算分析
3.1 计算条件
本节以某155 mm固定鸭舵双旋弹为研究对象, 在炮兵标准气象条件下进行弹道数值计算分析. 弹丸主要物理参数如表1所示, 仿真初始条件为: 初速930 m/s, 初始转速300 r/s, 射角45°, 其余弹道参数为0. 为便于分析, 给出原弹的
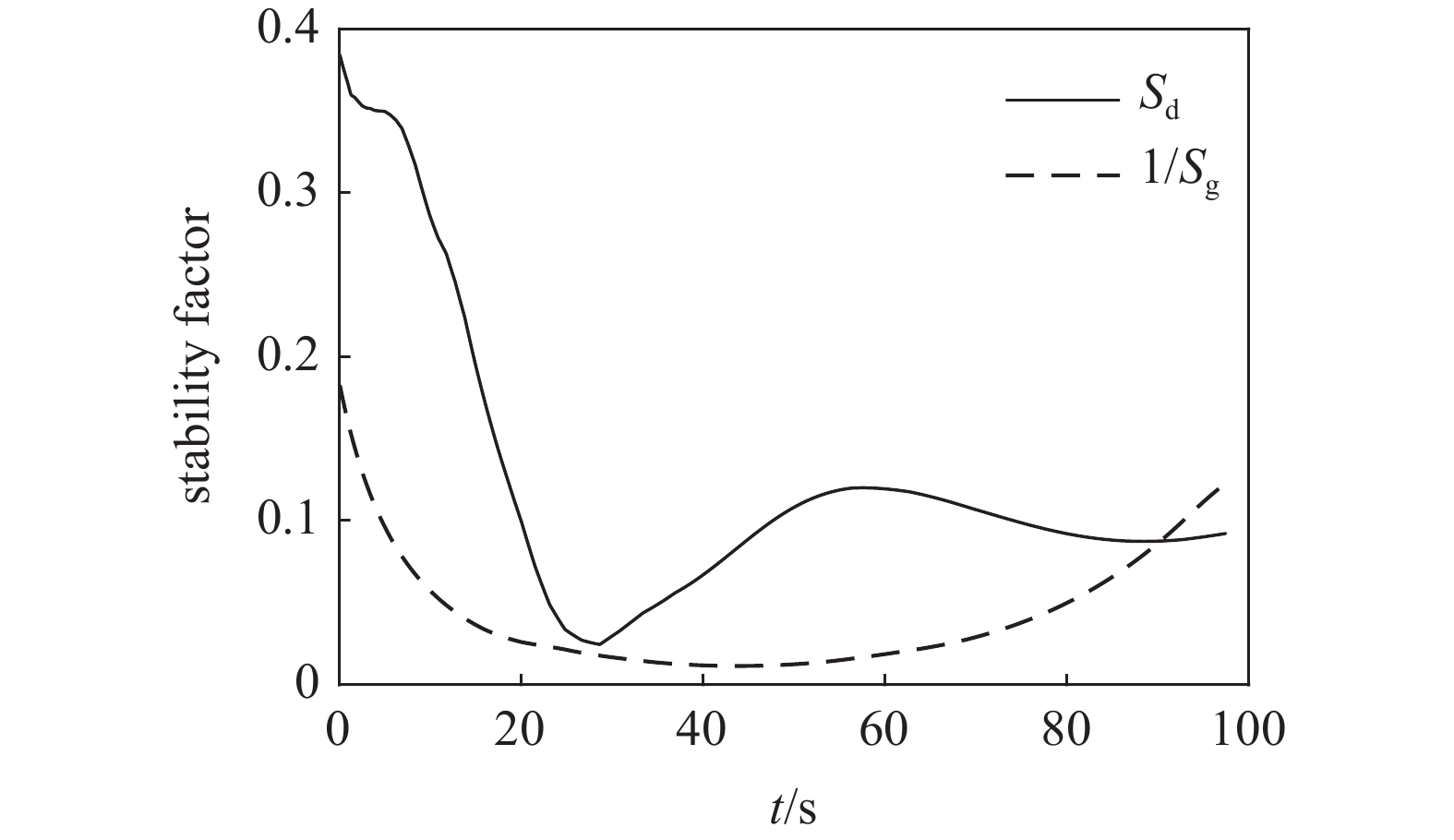
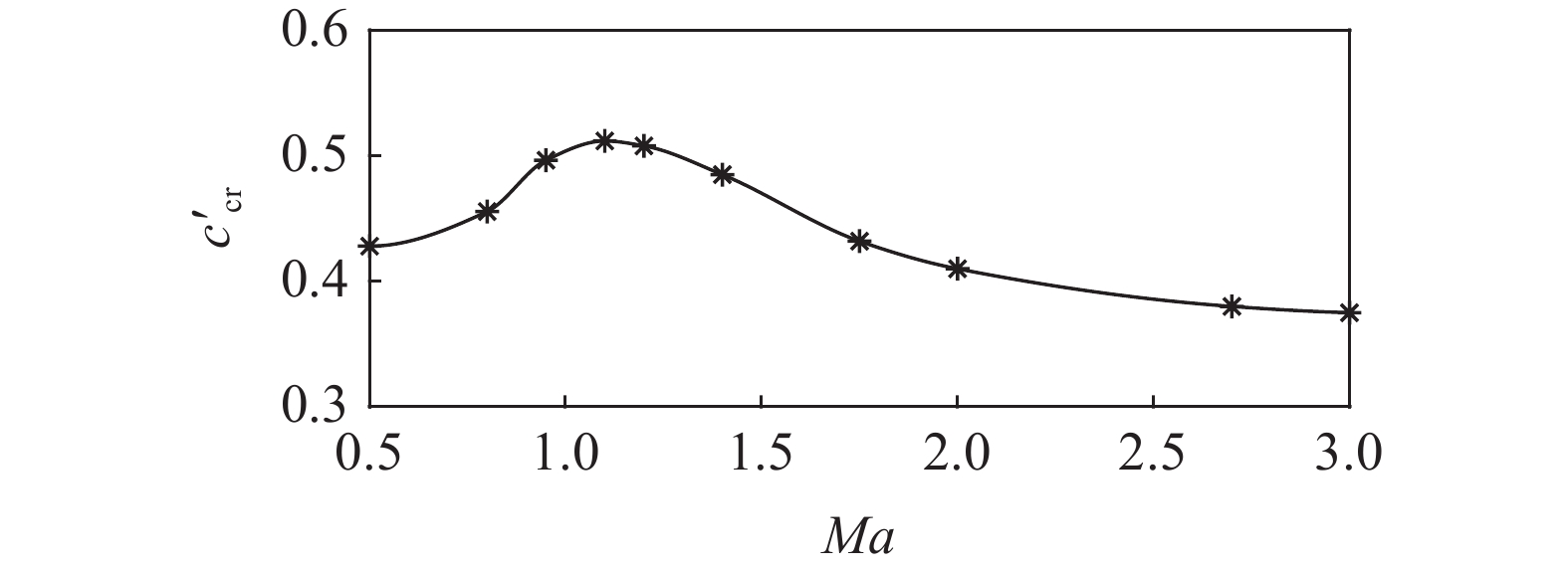
${S_{\text{d}}}$ 和${\text{1/}}{S_{\text{g}}}$ 如图3所示, 操纵舵的控制力系数导数如图4所示.表 1 弹丸物理参数Table 1. Physical parameters of projectilem/kg l/m C/(kg·m2) A/(kg·m2) L/m ${\delta _{\text{D}}}$/(°) 45.50 0.902 0.163 1.792 0.495 5 3.2 计算结果分析
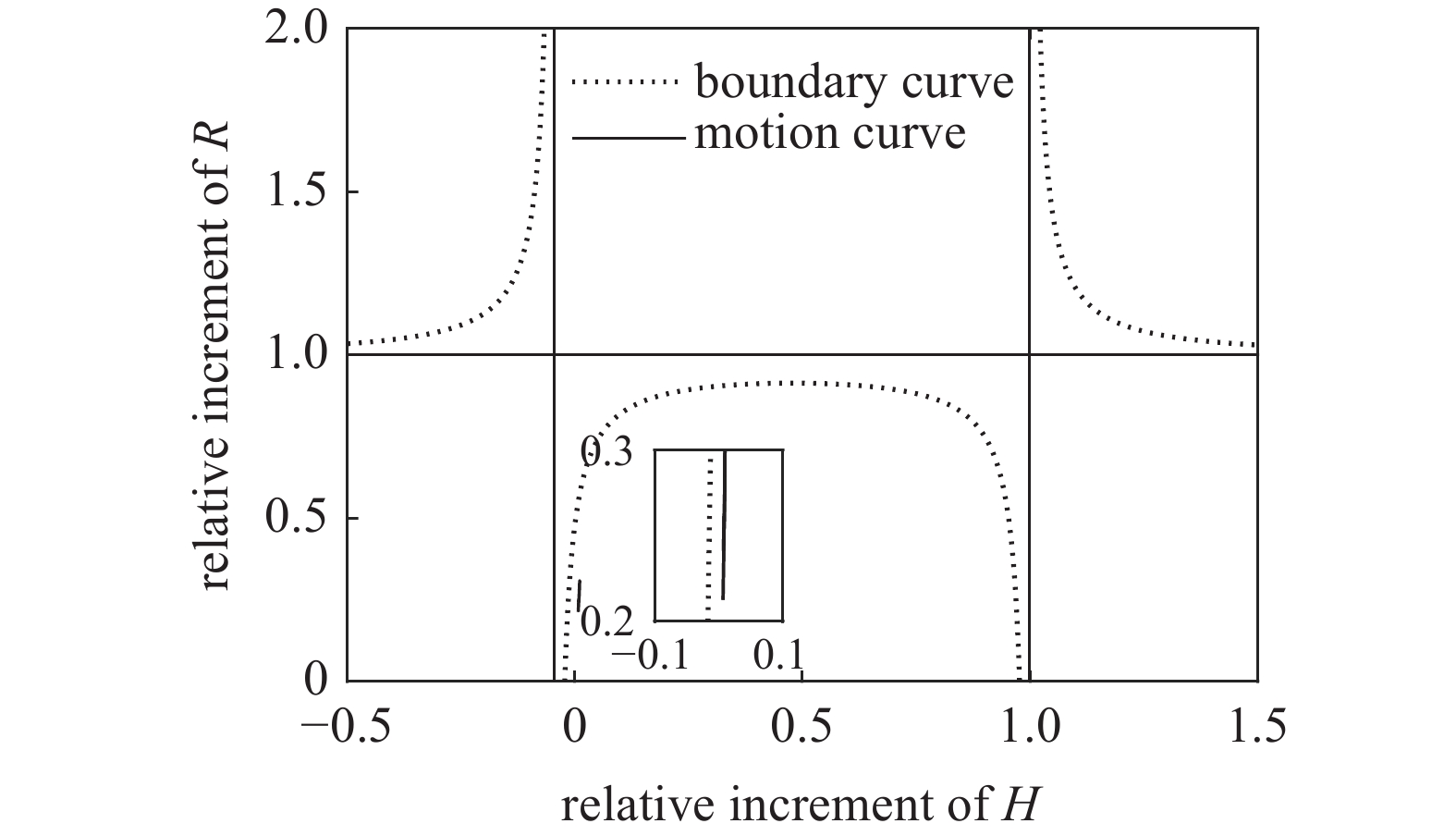
为了验证固定鸭舵双旋弹无控飞行时的动态稳定性判据和式(45)的舵面参数约束条件合理可行, 首先给出弹道初始段, 即t = 10 s时的H ~ R相对增量边界曲线如图5所示, 其中动态稳定域包括: 中间边界曲线以下、两侧边界曲线以下且在
$ \hat R $ =1轴以上. 依据本节的操纵舵参数图5还给出了H ~ R相对增量全弹道运动曲线, 其始终在动态稳定域内, 表明该弹在弹道初始段满足无控飞行时的动态稳定性条件.进一步分析无控飞行时全弹道的动态稳定性, 依据
${S_{\text{d}}} < 1$ 和${\text{1/}}{S_{\text{g}}} > 0$ , 由式(45)可知, 其他弹道点上的H ~ R相对增量边界曲线与图5类似, 只不过${S_{\text{d}}}$ 减小或${\text{1/}}{S_{\text{g}}}$ 增大会使中间部分的边界曲线收缩, 故由图3可知H ~ R相对增量运动曲线相对容易超出弹道末段的边界曲线. 图6给出弹道末段, 即t = 90 s时的H ~ R相对增量边界曲线, 易见H ~ R相对增量运动曲线靠近边界曲线, 但仍位于动态稳定域内, 表明该弹满足无控飞行时的动态稳定性条件.利用本节给出的计算条件进行弹道仿真, 在炮口和弹道顶点处各施加3°的初始扰动, 图7为无控飞行时复攻角的幅值变化曲线. 结果表明: ①复攻角的幅值在初始扰动作用后逐渐收敛, 故该弹无控飞行时动态稳定, 验证了固定鸭舵双旋弹无控飞行时的动态稳定性判据和舵面参数约束条件合理可行; ②炮口扰动在弹道初始段已逐渐收敛, 对弹道顶点附近起控后的复攻角运动影响不大, 为后文在零初始条件下分析有控飞行的动态稳定性提供了依据.
![]()
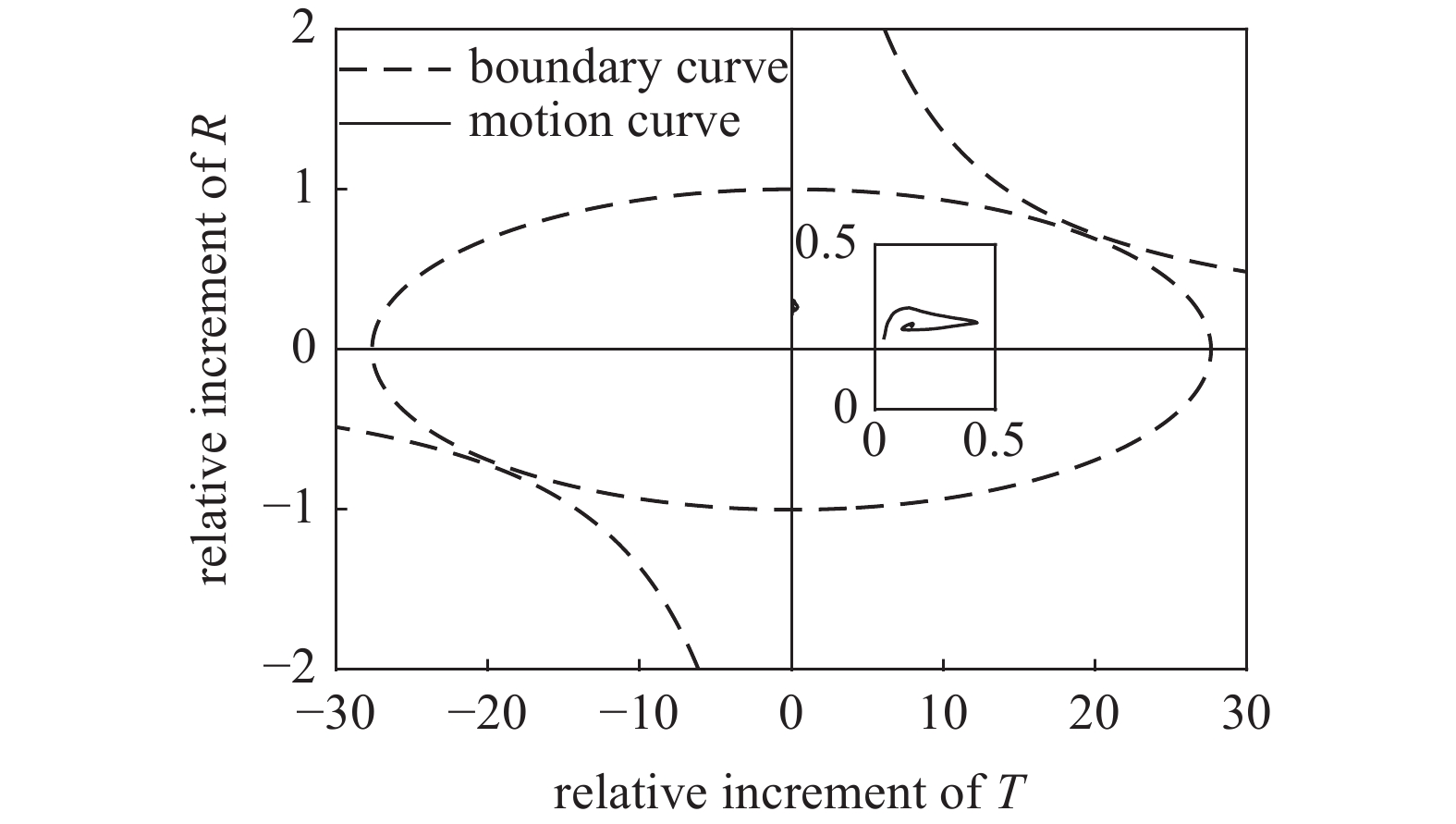
图 7 无控飞行时复攻角的幅值变化曲线Figure 7. Amplitude of complex attack angle in uncontrolled flight在满足无控飞行时动态稳定性条件的基础上, 进一步验证有控飞行时的动态稳定性判据和舵面参数约束条件合理可行. 结合图3给出的
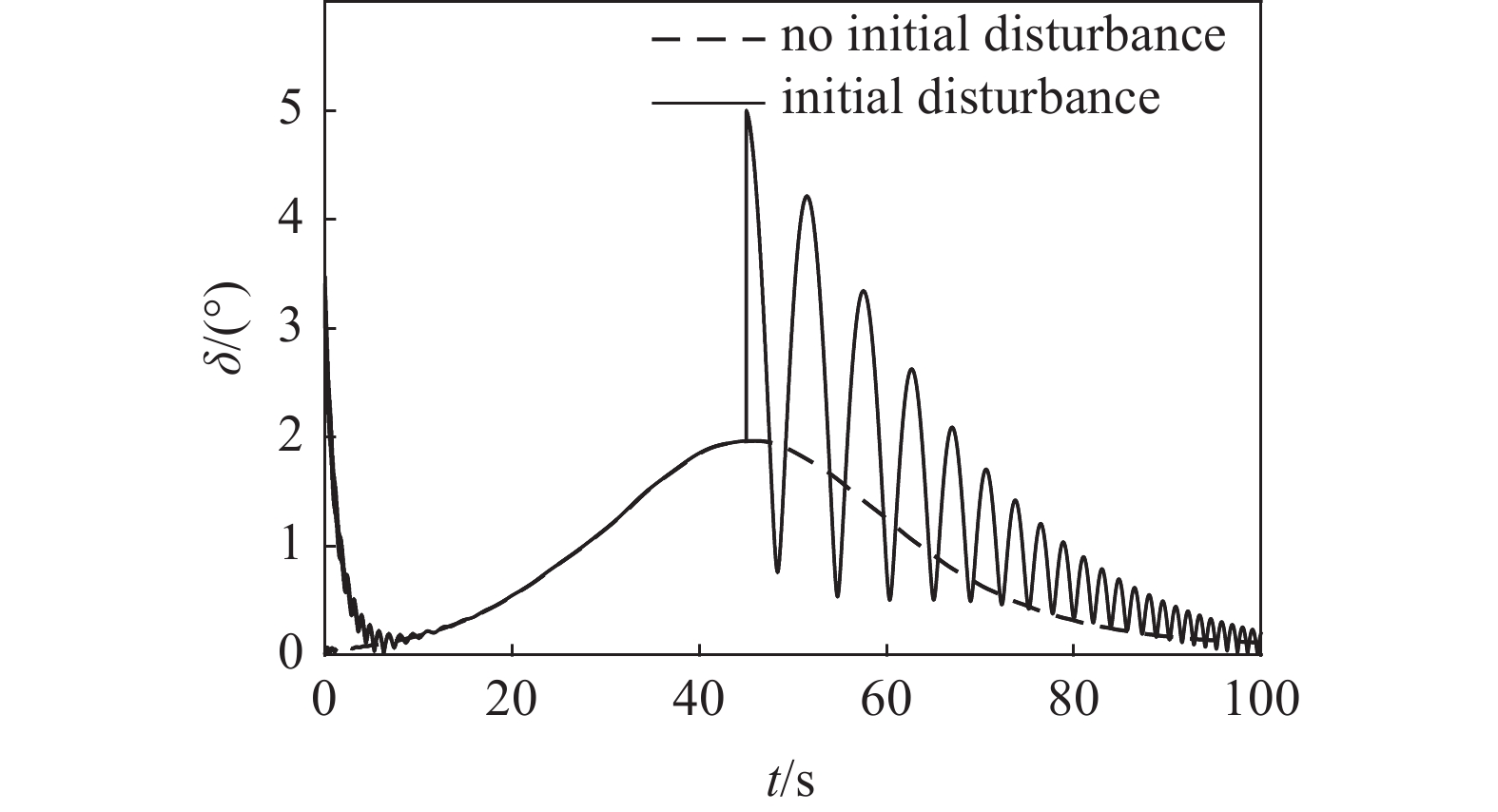
${S_{\text{d}}}$ 和${\text{1/}}{S_{\text{g}}}$ 取值范围分析式(46)可知,${S_{\text{d}}}$ 减小和${\text{1/}}{S_{\text{g}}}$ 增大对动态稳定域的椭圆边界影响不大, 但会使双曲线边界靠近原点, 可能导致T ~ R相对增量的取值范围缩小, 故T ~ R相对增量运动曲线相对容易超出弹道末段的边界曲线. 图8为弹道末段, 即t = 90 s时的T ~ R相对增量边界曲线, 易见T ~ R相对增量运动曲线始终在动态稳定域内并远离边界曲线, 故该弹在全弹道任意时刻均满足有控飞行时的动态稳定性条件.利用本节给出的计算条件进行弹道仿真, 假设固定鸭舵双旋弹在弹道顶点附近, 即t = 45 s时起控, 图9给出了前体滚转角控制方位分别为0°, 90°, 180°和270°时的复攻角运动曲线. 结合式(28)可知, 固定方位的控制力和力矩会产生控制平衡角, 其与重力产生的动力平衡角共同构成复攻角的强迫角运动, 并在起控瞬间引起与控制平衡角幅值相等、相位相反的初始扰动, 使复攻角以强迫角运动为中心做逐渐收敛的自由角运动, 表明该弹有控飞行时动态稳定, 验证了固定鸭舵双旋弹有控飞行时的动态稳定性判据和舵面参数约束条件合理可行.
![]()
图 9 不同控制方位下的复攻角运动曲线Figure 9. Complex attack angle motion under different control directions依据式(28), 在零初始条件下对包含固定方位控制力和力矩非齐次项的复攻角方程进行求解, 得到控制平衡角的表达式为
$$ {{{{{\varDelta}}}} _{\text{F}}} = \frac{{\sqrt {\left( {{P^2}b_c^2 + {N^2}} \right)\left( {{R^{\text{2}}} + {P^{\text{2}}}{T^{\text{2}}}} \right)} }}{{{R^{\text{2}}} + {P^{\text{2}}}{T^{\text{2}}}}}{\delta _{\text{D}}}{{\rm{e}}^{{\rm{i}}({\gamma _{\text{F}}} + {\phi _{\text{F}}}{{ + {\text{π}} }})}} $$ (48) 式中,
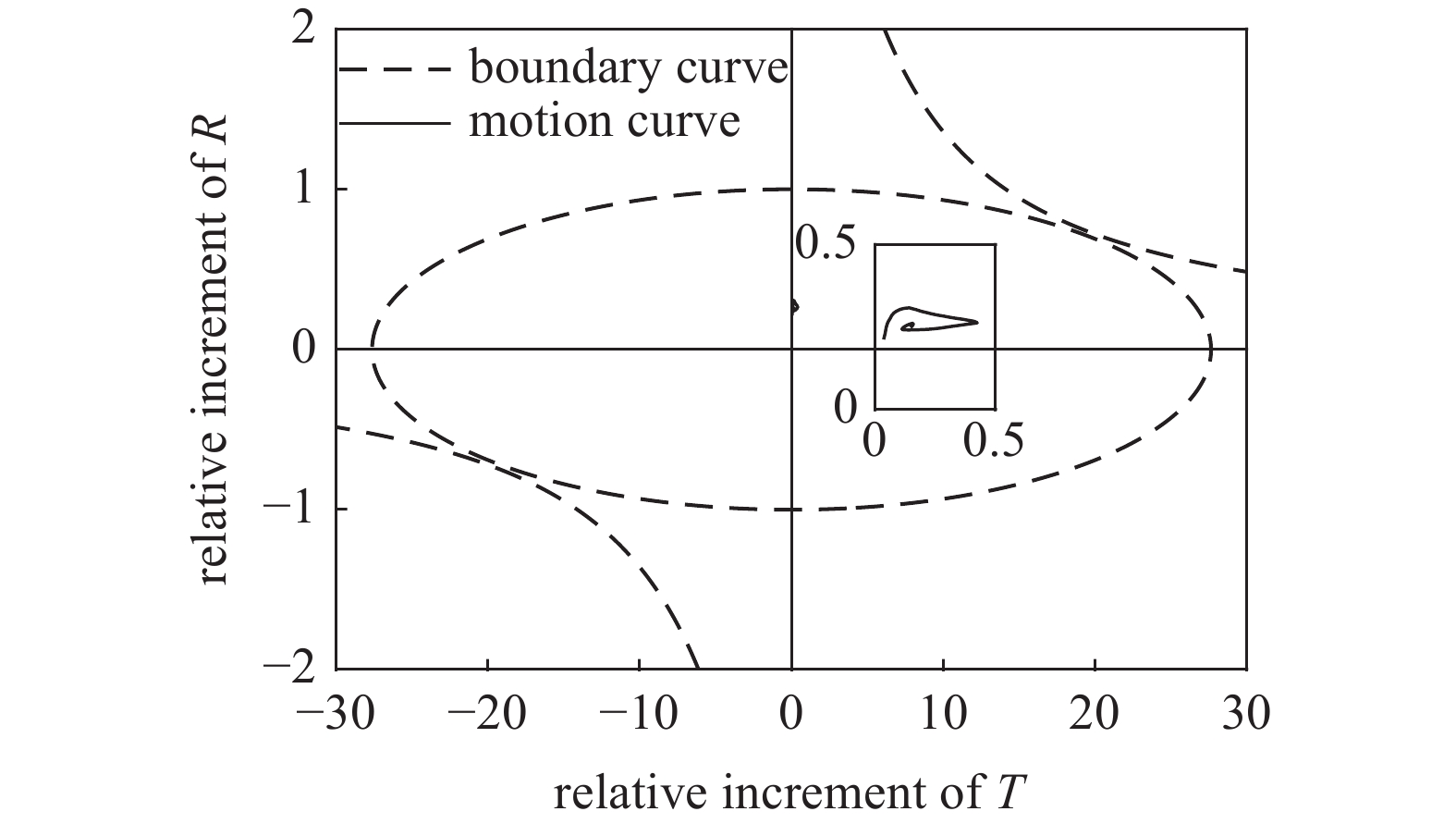
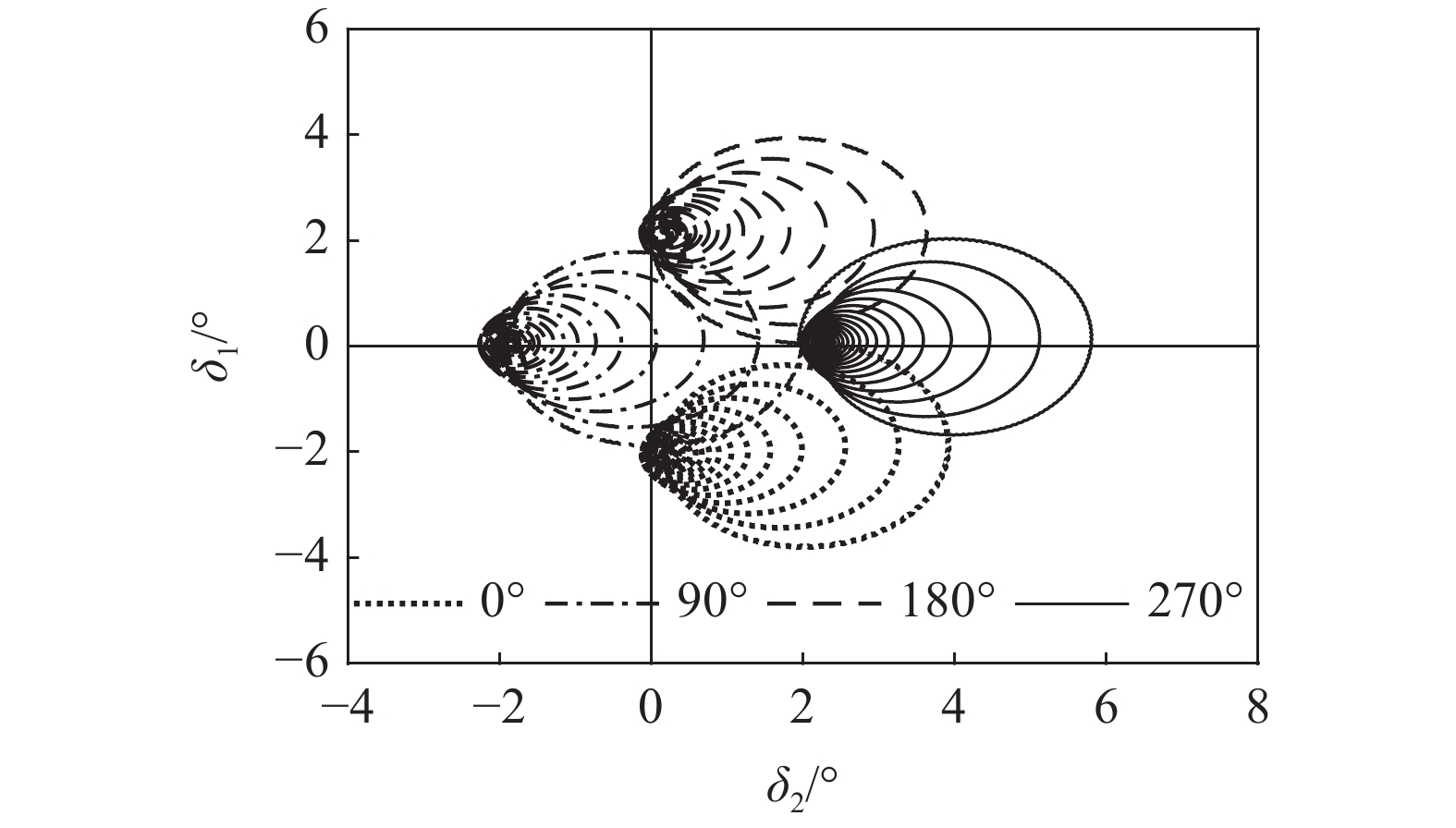
$ {\phi _{\text{F}}} = \arctan (P{b_c}{\text{/}}{k_c}) + \arctan ( - PT{\text{/}}R) $ . 对于本节研究的固定鸭舵双旋弹, 满足$ {\text{0}} < P{b_c} \ll N $ 和$ 0 < PT \ll R $ , 故$\left| {{{{{{\varDelta}}}} _{\text{F}}}} \right| \approx \hat R/(1 - \hat R){\delta _{\text{D}}}$ , 且$ {\phi _{\text{F}}} $ 为一较小角度, 即${{{{{\varDelta}}}} _{\text{F}}}$ 的幅值主要由$\hat R$ 和$ {\delta _{\text{D}}} $ 决定, 相位与$ {\gamma _{\text{F}}} $ 相差约180°. 结合图7可知, 当动力平衡角在弹道末段接近零时, 图9中不同控制方位下的强迫角运动主要由${{{{{\varDelta}}}} _{\text{F}}}$ 决定, 其幅值近似相等, 相位与前体滚转角控制方位相差约180°, 验证了上述结论合理, 为分析多次起控时的动态稳定性提供了理论依据.将控制周期设为15 s, 图10给出了多次起控, 前体滚转角控制方位依次为0°, 90°, 180°和270°时的复攻角运动曲线. 结合式(47)可知, 前体滚转角控制方位切换会使
${{{\varDelta}} _{\text{F}}}$ 的相位变为与切换后的$ {\gamma _{\text{F}}} $ 相差约180°, 这会导致复攻角的强迫角运动发生变化, 并在切换瞬间引起初始扰动, 使复攻角以当前强迫角运动为中心做逐渐收敛的自由角运动. 注意到在自由角运动未能收敛的条件下, 复攻角的强迫角运动多次变化容易使初始扰动幅值偏大, 可能导致$ \delta $ 超出某一界限, 因此为了保证弹丸具有良好的动态稳定性, 还须对前体滚转角控制方位切换时强迫角运动的变化量幅值$ {\delta _{\text{r}}} $ 进行限制.由于多次起控时强迫角运动变化量幅值主要由复控制平衡角的变化引起, 所以为了使
$ {\delta _{\text{r}}} $ 不会过大, 首先需要对$\left| {{{{{{\varDelta}}}} _{\text{F}}}} \right|$ 进行限制. 定义$ {\delta _{\max }} $ 为复控制平衡角的幅值允许限, 须满足$$ {\left| {{{{{{\varDelta}}}} _{\text{F}}}} \right|_{\max }} < {\delta _{{\text{max}}}} $$ (50) 依据
$\left| {{{{{{\varDelta}}}} _{\text{F}}}} \right| \approx \hat R/(1 - \hat R){\delta _{\text{D}}}$ , 在操纵舵控制力系数导数和安装位置确定的条件下, 即要求对$ {\delta _{\text{D}}} $ 进行限制. 此外, 注意到前体滚转角控制方位切换剧烈也会使$ {\delta _{\text{r}}} $ 较大, 故多次起控还应尽量避免$ {\gamma _{\text{F}}} $ 的切换幅度过大.![]()
图 10 控制方位多次切换的复攻角运动曲线Figure 10. Complex attack angle motion with multiple switching of control directions4. 结 论
本文通过建立复攻角的状态空间模型, 利用常规旋转弹的稳定性分析方法, 对固定鸭舵双旋弹全弹道的动态稳定性问题展开研究, 所得主要结论如下.
(1)由于前体滚转角的运动特性在不同飞行状态下存在差异, 为了保证固定鸭舵双旋弹全弹道飞行稳定, 须同时满足无控飞行和有控飞行时的动态稳定性判据.
(2)建立的固定鸭舵双旋弹动态稳定性判据与常规旋转弹的形式相似, 无控飞行时只是在升力和静力矩项中对应增加了舵面控制力和力矩项; 有控飞行时进一步增加了有关项相对增量的影响.
(3)在原弹气动参数确定时, 为使安装弹道修正组件后的固定鸭舵双旋弹全弹道飞行动态稳定, 需使
$\hat H \sim \hat R$ 落在由${S_{\text{d}}}$ 和${\text{1/}}{S_{\text{g}}}$ 确定的H ~ R相对增量边界曲线内, 且$\hat T \sim \hat R$ 位于由${\tilde S_{\text{d}}}$ 和${\text{1/}}{\tilde S_{\text{g}}}$ 确定的T ~ R相对增量边界曲线内, 据此可以对操纵舵的形状、尺寸和安装位置等参数进行设计.(4)对弹道进行多次控制, 在自由角运动尚未收敛时, 各控制周期的复控制平衡角相互干扰, 容易使
$\delta $ 过大, 导致弹丸飞行稳定性变差, 据此需对$ {\delta _{\text{D}}} $ 进行限制, 并尽量避免$ {\gamma _{\text{F}}} $ 切换幅度过大.考虑对弹道进行多次控制时容易使
$\delta $ 过大, 可能导致在原有小攻角假设下分析的稳定性判据等结果不再准确, 因此下一步拟通过建立固定鸭舵双旋弹的非线性角运动模型, 对其大攻角下的角运动特性和稳定性理论展开研究. -
![]()
图 7 无控飞行时复攻角的幅值变化曲线
Figure 7. Amplitude of complex attack angle in uncontrolled flight
![]()
图 9 不同控制方位下的复攻角运动曲线
Figure 9. Complex attack angle motion under different control directions
![]()
图 10 控制方位多次切换的复攻角运动曲线
Figure 10. Complex attack angle motion with multiple switching of control directions
表 1 弹丸物理参数
Table 1 Physical parameters of projectile
m/kg l/m C/(kg·m2) A/(kg·m2) L/m ${\delta _{\text{D}}}$/(°) 45.50 0.902 0.163 1.792 0.495 5 
下载: 导出CSV
-
[1] 王中原, 史金光, 常思江等. 弹道修正弹技术发展综述. 弹道学报, 2021, 33(2): 1-12 (Wang Zhongyuan, Shi Jinguang, Chang Sijiang, et al. Review on development of technology of trajectory correction projectile. Journal of Ballistics, 2021, 33(2): 1-12 (in Chinese) [2] 张民权, 刘东方, 王冬梅等. 弹道修正弹发展综述. 兵工学报, 2010, 31(S2): 127-130 (Zhang Minquan, Liu Dongfang, Wang Dongmei, et al. A summary for trajcectory correction projectiles. Acta Armamentarii, 2010, 31(S2): 127-130 (in Chinese) [3] Pettersson T, Buretta R, Cook D. Aerodynamics and flight stability for a course corrected artillery round//23rd International Symposium on Ballistics, Tarragona, Spain, 2007: 647-653
[4] Regan FJ, Smith J. Aeroballistics of a terminally corrected spinning projectile (TCSP). Journal of Spacecraft and Rockets, 1975, 12(12): 733-738 doi: 10.2514/3.57041
[5] Wernert P, Leopold F, Lehmann L. Wind tunnel tests and open-loop trajectory simulations for a 155 mm canards guided spin stabilized projectile, Honolulu, IA: AIAA, 2008. AIAA-2008-6881.
[6] 郝永平, 孟庆宇, 张嘉易. 固定翼二维弹道修正弹气动特性分析. 弹箭与制导学报, 2012, 32(3): 171-173 (Hao Yongping, Meng Qingyu, Zhang Jiayi. Aerodynamic characteristic analysis on two-dimensional trajectory corrector shell with fixed-wing. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(3): 171-173 (in Chinese) doi: 10.3969/j.issn.1673-9728.2012.03.047 [7] 纪秀玲, 王海鹏, 曾时明等. 可旋转鸭舵对旋转弹丸纵向气动特性的影响. 北京理工大学学报, 2011, 31(3): 265-268 (Ji Xiuling, Wang Haipeng, Zeng Shiming, et al. CFD prediction of longitudinal aerodynamics for a spinning projectile with fixed canard. Transactions of Beijing Institute of Technology, 2011, 31(3): 265-268 (in Chinese) [8] 冯斌, 于纪言, 鞠潭等. 双旋弹道修正弹弹体非对称载荷的数值研究. 兵工学报, 2018, 39(11): 2118-2126 (Feng Bin, Yu Jiyan, Ju Tan, et al. Numerical study of asymmetrical load on the body of dual-spin projectile. Acta Armamentarii, 2018, 39(11): 2118-2126 (in Chinese) doi: 10.3969/j.issn.1000-1093.2018.11.005 [9] 钟阳, 王良明, 李岩等. 旋转稳定二维修正弹鸭舵法向力计算模型研究. 弹道学报, 2019, 31(2): 48-54 (Zhong Yang, Wang Liangming, Li Yan, et al. Calculation model of normal force of canard on spin stabilized two-dimensional trajectory correction projectile. Journal of Ballistics, 2019, 31(2): 48-54 (in Chinese) [10] 黄智康, 陈少松, 魏恺等. 固定鸭舵双旋火箭弹超声速侧向气动特性. 弹道学报, 2021, 33(1): 55-64 (Hang Zhikang, Chen Shaosong, Wei Kai, et al. Lateral aerodynamics of a fixed-canard dual-spin rocket projectile at supersonic speed. Journal of Ballistics, 2021, 33(1): 55-64 (in Chinese) [11] 冯斌, 于纪言, 王晓鸣等. 固定鸭舵双旋火箭弹弹体绕流的数值研究. 弹道学报, 2021, 33(2): 21-27 (Feng Bin, Yu Jiyan, Wang Xiaoming, et al. Numerical study on the flow around dual-spin rocket projectile body. Journal of Ballistics, 2021, 33(2): 21-27 (in Chinese) [12] Costello M, Peterson A. Linear theory of a dual-spin projectile in atmospheric flight. Journal of Guidance, Control and Dynamic, 2000, 23(5): 789-797 doi: 10.2514/2.4639
[13] 常思江, 王中原, 刘铁铮. 鸭式布局双旋弹飞行动力学建模与仿真. 弹道学报, 2014, 26(3): 1-5, 16 (Chang Sijiang, Wang Zhongyuan, Liu Tiezheng. Modeling and simulation of flight dynamic for dual-spin stabilized projectile equipped with canards. Journal of Ballistics, 2014, 26(3): 1-5, 16 (in Chinese) doi: 10.3969/j.issn.1004-499X.2014.03.001 [14] 许诺, 于剑桥, 王亚飞等. 固定翼双旋弹动力学特性分析. 兵工学报, 2015, 36(4): 02-609 (Xu Nuo, Yu Jianqiao, Wang Yafei, et al. Analysis of dynamic characteristics of fixed-wing dual-spin projectiles. Acta Armamentarii, 2015, 36(4): 02-609 (in Chinese) [15] 许诺, 于剑桥, 王亚飞. 固定翼双旋弹动力学分岔特性分析. 航空学报, 2015, 36(12): 3798-3808 (Xu Nuo, Yu Jianqiao, Wang Yafei. Dynamic bifurcation characteristics analysis on fixed-canard dual-spin projectiles. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3798-3808 (in Chinese) [16] 许诺, 于剑桥, 王亚飞. 基于周期平均的固定翼双旋弹弹道修正方法. 航空学报, 2016, 36(9): 2892-2899 (Xu Nuo, Yu Jianqiao, Wang Yafei. Trajectory correct-ing method of fixed-canard of dual-spin projectiles based on period average. Acta Aeronautica et Astronautica Sinica, 2016, 36(9): 2892-2899 (in Chinese) [17] 马国梁. 基于修正质点弹道模型的双旋弹控制效果分析. 北京理工大学学报, 2019, 39(8): 777-783 (Ma Guoliang. Control effect analysis of dual-spin projectile based on modified mass point trajectory model. Transactions of Beijing Institute of Technology, 2019, 39(8): 777-783 (in Chinese) [18] Theodoulis S, Gassmann V, Wernert P, et al. Guidance and control design for a class of spin-stabilized fin-controlled projectiles. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 517-531 doi: 10.2514/1.56520
[19] 殷婷婷, 贾方秀, 于纪言等. 基于扩张状态观测器的双旋弹丸舵翼转速预测控制. 北京理工大学学报, 2019, 39(10): 1057-1062, 1068 (Yin Tingting, Jia Fangxiu, Yu Jiyan, et al. Direct model predictive rotating speed control for rudder in dual-spin projectile with output-feedback extended state observer. Transactions of Beijing Institute of Technology, 2019, 39(10): 1057-1062, 1068 (in Chinese) [20] 殷婷婷, 贾方秀, 于纪言等. 基于改进LuGre摩擦模型的双旋弹丸固定舵翼滚转位置鲁棒自适应控制算法. 兵工学报, 2019, 40(12): 2425-2432 (Yin Tingting, Jia Fangxiu, Yu Jiyan, et al. Robust adaptive control of roll position of fixed rudder for dual-spin projectile with improved LuGre friction model. Acta Armamentarii, 2019, 40(12): 2425-2432 (in Chinese) doi: 10.3969/j.issn.1000-1093.2019.12.005 [21] 张鑫, 姚晓先. 固定翼双旋弹修正组件滚转控制研究. 北京理工大学学报, 2020, 40(4): 386-395 (Zhang Xin, Yao Wenxian. Roll control of course correction fuze for dual-spin projectile with fixed-canards. Transactions of Beijing Institute of Technology, 2020, 40(4): 386-395 (in Chinese) [22] 冯斌, 于纪言, 王钰等. 固定鸭舵导引组件修正力模型改进及参数辨识. 兵工学报, 2019, 40(2): 257-264 (Feng Bin, Yu Jiyan, Wang Yu, et al. Improvement and parameter identification of correction force model for fixed-canard guidance kit. Acta Armamentarii, 2019, 40(2): 257-264 (in Chinese) [23] Wernert P, Theodoulis S. Modeling and stability analysis for a class of 155 mm spin-stabilized projectiles with course correction fuse (CCF)//Proceedings of AIAA Atmospheric Flight Mechanics Conference and Exhibit, Portland, OR, 2011
[24] Chang SJ. Dynamic response to canard control and gravity for a dual-spin projectile. Journal of Spacecraft and Rockets, 2016, 53(3): 558-566 doi: 10.2514/1.A33485
[25] 常思江, 王中原, 刘铁铮. 鸭式布局双旋稳定弹强迫运动理论研究. 兵工学报, 2016, 37(5): 829-839 (Chang Sijiang, Wang Zhongyuan, Liu Tiezheng. A theoretical study of forced motion for dual-spin-stabilized projectiles with canards. Acta Armamentarii, 2016, 37(5): 829-839 (in Chinese) doi: 10.3969/j.issn.1000-1093.2016.05.009 [26] 朱煌, 史金光, 谢飞等. 高旋二维弹道修正弹的角运动特性. 弹道学报, 2020, 32(1): 23-30 (Zhu Huang, Shi Jinguang, Xie Fei, et al. Angular motion characteristics of high-rotation two-dimension trajectory correction projectile. Journal of Ballistics, 2020, 32(1): 23-30 (in Chinese) [27] 赵新新, 史金光, 王中原等. 固定鸭舵双旋弹角运动特性与控制稳定性研究. 哈尔滨工业大学学报, 2022, 54(1): 123-131 (Zhao Xinxin, Shi Jinguang, Wang Zhongyuan, et al. Study on angular motion characteristics and control stability with the fixed canard dual-spin projectile. Journal of Harbin Institute of Technology, 2022, 54(1): 123-131 (in Chinese) [28] Zhu D, Tang S, Guo J, et al. Flight stability of a dual-spin projectile with canards. Proceedings of the Institute of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(4): 703-716 doi: 10.1177/0954410014539293
[29] 马国梁, 蔡红明, 常思江. 固定鸭舵双旋弹动态稳定性分析. 兵工学报, 2019, 40(10): 1987-1994 (Ma Guoliang, Cai Hongming, CHANG Si-jiang. Analysis of dynamic stability of fixed canard dual-spin Projectile. Acta Armamentarii, 2019, 40(10): 1987-1994 (in Chinese) [30] 李佳讯, 沈元川, 贾振岳等. 双旋弹非线性角运动特性分析. 弹箭与制导学报, 2021, 41(1): 1-7 (Li Jiaxun, Shen Yuanchuan, Jia Zhenyue, et al. Nonlinear angular motion analysis on dual-spin Projectile. Journal of Projectile,Rockets,Missiles and Guidance, 2021, 41(1): 1-7 (in Chinese) [31] 韩子鹏. 弹箭外弹道学. 北京: 北京理工大学出版社, 2008 Han Zipeng. Exterior Ballistics of Projectiles and Reckets. Beijing: Beijing Institute of Technology Press, 2008 (in Chinese)
-
期刊类型引用(5)
1. 杨东晓，曹信一，申强. 基于PID切换控制的弹道修正引信滚转角控制方法. 北京理工大学学报. 2025(02): 137-143 . 
百度学术
2. 李红云，申强，邓子龙. 鸭式布局二维修正双旋弹角运动及转向响应特性分析. 兵工学报. 2024(06): 1866-1876 . 百度学术
3. 赵新新，史金光，王中原，张宁. 鸭舵式双旋弹舵翼非线性控制力建模与分析. 兵工学报. 2024(08): 2607-2616 . 百度学术
4. 常思江，李东阳. 有控弹箭稳定性边界的解析预测模型. 航空兵器. 2023(01): 11-18 . 百度学术
5. 赵新新，史金光，王中原，张宁. 鸭舵式双旋弹非线性角运动及其分岔特性. 兵工学报. 2023(10): 3067-3078 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 1046
- HTML全文浏览量: 702
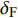
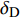
- PDF下载量: 125
- 被引次数: 5
