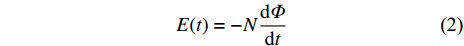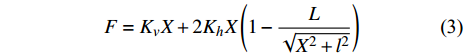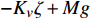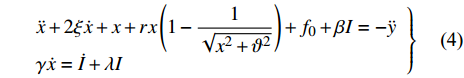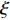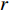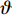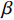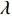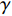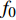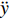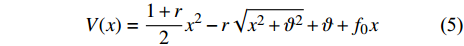SOME ADVANCES IN NONLINEAR VIBRATION ENERGY HARVESTING TECHNOLOGY
-
摘要: 随着工程中低功耗电子设备和自供能无线传感网络的迅速发展, 使得振动能量俘获在航空航天工程、机械工程、生物医学工程和可持续能源工程等领域得到了广泛地应用. 振动能量俘获不仅可以将振动能转化为可用的电能为微电子设备供电, 还能减少有害振动保护仪器设备. 根据振动能量不同转换机制, 可以将振动能量俘获系统分为静电式、电磁式、压电式、磁致伸缩式、摩擦起电式以及它们的混合式. 其中压电和电磁振动能量转化机制由于结构简单、容易组装、能量转换性能高等优点, 已被广泛应用于各种工程领域中. 受极端环境干扰, 工程中容易出现宽带、低频等振动, 迫使振动能量俘获技术向非线性方向迅猛发展, 进一步吸引了诸多学者对振动能量俘获系统的结构和电路进行优化设计研究. 本文首先综述了非线性振动能量俘获技术近十年来的研究进展, 主要包括设计技术基础、非线性结构设计、动力学分析等方面的研究现状. 其次, 重点阐述了振动能量俘获与振动抑制一体化的主要研究成果, 包括非线性准零刚度和非线性能量汇在振动能量俘获领域的应用. 最后, 总结了振动能量俘获外接电路和主动控制策略的优化设计, 分析了进一步提升非线性振动能量俘获效能的有效方法.Abstract: With the rapid development of low-power electronic equipment and self-powered wireless sensor networks in engineering, vibration energy harvesting has been widely used in aerospace engineering, mechanical engineering, biomedical engineering, and sustainable energy engineering. Vibration energy harvesting can not only convert vibration energy into usable electrical energy to power microelectronic equipment, but also reduce harmful vibrations to protect instruments and equipment. According to the different conversion mechanisms of vibration energy, the vibration energy harvesting system can be divided into electrostatic type, electromagnetic type, piezoelectric type, magnetostrictive type, triboelectric type and their hybrid type. Among them, piezoelectric and electromagnetic vibration energy conversion mechanisms have been widely used in various engineering fields due to their simple structure, easy assembly, and high energy conversion performance. Due to extreme environmental interference, broadband, low frequency and other vibrations are easy to occur in the engineering. It forces the rapid development of vibration energy harvesting technology in the direction of nonlinearity, which further attracts many scholars to study the optimal design of the structure and circuit of vibration energy harvesting. Firstly, this article summarizes the research progress of nonlinear vibration energy harvesting technology in the past ten years. It mainly includes the research status of design technology basis, nonlinear structure design, dynamic analysis and so on. Secondly, it focuses on the main research results of the integration of vibration energy harvesting and vibration suppression, including the application of nonlinear quasi-zero stiffness and nonlinear energy sink in the field of vibration energy harvesting. Finally, the optimized design of external vibration energy harvesting circuit and active control strategy are summarized, and effective methods to further improve the efficiency of nonlinear vibration energy harvesting are analyzed.
-
引 言
振动能量俘获是发展低功耗传感器和嵌入式电子设备, 建立结构健康监测、生命健康监测、环境监测、灾难性事故预防和军事侦察等必不可少的重要环节, 尤其在飞行器控制系统和遥测系统供电试验、海底传感器供电试验、人体健康监测试验等领域中发挥了重要的作用[1-3]. 通过振动能量俘获能够对电池进行充电或直接为设备供电, 以延长无线传感器网络和物联网等的工作时间, 提高设备的可靠性. 同时, 该技术还能减少有害振动保护仪器设备, 因此具有十分广阔的学术价值与工程应用前景.
实际环境激励普遍存在多方向、宽频带、多成分及低频非线性等特点, 从而制约了振动能量俘获试验效能的进一步提升. 例如, 人造地球卫星、载人飞船、空间探测器、武装直升机、战略导弹等先进飞行器的结构振动具有如下特征: 一是结构轻质、阻尼小、间隙多, 易产生低频非线性振动; 二是环境动载荷复杂, 具有多样性、多维性等特征. 振动能量俘获的核心在于设计与实际应用环境相匹配的高性能俘获系统, 主要涉及电路设计和结构设计[4-5]. 结构创新研究主要从最初的简单构型不断向宽频带、非线性、多稳态、多自由度等研究方向延伸. 电路优化设计主要关注最大输出功率、电路低功耗、低启动电压及自供电等方面.
在大多数情况下, 与线性系统相比, 使用非线性技术进行能量俘获会产生更大的有效工作带宽, 也可以导致更大的振幅响应[6-8]. 非线性单稳态和线性振动能量俘获系统之间的比较表明, 非线性耦合不仅可用于扩大频率响应范围, 还可以诱导更大的振幅响应. 非线性设计是提高振动能量俘获系统输出功率的和扩大频率响应范围的重要措施. 为了进一步提高俘获功率, 非线性双稳态设计需增加势阱之间的距离, 这将导致势阱之间的势垒高度增加, 在低强度激励下的能量俘获性能有待提高[9-10]. 虽然随着系统稳态数目的增加可以打破这种规律, 但因振子的质量和势垒高度的局限, 仍然无法实现超低频或低强度激励的能量俘获[11-12]. 根据非线性系统结构特征, 振动能量俘获系统可分为几何非线性[13-16]、磁耦合式[17]和内共振式[18-19]等; 按照系统的稳态数目, 振动能量俘获系统又可分为单稳态[20]、双稳态[21]、三稳态[22]及多稳态[23]等. 一般情况下, 通过振动能量俘获系统的非线性设计, 可实现对不同环境振动频率的能量俘获. 非线性机构或结构是最关键的部件, 决定了振动能量俘获系统的紧凑性和可靠性. 近些年不断涌现出各种非线性机构或结构, 譬如斜弹簧机构[24-26]、叉形结构[27]以及四边形连杆结构[28]等. 理论和实验研究均表明: 非线性振动能量俘获系统具有共振频率低、结构简单、输出功率高等优点. 另外, 实际环境中振动方向通常是多方向时变的, 这就要求振动能量俘获系统具有多方向振动敏感能力[29-30]. 采用多方向机构或结构是提高复杂振动环境下能量俘获效能的有效方法.
根据现代高新技术装备实际需求, 开展低频振动能量俘获理论与方法的研究, 探索其本质属性和复杂动力学机理, 是改善振动能量俘获技术效率不高的一个重要研究方向. 特别是在过去的十年里非线性振动能量俘获技术在工程各领域得到了广泛的关注和应用. 赵争鸣和王旭东[5]综述了电磁能量俘获技术的发展现状. 陈文艺等[31]重点阐明了微型振动能量俘获器实现大规模商业化产品的可能性. 张允等[32]回顾了振动能量俘获技术原理、材料、结构等方面的研究现状, 综述了国内外学者的主要研究成果, 详细阐述了多种收集方式的原理、特点和电学输出性能. 除了上述相关综述之外, 没有新的文章总结非线性振动能量俘获技术取得的最新研究成果和进展. 由于非线性振动能量俘获技术方面的研究成果很多, 本文仅对其中部分研究工作作一简要评述, 并对其进一步的研究做出展望.
1. 振动能量俘获设计理论
根据振动能量不同转换机制, 可以将振动能量俘获系统分为5种类型: 静电式、电磁式、压电式、磁致伸缩式和摩擦起电式. 其中, 由于结构简单、容易组装、能量转换性能高等优点, 基于压电效应和电磁感应定律的压电和电磁振动能量转化机制被广泛应用于各种工程领域中. 本节主要介绍与压电和电磁振动能量俘获相关的压电效应和电磁感应定律.
1.1 压电式振动能量俘获
压电式振动能量俘获是基于压电效应实现的. 压电效应是由法国著名物理学家皮埃尔·居里(Jacques Curie)和雅克·居里(Pierre Curie)发现, 可分为正压电效应和逆压电效应. 正压电效应为材料在外力作用下发生应变时在其两端感应出电势的现象, 而逆压电效应则相反地被定义为材料在暴露于电场时产生机械应变的现象. 压电效应是振动能量俘获的基础, 可以用压电本构方程表示为
$$ \left[ \begin{gathered} {\boldsymbol{\delta}} \hfill \\ {\boldsymbol{D}} \end{gathered} \right] = \left[ \begin{gathered} {s^{\rm{E}}}\begin{array}{*{20}{c}} {}&{{d^{\rm{t}}}} \end{array} \hfill \\ {d^{}}\begin{array}{*{20}{c}} {}&{{\varepsilon ^{\rm{T}}}} \end{array} \end{gathered} \right]\begin{array}{*{20}{c}} {} \\ {} \end{array}\left[ \begin{gathered} {\boldsymbol{\sigma}} \hfill \\ {\boldsymbol{E}} \end{gathered} \right] $$ (1) 其中,
$ {\boldsymbol{\sigma}} $ 和$ {\boldsymbol{\delta}} $ 是应变矢量和应力矢量; E和D分别是电场矢量和电位移矢量; s是恒定电场下的弹性系数,$ \varepsilon $ 是恒定应力下的介电系数, d是正逆压电效应常力矩阵. 上标t代表转置, 上标E和T表示恒定电场和恒定应力下的常数. 压电式振动能量俘获是从压电效应基本原理出发, 通过环境振动对压电材料施加压力, 使得压电层产生应变, 导致压电材料内部产生分离的正负电荷, 继而影响压电材料表面的电荷走向而形成电流, 最终产生电能.压电振动能量俘获最常用的是带有双晶/单晶压电材料的梁结构, 其优点在于这种结构在给定输入力的情况下能产生很高的平均应变[33-35]. 根据梁结构的不同边界条件, 通常可分为悬臂梁、一端固支一端可移动铰支梁、一端固支一端固定铰支梁以及两端固支梁等指的压电振动能量俘获系统. 图1(a)和图1(b)给出了基于悬臂梁结构的压电式振动能量俘获工作原理示意图. 环境振动通过悬臂梁的基座耦合到悬臂梁−质量系统中, 导致结构振动. 压电材料将振荡过程中的交变弯曲应变转化为交流电压. 在这种结构设计中, 最重要的是需要考虑频率匹配, 这需要环境振动频率与梁的固有振动频率的精确耦合. 当激励频率从谐振频率移开时, 振荡振幅将迅速下降. 由于大多数环境振动频率较低, 因此需要额外增加质量来降低能量俘获器的共振频率. 为了提高输出性能, 除了传统的矩形悬臂梁, 学者们还研究了三角形、锥形、S形和弧形等梁结构[36].
压电振动能量俘获技术由于其输出电压较大、加工艺简单、易于实现微型化、集成化及柔性化等, 已经被广泛地应用于便携式设备、可植入设备、微机电设备等领域. 压电式转换机制也存在电容性阻抗高、输出电流极小、易疲劳、使用寿命受压电材料限制等缺点. 但随着智能材料及其加工工艺的不断发展, 压电振动能量俘获的制作技术和应用开发也取得了许多重要的成果.
1.2 电磁式振动能量俘获
电磁式振动能量俘获是基于电磁感应定律实现的. 电磁感应定律是由英国著名物理学家迈克尔·法拉第(Michael Faraday)提出, 不仅揭示了电与磁之间的内在联系, 而且为它们之间的相互转换奠定了实验基础. 根据法拉第电磁感应定律, 当通过闭合线圈的磁通量发生变化时, 就会产生感应电动势和电流. 相应的感应电动势E(t)由下式给出
$$ E(t) = - N\frac{{{\rm{d}}\varPhi }}{{{\rm{d}}t}} $$ (2) 其中N是线圈匝数,
$\varPhi$ 是磁通量, t是时间.如图1(c)和图1(d)所示, 电磁式振动能量俘获技术是从法拉第电磁感应基本原理出发, 结合环境振动, 使得永磁体与线圈的相对位置发生变化, 进而线圈中的磁通量变化产生感应电动势, 引起感应线圈产生感应电流, 从而实现振动能到电能的转换. 电磁振动能量俘获器所使用的磁路需要一个由永(或硬)磁铁产生的磁场. 磁场也可以由电磁铁产生, 但这需要电流, 消耗电力. 因此, 在小型低功率器件的情况下, 使用电磁铁是不合适的. 设计电磁振动能量俘获器还需要考虑线圈的特性, 其中线圈的匝数和电阻是确定发电机电压和有效功率的重要参数.
电磁式转换机制的优点在于制作简单, 结构稳定, 输出电流与输出功率较大, 适合在低频环境中运行等. 因此, 到目前为止, 人们已经开发了各种基于电磁感应的创新结构, 如共振结构、旋转结构等[37-38]. 然而, 传统的电磁振动能量俘获系统也存在一些问题, 如受工作空间的限制难以实现微小尺寸下的高输出功率、微型化与集成化难度较大等.
1.3 压电−电磁混合式振动能量俘获
近年来, 随着传感器技术、MEMS、电子技术、材料科学与技术等的快速发展, 大量微型化、低功耗的无线传感器被应用到各种结构、设备、周围环境甚至人体的体内. 这些传感器对于结构健康监测、灾难性事故预防以及人体健康监测等均起着关键作用. 为了解决单个振动能量俘获器能量供给不足的问题, 学者们提出了混合能量俘获系统, 其基本原理如图1(e)所示. 混合式振动能量俘获不仅包括从多种振动来源获取能量, 还包括通过多种机电转换机制将振动量转化为电能[39-40]. 混合技术的优势在于其不仅可以提高空间利用效率, 还可以显著提高俘能器的输出功率.
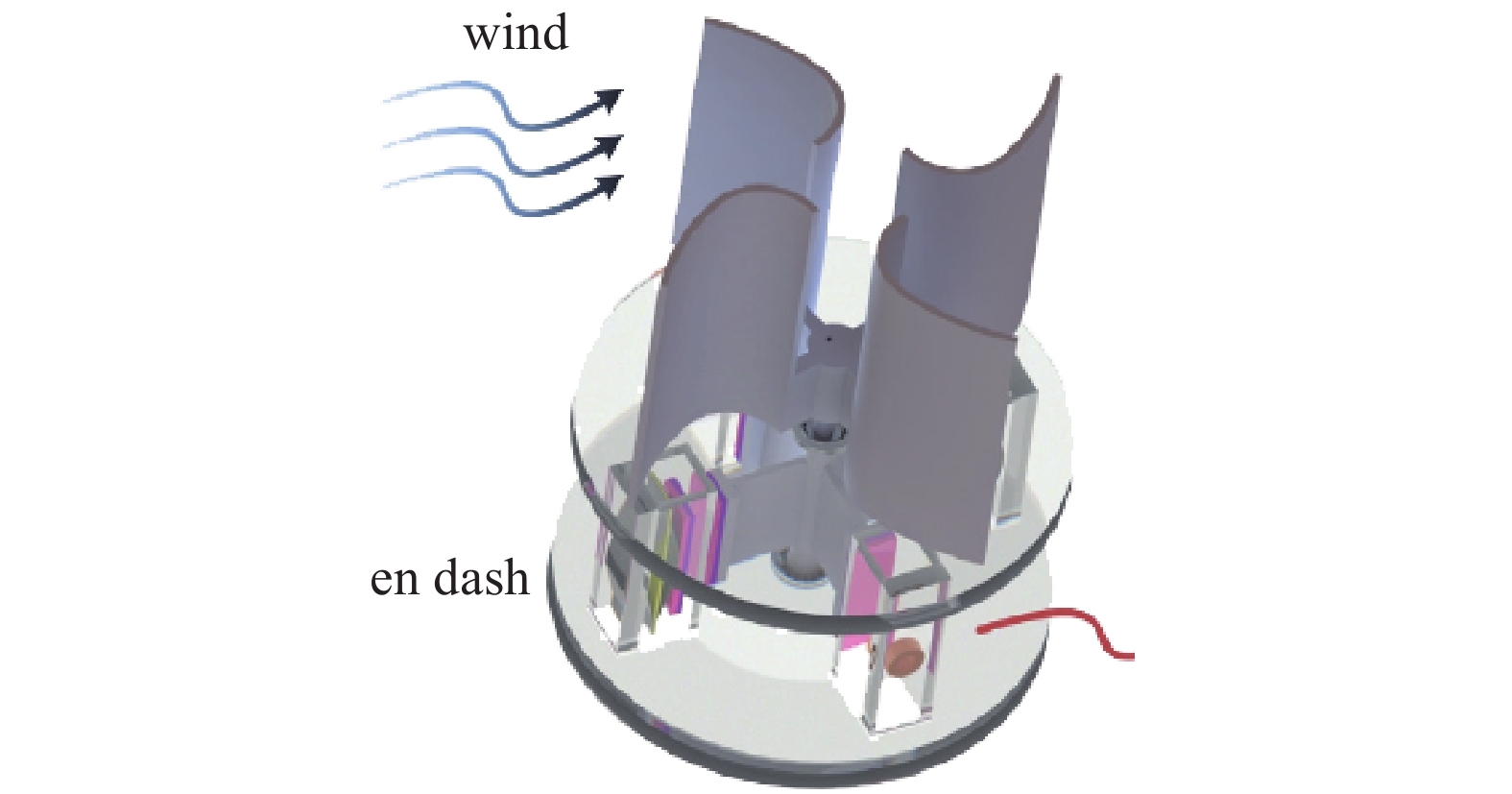
Challa等[41]基于悬臂梁模型设计了一种电磁−压电混合式振动能量俘获器, 悬臂梁采用双压电晶片式, 自由端附有永磁体, 永磁体下方固定有与之对应的一组感应线圈. 在最优激励频率和负载电阻下, 混合式振动能量俘获器的总输出功率为332 μW, 高于单独的振动能量俘获器的输出功率. Inman等[42-43]建立了压电−电磁混合式振动能量俘获器的理论模型, 分别分析了压电、电磁和混合能量俘获系统的输出功率. 在两种能量转换机制的耦合作用下, 研究发现压电−电磁混合式振动能量俘获器的谐振频率和阻尼效应发生一定的偏置, 且扩大了工作带宽和负载范围. Rajarathinam和Ali[44]设计了一种由悬臂梁和弹簧悬挂在悬臂梁自由端的永磁体组成的两自由度压电−电磁混合振动能量俘获器. 悬臂梁利用压电效应俘获电能, 而永磁体和铜线圈利用电磁感应定律俘获电能, 可在2.1 ~ 14.2 Hz的频率范围内实现高效能量俘获. Yang和Cao[25-26]基于几何非线性动力学理论设计了双稳态压电−电磁混合式振动能量俘获器. 基于随机平均法, 得到了系统的Fokker-Planck-Kolmogorov方程, 并揭示了与稳定概率密度、平均俘获功率和平均切换时间相关以及随机共振等相关的随机动力学. Zhao等[45]提出了一种使用磁耦合和力放大机制的新型混合压电−电磁混合式振动能量俘获器, 其结构如图2所示. 实验结果表明, 该俘获器可以连续运行超过100000次循环, 具有良好的机械耐久性, 而且在7.0 m/s的风速下可达到3157.7 μW的输出功率. Li等[46]提出了一种0.33 W混合压电−电磁能量俘获器, 以解决低频振动能量有效利用率低的问题.
2. 振动能量俘获动力学分析
2.1 多稳态振动能量俘获动力学
传统线性振动能量俘获的一个限制在于只能在共振频率附近获得高输出功率, 这严重限制了其工作范围[47]. 由于很小的频率误差都会导致输出功率的显着降低, 因此线性振动能量俘获器需要精确地按照该共振频率进行设计与制造, 才能保证其有效地工作. 为此, 学者们很快意识到, 这种设备不能用于从具有时间依赖性或宽带特性的激励中获取能量. 为了解决该问题, 最初的改进方案是设计具有可调谐特性的振动能量俘获器, 可调谐机构使用被动/主动设计手段来改变能量俘获器的基频, 以匹配激励的共振频率[48]. 经过大量的研究发现, 可调谐能量俘获器只能用来解释激励频率的缓慢漂移, 在随机或快速变化的频率输入下效率任然不高. 此外, 调谐机制通常需要外部电源或复杂的设计手段, 这将消耗部分能源, 对俘获能量的有效利用产生不利影响.
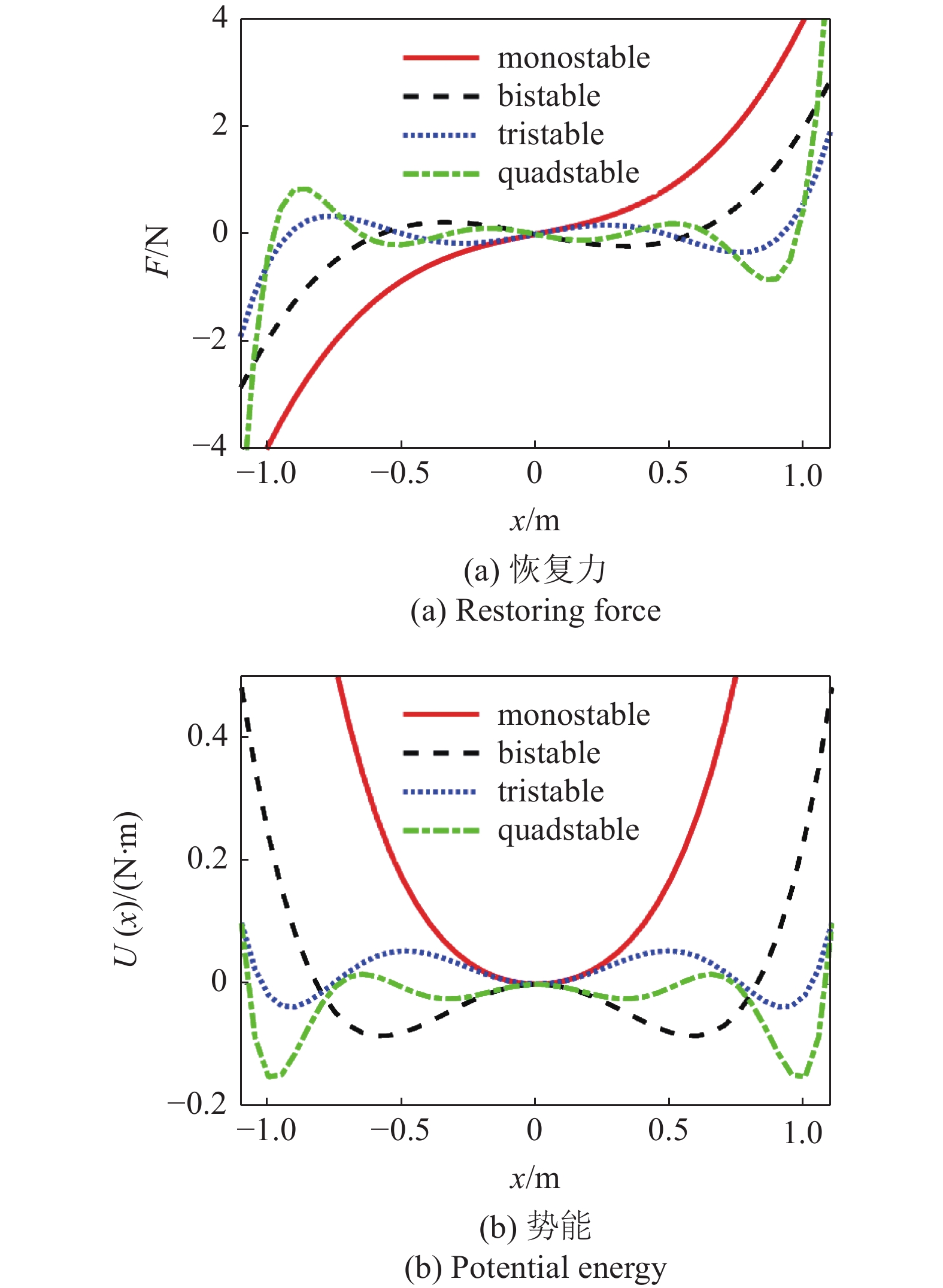
为了最大化振动能量俘获器的功率输出和有效工作范围, 许多研究者也有针对性地将非线性刚度型结构引入到振动能量俘获器的设计中. 非线性单、双、三和四稳态系统的恢复力和势能如图3所示. 非线性振动能量俘获器将单、双或多稳态宿结构与换能器和外接电路链接, 使得系统存在单、双或多个稳态, 从而实现低频宽带振动能量俘获. 非线性机构或结构是低频振动隔离与能量俘获的关键部件, 决定了振动能量俘获系统的紧凑性和可靠性, 是各工程领域亟待解决的瓶颈问题之一. 目前, 工程中的非线性机构或结构的研究主要集中于其复杂动力学行为及响应机理分析[49-53], 同时也为振动能量俘获结构创新设计提供了新思路.
非线性振动能量俘获的最简单形式是单自由度单稳态俘能器. 非线性单稳态俘能器与线性采集器的比较表明, 如果非线性采集器设计得当并集成到振动能量采集中, 非线性耦合不仅可以用来扩大频率响应范围, 而且可以引起更大的振幅响应[54-55]. 因此, 引入非线性设计是提高振动能量俘获系统输出功率和扩大频率响应范围的重要措施.
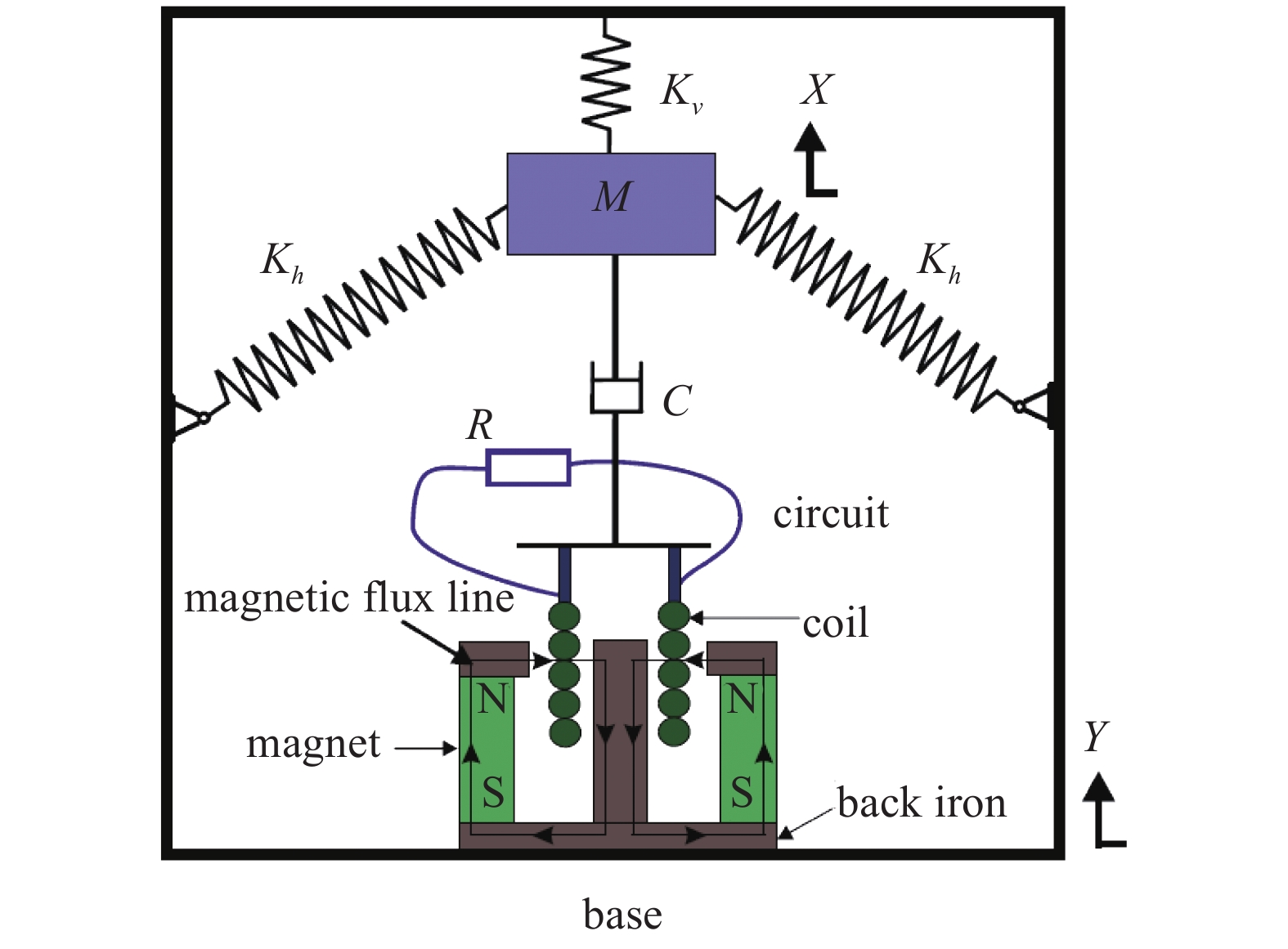
双稳态非线性跳跃机制是另一种扩大频率响应范围的重要方法. 合理设计双稳态非线性跳跃结构可以增加振动能量俘获的有效频率带宽范围. Ramlan等[56]基于具有双稳态特征的SD振子[57-58]提出了非线性双稳态振动能量俘获器, 研究了非线性跳跃机制中使用非线性刚度对振动能量俘获的潜在好处. 考虑振子的质量并结合电磁式机电转换机制, Yang等[59]提出了基于SD振子的双稳态电磁振动能量俘获器, 如图4所示. 在弹簧质量系统中, 竖直方向上作用力F和产生的位移X之间的关系为
$$ F = {K_v}X + 2{K_h}X\left( {1 - \frac{L}{{\sqrt {{X^2} + {l^2}} }}} \right) $$ (3) 为了分析不同加载质量对系统动力学的影响, 设竖直弹簧抵消振子重力后的常力为
$ - {K_v}\zeta + Mg $ . 其次, 考虑机电耦合作用, 图4所示双稳态电磁振动能量俘获器的动力学方程可以无量纲化为$$ \left. \begin{array}{l} \ddot x + 2\xi \dot x + x + rx\left( {1 - \dfrac{1}{{\sqrt {{x^2} + {\vartheta ^2}} }}} \right) + {f_0} + \beta I = - \ddot y \hfill \\ \gamma \dot x = \dot I + \lambda I \hfill \\ \end{array} \right\} $$ (4) 其中,
$ \xi $ 为无量纲线性阻尼系数,$ r $ 为无量纲非线性刚度系数,$ \vartheta $ 是无量纲几何参数,$\; \beta $ 为线性无量纲机电耦合系数,$ \lambda $ 是电阻和电感常数之间的比值,$ \gamma $ 电路方程中的电磁耦合项,$ {f_0} $ 为抵消重力后的无量纲常力,$ \ddot y $ 为基础激励. 系统的势能函数为$$ V(x) = \frac{{1 + r}}{2}{x^2} - r\sqrt {{x^2} + {\vartheta ^2}} + \vartheta + {f_0}x $$ (5) 当
$ {f_0} \ne 0 $ 时, 系统呈现出非对称的双稳态势能.Jiang和Chen[60]提出了一个基于非线性跳跃机制的耦合机电装置, 用以俘获振动能量, 并揭示了基于非线性跳跃机制的振动能量俘获器的性能优于线性振动能量俘获器. Liu等[61-62]证实了基于非线性跳跃机制的压电振动俘能器的宽带特性将提升能量俘获器的俘获功率, 尤其在低于谐振频率的频段内效果更明显. 通常, 基于非线性跳跃机制的振动俘能器结合了带宽和高输出功率密度的特点. 为了进一步提高能量俘获功率, 非线性双稳态设计需增加势阱之间的距离, 这将导致势阱之间的势垒高度增加.
由于传统双稳态和单稳态非线性俘能器的缺点, 非线性俘能器被设计为具有多阱势能特征的结构, 以实现更有效的低频宽带振动能量俘获. 一些与磁耦合三稳态压电振动能量俘获器具有相同或相似结构的有趣设备已被设计, 其目的在于揭示有效宽带振动能量俘获的广泛工程应用. Zhou等[63]提出了基于磁耦合的三稳态压电振动能量俘获器, 如图5所示, 分析表明基于磁耦合的三稳态压电振动能量俘获器在1 ~ 20 Hz谐波激励下具有更宽的高能阱间振荡能力. Panyam和Daqaq[64]讨论了设计参数对于三稳态振动能量俘获系统的带宽和有效输出功率的影响, 并通过实验验证了理论分析结果. 在考虑简谐激励和随机激励的不同情况下, Li等[65]对基于磁耦合的三稳态压电振动能量俘获器进行了优化设计, 从而有效提升了频率带宽, 并在相干共振条件下实现了高能量俘获效率. 仿真和实验结果表明, 在0 ~ 120 Hz频率范围内的高斯噪声激励下, 基于磁耦合的三稳态压电振动能量俘获器与传统的双稳态压电振动能量俘获器相比, 输出电压得到了显著提高[66]. Wang等[67]考虑了几何非线性和重力效应对三稳态压电振动能量俘获器性能的影响, 发现非对称势阱可以在低频激励下提高系统的输出性能, 并拓宽有效带宽.
为了进一步提升非线性振动能量俘获系统的带宽和有效输出功率, Zhou等[68-69]提出了四和五稳态的振动能量俘获器, 发现随着系统稳态数目的增加可以减小势阱之间的势垒高度. 但因非线性多稳态振子的质量、刚度的局限, 仍然难以实现超低频和超低强度激励下的能量俘获效能. 更为复杂的非线性设计是在超低频和超低强度激励下实现高效能量俘获的重要手段之一, 也是进一步提高能量俘获器输出功率, 扩大频响范围的重要措施. 对这类典型机械模型的研究还在继续, 研究成果凝聚了众多科研人员和机械设计人员的智慧.
2.2 多方向振动能量俘获动力学
在理想的单向简谐激励或随机激励下, 振动能量俘获器已显示出优越的能量俘获特性, 并具有广泛的应用前景. 但是实际环境中的振动通常是多向多源复合激励, 这就要求振动能量俘获器能够俘获多向振动能. 如果一个振动能能量俘获器可以俘获多个方向的振动能量, 其有效俘获功率将得到大大提升. 基于这一思想, 学者们设计了许多有趣的多向振动能量俘获器.
Kim等[70]设计了一种两方向压电能量收集器. 两个平行的悬臂梁共享相同的端部质量, 质量块可以沿套筒杆旋转或移动, 可以俘获两个方向的振动能量. Andò等[71]提出了一种由两个磁耦合和双稳态梁组成的双非线性双稳态振动能量俘获器, 可以实现两个方向的振动能量俘获. Park和Park[72]提出一种可以在二维平面内收集各个方向的振动能量的压电振动能量俘获器. 俘获器使用非对称惯性质量来俘获压电悬臂梁长度和厚度方向的振动. Su和Zu[73]设计了一种可以在3个相互垂直的方向俘获能量的宽带压电能量俘获器. 俘获器由横向摆动悬臂梁、垂直摆动悬臂梁和弹簧−质量系统组成, 其非线性恢复力通过磁铁引入, 且3个子系统的力是相互耦合的. 实验结果表明, 当负载电阻为1 MΩ时, 俘获器可以在超过5 Hz的带宽范围内输出超过2 V的电压. Chen等[74]设计了一种M型三方向压电振动能量俘获器, 其结构如图6所示. 俘获器在3个方向上的功率输出处于相似水平, 表明具有3个方向的振动能量俘获能力.
Xu和Tang[75-76]提出了末端带有摆锤的压电悬臂梁的振动能量俘获器, 这种结构可以收集空间中任意方向的摆动能. Chen等[77]提出了一种蒲公英形状的多向压电振动能量俘获器. 实验表明, 这种结构虽然在单个方向上俘获的能量较少, 但它可以在多个方向上俘获大量的能量. Feng等[78]设计了一种基于蜂窝状三电极的混合摩擦电和电磁发电机制的振动能量俘获器, 用于俘获海洋表面波的动能和势能. Gu等[79]提出了一种用于平面多向振动的非线性电磁振动能量俘获器. Zhang等[80]提出并设计了一种用于无人水下航行器的多向振动能量俘获器. Yang等[81]基于连杆机构提出了一种多向多稳态振动能量俘获器, 可以实现平面内振动能量的高效俘获. 值得注意的是, 多向宽带振动能量俘获技术的研究才刚刚起步, 还有很多理论和实验问题尚待探索.
2.3 随机振动能量俘获动力学
目前振动能量俘获系统的大部分研究都认为外部环境振动源是确定性的简谐激励, 但是这种假设过于理想化, 实际环境振动激励在大多数情况下往往是随机且随时间变化的. 物理学中用噪声或者随机力来刻画这种振动激励的普遍规律, 且噪声的存在会产生许多丰富和复杂的动力学行为. 因此在对振动能量俘获系统的研究中, 为了更好地接近于实际, 一般情形下, 可假设环境激励为概率密度函数服从正态分布的高斯噪声. 在振动能量俘获系统中, 噪声的出现使得系统产生了各种复杂的动力学行为, 例如双稳态机械系统中优化能量收集的随机共振[82]和噪声增强稳定性现象[26]、压电−电磁混合振动能量俘获系统中的随机分岔[83]以及基于压电梁振动能量俘获的随机相干共振[84]等.
Daqaq[85]给出了在高斯白噪声激励下压电振动能量俘获器的响应统计数据, 并证明了时间常数比和刚度非线性对平均功率的影响起着关键作用. Borowiec等[86]研究了噪声对振动能量俘获器性能的影响, 表明激励的噪声分量对系统稳定性有影响. Kumar等[87]推导了高斯白噪声激励下振动能量俘获器对应的Fokker-Planck方程, 并观察到通过选择适当的噪声强度可以提高所俘获的能量. 李海涛[88]使用随机线性化、Monte Carlo等方法研究了双稳态振动能量俘获器以及多稳态振动能量俘获器中的随机共振和相干共振现象. Xiao和Jin[89]观察到, 相关的加性和乘性高斯白噪声可以改善单稳态压电能量收集的性能.
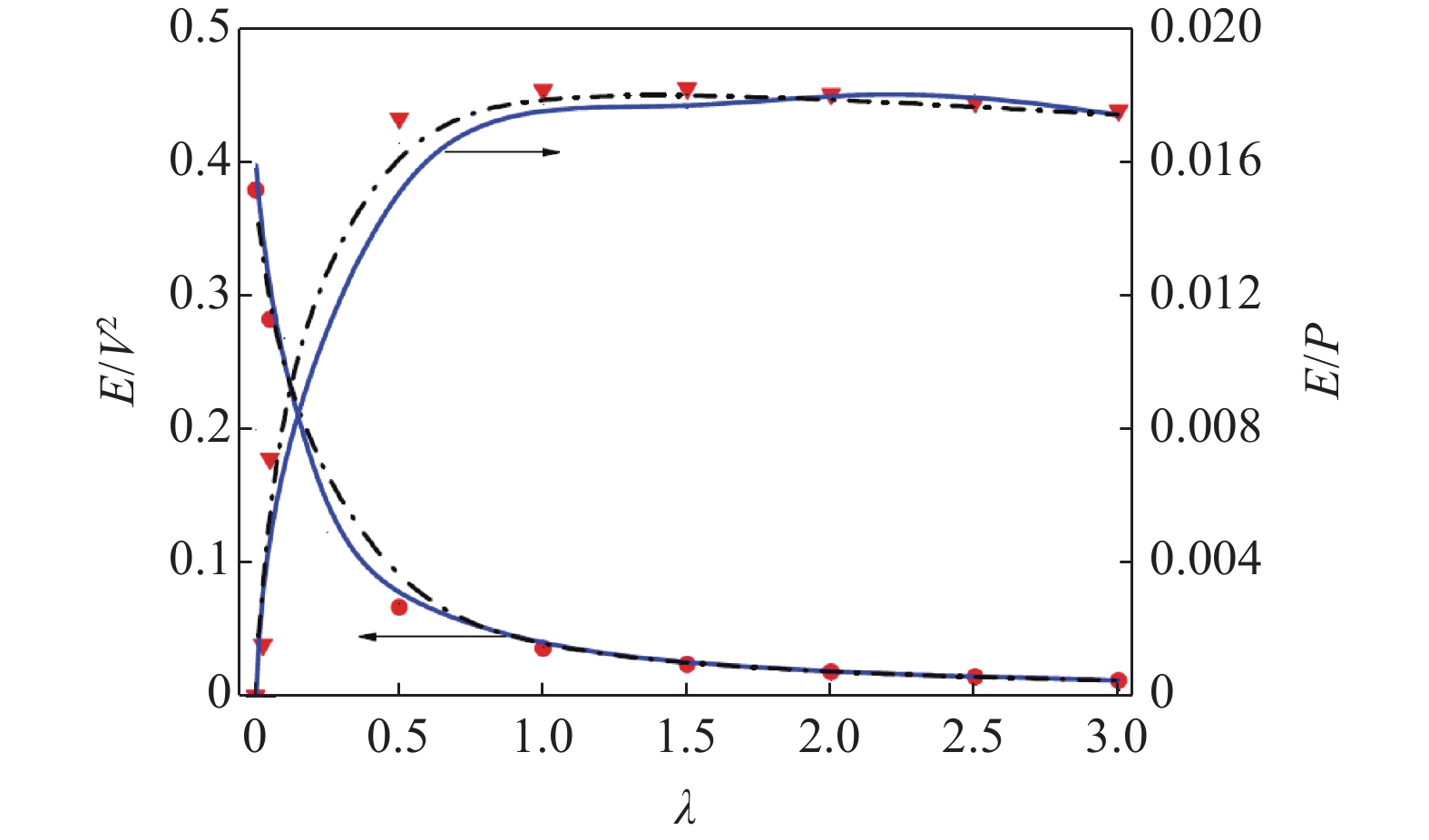
此外, 随机平均技术已广泛用于分析高斯噪声激励下振动能量俘获器系统的随机响应动力学. 为了解耦机电方程, Jin等[90-91]将广义谐波变换和等效非线性化技术引入到振动能量俘获系统的随机响应分析中, 导出了半解析解, 并提出了一种用于分析非线性振动能量俘获系统的均方电压和平均输出功率的随机平均方法, 其计算结果如图7所示[90]. 姜文安[92]发展了随机平均法, 并应用于各种不同类型的非线性振动能量俘获系统. 结合解析结果和Monte Carlo数值仿真, 分析了系统参数对输出功率的影响, 证明了随机激励下平方非线性系数可以对能量俘获功率有较大影响. Zhang和Jin[93]研究了加性和乘性有色噪声驱动下的旋转汽车轮胎振动能量俘获机理, 预测量系统的随机共振现象. 杨涛[15]发展了拓展平均法和Fokker-Planck-Kolmogorov方程分析法, 用于分析计算非线性多稳态振动能量俘获系统的均方电流、均方电压和平均收集功率等.
2.4 时滞振动能量俘获动力学
在机械系统中, 由于内部各部件间的相互作用、系统与外界环境间的相互作用以及能量的传输等需要一定的时间, 必然造成接受体所接受到物质、能量和信息在时间上具有延迟[94-97]. 时滞通常用于减小或抑制大振幅振动, 但在一定的延迟参数范围内, 也可以用来增大共振附近的振幅, 而大振幅振动对振动能量俘获是非常有益的. 因此, 通过时滞效应实现振动能量俘获系统性能控制及构建基于振动能量俘获技术的自供电时滞控制研究, 对振动能量俘获技术的发展和应用具有十分重要的意义.
振动能量俘获系统中的时滞效应通常存在于宿结构各部件间的相互作用、机械系统与电路系统耦合的过程及电路中的信号传输等. Ghouli等[98]考虑了压电振动能量俘获系统中由于系统组件位移变化引起的时滞对主共振现象的影响, 发现系统固有的时滞效应可以诱导大振幅准周期振动从而提升能量俘获性能. 考虑时滞来自于电磁振动能量俘获系统的机电耦合过程中, 发现系统固有的时间延迟可以引入电路以控制和优化系统的输出功率[99]. 研究还发现, 在考虑压电陶瓷固有时滞效应时, 适当的设计时间延迟组合参数, 存在一个超出共振的最佳激励频率范围, 其中基于准周期振动的能量俘获效率最大[100]. Yang和Cao[8,25]研究发现时间延迟在简谐和随机激励下均可改善振动能量俘获器的有益性能, 可以增强振动能量俘获系统的主共振和随机共振, 从而增加能量俘获器的输出功率.
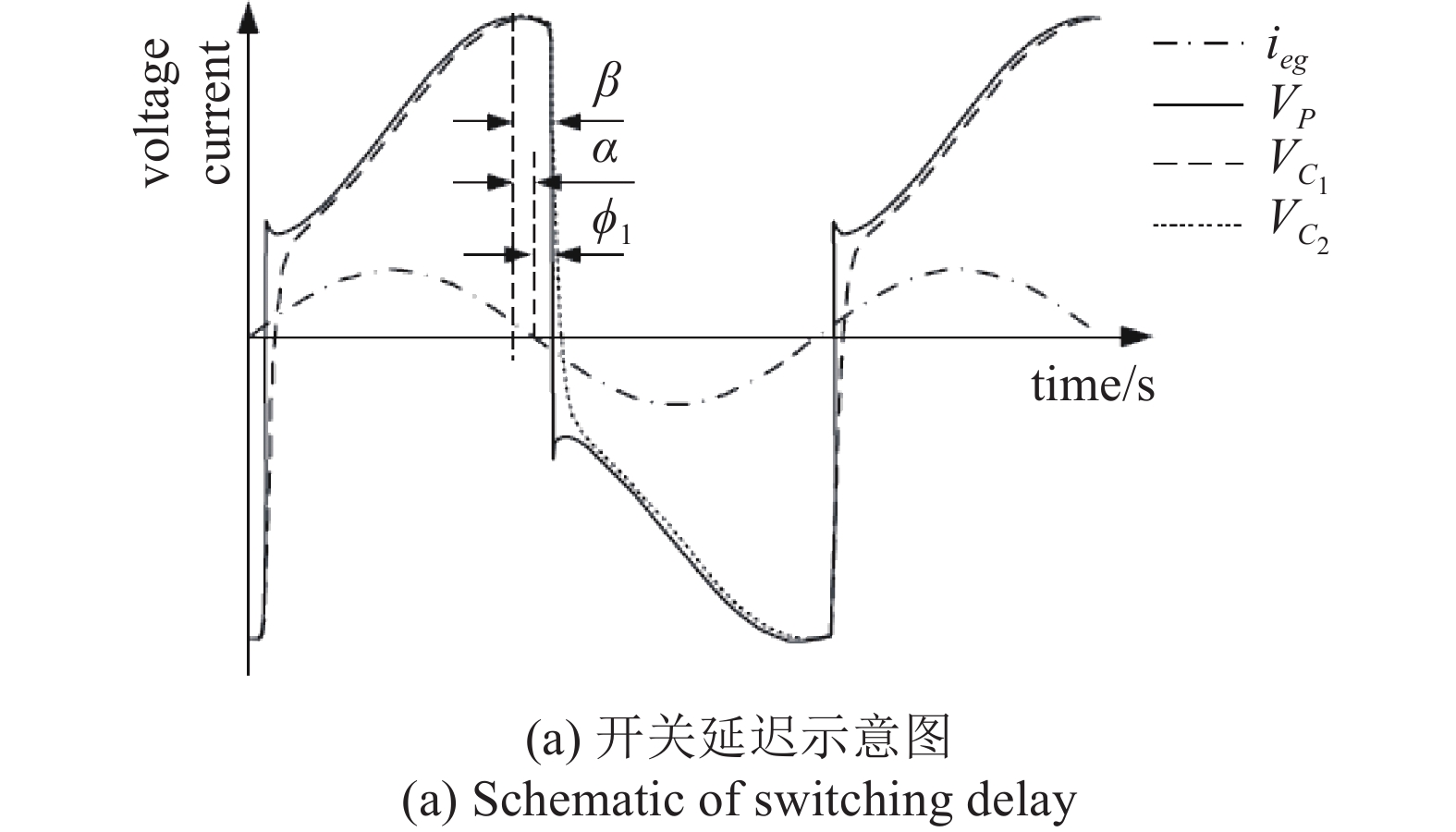
振动能量俘获系统中电感电路上的自供电同步开关在实际应用中, 由于非线性成分的存在, 开关不可能在峰值位移处同时接通, 因此开关延迟始终存在. 为了解决开关延迟带来的负面影响, Chen等[101]提出了一种改进的并联自供电同步开关. 开关延迟相位示意图和开关延迟随电阻的变化如图8所示. 实验研究表明, 在选择最佳元件的情况下, 改进后系统的平均俘获功率提高了11%左右. 时滞效应在工程中的研究虽然取得了许多卓有成效的成绩, 既可以减小或抑制大振幅振动, 也可以用于结构振动控制. 但时滞对于振动能量俘获效能的影响仍处于初期理论探索阶段, 存在许多亟待解决的关键科学问题. 特别是考虑自供能时滞反馈控制时, 其最大挑战在于控制系统消耗的功率应小于实际增加的功率, 这样引入复杂的主动控制提升输出功率才有意义.
3. 振动能量俘获与振动抑制一体化
振动是自然界普遍存在的一种现象, 能够给人类带来许多好处, 同时也会带来危害. 有利振动可以转化为可用的其他形式能源、产生美妙的音符、传递信号等, 对人类生活水平的提高和军事技术的发展带来很大的福利. 但当振动超过一定界限时就会对人体的健康和设施产生损坏, 使得仪器设备不能正常工作[102]. 例如复杂的路面环境引起的振动和噪声, 对战术类车载定向能武器系统的稳定性存在严重危害, 使得系统不能在行进过程中实现目标的有效打击, 抗干扰效能差. 将这些有害振动转化为能量, 既可以消除有害振动保护设备, 又可以俘获能量实现微电子设备供电. 因此, 振动控制与利用已成为现代高新技术装备结构设计和研制中的关键技术和难点.
近些年, 针对振动能量俘获与振动抑制一体化双重目标设计的研究也逐渐涌现出了. Tang和Zuo[103]研究了电磁能量俘获系统代替阻尼元件在主动调谐质量−阻尼器中的应用, 证明了振动抑制和能量俘获同时进行的可行性. Brennen等[104]对同时充当减振器和能量俘获器的弹簧−质量−阻尼器进行了研究. Davis和McDowell[105]提出了基于弯曲梁的结合隔振和能量收集性能的设备. 除此之外, 与振动抑制相关的非线性准零刚度隔振和非线性能量汇减振技术也在振动能量俘获与振动抑制一体化中得到了广泛应用.
3.1 非线性准零刚度用于振动能量俘获
非线性准零刚度(quasi-zero stiffness, QZS)振子因其高静低动刚度特征而具有良好的低频隔振性能, 但仍存在低频共振问题, 可用于低频振动能量俘获[106-108]. Drezet等[109]提出了准零刚度能量俘获理论, 提高了低频激励下的能量俘获效率. Cao等[110]设计了一种新型宽带压电振动能量采集器, 可提升低频振动范围的有效输出功率. Zou等[111]开发了一种能够定制非线性力的装置, 该装置可以很容易地应用于非线性振动能量俘获、准零刚度隔振和非线性能量汇减振的不同功能. Lu等[112]提出了一种具有准零刚度特征的电磁Stewart平台, 可以实现6个方向的振动抑制和能量俘获. Lu等[113]在基于双稳态压电复合板的研究中发现位移传递率和输出电压曲线中同时存在硬化和软化非线性现象. Yang等[114]提出了一种具有高阶准零刚度特性的新型非线性机械振荡器, 其结构如图9所示, 可以用于增强振动能量俘获和振动隔离的性能. 通过几何非线性参数设计, 该振荡器不仅可以在平衡位置附近获得任意小的刚度, 而且可以在超低频或低强度激励下实现隔振或高能阱间振荡. 目前准零刚度能量俘获受势阱宽度窄、准零刚度范围小的限制, 难以解决超低频或低强度能量俘获难题. 因此, 准零刚度能量俘获理论与实现方法还有待完善.
3.2 非线性能量汇用于振动能量俘获
非线性能量汇(nonlinear energy sink, NES)是一种减振器, 可将振动能量从主结构单向传递到耗能元件, 主要由非线性振子和阻尼元件两部分组成. 非线性振子提供非线性恢复力, 从而扩大减振器抑制振动的有效频带. 阻尼元件用以消耗非线性能量汇从主体结构吸收的振动能量, 最终达到耗能减振的目的. 由于非线性能量汇结构具有重量轻、鲁棒性强、频带宽等特点, 在振动能量俘获领域也备受关注, 应用研究主要集中于压电和电磁式两种振动能量俘获器.
Ahmadabadi和Khadem[115]通过非线性能量汇将振动抑制与振动能量俘获结合起来, 在冲击激励下对系统参数进行了全局优化, 以最大化非线性能量汇的能量耗散和增加俘获能量为目标. Zhang等[116]设计了一种基于非线性能量汇的压电能量收集系统, 该装置具有目标能量转移和初始能量依赖的特征, 可以同时实现宽带能量俘获和减振的目的. Li等[117]提出了一种两自由度非线性能量汇压电装置来抑制振动并获取振动能量, 在能量转移被吸收时, 同时也观察到连续的振动能量转换为电能. Xiong等[118]提出了一种基于非线性能量汇的压电振动能量俘获器, 该系统在谐波基极激励下的宽带动态响应和能量收集可以在交直流接口电路中实现. Kremer和Liu[119-120]开发了一个用于电磁振动能量俘获的非线性能量汇系统. 实验研究揭示了系统的瞬态行为和简谐强迫响应, 并确定了几个关键参数之间的关系, 能够以宽带方式实现振动抑制和能量收集的双重目标. Pennisi等[121]阐述了与电磁能量采集器耦合的非线性能量汇的理论设计和实验实现方法. Remick等[122]建造了一个带有非线性能量汇的能量俘获装置, 振动能量由电磁元件获得, 实验研究了由瞬态共振引起的单脉冲载荷作用下系统的高频动态不稳定性. Fang等[123-124]集成了非线性能量汇和超磁致伸缩材料, 研究表明目标能量传递对线性一次系统的振动响应具有非常有效的抑制作用. Zhang等[125]提出了格子夹层结构和带有悬浮电磁的非线性能量汇振动能量俘获器, 用于俘获振动能量和实现振动控制, 如图10所示. Zhang等[126]考虑将非线性减振器与悬浮磁电能俘获器集成在一起用于整个航天器系统, 实现较宽的频率范围俘获能量和有效降低振动, 并具有较高的输出电压. Tian等[127]提出了基于超磁致伸缩材料的非线性能量汇振动能量俘获器, 以抑制高超声速气流中悬臂梯形板的非线性气动弹性响应. Chiacchiari等[128]设计了一种具有立方非线性和负线性刚度特征的双稳态电磁能量俘获器, 用于俘获受激系统的小振幅和宽带振动能量.
4. 振动能量俘获的外接电路设计
除了非线性结构设计之外, 国内外研究者对于振动能量俘获器的外接匹配电路也开展了许多研究. 在基于压电效应和电磁感应式的振动能量俘获系统中, 由于压电贴片的变形和磁铁与线圈间的距离是交变的, 因此直接产生的电流也是交变的. 但是, 普通低功耗电子设备和自供能无线传感网络需要直流电源. 因此, 振动能量俘获需要具有整流和稳压功能的外接匹配电路[129-130]. 而复杂的电路设计使得描述电路中电流或电压变化的电路方程也是非线性的.
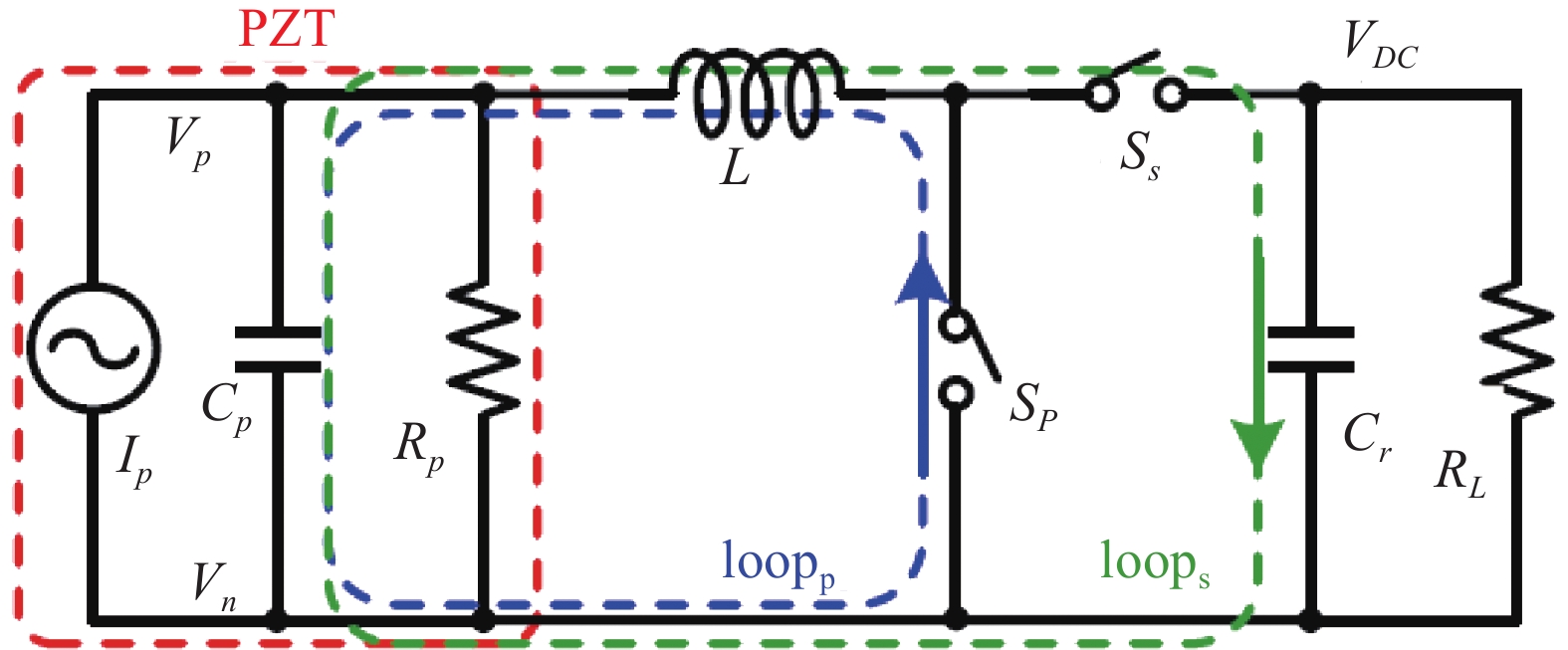
Wu等[131]设计了优化同步电荷提取电路, 实验结果表明该电路可以提高线性俘能系统在连接大范围负载电阻下的转换效率. Wang等[132]提出了一种用于弱输入功率和重负载的自供电、超低功率控制电路, 适合用于俘获经常中断的自然振动能量. 当使用大存储电容器和DR-DSSH电路时, 所提出的电路可以显著优于其他同步电路. Zhu等[133]对不同电子通断开关电路进行了理论分析. Shi等[134]提出了一种CMOS集成接口电路, 减少了电能转换过程中的能量消耗. Cheng等[135]设计了一种带可控最优电压的并联同步开关电感(COV-PSSHI), 通过优化电容和并联电感以及使用电压控制器调节优化两个阈值电压提高AC-DC能量转换效率, 可用于旋转式非线性双稳态压电俘能系统. Wang等[136]提出了一种用于压电振动能量俘获的无整流器同步开关采集电感(ReL-SSHI)接口电路, 如图11所示. 该电路可以两种不同的模式工作: 在压电换能器开路电压的正峰值时, 与负载串联的开关导通, 并在电感模式下以串联同步开关采集模式运行; 在压电换能器开路电压的负峰值时, 与负载并联的开关导通, 在电压同步反转模式工作. ReL-SSHI电路不需要整流桥, 降低了电路的功率损耗, 从而提高了电路的非线性压电振动能量俘获效率.
5. 振动能量俘获系统性能提升策略
虽然非线性振动能量俘获系统可以实现低频激励下的振动能量俘获, 但系统存在多解区实现高能阱间运动难、宽频优势难以有效利用等缺陷, 而且在超低频激励下能量俘获容易失效. 因此非线性振动能量俘获技术需要解决的一个这一问题是如何使得系统在多解区中的高能轨道运动, 并输出大幅值电压、得到较高的输出功率, 只有这样其宽频带优势才能得到切实发挥. 据此国内外学者对于振动能量俘获的性能提升策略开展了大量研究工作.
Zhou等[137-138]提出了一种基于碰撞原理的高能轨道实现方法, 通过对压电悬臂梁的自由端部施加碰撞, 使非线性俘能系统获得高能势阱间运动, 并具有较高的能量输出, 如图12所示. Fang等[139]将基于碰撞原理的高能轨道实现方法引入到旋转振动能量俘获系统中, 克服了以往分段线性模型不能反映驱动梁和发生梁变形对冲击力和能量输出影响的局限性. Mallicket等[140]提出了一种基于电气驱动实现高能轨道运动的方法. 其原理为通过电压源对线圈中施加短暂的高电压使得非线性振动系统获得足够的能量扰动而从多解区中的低能轨道跳跃到高能轨道稳定运动. Lan等[141]提出了通过负电阻原理对振动能量俘获系统施加电压扰动实现了高能轨道运动的方法. 施加电压扰动相当于对系统施加额外的激励, 使得非线性单稳态和双稳态压电振动能量俘获系统能在多解区中的高能轨道稳定运动. 以上研究表明, 通过对非线性振动能量俘获系统施加合适的扰动, 可使其实现高能轨道运动, 提高输出电压和功率. 上述性能提升方法最大挑战在于控制系统消耗的功率应小于实际增加的功率, 这样才具有实际意义.
6. 总结与展望
非线性振动能量俘获技术可以拓宽能量俘获器的有效工作频带, 提高能量俘获效率, 受到了航空航天工程、海洋工程、交通运输工程、结构工程、可持续能源工程、机械工程等各领域的青睐. 非线性振动能量俘获技术不仅可以将振动能转化为电能为微电子设备供电, 还可以消除有害振动保护精密设备, 其研究也逐步从理论研究过渡到应用研究.
本文致力于回顾高性能非线性振动能量俘获技术的若干最新研究进展, 分析了为实现高功率输出和宽频带而探索的各种方法, 主要包括结构设计、非线性动力学、多功能集成、匹配电路设计和优化控制策略等. 基于上述研究成果, 非线性振动能量俘获技术的设计与应用今后还可以在以下几个方面继续开展研究.
(1)非线性振动能量俘获系统结构优化设计. 非线性振动能量俘获结构设计目前主要集中于几何非线性结构和磁力非线性结构, 几何非线性结构利用弹簧、梁和板等通过几何构造实现非线性, 磁力非线性结构通过磁铁间的相互作用实现非线性. 根据不同的应用环境特点, 新型非线性结构的设计仍然是研究热点, 特别是材料非线性结构实现特殊的刚度非线性和阻尼非线性的研究还有待进一步深入.
(2)非线性振动能量俘获系统可靠性和稳定性研究. 目前对于非线性振动能量俘获系统的研究主要是对结构设计、动力学测试以及输出性能进行分析, 它们的可靠性和稳定性还没有得到很好的检验. 为了真正实现工程应用, 未来将有更多的研究工作来应对这些挑战.
(3)非线性振动能量俘获系统集成技术. 因非线性机构功能需求, 非线性机构的尺寸一般较大, 非线性振动能量俘获结构很难实现紧凑化. 为克服该限制, 需要进一步对非线性机构进行优化设计, 借助微电子技术实现系统的集成化. 其次利用同一非线性机构实现多功能的集成产品, 将形成更为广泛应用前景.
(4)非线性振动能量俘获系统复杂动力学研究. 由于非线性参数及外接电路参数均直接影响系统的动力学行为, 进而影响能量俘获效率. 因此, 揭示非线性振动能量俘获系统复杂动力学响应机理是研究重点之一, 特别是多方耦合激励、多激励耦合下的动力学行为值得进一步研究.
(5)非线性振动能量俘获系统应用研究. 在过去十年中, 非线性振动能量俘获技术取得了重大进步, 其应用领域已经辐射到自供能可穿戴电子设备、医疗设备和无线传感器监测等民用领域. 这些将有助于将振动能源俘获的研究成果转化为我们日常生活中的切实利益, 推进物联网和智能化应用场景落地.
-
-
[1] Priya S, Inman DJ. Energy Harvesting Technologies. New York: Springer, 2009
[2] Wei C, Jing X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renewable and Sustainable Energy Reviews, 2017, 74: 1-18 doi: 10.1016/j.rser.2017.01.073
[3] Yildirim T, Ghayesh MH, Li W, et al. A review on performance enhancement techniques for ambient vibration energy harvesters. Renewable Sustainable Energy Reviews, 2017, 71: 435-449 doi: 10.1016/j.rser.2016.12.073
[4] 刘祥建, 陈仁文. 压电振动能量收集装置研究现状及发展趋势. 振动与冲击, 2012, 31(16): 169-176 (Liu Xiangjian, Chen Renwen. Current situation and developing trend of piezoelectric vibration energy harvesters. Journal of Vibration and Shock, 2012, 31(16): 169-176 (in Chinese) doi: 10.3969/j.issn.1000-3835.2012.16.033 [5] 赵争鸣, 王旭东. 电磁能量收集技术现状及发展趋势. 电工技术学报, 2015, 30(13): 1-11 (Zhao Zhengming, Wang Xudong. The State-of-the-Art and the Future Trends of Electromagnetic Energy Harvesting. Transactions of China Electrotechnical Society, 2015, 30(13): 1-11 (in Chinese) doi: 10.3969/j.issn.1000-6753.2015.13.001 [6] Tan T, Yan Z, Zou H, et al. Renewable energy harvesting and absorbing via multi-scale metamaterial systems for internet of things. Applied Energy, 2019, 254: 113717 doi: 10.1016/j.apenergy.2019.113717
[7] Li W, Yang X, Zhang W, et al. Free vibration analysis of a spinning piezoelectric beam with geometric nonlinearities. Acta Mechanica Sinica, 2019, 35(4): 879-893 doi: 10.1007/s10409-019-00851-4
[8] Yang T, Cao Q. Delay-controlled primary and stochastic resonances of the SD oscillator with stiffness nonlinearities. Mechanical Systems and Signal Processing, 2018, 103: 216-235 doi: 10.1016/j.ymssp.2017.10.002
[9] Cao J, Wang W, Zhou S, et al. Nonlinear time-varying potential bistable energy harvesting from human motion. Applied Physics Letters, 2015, 107(14): 143904 doi: 10.1063/1.4932947
[10] Wang G, Liao WH, Zhao Z, et al. Nonlinear magnetic force and dynamic characteristics of a tri-stable piezoelectric energy harvester. Nonlinear Dynamics, 2019, 97(4): 2371-2397 doi: 10.1007/s11071-019-05133-z
[11] Gao M, Wang Y, Wang Y, et al. Experimental investigation of non-linear multi-stable electromagnetic-induction energy harvesting mechanism by magnetic levitation oscillation. Applied Energy, 2018, 220: 856-875 doi: 10.1016/j.apenergy.2018.03.170
[12] Wang C, Zhang Q, Wang W. Low-frequency wideband vibration energy harvesting by using frequency up-conversion and quin-stable nonlinearity. Journal of Sound and Vibration, 2017, 399: 169-181 doi: 10.1016/j.jsv.2017.02.048
[13] Cao Q, Xiong Y, Wiercigroch M. A novel model of dipteran flight mechanism. International Journal of Dynamics and Control, 2013, 1(1): 1-11 doi: 10.1007/s40435-013-0001-5
[14] 杨绍普, 曹庆杰, 张伟. 非线性动力学与控制的若干理论及应用. 北京: 科学出版社, 2011 Yang Shaopu, Cao Qingjie, Zhang Wei. Some Theories and Applications of Nonlinear Dynamics and Control. Beijing: Science Press, 2011 (in Chinese))
[15] 杨涛. 多稳态能量收集系统的非线性动力学行为及应用研究. [博士论文]. 哈尔滨: 哈尔滨工业大学, 2019 Yang Tao. Study on nonlinear dynamic behavior and application of multi-stable energy harvesting systems. [PhD Thesis]. Harbin: Harbin Institute of Technology, 2019 (in Chinese))
[16] Zou H, Zhang W, Li W, et al. Magnetically coupled flextensional transducer for wideband vibration energy harvesting: design, modeling and experiments. Journal of Sound and Vibration, 2018, 416: 55-79 doi: 10.1016/j.jsv.2017.11.041
[17] Zhou S, Cao J, Erturk A, et al. Enhanced broadband piezoelectric energy harvesting using rotatable magnets. Applied Physics Letters, 2013, 102(17): 173901 doi: 10.1063/1.4803445
[18] Chen LQ, Jiang WA, Panyam M, et al. A broadband internally resonant vibratory energy harvester. Journal of Vibration and Acoustics, 2016, 138(6): 061007 doi: 10.1115/1.4034253
[19] Chen LQ, Jiang WA. Internal resonance energy harvesting. Journal of Applied Mechanics, 2015, 82(3): 031004 doi: 10.1115/1.4029606
[20] Daqaq MF. Response of uni-modal Duffing-type harvesters to random forced excitations. Journal of Sound and Vibration, 2010, 329: 3621-3631 doi: 10.1016/j.jsv.2010.04.002
[21] 吴子英, 叶文腾, 刘强. 双稳态电磁式振动能量捕获器超谐波响应研究. 计算力学学报, 2017, 43(5): 623-630 (Wu Ziying, Ye Wenteng, Liu Qiang. Research on the superharmonic effects of bistable electromagnetic vibration energy harvester. Chinese Journal of Computational Mechanics, 2017, 43(5): 623-630 (in Chinese) [22] Wang G, Wu H, Liao WH, et al. A modified magnetic force model and experimental validation of a tri-stable piezoelectric energy harvester. Journal of Intelligent Material Systems and Structures, 2020, 31(7): 967-979 doi: 10.1177/1045389X20905975
[23] Wang C, Zhang Q, Wang W, et al. A low-frequency, wideband quad-stable energy harvester using combined nonlinearity and frequency up-conversion by cantilever-surface contact. Mechanical Systems and Signal Processing, 2018, 112: 305-318 doi: 10.1016/j.ymssp.2018.04.027
[24] Jiang WA, Chen LQ. Snap-through piezoelectric energy harvesting. Journal of Sound and Vibration, 2014, 333(18): 4314-4325 doi: 10.1016/j.jsv.2014.04.035
[25] Yang T, Cao Q. Time delay improves beneficial performance of a novel hybrid energy harvester. Nonlinear Dynamics, 2019, 96: 1511-1530 doi: 10.1007/s11071-019-04868-z
[26] Yang T, Cao Q. Dynamics and energy generation of a hybrid energy harvester under colored noise excitations. Mechanical Systems and Signal Processing, 2019, 121: 745-766 doi: 10.1016/j.ymssp.2018.12.004
[27] Wei C, Jing X. Vibrational energy harvesting by exploring structural benefits and nonlinear characteristics. Communications in Nonlinear Science and Numerical Simulation, 2017, 48: 288-306 doi: 10.1016/j.cnsns.2016.12.026
[28] Wang F, Sun X, Xu J. A novel energy harvesting device for ultralow frequency excitation. Energy, 2018, 151: 250-260
[29] 陈仁文, 任龙, 夏桦康等. 多方向宽频带压电式振动能量采集器研究进展. 仪器仪表学报, 2014, 35(12): 2641-2652 (Chen Renwen, Ren long, Xia Huakang, et al. Research advance in multi-directional wide-band piezoelectric vibration energy harvesters. Chinese Journal of Scientific Instrument, 2014, 35(12): 2641-2652 (in Chinese) [30] 岳喜海, 杨进, 文玉梅等. 多方向宽频磁电式振动能量采集器. 仪器仪表学报, 2013, 34(9): 1961-1967 (Yue Xihai, Yang Jin, Wen Yumei, et al. Multidirectional broadband magnetoelectric vibration energy collector. Chinese Journal of Scientific Instrument, 2013, 34(9): 1961-1967 (in Chinese) [31] 陈文艺, 孟爱华, 刘成龙. 微型振动能量收集器的研究现状及发展趋势. 微纳电子技术, 2013, 11: 715-720 (Chen Wenyi, Meng Aihua, Liu Chenglong. Research status and developing trend of micro vibration-based energy harvesters. Micronanoelectronic Technology, 2013, 11: 715-720 (in Chinese) [32] 张允, 王战江, 蒋淑兰等. 振动能量收集技术的研究现状与展望. 机械科学与技术, 2019, 7: 7-40 (Zhang Yun, Wang Zhanjiang, Jiang Shulan, et al. Retrospectives and perspectives of vibration energy harvest technologies. Mechanical Science and Technology for Aerospace Engineering, 2019, 7: 7-40 (in Chinese) [33] 何远钦. 压电能量收集概论. 装备制造技术, 2011, 8: 56-58 (He Yuanqin. Conspectus of piezoelectric energy harvesting. Equipment Manufacturing Technology, 2011, 8: 56-58 (in Chinese) doi: 10.3969/j.issn.1672-545X.2011.02.021 [34] 唐刚, 刘景全, 马华安等. 微型压电振动能量采集器的研究进. 机械设计与研究, 2010, 26(4): 61-64 (Tang Gang, Liu Jingquan, Ma Hua'an, et al. A survey on research of micro piezoelectric vibration energy harvesters. Mechanical Design and Research, 2010, 26(4): 61-64 (in Chinese) [35] 陈婧, 苏娟, 杜松怀等. 悬臂梁压电发电机输出特性及其影响因素分析. 电网与清洁能源, 2014, 30: 77-83 (Chen Jing, Su Juan, Du songhuai, et al. Analysis of the output characteristic and influence factors of the cantilever piezoelectric generator. Advances of Power System & Hydroelectric Engineering, 2014, 30: 77-83 (in Chinese) doi: 10.3969/j.issn.1674-3814.2014.08.018 [36] Li H, Tian C, Deng ZD. Energy harvesting from low frequency applications using piezoelectric materials. Applied Physics Reviews, 2014, 1(4): 041301 doi: 10.1063/1.4900845
[37] 吴鹏飞, 袁天辰, 杨俭. 非线性电磁振动能量采集的辨识研究. 振动工程学报, 2021, 34(1): 116-126 (Wu Pengfei, Yuan Tianchen, Yang Jian. System identification of single-DOF electromagnetic vibration energy collector. Journal of Vibration Engineering, 2021, 34(1): 116-126 (in Chinese) [38] Carneiro P, Santos MPS, Rodrigues A, et al. Electromagnetic energy harvesting using magnetic levitation architectures: A review. Applied Energy, 2020, 260: 114119
[39] 钱铄, 杨子杨, 崔丹凤等. 电磁−压电复合式机械能量收集器. 测试技术学报, 2019, 33: 60-66 (Qian Shuo, Yang Ziyang, Cui Danfeng, et al. Electromagnetic-piezoelectric hybrid generator for mechanical energy. Journal of Test and Measurement Technology, 2019, 33: 60-66 (in Chinese) [40] Liu H, Fu H, Sun L, et al. Hybrid energy harvesting technology: From materials, structural design, system integration to applications. Renewable and Sustainable Energy Reviews, 2021, 137: 110473 doi: 10.1016/j.rser.2020.110473
[41] Challa VR, Prasad MG, Fisher FT. A coupled piezoelectric-electromagnetic energy harvesting technique for achieving increased power output through damping matching. Smart Materials and Structures, 2009, 18(9): 95029 doi: 10.1088/0964-1726/18/9/095029
[42] Karami MA, Inman DJ. Equivalent damping and frequency change for linear and nonlinear hybrid vibrational energy harvesting systems. Journal of Sound and Vibration, 2011, 330(23): 5583-5597 doi: 10.1016/j.jsv.2011.06.021
[43] Lallart M, Inman DJ. Mechanical Effect of Combined Piezoelectric and Electromagnetic Energy Harvesting. Structural Dynamics and Renewable Energy. New York: Springer, 2011, 261-272
[44] Rajarathinam M, Ali SF. Energy generation in a hybrid harvester under harmonic excitation. Energy Conversion and Management, 2018, 155: 10-19 doi: 10.1016/j.enconman.2017.10.054
[45] Zhao L, Zou H, Yan G, et al. A water-proof magnetically coupled piezoelectric-electromagnetic hybrid wind energy harvester. Applied Energy, 2019, 239(1): 735-746
[46] Li Z, Li T, Yang Z, et al. Toward a 0.33W piezoelectric and electromagnetic hybrid energy harvester:Design, experimental studies and self-powered applications. Applied Energy, 2019, 255: 113805
[47] Beeby SP, Torah RN, Tudor MJ, et al. A micro electromagnetic generator for vibration energy harvesting. Journal of Micromechanics and microengineering, 2017, 17(7): 1257
[48] Challa V, Prasad M, Shi Y, et al. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Materials and Structures, 2008, 75: 1-10
[49] 韩彦伟. 一类几何非线性系统的动力学行为及应用研究. [博士论文]. 哈尔滨: 哈尔滨工业大学, 2015 Han Yanwei. Nonlinear dynamics of a class of geometrical nonlinear system and its application. [PhD Thesis]. Harbin: Harbin Institute of Technology, 2015 (in Chinese))
[50] Han Y, Cao Q, Chen Y, et al. A novel smooth and discontinuous oscillator with strong irrational nonlinearities. Science China Physics, Mechanics and Astronomy, 2012, 10: 1832-1843
[51] Han Y, Cao Q, Chen Y, et al. Chaotic thresholds for the piecewise linear discontinuous system with multiple well potentials. International Journal of Non-Linear Mechanics, 2015, 70: 145-152 doi: 10.1016/j.ijnonlinmec.2014.09.007
[52] Han N, Cao Q. Global bifurcations of a rotating pendulum with irrational nonlinearity. Communications in Nonlinear Science and Numerical Simulation, 2016, 36: 431-445
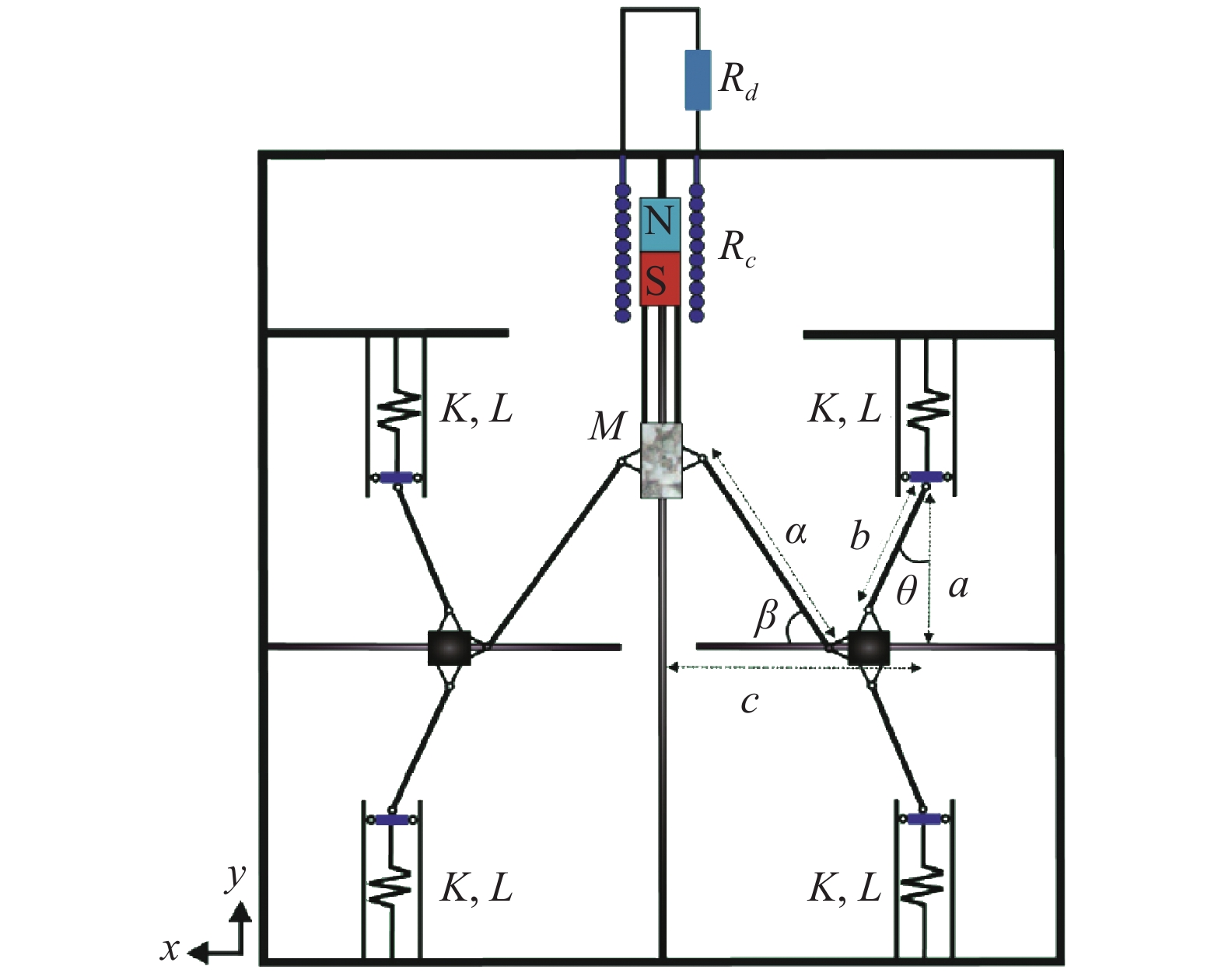
[53] Hao Z, Cao Q, Wiercigroch M. Nonlinear dynamics of the quasi-zero-stiffness SD oscillator based upon the local and global bifurcation analyses. Nonlinear Dynamics, 2017, 87(2): 987-1014 doi: 10.1007/s11071-016-3093-6
[54] Barton D, Burrow S, Clare L. Energy harvesting from vibrations with a nonlinear oscillator. Journal of Vibration and Acoustics, 2010, 132: 0210091
[55] Masana R, Daqaq MF. Electromechanical modeling and nonlinear analysis of axially-loaded energy harvesters. Journal of Vibration and Acoustics, 2011, 133: 011007 doi: 10.1115/1.4002786
[56] Ramlan R, Brennan MJ, Mace RB, et al. Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dynamics, 2010, 59: 545-558 doi: 10.1007/s11071-009-9561-5
[57] Cao Q, Wiercigroch M, Pavlovskaia EE, et al. Archetypal oscillator for smooth and discontinuous dynamics. Physical Review E, 2006, 74: 046218 doi: 10.1103/PhysRevE.74.046218
[58] Hao Z, Cao Q, Wiercigroch M. Two-sided damping constraint control strategy for high-performance vibration isolation and end-stop impact protection. Nonlinear Dynamics, 2016, 86: 2129-2144 doi: 10.1007/s11071-016-2685-5
[59] Yang T, Liu J, Cao Q. Response analysis of the archetypal smooth and discontinuous oscillator for vibration energy harvesting. Physica A, 2018, 507: 358-373 doi: 10.1016/j.physa.2018.05.103
[60] Jiang WA, Chen LQ. Stochastic averaging of energy harvesting systems. International Journal of Non-Linear Mechanics, 2016, 85: 174-187 doi: 10.1016/j.ijnonlinmec.2016.07.002
[61] Liu WQ, Badel A, Formosa F, et al. Wideband energy harvesting using a combination of an optimized synchronous electric charge extraction circuit and a bistable harvester. Smart Materials and Structures, 2013, 22: 125038 doi: 10.1088/0964-1726/22/12/125038
[62] Liu WQ, Badel A, Formosa F, et al. Novel piezoelectric bistable oscillator architecture for wideband vibration energy harvesting. Smart Materials and Structures, 2013, 22: 035013 doi: 10.1088/0964-1726/22/3/035013
[63] Zhou S, Cao J, Inman DJ, et al. Broadband tristable energy harvester: modeling and experiment verification. Applied Energy, 2014, 133: 33-39 doi: 10.1016/j.apenergy.2014.07.077
[64] Panyam M, Daqaq MF. Characterizing the effective bandwidth of tri-stable energy harvesters. Journal of Sound and Vibration, 2017, 386: 336-358 doi: 10.1016/j.jsv.2016.09.022
[65] Li H, Qin W, Lan C, et al. Dynamics and coherence resonance of Tri-stable energy harvesting system. Smart Materials and Structures, 2015, 25(1): 015001
[66] Leng Y, Tan D, Liu J, et al. Magnetic force analysis and performance of a Tri-stable piezoelectric energy harvester under random excitation. Journal of Sound and Vibration, 2017, 406: 146-160 doi: 10.1016/j.jsv.2017.06.020
[67] Wang G, Zhao Z, Liao WH, et al. Characteristics of a tri-stable piezoelectric vibration energy harvester by considering geometric nonlinearity and gravitation effects. Mechanical Systems and Signal Processing, 2020, 138: 106571 doi: 10.1016/j.ymssp.2019.106571
[68] Zhou Z, Qin W, Zhu P. Improve efficiency of harvesting random energy by snap-through in a quad-stable harvester. Sensors and Actuators A:Physical, 2016, 243: 151-158 doi: 10.1016/j.sna.2016.03.024
[69] Zhou Z, Qin W, Yang Y, et al. Improving efficiency of energy harvesting by a novel penta-stable configuration. Sensors and Actuators A:Physical, 2017, 265: 297-305 doi: 10.1016/j.sna.2017.08.039
[70] Kim IH, Jung HJ, Bo ML, et al. Broadband energy-harvesting using a two degree-of-freedom vibrating body. Applied Physics Letters, 2011, 98(21): 214102 doi: 10.1063/1.3595278
[71] Andò B, Baglio S, Maiorca F, et al. Analysis of two dimensional, wide-band, bistable vibration energy harvester. Sensors and Actuators A:Physical, 2013, 202(11): 176-182
[72] Park JC, Park JY. Asymmetric PZT bimorph cantilever for multi-dimensional ambient vibration harvesting. Ceramics International, 2013, 39: S653-S657 doi: 10.1016/j.ceramint.2012.10.155
[73] Su WJ, Zu J. An innovative tri-directional broadband piezoelectric energy harvester. Applied Physics Letters, 2013, 103(20): 203901 doi: 10.1063/1.4830371
[74] Chen K, Gao F, Liu Z, et al. A nonlinear M-shaped tri-directional piezoelectric energy harvester. Smart Materials and Structures, 2021, 30(4): 045017 doi: 10.1088/1361-665X/abe87e
[75] Xu J, Tang J. Multi-directional energy harvesting by piezoelectric cantilever-pendulum with internal resonance. Applied Physics Letters, 2015, 107(21): 213902 doi: 10.1063/1.4936607
[76] Xu J, Tang J. Modeling and analysis of piezoelectric cantilever-pendulum system for multi-directional energy harvesting. Journal of Intelligent Material Systems and Structure, 2017, 28(3): 323-338 doi: 10.1177/1045389X16642302
[77] Chen R, Long R, Xia H, et al. Energy harvesting performance of a dandelion-like multi-directional piezoelectric vibration energy harvester. Sensors and Actuators A:Physical, 2015, 230: 1-8 doi: 10.1016/j.sna.2015.03.038
[78] Feng L, Liu G, Guo H, et al. Hybridized nanogenerator based on honeycomb-like three electrodes for efficient ocean wave energy harvesting. Nano Energy, 2018, 47: 217-223 doi: 10.1016/j.nanoen.2018.02.042
[79] Gu Y, Liu W, Zhao C, et al. A goblet-like non-linear electromagnetic generator for planar multi-directional vibration energy harvesting. Applied Energy, 2020, 266: 114846 doi: 10.1016/j.apenergy.2020.114846
[80] Zhang Y, Yang F, Li Y, et al. Design and numerical investigation of a multi-directional energy-harvesting device for UUVs. Energy, 2020, 214: 118978
[81] Yang T, Cao Q, Li Q, et al. A multi-directional multistable device: Modeling, experiment verification and applications. Mechanical Systems and Signal Processing, 2021, 146: 106986 doi: 10.1016/j.ymssp.2020.106986
[82] Zheng R, Nakano K, Hu H, et al. An application of stochastic resonance for energy harvesting in a bistable vibrating system. Journal of Sound and Vibration, 2014, 333: 2568-2587 doi: 10.1016/j.jsv.2014.01.020
[83] Fokou IM, Buckjohn CND, Siewe MS, et al. Probabilistic distribution and stochastic P-bifurcation of a hybrid energy harvester under colored noise. Communications in Nonlinear Science and Numerical Simulation, 2018, 56: 177-197 doi: 10.1016/j.cnsns.2017.08.006
[84] Li H, Qin W. Dynamics and coherence resonance of a laminated piezoelectric beam for energy harvesting. Nonlinear Dynamics, 2015, 81: 1751-1757 doi: 10.1007/s11071-015-2104-3
[85] Daqaq MF. On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations. Nonlinear Dynamics, 2012, 69: 1063-1079 doi: 10.1007/s11071-012-0327-0
[86] Borowiec M, Litak G, Friswell MI, et al. Energy harvesting in a nonlinear cantilever piezoelastic beam system excited by random vertical vibrations. International Journal of Structural Stability and Dynamics, 2014, 14(8): 1440018 doi: 10.1142/S0219455414400185
[87] Kumar P, Narayanan S, Adhikari S, et al. Fokker-Planck equation analysis of randomly excited nonlinear energy harvester. Journal of Sound and Vibration, 2014, 333: 2040-2053 doi: 10.1016/j.jsv.2013.11.011
[88] 李海涛. 非线性能量采集系统的相干共振与动力学特性研究. [博士论文]. 西安: 西北工业大学, 2017 Li Haitao. Dynamics and coherence resonance of nonlinear energy harvesting system. [PhD Thesis]. Xi'an: Northwestern Polytechnical University, 2017 (in Chinese))
[89] Xiao S, Jin Y. Response analysis of the piezoelectric energy harvester under correlated white noise. Nonlinear Dynamics, 2017, 90(3): 2069-2082 doi: 10.1007/s11071-017-3784-7
[90] Xu M, Jin X, Wang Y, et al. Stochastic averaging for nonlinear vibration energy harvesting system. Nonlinear Dynamics, 2014, 78: 1451-1459 doi: 10.1007/s11071-014-1527-6
[91] Jin X, Wang Y, Xu M, et al. Semi-analytical solution of random response for nonlinear vibration energy harvesters. Journal of Sound and Vibration, 2015, 340: 267-282 doi: 10.1016/j.jsv.2014.11.043
[92] 姜文安. 振动能量非线性采集器的解析、数值和实验研究. [博士论文]. 上海: 上海大学, 2015 Jiang Wenan. Analysis, Simulation and Experiment of Vibration-based Nonlinear Energy Harvesting. [PhD Thesis]. Shanghai: Shanghai University, 2015 (in Chinese))
[93] Zhang Y, Jin Y. Stochastic dynamics of a piezoelectric energy harvester with correlated colored noises from rotational environment. Nonlinear Dynamics, 2019, 98(1): 501-515 doi: 10.1007/s11071-019-05208-x
[94] 胡海岩, 王在华. 非线性时滞动力系统的研究进展. 力学进展, 1999, 29(4): 501-512 (Hu Haiyan, Wang Zaihua. Review on nonlinear dynamic systems involving time delay. Advances in Mechanics, 1999, 29(4): 501-512 (in Chinese) doi: 10.3321/j.issn:1000-0992.1999.04.008 [95] 徐鉴, 裴利军. 非线性时滞动力系统的研究进展. 力学进展, 2006, 36(1): 17-30 (Xu Jian, Pei Lijun. Advances in dynamics for delay systems. Advances in Mechanics, 2006, 36(1): 17-30 (in Chinese) doi: 10.3321/j.issn:1000-0992.2006.01.008 [96] 蔡国平, 陈龙祥. 时滞反馈控制的若干问题. 力学进展, 2013, 43(1): 21-28 (Cai Guoping, Chen Longxiang. Some problems of delayed feedback control. Advances in Mechanics, 2013, 43(1): 21-28 (in Chinese) doi: 10.6052/1000-0992-12-014 [97] 张舒, 徐鉴. 时滞耦合系统非线性动力学的研究进展. 力学学报, 2017, 49(3): 565-587 (Zhang Shu, Xu Jian. Review on nonlinear dynamics in systems with coupling delays. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 565-587 (in Chinese) doi: 10.6052/0459-1879-17-123 [98] Ghouli Z, Hamdi M, Lakrad F, et al. Quasiperiodic energy harvesting in a forced and delayed duffing harvester device. Journal of Sound and Vibration, 2017, 407: 271-285 doi: 10.1016/j.jsv.2017.07.005
[99] Ghouli Z, Hamdi M, Belhaq M. Energy harvesting from quasi-periodic vibrations using electromagnetic coupling with delay. Nonlinear Dynamics, 2017, 89(3): 1625-1636 doi: 10.1007/s11071-017-3539-5
[100] Belhaq M, Ghouli Z, Hamdi M. Energy harvesting in a Mathieu-van der Pol-Duffing MEMS device using time delay. Nonlinear Dynamics, 2018, 94: 2537-2546 doi: 10.1007/s11071-018-4508-3
[101] Chen Z, He J, Liu J, et al. Switching delay in self-powered nonlinear piezoelectric vibration energy harvesting circuit: mechanisms, effects, and solutions. IEEE Transactions on Power Electronics, 2018, 34(3): 2427-2440
[102] 陆泽琦, 陈立群. 非线性被动隔振的若干进展. 力学学报, 2017, 49(3): 550-564 (Lu Zeqi, Chen Liqun. Some recent progresses in nonlinear passive isolations of vibrations. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 550-564 (in Chinese) [103] Tang X, Zuo L. Simultaneous energy harvesting and vibration control of structures with tuned mass dampers. Journal of Intelligent Material Systems and Structures, 2012, 23(18): 2117-2127 doi: 10.1177/1045389X12462644
[104] Brennan MJ, Tang B, Melo GP, et al. An investigation into the simultaneous use of a resonator as an energy harvester and a vibration absorber. Journal of Sound and Vibration, 2014, 333(5): 1331-1343 doi: 10.1016/j.jsv.2013.10.035
[105] Davis RB, McDowell MD. Combined Euler column vibration isolation and energy harvesting. Smart Materials and Structures, 2017, 26(5): 055001 doi: 10.1088/1361-665X/aa6721
[106] Zhang W, Zhao J. Analysis on nonlinear stiffness and vibration isolation performance of scissor-like structure with full types. Nonlinear Dynamics, 2016, 86(1): 17-36 doi: 10.1007/s11071-016-2869-z
[107] Wang K, Zhou J, Xu D, et al. Lower band gaps of longitudinal wave in a one-dimensional periodic rod by exploiting geometrical nonlinearity. Mechanical Systems and Signal Processing, 2019, 124: 664-678 doi: 10.1016/j.ymssp.2019.02.008
[108] Ding H, Chen LQ. Nonlinear vibration of a slightly curved beam with quasi-zero-stiffness isolators. Nonlinear Dynamics, 2019, 95(3): 2367-2382 doi: 10.1007/s11071-018-4697-9
[109] Drezet C, Kacem N, Bouhaddi N. Design of a nonlinear energy harvester based on high static low dynamic stiffness for low frequency random vibrations. Sensors and Actuators A: Physical, 2018, 283: 54-64 doi: 10.1016/j.sna.2018.09.046
[110] Cao D, Guo X, Hu W. A novel low-frequency broadband piezoelectric energy harvester combined with a negative stiffness vibration isolator. Journal of Intelligent Material Systems and Structures, 2019, 30(7): 1045389X1982983
[111] Zou D, Liu G, Rao Z, et al. A device capable of customizing nonlinear forces for vibration energy harvesting, vibration isolation, and nonlinear energy sink. Mechanical Systems and Signal Processing, 2020, 147: 107101
[112] Lu Z, Wu D, Ding H, et al. Vibration isolation and energy harvesting integrated in a Stewart platform with high static and low dynamic stiffness. Applied Mathematical Modelling, 2020, 89: 249-267
[113] Lu Z, Shao D, Fang Z, et al. Integrated vibration isolation and energy harvesting via a bistable piezo-composite plate. Journal Vibration and Control, 2019, 26(9-10): 107754631988981
[114] Yang T, Cao Q, Hao Z. A novel nonlinear mechanical oscillator and its application in vibration isolation and energy harvesting. Mechanical Systems and Signal Processing, 2021, 155: 107636 doi: 10.1016/j.ymssp.2021.107636
[115] Ahmadabadi ZN, Khadem SE. Nonlinear vibration control and energy harvesting of a beam using a nonlinear energy sink and a piezoelectric device. Journal of Sound and Vibration, 2014, 333: 4444-4457 doi: 10.1016/j.jsv.2014.04.033
[116] Zhang Y, Tang LH, Liu KF. Piezoelectric energy harvesting with a nonlinear energy sink. Journal of Intelligent Material Systems and Structures, 2017, 28: 307-322 doi: 10.1177/1045389X16642301
[117] Li X, Zhang Y, Ding H, et al. Integration of a nonlinear energy sink and a piezoelectric energy harvester. Applied Mathematics and Mechanics (English Edition)
, 2017, 38: 1019-1030 doi: 10.1007/s10483-017-2220-6 [118] Xiong L, Tang L, Liu K, et al. Broadband piezoelectric vibration energy harvesting using a nonlinear energy sink. Journal of Physics D:Applied Physics, 2018, 51: 185502 doi: 10.1088/1361-6463/aab9e3
[119] Kremer D, Liu K. A nonlinear energy sink with an energy harvester: Transient responses. Journal of Sound and Vibration, 2014, 333(20): 4859-4880 doi: 10.1016/j.jsv.2014.05.010
[120] Kremer D, Liu K. A nonlinear energy sink with an energy harvester: Harmonically forced responses. Journal of Sound and Vibration, 2017, 410: 287-302 doi: 10.1016/j.jsv.2017.08.042
[121] Pennisi G, Mann BP, Naclerio N, et al. Design and experimental study of a Nonlinear Energy Sink coupled to an electromagnetic energy harvester. Journal of Sound and Vibration, 2018, 437: 340-357 doi: 10.1016/j.jsv.2018.08.026
[122] Remick K, Quinn DD, McFarland DM, et al. High-frequency vibration energy harvesting from impulsive excitation utilizing intentional dynamic instability caused by strong nonlinearity. Journal of Sound and Vibration, 2016, 370: 259-279 doi: 10.1016/j.jsv.2016.01.051
[123] Fang Z, Zhang Y, Li X, et al. Integration of a nonlinear energy sink and a giant magnetostrictive energy harvester. Journal of Sound and Vibration, 2017, 391: 35-49 doi: 10.1016/j.jsv.2016.12.019
[124] Fang Z, Zhang Y, Li X, et al. Complexification-averaging analysis on a giant magnetostrictive harvester integrated with a nonlinear energy sink. Journal of Vibration and Acoustics, 2018, 140(2): 021009 doi: 10.1115/1.4038033
[125] Zhang Y, Su C, Ni Z, et al. A multifunctional lattice sandwich structure with energy harvesting and nonlinear vibration control. Composite Structures, 2019, 221: 110875 doi: 10.1016/j.compstruct.2019.04.047
[126] Zhang Y, Wang S, Ni Z, et al. Integration of a nonlinear vibration absorber and levitation magnetoelectric energy harvester for wholespacecraft systems. Acta Mechanica Solida Sinica, 2019, 32: 298-309 doi: 10.1007/s10338-019-00081-y
[127] Tian W, Li Y, Yang Z, et al. Suppression of nonlinear aeroelastic responses for a cantilevered trapezoidal plate in hypersonic airflow using an energy harvester enhanced nonlinear energy sink. International Journal of Mechanical Sciences, 2020, 172: 105417 doi: 10.1016/j.ijmecsci.2020.105417
[128] Chiacchiari S, Romeo F, McFarland DM, et al. Vibration energy harvesting from impulsive excitations via a bistable nonlinear attachment. International Journal of Non-Linear Mechanics, 2017, 94: 84-97 doi: 10.1016/j.ijnonlinmec.2017.04.007
[129] Shu YC, Lien IC, Wu WJ. An improved analysis of the SSHI interface in piezoelectric energy harvesting. Smart Materials and Structures, 2007, 16(6): 2253 doi: 10.1088/0964-1726/16/6/028
[130] Lallart M, Guyomar D. An optimized self-powered switching circuit for non-linear energy harvesting with low voltage output. Smart Materials and Structures, 2008, 17(3): 035030 doi: 10.1088/0964-1726/17/3/035030
[131] Wu Y, Badel A, Formosa F, et al. Piezoelectric vibration energy harvesting by optimized synchronous electric charge extraction. Journal of Intelligent Material Systems and Structures, 2013, 24(12): 1445-1458 doi: 10.1177/1045389X12470307
[132] Wang G, Li P, Wen Y, et al. Self-powered ultra-low-power low-threshold synchronous circuit for weak piezoelectric energy harvesting. Sensors and Actuators A:Physical, 2021, 322: 112632 doi: 10.1016/j.sna.2021.112632
[133] Zhu L, Chen R, Liu X. Theoretical analyses of the electronic breaker switching method for nonlinear energy harvesting interfaces. Journal of Intelligent Material Systems and Structures, 2012, 23(4): 441-451 doi: 10.1177/1045389X11435433
[134] Shi G, Xia Y, Wang X, et al. An efficient self-powered piezoelectric energy harvesting CMOS interface circuit based on synchronous charge extraction technique. IEEE Transactions on Circuits and Systems I: Regular Papers, 2018, 605(2): 804-817
[135] Cheng C, Chen Z, Xiong Y, et al. A high-efficiency, self-powered nonlinear interface circuit for bi-stable rotating piezoelectric vibration energy harvesting with nonlinear magnetic force. International Journal of Applied Electromagnetics and Mechanics, 2016, 51(3): 235-248 doi: 10.3233/JAE-150093
[136] Wang X, Xia Y, Shi G, et al. A self-powered rectifier-less synchronized switch harvesting on inductor interface circuit for piezoelectric energy harvesting. IEEE Transactions on Power Electronics, 2021, 36(8): 9149-9159 doi: 10.1109/TPEL.2021.3052573
[137] Zhou S, Cao J, Inman DJ, et al. Impact-induced high-energy orbits of nonlinear energy harvesters. Applied Physics Letters, 2015, 106(9): 093901 doi: 10.1063/1.4913606
[138] Zhou S, Cao J, Lin J. Theoretical analysis and experimental verification for improving energy harvesting performance of nonlinear monostable energy harvesters. Nonlinear Dynamics, 2016, 86(3): 1599-1611 doi: 10.1007/s11071-016-2979-7
[139] Fang S, Wang S, Miao G, et al. Comprehensive theoretical and experimental investigation of the rotational impact energy harvester with the centrifugal softening effect. Nonlinear Dynamics, 2020, 101(1): 123-152 doi: 10.1007/s11071-020-05732-1
[140] Mallick D, Amann A, Roy S. Surfing the High Energy Output Branch of Nonlinear Energy Harvesters. Physical Review Letters, 2016, 117(19): 197701 doi: 10.1103/PhysRevLett.117.197701
[141] Lan C, Tang L, Qin W. Obtaining high-energy responses of nonlinear piezoelectric energy harvester by voltage impulse perturbations. The European Physical Journal Applied Physics, 2017, 79(2): 20902 doi: 10.1051/epjap/2017170051
-
期刊类型引用(21)
1. 马丽骞,曹东兴,詹昌海. 音叉压电悬臂梁动力学建模及振动俘能特性分析. 振动工程学报. 2025(05): 984-993 .  百度学术
百度学术
2. 刘宗通,马建军,郭颖. 有限深度介质上梁非线性能量汇减振的Winkler地基实现. 振动与冲击. 2024(01): 237-245 .  百度学术
百度学术
3. 周坤涛,杨涛,葛根,郝淑英,冯晶晶,张琪昌. 变截面压电悬臂梁能量采集器在高斯白噪声激励下的稳态统计特性研究. 振动工程学报. 2024(05): 864-874 .  百度学术
百度学术
4. 伍芷娴,王锁,李支援,梅旭涛,周生喜. 旋转环境下的磁耦合双稳态能量俘获机理研究. 振动工程学报. 2024(06): 964-975 .  百度学术
百度学术
5. 王德莉,李晨莹,吴炳增,焦一宇,裴海清,徐伟. 联合噪声驱动下耦合记忆阻尼Rayleigh振子族的节律模式过渡分析. 力学学报. 2024(08): 2381-2396 .  本站查看
本站查看
6. 张湧崟,彭剑,易昱东,孙洪鑫,禹见达. 时滞作用下电磁-压电弹性梁的俘能特性分析. 噪声与振动控制. 2024(05): 39-43 .  百度学术
百度学术
7. 徐海涛,周生喜. 非线性俘能系统机电耦合动力学模型分析及故障诊断应用研究. 振动工程学报. 2024(10): 1714-1722 .  百度学术
百度学术
8. 姜文安,卞明礼,陈立群,毕勤胜. 簇发振荡能量采集动力学理论研究进展. 动力学与控制学报. 2024(08): 1-12 .  百度学术
百度学术
9. 刘国平,杨朝舒,何忠波,周景涛,孙民政. 面向微振信号的驻极体减振俘能装置设计与建模. 力学学报. 2023(01): 169-181 .  本站查看
本站查看
10. 杨楠,孙麟. 悬臂梁型混合俘能器研究进展. 节能. 2023(04): 94-96 .  百度学术
百度学术
11. 范圣平,李竞,李林勇,樊小鹏,李华亮,高南沙. 电磁阻尼器工作特性的理论模型与试验研究. 西北工业大学学报. 2023(04): 688-696 .  百度学术
百度学术
12. 孙成佳,靳艳飞,张艳霞. 具有时滞反馈控制的双稳态压电-电磁式俘能器的随机动力学. 动力学与控制学报. 2023(08): 75-81 .  百度学术
百度学术
13. 张野,王军雷. 基于翅片超表面钝体的流致振动俘能特性研究. 力学学报. 2023(10): 2199-2216 .  本站查看
本站查看
14. 赵林川,陈泽文,邹鸿翔,孟光,张文明. 机械能量采集动力学调控方法. 力学学报. 2023(10): 2094-2114 .  本站查看
本站查看
15. 李支援,吕文博,马小青,周生喜. 一种磁力滑动式翼型颤振能量俘获器. 力学学报. 2023(10): 2146-2155 .  本站查看
本站查看
16. 李猛,李孙飚,丁虎. 非线性能量汇胞元减振效率分析. 力学学报. 2023(11): 2614-2623 .  本站查看
本站查看
17. 陈晓哲,焦志成,石加联. 一种具有能量俘获自参数摆动力吸振器的设计及参数影响分析. 振动工程学报. 2023(06): 1657-1663 .  百度学术
百度学术
18. 张伟,刘爽,毛佳佳,黎绍佳,曹东兴. 磁耦合式双稳态宽频压电俘能器的设计和俘能特性. 力学学报. 2022(04): 1102-1112 .  本站查看
本站查看
19. 周碧柳,靳艳飞. 高斯色噪声和谐波激励共同作用下耦合SD振子的混沌研究. 力学学报. 2022(07): 2030-2040 .  本站查看
本站查看
20. 李岩,金亚斌. 超构材料波动功能调控研究进展. 复合材料学报. 2022(09): 4259-4273 .  百度学术
百度学术
21. 吴义鹏,李森,蓝春波,周圣鹏,谢维泰,裘进浩,季宏丽. 压电能量俘获结构及其升频转换技术的发展现状. 机械工程学报. 2022(20): 27-45 .  百度学术
百度学术
其他类型引用(32)



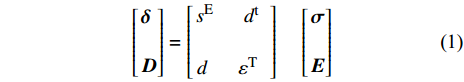
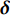

 下载:
下载: