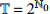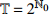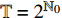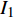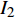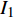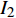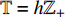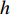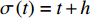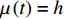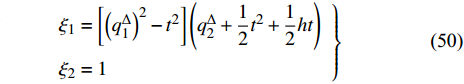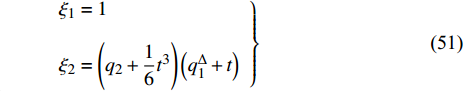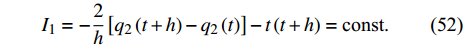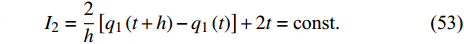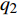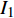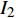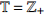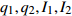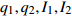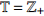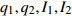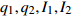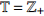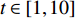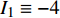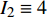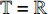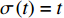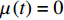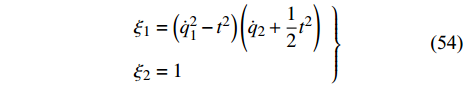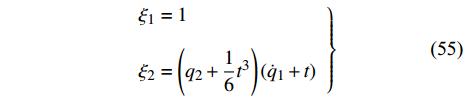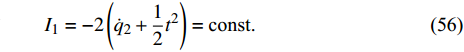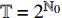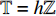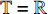HOJMAN CONSERVED QUANTITY FOR TIME SCALES LAGRANGE SYSTEMS
-
摘要: 利用对称性和守恒律, 可以简化动力学问题甚至求解力学系统的精确解, 更好地理解其动力学行为. 时间尺度分析将连续和离散动力学模型统一并拓展到时间尺度框架, 既避免了重复研究又可揭示两者之区别和联系. 因此, 通过对称性来探寻在时间尺度的框架下新的守恒定律很有必要. 本文首先建立了时间尺度上Lagrange方程, 利用时间尺度微积分性质导出了时间尺度上Lagrange系统的两个重要关系式; 其次, 依据微分方程在单参数Lie变换群下的不变性, 建立了时间尺度上Lie对称性的定义和确定方程; 最后, 建立了时间尺度上Lie对称性定理并利用上述关系式给出了证明, 得到了时间尺度上Lagrange系统的新守恒量. 当时间尺度取为实数集时, 该守恒量退化为著名的Hojman守恒量. 文末考察了一个两自由度时间尺度Lagrange系统, 在3种不同时间尺度情形下得到了该系统的Hojman守恒量, 数值计算结果验证了定理的正确性.
-
关键词:
- Lagrange系统 /
- Lie对称性 /
- Hojman守恒量 /
- 时间尺度
Abstract: By using symmetry and conservation laws, we can simplify dynamical problem and even obtain the exact solution of mechanical system, and better understand the dynamical behavior of system. Time scales analysis unifies and extends the continuous and discrete dynamics models to the time scales framework, which not only avoids repeated studies but also reveals the differences and connections between them. Therefore, it is necessary to explore new conservation laws in the framework of time scale through symmetry. Firstly, the Lagrange equations on time scales are established, and two important relations of time scales Lagrange system are derived by using the properties of time scales calculus. Secondly, according to the invariance of differential equation under the one-parameter Lie group of transformations, the definition of Lie symmetry on time scales and its determining equation are established. Thirdly, the Lie symmetry theorem on time scales is established and proved by using the above relations, and the new conservation laws of time scales Lagrange system are obtained. When the time scale is taken to the set of real numbers, the conservation laws degenerate to the famous Hojman conserved quantity. Finally, a two-degree-of-freedom time scales Lagrange system is investigated, and its Hojman conserved quantities are obtained in three different time scales, and the correctness of the theorem we obtained is verified by numerical calculation.-
Keywords:
- Lagrange system /
- Lie symmetry /
- Hojman conserved quantity /
- time scales
-
引 言
力学系统的对称性与守恒律密切相关. 通过研究对称性而探索或发现复杂力学系统的守恒律, 这是分析力学研究的一个重要方面[1-2]. Lie对称性[3-9]、Noether对称性[10-20]和Mei对称性[21-28]是3种概念不同的对称性方法. 利用对称性和守恒律, 可以简化动力学问题甚至求解力学系统的精确解, 从而更好地理解其动力学行为. 微分方程的Lie理论最早由Lutzky[29]引入力学系统, 所得守恒量是Noether型的. Hojman[30]由Lie对称性直接导出一类不属于Noether型的守恒量, 称之为Hojman守恒量[21]. Hilger[31]于1990年提出了测度链上的分析理论, 而时间尺度作为测度链的特殊情形备受关注[32-34]. 时间尺度分析不仅是连续分析和离散分析的统一, 而且是经典微积分对任意时间尺度的拓广. Bartosiewicz和Torres[35]首先开展时间尺度上Noether对称性的研究, 此后关于时间尺度上Noether定理及其证明的探讨至今仍方兴未艾[36-42]. 但是, 时间尺度上Lie对称性直到最近才有一些初步的研究且所得守恒量均为Noether型的[43-46]. 鉴于此, 本文将研究并给出由时间尺度上Lie对称性直接导出的非Noether型的新型守恒量.
1. 时间尺度微积分
为方便读者, 这里对时间尺度微积分做一简单介绍, 详见文献[32-33].
设
${{\mathbb{T}}}$ 是一个时间尺度, 即实数集${{\mathbb{R}}}$ 的任意非空闭子集, 如实数集${{\mathbb{R}}}$ 、整数集${\mathbb{Z}}$ 、非负整数集${{\mathbb{N}}_0}$ 或$\left[ {1,3} \right] \cup {\mathbb{N}}$ . 前跳算子$\sigma \left( t \right) = \inf \left\{ {s \in {{\mathbb{T}}}:s > t} \right\}$ 和后跳算子$\rho \left( t \right) = \sup \left\{ {s \in {{\mathbb{T}}}:s < t} \right\}$ 是关于时间尺度的两个重要的量. 若$\sigma \left( t \right) = t$ , 称点$t \in {{\mathbb{T}}}$ 右稠密,$\sigma \left( t \right) > t$ 则右发散; 若$\rho \left( t \right) = t$ , 称点$t \in {{\mathbb{T}}}$ 左稠密,$\rho \left( t \right) < t$ 则左发散. 相邻点的位置关系在时间尺度上可用向前或向后步差函数$\mu \left( t \right) = \sigma \left( t \right) - t$ 或$\upsilon \left( t \right) = t - \rho \left( t \right)$ 描述.由
${{\mathbb{T}}}$ 可定义集合${{{\mathbb{T}}}^k}$ 和${{{\mathbb{T}}}_k}$ : 当$\sup {{\mathbb{T}}} < \infty $ 时,${{{\mathbb{T}}}^k} = $ $ {{\mathbb{T}}}\backslash \left( {\rho \left( {\sup {{\mathbb{T}}}} \right),\sup {{\mathbb{T}}}} \right]$ , 而当$\sup {{\mathbb{T}}} = \infty $ 时,${{{\mathbb{T}}}^k} = {{\mathbb{T}}}$ ; 与之相对应, 当$\inf {{\mathbb{T}}} > - \infty $ 时,${{{\mathbb{T}}}_k} = {{\mathbb{T}}}\backslash \left[ {\sup {{\mathbb{T}}},\sigma \left( {\sup {{\mathbb{T}}}} \right)} \right)$ , 而当时$\inf {{\mathbb{T}}} = - \infty $ ,${{{\mathbb{T}}}_k} = {{\mathbb{T}}}$ .定义函数
$y:{{\mathbb{T}}} \to {{\mathbb{R}}}$ 在点$t \in {{{\mathbb{T}}}^k}$ 的delta导数为: 任给$\varepsilon > 0$ , 如果存在$\delta > 0$ , 使得$\left| y\left( {\sigma \left( t \right)} \right) - y\left( \tau \right) - \right. $ $ \left. {y^\Delta }\left( t \right)\left( {\sigma \left( t \right) - \tau } \right) \right| \leqslant \varepsilon \left| {\sigma \left( t \right) - \tau } \right|$ 对所有的$\tau \in U = ( t - \delta , $ $ t + \delta ) \cap {{\mathbb{T}}}$ 成立. 记为$ {y^\Delta }\left( t \right) $ 或$\dfrac{\Delta }{{\Delta t}}y\left( t \right)$ . 类似地, 在$t \in {{{\mathbb{T}}}_k}$ 的nabla导数定义为: 任给$\varepsilon > 0$ , 如果存在$\delta > 0$ , 使得$ \left| {y\left( {\rho \left( t \right)} \right) - y\left( \tau \right) - {y^\nabla }\left( t \right)\left( {\rho \left( t \right) - \tau } \right)} \right| \leqslant \varepsilon \left| {\rho \left( t \right) - \tau } \right| $ 成立. 记为$ {y^\nabla }\left( t \right) $ 或$\dfrac{\nabla }{{\nabla t}}y\left( t \right)$ .如果函数
$ y:{\mathbb{T}} \to {\mathbb{R}} $ 在$ {\mathbb{T}} $ 的右稠密点连续且在左稠密点的左极限存在, 则称$ y\left( t \right) $ 是$ {\text{rd}} $ 连续的.$ {\mathbb{T}} $ 上所有$ {\text{rd}} $ 连续的函数的集合记为$ C_{{\text{rd}}}^0\left( {\mathbb{T}} \right) $ , 而$ {{\mathbb{T}}^k} $ 上具有$ {\text{rd}} $ 连续的delta导数的delta可微函数的集合记为$ C_{{\text{rd}}}^{1,\Delta }\left( {\mathbb{T}} \right) $ .如果对所有的
$t \in {{{\mathbb{T}}}^k}$ , 有$ {Y^\Delta }\left( t \right) = y\left( t \right) $ , 则称$ Y:{\mathbb{T}} \to {\mathbb{R}} $ 为$ y:{\mathbb{T}} \to {\mathbb{R}} $ 的一个原函数. 定义函数$ y $ 的delta不定积分为$ \int {y\left( t \right)\Delta t = Y\left( t \right) + C} $ , delta定积分为$ \int_a^b {y\left( t \right)} \Delta t = Y\left( b \right) - Y\left( a \right) $ , 其中$ a,b \in {\mathbb{T}} $ ,$C$ 是任意常数.Dubois-Reymond引理: 令
$ y:\left[ {a,b} \right] \to {{\mathbb{R}}^n} $ ,$ y \in C_{{\text{rd}}}^0 $ , 对于任意的$ \eta \in C_{{\text{rd}}}^1 $ 且$ \eta \left( a \right) = \eta \left( b \right) = 0 $ , 积分$ \displaystyle\int_a^b {{y^T}\left( t \right)} {\eta ^\Delta }\left( t \right)\cdot $ $ \Delta t = 0$ 成立的充分必要条件是在$t \in {\left[ {a,b} \right]^k}$ 上$y\left( t \right) \equiv C$ .链式法则: 设函数
$g为\;{{{\mathbb{T}}}_1} \times {{{\mathbb{T}}}_2} \times \cdots \times {{{\mathbb{T}}}_n} \to {{\mathbb{R}}}$ 在点${t^0}$ 完全delta可微, 函数${\vartheta _j}\,\left( {j = 1,2, \cdots ,n} \right)$ 在点${\zeta ^0}$ 的delta导数存在, 其中$t_j^0 = {\vartheta _j}\left( {{\zeta ^0}} \right)$ , 则复合函数$G\left( \zeta \right) = g\left( {{\vartheta _1}\left( \zeta \right),{\vartheta _2}\left( \zeta \right), \cdots ,{\vartheta _n}\left( \zeta \right)} \right)$ 在该点的delta导数${G^\Delta }\left( {{\zeta ^0}} \right)$ 存在, 且有$$ \begin{array}{l} {G^\Delta }\left( {{\zeta ^0}} \right) = g_{{t_i}}^{{\Delta _i}}\left( {{t^0}} \right)\vartheta _i^\Delta \left( {{\zeta ^0}} \right)+\\ \quad g_{{t_{i - 1}}}^{{\Delta _{i - 1}}}\left[ {{\vartheta _1}\left( {{\zeta ^0}} \right),{\vartheta _2}\left( {{\zeta ^0}} \right), \cdots ,{\vartheta _{i - 1}}\left( {{\zeta ^0}} \right),{\sigma _i}\left( {{\vartheta _i}\left( {{\zeta ^0}} \right)} \right)}, \right. \\ \quad \left. {{\vartheta _{i + 1}}\left( {{\zeta ^0}} \right), \cdots ,{\vartheta _n}\left( {{\zeta ^0}} \right)} \right]\vartheta _{i - 1}^\Delta \left( {{\zeta ^0}} \right) + \cdots+ \\ \quad g_{{t_1}}^{{\Delta _1}}\left[ {{\vartheta _1}\left( {{\zeta ^0}} \right),{\sigma _2}\left( {{\vartheta _2}\left( {{\zeta ^0}} \right)} \right), \cdots ,{\sigma _i}\left( {{\vartheta _i}\left( {{\zeta ^0}} \right)} \right)}, \right. \\ \quad \left. {{\vartheta _{i + 1}}\left( {{\zeta ^0}} \right), \cdots ,{\vartheta _n}\left( {{\zeta ^0}} \right)} \right]\vartheta _1^\Delta \left( {{\zeta ^0}} \right)+ \end{array} $$ $$ \begin{array}{*{20}{l}} \quad g_{{t_{i + 1}}}^{{\Delta _{i + 1}}}\left[ {{\sigma _1}\left( {{\vartheta _1}\left( {{\zeta ^0}} \right)} \right),{\sigma _2}\left( {{\vartheta _2}\left( {{\zeta ^0}} \right)} \right) \cdots ,{\sigma _i}\left( {{\vartheta _i}\left( {{\zeta ^0}} \right)} \right)}, \right. \\ {\quad \left. {{\vartheta _{i + 1}}\left( {{\zeta ^0}} \right), \cdots ,{\vartheta _n}\left( {{\zeta ^0}} \right)} \right]\vartheta _{i + 1}^\Delta \left( {{\zeta ^0}} \right) + \cdots + }\\ \quad g_{{t_n}}^{{\Delta _n}}\left[ {{\sigma _1}\left( {{\vartheta _1}\left( {{\zeta ^0}} \right)} \right),{\sigma _2}\left( {{\vartheta _2}\left( {{\zeta ^0}} \right)} \right), \cdots ,{\sigma _{n - 1}}\left( {{\vartheta _{n - 1}}\left( {{\zeta ^0}} \right)} \right),} \right.\\ \left. {\quad {\vartheta _n}\left( {{\zeta ^0}} \right)} \right]\vartheta _n^\Delta \left( {{\zeta ^0}} \right) \end{array}$$ (1) 其中
$$ \begin{array}{l} g_{{t_i}}^{{\Delta _i}}\left( t \right){\buildrel \Delta \over =} \dfrac{{\partial g\left( t \right)}}{{{\Delta _i}{t_i}}} = \\ \mathop {\lim }\limits_{\begin{subarray}{l} {s_i} \to {t_i} \\ {s_i} \ne {\sigma _i}\left( {{t_i}} \right) \end{subarray}} \dfrac{\begin{array}{l} g\left( {{t_1},t_2, \cdots ,{t_{i - 1}},{\sigma _i}\left( {{t_i}} \right),{t_{i + 1}}, \cdots ,{t_n}} \right) - \\ g\left( {{t_1}, t_2,\cdots ,{t_{i - 1}},{s_i},{t_{i + 1}}, \cdots ,{t_n}} \right) \end{array}}{{{\sigma _i}\left( {{t_i}} \right) - {s_i}}} \end{array} $$ (2) 称为函数
$g\left( t \right)$ 在点$t$ 相对${t_i}$ 的delta偏导数.混合delta偏导数次序交换定理: 如果
$g_{{t_i}{t_j}}^{{\Delta _i}{\Delta _j}}\left( t \right)$ 和$g_{{t_j}{t_i}}^{{\Delta _j}{\Delta _i}}\left( t \right)$ 在点${t^0}$ 连续, 则$g_{{t_i}{t_j}}^{{\Delta _i}{\Delta _j}}\left( t \right) = g_{{t_j}{t_i}}^{{\Delta _j}{\Delta _i}}\left( t \right)$ .对于delta可微函数
$y\left( t \right)$ 和$z\left( t \right)$ , 在时间尺度上成立Leibniz公式$$ \begin{split} &{\left( {yz} \right)^\Delta }\left( t \right) = {y^\sigma }\left( t \right){z^\Delta }\left( t \right) + {y^\Delta }\left( t \right)z\left( t \right) =\\ & \;\;\;\;\;\;\;\; y\left( t \right){z^\Delta }\left( t \right) + {y^\Delta }\left( t \right){z^\sigma }\left( t \right) \end{split} $$ (3) 以及分部积分公式
$$ \begin{split} & \int_a^b {y\left( t \right)} {z^\Delta }\left( t \right)\Delta t = \\ &\qquad\left( {yz} \right)\left( b \right) - \left( {yz} \right)\left( a \right) - \int_a^b {{y^\Delta }\left( t \right){z^\sigma }\left( t \right)\Delta t} \end{split} $$ (4) 2. 时间尺度上运动微分方程
时间尺度上Lagrange方程为[28]
$$ \frac{\nabla }{{\nabla t}}\frac{{\partial L}}{{\partial q_s^\Delta }} - {\sigma ^\nabla }\left( t \right)\frac{{\partial L}}{{\partial {q_s}}} = 0, \;{s = 1,2, \cdots ,n} $$ (5) 其中
$ L\left( {{q_s},q_s^\Delta ,t} \right):{{{\mathbb{R}}}^n} \times {{{\mathbb{R}}}^n} \times {{{\mathbb{T}}}^k} \to {{\mathbb{R}}} $ 是时间尺度上Lagrange函数,${q_s}\left( t \right)$ 是时间尺度上广义坐标,$q_s^\Delta \left( t \right)$ 是广义速度. 假设这些函数都是$C_{{\text{rd}}}^1$ 函数.假设系统非奇异, 即
$D = \det \left( {\dfrac{{{\partial ^2}L}}{{\partial q_s^\Delta {\Delta _{n + k}}q_k^\Delta }}} \right) \ne 0$ , 则由方程(5)可解得所有广义加速度, 简记为$$ q_s^{\Delta \Delta } = {\alpha _s}\left( {{q_k},q_k^\Delta ,t} \right), \;{s = 1,2, \cdots ,n} $$ (6) 3. 时间尺度上Lagrange系统的两个重要关系式
本节推导时间尺度上Lagrange系统的两个重要关系式, 它们是推导时间尺度上Hojman守恒量的基础.
设函数
$ {\varOmega _s} = {\varOmega _s}\left( {{q_k},q_k^\Delta ,t} \right) $ 是delta可微的, 将$ {\varOmega _s} $ 按方程(6)对$t$ 求delta导数, 有$$ \frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = \frac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}q_k^\Delta + \frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}{\alpha _k} + \frac{{\partial {\varOmega _s}}}{{{\Delta _{2n + 1}}t}}\qquad\qquad $$ (7) $$ \begin{split} & \frac{{\bar \Delta }}{{\Delta t}}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = {\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}} \right)^\sigma }{\alpha _k} + \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}q_k^\Delta +\\ & \qquad {\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)^\sigma }\left( {\frac{{\partial {\alpha _k}}}{{{\Delta _j}{q_j}}}q_j^\Delta + \frac{{\partial {\alpha _k}}}{{{\Delta _{n + j}}q_j^\Delta }}{\alpha _j} + \frac{{\partial {\alpha _k}}}{{{\Delta _{2n + 1}}t}}} \right) +\\ & \qquad \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}{\alpha _k} + \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _k}{q_k}}}q_k^\Delta+ \\ & \qquad \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _{n + k}}q_k^\Delta }}{\alpha _k} + \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _{2n + 1}}t}} \end{split} $$ (8) 其中
$\dfrac{{\bar \Delta }}{{\Delta t}}\left( * \right)$ 表示$\left( * \right)$ 按方程(6)对时间$t$ 的delta导数, 即有$$ \frac{{\bar \Delta }}{{\Delta t}}\left( * \right) = \frac{\partial }{{{\Delta _k}{q_k}}}\left( * \right)q_k^\Delta + \frac{\partial }{{{\Delta _{n + k}}q_k^\Delta }}\left( * \right){\alpha _k} + \frac{\partial }{{{\Delta _{2n + 1}}t}}\left( * \right) $$ (9) 而符号
$\dfrac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}$ ,$\dfrac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}$ 和$\dfrac{{\partial {\varOmega _s}}}{{{\Delta _{2n + 1}}t}}$ 表示按照链式法则(1)函数${\varOmega _s}\left( {{q_1},q_2, \cdots ,{q_n},q_1^\Delta , q_2^\Delta,\cdots ,q_n^\Delta ,t} \right)$ 分别对${q_k}$ ,$q_k^\Delta $ 和时间$t$ 的delta偏导数, 即有$$ \dfrac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}} \buildrel \Delta \over = \dfrac{\partial }{{{\Delta _k}{q_k}}}{\varOmega _s}\left( {q_1^\sigma , q_2^\sigma,\cdots ,q_{k - 1}^\sigma ,{q_k}, \cdots ,{q_n},q_1^\Delta ,q_2^\Delta , \cdots ,q_n^\Delta ,t} \right)\quad\quad $$ (10) $$ \begin{array}{l} \dfrac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}\buildrel \Delta \over = \dfrac{\partial }{{{\Delta _{n + k}}q_k^\Delta }}{\varOmega _s}\left( q_1^\sigma , q_2^\sigma ,\cdots ,q_n^\sigma ,q_1^{\Delta \sigma }, q_2^{\Delta \sigma },\cdots ,\right. \\ \quad \left. q_{k - 1}^{\Delta \sigma },q_k^\Delta , \cdots ,q_n^\Delta ,t \right) \end{array}$$ (11) $$ \dfrac{{\partial {\varOmega _s}}}{{{\Delta _{2n + 1}}t}} \buildrel \Delta \over = \dfrac{\partial }{{{\Delta _{2n + 1}}t}}{\varOmega _s}\left( {q_1^\sigma , q_2^\sigma , \cdots ,q_n^\sigma ,q_1^{\Delta \sigma },q_2^{\Delta \sigma }, \cdots ,q_n^{\Delta \sigma },t} \right) \quad\quad\quad\quad\quad$$ (12) 再将式(7)两端分别对
${q_s}$ 和$q_s^\Delta $ 求普通偏导数和delta偏导数, 有$$ \begin{split} & \dfrac{\partial }{{\partial {q_s}}}\dfrac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = \dfrac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _k}{q_k}\partial {q_s}}}q_k^\Delta + \dfrac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial {q_s}}}{\alpha _k}+\\ &\qquad \dfrac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}\dfrac{{\partial {\alpha _k}}}{{\partial {q_s}}} + \dfrac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t\partial {q_s}}} \end{split}$$ (13) $$\begin{split} & \frac{\partial }{{{\Delta _s}{q_s}}}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _k}{q_k}{\Delta _s}{q_s}}}q_k^\Delta + {\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)^\sigma }\frac{{\partial {\alpha _k}}}{{{\Delta _s}{q_s}}}+\\ &\qquad \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta {\Delta _s}{q_s}}}{\alpha _k} + \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _s}{q_s}}} \end{split}$$ (14) $$ \begin{split} & \frac{\partial }{{\partial q_s^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _k}{q_k}\partial q_s^\Delta }}q_k^\Delta + \frac{{\partial {\varOmega _s}}}{{{\Delta _s}{q_s}}} +\\ &\qquad \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}{\alpha _k} + \frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }} + \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t\partial q_s^\Delta }} \end{split} $$ (15) $$ \begin{split} & \frac{\partial }{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = {\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}} \right)^\sigma } + \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _j}{q_j}{\Delta _{n + k}}q_k^\Delta }}q_j^\Delta+ \\ &\qquad {\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + j}}q_j^\Delta }}} \right)^\sigma }\frac{{\partial {\alpha _j}}}{{{\Delta _{n + k}}q_k^\Delta }} + \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{n + j}}q_j^\Delta {\Delta _{n + k}}q_k^\Delta }}{\alpha _j} +\\ &\qquad \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _{n + k}}q_k^\Delta }} \end{split} $$ (16) 将式(8)两端对
$q_s^\Delta $ 求普通偏导数, 有$$ \begin{split} & \frac{\partial }{{\partial q_s^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = \frac{\partial }{{\partial q_s^\Delta }}{\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}} \right)^\sigma }{\alpha _k} + {\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}} \right)^\sigma }\frac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }} +\\ &\qquad \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{{\Delta _s}{q_s}}} + \frac{\partial }{{\partial q_s^\Delta }}\left( {\frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}} \right)q_k^\Delta + \frac{\partial }{{\partial q_s^\Delta }}{\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)^\sigma }\cdot \\ &\qquad \left( {\frac{{\partial {\alpha _k}}}{{{\Delta _j}{q_j}}}q_j^\Delta + \frac{{\partial {\alpha _k}}}{{{\Delta _{n + j}}q_j^\Delta }}{\alpha _j} + \frac{{\partial {\alpha _k}}}{{{\Delta _{2n + 1}}t}}} \right) + \\ &\qquad {\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)^\sigma }\left( {\frac{{{\partial ^2}{\alpha _k}}}{{{\Delta _j}{q_j}\partial q_s^\Delta }}q_j^\Delta + \frac{{\partial {\alpha _k}}}{{{\Delta _s}{q_s}}}} \right. + \\ &\qquad \left. { \frac{{{\partial ^2}{\alpha _k}}}{{{\Delta _{n + j}}q_j^\Delta \partial q_s^\Delta }}{\alpha _j} + \frac{{\partial {\alpha _k}}}{{{\Delta _{n + j}}q_j^\Delta }}\frac{{\partial {\alpha _j}}}{{\partial q_s^\Delta }} + \frac{{{\partial ^2}{\alpha _k}}}{{{\Delta _{2n + 1}}t\partial q_s^\Delta }}} \right) +\\ &\qquad \frac{\partial }{{\partial q_s^\Delta }}\left( {\frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right){\alpha _k} + \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }} +\\ &\qquad \frac{{{\partial ^3}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _k}{q_k}\partial q_s^\Delta }}q_k^\Delta + \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _s}{q_s}}} +\\ &\qquad \frac{{{\partial ^3}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}{\alpha _k} + \frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t{\Delta _{n + k}}q_k^\Delta }}\frac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }} + \\ &\qquad\frac{{{\partial ^3}{\varOmega _s}}}{{{\Delta _{2n + 1}}{t^2}\partial q_s^\Delta }} \\[-5pt] \end{split}$$ (17) 将
$\dfrac{{\partial {\varOmega _s}}}{{\partial {q_s}}}$ 对时间$t$ 求delta导数, 得到$$ \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{\partial {q_s}}} = \frac{{{\partial ^2}{\varOmega _s}}}{{\partial {q_s}{\Delta _k}{q_k}}}q_k^\Delta + \frac{{{\partial ^2}{\varOmega _s}}}{{\partial {q_s}{\Delta _{n + k}}q_k^\Delta }}{\alpha _k} + \frac{{{\partial ^2}{\varOmega _s}}}{{\partial {q_s}{\Delta _{2n + 1}}t}} $$ (18) 比较式(13)和式(18), 假设
${\varOmega _s}$ 对变量${q_s}$ 和$q_s^\Delta $ 求delta偏导数和普通偏导数的次序可交换, 得到$$ \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{\partial {q_s}}} = \frac{\partial }{{\partial {q_s}}}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} - \frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\partial {\alpha _k}}}{{\partial {q_s}}} $$ (19) 再将式(15)对时间
$t$ 求delta导数, 得到$$ \begin{split} & \frac{{\bar \Delta }}{{\Delta t}}\frac{\partial }{{\partial q_s^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = {\left( {\frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _k}{q_k}\partial q_s^\Delta }}} \right)^\sigma }{\alpha _k} + \frac{{\bar \Delta }}{{\Delta t}}\frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _k}{q_k}\partial q_s^\Delta }}q_k^\Delta +\\ &\qquad \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{{\Delta _s}{q_s}}} + \frac{{\bar \Delta }}{{\Delta t}}\frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}{\alpha _k} +\\ &\qquad {\left( {\frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}} \right)^\sigma }\left( {\frac{{\partial {\alpha _k}}}{{{\Delta _j}{q_j}}}q_j^\Delta + \frac{{\partial {\alpha _k}}}{{{\Delta _{n + j}}q_j^\Delta }}{\alpha _j} + \frac{{\partial {\alpha _k}}}{{{\Delta _{2n + 1}}t}}} \right)+ \\ &\qquad {\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)^\sigma }\left( \frac{{{\partial ^2}{\alpha _k}}}{{\partial q_s^\Delta {\Delta _j}{q_j}}}q_j^\Delta + \frac{{{\partial ^2}{\alpha _k}}}{{\partial q_s^\Delta {\Delta _{n + j}}q_j^\Delta }}{\alpha _j} + \right.\\ &\qquad \left. \frac{{{\partial ^2}{\alpha _k}}}{{\partial q_s^\Delta {\Delta _{2n + 1}}t}} \right) + \frac{{\bar \Delta }}{{\Delta t}}\frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{2n + 1}}t\partial q_s^\Delta }} + \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }} \end{split}$$ (20) 类似地, 比较式(17)和式(20), 并假设函数
${\varOmega _s}$ 和${\alpha _s}$ 对变量${q_s}$ 和$q_s^\Delta $ 求delta偏导数以及普通偏导数的次序可交换, 有$$ \begin{split} & \frac{{\bar \Delta }}{{\Delta t}}\frac{\partial }{{\partial q_s^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} = \frac{\partial }{{\partial q_s^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s} - \frac{\partial }{{{\Delta _s}{q_s}}}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s}-\\ &\qquad \left[ {\frac{\partial }{{\partial q_s^\Delta }}{{\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _k}{q_k}}}} \right)}^\sigma } - {{\left( {\frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _k}{q_k}\partial q_s^\Delta }}} \right)}^\sigma }} \right]{\alpha _k} -\\ &\qquad \frac{\partial }{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}{\varOmega _s}\frac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }}- \\ &\qquad \left[ {\frac{\partial }{{\partial q_s^\Delta }}{{\left( {\frac{{\partial {\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)}^\sigma } - {{\left( {\frac{{{\partial ^2}{\varOmega _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}} \right)}^\sigma }} \right]\frac{{\bar \Delta }}{{\Delta t}}{\alpha _k} \end{split}$$ (21) 式(19)和式(21)是时间尺度上Lagrange系统导数运算的两个重要关系式.
4. 时间尺度上Lie对称性
在时间尺度上引进无限小变换
$$ {t^*} = t , \;q_s^*\left( {{t^*}} \right) = {q_s}\left( t \right) + \varepsilon {\xi _s}\left( {{q_k},q_k^\Delta ,t} \right) $$ (22) 式中
$\varepsilon $ 是无限小参数,$ {\xi _s} $ 是变换的生成元,${\kern 1pt} s,k = $ $ 1,2, \cdots ,n$ . 变换式(22)的无限小生成元向量${X^{\left( 0 \right)}}$ 及其一次拓展${X^{\left( 1 \right)}}$ 和二次拓展${X^{\left( 2 \right)}}$ 为[44]$$ \left. \begin{split} & {X^{\left( 0 \right)}} = {\xi _s}\frac{\partial }{{\partial {q_s}}} \\ & {X^{\left( 1 \right)}} = {X^{\left( 0 \right)}} + \frac{{\bar \Delta }}{{\Delta t}}{\xi _s}\frac{\partial }{{\partial q_s^\Delta }} \\ & {X^{\left( 2 \right)}} = {X^{\left( 1 \right)}} + \frac{{\bar \Delta }}{{\Delta t}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s}\frac{\partial }{{\partial q_s^{\Delta \Delta }}} \end{split}\right\}$$ (23) 依据微分方程在单参数Lie变换群下的不变性, 可定义时间尺度上Lagrange系统的Lie对称性, 即
定义1. 对于时间尺度上Lagrange系统(5), 当且仅当
$$ {X^{\left( 2 \right)}}\left[ {q_s^{\Delta \Delta } - {\alpha _s}\left( {{q_k},q_k^\Delta ,t} \right)} \right] = 0, \;{s = 1,2, \cdots ,n} $$ (24) 则变换式(22)是Lie对称性的.
方程(24)可写为
$$ \frac{{\bar \Delta }}{{\Delta t}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} - {X^{\left( 1 \right)}}\left( {{\alpha _s}} \right) = 0 $$ (25) 或
$$ \frac{{\bar \Delta }}{{\Delta t}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} - {\xi _k}\frac{{\partial {\alpha _s}}}{{\partial {q_k}}} - \frac{{\bar \Delta }}{{\Delta t}}{\xi _k}\frac{{\partial {\alpha _s}}}{{\partial q_k^\Delta }} = 0 $$ (26) 称方程(25)或式(26)为时间尺度上Lie对称性确定方程.
5. 时间尺度上Lie对称性定理
由Lie对称性可直接导出时间尺度上一类新守恒量, 即有:
定理1. 对于时间尺度上Lagrange系统(5), 如果变换式(22)是Lie对称性的, 并假设所有函数对其变量的混合delta偏导数连续, 且存在函数
$\psi = \psi \left( {{q_s}} \right)$ 使得$$ \frac{{\partial {\alpha _s}}}{{\partial q_s^\Delta }} + \frac{1}{\psi }\frac{{\partial \psi }}{{{\Delta _s}{q_s}}}q_s^\Delta = 0 $$ (27) 则该系统存在新的守恒量, 形如
$$ I = \frac{1}{\psi }\frac{\partial }{{\partial {q_s}}}\left( {\psi {\xi _s}} \right) + \frac{1}{\psi }\frac{\partial }{{\partial q_s^\Delta }}\left( {\psi \frac{{\bar \Delta }}{{\Delta t}}{\xi _s}} \right) + \varXi $$ (28) 其中
$$ \begin{split} & \varXi = \int_{{t_1}}^t {\Biggl\{{18} {\left( {\dfrac{\partial }{{{\Delta _s}{q_s}}} - \dfrac{\partial }{{\partial {q_s}}}} \right)\dfrac{{\bar \Delta }}{{\Delta t}}{\xi _s} + \left( {\dfrac{{\partial {\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta }} - \dfrac{{\partial {\xi _s}}}{{\partial q_k^\Delta }}} \right)\dfrac{{\partial {\alpha _k}}}{{\partial {q_s}}}} } +\\ &\qquad \left( {\dfrac{\partial }{{{\Delta _{n + k}}q_k^\Delta }} - \dfrac{\partial }{{\partial q_k^\Delta }}} \right)\dfrac{{\bar \Delta }}{{\Delta t}}{\xi _s}\dfrac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }} +\\ &\qquad \left[ {\dfrac{\partial }{{\partial q_s^\Delta }}{{\left( {\dfrac{{\partial {\xi _s}}}{{{\Delta _k}{q_k}}}} \right)}^\sigma } - {{\left( {\dfrac{{{\partial ^2}{\xi _s}}}{{{\Delta _k}{q_k}\partial q_s^\Delta }}} \right)}^\sigma }} \right]{\alpha _k} +\\ &\qquad \left[ {\dfrac{\partial }{{\partial q_s^\Delta }}{{\left( {\dfrac{{\partial {\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)}^\sigma } - {{\left( {\dfrac{{{\partial ^2}{\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}} \right)}^\sigma }} \right]\dfrac{{\bar \Delta }}{{\Delta t}}{\alpha _k} + \\ &\qquad \left[ {\dfrac{1}{\psi }\dfrac{{\partial \psi }}{{{\Delta _s}{q_s}}} - {{\left( {\dfrac{1}{\psi }\dfrac{{\partial \psi }}{{\partial {q_s}}}} \right)}^\sigma }} \right]\dfrac{{\bar \Delta }}{{\Delta t}}{\xi _s} +\\ &\qquad { \left[ {{X^{\left( 1 \right)}}\left( {\dfrac{1}{\psi }\dfrac{{\partial \psi }}{{{\Delta _s}{q_s}}}} \right) - {\xi _k}\dfrac{\partial }{{{\Delta _s}{q_s}}}\left( {\dfrac{1}{\psi }\dfrac{{\partial \psi }}{{\partial {q_k}}}} \right)} \right]q_s^\Delta } \Bigggr\}{18}\Delta \tau \end{split}$$ (29) 证明: 将式(28)按方程(6)对时间
$t$ 求delta导数, 得$$ \begin{split} & \frac{{\bar \Delta }}{{\Delta t}}I = \frac{{\bar \Delta }}{{\Delta t}}\left[ {\frac{1}{\psi }\frac{\partial }{{\partial {q_s}}}\left( {\psi {\xi _s}} \right) + \frac{1}{\psi }\frac{\partial }{{\partial q_s^\Delta }}\left( {\psi \frac{{\bar \Delta }}{{\Delta t}}{\xi _s}} \right)} \right]+ \\ &\qquad \left( {\frac{\partial }{{{\Delta _s}{q_s}}} - \frac{\partial }{{\partial {q_s}}}} \right)\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} + \left( {\frac{{\partial {\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta }} - \frac{{\partial {\xi _s}}}{{\partial q_k^\Delta }}} \right)\frac{{\partial {\alpha _k}}}{{\partial {q_s}}}+ \\ &\qquad \left( {\frac{\partial }{{{\Delta _{n + k}}q_k^\Delta }} - \frac{\partial }{{\partial q_k^\Delta }}} \right)\frac{{\bar \Delta }}{{\Delta t}}{\xi _s}\frac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }}+ \\ &\qquad \left[ {\frac{\partial }{{\partial q_s^\Delta }}{{\left( {\frac{{\partial {\xi _s}}}{{{\Delta _k}{q_k}}}} \right)}^\sigma } - {{\left( {\frac{{{\partial ^2}{\xi _s}}}{{{\Delta _k}{q_k}\partial q_s^\Delta }}} \right)}^\sigma }} \right]{\alpha _k} +\\ &\qquad \left[ {\frac{\partial }{{\partial q_s^\Delta }}{{\left( {\frac{{\partial {\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)}^\sigma } - {{\left( {\frac{{{\partial ^2}{\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}} \right)}^\sigma }} \right]\frac{{\bar \Delta }}{{\Delta t}}{\alpha _k} +\\ &\qquad \left[ {\frac{1}{\psi }\frac{{\partial \psi }}{{{\Delta _s}{q_s}}} - {{\left( {\frac{1}{\psi }\frac{{\partial \psi }}{{\partial {q_s}}}} \right)}^\sigma }} \right]\frac{{\bar \Delta }}{{\Delta t}}{\xi _s}+ \\ &\qquad \left[ {{X^{\left( 1 \right)}}\left( {\frac{1}{\psi }\frac{{\partial \psi }}{{{\Delta _s}{q_s}}}} \right) - {\xi _k}\frac{\partial }{{{\Delta _s}{q_s}}}\left( {\frac{1}{\psi }\frac{{\partial \psi }}{{\partial {q_k}}}} \right)} \right]q_s^\Delta \end{split} $$ (30) 根据假设, 所有函数对其变量的混合delta偏导数连续, 因此函数
${\xi _s}$ 和${\alpha _s}$ 对变量${q_s}$ 和$q_s^\Delta $ 求delta偏导数以及普通偏导数的次序可交换[33]. 利用关系式(19)和式(21), 有$$ \frac{{\bar \Delta }}{{\Delta t}}\frac{{\partial {\xi _s}}}{{\partial {q_s}}} = \frac{\partial }{{\partial {q_s}}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} - \frac{{\partial {\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\partial {\alpha _k}}}{{\partial {q_s}}} $$ (31) $$ \begin{split} & \frac{{\bar \Delta }}{{\Delta t}}\frac{\partial }{{\partial q_s^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} = \frac{\partial }{{\partial q_s^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} - \frac{\partial }{{{\Delta _s}{q_s}}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s}- \\ &\qquad \left[ {\frac{\partial }{{\partial q_s^\Delta }}{{\left( {\frac{{\partial {\xi _s}}}{{{\Delta _k}{q_k}}}} \right)}^\sigma } - {{\left( {\frac{{{\partial ^2}{\xi _s}}}{{{\Delta _k}{q_k}\partial q_s^\Delta }}} \right)}^\sigma }} \right]{\alpha _k} -\\ &\qquad \left[ {\frac{\partial }{{\partial q_s^\Delta }}{{\left( {\frac{{\partial {\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)}^\sigma } - {{\left( {\frac{{{\partial ^2}{\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}} \right)}^\sigma }} \right]\frac{{\bar \Delta }}{{\Delta t}}{\alpha _k} -\\ &\qquad \frac{\partial }{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\bar \Delta {\xi _s}}}{{\Delta t}}\frac{{\partial {\alpha _k}}}{{\partial q_s^\Delta }} \end{split}$$ (32) 注意到
$\psi = \psi \left( {{q_s}} \right)$ , 因此有$$ \frac{\Delta }{{\Delta t}}\left( {\frac{1}{\psi }\frac{{\partial \psi }}{{\partial {q_s}}}} \right){\xi _s} = \frac{\partial }{{{\Delta _k}{q_k}}}\left( {\frac{1}{\psi }\frac{{\partial \psi }}{{\partial {q_s}}}} \right)q_k^\Delta {\xi _s} $$ (33) 将式(31) ~ 式(33)代入式(30), 得到
$$ \begin{split} \frac{{\bar \Delta }}{{\Delta t}}I = \frac{\partial }{{\partial q_s^\Delta }}\left( {\frac{{\bar \Delta }}{{\Delta t}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} - {X^{\left( 1 \right)}}\left( {{\alpha _s}} \right)} \right) + {X^{\left( 1 \right)}}\left( {\frac{{\partial {\alpha _s}}}{{\partial q_s^\Delta }} + \frac{1}{\psi }\frac{{\partial \psi }}{{{\Delta _s}{q_s}}}q_s^\Delta } \right) \end{split} $$ (34) 将确定方程(25)和式(27)代入上式, 有
$$ \frac{{\bar \Delta }}{{\Delta t}}I = 0 $$ (35) 因此, 式(28)是该系统的守恒量. 证毕.
定理1可称为时间尺度上Lagrange系统的Lie对称性定理. 式(28)可称为时间尺度上Hojman守恒量, 它是由Lie对称性直接导致的.
对于任意时间尺度, 守恒量(28)中函数
$\varXi $ 一般不等于零. 函数$\varXi $ 出现的原因在于任意时间尺度上delta偏导数不同于普通偏导数, 而当时间尺度${{\mathbb{T}}} = {{\mathbb{R}}}$ 时两者是一致的. 实际上, 若取${{\mathbb{T}}} = {{\mathbb{R}}}$ , 则有$$ \left. \begin{split} & \frac{\partial }{{{\Delta _s}{q_s}}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} = \frac{\partial }{{\partial {q_s}}}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} \\ & \frac{\partial }{{{\Delta _{n + k}}q_k^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} =\frac{\partial }{{\partial q_k^\Delta }}\frac{{\bar \Delta }}{{\Delta t}}{\xi _s} \\ & \frac{{\partial {\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta }} = \frac{{\partial {\xi _s}}}{{\partial q_k^\Delta }}\\ & \frac{\partial }{{\partial q_s^\Delta }}{\left( {\frac{{\partial {\xi _s}}}{{{\Delta _k}{q_k}}}} \right)^\sigma } ={\left( {\frac{{{\partial ^2}{\xi _s}}}{{{\Delta _k}{q_k}\partial q_s^\Delta }}} \right)^\sigma } \\ & \frac{\partial }{{\partial q_s^\Delta }}{\left( {\frac{{\partial {\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta }}} \right)^\sigma } = {\left( {\frac{{{\partial ^2}{\xi _s}}}{{{\Delta _{n + k}}q_k^\Delta \partial q_s^\Delta }}} \right)^\sigma }\\ & \frac{1}{\psi }\frac{{\partial \psi }}{{{\Delta _s}{q_s}}} = {\left( {\frac{1}{\psi }\frac{{\partial \psi }}{{\partial {q_s}}}} \right)^\sigma } \\ & {X^{\left( 1 \right)}}\left( {\frac{1}{\psi }\frac{{\partial \psi }}{{{\Delta _s}{q_s}}}} \right) = {\xi _k}\frac{\partial }{{{\Delta _s}{q_s}}}\left( {\frac{1}{\psi }\frac{{\partial \psi }}{{\partial {q_k}}}} \right) \end{split}\right\}$$ (36) 因此
$\varXi = 0$ , 于是定理1退化为定理2. 对于经典Lagrange系统, 如果无限小变换(22)是Lie对称性的, 且存在函数
$\psi = \psi \left( {{q_s}} \right)$ 满足条件$$ \frac{{\partial {\alpha _s}}}{{\partial {{\dot q}_s}}} + \frac{{{\bar{\text{d}}}}}{{{\text{d}}t}}\ln \psi = 0 $$ (37) 则
$$ I = \frac{1}{\psi }\frac{\partial }{{\partial {q_s}}}\left( {\psi {\xi _s}} \right) + \frac{1}{\psi }\frac{\partial }{{\partial {{\dot q}_s}}}\left( {\psi \frac{{{\bar{\text{d}}}}}{{{\text{d}}t}}{\xi _s}} \right) = {\text{const}}. $$ (38) 是该系统的守恒量.
定理2与文献[30]的结果一致.
6. 算例
例. 设时间尺度为
${{\mathbb{T}}} = \left\{ {{2^m}:m \in {{\mathbb{N}}_0}} \right\}$ , 研究两自由度Lagrange系统, 其Lagrange函数为$$ L = \frac{1}{2}\left[ {{{\left( {q_1^\Delta } \right)}^2} + {{\left( {q_2^\Delta } \right)}^2}} \right] - {q_2}t - {q_1} $$ (39) 试研究该系统的Lie对称性, 并求出对应的Hojman守恒量.
时间尺度上Lagrange方程(5)给出
$$ \left. \begin{array}{l} \dfrac{\nabla }{{\nabla t}}q_1^\Delta + {\sigma ^\nabla } = 0\\ \dfrac{\nabla }{{\nabla t}}q_2^\Delta + {\sigma ^\nabla }t = 0 \end{array} \right\} $$ (40) 注意到, 对于时间尺度上任意函数
$u\left( t \right)$ , 有关系$$ \left. \begin{split} & \dfrac{\nabla }{{\nabla t}}{u^\sigma }\left( t \right) = {\sigma ^\nabla }{u^\Delta }\left( t \right) \\ & {\sigma ^\nabla }{u^{\Delta \rho \Delta }}\left( t \right) = {u^{\Delta \Delta \rho }}\left( t \right)\\ & {\sigma ^{\nabla \sigma }}\left( t \right) = {\sigma ^\Delta }\left( t \right) \end{split}\right\}$$ (41) 因此, 方程(40)可解出
$$\left. \begin{array}{l} q_1^{\Delta \Delta } = - {\sigma ^\Delta }\left( t \right) = {\alpha _1}\\ q_2^{\Delta \Delta } = - {\sigma ^\Delta }\left( t \right)\sigma \left( t \right) = {\alpha _2} \end{array} \right\} $$ (42) 确定方程(25)给出
$$ \left. \begin{array}{l} \dfrac{{\bar \Delta }}{{\Delta t}}\dfrac{{\bar \Delta }}{{\Delta t}}{\xi _1} = 0\\ \dfrac{{\bar \Delta }}{{\Delta t}}\dfrac{{\bar \Delta }}{{\Delta t}}{\xi _2} = 0 \end{array} \right\} $$ (43) 由于
${{\mathbb{T}}} = {2^{{{\mathbb{N}}_0}}}$ , 则$\sigma \left( t \right) = 2t$ ,$\mu \left( t \right) = t$ , 因此方程(43)有如下解$$ \left. \begin{array}{l} {\xi _1} = \left[ {{{\left( {q_1^\Delta } \right)}^2} - 4{t^2}} \right]\left( {q_2^\Delta + \dfrac{4}{3}{t^2}} \right)\\ {\xi _2} = 1 \end{array} \right\} $$ (44) $$ \left. \begin{array}{l} {\xi _1} = 1\\ {\xi _2} = \left( {{q_2} + \dfrac{4}{{21}}{t^3}} \right)\left( {q_1^\Delta + 2t} \right) \end{array} \right\} $$ (45) 与生成元式(44)和式(45)相应的变换是Lie对称的. 方程(27)给出
$$ \frac{1}{\psi }\frac{{\partial \psi }}{{{\Delta _1}{q_1}}}q_1^\Delta + \frac{1}{\psi }\frac{{\partial \psi }}{{{\Delta _2}{q_2}}}q_2^\Delta = 0 $$ (46) 方程(46)有解
$$ \psi = 1 $$ (47) 根据定理1, 由式(44), 式(45)和式(47), 得到
$$ {I_1} = - \frac{4}{t}\left[ {{q_2}\left( {2t} \right) - {q_2}\left( t \right)} \right] - \frac{{16}}{3}{t^2} = {\text{const}}. $$ (48) $$ {I_2} = \frac{2}{t}\left[ {{q_1}\left( {2t} \right) - {q_1}\left( t \right)} \right] + 4t = {\text{const}}. $$ (49) 这是时间尺度上Lie对称性式(44)和式(45)导致的Hojman守恒量. 如果取初始条件为
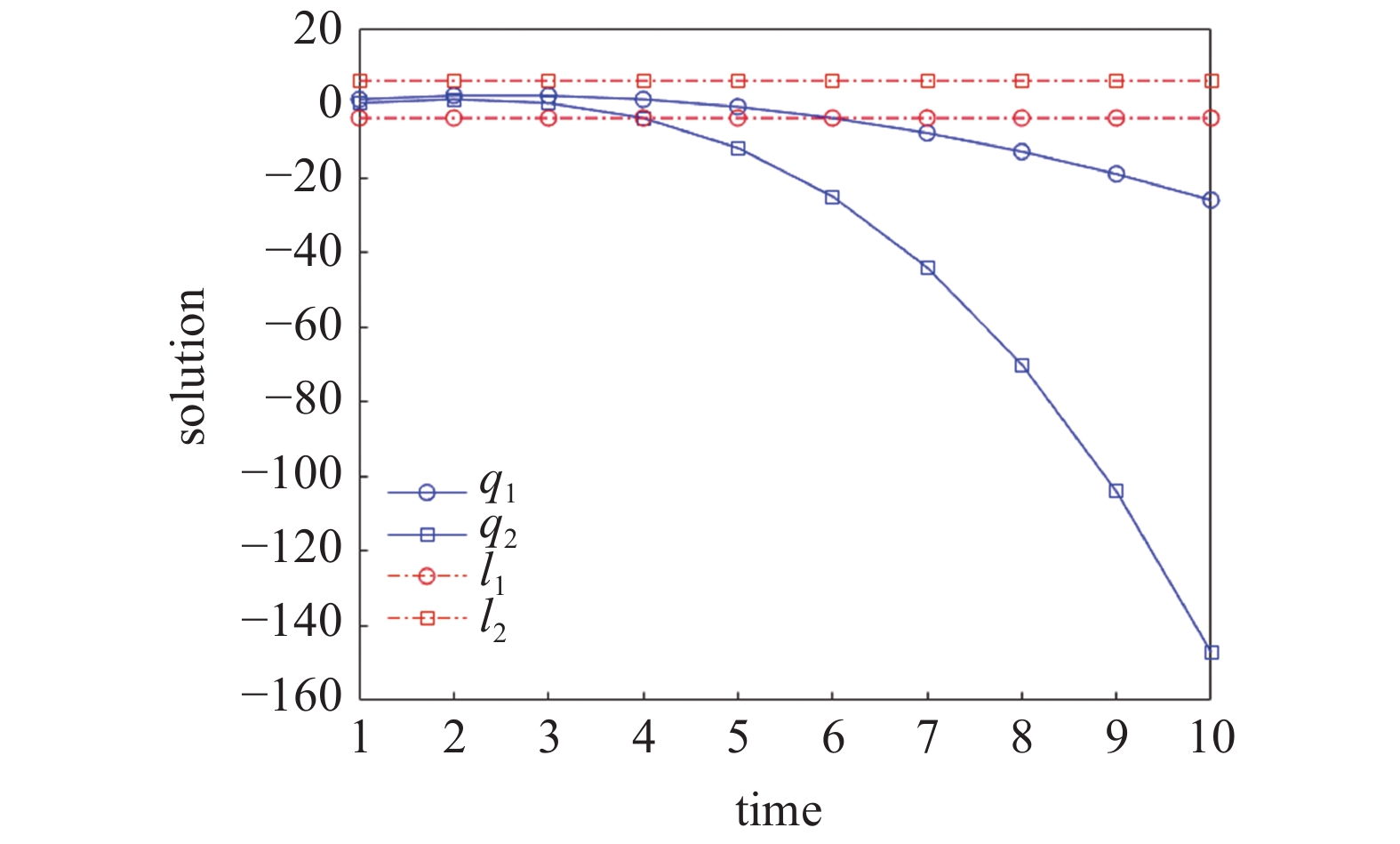
$ {q_1}\left( 1 \right) = 1 $ ,$ {q_2}\left( 1 \right) = 0 $ ,$ {q_1}\left( 2 \right) = 2 $ ,$ {q_2}\left( 2 \right) = 1 $ , 在时间尺度为${{\mathbb{T}}} = {2^{{{\mathbb{N}}_0}}}$ 上计算运动轨迹$ {q_1},{q_2} $ 和守恒量$ {I_1},{I_2} $ 的值, 其结果如图1所示. 图1中具体的数据如表1所示.表 1 时间尺度$ {{\mathbb{T}}} = {2^{{{\mathbb{N}}_0}}} $ 上$ {q_1},{q_2},{I_1},{I_2} $ 的值Table 1. The values of$ {q_1},{q_2},{I_1},{I_2} $ on the time scale$ {{\mathbb{T}}} = {2^{{{\mathbb{N}}_0}}} $ $ {\mathbb{T}}/{\rm{s}} $ $ {q_1}/{\rm{m}} $ $ {q_2}/{\rm{m}} $ $ {I_1} $ $ {I_2} $ 1 1 0 −9.33 6 2 2 1 −9.33 6 4 0 −5 −9.33 6 8 −20 −81 −9.33 6 16 −124 −745 −9.33 6 32 −588 −6169 −9.33 6 64 −2540 −49785 −9.33 6 从图1和表1可以看出, 在时间尺度
$ {{\mathbb{T}}} = {2^{{{\mathbb{N}}_0}}} $ 上, 由式(48)和式(49)所确定的$ {I_1} $ ,$ {I_2} $ 的值始终不变, 说明$ {I_1} $ 和$ {I_2} $ 确实是守恒量, 从而验证了定理1的正确性.如取
${{\mathbb{T}}} = h{{\mathbb{Z}}_ + }$ ,$h$ 为常数, 则$\sigma \left( t \right) = t + h$ ,$\mu \left( t \right) = h$ , Lie对称性式(44)和式(45)成为$$ \left. \begin{array}{l} {\xi _1} = \left[ {{{\left( {q_1^\Delta } \right)}^2} - {t^2}} \right]\left( {q_2^\Delta + \dfrac{1}{2}{t^2} + \dfrac{1}{2}ht} \right)\\ {\xi _2} = 1 \end{array} \right\}$$ (50) $$\left. \begin{array}{l} {\xi _1} = 1\\ {\xi _2} = \left( {{q_2} + \dfrac{1}{6}{t^3}} \right)\left( {q_1^\Delta + t} \right) \end{array} \right\} $$ (51) 守恒量式(48)和式(49)成为
$$ {I_1} = - \frac{2}{h}\left[ {{q_2}\left( {t + h} \right) - {q_2}\left( t \right)} \right] - t\left( {t + h} \right) = {\text{const}}. $$ (52) $$ {I_2} = \frac{2}{h}\left[ {{q_1}\left( {t + h} \right) - {q_1}\left( t \right)} \right] + 2t = {\text{const}}. $$ (53) 仍取上述初始条件, 令
$ h = 1 $ , 在时间尺度为${{\mathbb{T}}} = {{\mathbb{Z}}_ + }$ 上计算运动轨迹$ {q_1} $ ,$ {q_2} $ 和守恒量$ {I_1} $ ,$ {I_2} $ 的值, 其结果和数据如图2和表2所示.表 2 时间尺度${{\mathbb{T}}} = {{\mathbb{Z}}_ + }$ 上$ {q_1},{q_2},{I_1},{I_2} $ 的值.Table 2. The values of$ {q_1},{q_2},{I_1},{I_2} $ on the time scale${{\mathbb{T}}} = {{\mathbb{Z}}_ + }$ $ {\mathbb{T}}/{\rm{s}} $ $ {q_1} /{\rm{m}}$ $ {q_2}/{\rm{m}} $ $ {I_1} $ $ {I_2} $ 1 1 0 −4 4 2 2 1 −4 4 3 2 0 −4 4 4 1 −4 −4 4 5 −1 −12 −4 4 6 −4 −25 −4 4 7 −8 −44 −4 4 8 −13 −70 −4 4 9 −19 −104 −4 4 10 −26 −147 −4 4 这里只取了
$ t \in \left[ {1,10} \right] $ , 实际上随着时间的增加, 仍有$ {I_1} \equiv - 4 $ 和$ {I_2} \equiv 4 $ . 由此可知式(52)和式(53)是守恒量, 再次验证了定理1的正确性.若取
${{\mathbb{T}}} = {{\mathbb{R}}}$ , 则$\sigma \left( t \right) = t$ ,$\mu \left( t \right) = 0$ , Lie对称性式(44)和式(45)成为$$ \left. \begin{array}{l} {\xi _1} = \left( {\dot q_1^2 - {t^2}} \right)\left( {{{\dot q}_2} + \dfrac{1}{2}{t^2}} \right)\\ {\xi _2} = 1 \end{array} \right\}$$ (54) $$ \left. \begin{array}{l} {\xi _1} = 1\\ {\xi _2} = \left( {{q_2} + \dfrac{1}{6}{t^3}} \right)\left( {{{\dot q}_1} + t} \right) \end{array} \right\} $$ (55) 守恒量式(48)和式(49)成为
$$ {I_1} = - 2\left( {{{\dot q}_2} + \frac{1}{2}{t^2}} \right) = {\text{const}}. $$ (56) $$ {I_2} = 2\left( {{{\dot q}_1} + t} \right) = {\text{const}}. $$ (57) 这是经典情形的Hojman守恒量.
7. 结 论
本文将Lie对称性方法拓展到时间尺度上Lagrange系统, 给出了时间尺度上Hojman守恒量. 主要贡献在于: 一是利用时间尺度微积分的基本性质导出了时间尺度上Lagrange系统导数运算的两个重要关系式. 这是推导Hojman守恒量的基础; 二是由Lie对称性直接推导得到了时间尺度上Lagrange系统的Hojman类型的守恒量. 该守恒量不依赖于Lagrange函数的结构而仅取决于Lie对称性变换的生成元. 文中以时间尺度上两自由度系统为例, 给出了
${{\mathbb{T}}} = {2^{{{\mathbb{N}}_0}}}$ ,${{\mathbb{T}}} = h{\mathbb{Z}}$ 以及${{\mathbb{T}}} = {{\mathbb{R}}}$ , 3种情形下的Hojman守恒量, 并通过数值模拟验证了结果的正确性. 当时间尺度取为实数集时, 本文结果退化为经典Lagrange系统的Hojman守恒量. 文章的方法和结果可进一步推广和应用, 如时间尺度上非完整系统, 时间尺度上Birkhoff系统等. -
表 1 时间尺度
$ {{\mathbb{T}}} = {2^{{{\mathbb{N}}_0}}} $ 上$ {q_1},{q_2},{I_1},{I_2} $ 的值Table 1 The values of
$ {q_1},{q_2},{I_1},{I_2} $ on the time scale$ {{\mathbb{T}}} = {2^{{{\mathbb{N}}_0}}} $ $ {\mathbb{T}}/{\rm{s}} $ $ {q_1}/{\rm{m}} $ $ {q_2}/{\rm{m}} $ $ {I_1} $ $ {I_2} $ 1 1 0 −9.33 6 2 2 1 −9.33 6 4 0 −5 −9.33 6 8 −20 −81 −9.33 6 16 −124 −745 −9.33 6 32 −588 −6169 −9.33 6 64 −2540 −49785 −9.33 6 表 2 时间尺度
${{\mathbb{T}}} = {{\mathbb{Z}}_ + }$ 上$ {q_1},{q_2},{I_1},{I_2} $ 的值.Table 2 The values of
$ {q_1},{q_2},{I_1},{I_2} $ on the time scale${{\mathbb{T}}} = {{\mathbb{Z}}_ + }$ $ {\mathbb{T}}/{\rm{s}} $ $ {q_1} /{\rm{m}}$ $ {q_2}/{\rm{m}} $ $ {I_1} $ $ {I_2} $ 1 1 0 −4 4 2 2 1 −4 4 3 2 0 −4 4 4 1 −4 −4 4 5 −1 −12 −4 4 6 −4 −25 −4 4 7 −8 −44 −4 4 8 −13 −70 −4 4 9 −19 −104 −4 4 10 −26 −147 −4 4 -
[1] 梅凤翔, 吴惠彬, 李彦敏. 分析力学史略. 北京: 科学出版社, 2019 (Mei Fengxiang, Wu Huibin, Li Yanmin. A Brief History of Analytical Mechanics. Beijing: Science Press, 2019 (in Chinese))
[2] Mei FX, Wu HB, Zhang YF. Symmetries and conserved quantities of constrained mechanical systems. International Journal of Dynamics and Control, 2014, 2(3): 285-303 doi: 10.1007/s40435-013-0043-8
[3] Bluman GW, Anco SC. Symmetry and Integration Methods for Differential Equations. New York: Springer-Verlag, 2002
[4] Mei FX. Lie symmetries and conserved quantities of constrained mechanical systems. Acta Mechanica, 2000, 141(3): 135-148
[5] Han YL, Wang XX, Zhang ML, et al. Lie symmetry and approximate Hojman conserved quantity of appell equations for a weakly nonholonomic system. Nonlinear Dynamics, 2013, 71(3): 401-408 doi: 10.1007/s11071-012-0657-y
[6] Fu JL, Fu LP, Chen BY, et al. Lie symmetries and their inverse problems of nonholonomic Hamilton systems with fractional derivatives. Physics Letters A, 2016, 380(1): 15-21
[7] Zhang XT, He JM, Luo SK. A new type of fractional Lie symmetrical method and its applications. International Journal of Theoretical Physics, 2017, 56(3): 971-990 doi: 10.1007/s10773-016-3240-3
[8] Zhang Y, Wang XP. Lie symmetry perturbation and adiabatic invariants for dynamical system with non-standard Lagrangians. International Journal of Non-Linear Mechanics, 2018, 105: 165-172 doi: 10.1016/j.ijnonlinmec.2018.05.027
[9] 孟蕾, 项春, 丁明明等. 非完整蛇形机器人系统的Lie对称性和守恒量. 应用力学学报, 2021, 38(2): 441-449 (Meng Lei, Xiang Chun, Ding Mingming, et al. Lie symmetry and conserved quantity of non-holonomic snake robot system. Chinese Journal of Applied Mechanics, 2021, 38(2): 441-449 (in Chinese) [10] Bahar LY, Kwatny HG. Extention of Noether’s theorem to constrained non-conservative dynamical systems. International Journal of Nonlinear Mechanics, 1987, 22(2): 125-138 doi: 10.1016/0020-7462(87)90015-1
[11] Wang P, Xue Y, Liu YL. Noether symmetry and conserved quantities of the analytical dynamics of a Cosserat thin elastic rod. Chinese Physics B, 2013, 22(10): 104503 doi: 10.1088/1674-1056/22/10/104503
[12] Zhang Y, Zhai XH. Noether symmetries and conserved quantities for fractional Birkhoffian systems. Nonlinear Dynamics, 2015, 81(1-2): 469-480 doi: 10.1007/s11071-015-2005-5
[13] 张毅. 相空间中非保守系统的Herglotz广义变分原理及其Noether定理. 力学学报, 2016, 48(6): 1382-1389 (Zhang Yi. Generalized variational principle of Herglotz type for nonconservative system in phase space and Noether’s theorem. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(6): 1382-1389 (in Chinese) doi: 10.6052/0459-1879-16-086 [14] Atanacković TM, Janev M, Pilipović S. Noether’s theorem for variational problems of Herglotz type with real and complex order fractional derivatives. Acta Mechanica, 2021, 232(3): 1131-1146 doi: 10.1007/s00707-020-02893-3
[15] 张毅. Caputo导数下分数阶Birkhoff系统的准对称性与分数阶Noether定理. 力学学报, 2017, 49(3): 693-702 (Zhang Yi. Quasi-symmetry and Noether’s theorem for fractional Birkhoffian systems in terms of Caputo derivatives. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 693-702 (in Chinese) doi: 10.6052/0459-1879-16-350 [16] Zhang HB, Chen HB. Noether’s theorem of Hamiltonian systems with generalized fractional derivative operators. International Journal of Non-Linear Mechanics, 2018, 107: 34-41 doi: 10.1016/j.ijnonlinmec.2018.10.013
[17] Lazo MJ, Paiva J, Frederico GSF. Noether theorem for action-dependent Lagrangian functions: conservation laws for non-conservative system. Nonlinear Dynamics, 2019, 97: 1125-1136 doi: 10.1007/s11071-019-05036-z
[18] Zhang LJ, Zhang Y. Non-standard Birkhoffian dynamics and its Noether's theorems. Communications in Nonlinear Science and Numerical Simulation, 2020, 91: 105435 doi: 10.1016/j.cnsns.2020.105435
[19] 张毅. 弱非线性动力学方程的Noether准对称性与近似Noether守恒量. 力学学报, 2020, 52(6): 1765-1773 (Zhang Yi. Noether quasi-symmetry and approximate Noether conservation laws for weakly nonlinear dynamical equations. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1765-1773 (in Chinese) doi: 10.6052/0459-1879-20-242 [20] 梅凤翔. 关于Noether定理——分析力学札记之三十. 力学与实践, 2020, 42(1): 66-74 (Mei Fengxiang. On the Noether’s theorem. Mechanics in Engineering, 2020, 42(1): 66-74 (in Chinese) doi: 10.6052/1000-0879-19-332 [21] 梅凤翔. 约束力学系统的对称性与守恒量. 北京: 北京理工大学出版社, 2004 (Mei FX. Symmetries and Conserved Quantities of Constrained Mechanical Systems. Beijing: Beijing Institute of Technology Press, 2004 (in Chinese))
[22] Luo SK, Dai Y, Zhang XT, et al. A new method of fractional dynamics, i.e., fractional Mei symmetrical method for finding conserved quantity, and its applications to physics. International Journal of Theoretical Physics, 2016, 55(10): 4298-4309 doi: 10.1007/s10773-016-3055-2
[23] Wang P, Xue Y. Conformal invariance of Mei symmetry and conserved quantities of Lagrange equation of thin elastic rod. Nonlinear Dynamics, 2016, 83(4): 1815-1822 doi: 10.1007/s11071-015-2448-8
[24] Wu HB, Mei FX. Form invariance and conserved quantity for weakly nonholonomic system. Applied Mathematics and Mechanics (English Edition)
, 2014, 35(10): 1293-1300 doi: 10.1007/s10483-014-1863-9 [25] Jiang WA, Liu K, Xia ZW, et al. Mei symmetry and new conserved quantities for non-material volumes. Acta Mechanica, 2018, 229(9): 3781-3786 doi: 10.1007/s00707-018-2200-9
[26] Zhang Y, Wang XP. Mei symmetry and invariants of quasi-fractional dynamical systems with non-standard Lagrangians. Symmetry, 2019, 11: 1061 doi: 10.3390/sym11081061
[27] Zhai XH, Zhang Y. Mei symmetry of time-scales Euler-Lagrange equations and its relation to Noether symmetry. Acta Physica Polonica A, 2019, 136(3): 439-443 doi: 10.12693/APhysPolA.136.439
[28] Zhang Y. Mei's symmetry theorem for time scales nonshifted mechanical systems. Theoretical and Applied Mechanics Letters, https://doi.org/10.1016/j.taml.2021.100286
[29] Lutzky M. Dynamical symmetries and conserved quantities. Journal of Physics A: Mathematical and General, 1979, 12(7): 973-981 doi: 10.1088/0305-4470/12/7/012
[30] Hojman SA. A new conservation law constructed without using either Lagrangians or Hamiltonians. Journal of Physics A:Mathematical and General, 1992, 25(7): L291-L295 doi: 10.1088/0305-4470/25/7/002
[31] Hilger S. Analysis on measure chains - A unified approach to continuous and discrete calculus. Results in Mathematics, 1990, 18(1-2): 18-56 doi: 10.1007/BF03323153
[32] Bohner M, Peterson A. Dynamic Equations on Time Scales. Boston: Birkhäuser, 2001
[33] Bohner M, Georgiev SG. Multivariable Dynamic Calculus on Time Scales. Switzerland: Springer International Publishing AG, 2016
[34] Bohner M, Peterson A. Advances in Dynamic Equations on Time Scales. Boston: Birkhäuser, 2003
[35] Bartosiewicz Z, Torres DFM. Noether's theorem on time scales. Journal of Mathematical Analysis and Applications, 2008, 342(2): 1220-1226 doi: 10.1016/j.jmaa.2008.01.018
[36] Martins N, Torres DFM. Noether's symmetry theorem for nabla problems of the calculus of variations. Applied Mathematics Letters, 2010, 23(12): 1432-1438 doi: 10.1016/j.aml.2010.07.013
[37] Bourdin L. Nonshifted calculus of variations on time scales with
$ {\nabla} $ -differentiable σ. Journal of Mathematical Analysis and Applications, 2014, 411(2): 543-554 doi: 10.1016/j.jmaa.2013.10.013[38] Chen JY, Zhang Y. Time-scale version of generalized Birkhoffian mechanics and its symmetries and conserved quantities of Noether type. Advances in Mathematical Physics, 2021, 2021: 9982975
[39] Tian X, Zhang Y. Time-scales Herglotz type Noether theorem for delta derivatives of Birkhoffian systems. Royal Society Open Science, 2019, 6(11): 191248 doi: 10.1098/rsos.191248
[40] Anerot B, Cresson J, Belgacem KH, et al. Noether's-type theorems on time scales. Journal of Mathematical Physics, 2020, 61: 113502 doi: 10.1063/1.5140201
[41] Song CJ, Cheng Y. Noether’s theorems for nonshifted dynamic systems on time scales. Applied Mathematics and Computation, 2020, 374: 125086 doi: 10.1016/j.amc.2020.125086
[42] 田雪, 张毅. Caputo△型分数阶时间尺度Noether定理. 力学学报, 2021, 53(7): 2010-2022 (Tian Xue, Zhang Yi. Caputo △-type fractional time-scales Noether theorem. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(7): 2010-2022 (in Chinese) doi: 10.6052/0459-1879-21-108 [43] Cai PP, Fu JL, Guo YX. Lie symmetries and conserved quantities of the constraint mechanical systems on time scales. Reports on Mechanical Physics, 2017, 79(3): 279-298 doi: 10.1016/S0034-4877(17)30045-9
[44] Zhai XH, Zhang Y. Lie symmetry analysis on time scales and its application on mechanical systems. Journal of Vibration and Control, 2019, 25(3): 581-592 doi: 10.1177/1077546318790864
[45] Zhang Y. Lie symmetry and invariants for a generalized Birkhoffian system on time scales. Chaos, Solitons and Fractals, 2019, 128: 306-312 doi: 10.1016/j.chaos.2019.08.014
[46] Zhang Y. Adiabatic invariants and Lie symmetries on time scales for nonholonomic systems of non-Chetaev type. Acta Mechanica, 2020, 231(1): 293-303 doi: 10.1007/s00707-019-02524-6
-
期刊类型引用(6)
1. 舒莲莲,朱建青. 时间尺度上非迁移Emden方程的Lie对称性与守恒量. 苏州科技大学学报(自然科学版). 2024(01): 29-35 .  百度学术
百度学术
2. 宋传静,侯爽. 时间尺度上约束力学系统的Noether型绝热不变量. 力学学报. 2024(08): 2397-2407 .  本站查看
本站查看
3. 宋传静,翟相华. 经典导数的拓展——时间尺度上求导. 河南财政金融学院学报(自然科学版). 2024(03): 36-41 .  百度学术
百度学术
4. ZHANG Yi. A Study on Time Scale Non-Shifted Hamiltonian Dynamics and Noether's Theorems. Wuhan University Journal of Natural Sciences. 2023(02): 106-116 .  必应学术
必应学术
5. 沈世磊,宋传静. 分数阶奇异系统的Lie对称性与守恒量. 动力学与控制学报. 2023(09): 1-10 .  百度学术
百度学术
6. SONG Chuanjing,WANG Jiahang. Conserved Quantity for Fractional Constrained Hamiltonian System. Wuhan University Journal of Natural Sciences. 2022(03): 201-210 .  必应学术
必应学术
其他类型引用(3)







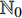
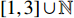
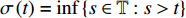
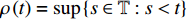
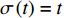
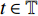
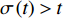
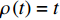
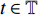
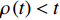
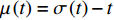
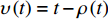

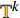
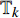
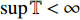
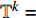
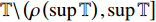
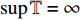
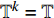
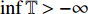
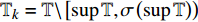
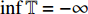
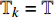
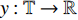
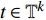
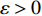
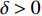
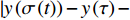
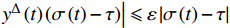
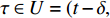
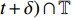
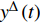
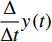
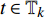
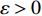
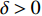
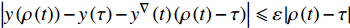
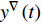
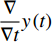
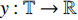

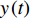

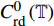
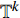
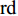
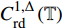
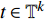
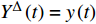

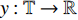
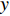
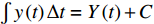
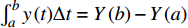

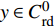
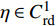
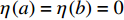
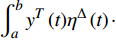
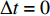
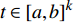
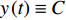
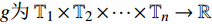
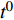
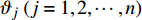
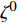
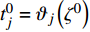
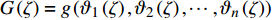
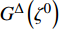
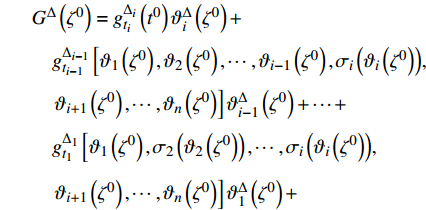
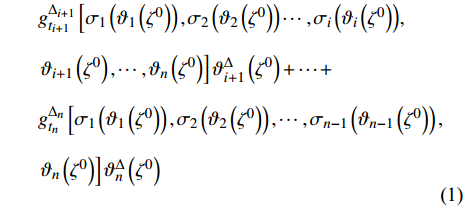
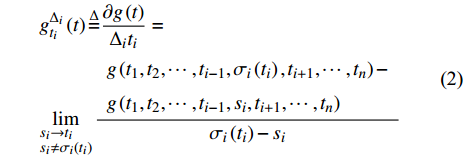
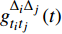
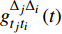
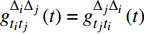
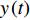
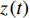
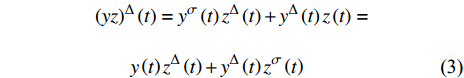
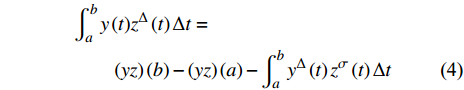
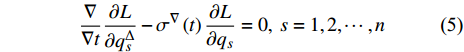
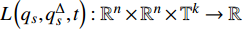
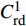
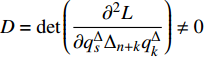
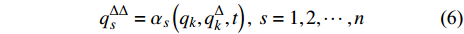
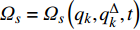
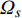
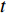
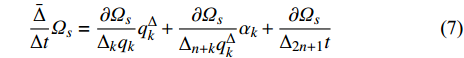
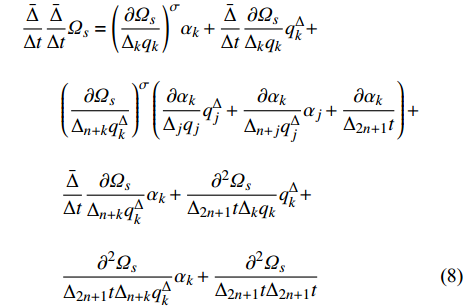
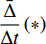

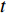
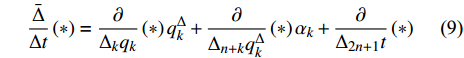
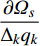
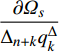
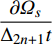
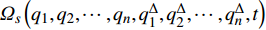
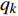
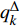
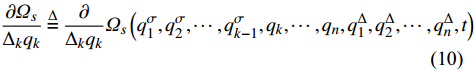
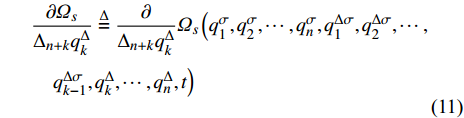
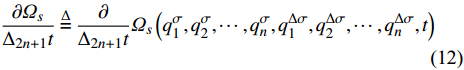
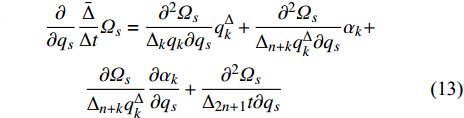
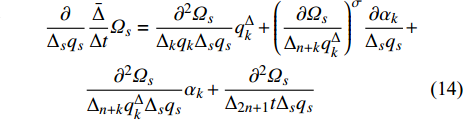
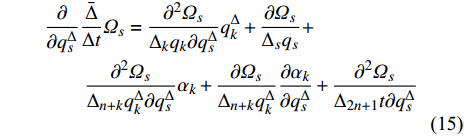
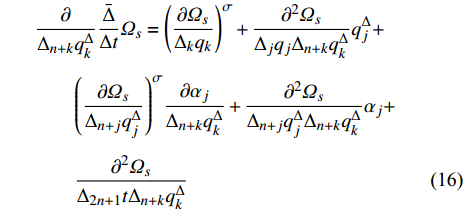
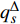
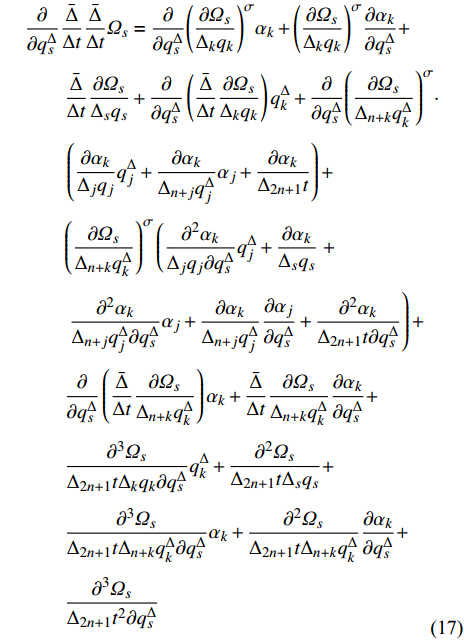
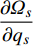
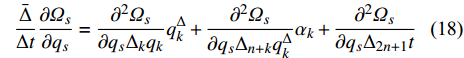
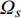
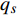
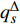
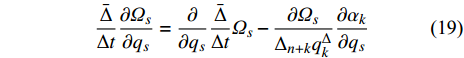
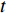
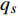
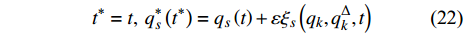
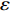
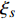
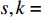
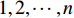
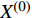
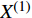
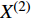
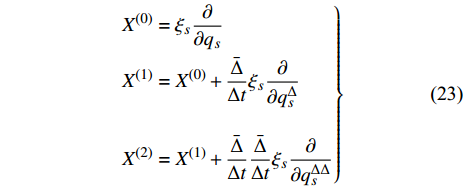
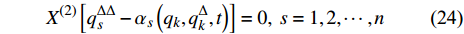
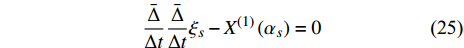
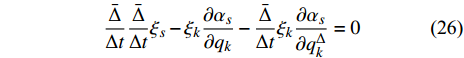
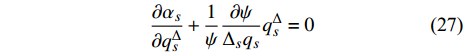
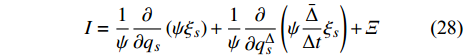
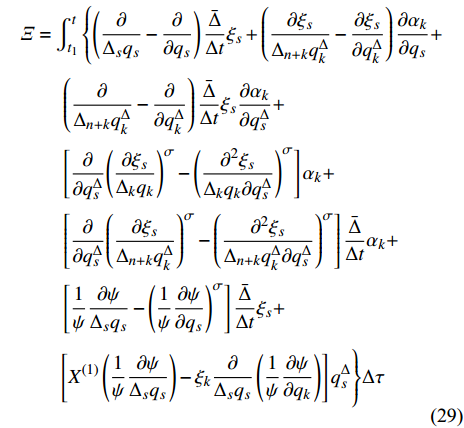
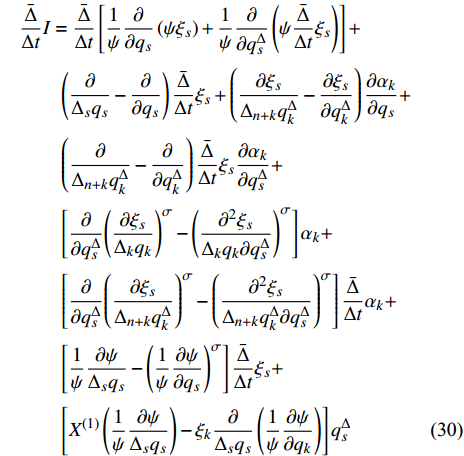
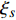
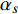
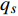
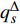
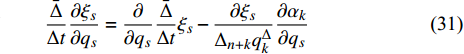
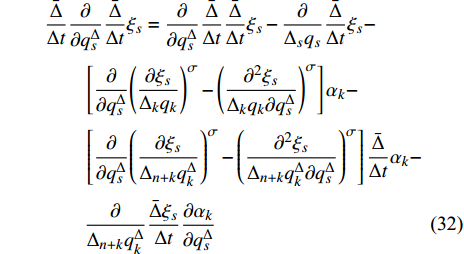
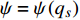
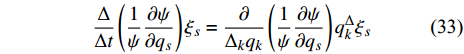
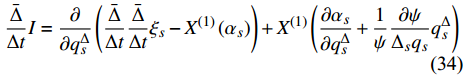
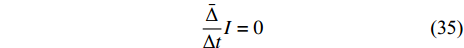
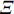
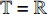
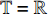
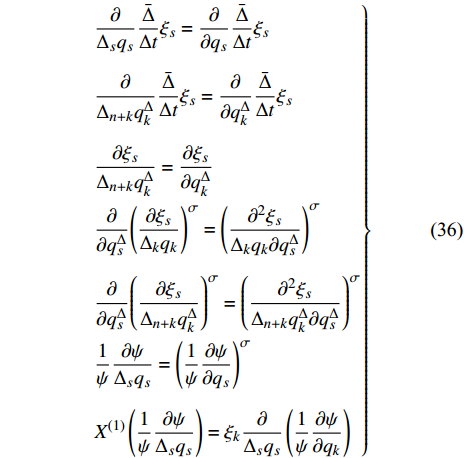

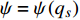
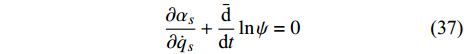
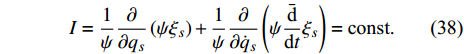
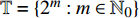
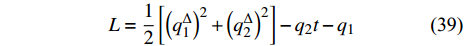
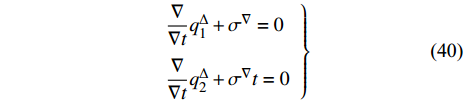
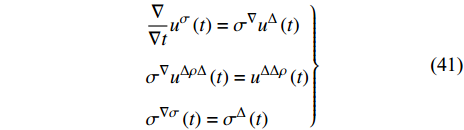
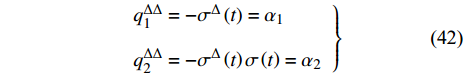
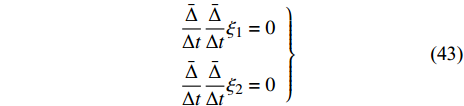
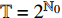
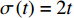
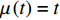
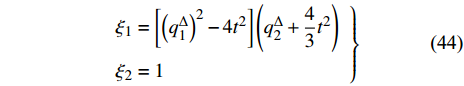
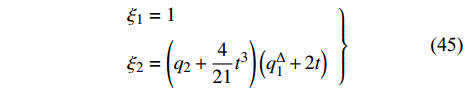
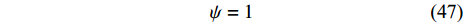
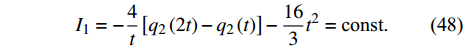
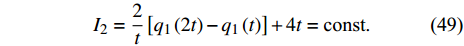
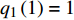
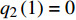
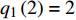
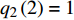
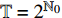
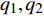
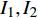

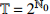
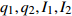
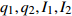
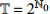
 下载:
下载: