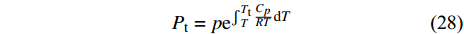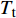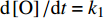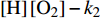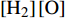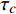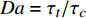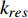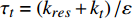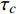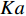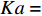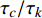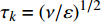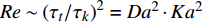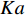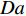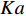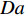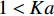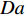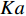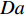LARGE EDDY SIMULATION OF HYPERSONIC COMBUSTION BASED ON DYNAMIC ZONE CONCEPT
-
摘要: 本文基于动态分区概念开展了亿级网格的高马赫数全尺寸超燃冲压发动机内外流耦合一体化改进延迟分离涡(IDDES)模拟研究. 研究建立了包括动态分区火焰面湍流燃烧模型(DZFM)、分区自适应化学(Z-DAC)和分区并行自适应建表(Z-ISAT)的完整动态分区燃烧模拟框架, 并通过1.15亿网格的马赫数12 REST标准高超声速燃烧室模型初步验证了分区模拟框架的保真性. DZFM通过分区解耦的思想既准确表征了当地湍流化学交互作用关系, 又有效提升了整场湍流燃烧的计算效率. Z-DAC和Z-ISAT通过在分区框架内对化学反应机理进行动态实时简化和建表查询, 可进一步提升当前分区内化学反应的求解效率. 基于1.25和1.4亿网格动态分区框架对比分析了马赫数10条件下中心支板(strut)和壁面撑挡型(pylon)两类构型氢气高超声速燃烧室特性. 支板或撑挡结构均诱发了明显的边界层分离和头部回流区, 由此两种燃烧室均出现了较长区域的喷注点前部燃烧现象. 基于Borghi图的数值分析表明当前氢气高超声速燃烧室中广泛存在扩散控制为主的火焰面模式, 效率提升的瓶颈在于高效增混. 壁面撑挡燃烧室具有较高的穿透深度和近场混合效率, 因而燃烧效率高于净推力准则80%, 相应的比冲1234 s也远高于中心支板燃烧室的437 s. 分区自适应化学方法在将近一半的计算域上降低了反应求解计算代价, 特别是在无燃料区反应机理的简化幅度更加明显. 相比与传统的有限速率PaSR模型, DZFM模型实现了高达11倍的加速比.Abstract: Based on the concept of dynamic zone partition, improved delayed detached eddy simulation (IDDES) modeling of high-Ma full-scale scramjets with more than 100 million cells was conducted for the integrated internal and external flow fields. A complete dynamic zonal combustion modeling framework was established, including dynamic zone flamelet model (DZFM), zonal dynamic adaptive chemistry (Z-DAC), and zonal in situ adaptive tabulation (Z-ISAT). The fidelity of the zonal modeling framework is preliminarily verified by the 115-million-cell modeling of a benchmark hypersonic combustor named REST, which was designed to operate at Mach 12. Through the idea of local flow-chemistry decoupling within each zone, DZFM not only accurately represents the local turbulence-chemistry interaction but also effectively improves the computational efficiency of turbulent combustion in the whole field. Z-DAC and Z-ISAT can further improve the resolving efficiency of chemical reactions in each zone by dynamically reducing the chemical mechanism and tabulating the thermochemical states. Then based on 125 and 140 million cells, respectively, the characteristics of hydrogen-fueled strut and pylon hypersonic combustors were comparatively analyzed for Mach 10. Both the pylon and strut structures induce obvious boundary layer separation and fore-body recirculation zone, resulting in long pre-combustion regions in front of the injection point in both combustors. Numerical analysis based on the Borghi diagram shows that the diffusion-dominated flame mode widely exists in the current hydrogen-fueled hypersonic combustor, and the bottleneck of efficiency improvement lies in efficient mixing. The pylon combustor has higher jet penetration depth and better near-field mixing, and thus the combustion efficiency of 80% is above the criterion of achieving net thrust. The specific impulse of 1234 s in the pylon combustor is also much higher than the 437 s in the strut combustor. Z-DAC reduces the computational cost of reaction systems in nearly half of the computational domain, especially in the fuel-free regions. Compared with the traditional finite-rate PaSR model, the DZFM model achieves an acceleration ratio of up to 11.
-
引 言
2004年, X-43 A在35 km高度的临近空间实现了接近马赫数10的高超声速飞行[1], 取得了大气层内吸气式飞行的最快速度. 近年来, 高马赫数飞行器引起了世界各国的高度重视, 成为各空天科技强国竞相争夺的科技制高点. 飞行马赫数上限达到12甚至更高的超燃冲压发动机是实现可重复使用天地往返飞行器的关键[2]. 目前反射激波风洞和激波膨胀风洞是能够产生马赫数大于8高焓气流的两种主要途径. 由于高焓气流地面模拟的困难, 目前世界上仅有为数不多的高马赫数风洞, 例如美国的NASA HYPULSE 激波风洞[3] 、日本的JAXA HIEST自由活塞驱动激波风洞[4]和澳大利亚昆士兰大学T4反射激波风洞[5]. 其中在T4风洞中针对飞行马赫数7.5 ~ 12[6-12]工况开展了一系列的矩形转椭圆(REST)高超声速燃烧室缩比模型测试. 由于高超声速实验测量手段和可获得数据均十分有限, 计算流体力学(CFD)成为燃烧内部流场分析和发动机性能优化的必需手段. 目前文献中已经开展了马赫数8, 12, 13和15[13-15]等对应飞行条件下的高超声速超燃冲压发动机模拟, 极大弥补了实验测量信息的不足. 然而, 随着飞行马赫数的提高, 湍流强度增加, 流动和化学反应特征时间相互重叠区域增加. 同时, 为了增加流动滞留时间以提高混合和燃烧效率, 相比于马赫数4 ~ 8的常规超燃冲压发动机, 马赫数大于8的高马赫数超燃冲压发动机流道尺寸大幅增加, 意味着巨大的全尺寸模拟计算代价. 高马赫数条件下内流与外流的耦合效应也显著增强, 为了提高模拟置信度一般计算区域需要至少包含部分飞行器前体. 上述独特性意味着高马赫数超燃冲压发动机数值模拟在兼顾模型保真度(复杂多重湍流−化学反应交互作用模式的表征)与计算代价(耦合详细化学反应动力学的高解析度大涡模拟)两方面均面临着极大的挑战.
空间上复杂而时间上多变的湍流化学反应交互作用关系(turbulence-chemistry interaction, TCI)是超声速燃烧室内部湍流燃烧的主要特点. 在超燃冲压发动机中, 其内部流场不仅存在混合控制为主的快速反应区和化学反应控制为主的慢速反应区, 甚至还存在预混、非预混和部分预混等复杂的湍流燃烧模式[16-20]. 跨越多个时间和空间尺度的湍流和化学反应不仅自身的模拟极为困难, 而且其交互作用所引起的复杂耦合效应进一步加剧了其模拟挑战性. 湍流燃烧模拟的核心在于对复杂的湍流−化学反应交互作用关系准确、高效建模. 目前的湍流燃烧模型大致可分为两类: 有限速率类和守恒标量类. 有限速率类模型包括近似层流模型(QL)[21]、部分搅拌反应器模型(PaSR)[22]、涡耗散/破碎模型(EDC/EBU)[23]、增厚火焰面模型[24]和线性涡模型(LEM)[25]等. 守恒标量类模型包括各类火焰面模型[26-28]、条件矩封闭模型(CMC)[29]、假定[30-31]/输运[32]概率密度函数模型等. 有限速率类模型适用范围较广但一般需要在每个网格节点上求解所有的组分输运方程, 因而计算量较大. 守恒标量类模型通过对流动和化学反应的解耦操作实现了湍流燃烧的降维求解, 一般可以显著降低计算量. 然而, 流动−化学反应可以解耦的前提是化学反应受湍流的影响模式单一, 以便选择适合的守恒变量−热力学参数空间分布去表征当前化学反应状态. 以火焰面模型为例, 当湍流化学反应交互处于火焰面或薄反应区模式(戴姆克拉数Da>10, 卡尔洛维奇数Ka<100)时, 适宜采用计算简便的稳态火焰面模型; 而当湍流化学反应模式处于慢反应区模式(Ka>100, Da<10)时, 此时化学反应速率小于湍流混合速率, 需要采用非稳态火焰面(UFM)或火焰面/进度变量(FPV)模型[33]; 在发动机燃烧室中还经常存在局部预混或部分预混模式, 此时需要采用火焰面模型的其他变种如G方程模型[34]或火焰面生成流形模型(FGM)[35] 等.
与亚声速流动相比, 超声速流动有如下特性: (1)滞留时间极短(毫秒量级), 和碳氢燃料的化学反应特征时间相当; (2)雷诺数一般高于5 × 105, 最小湍流尺度远小于火焰面厚度. 这意味着超声速燃烧中湍流和化学反应因特征时间和特征尺度相当, 存在强烈的耦合效应. 超声速燃烧场在不同局部区域存在差异性极大的湍流−化学反应交互作用模式, 反应状态参数对守恒标量的依赖存在极大的空间不均匀性, 因此采用单一火焰面去描述整场湍流反应状态将会带来严重的误差, 甚至一般认为火焰面模型不适用于超声速燃烧模拟. 尽管目前文献中已经发展了基于多重火焰面的表征火焰面模型[36], 但该模型仍然把整场作为一个火焰面分区, 并不能很好地区分受当地湍流影响的化学反应状态. 而如果能够根据局部流场状态自适应地采用单独的守恒标量反应状态参数空间去表征, 即局部表征火焰面模型的概念, 则可极大地提高整场计算的准确性. 局部火焰面模型的理论依据是, 尽管反应状态参数对守恒标量的依赖存在空间不均匀性, 但针对局部流场可以假设该依赖关系具有统计均一性. 分区模拟从物理本质上提高了火焰面模型在超声速燃烧模拟中的适用性, 从而为高效高保真超声速燃烧大涡模拟提供了一个独特的解决思路. 从针对各局部分区分别建立守恒标量与反应状态参数之间关联的角度看, 分区湍流燃烧模型与条件矩封闭模型类似[29]. 但是分区湍流燃烧模型的分区是基于局部流场的湍流−化学反应交互作用模式并且随流场演化而动态调整, 而条件矩封闭模型一般是单纯基于几何坐标位置(多为笛卡尔正交坐标)的固定分区. 对于瞬态流场而言, 局部湍流化学反应交互作用模式是动态变化的. 在分区火焰面模型中, 各分区的守恒标量−状态参数空间分布由一个表征火焰面(RIF)[37]描述. 表征火焰面描述的并非实际物理上的火焰面结构, 而是基于统计规律建立的近似映射关系. 因此该分区表征火焰面模型并不局限于传统的薄火焰面假设, 而是普遍适用于非平衡、瞬态和非均匀反应过程的模拟. 分区湍流燃烧模拟的前提是分区内湍流化学反应交互作用模式局部近似均匀, 不合适的分区会导致表征火焰面与实际的状态参数在守恒标量空间内分布差别较大. 为了准确描述局部化学反应动力学状态, 需要自适应地进行分区动态调整, 以便使得各分区内化学反应受湍流的影响模式局部单一.
近年来, 分区类燃烧模拟方法在发动机燃烧模拟中得到了较多关注[38-45]. 目前的分区燃烧模拟主要是依据化学反应热力学状态对燃烧场进行分区或聚类, 以便采用简化化学反应计算模型(如冻结反应、均匀混合和平衡态假设等)或基于分区对化学反应进行整体求解. 简单的分区一般基于几何空间分为未燃区、反应区/火焰锋面区和已燃区等[38-42,45], 复杂的分区对具有相似反应状态的单元(可以几何不相邻)进行聚类操作[43-44,46-48]. 然而现有分区燃烧模拟并未考虑湍流效应, 确切地说应该称之为“化学分区”. 已经有部分研究[49-50]在多燃烧模型耦合计算方面开展了初步的探索, 但是其所采用的方法需要提前初步评估各模型性能以指定分区, 难以在后续计算中动态调整分区, 因此不适用于瞬态性较强的超声速燃烧流场. 对各模型结合当前算例进行预测评估也需要额外的计算代价, 一定程度上降低了多模型耦合计算的效率优势. 此外, 有限速率类模型因计算代价过大, 难以耦合详细的化学反应机理, 与火焰面模型耦合使用时会产生“短板效应”, 严重降低整体计算效率, 因此具有不同理论基础的湍流燃烧模型分区耦合应用价值有限.
本文针对超声速燃烧模拟提出了一种基于当地湍流化学反应交互作用关系进行自适应流场分区和基于局部表征火焰面的分区湍流燃烧模拟方法. 该方法不仅可以极大提高存在复杂多重湍流燃烧模式的超声速燃烧模拟的保真度, 而且通过对局部湍流化学反应的解耦可取得极高的计算效率, 从而突破长期以来制约超声速燃烧模拟的流动−化学反应多尺度作用耦合建模这一关键瓶颈. 研究进一步结合该方法对不同构型的高超声速超燃冲压发动机进行了全尺寸内外流耦合一体化大涡模拟, 并对其中的流动、混合和燃烧机理进行了深入分析, 对比了两种构型高超声速燃烧室的性能, 展示了动态分区湍流燃烧模拟方法在超声速燃烧模拟基础研究和超声速燃烧室优化设计方面的应用.
1. 物理模型与数值方法
1.1 动态分区火焰面模型(DZFM)
定义当前局部分区内的表征火焰面结构函数为
${Q}_{\alpha }=\left\langle {{Y}_{\alpha }|\xi \left(x,t\right)=\eta ,x\in {\rm{zone}}} \right\rangle$ , 其中$ \eta $ 为混合分数空间的取样变量,$ x $ 代表空间物理坐标,$x\in {\rm{zone}}$ 表示条件平均统计局限于当前区域. 瞬态质量分数$ {Y}_{\alpha } $ 与表征质量分数$ {Q}_{\alpha } $ 的关联为$$ {Y}_{\alpha }(x,t)={Q}_{\alpha }\left(\eta =\xi \left(x,t\right),x\in {\rm{zone}},t\right) + {Y}_{\alpha }^{{'}}(x\in {\rm{zone}},t) $$ (1) 式中
$ {Y}_{\alpha }^{{'}} $ 表征瞬态值偏离对应当前混合分数$ \xi (x, t) $ 条件平均值的脉动,显然有条件平均脉动${Q}_{\alpha }^{{'}}= $ $ \left\langle {{Y}_{\alpha }^{{'}}|\eta ,x\in {\rm{zone}}} \right\rangle=0$ , 进一步得出当前分区平均脉动${\left\langle{{Q}_{\alpha }^{{'}}}\right\rangle}_{{\rm{zone}}}=\displaystyle\int {Q}_{\alpha }^{{'}}P\left(\eta \right){\rm{d}}\eta =0$ , 其中$ P\left(\eta \right) $ 为描述当前分区内瞬态混合分数$ \xi $ 分布的概率密度函数(PDF). 理想情况下$ {Y}_{\alpha }^{{'}}\to 0 $ , 局部火焰面结构函数完美表征当前分区化学反应状态. 然而实际中在点熄火等局部非稳态效应较强的区域当前分区内小脉动假设并不严格成立. 可进一步通过定义基于多重变量的分区准则, 即等同于多重条件映射的方法满足小脉动假设, 因此涉及$ {Y}_{\alpha }^{{'}} $ 的一阶或二阶项可以忽略, 从而从数学角度实现了湍流化学反应等非线性源项在矩空间的严格封闭.考虑相变效应和组分间差异扩散的描述质量守恒、瞬态混合分数
$ \xi $ 和组分质量分数$ {Y}_{\alpha } $ 的完整控制方程如下$$ \frac{\partial \rho }{\partial t} + {\boldsymbol{\nabla}} \cdot \left(\rho {\boldsymbol{U}}\right)={\dot{m}}_{p} $$ (2) $$ \begin{split} &\frac{\partial \rho \xi }{\partial t} + {\boldsymbol{\nabla}} \cdot \left(\rho {\boldsymbol{U}}\xi \right)=\left(\rho \frac{\partial \xi }{\partial t} + \rho {\boldsymbol{U}}\cdot {\boldsymbol{\nabla}} \xi \right) + \\ & \qquad \xi \left[\frac{\partial \rho }{\partial t} + {\boldsymbol{\nabla}} \cdot \left(\rho {\boldsymbol{U}}\right)\right] - {\boldsymbol{\nabla}} \cdot \left(\rho {D}_{\xi }{\boldsymbol{\nabla}} \xi \right)={\dot{m}}_{p}{\xi }_{l} \end{split} $$ (3) $$ \frac{\partial \rho {Y}_{\alpha }}{\partial t} + {\boldsymbol{\nabla}} \cdot \left(\rho {\boldsymbol{U}}{{Y}}_{\alpha }\right)=\left(\rho \frac{\partial {Y}_{\alpha }}{\partial t} + \rho {\boldsymbol{U}}\cdot {\boldsymbol{\nabla}} {{Y}}_{\alpha }\right) +$$ $$ \qquad {Y}_{\alpha }\left[\frac{\partial \rho }{\partial t} + {\boldsymbol{\nabla}} \cdot \left(\rho {\boldsymbol{U}}\right)\right]-{\boldsymbol{\nabla}} \cdot \left(\rho {D}_{\alpha }{\boldsymbol{\nabla}} {Y}_{\alpha }\right)={\dot{m}}_{p}{Y}_{l,\alpha } + \rho {W}_{\alpha } $$ (4) 其中
$ \rho $ 为密度,${\boldsymbol{U}}$ 为速度向量,$ {D}_{\xi } $ 和$ {D}_{\alpha } $ 分别代表混合物、单独组分的扩散速率,$ {W}_{\alpha } $ 为化学反应速率,$ {\dot{m}}_{p} $ 为相变/凝固等引起的质量增添,$ {Y}_{l,\alpha } $ 为其他相(如液滴)中的组分$ \alpha $ 的质量分数,$ {\xi }_{l} $ 为其他相的整体混合分数, 对于纯燃料液滴可取$ {\xi }_{l} $ =1.将式(1)差分后代入式(4), 并使用式(2)和式(3), 可得
$$ \begin{split} &\rho \frac{{\partial {Q_\alpha }}}{{\partial t}} + \rho {\boldsymbol{U}} \cdot {\boldsymbol{\nabla}} {Q_\alpha } + {{{Y}}_\alpha }{{\dot m}_p} - {{\dot m}_p}{Y_{l,\alpha }} - \rho {D_\alpha }{\left( {{\boldsymbol{\nabla}} \xi } \right)^2}\frac{{{\partial ^2}{Q_\alpha }}}{{\partial {\eta ^2}}} + \\ & \qquad\;\; \frac{{\partial {Q_\alpha }}}{{\partial \eta }}\left[ {\underbrace {\rho \frac{{\partial \xi }}{{\partial t}} + \rho {\boldsymbol{U}} \cdot {\boldsymbol{\nabla}} \xi - {\boldsymbol{\nabla}} \cdot \left( {\rho {D_\xi }{\boldsymbol{\nabla}} \xi } \right)}_{{{\dot m}_p}{\xi _l} - {{\dot m}_p}\xi }} \right] + \\ & \qquad\;\; \left(1 - \frac{{{D_\alpha }}}{{{D_\xi }}}\right){\boldsymbol{\nabla}} \cdot \left( {\rho {D_\xi }{\boldsymbol{\nabla}} \xi } \right)\frac{{\partial {Q_\alpha }}}{{\partial \eta }} + \Bigg[ \rho \frac{{\partial Q_\alpha '}}{{\partial t}} + \rho {\boldsymbol{U}} \cdot {\boldsymbol{\nabla}} Q_\alpha ' - \Bigg.\\ & \qquad\;\; \Bigg. {\boldsymbol{\nabla}} \cdot \left( {\rho {D_\alpha }{\boldsymbol{\nabla}} Q_\alpha '} \right) \Bigg] - \rho {D_\alpha }{\boldsymbol{\nabla}} \xi \cdot {\boldsymbol{\nabla}} \left( {\frac{{\partial {Q_\alpha }}}{{\partial \eta }}} \right){\rm{ - }}\\ & \qquad\;\; \rho {D_\alpha }{{\boldsymbol{\nabla}} ^{\rm{2}}}{Q_\alpha }{\rm{ = }}\rho {W_\alpha }\\[-14pt] \end{split} $$ (5) 对式(5)取条件平均
$ \xi (x,t)=\eta $ , 和位于当前分区内$ x\in {\rm{zone}} $ , 可得表征火焰面条件组分$ {Q}_{\alpha } $ 的最终控制方程为$$ \begin{split} &{\rho }_{\eta }\frac{\partial {Q}_{\alpha }}{\partial t} + {\left\langle {\rho {\boldsymbol{U}}|\eta } \right\rangle}_{{\rm{zone}}}\cdot {\boldsymbol{\nabla}} {Q}_{\alpha } + {E}_{{\rm{vap}}} + {E}_{{\rm{ZFM}}}=\\ & \qquad\quad {\rho }_{\eta }\frac{{D}_{\alpha }}{{D}_{\xi }}{\left\langle {\chi |\eta } \right\rangle}_{{\rm{zone}}} \frac{{\partial }^{2}{Q}_{\alpha }}{\partial {\eta }^{2}} + {\rho }_{\eta }\left(\frac{{D}_{\alpha }}{{D}_{\xi }}-1\right){M}_{\eta }\frac{\partial {Q}_{\alpha }}{\partial \eta } + \\ & \qquad\quad {\rho }_{\eta }\left\langle {{W}_{\alpha }|\eta } \right\rangle \end{split} $$ (6) 其中
$$ {E}_{{\rm{vap}}}={\left\langle{{\dot{m}}_{p}}\right\rangle}_{{\rm{zone}}}\left[{Q}_{\alpha }-{Y}_{l,\alpha } + \frac{\partial {Q}_{\alpha }}{\partial \eta }\left({\xi }_{l}-\eta \right)\right] $$ (7) $$\begin{split} &{E_{{\rm{ZFM}}}} = {\left\langle { {\underbrace {\rho \partial Q_\alpha '{\rm{/}}\partial t{\rm{ + }}\rho {\boldsymbol{U}} \cdot {\boldsymbol{\nabla}} {{Q}}_\alpha '{\rm{ - }}{\boldsymbol{\nabla}} \cdot \left( {\rho {D_i}{\boldsymbol{\nabla}} Q_i'} \right)}_{{e_Y}}} \Bigg|\eta } \right\rangle _{{\rm{zone}}}} - \\ &\qquad\;\; {\left\langle {\rho D{\boldsymbol{\nabla}} \xi \cdot {\boldsymbol{\nabla}} \left( {\frac{{\partial {Q_\alpha }}}{{\partial \eta }}} \right)\Bigg|\eta } \right\rangle _{{\rm{zone}}}} - {\left\langle {{\boldsymbol{\nabla}} \cdot \left( {\rho D{\boldsymbol{\nabla}} {Q_\alpha }} \right)\Bigg|\eta } \right\rangle _{{\rm{zone}}}} \end{split} $$ (8) $ {E}_{{\rm{vap}}} $ 表示相变效应贡献项, 在不涉及两相相变的情况下为零.$ \chi $ 是标量耗散率定义为$\chi =\left({D}_{\xi } + {D}_{{\rm{sgs}}}\right)\cdot $ $ {\left({\boldsymbol{\nabla}} \xi \right)}^{2}$ ,$ {\rho }_{\eta }=\left\langle {\rho |\eta } \right\rangle $ , 分区条件扩散$ {M}_{\eta }={\left\langle {{\boldsymbol{\nabla}} \cdot \left(\rho {D}_{\xi }{\boldsymbol{\nabla}} \xi \right)|\eta } \right\rangle}_{{\rm{zone}}} $ . 分区条件平均的引入意味着在每个分区内$ {Q}_{\alpha }^{{'}} $ 统计上遵循式(6)定义的守恒性. 式(6)中左端第二项表示局部小火焰在相邻区域之间流动的对流输运, 其物理意义为使得下游小火焰继承上游小火焰的反应状态, 这是准确模拟点火过程和火焰抬升现象的关键. 式(6)右端第1项和第2项分别模拟了因标量耗散和组分间差异扩散引起的混合分数空间内组分扩散, 第3项表示分区内组分因化学反应而发生的演化.分区内的化学反应受分区条件平均温度控制, 在本模型中采用基于当前分区内瞬态焓统计的方法获得[51]. 通过忽略焓脉动 (
$ {H}^{{'}} \sim O\left(0\right) $ )[52-54], 焓的概率密度分布$ \left\langle {H|\eta } \right\rangle $ 可以假设为以当前Favre平均值$ \tilde {H} $ 为中心的狄拉克$ \mathrm{\delta } $ 函数. 因此条件焓的$ \left\langle {H|\eta } \right\rangle $ 分布可以基于历史统计方法获得$$ \left\langle {H|\eta } \right\rangle=\left\langle {\tilde {H}|\tilde {\xi }=\eta } \right\rangle=\frac{1}{n} $$ (9) 其中
$ n $ 为符合$ \tilde {\xi }=\eta $ 的取样空间数据点. Thornber等[55]开展的高分辨率大涡模拟计算中采用了类似的统计方法以获取燃烧模型所需要的条件平均量. 条件温度通过条件统计平均焓与混合分数空间组分信息获得,$ {Q}_{T}=f(\left\langle {H|\eta } \right\rangle,{Q}_{\alpha }) $ . 该统计模型极大节省了直接求解条件能量方程的计算成本, 以及对超声速可压缩条件下条件能量源项建模的复杂度. 该统计条件温度模型的适用前提是分区内包含足够多的时间或空间采样样本, 以及数值模拟能够捕捉脉动瞬态值, 因此统计模型方法仅适用于大涡模拟(LES)和直接数值模拟(DNS)等高解析度模拟方法[55].对于
$ Re > {10}^{5} $ 的高雷诺数超声速流动, 通常有$ {\left\langle {\rho {D}_{\alpha }{\boldsymbol{\nabla}} \xi \cdot {\boldsymbol{\nabla}} \left({\partial Q}_{\alpha }/\partial \eta \right)|\eta } \right\rangle}_{{\rm{zone}}} \sim \rho {D}_{\alpha }\xi {D}_{\alpha }^{-1/2}\cdot {Q}_{\alpha } \sim {D}_{\alpha }^{1/2} $ ~${Re}^{-1/2} $ 和$ {\left\langle {{\boldsymbol{\nabla}} \cdot \left(\rho D{\boldsymbol{\nabla}} {Q}_{\alpha }\right)|\eta } \right\rangle}_{{\rm{zone}}} \sim \rho D\cdot {Q}_{\alpha } \sim {Re}^{-1} $ , 因此方程 (8) 右端第2项、第3项均可忽略. 在超声速流动中, 密度和速度很大程度上受压缩性(马赫数)影响, 与混合分数的直接关联度大大降低, 因此可近似认为$ \left\langle {{\boldsymbol{U}}|\eta } \right\rangle={\boldsymbol{U}} $ 和$ \left\langle {\rho |\eta } \right\rangle=\rho $ , 从而有$$ \begin{split} & \int {\left\langle {{e}_{Y}|\eta } \right\rangle}_{{\rm{zone}}}P\left(\eta \right){\rm{d}}\eta ={\left\langle{{e}_{Y}}\right\rangle}_{{\rm{zone}}}=\rho \partial {\left\langle{{Q}_{\alpha }^{{'}}}\right\rangle}_{{\rm{zone}}}/\partial t +\\ & \quad\quad\rho {\boldsymbol{U}}\cdot {\boldsymbol{\nabla}} {\left\langle{{Q}_{\alpha }^{{'}}}\right\rangle}_{{\rm{zone}}}-{\boldsymbol{\nabla}} \cdot {\left\langle{{\rho D{\boldsymbol{\nabla}} Q}_{\alpha }^{{'}}}\right\rangle}_{{\rm{zone}}} =0 \end{split} $$ (10) 上式表明式 (8) 右端第1项
$ {e}_{Y} $ 的作用为在每个分区对应的采样空间内重新分布条件平均量, 并且统计上重布效果相互抵消, 分区内整体质量分数脉动守恒. 通过动态更新火焰面分区使得每个火焰面分区对应一个较窄范围的混合分数子空间$\eta \in $ $ [{\bar{\xi }}_{{\rm{zone}}}-\mathrm{\Delta }\xi /2,{\bar{\xi }}_{{\rm{zone}}} + \mathrm{\Delta }\xi /2]$ . 其中$ {\bar{\xi }}_{{\rm{zone}}} $ 为当前分区平均混合分数,$ \mathrm{\Delta }\xi $ 为瞬态混合分数的脉动范围. 通过进一步细化分区, 当前分区混合分数变化幅度趋近于零$ \mathrm{\Delta }\xi \to 0 $ , 分区内标量概率密度分布坍缩为一个以$\eta ={\bar{\xi }}_{{\rm{zone}}}$ 为中心的狄拉克$ \mathrm{\delta } $ 函数. 据此有$\int {\left\langle {{e}_{Y}|\eta } \right\rangle}_{{\rm{zone}}}\mathrm{\delta } \cdot $ $ \left(\eta ={\bar{\xi }}_{{\rm{zone}}}\right) {\rm{d}}\eta =\left\langle {{e}_{Y}|\eta ={\bar{\xi }}_{{\rm{zone}}}} \right\rangle\approx {\left\langle {{e}_{Y}|\eta =\xi } \right\rangle}_{{\rm{zone}}}=0$ , 这意味着式 (8) 中的条件脉动输运项通过动态自适应分区可以被忽略.DZFM模型在四维空间(三维物理空间加一维混合分数空间)内求解火焰面的演化. 传统的火焰面模型可以看作是一个把整个计算区域当作一个单一分区的特殊分区火焰面模型, 属于低维流型模型(LDMM)的一种. 全组分输运湍流燃烧模型(如PaSR[22])需在三维物理空间离散网格单元逐一求解组分输运方程和化学反应, 计算代价一般远高于火焰面等流动−化学反应解耦模型. DZFM模型实现了流动和化学反应在当前分区内的局部解耦, 因而只需在火焰面分区单元上求解火焰面结构函数随空间的演化. 由于火焰面分区的空间分辨率通常远小于CFD网格数目, 所需求解的化学反应体系大幅减少, 因此整体上提高了计算效率. 注意DZFM模型的火焰面分区需随着流场而动态演化, 以满足湍流化学反应交互模式局部单一的前提假设.
1.2 分区自适应化学(Z-DAC)
在流场求解过程中动态地依据当地热化学反应状态进行实时机理简化的方法称之为动态自适应化学(DAC)[56-57]. 自适应化学方法通过发展并即时应用适用于当前局部和瞬态流场状态的简化机理可以在保证化学反应模拟准确性的前提下提高化学反应求解效率. 超声速燃烧中为了准确捕捉自点火和稳焰模态等流动−化学反应强耦合瞬态特征, 一般需要采用尽可能详细的化学反应机理. 对于需要直接积分(DI)的化学反应流求解, 其计算代价近似与组分数目的平方成正比[58]. 限于当前的计算技术水平, 目前超声速燃烧大涡模拟或直接数值模拟可接受的反应组分数目一般最多不超过50个组分[59]. 过度简化的机理往往降低了机理的适用范围, 而适用范围较广的机理尺寸又因尺寸过大无法应用于高解析度的三维反应流模拟. 此外, 流场中存在复杂而多变的热化学环境, 难以提前针对所有环境发展准确的简化反应机理[56]. 自适应化学方法通过冻结对目标组分和特性关联较小的反应路径和组分实现了在不同时间和空间流场中应用不同的反应机理, 其局部所应用的反应机理通常为更详细母反应机理的一个子集. 由于局部子机理的应用目标热化学环境变窄, 因此更容易在较少组分和反应步的情况下实现高化学反应保真度. 这里局部子机理既可以采用当前局部分区状态进行实时简化的方式, 也可以采用预估状态进行预先简化建库供后续查询的方式.
自适应化学准确应用的关键是选取合适的分区. 以往的研究中一般采用根据空间坐标分区的方法甚至直接采用并行分区的方式. 这种方式无法保证当前分区的热化学反应状态是均一的, 所简化的局部子机理甚至无法适用于当前分区内所有CFD节点状态. 对于采用并行分区的方法, 虽然建模框架搭建较为简便, 但是同样无法保证当前分区内热化学状态的均一性, 此外分区方式(如剖分算法、剖分数目)的改变也会影响计算结果.
本文提出了一种基于当地自适应分区的动态自适应化学方法(zonal dynamic adaptive chemsitry, Z-DAC). 该方法依据流场的反应状态变量(如混合分数和温度等)将计算区域划分为若干分区, 每个分区内的热化学反应状态相对均一. 在本文中选取了混合分数来表征当前组分的变化, 用温度来表征当前分区的化学反应活跃性. 如果包含对压力敏感的化学反应, 可进一步拓展加入压力指标体现压力不均匀性对反应路径的影响. 每个分区均对应某一特定的混合分数子空间、较窄的温度子空间以及压力子空间, 因此可认为分区内的热化学反应状态均匀, 从而为自适应子机理的匹配性与适用性提供了保障. 由于混合分数、温度和压力等反应状态参数是随时间动态变化的, 因此Z-DAC的分区同DZFM一样, 也是随流场更新而不断动态更新的. 通过判断当前CFD网格单元热化学反应状态参数, 自动匹配对应Z-DAC分区. 注意, Z-DAC分区同样可以是不规则形状, 甚至包含了离散的“孤岛”形CFD网格单元. 在应用中, 反应状态参数空间的网格划分在等当量比、临界点/熄火温度等反应活跃性剧变的区间需要局部加密以提高关键燃烧反应区域流动-化学耦合求解的准确性.
Z-DAC中的实时机理简化方法采用Lu和Law[60]提出的直接关系图法(DRG), 该方法基于组分之间的相互作用关系图谱, 评估其他组分对于某几类关键目标组分生成或者消耗速率的影响大小, 从而基于给定的误差阈值去除影响较弱的组分和相关反应步. DRG法尤其对于规模较大的机理具有高效率和高可靠性. 本文采用了基于误差传递的直接关系图法(DRGEP)[61], 其考虑不同反应路径的误差传递过程, 即考虑包含若干基元反应路径的整体重要性而非单个基元反应的重要性. 根据反应过程选择合适的目标组分, 如燃料、氧气、氮气和部分关键自由基. 根据基元反应关系图确定目标组分与所有其他相关组分的反应路径, 建立所有目标组分的依赖路径图谱. 在每条路径的相邻组分之间计算直接相关系数(DIC)
$$ \begin{split} &{{D}{I}{C}}_{\mathrm{A}\mathrm{B}}\equiv \frac{{\displaystyle\sum }_{i=1,Nr}\left|{\nu }_{\mathrm{A}i}{\omega }_{i}{\delta }_{\mathrm{B}i}\right|}{\mathrm{max}\left(\left|{P}_{\mathrm{A}}\right|,\left|{C}_{\mathrm{A}}\right|\right)} \\ &({\delta }_{\mathrm{B}i}=1,\;\mathrm{反}\mathrm{应}\;i\;\mathrm{涉}\mathrm{及}\mathrm{组}\mathrm{分}\mathrm{B};\mathrm{否}\mathrm{则}0) \end{split} $$ (11) 其中
$ Nr $ 为当前反应机理中所有反应的步数,$ {\omega }_{i} $ 为第i步反应的净反应速率,$ {\nu }_{\mathrm{A}i} $ 为反应i中组分A的计量系数,$ {P}_{\mathrm{A}} $ 和$ {C}_{\mathrm{A}} $ 分别为组分A的生成和消耗速率. 进而累计乘积路径上所有相邻组分之间的DIC得出路径相关系数(PIC). 定义总相关系数(OIC)为所有反应路径PIC的最大值. 由于OIC区分了受检组分与目标物组分的相对重要性, OIC低于指定OIC阈值的组分被视为不重要组分, 涉及该组分的反应路径被移除. 较之原始DRG方法, DRGEP方法中OIC考虑了包含多步基元反应的反应路径的相对重要性, 反应路径上距离目标组分越远的组分重要性越低. 调节OIC阈值可以确定原始机理中需要去除的不重要组分, 直至使给定工况条件下简化机理与原始机理计算的点火延迟误差达到最大允许偏差. DRGEP简化中用于起始路径搜索的目标组分选择对最终反应机理保留路径影响较大. 目标组分一般选取为燃料、氧化剂和主要产物(一般为H2O和CO2). 如果有需要与实验对比的关键中间自由基组分如OH和CH2O等, 也需要加入目标组分以在机理简化中保留这些中间组分及其关联反应路径. 一般而言, 当非最终产物(H2O和CO2)中C/H-O元素当量比高于某一特定值(如0.1)时则认为处于较活跃的燃烧反应区, 此时需加入CO和HO2等链式关键中间组分; 当反应区温度高于1000 K时则需加入NOx等氮氧化物组分.1.3 分区并行自适应建表(Z-ISAT)
碳氢燃料的详细反应动力学模型往往包含成百上千个基元反应, 其在实际的三维燃烧计算中的应用需要巨大的计算资源. 即便采用骨架或简化机理, 现有的计算机技术水平仍难以为继. 为了进一步提高化学反应源项的计算速度, 局部自适应建表(ISAT)方法[62-63]通过对局部热力学初始和最终状态建立映射存储从而大大节约了计算时间. 对于固定的反应机理, 特定时间步长之后反应热力学最终状态是初始状态的唯一解, 因此初始和最终状态之间存在一一对应的映射关系. 该方法首先按照常规方法通过积分计算某一化学热力学初始状态经过特定反应时间后的最终热力学状态, 然后存储起始状态和最终状态. 在后续的计算中, 通过在存储链表中对比当前热力学状态参数与存储参数, 将相似状态对应最终状态的插值近似作为当地特定反应时间之后的最终状态, 以替代冗长费时的积分过程. 理论上热力学状态的映射存储可以一次完整建立. 然而映射表的尺寸随反应组分数成幂次增长, 如果完整构建热力学状态参数空间, 即便是较小尺寸的反应系统存储都需要巨大的存储空间, 且后续的查找效率也较低. 事实上, 大多数反应系统仅涉及完整热力学状态参数空间的一个较小子空间. 该子空间的范围取决于实际燃烧条件, 如燃烧反应机理、热物性参数和湍流特性等. 由于事先无法确定, 必须在模拟过程中动态建立. 随着映射表的逐步建立, 化学反应的计算速率也逐步提高. 对于准稳态反应流, 在存储空间允许的范围内大部分化学反应都可以通过查表和插值近似得出, 从而极大地加速了复杂化学反应计算.
ISAT映射表的建立过程如下:
(1) 计算开始时, ISAT链表为空. 直接使用刚性反应求解器基于反应机理对初始组分Y0、温度T0和压力P0在特定时间步∆t上进行求解积分, 得到最终组分
$ {Y}_{1} $ 和温度T1(假设恒压反应). ISAT树状链表中单个叶节点存储信息为: 初始热力学参数$ {\boldsymbol{\phi }}_{0}= $ $ \left({Y}_{0}, {T}_{0}, {P}_{0}\right) $ , 最终热力学参数$ {\boldsymbol{\phi }}_{1}=\left({Y}_{1}, {T}_{1}, {P}_{1}\right) $ , 映射梯度矩阵$ \boldsymbol{A}=\partial {\boldsymbol{\phi }}_{1}/\partial {\boldsymbol{\phi }}_{0} $ 和在热力学参数空间内原点位于$ {\boldsymbol{\phi }}_{0} $ 的精度控制超椭球面(EOA).(2) 设有某初始热力学参数空间向量
$ {\boldsymbol{\phi }}_{\mathbf{q},0} $ , 在ISAT树形链表中查询与之最接近的节点设为$ {\boldsymbol{\phi }}_{0} $ , 根据映射梯度矩阵线性插值计算近似最终结果$ {\boldsymbol{\phi }}_{\mathbf{q},1}= $ $ {\boldsymbol{\phi }}_{1} + \boldsymbol{A}\left({\boldsymbol{\phi }}_{\mathbf{q},0}-{\boldsymbol{\phi }}_{0}\right) $ . 如果$ {\boldsymbol{\phi }}_{\mathbf{q},1} $ 位于EOA范围内, 则上述线性插值的结果在制定误差$ {\mathrm{\varepsilon }}_{{\rm{tot}}} $ 允许范围之内, 所计算结果将被取用. 否则, 则直接积分计算得到$ {\boldsymbol{\phi }}_{\mathbf{D}\mathbf{I},1} $ , 确定映射误差$ \mathrm{\varepsilon }=\left|\boldsymbol{B}\left({\boldsymbol{\phi }}_{\mathbf{D}\mathbf{I},1}-{\boldsymbol{\phi }}_{\mathbf{q},1}\right)\right| $ , 其中B为缩放矩阵. 若$ \mathrm{\varepsilon } < {\mathrm{\varepsilon }}_{\mathrm{t}\mathrm{o}\mathrm{t}} $ , 则选用$ {\boldsymbol{\phi }}_{\boldsymbol{q},1} $ , 同时扩张EOA范围以包括状态向量$ {\boldsymbol{\phi }}_{\mathbf{q},0} $ ; 否则$ {\boldsymbol{\phi }}_{\mathbf{q},0} $ 生成新叶节点.(3) 计算中按上述步骤依次查询或建立新的叶节点, 最终形成一个二叉树形链表. 当新的叶节点插入时, 最相似原始叶节点的位置将变成一个二叉结点, 重新连接原始叶节点和新的叶节点. 在二叉结点上将计算并存储其所属两片叶节点的超级分割平面. 计算中将以这个超级分割平面作为判据从树形链表的根部二叉结点依次往下层分支二叉结点上判断与
$ {\boldsymbol{\phi }}_{\mathbf{q},0} $ 最相似的叶节点.初始计算时, 大部分树形链表的操作都是增加叶节点(增操作)或扩张原有节点EOA(扩操作). 当大部分状态参数子空间都被树形链表的EOA区域覆盖时, 读取操作将更加频繁. 尽管初期的增、扩操作会耗费额外的计算时间, 但随着链表覆盖范围的完善, 计算效率将逐步提高. 注意, EOA扩操作包含了一定程度的近似, 即并不能保证EOA范围内的所有点的误差均在指定误差范围之内, 这是由于映射关系的非线性特性. 实际计算表明EOA范围内绝大部分状态参数子空间的误差都在指定的控制误差范围之内[64-65], 并且局部极个别的误差越界对整体计算精度影响可以忽略, 因此ISAT的EOA误差控制方法是符合计算需求的.
随着计算中增操作的进行, ISAT链表的尺寸会越来越大, 尤其是对于非稳态流场. 过大的二叉树链表尺寸一方面耗费存储空间另一方面增加了二叉树搜索深度. 由于先前历史中添加的叶节点被提取的概率逐渐降低, 可以定期对链表进行清理维护以保证每个叶节点都有较高的提取率. 本研究中实时记录每个节点被提取的次数并动态排名, 根据排名确定最常用叶节点双向链表. 当整个链表的尺寸超过设定上限后则清空整个二叉树形链表, 再以最常用双向链表中的节点信息重新建立二叉树形链表. 计算中发现, 一般最常用链表的尺寸上限设为整个树形链表尺寸上限20% ~ 50%可保持较好的加速比.
在并行计算中, 一般采取针对各并行分区建立独立的ISAT链表, 相互之间没有数据交换, 即纯粹本地建表(purely local processing, PLP)策略[66]. PLP策略的缺陷在于在强瞬态、非均匀燃烧流场中无法保证反应计算载荷均衡性. 特别是在超声速燃烧流场中, 不同分区之间热化学反应状态分布差异极大, 并且随时间演化而剧烈变化. 此时不同分区ISAT表的尺寸和成功取回率均差异较大. 一般主要反应区所需维护的ISAT链表尺寸较大, 而无反应区的ISAT链表尺寸甚至最小仅包含一个叶节点. 此外, 当并行分区方式或数目改变时, 原有的ISAT表需重新建立, 无法重复利用.
本文提出了基于热化学反应状态进行动态分区的ISAT建表策略, 即Z-ISAT (zonal ISAT). 该方法首先依据混合分数、温度、压力、反应进度变量等当地反应状态参数对流场进行动态分区, 并在每个分区建立单独的ISAT表. 由于每个分区的热化学反应状态相对单一, 因此ISAT表一旦建成即可保持尺寸长期稳定, 热化学状态点覆盖率和成功取回率效率也可大幅提升, 降低了ISAT链表树清理和重整频率. 不同于从初始起便固定的并行分区, 该基于热化学状态的动态分区建表策略尤其适用于强瞬态和空间非均匀燃烧场. 计算中为保持各建表分区与热化学状态子范围空间的严格对应关系, 需定期动态更新分区包含的CFD计算节点. 同样地, ISAT分区为不规则区域并且可以包含孤立的CFD节点. 对应每种热力学状态分区的ISAT表可以存储以便在计算重启或相似工况计算时再利用.
无通讯PLP-ISAT策略适用于反应区较集中而稳定的燃烧情形. 超燃冲压发动机中, 反应区一般集中于射流尾迹或凹腔, 但瞬态反应区存在剧烈的时空变化, 甚至在特殊的配置条件下还存在振荡燃烧模态[67]. 主反应区在各热力学状态分区之间频繁移动, 意味着相应的ISAT表存在频繁的节点插入和增长操作, 一方法增加了ISAT表的尺寸即内存需求, 另一方面降低了查表获取率, 加剧了直接积分需求. 为此本研究中发展了基于云计算的ISAT并行策略. 该云计算策略将本地热化学反应状态分为频繁取用和临时两类状态, 只有频繁取用的节点才存储ISAT链表, 而临时状态点则通过打包分配到其余空闲节点进行直接积分计算求解. 这里区分频繁取用的判据为ISAT 中被调用5次以上的状态点. 临时状态点的打包分发同样会占据内存带宽与通讯时间, 为此研究中发展了主节点统计各从节点待分配状态点数目, 绘制状态点重布向量地图, 各从节点再依据此重布向量地图直接采用点对点通讯交互数据的方式, 从而避免了集中分发所带来的额外通讯代价. 该云计算策略既保证了ISAT表较小的尺寸和极高的查询获取率, 又通过并行分发策略提高了强瞬态流场中化学反应计算求解的载荷均衡性.
1.4 控制方程
本数值研究中求解自变量为
$ \left(\bar{\rho },{\tilde {\boldsymbol{u}}}_{\boldsymbol{i}},{\tilde {H}}_{t},\tilde {\xi },{Q}_{\alpha }\right) $ 的完整非稳态三维Favre平均可压缩反应Navier-Stokes方程 (rNSE) [68-69]$$ \frac{\partial \bar{\rho }}{\partial t} + \frac{\partial \bar{\rho }{\tilde {\boldsymbol{u}}}_{{j}}}{\partial {\boldsymbol{x}}_{{j}}}=0 $$ (12) $$ \frac{\partial \bar{\rho }{\tilde {\boldsymbol{u}}}_{{i}}}{\partial t} + \frac{\partial \bar{\rho }{\tilde {\boldsymbol{u}}}_{{j}}{\tilde {\boldsymbol{u}}}_{{i}}}{\partial {\boldsymbol{x}}_{{j}}} + \frac{\partial \bar{p}}{\partial {\boldsymbol{x}}_{{i}}}-\frac{\partial {\tilde {\boldsymbol{\tau }}}_{{i}{j}}}{\partial {\boldsymbol{x}}_{{j}}}=-\frac{\partial {\boldsymbol{\tau }}_{{i}{j}}^{}}{\partial {\boldsymbol{x}}_{{j}}} $$ (13) $$ \begin{split} &\frac{\partial \bar{\rho }{\tilde {H}}_{t}}{\partial t} + \frac{\partial \bar{\rho }{\tilde {\boldsymbol{u}}}_{{j}}{\tilde {H}}_{t}}{\partial {\boldsymbol{x}}_{{j}}}-\frac{\partial }{\partial {\boldsymbol{x}}_{{j}}}\left(\bar{\rho }{D}_{T}\frac{\partial {\tilde {H}}_{t}}{\partial {\boldsymbol{x}}_{{j}}} + \sum _{\alpha =1}^{L}\bar{\rho }{D}_{\alpha }\frac{\partial {\tilde {Y}}_{\alpha }}{\partial {\boldsymbol{x}}_{{j}}}{\tilde {H}}_{\alpha }\right)-\\ &\qquad \frac{\partial \bar{p}}{\partial t}-\frac{\partial {{\tilde {\boldsymbol{u}}}_{{j}}\tilde {\boldsymbol{\tau }}}_{{i}{j}}}{\partial {\boldsymbol{x}}_{{j}}}=-\frac{\partial {\boldsymbol{\varPsi }}_{{T},{j}}}{\partial {{x}}_{{j}}} \end{split} $$ (14) $$ \frac{\partial \bar{\rho }\tilde {\xi }}{\partial t} + \frac{\partial \bar{\rho }{\tilde {\boldsymbol{u}}}_{{j}}\tilde {\xi }}{\partial {\boldsymbol{x}}_{{j}}}-\frac{\partial }{\partial {\boldsymbol{x}}_{{j}}}\left(\bar{\rho }{D}_{\xi }\frac{\partial \tilde {\xi }}{\partial {\boldsymbol{x}}_{{j}}}\right)=-\frac{\partial {\boldsymbol{\varPsi }}_{{\xi },{j}}^{}}{\partial {\boldsymbol{x}}_{{j}}} $$ (15) $$ \begin{split} &\frac{\partial \bar{\rho }\widetilde {{\xi }^{"2}}}{\partial t} + \frac{\partial \bar{\rho }{\tilde {\boldsymbol{u}}}_{{j}}\widetilde {{\xi }^{"2}}}{\partial {\boldsymbol{x}}_{{j}}}-\frac{\partial }{\partial {\boldsymbol{x}}_{{j}}}\left(\bar{\rho }{D}_{\xi }\frac{\partial \widetilde {{\xi }^{"2}}}{\partial {\boldsymbol{x}}_{{j}}}\right)={C}_{g}\bar{\rho }{D}_{\xi }{\left(\frac{\partial \tilde {\xi }}{\partial {\boldsymbol{x}}_{{j}}}\right)}^{2}-\\ &\qquad {C}_{d}\frac{2{D}_{\xi }}{{\Delta }^{2}}\widetilde {{\xi }^{"2}} \end{split} $$ (16) $$ \begin{split} &{\rho }_{\eta }\frac{\partial {Q}_{\alpha }}{\partial t} + {\left\langle {\rho {\boldsymbol{u}}_{{j}}|\eta } \right\rangle}_{{\rm{zone}}}\frac{\partial {Q}_{\alpha }}{\partial {\boldsymbol{x}}_{{j}}}={\rho }_{\eta }\frac{{D}_{\alpha }}{{D}_{\xi }}{\left\langle {\chi |\eta } \right\rangle}_{{\rm{zone}}}\frac{{\partial }^{2}{Q}_{\alpha }}{\partial {\eta }^{2}} +\\ &\qquad {\rho }_{\eta }\left(\frac{{D}_{\alpha }}{{D}_{\xi }}-1\right){M}_{\eta }\frac{\partial {Q}_{\alpha }}{\partial \eta } + {\rho }_{\eta }\left\langle {{W}_{\alpha }|\eta } \right\rangle \end{split} $$ (17) $$ \bar{p}=\bar{\rho }R\tilde {T} $$ (18) $$ {\tilde {H}}_{t}=\tilde {H} + 0.5{\tilde {\boldsymbol{u}}}_{{i}}{\tilde {\boldsymbol{u}}}_{{i}}={\tilde {H}}^{0} + {\int }_{0}^{T}{C}_{p}{\rm{d}}T + 0.5{\tilde {\boldsymbol{u}}}_{{i}}{\tilde {\boldsymbol{u}}}_{{i}} $$ (19) 上述公式中上标“-”和“ ~ ”分别代表平均和Favre平均量, t代表时间,
$ {\boldsymbol{x}}_{{i}} $ 是方向$ i $ 的笛卡尔坐标,$ \bar{\rho } $ 为密度,$ \tilde {\boldsymbol{u}} $ i 为$ i $ 方向的速度分量(空间维度 i = 1, 2, 3),$ \bar{p} $ 为压力,$ {\tilde {\boldsymbol{\tau }}}_{{i}{j}} $ 为黏性应力张量, 总绝对焓$ {\tilde {H}}_{t}=\tilde {H} + $ $ 0.5{\tilde {\boldsymbol{u}}}_{{i}}^{2} $ 为绝对焓$ \tilde {H} $ 和直接求解动能$ \tilde {K} $ 之和, 绝对焓$ \tilde {H} $ 为标准参考状态下生成焓$ {\tilde {H}}^{0} $ 和变化到当前温度T的显焓之和,$ {\tilde {Y}}_{\alpha } $ 为组分$ \alpha $ (α=1, 2, ···, L, L为总组分数目)的质量分数, 比热$ {C}_{p} $ 为混合组分浓度和温度的函数,$ {\bar{\omega }}_{\alpha } $ 为组分$ \alpha $ 的平均质量生成率(单位kg·m−3·s−1),$ {D}_{\alpha } $ 为组分$ \alpha $ 在混合物中的平均组分扩散率,$ {D}_{T} $ 为热扩散速率,$ \tilde {T} $ 为温度,$ R={{R}}_{{u}}/W $ 为气体常数,$ {{R}}_{{u}}= 8.314 $ $ {\rm{J}}\cdot {{\rm{mol}}}^{-1}\cdot {{\rm{K}}}^{-1} $ 为普适气体常数,$W={\left(\displaystyle\sum\nolimits_{\alpha =1}^{L}{Y}_{\alpha }/{W}_{\alpha }\right)}^{-1}$ 为多组分混合物的平均分子量. 式(13) ~ 式(15) 中的湍流雷诺应力$ {\boldsymbol{\tau }}_{{i}{j}}^{} $ 和湍流相关通量${\boldsymbol{\varPsi }}_{{T},{j}}$ 和${\boldsymbol{\varPsi }}_{{\xi },{j}}^{}$ 为未封闭项, 需要采用合适的湍流模型来模拟. 根据忽略体积黏性的Stokes假设, 牛顿流体的剪切应力张量表达式为$$ {\tilde {\boldsymbol{\tau }}}_{{i}{j}}=\stackrel-{\rho }\nu \left(\tilde {T}\right)\left(2{\tilde {\boldsymbol{S}}}_{{i}{j}}-\frac{2}{3}{\boldsymbol{\delta }}_{{ij}}{\tilde {\boldsymbol{S}}}_{{k}{k}}\right) $$ (20) 其中
$ \nu $ 为依赖于温度的运动黏性系数, 可解尺度的应变率张量为$$ {\tilde {\boldsymbol{S}}}_{{i}{j}}=\frac{1}{2}\left(\frac{\partial {\tilde {\boldsymbol{u}}}_{{i}}}{\partial {\boldsymbol{x}}_{{j}}} + \frac{\partial {\tilde {\boldsymbol{u}}}_{{j}}}{\partial {\boldsymbol{x}}_{{i}}}\right) $$ (21) 雷诺应力项
$ {\boldsymbol{\tau }}_{{i}{j}}^{}=\bar{\rho }\left(\widetilde {{\boldsymbol{u}}_{{i}}{\boldsymbol{u}}_{{j}}}-{\tilde {\boldsymbol{u}}}_{{i}}{\tilde {\boldsymbol{u}}}_{{j}}\right) $ 基于Boussinesq涡黏性假设模拟, 即假设其正比于可解尺度的应变率张量$ {\tilde {\boldsymbol{S}}}_{{i}{j}} $ $$\begin{split} &{{\boldsymbol{\tau }}_{{{ij}}}} = \underbrace {\left( {{{\boldsymbol{\tau }}_{{{ij}}}} - \frac{1}{3}{{\boldsymbol{\delta }}_{{{ij}}}}{{\boldsymbol{\tau }}_{{{kk}}}}} \right)}_{{\rm{deviatoric}}} + \underbrace {\frac{1}{3}{{\boldsymbol{\delta }}_{{{ij}}}}{{\boldsymbol{\tau }}_{{{kk}}}}}_{{\rm{isotropic}}} = \\ &\qquad - \bar \rho {\nu _{{\rm{sgs}}}}\left( {2{{\tilde {\boldsymbol{S}}}_{{{ij}}}} - \frac{2}{3}{{\boldsymbol{\delta }}_{{{ij}}}}{{\tilde {\boldsymbol{S}}}_{{{kk}}}}} \right) + \frac{2}{3}{{\boldsymbol{\delta }}_{{{ij}}}}\bar \rho {k_{{\rm{sgs}}}} \end{split}$$ (22) 其中
$ {\nu }_{{\rm{sgs}}} $ 为湍流模型解出的亚格子湍流黏性,$ {k}_{{\rm{sgs}}} $ 为不可解尺度的湍动能. 湍流焓通量$ {\boldsymbol{\varPsi }}_{{T},{j}}= \bar{\rho }(\widetilde {{\boldsymbol{u}}_{{j}}{H}_{t}}- $ $ {\tilde {\boldsymbol{u}}}_{{j}}{\tilde {H}}_{t}) $ 通常采用梯度扩散假设模拟$$ {\boldsymbol{\varPsi }}_{{T},{j}}=-2\bar{\rho }\frac{{\nu }_{{\rm{sgs}}}}{{{P}{r}}_{\mathrm{t}}}\frac{\partial {\tilde {H}}_{t}}{\partial {\boldsymbol{x}}_{{j}}} $$ (23) 其中
${{P}{r}}_{\mathrm{t}}$ = 1 为湍流普朗特数. 类似地, 湍流组分扩散通量${\boldsymbol{\varPsi }}_{\boldsymbol{\alpha },{j}}^{}=\bar{\rho }\left(\widetilde {{\boldsymbol{u}}_{{j}}{Y}_{\alpha }}-{\tilde {\boldsymbol{u}}}_{{j}}{\tilde {Y}}_{\alpha }\right)$ 模拟为$$ {\boldsymbol{\varPsi }}_{\boldsymbol{\alpha },{j}}^{}=-2\bar{\rho }\frac{{\nu }_{{\rm{sgs}}}}{{{S}{c}}_{\mathrm{t}}}\frac{\partial {\tilde {Y}}_{\alpha }}{\partial {\boldsymbol{x}}_{{j}}} $$ (24) 其中
${{S}{c}}_{\mathrm{t}}=$ 1 为湍流施密特数.动态分区火焰面模型[70]中求解了四维空间(三维物理空间加一维混合分数空间)中的条件组分输运方程 (17) 而不是传统的Favre平均组分输运方程. 平均组分质量分数
$ {\tilde {Y}}_{\alpha } $ 通过对混合分数空间内火焰面变量$ {Q}_{\alpha } $ 进行概率密度函数加权平均得到$$ {\tilde {{Y}_{}}}_{\alpha }=\int {Q}_{\alpha }P\left(\eta \right){\rm{d}}\eta $$ (25) 平均温度通过平均焓和已知组分信息反向迭代计算得出
$\tilde {T}=f\left(\tilde {H},\widetilde {{Y}_{\alpha }}\right)$ , 以考虑可压缩性对温度的影响. 本文采用$ \beta $ 函数形式的概率密度函数, 其为Favre平均混合分数$ \tilde {\xi } $ 及其脉动$\widetilde {{\xi }^{''2}}$ 的函数.$ \tilde {\xi } $ 及其脉动$\widetilde {{\xi }^{''2}}$ 通过额外的控制方程式(15)和式(16)求解得出[71], 模型参数Cg = 2.86, Cd = 2.0. 另一种计算混合分数脉动的方法为计算较为简便的代数梯度模型[72]$$ \widetilde {{\xi }^{''2}}={{C}}_{\mathrm{v}\mathrm{a}\mathrm{r}}{\mathrm{\Delta }}^{2}{\left(\frac{\partial \tilde {\xi }}{\partial {\boldsymbol{x}}_{{j}}}\right)}^{2} $$ (26) 其中模型参数
${{C}}_{\mathrm{v}\mathrm{a}\mathrm{r}}$ 在亚声速燃烧中校准为0.1[73], 但超声速燃烧中该值需进一步校准.1.5 物理模型与求解器细节
大部分发动机燃烧室模拟都必须要考虑壁面的摩擦和冷却效应, 相应地近壁区域的湍流模拟对发动机性能预测尤其重要. 目前近壁边界层模拟主要有3种方法: (1)直接数值模拟求解所有湍流尺度、(2)近壁湍流模型、(3)壁面函数方法. 在存在惯性子区的湍流中, 直接求解最小湍流尺度的单维度方向网格量需求为雷诺数的幂次方Re3/4, 求解最小耗散时间步需求为Re1/2[74]. 然而壁面附近不存在明显的惯性子区, 因此近壁边界层的模拟对网格有更加严苛的需求. 在保持相同无量纲近壁距离(
$ \Delta {{y}}_{{n}}^{ + }= $ $ \Delta {{y}}_{{n}}{\boldsymbol{u}}_{\boldsymbol{\tau }}/\mathrm{\nu } $ )的情况下, 近壁边界层直接数值模拟求解所需要的网格数量为$$ {{N}}_{{i}}=\frac{{L}}{\Delta {{y}}_{{n}}}=\frac{{L}}{\Delta {{y}}_{{n}}^{ + }\nu /{\boldsymbol{u}}_{\boldsymbol{\tau }}} \sim {{R}{e}}^{1-\mathrm{\zeta }/2} $$ (27) 其中摩擦速度
${\boldsymbol{u}}_{\boldsymbol{\tau }}={\left({\boldsymbol{\tau }}_{{{\rm{w}}}}/\rho \right)}^{1/2}={\left(0.5{{C}}_{\mathrm{f}}{\boldsymbol{U}}^{\mathrm{*}2}\right)}^{1/2}$ ,$ {\boldsymbol{\tau }}_{{{\rm{w}}}} $ 为壁面黏性剪切应力, U* 为边界外层速度. 根据经验数据拟合摩擦系数与雷诺数(Re)的关系为$ {{C}}_{\mathrm{f}} \sim {{R}{e}}^{-\mathrm{\zeta }} $ , 其中$ \mathrm{\zeta }\approx $ 0.2 ~ 0.25, 因此壁面附近网格需求近似为$ {{R}{e}}^{0.9} $ . 在保持相同网格纵横比的条件下, 近壁边界层模拟所需要的网格数目近似与$ {{R}{e}}^{2.6} $ 成正比[69]. 类似地, 近壁边界层求解时间步需求也为$ {{R}{e}}^{1-\mathrm{\zeta }/2}\approx {{R}{e}}^{0.9} $ . 因此边界层模拟所需要的计算代价近似为$ {{R}{e}}^{3.5} $ . 对于雷诺数$ {R}{e} > {10}^{5} $ 的超声速流动而言, 基于现有的计算机技术直接求解壁面边界层是不现实的. 近壁边界层一般可分为黏性子层、缓冲层和湍流层. 计算较为简便的方法为使用半经验公式即壁面函数近似模拟黏性子层和缓冲层的湍流黏性生成和速度分布, 而不需要在黏性子层分布网格. 然而壁面函数一般适用范围有限, 尤其是适用于高超声速边界层的壁面函数有待发展, 并且该方法无法准确预测边界层增厚和分离等逆压梯度较强的现象. 一种折中的方法是使用雷诺时均(RANS)湍流模型来求解直到黏性子层的壁面边界层, 而外流区域采用大涡模拟(LES)求解, 即分离涡模拟(DES)方法[75]. 作为对DES系列方法的发展, 改进延迟分离涡模拟(IDDES)方法解决了RANS和LES模拟区之间物理量不匹配导致的非物理过渡. 本研究中采用了基于一方程Spalart–Allmaras模型的IDDES方法[76], 其中近壁区域湍流由重新定义了特征尺度的Spalart–Allmaras模型[77]求解. 相比与原始的DES, IDDES的改进主要在于对近壁附近特征尺度的重新定义, 其不仅取决于当地网格尺度、近壁距离, 而且受当地湍流黏性影响, 并引入了隔离函数以防止网格诱导分离现象(grid induced separation, GIS)[78]. IDDES模型的特征尺度定义使得RANS模式可以覆盖完整的边界层. IDDES(改进延迟分离涡模拟)属于一种特殊类型的混合RANS/LES. 混合RANS/LES方法, 结合了RANS和LES方法的优点, 降低了计算代价, 从而满足全尺寸发动机模拟需求.高马赫数发动机中存在剧烈变化的温度和压力, 理想气体模型仅在一定范围内适用. 为此物性计算采用在热力学状态空间内分区计算, 具体为低于300 K, 低于1 kPa或高于临界压力时密度计算采用真实气体模型, 如广义对应状态法则[79]; 高温和中等压力条件下则采用计算较为简便的理想气体模型. 热扩散率和组分扩散率计算分别采用JANAF 格式热物性数据库[80]和CHEMKIN格式输运属性库[81]. 混合物平均黏性和热传导率的计算分别采用修正版Wilke定律和摩尔加权平均[82].
计算平台采用基于OpenFOAM开源框架[83]开发的可压缩密度基超声速燃烧求解器Amber (曾用版本名AstroFoam). 该求解器采用低耗散修正[84-85]二阶Kurganov-Tadmor中心迎风求解格式. 求解器已经在超声速燃烧工况模拟中得到广泛验证[16-18,70,86-89].
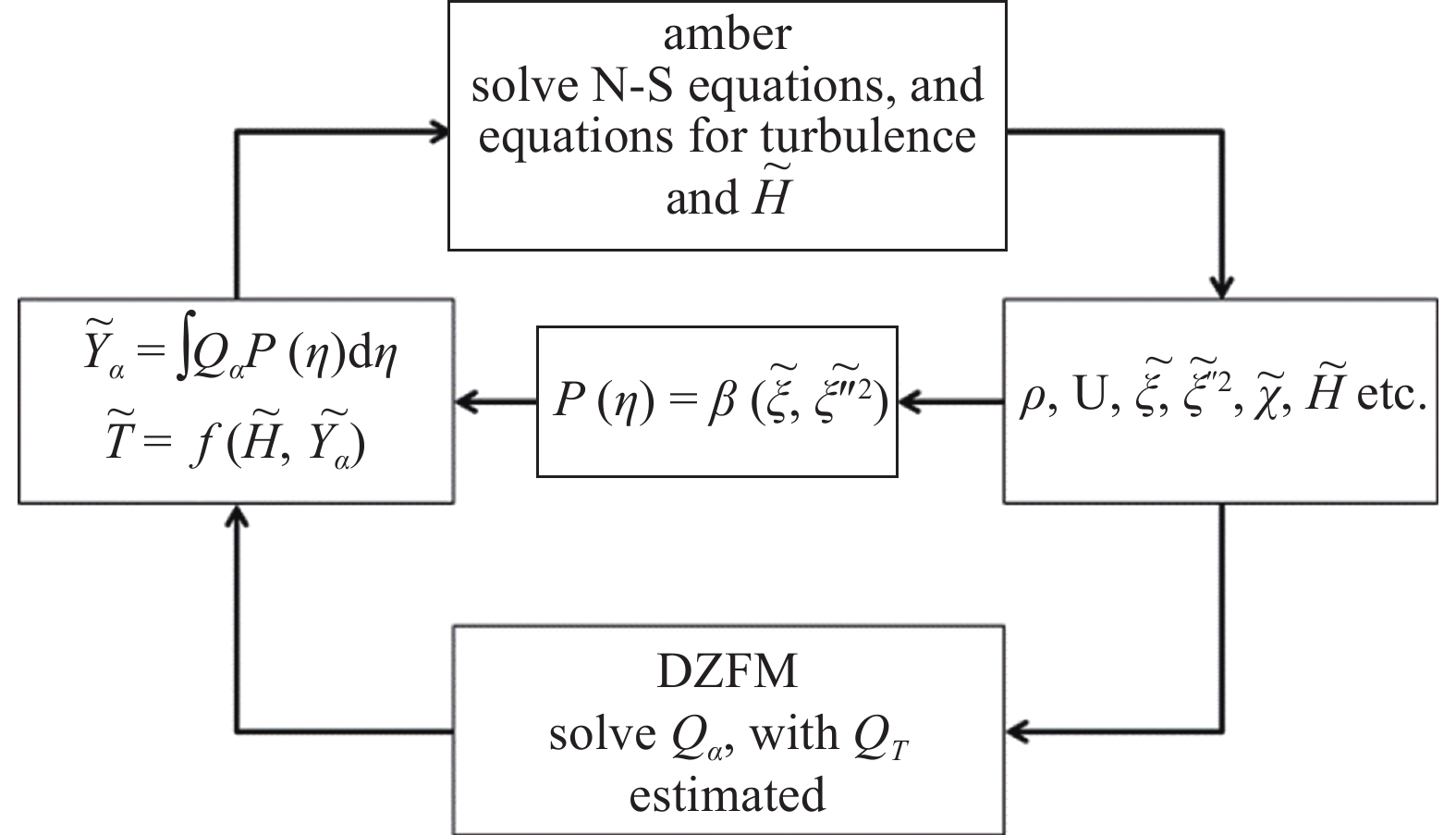
图1显示了计算中流动求解和湍流燃烧求解的耦合关系. 其中流动模块Amber求解式(12) ~ 式(16)基础N-S方程以及基于Spalart-Allmaras的IDDES湍流模型[90]. 与PaSR[22]等直接求解三维物理空间内的平均组分输运方程不同, DZFM湍流燃烧模型在四维空间内求解分区火焰面组分输运方程, 平均组分则通过对条件组分进行概率密度函数加权平均得到. 分区化学反应速率由条件温度控制, 其通过统计方法估算得到, 从而避免了复杂的可压缩非绝热条件温度建模与求解. 为体现可压缩效应, 平均温度由平均焓和平均组分反推得出. 化学反应采用Jachimowski [91]针对超声速燃烧开发的13组分33步反应详细氢气机理. 本研究中整个计算域被分割成18000个火焰面分区, 其中在主流动方向分割为200个薄片状区域, 进而对每个薄片区域依据当地混合分数分割为90个“年轮”状环带形子区域. 火焰面分区可以是不规则、非连续区域, 其随混合分数流场而动态更新以保证每个分区对应一个窄域的混合分数子空间.
1.6 测试工况
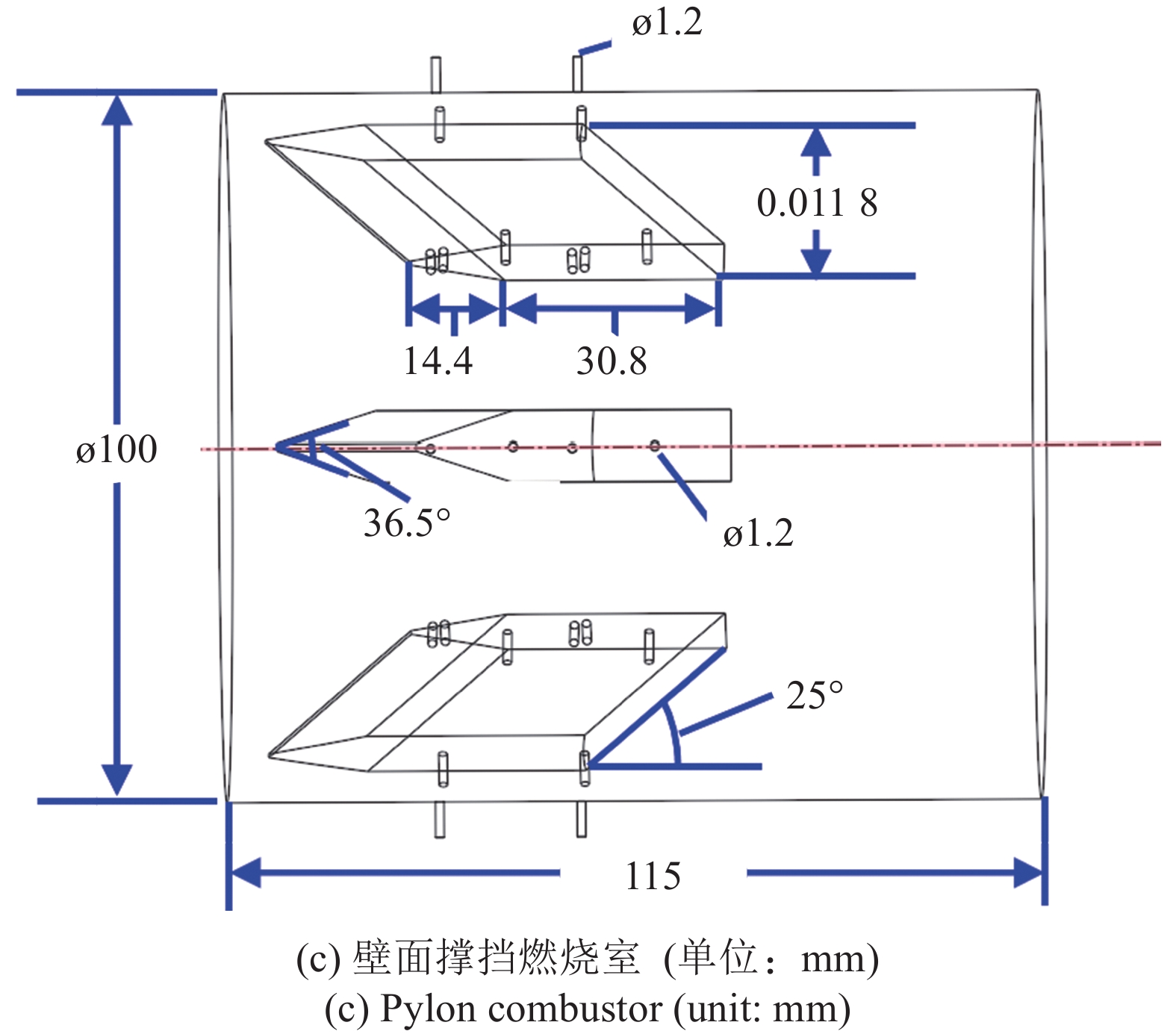
本文中选取了高超声速飞行中两种典型的发动机燃烧室构型进行对比测试. 该发动机目标飞行马赫数10, 飞行高度40 km. 如图2(a) 所示, 模型发动机包括进气道、隔离段、燃烧室和尾喷管4部分. 两种构型发动机的主要区别在于燃烧室中采用不同的被动增混方式, 分别为中心支板方式(如图2(b) 所示)和壁面撑挡方式(如图2(c) 所示). 发动机的整体长度为5.61 m, 计算中包括了一部分长度为0.67 m的外流部分以模拟自由流条件下的进气道特性. 进气道长度2.49 m, 采用基于Busemann基准流场的流线追踪法[92]设计, 其中边界层黏性修正采用参考温度法. 进气道的几何收缩比为10, 静压压缩比约为62. 隔离段平滑过渡进气道出口到圆形超声速燃烧室, 燃烧室包括一段0.985 m长的微扩张圆筒以过渡到单边扩张的尾喷管. 中心支板燃烧室共计有24个燃料喷孔, 其中6个燃料喷孔位于连接中心支板的支架侧面上, 其余18个燃料喷孔以3个为一组位于中心支板侧壁. 喷孔直径从0.8 ~ 1.5 mm直接变化以适应于当地横向流动速度增强射流穿透深度. 壁面撑挡超声速燃烧室同样采用了24个喷孔, 2个为一组均匀环绕周向分别从撑挡部件顶部(3组)和燃烧室壁面(9组)直接喷注.
本文中数值测试了上述两种典型构型高马赫数超燃冲压发动机在飞行马赫数10和海拔40 km高度的性能. 所模拟飞行工况参数如表1所示, 其中来流温度和压力均依据对应高度处大气层参数. 燃料流均为声速喷注, 总温为室温, 流量保持总包当量比为1.0.
表 1 测试飞行工况参数Table 1. Flight test conditionsFreestream Fuel stream (mass fraction YN2: 0.767, YO2: 0.233) (mass fraction YH2: 1.0) Ma H/km T/K p/Pa U/(m·s−1) q/Pa Pt/Pa Tt/K Qfuel/(kg·s−1) Tt/K Ma 10 40 250 287 3172 20099 2.7 × 107 4333.5 0.023 298 1 计算域包括外流和发动机内部区域, 其中中心支板发动机总网格数量为1.25亿, 壁面撑挡发动机总网格数量为1.4亿. 考虑到复杂的壁面突起结构和中心支板部件, 大部分区域(96.6%体积)采用无结构四面体网格剖分, 仅在拐角处采用少量楔形(3.39%体积分数)、棱柱形和金字塔形(共计0.01%体积分数)填充. 平均网格尺度0.8 mm, 在燃料喷孔附近局部加密至0.1 mm, 近壁边界层采用15层向内逐渐收缩的棱柱膨胀层, 无量纲近壁距离y + <1. 网格质量分析表明99.4%的网格正交性超过0.5, 99%的网格偏斜度小于0.5. 研究针对中心支板燃烧室开展了5413万、7176万、1.0477亿和1.251亿共4套网格的独立性验证, 其余3套较粗网格与最精细网格的平均壁面压力误差分别为1.7%, 1.2% 和0.8%, 随网格尺度呈指数递减, 因此可认为最精细网格的计算结果具有较好的网格独立性, 如图3所示.
2. 结果与讨论
2.1 REST算例验证
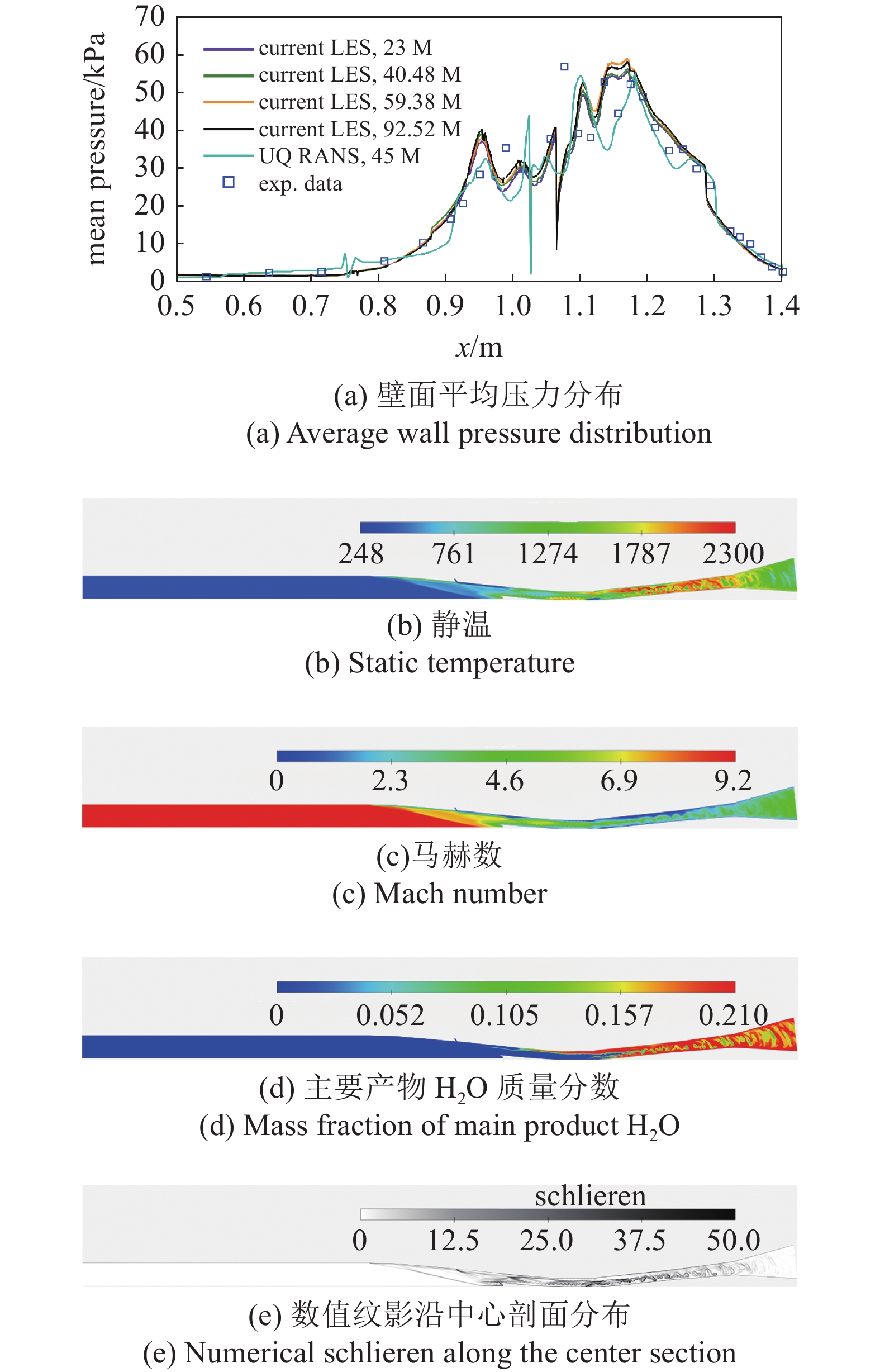
基于本研究的数值模型和方法框架对国际上已公开发表的澳大利亚昆士兰大学(简称UQ)矩形变椭圆高超声速燃烧室(REST)开展了计算验证. 昆士兰大学基于T4 反射激波风洞 (RST)开展了一系列的自由和半自由高马赫数超燃冲压发动机测试, 在马赫数 7.5[6], 8[7], 8.7[8], 10[9], 直到12[10-12]均观察到了正净推力. 与本研究类似, REST超燃冲压发动机的自由射流模拟[15]均包含了部分飞行器前体以模拟内外流一体化耦合过程. 验证REST算例对应飞行马赫数12和海拔36 km, 燃料为当量比1.0常温声速喷注氢气. 模拟中采用了1.15亿单元的无结构网格. 如图4(a)所示, 基于当前计算平台和数值框架所预测的平均压力与实验测量值吻合较好, 同时捕捉到了与文献中预测类似的双峰结构. 压力峰值位于燃烧室喷注点下游的微扩张段, 同时进气道喷注点附近也有初始燃烧但产生的压升弱于弓形激波反射产生的第二峰值压升. 如图4(b) ~ 图4(e) 所示, 计算中包含了0.5 m长的飞行器前体部分以模拟边界层等外流效应对发动机内流的影响. 上游喷注燃料的燃烧较为微弱, 从温度和产物分布看剧烈燃烧反应主要发生于下游喷注点之后的微扩张燃烧段. 马赫数分布表明燃烧室处于超燃冲压模式, 近壁面处特别是燃烧室上侧壁面处的燃烧造成了连续而狭长的局部亚声速区域. 数值纹影表明下游喷注点之前的进气道和隔离段存在多重反射激波并与剪切层相互作用, 而在剧烈燃烧下游因体积膨胀效应无明显激波存在但可见丰富的湍流漩涡结构.
2.2 中心支板与壁面撑挡燃烧室性能对比
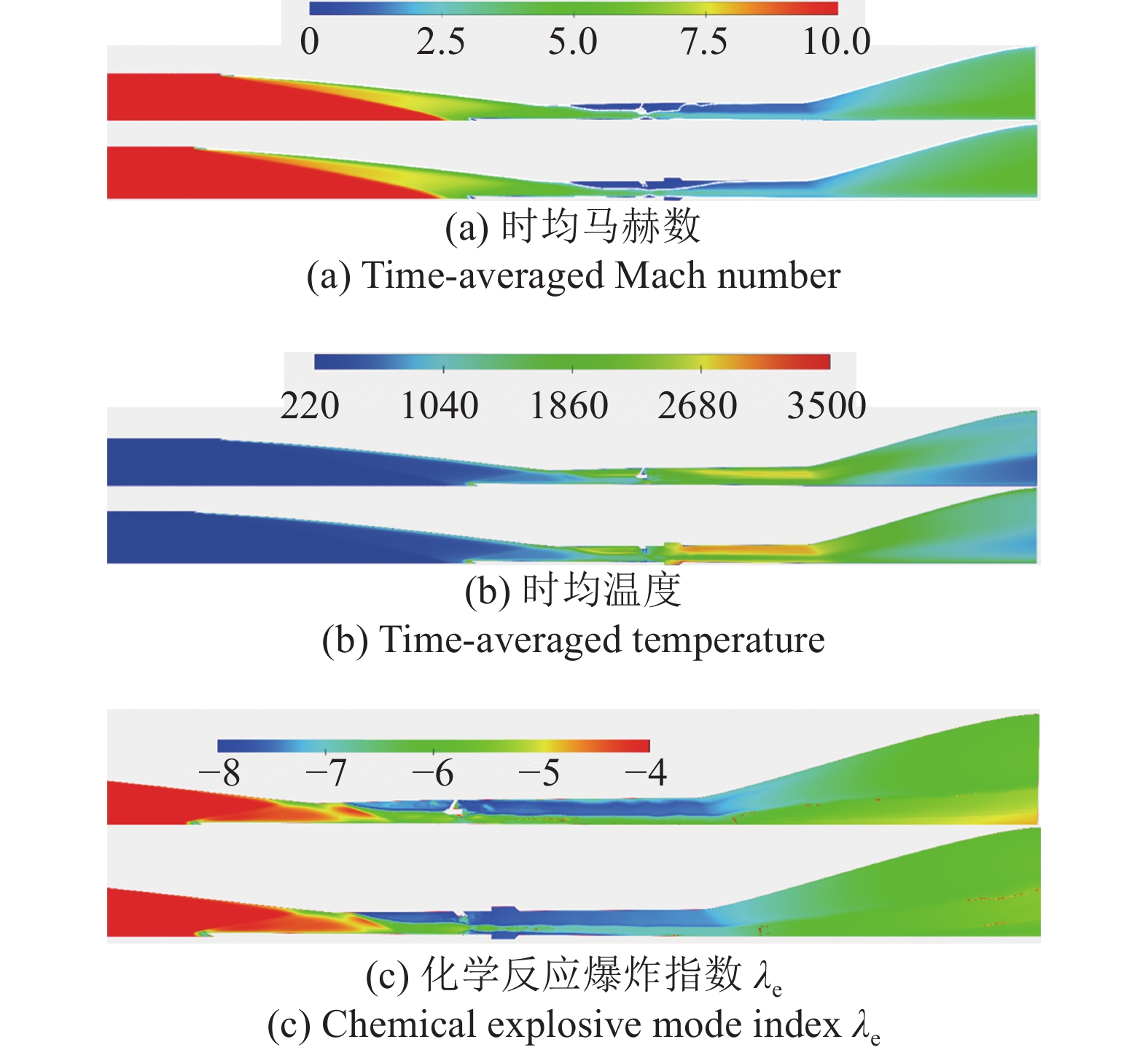
图5展示了两种构型高超声速燃烧室的内部流场结构. 从马赫数分布来看, 两种构型燃烧室均在支板或撑挡上下游出现了较大的亚声速区域, 并在支板或撑挡对侧壁面诱发了明显的边界层分离. 由于中心支板结构缩减, 加大了流通面积, 因此其对来流的减速效应更加明显, 表现为支板处的超声速射流核心缩窄至近乎壅塞. 壁面撑挡燃烧室由于凹腔的动量交换和稳焰助燃均进一步降低了局部马赫数, 因此其下游的亚声速区域延伸更长距离. 从温度分布来看, 两种构型均出现了较长区域的喷注点前部燃烧, 主要集中在燃料喷注撑挡一侧, 表明部分燃料在回流裹挟下被带到上游并在较高的边界层滞止温度(>1500 K)下被点燃. 中心支板燃烧室主要燃烧区域位于较靠下游区域, 表明燃料混合距离较长. 而壁面撑挡燃烧室中凹腔的稳焰作用比较明显, 上半部分在凹腔剪切层中出现了火焰, 下半部分在凹腔内部回流区实现了稳焰. 可见即使对于当地马赫数整体大于2.5的高超声速燃烧室, 凹腔的稳焰作用依然较为显著. 壁面撑挡燃烧室的H2O含量略高于中心支板回流区, 同时整体2400 K以上的温度也略高于整体2000 K左右的中心支板回流区, 表明壁面撑挡回流区反应强度更高. 从两个构型流场对比来看, 需要在燃烧室设计中一方面缩短两个喷注点的横向空间间距, 另一方面尽可能让射流喷注点远离外扩形壁面, 因其流动转向会增加下游尾迹的横向距离. CEMA指数λe是衡量燃烧化学反应剧烈程度的重要指标[15,93-94], 为化学反应速率雅可比矩阵的最大特征值, 通常正值表示爆炸模式, 负值表示趋于平衡的缓燃模式. 正值发生于预混点火区域, 而负值发生于扩散控制和后点火区域. 图中所示为带符号对数值signλe × lg|λe |, 本研究中燃烧室中均为负值, 表明燃烧主要由扩散控制, 高速流动中极短的滞留时间通常难以维持高温预混气团至点火状态. 其中对应温度高于2000 K的上游回流区、支板后主反应区和凹腔等燃烧剧烈处的λe均为108 s−1量级的特征反应速率. 尾喷管内因温度普遍低于1500 K, 即便仍有未完全反应的燃烧, 反应特征速率降为105 ~ 106 s−1. 由于反应机理中包含了部分O2, N2和H2O的离解反应, 因此空气来流区域也存在特征时间104 s−1量级的反应.
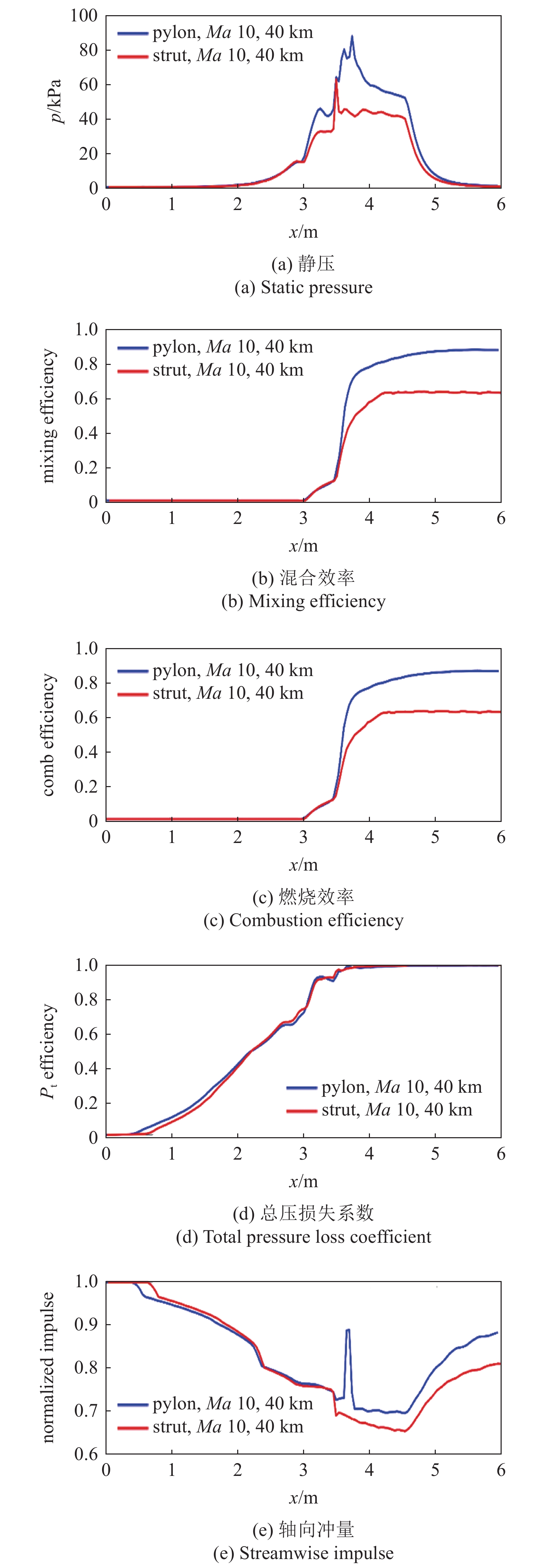
图6展示了沿程流向各截面提取参数对比. 壁面撑挡燃烧室静压峰值85 kPa, 为中心支板燃烧室压力峰值60 kPa的1.5倍. 继进气道压缩引起的压升之后, 回流区燃烧进一步提高了压力; 其中壁面撑挡燃烧室对应回流区反应更加剧烈因此压升效应更加明显并产生了一个较小的峰值. 壁面撑挡燃烧室的压力峰值位于凹腔处, 由剧烈燃烧诱导; 并在其后缓慢下降至尾喷管入口. 而中心支板燃烧室的压力峰值由支板或撑挡诱导的斜激波及其在壁面的反射激波引起, 支板下游未见明显的燃烧诱导峰值; 其后燃烧室压力出现了一个40 kPa的平台区, 燃烧近乎等压燃烧. 与冷态燃烧室不同, 燃烧条件下混合效率的计算应采用元素法[15], 即统计氢元素与氧元素的比例, 以考虑已反应部分的燃料以及组分间差异扩散效应. 回流区两种构型燃烧室的混合效率接近. 说明支板或撑挡之后, 壁面撑挡燃烧室的混合效率迅速升高远超中心支板燃烧室, 这是由于壁面撑挡燃烧室的射流穿透深度较高, 并且从图6(c) 凹腔前后燃料浓度分布可知凹腔顶部剪切层和内部回流区也起到了一定程度的增混作用. 混合效率在燃烧室下游靠近尾喷管入口处(x=4.2 m)趋于稳定值, 表明在尾喷管内平均马赫数5.0以上的高速流动发生的混合极少. 壁面撑挡燃烧室的最终混合效率为85.3%, 大幅高于中心支板燃烧室的61.2%. 燃烧效率的曲线与混合效率高度相似, 最终燃烧效率分别为83.9%和60.7%, 仅略低于混合效率, 表明高超声速燃烧室因滞止温度较高且氢气的特征反应时间极短(微秒级)存在混合即燃烧的特点. 这也与CEMA分析中指出的燃烧多为扩散混合控制的观察结果相符. 从这个角度上说, 高超声速燃烧室提高燃烧效率的关键在于增强混合. 总压计算中考虑了真实气体比热随温度变化的特性, 而理想情况下的非等熵关系式. 根据等熵关系式积分可得
$$ {P}_{\mathrm{t}}=p{{\rm{e}}}^{{\int }_{T}^{{T}_{\mathrm{t}}}\frac{{C}_{p}}{{R}T}{\rm{d}}T} $$ (28) 其中p和T为当前静压、静温,
$ {T}_{\mathrm{t}} $ 为总温, R为气体常数. 高超声速燃烧室的总压损失极高, 中心支板燃烧室的总压损失为99.3%, 壁面撑挡燃烧室的总压损失为99%, 意味着产生了接近2倍的熵增. 两种构型燃烧室的总压损失曲线基本一致, 其中壁面撑挡附近因局部动量交换更为剧烈导致总压损失更加迅速. 在设计中, 进气道型面微调为平滑过渡到燃烧室入口, 因此中心支板燃烧室的进气道略短导致总压损失起始延后, 但在保持相同几何压缩的条件下进气道末端的总压损失一致. 定义轴向冲量为$$ \boldsymbol{I}=pA + \rho \boldsymbol{U}A $$ (29) 其中A为流向面积, ρ为密度, U为流向速度. 根据动量守恒, 轴向推力F=∆I, 图6(e)中下降曲线(负梯度)表示阻力, 上升曲线段表示正推力. 一个很明显的结果是进气道因压缩来流是产生阻力的主要部件; 对应x=3.48 m处, 中心支板和壁面撑挡均产生了较大的阻力; 壁面撑挡燃烧室x=3.64 m处的轴向冲量突跃位于凹腔, 同时产生的推力和阻力, 总体上表现为阻力; 近等直燃烧段产生了微弱阻力; 尾喷管是获得推力的主要部件. 从以入口冲量无量纲化的冲量曲线对比可见, 两种构型燃烧室进气道阶段产生的阻力和尾喷管产生的推力均比较接近, 主要差别在于燃烧段的阻力差别较大: 特别是中心支板产生的阻力显著高于壁面撑挡, 凹腔虽然产生了一定程度的阻力但也有效增加了混合和燃烧, 其利弊需要进一步探索.
表2对比了两种构型燃烧室的总体性能. 其中壁面撑挡燃烧室的未装机净推力为344 N, 比冲比较理想为1234 s; 而中心支板燃烧室净推力较弱仅为99 N, 比冲437 s与常规火箭发动机性能接近, 体现不出吸气式发动机的优势. 壁面撑挡燃烧室的燃烧效率也较为理想, 高于通常认为的可产生推力的80% 准则[95]. 壁面撑挡燃烧室的压比16也显著高于中心支板燃烧室的11, 由此相比中心支板产生了增幅36% 的无黏(压力)推力. 同时, 中心支板燃烧室的阻力比壁面撑挡燃烧室高23%. 中心支板燃烧室进气道外形在保持几何压缩比的条件下做了一定的调整以适应微扩的隔离段, 因此其进气道捕获流量略低, 但计算中保持总当量比恒定.
表 2 壁面撑挡和中心支板燃烧室总体性能对比Table 2. Overall performance comparison between pylon and strut combustorsGlobal performance Pylon combustor Strut combustor air captured rate/(kg·s−1) 0.97619 0.79284 fuel flow rate/(kg·s−1) 0.028431 0.023091 inviscid Thrust/N 650.5093 477.038 viscous Drag/N 306.2568 377.9552 net Thrust/N 344.2525 99.0828 combustion efficiency 0.83833 0.60653 isolator pressure/kPa 5.1081 5.4449 peak pressure ratio 16.6474 11.1863 specific Impulse/s 1234.2698 437.4018 2.3 动态分区火焰面特性
如图7所示, 动态分区火焰面模型中火焰面结构函数随时间和空间而不断演化以准确表征当地燃烧化学反应状态. 分区条件平均温度取决于当前分区的焓增/减程度和反应进度, 用于控制当前分区反应速率. 随着流向距离增加, 分区条件平均温度随着反应趋向平衡递增, 并在燃烧室末端x=4.478 m处达到峰值, 后续在尾喷管内随着部分总焓转换为动能又逐渐降低. 上游的火焰面状态会被下游分区继承并继续反应, 因此随着反应趋于平衡产物H2O的浓度持续增加. 自由基O由O2在高于2500 K温度的离解反应生成, 并为在H2-O2的链式反应中起到重要作用的中间组分
${\rm{d}}\left[\mathrm{O}\right]/{\rm{d}}t={k_1}$ $\left[\mathrm{H}\right]\left[\mathrm{O}_2\right]-{k_2}$ $ \left[\mathrm{H}_2\right]\left[\mathrm{O}\right] $ , (k1和k2为反应速率常数). 一般认为燃烧反应过程中O的浓度在宽温度范围内相对恒定[96], 离解产生的过量O在燃烧段被逐渐消耗, 在温度低于离解温度(2500 K)仅有燃烧反应的尾喷管中保持相对恒定. 火焰面的演化除了在当前分区控制温度作用下演化以外, 还不断与相邻分区通过对流交互信息. 以O2浓度为例, 其在燃烧段被不断消耗的同时也不断从相邻未燃来流分区卷吸高浓度的O2, 因此在燃烧段其浓度甚至会短暂上升. 与H2O的不断生成对应, O2的浓度在自上游至下游的流动过程中被逐渐消耗, 而在尾喷管中因卷吸作用减弱, O2在反应中被逐渐消耗.动态分区火焰面的动态过程一方面是指火焰面的时空演化, 另一方面火焰面分区也不断自适应于流场而变化, 如图8(a)所示. 首先根据流向进行空间分区以区别不同流动阶段的火焰面. 精细的流向分区是准确捕捉点火距离的关键, 因其准确区分了从纯混合、点火到充分燃烧反应甚至熄火等不同阶段的反应状态. 分区独立性分析[70]表明, 当分区空间间隔小于一定程度时, 流场计算结果不再依赖于分区数目. 一般在超声速燃烧室模拟中, 一个合适的分区准则为分区间隔应不大于其点火距离, 并在燃烧段保证至少50个空间分区. 即空间上对流场进行分区后, 进一步在各“树墩”状剖分段依据当地混合分数进行分区. 图8(b) 展示了支板前、中、后典型位置处的混合分数分区情形. 其中在中段距离燃料喷注点附近, 当地混合分数覆盖从0到1的分布, 因此分区较为密集, 而前后段由于扩散效应仅覆盖低混合分数段, 因此分区数目减少. 再往上游或下游的更远端, 当地混合物状态为完全未预混的纯来流或已经混合较均匀的状态, 此时混合分数分区数目缩减为单个, 即单一火焰面即可充分表征当地反应状态. 在依据混合分数分区时, 为提高主反应区的表征保真度, 一般需要在当量比混合分数附近加密分区, 如图8(b) 所示. 从图中还可以看到, 混合分数分区形状不一定是规则的, 甚至可以是分散的孤岛集合, 在计算空间对流时依据格林公式沿交界面进行积分. 当流场不均匀性增大时, 可进一步增加分区指标. 例如根据当地温度、马赫数等进一步进行分区剖分以提高分区条件均一性.
2.4 分区自适应化学特性统计
图9 展示了分区自适应化学(Z-DAC)中各分区反应机理的统计. 从图9(a) 中可见前13步反应为在Z-DAC简化中几乎被始终保留的反应步, 而14 ~ 19步反应被使用的概率略低, 约为90% 左右. 20 ~ 33步反应则在63.5%的分区机理简化中被忽略. 前13步反应为H2的氧化反应, 在燃烧反应区被完整保留, 仅在纯空气来流区域被忽略. 第14 ~ 19步涉及过氧化氢(H2O2)的反应仅在OH浓度较高的活跃反应区才被激活. 而后14步涉及N元素的反应则在1800 K以上的高温区域才会被激活. 从各分区的反应机理尺寸统计来看, 64%的区域采用了31 ~ 33步反应, 27%的区域采用了19步反应, 8%的区域采用了11 ~ 13步反应. 另有极少的区域采用了7步反应, 为涉及N2和O2离解反应高温且无燃料区域. 可见分区自适应化学方法在将近一半的计算域上降低了反应求解计算代价, 特别是在无燃料区反应机理的简化幅度更加明显.
2.5 与传统燃烧模型效率对比
表3对比了DZFM模型与以PaSR为代表的传统有限速率模型的计算效率. PaSR模型除了需要对流场中所有CFD网格单元逐一积分求解当地化学反应外, 还需要求解全组分输运方程, 因此计算代价一般远高于流动−化学反应解耦模型. 超燃冲压发动机中的特征流通时间一般以毫秒为量级, 这里选取1 ms流动物理时间考察不同燃烧模型及加速方法的计算效率. 在相同并行规模504核(CPU型号Intel Xeon CPU E5-2640 , 单核主频2.40 GHz)的计算测试中, 纯PaSR模型的单毫秒的计算周期需要24 d, 采用Z-DAC加速后计算周期缩短为约20 d, 采用Z-ISAT加速缩短为14 d. 由于Z-DAC机理简化与ISAT建表查询方法近乎相互独立, 因此二者耦合使用的加速效率近似于二者单独加速比的乘积: 332.92 h × (468.16 h/582.61 h)=267.52 h=11 d, 仅略小于其耦合使用的12 d. ISAT与DAC的耦合使用的组合在部分文献[97]中被称为建表自适应化学(TDAC), 本研究中的方法为基于分区的Z-TDAC. 纯DZFM的单毫秒计算周期缩短为52 h, 对比纯PaSR的加速比高达11倍. 采用DZFM模型, 每个火焰面分区上仅有一维混合分数空间的若干状态点需要更新化学反应状态. Z-DAC尽管对当前分区反应机理进行了最大程度的简化, 然而因反应状态点数量大幅降低, 因此其加速效率不如与传统有限速率模型耦合时明显, 仅实现了5%的加速. 同样地, Z-ISAT的加速率也为5%. 二者耦合使用的Z-TDAC加速率略高, 也仅为8%. 表3列出了不同模型计算1 ms物理时间对应的CPU时间. 可见分区解耦湍流燃烧模拟将三维物理空间千万量级的化学反应状态点求解近似为较少的火焰面分区数目(本文中为1.8万个分区)乘以一维混合分数空间内的离散状态点上的反应求解, 从而极大地提升了加速比, 同时使得传统的反应计算加速方法加速效率相对不明显. 由于机理简化和建表查询均会产生一定的近似误差, 因此在加速比较低的情况下可以考虑优先提高精度.
表 3 DZFM模型与PaSR模型计算1 ms物理时间对应的CPU时间Table 3. CPU time of DZFM and PASR model calculation of 1 millisecond physical timeNo reaction acceleration Z-DAC Z-ISAT Z-DAC + Z-ISAT PaSR 582.61 × 504 CPU h 468.16 × 504 CPU h 332.92 × 504 CPU h 291.30 × 504 CPU h DZFM 52.02 × 504 CPU h 49.42 × 504 CPU h 49.42 × 504 CPU h 48.59 × 504 CPU h 图10基于Borghi图统计分析了以氢气为燃料的高超声速燃烧室中各分区的湍流化学反应交互作用关系(TCI). 其中戴姆克拉数Da 定义为湍流特征时间
$ {\tau }_{t} $ 与化学反应特征时间$ {\tau }_{c} $ 之比,$ Da={\tau }_{t}/{\tau }_{c} $ . 基于大涡模拟数据计算湍流特征时间时需要包括可解部分的湍流脉动$ {k}_{res} $ [98], 即$ {\tau }_{t}=\left({{k}_{res} + k}_{t}\right)/\varepsilon $ . 化学反应特征时间$ {\tau }_{c} $ 为CEMA指数的导数. 卡尔洛维奇数$ Ka $ 定义为化学反应特征时间与最小湍流尺度之比$ Ka= $ $ {\tau }_{c}/{\tau }_{k} $ , 其中Kolmogorov特征时间$ {\tau }_{k}={\left(\nu /\varepsilon \right)}^{1/2} $ . 据此有$ Re \sim {\left({\tau }_{t}/{\tau }_{k}\right)}^{2}={Da}^{2}\cdot {Ka}^{2} $ . 根据$ Ka $ 和$ Da $ 可将湍流化学反应交互作用关系分为3种模式: (1) 火焰面模式$ Ka $ <1且$ Da $ >10, (2) 薄反应区模式:$ 1 < Ka $ <100 且$ Da $ >10, (3) 慢反应模式:$ Ka $ >100 且$ Da $ <10. 从两种燃烧室的统计分析中可以看出, 超过90% 的绝大部分分区处于快速反应假设成立的火焰面模式, 5%左右的少部分分区处于薄反应区模式, 小于3%的分区处于慢速反应区. 氢气超声速燃烧与碳氢燃料超声速燃烧最大的区别在于, 碳氢超声速燃烧绝大部分处于薄反应区(大于50%)和慢速反应区(小于30%)[99]. 可见即便对于来流马赫数极高的高超声速燃烧室, 氢气反应速率仍然远快于滞留时间, 并且燃烧室中极高的滞止温度也进一步提高了氢气的反应速率, 在混合即燃烧的情况下决定燃烧效率的瓶颈在于高效增混. 高超声速燃烧室中雷诺数高达108, 最小湍流特征尺度为微米量级, 这意味直接求解高超声速燃烧的直接数值模拟计算代价仍然是目前计算机技术无法承受的, 同时也预示高超声速流场中跨越极广尺度的湍流与速率较慢的碳氢燃烧化学反应存在极其复杂的交互作用.3. 结 论
本文展示了基于动态分区概念的高马赫数全尺寸超燃冲压发动机的内外流耦合一体化改进延迟分离涡(IDDES)模拟研究. 研究建立了完整的动态分区燃烧模拟框架, 包括动态分区火焰面湍流燃烧模型(DZFM), 以及分区自适应化学(Z-DAC)和分区并行自适应建表(Z-ISAT)等化学反应加速模型. 前者通过分区解耦的思想既准确表征了当地湍流化学交互作用关系, 又有效提升了整场湍流燃烧的计算效率. 后两者通过在分区框架内对化学反应机理进行动态实时简化和建表查询, 可进一步提升当前分区内化学反应的求解效率. 沿不同空间位置处的火焰面结构函数的变化表明动态分区火焰面模型可以捕捉反应混合物微团内温度和组分等参数随反应进程逐渐演化的物理过程. 精细的流向分区准确区分了从纯混合、点火到充分燃烧反应甚至熄火等不同阶段的反应状态, 因而是准确捕捉点火距离的关键. 混合分数分区形状不必是规则的, 甚至可以是分散的孤岛集合, 其在不同流向距离处的分布密集程度也自适应于流场而变化.
首先通过对比有完备实验数据的马赫12 REST标准高超声速燃烧室模型, 验证了分区模拟框架的保真性. 分别基于1.25和1.4亿网格动态分区框架对马赫数10和海拔40 km条件下全尺寸的中心支板(strut)和壁面撑挡型(pylon)两类构型氢气高超声速燃烧室进行了深入的数值分析, 揭示了高超声速燃烧中一系列独特的规律和机理.
壁面撑挡燃烧室的未装机净推力为344 N, 比冲比较理想为1234 s; 而中心支板燃烧室净推力较弱仅为99 N, 比冲437 s. 壁面撑挡燃烧室的燃烧效率也较为理想, 高于通常认为的可产生推力的80% 准则. 壁面撑挡燃烧室的压比为16, 也显著高于中心支板燃烧室的压比11, 由此相比中心支板燃烧室产生了增幅为36%的无黏(压力)推力. 同时, 中心支板燃烧室的阻力也比壁面撑挡燃烧室高了23%. 两种构型燃烧室的总压损失均高达99%, 其中壁面撑挡附近因局部动量交换更为剧烈导致总压损失更加迅速.
基于Borghi图的数值分析表明, 上述两类燃烧室内燃烧的模式均为扩散主要控制的火焰面模式. 超过90% 的绝大部分分区处于快速反应假设成立的火焰面模式, 远大于碳氢超声速燃烧室中的约10% 的比例. 在混合即燃烧的情况下, 提高燃烧效率的关键在于增强混合. 壁面撑挡燃烧室中撑挡结构的燃料喷注由于处于亚声速区因而其穿透深度较中心支板钝体表面喷注更深, 从而取得了更好的混合效率, 进而提高了燃烧效率.
分区自适应化学Z-DAC在准确地区分了各分区的化学反应状态, 其中H2的氧化反应在燃烧反应区被完整保留, 涉及过氧化氢(H2O2)的反应仅在OH浓度较高的活跃反应区才被激活, 而涉及N元素的反应则在1800 K以上的高温区域才会被激活. 64%的区域采用了近乎完整的33步反应机理, 27%的区域采用了19步反应, 8%的区域采用了11 ~ 13步反应, 另有极少的高温纯空气离解区域采用了7步反应机理. 可见分区自适应化学方法在将近一半的计算域上降低了反应求解计算代价, 特别是在无燃料区反应机理的简化幅度更加明显.
相比于传统的有限速率PaSR模型, DZFM模型将三维物理空间千万量级的化学反应状态点求解近似为较少的火焰面分区数目(本研究中为1.8万个分区)乘以一维混合分数空间内的离散状态点上的反应求解, 实现了高达11倍的加速比, 同时使得传统的反应计算加速方法加速效率相对不明显. 由于机理简化和建表查询均会产生一定的近似误差, 因此在加速比较低的情况下可以考虑优先提高精度.
-
表 1 测试飞行工况参数
Table 1 Flight test conditions
Freestream Fuel stream (mass fraction YN2: 0.767, YO2: 0.233) (mass fraction YH2: 1.0) Ma H/km T/K p/Pa U/(m·s−1) q/Pa Pt/Pa Tt/K Qfuel/(kg·s−1) Tt/K Ma 10 40 250 287 3172 20099 2.7 × 107 4333.5 0.023 298 1 表 2 壁面撑挡和中心支板燃烧室总体性能对比
Table 2 Overall performance comparison between pylon and strut combustors
Global performance Pylon combustor Strut combustor air captured rate/(kg·s−1) 0.97619 0.79284 fuel flow rate/(kg·s−1) 0.028431 0.023091 inviscid Thrust/N 650.5093 477.038 viscous Drag/N 306.2568 377.9552 net Thrust/N 344.2525 99.0828 combustion efficiency 0.83833 0.60653 isolator pressure/kPa 5.1081 5.4449 peak pressure ratio 16.6474 11.1863 specific Impulse/s 1234.2698 437.4018 表 3 DZFM模型与PaSR模型计算1 ms物理时间对应的CPU时间
Table 3 CPU time of DZFM and PASR model calculation of 1 millisecond physical time
No reaction acceleration Z-DAC Z-ISAT Z-DAC + Z-ISAT PaSR 582.61 × 504 CPU h 468.16 × 504 CPU h 332.92 × 504 CPU h 291.30 × 504 CPU h DZFM 52.02 × 504 CPU h 49.42 × 504 CPU h 49.42 × 504 CPU h 48.59 × 504 CPU h -
[1] Marshall L, Bahm C, Corpening G. Overview with results and lessons learned of the x-43 a mach 10 flight//AIAA/CIRA 13 th International Space Planes and Hypersonics Systems and Technologies Conference, 2005
[2] Smart MK, Tetlow MR. Orbital delivery of small payloads using hypersonic airbreathing propulsion. Journal of Spacecraft and Rockets, 2009, 46(1): 117-125 doi: 10.2514/1.38784
[3] Rogers RC, Shih AT, Tsai CY. Scramjet tests in a shock tunnel at flight mach 7, 10, and 15 conditions. AIAA Paper, 2011-3241
[4] Barkmeyer D, Starkey R, Lewis M. Inverse waverider design for inward turning inlets//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2005
[5] Gai SL. Free piston shock tunnels developments and capabilities. Aerospace, 1992, 29(1): 1-41 doi: 10.1016/0376-0421(92)90002-Y
[6] Chan WYK, Razzaqi SA, Turner JC, et al. Freejet testing of the hifire 7 scramjet flowpath at mach 7.5. Journal of Propulsion and Power, 2018, 34(4): 844-853 doi: 10.2514/1.B36652
[7] Curran D, Wheatley V, Smart M. Investigation of combustion mode control in a mach 8 shape-transitioning scramjet. AIAA Journal, 2019, 57(7): 2977-2988 doi: 10.2514/1.J057999
[8] Suraweera MV, Smart MK. Shock-tunnel experiments with a mach 12 rectangular-to-elliptical shape-transition scramjet at offdesign conditions. Journal of Propulsion and Power, 2009, 25(3): 555-564 doi: 10.2514/1.37946
[9] Doherty LJ, Smart MK, Mee DJ. Experimental testing of an airframe-integrated three-dimensional scramjet at mach 10. AIAA Journal, 2015, 53(11): 3196-3207 doi: 10.2514/1.J053785
[10] Landsberg WO, Wheatley V, Smart MK, et al. Enhanced supersonic combustion targeting combustor length reduction in a mach 12 scramjet. AIAA Journal, 2018, 56(10): 3802-3807 doi: 10.2514/1.J057417
[11] Barth JE. Mixing and combustion enhancement in a mach 12 shape-transitioning scramjet engine. [PHD Thesis]. Brisbane: The University of Queensland, 2014
[12] Wise DJ, Smart MK. Experimental investigation of a three-dimensional scramjet engine at Mach 12//20th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2015
[13] Shenoy RR, Drozda TG, Norris AT, et al. Comparison of mixing characteristics for several fuel injectors at Mach 8, 12, and 15 hypervelocity flow conditions//2018 Joint Propulsion Conference, July 2018
[14] Bakos R, Tamagno J, Trucco R, et al. Mixing and combustion studies using discrete orifice injection at hypervelocity flight conditions. Journal of Propulsion and Power, 1992, 8(6): 1290-1296 doi: 10.2514/3.11475
[15] Yao W, Chen L. Large eddy simulation of rest hypersonic combustor based on dynamic zone flamelet model//AIAA Propulsion and Energy 2020 Forum, 2020
[16] Yao W, Wu K, Fan XJ. Influences of domain symmetry on supersonic combustion modeling. Journal of Propulsion and Power, 2019, 35(2): 451-465 doi: 10.2514/1.B37227
[17] Yao W, Lu Y, Wu K, et al. Modeling analysis of an actively cooled scramjet combustor under different kerosene/air ratios. Journal of Propulsion and Power, 2018, 34(4): 975-991 doi: 10.2514/1.B36866
[18] Yao W, Yuan YM, Li XP, et al. Comparative study of elliptic and round scramjet combustors fueled by RP-3. Journal of Propulsion and Power, 2018, 34(3): 772-786 doi: 10.2514/1.B36721
[19] Fan ZQ, Liu WD, Sun MB, et al. Theoretical analysis of flamelet model for supersonic turbulent combustion. Science China Technological Sciences, 2011, 55(1): 193-205
[20] 孙明波, 范周琴, 梁剑寒等. 部分预混超声速燃烧火焰面模式研究综述. 力学进展, 2010, 40(6): 634-641 (Sun Mingbo, Fan Zhouqin, Liang Jianhan, et al. Evalutaion of partially permixed flamelet approach in supersonic combustion. Anvances in Mechanics, 2010, 40(6): 634-641 (in Chinese) doi: 10.6052/1000-0992-2010-6-lxjzJ2009-127 [21] Davidenko D, Gökalp I, Dufour E, et al. Numerical simulation of hydrogen supersonic combustion and validation of computational approach//12th AIAA International Space Planes and Hypersonic Systems and Technologies, 2003
[22] Golovitchev VI, Nordin N, Jarnicki R, et al. 3-D diesel spray simulations using a new detailed chemistry turbulent combustion model. SAE Technical Paper, 2000
[23] Magnussen B. On the structure of turbulence and a generalized eddy dissipation concept for chemical reaction in turbulent flow//19th Aerospace Sciences Meeting, 1981
[24] Legiery JP, Poinsot T, Veynante D. Dynamically thickened flame LES model for premixed and non-premixed turbulent combustion//Proceedings of the 2000 Summer Program, 2000: 157-168
[25] Calhoon W, Menon S. Linear-eddy subgrid model for reacting large-eddy simulations - heat release effects//35th Aerospace Sciences Meeting and Exhibit. American Institute of Aeronautics and Astronautics, 1997
[26] Peters N. Laminar flamelet concepts in turbulent combustion//21st Symposium (International) on Combustion, 1986: 1231-1250
[27] Bray K. Laminar flamelets in turbulent combustion modeling. Combustion Science and Technology, 2016, 188(9): 1372-1375 doi: 10.1080/00102202.2016.1195819
[28] Cook DJ, Pitsch H, Chen JH, et al. Flamelet-based modeling of auto-ignition with thermal inhomogeneities for application to hcci engines. Proceedings of the Combustion Institute, 2007, 31(2): 2903-2911 doi: 10.1016/j.proci.2006.07.252
[29] Klimenkoa AY, Bilger RW. Conditional momen closure for turbulent combustion. Progress in Energy and Combustion Science, 1999, 25: 595-687 doi: 10.1016/S0360-1285(99)00006-4
[30] Ramanujachari V, Balakrishna S. Probability density function approach to non-premixed turbulent flames. Indian Journal of Pure and Applied Mathematics, 2000, 31: 1339-1351
[31] Huang C, Lipatnikov AN. Comparison of presumed PDF models of turbulent flames. Journal of Combustion, 2012, 2012: 1-15
[32] Pope SB. PDF methods for turbulent reactive flows. Progress in Energy and Combustion Science, 1985, 11: 119-192 doi: 10.1016/0360-1285(85)90002-4
[33] Pierce CD, Moin P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. Journal of Fluid Mechanics, 2004, 504: 73-97 doi: 10.1017/S0022112004008213
[34] Williams FA. Turbulent combustion//The Mathematics of Combustion, 1985, doi: 10.1137/1.9781611971064.Ch3
[35] Oijen JAV, Goey LPHD. Modelling of premixed laminar flames using flamelet-generated manifolds. Combustion Science and Technology, 2000, 161(1): 113-137 doi: 10.1080/00102200008935814
[36] Kundu P, Pei Y, Wang M, et al. Evaluation of turbulence-chemistry interaction under diesel engine conditions with multi-flamelet rif model. Atomization and Sprays, 2014, 24: 779-800 doi: 10.1615/AtomizSpr.2014010506
[37] Pitsch H, Barths H, Peters N. Three-dimensional modeling of nox and soot formation in di-diesel engines using detailed chemistry based on the interactive flamelet approach//International Fall Fuels & Lubricants Meeting& Exposition, San Antonio, Texas, 1996
[38] 刘昆, 张育林. 液体火箭发动机燃烧室的一种分区模型. 航空动力学报, 2002, 17(1): 135-139 (Liu Kun, Zhang Yulin. An innovative partition model of liquid rocket engine comubsution chambers. Journal of Aerospace Power, 2002, 17(1): 135-139 (in Chinese) doi: 10.3969/j.issn.1000-8055.2002.01.025 [39] Ge HW, Juneja H, Shi Y, et al. A two-zone multigrid model for si engine combustion simulation using detailed chemistry. Journal of Combustion, 2010, 2010: 1-12
[40] Saeed K, Stone CR. The modelling of premixed laminar combustion in a closed vessel. Combustion Theory and Modelling, 2006, 8(4): 721-743
[41] Kodavasal J, Keum SH, Babajimopoulos A. An extended multi-zone combustion model for pci simulation. Combustion Theory and Modelling, 2011, 15(6): 893-910 doi: 10.1080/13647830.2011.578663
[42] Men YF, Haskara I, Zhu GM. Multi-zone reaction-based modeling of combustion for multiple-injection diesel engines. International Journal of Engine Research, 2018, 21(6): 1012-1025
[43] Perini F. High-dimensional, unsupervised cell clustering for computationally efficient engine simulations with detailed combustion chemistry. Fuel, 2013, 106: 344-356 doi: 10.1016/j.fuel.2012.11.015
[44] Zhou DZ, Tay KL, Li H, et al. Computational acceleration of multi-dimensional reactive flow modelling using diesel/biodiesel/jet-fuel surrogate mechanisms via a clustered dynamic adaptive chemistry method. Combustion and Flame, 2018, 196: 197-209 doi: 10.1016/j.combustflame.2018.06.008
[45] Dai M, Xuna L, Liang Z. Detailed chemaical micro fluid combustion models for natural gas fueled hcci engines//19th International Conference on Computational Combustion, Stockholm, Sweden, 2017
[46] Raju M, Wang MJ, Dai MH, et al. Acceleration of detailed chemical kinetics using multi-zone modeling for cfd in internal combustion engine simulations. SAE Technical Paper Series, 2012
[47] Ingenito A, Flora M, Bruno C. LES modeling of scramjet combustion//44th AIAA Aerospace Sciences Meeting and Exhibit, 2006
[48] Liang L, Stevens JG, Farrell JT. A dynamic multi-zone partitioning scheme for solving detailed chemical kinetics in reactive flow computations. Combustion Science and Technology, 2009, 181(11): 1345-1371 doi: 10.1080/00102200903190836
[49] Wu H, See YC, Wang Q, et al. A pareto-efficient combustion framework with submodel assignment for predicting complex flame configurations. Combustion and Flame, 2015, 162(11): 4208-4230 doi: 10.1016/j.combustflame.2015.06.021
[50] Wu H, See YC, Wang Q, et al. A fidelity adaptive modeling framework for combustion systems based on model trust-region//53rd AIAA Aerospace Sciences Meeting, 2015
[51] Yao W, Fan XJ. Application of dynamic zone flamelet model to a gh2/go2 rocket combustor//AIAA Propulsion and Energy 2019 Forum, 2019
[52] Cuoci A, Frassoldati A, Faravelli T, et al. Kinetic modeling of soot formation in turbulent nonpremixed flames. Environmental Engineering Science, 2008, 25(10): 1407-1422 doi: 10.1089/ees.2007.0193
[53] Cleary M, Kent J. Modelling of species in hood fires by conditional moment closure. Combustion and Flame, 2005, 143(4): 357-368 doi: 10.1016/j.combustflame.2005.08.013
[54] Young KJ, Moss JB. Modelling sooting turbulent jet flames using an extended flamelet technique. Combustion Science and Technology, 1995, 105(1-3): 33-53 doi: 10.1080/00102209508907738
[55] Thornber B, Bilger RW, Masri AR, et al. An algorithm for LES of premixed compressible flows using the conditional moment closure model. Journal of Computational Physics, 2011, 230(20): 7687-7705 doi: 10.1016/j.jcp.2011.06.024
[56] Schwer DA, Lu P, Green WH. An adaptive chemistry approach to modeling complex kinetics in reacting flows. Combustion and Flame, 2003, 133(4): 451-465 doi: 10.1016/S0010-2180(03)00045-2
[57] Liang L, Stevens JG, Farrell JT. A dynamic adaptive chemistry scheme for reactive flow computations. Proceedings of the Combustion Institute, 2009, 32(1): 527-534 doi: 10.1016/j.proci.2008.05.073
[58] Lu TF, Law CK. Toward accommodating realistic fuel chemistry in large-scale computations. Progress in Energy and Combustion Science, 2009, 35(2): 192-215 doi: 10.1016/j.pecs.2008.10.002
[59] Yao W. Kerosene-fueled supersonic combustion modeling based on skeletal mechanisms. Acta Mechanica Sinica, 2019, 35(6): 1155-1177 doi: 10.1007/s10409-019-00891-w
[60] Lu TF, Law CK. A directed relation graph method for mechanism reduction. Proceedings of the Combustion Institute, 2005, 30(1): 1333-1341 doi: 10.1016/j.proci.2004.08.145
[61] Pepiotdesjardins P, Pitsch H. An efficient error-propagation-based reduction method for large chemical kinetic mechanisms. Combustion and Flame, 2008, 154(1-2): 67-81 doi: 10.1016/j.combustflame.2007.10.020
[62] Pope SB. Computationally efficient implementation of combustion chemistry usingin situadaptive tabulation. Combustion Theory and Modelling, 1997, 1(1): 41-63 doi: 10.1080/713665229
[63] Yang B, Pope SB. Treating chemistry in combustion with detailed mechanisms - in situ adaptive tabulation in principal directions - premixed combustion. Combustion and Flame, 1998, 112: 85-112 doi: 10.1016/S0010-2180(97)81759-2
[64] Liu BJD, Pope SB. The performance ofin situadaptive tabulation in computations of turbulent flames. Combustion Theory and Modelling, 2005, 9(4): 549-568 doi: 10.1080/13647830500307436
[65] 肖保国. 碳氢燃料简化动力学模型和当地自适应建表方法在超燃并行计算中的应用. [博士论文]. 中国空气动力研究与发展中心, 2009 Xiao Baoguo. Implementation of reduced chemical kinetics of hydrocarbon fuels and in situ adaptive tabulation in parallel computations of supersonic combustion. [PhD Thesis]. China Aerodynamics Research and Development Center, 2009 (in Chinese)
[66] Lu LY, Lantz SR, Ren ZY, et al. Computationally efficient implementation of combustion chemistry in parallel PDF calculations. Journal of Computational Physics, 2009, 228(15): 5490-5525 doi: 10.1016/j.jcp.2009.04.037
[67] Yuan YM, Zhang TC, Yao W, et al. Characterization of flame stabilization modes in an ethylene-fueled supersonic combustor using time-resolved CH* chemiluminescence. Proceedings of the Combustion Institute, 2017, 36(2): 2919-2925 doi: 10.1016/j.proci.2016.07.040
[68] Sankaran V, Genin F, Menon S. Subgrid mixing modeling for large eddy simulation of supersonic combustion//42nd AIAA Aerospace Sciences Meeting and Exhibit. American Institute of Aeronautics and Astronautics, 2004
[69] Piomelli U. Large-eddy and direct simulation of turbulent flows//Introduction to Turbulence Modelling, Von Karman Institute, Belgium, 2004
[70] Yao W. On the application of dynamic zone flamelet model to large eddy simulation of supersonic hydrogen flame. International Journal of Hydrogen Energy, 2020, 45(41): 21940-21955 doi: 10.1016/j.ijhydene.2020.05.189
[71] Jones WP, Whitelaw JH. Calculation methods for reacting turbulent flows: A review. Combustion and Flame, 1982, 48: 1-26 doi: 10.1016/0010-2180(82)90112-2
[72] Pierce CD, Moin P. A dynamic model for subgrid-scale variance and dissipation rate of a conserved scalar. Physics of Fluids, 1998, 10(12): 3041-3044 doi: 10.1063/1.869832
[73] Triantafyllidis A, Mastorakos E. Implementation issues of the conditional moment closure model in large eddy simulations. Flow, Turbulence and Combustion, 2009, 84(3): 481-512
[74] Nichols RH. Turbulence models and their application to complex flows. [PhD Thesis]. University of Alabama at Birmingham, 2014
[75] Spalart PR. Detached-eddy simulation. Annual Review of Fluid Mechanics, 2009, 41(1): 181-202 doi: 10.1146/annurev.fluid.010908.165130
[76] Shur ML, Spalart PR, Strelets MK, et al. A hybrid rans-LES approach with delayed-des and wall-modelled LES capabilities. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649 doi: 10.1016/j.ijheatfluidflow.2008.07.001
[77] Spalart PR, Allmaras SR. A one-equation turbulence model for aerodynamic flows. AIAA-92-0439, 1992
[78] Spalart PR, Deck S, Shur ML, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181-195 doi: 10.1007/s00162-006-0015-0
[79] McLinden MO, Klein SA, Perkins RA. An extended corresponding states model for the thermal conductivity of refrigerants and refrigerant mixtures. International Journal of Refrigeration, 2000, 23: 43-63 doi: 10.1016/S0140-7007(99)00024-9
[80] Chase MW. Nist-janaf thermochemical tables. (4th ed.). Journal of Physical and Chemical Reference Data, 1998, 9: 1-1952
[81] Kee RJ, Rupley FM, Miller JA. Chemkin-il: A fortran chemical kinetics package for the analysis of gas-phase chemical kinetics. Sandia National Laboratories, 1989
[82] Mathur S, Tondon PK, Saxena SC. Thermal conductivity of binary, ternary and quaternary mixtures of rare gases. Molecular Physics, 1967, 12(6): 569-579 doi: 10.1080/00268976700100731
[83] Weller HG, Tabor G, Jasak H, et al. A tensorial approach to computational continuum mechanics using object-oriented techniques. Computers in Physics, 1998, 12: 620
[84] Lee YC, Yao W, Fan XJ. Low-dissipative hybrid compressible solver designed for large-eddy simulation of supersonic turbulent flows. AIAA Journal, 2018, 56(8): 3086-3096 doi: 10.2514/1.J056404
[85] Chen SS, Yan C, Xiang XH. Effective low-mach number improvement for upwind schemes. Computers & Mathematics with Applications, 2018, 75(10): 3737-3755
[86] Yao W, Wang J, Lu Y, et al. Full-scale detached eddy simulation of kerosene fueled scramjet combustor based on skeletal mechanism//20th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2015
[87] Wu K, Zhang P, Yao W, et al. Numerical investigation on flame stabilization in dlr hydrogen supersonic combustor with strut injection. Combustion Science and Technology, 2017, 189(12): 2154-2179 doi: 10.1080/00102202.2017.1365847
[88] Yao W, Lu Y, Li XP, et al. Improved delayed detached eddy simulation of a high-ma active-cooled scramjet combustor based on skeletal kerosene mechanism//52nd AIAA/SAE/ASEE Joint Propulsion Conference, 2016.
[89] Wu K, Yao W, Fan XJ. Development and fidelity evaluation of a skeletal ethylene mechanism under scramjet-relevant conditions. Energy & Fuels, 2017, 31(12): 14296-14305
[90] Gritskevich MS, Garbaruk AV, Schütze J, et al. Development of ddes and iddes formulations for the k-ω shear stress transport model. Flow, Turbulence and Combustion, 2011, 88(3): 431-449
[91] Jachimowski CJ. An analysis of combustion studies in shock expansion tunnels and reflected shock tunnels. NASA Langley Technical Report Server, No. 19920019131, 1998
[92] Saarlas M. Reference temperature method for computing displacement thickness. AIAA Journal, 1964, 2(11): 2056-2057 doi: 10.2514/3.2741
[93] Lu TF, Yoo CS, Chen JH, et al. Three-dimensional direct numerical simulation of a turbulent lifted hydrogen jet flame in heated coflow: A chemical explosive mode analysis. Journal of Fluid Mechanics, 2010, 652: 45-64 doi: 10.1017/S002211201000039X
[94] Wu WT, Piao Y, Xie Q, et al. Flame diagnostics with a conservative representation of chemical explosive mode analysis. AIAA Journal, 2019, 57(4): 1355-1363 doi: 10.2514/1.J057994
[95] Smart MK. How much compression should a scramjet inlet do? AIAA Journal, 2012, 50(3): 610-619
[96] Law CK. Combustion Physics. Cambridge: Cambridge University Press, 2006
[97] Wu K, Contino F, Yao W, et al. On the application of tabulated dynamic adaptive chemistry in ethylene-fueled supersonic combustion. Combustion and Flame, 2018, 197: 265-275 doi: 10.1016/j.combustflame.2018.08.012
[98] Pope SB. Ten questions concerning the large-eddy simulation of turbulent flows. New Journal of Physics, 2004, 6: 35-35 doi: 10.1088/1367-2630/6/1/035
[99] Yao W, Wu K, Fan XJ. Development of skeletal kerosene mechanisms and application to supersonic combustion. Energy & Fuels, 2018, 32(12): 12992-13003
-
期刊类型引用(0)
其他类型引用(2)



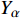
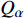
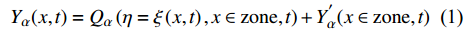
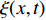
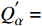
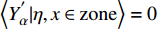
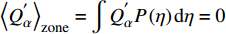
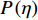
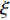
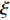
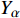

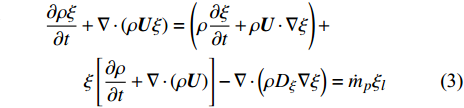
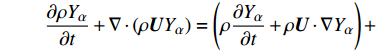
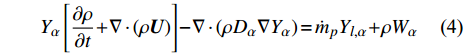
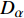
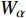
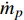
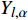
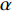
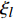
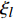
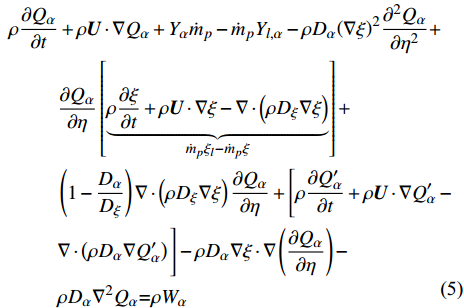
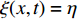
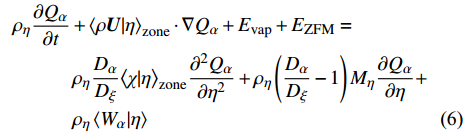
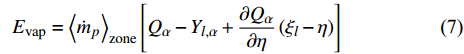
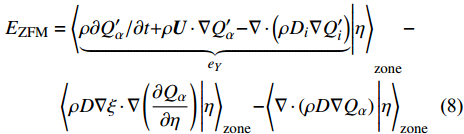
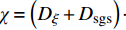
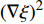
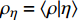
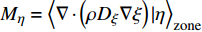
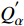
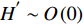
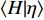
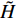
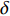
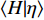
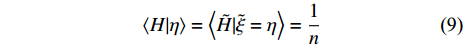
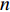
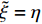
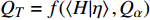
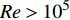
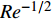
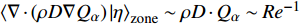
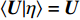
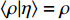
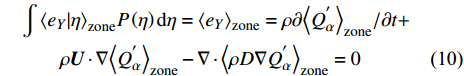
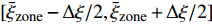
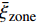
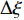
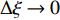
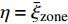
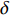
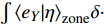

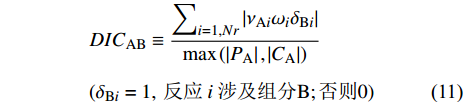
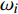
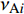
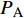
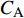
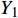
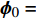
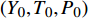
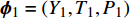
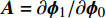
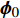
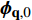
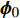
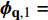
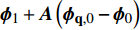
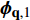
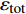
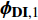
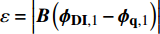
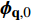
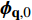
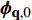
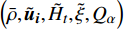

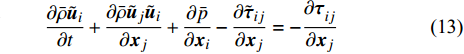
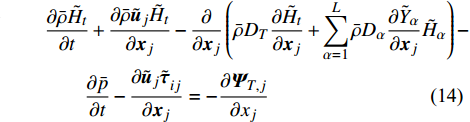
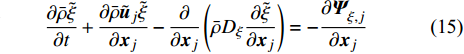
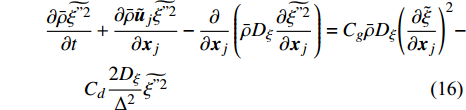
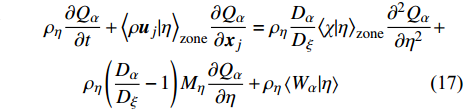

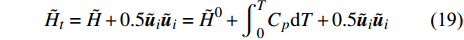
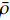
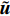
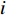
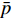
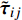
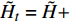
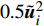
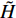
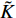
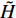
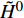
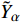
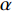
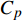
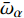
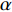
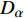
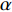
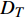
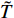
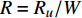
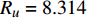
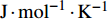
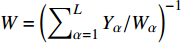
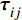
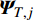
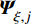
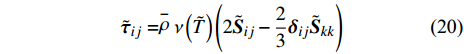
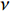
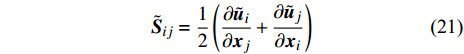
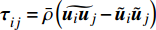
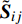
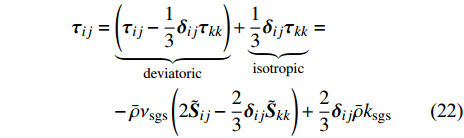
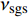
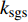
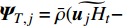
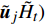
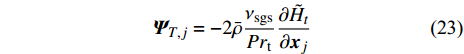
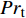
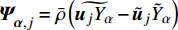
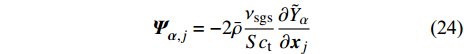
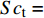
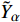
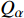
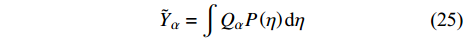
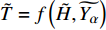
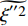
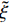
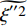
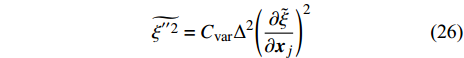
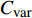
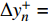
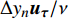
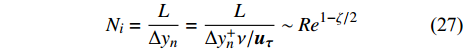
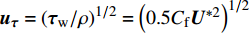
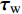
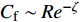
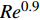
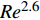
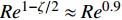
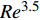
 下载:
下载: