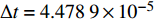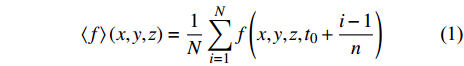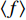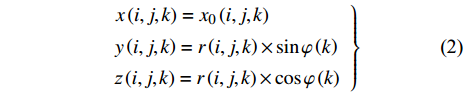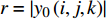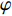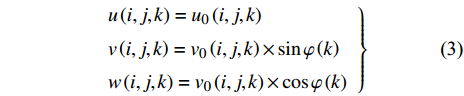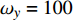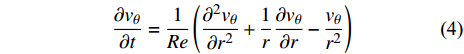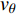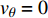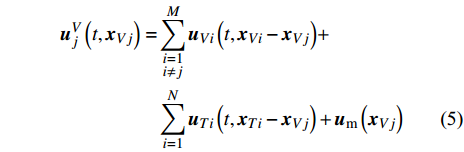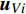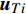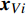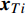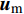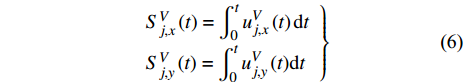STUDY ON INSTABILITY MECHANISM AND EVOLUTION MODEL OF PROPELLER TIP VORTICES
-
摘要: 螺旋桨尾流场的涡流特性是一个基础但又十分复杂的流体力学问题, 它的复杂性源于其蕴含复杂的漩涡系统, 且该漩涡系统会在高速的剪切层流动中不断演化, 其流体动力学行为, 如由稳定态演变为不稳定态的机理以及复杂工况环境中的流动现象, 一直是流体力学领域的难点和备受关注的热点问题. 从工程应用的角度看, 桨后梢涡的演化特性与船舶结构物的宏观特性直接相关, 更好地理解多工况下螺旋桨尾流的动力学特性, 将有助于改善与振动、噪声以及结构问题等相关的推进器性能, 对综合性能优良的下一代螺旋桨的设计和优化有着重要的现实意义. 本文基于延迟分离涡模拟、大涡模拟和无湍流模型模拟方法以及粒子图像测速流场测试分别开展了螺旋桨尾流动力学特性的数值与试验研究, 对螺旋桨尾流不稳定性的触发机理进行了揭示. 基于均匀来流中螺旋桨梢涡的演化机理, 提出了螺旋桨梢涡演化模型. 该模型能够较为准确地模拟螺旋桨梢涡的演化过程, 预测螺旋桨梢涡融合的时间和位置, 对螺旋桨流噪声预报和控制以及性能优良的螺旋桨设计具有重要意义.Abstract: The propeller wake dynamics is a fundamental but very complicated fluid mechanics problem. Its complexity comes from its sophisticated vortex system, which keeps evolving in high-speed shear layer flow. The mechanism of propeller wake behaviors such as the evolution from stable regime to unstable regime and the flow phenomenon in a complex operating environment have always been difficult and hot topics in the field of fluid mechanics. From the perspective of engineering applications, propeller wakes are directly related to the macroscopic characteristics of marine structures, a better understanding of the dynamic characteristic of the propeller wake under multiple operating conditions helps to improve the propulsion performance related to vibration, noise, and structure problems and has important practical significance for the design and optimization of next-generation propellers with good comprehensive performance. In this paper, the propeller wake dynamics are analyzed numerically using DDES, LES and NTM methods and experimentally based on PIV flow measurements, and the triggering mechanism of the instability of the propeller wake is revealed. Based on the evolution mechanism of the tip vortex in the uniform inflow, an evolution model of the tip vortices is proposed. The proposed model can accurately reproduce the evolution process of propeller tip vortex, predict the instant and position of tip vortex merging, which is of great significance to the prediction and control of propeller flow noise and the design of propellers with excellent performance.
-
引言
目前, 水面舰船和水下航行器主要采用螺旋桨推进方式. 螺旋桨的水动力性能、空化以及噪声性能等一直是船舶研究和设计建造人员非常关心的问题[1-3]. 螺旋桨尾流场的测量和精准模拟不仅关系到螺旋桨性能的评估, 同时也是螺旋桨型线优化、桨前后节能装置设计时需要考量的关键因素[4-5]. 截止到目前, 船舶螺旋桨尾流场这一高度复杂的湍流流动结构中依然包含着许多没有被完全揭示和理解的演化机理, 如椭圆不稳定性(短波不稳定性)、梢涡的融合、蛙跳、蜿蜒以及崩溃等复杂现象背后的物理机制. 更好地揭示它们的流动行为和特性往往能够帮助人们更准确地理解或预报螺旋桨的相关特性, 如梢涡融合以及短波不稳定性和长波不稳定性引起的涡系统崩溃, 都会导致流噪声的增加. 螺旋桨尾流的机理研究在工程应用中扮演着重要的角色, 并引起了足够的重视, 究其原因是这一基础问题与螺旋桨水动力性能、振动、噪声以及船舶结构问题等相关[6-7]. 另外, 从物理的观点来看, 螺旋桨尾流的特征也是造成能量损失的关键因素, 更好地理解螺旋桨尾流的物理本质, 对螺旋桨的优化设计以及新概念螺旋桨的发展十分重要[8].
螺旋桨尾流场计算的黏性方法仍主要采用计算流体力学方法进行[9-10], 但采用计算流体力学方法进行螺旋桨尾流非定常特性的研究时, 也面临着不小的挑战. 当螺旋桨尾流从近场向远场演化过程中的不稳定性问题成为关注的焦点时, 这一物理过程中精细涡结构的捕捉往往对数值模拟的时空分辨率要求较高[11-12].
国外在螺旋桨尾流场方面的研究较为深入和广泛, 对不同工况下螺旋桨的尾流场演化机理进行了揭示. 强光林等[13]研究了湍流模型效应对螺旋桨尾流模拟的影响, 分别讨论了雷诺平均方法和分离涡模拟方法在模拟尾涡中的限制和优势. 王巍等[14]基于分离涡模拟方法研究了斜流中的螺旋桨尾涡动力学特性, 对螺旋桨尾涡的不稳定性、湍动能进行了详细分析. Dubbioso等[15]采用雷诺平均方法研究了不同载况条件、不同斜流角情况下的螺旋桨水动力性能. 明尼苏达大学的Mahesh团队[16-18]在螺旋桨尾流场数值计算发面也开展了富有成效的研究. Jang和Mahesh[16]基于大涡模拟方法对反转螺旋桨的尾流特征进行了详细分析, 通过研究发现, 螺旋桨重载荷主要由于流动分离而产生. Kumar和Mahesh[17]利用大涡模拟方法对五叶螺旋桨设计工况下的尾流场稳定性进行了研究, 模拟结果揭示了梢涡相互干扰的不稳定性机理. Verma等[18]基于大涡模拟方法对两个进速系数条件下, 螺旋桨上游存在和不存在船体时的反转螺旋桨尾流场进行了数值分析, 重点考察了不同工况下反转螺旋桨侧向力产生的机理. 爱荷华大学的Chase和Carrica[19]探讨了分别采用雷诺平均、分离涡模拟、延迟分离涡模拟以及层流模型时, E1619螺旋桨尾流场的计算结果, 结果表明网格加密对推力和扭矩的计算结果影响不大, 但对尾流细节有着非常大的影响, 且采用雷诺平均方法时耗散较为严重.
国内在螺旋桨尾流动力学特性方面的研究不多. Zhu[20]基于雷诺平均方法对空化流中螺旋桨尾流场与螺旋桨侧斜角特征的关系进行了详细分析. 朱志峰等[21]利用多相流计算流体力学理论对螺旋桨模型的空化流特征进行了数值仿真, 其中滑移网格技术被用来实现螺旋桨的旋转运动, 给出了不同空化模型和湍流模型的模拟结果. 胡健等[22]基于雷诺平均方法计算并分析了螺旋桨尾流中速度分量的变化规律以及不同载荷工况下的流场特征.
本文针对螺旋桨尾流不稳定性机理问题, 基于粒子图像测速试验以及不同湍流模拟方法(大涡模拟、延迟分离涡模拟、无湍流模型模拟)为手段, 进行了不同进速系数条件下螺旋桨梢涡的不稳定性触发机制研究. 根据探索得到的螺旋桨尾流不稳定性触发机理提出了螺旋桨梢涡演化模型, 对梢涡的迁徙过程进行模拟, 并预测梢涡合并的时间和位置, 以期为基于流动控制技术的螺旋桨减振降噪设计提供基础性支撑.
1. 几何模型
本文的研究对象为七叶螺旋桨INSEAN E1658[23], E1658螺旋桨的主要几何参数如表1所示. 图1给出了E1658螺旋桨的几何模型示意图和参考系统, 其中x轴为旋转轴, 指向下游, z轴指向上, y轴由右手定则确定.
表 1 E1658螺旋桨的几何参数Table 1. Main parameters of E1658 propellerParameters Unit Value diameter mm 250 number of blades − 7 hub/diameter ratio − 0.227 chord at 0.95R mm 6.8 2. 试验设置
螺旋桨的尾流场测量试验在意大利国家研究委员会海洋工程研究所(CNR-INM)的空泡水筒中进行, 其测试段尺寸为0.6 m × 0.6 m × 2.6 m (高 × 宽 × 长), 总长度为13.9 m, 总高度为9.3 m. 该设备中来流的湍流度在2%以内, 平均轴向速度和垂向速度的不均匀度分别在1%以内和3%以内.
本文中螺旋桨的尾流场测量采用2D-PIV系统进行测量[24-25], 该粒子图像测速测量系统的照明由双腔Nd-Yag激光器(Quantel Twins, 每个脉冲200 mJ, 重复频率12.5 Hz, 波长532 nm)以及圆柱发散透镜(−15 mm焦距)和球面透镜组合提供(5000 mm焦距), 激光器的片光通过安装在测试截面处底部的窗户向上照射, 散射光是由多相机记录系统采集的, 该系统由LaVision的4台Imager sCMOS相机组成, 该相机能达到每秒50帧的帧速率, 其分辨率为2560 × 2160像素. 每个相机都配备了尼康的Nikkor AF-S 85 mm f/1.4G镜头, 其光圈设置为f/8. 照相机在光轴垂直于激光片的纵向上并排布置, 该试验设置方案已经在类似的实验研究中采用[26-27].
粒子图像测速采集系统会在螺旋桨被选定的参考叶片通过固定角位置时被触发, 该锁相测量是通过TTL信号将粒子图像测速相机系统和激光脉冲同步到螺旋桨每转一圈工作一次的频率来实现的, 该信号由安装在螺旋桨测力计上的每秒3600脉冲的旋转增量编码器提供, 这种同步是通过可编程计时单元(LaVision PTU)实现的. 粒子图像测速测量系统如图2所示.
3. 计算流体力学模拟
本文数值计算的工作主要基于REX求解器开展, REX[28]是一款通用的应用于船舶水动力学领域的自编程求解器, 它在爱荷华大学得到持续开发和维护. 该求解器中模型的运动通过动态重叠网格技术实现[29-30]. REX基于多块结构化贴体网格进行空间离散, 并支持局部网格的加密算法. 动量方程中速度与压力采用PISO算法进行解耦, 控制方程中的对流项采用四阶迎风格式进行离散, 而扩散项的离散则采用二阶中心格式处理, 时间项应用的是二阶隐式欧拉向后差分格式进行离散化, 延迟分离涡模拟模型中远场大涡模拟区域的正交网格区域采用的是二阶中心对流格式. 本文中采用的延迟分离涡模拟模型和大涡模拟模型的详细信息请参考文献[19]和文献[31].
计算域采用多块重叠/结构网格进行离散. 螺旋桨敞水条件下的计算并没有包含粒子图像测速试验中空泡水筒的壁面, 其计算域包括一个延伸到下游3.5倍螺旋桨直径的环形加密区. 这套网格以及笛卡尔尾流加密块均是正交的, 因此可以采用低耗散的二阶中心对流算法. 多块结构化网格划分以及计算核数分配细节如表2所示, 表中“Ref1”为一个长方体的背景网格加密区, 而“Ref2”为一个圆环状的柱体, 用来加密下游的梢涡演化区. 图3给出了E1658螺旋桨梢涡计算网格分布, 网格总数为1.927 × 108. 本文计算网格均满足壁面到第一层网格的无量纲距离y+ < 1这一条件. 数值模拟的无量纲时间步长
$\Delta t = 4.478\;9 \times {10^{ - 5}}$ , 它相当于螺旋桨每旋转0.4675°所需要的时间. 数值计算一共采用458核进行并行计算.表 2 螺旋桨网格系统Table 2. Details of the grid system for the propellerGrid Size Grid points/103 Grid type shaft 241 $ \times $ 91 $ \times $ 241 5285 O blades 7 $ \times $ 241 $ \times $ 61 $ \times $ 181 7 $ \times $ 2661 O tips 7 $ \times $ 145 $ \times $ 61 $ \times $ 101 7 $ \times $ 893 wrapped Ref1 603 $ \times $ 251 $ \times $ 251 37 990 cartesian Ref2 1141 $ \times $ 101 $ \times $ 1081 124 576 cylindrical total − 192 730 − 4. 结果与分析
4.1 螺旋桨尾流特性分析
本文中相平均流场采用下式进行计算
$$\left\langle f \right\rangle \left( {x,y,{\textit{z}}} \right) = \frac{1}{N}\sum\limits_{i = 1}^N {f\left( {x,y,{\textit{z}},{t_0} + \frac{{i - 1}}{n}} \right)} $$ (1) 式中
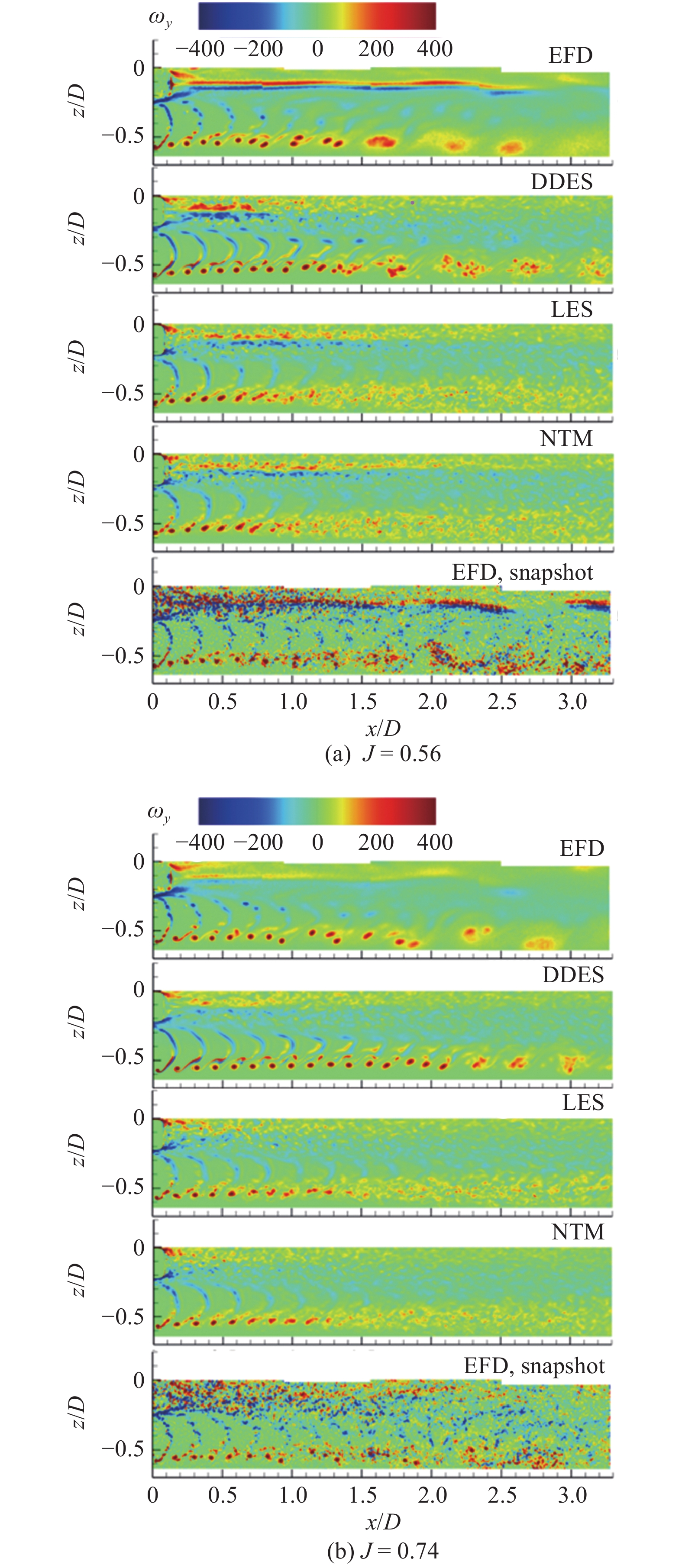
$\left\langle f \right\rangle $ 代表任一物理量f的相平均结果, N为所有参考桨叶在同一角位置时的瞬态流场总数, t0为流动充分发展之后开始采样的时刻, n为螺旋桨转速.图4给出了基于计算流体力学计算和粒子图像测速测量得到的不同工况条件下的相平均涡量场, 相平均结果是基于螺旋桨每旋转一周的锁相结果进行统计的, 目的是保证梢涡配对有一个螺旋桨旋转周期的观察时间. 其中, 计算流体力学计算的相平均结果是在螺旋桨旋转20圈、螺旋桨尾流达到稳定状态之后开始统计的, 有效避免了前期非稳定的结果对相平均统计的影响. 另外, 图4也包括了粒子图像测速试验测量得到的瞬态涡量场. 从图中可以看出, 计算流体力学和工程流体力学结果中都能清楚的观察到梢涡、桨叶随边泄出涡以及桨毂毂涡. 随边泄出涡存在于叶梢和根部的范围, 并很快在下游尾流中耗散了. 总体而言, 在同样的网格和物理条件下, 相比较于延迟分离涡模拟, 大涡模拟和无湍流模型模拟能求解出更多的湍流细节, 并且呈现出更早的梢涡不稳定性和随边涡的崩溃. 相比较于粒子图像测速试验结果, 大涡模拟和无湍流模型模拟似乎过早地失去了梢涡结构的连贯性, 且在超过x/D = 1范围的涡结构并没有出现. 在x/D > 1的范围内, 大涡模拟和无湍流模型模拟计算中的梢涡分解成了一系列小的涡结构. 对于J = 0.56工况的试验结果, 见图4(a)梢涡配对过程大约开始于x/D = 1的位置, 在x/D = 1.5位置处结束. 然而在相同的进速系数条件下, 延迟分离涡模拟预测的梢涡配对发生在下游更远的位置, 较为滞后. 产生这种现象的原因可能有两个, 一个是试验中螺旋桨进流中存在一定的湍流度, 从而触发了更早的尾流不稳定性; 另一个是试验中空泡水筒存在一定的阻塞效应. 值得注意的是, 计算流体力学中较差的统计(这是由于计算量和计算资源的限制, 导致计算流体力学模拟中可以用于相平均统计的样本远远没有粒子图像测速试验的多)导致梢涡配对发生时有噪音簇, 但是依然能观察到由于梢涡配对产生的较大涡处的涡量块. 粒子图像测速试验的瞬态流场结果表明在x/D > 1.4的范围内存在丰富的小尺度涡结构, 但是也存在一定有组织的大尺度涡结构, 这与延迟分离涡模拟的计算结果相似.
![]()
图 4 不同工况下的相平均涡量场Figure 4. Phase-averaged out-of-plane vorticity at different loading conditions桨叶随边泄出的涡结构呈现出小的局部涡结构, 它们的连贯性很快就随着继续演化后快速消失了, 这表明梢涡和桨叶随边泄出的这些小的涡结构的相互干扰效应并没有文献[17]描述的那么强, 这可能是螺旋桨几何形状以及工况不同的原因造成的. 但是这种干扰对梢涡不稳定性的影响是不容忽视的. 计算流体力学和工程流体力学结果在J = 0.74时表现出了与高载荷情况时相同的趋势, 见图4(b). 在这种高进速系数工况下, 梢涡不稳定性的触发点更加延后, 大概在螺旋桨盘面下游x/D = 1.4的位置, 并且可以在x/D > 1.75的位置观察到梢涡对.
另外可以看到, 在J = 0.56的工程流体力学结果中, 毂涡在下游很长的距离都能保持相对稳定, 然而延迟分离涡模拟的结果中, 毂涡较早就出现了崩溃的现象. 试验得到的瞬态涡量场中, 毂涡在x/D < 2.5的范围内都能保持连贯性. 值得注意的是, 大涡模拟和无湍流模型模拟方法能够捕捉到比延迟分离涡模拟方法连贯性更强的毂涡. 在J = 0.74时, 工程流体力学结果的毂涡耗散较为严重, 这与延迟分离涡模拟模拟较为一致.
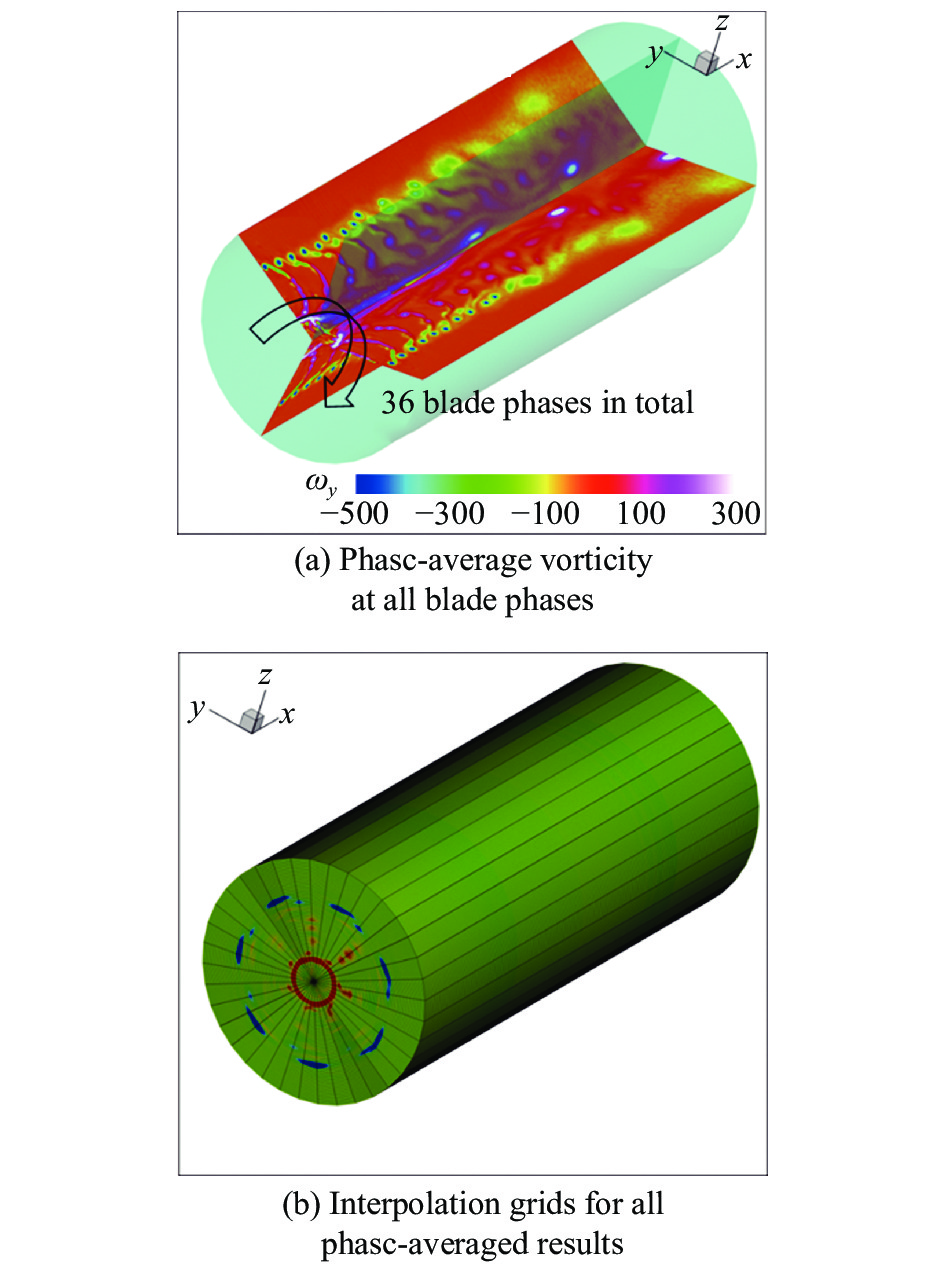
利用粒子图像测速试验测量得到的所有桨叶相(36个)的相平均结果, 进行螺旋桨尾流3D漩涡结构的重构. 如图5所示, 在圆柱坐标系统中导入流场试验得到的所有叶相的相平均流场, 并按照下式将网格插值到圆柱网格上
![]()
图 5 试验结果三维梢涡结构的插值方法Figure 5. Interpolation methods for calculating 3D tip vortex structures of experiments$$\left. \begin{array}{l} x\left( {i,j,k} \right) = {x_0}\left( {i,j,k} \right) \\ y\left( {i,j,k} \right) = r\left( {i,j,k} \right) \times \sin {\varphi \left( k \right)} \\ {\textit{z}}\left( {i,j,k} \right) = r\left( {i,j,k} \right) \times \cos {\varphi \left( k \right)} \end{array} \right\}$$ (2) 式中x, y, z为插值得到的新坐标,
$r = \left| {{y_0}\left( {i,j,k} \right)} \right|$ , x0, y0为原始相平均流场中的坐标, i和j分别为两个方向的索引, k为不同的桨叶相对应的流场索引,$\varphi $ 为不同叶相对应的角度. 流场按照下式插值到圆柱网格上$$\left. \begin{array}{l} u\left( {i,j,k} \right) = {u_0}\left( {i,j,k} \right) \\ v\left( {i,j,k} \right) = {v_0}\left( {i,j,k} \right) \times \sin {\varphi \left( k \right)} \\ w\left( {i,j,k} \right) = {v_0}\left( {i,j,k} \right) \times \cos {\varphi \left( k \right)} \end{array} \right\}$$ (3) 式中u, v, w和u0, v0分别为插值后的3个速度分量和原始相平均流场(2D-2C)中的两个速度分量.
图6给出了不同载荷条件下, 采用上述方法对工程流体力学结果重构的三维相平均漩涡结构, 其中涡结构采用无量纲轴向速度进行着色. 三维涡结构采用涡量等值面进行显示, 即
$ {\omega _y} = 100$ 的等值面. 为了显示清晰的梢涡结构, 图6中内半径处的涡结构即毂涡部分被移除了. 图6也给出了基于延迟分离涡模拟方法模拟得到的相平均三维涡结构, 漩涡分别定义为J = 0.56的Q = 15000等值面以及J = 0.74的Q = 20000等值面. 试验结果显示梢涡的最初合并是靠近螺旋桨盘面成对的, 然后是各对之间的合并. 由于漩涡的蜿蜒会引起相位平均涡度分辨率的损失, 使得很难识别到成对的、三重和四重漩涡. 相比于两种载况条件下的计算流体力学结果, 试验结果的初始漩涡合并更靠近螺旋桨盘面, 梢涡的不稳定性更早地被触发.![]()
图 6 不同工况下相平均三维涡结构Figure 6. Three-dimensional phase-averaged vortical structures at different loading conditions图7为基于延迟分离涡模拟、大涡模拟和无湍流模型模拟方法计算得到的瞬态螺旋桨尾涡结构, 对于J = 0.56工况, 漩涡结构由Q = 200000等值面显示, 对于J = 0.74, 漩涡结构由Q = 100000等值面显示. 这些瞬态视图更好地展现了相位平均结果的梢涡配对和不稳定性. 从不同工况以及不同数值方法得到的结果可以看到构成漩涡系统的梢涡、随边涡以及毂涡. 与延迟分离涡模拟方法计算得到的结果相比, 大涡模拟和无湍流模型模拟方法预测了更早的漩涡不稳定性和崩溃, 因此难以观测到试验中的梢涡配对现象. 在近场中可以观察到椭圆不稳定性, 随着梢涡彼此之间的距离越来越近, 椭圆不稳定性会不断增强. 漩涡合并会产生显著的顺流方向涡量, 并且在梢涡崩溃之前可以观察到更大范围的椭圆不稳定性现象. 在螺旋桨下游更远处, 梢涡趋于分解为逐渐变小的涡结构, 从而完全抑制了螺旋涡的合并. 在相同时间和网格分辨率下, 相比于大涡模拟模型, 无湍流模型模拟模型似乎能求解更多的湍流, 因此其预报的梢涡不稳定性发生的更早.
延迟分离涡模拟方法得到的结果显示了随着合并过程的发展梢涡是如何相互缠绕的, 但是梢涡的完全合并在瞬态计算结果中并未发生. 在J = 0.56时, 梢涡配对会更早的发生, 并且合并的漩涡在精细的计算域内会变得不稳定, 从而展现了漩涡系统崩溃的过程, 这在图6的相平均漩涡结构中表现为多个梢涡合并时的嘈杂尾流. 在J = 0.74时, 梢涡的合并进一步向下游延后, 并且在计算流体力学结果无法精细求解漩涡结构的梢涡加密区末端变得不稳定. 图7中延迟分离涡模拟结果在远场的漩涡结构与文献[26]中E779A螺旋桨的试验结果相似, 试验中E779A螺旋桨的梢涡分组但并未合并, 另外本文计算结果中的梢涡蛙跳现象和其他现象也与该试验中捕捉到的梢涡行为相近.
螺旋桨尾流结构被漩涡合并所支配. 图8给出了计算流体力学计算得到的梢涡合并过程, Q准则等值面显示的涡结构突出了梢涡的合并过程. 为了便于分析, 图8对从不同桨叶泄出的梢涡进行了编号. 从图8可以看到, 4号梢涡将3号梢涡推进内部轴向速度较高的尾流区, 本质上是包裹住梢涡以使其靠近并最终完成合并. 由于初始合并成对发生且当前螺旋桨有7个叶片, 因此合并对的角间隔应该在大约103°处发生, 这与1号梢涡和2号梢涡对相对于3号梢涡和4号梢涡对之间的距离接近. 同样, 如果螺旋桨叶片的数量是偶数, 则所有成对合并的梢涡都应该在螺旋桨盘面下游大约相同距离处产生互感. 涡对1 + 2和3 + 4确实在图8中的相同轴向位置合并. 在具有奇数个叶片的螺旋桨中, 必定有一个梢涡与已经合并的一对梢涡进行合并, 这是因为合并后的相邻涡对会产生更强的感应. 在图8中梢涡5会与6 + 7涡对合并, 形成新的组合涡5 + 6 + 7. 梢涡6和梢涡7在梢涡1 + 2和梢涡3 + 4合并的下游更远处合并, 这很可能是由于奇数叶片配置的螺旋桨的不对称效应引起的. 最后, 漩涡1 + 2, 3 + 4和5 + 6 + 7会产生进一步的互感效应, 导致漩涡1 + 2和漩涡3 + 4合并为漩涡1 + 2 + 3 + 4. 随着漩涡强度由于扩散而衰减(或漩涡由于不稳定性而崩溃), 并且由于合并而导致漩涡之间的距离增加, 因此在尾流中出现单个(理想状态下最终会合并成单个涡)涡之前, 该过程可能会停止. 另外, 图8也显示了漩涡合并之前和合并之后更加强烈的椭圆不稳定性的存在.
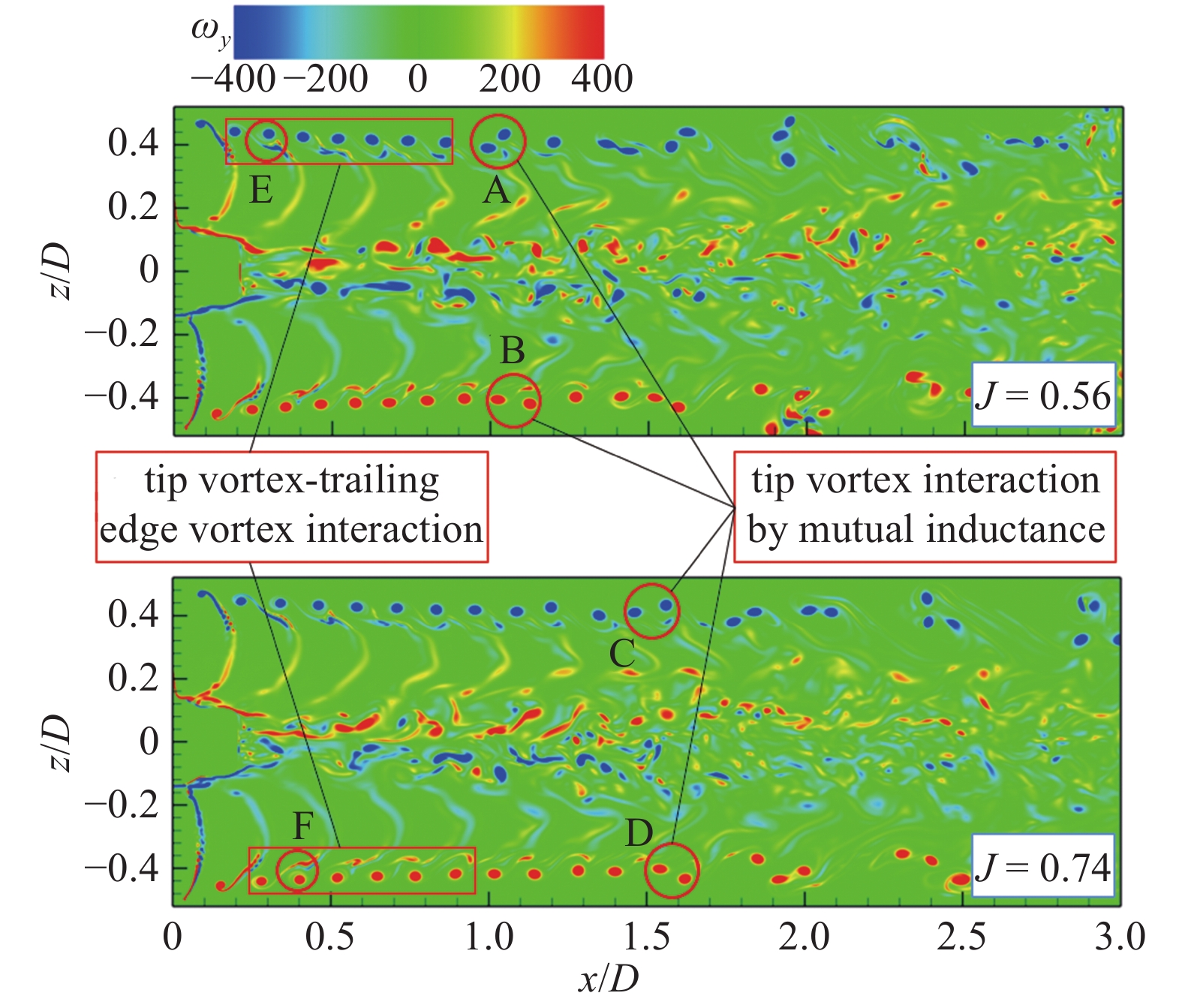
图9给出了两个工况条件下桨后的瞬态涡量云图, 图中可以清晰的看到梢涡不稳定性的触发过程. 梢涡和随边涡分别从桨叶的叶梢和随边泄出, 在向下游演化的过程中, 梢涡会与其上游相邻梢涡的随边涡产生干扰(如图9中的E区和F区所示), 并伴有各个梢涡之间的互感效应. 在继续向下游演化的过程中, 梢涡的不稳定性被触发, 如图9所示的A区、B区、C区和D区所示, 具体表现为这4个区域中的下游梢涡将上游梢涡推入内半径处高速剪切层流中, 这与图7中的分析一致, 产生这一现象的原因是梢涡在向下游演化的过程中, 其周向速度会逐渐出现扩散, 最终它们会有足够的周向速度来抵达相邻梢涡, 这会导致梢涡互感效应, 其中涡龄越大的梢涡(从桨叶泄出时间长, 即下游梢涡)周向速度扩散更为严重, 直到梢涡演化到流场中的某一点处时, 下游梢涡有足够的周向速度作用在相邻的上游梢涡上, 从而在高速剪切层流和随边涡的双重影响下, 触发梢涡的不稳定性.
![]()
图 9 不同工况下梢涡不稳定性触发过程Figure 9. Instability inception process of tip vortices under different conditions4.2 梢涡演化模型
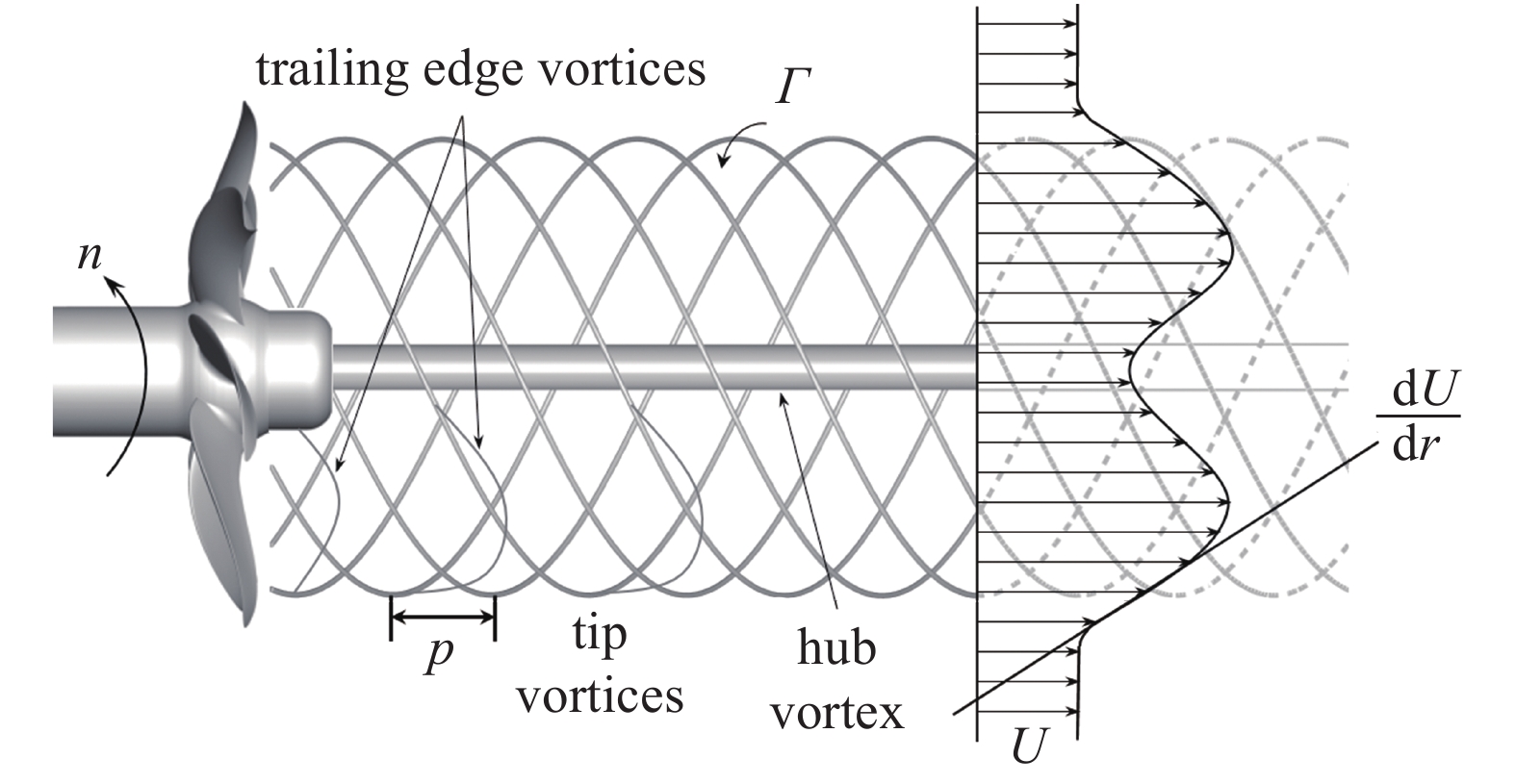
二维同向旋转漩涡的不稳定性和配对问题是湍流动力学中的重要问题, 受到了大量学者的关注[32-33]. 螺旋桨尾流中就包含着这一基本问题, 因为螺旋桨梢涡也是一系列天然的同向旋转漩涡, 但它们又在很多方面都比线性涡对复杂得多. 它们除了呈现出螺旋状的几何结构, 也同时沉浸在由螺旋桨推力和尾流中的高速区造成的剪切层中. 另外, 螺旋桨产生了一个尾流涡旋, 它的旋转速度取决于螺旋桨载荷, 大概是螺旋桨转速的1% ~ 5%. 更重要的是, 桨叶升力产生的随边涡可以与螺旋桨梢涡相互作用, 这都使得螺旋桨尾涡系统异常的复杂. 螺旋桨尾涡结构如图10所示, 其中p为梢涡螺距.
本文4.1节对螺旋桨尾流动力学特性包括不稳定性触发和梢涡配对进行了详细的计算流体力学和工程流体力学分析, 结论表明螺旋桨梢涡的互感效应以及梢涡−叶尾流(随边涡)的相互干扰是螺旋桨尾流不稳定性触发的主要原因(计算流体力学计算中不考虑来流中的背景湍流度), 其中梢涡周向速度随时间的耗散在梢涡互感效应中扮演者十分重要的作用, 相关定性的机理分析能够较好地对螺旋桨梢涡的不稳定性行为进行解释, 但有关螺旋桨梢涡演化规律的定量描述由于漩涡合并机制以及螺旋桨尾涡系统的复杂性至今仍没有公开发表的文献涉及, 大多数文献目前都只对这一问题进行了多工况下的多角度定性分析. 基于探索得到的均匀来流中螺旋桨梢涡的演化机理, 本文提出了螺旋桨梢涡的演化模型, 该模型基于涡−涡之间周向诱导速度相互作用的方式, 首次定量地描述了梢涡之间的互感效应和随边涡与梢涡之间的相互作用以及梢涡不稳定性的触发. 该模型包含了本文目前已探明的螺旋桨尾流不稳定性机理, 能够较为准确地模拟螺旋桨梢涡的演化规律, 预测螺旋桨梢涡融合的时间和位置, 相关研究为进一步理解螺旋桨尾流的动力学特征提供了指导作用.
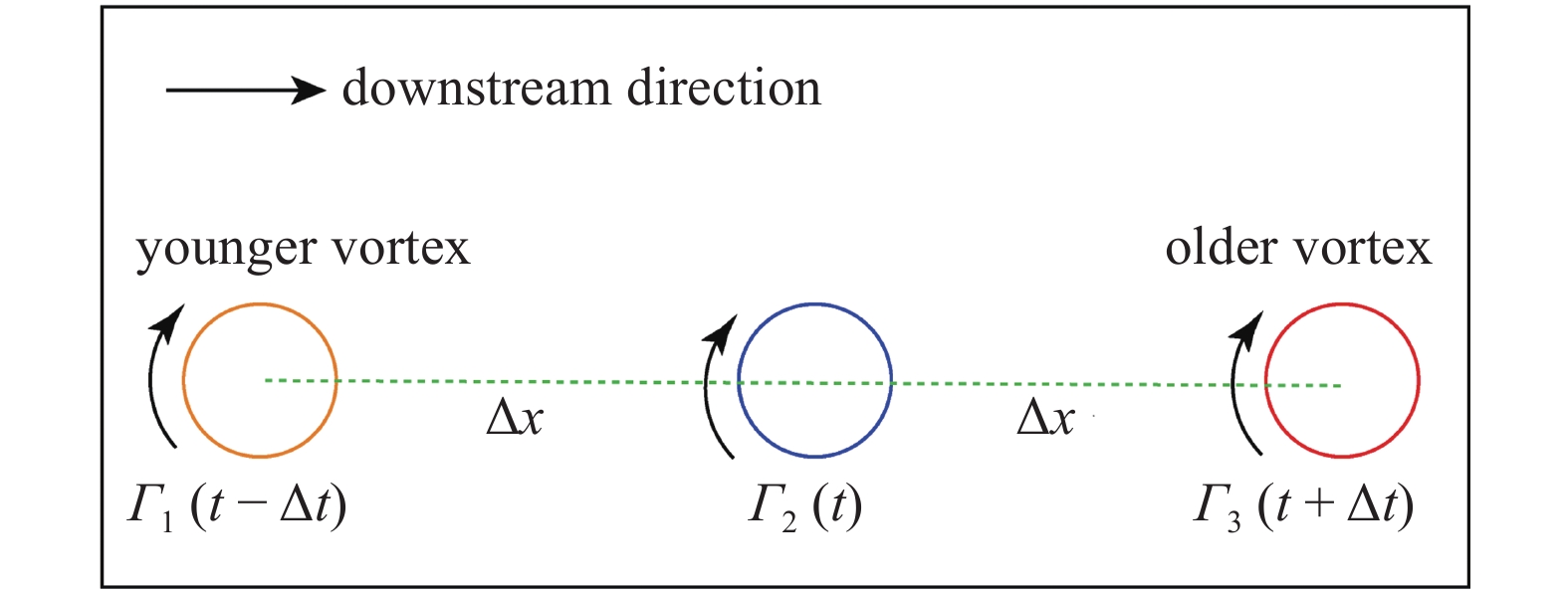
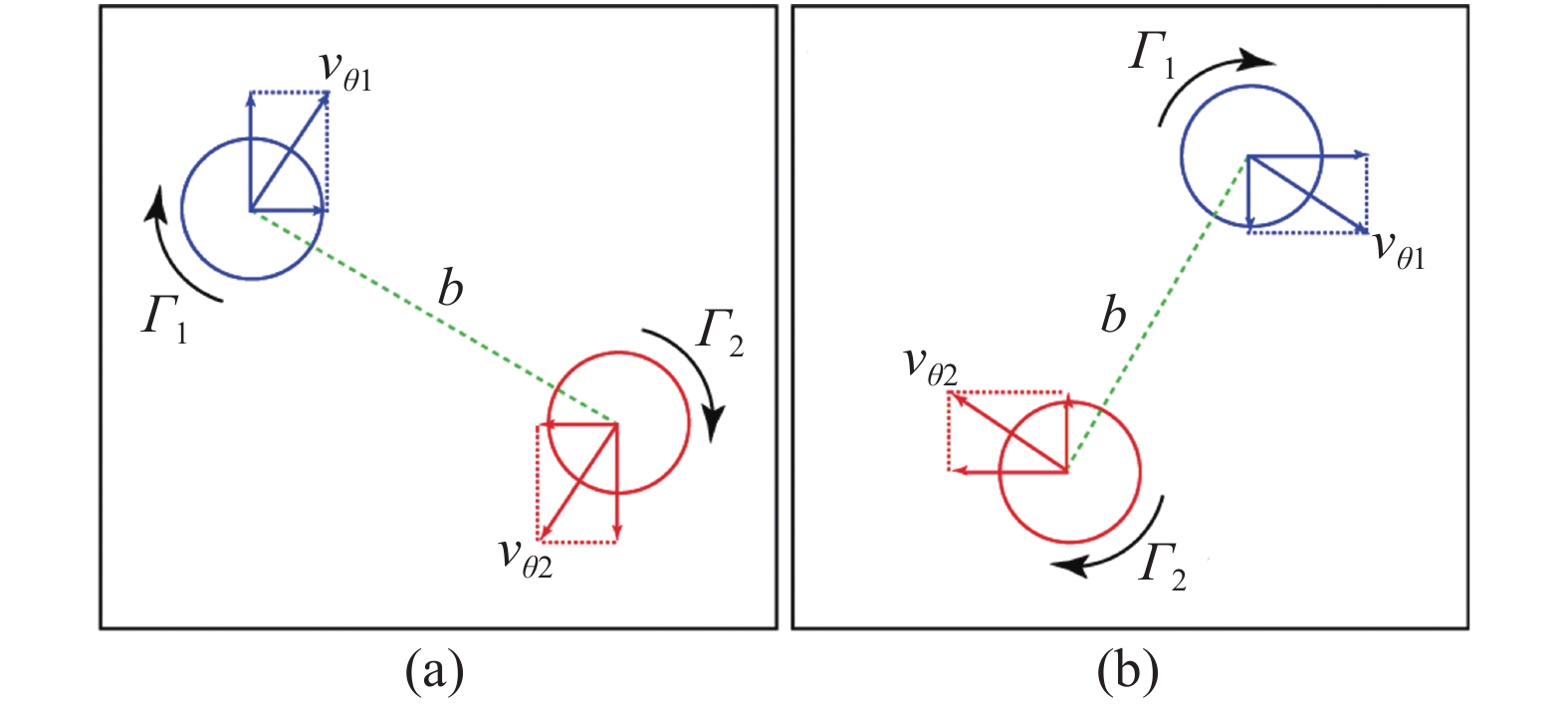
通过4.1节的分析可以知道, 对于某给定位置的梢涡, 其会分别受到一侧更年轻(涡龄越小, 即从桨叶泄出的时间越短)的梢涡和另一侧更老的梢涡周向诱导速度的影响, 且更老梢涡的影响更加强烈. 螺旋桨下游不同涡龄梢涡示意图如图11所示.
考虑二维梢涡周向速度由以下极坐标系下的无量纲方程控制
$$\frac{{\partial {v_{\theta} }}}{{\partial t}} = \frac{1}{{{{Re}} }}\left( {\frac{{{\partial ^2}{v_{\theta} }}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {v_{\theta} }}}{{\partial r}} - \frac{{{v_{\theta} }}}{{{r^2}}}} \right)$$ (4) 式中
${v_{\theta} }$ 为周向速度, 其初始速度剖面从计算流体力学结果中螺旋桨桨叶后的第一个参考梢涡中提取. 边界条件的选取也十分关键, 为了符合本模型的物理机理, 左右边界的边界条件均为${v_{\theta} } = 0$ , 需要注意的是, 如果右边界不为零, 得到的速度剖面数值解为Lamb−Oseen涡的速度剖面形式, 显然该形式不满足本模型的假设. 雷诺数计算的参考速度和参考长度与计算流体力学计算中保持一致, r为任意点到涡核中心的距离.螺旋桨尾涡与传统研究中同向旋转漩涡不稳定性问题的另一个区别是, 螺旋桨尾流中的梢涡存在轴向迁徙速度, 即螺旋桨尾涡系统中的涡结构在相互作用的同时也存在轴向迁徙. 风机需要从流场中抽取能量, 因此其尾流是向外径扩散的, 而螺旋桨工作的原理是加速尾流产生推力, 因此其尾流是收缩的. 螺旋桨后收缩尾流中的涡结构演化也给其不稳定性的研究带来了复杂性. 为了得到更加真实的涡系演化模拟结果, 本文提出的模型也考虑了中纵剖面内梢涡沿轴向和垂向的基础迁徙速度, 这两个速度从时间平均流场中双线性插值而来, 且取决于梢涡和随边涡在流场中的具体位置. 为了便于计算涡结构在每个时间步的位移, 涡结构上的诱导速度被分解为沿轴向和垂向的速度成分, 速度分解的原则如图12所示.
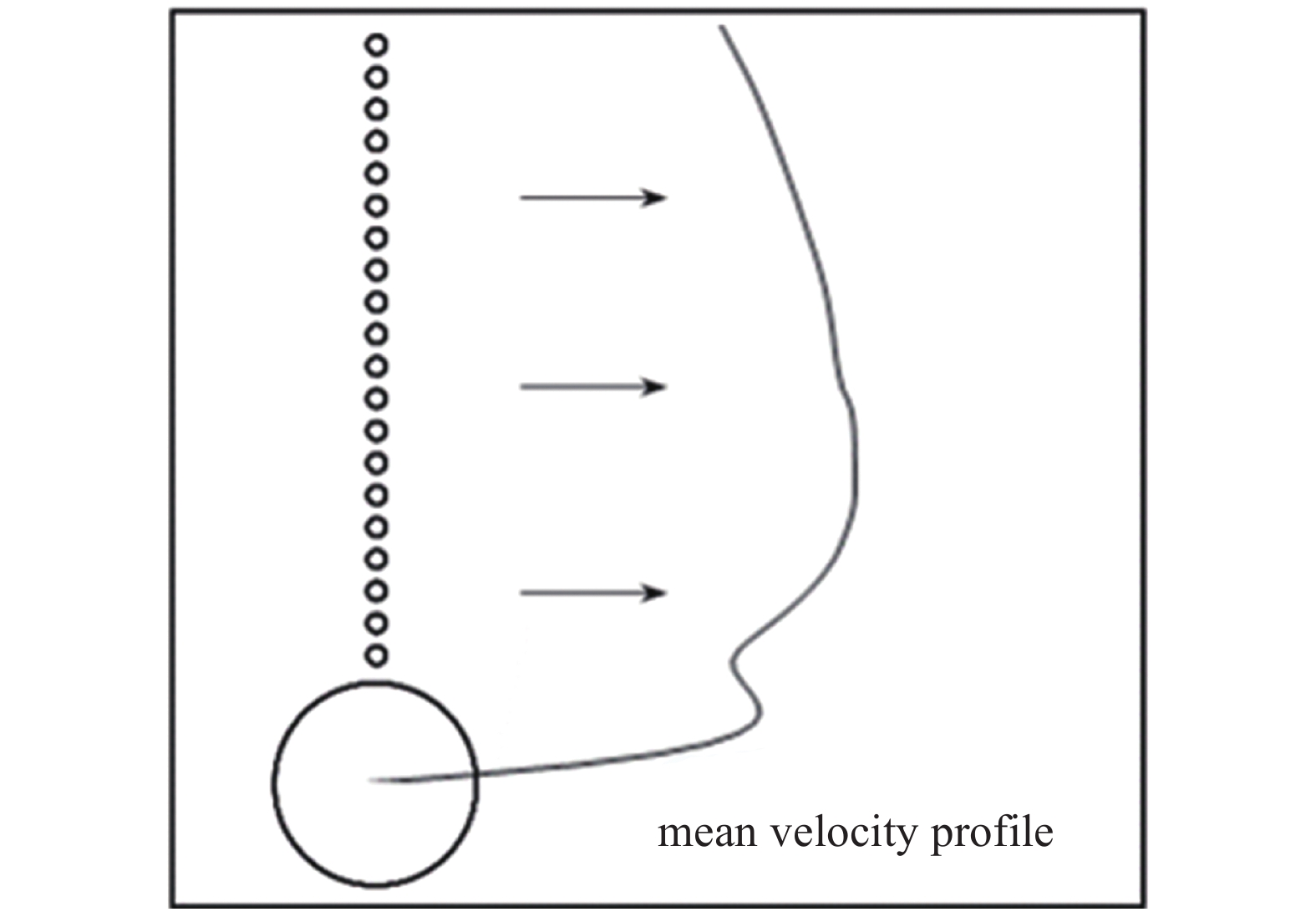
本模型中初始时刻漩涡系统配置的描述如图13所示, 图13中尺寸较大的圆代表桨后的梢涡, 而尺寸较小的一系列圆代表随边涡, 用来模拟桨叶尾流.
图13中, 以大圆的圆心为垂向位置的零点, 小圆则在垂向方向上等间距的排列, 与尾流中随边涡的特征尺度一致. 每过一个螺旋桨桨叶通道的时间, 就会初始化一套图13中的梢涡−随边涡系统, 这与螺旋桨在运行时生成桨后尾涡系统的过程一致.
涡结构之间的相互作用方式是本模型的核心问题之一, 为了简化涡结构之间的相互作用, 多个漩涡之间的作用采用线性叠加的方式进行评估. 假设t时刻, 流场中存在M个梢涡, N个随边涡, 则基于线型叠加得到的流场中第j个梢涡的诱导速度可以表示为
$$ \begin{split} {\boldsymbol{u}}_j^V\left( {t,{{\boldsymbol{x}}_{Vj}}} \right) =& \sum\limits_{\begin{subarray}{l} i = 1 \\ i \ne j \end{subarray}} ^M {{{\boldsymbol{u}}_{Vi}}\left( {t,{{\boldsymbol{x}}_{Vi}} - {{\boldsymbol{x}}_{Vj}}} \right)} + \\& \sum\limits_{i = 1}^N {{{\boldsymbol{u}}_{Ti}}} \left( {t,{{\boldsymbol{x}}_{Ti}} - {{\boldsymbol{x}}_{Vj}}} \right) + {{\boldsymbol{u}}_{\rm{m}}}\left( {{{\boldsymbol{x}}_{Vj}}} \right) \end{split}$$ (5) 式中
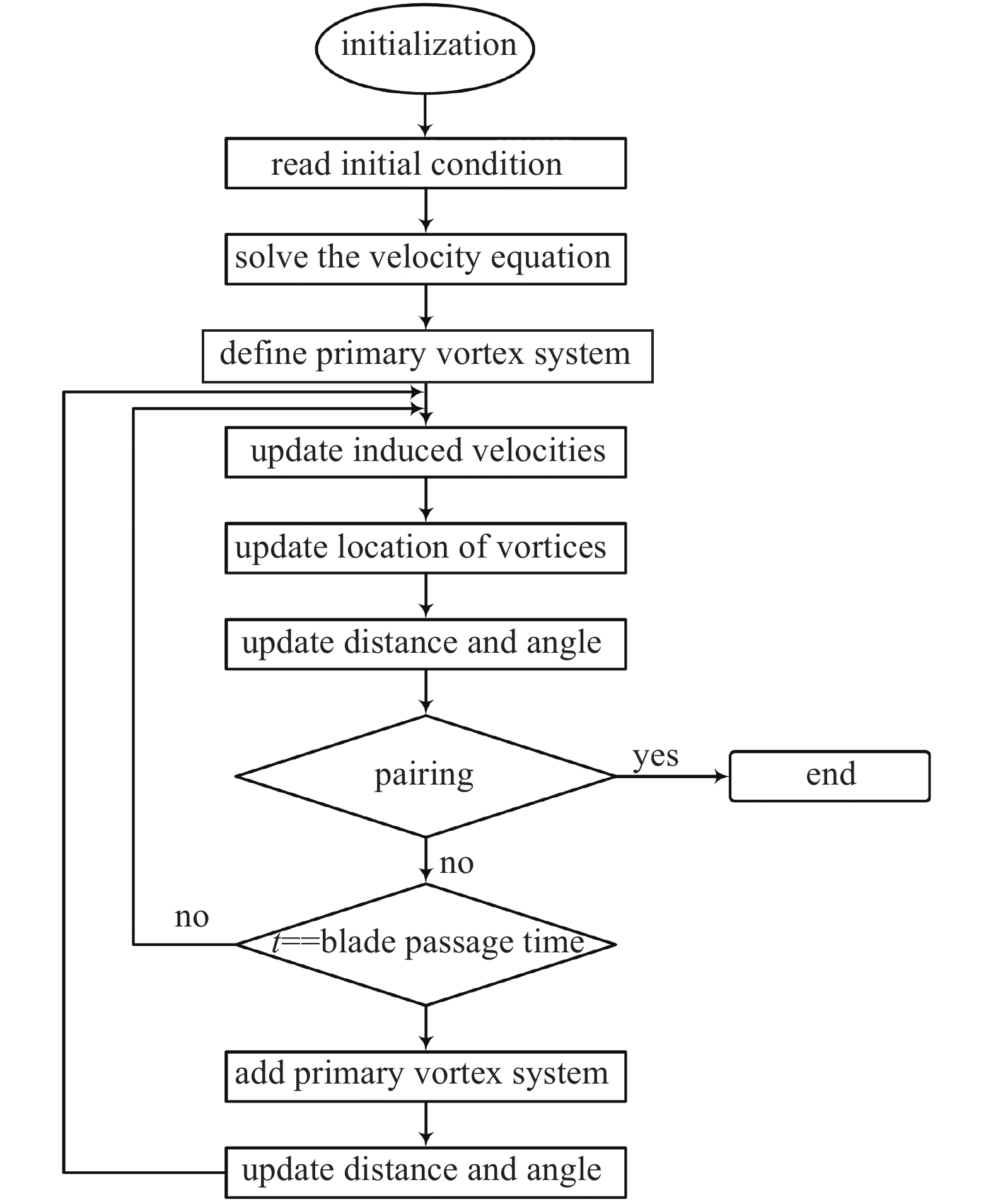
${{\boldsymbol{u}}_{Vi}}$ 是第i个梢涡诱导的速度,${{\boldsymbol{u}}_{Ti}}$ 是第i个随边涡诱导的速度,${{\boldsymbol{x}}_{Vi}}$ 代表第i个梢涡的位置,${{\boldsymbol{x}}_{Ti}}$ 代表第i个随边涡的位置.${{\boldsymbol{u}}_{\rm{m}}}$ 是从螺旋桨时间平均尾流场中获得的速度. 在每个时间步涡的速度计算完之后, 涡的位移可已通过速度对时间的积分计算, 例如流场中第j个梢涡的位移可通过下式计算$$\left. \begin{array}{l} S_{j,x}^V\left( t \right) = \displaystyle\int_0^t {u_{j,x}^V} \left( t \right){\rm{d}}t \\ S_{j,y}^V\left( t \right) = \displaystyle\int_0^t {u_{j,y}^V\left( t \right)} {\rm{d}}t \end{array} \right\}$$ (6) 图14给出了演化模型运行程序的流程图, 具体计算流程如下:
(1)准备涡系统. 读取初始条件, 求解诱导速度偏微分方程, 并给定初始漩涡的位置, 计算各漩涡之间的距离和分解角度, 读取各自的周向诱导速度, 开始迭代.
(2)更新诱导速度. 主要分为三部分. 第一, 梢涡在梢涡上产生的诱导速度; 第二, 梢涡在随边涡上产生的诱导速度; 第三, 随边涡在梢涡上产生的诱导速度. 并插值获得基本迁徙速度, 计算得到轴向和垂向速度分量.
(3)更新漩涡位置. 根据上一步中计算得到的速度分量获得轴向和垂向位移, 根据此位移计算得到漩涡新的位置.
(4)更新涡距和角度. 根据漩涡在流场中新的位置, 计算各个漩涡之间的涡距并计算它们的速度分解角度.
(5)判定计算是否满足停止条件, 即有两个梢涡在轴向上位置重合, 如是则计算停止, 如否则判定时间是否等于一个桨叶通道的时间, 如否继续从第2步开始迭代, 如是则向流场中添加新的梢涡和随边涡初始系统.
(6)更新新进梢涡和随边涡与流场中其他漩涡的涡距和速度分解角.
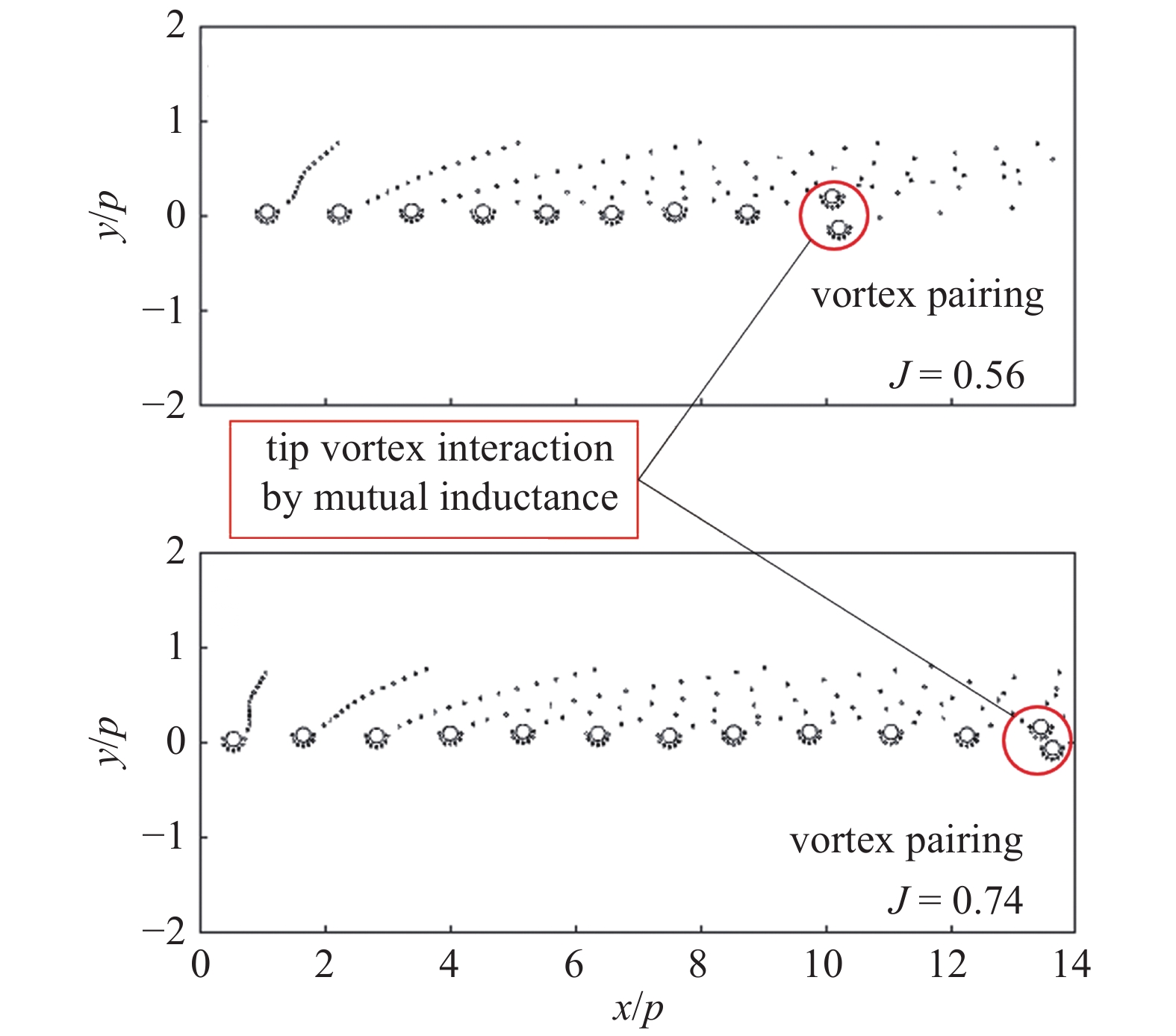
用来验证此模型的工况为计算流体力学计算中的J = 0.56和J = 0.74工况, 梢涡的周向速度剖面随时间的变化通过式(4)求解得到, 随边涡的初始周向速度在计算流体力学计算中从对应的垂向位置提取. 漩涡的基本迁徙速度采用双线性插值的方法在梢涡和随边涡对应位置的时间平均流场中提取. 图15给出了采用梢涡演化模型预报得到的J = 0.56和J = 0.74工况漩涡融合时对应的瞬态漩涡系统. 从图15中可以看出梢涡融合的位置和时间均与图9中的计算流体力学计算结果吻合较好, 表明本文挖掘的梢涡不稳定性触发物理机制较为准确, 提出的梢涡演化模型和算法能够有效地模拟梢涡的演化和梢涡的不稳定性触发过程.
![]()
图 15 采用模型预报得到的J = 0.56和J = 0.74时的瞬态漩涡系统Figure 15. Instantaneous vortex system predicted by proposed model at J = 0.56 and J = 0.745. 结论
长期以来, 螺旋桨尾流的不稳定性研究无论是从工程技术的角度, 还是作为一个基础的流体力学问题, 都一直深受广大学者的关注. 但就目前公开发表的文献来看, 不管是粒子图像测速试验还是高精度的计算流体力学模拟, 大多数有关螺旋桨尾流不稳定性的研究都是定性的, 往往都是通过观察到的流场信息和涡结构行为来定性的描述其不稳定性的机理, 这主要是由桨后涡系和演化过程本身的复杂性及其所处的剪切层流环境造成的. 计算流体力学模拟基于延迟分离涡模拟、大涡模拟和无湍流模型模拟模型开展, 结果表明与延迟分离涡模拟方法相比, 大涡模拟和无湍流模型模拟方法预测了更早的漩涡不稳定性和崩溃, 因此难以观测到试验中的梢涡配对现象. 延迟分离涡模拟模型能较好地捕捉到试验中的梢涡配对行为, 但预报的梢涡合并过程与粒子图像测速试验相比有所延后. 本文基于探索得到的均匀来流中螺旋桨梢涡的演化机理, 提出了螺旋桨梢涡的演化模型, 该模型基于涡−涡之间周向诱导速度相互作用的方式, 首次定量地描述了梢涡之间的互感效应和随边涡与梢涡之间的相互作用以及梢涡不稳定性的触发, 并能预测螺旋桨梢涡融合的时间和位置. 相关研究为进一步理解螺旋桨尾流的动力学特征、螺旋桨基于流动控制方法的降噪措施实施、以及新型螺旋桨的优化设计有着重要意义.
-
![]()
图 4 不同工况下的相平均涡量场
Figure 4. Phase-averaged out-of-plane vorticity at different loading conditions
![]()
图 5 试验结果三维梢涡结构的插值方法
Figure 5. Interpolation methods for calculating 3D tip vortex structures of experiments
![]()
图 6 不同工况下相平均三维涡结构
Figure 6. Three-dimensional phase-averaged vortical structures at different loading conditions
![]()
图 9 不同工况下梢涡不稳定性触发过程
Figure 9. Instability inception process of tip vortices under different conditions
![]()
图 15 采用模型预报得到的J = 0.56和J = 0.74时的瞬态漩涡系统
Figure 15. Instantaneous vortex system predicted by proposed model at J = 0.56 and J = 0.74
表 1 E1658螺旋桨的几何参数
Table 1 Main parameters of E1658 propeller
Parameters Unit Value diameter mm 250 number of blades − 7 hub/diameter ratio − 0.227 chord at 0.95R mm 6.8 
下载: 导出CSV
表 2 螺旋桨网格系统
Table 2 Details of the grid system for the propeller
Grid Size Grid points/103 Grid type shaft 241 $ \times $ 91 $ \times $ 241 5285 O blades 7 $ \times $ 241 $ \times $ 61 $ \times $ 181 7 $ \times $ 2661 O tips 7 $ \times $ 145 $ \times $ 61 $ \times $ 101 7 $ \times $ 893 wrapped Ref1 603 $ \times $ 251 $ \times $ 251 37 990 cartesian Ref2 1141 $ \times $ 101 $ \times $ 1081 124 576 cylindrical total − 192 730 −
下载: 导出CSV
-
[1] Long Y, Long X, Ji B, et al. Numerical simulations of cavitating turbulent flow around a marine propeller behind the hull with analyses of the vorticity distribution and particle tracks. Ocean Engineering, 2019, 189: 106310 doi: 10.1016/j.oceaneng.2019.106310
[2] 谢庆墨, 陈亮, 张桂勇等. 基于动力学模态分解法的绕水翼非定常空化流场演化分析. 力学学报, 2020, 52(4): 1045-1054 (Xie Qingmo, Chen Liang, Zhang Guiyong, et al. Analysis of unsteady cavitation flowover hydrofoil based on dynamic mode decomposition. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(4): 1045-1054 (in Chinese) [3] Wang L, Guo C, Su Y, et al. Numerical analysis of a propeller during heave motion in cavitating flow. Applied Ocean Research, 2017, 66: 131-145 doi: 10.1016/j.apor.2017.05.001
[4] Guo H, Zou Z, Wang F, et al. Numerical investigation on the asymmetric propeller behavior of a twin-screw ship during maneuvers by using RANS method. Ocean Engineering, 2020, 200: 107083 doi: 10.1016/j.oceaneng.2020.107083
[5] Wang L, Guo C, Xu P, et al. Analysis of the wake dynamics of a propeller operating before a rudder. Ocean Engineering, 2019, 188: 106250 doi: 10.1016/j.oceaneng.2019.106250
[6] 郭春雨, 徐鹏, 韩阳等. 自由面对潜艇尾流场流动特性影响研究. 力学学报, 2021, 53(1): 156-167 (Guo Chunyu, Xu Peng, Han Yang, et al. Research on the influence of free surface on the flow characteristics of submarine wake. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 156-167 (in Chinese) [7] Wang LZ, Guo CY, Su YM, et al. A numerical study on the correlation between the evolution of propeller trailing vortex wake and skew of propellers. International Journal of Naval Architecture and Ocean Engineering, 2018, 10(2): 212-224 doi: 10.1016/j.ijnaoe.2017.07.001
[8] Wang L, Guo C, Xu P, et al. Analysis of the performance of an oscillating propeller in cavitating flow. Ocean Engineering, 2018, 164: 23-39 doi: 10.1016/j.oceaneng.2018.06.036
[9] 李聪洲, 张新曙, 胡晓峰等. 高雷诺数下多柱绕流特性研究. 力学学报, 2018, 50(2): 233-243 (Li Congzhou, Zhang Xinshu, Hu Xiaofeng, et al. The study of flow past multiple cylinders at high Reynolds numbers. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(2): 233-243 (in Chinese) [10] 时北极, 何国威, 王士召. 基于滑移速度壁模型的复杂边界湍流大涡模拟. 力学学报, 2019, 51(3): 754-766 (Shi Beiji, He Guowei, Wang Shizhao. Large-eddy simulation of flows with complex geometries by using the slip-wall model. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 754-766 (in Chinese) [11] Muscari R, Mascio AD, Verzicco R. Modeling of vortex dynamics in the wake of a marine propeller. Computers & Fluids, 2013, 73(73): 65-79
[12] Di MA, Muscari R, Dubbioso G. On the wake dynamics of a propeller operating in drift. Journal of Fluid Mechanics, 2014, 754(9): 263-307
[13] 强光林, 杨易, 陈阵等. 基于车身绕流的低雷诺数湍流模型改进研究. 力学学报, 2020, 52(5): 1371-1382 (Qiang Guanglin, Yang Yi, Chen Zhen, et al. Research on improvements of LRN turbulence model based on flow around automobile body. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(5): 1371-1382 (in Chinese) [14] 王巍, 唐滔, 卢盛鹏等. 主动射流控制水翼空化的数值模拟与分析. 力学学报, 2019, 51(6): 1752-1760 (Wang Wei, Tang tao, Lu Shengpeng, et al. Numerical simulation and analysis of active jet control of hydrofoil cavitation. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(6): 1752-1760 (in Chinese) [15] Dubbioso G, Muscari R, Mascio AD. Analysis of the performances of a marine propeller operating in oblique flow. Computers & Fluids, 2013, 75(6): 86-102
[16] Jang, H, Mahesh, K. Large eddy simulation of flow around a reverse rotating propeller. Journal of Fluid Mechanics, 2013, 729: 151-179
[17] Kumar P, Mahesh K. Large eddy simulation of propeller wake instabilities. Journal of Fluid Mechanics, 2017, 814: 361-396 doi: 10.1017/jfm.2017.20
[18] Verma A, Jang H, Mahesh K. The effect of an upstream hull on a propeller in reverse rotation. Journal of Fluid Mechanics, 2012, 704(2): 61-88
[19] Chase N, Carrica PM. Submarine propeller computations and application to self-propulsion of DARPA Suboff. Ocean Engineering, 2013, 60(2): 68-80
[20] Zhu Z. Numerical study on characteristic correlation between cavitating flow and skew of ship propellers. Ocean Engineering, 2015, 99: 63-71 doi: 10.1016/j.oceaneng.2014.12.023
[21] 朱志峰, 方世良, 王晓燕. 空化螺旋桨非定常粘性流场特征分析. 中国科学: 技术科学, 2011, 41(2): 213-222 (Zhu Zhifeng, Fang Shiliang, Wang Xiaoyan. Characteristic analysis of unsteady viscous flow around a caviatating propeller. Scientia Sinica Technologica, 2011, 41(2): 213-222 (in Chinese) doi: 10.1360/ze2011-41-2-213 [22] 胡健, 马骋, 黄胜等. 螺旋桨尾流场的数值分析. 哈尔滨工程大学学报, 2008, 29(12): 1255-1260 (Hu Jian, Ma Cheng, Huang Sheng, et al. Numerical analysis of flow fields behind propellers. Journal of Harbin Engineering University, 2008, 29(12): 1255-1260 (in Chinese) doi: 10.3969/j.issn.1006-7043.2008.12.001 [23] Felli M, Falchi M. A parametric survey of propeller wake instability mechanisms by detailed flow measurement and time resolved visualizations//Proceedings of the 32nd Symposium on Naval Hydrodynamics, Hamburg, Germany. 2018: 5-10.
[24] 高天达, 孙姣, 范赢等. 基于PIV技术分析颗粒在湍流边界层中的行为. 力学学报, 2019, 51(1): 103-110 (Gao Tianda, Sun Jiao, Fan Yin, et al. PIV experimental investigation on the behavior of particle in the turbulent boundary layer. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(1): 103-110 (in Chinese) [25] 田海平, 伊兴睿, 钟山等. 基于Stereo-PIV技术的三维发卡涡结构定量测量研究. 力学学报, 2020, 52(6): 1666-1677 (Tian Haiping, Yi Xingrui, Zhong Shan, et al. Experimental study on quantitative measurement of three-dimensional structure of hairpin vortex by Stereo-PIV. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1666-1677 (in Chinese) [26] Felli M, Camussi R, Di Felice F. Mechanisms of evolution of the propeller wake in the transition and far fields. Journal of Fluid Mechanics, 2011, 682: 5-53 doi: 10.1017/jfm.2011.150
[27] Wang L, Carrica PM, Felli M. Experimental and CFD study of the streamwise evolution of propeller tip vortices//33rd Symposium on Naval Hydrodynamics, 2020.
[28] Li J, Carrica PM. An approach to couple velocity/pressure/void fraction in two-phase flows with incompressible liquid and compressible bubbles. International Journal of Multiphase Flow, 2018, 102: 77-94 doi: 10.1016/j.ijmultiphaseflow.2018.01.021
[29] Carrica PM, Wilson RV, Noack RW, et al. Ship motions using single-phase level set with dynamic overset grids. Computers & Fluids, 2007, 36(9): 1415-1433
[30] Wang L, Martin JE, Felli M, et al. Experiments and CFD for the propeller wake of a generic submarine operating near the surface. Ocean Engineering, 2020, 206: 107304 doi: 10.1016/j.oceaneng.2020.107304
[31] Germano M, Piomelli U, Moin P, et al. A dynamic subgrid-scale eddy viscosity model. Physics of Fluids A: Fluid Dynamics, 1991, 3(7): 1760-1765 doi: 10.1063/1.857955
[32] Meunier P, Leweke T. Three-dimensional instability during vortex merging. Physics of Fluids, 2001, 13(10): 2747-2750 doi: 10.1063/1.1399033
[33] Wang L, Guo C, Wang C, et al. Modified phase average algorithm for the wake of a propeller. Physics of Fluids, 2021, 33(3): 035146 doi: 10.1063/5.0030829
-
期刊类型引用(4)
1. 葛泽昊，王彧，刘政沅，刘辉，周波. 导管螺旋桨瞬时尾部涡演化数值研究. 大连理工大学学报. 2024(04): 403-411 . 
百度学术
2. 张维鹏，任建新，郭航，王子斌，胡健. 舵几何特征对桨-舵系统尾流场演化的影响. 力学学报. 2023(02): 318-329 . 本站查看
3. 谢超凡，柏铁朝，吴方良，张志国. 基于LES的螺旋桨精细流场特性分析与研究. 舰船科学技术. 2023(23): 39-43 . 百度学术
4. 陈卓，艾子涛，王恋舟. 不同工况下螺旋桨尾流场数值分析. 船舶工程. 2022(09): 89-94+100 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 1725
- HTML全文浏览量: 531
- PDF下载量: 174
- 被引次数: 8
