NON-PROBABILISTIC RELIABILITY ANALYSIS OF FLEXIBLE MANIPULATOR WITH JOINT CLEARANCE AND UNCERTAIN PARAMETERS
-
摘要: 由于加工制造精度以及空间环境等的影响, 空间机械臂的几何参数、材料参数等特征参数的不确定性会降低机械臂系统的运动精度及可靠性. 为了研究不确定参数和关节间隙对机械臂动态响应的影响, 解决由于空间机械臂实验样本数据不足难以获得精准的概率可靠性的问题. 本文建立了含关节间隙和不确定参数的柔性机械臂的动力学模型和非概率可靠性计算方法, 首先通过碰撞力模型和状态函数建立关节间隙数学模型, 采用假设模态法描述柔性机械臂的变形, 并利用Lagrange法建立含关节间隙柔性机械臂确定性动力学模型. 在此基础上, 考虑系统参数不确定性, 将系统的不确定参数描述为区间变量, 建立机械臂的不确定性动力学方程, 并利用基于Chebyshev多项式的区间算法求解含区间变量的机械臂的动力学方程. 针对空间机械臂的运动可靠性问题, 构建了极限状态函数, 并分别建立了4种非概率可靠性指标. 最后, 基于提出的不确定性动力学模型和4种非概率可靠性计算方法进行仿真分析, 数值仿真结果验证了所提出的动力学模型和非概率可靠性计算方法的有效性, 且可能性法相比Monte Carlo方法的计算效率更高, 实现了柔性机械臂的动力学响应预示与非概率可靠性分析.
-
关键词:
- 机械臂 /
- 关节间隙 /
- 不确定性 /
- Chebyshev多项式 /
- 非概率可靠性
Abstract: Due to the influence of manufacturing precision and space environment, the uncertainty of characteristic parameters such as geometric and material parameters of space manipulator reduces the motion accuracy and reliability of the manipulator system. In order to study the influence of uncertain parameters and joint clearance on the dynamic response of the manipulator, and the challenge of obtaining accurate probabilistic reliability due to insufficient experimental sample data of space manipulators. In this paper, a dynamic model and a non-probabilistic reliability calculation method for a flexible manipulator with joint clearance and uncertain parameters are established. Firstly, the clearance model is established by combining the collision force model and the state function, the deformation of the flexible manipulator is described by the hypothetical mode method. Then, utilizing the Lagrange method to establish the dynamic model of the flexible manipulator with joint clearance. On this basis, considering the uncertainty of the manipulator parameters, the uncertain parameters of the system are illustrated as interval variables to establish the uncertain dynamic model of the manipulator. Moreover, the dynamic equations of the flexible manipulator with interval variables are calculated by the interval algorithm based on Chebyshev polynomials. In response to the issue of motion reliability of the space manipulator, a limit state function and four types of non-probabilistic reliability method are presented respectively. Finally, simulation analysis was conducted based on the proposed uncertainty dynamics model and four non-probabilistic reliability calculation methods. The numerical simulation is implemented to verify the effectiveness of the proposed uncertain dynamic model and non-probabilistic reliability methods. The proposed method can achieve accurate dynamic prediction and non-probabilistic reliability analysis, and the possibility method presents higher computational efficiency compared to the Monte Carlo method.-
Keywords:
- manipulator /
- joint clearance /
- uncertainty /
- Chebyshev polynomial /
- non-probabilistic reliability
-
引 言
空间机械臂在执行在轨服务等空间任务中发挥着重要作用[1-2], 其功能繁杂、运动精度和可靠性要求较高[1]. 相较于刚性空间机械臂, 柔性空间机械臂是一个高度非线性和强耦合的动力系统, 以其质量轻、灵活性高、耗能低和工作空间大等特性, 在航空领域展现出巨大的应用潜力. 诸多学者对机械臂的动力学和概率可靠性做了大量研究, 但是对考虑间隙和不确定参数的空间柔性机械臂的动力学建模和非概率可靠性分析的研究较少. 由于认识的不完全、参数的变化和尺寸的公差, 机械系统模型中的参数不可避免地存在一定程度的不确定性[3]. 并且, 这些不确定参数的微小波动可能导致动态响应出现较大偏差[4-5]. 为了提高动力学模型的鲁棒性, 关于不确定性理论的研究越来越受到重视.
在理想或简化的模型中, 通常将研究对象视为确定性系统. 但是实际机械系统的参数是不确定的, 根据不确定性因素的产生机理和物理意义, 不确定性分析模型可分为随机模型、模糊模型和区间模型. 随机模型是以概率论和数理统计为基础, 通过随机概率来描述系统的不确定性. Gan等[6]采用随机模型, 考虑外部扰动不确定性与模型不确定性, 建立了系统运行状态的动力学模型和可靠性评估指标并进行了分析. 邱雪松等[7]基于运动弹性动力学, 建立极端温度下可展帆板间隙-机械臂耦合动力学模型, 将不确定参数以随机变量的形式来表示, 分析了帆板展开末端的位置可靠性. Fu等[8]考虑轴间轴承下的随机参数不确定性建立了多体系统的不确定动力学模型. 模糊模型将不确定性量表示为模糊变量, 这些变量不是精确的数值, 而是一组模糊集合中的元素. Nie等[9]用模糊数学原理的分解, 将模糊变量转换为区间变量, 建立了不确定性动力学模型, 并提出了一种基于直接积分法和椭球凸模型的模糊可靠性方法. Dourado等[10]基于模糊理论方法, 同时考虑了可能性和模糊状态的假设, 将不确定参数建模为模糊变量, 并设计了相关的优化. Hu等[11]针对工程中普遍存在的模糊状态下的时变可靠性, 分析模型的不足, 提出了模糊状态下的时变可靠性分析模型, 并提出了相应的安全寿命模型. Hu等[12]提出了一种定时自适应滑模控制方法, 选择高斯径向基函数神经网络逼近不确定性参数, 提高了系统的鲁棒性. Yao等[13]针对不确定非线性系统, 提出了一种自抗扰自适应控制器, 通过参数自适应来减小参数的不确定性, 提高了轨迹跟踪性能. 然而对于参数不确定性较大的系统, 自适应控制的跟踪性能较差. Pandy等[14]基于运动学模型提出了一种计算串联机械臂可靠性的方法. 考虑摩擦、接触和碰撞等非线性动力学因素的影响时, 基于运动学的可靠性方法无法实现评估. Jia等[15]为了提高计算效率, 采用自适应采样技术提出了一种具有间隙关节和不确定参数的空间并联机构可靠性分析方法.
区间模型通过界定一个明确的取值范围来表征不确定性变量, 为处理数据不明确时的不确定性问题提供了一种有效的方法. Chebyshev区间方法是计算代理模型边界最有效的方法之一. 蒋鑫等[16]针对Chebyshev区间方法在长时间分析中的响应边界精度下降问题, 结合信号分解技术和Chebyshev多项式, 提出了CIM-HHT和CIM-LMD两种区间不确定性分析方法. Jiang等[17]提出了一种二元子区间方法来处理机械系统中多个不确定参数且不确定程度较小的区间动态问题. Wang等[18]基于绝对节点坐标法对机械臂多体系统进行动力学建模, 采用Chebyshev张量积法求解区间参数, 得到不同间隙大小下的系统动力学响应.
含间隙机构与理想机构的模型存在误差, 从而导致机构实际运动与理想运动之间存在偏差[19]. 合理的运动副间隙可以使机构灵活运转, 不合理的运动副间隙会对机构的动态特性及可靠性产生影响. 关节处运动副元素的相对运动关系扩展为接触、分离和碰撞3种状态, 简称三状态模型[20-21]. Chen等[22]基于连续接触理论, 采用Lankarani-Nikravesh接触力模型[23]来描述销轴与轴套之间的接触碰撞现象. Miao等[24]研究了空间机械臂锁定过程中间隙对锁定精度的影响. Chen等[25]通过数值计算和实验研究了旋转副间隙对高精度曲柄滑块机构动力学的影响. Erkaya等[26-28]研究了具有关节间隙和柔性杆的平面4杆机构的运动学和动力学特性; 考虑摩擦效应并采用非线性弹簧-阻尼器模型建立了间隙关节的接触模型; 将间隙关节的动静摩擦系数及间隙大小视为不确定参数, 并研究多重不确定因素对系统动态响应的影响, 对提高机械系统的性能和可靠性具有重要的意义.
空间机械臂在外界环境、加工安装和摩擦磨损等因素的影响下, 存在着许多不确定参数和关节间隙, 这使得其动力学模型的建立和动态特性等分析变得尤为复杂. 此外, 由于成本限制, 无法获得大量的样本统计数据, 难以建立精准的概率分布特征[29], 所以需要研究非概率方法进行可靠性分析. 为了解决上述问题, 本文对考虑不确定参数的含间隙柔性机械臂的动力学响应和非概率可靠性进行研究. 首先考虑系统参数不确定性和关节间隙, 将系统的不确定参数描述为区间变量, 建立含间隙的柔性机械臂不确定性动力学模型, 并用Chebyshev多项式构建区间算法来求解含区间变量的动力学方程. 为了对机械臂可靠性进行快速有效的评估, 提出了4种非概率可靠性计算方法. 最后, 通过数值仿真验证含间隙不确定动力学模型的有效性, 并分析不同工况下的柔性机械臂的可靠性.
1. 含间隙的柔性机械臂动力学建模
1.1 柔性机械臂动力学建模
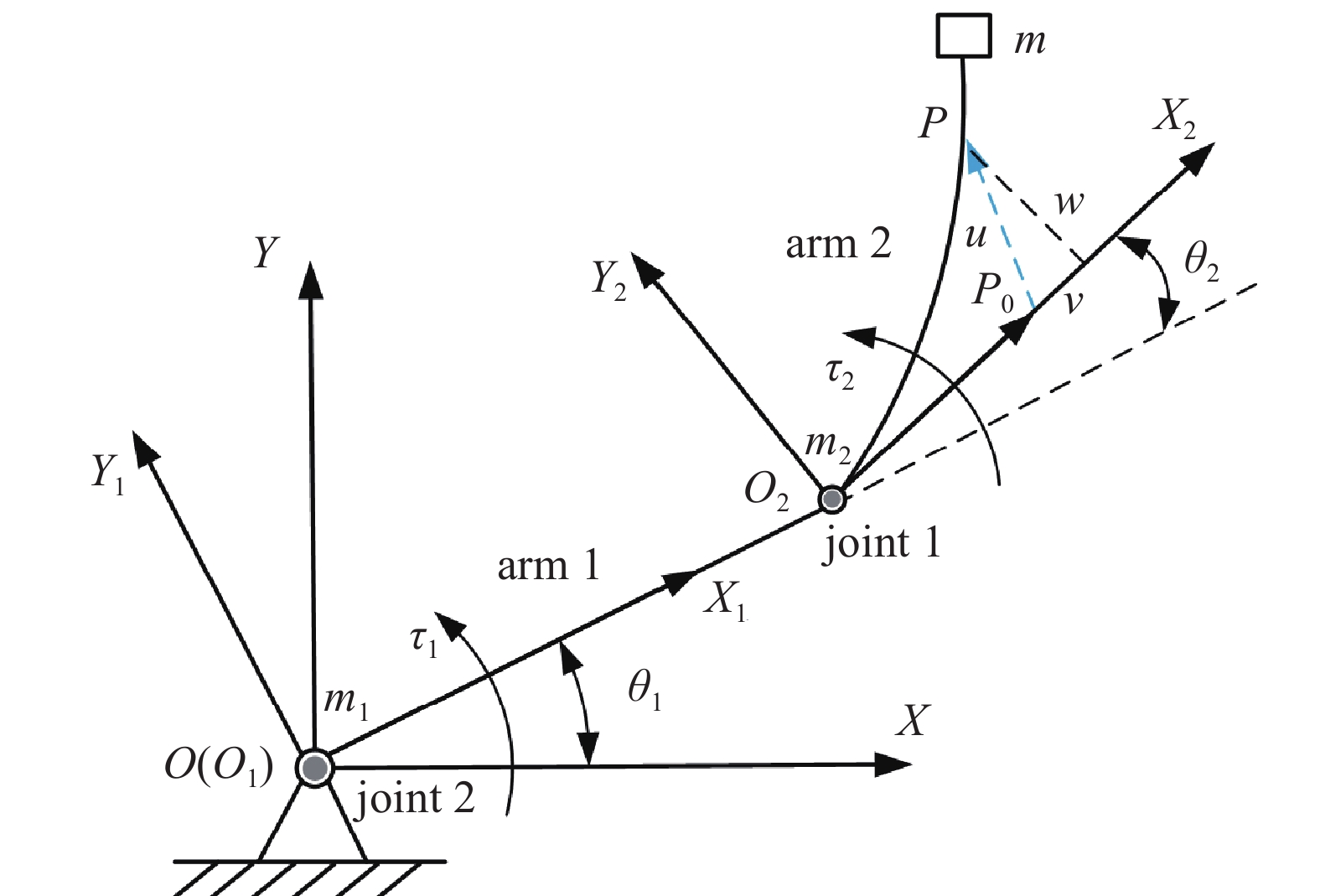
图1所示为在平面内作回转运动的柔性机械臂的简化模型, 臂1为刚性臂, 臂2为柔性臂, 关节均为转动副.
$ P $表示柔性臂轴线上变形后的任意一点, $ {P_0} $为未变形前的同一点, 假设点$ {P_0} $的坐标是$ (x,0) $, $ w(x,t) $和$ v(x,t) $分别表示柔性臂的径向变形和轴向变形. 柔性机械臂是等横截面的均质细长杆, 变形为小变形, 臂杆的长度远大于其截面尺寸, 且处在太空微重力环境下. 因此, 采用假设模态法[30], 基于Euler-Bernoulli梁模型[31-32]对柔性机械臂进行柔性变形描述. 柔性臂轴向振动的自由振动微分方程为
$$ {\rho _2}{A_2}\frac{{{\partial ^2}w(x,t)}}{{\partial {t^2}}} + \frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{E_2}{I_2}\frac{{{\partial ^2}w(x,t)}}{{\partial {x^2}}}} \right] = 0 $$ (1) 式中, $ {\rho _2} $, $ {A_2} $, $ {E_2} $和$ {I_2} $分别为柔性臂的单位体积质量、横截面面积、弹性模量和截面惯性矩. 利用分离变量法对式(1)进行求解, 假定自由振动微分方程解的形式为
$$ w(x,t) = \phi (x)q(t) $$ (2) 式中, $ \phi (x) $是柔性臂径向振动的模态振型函数, $ q(t) $是模态广义坐标. 将式(2)代入式(1), 简化得到的微分方程组如下所示
$$ - \frac{{\ddot q(t)}}{{q(t)}} = \frac{{EI}}{{\rho A}}\frac{{{\phi ^{(4)}}(x)}}{{\phi (x)}} $$ (3) 式中, 等号两端应等于常数, 记为$ {\omega ^2} $, 可以得到$ q(t) $和$ \phi (x) $应满足的微分方程为
$$ \left. \begin{aligned} & \ddot q(t) + {\omega ^2}q(t) = 0 \\ & {\phi ^{(4)}}(x) - \frac{{{\rho _2}{A_2}}}{{{E_2}{I_2}}}{\omega ^2}\phi (x) = 0 \end{aligned} \right\} $$ (4) 根据式(4)计算得到模态振型函数$ \phi (x) $和模态广义坐标$ q(t) $的通解分别为
$$ q(t) = a\cos (\omega t) + b\sin (\omega t) $$ (5) $$\begin{split} & \phi \left(x \right) = {C_1}\sin \left({\lambda x} \right) + {C_2}\cos \left({\lambda x}\right) + \\ &\qquad {C_3}\sinh \left({\lambda x} \right) + {C_4}\cosh \left({\lambda x}\right)\end{split} $$ (6) 式中, 令$ {\lambda ^4} = \dfrac{{{\rho _2}{A_2}}}{{{E_2}{I_2}}}{\omega ^2} $, $ \omega $是柔性臂的固有频率; $ {C_1} $, $ {C_2} $, $ {C_3} $和$ {C_4} $均是与边界条件有关的常数; $ a $和$ b $是与初始条件有关的常数. 柔性臂是一端固定且另一端自由的悬臂梁, 其边界条件为
$$ \left. \begin{split} & {w(0,t) = 0} \\ & {\frac{{\partial w(0,t)}}{{\partial x}} = 0} \\ & {{E_2}{I_2}\frac{{{\partial ^2}w({l_2},t)}}{{\partial {x^2}}} = 0} \\ & {{E_2}{I_2}\frac{{{\partial ^3}w({l_2},t)}}{{\partial {x^3}}} = 0} \end{split} \right\} $$ (7) 将柔性臂的边界条件(7)代入式(6), 可以计算得到频率方程如式(8)所示
$$ \cos (\lambda {l_2})\cosh (\lambda {l_2}) + 1 = 0 $$ (8) 式中, $ {l_2} $是柔性臂的长度. 对式(8)进一步求解可得
$$ \left. \begin{split} & {\lambda _1} = {{1.875\;1}}/{{{l_2}}} \\ & {\lambda _2} = {{4.694\;1}}/{{{l_2}}} \\ & {\lambda _3} = {{7.854\;8}}/{{{l_2}}} \\ & {{\lambda _4} = \frac{{(2i - 1)\text{π} }}{{2{l_2}}}}\quad {(i = 4,5, \cdots )} \end{split} \right\} $$ (9) 柔性臂的各阶固有频率可表示为
$$ {{\omega _i} = \lambda _i^2\sqrt {\frac{{{E_2}{I_2}}}{{{\rho _2}{A_2}}}} }\quad {(i = 1,2, \cdots )} $$ (10) 取前n阶模态, 柔性臂的径向变形可表示为
$$ w(x,t) = \sum\limits_{i = 1}^n {{\phi _i}(x){q_i}(t)} $$ (11) 进一步可得柔性臂的第i阶模态振型函数为
$$ \begin{split} &{\phi _i}(x) = \cos ({\lambda _i}x) - \cosh ({\lambda _i}x) + \\ &\qquad \frac{{\cos ({\lambda _i}{l_2}) + \cosh ({\lambda _i}{l_2})}}{{\sin ({\lambda _i}{l_2}) + \sinh ({\lambda _i}{l_2})}}\left[ {\sinh ({\lambda _i}x) - \sin ({\lambda _i}x)} \right] \end{split} $$ (12) 根据几何变形约束建立柔性臂的几何非线性位移表达式, 可以推导得出轴向变形和径向变形之间的关系式为
$$ v(x,t) = - \frac{1}{2}{\int_0^x {\left[ {\frac{{\partial w(\sigma ,t)}}{{\partial \sigma }}} \right]} ^2}{\mathrm{d}}\sigma $$ (13) Lagrange方法是求解柔性多体系统动力学模型应用最广泛的方法, 该方法计算量相对较小, 计算效率高. 如图1所示, 在t瞬时, 柔性臂径向变形用$ w $表示, 轴向变形用$ v $表示, $ \{ O\} $是柔性机械臂的固定坐标系, 坐标系$ \{ {O_1}\} $和$ \{ {O_2}\} $为该系统上分别固连在臂1和臂2上的动坐标系. $ {\tau _1} $和$ {\tau _2} $为关节处的电机扭矩, $ {m_1} $和$ {m_2} $为电机的集中质量, $ {l_1} $和$ {l_2} $为臂杆的长度, $ m $为柔性臂2末端的载荷质量, $ {\theta _1} $和$ {\theta _2} $为臂的关节转角.
$ {P_0} $点在动坐标系$ \{ {O_2}\} $下的坐标为$ (x,y) $. 臂杆为具有小变形能力的细长杆, $ P $点的运动可分解为臂杆转动和形变位移, 因此柔性机械臂上的点$ P $在固定坐标系$ \{ O\} $的坐标$ ({x_p},{y_p}) $可表示为
$$ \left.\begin{split} & {{x_p} = {l_1}\cos {\theta _1} + \left[ {(x + v)\cos ({\theta _1} + {\theta _2}) - w\sin ({\theta _1} + {\theta _2})} \right]} \\ & {{y_p} = {l_1}\sin {\theta _1} + \left[ {(x + v)\sin ({\theta _1} + {\theta _2}) + w\cos ({\theta _1} + {\theta _2})} \right]} \end{split}\right\} $$ (14) 式中, $ w $和$ v $可分别由式(11)和式(13)计算得到. 点$ P $的速度可表示为
$$ {\nu ^2_p} = \dot x_p^2 + \dot y_p^2 $$ (15) 式中, $ {\dot x_p} $和$ {\dot y_p} $是$ P $点位移的一阶导数. 刚性臂1和柔性臂2的动能分别为
$$\qquad\qquad {E_{k1}} = \frac{1}{6}{\rho _1}{A_1}{ {{{\dot \theta }_1}} ^2}l_1^3 $$ (16) $$\qquad\qquad {E_{k2}} = \frac{1}{2}{\rho _2}{A_2}\int_0^{{l_2}} {v_p^2} {\mathrm{d}}x $$ (17) 关节1处和2处电机的动能分别可表示为
$$ {T_1} = \frac{1}{2}{J_1}\dot \theta _1^2 $$ (18) $$ {T_2} = \frac{1}{2}{J_2}{\dot \theta _2}^2 + \frac{1}{2}{m_2}{\left( {{{\dot \theta }_1} {l_1}} \right)^2} $$ (19) 式中, $ {J_1} $和$ {J_2} $分别是电机1和电机2的转动惯量. 柔性臂末端负载的动能为
$$ {T_m} = \frac{1}{2}m{ {{\nu _m}} ^2} $$ (20) 式中, $ {\nu _m} $是负载的质心速度. 由以上可得系统的总动能为
$$ T = {E_{k1}} + {E_{k2}} + {T_1} + {T_2} + {T_m} $$ (21) 系统的总势能即柔性臂的变形能为
$$ V = \frac{1}{2}{E_2}{I_2}\int_0^{{l_2}} {{{\left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right)}^2}} {\mathrm{d}}x $$ (22) 将系统的总动能式(21)和总势能式(22)代入Lagrange方程可得
$$ L = T - V $$ (23) 基于第二类拉格朗日方程, 取广义坐标为$ {\boldsymbol{q}}(t) = {[{\theta _1},{\theta _2},{q_1},{q_2},{q_3}]^{\mathrm{T}}} $, 将动能和势能代入方程可得
$$ \left.\begin{aligned} & {\frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left(\frac{{\partial L}}{{\partial {{\dot \theta }_1}}}\right) - \frac{{\partial L}}{{\partial {\theta _1}}} = {\tau _1}} \\ & {\frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left(\frac{{\partial L}}{{\partial {{\dot \theta }_2}}}\right) - \frac{{\partial L}}{{\partial {\theta _2}}} = {\tau _2}} \\ &{\frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left(\frac{{\partial L}}{{\partial {{\dot q}_i}}}\right) - \frac{{\partial L}}{{\partial {q_i}}} = 0}&{{\text{ }}(i = 1,2,3)} \end{aligned}\right\} $$ (24) 将式(24)进行线性化处理, 得到柔性机械臂的动力学模型为
$$ {\boldsymbol{M\ddot q + C\dot q + Kq = Q}} $$ (25) 式中, 广义质量矩阵$ {\boldsymbol{M}} $和广义刚度矩阵$ {\boldsymbol{K}} $分别表示为
$$ {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{J_{11}}}&{{J_{12}}}&{{M_{m1}}}&{{M_{m2}}}&{{M_{m3}}} \\ {{J_{21}}}&{{J_{22}}}&{{M_{m1}}}&{{M_{m2}}}&{{M_{m3}}} \\ {{M_{m1}}}&{{M_{m1}}}&{{M_1}}&0&0 \\ {{M_{m2}}}&{{M_{m2}}}&0&{{M_2}}&0 \\ {{M_{m3}}}&{{M_{m3}}}&0&0&{{M_3}} \end{array}} \right] $$ (26) $$ {\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0 \\ 0&0&0&0&0 \\ 0&0&{{K_1}}&0&0 \\ 0&0&0&{{K_2}}&0 \\ 0&0&0&0&{{K_3}} \end{array}} \right] $$ (27) 式中
$$ \left.\begin{aligned} & {J_{11}} = {J_1} + {J_2} + \frac{1}{3}{\rho _1}{A_1}l_1^3 + \\ &\qquad {\rho _2}{A_2}\left(\frac{1}{3}l_2^3 + l_1^2{l_2}\right) + m(l_1^2 + l_2^2) \\ & {J_{12}} = {J_2} + \frac{1}{3}{\rho _2}{A_2}l_2^2 + ml_2^2 \\ & {J_{21}} = {J_2} + \frac{1}{3}{\rho _2}{A_2}l_2^2 + ml_2^2 \\ & {J_{22}} = {J_2} + \frac{1}{3}{\rho _2}{A_2}l_2^2 + ml_2^2 \\ & {{M_{mi}} = {\rho _2}{A_2}\int_0^{{l_2}} x {\phi _i}\left( x \right){\mathrm{d}}x + m{l_2}{\phi _i}\left( x \right)}\quad {\left( {i = 1,2,3} \right)} \\ & {{M_i} = {\rho _2}{A_2}\int_0^{{l_2}} {\phi _i^2} \left( x \right){\mathrm{d}}x + m\phi _i^2\left( x \right)}\quad {\left( {i = 1,2,3} \right)} \end{aligned} \right\} $$ (28) $$ {{K_i} = {E_2}{I_2}\int_0^{{l_2}} {{{\left[ {\frac{{{{\mathrm{d}}^2}{\phi _i}(x)}}{{{\mathrm{d}}{x^2}}}} \right]}^2}} {\mathrm{d}}x}\quad{(i = 1,2,3)} $$ (29) 在机械系统中, 由于变形、摩擦、磨损等现象, 造成系统能量损失, 所以在动力学模型中要考虑系统阻尼, 采用Rayleigh阻尼[33]作为系统的阻尼
$$ {\boldsymbol{C}} = {\alpha _0}{\boldsymbol{M}} + {\alpha _1}{\boldsymbol{K}} $$ (30) 其中, $ {\alpha _0} $和$ {\alpha _1} $是Rayleigh阻尼的比例常数.
1.2 旋转铰关节间隙模型
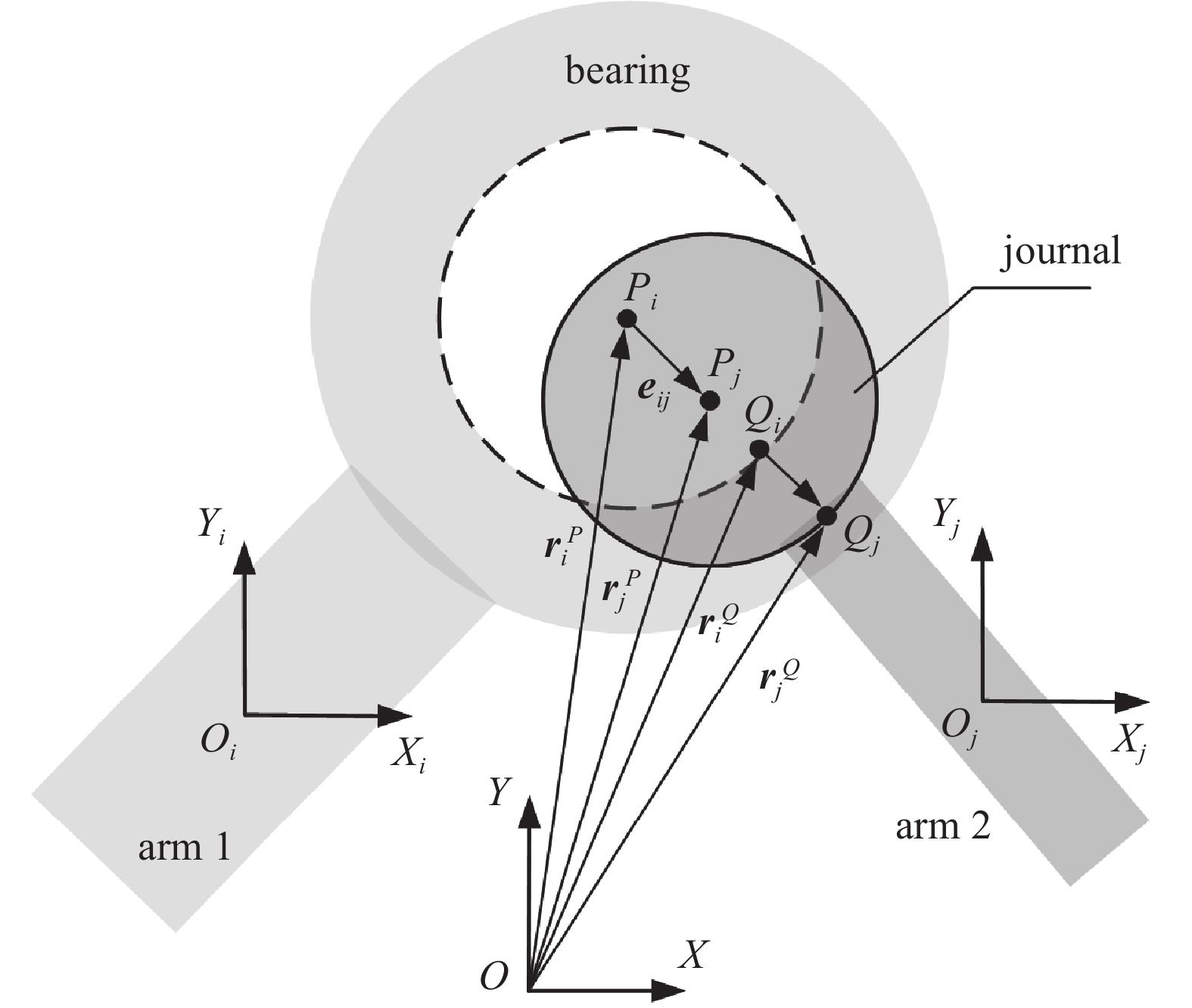
图2所示是处于碰撞状态的间隙关节模型. 在原有柔性机械臂中引入运动副间隙, 根据3状态模型, 运动副元素间的运动状态在自由运动、接触和碰撞之间不断切换, 需要根据运动副元素间不同的运动状态建立不同的动力学方程.
由图2可知, 臂杆1旋转中心与臂杆2旋转中心的中心距矢量$ {{\boldsymbol{e}}_{ij}} $和中心距$ {e_{ij}} $分别为
$$\qquad\qquad\quad {{\boldsymbol{e}}_{ij}}{\boldsymbol{ = r}}_i^p{\boldsymbol{ - r}}_j^p $$ (31) $$ \qquad\qquad\quad {e_{ij}} = \sqrt {{\boldsymbol{e}}_{ij}^\text{T}{{\boldsymbol{e}}_{ij}}} $$ (32) 轴承与销轴接触碰撞时产生的接触变形为
$$ \delta = {e_{ij}} - c $$ (33) 式中, $ c = {R_i} - {R_j} $为关节间隙, $ {R_i} $和$ {R_j} $分别是轴承半径和销轴半径. 撞时的法向相对速度${{\boldsymbol{v}}_n}$和切向相对速度${{\boldsymbol{v}}_t}$可分别表示为
$$\qquad\qquad\quad {{\boldsymbol{v}}_n} = {({{\boldsymbol{\dot r}}_j}^Q - {{\boldsymbol{\dot r}}_i}^Q)^\text{T}}{\boldsymbol{n}} $$ (34) $$\qquad\qquad\quad {{\boldsymbol{v}}_t} = {({{\boldsymbol{\dot r}}_j}^Q - {{\boldsymbol{\dot r}}_i}^Q)^\text{T}}{\boldsymbol{t}} $$ (35) 式中, ${\boldsymbol{n}}$和${\boldsymbol{t}}$分别是法向单位向量和切向单位向量, $ {\boldsymbol{n}} = \dfrac{{{{\boldsymbol{e}}_{ij}}}}{{\left| {{{\boldsymbol{e}}_{ij}}} \right|}} $, ${\boldsymbol{n}}$和${\boldsymbol{t}}$是正交向量. 当旋转铰处于自由运动状态时, 转动副中不存在约束, 柔性机械臂动力学方程为式(25); 当处于接触碰撞状态时, 满足接触碰撞条件, 运动副元素间产生碰撞力, 因此含关节间隙的柔性机械臂动力学方程为
$$ {\boldsymbol{M\ddot q + C\dot q + Kq = Q}} + {\boldsymbol{F}} $$ (36) 式中, $ {\boldsymbol{F}} $为接触力相对广义坐标的广义力列阵, 包含了铰间隙引起的法向接触力$ {F_N} $以及切向摩擦力$ {F_T} $. 基于Hertz接触理论和恢复系数的非线性弹簧阻尼模型, 定义法向接触力为
$$ {F_N} = {K_c}{\delta ^{1.5}} + D\dot \delta $$ (37) 式中, ${K_c}$为等效接触刚度系数, $D$为阻尼系数, $\delta $为接触变形, $\dot \delta $为接触速度. 由Hertz接触理论可知, 等效接触刚度系数和阻尼系数分别表示为
$$\qquad\qquad\quad {K_c} = \frac{4}{{3({\sigma _i} + {\sigma _j})}}\sqrt {\frac{{{R_i}{R_j}}}{{{R_i} - {R_j}}}} $$ (38) $$\qquad\qquad\quad D = \frac{{3K\left( {1 - {e^2}} \right){\delta ^{1.5}}}}{{4{{\dot \delta }^{\left( - \right)}}}} $$ (39) 其中
$$ {{\sigma _n} = \frac{{1 - {\nu _n}^2}}{{{E_n}}}}\quad {\left( {n = i,j} \right)} $$ (40) 式中, ${\nu _n}$和${E_n}$分别表示泊松比和杨氏模量, $e$为恢复系数, ${\dot \delta ^{\left( - \right)}}$为撞击点的初始相对速度. 根据Coulomb摩擦定律, 销轴受到的切向摩擦力为
$$ {F_T} = - \frac{{{{\boldsymbol{\nu }}_t}}}{{\left| {{{\boldsymbol{\nu }}_t}} \right|}}\mu {F_N} $$ (41) 式中, ${{\boldsymbol{\nu }}_t}$是接触点处的切向速度, 可由式(35)计算得到, $\mu $为摩擦系数. 根据接触碰撞变形$\delta $的大小来对机械系统作运动模式的判别, 引入状态函数$ W\left( \delta \right) $来表示运动状态
$$ W(\delta ) = \left\{\begin{aligned} & 0,\quad {\delta \leqslant 0} \\ & 1,\quad {\delta > 0} \end{aligned}\right. $$ (42) 式中, “0”代表自由和接触两种运动状态; “1”代表碰撞运动状态. 引入状态函数(42), 则式(37)和式(41)可进一步表示为
$$ \left.\begin{aligned} & {{F_N} = (K\delta + D\dot \delta )W(\delta )} \\ & {{F_T} = \left( - \frac{{{\nu _T}}}{{|{\nu _T}|}}\mu {F_N}\right)W(\delta )} \end{aligned}\right\}$$ (43) 2. 考虑参数不确定的机械臂动力学建模
2.1 考虑不确定参数的动力学模型
在实际工程中由于设计加工装配误差、摩擦和磨损等影响, 机械系统中机构的几何尺寸、密度、弹性模量、阻尼和摩擦系数等都是不确定的. 为了准确描述这些不确定性, 将不确定参数视为受上下边界限制的区间变量, 并采用区间模型进行表示
$$ {\boldsymbol{x}} = \left[ {\underline{x} ,\bar x} \right] $$ (44) 式中, $ \underline{x} $和$ \bar x $分别表示区间变量$ {\boldsymbol{ x}} $下边界和上边界. 在所建立的含间隙的动力学模型的基础上, 定义机械臂处于自由运动和接触碰撞状态的不确定性动力学方程分别为
$$\qquad\qquad {\boldsymbol{M}}{\boldsymbol{\ddot q}} + {\boldsymbol{C}}{\boldsymbol{\dot q}} + {\boldsymbol{K}}{\boldsymbol{q}} = {\boldsymbol{Q}} $$ (45) $$\qquad\qquad {\boldsymbol{M}}{\boldsymbol{\ddot q}} + {\boldsymbol{C}}{\boldsymbol{\dot q}} + {\boldsymbol{K}}{\boldsymbol{q}} = {\boldsymbol{Q}} + {\boldsymbol{F}} $$ (46) 式中
$$ {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{J}}_{11}}}&{{{\boldsymbol{J}}_{12}}}&{{{\boldsymbol{M}}_{m1}}}&{{{\boldsymbol{M}}_{m2}}}&{{{\boldsymbol{M}}_{m3}}} \\ {{{\boldsymbol{J}}_{21}}}&{{{\boldsymbol{J}}_{22}}}&{{{\boldsymbol{M}}_{m1}}}&{{{\boldsymbol{M}}_{m2}}}&{{{\boldsymbol{M}}_{m3}}} \\ {{{\boldsymbol{M}}_{m1}}}&{{{\boldsymbol{M}}_{m1}}}&{{{\boldsymbol{M}}_1}}&0&0 \\ {{{\boldsymbol{M}}_{m2}}}&{{{\boldsymbol{M}}_{m2}}}&0&{{{\boldsymbol{M}}_2}}&0 \\ {{{\boldsymbol{M}}_{m3}}}&{{{\boldsymbol{M}}_{m3}}}&0&0&{{{\boldsymbol{M}}_3}} \end{array}} \right] $$ (47) $$ {\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0 \\ 0&0&0&0&0 \\ 0&0&{{{\boldsymbol{K}}_1}}&0&0 \\ 0&0&0&{{{\boldsymbol{K}}_2}}&0 \\ 0&0&0&0&{{{\boldsymbol{K}}_3}} \end{array}} \right] $$ (48) 动力学模型系数为不确定变量, 所以在求解该类不确定动力学方程时, 需要采用特殊的区间算法来计算求解. 因此, 提出了一种基于Chebyshev多项式的区间求解算法.
2.2 不确定性动力学模型的求解
不确定的实数可以被视为包含不确定实数的所有可能值的实数区间数. 区间变量定义为
$$ {\boldsymbol{ x}} = \left[ {\underline{x} ,\bar x} \right] = \left\{{x \in {\bf{R}}:\underline{x} < x < \bar x} \right\} $$ (49) 在使用算术运算来计算区间之间的运算时, 会使所求解的区间范围变大, 所以需要采用区间算法进行求解, 以减小区间包裹效应, 减小运算误差. 一维的$ m $阶Chebyshev多项式定义为
$$ {{C_p}\left( x \right) = \cos (p\theta) ,}\quad {\theta = \arccos \left[ {\frac{{2x - (b + a)}}{{b - a}}} \right]} \in [0,\text{π} ] $$ (50) 区间$x \in \left[ {a,b} \right]$内的单变量连续函数$f\left( x \right)$可以近似表示为
$$ {f(x) \approx \frac{1}{2}{f_0} + \sum\limits_{p = 1}^m {{f_p}{C_p}\left( x \right)} }\quad {(p = 0,1,2, \cdots ,m)} $$ (51) 式中, $ {f_p} $是Chebyshev多项式的系数. 对于多维问题, Chebyshev多项式是每个一维多项式的张量积, ${\boldsymbol{x}} = {\left[ {{x_1},{x_2}, \cdots ,{x_k}} \right]^\text{T}}$的多维Chebyshev多项式可以表示为
$$ \begin{split} & {C_{{p_1},{p_{2,}} \cdots ,{p_k}}}({x_1},{x_2}, \cdots ,{x_k}) = \\ &\qquad{\cos ({p_1}{\theta _1})\cos ({p_2}{\theta _2}) \cdots \cos ({p_k}{\theta _k})}\quad {({p_k} = 0,1, 2,\cdots ,m}) \end{split} $$ (52) 式中, $ {p_k} $是多维Chebyshev多项式的系数的阶数, 插值点$ {\theta _k} = \arccos \left[ {\dfrac{{2{x_k} - ({b_k} + {a_k})}}{{{b_k} - {a_k}}}} \right] $. 多元函数$ f({x_1},{x_2}, \cdots, {x_k}) $可以近似为下式所示的多维$ m $阶Chebyshev多项式
$$ \begin{split} & f({x_1},{x_2}, \cdots ,{x_k}) \approx \\ &\qquad \sum\limits_{{p_1} = 0}^m { \cdots \sum\limits_{{p_k} = 0}^m {{f_{{p_1},{p_{2,}} \cdots ,{p_k}}}{C_{{p_1},{p_{2,}} \cdots ,{p_k}}}({x_1},{x_2}, \cdots ,{x_k})} }\end{split} $$ (53) 式中, $ l $表示下标$ {p_1},{p_2}, \cdots, {p_k} $等于0的数量. 基于Mehler积分, $ {f_{{p_1},{p_{2,}} \cdots ,{p_k}}} $可进一步表示为
$$\begin{split} & {f_{{p_1},{p_{2,}} \cdots ,{p_k}}} = {\left( {\frac{2}{{m + 1}}} \right)^k}\sum\limits_{{j_1} = 1}^{m + 1} { \cdots \sum\limits_{{j_k} = 1}^{m + 1} {f\left( {x_1^{{j_1}},x_2^{{j_2}}, \cdots ,x_k^{{j_k}}} \right)} } \cdot \\ &\qquad \cos ({p_1}\theta _1^{{j_1}})\cos ({p_2}\theta _2^{{j_2}}) \cdots \cos ({p_k}\theta _k^{{j_k}}) \end{split} $$ (54) 式中
$$ \left.\begin{aligned} & {\theta _k^{{j_k}} = \frac{{2{j_k} - 1}}{{m + 1}}\frac{\text{π} }{2},}\quad {{j_k} = 1,2, \cdots ,m + 1} \\ & {x_k^{{j_k}} = \frac{{{a_k} + {b_k}}}{2} + \frac{{{b_k} - {a_k}}}{2}\cos \theta _k^{{j_k}},}\quad {x_k^{{j_k}} \in \left[ {{a_k},{b_k}} \right]}\end{aligned}\right\} $$ (55) 3. 非概率可靠性分析方法
传统的随机可靠性与模糊可靠性模型都需要大量的数据计算不确定参数的概率分布函数, 非概率可靠性分析采用区间参数来表示系统的不确定信息, 只考虑系统参数的变化范围, 当统计数据缺乏或者难以得到实验数据时这种方法具有很大的优势. 考虑柔性机械臂的运动精度和运动的稳定性, 利用柔性臂的末端位移及角加速度建立系统的极限状态函数为
$$ g\left( X \right) = {\boldsymbol{\varepsilon}} - \Delta {\boldsymbol{\varepsilon}} $$ (56) 式中, $ {\boldsymbol{ \varepsilon}} \in \left[ {[ \underline{\varepsilon} ],[{\bar \varepsilon }]} \right] $表示许用位移偏差或许用加速度偏差, $ \Delta {\boldsymbol{\varepsilon}} $是考虑不确定参数时柔性臂末端位移偏差或加速度偏差. 极限状态函数$ g\left( X \right) $可以将不确定参数所构成的空间划分为失效区和安全区.
最短距离法[34]是在区间变量组成的区间里, 通过用无穷范数度量从坐标原点到失效平面上的最短距离, 作为非概率可靠性指标的衡量. 当$ - 1 \leqslant {\eta _1} \leqslant 1 $, 系统可能失效; 当$ {\eta _1} > 1 $, 系统安全, $ {R_{s1}} $值越大, 系统的安全程度越高; 当$ {\eta _1} < - 1 $, 系统失效. 基于最短距离法的非概率可靠性指标为
$$ {\eta _1} = \frac{{{{\left[ \varepsilon \right]}^c} - \Delta {\varepsilon ^c}}}{{{{\left[ \varepsilon \right]}^r} + \Delta {\varepsilon ^r}}} $$ (57) 式中, $ {\left[ \varepsilon \right]^c} $和$ {\left[ \varepsilon \right]^r} $分别表示$ \left[ \varepsilon \right] $的均值和偏差, $ \Delta {\varepsilon ^c} $和$ \Delta {\varepsilon ^r} $分别表示$ \Delta \varepsilon $的均值和偏差.
可能性法在最短距离法的基础上作了优化, 可以将基于可能性法[35]的非概率可靠性指标表示为
$$ {R_{s2}} = \min \left\{ {\max \left[\frac{1}{2}({\eta _1} + 1),0\right],1} \right\} $$ (58) 区间变量所构成的空间被失效面分成安全域和失效域, 整个系统的非概率可靠性度量为安全域的体积比上总体积. 基于体积比法[36]的非概率可靠性指标表示为
$$ {R}_{s3} = \frac{{V}_{{\mathrm{safe}}}}{{V}_{{\mathrm{all}}}} = 1-\frac{{\left(\Delta \overline{\varepsilon }-\left[\overline{\varepsilon }\right]\right)}^{2}}{8\Delta {\varepsilon }^{r}{\left[\varepsilon \right]}^{r}} $$ (59) 式中, $ \Delta \bar \varepsilon $和$ \left[ {\bar \varepsilon } \right] $分别表示偏差和许用偏差的区间上界. 当偏差$ \Delta {\varepsilon ^r} $越接近容差$ {\omega _{\Delta \varepsilon }} $时, 系统的可靠性越高; 反之, 当偏差$ \Delta {\varepsilon ^r} $越远离容差$ {\omega _{\Delta \varepsilon }} $时, $ {R_{{\text{s}}4}} $越小, 系统的可靠性越低. 基于容差法[37]的非概率可靠性指标表示为
$$ {R_{s4}} = 1 - \frac{{{{\left( {{\omega _{\Delta \varepsilon }} - \Delta {\varepsilon ^r}} \right)}^2}}}{{8\Delta {\varepsilon ^r}{{\left[ \varepsilon \right]}^r}}} $$ (60) 式(56) ~ 式(60)中, $ {R_{s2}} $, $ {R_{s3}} $和$ {R_{s4}} $越趋近于1, 系统安全程度越高, 当等于1时, 系统绝对安全; 当等于0时, 系统绝对失效.
4. 数值模拟与讨论
4.1 不同非概率可靠性模型的对比分析
基于所建立的4种非概率可靠性模型, 对含间隙的柔性机械臂进行数值仿真分析. 确定出计算结果与Monte Carlo方法最接近的一种模型, 并将这种模型与Monte Carlo方法的计算效率做了对比. 电机质量${m_2} = 1\text{ kg}$, 负载质量$m = 3.4\text{ kg}$, 关节扭矩${\tau _1} = 2\cos t\;{{\mathrm{N}}} \cdot {{\mathrm{m}}}$, ${\tau _2} = 4\;{{\mathrm{N}}} \cdot {{\mathrm{m}}}$, 将机械臂的关节间隙考虑为区间参数, 且$\left[ {{c_1}} \right] = \left[ {{c_2}} \right] = \left[ {0.8,1.2} \right]{\text{ mm}}$. 柔性机械臂的参数如表1所示.
表 1 柔性机械臂参数Table 1. Parameters for the flexible manipulatorGeometric size/m $ \rho $/(kg·m−3) $ E $/GPa arm 1 1 × 0.04 × 0.04 7800 215 arm 2 1 × 0.04 × 0.04 2700 71 图3所示是柔性机械臂末端的弹性变形, 形变位移随时间的变化遵循正弦函数的规律, 具有周期性和对称性. 随着时间的增加, 柔性臂末端弹性形变位移波动频率和幅值逐渐变小, 但是弹性变形区间的上下界偏差越来越大.
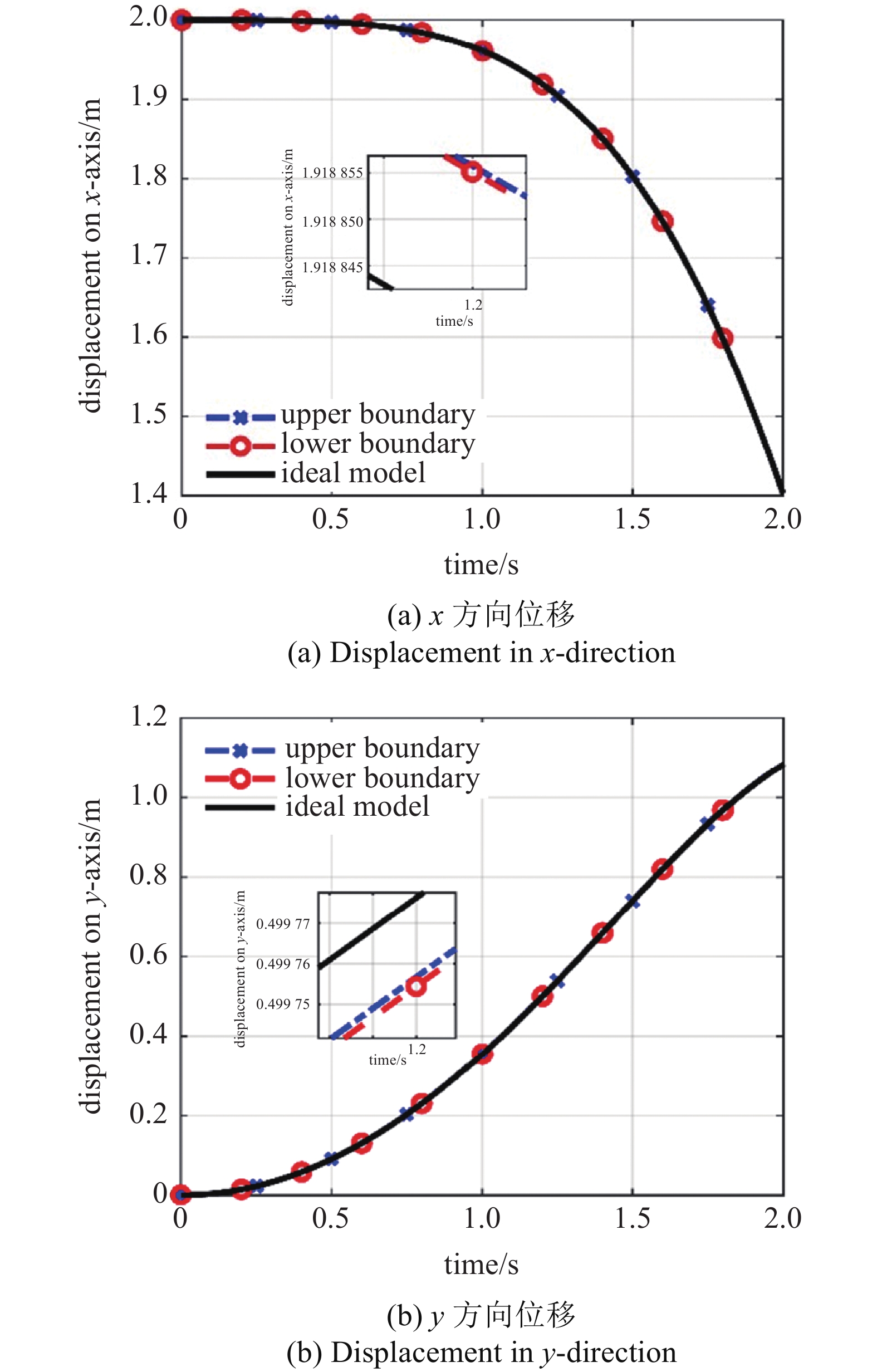
图4所示是在考虑间隙的情况下, 利用Chebyshev区间算法仿真得到位移上下边界的曲线, 以及不考虑关节间隙时的理想位移曲线. 运动副间隙对机械臂的运动精度具有比较大的影响. 空间机械臂内存在的关节间隙会使得运动精度越来越低, 所以分析运动副间隙对机构运动精度可靠性的影响具有非常重要的意义.
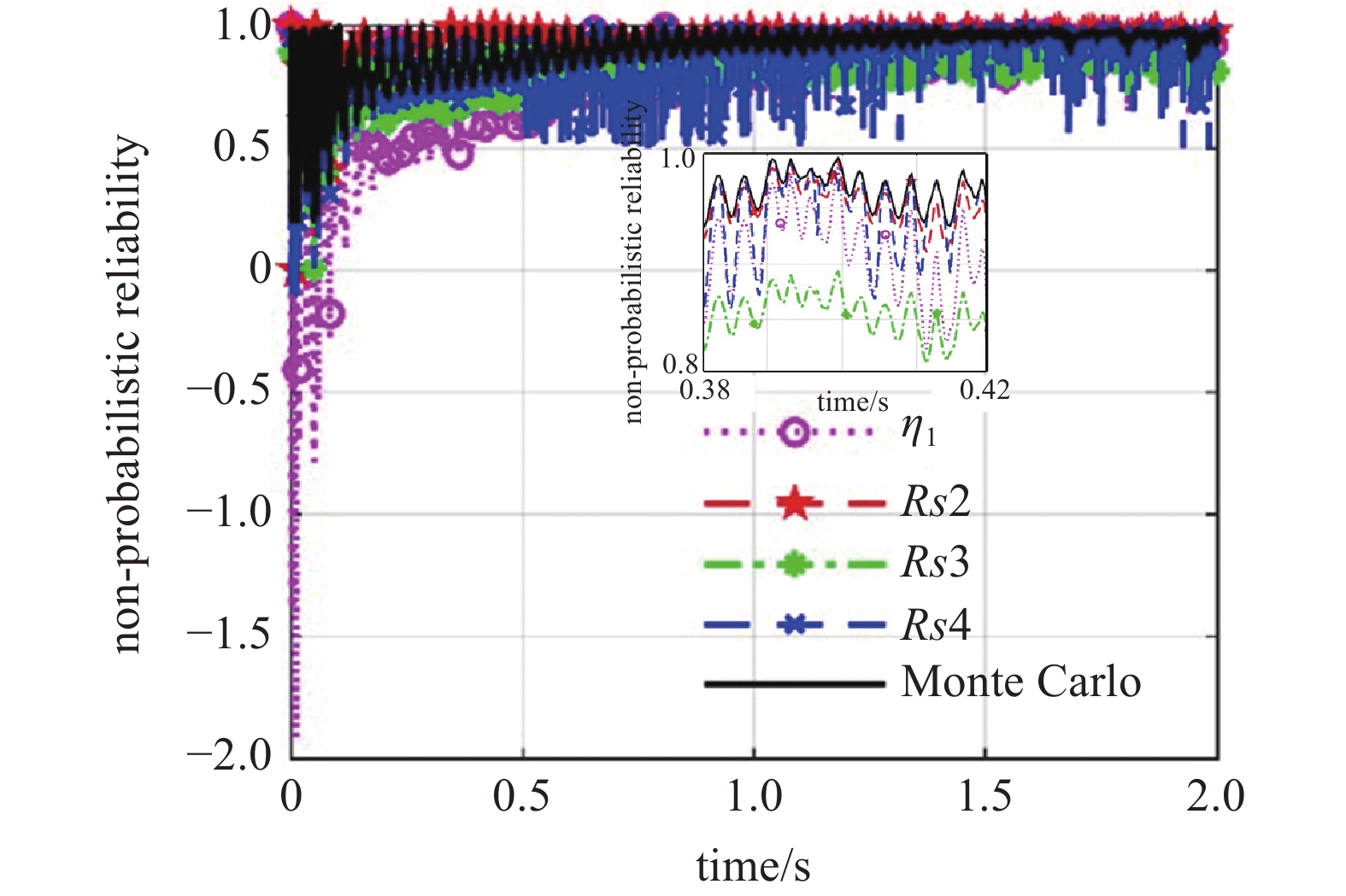
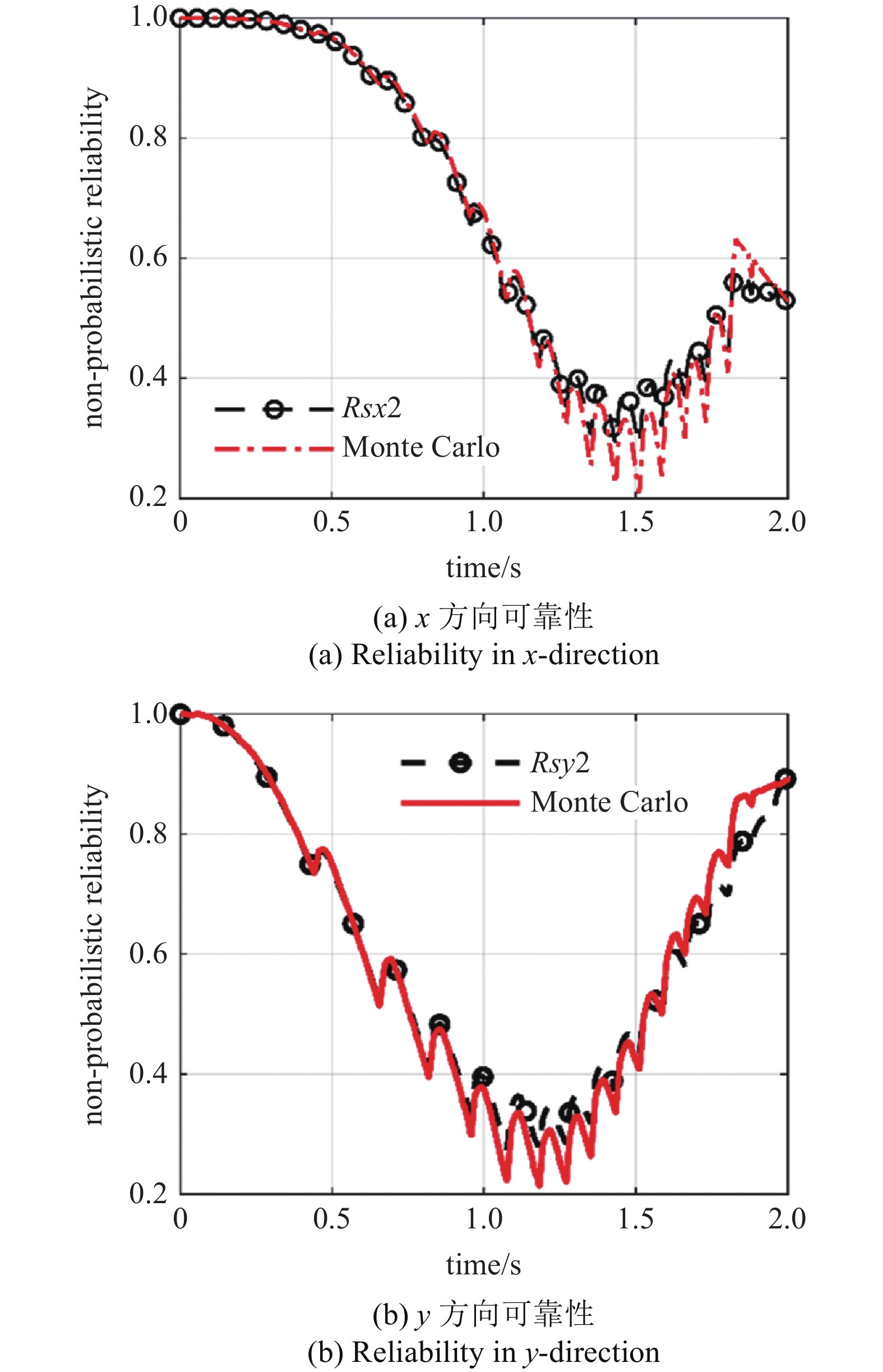
采用位移偏差构建评判系统可靠性的极限状态函数来评价系统的可靠性. 当x方向和y方向的许用位移偏差分别是$ \left[ {{\varepsilon _x}} \right] \in \left[ {0,5} \right]{\text{ mm}} $和$ \left[ {{\varepsilon _y}} \right] \in \left[ {0,10} \right]{\text{ mm}} $时, 得到5种非概率可靠性指标变化曲线, 如图5所示. 由图可知5种方法计算得到的可靠度整体变化趋势相似, 由于含间隙柔性机械臂是一个强耦合的非线性系统, 机械臂的动态响应随着运动时间动态变化. 在该仿真算例中, 机械臂的位移偏差随着运动时间先变大后变小, 进而机械臂运动可靠性随着工作时间增加先降低后增大. 此外, 基于可能性法的非概率可靠性值与Monte Carlo法所得到的值较为接近. 体积比法和容差法在计算可靠度时均存在分式的分母当中含有位移误差偏差, 当偏差较小的时候所得结果比较小, 所以会造成计算的结果偏差比较大.
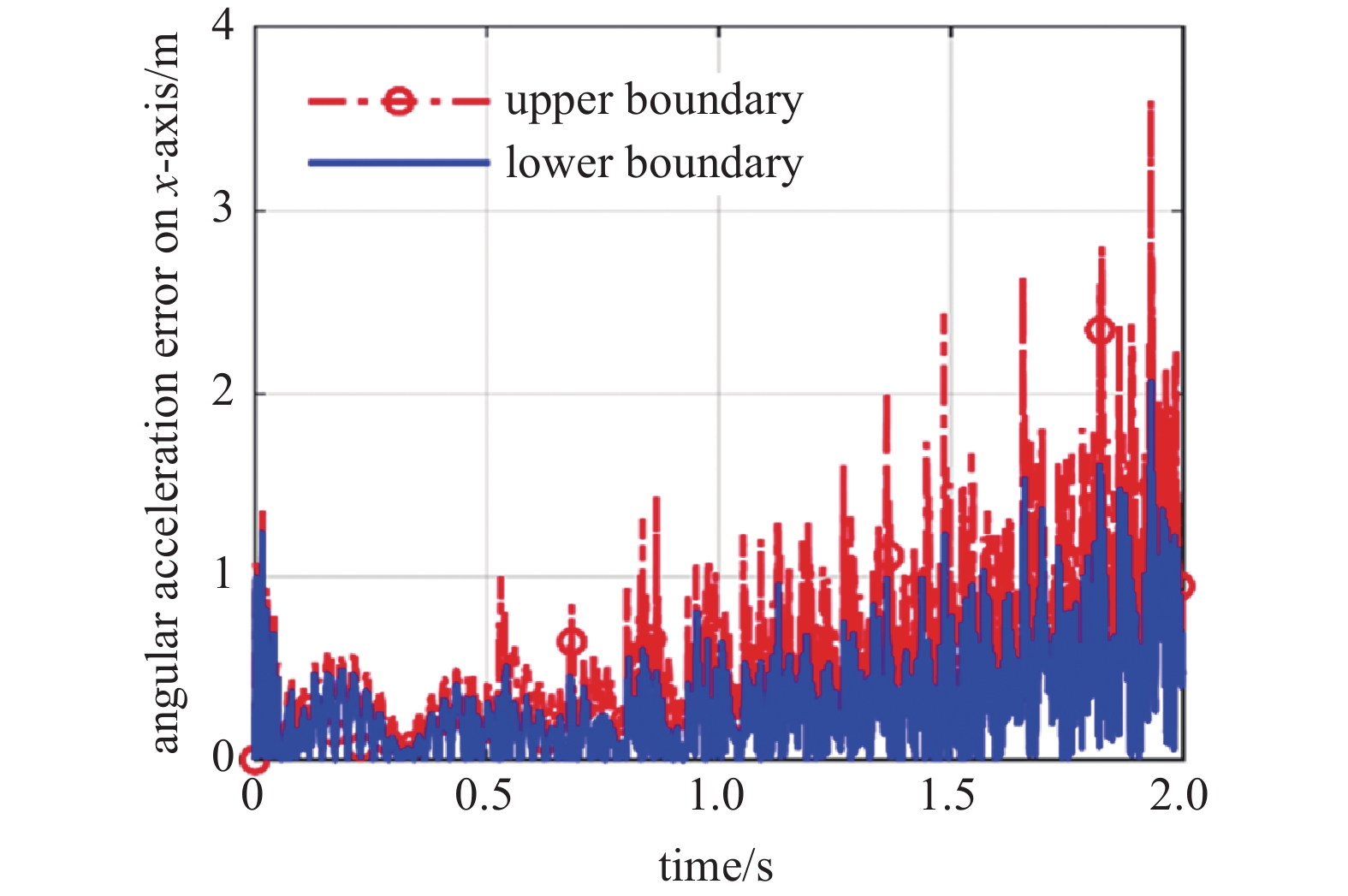
图6反映了在不考虑间隙以及将间隙考虑为区间变量的情况下的柔性臂关节角加速度的响应曲线. 在考虑间隙时, 机械臂的角加速度误差会逐渐增大, 这是由于系统的摩擦、磨损和受热变形等会改变间隙大小, 使碰撞力产生变化导致加速度的误差逐渐增大, 从而影响系统运动的稳定性和可靠性. 角加速度呈现出正弦波曲线样式的波动, 经过多次碰撞吸能, 波动的幅值和频率会逐渐减小.
采用角加速度偏差构建评判系统可靠性的极限状态函数来评价系统的可靠性. 当许用角加速度偏差$ \left[ {{\varepsilon _\alpha }} \right] \in \left[ {0,5} \right]\;{{\mathrm{rad/}}}{{{\mathrm{s}}}^{2}} $, 得到5种非概率可靠性指标变化曲线, 如图7所示. 随着时间的增加, 系统的可靠性指标在0 ~ 1之间不断震荡, 可靠性指标的波动范围逐渐减小. 其中, 可能性模型与Monte Carlo法所得到的结果的变化趋势较为接近. Monte Carlo法是一种随机模拟方法, 一般来说可以用它所得到的结果作为近似准确解.
Monte Carlo法作为一种计算机模拟方法, 样本点越多, 计算结果越精确, 同时计算所需的时间也增大. 仿真计算使用Intel Core i7-8750H的处理器, 16 G的RAM内存, 64位的Windows 10系统进行. 选取了
10000 个样本点, 基于可能性模型的仿真时间依次为0.673, 0.728和0.534 s; 基于Monte Carlo模型的仿真时间依次为2.527, 3.528和12.232 s, 相同条件下, 可能性法的计算效率更高.4.2 考虑多种不确定参数的动力响应分析
进一步, 本节研究考虑多种不确定区间参数的影响, 将关节间隙$c$、长度${L_2}$、密度${\rho _2}$和弹性模量${E_2}$考虑为不确定区间参数, 其余参数与4.1节相同. 取各区间参数的值为: $ {{{{c}}_1}} = {{{{c}}_2}} = \left[ {0.8,1.2} \right]{\text{ mm}}$, $ {{L_2}} = \left[ {0.99,1.01} \right]{\text{ m}} $, $ {{\rho _2}} = \left[{2650,2750} \right]{\;{\mathrm{kg}}/}{{{\mathrm{m}}}^3} $, $ {{E_2}} = \left[67.9, 72.1 \right]{\text{ GPa}} $. 在该种情况下的x方向的许用位移误差为$ {{\varepsilon _x}} = \left[ {0,5} \right]{\text{ mm}}$, y方向的许用位移误差为${{\varepsilon _y}} = \left[ {0,10} \right]{\text{ mm}}$, 柔性臂角加速度的许用误差为$ {{\varepsilon _a}} = \left[ {0,5} \right] {{\mathrm{rad}}/}{{{\mathrm{s}}}^{2}}$. 依据上述理论和数值仿真结果, 分析其动力学响应和非概率可靠性指标的变化规律.
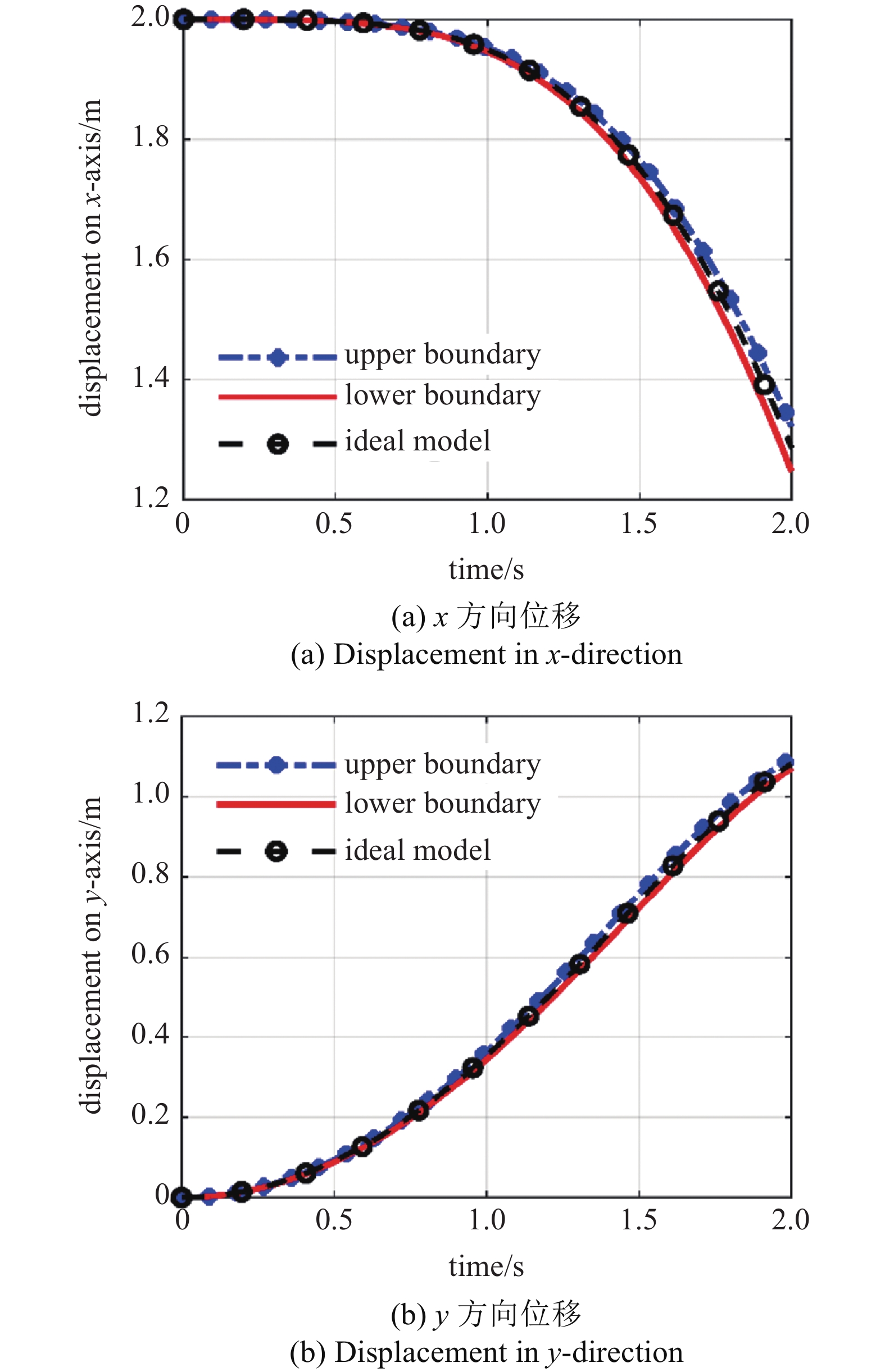
图8所示反映了在考虑4种混合区间变量时柔性臂末端位移的变化趋势与不确定参数在确定情况下的位移对比. 从图中可以看出, 不确定参数对末端位移具有很大的影响.
图9所示是机械臂末端位移误差的响应边界曲线. 反映了位移误差区间和误差的变化趋势是波动的, 其先增大后减小. 在$t = 0$时刻, 位移误差$ \Delta {\varepsilon _x} = \Delta {\varepsilon _y} = 0 $ mm. $x$方向位移的最大误差是
0.0049 m,$y$方向位移的最大误差是0.0084 m.以位移误差建立非概率可靠性模型, 并采用可能性法与Monte Carlo法计算得到可靠度, 图10给出了x方向和y方向的位移可靠性. 由图可知, 两种模型曲线的变化趋势是相近的, 两者的误差比较小, 所以可以通过可能性模型的非概率计算来判断系统的可靠性, 与图5得到的结论一致. 机械臂的长度${L_2}$、材料密度${\rho _2}$、弹性模量${E_2}$和关节间隙$c$等多种不确定参数对柔性臂末端位移的影响比较大, 随着时间的变化整个系统的可靠性指标在0 ~ 1内不断变化. 在接近2 s的位置, 整个系统的可靠性都有下降的趋势, 其中, x方向的位移可靠性指标的下降趋势比较大.
图11展示了在考虑多种区间参数情况下与理想情况下柔性臂角加速度的响应曲线. 多种不确定参数对机械臂角加速度的影响较为显著, 随着时间的增加, 角加速度的震荡频率和幅值也越来越大, 严重影响系统的稳定性. 图12所示是柔性机械臂角加速度误差的响应边界曲线, 系统的误差在不断变大, 波动频率和幅值不断增加.
图13所示反映了在多种区间参数下柔性机械臂的非概率可靠性指标的变化情况. 从图中可以看出, 可能性模型与Monte Carlo模型的变化趋势是相近的. 整体来看, 这些不确定参数使系统的可靠性降低, 影响系统的可靠性. 在$t = 0$时刻, 机械臂的可靠性$ {R_{s2}} = 1 $, 是完全可靠的, 随着时间的增加, 机械臂的可靠性呈现逐渐降低的趋势, 当可靠性$ {R_{s2}} = 0 $时, 系统将完全失效.
5. 结 论
本文基于Euler-Bernoulli模型和假设模态法, 利用Lagrange方程建立了柔性机械臂的不确定动力学模型. 然后, 基于Chebyshev多项式提出了不确定动力学的区间方法, 求解系统的响应边界, 重点研究了关节间隙和不确定参数对机械臂动力学响应的影响. 在此基础上, 针对空间机械臂难以获得大量实验样本来分析概率可靠性的问题, 提出了4种非概率可靠性计算方法, 并通过数值模拟研究, 得到如下主要结论.
(1) 考虑间隙和不确定性参数建立的柔性机械臂动力学模型可准确预示柔性机械臂的动力学响应, 且关节间隙和不确定参数严重影响机械臂的运动精度和运动的稳定性, 使得机械臂的可靠性降低.
(2) 相比于关节间隙, 臂杆的长度、密度和弹性模量等不确定参数对机械臂的动态特性的影响更为显著, 从而显著影响机械臂的运动稳定性. 而且, 机械臂的柔性会使得机械臂发生弹性形变, 对其运动精度具有显著影响.
(3) 4种非概率可靠性计算方法中, 可能性法与Monte Carlo法的可靠性指标求解结果最为接近, 计算精度最高, 且这种方法的计算效率比Monte Carlo方法更快.
-
表 1 柔性机械臂参数
Table 1 Parameters for the flexible manipulator
Geometric size/m $ \rho $/(kg·m−3) $ E $/GPa arm 1 1 × 0.04 × 0.04 7800 215 arm 2 1 × 0.04 × 0.04 2700 71 -
[1] Flores-Abad A, Ma O, Pham K, et al. A review of space robotics technologies for on-orbit servicing. Progress in Aerospace Sciences, 2014, 68: 1-26 doi: 10.1016/j.paerosci.2014.03.002
[2] Garcia-Luna F, Rodriguez-Ramirez A, Nandayapa M, et al. Augmented reality-based robotic system for in-space servicing. IEEE Aerospace and Electronic Systems Magazine, 2024, 39(1): 18-31 doi: 10.1109/MAES.2023.3335006
[3] Faes M, Moens D. Recent trends in the modeling and quantification of non-probabilistic uncertainty. Archives of Computational Methods in Engineering, 2020, 27(3): 633-671 doi: 10.1007/s11831-019-09327-x
[4] Jiang X, Bai Z. Dynamic analysis for mechanical system with clearance joint considering dependent interval parameters. Mechanics Based Design of Structures and Machines, 2024, 52(5): 2726-2748 doi: 10.1080/15397734.2023.2189944
[5] Zhang Y, Gu Y, Liu T, et al. Dynamic behavior and parameter sensitivity of the free-floating base for space manipulator system considering joint flexibility and clearance. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2019, 233(3): 895-910 doi: 10.1177/0954406218806927
[6] Gan CB, Wang YH, Yang SX. Nonparametric modeling on random uncertainty and reliability analysis of a dual-span rotor. Journal of Zhejiang University-Science A, 2018, 19(3): 189-202 doi: 10.1631/jzus.A1600340
[7] 邱雪松, 商阔, 丁锡浩等. 极端温度下含隙铰柔性帆板展开位置精度分析. 宇航学报, 2021, 42(3): 314-323 (Qiu Xuesong, Shang Kuo, Ding Xihao, et al. Precision analysis of deployable position of flexible solar array with gap hinges at extreme temperature. Journal of Astronautics, 2021, 42(3): 314-323 (in Chinese) doi: 10.3873/j.issn.1000-1328.2021.03.006 Qiu Xuesong, Shang Kuo, Ding Xihao, et al. Precision analysis of deployable position of flexible solar array with gap hinges at extreme temperature. Journal of Astronautics, 2021, 42(3): 314-323 (in Chinese) doi: 10.3873/j.issn.1000-1328.2021.03.006
[8] Fu C, Zhang K, Cheng H, et al. A comprehensive study on natural characteristics and dynamic responses of a dual-rotor system with inter-shaft bearing under non-random uncertainty. Journal of Sound and Vibration, 2024, 570: 118091 doi: 10.1016/j.jsv.2023.118091
[9] Nie XB, Li HB. A direct-integration-based structural reliability analysis method using non-probabilistic convex model. Journal of Mechanical Science and Technology, 2018, 32(11): 5063-5068 doi: 10.1007/s12206-018-1002-2
[10] Dourado ADP, Lobato FS, Cavalini AA, et al. Fuzzy reliability-based optimization for engineering system design. International Journal of Fuzzy Systems, 2019, 21(5): 1418-1429 doi: 10.1007/s40815-019-00655-5
[11] Hu Y, Lu Z, Lei J. Time-dependent reliability analysis model under fuzzy state and its safety lifetime model. Structural and Multidisciplinary Optimization, 2019, 60(6): 2511-2529 doi: 10.1007/s00158-019-02343-2
[12] Hu Y, Yan H, Zhang H, et al. Robust adaptive fixed-time sliding-mode control for uncertain robotic systems with input saturation. IEEE Transactions on Cybernetics, 2022, 53(4): 2636-2646
[13] Yao J, Deng W. Active disturbance rejection adaptive control of uncertain nonlinear systems: theory and application. Nonlinear Dynamics, 2017, 89(3): 1611-1624 doi: 10.1007/s11071-017-3538-6
[14] Pandy MD, Zhang X. System reliability analysis of the robotic manipulator with random joint clearances. Mechanism and Machine Theory, 2012, 58: 137-152 doi: 10.1016/j.mechmachtheory.2012.08.009
[15] Jia Y, Chen X, Zhang L, et al. Dynamic characteristics and reliability analysis of parallel mechanism with clearance joints and parameter uncertainties. Meccanica, 2023, 58(4): 813-842 doi: 10.1007/s11012-023-01650-9
[16] 蒋鑫, 白争锋, 宁志远等. 基于信号分解和Chebyshev多项式的多体系统区间不确定性分析方法. 力学学报, 2022, 54(6): 1694-1705 (Jiang Xin, Bai Zhengfeng, Ning Zhiyuan, et al. Interval uncertainty analysis methods for multibody systems based in signal decomposition and Chebyshev polynomials. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(6): 1694-1705 (in Chinese) doi: 10.6052/0459-1879-22-092 Jiang Xin, Bai Zhengfeng, Ning Zhiyuan, et al. Interval uncertainty analysis methods for multibody systems based in signal decomposition and Chebyshev polynomials. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(6): 1694-1705 (in Chinese) doi: 10.6052/0459-1879-22-092
[17] Jiang X, Bai Z. A bivariate subinterval method for dynamic analysis of mechanical systems with interval uncertain parameters. Communications in Nonlinear Science and Numerical Simulation, 2023, 125: 107377 doi: 10.1016/j.cnsns.2023.107377
[18] Xiang W, Yan S. Dynamic analysis of space robot manipulator considering clearance joint and parameter uncertainty: Modeling, analysis and quantification. Acta Astronautica, 2020, 169: 158-169 doi: 10.1016/j.actaastro.2020.01.011
[19] Jiang S, Zhao M, Liu J, et al. Dynamic response and nonlinear characteristics of multi-link mechanism with clearance joints. Archive of Applied Mechanics, 2023, 93(9): 3461-3493 doi: 10.1007/s00419-023-02449-6
[20] Liu Z, Zhang H, Meng L, et al. A new kinematic model for revolute clearance joints with noncircular bushing and pin in planar multibody systems. Nonlinear Dynamics, 2024, 112: 12965-12993
[21] Tan H, Li L, Huang Q, et al. Influence of two kinds of clearance joints on the dynamics of planar mechanical system based on a modified contact force model. Scientific Reports, 2023, 13(1): 20569 doi: 10.1038/s41598-023-47315-1
[22] Chen Y, Feng J, Peng X, et al. An approach for dynamic analysis of planar multibody systems with revolute clearance joints. Engineering with Computers, 2021, 37(3): 2159-2172 doi: 10.1007/s00366-020-00935-x
[23] Lankarani HM, Nikravesh PE. Continuous contact force models for impact analysis in multibody systems. Nonlinear Dynamics, 1994, 5(2): 193-207 doi: 10.1007/BF00045676
[24] Miao, H, Li B, Liu J, et al. Effects of revolute clearance joint on the dynamic behavior of a planar space arm system. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 233(5): 1629-1644 doi: 10.1177/0954410018760024
[25] Chen Y, Wu X, Wu K, et al. An experimental and analytical study on dynamic behaviors of high-precision mechanism including revolute clearance joints. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2022, 44(4): 120 doi: 10.1007/s40430-022-03421-1
[26] Erkaya S, Uzmay İ. Modeling and simulation of joint clearance effects on mechanisms having rigid and flexible links. Journal of Mechanical Science and Technology, 2014, 28(8): 2979-2986 doi: 10.1007/s12206-014-0705-2
[27] Erkaya S, Doğan S, Ulus Ş. Effects of joint clearance on the dynamics of a partly compliant mechanism: Numerical and experimental studies. Mechanism and Machine Theory, 2015, 88: 125-140 doi: 10.1016/j.mechmachtheory.2015.02.007
[28] Wang Z, Tian Q, Hu H, et al. Nonlinear dynamics and chaotic control of a flexible multibody system with uncertain joint clearance. Nonlinear Dynamics, 2016, 86(3): 1571-1597 doi: 10.1007/s11071-016-2978-8
[29] 战俊杰, 彭秀林, 白仲航. 考虑有界场的几何不确定性非概率可靠性拓扑优化. 力学学报, 2023, 55(9): 2056-2067 (Zhan Junjie, Peng Xiulin, Bai Zhonghang, et al. Non-probability reliability-based topology optimization against geometric uncertainty with a bounded field model. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(9): 2056-2067 (in Chinese) doi: 10.6052/0459-1879-23-207 Zhan Junjie, Peng Xiulin, Bai Zhonghang, et al. Non-probability reliability-based topology optimization against geometric uncertainty with a bounded field model. Chinese Journal of Theoretical and Applied Mechanics, 2023, 55(9): 2056-2067 (in Chinese) doi: 10.6052/0459-1879-23-207
[30] 李小彭, 尚东阳, 陈仁桢等. 基于机械臂位姿变换的柔性负载伺服驱动系统控制策略. 机械工程学报, 2020, 56(21): 56-69 (Li Xiaopeng, Shang Dongyang, Chen Renzhen, et al. Control strategy of flexible load servo drive system based on manipulator position and position transformation. Journal of Mechanical Engineering, 2020, 56(21): 56-69 (in Chinese) doi: 10.3901/JME.2020.21.056 Li Xiaopeng, Shang Dongyang, Chen Renzhen, et al. Control strategy of flexible load servo drive system based on manipulator position and position transformation. Journal of Mechanical Engineering, 2020, 56(21): 56-69 (in Chinese) doi: 10.3901/JME.2020.21.056
[31] Ranjan R, Dwivedy SK. Dynamic analysis and control of a string-stiffened single-link flexible manipulator with flexible joint. Mechanics Based Design of Structures and Machines, 2023, 51(11): 6329-6359 doi: 10.1080/15397734.2022.2040364
[32] Kumar P, Pratiher B. Nonlinear modelling and dynamics of spatial multi-link rigid-flexible manipulator with moving platform. International Journal of Intelligent Robotics and Applications, 2024, 8: 735-757
[33] Tokhi MO, Mohamed Z, Shaheed MH. Dynamic characterization of a flexible manipulator system. Robotica, 2001, 19(5): 571-580 doi: 10.1017/S0263574700003209
[34] Zhang Y, Liu Y, Yang X, et al. A global nonprobabilistic reliability sensitivity analysis in the mixed aleatory-epistemic uncertain structures. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014, 228(10): 1802-1814 doi: 10.1177/0954410014534201
[35] Marano GC, Quaranta G. A new possibilistic reliability index definition. Acta Mechanica, 2010, 210(3-4): 291-303 doi: 10.1007/s00707-009-0194-z
[36] Hong L, Li S, Chen M, et al. Non-probabilistic reliability analysis with both multi-super-ellipsoidal input and fuzzy state. Computer Methods in Applied Mechanics and Engineering, 2024, 429: 117154 doi: 10.1016/j.cma.2024.117154
[37] Wang R, Wang X, Wang L, et al. Efficient computational method for the non-probabilistic reliability of linear structural systems. Acta Mechanica Solida Sinica, 2016, 29(3): 284-299 doi: 10.1016/S0894-9166(16)30162-8



 下载:
下载: