ARTIFICIAL INTELLIGENT PREDICTION METHODS OF MATERIAL CONSTITUTIVE BEHAVIOR BASED ON CRYSTAL PLASTICITY FRAMEWORK
-
摘要: 人工神经网络(ANNs)已逐渐成为非线性材料多尺度本构建模的重要工具. 针对航空航天领域中广泛使用的镍基单晶合金开发了基于晶体塑性框架的材料本构行为智能预测方法. 提出的新方法在数据驱动的基础上结合了晶体塑性本构模型, 保留了晶体滑移系的求解框架, 将激活滑移系上的状态变量作为网络的输入, 建立了状态变量和滑移系剪切应变增量的物理联系, 引入了物理信息损失函数, 实现了应力的隐式求解, 从而准确预测了单晶材料的单调、循环力学行为. 进一步地, 探究了不同损失函数对模型训练结果的影响, 明确指出数据和物理约束共同作用下的模型性能显著提升. 物理信息的融入在一定程度上提升了模型的外插预测精度, 但在训练样本稀疏区域仍然无法做到精确预测. 为了解决在训练样本稀疏区域难以精确预测的问题, 在常规的离线学习策略上提出了在线学习策略, 使得神经网络模型根据残差大小进行自学习, 最终达到传统本构模型的预测精度. 提出的基于神经网络的晶体塑性本构行为预测框架为材料本构关系研究领域提供了创新且有效的思路, 有望进一步推动复杂材料的多尺度本构模型研究.
-
关键词:
- 循环晶体塑性 /
- 镍基单晶合金 /
- 物理信息神经网络(PINN) /
- 取向敏感性 /
- 在线学习机制
Abstract: Artificial neural networks (ANNs) have become a powerful and indispensable tool for multiscale constitutive modeling of nonlinear materials. This paper develops an intelligent prediction method for the constitutive behavior of nickel-based single-crystal alloys widely used in aerospace industries, based on the framework of crystal plasticity. The proposed approach integrates data-driven techniques with a conventional crystal plasticity constitutive model, resulting in a hybrid framework that enhances predictive capabilities while retaining the fundamental physical principles governing crystal slip systems. The solution framework preserves the conventional formulation for resolving slip systems, where state variables associated with these slip systems are used as inputs to the neural network. This enables the establishment of a physical relationship between the state variables and shear strain increments of the slip systems. A physics-informed loss function is employed to achieve the implicit stress integration, allowing the neural network to accurately predict the mechanical responses of single-crystal materials under both monotonic and cyclic loading conditions. The study also investigates the effects of different loss functions on the model training process, revealing that the combination of data-driven learning and physical constraints significantly improves the model’s performance. Integrating physical information within the loss function enhances the model's ability to extrapolate predictions beyond the range of training data, providing more accurate predictions for unseen scenarios. However, challenges remain in regions where training data is sparse, leading to less precise predictions. To address the limitations in sparse data regions, an innovative online training scheme is introduced on top of conventional offline learning strategies. This scheme enables the neural network to adaptively improve its performance by minimizing residual errors during predictions, essentially allowing the model to self-learn and refine its accuracy. As a result, the online-trained model achieves prediction accuracy comparable to that of conventional constitutive models, bridging the gap between data-driven approaches and established material modeling techniques. The neural network-based crystal plasticity framework proposed in this work offers a novel and effective approach for studying material constitutive relationships, with significant potential to further advance the development of multiscale constitutive models for complex material systems. -
引 言
材料本构模型在理解和预测材料的力学行为方面发挥着至关重要的作用[1]. 由于复杂的服役环境和载荷条件, 材料在多轴和循环等复杂应力状态下的行为仍未得到很好地刻画. 此外, 材料本构行为是一个宏微观结合的多尺度问题, 针对晶体塑性本构模型, 虽然晶体结构的滑移机制已经被学者们普遍接受, 但是各力学变量的演化方程仍未形成一致的共识, 尤其是高温服役过程中材料将发生微结构演化和性能衰退, 目前材料本构模型的适用性仍然有限, 难以考虑其多尺度时变特性[2]. 因此, 如何更好地描述材料本构行为有待进一步发展.
机器学习为材料本构模型建立提供了另一种选择. 机器学习从海量数据中总结自变量与因变量之间的规律, 其优势在于能够自主学习力学性能和微观机制等变量之间的潜在关联性, 从而发现一些难以直接观察的底层联系. 材料在不同的加载条件下可以表现出复杂的非线性行为, 这些行为可以通过机器学习算法捕获[3-4]. Ali 等[5]采用人工神经网络(ANN)来捕获多晶材料的本构行为和织构演化. Mozaffar等[6]和 Abueidda 等[7]使用循环神经网络(RNN)预测路径依赖的塑性流动行为. Yu等[8]采用门控循环单元(GRU)实现了复杂路径加载下的J2塑性本构的学习. Li等[9]建立了基于机器学习的 Johnson-Cook 塑性模型, 可以高精度地描述力-位移关系和局部表面应变. Weng等[10-11]引入了组构张量, 借助ANN来刻画多轴加载条件下J2塑性和晶体塑性的多尺度本构行为. Bonatti等[12]针对晶体塑性本构模型, 提出了利用RNN实现与输入路径的时间离散化无关的应力响应预测方法. Ibragimova等[13]通过机器学习实现了面心立方晶体的应力-应变行为及织构演化的预测. 总之, 机器学习方法能够建立各种条件下准确且通用的材料本构行为预测模型, 正在为材料本构建模领域带来新的变革.
为了更好地理解神经网络的内在运行逻辑, 研究兴趣从使用应力-应变作为直接输入和输出转变为考虑更多的材料状态变量. 作为研究基于神经网络的本构模型的早期先驱, Hasgash等[14]使用具有内部变量的 ANN 预测了材料的单轴迟滞行为. 最近, Jang等[15]用保留了传统力学框架的 ANN 模型取代了应力积分方案. Fazily等[16]进一步实现了各向异性塑性的进阶版本. 同样, Heider等[17]提出了一个融入力学信息的方法, 他将神经网络材料建模分解为几个步骤, 模拟弹塑性本构求解的基本流程. Liu等[18]也将类似的想法应用于疲劳寿命预测, 以分层渐进的方式建立了神经网络模型. 综上, 利用神经网络取代常规力学框架中的一部分, 或将框架解耦后分步建立成为材料行为智能预测的新方向, 这也有助于更好地看清内部变量的传递和预测过程.
尽管如此, 人工智能方法在力学、工程领域的应用仍然面临数据稀缺的困境. 为了克服神经网络对数据的依赖性, Raissi 等[19]提出了物理信息神经网络(physics-informed neural network, PINN)的概念, 其设计目的是将物理定律和约束纳入神经网络模型中. 数据驱动模型通常需要大量训练数据才能做出准确的预测. 相比之下, 即使在数据稀缺的条件下, PINN 也可以利用有限的数据和已知的物理原理来做出准确的预测. 通过编码基础物理的先验知识, PINN 可以强制执行基本关系, 例如守恒定律或边界条件, 这可以显著提高模型的准确性和泛化性. 由于PINN尊重底层物理原理, 能表现出良好的外插能力, 即使在没有可用训练数据的输入空间区域, 它们也可以提供可靠的预测[20]. Tandale等[21]针对Lemaitre-Chaboche的黏塑性模型开发了一种基于RNN的隐式积分算法, 其中使用了物理信息作为损失函数参与训练. Masi等[22-23]提出了满足热力学定律的物理信息神经网络本构模型. 在此基础上, Masi等[24]提出了演化的TANN (eTANN), 该方法的主要特点是以常微分方程的形式而不是增量离散时间形式来识别内部变量的演化方程. Niu等[25]提出了一种应用于有限弹塑性变形的PINN框架, 并通过有限元数值算例评估了PINN模型的准确性和稳定性. Haghighat等[26-27]在固体力学有限元模拟框架上, 将平衡方程、本构关系纳入PINN训练, 研究了线弹性和J2弹塑性下PINN的建立和性能. 然而, 目前PINN相关方法在晶体塑性框架的应用较少, 仍有待进一步发展.
本文基于晶体塑性框架提出了材料本构行为的智能预测方法, 该方法保留了晶体滑移理论, 能够实现对所有激活滑移系状态变量的预测. 同时, 为了减少神经网络模型对样本的依赖并提高其外插能力, 在神经网络训练模型时引入了物理约束, 并探讨了不同损失函数对于模型训练的影响. 本文验证了该方法的有效性, 也指出了现存问题和未来可能的发展.
1. 晶体塑性有限元模拟
1.1 本构模型
本文的主要目标是将晶体滑移机制引入神经网络本构行为预测中. 作为对该方法的初步探索, 本文以小变形问题为例, 开展后续数值仿真工作, 以简化问题的复杂性. Méric等[28]针对小变形问题提出了单晶合金循环晶体塑性模型, 它在连续介质力学框架内考虑了滑移变形机制, 目前仍有较广泛的应用. 本文将基于此模型开展研究和讨论.
在弹塑性问题中, 一般将总应变分解为弹性部分和塑性部分, 如
$$ {\boldsymbol{\dot \varepsilon }} = {{\boldsymbol{\dot \varepsilon }}^e} + {\text{ }}{{\boldsymbol{\dot \varepsilon }}^p} $$ (1) 应力${\boldsymbol{\sigma }}$可由弹性应变${{\boldsymbol{\dot \varepsilon }}^e}$确定
$$ {\boldsymbol{\dot \sigma }} = {\boldsymbol{C}}:{\text{ }}{{\boldsymbol{\dot \varepsilon }}^e} $$ (2) 其中, $ {\boldsymbol{C}} $是弹性模量张量. 对于呈立方弹性的单晶合金, $ {\boldsymbol{C}} $由3个独立参数${C_{11}},{C_{12}}$和${C_{44}}$组成. 在晶体塑性本构模型中, 塑性变形是由特定方向上的滑移引起. 对于镍基单晶合金的面心立方(FCC)晶体结构, 已知的可能启动的滑移系包括[29]: 八面体滑移系 <111> (110)、六面体滑移系 <100> (110)和十二面体滑移系 < 111 > (112). 将$\alpha $滑移系上的取向因子定义为
$$ {{\boldsymbol{P}}^{(\alpha )}} = \frac{1}{2}\left( {{\text{ }}{{\boldsymbol{m}}^{(\alpha )}} \otimes {{\boldsymbol{n}}^{(\alpha )}} + {\text{ }}{{\boldsymbol{n}}^{(\alpha )}} \otimes {{\boldsymbol{m}}^{(\alpha )}}} \right) $$ (3) 式中${{\boldsymbol{P}}^{(\alpha )}}$可作为方向乘数, 从而将应力应变与滑移系上的切应力应变建立联系. 这里, $ {{\boldsymbol{m}}^{(\alpha )}} $和$ {{\boldsymbol{n}}^{(\alpha )}} $是滑移系$\alpha $的滑移方向和滑移面法向量. $\alpha $滑移系$ {\tau ^{(\alpha )}} $中的剪应力可表示为
$$ {\tau ^{(\alpha )}} = {\text{ }}{{\boldsymbol{P}}^{(\alpha )}}:{\text{ }}{\boldsymbol{\sigma }} $$ (4) 通过一系列滑移系中的剪切应变计算宏观塑性应变, 得到关系式如下
$$ {{\boldsymbol{\dot \varepsilon }}^p} = \sum\limits_{\alpha = 1}^{{N_{sp}}} {\text{ }} {{\boldsymbol{P}}^{(\alpha )}}{\dot \gamma ^{(\alpha )}} $$ (5) 其中, $ {\dot \gamma ^{(\alpha )}} $是剪切应变率, 共有${N_{sp}}$个滑动系统. 由上式可见, 在晶体塑性框架下, 材料的塑性变量由各个启动的滑移系中的切应变贡献.
在塑性阶段, 晶体塑性框架下的应力应变关系需要依赖于滑移系建立, 其滑移剪切应变率方程可写为
$$ {\dot \gamma ^{(\alpha )}} = \dot \gamma _0^{(\alpha )}{\text{sign}}\left( {{\tau ^{(\alpha )}} - {X^{(\alpha )}}} \right){\left\langle {\frac{{\left| {{\tau ^{(\alpha )}} - {X^{(\alpha )}}} \right| - {r^{(\alpha )}}}}{{{g^{(\alpha )}}}}} \right\rangle ^n} $$ (6) 式中, 上标$\alpha $表示各个量所在的滑移系, $ {\tau ^{(\alpha )}} $是分解切应力, $ {r^{(\alpha )}} $和$ {X^{(\alpha )}} $分别是各向同性硬化和背应力项, $ \dot \gamma _0^{(\alpha )} $表示参考剪切应变率, $ {g^{(\alpha )}} $是取决于温度和滑移系统类型的材料常数. 指数$n$是与应变硬化相关的参数, 如果$n \to \infty $, 模型将接近理想塑性. 背应力$ {\alpha ^{(\alpha )}} $的演化方程为
$$ {\dot X^{(\alpha )}} = {c_1}{\dot \gamma ^{(\alpha )}} - {c_2}\left| {{{\dot \gamma }^{(\alpha )}}} \right|{X^{(\alpha )}} $$ (7) 各向同性硬化项$ {r^{(\alpha )}} $遵循以下等式
$$ {\dot r^{(\alpha )}} = bQ\sum\limits_\beta {{h_{\alpha \beta }}} {\dot \rho ^{(\beta )}} $$ (8) 式中, ${c_1},{c_2},b$和$Q$是模型常量, $ {r^{(\alpha )}} $的初始临界值为$r_0^{(\alpha )}$, ${h_{\alpha \beta }}$是交叉硬化矩阵, 反映了滑移系统耦合效应引起的潜在硬化. 引入状态变量${\rho ^{(\beta )}}$来描述晶滑中的位错硬化, 其演化方程为
$$ {\dot \rho ^{(\beta )}} = \left( {1 - b{\rho ^{(\beta )}}} \right)\left| {{{\dot \gamma }^{(\beta )}}} \right| $$ (9) 本模型未考虑非比例载荷的影响. 为了减少计算费用, 该模型目前基于小变形框架, 对于大变形问题可以在此基础上修改. 循环单晶塑性模型通过UMAT实现到通用有限元代码ABAQUS中, 有关算法和实现的更多详细信息可以参阅文献[30].
1.2 有限元实施
晶体塑性有限元的核心是求解滑移系上的剪切应变增量$\Delta \gamma $, 然而, 与用于传统弹塑性问题的返向映射方法不同, 晶体塑性框架中求解$\Delta \gamma $更加困难, 因为它与各个启动的滑移系相关. 切线系数法广泛应用于晶体塑性有限元模拟中$\Delta \gamma $的求解, 通过在$\Delta t$内采用线性插值, $\Delta \gamma $可以写为
$$ \Delta {\gamma ^{(\alpha )}} = \Delta t\left[ {(1 - \theta )\dot \gamma _t^{(\alpha )} + \theta \dot \gamma _{t + \Delta t}^{(\alpha )}} \right] $$ (10) 式中, 下标表示剪切应变率所在的时间步, 参数$\theta $的取值范围是0 ~ 1. 不难看出, 当$\theta = 0$时为简单显式积分法, 而$\theta = 1$时为欧拉隐式积分法, 建议$\theta $选择在0.5 ~ 1之间.
对$\dot \gamma _{t + \Delta t}^{(\alpha )}$进行泰勒展开, 可以得到$\Delta \gamma $的近似解
$$ \begin{split} & \Delta {\gamma ^{(\alpha )}} = \Delta t\left( {{{\dot \gamma }^{(\alpha )}}(t) + {{\left. {\theta \frac{{\partial {{\dot \gamma }^{(\alpha )}}}}{{\partial {\tau ^{(\alpha )}}}}} \right|}_t}\Delta {\tau ^{(\alpha )}}} \right. + \\ &\qquad \left. { {{\left. {\theta \frac{{\partial {{\dot \gamma }^{(\alpha )}}}}{{\partial {X^{(\alpha )}}}}} \right|}_t}\Delta {X^{(\alpha )}} + {{\left. {\theta \frac{{\partial {{\dot \gamma }^{(\alpha )}}}}{{\partial {r^{(\alpha )}}}}} \right|}_t}\Delta {r^{(\alpha )}}} \right) \end{split} $$ (11) 式中, $ \Delta {\tau ^{(\alpha )}} $, $ \Delta {X^{(\alpha )}} $和$ \Delta {r^{(\alpha )}} $是$ \Delta {\gamma ^{(\alpha )}} $的函数, $ \Delta {\tau ^{(\alpha )}} $可以根据式(2)和式(4)推导得到
$$ \Delta {\tau ^{(\alpha )}} = {{\boldsymbol{P}}^{(\alpha )}}:{\text{ }}{\boldsymbol{C}}:\left( {\Delta {\boldsymbol{\varepsilon }} - \sum\limits_{\alpha = 1}^{{N_{sp}}} {\text{ }} {{\boldsymbol{P}}^{(\alpha )}}\Delta {\gamma ^{(\alpha )}}} \right) $$ (12) $ \Delta {X^{(\alpha )}} $和$ \Delta {r^{(\alpha )}} $通过将式(7)和式(8)转变为增量形式得到
$$\qquad\quad \Delta {X^{(\alpha )}} = {c_1}\Delta {\gamma ^{(\alpha )}} - {c_2}\left| {\Delta {\gamma ^{(\alpha )}}} \right|{X^{(\alpha )}} $$ (13) $$\qquad\quad \Delta {r^{(\alpha )}} = bQ\sum\limits_\beta {{h_{\alpha \beta }}} \Delta {\rho ^{(\beta )}} $$ (14) 其中, $ \Delta {\rho ^{(\beta )}} $通过$ \Delta {\gamma ^{(\alpha )}} $表示为
$$ \Delta {\rho ^{(\beta )}} = \left( {1 - b{\rho ^{(\beta )}}} \right)\left| {\Delta {\gamma ^{(\beta )}}} \right| $$ (15) 因此, 式(11)是一个线性代数方程, 用于求解未知变量$ \Delta {\gamma ^{(\alpha )}} $. 由于一阶泰勒展开式存在误差, 泰勒展开估计值仅作为$\Delta \gamma $求解得初值, 后续需要通过Newton-Raphson迭代来消除残差.
1.3 材料与模型参数
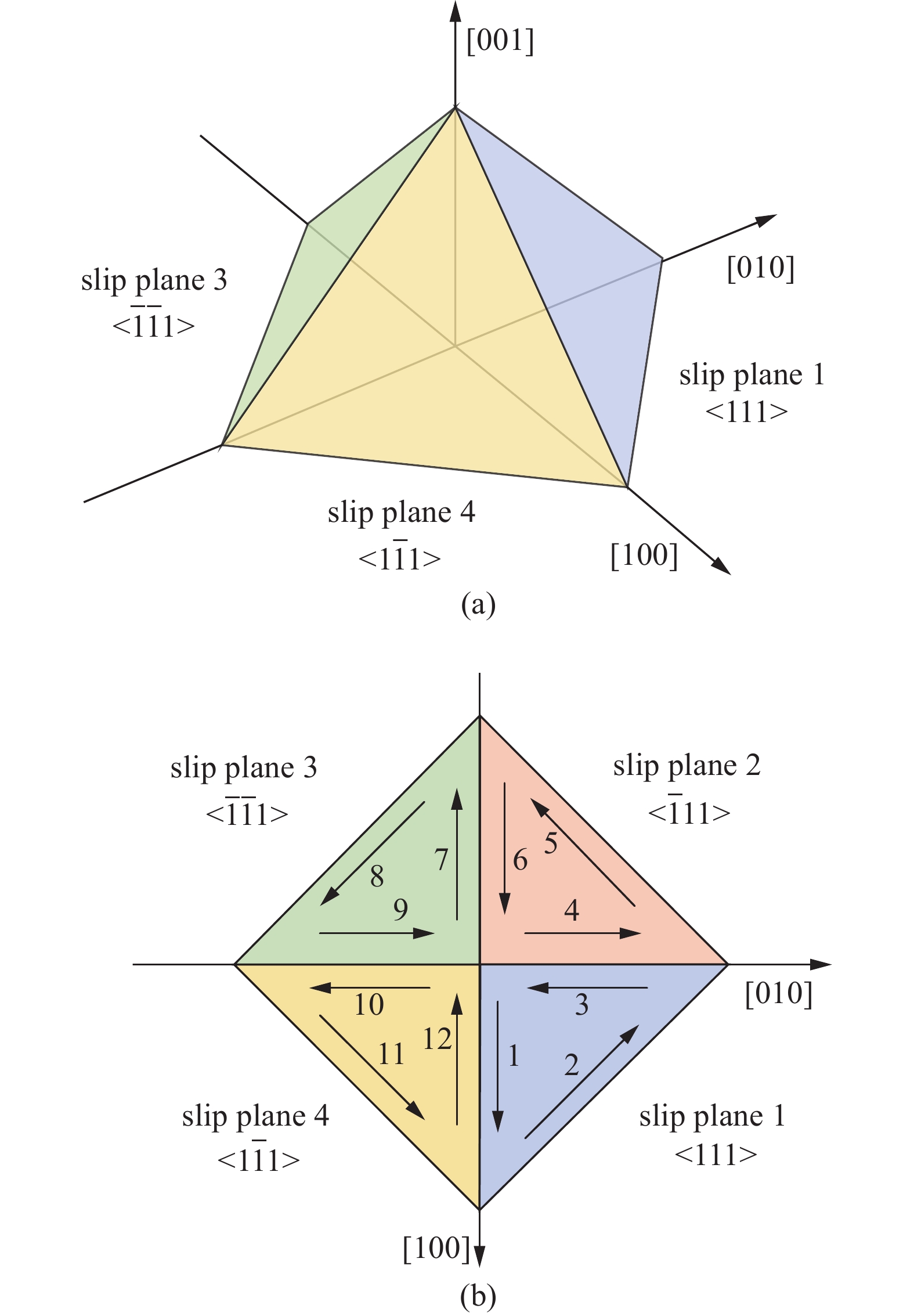
本文以国产第二代镍基单晶高温合金DD6为例开展讨论和研究. 镍基单晶高温合金是一类广泛应用于航空航天、燃气轮机发动机以及其他极端温度、载荷和腐蚀环境的高性能材料, 其制造过程涉及定向凝固, 其中合金以受控方式凝固以促进单晶的生长. 这种合金的变形通常由激活的滑移系控制, 例如此前提及的八面体、六面体和十二面体滑移系, 文献[31]表明, 在900 °C以下开动的滑移系为八面体滑移系, 在900 °C以上八面体滑移系和六面体滑移系同时开动. 由于本文主要研究DD6在900 °C以下本构行为预测方法, 因此, 在目前的工作中, 仅假设八面体滑移系统被激活. 八面体滑移系的滑移面和方向如图1所示, 由 4 个滑移面和每个平面上的 3 个滑移方向总共生成 12 个滑移系. 给定DD6合金的立方弹性参数[30,32], 即${C_{11}} = 169\;727$ MPa, ${C_{12}} = 104\;026$ MPa和${C_{44}} = 86\;000$ MPa. 由于本文为方法研究, 参数并不影响研究结论, 根据文献[28, 32]在合理区间内给出了晶体塑性参数, 见表1.
Parameter Value ${\dot \gamma _0}$/s−1 6.057 × 10−3 $n$ 3.9 $g$/MPa 322.5 ${c_1}$/MPa 100.0 ${c_2}$ 2.0 ${r_0}$/MPa 276.0 $b$ 42.0 $Q$/MPa 1.5 ${h_{\alpha \beta }}$ 1.0 2. 基于晶体塑性框架的物理信息神经网络
2.1 神经网络介绍
2.1.1 人工神经网络
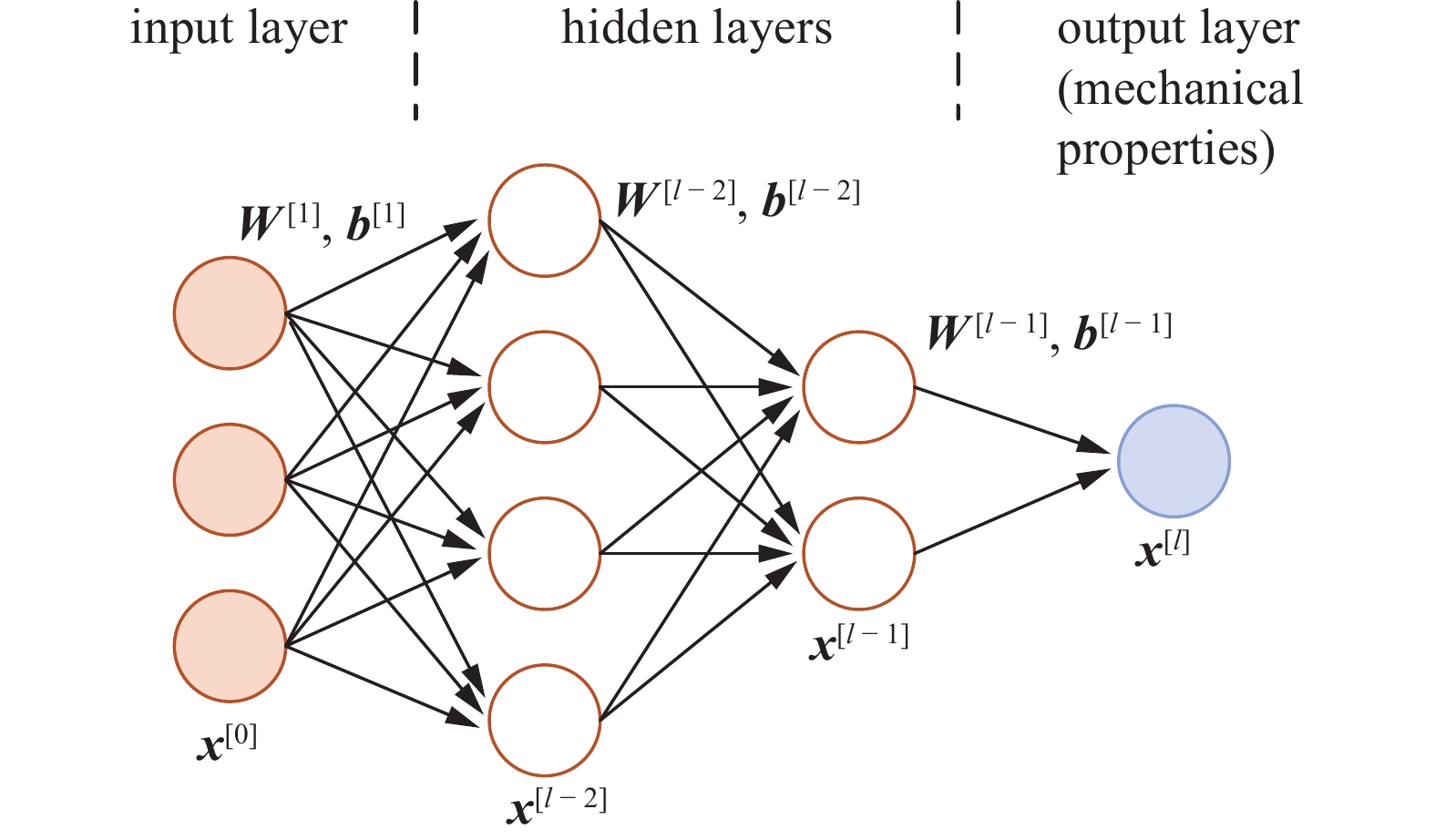
神经网络是一种试图模拟人脑工作方式的人工智能. 该网络由连接节点或“神经元”组成, 负责处理和传输信息. 在训练期间, 网络调整其连接的权重与偏置, 以提高其解决特定任务的能力, 实现高精度的预测. 全连接神经网络(FCNN)是一种最基础的人工神经网络, 其网络中每一层的所有神经元都与下一层神经元连接, 这意味着一层中的每个神经元接收来自上一层中所有神经元的输入, 并输出到下一层中的所有神经元. FCNN 中有3种类型的层: 输入层、隐藏层和输出层. 输入层接收输入数据的特征, 然后将其传递到隐藏层, 隐藏层对数据应用非线性变换以提取特征. 随后, 输出层根据处理后的特征最终生成分类或预测. 除了FCNN以外, 人工神经网络还包括卷积神经网络(CNN)、循环神经网络(RNN)等不同的类型, 本文主要采用FCNN, 因此, 对其他网络不做更多的介绍.
具体地, 给定一个由$L > 1$层组成的网络, 与层$l = 1,2,\cdots ,L$相关的数据和参数使用上标来区分, 例如${{\boldsymbol{x}}^{[l]}}$是${l^{{\text{th}}}}$层的输入. 输入${{\boldsymbol{x}}^{[l]}}$遵循等式
$$ {{\boldsymbol{x}}^{[l]}} = {\textit{π} ^{[l]}}\left( {{{\boldsymbol{W}}^{[l]}}{{\boldsymbol{x}}^{[l - 1]}} + {\text{ }}{{\boldsymbol{b}}^{[l]}}} \right) $$ (16) 其中, $ {\textit{π} ^{[l]}} $, $ {{\boldsymbol{W}}^{[l]}} $和$ {{\boldsymbol{b}}^{[l]}} $表示分别为${l^{{\text{th}}}}$层的激活函数、权重和偏置. 请注意, ${l^{{\text{th}}}}$层的输入也是${(l - 1)^{{\text{th}}}}$层的输出. 第一个输入层通常用${{\boldsymbol{x}}^{[0]}}$表示. 假设${{\boldsymbol{x}}^{[l]}} \in {{{\bf{R}}}^{{n^{[l]}}}}$和${{\boldsymbol{x}}^{[l - 1]}} \in {{{\bf{R}}}^{{n^{[l - 1]}}}}$, ${{\boldsymbol{W}}^{[l]}} \in {{{\bf{R}}}^{{n^{[l]}} \times {n^{[l - 1]}}}}$和${{\boldsymbol{b}}^{[l]}} \in {{{\bf{R}}}^{{n^{[l]}}}}$可以推导得到. 图2为一个具有两层隐藏层的FCNN示意图.
为了找到合适的权重和偏置, 神经网络的训练过程根据损失函数进行反向传播. 常用的损失函数例如均方误差 (MSE), 如下所示
$$ \mathcal{L}\left( {{\boldsymbol{T}}; {\boldsymbol{W}}, {\boldsymbol{b}}} \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{p_i} - {{\tilde p}_i}} \right)}^2}} $$ (17) 式中, $ {\boldsymbol{T}} $是包括输入数据和标签的采样点集合; $ {\boldsymbol{W}}和{\boldsymbol{b}} $表示整个神经网络中的权重和偏差; $N$是训练样本的数量; $ {p_i} $是神经网络的${i^{{\text{th}}}}$预测值, 而$ {\tilde p_i} $是${i^{{\text{th}}}}$标签值, 也是真实值, 本文采用有限元模拟值作为标签值. 然后, 权重和偏差根据训练期间的梯度进行优化. 层数、激活函数、训练周期等超参数应根据实际效果确定, 将在本文第2.4节介绍和给定.
2.1.2 物理信息神经网络
尽管FCNN具有强大的拟合能力, 但其“黑匣子”特性并没有得到力学界的充分认可. 物理信息神经网络的概念是由 Raissi等[19]提出, 并受到学界的广泛关注. PINN 是机器学习和计算物理领域的一种强大且创新的方法. PINN 背后的主要思想是将特定领域的知识(通常源自偏微分方程或其他物理法则)纳入神经网络的训练过程中. 这使得神经网络不仅可以从数据中学习, 还可以从系统的底层物理原理中学习, 使其在传统神经网络之后成为更有价值和前景的工具. 在常规神经网络的基础上, PINN的核心思想是在损失函数中加入物理信息相关的项, 使得参数训练优化过程中不仅需要与标签数据尽可能达到一致, 还需要使得输入输出尽可能达到物理协调条件, 因此是一个多目标优化问题. PINN的总损失函数可表示为
$$ \mathcal{L}\left( {{\boldsymbol{T}},{{\boldsymbol{L}}_1},{{\boldsymbol{L}}_2}, \cdots, {{\boldsymbol{L}}_n};{\boldsymbol{W}},{\boldsymbol{b}}} \right) = \sum\limits_{i = 1}^n {{\lambda _i}} {\mathcal{L}_i}\left( {{\boldsymbol{T}};{\boldsymbol{W}},{\boldsymbol{b}}} \right) $$ (18) 式中, $ {\mathcal{L}_i} $是第$i$个损失函数的值, $ {\lambda _i} $是各个损失函数的加权值. 除了数据驱动的损失函数外, 这些函数都是基于物理定律建立的. 因此, 网络参数将尽可能优化以满足物理规律, 这使得神经网络模型物理上可靠.
2.2 数据驱动的积分策略
开发基于神经网络的材料模型的最直接方法是使用应力和应变作为输入和输出, 最近的工作对此进行了充分研究[6,10-11]. 神经网络材料模型可写为
$$ {\boldsymbol{\varepsilon }} = \mathcal{N}\mathcal{N}\left( {\boldsymbol{\sigma }} \right)\quad {\text{or}}\quad {\boldsymbol{\sigma }} = \mathcal{N}\mathcal{N}\left( {\boldsymbol{\varepsilon }} \right) $$ (19) 尽管应用应力应变构建的神经网络预测精度良好, 但仍缺乏可解释性, 且对于不同加载路径下得到的不同分布数据预测精度难以保证, 进一步应用的稳定性和可靠性较低.
为了保留传统的弹塑性力学计算框架, Jang等[15]将经典的返向映射方法与神经网络结合, 其中神经网络只负责试应力到下一步应力的求解, 从而实现数据驱动的积分策略, 其神经网络模型可以表达为
$$ {\boldsymbol{\sigma }}_1^{n + 1},{\boldsymbol{\sigma }}_2^{n + 1} = \mathcal{N}\mathcal{N}\left[ {{\boldsymbol{\sigma }}_1^{TR},{\boldsymbol{\sigma }}_2^{TR},\rho ({{\bar \varepsilon }^{p,n}})} \right] $$ (20) 其中, ${\boldsymbol{\sigma }}_1^{n + 1}和{\boldsymbol{\sigma }}_2^{n + 1}$是下一步的两个主应力分量; ${\boldsymbol{\sigma }}_1^{TR} 和 {\boldsymbol{\sigma }}_2^{TR}$是两个试应力旋转至主应力空间的分量; $\rho $是屈服应力, 与当前步的等效塑性应变${\bar \varepsilon ^{p,n}}$相关. 该方法保留了弹塑性力学的基本框架, 实现了神经网络与弹塑性力学求解过程的融合, 且已推广至各向异性弹塑性力学[16].
然而, 由于晶体滑移求解基于各个激活的滑移系, 使得变量空间与问题复杂性都显著提升, 类似的思想尚未在晶体循环塑性力学得到很好的应用. 根据晶体塑性框架, 所有变量的计算都应基于激活的滑移系, 本文将神经网络作为隐式积分工具, 从而建立晶体材料状态变量与剪切应变增量的映射, 如下所示
$$ \Delta {\gamma ^{(*)}} = \mathcal{N}\mathcal{N}\left( {\tau _t^{(*)},X_t^{(*)},r_t^{(*)},\rho _t^{(*)},{{\boldsymbol{m}}^{(*)}},{{\boldsymbol{n}}^{(*)}},\Delta {\boldsymbol{\varepsilon }},\Delta t} \right) $$ (21) 所有变量的含义可以在1.1节中找到. 这里, *表示所有被激活滑移系上的变量都应该赋予神经网络. 例如, 针对八面体滑移系, 12个滑移系上的分切应力$\tau _t^{(1\sim 12)}$都应作为神经网络的输入. 在此基础上, 还可以将微结构特征赋予每个滑移系, 例如考虑单晶筏化后的通道宽度, 从而实现跨尺度模型的建立. 然而, 目前工作侧重于方法本身, 并没有讨论微观结构的演变. 上述模型中使用的数据可以从ABAQUS的场变量中提取.
2.3 物理信息驱动的积分策略
上述数据驱动的积分策略实现了神经网络本构建模从宏观向微观的迈进, 在此基础上, 输入的状态变量与剪切应变增量$ \Delta {\gamma ^{(*)}} $存在内在的关联, 从而可以为神经网络训练增加已知的物理信息[21]. 根据晶体塑性框架下的数据驱动积分策略如式(21)所示, $\Delta \gamma $可以根据提供的状态变量进行精确求解, 其具体流程可参考1.2节中的描述.
具体来说, 所提出的物理信息驱动的积分策略可以按以下步骤执行:
(1) 根据式(21) 求出$\Delta {\gamma ^{(*)}}$的初始值;
(2) 利用$\Delta {\gamma ^{(*)}}$初始值, 根据式(12) ~ 式(15)更新$X_{t + \Delta t}^{(*)},\;r_{t + \Delta t}^{(*)},\;\rho _{t + \Delta t}^{(*)}和\tau _{t + \Delta t}^{(*)}$;
(3) 在上一步获得$t$时刻和$t + \Delta t$时刻的状态变量后, 可以根据式(6)计算得到$\dot \gamma _t^{(\alpha )}$和$\dot \gamma _{t + \Delta t}^{(\alpha )}$, 进而根据式(10)利用$\dot \gamma _t^{(\alpha )}$和 $\dot \gamma _{t + \Delta t}^{(\alpha )}$计算得到$\Delta {\gamma ^{(*)}}$的更新值. 更新后的值记作$\Delta {\hat \gamma ^{(*)}}$以示区分, 当$\Delta {\gamma ^{(*)}}$与$\Delta {\hat \gamma ^{(*)}}$收敛到同一数值时, 则获得$\Delta {\gamma ^{(*)}}$的准确值, 该过程由损失函数控制;
(4) 最小化综合损失函数
$$ \mathcal{L} = \mathop {\underbrace {{\lambda _1}\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {\Delta \gamma _i^{(*)} - \Delta {\tilde \gamma }_i^{(*)}} \right)}^2}} }_{{{{\mathrm{data}} \text{-} {\mathrm{driven}}}}}}\limits_{} +\mathop {\underbrace {{\lambda _2}\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {\Delta \gamma _i^{(*)} - \Delta {\hat \gamma} _i^{(*)}} \right)}^2}} }_{{\text{physics-informed}}}}\limits_{} $$ (22) 同样, 式中用*代表了所有激活的滑移系, 从而省略了对各个滑移系的累加计算. $\Delta {\tilde \gamma ^{(*)}}$是FEM模拟得到的标签值, 而$\Delta {\hat \gamma ^{(*)}}$是由物理公式计算得到. ${\lambda _1}和{\lambda _2}$控制数据驱动和物理信息损失函数的影响比例. ${\lambda _1} = 1和{\lambda _2} = 0$是纯数据驱动的学习, 即退化回到章节2.2中的积分策略. ${\lambda _1} = 1和{\lambda _2} = 1$是数据驱动和物理信息驱动相结合的策略, 而${\lambda _1} = 0和{\lambda _2} = 1$是纯物理信息驱动的策略, 此时神经网络在不提供标签数据的情况下也可进行自学习, 使得残差最小化. 关于${\lambda _1}和{\lambda _2}$的讨论将在3.1节开展.
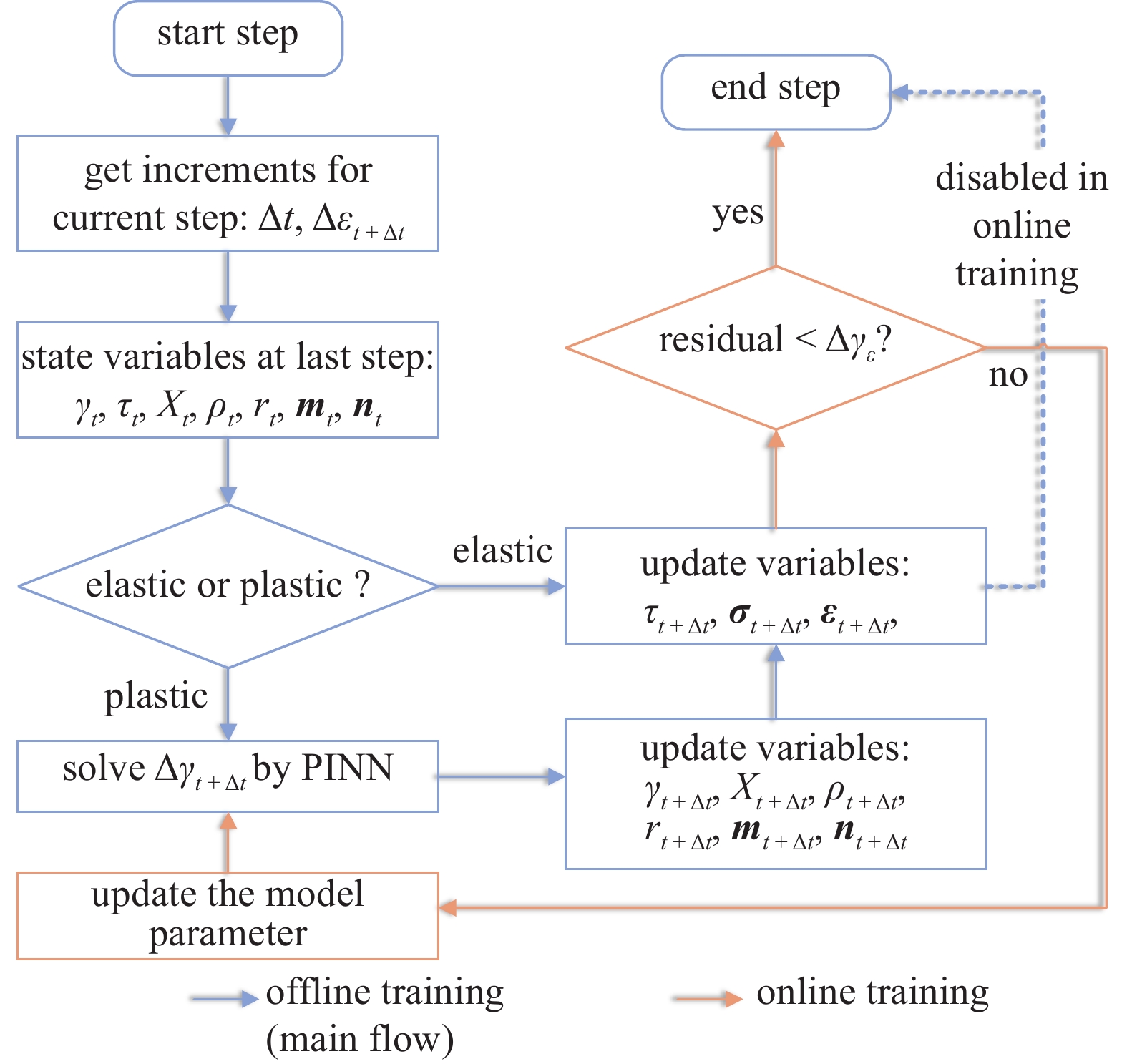
图3描述了训练物理信息神经网络以进行隐式积分的过程. 训练过程将残差最小化到可接受的值, 从而实现了类似Newton-Raphson迭代的功能. 需要注意的是, 目前的做法假设了单晶合金变形机理的正确性, 滑移变形的机理被普遍认可, 但其硬化方程的形式并没有形成统一, 后续的工作可放宽网络对部分方程的限制, 从而拓展模型的描述能力.
2.4 基于晶体塑性框架的实施
2.4.1 在线与离线学习机制
神经网络本构模型在与有限元模拟结合的过程中, 以神经网络参数是否更新区分在线和离线学习. 在线学习指观察到预测误差较大时更新模型参数以减少误差, 它类似于Newton-Raphson迭代, 使得残差始终保持在可接受范围之内. 与在线学习相反, 离线学习意味着使用神经网络时参数将保持不变, 这能大幅提高计算效率, 但需要神经网络具有很强的外插能力来保证预测精度.
本文分别开发了在线和离线学习机制下的PINN晶体塑性本构模型. 对于一个高斯积分点, $\Delta \gamma $求解及该点应力应变更新方案如图4所示. 离线学习和在线学习都符合晶体塑性本构模型的基本求解框架. 在当前载荷步求解中, 首先判断分切应力是否大于临界值, 从而确定目前材料表现为弹性还是塑性. 在弹性阶段材料满足胡克定理, 即应力应变满足简单的线性关系, 因此从计算精度和效率考虑都不需要引入神经网络. 离线和在线学习主要体现在塑性求解部分. $\Delta \gamma $求解过程中, 需要使用通过数据驱动或者物理信息驱动的方式训练得到的神经网络模型. 离线学习机制认为该模型计算结果满足要求, 不检查$\Delta \gamma $是否满足残差要求, 而在线学习确保参数小于容许值, 即
![]()
图 4 基于晶体塑性框架的在线与离线学习示意图Figure 4. Schematic diagram of online and offline learning based on crystal plasticity framework$$ \left| {\Delta \gamma - \Delta {{\hat \gamma }^{(*)}}} \right| < \Delta {\gamma _\varepsilon } $$ (23) 这里$\Delta {\hat \gamma ^{(*)}}$是通过物理方程计算得到的$\Delta \gamma $值, $\Delta {\gamma _\varepsilon }$是残差容许值. 在实际操作过程中, 可以将离线模型作为在线模型的初始值并冻结部分模型参数以提高训练速度, 这类似于迁移学习的思想. 后续再通过传统的基于梯度的方法对参数进行优化, 直到残差小于极限$\Delta {\gamma _\varepsilon }$, 这一过程实则实现了网络的自学习更新.
2.4.2 取向规范化
由于目前本构模型基于小变形框架, 因此假设晶体取向在加载过程中不发生变化, 滑移平面法向量${{\boldsymbol{m}}^{(*)}}$和滑移方向向量${{\boldsymbol{n}}^{(*)}}$将简化为能够反映材料取向的代号变量, 以有效减少神经网络输入变量. 例如{001}[100]大括号表示主晶向方向, 中括号表示次晶向方向, 该晶向即常规的主次晶向都与坐标系对齐的{001}取向的测试试验. 这样仅需增加6个变量即可判断材料取向. 若考虑大变形问题, 仍需要各个激活的滑移系的${{\boldsymbol{m}}^{(*)}}$和${{\boldsymbol{n}}^{(*)}}$向量参与运算. 另外需要注意的是, 这样的做法需要保证所有数据的滑移系按照一定顺序排列, 例如分切应力$\tau _t^{(1\sim 12)}$中, 1 ~ 12号滑移系的顺序是提前给定且不会改变的.
为了提升模型的预测效果, 注意到面心立方FCC晶体结构存在很强的对称性. 例如{100}[001]与{001}[100]两个晶体取向的加载完全相同, 但是对于神经网络的输入却是不同的. 在实际训练和预测阶段, 根据晶体对称性, 将晶体旋转至与之等效的取向, 使得其与{001}[100]、{011}[100]和{111}[$\bar 110$] 3个典型取向相近. 这样的做法在一定程度上减少了产生样本的计算量, 也能更好保证神经网络给出合理的预测结果.
2.4.3 数据生成
神经网络输入输出参数参照式(21), 包含了滑移系上所有状态变量, 预测目标为滑移系的塑性应变增量. 通过UMAT提取每一个加载步的状态变量以获得所需数据. PINN晶体塑性本构模型的验证主要以有限元模拟数据为基准开展. 本文以单调和循环拉伸加载下的材料行为来验证方法的可行性.
在商用有限元软件ABAQUS中, 创建了仅包含一个单元的有限元模型, 对其{001}[100]、{011}[100]和{111}[$\bar 110$]典型晶体取向以应变控制的方式施加单调拉伸载荷, 应变率在4.0 × 10−5 ~ 2.0 × 10−4 s之间, 拉伸至4%的应变后停止. 共获得单调拉伸曲线66条, 每条曲线包含40个等间隔载荷步, 共2640个数据. 类似地, 以应变控制的方式在3个取向上施加循环拉伸载荷, 应变率在1.25 × 10−5 ~ 2.0 × 10−4 s之间, 拉伸应变为$ \pm 1\% $, 进行10次循环后基本达到稳定, 认为第10个滞回环为稳定周应力应变关系. 据此, 共获得循环拉伸曲线90条, 包含10个循环, 每条循环包含40个等间隔载荷步. 循环加载训练仅使用了第一周循环的数据, 共计3600个数据点. 以8:1:1的比例划分训练集、验证集和测试集, 用于训练和评估模型表现.
此外, 为了更好地可视化模型预测效果, 在各个取向分别产生一条与此前数据应变率均不同的应力应变曲线, 用于验证模型对不同应变率的预测. 在不同取向上生成应力应变曲线, 检验模型的外插能力, 同时测试其是否能学习到晶体取向对称性等物理属性. 按照图4流程, 从0时刻开始进行材料行为的完整评估.
2.4.4 超参数选择
本文采用的神经网络由5层组成, 包括1个输入层、3个隐藏层和1个输出层, 其中隐藏层可以表示为[32, 32, 32], 激活函数选用了ReLU函数. 采用小批量(mini-batch)训练方法, 该方法有助于跳出局部最优, 加速收敛. 批量大小设置为数据量的十分之一. 本研究采用了改进的梯度下降型优化器Adam[33]. 梯度下降速率由学习率控制, 初始学习率确定为0.001, 每200轮训练衰减一半. 单调加载的训练轮数为500, 而循环加载由于收敛困难而增加到1500. 整个训练过程在PyTorch中进行.
2.4.5 数据规范化
由于参与神经网络训练的输入输出变量取值范围相差较大, 数据规范化对训练过程将产生较大的影响, 甚至将引起训练不收敛. 对神经网络的输入输出变量做规范化处理, 以分切应力$\tau $为例, 其规范化处理可表示为
$$ \tau _{{\mathrm{norm}}}^{(\alpha )} = \frac{{{\tau ^{(\alpha )}} - \tau _{{\mathrm{min}}}^{(*)}}}{{\tau _{{\mathrm{max}}}^{(*)} - \tau _{{\mathrm{min}}}^{(*)}}} $$ (24) 其中, ${\tau ^{(\alpha )}}$为$\alpha $滑移系上的分切应力, $\tau _{{\mathrm{min}}}^{(*)}和\tau _{{\mathrm{max}}}^{(*)}$指所有滑移系分切应力的最小值和最大值. 对神经网络的输入输出量都做上述规范化处理, 使得其取值范围落于[0, 1]之间. 注意在计算PINN损失值时, 需要将变量映射回原始值, 否则无法保证计算量纲匹配.
3. 基于PINN的晶体塑性行为预测
3.1 损失函数的影响
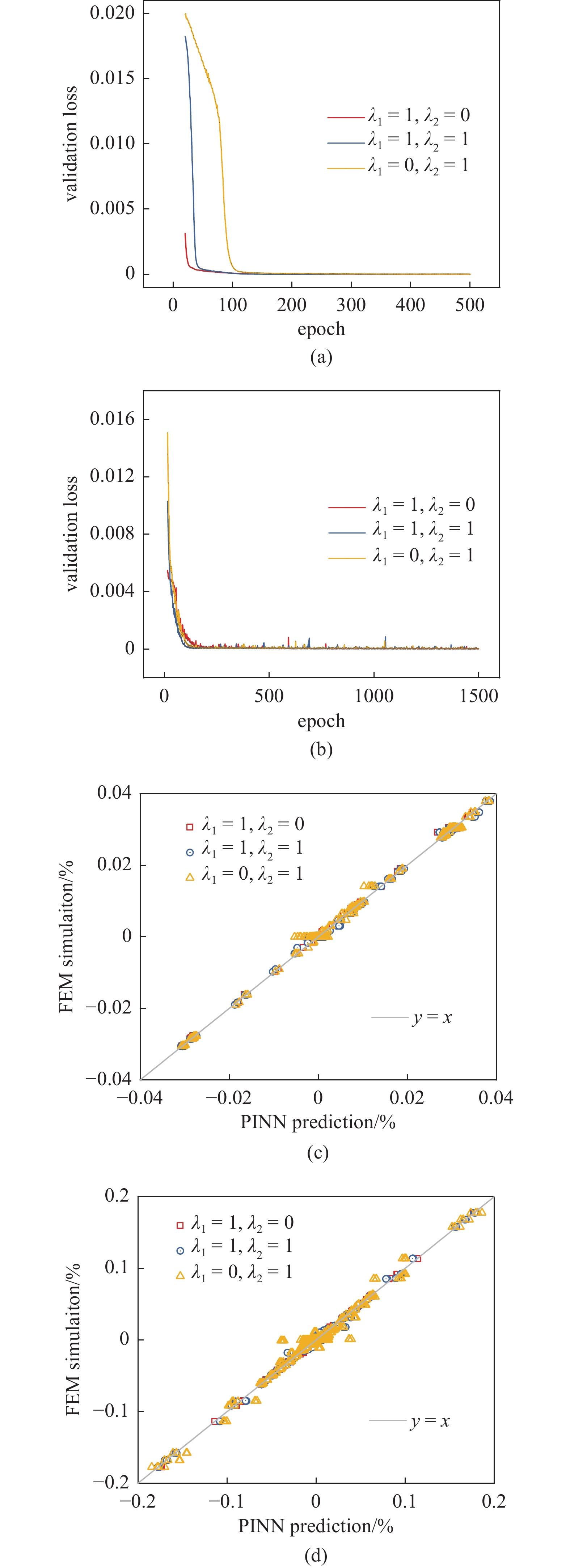
在 PINN 中, 物理定律被纳入损失函数中. 因此, 损失函数与各种控制参数${\lambda _1},{\lambda _2}$会影响收敛性和获得的模型. 在本节中, 首先研究损失函数的效果以确定控制参数并了解物理约束如何影响训练. 使用不同的${\lambda _1}和{\lambda _2}$值进行了3种情况. ${\lambda _1} = 1,{\lambda _2} = 0$表示纯数据驱动的损失函数, 而${\lambda _1} = 0,{\lambda _2} = 1$是仅受物理定律控制的损失函数. ${\lambda _1} = 1,{\lambda _2} = 1$考虑了两个损失项. 单调和循环训练数据集使用${\lambda _1}和{\lambda _2}$ 3种组合进行训练, 验证数据集上的收敛曲线和测试数据集上的性能如图5所示.
![]()
图 5 在 (a) 单调和 (b) 循环加载条件下验证数据集上不同$\lambda $值的迭代曲线. 在 (c) 单调和 (d) 循环加载条件下测试数据集上的 FE 模拟和 PINN 预测之间的比较Figure 5. Iteration curves of different $\lambda $ values on the dataset under (a) monotonic and (b) cyclic loading conditions. Comparison between FE simulations and PINN predictions on test datasets under (c) monotonic and (d) cyclic loading conditions首先比较收敛曲线. 在单调加载情况下, 不同损失函数的收敛速度表现出明显的差异, 如图5(a)所示. 具体来说, 最快的收敛是用纯数据驱动的损失函数, 即${\lambda _1} = 1,{\lambda _2} = 0$. 采用${\lambda _1} = 0,{\lambda _2} = 1$的纯物理信息损失函数似乎对神经网络训练更具挑战性, 收敛速度最慢, 在100代后才收敛至较小的误差. 这是因为物理公式会产生额外的梯度信息, 使得学习变得更加困难. 在${\lambda _1} = 1,{\lambda _2} = 1$的情况下, 由于数据驱动损失函数提供了初始解, 神经网络的收敛变得相对容易, 收敛速度处于中位. 有趣的是, 图5(b)展现的循环加载情况下各组收敛曲线并没有太大不同. 这可以归因于循环数据中线弹性数据更多, 因此可以很容易地用物理方程来描述, 对于神经网络产生额外的学习负担较少. 此外在循环加载下, 可以观察到神经网络模型需要更多的迭代才能收敛到可接受的精度, 其原因也是由于弹性数据较多导致模型学习塑性求解的机会变少. 当然, 在实际使用过程中弹性部分通过公式计算, 因此也可依此简化训练过程. 本文更加注重对方法的研究, 对于方法效率的提升可作为后续的研究课题.
PINN在测试集上的表现也值得关注. 从图5(c)和图5(d)中各点的分散程度可以看出, 单调加载条件下预测效果略优于循环加载. 从图中还可以发现神经网络在晶体塑性框架下对于零点附近的预测较差, 且主要发生在${\lambda _1} = 0,{\lambda _2} = 1$损失函数控制参数的情况下. 其原因可能是由于FCNN在预测历史相关问题方面的局限性. 然而, 接近零的不准确预测并不影响进一步的应用, 因为弹性部分的计算可以直接依赖于弹性模量张量. 因此, 由于对创新性的提升有限, 目前的工作中并未使用RNN等循环神经网络做进一步尝试.
3.2 单调加载的预测
本文提出的数据驱动以及PINN方法不再是一个完全的黑匣子. 由于模型是基于晶体塑性框架建立的, 因此所有内变量的预测情况都可以可视化. 在以下内容中将展示和讨论PINN本构模型在各个激活的滑移系中的预测效果以及存在的问题. 训练好的模型可以实现从0时刻开始完整的本构行为预测.
3.2.1 不同应变率的预测
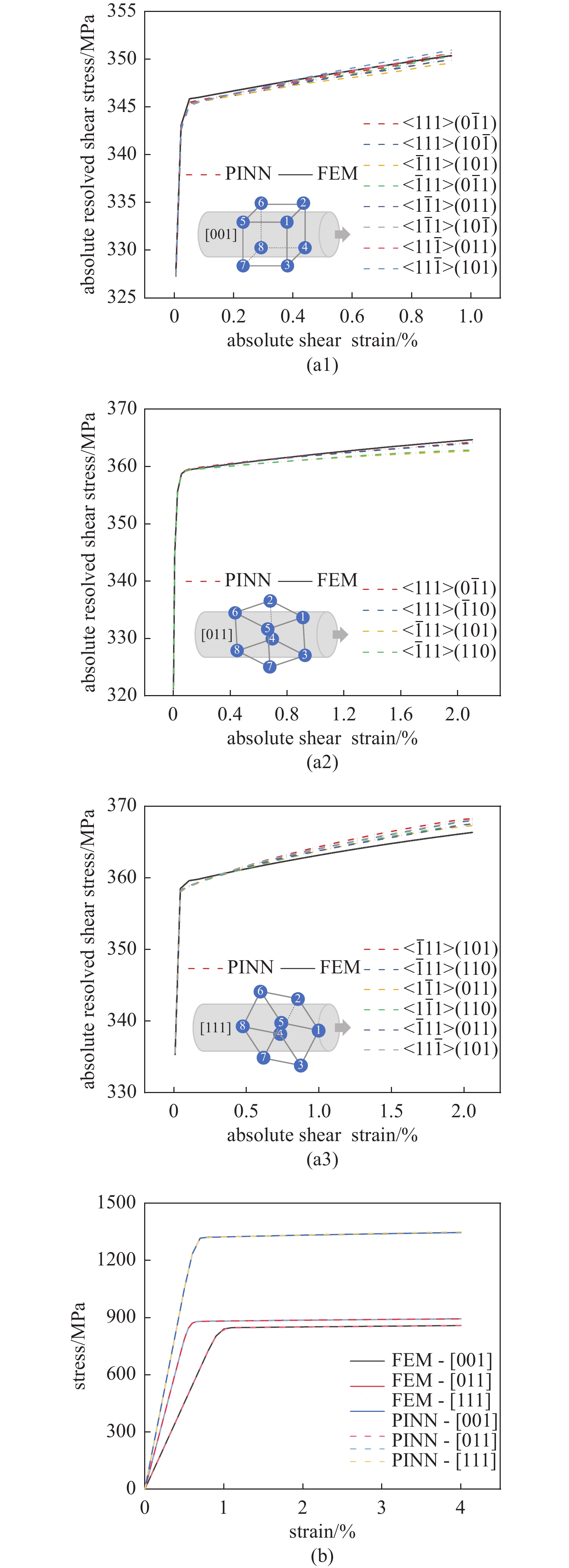
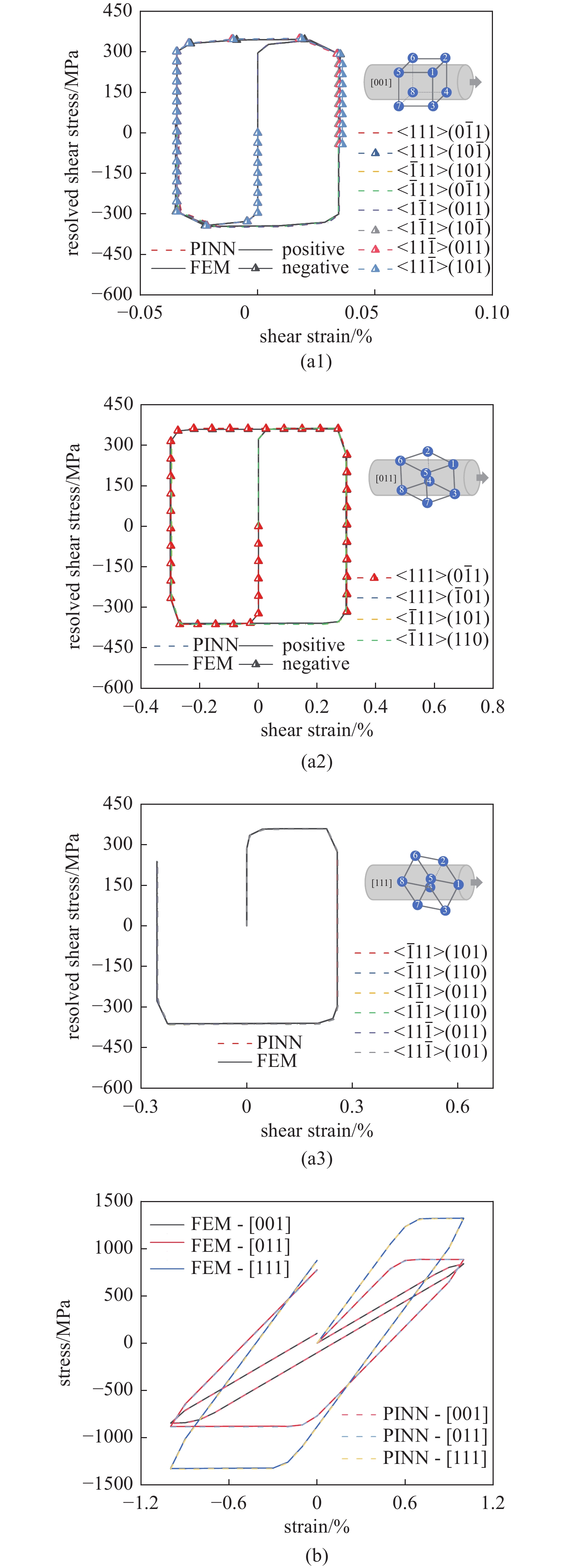
镍基单晶合金存在率相关的材料行为, 所采用的本构模型也能反映这种特征. 为了评估PINN模型对于应变率影响的预测能力, 在3个典型的晶体取向{001}[100]、{011}[100]和{111}[$\bar 110$]分别产生一条与训练、测试集加载速率都不同的应力应变曲线, 应变率为5.0 × 10−5 s−1. 在本节以{001}、{011}和{111}简化区分3个取向. {001}、{011}和{111}晶体取向的单轴拉伸测试的模拟和预测之间的比较如图6所示. 所有变量通过离线学习策略计算得到.
![]()
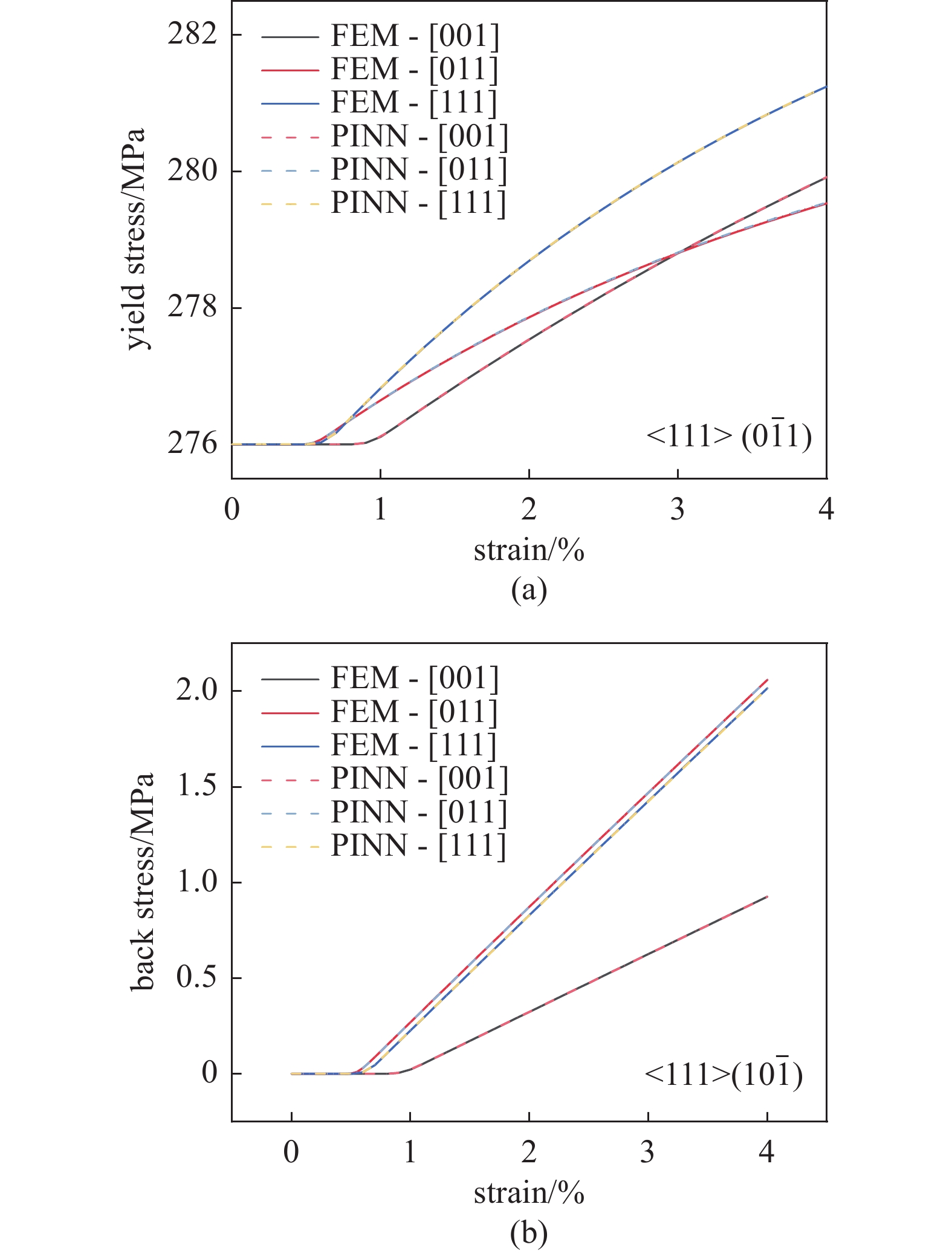
图 6 (a1) ~ (a3) {001}、{011}和{111}晶体取向剪切应力-应变曲线FEM模拟值与PINN预测值的比较. 绘制了启动的滑移系并将数值转换为绝对值. (b) FEM模拟值与PINN预测值在宏观应力-应变曲线上的比较Figure 6. (a1) ~ (a3) Comparison of shear stress-strain curves between FE simulations and PINN predictions for crystal orientations {001}, {011}, and {111}. The activated slip systems are illustrated, and the resolved shear stresses are converted to absolute values. (b) Comparison of FEM simulations and PINN predictions on the macroscopic stress-strain curve激活的滑移系上的剪切应力-应变曲线均绘制在图6(a1) ~ 图6(a3)中. {001}取向开启的滑移系最多, {011}取向最少. 根据图4的离线学习策略, 弹性部分由一般线弹性关系计算得到, 本节不做讨论. 总体上, PINN对于不同应变率的预测效果良好, 塑性部分的切应力预测偏差在5 MPa之内. 各个滑移系表现出较为一致的变化趋势, 表明神经网络基本学习到了晶体塑性模型中宏观力学响应和微观滑移系切应力-应变的关系. 宏观曲线的数值跨度较大, 因此不容易发现模拟和预测之间的细微差别, 预测结果完美. PINN在考虑与训练样本不同应变率时的泛化能力优越, 在微观与宏观均表现良好, 这也得益于训练时提供了足够的应变率变化样本. 另外, 其他状态变量的演化与预测结果也能够可视化, 以各向同性屈服应力以及背应力为例, 其结果如图7所示, 可见状态变量也可以被很好地预测, 这得益于神经网络准确的$\Delta \gamma $计算.
![]()
图 7 不同应变率下(a)屈服应力(各向同性硬化)和(b)背应力的FEM模拟和PINN预测Figure 7. FE Simulation and PINN prediction of (a) yield stress (isotropic hardening) and (b) back stress under different strain rates3.2.2 不同晶体取向的预测
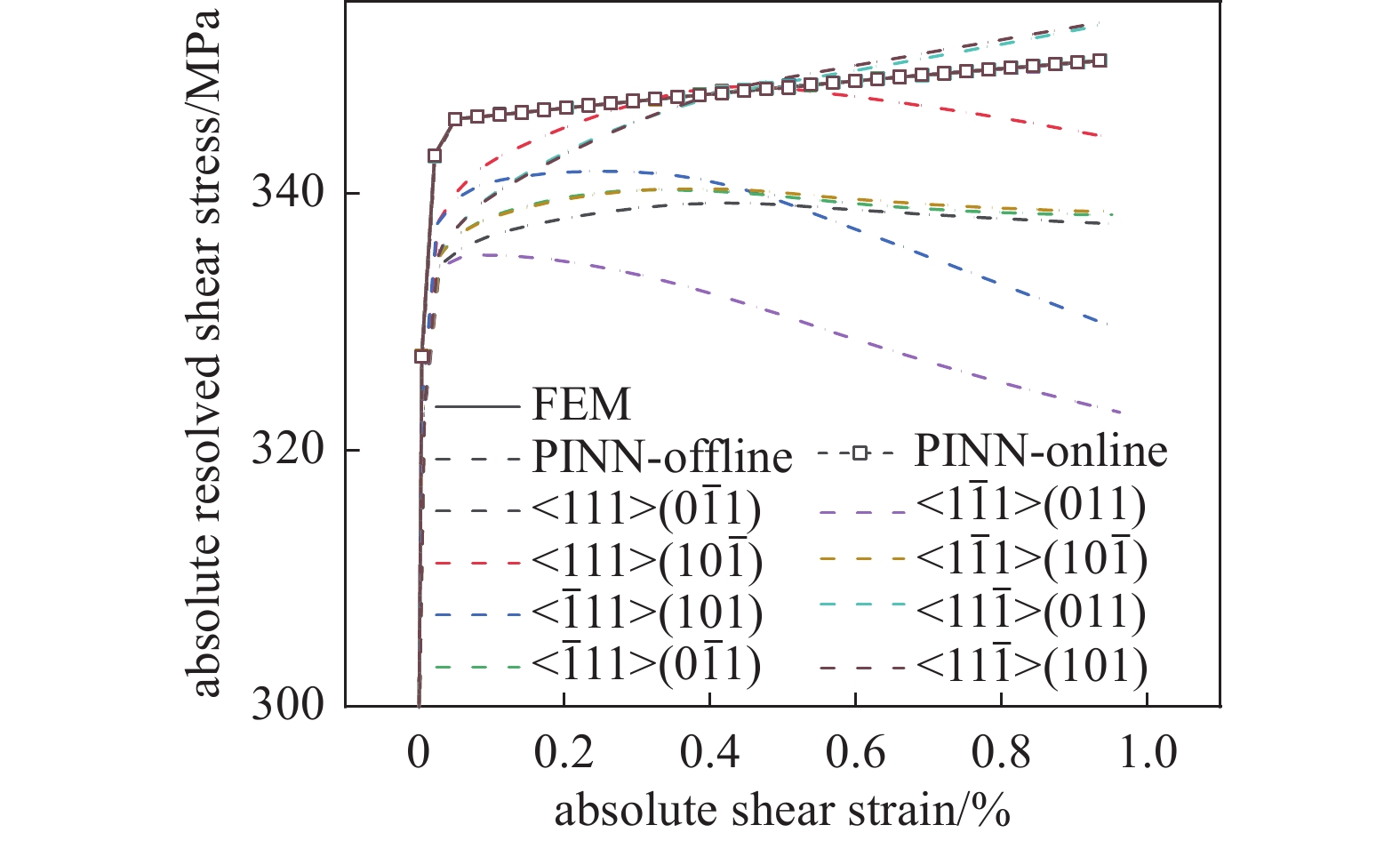
镍基单晶合金是典型的取向敏感性合金, 在神经网络训练过程中仅考虑了{001}[100]、{011}[100]和{111}[$\bar 110$] 3个晶体取向, 样本空间很小, 因此, 这一部分希望测试在样本稀缺的情况下PINN的泛化能力. 本节考虑晶体取向为{001}[110]的单调拉伸模拟作为检验. 虽然在单轴载荷作用下次晶向变化不影响材料的响应, 但是对于神经网络来说, 由于输入参数的改变, 这是一种与此前样本不同的情况(取向参数在节2.4.2中描述). 由于神经网络对于不同晶向样本的学习较为不足, 因此, 本节评估在样本稀缺的情况下, 不同的损失函数控制参量${\lambda _1},{\lambda _2}$对神经网络预测效果的影响, 如图8所示.
![]()
图 8 (a1) ~ (a3) 不同损失函数控制参数${\lambda _1},{\lambda _2}$下的FEM 模拟与 PINN 预测剪切应力-应变曲线的比较, 考虑了独立于原样本空间的{001}[110]取向数据, 绘制了启动的滑移系并将数值转换为绝对值, 其中PINN预测采用了离线学习策略. (b) FEM 模拟值与 PINN 预测值在宏观应力-应变曲线上的比较Figure 8. (a1) ~ (a3) Comparison of shear stress-strain curves between FE simulation and PINN prediction for {001}[110] orientation under different loss function control parameters ${\lambda _1},{\lambda _2}$. The activated slip systems are illustrated, and the resolved shear stresses are converted to absolute values. PINN predictions are obtained using the offline training scheme. (b) Comparison of FEM simulation values and PINN predicted values on the macroscopic stress-strain curve首先观察图8(a1): ${\lambda _1} = 1,{\lambda _2} = {\text{0}}$纯数据驱动的情况, 在纯数据驱动的损失函数下, 神经网络对于屈服应力能够较好地预测, 但是不同滑移系的切应力-应变曲线相差较大, 且趋势不符合材料行为的一般规律. 其次观察图8(a2): ${\lambda _1} = 1,{\lambda _2} = 1$数据与物理信息共同驱动的情况, 加入物理信息约束后, 预测曲线得到一定的改善, 以$ < 1\bar 11 > (011)$滑移系为例, 在图8(a1)中预测偏差极大, 而在图8(a2)显著向真实值靠拢. 最后观察图8(a3): ${\lambda _1} = {\text{0}}和{\lambda _2} = 1$为纯物理信息训练得到的模型, 从图中可以看出, 该模型预测得到的不同滑移系应力应变曲线一致性较好, 但是没有很好地捕捉到材料的屈服应力, 因此存在整体偏差. 在宏观应力应变曲线预测图8(b)中, 可以看到3种情况下得到的预测曲线误差处在可接受范围之内, ${\lambda _1} = 1 和 {\lambda _2} = 1$时, 误差最小.
综上, 对于不同取向材料行为的预测, 由于样本空间稀缺, 预测结果不是很理想, 尤其是微观不同滑移系的分切应力-应变曲线. 数据驱动的损失函数使得对材料屈服应力预测更准确, 而物理信息约束的损失函数能更好保证应力-应变曲线走势的合理性与一致性. 因此, ${\lambda _1} = 1和{\lambda _2} = 1$两者相结合的损失函数得到的模型最优, 且在宏观应力应变曲线的预测上表现也较为良好. 对于泛化误差较大的情况, 本文所提出的在线自学习策略可以有效解决这一问题, 见章节3.2.3. 当然, 为了获得更好的离线模型, 在后续使用中可以适当增加不同取向的样本数据, 从而提升网络对于取向相关性的学习.
3.2.3 在线学习与离线学习的比较
图4展示了在线和离线学习的差异. 在线学习的本质就是当残差较大时, 通过重新更新神经网络参数, 使得残差缩小到合理范围. 在上文PINN预测效果考察中, 采用的是离线学习策略, 对于不同取向的预测PINN离线预测结果不太理想. 因此这一部分采用在线学习策略进行修正, 设定容许的残差值为$\Delta {\gamma _\varepsilon }$ = 1.0 × 10−6, 在${\lambda _1} = 1,{\lambda _2} = 1$损失函数得到的模型基础上采用在线学习策略, 修正后的预测结果如图9所示.
![]()
图 9 离线和在线学习策略下的{001}[110]取向材料行为预测Figure 9. Predictions of material behavior for {001}[110] orientation under offline and online training schemes离线学习模型得到的结果此前已有过阐述, 各个滑移系有较大的偏差. 对比而言, 如图中带符号的短划线所示, 在线学习模型可以较好地求解每个增量步的$\Delta \gamma $, 从而使得所有启动的滑移系中切应力-应变曲线都能得到较好的预测. 在线学习策略也更好地保证了智能本构模型的推广使用.
3.3 循环加载的预测
上一部分主要探讨了PINN对于单调行为的预测效果. 本文采用的本构模型能够描述材料的循环晶体塑性行为. 循环塑性在材料的疲劳问题中备受关注, 因此本节主要讨论PINN模型对于循环晶体塑性行为的预测能力.
3.3.1 不同应变率的预测
循环加载的预测流程与单调加载相同, 这一部分同样采用图4中的离线学习策略. 由式(21)可以看到, 由于神经网络训练过程中已经包含了所有状态变量, 因此其训练和预测过程与单调情况没有区别. 类似地, 在{001}、{011}和{111} 3个典型晶体取向施加应变率不同的循环单轴载荷以获得不同于样本空间的测试样本, 应变率为5.0 × 10−5 s−1. FEM模拟值和PINN预测值的比较在图10中展示.
![]()
图 10 (a1) ~ (a3) {001}、{011}和{111}晶体取向循环剪切应力-应变曲线的 FEM 模拟与 PINN 预测的比较. 绘制了所有被激活的滑移系. 正向(positive)和负向(negative)用于区分剪应力方向引起的不同循环. (b) 宏观循环应力-应变曲线上的 FEM 模拟与 PINN 预测的比较Figure 10. (a1) ~ (a3) Comparison between FE simulation and PINN prediction of cyclic shear stress-strain curves for crystal orientations {001}, {011}, and {111}. All activated slip systems are plotted. Positive and negative are used to distinguish between different cycles induced by shear stress directions. (b) Comparison between FE simulation and PINN prediction on macroscopic cyclic stress-strain curves激活的滑移系上的循环剪切应力-应变曲线如图9(a1) ~ 图9(a3)所示, 循环载荷沿{001}、{011}和{111}晶体取向. 从图中难以发现明显的误差, 这意味着预测曲线与模拟曲线非常吻合. 宏观应力-应变曲线也吻合得很好. 然而, 如上所述, 循环情况下在零附近存在较大偏差, 如图9(d)所示. 这种偏差在实际计算流程中是可以避免的, 因为算法将首先识别是否发生塑性变形, 弹性部分采用线弹性理论进行计算, 因此0点附近预测不准确并不影响最终预测结果. 由目前展示的结果可见, 循环晶体塑性区域内, 即使采用离线方案, 神经网络也能表现良好. 与单调加载情况相似, PINN在考虑与训练样本不同应变率时的泛化能力优越.
3.3.2 后续循环的预测
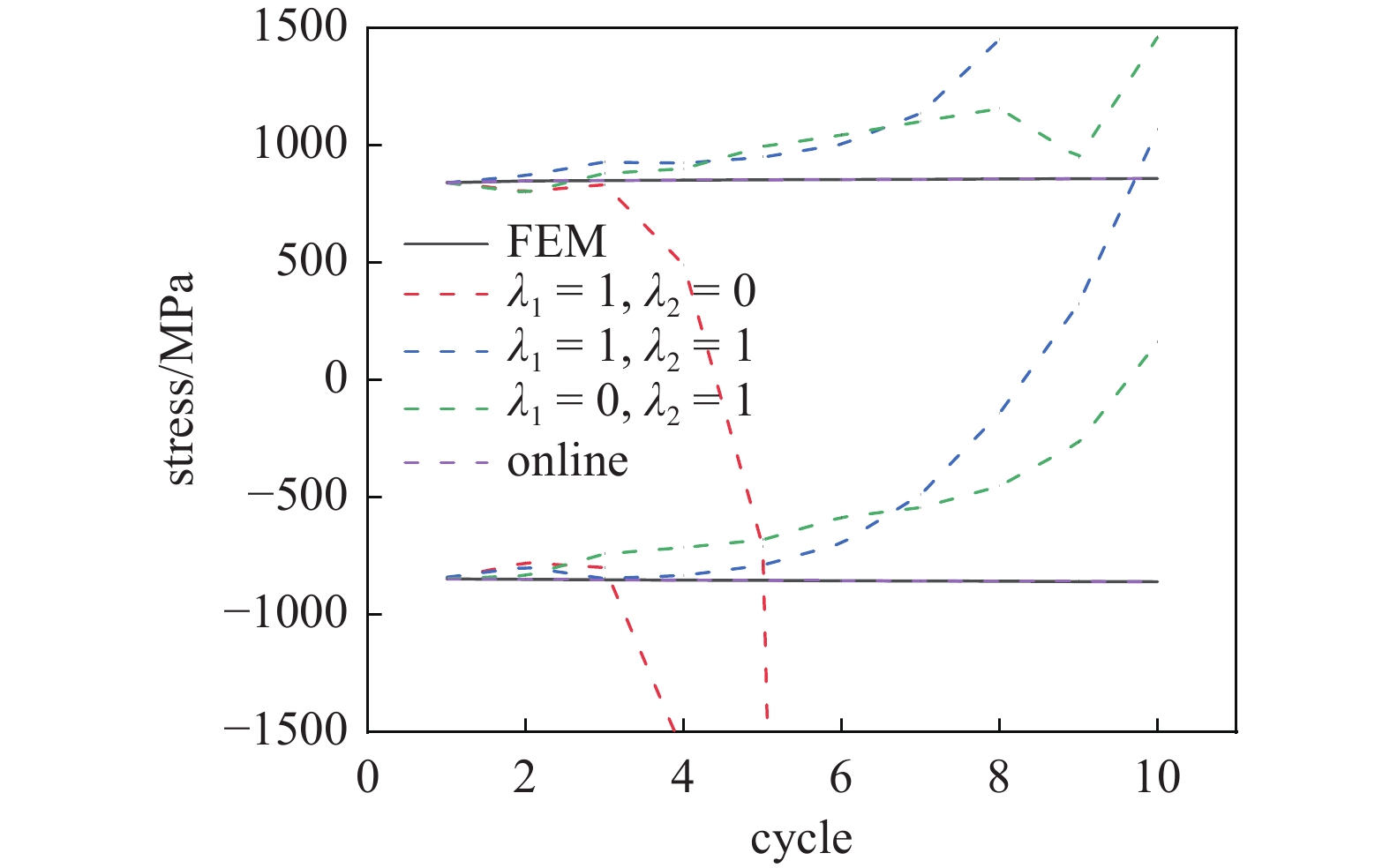
针对循环加载下材料行为, 第一周之后的循环预测也值得关注, 如在疲劳机理分析和寿命预测问题中常常需要循环稳定周的材料力学响应, 本节将讨论PINN对于后续循环预测的情况. 由于循环累积应变较小, 峰谷值演化较为稳定, 模拟和预测仅进行到第10周循环. 另外, 由于训练仅使用了第一周循环的数据, 虽然$\Delta \gamma $求解规律一致, 但是部分状态变量数值与训练时该变量取值范围相差较大, 以描述位错硬化的状态变量$\rho $为例见式(15), $\rho $随着加载时间的推进呈单调上升趋势, 因此$\rho $的取值范围脱离了原始的样本空间, 这影响了PINN实现稳定预测, 尤其是循环数较多时. 图11展示了不同损失函数控制下的离线学习模型以及在线学习模型对于循环峰谷值的预测, 以此评估仅以第一周数据作为训练样本的神经网络模型对于后续循环预测的效果.
![]()
图 11 {001}方向循环加载峰谷值预测Figure 11. Prediction of peak and valley values under cyclic loading for the {001} orientation从图中可以看到, 离线学习模型在前几周吻合较好, 但在后续循环预测中表现一般. ${\lambda _1} = 1,{\lambda _2} = 0$纯数据驱动情况下, 在前3周的预测效果良好, 但在第4周以后出现很大误差, 预测结果骤降, 这意味着数据驱动方法在大幅脱离原样本空间后将完全丧失预测能力. ${\lambda _1} = 1,{\lambda _2} = 1$损失函数的效果与${\lambda _1} = 0, {\lambda _2} = 1$接近, 且都优于${\lambda _1} = 1,{\lambda _2} = 0$, 这是因为物理信息的加入, 使得外插能力有所提升. ${\lambda _1} = 1,{\lambda _2} = 1$中预测峰谷值呈单调稳定上升趋势, ${\lambda _1} = 0,{\lambda _2} = 1$也类似, 除第9周的拐点外, 整体呈单调上升趋势, 另外, 可以注意到融入物理信息后, 峰谷值的差值较为稳定. 总体上, 融入物理信息后, 后续循环的预测稳定性有明显提升, 但是在第6周之后也出现了较大偏差. 为了更好地实现预测, 可以采用在线学习策略进行修正, 由图中可见修正后的曲线与FEM结果完全吻合. 在Weng等[11]的工作中, 也考虑了FCNN对于稳定循环周的预测. 在该研究中, 即使稳定循环周数据作为训练集参与神经网络训练, 采用应力应变对建立的全连接神经网络仍然难以很好地预测材料的后续循环行为. 本文基于晶体塑性框架的学习策略, 由于保留了一定的物理机制, 效果有明显的提升. 在本文的循环加载案例中仅采用了第一周循环的数据用于训练, 但是在后续循环的峰谷值预测中, 也能保持一定循环的合理性, 证明物理信息的融入有助于提升神经网络模型的泛化能力.
3.4 计算效率的讨论
本节针对传统方法和PINN智能本构方法的计算效率开展讨论. 所有代码均在Python环境下执行, 以控制编译环境对代码运行效率的影响. 考察了牛顿迭代解, 以及本文提出的离线和在线学习策略对于单步及应力应变曲线求解的运行时间, 结果如表2所示. 其中选择了3.2.1节和3.3.1节中{001}方向的单调和循环曲线(第一个循环)作为本节评估的对象, 单步为单调曲线上第一个塑性迭代步. 容许的残差$\Delta {\gamma _\varepsilon }$ = 10−5, 在线模型在修正过程中冻结了网络的前3层权重和参数, 从而提升其运行效率.
表 2 算法计算效率对比Table 2. Comparison of algorithm computational efficiencyNewton-Raphson
iterationPINN offline
schemePINN online
schemeRuntime/s single step 0.010 0.004 0.034 monotonic
loading0.112 0.117 0.387 cyclic loading
(1 cycle)0.096 0.038 0.104 首先比较单步计算效率, PINN离线模型可以将牛顿迭代的时间缩短至一半, 但PINN在线模型所需时间较长. 接着考察对于完整应力应变曲线的预测, 单调曲线的运行时间长于循环曲线的原因是单调曲线包含更多的塑性加载步, 而{001}方向的循环曲线表现为更多的弹性行为. 单调曲线预测中牛顿迭代解和PINN离线模型效率接近, 这是因为在后续加载步中, 基于泰勒展开的线性初解已满足残差要求, 因此无需牛顿迭代. 在线模型的运行时间约为前两者的3倍, 类似地, 在线模型依赖离线模型的初解, 当初解较为准确时, 则无需在线修正, 因此计算效率不如单步评估中悬殊. 循环曲线预测中, PINN离线模型表现最优, 比牛顿迭代解有超2倍的效率提升. 循环预测中PINN在线模型与牛顿迭代解运行效率接近.
总体上, PINN离线模型比传统计算方法可以获得约2倍的效率提升, 在线模型计算效率较低, 其主要作用是在离线模型预测失准时对模型进行修正, 然而会损失一定的计算效率. 由于本文的重点在于方法和框架的建立, 在计算效率上未做充分的优化, 其计算效率仍有提升空间. 另外, 对于复杂度及非线性程度更高的问题, PINN将体现出更显著的优势.
4. 结论
本文提出了基于神经网络和晶体塑性框架的材料行为智能预测方法. 该方法保留了晶体滑移理论, 将激活滑移系上的状态变量作为神经网络的输入, 实现了应力的隐式求解, 从而有效预测了单晶材料的单调、循环力学行为. 此外, 该方法在纯数据驱动的基础上融入了物理约束, 并提出了离线和在线的晶体塑性本构行为求解策略. 本文在具体模型评估过程中, 着重研究了数据驱动和物理信息损失函数对于模型的影响, 评估了对不同加载条件下模型的预测能力, 结论可以总结如下.
(1)物理信息损失函数的加入使得神经网络模型的物理一致性提升, 但由于方程的复杂性, 模型训练的收敛速度有一定程度的下降. 研究发现数据驱动和物理信息损失函数同时存在时, 对于本构行为的学习效果最好, 表现出较好的泛化能力.
(2)考察了PINN在不同应变率和不同取向的单调力学行为预测效果, 发现PINN的预测效果仍然会受到数据量的限制. 由于训练数据包含较多应变率的变化, 不同应变率的预测效果很好, 但是训练数据仅考虑了3个经典取向, 因此在不同取向的预测效果仍有较大提升空间, 后续可增加更多取向的训练样本. 另外, 数据驱动的损失函数使得对材料屈服应力预测更准确, 而物理信息约束的损失函数能更好保证应力-应变曲线走势的合理性.
(3)考察了PINN模型对循环力学行为的预测效果. PINN能够较好地预测第一周应力应变曲线. 然而, 由于神经网络模型训练时仅采用了第一周循环的数据, 部分晶体塑性状态变量在后续循环中将完全脱离最初训练的数据分布. 研究发现PINN模型具备一定的后续循环预测能力, 但在一定循环周次后出现较大的偏离. 总体上, 基于晶体塑性框架的神经网络在后续循环预测上要显著优于采用应力-应变进行训练的神经网络.
(4) PINN离线和在线模型实现了预测精度和计算效率的权衡. PINN离线模型比传统计算方法可以获得约2倍的效率提升. 在线学习策略根据滑移系切应变计算残差实时更新迭代, 可以有效解决离线模型外插精度不高的问题, 但会损失一定的计算效率.
(5)本工作是对晶体塑性智能本构建模的初步尝试, 仍有很大的发展空间. 在算法层面, 可采用循环神经网络RNN等进一步提升其处理历史相关问题的能力; 在变形机理层面, 可放宽对部分硬化方程的限制, 从而由神经网络拓展模型的描述能力. 此外, 还可以进一步考虑多轴载荷、多轴非比例载荷, 并且实现与FEM的整合.
-
![]()
图 4 基于晶体塑性框架的在线与离线学习示意图
Figure 4. Schematic diagram of online and offline learning based on crystal plasticity framework
![]()
图 5 在 (a) 单调和 (b) 循环加载条件下验证数据集上不同$\lambda $值的迭代曲线. 在 (c) 单调和 (d) 循环加载条件下测试数据集上的 FE 模拟和 PINN 预测之间的比较
Figure 5. Iteration curves of different $\lambda $ values on the dataset under (a) monotonic and (b) cyclic loading conditions. Comparison between FE simulations and PINN predictions on test datasets under (c) monotonic and (d) cyclic loading conditions
![]()
图 6 (a1) ~ (a3) {001}、{011}和{111}晶体取向剪切应力-应变曲线FEM模拟值与PINN预测值的比较. 绘制了启动的滑移系并将数值转换为绝对值. (b) FEM模拟值与PINN预测值在宏观应力-应变曲线上的比较
Figure 6. (a1) ~ (a3) Comparison of shear stress-strain curves between FE simulations and PINN predictions for crystal orientations {001}, {011}, and {111}. The activated slip systems are illustrated, and the resolved shear stresses are converted to absolute values. (b) Comparison of FEM simulations and PINN predictions on the macroscopic stress-strain curve
![]()
图 7 不同应变率下(a)屈服应力(各向同性硬化)和(b)背应力的FEM模拟和PINN预测
Figure 7. FE Simulation and PINN prediction of (a) yield stress (isotropic hardening) and (b) back stress under different strain rates
![]()
图 8 (a1) ~ (a3) 不同损失函数控制参数${\lambda _1},{\lambda _2}$下的FEM 模拟与 PINN 预测剪切应力-应变曲线的比较, 考虑了独立于原样本空间的{001}[110]取向数据, 绘制了启动的滑移系并将数值转换为绝对值, 其中PINN预测采用了离线学习策略. (b) FEM 模拟值与 PINN 预测值在宏观应力-应变曲线上的比较
Figure 8. (a1) ~ (a3) Comparison of shear stress-strain curves between FE simulation and PINN prediction for {001}[110] orientation under different loss function control parameters ${\lambda _1},{\lambda _2}$. The activated slip systems are illustrated, and the resolved shear stresses are converted to absolute values. PINN predictions are obtained using the offline training scheme. (b) Comparison of FEM simulation values and PINN predicted values on the macroscopic stress-strain curve
![]()
图 9 离线和在线学习策略下的{001}[110]取向材料行为预测
Figure 9. Predictions of material behavior for {001}[110] orientation under offline and online training schemes
![]()
图 10 (a1) ~ (a3) {001}、{011}和{111}晶体取向循环剪切应力-应变曲线的 FEM 模拟与 PINN 预测的比较. 绘制了所有被激活的滑移系. 正向(positive)和负向(negative)用于区分剪应力方向引起的不同循环. (b) 宏观循环应力-应变曲线上的 FEM 模拟与 PINN 预测的比较
Figure 10. (a1) ~ (a3) Comparison between FE simulation and PINN prediction of cyclic shear stress-strain curves for crystal orientations {001}, {011}, and {111}. All activated slip systems are plotted. Positive and negative are used to distinguish between different cycles induced by shear stress directions. (b) Comparison between FE simulation and PINN prediction on macroscopic cyclic stress-strain curves
![]()
图 11 {001}方向循环加载峰谷值预测
Figure 11. Prediction of peak and valley values under cyclic loading for the {001} orientation
Parameter Value ${\dot \gamma _0}$/s−1 6.057 × 10−3 $n$ 3.9 $g$/MPa 322.5 ${c_1}$/MPa 100.0 ${c_2}$ 2.0 ${r_0}$/MPa 276.0 $b$ 42.0 $Q$/MPa 1.5 ${h_{\alpha \beta }}$ 1.0 
下载: 导出CSV
表 2 算法计算效率对比
Table 2 Comparison of algorithm computational efficiency
Newton-Raphson
iterationPINN offline
schemePINN online
schemeRuntime/s single step 0.010 0.004 0.034 monotonic
loading0.112 0.117 0.387 cyclic loading
(1 cycle)0.096 0.038 0.104
下载: 导出CSV
-
[1] Sun J, Yuan H. Cyclic plasticity modeling of nickel-based superalloy Inconel 718 under multi-axial thermo-mechanical fatigue loading conditions. International Journal of Fatigue, 2019, 119: 89-101 doi: 10.1016/j.ijfatigue.2018.09.017
[2] Yang X, Cui X, Yuan H. Correlations between microstructure evolution and mechanical behavior of a nickel-based single crystal superalloy with long-term aging effects. Materials Characterization, 2020, 169: 110652 doi: 10.1016/j.matchar.2020.110652
[3] 胡雅楠, 余欢, 吴圣川等. 基于机器学习的增材制造金属力学性能预测研究进展与挑战. 力学学报, 2024: 56(7): 1892-1915 (Hu Yanan, Yu Huan, Wu Shengchuan, et al. Machine learned mechanical properties prediction of additively manufactured metallic alloys: Progress and challenges. Chinese Journal of Theoretical and Applied Mechanics, 2024: 56(7): 1892-1915 (in Chinese) Hu Yanan, Yu Huan, Wu Shengchuan, et al. Machine learned mechanical properties prediction of additively manufactured metallic alloys: Progress and challenges. Chinese Journal of Theoretical and Applied Mechanics, 2024: 56(7): 1892-1915 (in Chinese)
[4] Xu Y, Weng H, Ju X, et al. A method for predicting mechanical properties of composite microstructure with reduced dataset based on transfer learning. Composite Structures, 2021, 275: 114444 doi: 10.1016/j.compstruct.2021.114444
[5] Ali U, Muhammad W, Brahme A, et al. Application of artificial neural networks in micromechanics for polycrystalline metals. International Journal of Plasticity, 2019, 120: 205-219 doi: 10.1016/j.ijplas.2019.05.001
[6] Mozaffar M, Bostanabad R, Chen W, et al. Deep learning predicts path-dependent plasticity. Proceedings of the National Academy of Sciences, 2019, 116(52): 26414-26420 doi: 10.1073/pnas.1911815116
[7] Abueidda DW, Koric S, Sobh NA, et al. Deep learning for plasticity and thermo-viscoplasticity. International Journal of Plasticity, 2021, 136: 102852 doi: 10.1016/j.ijplas.2020.102852
[8] Yu Z, Han C, Yang H, et al. Elastoplastic constitutive modeling under the complex loading driven by GRU and small-amount data. Theoretical and Applied Mechanics Letters, 2022, 12(6): 100363 doi: 10.1016/j.taml.2022.100363
[9] Li X, Roth CC, Mohr D. Machine-learning based temperature-and rate-dependent plasticity model: Application to analysis of fracture experiments on DP steel. International Journal of Plasticity, 2019, 118: 320-344 doi: 10.1016/j.ijplas.2019.02.012
[10] Weng H, Luo C, Yuan H. ANN-aided evaluation of dual-phase microstructural fabric tensors for continuum plasticity representation. International Journal of Mechanical Sciences, 2022, 231: 107560 doi: 10.1016/j.ijmecsci.2022.107560
[11] Weng H, Yuan H. Quantitative representation of directional microstructures of single-crystal superalloys in cyclic crystal plasticity based on neural networks. International Journal of Plasticity, 2023, 170: 103757 doi: 10.1016/j.ijplas.2023.103757
[12] Bonatti C, Berisha B, Mohr D. From CP-FFT to CP-RNN: Recurrent neural network surrogate model of crystal plasticity. International Journal of Plasticity, 2022, 158: 103430 doi: 10.1016/j.ijplas.2022.103430
[13] Ibragimova O, Brahme A, Muhammad W, et al. A new ANN based crystal plasticity model for FCC materials and its application to non-monotonic strain paths. International Journal of Plasticity, 2021, 144: 103059 doi: 10.1016/j.ijplas.2021.103059
[14] Hashash YMA, Jung S, Ghaboussi J. Numerical implementation of a neural network based material model in finite element analysis. International Journal for Numerical Methods in Engineering, 2004, 59(7): 989-1005 doi: 10.1002/nme.905
[15] Jang DP, Fazily P, Yoon JW. Machine learning-based constitutive model for J2-plasticity. International Journal of Plasticity, 2021, 138: 102919 doi: 10.1016/j.ijplas.2020.102919
[16] Fazily P, Yoon JW. Machine learning-driven stress integration method for anisotropic plasticity in sheet metal forming. International Journal of Plasticity, 2023, 166: 103642 doi: 10.1016/j.ijplas.2023.103642
[17] Heider Y, Wang K, Sun WC. SO(3)-invariance of informed-graph-based deep neural network for anisotropic elastoplastic materials. Computer Methods in Applied Mechanics and Engineering, 2020, 363: 112875 doi: 10.1016/j.cma.2020.112875
[18] Liu Y, Yuan H. A hierarchical mechanism-informed neural network approach for assessing fretting fatigue of dovetail joints. International Journal of Fatigue, 2023, 168: 107453 doi: 10.1016/j.ijfatigue.2022.107453
[19] Raissi M, Perdikaris P, Karniadakis GE. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 2019, 378: 686-707 doi: 10.1016/j.jcp.2018.10.045
[20] 李道伦, 沈路航, 查文舒等. 基于神经算子与类物理信息神经网络智能求解新进展. 力学学报, 2023, 56: 1-15 (Li Daolun, Shen Luhang, Zha Wenshu, et al. New progress in intelligent solution of neural operators and physics-informed-based methods. Chinese Journal of Theoretical and Applied Mechanics, 2023, 56: 1-15 (in Chinese) doi: 10.6052/0459-1879-22-589 Li Daolun, Shen Luhang, Zha Wenshu, et al. New progress in intelligent solution of neural operators and physics-informed-based methods. Chinese Journal of Theoretical and Applied Mechanics, 2023, 56: 1-15 (in Chinese) doi: 10.6052/0459-1879-22-589
[21] Tandale SB, Bamer F, Markert B, et al. Physics-based self-learning recurrent neural network enhanced time integration scheme for computing viscoplastic structural finite element response. Computer Methods in Applied Mechanics and Engineering, 2022, 401: 115668 doi: 10.1016/j.cma.2022.115668
[22] Masi F, Stefanou I, Vannucci P, et al. Thermodynamics-based artificial neural networks for constitutive modeling. Journal of the Mechanics and Physics of Solids, 2021, 147: 104277 doi: 10.1016/j.jmps.2020.104277
[23] Masi F, Stefanou I. Multiscale modeling of inelastic materials with thermodynamics-based artificial neural networks (TANN). Computer Methods in Applied Mechanics and Engineering, 2022, 398: 115190 doi: 10.1016/j.cma.2022.115190
[24] Masi F, Stefanou I. Evolution TANN and the identification of internal variables and evolution equations in solid mechanics. Journal of the Mechanics and Physics of Solids, 2023, 174: 105245 doi: 10.1016/j.jmps.2023.105245
[25] Niu S, Zhang E, Bazilevs Y, et al. Modeling finite-strain plasticity using physics-informed neural network and assessment of the network performance. Journal of the Mechanics and Physics of Solids, 2023, 172: 105177 doi: 10.1016/j.jmps.2022.105177
[26] Haghighat E, Raissi M, Moure A, et al. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Computer Methods in Applied Mechanics and Engineering, 2021, 379: 113741 doi: 10.1016/j.cma.2021.113741
[27] Haghighat E, Abouali S, Vaziri R. Constitutive model characterization and discovery using physics-informed deep learning. Engineering Applications of Artificial Intelligence, 2023, 120: 105828 doi: 10.1016/j.engappai.2023.105828
[28] Méric L, Poubanne P, Cailletaud G. Single crystal modeling for structural calculations: Part 1—model presentation. Journal of Engineering Materials and Technology, 1991, 113: 162-170 doi: 10.1115/1.2903374
[29] 万建松. 基于有限变形晶体滑移理论的单晶力学行为及应用研究. [博士论文]. 西安: 西北工业大学, 2003 (Wan Jiansong. Study of mechanical behavior and application of single crystal superalloy base on finite deformation crystallographic theory. [PhD Thesis]. Xi’an: Northwestern Polytechnical University, 2003 (in Chinese) Wan Jiansong. Study of mechanical behavior and application of single crystal superalloy base on finite deformation crystallographic theory. [PhD Thesis]. Xi’an: Northwestern Polytechnical University, 2003 (in Chinese)
[30] 杨茜茜. 筏化镍基单晶合金本构模型及热机械疲劳研究. [博士论文]. 北京: 清华大学, 2022 (Yang Xixi Constitutive modeling and thermomechanical fatigue assessment for rafted nickel-based single crystal superalloys. [PhD Thesis]. Beijing: Tsinghua University, 2022 (in Chinese) Yang Xixi Constitutive modeling and thermomechanical fatigue assessment for rafted nickel-based single crystal superalloys. [PhD Thesis]. Beijing: Tsinghua University, 2022 (in Chinese)
[31] 丁智平, 刘义伦, 尹泽勇. 镍基单晶高温合金蠕变—疲劳寿命评估方法进展. 机械强度, 2003, 25(3): 254-259 (Ding Zhiping, Liu Yilun, Yin Zeyong, et al. Development on evaluating method of creep-fatigue life of single crystal nickel-based superalloys. Journal of Mechanical Strength, 2003, 25(3): 254-259 (in Chinese) Ding Zhiping, Liu Yilun, Yin Zeyong, et al. Development on evaluating method of creep-fatigue life of single crystal nickel-based superalloys. Journal of Mechanical Strength, 2003, 25(3): 254-259 (in Chinese)
[32] Weng H, Luo C, Yuan H, et al. Fatigue assessment of inclined film cooling holes in nickel-based single-crystal superalloy. AIAA Journal, 2024, https://doi.org/10.2514/1.J064178
[33] Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint, arXiv: 1412.6980, 201
计量
- 文章访问数: 256
- HTML全文浏览量: 43
- PDF下载量: 100
