NONLINEAR BENDING BEHAVIOR OF POROUS FUNCTIONALLY GRADED MATERIAL TUBES IN HYGRO-THERMAL ENVIRONMENT
-
摘要: 圆管作为重要的工程结构, 广泛应用于各个领域, 其几何特征特殊, 传统的梁理论不能满足其内外表面切应力为0的边界条件, 采用合适的梁理论对其进行研究至关重要. 文章采用一种修正的高阶剪切变形梁理论, 研究了湿热环境下多孔功能梯度圆管的非线性弯曲行为. 考虑材料物性与温度相关, 基于修正的高阶剪切变形梁理论和von Kármán非线性理论, 利用最小势能原理, 建立了多孔功能梯度圆管的非线性弯曲控制方程, 采用二次摄动法对控制方程进行求解, 通过数值算例讨论了孔隙分布模型、孔隙率、梯度指数、内半径、湿度和温度对多孔功能梯度圆管非线性弯曲行为的影响. 提出了针对湿热环境下多孔功能梯度圆管的非线性弯曲行为分析方法, 得到了该问题的半解析解, 将为优化多孔功能梯度圆管的结构和材料参数提供理论依据. 结果表明: 当孔隙率较大时, 非均匀孔隙分布模型比均匀孔隙分布模型的多孔功能梯度圆管具有更好的抗弯曲变形能力, 因此在实际轻量化设计过程中, 孔隙分布应优先采用非均匀分布模型.Abstract: Tubes, as important engineering structures, are widely used in various fields, its geometric characteristics are special, and the traditional beam theory can not satisfy the boundary condition that the shear stress on its inner and outer surfaces is zero. It is crucial to adopt a suitable beam theory to study it. A modified high-order shear deformation beam theory was used to study the nonlinear bending behavior of porous functionally graded material tubes under the hygro-thermal environment. Considering temperature-dependent material properties, basing on the modified high-order shear deformation beam theory and von Kármán nonlinear theory, the nonlinear bending control equations of porous functionally graded material tubes were derived by the principle of minimum potential energy. The control equations were solved by the two-step perturbation technique. The effects of porosity distribution types, porosity, gradient index, inner radius, humidity and temperature on the nonlinear bending behavior of the tubes were discussed by numerical examples. The nonlinear bending behavior analysis method of porous functionally graded tubes under hygro-thermal environment was proposed, and the semi-analytical solution of this problem was obtained, which will provide a theoretical basis for optimizing the structure and material parameters of porous functionally graded material tubes. The results show that when the porosity is relatively high, the porous functionally graded material tubes with uneven pore distribution models exhibit superior resistance to bending deformation compared to those with even pore distribution models. Consequently, in practical lightweight design processes, uneven pore distribution models are preferably adopted.
-
引 言
为开发性能更优的轻量化结构, 人们开始结合仿生复合材料进行结构创新[1], 通过模仿天然骨骼和木材引入内部孔隙, 从而改变材料的密度. 功能梯度材料[2](functionally graded materials, FGM)与孔隙结合就是重要的发展趋势之一. 多孔FGM结构具有分离过滤、阻燃防爆等功能, 在航空航天、土木工程、海洋工业等领域得到了广泛的应用[3-6].
功能梯度材料在温度和湿度不断变化的复杂环境中服役时, 其材料特性会发生变化. 近年来, 许多学者研究了复杂环境下FGM结构的力学行为. 李世荣等[7]研究了热环境中粘贴压电层功能梯度材料矩形梁的自由振动问题. 许新等[8]研究了FGM矩形截面微梁的热弹性阻尼. 范纪华等[9]研究了热环境下FGM变截面矩形梁的动力学问题. Nikrad等[10]研究了多孔FGM矩形截面曲梁的面内热弹性响应. Akbas[11]分析了湿热环境下FGM悬臂矩形梁的非线性弯曲行为. Tang等[12]研究了湿热环境下FGM矩形梁的非线性振动问题. Ansari等[13]对湿热环境下多孔FGM矩形梁进行振动分析. Wang等[14]研究了湿热环境下多孔FGM矩形梁的热弹性动力响应问题. 李清禄等[15]研究了湿热环境下多孔FGM矩形梁的后屈曲和屈曲问题. Wang等[16]研究了湿热环境下多孔FGM矩形微梁的屈曲行为. Wang等[17]研究了湿热环境下多孔FGM矩形微梁的弯曲和自由振动特性. Jouneghani等[18]研究了湿热环境下多孔FGM矩形微梁的弯曲行为. 戴婷等[19]研究了湿热环境下旋转变厚度多孔FGM圆板的湿热力学响应问题. Pham等[20]研究了湿热环境下多孔FGM矩形截面曲梁的自由振动问题.
上述文献中研究的是矩形截面梁和圆板. 圆管作为一种常见且重要的基本结构, 广泛应用于管道、支柱、横梁、机械设备和机器等部件中. 已有许多学者采取不同的梁理论对圆管进行研究. 基于Euler梁理论, 部分学者研究了圆管的静动力学问题[21-23]. 为考虑短粗梁中的横向剪切变形, Timoshenko梁理论被广泛应用于圆管的非线性静动力学问题[24-26]. Euler梁理论只适用于细长梁, Timoshenko梁理论可以分析含横向剪切变形的短粗梁, 然而Timoshenko梁理论针对不同的梁截面需要选取合适的剪切修正因子. 且上述两种梁理论均不能满足圆管内外表面剪应力为0的边界条件. 为此, Zhang等[27]提出了一种适用于圆管的高阶剪切变形梁理论, 该梁理论可以满足内外表面剪应力消失的应力边界条件, 能很好地反映圆截面的几何特征. 基于该梁理论, Liu等[28]研究了在不同分布载荷作用下层合管的非线性弯曲. She等[29-30]研究了多孔纳米管的非线性弯曲和振动[29]、屈曲和后屈曲[30]特性.
综上所述, 采用修正的高阶剪切变形梁理论对湿热环境下多孔FGM圆管的非线性弯曲行为的研究较少. 本文采用修正的高阶梁模型, 对多孔FGM圆管在湿热环境中的非线性弯曲行为进行研究. 基于修正的高阶剪切变形梁理论, 考虑温度对材料属性的影响, 通过最小势能原理, 得到湿热环境下多孔FGM圆管的非线性弯曲控制方程, 采用二次摄动法对控制方程进行求解, 并与已有文献的结果进行对比以验证本文方法的正确性, 通过数值算例讨论不同参数对多孔FGM圆管的非线性弯曲行为的影响.
1. 基本方程
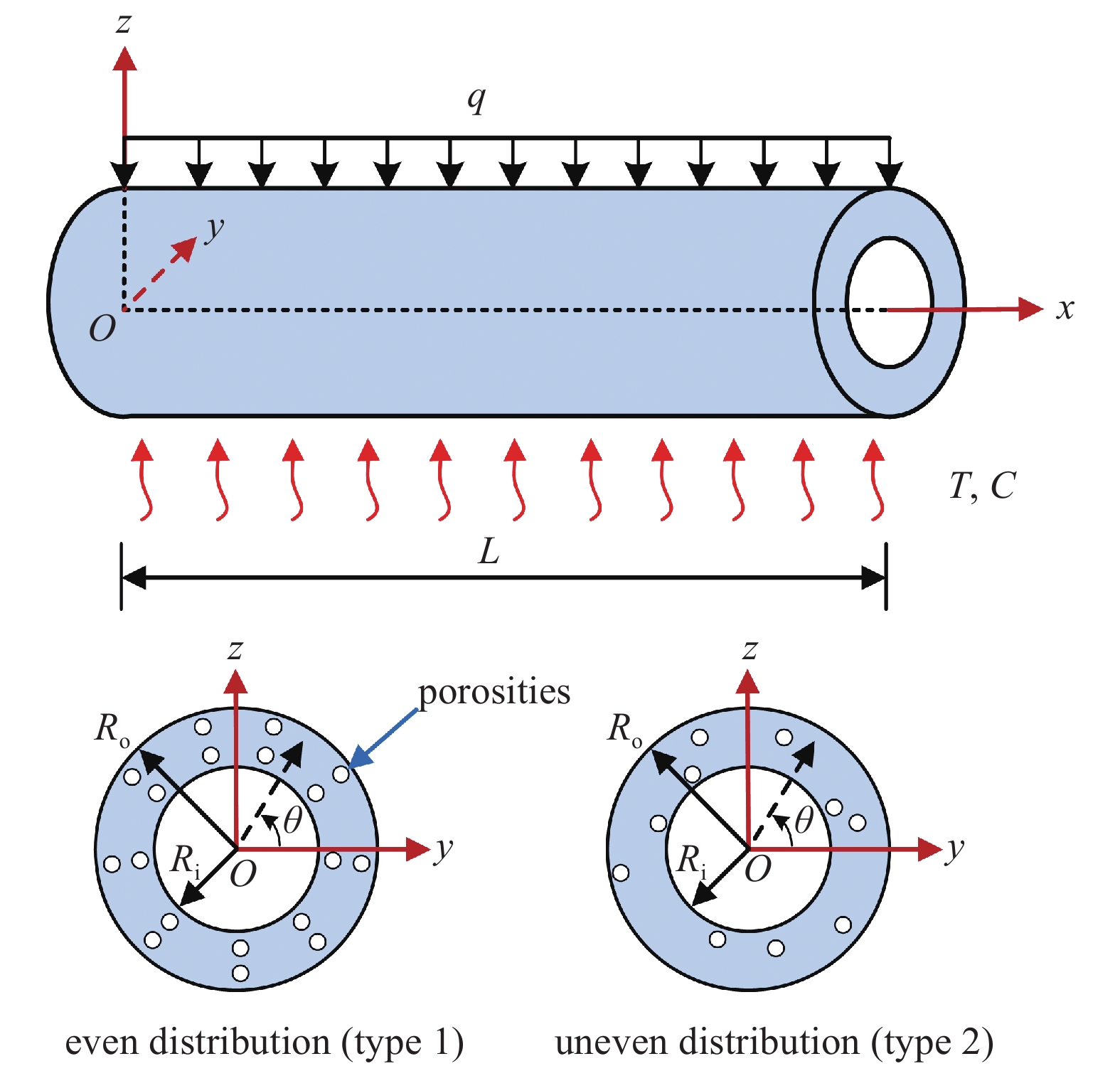
考虑处于湿热环境中, 并受横向均布载荷$q$作用的多孔FGM圆管, 其长度为$L$, 内半径为${R_{\text{i}}}$, 外半径为${R_{\text{o}}}$, 为便于研究, 建立直角坐标系$O\left( {x,y,z} \right)$和柱坐标系$O\left( {x,r,\theta } \right)$, 如图1所示. 显然, $y = r\cos \theta $, $z = r\sin \theta $, ${r^2} = {y^2} + {z^2}$.
均匀孔隙分布模型(type 1)如下
$$ {P_f}\left( r \right) = {P_m} + \left( {{P_c} - {P_m}} \right){\left( {\frac{{r - {R_{\text{i}}}}}{{{R_{\text{o}}} - {R_{\text{i}}}}}} \right)^N} - \frac{\zeta }{2}\left( {{P_c} + {P_m}} \right) $$ (1) 非均匀孔隙分布模型(type 2)如下
$$ \begin{split} & {P_f}\left( r \right) = {P_m} + \left( {{P_c} - {P_m}} \right){\left( {\frac{{r - {R_{\text{i}}}}}{{{R_{\text{o}}} - {R_{\text{i}}}}}} \right)^N} - \\ & \qquad \frac{\zeta }{2}\left( {{P_c} + {P_m}} \right)\left( {1 - \frac{{r - {R_{\text{i}}}}}{{{R_{\text{o}}} - {R_{\text{i}}}}}} \right) \end{split} $$ (2) 式中, $\zeta \left( {\zeta \ll 1} \right)$表示孔隙率, $N$是一个非负的梯度指数, $P$表示材料属性, 包括杨氏模量$E$、质量密度$\rho $、热膨胀系数$ \alpha $和湿膨胀系数$\beta $等. 下标$f$, $m$和$c$分别表示多孔FGM、金属和陶瓷.
基于Zhang等[27]的高阶剪切变形梁模型, 位移场如下
$$\left. \begin{split} & {u_1}\left( {x,y,z} \right) = {u_0} + f{w_{,x}} + g\varphi \\ & {u_3}\left( {x,y,z} \right) = w\left( x \right) \end{split} \right\}$$ (3) 式中
$$ \left.\begin{split} & f = \frac{z}{{{R_{\text{o}}}^2 + {R_{\text{i}}}^2}}\left( {{R_{\text{o}}}^2{R_{\text{i}}}^2{r^{ - 2}} - {r^2}{\text{/3}}} \right) \\ & g = f + z \end{split}\right\}$$ (4) 其中, ${u_1}$和${u_3}$是任意一点沿着$x$和$z$方向的位移, ${u_0}$和$w$分别为多孔FGM圆管中平面$x$方向和$z$方向的位移, $\varphi $为横截面的转角, 下标","表示对后面变量求偏导. 当$f = 0$时, 该梁模型退化为Timoshenko梁模型; 当$f = - z$时, 该梁模型退化为Euler梁模型.
由von Kármán非线性应变−位移关系可得轴向应变$ {\varepsilon _x} $、剪切应变$ {\gamma _{xy}} $和${\gamma _{xz}}$为
$$\left. \begin{split} & {\varepsilon _x} = {u_{1,x}} = {u_{0,x}} + \frac{1}{2}{{w_{,x}}^2} + f{w_{,xx}} + g{\varphi _{,x}} \\ & {\gamma _{xy}} = {u_{1,y}} = {f_{,y}}{w_{,x}} + {g_{,y}}\varphi = {f_{,y}}\left( {{w_{,x}} + \varphi } \right) \\ & {\gamma _{xz}} = {u_{1,z}} + {u_{3,x}} = {g_{,z}}({w_{,x}} + \varphi ) \end{split} \right\}$$ (5) 考虑湿热环境下多孔FGM圆管的物理方程为
$$\left. \begin{split} & {\sigma _x} = E{\varepsilon _x} - E{\alpha _x}\Delta T - E{\beta _x}\Delta C \\ & {\tau _{xy}} = G{\gamma _{xy}}{\text{ }} \\ & {\tau _{xz}} = G{\gamma _{xz}} \end{split} \right\}$$ (6) 其中, $ {\sigma _x} $表示轴向应力, $ {\tau _{xy}} $和$ {\tau _{xz}} $表示剪应力, $G$表示剪切模量, $ \Delta T和\Delta C $为温度和湿度的变化量.
多孔FGM圆管的非线性弯曲控制方程可由最小势能原理导出, 其总势能为
$$ \begin{split} & \varPi = U + {U_{\text{e}}}= \\ & \qquad \int_0^L {\int_A {\left( {{\sigma _x}{\varepsilon _x}{\text{ + }}{\tau _{xy}}{\gamma _{xy}}{\text{ + }}{\tau _{xz}}{\gamma _{xz}}} \right)} } {\text{d}}A{\text{d}}x - \int_L {qw{\text{d}}x} \end{split} $$ (7) 其中, $U$为应变能, ${U_{\text{e}}}$为外力势能, $A$表示多孔FGM圆管的横截面面积.
根据最小势能原理$ \delta \varPi {\text{ = 0}} $, 可得由内力表示的平衡方程
$$ \left.\begin{split} & \delta {u_0}:{N_{,x}} = 0 \\ & \delta w:{M_{1,xx}} - N{w_{,xx}} - {Q_{,x}} = q \\ & \delta \varphi :{M_{2,x}} - Q = 0 \end{split}\right\} $$ (8) 其中, 内力为
$$\left. \begin{split} & ({M_1},{M_2},N) = \int_A {({\sigma _{x}}f,{\sigma _{x}}g,} {\sigma _{x}}){\text{d}}A \\ & {\text{ }}Q{\text{ = }}\int_A {{\text{(}}{\tau _{xy}}{f_{,y}} + {\tau _{xz}}{g_{,z}}{\text{)d}}A} \end{split}\right\} $$ (9) 由式(9)可得
$$\left. \begin{split} & \left\{ {\begin{array}{*{20}{c}} N \\ {{M_1}} \\ {{M_2}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{A_0}}&0&0 \\ 0&{{A_1}}&{{A_2}} \\ 0&{{A_2}}&{{A_3}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u_{0,x}}{\text{ + }}w_{,x}^2/2} \\ {{w_{,xx}}} \\ {{\varphi _{,x}}} \end{array}} \right\}- \\ & \qquad \left\{ {\begin{array}{*{20}{c}} {{N_T}} \\ 0 \\ 0 \end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}} {{N_C}} \\ 0 \\ 0 \end{array}} \right\} \\ & Q = {A_4}({w_{,x}} + \varphi ) \end{split} \right\}$$ (10) 其中, ${N_T}和{N_C}$是由热载荷和湿载荷引起的轴力, 其表达式为
$$ {N_T} = \int_A {E{\alpha _x}\Delta T{\text{d}}A} ,{\text{ }}{N_C} = \int_A {E{\beta _x}\Delta C{\text{d}}A} $$ (11) 且${A_i}\;(i = 0,1,2,3,4)$的表达式为
$$ \begin{split} & ({A_0},{A_1},{A_2},{A_3}) = \int_A {(E,E{f^2},Efg,E{g^2}){\text{d}}A} \\ & {\text{ }}{A_4} = \int_A {G({f_{,y}}^2 + {g_{,z}}^2)} {\text{d}}A \end{split} $$ 考虑具有两端简支面内不可动支撑的多孔FGM圆管, 其边界条件为
$$ x = 0,L:{\text{ }}{u_0} = 0,w = 0,{M_1} = 0,{M_2} = 0 $$ (12) 由方程组(8)的第一式和边界条件(12)中的${u_0}(0) = {u_0}(L) = 0$, 可得
$$ N = \frac{{{A_0}}}{{2L}}\int_L {{w_{,x}}^2} {\text{d}}x - {N_T} - {N_C} $$ (13) 将式(5)和式(6)代入式(8), 可得由位移分量$w,\;\varphi $表示的控制方程
$$\left. \begin{split} & {A_1}{w_{,xxxx}} + {A_2}{\varphi _{,xxx}} - {A_4}({w_{,xx}} + {\varphi _{,x}}) - \\ & \qquad \left(\frac{{{A_0}}}{{2L}}\int_L {{w_{,x}}^2} {\text{d}}x - {N_T} - {N_C}\right){w_{,xx}} = q \\ & {A_2}{w_{,xxx}} + {A_3}{\varphi _{,xx}} - {A_4}({w_{,x}} + \varphi ) = 0 \end{split}\right\} $$ (14) 为方便研究, 引入如下无量纲参数
$$ \left. \begin{aligned} & W = \frac{w}{L},\xi = \text{π} \frac{x}{L},\varPhi = \frac{\varphi }{\text{π} },{\gamma _0} = \frac{{{A_0}{L^2}}}{{D{\text{π} ^2}}} \\ & ({\gamma _1},{\gamma _2},{\gamma _3}) = ({A_1},{A_2},{A_3})\frac{1}{D},{\gamma _4} = \frac{{{A_4}{L^2}}}{{D{\text{π} ^2}}} \\ & {\lambda _q} = \frac{{q{L^3}}}{{D{\text{π} ^4}}},{\lambda _T} = \frac{{{N_T}{L^2}}}{{D{\text{π} ^2}}},{\lambda _C} = \frac{{{N_C}{L^2}}}{{D{\text{π} ^2}}} \end{aligned} \right\} $$ (15) 其中
$$ D = \int_A {{E_0}{z^2}{\text{d}}A} $$ 式中${E_0}$为梯度指数$N = 0$时圆管的弹性模量.
将式(15)代入式(14), 得到无量纲控制方程为
$$\left. \begin{split} & {\gamma _1}{W_{,\xi \xi \xi \xi }} + {\gamma _2}{\varPhi _{,\xi \xi \xi }} - {\gamma _4}({W_{,\xi \xi }} + {\varPhi _{,\xi }}) - \\ &\qquad \left( {\int {\frac{{{\gamma _0}\text{π} }}{2}{W_{,\xi }}^2{\text{d}}\xi } - {\lambda _T} - {\lambda _C}} \right){W_{,\xi \xi }} = {\lambda _q} \\ & {\gamma _2}{W_{,\xi \xi \xi }} + {\gamma _3}{\varPhi _{,\xi \xi }} - {\gamma _4}({W_{,\xi }} + \varPhi ) = 0 \end{split}\right\} $$ (16) 2. 求解方法
式(16)为非线性常微分方程组, 采用二次摄动法[31]进行求解. 位移$W$、位移$ \varPhi $和载荷$ {\lambda _q} $展开为
$$\left. \begin{split} & W(\xi ,\varepsilon ) = \sum\limits_{k = 1} {{\varepsilon ^k}{w_k}(\xi )} \\ & \varPhi (\xi ,\varepsilon ) = \sum\limits_{k = 1} {{\varepsilon ^k}{\varphi _k}(\xi )} \\ & {\lambda _q}(\xi ,\varepsilon ) = \sum\limits_{k = 1} {{\varepsilon ^k}{\lambda _k}(\xi )} \end{split} \right\}$$ (17) 其中, $\varepsilon $为小摄动参数.
将式(17)代入式(16), 并按照$\varepsilon $的同次幂进行离散展开, 逐阶求解, 可得渐进解形式为
$$\left. \begin{split} & W(\xi ,\varepsilon ) = \varepsilon A_{10}^{(1)}\sin (m\xi) + {\varepsilon ^2}A_{20}^{(2)}\sin (2m\xi)+ \\ &\qquad {\varepsilon ^3}A_{30}^{(3)}\sin (3m\xi) + O({\varepsilon ^4}) \\ & \varPhi (\xi ,\varepsilon ) = \varepsilon B_{10}^{(1)}\cos (m\xi) + {\varepsilon ^2}B_{20}^{(2)}\cos (2m\xi) + \\ &\qquad {\varepsilon ^3}B_{30}^{(3)}\cos (3m\xi) + O({\varepsilon ^4}) \end{split}\right\} $$ (18) 且
$$ {\lambda _q} = \varepsilon {\lambda _1} + {\varepsilon ^2}{\lambda _2} + {\varepsilon ^3}{\lambda _3} + O({\varepsilon ^4}) $$ (19) 其中
$$ \begin{split} & B_{10}^{(1)} = - \frac{{{m^3}{\gamma _2} + m{\gamma _4}}}{{{m^2}{\gamma _3} + {\gamma _4}}}A_{10}^{(1)},A_{20}^{(2)} = B_{20}^{(2)} = 0,A_{30}^{(3)} = B_{30}^{(3)} = 0 \\ & {\lambda _1} = \frac{{m\text{π} }}{4}\Biggr[{m^4}\left( {{\gamma _1} - {\gamma _2}\frac{{{m^2}{\gamma _2} + {\gamma _4}}}{{{m^2}{\gamma _3} + {\gamma _4}}} - {\gamma _4}\frac{{{\gamma _2} - {\gamma _3}}}{{{m^2}{\gamma _3} + {\gamma _4}}}} \right) - \\ &\qquad {m^2}\left( {{\lambda _T} + {\lambda _C}} \right)\Biggr]A_{10}^{(1)} \\ & {\lambda _2} = 0 \\ & {\lambda _3} = \frac{{{m^5}{\text{π} ^3}{\gamma _0}}}{{16}}{\left(A_{10}^{(1)}\right)^3}\end{split} $$ 对于式(18), 取$ \xi = \dfrac{\text{π} }{{2 m}} $, 可得
$$ \varepsilon A_{10}^{(1)} = {W_m} $$ (20) 其中, $ {W_m} $为梁的中点挠度.
将式(20)代入式(19), 可得
$$ \frac{{q{L^3}}}{{D{\text{π} ^4}}} = A_W^{(1)}{W_m} + A_W^{(3)}W_m^3 $$ (21) 其中
$$\left. \begin{split} & A_W^{(1)} = \frac{{m\text{π} }}{4}\Bigg[{m^4}\left( {{\gamma _1} - {\gamma _2}\frac{{{m^2}{\gamma _2} + {\gamma _4}}}{{{m^2}{\gamma _3} + {\gamma _4}}} - {\gamma _4}\frac{{{\gamma _2} - {\gamma _3}}}{{{m^2}{\gamma _3} + {\gamma _4}}}} \right)- \\ &\qquad {m^2}\left( {{\lambda _T} + {\lambda _C}} \right)\Bigg] \\ & A_W^{(3)} = \frac{{{m^5}}}{{16}}{\text{π} ^3}{\gamma _0} \end{split} \right\}$$ (22) 3. 数值分析
表1为陶瓷(Si3N4)和金属(SUS304)的材料参数. 材料的温度相关性可由以下非线性方程描述
表 1 陶瓷(Si3N4)和金属(SUS304)的材料属性Table 1. Material properties for Si3N4 and SUS304Material Properties ${P_0}$ $ {P_{ - 1}} $ ${P_1}$ ${P_2}$ ${P_3}$ Si3N4 ${E_c}$/Pa 3.4843 × 1011 0 −3.07 × 10−4 2.160 × 10−7 −8.964 × 10−11 ${\alpha _c}$/K−1 5.8723 × 10−6 0 9.095 × 10−4 0 0 $ {\beta _c} $/(wt%H2O)−1 0 0 0 0 0 SUS304 $ {E_m} $/Pa 2.0104 × 1011 0 3.079 × 10−4 −6.534 × 10−7 0 $ {\alpha _m} $/K−1 1.233 × 10−5 0 8.086 × 10−4 0 0 $ {\beta _m} $/(wt%H2O)−1 0.0005 0 0 0 0 $$ P\left( T \right) = {P_0}\left( {{P_{ - 1}}{T^{ - 1}} + 1 + {P_1}T + {P_2}{T^2} + {P_3}{T^3}} \right) $$ (23) 其中, ${P_{ - 1}}$, ${P_0}$, ${P_{\text{1}}}$, ${P_{\text{2}}}$, ${P_{\text{3}}}$是与温度有关的材料系数.
考虑湿−热均匀分布
$$ T = {T_0} + \Delta T,\quad C = {C_0} + \Delta C $$ (24) 其中, $T$和$C$分别表示温度和湿度, ${T_0}$和${C_0}$表示无应力状态时的参考温度和湿度, 取${T_0} = 300{\text{ K}}$, ${C_0} = 0\% $.
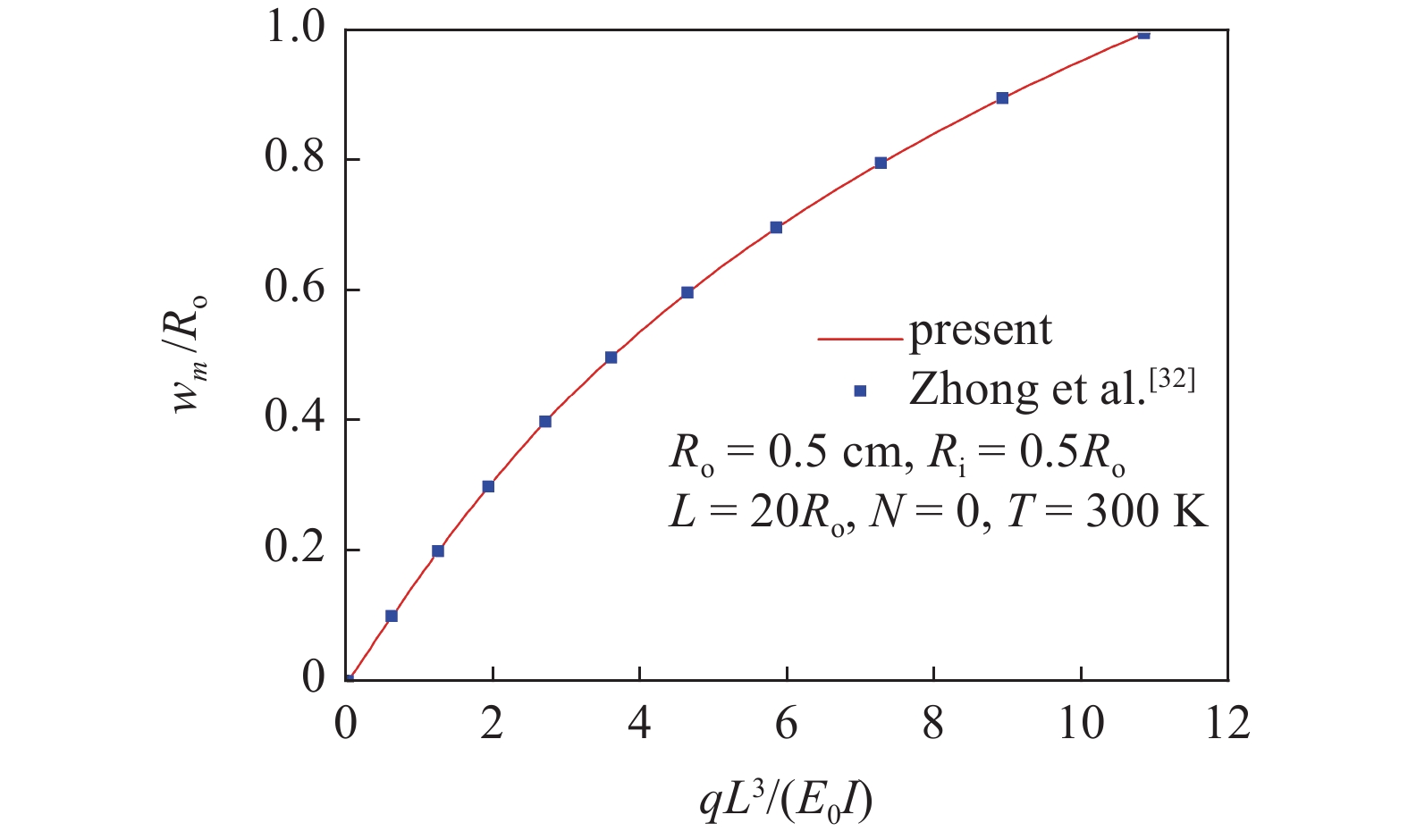
为验证本文模型和方法的正确性, 不考虑湿度和孔隙, 取材料参数和材料尺寸与文献[32]一致, 并将本文与其结果进行了对比, 如图2所示. 其中横坐标$ {{q{L^3}} \mathord{\left/ {\vphantom {{q{L^3}} {({E_0}}}} \right. } {({E_0}}}I) $是无量纲的载荷, $I = \displaystyle\int_A {{z^2}} {\text{d}}A$, 纵坐标${{{w_m}} \mathord{\left/ {\vphantom {{{w_m}} {{R_{\text{o}}}}}} \right. } {{R_{\text{o}}}}}$是无量纲的挠度. 由图2可知, 两文结果吻合, 表明了本文所采用的理论模型和求解方法的有效性.
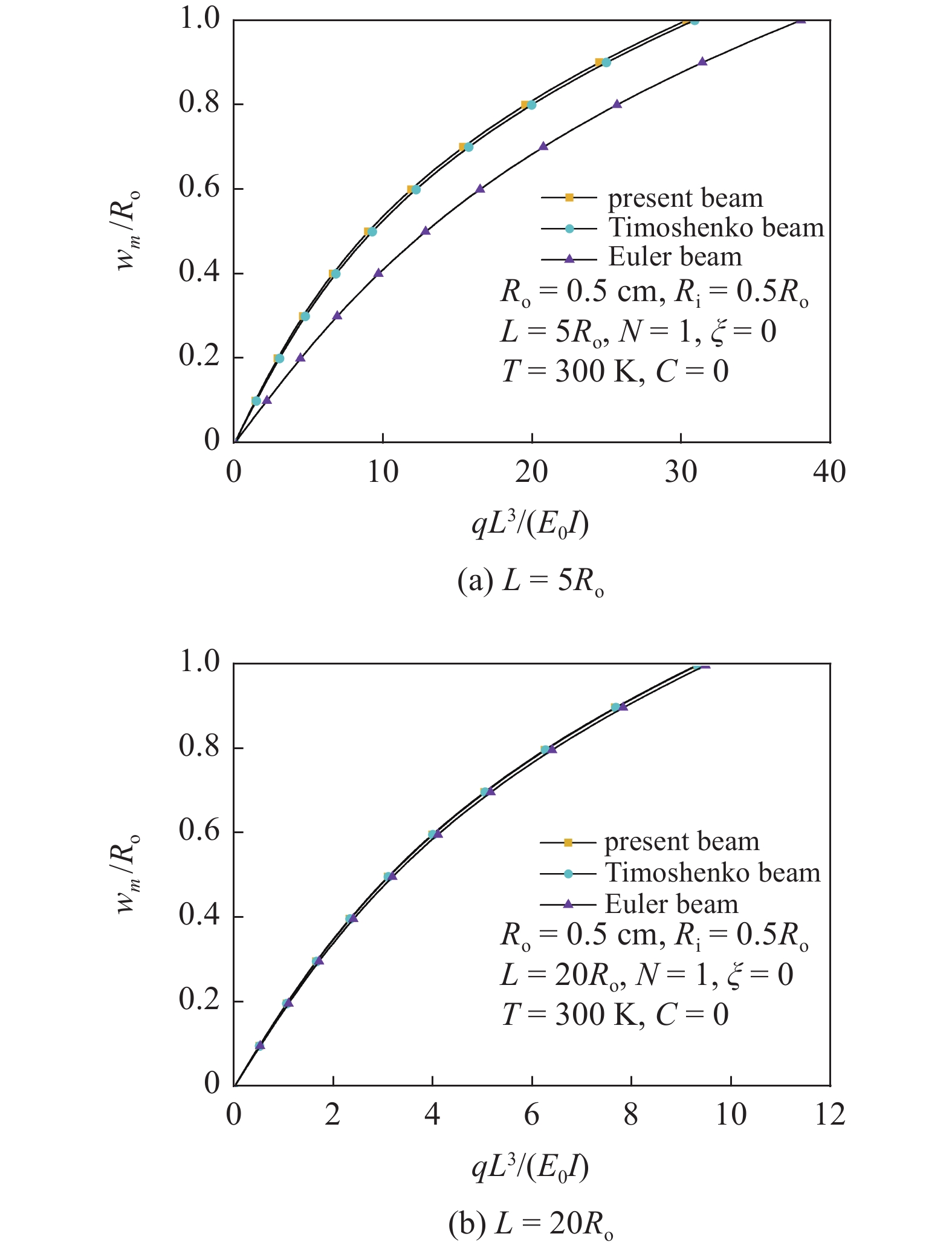
图3给出了不同梁模型下多孔FGM圆管的非线性弯曲响应曲线. 当$L = {\text{5}}{R_{\text{o}}}$时, 本文的高阶剪切梁模型和Euler梁模型所得的结果有一定差异; 当$L = 20{R_{\text{o}}}$时, 不同梁模型的结果基本相同. 这表明当圆管的长细比较小时, 圆管的横向剪切变形影响较为明显, 需要考虑剪切变形对弯曲的影响.
![]()
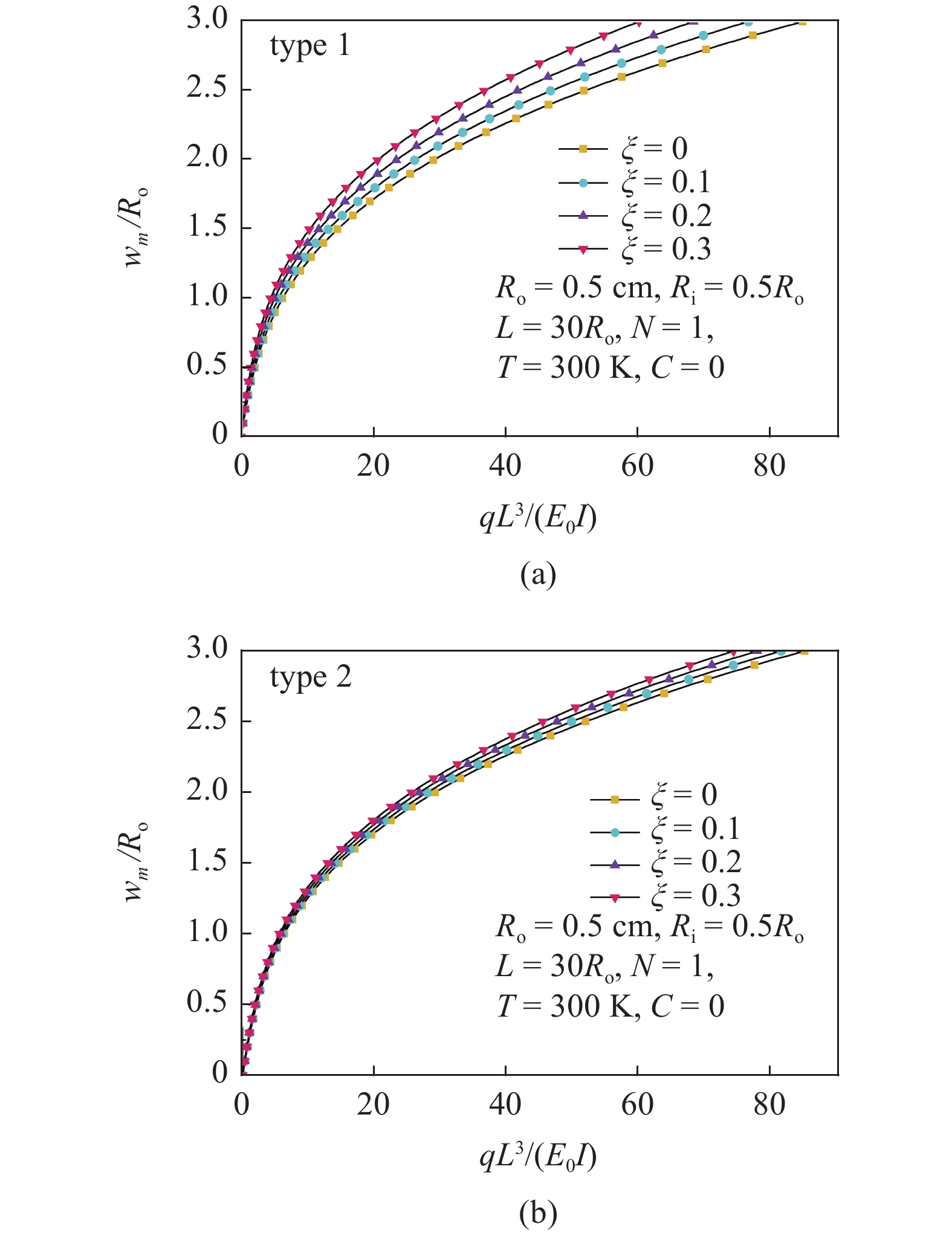
图 3 不同梁模型多孔FGM圆管的非线性弯曲响应Figure 3. Nonlinear bending responses of FGM porous tubes under different beam models图4和图5分别为孔隙率$\zeta $对多孔FGM圆管非线性和线性弯曲响应的影响. 由两图可知, 随着孔隙率$\zeta $的增加, 圆管的弯曲变形增大, 这是因为孔隙的增多导致圆管的弯曲刚度降低, 从而使圆管更容易发生变形; 当孔隙率越大, 均匀孔隙圆管的弯曲响应明显大于非均匀孔隙圆管的弯曲响应, 这表明在高孔隙率的情况下, 非均匀孔隙分布可以有效提高圆管的抗弯曲变形能力. 将图4和图5对比可知, 在弯曲变形较大时, 考虑非线性弯曲是十分必要的.
![]()
图 4 孔隙率$\zeta $对多孔FGM圆管非线性弯曲响应的影响Figure 4. Effect of porosity on nonlinear bending responses of FGM porous tubes![]()
图 5 孔隙率$\zeta $对多孔FGM圆管线性弯曲响应的影响Figure 5. Effect of porosity on linear bending responses of FGM porous tubes图6为梯度指数对多孔FGM圆管非线性弯曲响应的影响. 由图可知, 随着梯度指数的增加, 圆管的弯曲变形越明显, 原因是随着梯度指数的增加, 圆管的弹性模量会降低, 使得梁更容易发生变形.
![]()
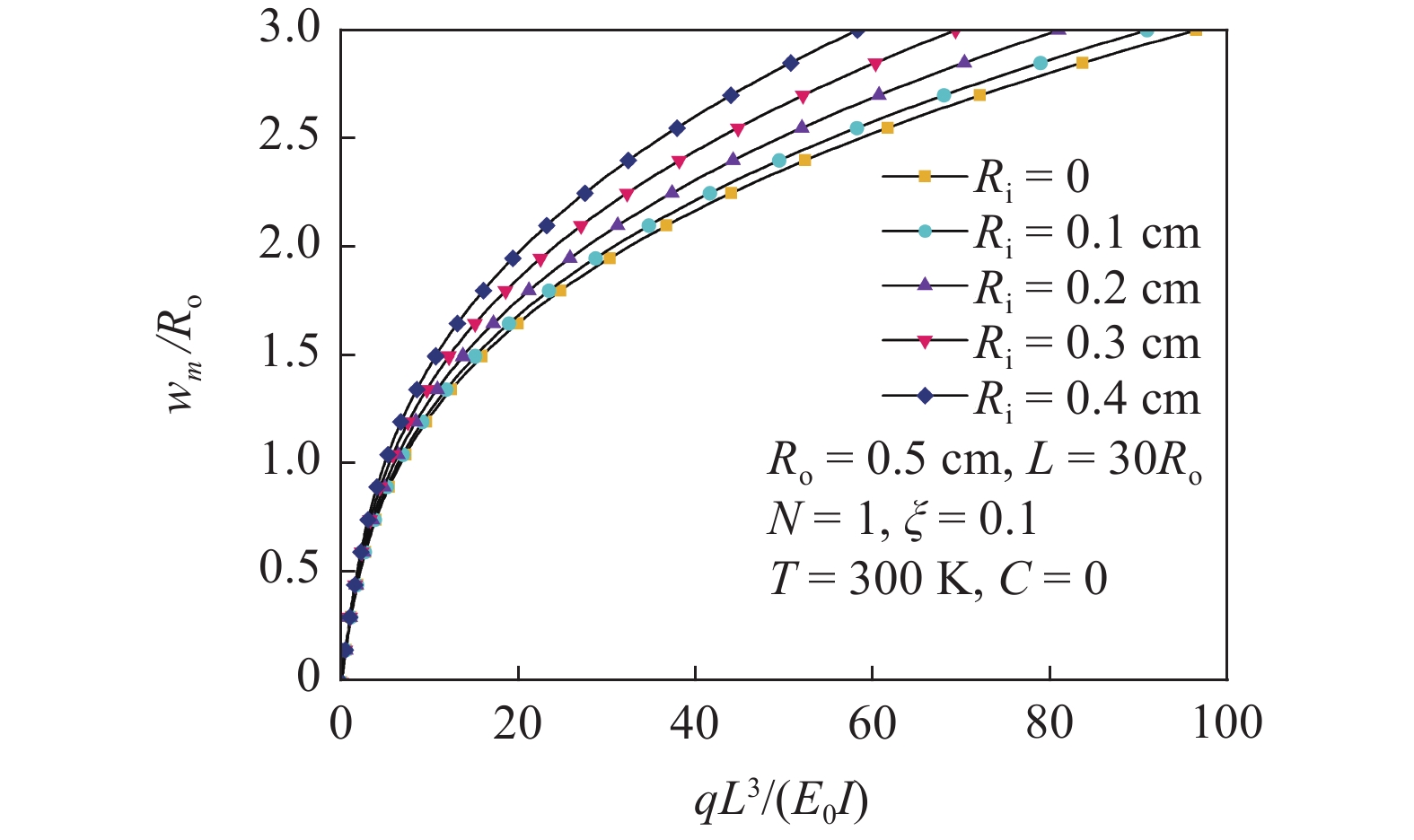
图 6 梯度指数对多孔FGM圆管非线性弯曲响应的影响Figure 6. Effect of volume fraction index on nonlinear bending responses of FGM porous tubes图7揭示了圆管内半径$ {R_{\text{i}}} $对多孔FGM圆管非线性弯曲响应的影响. 由图可知, 圆管内半径$ {R_{\text{i}}} $的增大导致其弯曲变形程度越明显, 原因是圆管内半径$ {R_{\text{i}}} $的增大会使圆管薄壁化, 这种薄壁化使得圆管的弯曲刚度降低, 让圆管更容易发生变形.
![]()
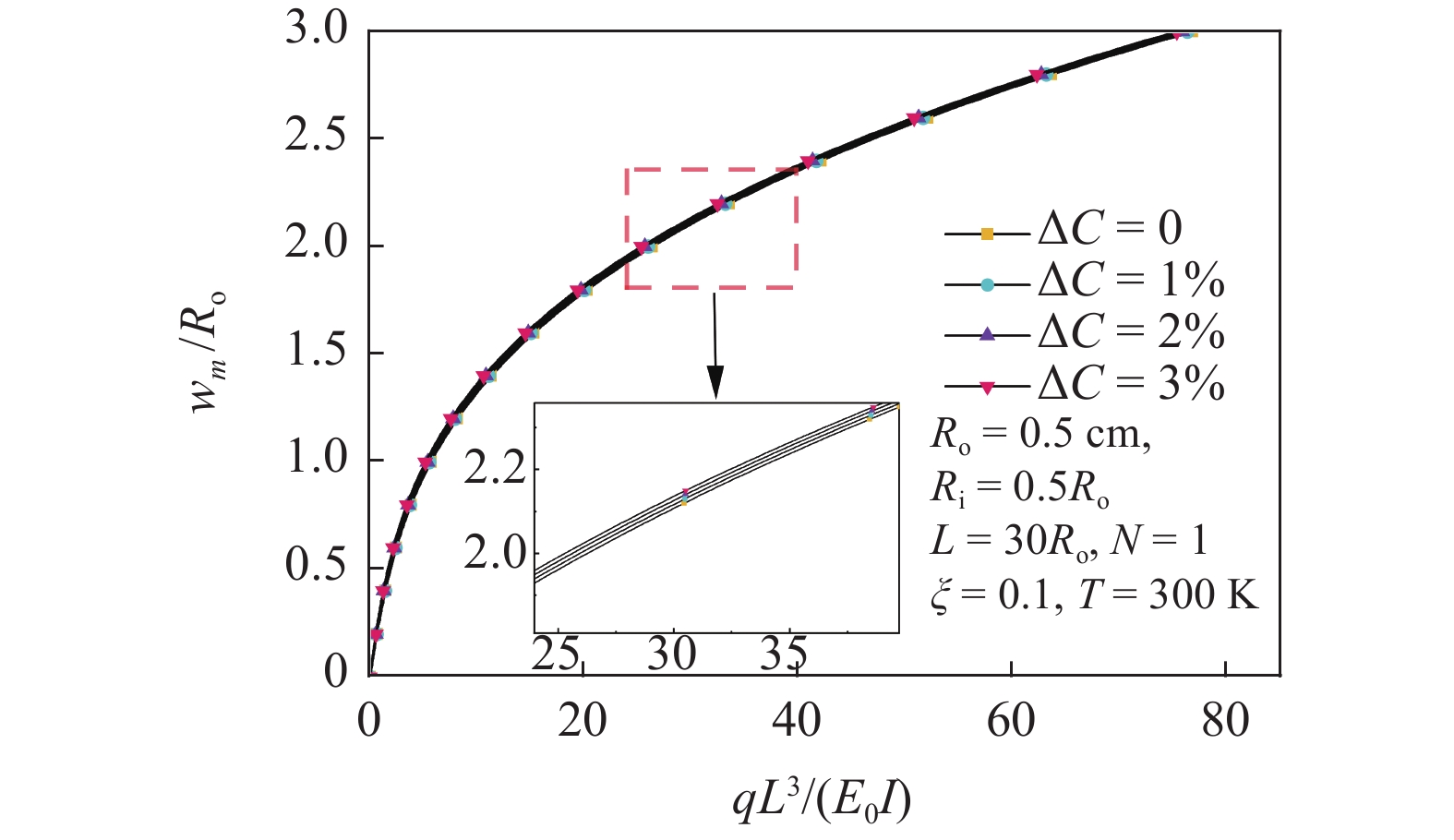
图 7 内半径$ {R_{\text{i}}} $对多孔FGM圆管非线性弯曲响应的影响Figure 7. Effect of inner radius ${R_{{\text{i}}}}$ on nonlinear bending responses of FGM porous tubes图8给出了湿度对多孔FGM圆管非线性弯曲响应的影响. 由图可知, 湿度越大, 圆管弯曲变形越大, 但湿度对于圆管弯曲变形影响很小, 这是因为材料的湿膨胀系数很低, 对湿度变化不敏感.
![]()
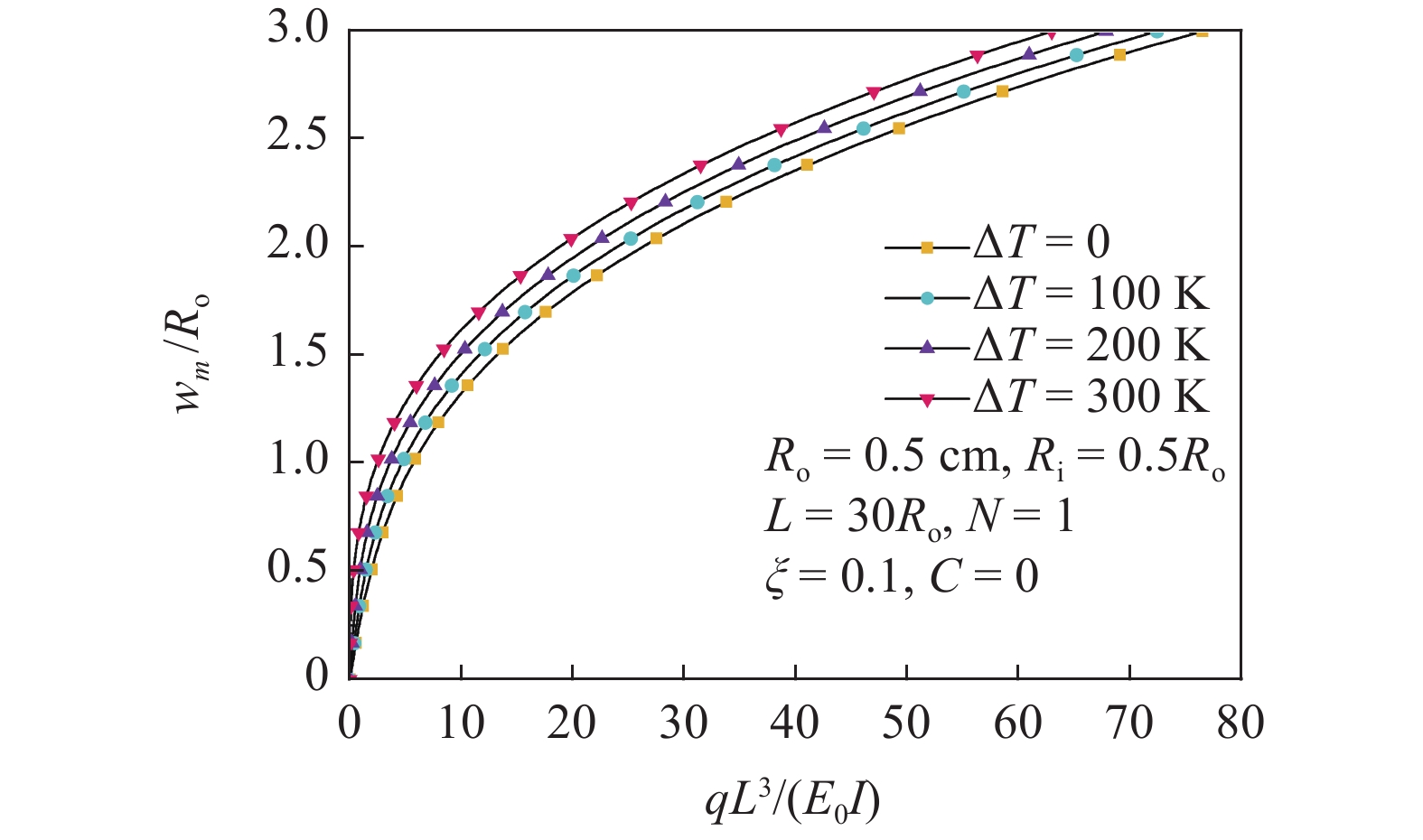
图 8 湿度对多孔FGM圆管非线性弯曲响应的影响Figure 8. Effect of humidities on nonlinear bending responses of FGM porous tubes图9研究了温度对多孔FGM圆管非线性弯曲响应的影响. 温度的升高会使得圆管弯曲变形增加.
![]()
图 9 温度对多孔FGM圆管非线性弯曲响应的影响Figure 9. Effect of temperature on nonlinear bending responses of FGM porous tubes4. 结论
本文基于一种修正的高阶剪切变形梁理论, 讨论了孔隙分布模型、孔隙率、梯度指数、内半径、湿度和温度对湿热环境下多孔FGM圆管的非线性弯曲行为的影响, 主要结论如下:
(1) 二次摄动法可以准确高效求解非线性弯曲问题, 并且能得到问题的半解析解, 便于对此类问题进行定量和定性的讨论;
(2) 当孔隙率较大时, 非均匀孔隙分布可以有效提升圆管的抗弯曲变形能力, 因此在实际轻量化设计过程时, 孔隙分布优先采用非均匀分布模型;
(3) 短粗梁需要考虑横向剪切变形, 采用的修正的高阶梁模型可以精确研究不同长细比的圆截面梁问题;
(4) 随着湿−热加剧, 多孔FGM圆管的弯曲变形越大, 考虑温度和湿度的影响对服役过程中的多孔FGM圆管十分必要.
-
![]()
图 3 不同梁模型多孔FGM圆管的非线性弯曲响应
Figure 3. Nonlinear bending responses of FGM porous tubes under different beam models
![]()
图 4 孔隙率$\zeta $对多孔FGM圆管非线性弯曲响应的影响
Figure 4. Effect of porosity on nonlinear bending responses of FGM porous tubes
![]()
图 5 孔隙率$\zeta $对多孔FGM圆管线性弯曲响应的影响
Figure 5. Effect of porosity on linear bending responses of FGM porous tubes
![]()
图 6 梯度指数对多孔FGM圆管非线性弯曲响应的影响
Figure 6. Effect of volume fraction index on nonlinear bending responses of FGM porous tubes
![]()
图 7 内半径$ {R_{\text{i}}} $对多孔FGM圆管非线性弯曲响应的影响
Figure 7. Effect of inner radius ${R_{{\text{i}}}}$ on nonlinear bending responses of FGM porous tubes
![]()
图 8 湿度对多孔FGM圆管非线性弯曲响应的影响
Figure 8. Effect of humidities on nonlinear bending responses of FGM porous tubes
![]()
图 9 温度对多孔FGM圆管非线性弯曲响应的影响
Figure 9. Effect of temperature on nonlinear bending responses of FGM porous tubes
表 1 陶瓷(Si3N4)和金属(SUS304)的材料属性
Table 1 Material properties for Si3N4 and SUS304
Material Properties ${P_0}$ $ {P_{ - 1}} $ ${P_1}$ ${P_2}$ ${P_3}$ Si3N4 ${E_c}$/Pa 3.4843 × 1011 0 −3.07 × 10−4 2.160 × 10−7 −8.964 × 10−11 ${\alpha _c}$/K−1 5.8723 × 10−6 0 9.095 × 10−4 0 0 $ {\beta _c} $/(wt%H2O)−1 0 0 0 0 0 SUS304 $ {E_m} $/Pa 2.0104 × 1011 0 3.079 × 10−4 −6.534 × 10−7 0 $ {\alpha _m} $/K−1 1.233 × 10−5 0 8.086 × 10−4 0 0 $ {\beta _m} $/(wt%H2O)−1 0.0005 0 0 0 0 
下载: 导出CSV
-
[1] Chen D, Gao K, Yang J, et al. Functionally graded porous structures: Analyses, performances, and applications—A review. Thin-Walled Structures, 2023, 191: 111046 doi: 10.1016/j.tws.2023.111046
[2] Koizumi M. The concept of FGM. Ceramic Transactions, 1993, 34: 3-10
[3] Lu TJ, Liu T, Deng ZC. Multifunctional design of cellular metals: A review. Mechanical Engineering, 2008, 30(1): 1-9
[4] Qiu X, Jing X, Du L, et al. Mode-merging design method for nonlocally reacting liners with porous materials. AIAA Journal, 2020, 58(6): 2533-2545 doi: 10.2514/1.J058958
[5] Geyer TF. Vortex shedding noise from finite, wall-mounted, circular cylinders modified with porous material. AIAA Journal, 2020, 58(5): 2014-2028 doi: 10.2514/1.J058877
[6] Qi FD, Xu GH. Research on multifunctional characteristics and application of ultralight porous metal materials based on structured. Materials Science Forum, 2020, 1: 67-72
[7] 李世荣, 苏厚德, 程昌钧. 热环境中粘贴压电层功能梯度材料梁的自由振动. 应用数学和力学, 2009, 30(8): 907-918 (Li Shirong, Su Houde, Cheng Changjun. Free vibration of functionally graded material beams with surface-bonded piezoelectric layers in thermal environment. Applied Mathematics and Mechanics, 2009, 30(8): 907-918 (in Chinese) doi: 10.3879/j.issn.1000-0887.2009.08.003 Li Shirong, Su Houde, Cheng Changjun . Free vibration of functionally graded material beams with surface-bonded piezoelectric layers in thermal environment. Applied Mathematics and Mechanics,2009 ,30 (8 ):907 -918 (in Chinese) doi: 10.3879/j.issn.1000-0887.2009.08.003[8] 许新, 李世荣. 功能梯度材料微梁的热弹性阻尼研究. 力学学报, 2017, 49(2): 308-316 (Xu Xin, Li Shirong. Analysis of thermoelastic damping for functionally graded material micro-beam. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 308-316 (in Chinese) doi: 10.6052/0459-1879-16-369 Xu Xin, Li Shirong . Analysis of thermoelastic damping for functionally graded material micro-beam. Chinese Journal of Theoretical and Applied Mechanics,2017 ,49 (2 ):308 -316 (in Chinese) doi: 10.6052/0459-1879-16-369[9] 范纪华, 陈立威, 王明强等. 旋转中心刚体-FGM梁刚柔热耦合动力学特性研究. 力学学报, 2019, 51(6): 1905-1917 (Fan Jihua, Chen Liwei, Wang Mingqiang, et al. Research on dynamics of a rigid-flexible-thermal coupling rotating HUB-FGM beam. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(6): 1905-1917 (in Chinese) doi: 10.6052/0459-1879-19-241 Fan Jihua, Chen Liwei, Wang Mingqiang, et al . Research on dynamics of a rigid-flexible-thermal coupling rotating HUB-FGM beam. Chinese Journal of Theoretical and Applied Mechanics,2019 ,51 (6 ):1905 -1917 (in Chinese) doi: 10.6052/0459-1879-19-241[10] Nikrad S, Kanellopoulos A, Bodaghi M, et al. Large deformation behavior of functionally graded porous curved beams in thermal environment. Archive of Applied Mechanics, 2021, 91: 2255-2278 doi: 10.1007/s00419-021-01882-9
[11] Akbas SD. Hygro-thermal nonlinear analysis of a functionally graded beam. Journal of Applied and Computational Mechanics, 2019, 5(2): 477-485
[12] Tang Y, Ding Q. Nonlinear vibration analysis of a bi-directional functionally graded beam under hygro-thermal loads. Composite Structures, 2019, 225: 111076 doi: 10.1016/j.compstruct.2019.111076
[13] Ansari R, Oskouie MF, Zargar M. Hygrothermally induced vibration analysis of bidirectional functionally graded porous beams. Transport in Porous Media, 2022, 142(1): 41-62
[14] Wang SY, Li QL. Thermoelastic dynamic responses near buckling of the non-conservative gradient porous beam in hygrothermal environments. Journal of Vibration Engineering & Technologies, 2023, in press
[15] 李清禄, 王思瑶, 张靖华. 湿−热−机耦合梯度多孔材料梁的非线性力学行为. 航空材料学报, 2022, 42(3): 38-44 (Li Qinglu, Wang Siyao, Zhang Jinghua. Nonlinear mechanical behavior of graded porous material beam subjected to moisture-heat-mechanics loads. Journal of Aeronautical Materials. 2022, 42(3): 38-44 (in Chinese) Li Qinglu, Wang Siyao, Zhang Jinghua. Nonlinear mechanical behavior of graded porous material beam subjected to moisture-heat-mechanics loads. Journal of Aeronautical Materials. 2022, 42(3): 38-44 (in Chinese)
[16] Wang S, Kang W, Yang W, et al. Hygrothermal effects on buckling behaviors of porous bi-directional functionally graded micro-/nanobeams using two-phase local/nonlocal strain gradient theory. European Journal of Mechanics - A/Solids, 2022, 94: 104554 doi: 10.1016/j.euromechsol.2022.104554
[17] Wang YQ, Zhao HL, Yang TH, et al. Thermo-hygro-mechanical bending and vibration of functionally graded material microbeams with microporosity defect. Journal of Thermal Stresses, 2019, 42(7): 815-834 doi: 10.1080/01495739.2019.1587325
[18] Jouneghani FZ, Dimitri R, Tornabene F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Composites Part B: Engineering, 2018, 152: 71-78 doi: 10.1016/j.compositesb.2018.06.023
[19] 戴婷, 戴宏亮, 李军剑等. 含孔隙变厚度FG圆板的湿热力学响应. 力学学报, 2019, 51(2): 512-523 (Dai Ting, Dai Hongliang, Li Junjian, et al. Hygrothermal mechanical behavior of a FG circular plate with variable thickness. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 512-523 (in Chinese) Dai Ting, Dai Hongliang, Li Junjian, et al. Hygrothermal mechanical behavior of a FG circular plate with variable thickness. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 512-523 (in Chinese)
[20] Pham QH, Tran VK, Nguyen PC. Hygro-thermal vibration of bidirectional functionally graded porous curved beams on variable elastic foundation using generalized finite element method. Case Studies in Thermal Engineering, 2022, 40: 102478 doi: 10.1016/j.csite.2022.102478
[21] Chang X, Zhou J. Static and dynamic characteristics of post-buckling of porous functionally graded pipes under thermal shock. Composite Structures, 2022, 288: 115373 doi: 10.1016/j.compstruct.2022.115373
[22] Fu GM, Wang X, Wang BY, et al. Dynamic behavior of axially functionally graded pipe conveying gas-liquid two-phase flow. Applied Ocean Research, 2024, 142: 103827 doi: 10.1016/j.apor.2023.103827
[23] Hou FX, Wu SB, Moradi Z, et al. The computational modeling for the static analysis of axially functionally graded micro-cylindrical imperfect beam applying the computer simulation. Engineering with Computers, 2022, 38(4): 3217-3235
[24] Tang Y, Xu J, Yang T. Natural dynamic characteristics of a circular cylindrical Timoshenko tube made of three-directional functionally graded material. Applied Mathematics and Mechanics, 2022, 43(4): 479-496 doi: 10.1007/s10483-022-2839-6
[25] Tan X, Tang YQ. Free vibration analysis of Timoshenko pipes with fixed boundary conditions conveying high velocity fluid. Heliyon, 2023, 9(4): e14716 doi: 10.1016/j.heliyon.2023.e14716
[26] Ghadirian H, Mohebpour S, Malekzadeh P, et al. Nonlinear free vibrations and stability analysis of FG-CNTRC pipes conveying fluid based on Timoshenko model. Composite Structures, 2022, 292: 115637 doi: 10.1016/j.compstruct.2022.115637
[27] Zhang P, Fu YM. A higher-order beam model for tubes. European Journal of Mechanics - A/Solids, 2013, 38: 12-19 doi: 10.1016/j.euromechsol.2012.09.009
[28] Liu T, Li ZM, Jin S. Nonlinear bending analysis of anisotropic laminated tubular beams based on higher-order theory subjected to different kinds of distributed loads. International Journal of Pressure Vessels and Piping, 2018, 163: 23-35
[29] She GL, Yuan FG, Ren YR, et al. Nonlinear bending and vibration analysis of functionally graded porous tubes via a nonlocal strain gradient theory. Composite Structures, 2018, 203: 614-623 doi: 10.1016/j.compstruct.2018.07.063
[30] She GL, Yuan FG, Ren YR, et al. On buckling and postbuckling behavior of nanotubes. International Journal of Engineering Science, 2017, 121: 130-142 doi: 10.1016/j.ijengsci.2017.09.005
[31] Shen HS. A Two-step Perturbation Method in Nonlinear Analysis of Beams, Plates and Shells. Singapore: John Wiley & Sons, 2013
[32] Zhong J, Fu YM, Wan D, et al. Nonlinear bending and vibration of functionally graded tubes resting on elastic foundations in thermal environment based on a refined beam model. Applied Mathematical Modelling, 2016, 40(17): 7601-7614
-
期刊类型引用(0)
其他类型引用(2)
计量
- 文章访问数: 259
- HTML全文浏览量: 74
- PDF下载量: 70
- 被引次数: 2
