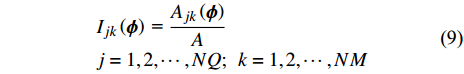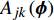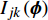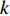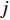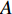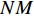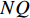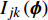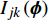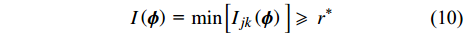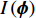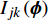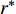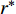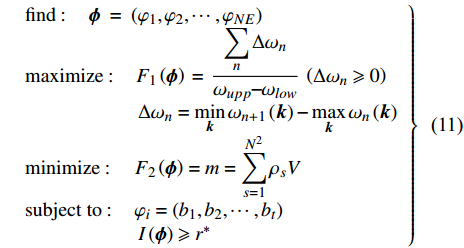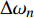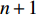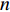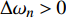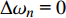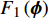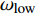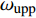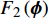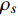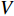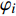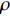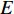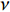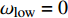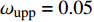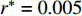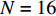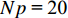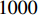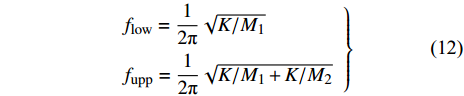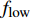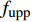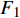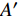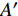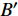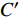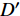MULTI-OBJECTIVE TOPOLOGY OPTIMIZATION OF PHONONIC CRYSTALS CONSIDERING MANUFACTURING CONSTRAINT
-
摘要: 对声子晶体进行拓扑优化可得到具有目标带隙特性的声子晶体结构, 在减振、隔声等领域具有潜在应用价值. 然而, 优化结果常会出现孤立材料单元而导致的制造困难问题. 针对该问题, 本文提出协同考虑带隙性能和可制造性约束的二维多相声子晶体多目标拓扑优化方法. 以在特定频率段带隙最宽和结构质量最小为优化目标, 在对微结构进行连通性分析的基础上, 引入考虑可制造性因素的附加约束, 并利用有限元法和具有精英选择策略的非支配排序遗传算法对该优化模型进行数值求解. 通过数值算例验证了本文模型及方法的合理性和有效性. 结果表明, 附加可制造性约束的拓扑优化模型可有效避免二维声子晶体构型中出现孤立材料单元的情况, 优化结果在满足带隙性能预期指标的同时也可兼顾到实际可制造性要求. 与仅仅考虑带隙性能的单目标优化结果相比, 本文提出的同时兼顾带隙性能和可制造因素的多目标优化模型可以针对实际应用和制造条件, 实现不同目标间的平衡, 具有显著优势和良好的应用前景.Abstract: Topology optimization of phononic crystals can achieve the structures with the targeted band-gap characteristics, which provides potential applications in the vibration reduction and sound insulation. However, the topology optimization results of phononic crystals often have isolated material elements, which are rather difficult to be manufactured. In this paper, a manufacturing-constrained topology optimization model considering both the band-gap performance and the manufacturability for the multi-objective topology optimization of two-dimensional (2D) multi-phase phononic crystals is proposed. The objective functions for maximizing the band-gap width in a specified frequency range and minimizing the structural weight are established. The manufacturing constraint is additionally introduced based on the connectivity analysis of the micro-structures of the constituent materials. The optimization problem is solved by the finite element method (FEM) and the non-dominated sorting genetic algorithm II (NSGA-II). The rationality and effectiveness of the proposed model and strategy are demonstrated by representative numerical examples. The results show that the isolated material elements can be avoided effectively by introducing an additional manufacturing constraint. Moreover, the optimized results can ensure both the band-gap performance and the manufacturability requirement. Compared with the results of the single-objective optimization (SOOP), the multi-objective optimization (MOOP) shows great advantages, since it can obtain non-dominated solution sets and achieve a balance between different optimization objectives.
-
引 言
声子晶体是一种新型周期性人工超材料, 它可以使得某些频率范围内弹性波的传播衰减或禁止, 其特有的带隙特性使其在负折射、声聚焦、声吸收、声隐身、声成像领域具有广阔的应用前景[1-2]. 带隙的产生和分布是声子晶体应用的关键问题, 因此, 利用拓扑优化方法进行声子晶体带隙设计与优化引起了国内外学者的广泛关注.
关于声子晶体的拓扑优化方法主要有两类: 梯度类算法和非梯度类算法. 梯度类算法通过处理目标函数和约束条件的灵敏度信息, 使可行解沿问题的梯度方向移动更新, 可通过较少迭代次数完成问题的求解. 目前, 该方面的研究主要采用移动渐近线算法(method of moving asymptotes, MMA)[3-6]和双向进化结构优化(bi-directional evolutionary structural optimization, BESO)方法[7-8]对声子晶体进行带隙优化. 虽然梯度类算法求解效率高, 但存在容易陷入局部最优解的弊端. 非梯度类算法是通过对适应度函数的不断评估和多次迭代, 在设计域内找到满足要求的近似全局最优解. 其中, 遗传算法在声子晶体拓扑优化中应用最为广泛, 如标准遗传算法(standard genetic algorithm, SGA)[9-15]、自适应遗传算法(adaptive genetic algorithm, AGA)[16-18]、多精英遗传算法(multiple elitist genetic algorithm, MEGA)[19]、快速非支配排序遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)[20-24]与不同的数值计算方法相结合皆可实现对声子晶体的带隙优化.
虽然声子晶体的拓扑优化近年来已经取得了一系列的重大进展, 但优化中存在的“棋盘格效应”使得结构中往往出现某种孤立材料单元、超细而导致刚度较弱的链接单元、微结构组元几何形貌十分复杂、微结构边界和各组元边界或界面粗糙等异常情况, 这对于实际加工制造十分不利, 因而大大限制了声子晶体的应用. 针对优化结果常常出现孤立材料单元这一问题, 本文开展考虑可制造性的二维多相声子晶体拓扑优化研究, 通过对优化过程中拓扑构型的连通性分析以限制最小材料连通域的占比, 避免出现孤立材料单元, 进而建立提高其可制造性的优化模型. 在此基础上, 应用NSGA-II对模型进行求解, 得到了多目标帕累托(Pareto)解集. 具有代表性的数值算例结果表明本文方法可在满足带隙性能等指标的前提下同时兼顾到制造可行性的要求, 有利于声子晶体优化结果的实际加工制造和推广应用.
1. 考虑可制造性的声子晶体拓扑优化方法
1.1 带隙计算理论模型
主要考虑二维声子晶体可视为非均质各向同性弹性材料的情况, 忽略体力影响时, 其弹性波动方程为
$$ \begin{gathered} \nabla \left\{{\left[ {\lambda \left( {\boldsymbol{r}} \right) + 2\mu \left( {\boldsymbol{r}} \right)} \right]\left( {\nabla \cdot {\boldsymbol{u}}} \right)}\right \} -\hfill \\ \quad \quad \quad \nabla \times \left[ {\mu \left( {\boldsymbol{r}} \right)\nabla \times {\boldsymbol{u}}} \right] + \rho {\omega ^2}{\boldsymbol{u }}= 0 \hfill \\ \end{gathered} $$ (1) 式中,
$ \;\rho $ ,$ \lambda $ 和$ \mu $ 分别是质量密度和拉梅常数,$ {\boldsymbol{u}} $ 是位移向量.$ \nabla $ 和$ \omega $ 分别为梯度算子和角频率. 假定弹性波仅在$ xy $ 平面内传播, 则有$ \partial u/\partial z = 0 $ , 于是方程(1)可分解为以下两个解耦的二维波动方程$$ \left. \begin{array}{l} \rho \left( {\boldsymbol{r}} \right){\omega ^2}{ {\boldsymbol{u}}_x} + \dfrac{\partial }{{\partial x}}\left[ {\lambda \left( {\boldsymbol{r}} \right)\left( {\dfrac{{\partial { {\boldsymbol{u}}_x}}}{{\partial x}} + \dfrac{{\partial { {\boldsymbol{u}}_y}}}{{\partial y}}} \right)} \right] + \dfrac{\partial }{{\partial x}}\left[ {2\mu \left( {\boldsymbol{r}} \right)\dfrac{{\partial { {\boldsymbol{u}}_x}}}{{\partial x}}} \right]+ \hfill \\ \qquad \dfrac{\partial }{{\partial y}}\left[ {\mu \left( {\boldsymbol{r}} \right)\left( {\dfrac{{\partial { {\boldsymbol{u}}_x}}}{{\partial y}} + \dfrac{{\partial { {\boldsymbol{u}}_y}}}{{\partial x}}} \right)} \right] = 0 \hfill \\ \rho \left( {\boldsymbol{r}} \right){\omega ^2}{ {\boldsymbol{u}}_y} + \dfrac{\partial }{{\partial y}}\left[ {\lambda \left( {\boldsymbol{r}} \right)\left( {\dfrac{{\partial { {\boldsymbol{u}}_x}}}{{\partial x}} + \dfrac{{\partial { {\boldsymbol{u}}_y}}}{{\partial y}}} \right)} \right] + \\ \qquad \dfrac{\partial }{{\partial y}}\left[ {2\mu \left( {\boldsymbol{r}} \right)\dfrac{{\partial { {\boldsymbol{u}}_y}}}{{\partial y}}} \right] + \dfrac{\partial }{{\partial x}}\left[ {\mu \left( {\boldsymbol{r}} \right)\left( {\dfrac{{\partial { {\boldsymbol{u}}_y}}}{{\partial x}} + \dfrac{{\partial { {\boldsymbol{u}}_x}}}{{\partial y}}} \right)} \right] = 0 \end{array} \right\} $$ (2) $$ \begin{gathered} \rho \left( {\boldsymbol{r}} \right){\omega ^2}{{\boldsymbol{u}}_z} + \frac{\partial }{{\partial x}}\left[ {\mu \left( {\boldsymbol{r}} \right)\left( {\frac{{\partial {{\boldsymbol{u}}_z}}}{{\partial x}}} \right)} \right] \frac{\partial }{{\partial y}}\left[ {\mu \left( {\boldsymbol{r}} \right)\left( {\frac{{\partial {{\boldsymbol{u}}_z}}}{{\partial y}}} \right)} \right] = 0 \hfill \\ \end{gathered} $$ (3) 仅考虑由式(2)描述的面内波动情形而不考虑由式(3)描述的面外或反平面波的传播. 根据周期性结构中的Bloch定理, 位移向量
$ u\left( r \right) $ 可用如下公式表示$$ {\boldsymbol{u}}\left( {\boldsymbol{r}} \right) = {{\rm{e}}^{{\text{i}}({\boldsymbol{k }}\cdot {\boldsymbol{r}})}}{ {\boldsymbol{u}}_k}\left( {\boldsymbol{r}} \right) $$ (4) 式中,
$ {{\boldsymbol{u}}_k}\left({\boldsymbol{ r}} \right) $ 为周期性函数,$ {\boldsymbol{k}} = {\boldsymbol{k}}(x,y) $ 为波矢. 利用有限元方法求解, 式(2)可转化为以下特征方程$$ \left( {{\kern 1pt} {\boldsymbol{K}}({\boldsymbol{k}}){\kern 1pt} - {\kern 1pt} \omega {{\kern 1pt} ^2}{\kern 1pt} {\boldsymbol{M}}{\kern 1pt} } \right)\,{\boldsymbol{U}}\,\; = \;0 $$ (5) 式中,
$ {\boldsymbol{K}} $ 和${\boldsymbol{ M}} $ 分别为整体刚度矩阵和整体质量矩阵,${\boldsymbol{ U}} $ 是节点位移向量. 给定波矢求解式(5)中的特征频率可得到能带结构或频散曲线. 为了方便起见, 能带结构图的纵坐标为带隙归一化频率$\varOmega = \omega a/\left( {2\text{π} {c_t}} \right)$ , 其中$ a $ 为晶格常数,$ {c_t} $ 为基体的剪切波波速.1.2 优化模型
实施声子晶体的拓扑优化, 主要思路是采用有限元网格对单胞结构进行离散化, 通过优化算法在网格中填充合适的材料, 得到满足优化目标要求的拓扑构型. 由于遗传算法采用二进制变量, 特别适合建立两相材料与拓扑构型之间的关系[12,19,24], 即采用0和1分别代表两种不同的材料, 故声子晶体的拓扑优化多采用遗传算法. 对于多相声子晶体, 可通过引入“二进制向量”的方式对离散单元的材料进行编码, 即
$$ \left.\begin{gathered} {\varphi _i} = ({b_1},{b_2}, \cdots ,{b_t}) \hfill \\ \;2{\,^{t - 1}} < \;\;NM\;\; \leqslant 2{\,^t} \hfill \\ {b_s} \in \left\{ {0\,,1\,} \right\},\;\; s \leqslant t \end{gathered} \right\}$$ (6) 式中,
$ {\varphi _i}(i = 1,2, \cdots ,NE) $ 为任意离散单元的二进制编码(NE为单元数),$ {b_s} $ 为二进制编码值,$ t $ 为向量长度,$ NM $ 为材料数. 以4相材料为例, 有$$ NM=4,\;\;t=2,\;\;{{{\varphi}}}_{i}=\left\{\begin{array}{c}(0,0),\;\;{\rm{material\,1}}\\ (0,1),\;\;{\rm{material\,2}}\\ (1,0),\;\;{\rm{material\,3}}\\ (1,1),\;\;{\rm{material\,4}}\end{array} \right.$$ (7) 对于更多相声子晶体, 可通过增加向量
$ {\varphi _i} $ 的长度$ t $ 来进行相应的编码. 由离散单元的“二进制向量”编码组合可得到整个设计域的材料分布，即$$ {\boldsymbol{\phi}} \; = \;\left( {{\varphi _1},{\varphi _2}, \cdots ,{\varphi _{NE}}} \right)$$ (8) 式中，
${\boldsymbol{\phi}} $ 为设计域的材料分布. 在优化问题求解中, 采用$ N \times N $ 的网格对单胞进行离散, 由于结构的平移周期性和点群对称性, 通过波矢遍历不可约布里渊区边界求解特征频率可得到能带结构, 则设计域内单元数目减少至$ (N/2)(1 + N/2)/2 $ , 对应遗传算法染色体长度为$ t (N/2)(1 + N/2)/2 $ .为了避免出现孤立材料单元而难以或无法实际制造的问题, 需要引入合适的可制造性约束条件. 本文试图通过控制连通单元的占比达到限制孤立单元的目的. 引入图像处理中四连通区域的定义, 即从区域内一点出发, 可通过上下左右4个方向的移动组合, 在不越出区域的前提下, 能达到区域内任一像素的区域定义为四连通区域. 将离散后的网格看作像素点, 则可将此定义扩展到材料连通单元中, 进一步由连通单元组成材料连通域, 如图1中所示. 红、绿、黑不同标记的网格分别由3种不同材料填充, 其中, 红色、绿色区域分别为独立的连通域, 而黑色区域虽在角点处相连接, 但属于两个连通域.
按照编码方式为元胞网格填充材料后, 可进行连通域的识别和其相对于元胞面积的占比计算, 即
$$ \begin{array}{l} {I_{jk}}\left( {\boldsymbol{\phi}} \right){\text{ = }}\dfrac{{{A_{jk}}\left( {\boldsymbol{\phi}} \right)}}{A} \hfill \\ {j = 1,2, \cdots ,NQ;\;\; k = 1,2,\cdots,NM} \end{array} $$ (8) 式中
$ {A_{jk}}\left( {\boldsymbol{\phi}} \right) $ 和$ {I_{jk}}\left( {\boldsymbol{\phi}} \right) $ 分别为第$ k $ 种材料的第$ j $ 个连通域的面积和其相对于元胞的面积占比;$ A $ 为元胞面积,$ NM $ 为材料数,$ NQ $ 为每种材料所包含的四连通域数目.$ {I_{jk}}\left( {\boldsymbol{\phi}} \right) $ 过小会使得声子晶体的可制造性下降, 故通过限制$ {I_{jk}}\left( {\boldsymbol{\phi}} \right) $ 值保障其可制造性, 相应的附加约束条件具体如下$$ I\left( {\boldsymbol{\phi}} \right){\text{ = }}\min \left[ {{I_{jk}}\left( {\boldsymbol{\phi}} \right)\;} \right] \geqslant \;{r^*} $$ (9) 式中,
$ I\left( {\boldsymbol{\phi}} \right) $ 为$ {I_{jk}}\left( {\boldsymbol{\phi}} \right) $ 的最小值,$ {r^*} $ 为阈值, 可根据实际对可制造性的要求和数值试验确定,$ {r^*} $ 越大则表示对结构可制造性要求越高.对于声子晶体的带隙优化研究, 常以最大化相对带隙宽度、最大化绝对带隙宽度、特定带隙中心频率等为优化目标. 本文主要以轻质结构的减振隔振为应用背景, 考虑到实际应用中通常是针对特定场合对特定频段的减振需求设计具有预期带隙的声子晶体, 同时, 往往还需兼顾结构轻量化设计的需求, 故本文以在特定频率段带隙最宽和结构质量最小为优化目标.
综上所述, 考虑可制造性约束的二维多相声子晶体多目标优化优化模型表述如下
$$\left. \begin{array}{l} {\rm{find}}:{\text{ }}\;\;\;{\boldsymbol{\phi}}\; = \;\left( {{\varphi _1},{\varphi _2}, \cdots ,{\varphi _{NE}}} \right) \hfill \\ {\rm{maximize}}:\;\;\;\;{F_1}\left( {\boldsymbol{\phi}} \right)\, = \,\dfrac{{\displaystyle \sum\limits_n {\Delta {\omega _n}} }}{{{\omega _{upp}} - {\omega _{low}}}}\; \left( {\Delta {\omega _n} \geqslant 0} \right) \hfill \\ \quad \quad \quad \quad \quad \;\; \; \Delta {\omega _n} = \mathop {\min }\limits_{\boldsymbol{k}} {\omega _{n + 1}}\left( {\boldsymbol{k}} \right) - \mathop {\max }\limits_{\boldsymbol{k}} {\omega _n}\left( {\boldsymbol{k}} \right) \hfill \\ {\rm{minimize}}:\quad {F_2}\left( {\boldsymbol{\phi}} \right) = m =\displaystyle \sum\limits_{s = 1}^{{N^2}} {{\rho _s}V} \hfill \\ {\rm{subject}}{\text{ }}{\rm{to}}:{\text{ }}{\kern 1pt} {\kern 1pt} \;\; {\varphi _i} = ({b_1},{b_2}, \cdots ,{b_t}) \\ \quad \quad \quad \quad \quad \;\;\; I\left( {\boldsymbol{\phi}} \right) \geqslant {r^*} \end{array} \right\}$$ (10) 式中,
$ {\boldsymbol{\phi}}$ 为设计域材料分布;$ \Delta {\omega _n} $ 为第n带隙的带隙宽度, 为了方便描述, 指定第n条能带和第n + 1能带之间存在的带隙为第n带隙, 即当第$ n + 1 $ 条能带的最小值大于第$ n $ 条能带的最大值时, 带隙宽度$ \Delta {\omega _n} > 0 $ , 反之带隙宽度$ \Delta {\omega _n}{\text{ = }}0 $ , 带隙不存在;$ {F_1}\left( {\boldsymbol{\phi}} \right) $ 为特定频率范围段内带隙宽度之和的占比, 其值越大表示带隙对特定频率段的覆盖率越高,$\omega_{ {{\rm{low}} }}$ 和$\omega_{{{{\rm{upp}}}}}$ 分别为特定频率范围的上、下界,$ {F_2}\left( {\boldsymbol{\phi}} \right) $ 为优化结构质量,$ N $ 为网格的离散规模,$ {\rho _s} $ 为单元质量密度,$ V $ 为单元面积.1.3 优化算法
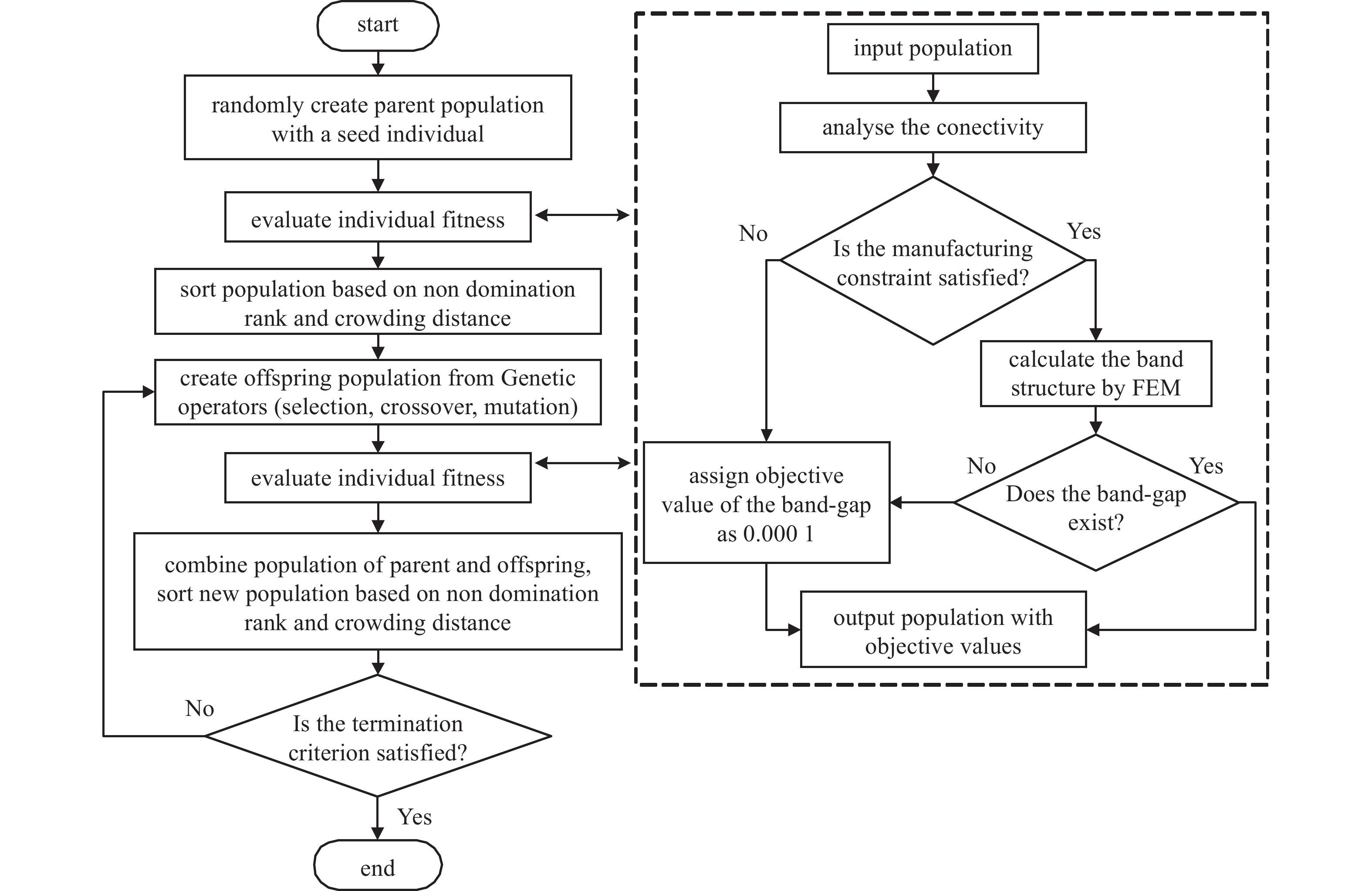
对于式(9)的多目标优化问题, 可采用快速非支配排序遗传算法
$ \text { NSGA-II } $ [25]进行求解, 该方法能够有效生成$ \text { Pareto } $ 解集, 使决策者能够根据需要从$ \text { Pareto } $ 解集中选择出最适合的解. 算法流程如图2所示.![]()
图 2 基于NSGA-II算法的声子晶体多目标优化流程图Figure 2. Flow chart of the multi-objective optimization of phononic crystals based on the NSGA-II algorithm在计算种群内个体的适应度值时, 将种群中不满足可制造性约束和虽满足可制造性约束但无带隙个体的带隙特性目标函数值赋予极小值0.0001, 可以增加满足可制造约束且存在带隙个体在非支配排序时处于更优的非支配排序层的可能性, 便于后续选择操作时对此类优秀个体的保留.
2. 数值算例
以二维正方晶格声子晶体面内模态为例, 晶格常数为0.01 m, 声子晶体单胞由4种材料组成, 即金(绿)、环氧树脂(灰)、硅橡胶(黄)和硫化橡胶(蓝), 材料名称、编码
$ {\varphi _i} $ 、质量密度$ \rho $ 、杨氏模量$ E $ 和泊松比$ \nu $ 如表1所示. 以在给定归一化频段0 ~ 0.05带隙最宽为优化目标, 有${\omega _{{{{\rm{low}}}}}} = 0$ ,${\omega _{{{{\rm{upp}}}}}} = 0.05$ ; 考虑可制造性约束要求, 取$ {r^*} = 0.005 $ ; 对单胞进行网格划分, 取$ N = 16 $ , 则设计域内的单元数目和染色体长度分别为36和72; 遗传算法的参数选取为: 种群规模20, 交叉率0.9, 变异率0.02, 采用二元锦标赛选择方式, 单点交叉方式, 设定迭代次数1000为终止条件.表 1 材料属性Table 1. Properties of the materialsName $ {\varphi _i} $ ρ/(kg·m−3) E/Pa $ \nu $ Au (0,0) 19500 8.75×1010 0.46 epoxy (0,1) 1180 4.35×109 0.368 sil (1,0) 1300 1.175×105 0.469 per (1,1) 1300 1×106 0.47 种群规模Np取值对优化结果不会产生影响, 但是会对优化收敛过程产生影响, 即Np取值越大, 所需得到Pareto解集的迭代次数越少. 对于本文考虑的问题而言, 因在每一步迭代中要对种群中所有个体的带隙进行有限元计算, 增大种群规模会导致单次迭代过程中有限元带隙计算次数大大增加, 加大单次迭代的计算成本. 因此, 综合考虑以上因素并通过数值试验, 本算例选取
$ Np{\text{ = 20}} $ . 为了提高算法的收敛速度, 在初始种群中引入具有带隙的“种子”结构, 其余个体随机产生, “种子”单胞构型如图3所示.图4为进化
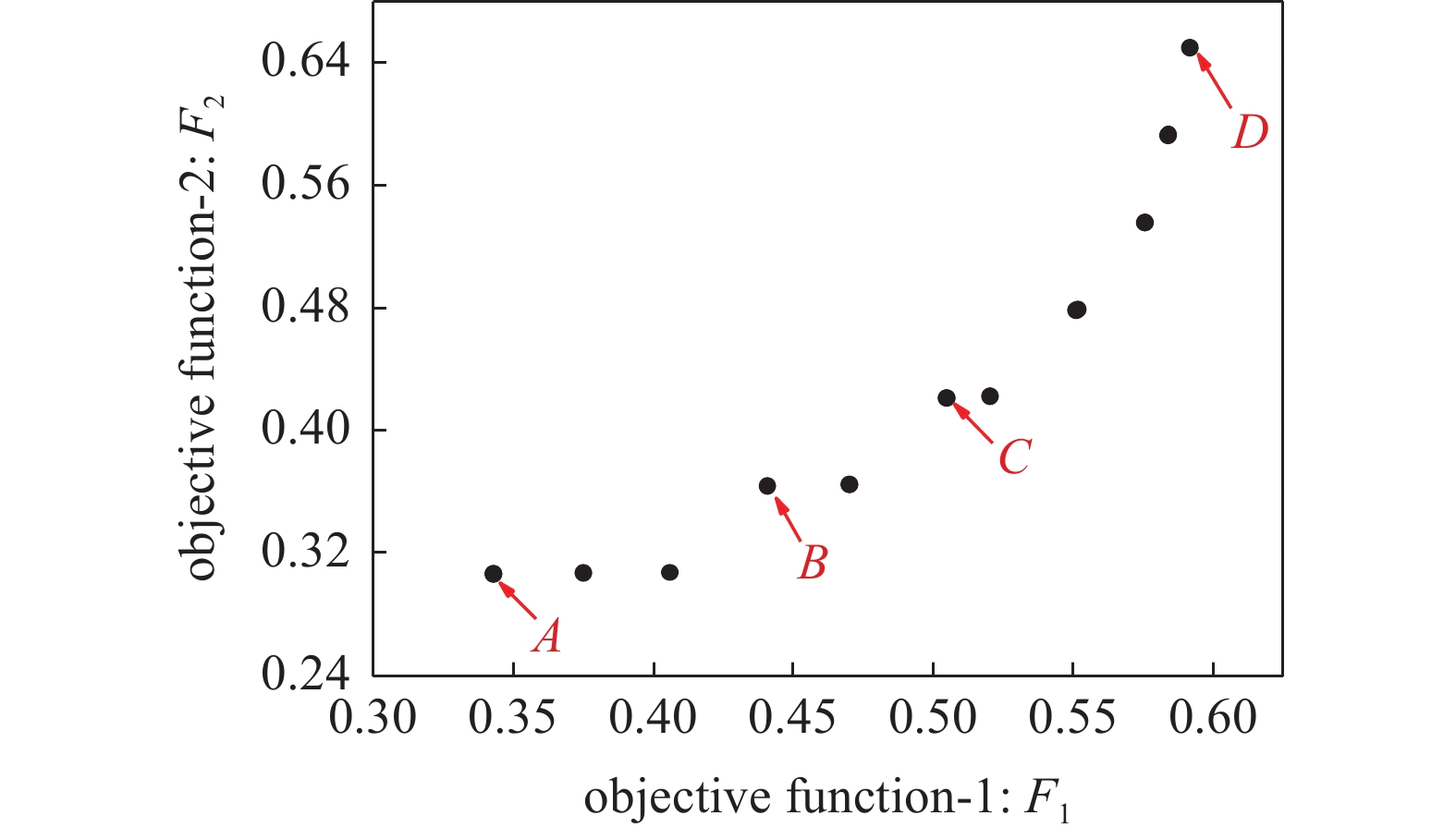
$ 1000 $ 代的Pareto解集, 横、纵坐标分别为目标函数$ F_{1} $ 和$ F_{2} $ 的值, 可以看出两个目标之间的制约关系, 即特定频段的带隙宽度之和的增大将使得结构质量也在同时变大.![]()
图 4 附加可制造性约束的多目标Pareto解集Figure 4. Pareto optimal solutions from the MOOP considering the manufacturing constraint从图4中选择4个非支配解A, B, C和D进行分析, 其拓扑构型、能带结构和透射谱如图5所示. 由图5(a)可以发现, 非支配解A, B, C和D的拓扑构型均由金、环氧树脂和硫化橡胶组成且具有相似的特征, 即由金和环氧树脂组成的夹杂体被硫化橡胶包覆层包裹后嵌入环氧树脂基体中. 图5(b)与图5(c)的对比表明能带结构的带隙范围与透射谱频率衰减范围吻合. 由图5(b)的能带结构可知, 解A, B, C和D的第3带隙充分打开, 其归一化带宽分别为0.0171,0.0220, 0.0252和0.0300, 计算得到的对应目标函数值如表2所示.
![]()
图 5 附加可制造性约束的多目标优化结果Figure 5. Pareto optimal solutions from the MOOP considering the manufacturing constraint表 2 附加可制造性约束优化结构目标函数值, S为单目标优化结果Table 2. The objective function values of the optimized structures from the MOOP and the SOOP considering the manufacturing constraintStructures $ {F_1} $ $ {F_2} $ A 0.3428 0.3064 B 0.4407 0.3640 C 0.5048 0.4216 D 0.5916 0.6504 S 0.6042 0.7656 由表2可知, 结构A, B, C的带隙特定频段的覆盖率比D分别小42%, 26%和15%, 结构质量比D分别小52%, 44%和35%, 因此, 决策者可根据实际应用情形的目标权重从Pareto解集中挑选自己所需要的声子晶体结构.
为进一步理解优化结果的带隙形成机理, 对图5(b1 ~ b4)带隙的上、下边界所对应的振动模态进行分析. 现以结构D为例进行说明(构型A, B, C的情况与之类似). 构型D的第3个带隙上、下边界处对应的振动模态如图6所示.
![]()
图 6 结构D的带隙边界所对应的振动模态Figure 6. Vibration modes corresponding to the band-gap edges of the optimized structure D由图6可以看出优化结果的带隙机理为局域共振型. 其振动特性可近似的通过简化的等效“弹簧-质量”系统进行描述, 相应的带隙上、下边界的频率可由下式进行估算[26-27]
$$ \left. {\begin{array}{*{20}{l}} {{f_{{\rm{low}}}} = \dfrac{1}{{2\text{π} }}\sqrt {K/{M_1}} }\\ {{f_{{\rm{upp}}}} = \dfrac{1}{{2\text{π} }}\sqrt {K/{M_1} + K/{M_2}} } \end{array}} \right\} $$ (11) 其中,
$ {f_{{\rm{low}}}} $ 和$ {f_{{\rm{upp}}}} $ 分别为带隙的下边界和上边界频率, K为包覆层(弹簧)的动态等效刚度, M1和M2分别为金散射体和环氧树脂基体的动态等效质量.由图5中的优化结果构型可以看出, 优化构型中仅剩下3种材料, 材料初始分布中的硅橡胶在优化过程中被淘汰掉, 包覆层全部由弹性模量更大的硫化橡胶构成, 使得弹性包覆层动态等效刚度增加. 由式(12)可知, 当其他参数不变时, K的增大将导致带隙起始(下边界)和截止(上边界)频率均会出现不同程度的上升. 由于截止(上边界)频率上升幅度更大, 因而带隙范围变宽, 带隙对特定频率段的覆盖率随之提高.
另外, 通过对比图5(a), 4种构型发现, 金散射体的占比不断提高, 即M1逐步增大, 而K与M2基本保持不变. 由式(12)可知, M1的增大将导致带隙起始(下边界)和截止(上边界)频率降低, 而起始(下边界)频率相比截止(上边界频率降幅更大, 因而带隙范围变宽, 带隙对特定频率段的覆盖率随之提高. 即F1与F2同时增大, 这种制约关系与图4十分吻合.
为了说明多目标和单目标优化结果的差异, 本文对只考虑了目标函数
$ {F_1} $ 的单目标带隙优化问题也进行了求解, 图7给出了单目标进化曲线、近似最优解S的拓扑构型、能带结构和透射谱.从图7(a)中可明显看出拓扑构型随迭代进程的演化过程, 即随着进化代数的增加, 包覆层的硅橡胶(黄)分布减小而硫化橡胶(蓝)分布增加, 金散射体分布变化不大; 进化800代左右后种群的最佳适应度收敛到稳定值, 表明种群进化趋于完善, 对应的个体即为近似最优解S, 其拓扑构型(图7(b))由硫化橡胶包覆着金嵌入环氧树脂基体中, 能带结构(见图7(c))显示可在第3和第4能带间打开归一化带宽为0.0302的带隙, 由此计算得到结构S的目标函数值同样在表2中给出以作对比. 对比D和S的结果发现, 两者对特定频段的覆盖率十分接近, 虽然S比D的特定频段覆盖率高2%, 但其质量却比D大18%, 所以从结构整体的角度来讲, 结构D比S更优, 这说明多目标优化不仅可以得到和单目标优化结果接近的非支配解, 还可以得到其他的多目标优化非支配解集, 因此较单目标优化更具有优越性.
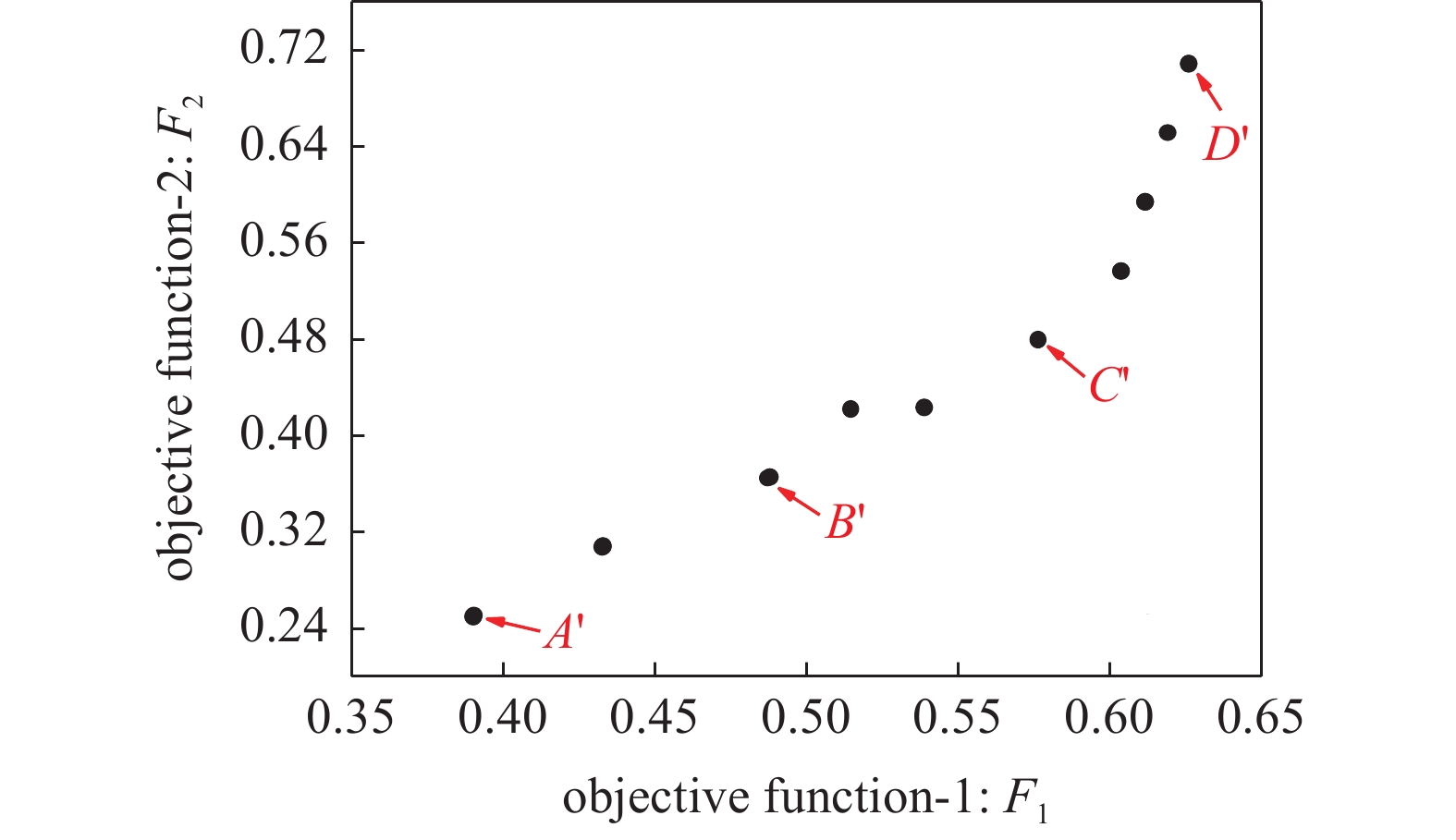
此外, 为说明考虑可制造性优化的有效性和优势, 图8给出了未附加可制造性约束的多目标优化Pareto解集. 从图8内选择与考虑可制造性约束的4个非支配解的目标函数值具有可比拟性的解
$ A' $ ,$ B' $ ,$ C' $ 和$ D' $ 分析, 其拓扑构型分别如图9所示.![]()
图 8 未附加可制造性约束多目标Pareto解集Figure 8. Pareto optimal solutions from the MOOP without the manufacturing constraint![]()
图 9 未附加可制造性约束多目标优化结果Figure 9. The optimized solutions from the MOOP without the manufacturing constraint从图9可以看出, 未考虑可制造性约束的结果构型中
$ A' $ 和$ B' $ 存在多个金(绿)、硅橡胶(黄)和环氧树脂(灰)孤立单元,$ C' $ 和$ D' $ 对角线位置存在多个环氧树脂(灰)孤立单元. 对4种结构单胞内的孤立材料单元进行统计, 结果如表3所示.表 3 单胞的孤立材料单元数Table 3. The number of the isolated elements in the unit-cellsStructures Au epoxy sil per $ A' $ 12 4 8 0 $ B' $ 0 16 0 8 $ C' $ 0 12 0 0 $ D' $ 0 4 0 0 由以上结果分析可见, 未考虑可制造性约束的多目标优化结果均存在孤立材料单元, 而图5中附加可制造性约束的优化结果则有效地避免了这种情况的发生, 表明本文所提出的考虑可制造性约束的声子晶体多目标拓扑优化方法可在满足带隙等性能指标的前提下同时兼顾到实际制造加工的可行性, 有效提高了优化结果的实用性.
3. 结论
本文针对声子晶体拓扑优化结果常会出现制造性能欠佳的问题, 通过引入可制造性附加约束, 建立了考虑可制造性约束的二维多相声子晶体多目标拓扑优化模型, 基于NSGA-II和有限元法对二维四相正方晶格声子晶体面内模态进行多目标拓扑优化设计, 得到了多目标Pareto解集, 数值算例表明了本文模型的有效性, 所得主要结论如下.
(1) 通过对比引入可制造性附加约束的多目标优化与相应的单目标拓扑优化结果发现, Pareto解集内可以找到与单目标优化结果接近的非支配解; 但多目标的优化解在一定程度上可优于单目标优化近似最优解, 表明多目标优化不仅可以得到和单目标优化结果近似非支配解, 还可以得到其他的多目标非支配解集.
(2) 通过对比引入和不考虑可制造性附加约束的多目标优化结果发现, 引入可制造性附加约束可有效避免通常优化结果中存在孤立材料单元的情况, 其优化结果在满足带隙性能指标的同时可兼顾到制造加工的可行性, 更具有实用价值.
本文算例针对二维正方晶格, 验证了协同考虑带隙性能和可制造性约束的多目标优化方法的可行性和有效性, 但该方法对其他类型的晶格, 比如二维三角晶格和六角蜂窝晶格、甚至三维体心立方晶格等等, 也同样适用. 其中, 单胞离散及材料编码方案的选择、可制造性约束的添加和优化算法的选择可根据具体问题进行确定. 对于三维晶格而言, 材料初始分布构型的选取、复杂三维网格的划分、计算规模大、优化效率低等仍是其拓扑优化问题的主要挑战[28], 同时也是该方面研究工作未来需要加强的一个方向.
最后需要强调指出的是, 影响声子晶体优化结果可制造性的因素很多, 比如孤立材料单元问题, 超细而导致刚度超弱链接单元问题, 不同材料连通域的个数问题, 微结构奇形怪状问题和微结构边界或组元界面非光滑问题等. 本文提出的多目标优化模型主要以避免出现孤立材料单元而提高多相声子晶体优化结构的可制造性能, 其他方法比如避免出现超细超弱链接单元[20, 29-30], 力求微结构边界或组元边界具有一定的光滑度[31]等也是提高其可制造性的有效措施, 值得引起科研和实用工作者的高度重视.
-
![]()
图 2 基于NSGA-II算法的声子晶体多目标优化流程图
Figure 2. Flow chart of the multi-objective optimization of phononic crystals based on the NSGA-II algorithm
![]()
图 4 附加可制造性约束的多目标Pareto解集
Figure 4. Pareto optimal solutions from the MOOP considering the manufacturing constraint
![]()
图 5 附加可制造性约束的多目标优化结果
Figure 5. Pareto optimal solutions from the MOOP considering the manufacturing constraint
![]()
图 6 结构D的带隙边界所对应的振动模态
Figure 6. Vibration modes corresponding to the band-gap edges of the optimized structure D
![]()
图 8 未附加可制造性约束多目标Pareto解集
Figure 8. Pareto optimal solutions from the MOOP without the manufacturing constraint
![]()
图 9 未附加可制造性约束多目标优化结果
Figure 9. The optimized solutions from the MOOP without the manufacturing constraint
表 1 材料属性
Table 1 Properties of the materials
Name $ {\varphi _i} $ ρ/(kg·m−3) E/Pa $ \nu $ Au (0,0) 19500 8.75×1010 0.46 epoxy (0,1) 1180 4.35×109 0.368 sil (1,0) 1300 1.175×105 0.469 per (1,1) 1300 1×106 0.47 
下载: 导出CSV
表 2 附加可制造性约束优化结构目标函数值, S为单目标优化结果
Table 2 The objective function values of the optimized structures from the MOOP and the SOOP considering the manufacturing constraint
Structures $ {F_1} $ $ {F_2} $ A 0.3428 0.3064 B 0.4407 0.3640 C 0.5048 0.4216 D 0.5916 0.6504 S 0.6042 0.7656
下载: 导出CSV
表 3 单胞的孤立材料单元数
Table 3 The number of the isolated elements in the unit-cells
Structures Au epoxy sil per $ A' $ 12 4 8 0 $ B' $ 0 16 0 8 $ C' $ 0 12 0 0 $ D' $ 0 4 0 0
下载: 导出CSV
-
[1] 田源, 葛浩, 卢明辉等. 声学超构材料及其物理效应的研究进展. 物理学报, 2019, 68(19): 194301 (Tian Yuan, Ge Hao, Lu Minghui, et al. Research advances in acoustic metamaterials. Acta Physica Sinica, 2019, 68(19): 194301 (in Chinese) doi: 10.7498/aps.68.20190850 [2] 曹蕾蕾, 朱旺, 武建华等. 基于人工神经网络的声子晶体逆向设计. 力学学报, 2021, 53(7): 1992-1998 (Cao Leilei, Zhu Wang, Wu Jianhua, et al. Inverse design of phononic crystals by artificial neural networks. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(7): 1992-1998 (in Chinese) doi: 10.6052/0459-1879-21-142 [3] Sigmund O, Jensen JS. Systematic design of phononic band-gap materials and structures by topology optimization. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2003, 361(1806): 1001-1019 doi: 10.1098/rsta.2003.1177
[4] Huang Y, Liu S, Zhao J. A gradient-based optimization method for the design of layered phononic band-gap materials. Acta Mechanica Solida Sinica, 2016, 29(4): 429-443 doi: 10.1016/S0894-9166(16)30245-2
[5] Yang XW, Lee JS, Kim YY. Effective mass density based topology optimization of locally resonant acoustic metamaterials for bandgap maximization. Journal of Sound and Vibration, 2016, 383: 89-107 doi: 10.1016/j.jsv.2016.07.022
[6] Zhang X, He J, Takezawa A, et al. Robust topology optimization of phononic crystals with random field uncertainty. International Journal for Numerical Methods in Engineering, 2018, 115(9): 1154-1173 doi: 10.1002/nme.5839
[7] Li YF, Huang X, Meng F, et al. Evolutionary topological design for phononic band gap crystals. Structural and Multidisciplinary Optimization, 2016, 54(3): 595-617 doi: 10.1007/s00158-016-1424-3
[8] Wang K, Liu Y, Wang B. Ultrawide band gap design of phononic crystals based on topological optimization. Physica B: Condensed Matter, 2019, 571: 263-272 doi: 10.1016/j.physb.2019.07.012
[9] Gazonas GA, Weile DS, Wildman R, et al. Genetic algorithm optimization of phononic bandgap structures. International Journal of Solids and Structures, 2006, 43(18-19): 5851-5866 doi: 10.1016/j.ijsolstr.2005.12.002
[10] 钟会林, 吴福根, 姚立宁. 遗传算法在二维声子晶体带隙优化中的应用. 物理学报, 2006, 55(1): 275-280 (Zhong Huilin, Wu Fugen, Yao Lining. Application of genetic algorithm in optimization of band gap of two-dimensional phononic crystals. Acta Physica Sinica, 2006, 55(1): 275-280 (in Chinese) doi: 10.3321/j.issn:1000-3290.2006.01.049 [11] Bilal OR, Hussein MI. Ultrawide phononic band gap for combined in-plane and out-of-plane waves. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 84(6): 065701 doi: 10.1103/PhysRevE.84.065701
[12] Dong HW, Su XX, Wang YS, et al. Topological optimization of two-dimensional phononic crystals based on the finite element method and genetic algorithm. Structural and Multidisciplinary Optimization, 2014, 50(4): 593-604 doi: 10.1007/s00158-014-1070-6
[13] 刘宗发, 吴斌, 何存富. 最优二维固/固声子晶体带隙特性研究. 固体力学学报, 2015, 36(4): 283-289 (Liu Zongfa, Wu Bin, He Cunfu. The characteristics of optimal two-dimensional solid/solid phononic crystals. Chinese Journal of Solid Mechanics, 2015, 36(4): 283-289 (in Chinese) [14] 刘坚, 陈俊煌, 夏百战等. 区间模型下声子晶体的带隙优化研究. 振动与冲击, 2018, 37(17): 115-121 (Liu Jian, Chen Junhuang, Xia Baizhan, et al. Bandgap optimization of phononic crystal based on interval model. Journal of Vibration and Shock, 2018, 37(17): 115-121 (in Chinese) [15] Chen L, Guo Y, Yi H. Optimization study of bandgaps properties for two-dimensional chiral phononic crystals base on lightweight design. Physics Letters A, 2021, 388(11): 127054
[16] Xie L, Xia B, Huang G, et al. Topology optimization of phononic crystals with uncertainties. Structural and Multidisciplinary Optimization, 2017, 56(6): 1319-1339 doi: 10.1007/s00158-017-1723-3
[17] Xie L, Xia B, Liu J, et al. An improved fast plane wave expansion method for topology optimization of phononic crystals. International Journal of Mechanical Sciences, 2017, 120: 171-181 doi: 10.1016/j.ijmecsci.2016.11.023
[18] Han XK, Zhang Z. Bandgap design of three-phase phononic crystal by topological optimization. Wave Motion, 2020, 93: 102496 doi: 10.1016/j.wavemoti.2019.102496
[19] Dong HW, Su XX, Wang YS, et al. Topology optimization of two-dimensional asymmetrical phononic crystals. Physics Letters A, 2014, 378(4): 434-441 doi: 10.1016/j.physleta.2013.12.003
[20] Hussein MI, Hamza K, Hulbert GM, et al. Multiobjective evolutionary optimization of periodic layered materials for desired wave dispersion characteristics. Structural and Multidisciplinary Optimization, 2006, 31(1): 60-75 doi: 10.1007/s00158-005-0555-8
[21] Dong HW, Su XX, Wang YS. Multi-objective optimization of two-dimensional porous phononic crystals. Journal of Physics D: Applied Physics, 2014, 47(15): 155301 doi: 10.1088/0022-3727/47/15/155301
[22] Dong HW, Wang YS, Wang YF, et al. Reducing symmetry in topology optimization of two-dimensional porous phononic crystals. AIP Advances, 2015, 5(11): 117149 doi: 10.1063/1.4936640
[23] Xu W, Ning J, Lin Z, et al. Multi-objective topology optimization of two-dimensional multi-phase microstructure phononic crystals. Materials Today Communications, 2020, 22: 100801 doi: 10.1016/j.mtcomm.2019.100801
[24] Qiu K, Jin J. Multi-objective optimization of two-dimensional phononic bandgap materials and structures using genetic algorithms. International Journal of Computational Methods, 2021, 18(6): 2140002 doi: 10.1142/S0219876221400028
[25] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197 doi: 10.1109/4235.996017
[26] Hirsekorn M. Small-size sonic crystals with strong attenuation bands in the audible frequency range. Applied Physics Letters, 2004, 84(17): 3364-3366 doi: 10.1063/1.1723688
[27] Wang G, Shao LH, Liu YZ, et al. Accurate evaluation of lowest band gaps in ternary locally resonant phononic crystals. Chinese Physics, 2006, 15(8): 1843-1848 doi: 10.1088/1009-1963/15/8/036
[28] Li W, Meng F, Li YF, et al. Topological design of 3D phononic crystals for ultra-wide omnidirectional bandgaps. Structural and Multidisciplinary Optimization, 2019, 60(6): 2405-2415 doi: 10.1007/s00158-019-02329-0
[29] Dong HW, Zhao SD, Wang YS, et al. Robust 2D/3D multi-polar acoustic metamaterials with broadband double negativity. Journal of the Mechanics and Physics of Solids, 2020, 137: 103889 doi: 10.1016/j.jmps.2020.103889
[30] Dong HW, Zhao SD, Wang YS, et al. Topology optimization of anisotropic broadband double-negative elastic metamaterials. Journal of the Mechanics and Physics of Solids, 2017, 105: 54-80 doi: 10.1016/j.jmps.2017.04.009
[31] Liang S, Gao L, Zheng Y, et al. A transitional connection method for the design of functionally graded cellular materials. Applied Sciences, 2020, 10(21): 7449 doi: 10.3390/app10217449
-
期刊类型引用(5)
1. 王燕，朱奕筱，吴圣川，亢战. 基于分析与设计序列迭代方法的三维声子晶体拓扑优化及参数分析. 振动与冲击. 2025(04): 97-104 . 
百度学术
2. 邱克鹏，陈智谋，张建刚，张卫红，燕群，孙向洋，彭涛. 基于形状记忆合金声子晶体的带隙优化设计. 力学学报. 2023(06): 1278-1287 . 本站查看
3. 孙维鹏，刘宸涵，郁小彬，胡珅，钟可欣，赵道利. 钝体表面附着物对低速水流压电俘能器性能影响研究. 力学学报. 2023(07): 1463-1472 . 本站查看
4. 陈昊宇，汪琳阁，陈名松. 基于遗传算法的防波通道拓扑优化. 新一代信息技术. 2023(16): 21-25 . 百度学术
5. 陈新华，张晨，陈猛，郭振坤，郝天琪. 分形凹角蜂窝结构声子晶体振动带隙特性. 人工晶体学报. 2022(08): 1343-1352+1360 . 百度学术
其他类型引用(6)
计量
- 文章访问数: 1518
- HTML全文浏览量: 633
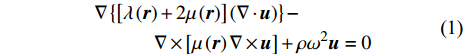
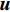
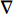
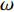
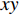
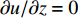
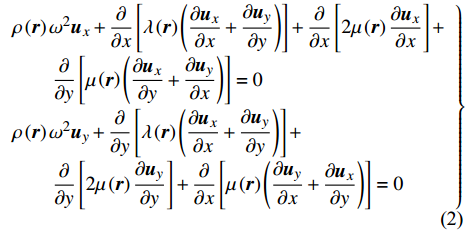
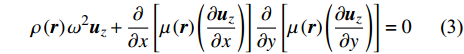
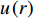
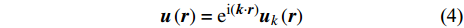
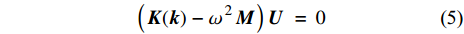
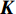
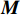
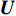
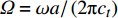
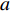
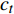
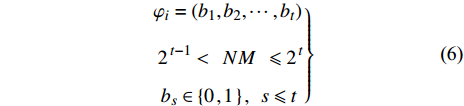
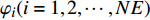
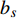
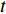
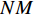
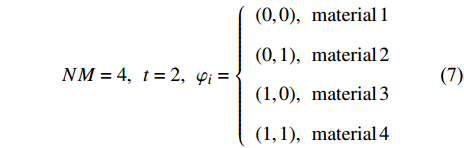
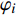
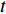
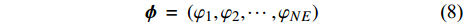
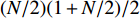
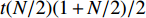
- PDF下载量: 149
- 被引次数: 11
