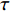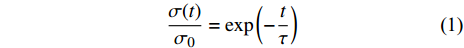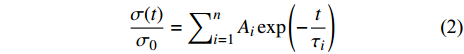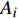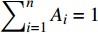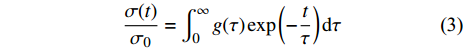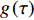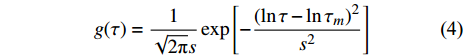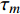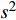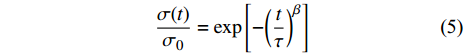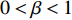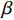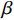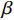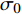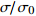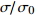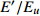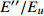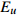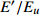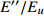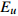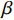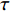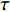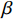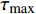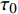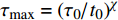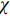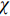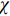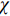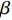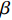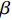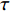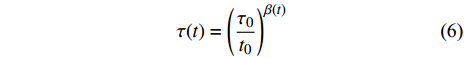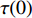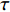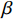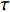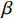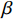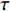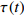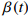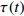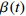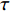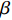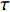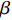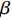STRESS RELAXATION DYNAMICS FOR AMORPHOUS ALLOYS BASED ON THE EVOLUTION OF MICROSTRUCTURAL HETEROGENEITY
-
摘要: 本文研究了Zr48(Cu5/6Ag1/6)44Al8 非晶合金应力松弛行为与固有微观结构非均匀性之间的关联. 非晶合金是典型非平衡固体, 其应力松弛过程伴随着老化效应, 本文首次考虑了经典KWW方程最可几特征时间
$\tau $ 和扩展指数$\beta $ 在应力松弛过程中的耦合演化, 这表明探究应力松弛过程中应力松弛响应必须考虑结构状态的时间依赖性. 基于所研究非平衡状态非晶合金结构状态的演化, 厘清了非晶合金应力松弛行为中老化效应. 研究结果表明, 非晶合金应力松弛行为具有典型非指数特征, 单一特征时间的指数弛豫形式与有限特征时间的有限谱方法均无法合理描述非晶合金应力松弛实验, 这是由于非晶合金微观结构非均匀性所导致的特征时间谱连续分布. 此外, 非晶合金的名义弹性区域应力松弛行为与初始应变无关, 这主要是因为非晶合金应力松弛行为的流变本质, 即弹性和滞弹性可逆性变形随时间推移逐渐转化为黏塑性不可逆变形. 最后, 考虑了老化效应引起的结构参量演化以及进一步导致的变形行为改变, 应力松弛特征时间随时间逐渐增加, 扩展指数随时间逐渐减小.Abstract: The correlation between stress relaxation behavior and the evolution of microstructural heterogeneity of Zr-based amorphous alloys was probed. Amorphous alloy is the typical non-equilibrium solid system. Stress relaxation process is accompanied by aging effect of the amorphous alloy. In the current work, the coupling evolution of the most probably characteristic time$\tau $ and stretched exponent$\;\beta $ in the classical stretched function is considered for the first time, indicating the time dependence of structural state in the stress relaxation process. Based on the evolution of the non-equilibrium structure state of the amorphous alloys, the aging effect in the stress relaxation behavior was clarified. The results demonstrated that the stress relaxation behavior of amorphous alloys has non exponential characteristics. The exponential relaxation form of single characteristic time and the finite spectrum method of finite characteristic time cannot describe accurately the experimental results. This phenomenon is ascribed to the continuous distribution of the characteristic time spectrum caused by the microstructural heterogeneity of amorphous alloys. In addition, the stress relaxation behavior in the apparent elastic region is independent of the initial strain, which is due to the macroscopic flow nature of the stress relaxation behavior. Elastic and anelastic reversible deformation is transformed into viscoplastic (irreversible) deformation. Finally, Evolution of structural parameters caused by aging during stress relaxation is considered, which is reflected in the increase of characteristic time$\tau $ and the decrease of stretched exponent$\;\beta $ .-
Keywords:
- amorphous alloy /
- stress relaxation /
- high temperature deformation /
- nonelastic deformation /
- aging
-
引 言
非晶合金作为一种新型亚稳态金属材料, 其兼具金属和玻璃的双重特性, 因而具有特殊的物理、化学与力学性能, 在材料科学、凝聚态物理以及工程领域具有重要价值[1-2]. 其优越性能包含高强度和硬度、高弹性极限、高断裂韧性和优异的耐腐蚀性能[3-5]. 然而非晶合金室温剪切变形局域化易导致宏观脆性断裂, 因而在工程领域作为结构材料应用受到较大限制[6-9]. 研究表明, 非晶合金低温变形(
$T < 0.8$ Tg, Tg为玻璃转变温度)不均匀, 局部变形远高于平均变形, 最终剪切带滑移导致宏观断裂; 在高温区域($T > 0.8$ Tg)或低应变速率下, 非弹性变形相对均匀分布于整个体系中, 具有较大塑性稳定性[10-11]. 在玻璃转变温度Tg附近, 非晶合金表现为超塑性行为, 变形甚至可达1000%以上[12].非晶合金上述变形特征在本质上与其通过熔体快速急冷到室温(或者更低温度)获得的无序结构特征有关. 传统晶体合金组成原子在三维空间周期性排列, 其中包含不同类型缺陷(空位、位错及晶界等), 依照此结构特征可建立晶体非弹性变形理论. 然而非晶合金原子在空间随机无序排列, 如何表征其原子结构、定义缺陷类型是研究非晶合金力学行为的关键课题之一[13-14]. 由于非晶合金宏观各向同性与组元均匀性, 其微观结构长期被认为是连续均匀的. 随着结构表征实验技术(动态原子力显微镜、超声显微镜以及固体核磁共振测量等)和原子级计算机模拟技术的不断发展, 通常认为, 非晶合金包含纳米级的微观结构非均匀区域, 这可能是在急速冷却过程中从金属熔体中冻结的结构特征[15-20]. 利用原子力声学显微镜(atomic force acoustic microscopy, AFAM), 可观察到PdCuSi非晶合金纳米尺度上局部压痕模量高斯分布, 模量大小差异达33%, 但晶化样品局部模量差异大大降低, 这进一步表明非晶合金存在微观结构非均匀性现象, 从而导致模量非均匀分布[21]. Liu等[15]从非晶合金表面局域能量耗散和模量变化角度, 利用振幅可调节动态原子力显微镜, 排除样品表面粗糙度影响后, 直接从实验中观察到能量耗散与模量不均匀, 结构非均匀性尺度约为2.5 nm. Fujita等[22]利用嵌入原子法(embeded atom method, EAM)进行分子动力学模拟, 揭示了Cu45Zr45Ag10非晶合金过冷液体动力学非均匀性、原子结构和化学短程序之间的关联.王云江等[1]对CuZr二元非晶合金分子动力学模拟过程中, 提出无序固体性能与结构亚纳米级空间关联特征密切相关. 非晶合金微观结构非均匀性和动力学非均匀性已经成为认识非晶合金原子扩散、弛豫行为和变形机制的基本出发点和切入口. 不同概念的结构缺陷, 如流变单元[23-24]、自由体积[25]、准点缺陷[26-27]等均是根据非晶固体局域密度、焓和熵等的波动所提出, 用以描述非晶合金的力学和物理性能.
如何构建微观结构(缺陷)与变形机制之间的关联是非晶合金尚未解决的重要科学问题, 这主要是因为将微观机制(如原子运动)纳入宏观塑性变形的本构模型仍然具有挑战性. Spaepen[28]基于描述液体输运的自由体积概念, 以自由体积为序参量, 提出了非晶合金稳态非均匀流动的微观机制, 该机制涉及两个相互竞争的过程: 应力诱导无序和扩散控制的重新排序过程. 随后, Argon[10]提出了一种非晶合金塑性变形理论, 该理论基于在外加剪切应力作用下在自由体积区域周围启动的两种热激活剪切转变模式, 预测了低温下非晶合金的极快剪切局部化. Falk等[29]利用分子动力学模拟研究了非晶合金的变形行为, 将经历局部剪切重排的基本变形单元定义为剪切转变区(STZ), 该理论是自由体积模型、剪切转变理论等流动缺陷理论的重要补充和延伸. 应注意, STZ理论本质上是一个平均场模型, 它将局部流动缺陷的密度和方向视为动态参量, 并没有考虑不同STZ之间的相关性. 此外, 塑性屈服过程中从堵塞到流动的过渡受外加应力控制. 当应力低于屈服应力时, 预屈服变形是一个简单的弹性过程; 一旦STZ在超过屈服应力的应力下激活, 就会发生屈服. 然而, 实验结果表明, 非晶合金即使在室温下也会发生滞弹性或永久变形. Yang等[30-31]提出了一个核壳模型, 通过考虑类固体原子的弹性背应力来解释滞弹性变形.
基于上述非晶合金微观结构非均匀性与相关变形研究, 可以设想结构缺陷、变形单元与宏观非弹性变形之间必然存在着内禀性关联. 当施加应力时, 首先激活变形单元从非晶合金诸多潜在位置中产生. 通常, 能量状态高、原子运动快的缺陷位点更易激活以产生原子重排. 事实上, 这些变形单元在低应变下在空间上是孤立的, 其所承载变形在消除应力后可恢复(滞弹性变形). 应力长时间作用下, 变形单元可以与邻近变形单元边界相互融合并失去其完整性, 由此产生的变形是不可逆的(塑性变形).
此外, 非晶态固体处于非平衡态, 无时无刻不在处于老化之中, 老化是非晶合金向平衡态(更低能量状态)迁移的过程. 当平衡过冷液体冷却至玻璃转变温度以下时, 原子运动部分冻结, 导致系统宏观上失去平衡, 其力学/物理性能表现为时间依赖性[2, 32]. 老化作为非晶合金的本征属性, 会极大改变非晶合金结构与性能, 因此可能导致一系列实际应用问题, 例如塑性变形能力在老化后的降低. 此外由于非晶合金力学参量的时间依赖性, 变形过程中必须考虑老化效应所带来的微观结构演化.
本文以热稳定性和玻璃形成能力好的Zr48(Cu5/6Ag1/6)44Al8 非晶合金为模型体系[33], 通过其应力松弛测试中所体现的重要特征, 研究非晶合金的微观结构非均匀性和宏观变形行为之间的关联. 本文主要考虑了非晶合金在应力松弛过程中的老化效应, 明晰了非晶合金微观结构非均匀性及对应宏观流动特征时间两者之间的耦合演化规律.
1. 实验方法
本研究所选取母合金采用电弧熔炼法获得, 其名义组分为Zr48(Cu5/6Ag1/6)44Al8 (at.%). 将各高纯金属组元按一定质量比配制并置于电弧熔炼炉铜坩埚中. 在高纯氩气气氛保护下, 反复熔炼六次以保证成分均匀, 采用铜模吸铸法制备尺寸为85 mm(长) × 10 mm(宽) × 2 mm(厚)的块体非晶合金. 非晶合金带材是采用高真空单辊甩带机制得的宽约0.9 mm、厚度约40 μm薄带.
非晶合金的玻璃特征采用X’Pert PRO型X射线衍射仪(X-ray diffraction, XRD)进行确认. 测试参数为Cu靶Kα, 扫描角度为20° ~ 90°, 扫描速度为5 °/min. 通过Netzsch DSC404型差示扫描量热仪测定实验样品的玻璃转变温度Tg和晶化初始温度Tx, 升温速率为20 K/min.
应力松弛是测量材料黏弹性性能和黏弹性参量的常用试验方法. 本研究中应力松弛测试在TA DMA Q800动态力学分析仪拉伸模式下进行. 首先将待测样品从室温以“equilibrium”模式升温至测试温度, 升温时间约10 min. 加载前保温一定时间, 以使整体温度平衡或引入老化效应. 加载阶段, 对条带样品在0.2 s时间内加载至特定应变并在此后保持应变值恒定, 测定维持该应变所需应力随时间的演化曲线.
动态力学分析测试是研究传统晶体合金、非晶态合金、软物质材料和新型功能材料缺陷弛豫过程和微结构变化的最有效测试手段之一. 本文中采用该试验手段确定给定温度下, 非晶合金结构状态随时间演化规律, 在TA DMA Q800动态力学分析仪单悬臂模式下进行. 动态力学分析指对样品施加交变力, 并分析材料对该力的响应. 测试参量为储能模量
$E'$ 和损耗模量$E''$ , 分别代表样品以弹性形式储存能量的能力和以热形式损耗能量的能力, 储能模量与损耗模量之比$\tan \delta = E''/E'$ 称为材料内耗, 也称阻尼. 待测样品为尺寸30 mm(长) × 2 mm(宽) × 1 mm (厚)的块体非晶合金, 加载频率为1 Hz.2. 实验结果与讨论
2.1 结构和热力学信息表征
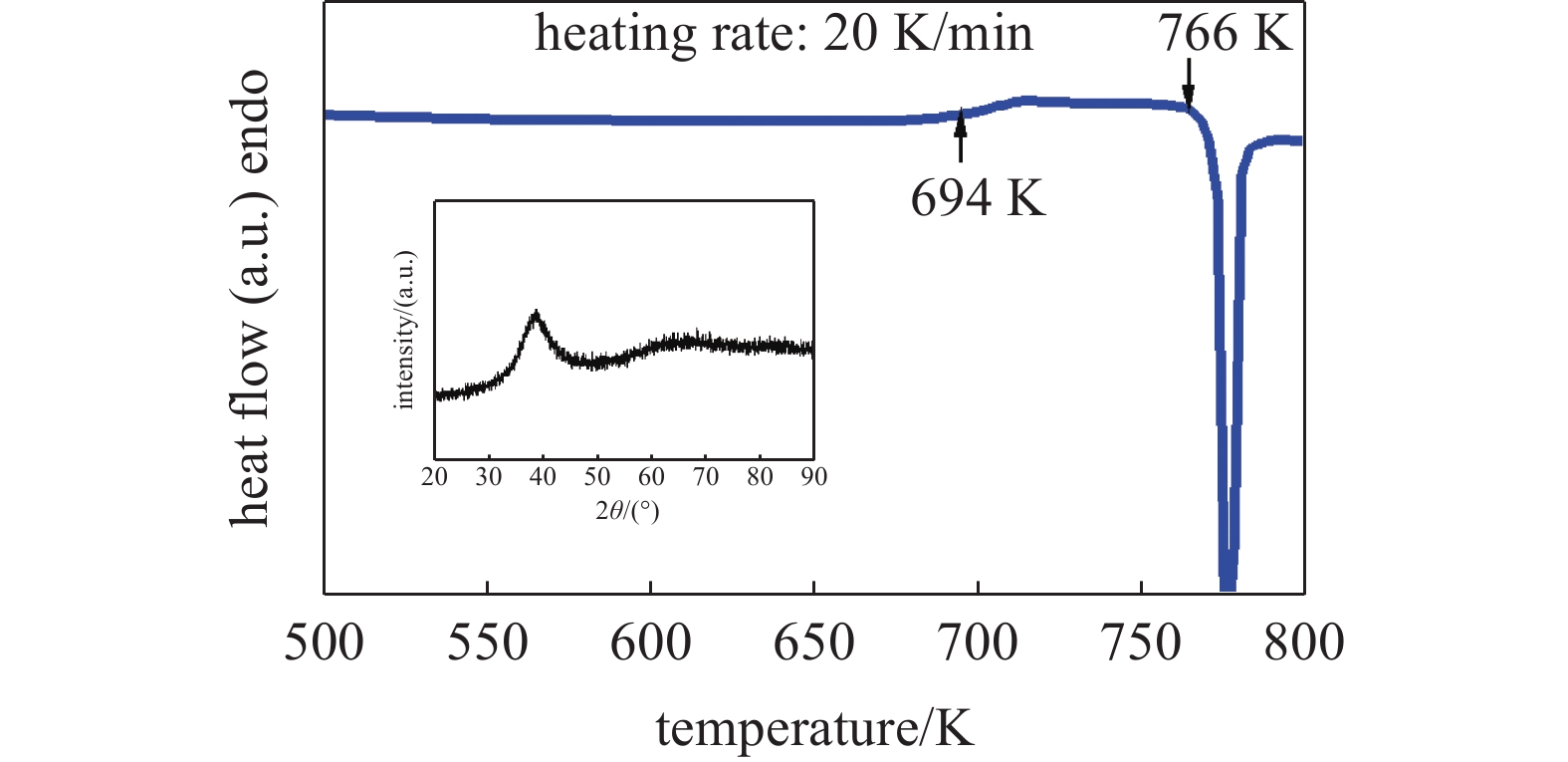
借助于差示扫描量热分析仪对待测样品进行相关热性能表征. 如图1所示为待测样品在给定升温速率(20 K/min)下的DSC曲线. 玻璃转变温度Tg和晶化初始温度Tx分别为694 K和766 K. 插图为模型合金体系的X射线衍射图谱, 仅可观察到宽广弥散馒头峰, 并未检测到尖锐晶化峰, 表明所制得模型合金为完全非晶态.
![]()
图 1 Zr48(Cu5/6Ag1/6)44Al8 非晶合金DSC曲线, 升温速率为20 K/min. 插图为X射线衍射图谱Figure 1. DSC curve of Zr48(Cu5/6Ag1/6)44Al8 metallic glass with a heating rate of 20 K/min. Inset shows the XRD pattern of the model alloy2.2 应力松弛的非指数行为: 结构起源
应力松弛作为黏弹性力学的主要变形行为之一, 不仅是实际工程应用领域(螺栓防松脱、沥青路面抗开裂)的常用试验方法, 其在晶态合金中位错或晶界部位原子级变形、聚合物黏弹性变形机制等科学研究领域也是被广泛应用的测试手段. 传统晶体合金应力松弛动力学可描述为单一过程, 具有单一弛豫时间
$ \tau $ , 其弛豫函数以指数形式衰减[34]$$ \frac{{\sigma (t)}}{{\mathop \sigma \nolimits_0 }} = \exp \left( { - \frac{t}{\tau }} \right) $$ (1) 式(1)也称为Debye弛豫模型. 在黏弹性力学理论中, Debye弛豫模型可通过基本黏弹性元件−弹簧和黏壶的简单串联推导得出.
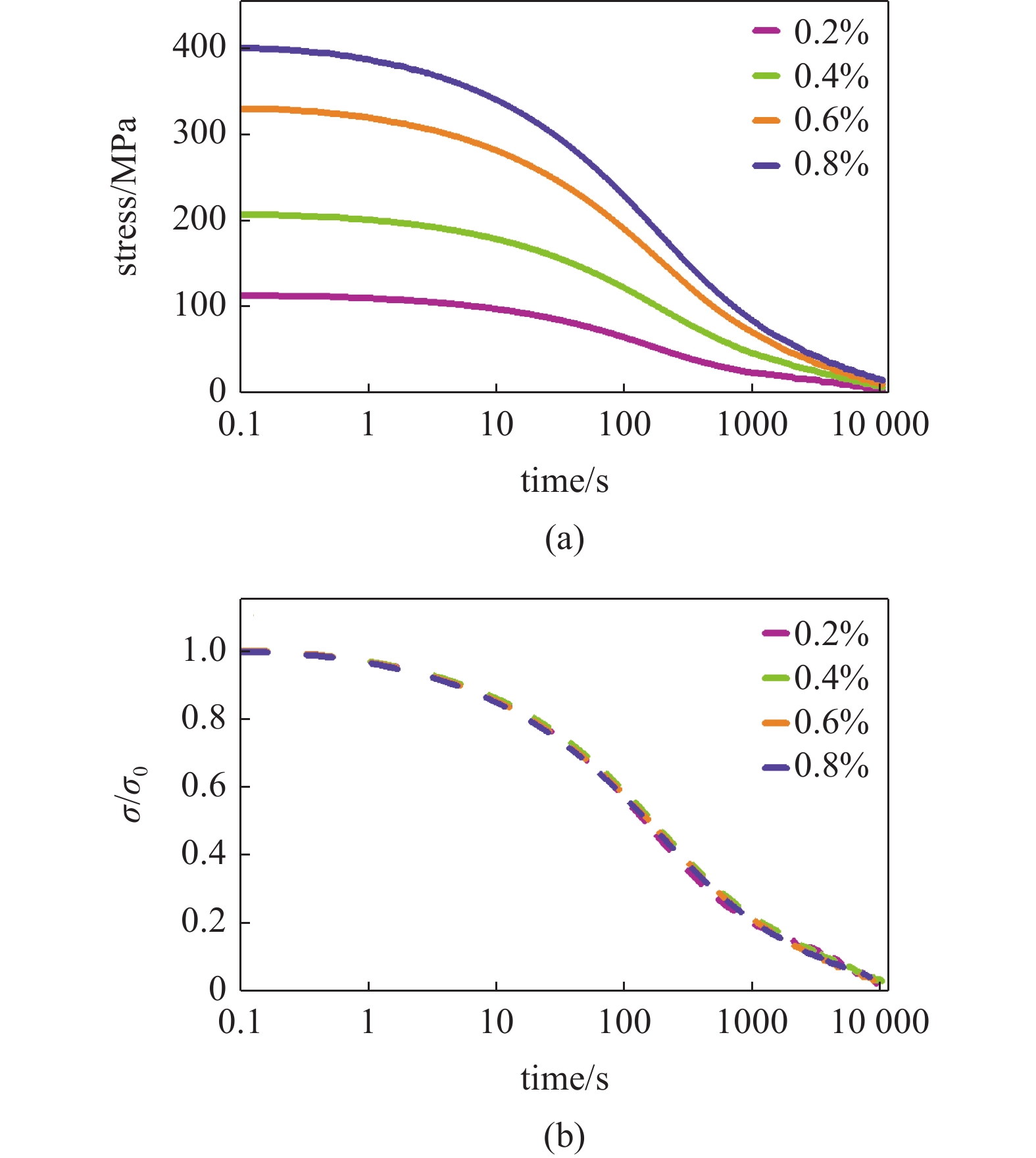
图2(a)为Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下加载应力随时间演化曲线(测试温度为620 K), 加载前保温120 min以使其结构状态相对稳定. 红色曲线为根据式(1)所得最小二乘拟合曲线. 可以发现非晶合金的应力松弛曲线与Debye弛豫公式所得曲线相差甚远. 这表明非晶合金弛豫位点特征时间的分布本质, 无法采用单一特征时间进行描述. 因此, 需要考虑多个特征时间的叠加, 式(1)可改写为[35]
![]()
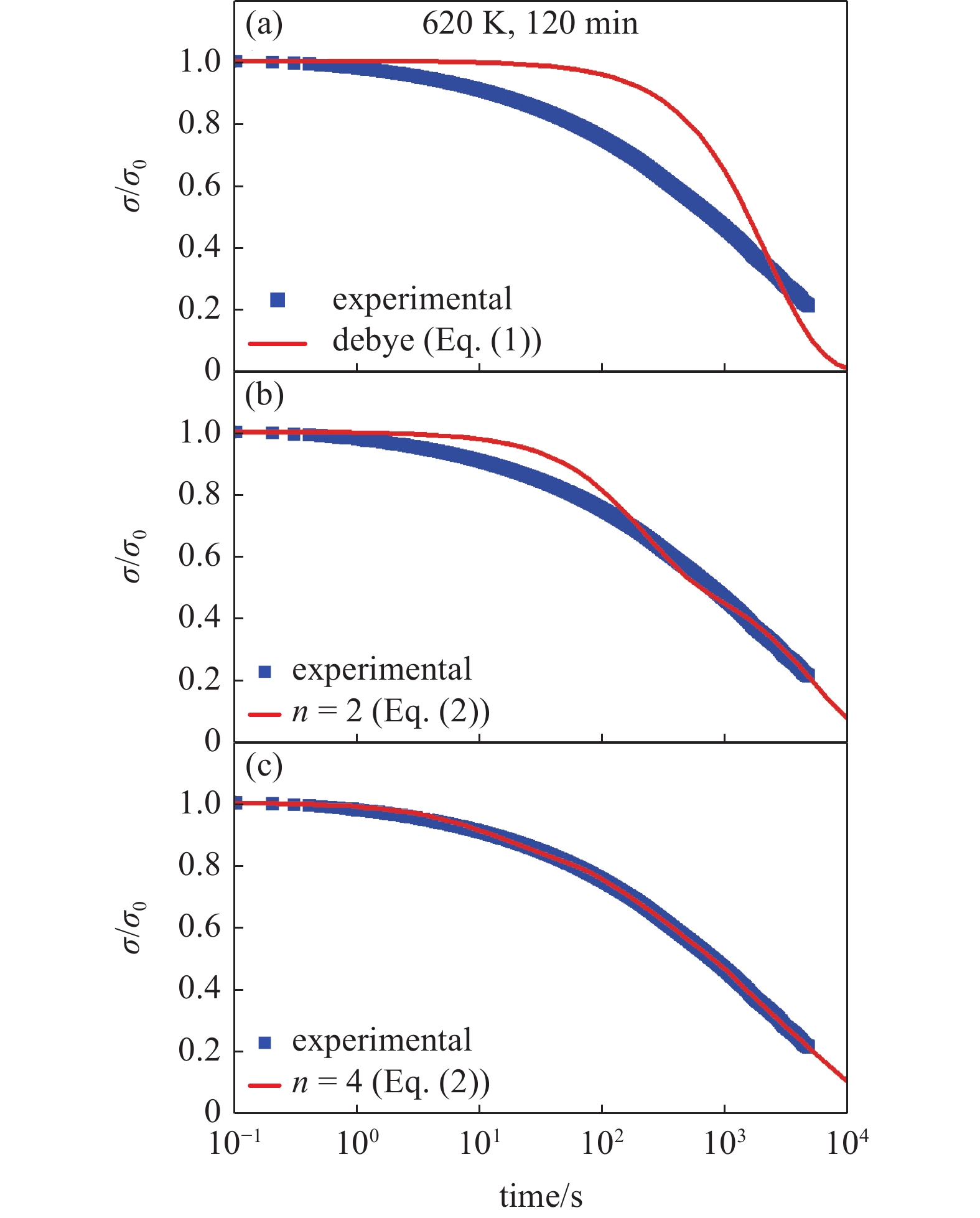
图 2 Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下的应力响应. 测试温度为620 K, 加载前保温120 min以使结构状态相对稳定. (a) Debye弛豫模型(式(1))拟合曲线; (b)和(c)分别为n = 2和n = 4情况下有限谱模型拟合曲线Figure 2. Stress response of Zr48(Cu5/6Ag1/6)44Al8 metallic glass at a given strain of 0.6%. The test temperature is 620 K, and the temperature is kept for 120 min before loading to make the structural state relatively stable. (a) Debye model fitting curve (Eq. (1)); (b) and (c) are the fitting curves of the finite spectrum approach when n = 2 and n = 4, respectively$$ \frac{{\sigma (t)}}{{\mathop \sigma \nolimits_0 }} = \sum\nolimits_{i = 1}^n {{A_i}\exp \left( { - \frac{t}{{{\tau _i}}}} \right)} $$ (2) 式中,
$ {A_i} $ 为$ {\tau _i} $ 所对应的弛豫强度, 且$ \displaystyle\sum\nolimits_{i = 1}^n {{A_i} = 1} $ . 考虑有限个数特征时间的方法可统称为有限谱法, 这在前期部分文献中已经被用于描述非晶态固体的应力松弛和蠕变等黏弹性行为, 通常人为给定3~5个可能特征时间并拟合获得其对应强度, 或直接拟合实验曲线以获得有限个特征时间及其对应强度[36]. 如图2(b)和图2(c)分别为n = 2和n = 4情况下根据式(2)的最小二乘拟合, 可知当n = 4时有限谱法与实验数据吻合较好.然而, 有限谱法的使用必须相当谨慎.一是由于非晶态固体的无序本质, 在宏观力学尺度考虑几个甚至数十个有限的离散特征时间的弛豫过程意义不大. 离散特征时间对应离散的能量等级, 这在量子力学所探究的微观尺度才有意义; 二是有限谱法所需参量随特征时间个数成倍增加, 例如n = 4时式(2)包含7个未知参量, 此时最小二乘拟合发散, 会导致解的不唯一性.
基于上述讨论与非晶态固体微观结构非均匀性的实验观察, 应当同时考虑特征时间的广泛连续分布, 此时应力松弛响应可以积分形式表示为
$$ \frac{{\sigma (t)}}{{\mathop \sigma \nolimits_0 }} = \int_0^\infty {g(\tau )} \exp \left( { - \frac{t}{\tau }} \right){\rm{d}}\tau $$ (3) 式中,
$ g\left(\tau \right) $ 代表特征时间在对数尺度上的Gauss形式连续谱, 可表示为$$ g(\tau ) = \frac{1}{{\sqrt {2{\text{π}} } s}}\exp \left[ { - \frac{{{{\left( {\ln \tau - \ln {\tau _m}} \right)}^2}}}{{{s^2}}}} \right] $$ (4) 式中,
${\tau _m}$ 为最可几特征时间;${s^2}$ 为方差, 与连续谱分布宽度相关.上式中正态分布的假设基于大量文献中非晶态固体活化能量谱和弹性常数实验测量的近似Gauss分布[21], 而激活能量谱分布可近似为特征时间的对数分布. 非晶合金在急速快冷过程中继承了其金属熔体微观尺度上的能量和密度涨落, 其内部存在大量纳米尺度上的“类固体”和“类液体”区域(图3(a)), 其不同区域的动力学特征时间可能相差几个数量级(图3(b)). 因此非晶合金在具有时(动力学特征)空(空间结构特征)非均匀性, 这与其原子扩散、弛豫行为和变形机制密切相关.
![]()
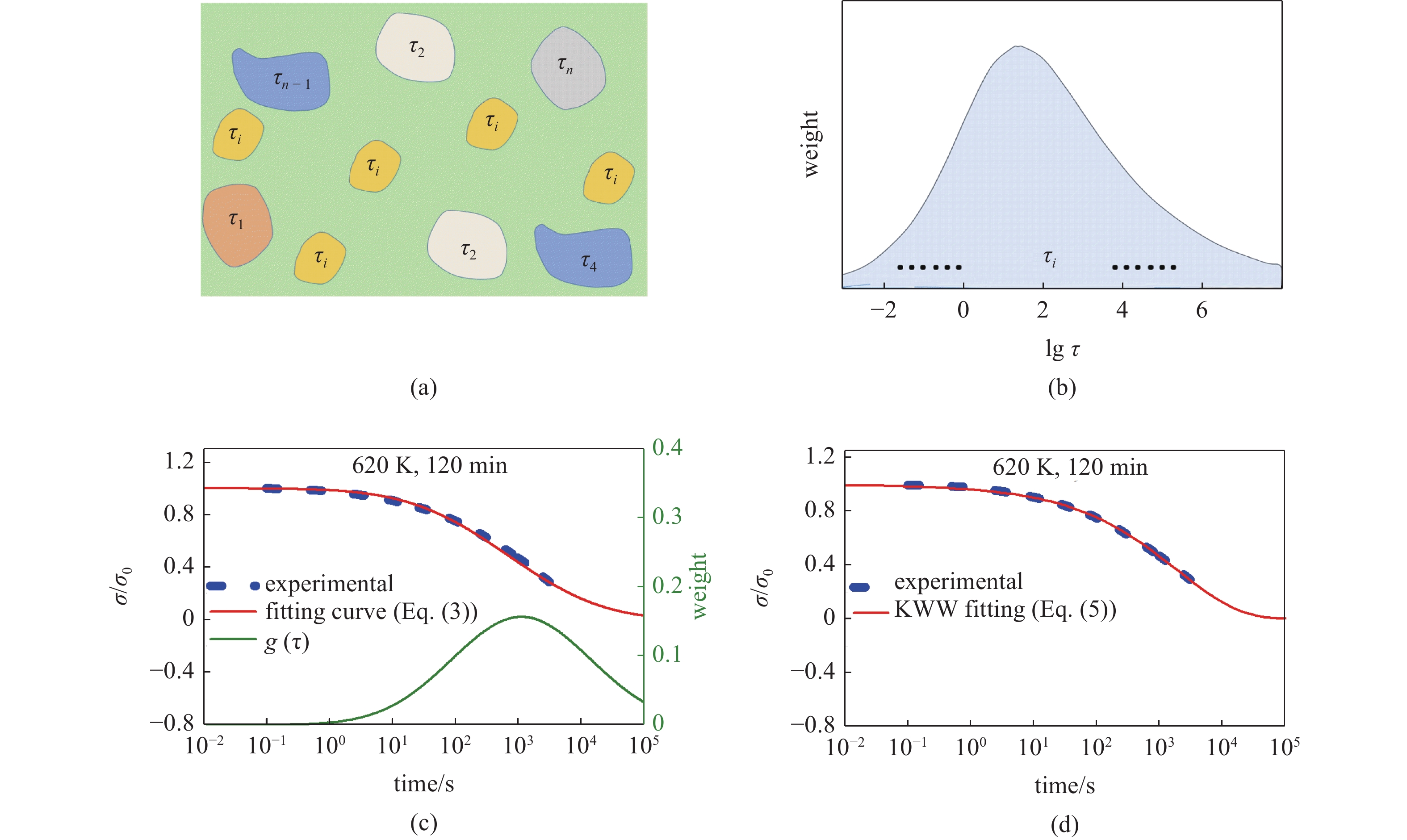
图 3 (a) 非晶合金微观结构非均匀性示意图; (b) 动力学特征时间分布; (c) Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下的应力响应. 红色曲线为式(3)计算曲线, 绿色曲线为特征时间Gauss形式连续谱; (d) 应力松弛实验曲线及KWW方程最小二乘拟合结果.Figure 3. (a) The schematic illustration of microstructural heterogeneity of MG. (b) Distribution of dynamic characteristic time. (c) The stress relaxation data at 620 K was calculated by Eq. (3), and the corresponding continuous$ \tau $ spectrum was obtained. (d) Comparison between theoretical calculations (lines) and experiments (symbols) for stress relaxation behavior图3(c)为Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变为0.6%条件下的典型应力松弛曲线, 测试温度为620 K, 加载前保温120 min以获得相对稳定结构状态. 红色曲线为采用连续谱方法(式(3))计算所得, 与实验结果相对吻合. 同时给出Gauss形式特征时间连续谱(绿色曲线), 其横跨多个数量级, 表明非晶合金局部变形单元特征时间广泛分布, 具有显著的动力学非均匀性, 这与非晶态无序固体本征结构非均匀性密切相关.
此外扩展指数(Kohlrausch-Williams-Watts, KWW)方程也可描述非晶态固体应力松弛行为[3]
$$ \dfrac{{\sigma (t)}}{{\mathop \sigma \nolimits_0 }} = \exp \left[ { - {{\left( {\frac{t}{\tau }} \right)}^\beta }} \right] $$ (5) 其中扩展指数
$0 < \beta < 1$ 用于衡量特征时间离散程度, 其值越大表明特征时间分布越窄. 当$ \;\beta $ 等于1时该方程退化为式(1)所示的指数形式. 如图3(d)所示为KWW方程(式(5))对应力松弛曲线的最小二乘拟合, 与实验结果吻合性较好. 事实上KWW方程中扩展指数$\; \beta $ 值在一定程度上等效于式(3)所考虑的特征时间连续谱分布, 两者唯一区别在于特征时间分布形式有微小差异. 由于式(4)中, 考虑了特征时间正态分布, 因而弛豫时间在对数尺度上的分布是对称的, 而式(5)中, 扩展指数$\; \beta $ 所体现的特征时间在分布对数尺度上是非对称的.2.3 应力松弛的宏观流变行为: 变形机制
在2.2节中非晶合金应力松弛行为的非指数特征表明了非晶态固体独特的微观结构非均匀性, 这种结构无序合金体系如何耗散外力、产生变形, 一直是凝聚态物理和固体力学领域的重要研究课题之一.
与整个玻璃体系的平均涨落相比, 部分位点处密度、焓和熵等参量变化更大, 能量状态更高, 在外加应力作用下必然优先产生原子重排, 耗散外力. 这一概念已在STZ理论和流变单元模型等非晶态固体经典模型中提及[32, 37], 那么非晶合金微观尺度纳米级微观区域的变形过程与宏观滞弹性、黏塑性变形究竟有何关联, 仍需进一步讨论.
图4为名义弹性区内, Zr48(Cu5/6Ag1/6)44Al8 非晶合金不同应变(0.2% ~ 0.4% ~ 0.6% ~ 0.8%)时典型应力松弛曲线, 测试温度为620 K. 可以发现给定应变越大, 初始应力
${\sigma _0}$ 越大, 在随后应力松弛过程中应力降也越明显. 非晶合金名义弹性区的应力松弛行为具有如下特点.(1) 应力最终松弛至0, 表明非晶合金变形中弹性和滞弹性分量随时间推移完全消失. 最近研究表明非晶态固体即使在室温下也表现一定滞弹性响应[38]. 从现象学角度看滞弹性与背应力效应相关, 这在剪切转变区(STZ)[39]、核壳模型[40]、流变单元模型[24]中均有所体现. 对于完全滞弹性响应, 由经典黏弹性理论(Kelvin模型)可知当应变完全固定时, 应力应立即松弛为某一确定值并在此后保持不变, 这种不完全松弛导致应力无法完全松弛到0. 此外完全滞弹性在外加载荷卸载后, 变形会回复初始值, 然而0应力表明即使在卸载后也无法产生可逆性回复应变.
(2) 名义弹性区, 不同应变处归一化应力松弛曲线重合(如图4(b)所示). 根据经典黏弹性理论(Maxwell模型)可知对于黏塑性流动, 其应力松弛应力随时间演化与初始应力无关. 该特征不仅应力松弛具有黏塑性流动本质, 亦证明2.2节提及的扩展指数方程(KWW方程)用于描述非晶合金应力松弛行为的合理性.
![]()
图 4 (a) Zr48(Cu5/6Ag1/6)44Al8 非晶合金不同应变(0.2% ~ 0.4% ~ 0.6% ~ 0.8%)典型应力松弛曲线. 测试温度为620 K, 加载前保温5 min; (b) 归一化应力松弛曲线${\sigma \mathord{\left/ {\vphantom {\sigma {{\sigma _0}}}} \right. } {{\sigma _0}}}$ Figure 4. (a) Typical stress relaxation curves at different given strain (0.2% ~ 0.4% ~ 0.6% ~ 0.8%). The test temperature is 620 K, and the temperature is kept for 5 min before loading. (b) Normalized stress relaxation curves${\sigma \mathord{\left/ {\vphantom {\sigma {{\sigma _0}}}} \right. } {{\sigma _0}}}$ 可见非晶合金应力松弛行为既表现为整体上的黏塑性流动本质, 又具有一定滞弹性可逆变形. 这表明非晶合金变形行为受到弹性、滞弹性和黏塑性三个分量共同控制, 在长时间应力松弛过程中弹性、滞弹性分量逐渐向黏塑性流动转变, 最终完全消失. 前期工作[13]已经提出非晶合金纳米级微区域的变形单元在外加应力下其内部局部原子重排激活后, 变形单元扩展, 此时变形单元边界原子仍保持其完整性以约束内部原子, 去除外加应力时使变形单元回复初始构型, 该过程为滞弹性本质. 在长时间应力作用下, 变形单元无法无限扩展, 这一方面是由于弹性边界能量有限性; 再者空间有限性导致发生邻近变形单元边界接触融合, 此时边界弹性能耗散, 发生不可逆黏塑性变形.
2.4 应力松弛的特征时间滞后行为: 老化动力学
非晶态固体的一个标志性特征是“遍历性破缺”,这是由于液体在急冷过程中原子运动急剧慢化, 在玻璃转变温度以下脱离热力学平衡态, 原子无法在特定实验时间内遍历探索所有构型, 此时固体结构仍处于高温状态所对应的结构状态[41]. 非平衡态非晶合金固体随时间推移向平衡方向迁移的过程称为结构弛豫, 也称为老化. 老化是非晶态固体的本质特征, 对于理解无序固体非平衡弛豫动力学和实现其大规模工程应用均至关重要.
如图5(a)所示, 老化导致非晶合金密度、焓和熵等结构和热力学参量的演化, 进而导致宏观力学与物理性能(强度、硬度、断裂韧性、比热等)随之变化[2, 32], 图中也给出了原子尺度缺陷位点在老化过程中湮灭示意图. 在2.3节提及变形优先在能量状态高的缺陷位点处发生, 在外加应力下有限发生原子重排以耗散外力. 部分缺陷位点在老化过程中消失因而无法在变形过程中形成变形单元. 图5(b)为Zr48(Cu5/6Ag1/6)44Al8 非晶合金在620 K退火时归一化储能模量和损耗模量随温度演化曲线, 可知非晶态固体老化伴随着物理性质的较大变化.
![]()
图 5 老化效应. (a)老化导致非晶态固体体积(V)、焓(H)、熵(S)等参量降低和缺陷位点湮灭; (b)归一化储能模量$E'/{E_u}$ 和损耗模量$E''/{E_u}$ 随退火时间演化.${E_u}$ 为室温未弛豫储能模量; (c)不同退火时间后应力松弛曲线, 测试温度为620 KFigure 5. Aging effect. (a) Evolution of volume (enthalpy, entropy) and annihilation of defect sites caused by aging. (b) Evolution of normalized storage modulus$E'/{E_u}$ and loss modulus$E''/{E_u}$ during annealing;${E_u}$ is unrelaxed storage modulus at room temperature. (c) Stress relaxation curves after annealing for different time从能量角度出发, 通常认为每个粒子均处于其与邻近原子构成的势阱中[41]. 老化对应于原子在不同势阱深度的热驱动跃迁, 随着老化时间的增加逐渐趋于低能状态, 因而老化必然增加原子重排的激活能垒, 导致跃迁时间增加. 而原子重排与非晶态固体宏观变形密切相关, 换言之老化增加了非晶态非弹性变形的激活能垒. 正如图5(c)所示, 随测试前退火时间增加, 应力松弛曲线向右偏移, 表明变形单元激活时间增加.
非晶态固体无时无刻不在处于老化过程中, 且其对微观结构和宏观性能均有显著影响, 前文在应力松弛过程中仅考虑单一的扩展指数
$ \;\beta $ 与特征时间$ \tau $ , 显然与实际不符. 图6为Zr48(Cu5/6 Ag1/6)44Al8 非晶合金在给定应变0.6%条件下应力松弛演化曲线, 测试温度为620 K. 红色曲线为采用扩展指数方程的最小二乘拟合, 与实验曲线差异较大. 需要注意, 在图3(d)采用扩展指数方程描述应力松弛曲线吻合相当好, 与图6并不矛盾. 图3(d)在实验开始前保温120 min, 且松弛时间仅有60 min, 因而在松弛过程中受老化效应的影响小. 而图6中加载前仅保温5 min, 且松弛时间长达180 min, 因而在松弛过程中受老化影响相当大, 无法采用固定$ \tau $ 和$\; \beta $ 的扩展指数方程拟合, 而必须考虑松弛过程中老化导致的两个参数的演化.![]()
图 6 Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下应力松弛曲线, 测试温度为620 K. 红色曲线为采用扩展指数方程的最小二乘拟合Figure 6. Stress relaxation curve at given strain of 0.6% (experimental temperature is 620 K). The red solid curve is the least square fitting using the KWW equationPalmer等[42]提出分级约束原子弛豫动力学理论,认为无序体系中由于其近邻结构单元束缚, 各结构单元包含从快到慢多个自由度等级, 最快的自由度可能涉及单原子运动. 其他原子或原子群只有在几个较快原子恰好以正确方式移动留下一个空穴或削弱相关成键作用力时, 才能发生移动. 更快的自由度依次约束较慢自由度, 进而产生广泛弛豫时间的分布与演化. 对比非晶合金老化过程分析, 考虑系统约束程度的变化似乎同样合理. Perez等[43]基于分级约束原子弛豫动力学理论, 推导了原子协同运动(
${\tau _{\max }}$ )和结构单元基本运动(${\tau _0}$ )两类原子运动之间有如下关系${\tau _{\max }} = {\left( {{{{\tau _0}} \mathord{\left/ {\vphantom {{{\tau _0}} {{t_0}}}} \right. } {{t_0}}}} \right)^{\chi} }$ . 相关工作[13]已经指出, 上述两类原子运动特征时间可用于变形单元的激活和融合, 以使非晶合金的非弹性变形行为合理化. 公式中关联因子$\chi $ 可视作结构序参量, 其与体系缺陷浓度正相关. 在玻璃转变温度以下, 通常认为玻璃体系结构被冻结, 此时关联因子$\chi $ 为常数. 老化会导致玻璃体系关联因子$\chi $ 值降低. 根据前期工作, 关联因子$\chi $ 似乎与广泛使用的KWW方程中扩展指数$\beta $ 概念类似, 两者均可作为无序固体结构非均匀性程度强弱的序参量[41].基于上述分析, 可以考虑应力松弛过程中老化效应造成的扩展指数
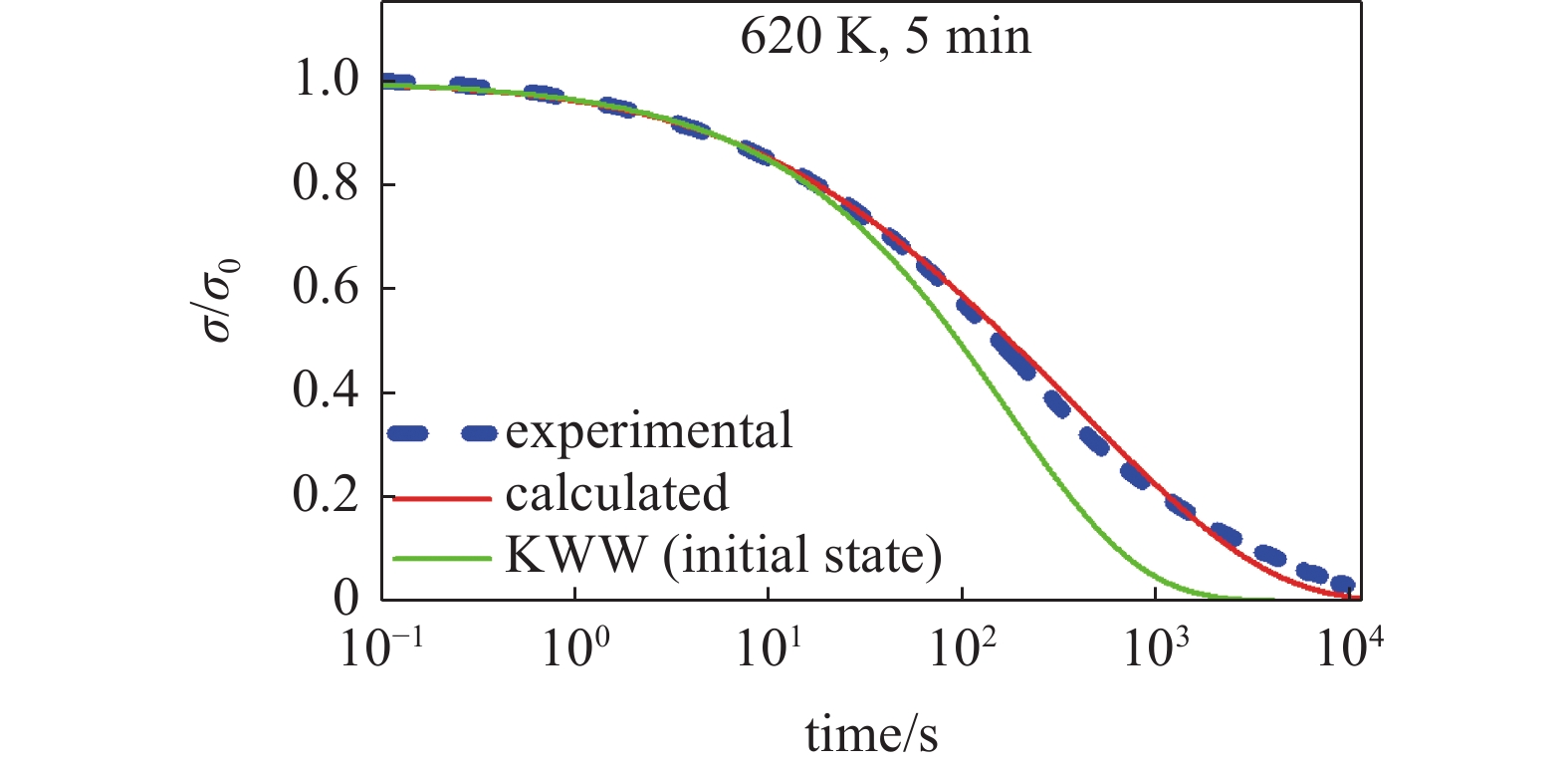
$\beta $ 以扩展指数方程形式降低, 并考虑$\beta $ 与特征时间$\tau $ 之间有关系$$ \tau (t) = {\left( {\frac{{{\tau _0}}}{{{t_0}}}} \right)^{\beta (t)}} $$ (6) 本文假设应力松弛时间在10 s内老化效应尚未对结构状态有明显改变, 并计算获得非晶合金初始态条件下特征时间
$\tau (0)$ 以及扩展指数$\;\beta (0)$ 分别为174.11 s和0.64, 如图7中绿色曲线所示. 红色实线为考虑$\;\beta $ 与$\tau $ 随应力松弛时间变化后的KWW方程对应力松弛行为计算结果, 与实验结果吻合较好.![]()
图 7 Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下应力松弛演化曲线, 测试温度为620 K, 加载前保温 5 min. 红色曲线为修正KWW方程计算结果. 绿色曲线为根据初始态参量计算曲线Figure 7. Stress relaxation curve at given strain of 0.6 %. The test temperature is 620 K, and the temperature is kept for 5 min before loading. The red solid curve is calculated by the modified KWW equation. The green solid curve is the calculated curve based on the initial state此外, 我们也给出应力松弛特征时间
$ \tau $ 和扩展指数$\;\beta $ 随应力松弛时间的演化(如图8所示). 应力松弛特征时间$ \tau $ 随时间逐渐增加, 扩展指数$\;\beta $ 随时间逐渐减小, 表明应力松弛过程中老化导致结构状态逐渐趋于稳定, 变形单元边界融合的最几特征时间相比于初始状态大大增加. 同时扩展指数$\;\beta $ 的减小, 表明变形单元特征时间的分布明显变宽. 需要注意, 此处KWW方程中的特征时间$ \tau $ , 其更具体含义为最可几弛豫时间, 其在系统众多弛豫时间中权重最大.![]()
图 8 Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下特征时间$ \tau \left(t\right) $ 和扩展指数$\; \beta \left(t\right) $ 随应力松弛时间的演化Figure 8. Evolution of characteristic time$ \tau \left(t\right) $ and stretched exponent$ \beta \left(t\right) $ caused by aging during stress relaxation process3. 结论
本文选用玻璃形成能力强、热稳定好的Zr48(Cu5/6Ag1/6)44Al8 非晶合金为模型体系, 系统研究了其应力松弛行为的几个重要特征, 并分析了其潜在结构起源与物理机制, 主要结论如下.
(1) 非晶合金应力松弛行为具有非指数特征, 无法采用单一特征时间的Debye弛豫模型进行描述. 采用有限个数特征时间的有限谱模型无法准确描述非晶固体应力松弛行为中特征时间分布本质. 真实非晶态固体系统微观结构为非均匀, 存在纳米尺度能量起伏, 因此应力松弛行为的准确描述应考虑特征时间的连续分布, 或采用以扩展指数表示分布特征的KWW方程.
(2)在名义弹性区不同应变处归一化应力松弛曲线完全重合, 这与初始应力无关, 且所有实验曲线均松弛至零应力. 表明非晶合金应力松弛行为虽然在一定时间尺度上具有滞弹性特征, 但在整体上由黏塑性流动控制, 在长时间应力松弛过程中弹性、滞弹性分量逐渐向黏塑性流动转变, 最终完全消失. 其纳米级微区域的变形单元在外加应力下其内部局部原子重排激活后, 变形单元扩展, 此时变形单元边界原子仍保持其完整性以约束内部原子, 去除外加应力时使变形单元回复初始构型, 该过程为滞弹性本质. 在长时间应力作用下, 变形单元无法无限扩展, 这一方面是由于弹性边界能量有限性; 再者空间有限性导致发生邻近变形单元边界接触融合. 此时边界弹性能耗散, 发生不可逆黏塑性变形.
(3)长时间应力松弛测试中KWW方程无法描述应力松弛行为, 这是由于老化效应. 非晶态固体无时无刻不在处于老化过程中, 且其对微观结构和宏观性能均有显著影响, 因此需考虑其结构参量演化. 本文基于Palmer等[42]提出的分级约束原子弛豫动力学理论, 首次考虑了经典KWW方程中特征时间
$ \tau $ 和扩展指数$\beta $ 在应力松弛过程中的耦合演化, 探究了应力松弛过程结构状态的时间依赖性. 其中应力松弛特征时间$ \tau $ 随时间逐渐增加, 扩展指数$\beta $ 随时间逐渐减小, 表明应力松弛过程中老化导致结构状态逐渐趋于稳定, 变形单元边界融合的特征时间相比于初始状态大大增加. 同时扩展指数$\beta $ 减小, 表明变形单元特征时间的分布明显变宽.因此, 本文不仅基于非晶合金宏观变形行为探究了其潜在的微观结构非均匀性特征, 而且我们详细揭示了非晶态固体纳米尺度结构在外加应力作用下激活为变形单元, 并扩展、融合以容纳变形的过程. 最重要的是, 我们同时考虑了老化效应引起的结构参量演化以及进一步导致的变形行为改变, 这为理解非晶合金这一非平衡固体变形行为所伴随的微观结构演化提供了新思路和新的切入口.
-
![]()
图 1 Zr48(Cu5/6Ag1/6)44Al8 非晶合金DSC曲线, 升温速率为20 K/min. 插图为X射线衍射图谱
Figure 1. DSC curve of Zr48(Cu5/6Ag1/6)44Al8 metallic glass with a heating rate of 20 K/min. Inset shows the XRD pattern of the model alloy
![]()
图 2 Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下的应力响应. 测试温度为620 K, 加载前保温120 min以使结构状态相对稳定. (a) Debye弛豫模型(式(1))拟合曲线; (b)和(c)分别为n = 2和n = 4情况下有限谱模型拟合曲线
Figure 2. Stress response of Zr48(Cu5/6Ag1/6)44Al8 metallic glass at a given strain of 0.6%. The test temperature is 620 K, and the temperature is kept for 120 min before loading to make the structural state relatively stable. (a) Debye model fitting curve (Eq. (1)); (b) and (c) are the fitting curves of the finite spectrum approach when n = 2 and n = 4, respectively
![]()
图 3 (a) 非晶合金微观结构非均匀性示意图; (b) 动力学特征时间分布; (c) Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下的应力响应. 红色曲线为式(3)计算曲线, 绿色曲线为特征时间Gauss形式连续谱; (d) 应力松弛实验曲线及KWW方程最小二乘拟合结果.
Figure 3. (a) The schematic illustration of microstructural heterogeneity of MG. (b) Distribution of dynamic characteristic time. (c) The stress relaxation data at 620 K was calculated by Eq. (3), and the corresponding continuous
$ \tau $ spectrum was obtained. (d) Comparison between theoretical calculations (lines) and experiments (symbols) for stress relaxation behavior![]()
图 4 (a) Zr48(Cu5/6Ag1/6)44Al8 非晶合金不同应变(0.2% ~ 0.4% ~ 0.6% ~ 0.8%)典型应力松弛曲线. 测试温度为620 K, 加载前保温5 min; (b) 归一化应力松弛曲线
${\sigma \mathord{\left/ {\vphantom {\sigma {{\sigma _0}}}} \right. } {{\sigma _0}}}$ Figure 4. (a) Typical stress relaxation curves at different given strain (0.2% ~ 0.4% ~ 0.6% ~ 0.8%). The test temperature is 620 K, and the temperature is kept for 5 min before loading. (b) Normalized stress relaxation curves
${\sigma \mathord{\left/ {\vphantom {\sigma {{\sigma _0}}}} \right. } {{\sigma _0}}}$ ![]()
图 5 老化效应. (a)老化导致非晶态固体体积(V)、焓(H)、熵(S)等参量降低和缺陷位点湮灭; (b)归一化储能模量
$E'/{E_u}$ 和损耗模量$E''/{E_u}$ 随退火时间演化.${E_u}$ 为室温未弛豫储能模量; (c)不同退火时间后应力松弛曲线, 测试温度为620 KFigure 5. Aging effect. (a) Evolution of volume (enthalpy, entropy) and annihilation of defect sites caused by aging. (b) Evolution of normalized storage modulus
$E'/{E_u}$ and loss modulus$E''/{E_u}$ during annealing;${E_u}$ is unrelaxed storage modulus at room temperature. (c) Stress relaxation curves after annealing for different time![]()
图 6 Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下应力松弛曲线, 测试温度为620 K. 红色曲线为采用扩展指数方程的最小二乘拟合
Figure 6. Stress relaxation curve at given strain of 0.6% (experimental temperature is 620 K). The red solid curve is the least square fitting using the KWW equation
![]()
图 7 Zr48(Cu5/6Ag1/6)44Al8 非晶合金在给定应变0.6%条件下应力松弛演化曲线, 测试温度为620 K, 加载前保温 5 min. 红色曲线为修正KWW方程计算结果. 绿色曲线为根据初始态参量计算曲线
Figure 7. Stress relaxation curve at given strain of 0.6 %. The test temperature is 620 K, and the temperature is kept for 5 min before loading. The red solid curve is calculated by the modified KWW equation. The green solid curve is the calculated curve based on the initial state
-
[1] 王云江, 魏丹, 韩懂等. 非晶态固体的结构可以决定性能吗? 力学学报, 2020, 52(2): 1-15 (Wang Yunjiang, Wei Dan, Han Dong, et al. Does structure determine property in amorphous solids? Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(2): 1-15 (in Chinese) [2] 乔吉超, 张浪渟, 童钰等. 基于微观结构非均匀性的非晶合金力学行为. 力学进展, 2022, 52(1): 117-152 (Qiao Jichao, Zhang Langting, Tong Yu, et al. Mechancial properties of amorphous alloys: In the framework of the microstructure heterogeneity. Advances in Mechanics, 2022, 52(1): 117-152 (in Chinese) doi: 10.6052/1000-0992-21-038 [3] Wang WH. The elastic properties, elastic models and elastic perspectives of metallic glasses. Progress in Materials Science, 2012, 57(3): 487-656 doi: 10.1016/j.pmatsci.2011.07.001
[4] Inoue A, Takeuchi A. Recent development and application products of bulk glassy alloys. Acta Materialia, 2011, 59(6): 2243-2267 doi: 10.1016/j.actamat.2010.11.027
[5] Khmich A, Hassani A, Sbiaai K, et al. Tuning of mechanical properties of Tantalum-based metallic glasses. International Journal of Mechanical Sciences, 2021, 204: 106546
[6] Sun BA, Song KK, Pauly S, et al. Transformation-mediated plasticity in CuZr based metallic glass composites: A quantitative mechanistic understanding. International Journal of Plasticity, 2016, 85: 34-51 doi: 10.1016/j.ijplas.2016.06.004
[7] Zhou HF, Qu SX, Yang W. An atomistic investigation of structural evolution in metallic glass matrix composites. International Journal of Plasticity, 2013, 44: 147-160 doi: 10.1016/j.ijplas.2013.01.002
[8] Jiang MQ, Ling Z, Meng JX, et al. Energy dissipation in fracture of bulk metallic glasses via inherent competition between local softening and quasi-cleavage. Philosophical Magazine, 2008, 88(3): 407-426 doi: 10.1080/14786430701864753
[9] Jiang MQ, Wilde G, Dai LH. Origin of stress overshoot in amorphous solids. Mechanics of Materials, 2015, 81: 72-83 doi: 10.1016/j.mechmat.2014.10.002
[10] Argon A. Plastic deformation in metallic glasses. Acta Metallurgica, 1979, 27(1): 47-58 doi: 10.1016/0001-6160(79)90055-5
[11] Cheng YT, Hao Q, Pelletier JM, et al. Modelling and physical analysis of the high-temperature rheological behavior of a metallic glass. International Journal of Plasticity, 2021, 146: 103107
[12] 汪卫华. 非晶态物质的本质和特性. 物理学进展, 2013, 33(5): 4-178 (Wang Weihua. The nature and properties of amorphous mater. Progress in Physics, 2013, 33(5): 4-178 (in Chinese) [13] Hao Q, Lyu GJ, Pineda E, et al. A hierarchically correlated flow defect model for metallic glass: Universal understanding of stress relaxation and creep. International Journal of Plasticity, 2022, 154: 103288 doi: 10.1016/j.ijplas.2022.103288
[14] Qiao JC, Wang Q, Pelletier JM, et al. Structural heterogeneities and mechanical behavior of amorphous alloys. Progress in Materials Science, 2019, 104: 250-329 doi: 10.1016/j.pmatsci.2019.04.005
[15] Liu YH, Wang D, Nakajima K, et al. Characterization of nanoscale mechanical heterogeneity in a metallic glass by dynamic force microscopy. Physical Review Letters, 2011, 106(12): 125504 doi: 10.1103/PhysRevLett.106.125504
[16] Yang Y, Zhou J, Zhu F, et al. Determining the three-dimensional atomic structure of an amorphous solid. Nature, 2021, 592(7852): 60-64 doi: 10.1038/s41586-021-03354-0
[17] Nomoto K, Ceguerra AV, Gammer C, et al. Medium-range order dictates local hardness in bulk metallic glasses. Materials Today, 2021, 44: 48-57 doi: 10.1016/j.mattod.2020.10.032
[18] Zhu F, Song SX, Reddy KM, et al. Spatial heterogeneity as the structure feature for structure–property relationship of metallic glasses. Nature Communications, 2018, 9(1): 3965 doi: 10.1038/s41467-018-06476-8
[19] Cheng YQ, Ma E. Atomic-level structure and structure-property relationship in metallic glasses. Progress in Materials Science, 2011, 56(4): 379-473 doi: 10.1016/j.pmatsci.2010.12.002
[20] Tang CG, Harrowell P. Anomalously slow crystal growth of the glass-forming alloy CuZr. Nature Materials, 2013, 12(6): 507-511 doi: 10.1038/nmat3631
[21] Wagner H, Bedorf D, Küchemann S, et al. Local elastic properties of a metallic glass. Nature Materials, 2011, 10(6): 439-442 doi: 10.1038/nmat3024
[22] Fujita T, Guan PF, Sheng HW, et al. Coupling between chemical and dynamic heterogeneities in a multicomponent bulk metallic glass. Physical Review B, 2010, 81(14): 140204 doi: 10.1103/PhysRevB.81.140204
[23] Zhu ZG, Wen P, Wang DP, et al. Characterization of flow units in metallic glass through structural relaxations. Journal of Applied Physics, 2013, 114(8): 083512 doi: 10.1063/1.4819484
[24] Wang Z, Wang WH. Flow units as dynamic defects in metallic glassy materials. National Science Review, 2019, 6(2): 304-323 doi: 10.1093/nsr/nwy084
[25] Turnbull D, Cohen MH. On the free-volume model of the liquid-glass transition. The Journal of Chemical Physics, 1970, 52(6): 3038-3041 doi: 10.1063/1.1673434
[26] Perez J. Quasi-punctual defects in vitreous solids and liquid-glass transition. Solid State Ionics, 1990, 39(1): 69-79
[27] Cheng YT, Hao Q, Qiao JC, et al. Effect of minor addition on dynamic mechanical relaxation in ZrCu-based metallic glasses. Journal of Non-Crystalline Solids, 2021, 553: 120496 doi: 10.1016/j.jnoncrysol.2020.120496
[28] Spaepen F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metallurgica, 1977, 25(4): 407-415 doi: 10.1016/0001-6160(77)90232-2
[29] Falk ML, Langer JS. Dynamics of viscoplastic deformation in amorphous solids. Physical Review E, 1998, 57(6): 7192-7205 doi: 10.1103/PhysRevE.57.7192
[30] Yang Y, Zeng JF, Volland A, et al. Fractal growth of the dense-packing phase in annealed metallic glass imaged by high-resolution atomic force microscopy. Acta Materialia, 2012, 60(13-14): 5260-5272 doi: 10.1016/j.actamat.2012.06.025
[31] Ke HB, Zeng JF, Liu C T, et al. Structure Heterogeneity in Metallic Glass: Modeling and Experiment. Journal of Materials Science and Technology, 2014, 30(6): 560-565 doi: 10.1016/j.jmst.2013.11.014
[32] Wang WH. Dynamic relaxations and relaxation-property relationships in metallic glasses. Progress in Materials Science, 2019, 106: 100561 doi: 10.1016/j.pmatsci.2019.03.006
[33] Hao Q, Qiao JC, Goncharova EV, et al. Thermal effects and evolution of the defect concentration based on shear modulus relaxation data in a Zr-based metallic glass. Chinese Physics B, 2020, 29(8): 086402 doi: 10.1088/1674-1056/ab969c
[34] Debye P. Polar Molecules. New York: Chemical Catalog Company, 1929
[35] Jiao W, Wen P, Peng HL, et al. Evolution of structural and dynamic heterogeneities and activation energy distribution of deformation units in metallic glass. Applied Physics Letters, 2013, 102(10): 101903 doi: 10.1063/1.4795522
[36] Taub A, Spaepen F. Ideal elastic, anelastic and viscoelastic deformation of a metallic glass. Journal of Materials Science, 1981, 16(11): 3087-3092 doi: 10.1007/BF00540316
[37] Schuh CA, Hufnagel TC, Ramamurty U. Mechanical behavior of amorphous alloys. Acta Materialia, 2007, 55(12): 4067-4109 doi: 10.1016/j.actamat.2007.01.052
[38] Ye JC, Lu J, Liu CT, et al. Atomistic free-volume zones and inelastic deformation of metallic glasses. Nature Materials, 2010, 9(8): 619-623 doi: 10.1038/nmat2802
[39] Atzmon M, Ju JD. Microscopic description of flow defects and relaxation in metallic glasses. Physical Review E, 2014, 90(4): 042313 doi: 10.1103/PhysRevE.90.042313
[40] Liu ZY, Yang Y. A mean-field model for anelastic deformation in metallic-glasses. Intermetallics, 2012, 26: 86-90 doi: 10.1016/j.intermet.2012.03.052
[41] Casalini R, Roland CM. Aging of the secondary relaxation to probe structural relaxation in the glassy state. Physical Review Letters, 2009, 102(3): 035701 doi: 10.1103/PhysRevLett.102.035701
[42] Palmer RG, Stein DL, Abrahams E, et al. Models of hierarchically constrained dynamics for glassy relaxation. Physical Review Letters, 1984, 53(10): 958-961 doi: 10.1103/PhysRevLett.53.958
[43] Perez J. Physics and Mechanics of Amorphous Polymers. CRC Press, 1998
-
期刊类型引用(2)
1. 张婧祺，郝奇，吕国建，熊必金，乔吉超. 基于微观结构非均匀性理解非晶态聚苯乙烯的应力松弛行为. 物理学报. 2024(03): 242-249 . 
百度学术
2. 朱凡，邢光辉，Jean-Marc Pelletier，乔吉超. Hf元素添加对Cu Zr基非晶合金动态弛豫的影响. 力学学报. 2024(08): 2282-2293 . 本站查看
其他类型引用(1)
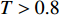
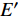
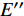
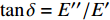
下载:
计量
- 文章访问数: 927
- HTML全文浏览量: 273
- PDF下载量: 168
- 被引次数: 3
