THE EFFECT OF IMPORTANT FACTORS ON THE GROWTH OF LITHIUM DENDRITES IN SOLID ELECTROLYTE WAS SIMULATED BASED ON PHASE FIELD THEORY
-
摘要: 锂枝晶的生长是固态电池安全性面临的重要挑战之一. 为了深入探讨锂枝晶的形成机制, 建立了电化学-力学耦合的相场模型, 以模拟重要因素对固态电解质中锂枝晶生长的影响. 该研究模拟了锂离子浓度场、电势场以及应力场的动态分布, 揭示了各向异性强度、反应常数、外界压力、环境温度以及初始成核形状等重要因素对锂枝晶生长形貌的影响规律, 并与针状和苔藓状枝晶的形态特征进行了对比分析. 结果表明: 降低各向异性强度和反应常数能在一定程度上抑制锂枝晶的生长; 增大外压和提高环境温度均能有效抑制锂枝晶的生长; 锂枝晶的初始成核形状会显著影响其分支方向. 对比3种不同形态的锂枝晶可知, 针状枝晶分支较少, 且应力主要集中在枝晶根部; 而苔藓状枝晶由于具备更高的空间生长自由度, 其分支结构更大, 在生长过程中会形成更高的内部应力水平; 树枝状枝晶则介于针状和苔藓状枝晶之间, 分支与应力分布较均匀. 本研究对优化固态电池的设计及提升其安全性具有重要意义.Abstract: The growth of lithium dendrites is one of the important challenges for the safety of solid-state batteries. In order to further investigate the formation mechanism of lithium dendrites, a phase field model of electrochemic-mechanical coupling was established to simulate the influence of important factors on the growth of lithium dendrites in solid electrolyte. In this study, the dynamic distribution of lithium ion concentration field, electric potential field and stress field was simulated, and the influence of anisotropy intensity, reaction constant, external pressure, ambient temperature and initial nucleation shape on the growth morphology of lithium dendrites were revealed, and the morphological characteristics of needle and moss dendrites were compared. The results show that reducing the anisotropy intensity and reaction constant can inhibit the growth of lithium dendrites to a certain extent. The growth of lithium dendrites can be effectively inhibited by increasing external pressure and ambient temperature. The initial nucleation shape of lithium by in creasing external pressure and ambient temperature. The initial nucleation shape of lithium dendrit- es can significantly affect their branching direction. The comparison of the three different forms of lithium dendrites shows that the acicular dendrites have fewer branches, and the stress is mainly concentrated in the dendrite root. Mossy dendrites have larger branch structure due to their higher spatial freedom of growth and higher internal stress level during growth. Dendritic dendrites are intermediate between acicular dendrites and moss dendrites, with uniform distribution of branches and stresses. This study is of great significance for optimizing the design of solid-state batteries and improving their safety.
-
Keywords:
- phase-field theory /
- solid electrolyte /
- lithium dendrite /
- stress
-
引 言
锂离子电池凭借循环寿命长、能量密度高等优势, 在家用电器、电动工具和医疗设备等众多领域中获得了广泛的应用[1]. 但随着电动汽车、航空航天和储能系统的快速发展, 人们对电池的能量密度、使用寿命和安全性等提出了更高的要求[2]. 在此背景下, 传统的液态锂离子电池已逐渐无法满足这些需求. 为了寻求更好的替代方案, 固态锂离子电池受到了越来越多的关注.
固态锂离子电池与传统液态锂离子电池的一个明显区别是电解质为高稳定性的固态电解质[3]. 首先, 固态锂离子电池具有不可燃、耐高温等特性, 安全性高. 其次, 固态电池一方面可以搭配更高能量密度的正负极材料, 另一方面因取消了电解液和隔膜, 结构紧凑、体积小, 故能量密度获得显著提高. 此外, 固态电解质的高稳定性可减少电池在充放电过程中的副反应, 从而可显著延长电池的使用寿命. 虽然固态电池具有显著的优势, 但在实际应用中仍需克服众多挑战, 比如在充放电过程中会有锂枝晶的形成[4], 锂枝晶的生长一方面可能会导致固态电解质的损坏, 增加电池的内阻, 降低电池的性能和循环寿命, 甚至刺穿固态电解质, 引发电池短路和热失控等严重的安全问题[5-7]. 另一方面锂枝晶的生长会导致锂离子在电极表面沉积不均匀, 形成“死锂”, 从而降低了电池的实际可用容量. 因此, 对锂枝晶生长的研究已经成为固态电池安全领域的重要课题[8-9].
相场法作为一种先进的数值模拟技术[10-12], 在锂电池微观结构演化预测领域展现出显著优势. 因其能够实时追踪锂金属-电解质界面的动态演化过程, 已成为研究锂枝晶生长动力学的重要工具[13]. 多年来, 研究者们已经利用各种相场模型模拟了枝晶生长的动态变化. 例如, Chen等[14]提出了一个热力学一致的非线性相场动力学模型. 重点研究了充电过程中施加电压和初始电极形态对树枝状形貌的影响. 分析得知, 较大的外加电压或界面处的平坦突起有助于枝晶的侧枝生长, 甚至促进不稳定的尖端分裂. Chen等[15]基于相场理论研究了固态电解质中锂枝晶渗透的机理及其抑制策略. 结果表明, 高的应力强度因子是由于锂中的高体积应力引起的, 固态电解质的高刚度并不抑制枝晶的穿透. Zhang等[16]基于非线性相场模型研究了外加电压、形核间距等因素对锂枝晶生长的影响. Zhang等[17]考虑将弹性能纳入吉布斯自由能来揭示应力在锂枝晶中的作用. Han等[18]利用相场模型研究了循环过程中的枝晶演化. 结果表明, 由于电势梯度的增加, 枝晶在恒电位条件下生长得更高更快. Hong等[19]借助一个完全热耦合的电沉积模型, 发现依赖于电化学反应势垒和离子扩散势垒, 自加热可以加速或减慢枝晶的形成. 这些研究存在一定的片面性.
近年来, 相场模型在锂枝晶生长机制研究中的应用呈现多维度发展趋势, 研究重点聚焦于揭示重要物化参数对枝晶演化的作用规律. Yurkiv等[20]提出了电化学-机械相场模型, 首次量化了表面能对枝晶形貌的调控机理. 研究表明充电速率与界面锂离子扩散能力的协同效应对固液界面稳定性具有决定性影响. 在此基础上, Jiang等[21]引入相场变量和损伤变量, 提出了力-电化学耦合相场模型, 揭示了电解质力学特性与枝晶裂纹扩展行为的非线性关联特征. Shen等[22]通过力-电化学相场模型揭示了外界压力对锂枝晶生长的抑制规律, 建立了压力参数与枝晶形貌演变的定量关系. Zhang等[23]建立了一个基于应力依赖过电位的相场模型来描述全固态电池中锂枝晶的生长. 与此同时, Ren等[24]聚焦固体复合电解质的微观结构设计, 发现引入一维纳米纤维阵列可产生双重抑制效应. Li等[25]研究了初始温度对锂枝晶生长的影响, 为未来在温度调控以控制枝晶生长方面的进展提供了有价值的见解.
目前众多研究虽然利用相场模型实现了枝晶形貌的多尺度表征, 然而现有工作大多聚焦于树枝状枝晶生长后期的形态演变, 对于初始成核阶段不同形状以及其他形貌类型的枝晶缺乏分析. 此外, 关于固态电解质在枝晶生长过程中膨胀状态改变的研究较为缺乏. 因此, 本文拟通过建立电化学-力学耦合的相场模型, 从多维度深入分析各重要因素对枝晶生长形貌的影响, 以期为固态电解质材料优化及锂枝晶抑制策略提供理论指导.
1. 模拟方法
1.1 相场方法
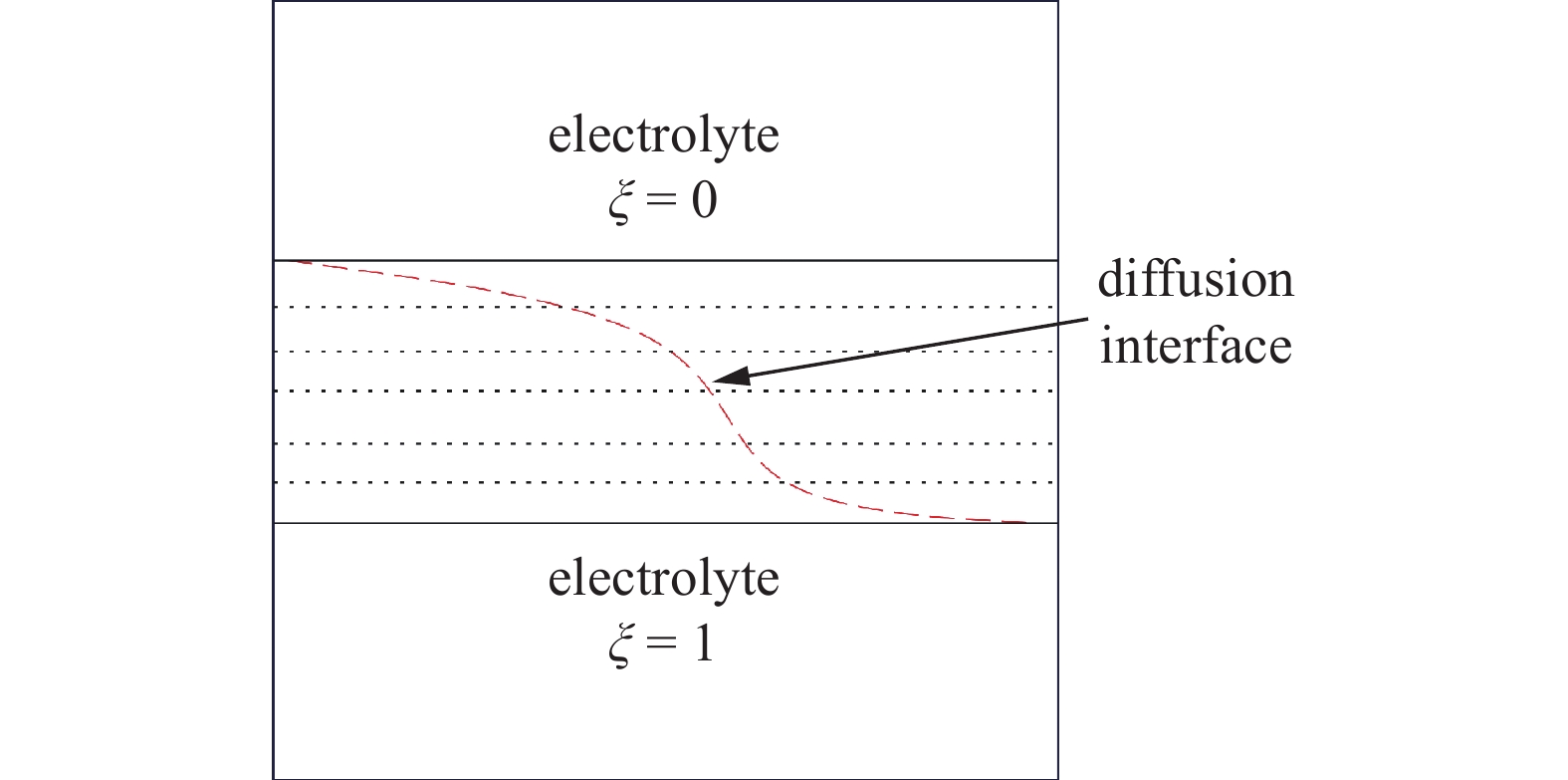
相场模型是一种用于描述和模拟多相系统中界面演化的数学模型. 在所研究的体系中存在电极和电解质两个相, 用相场序变量$\xi $来描述两相之间的变化以及物质状态[26], 其范围为0 ~ 1. 如图1所示为相场序参量示意图.
其中$\xi = 1$代表电极相, $\xi = 0$代表电解质相, $0 < \xi < 1$代表电极与电解质之间的扩散界面.
锂枝晶在固态电解质中生长时, 应力对枝晶的形貌有重要影响. 本研究以Chen等[14]提出的相场模型为基础, 引入了文献[17]中应变能的理论方法, 构建了电化学-力学耦合的相场模型. 其系统自由能函数表达式如下
$$ \begin{split} & F(\xi ,{c_i},\varphi ,{\boldsymbol{u}}) = \int_V {[{f_\text{ch}}\left( {\xi ,{c_i}} \right)} + \\ &\qquad {f_\text{grad}}(\nabla {c_i}) + {f_\text{elec}}(\xi ,{c_i},\varphi ) + {f_\text{ela}}(\xi ,{\boldsymbol{u}})]{\mathrm{d}}V\end{split} $$ (1) 式中主要包括4个变量: $\xi $为序参量; ${c_i}$为化学物质的摩尔分数; $\varphi $为电势; ${\boldsymbol{u}}$为位移.$ {f_\text{ch}}\left( {\xi ,{c_i}} \right) $是系统化学自由能密度; $ {f_\text{grad}}(\nabla {c_i}) $是与界面能相关的梯度能量密度; $ {f_\text{elec}}(\xi ,{c_i},\varphi ) $是电化学能量密度; $ {f_\text{ela}}(\xi ,{\boldsymbol{u}}) $是弹性应变能密度.
系统化学自由能密度为
$$ {f_\text{ch}}\left( {\xi ,{c_i}} \right) = g(\xi ) + {f_\text{ion}}({c_ + },{c_ - }) + {c_ + }\mu _ + ^* + {c_ - }\mu _ - ^* $$ (2) 其中, $ g(\xi ) = W{\xi ^2}{(1 - \xi )^2} $, 是基本的双势阱函数, $W$为势垒高度.$ {f_\text{ion}}({c_ + },{c_ - }) $为稀电解质溶液, 在固态电解质中忽略此项.$\mu _ + ^*$和$\mu _ - ^*$分别为${{\mathrm{Li}}^ + }$和阴离子的参考化学式.
梯度能量密度为
$$ {f_\text{grad}}(\nabla {c_i}) = \frac{1}{2}{k_\xi }{(\nabla \xi )^2} $$ (3) 式中, ${k_\xi } = {k_0}[1 + \delta \cos (\omega {\boldsymbol{\theta }})]$, ${k_0}$是界面能系数[27]; $\delta $是各向异性强度; $\omega $是各向异性模数; ${\boldsymbol{\theta }}$是参考轴与界面法向量之间的夹角. 其中各向异性强度影响锂枝晶在不同方向上的生长速率, 它体现了锂枝晶的生长具有方向性.
电化学能量密度为
$$ {f_\text{elec}}(\xi ,{c_i},\varphi ) = \rho \varphi $$ (4) 其中, $\rho $是局部电荷密度; $\varphi $是静电势.
弹性应变能密度$ {f_\text{ela}}(\xi ,u) $为
$$ {f_\text{ela}}(\xi ,u) = \frac{1}{2}{C_{ijkl}}\left( {{{\varepsilon }}_{{{ij}}}^{{T}} - {{\varepsilon }}_{{{ij}}}^{{0}}} \right) \cdot \left( {{{\varepsilon }}_{{{kl}}}^{{T}} - {{\varepsilon }}_{{{kl}}}^{{0}}} \right) $$ (5) 式中, ${{\varepsilon }}_{{{ij}}}^{{T}}$为总弹性应变张量; ${{\varepsilon }}_{{{ij}}}^{{0}}$为局部无特征应变张量, $\varepsilon _{ij}^0 = {\lambda _i}\xi {\delta _{ij}}$, 这与电化学沉积引发的相关应变有关, ${\lambda _i}$(i = 1,2,3)是特征值的集合; $ {C_{ijkl}} $表达式为
$$ {C_{ijkl}} = \frac{{Ev}}{{(1 + v)(1 - 2v)}}{\delta _{ij}}{\delta _{kl}} + \frac{E}{{2(1 + v)}}({\delta _{il}}{\delta _{jk}} + {\delta _{ik}}{\delta _{jl}}) $$ (6) 其中, ${\delta _{il}}{\delta _{jk}}$是克罗内克函数; $E$是杨氏模量; $v$为泊松比.
结合电化学能和弹性能, 相场模型中用于描述锂沉积过程的序参量$ \xi $的演化方程为[28]
$$\begin{split} & \frac{{\partial \xi }}{{\partial t}} = - {L_\sigma }\left[ {g'(\xi ) - {k_\xi }{\nabla ^2}\xi + {f_\text{ela}}^\prime (\xi ,{\boldsymbol{u}})} \right] - \\ &\qquad {L_\eta }h'(\xi )\left\{ {\exp \left[ {\frac{{n(1 - \alpha )F\eta }}{{RT}}} \right]} \right. -\left. {\frac{{{c_{{{\mathrm{Li}}^ + }}}}}{{{c_0}}}\exp \left[ {\frac{{ - n\alpha F\eta }}{{RT}}} \right]} \right\}\end{split} $$ (7) 式中, ${L_\sigma }$、${L_\eta }$、${\text{α }}$、${{F}}$、$\eta $、${{R}}$和$T$分别为界面迁移率、反应常数、电荷转移系数、法拉第常数、过电位、气体常数和温度.$n$为电荷转移数, 取值为1; $h(\xi )$为插值函数[29], 表达式为
$$ h(\xi ) = {\xi ^3}(6{\xi ^2} - 15\xi + 10) $$ 其中, $ - {L_\sigma }\left[ {g'(\xi ) - {k_\xi }{\nabla ^2}\xi + {f_\text{ela}}^\prime (\xi ,{\boldsymbol{u}})} \right] $对应于界面能; $ - {L_\eta }h'(\xi )\left\{ {\exp \left[ {\dfrac{{n(1 - \alpha )F\eta }}{{RT}}} \right]} \right. $$ \left. { - \dfrac{{{c_{{{\mathrm{Li}}^ + }}}}}{{{c_0}}}\exp \left[ {\dfrac{{ - n\alpha F\eta }}{{RT}}} \right]} \right\} $与电极反应的亲和力有关.
在枝晶生长过程中, 忽略阴离子传输的影响, ${{\mathrm{Li}}^ + }$在固态电解质中的演化方程为[30]
$$ \frac{{\partial {c_{{{\mathrm{Li}}^ + }}}}}{{\partial t}} = \nabla \left( {{D^\text{eff}}\nabla {c_{{{\mathrm{Li}}^ + }}} + \frac{{{D^\text{eff}}{c_{{{\mathrm{Li}}^ + }}}nF\nabla \varphi }}{{RT}}} \right) - \frac{{{c_s}}}{{{c_0}}}\frac{{\partial \xi }}{{\partial t}} $$ (8) 式中, ${D^\text{eff}}$为有效扩散系数, 表达式为
$$ {D^\text{eff}} = {D^e}h(\xi ) + {D^s}[1 - h(\xi )]$$ ${D^e}$为${{\mathrm{Li}}^ + }$在电极中的扩散系数; ${D^s}$为${{\mathrm{Li}}^ + }$在电解质中的扩散系数; ${c_s}$为电极初始浓度, ${c_0}$为电解质中锂离子浓度.
假设体系为中性, 体系的总电势守恒, 电位的变化反映了电化学反应中电荷的进入或释放. 静电势分布表示为[31]
$$ \nabla \left[ {{\sigma _\text{eff}}(\xi )\nabla \varphi } \right] - nF{c_s}\frac{{\partial \xi }}{{\partial t}} = 0 $$ (9) 式中, ${\sigma _\text{eff}} = {\sigma ^e}h(\xi ) + {\sigma ^s}[1 - h(\xi )]$, 其中${\sigma ^e}$为电极的电导率; ${\sigma ^s}$为电解质的电导率.
1.2 模型实现
本文采用COMSOL Multiphysics软件构建了电化学-力学耦合的相场模型, 以研究固态电解质Li3OCl中锂枝晶的生长. 电解质区域是100 μm × 100 μm的矩形网格, 将其划分为多个四边形网格. 选取
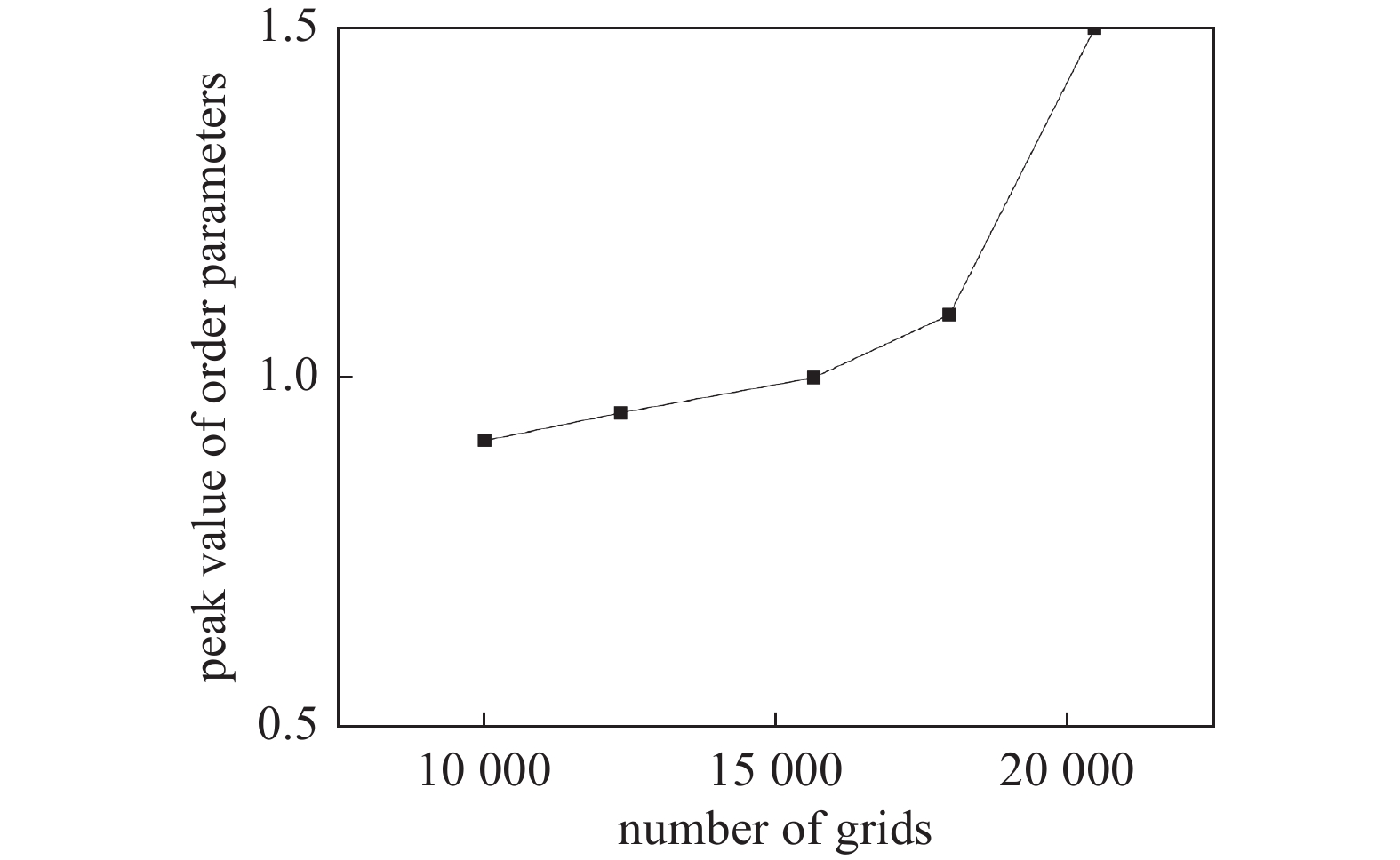
10000 、12321 、15625 、17956 和20449 这5套网格进行网格敏感性分析, 得到结果如图2所示. 由图可知, 网格数较少时, 序参量峰值小于1, 这会导致模拟出的锂枝晶形态较为粗糙, 只能显示出大致的生长方向和趋势; 网格数较多时, 序参量峰值远大于1, 导致序参量出现异常聚集现象, 无法正常扩散和分布. 因此网格数为15625 满足仿真要求, 其中最大网格设置为0.8 μm. 下边界设为阳极, 上边界设为阴极.确定网格尺寸后, 在阳极表面设置为半圆的初始成核点. 然后在一般偏微分方程模块中输入序参量、锂离子浓度和电势的演化方程, 其中初始值均设置为阶跃函数, 分别为step1($ {x}^{2} $ + $ {y}^{2} $)、{1−[step1($ {x}^{2} $ + $ {y}^{2} $)]}*$ {c}_{0} $、{1−[step1($ {x}^{2} $ + $ {y}^{2} $)]}*0.1. 同时, 在固体力学模块中输入相关方程及约束条件. 边界条件设置为: 浓度场的下边界为0, 上边界为1 mol/m3;电势场的下边界的初始电势为0 V, 上边界初始电势为1 V. 计算时间为10 s, 时间步长为0.02 s. 模型中的具体参数如表1所示.
表 1 相场模拟参数Table 1. Phase field simulation parametersParameter Value Reference gradient energy coefficient $ {k_0} $/(J·m−1) $4.17 \times {10^{ - 5}}$ [25] the strength of anisotropy $\delta $ $0.1$ [18] interfacial mobility ${L_\sigma }$/(m3·J−1·s−1) $2.5 \times {10^{ - 6}}$ [14] reaction constant ${L_\eta }$ $0.5$ [21] electrolyte diffusion coefficient${D^s}$/(m·s−1) $ 3.68 \times {10^{ - 10}} $ [25] electrode diffusion coefficient${D^e}$/(m·s−1) $3.68 \times {10^{ - 13}}$ [25] barrier height $W$/(J·m−3) $3.75 \times {10^5}$ [21] anisotropy modulus $\omega $ $4$ [21] electrolyte conductivity ${\sigma ^s}$/m−1 $1.2{\text{ S }}$ [20] electrode diffusion coefficient$ {\sigma ^e} $/m−1 $1 \times {10^7}{\text{S }}$ [20] symmetry factor$\alpha $ $0.5$ [21] standard volume concentration${c_0}$/(mol·m−3) $1 \times {10^3}$ [21] maximum Li ion concentration${c_s}$/(mol·m−3) $7.69 \times {10^4}$ [25] temperature $T$/K $298.15$ [25] Young’s modulus E/GPa $99.7$ [32] Poisson’s ratio $0.2$ [32] eigenvalues of stress tensors ${\lambda _i}$ $ - 0.866 \times {10^{ - 3}}$ [8] $ - 0.733 \times {10^{ - 3}}$ $ - 0.529 \times {10^{ - 3}}$ 2. 结果与讨论
2.1 树枝状锂枝晶的形态
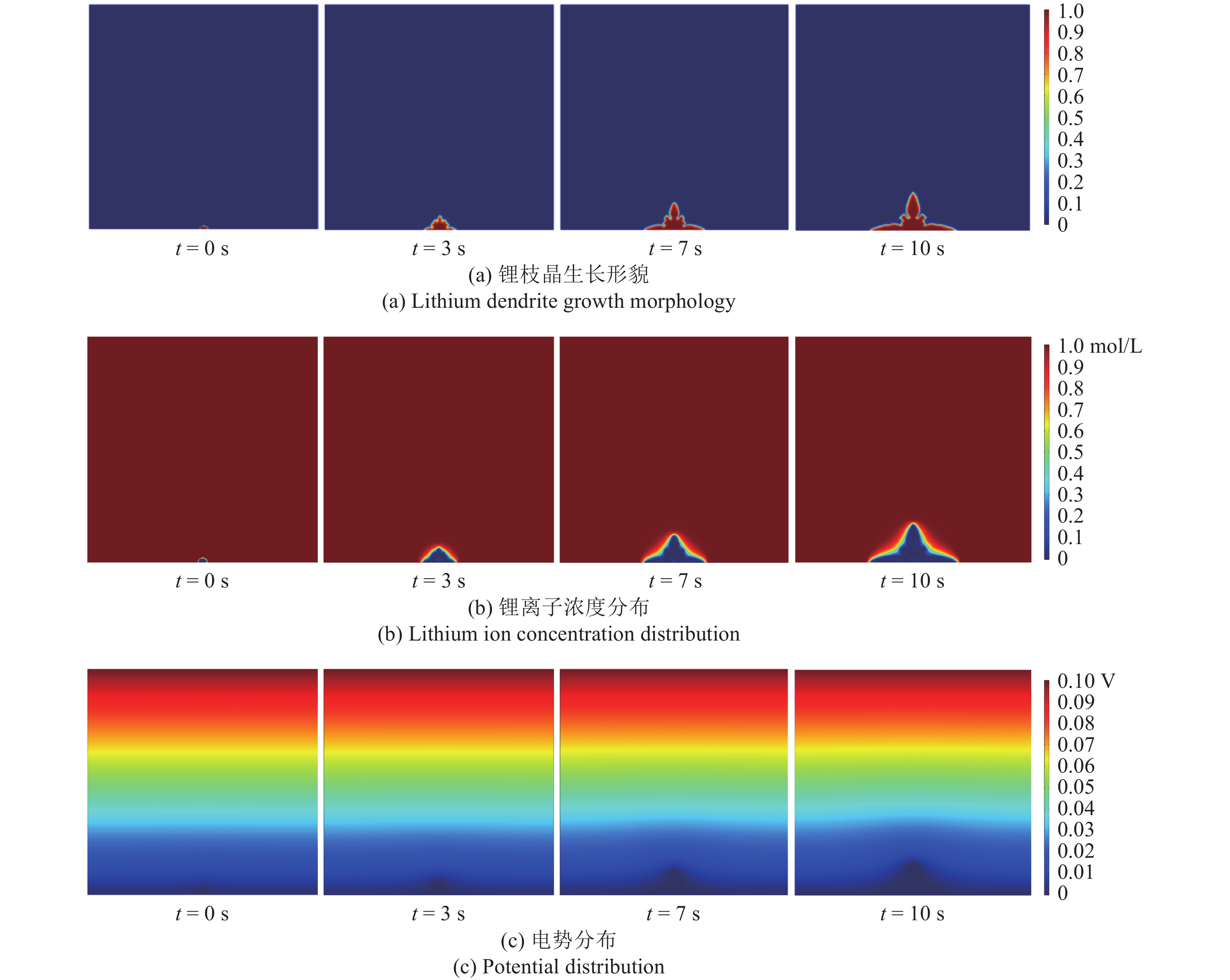
实际情况中电解质的内部结构复杂, 锂离子在其中难以均匀分布, 故假设锂枝晶已经完成半圆初始形核, 下文研究均以半圆成核形状为基础. 在电化学反应和应力的驱动下, 锂枝晶在固态电解质中的生长过程如图3所示. 可以看出锂枝晶的生长表现出明显的对称性, 对称轴两端有分支生成, 仿真结果与Ren等[24]结果相似.
![]()
图 3 不同时刻锂枝晶生长的模拟结果Figure 3. Simulation results of lithium dendrite growth at different time模拟过程中设置了4个时间点来展示不同时刻的枝晶生长形貌、锂离子浓度以及电势的分布情况, t = 0 s代表成核开始. 由于枝晶和固态电解质之间存在电位差和浓度梯度, 导致枝晶快速生长. 其中沿横轴和纵轴方向生长速度最快, 侧枝生长速度缓慢, 如图3(a) 所示. 这主要是因为固态电解质具有较高的机械强度和硬度, 难以产生侧向生长. 图3(b) 和图3(c) 分别为锂离子浓度和电势分布图. 由图可知枝晶内部在枝晶和电解质界面交汇处有明显的浓度和电势梯度. 这是由于锂离子的沉积速率超过了从电解质中补充的速率. 由于“尖端效应”, 会吸引更多的锂离子向尖端迁移, 导致尖端附近浓度迅速降低, 形成更大的浓度和电势梯度, 促使枝晶快速生长.
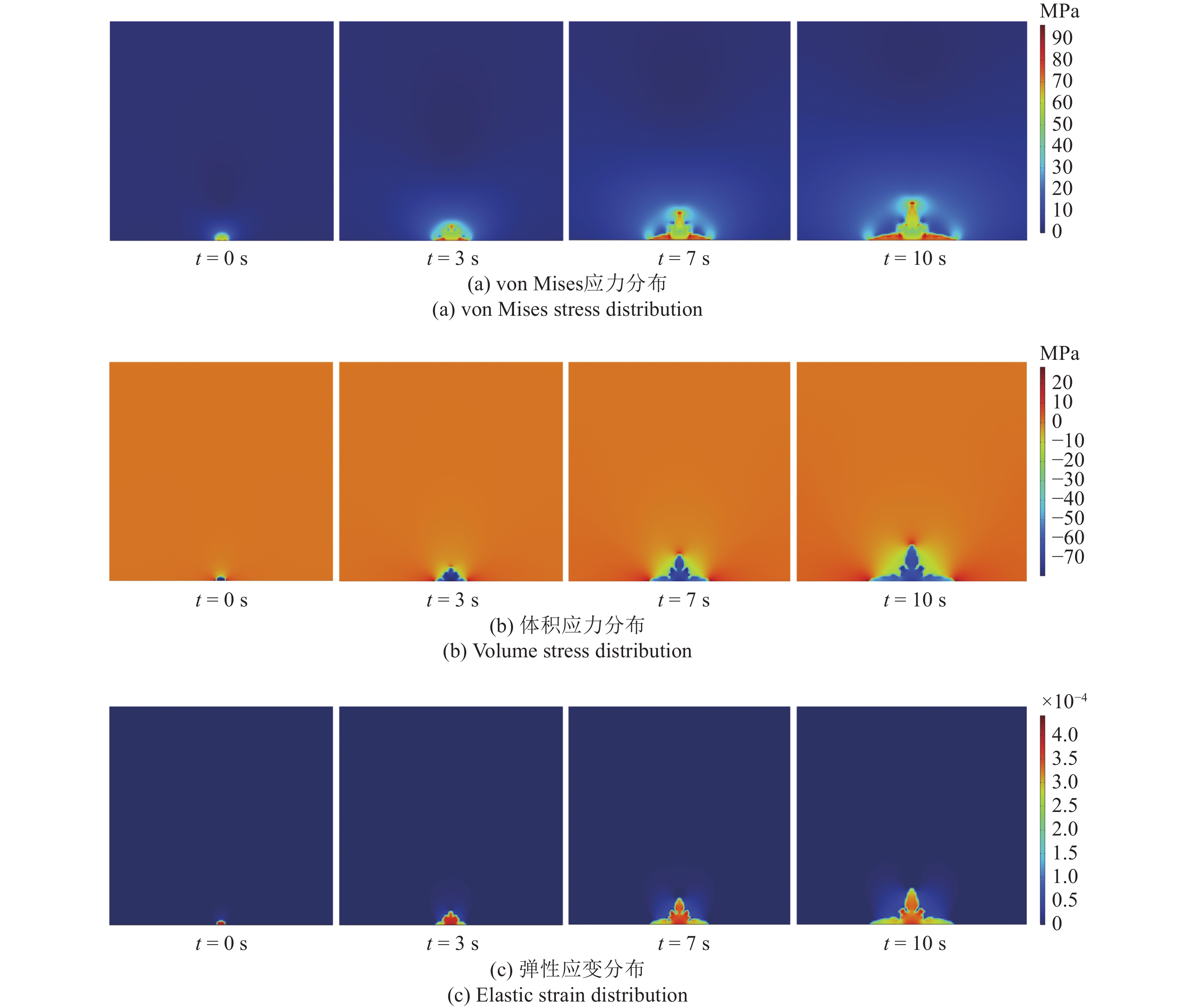
图4(a) 展示了锂枝晶内部的von Mises应力演化情况. 由图可知应力主要集中在枝晶尖端和电极附近. 这是因为枝晶尖端锂离子的沉积速率更快, 导致尖端体积增加, 使得尖端应力增大. 由于界面能差异, 枝晶根部区域的界面会产生拉伸或压缩应力, 使得该区域应力增大. 图4(b) 为体积应力的分布. 体积应力(即平均法向应力)主要表示该部分的体积变化, 正值表明该区域受到压缩, 负值表明该区域正在膨胀. 因为锂枝晶的生长会导致固态电解质受到压缩并发生形变, 所以枝晶尖端处的应力和枝晶与固态电解质接触处的应力会明显高于其他区域. 图4(c)展示了弹性应变(ɛ)的分布. 弹性应变的计算公式为 ɛ = (ɛxx + ɛyy + ɛzz). 由图可知最大值在4 × 10−4附近, 应变较小, 属于弹性范围之内, 不足以引起塑性变形, 后续研究不再展开分析.
2.2 初始成核形状对枝晶形貌的影响
枝晶的初始成核形状对枝晶形貌有重要影响. 在图5中, 本文以仿真区域下边界为x轴, 其中心为坐标原点, 在2.1节设置的半圆(图5(a))基础上, 设置了切割长轴半椭圆和切割短轴半椭圆(图5(c)) 3种初始成核形状. 并模拟了枝晶的生长过程, 不同初始成核形状下的枝晶形貌如图6所示. 由图6可知, 初始成核点为半圆、切割长轴半椭圆和切割短轴半椭圆时锂枝晶的形貌有很大的变化, 但应力变化趋势呈现一定的相似性, 整体差异不大. 其中半圆初始成核枝晶侧枝生长受到抑制, 切割长轴半椭圆成核向横轴两侧生长, 切割短轴半椭圆纵轴方向形成分叉. 当枝晶沿着长短轴方向继续生长时, 枝晶之间可能相互影响, 导致更多的侧枝和分支结构形成. 这样的结构变化会削弱枝晶的稳定性, 进而增加电池发生短路的风险.
![]()
图 5 锂枝晶初始成核形状示意图Figure 5. Schematic diagram of initial nucleation shape of lithium dendrites![]()
图 6 不同初始成核形状下锂枝晶的形貌Figure 6. Morphology of lithium dendrites under different initial nucleation shapes2.3 各向异性强度对枝晶形貌的影响
各向异性强度对锂离子在固态电解质中的扩散及迁移特性产生影响, 同时枝晶生长具有各向异性特质. 这种各向异性强度会显著左右枝晶的生长方向及侧枝分布情况, 从而决定枝晶的最终形态. 图7为不同各向异性强度下锂枝晶生长形貌. 从图7(a) 中可以看出, 不同各向异性强度下枝晶侧枝有明显的变化. 各向异性强度过大时, 枝晶侧枝生长受到抑制. 这是因为晶体沿着特定的方向快速生长, 使侧向的枝晶难以获得足够的锂离子供应, 进而导致侧枝生长受到抑制. 根据图7(b)和图7(c) 的应力分布特征, 可知不同各向异性强度下枝晶应力主要集中在枝晶尖端和根部. 其中由于尖端部分锂离子沉积速率较快, 驱动枝晶向外膨胀扩展.
![]()
图 7 不同各向异性强度下锂枝晶生长形貌Figure 7. Growth morphology of lithium dendrites under different anisotropy intensities2.4 反应常数对枝晶形貌的影响
反应常数决定了锂离子在电极/电解质界面处的沉积和溶解速率, 致使浓度梯度形成, 从而加剧锂的不均匀沉积, 影响锂枝晶的成核和生长. 图8为不同反应常数下枝晶的生长形貌. 由图可知, 较小反应常数, 意味着锂离子的沉积速率较低, 这会导致锂离子在电极表面分布更均匀, 生长的枝晶表面更加平滑, 枝晶生长得到抑制. 较大的反应常数会加速电化学反应, 使得枝晶的生长速度加快、长度增加, 短时间内长成更多的分支, 且在枝晶根部和尖端存在着更大的应力.
2.5 外界压力对锂枝晶形貌的影响
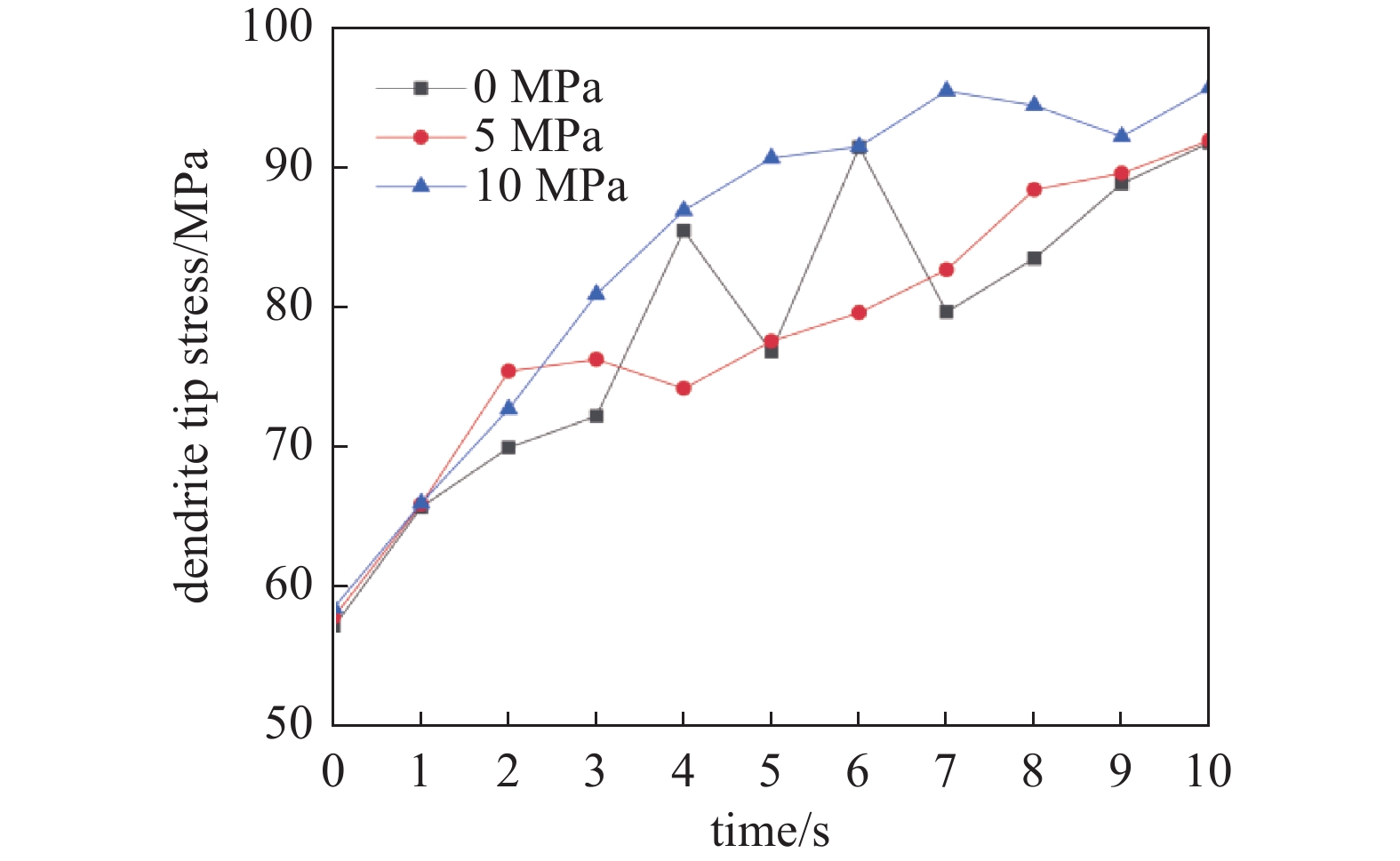
为探究外部压力对锂枝晶演化的影响, 将外界压力施加于几何模型的上边界. 图9给出了不同外界压力下锂枝晶的形貌图. 由图9(a) 可知, 在较低压力下, 锂枝晶纵向生长和横向拓展的抑制效果未呈现显著变化, 而当压力提升至更高范围时, 纵向生长和横向拓展的抑制效果开始显著增强. 由图9(b) 可知, 随着外界压力的增大, 纵轴方向上的枝晶所受的应力逐渐增大, 生长受到抑制, 枝晶逐渐沿横轴方向生长. 这是因为在外部压力的作用下, 电解质向内挤压, 导致内部应力增大, 从而抑制了锂的沉积反应速率. 在外界压力的作用下, 电解质区域也受到一定程度的压缩, 如图9(c) 所示. 图10展示了不同外压下, 枝晶尖端应力随时间变化的曲线. 随着时间推移, 在3种外压条件下的枝晶尖端应力均呈现随时间递增的趋势, 但存在一定波动. 这是由于电场分布、离子浓度梯度等因素的不均匀性导致锂枝晶生长速率和方向的变化, 进而引起尖端应力的波动. 随着外界压力的增大, 锂枝晶发生断裂的风险增大. 当压力过大时, 可能使局部von Mises应力超过锂的屈服强度, 进而导致枝晶发生断裂, 形成“死锂”, 造成库伦效率降低. 因此, 可以通过深入研究材料的力学性能和电化学特性, 来探索外部压力的最大可承受范围, 以确保电池在安全和高效的状态下运行.
![]()
图 10 不同外压下枝晶尖端应力随时间的变化Figure 10. The change of dendrite tip stress with time under different external pressures2.6 环境温度对枝晶形貌的影响
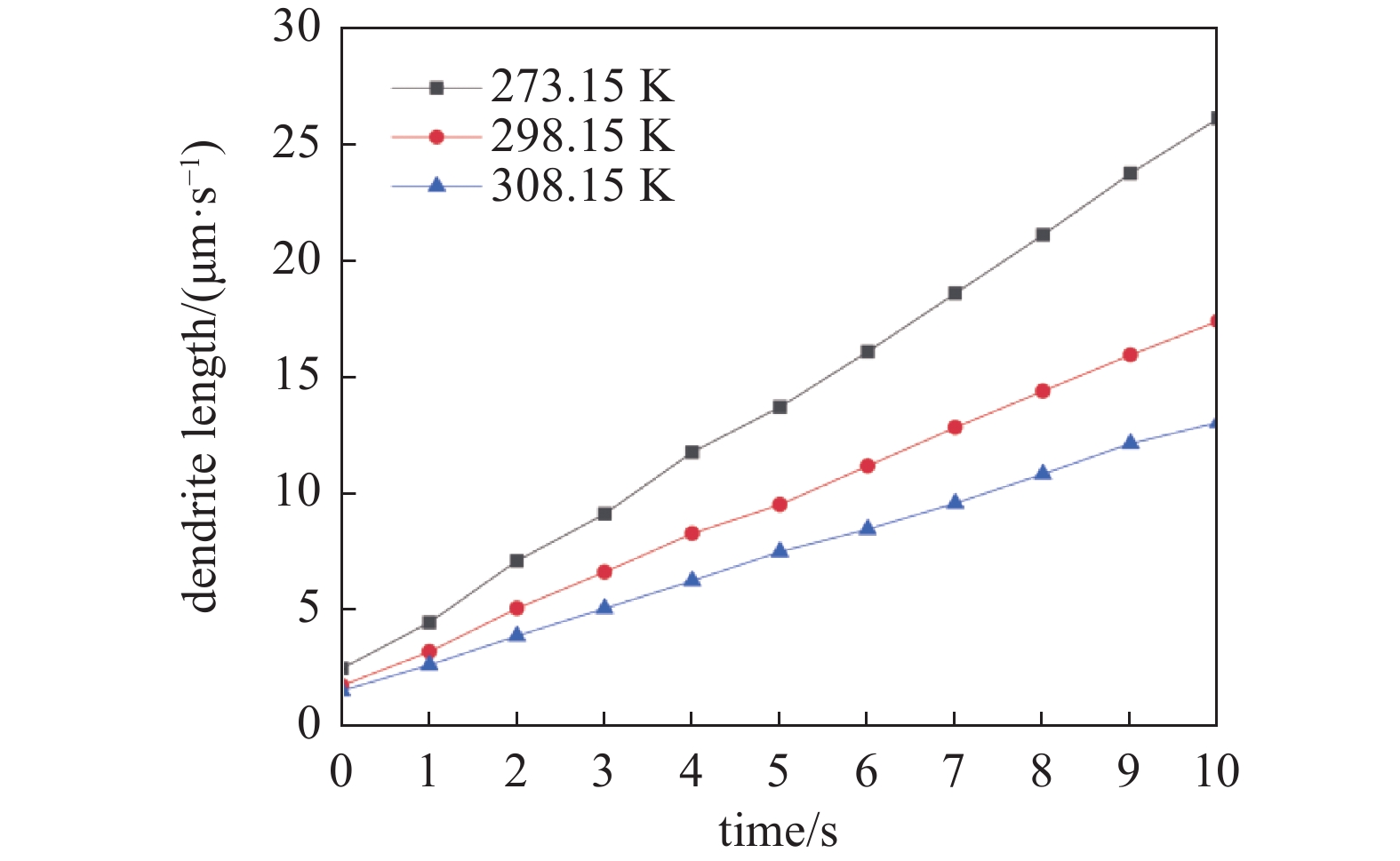
图11给出了273.15, 298.15和313.15 K 3个不同温度下锂枝晶生长形貌. 由图11(a) 可知, 随着环境温度的升高, 锂枝晶的尺寸逐渐变小, 横轴和纵轴上的侧枝数量减少, 生长速度得到抑制. 这是因为环境温度升高时, 锂离子在电解质中的扩散速率显著加快. 这使得锂离子在电极表面的分布更加均匀, 减小了因局部锂离子浓度差异而导致的枝晶生长驱动力, 从而抑制了锂枝晶的生长速度和侧枝的形成. 由图11(b)和图11(c) 可知, 随着温度的升高, 由于热应力逐渐累积并传递到锂枝晶内部, 导致锂枝晶内部应力变得更大、体积膨胀更显著. 图12给出了不同温度下枝晶长度(负极表面到枝晶尖端的距离)随时间的变化. 随着时间的增加, 3种不同温度下的枝晶长度也逐渐增加, 但枝晶生长速度会随着温度的升高而减慢, 这是因为温度升高抑制了其生长速率. 综合上述分析, 可知温度调控能抑制枝晶演化, 控制其生长速度和侧枝数量, 这对提升固态锂电池循环稳定性与安全性具有重要意义.
![]()
图 12 不同环境温度下枝晶长度随时间的变化Figure 12. Variation of dendrite length with time at different ambient temperatures2.7 锂枝晶的多种生长形态对比分析
锂枝晶在生长过程中, 除了上述常见的树枝状形态之外, 还可能呈现出针状、苔藓状等多种不同形状[33], 即使在固态电解质环境中, 这些多样化的形态也有可能出现[32]. 因此模拟对比不同形态的锂枝晶在固态电解质中的生长很有必要.
2.7.1 针状枝晶
针状生长是金属的固有趋势, 为了模拟针状枝晶的形成, 相场模型中采用差异化锂离子扩散系数进行参数配置, 即锂离子扩散系数沿横轴方向设为零, 纵轴方向上保持不变, 仿真结果如图13中左图所示. 与树枝状枝晶相比, 针状枝晶仅沿着纵轴方向生长, 并无侧枝生成. 由应力图可知, von Mises应力主要集中在枝晶根部, 这是因为针状枝晶生长时会出现应力积累, 这与Yurkiv等[20]的结论一致. 由于横向扩散受到抑制, 枝晶向纵轴生长, 所以电解质在纵轴方向更易受到挤压, 如图13(c) 所示. 在图13右图中, 横轴方向的扩散系数设置为$0.2{D^\text{eff}}$, 纵轴方向设置为$0.8{D^\text{eff}}$. 由于扩散系数的各向异性不同, 会导致浓度梯度的分布不均匀, 进而导致枝晶的结构发生变化. 如图13(a) 的右图所示, 针状枝晶在生长过程中在横轴方向上有侧枝生成. 因此, 在实际应用中需合理调控锂离子扩散系数, 同时关注根部应力积累.
2.7.2 苔藓状枝晶
锂枝晶除了有针状生长之外, 还可能生成苔藓状枝晶. 苔藓状枝晶的生成可能是锂离子通过SEI界面随机扩散至固态锂相所导致的[34]. 在固态电解质中, 因其成分多样性和结构复杂性, 采用传统实验技术很难对固态电解质的特性进行表征, 所以在方程中引入噪声项$ {f_\text{ns}}({c_i}) = h'(\xi )\chi \psi $来模拟随机扩散. 其中χ是一个随机数, ψ是波动幅度. 系统的自由能表达式为
$$ \begin{split} &F(\xi ,{c_i},\varphi ,u) = \int_V {[{f_\text{ch}}\left( {\xi ,{c_i}} \right)} + {f_\text{grad}}(\nabla {c_i}) +\\ &\qquad {f_\text{ela}}(\xi ,u) + {f_\text{elec}}(\xi ,{c_i},\varphi ) + {f_\text{ns}}({c_i})]{\mathrm{d}}V \end{split}$$ 图14(a) 展示了引入噪声项后锂枝晶的生长形貌. 与针状枝晶相比, 其生长更加自由, 二次分支更多. 这是由于电流密度不均匀等原因导致锂沉积的不均匀, 从而促进苔藓状枝晶的形成. 由图14(b) 可知, von Mises应力主要集中在枝晶分支的尖端, 这是由电流密度以及苔藓状枝晶的结构所造成的. 图14(c) 展示了固态电解质中枝晶体积应力的分布. 根据其应力分布特性可知, 相较于树枝状枝晶, 苔藓状枝晶所受的膨胀应力更为显著, 这可能导致枝晶呈现多孔、松散形貌, 诱发微裂纹和界面剥离, 进而影响电池的充放电效率, 增加电池短路的风险.
3. 结论与展望
本文建立了一个电化学-力学耦合的相场模型, 模拟分析了重要因素对固态电解质中锂枝晶生长的影响. 主要得到如下结论.
(1)当各向异性强度较小时, 锂枝晶容易形成侧枝; 随着各向异性强度增大, 侧枝生长逐渐受到抑制. 反应常数较小时, 锂离子沉积速率较低, 抑制枝晶扩展. 因此, 合理控制各向异性强度和反应常数的大小是优化锂枝晶生长的重要手段. 外界压力可抑制锂枝晶沿纵轴方向的生长, 迫使枝晶向横轴扩展, 但过大的压力可能导致枝晶断裂, 形成“死锂”. 环境温度升高时, 枝晶生长速度和侧枝数量均受到抑制, 对电解质的破坏作用也减小. 因此, 适当提高温度是抑制锂枝晶生长的有效策略.
(2)通过模拟3种初始成核形状发现: 切割长轴半椭圆形状在纵轴方向更易形成分支, 而切割短轴半椭圆形状在横轴方向更易产生分支. 可知, 当椭圆的焦点位于横轴时, 锂枝晶在纵轴方向呈现显著的各向异性特征, 从而更易形成分支结构; 反之, 当焦点位于纵轴时, 横轴方向则显示出更高的成核概率, 伴随明显的分支生长. 这表明枝晶的生长具有方向性.
(3)针状枝晶的生长依赖于锂浓度的分布, 分支较少且方向单一, 应力集中效应主要分布于根部区域. 苔藓状枝晶生长过程中表现出更高的自由度和分支数量, 对电解质的破坏性更大, 其生长过程中伴随着显著的体积膨胀现象. 树枝状枝晶则介于针状和苔藓状之间, 具有较为均匀的分支结构和应力分布, 对固态电解质的损伤也相对较小.
需要说明的是, 本研究虽然对于锂枝晶抑制策略具有一定的指导意义, 但也存在一定的局限性. 一方面, 模型未考虑电池内部产热, 且模拟仿真基于较理想条件, 忽略了固态电解质中的化学反应、裂纹和孔洞等对枝晶形貌的影响. 另一方面, 缺乏相应的实验验证. 后续研究可以聚焦于这些因素, 进一步完善分析, 来提高模型的准确性和实用性.
-
![]()
图 3 不同时刻锂枝晶生长的模拟结果
Figure 3. Simulation results of lithium dendrite growth at different time
![]()
图 5 锂枝晶初始成核形状示意图
Figure 5. Schematic diagram of initial nucleation shape of lithium dendrites
![]()
图 6 不同初始成核形状下锂枝晶的形貌
Figure 6. Morphology of lithium dendrites under different initial nucleation shapes
![]()
图 7 不同各向异性强度下锂枝晶生长形貌
Figure 7. Growth morphology of lithium dendrites under different anisotropy intensities
![]()
图 10 不同外压下枝晶尖端应力随时间的变化
Figure 10. The change of dendrite tip stress with time under different external pressures
![]()
图 12 不同环境温度下枝晶长度随时间的变化
Figure 12. Variation of dendrite length with time at different ambient temperatures
表 1 相场模拟参数
Table 1 Phase field simulation parameters
Parameter Value Reference gradient energy coefficient $ {k_0} $/(J·m−1) $4.17 \times {10^{ - 5}}$ [25] the strength of anisotropy $\delta $ $0.1$ [18] interfacial mobility ${L_\sigma }$/(m3·J−1·s−1) $2.5 \times {10^{ - 6}}$ [14] reaction constant ${L_\eta }$ $0.5$ [21] electrolyte diffusion coefficient${D^s}$/(m·s−1) $ 3.68 \times {10^{ - 10}} $ [25] electrode diffusion coefficient${D^e}$/(m·s−1) $3.68 \times {10^{ - 13}}$ [25] barrier height $W$/(J·m−3) $3.75 \times {10^5}$ [21] anisotropy modulus $\omega $ $4$ [21] electrolyte conductivity ${\sigma ^s}$/m−1 $1.2{\text{ S }}$ [20] electrode diffusion coefficient$ {\sigma ^e} $/m−1 $1 \times {10^7}{\text{S }}$ [20] symmetry factor$\alpha $ $0.5$ [21] standard volume concentration${c_0}$/(mol·m−3) $1 \times {10^3}$ [21] maximum Li ion concentration${c_s}$/(mol·m−3) $7.69 \times {10^4}$ [25] temperature $T$/K $298.15$ [25] Young’s modulus E/GPa $99.7$ [32] Poisson’s ratio $0.2$ [32] eigenvalues of stress tensors ${\lambda _i}$ $ - 0.866 \times {10^{ - 3}}$ [8] $ - 0.733 \times {10^{ - 3}}$ $ - 0.529 \times {10^{ - 3}}$ 
下载: 导出CSV
-
[1] 吴建营, 洪屹峰. 基于统一相场理论的锂电池电极颗粒断裂模拟研究. 力学学报, 2022, 54(9): 2472-2489 (Wu Jianying, Hong Yifeng. Phase-field cohesive modeling of fracture in storage particles of lithium-ion batteries. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(9): 2472-2489 (in Chinese) Wu Jianying, Hong Yifeng. Phase-field cohesive modeling of fracture in storage particles of lithium-ion batteries. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(9): 2472-2489 (in Chinese)
[2] 耿晓彬, 李顶根, 徐波. 固态电解质电池锂枝晶生长机械应力-热力学相场模拟研究. 物理学报, 2023, 72(22): 8-18 (Geng Xiaobin, Li Dinggen, Xu Bo. Mechanical stress-thermodynamic phase-field simulation of lithium dendrite growth in solid electrolyte battery. Acta Phys Sin, 2023, 72(22): 8-18 (in Chinese) Geng Xiaobin, Li Dinggen, Xu Bo. Mechanical stress-thermodynamic phase-field simulation of lithium dendrite growth in solid electrolyte battery. Acta Phys Sin, 2023, 72(22): 8-18 (in Chinese)
[3] 陈翔, 富忠恒, 高宇辰等. 机器学习在锂电池固态电解质研究中的应用. 硅酸盐学报, 2023, 51(2): 488-498 (Chen Xiang, Fu Zhongheng, Gao Yuchen, et al. Machine learning in lithium battery solid-state electrolytes. Journal of The Chinese Ceramic Society, 2023, 51(2): 488-498 (in Chinese) Chen Xiang, Fu Zhongheng, Gao Yuchen, et al. Machine learning in lithium battery solid-state electrolytes. Journal of The Chinese Ceramic Society, 2023, 51(2): 488-498 (in Chinese)
[4] 洪清和. 基于固态电解质电池模型的应力与枝晶生长仿真研究. [硕士论文]. 武汉: 华中科技大学, 2022 (Hong Qinghe. Simulation and research of stress and dendrite based on solid electrolyte battery model. [Master Thesis]. Wuhan: Huazhong University of Science and Technology, 2022 (in Chinese) Hong Qinghe. Simulation and research of stress and dendrite based on solid electrolyte battery model. [Master Thesis]. Wuhan: Huazhong University of Science and Technology, 2022 (in Chinese)
[5] 赵亚姿. 锂电池枝晶生长机理的相场法研究. [硕士论文]. 湘潭: 湘潭大学, 2021 (Zhao Yazi. Study on dendrite growth mechanism of lithium battery by phase field method. [Master Thesis]. Xiangtan: Xiangtan University, 2021 (in Chinese) Zhao Yazi. Study on dendrite growth mechanism of lithium battery by phase field method. [Master Thesis]. Xiangtan: Xiangtan University, 2021 (in Chinese)
[6] Lyu D, Ren B, Li S. Failure modes and mechanisms for rechargeable lithium-based batteries: A state-of-the-art review. Acta Mech, 2019, 230(3): 701-727 doi: 10.1007/s00707-018-2327-8
[7] Zhang X, Wang QJ, Harrison KL, et al. Rethinking how external pressure can suppress dendrites in lithium metal batteries. Journal of The Electrochem Society, 2019, 166(15): A3639 doi: 10.1149/2.0701914jes
[8] Yang H, Wang Z. Effects of pressure, temperature, and plasticity on lithium dendrite growth in solid-state electrolytes. Journal of Solid State Electrochemistry, 2023, 27(10): 2607-2618 doi: 10.1007/s10008-023-05560-4
[9] 罗霞, 谢浩杰, 魏继兴等. 全固态电池电解质研究进展及趋势分析. 浙江化工, 2024, 55(8): 12-18 (Luo Xia, Xie Haojie, Wei Jixing, et al. Research progress and trend analysis of electrolytes for all-solid-state batteries. Zhejiang Chemical Industry, 2024, 55(8): 12-18 (in Chinese) Luo Xia, Xie Haojie, Wei Jixing, et al. Research progress and trend analysis of electrolytes for all-solid-state batteries. Zhejiang Chemical Industry, 2024, 55(8): 12-18 (in Chinese)
[10] 徐波, 于超, 王宠等. 基于相场模拟的应力辅助时效的 NiTi 形状记忆合金功能性能研究. 力学学报, 2024, 56(12): 3507-3520 (Xu Bo, Yu Chao, Wang Chong, et al. Phase-field simulation on the functional propertiesof stress-assisted aging NiTi shape memory alloys. Chinese Journal of Theoretical and Applied Mechanics, 2024, 56(12): 3507-3520 (in Chinese) Xu Bo, Yu Chao, Wang Chong, et al. Phase-field simulation on the functional propertiesof stress-assisted aging NiTi shape memory alloys. Chinese Journal of Theoretical and Applied Mechanics, 2024, 56(12): 3507-3520 (in Chinese)
[11] Lin C, Ruan H. Panoramic modeling of lithium dendrite formation and crack penetration in solid-state electrolyte: Mechanism and suppression strategies. Journal of Power Sources, 2024, 598: 234137 doi: 10.1016/j.jpowsour.2024.234137
[12] Yurkiv V, Foroozan T, Ramasubramanian A, et al. Understanding Zn electrodeposits morphology in secondary batteries using phase-field model. Journal of The Electrochemical Society, 2020, 167(6): 060503 doi: 10.1149/1945-7111/ab7e91
[13] Liang L, Qi Y, Xue F, et al. Nonlinear phase-field model for electrode-electrolyte interface evolution. Physical Review E, 2012, 86(5
[14] Chen L, Zhang HW, Liang LY, et al. Modulation of dendritic patterns during electrodeposition: A nonlinear phase-field model. J Power Sources, 2015, 300(30): 376-385
[15] Lin C, Ruan HH. Mechano-electrochemical modeling of lithium dendrite penetration in a solid-state electrolyte: Mechanism and suppression. Journal of Energy Storage, 2023, 65: 107389
[16] Zhang C, Wang D, Lei C, et al. Effect of major factors on lithium dendrite growth studied by phase field modeling. Journal of The Electrochemical Society, 2023, 170(5): 052506 doi: 10.1149/1945-7111/acd587
[17] Zhang J, Liu Y, Wang C, et al. An electrochemical-mechanical phase field model for lithium dendrite. Journal of The Electrochemical Society, 2021, 168(9): 090522 doi: 10.1149/1945-7111/ac22c7
[18] Han D, Lin C. Numerical study of the formation of dead lithium during cycling and the mechanism of its effect on battery performance. Journal of Energy Storage, 2024, 83: 110641 doi: 10.1016/j.est.2024.110641
[19] Hong Z, Viswanathan V. Prospect of thermal shock induced healing of lithium dendrite. ACS Energy Letters, 2019, 4(5): 1012-1019 doi: 10.1021/acsenergylett.9b00433
[20] Yurkiv V, Foroozan T, Ramasubramanian A, et al. Phase-field modeling of solid electrolyte interface (SEI) influence on Li dendritic behavior. Electrochimica Acta, 2018, 265: 609-619 doi: 10.1016/j.electacta.2018.01.212
[21] Jiang W, Wang Z, Hu L, et al. Simulations of dendrite and crack and their interactions in solid electrolyte by phase field method. Journal of Energy Storage, 2024, 86: 111126 doi: 10.1016/j.est.2024.111126
[22] Shen X, Zhang R, Shi P, et al. How does external pressure shape Li dendrites in Li metal batteries. Advanced Energy Materials, 2021, 11(10): 2003416 doi: 10.1002/aenm.202003416
[23] Zhang Z H, Zhang Y, Liu C, et al. The influence of stress-dependent overpotential on dendrite growth in all-solid-state battery with cracks. Sci China Tech Sci, 2024, 67: 2493-2504 doi: 10.1007/s11431-023-2594-8
[24] Ren Y, Zhou Y, Cao Y. Inhibit of lithium dendrite growth in solid composite electrolyte by phase-field modeling. The Journal of Physical Chemistry C, 2020, 124(23): 12195-12204 doi: 10.1021/acs.jpcc.0c01116
[25] Li Y, Zhao W, Zhang G, et al. Unified picture on temperature dependence of lithium dendrite growth via phase-field simulation. Energy Material Advances, 2023, 4: 0053 doi: 10.34133/energymatadv.0053
[26] Chen Y, Yuan X, He C, et al. Mechanistic exploration of dendrite growth and inhibition for lithium metal batteries. Energies, 2023, 16(9): 3745 doi: 10.3390/en16093745
[27] Li Y, Yu Q, Ham S, et al. A phase-field model without artificial curvature effect for the crystal growth simulation. International Journal of Heat and Mass Transfer, 2023, 203: 123847 doi: 10.1016/j.ijheatmasstransfer.2023.123847
[28] Li Y, Zhang G, Chen B, et al. Understanding the separator pore size inhibition effect on lithium dendrite via phase-field simulations. Chinese Chemical Letters, 2022, 33(6): 3287-3290 doi: 10.1016/j.cclet.2022.03.065
[29] Schwen D, Aagesen LK, Peterson JW, et al. Rapid multiphase-field model development using a modular free energy based approach with automatic differentiation in moose/marmot. Computational Materials Science, 2017, 132: 36-45
[30] Lee H, Kwak T, Lee W, et al. Effect of surface topography on dendritic growth in lithium metal batteries. Journal of Power Sources, 2022, 552: 232264 doi: 10.1016/j.jpowsour.2022.232264
[31] Ren Y, Zhang K, Zhou Y, et al. Phase-field simulation and machine learning study of the effects of elastic and plastic properties of electrodes and solid polymer electrolytes on the suppression of Li dendrite growth. Acs Applied Materials & Interfaces, 2022, 14: 30658-30671
[32] Liu H, Chen Y, Chien P H, et al. Dendrite formation in solid-state batteries arising from lithium plating and electrolyte reduction. Nature Materials, 2025
[33] Baktash A, Demir B, Yuan Q, et al. Effect of defects and defect distribution on Li-diffusion and elastic properties of anti-perovskite Li3OCl solid electrolyte. Energy Storage Materials, 2021, 41: 614-622 doi: 10.1016/j.ensm.2021.06.039
[34] Steiger J, Richter G, Wenk M, et al. Comparison of the growth of lithium filaments and dendrites under different conditions. Electrochemistry Communications, 2015, 50: 11-14 doi: 10.1016/j.elecom.2014.11.002
计量
- 文章访问数: 43
- HTML全文浏览量: 3
- PDF下载量: 6
