EI、Scopus 收录
中文核心期刊
快速检索 年期检索 高级检索

可压缩流动问题笛卡尔网格模拟方法研究进展与展望

赵宁, 刘剑明, 田琳琳, 王镇明

赵宁, 刘剑明, 田琳琳, 王镇明. 可压缩流动问题笛卡尔网格模拟方法研究进展与展望. 力学学报, 2025, 57(2): 285-314. DOI: 10.6052/0459-1879-24-374
引用本文: 赵宁, 刘剑明, 田琳琳, 王镇明. 可压缩流动问题笛卡尔网格模拟方法研究进展与展望. 力学学报, 2025, 57(2): 285-314. DOI: 10.6052/0459-1879-24-374
shu
Zhao Ning, Liu Jianming, Tian Linlin, Wang Zhenming. Progress and prospects of Cartesian mesh simulation methods for compressible flow problems. Chinese Journal of Theoretical and Applied Mechanics, 2025, 57(2): 285-314. DOI: 10.6052/0459-1879-24-374
Citation: Zhao Ning, Liu Jianming, Tian Linlin, Wang Zhenming. Progress and prospects of Cartesian mesh simulation methods for compressible flow problems. Chinese Journal of Theoretical and Applied Mechanics, 2025, 57(2): 285-314. DOI: 10.6052/0459-1879-24-374
shu
赵宁, 刘剑明, 田琳琳, 王镇明. 可压缩流动问题笛卡尔网格模拟方法研究进展与展望. 力学学报, 2025, 57(2): 285-314. CSTR: 32045.14.0459-1879-24-374
引用本文: 赵宁, 刘剑明, 田琳琳, 王镇明. 可压缩流动问题笛卡尔网格模拟方法研究进展与展望. 力学学报, 2025, 57(2): 285-314. CSTR: 32045.14.0459-1879-24-374
shu
Zhao Ning, Liu Jianming, Tian Linlin, Wang Zhenming. Progress and prospects of Cartesian mesh simulation methods for compressible flow problems. Chinese Journal of Theoretical and Applied Mechanics, 2025, 57(2): 285-314. CSTR: 32045.14.0459-1879-24-374
Citation: Zhao Ning, Liu Jianming, Tian Linlin, Wang Zhenming. Progress and prospects of Cartesian mesh simulation methods for compressible flow problems. Chinese Journal of Theoretical and Applied Mechanics, 2025, 57(2): 285-314. CSTR: 32045.14.0459-1879-24-374
shu

可压缩流动问题笛卡尔网格模拟方法研究进展与展望

  • *.

    南京航空航天大学航空航天结构力学及控制全国重点实验室, 南京 210016

  • †.

    江苏师范大学数学与统计学院, 江苏徐州 221116

  • **.

    南京航空航天大学江苏省风力机设计高技术研究重点实验室, 南京 210016

  • ††.

    南京航空航天大学飞行器数学建模与高性能计算工信部重点实验室, 南京 210016

详细信息
    通讯作者:

    赵宁, 教授, 主要研究方向为流体力学. E-mail: zhaoam@nuaa.edu.cn

  • 中图分类号: O354, O355, V211

PROGRESS AND PROSPECTS OF CARTESIAN MESH SIMULATION METHODS FOR COMPRESSIBLE FLOW PROBLEMS

  • *.

    State Key Laboratory of Mechanics and Control for Aerospace Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

  • †.

    School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, Jiangsu, China

  • **.

    Jiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

  • ††.

    Key Laboratory of Mathematical Modelling and High Performance Computing of Air Vehicles, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

摘要

    摘要
  • 摘要: 计算网格是复杂流动问题精细化模拟的先决条件, 会对数值结果的准确性和可靠性产生重要影响. 然而, 高质量计算网格生成需要费时费力的人机交互过程且严重依赖于工程师的个人经验, 使得现阶段计算流体力学(CFD)自动化程度处于较低水平. 笛卡尔网格具备生成简单、内存要求低、计算效率高及自动性强等特点, 使其能够极大减少网格生成过程中的人工成本, 因而成为CFD社区的研究热点之一. 对此, 以笛卡尔网格可压缩流模拟为主线, 结合课题组多年的研究成果对其中涉及的关键技术和国内外发展现状展开综述. 首先简要概述了笛卡尔网格自适应方法及其数据结构, 随后系统阐述了切割单元、浸入边界、重叠笛卡尔网格和混合笛卡尔网格等方法的发展现状及存在的问题, 最后从自适应加密策略、动态并行技术、高保真计算方法、先进物理模型及实际工程应用等多个维度深入探讨了笛卡尔网格方法涉及的关键技术与未来发展趋势. 通过全面回顾和深入分析笛卡尔网格方法的研究现状和发展动态, 试图为读者提供一个清晰及全面的认识, 并为相关领域的研究提供有益的参考和启示.
    Abstract: The computational grid is an essential prerequisite for the accurate simulation of complex flow problems, significantly influencing the accuracy and reliability of the numerical results. However, generating high-quality computational meshes requires a time-consuming and laborious human-machine interaction process that heavily depends on the personal expertise of engineers, resulting in a relatively low level of automation in computational fluid dynamics (CFD) at this stage. Cartesian grids have the characteristics of simple generation, low memory requirements, high computational efficiency, and strong automation, which can substantially reduce labor costs during mesh generation. Consequently, they have emerged as a prominent research focus within the CFD community. This paper primarily examines Cartesian grid method for the compressible flow simulations, integrating years of research findings from our group and reviewing key technologies alongside domestic and international development trends. Firstly, this paper briefly summarizes the adaptive methods and data structures of Cartesian meshes. Subsequently, it systematically describes the development status and existing challenges of techniques such as cut-cell, immersed boundary, overlapping Cartesian mesh, and hybrid Cartesian mesh methods. Finally, this paper discusses critical technologies and future development trends of Cartesian grid methods from various perspectives, including adaptive refinement strategies, dynamic parallel technology, high-fidelity computing methods, advanced physical models, and practical engineering applications. Through comprehensive reviews and in-depth analyses of the current research status and development of the Cartesian grid methods, this paper aims to provide readers with a clear and comprehensive understanding, and offer valuable references and insights for related field research.
    • HTML全文

  • 引 言

    计算流体力学(computational fluid dynamics, CFD)能够实现几乎任意测试条件下的数值模拟, 快速生成数据库, 进而显著减少研发周期和成本, 已然成为航空、航天及武器装备等领域空气动力学研究的一大重要手段[1-6]. 近年来, 随着计算能力的提高、数值方法的改进以及物理模型的完善, 不断推动着CFD技术的发展. 但是, 随着研究的逐步深入以及所涉及的流动现象愈发复杂, 工程领域对模拟结果的保真度提出了更加严苛的需求, 从而给CFD技术带来了越来越多的困难和挑战[1-2, 4, 6]. 2014年, 美国NASA发布了《2030 CFD 愿景: 通向革命性计算航空科学之路》的技术报告[1], 我国学者也于2023年相继出版了《计算流体力学2035愿景》一书[2], 为未来CFD技术的发展指明了方向, 主要涉及网格技术、数值算法、物理模型及高性能计算等诸多方面.

    其中, 在网格方面, 高质量的计算网格与可压缩流动问题的高保真模拟密切相关, 是整个CFD计算的基石, 对CFD的计算结果有直接影响[1, 7]. 特别地, 对于下一代CFD技术, 自动化程度将是其性能评估的一个重要技术指标. 例如, 著名优化设计专家Martins[8]将全自动网格生成称为CFD的“圣杯(holy grail)”. 但是, 生成高质量的计算网格往往需要费时费力的人机交互过程, 且严重依赖于工程师的实践经验(一般占整个CFD计算过程中人力参与时间的70%左右), 使得现阶段的CFD计算自动化程度处于较低水平. 正如网格生成商业软件Pointwise总裁Chawner等[9]所言: 网格生成是CFD过程中的“首要瓶颈(principal bottleneck)”和“主要成本(dominant cost)”, 以至于大多数CFD分析过程变得“繁重(onerous)”. 因此, 自动高效的网格生成技术是CFD领域的一个重要研究方向.

    如图1所示, 目前CFD中的网格类型可以大致分为: 结构网格、非结构网格和笛卡尔网格等, 它们在不同领域针对不同问题都具有各自的优势与劣势[10]. 比如, 结构网格易于生成符合边界层流动特征的大纵横比单元, 同等条件下对于物面附近的可压缩流动能够产生更小的截断误差, 具有更高的黏性分辨率; 同时, 由于其网格之间具有明确的逻辑关系, 所以易于构造高阶空间精度的数值格式. 但是, 对于实际工程中广泛存在的多体或三维复杂外形问题, 结构网格的易用性逐渐减弱. 相对而言, 非结构网格更适合处理复杂几何构型, 但其计算存储量一般比结构网格高, 且高质量的非结构网格生成严重依赖于CFD工作者的个人经验. 此外, 在数值算法构造上, 由于非结构网格间的拓扑关系不够明确, 使得高精度格式的构造比较困难. 相比而言, 重叠网格或混合网格能够有效结合两者各自的优势, 缓解各自面临的问题, 因而在实际工程中应用广泛[7, 9-10].

    图  1  不同网格体系特点[10]
    Figure  1.  The features of different grid systems[10]
    下载: 全尺寸图片 幻灯片

    特别地, 笛卡尔网格作为一类特殊的网格体系, 其体网格的生成与几何表面离散单元相互解耦, 对输入几何体的复杂性并不敏感, 可以自动快速地生成高质量网格. 同时, 笛卡尔网格比较容易实现网格自适应(比如根据局部曲率、外形表面单元尺度和缝隙等几何特征或根据旋涡、激波和边界层等流动结构进行不同层级的自适应加密), 使其能够以更低的成本实现复杂多尺度共存流动的高效模拟, 进一步提升了其工程应用前景. 因此, 笛卡尔网格相关理论一直是CFD社区的研究热点, 也是降低CFD过程中人力成本的重要手段[7, 11-13]. 对此, 国内外诸多学者和研究团队开展了各具特色的理论研究, 并相继发展了诸多以(自适应)笛卡尔网格为核心的解算代码. 比如美国NASA艾姆斯研究中心的著名快速气动预研软件Cart3D[14-20]、波音公司的TRANAIR[21]、陆军的OVERFLOW-D[22]、国防部的Helios[23]以及佐治亚理工学院的NASCART-GT[24-26], 法国ONERA的FAST[27-29], 英国的CHAMPS[30], 意大利的URANOS[31], 日本东京大学的UTCart[32-36]及东北大学的FFVHC-ACE[37-42], 以及其他国家的SPLITFLOW[43]、GeULER3D[44]、Cflow[45]等. 国内方面, 笔者团队的纯笛卡尔网格解算器CABA[46-50]以及重叠笛卡尔网格解算器H-CABA[51-55], 中国空气动力研究与发展中心的ACGBuilder/CGESolver[56]、Cart-X[56-61], 西北工业大学的HLCE3D[62-64]以及北京荣泰创想公司的PiFlow等.

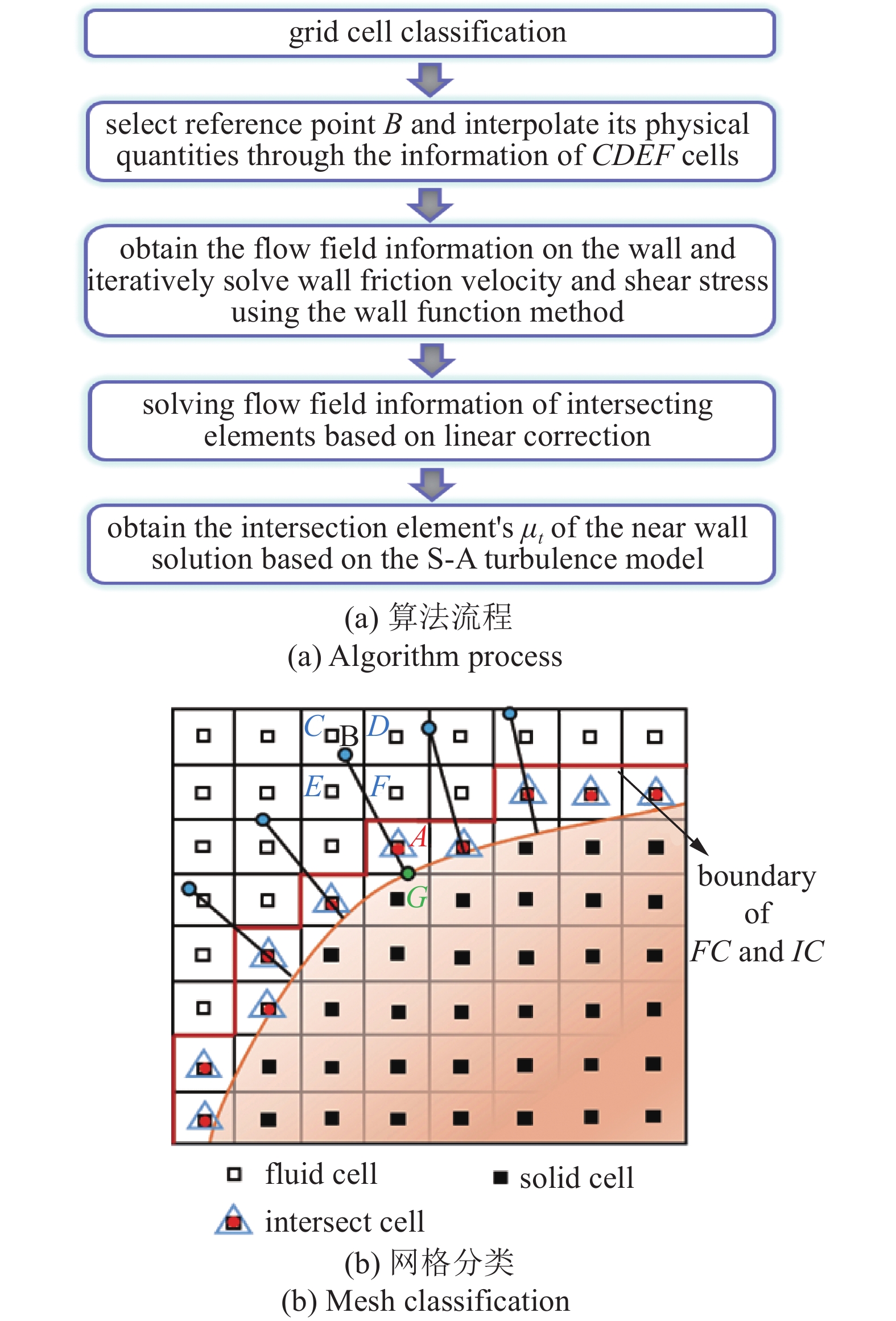
    虽然笛卡尔网格生成方法具备生成速度快、鲁棒性强、自动化程度高、网格质量好等优点, 但是其不可避免地带来了额外的困难. 主要体现在笛卡尔网格的非贴体性容易造成“阶梯形”的物面边界, 进而对模拟结果的可信度产生不利影响[7, 10-11, 25, 65]. 因此, 壁面处理成为制约笛卡尔网格工程应用的主要瓶颈. 对此, 常用的方法有4种(如图2所示): (1)切割单元方法; (2)浸入边界方法; (3)重叠笛卡尔网格方法; (4)混合笛卡尔网格方法. 它们有各自的优势及适用范围, 也存在相应的缺陷. 与此同时, 笛卡尔网格的各向同性特征使得其产生的网格量相比于其他网格高1 ~ 2个量级(如图3所示), 极易造成“网格灾难”问题[25]. 例如, 当雷诺数为106时, 对于二维翼型绕流问题, 纵横比为100和10的贴体网格所需网格量分别为103和104量级, 而所需笛卡尔网格数为105量级; 而对于三维问题, 笛卡尔网格数迅速增加到将近为109量级, 而贴体类网格仅为104 ~ 107量级[25]. 另一方面而言, 尽管自适应技术可以在一定程度上减少网格量, 同时提升关键流动模拟的精细程度. 但是, 动态变化的网格体系也给数据管理、并行计算、空间离散算法构造等带来了一定的挑战. 一方面, 区别于静态网格并行分区的“一劳永逸”, 自适应笛卡尔网格涉及频繁的几何自适应、解自适应、2:1平衡等动态变化过程, 给大规模网格数据管理、并行生成、并行计算以及高可扩展性等方面的实现带来了巨大困难. 另一方面, 动态变化的网格体系也加大了高精度、守恒、紧致和鲁棒的数值算法构造难度. 因此, 国内外学者针对自适应笛卡尔网格方法的理论及应用等方面开展了各具特色的研究, 本文将对其进行系统性的综述.

    图  2  笛卡尔网格方法分类(三维图分别来源于Cart3D网页[66]、笔者团队、桑为民等[64]以及Helios[67])
    Figure  2.  The classification of Cartesian grid methods (the three-dimensional diagrams are sourced from the Cart3D website[66], the author's group, Sang et al.[64], and Helios[67])
    下载: 全尺寸图片 幻灯片
    图  3  相同物理条件下贴体网格和笛卡尔网格数量比较[25]
    Figure  3.  Comparison of numbers between the body-fitted and Cartesian grids under the same physical conditions[25]
    下载: 全尺寸图片 幻灯片

    简而言之, 笛卡尔网格在可压缩流动问题模拟已有几十年的发展历史, 并取得了丰硕的成果. 但是, 据笔者所知, 国内外对此方法系统性的介绍尚未见到. 笔者团队在此方向开展了系统性的研究工作, 包括纯/混合笛卡尔网格生成理论、高精度格式、壁面处理方法、并行技术以及工程应用等. 因此, 本文结合我们在此领域多年的耕耘, 以自适应笛卡尔网格为主线, 对其中涉及的关键技术和国内外发展现状展开综述, 并结合现代CFD技术的发展对笛卡尔网格高保真模拟的发展方向给出展望.

    1.   笛卡尔网格自适应方法及数据结构

    正如前文所言, 笛卡尔网格具有生成自动化程度高、网格质量好和流场模拟能力强等优异特性, 但其内在的各向同性使得模拟包含激波、漩涡、边界层等多尺度共存问题时的代价是巨大的. 而自适应技术能够以相对更小的代价处理这类复杂流动问题, 是解决上述“网格灾难”难题的有力途径. 因此, 自适应笛卡尔网格方法具备更好的工程应用前景. 一般地, 常用的自适应技术包含以下几类[68-70]: (1)网格不断加密/粗化的h型自适应; (2)网格总数不变, 但网格点随流场移动的r型自适应; (3)网格单元内数值格式精度随流场变化的p型自适应; (4)混合型自适应(如hp型自适应). 对于笛卡尔网格而言, h型自适应能够很好地继承其正交性和层次性, 具备更好的工程实用性.

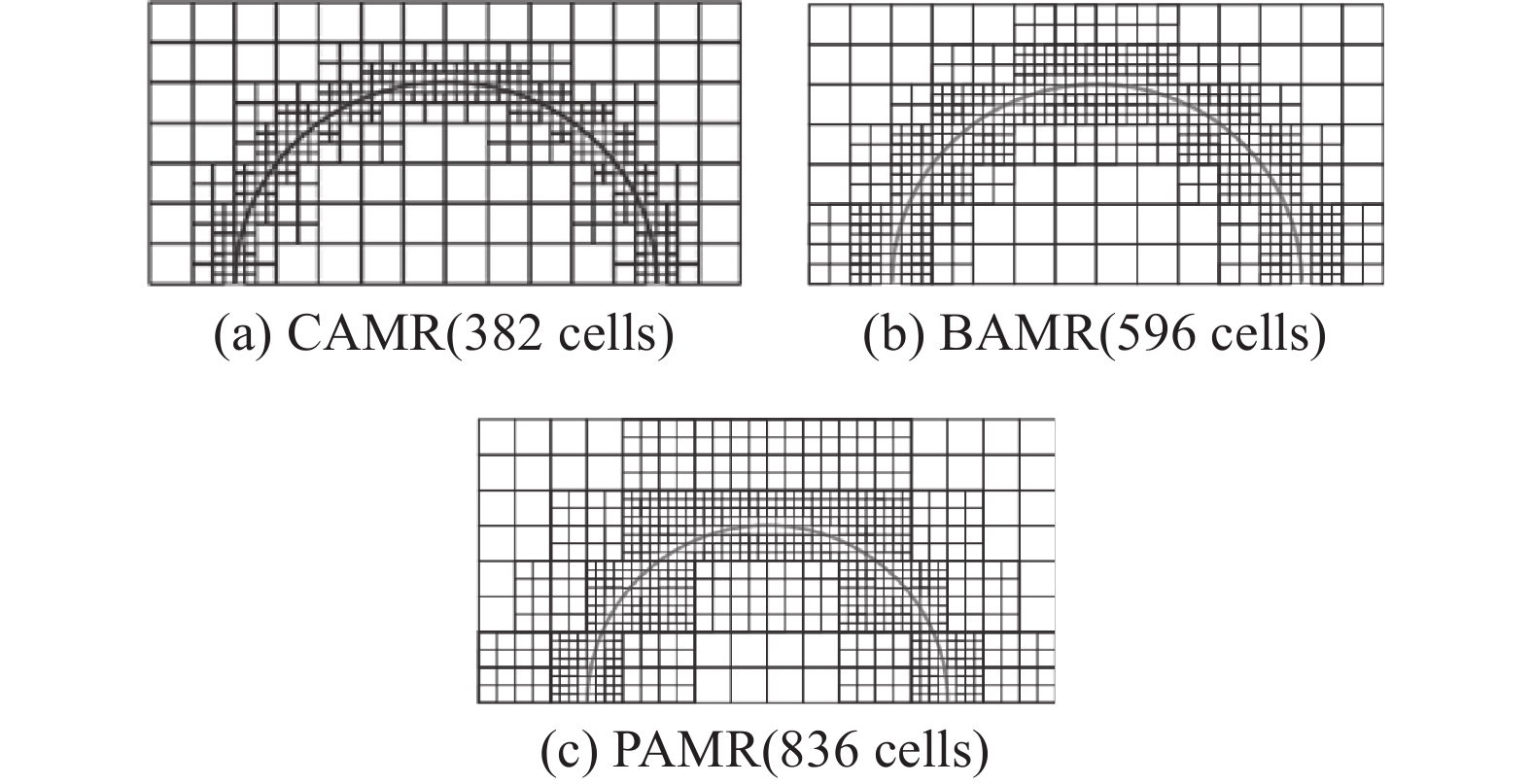
    然而, 对于h型自适应网格加密(adaptive mesh refinement, AMR)而言, 频繁进行的加密和粗化操作给网格单元的数据管理带来了巨大的困难, 如何构建高效的数据结构用于管理不同层级的网格将会对解算器的计算效率和空间存储产生重要影响[71-72]. 图4给出了目前常用的两种数据结构, 并衍生了3类h型自适应笛卡尔网格(如图5所示): (1) cell-based AMR (CAMR)[48-50, 61, 72-74]; (2) block-based AMR (BAMR)[23, 40, 75-79]; (3) patch-based AMR (PAMR)[71, 75, 80-81].其中, CAMR通常使用树结构来管理网格数据, 且允许叶子节点进行任意次数的加密/粗化和递归, 故而具备良好的数据管理能力和灵活的自适应能力. 同时, 为了保证不同层级网格之间过渡光滑, CAMR一般要求相邻网格单元之间的加密层级不超过1, 即遵循2: 1原则. 此外, 如图5(a)所示, 相比于其他两种方法, CAMR在同等条件下产生的加密网格单元数相对最少. 但是, 该方法的实现过程中存在大量不规则的内存使用, 进而影响代码的数据读取效率.

    图  4  不同自适应笛卡尔网格数据结构示意图
    Figure  4.  Schematic diagram of different adaptive Cartesian grid data structures
    下载: 全尺寸图片 幻灯片
    图  5  同等条件下三种自适应笛卡尔网格方法比较图[71]
    Figure  5.  Comparison diagram of three adaptive Cartesian grid methods under the same conditions[71]
    下载: 全尺寸图片 幻灯片

    BAMR和PAMR方法较为类似, 都采用补丁型数据结构进行管理, 将加密单元通过聚类算法分成若干个规则网格块(二维为矩形, 三维为长方体), 然后每个区域内部生成结构化的均匀笛卡尔网格. 因此, 部分学者也将此类方法称之为结构网格自适应(structured AMR, SAMR). 该方法在数据存储与访问、相邻单元查找和不同层级网格之间的信息传递等方面具有一定的优势, 并且其无需遵循2:1 准则, 允许任意跨度的网格过渡. 但是, 如图5(b) ~ 图5(c)所示, 由于其必须生成规则的网格块, 所以部分未被标记的单元也需要进行相应层级的加密, 进而使得其在同等条件下产生更多的网格单元. 特别地, 基于上述自适应笛卡尔网格架构和加密策略, 已相继搭建了许多较为成熟的AMR代码或管理库, 如: PARAMESH[82], SAMRAI[83], p4est[72], AMReX[84]以及文献[75]中列出的BoxLib, Cactus, Chombo, Enzo, FLASH和Uintah等, 并基于此发展了诸多解算代码用于计算流体力学、天体物理、磁流体力学等领域的工程问题模拟研究. 而从自主知识产权的自适应笛卡尔网格CFD软件架构的发展来看, 开发自适应笛卡尔网格管理库具有重要的意义.

    2.   基于笛卡尔网格的模拟方法及分类

    对于实际工程中广泛存在的绕流问题, 笛卡尔网格的非贴体性使其难以直接准确模拟物体表面附近的流动, 尤其是高雷诺数可压缩流动问题. 因此, 如何构造相应的壁面处理技术将直接决定笛卡尔网格方法的工程应用前景, 这也是目前国内外学者在这一方向重点关注的研究内容. 对此, 国内外学者相继发展了切割单元方法、浸入边界方法、重叠笛卡尔网格方法和混合笛卡尔网格方法等. 表1简要给出了上述4种方法各自的优势和劣势. 下面将详细综述各种方法的国内外研究现状及发展方向.

    表  1  各类笛卡尔网格方法优缺点
    Table  1.  Advantages and disadvantages of various Cartesian grid methods
    下载: 导出CSV 
    | 显示表格

    2.1   切割单元方法

    2.1.1   方法介绍及基本流程

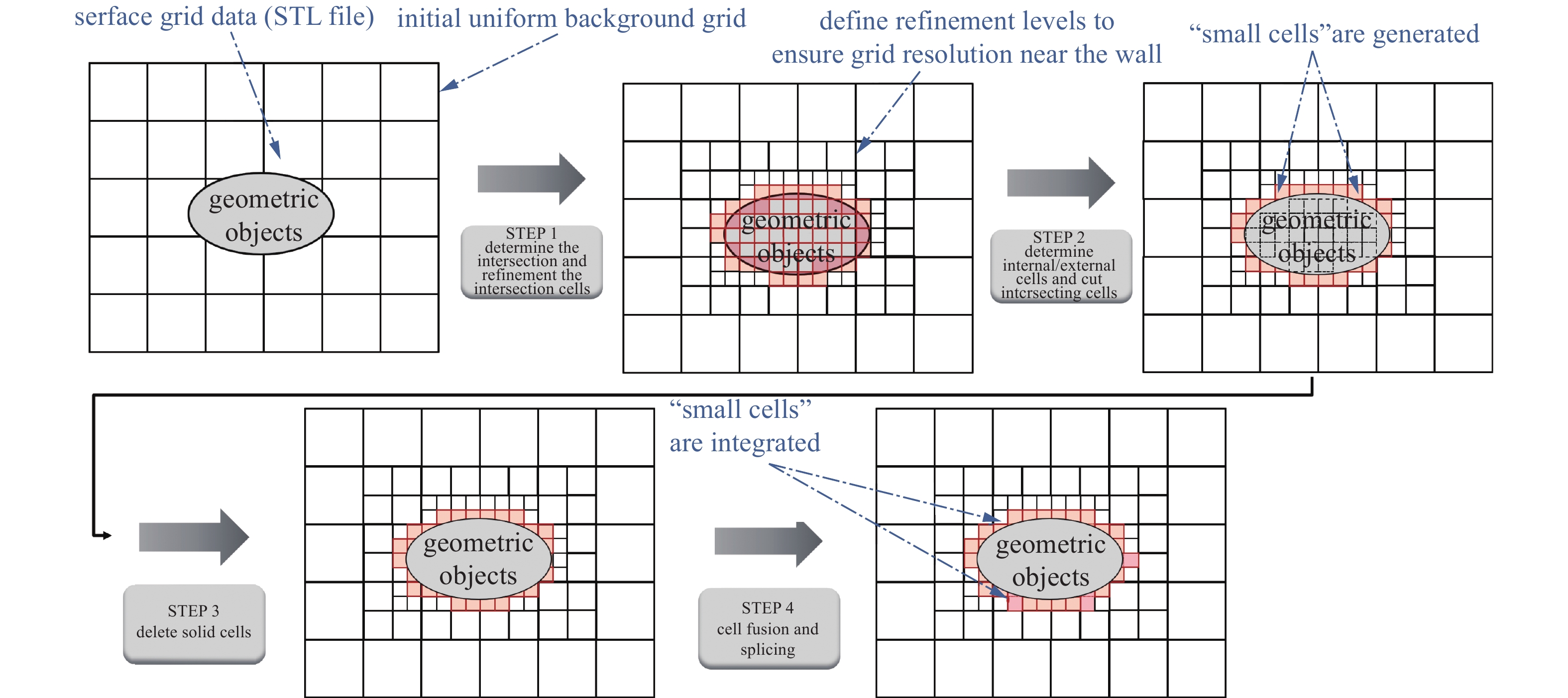
    切割单元方法通过笛卡尔网格与物面边界的几何关系将计算单元分为流场内部和物体内部区域, 然后去除所有物体内部区域的计算单元, 并将物面边界作为控制体单元的一部分. 图6给出了该方法的基本流程.

    图  6  切割单元方法基本流程
    Figure  6.  Basic process of the cut-cell method
    下载: 全尺寸图片 幻灯片
    2.1.2   国内外发展现状

    切割单元方法简单直接, 一方面充分继承了笛卡尔网格生成的直观、高效以及自动化特性, 同时由于几何外形是网格体系的一部分使其具备了较好的贴体性质. 因此, 诸多学者对此开展了广泛的研究. 1986年, Clarke等[85]首次将切割单元笛卡尔网格方法由位势方程推广到了无黏Euler方程, 并随后推广至三维情形[86]. De Zeeuw等[87]将其用于无黏定常三段翼以及三维复杂外形(喷气式商务机及侦察机)模拟研究[88]. 1997年, 美国NASA艾姆斯研究中心的Aftosmis等[14-15]在切割单元方法理论与应用方面做出了里程碑式工作, 与美国三院院士Berger等开发了著名的自适应笛卡尔网格全自动解算平台Cart3D[66], 并因此获得了2002年度NASA软件大奖. 作为全自动快速气动设计软件, 其能够全自动生成任意复杂外形的贴体自适应笛卡尔网格, 并快速给出气动参数数据库(尤其是飞行器初步设计阶段), 在航空航天领域的应用非常广泛(如图7所示), 其他应用可见其网页[66].

    图  7  切割单元软件Cart3D的典型计算结果[16, 66]
    Figure  7.  Typical computational results of the cut-cell software Cart3D[16, 66]
    下载: 全尺寸图片 幻灯片

    国内方面, 桑为民等[89-92]在笛卡尔非结构切割网格方法方面开展了系统性的研究; Li等[93]将各向异性加密思想融于各向同性自适应切割笛卡尔网格方法, 同等条件下能够节省30% ~ 40%的网格量; 逯雪铃等[94]于2009年提出了一种改进的射线求交法用于提升切割笛卡尔网格生成过程中内外判断的准确性等.

    2.1.3   黏性流动问题模拟

    对于黏性可压缩流动问题, 笛卡尔网格的各向同性极易造成“网格灾难”问题, 也极度考验切割网格方法壁面附近网格单元生成能力. 对此, Marshall等[26]基于切割自适应笛卡尔网格开发了NASCART-GT求解器, 并推广到非平衡化学反应流动模拟[95]. Kidron等[96]开展了高雷诺数湍流问题研究. Hartmann等[97]首次实现了三维切割网格单元方法的黏性流动问题模拟. 2012年, Berger等[20]基于Spalart-Allmaras湍流模型开展了黏性壁面边界处理技术的初步探索, 发展了切割单元壁模型, 实现了Cart3D软件的二维高雷诺数可压缩流动问题求解能力. Pasquariello等[98]基于切割笛卡尔网格发展了有限体积-有限元耦合方法用于流-固相互作用问题研究等.

    2.1.4   “小单元”处理方法

    由于几何外形的复杂性, 切割单元方法会产生任意形状的剪切单元, 其中的“小单元”会引起控制方程刚性增强和显式时间步长过小问题, 对数值算法的稳定性和计算效率产生重要影响, 尤其是高雷诺数湍流问题[99]. 同时, 壁面附近“不光滑过渡”的任意形状切割单元容易对气动参数的光滑性产生负面影响(尤其是表面摩擦力和热传导系数等导数量), 进而影响数值算法的收敛性[100-101].

    对此, 诸多学者针对切割单元方法产生的小单元问题展开了相应的研究. 1995年, Pember等[102]发展了通量重分布算法来解决剪切小单元产生的稳定性问题. Coirier等[100]设计了改进的多边形裁剪算法处理物面外形与笛卡尔网格相交的剪切单元. 随后, Yang等[103]发展了单元合并技术用于解决切割笛卡尔网格方法的稳定性问题. 1999年, Ye等[104]提出了融合切割单元方法, 将边界附近切割形成的小单元(小于未切割单元的50%)与最近的相邻单元进行融合, 解决“小单元问题”. Mondal等[105]发展了一种网格拼接算法, 其将笛卡尔网格点移至物面边界进而生成相对光滑的壁面网格用于计算. 2009年, Hartmann等[97]提出了一种三维单元合并/连接方法. 该方法允许使用更大的CFL条件数, 有效提升了数值稳定性. 2016年, Muralidharan等[106]提出了一种新的单元聚类算法用于重构小切割单元附近的多项式, 进而解决小单元引起的嵌入边界附近的数值振荡问题. Müller等[107]利用Level-Set方法确定固体边界, 并结合非浸入的单元合并技术用于避免小的或不规则切割单元问题. Gokhale[108]在切割网格方法理论及应用方面开展了系列工作, 提出了维度分裂笛卡尔网格切割方法, 构造了稳定的切割单元通量计算方法用于解决“小单元”稳定性问题, 并首次实现了汽车流场的WMLES切割笛卡尔网格模拟.

    2.1.5   运动问题模拟

    对于运动问题, 切割单元方法会在壁面附近产生非物理振荡. 一般认为, 产生该问题的根本原因是边界运动使得部分流场单元在下一时刻变成切割单元或物体内部单元, 而这种突然的不连续变化容易演变成非物理源项, 破坏边界附近的局部守恒性, 进而产生非物理振荡[109].

    对此, Seo等[110]提出了一种可以改善局部质量守恒的方法用于解决压力振荡问题. 2013年, Schneiders等[109]构造了一种精确的移动边界离散算子公式, 避免产生大小不连续的切割单元和非物理振荡, 并首次基于切割单元方法实现了三维黏性移动问题模拟. Muralidharan等[79]提出了一种新的单元聚类算法用于重构小切割单元附近的多项式, 解决了运动边界化学反应模拟中小单元引起的边界附近数值振荡问题. Schneiders等[111-112]对切割单元法的稳定性和守恒性展开了研究, 基于奇异值分解的加权Taylor级数方法提出了一种新的小剪切单元计算公式, 对于大位移问题也具有较好的守恒性.

    2.1.6   存在的问题

    需要注意的是, 虽然切割单元方法得到了较好的发展, 但必须承认的是其算法相对比较复杂, 特别是在三维流动模拟中. 如文献[99, 103, 113]中所示, 二维情形下, 几何外形与笛卡尔网格相交产生的切割单元有12种情形, 而延伸到三维情形高达上百种相交情况. 一方面, 需要大量的计算成本用于处理这些不同类型的切割单元. 另一方面, 切割单元方法会在预测的表面量中引入数值波动, 且这种波动不会随着网格分辨率的增加而消失. 同时, 将小单元与相邻较大的单元合并会产生表面单元体积的非光滑变化, 使得压力、表面摩擦和热通量等产生较大的波动, 容易得到非光滑数值解, 尤其是梯度量(如热通量)计算[101]. 因此, 不同类型切割单元之间的通量计算需要特别注意. 而在高雷诺数流动模拟中, 黏性效应主要集中在边界层内, 而切割网格单元方法在处理这类边界层流动时, 难以达到贴体网格所能提供的高长宽比网格效果. 要想解决此问题, 现在普遍通行的方法还得借助于壁面函数或者壁面模型来获得较为准确的边界条件.

    2.2   浸入边界方法

    2.2.1   方法介绍及基本流程

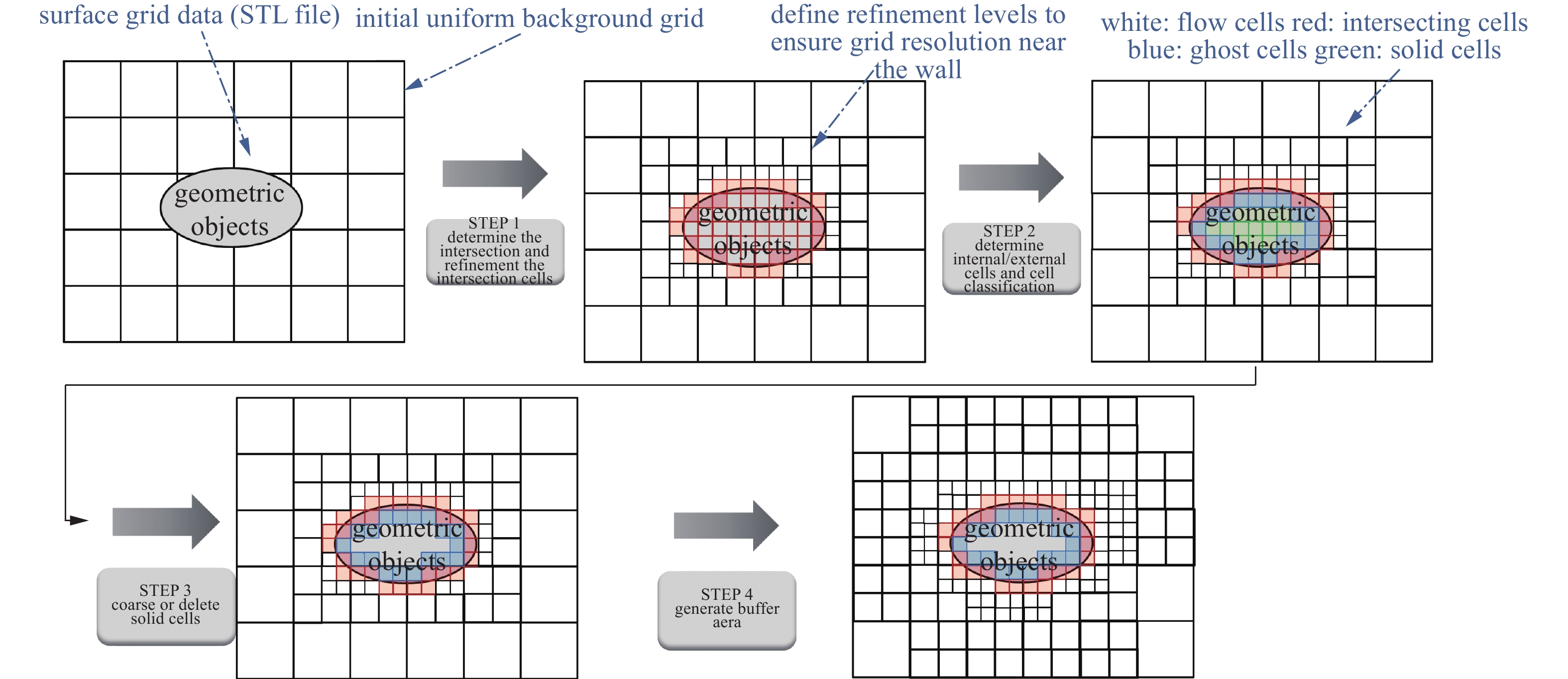
    浸入边界方法(immersed boundary method, IBM)分为连续力法和离散力法, 可以被视为数学建模方法或是数值离散方法, 它将物体边界与流体之间的相互作用通过在控制方程中添加体积力源项或修正边界条件的方式来体现[114]. “immersed boundary”一词最早由Peskin[115]于1972年提出, 并将其用于模拟心脏中的血液流动问题. 因此, Peskin也被誉为“IBM之父”[13]. 图8给出了IBM方法的一般性流程. 可以看出, IBM方法不需要对自动生成的笛卡尔网格进行进一步的切割处理, 编程实现较为简单, 避免了按照物体边界形状生成贴体网格所遇到的各种问题. 因此, 浸入边界方法持续受到流体力学工作者的青睐, 也一直是计算流体力学的一大研究热点[12-13, 99, 116-118].

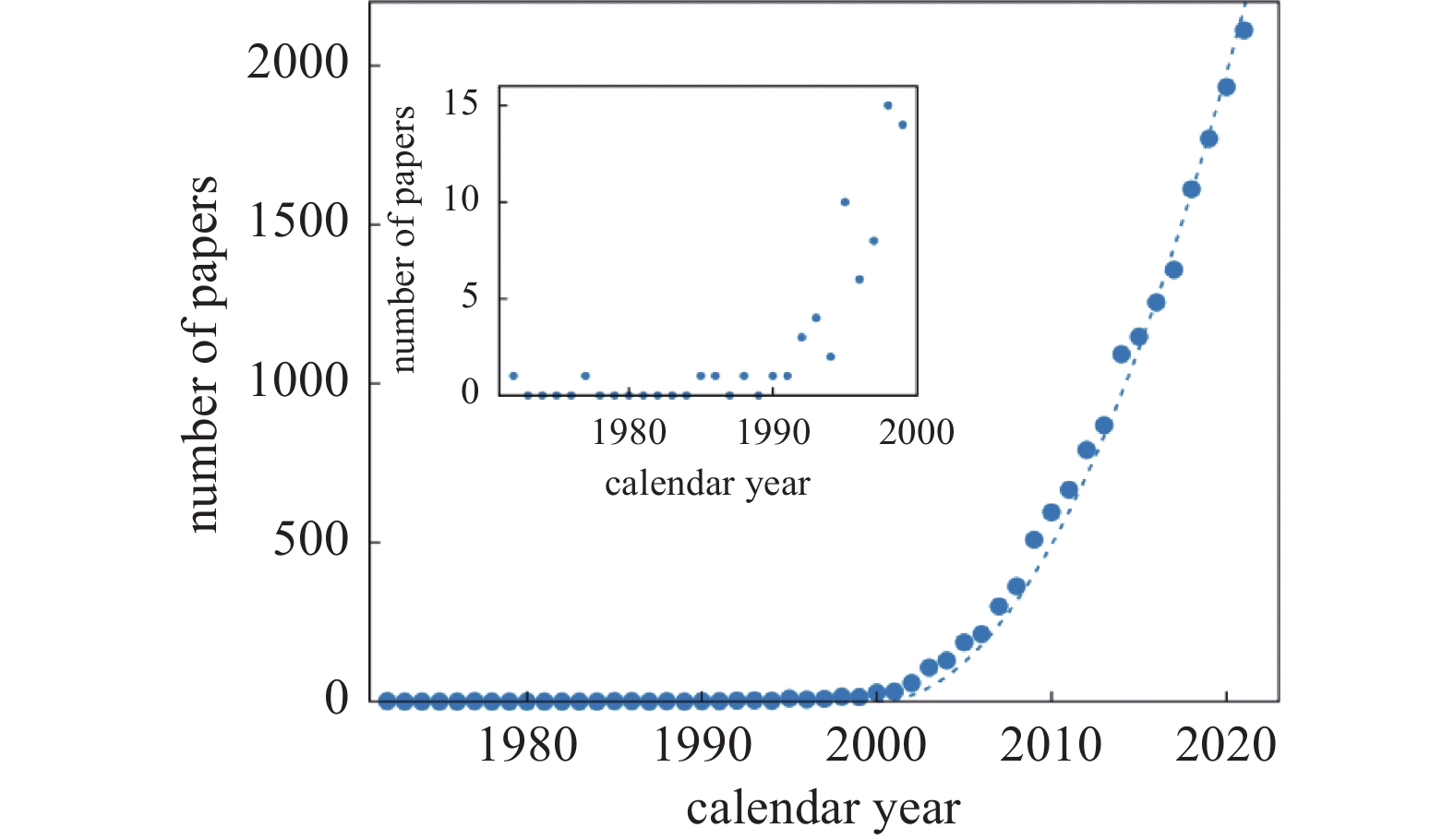
    2023年, Verzicco[13]在流体力学年鉴论文中系统介绍了IBM方法的起源、发展以及现阶段面临的问题和展望. 如图9所示, Verzicco检索了1970 ~ 2022年间标题中含“immersed boundary/boundaries”的论文数变化情况, 充分印证了IBM方法的关注热度[13]. 值得注意的是, 不可压缩流动问题的IBM方法研究相对更多[12-13, 114, 117-118], 而本文主要考虑可压缩流动. 因此, 后续将着重介绍可压缩流动IBM方法发展现状.

    图  8  浸入边界方法基本流程
    Figure  8.  Basic process of the immersed boundary method
    下载: 全尺寸图片 幻灯片
    图  9  1970—2022年间IBM有关论文变化趋势[13](图中统计数据来源于Scopus数据库, 统计时间截至2022年1月31日)
    Figure  9.  The trend of IBM-related papers from 1970 to 2022[13] (the statistical data in the figure is sourced from the Scopus database, with the data collection up to January 31, 2022)
    下载: 全尺寸图片 幻灯片
    2.2.2   国内外发展现状

    一般地, 在IBM方法中, 如何定义物面边界条件是其中的核心, 而对称反射(ST)方法是最为常用的物面边界处理技术. 但是, ST方法忽略了外形曲率的影响. 对此, Dadone等[119]提出了曲率修正对称(CCST)方法, 并在文献[120]中推广到笛卡尔网格, 命名为GBCM方法. 为了提升壁面求解精度, 美国劳伦斯伯克利国家实验室Colella等[121]提出了质量增量重分布思想, 发展了有限体积框架下的浸没边界方法. Capizzano[122]发展了各向异性自适应笛卡尔网格IBM方法用于减少网格量, 并提出了面边界条件模型用于解决近壁单元的守恒性问题, 同时在文献[123]中基于偏微分方程计算壁面距离用于解决传统遍历搜索法随着几何外形表面三角形数目及维数的增加效率急剧下降的问题. Kamatsuchi[124]基于自适应笛卡尔网格和浸入边界方法实现了F1方程式赛车复杂流动模拟(含140万几何外形表面单元). 国外团队的其他研究, 这里不再一一介绍, 详见文献[113, 116, 125-129].

    国内方面, 肖涵山等[56]于2003年开展了纯笛卡尔网格方法系列研究. 高正红团队[130]基于纯笛卡尔网格方法实现了三维无黏绕流问题模拟, 并推广至运动非定常问题[131]. 为了减小壁面附近的质量损失, Liu等[46, 73]率先提出了二/三维曲率校正虚拟单元-浸入边界方法, 并对浸入边界方法、径向基函数插值方法和内埋弹舱运动模拟等开展了系统性的研究[50, 132]. Zhang等[133]提出了无黏可压缩流动模拟的有限体积HCIB方法. 文献[134]中基于IBM方法系统研究了Dirichlet、Neumann和Robin 3种边界条件下的热传导问题. 2018年, 唐志共等[135]采用纯自适应笛卡尔网格技术模拟超声速流动问题, 并提出了一种改进的全线程树(FTT)数据结构用于提升自适应笛卡尔网格生成效率[57]. 2023年, 卢俊宇等[136]基于自适应笛卡尔网格和IBM方法介绍了一种有限差分自动化CFD计算新框架和初步实现方法. 特别地, 上述国内工作大多基于串行或OpenMP框架, 而动态网格对多核CPU并行IBM方法的实现带来了额外的挑战. 对此, Qi等[48]发展了一种自适应笛卡尔网格多核并行生成策略及计算框架. 国内其他团队有关IBM方法的工作见文献[60, 137-140], 这里不再叙述.

    基于上述研究, 国内外团队发展了诸多基于纯笛卡尔网格和IBM方法的解算器, 比如: 美国Arslanbekov等[101]的UFS、法国ONERA的FAST[27-29]、法国CEA-CESTA的HYPERION高超声速解算器[141]、英国牛津大学van Noordt团队[30]的CHAMPS (主要面向高超问题)、意大利De Vanna等[31]的URANOS、日本东京大学的UTCart[32-36]、日本东北大学Kawai团队的FFVHC-ACE[37-42]以及国内ACGBuilder/CGESolver[56]、Cart-X[57-60]和笔者团队的CABA[48-49, 55]等.

    2.2.3   网格生成效率

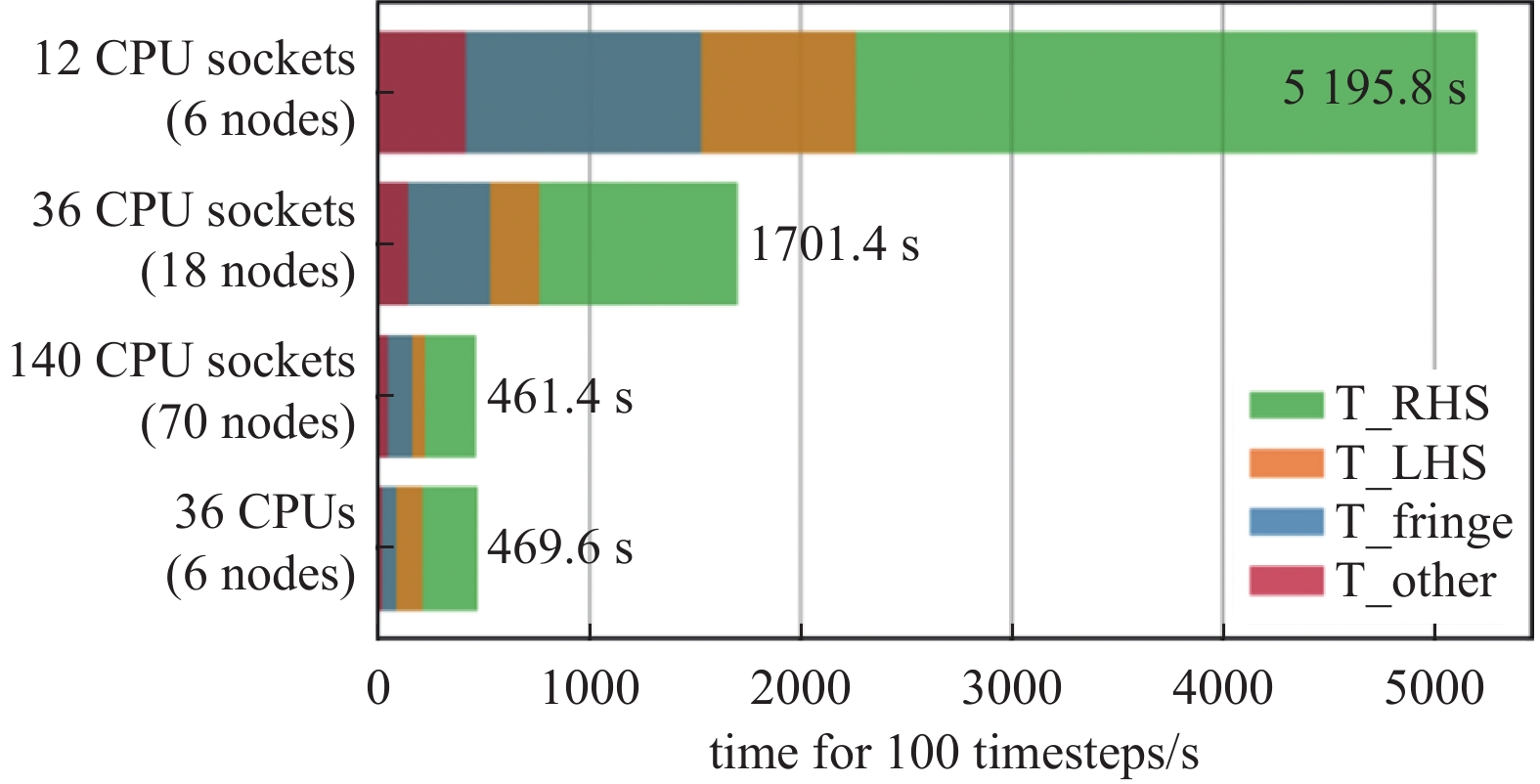
    特别地, 自适应笛卡尔网格的大规模生成能力和效率对IBM方法的应用前景至关重要. Nakahashi团队[142]发展的Building-Cube算法不需要完全水密的几何外形便可快速自动生成自适应笛卡尔网格, 同时具备“脏”几何处理能力, 多核CPU的PC上生成1亿网格仅需几分钟[78, 142]. 意大利航空航天研究中心Capizzano[123]采用完全非结构化的数据结构, 实现了自适应笛卡尔网格轻量级数据管理, 生成单个网格的时间约为$ 9.0\times10^{-5} $ s. 2021年, 法国ONERA纯笛卡尔网格求解器FAST[29]采用336核生成15亿网格仅需18 min. 中国空气动力研究与发展中心毕林团队[59, 143]提出了一种高效的笛卡尔网格生成策略. 2023年, 日本东北大学Kawai团队[42]发展的纯笛卡尔网格求解器FFVHC-ACE在日本超级计算机“富岳”实现了500亿网格并行生成与计算能力. 笔者团队发展了一种高效的笛卡尔网格内外/相交判断、壁面距离计算及网格生成策略, 如图10(a)所示. 图10(b)结果显示该方法在2048核下并行生成10.5亿网格仅需47.73 s (单个网格时间约为$ 9.3\times10^{-5} $s ), 且千核并行效率接近80%.

    图  10  纯自适应笛卡尔网格并行生成方法
    Figure  10.  Parallel generation method of purely adaptive Cartesian grids
    下载: 全尺寸图片 幻灯片

    从上述数据可以看出, 在自适应笛卡尔网格生成效率方面, 国内外发展水平相当, 但在计算能力方面依然存在一定的差距. 同时, 随着计算机硬件性能的提升和并行技术的发展, 自适应笛卡尔网格的生成效率仍有望突破至新的极限.

    2.2.4   镜像点插值方法

    IBM方法的核心是通过边界条件和流场内部信息得到固体内部虚拟单元的物理量. 其中, 流场内部信息一般为虚拟单元沿物面镜像点处的物理量. 但是, 虚拟单元的镜像对称点往往位于非网格点处, 需要通过其周围单元插值得到. 因此, 镜像点物理量的插值精度将会直接影响IBM方法的准确性.

    计算镜像单元值的经典方案是二维双线性插值(三维为三线性插值)[144-145]. 但是, 当镜像点非常靠近固体边界时, 可能会遇到插值点不在流体区域的情况. 对此, 可以通过零阶外推[146]或使用部分点进行插值[145]. 当然, 该方法也存在一定的缺陷, 比如前一种方法可能导致唯一的零阶外推, 而后一种方法在Neumann边界条件下难以实现. 逆距离加权(IDW)插值方法[144, 147-148]也常被用于构造锐利界面IBM方法中镜像点的物理量. 该方法对于重构光滑变化而不包含大梯度物理量的变量是稳定的, 而考虑到镜像点插值模板中可能存在间断, 容易导致近壁区域的不准确评估. 因此, 受高精度本质无振荡(ENO)格式的启发, Bridel-Bertomeu[149]发展了ENO型最小二乘插值方法, 类似的工作还有移动最小二乘(MLS)方法[110]、非线性加权镜像点插值方法[150]等. 需要注意的是, 上述方法的精度至多为二阶. 2010年, Tan等[151]发展了一种高精度逆Lax-Wendroff (ILW)插值方法, 可以实现5阶精度的边界处理. Brehm等[152]也提出了一种高精度边界处理技术(${L^\infty }$范数3阶和4阶). 其他有关镜像点插值方法的工作这里不再一一介绍, 比如基于PDE的镜像点插值方法[153]、改进的虚拟单元浸入边界方法[154]、局部坐标下的双线性/三线性镜像点插值方法[155]、带约束的MLS方法[156]等.

    国内方面, 刘剑明[132]发展了径向基函数(RBF)插值方法; Luo等[157]发展了适用于传热问题的逆距离插值和双线性插值方法; 何跃龙等[158]提出了一种指数镜像点插值方法, 根据速度、压力和温度等变量在壁面附近的物理特性使用不同的插值公式; Wang等[159]发展了BCGCM和HBCGCM镜像点插值方法用于提升IBM方法的精度和稳定性; Cheng等[160-161]将ILW方法推广到移动问题研究, 并在文献[162]中考虑壁面附近的迎风特性发展了相应的ILW高精度插值方法; 以及罗灿炎等[163]提出了双二次插值方法等.

    2.2.5   高雷诺数黏性流动模拟

    对于真实情况的黏性流动, 笛卡尔网格必须在所有方向上进行细化才能解析边界层内部结构, 而这将会带来难以承受的网格量(三维情形比贴体网格高2 ~ 4个量级[25]). 而随着雷诺数的增加, 边界层变薄, “网格灾难”问题将会越发严峻[13]. 因此, 高雷诺数流动一直是IBM方法的瓶颈问题. Ruffin等[25]提出的法向射线加密方法在一定程度上可以减少网格量, 但该方法尚处于初步理论研究阶段, 且如何根据几何外形合理分布法向射线、如何处理相邻法向射线间网格尺度变化大以及如何推广到三维情形还需要进行深入研究. 相对而言, 通过选择合适的壁面模型或壁面函数模化壁面附近的流动, 从而以更少的网格得到可接受的计算结果是目前能够从根本上缓解IBM方法“网格灾难”问题的有利途径.

    事实上, 对于贴体网格而言, 可以在壁面解析(wall-resolved)和壁面模型(wall-modeled)方法之间自由选择, 但对于IBM方法, 似乎只有后一种方法是可行的[13, 164]. 2006年, Lee[24]首次将壁面函数方法用于笛卡尔网格框架, 然后利用制动盘理论实现了旋翼直升机的高雷诺数湍流模拟. Capizzano结合双层壁模型[165]和壁扩散模型[166]用于提升高雷诺数压力诱导分离流模拟的准确性. 2016年, Bernardini等[167]结合基于S-A湍流模型的DDES方法和IBM方法用于复杂几何的高雷诺数可压缩湍流模拟, 其中流固界面处的边界条件根据自适应壁面函数[168]得到. 2017年, Tamaki等[32]基于UTCart提出了一种用于高雷诺数湍流模拟的IBM方法, 通过施加壁面边界处的滑移速度和改变S-A湍流模型中的阻尼函数, 实现了更为准确的表面摩擦预测, 并用于三维整机(NASA CRM构型和JAXA JSM高升力构型)[33]、起落架[34]以及三维旋翼[35]等问题研究. 此外, 由于近壁网格分辨率降低, 无法准确插值沿壁面法向上快速变化的物理量, 也难以准确计算其梯度, 容易产生虚假振荡. 对此, Cai等[164]发展了一种改进的IBM-壁面模型耦合方法用于抑制数值结果的虚假振荡, 得到更加光滑的壁面量(如壁面压力和表面摩擦力)以及更准确的积分量(如阻力和升力系数). 类似地, Constant等[27]基于FAST解算器提出一种改进的湍流壁模型IBM方法同样能够消除壁面压力和摩擦系数的虚假振荡.

    国内方面, 笔者团队[47, 169-171]率先开展了纯笛卡尔网格框架下壁面函数方法的系列研究. 图11给出了该方法的算法流程和二维示意图. 如图11(b)所示, 首先由近壁相交单元A中心沿物面法线方向朝着流场区域引出固定距离, 得到落在流体内部的参考点B. 随后, 以点B处的流场变量(周围单元插值得到)作为参考值代入壁面函数公式, 利用Newton迭代方法得到壁面摩擦速度及剪切应力, 进而通过点AB之间物理量的线性关系即可得到相交单元A处的流场变量. 壁面函数方法综合考虑了涡黏性和分子黏性的影响, 在边界层内的模拟效果较好, 能够大幅降低${y^ + }$的要求, 进而缓解笛卡尔网格处理高雷诺数流动问题时因各向同性带来的“网格灾难”问题. 图12给出了针对M6机翼绕流问题的千万量级网格全自动并行生成及计算[49]结果, 验证了课题组发展的纯笛卡尔网格解算器CABA, 得到了与实验和贴体网格吻合的数值结果.

    图  11  纯笛卡尔网格壁面函数壁面处理方法
    Figure  11.  Wall treatment method for wall functions in pure Cartesian grids
    下载: 全尺寸图片 幻灯片
    图  12  雷诺数DLR-F6绕流问题纯笛卡尔网格方法计算结果[49]
    Figure  12.  Computational results of high-Reynolds flow over DLR-F6 model using the pure Cartesian grid method[49]
    下载: 全尺寸图片 幻灯片

    此外, Chen等[172-173]基于Tamaki等[32]的壁面模型[32]实现了涡轮机械的非定常模拟. Zhou等[174-175]基于IBM方法开展了自适应壁面函数和双层墙模型[174]以及平衡型壁面模型[175]研究. 上海交通大学Yang等[176-177]采用IBM-壁面函数耦合方法模拟发动机内流问题. 特别地, IBM方法的参考点位置对高雷诺数湍流的准确性有重要影响. 对此, Wang等[178]提出了一种自适应强制距离技术. 陈浩等[179]介绍了在“国家数值风洞工程”资助下黏性自适应笛卡尔网格方法的研究进展等.

    2.2.6   存在的问题

    上述方法有力推动了IBM方法的工程应用前景, 但已有研究证明, 不同的壁面处理方式、与数值方法的耦合以及与外层湍流模型的适配性, 都会对计算结果的质量和可靠性产生直接影响, 需要进一步的深入研究. 而对于高雷诺数湍流模拟, 现有的壁面函数或壁面模型大多数都是基于简化边界层方程获得壁面速度分布, 往往忽略了非定常、压强梯度与对流项的影响, 而对于强压强梯度、分离流等不满足平衡状态假设的流动还不足以胜任. 此外, 壁面函数或壁面模型一般要求第一个网格至少落在对数律层, 而笛卡尔网格各项同性的特点难免造成第一个网格点落在外层尾迹区, 进而影响数值结果的准确性. 因此, 考虑边界层压缩性、对流和压力梯度的影响可能会提高IBM方法对大分离或高速流动的模拟能力. 而对于非平衡流体, 部分学者已逐渐开始将注意力投入到高温高速高焓边界层及气动热的应用研究, 但尚处于起步阶段, 亟需开展更加深入的研究. 另一方面, 针对高雷诺数流动问题的高精度IBM边界处理技术也是未来需要特别关注的地方.

    2.3   重叠笛卡尔网格方法

    2.3.1   方法介绍及基本流程

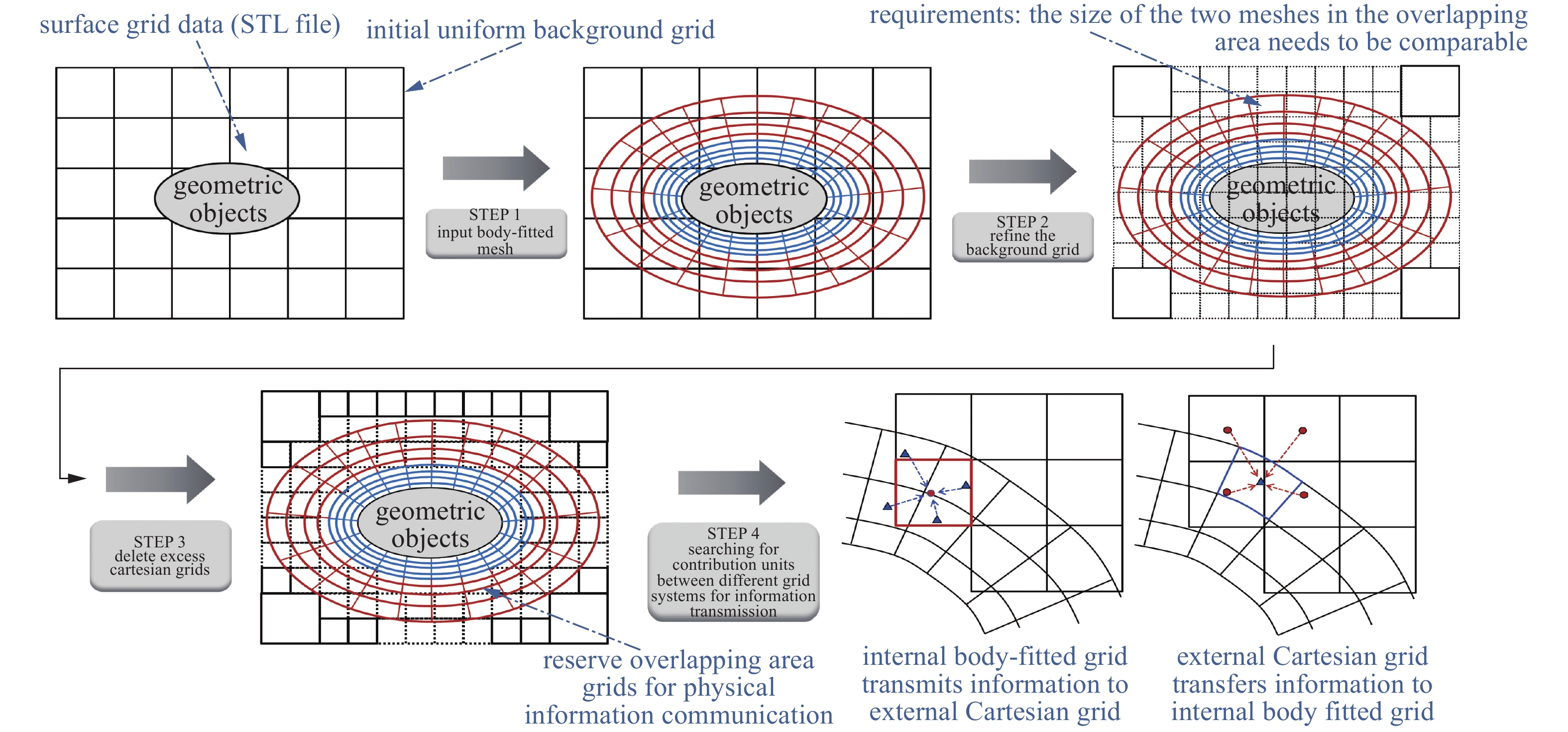
    第3类笛卡尔网格方法称为重叠笛卡尔网格方法, 如图2所示. 该方法在近壁区域使用结构或非结构贴体网格解析壁面附近的流动, 而在远离物面处采用自适应笛卡尔网格模拟远场流动特征. 图13给出了该方法的一般性流程.

    本质上来说, 这类方法属于重叠网格方法的一种, 巧妙地将前文提到的笛卡尔网格“壁面处理”难题转化为两套网格体系间的信息传递问题. 一方面, 其具备较好的贴体性质以及高雷诺数黏性流动问题处理能力, 同时又能充分发挥笛卡尔网格的优势. 另一方面, 其易于推广至多体或运动非定常问题, 具备极大的工程应用前景.

    图  13  重叠笛卡尔网格方法基本流程
    Figure  13.  Basic process of the overset Cartesian grid method
    下载: 全尺寸图片 幻灯片
    2.3.2   国内外发展现状

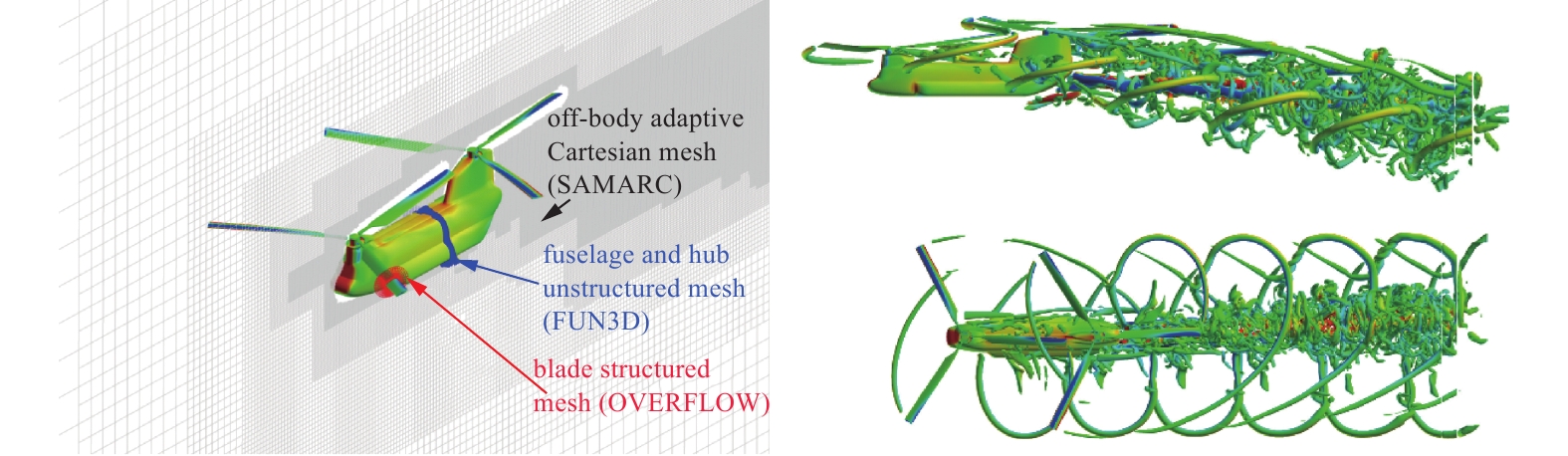
    1990年, Chesshire等[180]率先发展了重叠笛卡尔网格程序CMPGRD, 并用于求解偏微分方程. 1995年, NASA艾姆斯研究中心Meakin[181]发展了称之为Chimera的方法用于生成旋转部件的动态计算网格(内部结构网格, 外部自适应笛卡尔网格). 2002年, Strawn等[22]基于NASA的OVERFLOW代码开发了重叠笛卡尔网格版本OVERFLOW-D用于旋转部件模拟. Henshaw等[182]基于重叠笛卡尔网格开展了化学反应流问题模拟研究. 2006年, Luo等[183]结合近壁区无网格方法的灵活性和远场自适应笛卡尔网格方法的计算效率提出了一种用于可压缩流计算的混合方法. 该方法在一定程度上和内部采用结构或非结构贴体网格的重叠笛卡尔网格方法类似. 2007年, Saunier等[184]发展了3阶精度的重叠笛卡尔网格方法用于ONERA 7 A直升机旋翼悬停状态模拟, 而所需的CPU时间仅比传统的二阶方法高3%. 2007年, Kannan等[185]采用重叠笛卡尔网格对移动边界问题开展研究. Kirby等[186]基于重叠自适应笛卡尔网格体系搭建了风力机模拟平台W2A2KE3D. 该平台内部采用非结构NSU3D解算器, 外部采用dg4est代码(基于p4est开发的高精度DG代码), 并通过TIOGA实现两套网格之间的装配. 特别地, 美国国防部启动了HPCMP计划, 在其子项目CREATE资助下发展了目前最为先进和全面的旋翼直升机气动分析平台Helios[23, 67]. 如图14所示, 其在机身采用NASA开发的二阶非结构FUN3D解算器, 桨叶采用结构求解器OVERFLOW, 而在远离物体区域使用的是自适应笛卡尔SAMARC代码. 与Helios类似, 文献[187-189]中同样采用重叠笛卡尔网格模拟旋翼直升机流场.

    图  14  Helios软件计算结果[67]
    Figure  14.  Computational results using the Helios software[67]
    下载: 全尺寸图片 幻灯片

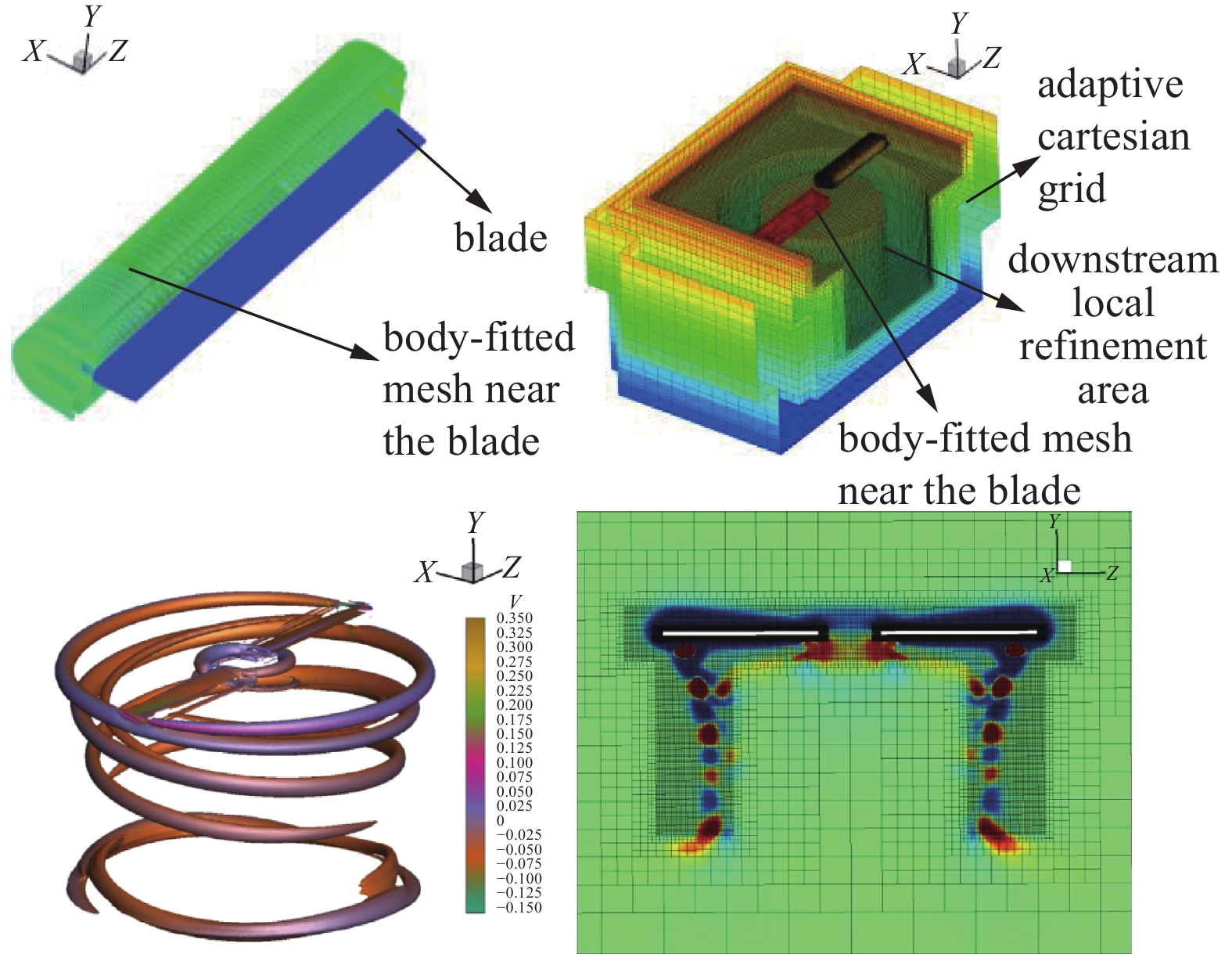
    国内方面, 笔者团队基于重叠笛卡尔网格方法开展了系统性的研究, 包括重叠笛卡尔网格生成方法[51, 190]、多段翼模拟[51]、俯仰振荡问题[52]、风力机模拟[53]和旋翼模拟[191](图15所示)等. 赵文梅等[192]采用混合笛卡尔网格方法对非定常旋涡-翼型相互作用问题进行了数值模拟研究. 2022年, 肖中云等[193]采用结构化贴体网格和SAMR框架自适应笛卡尔网格形成的重叠网格方法研究旋翼-机身相互干扰问题. 韩少强等[194]基于重叠笛卡尔网格对高速共轴刚性旋翼开展了非定常流动高精度数值模拟研究. 2023年, Fu等[195]基于重叠笛卡尔网格开展了高精度通量重构算法、p4est以及网格装配方法研究等.

    图  15  重叠自适应笛卡尔网格旋翼流场模拟
    Figure  15.  Simulation of rotor flow fields using the overset adaptive Cartesian grids
    下载: 全尺寸图片 幻灯片
    2.3.3   网格装配效率

    混合笛卡尔网格方法最为关键的技术就是如何判断多套网格体系的位置关系以及如何查找各网格相互之间信息传递的“供体单元”. 一般地, 这一过程被称为网格装配. 可以看出, 该过程将对重叠笛卡尔网格方法的计算效率及准确性产生直接影响. 而网格装配过程的核心就是快速点查找及位置判断问题.

    遍历法是最简单常用的贴体网格和笛卡尔网格位置关系判断方法. 但是, 在三维情况下, 其计算量将会急剧增加, 严重降低计算效率. 相邻单元搜索法[196]是改进的遍历方法, 可以在一定程度上提高网格装配的计算效率, 但对于三维网格来说计算量仍然较大. ADT算法[197]具备高效的数据查询结构, 可以有效降低网格装配的计算成本. 随后, KDT方法被提出用于解决ADT树结构不平衡问题, 可以进一步提升装配效率. 2023年, Wang等[198]提出了一种局部逆映射隐式全息切割网格装配方法. 该方法点标记和插值的计算成本在二维情况下仅占总计算成本的3%, 三维情况下占14%, 可以有效减少“供体单元”搜索的计算量和节省内存. 笔者团队[55]耦合最小有向包围盒、逆映射以及中位数的ADT树等技术发展了一种结构网格、非结构网格以及自适应笛卡尔网格间的通用型网格装配方法, 2000万量级网格并行装配仅需22 s. 需要强调的是, 由于重叠笛卡尔网格方法网格装配的本质依然是点查找及关系判断问题, 因此其他网格体系的网格装配算法同样适用于该方法, 这里不再举例叙述.

    2.3.4   不同网格体系间的信息传递及重叠区网格单元控制

    如何实现不同网格体系间快速、准确、守恒的信息传递也是重叠笛卡尔网格方法需要特别关注的研究内容. 对此, Gan等[191]对混合笛卡尔网格交界面附近的守恒性和精度开展了研究. 结果表明, 使用更多的插值点能够在一定程度上提升信息传递的精度和守恒性, 但是其容易产生点查找效率、信息存储、并行通讯等额外的问题, 需要进一步的研究.

    此外, 当生成重叠网格时, 一个主要的缺点是必须手动控制网格之间的重叠和插值区域中的网格间距, 使得整个网格系统保持两个约束: 一是两套网格在重叠区域内的单元面积/体积必须接近, 以防止插值误差破坏计算的精度; 二是两套网格之间必须存在一定的重叠, 以保证两套网格数值解的连续性. 为此, Benoit等[199]基于法国国家航空航天研究院的elsA软件发展了一种重叠笛卡尔网格自动网格生成算法. 该方法根据内部网格自动判断并生成符合要求的自适应笛卡尔网格, 但是其依然存在一定的局限性, 需要进一步的发展.

    2.3.5   存在的问题

    整体而言, 重叠笛卡尔网格方法在目前4种笛卡尔网格方法中最具工程应用前景, 尤其适用于多体或运动问题. 但是, 仍然需要在网格装配效率及准确性、网格信息传递的守恒性及精度及不同网格体系的全局并行负载平衡等方面进行深入研究, 以提升重叠笛卡尔网格的性能. 此外, 重叠自适应笛卡尔网格方法牺牲了笛卡尔网格生成自动化的优点, 仍然需要继续研究复杂几何表面网格自动生成方法.

    2.4   混合笛卡尔网格方法

    2.4.1   方法介绍及基本流程

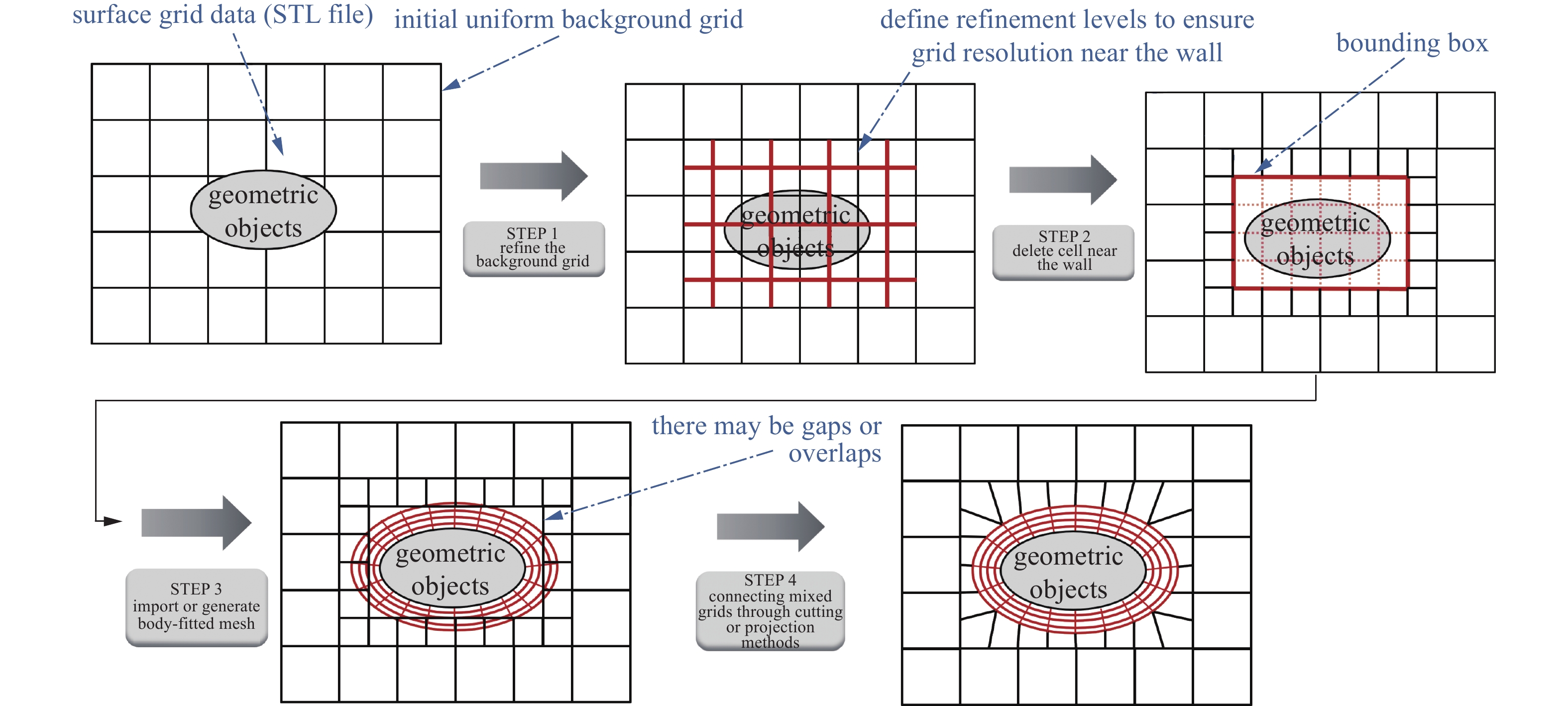
    第4类笛卡尔网格方法称为混合笛卡尔网格方法, 如图2所示. 该方法首先在物面附近区域自动或人工生成结构或非结构贴体网格, 然后外部区域采用笛卡尔网格填充, 并在相交区域使用剪切单元方法使其成为一套完整的非结构网格体系. 图16给出了混合笛卡尔网格的主要流程.

    此类方法可看作是介于切割单元方法和重叠笛卡尔网格方法之间的“衍生品”. 一方面, 其具备重叠笛卡尔网格方法的贴体性质以及黏性流动分辨率. 另一方面, 在两套网格体系过渡区域的网格填充可以直接借用切割单元方法中的单元剪切/合并算法. 同时, 由于混合笛卡尔网格方法内部网格界面相对更加简单, 所以能够在一定程度上缓解剪切单元方法面临的复杂几何相交剪切问题以及信息传递守恒性问题. 但是, 整体而言, 其受关注程度远不及切割单元方法和重叠笛卡尔网格方法, 研究相对较少.

    图  16  混合笛卡尔网格方法基本流程[45]
    Figure  16.  Basic process of the hybrid Cartesian grid method[45]
    下载: 全尺寸图片 幻灯片
    2.4.2   国内外发展现状

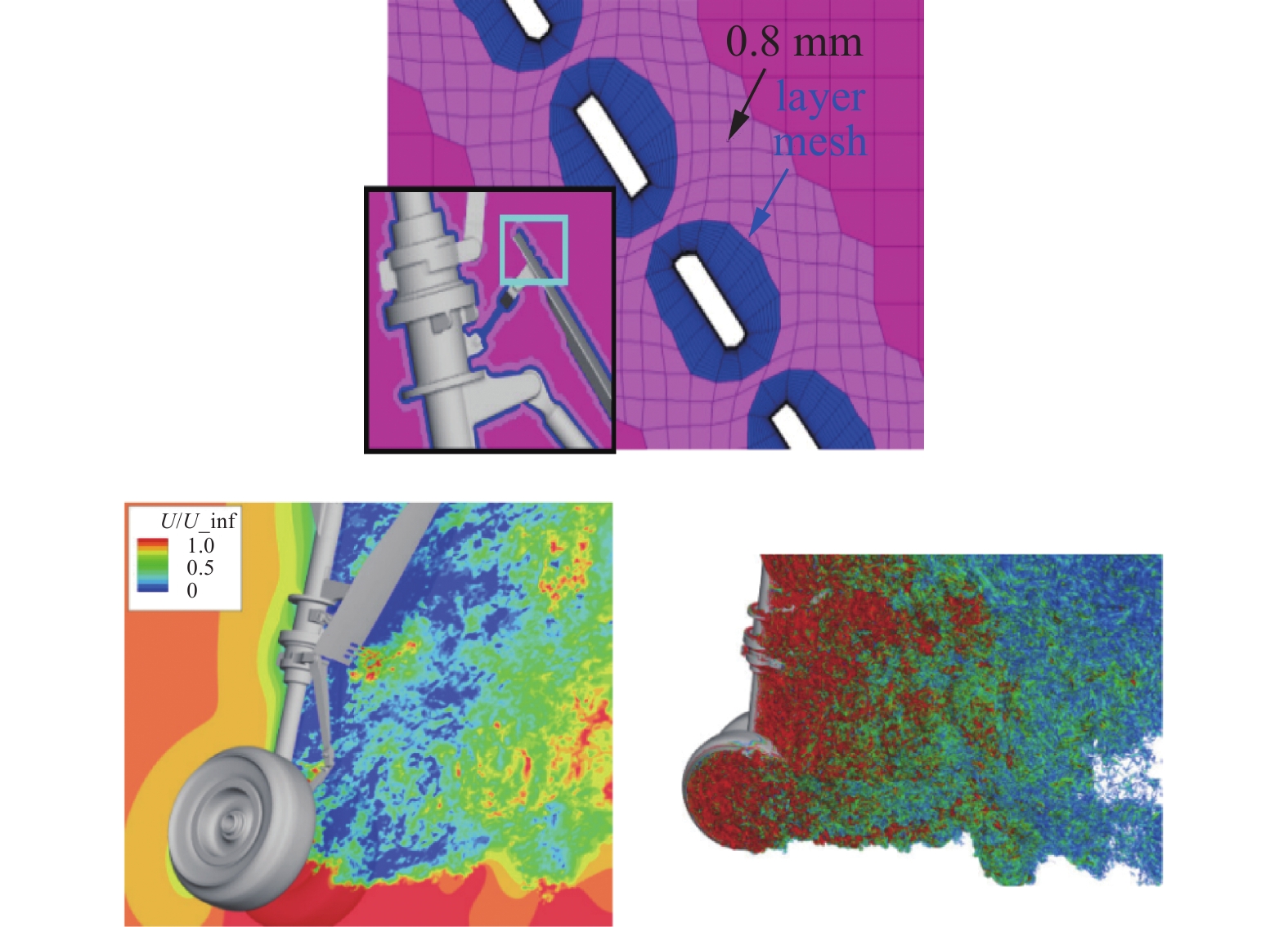
    1995年, Karman[43]率先发展了笛卡尔/棱柱非结构混合网格三维解算代码SPLITFLOW. 随后, Wang[200, 201]基于四叉树发展了笛卡尔/四边形混合网格快速生成及计算方法. 2008年, Kini等[202]发展了全自动的混合笛卡尔网格生成软件CFD-VisCART. 该软件无需完全水密的几何外形, 且具备很好的“脏”几何处理能力, 能够大幅缩短复杂几何的网格生成周期. 应用方面, Ashok等[203]基于混合笛卡尔网格方法开展了化学非平衡高超声速流动问题研究. Ueno等[45]基于混合笛卡尔网格解算器Cflow开展了起落架和高升力装置的噪声预测研究, 通过网格自适应显著改善了远场区域的非定常流动特性和噪声预测水平等. 图17给出了其基于混合笛卡尔网格方法的起落架噪声模拟结果.

    图  17  混合笛卡尔网格方法起落架噪声预测结果[45]
    Figure  17.  Prediction results of landing gear noise using the hybrid Cartesian grid method[45]
    下载: 全尺寸图片 幻灯片

    国内方面, Sang等[89, 204]于2002年提出了分区和面搭接技术用于生成混合笛卡尔网格, 并发展了三维解算器HLCE3D用于三维增升装置无黏流动模拟[62-64]. 2004年, 张来平等[205]建立了基于动态混合网格的高效非定常计算方法. 该混合网格由内层贴体四边形网格、外场自适应笛卡尔网格以及中间过渡区的三角形网格构成. 2009年, 刘周等[206]发展了适用于黏性计算的混合笛卡尔网格生成技术. 该方法首先基于物面曲率自适应的笛卡尔网格方法生成初始计算网格, 然后通过投影方法拟合壁面边界, 并通过特征恢复技术处理凹角和改进网格质量, 进而将柱形单元沿法向分层获得最终的计算网格. 但是, 该方法只能恢复简单特征, 全部特征的恢复是困难的, 且在几何变化复杂的区域网格质量有待提高. Liu等[207]提出了一种适用于动态非结构笛卡尔网格的网格变形算法用于运动边界非定常流动模拟等.

    2.4.3   存在的问题

    混合笛卡尔网格方法能够解决重叠笛卡尔网格方法不同网格体系间信息传递的守恒性和精度问题, 同时缓解切割单元方法单元剪切/合并算法的复杂性. 但是, 其同样面临重叠网格方法内部网格高质量生成难题以及切割单元方法面临的“小单元问题”. 同时, 其严重依赖于内部网格的生成方式, 在一定程度上降低了笛卡尔网格的自动化程度. 因此, 该方法在理论研究和工程应用都有一定的局限性. 但是, 随着结构或非结构网格自动生成技术的发展, 其未来在笛卡尔网格类方法中依然具备一定的竞争力.

    3.   关键技术及发展方向

    3.1   自适应加密判据

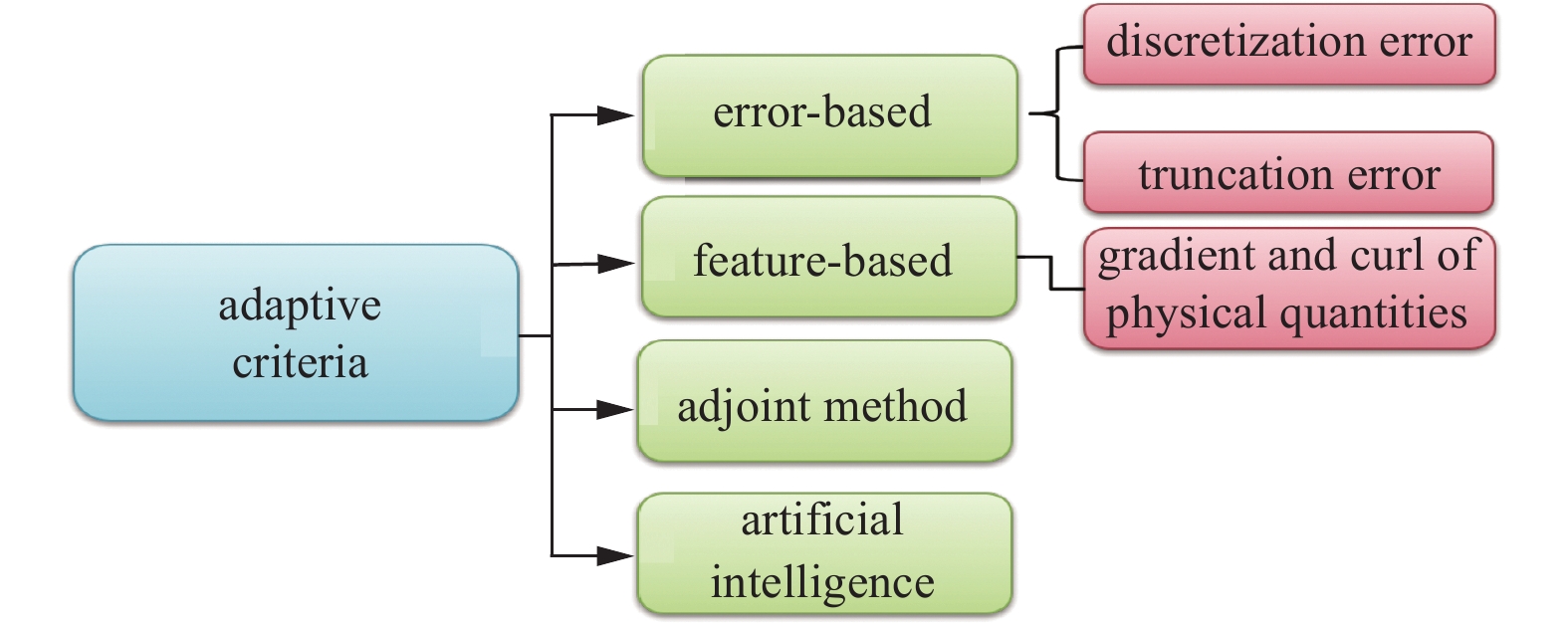
    自适应加密判据选择的合适与否将会对网格分布的优劣产生重要影响, 这一直是AMR方法的主要挑战之一. 适当的度量能够确保只有对离散误差有主要贡献的单元才被细化, 而如果加密判据选择不当, 则该过程可能会停滞或者产生过多非必要加密单元[208]. 同时, 不理想的网格加密会破坏解的精度, 而该过程引入的误差将会在整个计算过程中积累, 得到不如意的结果[68]. 如图18所示, 截至目前, 常用的自适应加密判据可分为基于误差、基于流场特征、伴随算子以及近些年兴起的人工智能等4类. 下面将简要介绍各自的基本原理及适用范围, 详细讨论可以参考文献[68-70, 209].

    图  18  自适应准则分类
    Figure  18.  Classification of adaptive criteria
    下载: 全尺寸图片 幻灯片
    3.1.1   基于误差的自适应准则

    首先是基于误差的自适应准则, 主要包含两个方面: (1)离散误差; (2)截断误差. 离散误差的基本定义是离散方程精确解与偏微分方程精确解之间的差. 一般地, 离散误差是最难估计的数值误差类型, 通常是最大的数值误差源, 其中还包括迭代误差、舍入误差和统计误差(如有). 因此, 离散误差会出现在每个CFD解决方案中, 通常是CFD模拟中整体不确定性的主要因素之一[210]. 对于自适应网格下的Euler/Navier-Stokes方程, 离散误差的精确求解是困难的, 因此出现了许多方法来估计离散误差[211]. 这些方法都可以作为自适应准则, 但相对而言, 研究较少. 截断误差的基本定义是偏微分方程与其离散近似值之间的差值, 其提供了局部离散化(网格单元大小、倾斜程度等)对离散化误差的贡献. 因此, 截断误差是启动网格自适应过程的良好指标. 基于截断误差自适应背后的一般概念是在整个计算域上等分布截断误差, 以达到总离散化误差最小化的目的. 对于简单的离散化方案, 可以直接计算截断误差. 但对于更复杂的方案, 难以直接评估截断误差, 需要截断误差估计方法, 如Richardson外推的局部截断误差估计方法[81]、基于残差的估计方法[209]. 因估计截断误差具备一定的简洁性, 使得基于该方法的网格自适应技术在商业CFD代码中更受欢迎[210].

    3.1.2   基于流场特征的自适应准则

    基于流场特征的自适应准则是目前最广泛使用的网格自适应方法. 该方法通常使用数值解的物理特征(如梯度和旋度)来驱动自适应过程. 基于流场特征的网格自适应技术可以自动判断流场中变化剧烈的区域(如激波和旋涡), 然后对流场计算网格进行动态的加密或粗化, 提高局部流场的分辨率, 进而使得整个流场计算结果更加精确. 但是, 如何选择合适的物理量以及流场特征是其中的关键一环. 对于流场中存在间断的区域, 其网格单元的梯度或散度能够较为明显地判断间断强度及位置, 是一种常用的捕捉激波的自适应判据[48-49, 135, 212]. 而旋涡的识别相对更加复杂, 由于目前其本身缺乏一种全面且准确的定义. 涡量和$Q$准则是常用的旋涡自适应加密判据. 但是, 其包含阈值以及人为参数, 需要根据特定问题进行调整. Kamkar等[213]系统比较了$Q$, ${\lambda _2}$, ${\lambda _{ci}}$和${\lambda _ + }$ 4种判据, 并提出了归一化特征检测无量纲方法用于提升涡识别加密判据的适用性. 此外, Pang等[214]提出了基于新型$\Omega $方法的涡识别敏感器开展尾流自适应网格加密算法研究. 在网格量减少30% ~ 50%的情况下, 该方法提高数值精度的同时能够高效稳定地处理弱涡旋流动.

    需要强调的是, 截至目前, 基于特征的自适应加密判据仍然是问题相关的, 且所含人为参数对数值结果的影响较大. 例如, 文献[208]中给出了一个基于特征自适应失败的案例, 并指出失败的原因可能是由用于测试算例的细化参数/阈值定义引起的. 因此, 未来需要针对性发展更具普适性的基于特征的细化准则, 尤其是多物理场耦合问题, 需要根据具体的模拟问题和流场特征进行权衡和调整.

    3.1.3   基于伴随算子的自适应准则

    基于伴随的自适应加密准则提供了一种稳健的方法, 通过有效的误差估计和网格自适应来估计和减少输出误差, 因而成为目前最受关注的网格自适应加密方法. 伴随方法可以估计任何感兴趣物理量解(如升力、阻力和力矩等)在每个单元中的离散化误差的局部贡献, 因此可以根据求解目标提供有针对性的网格自适应. Balasubramanian等[212]在非结构网格中系统比较了伴随自适应和特征自适应准则, 发现伴随方法对升力系数预测效果更好, 而特征方法收敛于较低估计. 同时指出, 特征方法受到初始网格分辨率较差的影响, 无法显著提高功能的准确性. 然而, 初始网格解对伴随自适应的结果影响不大, 但基于流场特征的方法需要一个更好的初始网格. 2008年, Nemec等[17-18]基于Cart3D软件发展了伴随自适应网格加密准则, 无需用户干预的情况下可自动生成高质量的气动数据库. Fidkowski等[215]给出了基于输出的误差估计和网格自适应研究的综述, 给出了其在实际实施及理论框架方面存在的挑战. 2016年, Ceze等[216]结合高精度间断Galerkin有限元方法和基于输出的自适应准则用于RANS方程求解, 得到了比二阶格式更快的阻力收敛结果. 2022年, Zastawny等[208]基于STAR-CCM+软件研究了基于伴随的自适应准则.

    虽然基于伴随的网格自适应方案正变得越来越流行(尤其是定常RANS计算), 但是由于其复杂性和代码实施难度, 它们尚未得到广泛应用, 特别是在商业CFD社区[210]. 此外, 对于非定常流模拟方法(如大涡模拟), 基于输出伴随方法的代价高得令人望而却步[217].

    3.1.4   基于人工智能方法的自适应准则

    近些年, 随着人工智能、机器学习、神经网络和深度学习方法的兴起, 流体力学研究已经进入新的范式, 而“智能自适应”已然成为重要的发展方向. 对此, 一些学者开始将其作为新的判据用于启动自适应过程. 2021年, Feng等[218]基于人工神经元训练了一种具有特征的冲击波指示器. 2021年, Chen等[217]提出了一种使用卷积神经网络(CNN)机器学习技术进行输出误差估计和网格自适应的方法, 给定由基于伴随的误差估计引导的自适应模拟数据, 训练代理模型来预测输出误差, 并仅以低保真度解作为输入来驱动网格自适应. 2023年, 李彩云等[219]利用BP神经网络(BPNN)实现DG有限元方法的自适应过程. 该方法首先采用 DG有限元法对 Navier-Stokes 方程进行非定常计算, 得到统计意义上的网格间断量, 然后以初始网格和间断量训练 BPNN回归模型, 用于预测任意位置节点的间断量.

    值得注意的是, 虽然这类方法能够提供一些新的视角, 具有一定潜力, 但是依然存在一定的发展空间. 例如, Chen等[217]指出, 在涉及强间断流动中CNN输出误差预测的准确性通常会降低. 同时, 算法的鲁棒性以及如何减少参数数量和提高训练效率依然需要进一步的研究.

    最后, 加密准则是驱动自适应过程的依据, 而加密或粗化后新现单元物理量赋值也是需要特别注意的地方. 插值精度及守恒性对自适应效果有重要影响. 不合适的插值会引入一定的数值误差, 而误差的积累将会破坏整个计算结果.

    3.2   动态并行技术

    高性能计算机的迅猛发展为科学研究提供了前所未有的发展机遇, 其计算能力已经从Peta级迈向了Exa级[220]. 而作为强烈依赖于计算机技术的流体力学仿真软件, 计算效率的提升一直是其永恒追求的主题. 随着实际工程问题中所涉及流动问题和物理模型越发复杂, CFD数值模拟的网格规模已由百万量级增加至千万甚至百亿量级(结构网格或非结构网格). 而相比于结构或非结构网格为基础的贴体体系, 为了实现同等精度的湍流黏性边界层流动模拟, 笛卡尔网格所需的网格量一般会高1 ~ 2个量级[25]. 因此, 基于笛卡尔网格的CFD软件对高性能计算的需求更加强烈, 而如何充分利用HPC集群的硬件性能实现其大规模计算能力显得尤为重要.

    3.2.1   自适应笛卡尔网格数据管理及存储结构

    区别于静态网格并行分区的“一劳永逸”, 自适应笛卡尔网格会频繁地涉及几何自适应、解自适应和2:1平衡等动态变化过程, 进而给大规模网格并行生成、并行计算以及高可扩展性等方面的实现带来巨大困难. 一方面, CFD软件必须具备强大的可扩展性来适应现阶段乃至未来计算规模的不断增加(一般要求能够实现至少千、万核量级的高度线性可扩展性并行计算能力). 而自适应笛卡尔网格求解器在网格自适应变化过程中信息的动态演变使得求解器需要更加频繁的集体通信操作, 进而造成其在大规模并行计算机中可扩展性较差. 另一方面, 网格的频繁变化给底层的编码方式及存储结构系统的搭建带来了巨大困难, 而如何实现变化网格下的动态分区至关重要. 此外, 动态分区后会使得各处理器中的计算负载变得极其不平衡, 而负载最多的处理器会严重损害求解器的全局并行效率. 同时, 为了减小并行通讯开销, 动态并行分区算法除了具备高负载平衡性能要求外, 还应具备聚类特性(同一进程的网格块尽可能相邻), 尽量减少并行交界面的数量, 保证物理上的几何连续性, 进而提升并行发送与接收的效率.

    2000年, 美国NASA MacNeice等[82]开发了用于管理八叉树自适应笛卡尔网格的开源软件包PARAMESH. 该软件提供了简单的自定义接口供用户将已有的笛卡尔网格串行代码转变成具有自适应功能的MPI并行代码. 美国劳伦斯利弗莫尔国家实验室开发了面向对象的自适应笛卡尔软件库SAMRAI[83], 提供了“即插即用”的灵活性, 可以基于此快速探索新的结构化自适应网格细化应用程序. 2002年, Lan等[221]发展了一种适用于SAMR的动态负载平衡技术, 并集成至著名的天体物理自适应笛卡尔网格代码ENZO. 相比于ENZO原始的动态负载平衡方案, 该方法的并行执行时间最多可减少57%, 负载平衡质量提高了6倍. 2010年, Ji等[222]基于哈希表提出了一种称之为CSAMR的数据结构用于维护AMR数据的连通性信息, 简化了AMR代码的实现和并行化过程. 其访问数据结构中单元或邻居搜索所产生的计算开销仅占流体动力学模拟总计算时间的10%左右. 相比之下, 文献[223]中基于树的FTT数据结构所占时间大约为20%. 2011年, Burstedde等[72]开发了CAMR框架的自适应笛卡尔网格管理库p4est, 并在美国NSF Ranger SUN/AMD超级计算机(超过62 000个CPU核)以及NCCS Jaguar Cray XT5超级计算机(超过220 000个CPU核)进行了测试, 结果验证了其具备优异的大规模并行可扩展性(1 min以内实现 1011量级的八叉树网格生成, 相应的2:1平衡算法仅需10 s). Dubey等[75]综述了国外知名机构基于BAMR框架开发的自适应笛卡尔网格管理库, 如美国劳伦斯伯克利国家实验室Chombo、美国能源部的FLASH以及德国马普引力物理研究所的Cactus等. 其在文中系统比较了它们的功能、适用领域及各方面性能, 如表2所示.

    表  2  国外知名结构自适应网格代码框架及性能[75]
    Table  2.  Overview of well-known foreign structured AMR code frameworks and their performance[75]
    Feature BoxLib Cactus Chombo Enzo FLASH Uintah
    subcycling optional optional optional required None required
    time step ratio same as refinement independent same as refinement independent same as refinement
    elliptic solver PETSc/Hypre/Trilinos native GMC user supplied PETSc/native GMG hypre native GMG hypre/native GMG PETSc(hypre)
    GMG with AMR sub or whole mesh sub or whole mesh single level whole mesh sub or whole mesh
    spherical AMR 1D multipatch 1D 1, 2, or 3D 1D
    cylindrical AMR 2D multipatch 2D 1, 2, or 3D 2D
    mixed dimensions yes
    highest dimension 4D up to 6D
    block size variable variable variable variable fixed variable
    refine factor 2/4 2 2/4 any integer 2 any integer
    parent blocks not unique not unique not unique unique unique unique
    regridding level tag cells per level tag cells per level tag cells per level tag cells per level tag blocks all atonce tag blocks all atonce
    space flling curve morton morton piano-Hilbert morton Hilbert+fast sorting
    OpenMP per block and loops dynamically tuned loops per block per block and loops per block and loops
    accelerators CUDA OpenCL CUDA CUDA
    parallel I/O native HDF5 HDF5 HDF5 HDF5 PnetCDF HDF5
    viz vist/yt vislt/yt vislt vislt/yt vislt/yt vislt
    FSI embedded boundary immersed boundary MPM method
    framework language C++/Fortran C/C++ C++ C++ Fortran C++
    user module language Fortran C/C++ Fortran Fortran Fortran Fortran
    下载: 导出CSV 
    | 显示表格
    3.2.2   自适应网格动态分区及负载平衡

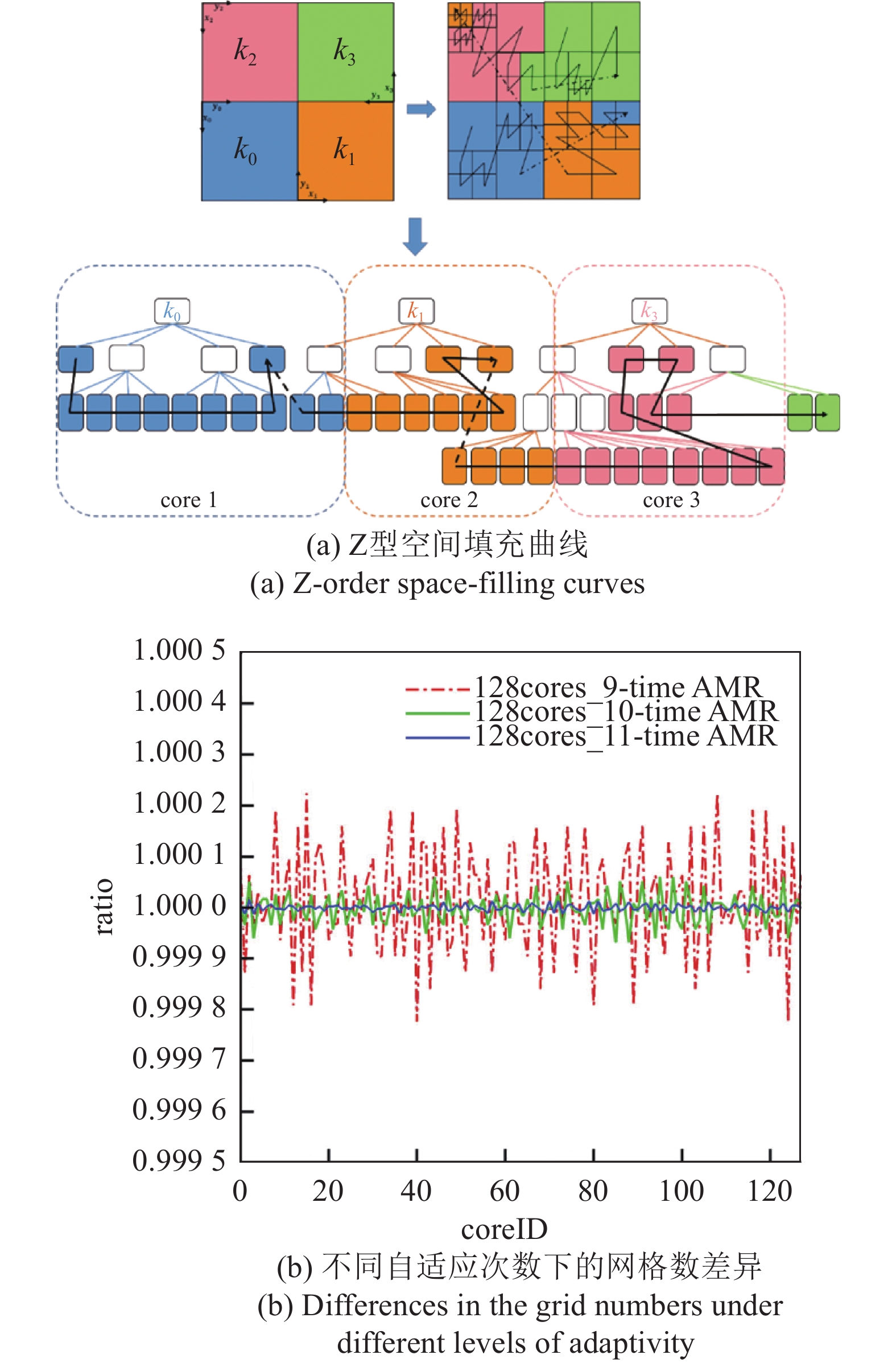
    对于自适应笛卡尔网格的大规模并行计算, 关键在于如何保证高可扩展性的同时实现自适应网格的动态分区以及保证负载平衡. 空间填充曲线技术是一种能够较好地实现自适应网格动态分区、负载平衡、高扩展性的大规模数据管理方法, 如: Peano-Hilbert曲线(U-order曲线)、Morton曲线(N-order或Z-order曲线)等. 该技术将高维自适应网格降维成一维动态问题, 进而可以实现变化网格的动态负载平衡分区以及自适应网格的分区管理及计算. 如前文提及的ENZO、Uintah以及著名的全自动快速气动设计软件Cart3D[16]采用的是Peano-Hilbert空间曲线技术; Chombo、FLASH以及p4est则采用Morton曲线实现了其大规模MPI并行计算功能. 国内方面, 笔者团队[49]以Z型空间填充曲线技术为基础实现了大规模自适应笛卡尔网格多核并行生成及计算, 如图19所示. 图19(b)给出了不同加密层级下不同核数之间网格数与理想网格数之间的比值, 结果表明差异均在1%以内, 具有优异的负载平衡性能. Pan等[224]实现了动态自适应并行框架下的高精度紧致有限体积变分重构方法构造. Wang等[225]利用Hilbert空间填充曲线算法开发了一套负载均衡的高精度并行AMR代码用于爆轰问题模拟. 2022年, 肖中云等[193]采用Z-order空间填充曲线的结构化自适应笛卡尔网格模拟旋翼流场. 需要说明的是, 采用空间填充曲线进行并行网格分区划分, 每个处理器都需要保存一个整体的信息, 对于超大规模计算($O({10^5})$核)的平衡与数据通讯迁移时间, 将会随着核数的增加而增加, 而采用基于扩散方法的平衡算法, 相关时间开销几乎是常数[226]. 未来为了满足超大规模的并行计算, 而目前上述自适应笛卡尔网格框架都不具有基于扩散方法的动态平衡算法功能, 需要进一步研究与开发.

    图  19  自适应笛卡尔网格并行生成负载平衡情况[49]
    Figure  19.  Load balancing situation of adaptive Cartesian grid parallel generation[49]
    下载: 全尺寸图片 幻灯片
    3.2.3   GPU异构并行加速

    随着具有大量图形处理单元(GPU)和协处理器的分层存储器架构的出现, CFD社区已开始逐渐将重心由传统的MPI并行框架转移到GPU异构并行技术的研究. 而对于自适应笛卡尔网格软件的超大规模并行计算, GPU异构并行架构有望解决传统CPU并行技术遇到的“强可扩展性瓶颈”难题. 但是, 除了CPU框架下的可扩展性以及负载平衡问题, 异构超级计算机具备的异构计算、存储、通信能力和编程环境会给自适应笛卡尔网格软件的开发带来额外的困难. 因此, 需要针对异构并行体系结构特征, 设计相应多层次可扩展的自适应笛卡尔网格并行算法, 实现软件与并行体系结构的“最佳适配”, 充分挖掘超高性能计算机的潜力. 在这方面, 国外团队早已对自适应笛卡尔网格的GPU并行技术展开了丰富的研究, 并已取得较好的成果.

    2015年, Backingsale[227]使用CUDA编程模型实现了块自适应笛卡尔网格库SAMRAI的GPU并行功能, 同等条件下模拟速度比CPU框架快4.8倍, 并展示了其在超过4000个节点上的扩展性. 2019年, Giuliani等[228]在GPU框架下实现了非结构自适应网格高精度DG有限元方法. 2021年, Dunning等[71]基于CAMR和PAMR提出了一种称之为Phantom-cell AMR的轻量化应用程序, 并在CPU和GPU架构下对其进行了详细的性能比较分析, 对将AMR方法推广到GPU架构所面临的问题及解决方案进行了详细讨论. 2022年, 美国陆军Jude等[229]发展了纯自适应笛卡尔网格GPU解算代码Orchard, 能够同时在CPU、GPU或混合架构运行, 在多达140个CPU卡槽和36个GPU上针对HART-II转子实现了11亿网格的自动生成与计算, 加速比为3.6 (如图20所示). 为了支持大规模异构并行计算, 美国能源部在百亿亿次计算项目ECP的资助下基于Boxlib开发了支持多核CPU和多种不同GPU加速器的可移植AMReX框架[84], 并以此为自适应底层架构实现了不同领域的研究与应用. 特别地, Dubey等[230]重新回顾了AMR包的发展, 特别关注异构体系结构的可移植性. 并指出, 为了支持GPU并行架构, 许多AMR库必须进行重大修改或完全重写, 而混合架构实现仍是一个持续的挑战. 相对于国外的蓬勃发展, 国内在这方面研究相对较少. Wei等[76]基于CUDA架构对自适应笛卡尔网格浸入边界方法展开了GPU并行加速初步研究, 对于二维无黏流动实现了近10倍的加速, 而对于无黏非定常问题实现了9.98 ~ 14.04的加速比[231].

    图  20  自适应笛卡尔网格GPU和CPU比较[229]
    Figure  20.  Comparison of adaptive Cartesian grids on GPU and CPU framework[229]
    下载: 全尺寸图片 幻灯片

    总而言之, 纵观国内外发展现状, 我国在该方向落后于欧美发达国家, 亟需发展自适应笛卡尔网格CPU/GPU并行技术及数据管理库, 为完全自主可控的自适应CFD模拟国产软件研发提供关键技术支撑.

    3.3   高保真计算方法

    随着工程问题的复杂性及对计算结果准确性要求的提高, 二阶格式本身固有的数值耗散与色散不足以满足关键流动精细化模拟的需求. 而高精度方法在同等网格水平上能够得到更为精细的高保真结果. 因此, 高阶精度方法逐渐受到各国学者和CFD工作者的重视[4]. 比如美国AIAA流体力学技术委员会成立了一个CFD算法讨论组用于解决高阶方法在CFD工程应用领域所面临的问题以及明确CFD高阶方法的发展方向[232]. 同时, 美国NASA发布的《CFD2030远景规划报告》[1]和我国学者出版的《计算流体力学2035愿景》一书[2]中也将高阶格式列为下一代CFD技术的重要方向. 另外, 欧盟启动了第六框架特别研究项目——ADIGMA[233], 旨在解决高精度格式在实际工程应用中面临的各种基础问题, IDIHOM[234]作为其后续项目, 开始关注高精度格式的应用情况.

    3.3.1   高精度空间离散方法

    对于自适应网格下的高精度格式, 可以在计算网格和数值算法层面同时提升结果的保真度, 达到事半功倍的效果. 但是, 相比于静态网格, 自适应笛卡尔网格频繁的加密/粗化操作给高精度格式的构造与实现带来不小挑战, 需要根据不同的自适应网格数据结构设计与之适配的高精度格式.

    对于BAMR/PAMR框架, 由于其在每个块/补丁内是规则的结构笛卡尔网格, 因此高精度有限差分格式无疑是最佳选择. 因此, 国内外诸多学者对此展开了相应的理论与应用研究. 2003年, 美国洛斯阿拉莫斯国家实验室的Li等[80]基于PAMR框架发展了高精度有限差分WENO格式, 系统研究了不同加密层级网格间的精度和守恒性问题. Chaudhuri等[148]基于WENO格式和IBM方法对激波-障碍物相互作用问题开展了研究. Shen等[235]在纯自适应笛卡尔网格下结合Berger的通量校正方法[236]发展了相应的高阶有限差分WENO格式. 2016年, Muralidharan等[106]在切割笛卡尔网格体系下实现了3阶精度的有限体积CENO格式. Nauleau等[141]采用IBM方法和高精度WENO-Z格式发展了HYPERION解算器用于高超声速黏性流动问题模拟. 除此之外, 还有TENO格式[31]、WENO-K格式[194]以及文[30, 74, 156, 176, 225]中的工作等.

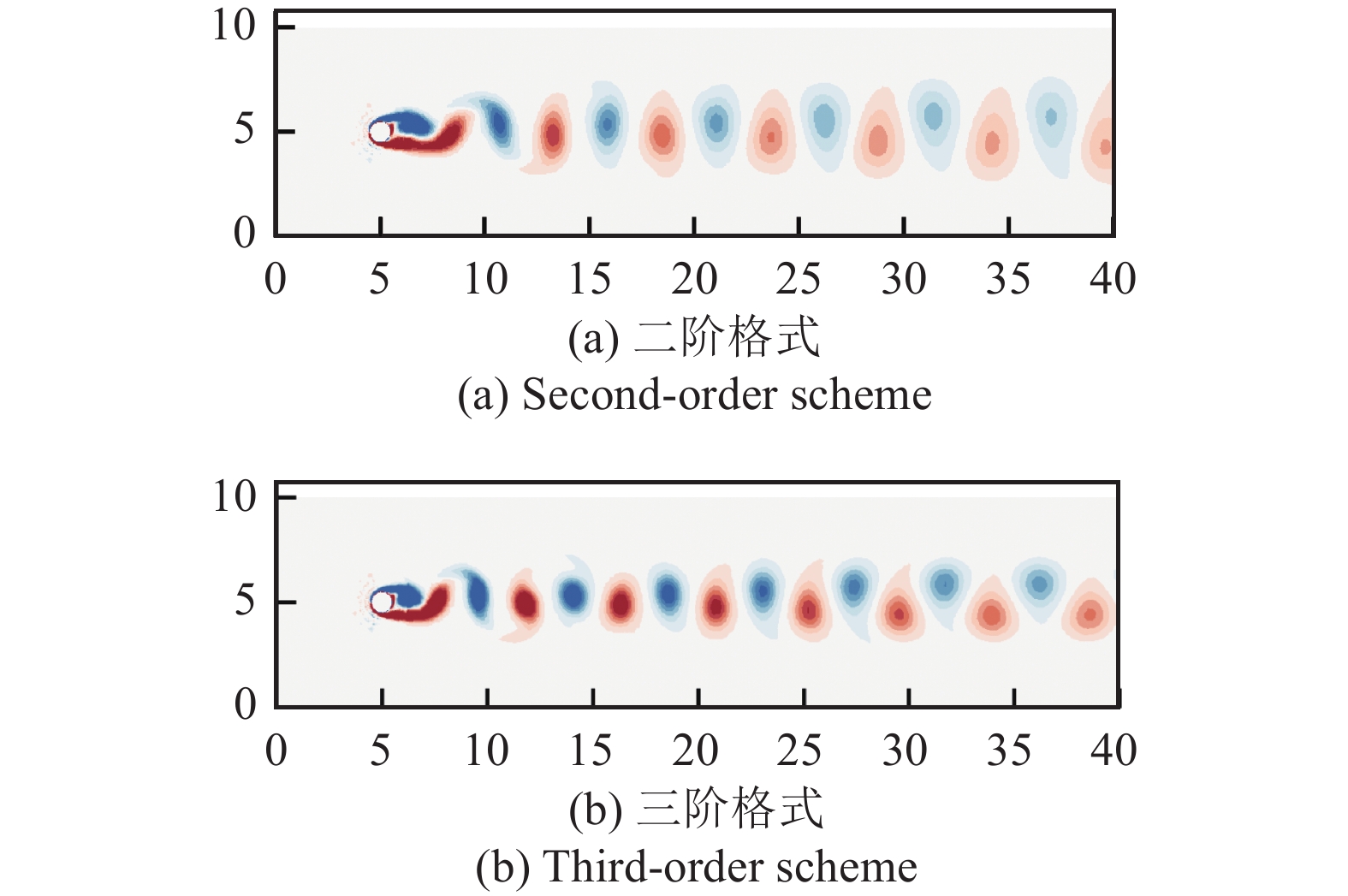
    而对于CAMR框架, 其网格单元之间的相邻关系极度不规则, 给高精度格式的构造带来了较大困难. 在此框架下, 紧致类高精度方法将是首选. 在这方面, 笔者团队率先基于IBM方法发展了高精度间断Galerkin (DG)有限元方法[237-238], 并相继构造了具备“操作紧致性”的有限体积U-MUSCL和WENO格式[54]以及DG-WENO方法[238-239]等. 图21给出了部分数值结果. 2017年, Müller等[107]构造了切割网格下的高精度DG方法, 并指出边界单元处高精度体积积分和面积分对实现数值格式的全收敛阶至关重要. Pan等[224]构造了自适应网格下的高精度有限体积紧致变分重构方法. 2022年, Kou等[240]基于体积惩罚IBM方法发展了高阶通量重构(FR)格式. 王婷婷等[241]基于体积惩罚方法和高精度DG有限元方法模拟了黏性可压缩问题. 2023年, Funada等[36]将高精度FR格式集成于UTCart软件. 文献[195]中在重叠笛卡尔网格中实现了高精度FR格式构造等.

    图  21  自适应网格圆柱绕流问题[238]
    Figure  21.  Flow around a cylinder on adaptive Cartesian grid[238]
    下载: 全尺寸图片 幻灯片
    3.3.2   守恒型“悬挂节点”重构方法及高精度边界处理技术

    特别地, 对于自适应笛卡尔网格, 不同层级网格过渡区域难以保证物理量的守恒性, 即所谓的“悬挂节点”问题. 因此, 自适应网格体系下的高精度格式一般难以实现预想的“$1 + 1 \geqslant 2$”效果. 正如文献[80]中所言, 不同层级网格界面处守恒型插值的阶数不大于2, 且高阶非守恒型插值效果并不比2阶守恒型插值更好, 在大多数情况下甚至更差. 对于低阶格式的“悬挂节点”问题, 已有部分工作. 比如: Berger[236]提出了通量校正方法; Kawai等[38, 40]提出了一种稳定无耗散的KEEP格式[38]以及随后提出的守恒型显式4阶通量滤波器[40]; 以及文献[74]的方法等. 但是, 对于高阶格式, 尚需深入研究, 进而设计出一致高阶、稳定且守恒的数值算法. 另一方面, 对于现阶段的自适应高精度方法, 其在物面附近最高往往只有二阶精度, 难以实现全场一致高阶精度, 尤其是浸入边界方法. 因此, 发展与之匹配的高精度边界处理技术也是特别需要关注的地方.

    3.4   其他

    除了前文所述的自适应加密准则、并行技术以及高精度计算方法以外, 下面简要介绍笛卡尔网格方法的其他发展方向.

    3.4.1   先进物理模型与自适应笛卡尔网格的适配性

    随着工程问题对分离流动模拟精度要求的提升, 传统的RANS方法已无法满足工程需求, 先进的物理模型应运而生. 而将其与自适应网格结合已然成为一个重要发展方向, 对非定常流动高保真模拟具有重要意义. 比如DES[45, 51], DDES[45], IDDES[194], LES方法[28-29, 39, 141, 176]和WMLES方法[30-31, 108]等等. 但是, 根据已有经验, 自适应加密准则、粗细网格间的信息传递和不同层级网格间物理量的守恒性等对物理模型的效果都有直接影响, 对此需要特别注意.

    3.4.2   复杂工程问题应用

    自适应笛卡尔网格类方法在动态问题(包括运动外形、非定常流动现象等)模拟中具有非常明显的优势, 本文此处仅介绍部分典型应用场景.

    声爆预测是超声速飞机设计的主要难点之一, 自适应网格能够根据压力信号自动加密, 得到更为准确的压力信号分布. 例如, Wintzer等[18]利用Cart3D软件和伴随自适应技术实现了F-5E 和SSBD超音速飞机近场压力信号的准确预测, 随后在文献[19]中利用伴随优化设计方法实现了升阻力不变的前提下噪声下降10 dB (如图22所示); 朱震浩等[242]利用伴随自适应笛卡尔网格方法实现了超声速民机声爆预测, 能够以更少的网格量实现流场中激波和膨胀波更精确的捕捉, 进而得到了更加准确的近场过压信号分布.

    图  22  Cart3D超声速民机声爆预测及优化结果[19]
    Figure  22.  Prediction and optimization results of supersonic civil aircraft sonic boom using Cart3D software [19]
    下载: 全尺寸图片 幻灯片

    旋转部件极易产生复杂的涡系结构, 而自适应网格能够以更低的成本对其演化过程进行更为准确的模拟. 因此, 旋转部件是自适应网格技术的主要应用对象, 例如发动机[176, 177]、风力机[53]以及旋翼直升机[193, 194]等. 图23给出了笔者团队采用重叠自适应笛卡尔网格模拟Phase VI风力机叶片的结果. 而对于飞行器结冰过程, 自适应笛卡尔网格能够根据冰形自动变化网格, 因此具有独到的优势, 笔者团队[243-244]率先对其开展了研究. 2024年, Nogi等[245]基于UTCart软件也开展了类似的研究. 同时, 自适应笛卡尔网格方法在旋翼无人机、智能飞行器、汽车和电动垂直起降(eVTOL)飞行器等领域也具有广泛的应用前景.

    图  23  风力机叶尖涡下游发展演化过程[53]
    Figure  23.  Downstream development and evolution of the tip vortex in the wind turbines[53]
    下载: 全尺寸图片 幻灯片

    4.   结束语

    网格生成和自适应是CFD流程中的重要瓶颈. 笛卡尔网格作为一种重要的网格体系, 具备生成速度快、自动化程度高、网格质量好等优点, 能够最大程度地减少CFD周期中的人力成本, 对新一代自动CFD解算器的研发具有重要意义. 随着计算能力的提高、数值方法的改进以及多学科的耦合, 笛卡尔网格方法近些年得到了充足的发展. 本文结合笔者多年系统性的理论与应用研究, 对可压缩流动的笛卡尔网格类方法进行了较为全面的综述, 填补了已有综述留下的空白. 在未来发展方向方面, 分别从大规模并行技术、自适应准则、数值算法以及在实际工程中的应用等几个方面对笛卡尔网格方法进行了展望, 给出了后续需要重点关注的研究方向. 比如, 结合人工智能技术实现“智能自适应”、发展适配的高保真计算方法、构建GPU架构下的动态网格管理以及与先进物理模型的适配性研究等都需投入更多的精力. 总而言之, 笛卡尔网格方法具有较好的工程前景, 也存在诸多亟需解决的瓶颈问题, 仍有大量工作需要进行更加深入的研究, 以期发展出更高效、更准确、更稳健、更智能的低人力成本CFD解算器, 进而为相关领域提供强有力的技术支撑.

    致谢

    本文主要围绕笔者团队近20年学术成果展开, 特别感谢胡偶、沈志伟、干雨新、杨宇辰、齐昕宇和陈航等博士研究生以及其他硕士生对本文相关内容的持续贡献.

  • 图  1   不同网格体系特点[10]

    Figure  1.   The features of different grid systems[10]

    下载: 全尺寸图片 幻灯片

    图  2   笛卡尔网格方法分类(三维图分别来源于Cart3D网页[66]、笔者团队、桑为民等[64]以及Helios[67])

    Figure  2.   The classification of Cartesian grid methods (the three-dimensional diagrams are sourced from the Cart3D website[66], the author's group, Sang et al.[64], and Helios[67])

    下载: 全尺寸图片 幻灯片

    图  3   相同物理条件下贴体网格和笛卡尔网格数量比较[25]

    Figure  3.   Comparison of numbers between the body-fitted and Cartesian grids under the same physical conditions[25]

    下载: 全尺寸图片 幻灯片

    图  4   不同自适应笛卡尔网格数据结构示意图

    Figure  4.   Schematic diagram of different adaptive Cartesian grid data structures

    下载: 全尺寸图片 幻灯片

    图  5   同等条件下三种自适应笛卡尔网格方法比较图[71]

    Figure  5.   Comparison diagram of three adaptive Cartesian grid methods under the same conditions[71]

    下载: 全尺寸图片 幻灯片

    图  6   切割单元方法基本流程

    Figure  6.   Basic process of the cut-cell method

    下载: 全尺寸图片 幻灯片

    图  7   切割单元软件Cart3D的典型计算结果[16, 66]

    Figure  7.   Typical computational results of the cut-cell software Cart3D[16, 66]

    下载: 全尺寸图片 幻灯片

    图  8   浸入边界方法基本流程

    Figure  8.   Basic process of the immersed boundary method

    下载: 全尺寸图片 幻灯片

    图  9   1970—2022年间IBM有关论文变化趋势[13](图中统计数据来源于Scopus数据库, 统计时间截至2022年1月31日)

    Figure  9.   The trend of IBM-related papers from 1970 to 2022[13] (the statistical data in the figure is sourced from the Scopus database, with the data collection up to January 31, 2022)

    下载: 全尺寸图片 幻灯片

    图  10   纯自适应笛卡尔网格并行生成方法

    Figure  10.   Parallel generation method of purely adaptive Cartesian grids

    下载: 全尺寸图片 幻灯片

    图  11   纯笛卡尔网格壁面函数壁面处理方法

    Figure  11.   Wall treatment method for wall functions in pure Cartesian grids

    下载: 全尺寸图片 幻灯片

    图  12   雷诺数DLR-F6绕流问题纯笛卡尔网格方法计算结果[49]

    Figure  12.   Computational results of high-Reynolds flow over DLR-F6 model using the pure Cartesian grid method[49]

    下载: 全尺寸图片 幻灯片

    图  13   重叠笛卡尔网格方法基本流程

    Figure  13.   Basic process of the overset Cartesian grid method

    下载: 全尺寸图片 幻灯片

    图  14   Helios软件计算结果[67]

    Figure  14.   Computational results using the Helios software[67]

    下载: 全尺寸图片 幻灯片

    图  15   重叠自适应笛卡尔网格旋翼流场模拟

    Figure  15.   Simulation of rotor flow fields using the overset adaptive Cartesian grids

    下载: 全尺寸图片 幻灯片

    图  16   混合笛卡尔网格方法基本流程[45]

    Figure  16.   Basic process of the hybrid Cartesian grid method[45]

    下载: 全尺寸图片 幻灯片

    图  17   混合笛卡尔网格方法起落架噪声预测结果[45]

    Figure  17.   Prediction results of landing gear noise using the hybrid Cartesian grid method[45]

    下载: 全尺寸图片 幻灯片

    图  18   自适应准则分类

    Figure  18.   Classification of adaptive criteria

    下载: 全尺寸图片 幻灯片

    图  19   自适应笛卡尔网格并行生成负载平衡情况[49]

    Figure  19.   Load balancing situation of adaptive Cartesian grid parallel generation[49]

    下载: 全尺寸图片 幻灯片

    图  20   自适应笛卡尔网格GPU和CPU比较[229]

    Figure  20.   Comparison of adaptive Cartesian grids on GPU and CPU framework[229]

    下载: 全尺寸图片 幻灯片

    图  21   自适应网格圆柱绕流问题[238]

    Figure  21.   Flow around a cylinder on adaptive Cartesian grid[238]

    下载: 全尺寸图片 幻灯片

    图  22   Cart3D超声速民机声爆预测及优化结果[19]

    Figure  22.   Prediction and optimization results of supersonic civil aircraft sonic boom using Cart3D software [19]

    下载: 全尺寸图片 幻灯片

    图  23   风力机叶尖涡下游发展演化过程[53]

    Figure  23.   Downstream development and evolution of the tip vortex in the wind turbines[53]

    下载: 全尺寸图片 幻灯片

    表  1   各类笛卡尔网格方法优缺点

    Table  1   Advantages and disadvantages of various Cartesian grid methods

    下载: 导出CSV

    表  2   国外知名结构自适应网格代码框架及性能[75]

    Table  2   Overview of well-known foreign structured AMR code frameworks and their performance[75]

    Feature BoxLib Cactus Chombo Enzo FLASH Uintah
    subcycling optional optional optional required None required
    time step ratio same as refinement independent same as refinement independent same as refinement
    elliptic solver PETSc/Hypre/Trilinos native GMC user supplied PETSc/native GMG hypre native GMG hypre/native GMG PETSc(hypre)
    GMG with AMR sub or whole mesh sub or whole mesh single level whole mesh sub or whole mesh
    spherical AMR 1D multipatch 1D 1, 2, or 3D 1D
    cylindrical AMR 2D multipatch 2D 1, 2, or 3D 2D
    mixed dimensions yes
    highest dimension 4D up to 6D
    block size variable variable variable variable fixed variable
    refine factor 2/4 2 2/4 any integer 2 any integer
    parent blocks not unique not unique not unique unique unique unique
    regridding level tag cells per level tag cells per level tag cells per level tag cells per level tag blocks all atonce tag blocks all atonce
    space flling curve morton morton piano-Hilbert morton Hilbert+fast sorting
    OpenMP per block and loops dynamically tuned loops per block per block and loops per block and loops
    accelerators CUDA OpenCL CUDA CUDA
    parallel I/O native HDF5 HDF5 HDF5 HDF5 PnetCDF HDF5
    viz vist/yt vislt/yt vislt vislt/yt vislt/yt vislt
    FSI embedded boundary immersed boundary MPM method
    framework language C++/Fortran C/C++ C++ C++ Fortran C++
    user module language Fortran C/C++ Fortran Fortran Fortran Fortran
    下载: 导出CSV
    • 参考文献(245)
  • [1]

    Slotnick J, Khodadoust A, Alonso J, et al. CFD vision 2030 study: A path to revolutionary computational aerosciences. NASA/CR-2014-218178, 2014
    [2] 陈坚强, 袁先旭, 涂国华等. 计算流体力学2035愿景. 北京: 科学出版社, 2023 (Chen Jianqiang, Yuan Xianxu, Tu Guohua, et al. Computational Fluid Dynamics 2035 Vision in China. Beijing: Science Press, 2023 (in Chinese)

    Chen Jianqiang, Yuan Xianxu, Tu Guohua, et al. Computational Fluid Dynamics 2035 Vision in China. Beijing: Science Press, 2023 (in Chinese)
    [3]

    Spalart PR, Venkatakrishnan V. On the role and challenges of CFD in the aerospace industry. The Aeronautical Journal, 2016, 120(1223): 209-232 doi: 10.1017/aer.2015.10
    [4]

    Mani M, Dorgan AJ. A perspective on the state of aerospace computational fluid dynamics technology. Annual Review of Fluid Mechanics, 2023, 55(1): 431-457 doi: 10.1146/annurev-fluid-120720-124800
    [5]

    Runchal A. 50 Years of CFD in Engineering Sciences. Springer, 2020
    [6] 阎超. 航空CFD四十年的成就与困境. 航空学报, 2022, 43(10): 21-57 (Yan Chao. Achievements and predicaments of CFD in aeronautics in past forty years. Acta Aeronautica et Astronautica Sinica, 2022, 43(10): 21-57 (in Chinese)

    Yan Chao. Achievements and predicaments of CFD in aeronautics in past forty years. Acta Aeronautica et Astronautica Sinica, 2022, 43(10): 21-57 (in Chinese)
    [7] 张来平, 常兴华, 赵钟等. 计算流体力学网格生成技术. 北京: 科学出版社, 2017 (Zhang Laiping, Chang Xinghua, Zhao Zhong, et al. Mesh Generation Technoques in Computational Fluid Dynamics. Beijing: Science Press, 2017 (in Chinese)

    Zhang Laiping, Chang Xinghua, Zhao Zhong, et al. Mesh Generation Technoques in Computational Fluid Dynamics. Beijing: Science Press, 2017 (in Chinese)
    [8]

    Martins JRRA. Aerodynamic design optimization: Challenges and perspectives. Computers & Fluids, 2022, 239: 105391
    [9]

    Chawner JR, Dannenhoffer J, Taylor NJ. Geometry, mesh generation, and the CFD 2030 vision//46th AIAA Fluid Dynamics Conference, Washington, 2016
    [10]

    Baker TJ. Mesh generation: Art or science? Progress in Aerospace Sciences, 2005, 41(1): 29-63
    [11]

    Nakahashi K. Aeronautical CFD in the age of petaflops-scale computing: from unstructured to Cartesian meshes. European Journal of Mechanics-B/Fluids, 2013, 40: 75-86 doi: 10.1016/j.euromechflu.2013.02.005
    [12]

    Griffith BE, Patankar NA. Immersed methods for fluid-structure interaction. Annual Review of Fluid Mechanics, 2020, 52: 421-448
    [13]

    Verzicco R. Immersed boundary methods: Historical perspective and future outlook. Annual Review of Fluid Mechanics, 2023, 55(1): 129-155
    [14]

    Aftosmis MJ. Solution adaptive Cartesian grid methods for aerodynamic flows with complex geometries//28th Computational Fluid Dynamics, von Karman Institute for Fluid Dynamics, 1997
    [15]

    Aftosmis MJ, Berger MJ, Melton JE. Robust and efficient Cartesian mesh generation for component-based geometry. AIAA Journal, 1998, 36(6): 952-960 doi: 10.2514/2.464
    [16]

    Aftosmis MJ, Berger MJ, Murman SE. Applications of space-filling curves to Cartesian methods for CFD//42nd Aerospace Sciences Meeting and Exhibit, Reno Nevada, 2004
    [17]

    Nemec M, Aftosmis MJ, Wintzer M. Adjoint-based adaptive mesh refinement for complex geometries//46th AIAA Aerospace Sciences Meeting and Exhibit, Nevada, 2008
    [18]

    Wintzer M, Nemec M, Aftosmis MJ. Adjoint-based adaptive mesh refinement for sonic boom prediction//26th AIAA Applied Aerodynamics Conference, Hawaii, 2008
    [19]

    Aftosmis MJ, Nemec M, Cliff SE. Adjoint-based low-boom design with Cart3D//29th AIAA Applied Aerodynamics Conference, Hawaii, 2011
    [20]

    Berger M, Aftosmis M. Progress towards a Cartesian cut-cell method for viscous compressible flow//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, 2012
    [21]

    Young DP, Melvin RG, Bieterman MB, et al. A locally refined rectangular grid finite element method: Approximation to computational fluid dynamics and computational physics. Journal of Computational Physics, 1991, 92: 1-66 doi: 10.1016/0021-9991(91)90291-R
    [22]

    Strawn RC, Djomehri MJ. Computational modeling of hovering rotor and wake aerodynamics. Journal of Aircraft, 2002, 39(5): 786-793 doi: 10.2514/2.3024
    [23]

    Wissink AM, Potsdam M, Sankaran V, et al. A dual-mesh unstructured adaptive Cartesian computational fluid dynamics approach for hover prediction. Journal of the American Helicopter Society, 2016, 61(1): 1-19
    [24]

    Lee JD. Development of an efficient viscous approach in a Cartesian grid framework and application to rotor-fuselage interaction. [PhD Thesis]. Atlanta: Georgia Institute of Technology, 2006
    [25]

    Ruffin SM, Zaki M, Sekhar S. A normal ray refinement technique for Cartesian-grid based Navier-Stokes solvers. International Journal of Computational Fluid Dynamics, 2012, 26(4): 231-246 doi: 10.1080/10618562.2012.691970
    [26]

    Marshall DD. Extending the functionalities of Cartesian grid solvers: Viscous effects modeling and MPI parallelization. [PhD Thesis]. Atlanta: Georgia Institute of Technology, 2002
    [27]

    Constant B, Péron S, Beaugendre H, et al. An improved immersed boundary method for turbulent flow simulations on Cartesian grids. Journal of Computational Physics, 2021, 435: 110240 doi: 10.1016/j.jcp.2021.110240
    [28]

    Renaud T, Benoit C, Peron S, et al. Validation of an immersed boundary method for compressible flows//AIAA Scitech 2019 Forum, California, 2019
    [29]

    Péron S, Benoit C, Renaud T, et al. An immersed boundary method on Cartesian adaptive grids for the simulation of compressible flows around arbitrary geometries. Engineering with Computers, 2021, 37(3): 2419-2437 doi: 10.1007/s00366-020-00950-y
    [30]

    van Noordt W, Ganju S, Brehm C. An immersed boundary method for wall-modeled large-eddy simulation of turbulent high-Mach-number flows. Journal of Computational Physics, 2022, 470: 111583 doi: 10.1016/j.jcp.2022.111583
    [31]

    De Vanna F, Baldan G, Picano F, et al. On the coupling between wall-modeled LES and immersed boundary method towards applicative compressible flow simulations. Computers & Fluids, 2023, 266: 106058
    [32]

    Tamaki Y, Harada M, Imamura T. Near-wall modification of Spalart-Allmaras turbulence model for immersed boundary method. AIAA Journal, 2017, 55(9): 3027-3039 doi: 10.2514/1.J055824
    [33]

    Tamaki Y. Turbulent flow simulations around aircraft using hierarchical Cartesian grids and the immersed boundary method. [PhD Thesis]. Tokyo: University of Tokyo, 2018
    [34]

    Imamura T, Tamaki Y. Unsteady flow simulation around two-wheel main landing gear based on compressible Navier-Stokes solver with immersed boundary method//AIAA Aviation 2020 Forum, Virtual Event, 2020
    [35]

    Sugaya K, Imamura T. Unsteady turbulent flow simulations on moving Cartesian grids using immersed boundary method and high-order scheme. Computers & Fluids, 2021, 231: 105173
    [36]

    Funada M, Imamura T. High-order immersed boundary method for inviscid flows applied to flux reconstruction method on a hierarchical Cartesian grid. Computers & Fluids, 2023, 265: 105986
    [37]

    Tamaki Y, Kawai S. Wall modeling for large-eddy simulation on non-body-conforming Cartesian grids. Physical Review Fluids, 2021, 6(11): 114603 doi: 10.1103/PhysRevFluids.6.114603
    [38]

    Kuya Y, Kawai S. A stable and non-dissipative kinetic energy and entropy preserving (KEEP) scheme for non-conforming block boundaries on Cartesian grids. Computers & Fluids, 2020, 200: 104427
    [39]

    Asada H, Kawai S. LES of full aircraft configuration using non-dissipative KEEP scheme with conservative explicit filter//AIAA SciTech 2022 Forum, San Diego & Virtual, 2022
    [40]

    Asada H, Kawai S. Conservative low-pass filter with compact stencils for hierarchical Cartesian mesh. Computers & Fluids, 2023, 252: 105769
    [41]

    Asada H, Tamaki Y, Takaki R, et al. Compressible flow solver FFVHC-ACE for fully automated LES of aeronautical flows//AIAA SCITECH 2023 Forum, National Harbor & Online, 2023
    [42]

    Asada H, Tamaki Y, Takaki R, et al. FFVHC-ACE: Fully automated Cartesian-grid-based solver for compressible large-eddy simulation. AIAA Journal, 2023, 61(8): 3466-3484 doi: 10.2514/1.J062593
    [43]

    Karman LJS. SPLITFLOW-A 3D unstructured Cartesian/prismatic grid CFD code for complex geometries//33rd Aerospace Sciences Meeting and Exhibit, Reno, 1995
    [44]

    Kara E, Kutlar AI, Aksel MH. An octree-based solution-adaptive Cartesian grid generator and Euler solver for the simulation of three-dimensional inviscid compressible flows. Progress in Computational Fluid Dynamics, 2016, 16(3): 131-145 doi: 10.1504/PCFD.2016.076247
    [45]

    Ueno Y, Ochi A. Airframe noise prediction using Navier-Stokes code with Cartesian and boundary-fitted layer meshes//25th AIAA/CEAS Aeroacoustics Conference, Delft, 2019
    [46]

    Liu J, Zhao N, Hu O. The ghost cell method and its applications for inviscid compressible flow on adaptive tree Cartesian grids. Advances in Applied Mathematics and Mechanics, 2009, 1(5): 664-682 doi: 10.4208/aamm.09-m0912
    [47] 胡偶, 赵宁, 刘剑明. 壁面函数在激波诱导分离流动中的应用. 航空计算技术, 2013, 43(6): 26-29 (Hu Ou, Zhao Ning, Liu Jianming. Wall function method for shock induced separated flows simulation. Aeronautical Computing Technique, 2013, 43(6): 26-29 (in Chinese) doi: 10.3969/j.issn.1671-654X.2013.06.007

    Hu Ou, Zhao Ning, Liu Jianming. Wall function method for shock induced separated flows simulation. Aeronautical Computing Technique, 2013, 43(6): 26-29 (in Chinese) doi: 10.3969/j.issn.1671-654X.2013.06.007
    [48]

    Qi X, Yang Y, Tian L, et al. A parallel methodology of adaptive Cartesian grid for compressible flow simulations. Advances in Aerodynamics, 2022, 4(1): 21 doi: 10.1186/s42774-022-00108-y
    [49]

    Yang Y, Qi X, Wang Z, et al. An immersed boundary method based on parallel adaptive Cartesian grids for high Reynolds number turbulent flow. International Journal of Computational Fluid Dynamics, 2022, 36(4): 319-341 doi: 10.1080/10618562.2022.2108807
    [50] 刘剑明, 赵宁, 胡偶等. 自适应笛卡尔网格Ghost Cell方法研究. 空气动力学学报, 2010, 28(1): 61-65 (Liu Jianming, Zhao Ning, Hu Ou, et al. Ghost cell methods on adaptive cartesian grids. Acta Aerodynamica Sinica, 2010, 28(1): 61-65 (in Chinese) doi: 10.3969/j.issn.0258-1825.2010.01.009

    Liu Jianming, Zhao Ning, Hu Ou, et al. Ghost cell methods on adaptive cartesian grids. Acta Aerodynamica Sinica, 2010, 28(1): 61-65 (in Chinese) doi: 10.3969/j.issn.0258-1825.2010.01.009
    [51] 沈志伟. 基于混合笛卡尔网格方法的非定常流动问题研究. [博士论文]. 南京: 南京航空航天大学, 2016 (Shen Zhiwei. Research on hybri-d cartesian grid method for simulating unsteady flows. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2016 (in Chinese)

    Shen Zhiwei. Research on hybri-d cartesian grid method for simulating unsteady flows. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2016 (in Chinese)
    [52] 干雨新, 赵宁. 预处理方法在混合笛卡尔网格中的应用研究. 空气动力学学报, 2018, 36(4): 651-657 (Gan Yuxin, Zhao Ning. Study of precondition method in hybrid Cartesian grid and its applications. Acta Aerodynamica Sinica, 2018, 36(4): 651-657 (in Chinese)

    Gan Yuxin, Zhao Ning. Study of precondition method in hybrid Cartesian grid and its applications. Acta Aerodynamica Sinica, 2018, 36(4): 651-657 (in Chinese)
    [53] 干雨新, 赵宁, 刘剑明. 基于混合笛卡尔网格的风力机问题数值模拟. 太阳能学报, 2019, 40: 1366-1372 (Gan Yuxin, Zhao Ning, Liu Jianming. Study on hybrid cartesian grid method for simulating wind turbine flows. Acta Energiae Solaris Sinica, 2019, 40: 1366-1372 (in Chinese)

    Gan Yuxin, Zhao Ning, Liu Jianming. Study on hybrid cartesian grid method for simulating wind turbine flows. Acta Energiae Solaris Sinica, 2019, 40: 1366-1372 (in Chinese)
    [54] 干雨新, 赵宁, 刘剑明. 基于混合笛卡尔网格的高精度格式研究. 航空计算技术, 2019, 49: 31-34 (Gan Yuxin, Zhao Ning, Liu Jianming. Study on high- order scheme in hybrid Cartesian grid. Aeronautical Computing Technique, 2019, 49: 31-34 (in Chinese) doi: 10.3969/j.issn.1671-654X.2019.04.008

    Gan Yuxin, Zhao Ning, Liu Jianming. Study on high- order scheme in hybrid Cartesian grid. Aeronautical Computing Technique, 2019, 49: 31-34 (in Chinese) doi: 10.3969/j.issn.1671-654X.2019.04.008
    [55] 杨宇辰. 可压缩流动模拟的自适应网格方法研究. [博士论文]. 南京: 南京航空航天大学, 2023 (Yang Yuchen. Research on adaptive mesh method for compressible flow simulation. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2023 (in Chinese)

    Yang Yuchen. Research on adaptive mesh method for compressible flow simulation. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2023 (in Chinese)
    [56] 肖涵山, 陈作斌, 刘刚等. 基于Euler方程的三维自适应笛卡尔网格应用研究. 空气动力学学报, 2003, 21(2): 202-210 (Xiao Hanshan, Chen Zuobin, Liu Gang, et al. Applications of 3-D adaptive Cartesian grid algorithm based on the Euler equations. Acta Aerodynamica Sinica, 2003, 21(2): 202-210 (in Chinese) doi: 10.3969/j.issn.0258-1825.2003.02.011

    Xiao Hanshan, Chen Zuobin, Liu Gang, et al. Applications of 3-D adaptive Cartesian grid algorithm based on the Euler equations. Acta Aerodynamica Sinica, 2003, 21(2): 202-210 (in Chinese) doi: 10.3969/j.issn.0258-1825.2003.02.011
    [57] 陈浩, 毕林, 华如豪等. 基于全线程树数据结构的笛卡尔网格高效生成技术. 航空学报, 2021, 40(12): 125170 (Chen Hao, Bi Lin, Hua Ruhao, et al. Efficient Cartesian mesh generation method based on fully threaded tree data structure. Acta Aeronautica et Astronautica Sinica, 2021, 40(12): 125170 (in Chinese)

    Chen Hao, Bi Lin, Hua Ruhao, et al. Efficient Cartesian mesh generation method based on fully threaded tree data structure. Acta Aeronautica et Astronautica Sinica, 2021, 40(12): 125170 (in Chinese)
    [58] 陈浩, 华如豪, 袁先旭等. 基于自适应笛卡尔网格的飞翼布局流动模拟. 航空学报, 2022, 43(8): 125674 (Chen Hao, Hua Ruhao, Yuan Xianxu, et al. Simulation of flow around fly-wing configuration based on adaptive Cartesian grid. Acta Aeronautica et Astronautica Sinica, 2022, 43(8): 125674 (in Chinese) doi: 10.7527/j.issn.1000-6893.2022.8.hkxb202208028

    Chen Hao, Hua Ruhao, Yuan Xianxu, et al. Simulation of flow around fly-wing configuration based on adaptive Cartesian grid. Acta Aeronautica et Astronautica Sinica, 2022, 43(8): 125674 (in Chinese) doi: 10.7527/j.issn.1000-6893.2022.8.hkxb202208028
    [59]

    Meng S, Zhou D, Yuan X, et al. Enhanced strategy for adaptive Cartesian grid generation with arbitrarily complex 3D geometry. Advances in Engineering Software, 2022, 174: 103304 doi: 10.1016/j.advengsoft.2022.103304
    [60] 孟爽, 周丹, 李雪亮等. 笛卡尔网格下精确高效的壁面距离计算方法. 空气动力学学报, 2023, 41(7): 93-101 (Meng Shuang, Zhou Dan, Li Xueliang, et al. Accurate and efficient wall distance calculation method for Cartesian grids. Acta Aerodynamica Sinica, 2023, 41(7): 93-101 (in Chinese) doi: 10.7638/kqdlxxb-2021.0359

    Meng Shuang, Zhou Dan, Li Xueliang, et al. Accurate and efficient wall distance calculation method for Cartesian grids. Acta Aerodynamica Sinica, 2023, 41(7): 93-101 (in Chinese) doi: 10.7638/kqdlxxb-2021.0359
    [61]

    Luo C, Zhou D, Meng S, et al. A novel cell-based adaptive Cartesian grid approach for complex flow simulations. Applied Sciences, 2024, 14(9): 3692 doi: 10.3390/app14093692
    [62] 桑为民, 李凤蔚. 采用自适应直角网格计算三维增升装置绕流. 力学学报, 2005, 37(1): 80-86 (Sang Weimin, Li Fengwei. Numerical analysis of flows around 3d high-lift system by adaptive Cartesian grid method. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(1): 80-86 (in Chinese) doi: 10.3321/j.issn:0459-1879.2005.01.011

    Sang Weimin, Li Fengwei. Numerical analysis of flows around 3d high-lift system by adaptive Cartesian grid method. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(1): 80-86 (in Chinese) doi: 10.3321/j.issn:0459-1879.2005.01.011
    [63]

    Sang W, Li F. Numerical simulations for transport aircraft high-lift configurations using adaptive Cartesian grid methods. Journal of Aircraft, 2006, 43(4): 1103-1111 doi: 10.2514/1.17886
    [64]

    Sang W, Yu J. Numerically analyzing more efficiently high-lift aerodynamics of wing/body model with omni-tree Cartesian grids. Aerospace Science and Technology, 2011, 15(5): 375-380 doi: 10.1016/j.ast.2010.09.001
    [65] 王力, 田方宝. 浸入边界法及其在可压缩流动中的应用和进展. 中国科学: 物理学 力学 天文学, 2018, 48(9): 094703 (Wang Li, Tian Fangbao. Recent progress of immersed boundary method and its applications in compressible fluid flow. Scientia Sinica (Physica, Mechanica & Astronomica ), 2018, 48(9): 094703 (in Chinese)

    Wang Li, Tian Fangbao. Recent progress of immersed boundary method and its applications in compressible fluid flow. Scientia Sinica(Physica, Mechanica & Astronomica), 2018, 48(9): 094703 (in Chinese)
    [66]

    Cart3D. [DB/OL]. (viewed on 26-06, 2024). https://www.nas.nasa.gov/publications/software/docs/cart3d/
    [67]

    Jain R, Biedron RT, Jones W, et al. Modularization and validation of NASA FUN3D as a HPCMP CREATE-AV helios near-body solver//54th AIAA Aerospace Sciences Meeting, San Diego, 2016
    [68]

    Alauzet F, Loseille A. A decade of progress on anisotropic mesh adaptation for computational fluid dynamics. Computer-Aided Design, 2016, 72: 13-39 doi: 10.1016/j.cad.2015.09.005
    [69]

    Park MA, Loseille A, Krakos J, et al. Unstructured grid adaptation: Status, potential impacts, and recommended investments towards CFD 2030//46th AIAA Fluid Dynamics Conference, Washington, 2016
    [70] 唐静, 崔鹏程, 张健等. 流体数值模拟网格自适应技术研究进展. 力学进展, 2023, 53(3): 661-692 (Tang Jing, Cui Pengcheng, Zhang Jian, et al. Review of mesh adaptation for fluid numerical simulation. Advances in Mechanics, 2023, 53(3): 661-692 (in Chinese) doi: 10.6052/1000-0992-23-013

    Tang Jing, Cui Pengcheng, Zhang Jian, et al. Review of mesh adaptation for fluid numerical simulation. Advances in Mechanics, 2023, 53(3): 661-692 (in Chinese) doi: 10.6052/1000-0992-23-013
    [71]

    Dunning DJ, Robey RW, Kuehn JA, et al. A performance analysis of phantom-cell adaptive mesh refinement on CPUs and GPUs. Journal of Computing and Information Science in Engineering, 2021, 21(1): 011011 doi: 10.1115/1.4048717
    [72]

    Burstedde C, Wilcox LC, Ghattas O. P4est: Scalable algorithms for parallel adaptive mesh refinement on forests of octrees. SIAM Journal on Scientific Computing, 2011, 33(3): 1103-1133 doi: 10.1137/100791634
    [73] 胡偶, 赵宁, 刘剑明等. 基于有限体积格式的自适应笛尔网格虚拟单元方法及其应用. 空气动力学学报, 2011, 29(4): 491-495 (Hu Ou, Zhao Ning, Liu Jianming, et al. A ghost cell method on finite volume adaptive Cartesiangrids and its applications. Acta Aerodynamica Sinica, 2011, 29(4): 491-495 (in Chinese) doi: 10.3969/j.issn.0258-1825.2011.04.016

    Hu Ou, Zhao Ning, Liu Jianming, et al. A ghost cell method on finite volume adaptive Cartesiangrids and its applications. Acta Aerodynamica Sinica, 2011, 29(4): 491-495 (in Chinese) doi: 10.3969/j.issn.0258-1825.2011.04.016
    [74]

    Saravanan V, Choung H, Lee S. Cell-based hybrid adaptive mesh refinement algorithm for immersed boundary method. International Journal for Numerical Methods in Fluids, 2021, 94(3): 272-294
    [75]

    Dubey A, Almgren A, Bell J, et al. A survey of high level frameworks in block-structured adaptive mesh refinement packages. Journal of Parallel and Distributed Computing, 2014, 74(12): 3217-3227 doi: 10.1016/j.jpdc.2014.07.001
    [76]

    Wei F, Jin L, Liu J, et al. GPU acceleration of a 2D compressible Euler solver on CUDA-based block-structured Cartesian meshes. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2020, 42(5): 250 doi: 10.1007/s40430-020-02290-w
    [77]

    Freret L, Williamschen M, Groth CPT. Enhanced anisotropic block-based adaptive mesh refinement for three-dimensional inviscid and viscous compressible flows. Journal of Computational Physics, 2022, 458: 111092 doi: 10.1016/j.jcp.2022.111092
    [78]

    Nakahashi K. Immersed boundary method for compressible Euler equations in the building-cube method//20th AIAA Computational Fluid Dynamics Conference, Hawaii, 2011
    [79]

    Muralidharan B, Menon S. Simulation of moving boundaries interacting with compressible reacting flows using a second-order adaptive Cartesian cut-cell method. Journal of Computational Physics, 2018, 357: 230-262 doi: 10.1016/j.jcp.2017.12.030
    [80]

    Li S, Hyman JM. Adaptive mesh refinement for finite difference WENO schemes. LA-UR-03-8927: Los Alamos, 2003
    [81]

    Li S. Comparison of refinement criteria for structured adaptive mesh refinement. Journal of Computational and Applied Mathematics, 2010, 233(12): 3139-3147 doi: 10.1016/j.cam.2009.08.104
    [82]

    MacNeice P, Olson KM, Mobarry C, et al. PARAMESH: A parallel adaptive mesh refinement community toolkit. Computer Physics Communications, 2000, 126(3): 330-354 doi: 10.1016/S0010-4655(99)00501-9
    [83]

    Hornung RD, Kohn SR. Managing application complexity in the SAMRAI object-oriented framework. Concurrency and Computation: Practice and Experience, 2002, 14(5): 347-368 doi: 10.1002/cpe.652
    [84]

    Zhang W, Myers A, Gott K, et al. AMReX: Block-structured adaptive mesh refinement for multiphysics applications. The International Journal of High Performance Computing Applications, 2021, 35(6): 508-526 doi: 10.1177/10943420211022811
    [85]

    Clarke DK, Salas MD, Hassan HA. Euler calculations for multielement airfoils using Cartesian grids. AIAA Journal, 1986, 24(3): 353-358 doi: 10.2514/3.9273
    [86]

    Gaffney JR, Hassan H. Euler calculations for wings using Cartesian grids//25th AIAA Aerospace Sciences Meeting, Reno, 1987
    [87]

    De Zeeuw D, Powell KG. An adaptively refined Cartesian mesh solver for the Euler equations. Journal of Computational Physics, 1993, 104: 56-68 doi: 10.1006/jcph.1993.1007
    [88]

    Powell KG. Solution of the Euler equations on solution-adaptive Cartesian grids. Computational Fluid Dynamics Review, 1998, 2: 65-92
    [89] 桑为民. 基于自适应直角切割及混合网格的Euler/N-S方程数值模拟. [博士论文]. 西安: 西北工业大学, 2002 (Sang Weimin. Numerical simulation of Euler/N-S equations based on adaptive right-angle cuts and hybrid grids. [PhD Thesis]. Xian: Northwestern Polytechnical University, 2002 (in Chinese)

    Sang Weimin. Numerical simulation of Euler/N-S equations based on adaptive right-angle cuts and hybrid grids. [PhD Thesis]. Xian: Northwestern Polytechnical University, 2002 (in Chinese)
    [90] 桑为民, 李凤蔚, 鄂秦. 应用笛卡尔非结构切割网格进行外挂物投放的数值模拟. 计算物理, 2002, 19(3): 268-272 (Sang Weimin, Li Fengwei, E Qin. Numerical simulation of the store separation usingunstructured cartesian cutted grid. Chinese Journal of Computational Physics, 2002, 19(3): 268-272 (in Chinese)

    Sang Weimin, Li Fengwei, E Qin. Numerical simulation of the store separation usingunstructured cartesian cutted grid. Chinese Journal of Computational Physics, 2002, 19(3): 268-272 (in Chinese)
    [91]

    Sang W, Shi Y. Comparison of octree and omni-tree Cartesian grid for civil-plane high-lift model simulations. Journal of Aircraft, 2013, 50(4): 1099-1105 doi: 10.2514/1.C032044
    [92]

    Sang WM, Li FW. Omni-tree and adaptive cartesian hybrid grid method in steady and unsteady flows//21st AIAA Applied Aerodynamics Conference, Orlando, 2003
    [93]

    Li K, Wu ZN. Nonet-Cartesian grid method for shock flow computations. Journal of Scientific Computing, 2003, 20(3): 303-329
    [94] 逯雪铃, 叶正寅. 笛卡尔网格生成过程中的内外判断问题. 西北工业大学学报, 2009, 27: 569-663 (Lu Xueling, Ye Zhengyin. Always proper inside/outside determination in Cartesian mesh generation. Journal of Northwestern Polytechnical University, 2009, 27: 569-663 (in Chinese) doi: 10.3969/j.issn.1000-2758.2009.05.014

    Lu Xueling, Ye Zhengyin. Always proper inside/outside determination in Cartesian mesh generation. Journal of Northwestern Polytechnical University, 2009, 27: 569-663 (in Chinese) doi: 10.3969/j.issn.1000-2758.2009.05.014
    [95]

    Lee JW. Parallelized Cartesian grid methodology for non-equilibrium hyperbolic flow analysis of ballutes. [PhD Thesis]. Atlanta: Georgia Institute of Technology, 2007
    [96]

    Kidron YE, Mor-Yossef Y, Levy Y. Robust Cartesian grid flow solver for high-Reynolds-number turbulent flow simulations. AIAA Journal, 2010, 48(6): 1130-1140 doi: 10.2514/1.45817
    [97]

    Hartmann D, Meinke M, Schröder W. A strictly conservative Cartesian cut-cell method for compressible viscous flows on adaptive grids. Computer Methods in Applied Mechanics and Engineering, 2011, 200(9-12): 1038-1052 doi: 10.1016/j.cma.2010.05.015
    [98]

    Pasquariello V, Hammerl G, Örley F, et al. A cut-cell finite volume-finite element coupling approach for fluid-structure interaction in compressible flow. Journal of Computational Physics, 2016, 307: 670-695 doi: 10.1016/j.jcp.2015.12.013
    [99]

    Bandringa H. Immersed boundary methods. [PhD Thesis]. Groningen: University of Groningen, 2010
    [100]

    Coirier WJ, Powell KG. Solution-adaptive Cartesian cell approach for viscous and inviscid flows. AIAA Journal, 1996, 34(5): 938-945 doi: 10.2514/3.13171
    [101]

    Arslanbekov R, Kolobov V, Frolova A. Analysis of compressible viscous flow solvers with adaptive Cartesian mesh//20th AIAA Computational Fluid Dynamics Conference, Hawaii, 2011
    [102]

    Pember RB, Bell JB, Colella P, et al. An adaptive Cartesian grid method for unsteady compressible flow in irregular regions. Journal of Computational Physics, 1995, 120: 278-304 doi: 10.1006/jcph.1995.1165
    [103]

    Yang G, Causon DM, Ingram DM, et al. A Cartesian cut cell method for compressible flows Part A: static body problems. The Aeronautical Journal, 1997, 101(1002): 47-56 doi: 10.1017/S0001924000066690
    [104]

    Ye T, Mittal R, Udaykumar HS, et al. An accurate Cartesian grid method for viscous incompressible flows with complex immersed boundaries. Journal of Computational Physics, 1999, 156: 209-240 doi: 10.1006/jcph.1999.6356
    [105]

    Mondal P, Munikrishna N, Balakrishnan N. Cartesian-like grids using a novel grid-stitching algorithm for viscous flow computations. Journal of Aircraft, 2007, 44(5): 1598-1609 doi: 10.2514/1.27854
    [106]

    Muralidharan B, Menon S. A high-order adaptive Cartesian cut-cell method for simulation of compressible viscous flow over immersed bodies. Journal of Computational Physics, 2016, 321: 342-368 doi: 10.1016/j.jcp.2016.05.050
    [107]

    Müller B, Krämer-Eis S, Kummer F, et al. A high-order discontinuous Galerkin method for compressible flows with immersed boundaries. International Journal for Numerical Methods in Engineering, 2017, 110(1): 3-30 doi: 10.1002/nme.5343
    [108]

    Gokhale NB. A dimensionally split Cartesian cut cell method for computational fluid dynamics. [PhD Thesis]. Cambridge: University of Cambridge, 2018
    [109]

    Schneiders L, Hartmann D, Meinke M, et al. An accurate moving boundary formulation in cut-cell methods. Journal of Computational Physics, 2013, 235: 786-809 doi: 10.1016/j.jcp.2012.09.038
    [110]

    Seo JH, Mittal R. A sharp-interface immersed boundary method with improved mass conservation and reduced spurious pressure oscillations. Journal of Computational Physics, 2011, 230(19): 7347-7363 doi: 10.1016/j.jcp.2011.06.003
    [111]

    Schneiders L, Günther C, Meinke M, et al. An efficient conservative cut-cell method for rigid bodies interacting with viscous compressible flows. Journal of Computational Physics, 2016, 311: 62-86 doi: 10.1016/j.jcp.2016.01.026
    [112]

    Seshadri PK. Sharp interface immersed boundary framework for all-speed flow solver. [PhD Thesis]. Kanpur: Indian Institute of Technology Kanpur, 2019
    [113]

    Lorensen WE, Cline HE. Marching cubes: A high resolution 3D surface construction algorithm. Computer Graphics, 1987, 21: 163-169 doi: 10.1145/37402.37422
    [114] 宫兆新, 鲁传敬, 黄华雄. 浸入边界法及其应用. 力学季刊, 2007, 28(3): 353-362 (Gong Zhaoxin, Lu Chuanjing, Huang Huaxiong. Immersed boundary method and its application. Chinese Quarterly of Mechanics, 2007, 28(3): 353-362 (in Chinese) doi: 10.3969/j.issn.0254-0053.2007.03.001

    Gong Zhaoxin, Lu Chuanjing, Huang Huaxiong. Immersed boundary method and its application. Chinese Quarterly of Mechanics, 2007, 28(3): 353-362 (in Chinese) doi: 10.3969/j.issn.0254-0053.2007.03.001
    [115]

    Peskin CS. Flow patterns around heart valves: A numerical method. Journal of Computational Physics, 1972, 10(2): 252-271 doi: 10.1016/0021-9991(72)90065-4
    [116]

    Roy S, De A, Balaras E. Immersed boundary method: Development and applications. Springer, 2020
    [117]

    Mittal R, Iaccarino G. Immersed boundary methods. Annual Review of Fluid Mechanics, 2005, 37(1): 239-261 doi: 10.1146/annurev.fluid.37.061903.175743
    [118]

    Sotiropoulos F, Yang X. Immersed boundary methods for simulating fluid-structure interaction. Progress in Aerospace Sciences, 2014, 65: 1-21 doi: 10.1016/j.paerosci.2013.09.003
    [119]

    Dadone A, Grossman B. Surface boundary conditions for the numerical solution of the Euler equations. AIAA Journal, 1994, 32(2): 285-293 doi: 10.2514/3.11983
    [120]

    Dadone A, Grossman B. Ghost-cell method for inviscid two-dimensional flows on Cartesian grids. AIAA Journal, 2004, 42(12): 2499-2507 doi: 10.2514/1.697
    [121]

    Colella P, Graves DT, Keen BJ, et al. A Cartesian grid embedded boundary method for hyperbolic conservation laws. Journal of Computational Physics, 2006, 211(1): 347-366 doi: 10.1016/j.jcp.2005.05.026
    [122]

    Capizzano F. A compressible flow simulation system based on Cartesian grids with anisotropic refinements//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, 2007
    [123]

    Capizzano F. Automatic generation of locally refined Cartesian meshes: Data management and algorithms. International Journal for Numerical Methods in Engineering, 2017, 113(5): 789-813
    [124]

    Kamatsuchi T. Turbulent flow simulation around complex geometries with Cartesian grid method//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, 2007
    [125]

    Gorsse Y, Iollo A, Telib H, et al. A simple second order cartesian scheme for compressible Euler flows. Journal of Computational Physics, 2012, 231(23): 7780-7794 doi: 10.1016/j.jcp.2012.07.014
    [126]

    De Palma P, De Tullio MD, Pascazio G, et al. An immersed-boundary method for compressible viscous flows. Computers & Fluids, 2006, 35(7): 693-702
    [127]

    Sekhar SK, Ruffin SM. Predictions of convective heat transfer rates using a Cartesian grid solver for hypersonic flows//44th AIAA Thermophysics Conference, San Diego, 2013
    [128]

    Piquet A, Roussel O, Hadjadj A. A comparative study of Brinkman penalization and direct-forcing immersed boundary methods for compressible viscous flows. Computers & Fluids, 2016, 136: 272-284
    [129]

    Ehsan Khalili M, Larsson M, Müller B. Immersed boundary method for viscous compressible flows around moving bodies. Computers & Fluids, 2018, 170: 77-92
    [130] 王俊杰, 高正红. 基于复合叉树的自适应笛卡尔网格应用研究. 应用力学学报, 2006, 23(4): 623-626 (Wang Junjie, Gao ZhengHong. Adaptive Cartesian grid based on an omni-tree. Chinese Journal of Applied Mechanics, 2006, 23(4): 623-626 (in Chinese) doi: 10.3969/j.issn.1000-4939.2006.04.023

    Wang Junjie, Gao ZhengHong. Adaptive Cartesian grid based on an omni-tree. Chinese Journal of Applied Mechanics, 2006, 23(4): 623-626 (in Chinese) doi: 10.3969/j.issn.1000-4939.2006.04.023
    [131] 王玉峰. 基于笛卡尔网格的非定常气动力计算. [硕士论文]. 西安: 西北工业大学, 2005 (Wang Yufeng. Unsteady aerodynamic calculations based on Cartesian grids. [Master Thesis]. Xi'an: Northwestern Polytechnical University, 2005 (in Chinese)

    Wang Yufeng. Unsteady aerodynamic calculations based on Cartesian grids. [Master Thesis]. Xi'an: Northwestern Polytechnical University, 2005 (in Chinese)
    [132] 刘剑明. 可压缩流体计算中的浸入边界方法及其应用. [博士论文]. 南京: 南京航空航天大学, 2010 (Liu Jianming. The immersed bounda-ry method in compressible flows and its applications. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2010 (in Chinese)

    Liu Jianming. The immersed bounda-ry method in compressible flows and its applications. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2010 (in Chinese)
    [133]

    Zhang Y, Zhou CH. An immersed boundary method for simulation of inviscid compressible flows. International Journal for Numerical Methods in Fluids, 2014, 74(11): 775-793 doi: 10.1002/fld.3872
    [134]

    Luo K, Zhuang Z, Fan J, et al. A ghost-cell immersed boundary method for simulations of heat transfer in compressible flows under different boundary conditions. International Journal of Heat and Mass Transfer, 2016, 92: 708-717 doi: 10.1016/j.ijheatmasstransfer.2015.09.024
    [135] 唐志共, 陈浩, 毕林等. 自适应笛卡尔网格超声速黏性流动数值模拟. 航空学报, 2018, 39(5): 121697 (Tang Zhigong, Chen Hao, Bi Lin, et al. Numerical simulation of supersonic viscous flow based on adaptive Cartesian grid. Acta Aeronautica et Astronautica Sinica, 2018, 39(5): 121697 (in Chinese)

    Tang Zhigong, Chen Hao, Bi Lin, et al. Numerical simulation of supersonic viscous flow based on adaptive Cartesian grid. Acta Aeronautica et Astronautica Sinica, 2018, 39(5): 121697 (in Chinese)
    [136] 卢俊宇, 陈洁, 刘君等. 基于笛卡儿网格的自动化CFD特点分析及一种新策略. 气动研究与试验, 2023, 1(3): 70-81 (Lu Junyu, Chen Jie, Liu Jun, et al. Characteristics analysis of automated cfd based on Cartesian grid and a new strategy. Aerodynamic Research & Experiment, 2023, 1(3): 70-81 (in Chinese)

    Lu Junyu, Chen Jie, Liu Jun, et al. Characteristics analysis of automated cfd based on Cartesian grid and a new strategy. Aerodynamic Research & Experiment, 2023, 1(3): 70-81 (in Chinese)
    [137]

    Ning J, Zhang H, Xu X, et al. A novel fluid-structure interaction algorithm for compressible flows and deformable structures. Journal of Computational Physics, 2021, 426: 109921 doi: 10.1016/j.jcp.2020.109921
    [138] 韩玉琪, 张常贤. 基于自适应笛卡尔网格的可压缩黏性流动数值模拟. 科学技术与工程, 2015, 15(4): 115-120 (Han Yuqi, Zhang Changxian. Numerical simulations of compressible viscous flows with adaptively refined Cartesian grid. Science Technology and Engineering, 2015, 15(4): 115-120 (in Chinese)

    Han Yuqi, Zhang Changxian. Numerical simulations of compressible viscous flows with adaptively refined Cartesian grid. Science Technology and Engineering, 2015, 15(4): 115-120 (in Chinese)
    [139]

    Qiu YL, Shu C, Wu J, et al. A boundary condition-enforced immersed boundary method for compressible viscous flows. Computers & Fluids, 2016, 136: 104-113
    [140] 刘旭, 朱君, 赵宁. 虚拟单元有限体积WENO5格式及其应用. 数值计算与计算机应用, 2016, 37(2): 152-164 (Liu Xu, Zhu Jun, Zhao Ning. The application of fvweno5 scheme and ghost cell method. Journal on Numerical Methods and Computer Applications, 2016, 37(2): 152-164 (in Chinese) doi: 10.12288/szjs.2016.2.152

    Liu Xu, Zhu Jun, Zhao Ning. The application of fvweno5 scheme and ghost cell method. Journal on Numerical Methods and Computer Applications, 2016, 37(2): 152-164 (in Chinese) doi: 10.12288/szjs.2016.2.152
    [141]

    Nauleau F, Bridel-Bertomeu T, Beaugendre H, et al. Immersed boundaries in hypersonic flows with considerations about high-fidelity and massive parallelism//The 8th European Congress on Computational Methods in Applied Sciences and Engineering, Norway, 2022
    [142]

    Ishida T, Takahashi S, Nakahashi K. Efficient and robust Cartesian mesh generation for building-cube method. Journal of Computational Science and Technology, 2008, 2(4): 435-446 doi: 10.1299/jcst.2.435
    [143]

    Li X, Yang M, Bi L, et al. An efficient Cartesian mesh generation strategy for complex geometries. Computer Methods in Applied Mechanics and Engineering, 2024, 418: 116564
    [144]

    Tseng YH, Ferziger JH. A ghost-cell immersed boundary method for flow in complex geometry. Journal of Computational Physics, 2003, 192(2): 593-623 doi: 10.1016/j.jcp.2003.07.024
    [145]

    Ghias R, Mittal R, Dong H. A sharp interface immersed boundary method for compressible viscous flows. Journal of Computational Physics, 2007, 225(1): 528-553 doi: 10.1016/j.jcp.2006.12.007
    [146]

    Deiterding R, Radovitzky R, Mauch SP, et al. A virtual test facility for the efficient simulation of solid material response under strong shock and detonation wave loading. Engineering with Computers, 2006, 22(3-4): 325-347 doi: 10.1007/s00366-006-0043-9
    [147]

    Bharadwaj SA, Ghosh S. Data reconstruction at surface in immersed-boundary methods. Computers & Fluids, 2020, 196: 104236
    [148]

    Chaudhuri A, Hadjadj A, Chinnayya A. On the use of immersed boundary methods for shock/obstacle interactions. Journal of Computational Physics, 2011, 230(5): 1731-1748 doi: 10.1016/j.jcp.2010.11.016
    [149]

    Bridel-Bertomeu T. Immersed boundary conditions for hypersonic flows using ENO-like least-square reconstruction. Computers & Fluids, 2021, 215: 104794
    [150]

    Choung H, Saravanan V, Lee S, et al. Nonlinear weighting process in ghost-cell immersed boundary methods for compressible flow. Journal of Computational Physics, 2021, 433: 110198 doi: 10.1016/j.jcp.2021.110198
    [151]

    Tan S, Shu CW. Inverse Lax-Wendroff procedure for numerical boundary conditions of conservation laws. Journal of Computational Physics, 2010, 229(21): 8144-8166 doi: 10.1016/j.jcp.2010.07.014
    [152]

    Brehm C, Hader C, Fasel HF. A locally stabilized immersed boundary method for the compressible Navier–Stokes equations. Journal of Computational Physics, 2015, 295: 475-504 doi: 10.1016/j.jcp.2015.04.023
    [153]

    Al-Marouf M, Samtaney R. A versatile embedded boundary adaptive mesh method for compressible flow in complex geometry. Journal of Computational Physics, 2017, 337: 339-378 doi: 10.1016/j.jcp.2017.02.044
    [154]

    Chi C, Lee BJ, Im HG. An improved ghost-cell immersed boundary method for compressible flow simulations. International Journal for Numerical Methods in Fluids, 2017, 83(2): 132-148 doi: 10.1002/fld.4262
    [155]

    Liu C, Hu C. An immersed boundary solver for inviscid compressible flows. International Journal for Numerical Methods in Fluids, 2017, 85(11): 619-640 doi: 10.1002/fld.4399
    [156]

    Qu Y, Batra RC. Constrained moving least-squares immersed boundary method for fluid-structure interaction analysis. International Journal for Numerical Methods in Fluids, 2017, 85(12): 675-692 doi: 10.1002/fld.4400
    [157]

    Luo K, Mao C, Zhuang Z, et al. A ghost-cell immersed boundary method for the simulations of heat transfer in compressible flows under different boundary conditions part-II: Complex geometries. International Journal of Heat and Mass Transfer, 2017, 104: 98-111 doi: 10.1016/j.ijheatmasstransfer.2016.08.010
    [158] 何跃龙, 李盾, 刘帅等. 基于指数插值的浸没边界法在可压缩流模拟中的应用研究. 空气动力学学报, 2016, 34(4): 426-432 (He Yuelong, Li Dun, Liu Shuai, et al. The application of power-law interpolation based immersed boundary method in compressible flow simulation. Acta Aerodynamica Sinica, 2016, 34(4): 426-432 (in Chinese)

    He Yuelong, Li Dun, Liu Shuai, et al. The application of power-law interpolation based immersed boundary method in compressible flow simulation. Acta Aerodynamica Sinica, 2016, 34(4): 426-432 (in Chinese)
    [159]

    Wang X, Deiterding R, Liang J, et al. A second-order-accurate immersed boundary ghost-cell method with hybrid reconstruction for compressible flow simulations. Computers & Fluids, 2022, 237: 105314
    [160]

    Cheng Z, Liu S, Jiang Y, et al. A high order boundary scheme to simulate complex moving rigid body under impingement of shock wave. Applied Mathematics and Mechanics, 2021, 42(6): 841-854 doi: 10.1007/s10483-021-2735-7
    [161]

    Liu S, Jiang Y, Shu CW, et al. A high order moving boundary treatment for convection-diffusion equations. Journal of Computational Physics, 2023, 473: 111752 doi: 10.1016/j.jcp.2022.111752
    [162]

    Lu J, Shu CW, Tan S, et al. An inverse Lax-wendroff procedure for hyperbolic conservation laws with changing wind direction on the boundary. Journal of Computational Physics, 2021, 426: 109940 doi: 10.1016/j.jcp.2020.109940
    [163] 罗灿炎, 周丹, 杜昊等. 笛卡尔网格高保真虚拟单元浸入边界法研究与应用. 中国科学: 物理学 力学 天文学, 2024, 54(3): 234611 (Luo Canyan, Zhou Dan, Du Hao, et al. A novel high-fidelity ghost-cell immersed boundary method for the Cartesian grid and its applications. Scientia Sinica (Physica, Mechanica & Astronomica ), 2024, 54(3): 234611 (in Chinese)

    Luo Canyan, Zhou Dan, Du Hao, et al. A novel high-fidelity ghost-cell immersed boundary method for the Cartesian grid and its applications. Scientia Sinica(Physica, Mechanica & Astronomica), 2024, 54(3): 234611 (in Chinese)
    [164]

    Cai SG, Degrigny J, Boussuge JF, et al. Coupling of turbulence wall models and immersed boundaries on Cartesian grids. Journal of Computational Physics, 2021, 429: 109995 doi: 10.1016/j.jcp.2020.109995
    [165]

    Capizzano F. Turbulent wall model for immersed boundary methods. AIAA Journal, 2011, 49(11): 2367-2381 doi: 10.2514/1.J050466
    [166]

    Capizzano F. Coupling a wall diffusion model with an immersed boundary technique. AIAA Journal, 2016, 54(2): 728-734 doi: 10.2514/1.J054197
    [167]

    Bernardini M, Modesti D, Pirozzoli S. On the suitability of the immersed boundary method for the simulation of high-Reynolds-number separated turbulent flows. Computers & Fluids, 2016, 130: 84-93
    [168]

    Knopp T, Alrutz T, Schwamborn D. A grid and flow adaptive wall-function method for RANS turbulence modelling. Journal of Computational Physics, 2006, 220(1): 19-40 doi: 10.1016/j.jcp.2006.05.003
    [169] 胡偶. 可压缩复杂流动笛卡尔网格方法研究及应用. [博士论文]. 南京: 南京航空航天大学, 2013 (Hu Ou. Development of cartesian grid method for complex compressible flows and its applications. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2013 (in Chinese)

    Hu Ou. Development of cartesian grid method for complex compressible flows and its applications. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2013 (in Chinese)
    [170]

    Hu O, Zhao N, Liu JM. A ghost cell method for turbulent compressible viscous flows on adaptive Cartesian grids. Procedia Engineering, 2013, 67: 241-249 doi: 10.1016/j.proeng.2013.12.023
    [171] 沈志伟, 赵宁, 胡偶. 可压缩黏性流动笛卡尔网格虚拟单元方法研究. 空气动力学学报, 2014, 32(6): 748-754 (Shen Zhiwei, Zhao Ning, Hu Ou. Numerical research of Cartesian based ghost cell method for compressible viscous flows. Acta Aerodynamica Sinica, 2014, 32(6): 748-754 (in Chinese)

    Shen Zhiwei, Zhao Ning, Hu Ou. Numerical research of Cartesian based ghost cell method for compressible viscous flows. Acta Aerodynamica Sinica, 2014, 32(6): 748-754 (in Chinese)
    [172]

    Chen C, Wang Z, Du L, et al. Simulating unsteady flows in a compressor using immersed boundary method with turbulent wall model. Aerospace Science and Technology, 2021, 115: 106834 doi: 10.1016/j.ast.2021.106834
    [173]

    Chen C, Wang Y, Wang Z, et al. Application of immersed boundary method in turbomachines. Chinese Journal of Aeronautics, 2023, 36(5): 268-279 doi: 10.1016/j.cja.2023.02.032
    [174]

    Zhou CH. RANS simulation of high-Re turbulent flows using an immersed boundary method in conjunction with wall modeling. Computers & Fluids, 2017, 143: 73-89
    [175]

    Pu TM, Zhou CH. An immersed boundary/wall modeling method for RANS simulation of compressible turbulent flows. International Journal for Numerical Methods in Fluids, 2018, 87(5): 217-238 doi: 10.1002/fld.4487
    [176]

    Liu X, Yang B, Ji C, et al. Research on the turbine blade vibration based on the immersed boundary method. Journal of Fluids Engineering, 2018, 140(6): 061402 doi: 10.1115/1.4038866
    [177]

    Yang B, Song M, Zhu G. Research on the ghost cell immersed boundary method for compressible flow. Processes, 2024, 12: 1182 doi: 10.3390/pr12061182
    [178]

    Wang Z, Du L, Gao F, et al. Adaptive forcing distance in an immersed boundary method for internal flow simulation at high Reynolds numbers. Computers & Mathematics with Applications, 2023, 140: 44-63
    [179] 陈浩, 袁先旭, 王田天等. 国家数值风洞(NNW)工程中的黏性自适应笛卡尔网格方法研究进展. 航空学报, 2021, 42(9): 625732 (Chen Hao, Yuan Xianxu, Wang Tiantian, et al. Advances in viscous adaptive Cartesian grid methodology of NNW Project. Acta Aeronautica et Astronautica Sinica, 2021, 42(9): 625732 (in Chinese)

    Chen Hao, Yuan Xianxu, Wang Tiantian, et al. Advances in viscous adaptive Cartesian grid methodology of NNW Project. Acta Aeronautica et Astronautica Sinica, 2021, 42(9): 625732 (in Chinese)
    [180]

    Chesshire G, Henshaw WD. Composite overlapping meshes for the solution of partial differential equations. Journal of Computational Physics, 1990, 90: 1-64 doi: 10.1016/0021-9991(90)90196-8
    [181]

    Meakin R. An efficient means of adaptive refinement within systems of overset grids//12th Computational Fluid Dynamics Conference, San Diego, 1995
    [182]

    Henshaw WD, Schwendeman DW. An adaptive numerical scheme for high-speed reactive flow on overlapping grids. Journal of Computational Physics, 2003, 191(2): 420-447 doi: 10.1016/S0021-9991(03)00323-1
    [183]

    Luo H, Baum JD, Löhner R. A hybrid Cartesian grid and gridless method for compressible flows. Journal of Computational Physics, 2006, 214(2): 618-632 doi: 10.1016/j.jcp.2005.10.002
    [184]

    Saunier O, Benoit C, Jeanfaivre G, et al. Third-order Cartesian overset mesh adaptation method for solving steady compressible flows. International Journal for Numerical Methods in Fluids, 2008, 57(7): 811-838 doi: 10.1002/fld.1646
    [185]

    Kannan R, Wang ZJ. Overset adaptive Cartesian/prism grid method for stationary and moving-boundary flow problems. AIAA Journal, 2007, 45(7): 1774-1779 doi: 10.2514/1.24200
    [186]

    Kirby AC, Yang Z, Mavriplis DJ, et al. Visualization and data analytics challenges of large-scale high-fidelity numerical simulations of wind energy applications//2018 AIAA Aerospace Sciences Meeting, Florida, 2018
    [187]

    Buning P, Pulliam T. Cartesian off-body grid adaption for viscous time-accurate flow simulations. //20th AIAA Computational Fluid Dynamics Conference, Hawaii, 2011
    [188]

    Péron S, Benoit C. Automatic off-body overset adaptive Cartesian mesh method based on an octree approach. Journal of Computational Physics, 2013, 232(1): 153-173 doi: 10.1016/j.jcp.2012.07.029
    [189]

    Sitaraman J, Floros M, Wissink A, et al. Parallel domain connectivity algorithm for unsteady flow computations using overlapping and adaptive grids. Journal of Computational Physics, 2010, 229(12): 4703-4723 doi: 10.1016/j.jcp.2010.03.008
    [190] 沈志伟, 赵宁. 基于混合笛卡尔网格方法的扑动翼型数值模拟. 航空计算技术, 2016, 46: 1-5 (Shen Zhiwei, Zhao Ning. Numerical simulation of airfoil flapping based on hybrid Cartesian grid method. Aeronautical Computing Technique, 2016, 46: 1-5 (in Chinese) doi: 10.3969/j.issn.1671-654X.2016.05.001

    Shen Zhiwei, Zhao Ning. Numerical simulation of airfoil flapping based on hybrid Cartesian grid method. Aeronautical Computing Technique, 2016, 46: 1-5 (in Chinese) doi: 10.3969/j.issn.1671-654X.2016.05.001
    [191]

    Gan Y, Liu J, Zhao N, et al. A numerical study on a Cartesian-based body-fitted adaptive grid method. International Journal of Computational Fluid Dynamics, 2018, 32(4-5): 186-202 doi: 10.1080/10618562.2018.1508659
    [192] 赵文梅, 赵军, 胡偶. 非定常旋涡-翼型相互作用问题数值模拟研究. 直升机技术, 2015(182): 6-12 (Zhao Wenmei, Zhao Jun, Hu Ou. Numerical simulation of unsteady airfoil-vortex interaction problem. Helicopter Technique, 2015(182): 6-12 (in Chinese) doi: 10.3969/j.issn.1673-1220.2015.01.002

    Zhao Wenmei, Zhao Jun, Hu Ou. Numerical simulation of unsteady airfoil-vortex interaction problem. Helicopter Technique, 2015(182): 6-12 (in Chinese) doi: 10.3969/j.issn.1673-1220.2015.01.002
    [193] 肖中云, 郭永恒, 张露等. 旋翼流动的块结构化网格自适应方法. 空气动力学学报, 2022, 40(2): 158-165 (Xiao ZhongYun, Guo Yongheng, Zhang Lu, et al. Block structured adaptive mesh refinement for rotor flows. Acta Aerodynamica Sinica, 2022, 40(2): 158-165 (in Chinese) doi: 10.7638/kqdlxxb-2021.0255

    Xiao ZhongYun, Guo Yongheng, Zhang Lu, et al. Block structured adaptive mesh refinement for rotor flows. Acta Aerodynamica Sinica, 2022, 40(2): 158-165 (in Chinese) doi: 10.7638/kqdlxxb-2021.0255
    [194] 韩少强, 宋文萍, 韩忠华等. 高速共轴刚性旋翼非定常流动高精度数值模拟. 航空学报, 2024, 45(09): 177-196 (Han Shaoqiang, Song Wenping, Han Zhonghua, et al. High-accuracy numerical-simulation of unsteady flow over high-speed coaxial rigid rotors. Acta Aeronautica et Astronautica Sinica, 2024, 45(09): 177-196 (in Chinese)

    Han Shaoqiang, Song Wenping, Han Zhonghua, et al. High-accuracy numerical-simulation of unsteady flow over high-speed coaxial rigid rotors. Acta Aeronautica et Astronautica Sinica, 2024, 45(09): 177-196 (in Chinese)
    [195]

    Fu H, Xia J, Tian S, et al. Dual-solver research based on the coupling of flux reconstruction and finite volume methods. Acta Mechanica, 2023, 234(8): 3173-3196 doi: 10.1007/s00707-023-03551-0
    [196]

    Noack R. SUGGAR: A general capability for moving body overset grid assembly//17th AIAA Computational Fluid Dynamics Conference, Toronto, 2005
    [197]

    Bonet J, Peraire J. An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems. International Journal for Numerical Methods in Engineering, 1991, 31(1): 1-17 doi: 10.1002/nme.1620310102
    [198]

    Wang J, Wu F, Xu Q, et al. Local inverse mapping implicit hole-cutting method for structured Cartesian overset grid assembly. Entropy (Basel), 2023, 25(3): 432 doi: 10.3390/e25030432
    [199]

    Benoit C, Jeanfaivre G. Three-dimensional inviscid isolated rotor calculations using chimera and automatic Cartesian partitioning methods//AHS Aeromechanics, Georigia, 2003
    [200]

    Wang ZJ. A fast nested multi-grid viscous flow solver for adaptive Cartesian/Quad grids//AIAA Fluid Dynamics Conference, New Orleans, 1996
    [201]

    Wang ZJ. A quadtree-based adaptive Cartesian/Quad grid flow solver for Navier-Stokes equations. Computers & Fluids, 1998, 27(4): 529-549
    [202]

    Kini S, Thoms R, Zhu FL. A fast and fully automated Cartesian meshing solution for dirty CAD geometries//Motorsports Engineering Conference, North Carolina, 2008
    [203]

    Ashok V, Adimurthy V, Joseph G. Computation of non-equilibrium chemically reacting hypersonic flow from a Cartesian mesh with near wall viscous resolution. Journal of Applied Fluid Mechanics, 2014, 7(2): 217-226
    [204]

    Sang W, Li F. An unstructured/structured multi-layer hybrid grid method and its application. International Journal for Numerical Methods in Fluids, 2006, 53(7): 1107-1125
    [205] 张来平, 王志坚, 张涵信. 动态混合网格生成及隐式非定常计算方法. 力学学报, 2004, 36(6): 664-672 (Zhang Laiping, Wang Zhijian, Zhang Hanxin. Dynamic hybrid mesh generation and implicit nonconstant computational methods. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(6): 664-672 (in Chinese) doi: 10.3321/j.issn:0459-1879.2004.06.004

    Zhang Laiping, Wang Zhijian, Zhang Hanxin. Dynamic hybrid mesh generation and implicit nonconstant computational methods. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(6): 664-672 (in Chinese) doi: 10.3321/j.issn:0459-1879.2004.06.004
    [206] 刘周, 周伟江. 适于黏性计算的自适应笛卡儿网格生成及其应用. 航空学报, 2009, 30(12): 2280-2287 (Liu Zhou, Zhou Weijiang. Adaptive viscous Cartesian grid generation and application. Acta Aeronautica et Astronautica Sinica, 2009, 30(12): 2280-2287 (in Chinese) doi: 10.3321/j.issn:1000-6893.2009.12.007

    Liu Zhou, Zhou Weijiang. Adaptive viscous Cartesian grid generation and application. Acta Aeronautica et Astronautica Sinica, 2009, 30(12): 2280-2287 (in Chinese) doi: 10.3321/j.issn:1000-6893.2009.12.007
    [207]

    Liu X, Zhou W, Ji C. Applications of dynamic Cartesian grids method on unsteady flows involving moving boundaries. Procedia Engineering, 2015, 126: 633-638 doi: 10.1016/j.proeng.2015.11.252
    [208]

    Zastawny M, Biava M. Assessment of adjoint-based adaptive mesh refinement strategies for steady RANS//AIAA Scitech 2022 Forum, San Diego & Virtual, 2022
    [209]

    Sadrehaghighi I. Adaptive meshing. [M/OL]. 2022. https://www.researchgate.net/publication/339292239_Adaptive_Meshing
    [210]

    Roy CJ. Strategies for driving mesh adaptation in CFD//47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Florida, 2009
    [211]

    Roy C. Review of discretization error estimators in scientific computing//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, 2010
    [212]

    Balasubramanian R, Newman JC. Comparison of adjoint-based and feature-based grid adaptation for functional outputs. International Journal for Numerical Methods in Fluids, 2007, 53(10): 1541-1569 doi: 10.1002/fld.1361
    [213]

    Kamkar SJ, Wissink AM, Sankaran V, et al. Feature-driven Cartesian adaptive mesh refinement for vortex-dominated flows. Journal of Computational Physics, 2011, 230(16): 6271-6298 doi: 10.1016/j.jcp.2011.04.024
    [214]

    Pang C, Yang H, Gao Z, et al. Enhanced adaptive mesh refinement method using advanced vortex identification sensors in wake flow. Aerospace Science and Technology, 2021, 115: 106796 doi: 10.1016/j.ast.2021.106796
    [215]

    Fidkowski KJ, Darmofal DL. Review of output-based error estimation and mesh adaptation in computational fluid dynamics. AIAA Journal, 2011, 49(4): 673-694 doi: 10.2514/1.J050073
    [216]

    Ceze MA, Fidkowski KJ. High-order output-based adaptive simulations of turbulent flow in two dimensions. AIAA Journal, 2016, 54(9): 2611-2625 doi: 10.2514/1.J054517
    [217]

    Chen G, Fidkowski KJ. Output-based adaptive aerodynamic simulations using convolutional neural networks. Computers & Fluids, 2021, 223: 104947
    [218]

    Feng Y, Liu T, He X, et al. A characteristic-featured shock wave indicator for simulating high-speed inviscid flows on 3D unstructured meshes. Advances in Aerodynamics, 2021, 3: 27 doi: 10.1186/s42774-021-00084-9
    [219] 李彩云, 安慰, 刘学军等. 基于机器学习的非定常流场网格自适应. 空气动力学学报, 2023, 41(6): 89-101 (Li Caiyun, An Wei, Liu Xuejun, et al. Mesh adaptation for unsteady flow field based on machine learning. Acta Aerodynamica Sinica, 2023, 41(6): 89-101 (in Chinese) doi: 10.7638/kqdlxxb-2022.0034

    Li Caiyun, An Wei, Liu Xuejun, et al. Mesh adaptation for unsteady flow field based on machine learning. Acta Aerodynamica Sinica, 2023, 41(6): 89-101 (in Chinese) doi: 10.7638/kqdlxxb-2022.0034
    [220] 张来平, 邓小刚, 何磊等. E级计算给CFD带来的机遇与挑战. 空气动力学学报, 2016, 34(4): 405-417 (Zhang Laiping, Deng Xiaogang, He Lei, et al. The opportunity and grand challenges in computational fluid dynamics by exascale computing. Acta Aerodynamica Sinica, 2016, 34(4): 405-417 (in Chinese)

    Zhang Laiping, Deng Xiaogang, He Lei, et al. The opportunity and grand challenges in computational fluid dynamics by exascale computing. Acta Aerodynamica Sinica, 2016, 34(4): 405-417 (in Chinese)
    [221]

    Lan Z, Taylor VE, Bryan G. A novel dynamic load balancing scheme for parallel systems. Journal of Parallel and Distributed Computing, 2002, 62: 1763-1781 doi: 10.1016/S0743-7315(02)00008-4
    [222]

    Ji H, Lien FS, Yee E. A new adaptive mesh refinement data structure with an application to detonation. Journal of Computational Physics, 2010, 229(23): 8981-8993 doi: 10.1016/j.jcp.2010.08.023
    [223]

    Khokhlov AM. Fully threaded tree algorithms for adaptive refinement fluid dynamics simulations. Journal of Computational Physics, 1998, 143: 519-543 doi: 10.1006/jcph.1998.9998
    [224]

    Pan J, Wang Q, Zhang Y, et al. High-order compact finite volume methods on unstructured grids with adaptive mesh refinement for solving inviscid and viscous flows. Chinese Journal of Aeronautics, 2018, 31(9): 1829-1841 doi: 10.1016/j.cja.2018.06.018
    [225]

    Wang C, Dong X, Shu CW. Parallel adaptive mesh refinement method based on WENO finite difference scheme for the simulation of multi-dimensional detonation. Journal of Computational Physics, 2015, 298: 161-175 doi: 10.1016/j.jcp.2015.06.001
    [226]

    Schornbaum F, RüDe U. Extreme-scale block-structured adaptive mesh refinement. SIAM Journal on Scientific Computing, 2018, 40(3): C358-C387 doi: 10.1137/17M1128411
    [227]

    Backingsale DA. Towards scalable adaptive mesh refinement on future parallel architectures. [PhD Thesis]. Coventry: University of Warwick, 2015
    [228]

    Giuliani A, Krivodonova L. Adaptive mesh refinement on graphics processing units for applications in gas dynamics. Journal of Computational Physics, 2019, 381: 67-90 doi: 10.1016/j.jcp.2018.12.019
    [229]

    Jude D, Sitaraman J, Wissink A. An octree-based, Cartesian Navier-Stokes solver for modern cluster architectures. The Journal of Supercomputing, 2022, 78(9): 11409-11440 doi: 10.1007/s11227-022-04324-7
    [230]

    Dubey A, Berzins M, Burstedde C, et al. Structured adaptive mesh refinement adaptations to retain performance portability with increasing heterogeneity. Computing in Science & Engineering, 2021, 23(5): 62-66
    [231]

    Wei F, Jin L, Liu J, et al. Acceleration of a 2D unsteady Euler solver with GPU on nested Cartesian grid. Acta Astronautica, 2019, 159: 319-330 doi: 10.1016/j.actaastro.2019.03.020
    [232]

    Wang ZJ, Fidkowski K, Abgrall R, et al. High-order CFD methods: Current status and perspective. International Journal for Numerical Methods in Fluids, 2013, 72(8): 811-845 doi: 10.1002/fld.3767
    [233]

    Kroll N. ADIGMA: A European project on the development of adaptive higher order variational methods for aerospace applications//47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Florida, 2009
    [234]

    Kroll N, Hirsch C, Bassi F, et al. IDIHOM: Industrialization of high-order methods-A top-down approach: Results of a collaborative research project funded by the European Union, 2010-2014. Springer, 2015
    [235]

    Shen C, Qiu JM, Christlieb A. Adaptive mesh refinement based on high order finite difference WENO scheme for multi-scale simulations. Journal of Computational Physics, 2011, 230(10): 3780-3802 doi: 10.1016/j.jcp.2011.02.008
    [236]

    Berger MJ. Adaptive mesh refinement for hyperbolic partial differential equations. [PhD Thesis]. California: Stanford University, 1982
    [237]

    Liu J, Qiu J, Hu O, et al. Adaptive Runge-Kutta discontinuous Galerkin method for complex geometry problems on Cartesian grid. International Journal for Numerical Methods in Fluids, 2013, 73: 847-868 doi: 10.1002/fld.3825
    [238]

    Qi X, Wang Z, Zhu J, et al. High-order discontinuous Galerkin method with immersed boundary treatment for compressible flows on parallel adaptive Cartesian grids. Physics of Fluids, 2024, 36(11): 116139 doi: 10.1063/5.0238605
    [239]

    Qi X, Wang Z, Zhu J, et al. A high-order nonlinear limiter for discontinuous Galerkin method on parallel adaptive Cartesian grids. Physics of Fluids, 2023, 35(3): 036108 doi: 10.1063/5.0138993
    [240]

    Kou J, Joshi S, Hurtado-De-Mendoza A, et al. Immersed boundary method for high-order flux reconstruction based on volume penalization. Journal of Computational Physics, 2022, 448: 110721 doi: 10.1016/j.jcp.2021.110721
    [241] 王婷婷, 吕宏强, 安慰. 基于高阶间断伽辽金数值方法的浸没边界法. 空气动力学学报, 2023, 41(9): 96-106 (Wang Tingting, Lyu Hongqiang, An Wei. Immersed boundary method based on high-orderdiscontinuous Galerkin method. Acta Aerodynamica Sinica, 2023, 41(9): 96-106 (in Chinese) doi: 10.7638/kqdlxxb-2022.0138

    Wang Tingting, Lyu Hongqiang, An Wei. Immersed boundary method based on high-orderdiscontinuous Galerkin method. Acta Aerodynamica Sinica, 2023, 41(9): 96-106 (in Chinese) doi: 10.7638/kqdlxxb-2022.0138
    [242] 朱震浩, 肖天航, 徐雅楠等. 基于直角网格伴随自适应的声爆预测. 北京航空航天大学学报, 2023, 49(9): 2432-2441 (Zhu Zhenhao, Xiao Tianhang, Xu Yanan, et al. Adjoint-based adaptive Cartesian mesh refinement for sonic boom prediction. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(9): 2432-2441 (in Chinese)

    Zhu Zhenhao, Xiao Tianhang, Xu Yanan, et al. Adjoint-based adaptive Cartesian mesh refinement for sonic boom prediction. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(9): 2432-2441 (in Chinese)
    [243]

    Zhu CX, Zhao HY, Zhao N, et al. An adaptive Cartesian method for prediction of the unsteady process of aircraft ice accretion. Communications in Computational Physics, 2021, 30(2): 515-535 doi: 10.4208/cicp.OA-2018-0228
    [244] 李胜超. 三维笛卡尔网格的结冰数值模拟. [博士论文]. 南京: 南京航空航天大学, 2019 (Li Shengchao. Numerical simulation of icing based on three-dimensional Cartesian grids. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2019 (in Chinese)

    Li Shengchao. Numerical simulation of icing based on three-dimensional Cartesian grids. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautic, 2019 (in Chinese)
    [245]

    Nogi K, Imamura T. Numerical simulation of rime ice accretion on airfoil using rigid sphere model. Computers & Fluids, 2024, 275: 106244
    • 相关文章
    • 施引文献
    • 资源附件(0)
图(23)  /  表(2)
计量
  • 文章访问数:  207
  • HTML全文浏览量:  38
  • PDF下载量:  111
  • 被引次数: 0
出版历程
  • 收稿日期:  2024-08-01
  • 录用日期:  2025-01-17
  • 网络出版日期:  2025-01-17
  • 发布日期:  2025-01-18
  • 刊出日期:  2025-02-17

目录

摘要
HTML全文

  • 引 言

  • 1.   笛卡尔网格自适应方法及数据结构

  • 2.   基于笛卡尔网格的模拟方法及分类

  • 2.1   切割单元方法

  • 2.1.1   方法介绍及基本流程
  • 2.1.2   国内外发展现状
  • 2.1.3   黏性流动问题模拟
  • 2.1.4   “小单元”处理方法
  • 2.1.5   运动问题模拟
  • 2.1.6   存在的问题

  • 2.2   浸入边界方法

  • 2.2.1   方法介绍及基本流程
  • 2.2.2   国内外发展现状
  • 2.2.3   网格生成效率
  • 2.2.4   镜像点插值方法
  • 2.2.5   高雷诺数黏性流动模拟
  • 2.2.6   存在的问题

  • 2.3   重叠笛卡尔网格方法

  • 2.3.1   方法介绍及基本流程
  • 2.3.2   国内外发展现状
  • 2.3.3   网格装配效率
  • 2.3.4   不同网格体系间的信息传递及重叠区网格单元控制
  • 2.3.5   存在的问题

  • 2.4   混合笛卡尔网格方法

  • 2.4.1   方法介绍及基本流程
  • 2.4.2   国内外发展现状
  • 2.4.3   存在的问题

  • 3.   关键技术及发展方向

  • 3.1   自适应加密判据

  • 3.1.1   基于误差的自适应准则
  • 3.1.2   基于流场特征的自适应准则
  • 3.1.3   基于伴随算子的自适应准则
  • 3.1.4   基于人工智能方法的自适应准则

  • 3.2   动态并行技术

  • 3.2.1   自适应笛卡尔网格数据管理及存储结构
  • 3.2.2   自适应网格动态分区及负载平衡
  • 3.2.3   GPU异构并行加速

  • 3.3   高保真计算方法

  • 3.3.1   高精度空间离散方法
  • 3.3.2   守恒型“悬挂节点”重构方法及高精度边界处理技术

  • 3.4   其他

  • 3.4.1   先进物理模型与自适应笛卡尔网格的适配性
  • 3.4.2   复杂工程问题应用

  • 4.   结束语

  • 致谢

参考文献(245)
相关文章
施引文献
资源附件(0)

/

返回文章
返回

下载中心

作者中心

版权所有 © 《力学学报》编辑部备案号：京ICP备05039218号-1

通讯地址：北京市海淀区北四环西路15号邮政编码：100190

联系电话：010-62536271

邮箱：lxxb@cstam.org.cn

微信公众号
RSS

本系统由 北京仁和汇智信息技术有限公司 开发  百度统计