THREE DIMENSIONAL NUMERICAL SIMULATION OF WAVE INTERACTION WITH A NEW TYPE OF DOUBLE ROW PERFORATED CYLINDER BREAKWATER
-
摘要: 双排开孔圆筒防波堤是基于圆筒、板式结构的一种复合式新型结构型式; 基于不可压缩两相流模型建立三维数值波浪水槽, 通过RNG k-ε湍流模型进行湍流封闭, 并采用TruVOF方法捕捉自由液面, 开展波浪与双排开孔圆筒防波堤相互作用数值模拟, 探究相对排间距、开孔率对新型双排开孔圆筒防波堤消浪性能的影响, 分析了后排开孔圆筒防波堤附近的复杂水动力现象和流动特性. 结果表明, 在本文研究工况范围内, 沿程平均波高随相对排间距的增大先增大后减小, 随开孔率的增大而增大, 周期对沿程平均波高的影响没有明显规律; 当B/D = 9, e = 23.11%时, 新型双排开孔圆筒防波堤消浪效果最优, 反射系数在0.4 ~ 0.46之间, 透射系数在0.3 ~ 0.35之间, 耗散系数在0.8 ~ 0.85之间; 自由液面破碎、水气掺混、环状涡运动演化是新型双排开孔圆筒防波堤紊动耗能消波的主要原因; 相对排间距会引起后排防波堤附近涡量分布以及剪切层形态的变化, 从而导致不同的紊动特性, 影响双排开孔圆筒防波堤消浪特性. 研究结果可以为新型双排开孔圆筒防波堤工程设计与消浪机理研究提供理论支撑.Abstract: The double row perforated cylinder breakwater is a new composite structure based on the cylinder and plate breakwater. The three-dimensional numerical wave flume is established based on the incompressible two-phase flow model. The turbulent closure is carried out by RNG k-ε turbulence model, and the TruVOF method is used to capture the free liquid surface. The influence of relative row spacing and opening rate on the wave dissipation performance of double row perforated cylinder breakwater is explored, and the special hydrodynamic phenomena and flow characteristics near the back row perforated cylinder breakwater are analyzed. The results show that in the range of working conditions studied in this paper, the along-range average wave height increases and then decreases with the increase of relative row spacing, and increases with the increase of opening rate, and the effect of period on the along-range average wave height has no obvious rule; when B/D = 9, e = 23.11%, the double row perforated cylinder breakwater has the best wave dissipation effect, the reflection coefficient ranges from 0.4 to 0.46,the transmission coefficient is between 0.3 ~ 0.35, the dissipation coefficient is between 0.8 ~ 0.85. Free surface fragmentation, water-air mixing and annular eddy motion evolution are the main causes of wave dissipation and energy dissipation of double-row cylinder breakwater. The jet stage occurred more violent free liquid surface fragmentation and water-gas mixing, resulting in the increase of turbulent kinetic energy after the dike, the peak turbulent kinetic energy after the increase is about 2.5 times of that before the jet, and the violent turbulent energy dissipation occurred. The relative row spacing will cause the changes of vorticity distribution and shear layer morphology near the rear breakwater, which will lead to different turbulent characteristics and affect the wave breaking characteristics of the double row perforated cylinder breakwater. The research results can provide theoretical support for the engineering design of a new type of double-arranged cylindrical breakwater and the study of wave dissipation mechanism.
-
Keywords:
- wave dissipation characteristics /
- flow characteristics /
- jet flow /
- shear layer /
- Q criterion /
- ring-vortex
-
引 言
当前, 我国涉海工程逐渐从近岸近海向深海远海发展, 并向生态、绿色、环保理念转变. 传统防波堤由于其掩护水域与外海间的水体交换能力差, 易造成掩护水域内的泥沙淤积、水质污染等问题, 越来越不能满足工程建设的新要求. 透空式防波堤具有良好的水体交换能力, 能够改善港内外水体循环从而解决港内泥沙淤积、水质污染等问题; 且透空式结构波浪反射较小, 所受波浪力较小, 在不增加建设成本的前提下能够增强防波堤的稳定性[1], 具有良好的应用前景.
透空式防波堤型式主要有板式、桩式、开孔结构等[2]. 前人通过理论研究、水槽试验、数值模拟手段开展了大量透空式防波堤消浪特性的研究. 其中板式结构相对简单, Longuet-Higgins[3] 在1957年率先从理论层面分析了长波作用下固定浮板的波浪透射系数; Yu等[4]采用特征值展开法求解有限水深平板的绕射问题. 与此同时, 部分学者[5-7] 基于水槽试验研究发现相对板宽、相对板间距、相对水深是影响双层、多层平板式防波堤消浪能力的主要原因. 在数值模拟方面, Li等[8]建立数值模型分析了双层水平板消浪特性并拟合出透射系数经验公式; Li等[9]基于有限体积法建立二维数值模型对比分析双平板和双弧板式防波堤透反射系数、耗能系数, 得出双弧板式防波堤有更好的消浪效果; 潘春昌等[10]提出多层圆弧板组成的透空式防波堤, 其研究结果也表明圆弧板透空式结构消波效果优于平板式结构. 此外, 相关研究[11-12]也表明, 与直立壁面相比, 圆弧壁面能承受更大的波浪载荷; 但圆弧板式防波堤施工难度大且稳定性较差, 而桩式防波堤施工方便且稳定性更好. 以圆柱型为代表的桩式防波堤在实际工程中得到广泛应用.
近年来前人针对桩式防波堤消浪效果进行了大量的研究. 在理论方面, Weigel[13] 于1961年首次提出了单排密排桩波浪透射系数的理论公式, 由于忽略了衍射效应, 该公式对试验结果的预测误差达25%. 部分学者[14-15]通过开展规则波、随机波作用下单排圆柱消浪特性试验研究得出, 相对桩距是影响透射系数的主要因素; Suvarna等[16]开展了新型圆台式单排桩消浪特性试验, 并建立了预测透射系数的混合理论模型, 研究表明圆台式的设计能有效提高单排桩的消浪效果. 在数值模拟方面, Rao等[17]通过数值模拟分析单排桩与双排桩的消浪特性, 结果表明双排桩的消浪效果优于单排桩; 许栋等[18]等在前人板式防波堤与桩式防波堤研究基础上, 提出了一种双排圆柱筒与挡浪板结合的新型结构型式, 研究表明透射系数在0.34 ~ 0.5之间, 此结构相较于传统单一的板式、桩式防波堤具有更好的消浪效果. 此外, 少量学者提出在防波堤上开孔以增加波浪的衰减, 如Jarlan[19]最早提出沉箱防波堤前壁开孔结构, 发现该结构可通过减少波浪反射、增大波浪与防波堤间相互作用从而增大波能耗散; Rao等[20]通过开展双排圆柱、双排穿孔圆筒试验研究了透射系数随相对间距、波陡的关系, 并基于Reef 3D建立三维数值模型, 对比分析单排无孔圆柱与单排开孔圆筒的消浪特性[21]; Suvarna等[22]在新型圆台式防波堤的基础上对上圆台开孔进行消浪效果试验, 分析了开孔百分比、开孔尺寸、开孔位置对防波堤消浪效果的影响; 部分学者基于势流理论, 引入黏性效应, 建立半解析模型开展波浪与圆柱、透空圆筒结构的数模研究, 此类方法内存占用小、计算效率高, 但仅能捕捉到部分黏性效应, 且“修正黏性系数”“耗散面”的选择多依赖于物模试验或CFD方法[23-26].
综上所述, 新型透空式双排圆筒防波堤结合了桩式防波堤与板式防波堤的优点, 有更好的消浪效果, 而现有研究表明结构上局部开孔可增加波浪与结构的相互作用, 从而加大波浪的能量耗散; 但开孔后结构复杂, 波浪与结构的相互作用过程具有非常复杂的三维特征, 流体的黏性效应更强, 现有研究大多针对于透空堤消浪特性, 缺少波浪作用下透空堤附近水流三维流动特性的研究. 因此, 本文在许栋[18]的研究基础上对圆筒进行局部开孔, 采用有限差分法结合RNG
$k-\varepsilon $ 湍流模型建立波浪与新型双排开孔圆筒防波堤相互作用的三维数值模型, 模拟了波浪与这种新型结构的相互作用过程, 并重点对双排开孔圆筒防波堤消浪特性、流动特性等进行分析, 为探究新型双排开孔圆筒防波堤消浪特性、揭示双排开孔圆筒防波堤消浪机理提供理论基础.1. 数值模型
1.1 数值模型的建立
基于Navier-Stokes (N-S)方程求解三维两相不可压缩黏性流体运动, 控制方程具体表达式如下
$$ \frac{\partial \bar{u_{i}}}{\partial x_{{i}}} = 0 $$ (1) $$ \begin{split} & \frac{\partial \bar{u_i}}{\partial t}+\bar{u_j} \frac{\partial \bar{u_i}}{\partial x_j}=-\frac{1}{\rho} \frac{\partial \bar{p}}{\partial x_i}+g_i+ \\ &\qquad \frac{1}{\rho} \frac{\partial}{\partial x_j}\left[\mu\left(\frac{\partial \bar{u}_i}{\partial x_j}+\frac{\partial \bar{u_j}}{\partial x_i}\right)-\rho { \bar u'_i \bar u'_j}\right] \end{split} $$ (2) 式中, 对于三维流体运动, i, j = 1, 2, 3; xi和xj为笛卡尔坐标系下三个方向空间坐标分量;
$\bar {u_{i}}$ 为i方向平均速度分量; t为时间;$ \rho $ 为流体密度;$ \bar{p} $ 为平均压应力; gi为i方向的重力加速度;$ \mu $ 为动力黏滞系数;$u'_{i}$ 和$u'_{j}$ 分别为i和j方向的脉动速度分量;$- \rho {\overline {u'_i u'_j}}$ 为雷诺应力.为了封闭上述方程组, 引入RNG
$ k-\varepsilon $ 湍流模型进行求解[27]. 与标准$ k-\varepsilon $ 模型相比, 它可以考虑小尺度涡体运动的影响, 同时对于旋转流动、急变流及低雷诺数流体模拟有更高的精度. RNG$ k-\varepsilon $ 湍流模型求解湍动能k方程、耗散率$ \varepsilon $ 方程具体表达式如下$$ \begin{split} &\frac{\partial k}{\partial t} + { \bar u_{j}} \frac{\partial k}{\partial x_{j}} = \frac{\partial}{\partial x_{j}}\left[\left(\frac{v_{t}}{\sigma_{k}} + v\right) \frac{\partial k}{\partial x_{j}}\right] + \\ &\qquad v_{t}\left(\frac{\partial {\bar u_{i}}}{\partial x_{j}} + \frac{\partial {\bar u_{j}}}{\partial x_{i}}\right) \frac{\partial {\bar u_{i}}}{\partial x_{j}}-\varepsilon \end{split} $$ (3) $$ \begin{split} &\frac{\partial \varepsilon}{\partial t} + {\bar u_{j}} \frac{\partial \varepsilon}{\partial x_{j}} = \frac{\partial}{\partial x_{j}}\left[\left(\frac{v_{t}}{\sigma_{\varepsilon}} + v\right) \frac{\partial \varepsilon}{\partial x_{j}}\right] + \\ &\qquad C_{1 \varepsilon} \frac{\varepsilon}{k} v_{t}\left(\frac{\partial {\bar u_{i}}}{\partial x_{j}} + \frac{\partial {\bar u_{j}}}{\partial x_{i}}\right) \frac{\partial \bar{u}_{i}}{\partial x_{j}}-C_{2 \varepsilon} \frac{\varepsilon^{2}}{k} \end{split} $$ (4) 式中,
$v_{t} = C_{\mu} k^{2} / \varepsilon$ 为湍流黏性系数;$v = \mu / \rho$ 为运动黏滞系数; 常数项$ C_{\mu} = 0.09 $ ,$C_{k} = 1.0$ ,$ \sigma_{k} = 1.0 $ ,$\sigma_\varepsilon = 1.3$ ,$C_{\mathrm{l}\varepsilon } = 1.44$ ,$C_{2 \varepsilon } = 1.92$ .对于自由表面的处理, 采用优化后的TruVOF方法, 该方法忽略只有气体的控制单元, 只计算有流体存在的控制单元, 减少模型计算收敛的同时对自由液面的追踪及飞溅液滴的捕获也更为精确[28]. 其控制方程如下
$$ \frac{\partial F}{\partial t} + {\bar u_{i}}\cdot \nabla F = 0 $$ (5) 式中,
${\bar u_{i}}$ 为混合流体的平均速度, t为时间,$ \nabla $ 为哈密顿算子; F为流体体积分数, F = 1为流体单元; F = 0为空气单元; 0 < F < 1为混合单元.数值模型采用非均匀交错网格和有限差分法对计算区域进行离散、两步映射法求解N-S方程, 压力项采用GMRES (generalized minmal residual method)方法进行求解. 数值模型中, 水槽底边界采用固壁无滑移界条件; 水槽上边界采用压力边界条件; 水槽前后两侧边界采用固壁滑移边界条件; 水槽左端进口边界采用基于线性波理论的速度入口造波边界条件造波; 水槽右端出口边界采用出流边界条件, 即为Orlanski[29]于1976年首次提出的Sommerfeld辐射边界条件.
1.2 数值模型的验证
1.2.1 网格无关性验证
为避免计算网格的尺寸和数量对模拟结果产生影响, 需进行网格无关性验证. 在保证x和y方向网格分辨率不变的情况下, 在沿波高方向考虑三套网格分辨率: 一个波高范围内划分15个网格(Δz = 0.0040 m, 粗网格)、一个波高范围内划分20个网格(Δz = 0.0030 m, 中网格)、一个波高范围内划分25个网格(Δz = 0.0024 m, 细网格). 数值造波参数为: 水深h = 0.5 m, 波高H = 0.06 m, 周期T = 1.4 s. 分别在x = 10 m, x = 13 m, x = 16 m, x = 29 m处设置4个浪高仪用来记录水面历时变化, 数值水槽计算结果与理论值对比如图1所示. 由图1(a) ~ 图1(c)可知, 三套网格计算结果差别不大且与理论值都有较好的吻合度, 对应的Skill数分别为0.99059, 0.99466, 0.99469. 考虑计算效率, 研究选取中网格进行后续计算. 此外, 为了解消波区的消浪效果, 图1(d)为消波区波高监测值变化, 最大波高仅为理论值的7.9%, 消浪效果良好.
![]()
图 1 不同测点处波高时间序列对比图Figure 1. Comparison of wave height time series at different measuring points1.2.2 规则波作用下圆柱式群桩结构物消浪验证
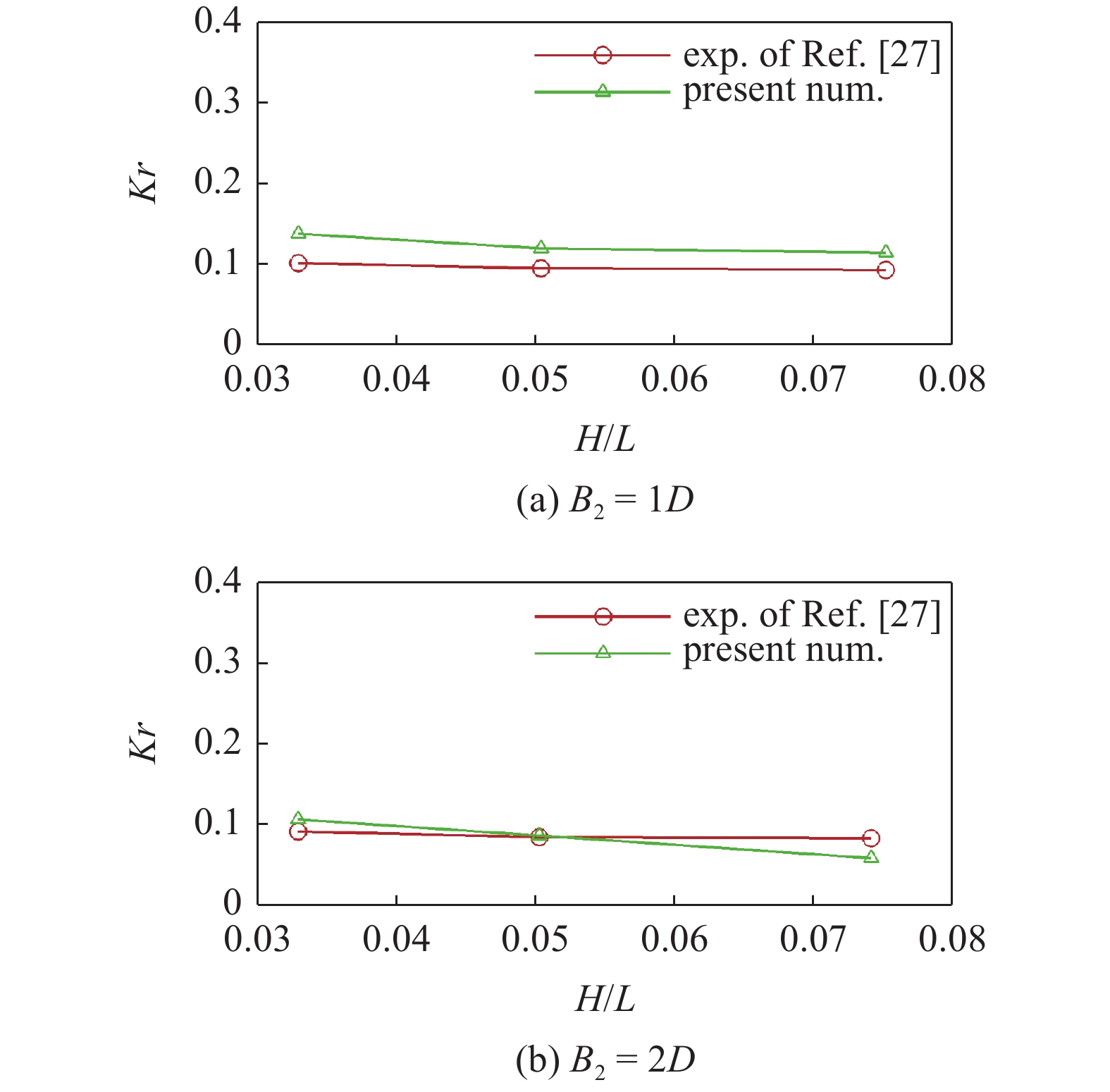
为进一步验证本数值模型能够较精确地模拟波浪与圆柱式群桩结构物相互作用过程, 本节参照Wheele等[30]物模试验进行圆柱式群桩结构物消浪性能的数值模拟. 数值模型参数设定与试验参数保持一致. 试验共布置16个圆柱, 圆柱直径D = 0.019 m, 沿波浪传播方向圆柱间距B1 = 2D, 垂直于波浪传播方向圆柱间距分别为B2 = 1D, 2D, 沿波浪传播方向共布置4个数值浪高仪用于监测波面历时数据, 采用Goda等[31]分离入射波与反射波. 如图2所示, 将反射系数计算结果与前人物模试验结果进行对比, 可以看出数模计算结果与前人研究结果吻合较好. 当B2 = 1D时两者的均方根误差RMSE为0.0283, 当B2 = 2D时两者均方根误差RMSE为0.0169, 误差在合理范围之内. 两者误差可能由于物模试验模型所用材料表面粗糙率与数值模型粗糙率有差异. 综上所述, 本文所搭建的三维数值模型能较好地模拟波浪与多圆柱桩式结构物相互作用过程, 可用于进一步研究.
![]()
图 2 不同柱间距Kr试验值与数模值对比图Figure 2. Comparison of Kr test value and numerical value with different column spacing2. 模型与工况设置
数值计算模型布置如图3所示. 数值水槽长30 m、宽0.9 m、高0.7 m; 第一排开孔圆筒高h1 = 0.55 m, 固定放置于x = 12 m处, 其距左端造波边界3 ~ 5倍波长; 第二排开孔圆筒高h2 = 0.7 m放置其后, 其与第一排开孔圆筒的距离设为B; 圆筒直径D1 = 0.2 m, 开孔直径D2 = 0.04 m, 考虑到波浪能量主要集中在一倍波高范围之内, 故静水面以下0.3 m至圆筒顶部之间开孔, 共设置三种开孔率; 为了避免水槽右端波浪反射的影响, 结合出流边界在水槽右端设置12 m长的消波区; 如图3所示沿波浪传播方向共布置6个浪高仪记录波面历时数据, 采用Goda等[31]两点法分离入射波与反射波. 采用局部加密的分块网格和嵌套网格技术对计算域进行网格划分, 最小网格尺寸为Δx = 0.011 m, Δy = 0.011 m, Δz = 0.003 m, 网格总数达532万, 图4为开孔圆筒防波堤附近网格细节图. 具体计算工况设置为: 结构开孔率e = 23.11%, 34.67%, 46.22%; 排间距B = 1.0 m, 1.2 m, 1.4 m, 1.8 m; 波高H = 0.06 m, 0.07 m, 0.09 m, 0.11 m; 周期T = 1.4 s, 1.5 s, 1.6 s, 1.8 s; 4个参数共72组工况.
![]()
图 3 模型布置图: (a)立面视图和(b)平面视图Figure 3. Layout of the model: (a) the elevation view and (b) the vertical view![]()
图 4 双排开孔圆筒防波堤附近网格细节图Figure 4. Mesh details near the double row perforated cylinder breakwater3. 结果与分析
3.1 沿程平均波高变化
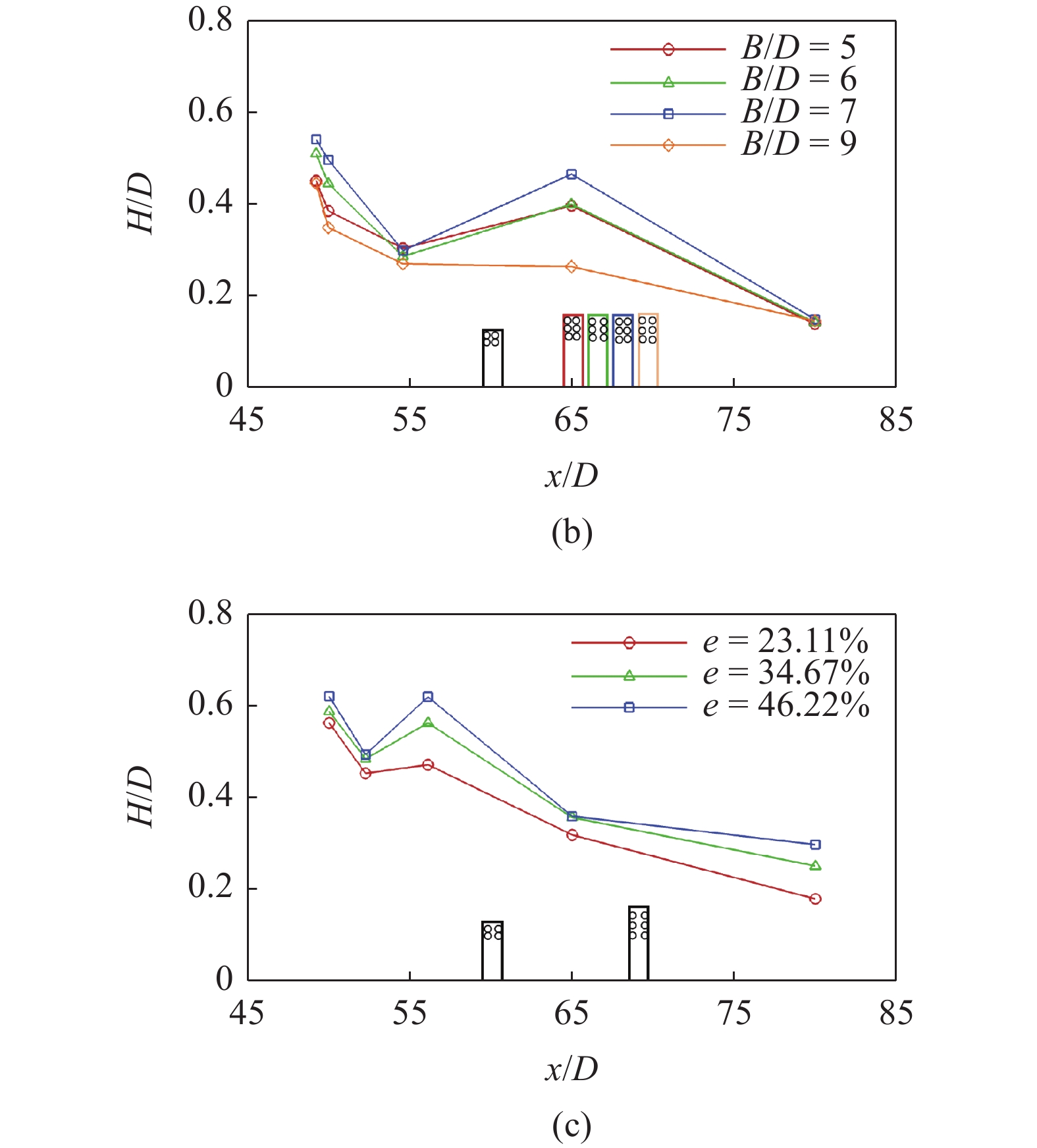
图5给出了防波堤附近WG1 ~ WG5各测点处平均波高随周期、相对排间距、开孔率的变化关系. 如图5(a)所示, 在B/D = 6, e = 46.22%, H = 0.06 m工况下, 平均波高随周期的增大而上下波动, 沿程平均波高随周期的变化没有明显规律; 由图5(b)可知, 在e = 46.22%, T = 1.8 s , H = 0.09 m工况下, 沿程平均波高随相对排间距的增大先增大后减小, 当B/D = 7时沿程平均波高最大, 当B/D = 9时沿程平均波高最小; 如图5(c)所示, 在B/D = 9, T = 1.4 s, H = 0.09 m工况下, 沿程平均波高随开孔率的增大而增大, 呈正相关关系.
3.2 结构参数对防波堤消浪特性的影响
本研究采用波浪与双排开孔圆筒防波堤相互作用下的反射系数(Kr)、透射系数(Kt)、耗散系数(Kd)评估防波堤的消浪效果, 分析无量纲参数相对排间距(B/D = 5, 6, 7, 9)、开孔率(e = 23.11%, 34.67%, 46.22%)对防波堤消浪性能的影响, 相应计算公式为
$$\qquad\qquad K_{r} = \frac{H_{r}}{H_{i}} $$ (6) $$\qquad\qquad K_{t} = \frac{H_{t}}{H_{i}} $$ (7) $$\qquad\qquad K_{d} = \sqrt{1-\left(K_{r}^{2} + K_{t}^{2}\right)} $$ (8) 式中, Hi为入射波高, Hr为反射波高, Ht为透射波高.
3.2.1 相对排间距对防波堤消浪特性的影响
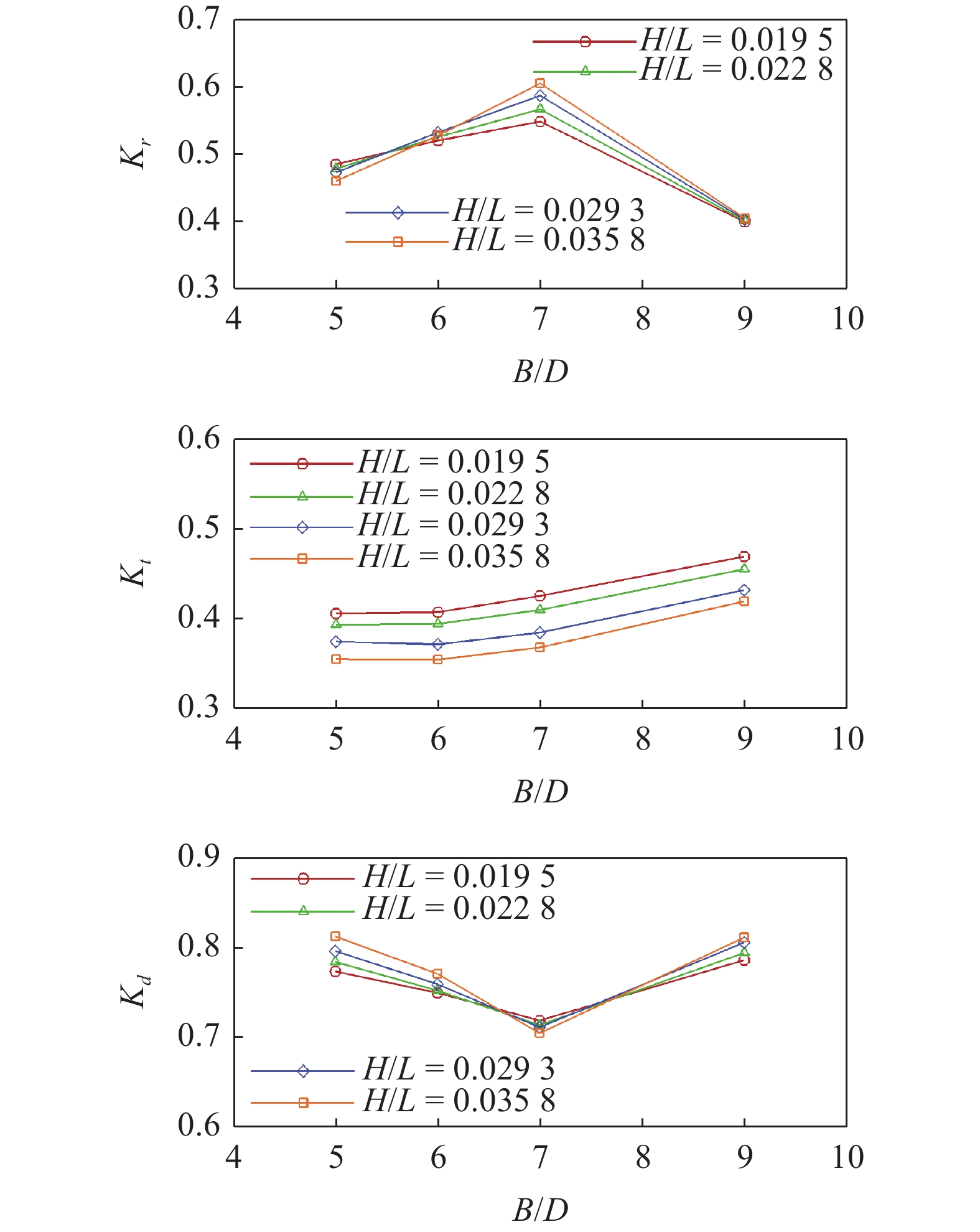
图6给出了波高H = 0.06, 0.07, 0.09, 0.11 m, T = 1.6 s, e = 34.67%工况下, 双排开孔圆筒防波堤的反射系数、透射系数、耗散系数随相对排间距的变化情况. 结果表明, 相对排间距对反射系数、透射系数、耗散系数影响较为显著; 不同波陡条件下, 反射系数随相对排间距的增大均呈先增大后减小的趋势, 当B/D = 7时反射系数达到最大, 当B/D = 9时反射系数最小, 防波堤对波浪的反射效果较弱, 相较于B/D = 7的反射系数减小约33%; 透射系数整体均呈增大的趋势, 但增幅不大, 透射系数均在0.45以下, 当B/D = 6时波浪的透过率最低, 此时相较于最大透射系数可减小约15.5%; 耗散系数均呈先减小后增大的趋势, 耗散系数均在0.7以上, 双排开孔圆筒防波堤通过改变自由液面附近水质点的横向和竖向运动轨迹耗散大量波能, 当B/D = 9时防波堤对波能的耗散能力最大, 耗散系数可达0.81, 相较于最小耗散系数可提升约15.1%. 因此, 当B/D = 9时, 在保证透射系数增幅不大的前提下可降低反射系数、增大耗散系数, 消浪效果最优.
![]()
图 6 相对排间距对防波堤消浪特性的影响Figure 6. The influence of relative row spacing on wave dissipation characteristics of breakwater3.2.2 开孔率对防波堤消浪特性的影响
图7给出了波高H = 0.06, 0.07, 0.09, 0.11 m, T = 1.6 s, B/D = 9 工况下双排开孔圆筒防波堤对波浪的反射系数、透射系数、耗散系数随开孔率的变化情况. 由结果可知, 开孔率对反射系数、透射系数、耗散系数影响较为显著; 不同波陡条件下, 随着开孔率的增加防波堤对波浪的反射作用减小, 最大反射系数在0.44左右, 最小反射系数在0.36左右; e = 23.11%相较于e = 46.22%工况下透射系数可降低39.8%左右, 当e = 23.11%时透射系数在0.3 ~ 0.35之间, 此时防波堤有较好的消浪效果; 耗散系数与开孔率呈负相关关系, 其值均在0.75以上, 最大可达0.85, e = 23.11%相较于e = 46.22%工况耗散系数可提升11%左右. 由此可知, 当e = 23.11%时双排开孔圆筒防波堤透射系数较小、耗散系数较大, 改变水质点运动的能力最强, 波浪破碎更为剧烈, 波能衰减更为显著, 消浪效果最优.
![]()
图 7 开孔率对防波堤消浪特性的影响Figure 7. The effect of opening rate on the wave dissipation characteristics of breakwater综上可得, 在本研究范围内, 相较于传统的桩式防波堤, 本文提出的新型双排开孔圆筒防波堤有良好的消浪效果. 对比Suvarna等[22]的研究成果, 本研究耗散系数增大约16.4%, 透射系数降低约 39.7%, 表明结构开孔能充分利用水体剪切紊动进行消能, 可促进掩护水域水体的交换, 并有利于结构的稳定.
3.3 波浪与双排开孔圆筒防波堤相互作用过程流动特性
3.3.1 流场分析
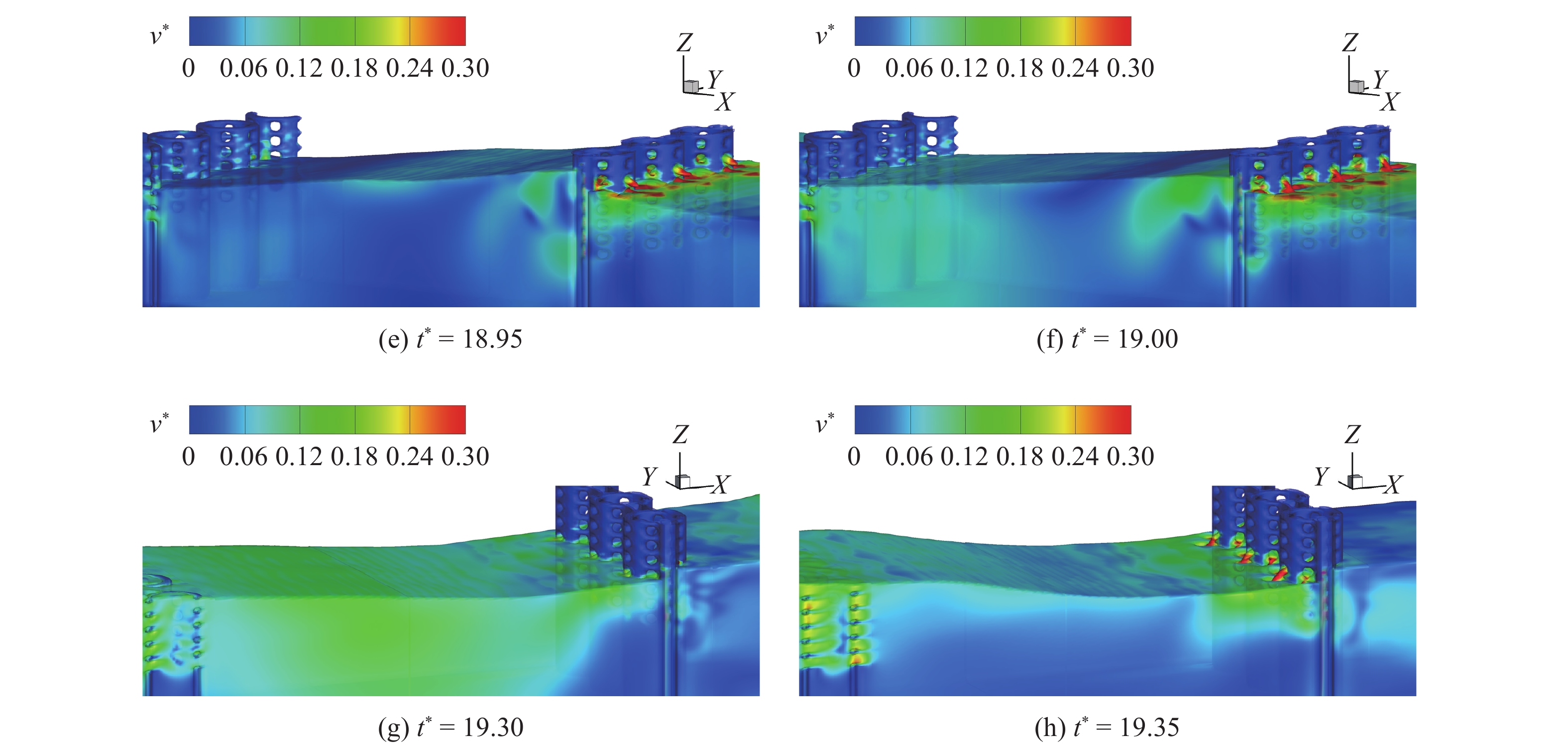
图8为波浪与双排开孔圆筒防波堤相互作用一个周期内波面演化过程三维速度云图, 其中时间t、速度v已无量纲化 :
$ {t^*} = t/T $ ,$ {v^*} = v \cdot T/L $ . 可将波浪与新型双排开孔圆筒防波堤相互作用过程分为四个阶段: 漫顶阶段(图8(a)和8(b))、雍水阶段(图8(c)和8(d))、射流阶段(图8(e)和8(f))、回涌阶段(图8(g)和8(h)). 从图8(a)和8(b)可观察到, 当波峰到达前排防波堤时, 圆筒上方自由液面发生明显的波动变形, 此处水体存在速度梯度, 形成了湍流, 引起了波能的紊动耗散. 由图8(c)和8(d)可知, 波峰到达后排防波堤, 部分水体穿过小孔进入后排圆筒内, 另一部分水体由于直立板和后排圆筒壁面的阻碍, 不断爬升, 在堤前形成雍水, 此时后排防波堤前的水体速度变小、势能增大. 如图8(e)和8(f)所示, 由于堤前雍水导致后排防波堤前后存在水头差, 在重力作用下圆筒内的水体穿过小孔脱离固体边界的约束, 与周围水体产生速度不连续的间断面, 形成小孔紊动射流; 向下回落的小孔射流卷入一部分空气进入堤后水体, 造成堤后水体自由液面破碎与水气掺混现象, Frantzis等[32]指出波浪破碎与水气掺混对能量耗散有较大影响. 从图8(g)和8(h)可观察到, 波谷到达后排防波堤, 出现了堤后水头高于堤前水头的逆水头差, 引起了水体倒流, 在堤前出现了类似于图8(e)和8(f)所示的反向射流, 再次出现自由液面破碎和水气掺混现象, 导致波能进一步耗散.![]()
图 8 波浪与双排开孔圆筒防波堤相互作用速度云图Figure 8. Velocity cloud image of wave interaction with a double row perforated cylinder breakwater![]()
8 波浪与双排开孔圆筒防波堤相互作用速度云图 (续)8. Velocity cloud image of wave interaction with a double row perforated cylinder breakwater (continued)图9为上述四个阶段部分时刻的湍动能云图, 湍动能计算公式为
![]()
图 9 波浪与双排开孔圆筒防波堤相互作用湍动能云图Figure 9. Turbulent kinetic energy cloud image of wave interaction with a double row perforated cylinder breakwater$$ K{\text{ = }}\frac{1}{2}\left( {{u'}^2 + {v'}^2 + {w'}^2} \right) $$ (9) 式中
$u',v'和w'$ 分别为三个方向的脉动速度. 湍动能K已无量纲化:$ {K^*} = K \cdot {T^2}/{L^2} $ , 可知在漫顶阶段(图9(a))前排防波堤堤顶附近水体存在较小的湍动能, 在其他三个阶段前排防波堤附近区域水体也存在较小的湍动能, 堤后湍动能最大K*约为0.001; 在漫顶阶段(图9(a))、雍水阶段(图9(b))、回涌阶段(图9(d))后排防波堤前的水体湍动能均较大, K*最大值约为0.0038; 由图9(b)和9(c)可知, 射流引起堤后湍动能增大, 湍动能峰值约为射流之前的2.5倍, 印证了前文流速场四个阶段关于紊动耗能的分析. 通过流速场及湍动能分析可知, 后排防波堤水流的紊动现象较前排更明显、更复杂, 发生了更为剧烈的能量转化、耗散.为进一步分析波浪与后排开孔圆筒防波堤相互作用过程的流动特性, 图10给出了后排防波堤附近水体的三维流管数值演化过程, 可将此过程分为三个典型阶段: 堤前未开孔位置旋涡的形成、堤前开孔位置旋涡的形成、堤后旋涡的形成. 如图10(a)所示, 圆筒开孔位置的堤前的流管v*值约为0.15, 圆筒未开孔位置的堤前流管v*值较小仅为0.025左右, 开孔位置分界处的水体存在流速梯度; 图10(b)中, 圆筒开孔位置前的部分流管进入圆筒且流速值仍然较大, 而未开孔位置前的流管受到圆筒壁的阻碍发生反射, 与来流发生碰撞, 因此相较于图10(a), 部分流管流速值变得更小; 上述两部分流管流向相反且存在明显的速度梯度差, 故存在水流剪切力, 在剪切力作用下圆筒未开孔位置前形成小旋涡. 由图10(c)和10(d)可知, 在雍水阶段向射流阶段发展过程中, 圆筒开孔位置前会逐渐形成一个尺寸较大的旋涡. 图10(e)和10(f)可知, 射流阶段向回涌阶段发展过程中, 穿过圆筒的流管顺时针旋转, 逐渐变得规律、排列紧密, 最终演化成大旋涡.
综上可得, 漫顶阶段、射流阶段、回涌阶段均有自由液面的破碎和水气掺混现象, 且有不同尺度的旋涡产生. 流体的本质是涡, 因为流体经不住“搓”, 一“搓”就“搓”出了涡[33]. 湍流中存在着各种尺度不一和强度各异的涡结构, 这些涡结构在湍流生成和维持过程中发生着关键性作用[34]. 因此, 自由液面破碎、水气掺混、涡的产生是双排开孔圆筒防波堤湍动耗能、消浪的重要原因.
![]()
图 10 第二排开孔圆筒防波堤附近三维流管演化图Figure 10. 3D flow pipe diagram near the second row of perforated cylinder breakwater3.3.2 涡量场分析
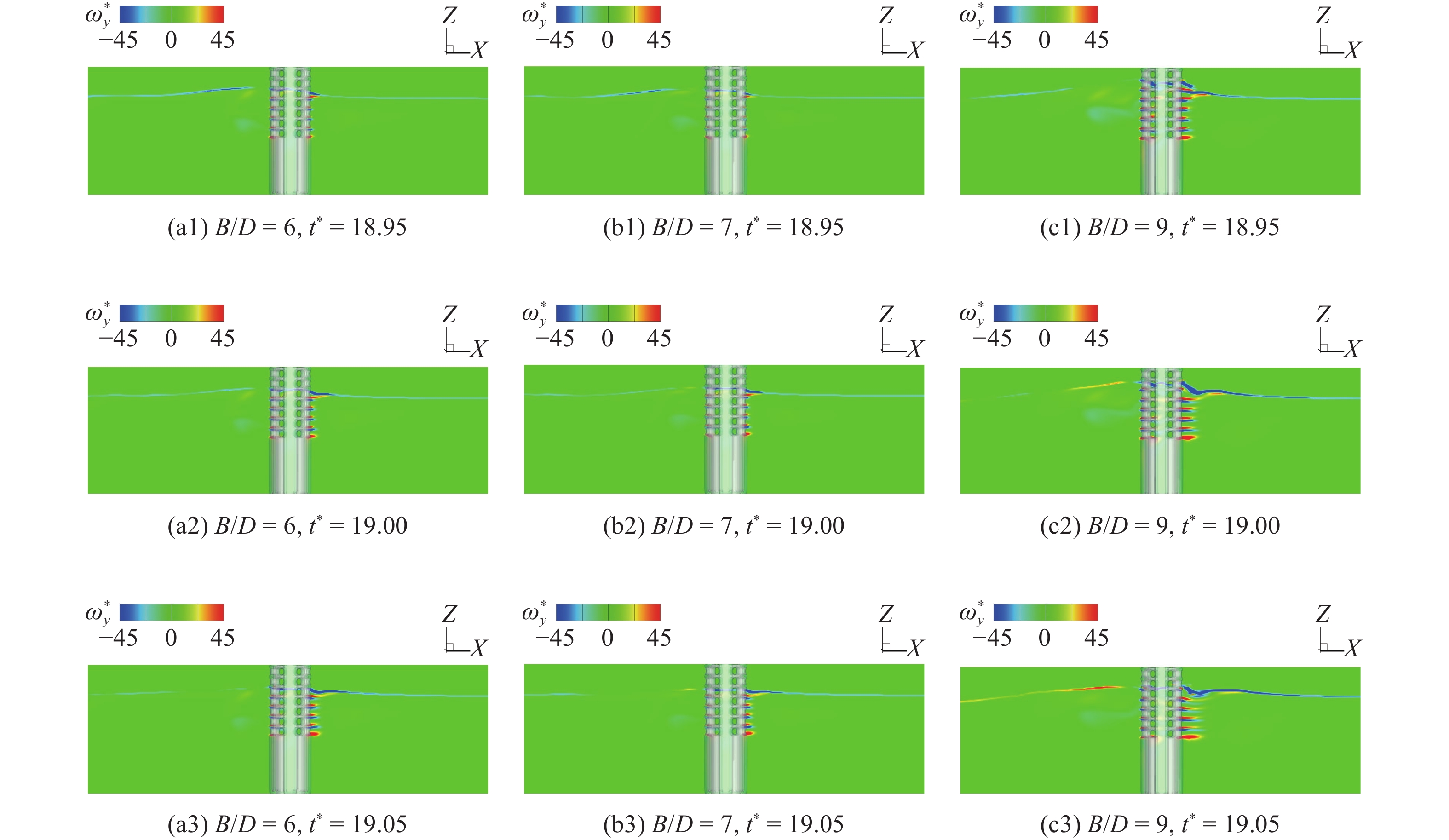
涡量表示速度矢量的旋度, 是描述旋涡运动的重要物理量. 为进一步分析旋涡演变与防波堤消浪特性之间的关系, 图11给出了不同相对排间距(B/D = 6, 7, 9)工况下射流阶段后排防波堤附近x-z平面内涡量演化图, 其中, y方向的涡量表示为
$$ \omega _{y} = \frac{\partial u}{\partial z}-\frac{\partial w}{\partial x} $$ (10) 式中, u为x方向的速度, w为z方向的速度.
如图11(a1), 11(b1)和11(c1)所示, y方向的涡量已无量纲化:
${\omega^* _y} = {\omega _y} \cdot T$ , 堤前自由液面处分布着少量负涡量; 穿过小孔到达堤后的水质点与堤后本身存在的水质点存在速度梯度, 在剪切力作用下水质点顺时针旋转生成正涡量、逆时针旋转生成涡量集中分布在开孔位置; 当相对排间距由6增大到7时, 堤后正负涡量分布均会减少, 剪切层在流动方向缩短, 当相对排间距由7增大到9时, 堤后正负涡量分布均会增大, 剪切层在流动方向伸长, 且开孔位置演化出许多新的剪切层, 剪切层附近的水质点涡动引起波能耗散. 由图11(a2), 11(b2)和11(c2)及图11(a3), 11(b3)和11(c3)可观察到, 三种相对排间距工况下, 堤后的涡量分布相较于上一时刻均增大, 这是因为小孔射流回落过程中卷入了一部分空气进入堤后水体, 空气在水流的挤压下发生变形、破碎, 从而影响涡量和动能的变化[35], 由此推断, 不同相对排间距条件下射流回落过程卷入空气后形成气腔的尺寸、数量可能对紊动耗能产生了影响, 有待开展进一步研究; 涡量分布、剪切层长度变化随相对排间距的变化情况与图11(a1), 11(b1)和11(c1)所示一致: 相对排间距为7时, 涡量分布最少, 相对排间距为9时, 涡量分布最多, 相对排间距由6增大到9过程中, 堤后各剪切层先缩短后伸长, 紊动特性先减弱后增强, 即防波堤波能耗散能力先减小后增大, 这与前文3.2.1节中耗散系数随相对排间距的变化趋势一致. 由此可知, 改变相对排间距会引起后排防波堤附近涡量分布以及剪切层长度的变化, 从而导致不同的紊动特性, 引起不同的波能耗散. 由前文三维流管部分的分析可知, 从雍水阶段发展到射流阶段的过程中, 堤前会有大旋涡生成, 但涡量图中并未显示出此旋涡, 说明存在流体旋转强度大但涡量小的区域[36]. 因此, 涡量并不能全面地表示各尺度、各强度的旋涡运动演化过程.![]()
图 11 第二排开孔圆筒防波堤附近y方向涡量对比图Figure 11. y-vorticity near the second row perforated cylinder breakwater3.3.3 基于Q准则涡结构分析
涡识别技术可以分为三代[37], 其中Q准则[38]在第二代涡识别方法中应用最为广泛, 能够剔除绝大部分的剪切层影响并合理地反映涡在流场中的位置、尺寸和强度[39], 也能很好地描述水体绕流柱型结构物后的旋涡结构形态演化过程[40]. 因此, 基于Q准则分析波浪与双排开孔防波堤相互作用过程中旋涡结构的运动演化对流场的影响具有重要参考价值. Q准则是速度梯度张量的二次不变量, 表达式为
$$ Q = \frac{1}{2}\left(\varOmega_{ij} \varOmega_{ij}-S_{ij} S_{ij}\right) $$ (11) 式中
$\varOmega_{ij}$ 表示旋转率张量的分量,$S_{ij}$ 表示应变率张量的分量. 若$ Q>0 $ , 表示流体的旋转速率大于应变速率, 则判断为有旋涡存在.图12给出了Q准则下(阈值为0.46)波浪与后排开孔圆筒防波堤相互作用涡结构演化过程三维局部视图, 其中图12(a)为堤前视角, 图12(b)为堤后视角. 如图12(a1)所示, 大量不规则碎涡集中在圆筒开孔位置处, 堤前生成了两个涡腿较粗且短的主涡结构, 可知此主涡即为前文图10(a)和10(b)分析中两部分流管对流剪切所生成. 由图12(a2) ~ 图12(a5)可观察到堤前演化出两排“半环状涡”, 由此可知, 前文中图10(c)和10(d)所示的大涡旋生成演化过程与两排半环状涡相互作用密切相关, 雍水阶段的湍动能(图9(b))是由两排“半环状涡”附近水质点涡动引起的. 由图12(b1)和12(b2)可以观察到, 堤后有环状涡生成, 由于水面附近流速较大, 环状涡上部受到剪切作用被拉伸并沿流向弯曲变形, 环状涡向下游演化过程中尺寸变小、弯曲程度变大; 由于持续的剪切作用, 环状涡上部逐渐变细, 最终断裂, 在自身诱导作用下其下部也发生断裂, 演化为两条“肋状”涡结构, 随后脱落消失, 堤后重新演化出新的环状涡, 如图12(b3) ~ 图12(b5)所示. 涡结构运动演化过程与上文三维流管演化过程相关分析基本一致, 说明Q准则能较好地识别波浪与后排开孔圆筒防波堤相互作用过程中旋涡的生成、演化过程及涡结构特征, 结合前文湍动能相关分析, 也说明了防波堤附近环状涡的运动演化是引起波能耗散的重要原因.
![]()
图 12 Q准则下涡结构演化过程图: (a1) ~ (a5)为堤前视角和(b1) ~ (b5)为堤后视角Figure 12. Evolution process of vortex structure under the Q criterion: (a1) ~ (a5) is the perspective in front of the breakwater and (b1) ~ (b5) is the perspective behind the breakwater4. 结论
本文基于Navier-Stokes方程建立波浪与新型双排开孔圆筒防波堤相互作用三维数值模型, 模拟了不同工况下波浪与新型双排开孔圆筒防波堤相互作用过程, 探究结构参数对消浪特性的影响以及流动特性对波能耗散的作用, 主要得出以下结论.
(1)在e = 46.22%, T = 1.8 s , H = 0.09 m工况下, 沿程平均波高随相对排间距的增大先增大后减小, 当相对排间距为 7时沿程平均波高最大, 当相对排间距为 9时沿程平均波高最小; 在B/D = 9, T = 1.4 s, H = 0.09 m工况下, 沿程平均波高随开孔率的增大而增大, 呈正相关关系.
(2)相对排间距、开孔率对新型双排开孔圆筒防波堤消浪特性的影响较为显著; 水深为0.5 m, 波陡在0.0195 ~ 0.0358范围内, 相对排间距为9、开孔率为23.11%时防波堤消浪效果最优, 透射系数在0.3 ~ 0.35之间, 耗散系数均在0.8以上, 最大可达0.85; 相较于传统的桩式防波堤, 新型双排开孔圆筒防波堤能充分利用水体剪切紊动进行消能, 具有良好的消浪效果, 且能促进水体交换和结构稳定; 实际工程应用中, 可根据不同的工程条件选择合适的开孔率和相对排间距, 以达到最优消浪效果.
(3) 波浪与新型双排开孔圆筒防波堤相互作用过程可分为四个阶段: 漫顶阶段、雍水阶段、射流阶段、回涌阶段, 其中射流阶段发生了较为剧烈的自由液面破碎和水气掺混, 导致堤后湍动能增大, 增大后的湍动能峰值约为射流之前的2.5倍, 发生了剧烈的紊动耗能.
(4) 波浪与新型双排开孔圆筒防波堤相互作用过程中后排防波堤前后均有环状涡的生成, 环状涡的生成、脱落、断裂过程引起了涡动耗能; 增大相对排间距, 后排防波堤附近涡量分布、剪切层长度先减小后增大, 与耗散系数变化趋势一致.
本文仅对开孔率、相对排间距两个无量纲参数进行了研究, 在此基础上考虑更多极端波况、结构布置等参数进行优化研究, 同时开展相应的载荷及稳定性分析, 为新型双排开孔圆筒防波堤消浪机理和工程设计提供更全面的技术支撑.
-
![]()
图 10 第二排开孔圆筒防波堤附近三维流管演化图
Figure 10. 3D flow pipe diagram near the second row of perforated cylinder breakwater
![]()
图 1 不同测点处波高时间序列对比图
Figure 1. Comparison of wave height time series at different measuring points
![]()
图 2 不同柱间距Kr试验值与数模值对比图
Figure 2. Comparison of Kr test value and numerical value with different column spacing
![]()
图 3 模型布置图: (a)立面视图和(b)平面视图
Figure 3. Layout of the model: (a) the elevation view and (b) the vertical view
![]()
图 4 双排开孔圆筒防波堤附近网格细节图
Figure 4. Mesh details near the double row perforated cylinder breakwater
![]()
图 6 相对排间距对防波堤消浪特性的影响
Figure 6. The influence of relative row spacing on wave dissipation characteristics of breakwater
![]()
图 7 开孔率对防波堤消浪特性的影响
Figure 7. The effect of opening rate on the wave dissipation characteristics of breakwater
![]()
图 8 波浪与双排开孔圆筒防波堤相互作用速度云图
Figure 8. Velocity cloud image of wave interaction with a double row perforated cylinder breakwater
![]()
8 波浪与双排开孔圆筒防波堤相互作用速度云图 (续)
8. Velocity cloud image of wave interaction with a double row perforated cylinder breakwater (continued)
![]()
图 9 波浪与双排开孔圆筒防波堤相互作用湍动能云图
Figure 9. Turbulent kinetic energy cloud image of wave interaction with a double row perforated cylinder breakwater
![]()
图 11 第二排开孔圆筒防波堤附近y方向涡量对比图
Figure 11. y-vorticity near the second row perforated cylinder breakwater
-
[1] Li A, Liu Y, Liu X, et al. Analytical and experimental studies on water wave interaction with a submerged perforated quarter-circular caisson breakwater. Applied Ocean Research, 2020, 101: 102267 doi: 10.1016/j.apor.2020.102267
[2] Karthik RS, Sannasiraj SA, Sundar V. Hydrodynamic performance of pile supported breakwaters—A review//Proceedings of the 10th International Conference on Asian and Pacific Coasts, 2019, Hanoi, Vietnam. Springer Singapore, 2020: 929-935
[3] Longuet-Higgins MS. Reviews water waves//The Mathematical Theory with Applications. New York Stroker JJ: Interscience Publishers, 1958, 4(4): 435-439
[4] Yu X, Chwang AT. Analysis of wave scattering by submerged circular disk. Journal of Engineering Mechanics, 1993, 119(9): 1804-1817 doi: 10.1061/(ASCE)0733-9399(1993)119:9(1804)
[5] Neelamani S, Gayathri T. Wave interaction with twin plate wave barrier. Ocean Engineering, 2006, 33(3-4): 495-516 doi: 10.1016/j.oceaneng.2005.03.009
[6] 王国玉, 王永学, 李广伟. 多层水平板透空式防波堤消浪性能试验研究. 大连理工大学学报, 2005, 6: 865-870 (Wang Guoyu, Wang Yongxue, Li Guangwei. Experimental study of wave damping performance of multiple layer breakwater. Journal of Dalian University of Technology, 2005, 6: 865-870 (in Chinese) doi: 10.3321/j.issn:1000-8608.2005.06.018 [7] 王晶, 程永舟, 杨小桦等. 新型透空板式防波堤消浪效果试验研究. 船舶力学, 2015, 19(Z1): 86-94 (Wang Jing, Cheng Yongzhou, Yang Xiaohua. Experimental study on wave dissipation of new plate breakwaters. Journal of Ship Mechanics, 2015, 19(Z1): 86-94 (in Chinese) [8] Li JB, Zhang NC, Guo CS. Numerical simulation of waves interaction with a submerged horizontal twin-plate breakwater. China Ocean Engineering, 2010, 24(4): 627-640
[9] Li XY, Xie T, Wang Q, et al. Numerical study of the wave dissipation performance of two plate-type open breakwaters based on the Navier–Stokes equations. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2021, 43(4): 1-18
[10] 潘春昌, 王国玉, 任冰等. 圆弧板透空式防波堤消波性能试验研究. 海洋工程, 2014, 32(4): 33-40 (Pan Chunchang, Wang Guoyu, Ren Bing, et al. Experimental study on the performance of arc-plate type breakwater. The Ocean Engineering, 2014, 32(4): 33-40 (in Chinese) doi: 10.16483/j.issn.1005-9865.2014.04.012 [11] Chen J, Wen HJ, Wang YX, et al. Experimental investigation of an annular sector OWC device incorporated into a dual cylindrical caisson breakwater. Energy, 2020, 211: 118681 doi: 10.1016/j.energy.2020.118681
[12] Tanimoto K, Takahashi S. Design and construction of caisson breakwaters—the Japanese experience. Coastal Engineering, 1994, 22(1-2): 57-77 doi: 10.1016/0378-3839(94)90048-5
[13] Wiegel RL. Closely spaced piles as a breakwater. Dock and Harbor Authority, 1961, 42(491): 150
[14] Hayashi T, Hattori M, Kano T, et al. Hydraulic research on the closely spaced pile breakwater. Coastal Engineering in Japan, 1966, 9(1): 107-117 doi: 10.1080/05785634.1966.11924676
[15] Truitt CL, Herbich JB. Transmission of random waves through pile breakwaters//Proceedings of 20th conference on Coastal Engineering. ASCE, 1986, 169: 2303-2313
[16] Suvarna PS, Sathyanarayana AH, Umesh P, et al. Laboratory investigation on hydraulic performance of enlarged pile head breakwater. Ocean Engineering, 2020, 217: 107989 doi: 10.1016/j.oceaneng.2020.107989
[17] Rao PSB, Mathew SE, Suvarna P, et al. Numerical investigation of wave interaction with pile breakwater//Proceedings of the International Conference on Industrial Engineering and Operations Management, Washington DC, USA, 2018: 1618-1628
[18] 许栋, 孙家聪, 李斌等. 透空式双排圆筒防波堤消波性能数值模拟研究. 水道港口, 2022, 43(1): 16-21 (Xu Dong, Sun Jiacong, Li Bin, et al. Numerical study on of wave-damping performance of double-row cylindrical. Journal of Waterway and Harbor, 2022, 43(1): 16-21 (in Chinese) doi: 10.3969/j.issn.1005-8443.2022.01.004 [19] Jarlan GE. A perforated vertical wall breakwater. The Dock and Harbour Authority, 1961, 486: 394-398
[20] Rao S, Rao NBS, Sathyanarayana VS. Laboratory investigation on wave transmission through two rows of perforated hollow piles. Ocean Engineering, 1999, 26(7): 675-699 doi: 10.1016/S0029-8018(98)00021-3
[21] Rao N, Rao PSB, Nayak K, et al. Numerical investigation on wave transmission characteristics of perforated and non-perforated pile breakwater. Journal of Physics: Conference Series, 2019, 1276(1): 012021 doi: 10.1088/1742-6596/1276/1/012021
[22] Suvarna PS, Sathyanarayana AH, Umesh P, et al. Hydraulic performance of perforated enlarged pile head breakwaters through laboratory investigation. Ocean Engineering, 2021, 241: 110089 doi: 10.1016/j.oceaneng.2021.110089
[23] Bai W, Feng X, Taylor RE, et al. Fully nonlinear analysis of near-trapping phenomenon around an array of cylinders. Applied Ocean Research, 2014, 44: 71-81 doi: 10.1016/j.apor.2013.11.003
[24] Feng X, Chen XB, Dias F. A potential flow model with viscous dissipation based on a modified boundary element method. Engineering Analysis with Boundary Elements, 2018, 97: 1-15 doi: 10.1016/j.enganabound.2018.09.004
[25] 赵玄烈, 宁德志, 康海贵等. 波浪作用下上部带有透空结构的圆筒垂向水动力特性的解析研究. 工程力学, 2017, 34(12): 239-247 (Zhao Xuanlie, Ning Dezhi, Kang Haigui, et al. Analytical study on the vertical hydrodynamics of a truncated cylinder with upper porous wall and inner column. Engineering Mechanics, 2017, 34(12): 239-247 (in Chinese) [26] 王广原, 王多银, 房皓等. 规则波作用下开孔圆盘阵列绕射效应研究. 工程力学, 2022, 39: 1-10 (Wang Guangyuan, Wang Duoyin, Fang Hao, et al. Study on diffraction effect of porous plate array under regular wave. Engineering Mechanics, 2022, 39: 1-10 (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.05.0379 [27] Lin P, Liu PLF. A numerical study of breaking waves in the surf zone. Journal of Fluid Mechanics, 1998, 359: 239-264 doi: 10.1017/S002211209700846X
[28] Bombardelli FA, Hirt CW, García MH, et al. Computations of curved free surface water flow on spiral concentrators. Journal of Hydraulic Engineering, 2001, 127(7): 629-631 doi: 10.1061/(ASCE)0733-9429(2001)127:7(629)
[29] Orlanski I. A simple boundary condition for unbounded hyperbolic flows. Journal of Computational Physics, 1976, 21(3): 251-269 doi: 10.1016/0021-9991(76)90023-1
[30] Wheele BL, Herbich JB. Wave reflection and transmission for pile arrays//Proceedings of 13th Conference on Coastal Engineering, ASCE, 1972
[31] Goda Y, Suzuki Y. Estimation of incident and reflected waves in random wave experiments//Proceedings of the 15th Conference on Coastal Engineering Conference, 1976
[32] Frantzis C, Grigoriadis DGE, Dimas AA. Numerical study of solitary waves past slotted breakwaters with a single row of vertical piles: wave processes and flow behavior. Ocean Engineering, 2020, 211: 107667 doi: 10.1016/j.oceaneng.2020.107667
[33] 吴介之. 涡动力学引论. 北京: 高等教育出版社, 1993 Wu Jiezhi. Introduction to Vortex Dynamics. Beijing: Higher Education Press, 1993 (in Chinese))
[34] 刘超群. Liutex-涡定义和第三代涡识别方法. 空气动力学学报, 20 20, 38(3): 413-431, 478 Liu Chaoqun. Liutex third generation of vortex definition and identification methods. Acta Aerodynamica Sinica, 2020, 38 (3): 413-431, 478 (in Chinese))
[35] 邓斌, 王孟飞, 黄宗伟等. 波浪作用下直立结构物附近强湍动掺气流体运动的数值模拟. 力学学报, 2020, 52(2): 408-419 (Deng Bin, Wang Mengfei, Huang Zongwei, et al. Numerical simulation of the hydrodynamic characteristics of violent aerated flows near vertical structure under wave action. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(2): 408-419 (in Chinese) doi: 10.6052/0459-1879-20-029 [36] Wang Y, Yang Y, Yang G, et al. DNS study on vortex and vorticity in late boundary layer transition. Communications in Computational Physics, 2017, 22(2): 441-459 doi: 10.4208/cicp.OA-2016-0183
[37] 王义乾, 桂南. 第三代涡识别方法及其应用综述. 水动力学研究与进展 (A 辑), 2019, 34(4): 413-429 (Wang Yiqian, Gui Nan. A review of the third-generation vortex identification method and its applications. Chinese Journal of Hydrodynamics, 2019, 34(4): 413-429 (in Chinese) [38] Hunt JCR, Wray AA, Moin P. Eddies, stream, and convergence zones in turbulent flows. Summer Program Center Turbulence Research, 1988: 193-208
[39] 赵斌娟, 谢昀彤, 廖文言等. 第二代涡识别方法在混流泵内部流场中的适用性分析. 机械工程学报, 2020, 56(14): 216-223 (Zhao Binjuan, Xie Yuntong, Liao Wenyan, et al. Adaptability analysis of second generation vortex recognition method in internal flow field of mixed flow pumps. Journal of Mechanical Engineering, 2020, 56(14): 216-223 (in Chinese) doi: 10.3901/JME.2020.14.216 [40] 刘健, 邹琳, 陶凡等. 串列双锥柱绕流流动特性的大涡模拟研究. 力学学报, 2022, 54(5): 1209-1219 (Liu Jian, Zou Lin, Tao Fan, et al. Large eddy simulation of flow past two conical cylinders in tandem arrangement. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(5): 1209-1219 (in Chinese) -
期刊类型引用(3)
1. 黄波林，殷跃平，李仁江，蒋树，秦臻，张鹏，闫国强. 滑坡涌浪综合防控工程措施研究进展与挑战. 工程地质学报. 2025(01): 159-170 . 
百度学术
2. 邓斌，王玲，何军，尹龙斌，蒋昌波，陈杰，伍志元. 基于SSA-CNN模型的双排开孔圆筒防波堤透射系数预测. 海洋学报. 2024(04): 122-132 . 百度学术
3. 石晓，蒋勤，钟振宇. 波浪对水平板冲击作用水气二相流数值模拟研究. 力学学报. 2024(10): 2878-2887 . 本站查看
其他类型引用(0)
下载:
计量
- 文章访问数: 859
- HTML全文浏览量: 312
- PDF下载量: 111
- 被引次数: 3
