页岩气是一种主要以吸附状态储存在页岩中的非常规天然气,储量丰富,清洁高能,随着美国页岩气开采的迅速发展,美国能源行业发生了巨大转变.中国虽起步较晚,但据美国能源信息署2014年简报,中国拥有世界上最大的页岩气技术可采储量,2014年7月,中石化涪陵页岩气田的正式投产标志着中国页岩气商业开发的开始.页岩气储层与常规油气储层不同,致密低渗使其必须通过水力压裂等储层改造技术才能获得工业产能.水力压裂法是利用高压泵组以超过油气储层吸收能力的排量注入较高黏度的压裂液,在压裂目标层形成高压[1-2],当压力超过井底岩石的破裂强度时,储层产生裂缝.裂缝的形成与沟通大大提高了储层渗透性,达到油气资源增产增注效果 [3-4].岩石是典型的脆性材料,陈昀等[5]基于能量耗散法对岩石进行了脆性评价.页岩储层具有典型的层理性,层理对水力压裂裂纹扩展的干扰使均质储层水力压裂裂纹扩展理论不再完全适用[6],研究天然层理发育对水力压裂裂纹扩展的影响对页岩气的全面开发至关重要[7-8].
学者[9-18]主要针对含天然裂缝储层水力压裂过程进行了实验研究,建立了水力裂缝穿过天然裂缝的准则.实验利用真三轴压裂模拟系统对含有预制裂缝的水泥块进行压裂,模拟天然裂缝性储层中水力裂缝的扩展规律,研究天然裂缝方位、原始地应力场等因素对裂缝扩展的影响,证实了压裂裂缝遇天然裂缝后的扩展模式受地应力及天然裂缝与压裂裂纹的相交角影响.与天然裂缝不同的是层理弱面强度比岩石基体低,但仍为连续性介质,压裂裂纹遇层理弱面后的扩展模式除受地应力及层理弱面方位影响外,岩石基体抗拉强度和层理弱面抗拉强度对裂纹的扩展影响不可忽略.孙可明等[19-25]分别采用离散元法、数值流形法、扩展有限元等方法进行了水力压裂裂纹扩展的数值模拟,其中扩展有限元方法不需重画网格及预设裂纹扩展路径,发展较为完善.曾冬青等[26-32]基于扩展有限元方法对天然裂缝储层及页岩储层的水力压裂裂纹扩展规律进行了数值模拟,实现了裂纹任意路径扩展计算.数值计算结果分散性大,对层理性页岩储层压裂裂纹的扩展机理研究不够完善,目前国内外对含层理弱面储层的水力压裂裂缝扩展规律深入研究较少.本文基于复变函数保角变换推导得出裂纹尖端应力状态,进而得出水力压裂裂纹在斜交层理后的扩展判据,并对扩展规律进行解析,为页岩储层的水力压裂作业提供理论指导.
1 压裂裂纹面尖端应力集中解现做如下假设:(1)压裂裂纹与层理相遇前垂直最小地应力方向稳定扩展;(2)裂纹几何形态为扁状椭球形,稳定扩展时裂纹面长轴与短轴比值不变;(3)裂纹垂面可看作短轴为零的椭圆;(4)裂缝尖端流体压力均匀分布且不存在流体滞后现象.
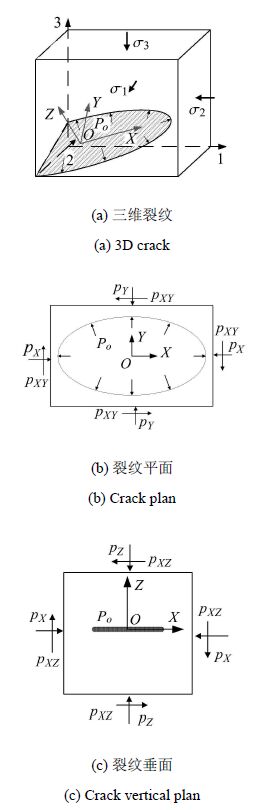
图 1为裂纹示意图. 图 1(a) 中阴影为三维空间任意方向裂纹,裂纹尖端应力状态可由裂纹面尖端应力状态及裂纹垂面裂尖应力状态确定,以裂纹面为$XOY$面建立坐标系$OXYZ$,则裂纹面尖端及裂纹任意垂面裂尖受力状态可由坐标变换得出[33]
| $ {\sigma} = { K}{\sigma} { K}^{\rm T}$ | (1) |
|
图 1 裂纹示意图 Figure 1 The figure of crack |
式中,${\sigma}$为主应力坐标系下的应力,${\sigma}$为裂纹平面及所选取的裂纹垂面组成的坐标系下应力,${K}$为坐标变换矩阵.
裂纹面长轴$2a$,短轴$2b$,受力情况为无限远处地应力$p_X $,$p_Y $和$p_{XY} $以及椭圆孔边水压力$P_o$.建立如图 2所示的复平面.

|
图 2 裂纹面的保角变换 Figure 2 The conformal transformation of crack plan |
复平面$z = x + {\rm i}y$,将$z$平面上的椭圆孔外部通过保角变换,变换到$\zeta $平面上单位圆内部,变换式$z = \omega (\zeta ) = R(\zeta ^{-1} + m\zeta )$,$\zeta = \rho {\rm e}^{{\rm i}\theta }$,单位圆$\vert \zeta \vert = 1$对应椭圆孔口边界,$\rho $,$\theta $为$\zeta $平面内极坐标,$R = (a + b) / 2$,$m = (a - b) / (a + b)$. 以拉为正,由曲线坐标中应力分量的复变函数表示[34]可知
| $\left. \begin{array}{*{35}{l}} {{\sigma }_{\theta }}+{{\sigma }_{\rho }}=4\text{Re}\Phi (\zeta ) \\ {{\sigma }_{\theta }}-{{\sigma }_{\rho }}+2\text{i}{{\tau }_{\rho \theta }}= \\ \frac{2{{\zeta }^{2}}}{{{\rho }^{2}}\overline{{\omega }'(\zeta )}}[\overline{\omega (\zeta )}{{\Phi }^{\prime }}(\zeta )+{\omega }'(\zeta )\psi (\zeta )] \\ \end{array} \right\}$ | (2) |
其中
| $\left.\!\! \varPhi (\zeta ) = {\varphi }'(\zeta ) / {\omega }'(\zeta ) ,\ \varPsi (\zeta ) = {\psi }'(\zeta ) / {\omega }'(\zeta ) \\ \varphi (\zeta ) = \dfrac{1 + \mu }{8\pi }(\bar {F}_x + {\rm i}\bar {F}_y )\ln \zeta + B\omega (\zeta ) + \varphi _0 (\zeta ) \\ \psi (\zeta ) = - \dfrac{3 - \mu }{8\pi }(\bar {F}_x - {\rm i}\bar {F}_y )\ln \zeta + ({B}' + {\rm i}{C}')\omega (\zeta ) + \psi _0 (\zeta ) \!\!\right\} $ | (3) |
$\bar {F}_x$,$\bar {F}_y$由应力边界条件确定,根据无穷远处 $\sigma _x = - p_X$,$\sigma _y = - p_Y$,$\tau_{xy} = - p_{XY}$及柯西积分公式,推导得
| $\left. \begin{matrix} \varphi (\zeta )=-R{{\xi }^{-1}}({{p}_{Y}}+{{p}_{X}})/4+(m-2)R\zeta {{p}_{X}}/4+ \\ (m+2)R\zeta {{p}_{Y}}/4-\text{i}{{p}_{XY}}R\zeta -{{P}_{o}}Rm\zeta \\ \psi (\zeta )={{P}_{o}}R\zeta \frac{1+{{m}^{2}}}{m{{\zeta }^{2}}-1}+R{{\zeta }^{-1}}[({{p}_{X}}-{{p}_{Y}})/2+\text{i}{{p}_{XY}}]+ \\ \frac{1}{2}{{p}_{X}}R\zeta \frac{{{\zeta }^{2}}-{{m}^{2}}+m-1}{m{{\zeta }^{2}}-1}- \\ \frac{1}{2}{{p}_{Y}}R\zeta \frac{{{\zeta }^{2}}+{{m}^{2}}+m+1}{m{{\zeta }^{2}}-1}+\text{i}R{{p}_{XY}}\zeta \frac{{{\zeta }^{2}}+m}{m{{\zeta }^{2}}-1} \\ \end{matrix} \right\}$ | (4) |
将$\zeta = \rho {\rm e}^{{\rm i}\theta } = \rho (\cos \theta + {\rm i}\sin \theta )$代入式(4),联合式(2)可求得孔边应力:$\sigma _\rho = - P_o $,$\tau _{\rho \theta } = 0$,
| $ \sigma _\theta = p_X \dfrac{m^2 - 2m + 2\cos 2\theta - 1}{m^2 - 2m\cos 2\theta + 1} + \\ p_Y \dfrac{m^2 + 2m - 2\cos 2\theta - 1}{m^2 - 2m\cos 2\theta + 1} -\\ 4p_{XY} \dfrac{\sin 2\theta }{m^2 - 2m\cos 2\theta + 1} - \\ P_o \dfrac{3m^2 + 2m\cos 2\theta - 1}{m^2 - 2m\cos 2\theta + 1}$ | (5) |
为简化计算,式中取$a = 2b$,则$m = 1 / 3$,即
| $\begin{align} & {{\sigma }_{\theta }}=\frac{1}{5-3\cos 2\theta }[3(1-\cos 2\theta ){{P}_{o}}-(7{{p}_{X}}+{{p}_{Y}})+ \\ & 9\cos 2\theta ({{p}_{X}}-{{p}_{Y}})-18{{p}_{XY}}\sin 2\theta ]\text{ } \\ \end{align}$ | (6) |
式中,$\sigma _\theta $为裂纹面内环向应力,$\theta $为裂纹面内环向角,$P_o $为裂纹尖端水压力,$p_X $,$p_Y $和$p_{XY} $为$XOY$面上裂纹所受正应力和剪应力.
同理,压裂裂纹垂面通过保角变换可得出裂纹尖端应力$\sigma _X $,$\sigma _Z$以及$\tau _{XZ} $,根据直角坐标向极坐标的变换,可得尖端环向应力
| $ \sigma _{\theta }' = (P_o - p_Z )\sqrt {\dfrac{a}{2r}} \cos ^3\dfrac{{\theta }'}{2} + \\ p_{XZ} \sqrt {\dfrac{a}{2r}} \Big (\sin ^3\dfrac{{\theta }'}{2} - \sin \dfrac{5{\theta }'}{2} \Big )$ | (7) |
式中,$\sigma _{\theta }' $为裂纹垂面裂纹尖端极坐标的环向应力,$r$为极坐标的极径,${\theta }'$为极角,$a$为裂纹尖端长度,$P_o $为裂纹尖端水压力,$p_Z $和$p_{XZ} $分别为$XOZ$面正应力和剪应力.
式(5)和式(6)中$\sigma _\theta$,$\sigma _{\theta }' $以及$\theta $,${\theta }'$见图 3.

|
图 3 裂纹尖端应力 Figure 3 The stresses of crack tip |
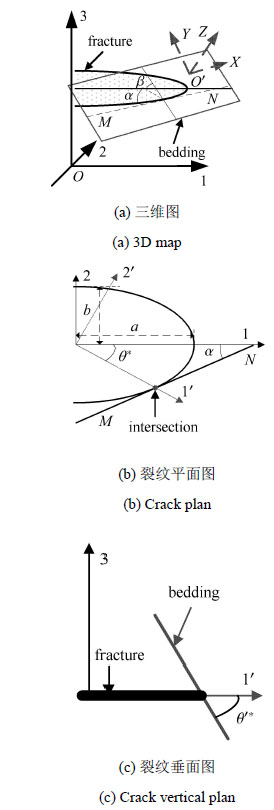
垂直于最小地应力方向裂纹与任意方向层理弱面斜交,相交位置的不同决定交点处应力状态不同,因而需先确定压裂裂纹与层理的相交点. 当储层地应力中垂向地应力最小时,水力压裂裂纹稳定时沿水平扩展,设层理走向线$MN$与第一主应力的夹角为层理走向角$\alpha$,层理弱面相对水平面的倾角$\beta $,岩石基体抗拉强度为$S_{\rm t}$,层理弱面抗拉强度为$S_{\rm t}^\ast $. 通过对椭圆和走向线相切确定交点,设层理与裂纹交点所对应主平面$1O2$上极角为$\theta ^\ast $,主坐标系下满足$\tau _{12} =0$. 保持坐标系原点及3轴不变,绕3轴旋转使交点落在${1}'$轴,交点垂面${1}'O{2}'$上裂纹尖端极坐标角${\theta }'^\ast $,根据坐标变换可知$\tau _{{1}'3} = 0$,如图 4所示.
|
图 4 水力压裂裂纹与层理斜交 Figure 4 Hydraulic fracture meet bedding oblique |
当$\alpha \ne 0$时,满足
| $ \tan \theta ^\ast = - \dfrac{1}{4\tan \alpha } , \quad {\theta }'^\ast = - \beta $ | (8) |
则有尖端环向应力
| $\left. \begin{matrix} _{\theta }{{|}_{\theta ={{\theta }^{*}}}}=\frac{1}{4{{\tan }^{2}}\alpha +1}[\frac{3}{4}{{P}_{o}}+(4{{\tan }^{2}}\alpha -2){{\sigma }_{1}}- \\ \sigma (20{{\tan }^{2}}\alpha -1){{\sigma }_{2}}] \\ {{\sigma }_{{{\theta }'}}}{{|}_{{\theta }'={{{{\theta }'}}^{*}}}}=({{P}_{o}}-{{\sigma }_{3}})\sqrt{\frac{a}{2r}}{{\cos }^{3}}\frac{\beta }{2} \\ \end{matrix} \right\}$ | (9) |
由式(6)可知,裂纹在垂直最小地应力方向扩展需满足主平面$1O3$上裂纹尖端环向应力最大值大于抗拉强度,即
| $ \sigma _{\theta }'^{\max } = (P_o - \sigma _3 )\sqrt {\dfrac{a}{2r}} ≥ S_{\rm t} $ | (10) |
得出裂纹沿原方向扩展所需的裂缝尖端水压力$P_o^{\rm f} $ (上标f为fracture缩写)为
| $ P_o^{\rm f} = \sigma _3 + \sqrt {\dfrac{2r}{a}} S_{\rm t}$ | (11) |
均质储层不考虑滤失时水平缝破裂压力[35]
| $ P_o^{\rm f} = \sigma _v + S_{\rm t } $ | (12) |
由此,式中取$\sqrt {\dfrac{2r}{a}} = 1$.
2.2.2 垂直最小地应力压裂裂纹在层理起裂条件裂纹在层理方向起裂需满足层理方向环向应力大于层理抗拉强度,即式(9)中$ \sigma _\theta $和$ \sigma _{\theta }' $满足
| $ \max \{\sigma _\theta \vert _{\theta = \theta ^ * } ,\sigma _{\theta }' \vert _{{\theta }' = {\theta }'^ * } \} ≥ S_{\rm t}^ * $ | (13) |
设由$\sigma _\theta \vert _{\theta = \theta ^ * } = S_{\rm t}^\ast $确定的裂缝尖端水压力为$P_{o1}^{\rm i} $ (上标i为initiation缩写),$\sigma _{\theta }' \vert _{{\theta }' = {\theta }'^ * } = S_{\rm t}^\ast $确定的裂缝尖端水压力为$P_{o2}^{\rm i} $
| $\left. \begin{matrix} P_{o1}^{\text{i}}=\frac{4}{3}[(4{{\tan }^{2}}\alpha +1)S_{\text{t}}^{*}-(4{{\tan }^{2}}\alpha -2){{\sigma }_{1}}+ \\ (20{{\tan }^{2}}\alpha -1){{\sigma }_{2}}] \\ P_{o2}^{\text{i}}={{\sigma }_{3}}+S_{\text{t}}^{*}/{{\cos }^{3}}\frac{\beta }{2} \\ \end{matrix} \right\}$ | (14) |
则裂纹在层理处起裂的裂缝尖端水压力$P_o^{\rm i} $满足
| $ P_o^{\rm i} = \min \{P_{o1}^{\rm i} ,P_{o2}^{\rm i} \}$ | (15) |
在层理弱面上建立如图 4(a)所示局部坐标系${O}'XYZ$,则裂纹在层理方向扩展需$X{O}'Z$面上满足
| $ \sigma _{\theta ^\prime }^{\max } > S_{\rm t}^ * $ | (16) |
通过坐标变换,由式(15)所得裂纹在层理弱面扩展所需裂缝尖端水压力$P_o^{\rm e} $ (上标e为extend缩写)
| $ P_o^{\rm e} = (\sigma _1 \sin ^2\alpha + \sigma _2 \cos ^2\alpha )\sin ^2\beta + \sigma _3 \cos ^2\beta + S_{\rm t}^\ast $ | (17) |
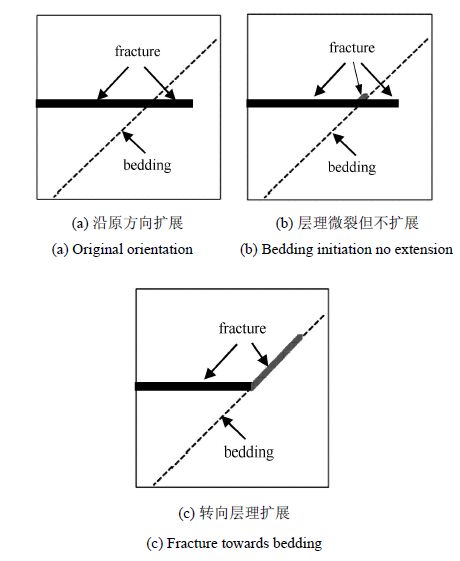
比较裂纹沿垂直最小地应力方向扩展的裂缝尖端水压力$P_o^{\rm f} $和压裂裂纹在层理起裂和扩展的主裂缝尖端水压力$P_o^{\rm i} $和$P_o^{\rm e} $,当$P_o^{\rm f} < P_o^{\rm i} $,且$P_o^{\rm f} < P_o^{\rm e} $时,裂纹遇层理后仍按原方向扩展;当$P_o^{\rm i} < P_o^{\rm f} $,而$P_o^{\rm f} < P_o^{\rm e} $时,裂纹遇层理后可在层理处产生微裂纹,但仍按原方向扩展;当$P_o^{\rm i} < P_o^{\rm f} $,且$P_o^{\rm e} < P_o^{\rm f} $时,裂纹遇层理后转向层理扩展,如图 5所示.
|
图 5 压裂裂纹遇层理后扩展模式 Figure 5 Hydraulic fracture propagation modes meeting bedding |
定义层理弱面抗拉强度与岩石基体抗拉强度比为$S_{\rm r} $ (以下简称为强度比),$S_{\rm r} = S_{\rm t}^ * / S_{\rm t} $. 因为层理弱面抗拉强度与基体抗拉强度满足$0 ≤ S_{\rm t}^ * < S_{\rm t} $ ,故$0 ≤ S_{\rm r} <1$. $S_{\rm r}^{\rm i} $为水力压裂裂纹遇层理时刚好满足在层理处起裂临界条件的强度比,简称层理起裂临界强度比,$S_{\rm r}^{\rm e} $为水力压裂裂纹刚好满足沿层理扩展临界条件的强度比,简称层理扩展临界强度比.层理起裂临界强度比和层理扩展临界强度比由地应力、层理方位及岩石基体抗拉强度共同确定,以此衡量压裂裂纹遇层理时在层理处起裂和沿层理扩展所需的层理弱面强度范围.
3.1 压裂裂纹在层理处起裂判据解析分析由$P_o^{\rm f} > P_o^{\rm i} $可推导得出层理起裂临界强度比$S_{\rm r}^{\rm i} $,$S_{\rm r}^{\rm i} $与地应力状态、层理方位以及岩石基体抗拉强度有关,由$P_o^{\rm f} > P_{o1}^{\rm i} $得
| $ S_{\rm r1}^{\rm i} = \dfrac{1}{4(4\tan ^2\alpha + 1)S_{\rm t} }\Big[(16\tan ^2\alpha - 8)\sigma _1 +\\ (4 - 80\tan ^2\alpha )\sigma _2 + 3\sigma _3 + 3S_{\rm t} $ |
由$P_o^{\rm f} > P_{o2}^{\rm i} $得$S_{\rm r2}^{\rm i} = \cos ^3\dfrac{\beta }{2}$,由于裂纹总是沿最易开裂方向扩展,因当$P_o^{\rm f} > P_{o1}^{\rm i} $与$P_o^{\rm f} > P_{o2}^{\rm i} $满足其一时,水力压裂裂纹在层理处起裂,即
| $ S_{\rm r}^{\rm i} = \max \{S_{\rm r1}^{\rm i} \;,\;S_{\rm r2}^{\rm i} \} $ | (18) |
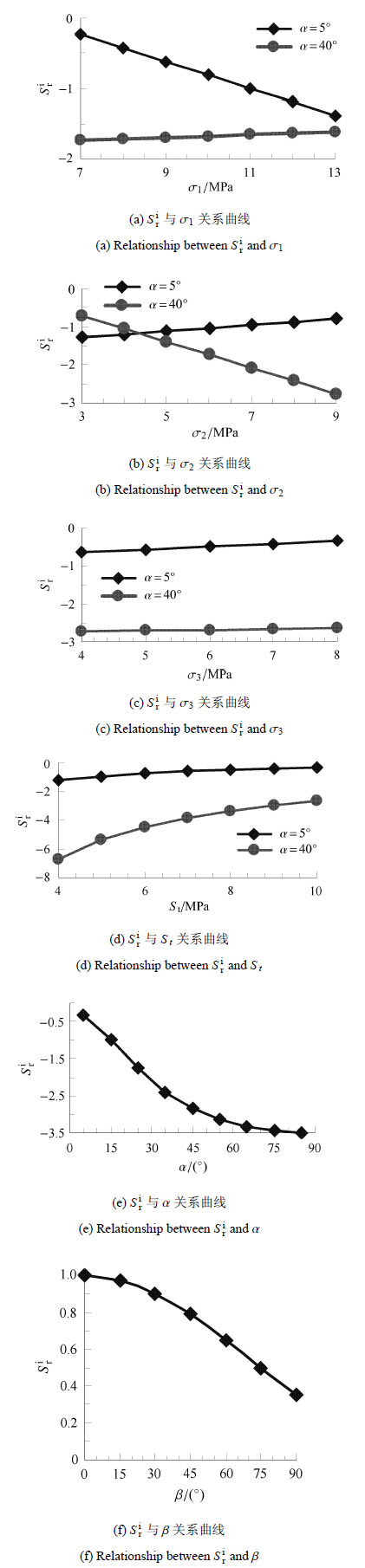
图 6为层理起裂临界强度比($S_{\rm r}^{\rm i}$)随地应力$(\sigma)$、岩石基体强度($S_t$)及层理方位($\alpha, \beta$)的变化曲线. 当$S_{\rm r1}^{\rm i} > S_{\rm r2}^{\rm i} $时,即$S_{\rm r}^{\rm i} = S_{\rm r1}^{\rm i} $,层理起裂临界强度比由$\sigma _1 ,\sigma _2 ,\sigma _3 ,\alpha ,S_{\rm t} $确定. 当$\alpha <35.26^ \circ $时,$S_{\rm r}^{\rm i} $随$\sigma _1 $的增大而减小;当$\alpha > 35.26^ \circ $时,$S_{\rm r}^{\rm i} $随$\sigma _1 $的增大而增大;当$\alpha < 12.6^ \circ $时,$S_{\rm r}^{\rm i} $随$\sigma _2 $的增大而增大;当$\alpha > 12.6^ \circ $时,$S_{\rm r}^{\rm i} $随$\sigma _2 $的增大而减小;$S_{\rm r}^{\rm i} $随$\sigma _3 ,S_{\rm t} $的增大而增大,随$\alpha $的增大而减小. 当$S_{\rm r1}^{\rm i} < S_{\rm r2}^{\rm i} $时,即$S_{\rm r}^{\rm i} = S_{\rm r2}^{\rm i} $,层理起裂临界强度比随$\beta $增大而减小.
|
图 6 层理起裂临界强度比曲线 Figure 6 The curves of bedding crack initiation critical strength ratio |
从图中曲线分析可知,$S_{\rm r}^{\rm i} = \;S_{\rm r1}^{\rm i} $时,仅当$\alpha $较小、岩石基体抗拉强度较大,且三向主地应力接近时,才有$S_{\rm r}^{\rm i} > 0$成立,故压裂裂纹在层理处起裂条件主要由$S_{\rm r}^{\rm i} = S_{\rm r2}^{\rm i} $确定,即层理起裂临界强度比主要受$\beta $影响,由于$S_{\rm r2}^{\rm i} ≥ \sqrt 2 / 4$,故曲线$S_{\rm r}^{\rm i} < \sqrt 2 / 4$部分舍弃.
$S_{\rm r}^{\rm i}$增大,表示压裂裂纹在层理处起裂所需要的层理强度范围变大,即压裂裂纹在层理处更易起裂;$S_{\rm r}^{\rm i} $减小,表示满足压裂裂纹在层理处起裂的层理强度范围变小,即压裂裂纹在层理处较难起裂.
3.2 压裂裂纹沿层理扩展判据解析分析由$P_o^{\rm f} > P_o^{\rm e} $可推导得出层理扩展临界强度比$S_{\rm r}^{\rm e} $,$S_{\rm r}^{\rm e} $由地应力差 $\sigma _1 - \sigma _3 $和 $\sigma _2 - \sigma _3 $、岩石基体强度$S_{\rm t} $以及层理方位$\alpha ,\beta $决定
| $ S_{\rm r}^{\rm e} = 1 - [(\sigma _1 - \sigma _{3} )\sin ^2\alpha + (\sigma _2 - \sigma _3 )\cos ^2\alpha] \cdot \sin ^2\beta / S_{\rm t}$ | (19) |
$S_{\rm r}^{\rm e} <0$时,表示即便层理弱面发育为天然裂纹,压裂裂纹也不会沿层理扩展; $0 ≤ S_{\rm r}^{\rm e} <1$时,弱面强度需满足 $0 ≤ S_{\rm r} < S_{\rm r}^{\rm e}$,压裂裂纹遇层理弱面时沿层理扩展. $S_{\rm r}^{\rm e} $越大,表示满足压裂裂纹沿层理扩展的层理弱面强度范围越大,即裂纹更易沿层理扩展;$S_{\rm r}^{\rm e} $越小,表示满足压裂裂纹沿层理扩展的层理弱面强度范围越小,即裂纹更难沿层理扩展.
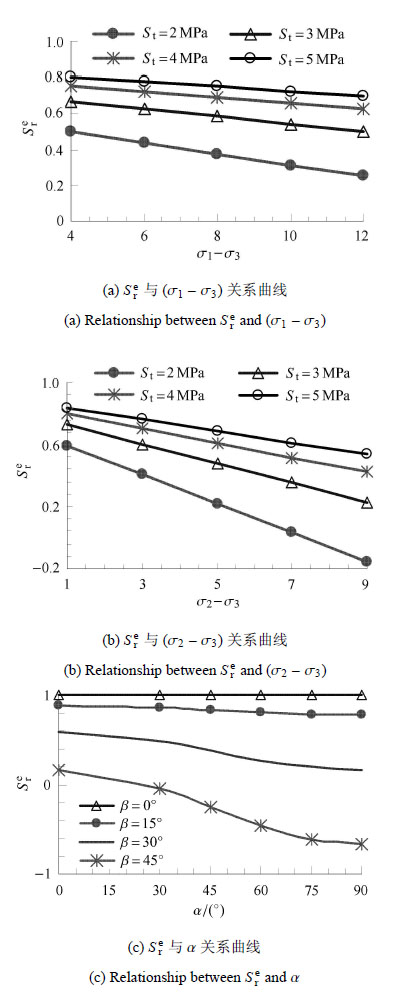
根据页岩力学参数统计范围,图 7(a)和图 7(b)为不同岩体抗拉强度下层理扩展临界强度比随地应力差变化曲线,图 7(c)为不同层理倾角下层理扩展临界强度比随层理方位角的变化曲线. 从中可以得出:随着地应力差和层理走向角及倾角的增大,层理扩展临界强度比降低,裂纹沿层理弱面扩展变难;随着岩石基体强度的增大,层理扩展临界强度比增大,裂纹更易于沿层理弱面扩展.
|
图 7 层理扩展临界强度比曲线 Figure 7 The curves of bedding crack propagation critical strength ratio |
层理弱面对页岩储层水力压裂过程中裂纹的扩展有重要影响,本文通过复变函数法的保角变换,推导出裂纹尖端的应力状态,通过比较水力压裂裂纹沿垂直最小地应力方向扩展和压裂裂纹在层理处起裂及沿层理扩展所需的裂缝尖端水压力,得到水力压裂遇层理弱面后在层理起裂及沿层理扩展的判据,通过对判据的分析,得出以下结论:
(1) 层理起裂临界强度比主要受层理倾角影响,随层理倾角的减小,层理起裂临界强度比增大.
(2) 当三向地应力值接近,岩石基体抗拉强度较大,层理走向角较小,且层理倾角较大时,层理起裂临界强度比受主地应力、岩石基体抗拉强度以及层理走向角影响. 层理起裂临界强度比随第一主地应力和层理走向角的增大而减小,随第二、第三主地应力以及岩石基体抗拉强度的增大而增大.
(3) 裂纹沿层理扩展临界强度比受地应力差、岩石基体强度以及层理方位多种因素影响. 随着地应力差、层理走向角、倾角的增大,层理扩展临界强度比降低,裂纹沿层理弱面扩展变难;随着岩石基体强度的增大,层理扩展临界强度比增大,裂纹更易于沿层理弱面扩展.
| 1 |
冯彦军, 康红普. 水力压裂起裂与扩展分析.
岩石力学与工程学报,2013, 32 (S2) : 3169-3179.
( 0) 0)
|
| 2 |
赵金洲, 王松, 李勇明. 页岩气藏改造难点与技术.
天然气工业,2012, 32 (4) : 46-49.
( Zhao Jinzhou, Wang Song, Li Yongming. Di culties and key techniques in fracturing treatment of shale gas reservoirs.
Natural Gas Industry,2012, 32 (4) : 46-49.
(in Chinese) ) ( 0) 0)
|
| 3 |
柳占立, 王涛, 高岳, 等. 页岩水力压裂的关键力学问题.
固体力学学报,2016, 37 (1) : 34-49.
( Liu Zhanli, Wang Tao, Gao Yue, et al. The key mechanical problems on hydraulic fracture in shale.
Chinese Journal of Solid Mechanics,2016, 37 (1) : 34-49.
(in Chinese) ) ( 0) 0)
|
| 4 |
Daneshy AA,Herman DS,Tymko DW. Investigation of horizontal well fracture extension pattern based on downhole pressure data. In:SPE Hydraulic Fracturing Technology Conference, Texas, USA, 2012
( 0) 0)
|
| 5 |
陈昀, 金衍, 陈勉. 基于能量耗散的岩石脆性评价方法.
力学学报,2015, 47 (6) : 984-993.
( Chen Yun, Jin Yan, Chen Mian. A rock brittleness evaluation method based on energy dissipation.
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (6) : 984-993.
(in Chinese) ) ( 0) 0)
|
| 6 |
程万, 金衍, 陈勉, 等. 三维空间非连续面对水力压裂影响的试验研究.
岩土工程学报,2015, 37 (3) : 559-563.
( Cheng Wan, Jin Yan, Chen Mian, et al. Experimental investigation on influence of discontinuities on hydraulic fracture propagation in threedimensional space.
Chinese Journal of Geotechnical Engineering,2015, 37 (3) : 559-563.
(in Chinese) ) ( 0) 0)
|
| 7 |
Wang SL, Li Y, Liu H, et al. Hydraulic fracture propagation in unconventional reservoirs:the role of bedding plane.
Synlety,2012, 8 (3) : 173-191.
( 0) 0)
|
| 8 |
Zhao HF, Chen M. Extending behavior of hydraulic fracture when reaching formation interface.
Journal of Petroleum Science and Engineering,2010, 74 (12) : 26-30.
( 0) 0)
|
| 9 |
程万, 金衍, 陈勉, 等. 三维空间中水力裂缝穿透天然裂缝的判别准则.
石油勘探与开发,2014, 41 (2) : 1-6.
( Cheng Wan, Jin Yan, Chen Mian, et al. A criterion for identifying hydraulic fractures crossing natural fractures in 3D space.
Petroleum Exploration and Development,2014, 41 (2) : 1-6.
(in Chinese) ) ( 0) 0)
|
| 10 |
Zhou J, Jin Y, Chen M. Experimental investigation of hydraulic fracturing in random naturally fracture blocks.
International Journal of Rock Mechanics and Mining Science,2010, 47 (7) : 1193-1199.
DOI: 10.1016/j.ijrmms.2010.07.005. ( 0) 0)
|
| 11 |
郭印同, 杨春和, 贾长贵, 等. 页岩水力压裂物理模拟与裂缝表征方法研究.
岩石力学与工程学报,2014, 33 (1) : 52-59.
( Guo Yintong, Yang Chunhe, Jia Changgui, et al. Research on hydraulic fracturing physical simulation of shale and fracture characterization methods.
Chinese Journal of Rock Mechanics and Engineering,2014, 33 (1) : 52-59.
(in Chinese) ) ( 0) 0)
|
| 12 |
Wang S, Zhao JZ, Li YM. Hydraulic fracturing simulation of complex fractures growth in naturally fractured shale gas reservoir.
Arabian Journal for Science and Engineering,2014, 39 : 7411-7419.
DOI: 10.1007/s13369-014-1221-5. ( 0) 0)
|
| 13 |
Reza KH, Sajad JL. Building a mechanical earth model and its application in a geomechanical analysis of hydraulic fracture behaviour in naturally fractured reservoirs.
European Journal of Environmental and Civil Engineering,2013, 18 (3) : 336-357.
( 0) 0)
|
| 14 |
张然, 李根生, 赵志红, 等. 压裂中水力裂缝穿过天然裂缝的判断准则.
岩土工程学报,2014, 36 (3) : 585-588.
( Zhang Ran, Li Gensheng, Zhao Zhihong, et al. New criteria for hydraulic fracture crossing natural fractures.
Chinese Journal of Geotechnical Engineering,2014, 36 (3) : 585-588.
(in Chinese) ) ( 0) 0)
|
| 15 |
Chuprakov DA, Akulich AV, Siebrits E, et al. Hydraulic fracture propagation in a naturally fractured reservoir.
SPE Production & Operations,2011, 26 (1) : 88-97.
( 0) 0)
|
| 16 |
Zhou DS, Zheng P, He P, et al. Hydraulic fracture propagation direction during volume fracturing in unconventional reservoirs.
Journal of Petroleum Science and Engineering,2016, 141 : 82-89.
DOI: 10.1016/j.petrol.2016.01.028. ( 0) 0)
|
| 17 |
Ali ND, Kamran G, Kaveh A, et al. The effect of natural fracture dip and strike on hydraulic fracture propagation.
International Journal of Rock Mechanics & Mining Sciences,2015, 75 : 210-215.
( 0) 0)
|
| 18 |
赵金洲, 李勇明, 王松, 等. 天然裂缝影响下的复杂压裂裂缝网络模拟.
天然气工业,2014, 34 (1) : 68-73.
( Zhao Jinzhou, Li Yongming, Wang Song, et al. Simulation of a complex fracture network influenced by natural fractures.
Natural Gas Industry,2014, 34 (1) : 68-73.
(in Chinese) ) ( 0) 0)
|
| 19 |
孙可明, 王松, 张树翠. 页岩气储层水力压裂裂纹扩展数值模拟.
辽宁工程技术大学学报(自然科学版),2014, 33 (1) : 5-10.
( Sun Keming, Wang Song, Zhang Shucui. A numerical simulation on rules of crack extension during hydraulic fracturing in shale gas reservoir.
Journal of Liaoning Technical University (Natural Science),2014, 33 (1) : 5-10.
(in Chinese) ) ( 0) 0)
|
| 20 |
孙可明, 张树翠, 辛利伟. 页岩气储层层理方向对水力压裂裂纹扩展的影响.
天然气工业,2016, 36 (2) : 45-51.
( Sun Keming, Zhang Shucui, Xin Liwei. Impacts of bedding directions of shale gas reservoirs on hydraulically induced crack propagation.
Natural Gas Industry,2016, 36 (2) : 45-51.
(in Chinese) ) ( 0) 0)
|
| 21 |
王杰, 李世海, 张青波. 基于单元破裂的岩石裂纹扩展模拟方法.
力学学报,2015, 47 (1) : 105-118.
( Wang Jie, Li Shihai, Zhang Qingbo. Simulation of crack propagation of rock based on splitting elements.
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (1) : 105-118.
(in Chinese) ) ( 0) 0)
|
| 22 |
徐栋栋, 郑宏, 杨永涛, 等. 多裂纹扩展的数值流形法.
力学学报,2015, 47 (5) : 471-481.
( Xu Dongdong, Zheng Hong, Yang Yongtao, et al. Multiple crack propagation based on the numerical manifold method.
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (5) : 471-481.
(in Chinese) ) ( 0) 0)
|
| 23 |
王理想, 唐德弘, 李世海, 等. 基于混合方法的二维水力压裂数值模拟.
力学学报,2015, 47 (6) : 973-983.
( Wang Lixiang, Tang Dehong, Li Shihai, et al. Numerical simulation of hydraulic fracturing by a mixed method in two dimensions.
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (6) : 973-983.
(in Chinese) ) ( 0) 0)
|
| 24 |
曾青冬, 姚军. 基于扩展有限元的页岩水力压裂数值模拟.
应用数学和力学,2014, 35 (11) : 1239-1248.
( Zeng Qingdong, Yao Jun. Numerical simulation of shale hydraulic fracturing based on the extended element method.
Applied Mathematics and Mechanics,2014, 35 (11) : 1239-1248.
(in Chinese) ) ( 0) 0)
|
| 25 |
Hiroyuki SM, Sumihiko MR, Tsuyoshi IS. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution.
International Journal of rock Mechanics & Mining Sciences,2011, 48 : 712-727.
( 0) 0)
|
| 26 |
曾青冬, 姚军, 孙致学. 页岩气藏压裂缝网扩展数值模拟.
力学学报,2015, 47 (6) : 994-999.
( Zeng Qingdong, Yao Jun, Sun Zhixue. Numerical modeling of fracture network propagation in shale reservoirs.
Chinese Journal of Theoretical and Applied Mechanics,2015, 47 (6) : 994-999.
(in Chinese) ) ( 0) 0)
|
| 27 |
Weng XW. Modeling of complex hydraulic fractures in naturally fractured formation.
Journal of Unconventional Oil and Gas Resources,2015, 9 : 114-135.
DOI: 10.1016/j.juogr.2014.07.001. ( 0) 0)
|
| 28 |
王涛, 高岳, 柳占立, 等. 基于扩展有限元法的水力压裂大物模实验的数值模拟.
清华大学学报(自然科学版),2014, 54 (10) : 1304-1309.
( Wang Tao, Gao Yue, Liu Zhanli, et al. Numerical simulations of hydraulic fracturing in large objects using an extended finite element method.
Journal of Tsinghua University (Sci & Technol),2014, 54 (10) : 1304-1309.
(in Chinese) ) ( 0) 0)
|
| 29 |
陈军斌, 魏波, 谢青, 等. 基于扩展有限元的页岩水平井多裂缝模拟研究.
应用数学和力学,2016, 37 (1) : 73-83.
( Chen Junbin, Wei Bo, Xie Qing, et al. Simulation of multi-hydrofracture horizontal wells in shale based on the extended finite element method.
Applied Mathematics and Mechanics,2016, 37 (1) : 73-83.
(in Chinese) ) ( 0) 0)
|
| 30 |
Taghichian A, Zaman M, Devegowda D. Stress shadow size and aperture of hydraulic fractures in unconventional shales.
Journal of Petroleum Science and Engineering,2014, 124 : 209-221.
DOI: 10.1016/j.petrol.2014.09.034. ( 0) 0)
|
| 31 |
Taleghani A D.
Analysis of hydraulic fracture propagation in fractured reservoirs:an improved model for the interaction between induced and natural fractures. Beijing: The University of Texas, 2009 .
( 0) 0)
|
| 32 |
Mohammad R,Mohammad AA,Abdul RS. Numerical modeling of fully coupled hydraulic fractured propagation in naturally fracture poro-elastic reservirs. 2009,SPE-121903-MS:427-433
( 0) 0)
|
| 33 |
Yew CH, Weng XW. Mechanics of Hydraulic Fracturing (second edition).
Elsevier,2015 : 69-73.
( 0) 0)
|
| 34 |
吴家龙.
弹性力学. 北京: 高等教育出版社, 2001 : 174 -213.
( Wu Jialong.
Elasticity. Beijing: Higher Education Press, 2001 : 174 -213.
(in Chinese) ) ( 0) 0)
|
| 35 |
陈勉, 金衍, 张广清.
石油工程岩石力学. 北京: 科学出版社, 2008 : 162 -166.
( Chen Mian, Jian Yan, Zhang Guangqing.
Petroleum Engineering Rock Mechanics. Beijing: Science Press, 2008 : 162 -166.
(in Chinese) ) ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48
