骨是一种多孔弹性材料,在日常的生活活动(如行走、跑步等)中经常受到循环载荷的刺激[1].这些载荷能使骨"感受"并做出"反应",这便是骨的力传导机理.载荷刺激传递到骨的微观结构------骨单元会引起其内部与液体相关的一系列物理效应,如压力梯度、流速、流体切应力及流动电位等等. 这些物理效应又被细胞感知并做出破骨或成骨等反应,来使骨适应外部载荷环境[2],这是骨的力传导可能进一步的基本机制.尽管骨超微结构下的液体流动信号通路还不是很清楚,但液体流动在骨重建过程中起到了至关重要的作用.
力传导的研究至少应该从骨单元尺度开始[1]. 骨单元是由一层层的骨板层围绕中间的哈弗管构成,形成一个大约半径为100$\sim$150 μm的圆柱体[3].骨小管放射状地横穿骨板层,一端起始于哈弗管另一端终止于黏合线,其间也连接着骨陷窝. 骨陷窝和骨小管组成骨单元内的第二大孔隙(哈弗管和福尔克曼氏管为第一大孔隙).在载荷的作用下,液体将在这些孔隙中流动(在骨单元壁中扩散),并产生上面提到的内生性和外生性的物理化学效应[4],同时也起到对骨细胞(在骨陷窝内) 输送营养和排泄代谢废物的作用[1, 3].
骨小管被认为是实现力传导的最佳通道[3, 5],因为其连通着骨陷窝内的主要力学信号感受细胞------骨细胞. 骨细胞主要通过骨小管内的液体切应力感知外界信号.由于这一机理,流体切应力对细胞的作用[5-6]被广泛研究.一些学者基于各向同性的骨材料试件[7-8]或骨单元[9-14]力学模型来描述内部骨液的流动行为,但是没有把外界载荷与骨小管尺度的液体流动偶联起来. 最近,基于Cowin等[15]的骨单元多孔弹性理论模型, Liu等[16]建立了一种骨小管的流动模型,其骨单元的外边界是刚性约束且不可渗透,并考虑了哈弗管中的血液脉动.另外,Wu等[17-19]也在自己建立的横观各向同性的骨单元多孔弹性力学模型的基础上,建立一种骨小管的流动电位模型[20],将骨单元尺度的载荷与骨小管尺度的液体流动联系起来.本文将在此模型的基础上构建骨小管的流体切应力模型.骨小管模型的建立分别基于中空和考虑哈弗液体的骨单元模型,并考虑了骨单元外壁的弹性约束和刚性位移约束两种边界条件.最终得到骨单元受外部轴向载荷作用下,骨小管内部液体的流量及流体切应力的解析解.该模型的建立有望进一步研究小管内液体流动对细胞和骨陷窝的作用等.
1 模型建立 1.1 骨单元模型骨单元的多孔介质弹性力学本构方程可以用下面的式子来描述[21]
| $\sigma _{ij} = C_{ijkl} \varepsilon _{kl} - \alpha _{ij} p $ | (1) |
| $p = M\left( {\xi - \alpha _{ij} \varepsilon _{ij} } \right) $ | (2) |
其中,$\sigma _{ij} $ 和 $\varepsilon _{kl} $分别是总的应力和应变张量,$p$为骨单元内部液体的压力,$\alpha _{ij} $和$M$分别为Biot系数张量和模量,$C_{ijkl} $是脱水的固体骨架弹性系数张量[21],$\xi $为液体单位体积的变化率.
在忽略体力的情况下,平衡方程为
| $ \sigma _{ij,j} = \rho \ddot {u}_i ^{\rm s} $ | (3) |
其中,$\ddot {u}_i ^{\rm s}$表示固体项的位移分量对时间的两阶导数,$\rho $是固液混合密度,可以定义为$\rho =\phi \rho _{\rm f} + (1 - \phi )\rho _{\rm s} $,其中$\phi $,$\rho _{\rm f} $和$\rho _{\rm s} $分别为孔隙率、液体和固体的密度.
液体单位体积的变化率$\dot {\xi }$与速度分量$q_i $的关系
| $ \dot {\xi } = - q_{i,i} $ | (4) |
不计孔隙摩擦,达西定律可描述为[12]
| $ q_i = - \dfrac{k_{ij} }{\mu }(p_{,i} + \rho _{\rm f} \ddot {u}_i^{\rm s}) $ | (5) |
式中,$k_{ij}$ 为渗透系数张量,$\mu $为液体的动力黏度系数.
整理以上方程可得骨单元的多孔介质弹性力学模型的控制方程
| $\left. \begin{array}{*{35}{l}} \rho \ddot{u}_{i}^{\text{s}}={{C}_{ijkl}}{{\varepsilon }_{kl,j}}-{{\alpha }_{ij}}{{p}_{,j}} \\ \dot{p}-M\left[ \left( {{k}_{ij}}/\mu \right)\left( {{p}_{,ii}}+{{\rho }_{\text{f}}}\ddot{u}_{i,i}^{\text{s}} \right)-{{\alpha }_{ij}}{{{\dot{\varepsilon }}}_{ij}} \right]=0 \\ \end{array} \right\}$ | (6) |
考虑到人体日常活动中的载荷频率(几个赫兹),略去方程(6)中的惯性项和高阶项得到
| $\left. \begin{array}{*{35}{l}} {{C}_{ijkl}}{{\varepsilon }_{kl,j}}-{{\alpha }_{ij}}{{p}_{,j}}=0 \\ \dot{p}-M\left[ \left( {{k}_{ij}}/\mu \right){{p}_{,ii}}-{{\alpha }_{ij}}{{{\dot{\varepsilon }}}_{ij}} \right]=0 \\ \end{array} \right\}$ | (7) |
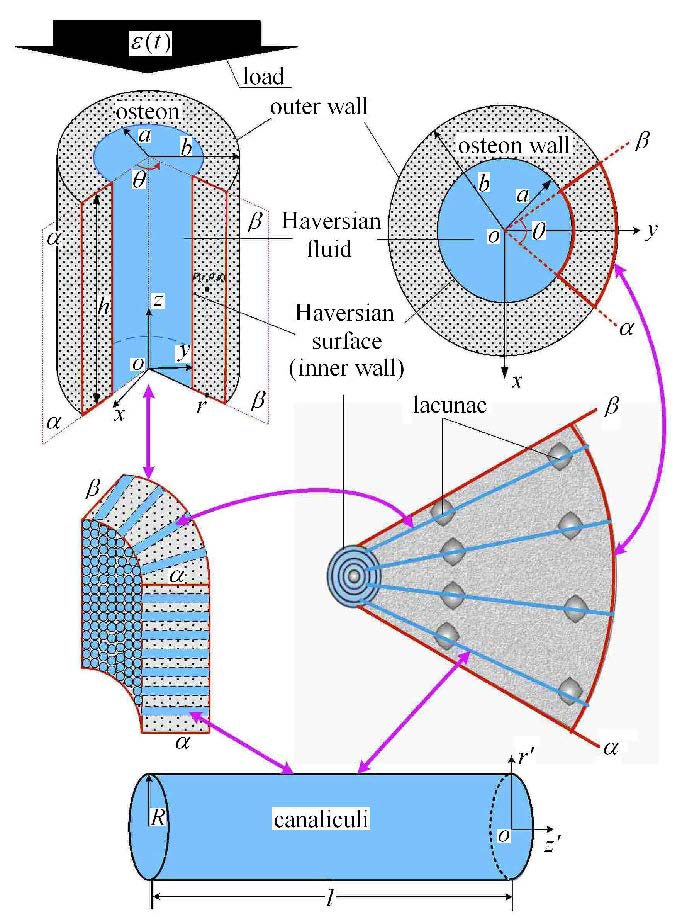
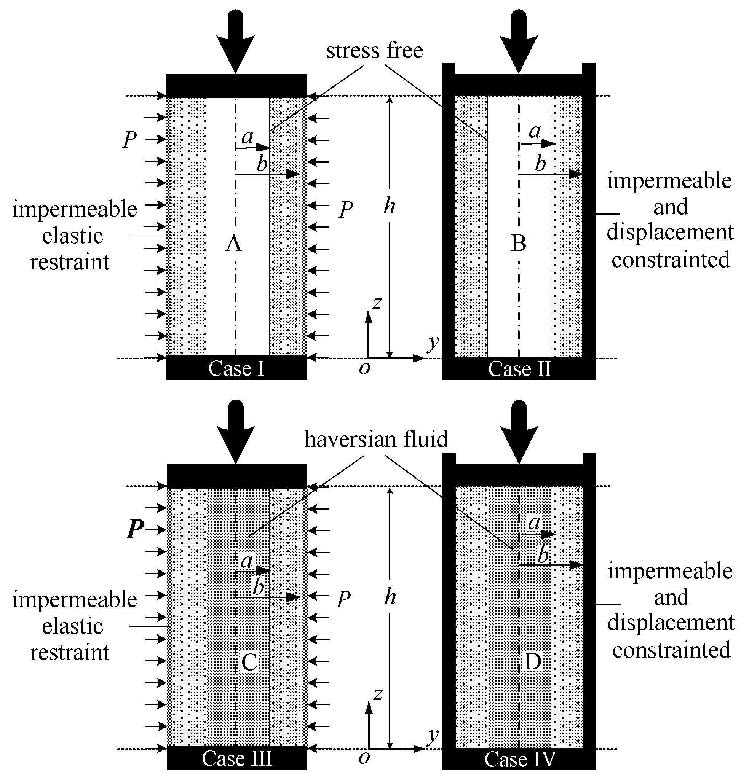
在柱坐标系($r$,$\theta $,$z$)下,如图 1所示[20],骨单元可以看成横观各向同性的圆柱体[17-19] (内外半径和高分别为$a$,$b$和$h$). 本文考虑两种模型4种边界条件,如图 2所示[17, 20].一种为中空骨单元模型(图 2中的A和B),一种为考虑哈弗液体压力的骨单元模型(图 2中的C和D). Case I和Ⅲ:外边界受到周围组织的弹性约束且不可渗透(图 2中的A和C);Case Ⅱ和Ⅳ:外边界受到周围组织的刚性约束且不可渗透(图 2中的B和D). 根据文献[19-20],各自边界条件下骨单元中的压力为
| $\begin{align} & {{p}_{m}}=\frac{M{{C}_{11}}\left( \alpha {{c}_{m}}+{\alpha }'{{\varepsilon }_{z0}} \right)}{{{C}_{11}}+M{{\alpha }^{2}}}\cdot \\ & \left[ \frac{{{\text{I}}_{0}}\left( Cr \right){{\text{K}}_{1}}\left( Cb \right)+{{\text{K}}_{0}}\left( Cr \right){{\text{I}}_{1}}\left( Cb \right)}{{{\text{I}}_{0}}\left( Ca \right){{\text{K}}_{1}}\left( Cb \right)+{{\text{I}}_{1}}\left( Cb \right){{\text{K}}_{0}}\left( Ca \right)}-1 \right]{{\text{e}}^{\text{i}\omega t}} \\ \end{align}$ | (8) |
| $\begin{align} & {{p}_{n}}=\left\{ \left( {{p}_{hn}}+\frac{M{{C}_{11}}\left( \alpha {{c}_{n}}+{\alpha }'{{\varepsilon }_{z0}} \right)}{{{C}_{11}}+M{{\alpha }^{2}}} \right) \right.\cdot \\ & \left[ \frac{{{\text{K}}_{1}}\left( Cb \right){{\text{I}}_{0}}\left( Cr \right)+{{\text{I}}_{1}}\left( Cb \right){{\text{K}}_{0}}\left( Cr \right)}{{{\text{I}}_{0}}\left( Ca \right){{\text{K}}_{1}}\left( Cb \right)+{{\text{I}}_{1}}\left( Cb \right){{\text{K}}_{0}}\left( Ca \right)} \right]- \\ & \left. \frac{M{{C}_{11}}\left( \alpha {{c}_{n}}+{\alpha }'{{\varepsilon }_{z0}} \right)}{{{C}_{11}}+M{{\alpha }^{2}}} \right\}{{\text{e}}^{\text{i}\omega t}} \\ \end{align}$ | (9) |
|
图 1 骨单元系统的分层结构示意图 Figure 1 The hierarchical model for osteon system. |
|
图 2 两种骨单元模型 Figure 2 Two osteon models |
其中,$p_{m}=p_{0m}(r) {\rm e}^{{\rm i}\omega t }$和$p_{n}=p_{0n}(r) {\rm e}^{{\rm i}\omega t}$ ($\omega = 2\pi f$,$f$为载荷频率,$m =1$和2分别对应Case Ⅰ和Ⅱ,$n =3$和4分别对应Case Ⅲ和Ⅳ); $C_{11} =E_r (E_z - E_r \mu _z ^2)(1 + \mu _r )^{ - 1} (E_z - E_z \mu _r - 2E_r \mu _z ^2)^{ -1}$为脱水刚度矩阵中的一个分量,$E_{r}$ 和 $E_{z }$分别是径向和轴向的弹性模量,$\mu_{r}$和$\mu_{z}$分别是径向和轴向的泊松比;$\alpha $和 ${\alpha }'$分别是径向和轴向的Biot系数;${\rm I}_{n}$ 和${\rm K}_{n}$ ($n =0$,1)分别是$n$阶变形的第一类及第二类贝塞尔函数. 常数$C$为[1, 17, 19]
| $ C = \sqrt { {\rm i}\omega \mu \left( {C_{11} + M\alpha ^2} \right) / \left( {kMC_{11} } \right)} $ | (10) |
其中${\rm i} = \sqrt { - 1} $.
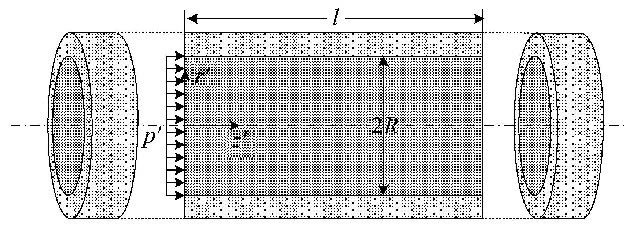
1.2 骨小管液体流动及切应力模型图 3所示为简化的骨小管模型[20],假设骨小管的长度为$l=b-a$;小管半径为$R$. 并假设:(1)组织液在骨小管中的流动可用Stokes方程来描述,但略去方程中的惯性项和体力(低频);(2)每根骨小管为一直管,且均匀分布于骨单元壁中(渗透率为一常数);(3)发生一维的轴向流动,忽略骨陷窝中的液体交换.
|
图 3 骨小管模型 Figure 3 Fluid flow model of the canalicular canal |
根据文献 [20]可以得到骨小管内压力分布及$p'$和流速$u$
| ${p}'({z}') = \left[{p_0 (a) + \dfrac{p_0 (b) - p_0 (a)}{l}\left( {{z}' - a} \right)} \right] {\rm e}^{{\rm i}\omega t} $ | (11) |
| $u({r}') = \dfrac{p_0 (a) - p_0 (b)}{{\rm i}\omega \rho _{\rm f} l} \left[{1 - \dfrac{{\rm I}_0 \left( {\beta {r}'} \right)}{{\rm I}_0 \left( {\beta R} \right)}} \right] {\rm e}^{{\rm i}\omega t} $ | (12) |
其中,常数$\beta $ 为
| $ \beta = \sqrt {{\rm i}\omega / \mu }$ | (13) |
根据文献[22],液体流量$Q$,小管壁的切应力$\tau_{\rm w}$可以表示为
| $Q = \int_0^R {2\pi {r}'} u({r}') d {r}'$ | (14) |
| $\tau _{\rm w} = \mu \left. {\dfrac{\partial u({r}')}{\partial {r}'}} \right|_{{r}' = R} $ | (15) |
最终可以得到
| $Q_s = \dfrac{2\pi }{{\rm i}\omega \rho _{\rm f} l}p_{0s} (b) \left[{\dfrac{R} {\beta }\dfrac{{\rm I}_1 \left( {\beta R} \right)}{ {\rm I}_0 \left( {\beta R} \right)} - \dfrac{R^2}{2}} \right] {\rm e}^{{\rm i}\omega t} $ | (16) |
| $ \tau _{ws} = \dfrac{\mu \beta }{{\rm i}\omega \rho _{\rm f} l}p_{0s} (b)\dfrac{{\rm I}_1 \left( {\beta R} \right)}{ {\rm I}_0 \left( {\beta R} \right)} {\rm e}^{{\rm i}\omega t} $ | (17) |
其中$s=1$,2,3,4分别对应case Ⅰ,Ⅱ,Ⅲ,Ⅳ.
2 数值参数模型所需要的材料和几何常数见表 1. 参数对骨小管内流量及切应力的影响主要从以下几个方面内容展开:(1)载荷大小(应变幅值:0.04%$\sim$0.3% [1, 17, 19])和载荷频率;(2)骨小管半径(100$\sim$1 000 nm[23, 24]); (3)特定载荷(应变率一定)下的流量及切应力随载荷频率和时间的变化;(4)渗透率;(5)含哈弗管模型与中空骨单元模型的对比.
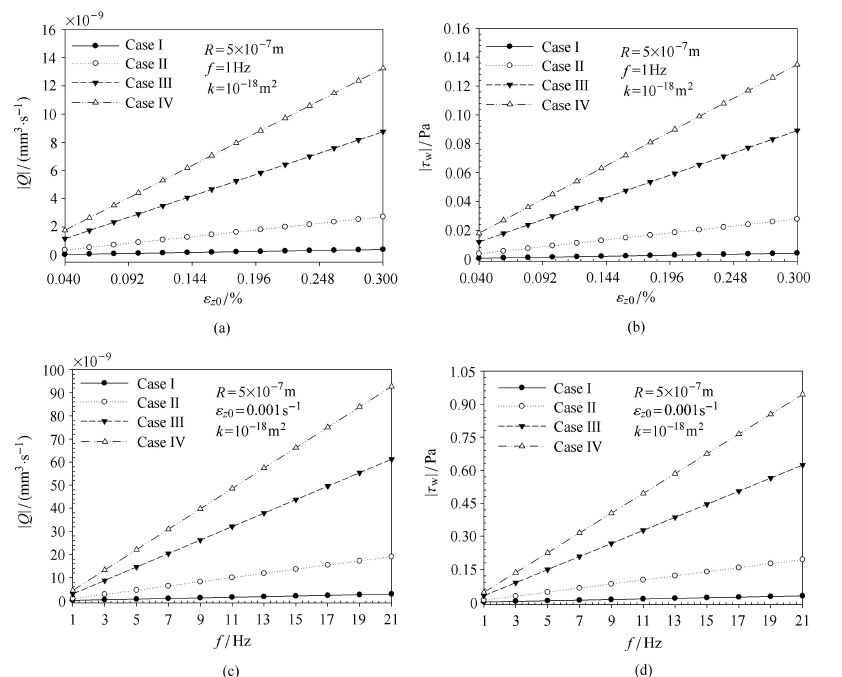
3 结果 3.1 载荷幅值和频率图 4绘制了4种情况下,流量($\left| Q \right|)$及切应力幅值($\left| {\tau _w } \right|)$与应变幅值($\varepsilon_{z0})$、频率( $\omega $)的关系曲线. 从图中可以看出,当应变和频率两参数之一恒定时,流量及切应力随另一参数增加而线性增加. 同时在相同的载荷频率和幅值下,Case Ⅲ和Ⅳ产生流量及切应力皆大于Case I和Ⅱ.
|
图 4 载荷大小(应变幅值)和载荷频率对流量($\left| Q \right|)$及切应力幅值($\left| {\tau _{\rm w} } \right|)$的影响 Figure 4 Effects of the loading frequency and strain amplitude on fluid flow rate amplitude($\left| Q \right|$) and fluid shear stress amplitude ($\left| {\tau _{\rm w} } \right|$) |
定义应变率幅值为[17, 20] $\dot {\varepsilon }_z =\left| {{\rm i}\omega \varepsilon_{z0} {\rm e}^{{\rm i}\omega t}} \right|=\varepsilon _{z0} \omega $,那么式(16)和式 (17)可表示为
| $\left| {Q_s } \right| = \left| {\dfrac{2\pi }{{\rm i}\omega ^2\rho _{\rm f} l}p_{0s}^\ast (b)\left( {\dfrac{R}{\beta }\dfrac{{\rm I}_1 \left( {\beta R} \right)}{{\rm I}_0 \left( {\beta R} \right)} - \dfrac{R^2}{2}} \right)} \right|\dot {\varepsilon }_z $ | (18) |
| $\left| {\tau _{{\rm w}s} } \right| = \left| {\dfrac{\mu \beta }{{\rm i}\omega ^2\rho _{\rm f}l}p_{0s}^\ast (b) \dfrac{{\rm I}_1 \left( {\beta R} \right)}{{\rm I}_0 \left( {\beta R} \right)}} \right|\dot {\varepsilon }_z $ | (19) |
其中,$p_{0s}^\ast (b) = p_{0s} (b) / \varepsilon _{z0} $ ($s=1$,2,3,4).从上式中可以看出流量及切应力幅值正比于应变率幅值.图 4中频率为1 Hz,所以也可以看成是流量及切应力幅值随应变率从0.004 s$^{-1}$到0.003 s$^{-1}$的变化曲线.
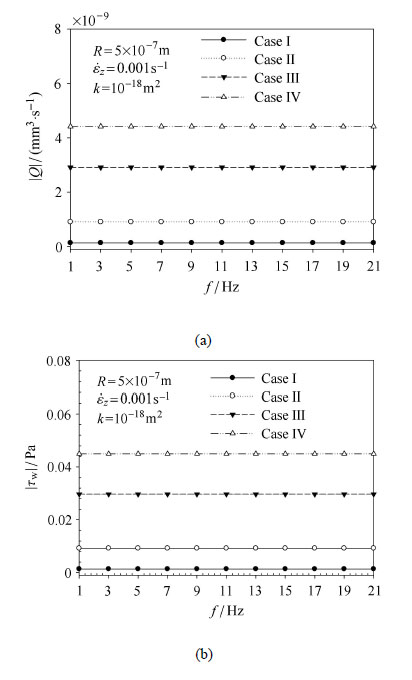
图 5绘制了应变率一定的情况下,载荷频率对流量及切应力幅值的影响,其中应变率控制为0.001 s$^{-1}$,频率的变化范围为:1$\sim$21 Hz. 从图中可以看出当应变率保持不变时,流量及切应力幅值保持不变.可见,真正决定骨小管流量及切应力的是应变率. 另外,在相同的应变率幅值下,Case Ⅱ产生的流量及切应力大于Case I产生的(大约6.7倍于Case I). Case Ⅳ产生的流量及切应力大于Case Ⅲ产生的(大约1.5倍于Case Ⅲ). Case Ⅲ和Ⅳ是考虑了哈弗液体的存在的骨单元模型,可见其产生的流量及切应力均大于中空的模型,并且他们的具体数量关系为
| $\left| {{Q}_{4}} \right|(\left| {{\tau }_{\text{w4}}} \right|)=1.5\left| {{Q}_{3}} \right|(\left| {{\tau }_{\text{w3}}} \right|)=4.9\left| {{Q}_{2}} \right|(\left| {{\tau }_{\text{w2}}} \right|)=32.6\left| {{Q}_{1}} \right|(\left| {{\tau }_{\text{w1}}} \right|)$ |
|
图 5 应变率一定的情况下,频率对流量及切应力幅值的影响 Figure 5 The amplitudes of fluid flow rates (FFRA) and shear stress (FSSA)as a function of the loading frequency with the strain \rater kept onstant |
Case Ⅲ和Ⅳ中的压力和流速场均高于中空的骨单元模型,这样含哈弗液体的骨单元模型内液体(骨小管中)的流量(流速)高于中空模型,从而导致产生的切应力较大.
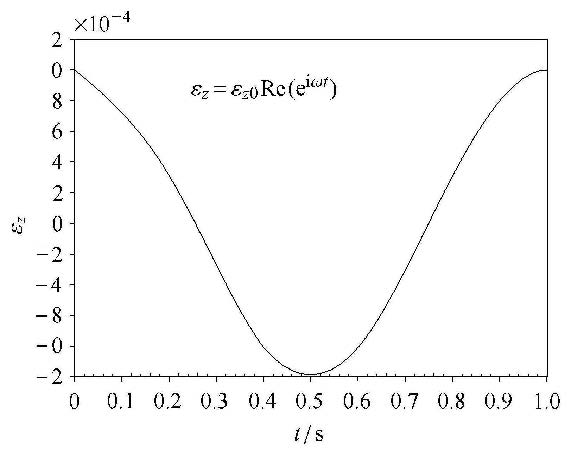
3.3 时间图 6为轴向应变载荷幅值为0.001及频率为1Hz 时的时程曲线,图 7(a)和图 7(b)分别是对应的流量及切应力时程曲线.由图 7可以看出,载荷和流量切应力不是同步达到最大值. 当载荷达到最大值时($t =0.5$ s)流量和切应力为最小值0,载荷的变化率最大时候($t =0.25$ s)流量和切应力同时达到最大值. 可以看出流量.从图中还可以看出,Case Ⅳ 中产生的流量和切应力最大.
|
图 6 应变率为$\dot {\varepsilon }_z = 0.001$ s$^{-1}$时,应轴向应变随时间的变化,\Re( ) 表示复数取虚部 Figure 6 History of strain loads at $\dot {\varepsilon }_z = 0.001$ s$^{-1}$, the operator Re( ) gives the real part of the complex number |

|
图 7 流量与切应力随时间的变化 Figure 7 Time responses of FFR and FSS |
图 8绘制了流量及切应力幅值随着骨小管半径变化的关系曲线. 从图中可以看出流量及切应力幅值随着骨小管半径的增大而增大,具体地,流量幅值呈现非线性增大趋势,而切应力呈现线性增大趋势.

|
图 8 流量及切应力幅值与骨小管半径的关系 Figure 8 Evolutions of FFRA and FSSA with canalicular radius |
渗透率对流量速率及切应力的影响分别如图 9(a)和图 9(b). 渗透率的变化范围是10$^{ - 23}$$\sim$ 10$^{ -18}$m$^{2}$[25-26],在上面的研究中取的是最大值10$^{ - 18 }$m$^{2}$.从图 9中可以看出流量速率和切应力随着渗透率的增大而减小.

|
图 9 流量及切应力幅值与渗透率的关系 Figure 9 Evolutions of FFRA and FSSA with permeability |
一种骨小管的理论模型被建立并用来描述其内部液体的流动及切应力.本模型将骨小管内部的液体流动与骨单元所受到的外部载荷联系了起来.该模型可以进一步用于骨的力传导及力-电传导的研究.在骨单元尺度,其边界条件和载荷参数均影响骨小管内部液体的流动行为.
骨单元的生理边界条件一直是讨论热点[27-28],一些研究选用的是中空的骨单元模型[12-14,17, 29],并不考虑中间哈弗管的影响.特别地,本文考虑了中间哈弗液体的影响,根据对比可以发现哈弗液体能使骨小管产生较高的流量和切应力,如图 5和图 8.Case I 和 Ⅲ与Case Ⅱ 和 Ⅳ分别代表两种边界条件------一种是受到周围组织的弹性约束且液体不可渗透,另一种是刚性位移约束液体也不可渗透.在骨单元外壁一般认为是液体不可渗透的,只是确切的受力边界条件还不清楚,大多数研究认为是刚性位移约束[10-14].在此基础上我们也发展了几种可能存在的边界条件[17],包括自由(用来模拟黏合线破裂)、弹性约束和刚性位移约束.弹性约束条件下骨单元中的液体压力和流速均小于刚性位移约束条件[18].本研究中也发现:相同的载荷条件下,弹性约束条件下骨小管中液体流动产生的流量及切应力均小于刚性位移约束条件下产生的,如图 5和图 8.
载荷的幅值和频率均对骨小管内液体的流动产生影响. 流量及切应力均随着载荷幅值和频率的增大而线性增大,如图 4.但其决定因素是应变率,如图 5,当应变率为0.001 s$^{- 1}$的时候,流量及切应力均不再随着载荷频率的增大而增大.生理载荷下,骨发生的应变范围为[30] (1.2$\sim$1.9)$\times 10^{-3}$,能使得细胞产生响应的切应力为0.2$\sim$6 Pa[10, 30]. 在本研究中,当应变率为0.001 s$^{- 1}$的时候Case IV产生的最大切应力大约为0.05 Pa(如图 5),因此如果为了引起细胞的反应,应变率至少需要增大到5倍,当然可以通过增大载荷幅值和频率实现. 载荷幅值和频率是一组耦合载荷,当固定其中一个,另一个可以充当替补参数.这也是Fritton等[31]试验中发现低幅高频和高幅低频具有相同的骨形成效果的原因.对骨来说,生理载荷幅值和频率是一对耦合参数,两者的乘积$\varepsilon_{z0} \omega $ 作为描述骨的生理载荷参数是合理的和有效的.
骨小管内液体的流动行为不但受到载荷参数的影响,而且也受到几何参数的影响.如图 8可以看出,其流量和切应力随着骨小管的半径增大而增大.具体地,流量幅值呈现非线性增大趋势,而切应力呈现线性增加趋势.可能的机理为:随着骨小管的半径的增大,单位时间内通过的液体的流量也增大,从而导致切应力的增大.渗透率是一个反映微观尺度下液体穿透介质的能力的宏观物理量,由孔隙率、微观结构等决定,是孔隙介质的一个固有参数.当然渗透率可表现出一定的几何非线性,在骨单元的粘合线处的渗透率系数相对哈弗管附近的小[32],在关节软骨中,渗透率系数沿着深度方向显示出几何非线性.Guo等[33]利用两相超弹性有限元方法研究了关节软骨在围限压缩时表层区的力学行为,研究发现当施加0.2 MPa的压应力时表面的渗透率减少到12%. 在本研究中我们选择10$^{ - 18}$ m$^{2}$作为骨单元中骨小管的孔隙尺度.
在本文的结果考察中选用了两个指标:一个是流量,另一个是切应力.当密度为常数时候,流量代表的物理意义是质量流速,一定程度上可以反映其物质质量的运输速率.根据结果3.1,在载荷幅值及频率增大的时候,骨小管中的液体流量也增大,这预示着为骨细胞的营养运输及废物排泄速率也加快,一定程度上加快了骨细胞的新陈代谢.根据结果3.2可知,其物质的运输速率的决定因素为应变率,同时也受到整体骨单元渗透率的影响(如图 9).此外,细胞对骨小管内液体的流速变化比较敏感,这个速度的梯度变化反映的就是流体切应力(式15).流体切应力对细胞的作用是研究的热点,并且细胞对这一尺度下力信号的感知也主要是通过流体切应力这一途径.切应力可能是液体流动给细胞作用的第一主要刺激,也是第一物理效应,其次才是流动电位、电化学运输等滞后效应.在本文的考察结果中,骨小管中的流体切应力随着载荷幅值及频率的增大而增大,这样意味着增大宏观尺度的载荷信号可以增大微观尺度上细胞所感受的流体切应力信号,但应变率是决定因素.可见,骨受到的外部载荷一定程度上影响细胞尺度下的力学微环境,其中力学信号的跨尺度传递机理也是急需研究的课题.本模型的建立也为这一机理的研究提供了基础.
骨内液体的流动研究应该从骨的微观结构基础------骨单元尺度进行,这是一个完整的分层结构系统,是骨重建内容中细观、微观和分子信号水平的偶联的研究平台.与液体流动相关的其他骨重建内容,如流体压力、流体切应力、流动电位、物质运输、电渗流动等研究均可以在这一尺度下开展.本工作中的骨小管流动模型存在以下不足:(1)骨单元的几何和边界条件是理想化. (2)每个骨小管为一直管均匀分布于骨单元壁中(渗透率为一常数),并且发生一维的轴向流动.(3)不考虑骨陷窝的作用(液体交换).(4)并没与考虑流动电位对液体的流动的影响(电渗流动).
5 结论通过骨单元的分层结构,我们建立了单根骨小管内液体流动并产生切应力的理论模型,从而将骨单元尺度的外部载荷与骨小管尺度的液体流动联系起来. 本模型可为以后的骨重建中的力传导和力-电传导提供参考.尽管模型有一定的缺陷,但可以初步得出下列参考结论:
(1) 骨小管中的液体流量和切应力均跟骨单元受到的外部载荷幅值和频率呈线性关系.进一步研究表明,应变率是流量和切应力的生理载荷决定因素.
(2) 骨小管的半径越大,产生的流量和切应力越大.
(3) 在骨单元尺度,流量和切应力随着渗透率的增大而减小.
(4) 相对于中空的骨单元模型,哈弗液体能使骨小管产生较大的流量和切应力.
| 1 |
Wu X, Chen W, Gao Z, et al. The effects of Haversian fluid pressure and harmonic axial loading on the poroelastic behaviors of a single osteon.
Science China Physics, Mechanics and Astronomy,2012, 55 (9) : 1646-1656.
DOI: 10.1007/s11433-012-4829-z. ( 0) 0)
|
| 2 |
Wang L, Ciani C, Doty SB, et al. Delineating bone's interstitial fluid pathway in vivo.
Bone,2004, 34 (3) : 499-509.
DOI: 10.1016/j.bone.2003.11.022. ( 0) 0)
|
| 3 |
Cowin SC. Bone poroelasticity.
Journal of Biomechanics,1999, 32 (3) : 217-238.
DOI: 10.1016/S0021-9290(98)00161-4. ( 0) 0)
|
| 4 |
Anderson EJ, Kaliyamoorthy S, Alexander JID, et al. Nano-microscale models of periosteocytic flow show differences in stresses imparted to cell body and processes.
Annals of Biomedical Engineering,2005, 33 (1) : 52-62.
DOI: 10.1007/s10439-005-8962-y. ( 0) 0)
|
| 5 |
Ahn AC, Grodzinsky AJ. Relevance of collagen piezoelectricity to "Wolff's Law":A critical revie.
Med Eng Phys,2009, 31 (7) : 733-741.
DOI: 10.1016/j.medengphy.2009.02.006. ( 0) 0)
|
| 6 |
Brown TD. Techniques for mechanical stimulation of cells in vitro:a review.
Journal of Biomechanics,2000, 33 (1) : 3-14.
DOI: 10.1016/S0021-9290(99)00177-3. ( 0) 0)
|
| 7 |
Salzstein RA, Pollack SR, Mak AF, et al. Electromechanical potentials in cortical bone-I. A continuum approach.
Journal of Biomechanics,1987, 20 (3) : 261-270.
DOI: 10.1016/0021-9290(87)90293-4. ( 0) 0)
|
| 8 |
Srinivasan S, Gross T. Canalicular fluid flow induced by bending of a long bone.
Medical Engineering & Physics,2000, 22 (2) : 127-133.
( 0) 0)
|
| 9 |
Cowin S, Weinbaum S, Zeng Y. A case for bone canaliculi as the anatomical site of strain generated potentials.
Journal of Biomechanics,1995, 28 (11) : 1281-1297.
DOI: 10.1016/0021-9290(95)00058-P. ( 0) 0)
|
| 10 |
Zeng Y, Cowin S, Weinbaum S. A fiber matrix model for fluid flow and streaming potentials in the canaliculi of an osteon.
Annals of Biomedical Engineering,1994, 22 (3) : 280-292.
DOI: 10.1007/BF02368235. ( 0) 0)
|
| 11 |
Zhang D, Weinbaum S, Cowin SC. On the calculation of bone pore water pressure due to mechanical loading.
International Journal of Solids and Structures,1998, 35 (34) : 4981-4997.
( 0) 0)
|
| 12 |
Nguyen V-H, Lemaire T, Naili S. Anisotropic poroelastic hollow cylinders with damaged periphery under harmonic axial loading:relevance to bone remodelling.
Multidiscipline Modeling in Materials and Structures,2009, 5 (3) : 205-222.
DOI: 10.1163/157361109789017005. ( 0) 0)
|
| 13 |
Rémond A, Naili S, Lemaire T. Interstitial fluid flow in the osteon with spatial gradients of mechanical properties:A finite element study.
Biomech Model Mechanobiol,2008, 7 (6) : 487-495.
DOI: 10.1007/s10237-007-0111-0. ( 0) 0)
|
| 14 |
Nguyen VH, Lemaire T, Naili S. Poroelastic behaviour of cortical bone under harmonic axial loading:A finite element study at the osteonal scale.
Med Eng Phys,2010, 32 (4) : 384-390.
DOI: 10.1016/j.medengphy.2010.02.001. ( 0) 0)
|
| 15 |
Cowin SC, Gailani G, Benalla M. Hierarchical poroelasticity:movement of interstitial fluid between porosity levels in bones.
Philosophical Transactions of the Royal Society of London A:Mathematical, Physical and Engineering Sciences,2009, 367 (1902) : 3401-3444.
DOI: 10.1098/rsta.2009.0099. ( 0) 0)
|
| 16 |
Liu S, Wang F, Liu R. Fluid flow and fluid shear stress in canaliculi induced by external mechanical loading and blood pressure oscillation.
Applied Mathematics and Mechanics,2015, 36 (5) : 681-692.
DOI: 10.1007/s10483-015-1932-7. ( 0) 0)
|
| 17 |
Wu XG, Chen WY. A hollow osteon model for examining its poroelastic behaviors:Mathematically modeling an osteon with different boundary cases.
European Journal of Mechanics-A/Solids,2013, 40 : 34-49.
DOI: 10.1016/j.euromechsol.2012.12.005. ( 0) 0)
|
| 18 |
Wu XG, Chen WY, Wang DX. Mathematical osteon model for examining poroelastic behaviors.
Applied Mathematics and Mechanics,2013, 34 (4) : 405-416.
DOI: 10.1007/s10483-013-1680-x. ( 0) 0)
|
| 19 |
Wu XG, Chen WY. Poroelastic behaviors of the osteon:A comparison of two theoretical osteon models.
Acta Mechanica Sinica,2013, 29 (4) : 612-621.
DOI: 10.1007/s10409-013-0053-y. ( 0) 0)
|
| 20 |
Wu XG, Yu WL, Cen HP, et al. Hierarchical model for strain generalized streaming potential induced by the canalicular fluid flow of an osteon.
Acta Mechanica Sinica,2015, 31 (1) : 112-121.
DOI: 10.1007/s10409-015-0002-z. ( 0) 0)
|
| 21 |
Cheng AD. Material coefficis of anisotropic poroelasticity.
International Journal of Rock Mechanics and Mining Sciences,1997, 34 (2) : 199-205.
DOI: 10.1016/S0148-9062(96)00055-1. ( 0) 0)
|
| 22 |
You L, Cowin SC, Schaffler MB, et al. A model for strain amplification in the actin cytoskeleton of osteocytes due to fluid drag on pericellular matrix.
Journal of Biomechanics,2001, 34 (11) : 1375-1386.
DOI: 10.1016/S0021-9290(01)00107-5. ( 0) 0)
|
| 23 |
Boyde A. Scanning electron microscope studies of bone.
The Biochemistry and Physiology of Bone,1972, 1 : 259-310.
( 0) 0)
|
| 24 |
Cooper RR, Milgram JW, Robinson RA. Morphology of the osteon.
The Journal of Bone & Joint Surgery,1966, 48 (7) : 1239-1271.
( 0) 0)
|
| 25 |
Nguyen VH, Lemaire T, Naili S. Numerical study of deformationinduced fluid flows in periodic osteonal matrix under harmonic axial loading.
Comptes Rendus Mecanique,2009, 337 (5) : 268-276.
DOI: 10.1016/j.crme.2009.06.033. ( 0) 0)
|
| 26 |
Buckley M, Banes A, Levin L, et al. Osteoblasts increase their rate of division and align in response to cyclic, mechanical tension in vitro.
Bone and Mineral,1988, 4 (3) : 225-236.
( 0) 0)
|
| 27 |
Wang L, Fritton SP, Cowin SC, et al. Fluid pressure relaxation depends upon osteonal microstructure:modeling an oscillatory bending experiment.
Journal of Biomechanics,1999, 32 (7) : 663-672.
DOI: 10.1016/S0021-9290(99)00059-7. ( 0) 0)
|
| 28 |
Qin YX, Kaplan T, Saldanha A, et al. Fluid pressure gradients, arising from oscillations in intramedullary pressure, is correlated with the formation of bone and inhibition of intracortical porosity.
Journal of Biomechanics,2003, 36 (10) : 1427-1437.
DOI: 10.1016/S0021-9290(03)00127-1. ( 0) 0)
|
| 29 |
Nguyen VH, Lemaire T, Naili S. Influence of interstitial bone microcracks on strain-induced fluid flow.
Biomech Model Mechanobiol,2011, 10 (6) : 963-972.
DOI: 10.1007/s10237-011-0287-1. ( 0) 0)
|
| 30 |
Beno T, Yoon YJ, Cowin SC, et al. Estimation of bone permeability using accurate microstructural measurements.
J Biomech,2006, 39 (13) : 2378-87.
DOI: 10.1016/j.jbiomech.2005.08.005. ( 0) 0)
|
| 31 |
Fritton SP, McLeod KJ, Rubin CT. Quantifying the strain history of bone:spatial uniformity and self-similarity of low-magnitude strains.
Journal of Biomechanics,2000, 33 (3) : 317-325.
DOI: 10.1016/S0021-9290(99)00210-9. ( 0) 0)
|
| 32 |
Rémond A, Naili S, Lemaire T. Interstitial fluid flow in the osteon with spatial gradients of mechanical properties:a finite element study.
Biomechanics and Modeling in Mechanobiology,2008, 7 (6) : 487-495.
DOI: 10.1007/s10237-007-0111-0. ( 0) 0)
|
| 33 |
Guo H, Maher SA, Torzilli PA. A biphasic finite element study on the role of the articular cartilage superficial zone in confined compression.
Journal of Biomechanics,2015, 48 (1) : 166-170.
DOI: 10.1016/j.jbiomech.2014.11.007. ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48

