两种不同密度的流体相互作用时，界面处存在的扰动使密度梯度与压力梯度不在同一个方向上($\triangledown p\times \triangledown \rho e {\bf 0}$)，在界面上产生一定的斜压涡量. 这些斜压涡量的存在会引起Richtmyer-Meshkov(R-M)不稳定性，促使界面失稳，以致两侧的流体发生混合^[1]. 在惯性约束聚变(intertial confinement fusion,ICF)^[2-4]的内爆压缩过程中，R-M不稳定性可能使燃料层提前发生混合导致点火失败；而在超燃超压发动机^[5-6]中，R-M不稳定性可增强液体燃料同空气的混合，提高燃烧效率.此外，R-M不稳定性引起的混合还在超新星爆炸产物层化^[7-8]、爆燃转爆轰^[9]等问题中扮演着重要角色，该问题引起了工程界和学术界浓厚的兴趣.

激波管实验是研究R-M不稳定性的主要实验手段，其中大部分实验采用弱激波，通常以纹影^[10]、高速摄影^[11]等技术为诊断手段，研究对象主要为气柱^[12]、气帘^[13]、气泡^[14]等界面的失稳演化机理.在早期的实验研究中，大多采用肥皂泡、硝化纤维薄膜等形成间断型气体界面^[15-16].但薄膜破裂后形成的碎片对流场会产生一定的干扰，同时碎片对激光的反射和散射严重影响了测试的准确度.为了消除碎片带来的干扰，Jacobs^[17]发展了无膜气柱生成技术，利用气体的自身重力作用形成具有扩散型边界的气柱界面，该方法在后来的相关实验中得到了广泛的应用. 在单圆柱界面的基础上，椭圆形气柱界面^[18-19]、多边形气柱界面^[20-21]、 多气柱排列^[22] 等复杂构型界面也得到了细致的研究，其焦点主要集中于界面与激波的相互作用，以及气柱间的相互干扰效应.随着高精度粒子图像测速(particle image velocimetry,PIV)、平面激光诱导荧光(planar laser-induced fluorescence,PLIF)诊断技术的不断成熟，实验精度得到了大幅提升，由此获得了汇聚激波引起的射流、演化后期的二次不稳定性等小尺度结构^[23]的演化特征和发展规律.PIV-PLIF的联合同步测试技术为研究失稳演化后期的湍流混合提供了丰富的实验数据^[24].利用浓度场(摩尔分数)和速度场计算脉动速度^[25]、界面混合率^[26]、浓度的概率密度函数^[27]、密度自相关系数^[28]等物理量，初步实现了对界面失稳演化中湍流混合阶段的定量研究.

一直以来，对界面失稳后期湍流混合的研究都是学术界的一个热点和难点^[29-31].但由于测试技术和分析手段的限制，相关进展较为缓慢. 特别是国内对R-M不稳定性的实验研究主要还集中在早期演化的失稳机理上，对失稳过程中的混合问题还少有触及. 本工作以斜压机制为出发点，从气柱界面失稳形态、混合率的分布等方面分析界面的R-M失稳混合.

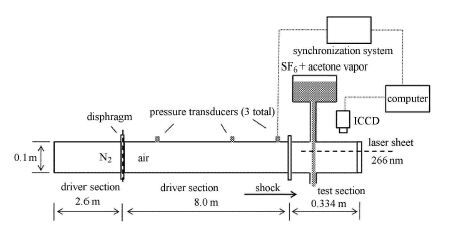
实验在水平激波管中进行，实验装置如图 1所示. 在驱动段中充入高压氮气，驱动段与被驱动段之间由塑料膜片分隔.电阻丝通电发热后膜片瞬间破裂，被驱动段内的空气受高压氮气的驱动，产生从左向右传播的马赫数$M a =1.25$的平面激波. 被驱动段上装有压力传感器，用以测量激波传播速度和触发测试系统.激波作用于测试段内的SF$_{6}$气柱，引起气柱界面的R-M不稳定性演化. 激光通过光学透镜组合，形成厚度约1 mm的片状光束,从尾端窗口射入测试段，片光平面位于测试段内气体入口下方20 mm处. 信号接收端采用带有像增强功能的高性能数字化相机(Andor's iStar ICCD DH740)，并且在镜头前加装窄带滤光片以提高信噪比.

图 1(Figure 1)

图 1 激波管装置 Figure 1 Schematic of the shock tube facility

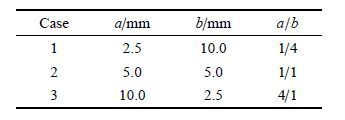
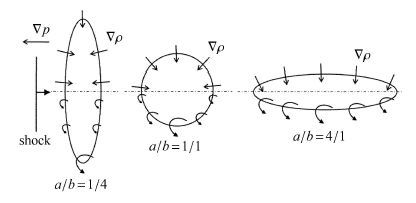
测试技术采用高精度的PLIF技术，该技术常用于诊断不同气体间的混合.将丙酮液体置于恒温水浴环境中，SF$_{6}$气体匀速通过丙酮液体后得到SF$_{6}$和丙酮的混合气体.该方法保证了单位时间内丙酮的挥发量和SF$_{6}$气体的进入量均保持恒定，同时也使得实验过程中混合气体的组分保持一致.混有丙酮蒸汽的SF$_{6}$气体进入激波管上方的储气盒，储气盒具有稳定气体的作用.在重力作用下，SF$_{6}$气体从底部装有模具的喷口处流出，形成特定形状的椭圆形气柱.由于界面形状为曲面，激波经过后界面上将产生斜压涡量，引起R-M失稳，如图 2所示.实验中选取了3种不同气柱构型：圆形气柱、长短轴比($a/b$)分别为1/4和4/1的椭圆形气柱，气柱模具的几何尺寸如表 1所示.这3种构型界面具有相同的面积(78.54 mm$^{2})$，但不同的长短轴比使得激波经过时界面上产生的斜压涡量不同，因此各界面失稳混合的演化速度和演化形态均各不相同. 采用这3种构型界面，既保证了扩散型界面样本的多样性，也可进一步理解初始形状对失稳混合的影响.

图 2(Figure 2)

图 2 气柱界面 Figure 2 Interface of gas cylinder

表 1(Table 1)

表 1 气柱构型几何尺寸 Table 1 Geometry of gas cylinders

表 1 气柱构型几何尺寸 Table 1 Geometry of gas cylinders

实验开始前，将混合气体充满测试段，以检测激发片光的均匀性，并对荧光图像进行修正.实验中分别捕捉3种气柱界面的初始状态以及激波作用后0.4 ms,0.6 ms和0.8 ms时刻的演化图像.

在气体分子扩散作用下，初始界面气体浓度(摩尔分数)呈近似Gaussian分布^[29].通过对荧光图像进行标定，得到圆形初始界面中心像素点处SF$_{6}$摩尔分数为84%^[24]，设定无荧光信号像素点为0%，进一步得到气柱界面摩尔分数，如图 3所示.初始状态时3种气柱界面的边界处都存在明显的扩散层，中心处浓度最大，大部分界面浓度为中心最大值的1/2左右.由于各界面具有不同的初始形状，激波作用后在界面上产生不同大小的涡量，导致各界面的演化速度和形态均存在较大差异.

图 3(Figure 3)

图 3 浓度分布 Figure 3 Distribution of concentration

从图 3(a)可以看出，$a/b =1/4$的椭圆形界面在考察时间内的不稳定性演化发展最慢. 主涡在卷曲过程中轮廓范围不断扩大，SF$_{6}$气体在主涡的带动下向下游转移. 0.8ms时，主涡对的连接处拉伸变细(图中"1"所示)，上下两个主涡呈现出分离开的趋势；主涡右界面处局部浓度升高，说明该处出现气体堆积. 从图 3(b)可以看出,圆形界面主涡界面下游区域在0.6 ms时刻出现波浪形结构(图中"2"所示)，这主要是由于Kelvin-Helmholtz (K-H)失稳引起的. 此时两个主涡的下游部分发生接触，外轮廓边界处浓度相对较高. 随着主涡对进一步的相互作用，右界面出现了向下游突出的尾部结构. 与前两种界面不同，$a/b =4/1$的椭圆形界面(图 3(c))失稳演化速度最快. 由于主涡中堆积的涡量大且涡距较小，主涡对之间的相互作用更加剧烈. 0.4 ms时主涡右界面在相互作用下向两侧分开形成外翻型结构，并且在主涡对交界处产生明显的射流结构(图中"3"所示)，再现了数值模拟结果^[29]. 0.6 ms时，尾部射流结构继续发展呈扇形喷射状.

由以上分析可以看出，随着$a$/$b$比值增大，界面演化速度明显加快. 由图 2可知，$a$/$b$比值较大的界面上产生了更多的斜压涡量，同时，形成的涡对的涡间距更小. 涡量的增多和涡对间距的减小使得界面不稳定性演化的"驱动"增强，加速了不稳定性的发展.

气体间的混合本质上是气体间的对流和扩散. 为更直观地研究界面失稳演化中的混合机制，定义混合率$\chi (x,t)=D\cdot(\triangledown c\cdot \triangledown c)$，其中$D$为界面气体扩散率，$\triangledown c$为界面浓度梯度.瞬时混合率即流场中浓度的瞬时耗散率，代表了由于扩散引起的分子间混合的剧烈程度，常用于表征小尺度的湍流流动^[23]. Tomkins等^[24]在研究由R-M失稳引起的混合时首次引入了混合率，后来该参数又多次被用来研究其他失稳混合的相关问题.

初始界面气体中，SF$_{6}$的扩散率为0.97×10$^{-5 }$m$^{2}$/s，丙酮蒸汽的扩散率为1.04$\times$10$^{-5}$m$^{2}$/s； 根据参考文献^[24]的测算，取SF$_{6}$和丙酮的混合气体扩散率$D=0.98\times10^{-5}$m$^{2}$/s，浓度梯度采用中心差分法计算^[30].为减小误差，分别采用目标像素点网格方向的4个像素点和斜45$^{\circ}$方向的4个像素点计算，取平均值.同图 3相对应，规范化后的界面混合率如图 4所示.由前文分析可知，由于3种界面的演化速度不同，实际上在相同的演化时间内各自处于不同的演化阶段.因此各界面混合率的分布具有不同演化阶段的显著特征.

图 4(Figure 4)

图 4 规范化后的气柱界面混合率($\chi (x,t)/c^{2}_{\max}$,$c_{\max}$为浓度最大值) Figure 4 Normalized mixing rate of interface ($\chi (x,t)/c^{2}_{\max}$,$ c_{\max}$ is the maximum concentration)

当$a/b =1/4$时(图 4(a))，在界面失稳早期,浓度主要集中于左界面，导致该处浓度梯度较大.此时左界面同周围空气交界处分子混合较为剧烈，因而混合率相对较高.在主涡的带动下界面拉伸卷曲，左界面混合率减小，右界面混合率升高，分子混合速率加快(0.8 ms).在涡卷内部，浓度梯度相对较小，因扩散产生的分子混合较缓慢.界面外轮廓区域的混合率远高于涡卷内部，说明此时界面外轮廓处在高浓度梯度作用下分子混合更为剧烈，而涡卷内部的混合主要通过界面的卷曲发展以对流的形式进行.

从图 4(b)可以看出,圆形初始界面在发展早期同样出现上述现象，当下游界面出现二次不稳定性时(0.6ms)，浓度梯度迅速下降，由浓度梯度引起的分子间的混合速率也因此减小. 二次不稳定性的出现加强了小尺度的对流，因而加速了界面的混合，使得浓度梯度降低. 当失稳进入中后期(0.8ms)，主涡对发生接触，涡核的卷曲受到破坏. 受此影响，外轮廓界面气体进入涡核区域，致使外轮廓浓度梯度大幅降低，分子混合速率降低. 由于界面气体的进入，涡核区域内浓度梯度增大，混合速率略有提高. 总体来看，界面混合率较小且分布较为均匀，说明界面已完成了一定程度的混合，此时界面的混合主要由小尺度对流驱动.

由于$a/b =4/1$的椭圆形初始界面(图 4(c))失稳演化较快，在测试时间内其演化进程已相对靠后，故界面上高混合率区域很少，界面混合程度普遍较高. 激波作用后，初始界面上堆积的涡量大且主涡对之间相距较近，在强相互作用下气体在界面下游处堆积使梯度升高，右界面混合率明显高于左界面. 涡对"碰撞"产生射流结构后(0.6 ms)，左界面混合率进一步减小，趋于均匀. 此时左界面的混合率较小且分散，说明该区域气体混合程度较高. 之后界面混合区域继续扩大，尾部射流结构在拉伸发展过程中混合率进一步减小. 左界面的混合率并没有发生明显的改变，只是射流结构在拉伸发展中浓度梯度迅速减小.

综合3种界面的混合过程可以发现，随着$a$/$b$比值的增大，在考察时间段内界面混合率降低且分散，其失稳混合进程逐渐加快. 在失稳发展的初期，在斜压涡诱导下界面发生简单的拉伸卷曲，以致浓度梯度增大，促进界面气体与空气混合. 在外轮廓界面处界面混合率较高，分子混合较为剧烈. 随着失稳的发展，涡核区域率先达到较高混合度. 由二次不稳定性引发的小尺度对流进一步加速了界面的混合，使局部浓度梯度快速降低. 由此可见，界面的混合主要由斜压涡和二次不稳定性共同主导：前者在演化初期引起大尺度的界面变形，使得局部浓度梯度增大，加强了局部扩散从而促进混合，但无法引起更小尺度的湍流混合；后者则是在失稳发展到一定阶段才出现，产生更小尺度的速度梯度，引起小尺度的对流，加速了界面的混合，甚至产生湍流混合.

为了定量地比较3种界面演化过程中的混合，考察各演化时刻的界面的整体平均混合率$\chi_{ave}$，如图 5所示. $\chi _{\rm ave} = \left( \iint \chi \left( { { x},t} \right) / c_{\max }^2 d x d y \right) /A$，其中$A$为界面面积.整体平均混合率中包含了由简单拉伸和二次不稳定性所产生的浓度梯度变化，同时消除了界面面积变化的影响.整体平均混合率可反映该时刻由于扩散引起的界面的整体分子混合强度. 从图 5可以看到，3种初始界面的整体平均混合率随失稳的发展均表现出先升后降的趋势(如图中箭头所示).

图 5(Figure 5)

图 5 不同初始界面的整体平均混合率$\chi_{\rm ave}$ Figure 5 Ensemble-averaged mixing rate $\chi_{\rm ave }$ in different initial condition

尽管$a/b$比值较小的初始界面失稳演化速度更慢，但在波后相同时刻却具有更大的整体平均混合率，由浓度梯度引起的分子混合更加剧烈. 由于$a$/$b$比值较小的初始界面上堆积的大涡量斜压涡位置更加集中(如图 2所示)，界面在随后的演化过程中更趋近于简单的拉伸和卷曲且变形速率缓慢. 拉伸的界面具有一定的"张力"，除涡核区域外的界面气体难以通过对流的形式与空气进行小尺度的混合. 相对而言，$a/b$比值较大的初始界面周围堆积的斜压涡分布更广且涡量大，斜压涡之间的相互作用更加强烈，使界面变形更加剧烈. 在大量斜压涡的作用下，界面失稳发展加快甚至出现二次不稳定性，界面气体的小尺度对流更加活跃. 更多的分子间混合通过对流来完成，加速降低甚至消除浓度梯度. 由于快速的失稳演化，界面本身已完成一定程度的混合，整体平均混合率的降低也表明界面混合程度的提高.

因此，在演化过程中即使$a$/$b$比值较大的初始界面拥有更大的面积增长(如图 3所示)，但界面的整体平均混合率却更小，说明由扩散驱动的分子间混合更加弱势. 这也从侧面反映了其失稳演化更加迅速，混合程度更高.与此相似，Orlicz等^[26]在研究不同马赫数激波作用下的气帘界面失稳混合问题时，也发现了类似的现象：界面失稳发展得越快，浓度梯度对界面混合的促进作用也会减弱得越快.事实上，进入失稳演化后期的界面同空气的混合同初期相比更加剧烈，但扩散式的混合速率却降低，说明此时对流式的混合迅速增强并占据主导.

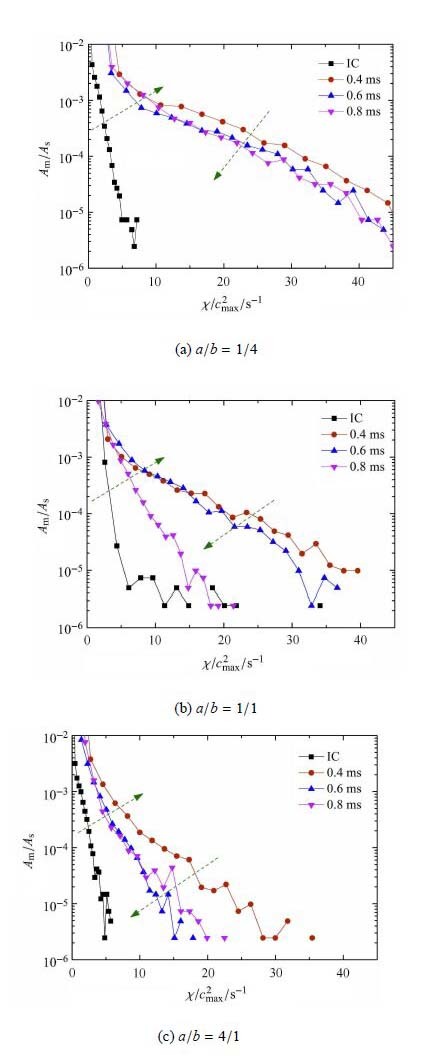
图 6为给定混合率的面积$A_{\rm m}$占混合率图像总面积$A_{\rm s}$的比例，代表了界面混合率随演化发展的概率密度分布. 可以看到，3种界面的混合率分布在失稳演化过程中具有相同的发展趋势：激波作用后高混合率区域迅速增多，随着演化的发展，高混合率区域又随演化时间减少. $a/b =1/4$的椭圆形界面混合率较大，且其分布变化幅度较小，说明该界面浓度梯度所驱动的分子间混合持续较强.随着$a$/$b$比值的增大，相同演化时刻由于对流引起的界面混合程度更高，降低了高浓度梯度区域所占面积，导致界面高混合率区域减小.

图 6(Figure 6)

图 6 界面混合率的概率密度分布 (IC为初始状态；箭头方向为变化趋势) Figure 6 Probability density of mixing rate \\vskip -1mm(IC is the initial condition; the evolution trend is pointed by arrow)

通过以上分析表明，在界面失稳发展初期，通过扩散作用实现的分子间混合主要集中于外轮廓界面上.当涡卷发展到一定程度，主涡区域规则的卷曲运动遭到破坏，同时对外轮廓界面形成扰动，使得浓度梯度迅速降低，界面内部的混合得到加强.二次不稳定性的出现加速了界面的混合，使浓度梯度进一步减小.由于$a$/$b$比值较大的初始界面失稳发展迅速，在大量斜压涡的作用下变形更加复杂剧烈，相同演化时刻界面通过小尺度的对流所引起的的混合程度迅速提高，由浓度梯度驱动产生的分子间混合逐步减弱.

利用浓度分布计算并分析了多种扩散型气柱界面的瞬时混合率发展情况，发现演化初期在斜压涡影响下，界面通过增大浓度梯度来促进界面同周围空气的混合. 当二次不稳定性出现后，小尺度的对流增强，加速了失稳界面的混合. 二次不稳定性的出现迅速降低了局部浓度梯度，使得由浓度梯度引起的分子间混合减弱. $a$/$b$比值较大的初始界面失稳发展更加迅速，随着混合程度的提高，由浓度梯度驱使的分子间混合逐渐减弱. 由浓度梯度引起的扩散和由二次不稳定性引起的对流共同主导了界面的混合，前者在演化初期的主导地位随着失稳演化的进行逐渐被后者所取代.

参考文献

1	王显圣, 司廷, 罗喜胜, 等. 反射激波冲击重气柱的RM不稳定性数值研究. 力学学报,2012, 44 (4) : 664-672. ( Wang Xiansheng, Si Ting, Luo Xisheng, et al. Numerical study on the RM instability of a heavy-gas cylinder interacted with reshock. Chinese Journal of Theoretical and Applied Mechanics,2012, 44 (4) : 664-672. (in Chinese) ) (0)
2	Samtaney R, Meiron DI. Hypervelocity Richtmyer-Meshkov instability. Physics of Fluids,1997, 9 (6) : 1783-1803. DOI: 10.1063/1.869294. (0)
3	Anderson MH, Puranik BP, Oakley JG, et al. Shock tube investigation of hydrodynamic issues related to inertial confinement fusion. Shock Waves,2000, 10 : 377-387. DOI: 10.1007/s001930000067. (0)
4	Tian BL, Fu DX, Ma YW. Numerical investigation of Richtmyer-Meshkov instability driven by cylindrical shocks. Acta Mechanica Sinica,2006, 22 : 9-16. DOI: 10.1007/s10409-005-0083-1. (0)
5	Yang J, Toshi K, Zukoski EE. Applications of shock-induced mixing to supersonic combustion. AIAA Journal,1993, 31 (5) : 854-862. DOI: 10.2514/3.11696. (0)
6	李平, 柏劲松, 王涛, 等. 激波作用下气柱不稳定性发展诱发湍流大涡数值模拟. 中国科学:物理学力学天文学,2009, 39 (9) : 1241-1247. ( Li Ping, Bai Jinsong, Wang Tao, et al. Large eddy simulation of a shocked gas cylinder instability induced turbulence. Science China:Physics Mechanics & Astronomy,2009, 39 (9) : 1241-1247. (in Chinese) ) (0)
7	Arnett D. The role of mixing in astrophysics. The Astrophysical Journal Supplement Series,2000, 127 : 213-217. DOI: 10.1086/apjs.2000.127.issue-2. (0)
8	王涛, 柏劲松, 李平, 等. 冲击波加速矩形界面的Richtmyer-Meshkov不稳定性大涡模拟. 中国科学:物理学力学天文学,2009, 39 (12) : 1770-1778. ( Wang Tao, Bai Jinsong, Li Ping, et al. Large-eddy simulations of the Richtmyer-Meshkov instability of rectangular interfaces accelerated by shock weaves. Science China:Physics Mechanics & Astronomy,2009, 39 (12) : 1770-1778. (in Chinese) ) (0)
9	Khokhlov AM, Oran ES, Thomas GO. Numerical simulation of deflagration-to-detonation transition-the role of shock-flame interactions in turbulent flames. Combustion and Flame,1999, 117 : 323-339. DOI: 10.1016/S0010-2180(98)00076-5. (0)
10	Brouillette M, Bonazza R. Experiments on the Richtmyer-Meshkov instability:Wall effects and wave phenomena. Physics of Fluids,1999, 11 (5) : 1127-1143. DOI: 10.1063/1.869983. (0)
11	Rightley PM, Vorobie P, Martin R, et al. Evolution of a shockaccelerated thin fluid layer. Physics of Fluids,1997, 9 (6) : 1770-1782. DOI: 10.1063/1.869299. (0)
12	Jacobs JW. The dynamics of shock accelerated light and heavy gas cylinders. Physics of Fluids A,1993, 5 : 2239-2247. DOI: 10.1063/1.858562. (0)
13	Jacobs JW, Jenkins DG, Klein DL, et al. Nonlinear growth of the shock-accelerated instability of a thin fluid layer. Journal of Fluid Mechanics,1995, 295 : 23-42. DOI: 10.1017/S002211209500187X. (0)
14	Layes G, Jourdan G, Houas L. Experimental study on a plane shock wave accelerating a gas bubble. Physics of Fluids,2009, 21 : 074102. DOI: 10.1063/1.3176474. (0)
15	Haas JF, Sturtevant B. Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities. Journal of Fluid Mechanics,1987, 181 : 41-76. DOI: 10.1017/S0022112087002003. (0)
16	Prasad JK, Rasheed A, Kumar S, et al. The late-time development of the Richtmyer-Meshkov instability. Physics of Fluids,2000, 12 (8) : 2108-2115. DOI: 10.1063/1.870456. (0)
17	Jacobs JW. Shock-induced mixing of a light-gas cylinder. Journal of Fluid Mechanics,1992, 234 : 629-651. DOI: 10.1017/S0022112092000946. (0)
18	Zou LY, Liu CL, Tan DW, et al. On interaction of shock wave with elliptic gas cylinder. Journal of Visualization,2010, 13 : 347-353. DOI: 10.1007/s12650-010-0053-y. (0)
19	Zou LY, Liao Shenfei, Liu Cangli, et al. Aspect ratio effect on shock-accelerated elliptic gas cylinders. Physics of Fluids,2016, 28 : 036101. DOI: 10.1063/1.4943127. (0)
20	Wang MH, Si T, Luo XS. Generation of polygonal gas interfaces by soap film for Richtmyer-Meshkov instability study. Experiments in Fluids,2013, 54 : 1427. DOI: 10.1007/s00348-012-1427-9. (0)
21	Wang MH, Si T, Luo XS. Experimental study on the interaction of planar shock wave with polygonal helium cylinders. Shock Waves,2015, 25 : 347-355. DOI: 10.1007/s00193-014-0528-1. (0)
22	邹立勇, 廖深飞, 刘金宏, 等. 双椭圆界面Richtmyer-Meshkov流动中的相互干扰效应. 高压物理学报,2015, 29 (3) : 191-198. ( Zou Liyong, Liao Shenfei, Liu Jinhong, et al. Interaction effect of two ellipse Richtmyer-Meshkov flows. Chinese Journal of High Pressure Physics,2015, 29 (3) : 191-198. (in Chinese) ) (0)
23	Su LK, Clemens NT. The structure of fine-scale scalar mixing in gas-phase planar turbulent jets. Journal of Fluid Mechanics,2003, 488 : 1-29. DOI: 10.1017/S002211200300466X. (0)
24	Tomkins CD, Kumar S, Orlicz G, et al. An experimental investigation of mixing mechanisms in shock-accelerated flow. Journal of Fluid Mechanics,2008, 611 : 131-150. (0)
25	Balakumar BJ, Orlicz GC, Tomkins CD, et al. Simultaneous paticleimage velocimetry-planar laser-induced fluorescence measurments of Richtmyer-Meshkov instability growth in a gas curtain with and without reshock. Physics of Fluids,2008, 20 : 124103. DOI: 10.1063/1.3041705. (0)
26	Orlicz GC, Balakumar BJ, Tomkins CD, et al. A Mach number study of the Richtmyer-Meshkov intability in a varicose, heavy-gas curtain. Physics of Fluids,2009, 21 : 064102. DOI: 10.1063/1.3147929. (0)
27	Balasubramanian S, Orlicz GC, Prestridge KP, et al. Experimental study of initial condition dependence on Richtmyer-Meshkov instability in the presence of reshock. Physics of Fluids,2012, 24 : 034103. DOI: 10.1063/1.3693152. (0)
28	Tomkins CD, Balakumar BJ, Orlicz GC, et al. Evolution of the density self-correlation in developing Richtmyer-MeshkJov turbulence. Journal of Fluid Mechanics,2013, 735 : 288-306. DOI: 10.1017/jfm.2013.430. (0)
29	Bai JS, Zou LY, Wang T, et al. Experimental and numerical study of shock-accelerated elliptic heavy gas cylinders. Physical Review E,2010, 82 : 056318. DOI: 10.1103/PhysRevE.82.056318. (0)
30	Buch KA, Dahm JA. Experimental study of the fine-scale structure of conserved scalar mixing in turbulent shear flows. Part 1. Sc 1. Journal of Fluid Mechanics,1996, 317 : 21-71. DOI: 10.1017/S0022112096000651. (0)
31	罗喜胜, 翟志刚, 司廷, 等. 激波诱导下的气体界面不稳定性实验研究. 力学进展,2014, 44 : 201407. ( Luo Xisheng, Zhai Zhigang, Si Ting, et al. Experimental study on the interfacial instability induced by shock waves. Advances in Mechanics,2014, 44 : 201407. (in Chinese) ) (0)

Huang Xilong, Liao Shenfei, Zou Liyong, Liu Jinhong, Cao Renyi