0 引言

1988年，Bendsoe和Kikuchi^[1]提出了基于均匀化理论的拓扑优化方法.在此之后，连续体拓扑优化的理论方法不断被完善，在工程设计中逐渐成为初始概念设计的重要工具^[2].在这其中使用最为广泛的拓扑优化方法是以(solid isotropic material with penalization,SIMP)方法^[3-4]为代表的变密度方法.

拓扑优化问题通常是非凸问题，存在许多局部最优解，寻找拓扑优化的最优解一直是学术界所关心的问题.然而在实际工程问题中，耗费大量资源求解单一"最优解"未必是拓扑优化设计的主要目的.由于拓扑优化往往作为概念性阶段的设计工具，为后续的形状和尺寸优化提供可试探的初始设计构型^[5-7]，所以，在实际设计中迫切的需要能基于拓扑优化给出若干个满足要求的初始设计构型的方法.因为不同的初始设计会更加丰富设计人员对产品设计的认识，引导设计人员获得不同的精细设计方案.

在产品或结构的设计过程中，大体上有两种情况希望获得多个不同的设计方案，或多样性设计.第一种情况是，对于一个设计，我们已经知道应该关心哪些性能，这些性能可能互相矛盾，我们希望通过优化求得多个不同的设计，它们的这些性能各有长处，供决策者最后选择.多目标优化为这样的设计多样性提供工具^[8-12].

第二种情况，在设计初期阶段，设计人员无法全面的认知整个产品设计需求，往往采用较为简单的结构模型和简化过的数学模型.如Zhou和Rozvang^[3]采用最小化柔顺性做为优化目标，结构体积作为约束条件；程耿东等^[13]、隋允康等^[14]采用最小化结构重量作为优化目标，单元应力作为约束条件；Pedersen^[15]采用最大结构自振频率作为优化目标.而在后续精细设计阶段，随着分析模型的逐步细化、设计需求逐步明确，往往会增加一些其他的设计目标和约束.当进入后续精细设计阶段时，我们前期耗费大量资源基于拓扑优化方法所获得的单一"最优解"可能无法被采用^[16-19]. 多个不同的优化设计能够减小上述风险^[20]，因此本文希望在初始设计阶段能够获得若干多样性拓扑设计.

为了得到多个不同的优化设计，Villanueva^[21]通过对设计域自动分区并建立代理模型，可以同时求得设计域中的所有的全局最优解和局部最优解.然而，对于高维问题找寻所有的全局最优解和局部最优解十分困难，并不适合求解拓扑优化问题.随后，Zhou等^[22]提出了一个多样性可竞争设计优化列式，能够在高维问题中同时获得多个具有多样性的可竞争解.

本文提出了基于变密度拓扑优化的多样性设计问题.这里，多样性是指求得的优化设计间的几何构型存在差异，并且它们的目标性能比较相近.第1节提出了拓扑优化设计中多样性设计求解方法(multiple designs approach，MDA)的一般优化列式，给出了多样性约束函数并进行了讨论；第2节对结构拓扑优化中的最小柔顺性问题给出基于SIMP法的MDA优化列式及敏度分析；第3节对两个算例进行求解，研究了不同约束对结果的影响，并对目标函数之外的其他潜在结构性能进行了讨论和比较；第4节，讨论了目标函数的加权系数对结果的影响；第5节给出了结论与展望.

1 拓扑优化设计中的多样性可竞争解 1.1 MDA的基本优化列式

拓扑优化是为了在设计域$\Omega $内寻找最优的拓扑材料分布$\rho \left( {{ x}}\right)$，使得目标函数$F$最小，并且满足一定的约束条件.给出拓扑优化问题的一般列式^[23]

$\begin{equation}\label{eq1} \left.\begin{array}{lll} \mathop{\min}\limits_\rho :F({{ u}}(\rho ),\rho ) \\ {\rm s.t.}: G_0 (\rho) = \dfrac{\int_{\Omega}\rho {\rm d}V}{\int_{\Omega}{{\rm d}V}}-V_{f} \le 0 \\G_i ({{ u}}(\rho ),\rho ) \le 0,~i = 1,2,...,m \\\rho ({{ x}}) = 0 ~~{\rm or }~~1,~\forall {{ x}} \in \Omega \\ \end{array}\right\}\end{equation}$

(1)

其中$F$为目标函数，${{ u}}$物理场分布函数，${{x}}$是物质点坐标，$\rho ({{ x}})$是密度场分布函数,$G_0$为材料用量约束，$G_i $为功能约束函数，$m$为功能约束函数个数，$V_{f} $材料用量体分比.

在变密度法连续体拓扑优化中，为了能够通过梯度类优化算法求解，需要对材料分布函数进行插值，保证其连续光滑

$\begin{equation}\label{eq2} \rho \left( {{ x}} \right) \in \left[{0,1}\right],\forall {{ x}} \in {\Omega }\end{equation}$

(2)

对于拓扑优化的多样性可竞争设计问题，我们可以同时求解得到两个或两个以上的优化设计.以求解两个设计为例，需要在设计域$\Omega $内寻找两种不同的材料分布$\rho ^{1}\left( {{ x}}\right)$和$\rho ^{2}\left( {{ x}}\right)$，使得双目标$F^{1}$和$F^{2}$最小.同时需要额外满足多样性约束$G\left( {\rho ^{1},\rho ^{2}} \right)\le \eta $. 上标标识不同设计构型的物理量.这样MDA的优化列式可以写为

$\begin{equation}\label{eq3} \left.\begin{array}{l} \mathop {\min }\limits_{\rho ^1,\rho ^2}:F^{1}\left( {\rho ^{1}}\right),~~F^{2}\left( {\rho ^{2}} \right) {0.5mm}\\ {\rm s.t.}: G_0^1 \left( {\rho ^{1}} \right) \le 0 {0.5mm}\\ G_0^2 \left( {\rho ^{2}} \right) \le 0 {0.5mm}\\ G_i^1 \left( {\rho ^{1}} \right) \le 0 {0.5mm}\\ G_i^2 \left( {\rho ^{2}} \right) \le 0,~~i = 1,2,\ldots ,m {0.5mm}\\ G\left( {\rho ^{1},\rho ^{2}} \right) \le \eta {0.5mm}\\ \rho ^{1}\left( {{ x}} \right) \in [0,1],\rho ^{2}\left({{ x}} \right) \in [0,1],\forall {{ x}} \in \Omega \\ \end{array}\right\}\end{equation}$

(3)

通过对这两个目标的加权求和，我们可以得到

$\begin{equation}\label{eq4} F = \alpha F^{1} + \left( {1-\alpha } \right)F^{2}\end{equation}$

(4)

其中$\alpha \in [0,1]$是权系数，{$\alpha $}的大小平衡了所求最优设计的目标函数性能与多样性之间的关系.我们将在第四节进行讨论.

如果要获得$n$个设计构型，需要施加$n\left( {n-1} \right) / 2$个多样性约束. 优化列式可以写为

$\begin{equation}\label{eq5} \left.\begin{array}{l} \mathop {\min }\limits_{\rho ^i} :F = \sum_{i = 1}^n \alpha ^iF^i,\sum _{i = 1}^n \alpha ^i = 1 \\ {\rm s.t.}:G_0^i \left( {\rho ^i} \right) \le 0 \\ G_j^i \left( {\rho ^i} \right) \le 0 \\ \rho ^i\left( {{ x}} \right) \in \left[{0,1}\right],\forall {{ x}} \in \Omega ,\\ i = 1,2,\ldots ,n,j = 1,2,\ldots ,m \\ G\left( {\rho ^p,\rho ^q} \right) \le \eta ,p,q = {1,2,}\ldots ,n\mbox{ and }p e q \\ \end{array}\right\}\end{equation}$

(5)

1.2 多样性约束

以为了获得两个不同的拓扑构型为例，上一节中，我们定义一个多样性函数$G\left({\rho ^1,\rho ^2} \right)$ 作为约束.这个函数需要可以定量地描述两个拓扑构型间的几何差异，并保证连续光滑以便能够通过梯度类算法进行求解.

在图形学中，图像间的相似性有很多种度量方法，包括互相关系数法(cross-correlation,CC)、加和方差法(sum of squared differences,SSD)、加和绝对距离法(sum of absolute differences,SAD)等以及它们的衍生算法^[24].参照CC法，这里我们给出一个多样性函数的简单度量

$\begin{equation}\label{eq6} \left.{\begin{array}{lll} {G = SF\left( {\rho ^1,\rho ^2} \right) = \frac{\int _{\Omega } g\left( {\rho ^1\left( {{ x}} \right),\rho ^2\left( {{ x}} \right)} \right){\rm d}V}{ \int_{\Omega } {\rm d}V}} \\ {g\left( {\rho ^1\left( {{ x}} \right),\rho ^2\left( {{ x}}\right)} \right) = \rho ^1\left( {{ x}} \right)\rho ^2\left( {{ x}} \right),\forall {{ x}} \in \Omega } \\\end{array} }\right\}\end{equation}$

(6)

我们称SF为相似度函数(similarity function)，其中$g$为单点相似度衡量指标.其中，$g(0,0)=0$，$g(1,0)=0$，$g(0,1)=0$，$g(1,1)=0$，$g$在域内连续且光滑.

上述定义可以看出，相似度函数通过描述两拓扑构型间材料重叠比例来描述其差异.对于两个完全0-1的拓扑构型，材料重叠部分越大，相似度函数值越接近于1，结构越相似；材料重叠部分越小，相似度函数值越接近于0，结构差异越大.

1.3 相似度函数测试

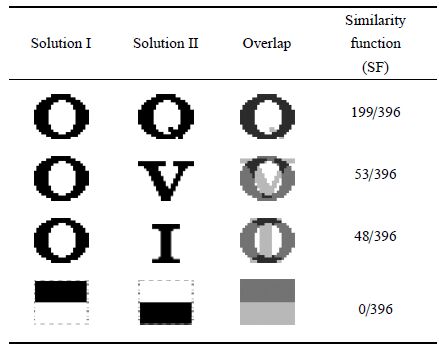
本节通过 4个字母(O,Q,I,V)的黑白拓扑图形对相似度函数进行测试.图形测试域大小为$18\times 22$，离散成396个拓扑变量.此外，我们同时给出测试域上半部分或下半部分全黑的图形作为对比.

表 1中列举了4组不同构型的相似度.在表 1第4组中，相似度函数值为0，差异性最大；最为相近的图形O与Q的相似度函数值最大；O和I,O和V拓扑差异较大，相似度函数值较小.从结果中可以看到，相似度函数值随图像差异增大而减小.因此，为了保证拓扑构型间的差异性，需要约束相似度函数小于一定阈值.

1.4 相似度函数与体分比的关系

在两个0-1构型中材料体分比$V_{f}$相同时，相似度函数的值域范围与材料体分比是具有联系的.下面给出一个由3个离散变量控制的$3\times 1$图像的例子来说明.

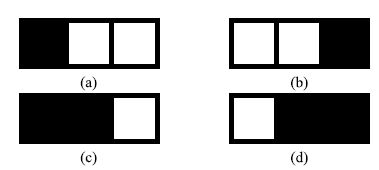
对于材料体积为1的构型，如图 1 (a)和图 1(b)，材料体分比为1/3，(a)对(b)的相似度函数值为0(下限)，(a)对(a)的多样性函数值为1/3(上限).

对于材料体积为2的构型，如图 1(c)和图 1(d)，材料体分比为2/3，由于必有材料重叠，(c)对(d)的多样性函数值为1/3(下限)，(c)对(c)的多样性函数值为2/3(上限).

可以看出相似度函数值的上限取决于材料的体分比，下限取决于材料的最小重叠体积.假设构型1和构型2重叠部分体积比为$v_0$，构型1非重叠部分体积比为$v_1 $，非重叠部分体积比为$v_2 $.他们与$V_{f} $ 满足不等式约束

$\begin{equation}\label{eq7} \left\{ {\begin{array}{l} v_0 + v_1 + v_2 \le 1 \\ v_0 + v_1 = V_{f} \\ v_0 + v_2 = V_{f} \\ v_0 \ge 0,v_2 \ge 0,v_2 \ge 0 \\ \end{array}} \right. \Rightarrow \mbox{ }\left\{ {{\begin{array}{*{20}c} {v_0 \ge 2V_{ f}-1} \\ {0 \le v_0 \le V_{f} } \\\end{array} }} \right.\end{equation}$

(7)

可以通过两集合并集确定来得到

$\begin{equation}\label{eq8} SF = v_0 \in [\max \left( {0,2V_{f}-1} \right),V_{f}] \end{equation}$

(8)

因此，在设计域材料用量不同时，需要根据体分比调整多样性约束函数值，保证其在多样性函数的值域内.

由于不同的体分比下相似度函数的值域不同，为了更好地描述拓扑构型的差异性，我们给出了统一的度量准则.这里，将根据值域的范围对相似度函数进行归一化，定义差异度函数DF(diversity function)

$\begin{equation}\label{eq9} DF = 1-\frac{SF-\max \left( {0,2V_{f}-1}\right)}{V_{\rm f}-\max \left( {0,2V_{f}-1} \right)}\end{equation}$

(9)

差异度函数的取值范围为[0,1]，差异度函数越接近于0表示拓扑构型越相似，越近于1表示拓扑图形差异越大.相似度函数与差异度函数之间呈线性关系.

2 最小柔顺性拓扑优化问题描述

最小柔顺性问题的两构型设计MDA优化列式为

$\begin{equation}\label{eq10} \left.\begin{array}{l} \mathop {\min }\limits_{\rho _1 ,\rho _2 } :c = \alpha c_1 + (1-\alpha )c_2 =\\ \alpha {{ P}}^{\rm T}{{ U}}_{{ 1}} + (1-\alpha ){\rm { P}}^{\rm T}{{ U}}_{{ 2}} \\ {\rm s.t.}:{{ K}}_{{ 1}} \left( {\rho _1 } \right){\rm {U}}_{{ 1}} = {{ P}},~{{ K}}_{{ 2}} \left( {\rho _2 } \right){{ U}}_{{ 2}} = {{ P}} \\ G_1 \left( {\rho _1 } \right) = \dfrac{\sum\limits_i {\rho _1^i v^i}}{V}-V_{f} \le 0 \\ G_2 \left( {\rho _2 } \right) = \dfrac{\sum\limits_i {\rho _2^i v^i}}{V}-V_{f} \le 0 \\ DF\left( {\rho _1 ,\rho _2 } \right) \ge \eta \\ 0 \le \rho _1^i ,\rho _2^i \le 1,i = 1,2,\ldots ,n \\ \end{array}\right\}\end{equation}$

(10)

其中$\rho _1 $和$\rho _2$是作为优化设计变量的单元伪密度，设计域单元总数为$n$.$c$为加权目标函数，$c_1 $和$c_2 $为两拓扑构型柔顺性值，$\alpha $为加权系数. $V$是设计域体积，$V_{\rm f} $是设计域体积约束体分比.$v^i$是第$i$号单元体积，$\rho _1^i $和$\rho _2^i $是第$i$号单元密度. $\eta $是差异度函数约束值. ${{ K}}_{\rm {1}} $,${{ K}}_{{ 2}} $；${{ U}}_{{ 1}} $,${{U}}_{{ 2}} $ ，分别为两拓扑构型总刚度阵与位移向量.$P$为外载荷向量. 总刚度阵通过下式计算

$\begin{equation}\label{eq11} {{ K}} = \mathop \sum \limits_{e = 1}^n {{K}}^e\left( {E^e\left( {\rho ^e} \right)} \right)\end{equation}$

(11)

其中上标$e$表示单元变量，${{K}}^e$是单元刚度阵(总刚下)，$E^e$单元材料弹性模量，材料插值模型采用SIMP插值格式^[4]

$\begin{equation}\label{eq12} E^e\left( \rho \right) = E_{\min} + (\rho ^e)^p\left({E_0-E_{\min} } \right)\end{equation}$

(12)

其中$E_0 $为材料弹性模量上限，$E_{\min}$为材料弹性模量下限，$p$是罚系数.

这样，目标函数、约束函数的敏度可以表示为以下形式

$\begin{equation}\label{eq13} \left.\begin{array}{l} \dfrac{\partial c}{\partial \rho _1^e } = \alpha \dfrac{\partial c_1 }{\partial \rho _1^e } =-\alpha u_1^T \dfrac{\partial k^e}{\partial \rho _1^e }u_1 \\ \dfrac{\partial c}{\partial \rho _2^e } = \left( {1-\alpha }\right)\dfrac{\partial c_2 }{\partial \rho _2^e } =-\left( {1-\alpha }\right)u_2^T \dfrac{\partial k^e}{\partial \rho _2^e }u_2 \\ \dfrac{\partial k_e }{\partial \rho ^e} = p\left( {E_0-E_{min} }\right)(\rho ^e)^{p-1}k_0^e \\ \dfrac{\partial G_1 }{\partial \rho _1^e } = V^e \\ \dfrac{\partial G_1 }{\partial \rho _2^e } = 0 \\ \dfrac{\partial G_2 }{\partial \rho _1^e } = 0 \\ \dfrac{\partial G_2 }{\partial \rho _2^e } = V^e \\ \dfrac{\partial DF}{\partial \rho _1^e } = \dfrac{\rho _2^e }{V_{\rm f}-\max \left( {0,2V_{f}-1} \right)} \\ \dfrac{\partial DF}{\partial \rho _2^e } = \dfrac{\rho _1^e }{V_{\rm f}-\max \left( {0,2V_{f}-1} \right)} \end{array}\right\}\end{equation}$

(13)

为了避免棋盘格效应且不影响结构拓扑的多样性，这里采用敏度过滤^[4]的方法，并采用较小的过滤半径.这里针对两拓扑构型的柔顺性$c_1 $和$c_2 $分别进行敏度过滤.

$\begin{equation}\label{eq14} \left.\begin{array}{l} \overline {\dfrac{\partial c_1 }{\partial \rho _1^e }} = \dfrac{\sum _{i \in N^e} w\left( {{{ x}}_i } \right)\rho _1^i \dfrac{\partial c_1 }{\partial \rho _1^i}}{\rho _1^e \sum _{i \in N^e} w\left( {{{ x}}_i } \right)} \\ \overline {\dfrac{\partial c_2 }{\partial \rho _2^e }} = \dfrac{\sum _{i \in N^e} w\left( {{{ x}}_i } \right)\rho _2^i \dfrac{\partial c_2 }{\partial \rho _2^i}}{\rho _2^e \sum _{i \in N^e} w\left( {{{ x}}_i } \right)} \\ N^e = \{i\left| {\vert \vert {{ x}}^i-{{ x}}^e\vert \vert \le R} \right.\} \\ w\left( {{{ x}}^i} \right) = R-\vert \vert {{ x}}^i-{{ x}}^e\vert \vert \\ \end{array}\right\}\end{equation}$

(14)

优化的迭代初值为均匀灰度，所有单元密度大小等于约束体分比.由于两构型在相同的初始设计变量下目标函数与约束函数的敏度相同，需要给两初始构型一个相异的扰动(在两构型的第一个设计变量，即第一个单元伪密度给予$\pm $0.01的扰动)，驱动构型分离.

3 数值算例 3.1 不同多样性约束下MBB梁结果对比

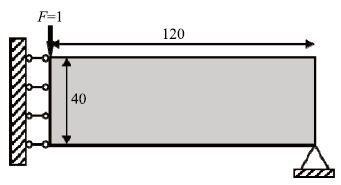
MBB梁模型设计域如图 2 所示.设计域取对称结构的一半，大小为$120\times 40$，离散为4800个$1\times 1$的双线性单元. 弹性模量$E_0 =1$，弹性模量下限$E_{\rm min} = 1\times 10^{-6}$，泊松比$\nu =0.3$.材料罚函数取3，过滤半径取1.5，体积约束为设计域总体积的50%.MBB梁对称模型左端约束横向位移，右下角点约束竖向位移，左上角点施加向下单位力.加权目标函数的加权系数$\alpha $取0.5.保证其差异度函数DF的约束值$\eta $分别取0.8,0.6,0.4,0.2和0.0.

表 2 给出了在权重系数$\alpha $=0.5时，MBB梁在不同差异度约束下的多样性设计结果.表 2中第二列为第一个拓扑优化解构型及其柔顺性值；第三列为第二个拓扑优化解构型及其柔顺性值；第四列为目标函数值.从表中可知，差异度函数越小，构型的重叠部分越大.增大构型之间的差异度能够有效地增大它们之间的差异.另外，由于体分比较高(50%)，较紧的差异度约束(如DF=0.8)会使两个结构拓扑构型形成局部互斥的构型，这时多样性的获得是以牺牲结构性能为代价的.

3.2 MBB梁潜在结构性能多样性分析

在进入精细设计阶段后，我们可能会对优化设计提出更多更复杂的性能要求.这往往不能在初始设计阶段通过简单的多目标设计来求解.在本文中，我们通过多设计求解方法来得到不同的拓扑构型，并尝试围绕可能关注的结构性能(并不限于这些)对获得的多样性拓扑构型进行分析和比较，以此对不同构型进行评判.

这里对在$\alpha =0.5$时得到的MBB梁的不同构型进行强度、稳定性和自振频率的分析.表 3给出了最大单元平均von Mises应力、屈曲特征值和一阶自振频率^[25-26]等潜在的结构性能.将这些性能按式(15)进行归一化，用雷达图表示，结果如表 4 所示.

$\begin{equation}\label{eq15} \left.\begin{array}{l} I_C = 1-\dfrac{C-C_{\rm lower} }{C_{\rm upper}-C_{\rm lower} } \\ I_\sigma = 1-\dfrac{\sigma-\sigma _{\rm lower} }{\sigma _{\rm upper}-\sigma _{\rm lower} } \\ I_\lambda = \dfrac{\lambda-\lambda _{\rm lower} }{\lambda _{\rm upper}-\lambda _{\rm lower} } \\ I_f = \dfrac{f-f_{\rm lower} }{f_{\rm upper}-f_{\rm lower} } \end{array}\right\}\end{equation}$

(15)

其中$I_{\left( \cdot \right)}$表示归一化性能指标，越接近1相对性能越好，越接近0相对性能越差.下标upper表示性能上限，下标lower表示性能下限.

从表 4中可以看出，在差异度函数较大(0.8,0.6,0.4)时，构型普遍差异大，构型结构潜在性能差异也大.以DF=0.4为例，构型I的柔顺性为194.64，低于构型2的196.08，同时构型I的屈曲特征值0.1330高于构型2的0.066 4；但是构型Ⅱ的一阶自振频率为2.9908高于构型I的2.422 3. 两个构型在不同性能表现上各有优势.当差异度函数较小(0.2,0)时，构型差异小，构型潜在性能也越趋于相同.如果只能得到两个相近的结构，当其中一个构型不满足潜在性能设计要求时，另一个构型很可能也无法满足.

3.3 不同多样性约束下L型梁结果对比

L型梁模型如图 3 所示. 设计域外边长80，内边长40，宽40，离散为4800个$1\times 1$的双线性单元. 弹性模量$E_0 =1$，弹性模量下限$E_{\min} = 10^{-6}$，泊松比$\nu = 0.3$.材料罚函数取3，过滤半径取1.5，体积约束为设计域总体积的50%.模型上边固支，右上角点受向下单位力载荷.保证其差异度函数DF的约束值$\eta $分别取0.8,0.6,0.4,0.2和0. 加权目标函数的加权系数$\alpha $取0.5.

表 5给出了在权重系数$\alpha =0.5$时，L型梁在不同差异度函数下的多样性设计优化结果.从表 5中可以看出，与MBB梁算例相似，差异度函数越小，得到的两个构型之间的重叠部分越大；而差异度函数越大，构型越不相同.较大的差异度能够有效地驱使构型增大差异，并收敛于两个相异解.

3.4 L型梁潜在结构性能多样性分析

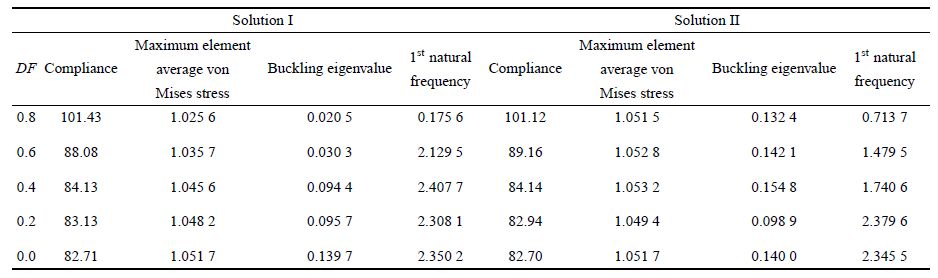
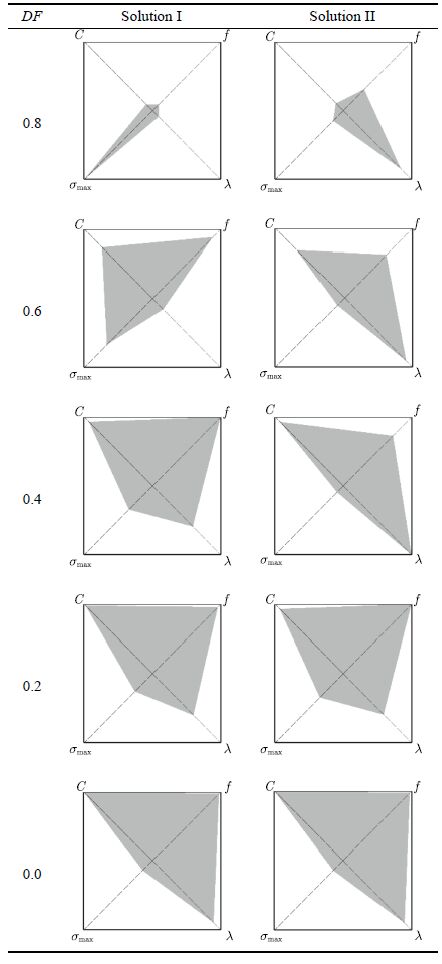
为了验证不同的拓扑构型是否对潜在的结构性能存在多样性，对在$\alpha =0.5$时得到的L型梁的多样性构型进行强度、稳定性和自振频率的分析.表 6和表 7给出了L型梁优化得到的各个构型的性能值及雷达图.

从表 6中可以看出，与MBB梁算例相似，在差异度函数较大(DF=0.8,0.6,0.4)时，构型差异大，构型结构潜在性能差异也大.以DF=0.4为例，两构型柔顺性值基本接近，同时构型I的屈曲特征值0.094 4远低于构型Ⅱ的0.154 8；但是构型I的一阶自振频率为2.407 7高于构型Ⅱ的1.740 6. 两个构型在不同性能表现上各有优势.而在差异度函数较小(0.2,0.0)时，构型差异小，构型结构潜在性能也越趋于相同.

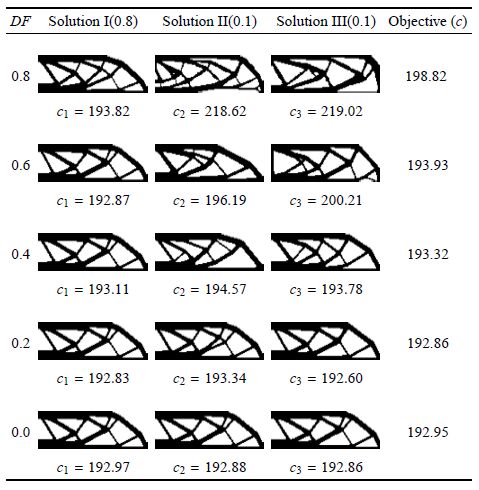
4 加权目标函数的加权系数α与最优拓扑构型的关系

取加权系数分别为0.8，0.1和0.1,当同时优化3个构型时，其他参数与第3节算例相同.同时优化3构型时，类似式(7)相似度函数取值范围会变为

$\begin{equation}\label{eq16} SF \in \left[\max \left( {0,\dfrac{3V_{\rm f}-1}{3}} \right),V_{f} \right] \end{equation}$

(16)

差异度函数DF变为

$\begin{equation}\label{eq17} DF = 1-\dfrac{SF-\max \left( {0,\dfrac{3V_{f}-1}{3}} \right)}{V_{\rm f}-\max \left( {0,\dfrac{3V_{f}-1}{3}}\right)}\end{equation}$

(17)

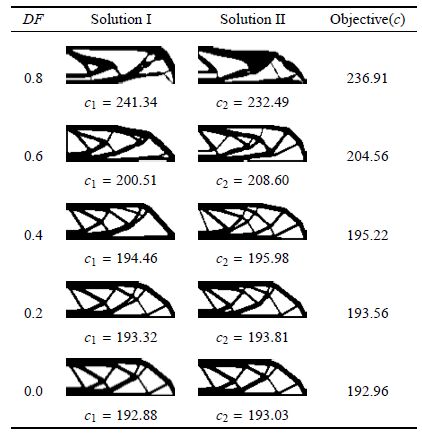
表 8和表 9 给出了MBB梁和L型梁在不同加权系数时的多样性设计结果.从结果可以看出，构型I的加权系数为0.8，对目标函数的影响较大；构型Ⅱ、构型Ⅲ的加权系数为0.1，对目标函数的影响较小.从表中可以看出，构型I更接近于传统单目标拓扑优化得到的优化设计.随着差异度约束的增大，构型Ⅱ、构型Ⅲ与构型I的差异性越来越大，目标函数性能也越来越差.

5 结论

本文提出了基于拓扑优化的多设计优化问题，在SIMP框架下给出了MDA优化算法.本文定义了一种基于图形学的相似度/差异度函数作为多样性约束，并且对其进行了讨论.

本文求解了MBB梁和L型梁这两个算例的多设计问题.从结果可以看到，差异度越大，拓扑构型间的差异就越大，潜在结构性能也越不相同，这给设计者在精细设计阶段提供了不同的选择.差异度的选取是有范围的，差异度太小容易导致获得的拓扑构型过于相似，多个设计都趋近于传统单目标拓扑优化结果；差异度太大容易导致获得的拓扑构型性能过差，未必适合进一步的精细优化设计.文章还讨论了加权系数对优化结果的影响，结果发现权重系数较大的拓扑构型会更接近传统单目标拓扑优化结果.

值得说明的是，文中所给出的多样性约束并不是唯一的.是否存在更好的多样性约束函数是我们下一步将研究的工作.