近年来,随着机器人技术的迅猛发展以及对机器人所执行任务的多样性与复杂性要求的不断提高,具备感知能力的智能机器人已被公认为当今机器人发展的主流趋势.在诸多传感器中,视觉传感器因其信息量大、适用范围广、非接触性等特点已成为最重要的机器人传感器之一.将视觉传感器引入机器人控制系统,可增加机器人对周围环境的自适应性,拓宽机器人的应用领域[1-2].这一思路也直接催生了机器人视觉伺服控制技术.机器人的视觉伺服控制是采用视觉传感器来间接检测机器人当前位姿或机器人相对目标物体的相对位姿,在此基础上,实现机器人的定位控制或者轨迹跟踪[3],是对包括高速图像处理、运动学、动力学、控制理论、实时计算在内的多种基本领域的融合[4].
机器人视觉伺服系统的基本构成,包括机器人系统与视觉系统两大部分.机器人系统与视觉系统在作业之前均需要进行系统的标定. 因此对于视觉伺服系统而言,其标定内容包括:相机标定、机器人标定、机器人与相机相对位置标定(也称手眼标定).传统的机器人视觉伺服系统的性能高度依赖于标定精度[5].但是,视觉伺服的系统标定在很多情况下会受到诸多限制:
(1)系统标定结果只在标定条件下有效,细微的结构改变也可能需要重新标定[6]. 例如视觉伺服系统在较大振动的条件下作业时,可能带来的手眼关系的改变.
(2)在很多工况下,系统标定的参数可能会缓慢变化[7],例如在有辐射条件下,相机参数会发生退化.
(3)由于相机畸变等因素,相机的标定区域一般限制在有限的区域,限制了机器人的工作范围[4].
(4)系统的标定通常繁琐,需要专门的标定环节与专业人员,标定成本较高[8].
基于上述原因,无标定视觉伺服作为一种新的视觉伺服形式逐渐得到了众多学者的关注.所谓的无标定视觉伺服是指在不预先标定摄像机模型和参数或者机器人运动学模型的情况下,直接利用图像上的系统误差,通过研究控制规律进而驱动机器人运动,使系统收敛到一个容许的误差域内的控制方法[3].无标定视觉伺服省去了繁琐的标定过程,在控制效率、应用的便利性以及性能上均有较大的优势,得到了广泛的关注[4, 9-12].
无标定视觉伺服的控制目标可以通过以下目标函数(task function)描述
| $e\left( t \right)=s\left( m(t),a \right)-{{s}^{*}}$ | (1) |
其中,s与s*分别为系统的当前状态和期望状态;m(t)是图像测量值,而a为相关模型参数,如相机焦距等[13];视觉伺服控制均以使得目标函数(1)最小化为控制目标.从上式可以看出,选择何种信号作为描述系统特征的状态向量s,即如何构造目标函数作为控制目标是视觉伺服研究的第一个任务;在确定目标函数的形式后,如何设计控制器,实现目标函数的最小化是另一个任务[14-15];此外,在控制过程中,机器人选择何种中间状态实现更优运动轨迹,也是值得关注的问题.基于此,本文从机器人无标定视觉伺服控制的目标函数选择、控制器设计以及轨迹规划3个角度对机器人无标定视觉伺服控制技术的发展现状展开综述.
1 无标定视觉伺服的目标函数按照目标函数中所选择的反馈信号的不同,无标定的视觉伺服和视觉伺服一样可以分为基于位置的视觉伺服(三维视觉伺服)、基于图像的视觉伺服(二维视觉伺服)以及混合视觉伺服(2.5维视觉伺服)[12].
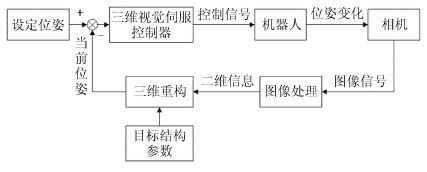
1.1 基于位置的视觉伺服PBVS基于位置的视觉伺服(position based visual servoing,PBVS)系统基本结构如图 1所示.对于PBVS而言,其目标函数所选择的控制信号s是机器人的位姿信息. 在控制过程中,通常需要利用相机所采集的图像信息以及相机模型、目标物的结构模型等信息进行三维重构,进而获取机器人的位姿信息.最后基于当前位姿与设定位姿设计反馈控制律,完成伺服控制. 由于需要利用三维空间信息,该方法又称为三维视觉伺服.
|
图 1 基于位置的视觉伺服结构 Fig.1 Scheme of position based visual servoing |
PBVS将视觉传感器视作一个三维传感器,此类方法虽然有笛卡尔空间轨迹最优的优点,但其高度依赖对模型的标定(包括相机内参数以及手眼关系、机器人模型等). 因此,从原理上考虑,PBVS并不适用于无标定视觉伺服.仅有少数文献提出了一些部分标定(通常是相机标定)情况下的PBVS视觉伺服控制方法. 例如文献[16]针对相机安装在机器人末端执行器的结构(又称为eye-in-hand结构,简记为EIH),选择了相机内参数已知而机器人模型以及手眼关系未知的部分无标定方案,并在此基础上解决了遥操作式爆炸物处理机器人的控制问题.该方案尽管并非完全无标定,但是其控制理念与无标定方法近似,显著地提高了遥操作机器人的人机体验,因此也有较大的借鉴意义.此外,文献[6]提出了双目相机安装在机器人以外的固定位置(又称为eye-to-hand结构,简记为ETH)的结构下的无标定视觉伺服方法.该方法在相机内参数已知,但手眼关系未知情况下,实现了机器人对动态目标的跟踪以及障碍规避.
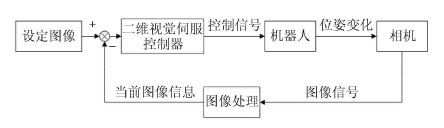
1.2 基于图像的视觉伺服基于图像的视觉伺服(image based visual servoing,IBVS)基本结构如图 2 所示.IBVS的目标函数中所选择的控制信号是纯粹的图像信息,因而又称为二维视觉伺服. 相比于PBVS,IBVS控制结构更为简单.由于只需要使用图像信息进行比较而不需要进行三维重构,因此IBVS对于相机的标定误差有更高的鲁棒性.在无标定的限制条件下,IBVS控制信号的获取不再依赖相机、机器人的系统参数,因此从原理上分析,IBVS更适合无标定视觉伺服,目前成为无标定视觉伺服控制的主流技术[8, 13, 15, 17-18].
|
图 2 基于图像的视觉伺服结构 Fig.2 Scheme of image based visual servoing |
图像虽然是二维信息,但是对于无标定的IBVS而言,可以用作控制信号的二维信息类型依然相当丰富. 常见的用于视觉伺服控制的图像特征包括点特征、线特征、图像矩等等.
通过对点特征图像坐标的变化速度与机器人运动的速度的运动学分析可直接获取点特征图像坐标与机器人速度之间的映射关系,因此,点特征成为大多数无标定IBVS系统的优先选择. 单个点特征可以建立两个运动学方程. 对于拥有6自由度的机器人而言,理论上3个点特征即可构造机器人的运动学控制模型,实际应用中,从稳定性与避免奇异性考虑,通常选择4个以上的特征点[13]作为目标特征. 通过图像空间中的点特征与任务空间中机器人的速度关系,可以获取下文中重点讨论的图像雅克比矩阵,通过对图像雅克比矩阵进行估计,即可设计出IBVS的反馈控制律,这也是大部分无标定视觉伺服所采用的思路[19- 22].
虽然多数IBVS都采用点特征作为建立目标函数的特征,但在实现世界中,多面体结构的物体更为常见,因此线特征相对于点特征更易于检测,且其对图像噪声有更强的鲁棒性,因此也有学者提出在相机参数已知的情况下,使用线特征进行视觉伺服控制[23-25]. 而无标定情况下,Malis等[26]最早考虑了在相机内参数未知的条件下使用线特征进行视觉伺服;Wang等[27]针对EIH结构的视觉伺服系统,首次在考虑机器人动力学的情况下,利用无标定视觉伺服控制技术对静态目标实现了机器人的精确定位.
除了点特征与线特征以外,还可利用更为自由的形状进行视觉伺服,从而有效放宽IBVS无标定视觉伺服技术的限制条件. 因此有学者提出采用更为一般化的形状图像特征实现无标定动力学视觉伺服,并给出了几何参数未知的一般化图像特征所对应的深度无关雅克比矩阵的形式与成立条件[28]. 解决不规则形状的图像信息用于视觉伺服另一个主要思路就是从不规则的图像信息中抽取出有共性特征的信息,图像矩就是典型的一种. 传统的基于图像的视觉伺服方法中,图像几何特征的标记、提取与匹配过程复杂且通用性较差. 以图像矩作为视觉特征,可以为针对复杂形状的视觉伺服提供更为可靠的解决方法. 文献 [29-30]提出了各种不同图像矩作为目标函数时的雅克比矩阵形式,并指出图像矩特征有助于提高视觉伺服系统性能. 通过选择不同的图像矩还可实现解耦控制,实现空间轨迹的优化[31]. 经过试验证明,在空间轨迹、收敛速度等方面,采用图像矩作为目标函数的IBVS 比采用普通点特征的IBVS拥有更优异的性能[32]. 此外,还有学者将图像矩描述算子与BP神经网络结合起来,映射图像矩特征与机器人关节角度变化,避免了传统视觉伺服技术中图像特征提取匹配复杂的问题[33].
上述用于IBVS的特征,不仅可以针对单目视觉系统,对于双目或多目视觉系统,其误差函数的构造方式依然可以使用,通常的做法是将不同相机所获取的图像信号串联成列向量[19, 34-38],本质上等价于增加了特征点的个数.
此外,除直接利用图像信息的无标定IBVS方法以外,近年来,也有不少学者试图通过探究图像信息更多的内涵构造新的控制信号与目标函数. 例如文献 [14, 39]提出了一种虚拟复合视觉系统以及新的立体视觉模型,分别将任务空间中的点的位置信息以及机器人位姿信息映射到新的三维视觉笛卡尔空间(3D visual cartesian space)中,该空间中的三维位置是采用像素进行测量的. 这种模型可以构建出满秩的图像雅克比矩阵,从而应对经典IBVS中图像空间奇异以及局部最小值的问题;针对无标定IBVS只有初始位置在目标位置附近时方能保证较高的成功率这一局部稳定限制[13, 40-41],文献[42]提出使用初始时刻、当前时刻、目标位置三幅图像之间的三视图射影几何关系构建新的目标函数,即使用三视张量的各个元素作为目标特征,构建目标函数,通过在线估计机器人关节空间与三视张量各个元素之间的雅克比矩阵,首次实现了基于三视张量的6自由度机械臂的无标定视觉伺服.
1.3 混合视觉伺服经典的IBVS与PBVS均有明显的缺陷与局限性.对于PBVS而言,除了高度依赖于标定与模型精度以外,由于图像信号处于控制环路之外,因此目标容易脱离相机视场范围[1, 40].IBVS得益于其直接对图像特征进行控制的控制目标选择[23],对相机参数等模型参数的标定误差有更好的鲁棒性,但仍存在一定的缺陷,如:图像雅克比矩阵的奇异点难以规避;仅能保证局部收敛性,即IBVS的稳定性区域较小,当初始位姿误差较大时,无法保证收敛[43];存在局部最小值,即当误差函数取值位于图像雅克比矩阵的零空间时,误差尚未收敛到0,但是机器人速度为[13];机器人工作空间轨迹无法控制,会出现包括肖梅特难题(Chaumette Conundrum)在内的空间轨迹问题[44]. 为了克服上述两种方法的缺陷,Malis等[45]提出了部分使用3维信息和2维信息的2.5维视觉伺服,其核心思路是,利用当前图像与目标图像信息计算获取单应性矩阵.通过对单应性矩阵进行分解,获取当前位姿与理想位姿的姿态误差,进行旋转控制;同时使用扩展图像坐标,在图像空间进行位置控制.2.5维视觉伺服也称为基于单应性矩阵的混合视觉伺服(homography based visual servoing,HBVS),结构如图 3所示.

|
图 3 2.5维视觉伺服结构 Fig.3 Scheme of 2.5D visual servoing |
HBVS对于标定误差有着很高的鲁棒性[46-47],而且可以避免IBVS和PBVS的诸多缺陷,因此也是无标定视觉伺服的重要技术路线之一.在无标定条件下应用HBVS的核心思想在于:将经典HBVS算法中的欧几里得单应性矩阵转化为仅利用图像信息即可获取的射影单应性矩阵;通过建立自适应控制律,在模型参数未知的情况下,实现稳定的控制.
从目标函数的角度分析,由于HBVS的误差分为位置误差和姿态误差,所以通常采用不同的目标函数对位置误差和姿态误差进行描述.
经典表达式:在无标定条件下,依然可以沿用经典HBVS的目标函数表达式,即分别使用扩展图像坐标描述位置误差,使用旋转轴与旋转角描述姿态误差. 例如,Chen等[48]提出在缺少深度信息且相机参数不确定的情况下,首先利用射影单应性矩阵与欧几里得单应性矩阵之间的相似关系,基于分解算法获取新的旋转轴角表达式,进而得到姿态误差函数;同时根据图像信息建立位置误差函数,对误差函数中的包括深度信息在内的未知参数,则设计了自适应控制器进行自适应估计. Fang等[49]也采用类似的姿态控制器,但是采用新的混合位置控制器,实现指数收敛.
四元数表达式: Hu等[50-52]利用目标平面中消失点(vanishing points)计算射影单应性矩阵,借助无穷远平面的几何特性,直接获取旋转矩阵的估计值. 为了更好地处理实际旋转矩阵与估计旋转矩阵之间的关系,Hu等[50-52]提出了采用四元数的描述姿态误差,而对于位置误差则采用扩展的图像坐标描述,从而实现了姿态控制与平移控制的解耦.
2 无标定视觉伺服的控制器设计控制器设计的主要任务是根据目标函数设计控制律,以使目标函数收敛于0. 视觉伺服按照控制器的设计过程中是否考虑机器人的动力学特性,可以分为运动学无标定视觉伺服与动力学无标定视觉伺服[8, 53].
2.1 考虑机器人运动学的无标定视觉伺服运动学无标定视觉伺服不考虑机器人系统的非线性力对机器人产生的影响,仅考虑机器人运动速度与视觉信息之间的关系.因此其设计目标即为速度控制器[13]. 机器人的视觉伺服控制本质是需要对手眼关系进行映射.如何获取手眼映射关系是控制律设计的关键.手眼关系的映射存在着高度非线性,从简化研究的角度可以将其视为一系列局部范围内的非线性关系的线性近似.这种对视觉空间与机器人任务空间或关节空间映射关系的近似,即为雅克比矩阵.最为常见的雅克比矩阵定义如下:在选定目标函数e的情况下,构建如下的开环系统
| $\dot{e}={{L}_{e}}{{\upsilon }_{c}}$ | (2) |
其中,
在无标定视觉伺服系统中有多种雅克比矩阵:式(2)中关联图像特征变化速率与机器人末端在欧氏空间中的速度的矩阵[13],称为互作用矩阵(interaction matrix)或者特征矩阵(feature matrix);机器人在任务空间(欧式空间)中的运动速度与关节空间的运动速度之间的关系,为机器人雅克比[36, 54];针对使用图像特征作为控制信号的IBVS而言,将互作用矩阵与机器人雅克比的乘积称为组合图像雅克比(image jacobian)[34]或复合雅克比(composite Jacobian)[36]或视觉运动雅克比(visual-motor Jacobian)[55].除此以外,对于基于视觉的动态目标跟踪,有下式
| $\dot{e}=\frac{ds}{dt}=\frac{\partial s}{\partial t}+\frac{\partial s}{\partial \theta }\frac{\partial \theta }{\partial t}=\frac{\partial s}{\partial t}+{{L}_{q}}\dot{\theta }$ | (3) |
其中, Lq复合雅克比矩阵,θ 为机器人的关节角度.由此可见目标函数的变化不仅与机器人运动相关,还与目标自身的运动有关,通常需要增加物体运动的速度预测VPC [18, 22],构成所谓的完全雅克比(total Jacobian) [20].
对于运动学无标定视觉伺服而言,其控制律的设计通常思路就是对雅克比矩阵进行在线估计,然后使用雅克比矩阵的逆(广义逆)矩阵构造比例积分反馈控制器完成控制[56]. 即根据上述开环系统可以设计简单的速度控制器
| $\theta =-\lambda L_{e}^{+}e$ | (4) |
保证目标函数指数收敛到0.Le+式中为雅克比矩阵的广义逆[13, 55]. 由此可见,无标定视觉伺服的性能主要依赖于雅克比矩阵在线估计的速度与精度[19].
在无标定视觉伺服控制器设计过程中,雅克比矩阵的求取方式分为两种:解析法与数值法.解析法是在线精确地获取每个控制周期内系统的各个参数值,然后代入雅克比矩阵的各个元素中进行精确计算.其缺陷在于,无标定的情况下,精确系统参数难以获取.数值法则是在不显式地应用运动学模型获取雅克比矩阵解析表达式的前提下,采用数值估计的方法直接对雅克比矩阵的各个元素进行整体的估计.研究表明,采用估计雅克比矩阵设计运动控制器,控制效果与采用解析的雅克比矩阵相当 ,甚至有部分指标更优[35-37, 57]. 且数值法可以省去冗杂的标定、重构等工作.因此,对于无标定视觉伺服而言,采用数值法估计雅克比矩阵更为可取.
2.1.1 基于非线性优化方法鉴于无标定视觉伺服任务的控制目标均为通过反馈控制最小化目标函数. 因此无标定视觉伺服也可以被视作最优化问题. 从而最优化理论与方法也成为无标定视觉伺服控制的一种主要解决思路.
(1) 动态Gauss-Newton法
为应用经典的最优化理论,需要对目标函数进行改造,构造新的目标函数
| $F(\theta ,t)=\frac{1}{2}{{e}^{\text{T}}}(\theta ,t)e(\theta ,t)$ | (5) |
其中,e为图像误差函数,与机器人关节角度θ以及时间$t$有关.此时目标函数的最小化问题转化为非线性优化问题,一系列成熟的非线性优化算法均可应用.其中较为有代表性的方法是针对此类非线性最小二乘问题的Gauss-Newton方法.此方法通过迭代搜索下降方向与步长获得目标函数的全局或局部最小值.
在迭代获取下降方向的过程中,需要对复合雅克比矩阵进行估计(对于动态跟踪问题,则需要对完全雅克比矩阵进行估计). 针对雅克比矩阵的求取,主要有以下方法.
① Broyden法. 为了避免非线性优化的经典牛顿法中Hesse矩阵的求取难题,通常采用拟牛顿方法构造Hesse矩阵的近似矩阵,使之满足拟牛顿条件[58]. 其中,Broyden法是一种经 典的拟牛顿方法,在ETH结构下的无标定视觉伺服已经得到成功应用[21, 59].
② 递归最小二乘法(recursive least squares,RLS).在Gauss-Newton法求非线性目标函数最小值的架构下,通过如下原则选择目标函数的下降方向:所选下降方向应当使当前时刻误差函数值与此前各个时刻的误差函数值之差的加权和最小.在此基础上可推演出带遗忘因子的递归最小二乘法架构. 文献 [22, 60-63]中,针对固定式相机的无标定动态目标跟踪任务,采用RLS法对雅克比矩阵进行在线估计,并通过实验证明RLS方法相对于Broyden方法有更好的鲁棒性.Piepmeier等[64]针对流体环境中的微型机电系统难以标定、环境容易受到扰动的特点,使用RLS法在线估算流体环境中的磁力驱动微型机器人的图像雅克比矩阵,取得了良好的控制效果.RLS法用于雅克比矩阵在线求取在实际应用中会受到由图像传输、采集、处理等过程带来的时延的影响,可采用局部拟合多项式的方法补偿时延,提高RLS方法的的估计精度[65].
③ 分块的 Broyden法(partitioned Broyden update).对于EIH手眼关系下的无标定目标动态跟踪任务,由于目标图像信息的变化不仅与机器人运动相关,而且与目标自身的运动相关,因此,复合雅克比矩阵已经不能完整地表示图像空间与机器人关节空间的关系.针对这一挑战,可将图像雅克比矩阵扩展成分块矩阵,构成完全雅克比矩阵[20, 22],其中两个分块分别为图像雅克比矩阵与图像变化的时间微分,表征关节空间运动与目标自身运动带来的影响.然后采用与前述RLS法类似的求解方法,获得分块矩阵的迭代公式.
④ 递归Gauss-Newton法.前述的Gauss-Newton框架下的方法,无论是Broyden法还是RLS法,均只对复合雅克比矩阵提出递归估计,而对于控制量即机器人的关节角度没有进行递归估计[18].文献[22]提出一种对雅克比矩阵以及机器人关节角都进行递归估计的方法,该方法将动态Gauss-Newton架构扩展成具有指数权重的递归最小二乘形式,其优化目标为使目标函数的仿射函数在各个历史时刻的函数模值的加权和最小化.
(2) Levenberg-Marquadt法
针对式(5)所示的非线性最小二乘优化问题,前述的Gauss-Newton框架下的方法要求雅克比矩阵列满秩.而另一种最小二乘问题的解决方法:Levenberg-Marquadt法,则可以放宽这一限制. 文献[35-37]提出了一种引入基本矩阵(fundamental matrix)雅克比矩阵估计方法,在ETH结构下,通过极线几何关系与基本矩阵,构造图像雅克比的迭代公式,然后采用Levenberg-Marquadt法,对其图像雅克比进行在线的估计.实验对比证明,相对传统雅克比估计方法,该方法拥有更高运算效率以及鲁棒性.
(3) 基于群体的Broyden法
Gauss-Newton型的非线性优化方法均在一定程度上依赖于割线模型. 例如上文中提到的Broyden法就是割线模型的一种.但Broyden法对噪声相当敏感,其原因主要是因为只考虑与当前时刻相邻的一个控制周期的迭代数据的情况.一种可行的改进思路是:使用多个历史数据进行迭代更新,实现Gauss-Newton法中雅克比矩阵的迭代估计.这种方法称为基于群体的Broyden(BP)迭代方法.实验证明,对于ETH手眼关系下的无标定目标动态跟踪,BP法拥有更高的稳定性与跟踪精度,其性能会随着所选择的历史数据步数的增加而提升,但计算负担会显著增加.如何选择适当的历史步数以权衡性能与计算效率,尚未有定论,目前也是研究热点之一[57, 66].
(4) 残差估计法
Gauss-Newton法非线性最优化的过程中,通常认为Hesse矩阵(即含有二阶导数的残差部分)较小,可以忽略.当残差较大时,这种忽略显然会带来较大的误差. 因此通过对残差的估计也可以有效地提高雅克比矩阵的估计精度.残差估计可以通过使用割线近似的方法来实现[67].此外,Munnae等[68]在机器人趋近于理想位姿之后保留了Hesse矩阵的完全形式,采用启发式准则(heuristic criteria)在Gauss-Newton法与拟牛顿法之间进行切换,以应对大残差问题;赵杰等[69]基于误差函数的仿射模型,采用拟牛顿法对图像雅克比矩阵进行估计,并仿照雅克比矩阵递归公式的割线模型,提出了全局Hesse逆矩阵的估计方法;杨诚等[70]则基于拟牛顿法中的BFGS法,通过直接估计包含残差项的全局Hesse矩阵之逆,简化了直接计算残差项的计算量,并保证了逆矩阵的可逆性.
(5) 回归方法
雅克比矩阵的在线估计问题本质上是建立机器人各个位姿下,图像空间的变化量与关节空间变化量之间的映射关系.在线估计雅克比矩阵实际上是利用某一位姿附近的多组图像空间变化量与对应的关节变化量拟合一个超平面.因此雅克比矩阵的在线估计也可以被视作回归问题,各种回归方法均有应用潜力.
① 传统的最小二乘回归方法. 文献 [71]提出一种局部最小二乘法.其主要的思路是建立一个存储空间,用于记录各个时刻机器人的姿态与对应的目标图像坐标,组成视觉运动数据对(visual motion data pairs). 此后对于任意时刻的机器人姿态,均可以获取该位姿附近的历史视觉运动数据对.求取雅克比矩阵来拟合这些数据实质上是一个超平面拟合问题.将优化目标设置为最小化当前数据对与附近的历史数据对的残差的二范数之和,从而将雅克比矩阵的求取问题转化为最小二乘规划问题.
② 支持向量回归方法. 文献[72]使用支持向量回归(SVR)的方法,使用高斯径向基函数的核函数将关节角度的每一个特征分量非线性映射到图像特征空间,对每个关节角度均构造出一个支持向量回归机,进而得到图像雅克比矩阵的表达式.此方法在EIH和ETH两种手眼关系下的焊接机器人上均进行了试验验证. 文献 [73]提出了基于内核的递归最小二乘法(kernel recursive least squares)用于估计雅克比矩阵.该方法与SVR思路相似,将目标矢量映射到高维空间,然后采用递归最小二乘进行回归.
2.1.2 基于状态估计方法雅克比矩阵对于无标定视觉伺服系统而言,是在不同时刻下,用于描述目标函数空间与机器人关节空间的系统固有属性,因此若将无标定视觉伺服控制系统的雅克比矩阵视作系统的状态参量,采用成熟的状态估计理论对其进行最优估计.
(1) Kalman滤波
Kalman滤波器是一种对理想线性系统在高斯噪声影响下进行的最小方差状态估计,普遍应用于最小二乘条件下的实时状态估计、系统参数辨识、目标跟踪等领域.
最早将经典的Kalman滤波应用于无标定视觉伺服领域的是上海交通大学的苏剑波团队[34]. 其思路是将雅克比矩阵的元素按行串联成列向量,然后将系统开环误差函数改写成Kalman滤波状态方程用于估计雅克比矩阵,并完成了双目视觉ETH手眼关系下的动态目标跟踪. 该团队进一步证明了相对于RLS,基于Kalman滤波的方法拥有更高的鲁棒性与抗干扰能力[19]. 此后,陆续有学者应将此方法扩展到单目EIH结构下的无标定视觉伺服[18, 32, 57],并证明了Kalman滤波估计雅克比矩阵的可控与可观性[74]. 然而经典的Kalman滤波在无标定视觉伺服系统的实际应用中有诸多局限.
首先,经典的Kalman滤波算法高度依赖于噪声的统计特性是否已知.但是实际的机器人视觉任务中,噪声的统计特性通常难以确定的. 未知的噪声统计特性会导致滤波精度的下降甚至发散.因此如何确定过程噪声与观测噪声,一直是制约Kalman滤波从无标定视觉伺服控制理论迈向工程实践的重大障碍.针对kalman滤波算法中噪声模型不精确的难题,可以采用自适应的方法对Kalman滤波的参数进行调校.例如,利用模糊自适应Kalman滤波器在线调节噪声参数,提高动态环境下的矩阵估计精度[75].此方法的缺陷在于滤波器参数的增量难以确定,不适于动态未知环境下的应用,而且模糊逻辑自适应控制器没有统一的设计标准,增加了实际应用难度[76]. 另一种自适应方法是将Sage-Husa自适应Kalman滤波应用于图像雅可比矩阵的在线估计,在线估计和调节滤波参数,提高雅可比矩阵辨识模型的自适应能力[77].此外,将Kalman滤波与智能算法相结合的智能滤波也是雅克比矩阵在线估计的一种方案. 例如,文献 [78]提出一种Kalman神经网络法,利用神经网络法对机器人系统的摄动引起的非线性建模误差以及由于有色噪声引起的噪声统计误差进行在线的估计与补偿,提高Kalman滤波法的稳定性.
Kalman滤波法在实际应用中面临的另一个重大挑战是由于图像传输、采集、处理等过程的时延对估计产生的影响.目前也有不少学者探索其解决方法,如刘文芳等[79]提出不对图像雅可比矩阵和图像特征运动本身进行任何假设,利用Kalman滤波算法估计特征点在图像空间中的位置和速度,进而估计出当前时刻准确的图像雅可比矩阵.王新梅等[80]从图像特征空间的角度进行时延情况下图像雅可比矩阵估计补偿的研究,对Kalman滤波模型进行修正,消除噪声互相关性;并采用多项式拟合的方法获取时延期间的观测向量,对雅克比矩阵、图像空间中的目标状态实现更精确的估计.
此外,除了将Kalman滤波用于雅克比矩阵估计,还可利用其最优估计的特性,直接构造控制器.具体方法是首先使用其他方法(如RLS)进行雅克比矩阵估计,进而使用雅克比矩阵的估计值作为Kalman滤波器的观测矩阵,以关节角度误差作为状态矢量,以图像误差作为观测矢量.这样通过滤波估计可直接得到估计的关节角度误差.Marshall等[15]通过仿真证明,无论是静止目标的定位还是动态目标的跟踪,Kalman滤波控制法拥有比Gauss-Newton法更高的鲁棒性.
值得一提的是,前述基于非线性优化的方法中,用于求取雅克比矩阵的Broyden法以及RLS法,从本质上说,也是一种Kalman滤波器[22],基于此,清华大学 Hao等[18]建立了一个通用的基于状态空间的无标定视觉伺服框架,并将非线性优化方法,如Broyden-Gauss-Newton,Broyden-RLS以及基于群体的Broyden法均转化成了状态空间的表达形式,并与Kalman滤波估计方法进行了系统的比较,得出以下结论:对于静态目标定位以及直线运动等方向变化较少的运动跟踪类型,基于RLS的方法性能更好;对于目标运动方向不断缓慢变化的情形,基于群体的Broyden法有一定的性能优势;而对于的方向突发剧烈变化的运动形式,基于Kalman滤波的方法和基于群体的Broyden法均有较佳的性能.
(2) 粒子滤波
经典Kalman滤波只能应对高斯噪声,而粒子滤波对于非高斯噪声的处理能力,使其成为无标定条件下视觉伺服控制的一种潜在可行方法.
针对非高斯噪声的情况,同样可以将雅克比矩阵的各个分量作为状态向量,然后采用粒子滤波进行雅克比估计[20]. 进一步,若采用模糊自适应粒子滤波,通过设计模糊规则,根据估计误差的大小,自适应的调整粒子数量,实现更快的收敛速度与更高的跟踪精度[81]. 不过粒子滤波需要知道实际系统噪声的分布特性,从目前的文献情况来看,通常需要假设一种特定形式的非高斯噪声,并没有应用于实际系统中[76].
Music等[57]也对动态Broyden-Gauss-Newton法、基于群体的Broyden法、Kalman滤波法以及粒子滤波法进行了系统的对比,得出以下结论:对静态定位以及动态跟踪,粒子滤波在各级噪声条件下都有最高的精度,且轨迹更优,但是计算效率几乎是其他估计方法的6倍;从机械系统动态性能的角度考虑,粒子滤波由于在目标位置附近有振荡特性,因而有最大的跃度(jerk),对于静止或者低速目标跟踪,基于群体的Broyden法的跃度最小,而Kalman滤波在高速物体跟踪时有最低的跃度.
(3) 信息滤波
基于Kalman滤波、模糊自适应Kalman滤波和粒子滤波的图像雅可比矩阵在线估计有一些共同的缺陷,如三者都采用线性近似的模型,并将系统噪声假设为特定的形式(对于Kalman滤波,设为高斯分布;对于粒子滤波,设为特定的非高斯分布).此类线性近似给状态估计算法在无标定视觉伺服的实际应用带来了较大障碍.如果将线性近似环节所产生的模型误差视作系统噪声的一部分,并假设为有界的随机信号,可进一步提高未知环境下的系统估计精度.文献[76]选择基于滤波理论的估计框架,对系统模型进行调整,用鲁棒信息滤波器在线估计图像雅可比矩阵,该滤波算法对任意分布的有界噪声都具有较强的鲁棒性.仿真和实验结果表明,在未知系统噪声的情况下,该算法仍可以实现图像雅可比矩阵的精确估计.
(4) 非线性状态观测
机器人视觉伺服系统是典型的不确定非线性系统,在无标定情况下,不仅包含模型与参数的不确定性,在运行过程中还会受到噪声以及外部干扰的影响.
目前,考虑运动学的无标定视觉伺服控制方法所主要采用的图像雅克比矩阵是基于对非线性系统的局部线性近似原理,模型本身具有一定的误差. 而非线性系统理论方法的完善也为无标定视觉伺服提供了一种新的解决思路.
从控制的观点看,无标定手眼系统可以视作动力学系统,而未知的手眼关系(即随时空变化特性的雅克比矩阵)可以视作未建模动态(unmodeled dynamics),目前已有多种成熟的方法对未建模动态进行估计并在控制系统中进行补偿.
例如,可以将状态观测的思想引入无标定视觉伺服控制中,设计无标定视觉伺服系统的自抗扰控制器(ADRC):针对无标定视觉伺服系统设计扩张状态观测器(ESO),在线估计图像雅克比矩阵以及由于模型不确定性和外界干扰所带来的系统扰动总量,在非线性控制器中进行补偿[82];此外,还可在图像雅克比矩阵中采用非线性映射模型,将这种非线性映射关系视作系统的未建模动态;使用扩展状态观测器对系统的未建模动态以及外部扰动进行估计.针对估计结果,使用非线性状态误差反馈控制原理,设计系统的非线性控制器[83-84];另一种状态观测的思路是应用基于扰动观测器(DOB)的鲁棒控制方法,以同时解决外部干扰与噪声的影响. 此方法将模型不确定性、噪声以及外部干扰均视为等价的扰动,通过一系列的局部区域的图像雅克比描述手眼关系,而雅克比的不确定性则通过基于H$\infty$的控制方案设计的DOB去除,从而形成标称形式的雅克比,避免矩阵奇异与局部最小值[38].
2.1.3 鲁棒估计方法视觉伺服控制的有效性高度依赖于理想图像中的特征与实时获取的图像中的特征之间的一一对应性[85].而实际上,由于图像处理技术无法保证特征点的匹配准确无误,将不可避免地存在特征匹配误差.由于匹配误差产生的异常值(outlier)将会对视觉伺服控制过程产生严重影响.这种异常值出现的原因很多,例如:目标特征的遮挡、目标特征的匹配失误、高速运动时的跟踪误差等[55].
若将机器人的姿态用各关节角度组成的向量表示,则机器人的所有姿态对应的向量可以组成一个空间,称为构型空间(configuration space);将某时刻图像特征的变化用向量表示,则各个时刻的图像特征变化向量可以组成一个视觉空间(visual space).构型空间与视觉空间可以共同组成一个视觉-运动空间(visual-motion configuration)[86].对于无标定的视觉伺服控制而言,前述的匹配误差所产生的异常值可以反映为视觉运动空间中视觉-运动数据对(visual-motion data pair)的异常. 对于特定采样周期内,机器人的运动会带来视觉特征的变化.若在图像处理与特征匹配过程中存在误差,则此周期内的机器人运动与视觉测量数据将无法有效的表征二者的关联,从而出现异常值.此时,如何在异常值存在的情况下,实现雅克比矩阵有效估计,也成为无标定视觉伺服控制研究的一个前沿问题.
文献[55]提出了一种鲁棒回归方法.该方法针对文献[71]中的局部最小二乘法利用当前视觉运动数据对附近的残差的二范数作为目标函数对噪声敏感的缺陷,提出了使用M 估计器(M-estimator)调整目标函数的方法. 该方法的核心在于M 估计器的设计.对于局部最小二乘法而言,M估计器是简单的二次函数,即当前机器人位姿附近的所有数据,无论残差大小,对于估计结果的有相同权重的影响. 而文章选择的Geman-McClure估计器,通过其影响函数(influence function)与权重函数(weight function),对不同的视觉-运动数据对进行权重分配,从而实现对于超平面的鲁棒拟合,显著的降低偏差较为严重的数据对于雅克比矩阵计算的影响,最终达到提升对异常值鲁棒性的目的.此方法的另一大优势是,随着机器人的运行,数据对不断增加,其雅克比矩阵的估算精度会不断提高.此方法不仅在IBVS的目标函数下效果显著,也可以用于诸如基于三视张量的视觉伺服中[42],体现了良好的扩展性.
此外文献[36]提出了雅克比计算可靠性系数的概念,对当前控制周期之前的多个周期中对应的视觉运动数据对进行计算可靠性分析,并选择其中可靠度较高的视觉运动对进行雅克比计算.
2.2 考虑机器人动力学的无标定视觉伺服从控制的角度来看,纯运动学的控制由于忽略了非线性力,很难保证机器人控制动力学性能与稳定性. 因此考虑机器人动力学的视觉伺服也成为视觉伺服领域的重要研究方向.
对于动力学无标定视觉伺服而言,关联图像空间与机器人关节空间的图像(复合)雅克比矩阵同样重要. 不同于运动学无标定视觉伺服方法中常用的雅克比矩阵数值化估计的方法,动力学无标定视觉伺服通常采用各种自适应算法对包括相机内参在内的系统参数进行在线辨识[14],其整体思路相对而言更倾向于解析的雅克比矩阵的获取. 在获取系统参数后,可设计自适应控制律进行控制,采用李雅普诺夫法进行控制律稳定性的分析[10, 27, 87-90]. 此外,通过对图像雅克比矩阵的解析式进行分析可以看出,除了相机内参未知以外,目标特征在笛卡尔空间中的深度信息也是无法直接获取的. 如何处理包括深度信息在内的各种系统参数的不确定性也一直是动力学无标定视觉伺服的重要研究内容[7, 13, 17, 91].
2.2.1 雅克比自适应估计机器人的动力学自适应控制研究已得到业界的长期广泛关注,已形成相对丰富的理论体系.常见的机器人动力学自适应控制器主要基于机械臂动力学模型中未知参数的线性性[88, 92-94].文献[93-94]分别为机器人运动学和动力学的参数不确定性问题提供了良好的分析框架[95],其主要思路是使用自适应的回归器,在线估计的系统变量,进行雅克比矩阵的自适应估计.对于无标定的视觉伺服系统而言,最为直接的思路就是将上述较为成熟的机器人动力学自适应控制扩展到无标定视觉伺服的动力学自适应控制中.这一思路最大的难点在于,基于图像的视觉伺服系统所采用的图像雅克比矩阵中,深度信息以倒数形式非线性的呈现在控制闭环中,无法满足上述模型中未知参数线性化表述的要求.对此,Cheah等[87, 94]指出,在视觉伺服系统中,当特征点的深度信息保持不变时,则用于描述关节空间与图像空间的动力学系统模型将可以使用未知参数的进行线性化描述,这为自适应控制用于无标定动力学视觉伺服提供了有力的理论支撑.
Cheah等[87]在文献[94]的基础上,率先提出无标定情况下,对深度信息不断变化的目标进行跟踪的动力学视觉伺服方法. 其核心创新点是提出了深度信息的自适应律.根据由图像雅克比矩阵所表征的图像空间与关节空间的开环误差关系,可单独获取深度信息的线性参数表达式.通过构造图像误差与关节速率的滑模矢量,结合动力学模型与图像雅克比矩阵,可构造动力学参数自适应律以及深度信息自适应律.而文献[90]则将上述方法扩展到ETH手眼关系下的静态目标定位问题,并在稳定性分析中考虑了动力学与运动学的不确定性带来的影响.文献[89]应用此方法实现未知物体的表面的跟踪定位,通过无标定视觉伺服技术为机器人动力学控制提供力位控制依据.
此外,文献[96]对自适应参数时的过度参数化问题,提出了两层串联的控制结构:内层结构为确定性等价的自适应控制器,用于稳定快速变化的机器人动力学模型;外层为新型的控制架构,用于处理视觉系统动力学的非线性参数化问题. 文献 [11]提出将开环误差方程改写成未知系统参数的函数形式,进而针对新的误差函数表达形式构造滑模变量,构造自适应律,实现系统参数的在线估计;文献 [97]根据图像雅克比矩阵的表达形式,将相机焦距与深度信息的比值作为参数,并利用EPnP以及UPnP算法,对该比值进行在线估计. 在相机光轴位置与垂直度弱假设的条件下,该方法可以对雅克比进行较好的近似,对标定误差以及视场缩放有着良好的适应性,在无人机的垂直起降控制中体现出良好的性能.
大多数基于图像的视觉伺服控制算法,无论是否有标定,均需要对特征图像的速度进行精确测量,以期通过雅克比矩阵将关节变化与图像误差变化关联起来.但是实际应用过程中,图像误差的获取很容易受到噪声、采样周期过长等内外干扰因素的影响,从而导致视觉伺服任务失败.Cheah等[98]最早对不需要视觉特征变化速度测量的视觉伺服方法进行了研究,在目标的深度信息缓慢变化时实现无标定视觉伺服.Lizarralde等[99]将相机的在线标定问题视作一个多输入多输出(MIMO)的自适应控制问题,并使用模型参考自适应控制(MRAC)方法中的基于SDU分解的方法对此问题进行求解,从而实现模型的在线标定.Wang[100]提出了一种基于非线性观测器的控制方案,在不测量图像空间速度的前提下,实现目标深度变化的三维跟踪.其自适应控制器实现了深度信息、深度无关的运动学模型参数以及动力学参数这3种不同层次的参数不确定性的分离,避免了过度参数化,简化了控制结构.
2.2.2 深度独立雅克比矩阵在考虑动力学的无标定视觉伺服控制中,雅克比矩阵自适应估计通常需要假设深度信息为固定值或者是缓变值,以便于未知系统变量的线性参数化与自适应律对这些变量进行在线估计.此外,从图像雅克比矩阵的表达式分析,其最大的特点就是矩阵的各个元素不是相机内外参数的线性函数,即无法通过未知的相机参数的线性参数化实现自适应控制律的设计.
为克服这一限制,Liu 等[8]针对ETH手眼关系的动力学无标定视觉伺服定位系统提出了深度独立雅克比矩阵的方法.该深度独立雅克比矩阵单独提取与深度信息相关的项,作为一个比例项,故矩阵内部不包含深度信息,从而使未知参数线性的出现在闭环动力学系统中.在对系统未知参数进行估计的过程中,为了实现输出控制,将用于状态控制的Slotine-Li自适应算法与图像误差在线梯度最小下降法结合起来,在线估计未知参数同时实现特征点图像坐标的渐进收敛.在此论文的基础上,Wang等[53]进行了一系列研究,陆续解决了ETH与EIH手眼关系下的静态定位与动态跟踪问题.
Wang等[53]首先将此方法从ETH的静态定位问题扩展到了ETH结构下多个特征点的动态轨迹跟踪问题,且保证了机器人在任务空间中路径的唯一性. 与视觉定位相比,视觉跟踪的自适应算法还保证了深度独立雅可比广义逆矩阵的存在性. 但是文献[53]的自适应控制律中要求使用准确的特征深度信号向量,而实际使用的是估计的特征深度值,因而难以保证系统闭环稳定性.基于此,Liang等[101]提出采用了一个由特征点深度信息估计值定义的向量信号来构造自适应律,保证系统的渐进收敛性.Wang 等[102-103]也针对文献[53]中使用深度估计值代替精确深度信息的问题,提出了新的自适应算法.该算法在估计未知系统参数时,所有已知参数均只与测量值有关,并基于李雅普诺夫法证明了全局稳定性.
此外,针对EIH手眼关系的静态定位问题,Wang等[27]建立了点特征与线特征的深度无关雅克比矩阵,实现了未知系统参数以及目标特征的三维结构的同步估算,完成了静态目标的定位. 进一步,该团队还建立了更一般化的图像特征所对应的深度独立雅克比矩阵的表达形式,给出了能够通过图像特征的未知几何参数对深度独立雅克比矩阵进行线性化描述的情形,并建立新的误差函数对参数进行了估计 [28].
对于无标定动力学视觉伺服在EIH手眼关系下的动态跟踪问题,由于使用基于深度独立图像雅克比矩阵对移动目标进行跟踪时,目标的未知位置在闭环动力学系统中是呈现出线性特征的. Wang等[104]进一步提出一种新的非线性观测器来估计目标在笛卡尔空间的三维运动,并在此基础上设计了基于深度独立雅克比矩阵的动态跟踪控制器.
此外,针对文献[98]提出的不需要视觉特征速度测量的自适应控制器要求目标深度信息缓慢变化的限制条件,Wang等[10]首度提出在无标定且不对目标深度信息作出任何假设的条件下,不测量图像误差变化速度,实现ETH手眼关系下的目标动态跟踪.主要思路是使用图像雅克比矩阵与关节空间的速度对图像空间的速度进行估计,然后使用深度无关雅克比矩阵将估计的图像速度映射到机器人的关节空间,实现机器人的运动控制. 其中未知的系统参数通过自适应估计算法进行估计.此外,在由于外部干扰或系统建模偏差导致关节速度无法测量或者测量误差较大的情况下实现无标定视觉伺服,也引起了部分学者的关注.Hua等[105]在使用深度无关矩阵实现参数线性表达的基础上,采用浸没与不变(immersion and invariance)观测器对关节速度进行观测,在关节速度无法测量的条件下实现机器人动力学无标定视觉伺服.
3 无标定视觉伺服的路径规划由于IBVS与HBVS相对于PBVS,对模型误差与相机标定误差有更高的鲁棒性与局部稳定性,因此更适用于无标定视觉伺服.但是IBVS在应用过程中存在以下缺陷:首先是全局稳定性问题,即初始相机位姿与目标相机位姿相差过大时,系统无法收敛[40];此外,由于利用图像信息设计的控制律没有对相机的空间运动进行直接控制,只能保证图像轨迹的最优,但是空间轨迹往往不理想,由此可能出现障碍物碰撞、超出关节极限位置等情况[43].而HBVS由于是部分基于图像,因此其对图像误差的鲁棒性无法完全获取;同时当相机初始位姿与目标位姿相距过大时,单应矩阵的计算与分解对测量的波动会很敏感,从而带来稳定性与收敛性问题[106].
鉴于上述情况,对视觉伺服系统进行轨迹规划有重大意义.视觉伺服的轨迹规划主要思路就是:在考虑环境与自身结构约束条件的前提下,规划并生成合适的图像轨迹(通常是一系列图像),然后通过IBVS的控制律,控制机器人跟踪所设计的图像轨迹.此思路将单一控制周期内的图像误差细分到足够小,从而能够充分地利用IBVS的优良局部稳定性与鲁棒性[106-107],即便对于较大的初始位姿误差,也能实现稳定控制,且保证空间轨迹的优异性.因此近十年来,大量学者对图像轨迹的生成算法进行了研究.传统的视觉伺服的轨迹规划策略主要是利用相机所获取的视觉信息以及相机模型,完全或部分地重构出当前机器人位姿与目标机器人位姿间的误差,根据此误差在笛卡尔空间中进行轨迹规划,然后再次利用相机模型将规划出的中间位姿对应的假想图像虚拟出来,作为图像轨迹的中间参考点,在此基础上对参考点进行插值,完成图像空间的轨迹规划.最后以图像轨迹作为目标,利用IBVS的方法进行轨迹跟踪[108-112].
在有标定的视觉伺服系统中,对于视觉伺服的轨迹规划而言,相机模型等系统参数的获取至关重要.而在无标定条件下,最大的挑战来自于包括相机模型在内的模型参数不再已知.因此,目前业界对模型参数不精确获取时的视觉伺服轨迹规划研究并不充分,尤其是完全无标定条件下的轨迹规划,依然是一个研究的热门话题.
3.1 轨迹优化问题由于无标定状态下无从获取包括相机模型在内的系统参数,因此只能利用仅有的图像信息完成三维空间的轨迹规划. 最为常见的思路是转化规划空间,将轨迹规划的目标空间从机器人的任务空间(笛卡尔空间)转换到图像空间或者与图像有关的其他空间. 此思路的理论依据是笛卡尔空间与图像空间之间对应的内在几何关系. 如,Mezouar等[106]提出的相机无标定运动轨迹最优化的方法,其总体思路是:根据图像信息可以求取射影单应性矩阵. 从而将笛卡尔空间的轨迹规划问题转化为射影单应性矩阵空间的轨迹规划问题. 先对射影单应性矩阵的取值设置规划约束,获得射影单应性矩阵的矩阵函数,该函数可保证空间轨迹的旋转部分是测地线,而位移部分是直线;然后根据射影单应性矩阵路径获取对应的图像轨迹,最后根据图像轨迹,使用IBVS的控制方法,获得了满意的实验效果. 在文献[106]的基础上,Schramm等[113-116]对EIH手眼关系下,无标定视觉伺服的轨迹规划问题进行了一系列深入的研究. 同样通过射影关系将空间轨迹的约束反映到图像空间. 除了使用射影单应性矩阵(消失点),还可以采用4个不共面的点以及控制初始阶段的由纯平移运动产生的一副附加图像,进而分别计算旋转矩阵的相似矩阵以及平移向量相关的分量,然后对旋转矩阵的相似矩阵进行特征值分解,利用旋转矩阵特征值的性质,设计旋转矩阵的轨迹;利用直线收敛设计平移向量轨迹,最后合成计算出图像轨迹. 与此同时也考虑了视场约束,包括单一特征点约束以及所有特征点约束.
相比于EIH的单目无标定视觉伺服轨迹规划,ETH的单目的视觉伺服轨迹规划除了需要应对由于相机参数未知以及目标位姿与当前位姿的未知性以外,还需要处理相机坐标系与初始机器人末端坐标系相对位姿的未知性[107].
为应对上述问题,Liang等[107]在文献[115]的基础上进行了扩展. 由于无法获取相机参数,所以考虑在射影单应矩阵空间中进行插值. 但是为了获取射影空间的参数,对于EIH结构的单目系统而言,利用由平移运动产生的一副附加图像即可[115];对于ETH结构的双目系统,不需要附加运动即可利用双目视觉的极线几何关系获取[117];对于ETH结构的单目系统,则需要两次附加运动得到两幅附加图像. 通过获取的射影参数,可以直接对旋转运动进行测地线路径的插值,对平移运动进行直线插值,从而可以得到图像特征轨迹,然后使用IBVS对目标轨迹进行跟踪[107].
3.2 障碍规避问题除了轨迹优化以外,机器人工作空间中的障碍物规避、视场约束、关节极限约束等限制条件也是无标定视觉伺服轨迹规划需要应对的一系列挑战.
Shademan等[86]提出在考虑将轨迹规划纳入无标定视觉伺服的同时,实现鲁棒的轨迹规划与视觉伺服控制. 与文献[55]类似,该方法需要建立数据库,数据库中的元素都是视觉-运动空间中的点.不同的是需要建立两个离线数据库:目标数据库与障碍物数据库,分别记录目标与障碍物的图像及对应的构型.路径规划也就是在视觉-运动空间进行规划:通过障碍物数据库与其他的系统约束,可以排除视觉-运动空间中与约束冲突的点,剩余的自由点即可以用于路径规划;随后基于采样的规划器,该规划器是基于快速搜索随机树(rapidly-exploring random tree,RRT)算法,迭代地在相机空间与图像空间进行搜索,快速寻找满足各种约束(如视场范围、关节极限位置、障碍物等)的路径;在寻找到合适的路径后,使用文献[55]中的鲁棒估计方法估计雅克比矩阵,进行轨迹的跟踪.
除了静态定位任务的避障与轨迹规划以外,Fu等[118]针对无标定的机器人动态目标跟踪任务,提出在ETH手眼关系下,实现对静止障碍物的规避,并保证避开障碍物之后机器人可以继续跟踪目标;文献[6]则在此基础上,针对运动的障碍物提出了避障算法.在相机内参数已知而手眼关系未知的情况下,利用双目固定视觉系统以及虚拟阻抗控制器,在跟踪动态目标的过程中,可同时实现对包括人的活动产生的障碍在内的各种运动障碍物的规避,因此在实际生产作业中有广阔的应用前景.
4 研究展望随着科技的不断进步,机器人作业任务将日趋复杂化、多样化. 可以预见,视觉伺服控制技术将成为机器人控制的主要手段之一. 机器人技术也将从专业技术领域逐步渗透到社会生活的各个方面. 因此,在机器人技术的推广过程中,不需要专业标定环节的无标定视觉伺服方法凭借其更高的灵活性与适应性,势必会成为视觉伺服领域最为重要的分支之一. 目前无标定视觉伺服技术虽然取得了较为丰硕的成果,但是远未达到成熟可靠的境界,亟需进一步的深入研究. 结合本文内容分析,笔者认为无标定视觉伺服技术的研究可以从以下方面展开.
(1) 目标函数的创新.目前无标定视觉伺服方法中使用的目标函数,普遍需要从图像中提取特定的信息,如点特征、线特征、图像矩等等.此类方法在精度上和速度上均存在一定缺陷:由于特征提取匹配算法可能出现的错误匹配、漏匹配等问题,易导致视觉伺服控制失败;对于有较高实时性要求的视觉伺服任务而言,图像处理速度也成为限制系统实时性的瓶颈.因此,目前也有学者提出采用非尺度化(nonmetric)[119]、光度测定的(photometric)[120]的图像特征作为视觉伺服控制的目标函数,从而降低目标函数对图像处理的依赖程度. 但从目前的情况来看,尚未在无标定情况下以上述思路进行研究.
(2) 雅克比矩阵估计优化. 雅克比矩阵在机器人运动学、动力学无标定视觉伺服控制中均扮演着核心角色. 目前,雅克比矩阵的估计方式普遍在噪声的自适应处理方面有较多的限制,例如,需要已知噪声形式、鲁棒性不够等,尚未达到在实际生产生活中稳定应用的成熟度. 此外,雅克比矩阵的计算效率与时效性也需进一步提升[19].
(3) 操作对象的自适应性问题. 目前的无标定视觉伺服技术,大部分仍处在实验环境下的算法研究阶段,所选择的目标对象通常是形状规则的刚体. 而在实际应用中,机器人将普遍面临形状随机的可变形操作对象. 例如在手术机器人、康复机器人等生物医疗环境中,要求机器人对柔性目标有更高的适应性. 目前也有学者开展可变形物体的无标定视觉伺服工作[121-122],可以预见,这也是将来无标定视觉伺服领域的热点之一.
(4) 空间轨迹规划问题. 随着未来机器人应用环境的愈发复杂,单纯的轨迹优化以及简单的避障能力将无法满足需求. 因此,无标定视觉伺服在轨迹规划方面的研究应包含以下目标:在完全无标定的情况下,即视觉系统和机器人运动学参数以及手眼关系均不确定的情况下,使机器人通过视觉信息自主的感知工作空间中的形状复杂且运动状态不确定的障碍物,在不需要离线学习或者构建数据库等额外操作的情况下,实现最优化的运动轨迹.
(5) 人工智能控制算法的应用. 人工智能的发展,是机器人行业发展的重要契机.在无标定视觉伺服领域,尽管有一系列智能控制方法的应用尝试[33, 123-125],但是大部分算法需要离线学习过程,从目前的智能算法在无标定视觉伺服领域的应用情况来看,其离线学习训练的成本相对于系统标定的成本而言,有过之而无不及.这就失去了无标定算法在提高使用便捷性方面的重要意义,对于高速发展的机器人行业与日益扩大的应用需求均是重大制约.如何实现在线学习与自我进化,实现无标定、非结构化环境下视觉伺服,也是具有广阔前景的研究方向.
| [1] |
方勇纯. 机器人视觉伺服研究综述[J].
智能系统学报,2008, 3 (2) : 109-114.
( Fang Yongchun. A survey of robot visual servoing[J].
CAAI Transactions on Intelligent Systems,2008, 3 (2) : 109-114.
(in Chinese) ) ( 0) 0)
|
| [2] |
贾丙西, 刘山, 张凯祥, 等. 机器人视觉伺服研究进展: 视觉系统与控制策略[J].
自动化学报,2015, 41 (5) : 861-873.
( Jia Bingxi, Liu Shan, Zhang Kaixiang, et al. Survey on robot visual servo control: vision system and control strategies[J].
Acta Automatica Sinica,2015, 41 (5) : 861-873.
(in Chinese) ) ( 0) 0)
|
| [3] |
李牧. 机器人无标定视觉伺服关键技术的研究. [博士论文]. 哈尔滨: 哈尔滨工业大学, 2008
( Li Mu. Research on robot uncalibrated visual servoing key technique. [PhD Thesis]. Harbin: Harbin Institute of Technology, 2008 (in Chinese)
) ( 0) 0)
|
| [4] |
苏剑波.
机器人无标定手眼协调[M]. 北京: 电子工业出版社, 2010 .
( Su Jianbo.
Uncalibrated Robot Hand-Eye Coordination[M]. Beijing: Publishing House of Electronics Industry, 2010 .
(in Chinese) ) ( 0) 0)
|
| [5] |
辛菁. 机器人无标定视觉伺服控制系统研究. [博士论文]. 西安: 西安理工大学, 2007
( Xin Jing. Research on robot uncalibrated visual servoing control system. [PhD Thesis]. Xi'an: Xi'an University of Technology, 2007 (in Chinese)
) ( 0) 0)
|
| [6] |
Cai C, Somani N, Nair S, et al. Uncalibrated stereo visual servoing for manipulators using virtual impedance control. In: Control Automation Robotics & Vision (ICARCV), 2014 13th International Conference, 2014. 1888-1893
( 0) 0)
|
| [7] |
Liang XW, Wang HS, Liu YH, et al. A unified design method for adaptive visual tracking control of robots with eye-in-hand/fixed camera configuration[J].
Automatica,2015, 59 : 97-105.
DOI: 10.1016/j.automatica.2015.06.018. ( 0) 0)
|
| [8] |
Liu YH, Wang HS, Wang CY, et al. Uncalibrated visual servoing of robots using a depth-independent interaction matrix[J].
IEEE Transactions on Robotics,2006, 22 (4) : 804-817.
DOI: 10.1109/TRO.2006.878788. ( 0) 0)
|
| [9] |
Liu M, Pradalier C, Siegwart R. Visual homing from scale with an uncalibrated omnidirectional camera[J].
IEEE Transactions on Robotics,2013, 29 (6) : 1353-1365.
DOI: 10.1109/TRO.2013.2272251. ( 0) 0)
|
| [10] |
Wang HS, Liu YH, Chen WD. Uncalibrated visual tracking control without visual velocity[J].
IEEE Transactions on Control Systems Technology,2010, 18 (6) : 1359-1370.
( 0) 0)
|
| [11] |
Hua CC, Wang YQ, Guan XP. Visual tracking control for an uncalibrated robot system with unknown camera parameters[J].
Robotics and Computer-Integrated Manufacturing,2014, 30 (1) : 19-24.
DOI: 10.1016/j.rcim.2013.06.002. ( 0) 0)
|
| [12] |
徐德, 谭民, 李原.
机器人视觉测量与控制[M]. 北京: 国防工业出版社, .
( Xu De, Tan Min, Li Yuan.
Visual Measurement and Control for Robots[M]. Beijing: National Defence Industry Press, .
(in Chinese) ) ( 0) 0)
|
| [13] |
Chaumette F, Hutchinson S. Visual servo control. I. Basic approaches[J].
IEEE Robotics & Automation Magazine,2016, 13 (4) : 82-90.
( 0) 0)
|
| [14] |
Cai CX, Dean-Leon E, Mendoza D, et al. Uncalibrated 3D stereo image-based dynamic visual servoing for robot manipulators. In: 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2013, 63-70
( 0) 0)
|
| [15] |
Marshall M, Lipkin H. Kalman filter visual servoing control law. In: 2014 IEEE International Conference on Mechatronics and Automation (ICMA), 2014
( 0) 0)
|
| [16] |
Marshall M, Matthews M, Hu AP, et al. Uncalibrated Visual Servoing for Intuitive Human Guidance of Robots. In: 2012 IEEE International Conference on Robotics and Automation (ICRA), 2012, 4463-4468
( 0) 0)
|
| [17] |
Hutchinson S, Hager GD, Corke PI. A tutorial on visual servo control[J].
IEEE Transactions on Robotics and Automation,1996, 12 (5) : 651-670.
DOI: 10.1109/70.538972. ( 0) 0)
|
| [18] |
Hao M, Sun ZQ. A universal state-space approach to uncalibrated model-free visual servoing[J].
IEEE-ASME Transactions on Mechatronics,2012, 17 (5) : 833-846.
DOI: 10.1109/TMECH.2011.2131149. ( 0) 0)
|
| [19] |
Su J, Zhang Y, Luo Z. Online estimation of image jacobian matrix for uncalibrated dynamic hand-eye coordination[J].
International Journal of Systems, Control and Communications,2008, 1 (1) : 31-52.
DOI: 10.1504/IJSCC.2008.019582. ( 0) 0)
|
| [20] |
Zhao QJ, Zhang LQ, Chen YJ. Online estimation technique for Jacobian matrix in robot visual servo systems. In: IEEE Conference on Industrial Electronics and Applications, 2008. 1270-1275
( 0) 0)
|
| [21] |
Piepmeier JA, McMurray GV, Lipkin H. A dynamic quasi-Newton method for uncalibrated visual servoing. In: IEEE International Conference on Robotics and Automation, New York, 1999. 1595-1600
( 0) 0)
|
| [22] |
Piepmeier JA, Lipkin H. Uncalibrated eye-in-hand visual servoing[J].
International Journal of Robotics Research,2003, 22 (10-11) : 805-819.
( 0) 0)
|
| [23] |
Espiau B, Chaumette F, Rives P. A new approach to visual servoing in robotics[J].
IEEE Transactions on Robotics and Automation,1992, 8 (3) : 313-326.
DOI: 10.1109/70.143350. ( 0) 0)
|
| [24] |
Andreff N, Espiau B, Horaud R. Visual servoing from lines[J].
International Journal of Robotics Research,2002, 21 (8) : 679-699.
DOI: 10.1177/027836402761412430. ( 0) 0)
|
| [25] |
Mahony R, Hamel T. Image-based visual servo control of aerial robotic systems using linear image features[J].
IEEE Transactions on Robotics,2005, 21 (2) : 227-239.
DOI: 10.1109/TRO.2004.835446. ( 0) 0)
|
| [26] |
Malis E, Borrelly JJ, Rives P. Intrinsics-free visual servoing with respect to straight lines. In: 2002 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2002. 384-389
( 0) 0)
|
| [27] |
Wang HS, Liu YH, Zhou DX. Adaptive visual servoing using point and line features with an uncalibrated eye-in-hand camera[J].
IEEE Transactions on Robotics,2008, 24 (4) : 843-857.
DOI: 10.1109/TRO.2008.2001356. ( 0) 0)
|
| [28] |
Liu Y-H, Wang H, Chen W, et al. Adaptive visual servoing using common image features with unknown geometric parameters[J].
Automatica,2013, 49 (8) : 2453-2460.
DOI: 10.1016/j.automatica.2013.04.018. ( 0) 0)
|
| [29] |
Chaumette F. Image moments: A general and useful set of features for visual servoing[J].
IEEE Transactions on Robotics and Automation,2004, 20 (4) : 713-723.
DOI: 10.1109/TRO.2004.829463. ( 0) 0)
|
| [30] |
Tahri O, Chaumette F. Point-based and region-based image moments for visual servoing of planar objects[J].
IEEE Transactions on Robotics,2005, 21 (6) : 1116-1127.
DOI: 10.1109/TRO.2005.853500. ( 0) 0)
|
| [31] |
Tahri O, Mezouar Y, Chaumette F, et al. Decoupled image-based visual servoing for cameras obeying the unified projection model[J].
IEEE Transactions on Robotics,2010, 26 (4) : 684-697.
DOI: 10.1109/TRO.2010.2051593. ( 0) 0)
|
| [32] |
Zhang J, Liu D. Calibration-free and model-independent method for high-DOF image-based visual servoing[J].
Journal of Control Theory and Applications,2013, 11 (1) : 132-140.
DOI: 10.1007/s11768-013-0271-7. ( 0) 0)
|
| [33] |
李优新, 毛宗源, 田联房. 基于图像矩与神经网络的机器人四自由度视觉伺服[J].
控制理论与应用,2009, 26 (10) : 1162-1166.
( Li Youxin, Mao Zongyuan, Tian Lianfang. Visual servoing of 4DOF using image moments and neural network[J].
Control Theory & Applications,2009, 26 (10) : 1162-1166.
(in Chinese) ) ( 0) 0)
|
| [34] |
Qian J, Su JB. Online estimation of image Jacobian matrix by Kalman-Bucy filter for uncalibrated stereo vision feedback. In: IEEE International Conference on Robotics and Automation, 2002
( 0) 0)
|
| [35] |
Pari L, Sebastian JM, Traslosheros A, et al. Image based visual servoing: estimated image Jacobian by using fundamental matrix vs analytic Jacobian[J].
Image Analysis and Recognition,2008, 5112 : 706-717.
DOI: 10.1007/978-3-540-69812-8. ( 0) 0)
|
| [36] |
Sebastian JM, Pari L, Angel L, et al. Uncalibrated visual servoing using the fundamental matrix[J].
Robotics and Autonomous Systems,2009, 57 (1) : 1-10.
DOI: 10.1016/j.robot.2008.04.002. ( 0) 0)
|
| [37] |
Pari L, Sebastian JM, Traslosheros A, et al. A comparative study between analytic and estimated image jacobian by using a stereoscopic system of cameras. In: IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems (IROS 2010), 2010: 6208-6215
( 0) 0)
|
| [38] |
Ma Z, Su J. Robust uncalibrated visual servoing control based on disturbance observer. In: ISA Transactions, 2015
( 0) 0)
|
| [39] |
Cai CX, Dean-Leon E, Somani N, et al. 6D image-based visual servoing for robot manipulators with uncalibrated stereo cameras. In: 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (Iros 2014), 2014. 736-742
( 0) 0)
|
| [40] |
Chaumette F. Potential problems of stability and convergence in image-based and position-based visual servoing. In: The Confluence of Vision and Control, Springer, 1998. 66-78
( 0) 0)
|
| [41] |
Marey M, Chaumette F. Analysis of classical and new visual servoing control laws. In: 2008 IEEE International Conference on Robotics and Automation, 2008. 3244-3249
( 0) 0)
|
| [42] |
Shademan A, Jagersand M. Three-view uncalibrated visual servoing. In: IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems (IROS 2010), 2010
( 0) 0)
|
| [43] |
Kazemi M, Gupta K, Mehrandezh M. Path-planning for visual servoing: A review and issues. In: Visual Servoing via Advanced Numerical Methods, Springer, 2010: 189-207
( 0) 0)
|
| [44] |
Corke PI, Hutchinson SA. A new partitioned approach to imagebased visual servo control[J].
IEEE Transactions on Robotics and Automation,2001, 17 (4) : 507-515.
DOI: 10.1109/70.954764. ( 0) 0)
|
| [45] |
Malis E, Chaumette F, Boudet S. 2-1/2-D visual servoing[J].
IEEE Transactions on Robotics and Automation,1999, 15 (2) : 238-250.
DOI: 10.1109/70.760345. ( 0) 0)
|
| [46] |
Malis E, Chaumette F. 2 1/2 D visual servoing with respect to unknown objects through a new estimation scheme of camera displacement[J].
International Journal of Computer Vision,2000, 37 (1) : 79-97.
DOI: 10.1023/A:1008181530296. ( 0) 0)
|
| [47] |
Malis E, Chaumette F. Theoretical improvements in the stability analysis of a new class of model-free visual servoinor methods[J].
IEEE Transactions on Robotics and Automation,2002, 18 (2) : 176-186.
DOI: 10.1109/TRA.2002.999646. ( 0) 0)
|
| [48] |
Chen J, Behal A, Dawson DM, et al. Adaptive visual servoing in the presence of intrinsic calibration uncertainty. In: 42nd IEEE Conference on Decision and Control, New York, 2003. 5396-5401
( 0) 0)
|
| [49] |
Fang Y, Dixon WE, Dawson DM, et al. An exponential class of model-free visual servoing controllers in the presence of uncertain camera calibration. In: 2003 Proceedings 42nd IEEE Conference, the Decision and Control, 2003
( 0) 0)
|
| [50] |
Hu G, MacKunis W, Gans N, et al. Homography-based visual servocontrol via an uncalibrated camera. In: 2008 American Control Conference, New York, 2008. 4791-4796
( 0) 0)
|
| [51] |
Hu G, MacKunis W, Gans N, et al. Homography-based visual servo control with imperfect camera calibration[J].
IEEE Transactions on Automatic Control,2009, 54 (6) : 1318-1324.
DOI: 10.1109/TAC.2009.2015541. ( 0) 0)
|
| [52] |
Hu G, Dixon WE, Gupta S, et al. A quaternion formulation for homography-based visual servo control. In: 2006 IEEE International Conference on Robotics and Automation. New York, 2006. 2391-2396
( 0) 0)
|
| [53] |
Wang HS, Liu YH, Zhou DX. Dynamic visual tracking for manipulators using an uncalibrated fixed camera[J].
IEEE Transactions on Robotics,2007, 23 (3) : 610-617.
DOI: 10.1109/TRO.2007.895091. ( 0) 0)
|
| [54] |
熊有伦.
机器人技术基础. 武汉: 华中科技大学出版社[M]. 1996 .
( Xiong Youlun.
Fundamentals of Robot Techniques[M]. Wuhan: Huazhong University of Science and Technology Press, 1996 .
(in Chinese) ) ( 0) 0)
|
| [55] |
Shademan A, Farahmand AM, Jägersand M. Robust jacobian estimation for uncalibrated visual servoing. In: 2010 IEEE International Conference on the Robotics and Automation (ICRA), 2010
( 0) 0)
|
| [56] |
Janabi-Sharifi F, Deng LF, Wilson WJ. Comparison of basic visual servoing methods[J].
IEEE-ASME Transactions on Mechatronics,2011, 16 (5) : 967-983.
DOI: 10.1109/TMECH.2010.2063710. ( 0) 0)
|
| [57] |
Music J, Bonkovic M, Cecic M. Comparison of uncalibrated modelfree visual servoing methods for small-amplitude movements: a simulation study[J].
International Journal of Advanced Robotic Systems,2014, 11 (1) : 1-16.
( 0) 0)
|
| [58] |
王宜举, 修乃华.
非线性最优化理论与方法[M]. 北京: 科学出版社, 2012 .
( Wang Yiju, Xiu Laihua.
Nonlinear Optimization Theory and Method[M]. Beijing: Science Press, 2012 .
(in Chinese) ) ( 0) 0)
|
| [59] |
Jägersand M, Fuentes O, Nelson R. Experimental evaluation of uncalibrated visual servoing for precision manipulation. In: Proceedings of 1997 IEEE International Conference, the Robotics and Automation, 1997
( 0) 0)
|
| [60] |
Piepmeier JA, McMurray GV, Lipkin H. Uncalibrated dynamic visual servoing[J].
IEEE Transactions on Robotics and Automation,2004, 20 (1) : 143-147.
DOI: 10.1109/TRA.2003.820923. ( 0) 0)
|
| [61] |
Piepmeier JA, McMurray GV, Lipkin H. Experimental results using vision-based control for uncalibrated robotic systems. In: Proceedings of the Photonics East'99, 1999
( 0) 0)
|
| [62] |
Hosoda K, Asada M. Versatile visual servoing without knowledge of true Jacobian. In: Proceedings of the Intelligent Robots and Systems' 94'Advanced Robotic Systems and the Real World, 1994
( 0) 0)
|
| [63] |
Munnae J, Lipkin H. Kinematic robot tracking using uncalibrated cameras. In: 13th World Congress in Mechanism and Machine Science, 2011
( 0) 0)
|
| [64] |
Piepmeier JA, Firebaugh S, Olsen CS. Uncalibrated visual servo control of magnetically actuated microrobots in a fluid environment[J].
Micromachines,2014, 5 (4) : 797-813.
DOI: 10.3390/mi5040797. ( 0) 0)
|
| [65] |
高振东, 苏剑波. 带有时延补偿的图像雅可比矩阵估计方法[J].
控制理论与应用,2009, 26 (1) : 23-27.
( Gao Zhendong, Su Jianbo. The estimation of image Jacobian matrix with time-delay compensation for uncalibrated visual servoing[J].
Control Theory & Applications,2009, 26 (1) : 23-27.
(in Chinese) ) ( 0) 0)
|
| [66] |
Bonkovic M, Hace A, Jezernik K. Population-based uncalibrated visual servoing[J].
IEEE-ASME Transactions on Mechatronics,2008, 13 (3) : 393-397.
DOI: 10.1109/TMECH.2008.924135. ( 0) 0)
|
| [67] |
Kim GW. Uncalibrated visual servoing through the efficient estimation of the image jacobian for large residual[J].
Journal of Electrical Engineering & Technology,2013, 8 (2) : 385-392.
( 0) 0)
|
| [68] |
Munnae J. Uncalibrated robotic visual servo tracking for large residual problems. [PhD Thesis]. Georgia Institute of Technology, 2010
( 0) 0)
|
| [69] |
赵杰, 李牧, 李戈, 等. 一种无标定视觉伺服控制技术的研究[J].
控制与决策,2006, 21 (9) : 1015-1019.
( Zhao Jie, Li Mu, Li Ge, et al. Study on uncalibrated visual servoing technique[J].
Control and Decision,2006, 21 (9) : 1015-1019.
(in Chinese) ) ( 0) 0)
|
| [70] |
杨诚, 匡森, 宋彩温. 基于动态BFGS 法的无标定视觉伺服控制[J].
中国科学技术大学学报,2015, 45 (1) : 1-8.
( Yang Cheng, Kuang Sen, Song Caiwen. Dynamic BFGS method for uncalibrated visual servoing[J].
Journal of University of Science and Technology of China,2015, 45 (1) : 1-8.
(in Chinese) ) ( 0) 0)
|
| [71] |
Farahmand AM, Shademan A, Jagersand M. Global visual-motor estimation for uncalibrated visual servoing. In: 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007. 1975-1980
( 0) 0)
|
| [72] |
李鹤喜, 石永华, 王国荣. 采用SVR 雅可比估计器的焊接机器人视觉导引[J].
华南理工大学学报(自然科学版),2013, 41 (7) : 19-25.
( Li Hexi, Shi Yonghua, Wang Guorong. Vision-guided welding robot based on SVR-Jacobian estimator[J].
Journal of South China University of Technology (Natural Science Edition),2013, 41 (7) : 19-25.
(in Chinese) ) ( 0) 0)
|
| [73] |
Kale A, Meena ML, Gopal M. Kernel machines for uncalibrated visual servoing of robots. In: 2013 IEEE International Symposium on Intelligent Control, 2013. 364-369
( 0) 0)
|
| [74] |
Liu SQ, Liu SY. Online-estimation of image jacobian based on adaptive Kalman filter. In: Proceedings of the Control Conference, 2015
( 0) 0)
|
| [75] |
Lü XD, Huang XH. Fuzzy adaptive Kalman filtering based estimation of image Jacobian for uncalibrated visual servoing. In: 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2006. 2167-2172
( 0) 0)
|
| [76] |
张捷, 刘丁. 基于鲁棒信息滤波器的图像雅可比矩阵在线估计[J].
西安理工大学学报,2011, 27 (2) : 133-138.
( Zhang Jie, Liu Ding. Online estimation of image jacobian matrix based on robust information filter[J].
Journal of Xi'an University of Technology,2011, 27 (2) : 133-138.
(in Chinese) ) ( 0) 0)
|
| [77] |
辛菁, 白蕾, 刘丁. 基于自适应Kalman 滤波的机器人6DOF 无标定视觉定位[J].
系统仿真学报,2014, 26 (3) : 586-591.
( Xin Jing, Bai Lei, Liu Ding. Adaptive Kalman filter-based robot 6DOF uncalibrated vision positioning[J].
Journal of System Simulation,2014, 26 (3) : 586-591.
(in Chinese) ) ( 0) 0)
|
| [78] |
Zhong XG, Zhong XY, Peng XF. Robots visual servo control with features constraint employing Kalman-neural-network filtering scheme[J].
Neurocomputing,2015, 151 : 268-277.
DOI: 10.1016/j.neucom.2014.09.043. ( 0) 0)
|
| [79] |
刘文芳, 邴志刚, 卢胜利, 等. 带时延补偿的图像雅可比矩阵在线估计方法[J].
计算机工程与应用,2010, 46 (21) : 181-184.
( Liu Wenfang, Bing Zhigang, Lu Shengli, et al. Online estimation of image Jacobian matrix with time-delay compensation[J].
Computer Engineering and Applications,2010, 46 (21) : 181-184.
(in Chinese) ) ( 0) 0)
|
| [80] |
王新梅, 魏武, 刘玮, 等. 鲁棒卡尔曼滤波下的图像雅可比矩阵带时延补偿的估计[J].
控制理论与应用,2015, 32 (8) : 1052-1057.
( Wang Xinmei, Wei Wu, Liu Wei, et al. Estimation of image Jacobian matrix with time-delay compensation based on robust Kalman filtering[J].
Control Theory & Applications,2015, 32 (8) : 1052-1057.
(in Chinese) ) ( 0) 0)
|
| [81] |
Ma J, Zhao Q. Robot visual servo with fuzzy particle filter[J].
Journal of Computers,2012, 7 (4) : 842-845.
( 0) 0)
|
| [82] |
Su JB, Ma HY, Qiu WB, et al. Task-independent robotic uncalibrated hand-eye coordination based on the extended state observer[J].
IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics,2004, 34 (4) : 1917-1922.
DOI: 10.1109/TSMCB.2004.827615. ( 0) 0)
|
| [83] |
Su JB, Qiu WB, Ma HY, et al. Calibration-free robotic eye-hand coordination based on an auto disturbance-rejection controller[J].
IEEE Transactions on Robotics and Automation,2004, 20 (5) : 899-907.
DOI: 10.1109/TRO.2004.829458. ( 0) 0)
|
| [84] |
Su JB. Convergence analysis for the uncalibrated robotic hand-eye coordination based on the unmodeled dynamics observer[J].
Robotica,2010, 28 : 597-605.
DOI: 10.1017/S0263574709990270. ( 0) 0)
|
| [85] |
Comport AI, Marchand E, Chaumette F. Statistically robust 2-D visual servoing[J].
IEEE Transactions on Robotics,2006, 22 (2) : 416-421.
( 0) 0)
|
| [86] |
Shademan A, Jagersand M. Robust sampling-based planning for uncalibrated visual servoing. In: 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2012. 2663-2669
( 0) 0)
|
| [87] |
Cheah CC, Liu C, Slotine JJE. Adaptive vision based tracking control of robots with uncertainty in depth information. In: Proceedings of the 2007 IEEE International Conference on Robotics and Automation, 2007. 2817-2822
( 0) 0)
|
| [88] |
Dixon WE. Adaptive regulation of amplitude limited robot manipulators with uncertain kinematics and dynamics[J].
IEEE Transactions on Automatic Control,2007, 52 (3) : 488-493.
DOI: 10.1109/TAC.2006.890321. ( 0) 0)
|
| [89] |
Cheah CC, Hou SP, Zhao Y, et al. Adaptive vision and force tracking control for robots with constraint uncertainty[J].
IEEE-ASME Transactions on Mechatronics,2010, 15 (3) : 389-399.
DOI: 10.1109/TMECH.2009.2027115. ( 0) 0)
|
| [90] |
Cheah CC, Liu CA, Slotine JJE. Adaptive Jacobian vision based control for robots with uncertain depth information[J].
Automatica,2010, 46 (7) : 1228-1233.
DOI: 10.1016/j.automatica.2010.04.009. ( 0) 0)
|
| [91] |
Chaumette F, Hutchinson S. Visual servo control. II. Advanced approaches[J].
IEEE Robotics & Automation Magazine,2007, 14 (1) : 109-118.
( 0) 0)
|
| [92] |
Braganza D, Dixon WE, Dawson DM, et al. Tracking control for robot manipulators with kinematic and dynamic uncertainty[J].
International Journal of Robotics & Automation,2008, 23 (2) : 117-126.
( 0) 0)
|
| [93] |
Cheah CC, Liu C, Slotine J. Adaptive Jacobian tracking control of robots with uncertainties in kinematic, dynamic and actuator models[J].
IEEE Transactions on Automatic Control,2006, 51 (6) : 1024-1029.
DOI: 10.1109/TAC.2006.876943. ( 0) 0)
|
| [94] |
Cheah CC, Liu C, Slotine JJE. Adaptive tracking control for robots with unknown kinematic and dynamic properties[J].
International Journal of Robotics Research,2006, 25 (3) : 283-296.
DOI: 10.1177/0278364906063830. ( 0) 0)
|
| [95] |
梁新武. 机械手无标定动态视觉伺服研究. [博士论文]. 武汉: 华中科技大学, 2011
( Liang Xinwu. Research on the unealibrated dynamic visual servoing of robotic manipulator. [PhD Thesis]. Wuhan: Huazhong University of Science and technology, 2011 (in Chinese)
) ( 0) 0)
|
| [96] |
Akella MR. Vision-based adaptive tracking control of uncertain robot manipulators[J].
IEEE Transactions on Robotics,2005, 21 (4) : 748-753.
( 0) 0)
|
| [97] |
Santamaria-Navarro A, Andrade-Cetto J. Uncalibrated image-based visual servoing. In: 2013 IEEE International Conference on Robotics and Automation (ICRA), 2013, 5247-5252
( 0) 0)
|
| [98] |
Cheah CC, Liu C, Slotine J. Adaptive Jacobian tracking control of robots based on visual task-space information. In: Proceedings of 2005 IEEE International Conference the Robotics and Automation, 2005
( 0) 0)
|
| [99] |
Lizarralde F, Leite AC, Hsu L, et al. Adaptive visual servoing scheme free of image velocity measurement for uncertain robot manipulators[J].
Automatica,2013, 49 (5) : 1304-1309.
DOI: 10.1016/j.automatica.2013.01.047. ( 0) 0)
|
| [100] |
Wang HL. Adaptive visual tracking for robotic systems without image-space velocity measurement[J].
Automatica,2015, 55 : 294-301.
DOI: 10.1016/j.automatica.2015.02.029. ( 0) 0)
|
| [101] |
Liang XW, Huang XH, Wang M, et al. Improved stability results for visual tracking of robotic manipulators based on the depthindependent interaction matrix[J].
IEEE Transactions on Robotics,2011, 27 (2) : 371-379.
DOI: 10.1109/TRO.2011.2106331. ( 0) 0)
|
| [102] |
Wang H, Liu YH, Chen W. Visual tracking of robots in uncalibrated environments[J].
Mechatronics,2012, 22 (4) : 390-397.
DOI: 10.1016/j.mechatronics.2011.09.006. ( 0) 0)
|
| [103] |
Wang HS, Jiang MK, Chen WD, et al. Visual servoing of robots with uncalibrated robot and camera parameters[J].
Mechatronics,2012, 22 (6) : 661-668.
DOI: 10.1016/j.mechatronics.2011.05.007. ( 0) 0)
|
| [104] |
Wang HS, Liu YH, Chen WD, et al. A new approach to dynamic eye-in-hand visual tracking using nonlinear observers[J].
IEEE-ASME Transactions on Mechatronics,2011, 16 (2) : 387-394.
DOI: 10.1109/TMECH.2009.2039941. ( 0) 0)
|
| [105] |
Hua CC, Liu YJ, Yang YA. Image-based robotic control with unknown camera parameters and joint velocities[J].
Robotica,2015, 33 (8) : 1718-1730.
DOI: 10.1017/S0263574714001015. ( 0) 0)
|
| [106] |
Mezouar Y, Chaumette F. Optimal camera trajectory with imagebased control[J].
International Journal of Robotics Research,2003, 22 (10-11) : 781-803.
( 0) 0)
|
| [107] |
Liang XW, Huang XH, Min W. Uncalibrated path planning in the image space for the fixed camera configuration[J].
Acta Automatica Sinica,2013, 39 (6) : 759-769.
DOI: 10.1016/S1874-1029(13)60053-1. ( 0) 0)
|
| [108] |
Chesi G, Hung YS. Global path-planning for constrained and optimal visual servoing[J].
IEEE Transactions on Robotics,2007, 23 (5) : 1050-1060.
DOI: 10.1109/TRO.2007.903817. ( 0) 0)
|
| [109] |
Chesi G, Prattichizzo D, Vicino A. Straight line path-planning in visual servoing[J].
Journal of Dynamic Systems Measurement and Control-Transactions of the ASME,2007, 129 (4) : 541-543.
DOI: 10.1115/1.2745882. ( 0) 0)
|
| [110] |
Deng LF, Janabi-Sharifi F, Wilson WJ. Hybrid motion control and planning strategies for visual servoing[J].
IEEE Transactions on Industrial Electronics,2005, 52 (4) : 1024-1040.
DOI: 10.1109/TIE.2005.851651. ( 0) 0)
|
| [111] |
Mezouar Y, Chaumette F. Path planning for robust image-based control[J].
IEEE Transactions on Robotics and Automation,2002, 18 (4) : 534-549.
DOI: 10.1109/TRA.2002.802218. ( 0) 0)
|
| [112] |
Allotta B, Fioravanti D. 3D motion planning for image-based visual servoing tasks. In: 2005 IEEE International Conference on Robotics and Automation (ICRA), 2005. 2173-2178
( 0) 0)
|
| [113] |
Schramm F, Morel G. A calibration free analytical solution to image points path planning that ensures visibility. In: Proceedings of International Conference on the Robotics and Automation, 2004
( 0) 0)
|
| [114] |
Schramm F, Micaelli A, Morel G. Calibration free path planning for visual servoing yielding straight line behaviour both in image and work space. In: 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2005. 2688-2693
( 0) 0)
|
| [115] |
Schramm F, Morel G. Ensuring visibility in calibration-free path planning for image-based visual servoing[J].
IEEE Transactions on Robotics,2006, 22 (4) : 848-854.
DOI: 10.1109/TRO.2006.878955. ( 0) 0)
|
| [116] |
Schramm F, Ge ard F, Morel G, et al. Calibration free image point path planning simultaneously ensuring visibility and controlling camera path. In: Proceedings of the IEEE International Conference on Robotics and Automation, 2007
( 0) 0)
|
| [117] |
Park JS, Chung MJ. Path planning with uncalibrated stereo rig for image-based visual servoing under large pose discrepancy[J].
IEEE Transactions on Robotics and Automation,2003, 19 (2) : 250-258.
DOI: 10.1109/TRA.2003.808861. ( 0) 0)
|
| [118] |
Fu QS, Zhang ZS, Shi JF, et al. Uncalibrated visual servoing with obstacle avoidance using SQP method. In: 2009 IEEE International Conference on Mechatronics and Automation, 2009. 2031-2036
( 0) 0)
|
| [119] |
Silveira G. On intensity-based nonmetric visual servoing[J].
IEEE Transactions on Robotics,2014, 30 (4) : 1019-1026.
DOI: 10.1109/TRO.2014.2315712. ( 0) 0)
|
| [120] |
Bakthavatchalam M, Chaumette F, Tahri O. An improved modelling scheme for photometric moments with inclusion of spatial weights for visual servoing with partial appearance/disappearance. In: Proceedings of the IEEE Int Conf on Robotics and Automation, 2015
( 0) 0)
|
| [121] |
Navarro-Alarcon D, Liu YH, Romero JG, et al. On the visual deformation servoing of compliant objects: Uncalibrated control methods and experiments[J].
International Journal of Robotics Research,2014, 33 (11) : 1462-1480.
DOI: 10.1177/0278364914529355. ( 0) 0)
|
| [122] |
Navarro-Alarcon D, Liu YH, Romero JG. Model-free visually servoed deformation control of elastic objects by robot manipulators[J].
IEEE Transactions on Robotics,2013, 29 (6) : 1457-1468.
DOI: 10.1109/TRO.2013.2275651. ( 0) 0)
|
| [123] |
Kumar S, Behera L. Implementation of a neural network based visual motor control algorithm for a 7 DOF redundant manipulator. In: 2008 IEEE International Joint Conference on Neural Networks, 2008. 1344-1351
( 0) 0)
|
| [124] |
Su JB. Performance analysis of neural network-based uncalibrated hand-eye coordination. In: Advances in Neural Networks-ISNN 2005, 2005, 3498: 222-227
( 0) 0)
|
| [125] |
李优新. 机器人无标定视觉伺服的多种智能控制方法研究. [博士论文]. 广州: 华南理工大学, 2009
( Li Youxin. Research on robot uncalibrated visual servoing system based on multi-intellegent control methods. [PhD Thesis]. Guangzhou: South China University of Technology, 2009 (in Chinese)
) ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48
