对于传统的高超声速激波风洞，由于其瞬态流场和极短的有效试验时间(一般500 $\mu$s$\sim$20 ms)^{[1, 2, 3, 4]}，模型-天平-支撑(model-balance-support,MBS)系统的机械振动被激起并且在试验时间内不能通过阻尼特性快速衰减掉.因此，在有效试验时间内，为了得到较好的测力结果，测力支撑系统的低频振动信号应至少具有5个以上的周期^[2].对于试验时间在几毫秒的典型激波风洞，可能最低频率在1 000 Hz以上才能确保试验结果具有较好的精度.因为高频率的信号可以采取直接平均处理，从而避免应用诸如惯性补偿等更加复杂的方法对信号进行人为干预.针对以上的技术难题，为了在高超声速风洞测力试验中得到更高精度的测量结果，很多测力天平专家也提出了多类采用特种天平(加速度计天平^{[5, 6, 7]}、应力波天平^[8]及其混合技术天平^{[9, 10]}等)进行脉冲式风洞气动力测量的技术，并且以上特种天平技术所针对的风洞均为短试验时间的情况.

对于有效试验时间极短的脉冲型风洞，如激波风洞，应变天平的使用遇到了瓶颈.中国科学院力学研究所复现高超声速激波风洞JF12的建成在某种程度上缓解了这个难题，使得我们可以再次考虑应变天平在动态测力中的应用.JF12长试验时间激波风洞突破了毫秒级试验时间的技术难题，使得有效试验时间超过100 ms，同时其具有复现高空高超声速真实飞行条件的能力^[11].基于其较长的有效试验时间，我们认为一个具有优化结构测力单元的应变天平可以保证输出足够周期的天平信号，从而得到满足要求的测力结果.因此，对于JF12长试验时间激波风洞的气动力测量试验，我们仍考虑采用传统的应变计天平，其中主要是基于应变天平技术较为成熟，结构简单并且成本低廉^{[12, 13, 14, 15, 16]}.但是，传统的内置应变天平的结构刚度是很难保证信号有足够的处理周期的.

针对这个难题，我们优化设计天平的测力单元结构以适用于这种脉冲型动态测力试验，并相应提出一套有限元结构优化方案^[17]. 针对JF12长试验时间激波风洞，我们加工制造了大刚度、高灵敏度的系列脉冲型应变天平，结构形式包含了杆式和盒式，最大载荷从1 kN到30 kN，同时具备尾式支撑和背式支撑两种测力模型的支撑形式，以满足不同尺度、不同外形的飞行器测力试验需求.同时，应用不同尺度的标模对研制的脉冲型天平，在JF12激波风洞进行了动态测力试验^[18]，其试验结果与常规高超声速风洞的测力数据具有较好的一致性，JF12系列脉冲型天平均表现出优异的结构特性和测力性能.

中科院力学所高温气体动力学国家重点实验室历时四年多，研制成功了JF12复现高超声速飞行条件激波风洞，应用其进行气动力测量将可以满足越来越迫切的高超声速研究高端测力试验的需求^{[19, 20]}.JF12激波风洞的运行特点为可复现25$\sim $ 50 km高空马赫数5$\sim$9的飞行，喷管出口直径为1.5 m或2.5 m，试验气体为纯净空气并且有效试验时间超过了100 ms.风洞主体结构全长约280 m，包括爆轰驱动段、激波管段、喷管(喉道可更换)、试验段、真空段和卸爆段等主体部分，爆轰驱动段与激波管段、激波管段与喷管、爆轰驱动段与卸爆段之间分别由三道不同的膜片隔开.该风洞利用了反向爆轰驱动技术^[21]，驱动能力强，同时集成应用一系列的延长试验时间的创新技术^{[22, 23, 24]}，从而实现了高超声速飞行器地面试验的复现能力，为我国重大工程项目关键技术研究和高温气体动力学基础研究提供了可靠的地面试验手段.图1为JF激波风洞.

图1(Fig.1)

图1 JF12长试验时间激波风洞 Fig.1 JF12 long-test duration shock tunnel

对于应用激波风洞进行气动力测量试验，目前仍然存在诸多未解决的关键技术问题^{[25, 26]}. JF12高超声速激波风洞由于流场瞬时建立，在进行气动力试验时，较大的冲击载荷使模型-天平-支撑系统受到充分激励，从而产生瞬态冲击载荷,激发起模型、测力元件、支撑系统及风洞部件的振动，这种振动必然会对测力元件输出信号产生干扰^[27].惯性干扰力与真实气动力混杂在一起，甚至完全覆盖气动力，大大降低试验精准度，出现气动信号无法使用的情况，给激波风洞气动力测量带来了较大困难，使得试验模型的尺度、质量也受到极大的限制^[28].因此，应用激波风洞进行测力试验仍存在诸多难题，尤其对于大尺寸、较重模型的测力试验，更是鲜有相关技术报道和文章发表.因此，探索新型结构天平和实施方案，设计优化专用应变天平才可以充分发挥JF12激波风洞的特长，大大提高这种脉冲风洞气动力测量结果的精准度.同时，基于对冲击振动载荷进行的系统的理论、数值及试验(模态)分析结果，可以对模型-天平-支撑系统进行试验前的预评估，这将大大改善和提高测力结果的精确度.

根据JF12激波风洞的运行特点及来流参数，加工制造了JF12系列脉冲型应变天平(见图2)，这些天平具有刚度大、灵敏度高、分量间干扰小等特点，实现应变计测力传感器在脉冲型风洞的有效应用. 应变天平结构形式为杆式和盒式两种.其中，杆式天平主要以传统尾部支撑为主，这种支撑结构简单，易于安装拆卸，对模型位置流场干扰相对较小，可适用于绝大多数的常规测力试验要求；盒式天平主要采用背部支撑形式，这种支撑结构最大特点是可以进行重模型(100 kg以上)的测力试验，但是对模型底部位置流场具有一定干扰影响. 背部支撑除了可以应用于重模型的气动力测量试验，也可满足多数非常规测力试验.表1和表2列出了JF12激波风洞目前正在投入使用的系列脉冲型应变天平详细参数和载荷指标.

图2(Fig.2)

图2 JF12系列应变天平照片：(a) S01、S02、S03 (依次从左至右),(b) B01 Fig.2 JF12 series strain-gaged balances: (a) S01,S02,S03,(b) B01

表1(Table 1)

表1 目前投入使用的JF12系列脉冲型应变天平Table 1 Parameters of JF12 series pulse-type strain-gaged balance Serial No. Type Component number Dimension/ mm JF12-ISG3-D053-S01(S01) sting 3 $\Phi 53$ JF12-ISG6-D034-S02(S02) sting 6 $\Phi 34$ JF12-ISG6-D106-S03(S03) sting 6 $\Phi 106$ JF12-ISG6-L315-B01(B01) cassette 6 L315 JF12-ISG6-L600-B02(B02) cassette 6 L600

表1 目前投入使用的JF12系列脉冲型应变天平 Table 1 Parameters of JF12 series pulse-type strain-gaged balance

表2(Table 2)

表2 各天平载荷量程Table 2 Limited loads for JF12 series balances Serial No. Normal force Y/ N Pitching moment Mz/Nm Axial force X/ N Side force Z/N Yawing moment My/ Nm Rolling moment Mx/Nm S01 2 000 100 1 000 --- --- --- S02 1 000 60 500 150 20 10 S03 6 500 1 000 1 000 3 000 150 100 B01 20 000 5 000 7 000 5 000 1 000 1 000 B02 30 000 7 500 10 000 10 000 3 000 1 500

表2 各天平载荷量程 Table 2 Limited loads for JF12 series balances

应变天平的结构设计需要充分考虑多方面的技术问题，比如风洞参数指标、测力系统结构的配合问题、数据采集方案及天平的结构形式等等. 在JF12脉冲型系列天平的设计中，重点考察天平的结构对整体测力性能的影响.从结构特性的观点，集中关注以下几个方面：(1)较低的结构干扰；(2)较大的刚度；(3)在应变计粘贴位置需有较小的应力变化；(4)结构简单化；(5)基于相对较短的运行时间，暂不考虑温度对天平的影响.在这些具体的设计要求中，(1)和(2)为脉冲型天平结构设计中最重要的两个特性，本文对其进行了重点研究和探讨，并利用有限元优化设计方法解决大刚度和高灵敏度的矛盾问题.

关于杆式脉冲型应变天平的优化设计，本文选取S01天平为例进行说明.S01天平为三分量天平，从轴向载荷与法向力载荷的匹配 (见表2)可以看出，主要应用于的高超声速飞行器的气动力测量.法向力和俯仰力矩分量的测量单元结构以"结构简单化"为原则，选取最简单的矩型截面梁结构，并通过有限元优化计算，取得最优长宽比.为了增大天平的整体刚度，采用单侧矩型截面梁结构，其设计相对简单，在这里不再赘述.轴向力单元结构是杆式应变天平六个分量结构中最复杂也是最难设计的单元，因此轴向力单元的设计是本文研究的重点.

本文考虑并提出3个轴向力测量单元结构类型，并着重分析各个类型的优缺点，最终确认最优方案.结构优化的原则是在保证单元结构受相同载荷的情况下，各个载荷分量之间干扰要尽可能小，应变输出要大，从而保证天平测力单元具有较高的测量灵敏度.轴向力单元的刚度特性则通过设置较多的支撑片(S01天平的支撑片为108片)来进一步保证.在最优方案的基础上，单元结构的尺寸最终是通过强度计算来确定，即在保证强度校核合格的基础上，结构具有最小尺寸，从而天平的质量更轻.

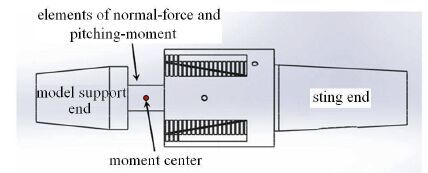
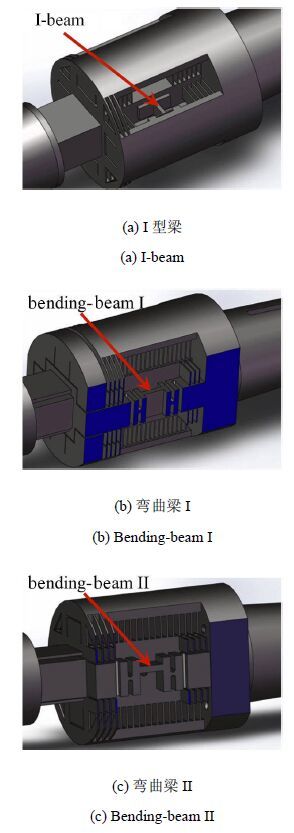
图3为S01天平的结构示意图，力矩参考中心位于矩形截面梁中心位置.作为应变天平最复杂和最关键的测量单元结构，对轴向力单元进行了重点优化设计.图4列出了轴向力测力单元结构设计方案并归类为3个结构类型，即Ⅰ型梁、弯曲梁Ⅰ及Ⅱ.

图3(Fig.3)

图3 S01天平结构示意图 Fig.3 S01 balance's structure

图4(Fig.4)

图4 S01天平轴向力测量单元设计优化方案 Fig.4 Different geometries for the axial force element of S01

其中，Ⅰ型梁为已成熟应用的一种结构形式. 弯曲梁Ⅰ是在Ⅰ型梁结构的基础上，进行有限元结构计算后改进的一种结构.这种改良在应变天平整体刚度不变的情况下使得轴向力测量单元的应变输出增大.将1 kN轴向力作用在天平上后，相比Ⅰ型梁，弯曲梁的应变输出增大了3倍以上，这将使应变天平的精准度有较大幅度的提高.但是，在检验各个分量之间的干扰时发现，单独作用法向力和俯仰力矩载荷时，弯曲梁Ⅰ类型的轴向力测量单元上仍存在相对较大的应变输出，这意味着这两个载荷对这种结构的轴向力输出具有大的干扰，并且这种干扰无疑会对天平校准的精准度有负面影响. 因此，在弯曲梁Ⅰ的基础上，提出了弯曲梁Ⅱ结构.计算结果表明，法向力和俯仰力矩载荷对这种结构轴向力单元的干扰降到了5%以内.

进一步的有限元结构数值计算表明，当其他载荷作用到天平参考中心时，弯曲梁Ⅱ结构具有最小的干扰影响，同时也具有最大的应变输出(参见表3)，这意味着弯曲梁Ⅱ的结构具有更高的测量灵敏度. 因此，弯曲梁Ⅱ型结构被确定为轴向力单元结构最优方案. 此外，基于结构的复杂性，理论计算部分不作为重点分析，不在本文中给出.

表3(Table 3)

表3 1 kN轴向力作用下各单元结构平均应变(S01天平)Table 3 Averaged strain by 1 kN axial load acting on the moment center (S01) Structure Ⅰ beam Bending beam Ⅰ Bending beam Ⅱ $\varepsilon_{\rm ave}$ 84×10$^{-6}$ 265×10$^{-6}$ 336×10$^{-6}$

表3 1 kN轴向力作用下各单元结构平均应变(S01天平) Table 3 Averaged strain by 1 kN axial load acting on the moment center (S01)

为了评估应变天平应用的安全性和适用性，分别对S01天平整体结构进行了强度校核和应变计算.一方面，有限元计算结果表明，目前的结构方案符合设计要求并且在最大载荷作用下天平结构是安全可靠的.表4列出了3个载荷(轴向力、法向力及俯仰力矩)分别作用时最大应力的计算结果；另一方面，应变计算的结果显示，S01应变天平(弯曲梁Ⅱ结构)具有最高的测量敏感度. 表5列出了各个分量载荷作用下应变计黏贴位置的最大和平均应变计算结果.相对于常规高超声速风洞使用的传统杆式应变天平，本文中脉冲型应变天平在保证整体刚度较大的同时具有更高的测量敏感度.

表4(Table 4)

表4 S01天平三载荷单独作用下最大应力Table 4 Maximum von Mises stress of S01 for three individual load components Component $X$ $Y$ $Mz$ load 1 kN 2 kN 100 Nm maximum stress ${a_{\max }}/{\rm{MPa}}$ 154 312 173

表4 S01天平三载荷单独作用下最大应力 Table 4 Maximum von Mises stress of S01 for three individual load components

表5(Table 5)

表5 S01天平三载荷单独作用下的应变结果Table 5 Maximum strain of S01 for three individual load components Component $X$ $Y$ $Mz$ loads 1 kN 2 kN 100 Nm maximum strain ${\varepsilon _{\max }}/{10^{ - 6}}$ 823 1 664 923 averaged Strain ${\varepsilon _{ave}}/{10^{ - 6}}$ 336 595 722

表5 S01天平三载荷单独作用下的应变结果 Table 5 Maximum strain of S01 for three individual load components

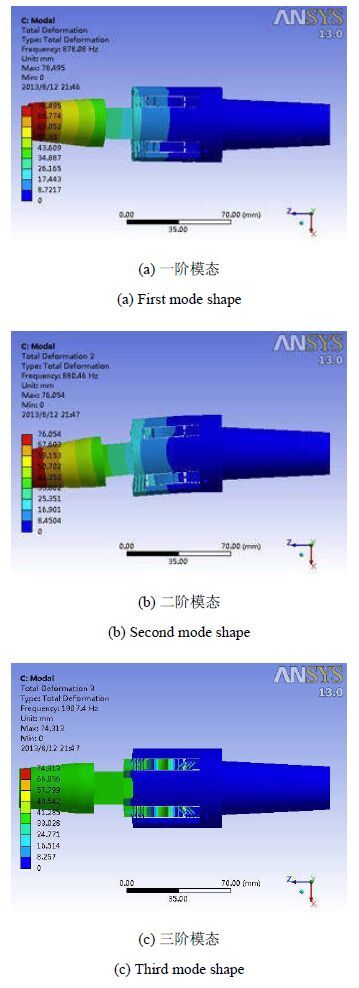
为了更好地评估目前设计的天平结构特性，对S01天平应用有限元数值方法进行了结构模态振型和频率的计算分析.结果表明，S01天平结构的前三阶模态频率分别为878 Hz,880 Hz和1 907 Hz.这表明其具有较高的刚度特性，天平输出电压信号将具有更好的周期性，从而保证测力结果具有更高的精准度.这一点在JF12激波风洞测力试验中也得到了验证.

图5为S01天平的前三阶模态振型.前两阶模型分别沿$X$和$Y$轴(计算坐标系)弯曲，第三阶振型为轴向振动，这意味着天平轴向力电压输出信号的主频率是较高的. 因此，目前的S01脉冲型应变天平符合设计预期，可以满足使用要求.

图5(Fig.5)

图5 S01天平前三阶模态振型 Fig.5 First three mode shapes (top view)

表6和表7中列出的静态校准指标可以看出其具有非常好的重复性和较高的精准度.尤其是轴向力测量精度达到0.03%，这个指标已经远超过了国军标GJB2244A-2011中对精度要求的先进指标(0.1%)^[29]，这意味着目前的设计方案达到甚至超过了研制预期目标.

表6(Table 6)

表6 S01天平静态校准均方误差指标Table 6 The mean squared error of S01 by the static calibration Component $Y$ $Mz$ $X$ $\sigma $/% 0.26 0.12 0.03

表6 S01天平静态校准均方误差指标 Table 6 The mean squared error of S01 by the static calibration

表7(Table 7)

表7 S01天平静态校准精度指标Table 7 The precision of the S01 balance $Y$ $Mz$ $X$ precision/% 0.03 0.05 0.03

表7 S01天平静态校准精度指标 Table 7 The precision of the S01 balance

目前，大尺度(或全尺度)高超声速飞行器的气动力测量试验越来越受到关注，一些飞行器测力模型的长度甚至超过了7 m.因此，JF12激波风洞在大、重模型的气动力测量方面也更加凸显出其尺度上的优势.但是，对于长度超过4m的飞行器模型，基于目前的加工制造技术，其重量也较难控制在尾式支撑方式可以接受的范围.因此，对于超大尺度的测力模型，考虑采用刚度更好的盒式天平，并结合背部支撑测力形式.

盒式天平的尺寸一般较大，整体结构也更加复杂. 对于脉冲型盒式应变天平的结构优化，借鉴杆式脉冲型天平的优化设计经验，仍然采取保证较大刚度的同时提高测量灵敏度的设计思路，同时结合JF12激波风洞的运行特性，载荷量程和信号输出尽可能满足不同尺度、重量模型的测力要求.

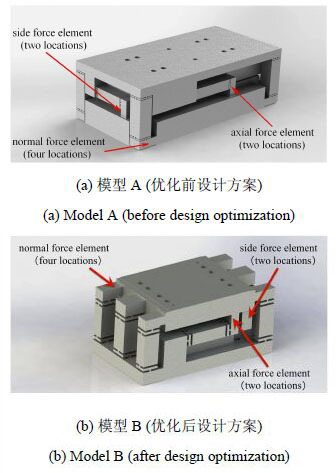
图6为B01盒式脉冲型应变天平在加工制造之前所进行的优化设计方案的对比. 优化前的(模型A)与优化后的天平(模型B)在整体结构和重量上都有较大的差别.

图6(Fig.6)

图6 B01天平结构优化设计方案比较 Fig.6 Design optimization of B01 balance

模型A的外形尺寸为464 mm × 234 mm × 146 mm，质量超过105 kg. 模型B整体外形尺寸为315 mm× 178 mm × 150 mm，天平质量减小到46.6 kg.在重量方面，模型B比A轻了近50 kg，这将使得激波风洞的冲击载荷产生的惯性力有较大程度的降低.同时，更小的尺寸可以为飞行器内部结构设计提供更大的设计空间. 表8为优化前后两个模型的模态频率分析结果.显然，相对于模型A，模型B具有更好的整体刚度特性.下文中测力信号输出结果显示其完全满足JF12激波风洞的测力需求，盒式脉冲型应变天平结构优化符合设计预期.

表8(Table 8)

表8 B01盒式天平优化前后的模态频率比较Table 8 Mode frequencies of B01's models A and B Model Mode 1 Mode 2 Mode 3 Mode 4 Mode 5 Mode 6 A 292 322 400 519 648 720 B 428 467 648 831 1 019 1 809

表8 B01盒式天平优化前后的模态频率比较 Table 8 Mode frequencies of B01's models A and B

图7列出了两个模型详细的前三阶模态振型及其应变分布. 可以看出，模型A的一阶模态振动为轴向振动，而模型B的轴向振动则对应其二阶模态，且模态振动频率远高于模型A.因此，模型B的轴向力测力单元具有更好的刚度特性，也意味着在有效试验时间内轴向力应变输出将具有相对模型A更好的周期信号.同时注意到，模型A的法向振动出现在第三阶模态振型，频率仅为400 Hz，而模型B的法向振动模态频率则达到了831 Hz.因此，在进行了有限元结构优化后，模型B的整体结构刚度特性要优于模型A，且重量更轻.

图7(Fig.7)

图7 B01天平模型A 和B的前三阶模态振型 Fig.7 First third mode shapes for models A and B of B01 balance

表9中列出了优化后的B01天平在满量程载荷下的应变输出情况. 模型B的6个分量的测力单元均具有较大的应变输出.显然，在保证其具有较高灵敏度的同时，也确保了各个分量之间具有较小的干扰输出.因此，在天平应变输出特性上，模型B也具有更高的测量灵敏度，其符合设计预期，可满足JF12激波风洞测力使用要求.

表9(Table 9)

表9 B01脉冲型天平(模型B)各元桥路应变输出Table 9 Strain output of B01's model B Component $Y$ $Mz$ $Mx$ $X$ $Z$ $My$ $Y$ 360 $-3$ 1 $-2$ $-1$ $-7$ $Mz$ $-1$ 651 0 11 14 1 $Mx$ $-2$ 2 1 233 $-18$ $-3$ $-1$ $X$ 1 30 $-1$ 700 $-2$ 2 $Z$ 0 $-9$ $-1$ $-6$ $-423$ 1 $My$ $-29$ 0 0 $-4$ $-2$ 970

表9 B01脉冲型天平(模型B)各元桥路应变输出 Table 9 Strain output of B01's model B

JF12系列脉冲型应变天平在加工及静态校准完毕后，均需在JF12激波风洞进行动态校准与测试.杆式应变天平校准测试模型选定为半锥角10°尖锥模型，并且根据天平量程匹配不同尺度的两个测力模型^[30].盒式天平的测试工作更为复杂，其主要原因在于天平和模型重量、更大的模型尺度以及支撑结构形式等都要与JF12激波风洞脉冲型测力方式相匹配.所以，作为动态测力的第一步，选定我们自行设计的重达200 kg、长2 m的超燃冲压发动机模型对其输出信号的可靠性进行动态测试.本文给出了部分信号的数据图及其初步分析结果.

表10为选定的JF12激波风洞天平动态测试的标准来流条件，本文中脉冲型天平的动态测力试验均采用这个来流状态进行.

表10(Table 10)

表10 试验来流条件Table 10 Freestream conditions $Ma$ $\alpha $ $T_{0}$ $P_{0}$ $Re(L) $ 7 5° 2 200 K 2.5 MPa 6.0×10$^{5}$

表10 试验来流条件 Table 10 Freestream conditions

测力模型采用半锥角为10°的尖锥模型. 这个模型由于拥有大量的国内外风洞的测力试验数据及理论分析结果^{[31, 32]}，因此常被作为标准模型应用于新建或改造风洞的流场校测.在脉冲型风洞进行气动力测量，模型的重量被认为是决定试验成败的一个十分重要的影响因素.因此，采用轻模型将大大降低风洞应变天平及模型支撑系统的设计难度.所以，对于目前的尖锥模型，除顶尖部分采用合金钢材料外，其余部分为铝合金材料加工，最大限度地保证模型具有较轻的重量.

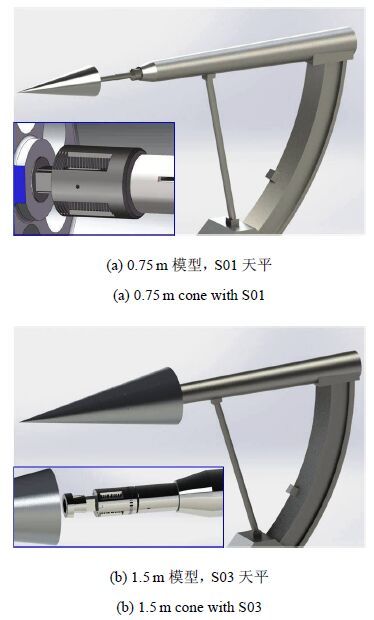
动态测力试验中，S01和S02天平的测力试验选定长为0.75 m的尖锥模型，而S03天平由于尺寸、重量和量程均较大，所以匹配了1.5 m长的尖锥模型(见图8). 模型与天平连接采用尾式支撑形式并设定攻角为5°，侧滑角为0°.

图8(Fig.8)

图8 尖锥模型应变天平支撑测力系统 Fig.8 MBS system for the cone model

此外，这两个模型的尺寸均达到激波风洞尖锥测力模型尺度之最，尤其是1.5 m尖锥模型，目前可查到的文献中的激波风洞尖锥模型均远低于它的尺寸和重量参数指标. 表11列出了各风洞测力尖锥模型的尺寸及重量参数.

表11(Table 11)

表11 不同风洞使用的尖锥标准模型参数Table 11 Dimensions of the cones employed in different wind tunnel Wind tunnel Length/m Area/m$^{2}$ Weight/kg JF12 1.5 0.219 8 29.5 JF12 0.75 0.054 9 6.9 FD-03 0.141 78 0.001 96 --- Langley 11 inch 0.085 5 0.000 7 ---

表11 不同风洞使用的尖锥标准模型参数 Table 11 Dimensions of the cones employed in different wind tunnel

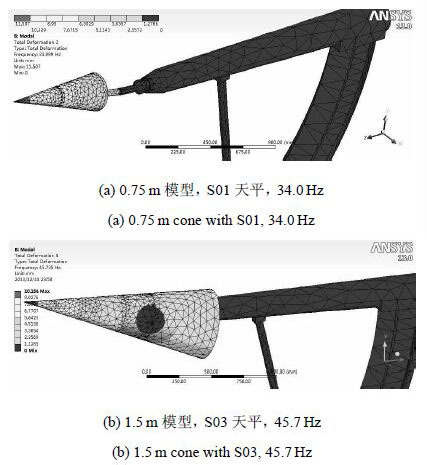
在各个脉冲型应变天平进行风洞测力试验之前，对模型-天平-支撑系统进行建模(见图9)和有限元振动分析，包括静态、动态模拟和模态分析，从而进一步预评估测力支撑系统特性和天平应变信号输出.图10为S01和S03天平的模型-天平-支撑系统法向模态振动应变分布图以及相应的固有振动频率.从振动频率的结果可以看出，S03天平测力支撑系统相对具有更好的结构刚度特性，尤其是法向振动特性，这意味着在有效试验时间内，S03天平的法向力输出电压信号将可以找到更多的信号周期. 同时，有限元模态分析结果显示，S系列天平的轴向力振动均具有较高的频率.(详见下节中的信号分析)

图9(Fig.9)

图9 MBSS三维计算模型 Fig.9 FEM computational modeling

图10(Fig.10)

图10 两模型法向振动模态振型 Fig.10 Mode shapes in normal direction

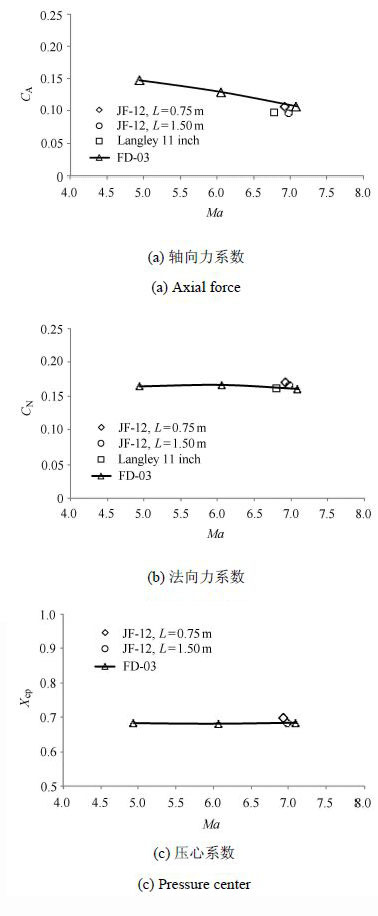
应用新研制的脉冲型杆式应变天平，在JF12复现大尺度激波风洞进行了一系列尖锥模型的测力试验. 图11列出了S01天平($L=0.75$ m尖锥模型)和S03天平($L=1.5$ m尖锥模型)的测力结果并且与其他常规高超声速风洞的测力数据进行了比较. 目前的试验结果与其他风洞数据以及理论结果均具有较好的一致性. 同时，应该注意到："美国国家航空航天局兰利11英寸"风洞和国内FD-03风洞的总温均在600 K左右，而目前试验选取的总温2 200 K的试验状态可复现飞行条件，这种由于总温(试验来流焓值)条件对气动力的影响较为复杂，目前仍在研究中，本文不做分析. 此外，美国国家航空航天局的试验条件为：马赫数$Ma=6.8$；雷诺数$Re(L)=0.81 \times 10^{6}$. 所以比较数据后发现：法向力和轴向力系数的偏差分别为2.61%和4.69%(S01天平结果).

图11(Fig.11)

图11 尖锥标模气动力系数比较($Ma\approx 7$) Fig.11 Aerodynamic force comparison ($Ma\approx 7$)

表7给出了$L=0.75$ m尖锥模型使用S01天平测力试验数据的精度指标，可以看出在JF12激波风洞测力试验中，针对其风洞特点研制的脉冲型应变天平输出具有好的重复性.

表12中

表12(Table 12)

表12 S01天平部分测力数据精度指标Table 12 The precision of the test data (Balance S01) $\sigma _{C_{\rm N}}$ $\sigma _{C_{\rm M}}$ $\sigma _{C_{\rm A}}$ $\sigma _{X_{\rm cp}}$ 0.242% 0.186% 0.537% 0.283%

表12 S01天平部分测力数据精度指标 Table 12 The precision of the test data (Balance S01)

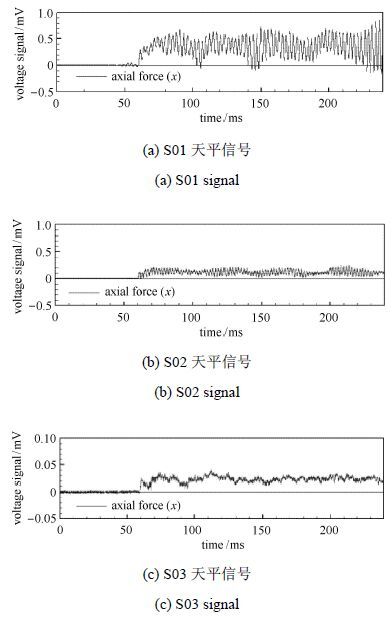
为了进一步评估和说明JF12系列杆式天平的测力重复性指标，图12和图13分别列出了相同来流状态下尖锥标模测力试验的各个天平轴向力和法向力电压信号曲线.

图12(Fig.12)

图12 JF12系列杆式天平轴向力电压输出信号 Fig.12 Axial force signals of JF12 series sting balances

图13(Fig.13)

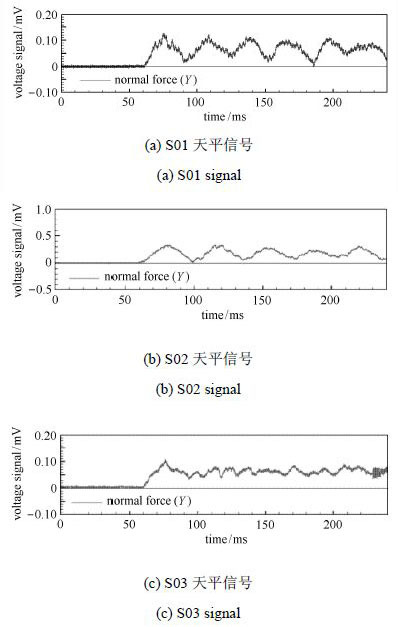
图13 JF12系列杆式天平法向力电压输出信号 Fig.13 Normal force signals of JF12 series sting balances

从轴向力电压信号可以看出，S01天平具有最大的应变输出，即其有较高的测量灵敏度；S02天平刚度相对较低，信号频率也相对低；S03天平具有最大的刚度，同时，也因为保证了大刚度特性，所以输出很小，在3个天平中，具有最小应变输出，测量灵敏度也相对较低.

在天平结构的优化设计中，通过有限元结构优化保证了天平具有较大的刚度，即有较高的自振频率.但在实际的测力试验中，模型-天平-支撑测力系统，即模型-天平-支撑系统的振动频率对输出信号周期的影响较大. 大刚度脉冲型应变天平在测力系统中充分保证了"天平"环节在刚度方面的要求.因此，大刚度的测力天平将提高整个系统的刚度特性. 这在计算中得到了验证.例如，采用一阶自振频率为335 Hz的天平模型通过建模安装到模型-天平-支撑系统中后，其法向振动频率为21 Hz；而将自振频率为878 Hz的S01天平装配到相同模型-天平-支撑系统中后，经计算得到的一阶法向频率为34 Hz.

上一节中对测力模型支撑系统的结构特性分析中，已经对法向力信号进行了初步的预估分析.对于S01和S03天平测力系统，法向振动频率分别为34 Hz和45.7 Hz(见3.1.1节)，这样的频率意味着在100 ms的有效试验时间内，这两个天平的法向力应变输出信号分别可以找到约3个和5个周期.事实上，图13中S01和S03天平法向力信号结果也验证了数值分析的可靠性和准确性，即采用有限元结构分析可以对整个测力支撑系统激波风洞测力可行性进行较为精确评估. 尤其是S01天平的法向力信号，对其进行快速傅里叶变换(fast Fouriertransformation)数据处理后，找到了两个主要的干扰频率，分别为30.52 Hz和61.04 Hz.这两个频率与模型-天平-支撑系统有限元模态分析的两个模态频率的结果(34 Hz和60 Hz)相互吻合，这意味着法向振动的第三和第六阶模态频率对天平的法向力电压信号产生了最主要的干扰影响；同时，有限元模态分析方法在测力试验之前成功地预测评估了模型-天平-支撑系统的结构特性和天平信号影响因素.

盒式天平基于其较大的体积、重量以及较好的刚度特性，常被用于常规风洞中较大尺度模型的气动力测量试验.JF12激波风洞具有超过100 ms的有效试验时间，对于长度尺寸超过3 m的模型，我们考虑将盒式天平作为保守、可靠的测力技术之一进行发展研制，并在JF12风洞开展动态测力试验.

在盒式天平研制之前，由于测力模型均考虑尾式支撑形式，因此模型尺度，尤其是重量，都受到严格限制.所以，为了进行盒式天平的气动力测试，采用了自行设计研制的超燃冲压发动机模型，其200 kg的重量考虑作为盒式天平的初步测试.

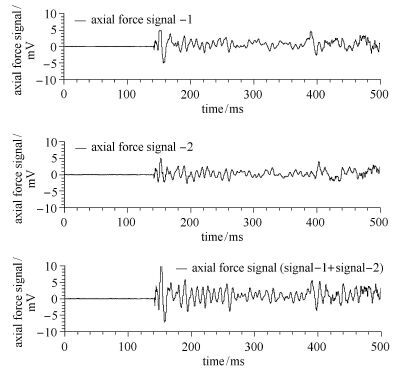
根据B01天平的结构特点，左右两侧轴向力单元结构(见图6(b))应变输出的叠加结果作为为其轴向力输出结果.图14为盒式天平B01的初步信号结果.其中，前两个信号为盒式天平两个轴向力测力单元输出信号，第3个信号为其叠加合成信号.从第3个信号可以看出其周期性非常好，尤其是在大约60 ms ($t=200\sim260$ ms)有效试验时间内，找到了约6个周期，即轴向力测力单元的振动频率达到了100 Hz以上.这个特性使得B01天平可以满足对发动机甚至飞行器一体化试验的要求.

图14(Fig.14)

图14 B01天平轴向力应变信号及其叠加信号分析 Fig.14 Axial force signal (superimposed signal) of B01 balance

同样，法向力测力应变输出结果为4个测力单元结构应变输出的叠加(见图15). 图中，信号的周期性非常好，从大约60 ms ($t$为$250\sim 310$ ms)有效试验时间内，我们可以很容易找到两个周期，即频率超过30 Hz.从而反映出B01天平结构整体较好的刚度特性以及较高的输出灵敏度，这个结构特性可以满足JF12激波风洞大、重模型的气动力测量试验.

图15(Fig.15)

图15 B01天平法向力应变信号 Fig.15 Normal force signal of B01 balance

JF12复现飞行条件高超声速激波风洞有效试验时间超过了100 ms，针对其运行特点和试验性能，采用应变计测量技术，设计研制了JF12系列脉冲型应变天平，以专门针对其进行气动力测量试验.脉冲型应变天平的类型包括了传统的杆式天平和盒式天平，其载荷量程涵盖了从1 kN到30 kN的较宽范围，以满足JF12激波风洞大尺度模型的测力试验需求.这个系列天平的特点为刚度大、各个分量之间干扰低、灵敏度高，从而保证风洞测力数据具有较高的精准度.在结构设计方面，充分考虑JF12激波风洞启动和运行特点，应用有限元结构优化和数值计算对整个模型-天平-支撑系统进行建模及测力输出评估.在此基础上，确定脉冲型应变天平的结构和性能参数.一系列的动态测力试验结果表明：对于100 ms以上试验时间的脉冲型风洞，应变计测力传感器完全可以满足试验需求，但前提条件是要对其结构进行优化设计；目前设计研制的JF12系列脉冲型应变计天平完全适应JF12风洞的运行特点，对大尺度、较重模型的测力试验更具优势；脉冲型盒式应变天平的性能指标表明其可以满足大尺度飞行器一体化试验的需求.

Wang Yunpeng, Liu Yunfeng, Yuan Chaokai, Luo Changtong, Wang Chun, Hu Zongmin, Han Guilai, Zhao Wei, Jiang Zonglin