2. 天津市现代工程力学重点实验室, 天津 300072
在工程技术中,湍流边界层是典型的湍流流动形态之一,大量的工程湍流问题均与湍流边界层密切相关,如飞行器和船舶固壁表面流动、流体机械内部叶片表面流动等等. 随着湍流研究的深入和流体力学实验技术的发展,人们逐渐发现了湍流边界层中存在间歇的、可重复的、有组织的大尺度涡结构,被称为相干结构[1, 2]. 自此,人们对湍流本质的认识从完全随机的阶段进入到有序和无序并存的新阶段[3]. 研究表明,壁湍流的产生、维持和演化主要与相干结构的猝发过程有关[4]. 湍流边界层相干结构的猝发过程,包括低速流体远离壁面向外喷射,以及高速流体向壁面扫掠,其中扫掠过程是平板湍流边界层中摩擦阻力的主要来源[5, 6, 7, 8, 9]. 因此,对湍流边界层相干结构进行控制就应从抑制猝发过程入手,且着重考虑对扫掠事件的影响.
20世纪80年代以来,湍流边界层相干结构的控制一直是湍流研究的前沿课题.根据是否有外部能量的输入,湍流控制方案可以分为被动控制和主动控制,近年来,湍流的主动控制成为湍流控制技术研究的热点[10, 11, 12, 13, 14].Jung等[15]利用直接数值模拟的方法,通过高频的壁面展向振荡对壁湍流边界层相干结构进行主动控制,得到了最大40%的减阻率,同时湍流度与雷诺应力等统计量也有所减小. Choi等[16]在实验中也实现了壁面的展向振荡,减阻率可达45%.Choi等[17]利用直接数值模拟对湍流边界层进行了反向控制,即在$y^{+ }=10$的平面对法向速度进行检测,同时在壁面的对应位置通过吹、吸施加大小相同、方向相反的法向速度,实现了对流向涡的抑制以及最大30%的减阻率.Berger等[18]在直接数值模拟中对低雷诺数流体施加展向振荡的Lorentz力,进行了开环控制实验,最大减阻率约为40%.Park等[19]在平板壁面上切割一条展向窄缝,利用扬声器施加可变频率的局部扰动,从而在物理实验中实现了对湍流边界层的周期性扰动,表明周期性扰动可以减小壁面摩擦阻力.Du等[20, 21]在对流场的直接数值模拟中施加横向行波,实现了减阻以及对近壁条带结构的控制.
在众多主动控制方案中,壁面变形是较为可靠、高效的一种.Grosjean等[22]测试了基于微机电(MEMS)技术的气动壁面变形装置,结果表明在温度变化很大的跨声速飞行中这种装置也是可靠的.Segawa等[23]设计了一套致动器阵列来产生壁面法向振荡的装置,有效地降低了近壁条带结构的规则性.Itoh等[24]利用扬声器激励壁面上的一块聚乙烯薄片,使其沿法向振荡,得到了约7.5%的减阻率.
压电陶瓷作为一种能够将电信号直接转化为陶瓷片振动的特殊材料,可以利用它的特性制作动作元件,应用到湍流边界层主动控制方案中.在Rathnasingharm[25]的主动控制实验中,将一块镀镍压电陶瓷片粘贴在薄膜上,压电陶瓷片的振动可以带动薄膜把空腔中的空气从平板的小孔中吹出,构成法向吹、吸装置.Cattafesta等[26]给出了用于主动控制实验的压电振子的一种形式,即由压电陶瓷片与钢片粘结而成的悬臂梁的形式,并通过最优化算法推导出压电振子的频率响应函数.Cattafesta等[27]对各种主动控制方案中使用的致动装置进行了总结,压电振子为重要的主动控制方式之一.
本文利用沿流向安装于壁面上的单个压电振子,通过对其施加不同幅值和频率的交流电,使其产生不同振幅和频率的振动,从而实现振子对湍流边界层多尺度相干结构的干扰和控制,在下游采集湍流速度信号,研究压电振子振动对大尺度相干结构的影响,寻找具有最佳减阻效果的工况. 本研究采用的控制方案为开环式主动控制.
1 压电振子模型实验中的压电振子由宽3.6 mm、厚0.2 mm的铜片和宽3.6 mm、厚0.22 mm的压电陶瓷片粘结而成,两薄片一端对齐,另一端铜片多出的部分则固定在平板上,有效振动长度为30 mm,振子以悬臂梁的形式平行悬挂在平板的空腔之上,如图1(a)所示,空腔深度为5 mm. 为了使空腔内空气能顺利排出,振子与周围平板之间均有1 mm的间隙,同时避免了振子振动时与壁面触碰.

|
图1 压电振子示意图 Fig.1 Schematic diagram of piezoelectric oscillator |
压电陶瓷片的两个电极是其上下两面,因此一根导线直接焊在压电陶瓷片的下面,而另一根导线则焊在铜片上,通过铜片的传导与压电陶瓷片上面连通. 当两根导线接在交流电源上时,压电陶瓷片会产生轴向的伸缩振动,在粘结了自身不振动的铜片后,可以转化为整个压电振子在壁面法向上的振动. 两根导线穿过空腔下方的小孔,伸入平板的背面,而后与风洞外的交流电源连接,不会对平板正面的流场造成影响. 压电振子的实物图见图1(b).
根据Cattafesta等[26]的研究可知,本研究中压电振子的频率响应函数为
\[H(\omega ) = \frac{{{K_0}}}{{1 - {{\left( {\omega /{\omega _n}} \right)}^2}}}\]
(1)
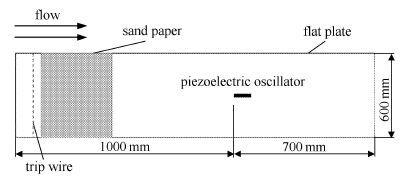
实验在三元回流闭口式风洞中进行. 风洞为木质结构,实验段长1 500 mm,横截面为切角的矩形,宽800 mm,高600 mm. 实验段风速在0.5 m/s到40 m/s之间连续可调,背景湍流度小于0.2%. 如图2所示,产生湍流边界层的平板为15 mm厚的有机玻璃板,长1 700 mm,宽600 mm,竖直固定在风洞实验段,前缘为楔形,并设有绊线和砂纸,以加速流场转捩,得到充分发展湍流. 压电振子位于距离平板前缘1 000 mm处,沿流向布置,其固定端在上游位置,自由端在下游位置. 为压电振子供电的电源是远方GK10005交流变频稳压电源,其输出电压的幅值和频率可精细调节,耗电功率实时显示,且采用过流保护以确保安全.
|
图2 实验平板示意图 Fig.2 Schematic diagram of the flat plate |
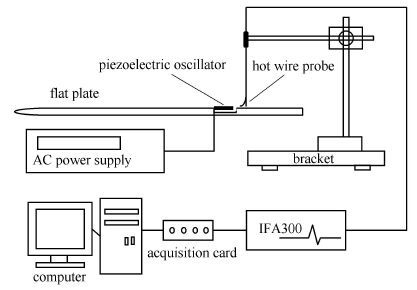
测速仪器为TSI-IFA300型恒温热线风速仪和TSI-1621A-T1.5型单丝热线探针,热线敏感材料为直径4 μm钨丝,探针在使用前在TSI-1128型热线探针校准器上进行了标定. 数据采集卡采用美国UEI公司生产的WIN-30DS4型12位A/D卡. 热线探针支杆由CCTS-1193E型三维自动控制坐标架固定. 实验装置连接如图3所示.
|
图3 实验测量系统示意图 Fig.3 Schematic diagram of experimental measurement system |
实验时风洞实验段自由来流速度控制在$U_\infty = 9.0$ m/s,动量损失雷诺数$Re_\theta = 2 183$. 热线探针在压电振子下游2 mm处,测量湍流边界层不同法向位置的流向速度信号. 采样频率为100 kHz,每个空间点样本数量为4 194 304,采样时间长度41.9 s.
本实验中交流电源输出电压的幅值选用20 V,60 V和 100 V,频率分别为80 Hz,160 Hz和 240 Hz,此外,设置一组无控制的工况(电源无输出,振子不振动)作为对照,共10种工况.压电振子的振动频率与交流电源的频率相同,振幅可由频率响应函数(式1)计算得到,计算结果如表1所示.
| 表1 各工况压电振子振幅 Table 1 Amplitude of piezoelectric oscillator for each condition |
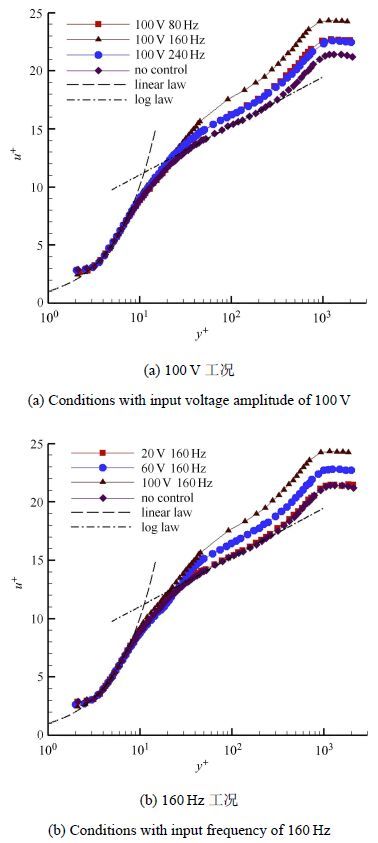
图4(a)为电压幅值为100 V时3种工况的平均速度剖面. 无量纲量$y^ + = {yu_\tau } /\nu $,$u^ + = u / {u_\tau }$,其中$\nu $为运动学黏性系数,$u_\tau $为壁面摩擦速度,是由黏性底层的线性律$u^ + = y^ + $拟合而得.从图中可以发现,施加控制的3种工况与无控制的工况相比,平均速度剖面对数律的斜率均相同,但是相比于无控制的工况,施加控制的工况下对数律与$u^ + = y^ + $交点的横坐标更加远离壁面,即对数律层上移,这与前人在大涡破碎器[28]等研究中的结论吻合.也就是说,加100 V电压控制的3种工况都具有减阻效果,其中,100 V和160 Hz的工况对数律层上移的现象最明显,说明其减阻效果最佳,而另外两工况减阻效果相近.同样,对于电压幅值为20 V和60 V的工况,平均速度剖面也存在对数律层上移的现象,但上移程度各不相同.各种工况的减阻效果可以通过减阻率定量比较.
|
图4 无控制与施加控制各工况平均速度剖面 Fig.4 Mean velocity profile on conditions of unmanipulated wall and manipulated wall |
图4(b)为频率为160 Hz时3种工况的平均速度剖面. 由图可知,控制频率为160 Hz不变,电压幅值由20 V变化到60 V和100 V时,对数律层上移的程度依次增大,减阻效果也愈加明显.此外,20 V和160 Hz工况的平均速度剖面与无控制工况的差别很小,减阻效果不明显.
3.2 各工况减阻率
由上一小节中拟合出的壁面摩擦速度$u_\tau $可以计算壁面剪应力
\[{\tau _{\rm{w}}} = \rho u_\tau ^2\]
(2)
\[{C_f} = \frac{{{\tau _{\rm{w}}}}}{{\frac{1}{2}\rho U_\infty ^2}}\]
(3)
\[\eta = \left( {1 - \frac{{{C_{{\rm{fm}}}}}}{{{C_{{\rm{fu}}}}}}} \right) \times 100\% \]
(4)
| 表2 各工况壁面摩擦速度与减阻率 Table 2 Wall friction velocity and drag reduction rate for each condition |
由表中数据可知,减阻率不仅与压电振子的振幅有关,还与其振动频率密切相关. 当频率固定时,在一定范围内(压电振子在工作时有一定的额定电压),电压幅值越大,即振子振幅越大,减阻效果越明显;而对于同一电压幅值的情况,输入交流电频率为160 Hz,即压电振子振动频率为160 Hz时,能够得到最佳减阻效果. 在本文研究的九种施加控制的方案中,100 V和160 Hz的工况减阻率最大.
3.3 脉动动能随尺度分布与平均猝发周期检测
一维速度信号$u(t)$在子波函数$W_{ab}(t)$下的子波变换$W_{u}(a,b)$定义为
\[{W_u}(a,b) = \int_{ - \infty }^{ + \infty } u (t)\overline {{W_{ab}}(t)} dt\]
(5)
\[{W_{ab}}(t) = \frac{1}{{\sqrt a }}W(\frac{{t - b}}{a})\]
(6)
根据子波系数$W_{u}(a,b)$,速度信号$u(t)$的能量可以分解为
\[\int_{ - \infty }^{ + \infty } {{{\left| {u(t)} \right|}^2}dt} = \int_0^{ + \infty } {\frac{{E(a)}}{{{a^2}}}da} \]
(7)
\[E(a) = \frac{2}{{{C_W}}}\int_{ - \infty }^{ + \infty } {{{\left| {{W_u}(a,b)} \right|}^2}db} \]
(8)
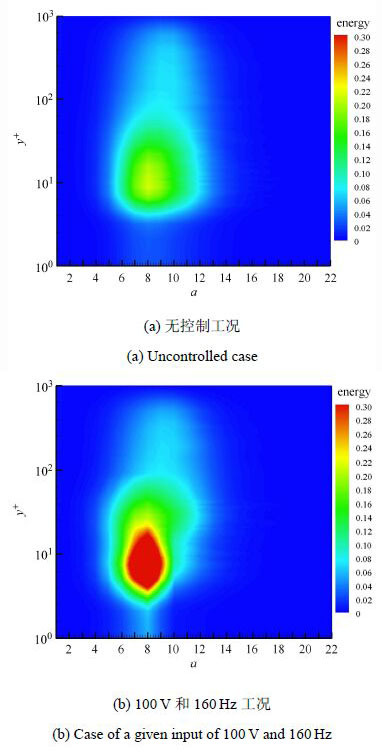
对无控制和100 V和160 Hz工况,不同法向位置的速度信号进行子波变换,得到分尺度脉动动能随尺度参数的分布[29],如图5所示. 缓冲层附近区域的各法向位置均在第8尺度达到能量最大尺度,为相干结构猝发的时间尺度.由图5(b)可知,压电振子振动产生的周期扰动使能量最大尺度的能量达到无控制工况最大能量的3倍,这表明振子以固定频率振动,可以产生与相干结构猝发频率相同的扰动,对大尺度相干结构的运动进行干扰和调制.
|
图5 各法向位置能量随尺度分布云图 Fig.5 Contours of energy as a function of wavelet scale for each wall-normal position |
对无控制的工况中能量最大尺度(第8尺度)子波系数进行自相关分析[30],得到该尺度相干结构的平均猝发周期约为 5.92 ms,即猝发频率为168 Hz,与160 Hz非常接近.结合前面得到的减阻率可知,当压电振子振动频率接近能量最大尺度对应的猝发频率时,压电振子产生的扰动对猝发影响最显著,减阻率最大;当压电振子频率偏离能量最大尺度对应的猝发频率时,减阻效果不明显.
3.4 子波系数等值云图图6给出了施加100 V和160 Hz振动前后$y^+=15$处用公式(5)对流向速度进行子波变换的子波系数等值云图. 从图6可以看出,施加扰动前的相干结构猝发间隔具有一定的随机性,尺度跨度具有一定的不规则形,强度有强有弱;施加周期扰动后,施加周期扰动对相干结构猝发产生调制作用,使猝发间隔更加均匀,尺度跨度趋于一致,强度更加均匀.

|
图6 $ y^{ + } =15$ 处流向速度子波系数等值云图 Fig.6 Contours of wavelet coefficients for longitudinal velocity component at $y^{ + } =15$ |
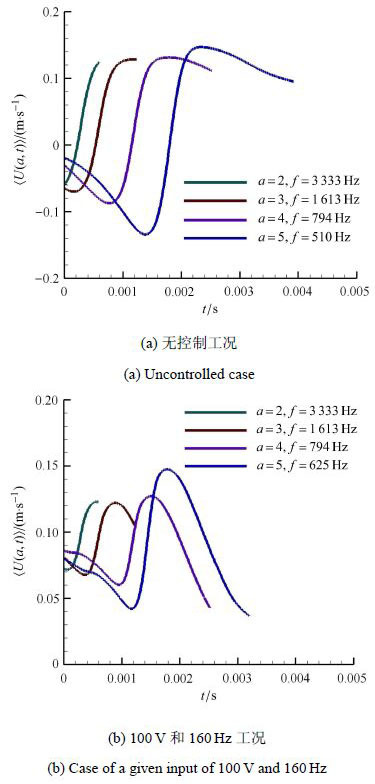
根据上面得到的子波系数,利用姜楠[31, 32]的子波系数瞬时强度因子和平坦因子检测多尺度相干结构的条件采样方法,检测无控制和100 V和160 Hz两种工况下法向位置$y^{ + }=15$处的条件相位平均波形,结果如图7所示.
|
图7 $y^{ + } =15$处的条件相位平均波形 Fig.7 Conditional sampling phase-averaged waveforms at the position of $y^{ + } =15$ |
由以上两种工况下的条件相位平均波形可以看出,施加控制工况中波形的均值位于$\langle U \rangle=0.1$附近,比无控制的工况明显增大,且波形整体都位于$\langle U\rangle =0$以上,说明压电振子的振荡以及空腔中空气的喷出使振子下游2 mm处的流向速度在空腔中空气喷出的局部时间段内明显增大,这种瞬态速度提升对当地总体平均速度有一定的贡献,但在整个湍流过程中还是属于脉动速度的范畴,在总体上还是属于对脉动动能的贡献. 这也解释了3.3节中施加控制工况总体脉动动能的显著增加的原因. 此外,尽管扰动使瞬态平均速度增大,但施加扰动的周期调制作用使得近壁扫掠过程中当地速度加速以后要迅速衰减,不能像通常扫掠那样使速度持续增长较长时间,所以施加控制后相位平均速度波形的脉动振幅减小,使施加控制的工况中条件相位平均波形的振幅比无控制的工况减小了一半以上,说明压电振子的振动对近壁区域相干结构的扫掠过程具有明显的抑制作用,抑制了高速流体的强烈剪切过程,达到了减阻的目的.
两种工况中的条件相位平均波形均包含了一个扫掠事件,即波形由波谷变化到波峰的过程,探针所处空间点经历了高速流体向壁面强烈下扫,从而流向脉动速度由最小值变化为最大值.此时高速流体与壁面强烈剪切,壁面摩擦阻力最大,因此扫掠事件是壁面摩擦阻力的最主要来源.然而对比两种工况的波形可以发现,无控制的工况中波峰衰减缓慢,流体保持高速下扫状态的时间较长,约2 ms,而施加控制的工况中波峰衰减很快,高速下扫的状态也很短,仅为0.2 ms,缩短了下扫的持续时间,减小了湍流高幅值脉动的产生,从而减小了壁面摩擦阻力.
利用同样的方法,检测无控制和100 V 和160 Hz两种工况下法向位置$y^{ + } =185$处的条件相位平均波形,结果如图7所示. 从图中可以看出,两种相位平均波形的形状和幅值大小都十分相似,说明压电振子振动在$y^{+ } =185$处已不起作用,压电振子的振动对远离壁面的区域没有影响. 从3.3的能量分布中也可以看出,在远离壁面的位置两种工况的能量随尺度分布基本相同.
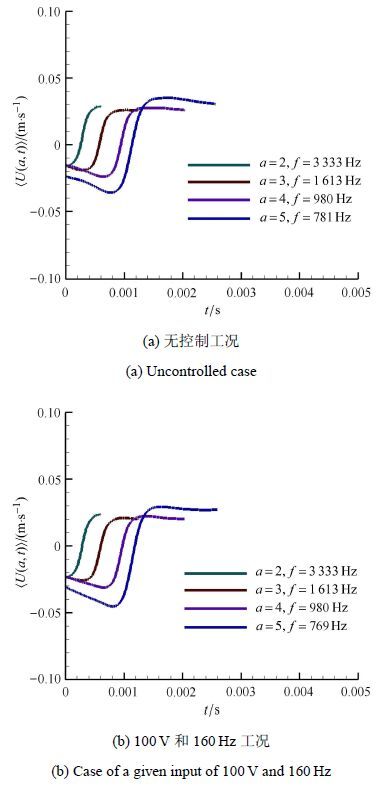
|
图8 $y^{+} =185$处的条件相位平均波形 Fig.8 Conditional sampling phase-averaged waveforms at the position of $y^{+} =185$ |
本文从平均速度剖面、不同法向位置的分尺度脉动动能随尺度的分布和相干结构猝发的条件相位平均波形等方面研究了不同振幅和频率的单个压电振子对湍流边界层的影响,得出以下结论:
(1)压电振子的振动能实现减阻,但减阻率有所差别. 当压电振子振动频率一定时,其振幅越大,减阻率越大;当振幅一定时,振动频率越靠近壁湍流能量最大尺度的猝发频率,则减阻率越大. 本研究所涉及到的工况中,对压电振子施加100 V和160 Hz的交流电时减阻率最大,最大减阻率为25.02%.
(2)利用子波变换,分解不同法向位置的脉动速度时间序列信号,并计算各尺度的湍流脉动动能,找出了各法向位置的能量最大尺度. 对比最大减阻率工况和无控制工况的能量随尺度分布,发现压电振子可以使脉动动能更大程度地集中在能量最大尺度周围,使能量出现一个很大的峰值. 压电振子以固定频率振动,可以抑制较大和较小尺度的湍流脉动,使能量更加集中.
(3)通过检测、对比最大减阻率工况和无控制工况在$y^{+}=15$处的条件相位平均波形,发现施加控制工况的条件相位平均波形均值增大,幅值降低,且下扫的时间明显缩短,说明压电振子的振动可以使近壁区域的流体抬升,并抑制下扫过程的幅值和持续时间,从而实现减阻.
(4)压电振子的影响仅限于近壁区域,对远离壁面的区域没有影响.
| [1] | Robinson SK. Coherent motions in the turbulent boundary layer. Annual Review of Fluid Mechanics, 1991, 23: 601-639 |
| [2] | 许春晓. 壁湍流相干结构和减阻控制机理. 力学进展, 2015, 45:111-139 (Xu Chunxiao. Coherent structures and drag-reduction mechanism in wall turbulence. Advances in Mechanics, 2015, 45:111-139 (in Chinese)) |
| [3] | Zhang ZS, Cui GX, Xu CX. Modern turbulence and new challenges. Acta Mechanica Sinica, 2002, 18(4): 309-327 |
| [4] | Kravchenko AG, Choi H, Moin P. On the generation of near-wall streamwise vorticesto wall skin friction in turbulent boundary layers. Phys Fluids, 1993, A5: 3307-3309 |
| [5] | 葛铭纬, 许春晓, 黄伟希等. 基于壁面主动变形的湍流减阻控制研究. 力学学报, 2012, 44 (4): 653-663 (Ge Mingwei, Xu Chunxiao, Huang Weixi, et al. Drag reduction control based on active wall deformation. Chinese Journal of Theoretical and Applied Mechanics,2012, 44 (4): 653-663 (in Chinese)) |
| [6] | Deng BQ, Xu CX. Influence of active control on STG-based generation of streamwise vortices in near-wall turbulence. J Fluid Mech,2012, 710: 234-259 |
| [7] | 黄伟希, 许春晓, 崔桂香等. 壁面展向周期振动的槽道湍流减阻机理的研究. 力学学报, 2004, 36(1): 24-30 (HuangWeixi, Xu Chunxiao, Cui Guixiang, et al. Mechanism of drag reduction by spanwise wall oscillation in turbulent channel flow. Acta Mechanica Sinica,2004, 36(1): 24-30 (in Chinese)) |
| [8] | 杨歌, 许春晓, 崔桂香. 槽道湍流减阻次优控制方案研究. 力学学报, 2010, 42(5): 818-829 (Yang Ge, Xu Chunxiao, Cui Guixiang. Study on suboptimal control schemes for skin-friction reduction in turbulent channel flow. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(5): 818-829 (in Chinese)) |
| [9] | 罗世东, 许春晓, 崔桂香. 圆管湍流减阻电磁力控制的直接数值模拟. 力学学报, 2007, 39(3): 311-319 (Luo Shidong, Xu Chunxiao, Cui Guixiang. Direct Numerical simulation of turbulent pipe flow controlled by MHD for drag reduction. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(3): 311-319 (in Chinese)) |
| [10] | Kral LD. Active flow control technology. ASME Fluids Engineering Division Newsletter, 1999: 1-3 |
| [11] | Kim J. Control of turbulent boundary layers. Phys Fluids, 2003,15(15): 1093-1105 |
| [12] | Karniadakis GE, Choi KS. Mechanisms on transverse motions in turbulent wall flows. Annual Review of Fluid Mechanics, 2003,35(1): 45-62 |
| [13] | Gad-El-Hak M. Flow Control: Passive, Active, and Reactive Flow Management. Cambridge: Cambridge University Press, 2000 |
| [14] | Kasagi N, Suzuki Y, Fukagata K. Microelectromechanical systems- based feedback control of turbulence for skin friction reduction. Annual Review of Fluid Mechanics, 2009, 41(41): 231-251 |
| [15] | Jung WJ, Mangiavachi N, Akhavan R. Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations. Phys Fluids, 1992, 4 (8): 1605-1607 |
| [16] | Choi KS, Debisschop JR, Clayton BR. Turbulent boundary-layer control by means of spanwise-wall oscillation. AIAA J , 1998, 36(7):1157-1163 |
| [17] | Choi H, Moin P, Kim J. Active turbulence control for drag reduction in wall-bounded flows. J Fluid Mech, 1994, 262: 75-110 |
| [18] | Berger TW, Kim J, Lee C, et al. Turbulent boundary layer control utilizing the Lorentz force. Phys. Fluids, 2000, 12(3): 631-649 |
| [19] | Park SH, Lee I, Sung HJ. E ect of local forcing on a turbulent boundary layer. Exp in Fluids, 2001, 31: 384-393 |
| [20] | Du Y, Karniadakis GE. Suppressing wall turbulence by means of a transverse traveling wave. Science, 2000, 288(5469): 1230-1234 |
| [21] | Du Y, Symeonidis V, Karniadakis GE. Drag reduction in wallbounded turbulence via a transverse travelling wave. J Fluid Mech,2002, 457(5):1-34 |
| [22] | Grosjean C, Lee GB, Hong W, et al. Micro balloon actuators for aerodynamic control. In: Proceedings of the 11th MEMS Workshop, Heidelberg, 25-29 January, 1998: 166-171 |
| [23] | Segawa T, Kawaguchi Y, Kikushima Y, et al. Active control of streak structures in wall turbulence using an actuator array producing inclined wavy disturbances. Journal of Turbulence, 2002, 3(1): 1-15 |
| [24] | Itoh M, Tamano S, Yokota K, et al. Drag reduction in a turbulent boundary layer on a flexible sheet undergoing a spanwise traveling wave motion. Journal of Turbulence, 2006, 7(27): 1-17 |
| [25] | Rathnasingham R. System identification and active control of a turbulent boundary layer. [PhD Thesis]. Boston: Massachusetts Institute of Technology, 1997: 64-69 |
| [26] | Cattafesta LN, Garg S, Shukla D. Development of piezoelectric actuators for active flow control. American Institute of Aeronautics and Astronautics, 2001, (8): 1562-1568 |
| [27] | Cattafesta LN, Sheplak M. Actuators for active flow control. Annual Review of Fluid Mechanics, 2011, 43(5): 247-272 |
| [28] | Bandyopadhyay PR. Review: mean flow in turbulent boundary layers disturbed to alter skin friction. Journal of Fluids Engineering,1986, 108(2): 127-140 |
| [29] | 姜楠, 王振东, 舒玮. 子波分析辨识壁湍流猝发事件的能量最大准则. 力学学报, 1997, 29 (4): 406-411 (Jiang Nan, Wang Zhendong, Shu Wei. Maximum energy criterion for identifying burst events in wall turbulence using wavelet analysis. Acta Mechanica Sinica,1997, 29 (4): 406-411 (in Chinese)) |
| [30] | 舒玮, 姜楠. 湍流中涡的尺度分析, 空气动力学报, 2000, 18(增):89-95 (Shu Wei, Jiang Nan. Eddy scale analysis in turbulence. Acta Aerodynamica Sinica, 2000, 18(S): 89-95 (in Chinese)) |
| [31] | Jiang N, Zhang J. Detecting multi-scale coherent eddy structures and intermittency in turbulent boundary layer by wavelet analysis. Chinese Physics Letter, 2005, 22(8): 1968-1971 |
| [32] | Jiang N, LiuW, Liu JH, et al. Phase-averaged waveform of Reynolds stress in wall turbulence during the burst events of coherent structures. Science in China, 2008, 51(7): 857-866 |
2. Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300072, China
 2016, Vol. 48
2016, Vol. 48