随着纳米科学与机械工艺的进步,纳米机电系统(nano electro mechanical systems, NEMS)成为当今微电子工程领域的研究热点[1, 2]. 纳米机电系统[3]具有尺度小、重量轻、灵敏度高、能耗低以及信 息存储量大的特点. 郑泉水等[4, 5]发现两端开口的多壁碳纳米管在范德华力驱动下会出现高频振荡. 郭万林等[6]在 对吉赫兹量级振动器的能量耗散进行研究时发现:具有对称结构的振荡器能量耗散更大. 王琳[7]分析了载流管的动力学特性及稳 定性. 王琳等[8, 9, 10]还研究了弯曲载流碳纳米管的动态响应问题. 王立峰[11]分别以弹性杆、壳模型和分子动力学模 型,研究了碳纳米管纵波频散特性. 吉布森等[12]综述了有关碳纳米管的力学特性、动力学模型. Zhang等[13]分析了轴向载荷 下双壁碳纳米管的横向振动问题. 尹 等[14, 15]分别基于欧拉-伯努利梁理论和铁木辛柯梁理论,研究了 碳纳米管波传播问 题并且提出:对于太赫兹频率下的波传播分析,铁木辛柯梁理论更为准确. Wang等[16]对单、双壁碳纳米管波传播特性, 均做了理论及数值分析. 目前,在国际上应用非局部连续介质力学理论[17, 18, 19]研究碳纳米管的力学性能仍然是一个 热点[20, 21, 22].
钟万勰[23]将对偶体系引入到弹性力学,建立了弹性力学哈密顿系统辛求解的一般方法. 张洪武等[22]将应用力学辛体系应用在碳纳米管的色散关系的计算中,阐述了辛数学理论在波的界带分析上具有优势. 邓子辰[24]将辛数学方法应用到高频振荡系统中,而碳纳米管的特殊力学性能恰好可以实现高频振荡的需求. 因此,将辛体系应用于碳纳米管的振动分析以及波传播研究是必要的. 钟万勰[23]提出铁木辛柯梁的哈密顿对偶方程,并研究了铁木辛柯梁的波散射与波共振问题. 吴锋等[25]在此基础上,分析了铁木辛柯梁的能带结构以及波散射问题. 本文以铁木辛柯梁理论为基础,将辛弹性力学 理论[23, 26]应用于研究载流碳纳米管的波传播 问题[27, 28].
1 载流碳纳米管动力学模型本文基于铁木辛柯梁理论,应用能量变分法建立出载流碳纳米管振动分析模型[27].
|
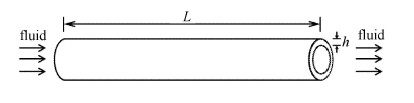
图 1 载流碳纳米管几何结构 Fig.1 Geometry of fluid-conveying single-walled carbon nanotubes (SWCNTs) |
载流碳纳米管无量纲振动控制方程[27]
| $\left. \begin{array}{l} \left( {1 - {\lambda _{\rm{e}}}} \right)\frac{{{\partial ^2}\bar w}}{{\partial {\xi ^2}}} + \frac{{\partial \bar \phi }}{{\partial \xi }} - \left( {1 + {\lambda _{\rm{d}}}} \right)\frac{{{\partial ^2}\bar w}}{{\partial {\eta ^2}}} = 0\\ \frac{{{\partial ^2}}}{{\partial {\xi ^2}}}\left[{{\lambda _{\rm{a}}} + \mu \left( {{\lambda _{\rm{b}}} + {\lambda _{\rm{c}}}} \right)\frac{{{\partial ^2}}}{{\partial {\eta ^2}}}} \right]\bar \phi - \left( {{\lambda _{\rm{b}}} + {\lambda _{\rm{c}}}} \right)\frac{{{\partial ^2}\bar \phi }}{{\partial {\eta ^2}}} - \\ \qquad \left( {\frac{{\partial \bar w}}{{\partial \xi }} + \bar \phi } \right) = 0 \end{array} \right\}$ | (1) |
由振动理论可知,方程(1)的波动解[23]为
| $\bar w\left( {\xi ,\eta } \right) = W\left( {\xi ,\omega } \right){{\rm{e}}^{ - {\rm{i}}\omega \eta }}\bar \phi \left( {\xi ,\eta } \right) = \Phi \left( {\xi ,\omega } \right){{\rm{e}}^{ - {\rm{i}}\omega \eta }}$ | (2) |
其中,$\omega $为无量纲激励频率.
将方程(2)代入方程(1),动力学方程为
| $\left. \begin{array}{l} \frac{{{{\rm{d}}^2}W}}{{{\rm{d}}{\xi ^2}}} + \frac{{{\rm{d\Phi }}}}{{{\rm{d}}\xi }} + {\omega ^2}W + {\lambda _{\rm{d}}}{\omega ^2}W - {\lambda _{\rm{e}}}\frac{{{{\rm{d}}^2}W}}{{{\rm{d}}{\xi ^2}}} = 0\\ {\lambda _{\rm{a}}}\frac{{{{\rm{d}}^2}{\rm{\Phi }}}}{{{\rm{d}}{\xi ^2}}} - \left( {\frac{{{\rm{d}}W}}{{{\rm{d}}\xi }} + {\rm{\Phi }}} \right) + \left( {{\lambda _{\rm{b}}} + {\lambda _{\rm{c}}}} \right){\omega ^2}{\rm{\Phi }} = 0 \end{array} \right\}$ | (3) |
为了将拉格朗日函数导入哈密顿体系,引入对偶变量q[23]
| $p = \frac{{\partial L}}{{\partial \dot q}} = {K_{22}}\dot q + {K_{21}}q = \left[{\begin{array}{*{20}{c}} \begin{array}{l} {Q_x}\\ - {M_x} \end{array} \end{array}} \right]$ | (4) |
引入向量$v = {\left[{\begin{array}{*{20}{c}} q&p \end{array}} \right]^{\rm{T}}}$,方程(3)重新表示为[25]
| $\dot{ v} = { H v}$ | (5) |
对于给定的$\omega ^2$,位移约束
| $\dot{ q} = {\rm i}\mu { q}$ | (6) |
| $\left[{ { K }_{ {\rm qs}\mu } - \omega ^2{ M }_{ {\rm q}\mu } } \right]{ q} = 0$ | (7) |
其中,$\mu $是波数.
| $\begin{array}{l} \left. \begin{array}{l} {M_{{\rm{q}}\mu }} = \left[\begin{array}{l} 1 + {\lambda _{\rm{d}}}\;\;\;\;0\\ 0\;\;\;\;\;{\lambda _{\rm{b}}} + {\lambda _{\rm{c}}} \end{array} \right]\\ {K_{{\rm{qs}}\mu }} = \left[\begin{array}{l} {\mu ^2}\left( {1 - {\lambda _{\rm{e}}}} \right)\;\;\; - {\rm{i}}\mu \\ {\rm{i}}\mu \;\;\;\;{\lambda _{\rm{a}}}{\mu ^2} + 1 \end{array} \right] \end{array} \right\}\\ \;\;\; \end{array}$ | (8) |
令方程(7)的系数矩阵的行列式为零,这样可以得到载流碳纳米管的波传播特征方程
| $ a{\left( {{\omega ^2}} \right)^2} + b{\omega ^2} + c = 0$ | (9) |
其中
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} a = \left( {1 + {\lambda _{\rm{d}}}} \right)\left( {{\lambda _{\rm{b}}} + {\lambda _{\rm{c}}}} \right)\\ b = - \left[{\left( {1 + {\lambda _{\rm{d}}}} \right)\left( {{\lambda _{\rm{a}}}{\mu ^2} + 1} \right) + \left( {1 - {\lambda _{\rm{e}}}} \right)\left( {{\lambda _{\rm{b}}} + {\lambda _{\rm{c}}}} \right){\mu ^2}} \right]\\ c = \left( {1 - {\lambda _{\rm{e}}}} \right)\left( {{\lambda _{\rm{a}}}{\mu ^2} + 1} \right){\mu ^2} - {\mu ^2} \end{array} \end{array}} \right\}$ | (10) |
波在单壁铁木辛柯梁中的传播,只存在高频的剪切波和低频的弯曲波[27],相应频率分别为
| $\omega = \sqrt {\frac{{b \pm \sqrt {{b^2} - 4ac} }}{{2a}}} $ | (11) |
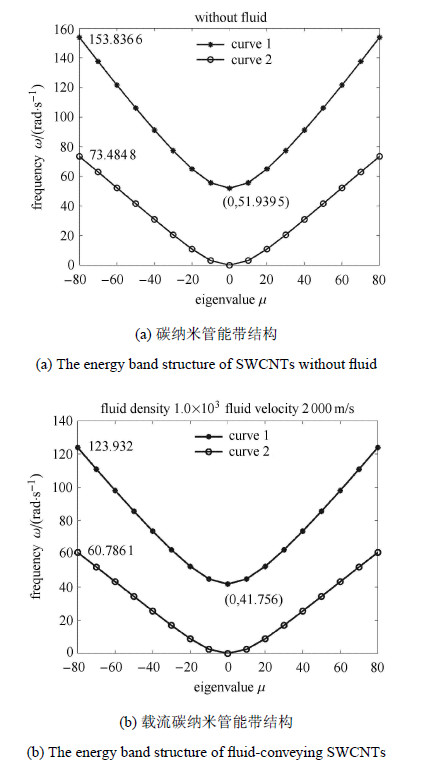
图 2分别给出了碳纳米管无流体和有流体的能带曲线. 图 2中,曲线1 (Curve 1)表示剪切波色散曲线,曲线2 (Curve 2)表示弯曲波色散曲线. 由图 2不难发现:相比于无流体情况,载流碳纳米管的频率区段$[0,\omega _{\min } ]$变窄(其中$\omega _{\min } $为波数$\mu $为零时的剪切频率,在图 2中分别对应51.9395和41.7560);同时,随着碳纳米管中流体的加入,碳纳米管的弯 曲频率与剪切频率均减小. 可以得到结论:由于碳纳米管内流体加入,碳纳米管会变得更"柔软"[27]. 另外,可以发现无量纲的弯曲频率是从零开始,剪切波传播是截止频率之后开始[28].
|
图 2 碳纳米管内有无流体频率对比 Fig.2 Comparison between the energy band structure of SWCNTs with and without fluid |
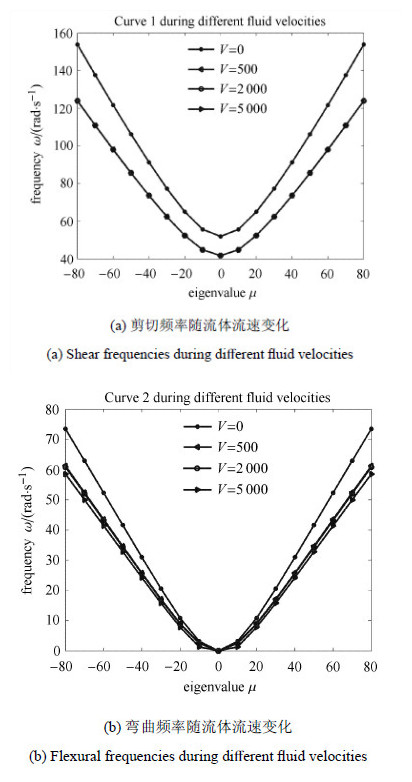
图 3描述了碳纳米管能带结构随流速变化色散曲线,其中,图 3(a)表示同一流体在不同流速下碳纳米管的剪切波色散曲线,图 3(b)为相应的 弯曲波色散曲线. 将图 3中剪切波色散曲线(Curve 1)的最小频率值记为$\omega _{\min } $,频率区段$[\omega _{\min } , + \infty]$内的状态向量均由两对通带本征向量构成,其物理意义为沿相反传播的两对波.
|
图 3 能带结构随流体流速变化 Fig.3 The energy band structure during different fluid velocities |
观察图 3可以发现:随着碳纳米管管内流体流速的增加,载流碳纳米管的弯曲频率与剪切频率均减小. 通过对这一现象的分析,可以得到结论:由于碳纳米管内流体流速的增加,碳纳米管会变得更"柔软"[27]. 这一现象的发生可以由方程(8)中的$\lambda_{\rm e} $得以解释,因此,在研究载流碳纳米管力学问题时,流速对剪切频率的作用应当考虑.
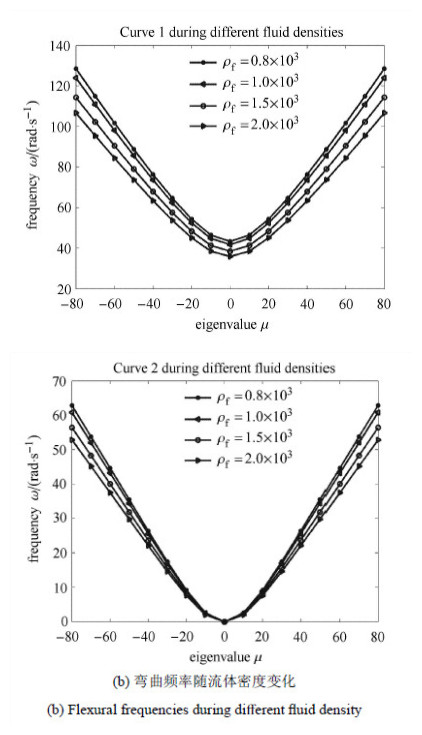
图 4描述了碳纳米管能带结构随流体密度变化曲线,其中, 图 4(a)表示不同密度的流体在相同流速2000m/s下通过碳纳米管时,碳纳米管的剪切波色散曲线;图 4(b)为弯曲波色散曲线. 将图 4中剪切波色散曲线(Curve 1)的最小频率值记为$\omega _{\min } $,频率区段$[0,\omega _{\min } ]$内的状态向量由一对通带本征向量,与一对禁带本征向量构成,通带本征向量表示的物理意义为:一对相反方向传播的波,而 禁带本征向量表示的物理意义为:按模态就地振动.
|
图 4 能带结构随流体密度变化 Fig.4 The energy band structure during different fluid density |
观察图 4还可以发现:随着碳纳米管管内流体密度的增加,载流碳纳米管的弯曲频率与剪切频率均减小. 通过对这一现象的分析,可以得到结论:由于碳纳米管内流体流速的增加,碳纳米管会变得更"柔软". 此结论不同于纳伦德拉等[28]在非局部弹性理论下的结论. 原因在于本文在哈密顿系统讨论波的传播问题,不同于文献[28]的拉格朗日系统. 这一现象的发生可以由方程(8)中的$\lambda _{\rm c} ,\lambda _{\rm d} ,\lambda _{\rm e} $得以解释,因此,在研究载流碳纳米管力学问题时,流体密度对剪切频率的作用应当考虑.
3.2 散射矩阵计算载流碳纳米管的散射矩阵[28]
| ${S_{{\rm{ca}}}} = - {\left( {{P_{\rm{a}}} - {K_{\rm{r}}}{Q_{\rm{a}}}} \right)^{ - 1}}\left( {{P_{\rm{b}}} - {K_{\rm{r}}}{Q_{\rm{b}}}} \right)$ | (12) |
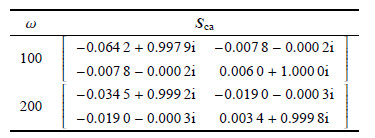
表 1给出了不同频率下的散射矩阵${\pmb S }_{\rm ca} $. 研究发现,散射矩阵${S_{{\rm{ca}}}} $是对称矩酉矩阵,即满足$S_{{\rm{ca}}}^{\rm{T}} = {S_{{\rm{ca}}}}$和$S_{{\rm{ca}}}^{\rm{H}}{S_{{\rm{ca}}}} = I$. 同时表明:通过载流碳纳米管的入射波功率流等于反射波的功率流,满足功率流守恒的要求,体现了辛方法的优越性.
| 表 1 散射矩阵 Table 1 cattering matrix |
本文基于辛弹性力学理论和铁木辛柯梁理论,研究了载流碳纳米管的波传播问题. 通过勒让德变换,引入对偶变量,建立了辛体系下的 动力学方程;采用波传播分析方法解析得到了载流碳纳米管的能带结构表达式;同时计算了载流碳纳米管的散射矩阵. 此外,可以将本文的方法推广应用到具有周期性结构的二维碳纳米管阵列的能带分析,为纳米机电系统的力学行为研究提供了良好的理 论分析方法.
| 1 | 白春礼. 纳米科技及其发展前景. 科学通报, 2001, (02): 89-92 (Bai Chunli. Nano science and technology and its development prospect. Chinese Science Bulletin, 2001, (02): 89-92 (in Chinese)) |
| 2 | Craighead HG. Nanoelectromechanical systems. Science, 2000,290(5496): 1532-1535 |
| 3 | 郑泉水, 徐志平, 王立峰. 碳纳米管的力学. 力学进展, 2004, 34(1):97-138 (Zheng Quanshui, Xu Zhiping, Wang Lifeng. Mechanics of carbon nanotubes. Advances in Mechanics, 2004, 34(1): 97-138 (in Chinese)) |
| 4 | Liu JZ, Zheng Q, Jiang Q. E ect of a rippling mode on resonances of carbon nanotubes. Physical Review Letters, 2001, 86(21): 4843-4846 |
| 5 | Zheng Q, Jiang Q. Multiwalled carbon nanotubes as gigahertz oscillators. Physical Review Letters, 2002, 88(4): 045503 |
| 6 | Guo W, Guo Y, Gao H, et al. Energy dissipation in gigahertz oscillators from multiwalled carbon nanotubes. Physical Review Letters,2003, 91(12): 125501 |
| 7 | Wang L. Flutter instability of supported pipes conveying fluid subjected to distributed follower forces. Acta Mechanica Solida Sinica,2012, 25(1): 46-52 |
| 8 | Xia W, Wang L. Vibration characteristics of fluid-conveying carbon nanotubes with curved longitudinal shape. Computational Materials Science, 2010, 49(1): 99-103 |
| 9 | Wang L, Hu H. Flexural wave propagation in single-walled carbon nanotubes. Physical Review B, 2005, 71(19): 195412 |
| 10 | Wang L, Ni Q, Li M, et al. The thermal e ect on vibration and instability of carbon nanotubes conveying fluid. Physica E: Lowdimensional Systems and Nanostructures, 2008, 40(10): 3179-3182 |
| 11 | 王立峰. 一维纳米结构的若干力学问题. [博士论文]. 南京:南京航空航天大学, 2005 (Wang Lifeng. On some mechanics problems in one dimensional nanostructures. [PhD Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005 (in Chinese)) |
| 12 | Gibson RF, Ayorinde EO, Wen YF. Vibrations of carbon nanotubes and their composites: A review. Composites Science and Technology,2007, 67(1): 1-28 |
| 13 | Zhang Y, Liu G, Han X. Transverse vibrations of double-walled carbon nanotubes under compressive axial load. Physics Letters A,2005, 340(1-4): 258-66 |
| 14 | Yoon J, Ru CQ, Mioduchowski A. Timoshenko-beam e ects on transverse wave propagation in carbon nanotubes. Composites Part B: Engineering, 2004, 35(2): 87-93 |
| 15 | Yoon J, Ru CQ, Mioduchowski A. Vibration and instability of carbon nanotubes conveying fluid. Composites Science and Technology,2005, 65(9): 1326-1336 |
| 16 | Wang Q, Varadan VK. Wave characteristics of carbon nanotubes. International Journal of Solids and Structures, 2006, 43(2): 254-65 |
| 17 | Chang TP. Thermal-mechanical vibration and instability of a fluid conveying single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory. Applied Mathematical Modelling, 2012, 36(5): 1964-1973 |
| 18 | Soltani P, Farshidianfar A. Periodic solution for nonlinear vibration of a fluid-conveying carbon nanotube, based on the nonlocal continuum theory by energy balance method. Applied Mathematical Modelling, 2012, 36(8): 3712-3724 |
| 19 | Soltani P, Kassaei A, Taherian M, et al. Vibration of wavy singlewalled carbon nanotubes based on nonlocal Euler Bernoulli and Timoshenko models. International Journal of Advanced Structural Engineering, 2012, 4(1): 1-10 |
| 20 | Kiani K. Transverse wave propagation in elastically confined singlewalled carbon nanotubes subjected to longitudinal magnetic fields using nonlocal elasticity models. Physica E: Low-dimensional Systems and Nanostructures, 2012, 45: 86-96 |
| 21 | Li BH, Gao HS, Liu YS, et al. Free vibration analysis of micropipe conveying fluid by wave method. Results in Physics, 2012, 2: 104-109 |
| 22 | Zhang HW, Yao Z, Wang JB, et al. Phonon dispersion analysis of carbon nanotubes based on inter-belt model and symplectic solution method. International Journal of Solids and Structures, 2007,44(20): 6428-6449 |
| 23 | 钟万勰. 应用力学的辛数学方法. 北京:高等教育出版社, 2006 (Zhong Wanxie. Symplectic Method in Applied Mechanics. Beijing: Higher Education Press, 2006 ( in Chinese)) |
| 24 | Li W, Deng Z, Zhang S. Numerical algorithms for highly oscillatory dynamic system based on commutator-free method. Journal of Sound and Vibration, 2007, 302(1-2): 39-49 |
| 25 | 吴锋,徐小明,高强等. 基于辛理论的Timoshenko 梁波散射分析. 应用数学和力学, 2013, 34(12): 1225-35 (Wu Feng, Xu Xiaoming, Gao Qiang, et al. Analyzing the wave scattering in Timoshenko beam based on the symplectic theory. Applied Mathematics and Mechanics,2013, 34(12): 1225-35 (in Chinese)) |
| 26 | 姚伟岸,钟万勰. 辛弹性力学. 北京:高等教育出版社, 2002 (Yao Weian, Zhong Wanxie. Symplectic Elasticity. Beijing: Higher Education Press, 2002 (in Chinese)) |
| 27 | Wang B, Deng Z, Ouyang H, et al. Wave characteristics of single-walled fluid-conveying carbon nanotubes subjected to multiphysical fields. Physica E: Low-dimensional Systems and Nanostructures,2013, 52: 97-105 |
| 28 | Narendar S, Gopalakrishnan S. Terahertz wave characteristics of a single walled carbon nanotube containing a fluid flow using the nonlocal Timoshenko beam model. Physica E: Low-dimensional Systems and Nanostructures, 2010, 42(5): 1706-12 |
 2016, Vol. 48
2016, Vol. 48