拥有两串列扑翼的昆虫,比如蜻蜓,能够获得大的气动力和高的效率通过主动调节翅翼运动,比如扑动的幅值和前后翅翼之间的相位差[1, 2]. 它们引人注目的飞行能力与前后翅的前缘涡的产生以及相互作用密不可分[3, 4].前后翅翼之间的相位差对前缘涡的相互作用有重要的影响,因此对翅翼气动力的产生和变化也会产生重要影响.理解相位差的重要作用,对研发高效的串列式微型仿生扑翼飞行器具有重要的理论意义和工程应用价值[5, 6, 7, 8]. 实际的扑翼运动是周期性的平动、 转动和摆动的叠加[9].周期性的平动是昆虫扑翼运动基本模式中最重要的一个. 本文主要研究相位差对做平动运动的串列扑翼平均推力的影响机理.
Konller[10]和Betz[11] 首先观察到在有来流的工况下,一个平动的翼型会产生净推力.由上拍和下拍造成的相对垂直速度,会使叶片和来流有一个有效攻角,从 而使合力向前倾斜.因此,就会得到一个推力分量,如图1所示. Karman和Burgers [12]基于观测到的尾流涡的位置和方向首先提出了关于推力产生的理论解释.从此,许多数值和实验研究就致力于量化扑翼产生的推力以及其周围的流场结构[3, 13, 14, 15].
前翅或后翅的推力都会受到相位差的影 响[16, 17, 18, 19]. Broering等[17]数值研究了相位差对在飞行模式下两串列扑翼 气动力的影响.翼型的运动方式为平动加转动,实验间距为一个弦长,相位差为前翅领先后翅0°,180°和270°.他们发现相对于单翼的平均推力,前翅的平均推力在实验所研究的3个相位差下都有所提升;后翅的平均推力在0°时有提升而在180°和270°时候下降. Yilmaz等[19]的数值研究是在相位差为0°和180°,间距为一个弦长的工况下进行的.他们的研究结果表明:当相位差为0°时,前翅和后翅的平均推力均高于单翼值;当相位差为180°,前翅的平均推力值略低于单翼值,而后翅的平均推力竟为负值.通过文献[17, 18, 19],我们可以得出:在特定的相位差下,前后翅翼之间发生了强烈的相互作用,才造成前翅或后翅的平均推力值与单翼值相差较大.此外,文献 [17, 18, 19]中前翅和后翅各自的平均推力值也是不尽相同的,这可能是由来流工况和运动模式不同造成的.同时,这也表明了两扑翼相互作用的复杂性,因此,在这个领域内,需要更为广泛和深入的研究.
相位差对翅翼受力的影响和前后翅翼之间的涡相互作用紧密相联[18]. Broering和Lian[18]的数值研究结果表明:相位差影响前翅脱落前缘涡和后翅前缘涡之间相互作用的时机,从而改变后翅前缘涡产生和脱落的过程.最终使后翅的受力区别于单翼.他们的研究主要揭示了前翅对后翅前缘涡的影响,但是关于后翅对前翅脱落涡的影响并没有深入讨论.这两个重要方面在本文中都会进行进一步的讨论.
本文实验研究了相位差对两串列扑翼推力的影响. 实验是在一低雷诺数循环水洞中进行的.翼型的扑动运动被简化为二维的平动. 为了对 比研究,首先测量单翼运动.一个三分量的Kistler压力传感器被用来测量叶片上的瞬时力;一个TSIDPIV系统被用来测量叶片的前缘涡以及其周围的流场.本文通过分析前后翅翼的平均推力以及其周围的速度矢量场和涡量场,重点揭示在不同相位差下前后翅翼相互作用机理.
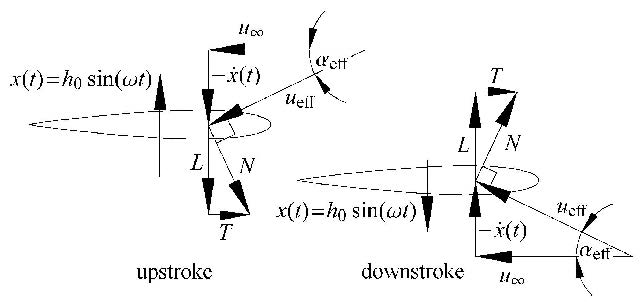
|
图1 扑翼的推力和升力 Fig.1 Thrust $T$ and lift $L$ on a plunging wing |
实验是在西安交通大学能动学院,一个低雷诺数的循环水洞中进行的,如图2所示. 使用多普勒测速仪(LDV)来测量测试段进口处的水流速度和湍流强度. 在本次实验中,测试段进口处来流速度$U_{\infty }$固定在0.2 m/s;对应的湍流强度低于3%. 叶片截面是NACA0012翼型,弦长是50 mm,翼展是260 mm,因此,基于弦长的雷诺数是1.0×10$^{4}$. 每个叶片的运动都由一套偏心轮和滑块机构来驱动. 每一个偏心轮都由一个电机单独驱动,因此,前后翅翼之间的相位差,能够通过调节两个电机起始运转之间的时间差来完成. 这种调节是在LabVIEW平台上通过编程控制实现的,对应相位差调节误差是0.5°.
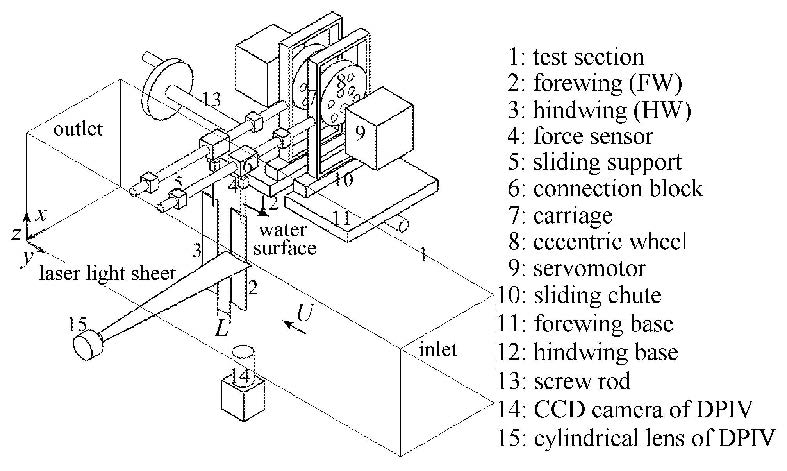
|
图2 实验台 Fig.2 Test rig |
作用在叶片上的力由三分量压力传感器测量得到(Kistler,Type9317B). 传感器测量的不确定度是1.0%,分辨率是1.0mN. 在测量开始前我们采用静态卸载校准的方法对传感器进行了校准,得到了力和输出电压稳定的线性关系.
叶片周围的流场通过TSI DPIV系统进行测量. 示踪粒子是SiC,直径约为1.5 μm,密度为3.2 g/cm$^3$.粒子的响应时间定义为$d_{p}^{2} \rho_{p}/(18\mu) $[20],$d_{p}$ 和$\rho _{p}$分别是粒子的直径和密度;$\mu $ 是流体的动力黏性系数.SiC粒子的响应时间为0.26 μs,大大低于来流速度的时间尺度. 因此,SiC粒子能够完好地跟踪流体.
DPIV系统激光脉冲的功率是300 mJ,CCD相机的分辨率是1 024×1 024.激光面垂直叶片的横截面,其厚度约为1 mm,如图2所示. 一对激光脉冲之间的时间间隔选定为250 μs,这是依据问询窗口内粒子的最大位移而定的. 为了提高视场的分辨率,每次拍摄视场的范围为43 mm×43 mm.至于图像处理,问询窗口的尺寸是32×32像素有50%的重叠,所以在PIV测量中速度矢量场的空间分辨率是$0.013 4c$,约为0.67 mm,其中$ c$ 是叶片的弦长.因为拍摄视场的边长43 mm小于叶片的弦长50 mm,为了完整地反映叶片周围的流场,叶片周围的流场必须被分成两部分并分别拍摄,然后再把分别拍摄的图片合成为一张完整的流场图. 两段区域的重叠范围为8.5 mm,拼接后的流量范围是77.5 mm×43 mm.
速度测量的不确定度是由粒子位移测量的不确定度决定的.根据PIV的使用手册,粒子位移测量的不确定度是0.1个像素,因此,实际PIV测量中速度误差是16.8 mm/s (=43 mm/1 024×0.1/250 μs). 实验中叶片周围流体最大速度约为0.43 m/s,因此在PIV测量中相对于最大流动速度的误差为3.9% (=16.8×10$^{ - 3}$/0.43).
1.3 叶片的运动方程
对于单翼试验,最主要的目的是评价扑动幅值对叶片推力的影响,以及验证实验测量的准确性. 其结果可以为双翼实验提供一个参考对比的对象. 其运动方程是
\[x(t) = {h_0}\sin (2\pi ft)\]
(1)
\[St = fA/{U_\infty }\]
(2)
对于做三维扑动的叶片而言,在扑动平面上,它的移动速度从根部到叶尖逐渐增加.当流动在叶尖发生分离的时候,也许在叶 根的部位就没有产生涡的脱落.在这种情况下,就会产生翼展方向的流动,并且带来三维效应.而在此,我们主要集中研究前后翅翼之间的相互作用机理,因此,我们把三维扑翼运动简化为二维扑动运动,这样就能够减去其他变量,更加清楚地研究翼-翼相互作用. 两个翅翼是前后并排放置,如图2所示.扑动的前后翅翼的运动方程可以描述为
\[前翅 x(t) = {h_0}\sin (2\pi ft)\]
(3)
\[后翅 x(t) = {h_0}\sin (2\pi ft - \varphi )\]
(4)
基于NI LabVIEW 平台,我们编写了力数据采集以及运动控制的程序.在力采集的过程中,为了消除叶片在起始和停止运动时期的不利因素,力数据采集是在叶片运动10个周期后开始,并且在叶片运动结束前5个周期结束.力数据采样频率是1 000 Hz,并且记录至少10个连续周期内的数据.在每一个工况点,力数据采集均重复3次,来确保其高可信度.
在力测量中,为了把叶片瞬时力和其位置对应起来,LabVIEW程序会发出一个连续的方波信号,来识别叶片扑动周期的开始和结束.方波的频率和叶片扑动的频率相同,每个方波的上升沿和扑动周期开始同步. 发出的方波信号和力的信号又同时被采集.通过这些方波信号,可以把采集到的连续的力的信号分割成每一个独立的循环部分的信号.然后对10个周期内的力的信号进行集平均,最后通过这个集平均后的一个周期内的瞬时力来得到一个周期内的平均力.
在流场测量中,LabVIEW程序会产生一个连续的方波信号,该信号通过数据采集卡输入到PIV系统,控制激光器的曝光频率,并使相机拍照频率和翼型的运动频率相同. 从而实现对PIV系统的锁相触发.为了得到某时刻叶片周围的流场,除去叶片开始运动的10个周期以及结束前的5个周期,连续拍摄300周期,进行集平均处理后得到一张流场图.
平均推力系数$C_{\rm T }$代表了一个扑动翼型的推力能力. 它的定义为
\[{C_{\rm{T}}} = \frac{{2\bar F}}{{\rho U_\infty ^2cs}}\]
(5)
\[\bar F = \frac{1}{T}\int_1^T {F(t)dt} \]
(6)
对于单个做正弦运动的翼型,推力的大小主要受缩减频率和扑动幅值的影响[22]. 缩减频率$k = \omega c/{U_\infty } = 2\pi fc/{U_\infty }$. 对于单翼,无量纲的扑动幅值$h$ 从0.3增加到1.1,对应的$St$数从0.15增加到0.55,实验测量得到的平均推力系数如图3所示. 通过图3,我们得知测量得到的平均推力系数和Platzer等[22]所提到的数值模拟结果有略微的差别.原因可能是在我们的实验中缩减频率是1.57,低于Platzer等[22]所提到模拟结果中的2.00.他们的结果[22]已经表明在一定的范围内平均推力系数随缩减频率的增加而增加.Platzer等[23]发现当$St$数分别是0.092,0.146和0.191,尾流涡结构分别代表阻力产生,无推力和推力产生3种尾流. 我们实验最小的$St$数是0.15,非常接近于文献[23]中的0.146,其对应的平均推力系数是0.056,接近于0.所以我们的结论和Platzer等在文献[23]中的结论一致,即无推力产生的尾流发生在$St= 0.146$.
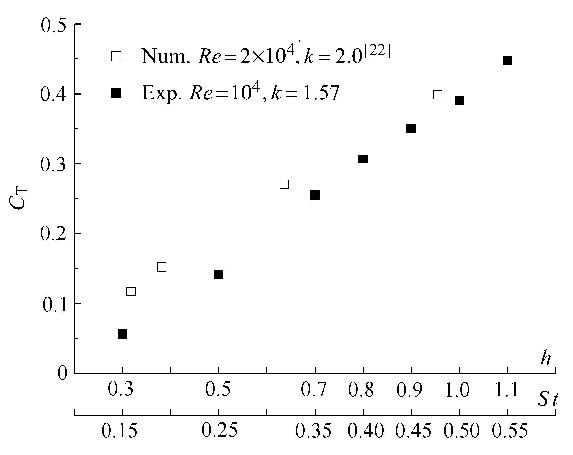
|
图3 单翼的平均推力系数$C_{\rm T}$ Fig.3 Mean thrust coefficient $C_{\rm T }$ of the single plunging wing |
图4描绘了在不同扑动幅值下单翼在两个周期内的瞬时力. 最大的瞬时推力基本都在$t/T$ = 0 和0.5处取得,并且随着扑动幅值$h$的增加明显增加. 单翼诱导的最大有效攻角是在其经过平衡位置$t/T= 0$和 0.5的时 候取得,它可以表示为 $\alpha_{\max }={\rm atan}(kh)$[22].本文中,缩减频率$k$是常量1.57,无量纲的扑动幅值$h$ 是变量.因此,最大攻角$\alpha_{\max}$随着$h$的增加而增加. 通过图4可以得知,更高的$\alpha_{\max}$导致了更高的瞬时推力峰值;然后,更高的平均推力就得到了.
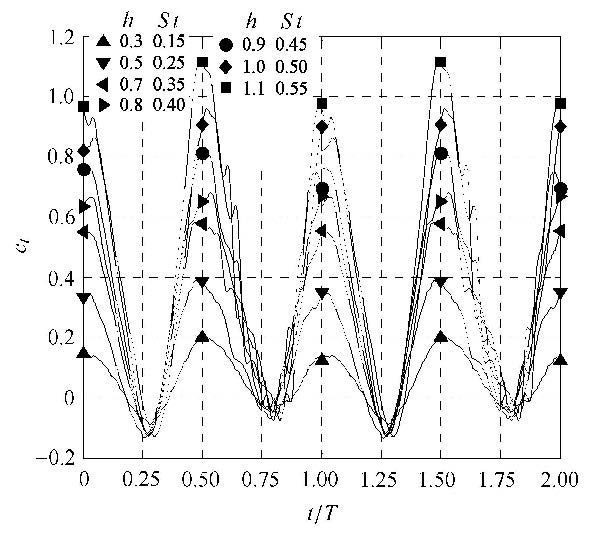
|
图4 单翼的瞬时推力系数$c_{t}$ Fig.4 Instantaneous thrust coefficient $c_{t}$ of a single plunging wing |
在这一部分中,前后翅翼之间的相位差对前翅或后翅平均推力的影响将会被详述,并将深入讨论后翅的前缘涡以及其周围的滞止区域对前翅性能的影响,以及前翅的脱落涡对后翅性能的影响.
3.1 前翅图5描述了在间距为0.5$c$下,前翅平均推力系数随着相位差变化的规律. 虚线表示单个扑翼的平均推力系数,其值为0.255. 可以观察到其平均推力系数几乎是相位差的正弦函数,并在相位差为315°的时候取得最大值,达到0.380,远大于单翼值. 最小的平均推力系数在大约112.5°相位差时取得,略低于单翼值.
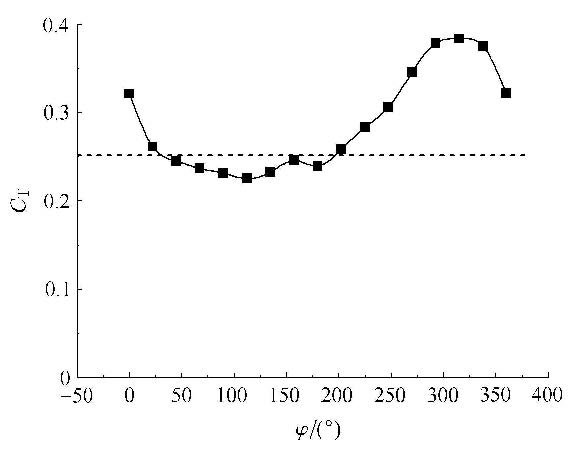
|
图5 前翅平均推力系数随相位差变化规律 Fig.5 Variation of mean thrust coefficient of the forewing with phase difference |
根据以上关于图4的讨论我们得知:如果单翼经过平衡位置时候的瞬时推力值较大,那么平均推力值也较大,反之亦然.因为前 后翅和单翼的运动模式一样,所以,上述结论也同样适用于前翅或后翅.因为瞬时力大小严重依赖于叶片周围的瞬时流场,所以测量和分析当叶片通过平衡位置时候其周围的流场就显得尤为重要.图6(a)和图6(b)分别展示了在间距为0.5倍弦长,相位差为112.5°和315°下,前翅经过平衡位置时候的速度场图和涡量场图.在这两个相位差下,前翅的平均推力分别取得最小值和最大值. 图6(c)表示参考坐标系固定在运动中的前翅上的流线图,即为前翅周围的相对流线图.前翅或后翅诱导的有效攻角不仅仅依赖于其运动速度,还和前后翅翼之间涡的相互作用密切相关.有效攻角沿着弦长方向发生改变,因此取经过叶片上滞止点的流线和弦长的夹角为有效攻角.有效攻角大小和位置标注在相对流线图上(见图6(c)). 图6(d)是一幅涡相互作用示意图.
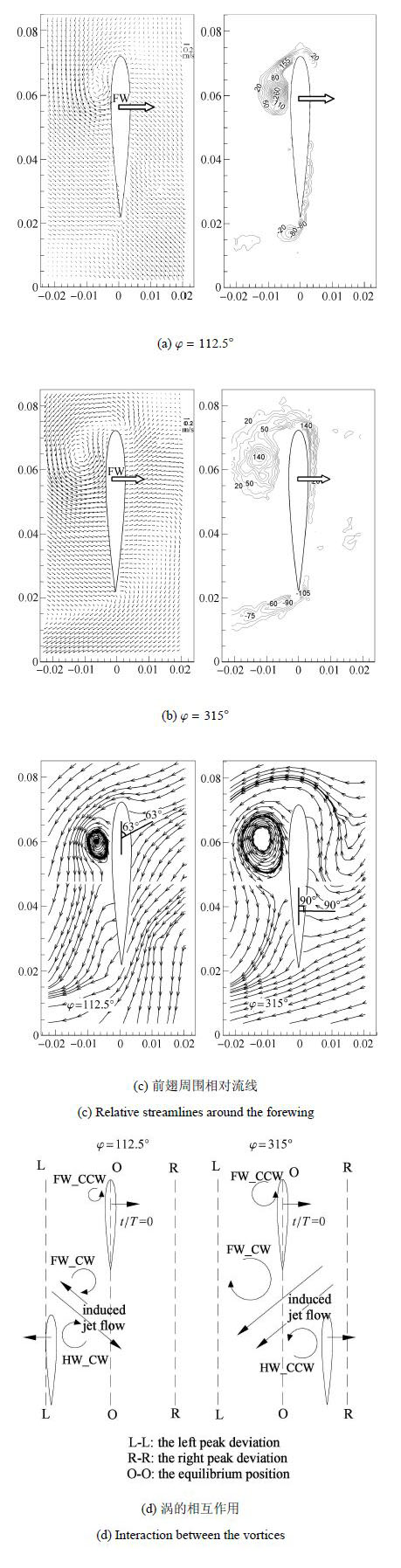
|
图6 用PIV测量的前翅周围的速度场,涡量场和相对流线,时刻$t/T $= 0,翅间距$L/c =0.5$. FW表示前翅,HW表示后翅;CCW表示逆时针,CW表示顺时针 Fig.6 Velocity fields,vorticity contours and relative streamlines around the forewing measured by DPIV at $t/T = 0$ and $L/c = 0.5$. FW denotes the forewing,HW denotes the hindwing,CCW denotes the counter clock wise,and CW the clock wise |
当相位差是315°的时候,此刻后翅已经经过平衡位置并且正在向右边移动.后翅已经产生了一个逆时针方向的前缘涡,如图6(c)所示.它的旋转方向和前翅脱落的顺时针旋转的前缘涡刚好相反,这两个涡诱导他们之间的流体向左下方运动(见图6(b)和图6(d)).而此刻前翅运动方向是向右,这会导致更大的有效攻角(接近于90°,见图6(c)),从而导致瞬时推力峰值和平均推力的增加.
当相位差是112.5°的时候,此刻后翅已经经过平衡位置并且正在向左边移动. 由于后翅右上角的顺时针旋向的前缘涡的强度高于前翅左下角脱落的顺时针前缘涡的强度,因此这两个涡之间诱导的流体向右下方运动(见图6(a)和图6(d)). 此刻前翅也是向右运动,所以这会减小前翅的有效攻角(大约63°,见图6(c)),从而导致瞬时推力峰值和平均推力的减小.
另外,在后翅的前缘会有一个滞止区域,在这个区域内,流体速度减小压力增大. 当这个区域接近前翅的时候,就会影响前翅周围速度的分布. 如图6(d)示,当相位差为315°的时候,后翅的滞止区域位于前翅的右下方,能够抑制或者阻止前翅右侧压力面的流体流动. 因为前翅是从左向右移动,所以这个滞止区域会相对增加前翅的有效攻角,从而导致前翅产生更大的推力. 当相位差为112.5°的时候,情况正好相反. 后翅的滞止区域位于前翅的左下角在叶片吸力面的下面,它的作用是相对增加叶片左侧吸力面的压力,从而相对减小了前翅的有效攻角,并且导致前翅产生较小的推力.
Broering等[17]发现在相位差为0°,180°和270°时前翅的平均推力较单翼均有所提升;我们发现当相位差从0°到360°时前翅的平均推力随相位差正弦波动,或低或高于单翼值.后翅的前缘涡以及滞止区域是前翅平均推力偏离单翼值的主要原因.从前翅的流场图和涡量图中,我们观测到由于大的压力梯度涡主要从叶片前缘产生,因此称之为前缘涡.前缘涡沿着叶片表面向下游漂移在叶片正弦扑动的过程中,最后从尾缘脱落.脱落的前缘涡在尾流中形成逆向卡门涡街,产生射流,从而产生平均推力. 因此,涡对叶片的受力产生重要影响.Zhong等[24, 25, 26]在研究薄圆盘在静止的水中自由落体的时候,通过PIV观测流场发现圆盘运动轨迹和薄圆盘诱导的涡结构紧密相关.Zhong等[24, 25, 26]的结果表明在分析非定常运动时,涡的作用应该被考虑因为涡影响薄圆盘受力.在本文中主要考虑前翅脱落前缘涡与后翅前缘涡之间的相互作用.
3.2 后 翅图7表示在间距为0.5$c$下后翅的平均推力系数随相位差的变化规律. 虚线表示单翼的平均推力值.可以观察到后翅的平均推力系数 随相位差变化有一个明显的V字形低谷特征. 在此处,后翅的平均推力值取得最小值.最小的平均推力意味着前翅对后翅最强的破环性作用[27].前翅和后翅平均推力系数的合值定义为在同样相位差下前翅的值加上后翅的值,如图8所示.可以看到合力也有一个明显的V字形低谷,其所在的相位差和后翅相同,均为135°.图8中虚线表示单翼平均推力系数的两倍. 观察到推力系数的合值高于单翼值的两倍在相位差$\phi = 0^\circ$ $\sim $75°和215° $\sim $ 360°处,尤其是相位差为290°时,平均推力系数合值达到了最大值0.667.
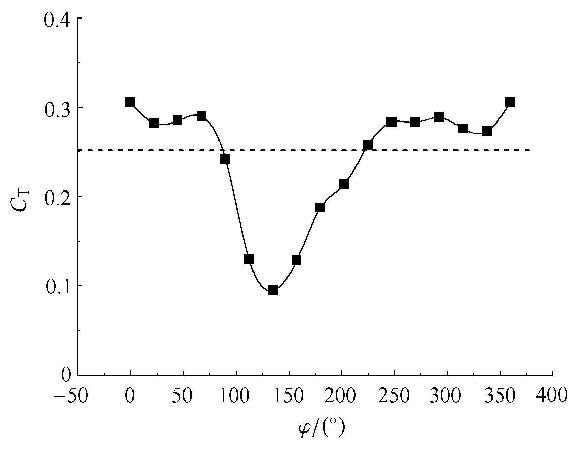
|
图7 后翅平均推力系数随相位差变化规律 Fig.7 Variation of mean thrust coefficient of the hindwing with phase difference |

|
图8 前翅和后翅平均推力系数的合值 Fig.8 The combined mean thrust coefficient of the forewing and hindwing |
为了解释前翅脱落涡对后翅推力的不利影响,我们测量了在135°相位差下,后翅由左向右经过平衡位置时候其周围的速度矢量场和涡量场,如图9(b)所示.作为对比,相位差135°周围的两个相位差90°和180°的工况也在图9(a)和图9(c)中展示.图9(d)表示3个相位差下后翅周围的相对流线图,其参考坐标系固定在运动中的后翅上.此刻后翅在3个相位差下的有效攻角均标注在图9(d)中. 图9(e)是一幅涡之间相互作用的示意图.
当相位差为135°,前翅脱落的逆时针方向的前缘涡正好漂移到后翅的右上角,这将会导致后翅右上角的流体向右方运动(见图9(b)).诱导流体的运动方向和后翅的运动方向相同,这将会相对减小后翅的运动速度,导致较小的有效攻角(约为20°).文献[21, 28, 29]表明:大的有效攻角有利于前缘涡的形成.而在图9(b)中,我们观察到前翅脱落的逆时针涡抑制了后翅的逆时针旋向的前缘涡的形成.这也意味着此刻后翅有一个较低的瞬时攻角.因此,依据前面的讨论,将会产生较低的瞬时推力峰值,从而导致平均推力的降低.其实,当相位差为135°时,此时的平均推力是最低的(见图7).
比较相位差90°和135°,当后翅穿过平衡位置的时候,前翅脱落的逆时针涡在垂直来流的方向和后翅的间距大大增加(见图9(a),图9(b)和图9(e)).因此,在相位差为90°时前翅脱落涡的破坏性的作用就会大大减弱,有效攻角也会有所增加(约为40°),从而后翅的平均推力就会快速升高. 比较相位差180°和135°,当后翅穿过平衡位置的时候,前翅脱落的逆时针涡已经漂移到后翅的右边,并且它的强度也已经减弱(见图9(b),图9(c)和图9(e)).在相位差为180°时,后翅前缘逆时针旋向涡的强度有所增强,对应的有效攻角也有所提升(约为38°),所以平均推力值也有所提高.总之,后翅的平均推力在相位差为90°和180°的时候都有或多或少的提高,但仍然低于单翼值.
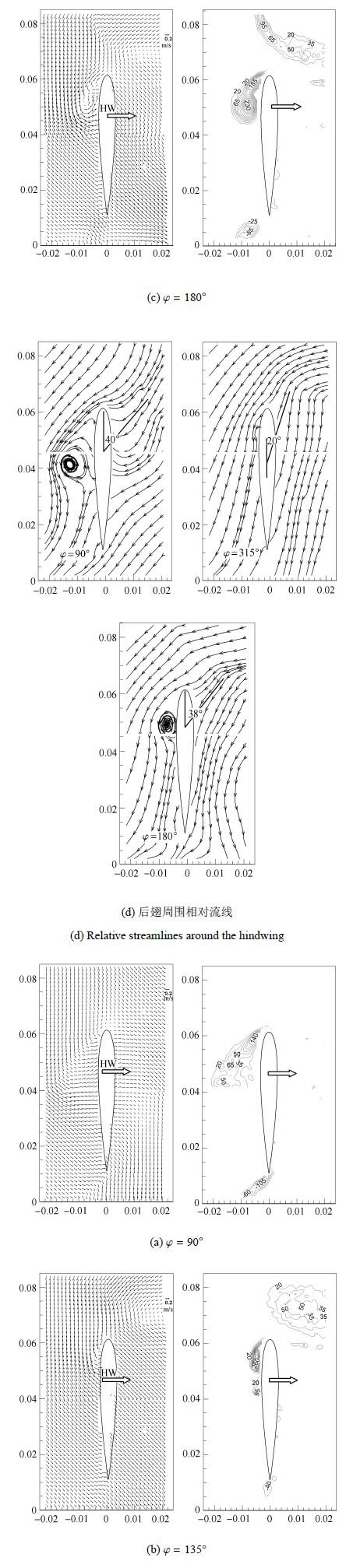
|
图9 后翅周围的速度场,涡量场和相对流线 Fig.9 Velocity fields,vorticity contours and relative streamlines around the hindwing measured by DPIV at $t/T = 0$ and $\varphi = 315^\circ$ |
Broering等[17]发现在间距为1$c$时,后翅平均推力最小值0.088在3个相位差0°,180°和270°中的180°取得. 我们的结果表明在0.5$c$时后翅平均推力最小值0.094在135°取得.后翅最小平均推力意味着前翅脱落涡对后翅具有强烈的作用.间距从1$c$减小到0.5$c$,前翅前缘涡从脱落到作用于后翅的时间减小,所以相应的前翅领先于后翅的相位差也会随之减小.而在Broering等数值模拟中,叶片是转动加平动,对应的无量纲扑动幅值是0.5,平均攻角为5°;我们实验中叶片是平动,相应的值分别为0.7和0°.这些因素导致叶片在一个扑动周期内有效攻角变化规律不同,所以对应的后翅最小平均推力数值有所差异.
4 结 论在一个低雷诺数水洞中,我们实验研究了做二维扑动的单翼和两串列翼型. 一个三分量压力传感器和一套二维DPIV系统分别用来测量叶片的气动力以及叶片周围的前缘涡结构.实验结果表明:平均推力系数的变化趋势主要由经过平衡位置时刻扑翼的瞬时推力值决定.相位差对前翅和后翅的平均推力有重要影响. 前翅的平均推力系数几乎是相位差的正弦函数,取得的最大值为0.380.其值的增加是由于后翅的前缘涡以及其滞止区域提高了前翅的有效攻角.后翅的平均推力系数随着相位差变化的时候,有一明显的V字型特征,取得的最小值为0.095.其值的减小是由于前翅的脱落涡抑制了后翅前缘涡的形成,并且减小了后翅的有效攻角.前后翅翼平均推力系数的合值取得的最大值是0.667,远高于单翼值的两倍. 在本次试验中.本文提供了详细的实验步骤和参数,同时,实验结果也得到了详细的陈述和讨论.因此,本文可以为验证和发展一个稳健的数值方法或者程序代码提供有利的参考.
| [1] | Usherwood JR, Lehmann FO. Phasing of dragonfly wings can improve aerodynamic efficiency by removing swirl. Journal of The Royal Society Interface, 2008, 5(28): 1303-1307 |
| [2] | Lehmann FO. When wings touch wakes: Understanding locomotor force control by wake wing interference in insect wings. Journal of Experimental Biology, 2008, 211(2): 224-233 |
| [3] | Triantafyllou GS, Triantafyllou MS, Grosenbaugh MA. Optimal thrust development in oscillating foils with application to fish propulsion. Journal of Fluids and Structures, 1993, 7(2): 205-224 |
| [4] | Hall KC, Hall SR. Minimum induced power requirements for flapping flight. Journal of Fluid Mechanics, 1996, 323(25): 285-315 |
| [5] | Tuncer IH, Platzer MF. Thrust generation due to airfoil flapping. AIAA Journal, 1996, 34(2): 324-331 |
| [6] | Streitlien K, Triantafyllou GS, Striantafyllou MS. Efficient foil propulsion through vortex control. AIAA Journal, 1996, 34(11): 2315-2319 |
| [7] | Jones KD, Platzer MF. Numerical computation of flapping-wing propulsion and power extraction. AIAA Paper, 1997, 97: 826 |
| [8] | Fenercioglu I, Cetiner O. Categorization of flow structures around a pitching and plunging airfoil. Journal of Fluids and Structures, 2012, 31: 92-102 |
| [9] | Lian Y, Broering T, Hord K, et al. The characterization of tandem and corrugated wings. Progress in Aerospace Sciences, 2014, 65: 41-69 |
| [10] | Knoller R. Die Gesetze des Luftwiderstandes. Flug-und Motortechnik (Wien). 1909, 3(21): 1-7 |
| [11] | Betz A. Ein Beitrag zur Erklaerung Segelfluges. Zeitschrift f" ur Flugtechnik und Motorluftschiffahrt, 1912, 3: 269-272 |
| [12] | Von K. General Aerodynamic Theory. Perfect fluids. Aerodynamic Theory, 1963, 2: 328 |
| [13] | Bohl DG, Koochesfahani MM. MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency. Journal of Fluid Mechanics, 2009, 620: 63-88 |
| [14] | Ramamurti R, Sandberg W. Simulation of flow about flapping airfoils using finite element incompressible flow solver. AIAA Journal, 2001, 39(2): 253-260 |
| [15] | Koochesfahani MM. Vortical patterns in the wake of an oscillating airfoil. AIAA Journal, 1989, 27(9): 1200-1205 |
| [16] | Broering TM, Lian Y, Henshaw W. Numerical investigation of energy extraction in a tandem flapping wing configuration. AIAA Journal, 2012, 50(11): 2295-2307 |
| [17] | Broering TM, Lian Y, Henshaw W. Numerical study of two flapping airfoils in tandem configuration. In: Proc. of 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2010 |
| [18] | Broering TM, Lian Y. The effect of phase angle and wing spacing on tandem flapping wings. Acta Mechanica Sinica, 2012, 28(6): 1557-1571 |
| [19] | Yilmaz SB, Sahin M, Unal MF. Thrust enhancement of flapping wings in tandem and biplane configurations by pure plunging motion. Bulletin of the American Physical Society, 2012, 1: 26009 |
| [20] | Raffel M. Particle Image Velocimetry: A Practical Guide. Springer, 2007: 16 |
| [21] | Anderson JM, Streitlien K, Barrett DS, et al. Oscillating foils of high propulsive efficiency. Journal of Fluid Mechanics, 1998, 360(1): 41-72 |
| [22] | Platzer MF, Jones KD, Young J, et al. Flapping wing aerodynamics: Progress and challenges. AIAA Journal, 2008, 46(9): 2136-2149 |
| [23] | Jones KD, Dohring CM, Platzer MF. Experimental and computational investigation of the Knoller-Betz effect. AIAA Journal, 1998, 36(7): 1240-1246 |
| [24] | Zhong H, Lee C, Su Z, et al. Experimental investigation of freely falling thin disks. Part 1. The flow structures and Reynolds number effects on the zigzag motion. Journal of Fluid Mechanics, 2013, 716: 228-250 |
| [25] | Lee C, Su Z, Zhong H, et al. Experimental investigation of freely falling thin disks. Part 2. Transition of three-dimensional motion from zigzag to spiral. Journal of Fluid Mechanics, 2013, 732: 77-104 |
| [26] | Zhong H, Chen S, Lee C. Experimental study of freely falling thin disks: Transition from planar zigzag to spiral. Physics of Fluids, 2011, 23(1): 11702 |
| [27] | Maybury WJ, Lehmann FO. The fluid dynamics of flight control by kinematic phase lag variation between two robotic insect wings. Journal of Experimental Biology, 2004, 207(26): 4707-4726 |
| [28] | Hover FS, Haugsdal O, Triantafyllou MS. Effect of angle of attack profiles in flapping foil propulsion. Journal of Fluids and Structures, 2004, 19(1): 37-47 |
| [29] | Xiao Q, Liao W. Numerical investigation of angle of attack profile on propulsion performance of an oscillating foil. Computers & Fluids, 2010, 39(8): 1366-1380 |
 2015, Vol. 47
2015, Vol. 47